





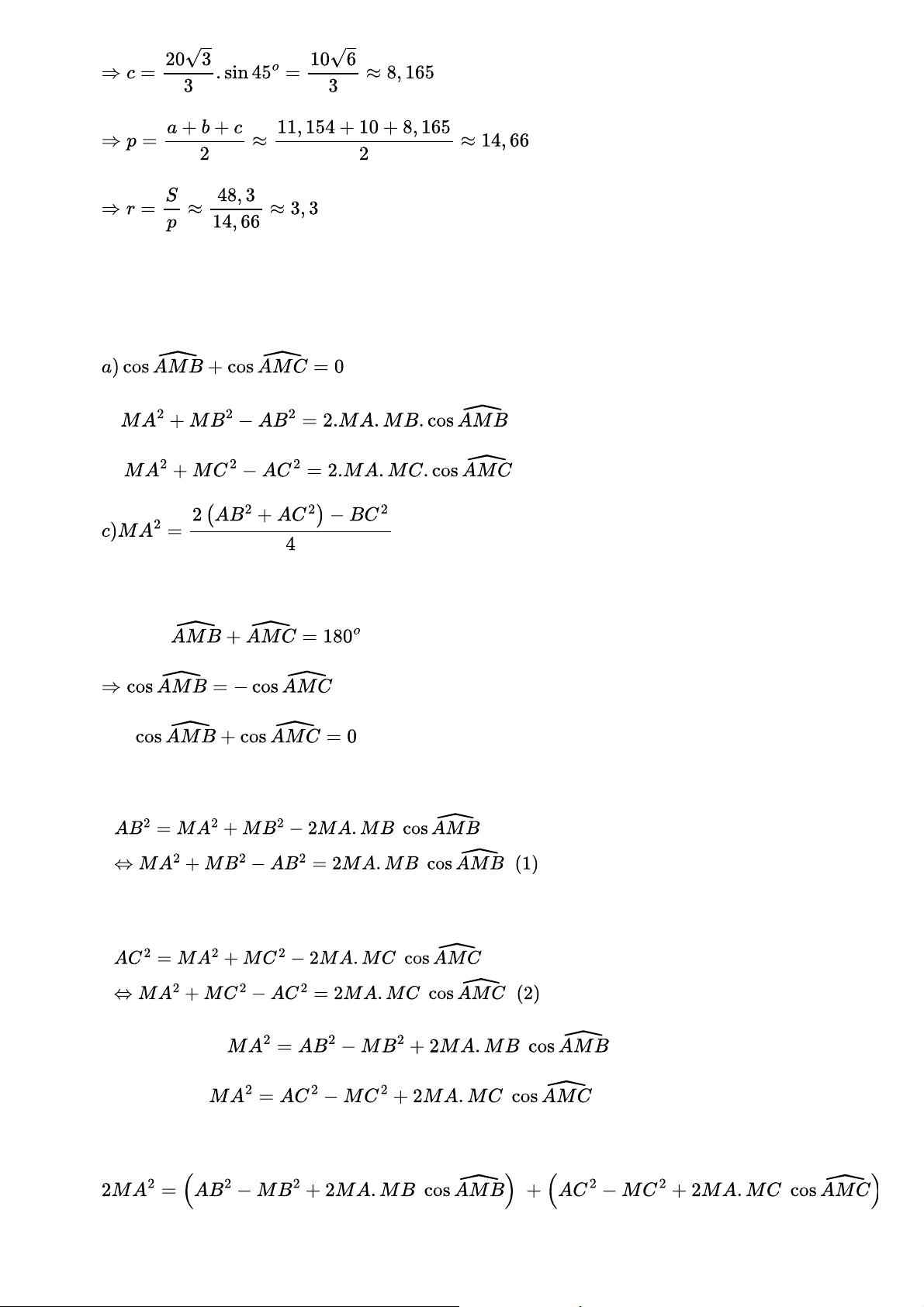




Preview text:
Giải Toán 10 trang 44, 45 Kết nối tri thức tập 1 Bài 3.12 trang 44 Cho tam giác ABC có
. Khẳng định nào sau đây là đúng? Gợi ý đáp án: Diện tích tam giác ABC: Mà Chọn D LG b Gợi ý đáp án: Theo định lí sin, ta có: A đúng Mà Vậy B sai.
(Loại vì không có dữ kiện về góc C nên không thể tính R theo c.)
(Loại vì không có dữ kiện về góc A nên không thể tính R theo a.) Chọn A LG c Gợi ý đáp án: (Loại)
Vì: Theo định lí cos ta có:
Không đủ dữ kiện để suy ra (Loại) Theo định lí sin, ta có: (sai vì theo câu a, ) Theo định lý cos ta có: Mà Thay vào (*) ta được: => D đúng. Chọn D Bài 3.13 trang 44
Cho tam giác ABC. Khẳng định nào sau đây là đúng? LG a Gợi ý đáp án: a) Chọn đáp án B Ta có: . Mà r < Rnên suy ra Vậy A sai. Ta có: Mà Vậy B đúng
Sai vì theo định lí cos ta có: D. Sai vì b) Chọn đáp án A Ta có: Vậy A đúng. Sai vì
Không đủ dữ kiện để kết luận. Nếu ì Nếu thì Ta có Mà b,c > 0 Vậy D sai. LG b Gợi ý đáp án: Ta có: => A đúng. Sai vì
Không đủ dữ kiện để kết luận. Nếu thì Nếu thì Ta có Mà b,c > 0 => D sai. Chọn A Bài 3.14 trang 44
Tính giá trị của các biểu thức sau: Gợi ý đáp án Ta có: Thay vào M, ta được: Ta có: Thay vào N, ta được: Ta có: Thay vào P, ta được: d) Ta có: Thay vào P, ta được: Bài 3.15 trang 44 Cho tam giác ABC có í Gợi ý đáp án Theo định lí sin: +) Ta có: Mà +) Mặt khác: Mà
+) Diện tích tam giác ABC là: +) Lại có: Bài 3.16 trang 44
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng: b) và
(công thức đường trung tuyến). Gợi ý đáp án a) Ta có: Hay
b) Áp dụng định lí cos trong tam giác AMB ta có:
Tương tự, Áp dụng định lí cos trong tam giác AMB ta được: c) Từ (1), suy ra Từ (2), suy ra
Cộng vế với vế ta được: Mà: (do AM là trung tuyến) (đpcm) Bài 3.17 trang 44
Cho tam giác ABC. Chứng minh rằng: a) Nếu góc A nhọn thì b) Nếu góc A tù thì c) Nếu góc A vuông thì Gợi ý đáp án Theo định lí cos ta có: a) Nếu góc A nhọn thì Từ (1), suy ra b) Nếu góc A tù thì Từ (1), suy ra c) Nếu góc A vuông thì Từ (1), suy ra Bài 3.18 trang 45
Trên biển, tàu B ở vị trí cách tàu A 53 km về hương N340E. Sau đó, tàu B chuyển động thẳng
đều với vận tốc có độ lớn 30km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc
có độ lớn 50km/h để đuổi kịp tàu B.
a) Hỏi tàu A cần phải chuyển động theo hướng nào?
b) Với hướng chuyển động đó thì sau bao lâu tàu A đuổi kịp tàu B? Hướng dẫn giải Định lí cosin: a2 = b2 + c2 – 2bc.cosA b2 = a2 + c2 – 2ac.cosB c2 = a2 + b2 – 2ab.cosC Định lí sin: Trong tam giác ABC có:
Học sinh xem lại các công thức tính diện tích tam giác đã được học. Gợi ý đáp án
a) Gọi thời gian tàu A đuổi kịp tàu B ở vị trí C là x (giờ) (x > 0)
Vì tàu B chuyển động thẳng đều với vận tốc có độ lớn 30km/h đến C nên quãng đường BC là 30x (km)
Vì tàu A chuyển động thẳng đều với vận tốc có độ lớn 50km/h để đuổi kịp tàu B nên quãng đường AC là 50x (km) Xét tam giác ABC ta có:
AC2 = BC2 + AB2 – 2AB.BC.cosB
=> 2500x2 = 900x2 + 532 – 2.53.30x.cos1240
=> 1600x2 – 1778x – 2809 = 0
Do đó tàu A mất 1,99 giờ đuổi kịp tàu B.
=> BC = 30.x = 30.1,99 = 59,7; AC = 50.x = 50.1,99 = 99,5 Ta lại có:
=> AC hợp với phương nam một góc 340 + 29,830 = 63,830
Vậy tàu A chuyển động theo hướng N63,830E Bài 3.19 trang 45
Trên sân bóng chày dành cho nam, các vị trí gôn nhà (Home plate), gôn 1 (First base), gôn
2(Second base), gôn 3 (Third base) là bốn đỉnh của một hình vuông có cạnh dài 27,4m. Vị trí
đứng ném bóng (Pitcher’s mound) nằm trên đường nối gôn Nhà với gôn 2 và cách gôn nhà
18,44m. Tính các khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3. Hướng dẫn giải Định lí cosin: a2 = b2 + c2 – 2bc.cosA b2 = a2 + c2 – 2ac.cosB c2 = a2 + b2 – 2ab.cosC Định lí sin: Trong tam giác ABC có:
Học sinh xem lại các công thức tính diện tích tam giác đã được học. Gợi ý đáp án
A là vị trí gôn nhà, B là vị trí gôn 1, C là vị trí gôn 2, D là vị trí gôn 3, E là vị trí ném bóng. Xét tam giác ABE ta có:
BE2 = AB2 + AE2 – 2.AB.AE.cos
=> BE2 = 27,42 + 18,442 – 2.27,4.18,44.cos450 => BE2 ≈ 376,25 => BE ≈ 19,4 m.
Xét tam giác ABE và tam giác ADE ta có: AB = AD (gt) AE chung
=> ΔABE = ΔCDE (c – g – c)
=> BE = DE (hai cạnh tương ứng) => DE ≈ 19,4 m
Vậy khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3 là 19,4 m.




