









Preview text:
Anh Giáo Kid An – h Ch G uyên L iáo Kid u – yệ Chn u Th yê i T n L o uán C yện ấp Th Tố i T c o án Cấp Tốc 2x − 3
Câu 1. [KID] Tiệm cận ngang của đồ thị hàm số y = là: 7 − 6x 2 7 1 3 A. y = . B. x = . C. y = − . D. x = . 7 6 3 2
Câu 2. [KID] Cho hàm số f ( x) = x ( x − )(x + )3 2 2
3 liên tục trên . Số điểm cực trị của hàm số y = f (x) là: A. 2. B. 1. C. 3. D. 4.
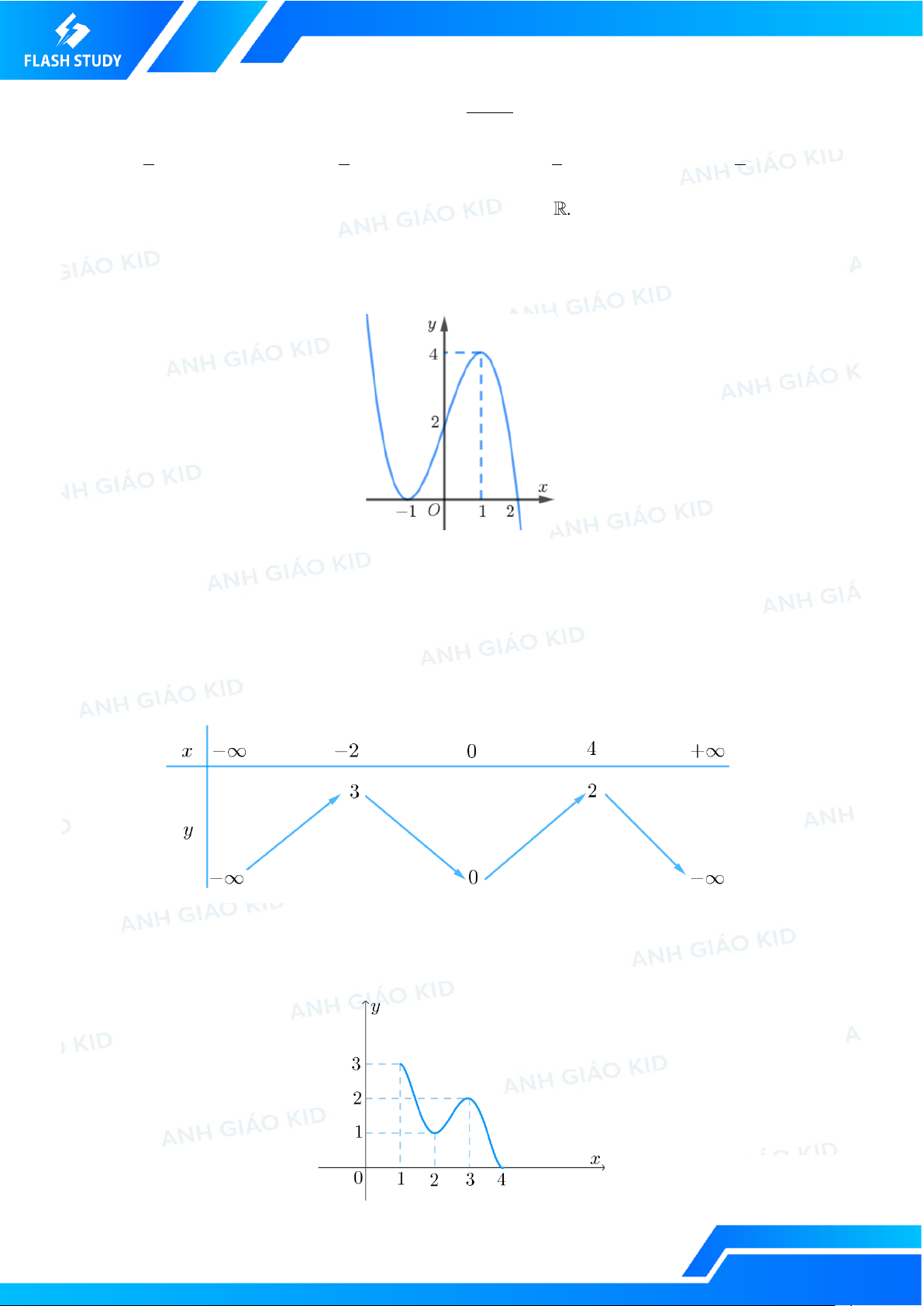
Câu 3. [KID] Cho hàm số y = f (x) có đồ thị như hình vẽ dưới đây:
Hàm số y = − f (x) nghịch biến trên khoảng nào trong các khoảng sau đây? A. ( ; − 0). B. ( 1 − ; ) 1 . C. (1;+). D. (0;+).
Câu 4. [KID] Tập xác định của hàm số y = log 2x − 4 là: 2 ( ) A. x 2. B. (0;+). C. x 2. D. (2;+).
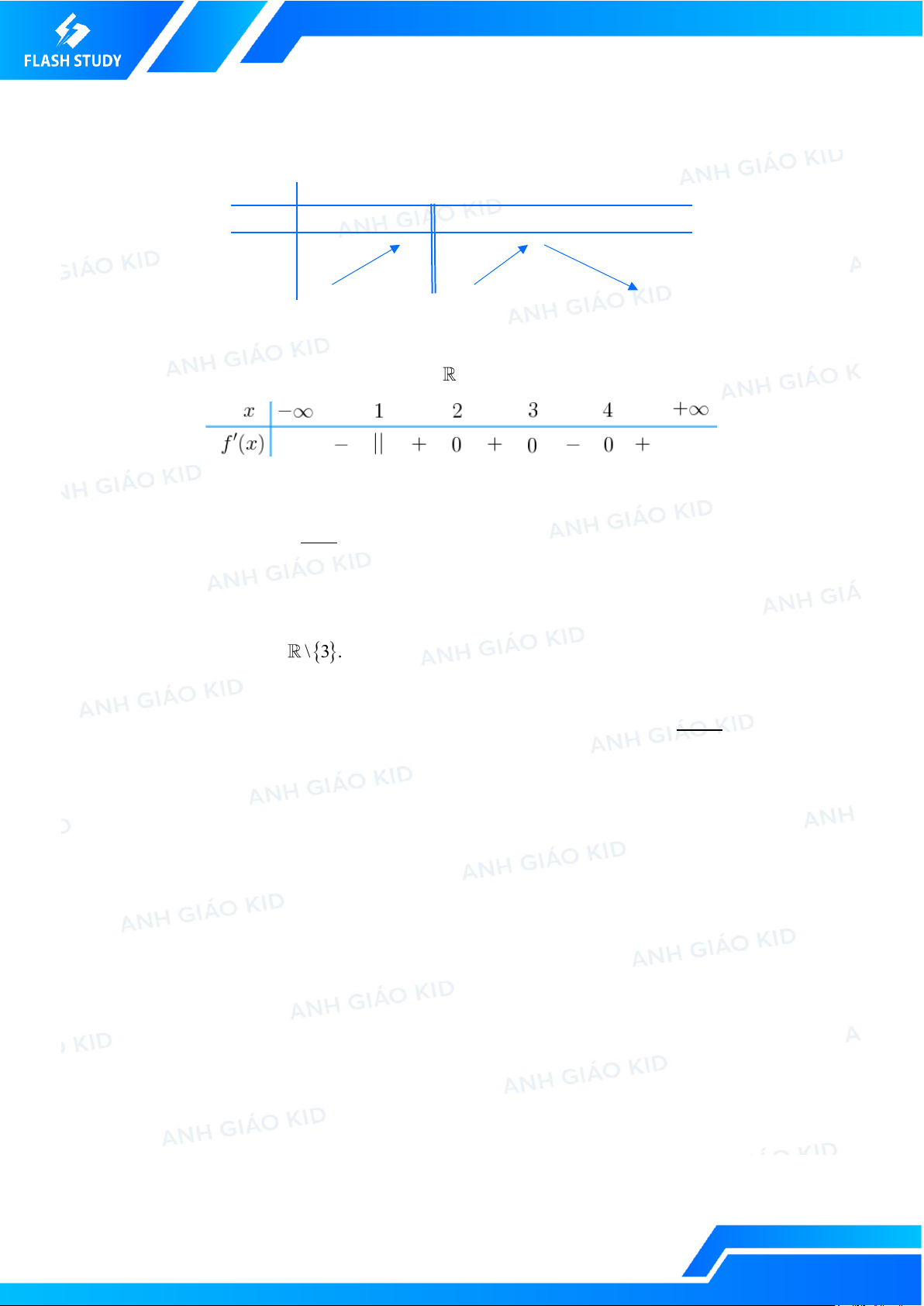
Câu 5. [KID] Cho hàm số y = f (x) có bảng biến thiên của f ( x) như hình vẽ: ,
Số điểm cực trị của hàm số y = f (x) là: A. 4. B. 1. C. 2. D. 3.
Câu 6. [KID] Cho hàm số y = f (x) liên tục trên đoạn 1;4có đồ thị như hình vẽ: Trang 1
FLASH STUDY x RIKI NIHONGO x TIẾNG TRUNG HANKI Anh Giáo Kid An – h Ch G uyên L iáo Kid u – yệ Chn u Th yê i T n L o uán C yện ấp Th Tố i T c o án Cấp Tốc
Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn 1;
3 . Giá trị của M + m là: A. 3. B. 5. C. 4. D. 2.
Câu 7. [KID] Cho hàm số y = f (x) có bảng biến thiên như hình vẽ: x − 1 − 0 + y + + 0 − 2 5 y − − −
Số nghiệm của phương trình f (x) − 4 = 0 là: A. 3. B. 1. C. 0. D. 2.
Câu 8. [KID] Cho hàm số y = f (x) liên tục trên và có bảng xét dấu đạo hàm dưới đây:
Số điểm cực trị của hàm số là: A. 1. B. 3. C. 2. D. 4. x + 2
Câu 9. [KID] Cho hàm số y =
. Khẳng định nào dưới đây đúng? 3 − x
A. Hàm số đồng biến trên khoảng (− ; ) 3 (3;+).
B. Hàm số nghịch biến trên khoảng ( ; − ) 1 .
C. Hàm số đồng biến trên \ 3 .
D. Hàm số đồng biến trên các khoảng ( ;3 − ) và (3;+). 5 − 2x
Câu 10. [KID] Gọi I là giao điểm của các đường tiệm cận của đồ thị hàm số y = . Toạ độ của điểm x − 3 I là: A. (3; 2 − ). B. (3;5). C. ( 3 − ;5). D. ( 3 − ; 2 − ).
Câu 11. [KID] Cho hàm số 3
y = x − 3x +1 có đồ thị (C). Hệ số góc của tiếp tuyến với đồ thị hàm số (C)
tại điểm có tung độ bằng 1 là: A. 3. − B. 0. C. 6. D. −3 hoặc 6. Trang 2
FLASH STUDY x RIKI NIHONGO x TIẾNG TRUNG HANKI Anh Giáo Kid An – h Ch G uyên L iáo Kid u – yệ Chn u Th yê i T n L o uán C yện ấp Th Tố i T c o án Cấp Tốc ax + b
Câu 12. [KID] Hình vẽ dưới là đồ thị của hàm số y =
. Mệnh đề nào dưới đây là đúng? cx + d
A. bd 0,ad 0.
B. bd 0,ab 0.
C. ad 0,ab 0.
D. ab 0,ad 0.
Câu 13. [KID] Hàm số 3 2 x y = có đạo hàm là: A. 3x 1 2 − . B. 3x 1 2 + ln 2. C. 3 2 x ln 2. D. 3 3.2 x ln2.
Câu 14. [KID] Đồ thị hàm số y = f (x) của hàm số y = f (x) trong đoạn 4 − ;
3 được cho trong hình vẽ dưới đây.
Điểm cực tiểu của hàm số y = f (x) trong đoạn 4 − ; 3 là: A. x = 3. − B. x = 2. − C. x = 1. − D. x =1.
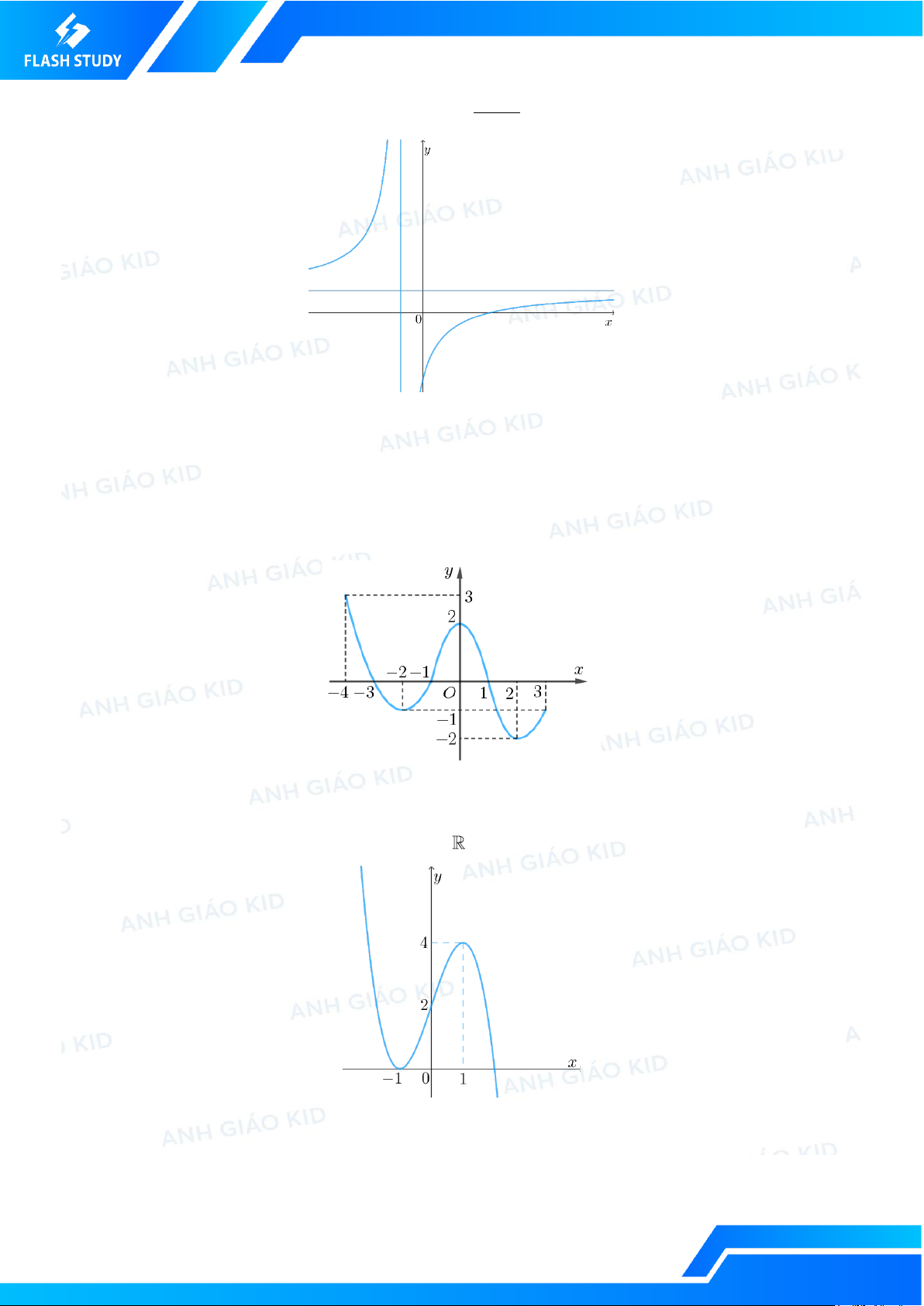
Câu 15. [KID] Cho hàm số y = f (x) liên tục trên và có đồ thị như hình vẽ:
Khẳng định nào sau đây đúng về hàm số y = − f (x) ?
A. Hàm số đạt cực đại tại x =1.
B. Giá trị cực tiểu của hàm số bằng 1. −
C. Hàm số không có cực trị.
D. Điểm cực đại của đồ thị hàm số là ( 1 − ;0). Trang 3
FLASH STUDY x RIKI NIHONGO x TIẾNG TRUNG HANKI Anh Giáo Kid An – h Ch G uyên L iáo Kid u – yệ Chn u Th yê i T n L o uán C yện ấp Th Tố i T c o án Cấp Tốc
Câu 16. [KID] Cho hàm số y = f (x) xác định trên \ 1
− , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình sau: x − 1 − 1 + y ' + + 0 − 4 y 3 2 − 1 −
Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số là: A. 0. B. 1. C. 2. D. 3.
Câu 17. [KID] Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau: Biết f ( 2 − ) = f (0) = 3
− . Giá trị lớn nhất của hàm số y = f ( x) trên đoạn 2 − ;0 là: A. f (− ) 1 . B. 3. − C. − f (− ) 1 . D. 3.
Câu 18. [KID] Tập giá trị của hàm số y = sin 2x là: A. . B. 2 − ;2. C. \ 1 . D. 1 − ; 1 .
Câu 19. [KID] Cho hàm số 4 3
y = x − 4x . Hàm số y = f (x) nghịch biến trên khoảng nào trong các khoảng sau? A. (0;3). B. (3;+). C. (0;2). D. ( ; − 3).
Câu 20. [KID] Tập xác định của hàm số y = ( x − )783 2 là: A. . B. \ 2 . C. 2;+). D. (2;+).
Câu 21. [KID] Tập nghiệm của bất phương trình log x +1 0 là: 1 ( ) 2 1 − A. 1 − ; . B. 0;+). C. ( 1 − ;0. D. ( ;0 − . 2 1 x
Câu 22. [KID] Tập nghiệm S của bất phương trình 8 là: 2 A. S = ( 3 − ;+). B. S = (− ; − ) 3 . C. S = (− ; ) 3 .
D. S = (3;+).
Câu 23. [KID] Tìm tập nghiệm S của phương trình x 1 4 + = 8. 1 A. S = 0 .
B. S = . C. S = 2 . D. S = 1 . 2 Trang 4
FLASH STUDY x RIKI NIHONGO x TIẾNG TRUNG HANKI Anh Giáo Kid An – h Ch G uyên L iáo Kid u – yệ Chn u Th yê i T n L o uán C yện ấp Th Tố i T c o án Cấp Tốc 2 3 1 − x
Câu 24. [KID] Giải bất phương trình 2x 1 3 + ta được tập nghiệm: 3 1 − 1 − 1 − A. − ; (1;+ ) . B. ; − . C. (1;+) . D. ;1 . 3 3 3
Câu 25. [KID] Bất phương trình x x 1 9 4.3 + −
+ 27 0 có tập nghiệm là: A. 1;2. B. 1;2) . C. (1; 2 . D. (1;2) .
Câu 26. [KID] Cho cấp số nhân (u với u = 3 và công bội q = 2. Giá trị của u bằng: n ) 1 3 3 A. 64. B. 81. C. . D. 12. 4
Câu 27. [KID] Cho cấp số cộng (u có u = 2 và công sai d = 2
− . Giá trị của u là: n ) 1 5 A. 10 . B. 6 . C. −6 . D. 32 .
Câu 28. [KID] Cho cấp số nhân có u = 2;u = 486 . Tính công bội q của cấp số nhân đã cho. 1 6 A. q = 2 − . B. q = 3 − .
C. q = 2 . D. q = 3.
Câu 29. [KID] Cho cấp số nhân (u biết u = 2,u =1. Công bội của cấp số nhân đó là: n ) 1 2 1 1 A. 2 . B. 2 − . C. . D. − . 2 2 1
Câu 30. [KID] Cho cấp số nhân (u có số hạng đầu u = và u = 3. Khi đó, công bội của cấp số nhân n ) 1 3 2 này là: 8 1 A. . B. 1. C. . D. 9 . 3 9
Câu 31. [KID] Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y = x + 2x +1, trục hoành và
hai đường thẳng x = 1 − , x = 3. 37 68 64 56 A. S = . B. S = . C. S = . D. S = . 3 3 3 3
Câu 32. [KID] Cho đồ thị hàm số y = f (x) . Diện tích hình phẳng (phần tô đậm trong hình) là: 4 A. f
(x)dx. 3 − 0 0 B. f
(x)dx+ f
(x)dx. 3 − 4 0 4 C. f
(x)dx+ f
(x)dx. 3 − 0 3 − 4 D. f
(x)dx+ f (x)dx. 0 0 Trang 5
FLASH STUDY x RIKI NIHONGO x TIẾNG TRUNG HANKI Anh Giáo Kid An – h Ch G uyên L iáo Kid u – yệ Chn u Th yê i T n L o uán C yện ấp Th Tố i T c o án Cấp Tốc 5 5 7
Câu 33. [KID] Nếu f
(x)dx = −2 và f (x)dx = 6 −
thì f ( x)dx bằng: 1 7 1 A. 12 − . B. −8 . C. 4 . D. 8 . 2
Câu 34. [KID] Giá trị của tích phân cos x dx bằng: 0 A. 1. B. 1 − . C. 0 . D. 2 . 1 1 1
Câu 35. [KID] Cho f
(x)dx = 2 và f
(x)−2g(x)dx = 8 −
. Tính tích phân g ( x)dx . 0 0 0 A. −6. B. −3 . C. 5 . D. −5 . 2 2 1
Câu 36. [KID] Cho f
(x)dx = 9 và f
(x)dx = 2 thì f
(x)dx bằng: 2 − 1 2 − A. 7 . B. 3 . C. 11. D. −7 .
Câu 37. [KID] Cho hàm số f (x) = x + cos x . Khẳng định nào sau đây đúng? A. f
(x)dx =1−sin x+C B. f
(x)dx =1+sin x+C 2 x 2 x C. f
(x)dx = +sin x +C D. f
(x)dx = −sin x+C 2 2 e
e 1+ xf ( x)
Câu 38. [KID] Nếu tích phân f
(x)dx = −1 thì dx bằng: x 1 1 1 A. 1 − . B. − . C. e −1. D. 0 . 2 e
Câu 39. [KID] Tìm họ nguyên hàm của hàm số ( ) = 2sin 2 −3 x f x x e . x 1 3e + A. f
(x)dx = −cos2x − + C .
B. ( ) = cos2 −3 x f x dx x e + C . x +1 x 1 3e + C. f
(x)dx = cos2x − + C .
D. ( ) = −cos2 −3 x f x dx x e + C . x +1 2 3 3 Câu 40. [KID] Nếu f
(x)dx = 7 và f
(x)dx = −2 thì f (x)dx bằng: 1 2 1 A. −9 . B. 5 . C. 9 . D. −5 .
Câu 41. [KID] Cho hàm số f (x) có đạo hàm là f (x) = 3−5cos x , x
và f (0) = 5. Biết F (x) là
nguyên hàm của hàm f (x) thỏa mãn F (0) = 5. Khi đó F thuộc khoảng nào dưới đây? 2 A. (12;1 ) 3 B. (11;12) C. (9;10) D. (10;1 ) 1
Câu 42. [KID] Cho hàm số f (x) 2
= x −1. Khẳng định nào dưới đây là đúng? 3 x A. f
(x)dx = 2 .x B. f
(x)dx = − x +C. 3 3 x C. f
(x)dx = − .x D. f
(x)dx = 2x +C. 3 Trang 6
FLASH STUDY x RIKI NIHONGO x TIẾNG TRUNG HANKI Anh Giáo Kid An – h Ch G uyên L iáo Kid u – yệ Chn u Th yê i T n L o uán C yện ấp Th Tố i T c o án Cấp Tốc
Câu 43. [KID] Cho (H ) là hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − x và trục hoành. Quay hình
phẳng (H ) quanh trục hoành ta được một khối tròn xoay có thể tích là: 1 1 A. 2
V = x − xdx .
B. V = ( 2x − x)dx . 0 0 1 1 2 2
C. V = ( 2x − x) dx .
D. V = ( 2x − x) dx. 0 0 2 2 2
Câu 44. [KID] Nếu f
(x)dx =3 và g(x)dx = 1 − thì f
(x)−5g(x)− xdx bằng: 0 0 0 A. 10 . B. 6 . C. 12. D. 8 .
Câu 45. [KID] Cho hàm số f (x) = 2 + cos x có một nguyên hàm là hàm số F (x) thỏa F (0) = 2022 .
Khẳng định nào đưới đây đúng?
A. F (x) = 2x +sin x +C .
B. F (x) = 2x +sin x .
C. F (x) = 2x +sin x + 2022 .
D. F (x) = 2x −sin x + 2022 .
Câu 46. [KID] Cho hình thang cong (H ) giới hạn bởi các đường y = x , y = 0, x = 0 , x = 4 . Đường
thẳng x = k (0 k 4) chia (H ) thành hai phần có diện tích S và S như hình vẽ. 1 2
Để S = 3S thì giá trị k thuộc khoảng nào sau đây? 1 2 A. (3,1;3,3) . B. (3,3;3,5). C. (3,8;3,9) . D. (3,5;3,8). 1 1 1
Câu 47. [KID] Nếu 3 f
(x)+2g(x) dx = 7
và g ( x)dx = 1 −
thì f (x)dx bằng: 0 0 0 A. 3 . B. 1 . C. −3 . D. 1 − .
Câu 48. [KID] Trên khoảng (0;+ ), họ nguyên hàm của hàm số 3 y = x là: 1 1 1 A. f (x) 3
dx = x + C . B. f (x) 3
dx = 3x + C . 3 4 1 4 3 C. f (x) 3
dx = x + C . D. f (x) 3
dx = x + C . 4 4 3
Câu 49. [KID] Cho hàm số y = f (x) thỏa mãn f (0) = 3 , f ( x) liên tục trên và f
(x)dx = 9. Giá trị 0 của f (3) là: A. 6 . B. 3 . C. 12. D. 9 . Trang 7
FLASH STUDY x RIKI NIHONGO x TIẾNG TRUNG HANKI Anh Giáo Kid An – h Ch G uyên L iáo Kid u – yệ Chn u Th yê i T n L o uán C yện ấp Th Tố i T c o án Cấp Tốc
Câu 50. [KID] Cho hình phẳng (H ) giới hạn bởi parabol (P) 2
: y = x và đường thẳng d: y = 2x . Thể tích
khối tròn xoay sinh bởi (H ) khi quay quanh trục Ox bằng: 64 16 256 4 A. . B. . C. . D. . 15 15 15 3
Câu 51. [KID] Trong không gian Oxyz , phương trình nào dưới đây không phải là phương trình của một mặt cầu? A. 2 2 2
x + y + z − 2x = 0 . B. 2 2 2
x + y + z −8x + 2y +1 = 0 . C. 2 2 2
x + y − z + 2x − 4y + 6z + 7 = 0 . D. 2 2 2
x + y + z − 2x + y − z −1 = 0 .
Câu 52. [KID] Trong không gian , cho mặt cầu (S ) x + ( y + )2 + ( z + )2 2 : 2
1 = 9 . Bán kính của (S ) bằng: A. 3 . B. 6 . C.8 . D. 9 .
Câu 53. [KID] Trong không gian Oxyz , hình chiếu vuông góc của điểm A(3;5;2) trên mặt phẳng (Oxy) có tọa độ là: A. (5;3;0) . B. (3;5;0) . C. (0;5;2). D. (3;0;2). x − 3 y +1 2 − z
Câu 54. [KID] Trong không gian Oxyz , cho đường thẳng d : = =
. Vectơ nào dưới đây là 4 1 − 3 −
một vectơ chỉ phương của d ?
A. u = 3;−1;2 .
B. u = 4;−1;− 3 .
C. u = 4;−1;3 . D. u = 3;1;2 . 1 ( ) 4 ( ) 2 ( ) 3 ( )
Câu 55. [KID] Trong không gian Oxyz , cho điểm M (1;1; )
1 . Đường thẳng đi qua M đồng thời cắt và
vuông góc với trục Oy có phương trình tham số là: x = t x =1+ t x = 1 x = t
A. y =1,t R .
B. y =1, t R .
C. y = t, t R .
D. y = t, t R . z = t z = t z = 1 z = t
Câu 56. [KID] Trong không gian Oxyz , cho ba điểm A( 1
− ;0;0),B(0;2;0),C(0;0;3) . Mặt phẳng ( ABC) có phương trình là: x y z x y z x y z x y z A. + + = 0. B. + + =1. C. + + =1. D. + + =1. 1 2 − 3 − 1 − 2 − 3 1 2 − 3 − 1 − 2 3
Câu 57. [KID] Trong không gian Oxyz , phương trình mặt cầu có tâm I (0;2;0) và đi qua điểrm M (2;0;0) là: A. ( x − )2 2 2
2 + y + z = 2 2 .
B. x + ( y − )2 2 2 2 + z = 8 . C. ( x − )2 2 2
2 + y + z = 8 .
D. x + ( y − )2 2 2 2 + z = 2 2 .
Câu 58. [KID] Trong không gian Oxyz , cho các điểm A(1;0;2) , B(1;2; )
1 , C (3;2;0) , và D(1;1;3) .
Đường thẳng đi qua A và vuông góc với mặt phẳng (BCD) có phương trình là: x = 2 − t x = 1+ t x =1+ t x =1− t
A. y = 4 − 4t .
B. y = 2 + 4t . C. y = 4 − t .
D. y = 4t . z = 4 − 2t z = 2 + 2t z = 2 + 2t z = 2 + 2t Trang 8
FLASH STUDY x RIKI NIHONGO x TIẾNG TRUNG HANKI Anh Giáo Kid An – h Ch G uyên L iáo Kid u – yệ Chn u Th yê i T n L o uán C yện ấp Th Tố i T c o án Cấp Tốc
Câu 59. [KID] Trong không gian Oxyz , đường thẳng d đi qua điểm A(1; 1
− ;2) nằm trong mặt phẳng ( x −1 y +1 z −1
P) có phương trình (P): x + y + z − 2 = 0 và vuông góc với đường thẳng : = = có 2 1 − 2 phương trình là: x =1+ t x = 1+ t x = 1+ t x = 1+ t
A. d : y = 1 − + 2t .
B. d : y = −1− t .
C. d : y = −1+ t .
D. d : y = −1 . z = 2−3t z = 2 z = 2 − 2t z = 2 − t x y z
Câu 60. [KID] Trong không gian Oxyz , mặt phẳng (P) : + +
=1 có một vectơ pháp tuyến là: 2 2 1 − A. n = 2;2; 1 − . B. n = 1;1; 2 − . C. n = 2; 2 − ; 1 − . D. n = 2 − ; 2 − ;1 . 2 ( ) 1 ( ) 4 ( ) 3 ( ) x +1 2 − y z
Câu 61. [KID] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d : = = , vectơ nào 1 3 2 −
dưới đây là một vectơ chỉ phương của đường thẳng d ? A. u = 1 − ;3; 2 − .
B. u = 1;3;2 . C. u = 1; 3 − ; 2 − . D. u = 1 − ; 3 − ;2 . 2 ( ) 2 ( ) 1 ( ) 4 ( )
Câu 62. [KID] Trong không gian Oxyz , hình chiếu của điểm A(1;2;− )
1 trên mặt phẳng (Oxy) là điểm nào sau đây? A. Q( 1 − ;− 2; ) 1 . B. P( 1 − ;− 2;0) . C. M (1;2; ) 1 . D. N (1;2;0) . x = 1 − + 2t
Câu 63. [KID] Trong không gian Oxyz , đường thẳng (d ) : y = t
− + 3 có một vectơ chỉ phương là: z = 2+t A. u (2;−1; ) 1 . B. v( 1 − ;3;2) . C. a( 1 − ;2;3) . D. b = (2;3; ) 1 .
Câu 64. [KID] Trong không gian Oxyz, gọi là góc giữa hai mặt phẳng (P): x + 2y − z + 2 = 0 và
(Q):2x− y − z +4 = 0. Tính cos . 2 3 1 1 − A. cos = . B. cos = . C. cos = . D. cos = . 3 4 6 6
Câu 65. [KID] Trong không gian Oxyz, cho mặt cầu (S): 2 2 2
2x + 2y + 2z −8x + 4y − 2 = 0 . Tâm và bán kính của (S) là: A. I (2; 1 − ;0),R = 6 B. I ( 2 − ;1;0),R = 6 C. I (2; 1
− ;0),R = 5 D. I (4; 2 − ;0), R = 19
Câu 66. [KID] Trong không gian Oxyz , cho hai điểm A(1;1;2) và B(3;1;0). Phương trình mặt phẳng
trung trực của đoạn thẳng AB là:
A. x − z −1 = 0
B. x + z − 3 = 0 C. x = 2 D. y =1
Câu 67. [KID] Trong không gian Oxyz , phương trình nào sau đây không phải là phương trình tham số của
đường thẳng đi qua hai điểm A(1;2; ) 3 và B(3;4;5) ? A. x = 1 − +t; y = 2 − +t;z = 3 − +t
B. x = 3− 2t; y = 4 − 2t; z = 5− 2t
C. x =1+ 2t; y = 2 + 2t; z = 3+ 2t
D. x = 2+t; y = 3+t; z = 4+t
Câu 68. [KID] Trong không gian Oxyz , cho điểm M ( 1 − ;2;− )
3 . Tọa độ điểm M đối xứng với M qua
mặt phẳng (Oxz) là: A. (1; 2 − ; ) 3 B. ( 1 − ; 2 − ; 3 − ) C. (1;2; ) 3 − D. ( 1 − ;2;3) Trang 9
FLASH STUDY x RIKI NIHONGO x TIẾNG TRUNG HANKI Anh Giáo Kid An – h Ch G uyên L iáo Kid u – yệ Chn u Th yê i T n L o uán C yện ấp Th Tố i T c o án Cấp Tốc x −1 y − 2 z + 3
Câu 69. [KID] Trong không gian Oxyz , cho đường thẳng d: = =
. Điểm nào sau đây không 2 1 1 −
thuộc đường thẳng d ? A. (1;2; ) 3 − B. (3;3; 4 − ) C. ( 1 − ;1; 2 − ) D. (5;4; 4 − )
Câu 70. [KID] Điều kiện của tham số m để phương trình 2 2 2
x + y + z − 2x − 4y + 6z + m = 0 là phương
trình của một mặt cầu là: A. m 14 B. m 14 C. m 14 D. m 0
Câu 71. [KID] Trong không gian Oxyz , cho đường thẳng d đi qua M (1;2; )
3 và có vectơ chỉ phương u = (0;1; 2
− ). Phương trình nào sau đây là phương trình của d? x = 1 x = 1+ t x −1 y − 2 z − 3 A. = =
B. y = 2 + t
C. y = 2 + t
D. x =1; y + z = 5 0 1 2 − z = 3− 2t z = 3 − 2t
Câu 72. [KID] Trong không gian Oxyz , cho hai vectơ u = (1; 1
− ;2) và v = (2;4; )
1 . Tích vô hướng u v có giá trị là: A. 0 B. (0,0,0) C. (2, 4 − ,2) D. 4 −
Câu 73. [KID] Trong không gian Oxyz , cho mặt phẳng (P): 2y −3z −3 = 0 và hai đường thẳng x = 1 − + 2t x y −1 z + 2 d : = =
; d : y =1+ t
. Đường thẳng nằm trong mặt phẳng (P) , đồng thời cắt cả hai 1 2 1 − 1 2 z =1
đường thẳng d ,d có phương trình là: 1 2 x − 2 y z +1 x + 2 y z −1 x + 2 y z −1 x − 2 y z +1 A. = = . B. = = . C. = = . D. = = . 1 3 2 1 3 − 2 1 3 2 1 3 − 2 x = 2 + t
Câu 74. [KID] Trong không gian Oxyz , đường thẳng d : y = 3 − t đi qua điểm nào trong các điểm có z = −2+t tọa độ dưới đây? A. C(3; 2 − ;− ) 1 . B. B(3;2;− ) 1 . C. D( 3 − ; 2 − ; ) 1 . D. A(1;2;− ) 1 .
Câu 75. [KID] Phương trình mặt phẳng đi qua ba điểm O(0;0;0) , A(5;0;0) và B(0;2;0) là x y
A. z = 0 B. + =1
C. 2x +5y = 0
D. 2x +5y + z = 0 5 2
Câu 76. [KID] Cho khối chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy và SA = a .
Thể tích của khối chóp V đã cho bằng: S .ABC 3 2a 3 a 3 a A. . B. . C. 3 a . D. . 3 6 3
Câu 77. [KID] Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a . Thể tích của khối chóp S.ABC bằng: 2 2 2 2 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 12 6 4 2 Trang 10
FLASH STUDY x RIKI NIHONGO x TIẾNG TRUNG HANKI Anh Giáo Kid An – h Ch G uyên L iáo Kid u – yệ Chn u Th yê i T n L o uán C yện ấp Th Tố i T c o án Cấp Tốc
Câu 78. [KID] Cho hình chóp S.ABCD có SA vuông góc với đáy và đáy là hình thang vuông tại A và B
. Biết cạnh AB = BC = ,
a SA = a 2, AD = 2a , khi đó góc giữa đường thẳng SC và mặt phẳng đáy bằng: A. 90 . B. 30 . C. 60 . D. 45 .
Câu 79. [KID] Cho hình chóp S.ABCD đáy là hình vuông cạnh bằng a 2 , cạnh bên SA vuông góc với
đáy và SA = a 3 . Số đo của góc nhị diện S, B , D A bằng A. 30 . B. 45. C. 90 . D. 60 .
Câu 80. [KID] Cho hình chóp S.ABCD có đáy là hình thoi tâm ,, S a 6
SO ⊥ ( ABCD) , SO =
và BC = SB = a (tham khảo hình vẽ). Khoảng 3
cách từ điểm , đến mặt phẳng (SBC) bằng: 2a 3 a 3 D A. . B. . C 3 6 O a 6 a 6 A C. . D. . B 6 2
Câu 81. [KID] Cho hai biến cố A và B là hai biến cố ngẫu nhiên mà ( P ) A 0 , ( P )
B 0 , công thức Bayes là
P B .P A | B
P A .P A | B
A. P(B | A) ( ) ( ) =
B. P(B | A) ( ) ( ) = P( A) P(B)
P B .P B | A
P A .P B | A
C. P(B | A) ( ) ( ) =
D. P(B | A) ( ) ( ) = P( A) P(B)
Câu 82. [KID] Chọn khẳng định đúng.
P B .P B | A
A. Với hai biến cố ,
A B , ta có P(B | A) ( ) ( ) = . P( A)
P A .P A | B
B. Với hai biến cố ,
A B , ta có P(B | A) ( ) ( ) = . P(B)
P B .P A | B
C. Với hai biến cố , A B mà ( P ) A 0, ( P )
B 0 , ta có P(B | A) ( ) ( ) = . P( A)
P A .P A | B
D. Với hai biến cố , A B mà ( P ) A 0, ( P )
B 0 , ta có P(B | A) ( ) ( ) = . P(B)
Câu 83. [KID] Cho hai biến cố , A B sao cho ( P ) B = 0,7 và ( P A ) B = 0,2 . Tính ( P A| ) B . 7 2 7 1 A. B. C. D. 10 7 50 2
Câu 84. [KID] Cho hai biến cố A và B độc lập, biết P( A) = 0,4;P(B) = 0,7. Khi đó P(B | A) bằng 7 4 7 3 A. B. C. D. 10 7 25 10
Câu 85. [KID] Cho hai biến cố A và B biết P(B) = 0,6; P( A| B) = 0,3; P(A| B) = 0,8 . Tính P( A)
A. P( A) = 0,3
B. P( A) = 0,4
C. P( A) = 0,5
D. P( A) = 0,6 Trang 11
FLASH STUDY x RIKI NIHONGO x TIẾNG TRUNG HANKI Anh Giáo Kid An – h Ch G uyên L iáo Kid u – yệ Chn u Th yê i T n L o uán C yện ấp Th Tố i T c o án Cấp Tốc
Câu 86. [KID] Cho hai biến cố A và B , với P(B) = 0,8 , P( A| B) = 0,7 , P( A| B) = 0,45 . Giá trị P( A) bằng A. 0,25 B. 0,65 C. 0,55 D. 0,5
Câu 87. [KID] Cho P( A) = 0,4; P(B A) = 0,2 . Giá trị của P(BA) là A. 0,2 B. 0,08 C. 0,4 D. 0,12
Câu 88. [KID] Cho hai biến cố A và B là hai biến cố độc lập, với P( A) = 0,2024, P(B) = 0,2025. Tính
P( A| B) . A. 0,7976 B. 0,7975 C. 0,2025 D. 0,2024
Câu 89. [KID] Cho hai biến cố A và B , với P( A) = 0,8 , P(B) = 0,65 , P( A B) = 0,55 . Tính
P( A B). A. 0,25 B. 0,1 C. 0,15 D. 0,35
Câu 90. [KID] Cho hai biến cố ,
A B có xác suất P( A) = 0,4;P(B) = 0,3;P( A| B) = 0,25. Tính xác suất
P(B | A) . 1 A. 0,1875 B. 0,48 C. D. 0,95 3
Câu 91. [KID] Cho một hộp kín có 6 thẻ ATM của ACB và 4 thẻ ATM của Vietcombank. Lấy ngẫu nhiên
lần lượt 2 thẻ (lấy không hoàn lại). Tìm xác suất để lần thứ hai lấy được thẻ ATM của Vietcombank nếu
biết lần thứ nhất đã lấy được thẻ ATM của ACB. 1 2 2 4 A. B. C. D. 3 3 9 9
Câu 92. [KID] Để được chọn vào đội tuyển học sinh giỏi môn Toán cấp thành phố, mỗi thí sinh phải vượt
qua hai vòng thi. Bạn Hà tham dự cuộc tuyển chọn này. Xác suất để Hà qua được vòng thứ nhất là 0,8 .
Nếu qua được vòng thứ nhất thì xác suất để Hà qua được vòng thứ hai là 0,7 . Xác suất để bạn Hà được
chọn vào đội tuyển này là A. 0,06 B. 0,24 C. 0,56 D. 0,875
Câu 93. [KID] Một mảnh đất chia thành hai khu vườn. Khu A có 150 cây ăn quả, khu B có 200 cây ăn quả.
Trong đó, số cây Táo ở khu A và khu B lần lượt là 50 cây và 100 cây. Chọn ngẫu nhiên 1 cây trong mảnh
đất. Xác suất cây được chọn là cây Táo , biết rằng cây đó ở khu B, là : 1 1 1 2 A. B. C. D. 2 4 3 3
Câu 94. [KID] Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của các dự án I và II lần lượt là 0,4 và
0,5 . Khả năng thắng thầu của hai dự án là 0,3 . Gọi ,
A B lần lượt là biến cố thắng thầu dự án I và dự án II.
Biết công ty thắng thầu dự án I, tìm xác suất công ty thắng thầu dự án II. A. 0,25 B. 0,5 C. 0,75 D. 0,125
Câu 95. [KID] Gieo hai con xúc sắc cân đối và đồng chất. Tính xác suất để tổng số chấm xuất hiện trên
hai con xúc xắc bằng 6 . Biết rằng con xúc xắc thứ nhất xuất hiện mặt 4 chấm. 2 1 1 5 A. B. C. D. 6 2 6 6
Câu 96. [KID] Một lớp có 50 học sinh, trong đó có 30 học sinh nam và 20 học sinh nữ. Có 5 học sinh nam
được học sinh giỏi và có 6 học sinh nữ được học sinh giỏi. Xác suất để chọn được một bạn nữ là học sinh giỏi 5 2 7 3 A. B. C. D. 9 3 9 10 Trang 12
FLASH STUDY x RIKI NIHONGO x TIẾNG TRUNG HANKI Anh Giáo Kid An – h Ch G uyên L iáo Kid u – yệ Chn u Th yê i T n L o uán C yện ấp Th Tố i T c o án Cấp Tốc
Câu 97. [KID] Một lớp học có 40 học sinh, mỗi học sinh giỏi ít nhất một trong hai môn Văn hoặc môn
Toán. Biết rằng có 30 học sinh giỏi môn Toán và 15 học sinh giỏi môn Văn. Chọn ngẫu nhiên một học
sinh. Tính xác suất để học sinh đó học giỏi môn Toán, biết rằng học sinh đó giỏi môn Văn. 1 1 1 1 A. B. C. D. 2 6 3 5
Câu 98. [KID] Khảo sát về sở thích uống trà sữa của 200 em học sinh theo giới tính và loại trà sữa ta được bảng số liệu sau: Loại trà Nam Nữ Matcha 40 50 Hồng trà 30 80
Chọn ngẫu nhiên một bạn học sinh. Nếu đã chọn được một bạn nữ thì xác suất để bạn nữ thích uống vị hồng trà là bao nhiêu? 8 5 3 2 A. B. C. D. 13 8 4 5
Câu 99. [KID] Một trường trung học phổ thông có 600 học sinh, trong đó có 245 học sinh nam và 355 học
sinh nữ. Tổng kết học kỳ I, có 170 học sinh đạt danh hiệu học sinh giỏi, trong đó có 80 học sinh nam và 90
học sinh nữ. Chọn ra ngẫu nhiên một học sinh trong số 600 học sinh đó. Tính xác suất để học sinh được
chọn có danh hiệu học sinh giỏi và là nam (làm tròn kết quả đến hàng phần trăm). 5 12 11 2 A. B. C. D. 19 31 45 15
Câu 100. [KID] Một hộp chứa 8 bi xanh, 2 bi đỏ. Lần lượt bốc từng bi và không hoàn lại. Giả sử lần đầu
tiên bốc được bi xanh. Xác định xác suất lần thứ 2 bốc được bi đỏ. 1 2 8 2 A. B. C. D. 10 9 9 5 --------HẾT------- Trang 13
FLASH STUDY x RIKI NIHONGO x TIẾNG TRUNG HANKI




