Toán Thực Tế Tích Phân Trong Hình Học | Tài liệu môn Toán

TOÁN THỰC TẾ TÍCH PHÂN TRONG HÌNH HỌC
DẠNG 1. ỨNG DỤNG TÍNH DIỆN TÍCH VD1:
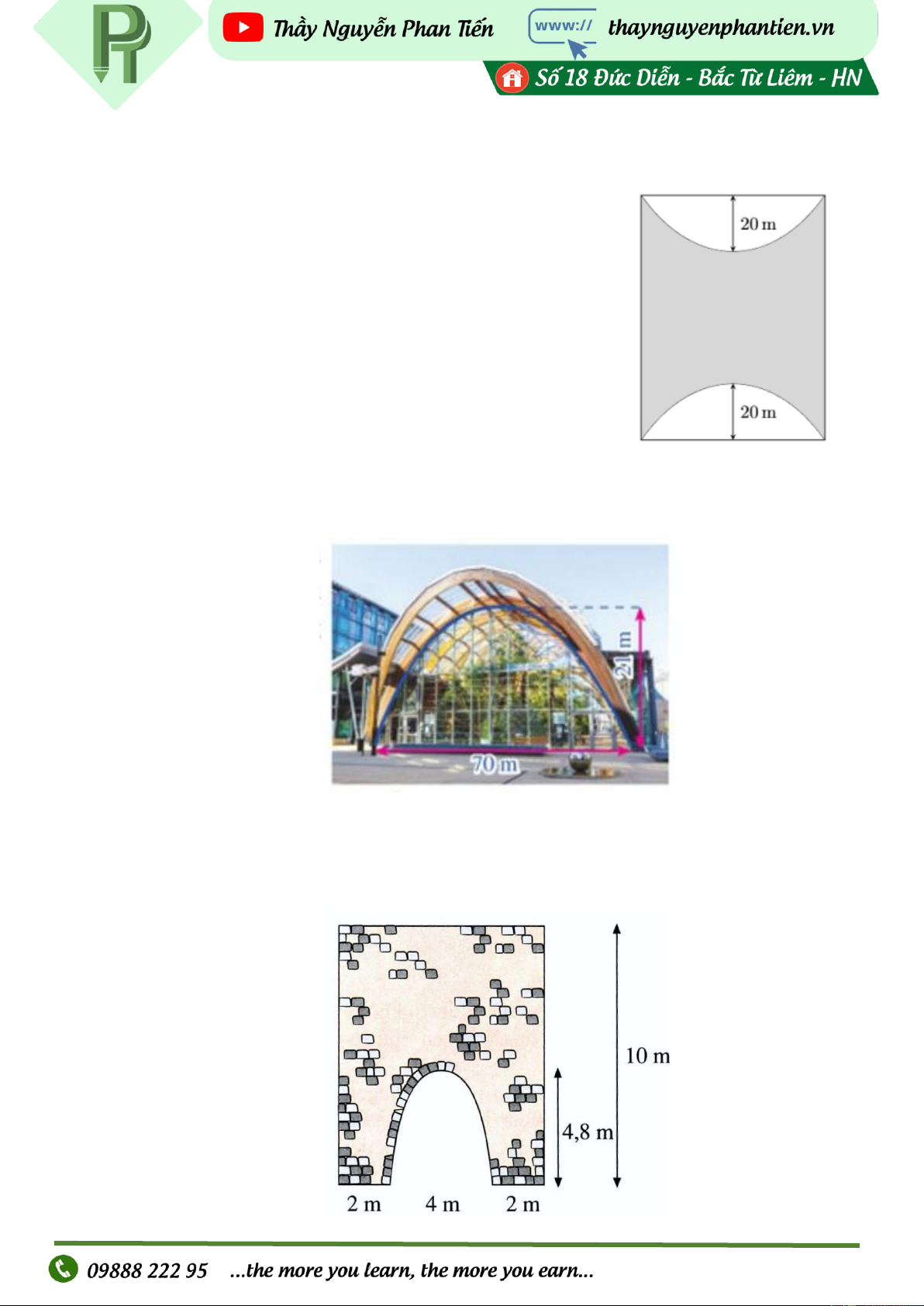
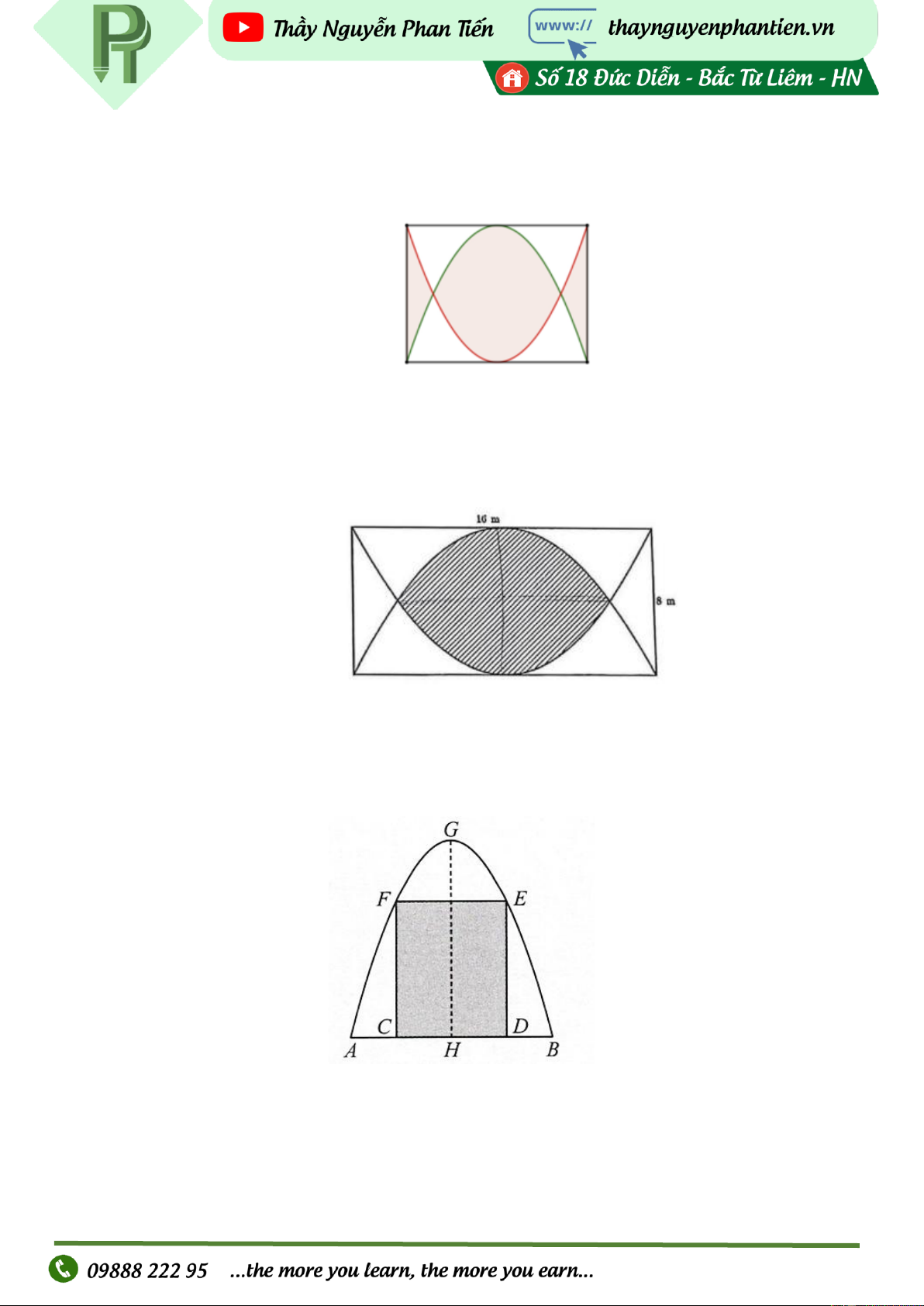
Kiến trúc sư thiết kế một khu sinh hoạt cộng đồng có dạng hình
chữ nhật với chiều rộng và chiều dài lần lượt là 60 m và 80 m.
Trong đó, phần được tô màu đậm là sân chơi, phần còn lại để
trồng hoa. Mỗi phần trồng hoa có đường biên cong là một phần
của parabol với đỉnh thuộc một trục đối xứng của hình chữ nhật
và khoảng cách từ đỉnh đó đến trung điểm cạnh tương ứng của
hình chữ nhật bẳng 20 m (xem hình minh họa). Diện tích của
phần sân chơi là bao nhiêu mét vuông? VD2:
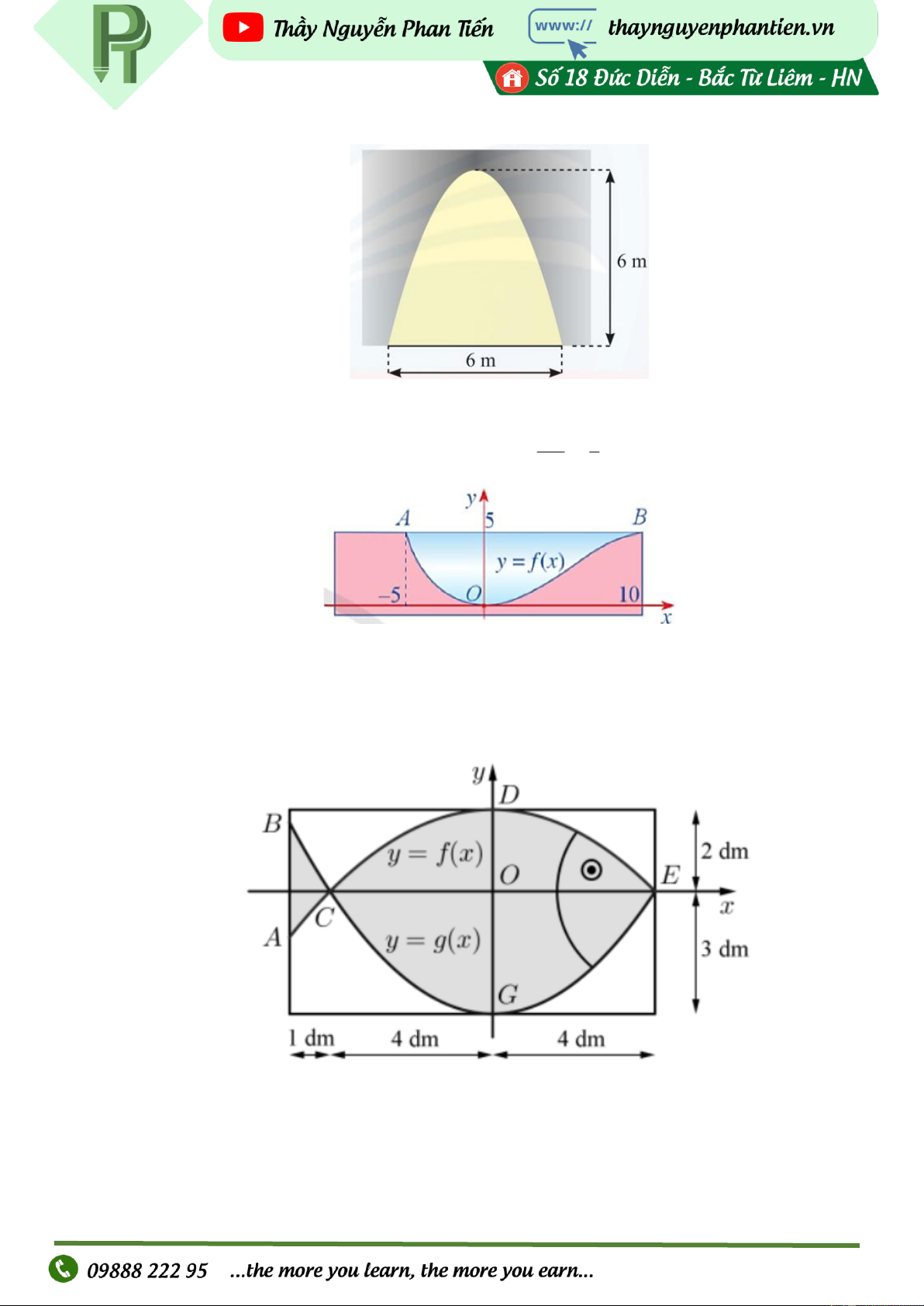
Người ta dự định lắp kính cho cửa của một mái vòm có dạng hình parabol. Hãy tính diện tích
mặt kính cần lắp vào, biết rằng vòm cửa cao 21 m và rộng 70 m (Hình). VD3:
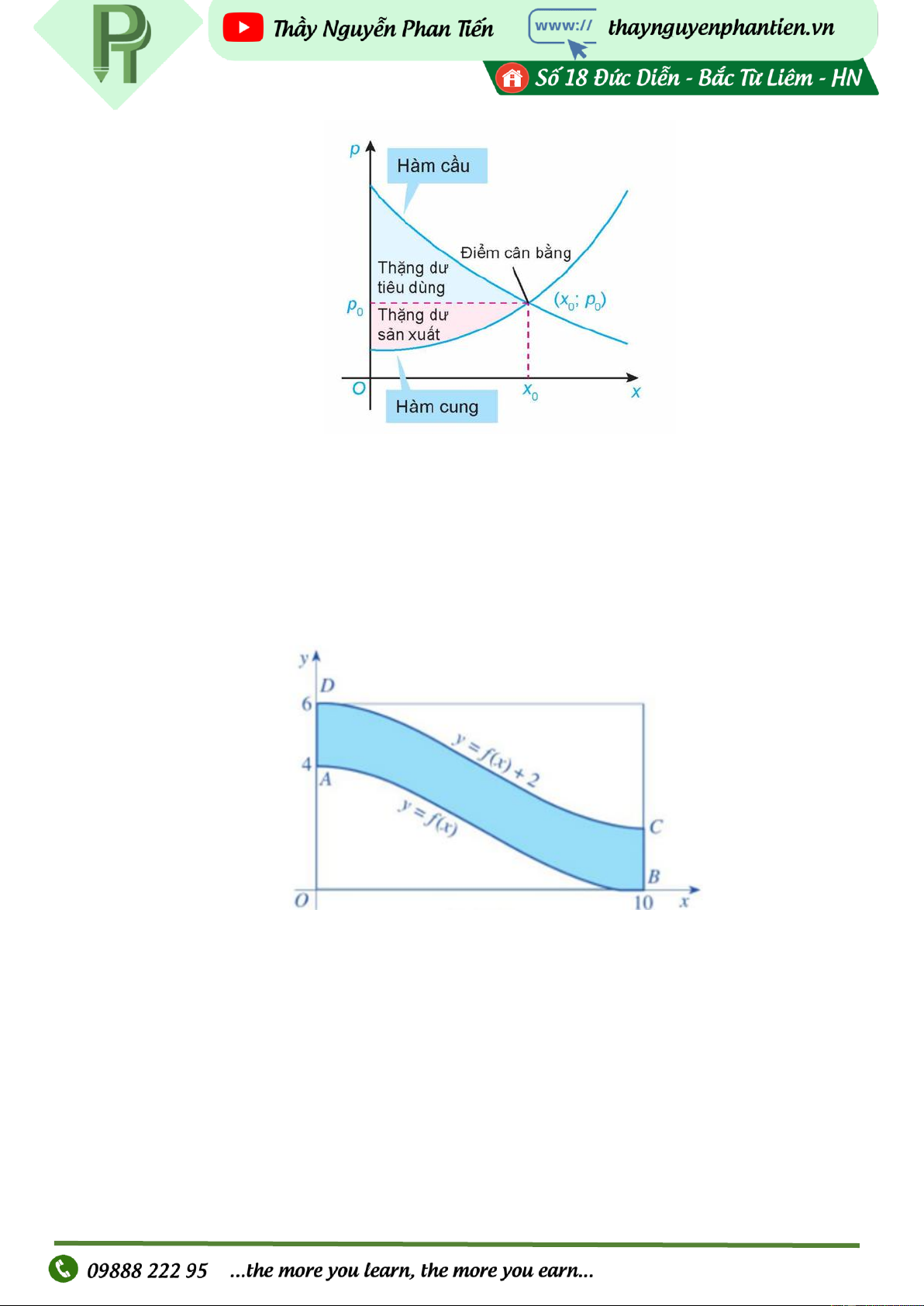
Hình minh hoạ mặt cắt đứng của một bức tường cũ có dạng hình chữ nhật với một cổng ra vào
có dạng hình parabol với các kích thước được cho như trong hình đó. Người ta dự định sơn lại
mặt ngoài của bức tường đó. Chi phí để sơn bức tường là 15000 đồng/ 2
1 m . Tổng chi phí để sơn
lại toàn bộ mặt ngoài của bức tường đó sẽ là bao nhiêu? Page | 1 VD4:
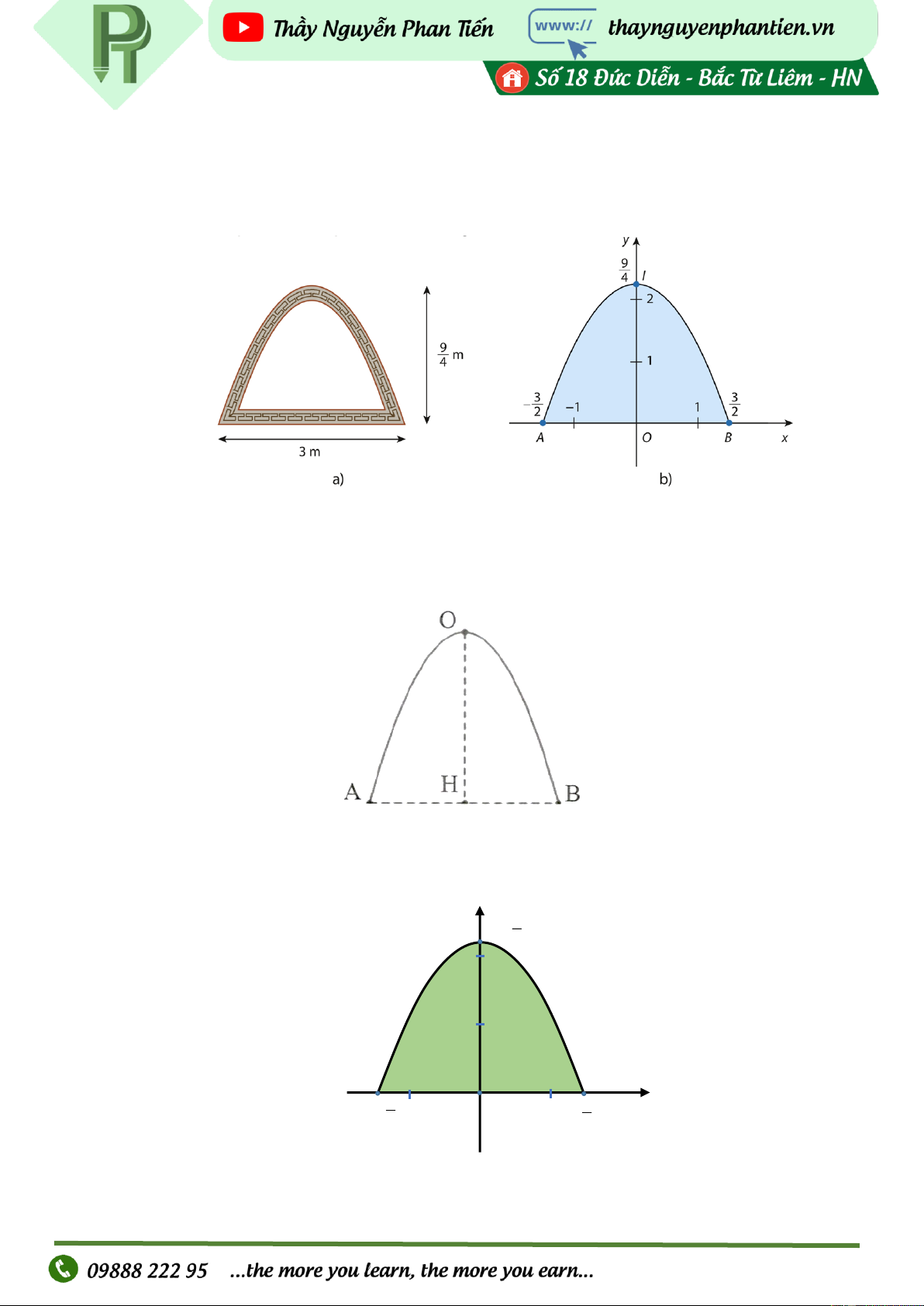
Mặt cắt của một cửa hầm có dạng là hình phẳng giới hạn bởi một parabol và đường thẳng nằm
ngang như Hình. Tính diện tích của cửa hầm. VD5:
Hình minh hoạ mặt cắt đứng của một con kênh đặt trong hệ trục toạ độ Oxy . Đáy của con kênh 3  1 
là một đường cong cho bởi phương trình 3 2
y = f (x) = − x + 5x   100  3 
Hãy tính diện tích hình phẳng tô màu xanh trong Hình, biết đơn vị trên mỗi trục tọa độ là mét. VD6:
Trên cửa sổ có dạng hình chữ nhật, hoạ sĩ thiết kế logo hình con cá cho một doanh nghiệp kinh
doanh hải sản. Logo là hình phẳng giới hạn bởi hai parabol với các kích thước được cho trong
Hình (đơn vị trên mỗi trục toạ độ là decimét).
a) Lập phương trình các parabol y = f (x) và y = g(x) .
b) Tính diện tích của logo. Page | 2 VD7:
Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hoá bởi: Hàm cầu: p = 0
− ,36x + 9 và hàm cung: p = 0,14x + 2, trong đó x là số đơn vị sản phẩm.
Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này. VD8:
Cô Hạnh đổ bê tông một đường đi trong vườn (phần được tô màu) với kích thước được cho trong
Hình. Biết rằng đường cong AB được cho bởi đồ thị của một hàm số liên tục và đường cong
DC nhận được từ đường cong AB bằng cách tịnh tiến theo phương thẳng đứng lên phía trên 2 m .
Ngoài ra, cô Hạnh quyết định đổ lớp bê tông dày 15 cm và giá tiền 3
1 m bê tông là 1080000 đồng.
Tính số tiền cô Hạnh cần dùng để đổ bê tông con đường đó. Page | 3
BÀI TẬP TỰ LUYỆN 1 Câu 1.
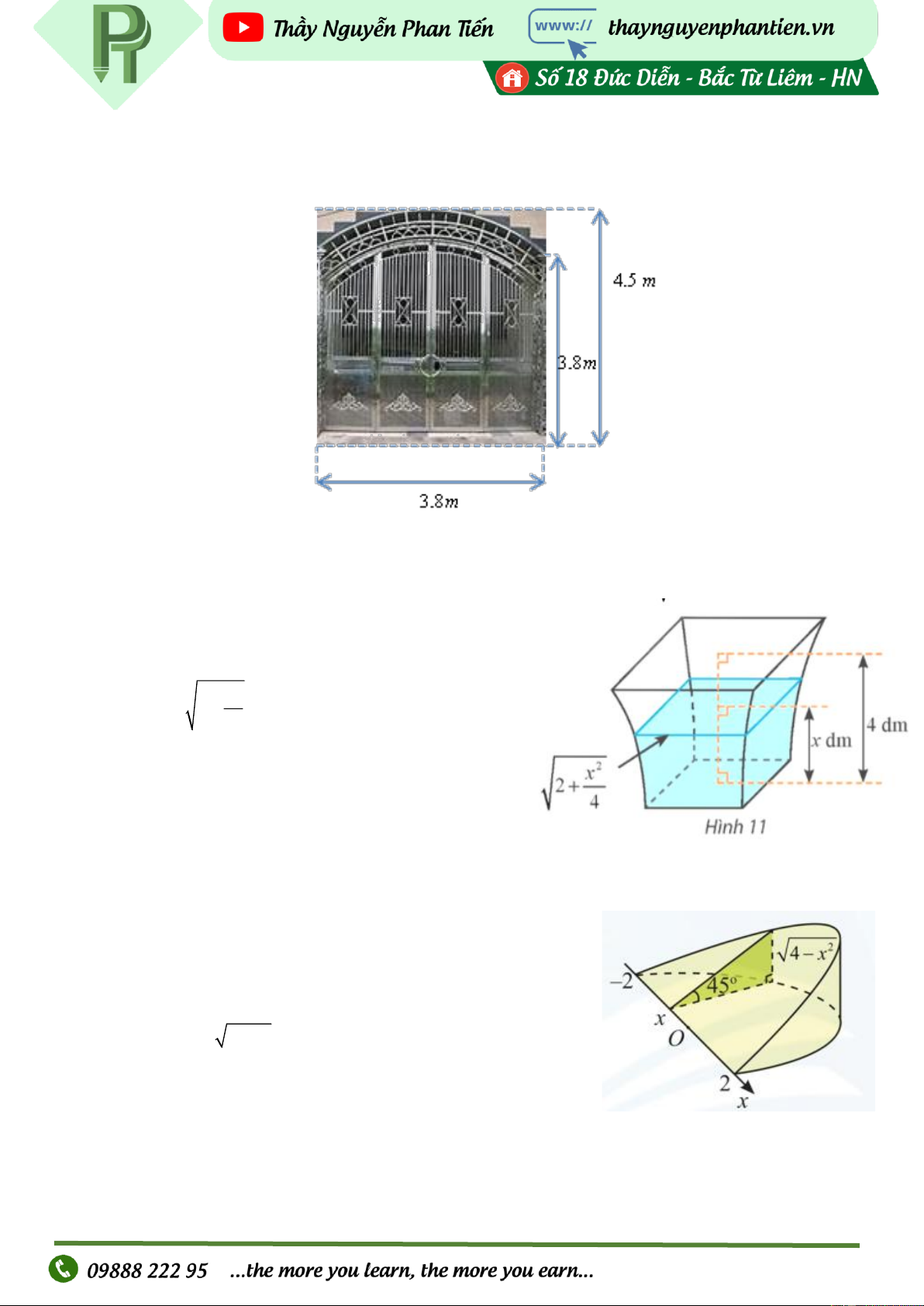
Cửa vòm lấy ánh sáng của một toà nhà được thiết kế với kích thước như Hình a. Cửa có hình
dạng một parabol có đỉnh I và đi qua hai điểm ,
A B như Hình b. Người ta dự định lắp kính cho
cửa này. Tính diện tích kính cần lắp, biết rằng người ta chỉ sử dụng một lớp kính và bỏ qua diện tích khung cửa. Câu 2.
Mặt cắt đứng của một cái cổng có dạng một đường parabol với chiều cao OH = 4 m và khoảng
cách giữa hai chân cổng là AB = 4 m (hình bên). Diện tích hình phẳng giới hạn bởi đường
parabol và đoạn thẳng AB bằng bao nhiêu mét vuông? (Làm tròn kết quả đến hàng phần mười) Câu 3.
Bác Năm làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là 2, 25 mét, chiều
rộng tiếp giáp với mặt đất là 3 mét. Giá thuê mỗi mét vuông là 1500000 đồng. Vậy bác Năm
phải trả bao nhiêu nghìn đồng? y  9  I 0;    4  2 1 − 1 1  3  O  3  x A − ; 0   B ; 0    2   2  Page | 4 Câu 4.
Ông A trồng hoa cảnh trên khuôn viên đất ở trong vườn là phần hình phẳng giới hạn bởi hai
đường parabol và hình chữ nhật có chiều rộng 6m và chiều dài 8m (phần tô đậm trong hình vẽ
dưới), các đỉnh của parabol là điểm chính giữa các cạnh chiều dài hình chữ nhật. Biết chi phí
trồng hoa cảnh xong là 500000 đồng 2
1 m . Tổng chi phí mà ông A phải trả để trồng xong vườn
hoa cảnh bằng bao nhiêu triệu đồng? (làm tròn đến hàng phần mười) Câu 5.
Ông Năm có một khu đất dạng hình chữ nhất với chiều dài là 16m và chiều rộng là 8m . Ông
Năm trồng rau sạch trên một mảnh vườn được giới hạn bởi hai parabol. Biết rằng mỗi parabol
có đỉnh là trung điểm của cạnh dài và đi qua hai điểm đầu mút của cạnh dài đối diện (phần gạch
sọc như hình vẽ minh họa).
Biết chi phí để trồng rau là 45000 đồng 2
/m . Hỏi ông Năm cần bao nhiêu triệu đồng để trồng
rau trên phần mảnh vườn đó (làm tròn kết quả đến hàng phần mười) Câu 6.
*Một cánh cổng của một toà nhà có dạng parabol gồm hai phần: phần hai cánh cửa hình chữ
nhật CDEF , còn lại là phần xiên hoa trang trí (Hình). Biết rằng GH = 4 ,
m AB = 4 m và AC = BD = 0,9 m . Diện tích phần cổng làm xiên hoa trang
trí (kết quả làm tròn đến hàng phần trăm) bằng bao nhiêu mét vuông? Page | 5 Câu 7.
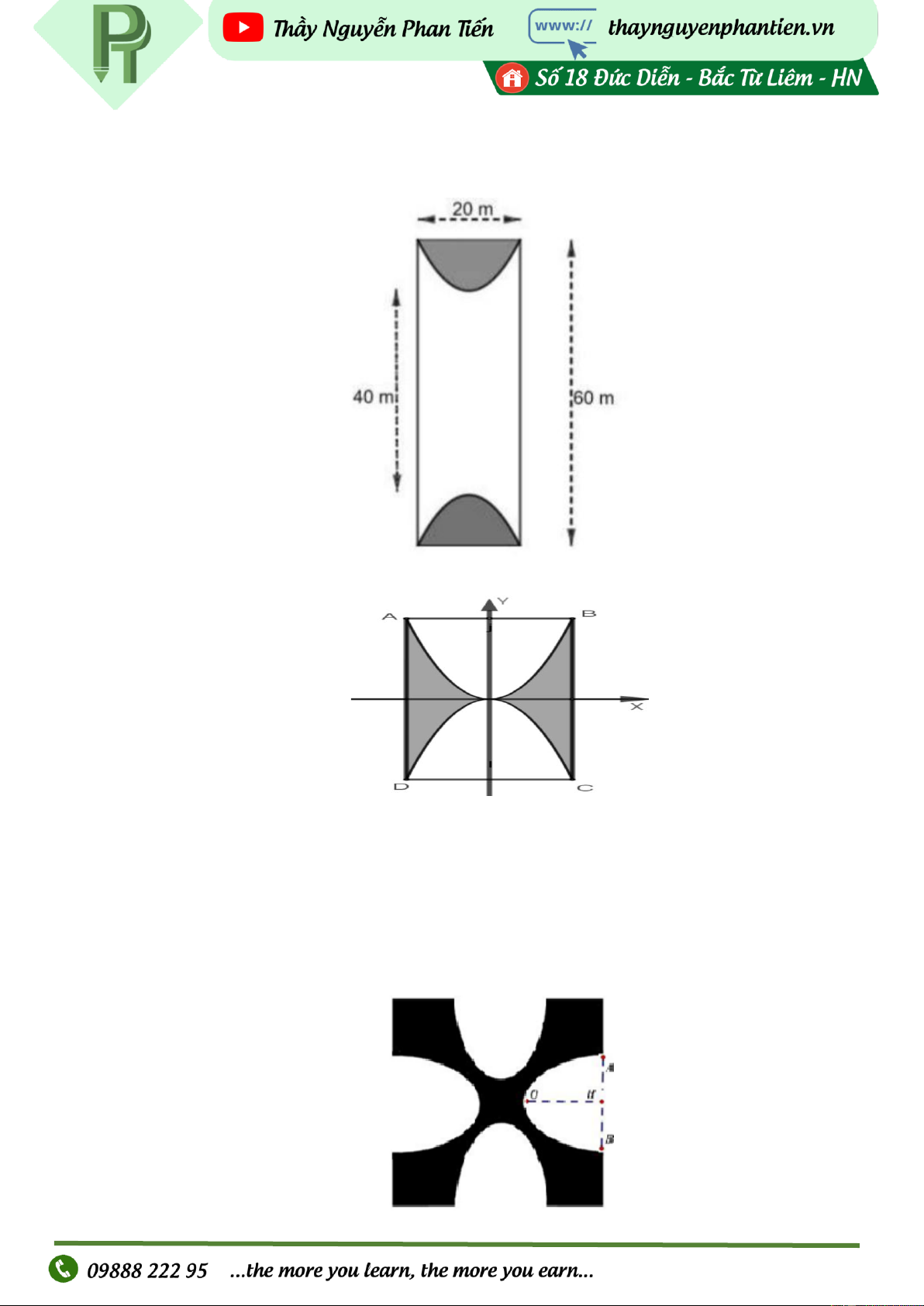
Một mành đất hình chữ nhật có chiều dài 60 m , chiều rộng 20 m . Người ta muốn trồng cỏ ở hai
đầu của mảnh đất hai hình bằng nhau giới hạn bởi hai đường Parabol có hai đỉnh cách nhau
40 m (như hình vẽ bên). Phần còn lại của mảnh đất người ta lát gạch với chi phí là 200.000 đồng 2
/m . Hỏi cần tổng bao nhiêu triệu đồng đề lát gạch (làm tròn đến hàng đơn vị) Câu 8.
Một họa tiết hình cánh bướm như hình vẽ bên.
Phần tô đậm được đính đá với giá thành 2
500.000đ/m . Phần còn lại được tô màu với giá thành 2 250.000đ / m . Cho AB = 4d ; m BC = 8d .
m Hỏi để trang trí 1000 họa tiết như vậy cần bao nhiêu triệu đồng? (Số
tiền được làm tròn đến hàng đơn vị) Câu 9.
Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng 10 cm bằng
cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết AB = 5 cm, OH = 4
cm. Tính diện tích bề mặt hoa văn đó (làm tròn kết quả đến hàng đơn vị) Page | 6
Câu 10. Ông X muốn làm cửa rào sắt có hình dạng và kích thước như hình vẽ bên, biết đường cong phía
trên là một Parabol, chất liệu làm là inox. Giá 2
1m vật tư và công làm là 1.300.000 đồng. Hỏi
ông X phải trả bao nhiêu triệu đồng để làm cái cửa sắt như vậy (làm tròn đến hàng đơn vị).
DẠNG 2. ỨNG DỤNG THỂ TÍCH – TOÁN THỰC TẾ VD9:
Một bình chứa nước có hình dạng như Hình.
Biết rằng khi nước trong bình có chiều cao
x(dm)(0  x  4) thì mặt nước là hình vuông có 2 x cạnh 2 +
(dm) . Tính dung tích của bình. 4 VD10:
Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc
với trục Ox tại điểm có hoành độ x( 2
−  x  2) , mặt cắt là
tam giác vuông có một góc 45 và độ dài một cạnh góc vuông là 2 4 − x (d )
m . Tính thể tích của vật thể. Page | 7 VD11:
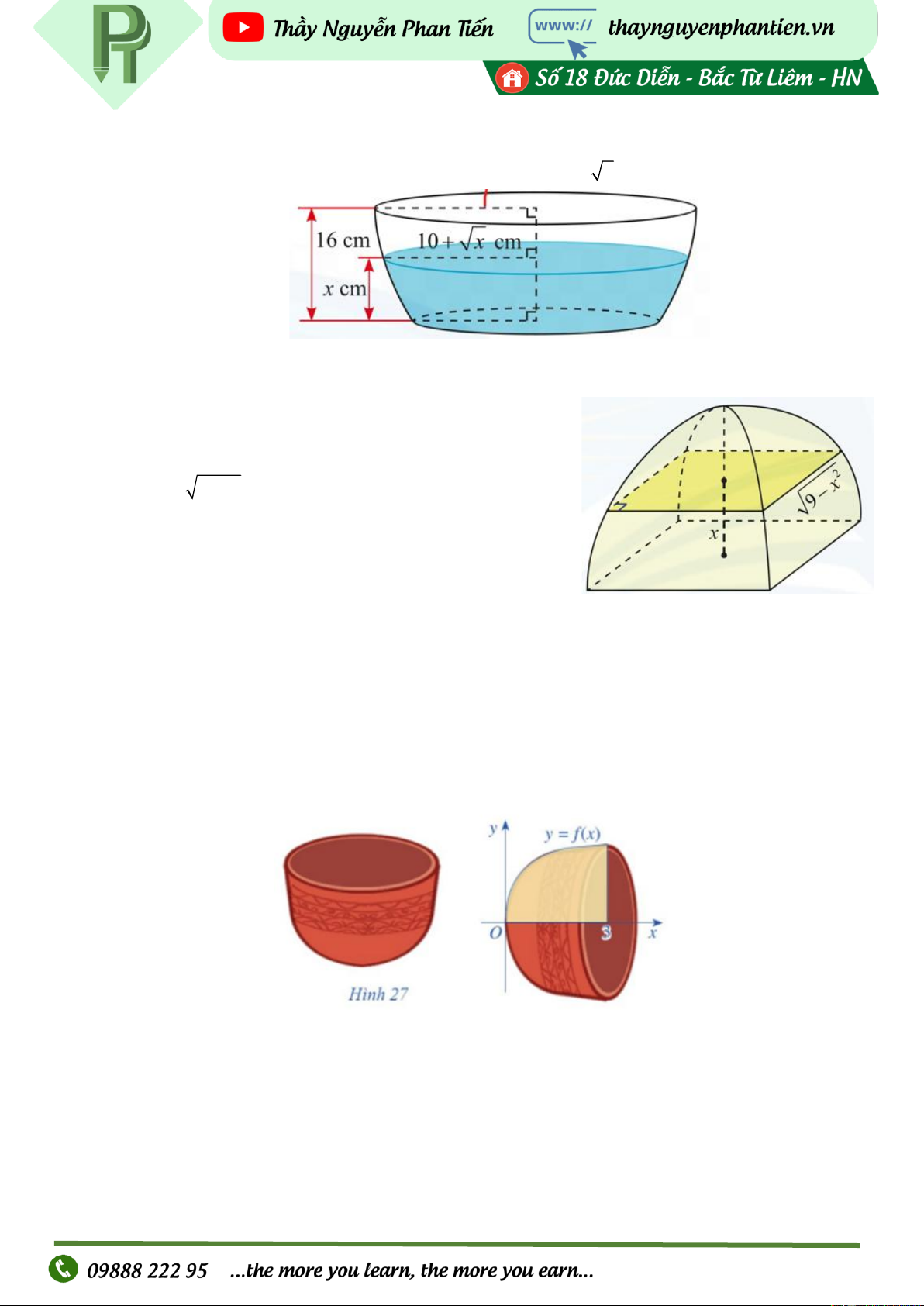
Nếu cắt chậu nước có hình dạng như Hình bằng mặt phẳng song song và cách mặt đáy
x( cm)(0  x  16) thì mặt cắt là hình tròn có bán kính (10 + x )(c )
m . Tính dung tích của chậu VD12:
Một chiếc lều mái vòm có hình dạng như Hình. Nếu cắt
lều bằng mặt phẳng song song với mặt đáy và cách mặt
đáy một khoảng x( m)(0  x  3) thì được hình vuông có cạnh 2 9 − x ( )
m . Tính thể tích của lều. VD13:
Xét chiếc chén trong bộ ấm chén uống trà ở phần mở đầu, bạn Dương ước lượng được rằng chiếc
chén được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số 3 2
f (x) = 0,14x − 0,87x +1,92x + 0,85 , trục hoành và hai đường thẳng x = 0, x = 3 quay quanh
trục Ox (đơn vị trên mỗi trục tọa độ là centimét).
Tính thể tích của chiếc chén (làm tròn đến hàng đơn vị của centimét khối). Page | 8 VD14:
Sau khi đo kích thước của thùng rượu vang (Hình), bạn Quân xác định thùng rượu vang có dạng
hình tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số 2 y = 0
− ,011x − 0,071x + 40, trục Ox và hai đường thẳng x = 35
− , x = 35 quay quanh trục Ox .
Tính thể tích thùng rượu vang đó, biết đơn vị trên mỗi trục tọa độ là centimét. VD15:
Hình b mô phỏng phần bên trong của một chậu cây có dạng khối tròn xoay tạo thành khi quay 3
một phần của đồ thị hàm số y = x +
với 0  x  4 quanh trục hoành. Tính thể tích phần bên 2
trong (dung tích) của chậu cây, biết đơn vị trên các trục Ox, Oy là decimét.
BÀI TẬP TỰ LUYỆN 2
Câu 11. Một khối bê tông cao 2 m được đặt trên mặt đất phẳng.
Nếu cắt khối bê tông này bằng mặt phẳng nằm ngang,
cách mặt đất x( m)(0  x  2) thì được mặt cắt là hình
chữ nhật có chiều dài 5 m, chiều rộng (0,5)x ( ) m (Hình).
Tính thể tích của khối bê tông (kết quả làm tròn đến hàng
phần trăm của mét khối). Page | 9 3
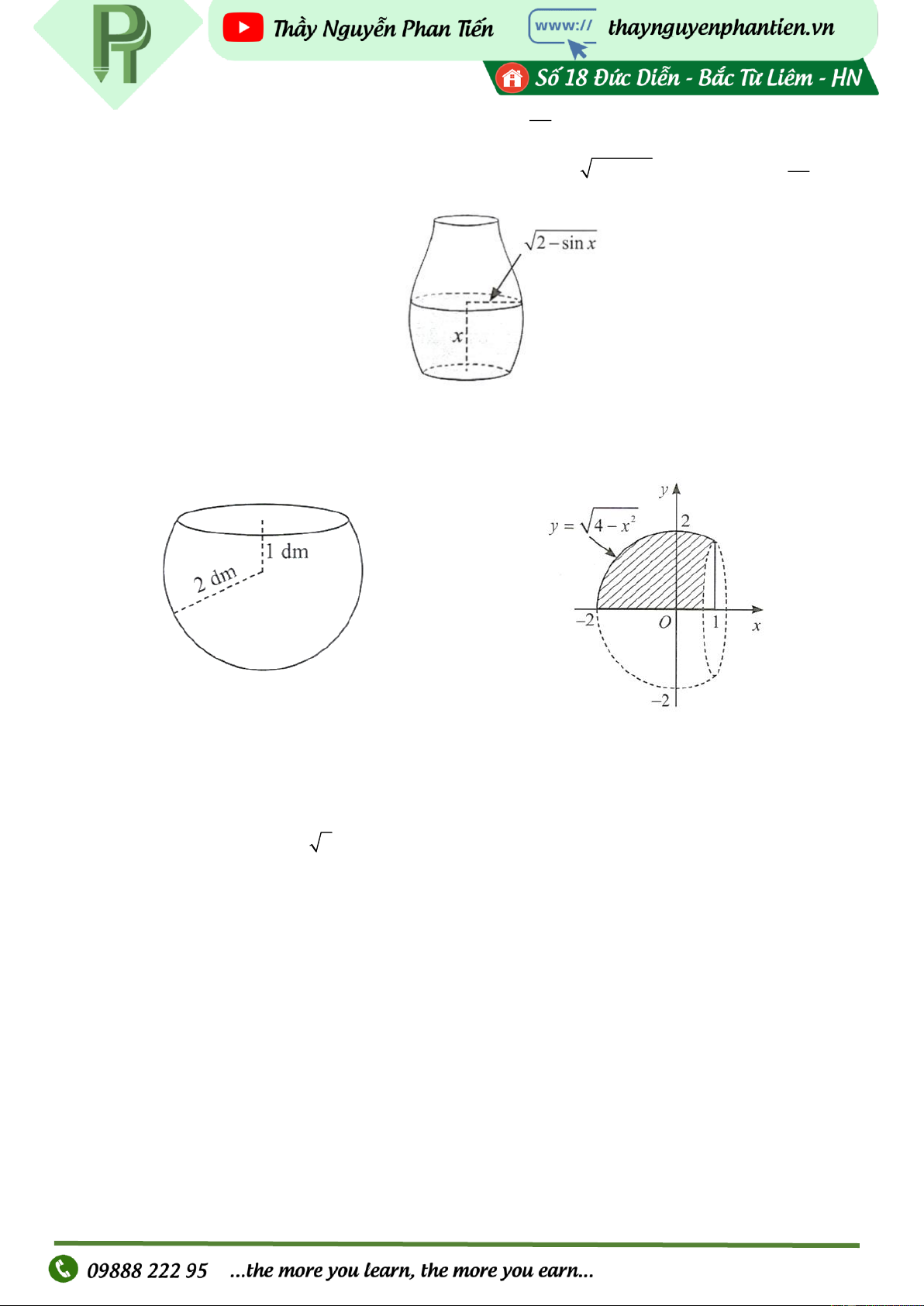
Câu 12. Một bình chứa nước dạng như hình có chiều cao là
dm. Nếu lượng nước trong bình có 2 3
chiều cao là x (dm) thì mặt nước là hình tròn có bán kính 2 − sin x (dm) với 0  x  2
Tính dung tích của bình (kết quả làm tròn đến hàng phần trăm của đềximét khối).
Câu 13. Một bể cá có dạng là một phần hình cầu được tạo thành khi cắt hình cầu bán kính 2 dm bằng
mặt phẳng cách tâm của hình cầu 1 dm (Hình). Gợi ý:
Tính dung tích của bể cá (kết quả làm tròn đến hàng phần mười của đềximét khối).
Câu 14. Khi sử dụng phần mềm mô phỏng để thiết kế một chậu cây, người ta quay hình phẳng giới hạn
bởi đồ thị hàm số y =
x + 2 , trục hoành và hai đường thẳng x = 0, x = 4 quanh trục hoành.
Biết đơn vị trên các trục toạ độ là đềximét. Thể tích của chậu cây (kết quả làm tròn đến hàng
phần mười) bằng bao nhiêu đềximét khối?
Câu 15. Một chi tiết máy được thiết kế bằng cách quay hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 4x + 5 , trục hoành và các đường thẳng x = 1, x = 4 quanh trục hoành. Biết đơn vị trên
các trục tọa độ là centimét. Thể tích của chi tiết máy đó (kết quả làm tròn đến hàng đơn vị)
bằng bao nhiêu centimét khối? Page | 10
Câu 16. (Chuyên Vinh 2024) Một vât trang trí có dạng một khối tròn xoay được tạo thành khi quay
miền (H ) (phần màu xám trong hình vẽ bên) quanh trục AC . Biết rằng AC = 2 c , m B là trung
điểm của AC . Miền (H ) được giới hạn bởi đoạn thẳng BC và các cung tròn bán kính 1 cm có
tâm A và B . Tính thể tích của vật trang trí đó (làm tròn kết quả đến hàng phần mười).
Câu 17. Cho một mô hình 3− D mô phỏng một đường hầm như hình vẽ bên. Biết rằng đường hầm mô
hình có chiều dài 5(cm) ; khi cắt hình này bởi mặt phẳng vuông góc với đấy của nó, ta được
thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao parabol. Chiều cao của mỗi thiết 2
diện parobol cho bởi công thức y = 3 −
x (cm) , với x (cm) là khoảng cách tính từ lối vào lớn 5
hơn của đường hầm mô hình. Tính thể tích (theo đơn vị 3
cm ) không gian bên trong đường hầm
mô hình ( làm tròn kết quả đến hàng đơn vị)
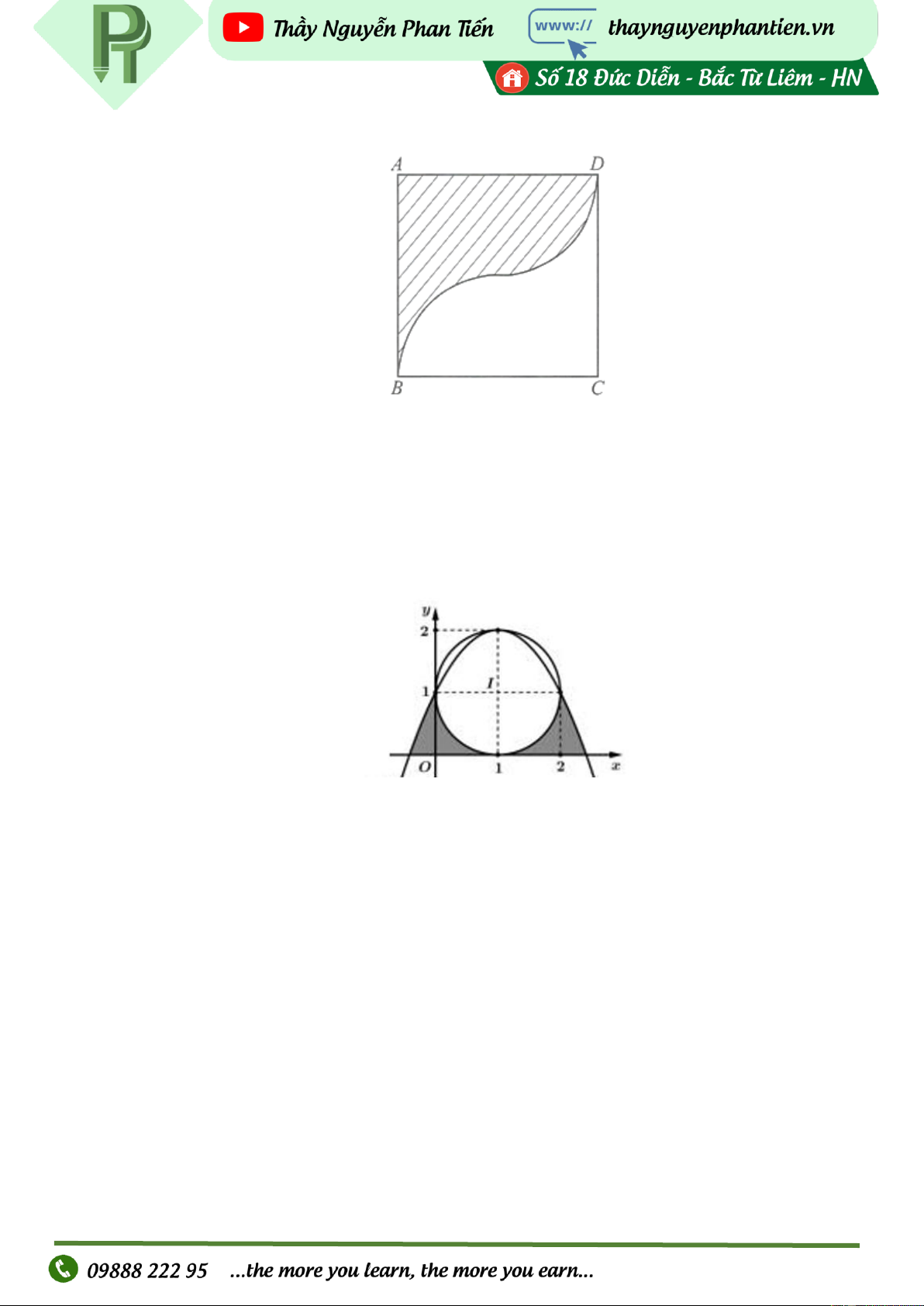
Câu 18. *Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền (R) (phần được tô
màu trong hình vẽ bên) quanh trục AB . Miền (R) được giới hạn bởi các cạnh AB , AD của
hình vuông ABCD và các cung phần tư của các đường tròn bán kính bằng 1m với tâm lần lượt
là trung điểm của các cạnh AD , AB .
Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười. Page | 11
Câu 19. *Một vật trang trí có dạng là khối tròn xoay được tạo thành khi quay miền (R) (phần gạch
chéo trong hình bên) quanh trục AB .
Miền (R) được giới hạn bởi các cạnh AB, AD của hình vuông ABCD và các cung phần tư của
các đường tròn bán kính bằng 1 cm với tâm lần lượt là trung điểm các cạnh BC, AD . Thể tích
của vật trang trí đó (làm tròn kết quả đến hàng phần mười) bằng bao nhiêu centimét khối? (Trích
đề Minh hoạ tốt nghiệp THPT năm 2024).
Câu 20. *(Sở Nam Định 2024) Hình phẳng được tô đậm trong hình bên được giới hạn bởi đường tròn,
đường parabol, trục hoành. Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng đã
cho quanh trục Ox . (làm tròn kết quả đến hàng phần trăm). --HẾT-- Page | 12