Tóm tắt chương 4 bộ môn toán khoa toán kinh tế

KHOA TOÁN KINH TẾ BỘ MÔN TOÁN CƠ BẢN Bài giảng TOÁN CHO CÁC NHÀ KINH TẾ TÓM TẮT CHƯƠNG 4
Tóm tắt chương 4 - Lãi suất gộp liên tục
Giả sử một khoản tiền gốc được
Giá trị hiện tại của một
đầu tư với lãi suất hàng năm khoản tiền được nhận
trong năm để tích lũy giá trị
sau năm với lãi suất hàng tương lai . Nếu lãi suất
năm được tính gộp lần
được tính gộp lần mỗi năm thì mỗi năm bằng
và nếu lãi suất được tính gộp
và nếu lãi suất được tính liên tục thì gộp liên tục thì 2
Tóm tắt chương 4 - Đạo hàm của hàm mũ và loga       3
Tóm tắt chương 4 - Nguyên hàm và tích phân bất định  Hàm số
được gọi là một nguyên hàm của hàm số nếu
 Tích phân bất định của hàm số là trong đó
là một nguyên hàm của hàm số . 4
Tóm tắt chương 4 - Một số quy tắc tính tích phân
Quy tắc tính tích phân với các hàm thường gặp Quy tắc hằng: với là hằng số Quy tắc lũy thừa: với mọi Quy tắc logarit: với mọi Quy tắc mũ: với là hằng số 5
Tóm tắt chương 4 - Các quy tắc đại số
Quy tắc nhân với hằng số: với là hằng số Quy tắc tổng: Quy tắc hiệu : 6
Tóm tắt chương 4 - Phương trình vi phân
 Phương trình vi phân là phương trình có chứa các vi phân hoặc
đạo hàm; một hàm số thỏa mãn phương trình như vậy được gọi là nghiệm.
 Phương trình vi phân phân ly biến số có dạng:
và có thể giải được bằng cách phân ly biến: 7
Tóm tắt chương 4 - Bài toán giá trị ban đầu
 Nghiệm của phương trình vi phần chứa hằng số C được gọi là
nghiệm tổng quát (ứng với toàn bộ họ nghiệm ) của phương trình.
 Bài toán giá trị ban đầu là phương trình vi phân + một điều kiện
(ban đầu) để có thể tìm ra hằng số trong nghiệm tổng quát. Khi
đó ta giải ra nghiệm riêng của bài toán giá trị ban đầu. 8
Tóm tắt chương 4 - Tính tích phân bằng phương pháp đổi biến Xét tích phân . 1. Chọn hàm .
2. Biểu diễn tích phân theo biến với . 3. Tìm nguyên hàm của . 4. Thay để được kết quả 9
Tóm tắt chương 4 - Tính tích phân bằng phương pháp đổi biến
 Nếu tích phân chứa căn thức, có thể đặt căn thức bằng một biến mới.
 Nếu biểu thức trong dấu tích phân chứa và thì nên đặt , khi đó .  Với tích phân dạng
có thể đổi biến tuyến tính: 10
Tóm tắt chương 4 - Mô hình điều chỉnh giá Lượng cung và lượng cầu ban đầu chưa bằng nhau: tại
Mô hình giả định tốc độ thay đổi giá tỷ lệ thuận với mức thiếu hụt Ta có thể giải ra
từ phương trình phân ly biến số trên. 11
Tóm tắt chương 4 - Khái niệm tích phân xác định  Hàm liên tục trên đoạn .  Chia
thành đoạn con bằng nhau có độ dài và là
số bất kỳ thuộc đoạn con thứ .  Tổng Riemann: .
 Tích phân xác định của trên là: 12
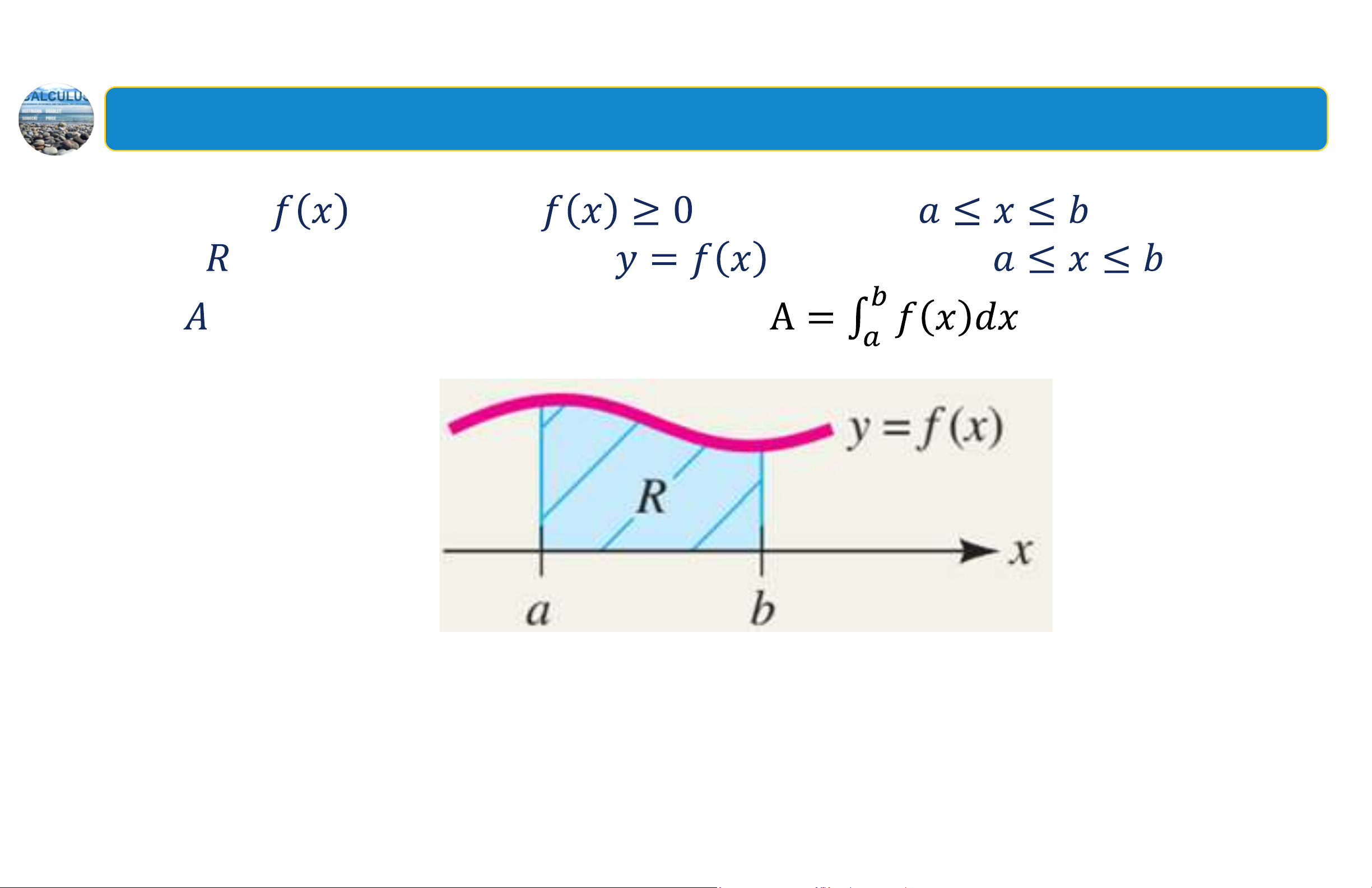
Tóm tắt chương 4 - Tính diện tích bằng tích phân xác định: Nếu hàm liên tục và trên khoảng . Khi đó
miền bên dưới đường cong trên khoảng có diện
tích được cho bởi tích phân xác định . 13
Tóm tắt chương 4 - Định lý cơ bản của giải tích Nếu hàm số liên tục trên khoảng thì
Khi áp dụng định lý cơ bản, ta sử dụng ký hiệu Như vậy 14
Tóm tắt chương 4 - Các quy tắc tính tích phân xác định Cho các hàm liên tục trên đoạn , khi đó:
• Quy tắc nhân với hằng số: • Quy tắc tổng: • Quy tắc hiệu: 15
Tóm tắt chương 4 - Các quy tắc tính tích phân xác định • Quy tắc phân đoạn: 16
Tóm tắt chương 4 - Phép đổi biến trong tích phân xác định
Khi sử dụng phép đổi biến để tính ta có hai cách: 1. Tìm ra nguyên hàm rồi đổi lại và thay hai cận vào.
2. Thay cận lấy tích phân là bởi các cận mới
rồi áp dụng trực tiếp với hàm . 17
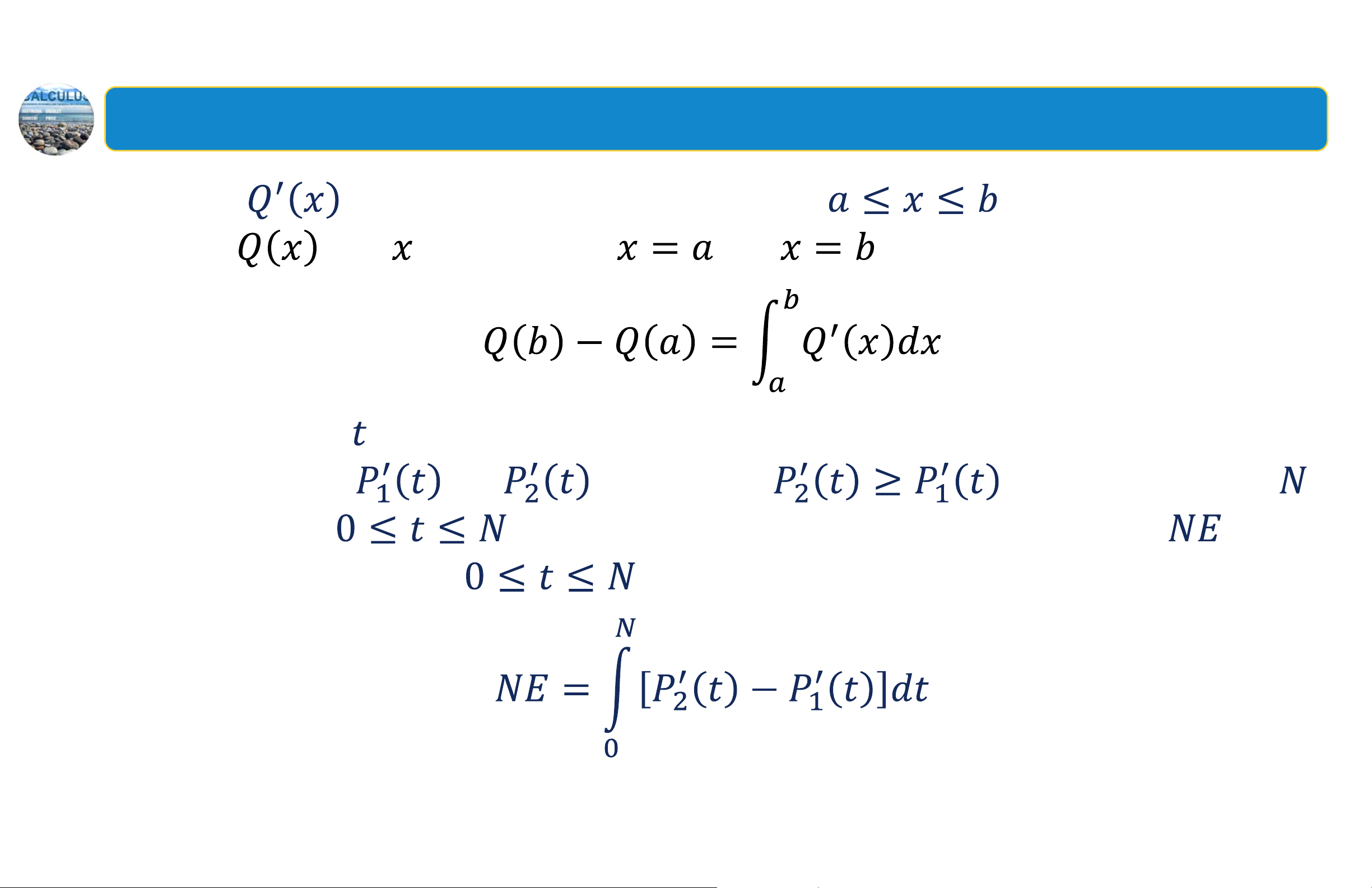
Tóm tắt chương 4 - Thay đổi ròng (Net Change)  Nếu
là hàm liên tục trên khoảng thì thay đổi ròng của khi thay đổi từ tới được xác định bởi:
 Giả sử sau năm (kể từ bây giờ), hai dự án đầu tư có tốc độ sinh lợi lần lượt là và thỏa mãn trong thời gian năm tới (
). Khi đó, lợi nhuận vượt trội ròng trên khoảng thời gian
được xác định bởi tích phân xác định: 18
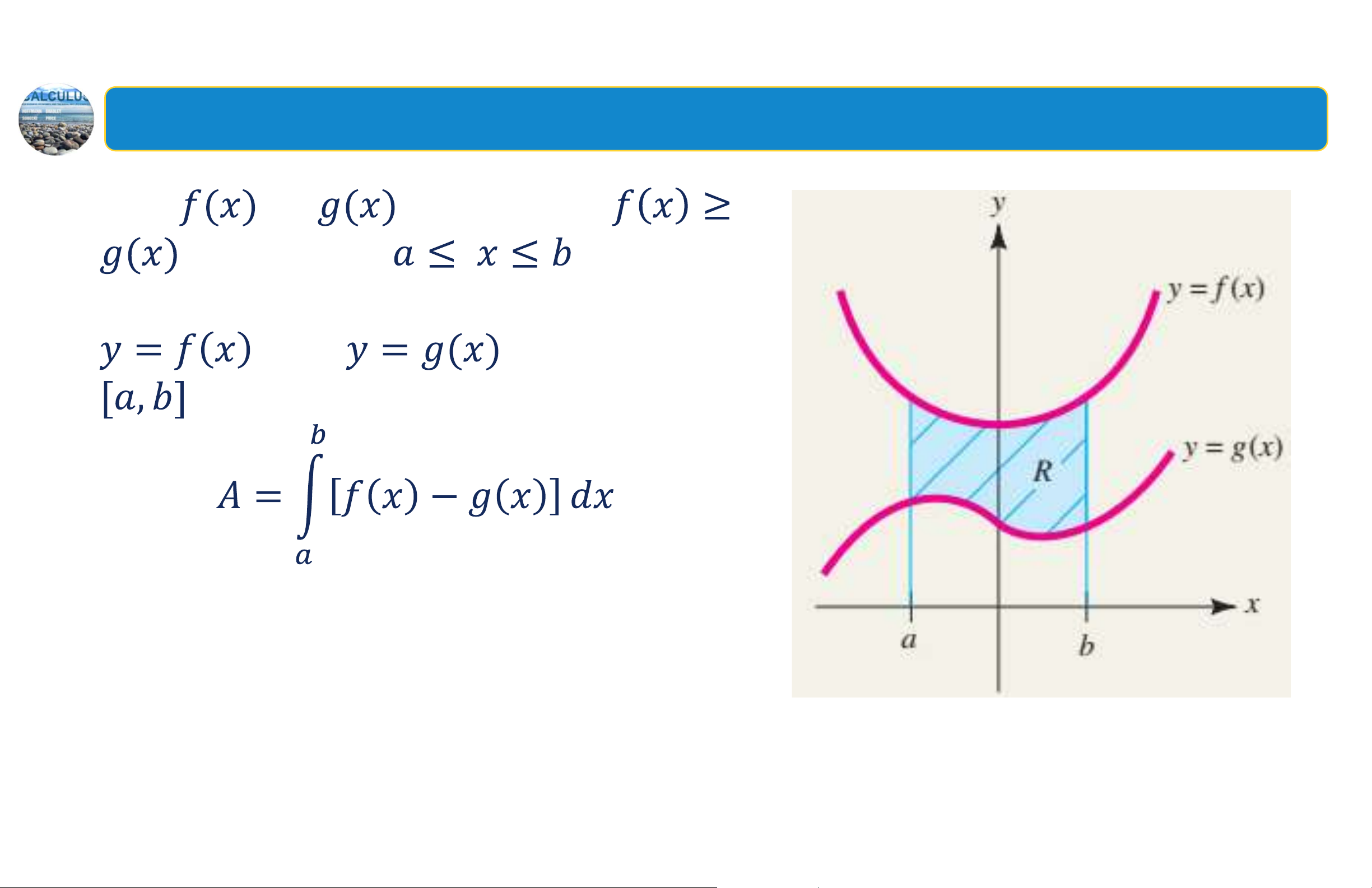
Tóm tắt chương 4 - Diện tích miền giới hạn bởi hai đường cong Nếu và liên tục với trên đoạn thì diện
tích A của miền nằm giữa hai đường và trên đoạn được xác định bởi: 19
Tóm tắt chương 4 - Đường cong Lorenz và chỉ số Gini
Đường cong Lorenz đối với nền kinh tế của một xã hội là đồ thị của hàm
, biểu thị tỷ phần trong tổng thu nhập quốc dân hàng năm của
người được trả lương thấp nhất trong xã hội, với . Nếu
là phương trình của đường cong Lorenz thì chỉ số
Gini (GI) đo sự bất bình đẳng trong phân phối thu nhập thu nhập được
xác định bởi công thức 20