Tóm tắt công thức Hệ Thức Lượng trong Tam Giác Vuông - TGL 101

- Tổng hợp tất cả các công thức về HỆ THỨC LƯỢNG TRONG TAM GIÁC –
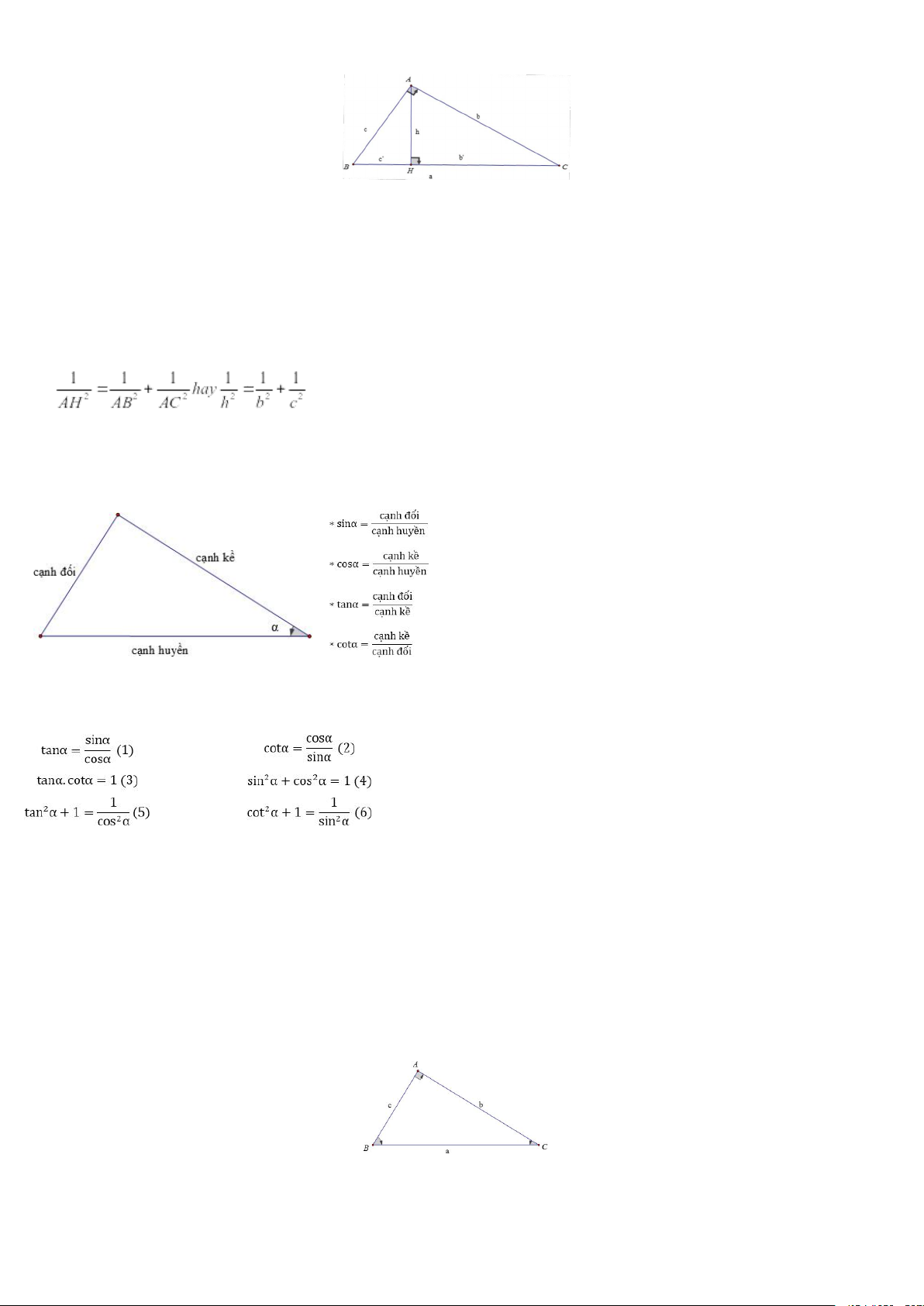
Chủ đề 1: Hệ thức về cạnh và đường cao trong tam giác vuông
Cho ΔABC, góc A bằng 900, AH ⊥ BC, AB = c, AC = b, BC = a, AH = h thì:
+ BH = c' được gọi là hình chiếu của AB xuống BC
+ CH = b' được gọi là hình chiếu của AC xuống BC Khi đó, ta có: 1) AB2 = BH.BC hay c2 = a.c' AC2 = CH.BC hay b2 = a.b' 2) AH2 = CH.BH hay h2 = b'.c' 3) AB.AC = AH.BC hay b.c = a.h 4)
5) AB2 + AC2 = BC2 hay b2 + c2 = a2 (Định lý Pytago)
6) Cạnh huyền trong tam giác bình phương bằng tổng bình phương của hai cạnh góc vuông trong tam giác đó.
Chủ đề 2: Tỉ số lượng giác của góc nhọn 1. Định nghĩa 2. Định lí
Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bằng cotang góc kia.
3. Một số hệ thức cơ bản
4. So sánh các tỉ số lượng giác
a) Cho α, β là hai góc nhọn. Nếu α < β thì
* sinα < sinβ; tanα < tanβ
*cosα > cosβ; cotα > cotβ
b) sinα < tanα; cosα < cotα
Chủ đề 3: Hệ thức về góc và cạnh trong tam giác vuông 1. Các hệ thức
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
a) Cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề
b) Cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề b = a.sinB = a.cosC c = a.sinC = a.cosB b = c.tanB = c.cotC c = b.tanB = b.cotC
2. Định lý lượng giác trong tam giác vuông
m giác vuông được tổng hợp để các bạn học sinh dễ học và dễ hình dung hơ
- Các định lý lượng giác trong ta n:
3. Tỉ số lượng giác của góc nhọn
- Nếu α cho trước là một góc nhọn bất kỳ thì: • 0 < sinα <1 •
0< cosα <1, tanα > 0 •
cotα > 0, sin2α + cos2α = 1 •
tanα.cotα = 1; tanα = sinα.cosα • cotα = cosα.sinα • 1 + tan2α = 1cos2α • 1 + cot2α = 1sin2α
• Chủ đề 3: Hệ thức về góc và cạnh trong tam giác vuông 1. Định lý cosin
Định lí: Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạn
đó nhân với cosin của góc xen giữa chúng.
Ta có các hệ thức sau:
Hệ quả của định lí cosin:
Áp dụng: Tính độ dài đường trung tuyến của tam giác:
Cho ∆ ABC có các cạnh BC = a, CA = b và AC = c. Gọi ma, mb và mc là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B, C c tam giác. Ta có: 2. Định lý Sin:
Định lí: Trong tam giác ∆ ABC bất kỳ, tỉ số giữa một cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là:
với R là bán kính đường tròn ngoại tiếp tam giác
* Công thức tính diện tích tam giác:
Diện tích S của ∆ ABC được tính theo một trong các công thức sau:
3. Giải tam giác và ứng dụng vào việc đo đạc
Giải tam giác: Giải tam giác là đi tìm các yếu tố (góc, cạnh) chưa biết của tam giác khi đã biết một số yếu tố của tam giác đó.
Muốn giải tam giác ta cần tìm mối liên hệ giữa các góc, cạnh đã cho với các góc, các cạnh chưa biết của tam giác thông qua các hệ thức đã
được nêu trong định lí cosin, định lí sin và các công thức tính diện tích tam giác.
Các bài toán về giải tam giác: Có 3 bài toán cơ bản về gỉải tam giác:
a) Giải tam giác khi biết một cạnh và hai góc.
=> Dùng định lí sin để tính cạnh còn lại.
b) Giải tam giác khi biết hai cạnh và góc xen giữa
=> Dùng định lí cosin để tính cạnh thứ ba.
Sau đó dùng hệ quả của định lí cosin để tính góc.
c) Giải tam giác khi biết ba cạnh
Đối với bài toán này ta sử dụng hệ quả của định lí cosin để tính góc: Chú ý:
1. Cần lưu ý là một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một yếu tố độ dài (tức là yếu tố góc không được quá 2)
2. Việc giải tam giác được sử dụng vào các bài toán thực tế, nhất là các bài toán đo đạc.
Document Outline

• - Tổng hợp tất cả các công thức về HỆ THỨC LƯỢNG
• 3.Một số hệ thức cơ bản
• 1.Các hệ thức
• 2.Định lý lượng giác trong tam
• 3.Tỉ số lượng giác của góc nhọn
• •Chủ đề 3: Hệ thức về góc và cạnh trong tam giác vu
• 2.Định lý Sin:
• * Công thức tính diện tích tam giác:
• 3.Giải tam giác và ứng dụng vào việc đo đạc