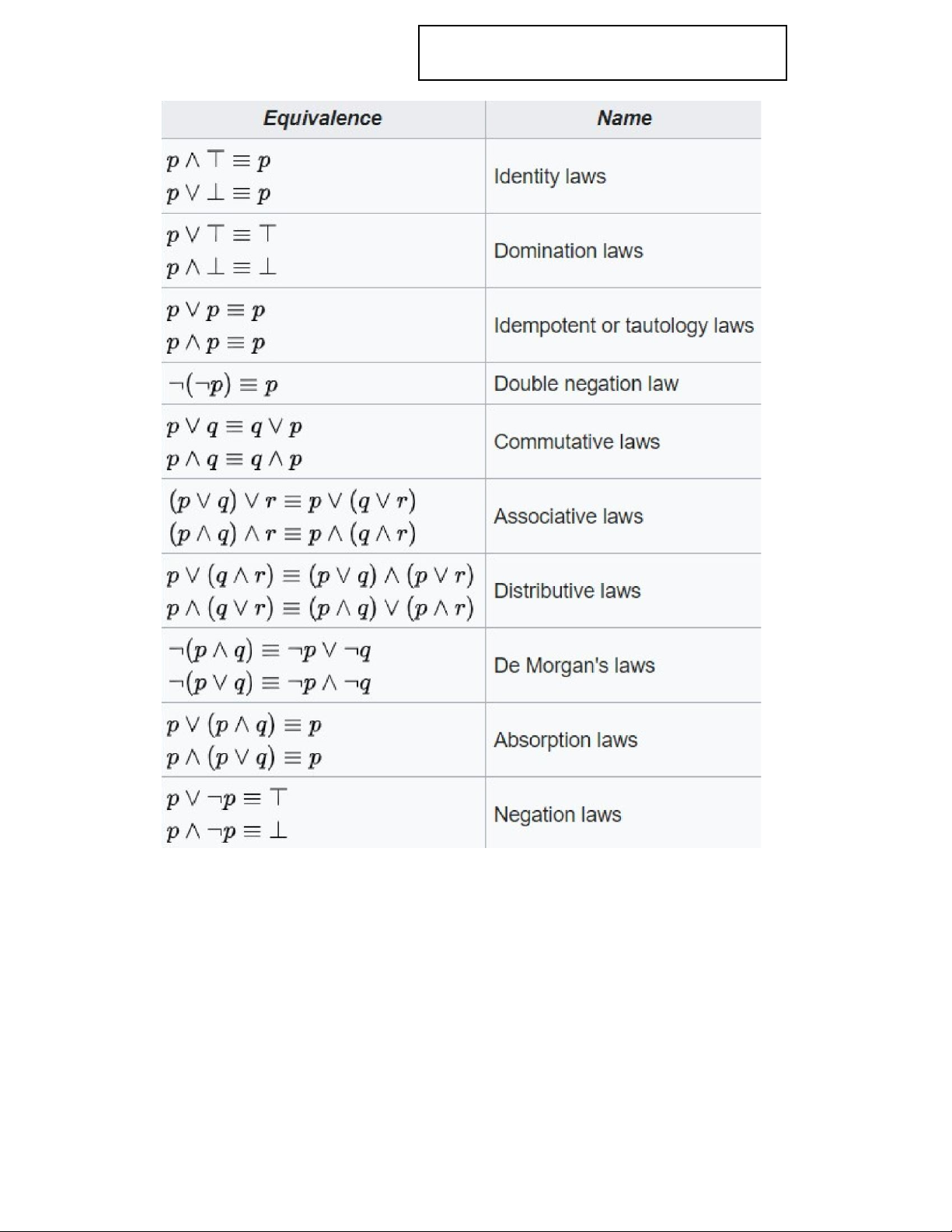


Preview text:
lOMoAR cPSD| 58488183 Thứ tự ưu tiên:
¬→∧→∨→→→↔ lOMoAR cPSD| 58488183 Definition:
n is even if there is k such that n = 2k n
is odd if there is k such that n = 2k + 1
1. Mệnh đề phủ định:
∀ x. P (x ) →∃ x.¬P(x)
∀ x. P (x ) →Q ( x )→∃x .P ( x )→¬Q(x) ∃x
.P ( x )→ ∀ x.¬P(x)
∃x .P ( x )∧Q( x ) →∀ x.¬(p (x ) →Q ( x ))
2. Chứng minh trực tiếp, gián tiếp a. Contrapositive:
Theorem: For any n∈Z, if n2 is even, then n is even
Proof: By contrapositive: we prove that if n is odd, then n2 is odd
Let n be an arbitrary odd integer
Since n is odd. There is an integer k such that n = 2k + 1
Squaring both sides of this equality and simplitying gives the following: n2=(2k+1)2 ¿4 k2+4 k+1 ¿2 (2k2+2k)+1
From this, we see that there is an integer m(namely, 2k2+2k) such that n2=2m+1 Therefore: n2 is odd lOMoAR cPSD| 58488183
Lưu ý: Dạng bài: P ( x )iff Q( x ). Chứng minh 2 lemma: + if P then Q + if Q then P
Thường sẽ có 1 lemma dùng direct, 1 dùng contrapositive b. Contradiction
Theorem: There is no longer set
Proof: Assume for the sake of contradiction that there is a largest set: call it s Now consider the set P(s)
By Cantor’s theorem, we know that |S| < |P(s)|, so P(s) is a larger set than S.
This contradicts the fact that S is the largest set.
We have reached a contradiction, so our asumption must have been wrong.
Therefore, there is no largest set.
3. First – order logic
a. Predicate: Nhận vào object -> trả về proposition (có tính chất T/F)
b. Function: Nhận vào object -> trả về 1 object
c. Translate: ∀ x.(P ( x )→Q(x))
¬(∀ x. P( x ))≡∃x.¬P(x)
∃x .(P ( x) ∧Q(x))
¬( ∃x. P (x )) ≡∀ x .¬P(x)



