









Preview text:
Ch đ 1 : Dao đ ng đi u hòa
CH Đ 1: DAO Đ NG ĐI U HÒA
A. TịM T T Lụ THUY T
1. Dao động điều hòa
+ Dao động điều hòa là dao động trong đó li độ c a vật là một hàm côsin (hay sin) c a thời gian.
+ Phương trình dao động: x = Acos(t + ).
+ Điểm P dao động điều hòa trên một đoạn th ng luôn có thể được coi là hình chiếu c a một điểm M chuyển động
tròn đều trên đường tròn có đường kính là đoạn th ng đó.
2. Các đại lượng đặc trưng của dao động điều hoà: Trong phương trình x = Acos(t + ) thì:
Các đại lượng đặc ụ nghĩa Đ n v trưng A
biên độ dao động; xmax = A >0 m, cm, mm
(t + )
pha c a dao động tại thời điểm t (s) Rad; hay độ
pha ban đầu c a dao động, Rad; hay độ
tần số góc c a dao động điều hòa rad/s. T
Chu kì T c a dao động điều hòa là kho ng thời gian để thực s ( giây) 2
hiện một dao động toàn phần : t T = = N f
Tần số f c a dao động điều hòa là số dao động toàn phần thực Hz ( Héc) hay 1/s
hiện được trong một giây . 1 f T
Liên h gi a , T vƠ f: 1 2 T f 2 So_dao_dong N 2 f 2 T ;f f T 2 thoi _ gian t 2 2f T
Biên độ A và pha ban đầu phụ thuộc vào cách kích thích ban đầu làm cho hệ dao động,
Tần số góc (chu kì T, tần số f) chỉ phụ thuộc vào cấu tạo c a hệ dao động.
3. Mối liên hệ gi a li độ , vận tốc và gia tốc của vật dao động điều hoà:
Đại lượng Biểu thức
So sánh, liên hệ Ly đ
x = Acos(t + ): là nghiệm c a phương trình : Li độ c a vật dao động điều hòa biến thiên điều
x’’ + 2x = 0 là phương trình động lực học c a dao động điều hòa.
hòa cùng tần số nhưng trễ pha hơn so với với 2 xmax = A vận tốc. V n t c
v = x' = - Asin(t + )
-Vận tốc c a vật dao động điều hòa biến thiên
v= Acos(t + + )
điều hòa cùng tần số nhưng sớm pha hơn so 2 2
-Vị trí biên (x = A), v = 0. với với li độ.
-Vị trí cân bằng (x = 0), |v| = v
- Khi vật đi từ vị trí biên về vị trí cân bằng thì vận max = A.
tốc có độ lớn tăng dần, khi vật đi từ vị trí cân bằng
về biên thì vận tốc có độ lớn gi m dần. Gia t c
a = v' = x’’ = - 2Acos(t + )
-Gia tốc c a vật dao động điều hòa biến thiên điều a= - 2x.
hòa cùng tần số nhưng ngược pha với li độ x(sớm
Véc tơ gia tốc c a vật dao động điều hòa luôn
hướng về vị trí cân bằng, có độ lớn tỉ lệ với độ pha so với vận tốc v). lớn c a li độ. 2
-Khi vật đi từ vị trí cân bằng đến vị trí biên, a
- biên (x = A), gia tốc có độ lớn cực đại: a
ngược chiều với v ( vật chuyển động chậm dần) max = 2A.
- vị trí cân bằng (x = 0), gia tốc bằng 0.
-Khi vật đi từ vị trí biên đến vị trí cân bằng,
a cùng chiều với v ( vật chuyển động nhanh dần).
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 1
Ch đ 1 : Dao đ ng đi u hòa L c kéo v
F = ma = - kx = -kAcos(t + )
- Chuyển động nhanh dần : a.v>0, F v ;
Lực tác dụng lên vật dao động điều hòa luôn
hướng về vị trí cân bằng, gọi là lực kéo về (hồi phục).
- Chuyên động chậm dần a.v<0 , F v F max = kA
( F là hợp lực tác dụng lên vật)
4.Hệ thức độc lập đối với thời gian : 2 2 x v
+S đ công th c gi a tọa đ vƠ v n t c: 1 2 2 2 A A 2 v 2 v 2 2 v 2 x A 2 A x v A x 2 2 2 2 A x
+S đ công th c gi a gia t c vƠ v n t c: 2 2 v a 2 2 v a 2 a 2 4 2 2 2 1 2 A 2 2 2 v A
a .A .v 2 2 4 2 A A 2 4 2
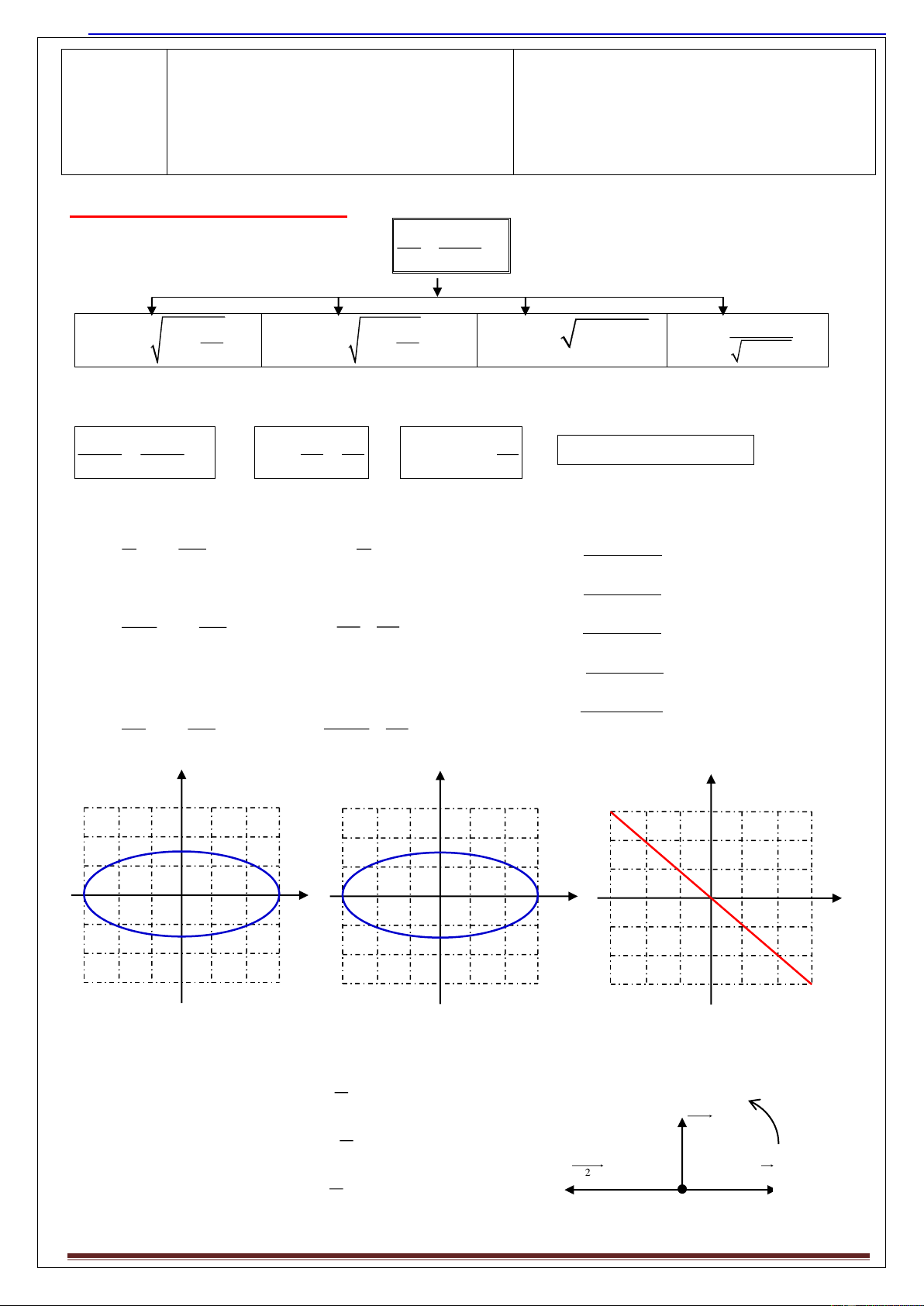
+Các h th c đ c l p vƠ đ th : 2 2 2 x v v 2 2 a) + =1 A = x +
a) đồ thị c a (v, x) là đường elip. A Aω ω b) a = - 2x
b) đồ thị c a (a, x) là đoạn thẳng đi qua gốc tọa độ. a 2 v 2 2 2 a v c) + = 1 2 A = +
c) đồ thị c a (a, v) là đường elip. 2 Aω Aω 4 2 ω ω
d) đồ thị c a (F, x) là đoạn thẳng đi qua gốc tọa độ d) F = -kx 2 2 e) đồ thị c a (F, v) là đường elip. F v 2 2 F v e) + = 1 2 A = + kA A ω 2 4 2 m ω ω v a a ω2A ωA ω2A - A A x -ωA ωA v -A A x O O O -ωA -ω2A -ω2A Đồ thị v theo x là elip Đồ thị a theo v là elip
Đồ thị a theo x là đoạn th ng
+Quan h v pha c a ly đ x, v n t c v vƠ gia t c a trong dao đ ng đi u hòa:
- Vận tốc biến đổi điều hòa sớm pha so với li độ. 2 v A +
=> Ly dộ biến đổi điều hòa trễ pha so với vận tốc . 2 2 a A A
- Gia tốc biến đổi điều hòa sớm pha so với vận tốc. x 2 O
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 2
Ch đ 1 : Dao đ ng đi u hòa
=> Vận tốc biến đổi điều hòa trễ pha so với gia tốc. 2
- Gia tốc biến đổi điều hòa ngược pha so với li độ. +Chú Ủ:
* Với hai thời điểm t1, t2 vật có các cặp giá trị x1, v1 và x2, v2 thì ta có hệ thức tính ω,A & T như sau: 2 2 2 2 v - v x - x 2 1 1 2 ω = T = π 2 2 2 2 2 2 2 2 2 2 2 2 x - x v - v
x v x v x - x v - v 1 2 2 1 1 1 2 2 1 2 2 1 + = + = 2 2 2 2 A A 2 2 2 2
ω A Aω A A ω v x .v - x .v 2 1 1 2 2 1 A = x + = 1 2 2 ω v - v 2 1 5.Các l u Ủ:
5.1) S đổi chiều các đại lượng:
Các vectơ a , F đổi chiều khi qua VTCB. Vectơ v đổi chiều khi qua vị trí biên.
* Khi đi từ vị trí cân bằng O ra vị trí biên:
Nếu a v chuyển động ch m d n. (Không ph i chậm dần “đều” )
Vận tốc gi m, ly độ tăng động năng gi m, thế năng tăng độ lớn gia tốc, lực kéo về tăng.
* Khi đi từ vị trí biên về vị trí cân bằng O:
Nếu a v chuyển động nhanh d n. (Không ph i nhanh dần “đều” )
Vận tốc tăng, ly độ gi m động năng tăng, thế năng gi m độ lớn gia tốc, lực kéo về gi m.
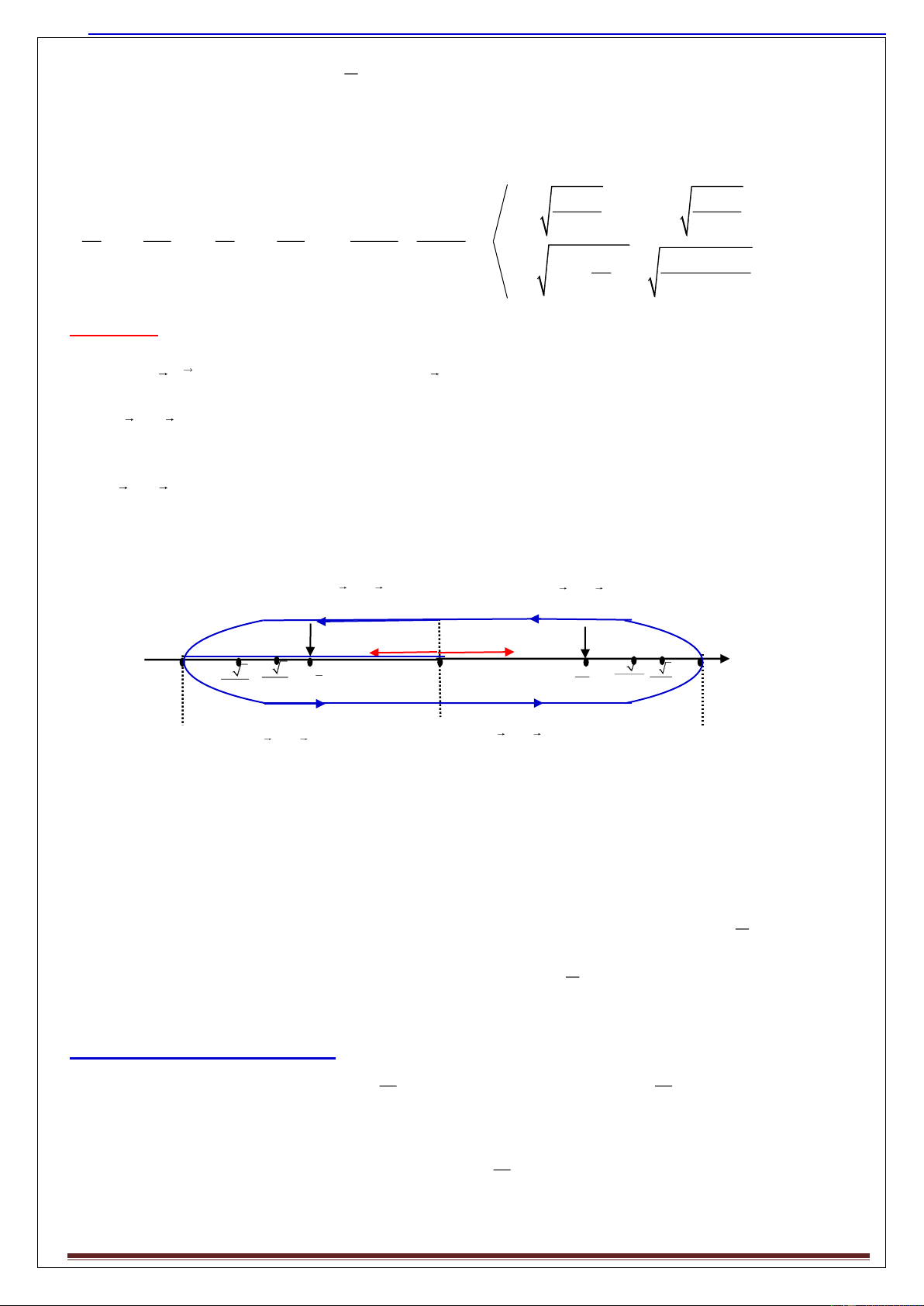
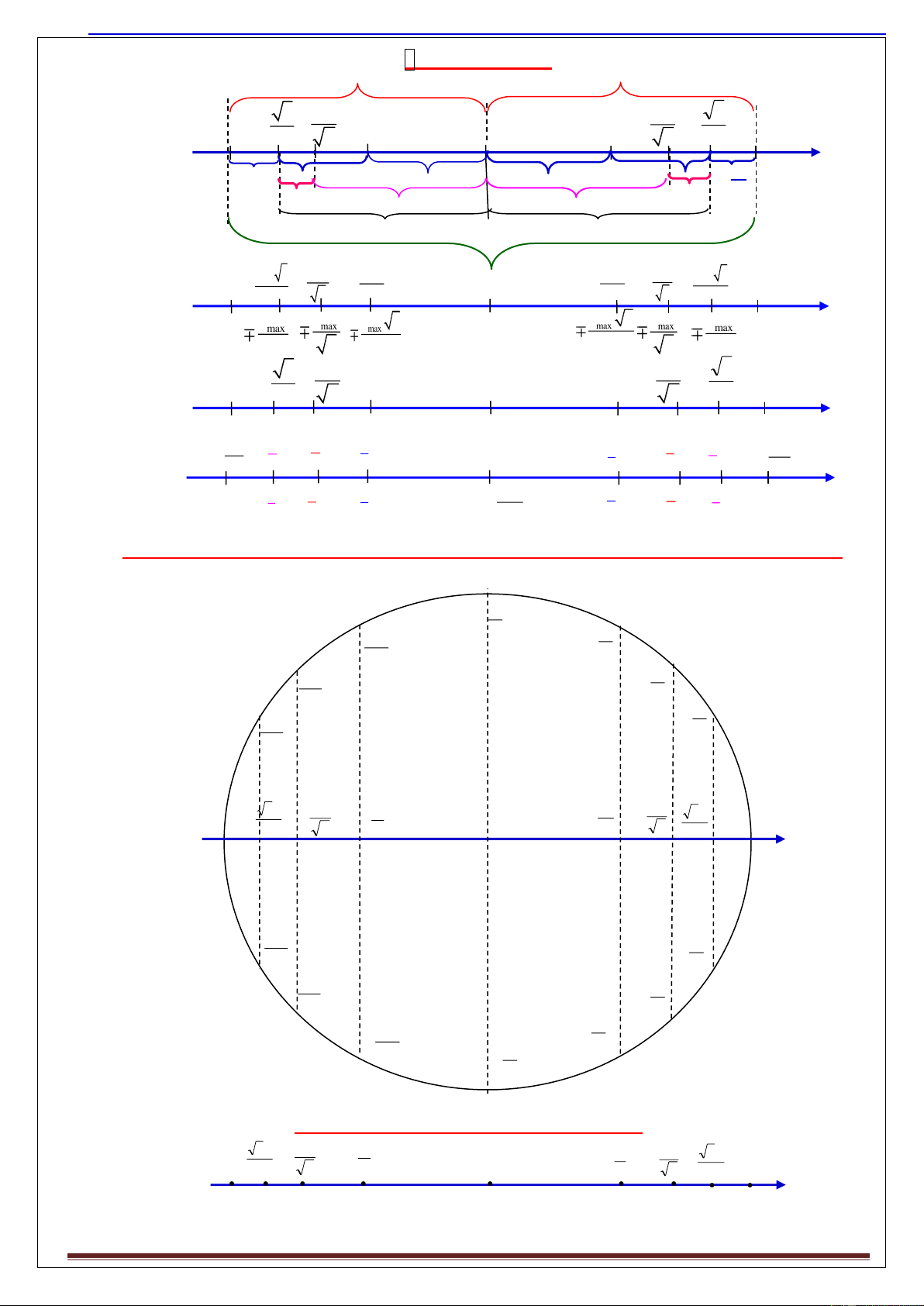
* Sơ đồ mô tả quá trình dao động trong 1 chu kì:
CĐ chậm dần v a
CĐ nhanh dần v a x= -A x=A -A vmin= -Aω vmax= Aω +A x 3 2 0 A A A 3 cos A A A 2 2 2 2 2 2 2 CĐ chậ X=0 m dần CĐ nhanh dần v= 0 v= 0 vmax= ωA v v a a A min= -Aω2 A max= Aω2 a= 0 W W tmax= 0,5mω2A2 tmax= 0,5mω2A2 Wđmax= 0,5mω2A2 Wđmin= 0 Wđmin= 0 Wtmin= 0 5.2)Các h qủ: T
+ Qũ đạo dao động điều hòa là 2A + Thời gian nǵn nhất để đi từ biên này đến biên kia là 2 T
+ Thời gian nǵn nhất để đi từ VTCB ra VT biên học ngược lại là 4
+ Quưng đường vật đi được trong một chu k̀ là 4A. 5.3) M t vƠi ph
ng trình c n l u Ủ:
x Asin(t) Acos(t
); x Acos(t) Asin(t ); 2 2
x Acos( t) Acos(t ); x Asin(t ) Asin(t );
x Asin(t ) A cos(t ). 2
x A cos(t ) A cos(t )
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 3
Ch đ 1 : Dao đ ng đi u hòa *Ph ng trình đ c bi t. Biên độ : A
Tọa độ VTCB : x a
a) x a ± Acos(t + φ) với a const
Tọa độ vị trí biên : x a ± A A
b) x Acos2(t + φ) Biên độ :
; ’ 2 ; φ’ 2φ. 2 2 t 2f;T ; T N 2 2 2
5.4)Cách lập phương trình dao động : v a v 2 A 2 xọ a độ 2 ị 4 trí biê n : x a ± A 2 x t=0 shift cos A V 0 0 t 0 x
cos = 0 (lấy nghiệm "-" khi v0 > 0; lấy nghiệm "+" khi v0 < 0) ; A
(với x0 và v0 là li độ và vận tốc tại thời điểm ban đầu t = 0).
Các b c l p ph ng trình dao đ ng dao đ ng đi u hoƠ: ☞ * Tính * Tính A x Acos
* Tính dựa vào điều kiện đầu: lúc t = t 0 (thường t0 = 0) v sin A
L u Ủ: + Vật chuyển động theo chiều dương thì v > 0, ngược lại v < 0
+ Trước khi tính cần xác định rõ thuộc góc phần tư thứ mấy c a đường tròn lượng giác
(thường lấy -π < ≤ π)
*Phương pháp: sodaodong N +Tìm T: khoangthoigian t T Tìm f : f sodaodong N khoangthoigian t 1 2 v a a
+Công th c liên h f T n s góc: max max max 2 f T 2 T A A vmax 2 v 2W v a +Biên đ 2 2 2 max max chieudaiquydao A: A x A A 2 ; ; k 2 2
6. Xác định thời điểm vật đi qua ly độ x0 -vận tốc vật đạt giá trị v0 x
6.1) Khi v t đi qua ly đ x0 thì x0= Acos(t + ) cos(t + ) = 0 t= ? Tìm t A v
6.2) Khi v t đ t v n t c v
0 thì v0 = -Asin(t + ) sin(t + ) = 0 t= ? A 2 2 6.3) Tìm ly đ v v
v t khi v n t c có giá tr v 2 2 1 2 1 1: A
x x A 2 6.4) Tìm v v n t c khi qua ly đ x 2 2 2 2 1: A x v A x 1 1
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 4
Ch đ 1 : Dao đ ng đi u hòa 7.Năng l
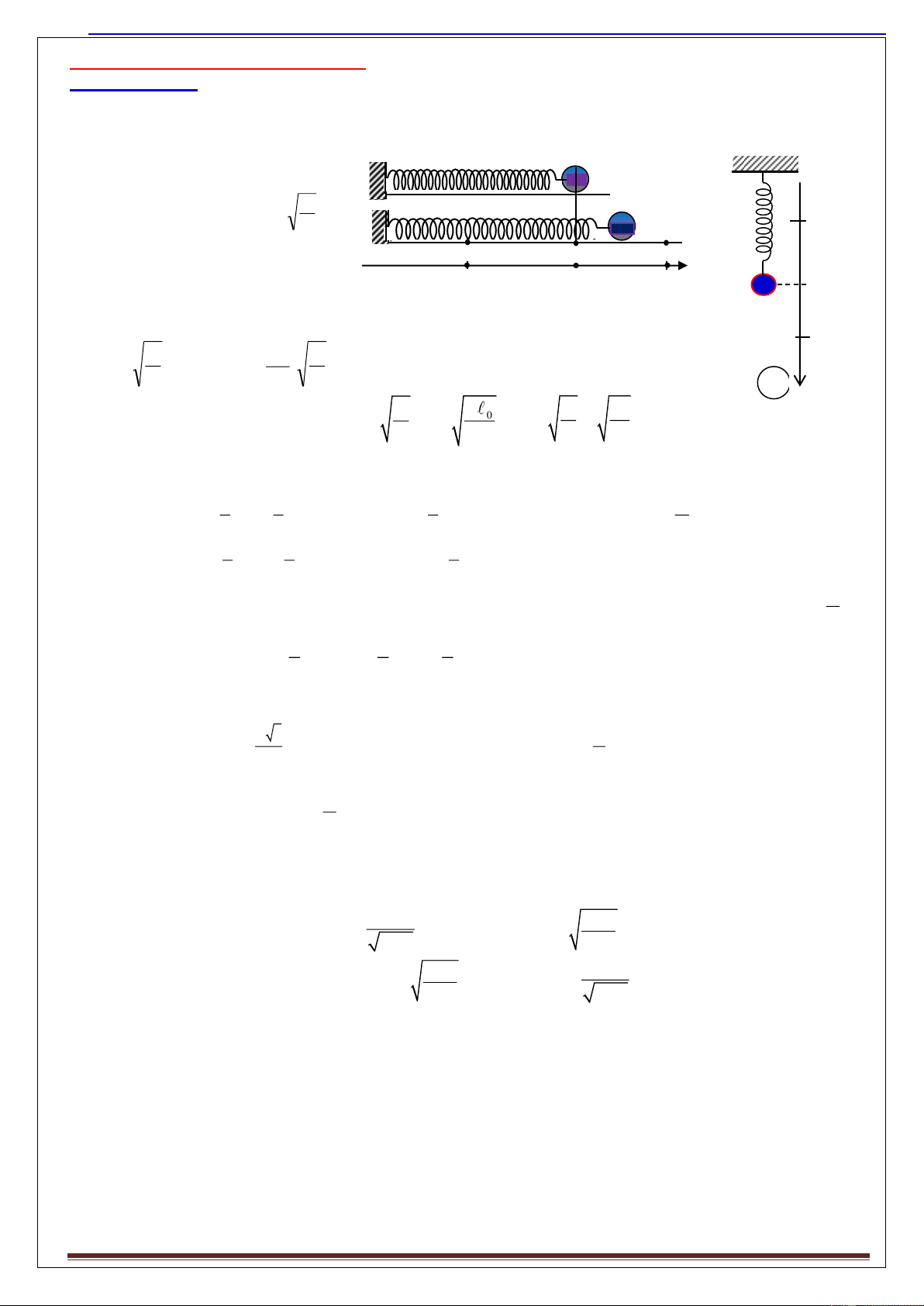
ng c a dao đ ng đi u hoƠ: a) Con lắc lò xo:
+ Mô t̉: Con ĺc lò xo gồm một lò xo có độ cứng k,
khối lượng không đáng kể, một đầu ǵn cố định, đầu kia ǵn với vật ṇng khối lượng m, được đ̣t theo phương
ngang học treo th ng đứng. k VTCB + Ph ng trình dao đ ng: m
x = Acos(t + ); với: = k ; k k m m
k: độ cứng c a lò xo(N/m); A x x
m: khối lượng vật ṇng (kg); -A O O A m O
ω: tần số góc (rad/s)
+Chu kì, t n s c a con l c lò xo: A m 1 k Hình vẽ con ĺc lò xo T = 2
; Tần số: f = . k 2 m + x m k g
+Chu kì con l c lò xo thẳng đ ng: 0 T 2 2 ; k g m l
b) Năng lượng của con lắc lò xo: 1 1 1 k + Th năng: W m ω2 t = kx2 = kA2cos2(t + φ) = .A2cos2(t + φ) ( Với 2 2 k . m ) 2 2 2 m 1
+ Đ ng năng: Wđ mv2 1 m2A2sin2(t + φ) 1 kA2sin2(t + φ) ; với k m2 2 2 2 T
Động năng, thế năng c a vật dao động điều hòa biến thiên tuần hoàn với ’ = 2, tần số f’ = 2f, chu kì T’ = . 2 1 1 1 2 2 2 2 2 + C năng: W=W W m A kA m 2 f A ñ t 2 2 2 = const C) Chú ý: + Khi W t
Wđ x A 2 kho ng thời gian để Wt = Wđ là : Δt T 2 4
(Trong một chu kì có 4 lần động năng và thế năng c a vật bằng nhau nên kho ng thời gian liên tiếp giữa hai lần động năng và thế T năng bằng nhau là .) 4
+ Khi vật dao động điều hòa với tần số f, tần số góc chu k̀ T thì Thế năng và động năng c a vật biến thiên tuần
hoàn với cùng tần số góc ’2, tần số dao động f’ =2f và chu kì T’ T/2.
+ Khi tính năng l ng ph̉i đổi kh i l
ng v kg, v n t c v m/s, ly đ v mét A n
+Tại vị trí có Wđ = n.Wt Tọa độ: x
; Vận tốc : v A n 1 n 1 n A +Tại vị trí có W
t = n.Wđ Tọa độ: x A ; Vận tốc : v n 1 n 1
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 5
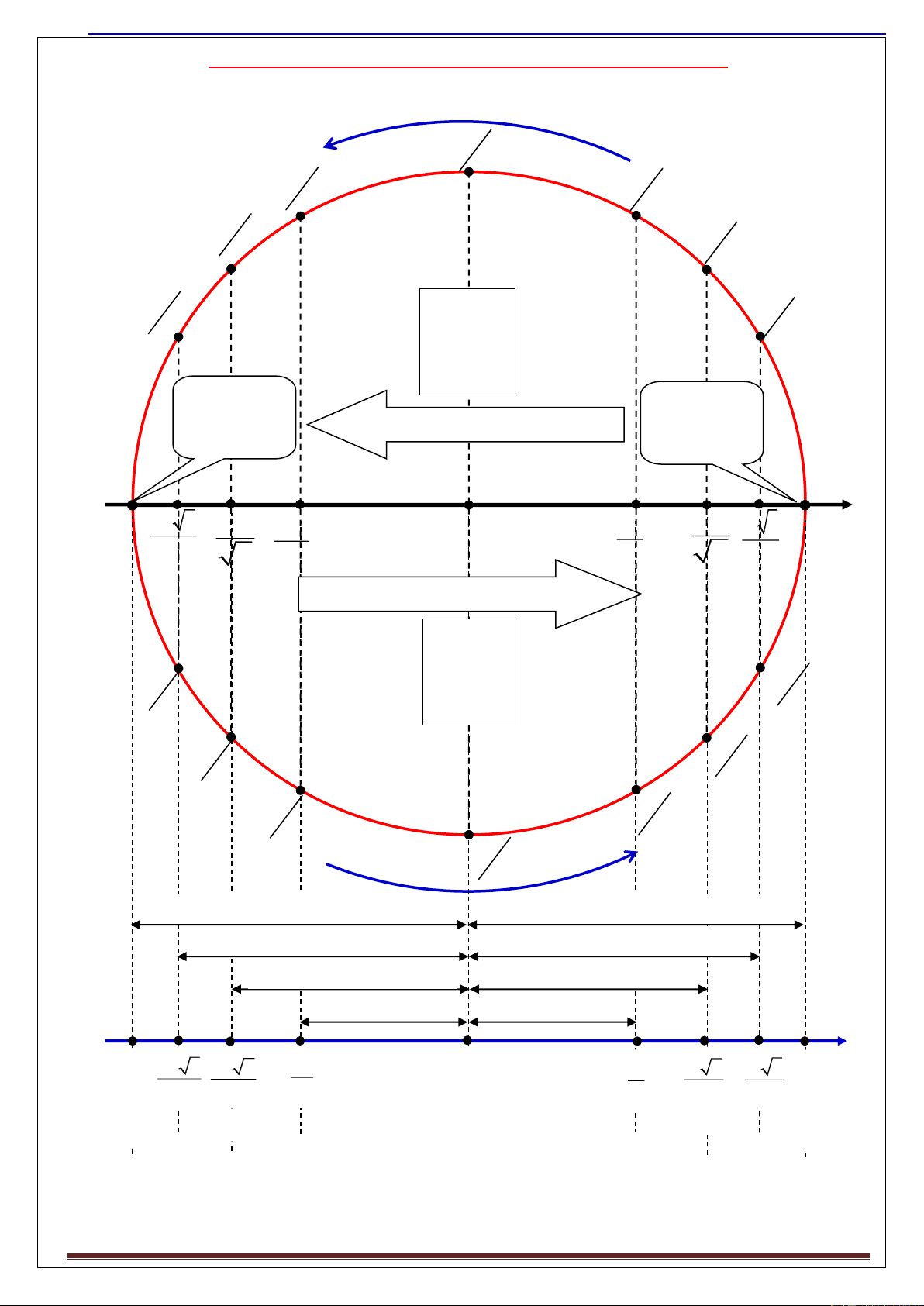
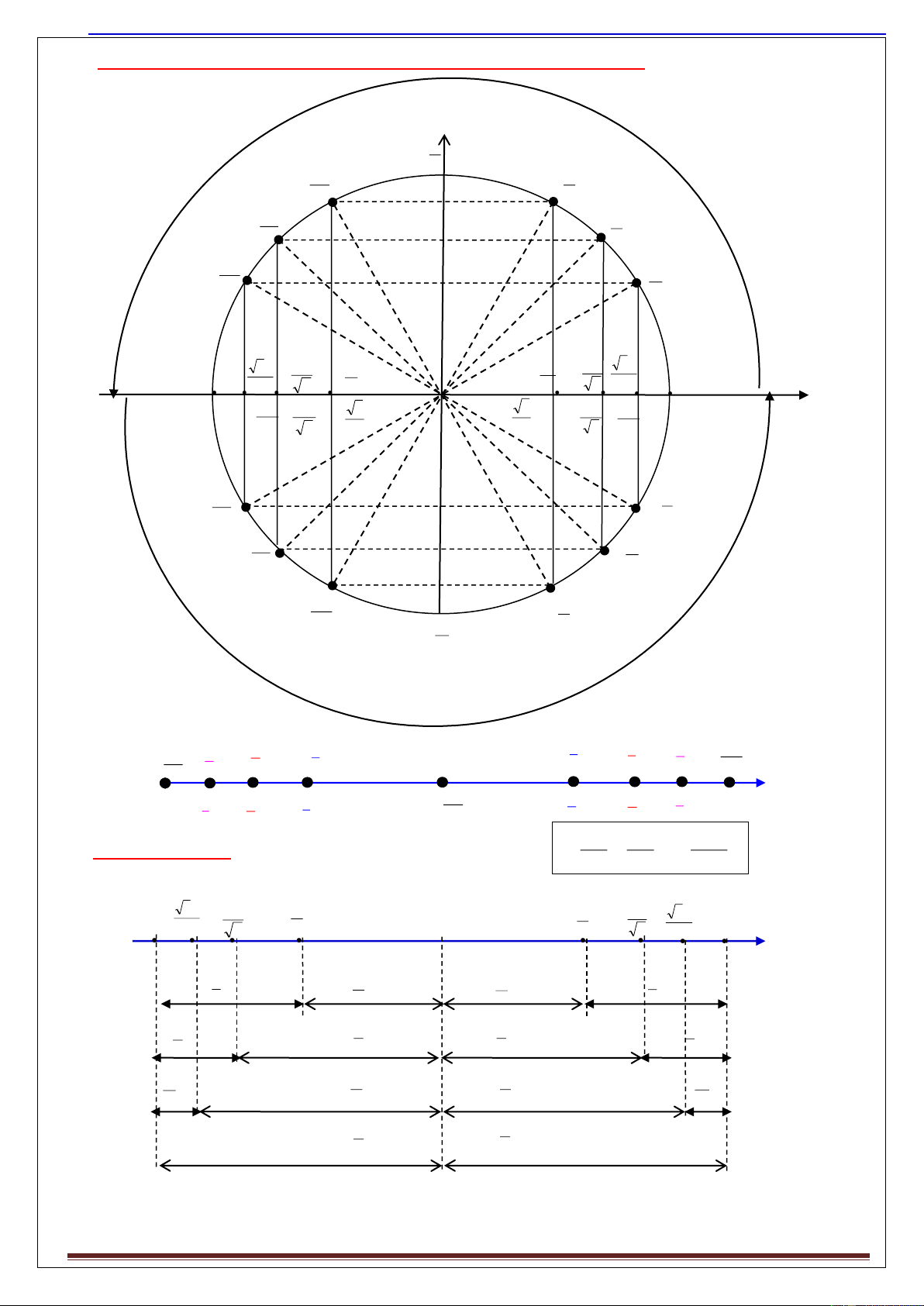
Ch đ 1 : Dao đ ng đi u hòa 8.VÒNG TRÒN L
NG GIÁC- GịC QUAY VÀ TH I GIAN QUAY
Các góc quay vƠ th i gian quay đ c tính từ g c A π 2 2π π 3 3 3π π 4 4 5π x=0 π 6 v =-Aω 6 min a=0 xmin = -A xmax = A amax = Aω2
Chuy n đ ng theo chi u ơm v<0 amin = -Aω2 v = 0 v = 0 π VTCB 0 -A -A 3 -A -A O A A A 3 A 2 2 2 2 2 2
Chuy n đ ng theo chi u d ng v>0 x=0 v =Aω 5π max π a=0 6 6 3π π 4 4 2π π 3 3 π 2 T/4 T/4 T/6 T/6 T/8 T/8 T/12 T/12 -A -A 3 -A 2 -A O A A 2 A 3 A 2 2 2 2 2 2 Wđ=0 Wđmax W đ=0 W W Wt=Wđ t=Wđ W tmax Wt=0 tmax W W t=3Wđ W đ=3Wt đ=3Wt Wt=3Wđ
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 6
Ch đ 1 : Dao đ ng đi u hòa 9. S đ th i gian 1: T/4 T/4 3 A A 3 A A -A -A/2 2 2 O A/2 2 2 A x T/12 T/12 T/12 T/12 T/12 T/12 T/24 T/24 T/8 T/8 T/6 T/6 a a a a a 3 max max max T/2 a 3 Gia t c: max max max ω2A -ω2A 2 2 2 2 2 x O 2 V n t c: v v v 3 v 3 v v 0 max max max max 0 max max 2 2 2 2 2 2 3 A A 3 A A Ly đ x: -A -A/2 2 2 O A/2 2 2 A x 2 kA 2 3 1 1 1 3 kA W Wt= W W 1 W Wt=0 W W W W 2 4 2 4 O 4 2 4 2 2 Wd= 1 1 3 kA 3 1 0 W W W W W 1 W W 0 4 2 4 2 4 2 4 10.Đ
ng tròn l ng giác liên h gi a các v trí đ c bi t vƠ góc quay t ng ng( đ vƠ rad) 900 1200 600 2 2 450 1350 3 3 3 1500 300 4 4 5 6 6 3A A A A A 3A -A 1800 2 O A • 2 2 2 2 2 • • • • • • • • x 5 6 6 3 -300 -1500 4 4 2 -1350 -450 3 3 -1200 2 -600 -900
11.Các vị trí đặc biệt trong dao động điều hoà 3A A A A A -A 3A O A 2 2 2 2 2 x 2 • • • • • • • • • • B- C3-/2 HD- NB- CB NB+ HD+ C3+/2 B+
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 7
Ch đ 1 : Dao đ ng đi u hòa
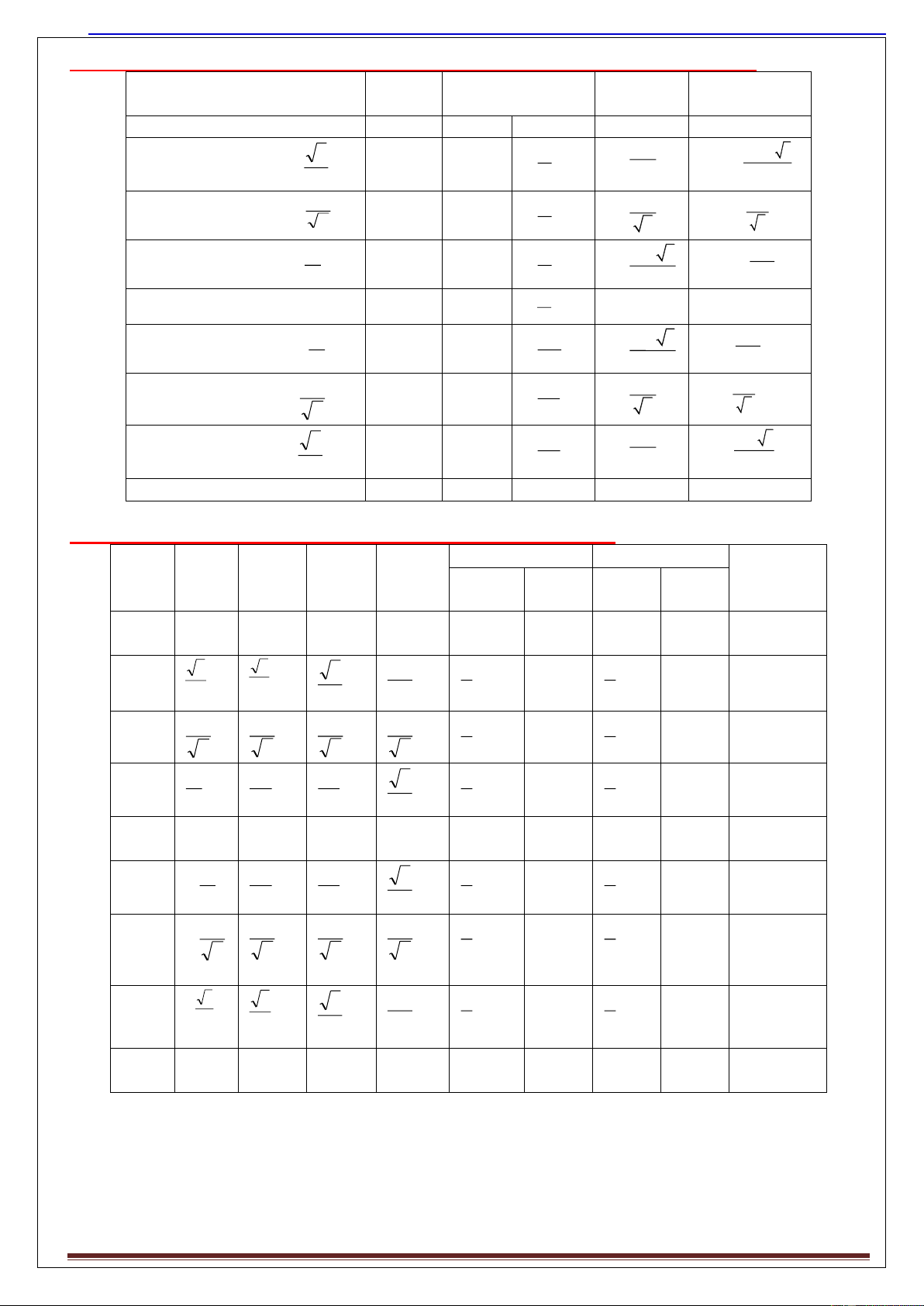
12.Bảng: Giá trị của các đại lượng , v, a ở các vị trí đặc biệt trong dao động điều hòa:
Tên gọi c a 9 v trí x Kí hi u Góc pha
T c đ t i Giá tr gia t c
đ c bi t trên tr c x’Ox li đ x t i li đ x Biên d ng A: x = A B+ 00 0 rad V= 0 -amax = -ω2A C3/2+ ±300 v a 3
Nửa căn ba d ng: x = 3 max A v max a 2 2 6 2
Hi u d ng d ng: x = A HD+ ±450 v a max v max a 2 4 2 2 a Nửa biên d ng: x = A NB+ ±600 v 3 max v max a 2 3 2 2 Cơn bằng O: x = 0 CB ±900 V = ωA max a=0;Fhp=0 2 a
Nửa biên ơm: : x = A NB- ±1200 2 v 3 - max v max a 2 3 2 2 a
Hi u d ng ơm: x = A HD- ±1350 3 vmax - v max a 2 4 2 2 C3/2- ±1500 5 v a 3
Nửa căn ba ơm: x = 3 max v max - A a 2 2 6 2 Biên ơm: x = -A B- 1800 V= 0 amax = ω2A
13.Bảng : Giá trị của các đại lượng F, a, v, Wđ, Wt ở các vị trí đặc biệt Vị trí Wđ Wt So x F a v Độ lớn Phần Độ Phần sánh trăm lớn trăm B+ A Fm am 0 0 0% Wtmax 100% =W 3 3 V 1 3 F 3 m W W C3+/2 A m a 2 2 m 25% 75% W 2 2 4 4 t=3Wđ HD+ A F a V 1 50% 1 50% Wt=Wđ m m m W W 2 2 2 2 2 2 NB+ A F a 3 75% 1 25% m m 3 V W W 2 2 2 m Wđ=3W 2 4 4 t CB 0 0 0 Vm Wđmax= 100% 0 0% W NB- A F a 3 75% 1 25% Wđ=3Wt m m 3 V W W 2 2 2 m 2 4 4 A F a V 1 1 m m m W W HD- 2 2 2 2 2 50% 2 50% Wt=Wđ 3 3 V 1 3 A 3 m W W C3-/2 F 2 m a 2 m 25% 75% W 2 2 4 4 t=3Wđ B- - A Fm am 0 0 0% Wtmax 100% =W
- Khi xét mối liên hệ giữa dao động điều hoà và chuyển động tròn đều ta thấy dao động điều hoà theo chiều
dương ứng với góc pha âm (nửa đường tròn lượng giác phía dưới), và dao động theo chiều âm ứng với góc
pha dương (nửa đường tròn lượng giác phía trên).
Khi ωt+φ > 0 thì v < 0
Khi ωt+φ < 0 thì v > 0 -
Xét dấu riêng góc pha ban đầu φ cho ta kết qu chiều dao động tại thời điểm chọn mốc thời gian.
Khi φ > 0 thì v < 0
Khi φ < 0 thì v > 0
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 8
Ch đ 1 : Dao đ ng đi u hòa 14.L
c đ đ ng tròn l ng giác liên h các đ i l ng trong DĐĐH V< 0 sin W W đ đ = max = W W 2 đ = 3 2 Wt 3 W t Wtmin = 0 3 3 W đ = Wt W đ = Wt 3 4 4 Wt = 5 Wt = 3W 3W đ đ 6 6 O -A 3A A A A A 3A A 2 2 2 2 2 2 0 • X cos • • • • • • • • Vm Vm Wtmax = W 3 3 Vm Vm Vm W Vm tmax = W 2 2 2 ±Vm 2 2 2 Wđmin = 0 Wđmin = 0 5 Wt = 6 6 W t = 3W đ 3 3Wđ 4 4 Wđ = Wt Wđ = Wt 2 3 3 W đ = 2 Wđ = W 3W đmax = W 3W t t Wtmin = 0 V > 0 Wt= 2 1 2 1 1 1 3 kA kA 3 W W W Wt= 0 W W W 4 4 2 4 O 2 4 2 2 x 2 kA 1 0 1 1 3 3 1 0 W d W W W Wd= W W W 2 4 2 4 4 2 4 0
15.Sơ đồ thời gian 2: Cự thể liên hệ với vòng tròn lượng giác: t .T .T 0 2 360 3A A -A A O A A 3A A x • 2 2 2 2 2 2 • • • • • • • • B- C3/2- HD- NB- CB NB+ HD+ C3/2+ B+ T T T T 6 12 12 6 T T T T 8 8 8 8 T T T T 12 6 6 12 T T 4 4
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 9
Ch đ 1 : Dao đ ng đi u hòa
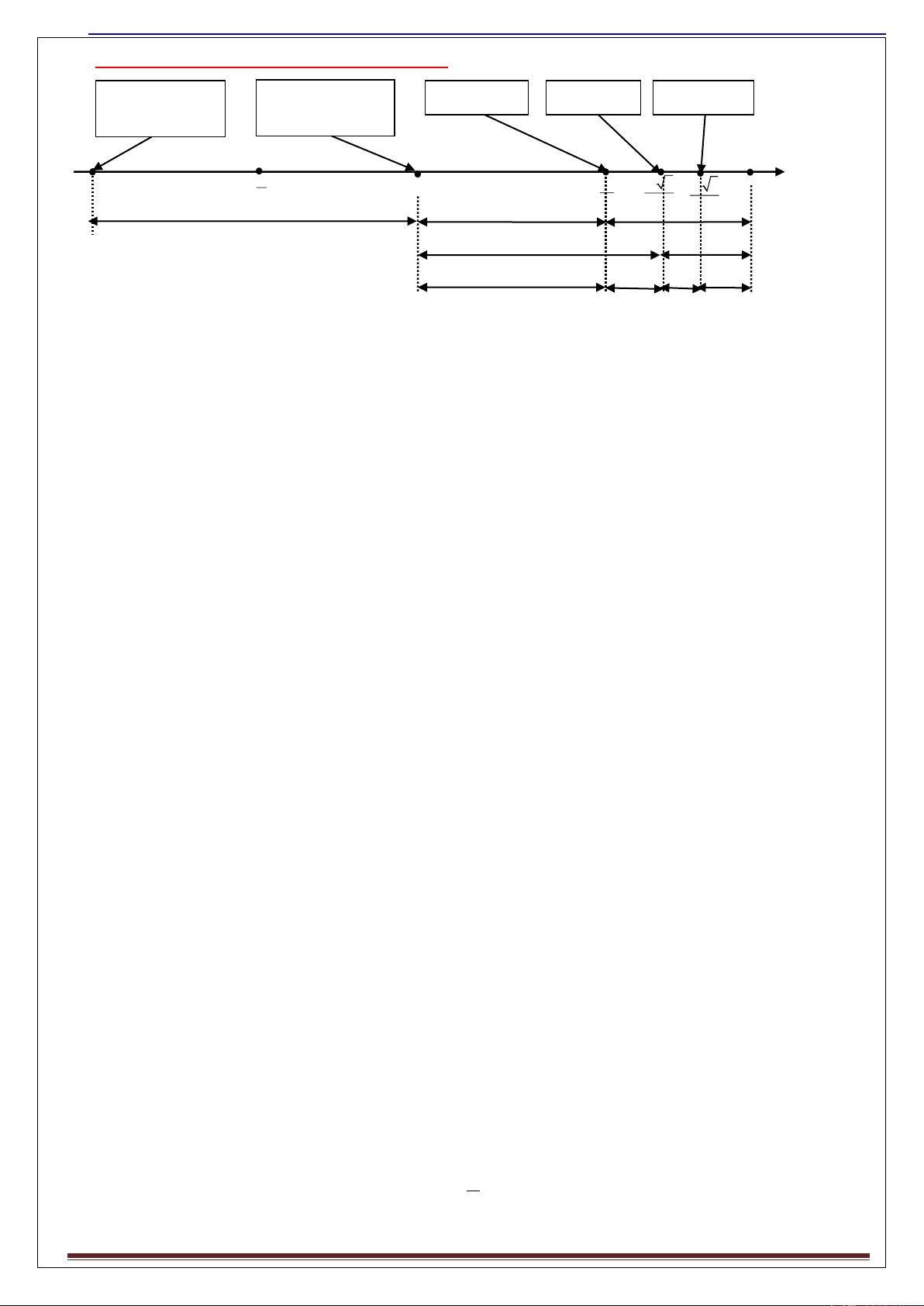
16. S đ : V th i gian vƠ năng l ng trong DĐĐH: W đmax = ½ kA2 Wđ = 0 Wđ = 3 Wt Wđ = Wt Wt = 3 Wđ W t = 0 W = ½ kA2 tmax cos A A 2 -A A O A 3 A 2 2 2 2 T/4 T/12 T/6 T/8 T/8 T/12 T/24 T/24 T/12
B. TR C NGHI M Lụ THUY T
I.1: Chọn câu đúng khi nói về dao động điều hòa c a một vật.
A. Li độ dao động điều hòa c a vật biến thiên theo định luật hàm sin học cosin theo thời gian.
B. Tần số c a dao động phụ thuộc vào cách kích thích dao động.
C. vị trí biên, vận tốc c a vật là cực đại.
D. vị trí cân bằng, gia tốc c a vật là cực đại.
I.2: Trong phương trình dao động điều hoà đại lượng nào sau đây thay đổi theo thời gian A. li độ x B. tần số góc C. pha ban đầu D. biên độ A
I.3. Chọn câu sai khi nói về chất điểm dao động điều hoà:
A. Khi chuyển động về vị trí cân bằng thì chất điểm chuyển động nhanh dần đều.
B. Khi qua vị trí cân bằng, vận tốc c a chất điểm có độ lớn cực đại.
C. Khi vật vị trí biên, li độ c a chất điểm có độ lớn cực đại.
D. Khi qua vị trí cân bằng, gia tốc c a chất điểm bằng không.
I.4: Trong dao động điều hoà x = Acos(t + ), phát biểu nào sau đây là không đúng?
A. Vận tốc c a vật đạt giá trị cực đại khi vật chuyển động qua vị trí cân bằng.
B. Gia tốc c a vật đạt giá trị cực đại khi vật chuyển động qua vị trí cân bằng.
C. Vận tốc c a vật đạt giá trị cực tiểu khi vật một trong hai vị trí biên.
D. Gia tốc c a vật bằng không khi vật chuyển động qua vị trí cân bằng.
I. 5: Một vật dao động điều hòa theo phương trình: x A os c
(t ) . Vận tốc c a vật tại thời điểm t có biểu thức: A. v A os c (t ) B. 2 v A o c s( t ) .
C. v Asin(t ) D. 2
v A sin( t ).
I.6: Con ĺc lò xo dao động điều hoà theo phương trình : x=Acos(t ). Phương trình gia tốc là A. a = 2
A cos(t ) B. a = - 2
A cos(t ) C. a = 2
A sin(t ) D. a = - 2
A 2cos(t )
I.7: Một vật dao động điều hòa theo phương trình: x A o
c s(t) Gia tốc c a vật tại thời điểm t có biểu thức: A. a A os c (t ) B. 2 a A o c s( t )
C. a A sin t D. 2
a A sin t
I.8: Trong dao động điều hòa, giá trị cực đại c a vận tốc là: A. v . B. v 2 A C. v D. v 2 A max A max A max max
I.9: Trong dao động điều hòa, giá trị cực đại c a gia tốc là: A. a B. a 2 A C. a D. a 2 A max A max A max max
I.10: Một vật dao động điều hoà, khi qua vị trí cân bằng thì:
A. Vận tốc bằng 0, gia tốc bằng 0
B. Vận tốc cực đại, gia tốc bằng 0
C. Vận tốc bằng 0, gia tốc cực đại
D. Vận tốc cực đại, gia tốc cực đại.
I.11: Trong dao động điều hòa với biên độ A thì:
A.qũ đạo là một đoạn th ng dài l=A.
B. lực phục hồi là lực đàn hồi.
C. vận tốc biến thiên điều hòa.
D. gia tốc tỉ lệ thuận với thời gian.
I.12: Vận tốc trong dao động điều hòa A. luôn luôn không đổi.
B. đạt giá trị cực đại khi đi qua vị trí cân bằng.
C. luôn luôn hướng về vị trí cân bằng và tỉ lệ với li độ. T
D. biến đổi theo hàm cosin theo thời gian với chu k̀ . 2
I.13: Gia tốc c a vật dao động điều hòa có giá trị bằng không khi:
A. vật vị trí có li độ cực đại.
B. vận tốc c a vật cực tiểu.
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 10
Ch đ 1 : Dao đ ng đi u hòa
C. vật vị trí có li độ bằng không.
D. vật vị trí có pha ban dao động cực đại.
I.14: Gia tốc trong dao động điều hòa: A. luôn luôn không đổi.
B. đạt giá trị cực đại khi đi qua vị trí cân bằng.
C. luôn luôn hướng về vị trí cân bằng và tỉ lệ với li độ. T
D. biến đổi theo hàm cosin theo thời gian với chu k̀ . 2
I.15: Phát biểu nào sau đây về sự so sánh li độ, vận tốc và gia tốc là đúng ?
Trong dao động điều hòa li độ, vận tốc và gia tốc là ba đại lượng biến đổi điều hòa theo thời gian và có A. cùng biên độ. B. cùng pha. C. cùng tần số góc. D. cùng pha ban đầu.
I.16: Phát biểu nào sau đây về mối quan hệ giữa li độ, vận tốc và gia tốc là đúng ?
A. Trong dao động điều hòa vận tốc và li độ luôn cùng chiều.
B. Trong dao động điều hòa vận tốc và gia tốc luôn ngược chiều.
C. Trong dao động điều hòa gia tốc và li độ luôn ngược chiều.
D. Trong dao động điều hòa gia tốc và li độ luôn cùng chiều.
I.17 (TNậ2009): Một vật nhỏ dao động điều hòa theo một trục cố định. Phát biểu nào sau đây đúng?
A. Qũ đạo chuyển động c a vật là một đoạn th ng.
B. Lực kéo về tác dụng vào vật không đổi.
C. Qũ đạo chuyển động c a vật là một đường hình sin.
D. Li độ c a vật tỉ lệ với thời gian dao động.
I.18.( TN- 2010):Nói về một chất điểm dao động điều hòa, phát biểu nào dưới đây đúng?
A. vị trí biên, chất điểm có vận tốc bằng không và gia tốc bằng không.
B. vị trí cân bằng, chất điểm có vận tốc bằng không và gia tốc cực đại.
C. vị trí cân bằng, chất điểm có độ lớn vận tốc cực đại và gia tốc bằng không.
D. vị trí biên, chất điểm có độ lớn vận tốc cực đại và gia tốc cực đại.
I.19: Trong dao động điều hoà c a chất điểm, chất điểm đổi chiều chuyển động khi lực tác dụng
A. đổi chiều. B. bằng không. C. có độ lớn cực đại. D. thay đổi độ lớn.
I.20:Một vật dao động điều hòa với li độ x = Acos (t + ) và vận tốc v = - Asin(t + ):
A. Vận tốc dao động cùng pha với li độ B. Vận tốc dao động sớm pha / 2 so với li độ
C. Li độ sớm pha /2 so với vận tốc D. Vận tốc sớm pha hơn li độ một góc .
I.21.( TN- 2014): Khi nói về dao động điều hòa c a một vật, phát biểu nào sau đây đúng?
A. Khi vật vị trí biên, gia tốc c a vật bằng không.
B. Véctơ gia tốc c a vật luôn hướng về vị trí cân bằng.
C. Véctơ vận tốc c a vật luôn hướng về vị trí cân bằng.
D. Khi đi qua vị trí cân bằng, vận tốc c a vật bằng không. I.1: A I.2: A I.3: A I.4: B I.5: C I.6: B I.7: B I.8: A I.9: B I.10:B I.11:C I.12: B I.13: C I.14: C I.15: C I.16: C I.17:A I.18: C I.19:C I.20:B I.21:B I.22: ĐÓN ĐỌC:
1.TUY T Đ NH CÔNG PHÁ CHUYÊN ĐỀ V T Lệ ( 3 t p )
Tác gỉ: Đoàn Văn Lượng ( Chủ biên)
ThS Nguyễn Thị Tường Vi – ThS.Nguyễn Văn Giáp
2.TUY T PHẨM CÁC CHUYÊN ĐỀ V T Lệ ĐI N XOAY CHIỀU.
Tác gỉ: Hoàng Sư Điểu - Đoàn Văn Lượng
NhƠ sách Khang Vi t phát hƠnh.
Website: WWW.nhasachkhangviet.vn
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 11
Ch đ 1 : Dao đ ng đi u hòa CÁC D NG BÀI T P
Dạng 1: Xác đ nh các đ i l
ng đ c tr ng trong dao đ ng đi u hòa.
Cơu 1. Một vật dao động điều hòa với phương trình x = cos(t + π) cm. Xác định biên độ, pha ban đầu, tần số và chu kì c a dao động.
A.1cm; π; 0,5Hz; 2s. B. 0; π; 0,5Hz; 2s C. 1cm; π; 1Hz; 1s D.0; π; 5Hz; 0,2s
BƠi gỉi: Phương trình tổng quát: x= A cos (ω t + )
Phương trình cụ thể: x = 1 cos (π t +π ) cm x c A os ( t ω ) Ta có: A 1c ;
m rad / s T 2 ;
s f 0,5Hz; . Đáp án A. x 1cos ( t ) Cơu
2. Một vật dao động điều hòa theo phương trình: x 5
cos(t )cm . Xác định biên độ, pha ban đầu, tần số 2 và chu kì c a dao động.
A.5cm; π/2; 0,5Hz; 2s.
B. 5cm; -π/2; 0,5Hz; 2s. C. -5cm; -π/2; 0,5Hz; 2s
D. -5cm; -π/2; 0,5Hz; 2s.
BƠi gỉi: Phương trình tổng quát: x= A cos (ω t + )
Phương trình cụ thể: x = -5 cos (π t –π/2 )= 5 cos (π t –π/2+π )= 5 cos (π t +π/2) x c A os ( t ω ) Ta có:
A 5c ;
m rad / s T 2s; f 0,5Hz; / 2 . Đáp án A.
x 5cos (t ) 2
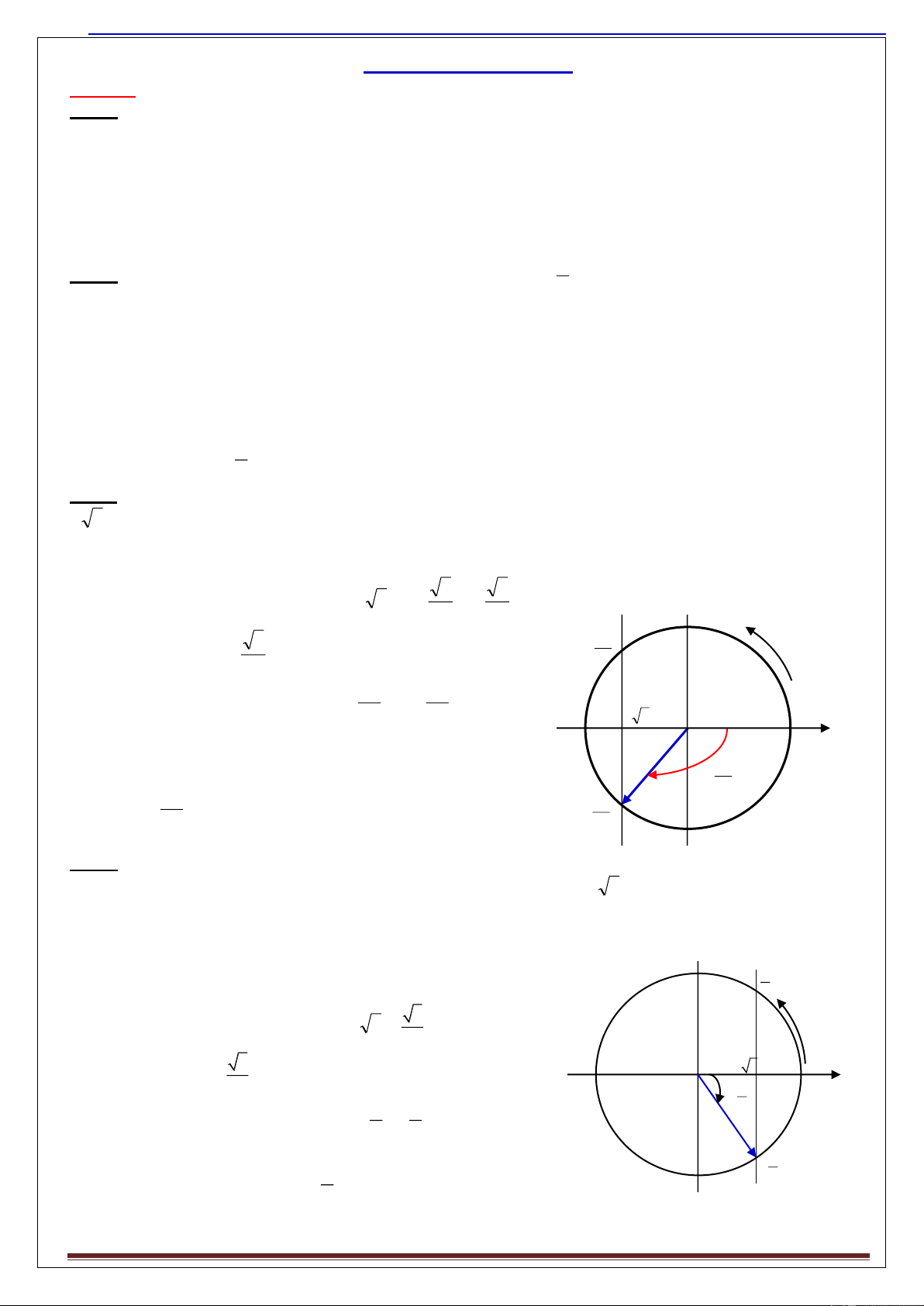
Cơu 3. Một vật dao động điều hòa với phương trình x = 4cos(t + ). Thời điểm ban đầu vật qua vị trí có li độ x = -
2 3 cm và động năng c a vật đang tăng. Xác định pha ban đầu ?
A. = -5/6 B. = - /6 C. = 5/6 D. = /6 BƠi gỉi: 3 3
- Gốc thời gian được chọn tại vị trí x 0 = -2 3 = - 4 A 2 2 , đây là vị trí -C3/2. (d) 3 5 + - Từ vị trí -C3/2: x
, ta dựng đường th ng (d) 0 = A Ox , 6 2 v0<0
(d) ćt đường tròn lượng giác tại hai góc: 5 5 và 6 6 -4 2 3 x 4
- Do mốc thời gian động năng tăng nên độ O
lớn vận tốc tăng, vật đi về vị trí cân bằng tức
là đi theo chiều dương, do đó pha ban đầu âm. 5 6 5 v0>0 Vậy φ = . Đáp án A 5 6 6
Cơu 4. Một vật dao động điều hòa có quĩ đạo là đoạn th ng dài 8cm. Vật đi từ vị trí biên dương đến vị trí biên âm
với thời gian nǵn nhất là 1s. Thời điểm ban đầu vật qua vị trí có li độ x = 2 3 cm theo chiều dương. Xác định chu
kì dao động và pha ban đầu ?
A.2s; = -/6 B. 1s; = - 5/6 C. 2s; = 5/6 D. 1s; = /6
BƠi gỉi:-Biên độ: A =l/2 = 8/2 =4cm. (d)
-Chu kì: Vật từ biên dương đến biên âm với thời gian nǵn nhất là T/2, nên: T= 2.1 =2s. 6 v 3 0<0 +
- Gốc thời gian được chọn tại vị trí x0 = 2 3 =
A , đây là vị trí C3/2. 2 3 -4 2 3 x - Từ vị trí C3/2: x 4 0 =
A , ta dựng đường th ng (d) Ox , 2 O
(d) ćt đường tròn lượng giác tại hai góc: và 6 6 6
- Do mốc thời gian vật đi theo chiều dương vận tốc dương, v0>0
do đó pha ban đầu âm. Vậy φ = . Đáp án A 6 6
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 12
Ch đ 1 : Dao đ ng đi u hòa
Dạng 2: Tính v n t c, gia t c c a v t dao đ ng đi u hòa. 1.Ki n th c căn b̉n:
Vận tốc vật tài thời điểm t . v Asin t
; Gia tốc vật tài thời điểm t . 2 a A o c s t 0 0 0 0 2 v
Vận tốc vật tại vị trí x: 2 2 2 2 A x v
A x ; Gia tốc vật tài thời điểm x: 2 a x 2
2.H th c đ c l p đ i v i th i gian : 2 2 x v
+S đ công th c gi a tọa đ vƠ v n t c: 1 2 2 2 A A 2 v 2 v 2 2 v 2 x A 2 A x v A x 2 2 2 2 A x
+S đ công th c gi a gia t c vƠ v n t c: 2 2 v a 2 2 v a 2 a 2 4 2 2 2 1 2 A 2 2 2 v A
a .A .v 2 2 4 2 A A 2 4 2
3.Các s đ gỉi nhanh: a a a a a 3 max max max a 3 Gia t c: max max max ω2A -ω2A 2 2 2 2 2 x O 2 V n t c: v v v 3 v 3 v v 0 max max max max 0 max max 2 2 2 2 2 2 3 A A 3 A A Ly đ x: -A -A/2 2 2 O A/2 2 2 A x 2 kA 2 3 1 1 1 3 kA W Wt= W W 1 W Wt=0 W W W W 2 4 2 4 O 4 2 4 2 2 Wd= 1 1 3 kA 3 1 0 W W W W W 1 W W 0 4 2 4 4 2 2 4 A. Các ví d :
Ví d 1: Chọn câu trả lời đúng.
Một vật dao động điều hòa theo phương trình: x 4cos t
(cm).Vận tốc c a vật khi nó qua li độ 2 x cm 2 là:
A. 2 3 cm / s
B. 2 3 cm / s C. C A, B đều đúng D. Một kết qu khác 2 Hướ 2 2 v
ng dẫn : Công thức độc lập với thời gian: A x 2 2 2
Vận tốc c a vật là: v A x 2
3 cm/ s .Đáp án C.
Cách 2: Dùng sơ đồ gi i nhanh: x=A/2 => A 3 4 v 3 2 3 cm / s 2 2
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 13
Ch đ 1 : Dao đ ng đi u hòa
Ví d 2: Một chất điểm dao động điều hòa với chu kì 0,314 s và biên độ 8 cm. Tính vận tốc c a chất điểm khi nó
qua vị trí cân bằng và khi nó qua vị trí có li độ 4 cm.
Hướng dẫn : 2 2 - Tìm ω = ? 20rad/s T 0,314
- Khi vật qua vị trí cân bằng thì vận tốc c a vật đạt giá trị cực đại: v
A 20.8 160 cm/s max
- Khi vật qua vị trí có li độ x = 4 cm thì: 2 v 2 2 2 2 2 2 x
A v A x 2 0. 8 4 1 39 cm/s 2
Cách 2: Dùng sơ đồ gi i nhanh: x= A 3 8* 20 4 =A/2 => v 3 8 0 3 cm / s 2 2 Ví d 3
: Một chất điểm (vật) dao động điều hòa theo phương trình: x = 6cos 10
( t ) (cm). 3
a. Tính vận tốc và gia tốc cực đại c a vật.
b. Tính li độ, vận tốc và gia tốc c a vật tại thời điểm t = 0,1π.s
c. Tính vận tốc c a vật tại vị trí động năng bằng 1 thế năng. Biết m = 200g. 3
Hướng dẫn :
a.- Vận tốc cực đại : v .
A 6.10 60cm / s max 2 2
- Gia tốc cực đại: a .
A 600cm / s max
b. - Li độ c a vật tại thời điểm t = 0,1 π s 4 x = 6cos(10 .0,1+ ) (cm) x = 6cos(
) (cm) x = -3 (cm). 3 3
- Vận tốc c a vật tại thời điểm t = 0,1 π s 4 v = -60sin(10 .0,1+ ) v = - 60sin( ) v = 30. 3 cm/s 3 3
- Gia tốc c a vật tại thời điểm t = 0,1 π s 4 a = -600cos(10 .0,1+ ) (cm/s2) a = -600cos( )(cm/s2) a = 300 (cm/s2). 3 3
c. Vận tốc c a vật tại vị trí động năng bằng 1 thế năng 3 Ta có: W 1
đ W W 3 Wđ; mà W = Wđ + Wt 3 t t 1 1 2 2 A 100.36 2 2 2
m A 4 mv 2 2 2
A 4v v 30cm / s 2 2 4 4
Ví d 4: Một vật dao động điều hòa tần số 2Hz, biên độ A = 5 cm. Lấy ² = 10. Khi vận tốc c a vật có độ lớn là
16 cm/s thì gia tốc c a vật có độ lớn là: A.6,4m/s²
B. 4,8m/s² C. 2,4 m/s² D. 1,6m/s² Hướ 2 4 2 2 2
ng dẫn : a .A .v . Th s : 2 a ( 4 2 2 4 ) .(5.10 ) ( 2 4 ) .(0,1 2 6 ) 4 25600.25.10
160.0,256 64 40,96 a 2 4,8m / s Đáp án B
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 14
Ch đ 1 : Dao đ ng đi u hòa
C. BÀI T P T LUY N D NG 2
Cơu 1: Trong dao động điều hòa :
A. Vận tốc biến đổi điều hòa cùng pha với li độ. B. Vận tốc biến đổi điều hòa ngược pha với li độ
C. Vận tốc biến đổi điều hòa sớm pha
với li độ. D. Vận tốc biến đổi điều hòa trễ pha với li độ 2 2
Cơu 2: Một vật dao động điều hòa với tần số f thì vận tốc cực đại có giá trị là v . Nếu chu kì dao động c a vật tăng 1
2 lần thì vận tốc cực đại có giá trị v . Mệnh đề nào sau đây đúng: 2 A. v 2 v B. v 2v C. v 2v D. v 2 v 1 2 1 2 2 1 2 1
Cơu 3: Một vật nhỏ chuyển động tròn đều theo một qũ đạo tâm O, bán kính R. Trong 12s vật quay được 18 vòng.
Gọi P là hình chiếu vuông góc c a vật trên trục tung. Biết bán kính qũ đạo tròn là 3 2cm ; lấy 2 10. Số đo
vận tốc cực đại và gia tốc cực đại chuyển động c a P là: A. cm s 2 9 2 /
; 270 2 cm / s B. cm s 2 8 2 /
; 240 2 cm / s C. cm s 2 9 2 /
; 270 cm / s D. cm s 2 8 2 /
; 240 cm / s
Cơu 4: Một vật dao động điều hòa với tần số 1Hz. Lúc t 0, vật qua vị trí M mà x 3 2cm với vận tốc M
6 2 cm / s . Biên độ c a dao động là: A. 6cm B. 8cm C. 4 2cm D. 6 2cm
Cơu 5: Trong dao động điều hòa, độ lớn cực đại c a vận tốc là: A. v A B. 2 v
A C. v A D. 2 v A max max max max
Cơu 6: Cho một vật dao động điều hoà với phương trình x = 10cos(10t) cm. Vận tốc c a vật có độ lớn 50cm/s lần
thứ 2016 tại thời điểm 6047 6047 6043 504 A. s B. s C. s D s s 30 60 60 5
Cơu 7: Một vật nhỏ dao động điều hòa với chu k̀ T=1s. Tại thời điểm t1 nào đó, li độ c a vật là -2cm. Tại thời điểm
t2 = t1+0.25s,vận tốc c a vật có giá trị : A: 4 cm/s B:-2 m/s C:2cm/s D:- 4m/s
Cơu 8: Một vật dao động điều hòa ph i mất 0,025s để đi từ điểm có vận tốc bằng không tới điểm tiếp theo cũng có
vận tốc bằng không, hai điểm ấy cách nhau 10cm. Chon đáp án Đúng
A.chu kì dao động là 0,025s
B.tần số dao động là 10Hz
C.biên độ dao động là 10cm
D.vận tốc cực đại c a vật là 2cm / s
Cơu 9: Một vật dao động điều hoà theo phương trình : x = 10 cos ( 4t ) cm. Gia tốc cực đại vật là 3
A. 10cm/s2 B. 16m/s2 C. 160 cm/s2 D. 100cm/s2
Cơu 10. Một vật dao động điều hòa có phương trình : x 2cos(2πt – π/6) (cm, s) Li độ và vận tốc c a vật lúc t 0,25s là :
A. 1cm ; ±2 3 π.(cm/s). B. 1,5cm ; ±π 3 (cm/s). C. 0,5cm ; ± 3 cm/s. D. 1cm ; ± π cm/s.
Cơu 11. Một vật dao động điều hòa có phương trình : x 5cos(20t – π/2) (cm, s). Vận tốc cực đại và gia tốc cực đại c a vật là : A. 10m/s ; 200m/s2.
B. 10m/s ; 2m/s2. C. 100m/s ; 200m/s2. D. 1m/s ; 20m/s2. Cơu
12. Vật dao động điều hòa theo phương trình : x 10cos(4πt +
)cm. Biết li độ c a vật tại thời điểm t là 8
4cm. Li độ c a vật tại thời điểm sau đó 0,25s là : A. -4cm B. 10cm C. 4 2cm D. 6 2cm Cơu 13:
Một vật dao động điều hòa theo phương trình: x 3cos(2t ) , trong đó x tính bằng cm, t tính bằng 3
giây. Gốc thời gian đư được chọn lúc vật có trạng thái chuyển động như thế nào?
A. Đi qua Vị trí có li độ x = - 1,5 cm và đang chuyển động theo chiều dương trục Ox
B. Đi qua vị trí có li độ x = 1,5 cm và đang chuyển động theo chiều âm c a trục Ox
C. Đi qua vị trí có li độ x = 1,5 cm và đang chuyển động theo chiều dương trục Ox
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 15
Ch đ 1 : Dao đ ng đi u hòa
D. Đi qua vị trí có li độ x = - 1,5cm và đang chuyển động theo chiều âm trục Ox Cơu 14 3
. Một vật dao động điều hòa với chu k̀ T = 1s. thời điểm pha dao động là
rad vận tốc c a vật có giá 4
trị là v = - 4 2 cm/s. Lấy 2 = 10. Gia tốc c a vật thời điểm đư cho nhận giá trị nào?
A. 0,8 2 m/s2 B. -0,8 2 m/s2 C.0,4 2 m/s2 D.-0,4 2 m/s2
Cơu 15. Một con ĺc lò xo gồm lò xo có độ cứng 20 N/m và viên bi có khối lượng 0,2 kg dao động điều hòa. Tại
thời điểm t, vận tốc và gia tốc c a viên bi lần lượt là 20 cm/s và 2
2 3m / s . Biên độ dao động c a viên bi là A. 4 cm. B. 16 cm. C. 10 3cm D. 4 3cm
Cơu 16. Chọn câu tr lời đúng .
Một chất điểm dao động điều hòa với phương trình: x 6cos 20t (c ) m .
. thời điểm t s, vật có: 2 15
A. Vận tốc 60 3 cm / ,s , gia tốc 2
12 m / s , và đang chuyển động theo chiều dương quĩ đạo. B. Vận tốc 6
0 3 cm / ,s , gia tốc 2 1
2 m / s , và đang chuyển động theo chiều âm quĩ đạo.
C. Vận tốc 60 cm / ,s , gia tốc 2
12 3 m / s , và đang chuyển động theo chiều dương quĩ đạo. D. Vận tốc 6
0 cm / ,s , gia tốc 2 1
2 3 m / s , và đang chuyển động theo chiều âm quĩ đạo.
Cơu 17: Một vật dao động điều hòa dọc theo trục Ox, gọi Δt là kho ng thời gian giữa hai lần tiên tiếp vật
cách vị trí cân bằng một kho ng như cũ. Tại thời điểm t vật qua vị trí có tốc độ 8π 3 cm/s với độ lớn gia
tốc 96π2 cm/s2, sau đó một kho ng thời gian đúng bằng Δt vật qua vị trí có độ lớn vận tốc 24π cm/s. Biên độ c a vật là A.8cm B.4. 3 cm C.2. 2 cm D.5. 2 cm
Đáp án & Hướng dẫn chi tiết: Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 A A A A A B A D B A Câu 11 Câu 12 Câu 13 Câu 14 Câu 15 Câu 16 Câu 17 Câu 18 Câu 19 Câu 20 D A C A A D B
Cơu 1: HD: Ta có: x A o c s t+
v A sin t+ A sin t+ A o
c s t+ A o
c s t+ 2 2 Cơu 1 2 2 2 v
2: HD: T
; v A A ; T 2 T ; 1
v A A A v 2 v 1 f 1 1 2 2 T 2 1 T 1 2 2T 2 1 2 1 Cơu 3: 2 2 2 .3
HD: Chu kì: T s
3 rad / s 3 T 2 2
Vận tốc cực đại: v A . A
3 2.3 9 2 cm/ s ax m T Gia tốc cực đại: 2 2 a
A 9 .3 2 270 2 cm s m 2 / ax 2 2 Cơu 4: v 2.36
HD: Ta có: 2 f 2 rad / s ; 2 2 M A x 18
36 A 6cm M 2 2 4
Cơu 5: HD: Chọn A. v A max
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 16
Ch đ 1 : Dao đ ng đi u hòa Cơu 6 2 : Gỉi: chu kì : T =
= 0,2 (s);x = 10cos(10t) cm => v = x’ = - 100sin10t (cm/s) 10
v = 50cm/s => sin10t = ± 0,5 => x = ± 5 3 cm
Trong một chu kì có 4 lần vật có độ lớn vận tốc bằng 50cm/s
Khi t = 0 vật biên dương. Nên lần thứ 2016 vật có độ lớn vân tốc bằng 50cm/s khi x = 5 3 cm
và đang chuyển động theo chiều dương về biên dương vào thời điểm: 1 6035 6047 6047
t = (2016:4) T – T/12 = (504 - ) T = .0, 2 s . Chọn B 12 12 12 60 Cơu 7 2
: Gỉi: Gi sử phương trình dao động c a vật có dạng x = Acos t (cm) T 2 x1 = Acos t1 (cm) T 2 2 T 2 2 x2 = Acos t2 = Acos (t1+ ) = Acos( t1 + ) (cm) = - Asin t1 T T 4 T 2 T 2 2 2 2 v2 = x’2 = - Asin( t1 + ) = - Acos
t1 = 4 (cm/s). Chọn A T T 2 T T T 0,025 T
2.0,025 0,05(s) Cơu 8 : Chọn D. Gỉi: 2 2 10
v .A
.A 2 m / s ax m l A
5cm 0,05m T A 2 2
Cơu 9: Chọn B. Gia tốc cực đại: 2 2 2 a
A (4 ) .A 160.10 16m / s max
Cơu 10. Từ phương trình x 2cos(2πt – π/6) (cm, s) v 4πsin(2πt – π/6) cm/s.
Thay t 0,25s vào phương trình x và v, ta được :x 1cm, v ±2 3 (cm/s) Chọn : A. Cơu 11. Áp dụng : v A và a 2A Chọn : D max max Cơu 12.
Tại thời điểm t : 4 10cos(4πt + π/8)cm. Đ̣t : (4πt + π/8) α 4 10cosα
Tại thời điểm t + 0,25: x 10cos[4π(t + 0,25) + π/8] 10cos(4πt + π/8 + π) 10cos(4πt + π/8) 4cm.
Vậy : x 4cm x 3cos 2
.0 1,5cm 0 Cơu 3 13. Đáp án C '
v x 6 sin 2
.0 3 3cm / s 0 0 3 Cơu 14 3
. Đáp án A. v Asin( t ) 4 2 2
Asin( ) A 4cm 4 3 2 2 2 2 2 2 a Acos( t
) a (2) 4cos( ) (2) 4( ) 8 2cm/ s 4 2
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 17
Ch đ 1 : Dao đ ng đi u hòa Cơu k
15: Đáp án A.Ta có: - Tần số góc:
10rad / s m a
-Li độ tại thời điểm t: 2 a
x x 2 3 cm 2 2 2 2 v 20 - Biên độ dao động: 2 A x 2
3 4 cm 2 10 Cơu
16: Biểu thức vận tốc: v x' 1 20sin 20t (cm / s), 2 5 Khi t s : v 1 20sin 20.
120sin 60(cm /s), 15 15 2 6
v 0 chuyển động theo chiều âm quĩ đạo Biểu thức gia tốc: 2 a v' 2 400cos 20t (cm / s ) 2 2 4cos 20t m / s ). 2 2 5 Khi t s : 2 a 2 4cos 20.
24cos 12 3 m / s .Đáp án: D 15 15 2 6 Cơu 17: Gỉi :
Do ∆t là kho ng thời gian giữa hai lần liên tiếp vật cách vị trí cân bằng một kho ng như cũ nên 2 2 ∆ T v v t = => Sau ∆t thì v 1 2 2 2 2 1 và v2 vuông pha:
1 v v ( ) A . 4 2 2 1 2 ( ) A ( ) A 16 3 Thế số: 2 2 2
(8 3) (24 ) ( ) A
A 16 3 A . (1) 2 2 2 2 2 v a a (96 )
Ṃt khác, ta có v và a vuông pha: 1 1 2 1 2 2 2 1 v ( ) A (8 3) ( ) A . (2) 2 2 2 1 2 2 ( ) A ( ) A 2 2 (96 ) Từ (1) và (2) => 2 2 2 2 2 ( )
A (8 3) (16 3) (8 3) (24 ) . 2 2 2 (96 ) => 2 2
(4) 4 rad / .s (3). 2 (24 ) 16 3 16 3
Thế (3) vào (1) ta được: A 4 3 cm . Đáp án B 4
*So sánh về pha của ly độ x, vận tốc và gia tốc a của DĐĐH v + + -A O x A a x + x = Acos(t + )
v=x’ = -Asin(t + ) = Acos(t + + π/2) 2 2
a x ' x Acos( t )
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 18
Ch đ 1 : Dao đ ng đi u hòa Nhận xét:
v nhanh pha hơn x góc π/2 => x chậm pha thua v góc π/2
a nhanh pha hơn v góc π/2 => v chậm pha thua a góc π/2 a và x ngược pha nhau 2 2 2 2 v vuông pha vớ x v v a i x : 1 1 2 2 2 A ; v vuông pha với a : A 2 2 4 2 A A
Dạng 3: Liên hệ x, v và a của vật dao động điều hòa.
A. Ki n th c căn b̉n:
a) Từ các phương trình c a vận tốc và li độ ta có 2 2 x A cos t x v 1, 1 v A sin t A A
(1) được gọi là hệ thức liên hệ c a x, A, v và ω không phụ thuộc vào thời gian t. 2 v 2 v + 2 1 A x + 2 1 x A 2 2 + 2 2 1 v
A x ; nếu v là tốc độ thì 2 2 v A x v + 1 2 2 A x
+ Với hai thời điểm t1, t2 vật có các c̣p giá trị x1, v1 và x2, v2 thì ta có hệ thức sau: 2 2 v v 1 2 2 2 2 2 2 2 2 2 2 2 x x x v x v x x v v 1 2 1 1 2 2 1 2 1 2 2 2 2 2 2 A A A A A A x x 1 2 T 2 2 2 v v 1 2
b) Từ các phương trình c a vận tốc và gia tốc ta có 2 2 2 2 v A sin t a v a v 1 1, 2 2 2 4 2 2 2 a A cos t A A A A
(2) được gọi là hệ thức liên hệ c a a, A, v và ω không phụ thuộc vào thời gian t. 2 v 2 2 a v c) Liên hệ 2 2 , A x à
v v: A x ; Liên hệ 2 , A v à v a: A . 2 4 2
d) Lực kéo về ( hay lực hồi phục): F kx F KA. KV KV ax m A v 3 A v A 3 v e) a m x a m x max
Khi x 0 v ; A Khi x v ; Khi x v ; Khi x v ax m 2 2 2 2 2 2 Chú Ủ:
+ Từ (1) ta thấy đồ thị c a (v, x) là đ ng elip.
+ Từ (2) ta thấy đồ thị c a (a, v) là đ ng elip.
+ Từ a = –ω2x ta thấy đồ thị c a (a, x) là đo n thẳng. B. Các ví d :
Ví d 1: Một vật dao động điều hòa: khi vật có li độ x 3 cm . Thì vận tốc là v 4 cm / s , khi vật có li độ 1 1
x 4 cm thì vận tốc là v 3 cm / s . Tìm tần số góc và biên độ c a vật? 2 2
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 19
Ch đ 1 : Dao đ ng đi u hòa
Hướng dẫn : v 4 1 2 2 2 2 2 2 A x A 3 1 2 2
rad / s Từ 2 v A x 3 2 A 5cm 2 2 2 2 2 2 2 A 4 2
Ví d 2: Một vật dao động điều hòa với phương trình x = 5cos(ωt + π/3) cm. Lấy π = 10.
a) Khi vật qua vị trí cân bằng có tốc độ 10π (cm/s). Viết biểu thức vận tốc, gia tốc c a vật.
b) Tính tốc độ c a vật khi vật có li độ 3 (cm).
c) Khi vật cách vị trí cân bằng một đoạn 5 2 cm thì vật có tốc độ là bao nhiêu ? 2
Hướng dẫn :
a) Khi vật qua vị trí cân bằng thì tốc độ c a vật đạt cực đại nên v 10 2 max v A 10 rad / s max A 5 v x ' 10 sin t Khi đó 3 x 5 cos 2 t cm 3 2 2 2 a A 4 .5cos 2 t cm / s 3
b) Khi x = 3 cm, áp dụng hệ thức liên hệ ta được 2 2 x v 2 2 2 2 1 v 2 A x 2 5 3 8 cm / s A A
c) Khi vật cách vị trí cân bằng một đoạn 5 2 cm , tức là 2 2 5 2 2 5 2 x cm v 2 5 5 2 cm / s 2 2
Ví d 3: Một vật dao động điều hòa có 2 v 16 cm / s ;a 6, 4 m / s max max
a) Tính chu k̀, tần số dao động c a vật.
b) Tính độ dài qũ đạo chuyển động c a vật.
c) Tính tốc độ c a vật khi vật qua các li độ A A 3 x ; x . 2 2
Hướng dẫn : v 16 cm / s a a) Ta có max 640 40 max 4 rad / s 2 2 a 6, 4 m / s 640 cm / s v 16 . max max 2 T 0, 5 s
Từ đó ta có chu k̀ và tần số dao động là f 2 Hz 2 v
b) Biên độ dao động A thỏa mưn 16 max A 4 cm 4
Độ dài qũ đạo chuyển động là 2A = 8 (cm).
c) Áp dụng công thức tính tốc độ c a vật ta được: 2 A 2 2 2 A 4 A 3 khi x v A x 4 A 8 3 cm / s 2 4 2 2 A 3 2 2 2 3A 4 A khi x v A x 4 A 8 cm / s 2 4 2
http://thuvienvatly.com/u/32950 - GV: Đoàn Văn Lượng - Email: doanvluong@gmail.com Trang. 20




