Tóm tắt lý thuyết và bài tập Chương 2: Phần 2 - Các phương pháp giải mạch điện hình Sin xác lập | Môn Kỹ thuật điện - Điện tử - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58759230
KỸ THUẬT ĐIỆN – ĐIỆN TỬ
Chương 2: Phần 2 - Các phương pháp giải mạch điện hình SIN xác lập
TÓM TẮT LÝ THUYẾT
1. Định luật Kirchhoff 1 và Kirchhoff 2
• Định luật Kirchhoff 1 về dòng điện: Tổng đại số các dòng điện đến một nút bằng không : ∑ 𝑖𝑛= 0 i
Chiều dương dòng điện tùy chọn. Nếu xem các dòng điện vào nút là dương, dòng ra 3 i 1
nút là âm thì ta có: i1 + i2 + (-i3) + (-i4) = 0 i 4 i 2
Hoặc ta có thể viết: i1 + i2 = i3 + i4 (tổng dòng đến nút = tổng dòng rời nút)
• Định luật Kirchhoff 2 về điện áp: Tổng đại số các điện áp dọc theo một vòng bằng không: ∑ 𝑣𝑛= 0 A + u 1 B -
Các dấu + điện áp u1, u2, u3, u4 là tùy ý chọn. + + u 4 u 2
Nếu chọn chiều chạy là ABCDA, ta có u1 + u2 – u3 – u4 = 0 - - D
Nếu chọn chiều chạy là ADCBA, ta có u4 + u3 – u2 – u1 = 0 + u 3 - C 𝑍̇ 1 𝑍̇ 2 𝑍̇ 𝑛 …
+ 𝑈̇ 1 - + 𝑈̇ 2 - 𝑈̇ 𝑘 + 𝑈̇ 𝑛 - ̇ ̇ ̇
2. Phương pháp biến đổi tương đương: ̇ ̇ ̇ ̇
• Ghép tổng trở nối tiếp:
Tổng trở tương đương 𝑍̇̇𝑡𝑑 của các tổng trở nối tiếp là:
Nếu U là điện áp tổng thì các điện áp 𝑈̇̇1, 𝑈̇̇2, .. , 𝑈̇̇𝑛 rơi trên các điện trở là:
Dòng điện qua các điện trở bằng nhau: 𝐼1̇ = 𝐼2̇ = .. = 𝐼𝑛̇
• Ghép tổng trở song song
Tổng trở tương đương 𝑍̇̇𝑡𝑑 của các tổng trở song song 𝑍̇̇1, 𝑍̇̇2, .. 𝑍̇̇𝑛 là: 1 … 𝑍̇̇ + 𝐼 𝑡𝑑 = 1 𝐼 𝑛 1 𝐼 2 11 ̇ ̇ 𝑈̇ … 𝑍̇ 1 𝑍̇ 2 𝑍̇ 𝑛 - … ̇ ̇ ̇ ̇
Nếu I là dòng tổng thì các dòng rẽ
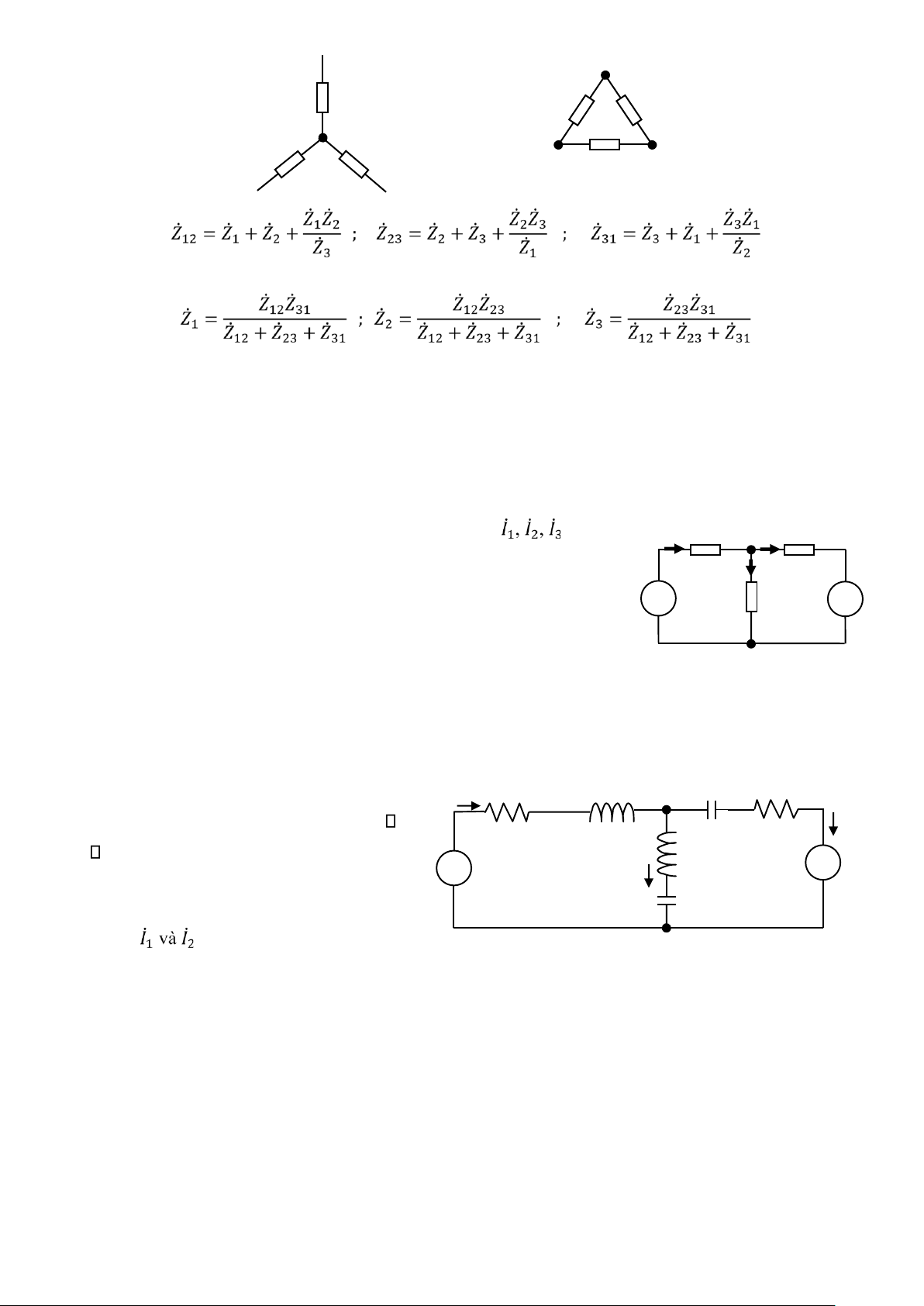
• Biến đổi Y – Δ và Δ – Y lOMoAR cPSD| 58759230 1 ̇ 1 ̇ 𝑍̇ 1 𝑍̇ ̇ ̇ 31 𝑍̇ 12 𝑍̇ 3 𝑍̇ 2 2 3 𝑍̇ 23 Nếu có mạch hình Y, 3
2 mạch điện tương đương của dạng Δ của nó có các giá trị:
Nếu có mạch hình Δ, mạch điện tương đương của dạng Y của nó có các giá trị:
3. Phương pháp dòng nhánh:
Nguyên lý của phương pháp này là chọn các dòng nhánh làm ẩn. Viết các phương trình cân bằng điện tại các
nút và vòng để giải hệ phương trình các ẩn dòng. Ta có các bước như sau: (ví dụ mạch hình bên)
Bước 1: Chọn 3 dòng nhánh 𝐼1̇ , 𝐼2̇ , 𝐼3̇ với chiều tùy ý.
Bước 2: Viết các phương trình cân bằng của mạch dùng Kirchhoff 1,
Kirchhoff 2 và định luật Ohm để có hệ 3 phương trình chứa 𝐼 + 𝑈̇ 1 - 1 A + 𝑈̇ 2 - 𝐼 2 -
Áp dụng Kirchhoff 1 tại nút A: 𝐼1̇ = 𝐼2̇ + 𝐼3̇ - Áp dụng Kirchhoff 2 tại 𝐼 3 𝑍̇ 1 𝑍̇ 2 + + vòng chứa + 𝐼1̇ và 𝐼2̇ : E 1 𝑈̇ 3 𝑍̇ 3 E 2 - - -
𝑈̇̇1 + 𝑈̇̇3 = 𝐸1  𝑍̇̇1𝐼1̇ + 𝑍̇̇3𝐼3̇ = 𝐸1
𝑈̇̇2 − 𝑈̇̇3 = −𝐸2  𝑍̇̇2𝐼2̇ − 𝑍̇̇3𝐼3̇ = −𝐸2
Bước 3: Giải hệ phương trình ta tìm được 𝐼1̇ , 𝐼2̇ , 𝐼3̇
Ví dụ 1: Trong hình bên, cho R1=2Ω; R2=1Ω; ̇ 𝐼 L C 1 R 1 1 1 R 2
L1=j1Ω; L2=j2Ω; C1= -j2Ω; C2=-j1Ω; E1=10 00; 𝐼 2
E2=5 -900. Tính 𝐼1̇ và 𝐼2̇ + L 2 + - 𝐸 𝐸 - 2 -
Áp dụng Kirchhoff 1 tại nút A: 1 𝐼 𝐼 3 1̇ = 𝐼2̇ + 𝐼3̇ C 2 ̇ ̇ - Áp dụng Kirchhoff 2 tại vòng chứa :
(2 + 𝑗1)𝐼1̇ + (𝑗2 − 𝑗1)𝐼3̇ = 𝐸1
(−𝑗2 + 1)𝐼2̇ − (𝑗2 − 𝑗1)𝐼3̇ = −𝐸2
Khử 𝐼3̇ trong hai phương trình trên ta được hệ:
{(2 + 𝑗2)𝐼1̇ − 𝑗𝐼2̇ = 10
−𝑗𝐼1̇ + (1 − 𝑗)𝐼2̇ = 𝑗5 Giải hệ bằng quy tắc Cramer: lOMoAR cPSD| 58759230 ; ;
4. Phương pháp dòng vòng:
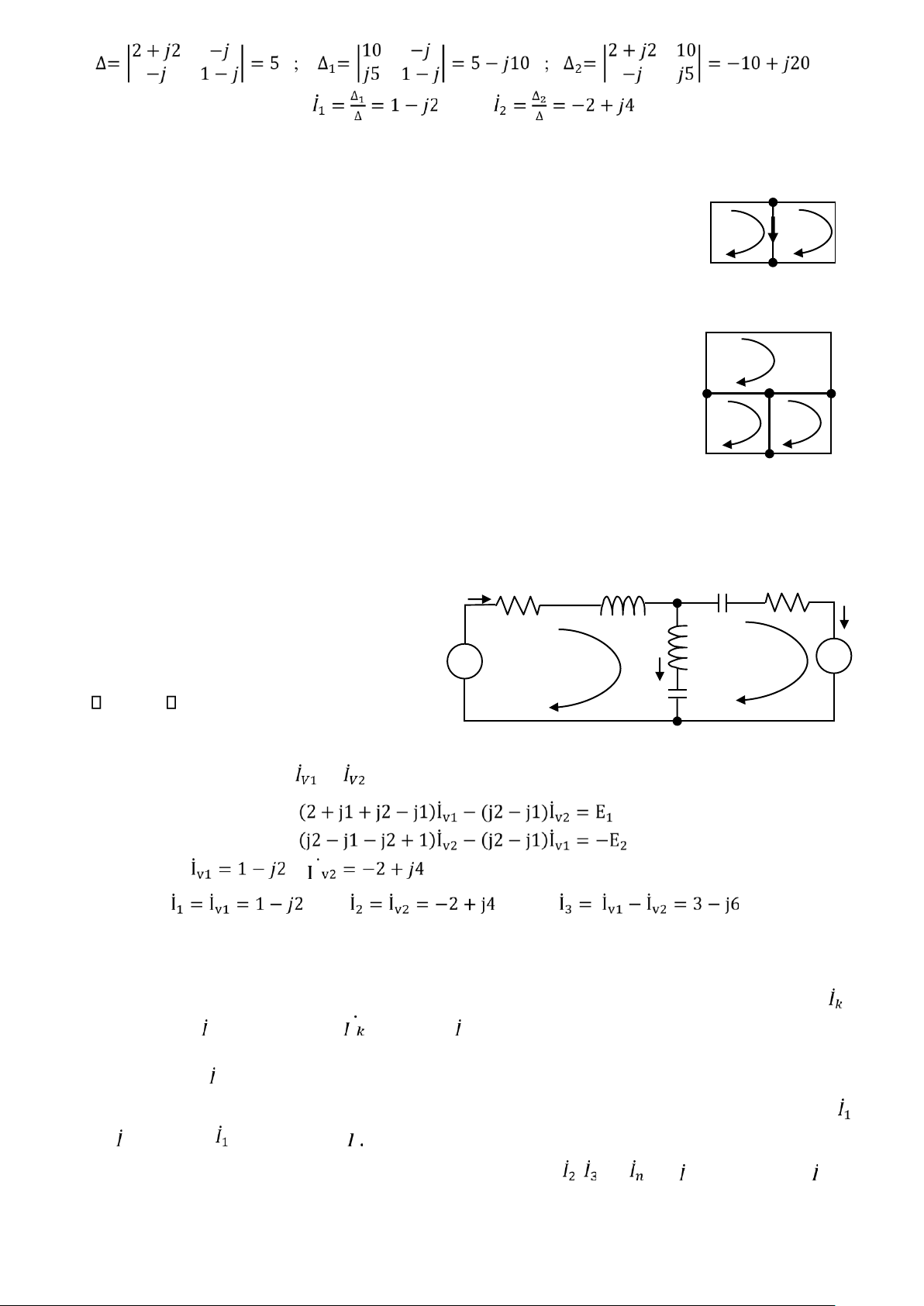
Nguyên lý của phương pháp này giả thiết mỗi vòng kín chỉ có dòng điện 𝐼 ̇ chạy A B C
trong vòng. Viết phương trình cân bằng cho tất cả các vòng kín trong mạch (với ̇ 𝐼 𝐵𝐸
nguồn E trong vòng sẽ mang dấu + khi dòng điện 𝐼
𝐼 ̇ chạy ra đầu + của nguồn; ̇ 1 𝐼 2 ̇ D E F
ngược lại mang dấu -). Giải hệ phương trình ta được các dòng 𝐼 ̇ trong các vòng
kín. Rồi áp dụng nguyên lý xếp chồng dòng điện để tính dòng cụ thể qua các A B
nhánh. (cùng chiều thì +, ngược chiều thì -) 𝐼 1
Bước 1: Giả thiết dòng điện chạy trong các vòng kín là 𝐼1̇ , 𝐼2̇ , . . , 𝐼𝑛̇ với chiều tùy C D E
chọn. (chọn cùng chiều cho dễ tính toán) 𝐼 2 𝐼 3
Bước 2: Viết n phương trình Kirchhoff 2 cho n vòng để tìm 𝐼1̇ , 𝐼2̇ , . . , 𝐼𝑛̇ ̇ ̇ F G H
Bước 3: Dùng nguyên lý xếp chồng (tổng đại số) để tính dòng chạy qua các
nhánh thực tế. (VD: 𝐼𝐵𝐸̇ = 𝐼1̇ − 𝐼2̇ )
Ví dụ 2: Giải mạch điện ở ví dụ 1 bằng phương 𝐼 L C 1 R 1 1 1 R 2
pháp dòng vòng. R1=2Ω; R2=1Ω; L1=j1Ω; 𝐼 2 ̇ + L + L 2
2=j2Ω; C1= -j2Ω; C2=-j1Ω; - 𝐸 𝐸 - 2 1 𝐼 𝑉 1 𝐼 𝐼 𝑉 2 3 E C 2 1=10 00; E2=5 -900. ̇ ̇
Gọi dòng điện trong hai vòng là và
. Áp dụng Kirchhoff 2 vào 2 vòng này ta được hệ: Giải hệ ta tìm được và . Suy ra các dòng nhánh: ; ; và
5. Phương pháp xếp chồng
Nguyên lý của phương pháp này là lần lượt giả thiết chỉ một nguồn làm việc, các nguồn còn lại nghỉ (ngắn
mạch nguồn áp hoặc hở mạch nguồn dòng). Dùng các định luật cân bằng điện để giải tìm các thành phần của
dòng thực tế cần tìm tại một nhánh (vẽ cùng chiều ) . Khi tất cả n nguồn cùng làm việc thì dòng thực tế là
tổng của các dòng thành phần. Lưu ý nếu mạch có nguồn một chiều, thì khi tính thành phần một chiều (các
nguồn khác nghỉ) của , ta phải ngắn mạch cuộn cảm và hở mạch tụ điện.
Bước 1: Chỉ cho một nguồn làm việc, các nguồn 2, 3, …n nghỉ. Giải mạch thứ nhất này để tìm thành phần
của dòng cần tìm (vẽ cùng chiều với )
Bước 2: Tiếp tục với các nguồn 2, 3, …n, ta tìm được các thành phần , , …, của . Dòng tổng hợp khi tất cả nguồn làm việc là lOMoAR cPSD| 58759230
Ví dụ 3: Tính dòng điện trong mạch điện ví dụ 1 bằng phương pháp xếp chồng.
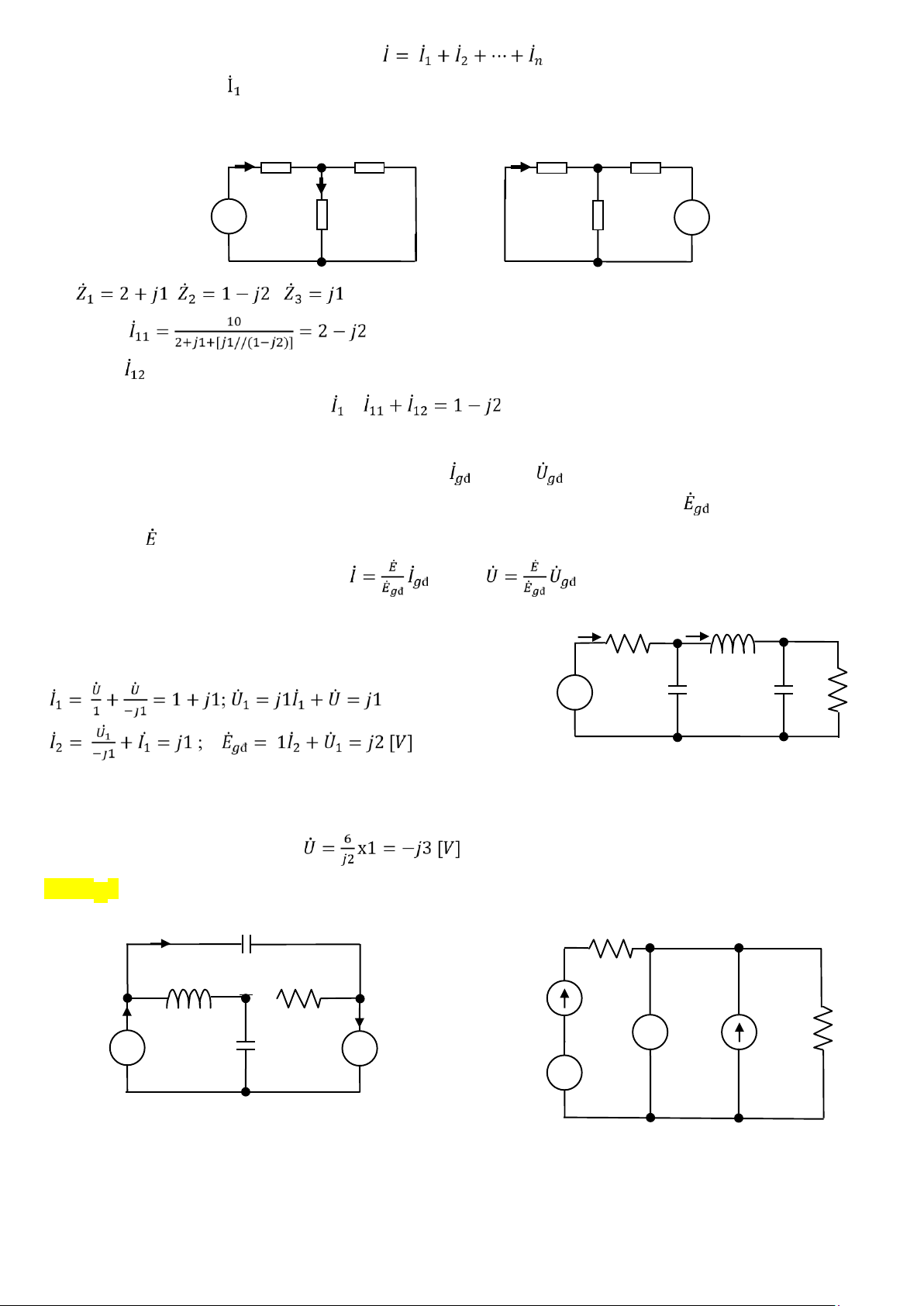
Khi cho nguồn E2 nghỉ và nguồn E1 nghỉ, ta được các mạch điện sau: 𝐼 11 𝐼 12 𝑍̇ 1 𝑍̇ 2 𝑍̇ 1 𝑍̇ 2 + E + 1 𝑍̇ 3 - 𝑍̇ 3 E 2 - Với ; ; ; E1 = 10 ; E2 = -j5 Tính dòng
(phương pháp biến đổi tương đương) Tính dòng = … = -1
Khi cả hai nguồn cùng làm việc, dòng =
6. Phương pháp tỷ lệ
Nguyên lý của phương pháp này là tự ý giả định dòng hoặc áp
cần tìm trong mạch có một giá trị tùy ý
(thường chọn giá trị đơn giản nhất). Rồi dùng giá trị giả định đó tính ngược lại nguồn (giả định) Khi
nguồn thật là (theo đề bài) thì dòng hoặc áp thật cần tìm là số tỷ lệ: hoặc
Ví dụ 4: Tính điện áp 𝑈̇̇ qua điện trở R2 trên mạch điện bên. Biết: ̇ 𝐼 R L 2 1 𝐼 1 1
R1= 1Ω; R2= 1Ω; C1= -j1Ω; C2= -j1Ω; L1= j1Ω; 𝑈̇̇ = 6∠00 [V] + Giả sử + 𝑈̇̇ = 1V. + 𝐸 𝑈̇ C 1 1 C 2 𝑈̇ R 2 Tính ngược về - - - nguồn để tìm 𝐸̇ ̇ ̇ ̇
Vậy giá trị thật của 𝑈̇̇ khi E=6 là:
BÀI T Ậ P 𝐼 C 1 A 3 2Ω B L R D C E 2 A 𝐼 𝐼 1 2 + + 1 V C + 1 A 1Ω 𝑒 2 - 1 - - 𝑒 2 + 5 V - F H G ̇ Hình 1 Hình 2
Bài tập 1: Cho mạch điện như hình 1. e1 và e2 là các nguồn áp.
a. Tính các dòng iCD, iDE, iDG theo i1, i2, i3 lOMoAR cPSD| 58759230
b. Viết phương trình cân bằng áp (Kirchhoff 2) cho các vòng CDGFC, DEHGD, và ABEDCA c. Tìm
phương trình vi tích phân để tính i1, i2, i3.
Bài tập 2: Xác định công suất do từng phân tử trong mạch hình 2 tiêu thụ hoặc phát ra. Hình 3 Hình 4
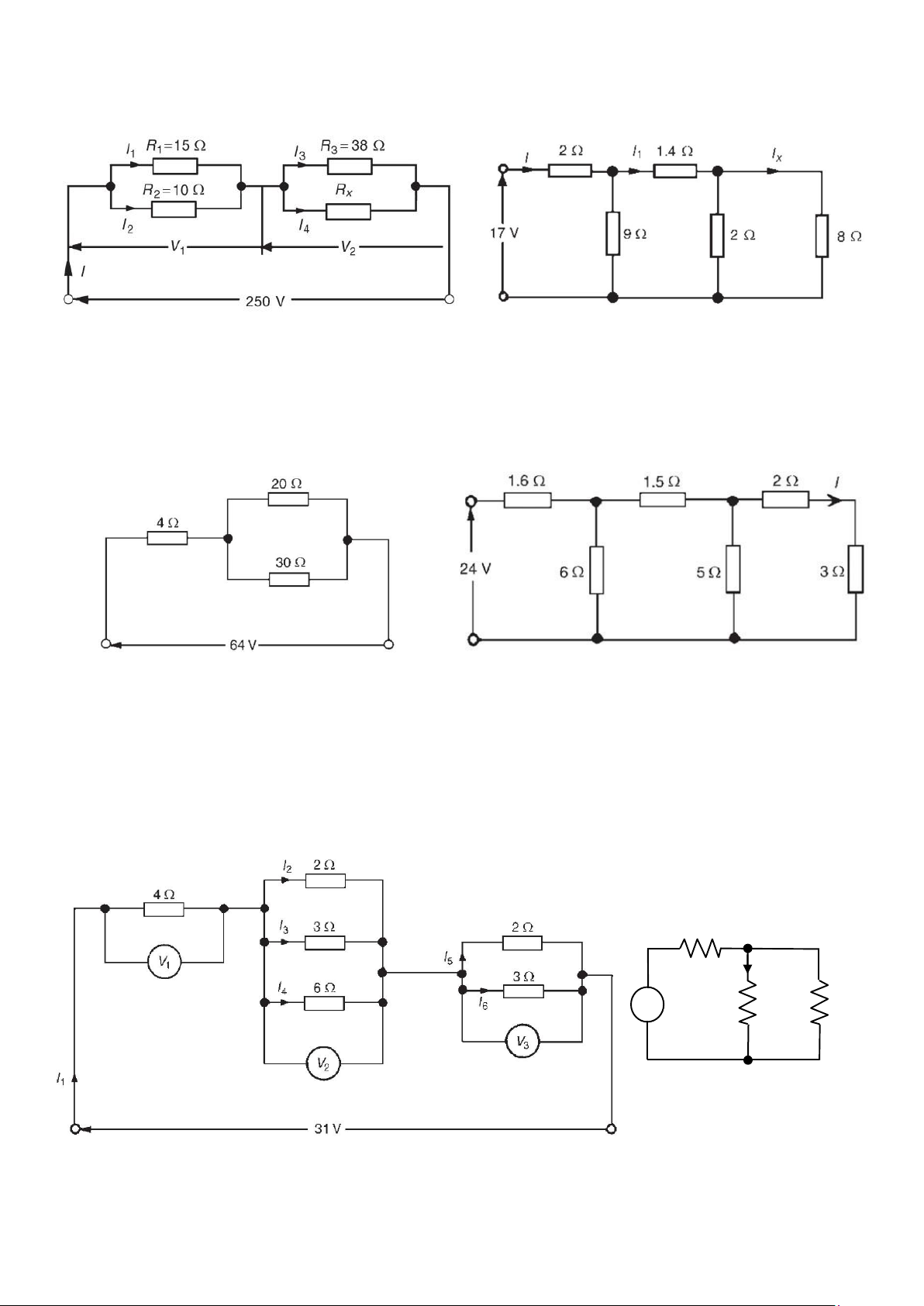
Bài tập 3: Trong mạch điện hình 3 tổng công suất của mạch là 2.5kW a. Tìm giá trị của Rx
b. Tính dòng điện chạy qua các điện trở
Bài tập 4: Trong mạch điện hình 4, tìm giá trị dòng Ix Hình 5 Hình 6
Bài tập 5: Trong mạch điện hình 5,
a. Tính dòng điện chạy qua điện trở 30 Ω
b. Xác định giá trị điện trở thêm vào song song với điện trở 20 Ω và 30 Ω để dòng điện ra từ nguồn cấp là
8A (điện áp nguồn không đổi)
Bài tập 6: Tìm giá trị dòng điện I trong mạch hình 6.
Bài tập 7: Tính dòng điện và điện áp (V1, V2, V3, I1, I2, I3, I4, I5, I6) ký hiệu trên mạch điện hình 7 4Ω A 6 + - 50 V R 9Ω Hình 8 Hình 7
Bài tập 8: Tính giá trị điện trở R trong mạch điện hình 8 lOMoAR cPSD| 58759230
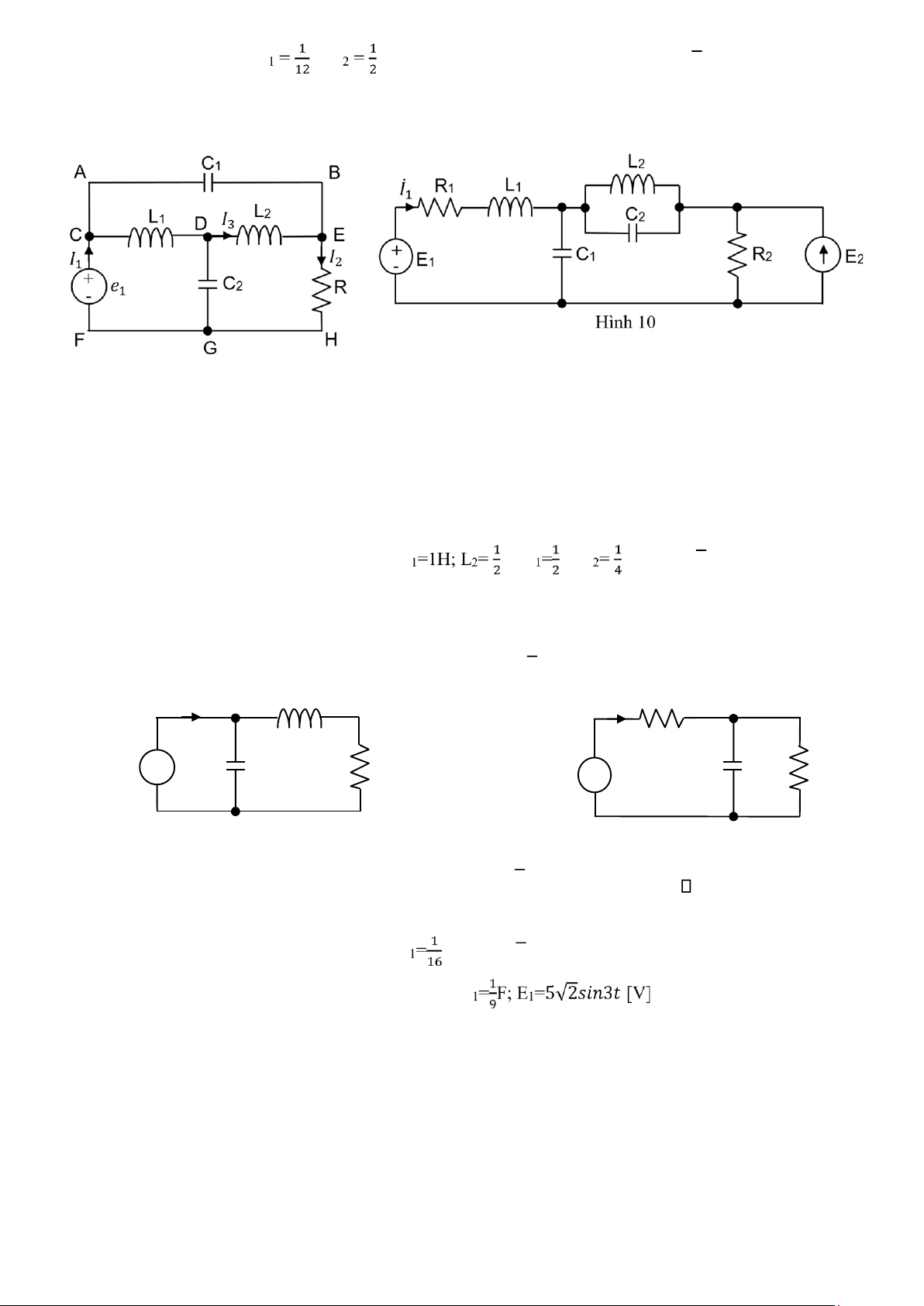
Bài tập 9: Trong hình 9, cho C F; C
F; L1 = 2H; L2 = 1H; R = 1Ω ; e1(t) = 50√2sin2t [V]. Tìm các
dòng điện 𝐼1̇ , 𝐼2̇ , 𝐼3̇ . ̇ ̇ ̇ Hình 9
Bài tập 10: Trong hình 10, cho R1=3Ω; R2=1Ω; L H; C F; C F;
E1=5√2𝑠𝑖𝑛2𝑡 [V]; E2 = 4A. Tìm 𝐼1̇ ?
Bài tập 11: Trong hình 11, cho C1=0.1F; L1=0.4H; R1=1Ω. E1=√2𝑠𝑖𝑛5𝑡 [V]. Tìm dòng điện 𝐼1̇ 𝐼 L 1 R 1 1 𝐼 1 + E 1 C 1 R C 1 - 1 E 1 R 2 + - Hình 11 Hình 12
Bài tập 12: Trong hình 12, cho R1=2Ω; R2=1Ω; C1=1F; E1=𝑈̇√2𝑠𝑖𝑛𝜔𝑡 [V]. Xác định sao cho dòng 𝐼1̇ sớm phase 100 so với áp E1.
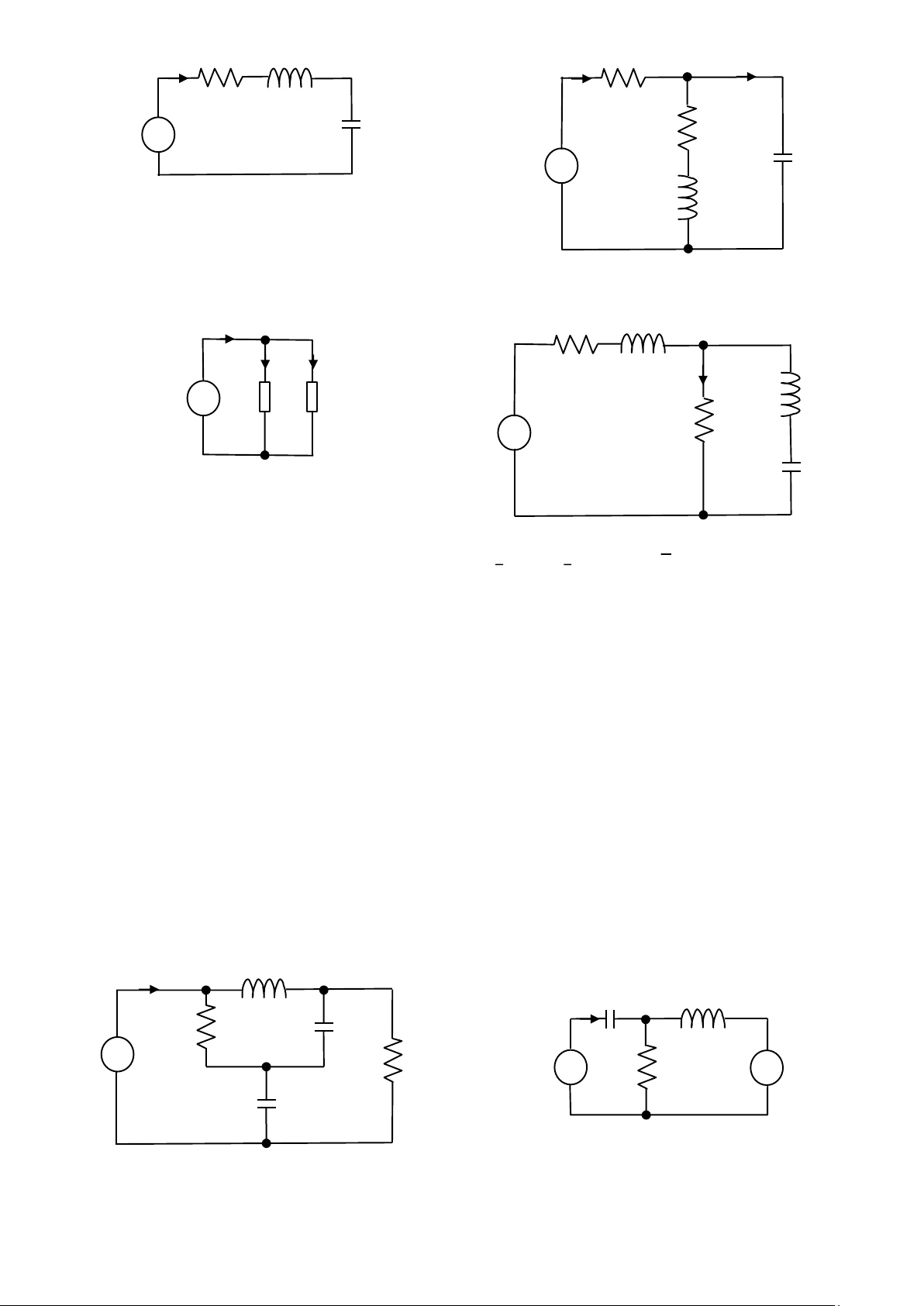
Bài tập 13: Trong hình 13, cho R1=8Ω; L1=1H; C F;
E1=5√2𝑠𝑖𝑛8𝑡 [V]. Tìm 𝐼1̇ và uc(t).
Bài tập 14: Trong hình 14, cho R1=1Ω; R2=3Ω; L1=1H; C . Tìm 𝐼1̇ và 𝐼𝐶̇ lOMoAR cPSD| 58759230 R 1 L 𝐼 R 1 1 1 𝐼 1 𝐼 𝐶 + C 1 R - E 1 2 + C 1 - E 1 Hình 13 L 1 Hình 14
Bài t ậ p 15 : Trong hình 15, cho 𝑈̇ = 100∠
0 0 ; 𝑍̇ 1 = 5 + 𝑗 5 ; 𝑍̇ 2 = 3 + 𝑗 10 . Tính 𝐼 1 , 𝐼 2 , 𝐼 3 𝐼 R 1 L 1 𝐼 1 𝐼 2 + 𝐼 + L 2 𝑈̇ 𝑍̇ 𝑍̇ 1 - 2 + R 2 - - E 1 Hình 15 C 1 Hình 16
Bài t ậ p 16 : Trong hình 16, cho R 1 Ω; =3 R 2 Ω; =1 L 1 =1 H; L 2 = 1 2 H; C 1 = 1
4 F; E 1 = 1 8 √ 2 𝑠𝑖𝑛 8 𝑡 [ V ] . Tìm bi ể u th ứ c ̇ ̇ của i(t).
Bài tập 17: Trong hình 17, cho R1=10Ω; R2=10Ω; L1=j10Ω; C1=-j10Ω; C2=-j10Ω; E1=100∠00 [V]. Tìm biểu thức của i(t). L 1 𝐼 ̇ C L 𝐼 1 1 R 1 C 1 + - E 1 R 2 + + - E 1 R 1 E 2 - C 2 Hình 18 Hình 17 lOMoAR cPSD| 58759230
Bài tập 18: Trong hình 18, cho R1=10Ω; C2=0.02F; L1=2H; E1 = 100√2sin10t [V]; E2 =
200√2sin10t [V]. Tìm dòng 𝐼 ̇ và viết biểu thức của i(t).
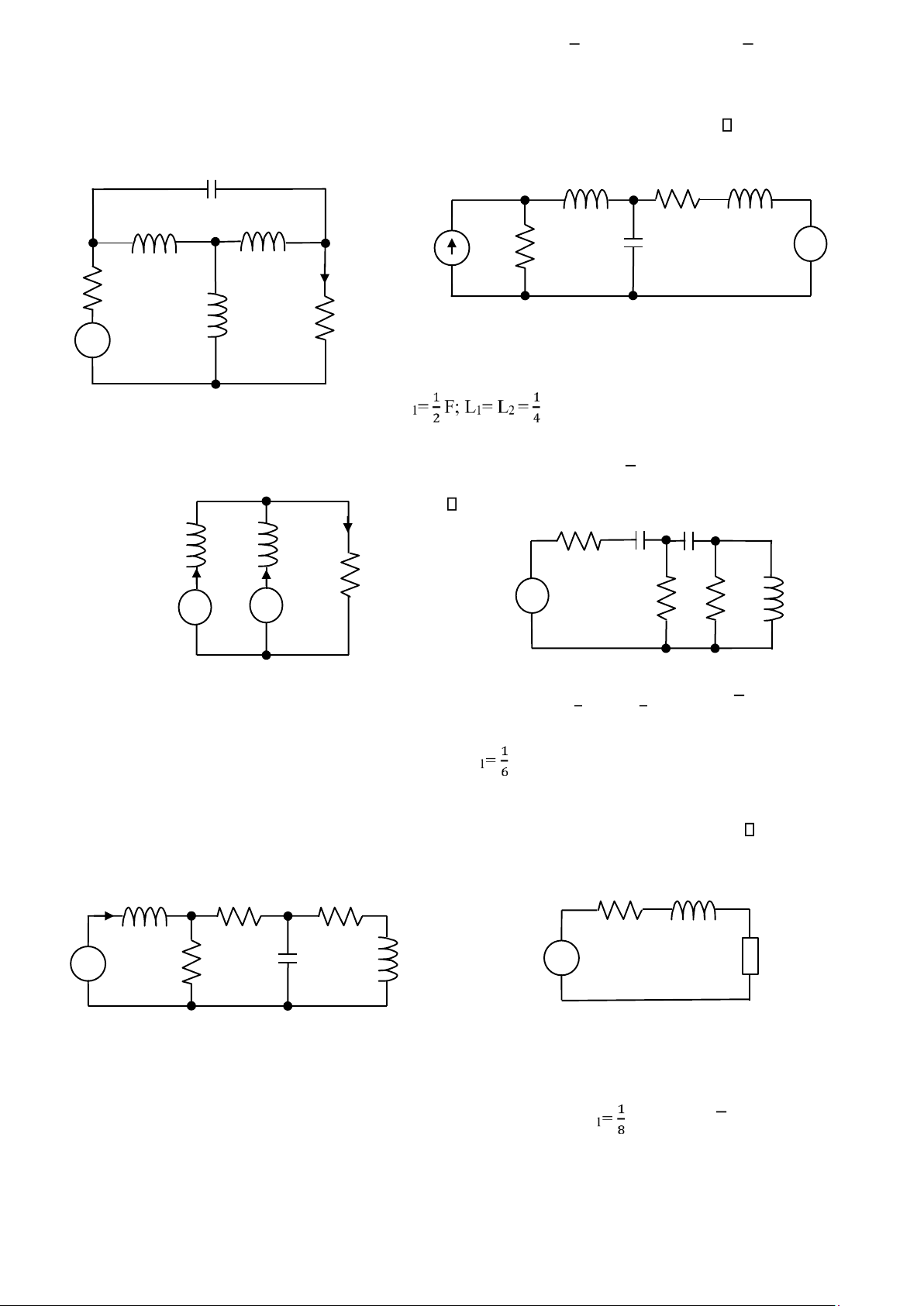
Bài tập 19: Trong hình 19, cho R1=1Ω; R2=1Ω; C1=-j4Ω; L1=j2Ω; L2=j2Ω; L3=j1Ω; E1 = 5 00 [V]; Tìm dòng 𝐼 ̇
và viết biểu thức của i(t). ̇ C 1 L 1 R 2 L 2 L L 1 2 + E C 1 R 1 1 E 2 - 𝐼 R 1 L 3 R 2 Hình 20 + 𝑒 - 1 Hình 19
Bài tập 20: Trong hình 20, cho R1=1Ω; R2=1Ω; C
H; E1 = 4 [A]; E2 = 8cos4t [V]. Tính điện áp
qua điện trở R1. (gợi ý: sử dụng phương pháp xếp chồng)
Bài tập 21: Trong hình 21, cho R1=3Ω; L1= j5Ω; L2 = j200Ω ; E1 1 2 = E2 = 100√2sin t [V]. Tính R 1 C 1 C 2 𝐼, ̇ 𝐼̇ , 𝐼̇ . 𝐼 L 1 L 2 R 1 ̇ 𝐼 1 𝐼 2 + + + - E 1 R 2 R 3 E E 1 2 L 1 - - ̇ ̇ Hình 22 Hình 21 2 = 1 2 1 = 1 2
Bài tập 22: Trong hình 22, cho R1=4Ω; R2=3Ω; R3=1Ω; C F ; C
F; L H; E1 = 7√2sin2t [V]. Tính
dòng và áp trong toàn mạch.
Bài tập 23: Trong hình 23, cho R1=3Ω; R2=1Ω; R3=4Ω; L1 = j1Ω; L2 = j4Ω; C1 = -j2Ω; E1 = 8 00 [V]. Tính dòng 𝐼 ̇ . L R L 1 R 1 1 𝐼 R 2 3 + + C E 1 Z 1 - E 1 1 L 2 - R 1 ̇ Hình 23 Hình 24
Bài tập 24: Trong hình 24, cho R1=2Ω; E1 = 440 [V]. Nguồn E1 hình sin có trị hiệu dụng 440V và phát ra
7200W. Tổng trở 𝑍̇1̇ có Z1 = 20Ω và tiệu thụ 6400W. Tính dòng điện trong mạch 𝐼 ̇ , UZ1 và HSCS của 𝑍̇1̇ .
Bài tập 25: Trong hình 25, cho R1=6Ω; R2=2Ω; R3=2Ω; L1=2H; L2=1H; C F ; E1=18√2sin2t
[V]. Tính công suất tác dụng và/hoặc phản kháng do từng phần tử tiêu thụ hoặc phát ra. lOMoAR cPSD| 58759230 R 1 L R R 1 3 L 2 1 L 1 + C + 1 - E 1 E R 1 C 2 - 1 R 2 Hình 25 Hình 26
Bài tập 26: Trong hình 26, cho R1=6Ω; R2=2Ω; L1=1H; C
F ; E1=10√2sin2t [V]. Tính công suất tác dụng
và/hoặc phản kháng do từng phần tử tiêu thụ hoặc phát ra.