


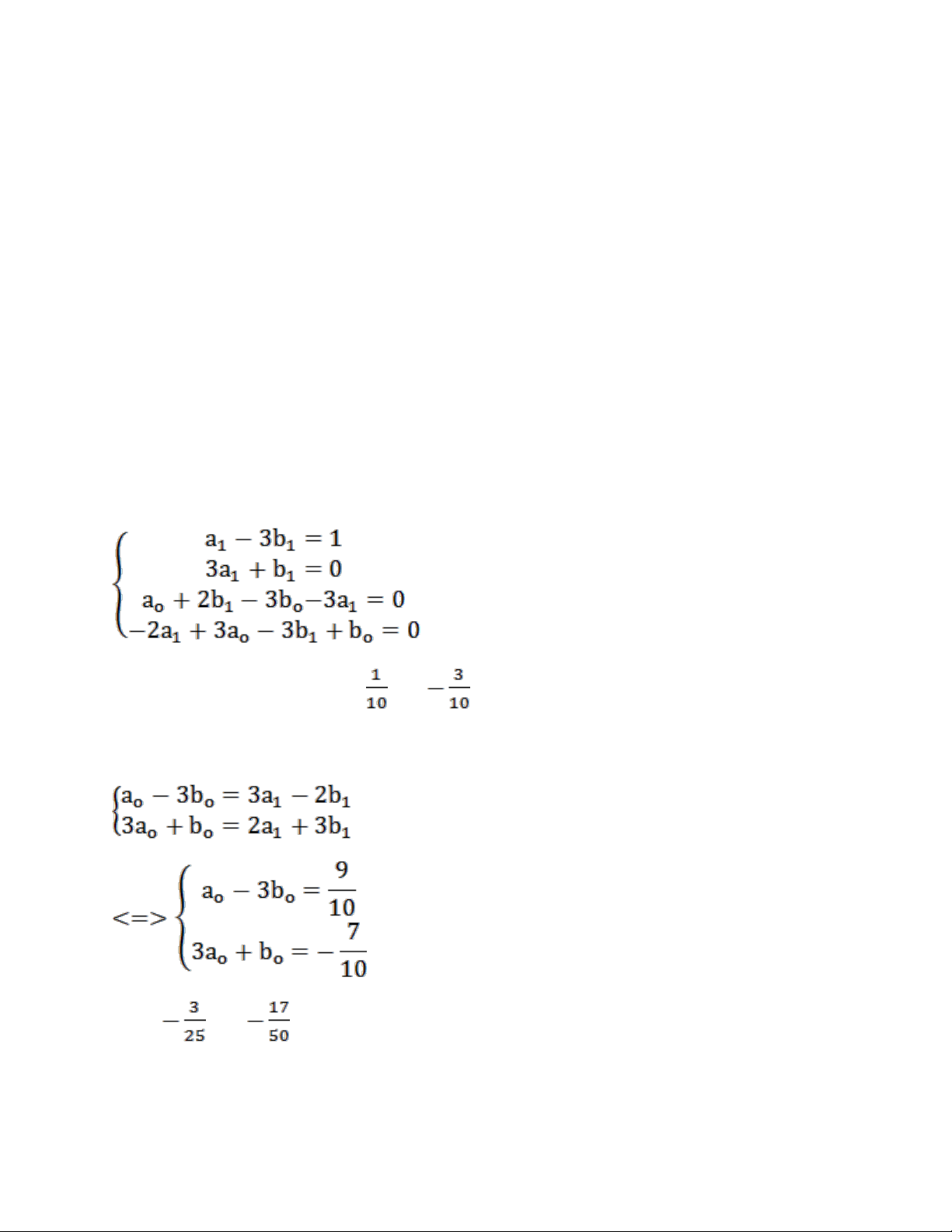
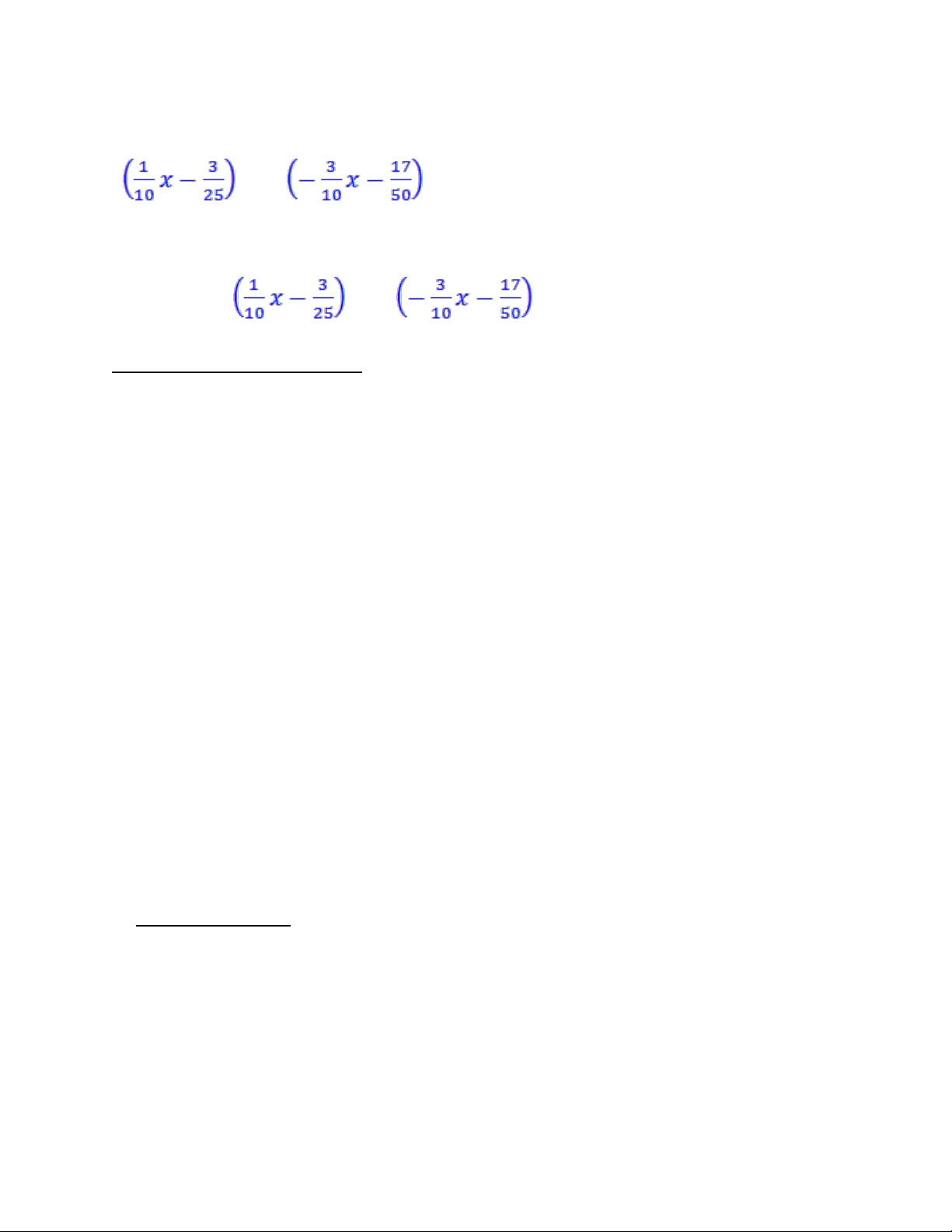



Preview text:
1) y" + 3y' - 4y =e^ -4x + xe^ -x 2) y" - 3y' + 2y = xcosx
3) y" - 4y' + 8y = e^ 2x + sin 2x
4) y" - 3y' + 2y = 3x + 5sin2x Giải:
1) y" + 3y' - 4y =e-4x + xe-x
phương trình thuần nhất tương ứng là: y" + 3y' - 4y =0
ð phương trình đặc trưng: ð k2+3k-4=0 (I)
ð phương trình có 2 nghiệm phân biệt là k1=1 và k2=-4. Do đó nghiệm tổng quát của phương trình là:
ð y=C1ex+C2e-4x trong đó C là hằng số. (@)
ð bây giờ ta tìm nghiệm riêng nữa là xong:
(nghiệm tổng quát cần tìm=nghiệm tổng quát của phương trình thuần nhất+nghiệm riêng)
Vế phải là e-4x + xe-x ta không đưa được về dạng tổng quát nên mình xét 2 phương trình con: (*) y" + 3y' - 4y =e-4x.
Vế phải có dạng eaxPn(x), a=-4 là nghiệm của (I)
Nên có nghiệm riêng dạng: y=xe-4xa0
=>y'=aoe-4x-4aoxe-4x=(1-4x) aoe-4x
=>y''=-4 aoe-4x-4(1-4x) aoe-4x=-4(2-4x) aoe-4x Thay lên ta được:
-4(2-4x) aoe-4x+3(1-4x) aoe-4x-4xe-4xa0= e-4x. <=>-5aoe-4x= e-4x =>ao=- =>y=- xe-4x (1) (**)y" + 3y' - 4y =xe-x
Vế phải có dạng eaxPn(x):a=-1 không phải là nghiệm của phương trình (I) nên nó có nghiệm riêng dạng: y=e-x(a1x+ao)
=>y'=a1e-x- e-x(a1x+ao)=e-x(-a1x-ao+a1)
=>y''=- e-x(-a1x-ao+a1)-a1e-x= e-x(a1x+ao-2a1) Thay lên ta được:
e-x(a1x+ao-2a1)+3e-x(-a1x-ao+a1)-4e-x(a1x+ao)=xe-x
<=>(-6a1) xe-x+(a1-6ao) e-x =xe-x
Để cho nó đồng nhất:(có nghĩa là giống nhau) thì:
Từ (1),(2) suy ra có có nghiệm riêng: (@@)
Từ (@),(@@) suy ra nghiệm tổng quát là: y=C1ex+C2e-4x
2) y" - 3y' + 2y = xcosx
ta có phương trình thuần nhất tương ứng: y" - 3y' + 2y =0
=>phương trình đặc trưng: k2-3k+2=0
phương trình có 2 nghiệm phân biệt k=1 và k=2. Do đó nghiệm tổng quát của phương trình là: y=C1ex+C2e2x
bây giờ ta tìm nghiệm riêng của phương trình: y" - 3y' + 2y = xcosx
vế là xcosx có dạng f(x)=eax[Pn(x)cosbx+Qm(x)sinbx]
trong đó a=0, b=1, max{n,m}=1
a+ib=0+i=i không là nghiệm của phương trình:
nên nó có nghiệm riêng dạng:
y=eax[(a1x+a0)cosbx+(b1x+bo)sinbx]
=(a1x+a0)cosx+(b1x+bo)sinx (do a=0,b=1)
=>y'=a1cosx-(a1x+a0)sinx+b1sinx+(b1x+bo)cosx
=( b1x+bo+ a1)cosx+(-a1x-a0+b1)sinx
=>y''=-( a1+ b1x+bo)sinx+b1cosx-a1sinx+(b1-a1x-a0)cosx
=-( b1x+bo+2a1)sinx+(-a1x-a0+2b1)cosx
Thay vào: y" - 3y' + 2y = xcosx
<=>-( b1x+bo+2a1)sinx+(-a1x-a0+2b1)cosx
-3[( b1x+bo+ a1)cosx+(-a1x-a0+b1)sinx]
+2[(a1x+a0)cosx+(b1x+bo)sinx]= xcosx
<=>[( a1-3b1)x+a0+2b1-3bo-3a1]cosx+[(b1+3a1)x-2a1+3ao-3b1+bo]sinx=xcosx
Để cho nó đồng nhất (tức là 2 vế giống nhau) thì:
Giải (1) và (3) bấm máy=>a1= , b1=
Thay vào (2) và (3) ta được: =>ao= , bo= Vậy ta có nghiệm riêng: y=(a1x+a0)cosx+(b1x+bo)sinx = cosx+ sinx
Vậy nghiệm tổng quát của phương trình là: y=C1ex+C2e2x+ cosx+ sinx (C là hằng số)
3) y" - 4y' + 8y = e 2x + sin 2x
Ta có phương trình thuần nhất: y" - 4y' + 8y = 0
=>phương trình đặc trưng k2-4k+8=0
phương trình vô nghiệm thực, có 2 nghiệm phức: k1=2+2i và k2=2-2i: =>p=q=2
=> phương trình có nghiệm tổng quát dạng: y=epx(C1cosqx+C2sinqx) =e2x(C1cos2x+C2sìn2x)
Bây giờ ta chỉ cần đi tìm nghiệm riêng của phương trình:
Lúc này do không đưa được về dạng tổng quát nên ta xét 2 phương trình con:
(*)y" - 4y' + 8y = e 2x
Vế phải f(x)=e2x có dạng eaxPn(x) với a=2 và n=0
a=2 không phải là nghiệm của phương trình đặt trưng nên nó có nghiệm riêng dạng: y=eaxao=aoe2x. =>y'=2aoe2x. =>y''=4aoe2x
Thay vào: y" - 4y' + 8y = e 2x.
<=>4aoe2x-4.2aoe2x+8aoe2x= e2x <=>4aoe2x= e2x
Để nó đồng nhất(giống nhau) thì: 4ao=1=>ao= Vậy ta có: y= e2x.
(**)y" - 4y' + 8y = sin 2x
Vế phải f(x)=sìn2x có dạng y=eax[Pn(x)cosx+Qm(x)sinx] với a=0, b=2, max{n,m}=0 =>y=a0cos2x+b0sin2x =>y'=-2aosin2x+2bocos2x =>y''=-4aocos2x-4bosin2x
Thay vào: y" - 4y' + 8y=sin2x
<=>-4aocosx-4bosinx-4(-2aosinx+2bocosx)+8 (a0cosx+b0sinx)=sin2x
<=>(4a0-8bo)cos2x+(8ao+4 b0)sin2x=sin2x
Để cho nó đồng nhất (giống nhau) thì: =>ao= , bo=
Vậy ta có nghiệm riêng: y= cos2x+ sin2x
Từ (*),(**) ta có nghiệm riêng của phương trình: y= e2x+ cos2x+ sin2x
kết luận nghiệm tổng quát của phương trình là: y=e2x(C1cos2x+C2sìn2x)+ e2x+ cos2x+ sin2x
4) y" - 3y' + 2y = 3x + 5sin2x
Ta có phương trình thuần nhất: y" - 3y' + 2y = 0
ð Phương trình đặc trưng: ð k2-3k+2=0
phương trình có 2 nghiệm phân biệt k1=1 và k2=2, nó có nghiệm tổng quát: y=C1 +C2 =C1ex+C2e2x
Bây giờ chỉ cần tìm nghiệm riêng nữa là hết: (*)xét phương trình con: y" - 3y' + 2y = 5sin2x
vế phải f(x)= 5sin2x có dạng:
eax[Pn(x)cosbx+Qm(x)sinbx], với a=0, b=2, max{n,m}=0.
a+ib không là nghiệm của phương trình thuần nhất, nên nó có nghiệm riêng dạng: y=eax[aocosbx+bosinbx] = aocos2x +bosin2x (b=2, a=0) =>y'=-2aosin2x+2bocos2x =>y''=-4aocos2x-4bosin2x
Thay vào phương trình: y" - 3y' + 2y = 5sin2x
=>-4aocos2x-4bosin2x-3[-2aosin2x+2bocos2x]+2[ aocos2x +bosin2x] = 5sin2x
<=>(-2ao-6bo)cos2x+(6ao-2bo)sin2x=5sin2x
Để cho nó đồng nhất(giống nhau)thì: =>ao=3/4; bo=-1/4 Vậy ta có nghiệm riêng: y= cos2x + sin2x
(**)xét phương trình con: y" - 3y' + 2y=3x
Vế phải f(x)=3x có dạng eaxPn(x), với a=0 và n=1
a=0 không phải nghiệm của phương trình thuần nhất nên nó có nghiệm riêng dạng: y=eax(a1x+ao)=a1x+ao, do a=0 =>y'=a1 =>y''=0
Thay vào phương trình: y" - 3y' + 2y=3x <=>0-3a1+2(a1x+ao)=3x <=>2a1x-3a1+2ao=3x
Để nó đồng nhất thì: 2a1=3=>a1=3/2
=>2ao=3a1<=>2a0=3.3/2=>a0=9/4
Vậy ta có nghiệm riêng: y= a1x+ao= x+
Từ (*), (**) ta có nghiệm riêng của phương trình là: y= cos2x + sin2x+ x+
kết luận nghiệm tổng quát của phương trình là: y=C1ex+C2e2x+ cos2x + sin2x+ x+





