

















































Preview text:
ĐẠI HỌC ĐÀ NẴNG
TRƯỜNG ĐẠI HỌC SƯ PHẠM KHOA VẬT LÝ
BÀI TẬP VẬT LÝ 2
(NHIỆT , QUANG, & VẬT LÝ HIỆN ĐẠI)
DÙNG CHO SINH VIÊN KHỐI ĐẠI TRÀ
TRƯỜNG ĐẠI HỌC BÁCH KHOA
LƯU HÀNH NỘI BỘ Đà Nẵng, 2017-2018
Phần I: NHIỆT HỌC
Chương 1: THUYẾT ĐỘNG HỌC PHÂN TỬ
(Không có bài tập)
---------------------------------------------------------------------------
Chương 2: NGUYÊN LÝ I CỦA NHIỆT ĐỘNG LỰC HỌC
I. CÁC CÔNG THỨC CẦN GHI NHỚ
A. Các định luật thực nghiệm về chất khí
1. Định luật Boyle-Mariotte cho quá trình đẳng nhiệt: pV = const
trong đó p và V là áp suất và thể tích của khối khí.
2. Định luật Gay-Lussac cho quá trình đẳng áp: V = V0(1 + t) = V0T hay V/T = const.
Định luật Charles cho quá trình đẳng tích: P = p0(1+t) = p0T hay P/T = const. trong đó V 0
0 và p0 là thể tích và áp suất của khối khí ở 0 C; V và p là thể tích và áp 1
suất của khối khí ở t (0C) ứng với T (K),
độ -1 là hệ số giãn nở nhiệt của 273 chất khí.
3. Phương trình trạng thái của khí lý tưởng (phương trình Mendeleep – Claperon):
a. Phương trình trạng thái cho một Kmol khí: PV = RT.
b. Phương trình trạng thái cho một khối khí bất kỳ: m pV RT
trong đó p, V và T là áp suất, thể tích và nhiệt độ của khối khí có khối lượng m,
là khối lượng của 1 kilômol khí đó; R là hằng số khí lý tưởng. Trong hệ SI: 3 8,31.10 J R
8,31J / mo .lK kmo . l K
4. Nội năng và khối lượng riêng của khí lý tưởn g m i
a. Nội năng của một khối khí lý tưởng khối lượng m: U RT 2 1
b. Khối lượng riêng của khối khí lý tưởng khối lượ m ng m: v
B. Nguyên lý thứ nhất nhiệt động học và các hệ quả
1. Nguyên lý thứ nhất nhiệt động học U = A + Q
Nó có thể viết dưới dạng vi phân: dU = A + Q
trong đó: dU là độ biến thiên nội năng của hệ, A = -pdV là công và Q là nhiệt
lượng mà hệ nhận được trong suốt quá trình biến đổi.
2. Độ biến thiên nội năng của khí lý tưởng m i m dU RdT C dT 2 v
3. Công mà khối khí nhận được trong quá trình biến đổi đẳng nhiệt: m V m p 1 2 A RT ln RT ln V p 2 1 4. Nhi
ệt dung riêng của một chất: Q c
trong đó m là khối lượng của hệ. mdT
- Nhiệt dung phân tử của một chất: C = c , với là khối lượng của 1 mol chất đó.
- Nhiệt dung phân tử đẳng tích và nhiệt dung phân tử đẳng áp của một chất khí i 2 iR C ; C
R C R v 2 p 2 v Cp i 2 - Hệ số Poisson: C i v
5. Phương trình của quá trình đoạn nhiệt: 1 pV = const hoặc: TV-1 = const
hoặc Tp const
6. Công mà khối khí nhận được trong quá trình đoạn nhiệt: 1 p V V 1 1 2 A 1 1 1 V m RT T Hoặc: p V p V 2 2 1 1 A hoặc: 1 2 A 1 1 1 1 T
Trong đó p1 và V1 là áp suất và thể tích của khối khí ở nhiệt độ T1; p2 và V2 là
áp suất và thể tích của khối khí ở nhiệt độ T2. 2 II. BÀI TẬP Bài 1.
6,5 gam Hydro ở nhiệt độ 270C, nhận được nhiệt nên thể tích giản nở gấp
đôi, trong điều kiện áp suất không đổi. Tính : a. Công mà khí sinh ra
b. Độ biến thiên nội năng của khối khí
c. Nhiệt lượng đã cung cấp cho khối khí. Bài 2.
10 gam khí Oxy ở nhiệt độ 100C, áp suất 3.105 N/m2. Sau khi hơ nóng đẳng
áp, thể tích khí tăng đến 10 lít. Tìm:
a. Nhiệt lượng mà khối khí nhận được
b. Nội năng của khối khí trước và sau khi hơ nóng.
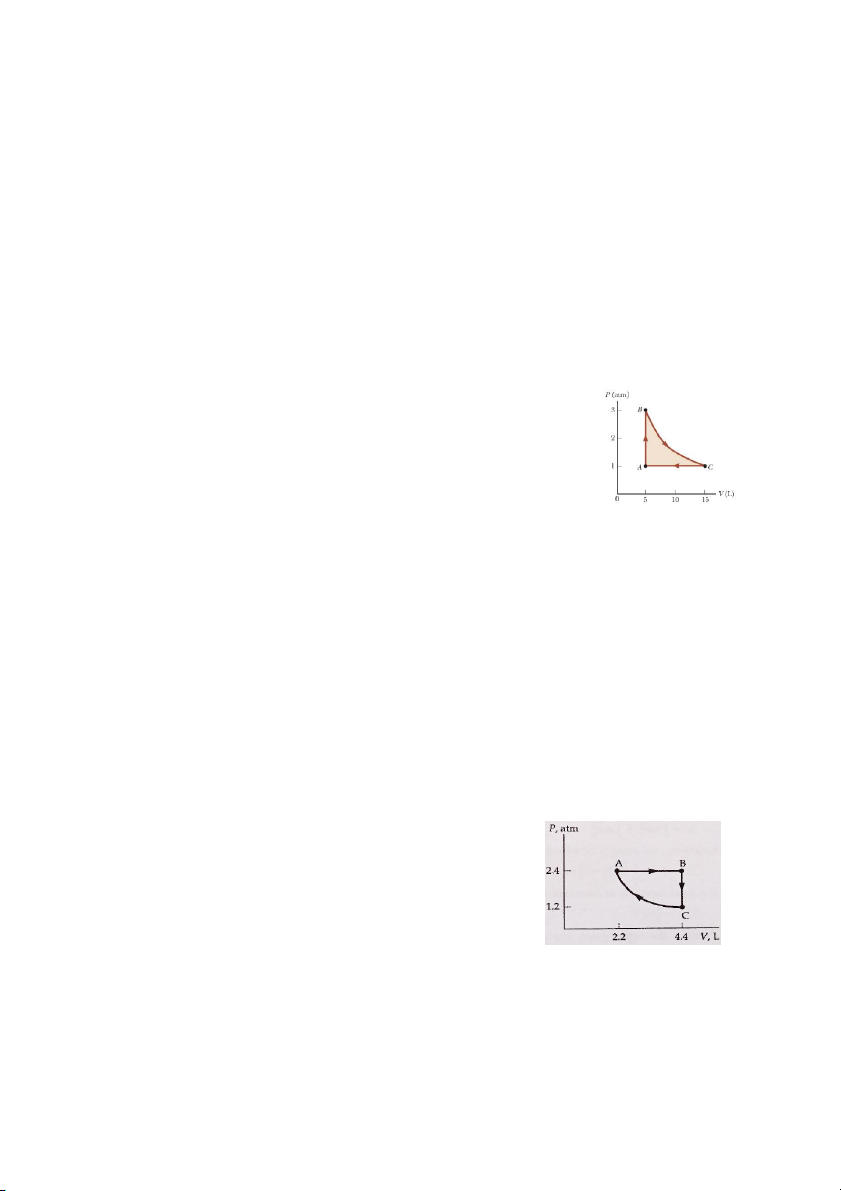
Bài 3. Cho một khí lý tưởng đơn nguyên tử có thể tích 5 lít ở áp
suất 1 atm và nhiệt độ 300 K (A). Khí thực hiện quá trình
biến đổi đẳng tích đến áp suất 3 atm (B), sau đó giãn đẳng
nhiệt về áp suất 1 atm (C). Cuối cùng, khí được làm lạnh
đẳng áp đến thể tích ban đầu (A). Tính:
a. Nhiệt độ tại B và C.
b. Nhiệt hệ nhận và công khối khí thực hiện trong chu trình trên.
Bài 4. Một mol khí lý tưởng được làm nóng đẳng áp từ 170C đến 750C, khi đó khí hấp
thụ một nhiệt lượng là 1200 J. Tìm:
a. Hệ số Poátxông =Cp/CV
b. Độ biến thiên nội năng U của khối khí và công mà khí sinh ra.
Bài 5. Để nén 10 lít không khí đến thể tích 2 lít, người ta có thể tiến hành theo hai cách: nén
đẳng nhiệt hay nén đoạn nhiệt. Hỏi cách nén nào tốn công ít hơn?
Bài 6. Một mol khí lý tưởng lưỡng nguyên tử thực hiện biến đổi như sau: từ trạng thái (1) với áp suất P o
1; thể tích V1 và nhiệt độ T1 = 27 C khí giãn đẳng nhiệt đến
trạng thái (2) có thể tích V2 = 2V1. Sau đó, khí lý tưởng tăng áp đẳng tích đến
trạng thái (3) có P3 = 2P1.
a. Vẽ đồ thị biến đổi trên giản đồ (P,V).
b. Tính trong toàn bộ quá t ì r nh: Nhiệt mà khối khí
nhận được và công khối k í h sinh ra.
Bài 7. 0,32 mol khí lý tưởng đơn nguyên tử thực hiện
biến đổi như sau: từ trạng thái (A) với áp suất p1 =
2,4 atm, thể tích V1 = 2,2 lit được nung nóng và
giãn đẳng áp đến trạng thái (B) có thể tích V2 =
2V1. Sau đó, khối khí được làm lạnh đẳng tích đến trạng thái (C) có P3 = P1/2 =
1,2 atm. Từ (C) nén đẳng nhiệt thì khối khí trở về trạng thái (A). Hãy xác định: 3
a. Nhiệt độ tại các trạng thái A, B, và C
b. Công hệ sinh, nhiệt hệ nhận, và độ biến thiên nội năng trong mỗi quá t ì r nh. Bài 8.
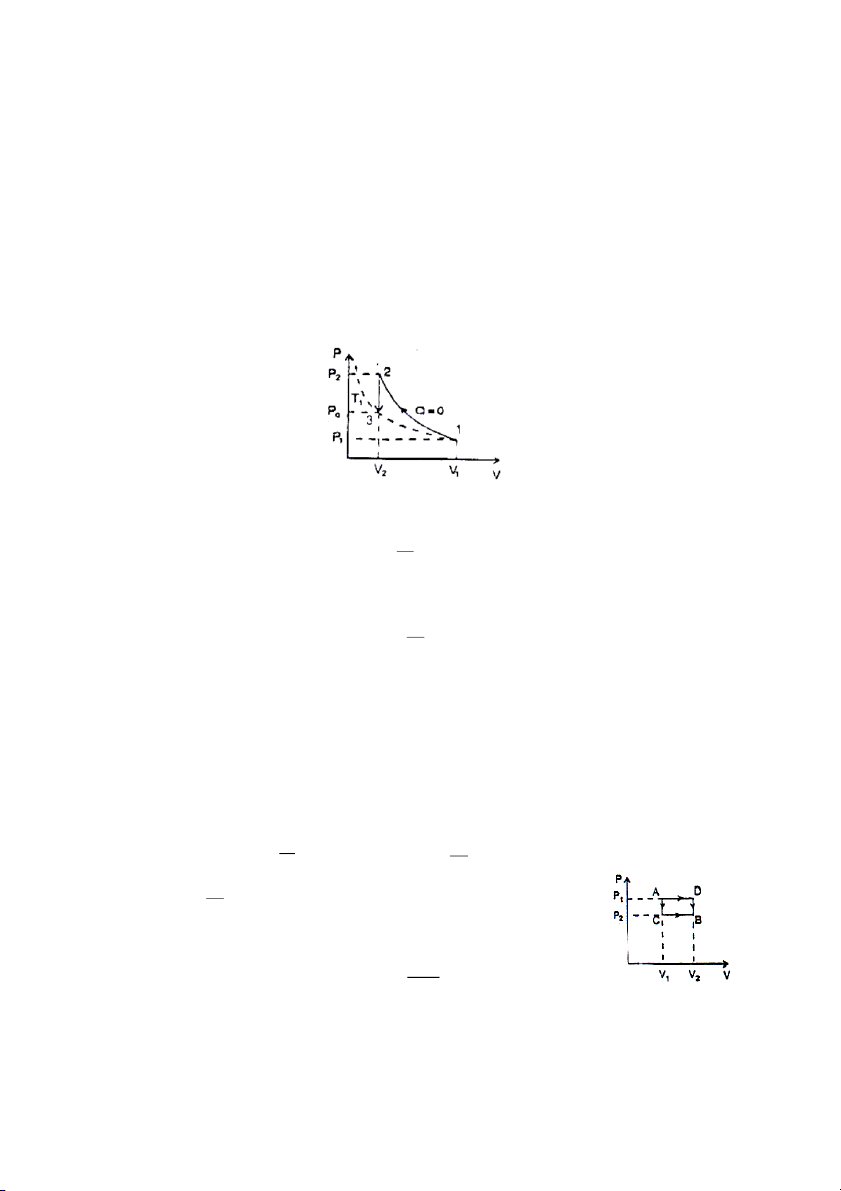
Một chất khí lưỡng nguyên tử có thể tích V1 = 0,5lít, ở áp suất p1 = 0,5 at.
Nó bị nén đoạn nhiệt tới thể tích V2 và áp suất p2. Sau đó người ta giữ nguyên
thể tích V2 và làm lạnh nó đến nhiệt độ ban đầu. Khi đó áp suất của khí là p0 = 1at.
a. Vẽ đồ thị của quá trình đó.
b. Tìm thể tích V2 và áp suất p2
Bài 9. Một lượng khí Oxy chiếm thể tích V1 = 3 lít, ở nhiệt độ 270C và áp suất p 5 2
1 = 8,2.10 N/m . Ở trạng thái thứ hai, khi có các thông số V 5 2
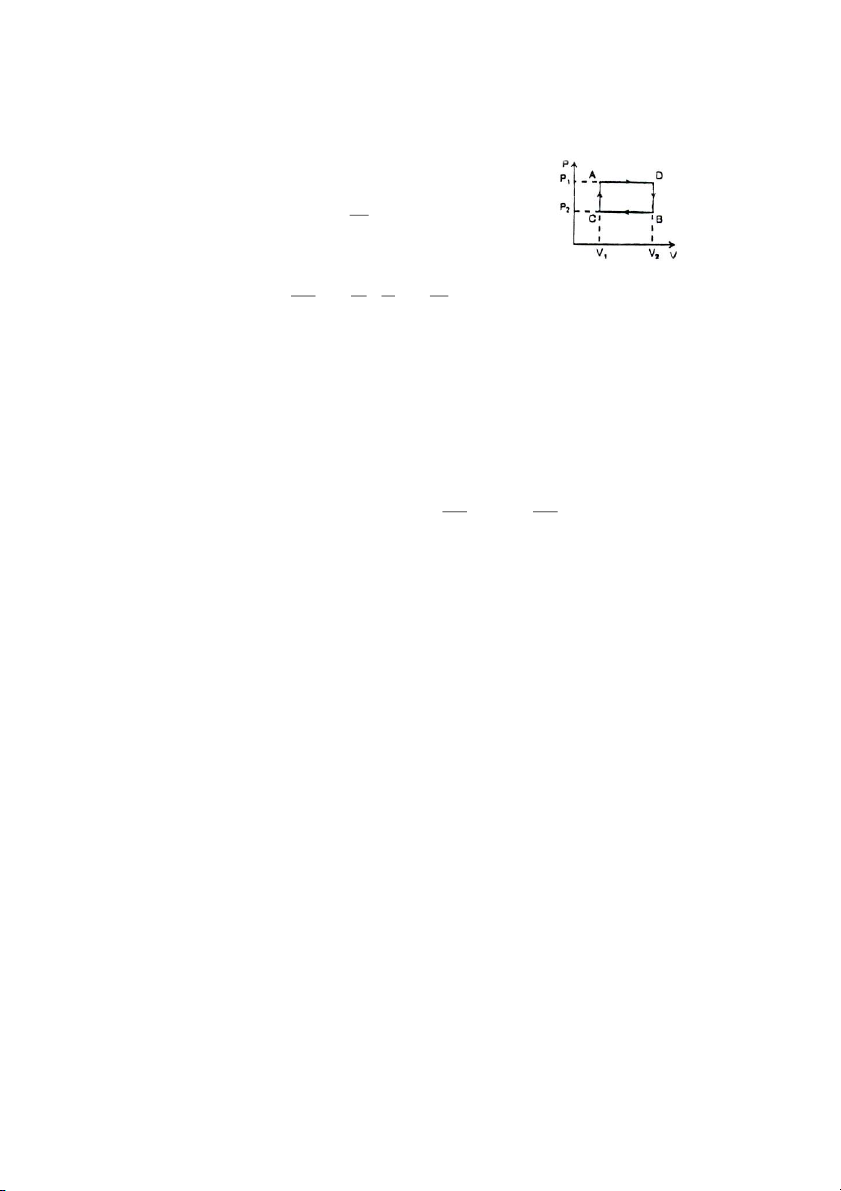
2 = 4,5 lít và p2 = 6.10 N/m (hình vẽ)
Tìm nhiệt lượng mà khí sinh ra khi giãn nở và độ biến thiên
nội năng của khối khí. Giải hai bài toán trong trường hợp
biến đổi khí từ trạng thái thứ nhất sang trạng thái thứ hai theo hai con đường. a. ACB b. ADB
Bài 10. Một mol khí lưỡng nguyên tử thực hiện một
chu trình (như được minh họa ở hình bên) gồm 2
quá trình đẳng nhiệt ứng với nhiệt độ 𝑇1 =
700 K, 𝑇2 = 300 K; và 2 quá trình đẳng tích ứng
với thể tích 𝑉1 và 𝑉2 = 2𝑉1. P P
a. Chứng minh rằng: A p P P B C
b. Tính công và nhiệt mà hệ trao đổi với môi
trường và độ biến thiên nội năng của hệ trong mỗi quá trình.
III. HƯỚNG DẪN VÀ ĐÁP SỐ Bài 1.
Cho: quá trình đẳng áp p=const Tìm: 6,5gam =65.10-4kg
a.Công mà khối khí sinh ra: A’. t o o 1= 27 CT1= 300 K
b.Độ biến thiên nội năng: U. V2=2V1, =2kg/Kmol, i=5
c. Nhiệt lượng dã cung cấp cho khối
khí ( nhiệt mà khối khí nhận được) :Q.
a. Quá trình giản nở là đẳng áp nên: m A= p. V = pV 3 1 = - RT J 1 = - 8,1.10 4
b.Độ biến thiên nội năng của khối khí: U = m i T ( R T ) 2 2 1 Tìm T V2
2 từ phương trình của quá trình đẳng áp: T2 = T1 T 2 1 V1 m Do đó: U = i 3
RT 20, 2.10 J 1 2
c. Theo nguyên lý I NĐH: U= A+Q => Q=U –A = 28,3.103J Bài 2.
Cho: quá trinh đẳng áp p=const Tìm:
10gam =.10-2kg a.Nhiệt mà khối khí nhận được :Q. t o o 1= 10 CT1= 283 K b. U1 , U2. V -2 2=10lit = 10 m3, =32kg/Kmol, i=5
a. Vì quá trình hơ nóng là đẳng áp, nên: Q = m m i 2 C T
R (T T ) p 2 1 2
Tìm T2 từ phương trình của quá trình đẳng áp. m RT ; trong đó V 1 1 = . p1
Kết quả là: Q = 7,9.103J
b. Nội năng của khối khí trước khi hơ nóng: m i 8 U RT 1 . 8 , 1 0 J 1 1 2 m i Và sau khi hơ nóng: U 3 2 = RT 1 . 6 , 7 0 J 2 1 Bài 3. ĐS:
- Nhiệt độ 𝑇𝐵 = 𝑇𝐶 = 900 K - Công 𝐴′𝐵𝐶 = 1648 J 𝐴′𝐶𝐴 = −1000 J - Suy ra: 5 𝐴′ = 648 J
- Nhiệt hệ nhận trong cả chu trình: 𝑄 = −𝐴 = 𝐴′ = 648 J Bài 4. ĐS: a) Tính 𝑚 𝑄 1200 𝐽
𝑄 = 𝜇 𝐶𝑃∆𝑇 → 𝐶𝑃 = 𝑚 = 75 − 17 = 20,69𝑚𝑜𝑙.𝐾. 𝜇 ∆𝑇 𝐶 𝐶 20,69 𝛾 = 𝑃 𝑃 𝐶 = = 1,67 𝑉
𝐶𝑃 − 𝑅 = 20,69 − 8,31 b) Tính ∆𝑈 và 𝐴′ 𝑚 𝑖 𝑚 ∆𝑈 = 𝜇 2𝑅∆𝑇 = ( )
𝜇 𝐶𝑉∆𝑇 = 12,38 75 − 17 = 720𝐽
𝐴′ = −𝐴 = 𝑄 − ∆𝑈 = 1200 − 720 = 480𝐽 Bài 5. Cho: V -2 -3
1 =10lit =10 m3; V2 =2lit =2.10 m3
Nén theo quá trình nào mà ít tốn công hơn thì lợi hơn.
Nếu nén đẳng nhiệt, thì công mà khí phải nhận vào là: A m V1 1 = RT ln 1 V2 1
Nếu nén đọan nhiệt, thì A m R 1 T 2 V 2 = 1 l 1 V i 2 Với = ; i (không khí) = 5 2 Xét tỷ số
; suy ra là nén đẳng nhiệt lợi hơn. Bài 6. ĐS:
b. Nhiệt hệ nhận: 𝑄 = 𝑄12 + 𝑄23 = (𝑙𝑛2 + 15 ) 𝑅𝑇 2 1 = 20427 J
Công hệ sinh: 𝐴′ = 𝐴′ ′ 12 + 𝐴23 = 1701 J Bài 7. ĐS: a. TA = TC = 199 K; TB = 398 K
b. Tính 𝑄, 𝐴′ và ΔU
- Quá trình 1 (A → B): Q1 = 1323 J; A’1 = 528 J; ΔU1 = 795 J 6
- Quá trình 2 (B → C): A’2 = 0; Q2 = - 795 J; ΔU2 = -795 J
- Quá trình 3 (C → C): ΔU3 = 0; A3 = - Q3 = 367 J Bài 8. Cho: p 4
1=0,5at= 0,5.9,81.10 N/m2 Tìm: P 4
o=1at= 9,81.10 N/m2 a.Vẽ đồ thị của quá trình đó. V -4 1=0,5lit = 5.10 m3 b. V2 , p2. i=5. a. Đồ t ị h biểu diễn quá trình b. Xét trạng thái 1 và
3 ta tìm được (quá trình đẳng nhiệt): p V 1 2 = V 2 , 0 l 5 p 1 2
Quá trình biến đổi từ (1) đến (2) là đoạn nhiệt Q = 0, ta có: V y p p 1 3 , 1 a 2 t 2 1 V 2 Bài 9. Cho: V -3 3 5 2
1=3lit=3.10 m , p1 = 8,2.10 N/m Tìm: t o o 1= 27 CT1=300 K = TA
a.Nhiệt lượng mà khí sinh ra.
V2= 4,5lit, p2=6.105 N/m2 . b.Độ biến thiên nội năng của khối khí.
Vì nhiệt lượng trao đổi phụ thuộc vào độ biến thiên nhiệt độ, nên phải tìm nhiệt độ
của những trạng thái C, B, D. T P2 0 V C = T 220 K ; TB = T2 = T 2 0 ; TD = T 1 330 P C K 1 1 V1 V2 4500K V1
Tính khối lương khí từ trạng thái 1: PV 1 1 m R 1 T 7
Nhiệt hệ nhận được khi biến đổi khí từ trạng thái thứ nhất
sang trạng thái thứ hai theo hai con đường: Q m m ACB= QA C + QCB = C T + C T =1,55KJ . V AC P CB Tương tự Q m m ADB= QA D + QDB = C T + C T =1,88KJ . P AD V DB
Công hệ nhận được khi biến đổi khí từ trạng thái thứ nhất sang trạng thái thứ hai theo hai con đường: AACB= AA
C + ACB =0 –p2(VB-VC) =–p2(V2-V1)= -0,92KJ Tương tự AADB= AA
D + ADB = –p1(VD-VA) =–p1(V2-V1)= -1,25KJ
Độ biến thiên nội năng khi biến đổi khí từ t ạ
r ng thái thứ nhất sang trạng thái thứ hai theo hai con đường: UACB = AACB+ QACB =0,63KJ UADB = AAD + B QAD B =0,63KJ
U = UV=const + Up =const ; Q = QV= const + Qp=const ; A = - p.V Ta tính được:
QACB = 1,55KJ : QADB = 1,88KJ ; AACB = 0,92KJ ; AADB = 1,25KJ
UACB = 0,63KJ ; UADB = 0,63KJ Bài 10. ĐS:
a. Đối với các quá trình đẳng nhiệt AB và CD, ta có: P V P V p P A 2 và D 2 do đó A D P V P V P P B 1 C 1 B C b.
Quá trình từ A→ B: 𝐴𝐴𝐵 = −4,032 kJ; 𝑄
𝐴𝐵 = −𝐴𝐴𝐵 = 4,032 kJ
Quá trình BC: 𝑄𝐵𝐶 = −8,31 kJ;
Quá trình từ C → D: 𝐴𝐶𝐷 = 1,728kJ; 𝑄𝐶𝐷 = −𝐴𝐶𝐷 = −1,728kJ;
Quá trình DA: 𝑄𝐷𝐴 = 8,31kJ
--------------------------------------------------------------------------- 8
Chương 3: NGUYÊN LÝ II CỦA NHIỆT ĐỘNG LỰC HỌC
I. CÁC CÔNG THỨC CẦN GHI NHỚ
1. Hiệu suất của một động cơ nhiệt: A ' Q Q ' 1 2 Q Q 1 1
Trong đó Q1 là nhiệt mà tác nhân nhận được của nguồn nóng và Q'2 là nhiệt
mà tác nhân nhả cho nguồn lạnh.
2. Hiệu suất của chu trình Carnot: 2 1 T T1
3. Hệ số làm lạnh của máy làm lạnh: 2 Q 2 Q ' A Q Q 1 2
Trong đó A là công tiêu tốn trong một chu trình làm lạnh, Q2 nhiệt mà tác nhân
nhận được của nguồn lạnh trong chu trình đó, Q'1 nhiệt mà tác nhân nhả cho
nguồn nóng trong 1 chu trình.
Đối với máy làm lạnh hoạt động theo chu trình Carnot: T2 T T 1 2 II. BÀI TẬP
Bài 1. Một động cơ nhiệt làm việc theo chu trình Cacnô có công suất P = 73.600W.
Nhiệt độ của nguồn nóng là 1000C nhiệt độ của nguồn lạnh là 00C. Tính:
a. Hiệu suất của động cơ.
b. Nhiệt mà tác nhân thu được từ nguồn nóng trong 1 phút.
c. Nhiệt mà tác nhân nhả cho nguồn lạnh trong 1 phút
Bài 2. Một máy hơi nước có công suất 14,7KW, tiêu thụ 8,1 kg than trong 1 giờ. Năng
suất tỏa nhiệt của than là 7800 kcal/kg. Nhiệt độ của nguồn nóng là 2000C, nhiệt
độ của nguồn lạnh là 580C. Tìm hiệu suất thực tế của máy. So sánh hiệu suất đó
với hiệu suất lý tưởng của máy nhiệt làm việc theo chu trình Carnot với những nguồn nhiệt kể trên.
Bài 3. Một máy làm lạnh làm việc theo chu trình Carnot nghịch, tiêu thụ công suất
36800W. Nhiệt độ của nguồn lạnh là -100C, nhiệt độ của nguồn sóng là 170C. Tính:
a. Hệ số làm lạnh của máy.
b. Nhiệt lượng lấy được từ nguồn lạnh trong 1 giây
c. Nhiệt lượng tỏa ra cho nguồn nóng trong 1 giây.
Bài 4. Một máy hơi nước chạy theo chu trình Stilin gồm hai quá trình đẳng nhiệt và
hai quá trình đẳng tích.
a. Tính hiệu suất của chu trình 9
b. So sánh hiệu suất này với hiệu suất của chu trình Carnot có cùng nhiệt độ của
nguồn nóng và nguồn lạnh
Bài 5. Một động cơ nhiệt có nhiệt độ của nguồn nóng là 200oC và nhiệt độ của nguồn
lạnh là 57oC. Động cơ nhận nhiệt lượng 45000 kJ trong 1 giờ và có công suất là 2,5 kW.
a. Tính hiệu suất thực của động cơ.
b. Giả sử động cơ nhiệt đó hoạt động theo chu trình Carnot thì công suất của nó tăng lên bao nhiêu lần.
Bài 6. Một máy nhiệt lý tưởng chạy theo chu trình Carnot thuận nghịch có nguồn nóng
ở nhiệt độ 1270C và nguồn lạnh ở 270C. Máy nhận một nhiệt lượng 63 kcal từ
nguồn nóng trong 1 s. Tính: a) Hiệu suất của máy.
b) Nhiệt lượng tỏa ra cho nguồn lạnh trong 1 giây. c) Công suất của máy.
Bài 7. Tua bin hơi của nhà máy phát điện nguyên tử công suất 1000MW nhận nhiệt từ
nguồn hơi ở nhiệt độ 7270C và thải nhiệt ra môi trường ở nhiệt độ 1270C. Giả
thiết hiệu suất thực tế của tua bin hơi bằng 50% hiệu suất của chu trình Carnot. Hãy tính:
a) Hiệu suất thực tế của chu trình tuabin hơi.
b) Nhiệt do nhà máy thải ra nguồn nước (sông) làm lạnh trong 1 giây.
c) Nhiệt độ tăng của nước sông nếu dòng chảy có lưu lượng 106kg/s. Cho nhiệt
dung riêng của nước là: c = 4,19 kJ/kg. độ.
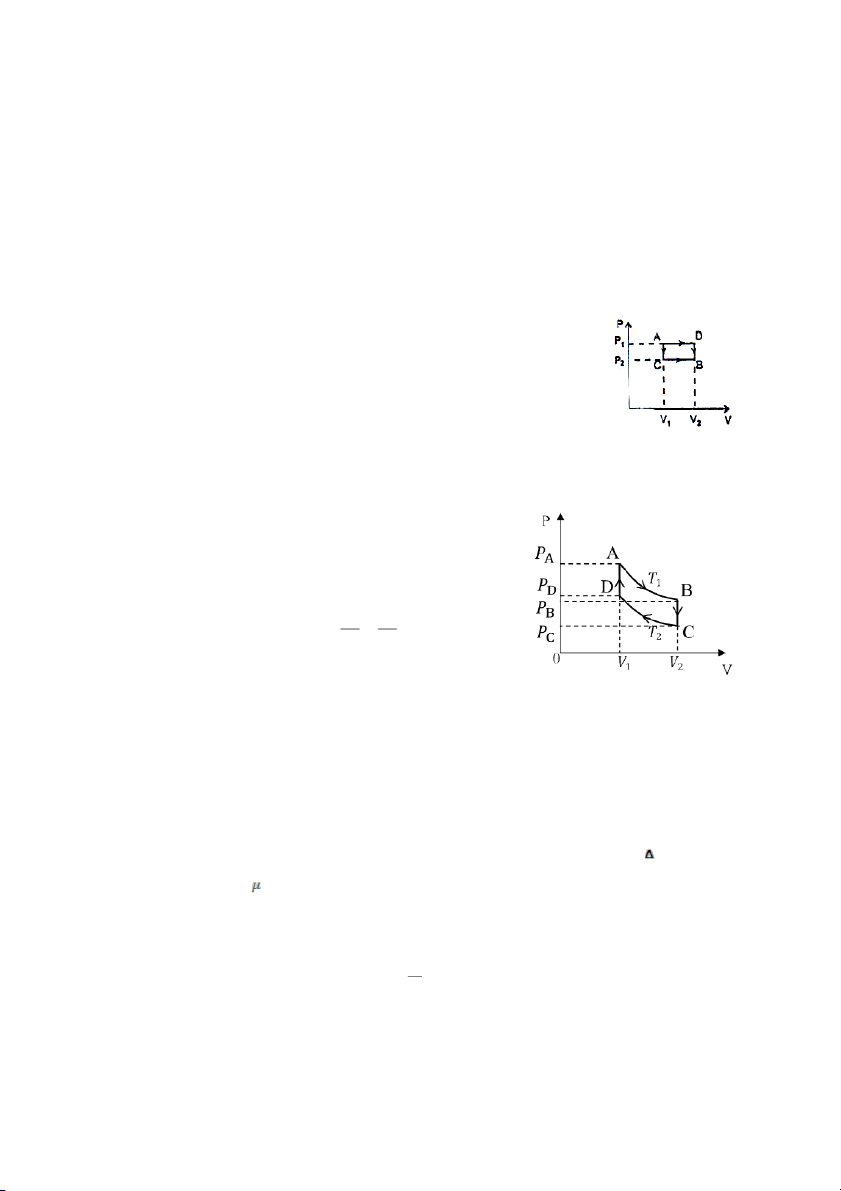
Bài 8. Động cơ đốt trong 4 thì hoạt động theo chu trình Otto (Đồ thị)
Hút: O→A hỗn hợp nhiên liệu và không khí hút vào
xi lanh, thể tích tăng từ V2 đến V1
Nén đoạn nhiệt từ A→B
Đốt, tỏa nhiệt Q1 từ B→C
Sinh công: giãn đoạn nhiệt từ C→D
Xả từ D→A→O, tỏa nhiệt Q2 cho môi trường.
a) Hãy tính hiệu suất của chu trình Otto, biểu diễn hiệu suất thông qua nhiệt độ
TA, TB, TC, TD và hệ số nén r = V1/V2.
b) So sánh với hiệu suất chu trình Carnot.
Bài 9. Một cục nước đá có khối lượng 0,1kg ở nhiệt độ 2400K, được biến thành hơn
nước ở 3730K. Tính độ biến thiên Entropi trong quá trình biến đổi trên nếu cho
rằng nhiệt dung của nước đá và nước không phụ thuộc nhiệt độ. Áp suất trong 10
quá trình biến đổi là áp suất khí quyển. Nhiệt dung riêng của nước là
1,8.103J/kg độ, của nước là 4,18.103J/kg độ, nhiệt nóng chảy riêng của nước đá
là 3,35.105J/kg độ. Nhiệt hóa hơi riêng của nước là 2,26.106 J/kg.
Bài 10. Tính độ biến thiên Entrôpi khi hơ hóng đẳng áp 6,5 gam Hydro, thể tích khí tăng gấp đôi.
Bài 11. Tính độ biến thiên Entrôpi khi biến đổi 1g nước đá ở 00C thành hơi nước ở 1000C.
Bài 12. 10 gam Oxy được hơ nóng từ t1 = 500C tới t2 = 1500C.Tính độ biên thiên
Entrôpi nếu quá trình hơ nóng là: a. Đẳng tích b. Đẳng áp
Bài 13. Tính độ biến thiên Entrôpi của một chất khí lý tưởng khi
trạng thái của nó thay đổi từ A đến B (hình vẽ) theo: a) Đường ACB;
b) Đường ADB. Cho biết: V 5 1 = 3 lít, P1 = 8,31.10 N/m2 t 0 5 2
1 = 27 C, V2 = 4,5 lít; P2 = 6.10 N/m .
Bài 14: 200 gam sắt ở 1000C được bỏ vào một nhiệt lượng kế chứa 300g nước ở
120C. Entrôpi của hệ thế nào khi hệ đạt tới trạng thái cân bằng nhiệt.
III. HƯỚNG DẪN VÀ ĐÁP SỐ Bài 1. T T 373 273
a. Hiệu suất của động cơ chạy theo chu trình Carnot: = 1 2 27% T 373 1
b. Trong 1 giây, động cơ sinh một công A’ = P.t = 73600J và nhận từ nguồn nóng nhiệt lượng: A' Q1 =
Trong một phút động cơ nhận được nhiệt lượng: ' A 73600 Qlp = 60Q1 = 60 60. 16470J 0,27
c. Trong thời gian 1 giây tác nhân nhả cho nguồn lạnh nhiệt lượng: Q’2 = Q1 - A’
Nếu thời gian là 1 phút thì nhiệt lượng đó là: 60.Q’ ' 2 = 60 (Q1 - A ) = 12054 KJ. Bài 2.
Hiệu suất thực tế của động cơ nhiệt chạy theo chu trình Carnot với cùng 2 nguồn nhiệt là: 11 ' A 2 % 0 Q1
Hiệu suất lý tưởng của động cơ nhiệt chạy theo chu trình Carnot với cùng 2 nguồn nhiệt là: T 1 2 2 3 % 0 T1 2 Vậy 1 2 3 Bài 3. Đáp số: a. Q T 2 2 7 , 9 4 A T T 1 2
b. Q2 = A = Pt = 86000 Calo c. Q 1 = Q2 +A = 94.800 Calo Bài 4. Q'
Hiệu suất của máy hơi nước x = 1y - với Q' là nhiệt Q
mà máy tỏa ra và Q là nhiệt mà máy nhận vào trong toàn chu trình. m m 2
Q Q Q
C (T T ) RT ln V 23 34 V 1 2 1 V1 Q' = m V m 2 Q' Q RT ln
C (T T ) 12 11 2 V 1 2 1 V T T 1 T 2 T và 1 2 ; X
C (T T ) c T v 1 2 T 1 1 V2 Rln 1 V Vậy . x c
Bài 5. ĐS: 𝜂𝑡 = 20%; 𝜂𝑐 = 30% 𝑃𝑐𝑃 =1,5
→ Công suất tăng 1,5 lần Bài 6. Đáp số: T 300 a) 2 1 1 25% T 400 1 12 b) ' Q Q 1 3 47,25.10 cal / . 2 1 s ' ' A Q Q c) 1 2 P 65,835 w k . t 1s 1 T 1 400
Bài 7. a) Hiệu suất thực tế: 2 1 1 30% 2 T 2 1000 1
b) Nhiệt do nhà máy thải ra trong 1 giây: ' ' A A 7 7 ' ' Q A . P t ' ' 2 Q A Q 3 3 1 2 ' 9 Q 2,33.10 2 J ' Q c) Nhiệt độ tăng: 2 T 0,56K c.m
Bài 8. a) Tính hiệu suất: Công ' ' A 1 Q Q2
Hai quá trình đẳng tích: Q nC T T 1 v c B ' 2 Q nC T T v D A ' A' Q T T Hiệu suất: 2 1 1 D A . Q Q T T 1 1 C B
Do hai quá trình A → B và C → D là đoạn nhiệt nên 1 TV c onst 1 1 T V T V (1) và 1 1 T V T V (2) c 2 D 1 B 2 A 1 Suy ra: T T V T T V D A 1 c B 1 1 2 1 V V 1 2 1 . Đặt 1 r 1 V 1 V r 1 2 1 V T T So sánh: Từ (1) và (2) 2 D A 1 V T T C B T - Chu trình Carnot: 1 A c TC T - Chu trình Otto: 1 D . Do o T T nên T D A c o C Bài 9. 13
Trong quá trình đưa nước đá ở T 0 0
1 = 240 K thành nước đá ở T0= 273 K thì: dT S MC MC (ln T ln T ) 1 d O T d O 1 T 1 T
Trong quá trình nước đá. Ở T 0 0
0 = 273 K biến thành nước ở T0 = 273 K thì: M S 2 0 T với = 3,35.105J/kgK
Trong quá trình trình nước ở T 0 0
0 = 273 K biến thành nước ở T2 = 373 K thì: T 2 dT S MC
MC (lnT lnT ) 3 n n 2 0 0 T T
Trong quá trình nước ở T ML
2 = 2730K biến thành hơi nước ở T2 = 3730K thì S với L = 4 T2 2,26.106 J/kg. Độ biến thiên Entrôpi trong cả 4 quá trình trên là: S S S S S 83 J 3 / độ. 4 1 2 3 4 Bài 10. 2 Q m S
với quá trình đẳng áp thì: Q C dT 1 T p T V m 2 m V S
Cp ln T Mặt khác ta có: 2 2 . Vậy : 2 S C ln 66,3J T T V p V 1 1 1 1 /độ. Bài 11. S S S 1 2
S1 = độ tăng Entrôpi trong quá trình biến đổi nước ở 00C thành nước ở 1000C.
S1 = độ tăng Entrôpi trong quá trình nước ở 1000C thành hơi nước ở 1000C.
Tương tự bài 6 ta có: S = 7,4J/độ Bài 12. m P m T a. 2 2 S C ln C ln 1,6J /độ v v v 1 P 1 T m T b. S C ln 2 4 , 2 J /độ p p T1 Bài 13. 14
Độ biến thiên của Entrôpi không phụ thuộc
đường đi mà chỉ phụ thuộc vào trạng thái đầu và trạng thái cuối. A Q S S ACB ADB B T S S S ACB AC CB = m P m V C ln 1 C ln 2 J 5 , 5 /độ v P p V 2 1 Bài 14:
Gọi nhiệt độ lúc hệ cân bằng nhiệt là T (0C): M1C1 (100 - T) = M2C2 (T - 12)
Với M1, C1 là khối lượng và nhiệt dung riêng của sắt
M2,C2 là khối lượng và nhiệt dung riêng của nước Rút ra : T = 190C = 2920K
Độ biến thiên Entrôpi của hệ bằng tổng độ biến thiên Entrôpi của sắt và độ biến 292 292
thiên Entrôpi của nước: S M C ln M C ln 3,26 1 1 2 2 J /độ. 373 285
---------------------------------------------------------------------------
Chương 4: KHÍ THỰC (SV tự đọc)
(Không có bài tập)
---------------------------------------------------------------------------
Phần II: DAO ĐỘNG VÀ SÓNG (SV TỰ ĐỌC)
Chương 5: DAO ĐỘNG CƠ VÀ DAO ĐỘNG ĐIỆN TỪ
(Không có bài tập)
Chương 6: SÓNG CƠ VÀ SÓNG ĐIỆN TỪ
(Không có bài tập)
---------------------------------------------------------------------------
Phần III: QUANG HỌC
Chương 7: GIAO THOA ÁNH SÁNG
I. CÁC CÔNG THỨC CẦN GHI NHỚ
1. Điều kiện cho cực trị giao thoa:
a. Cực đại: L2 - L1 = k (k = 0, 1, 2…) 15
b. Cực tiểu: L2 - L1 = 2k 1
(k= 0,–1; 1, –2; 2, –3…) 2
Với: L1, L2 là quang lộ của tia sáng từ nguồn thứ nhất và thứ hai tới điểm quan sát
là bước sóng của ánh sáng trong chân không
k là bậc giao thoa (khái niệm bậc giao thoa chỉ dùng cho vân sáng, vân tối
không có khái niệm bậc giao thoa)
2. Giao thoa gây bởi khe Young
a. Hiệu quang lộ 2 tia giao thoa: ax L L 2 1 D
Với: a là khoảng cách hai khe hẹp.
D là khoảng cách từ hai khe hẹp đến màn quan sát.
x là vị trí của một điểm M trên màn. b. Vị trí vân sáng: D x k S a c. Vị trí vân tối: D D x k k t 1 2 1 2 a 2 a
d. Khoảng cách vân (khoảng cách hai vân sáng hoặc hai vân tối kế tiếp): D i a
3. Giao thoa gây bởi bản mỏng:
a. Bản mỏng có độ dày thay đổi vân cùng độ dày:
Hiệu quang lộ giữa hai tia phản xạ trên hai mặt của bản : L L 2 2
d n sin 2 i 2 1 2
b. Nêm không khí và bản cho vân tròn Niutơn :
- Vị trí của các vân tối : k d ; k = 0, 1, 2, ... 2
- Vị trí của các vân sáng: d 2k 1 ; k = 1, 2, ... 4
Với d là chiều dày của nêm.
* Đối với bản cho vân tròn Niutơn thì bán kính vân tối thứ k là : r R . k k
Với R là bán kính mặt cong của thấu kính. 16
c. Bản có độ dày không đổi - Vân cùng độ nghiêng :
Hiệu quang lộ giữa hai tia phản xạ trên hai mặt bản mỏng: L L 2 2
d n sin 2 i 2 1 2
Với: d là bề dày của bản, n là chiết suất của bản, i là góc tới của ánh sáng tới mặt bản
là bước sóng của ánh sáng tới. II. BÀI TẬP:
Bài 1. Khoảng cách giữa hai khe trong máy giao thoa khe Young a = 1mm. Khoảng
cách từ màn quan sát E tới mặt phẳng chứa hai khe D = 1m. Đặt toàn bộ hệ
thống trong không khí, hai khe được chiếu bởi ánh sáng đơn sắc có bước sóng = 0,49m.
a. Xác định vị trí của 3 vân sáng đầu tiên và vị trí vân tối thứ 4. Nêu nhận xét
b. Thay ánh sáng đơn sắc khác có bước sóng ’, hệ thống trên cho các vân giao thoa
với khoảng cách vân bằng 0,66mm. Tính ’.
c. Sử dụng ánh sáng có bước sóng = 0,49m. Đổ vào khoảng giữa màn ảnh và mặt
phẳng chứa hai khe một chất lỏng có chiết suất n. Tính chiết suất n của chất lỏng đó, biết
rằng khoảng cách vân trong trường hợp này bằng 0,36mm. Nêu nhận xét?
Bài 2. Trong thí nghiệm giao thoa với máy giao thoa khe Young, 2 khe cách nhau a =
1mm. Màn quan sát E đặt song song và cách mặt phẳng chứa 2 khe một đoạn D = 1m.
Nguồn S đặt cách đều hai khe và cách mặt phẳng chứa hai khe một đoạn là d = 0,5m
phát ánh sáng đơn sắc có bước sóng = 0,6m.
a. Dời khe S song song với mặt phẳng chứa hai khe S1, S2 tới vị trí S’ và SS’ = 1mm.
Xác định chiều và khoảng dịch chuyển của vân trung tâm.
b. Lại đưa khe S về vị trí cũ nhưng đặt trước S1 một bản mặt song song có chiều dày e
= 8m, chiết suất n = 1,5. Vân sáng trung tâm sẽ dời chỗ như thế nào ?
Bài 3. Trong thí nghiệm giao thoa với máy giao thoa khe Young, khoảng cách giữa hai
khe là a = 1mm, khoảng cách từ hai khe tới màn quan sát là D = 2m. Chiếu đồng thời
hai khe bởi hai bức xạ có bước sóng 1 và 2. Khoảng cách giữa 5 vân sáng liên tiếp của
bức xạ 1 là 4,8mm, khoảng cách từ vân sáng thứ 2 đến vân sáng trung tâm của bức xạ 2 là 1,92mm.
a. Tìm bước sóng của hai bức xạ trên.
b. Trong vùng có giao thoa MN = 23mm có :
- Bao nhiêu vân sáng và tối của từng bức xạ trên?
- Mấy vị trí có sự chồng nhau của vân sáng của hai loại bức xạ trên? 17
Bài 4. Chiếu một chùm ánh sáng trắng (0,4 μm ≤ λ ≤ 0,7 μm) lên một màng nước xà
phòng có chiết suất n = 1,33.
a. Chiếu theo phương vuông góc với màng xà phòng. Cho bề dày của màng xà phòng e
= 0,4 µm. Hỏi trong phạm vi quang phổ thấy được của chùm sáng trắng, những chùm
tia phản chiếu có bước sóng nào sẽ được tăng cường.
b. Chiếu theo phương xiên góc 450 lên màng xà phòng. Tìm bề dày nhỏ nhất của màng
để tia phản chiếu có màu vàng với bước sóng λ = 0,6 µm.
Bài 5. Một màng mỏng có bề dày d, chiết suất n = 1,3. Một chùm ánh sáng đơn sắc
song song có bước sóng = 0,6m chiếu vào màng mỏng dưới góc tới i = 300. Hỏi bề
dày nhỏ nhất của màng phải bằng bao nhiêu để ánh sáng phản chiếu giao thoa có cường độ: a. Cực đại b. Cực tiểu
Bài 6. Trên một bản mỏng thủy tinh phẳng (có chiết suất n = 1,5), người ta phủ một
màng rất mỏng của chất có chiết suất n’ = 1,4. Một chùm tia sáng đơn sắc, song song có
bước sóng = 0,6m được chiếu thẳng góc với bản mặt. Xác định bề dày nhỏ nhất của
màng mỏng khi hiện tượng giao thoa cho chùm tia phản xạ có:
a. cường độ cực tiểu.
b. cường độ cực đại.
Bài 7. Một nêm thủy tinh có góc nghiêng =2’, chiết suất n. Người ta chiếu thẳng
góc với nêm ánh sáng đơn sắc có bước sóng 0,5216 m.
a) Vẽ hình và thiết lập biểu thức điều kiện độ dày để có vân tối
b) Tìm chiết suất của nêm, biết rằng khoảng cách giữa 2 vân tối liên tiếp trên bề
mặt của nêm bằng 0,3 mm .
c) Độ dày nêm tại vị trí có vân tối thứ 4;
Bài 8. Chiếu một chùm tia sáng đơn sắc, song song và thẳng góc với mặt dưới của một
nêm không khí. Ánh sáng tới có bước sóng λ = 0,6µm.
a. Xác định góc nghiêng của nêm, biết rằng trên 1cm chiều dài của mặt nêm, người ta
quan sát thấy 10 vân giao thoa.
b. Nếu chiếu đồng thời hai chùm tia sáng đơn sắc có bước sóng lần lượt là λ1 = 0,5 µm
và λ2 = 0,6 µm xuống mặt nêm thì hệ thống vân trên mặt nêm có gì thay đổi? Xác định
vị trí tại đó các vân tối của hai hệ thống vân trùng nhau.
Bài 9. Một thấu kính hội tụ phẳng lồi được đặt trên một bản thủy tinh để tạo thành hệ
thống cho vân tròn Newton. Mặt lồi của thấu kính có bán kính R = 4 m. Chiếu ánh
sáng đơn sắc thẳng góc vào mặt phẳng của thấu kính thì khoảng cách giữa vân tối thứ 9 và thứ 4 là 1,6 mm. 18
a. Tìm bước sóng của ánh sáng.
b. Tìm bề dày của lớp không khí tại vị trí vân tối thứ 4.
Bài 10. Một thấu kính được đặt trên một bản thủy tinh, nhưng do một hạt bụi dày nằm
giữa thấu kính và bản thủy tinh nên chúng không tiếp xúc với nhau. Đường kính của vân
tối thứ 5 và thứ 15 là 0,7mm và 1,7mm, bước sóng của ánh sáng rọi vuông góc vào mặt
phẳng của thấu kính là 0,59m. Xác định bán kính cong của thấu kính.
III. HƯỚNG DẪN VÀ ĐÁP SỐ Tóm tắt: M d1 a = 1mm S1 d x 2 D = 1m a O = 0,49m S2 D
a. xStt; xS1; xS2; xS3; xt4.
b. Thay ’; i’ = 0,66mm. ’ = ?
c. = 0,49m, đổ n = ? với i’’ = 0,36mm. Nhận xét? Hướng dẫn: 6 D 0,49.10 .1 a. - Khoảng cách vân : -3 i = 0,49.10 m 3 a 10
- Vị trí 3 vân sáng đầu tiên:
Vân sáng trung tâm (k = 0) ứng với: 𝑥𝑆𝑡𝑡 = 0𝑖 = 0
Vân sáng bậc 1 (k = 1) ứng với: 𝑥 −3
𝑆1 = 𝑘 𝜆𝐷 = 1. 𝑖 = 0,49. 10 𝑚 𝑎
Vân sáng bậc 2 (k = 2) ứng với: 𝑥 −3
𝑆2 = 𝑘 𝜆𝐷 = 2. 𝑖 = 0,98. 10 𝑚 𝑎
Vân sáng bậc 3 (k = 3) ứng với: 𝑥 −3
𝑆3 = 𝑘 𝜆𝐷 = 3. 𝑖 = 1,47. 10 𝑚 𝑎
Nhận xét: Các vân sáng cách đều nhau.
- Vị trí vân tối bậc 4 (k = 3) ứng với: D x 2k i = 3,5i = 1,715mm. 2a
b. Khi thay ánh sáng có bước sóng bởi ánh sáng có bước sóng thì khoảng cách vân: ' i 'a 0,66.1 ' D -3 i ' = 0,66 . 10 mm = 0,66 m a 3 D 10
c. Tính chiết suất của chất lỏng :
- Hiệu quang lộ tại M của 2 tia sáng từ S1 và S2: L2 - L1 = nd2 - nd1 = n(d2 - d1) = ax n D 19
- Điều kiện xác định vị trí các vân sáng: ax
L L n k 2 1 D D i Tọa độ vân sáng: x k k na n
Khoảng cách vân (khoảng cách giữa 2 vân sáng liên tiếp) là : ' 1 i ki i i k n n n 𝑖′ = 𝑖 𝑛 i , 0 49 1 . 03
Do đó chiết suất chất lỏng: n 3 , 1 6 i' 3 , 0 6 1 . 03
* Nhận xét: Khoảng vân giảm n lần, tức là hệ thống vân sít lại gần nhau một đoạn Δi =
i – i’ = (0,49 – 0,36).10–3 khi được đặt trong chất lỏng có chiết suất n = 1,36. Bài 2. Tóm tắt: O’ d 1 a = 1mm; S1 x d 2 d ’ 1 S a D = 1m; O S’ = 0,6m; d ’ 2 S2 D d = 0,5m. d a. Dời S với SS’=1mm. O’ d1 Xác định chiều và S1 d x 2 khoảng dịch chuyển? a O
b. Bản mặt e = 8m vào S1. S2 D
Vân sáng trung tâm dời chỗ như thế nào? Hướng dẫn:
a. Khi nguồn sáng di chuyển tới vị trí mới S’ thì hiệu quang lộ của hai tia sáng xuất phát từ S’ tới O' là:
L2 - L1 = (d2’ + d2) – (d1’ + d1) = (d2 - d1) + (d2’ - d1’)
Hiệu khoảng cách từ điểm ta xét đến 2 nguồn S1 và S2: d2 - d1 = xa D x ' Do đó: d a 2’ - d1’ = d x 'a xa
Suy ra : L L 2 1 d D 20 x '
- Điều kiện để tại O' có vân sáng: L a xa 2 - L1 = k d D x 'a xa
Vân sáng trung tâm ứng với k = 0: 0. d D Suy ra : D 1 x x ' 1. = –2mm d 0,5
Dấu (–) chứng tỏ vân sáng trung tâm dời ngược chiều di chuyển của nguồn S,
khoảng dịch chuyển là 2mm.
b. Giả sử bản mặt song song đặt trước nguồn S1.
Hiệu quang lộ từ 2 nguồn sáng S1 và S2 đến điểm M (2 tia S2M và S1M) là: L xa
2 – L1 = d2 – [(d1 – e) + ne)] = (d2 – d1).n – (n – 1).e = – (n – 1).e D
Điều kiện để tại M cho vân sáng: L2 – L1 = xa – (n – 1).e = k D kD n 1 eD
Suy ra công thức xác định tọa độ vân sáng: x a a n 1eD 1
Vân sáng trung tâm k = 0 3 -3 x 1,5 1 8. = 4.10 m = 4.10 m 0 3 a 10
Vậy vân sáng trung tâm mới nằm cách vân sáng trung tâm cũ một đoạn: (𝑛 − 1)𝑒𝐷 𝑥0 = 𝑎 = 4. 10−3𝑚
* Do n > 1 nên x0 > 0, nghĩa là vân sáng giữa về phía có đặt bản mặt song song, trong
trường hợp này là dời về phía nguồn S1. Bài 3. Tóm tắt: M d 1 a = 1mm; D = 2m; λ1 và λ2. S1 x d 2
Cho: xS(k+3) (λ1) – xSk (λ1) = 4,8mm a O
xS2 (λ2) – xStt (λ2) = 1,92mm S2 D a. λ1 và λ2 = ? b. MN = 23mm. - Số vân sáng; vân tối ?
- Vị trí trùng nhau của λ1 và λ2 trong MN. Hướng dẫn: 21 a. * Theo giả thiết:
xS(k+3) (λ1) – xSk (λ1) = 4.i1 = 4,8mm
Suy ra khoảng vân của bức xạ λ1: i1 = 1,2mm Bước sóng λ 1
1 = 𝑖 𝑎 = 1,2.10−3.1.10−3 = 0,6. 10−6𝑚 = 0,6𝜇𝑚 𝐷 2 * Theo giả thiết:
xS2 (λ2) – xStt (λ2) = 2.i2 = 1,92mm
Suy ra khoảng vân của bức xạ λ2: i2 = 0,96mm Bước sóng λ 2 −6
2 = 𝑖 𝑎 = 0,96.10−3.1.10−3 = 0,48. 10 𝑚 = 0,48𝜇𝑚 𝐷 2 b. Ta có: 1 1
2𝑏ề 𝑟ộ𝑛𝑔 𝑣ù𝑛𝑔 𝑔𝑖𝑎𝑜 𝑡ℎ𝑜𝑎 = 2.23 = 9,58 λ có 19 vân sáng và 20 vân tố 𝑖 1 i 1 1,2 1 𝑛𝑔 𝑛𝑔 𝑜𝑎 1
2𝑏ề 𝑟ộ 𝑣ù 𝑔𝑖𝑎𝑜 𝑡ℎ
= 2.23 = 11,98 λ có 23 vân sáng và 24 vân tối 𝑖 2 1 0,96
* Khi vân sáng của hai bức xạ trung nhau: k1.λ1 = k2.λ2 k1.0,6 = k2.0,48 k1 = 4.k 5 2 Khi k1 = k2 = 0: xStt = 0.
Khi k1 = ±4; k2 = ±5: xS 1= ±4,8mm
Khi k1 = ±8; k2 = ±10: xS 2= ± 9,6mm
Vậy có 5 vị trí trên màn ảnh cho các vân sáng trùng nhau. Bài 4. ĐS:
a. Bước sóng: λ = 0,4256μm b. d -5 min = 1,33.10 cm. Bài 5. 22 Tóm tắt: S R R’ Màn mỏng d; n = 1,3 N
Chiếu = 0,6m; i = 300. i i i d H i min = ? để: I L
a. Giao thoa có cường độ cực đại r r
b. Giao thoa có cường độ cực tiểu r K Hướng dẫn:
Đây là hiện tượng giao thoa do bản mỏng cùng độ dày gây ra.
Hiệu quang lộ của 2 tia phản chiếu từ 2 mặt màng (tia IR và LR’) là : L L 2 2 d n s in 2 i 2 1 2
a. Cường độ sáng phản chiếu cực đại khi : 2 d 2 2 n sin i k 2
Suy ra: d = (2k + 1) 4 n2 2 sin i
Bề dày cực tiểu của bản mỏng ứng với k = 0: d min = 7 2 , 1 5 1 . 0 m 2 2 4 n s in i
b. Cường độ ánh sáng phản chiếu cực tiểu khi : 2 2
2d n sin i 2k 1 2 2
Suy ra: d k 1 2 2 2 n sin i
Bề dày cực tiểu của bản mỏng ứng với k = 0: d -7 min = 2,5 . 10 m. 2 2 2 n sin i
* Trường hợp riêng: Khi tia sáng được chiểu vuông góc với màng mỏng góc tới i =
00 nên bề dày cực tiểu của bản mỏng khi:
- Cường độ sáng phản chiếu cực đại: 𝑑𝑚𝑖𝑛 = 𝜆 4𝑛 23
- Cường độ sáng phản chiếu cưc tiểu: 𝑑𝑚𝑖𝑛 = 𝜆 2𝑛 Bài 6. Tóm tắt: S S 1 2 Bản mỏng n = 1,5
Phủ lớp mỏng n’ = 1,4. I I = 0,6m. 1 2 e e = ? khi: N N 1 2
a. cường độ giao thoa cực tiểu.
b. cường độ giao thoa cực đại. Hướng dẫn:
Xét tia sáng S1I1, khi tới mặt của màng mỏng, một phần tia sáng này sẽ phản xạ
ở mặt trên của màng tại I1, một phần sẽ đi qua màng mỏng và phản xạ ở mặt dưới của
màng mỏng tại N1. Quang lộ của cả hai tia sáng phản xạ tại I1 và N1 đều bị dài thêm
một đoạn 𝜆 do phản xạ trên môi trường chiết quang hơn. Hai tia phản xạ này sẽ giao 2
thoa với nhau tại mặt trên của màng mỏng.
- Quang lộ của tia S1I1S1 phản xạ tại I1: 𝜆 𝐿 1 = 𝑆1𝐼1𝑆1 + 2
- Quang lộ của tia S1I1N1I1S1 phản xạ N1: 𝜆 𝐿 ′ ′ 𝜆
2 = 𝑆1𝐼1𝑆1 + 2𝑛 . 𝐼1𝑁1 + + 2𝑛 𝑒 + 2 = 𝑆1𝐼1𝑆1 2
Hiệu quang lộ của hai tia phản xạ: L2 – L1 = 2𝑛′𝑒
a. Khi cường độ sáng của chùm tia giao thoa này cực đại thì:
𝐿2 − 𝐿1 = 2𝑛′𝑒 = 𝑘𝜆
Do đó bề dày của màng mỏng được xác định bởi công thức: 𝑘𝜆 𝑒 = 2𝑛′
Ứng với k = 1: 𝑒1 = 𝜆 = 0,6 = 0,214𝜇𝑚 2𝑛′ 2.1,4
Ứng với k = 2: 𝑒1 = 2𝜆 = 3.0,6 = 0,428𝜇𝑚 2𝑛′ 4.1,4 …
b. Khi cường độ sáng của chùm tia giao thoa này cực tiểu thì: 24
𝐿2 − 𝐿1 = 2𝑛′𝑒 = (2𝑘 + 1) 𝜆2
Do đó bề dày của màng mỏng được xác định bởi công thức: 𝑒 = (2𝑘 + 1) 𝜆 4𝑛′
Ứng với k = 0: 𝑒0 = 𝜆 = 0,6 = 0,11𝜇𝑚 4𝑛′ 4.1,4
Ứng với k = 1: 𝑒1 = 3𝜆 = 3.0,6 = 0,33𝜇𝑚 4𝑛′ 4.1,4 … Bài 7. Tóm tắt: S =2’; chiết suất n λ = 0,539m k R k–1 x = x O k – xk–1 = 0,3mm I α Xác định n=? α K Hướng dẫn:
a) Tia tới SI khi đến gặp mặt phân cách giữa hai môi trường trong suốt không khí-thủy tinh thì tách làm 2 tia:
- Tia SIR phản xạ tại I (quang lộ của tia SIR bị dài thêm một đoạn 𝜆 do phản xạ 2
trên thủy tinh là môi trường chiết quang hơn)
- Tia truyền qua SIKIR’. Tia IK bị phản xạ tại K và quay lại theo phương KI rồi
giao thoa với tia IR tại I.
Vân giao thoa xuất hiện ở bề mặt trên của nêm.
Tại I hiệu quang lộ của 2 tia là:
L2 – L1 = 2.IK.n – = 2dKn – (với d 2 2 k = IK)
b) Các vân tối thỏa mãn: L2 – L1 = 2dKn – = (2k + 1). dK = (k + 1). 2 2 n 2 d k k K 1 1
Gọi xK là khoảng cách từ cạnh nêm 0 tới vân tối thứ k: xk = sin 2n sin 2n
Khoảng cách giữa 2 vân tối liên tiếp : x = xk – xk - 1 = n 2 25
Suy ra chiết suất của nêm là: n = 1,55 2 x c) Độ dày vân t i ố th 4:
ứ 𝑑4 = 4𝜆 = 0.695 m 2𝑛 Bài 8. Tóm tắt: S2 Cho λ = 0,6µm S1 a. N = 10 vân/cm α = ? b. λ I2 1 = 0,5µm; λ2 = 0,6µ m I - Thay đổi ntn? 1 0 α 1 + k k d
- Xác định vị trí trùng nhau? d N N α 1 2 Hướng dẫn:
a. Tia tới S1I1 khi đến gặp mặt phân cách giữa hai môi trường trong suốt thủy tinh-
không khí thì chia ra làm hai tia:
- Tia S1I1R1 phản xạ tại I1 - Tia truyền qua S 𝜆
1I1N1I1R1’ phản xạ tại N1, tia này có quang lộ dài thêm một đoạn 2
do phản xạ trên thủy tinh là môi trường chiết quang hơn.
Vân giao thoa xuất hiện ở mặt trên của nêm không khí.
Tại I1, hiệu quang lộ của hai tia: 𝜆
∆𝐿 = 𝐿2 − 𝐿1 = 2.𝑑𝑘 + 2
* Điều kiện để cho vân sáng: ∆𝐿 = 𝐿2 − 𝐿1 = 2. 𝑑𝑘 + 𝜆 = 𝑘𝜆 2
Suy ra công thức xác định vị trí vân sáng thứ k của nêm không khí:
𝑑𝑘 = (2𝑘 − 1) 𝜆4
Khoảng cách từ cạnh nêm đến vân sáng thứ k: 𝑑 𝑑 𝜆 𝑥 𝑘 𝑘
𝑘 = sin𝛼 ≈ 𝛼 = (2𝑘 − 1)4𝛼
Khoảng vân: 𝑖 = 𝑥𝑘+1 − 𝑥𝑘 = 𝜆 2𝛼
Khoảng cách giữa 10 vân sáng = 9 khoảng vân: 26 𝜆 𝐼1𝐼2 = 9𝑖 = 92𝛼 9𝜆
→ 𝛼 = 2𝐼 = 2,7 × 10−4 𝑟𝑎𝑑 1𝐼2
Lưu ý: Có thể dựa vào điều kiện cho vân tối để giải bài toán này.
b. Tương tự câu a, tại I1, hiệu quang lộ của hai tia: 𝜆
∆𝐿 = 𝐿2 − 𝐿1 = 2.𝑑𝑘 + 2
* Điều kiện để cho vân tối: ∆𝐿 = 𝐿2 − 𝐿1 = 2. 𝑑𝑘 + 𝜆 = (2𝑘 + 1) 𝜆 2 2
Suy ra công thức xác định vị trí vân tối thứ k của nêm không khí: 𝑘𝜆 𝑑𝑘 = 2
Vân tối thứ k+1: 𝑑𝑘+1 = (𝑘 + 1) 𝜆 2
Khoảng vân là khoảng cách giữa hai vân tối liên tiếp: 𝑖 = 𝑥𝑘+1 − 𝑥𝑘 = 𝑑𝑘+1−𝑑𝑘 = 𝜆 𝛼 2𝛼
Vậy, khoảng vân của bức xạ: 𝑖1 = 𝜆1; 𝑖
. Do đó sẽ có vị trí tại đó vân giao thoa 2𝛼 2 = 𝜆2 2𝛼
của hai hệ thống trùng nhau.
* Vị trí của các vân tối được xác định: 𝜆 𝜆 𝑦 1 2
𝑡1 = 𝑘1 2𝛼 ; 𝑦𝑡2 = 𝑘2 2𝛼
Khi hai vân trùng nhau: yt1 = yt2 k1λ1 = k2λ2 𝑘1 = 6 𝑘 5 2
- k1 = k2 = 0 yt1 = yt2 = 0
- k1 =6; k2 = 5 yt1 = yt2 = 0,3cm
- k1 = 12; k2 = 10 yt1 = yt2 = 0,6cm …
Vậy cứ cách cạnh nêm một khoảng bằng một bội số nguyên lần 0,3cm thì hai vân tối
của hai hệ thống vân lại trùng nhau. Bài 9. 27 Tóm tắt:
Hệ thống vân tròn Newton R R = 4m r9 – r4 = 1,6mm a. = ? rk M dk b. d4 = ? Hướng dẫn:
a. Bán kính của vân tối thứ K là : rK = K R
Bán kính vân tối thứ 9 là : r9 = 9 R 3 R . 3 2
Bán kính vân tối thứ 4 là : r4 = 4 R 2 R 2.2
Khoảng cách giữa vân tối thứ 9 và vân tối thứ 4 là: r 9 - r4 = 3
6 4 2 1,6 .10 m
= (0,8 . 10-3)2 = 0,64 . 10-6m = 0,64m k 4
b. Bề dày lớp không khí tại vị trí vân tối thứ 4 là : d d = 2 = 1,28m K 4 2 2 Bài 10. Tóm tắt:
Hệ thống vân tròn Newton, hạt bụi e. k1 = 5 D1 = 0,7mm k2 = 15 D2 = 1,7mm λ = 0,59µm R = ? Hướng dẫn: Gọi e là đ ờ
ư ng kính của hạt bụi. 𝐷𝑘 là đường kính vân tròn Newton thứ k
Hiệu quang lộ giữa hai tia phản xạ tại điểm giao thoa M: 𝐿2 − 𝐿1 = 2(𝑑𝑘 + 𝑒) + 𝜆 2
Điều kiện cho vân tối: 𝐿2 − 𝐿1 = 2(𝑑𝑘 + 𝑒) + 𝜆 = (2𝑘 + 1). 𝜆 2 2 28
Suy ra: 𝑑𝑘 = 𝑘 𝜆 − 𝑒 (1) 2
Trong tam giác vuông ABM, ta có: 𝐷2𝑘
4 = 𝑅2 − (𝑅 − 𝑑𝑘)2 = 𝑑𝑘(2𝑅 − 𝑑𝑘) ≈ 2𝑅𝑑𝑘 2 Suy ra: 𝑑𝑘 = 𝐷𝑘 (2) 8𝑅 Từ (1) và (2), suy ra: 𝜆 𝐷2 𝑘 𝑘 2 − 𝑒 = 8𝑅
Thay các điều kiện trong bài toán: 𝐷2 − 𝐷2 𝑅 = 2 1 4𝜆(𝑘2 − 𝑘1) Thế số: R = 10,2cm.
---------------------------------------------------------------------------
Chương 8: NHIỄU XẠ ÁNH SÁNG
I. CÁC CÔNG THỨC CẦN GHI NHỚ
1. Nhiễu xạ qua 1 khe hẹp : Vị trí của cực đại giữa ứng với sin = 0;
Vị trí cực tiểu : Sin = k ; k = 1, 2... ; b
Vị trí cực đại : Sin = (2k + 1)
; k = 1, 2, 3... ; Với là góc nhiễu xạ. b 2
2. Nhiễu xạ qua nhiều khe hẹp - Cách tử nhiễu xạ:
Cực đại nhiễu xạ : Sin = k ; K = 0, 1, 2 ... d là chu kỳ cách tử. d 1
n = là số khe trên một đơn vị dài của cách tử. d
3. Nhiễu xạ trên mạng tinh thể :
Công thức nhiễu Bragg cho cực đại nhiễu xạ:
2d sin = k với k = 0, 1, 2...
d là khoảng cách giữa hai mặt phẳng nguyên tử liên tiếp.
là góc nhiễu xạ theo phương phản xạ gương. 29 II. BÀI TẬP
Bài 1. Bề rộng cực đại giữa của hình nhiễu xạ trên màn M bằng 2,4 cm. Màn cách
thấu kính đặt ngay sau một khe hẹp chữ nhật một khoảng 2 m. Tìm bước sóng
của chùm ánh sáng song song chiếu vuông góc với khe, biết bề rộng của khe bằng 0,1mm.
Bài 2. Một cách tử có 20.000 vạch có chiều dài 4cm. Tìm sự tách góc của toàn bộ phổ
nhìn thấy đối với quang phổ bậc 1 và bậc 2 nếu chùm sáng song song chiếu
thẳng góc với cách tử có bước sóng từ 3,9.10-7 m tới 7,7.10-7m.
Bài 3: Chiếu một chùm tia sáng ( = 0,5m) thẳng góc với một cách tử nhiễu xạ. Gần
cách tử có một thấu kính hội tụ. Khoảng cách từ màn ảnh tới thấu kính bằng 1m.
Khoảng cách giữa 2 cực đại chính bậc 1 bằng 20,2cm. Hãy xác định :
a. Chu kỳ d của cách tử.
b. Số vạch n trên 1cm cách tử.
c. Tổng số vạch sáng cực đại ứng với góc lệch lớn nhất cho bởi cách tử.
d. Góc nhiễu xạ max ứng với vạch quang phổ ngoài cùng.
Bài 4. Quang phổ của nguyên tử Hydro có một vạch đỏ có bước sóng 656 nm và một
vạch tím có bước sóng 434 nm. Tìm sự tách góc giữa các cực đại nhiễu xạ của hai
bước sóng trên ở tất cả các bậc quang phổ thu được qua một cách tử có 4500 khe/cm?
Bài 5. Chiếu sáng vuông góc với mặt phẳng của một cách tử nhiễu xạ truyền qua,
quan sát hình nhiễu xạ bằng một thị kính. Khi quay thị kính một góc nào đó,
người ta quan sát thấy vạch quang phổ bậc ba ứng với bước sóng = 4,4.10-4
mm. Hỏi dưới cùng một góc đó, người ta có thể quan sát thấy vạch quang phổ
ứng với bước sóng nào nằm trong giới hạn từ -4 -4
1 = 4.10 mm đến 2 = 7.10 mm.
Vạch đó thuộc quang phổ bậc mấy.
Bài 6. Một cách tử nhiễu xạ có chu kỳ cách tử 𝑑 = 2 × 10−6 m. Chiếu chùm tia sáng
đơn sắc song song có bước sóng bằng 0,589 µm thẳng góc với cách tử.
a) Hãy xác định số vạch cực đại chính tối đa cho bởi cách tử.
b) Nếu thay ánh sáng nói trên bằng ánh sáng khác thì bước sóng lớn nhất có thể
quan sát được nhiễu xạ là bao nhiêu?
Bài 7. Khi chiếu ánh sáng đơn sắc với bước sóng 1 = 0,6 m thẳng góc với một cách
tử phẳng thì góc lệch ứng với quang phổ bậc 1 là 1708’.
a. Tìm góc lệch ứng với vạch quang phổ bậc 2 của ánh sáng đơn sắc có bước sóng 2 = 0,5 m.
b. Tìm số vạch trên 1 cm chiều dài của cách tử.
c. Với góc lệch bằng bao nhiêu thì vạch quang phổ của 2 ánh sáng trên trùng nhau. 30
Bài 8. Khoảng cách giữa 2 cực đại ở kề hai bên cực đại giữa trên màn ảnh là 3,6cm.
Màn cách thấu kính đặt ngay sau khe hẹp một đoạn 2m và ở tiêu diện của thấu
kính này. Ánh sáng chiếu vuông góc vào khe hẹp có bước sóng 0,6 m. Tìm bề rộng của khe hẹp.
Bài 9. Một chùm tia Rơnghen hẹp tới đập vào mặt tự nhiên của đơn tinh thể NaCl thu
được góc nhiễu xạ theo phương phản xạ gương bằng 300. Theo phương phản xạ
gương trên mặt tinh thể người ta quan sát thấy cực đại nhiễu xạ bậc hai. Xác
định khoảng cách giữa hai mặt phẳng nguyên tử liên tiếp, biết rằng ánh sáng tới
có bước sóng là 1,41.10-10m.
Bài 10. Cho một nguồn sáng song song có bước sóng 500 nm chiếu vuông với một
cách tử nhiễu xạ. Cực đại nhiễu xạ bậc 3 quan sát được ở góc lệch 32.0°. Tính: a. Số khe trên 1 cm.
b. Số cực đại chính có thể quan sát được trong trường hợp trên.
III. HƯỚNG DẪN VÀ ĐÁP SỐ Bài 1.
Bề rộng cực đại giữa của hình nhiễu xạ là
khoảng cách giữa 2 cực tiểu bậc một. Vị trí M
của 2 cực tiểu đó, xác định từ:
bsin = k với k = 1 b
Bề rộng cực đại giữa là: O B I
l = 2.OB.tg 2.OB.sin
(do nhỏ). l = 2. OB . P b L Sin l
= b = 0,6 m. 2OB Bài 2.
Chu kỳ của cách tử : d = 4.10-2m/20.000 = 2.10-6m
Cực đại nhiễu xạ xác định từ công thức: sin = k d
1. Với quang phổ bậc 1 (k = 1) ta có: sin = d
+ Với ánh sáng tím có -6 t = 0,39.10 m thì 6 3 , 0 . 9 10 sin t 0 t = = = 0,195 t = 11 15’ d 6 . 2 10
+ Với ánh sáng đỏ có -6 d = 0,77.10 m thì 31 6 7 , 0 . 7 10 sin 0 đ = đ = = 0,385 đ = 22 39’ d 6 . 2 10
Sự tách góc của quang phổ bậc một là 0 đ - t = 11 24’ 2
2. Với quang phổ bậc 2 (k = 2) thì : Sin = d 2
+ Với ánh sáng tím: Sin t 0 t = = 0,39 t = 22 57’ d 2
+ Với ánh sáng đỏ: Sin 0 đ = đ = 0,77 đ = 50 21’ d
Sự tách góc của quang phổ bậc 2 là 0 d - t = 27 24’ Bài 3.
a. Tìm d: Công thức xác định vạch cực đại: dsin = k
Với quang phổ bậc 1: d = sin M l
Mà tg = BM với BM = và OB = f OB 2 l
khi đó ta có tg
. Do nhỏ nên tg = sin 2 f l si n = 2 f 4 2 f 2.0,5.10 .100 Vậy: d = = 4,95.10-4cm l 20,2 1 1 b. Tìm n : n = = 2020 vạch/cm 4 d 9 , 4 . 5 10
c. Tìm Nmax: Số vạch cực đại quang phổ xác định từ :
dsin = k ; k = 0, 1, 2, ... Ta có: sin d d k
; Vì 1 sin 1 k 9.9 k 9.9 k 9 max d
Tổng số vạch sáng ứng với góc lệch lớn nhất là: Nmax = 2kmax + 1 = 2.9 + 1 + 19 vạch
d. Góc nhiễu xạ ứng với vạch cực đại ngoài cùng là : max 5 , 0 . 9 Sin 0 max = kmax = 9 , 0 1 max = 65 30' d 9 , 0 5
Bài 4. ĐS: Δ𝜃1 = 5,91𝑜, Δ𝜃2 = 13,2𝑜, Δ𝜃3 = 26,5𝑜 32 Bài 5.
Vị trí vạch quang phổ xác định bởi: dsin = k = 3.4,4.10-4 mm = 13,2.10-7m 7 Ta có : ’ = 13,2.10
. Trong giới hạn ' ' m 1 2 k 7 13,2.10 7 1 , 3 1 . 2 0 Phải có: k ' 1,9 < k’ < 3,3 2 1
Do k’ nguyên, nên ta lấy: k’= 2, 3. Vậy dưới cùng một góc trên, có thể quan sát thấy 7 13,2.10
thêm vạch quang phổ bậc 2 có =
= 0,66.10-6m (ngoài vạch cực đại đã cho 2 trong bài ứng với k= 3).
Bài 6. ĐS: a. Nmax=7; b. λ max=d=2µm Bài 7.
a. Ta có góc lệch ứng với phổ bậc một của bước sóng 1 1 1: sin 1 k1 d d
Góc lệch ứng với phổ bậc hai của bước sóng 2: 2 2 sin k 2 2 2 d d 0 sin 2 2.0,5 5 5.sin(17 8') 2 2 0 sin 29 24' 2 2 sin 0,6 3 3 1 1
b. Số vạch trên 1cm chiều dài 0 1 sin sin(17 8') Ta có: 1 n 4910 vạch/cm 5 d 6.10 1
c. Điều kiện vạch quang phổ của hai ánh sáng trên trùng nhau: k k 1 2
sin sin 1 2 1 k 1 k2 2 5 6
Vì k1 và k2 nguyên (k1=5, k2=6); (k1=10, k2=12)… 1 0 (sin ) 5 5.sin(17 8') 1.47 1 1 min d
Không có nào thỏa mãn để quang phổ của hai vạch sáng trùng nhau. Bài 8.
Khoảng cách giữa hai cực đại ở kề hai bên cực đại giữa là cực đại bậc 1. Vì vậy,
ta có điều kiện cho cực đại nhiễu xạ qua 1 khe hẹp: 3 sin (2k 1) 2d 2d Vì góc nhỏ 33 3 sin tan 2 f 2b 2 f 6 3 f 3.0,6.10 .2 4 b
10 (m) 0,1(m ) m 2 3,6.10 Bài 9. Đáp số: d = 2,82.10-10m . Bài 10. Đáp số:
a. n = 3530 vạch/cm; b. N = 11
---------------------------------------------------------------------------
Chương 9: PHÂN CỰC ÁNH SÁNG
I. CÁC CÔNG THỨC CẦN GHI NHỚ
1. Định luật Maluýt: I2 = I1cos2
là góc tạo bởi 2 quang trục của kính phân cực và kính phân tích, I1, I2 là cường
độ sáng sau 2 kính trên.
2. Phân cực ánh sáng do phản xạ - Góc Briuxtơ: Khi ánh sáng tự nhiên tới mặt
phân cách hai môi trường với góc tới iB, nếu tgiB = n2 .1 (n21 là chiết suất tỷ đối của
môi trường chứa tia khúc xạ và tia tới) thì ánh sáng phản xạ phân cực toàn phần.
3. Cường độ sáng sau các lăng kính Nicôn: I 2 2 = I cos
: góc tạo bởi tiết diện chính của 2 Nicôn.
I1, I2 là cường độ sáng sau Nicôn khi có ánh sáng tự nhiên rọi vào chúng.
4. Sự quay mặt phẳng phân cực:
Anh sáng tự nhiên rọi theo phương quang trục thì hai mặt phẳng phân cực bị quay một góc :
a. Với tinh thể đơn trục : = [ ] d
: Khối lượng riêng của tinh thể đơn trục; d : Chiều dày của bản tinh thể.
b. Với chất quang hoạt : = [ ] Cd
C : Nồng độ của chất quang hoạt ; d : Chiều dày của lớp dung dịch. II. BÀI TẬP
Bài 1. Một tia sáng đập vào một tinh thể canxít, tinh thể này có mặt song song với
quang trục. Giả thiết rằng mặt phẳng tới vuông góc với quang trục và góc tới
bằng 500. Tìm góc tách giữa tia thường và tia bất thường. 34
(Cho biết đối với Canxit, chiết suất tia bất thường là ne = 1,4864 và đối với tia thường là n0 = 1,6583).
Bài 2. Một chùm ánh sáng phân cực thẳng có bước sóng trong chân không bằng
5,9.10-7m rọi vuông góc với quang trục của 1 tinh thể canxit. Tìm bước sóng của
tia thường và tia bất thường, tần số ứng với mỗi tia. Cho no = 1,658 , ne = 1,486
Bài 3. Hỏi góc nghiêng của tia sáng mặt trời so với chân trời (mặt phẳng nằm ngang)
phải bằng bao nhiêu để những tia sáng mặt trời phản chiếu trên mặt nước hồ bị
phân cực toàn phần ? Biết rằng chiết suất của nước hồ là n = 1,33.
Bài 4. Một chùm sáng tự nhiên truyền qua 2 bản Tuamalin T1 và T2 có các mặt bản
song song với nhau. Xác định góc hợp bởi hai tiết diện chính của 2 bản, nếu
cường độ sáng sau bản T2 giảm đi 4 lần so với cường độ sáng sau bản T1.
Bài 5. Dung dịch đường glucôz nồng độ C1 = 0,28g/cm3 đựng trong một bình trụ thủy
tinh sẽ làm quay mặt phẳng phân cực của ánh sáng xanh đi qua bình một góc 1
= 320. Hãy xác định nồng độ C2 của một dung dịch cũng đựng trong bình trụ
giống như trên, biết rằng nó làm quay mặt phẳng phân cực của ánh sáng một góc 0 2 = 24 .
Bài 6. Chất nicôtin (lỏng tinh khiết) đựng trong một bình hình trụ thủy tinh dài l =
8cm sẽ làm quay mặt phẳng phân cực của ánh sáng vàng natri một góc =
136,60. Khối lượng riêng của nicôtin là = 1,01g/cm3 . Xác định góc quay riêng [ ] của nicôtin.
Bài 7. Một bản thạnh anh dày d = 2mm được cắt vuông góc với quang trục, sau đó được đặt
vào giữa 2 Nicôn song song. Mặt phẳng phân cực của ánh sáng bị quay 1 góc = 530.
Hỏi chiều dày của bản phải bằng bao nhiêu để ánh sáng đơn sắc dùng trong thí nghiệm
không qua được Nicôn phân tích.
III. HƯỚNG DẪN VÀ ĐÁP SỐ Bài 1.
Anh sáng tới nằm trong mặt phẳng tới vuông góc với quang trục, nên tia tới
vuông góc với quang trục. Khi đó tia thường truyền trong tinh thể với vận tốc
v0, tia bất thường truyền trong tinh thể với vận tốc ve # v0, chiết suất của canxit
đối với hai tia là n0 và ne. sin i sin i
Theo định luật khúc xạ : n 6 , 1 583 ; n 4 , 1 864 sin r 0 sin r e 0 e Thay i = 500, ta có : r 0
0’ = 27030’ ; re = 31 35’. Vậy góc tách giữa 2 tia là : re - ro = 3035’ Bài 2. 35 Ta có n c cT c cT O = ; ne = o e v v T n v v T n o o o o e e e e Thay số ta được : -7 -7
o = 3,55.10 m ; e = 3,97.10 m
Vận tốc của tia thường và tia bất thường trong tinh thể khác nhau, nhưng tần số
của chúng không thay đổi và bằng tần số của ánh sáng tới: f = c v v O e = O e 5,08.1014Hz Bài 3. Đáp số: = 36055’ Bài 4.
Ap dụng định lý Maluýt : I 1 1 1 2 = I1 cos2 = ; cos2 = cos = 4 4 2 / 3 4/ 3 Bài 5. 1 = [ ]lC1 ; 2 = [ ]lC2 Suy ra: C 2 2 2 C C 3 1 = 0,21g/cm 2 C 1 1 1 Bài 6. m 3 â c âäü m = [ ] V . lC = [ ]1 = [ ]1
; = [ ]1 [ ] = 16,9 v V l c . g m Bài 7.
Bề dày của bản phải sao cho mặt phẳng phân cực quay đi 1 góc 900. Từ hai điều kiện đã cho ta có: 90 2 1 = [ ] d ; 2 = [ ] d d2 = d . d . , 3 m 4 m 1 2 1. 1 53 1
--------------------------------------------------------------------------- 36
Phần IV: VẬT LÍ HIỆN ĐẠI
Chương 10: CƠ HỌC TƯƠNG ĐỐI
(Không có bài tập)
---------------------------------------------------------------------------
Chương 11: QUANG LƯỢNG TỬ
I. CÁC CÔNG THỨC CẦN GHI NHỚ A. BỨC XẠ NHIỆT
1. Năng suất phát xạ xa toàn phần của vật đen tuyệt đối (Định luật Stephan- Boltzmann) R 4 -8 W T = r
d T với = 5,67.10 : hệ số Stephan-Boltzmann T 2 4 m K 0
2. Bước sóng bức xạ mang nhiều năng lượng nhất (Định luật Wien) b
max = với b = 2,896.10-3m K T
3. Công thức Planck về năng suất phát xạ của vật đen tuyệt đối 2 f (v, T) = -34
f ,T h h
, với h = 6,625.10 J.s : hằng số Planck; c = 2 h c kT e 1 3.108 m/s
B. TÍNH CHẤT HẠT CỦA BỨC XẠ ĐIỆN TỪ
1. Năng lượng, khối lượng, động lượng của photôn có tần số , bước sóng c : W = h W h h h = hc ; m = ; P mc 2 2 c c c 2. Tán xạ Compton
= ’ - = 2c sin2 ; 2
là bước sóng tới, ’ là bước sóng tán xạ, là góc tán xạ. -12 c = 2,4.10 m là bước sóng Compton.
3. Thuyết lượng tử ánh sáng của Einstein : 37 Công thức Einstein: c 1 2 h h A mv th max 2 II. BÀI TẬP
Bài 1. Một vật (xem là vật đen tuyệt đối) được nung nóng để nhiệt độ của nó tăng từ 1000 K đến 3000 K.
a) Tính bước sóng có năng suất phát xạ cực đại của vật ở nhiệt độ ban đầu.
b) Năng suất phát xạ toàn phần của nó tăng lên bao nhiêu lần sau khi nung nóng?
Bài 2. Bước sóng của bức xạ mang nhiều năng lượng nhất được phát ra từ mặt trời là
m = 0,48 m. Xem mặt trời là một vật đen tuyệt đối. Hãy tính.
a. Nhiệt độ của mặt trời
b. Công suất phát xạ toàn phần của mặt trời
Biết rằng mặt trời có bán kính R 5 0 = 7.10 km.
Bài 3. Dây tóc Vônfram trong đèn điện có đường kính là d = 0,03cm và độ dài là l =
5cm, khi mắc vào mạch điện 127 vôn thì dòng điện qua đèn là I = 0,3Ampe. Tỉ
số giữa năng suất phát xạ toàn phần của Vônfram và năng suất phát xạ toàn
phần của vật đen tuyệt đối ở cùng một nhiệt độ là = 0,31. Giả sử ở trạng thái
cân bằng nhiệt tất cả nhiệt do đèn phát ra đều ở dạng bức xạ. Tìm nhiệt độ của đèn.
Bài 4. Bề mặt da người có nhiệt độ trung bình 35oC, diện tích 1,6m2. Áp dụng các
công thức dùng cho vật đen tuyệt đối với giả thiết RT của người chỉ bằng 10%
vật đen tuyệt đối. Hãy tính:
a) Bước sóng bức xạ mang nhiều năng lượng nhất do con người phát xạ.
b) Tổng năng lượng phát xạ của một người trong một ngày đêm.
Bài 5. Công suất bức xạ của một vật đen tuyệt đối tăng bao nhiêu lần nếu trong quá
trình nung nóng bước sóng của bức xạ mang nhiều năng lượng nhất dịch chuyển từ 0,6 m đến 0,5m.
Bài 6. Nhiệt độ của sợi dây tóc của bóng đèn điện luôn biến đổi vì được đốt nóng bằng
dòng điện xoay chiều. Hiệu số giữa nhiệt độ cao nhất và thấp nhất là 800K, nhiệt độ
trung bình là 23000K. Hỏi công suất bức xạ biến đổi bao nhiêu lần, nếu coi dây tóc
bóng đèn như một vật đen tuyệt đối.
Bài 7. Trong hiện tượng tán xạ Compton, chùm tia X tới có có bước sóng bằng bao
nhiêu? Nếu electron bắn ra có động năng cực đại là 0,19MeV.
Bài 8. Photon có năng lượng 0,25MeV bay đến va chạm với một electron đứng yên và
tán xạ theo góc 1200 (tán xạ Compton). Xác định năng lượng của electron tán xạ.
Bài 9. Một tấm kim loại có diện tích bề mặt S = 10 cm2, có nhiệt độ 2500 K, trong 1 phút
phát ra một năng lượng 4.104 J dưới dạng bức xạ điện từ. 38
a. Tính năng lượng phát xạ của một vật đen tuyệt đối có cùng diện tích bề mặt và
cùng nhiệt độ với vật trên trong 1 phút.
b. Nhiệt độ của tấm kim loại giảm đi 500 K. Tính công suất phát xạ của tấm kim loại trên.
Bài 10. Xác định năng lượng, khối lượng và xung lượng của photon có bước sóng tương ứng : a. -6 -10 -10 1 = 0,7.10 m; b.2 = 0,25.10 m ; c.3 = 0,016.10 m
III. HƯỚNG DẪN VÀ ĐÁP SỐ Bài 1. a. Bước sóng ở 𝑇 −3
1: 𝜆1 = 𝑏 = 2,9 × 10 /1000 = 2,9 𝜇m. 𝑇1
b. Năng suất bức xạ toàn phần của vật đen tuyệt đối: 𝑅(𝑇) = 𝜎𝑇4 4 Do đó: 𝑅2 = (𝑇2) = 34 = 81 𝑅1 𝑇1 → tăng lên 81 lần Bài 2. 3 b 2,9.10
a. Nhiệt độ của mặt trời: T 6042K 7 4,8.10 max
b. Công suất bức xạ của mặt trời là năng lượng do mặt trời phát ra trong một giây. W P = R 2 T.S = T4 4R0 t S = 4R 2
0 là diện tích của mặt trời. 4 Ta có P = 4 b 2 .R = 4,9.1025W 0 max
Bài 3. Công suất bức xạ của dây tóc Vônfram bằng công suất tiêu thụ của đèn: P = U.I
Năng suất phát xạ toàn phần của dây tóc Vônfram hình trụ có diện tích S = dl
là năng lượng bức xạ toàn phần của một đơn vị diện tích của nó. Rv = P UI S dl
Năng suất phát xạ toàn phần của vật đen là RT = T4 Từ điện kiện: R UI V = 4 R
d .lT T
Ta tìm được nhiệt độ của dây tóc là : T = 4 UI = 2620K dl Bài 4. ĐS: a. λ -6 max = 9,4.10 m 39
b. Tổng năng lượng phát xạ: E = 7,54.103 kJ b
Bài 5. Ta có : max = và P = .T4.S T P T 4 4 2 2 1 2,07 lần P T 1 1 2 4 P T Bài 6 . P = R max max TS = T4S; = 1,15 P T min min Bài 8.
a. + Năng lượng toàn phần trước tán xạ: 2 1 W m C h e 2
+ Năng lượng toàn phần sau tán xạ là: m C e W h ' 2 2 1 v 2 c
Theo định luật bảo toàn năng lượng: W2 = W1 2 2 2 hc m c hc m c e e 2 hc hc hc hc m c E m c e 2 ' đ 2 e ' v v 1 1 2 2 c c hc hc E đ 2C sin 2 2 2 2 Và : E hc hc hc C đmax khi sin 1 E đ 2 max 2 2 C C = 0,037A0
Bài 8. Năng lượng của photon tán xạ : E' hc hc ' 2 sin2 C 2 và : hc
; với E là năng lượng của photon tới E hc E' = 0,144MeV. hc 2 sin 2 C E 2 Bài 9. ĐS: a. 5
E = 1,33x10 J; b. P = 27,28 W Bài 10. 40
Ta có : năng lượng, khối lượng và xung lượng của photon được xác định bởi các công hc thức lần lượt là : h h ; m ; p c 2 a. -6 -19 -36 -28 1 = 0,7.10 m : = 2,839.10
J, m = 3,16.10 kg, p = 9,466.10 kgm/s b. -10 -15 -32 -23 2 = 0,25.10
m : = 7,95.10 J, m = 8,84.10 kg, p = 2,65.10 kgm/s c. -10 -13 -30 -22 3 = 0,016.10
m : = 1,24.10 J, m = 1,38.10 kg, p = 4,14.10 kgm/s
---------------------------------------------------------------------------
Chương 12: CƠ HỌC LƯỢNG TỬ
I. CÁC CÔNG THỨC CẦN GHI NHỚ
1. Hệ thức de Broglie: Vì hạt tự do có năng lượng E, động lượng P tương ứng với
sóng phẳng đơn sắc có tần số và bước sóng : E ; h h p
2. Hệ thức bất định Heisenberg :
a. Hệ thức giữa độ bất định về tọa độ và độ bất định về động lượng của vi hạt : x . Px h h : hằng số Plăng
b. Hệ thức giữa độ bất định năng lượng và thời gian sống của vi hạt: E . t h 3. Hàm sóng : i
a. Hàm sóng phẳng đơn sắc : = 0 exp [- i (t - kr)] = 0 exp
Et pr h với h h 2
b. Ý nghĩa của hàm sóng: - Mật độ xác suất tìm hạt = 2
- Xác suất tìm hạt trong yếu tố thể tích dV là : 2 dV = *dV
- Xác suất tìm hạt trong toàn không gian : 2 dV = 1
4. Phương trình Schrodinger mô tả chuyển động của vi hạt :
− ℏ2 Δ𝜓(𝑟) + 𝑈(𝑟)𝜓(𝑟) = 𝐸𝜓(𝑟) 2𝑚
với 𝜓(𝑟) là hàm sóng không phụ thuộc thời gian. II. BÀI TẬP:
Bài 1. Hạt electron có vận tốc ban đầu bằng 0 được gia tốc qua 1 hiệu điện thế U. Xác
định bước sóng de Broglie của electron sau khi gia tốc trong 2 trường hợp : 41 a. U = 51V b. U = 510 KV
Bài 2. Động năng của electron trong nguyên tử hydrô có giá trị vào cỡ 10eV. Dùng hệ
thức bất định hãy đánh giá kích thước nhỏ nhất của nguyên tử.
Bài 3. Trong một thí nghiệm cho chùm hạt xuyên qua 2 khe hẹp A và B, người ta xác
định được biên độ của sóng đi qua 2 khe này tại 1 điểm nào đó trên màn hứng
lần lượt bằng + 3 và + 5 và tốc độ đếm (số hạt đếm được trong một đơn vị thời
gian) nếu chỉ mở khe A bằng 60 hạt/giây.
a. Hỏi tốc độ đếm nếu chỉ mở khe B ?
b. Hỏi tốc độ đếm nếu mở cả 2 khe ?
Bài 4. Một phôtôn và 1 electron có động năng bằng nhau. Hãy so sánh bước sóng de
Broglie của phôtôn và electron ?
Bài 5. Tính độ bất định về tọa độ x của hạt electron trong nguyên tử hydrô biết rằng
vận tốc electron bằng v = 1,5.106 m/s và độ bất định về vận tốc v = 10% của
V. So sánh kết quả tìm được với đường kính d của quỹ đạo Bohr thứ nhất và xét
xem có thể áp dụng khái niệm quỹ đạo cho trường hợp kể trên không ?
Bài 6. Prôtôn có năng lượng bằng 103 MeV. Bước sóng de Broglie của prôtôn này
bằng bao nhiêu ? Cho khối lượng nghỉ của prôtôn là 1,67.10-27 kg.
Bài 7. Một vi hạt trong giếng thế năng một chiều sâu vô hạn có bề rộng 0 ≤ 𝑥 ≤ 𝑎 được
mô tả bởi hàm sóng 𝜓(𝑥) = 𝜓 𝑛𝜋 0 sin 𝑥. 𝑎
a) Hãy xác định biên độ sóng 𝜓 t 0 ừ đ ề i u kiện chuẩn hoá.
b) Hạt ở trạng thái kích thích có 𝑛 = 2. Xác định những vị trí ứng với cực đại
và cực tiểu của mật độ xác suất tìm thấy hạt trong vùng 0 ≤ 𝑥 ≤ 𝑎/2.
Bài 8. Chiếu một chùm electron có năng lượng 0,083eV lên một mẫu tinh thể, người ta
quan sát thấy góc trượt ứng với nhiễu xạ bậc nhất ằ
b ng 220. Tìm hằng số mạng
d của tinh thể nói trên.
Bài 9.Một hạt bị nhốt giữa hai bức tường rắn nằm cách nhau một khoảng L. Biết rằng
hạt ở trạng thái năng lượng thấp nhất và có hàm sóng là 𝜋𝑥
Ψ(𝑥) = 𝐴 sin 𝐿 (𝑣ớ𝑖 𝐴 = √2𝐿)
Tính xác suất tìm thấy hạt giữa các điểm. a. Từ x L L L 2 L 2 1 = 0 đến x2 = b. Từ x1 = đến x2 = c. Từ x1 = đến x2 = 3 3 3 3 L
Bài 10. Tìm vận tốc và bước sóng của một electron có động năng tương đối tính bằng
năng lượng nghỉ của nó. 42
III. HƯỚNG DẪN VÀ ĐÁP SỐ Bài 1.
Hạt electron khi được gia tốc của hiệu điện thế U sẽ nhận được một lượng năng
lượng W = eU. Toàn bộ năng lượng này chuyển thành động năng Wđ của eclectron.
a. Vì hiệu điện thế U không lớn lắm nên động năng của electron không lớn, do đó
vận tốc của nó cũng không lớn. Trong trường hợp này ta có thể sử dụng được cơ học cổ điển : 2 2 2 2 m v m v P e e eU W P m 2 eU đ 2 2m 2m e e e h h
Mặt khác, theo giả thiết Đơbrơi : h P (1) P m 2 eU e Thay số : h = 6,625 . 10-34 J.S ; m -31 e = 9,1 . 10 kg e = 1,6 . 10-19 C ; U = 51V
Vào biểu thức (1) ta được : = 1,7.10-9m = 1,7A0
b. Vì hiệu điện thế U khá lớn, nên động năng của electron lớn, như vậy vận tốc
của nó cũng lớn. Trong trường hợp này ta không thể áp dụng cơ học cổ điển
được mà phải áp dụng cơ học tương đối : Wđ = W - W0
Trong đó W=mc2 là năng lượng toàn phần của electron, W0 =mec2 là năng
lượng nghỉ của electron. Do đó : eU = W 2 đ = mc - mec2
Theo cơ học tương đối ta có biểu thức liên hệ giữa năng lượng và động lượng
của hạt: 𝑊2 = 𝑚2𝑐4 = 𝑚2 2 2 𝑒 𝑐4 + 𝑝2𝑐2
nên 𝑚𝑐2 = √𝑚𝑒 𝑐4 + 𝑝 𝑐2 . Do đó:
eU = √𝑚2𝑒𝑐4 + 𝑝2𝑐2 − 𝑚𝑒𝑐2 ⇒ 𝑚2 2 𝑒𝑐4 2
+ 𝑝2𝑐2 = 𝑒2𝑈2 + 2𝑒𝑈𝑚𝑒𝑐 + 𝑚𝑒 𝑐4 2 2 2 e U 2eUm c 1
Từ đây ta rút ra được: e p p eU 2 eU 2m c e 2 c c Do: h hc
Thay số vào ta được = 0,014A0 p eU 2 eU 2m c e Bài 2.
Theo hệ thức bất định ta có : ∆𝑥. ∆𝑝𝑥 ≈ ℎ
Vì trong nguyên tử, electron chỉ chuyển động trong phạm vi kích thước nguyên tử nên : 43
x = r0 (bán kính nguyên tử) Do đó : 𝑟 h
0. ∆𝑝𝑥 ≈ ℎ r0 do ∆𝑝𝑥 ≤ 𝑝 = p x √2𝑚𝑒𝑊đ 3 4 h h 6,625.10 Nên : romin = 3 1 1 9 p 2m W x a m x e đ 2.9,1.10 .1,6.10 .10 Vậy : r -9 omin = 0,39.10 m Bài 3.
Vì vi hạt có lưỡng tính sóng hạt, nên cường độ sáng tỷ lệ thuận với bình phương
biên độ sóng hoặc với số hạt đếm được trong 1 giây.
Gọi : IA , IB lần lượt là cường độ sóng qua khe A, B. I 52 N 2 a. Ta có : 5 25.60 B B N N = 167 hạt/giây I B A A 32 N A 32 9 I 5 3 N N AB 2 b. AB AB N = 420 hạt/giây AB 2 I 3 N 60 A A Bài 4.
Gọi W là năng lượng toàn phần của hạt, Wđ là động năng của hạt và W0 là năng
lượng nghỉ của hạt. Ta có : Wđ = W - W0 M à W = 2 2 2 c m c P 0
* Nên đối với hạt electron ta có : 2 2 2 2
W c m c P m c e đ 0 0
* Đối với phôtôn do khối lượng nghỉ của hạt phôtôn m0 = 0 nên với hạt phôtôn ta có : 𝑊đ𝑓 = 𝑐. 𝑃𝑓 Theo giả thiết: W 2 2 2 đf = Eđe Nên : 2 c m c P m c = cPf 0 0 Hay : 2 4 2 2 2 m c Pe c m c = cpf 0 e Nhưng : 2 4 2 2 2 m c P c m c < cP 2 2 e do - A < B 0 0 A B Nên : cP h h f < cPe c c . Vậy: f > e f e Bài 5.
Theo hệ thức bất định Heisenberg: 44 ℎ ℎ
∆𝑥. ∆𝑝 ≈ ℎ ⟹ ∆𝑝 ≈ ∆𝑥 ⟹ 𝑚𝑒∆𝑥 ≈ ∆𝑝 ℎ ℎ 10−34
⟹ ∆𝑥 ≈ 𝑚𝑒∆𝑣 = 𝑚𝑒.10%.𝑣 = 6,625 .9,1.10−31.10%.1.5.106 = 0,48.10−8𝑚
Bán kính quỹ đạo Bohr: 𝑟0 = 5,3.10−11𝑚
⟹ đườ𝑛𝑔 𝑘í𝑛ℎ 𝑞𝑢ỹ đạ𝑜 𝐵𝑜ℎ𝑟: 𝑑 = 2𝑟 −10 0 = 1,06.10
𝑚 nhỏ hơn nhiều với độ bất
định về tọa độ ∆𝑥. Vì vậy khái niệm quỹ đạo nguyên tử không phù hợp trong trường hợp này. Bài 6.
Ta có hệ thưc liên hệ giữa năng lượng và động lượng trong cơ học tương đối
𝑊2 = 𝑚2𝑐4 = 𝑚 20𝑐4 + 𝑝2𝑐2 1 ⟹ 𝑝 = 2𝑐4 𝑐 √𝑊2 − 𝑚0
Vậy bước sóng Dơbrơi của proton này là : ℎ ℎ𝑐 𝜆 = 𝑝 = = 3,7.10−15𝑚 √𝑊2 − 𝑚 20𝑐4 Bài 7. a. Biên độ sóng : Điều kiện chuẩn hoá: 𝑎
∫|𝜓(𝑥)|2𝑑𝑥 = 𝜓20∫ sin2 𝑛𝜋 𝑎 𝑥 𝑑𝑥 = 1 0 𝑎 1 2𝑛𝜋
→ 𝜓20 ∫2(1 − cos 𝑎 𝑥)𝑑𝑥 = 1 0 → 𝜓0 = √2/𝑎 b. Mật độ xác suất:
- Hàm sóng ở trạng thái 𝑛 = 2: 𝜓(𝑥) = √2sin 2𝜋 𝑥 𝑎 𝑎
- Mật độ xác suất: |𝜓(𝑥)|2 = 2sin2 2𝜋 𝑥 𝑎 𝑎
- Cực trị: 𝑑 |𝜓(𝑥)|2 = 8𝜋cos 2𝜋 𝑥 sin 2𝜋 𝑥 = 4𝜋 sin 4𝜋 𝑥 = 0 𝑑𝑥 𝑎2 𝑎 𝑎 𝑎2 𝑎 45 4𝜋 𝑎 𝑎
→ sin 𝑎 𝑥 = 0 → 𝑥 = 0, 4,2
Trong vùng 0 ≤ 𝑥 ≤ 𝑎/2
+ 𝑥 = 0 → |𝜓(𝑥)|2 = 0: cực tiểu
+ 𝑥 = 𝑎/4 → |𝜓(𝑥)|2 = 2/𝑎: cực đại
+ 𝑥 = 𝑎/2 → |𝜓(𝑥)|2 = 0: cực tiểu Bài 8.
Năng lượng của electron chính là động năng của nó. Sử dụng cơ học cổ điển ta có: 𝑚 𝑚2𝑣2 𝑝2 𝑊 𝑒𝑣2 𝑒 đ = 2 = 2𝑚 = ⟹ 𝑝 = √2𝑚𝑒𝑊đ 𝑒 2𝑚𝑒
Từ đó ta có được bước sóng Dơbrơi của chùng electron ℎ ℎ 𝜆 = 𝑝 = √2𝑚𝑒𝑊đ
Trong chương nhiễu xạ ánh sáng ta có công thức Vunfơ-Brêgơ cho cực đại nhiễu xạ
trên mạng tinh thể: 2𝑑𝑠𝑖𝑛𝜑 = 𝑘𝜆 hay 𝑑 = 𝑘𝜆/2𝑠𝑖𝑛𝜑. Góc nhiễu xạ bậc nhất ứng với 𝑘 = 1 𝜆 ℎ 6,625.10−34 𝑑 = 2𝑠𝑖𝑛𝜑 = =
2𝑠𝑖𝑛𝜑√2𝑚𝑒𝑊đ 2𝑠𝑖𝑛22𝑜√2.9,1.10−31.0.083.1,6.10−19 = 5,7.10−9𝑚 Bài 9.
Theo có học lượng tử, bình phương modul hàm sóng tỉ lệ với mật độ xác suất tìm thấy hạt.
Vì vậy mật độ tìm thấy hạt trong thể tích V nào đó là : ∫ |Ψ(𝑥)|2𝑑𝑉 𝑉
Trong bài toán này hàm sóng là hàm một chiều theo x nên ta có xác suất tìm thấy hạt: a.
Từ 𝑥1 = 0 đến 𝑥2 = 𝐿/3 l : à 𝐿 𝐿 3 3 𝜋𝑥 2 2 𝜋𝑥
∫ | Ψ(𝑥)|2𝑑𝑉 = ∫|𝐴 sin 𝑑𝑥 =
𝐿 | 𝑑𝑥 = ∫𝐿 sin2 𝐿 𝑉 0 0 46 𝐿 3 1 2𝜋𝑥 1 1 2𝜋
= 𝐿∫(1 − cos 𝐿 ) 𝑑𝑥 = 3 −2𝜋.sin 3 = 0.196 0 b.
Tương tự từ 𝑥1 = 𝐿/3 đến 𝑥2 = 2𝐿/3 2𝐿/3 ∫ 𝜋𝑥 | 2
Ψ(𝑥)|2𝑑𝑉 = ∫ 𝐿sin2 𝐿 𝑑𝑥 = 0.608 𝑉 𝐿/3 c.
Từ 𝑥1 = 2𝐿/3 đên 𝑥2 = 𝐿 𝐿 ∫ 𝜋𝑥 | 2
Ψ(𝑥)|2𝑑𝑉 = ∫ 𝐿sin2 𝐿 𝑑𝑥 = 0.196 𝑉 2𝐿/3 Bài 10.
Theo cơ học tương đối tính, năng lượng toàn phần của hạt bằng tổng năng lượng nghỉ và động năng:
𝑚𝑐2 = 𝑚0𝑐2 + 𝑊đ
Theo giả thiết động năng bằng năng lượng nghỉ nên 𝑚𝑐2 = 2𝑚 hay 0𝑐2 𝑚 = 2𝑚0
Mặt khác ta có khối lượng tương đối của hạt 𝑚 = 𝑚0 = 2𝑚 2 2
0 suy ra 𝑐 = 4(𝑐 − 𝑣2) √1−𝑣2 𝑐2
⇒ 𝑣 = 𝑐√3/4 = 2,55 108𝑚/𝑠 𝑚2𝑐4 = 4𝑚^2 4 2
0𝑐 = 𝑚0 𝑐4 + 𝑝2𝑐2 ⇒ 𝑝 = √3𝑚0𝑐 Bước sóng
𝜆 = ℎ = ℎ = 1,40.10−12m 𝑝 √3𝑚0𝑐 Đáp số : 2,55.108 m/s; 1,40.10-12m
---------------------------------------------------------------------------
Chương 13: VẬT LÝ NGUYÊN TỬ
I. CÁC CÔNG THỨC CẦN GHI NHỚ
1. Nguyên tử Hyđrô : 47
a. Trạng thái của electron mô tả bởi hàm sóng :
nlm (r, , ) = Rnl (r) . Ylm (, )
n = 1, 2, 3... số lượng tử chính;
l = 0, 1, ... n - 1 : số lượng tử quỹ đạo;
m = 0, -1 . 2 . 1 : số lượng tử từ.
b. Năng lượng của vi hạt : 1 𝑒2 1 1 2 𝑚 1 13,6 𝐸 𝑒𝑒4 𝑛 = − 4𝜋𝜖 ( ) 0 2𝑎0 𝑛2) = − (4𝜋𝜖0
2ℏ2 (𝑛2) = − 𝑛2 eV (𝑛 = 1, 2, 3, … )
2. Nguyên tử kim loại kiềm :
a. Trạng thái electron hóa trị vẫn phụ thuộc 3 số lượng tử : n, l, m Rh
b. Năng lượng electron hóa trị : Enl = n 2 l
l là số bổ chính phụ thuộc vào 1 và phụ thuộc vào từng nguyên tử.
c. Ký hiệu năng lượng là : nx với x = S, P, D, F... khi 1 = 0, 1, 2, 3...
Qui tắc lựa chọn khi chuyển mức năng lượng : l = 1
3. Mômen động lượng quỹ đạo của electron : L l l 1
Hình chiếu 𝐿 trên phương z : 𝐿𝑧 = 𝑚ℏ
4. Mômen từ quỹ đạo của electron : 𝑒
𝜇 = − 2𝑚 𝐿 𝑒
Hình chiếu từ 𝜇 trên phương z: −24 z = - mB
với 𝜇𝐵 = − 𝑒ℏ = 9,27 × 10 Am2 gọi là Manhêtôn Bo. 2𝑚𝑒
5. Mômen spin của electron có giá trị :
S s s 1 1 h ;
s là số lượng tử Spin. 2
Hình chiếu của 𝑆 trên phương z : 𝑆 1 𝑧 = 𝑚𝑠ℏ; ms =
: số lượng tử hình chiếu Spin. 2
6. Mômen động lực toàn phần của electron :
Dạng vector: 𝐽 = 𝐿 + 𝑆 48
Độ lớn: 𝐽 = √𝑗(𝑗 + 1)ℏ 1 Với j = l
: số mô men lượng tử toàn phần 2
7. Trạng thái của electron khi kể tới spin
Phụ thuộc vào 4 số lượng tử n, 1, m, ms. n 1
Với n xác định, có : 2 l2
1 = 2n2 trạng thái electron. l 0
8. Sự chuyển mức năng lượng phải tuân theo qui tắc lựa chọn : n 0 ; l = 1; m = 0, 1 II BÀI TẬP :
Bài 1. Để tất cả các vạch quang phổ hyđrô đều xuất hiện, hỏi các “viên đạn” electron
kích thích nguyên tử hyđrô phải có a) động năng nhỏ nhất và b) vận tốc nhỏ nhất bằng bao nhiêu?
Bài 2. Nguyên tử hyđrô ban đầu ở trạng thái cơ bản, hấp thụ một phôtôn để chuyển
sang trạng thái kích thích P. Hãy xác định độ biến thiên của mô men động
lượng quĩ đạo của electron trong nguyên tử đó.
Bài 3. Trong nguyên tử hyđrô, electron chuyển từ trạng thái 3p về trạng thái cơ bản.
Xác định độ biến thiên của hình chiếu mômen từ quỹ đạo của electron trong quá trình đó.
Bài 4. Đối với electron hóa trị trong nguyên tử Na, hỏi những trạng thái năng lượng
nào có thể chuyển về trạng thái ứng với n = 3 ? Xét cho 2 trường hợp :
a. Khi không chú ý tới Spin.
b. Khi có chú ý tới Spin.
Bài 5. Electron trong nguyên tử hydro ở trạng thái có momen động lượng quỹ đạo 𝐿 = √2ℏ. Tìm :
a. Số góc định hướng của 𝐿 đối với phương z.
b. Mômen động lượng toàn phần của electron.
c. Độ biến thiên của hình chiếu của mômen động lượng quĩ đạo của electron khi
nó chuyển về trạng thái cơ bản.
Bài 6. a) Vẽ và giải thích sơ đồ chuyển mức của electron hóa trị trong kim loại Li ứng
với chuyển dời từ mức 3P về 2S khi tính đến spin.
b) Tìm độ biến thiên của độ lớn momen động lượng quỹ đạo và hình chiếu momen
từ quỹ đạo của electron trong các dịch chuyển được mô tả trong sơ đồ trên. 49
Bài 7. Một vạch quang phổ của nguyên tử kim loại kiềm khi chưa chú ý đến spin có
tần số : 4D 3P. Nếu chú ý đến spin thì vạch quang phổ trên có bao nhiêu
vạch? Hãy giải thích sự xuất hiện các vạch trên và vẽ sơ đồ chuyển mức.
Bài 8. Tính năng lượng ion hóa nguyên tử hyđrô khí electron chuyển động trên các quĩ đạo K, L, M.
Bài 9. a. Gọi 1, 2 lần lượt là tần số lớn nhất của các vạch phổ trong dãy Laiman và Banme. Tìm 1 . 2
b. Gọi 1, 2 lần lượt là bước sóng dài nhất và ngắn nhất của các vạch phổ trong
dãy Laiman và Banme. Tìm 1 . 2
Bài 10. Khi nguyên tử Hydro ở trạng thái cơ bản được rọi bởi ánh sáng đơn sắc thì đã
phát ra 6 vạch quang phổ. Tính năng lượng của phô tôn tới và xác định các vạch thuộc các dãy phổ nào.
Bài 11. Khi chiếu chùm photon đơn sắc vào nguyên tử Hydro ở trạng thái cơ bản,
người ta thấy phát ra quang phổ gồm 10 vạch.
a) Tính năng lượng của photon tới .
b) Xác định các vạch quang phổ nói trên thuộc dãy phổ nào?
c) Tính tỉ số giữa bước sóng lớn nhất và bé nhất trong 10 vạch quang phổ trên .
Bài 12. Electron trong nguyên tử từ trạng thái có số lượng tử mômen toàn phần 3 j 2
chuyển về trạng thái cơ bản. Tìm độ biến thiên hình chiếu của mômen động
lượng và mômen từ quĩ đạo của điện từ trong sự chuyển trạng thái trên.
III. HƯỚNG DẪN VÀ ĐÁP SỐ Bài 1.
a. Để tất cả các vạch quang phổ hyđrô đều xuất hiện thì các “viên đạn” electron
kích thích nguyên tử hyđrô phải có năng lượng tối thiểu bằng năng lượng cần
thiết để đưa electron trong nguyên tử hyđrô nhảy từ trạng thái cơ bản ứng với
năng lượng E1, lên trạng thái kích thích ứng với năng lượng E, do đó: 13,6
𝑊đ𝑚𝑖𝑛 = 𝐸∞ − 𝐸1 = − ∞2 + 13,6 = 13,6 eV b. Vận tốc nhỏ nhất: 2 2. W m v min Wđ e min 6 đmin = v = 2,19×10 m/ s min 2 me Bài 2. 50
Ban đầu nguyên tử hyđrô ở trạng thái cơ bản là trạng thái 1𝑠 ứng với 𝑙 = 0
Momen động lượng quĩ đạo ban đầu:
𝐿𝑠 = √𝑙(𝑙 + 1)ℏ = 0
Sau khi hấp thụ phôtôn electron ở trạng thái kích thích P ứng với 𝑙 = 1.
Momen động lượng quỹ đạo lúc sau:
𝐿𝑝 = √𝑙(𝑙 + 1)ℏ = √2ℏ
Độ biến thiên của mômen động lượng quĩ đạo của electron trong nguyên tử:
Δ𝐿 = 𝐿𝑝 − 𝐿𝑠 = √2ℏ Bài 3.
Các số lượng tử của electron ở trạng thái 3p: 𝑙 = 1, 𝑚 𝑙 = −1, 0, 1.
Hình chiếu momen từ quỹ đạo trên trục z: 𝜇𝑧 = −𝑚𝑙𝜇 B
Suy ra: 𝜇𝑧_p = 𝜇B, 0, −𝜇 B
Các số lượng tử của electron ở trạng thái cơ bản 1s: 𝑙′ = 0, 𝑚′𝑙 = 0
Hình chiếu momen từ quỹ đạo trên trục z: 𝜇 ′
𝑧_1s = −𝑚𝑙𝜇B = 0
Độ biến thiên hình chiếu momen từ quỹ đạo:
Δ𝜇𝑧 = 𝜇𝑧_p − 𝜇𝑧_s = 𝜇B, 0, −𝜇B Bài 4.
a. Chưa kể tới Spin thì những trạng thái ứng với n = 3 có thể là 3S (l = 0), 3P (l = 1), 3D (l = 2).
Sự chuyển trạng thái tuân theo qui tắc lựa chọn đối với n là chuyển từ cao về
thấp, n > 3, và đối với l là l = 1.
b. Khi tính tới Spin thì trạng thái của electron được biểu diễn bởi n2xj mà j = 1 l
nên những trạng thái ứng với n = 3 có thể là : 2 32S 2 2 2 2 1/2 ; 3 P1/2 ; 3 P3/2 ; 3 D3/2 ; 3 D5/2
Ngoài 2 quy tắc giống như trong câu a, sự chuyển trạng thái còn phải tuân theo qui
tắc lựa chọn đối với j : j = 0 ; 1
Do đó, những trạng thái có thể chuyển - Về 32S 2 2 1/2 là: n P1/2 và n P3/2 với n = 3, 4, 5, ... - Về 32P1/2 là: 51 n2S1/2 với n = 4, 5, 6 ... n2D3/2 với n = 3, 4, 5 ... - Về 32P3/2 là : n2S1/2 với n = 4, 5, 6 ... n2D3/2 với n = 3, 4, 5 ... n2D5/2 với n = 3, 4, 5 ... - Về 32D3/2 là : n2P1/2 với n = 4, 5, 6 ...
n2P3/2 với n = 4, 5, 6 ... ; n2F5/2 với n = 3, 5, 6 ... - Về 32D5/2 là : n2P3/2 với n = 4, 5, 6 ...
n2F5/2 với n = 3, 5, 6 ... ; n2F7/2 với n = 3, 5, 6 ... Bài 5.
a. Từ 𝐿 = √𝑙(𝑙 + 1)ℏ = √2ℏ. Suy ra: 𝑙 = 1 và 𝑙 = −2 (loại )
Với 𝑙 = 1 thì m = 0, 1, nên theo công thức 𝐿 thì có 3 tr c ng 𝑧 = 𝑚ℏ ị ủa 𝐿𝑧 ứ
với 3 góc định hướng của 𝐿 đối với phương z.
Với 𝑚 = −1 → cos 𝜃1 = − 1 → 𝜃 √2 1 = −450
Với 𝑚 = 0 → cos 𝜃2 = 0 → 𝜃2 = 900
Với 𝑚 = 1 → cos 𝜃3 = 1 → 𝜃 √2 3 = 450
b. Với 𝑙 = 1 thì 𝑗 = |𝑙 ± 1| = 1 và 3 2 2 2
Với 𝑗 = 𝑗1 = 1, suy ra: 2
𝐽1 = √𝑗1(𝑗1 + 1)ℏ = √3 2 ℏ
Với 𝑗 = 𝑗2 = 3, suy ra: 2
𝐽2 = √𝑗2(𝑗2 + 1)ℏ = √15 2 ℏ
c. Ta có: 𝐿 = √𝑙(𝑙 + 1)ℏ = √2ℏ → 𝑙 = 1 → 𝑚𝑙 = −1, 0, 1
Hình chiếu momen động lượng: 𝐿𝑧 = 𝑚𝑙ℏ = −ℏ, 0, ℏ 52
Khi chuyển về trạng thái cơ bản: 𝑙′ = 0 → 𝑚′ ′ 𝑙 = 0 → 𝐿𝑧 = 0 Độ biến thiên: Δ𝐿 ′
𝑧 = 𝐿𝑧 − 𝐿𝑧 = −ℏ, 0, ℏ Bài 6. a. Vẽ hình
b. Ta có moment động lượng quỹ đạo 𝐿 = √𝑙(𝑙 + 1)ℏ và hình chiếu của moment từ
quỹ đão 𝜇𝑧 = −𝑚𝜇 𝐵
+ Ở trạng thái đầu (3P: 𝑙 = 1, 𝑚 = 0, ±1): 𝐿3𝑃 = √2ℏ, 𝜇𝑧 = 0, ∓𝜇 3𝑃 𝐵
+ Ở trạng thái cuối (2S: 𝑙 = 0, 𝑚 = 0): 𝐿2𝑆 = 0, 𝜇𝑧 = 0 2𝑆
Suy ra: Δ𝐿 = −√2ℏ, Δ𝜇𝑧 = 0, ±𝜇𝐵 Bài 7.
Khi tính đến spin: 1 vạch quang phổ : 4D 3P sẽ tách thành 3 vạch:
𝜈1: 42𝐷5/2 → 32𝑃3/2 𝜈 2 2: 4 𝐷3/2 → 32𝑃3/2 𝜈 2
3: 4 𝐷3/2 → 32𝑃1/2 Sơ đồ chuyển mức:
Bài 8. Đáp số : 13,5 eV; 3,375 eV; 1,5 eV
Bài 9. Đáp số : a. 1 = 4; b. 1 = 3. 2 2
Bài 10. Đáp số : số vạch N = n(n-1)/2 n = 4, ΔE = 12,66 eV
3 vạch dãy Laiman; 2 vạch dãy Bame; 1 vạch dãy Pasen
Bài 11. Đáp số:
a. Ta có: số vạch N = n(n-1)/2 n = 5 ΔE = 13,06eV. 53
a) Gồm: 4 vạch dãy Laiman, 3 vạch dãy Banme, 2 vạch dãy Pasen và 01 vạch dãy Bracket. b) * λ 2
max (trong dãy Bracket), ν1 = R(1/4 -1/52) = R.0,0225; λ 2
min (trong dãy Laiman), ν2 = R(1-1/5 ) = R.0,96 ;
* λ = c/ν → λmax / λmin = 0,96/0,0225 = 42,67
Bài 12. Đáp số : (0, ±1)ℏ; (0, 1)B
---------------------------------------------------------------------------
Chương 14: HẠT NHÂN NGUYÊN TỬ (SV tự đọc)
(Không có bài tập)
--------------------------------------------------------------------------- 54




