














Preview text:
VIII. BÀI TOÁN TẦN SỐ f BIẾN THIÊN
Ví dụ 1: Cho đoạn mạch RLC mắc nối tiếp, hiệu điện thế hiệu dụng hai đầu đoạn mạch là U và tần số góc
của dòng điện thay đổi được, cho biết 2L CR2 .
1. Tìm để công suất, hiệu điện thế giữa hai đầu điện trở và dòng điện trong mạch đạt giá trị cực đại.
2. Tìm để hiệu điện thế hiệu dụng giữa hai đầu cuộn cảm đạt giá trị cực đại. Tính giá trị cực đại đó.
3. Tìm để hiệu điện thế hiệu dụng giữa hai đầu tụ điện đạt giá trị cực đại. Tính giá trị cực đại đó.
4. Tìm mối liên hệ giữa hai tần số tìm được ở câu 2 và 3. Lời giải
1. Tìm để công suất, hiệu điện thế giữa hai đầu điện trở và dòng điện trong mạch đạt giá trị cực đại. U U 2 ; 2 2 R Z Z 2 1 L C R IR I ;P I R R L C U Ta có:
Vì R không đổi nên P U, R lớn nhất khi I lớn nhất. Vậy ta chỉ cần tìm để I lớn nhất là xong. Ta có: U U U U 2 2 2 R Z Z 2 1 R L C I R L C R 1 2 1
I,P, UR đạt giá trị lớn nhất khi 2 1 . Từ này, ta
Đẳng thức xảy ra khi L 0 nên C LC LC 2 1 1 . kí hiệu R LC
2. Tìm để UL đạt cực đại. Tính UL max
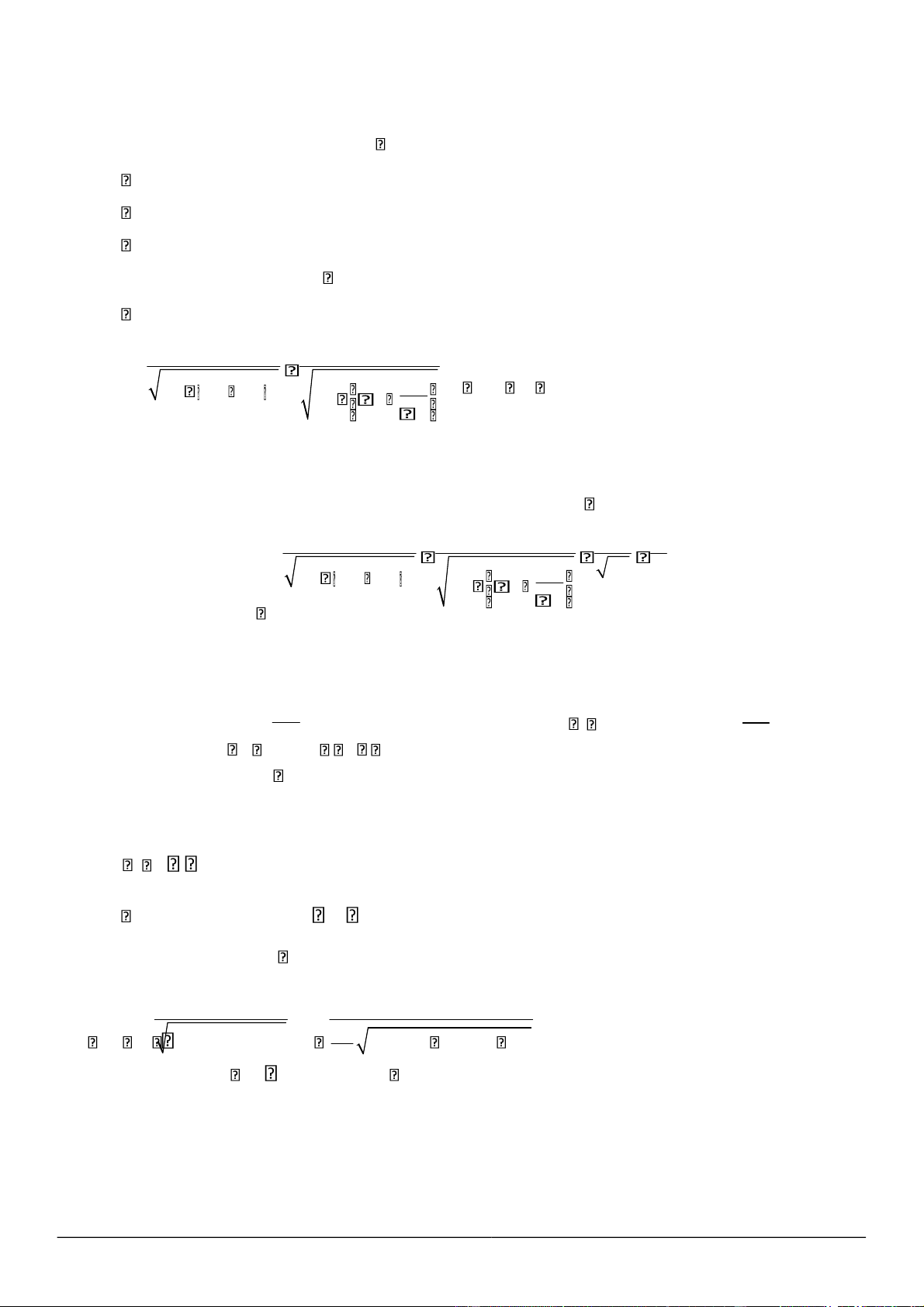
Ta sẽ viết biểu thức UL theo và xem xét khi nào thì UL đạt cực đại. Ta có U U UL IZL R 2 ZL 1 2 ZL2 2Z ZL C ZC2 2 ZL ZC R Trang 1 ZL U U 2 1 2 2 2 1 1 R 2 1 R L 2 L 1 2 2 2 2 2 4 2 2 L C C C LC LC U 2 2 1 1 R 2 1 . . 1 2 2 2 2 2 LC L LC 1 x 2 1 R Đặt y 1 . 2 2 2 1 1 .x2 RL22 LC2 .x 1 L C22 2 L2 LC . 2 1 L C2 2
Ta thấy UL đạt giá trị lớn nhất nếu y đạt giá trị nhỏ nhất. Rõ ràng y là một tam thức bậc hai có hệ số của x2
luôn dương nên y sẽ đạt giá trị nhỏ nhất tại 2 2 2 R 2 L RC 2 2 L RCC 2 2 1 b 2 2 2 2 L RCC L LC LC LC x 2 2 a 1 1 1 2 2. 2. 2. 2 2 2 2 2 2 LC LC LC 2 1 2 L 2 2 L L RCC C 2 L 2 R C 1 2 2 Vậy giá trị của L để U L cực đại là C 2 L 2 R C Tính U L . max R2 2 2 1 R4 2 R2 4 1 L2 LC 4.
Ta có ymin 4 a
4. L C 21 2 L C22 L4 2. LC L4.2 L C 21L C222 4.L C2 2 R4 2 R2
4R L2 R C4 4R LC4 R C42 2. L4 LC L2 L C4 L C42 4R LC2 R C42 1 1 1 4L2 Trang 2 4. L C22 4. L C22 4. L C22 Từ đó suy ra U U 2 UL 2 UL U L max 2 4 2 2 4 2 2 2 ymin 4 RLC RC 4 RLC RC R 4 LC RC 2 4 L 2 UL Vậy UL max 2 2
R 4 LC RC
3. Tìm để UC đạt cực đại. Tính UC max
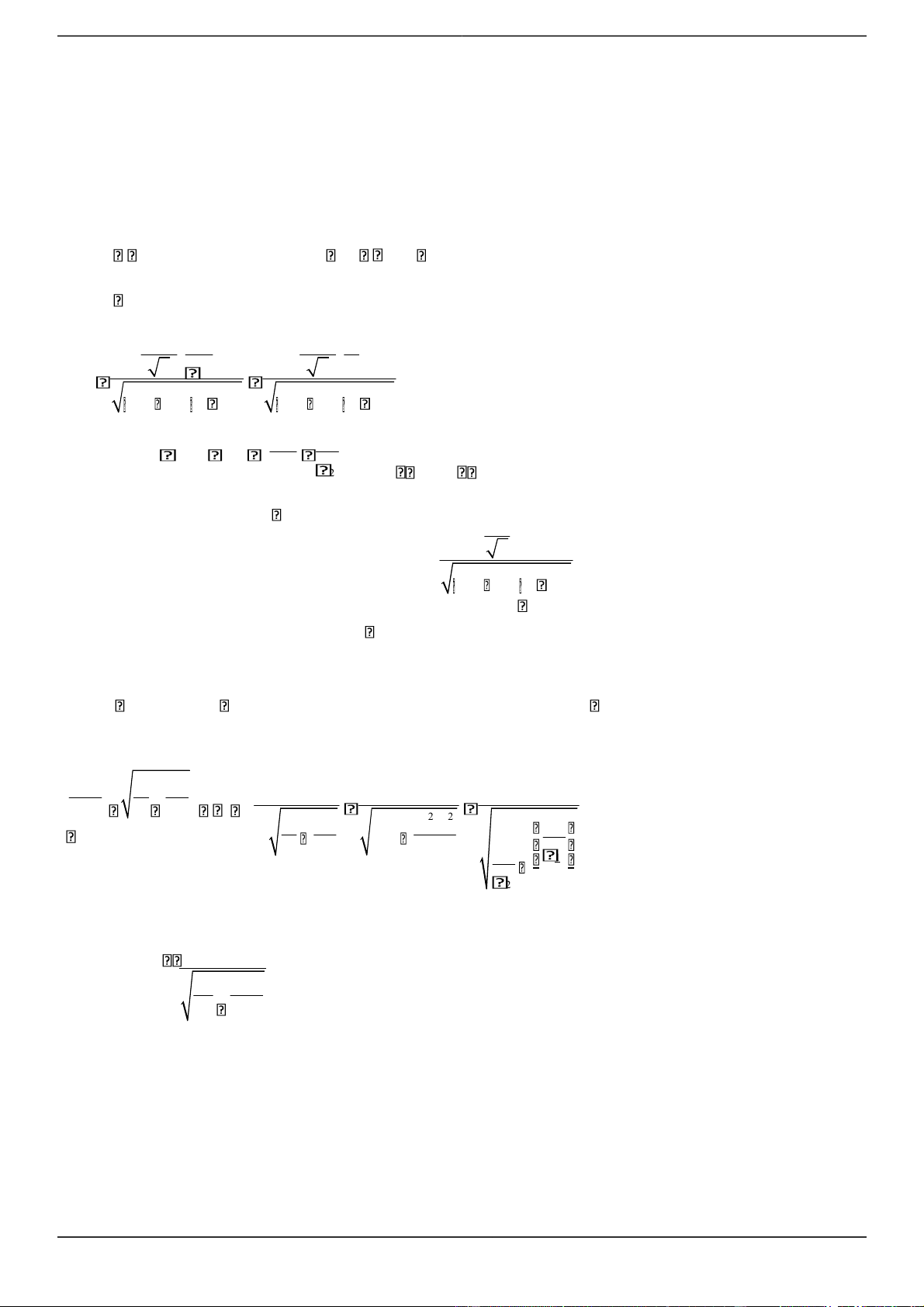
Ta sẽ viết biểu thức UC theo và xem xét khi nào thì UC đạt cực đại. Ta có U U UC IZC R2
ZL ZC 2 ZC 1 ZC
R2 ZL2 2Z ZL C ZC2 U U x 2 2 2 2 2 2 4 2 2 2 2 1 1 RC LC 2 LC 1 C R L 2 L 2 2 C C U 2 2 2 2 2 2 2 LC . RC 2 LC . 1 Đặt 2 2 2 2 R C2 2 2LC 2 1
L C2 2 x2 R C2 2 2LC x 1 y L C
UC đạt giá trị lớn nhất nếu y đạt giá trị nhỏ nhất. Rõ ràng y là một tam thức bậc hai có hệ số của x2 luôn
dương nên y sẽ đạt giá trị nhỏ nhất tại 2L R2 2 2 2 2 2 b RC
2 LC 2 LC RC C x 2 2 2 2 2 2 a 2. LC 2 LC 2 L 2 L 2 2 L 2 R 1 R C . C C 2 2 L L 2 2 L 2 Vậy giá trị của R để U C cực đại là 1 C 3 C L 2
Tính UC max . Ta có ymin 4 a R C22 24LCL C2 22 4L C2 2 Trang 3
R C4 4 4R LC2 3 4L C2 2 4L C2 2 4R LC2 R C4 2 2 2 2 4 LC 4 L U U 2 UL 2 UL U C max 2 4 2 2 4 2 2 2 ymin 4 RLC RC 4 RLC RC R 4 LC RC 2 4 L 2 UL Vậy UC max 2 2
R 4 LC RC
4. Mối liên hệ giữa hai tần số L và C 2 L 2 1 R 2 1 1 . C . . C 2 L 2 L 2 LC R
Từ biểu thức (2) và (3), ta có: C L C 1 2 2 Mà theo (1) ta có
R nên do đó ta có biểu thức liên hệ R L C LC
Ví dụ 2: Cho mạch điện RLC nối tiếp có 2L CR2 , được nối hiệu điện thế xoay chiều có hiệu điện thế
hiệu dụng không đổi nhưng tần số thay đổi được. Tăng dần tần số để hiệu điện thế hiệu dụng giữa hai
đầu mỗi thiết bị UR;UL hoặc UC đạt giá trị cực đại. Hãy chỉ ra thứ tự cực đại của các hiệu điện thế trên
A. UR;UC;UL.
B. UC;UR;UL.
C. U UL; R;UC.
D. UC;U UL; R. Lời giải
Mạch RLC hiệu điện thế hiệu dụng không đổi, thay đổi tần số để hiệu điện thế hiệu dụng UR đạt giá trị 1 lớn nhất thì: R 1 LC
Mạch RLC hiệu điện thế hiệu dụng không đổi, thay đổi tần số để hiệu điện thế hiệu dụng UC đạt giá trị lớn nhất thì: 2 L 2 1 R C L 2 2 C
C LC1 2RL22 LC1
R2 C R 2
Mạch RLC hiệu điện thế hiệu dụng không đổi, thay đổi tần số để hiệu điện thế hiệu dụng U đạt giá trị lớn nhất thì: 2 1 2 2 Trang 4 1 2 L
L C2 2L 2 2LC R C2 2 C 2 L 2 R C 1R R C L2 2 LC
R2 L R 3 2 2 1 RC LC
(Ta cũng có thể dựa theo hệ thức 2
L C R , mà L R C R
Từ (2) và (3) suy ra: C R L . Như vậy khi tăng dần tần số thì thứ tự cực đại của các hiệu điện thế
hiệu dụng là UC,UR,UL. Đáp án B.
Ví dụ 3: Cho mạch điện RLC mắc nối tiếp, cuộn dây thuần cảm có 2L CR2 , hiệu điện thế hai đầu mạch
có giá trị hiệu dụng không đổi nhưng tần số góc thay đổi được. Thay đổi thấy tồn tại L ; C để lần lượt
hiệu điện thế hiệu dụng hai đầu mỗi thiết bị L và C cực đại. Tính hiệu điện thế cực đại (UL)max và (UC)max ? U U
UL max UC max . 2
UL max UC max . 2 A. B. 1 L 1 C 2 2 C L U U 4 4 U 1 C 1 L L max UC max . 4
UL max UC max . 4 L C C. D. Lời giải
Khi thay đổi, hiệu điện thế hai đầu cuộn cảm hoặc tụ điện đạt giá trị lớn nhất. Ta có: 1 2 2 1 2 2 . L L 2 2 2 C 2 L 2 C 2 L 2 2 LC R C R R C C 2 L 2 2 L 2 R R 2 1 C 2 1 2 L C . R C C C 2 2 L 2 L 2 2 L C U.2 L U U L max C max 2 2
R 4 LC R C . Trang 5 2L R C2 C2 1 2L C22
12L2 L C2R C2.2LC 2R C2
2 1 2L 4LR C22 2 Ta có: 1 2 L 2LC R C2 2 2 2 2 2 2 2 2 4 2
4 L 4 L 4LRC RC R 4 LC RC C 1 2 2 2 4 L 4 L L 2 2 2 2
R 4 LC RC R L C 1 2 2 2 1 4 LC RC 2 2 2 2 2 4 L 2 L L R 4 LC 1 RC C 2 L
Nhân hai vế với U ta được 2UL U U L UL max UC max 2 2 2 2 2
R 4LC R C 1 C2 L C L Đáp án B.
Ví dụ 4: Cho mạch điện RLC mắc nối tiếp, cuộn dây thuần cảm có 2L CR2 , hiệu điện thế hai đầu đoạn
mạch có giá trị hiệu dụng không đổi nhưng tần số góc có thể thay đổi được. Thay đổi thấy tồn tại R ;
L để lần lượt hiệu điện thế hiệu dụng hai đầu mỗi thiết bị R, L đạt giá trị lớn nhất. Tính hiệu điện thế lớn nhất UL max ? U U UL 2 max . UL max . 4 A. B. 1 1 R L 2 4 L R U U 4 2 U 1 1 L R L 4 max . UL max . 2 C. D. L R Lời giải 2 1
Khi thay đổi, hiệu điện thế hai đầu dây điện trở cực đại khi R LC
Khi thay đổi, hiệu điện thế hai đầu cuộn cảm cực đại khi Trang 6 1 2 2 1 2 2 L L 2 2 2 C 2 L 2 C 2 L 2 2 LC RC R R C C U.2 L U U L max C max 2 2 .4 R LC RC 1 2 2 2 2 4 2 LC 2 L RC 2 L RC Ta có: R 1 1 1 1 4 2 4 4 4 L L 2 2 2 2 LC RC 4 1 R 2L R C2 4 1 2 2 2 4 4 L 4 L L L 2 4L2 4 2 2
R 4 LC RC 1 2 L 1 R 4L2 4LR C2 R C4 2 4 4 2 2 2 L L R 4 LC RC R 1 4 R2 4LC R L C2 2 2 2 UL U U L U L Nhân cả hai vế với max U ta được: 2 2 4 4 4
R 4 LC RC . 1 R L R 4 L Đáp án C.
Ví dụ 5: Cho mạch điện RLC mắc nối tiếp, cuộn dây thuần cảm có 2L CR2 , hiệu điện thế hai đầu đoạn
mạch có giá trị hiệu dụng không đổi nhưng tần số góc có thể thay đổi được. Thay đổi thấy tồn tại R ;
C để lần lượt hiệu điện thế hiệu dụng hai đầu mỗi thiết bị R, L đạt giá trị lớn nhất. Tính hiệu điện thế lớn nhất UC max ? U U UC 2 max . UC max . 4 A. B. 1 1 R C 2 4 C R U U 4 2 U 1 R 1 C C 4 max . UC max . 2 C R C. D. Trang 7 Lời giải 2 1
Khi thay đổi, hiệu điện thế hai đầu dây điện trở cực đại khi R LC
Khi thay đổi, hiệu điện thế hai đầu tụ điện cực đại khi 2 L 2 2 L 2 R R 2 1 C 2 1 2 L . RC C C C 2 2 L 2 L 2 2 LC U.2 L U C ma x 2 2 .
R 4 LC RC 4 2 2 2 2 4 2 2 2 2 2 LC RC LC 2 L RC 2 L RC Ta có: C 1 1 1 1 4 4 2 2 1 1 4 LC 4 L R 2 LC 2 2 4 2 2 2 4 2 2 2 2 2 L RC
4 L 4 L 4LRC RC
R 4 LC RC C 1 1 4 2 2 2 4 L 4 L 4 L R 4 2 2
R 4 LC RC 1 2 L 1 C 4 4 2 2 2 L R R 4 LC 1 RC C 4 R 2 2 UL U U R U C Nhân cả hai vế với max U ta được: 2 2 4 4 4
R 4 LC RC . 1 C R C 4 R
Chú ý: (Cách của thầy Lê Văn Thành): Ta cũng có thể thiết lập các công thức giải nhanh trong các ví dụ 4
và ví dụ 5 dựa trên kết quả của ví dụ 3 như sau: thay đổi tồn tại C R L để tương ứng các giá trị R C hiệu dụng U 2
C;UR;UL đạt giá trị lớn nhất, ta có: R L C L R2 2 CL RL2 CR2 U U U UL max UC max 2 4 4
Từ kết quả Ví dụ 3, ta có 1 C 1 R4 1 C4 2 L L R Trang 8
Trong các công thức trên để cho không nhầm lẫn thì ta cần hiểu các biểu thức trong căn luôn dương, do
đó tỉ số các tần số góc trong căn luôn nhỏ hơn 1 C22 1; R44 1; C44 1 . L L R
Như vậy tần số góc trên tử phải nhỏ hơn tần số góc dưới mẫu theo đúng tính chất đã chứng minh C22 1; R44 1; C44 1 L L R 0 C L 0
R L C R L 0 C R
Ví dụ 6: Cho mạch điện RLC mắc nối tiếp, cuộn dây thuần cảm có 2L CR2 , hiệu điện thế hai đầu đoạn
mạch có giá trị hiệu dụng không đổi nhưng tần số góc có thể thay đổi được. Thay đổi thấy tồn tại L để
hiệu điện thế hiệu dụng hai đầu cuộn dây đạt giá trị lớn nhất. Tìm mối liên hệ giữa độ lệch pha của cường
độ dòng điện với hiệu điện thế hai đầu mạch và hiệu điện thế uRC . 1
B. tan RC tan 1. A. tan 2 RC tan .
C. tan RC tan 2. D. tan RC tan . Lời giải
thay đổi, hiệu điện thế hai đầu cuộn cảm cực đại khi: 1 2 1 2 C 2 L 2 C 2L R L L 2 R C C L 1 L Z Z Z 1 L C . C 2 Z Z 2 L C R2 tan .tan RC 1. ZC 2 R R 2
Như vậy: thay đổi, khi UL max thì tan .tan RC . Đáp án D.
Ví dụ 7: Cho mạch điện RLC mắc nối tiếp, cuộn dây thuần cảm có 2L CR2 , hiệu điện thế hai đầu đoạn
mạch có giá trị hiệu dụng không đổi nhưng tần số góc có thể thay đổi được. Thay đổi thấy tồn tại C để
hiệu điện thế hiệu dụng hai đầu tụ điện đạt giá trị lớn nhất. Tìm mối liên hệ giữa độ lệch pha của cường độ
dòng điện với hiệu điện thế hai đầu mạch và hiệu điện thế uRL . 1
B. tan RL.tan 1. A. tan 2 RL.tan . Trang 9
C. tan RL.tan 2. D. tan RL.tan . Lời giải
thay đổi, hiệu điện thế hai đầu cuộn cảm cực đại khi: 2 L 2 L C 2 2 R 1 R C C C C CL L 2 2 2 R Z 1 C . L 2 Z 2 L Z ZL C ZL Z tan .tan RL 1 2 R R 2
Như vậy: thay đổi, khi UC max thì
Đáp án D. Ví dụ 8: Cho mạch điện RLC mắc nối tiếp, cuộn dây thuần cảm có 2L CR2 , hiệu
điện thế hai đầu đoạn mạch có giá trị hiệu dụng không đổi nhưng tần số góc có thể thay đổi được. Thay đổi thấy rằng khi 1 hoặc
2 thì hiệu điện thế hiệu dụng hai đầu cuộn cảm có giá trị bằng nhau. Hỏi thay đổi tần số
góc bằng bao nhiêu thì hiệu điện thế hiệu dụng hai đầu cuộn cảm đạt giá trị lớn nhất? A. 2 2 2 . B. 1 11 1 2 2 12. 12 22 . 1 1 1 1 2 2 2. C. 2 2 12 22 . D. 1 2 Lời giải U Ta có: UL ZL R2 ZL ZC 2 UUL
2 R2 ZL2 ZZL2C2 2Z ZL C 2 U R2 ZC 2 Z U 2 R2 1 1 U
Z 2 1 ZL 2 ZCL UL 2L2 1 L C2 2 4 2 LC 2 L L 1 1 R2 2 1 U 2 2 2 . 4 L2 LC . 2 1 U L 0 L C 1 Trang 10
Đây là một phương trình bậc 2 theo biến 2 , theo định lí Viet ta có R2 2 b
x1 x2 a L2 1 LC 2LC R C2 2 2. 12 L C22 LC R C2 2 1 1 1 1 1 1 1 2 2 2 2 2 2 12 22 12 L L
Đáp án C. Ví dụ 9: Cho mạch điện RLC mắc nối tiếp, cuộn dây thuần cảm có 2L CR2 , hiệu
điện thế hai đầu đoạn mạch có giá trị hiệu dụng không đổi nhưng tần số góc có thể thay đổi được. Thay đổi thấy rằng khi 1 hoặc
2 thì hiệu điện thế hiệu dụng hai đầu tụ điện có giá trị bằng nhau. Hỏi thay đổi tần số góc
bằng bao nhiêu thì hiệu điện thế hiệu dụng hai đầu tụ điện đạt giá trị lớn nhất? 1 1 1 1 B. 2 A. 2 2 2 . . 12 22 . 1 2 2 1 1 1 1 C. 2 1 2 2 2 2 . D. 2 12 22. Lời giải Ta có: UC ZC
R2 UZ Z 2 UUC
2 R2 ZL2 ZZC2C2 2Z ZL C L C 2 1 U U ZR22 ZZCL 2 2 ZZCL UUC 2 R C22 2 1 L C2 2 4 2LC 2 C C 2 L C2 2. 4
R C22 2LC . 2 1 U UC 0
Đây là một phương trình bậc 2 theo biến , theo định lí Viet ta có
R C2 2 2LC 2 R2 1 2 R2 x1 x2 L C 2. 2 2 LC L2 2 LC L2 Trang 11 2 2
2 C2 C2 12 12 22 1 2 Đáp án B.
Ví dụ 10: Cho mạch điện gồm điện trở thuần R, cuộn dây thuần cảm L và tụ điện C mắc theo thứ tự
L R C , M nằm giữa L và R, N nằm giữa R và C. Đặt vào hai đầu AB một điện áp xoay chiều có biểu
thức: uAB U 2 cos t V , tần số góc thay đổi được. Khi 1 thì điện áp giữa hai đầu các đoạn mạch
AN và MB vuông pha với nhau. Khi đó UAN 50 5 V ;UMB 100 5 V và mạch tiêu thụ công suất P
50W . Khi thay đổi tần số góc đến giá trị 2 100 2 (rad/s) thì điện áp hiệu dụng giữa hai đầu cuộn
dây đạt giá trị cực đại. Giá trị của 1 là A. 1 100 rad s/ . B. 1 120 rad s/ .
C. 1 50 rad s/ .
D. 1 60 rad s/ . Lời giải
Khi 1 thì điện áp giữa hai đầu các đoạn mạch AN và MB vuông pha với nhau nên ta có 1 1 1
UR2 UAN2 UMB2 UR 100 V U
AN 50 5 UR2 UL21 U L1 50 V Mặt khác
UMB 100 5 UR2 UC21 U C1 200 V U UR2 UL 1 UC1 2 50 13 U R2
Mà công suất P 50W nên ta có P 2 ZL ZC 2 50 R R2 ZL 1 ZC1 2 ZL1 ZC1 650 650 1 R R R 1 L1 C 2 1 R R 200 UR Trang 12 1 U U 650 U 1 L 100 1 1L 40000 Z C
Từ đó suy ra I RR 2 A ZC1 400 11C C 4001 1 1 1 Khi 2 100 2 thì ta có 2 L R2 2 C C 2
Từ (1) và (2) và giá trị của R, thay vào ta được 2 2 2 1 1 50 (rad/s). Đáp án C.
Ví dụ 11: Cho đoạn mạch RLC nối tiếp (cuộn dây thuần cảm với CR2 2L . Đặt vào hai đầu đoạn mạch
điện áp u U0 cos t (V) với thay đổi được. Điều chỉnh để điện áp hiệu dụng giữa hai bản tụ đạt cực đại,
khi đó điện áp hiệu dụng trên điện trở gấp 5 lần điện áp hiệu dụng trên cuộn dây. Hệ số công suất của đoạn mạch đó là: 5 2 5 3 A. 31. B. 29. C. 29. D. 19. Lời giải
Điều chỉnh để điện áp hiệu dụng giữa hai bản tụ đạt cực đại ta có L R2 C 2 ZL .
Mặt khác UR 5UL 2 2 2 2 L R R L R 27 R 27 R 5 Z R 5 . ZZ Z R L C 2 LC C 25 C 2 50 10 R R 2 cos Hệ số công suất: 2 2 25 29 R Z Z L C 2 2 R R 4 Đáp án B.
Ví dụ 12: Một máy phát điện xoay chiều một pha có roto là một nam châm điện có một cặp cực, quay đều
với tốc độ n (vòng/s). Một đoạn mạch RLC nối tiếp được mắc vào hai cực của máy. Khi roto quay với tốc
độ n1 60 (vòng/phút) thì dung kháng của tụ điện bằng R; khi roto quay với tốc độ n2 80 Trang 13
(vòng/phút) thì điện áp hiệu dụng ở hai đầu tụ điện đạt giá trị cực đại. Bỏ qua điện trở thuần ở các cuộn dây
phần ứng máy phát. Để cường độ dòng điện hiệu dụng qua mạch đạt giá trị cực đại thì roto phải quay với tốc độ bằng A. 240 vòng/phút. B. 120 vòng/phút. C. 48 vòng/phút. D. 68 vòng/phút. Lời giải
Khi n n1 60 (vòng/phút) ta có R ZC1 1RC 1.
Khi n n2 ta có hiệu điện thế hiệu dụng giữa hai đầu tụ C là 1 2 C 2 C UC 2 2 2 2 Z Z R Z Z R L C L C 1 1 Từ đó UC Z Z . max L C 2 LC 2 0 . 1 0 . 0 2 2 2 Z Z R L C . Cường
độ dòng điện hiệu dụng trong mạch là I
Khi n n3 , thay đổi để Imax trong trường hợp này tương tự thay đổi để UL trong mạch RLC mắc nối max
tiếp. Khi đó ta có kết quả 1 L R2 1 1 1 3 2 2 2 L R RC 1 C 3C C 2 LC 2 C 2 2 1 1 2 2 2 1 n3 240 Vậy ta có 1 1 (vòng/phút). n22 2.n12 Đáp án A.
Ví dụ 13: Lần lượt đặt các điện áp xoay chiều u u1, 2 và u3 có cùng giá trị hiệu dụng nhưng tần số khác nhau
vào hai đầu một đoạn mạch có R, L, C nối tiếp thì cường độ dòng điện trong mạch tương ứng là: Trang 14
i1 I 2 cos 150 t 3 , i2 I 2 cos 2000 t 3
và i3 I cos 100 t 3 . Phát biểu nào sau đây đúng?
A. i2 sớm pha so với u2 .
B. i3 sớm pha so với u3 .
C. i1 trễ pha so với u1 .
D. i1 cùng pha với i2 . Lời giải
- Ta thấy khi 1 150 hoặc 1 200 thì cường độ hiệu dụng là như nhau, bằng I nên phương trình sau có hai nghiệm 2 2 U 2L2 2CL 21C2 R2 UI 2 0 R Z Z L C I 4 2 L 2 U C L I 2 2 1 0 C2 2 2 1 1 2
- Theo định lí Viet, ta có 1 2 L C2 2 1 2 LC 0
- Trong đó 0 là giá trị để cường độ hiệu dụng đạt giá trị cực đại, có giá trị là 0 1. 2 150 .200 173 2
1 ZL3 ZC3 tan 3 ZL3 ZC3 0 3 0. - Từ đó ta có 3 0 3 LC R
- Vậy i3 sớm pha hơn so với u3 . Đáp án B.
Ví dụ 14: Đặt điện áp u U 2 cos2 ft (f thay đổi được, U tỉ lệ thuận với f ) vào hai đầu đoạn mạch AB gồm
đoạn mạch AM mắc nối tiếp với đoạn mạch MB. Đoạn mạch AM gồm điện trở thuần R mắc nối tiếp với tụ
điện có điện dung C, đoạn mạch MB chỉ có cuộn cảm thuần có độ tự cảm L. Biết 2L R C2 . Khi f 60 Hz
hoặc f 90 Hz thì cường độ dòng điện hiệu dụng trong mạch có cùng giá trị. Khi f 30 Hz hoặc f 120 Hz Trang 15
thì điện áp hiệu dụng hai đầu tụ điện có cùng giá trị. Khi f f1 thì điện áp ở hai đầu đoạn mạch MB lệch pha
một góc 135 so với điện áp ở hai đầu đoạn mạch AM. Giá trị của f1 bằng A. 60 Hz. B. 80 Hz. C. 50 Hz. D. 120 Hz. Lời giải
- Vì U tỉ lệ thuận với f nên u giống với u của máy phát điện xoay chiều 1 pha.
- Hai giá trị của tần số f2 và f3 cho cùng I, nên ta có: I 2 2 2 1 2 1 R L R L C C 2 2 2 2 1 k 2 1 1 L R 1 2 k R . L 2 . L 0 2 2 4 2 C I C C 2 I U k 1 1 2
Theo Viet, ta có 2 2 2LC RC . 1 2 3 1 1 1 - C
Hai giá trị của tần số f4 và f5 cho cùng UC , ta có: UC U C k C Z Z Z
Nhận xét rằng tử số không thay đổi khi thay đổi. Như vậy, bài toán “Mạch RLC có U tỉ lệ thuận với f, khi
thay đổi f thấy có 2 giá trị của f làm cho UC như nhau” giống với bài toán: “Mạch RLC có U không 1
đổi, khi thay đổi f thấy có 2 giá trị của f làm cho UR như nhau”, ta có ngay kết quả: 4 5 2 LC
Khi f f1 ta có uAM trễ pha 135 so với uMB , mà uR trễ pha 90 so với uMB , nên UR sớm pha 45 so với uAM .
Tức là cường độ dòng điện sớm pha 45 so với uAM . ZC1 ZC1 R hay 1 1
Ta có tan AM tan 45 R , nên suy ra RC Trang 16 1 2 1 1 - Tha
y (2) vào (1) ta rút được RC 2 2 1 4 5 3 1 f 80, 1 5 - Từ đó suy r a 2 1 1 Hz. 2 2 ff f 4 f 5 2 3 Đáp án B.
IX. BÀI TOÁN VỀ MÁY BIẾN ÁP, TRUYỀN TẢI ĐIỆN NĂNG 1. Phương pháp
Bạn đọc xem lại phần lí thuyết về máy biến áp và truyền tải điện năng. Phần bài tập truyền tải điện năng
có thể tham khảo thêm phương pháp chuẩn hóa đã trình bày. 2. Ví dụ minh họa
2.1. Bài toán về máy phát điện
Ví dụ 1: Khi máy phát điện xoay chiều một pha đang hoạt động bình thường và tạo ra hai suất điện động
có cùng tần số f . Roto của máy thứ nhất có p1 cặp cực và quay với tốc độ n1 1800 vòng/phút. Roto của
máy thứ hai có p2 4 cặp cực và quay với tốc độ n2 . Biết n2 có giá trị trong khoảng từ 12 vòng/giây đến
18 vòng/giây. Giá trị của f là A. 54 Hz. B. 60 Hz. C. 48 Hz. D. 50 Hz. Lời giải
Khi máy phát điện xoay chiều một pha đang hoạt động bình thường và tạo ra hai suất điện động có cùng
tần số f nên ta có f n p1 1 n p2 2
.p1 n2.4 n2 7,5p1
Vì 12 n2 18 nên 12 7,5p1 18 1,6 p1 2,4 p1 2.
Từ đó suy ra tần số cần tìm là f .2 60Hz. Đáp án B.
Ví dụ 2: Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch A, B mắc nối tiếp
gồm điện trở f, cuộn cảm có độ tự cảm L và tụ điện có điện dung 176,8 F . Bỏ qua điện trở thuần của các
cuộn dây của máy phát. Biết roto máy phát có hai cặp cực. Khi roto quay đều với tốc độ n1 1350 vòng/phút
hoặc n2 1800 vòng/phút thì công suất tiêu thụ của đoạn mạch AB là như nhau. Độ
tự cảm L có giá trị gần giá trị nào nhất sau đây? A. 0,7 H. B. 0,8 H. C. 0,6 H. D. 0,2 H. Lời giải
Công suất tiêu thụ như nhau thì cường độ hiệu dụng cũng như nhau. Trang 17




