CÁC DẠNG BÀI TẬP VỀ TÍCH PHÂN KÉP 1. Các tính chất. 
 fx, y gx, y dxdy fx, ydxdygx, ydxdy .  D D D
  k . fx, ydxdy k . fx, ydxdy . D D
 Nếu D D1 D2 với D1 và D2 không có điểm chung thì :
 fx , ydxdy fx , ydxdy fx , ydxdy . D D1 D2
2. Các tính chất tích phân kép trong tọa độ đề-các.        Trường hợp 1:
: a  b, c z D M x, y x y d và f
x, y liên tục trên D thì:    b d   b d    
f x, y dxdy   dx. f  x, y dy f x, y  dy dx (1) . D a c a c   d b d b    dxdy      Hoặc: f x, y    f   f x, y  dy. x, y dx dx dy (2) . c D c a a  d   
*) Chú ý :-Trong biểu thức (1) khi tính f
x , y dy thì ta coi x là hằng số. c b   
- Trong biểu thức (2) khi tính
f x , y dx thì ta coi y là hằng số. a
fx, y gx.hyvà D : a x b,c - Nếu y d thì:  b d  
dxdy       f x , y  g x dx. h y dy  D a c Phương  Trườ pháp:
ng hợp 2: DMx, y: a x b, y1x y y2xvà x
xu,v z  Bước 1:
 fx, y Đặt x y  y y  
u,v. b 2      
b  y2 x      dxdy x, y  f x, y  dx. f dy 
f x, y dydx (3) 1    1    D a y x a y x 
 Trường hợp 3: DMx, y: x1y x x2y, c y dvà
z fx, y   x   d 2 y    
d  x2  y      dxdy x, y  f x, y  dy. f dx 
f x, y dxdy (4) 1     1   D c x y c x y 
3. Đổi biến số trong hệ đề-các. liên tục trên D thì: liên tục trên D thì:  x' x'  Bước 2: Tính u v dxdy J du.dv J y' y'  u v  D ' Bước 3: Xác định
x , y D u ,v .
 Bước 4: Tính I fxu , v, J dudv.
yu , v. D'
4. Tích phân trong tọa độ cực.
DÊu hiÖu nhËn biÕt: fx, ydxdy mà D chứa biểu thức: x x 2 y 2 2 y2 ;  . a 2 b 2 D  Phương pháp:
x r cos  Đặt:  x ' x ' y Tính: r 
 cos r sin ' 
r dxdy rdr .d . y ' J r sin r cos    Xác định D '
x , y D r, .
 Tính I fr cos , r sin.rdrd. D'
 Trường hợp 1: Gốc cực O nằm ngoài miền D.
Xác định hai tia xuất phát từ O giới hạn miền (D). Giả sử là: 1, 2
12suy ra cận : 12 Thay x 
 r cos vào biên D. y   r sin
 r r1 , r
r1 r2 . r2suy
ta cận r: r1 r r2.    1 2 Vậy: D ' : (Tính theo r
r1 r r2   trước, sau).
Trường hợp 2: Gốc cực O nằm trong miền D. Luôn có:  02.  x Thay 
   r cos vào biên D r r. Khi đó: 0 r r  y r sin 02   Vậy D ' : . 0   r 
 Trường hợp 3: Gốc cực O nằm trên biên của miền D.
Xác định hai tia xuất phát từ O giới hạn miền (D). Giả sử là:
 1 ,212suy ra cận : 12 x
Thay  r cos vào biên D y   r sin 
Vậy: D ' : 12 r  0  0 r
0 r r  r   r  r 
BÀI TẬP TÍCH PHÂN KÉP
(Lưu ý: Tài liệu đã cho chưa được thẩm định nên có phần chưa chính xác hoàn toàn) y
Tính các tích phân kép: y = x2
Cho x2 = 2 – x để xác định giao điểm của hai đường: x1= 2 x = y = x 2và y = 2 – x 2 x
x2 + x = 0 có 2 nghiệm: x1 = 1 và x2 = – 2 y= Vậy:
Vì đường y = 2 – x nằm trên đường y = x2
Tính tích phân theo y, coi x như hằng số:
Để cho “dễ nhìn, quen mặt”, ta đặt x = y
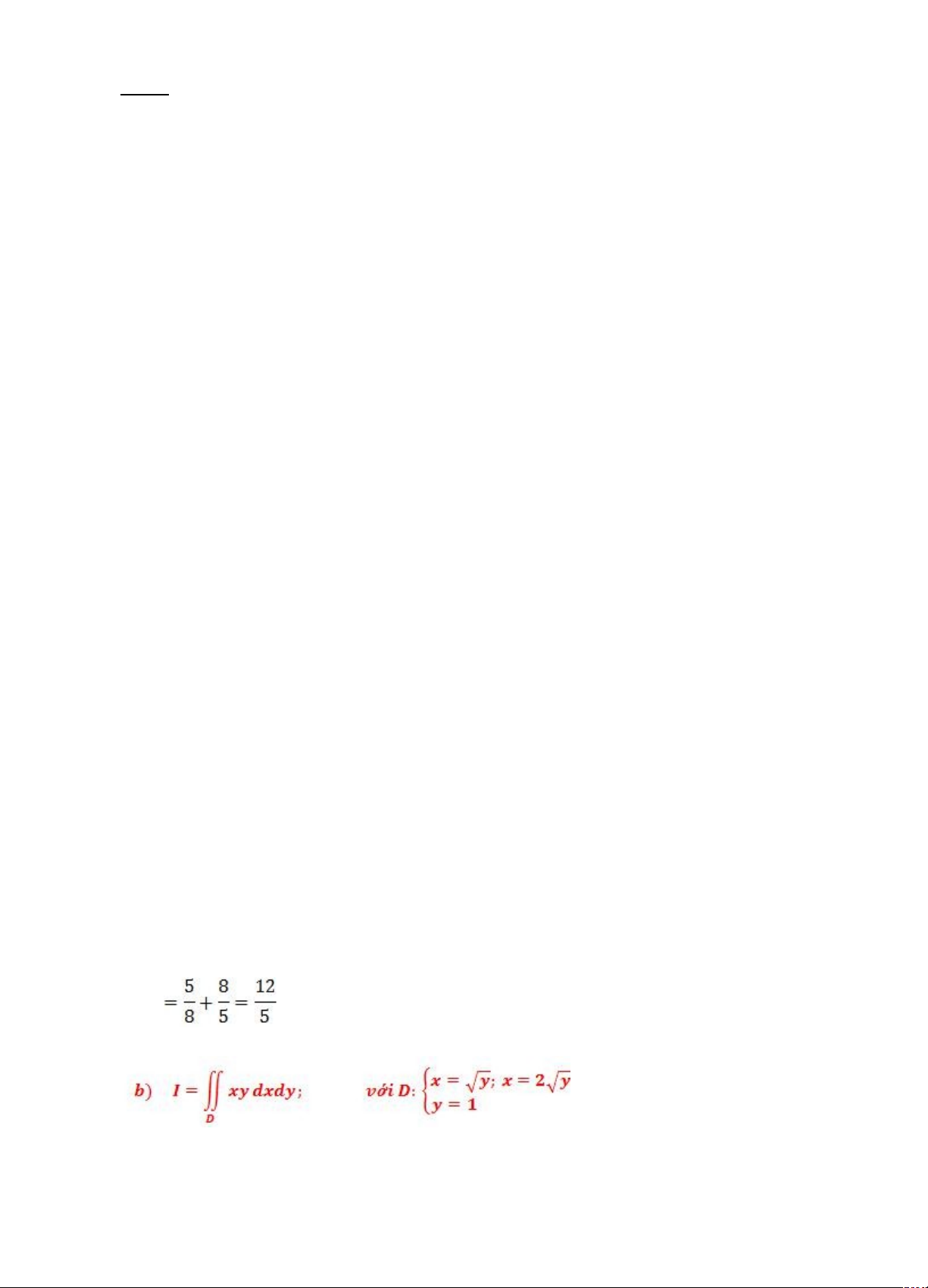
Bài tập Tích phân kép dx = dy. y=2 Tích phân I không đổi. 2 Vẽ : y= x = 0, y = 0; 1 x = 1, y = 1; x = 4, y = 2. x Vẽ 4 x = 1 Vậy: D: nên: y= đổi trục tọa độ: x = rcos y = rsin 1 r2cos2 + r2sin2 1 r2(cos2 + sin2 1 r2 ((cos2 + sin2 y = 12 r2 22 1 r x y
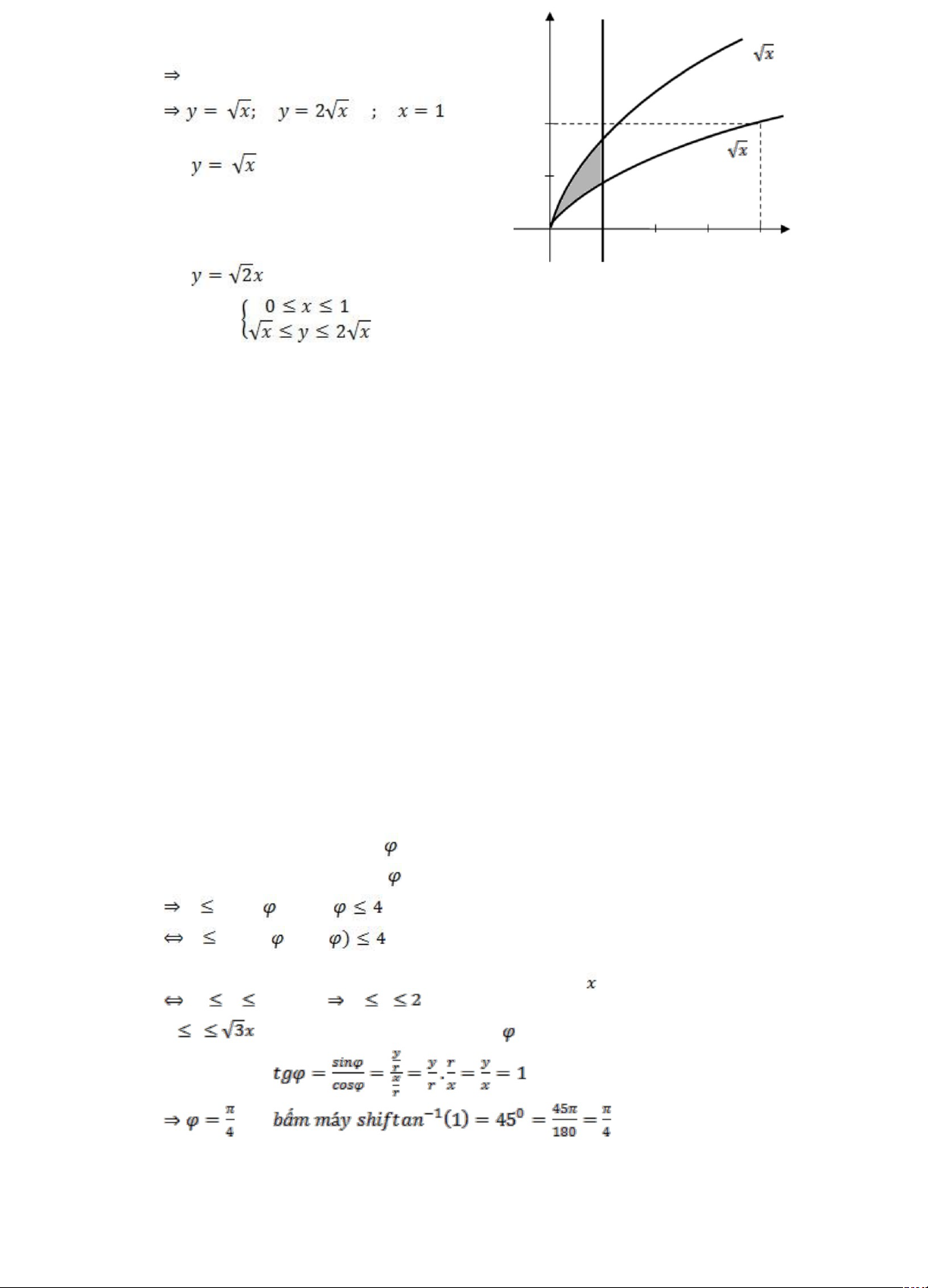
lấy dấu = để tính 2 con x = y ; (vì x = y) y = ; Bấm máy y sai đặt: x – 1 = rcos r2cos2 + r2sin2 =12 x đúng y = rsin r2 =12 vậy: vì y (vì r không âm) (thì sin y x Trang 3 Xét: Đặt lại: x = rcos y = rsin r2 =2rcos r = 2cos Đổi biến: D: y x2 + y2 r2 r2 22 Nhìn vào hình: x hay y = x 2y =
(a) Đường tròn tâm I(0, 1) bán kính r = 1. y y = x (b) Đường
tròn tâm I1(0, 2) bán kính r1 = 2. (a) (b) 1 2 x Kết hợp: y x cận dưới x 0 cận trên Xét