10 trang 107 lượt tải

Tổng hợp công thức giải nhanh Oxyz - Tài liệu tổng hợp

214

Tổng hợp công thức giải nhanh Oxyz - Tài liệu tổng hợp. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !

Môn: Tài liệu Tổng hợp 2.3 K tài liệu

Trường: Tài liệu khác 2.5 K tài liệu

Tác giả:

Phạm Thị Huyền

5 tháng trước

Danh sách Quiz

Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/

_________________________________________________________________________________________________________________________________________________________________________________________________________________

Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 1

Tài liệu này tóm tắt các công thức, phương pháp giải nhanh Oxyz thầy Đức biên soạn cho

học sinh của khóa học.

Tọa độ điểm thuộc trục tọa độ, các mặt phẳng tọa độ

Xét điểm





; ; .

M M M

M x y z







;0;0 ;

M Ox M x 







0; ;0 ;

M Oy M y 







0;0; .

M Oz M z

 











; ;0 ;

M M

M Oxy M x y 











0; ; ;

M M

M Oyz M y z

 











;0; .

M M

M Ozx M x z

 

2. Điểm đối xứng với 1 điểm qua trục tọa độ, mặt phẳng tọa độ

Xét điểm





; ; .

M M M

M x y z

Điểm



đối xứng với

qua:

Trục





; ; .

M M M

Ox M x y z



  

Trục





; ;

M M M

Oy M x y z



  

Trục





; ; .

M M M

Oz M x y z



  











; ;

M M M

Oxy M x y z



 











; ;

M M M

Oyz M x y z



 











; ;

M M M

Ozx M x y z



 

Hình chiếu của 1 điểm lên các trục tọa độ

Xét





; ; .

M M M

M x y z

Chiếu lên





: ;0;0 .

x M

Ox M x

Chiếu lên





: 0; ;0 .

y M

Oy M y

Chiếu lên





: 0;0; .

z M

Oz M z

4. Hình chiếu của 1 điểm lên các mặt phẳng tọa độ

Xét





; ; .

M M M

M x y z

Chiếu lên









: 0; ; .

M M

Oyz M y z



Chiếu lên









: ; ;0 .

M M

Oxy M x y



Chiếu lên





Ozx





;0; .

M M

M x z



5. Khoảng cách 1 từ 1 điểm lên các mặt phẳng tọa độ

Xét





; ; .

M M M

M x y z











;

d M Oxy z













;

d M Oyz x













;

d M Ozx y



6. Khoảng cách từ 1 điểm tới các trục tọa độ

Xét





; ; .

M M M

M x y z



 

2 2

; ;

M M

d M Ox y z

 



 

2 2

; ;

M M

d M Oy z x

 



 

2 2

; .

M M

d M Oz x y

 

Ba điểm thẳng hàng

Xét 3 điểm

, ,

A B C

đã biết tọa độ.



, ,

A B C

thẳng hàng khi và chỉ khi

Cách 1. Tồn tại





để

AB k AC



 

Cách 2. Tồn tại

,p q





để

IA pIB qIC

p q



 





 





  

Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/

Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 2

8. Tích có hướng của hai vectơ

 Định nghĩa

Cho hai vectơ





1 1 1

, ,

u x y z





và





2 2 2

, , .

v x y z





Tích có hướng của hai vectơ



và



là một vectơ, được kí

hiệu:





u v

 

và được xác định:

 

1 1 1 1 1 1

2 2 2 2 2 2

, ; ; .

y z z x x y

u v

y z z x x y

 



 

 

 



ính ch

ấ



át bi

ể







 

u v u

u v v















  

Tích có hướng của hai vectơ vuông góc với các vectơ thành phần











, ,

u v v u

 

   

Khi ta đổi thứ tự hai vectơ, ta được vectơ đối











, . .sin , .

u v u v u v



     

Độ dài của vectơ tích có hướng















, , ,

u v u mv v u v ku

   

       

, .

m k

 



Nếu thay



bởi

u kv



 

giá trị tích có hướng không đổi.

9. Hai vectơ cùng phương

Xét hai vectơ









; ; , , , .

u a b c v a b c

  

 

 

Hai vectơ này cùng phương khi và chỉ khi



k u kv

  

 



; ;

a ka b kb c kc

  

   







, 0.

u v





 

 Hệ quả:

, ,

A B C

thẳng hàng

, 0.

AB AC

 

 

 

  

10.

Ba vectơ đồng phẳng – tích hỗn tạp

 Ba vectơ

, ,

u v w

  

đồng phẳng khi và chỉ khi





, . 0

u v w



  

 Hệ quả:

Cho 4 điểm

, , ,

A B C D

, xét

, . .

k AB AC AD

 



 

  

Nếu



thì

, , ,

A B C D

đồng phẳng

Nếu



thì

, , ,

A B C D

không đồng phẳng

11. Tọa độ trung điểm

 Cho





; ;

A A A

A x y z

và





; ; .

B B B

B x y z

Trung điểm

của

; ; .

2 2 2

A B A B A B

x x y y z z

  

 

 

 

12.

Tọa độ trọng tâm



m gi

ác



ứ

ệ

; ;

3 3 3

A B C A B C A B C

x x x y y y z z z

     

 

 

 

A B C D

x x x x

y y y y

z z z z

  







  









  









13. Tìm tọa độ trực tâm H

Cho

ABC



đã biết tọa độ 3 đỉnh

, , .

A B C

. 0

. 0 .

, , ,

, . 0

BH AC

CH AB CH AB

A B C H dong phang

AB AC AH











 

  

 

 

 







 



 

  

14. Tọa độ tâm đường tròn ngoại tiếp I.

Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/

Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 3

Cho

ABC



đã biết tọa độ 3 đỉnh

, , .

A B C

2 2 2 2

, , ,

, . 0

IA IB IA IB

IA IC IA IC

A B C I dong phang

AB AC AI



 



  

 

 

 







 



  

15. Tọa độ chân đường phân giác trong của một góc trong tam giác

Cho

ABC



phân giác trong





AD D BC





DB AB

DC AC

 

chia

theo tỉ số

 



; ;

1 1 1

B C B C B C

x kx y ky z kz

k k k

  

 

 

  

 

(

B kC







16. Tâm tỉ cự hệ 3 điểm

 Cho 3 điểm

, ,

A B C

đã biết tọa độ và bộ 3

số thực

, ,

a b c

thỏa mãn

a b c

  

Xét điểm

thỏa mãn

aIA bIB cIC

  

   

(Điểm I gọi là tâm tỉ cực của hệ 3 điểm A, B,

C ứng với bộ 3 số a, b, c).

 Tọa độ điểm

A B C

ax bx cx

a b c

ay by cy

a b c

az bz cz

a b c

 







 



 







 



 







 



(Nhớ:

aA bB cC

a b c

 



 

)

Với 1 điểm

bất kì







aMA bMB cMC a b c MI

    

   



 

2 2 2

2 2 2 2

aMA bMB cMC

aIA bIB cIC a b c MI

 

     

17.

Tọa độ tâm đường tròn nội tiếp J

 Cho

ABC



đã biết tọa độ 3 đỉnh, gọi

là

tâm đường tròn nội tiếp

ABC



aA bB cC

a b c

 



 

(với

; ;

a BC b CA c AB

  

)

Ta có:

A B C

ax bx cx

a b c

 



 

;

A B C

ay by cy

a b c

 



 

;

A B C

az bz cz

a b c

 



 

18. Diện tích hình bình hành

 Xét hình bình hành

ABCD



S AB AD

 



 

 

 Hệ quả (diện tích tam giác): Cho

ABC



khi đó

, .

ABC

S AB AC

 



 

 

19.

Thể tích của khối hộp

Cho khối hộp

. .

ABCD A B C D

   

Khi đó



, .

V AB AD AA

 





 

  

Hệ quả (thể tích tứ diện): Cho tứ diện

ABCD

khi đó

, . .

ABCD

V AB AC AD

 



 

  

20.

Tính bán kính đường tròn ngoại tiếp tam giác

Cho

ABC



đã biết tọa độ 3 điểm



. . . .

2 ,

ABC

AB BC CA AB BC CA

AB AC

 

 

 

 

21.

Phương trình các mặt phẳng tọa độ





: 0

Oxy z







: 0

Oyz x







: 0

Ozx y



Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/

Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 4

22. Phương trình mặt phẳng chứa các trục tọa độ

Chứa

by cz

 





2 2

b c

 

Chứa





2 2

0 0

ax cz a c

   

Chứa





2 2

0 0

ax by a b

   

23. Phương trình mặt chắn

Cho





 

;0;0

0; ;0

0;0;

A a Ox

B b Oy

C c Oz





















abc



Phương trình mặt phẳng





ABC

x y z

a b c

  

24.

Tìm tọa độ 1 điểm thuộc đường thẳng, mặt phẳng

 Đường thẳng

x x at

d y y bt

z z ct

 





 





 



 Mặt phẳng





: 0.

P ax by cz d

   

 Lấy

t t



bất kì, ta có





0 0 0 0 0 0

; ;

M x at y bt z ct

  

 Gọi









; ; ,

M M M

M x y z P

 khi đó

M M M

ax by cz d

   

Chọn

M M

x y

bất kì để tìm

Từ đó tìm được tọa độ điểm

25. Tìm tọa độ 1 điểm thuộc giao tuyến của hai mặt phẳng

 Xét





 

: 0

P ax by cz d

Q a x b y c z d

   





   

   





 Nếu





 

M P

M Q













thì

M M M

ax by cz d

a x b y c z d

   





   

   



 Cho

bất kì, giải hệ tìm

và

26.

Phương trình đường giao tuyến của 2 mặt phẳng

 Qua điểm:





 

M P

M Q













 Vectơ chỉ phương:





1 2

u n n



  

27. Tìm giao điểm của đường thẳng và mặt phẳng

 Đường thẳng:

: ;

x x at

d y y bt

z z ct

 





 





 



 Mặt phẳng





: 0.

P Ax By Cz D

   

 Vì





0 0 0

; ;

M d M x at y bt z ct

    







     

0 0 0

M P

A x at B y bt C z ct D



       

 Tìm được

(nên dùng CASIO), sau đó tìm

28. Tìm giao điểm của đường thẳng và mặt cầu

 Đường thẳng:

: ;

x x at

d y y bt

z z ct

 





 





 



 Mặt cầu

       

2 2 2

S x A y B z C R

     

 Vì





0 0 0

; ;

M d M x at y bt z ct

    







     

2 2 2

0 0 0

M S

x at A y bt B z ct C R

 

        

 Từ đó tìm được



tìm được

29.

Khoảng cách từ 1 điểm tới 1 mặt phẳng

 Cho điểm





; ;

M M M

M x y z

 Mặt phẳng





: 0.

P ax by cz d

   



 

2 2 2

; .

M M M

ax by cz d

d M P

a b c

  



 

30. Khoảng cách từ 1 điểm tới 1 đường thẳng

 Cho điểm





; ;

M M M

M x y z



 

; .

u MM

d M

 



 

 





Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/

Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 5

 Đường thẳng





 

0 0 0

; ;

: .

: ; ;

Qua M x y z

VTCP u a b c



















31. Khoảng cách giữa hai đường thẳng chéo nhau

 Cho

: ; : .

: :

Qua M Qua M

VTCP u VTCP u



 



 

 



 

 



 





, .

u u MM

u u

 



  





 

32.

Khoảng cách giữa hai mặt phẳng song song

 Cho





 

: 0

P ax by cz d

Q ax by cz d

   









   







   

 

2 2 2

, .

d d

d P Q

a b c







 

33. Vị trí tương đối của hai mặt phẳng

 Xét





 

: 0

P ax by cz d

Q a x b y c z d

   





   

   





 Song song:

a b c d

  

   

(hay

: : : :

: : : : : :

a b c a b c

a b c d a b c d

  







   





 Trùng nhau:

a b c d

  

   

(hay

: : : : : :

a b c d a b c d

   



)

 Cắt nhau:

: : : : .

a b c a b c

  



34. Vị trí tương đối của hai đường thẳng

 Xét

: ;

Qua M

VTCT u









: .

Qua M

VTCP u















 Tính





, .

n u u





  





 Song song:

M d





 Trùng nhau:

M d









 Chéo nhau:

. 0.

n MM









 Cắt nhau:

. 0.

n MM









35. Hình chiếu của 1 điểm lên 1 mặt phẳng

 Xét





; ;

M M M

M x y z

và





: 0.

P ax by cz d

   







; ;

M M M

H x at y bt z ct

  

với

2 2 2

M M M

ax by cz d

a b c

  

 

 

36. Hình chiếu của 1 điểm lên 1 đường thẳng

 Cho





 

0 0 0

; ;

: ; ;

Qua I x y z

VTCP u a b c















và điểm

 Từ





0 0 0

; ; .

H d H x at y bt z ct

    

 Vì

. 0

MH d MH u

  





, ta tìm được

37.

Hình chiếu của một đường thẳng lên một phẳng phẳng

 Cho đường thẳng





 

0 0 0

; ;

: ; ;

Qua I x y z

VTCP u a b c















và mặt phẳng





: 0.

P Ax By Cz D

   

 Nếu





d P

 Nếu









d P M

 

 Chọn

M d



bất kì (có thể chọn

M I



)

 Xác định





 

MH P

H P















: .

Qua H

VTCP u u











 



 

: , ,

Qua M

VTCP u n u n









 





 



   

38. Đường thẳng đối xứng của một đường thẳng khác qua một mặt phẳng

 Cho đường thẳng





 

0 0 0

; ;

: ; ;

Qua I x y z

VTCP u a b c















và mặt phẳng





: 0.

P Ax By Cz D

   

Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/

Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 6

 Nếu





d P

 Nếu









d P M

 

 B1 : Tìm điểm



đối xứng với

qua





 B2:

: .

Qua I

VTCP u













 B1. Xác định tọa độ giao điểm

 B2. Chọn điểm

N d



(

không trùng với

 B3. Dựng



đối xứng với

qua





 B4.

: .

Qua N

VTCP MN



















39. Đường vuông góc chung của 2 đường thẳng chéo nhau

 Cho

Qua A

VTCP u









và

Qua A

VTCP u















Viết phương trình đường thẳng



là đường

vuông góc chung của

và



 B1.

 

, .

u u u



 





 





 



  

 B2. Viết phương trình mp





chứa



 

 

: .

Qua A

n u u















  

 B3. Xác định giao điểm:









d P M



 

 B4.

 

: , .

Qua M

VTCP u u u



















  

40. Góc

 Xét đường thẳng

và



có VTCP



và





mặt phẳng





và







có VTPT



và















cos , cos ,

d d u u

 



 



















cos , cos ,

P P n n

 



 















sin , cos ,

d P u n



 

ng l

ạ

i l

ác

ạ

i l

à sin

41. Phương trình mặt chắn qua trọng tâm tam giác







Qua













;0;0 , 0; ;0 , 0;0;

A a B b C c





; ;

G G G

G x y z

làm trọng tâm của

ABC









3 3 3

G G G

x y z

  

42. Phương trình mặt chắn đi qua trực tâm của tam giác







: Qua













;0;0 , 0; ;0 , 0;0;

A a B b C c





; ;

H H H

H x y z

làm trực tâm của

ABC









2 2 2

H H H H H H

P x x y y z z x y z

    

43.

Phương trình mặt chắn đi qua tâm đường tròn ngoại tiếp của tam giác







: Qua













;0;0 , 0; ;0 , 0;0;

A a B b C c





; ;

I I I

I x y z

làm tâm ngoại của

ABC





 

: 1

x y z

a b c

  

, ta có:

2 2

I I I

IA IB

IA IC

x y z

a b c



 









  



44. Phương trình mặt phẳng chứa 1 đường thẳng và đi qua 1 điểm







: Chứa

Qua M

VTCP u









và





A P







A d





 

: .

: ,

Qua A

VTPT n u AM







 





 





 

Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/

Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 7

45. Phương trình mặt phẳng chứa 1 đường thẳng và vuông góc với 1 mặt phẳng







: Chứa

Qua M

VTCP u









và









P Q

 

 

: .

: ,

Qua M

VTPT n n u







 





 



  

46. Đường thẳng đi qua 1 điểm, cắt và vuông góc với 1 đường thẳng cho trước



Qua M

VTCP u









, viết PTĐT:

: .

Qua A

Cat d





 









: .

: , ,

Qua A

VTCP u u u MA











 





 





  

47.

Đường thẳng đi qua 1 điểm, cắt 1 đường thẳng d và vuông góc với d’



Qua M

VTCP u









;

Qua M

VTCP u















và điểm

Viết PTĐT



qua

cắt

và vuông góc với





: .

, ,

Qua A

u u u MA











 







 





  

48. Đường thẳng nằm trong (P), cắt cả hai đường thẳng d và d’

 Viết PTĐT nằm trong





cắt cả

và



 B1. Xác định giao điểm của

với





và của



với





(gọi là

và

 B2:

: .

Qua A

VTCP u AB



















49. Đường thẳng đi qua 1 điểm và cắt cả hai đường thẳng cho trước



Qua M

VTCP u









;

Qua M

VTCP u















và điểm

Viết PTĐT qua

cắt cả

và



Cách 1: Gọi giao điểm





B t d



và





B t d

  

 Dựa vào

, ,

A B B



thẳng hàng, ta tìm được

và



Cách 2:

B1. Viết phương trình mặt phẳng





chứa

và

có:

 

: .

Qua A

n u AM







 





 





 

B2. Xác định









d P B



 

B3.

: .

Qua A

VTCP u AB





















50. Đường thẳng song song với



, cắt cả d và d’



Qua M

VTCP u











;

Qua M

VTCP u









và

Qua M

VTCP u















Viết PTĐT song song với



cắt cả

và



Cách 1. Gọi









, .

A a d B b d



 

Dựa vào



, ta tìm

được

và

Cách 2.

B1. Viết phương trình mặt phẳng





chứa

và song song

với



Ta có

 

 

: .

P d

Qua M

n u u















  

B2. Xác định









d P B



 

B3.

: .

Qua B

VTCP u u



 













 

51. Phương trình đường trung tuyến của tam giác

Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/

Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 8

 Cho

ABC



đã biết tọa độ các đỉnh.

Viết phương trình trung tuyến

B1. Xác định

; ; .

2 2 2

B C B C B C

x x y y z z

  

 

 

 

B2.

: .

VTCP:

Qua A

u AM

















52. Phương trình đường cao của tam giác

 Cho

ABC



đã biết tọa độ các đỉnh.

Viết phương trình đường cao

: .

VTCP: , ,

Qua A

u BC BC BA







 





 



  



53. Phương trình đường trung trực của BC

 Cho

ABC



đã biết tọa độ các đỉnh.

Viết phương trình đường trung trực của BC

B1. Xác định

; ; .

2 2 2

B C B C B C

x x y y z z

  

 

 

 

B2.

: .

VTCP: , ,

Qua M

u BC BC BA







 





 



  



54. Phương trình đường phân giác trong và ngoài góc A

 Cho

ABC



đã biết tọa độ các đỉnh. Viết phương trình đường phân giác trong và ngoài của góc A

 Phân giác trong

: .

VTCP:

Qua A

AB AC







 





 



 Phân giác ngoài

: .

VTCP:

Qua A

AB AC









 





 



55. Mặt cầu đã biết tâm và tiếp xúc với 1 mặt phẳng

 Viết PTMC





có tâm

tiếp xúc với





đã biết



 

Tam I

R d I P













56. Mặt cầu đi qua 4 điểm

 Viết PTMC





đi qua 4 điểm

, , ,

A B C D

đã biết tọa độ

 Gọi phương trình mặt cầu:





2 2 2

: 0.

S x y z ax by cz d

      





 

A S

B S

C S

D S























hệ 4 phương trình, 4 ẩn, tìm

, , , .

a b c d

57. Mặt cầu đi qua 3 điểm và có tâm thuộc 1 mặt phẳng

 Viết PTMC





đi qua 3 điểm

, ,

A B C

đã

biết tọa độ và có tâm thuộc





đã biết

 Gọi phương trình mặt cầu:





2 2 2

: 0.

S x y z ax by cz d

      





 

A S

B S

C S

I P























hệ 4 phương trình, 4 ẩn, tìm

, , , .

a b c d

58. Mặt cầu đi qua 2 điểm và có tâm thuộc 1 đường thẳng đã biết

 Viết PTMC





đi qua 2 điểm

A B

đã biết

tọa độ và có tâm thuộc đường thẳng

đã biết

Cách 1.

Gọi tâm

theo tham số

Từ

2 2

IA IB



tìm được

Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/

Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 9

Cách 2.

B1. Viết phương trình





trung trực của

B2. Tìm









d P I

  là tâm của mặt cầu

B3.

ính

R IA



à b

án k

ính m

ặ

t c

ầ

59. Mặt cầu đi qua 1 điểm, có tâm thuộc 1 đường thẳng và tiếp xúc với 1 mặt phẳng

 Viết PTMC





đi qua

có tâm thuộc

và tiếp xúc với mặt phẳng





B1. Gọi tâm

theo tham số t (vì

I d



)

B2. Xử lý









, ,

IA d I P

 tìm được t.

B3. Xác định

I R

và viết PTMC





60. Mặt cầu biết tâm I, mặt phẳng (P) cắt (S) theo giao tuyến là đường tròn biết bán kính

 Viết PTMC





có tâm

biết





cắt





theo giao tuyến là đường tròn đã biết bán

kính (hoặc chu vi, diện tích)

B1. Tìm









d I P

và

(nếu đề cho

hoặc

), chú ý

rằng

S r

C r













B2. Tìm









2 2 2

R r d I P

 

B3. Viết PTMC





có tâm

bán kính

61. Mặt cầu biết tâm I, cắt đường thẳng d theo 1 đoạn thẳng có độ dài đã biết

 Viết PTMC





có tâm

biết đường

thẳng

cắt





theo cát tuyến là đoạn thẳng

có độ dài

B1. Tìm









d I d

B2. Xác định

 

2 2

, .

R d I d 

B3. Viết PTMC





có tâm

bán kính

Ộ

T S

Ố

Ạ

NG T

OÁN C

Ự

C TR

Ị

QUEN THU

Ộ

62. Mặt phẳng đi qua điểm A và cách M một khoảng lớn nhất







đi qua điểm A và cách M một khoảng

lớn nhất

 

: .

Qua A

n MA

















63.

Đường thẳng nằm trong mặt phẳng (P), song song với d (d//(P)) và cách d khoảng nhỏ nhất

 Cho





và đường thẳng





// .

d P

PTĐT



thỏa mãn





 

min

d d

 











B1. Lấy

A d



B2. Xác định









| .

A P AA P

 

 

B3.

: .

VTCP:

Qua A

u u













 

64. Đường thẳng qua 1 điểm thuộc mặt phẳng, cách 1 điểm khác một khoảng lớn nhất

 Cho





A P

 và điểm





M P



không vuông góc với





PTĐT



thỏa mãn:





 

max

;

d M



 













: .

VTCP: ,

Qua A

u n AM









 





 





 

Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/

Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 10

65. Đường thẳng qua 1 điểm thuộc mặt phẳng, cách 1 điểm khác một khoảng nhỏ nhất

 Cho





A P

 và điểm





M P



không vuông góc

với





PTĐT



thỏa mãn:





 

min

;

d M

 













B1. Xác định

là hình chiếu của

lên





B2.

: .

VTCP:

Qua A

u AH



















Hoặc

, , .

u n n AM

 



 



  

66. Mặt phẳng chứa 1 đường thẳng d và cách điểm M một khoảng lớn nhất







chứa

và cách

M d



một khoảng lớn nhất

B1. Lấy

A d



bất kì

B2.

 

VTPT: , ,

d d

Qua A

n u AM u







 





 





  

67. Đường thẳng nằm trong mặt phẳng (P), qua A và cách d một khoảng lớn nhất (d cắt (P))

 Cho





, điểm





A P

 và

đường thẳng

cắt





tại

Viết PTĐT

   

 

max

: .

Qua A

d d





  









B1. Lấy

B d



bất kì

B2:

 

: .

, , ,

P d d

Qua A

u n u u AB









 





 





   

68. Mặt phẳng chứa đường thẳng



, tạo với đường thẳng d một góc lớn nhất

 Cho hai đường thẳng



và

ngoài nhau và không vuông

góc với nhau

 Viết PTMP





chứa



tạo với

một góc lớn nhất

Cách làm:

 Lấy

bất kì thuộc



 Mặt phẳng





được xác định:

 





 

, ,

P d

A P

n u u u

 







 





 



   

69. Đường thẳng đi qua A, nằm trong (P) và tạo với d một góc nhỏ nhất

 Cho điểm A nằm trong





và đường thẳng

(

cắt





và

không vuông góc với





 Viết PTĐT



qua A, nằm trong





, tạo với

góc nhỏ nhất.

Công thức:





, , .

P P d

u n n u



 



 

   

Thầy Đỗ Văn Đức

Nhớ theo dõi page: https://www.facebook.com/dovanduc2020 để cập nhật bài giảng nhanh nhất nha.

Yêu các em nhìu

󰄮󰄯

Bấm Tải xuống để xem toàn bộ.

Preview text:

Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/
Tài liệu này tóm tắt các công thức, phương pháp giải nhanh Oxyz thầy Đức biên soạn cho học sinh của khóa học.
1. Tọa độ điểm thuộc trục tọa độ, các mặt phẳng tọa độ
Xét điểm M  x ; y ; z . M M M
 M Ox  M  x ;0;0;
 M Oxy  M  x ; y ;0 M M ; M
 M Oy  M 0; y ;0;
 M Oyz  M 0; y ; z M M  ; M
 M Oz  M 0;0; z .
 M Ozx  M  x ;0; z M M . M
2. Điểm đối xứng với 1 điểm qua trục tọa độ, mặt phẳng tọa độ
Xét điểm M  x ; y ; z . Điểm M  đối xứng với M qua: M M M
Trục Ox  M  x ; y ; z .
 Oxy  M  x ; y ;  z M M M  M M M
Trục Oy  M x ; y ; z
 Oyz  M x ; y ; z M M M  M M M 
Trục Oz  M x ; y ; z .
 Ozx  M  x ; y ; z M M M  M M M
3. Hình chiếu của 1 điểm lên các trục tọa độ
Chiếu lên Ox : M  x ;0;0. x M Xét M  x ; y ; z . Chiếu lên Oy : M y y  0 ; ;0 M . M M M
Chiếu lên Oz : M 0;0; z . z M
4. Hình chiếu của 1 điểm lên các mặt phẳng tọa độ
Chiếu lên Oyz : M 0; y ; z . M M Xét M  x ; y ; z .
Chiếu lên Oxy : M  x ; y ;0 M M . M M M
Chiếu lên Ozx : M  x ;0; z . M M
5. Khoảng cách 1 từ 1 điểm lên các mặt phẳng tọa độ
 d M ;Oxy  z M Xét M  x ; y ; z .
 d M ;Oyz  x M M M M
 d M ;Ozx  y M
6. Khoảng cách từ 1 điểm tới các trục tọa độ  d M Ox 2 2 ;  y  z ; M M Xét M  x ; y ; z .   M M M  d M Oy 2 2 ; z x ; M M  d M Oz 2 2 ;  x  y . M M 7. Ba điểm thẳng hàng   Xét 3 điểm ,
A B, C đã biết tọa độ.
Cách 1. Tồn tại k   để AB  k AC.  ,
A B, C thẳng hàng khi và chỉ khi    IA  pIB  qIC
Cách 2. Tồn tại p, q   để   p  q 1
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 1
Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/
8. Tích có hướng của hai vectơ  Định nghĩa    
Cho hai vectơ u   x , y , z và v   x , y , z . Tích có hướng của hai vectơ u và v là một vectơ, được kí 2 2 2  1 1 1     y z z x x y   
hiệu: u,v và được xác định: u,v 1 1 1 1 1 1   ; ; . y z z x x y  2 2 2 2 2 2   Tính chất  Phát biểu    u, v    u    
Tích có hướng của hai vectơ vuông góc với các vectơ thành phần  u v   . ,  v    
 u,v  v,u
Khi ta đổi thứ tự hai vectơ, ta được vectơ đối      
 u,v  u . v .sin u,v . Độ dài của vectơ tích có hướng        
 u,v  u  mv,v  u,v  ku   
Nếu thay u bởi u  kv, giá trị tích có hướng không đổi. m  , k  .  9. Hai vectơ cùng phương  
Xét hai vectơ u  a;b;c, v  a , b , c. Hai vectơ này cùng phương khi và chỉ khi       k
   :u  kv  a  ka ; b  kb ; c  kc  u ,v  0.     Hệ quả: ,
A B, C thẳng hàng   AB , AC   0.  
10. Ba vectơ đồng phẳng – tích hỗn tạp      
 Ba vectơ u, v, w đồng phẳng khi và chỉ khi u,v.w  0  Hệ quả: Nếu k  0 thì , A B, C, D đồng phẳng Cho 4 điểm , A B, C, D , xét
   Nếu k  0 thì ,
A B, C, D không đồng phẳng k   AB, AC.A . D   11. Tọa độ trung điểm
 x  x y  y z  z 
 Cho A x ; y ; z và B  x ; y ; z Trung điểm I của AB : A B I ; A B ; A B . B B B  . A A A     2 2 2  12. Tọa độ trọng tâm Tam giác Tứ diện  x  x  x  x A B C D x   G 4   x  x  x y  y  y z  z  z   y  y  y  y A B C G ; A B C ; A B C   A B C D  y  .  3 3 3  G 4   z  z  z  z A B C D z   G  4
13. Tìm tọa độ trực tâm H   BH  AC BH.AC  0    
Cho ABC đã biết tọa độ 3 đỉnh , A B, C. C  H  AB  C  H.AB  0 . 
   , A B, C, H dong phang    AB, AC.AH  0  
14. Tọa độ tâm đường tròn ngoại tiếp I.
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 2
Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/ 2 2  2 2 IA  IB IA  IB   
Cho ABC đã biết tọa độ 3 đỉnh , A B, C. 2 2 2 2 IA  IC  IA  IC . 
   , A B, C, I dong phang   AB , AC .AI  0  
15. Tọa độ chân đường phân giác trong của một góc trong tam giác DB AB AB  
 D chia BC theo tỉ số k   . DC AC AC Cho A
 BC, phân giác trong AD D  BC.  x  kx y  ky z  kz  B  kC  B C D ; B C ; B C   ( D  ).  1 k 1 k 1 k  1 k
16. Tâm tỉ cự hệ 3 điểm  ax  bx  cx A B C x   I a  b  c  Cho 3 điểm ,
A B, C đã biết tọa độ và bộ 3   ay  by  cy số thực a, ,
b c thỏa mãn a  b  c  0.  Tọa độ điểm I : A B C  y      I a  b  c 
Xét điểm I thỏa mãn aIA  bIB  cIC  0.  az  bz  cz
(Điểm I gọi là tâm tỉ cực của hệ 3 điểm A, B, A B C z   I   
C ứng với bộ 3 số a, b, c). a b c aA  bB  cC (Nhớ: I  .) a  b  c    
 aMA  bMB  cMC  a  b  c MI. 2 2 2 aMA  bMB  cMC
Với 1 điểm M bất kì  2 2 2
 aIA  bIB  cIC  a  b  c 2 MI
17. Tọa độ tâm đường tròn nội tiếp J aA  bB  cC J  (với a  BC; b  C ; A c  AB ) a  b  c
 Cho ABC đã biết tọa độ 3 đỉnh, gọi J là ax  bx  cx ay  by  cy Ta có: A B C x  ; A B C y  ;
tâm đường tròn nội tiếp ABC. J a  b  c J a  b  c az  bz  cz A B C z  J a  b  c
18. Diện tích hình bình hành  
 Xét hình bình hành ABCD  S   AB , AD   1  
 Hệ quả (diện tích tam giác): Cho A  BC, khi đó S  AB , AC . ABC 2  
19. Thể tích của khối hộp
   Cho khối hộp ABC . D AB C  D  . Khi đó V   AB , AD.AA  
1   
Hệ quả (thể tích tứ diện): Cho tứ diện ABCD, khi đó V   AB , AC.AD . ABCD 6  
20. Tính bán kính đường tròn ngoại tiếp tam giác A . B BC.CA A . B BC.CA  
Cho ABC đã biết tọa độ 3 điểm  R .   4S   ABC 2 AB , AC  
21. Phương trình các mặt phẳng tọa độ Oxy: z  0 Oyz: x  0 Ozx: y  0
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 3
Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/
22. Phương trình mặt phẳng chứa các trục tọa độ Chứa Ox : Chứa Oy : Chứa Oz : by  cz  0  2 2 b  c  0 ax  cz   2 2 0 a  c  0 ax  by   2 2 0 a  b  0
23. Phương trình mặt chắn Aa;0;0Ox  x y z
Cho B 0;b;0Oy abc  0
Phương trình mặt phẳng  ABC :   1.  a b c C  0;0;cOz
24. Tìm tọa độ 1 điểm thuộc đường thẳng, mặt phẳng x  x  at 0 
 Đường thẳng d : y  y  bt
 Mặt phẳng P : ax  by  cz  d  0. 0 z  z  ct  0 
 Lấy t  t bất kì, ta có  Gọi M  x ; y ; z  P, khi đó M M M 0    
M  x  at ; y  bt ; z  ct ax by cz
d 0. Chọn x , y bất kì để tìm z . M M M M M M 0 0 0 0 0 0 
Từ đó tìm được tọa độ điểm M .
25. Tìm tọa độ 1 điểm thuộc giao tuyến của hai mặt phẳng  M   P
ax  by  cz  d  0  P
  : ax  by  cz  d  0  Nếu  thì M M M  .  Xét          M   Q a x b y c z d  0   Q M M M   . : a x   b y   c z  d  0
 Cho x bất kì, giải hệ tìm y và z . M M M
26. Phương trình đường giao tuyến của 2 mặt phẳng M   P     Qua điểm: 
 Vectơ chỉ phương: u  n ,n 1 2  M   Q
27. Tìm giao điểm của đường thẳng và mặt phẳng x  x  at      0  Vì M d M  x at ; y bt ; z ct 0 0 0  
 Đường thẳng: d : y  y  bt ; 0 M P z  z ct   0
 A x  at  B y  bt  C z  ct  D  0 0   0   0 
 Mặt phẳng P : Ax  By  Cz  D  0.
 Tìm được t (nên dùng CASIO), sau đó tìm M .
28. Tìm giao điểm của đường thẳng và mặt cầu x  x  at 0 
 Vì M  d  M  x  at ; y  bt ; z  ct 0 0 0 
 Đường thẳng: d : y  y  bt ; 0  M S   z  z  ct  0  2 2 2 2  Mặt cầu
x  at  A  y bt  B  z  ct C  R 0   0   0 
S x  A2   y  B2 z C2 2 :  R .
 Từ đó tìm được t  tìm được M .
29. Khoảng cách từ 1 điểm tới 1 mặt phẳng
 Cho điểm M  x ; y ; z    M M M  ax by cz d  d M ;P M M M  .
 Mặt phẳng P : ax  by  cz  d  0. 2 2 2 a  b  c
30. Khoảng cách từ 1 điểm tới 1 đường thẳng   u, MM 
 Cho điểm M  x ; y ; z   M M M   d M ;  .  u
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 4
Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/ Q  ua M   x ; y ; z 0 0 0 
 Đường thẳng  :   V  TCP u   a b c. : ; ;
31. Khoảng cách giữa hai đường thẳng chéo nhau    Q  ua M Q  ua M  u,u.MM  Cho  :  ;  :   .   d ,   VTCP : u VTCP : u     u,u
32. Khoảng cách giữa hai mặt phẳng song song   P
  : ax  by  cz  d  0 d  d  Cho d  P , Q          .  Q
  : ax  by  cz  d  0 2 2 2 a  b  c
33. Vị trí tương đối của hai mặt phẳng a b c d  Song song:    . a b c d
a : b : c  a : b : c   P
  : ax  by  cz  d  0 (hay  ).  Xét
a : b : c : d  a : b : c : d    Q   : a x   b y   c z  d  0 a b c d  Trùng nhau:    . a b c d
(hay a : b : c : d  a : b : c : d )
 Cắt nhau: a : b : c  a : b : c .
34. Vị trí tương đối của hai đường thẳng Q  ua M Q  ua M     Song song: M  d .  Xét d :  ;  d:  .  n  0 V    TCT : u VTCP : u   Trùng nhau: M d .    Tính  
 Chéo nhau: n.MM   0.    n  0   n  u,u.  Cắt nhau: . n MM   0.
35. Hình chiếu của 1 điểm lên 1 mặt phẳng     Xét M  x ; y ; z và  H x at ; y bt ; z ct M M M  M M M   ax  by  cz  d
P : ax  by  cz  d  0. với M M M t   . 2 2 2 a  b  c
36. Hình chiếu của 1 điểm lên 1 đường thẳng Q  ua I  x ; y ;z
 Từ H  d  H  x  at ; y  bt ; z  ct . 0 0 0  0 0 0   Cho d :   và điểm M .  V   TCP : u   a;b;c
 Vì MH  d  MH.u  0 , ta tìm được t. d
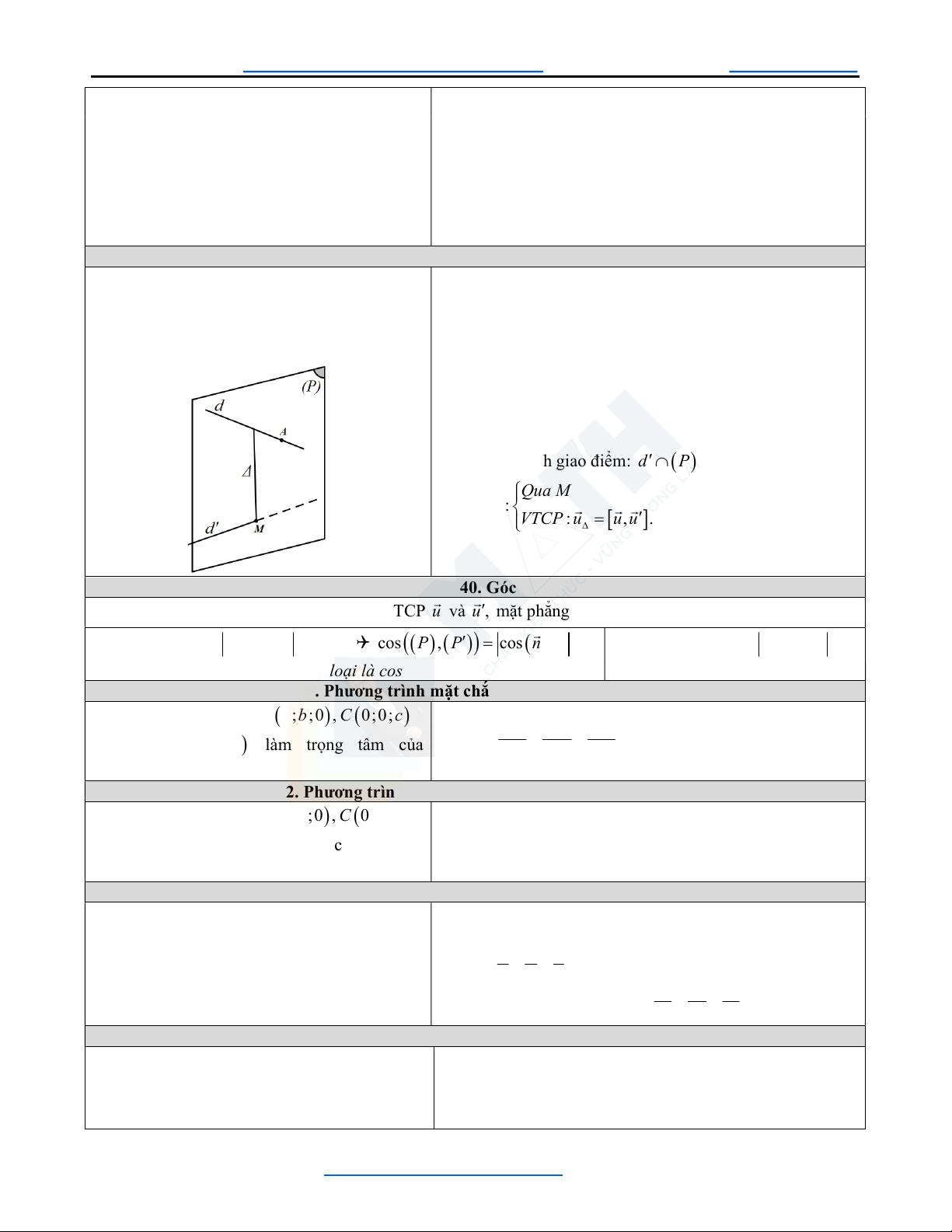
37. Hình chiếu của một đường thẳng lên một phẳng phẳng Q  ua I  x ; y ;z 0 0 0 
 Cho đường thẳng d :  
và mặt phẳng P : Ax  By  Cz  D  0. V  TCP : u   a;b;c  Nếu d // P
 Nếu d  P  M.
 Chọn M  d bất kì (có thể chọn M  I )  Xác định H | Q  ua M  MH    P Q  ua H  d :      VTCP : u   n,u      d :  .   , n d  H   P VTCP : u  u  d
38. Đường thẳng đối xứng của một đường thẳng khác qua một mặt phẳng Q  ua I  x ; y ;z 0 0 0 
 Cho đường thẳng d :  
và mặt phẳng P : Ax  By  Cz  D  0. V  TCP : u   a;b;c
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 5
Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/  Nếu d // P
 Nếu d  P  M.
 B1. Xác định tọa độ giao điểm M
 B1 : Tìm điểm I đối xứng với I qua P.  B2. Chọn điểm N d ( N không trùng với M ).
 B3. Dựng N đối xứng với N qua P. Q  ua I  B2: d :  .    V Qua N  TCP : u   B4. d :  . V  TCP : MN
39. Đường vuông góc chung của 2 đường thẳng chéo nhau Q  ua A Q  ua A  Cho d :   và d:   . V  TCP : u VTCP : u    d
Viết phương trình đường thẳng  là đường     B1.   u  u,u.
vuông góc chung của d và d .   d  
 B2. Viết phương trình mp P chứa d, chứa  :   Q  ua A  P :    n   u u. ,
 B3. Xác định giao điểm: d  P  M. Q  ua M   B4.  :     V  TCP : u   u,u  . 40. Góc  
 Xét đường thẳng d và d có VTCP u và u ,
 mặt phẳng P và P có VTPT n và n.  cosd,d    cos u,u
 cosP,P    cos n, n  sin d,P    cosu, n Cùng loại là cos Khác loại là sin
41. Phương trình mặt chắn qua trọng tâm tam giác
 P : Qua Aa;0;0, B 0;b;0, C 0;0;c x y z
G  x ; y ; z làm trọng tâm của  P :    1. G G G  3x 3y 3z G G G ABC.
42. Phương trình mặt chắn đi qua trực tâm của tam giác
 P : Qua Aa;0;0, B 0;b;0, C 0;0;c
H x ; y ; z làm trực tâm của  P 2 2 2
: x x  y y  z z  x  y  z H H H  H H H H H H ABC.
43. Phương trình mặt chắn đi qua tâm đường tròn ngoại tiếp của tam giác  2 2
 P : Qua Aa;0;0, B 0;b;0, C 0;0;c IA  IB x y z  2 2
I  x ; y ; z làm tâm ngoại của
 P :    1, ta có: IA  IC . I I I  a b c  ABC. x y z I I I     1  a b c
44. Phương trình mặt phẳng chứa 1 đường thẳng và đi qua 1 điểm Q  ua M  P : Chứa d :   và AP Q  ua A  V  TCP : u  P :     .     VTPT : n u, AM A d    
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 6
Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/
45. Phương trình mặt phẳng chứa 1 đường thẳng và vuông góc với 1 mặt phẳng Q  ua M Q  ua M   P : Chứa d :   và P  Q  P :  .    V  TCP : u VTPT : n  n ,u    Q 
46. Đường thẳng đi qua 1 điểm, cắt và vuông góc với 1 đường thẳng cho trước Q  ua A Q  ua A Q  ua M     :      .  d : 
 , viết PTĐT:  :  d .
VTCP : u  u, u, MA V  TCP : u       C  at d 
47. Đường thẳng đi qua 1 điểm, cắt 1 đường thẳng d và vuông góc với d’ Q  ua M Q  ua M   d :   ; d:   và điểm . A Q  ua A V  TCP : u VTCP : u     :     . Viết PTĐT  qua ,
A cắt d và vuông góc với u  u , u, MA       d .
48. Đường thẳng nằm trong (P), cắt cả hai đường thẳng d và d’
 B1. Xác định giao điểm của d với P và của d với P (gọi là A và B ).
 Viết PTĐT nằm trong P, cắt cả d và d . Q  ua A   B2:  :   . V  TCP :u  AB
49. Đường thẳng đi qua 1 điểm và cắt cả hai đường thẳng cho trước
Cách 1: Gọi giao điểm B t d và Bt d . Dựa vào ,
A B, B thẳng hàng, ta tìm được t và t . Cách 2:
B1. Viết phương trình mặt phẳng P chứa A và d. Ta Q  ua M Q  ua M  Q  ua A   d :   ; d:   và điểm . A có: P :    . V  TCP : u VTCP : u  n  u, AM   P    Viết PTĐT qua , A cắt cả d và d .
B2. Xác định d  P    B . Q  ua A  B3.  :   . V  TCP : u  AB  
50. Đường thẳng song song với  , cắt cả d và d’
Cách 1. Gọi Aa d, Bb d . Dựa vào AB //  , ta tìm được a và . b Q  ua M Q  ua M Cách 2.   :   ; d :   và
B1. Viết phương trình mặt phẳng P chứa d và song song V  TCP : u V  TCP : u Q  ua M  Q  ua M  d :   với .  Ta có P :  .    VTCP : u n   u ,u P d   
Viết PTĐT song song với , cắt cả d và d . B2. Xác định d   P    B . Q  ua B B3.  :  .   VTCP : u    u
51. Phương trình đường trung tuyến của tam giác
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 7
Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/  x  x y  y z  z  B1. Xác định B C M ; B C ; B C .    2 2 2 
 Cho ABC đã biết tọa độ các đỉnh. Q  ua A
Viết phương trình trung tuyến AM .  B2. AM :   . VTCP:u  AM
52. Phương trình đường cao của tam giác Q  ua A
 Cho ABC đã biết tọa độ các đỉnh.  AH :  
   .
Viết phương trình đường cao AH.
VTCP: u  BC, BC, BA    
53. Phương trình đường trung trực của BC  x  x y  y z  z  B1. Xác định B C M ; B C ; B C .  
 Cho ABC đã biết tọa độ các đỉnh.  2 2 2 
Viết phương trình đường trung trực của BC Q  ua M  B2. d :  
   .
VTCP: u  BC, BC, BA    
54. Phương trình đường phân giác trong và ngoài góc A
 Cho ABC đã biết tọa độ các đỉnh. Viết phương trình đường phân giác trong và ngoài của góc A  Phân giác trong Q  ua A Q  ua A      
 Phân giác ngoài At :  . At :  .   AB AC AB AC VTCP: u   VTCP: u     AB AC AB AC
55. Mặt cầu đã biết tâm và tiếp xúc với 1 mặt phẳng
 Viết PTMC S  có tâm I, tiếp xúc với T  am I    S  :  P đã biết R  d  I,P
56. Mặt cầu đi qua 4 điểm
 Gọi phương trình mặt cầu: S 2 2 2
: x  y  z  ax  by  cz  d  0. AS 
 Viết PTMC S  đi qua 4 điểm , A B, C, D  đã biết tọa độ B   S 
 hệ 4 phương trình, 4 ẩn, tìm a, b, c, d. C   S D  S
57. Mặt cầu đi qua 3 điểm và có tâm thuộc 1 mặt phẳng
 Gọi phương trình mặt cầu: S 2 2 2
: x  y  z  ax  by  cz  d  0.
 Viết PTMC S  đi qua 3 điểm , A B, C đã AS  
biết tọa độ và có tâm thuộc mp P đã biết B   S 
 hệ 4 phương trình, 4 ẩn, tìm a, b, c, d. C   S I   P
58. Mặt cầu đi qua 2 điểm và có tâm thuộc 1 đường thẳng đã biết
 Viết PTMC S  đi qua 2 điểm , A B đã biết Cách 1.
tọa độ và có tâm thuộc đường thẳng d đã biết Gọi tâm I theo tham số t. Từ 2 2 IA  IB tìm được t.
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 8
Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/ Cách 2.
B1. Viết phương trình mp P trung trực của A . B
B2. Tìm d  P  I là tâm của mặt cầu
B3. Tính R  IA là bán kính mặt cầu.
59. Mặt cầu đi qua 1 điểm, có tâm thuộc 1 đường thẳng và tiếp xúc với 1 mặt phẳng
B1. Gọi tâm I theo tham số t (vì I  d )
 Viết PTMC S  đi qua , A có tâm thuộc
B2. Xử lý IA  d I,P, tìm được t.
d, và tiếp xúc với mặt phẳng P.
B3. Xác định I , R và viết PTMC S 
60. Mặt cầu biết tâm I, mặt phẳng (P) cắt (S) theo giao tuyến là đường tròn biết bán kính
B1. Tìm d I,P và r (nếu đề cho S hoặc C ), chú ý 2 S   r
 Viết PTMC S  có tâm I, biết P cắt rằng  .  C  2  r
S  theo giao tuyến là đường tròn đã biết bán B2. Tìm R :
kính (hoặc chu vi, diện tích) 2 2 2 R  r  d I,P
B3. Viết PTMC S  có tâm I, bán kính . R
61. Mặt cầu biết tâm I, cắt đường thẳng d theo 1 đoạn thẳng có độ dài đã biết B1. Tìm d I,d 
 Viết PTMC S  có tâm I, biết đường 2 a
thẳng d cắt S  theo cát tuyến là đoạn thẳng B2. Xác định 2 2 R  d I, d   . 4 có độ dài . a
B3. Viết PTMC S  có tâm I, bán kính . R
MỘT SỐ DẠNG TOÁN CỰC TRỊ QUEN THUỘC
62. Mặt phẳng đi qua điểm A và cách M một khoảng lớn nhất
 P đi qua điểm A và cách M một khoảng Q  ua A  lớn nhất P: . n  MA
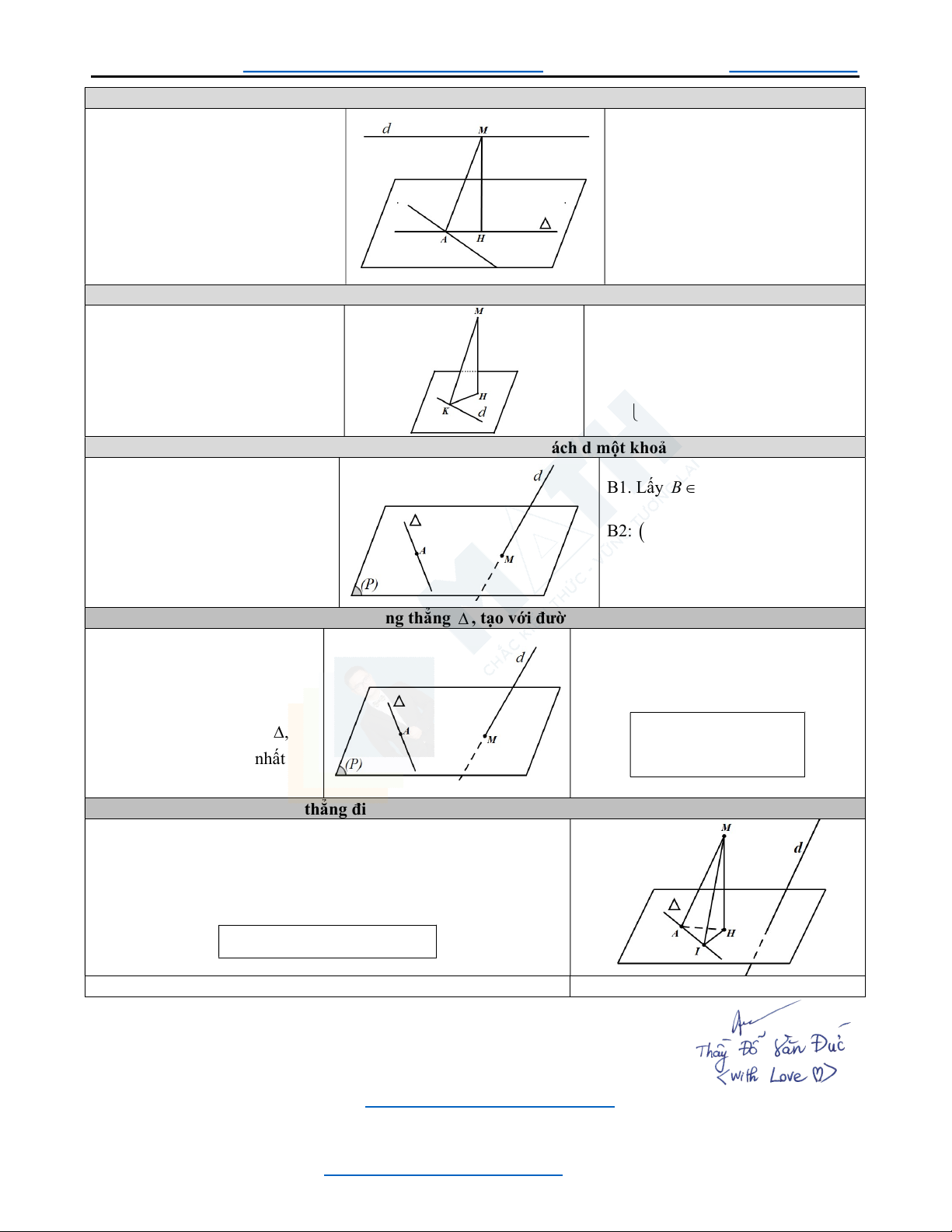
63. Đường thẳng nằm trong mặt phẳng (P), song song với d (d//(P)) và cách d khoảng nhỏ nhất B1. Lấy A d.
 Cho P và đường thẳng d // P. B2. Xác định    P
AP | AA  P. PTĐT  thỏa mãn  d   d  . , Q  ua A min B3.  :  .   VTCP: u  u  d
64. Đường thẳng qua 1 điểm thuộc mặt phẳng, cách 1 điểm khác một khoảng lớn nhất
 Cho AP và điểm M  P, AM
không vuông góc với P. Q  ua A    P  :     .  VTCP: u  n, AM   PTĐT  thỏa mãn:    A  . d M ;  max
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 9
Thầy Đỗ Văn Đức – https://www.facebook.com/dovanduc2020 Website: http://thayduc.vn/
65. Đường thẳng qua 1 điểm thuộc mặt phẳng, cách 1 điểm khác một khoảng nhỏ nhất  Cho AP và điểm
B1. Xác định H là hình chiếu của
M P, AM không vuông góc M lên P. với P. Q  ua A     B2.  :   . P    VTCP: u AH
PTĐT  thỏa mãn: A  .          Hoặc u n, n, AM .    d M ;   min
66. Mặt phẳng chứa 1 đường thẳng d và cách điểm M một khoảng lớn nhất B1. Lấy A d bất kì
 P chứa d và cách M  d B2. một khoảng lớn nhất Q  ua A  P:    
VTPT: n  u , AM  ,u   d d    
67. Đường thẳng nằm trong mặt phẳng (P), qua A và cách d một khoảng lớn nhất (d cắt (P))
 Cho P , điểm A P và B1. Lấy B  d bất kì
đường thẳng d cắt P tại M Q  ua A  Q  ua A B2:  :      .  u 
 n , u , u , AB  Viết PTĐT  : P d d        P .   d , d   max
68. Mặt phẳng chứa đường thẳng  , tạo với đường thẳng d một góc lớn nhất Cách làm:
 Cho hai đường thẳng  và
 Lấy A bất kì thuộc . 
d ngoài nhau và không vuông
 Mặt phẳng P được xác định: góc với nhau
 Viết PTMP P chứa , A  P P:   
tạo với d một góc lớn nhất n  u ,     u ,u P  d 
69. Đường thẳng đi qua A, nằm trong (P) và tạo với d một góc nhỏ nhất
 Cho điểm A nằm trong P, và đường thẳng d ( d cắt P và
d không vuông góc với P ).
 Viết PTĐT  qua A, nằm trong P , tạo với d góc nhỏ nhất.     Công thức: u  n ,  n ,u    . P P d  Thầy Đỗ Văn Đức
Nhớ theo dõi page: https://www.facebook.com/dovanduc2020 để cập nhật bài giảng nhanh nhất nha. Yêu các em nhìu
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức – Facebook: http://facebook.com/thayductoan 10

Tổng hợp công thức giải nhanh Oxyz - Tài liệu tổng hợp

Tài liệu liên quan:

Lời chia buồn đám tang cảm động, ý nghĩa nhất

Án tử hình thực hiện như thế nào? Nên duy trì hay loại bỏ án tử hình?

Kiểm soát là gì? Mục đích, vai trò, ý nghĩa, nguyên tắc kiểm soát

Ký tên và đóng dấu vào văn bản như thế nào là đúng luật?

Cô ta (QUOTA) là gì? Phân loại Quota và hạn ngạch xuất nhập khẩu