Tổng hợp đề thi giữa kì học phần Giải tích 1 | Đại học Bách Khoa Hà Nội

Tổng hợp đề thi giữa kì học phần Giải tích 1 | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!

12 6 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Giải tích 1

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

27 trang 2 tháng trước

Tác giả:

Profile Thùy Dương
PHẦN 1: T NG H THI GI A K Ổ ỢP ĐỀ Ữ Ỳ CÁC NĂM
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 1 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20193
Nhóm 1: MI1111. Khóa: K64. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1. Tìm hàm ngược của hàm số
1
x
y
x
.
Câu 2. Tìm t nh c a hàm s ập xác đị ủ ố
2
2 1 arccos 1y x x
.
Câu 3. So sánh hai vô cùng bé
arcsin , arctan ln 1f x x x g x x x
khi
0x
.
Câu 4. Tìm gi i h n ớ ạ
2
1
0
tan
lim
x
x
x
x
.
Câu 5. Tìm c c tr c a hàm s ự ị ủ ố
2
1y x x
.
Câu 6. Tính đạo hàm cấp cao
10
0y
c a hàm s ủ ố
.
Câu 7. Tính g vi phân ần đúng nhờ
5
32,5A
.
Câu 8. Tính các tích phân sau
a)
2
2
ln 1
1
x x
dx
x
b)
2 5
x
dx
Câu 9. Cho các s a mãn ố thực a, b, c thỏ
3 2 0a b c
. Ch ng minh rứ ằng phương trình
5 3
7 15 4 0ax bx c
có ít nh t m t nghi m th c thu c kho ng ấ ộ ệ ự ộ ả
0,1
.
Thang điể Câu 2 điểm: m: Câu 8.
m: Câu 1, 2, 3, 4, 5, 6, 7, 9.Câu 1 điể
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 3 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20193
Mã HP: MI1112 (nhóm 2). Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1. Xét tính ch n l c a hàm s ẵ ẻ ủ ố
3 3
2 2f x x x
.
Câu 2. Tìm hàm ngược của hàm số
2
1
x
x
e
y
e
nh trên xác đị
1,
.
Câu 3. So sánh các vô cùng bé sau khi
0x
:
2
x x
e e
x
và
1
x
x e
.
Câu 4. Cho hàm s ố
1
arctan 0,
0.
2
khi x
x
f x
khi x
Xét tính kh vi c a hàm s tả ủ ố ại
0x
.
Câu 5. Với n bằng bao nhiêu thì hàm số sau liên tục tại
0x
( n nguyên dương).
sin 2
0,
2 0.
n
x
khi x
f x
x
khi x
Câu 6. Tìm khai tri n Macloranh c a hàm s ể ủ ố
ln cosf x x
n s h ng đế ố ạ
2
x
.
Câu 7. Cho hàm s ố
2
1
1
f x
x
. Tính
1000
0f
.
Câu 8. Cho
b a
. CMR
cos sin
2 2 2 2
a b a b a b b a
.
Câu 9. Tìm ti m c n c a hàm s ệ ậ ủ ố
ln 1
x
f x e
.
Câu 10. Cho hàm s liên tố ục
: 0,2 0,2f
. CMR t n tồ ại
0,2c
sao cho
f c c
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 5 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20193
Nhóm 3. Mã h c ph n: MI 1113. Th i gian: 60 phút ọ ầ ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1. Tìm hàm ngược của hàm
, 0
2
x x
e e
y x
.
Câu 2. Tìm gi i h n c a dãy s ớ ạ ủ ố
n
x
a mãn thỏ
1
2 1
3 3
n n
x x
.
Câu 3. Tìm hàm s sau liên t c ta để ố ụ ại
0x
:
2
2
sin 2 tan arcsin
, 0
arctan 3 ln 1
, 0
x x x x
x
x xf x
a x
.
Câu 4. Cho
2 3 4
ln 1 arccos arctan 1f x x x x
. Tính
0
f
.
Câu 5. Cho hàm s ố
2x
f x xe
. Tính
100
0f
.
Câu 6. Tìm khai tri n Maclaurin c a hàm s ể ủ ố
2x
f x xe
n đế
4
x
.
Câu 7. Tìm giá tr l n nh t và nh nh t cị ớ ấ ỏ ấ ủa
2
x
e
f x
x
n trên đoạ
1;2
.
Câu 8. Tìm ti m c n c ng cong cho b i tham sệ ậ ủa đườ ở ố:
1
1
t
x t
t
y t
t
.
Câu 9. Tính tích phân
2
6 17 6
2 3
x x
dx
x x x
.
Câu 10. Tính
2
sin
2 2
0
1
2
lim
arcsin .ln 1
x
x
x
e x
x x
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 1 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20191
Mã s MI111. Nhóm ngành 1/L p BK. Th i gian: 60 phút ố ớ ờ
Chú ý: Thí sinh không c s d ng tài li u và giám th i ký xác nh n s vào bài thi. đượ ử ụ ệ ị phả ậ ố đề
Câu 1. Tìm hàm s liên t a để ố ục:
2
2 2
1 , 0
, 0
x
e x x
f x
a x
.
Câu 2. Cho
1y x
. Xét tính kh vi tả ại
1x
.
Câu 3. Tính
lim sin 2 sin 2
x
x x

.
Câu 4. Tính
40
1y
, ở đó
1
2
1
x
y x e
.
Câu 5. Cho
0a b c
. Ch ng minh rứ ằng phương trình
3 2
4 3 0ax bx c
, luôn có nghi m thuệ ộc
0;1
.
Câu 6. Tìm c c tr c a hàm s ự ị ủ ố
2
3
2y x x
.
Câu 7. Tính
2
2
2 2
x
dx
x x
.
Câu 8. Tìm các ti m c n c hàm s ệ ậ ủa đồ thị ố
1
lnf x x e
x
.
Câu 9. Tính gần đúng
0,1
e
v i sai s ớ ố bé hơn
4
10
.
Câu 10. Tính
4 2
3 5
0
1 1 cos
lim
arctan
x
x x
x x
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
3 THI GI A KÌ MÔN GI I TÍCH 1 H C KÌ 20191 ĐỀ ĐỀ Ữ Ả – Ọ
Mã s : MI 111. Nhóm ngành 1/L p BK. i gian: 60 phút ố ớ Thờ
Chú ý: - Thí sinh không được sử dụng tài liệu.
- Giám th ph i kí xác nh n s vào bài thi.ị ả ậ ố đề
Câu 1. (1 điểm) Tìm
a
hàm s liên t c: để ố ụ
1
1 sin , 1
1
1
x x
f x
x
a x
.
Câu 2. (1 điểm) Tìm t nh và t p giá tr c a hàm sập xác đị ậ ị ủ ố:
1 1
sin cosy
x x
.
Câu 3. (1 điểm) Tính
3
0
lim
x
x
x
x
.
Câu 4. (1 điểm) Dùng vi phân tính gần đúng
3
8, 012
.
Câu 5. (1 điểm) Khai tri n hàm s ể ố
4
f x x
a ctheo lũy thừ ủa
2x
.
Câu 6. (1 điểm) Tìm giá tr l n nh t và bé nh t c a hàm s ị ớ ấ ấ ủ ố
cos 2y x x
n trên đoạ
0;
4
.
Câu 7. (1 điểm) Tính
arcsin
1
x
dx
x
.
Câu 8. (1 điểm) Tìm các ti m c n c hàm s ệ ậ ủa đồ thị ố
3 3
1f x x
.
Câu 9. (1 điểm) Tính
2
2
2
1
lim
1
n
n
n
n

.
Câu 10. (1 điểm) ng minh r ng: Chứ ằ
6arctan 5arctan 2 11arctan 1 , 0x x x x
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 5 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20191
Nhóm 2: Mã h c ph n MI1112. Th i gian: 60 phút ọ ầ ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1. Cho hàm s ố
f x
và
g x
v i các giá tr c cho trong b ng sau: ớ ị đượ ả
x
1
2
3
4
5
6
7
8
9
f x
5
8
4
6
3
2
1
7
9
g x
9
2
5
4
3
1
7
8
6
Tính
1
g
.
Câu 2. Tính gi i h n: ớ ạ
a)
1
lim
2
x
x
x
x

b)
2
1
arctan 2
0
lim cosh
x
x
x
.
Câu 3. Tìm hàm ngược của hàm số
2
ln 1 ,f x x x x
ℝ.
Câu 4.
0x
n lo i gì c a hàm s là điểm gián đoạ ạ ủ ố
sin x
y x
x
?
Câu 5. Cho hàm s ố
2
1
0
0 0
x
e khi x
f x
khi x
.
a) Xét tính liên t c c a hàm s tụ ủ ố ại
0x
.
b) Xét tính kh vi c a hàm s tả ủ ố ại
0x
.
Câu 6. Cho hàm s ố
2
sinhf x x x
. Tính
2019
0f
.
Câu 7. Xác đị ụng định giá trị khi áp dc nh lý Lagrange vào hàm số
sinf x x
n trên đoạ
0,
2
.
Câu 8. Tìm khai tri n Maclaurin c a hàm s ể ủ ố
sin x
f x e
n s h ng đế ố ạ
4
x
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 2 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20183
Mã HP: MI1111, Khóa: K63, Nhóm ngành 1, Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1. Tìm t nh và t p giá tr c a hàm s ập xác đị ậ ị ủ ố
sin arccosy x
.
Câu 2. Cho hàm s ố
3
cosf x x x
. Hàm s ố
f x
có là hàm s l không? Vì sao? ố ẻ
Câu 3. So sánh cặp vô cùng bé sau đây khi
0x
:
3
1 cos 2x x
và
2
x x x
.
Câu 4. Tính gi i h n ớ ạ
1
1 2 1
0
lim 1 4
x
x
x
.
Câu 5. Cho
2 6
1 sin 2
, 0,
2
0 , 0
x
e x
neu x
f x
x x
neu x
. Tính
0
f
.
Câu 6. Cho
2
ln 3 2y x x
. Tính đạo hàm cấp cao
10
0y
.
Câu 7. Tìm c c tr c a hàm s ự ị ủ ố
2
1
x
y
x
.
Câu 8. Tính tích phân
3 2
2
x x
I e e dx
.
Câu 9. Tính tích phân
2
ln 1I x x dx
.
Câu 10. Tìm
f x
biết
2 3
2019
d
f x x
dx
và
0 0f
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 1 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20181
Mã HP: MI1111, Khóa: K63, Nhóm ngành 1, Th i gian: 60 phút ờ
Chú ý: Thí sinh c s d ng tài li u và giám th i ký xác nh n s vào bài thi. không đượ ử ụ ệ ị phả ậ ố đề
Câu 1 (1đ). Chứng minh
2
cos(arcsin ) 1 , 1,1x x x
.
Câu 2 (1đ). So sánh cặp vô cùng lớn sau khi
x
2
( ) , ( ) 1
x
x x x x e
.
Câu 3 (1đ). Tìm hàm ngược của hàm số
1
ln , ( 1,1)
1
x
y x
x
1
ln , ( 1,1)
1
x
y x
x
.
Câu 4 (1đ). Tìm và phân loại điểm gián đoạn của hàm số
1
cot arctany
x
.
Câu 5 (1đ). Tìm hàm số
ln( cos ),
( )
0,
x x
f x
0
0
neu x
neu x
Tính
'
(0)f
.
Câu 6 (1đ). Tính giới hạn
2 3
0
lim
ln(1 )
x
x x
x x
.
Câu 7 (1đ). Tính tích phân
2
3
2
1
x
dx
x
.
Câu 8 (1đ). Cho
2
3
3
1
x
y
x
o hàm c p cao . Tính đạ ấ
(5)
(0)y
.
Câu 9 (1đ). Tính giới hạn của dãy số
2
lim 2
n
n
n

Câu 10 (1đ). Viết phương trình tiế ủa đườp tuyến c ng cong
2 cosr
Tại điểm ứng với
0
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 2 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20181
Mã HP: MI1111, Khóa: K63, Nhóm ngành 1, Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1 (1đ). Chứng minh
2
sin(arccos ) 1 , 1,1x x x
.
Câu 2 (1đ). So sánh cặp vô cùng lớn sau khi
x
2
( ) , ( ) ln(1 )x x x x x
.
Câu 3 (1đ). Tìm hàm ngược của hàm số
1
ln , ( 1,1)
1
x
y x
x
1
ln , ( 1,1)
1
x
y x
x
.
Câu 4 (1đ). Tìm và phân loại điểm gián đoạn của hàm số
1
tan arccoty
x
.
Câu 5 (1đ). Tìm hàm số
ln( ),
( )
0,
x
x e
f x
0
0
neu x
neu x
Tính
'
(0)f
.
Câu 6 (1đ). Tính giới hạn
3 4
0
lim
sin
x
x x
x x
.
Câu 7 (1đ). Tính tích phân
2
3
2
1
x x
dx
x
.
Câu 8 (1đ). Cho
2
2
1
x
y
x
o hàm c p cao . Tính đạ ấ
(7 )
(0)y
.
Câu 9 (1đ). Tính giới hạn của dãy số
2
lim 1
n
n
n

Câu 10 (1đ). ết phương trình tiếVi p tuyến c ng cong ủa đườ
1 cosr
Tại điểm ứng với
0
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 3 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20181
Mã HP: MI1111, Khóa: K63, Nhóm ngành 1, Th i gian: 60 phút ờ
Chú ý: Thí sinh c s d ng tài li u và giám th i ký xác nh n s vào bài thi. không đượ ử ụ ệ ị phả ậ ố đề
Câu 1 (1đ). Hàm số
arctany x
có tu n hoàn không? T i sao? ầ ạ
Câu 2 (2đ). Tính các giới hạn
a)
1
sin
0
lim(cos )
x
x
x
, b)
3
0
sin cos
lim
x
x x x
x
.
Câu 3 (1đ). Cho hàm số
1
neu 0
( )
1
neu 0
ln
x
a e x
f x
x
x
Tìm
a
để
0x
n b c c a hàm s là điểm gián đoạ ỏ đượ ủ ố
( )f x
Câu 4 (1đ). Tìm
lim [sin(ln ) sin(ln( 1))]
n
n n

lim [sin(ln ) sin(ln( 1))]
n
n n

Câu 5 (1đ). Tìm
,a b
để hai vô cùng bé sau là tương đương khi
0x
2 3 2
( ) , ( ) sin( )x ax bx x x x
Câu 6 (1đ). Ứ ần đúng ng dụng vi phân, tính g
4
2
2 0, 02
.
Câu 7 (1đ). Tính tích phân
2
arccos xdx
.
Câu 8 (1đ). Viết phương trình tiế ủa đườp tuyến c ng cycloid
sin ,
1 cos
x t t
y t
Tại điểm ứng với
2
t
.
Câu 9 (1đ). Cho hàm số
( )f x
o hàm trên . Ch ng minh r ng n u xác định và có đạ ℝ ứ ằ ế
( )f x
là m t hàm s l ộ ố ẻ
thì
'( )f x
là m t hàm s n.ộ ố chẵ
N TOÁN D NG VÀ TIN H C VIỆ ỨNG Ụ Ọ
Đề ĐỀ Ả – ọ 4 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20181
Mã HP: MI1111, Khóa: K63, Nhóm ngành 1, Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1 (1đ). Hàm số
arccoty x
có tu n hoàn không? T i sao? ầ ạ
Câu 2 (2đ). Tính các giới hạn
b)
1
tan
0
lim(cos )
x
x
x
, b)
2
0
sin
lim
x
x
x xe
x
.
Câu 3 (1đ). Cho hàm số
1
1
neu 0
ln( )
( )
a+e neu 0
x
x
x
f x
x
Tìm
a
để
0x
n b c c a hàm s là điểm gián đoạ ỏ đượ ủ ố
( )f x
Câu 4 (1đ). Tìm
lim [sin(ln( 1)) sin(ln )]
n
n n

Câu 5 (1đ). Tìm
,a b
để hai vô cùng bé sau là tương đương khi
0x
2 3 4 3
( ) , ( ) sin( )x ax bx x x x
Câu 6 (1đ). Ứ ần đúng ng dụng vi phân, tính g
4
2
2 0, 02
.
Câu 7 (1đ). Tính tích phân
2
arcsin xdx
.
Câu 8 (1đ). Viết phương trình tiế ủa đườp tuyến c ng cycloid
cos ,
1 sin
x t t
y t
Tại điểm ứng với
2
t
.
Câu 9 (1đ). Cho hàm số
( )f x
o hàm trên . Ch ng minh r ng n u xác định và có đạ ℝ ứ ằ ế
( )f x
là m t hàm s ộ ố
chẵn thì
'( )f x
là m t hàm s l .ộ ố ẻ
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 5 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20181
Mã HP: MI1112, Khóa: K63, Nhóm ngành 2, Th i gian: 60 phút ờ
Chú ý: Thí sinh c s d ng tài li u và giám th i ký xác nh n s vào bài thi. không đượ ử ụ ệ ị phả ậ ố đề
Câu 1. (1đ). Tìm tập xác định và tập giá trị của hàm số
2
arccot 3y x
.
Câu 2. (1đ). Chứng minh rằng với mọi
,x y
ℝ:
sinh sinh cosh sinh coshx y x y y x
.
Câu 3. (1đ). Phân loại điểm gián đoạn
1x
c a hàm s ủ ố
1
arctan 2
x
x
y
.
Câu 4. (1đ). Tìm cực trị của hàm số
2
2 1
1
x
y
x
.
Câu 5. (1đ). Tìm sau có đạa để hàm số o hàm tại
0x
:
sin 0
cos 0
x
e a x khi x
f x
x khi x
.
Với a v c tính ừa tìm đượ
0
f
.
Câu 6. d ng vi phân c p m t, tính g(1đ). Sử ụ ấ ộ ần đúng
3
7, 76
.
Câu 7. (1đ). Cho hàm số
1 lny x x
. Tính đạo hàm
20
1y
.
Câu 8. (1đ). So sánh các vô cùng bé sau khi
0x
:
2
ln 2 sin 2x x e x x x
;
1 cos 2x x
.
Câu 9. (1đ). Tính giới hạn
2
3
0
2sin 1
lim
ln 1 2sin
x
x
e x
x x x
.
Câu 10. (1đ). Cho ba số a, b, c thỏa mãn
b a c
. Ch ng minh rứ ằng phương trình
4 2
5 3 0ax bx c
có ít
nhất một nghiệm trong khoảng
0,1
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 6 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20181
Mã HP: MI1112, Khóa: K63, Nhóm ngành 2, Th i gian: 60 phút ờ
Chú ý: Thí sinh c s d ng tài li u và giám th i ký xác nh n s vào bài thi. không đượ ử ụ ệ ị phả ậ ố đề
Câu 1 (1đ). Tìm t nh và t p giá tr c a hàm s ập xác đị ậ ị ủ ố
2
arccot 1y x
.
Câu 2 (1đ). Chứ ằ ọng minh r ng với m i
,x y
ℝ:
cosh cosh cosh sinh sinhx y x y x y
.
Câu 3 (1đ). Phân lo n ại điểm gián đoạ
1x
c a hàm s ủ ố
1
arctan 2
x
x
y
.
Câu 4 (1đ). Tìm c c tr c a hàm s ự ị ủ ố
2
2 1
1
x
y
x
.
Câu 5 (1đ). Tìm hàm s o hàm ta để ố sau có đạ ại
0x
:
1 sin 0
0
x
ax khi x
f x
e khi x
.
Với v c tính a ừa tìm đượ
0
f
.
Câu 6 (1đ). Sử d ng vi phân c p m t, tính gụ ấ ộ ần đúng
3
8,12
.
Câu 7 (1đ). Cho hàm s ố
2 lny x x
. Tính đạo hàm
20
1y
.
Câu 8 (1đ). So sánh các vô cùng bé sau khi
0x
:
2 33
1 1 4x x x
;
sin
1
x x
x e
.
Câu 9 (1đ). Tính gi i h n ớ ạ
2
3
0
2 cos 1
lim
ln 1 2 arcsin
x
x
e x
x x x
.
Câu 10 (1đ). Cho ba s a mãn ố a, b, c thỏ
b a c
. Ch ng minh rứ ằng phương trình
4 2
5 3 0ax bx c
có ít nhất
một nghi m trong kho ng ệ ả
0,1
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
ĐỀ ĐỀ Ả – ọ 7 THI GIỮA KÌ MÔN GI I TÍCH I H c kì 20181
Khóa: 63 - Nhóm ngành 3 - Mã HP: MI1113. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1 (1 điể ập xác địm). Tìm t nh của hàm số
lg cosy x
.
Câu 2 (1 điểm). Tính
0
1 2 1
lim
tan 3
x
x
x
.
Câu 3 (1 điể ại điểm gián đoạm). Tìm và phân lo n của hàm số
1
arctany
x
.
Câu 4 (1 điểm). Khi
0x
i sao? các vô cùng bé sau có tương đương không? Tạ
sin5x x
,
5 2
1
x
x e x
.
Câu 5 (1 điểm). Dùng định nghĩa, tính đạo hàm
0
y
v i ớ
3
arcsiny x x
.
Câu 6 (1 điểm). Tính
2
4
1
x
x
e
dx
e
.
Câu 7 (1 điểm). Tính
2
arctan x
dx
x
.
Câu 8 (1 điểm). Tính
0
1 1
lim cot
x
x
x x
.
Câu 9 (1 điể ủa đồm). Tìm các tiệm cận xiên c thị hàm số
1
2
1
x
x
y xe
.
Câu 10 (1 điểm). Cho
f x
kh vi trên ả
,a b
,
0 a b
. Ch ng minh r ng ứ ằ
,a b
sao cho
1 1
f b f a
f f
b a b a
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
ĐỀ ĐỀ Ả – ọ 8 THI GIỮA KÌ MÔN GI I TÍCH I H c kì 20181
Khóa: 63 - Nhóm ngành 3 - Mã HP: MI1113. Th i gian: 60 phút ờ
Chú ý: Thí sinh c s d ng tài li u và giám th i ký xác nh n s vào bài thikhông đượ ử ụ ệ ị phả ậ ố đề
Câu 1 (1 điể ập xác địm). Tìm t nh của hàm số
lg siny x
.
Câu 2 (1 điểm). Tính
0
1 4 1
lim
tan 5
x
x
x
.
Câu 3 (1 điể ại điểm gián đoạm). Tìm và phân lo n của hàm số
1
arccoty
x
.
Câu 4 (1 điểm). Khi
0x
i sao? các vô cùng bé sau có tương đương không? Tạ
sin3x x
,
3 2
1
x
x e x
.
Câu 5 (1 điểm). Dùng định nghĩa, tính đạo hàm
0
y
v i ớ
5
arcsiny x x
.
Câu 6 (1 điểm). Tính
3
4
1
x
x
e
dx
e
.
Câu 7 (1 điểm). Tính
2
arccot x
dx
x
.
Câu 8 (1 điểm). Tính
0
2 1
lim cot
x
x
x x
.
Câu 9 (1 điể ủa đồm). Tìm các tiệm cận xiên c thị hàm số
1
3
1
x
x
y xe
.
Câu 10 (1 điểm). Cho
f x
kh vi trên ả
,a b
,
0 a b
. Ch ng minh r ng ứ ằ
,a b
sao cho
1 1
f b f a
f f
b a b a
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 1 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20173
Nhóm ngành 1. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1. Tìm t nh c a hàm s ập xác đị ủ ố
3 1
2 1 4 arcsin
2
x
y x
.
Câu 2. Tìm và phân lo n c a hàm s ại điểm gián đoạ ủ ố
sin
1
x
y
x x
.
Câu 3. Tính
2 3
0
ln 1 2
lim
3 4sin
x
x x
x x
.
Câu 4. Tìm các ti m c n c hàm s ệ ậ ủa đồ thị ố
1
2
x
y xe
.
Câu 5. Tính
sin ln x dx
.
Câu 6. Tính
3
sin
cos
x
dx
x
.
Câu 7. Tính
2
2
2
2 2
x
dx
x x
.
Câu 8. Kiểm tra định lý Fernat cho hàm số
1y x
trên
0;2
.
Câu 9. Tính
4 2
5 3
0
1 1 2 cos 2
lim
ln 1 2
x
x x
x x
.
Câu 10. Xét s h i t và tìm gi i h n (n u có) c a dãy s ự ộ ụ ớ ạ ế ủ ố
1 1
1 1
: 0, , 1
2
n n n
n
x x x x n
x
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 1 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 2017.1
Khóa: K62. Mã HP: MI1111. Nhóm ngành 1. Th i gian: 60 phút ờ
Chú ý: Thí sinh c s d ng tài li u và giám th i ký xác nh n s vào bài thi. không đượ ử ụ ệ ị phả ậ ố đề
Câu 1. Tìm t nh c a hàm s ập xác đị ủ ố
6 arccot 5y x
.
Câu 2. Tìm t t c hàm s liên tấ ả ố ục
f x
a mãn thỏ
,f x x x
ℝ.
Câu 3. Tính
0
ln 1 4sin
lim
3 1
x
x
x
I
.
Câu 4. Tìm
,a b
ℝ hàm s để ố
3
1,
1
x x khi x
y
ax b khi x
kh vi tả ại
1x
.
Câu 5. Tính đạo hàm cấp cao
5
y x
với
2
ln 2y x x
.
Câu 6. Tính
2
cot
0
lim
sin
x
x
x
I
x
.
Câu 7. Tính tích phân
3
2 3
1
x
dx
x
.
Câu 8. Tính tích phân
2
tan x dx
.
Câu 9. Sử d ng khai tri n Maclaurin c a hàm s ụ ể ủ ố
3
1y x
n đế
3
x
tính gđể ần đúng
3
1, 09
, (quy tròn đến
6
10
).
Câu 10. Bơm nướ ốc độc vào một bể chứa hình cầu bán kính 4 vm ới t
3
1m
/1 phút. Tính t c thốc độ tăng lên tứ ời
của chiều cao m c khi chiực nướ ều cao m c là 3ực nướ m.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 2 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 2017.1
Khóa: K62. Mã HP: MI1111. Nhóm ngành 1. Th i gian: 60 phút ờ
Chú ý: Thí sinh c s d ng tài li u và giám th i ký xác nh n s vào bài thi. không đượ ử ụ ệ ị phả ậ ố đề
Câu 1. Tìm t nh c a hàm s ập xác đị ủ ố
4 arccot 3y x
.
Câu 2. Tìm t t c hàm s liên tấ ả ố ục
f x
a mãn thỏ
2
,f x x x
ℝ.
Câu 3. Tính
3
0
log (1 4 tan )
lim
1
x
x
x
I
e
.
Câu 4. Tìm
,a b
ℝ hàm s để ố
3
2 1,
1
ax x khi x
y
x b khi x
kh vi tả ại
1x
.
Câu 5. Tính đạo hàm cấp cao
6
y x
với
2
lny 3x x
.
Câu 6. Tính
2
cot
0
lim
tan
x
x
x
I
x
.
Câu 7. Tính tích phân
3
3 2
1
x
dx
x
.
Câu 8. Tính tích phân
2
cot x dx
.
Câu 9. Sử d ng khai tri n Maclaurin c a hàm s ụ ể ủ ố
4
1y x
n đế
3
x
tính gđể ần đúng
4
1, 04
, (quy tròn đến
7
10
).
Câu 10. Bơm nướ ốc độc vào một bể chứa hình cầu bán kính 6 vm ới t
3
1m
/1 phút. Tính t c thốc độ tăng lên tứ ời
của chiều cao m c khi chiực nướ ều cao m c là 5 ực nướ m.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 3 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 2017.1
Khóa: K62. Mã HP: MI1111. Nhóm ngành 1. Th i gian: 60 phút ờ
Chú ý: Thí c s d ng tài li u và giám th i ký xác nh n s vào bài thi. sinh không đượ ử ụ ệ ị phả ậ ố đề
Câu 1. Tìm hàm s c c a hàm s ố ngượ ủ ố
2arcsin , 1;1y x x
.
Câu 2. Tìm hàm s a để ố
1
arctan 0,
0
khi x
y
x
a khi x
liên t c tụ ại
0x
.
Câu 3. Tính
4
3
0
ln arcsin ln
lim
x
x x x
I
x
.
Câu 4. Tính vi phân c a hàm s ủ ố
ln tan 2y x
.
Câu 5. Tìm c c tr c a hàm s ự ị ủ ố
2 2
2 ln 4 ln 4y x x+3x x x x
.
Câu 6. Tính
tan
0
lim sin
x
x
I x
.
Câu 7. Tính tích phân
2 cos
x
xe xdx
.
Câu 8. Tính tích phân
1 arccot 2x x dx
.
Câu 9. Tìm nghi m x p x 6 cệ ấ ỉ thứ ủa phương trình
5
10x x
i x p x u theo phương pháp Newton vớ ấ ỉ ban đầ
1
2x
, (quy tròn đến
9
10
).
Câu 10. Tính bán kính l n nh t c a m t qu c u có th di chuy c m t c ng hình Parabol v i kích ớ ấ ủ ộ ả ầ ể ển vào đượ ộ ổ ớ
thước như hình vẽ bên.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 4 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 2017.1
Khóa: K62. Mã HP: MI1111. Nhóm ngành 1. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1. Tìm hàm s c c a hàm s ố ngượ ủ ố
3arccos , 1;1y x x
.
Câu 2. Tìm hàm s a để ố
1
arccot 0,
0
khi x
y
x
a khi x
liên t c tụ ại
0x
.
Câu 3. Tính
3
2
0
ln arcsin ln
lim
x
x x x
I
x
.
Câu 4. Tính vi phân c a hàm s ủ ố
ln cot 2y x
.
Câu 5. Tìm c c tr c a hàm s ự ị ủ ố
2 2
2 ln 2 ln 2y x x x x x x
.
Câu 6. Tính
sin
0
lim tan
x
x
I x
.
Câu 7. Tính tích phân
2 sin
x
xe xdx
.
Câu 8. Tính tích phân
1 arctan 3x x dx
.
Câu 9. Tìm nghi m x p x 6 cệ ấ ỉ thứ ủa phương trình
4
10x x
i x p x u theo phương pháp Newton vớ ấ ỉ ban đầ
1
2x
, (quy tròn đến
9
10
).
Câu 10. Tính bán kính l n nh t c a m t qu c u có th di chuy c m t c ng hình Parabol v i kích ớ ấ ủ ộ ả ầ ể ển vào đượ ộ ổ ớ
thước như hình vẽ bên.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 5 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 2017.1
Khóa: K62. Mã HP: MI1112. Nhóm ngành 2. Th i gian: 60 phút ờ
Chú ý: Thí sinh c s d ng tài li u và giám th i ký xác nh n s vào bài thi. không đượ ử ụ ệ ị phả ậ ố đề
Câu 1. Tìm t nh và t p giá tr c a hàm s ập xác đị ậ ị ủ ố
sin arccosy x
.
Câu 2. So sánh cặp vô cùng bé sau đây khi
0x
:
3 2
sinx x x
,
3
1 cosx x
.
Câu 3. Tìm hàm ngược của hàm số
2
2 , 1,y x x x
.
Câu 4. Tìm và phân lo n c a hàm s ại điểm gián đoạ ủ ố
2
1
arctany x
x
.
Câu 5. Tìm m t hàm s ộ ố
f x
và s sao cho ố thực a
4
0
3 81
lim
h
h
f a
h
.
Câu 6. Tính gi i h n ớ ạ
2
4
0
1 cos 2 2
lim
x
x x
x
.
Câu 7. Tìm ng tha để đẳ ức sau đúng
lim
x
x
x a
e
x a

.
Câu 8. Cho
2
ln 1y x x
. Tính đạo hàm cấp cao
9
0y
.
Câu 9. Cho ba s a mãn ố thực a, b, c thỏ
0a b c
. Ch ng minh rứ ằng phương trình
2
2 4 5 0ax bx c
có ít
nhất một nghiệm thuộc khoảng
1,
.
Câu 10. Tìm
,a b
sao cho ℝ
2
4
0
ln cos
lim 1
x
ax b x
x
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 6 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 2017.1
Khóa: K62. Mã HP: MI1112. Nhóm ngành 2. Th i gian: 60 phút ờ
Chú ý: Thí sinh c s d ng tài li u và giám th i ký xác nh n s vào bài thi. không đượ ử ụ ệ ị phả ậ ố đề
Câu 1. Tìm t nh và t p giá tr c a hàm s ập xác đị ậ ị ủ ố
cos arcsiny x
.
Câu 2. So sánh cặp vô cùng bé sau đây khi
0x
:
2 3
sinx x x
,
3
1 cosx x
.
Câu 3. Tìm hàm ngược của hàm số
2
2 , 1,y x x x 
.
Câu 4. Tìm và phân lo n c a hàm s ại điểm gián đoạ ủ ố
3
1
arctany x
x
.
Câu 5. Tìm m t hàm s ộ ố
f x
và s sao cho ố thực a
5
0
2 32
lim
h
h
f a
h
.
Câu 6. Tính gi i h n ớ ạ
2
4
0
1 cos 4 8
lim
x
x x
x
.
Câu 7. Tìm ng tha để đẳ ức sau đúng
lim
x
x
x a
e
x a

.
Câu 8. Cho
2
ln 1y x x
. Tính đạo hàm cấp cao
9
0y
.
Câu 9. Cho ba s a mãn ố thực a, b, c thỏ
0a b c
. Ch ng minh rứ ằng phương trình
2
2 3 4 0ax bx c
có ít
nhất một nghiệm thuộc khoảng
1,
.
Câu 10. Tìm
,a b
sao cho ℝ
3
0
sin sin
lim 1
x
ax b x
x
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 7 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 2017.1
Khóa: K62. Mã HP: MI1113. Nhóm ngành 3. Th i gian: 60 phút ờ
Chú ý: Thí sinh c s d ng tài li u và giám th i ký xác nh n s vào bài thi. không đượ ử ụ ệ ị phả ậ ố đề
Câu 1(1đ). Tìm và phân lo n c a hàm s ại điểm gián đoạ ủ ố :
2
1
( 1)
( ) 3
x x
f x
Câu 2(1đ). So sánh các vô cùng bé sau, khi 1: x →
3
( 1)
( ) 1; ( ) cot
2
x
x
x e x
Câu 3(1đ). Tính
1
0
1
lim
1 ln
x
x
x
x x
Câu 4(1đ). Tìm c c tr hàm s ự ị ố
2
5
( ) ( 1)f x x x
Câu 5(1đ). Tính
2
arcsin xdx
Câu 6(1đ). Viết công th c Maclaurin cho hàm ứ
2
siny x x
đến lũy thừa
11
x
Câu 7(1đ). Cho
| 2 |
x
y x x
. Tính
'(1); '(2).y y
Câu 8(1đ). Tính
8 6
1
dx
x x
Câu 9(1đ) . Cho
4
( 1)
( ) ln(2 )
5!
x
f x x
. Tính
10
(1).d f
Câu 10(1đ). Cho
a b c d
.CMR phương trình
5 4 3
6 5 4 0ax bx cx d
có nghi m trong kho ng (-1;0)ệ ả
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 8 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 2017.1
Khóa: K62. Mã HP: MI1113. Nhóm ngành 3. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1(1đ). Tìm và phân lo n c a hàm s ại điểm gián đoạ ủ ố :
2
1
( 2) (1 )
( ) 2
x x
f x
Câu 2(1đ). So sánh các vô cùng bé sau, khi 1: x →
2
3
( 1)
( ) 1; ( ) cot
2
x
x
x e x
Câu 3(1đ). Tính
0
sin
lim
1
x
x
x x
x x
Câu 4(1đ). Tìm c c tr hàm s ự ị ố
2
5
( ) ( 1)f x x x
Câu 5(1đ). Tính
2
arccos xdx
Câu 6(1đ). Viết công th c Maclaurin cho hàm ứ
2
cosy x x
đến lũy thừa
9
x
Câu 7(1đ). Cho
| 1|
x
y x x
. Tính
'(1); '(2).y y
Câu 8(1đ). Tính
8 6
1
dx
x x
Câu 9(1đ) . Cho
4
( 2)
( ) ln(3 )
5!
x
f x x
. Tính
10
(2).d f
Câu 10(1đ). Cho
a b c d
.CMR phương trình
5 4 3
6 5 4 0ax bx cx d
có nghi m trong kho ng (0;1) ệ ả
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 2 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20161
Khóa: K61. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1. Tìm t nh và t p giá tr c a hàm s ập xác đị ậ ị ủ ố
arccos sin 2y x
.
Câu 2. So sánh cặp vô cùng bé sau đây khi
0x
:
,
tan
1
x
x e
.
Câu 3. Tính
0
f
, biết
2
tan , 0
, 0
x neu x
f x
x x neu x
.
Câu 4. Chứng minh r ng ằ
2 2
arctan arctan
1 1
b a b a
b a
b a
v i mớ ọi
0 a b
.
Câu 5. Tính gi i h n ớ ạ
2
0
sin ln 1
lim
x
x x
x
.
Câu 6. Tìm các c c tr c a hàm s ự ị ủ ố
sin
2 cos
x
y
x
trong kho ng ả
0,2
.
Câu 7. Tính tích phân
2
1
2016
dx
x x
.
Câu 8. Cho
,f x g x
là các hàm s nh trên và tu n hoàn v i chu kì l t là ố xác đị ầ ớ ần lượ
1 2
0, 0T T
. Bi t t ế ỉ
số
1
2
T
T
là m t s h u t . Ch ng minh r ng ộ ố ữ ỉ ứ ằ
f x g x
t hàm s n hoàn. cũng là mộ ố tuầ
Câu 9. Tính đạo hàm cấp cao
10
0y
với
2
x
y x e
.
Câu 10. Tính tích phân
2
ln 1x x x dx
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 3 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 2016.1
Khóa: K61. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1. Tìm hàm ngược của hàm số sau
1
2 1
x
y
x
.
Câu 2. Tính gi i h n ớ ạ
2
0
1
lim
x
x
e
x x
.
Câu 3. Điểm
2
x
n lo i gì c a hàm s là điểm gián đoạ ạ ủ ố
tan
1
1 2
x
f x
.
Câu 4. Sử d ng vi phân, tính gụ ần đúng
3
7, 97
.
Câu 5. Tính đạo hàm cấp cao
60
2
1
x x
.
Câu 6. Tính gi i h n ớ ạ
2
0
1
1
lim
x
x
e
x
x
.
Câu 7. Tính tích phân
3
arctanx xdx
.
Câu 8. Tính đạo hàm cấp cao
9
0y
với
arccoty x x
.
Câu 9. Tìm các ti m c n c ng cong cho b ệ ậ ủa đườ ởi phương trình tham số
2
2
3
2016
1
2016
1
t
x
t
t
y
t
.
Câu 10. Tính tích phân
1
1
1 ln
x
x x dx
x
.
N TOÁN NG D NG VÀ TIN H C VIỆ Ứ Ụ Ọ
Đề ĐỀ Ả – ọ 5 THI GIỮA KÌ MÔN GI I TÍCH 1 H c kì 20161
Khóa: K61. Th i gian: 60 phút ờ
Chú ý: Thí sinh c s d ng tài li u và giám th i ký xác nh n s vào bài thi. không đượ ử ụ ệ ị phả ậ ố đề
Câu 1. Xét tính ch n l c a hàm s ẵ ẻ ủ ố
tan siny x
.
Câu 2. Tìm hàm s sau liên t c tm để ố ụ ại
1x
.
2
1 , 1
1 , 1
x m x x neu x
f x
m neu x
.
Câu 3. Tính gi i h n ớ ạ
2
0
1
lim
ln 1 3
x
x
e
x
.
Câu 4. Tính đạo hàm cấp cao
50
2
sin 2x x
.
Câu 5. Tính gi i h n ớ ạ
2
0
ln 1 sin
lim
x
x x
x
.
Câu 6. Tìm các c c tr c a hàm s sau ự ị ủ ố
2
2
1
x
y
x
.
Câu 7. Tính tích phân
2
sin 2x xdx
.
Câu 8. Hãy ch ra m t hàm s ỉ ộ ố
f x
nh trên , liên t c txác đị ℝ ụ ại các điểm
0 1
1, 2x x
nhưng không có đao
hàm t m này. ại các điể
Câu 9. Tính tích phân
2 2
2 3
xdx
x x
.
Câu 10. Tìm
f x
n u biế ết
2
2016
d
f x x
dx
.
| 1/27
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHẦN 1: TỔNG HỢP ĐỀ THI GIỮA KỲ CÁC NĂM
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 1 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20193
Nhóm 1: MI1111. Khóa: K64. Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi. x
Câu 1. Tìm hàm ngược của hàm số y  . x 1 Câu 2. Tìm t nh c ập xác đị a hàm s ủ ố y x    2 2 1 arccos 1 x  .
Câu 3. So sánh hai vô cùng bé f x  xarcsin ,
x g x  arctan x ln 1 x khi x  0 . 1 2  tan x x
Câu 4. Tìm giới hạn lim   . x0  x
Câu 5. Tìm cực trị c a hàm s ủ ố 2
y x 1 x . Câu 6. 1  Tính đạo hàm cấp cao 0 y   0 c a hàm s ủ
ố y  2x   1 sin x. Câu 7. Tính g vi phân ần đúng nhờ 5 A  32,5 .
Câu 8. Tính các tích phân sau x ln  2 1 x dx a) dx  b)  2 x 1 x 2 5 Câu 9. Cho các s
ố thực a, b, c th a mãn ỏ
a  3b  2c  0. Ch ng minh r ứ ằng phương trình 5 3
7ax 15bx  4c  0 có ít nhất m t nghi ộ ệm thực thu c kho ộ ảng 0,  1 .
Thang điểm: Câu 2 điểm: Câu 8.
m: Câu 1, 2, 3, 4, 5, 6, 7, 9. Câu 1 điể
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 3 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20193
Mã HP: MI1112 (nhóm 2). Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1. Xét tính chẵn lẻ c a hàm s ủ ố f x  3 3
 2  x  2  x . x Câu 2. 2e
Tìm hàm ngược của hàm số y
xác định trên 1, . x e 1
Câu 3. So sánh các vô cùng bé sau khi x  0 : xx
  e e x  và    x x e 1. 2   1  a  rctan   khi x  0,    Câu 4. x Cho hàm s ố f x      khi x 0. 2  Xét tính khả vi c a hàm s ủ t ố ại x  0 .
Câu 5. Với n bằng bao nhiêu thì hàm số sau liên tục tại x  0 ( n nguyên dương). sin 2x    f x khi x 0, n   x 2 khi x 0. 
Câu 6. Tìm khai triển Macloranh c a hàm s ủ
ố f x   ln  cos x  đến s h ố ạng 2 x . Câu 7. 1 1000 Cho hàm s
ố f x  . Tính f 0 . 2 1 x a ba b
a b b a
Câu 8. Cho b a . CMR  cos sin      . 2  2   2  2
Câu 9. Tìm tiệm cận c a hàm s ủ ố   ln 1 x f x e    .
Câu 10. Cho hàm s liên t ố
ục f : 0,2 0,2. CMR tồn tại c   0, 
2 sao cho f c  c .
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 5 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20193 Nhóm 3. Mã h c ph ọ n: MI 1113. Th ầ i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi. xxCâu 1. e e
Tìm hàm ngược của hàm y  , x  0. 2 Câu 2. 2 1 Tìm giới hạn c a dãy s ủ ố x th a mãn ỏ xx  . nn 1  n 3 3 Câu 3. Tìm
a để hàm s sau liên t ố c t ụ ại x  0 : 2
sin 2x  tan x x arcsin x   f x x
  arctan 3x ln , 0 2 1 x  . a , x   0
Câu 4. Cho f x   2 x    3x 4 ln 1 arccos
arctan x 1 . Tính f    0 . Câu 5. Cho hàm s ố   2x
f x xe . Tính 10 0 f   0 .
Câu 6. Tìm khai triển Maclaurin của hàm s ố   2x
f x xe đến 4 x . 2 x e
Câu 7. Tìm giá trị lớn nhất và nh nh ỏ
ất của f x  trên đoạn 1;2. x    t x t   Câu 8. t  1 Tìm tiệm cận c ng cong cho b ủa đườ ởi tham số:  . yt 1   t 2   Câu 9. 6x 17 x 6 Tính tích phân   dx .
x x  2  x3  2 sin x x e 1 x Câu 10. Tính 2 lim . 2 x arcsin x .ln  2 0 1 x
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 1 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20191
Mã s MI111. Nhóm ngành 1/L ố
ớp BK. Thời gian: 60 phút
Chú ý: Thí sinh không c s
đượ ử dụng tài liệu và giám thị phải ký xác nh n s ậ
ố đề vào bài thi. Câu 1. Tìm a để hàm s liên t ố ục :  2 2 x e 1 2    f xx , x 0   . a , x  0 
Câu 2. Cho y x 1 . Xét tính khả vi tại x 1.
Câu 3. Tính lim sin x 2 sin x 2 . x  Câu 4. Tính 40 y
1, ở đó      1 2 1 x y x e .
Câu 5. Cho a b c  0. Ch ng minh r ứ ằng phương trình 3 2
4ax  3bx c  0 , luôn có nghiệm thuộc 0;  1 .
Câu 6. Tìm cực trị c a hàm s ủ
ố y x x  2 3 2 .  Câu 7. x 2 Tính dx  . 2 x  2 x  2  
Câu 8. Tìm các tiệm cận của đồ thị hàm s ố f x 1  x ln e    .  x
Câu 9. Tính gần đúng 0,1 e với sai s ố bé hơn 4 10 . 4 1 1 x cos 2 x Câu 10. Tính lim . 3 xx arctan  5 0 x
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 3
ĐỀ THI GIỮA KÌ MÔN GIẢI TÍCH 1 H – ỌC KÌ 20191 Mã s : MI 111. ố Nhóm ngành 1/L p BK. ớ
Thời gian: 60 phút Chú ý:
- Thí sinh không được sử dụng tài liệu.
- Giám thị ph i kí xác nh ả n s ậ
ố đề vào bài thi.   x x
Câu 1. (1 điểm) Tìm a để hàm s liên t ố c: ụ f x   1 1 sin , 1   x 1 .  a x  1  1 1
Câu 2. (1 điểm) Tìm t nh và t ập xác đị
ập giá trị của hàm số: y  sin  cos . x x 3 x
Câu 3. (1 điểm) Tính lim x x . x 0 
Câu 4. (1 điểm) Dùng vi phân tính gần đúng 3 8, 012 .
Câu 5. (1 điểm) Khai triển hàm s ố   4
f x x theo lũy thừa của x  2.   
Câu 6. (1 điểm) Tìm giá trị lớn nhất và bé nhất của hàm s
ố y x  co  s 2  x trên đoạn 0;  . 4    Câu 7. arcsin x (1 điểm) Tính dx  . 1 x
Câu 8. (1 điểm) Tìm các tiệm cận của đồ thị hàm s ố f x 3 3  1 x . 2 2 n    Câu 9. n 1
(1 điểm) Tính lim  . 2 n n  1  
Câu 10. (1 điểm) Ch ng minh r ứ
ằng: 6arctan x  5arctan x  2 11arctan x   1 , x   0 .
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 5 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20191 Nhóm 2: Mã h c ph ọ n MI1112. Th ầ i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi. Câu 1. Cho hàm s
ố f x và g x với các giá trị được cho trong bảng sau: x 1 2 3 4 5 6 7 8 9 f x  5 8 4 6 3 2 1 7 9 g x 9 2 5 4 3 1 7 8 6 Tính 1 g  .
Câu 2. Tính giới hạn: xx 1  1 a) lim   b) lim cosh x 2 arctan 2 x .
x   x  2  x 0 
Câu 3. Tìm hàm ngược của hàm số f x   2
ln x x 1 , x ℝ. Câu 4. x  0 n lo là điểm gián đoạ ại gì của hàm s ố   sin x y x  ? x 1    Câu 5. x Cho hàm s ố f x 2 e khi x  0   . 0  khi x  0  a) Xét tính liên t c c ụ ủa hàm s t ố ại x  0 .
b) Xét tính khả vi c a hàm s ủ t ố ại x  0 . Câu 6. 2019 Cho hàm s ố f x 2
x sinh x . Tính f 0 .  
Câu 7. Xác định giá trị c khi áp dụng định lý Lagrange vào hàm số f x  sin x trên đoạn 0,  . 2   
Câu 8. Tìm khai triển Maclaurin của hàm s ố   sinx f x e đến s h ố ạng 4 x .
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 2 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20183
Mã HP: MI1111, Khóa: K63, Nhóm ngành 1, Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi. Câu 1. Tìm t nh và t ập xác đị ập giá trị c a hàm s ủ
ố y  sinarccos  x . Câu 2. Cho hàm s ố f x 3
x  cos x. Hàm số f x có là hàm s l ố ẻ không? Vì sao?
Câu 3. So sánh cặp vô cùng bé sau đây khi x  0:  x 3
 1 cos 2x và   2
x x x .
Câu 4. Tính giới hạn lim1 4x 1 1 2x 1 . x 0 
 xe  1sin2x  , neu x  0,
Câu 5. Cho f x 2 6  x  2x . Tính f 0 . 0 , neu x  0 Câu 6. 10  Cho y   2
ln x  3x  2 . Tính đạo hàm cấp cao y 0. 2 Câu 7. x Tìm cực trị c a hàm s ủ ố y  . x 1
Câu 8. Tính tích phân 3 2  2 x x I e e dx  .
Câu 9. Tính tích phân I   2 ln x x   1dx. Câu 10. d
Tìm f x biết
f  2x  3
 2019x và f 0 0 . dx
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 1 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20181
Mã HP: MI1111, Khóa: K63, Nhóm ngành 1, Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nh n s ậ
ố đề vào bài thi.
Câu 1 (1đ). Chứng minh 2 cos(arcsin )
x  1 x , x   1  ,  1 .
Câu 2 (1đ). So sánh cặp vô cùng lớn sau khi x   2  ( )  , ( ) x x x x x e  1. 1 x 1 x
Câu 3 (1đ). Tìm hàm ngược của hàm số y  ln , x ( 1  ,1) y ln , x ( 1  ,1) . 1 x 1 x
Câu 4 (1đ). Tìm và phân loại điểm gián đoạn của hàm số  1  y  cot arctan   .  x  l
 n(x cos x), neu x  0
Câu 5 (1đ). Tìm hàm số f (x)    0, neu x  0 Tính ' f (0) .  2 3 x x
Câu 6 (1đ). Tính giới hạn lim . x 0
x  ln(1 x) 2 x  2
Câu 7 (1đ). Tính tích phân dx  . 3 x 1 2 Câu 8 3x (1đ). Cho y
. Tính đạo hàm cấp cao (5) y (0) . 3 x 1
Câu 9 (1đ). Tính giới hạn của dãy số n 2 lim n  2 n
Câu 10 (1đ). Viết phương trình tiếp tuyến của đường cong r  2  cos
Tại điểm ứng với   0
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 2 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20181
Mã HP: MI1111, Khóa: K63, Nhóm ngành 1, Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1 (1đ). Chứng minh 2
sin(arccos x)  1 x , x   1  ,  1 .
Câu 2 (1đ). So sánh cặp vô cùng lớn sau khi x   2
 (x) xx , (x) ln(1 x). 1 x 1 x
Câu 3 (1đ). Tìm hàm ngược của hàm số y  ln , x ( 1  ,1) y ln , x ( 1  ,1) . 1 x 1 x
Câu 4 (1đ). Tìm và phân loại điểm gián đoạn của hàm số  1  y  tan arccot   .  x  ln( x
x e ), neu x  0
Câu 5 (1đ). Tìm hàm số f ( ) x   0,  neu x  0 Tính ' f (0) .  3 4  Câu 6 x x (1đ). Tính giới hạn lim .
x0 x  sin x 2 
Câu 7 (1đ). Tính tích phân x 2x dx  . 3 x 1 2x
Câu 8 (1đ). Cho y
. Tính đạo hàm cấp cao (7) y (0) . 2 x 1 
Câu 9 (1đ). Tính giới hạn của dãy số n 2 lim n 1 n
Câu 10 (1đ). V ết phương trình tiế i
p tuyến của đường cong r 1 cos 
Tại điểm ứng với   0
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 3 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20181
Mã HP: MI1111, Khóa: K63, Nhóm ngành 1, Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nh n s ậ
ố đề vào bài thi.
Câu 1 (1đ). Hàm số y  arctan x có tuần hoàn không? Tại sao?
Câu 2 (2đ). Tính các giới hạn 1
sin x xcos x a) sin lim(cos x) x , b) lim . 3 x 0  x 0  x 1  x
a e neu x  0
Câu 3 (1đ). Cho hàm số f (x)   1  neu x  0 ln x
Tìm a để x  0 n b là điểm gián đoạ ỏ được của hàm s ố f (x)
Câu 4 (1đ). Tìm lim [sin(ln )
n  sin(ln( n 1))] lim [sin(ln ) n sin(ln( n 1  ))] n n
Câu 5 (1đ). Tìm a,b để hai vô cùng bé sau là tương đương khi x  0 2 3 2
 (x) axbx x , ( ) x  sin(x ) Câu 6 2
(1đ). Ứng dụng vi phân, tính gần đúng 4 . 2  0, 02
Câu 7 (1đ). Tính tích phân 2 arccos xdx  .
Câu 8 (1đ). Viết phương trình tiếp tuyến của đường cycloid
x t sin t,  y  1  cost  
Tại điểm ứng với t  . 2
Câu 9 (1đ). Cho hàm số f (x) xác định và có đạo hàm trên ℝ. Chứng minh rằng nếu f (x) là m t hàm s ộ l ố ẻ
thì f '(x) là m t hàm s ộ ố chẵn.
VIỆN TOÁN ỨN D
G ỤNG VÀ TIN HỌC Đề 4 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20181
Mã HP: MI1111, Khóa: K63, Nhóm ngành 1, Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi.
Câu 1 (1đ). Hàm số y  arccot x có tuần hoàn không? Tại sao?
Câu 2 (2đ). Tính các giới hạn 1 sin x x xe b) tan lim(cos x) x , b) lim . x 0 2 x0 x  1 neu x  0  Câu 3 ln( ) x
(1đ). Cho hàm số f ( x)   1  
a+e x neu x  0 
Tìm a để x  0 n b là điểm gián đoạ ỏ được của hàm s ố f (x)
Câu 4 (1đ). Tìm lim [sin(ln( n1))  sin(ln )] n n
Câu 5 (1đ). Tìm a,b để hai vô cùng bé sau là tương đương khi x  0 2 3 4 3
 (x) ax bx x , ( ) x  sin(x ) Câu 6 2
(1đ). Ứng dụng vi phân, tính gần đúng 4 . 2  0, 02
Câu 7 (1đ). Tính tích phân 2 arcsin xdx  .
Câu 8 (1đ). Viết phương trình tiếp tuyến của đường cycloid
x t  cost,  y  1 sint  
Tại điểm ứng với t  . 2
Câu 9 (1đ). Cho hàm số f (x) xác định và có đạo hàm trên ℝ. Chứng minh rằng nếu f (x) là m t hàm s ộ ố
chẵn thì f '(x) là m t hàm s ộ l ố ẻ.
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 5 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20181
Mã HP: MI1112, Khóa: K63, Nhóm ngành 2, Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nh n s ậ
ố đề vào bài thi.
Câu 1. (1đ). Tìm tập xác định và tập giá trị của hàm số 2
y  arccot 3  x .
Câu 2. (1đ). Chứng minh rằng với mọi x, y ℝ:
sinh x y  sinh x cosh y sinh y cosh x .
Câu 3. (1đ). Phân loại điểm gián đoạn x 1 c a hàm s ủ ố x 1 arctan 2 x y   . 2x  1
Câu 4. (1đ). Tìm cực trị của hàm số y  . 2 x 1
Câu 5. (1đ). Tìm a để hàm số sau có đạ o hàm tại x  0 : x    f x e asin x khi x 0   . cos x khi x  0 
Với a vừa tìm được tính f 0 .
Câu 6. (1đ). Sử d ng vi phân c ụ ấp m t, tính g ộ ần đúng 3 7, 76 . Câu 7. 20
(1đ). Cho hàm số y  x  
1 ln x. Tính đạo hàm y  1 .
Câu 8. (1đ). So sánh các vô cùng bé sau khi x  0 :
 x  x  2
ln e  2x   x sin 2x ;  x 1 cos 2x .
Câu 9. (1đ). Tính giới hạn 2x e 2sin x 1  lim . xx ln1 x 3 0  2sin x
Câu 10. (1đ). Cho ba số a, b, c thỏa mãn b a c . Ch ng minh r ứ ằng phương trình 4 2
5ax  3bx c  0 có ít
nhất một nghiệm trong khoảng 0,  1 .
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 6 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20181
Mã HP: MI1112, Khóa: K63, Nhóm ngành 2, Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nh n s ậ
ố đề vào bài thi. Câu 1 (1đ). Tìm t nh và t ập xác đị ập giá trị c a hàm s ủ ố 2
y  arccot 1 x .
Câu 2 (1đ). Chứng minh rằng với mọi x, y ℝ:
cosh x y   cosh x cosh y sinh xsinh y. Câu 3 (1đ). Phân lo n
ại điểm gián đoạ x  1  c a hàm s ủ ố x 1 arctan 2 x y   . 2x  1
Câu 4 (1đ). Tìm cực trị c a hàm s ủ ố y  . 2 x 1 Câu 5 (1đ). Tìm a để hàm s ố o hàm t sau có đạ ại x  0 : 1  sin ax   f x khi x 0   . xe khi x  0 
Với a vừa tìm được tính f    0 .
Câu 6 (1đ). Sử d ng vi phân c ụ ấp m t, tính g ộ ần đúng 3 8,12 . Câu 7 20  (1đ). Cho hàm s
ố y   x  2ln x . Tính đạo hàm y   1 .
Câu 8 (1đ). So sánh các vô cùng bé sau khi x  0 :  x 3 2 3
1 1 4x x x x ;   x  sin  e  1.
Câu 9 (1đ). Tính giới hạn 2 x
e  2 cos x  1 lim . x ln 3 0
1  2x   x arcsin x
Câu 10 (1đ). Cho ba s ố a, b, c th a mãn ỏ
b a c. Ch ng minh r ứ ằng phương trình 4 2
5ax  3bx c  0 có ít nhất
một nghiệm trong khoảng 0,1 .
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 7 ĐỀ THI GIỮ Ả
A KÌ MÔN GI I TÍCH I – Học kì 20181
Khóa: 63 - Nhóm ngành 3 - Mã HP: MI1113. Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1 (1 điểm). Tìm tập xác định của hàm số y  lg cos x . 1 2 x 1 
Câu 2 (1 điểm). Tính lim . x 0 tan 3x
Câu 3 (1 điểm). Tìm và phân loại điểm gián đoạn của hàm số 1 y  arctan . x
Câu 4 (1 điểm). Khi x  0 i sao?
các vô cùng bé sau có tương đương không? Tạ
 x  sin5x,  x 5x 2
e 1 x .
Câu 5 (1 điểm). Dùng định nghĩa, tính đạo hàm y   0 với 3
y x arcsin x . 2x e
Câu 6 (1 điểm). Tính dx  . 4 x e 1 Câu 7 arctan x (1 điểm). Tính dx  . 2 x 1  1 
Câu 8 (1 điểm). Tính lim  cot x   .
x 0 x xx1 2
Câu 9 (1 điểm). Tìm các tiệm cận xiên của đồ thị hàm số x 1 y xe .
Câu 10 (1 điểm). Cho f x khả vi trên  ,
a b, 0  a b . Ch ng minh r ứ
ằng a,b sao cho f bf a   
  f   f   1 1      . b ab a
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 8 ĐỀ THI GIỮ Ả
A KÌ MÔN GI I TÍCH I – Học kì 20181
Khóa: 63 - Nhóm ngành 3 - Mã HP: MI1113. Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị ph i ký xác nh ả
ận số đề vào bài thi
Câu 1 (1 điểm). Tìm tập xác định của hàm số y  lg sin x . 1 4 x 1 
Câu 2 (1 điểm). Tính lim . x 0 tan 5x
Câu 3 (1 điểm). Tìm và phân loại điểm gián đoạn của hàm số 1 y  arccot . x
Câu 4 (1 điểm). Khi x  0 i sao?
các vô cùng bé sau có tương đương không? Tạ
 x  sin3x ,  x 3x 2
e 1 x .
Câu 5 (1 điểm). Dùng định nghĩa, tính đạo hàm y   0 với 5
y x arcsin x . 3x e
Câu 6 (1 điểm). Tính dx  . 4 x e 1 Câu 7 arccot x (1 điểm). Tính dx  . 2 x 2  1 
Câu 8 (1 điểm). Tính lim  cot x   .
x 0 x xx 1  3
Câu 9 (1 điểm). Tìm các tiệm cận xiên của đồ thị hàm số x1 y xe .
Câu 10 (1 điểm). Cho f x khả vi trên  ,
a b, 0  a b . Ch ng minh r ứ
ằng a,b sao cho f bf a   
  f   f   1 1      . b ab a
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 1 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20173
Nhóm ngành 1. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi. Câu 1. x Tìm t nh c ập xác đị a hàm s ủ ố 3 1 y  2x 1   4 arcsin . 2 Câu 2. sin x Tìm và phân lo n c ại điểm gián đoạ ủa hàm s ố y  . xx   1 l
x n 1  2 xCâu 3. Tính lim . 2 3
x 0 3x  4sin x 1 
Câu 4. Tìm các tiệm cận của đồ thị hàm s ố x y xe  2.
Câu 5. Tính sin ln x dx  . 3 Câu 6. sin x Tính dx  . cos x x  2 Câu 7. Tính   dx .
x  2x  2 2 2
Câu 8. Kiểm tra định lý Fernat cho hàm số y x 1 trên 0;2. 4 1 1 2x cos  2 2x Câu 9. Tính lim . 5 x x ln  3 0 1  2x    Câu 10. 1 1 Xét sự h i t ộ và tìm gi ụ
ới hạn (nếu có) c a dãy ủ số x x x     x n . n  : 0, , 1 1 n 1 2 n xn
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 1 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 2017.1
Khóa: K62. Mã HP: MI1111. Nhóm ngành 1. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nh n s ậ
ố đề vào bài thi. Câu 1. Tìm t nh c ập xác đị a hàm s ủ
ố y  6 arccot x  5 .
Câu 2. Tìm tất cả hàm s liên t ố
ục f x th a mãn ỏ
f x   x , x   ℝ. ln1 4sin  x
Câu 3. Tính I  lim .  0 3x x 1  3    Câu 4. x x khi x 1,
Tìm a,b ℝ để hàm s ố y  
khả vi tại x  1 .
ax b khi x  1  Câu 5.   Tính đạo hàm cấp cao 5
y x với y   2
ln 2x x . 2 cot x   Câu 6. x Tính I  lim   . x 0   sin x   Câu 7. 2x 3 Tính tích phân dx  . 3 x 1
Câu 8. Tính tích phân 2 tan  xdx  .
Câu 9. Sử d ng khai tri ụ ển Maclaurin của hàm s ố 3
y  1 x đến 3
x để tính gần đúng 3 1, 09 , (quy tròn đến 6 10 ).
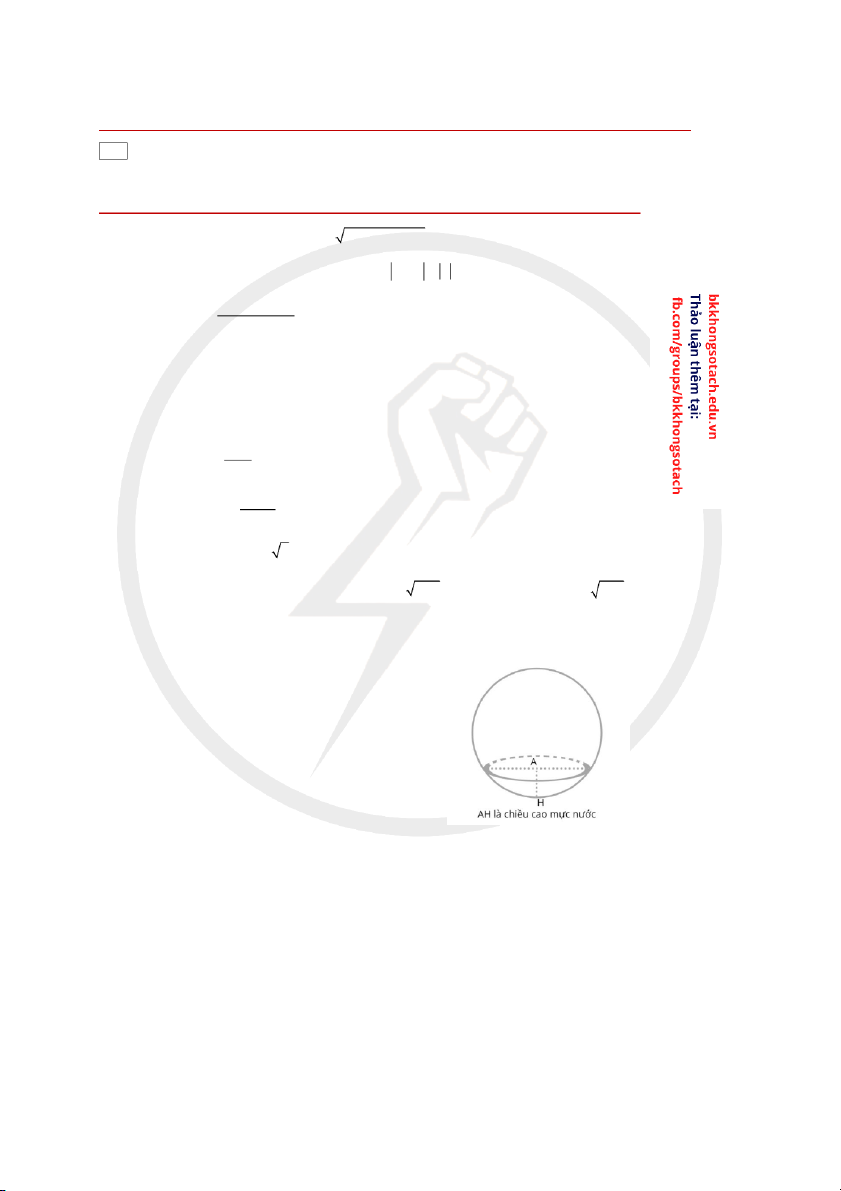
Câu 10. Bơm nước vào một bể chứa hình cầu bán kính 4m với tốc độ 3
1m /1 phút. Tính tốc độ tăng lên tức thời của chiều cao m c khi chi ực nướ ều cao m c là 3 ực nướ m.
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 2 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 2017.1
Khóa: K62. Mã HP: MI1111. Nhóm ngành 1. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nh n s ậ
ố đề vào bài thi. Câu 1. Tìm t nh c ập xác đị a hàm s ủ
ố y  4 arccot x  3 .
Câu 2. Tìm tất cả hàm s liên t ố
ục f x th a mãn ỏ f x 2  x , x  ℝ.  Câu 3. log (1 4 tan ) x Tính 3 I  lim . 0 x x e 1  3 a
x 2 x khi x 1,
Câu 4. Tìm a,b ℝ để hàm s ố y  
khả vi tại x  1.
x b khi x 1 Câu 5. 6
Tính đạo hàm cấp cao y
x  với y   2
ln 3x x . 2 cot x   Câu 6. x Tính I  lim   . x 0   tan x   Câu 7. 3x 2 Tính tích phân dx  . 3 x 1
Câu 8. Tính tích phân 2 cot  xdx  .
Câu 9. Sử d ng khai tri ụ ển Maclaurin của hàm s ố 4
y  1 x đến 3
x để tính gần đúng 4 1, 04 , (quy tròn đến 7 10 ).
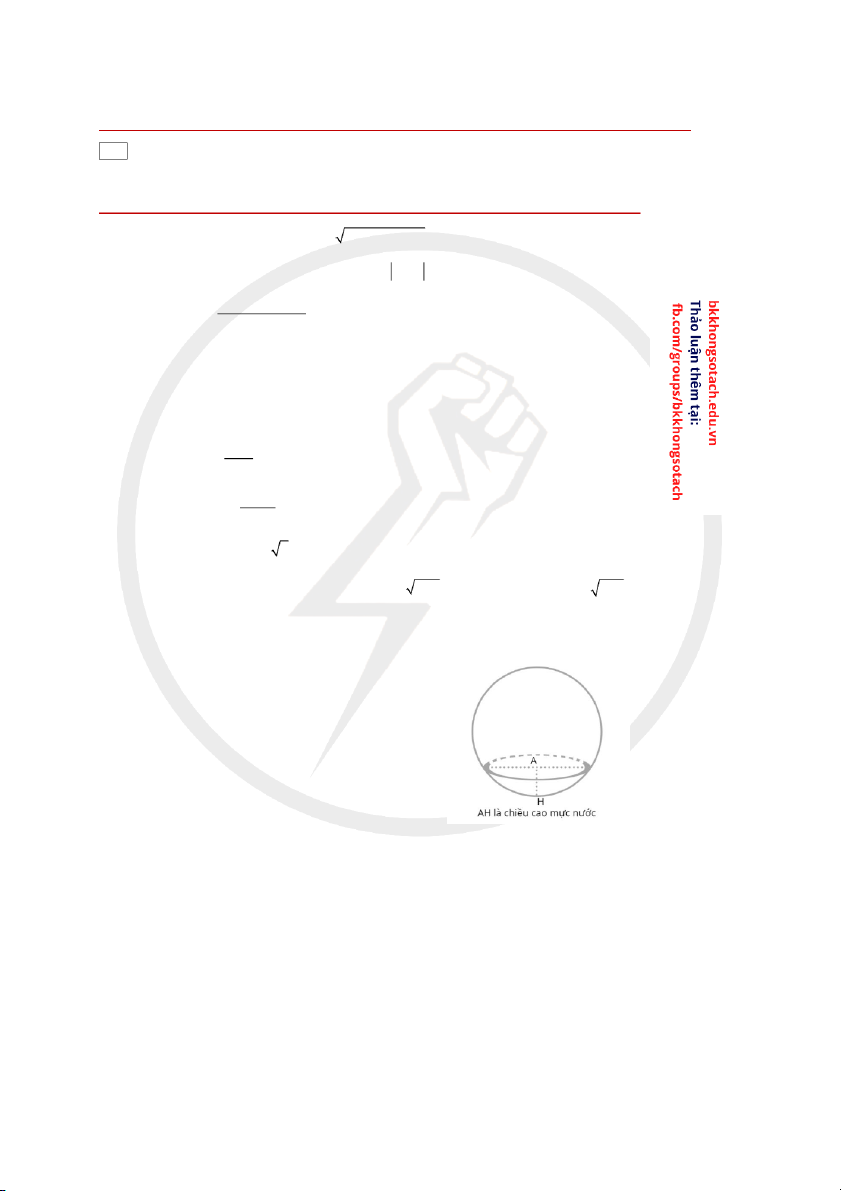
Câu 10. Bơm nước vào một bể chứa hình cầu bán kính 6 m với tốc độ 3
1m /1 phút. Tính tốc độ tăng lên tức thời của chiều cao m c khi chi ực nướ ều cao m c là 5 ực nướ m.
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 3 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 2017.1
Khóa: K62. Mã HP: MI1111. Nhóm ngành 1. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nh n s ậ
ố đề vào bài thi. Câu 1. Tìm hàm s ố ngược c a hàm s ủ
ố y  2arcsin x, x   1  ;  1 .   1  arctan khi x  0,   Câu 2. Tìm a để hàm s ố y    x  liên t c t ụ ại x  0 . a khi x   0 ln  4
x  arcsin x   ln x
Câu 3. Tính I  lim .  3 x0 x
Câu 4. Tính vi phân c a hàm s ủ
ố y  ln tan 2x .
Câu 5. Tìm cực trị c a hàm s ủ ố 2 2
y  2x ln x+3x  4x ln x  4x . Câu 6. x
Tính I  lim  sin x .  tan x0
Câu 7. Tính tích phân 2 x xe cos xdx  .
Câu 8. Tính tích phân  x   
1 arccot  2xdx .
Câu 9. Tìm nghiệm xấp xỉ thứ 6 của phương trình 5
x x  10 theo phương pháp Newton với xấp xỉ u ban đầ
x  2 , (quy tròn đến 9 10 ). 1
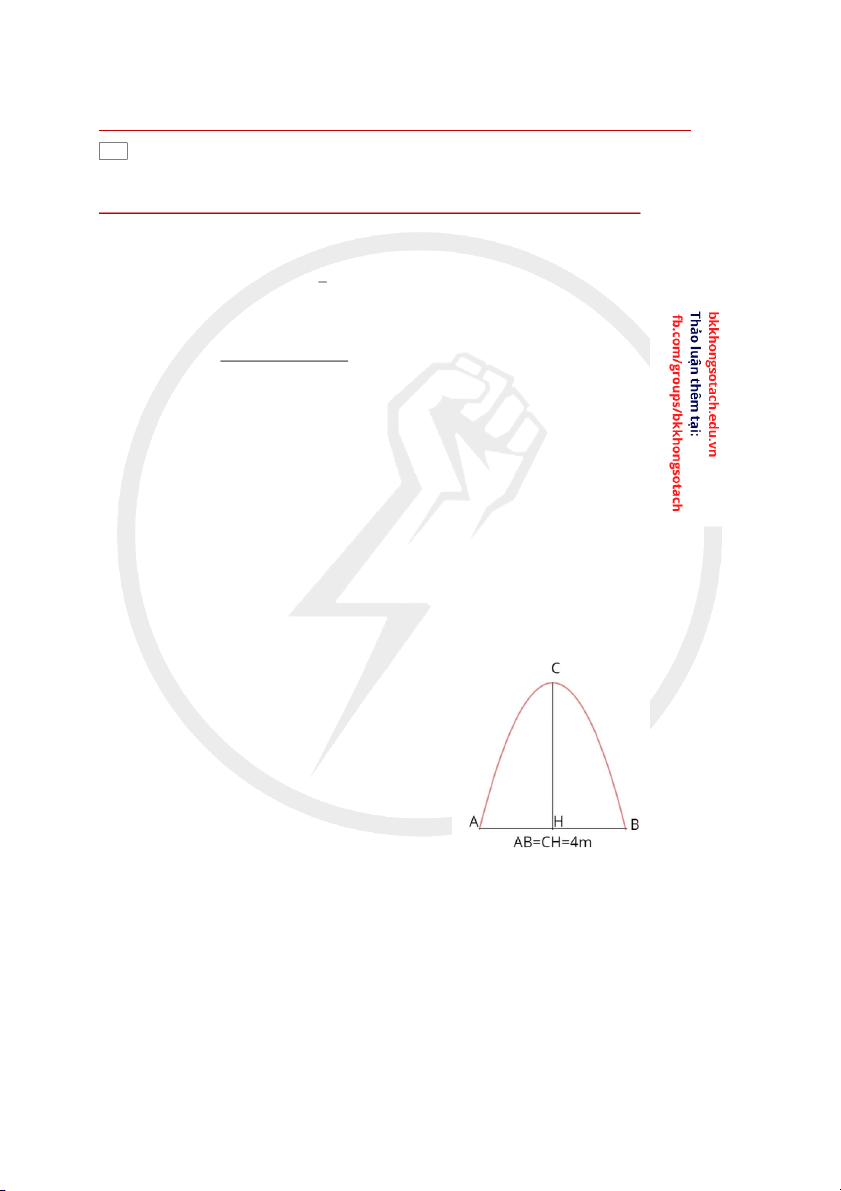
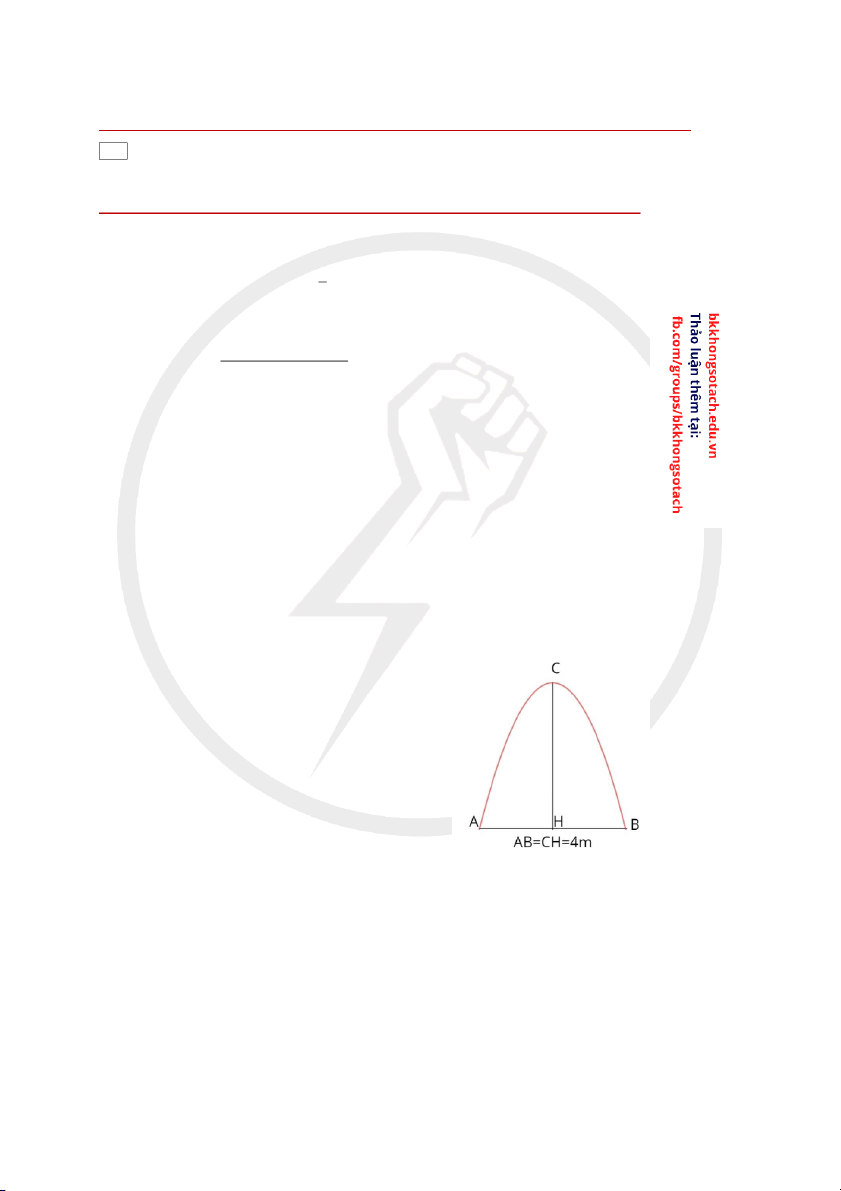
Câu 10. Tính bán kính lớn nhất c a m ủ t qu ộ
ả cầu có thể di chuyển vào được m t c ộ ng hình Parabol v ổ ới kích
thước như hình vẽ bên.
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 4 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 2017.1
Khóa: K62. Mã HP: MI1111. Nhóm ngành 1. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi. Câu 1. Tìm hàm s ố ngược c a hàm s ủ
ố y  3arccos x , x 1  ;  1 .   1  arccot khi x  0,   Câu 2. Tìm a để hàm s ố y    x  liên t c t ụ ại x  0 . a khi x   0 ln  3
x  arcsin x   lnx
Câu 3. Tính I  lim .  2 x0 x
Câu 4. Tính vi phân c a hàm s ủ
ố y  ln cot 2x .
Câu 5. Tìm cực trị c a hàm s ủ ố 2 2
y  2x ln x x  2x ln x  2x . Câu 6. x
Tính I  lim  tan x .  sin x0
Câu 7. Tính tích phân 2 x xe sin xdx  .
Câu 8. Tính tích phân  x   
1 arctan 3xdx .
Câu 9. Tìm nghiệm xấp xỉ thứ 6 của phương trình 4
x x  10 theo phương pháp Newton với xấp xỉ u ban đầ
x  2 , (quy tròn đến 9 10 ). 1
Câu 10. Tính bán kính lớn nhất c a m ủ t qu ộ
ả cầu có thể di chuyển vào được m t c ộ ng hình Parabol v ổ ới kích
thước như hình vẽ bên.
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 5 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 2017.1
Khóa: K62. Mã HP: MI1112. Nhóm ngành 2. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nh n s ậ
ố đề vào bài thi. Câu 1. Tìm t nh và t ập xác đị ập giá trị c a hàm s ủ
ố y  sinarccos  x .
Câu 2. So sánh cặp vô cùng bé sau đây khi x  0:   3 2
x x  sin x ,  x  3 1 cos x .
Câu 3. Tìm hàm ngược của hàm số 2 y x  2 ,
x x 1,  . Câu 4. 1 Tìm và phân lo n c ại điểm gián đoạ ủa hàm s ố 2 y x arctan . x 3 h4  81 Câu 5. Tìm m t hàm s ộ
ố f x và s ố thực sao cho a lim
f  a  . h 0 h 2   Câu 6. 1 cos 2 x 2 x Tính giới hạn lim . 4 x 0 x x    Câu 7. x a Tìm
a để đẳng thức sau đúng lim  e   .
x   x a Câu 8. 9 Cho y   2
ln 1 x x  . Tính đạo hàm cấp cao y 0 . Câu 9. Cho ba s
ố thực a, b, c thỏa mãn a b c  0 . Ch ng minh r ứ ằng phương trình 2
2ax  4bx  5c  0 có ít
nhất một nghiệm thuộc khoảng 1, . 2
ax bln cos x
Câu 10. Tìm a,b  sao cho ℝ lim  1. 4 x 0 x
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 6 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 2017.1
Khóa: K62. Mã HP: MI1112. Nhóm ngành 2. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nh n s ậ
ố đề vào bài thi. Câu 1. Tìm t nh và t ập xác đị ập giá trị c a hàm s ủ
ố y  cosarcsin x .
Câu 2. So sánh cặp vô cùng bé sau đây khi x  0:  x 2 3
x  sin x ,  x 3 1 cos x .
Câu 3. Tìm hàm ngược của hàm số 2 y x  2 ,
x x 1,  . Câu 4. 1 Tìm và phân lo n c ại điểm gián đoạ ủa hàm s ố 3 y x arctan . x 2  h5 32 Câu 5. Tìm m t hàm s ộ
ố f x và s ố thực sao cho a lim
f  a. h 0 h 2   Câu 6. 1 cos 4x 8 x Tính giới hạn lim . 4 x 0 x x    Câu 7. x a Tìm
a để đẳng thức sau đúng lim  e   .
x   x a Câu 8. 9 Cho y   2
ln 1 x x  . Tính đạo hàm cấp cao y 0 . Câu 9. Cho ba s
ố thực a, b, c thỏa mãn a b c  0 . Ch ng minh r ứ ằng phương trình 2
2ax  3bx  4c  0 có ít
nhất một nghiệm thuộc khoảng 1, .
axbsin sin  x
Câu 10. Tìm a,b  sao cho ℝ lim  1. 3 x 0 x
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 7 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 2017.1
Khóa: K62. Mã HP: MI1113. Nhóm ngành 3. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nh n s ậ
ố đề vào bài thi. 1 2 Câu 1(1đ). Tìm và phân lo n c ại điểm gián đoạ a hàm s ủ ố : ( 1) ( ) 3x x f x     x
Câu 2(1đ). So sánh các vô cùng bé sau, khi x 1: → 3 ( x 1)  (x)  e  1; (x) cot 2 1 Câu 3(1đ).  x 1 x  Tính lim     x 0 1 x ln x  Câu 4(1đ). Tìm c c tr ự ị hàm s ố 5 2 f (x)  ( x x 1) Câu 5(1đ). Tính 2 arcsin xdx
Câu 6(1đ). Viết công th c Maclaurin cho hàm ứ 2
y x sin x đến lũy thừa 11 x Câu 7(1đ). Cho x
y x  | x  2 |. Tính y '(1); y '(2). 1 Câu 8(1đ). Tính dx  8 6 x x 4  Câu 9(1đ) . (x 1) Cho f (x)  ln(2  x) . Tính 10 d f (1). 5!
Câu 10(1đ). Cho a b c d .CMR phương trình 5 4 3
6ax  5bx  4cx d  0 có nghiệm trong khoảng (-1;0)
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 8 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 2017.1
Khóa: K62. Mã HP: MI1113. Nhóm ngành 3. Th i gian: 60 phút ờ
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi. 1 2 Câu 1(1đ). Tìm và phân lo n c ại điểm gián đoạ a hàm s ủ ố : ( 2) (1 ) ( ) 2 x x f x    2   Câu 2(1đ). 3 x x
So sánh các vô cùng bé sau, khi x 1: → ( 1)  (x)  e  1; (x)  cot 2 x   Câu 3(1đ). x sin x Tính lim     x 0 1 x x  Câu 4(1đ). Tìm c c tr ự ị hàm s ố 5 2 f (x)  ( x x 1) Câu 5(1đ). Tính 2 arccos xdx
Câu 6(1đ). Viết công th c Maclaurin cho hàm ứ 2
y x cos x đến lũy thừa 9 x Câu 7(1đ). Cho x
y x  | x  1|. Tính y '(1); y '(2). Câu 8(1đ). 1 Tính dx  8 6 x x 4  Câu 9(1đ) . (x 2) Cho f (x)  ln(3  x) . Tính 10 d f (2). 5!
Câu 10(1đ). Cho a b c d .CMR phương trình 5 4 3
6ax  5bx  4cx d  0 có nghiệm trong khoảng (0;1)
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 2 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20161
Khóa: K61. Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi. Câu 1. Tìm t nh và t ập xác đị ập giá trị c a hàm s ủ
ố y  arccos sin 2x .
Câu 2. So sánh cặp vô cùng bé sau đây khi x  0:    5 4 5 x
x x ,    tan x x e 1 . t  an , x neu x  0
Câu 3. Tính f 0 , biết f x   . 2  x  , x neu x  0  b a b a
Câu 4. Chứng minh rằng
 arctan b arctan a
với mọi 0  a b. 2 2 1 b 1 a
sinx  ln1 x
Câu 5. Tính giới hạn lim . 2 x 0 x Câu 6. x
Tìm các cực trị c a hàm s ủ ố sin y
trong khoảng 0, 2 . 2  cos x Câu 7. 1 Tính tích phân dx  . 2 x  2016 x
Câu 8. Cho f x , g x là các hàm s
ố xác định trên và tuần hoàn với chu kì lần lượt là T  0, T  0 . Biết tỉ 1 2 T số 1 là m t s ộ h
ố ữu tỉ. Chứng minh rằng f xgx t hàm s cũng là mộ ố tuần hoàn. T2
Câu 9. Tính đạo hàm cấp cao 10 y 0 với   2 x y x e  .
Câu 10. Tính tích phân x  2 ln x x   1 dx .
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 3 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 2016.1
Khóa: K61. Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi. Câu 1. x 1
Tìm hàm ngược của hàm số sau y  . 2 x 1 x Câu 2. e 1 Tính giới hạn lim . x 0  2 xxCâu 3. 1 Điểm x   n lo là điểm gián đoạ ại gì c a hàm s ủ
ố f x  . 2 tan 1  2 x
Câu 4. Sử d ng vi phân, tính g ụ ần đúng 3 7, 97 . 60    Câu 5. 1
Tính đạo hàm cấp cao   . 2  x x  1 x e Câu 6.  Tính giới hạn 1 lim x . 2 x 0 x
Câu 7. Tính tích phân 3 x arctan xdx  . Câu 8.   Tính đạo hàm cấp cao 9 y
0 với yx  arccot x .  2016t x   2   Câu 9. 1 t Tìm các tiệm cận c ng cong cho b ủa đườ
ởi phương trình tham số  . 2 2016ty  3  1 tCâu 10. x  1 Tính tích phân 1 x 1  ln x dx    .  x
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC Đề 5 ĐỀ THI GIỮ Ả A KÌ MÔN GI –
I TÍCH 1 Học kì 20161
Khóa: K61. Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nh n s ậ
ố đề vào bài thi.
Câu 1. Xét tính chẵn lẻ c a hàm s ủ
ố y  tan sin x.
Câu 2. Tìm m để hàm s sau liên t ố c t ụ ại x 1. 2      f x
x mx x 1, neu x 1   . 1   , m neu x 1  2x Câu 3. e 1 Tính giới hạn lim .
x 0 ln1 3x 50
Câu 4. Tính đạo hàm cấp cao  2
x sin 2x  . l  n 1  x  sin x
Câu 5. Tính giới hạn lim . 2 x 0 x 2x
Câu 6. Tìm các cực trị c a hàm s ủ sau ố y  . 2 x  1
Câu 7. Tính tích phân 2 x sin 2xdx  .
Câu 8. Hãy chỉ ra m t hàm s ộ
ố f x xác định trên , liên t ℝ c t
ụ ại các điểm x  1, x  2 nhưng không có đao 0 1 hàm tại các điểm này. xdx
Câu 9. Tính tích phân   . 2 x   2 2 x 3 Câu 10. d
Tìm f  x  nếu biết  f x  2 2016   x   . dx