









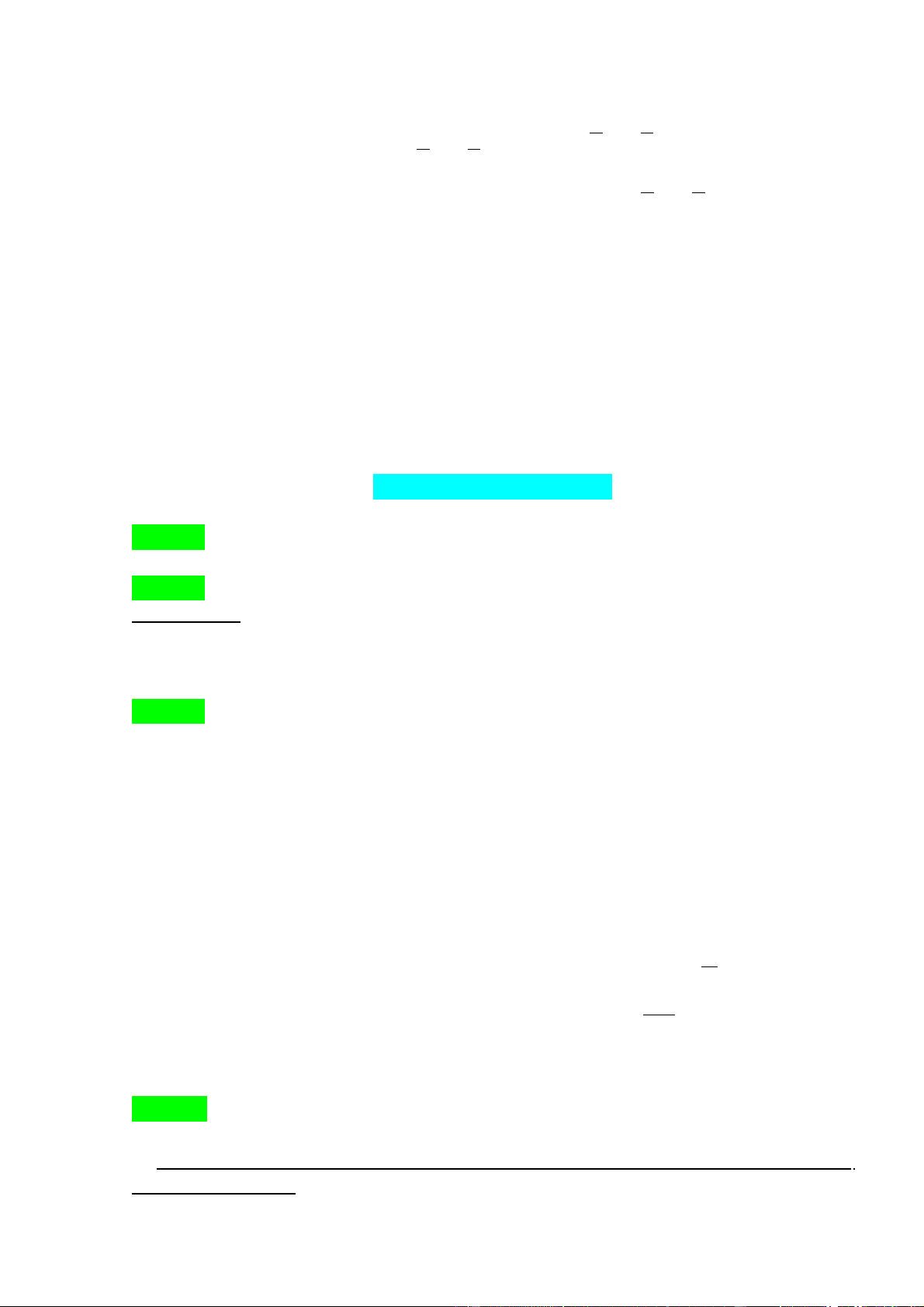


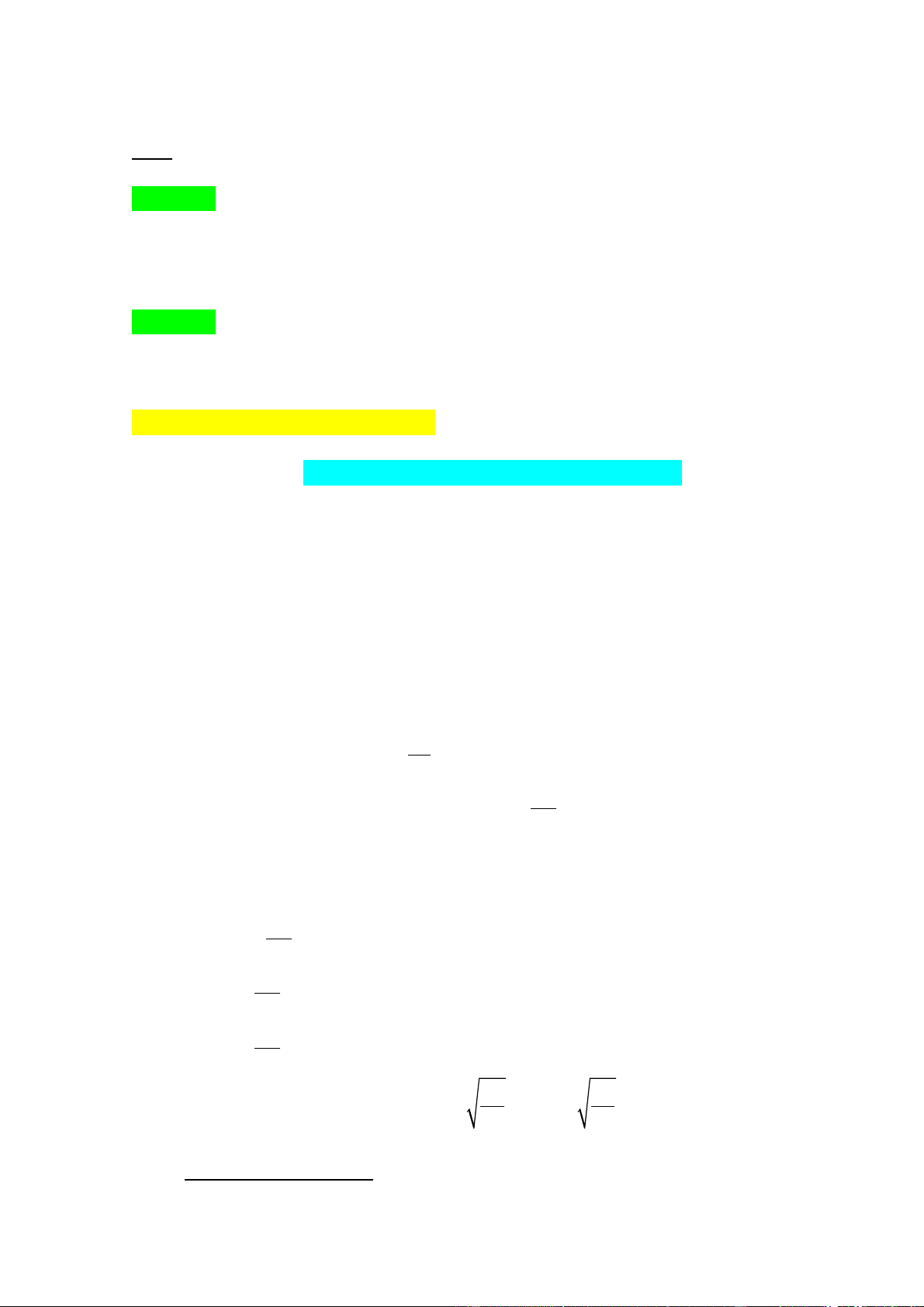












Preview text:
TæNG HîP KIÕN THøC —²™ M«n : §¹i Sè - THCS
I - C¸c lo¹i ph¬ng tr×nh
1. Ph¬ng tr×nh bËc nhÊt
- Ph¬ng tr×nh bËc nhÊt lµ ph¬ng tr×nh cã d¹ng ax + b = 0 (a ≠ 0)
- Ph¬ng tr×nh cã nghiÖm duy nhÊt x = b − a
- Chó ý: NÕu ph¬ng tr×nh chøa tham sè ta chuyÓn vÒ d¹ng Ax = B vµ xÐt c¸c trêng hîp sau:
NÕu A ≠ 0 ph¬ng tr×nh cã nghiÖm x = B − A
NÕu A = 0 , B ≠ 0 ph¬ng tr×nh trë thµnh 0.x = B
=> ph¬ng tr×nh v« nghiÖm
NÕu A = 0, B = 0 => ph¬ng tr×nh v« sè nghiÖm 2. Ph¬ng tr×nh tÝch
- Ph¬ng tr×nh tÝch cã d¹ng A(x).B(x) = 0
- C¸ch gi¶i: A(x).B(x) = 0 <=> A(x) = 0 hoÆc B(x) = 0 A(x) = 0
- Tr×nh bµy gän : A(x).B(x) = 0 <=> B(x) = 0 A(x) = 0
- Më réng: A(x).B(x).C(x) = 0 <=> B(x) = 0 C(x) = 0
3. Ph¬ng tr×nh chøa Èn ë mÉu
- Gi¶i ph¬ng tr×nh chøa Èn ë mÉu ta thùc hiÖn theo 4 bíc:
Bíc 1: T×m §KX§ cña ph¬ng tr×nh
Bíc 2: Quy ®ång mÉu hai vÕ cña ph¬ng tr×nh råi khö mÉu
Bíc 3: Gi¶i ph¬ng tr×nh võa nhËn ®îc
Bíc 4: (kÕt luËn)
Trong c¸c gi¸ trÞ cña Èn t×m ®îc ë bíc 3, c¸c gi¸ trÞ tháa m·n §KX§
chÝnh lµ nghiÖm cña ph¬ng tr×nh ®· cho, gi¸ trÞ cña x kh«ng thuéc
§KX§ lµ nghiÖm ngo¹i lai (lo¹i ®i)
4. Ph¬ng tr×nh chøa dÊu gi¸ trÞ tuyÖt ®èi A nÕu A ≥ 0
- §Þnh nghÜa: A = −A nÕu A < 0
- C¸c d¹ng ph¬ng tr×nh
f ( x) = 0 <=> f ( x) = 0
f ( x) = k( k > 0) <=> f ( x) = ±k f (x) = g(x)
f ( x) = g( x) <=> f(x) = −g(x) Hay = <=> [ ]2 = [ ]2 f ( x ) g( x) f ( x)
g( x) , ®a vÒ ph¬ng tr×nh tÝch f(x) ≥ 0 g(x) ≥ 0 f ( x) = g(x) f ( x) = g(x)
f ( x) = g( x) <=> hoÆc <=> f (x) ≤ 0 g(x) ≥ 0 f (x) = −g(x) f (x) = −g(x) g(x) ≥ 0 HoÆc <=> f(x) = g(x) hoÆc f (x) = −g(x) g(x) ≥ 0
HoÆc <=> [f(x) ]2 = [g(x)]2 - Chó ý: 2 2
A = A ; A ≥ ± A vµ A − B ≤ A ± B ≤ A + B
5. Ph¬ng tr×nh v« tØ 2
f (x) = A( A ≥ 0) <=> f (x) = A (víi f(x) lµ mét ®a thøc) f ( x) ≥ 0 g(x) ≥ 0
f ( x) = g(x) <=> f(x)= [g(x)]2 f(x) ≥ 0
f (x) = g(x) <=> g(x) ≥ 0 f(x) = g(x)
*)Lu ý: HÇu hÕt khi gi¶i ph¬ng tr×nh chøa Èn trong c¨n, ta cÇn x¸c ®Þnh
®iÒu kiÖn cã nghÜa cña ph¬ng tr×nh vµ c¸c ®iÒu kiÖn t¬ng
®¬ng. NÕu kh«ng cã thÓ thö l¹i trùc tiÕp.
6. Ph¬ng tr×nh trïng ph¬ng Ph¬ng tr×nh
trïng ph¬ng lµ ph¬ng tr×nh cã d¹ng: 4 2 ax + bx + c = 0 (a ≠ 0)
§Æt x2 = t ( t ≥ 0 ), ph¬ng tr×nh trïng ph¬ng trë thµnh ph¬ng tr×nh bËc hai Èn t : 2 at + bt + c = 0 (*)
Gi¶i ph¬ng tr×nh (*), lÊy nh÷ng gi¸ trÞ thÝch hîp tháa m·n t ≥ 0
Thay vµo ®Æt x2 = t vµ t×m x = ?
7. Ph¬ng tr×nh bËc cao
a) Ph¬ng tr×nh bËc ba d¹ng: ax3 + bx2 + cx + d = 0
Híng dÉn: NhÈm nghiÖm (nÕu cã nghiÖm nguyªn th× nghiÖm ®ã lµ íc cña
h¹ng tö tù do d) hoÆc dïng s¬ ®å Hooc- ne hoÆc dïng m¸y tÝnh ®Ó t×m
nhanh nghiÖm nguyªn cña ph¬ng tr×nh, khi ®· biÕt mét nghiÖm th× dÔ dµng
ph©n tÝch VT díi d¹ng tÝch vµ gi¶i ph¬ng tr×nh tÝch (hoÆc chia ®a thøc)
b) Ph¬ng tr×nh bËc bèn d¹ng: ax4 + bx3 + cx2 + dx + e = 0
Híng dÉn: Ph¬ng ph¸p t¬ng tù nh ph¬ng tr×nh bËc ba trªn
c) Ph¬ng tr×nh bËc bèn d¹ng: 2
x4 + ax3 + bx2 + cx + d = 0 (víi d = c ). a ÷ P h ¬ng ph¸p:
Víi x = 0, thay vµo ph¬ng tr×nh vµ kiÓm tra xem x = 0 cã lµ nghiÖm hay kh«ng ?
Víi x ≠ 0. Chia c¶ hai vÕ cho x2, sau ®ã ta ®Æt t = x + c ax
d) Ph¬ng tr×nh bËc 4 d¹ng:
(x + a)(x + b)(x + c)(x + d) = k (víi a + b = c + d = m) P h ¬ng ph¸p: §Æt t = x ab cd 2 + mx + + 2
e) Ph¬ng tr×nh bËc bèn d¹ng:
(x + a)(x + b)(x + c)(x + d) = kx2 (víi ab = cd = k) P h ¬ng ph¸p:
Chia c¶ hai vÕ cho x2. §Æt t = x + k x
II- BÊt ph¬ng tr×nh bËc nhÊt mét Èn 1) §Þnh nghÜa:
Mét bÊt ph¬ng tr×nh d¹ng ax + b > 0 (hoÆc ax + b < 0) víi a ≠ 0
®îc gäi lµ mét bÊt ph¬ng tr×nh bËc nhÊt mét Èn
2) C¸ch gi¶i: ax + b > 0 <=> ax > - b b
NÕu a > 0 th× x > − ab
NÕu a < 0 th× x < − a
3) KiÕn thøc cã liªn quan:
Hai bÊt ph¬ng tr×nh ®îc gäi lµ t¬ng ®¬ng nÕu chóng cã cïng tËp nghiÖm vµ
dïng kÝ hiÖu <=> ®Ó chØ sù t¬ng ®¬ng ®ã
Quy t¾c chuyÓn vÕ: Khi chuyÓn mét h¹ng tö (lµ sè hoÆc ®a thøc) tõ vÕ nµy
sang vÕ kia cña bÊt ph¬ng tr×nh ta ph¶i ®æi dÊu h¹ng tö ®ã => ta cã thÓ
xãa hai h¹ng tö gièng nhau ë hai vÕ
Quy t¾c nh©n: Khi nh©n hai vÕ cña mét bÊt ph¬ng tr×nh víi cïng mét sè
kh¸c 0, ta ph¶i: Gi÷ nguyªn chiÒu BPT nÕu sè ®ã d¬ng; ®æi chiÒu BPT nÕu sè ®ã ©m.
4) TÝnh chÊt c¬ b¶n cña bÊt ®¼ng thøc
- Víi mäi sè thùc a, b, c ta cã : a > b <=> a + c > b + c
- Víi mäi sè thùc a, b, c, d ta cã : a > b, b > c => a > c (t/c b¾c cÇu)
a > b, c > d => a + c > b + d
a > b > 0, c > d > 0 => ac > b
- Víi mäi sè thùc a, b, c,
+ NÕu c > 0 th× a > b <=> ac > bc
+ NÕu c < 0 th× a > b <=> ac < bc
- Víi a, b lµ hai sè thùc : a > b <=> 3 3 a
> b vµ a > b <=> 3 3 a > b
- NÕu a ≥ 0,b ≥ 0 th× a > b <=> a > b vµ a > b <=> 2 2 a > b
- Gi¸ trÞ tuyÖt ®èi cña mét biÓu thøc A A, nÕu A ≥ 0 A = −A, nÕu A < 0.
Ta cã: A2 ≥ 0, |A| ≥ 0, 2 A = A
- BÊt ®¼ng thøc C« - si: Cho a, b lµ hai sè thùc kh«ng ©m, ta cã: a + b ≥ ab DÊu =
“ ” x¶y ra <=> a = b 2
III – C¸c d¹ng bµi tËp cã liªn quan ®Õn biÓu thøc h÷u tØ, c¨n bËc hai, c¨n bËc ba.
1. D¹ng 1 : Rót gän vµ tÝnh gi¸ trÞ c¸c biÓu thøc h÷u tØ
- Khi thùc hiÖn rót gän mét biÓu thøc h÷u tØ ta ph¶i tu©n theo thø tù thùc
hiÖn c¸c phÐp to¸n : Nh©n chia tríc, céng trõ sau. Cßn nÕu biÓu thøc cã c¸c dÊu
ngoÆc th× thùc hiÖn theo thø tù ngoÆc trßn, ngoÆc vu«ng, ngoÆc nhän.
- Víi nh÷ng bµi to¸n t×m gi¸ trÞ cña ph©n thøc th× ph¶i t×m ®iÒu kiÖn cña
biÕn ®Ó ph©n thøc ®îc x¸c ®Þnh (mÉu thøc ph¶i kh¸c 0)
2. D¹ng 2 : T×m ®iÒu kiÖn ®Ó biÓu thøc cã nghÜa
- BiÓu thøc cã d¹ng A
B x¸c ®Þnh (cã nghÜa) khi B ≠ 0
- BiÓu thøc cã d¹ng A x¸c ®Þnh (cã nghÜa) khi A ≥ 0 A
- BiÓu thøc cã d¹ng
x¸c ®Þnh (cã nghÜa) khi B > 0 B B A ≥ 0
- BiÓu thøc cã d¹ng A +
x¸c ®Þnh (cã nghÜa) khi C C > 0 A ≥ 0
- BiÓu thøc cã d¹ng B
A + C x¸c ®Þnh (cã nghÜa) khi C ≠ 0
3. D¹ng 3 : Rót gän c¸c biÓu thøc chøa c¨n bËc hai, c¨n bËc ba LÝ thuyÕt chung:
a) C¸c c«ng thøc biÕn ®æi c¨n thøc 1) 2 A = A 2) AB = A B ( víi A ≥ 0 vµ B ≥ 0) 3) A A = (víi A ≥ 0 vµ B > 0) B B 4) 2 A B = A B (víi B ≥ 0) 5) 2
A B = A B (víi A ≥ 0 vµ B ≥ 0) 2
A B = − A B (víi A < 0 vµ B ≥ 0) 6) A 1 = AB (víi AB ≥ 0 vµ B ≠ 0) B B 7) A A B = (víi B > 0) B B C( A B m C ) 8) 2 = (víi A ≥ 0 vµ A ≠ B ) 2 A ± B A − B C( A m B C ) 9) =
(víi A ≥ 0 , B ≥ 0 vµ A ≠ B) A − B A ± B *) L u ý :
§Ó rót gän biÓu thøc chøa c¨n thøc bËc hai ta lµm nh sau :
- Quy ®ång mÉu sè chung (nÕu cã)
- §a bít thõa sè ra ngoµi dÊu c¨n (nÕu cã)
- Trôc c¨n thøc ë mÉu (nÕu cã)
- Thùc hiÖn c¸c phÐp tÝnh lòy thõa, khai c¨n, nh©n, chia , … theo thø
tù ®· biÕt ®Ó lµm xuÊt hiÖn c¸c c¨n thøc ®ång d¹ng
- Céng, trõ c¸c biÓu thøc ®ång d¹ng (c¸c c¨n thøc ®ång d¹ng)
b) C¸c h»ng ®¼ng thøc quan träng, ®¸ng nhí: 1) (a + b)2 = a2 + 2ab + b2 + 2 ( a b) = a + 2 a.b + b (a,b ≥ 0) 2) (a - b)2 = a2 - 2ab + b2 − 2 ( a b) = a − 2 a.b + b (a,b ≥ 0) 3) a2 - b2 = (a + b).(a - b) a − b = ( a + b).( a − b) (a,b ≥ 0)
4) (a + b)3 = a3 + 3a2b + 3ab2 + b3
5) (a - b)3 = a3 - 3a2b + 3ab2 - b3 6) 3 + 3 = + 2 − + 2 a b (a b)(a ab b ) 3 3 + = 3 + 3 a a b b a
b = ( a) + ( b) = ( a + b)(a − ab + b) (a,b ≥ 0) 7) 3 − 3 = − 2 + + 2 a b (a b)(a ab b ) 3 3 − = 3 − 3 a a b b a
b = ( a) − ( b) = ( a − b)(a + ab +b) (a,b ≥ 0)
8) (a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc 9) + + 2 ( a b
c) = a + b + c + 2 ab + 2 ac + 2 bc (a,b,c ≥ 0) 10) 2 a = a
IV – C¸c d¹ng to¸n vÒ hµm sè LÝ thuyÕt chung
1) Kh¸i niÖm vÒ hµm sè (kh¸i niÖm chung).
NÕu ®¹i lîng y phô thuéc vµo ®¹i lîng thay ®æi x sao cho víi mçi gi¸ trÞ cña
x ta lu«n x¸c ®Þnh ®îc chØ mét gi¸ trÞ t¬ng øng cña y th× y ®îc gäi lµ hµm sè
cña x vµ x ®îc gäi lµ biÕn sè.
*) VÝ dô: y = 2x; y = - 3x + 5; y = 2x + 3 ; ... *) Chó ý:
Khi ®¹i lîng x thay ®æi mµ y lu«n nhËn mét gi¸ trÞ kh«ng ®æi th× y ®îc gäi lµ hµm h»ng.
*) VÝ dô: C¸c hµm h»ng y = 2; y = - 4; y = 7; ...
2) C¸c c¸ch thêng dïng cho mét hµm sè
a) Hµm sè cho bëi b¶ng.
b) Hµm sè cho bëi c«ng thøc.
- Hµm h»ng: lµ hµm cã c«ng thøc y = m (trong ®ã x lµ biÕn, m ∈ ¡ )
- Hµm sè bËc nhÊt: Lµ hµm sè cã d¹ng c«ng thøc y = ax + b
Trong ®ã: x lµ biÕn, a,b ∈ ¡ , a ≠ 0 .
a lµ hª sè gãc, b lµ tung ®é gèc.
Chó ý: NÕu b = 0 th× hµm bËc nhÊt cã d¹ng y = ax (a ≠ 0 )
- Hµm sè bËc hai: Lµ hµm sè cã c«ng thøc y = ax2 + bx + c
(trong ®ã x lµ biÕn, a,b,c ∈ ¡ , a ≠ 0 ).
Chó ý: NÕu c = 0 th× hµm bËc hai cã d¹ng y = ax2 + bx (a ≠ 0 )
NÕu b = 0 vµ c = 0 th× hµm bËc hai cã d¹ng y = ax2 (a ≠ 0 )
3) Kh¸i niÖm hµm ®ång biÕn vµ hµm nghÞch biÕn.
Cho hµm sè y = f(x) x¸c ®Þnh víi mäi x ∈ ¡ . Víi x1, x2 bÊt k× thuéc R
a) NÕu gi¸ trÞ cña biÕn x t¨ng lªn mµ gi¸ trÞ t¬ng øng f(x) còng t¨ng lªn th× hµm
sè y = f(x) ®îc gäi lµ hµm ®ång biÕn. NÕu 1 x < x2 mµ f( 1
x ) < f(x2 ) th× hµm sè y = f(x) ®ång biÕn trªn R
b) NÕu gi¸ trÞ cña biÕn x t¨ng lªn mµ gi¸ trÞ t¬ng øng f(x) gi¶m ®i th× hµm sè y
= f(x) ®îc gäi lµ hµm nghÞch biÕn. NÕu 1 x < x2 mµ f( 1
x ) > f(x2 ) th× hµm sè y = f(x) nghÞch biÕn /R
4) DÊu hiÖu nhËn biÕt hµm ®ång biÕn vµ hµm nghÞch biÕn.
a) Hµm sè bËc nhÊt y = ax + b (a ≠ 0 ).
- NÕu a > 0 th× hµm sè y = ax + b lu«n ®ång biÕn trªn ¡ .
- NÕu a < 0 th× hµm sè y = ax + b lu«n nghÞch biÕn trªn ¡ .
b) Hµm bËc hai mét Èn sè y = ax2 (a ≠ 0 ) cã thÓ nhËn biÕt ®ång biÕn vµ nghÞch
biÕn theo dÊu hiÖu sau:
- NÕu a > 0 th× hµm ®ång biÕn khi x > 0, nghÞch biÕn khi x < 0.
- NÕu a < 0 th× hµm ®ång biÕn khi x < 0, nghÞch biÕn khi x > 0.
5) Kh¸i niÖm vÒ ®å thÞ hµm sè.
§å thÞ cña hµm sè y = f(x) lµ tËp hîp tÊt c¶ c¸c ®iÓm biÓu diÔn c¸c cÆp gi¸
trÞ t¬ng øng (x; f(x)) trªn mÆt ph¼ng to¹ ®é. Chó ý: D¹ng ®å thÞ: a) Hµm h»ng.
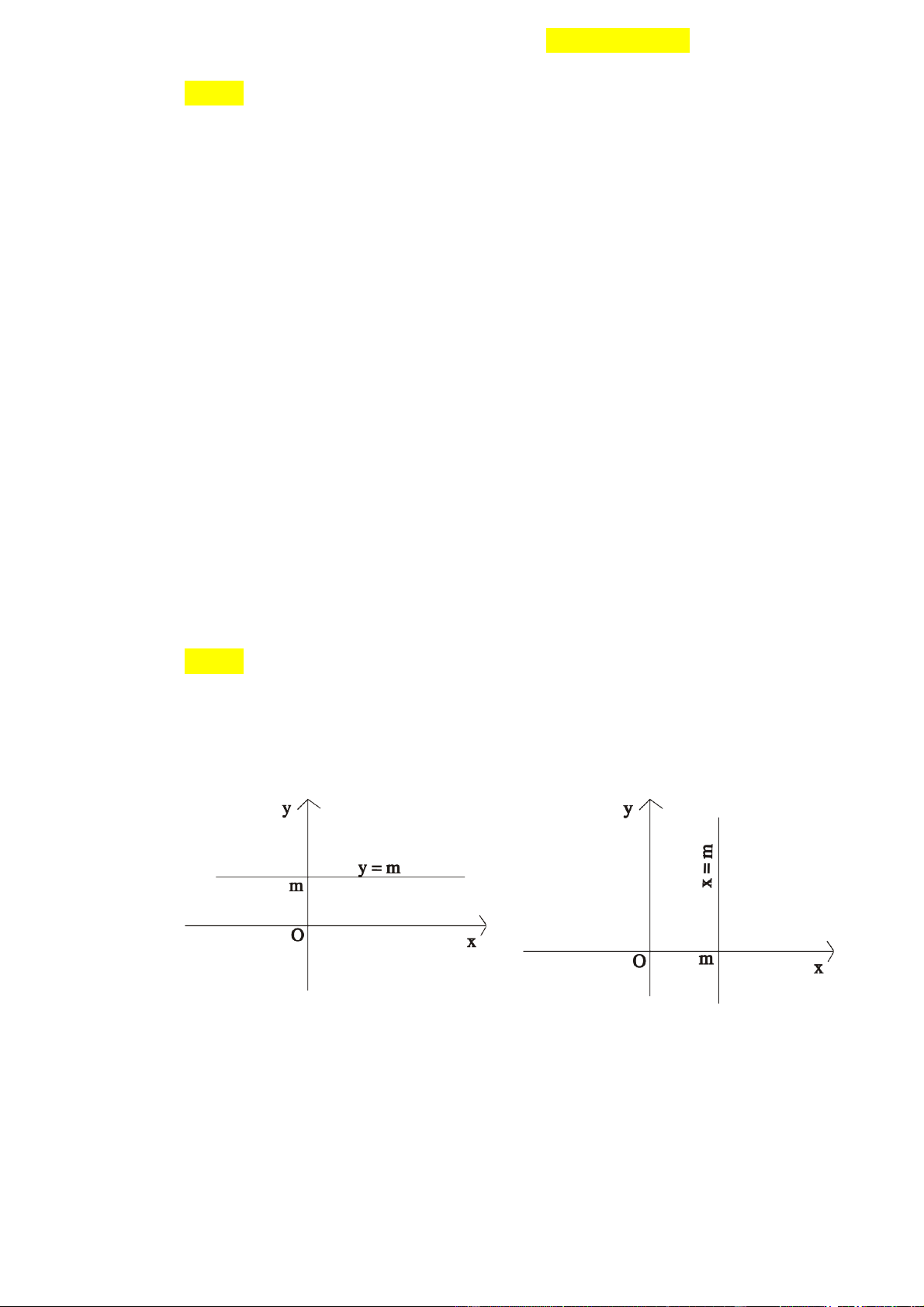
§å thÞ cña hµm h»ng y = m (trong §å thÞ cña hµm h»ng x = m (trong ®ã
®ã x lµ biÕn, m ∈ ¡ ) lµ mét ®êng y lµ biÕn, m ∈ ¡ ) lµ mét
th¼ng lu«n song song víi trôc Ox.
®êng th¼ng lu«n song song víi trôc Oy.
b) §å thÞ hµm sè y = ax ( a ≠ 0 ) lµ mét ®êng th¼ng (h×nh ¶nh tËp hîp c¸c
®iÓm) lu«n ®i qua gèc to¹ ®é.
*) C¸ch vÏ: LÊy mét ®iÓm thuéc ®å thÞ kh¸c O(0 ; 0), ch¼ng h¹n ®iÓm A(1 ;
a). Sau ®ã vÏ ®êng th¼ng ®i qua hai ®iÓm O(0 ; 0) vµ A(1 ; a) ta ®îc ®å thÞ
hµm sè y = ax (a ≠ 0 )
c) §å thÞ hµm sè y = ax + b ( a,b ≠ 0) lµ mét ®êng th¼ng (h×nh ¶nh tËp hîp
c¸c ®iÓm) c¾t trôc tung t¹i ®iÓm (0; b) vµ c¾t trôc hoµnh t¹i ®iÓm ( −b , 0). a
*) C¸ch vÏ: Cã hai c¸ch vÏ c¬ b¶n
+) C¸ch 1: X¸c ®Þnh hai ®iÓm bÊt k× nµo ®ã thuéc ®å thÞ, ch¼ng h¹n nh sau:
Cho x = 1 => y = a + b, ta ®îc A(1 ; a + b)
Cho x = -1 => y = - a + b, ta ®îc A(-1 ; - a + b)
VÏ ®êng th¼ng ®i qua hai ®iÓm A vµ B ta ®îc ®å thÞ hµm sè
y = ax + b (a,b ≠ 0)
+) C¸ch 2: T×m giao ®iÓm cña ®å thÞ víi c¸c trôc täa ®é, cô thÓ:
Cho x = 0 => y = b, ta ®îc M(0 ; b) ∈ Oy Cho y = 0 => x = b − − a , ta ®îc N( b a ; 0) ∈ Ox
VÏ ®êng th¼ng ®i qua hai ®iÓm M vµ N ta ®îc ®å thÞ hµm sè
y = ax + b (a,b ≠ 0)
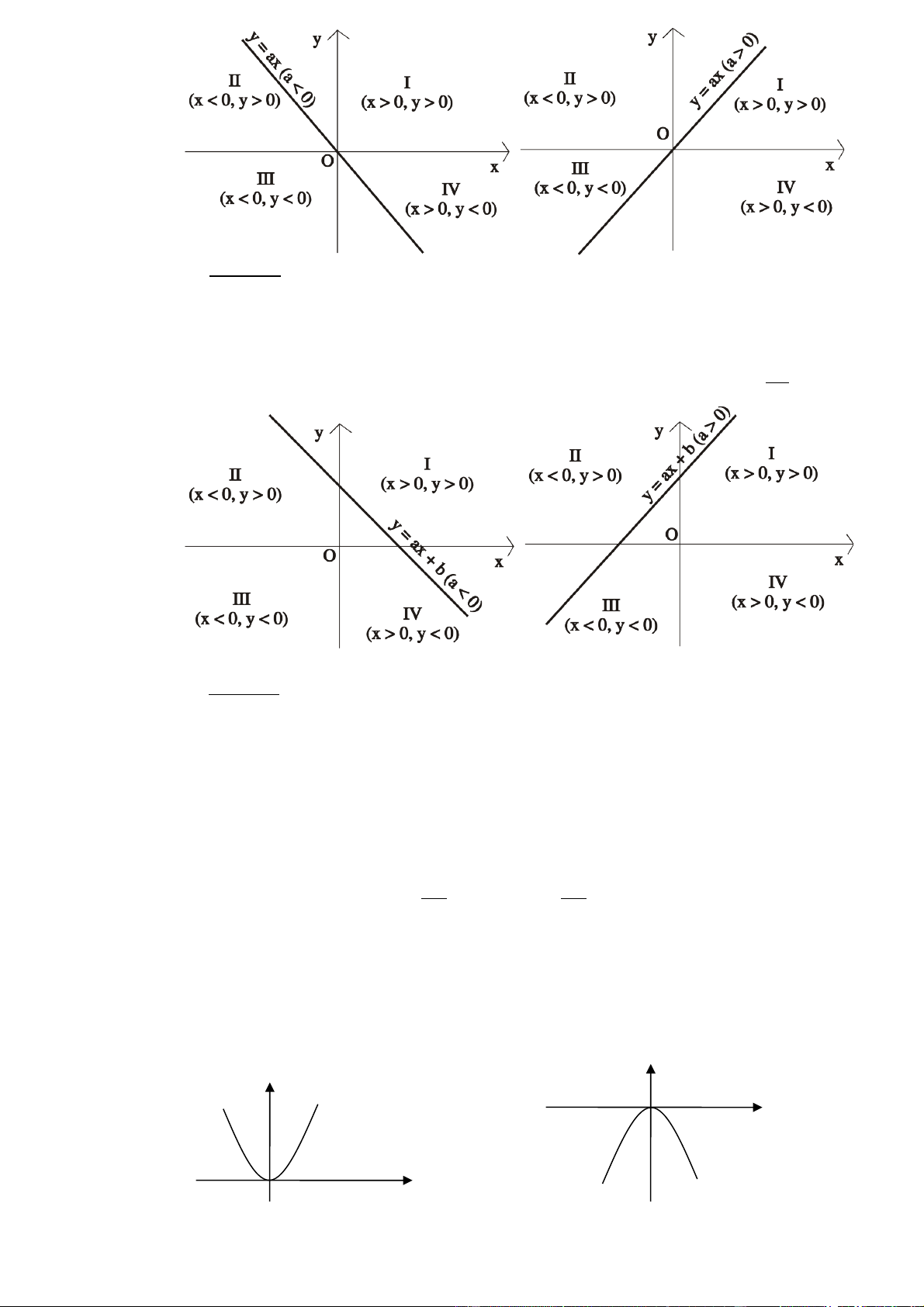
d) §å thÞ hµm sè y = ax2 (a ≠ 0 ) lµ mét ®êng cong Parabol cã ®Ønh O(0;0).
NhËn trôc Oy lµm trôc ®èi xøng
- §å thÞ ë phÝa trªn trôc hoµnh nÕu a > 0.
- §å thÞ ë phÝa díi trôc hoµnh nÕu a < 0. y y O x a > 0 a < 0 x O
6) VÞ trÝ t¬ng ®èi cña hai ®êng th¼ng
*) Hai ®êng th¼ng y = ax + b (a ≠ 0 ) vµ y = a x + ’ b ( ’ a' ≠ 0 )
+ Trïng nhau nÕu a = a , b = ’ b .’
+ Song song víi nhau nÕu a = a , b ’ ≠ b’.
+ C¾t nhau nÕu a ≠ a’.
+ Vu«ng gãc nÕu a.a = ’ -1 .
*) Hai ®êng th¼ng ax + by = c vµ a x + ’ b y = ’ c ( ’ a, b, c, a , b ’ , c ’ ’≠ 0)
+ Trïng nhau nÕu a b c = = a ' b' c '
+ Song song víi nhau nÕu a b c = ≠ a ' b' c '
+ C¾t nhau nÕu a b ≠ a ' b'
7) Gãc t¹o bëi ®êng th¼ng y = ax + b (a ≠ 0 ) vµ trôc Ox
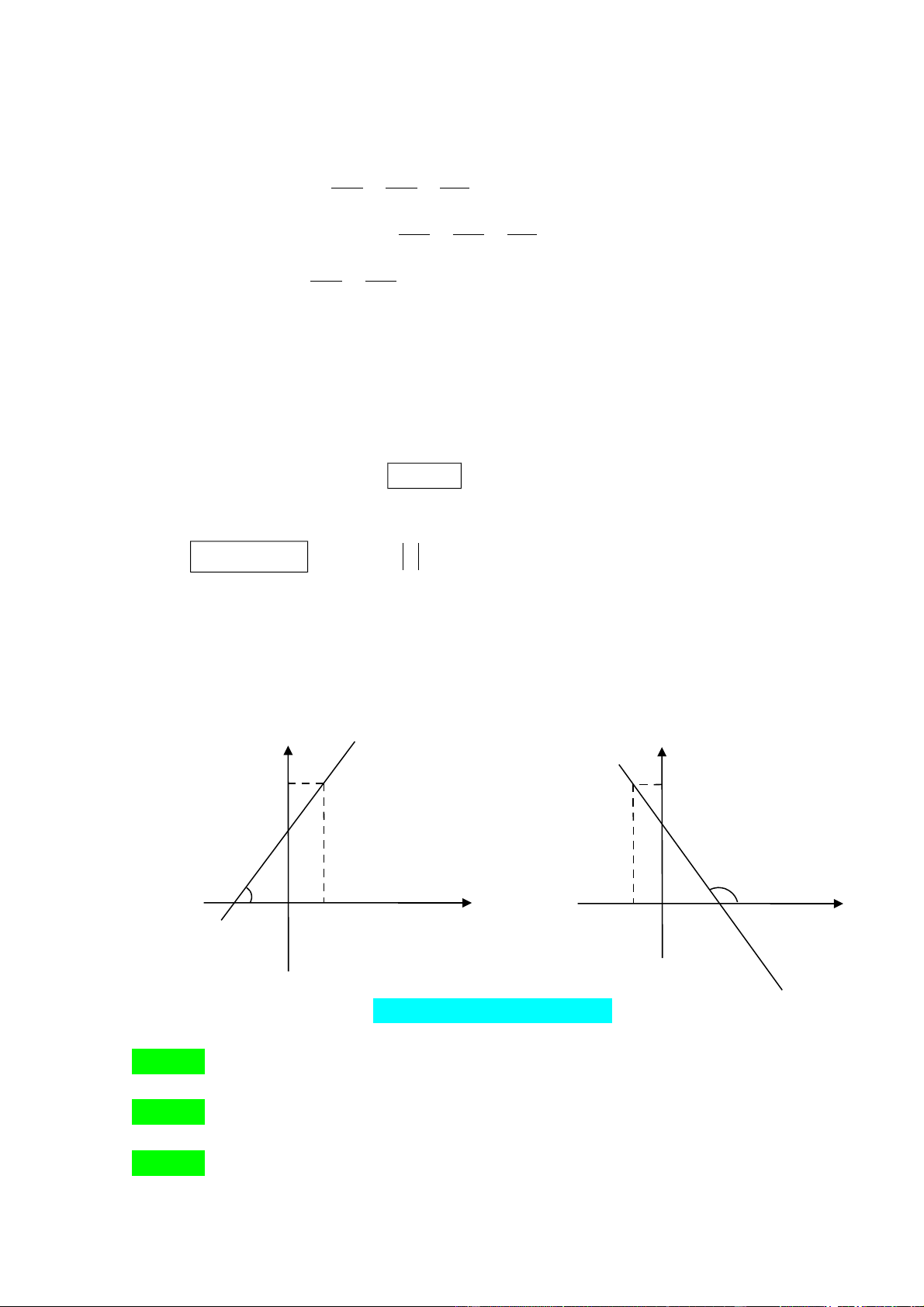
Gi¶ sö ®êng th¼ng y = ax + b ( a ≠ 0 ) c¾t trôc Ox t¹i ®iÓm A.
Gãc t¹o bëi ®êng th¼ng y = ax + b ( a ≠ 0) lµ gãc t¹o bëi tia Ax vµ tia AT
(víi T lµ mét ®iÓm thuéc ®êng th¼ng y = ax + b cã tung ®é d¬ng).
- NÕu a > 0 th× gãc α t¹o bëi ®êng th¼ng y = ax + b víi trôc Ox ®îc tÝnh
theo c«ng thøc nh sau: tgα=a (cÇn chøng minh míi ®îc dïng).
NÕu a < 0 th× gãc α t¹o bëi ®êng th¼ng y = ax + b víi trôc Ox ®îc tÝnh
- theo c«ng thøc nh sau: α= 0
180 −β víi tgβ = a (cÇn chøng minh míi ®îc dïng). y y y = a x + b Y T T (a > 0) (a < 0) α βα A x O A Y x O y = ax + b
Ph©n d¹ng bµi tËp chi tiÕt
D¹ng 1: NhËn biÕt hµm sè
D¹ng 2: TÝnh gi¸ trÞ cña hµm sè, biÕn sè.
D¹ng 3: Hµm sè ®ång biÕn, hµm sè nghÞch biÕn.
a) Hµm sè bËc nhÊt y = ax + b (a ≠ 0 ).
- NÕu a > 0 th× hµm sè y = ax + b lu«n ®ång biÕn trªn ¡ .
- NÕu a < 0 th× hµm sè y = ax + b lu«n nghÞch biÕn trªn ¡ .
b) Hµm bËc hai mét Èn sè y = ax2 (a ≠ 0 ) cã thÓ nhËn biÕt ®ång biÕn vµ nghÞch
biÕn theo dÊu hiÖu sau:
- NÕu a > 0 th× hµm ®ång biÕn khi x > 0, nghÞch biÕn khi x < 0.
- NÕu a < 0 th× hµm ®ång biÕn khi x < 0, nghÞch biÕn khi x > 0.
D¹ng 4: VÏ ®å thÞ hµm sè
§å thÞ cña hµm sè y = f(x) lµ tËp hîp tÊt c¶ c¸c ®iÓm biÓu diÔn c¸c cÆp gi¸
trÞ t¬ng øng (x; f(x)) trªn mÆt ph¼ng to¹ ®é. Chó ý: D¹ng ®å thÞ: a) Hµm h»ng.
§å thÞ cña hµm h»ng y = m (trong §å thÞ cña hµm h»ng x = m (trong ®ã
®ã x lµ biÕn, m ∈ ¡ ) lµ mét ®êng y lµ biÕn, m ∈ ¡ ) lµ mét
th¼ng lu«n song song víi trôc Ox.
®êng th¼ng lu«n song song víi trôc Oy.
b) §å thÞ hµm sè y = ax ( a ≠ 0 ) lµ mét ®êng th¼ng (h×nh ¶nh tËp hîp c¸c
®iÓm) lu«n ®i qua gèc to¹ ®é.
*) C¸ch vÏ: LÊy mét ®iÓm thuéc ®å thÞ kh¸c O(0 ; 0), ch¼ng h¹n ®iÓm A(1 ;
a). Sau ®ã vÏ ®êng th¼ng ®i qua hai ®iÓm O(0 ; 0) vµ A(1 ; a) ta ®îc ®å thÞ
hµm sè y = ax (a ≠ 0 )
c) §å thÞ hµm sè y = ax + b ( a,b ≠ 0) lµ mét ®êng th¼ng (h×nh ¶nh tËp hîp
c¸c ®iÓm) c¾t trôc tung t¹i ®iÓm (0; b) vµ c¾t trôc hoµnh t¹i ®iÓm ( −b , 0). a
*) C¸ch vÏ: Cã hai c¸ch vÏ c¬ b¶n
+) C¸ch 1: X¸c ®Þnh hai ®iÓm bÊt k× nµo ®ã thuéc ®å thÞ, ch¼ng h¹n nh sau:
Cho x = 1 => y = a + b, ta ®îc A(1 ; a + b)
Cho x = -1 => y = - a + b, ta ®îc A(-1 ; - a + b)
VÏ ®êng th¼ng ®i qua hai ®iÓm A vµ B ta ®îc ®å thÞ hµm sè
y = ax + b (a,b ≠ 0)
+) C¸ch 2: T×m giao ®iÓm cña ®å thÞ víi c¸c trôc täa ®é, cô thÓ:
Cho x = 0 => y = b, ta ®îc M(0 ; b) ∈ Oy Cho y = 0 => x = b − − a , ta ®îc N( b a ; 0) ∈ Ox
VÏ ®êng th¼ng ®i qua hai ®iÓm M vµ N ta ®îc ®å thÞ hµm sè
y = ax + b (a,b ≠ 0)
d) §å thÞ hµm sè y = ax2 (a ≠ 0 ) lµ mét ®êng cong Parabol cã ®Ønh O(0;0).
NhËn trôc Oy lµm trôc ®èi xøng
- §å thÞ ë phÝa trªn trôc hoµnh nÕu a > 0.
- §å thÞ ë phÝa díi trôc hoµnh nÕu a < 0. y y O x a > 0 a < 0 x O
D¹ng 5: §iÓm thuéc vµ kh«ng thuéc ®å thÞ hµm sè.
*) §iÓm thuéc ®êng th¼ng.
- §iÓm A(xA; yA) ∈(d): y = ax + b (a ≠ 0) khi vµ chØ khi yA = axA + b
- §iÓm B(xB; yB) ∈(d): y = ax + b (a ≠ 0) khi vµ chØ khi yB= axB + b
*) §iÓm thuéc Parabol : Cho (P) y = ax2 (a ≠ 0 ) - §iÓm A(x 2 0; y0) ∈(P) ⇔ y0 = ax0 . - §iÓm B(x 2 1; y1) ∉(P) ⇔ y1 ≠ ax1 .
D¹ng 6: X¸c ®Þnh hµm sè
D¹ng 7: X¸c ®Þnh ®iÓm cè ®Þnh cña hµm sè * ) Ph ¬ng p h¸p:
§Ó t×m ®iÓm cè ®Þnh mµ ®êng th¼ng y = ax + b ( a ≠ 0 ; a,b cã chøa tham sè)
lu«n ®i qua víi mäi gi¸ trÞ cña tham sè m, ta lµm nh sau:
Bíc 1: Gäi ®iÓm cè ®Þnh lµ A(x0; y0) mµ ®êng th¼ng y = ax + b lu«n ®i qua
víi mäi gi¸ trÞ cña tham sè m 10
Bíc 2: Thay x = x0; y = y0 vµo hµm sè ®îc y0 = ax0 + b, ta biÕn ®æi vÒ d¹ng
<=> A(x0 ,y0 ).m + B(x0 ,y0 ) = 0 , ®¼ng thøc nµy lu«n ®óng víi mäi gi¸ trÞ
cña tham sè m hay ph¬ng tr×nh cã v« sè nghiÖm m
Bíc 3: §Æt ®iÒu kiÖn ®Ó ph¬ng tr×nh cã v« sè nghiÖm. A(x ,y ) 0 0 0 =
( A(x0 ,y0 ).m + B(x0 ,y0 ) = 0 , cã v« sè nghiÖm ⇔ ) B(x ,y ) 0 0 0 =
D¹ng 8: T×m giao ®iÓm cña hai ®å thÞ
8.1: T×m giao ®iÓm cña hai ®êng th¼ng.
Giao ®iÓm cña hai ®êng th¼ng (d1): y = a1x + b1 ; (d2): y = a2x + b2 y = a x + b
Lµ nghiÖm cña hÖ ph¬ng tr×nh 1 1 y = a x +b 2 2
8.2: T×m to¹ ®é giao ®iÓm cña Parabol víi ®êng th¼ng.
Cho (P) : y = ax2 (a ≠ 0) vµ (d) : y = mx + n.
XÐt ph¬ng tr×nh hoµnh ®é giao ®iÓm ax2 = mx + n.
Gi¶i ph¬ng tr×nh t×m x.
Thay gi¸ trÞ x võa t×m ®îc vµo hµm sè y = ax2 hoÆc y = mx + n ta t×m ®- îc y.
+ Gi¸ trÞ cña x t×m ®îc lµ hoµnh ®é giao ®iÓm.
+ Gi¸ trÞ cña y t×m ®îc lµ tung ®é giao ®iÓm.
8.3: T×m sè giao ®iÓm cña ®êng th¼ng vµ Parabol.
Cho (P) : y = ax2 (a ≠ 0) vµ (d) : y = mx + n.
XÐt ph¬ng tr×nh hoµnh ®é giao ®iÓm ax2 = mx + n. (*)
+ Ph¬ng tr×nh (*) v« nghiÖm ( ∆ < 0) ⇔ (d) vµ (P) kh«ng cã ®iÓm chung.
+ Ph¬ng tr×nh (*) cã nghiÖm kÐp ( ∆ = 0) ⇔ (d) tiÕp xóc víi (P).
+ Ph¬ng tr×nh (*) cã hai nghiÖm ph©n biÖt ( ∆ > 0 hoÆc ac < 0)
⇔ (d) c¾t (P) t¹i hai ®iÓm ph©n biÖt.
8.4: T×m gi¸ trÞ cña mét tham sè khi biÕt giao ®iÓm cña hai ®êng th¼ng.
8.5: T×m gi¸ trÞ cña 2 tham sè khi biÕt giao ®iÓm cña hai ®êng th¼ng.
8.6: T×m gi¸ trÞ cña tham sè khi biÕt sè giao ®iÓm cña Parabol vµ ®êng th¼ng.
Cho (d) : y = ax + b vµ (P): y = a’x2 (a’ ≠ 0)(a’, a, b cã chøa tham sè)
XÐt ph¬ng tr×nh hoµnh ®é giao ®iÓm a’x2 = ax + b. (*)
+ (d) vµ (P) kh«ng cã ®iÓm chung
⇔Ph¬ng tr×nh (*) v« nghiÖm (∆ < 0)
+ (d) tiÕp xóc víi (P) ⇔ Ph¬ng tr×nh (*) cã nghiÖm kÐp ( ∆ = 0).
NghiÖm kÐp lµ hoµnh ®é ®iÓm tiÕp xóc
+ (d) c¾t (P) t¹i hai ®iÓm ph©n biÖt ⇔Ph¬ng tr×nh (*) cã hai
nghiÖm ph©n biÖt ( ∆ > 0 hoÆc ac < 0). Hai nghiÖm ®ã lµ hoµnh ®é cña hai giao ®iÓm
8.7: T×m gi¸ trÞ cña tham sè khi biÕt to¹ ®é giao ®iÓm cña Parabol vµ ®êng
th¼ng.Cho (d): y = ax + b vµ (P): y = a’x2 (a’≠0)
(a’, a, b cã chøa tham sè)
T×m gi¸ trÞ cña tham sè ®Ó (d) vµ (P) c¾t nhau t¹i A(xA; yA).
C¸ch lµm: Thay täa ®é cña A vµo hµm sè cña (d); (P) ®Ó t×m gi¸ trÞ cña tham sè. 11
Dang 9: LËp ph¬ng tr×nh ®êng th¼ng ®i qua hai ®iÓm
9.1: LËp ph¬ng tr×nh ®êng th¼ng ®i qua hai ®iÓm
A(xA; yA) vµ B(xB; yB) trong ®ã xA ≠ xB vµ yA ≠ yB. P h ¬ng p h¸p:
Gäi ph¬ng tr×nh ®êng th¼ng (d) cÇn lËp ®i qua A vµ B cã d¹ng y = ax + b (a ≠ 0).
Do A∈(d) thay x = xA; y = yA vµo y = ax + b ta cã yA = axA + b (1)
Do B∈(d) thay x = xB; y = yB vµo y = ax + b ta cã yB = axB + b (2) y ax b A = A +
Tõ (1) vµ (2) ta cã hÖ ph¬ng tr×nh: y ax b B = B +
Gi¶i hÖ ph¬ng tr×nh nµy t×m ®îc a, b vµ suy ra ph¬ng tr×nh ®êng th¼ng (d) cÇn lËp
9.2: LËp ph¬ng tr×nh ®êng th¼ng ®i qua M(x0 ; y0) vµ cã hÖ sè gãc lµ k.
Bíc 1: Ph¬ng tr×nh ®êng th¼ng cã hÖ sè gãc k cã d¹ng y = kx + b
Bíc 2: §êng th¼ng nµy ®i qua M(x y = kx + b 0 ; y0) => 0 0 => b = y0 − kx0
Bíc 3: Ph¬ng tr×nh ®êng th¼ng cÇn t×m lµ y = kx + y0 − kx0
9.3: LËp ph¬ng tr×nh ®êng th¼ng ®i qua hai ®iÓm
A(m; yA) vµ B(m; yB) trong ®ã yA ≠ yB. P h ¬ng p h¸p: Do A(m; yA) ∈(d): x = m; Do B(m; yB) ∈(d) : x = m;
VËy ph¬ng tr×nh ®êng th¼ng cÇn lËp lµ: (d): x = m
9.4: LËp ph¬ng tr×nh ®êng th¼ng ®i qua hai ®iÓm
A(xA; n) vµ B(xB; n) trong ®ã xA ≠ xB. P h ¬ng p h¸p: Do A(xA; n) ∈(d): y = n; Do B(xB; n) ∈(d) : y = n;
VËy ph¬ng tr×nh ®êng th¼ng cÇn lËp lµ: (d): y = n
9.5: LËp ph¬ng tr×nh ®êng th¼ng ®i qua ®iÓm A(xA ; yA) vµ tiÕp xóc víi ®êng cong 2 y = ax (a ≠ 0)
Bíc 1: Gi¶ sö ph¬ng tr×nh cÇn lËp lµ y = a’x + b’
Bíc 2: §êng th¼ng nµy tiÕp xóc víi ®êng cong 2 y = ax (a ≠ 0)
khi vµ chØ khi ph¬ng tr×nh hoµnh ®é giao ®iÓm 2 ax = a'x + b' cã nghiÖm
kÐp. Ta cho ∆ = 0 , t×m ra mét hÖ thøc gi÷a a’ vµ b’ (1)
Bíc 3: §êng th¼ng ®i qua A(x y = a'x + b' A ; yA) => A A (2)
Bíc 4: Tõ (1) vµ (2) ta cã mét hÖ ph¬ng tr×nh hai Èn lµ a’ vµ b’. Gi¶i hÖ t×m
®îc a’ vµ b’ => ph¬ng tr×nh cÇn lËp
9.6: LËp ph¬ng tr×nh ®êng th¼ng cã hÖ sè gãc lµ k vµ tiÕp xóc víi ®êng cong 2 y = ax (a ≠ 0)
Bíc 1: Ph¬ng tr×nh ®êng th¼ng cÇn t×m gi¶ sö lµ y = ax + b
V× ®êng th¼ng cã hÖ sè gãc lµ k nªn a = k => y = kx + b
Bíc 2: §êng th¼ng y = kx + b tiÕp xóc víi ®êng cong 2 y = ax (a ≠ 0) <=>
ph¬ng tr×nh hoµnh ®é giao ®iÓm 2 2
kx + b = ax <=> ax − kx − b = 0 cã nghiÖm kÐp 12
Cho ∆ = 0(∆ ' = 0) => b = ? Bíc 3: Tr¶ lêi
D¹ng 10: Ba ®iÓm th¼ng hµng
10.1: Chøng minh ba ®iÓm th¼ng hµng.
Bíc 1: LËp ph¬ng tr×nh ®êng th¼ng ®i qua hai ®iÓm.
Bíc 2: Chøng minh ®iÓm cßn l¹i thuéc ®êng th¼ng võa lËp.
10.2: T×m gi¸ trÞ cña tham sè ®Ó ba ®iÓm th¼ng hµng.
Bíc 1: LËp ph¬ng tr×nh ®êng th¼ng ®i qua hai ®iÓm cã to¹ ®é ®¬n gi¶n nhÊt.
Bíc 2: Thay to¹ ®é cña ®iÓm cßn l¹i vµo ph¬ng tr×nh ®êng th¼ng võa lËp.
Gi¶i ph¬ng tr×nh vµ t×m tham sè.
D¹ng 11: Ba ®êng th¼ng ®ång qui
11.1: Chøng minh ba ®êng th¼ng ®ång qui.
Bíc 1: T×m giao ®iÓm cña hai ®êng th¼ng.
Bíc 2: Chøng minh giao ®iÓm ®ã thuéc ®êng th¼ng cßn l¹i.
11.2: T×m gi¸ trÞ cña tham sè ®Ó ba ®êng th¼ng ®ång qui.
Bíc 1: T×m giao ®iÓm cña hai ®êng th¼ng ®¬n gi¶n nhÊt.
Bíc 2: Thay to¹ ®é giao ®iÓm trªn vµo ph¬ng tr×nh ®êng th¼ng cßn l¹i. Gi¶i
ph¬ng tr×nh vµ t×m tham sè.
D¹ng 12: VÞ trÝ t¬ng ®èi cña hai ®å thÞ cña hai hµm sè
12.1: VÞ trÝ t¬ng ®èi cña hai ®å thÞ cña hai hµm sè bËc nhÊt
Cho hai ®êng th¼ng : (d1): y = a1x + b1 ; (d2): y = a2x + b2
+) (d1) c¾t (d2) ⇔ a1 ≠ a2 +) (d1) // (d2) ⇔ a1 = a2
+) (d1) ≡ (d2) ⇔ a1 = a2 vµ b1 = b2
+) (d1) ⊥ (d2) ⇔ a1.a2 = -1 (ph¶i chøng minh míi ®îc dïng)
12.2: T×m ®iÒu kiÖn ®Ó hai ®êng th¼ng c¾t nhau t¹i mét ®iÓm trªn trôc tung.
Cho (d1): y = a1x + b1 vµ (d2): y = a2x + b2 a a (1) 1 ≠ §Ó (d 2
1) c¾t (d2) t¹i mét ®iÓm trªn trôc tung th× b b (2) 1 = 2 Gi¶i (1)
Gi¶i (2) vµ chän nh÷ng gi¸ trÞ tho¶ m·n (1).
12.3: T×m ®iÒu kiÖn ®Ó hai ®êng th¼ng c¾t nhau t¹i mét ®iÓm trªn trôc hoµnh.
Cho (d1): y = a1x + b1 vµ (d2): y = a2x + b2 a a (1) 1 ≠ 2
§Ó (d1) c¾t (d2) t¹i mét ®iÓm trªn trôc hoµnh th× −b b 1 − = 2 (2) a a 1 2
Lu ý: ChØ nªn ¸p dông khi hai ph¬ng tr×nh ®Òu chøa tham sè.
D¹ng 13: X¸c ®Þnh gi¸ trÞ cña tham sè m ®Ó ®êng th¼ng
y = ax + b c¾t hai trôc täa ®é Ox, Oy t¹o thµnh mét tam gi¸c cã diÖn tÝch b»ng c
Bíc 1: §Ó ®å thÞ hµm sè y = ax + b c¾t hai trôc täa ®é t¹o thµnh mét tam
gi¸c th× ta cã ®iÒu kiÖn cÇn lµ: a ≠ 0,b ≠ 0 => ®iÒu kiÖn cña m
Bíc 2: T×m giao ®iÓm cña ®å thÞ víi hai trôc täa ®é; gi¶ sö A vµ B lÇn lît lµ
giao ®iÓm cña ®å thÞ víi trôc tung vµ trôc hoµnh A(0 ; b) vµ B( −b ;0 a )
Bíc 3: XÐt tam gi¸c vu«ng OAB cã 13 S 1 1 OA.OB b . − = × = c OAB = b 2 2 a
=> m = ? (kiÓm tra víi ®iÒu kiÖn ë bíc 1)
D¹ng 14: X¸c ®Þnh gi¸ trÞ cña tham sè m ®Ó ®êng th¼ng
y = ax + b c¾t hai trôc täa ®é Ox, Oy t¹o thµnh mét tam gi¸c c©n C¸ch 1:
Bíc 1: §Ó ®å thÞ hµm sè y = ax + b c¾t hai trôc täa ®é t¹o thµnh mét tam
gi¸c th× ta cã ®iÒu kiÖn cÇn lµ: a ≠ 0,b ≠ 0 => ®iÒu kiÖn cña m
Bíc 2: T×m giao ®iÓm cña ®å thÞ víi hai trôc täa ®é; gi¶ sö A vµ B lÇn lît lµ
giao ®iÓm cña ®å thÞ víi trôc tung vµ trôc hoµnh A(0 ; b) vµ B( −b ;0 a )
Bíc 3: Tam gi¸c OAB c©n <=> OA = OB <=> −b b = a (*)
Gi¶i ph¬ng tr×nh (*) ta t×m ®îc gi¸ trÞ cña m (kiÓm tra ®iÒu kiÖn ë bíc1)
C¸ch 2: §å thÞ hµm sè c¾t hai trôc täa ®é t¹o thµnh mét tam gi¸c c©n khi vµ chØ
khi ®êng th¼ng y = ax + b song song víi ®êng th¼ng
y = x hoÆc song song víi ®êng th¼ng y = - x
D¹ng 15: X¸c ®Þnh gi¸ trÞ cña tham sè ®Ó giao ®iÓm cña hai
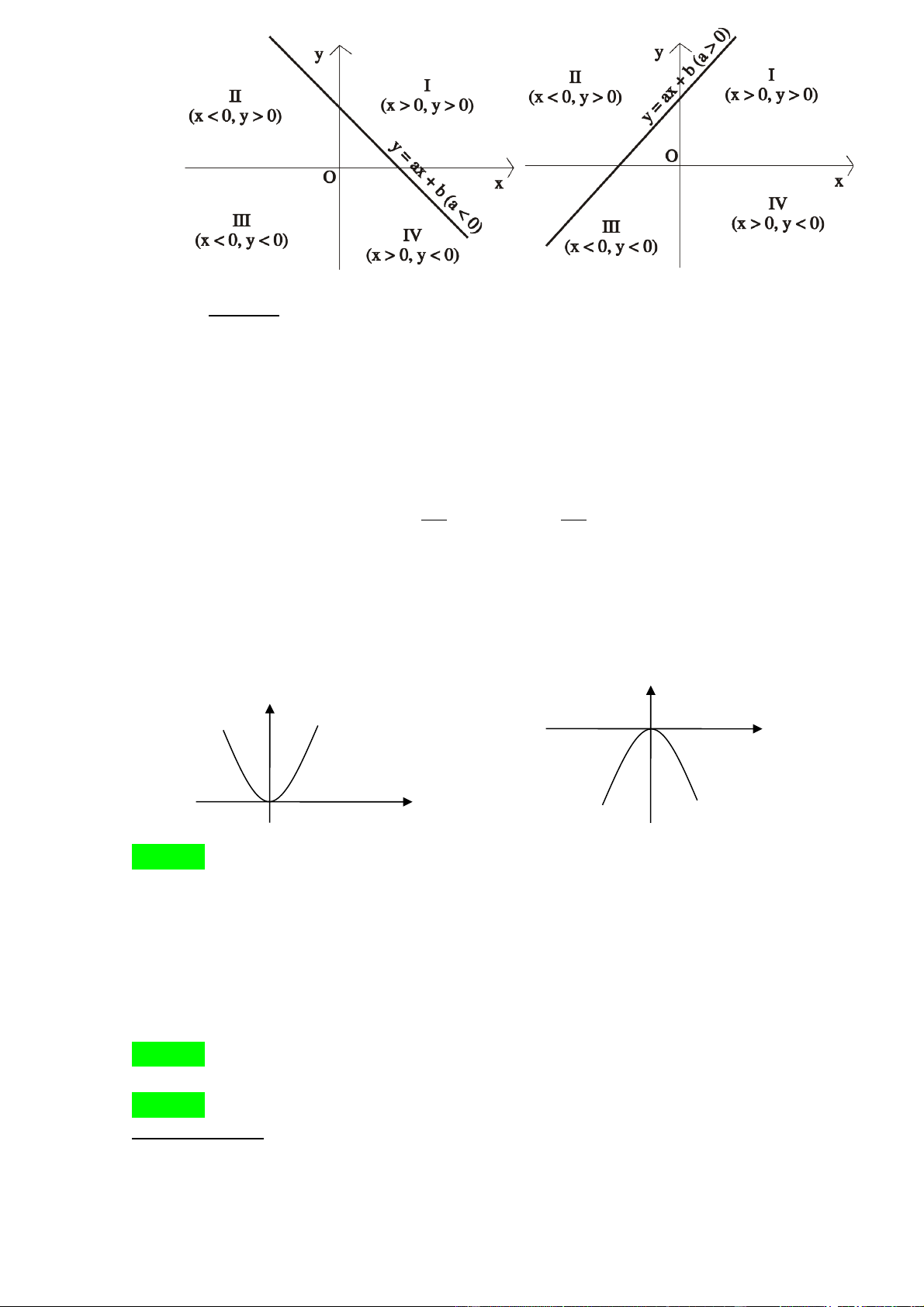
®êng th¼ng ax + by = c vµ a’x + b’y = c’ n»m trong c¸c gãc phÇn t cña hÖ trôc täa ®é.
Bíc 1: T×m täa ®é giao ®iÓm A(x ; y) cña hai ®êng th¼ng, chÝnh lµ nghiÖm ax + by = c cña hÖ ph¬ng tr×nh: a'x + b'y = c' Bíc 2: x > 0
+) NÕu A n»m trong gãc phÇn t thø I th× ®iÒu kiÖn lµ: y > 0 x < 0
+) NÕu A n»m trong gãc phÇn t thø II th× ®iÒu kiÖn lµ: y > 0 x < 0
+) NÕu A n»m trong gãc phÇn t thø III th× ®iÒu kiÖn lµ: y < 0 x > 0
+) NÕu A n»m trong gãc phÇn t thø IV th× ®iÒu kiÖn lµ: y < 0 Bíc 3: T×m m = ? D¹ng 16:
X¸c ®Þnh gi¸ trÞ tham sè ®Ó ®a thøc f(x) = Ax + B b»ng ®a thøc 0 A = 0
Bíc 1: §a thøc f(x) = Ax + B b»ng ®a thøc 0 <=> B = 0
Bíc 2: Gi¶i hÖ nµy t×m ®îc gi¸ trÞ cña tham sè
V - C¸c d¹ng to¸n vÒ hÖ ph¬ng tr×nh LÝ thuyÕt chung 14
1. §Þnh nghÜa:
HÖ hai ph¬ng tr×nh bËc nhÊt hai Èn cã d¹ng tæng qu¸t lµ: ax + by = c (I)
(trong ®ã a, b, c, a , b ’ , c ’ cã ’ thÓ chøa tham sè) a'x + b'y = c'
2. §Þnh nghÜa nghiÖm, tËp nghiÖm
- NghiÖm (x0 ; y0) cña hÖ (I) lµ nghiÖm chung cña hai ph¬ng tr×nh trong hÖ
- NÕu hai ph¬ng tr×nh trong hÖ kh«ng cã nghiÖm chung th× hÖ ph¬ng tr×nh v« nghiÖm
- Gi¶i hÖ ph¬ng tr×nh lµ t×m tÊt c¶ c¸c nghiÖm (t×m tËp nghiÖm) cña nã. *) §
iÒu kiÖn ®Ó hÖ hai ph ¬ng
tr×nh bËc nhÊt hai Èn cã nghiÖm duy nhÊt, cã
v« sè nghiÖm, v« nghiÖm. ax + by = c
(a, b, c, a’, b’, c’ kh¸c 0) a' x + b'y = c' a b c
+ HÖ cã v« sè nghiÖm nÕu = = a' b' c ' a b c + HÖ v« nghiÖm nÕu = ≠ a' b' c ' a b
+ HÖ cã mét nghiÖm duy nhÊt nÕu ≠ a' b'
+ §iÒu kiÖn cÇn ®Ó hÖ v« nghiÖm hoÆc v« sè nghiÖm lµ
ab’ – a’b = 0
3. C¸c ph¬ng ph¸p gi¶i hÖ hai ph¬ng tr×nh bËc nhÊt hai Èn . ax + by = c a' x + b'y = c'
a) Ph¬ng ph¸p céng ®¹i sè.
*) C¸ch gi¶i hÖ ph¬ng tr×nh b»ng ph¬ng ph¸p céng ®¹i sè
Bíc1: Nh©n hai vÕ cña mçi ph¬ng tr×nh víi mét sè thÝch hîp (nÕu
cÇn) sao cho c¸c hÖ sè cña mét Èn nµo ®ã trong hai ph¬ng tr×nh cña
hÖ b»ng nhau hoÆc ®èi nhau.
Bíc 2: ¸p dông quy t¾c céng ®¹i sè ®Ó ®îc hÖ ph¬ng tr×nh míi, trong
®ã cã mét ph¬ng tr×nh mµ hÖ sè cña mét trong hai Èn b»ng 0 (tøc lµ ph¬ng tr×nh mét Èn)
Bíc 3: Gi¶i ph¬ng tr×nh mét Èn võa thu ®îc, råi suy ra nghiÖm cña hÖ ®· cho *) Tæng qu¸t: ax + by = c (b + b')y = c + c' + NÕu cã ⇔ −ax + b'y = c' −ax + b'y = c' ax + by = c ( b − b')y = c − c' + NÕu cã ⇔ ax + b'y = c' ax + b'y = c' ax + by = c k.ax + kby = kc ( kb − b')y = k.c − c' + NÕu cã ⇔ ⇔ k.ax + b'y = c' k.ax + b'y = c' ax + by = c b) Ph¬ng ph¸p thÕ.
*) C¸ch gi¶i hÖ ph¬ng tr×nh b»ng ph¬ng ph¸p thÕ
Bíc 1: Dïng quy t¾c thÕ biÕn ®æi hÖ ph¬ng tr×nh ®· cho ®Ó ®îc mét hÖ
ph¬ng tr×nh míi, trong ®ã cã mét ph¬ng tr×nh mét Èn 15
Bíc 2: Gi¶i ph¬ng tr×nh mét Èn võa cã, råi suy ra nghiÖm cña hÖ ®· cho *) Tæng qu¸t: a c a c y = − x + ax + by = c y = − x + b b ⇔ b b ⇔ a' x + b'y = c' a c a' x + b'y = c' a' x + b' − x + = ÷ c ' b b
c) Ph¬ng ph¸p ®å thÞ
- VÏ hai ®êng th¼ng biÓu diÔn hai tËp nghiÖm cña hai ph¬ng tr×nh trong hÖ
- Dùa vµo ®å thÞ, xÐt vÞ trÝ t¬ng ®èi cña hai ®êng th¼ng
+) NÕu hai ®êng th¼ng c¾t nhau th× hÖ cã nghiÖm duy nhÊt, dùa vµo
®å thÞ ®o¸n nhËn nghiÖm duy nhÊt ®ã, sau ®ã thö l¹i vµ kÕt luËn nghiÖm cña hÖ
+) NÕu hai ®êng th¼ng song song th× hÖ v« nghiÖm
+) NÕu hai ®êng th¼ng trïng nhau th× hÖ cã v« sè nghiÖm
Chó ý: Cã thÓ ®Æt Èn phô tríc khi ¸p dông c¸c ph¬ng ph¸p gi¶i hÖ: (¸p dông
cho c¸c hÖ ph¬ng tr×nh chøa Èn ë mÉu, díi dÊu c¨n bËc hai.)
Ph©n d¹ng bµi tËp chi tiÕt
D¹ng 1: Gi¶i hÖ ph¬ng tr×nh kh«ng chøa tham sè
D¹ng 2: Gi¶i hÖ ph¬ng tr×nh khi biÕt gi¸ trÞ cña tham sè P h ¬ng p h¸p:
Bíc 1: Thay gi¸ trÞ cña tham sè vµo hÖ ph¬ng tr×nh
Bíc 2: Gi¶i hÖ ph¬ng tr×nh kh«ng chøa tham sè võa thu ®îc.
D¹ng 3: Gi¶i vµ biÖn luËn hÖ ph¬ng tr×nh theo tham sè
- Dïng ph¬ng ph¸p céng hoÆc thÕ ®Ó t×m x theo tham sè m (hoÆc y theo tham sè
m), lµm xuÊt hiÖn ph¬ng tr×nh cã d¹ng : Ax = B (1) (hoÆc Ay = B)
NÕu A = 0 th× ph¬ng tr×nh (1) cã d¹ng 0x = B.
+) Khi B = 0 th× ph¬ng tr×nh (1) cã d¹ng 0x = 0
⇒ ph¬ng tr×nh cã v« sè nghiÖm
=> hÖ ph¬ng tr×nh cã v« sè nghiÖm
+) Khi B ≠ 0 ph¬ng tr×nh (1) v« nghiÖm
=> hÖ ph¬ng tr×nh v« nghiÖm B
NÕu A ≠ 0 th× ph¬ng tr×nh (1) cã mét nghiÖm duy nhÊt A B x =
=> hÖ ph¬ng tr×nh cã nghiÖm duy nhÊt A y = y(m)
D¹ng 4: T×m gi¸ trÞ cña tham sè ®Ó hÖ ph¬ng tr×nh cã nghiÖm duy nhÊt, v« nghiÖm, v« sè nghiÖm. *) §
iÒu kiÖn ®Ó hÖ hai ph ¬ng
tr×nh bËc nhÊt hai Èn cã nghiÖm duy nhÊt, cã v« sè nghiÖm, v« nghiÖm. 16 ax + by = c
(a, b, c, a’, b’, c’ kh¸c 0) a' x + b'y = c ' a b c
+ HÖ cã v« sè nghiÖm nÕu = = a' b' c ' a b c + HÖ v« nghiÖm nÕu = ≠ a' b' c ' a b
+ HÖ cã mét nghiÖm duy nhÊt nÕu ≠ a' b'
D¹ng 5: T×m gi¸ trÞ tham sè khi biÕt dÊu cña nghiÖm cña hÖ ph¬ng tr×nh
D¹ng 6: T×m gi¸ tham sè khi biÕt nghiÖm cña hÖ ph¬ng tr×nh
6.1: T×m mét gi¸ trÞ tham sè khi biÕt nghiÖm cña hÖ ph¬ng tr×nh. ax + by = c (1) Cho hÖ ph¬ng tr×nh : ′ a x + b′y = c′ (2) x = x
T×m gi¸ trÞ tham sè ®Ó hÖ ph¬ng tr×nh cã nghiÖm 0 y = y 0 C¸ch 1:
Thay x = x0; y = y0 lÇn lît vµo (1) vµ gi¶i.
Thay x = x0; y = y0 lÇn lît vµo (2) vµ gi¶i. C¸ch 2:
Thay x = x0; y = y0 vµo c¶ hai ph¬ng tr×nh vµ gi¶i hÖ ph¬ng tr×nh chøa Èn lµ tham sè
6.2: T×m hai gi¸ trÞ tham sè khi biÕt nghiÖm cña hÖ ph¬ng tr×nh. ax + by = c x = x Cho hÖ ph¬ng tr×nh: cã nghiÖm 0 a x ′ + b y ′ = c′ y = y 0
Bíc 1: Thay x = x0; y = y0 vµo c¶ hai ph¬ng tr×nh cña hÖ ph¬ng tr×nh ta ®îc ax + by = c 0 0 a′x +b y′ = c′ 0 0
Bíc 2: Gi¶i hÖ ph¬ng tr×nh chøa Èn lµ tham sè.
D¹ng 7: T×m gi¸ trÞ tham sè khi biÕt hÖ thøc liªn hÖ gi÷a x vµ y. ax + by = c (1) Cho hÖ ph¬ng tr×nh : (I) a ′x + b y ′ = c′ (2)
Cã nghiÖm (x; y) tho¶ m·n: px + qy = d (3)
Bíc 1: Tríc hÕt cÇn t×m ®iÒu kiÖn cña tham sè ®Ó hÖ (I) cã nghiÖm duy nhÊt
Bíc 2: Do (x; y) lµ nghiÖm cña hÖ (I) vµ tho¶ m·n (3) ⇒ (x; y) lµ nghiÖm
cña (1), (2), (3). KÕt hîp 2 ph¬ng tr×nh ®¬n gi¶n nhÊt ®Ó ®îc mét hÖ ph¬ng
tr×nh => Gi¶i hÖ t×m nghiÖm thay vµo ph¬ng tr×nh cßn l¹i
Bíc 3: Gi¶i ph¬ng tr×nh chøa Èn lµ tham sè
D¹ng 8: T×m gi¸ trÞ tham sè m ®Ó hÖ ph¬ng tr×nh cã nghiÖm duy nhÊt (x0 ; y0) lµ nh÷ng sè nguyªn
Bíc 1: T×m ®iÒu kiÖn cña tham sè m ®Ó hÖ cã nghiÖm duy nhÊt
Bíc 2: Ph©n tÝch x0 ; y0 díi d¹ng b x0 = a + víi a, b ∈ Z A(m) 17 d y0 = c + víi c, d ∈ Z B(m) b x0 ∈Z <=> ∈ Z <=> A(m) ¦ ∈ (b) A(m) => m = ? d y0 ∈Z <=> ∈ Z <=> B(m) ¦ ∈ (d) B(m) *) §Æc biÖt nÕu : b x0 = a + víi a, b ∈ Z A(m) d y0 = c + víi c, d ∈Z A(m)
=> x0 ,y0 ∈ Z <=> A(m)∈¦ C(b,d) => m = ?
D¹ng 9: T×m gi¸ trÞ tham sè ®Ó biÓu thøc liªn hÖ gi÷a x, y lµ
P(x,y) = ax2 + bx + c nhËn gi¸ trÞ lín nhÊt, nhá nhÊt. C¸ch 1:
Bíc 1: Tríc hÕt t×m ®iÒu kiÖn cña tham sè ®Ó hÖ ph¬ng tr×nh cã nghiÖm duy nhÊt
Bíc 2: BiÕn ®æi biÓu thøc liªn hÖ gi÷a x vµ y lµ:
P(x,y) = kA2(x) + d (d lµ h»ng sè).
k < 0 ⇒ kA2(x) ≤ 0 ⇒ kA2(x) + d ≤ d ⇒P(x,y) ≤ d
Gi¸ trÞ lín nhÊt cña P(x,y) b»ng d ®¹t ®îc khi A(x) = 0.
k > 0 ⇒ kA2(x) ≥ 0 ⇒ kA2(x) + d ≥ d ⇒P(x,y) ≥ d
Gi¸ trÞ nhá nhÊt cña P(x,y) b»ng d ®¹t ®îc khi A(x) = 0. C¸ch 2:
P(x,y) = ax2 + bx + c ⇔ ax2 + bx + c – P(x,y) = 0
Bíc 1: TÝnh ∆ hoÆc ∆' .
Bíc 2: §Æt ®iÒu kiÖn ∆ ≥ 0 (∆' ≥0)
⇒ Gi¶i bÊt ph¬ng tr×nh chøa Èn P(x,y).
P(x,y) ≥ e ⇒Gi¸ trÞ nhá nhÊt cña P(x,y) b»ng e ®¹t ®îc khi ∆ − b − ' = ∆' = 0 ⇔ b x = = . 2a a
P(x,y) ≤ e ⇒Gi¸ trÞ lín nhÊt cña P(x,y) b»ng e ®¹t ®îc khi ∆ − b − ' = ∆' = 0 ⇔ b x = = 2a a
D¹ng 10: T×m hÖ thøc liªn hÖ gi÷a x vµ y kh«ng phô thuéc vµo tham sè 1. P h ¬ng p h¸p : ax + by = c Cho hÖ ph¬ng tr×nh:
trong ®ã a, b, c, a’, b’, c’ chøa tham sè a ' x + b'y = c '
m. T×m hÖ thøc liªn hÖ gi÷a x vµ y kh«ng phô thuéc vµo tham sè m ? *) C¸ch 1:
Bíc 1: Tõ mét ph¬ng tr×nh cña hÖ ta rót m theo x vµ y lµ m = A(x,y)
Bíc 2: Thay m = A(x,y) vµo ph¬ng tr×nh thø hai cña hÖ ta
®îc hÖ thøc liªn hÖ gi÷a x vµ y kh«ng phô thuéc vµo tham sè m
*) C¸ch 2: Sö dông ®èi víi hÖ ph¬ng tr×nh cã tham sè m díi d¹ng bËc nhÊt 18 ax + by = c m = A(x,y)
Bíc 1: Tõ hÖ ph¬ng tr×nh => a ' x + b'y = c' m = B(x,y)
Bíc 2: Cho A(x,y) = B(x,y). §©y lµ hÖ thøc liªn hÖ gi÷a x vµ y kh«ng phô thuéc vµo tham sè m L u ý
: Ta cÇn rót gän c¸c hÖ thøc sao cho ng¾n gän, ®¬n gi¶n nhÊt
D¹ng 11: T×m gi¸ trÞ cña tham sè ®Ó hai hÖ ph¬ng tr×nh t¬ng
®¬ng - Hai hÖ ph¬ng tr×nh ®îc gäi lµ t¬ng ®¬ng nÕu chóng cã cïng mét tËp
nghiÖm (tøc lµ mäi nghiÖm cña hÖ nµy ®Òu lµ nghiÖm cña hÖ kia vµ ngîc l¹i)
D¹ng 12: Gi¶i hÖ phư¬ng tr×nh theo ph¬ng ph¸p ®Æt Èn phô vµ
gi¶i mét sè hÖ ph¬ng tr×nh kh«ng ë d¹ng hÖ hai ph¬ng tr×nh bËc nhÊt hai Èn (hÖ ®Æc biÖt)
VI – Ph¬ng tr×nh bËc hai mét Èn
PhÇn I: Ph¬ng tr×nh kh«ng chøa tham sè
I. §Þnh nghÜa: Ph¬ng tr×nh bËc hai mét Èn (nãi gän lµ ph¬ng tr×nh bËc hai) lµ
ph¬ng tr×nh cã d¹ng 2
ax + bx + c = 0 (a ≠ 0)
Trong ®ã: x lµ Èn; a, b, c lµ nh÷ng sè cho tríc gäi lµ c¸c hÖ sè II. Ph©n lo¹i.
1. Ph¬ng tr×nh khuyÕt c: ax2 + bx = 0 (a ≠ 0) Ph¬ng ph¸p gi¶i:
ax2 + bx = 0 (a, b ≠ 0) x = 0
⇔ x(ax + b) = 0⇔ b − x = a −b
Ph¬ng tr×nh cã hai nghiÖm x1 = 0; x2 = a
2. Ph¬ng tr×nh khuyÕt b: ax2 + c = 0 (a, c ≠ 0) Ph¬ng ph¸p gi¶i:
ax2 + c = 0 (a ≠ 0) ⇔ −c 2 x = a +) −c NÕu
< 0 ⇒ Ph¬ng tr×nh v« nghiÖm. a −c +) NÕu
> 0 ⇒ Ph¬ng tr×nh cã hai nghiÖm ph©n biÖt: a −c c x ; − x2 = − 1 = a a
3. Ph¬ng tr×nh bËc hai ®Çy ®ñ: ax2 + bx + c = 0 (a , b, c ≠ 0) *) C«ng thøc nghiÖm: ∆ = b2 - 4ac
+) ∆ < 0 ⇒ Ph¬ng tr×nh v« nghiÖm 19
+) ∆ > 0 ⇒ ph¬ng tr×nh cã hai nghiÖm ph©n biÖt: x b b 1 = − + ∆ ; x 2a 2 = − − ∆ 2a b −
+) ∆ = 0 ⇒ Ph¬ng tr×nh cã nghiÖm kÐp: x1 = x2 = 2a
* ) C«ng thøc nghiÖm thu gän b NÕu b = 2b ( ’ b = ’
)→ ta cã : ∆’ = b 2 ’2 - ac
+ NÕu ∆’ > 0 → ph¬ng tr×nh cã hai nghiÖm ph©n biÖt lµ : b − '+ ∆ ' b − '− ∆ ' x = ; x = 1 2 a a
+ NÕu ∆’ = 0 → ph¬ng tr×nh cã nghiÖm kÐp b − ' x1 = x2 = a
+ NÕu ∆’ < 0 → ph¬ng tr×nh v« nghiÖm
PhÇn II – C¸c d¹ng ph¬ng tr×nh chøa tham sè
D¹ng 1: Gi¶i ph¬ng tr×nh khi biÕt gi¸ trÞ cña tham sè
Thay gi¸ trÞ cña tham sè vµo ph¬ng tr×nh vµ gi¶i ph¬ng tr×nh
D¹ng 2: Gi¶i vµ biÖn ph¬ng tr×nh theo tham sè Tæng qu¸t:
Víi a = 0: Ph¬ng tr×nh trë thµnh ph¬ng tr×nh bËc nhÊt bx + c = 0.
+ NÕu b ≠ 0 th× ph¬ng tr×nh cã nghiÖm x = −c b
+ NÕu b = 0 vµ c ≠ 0 th× ph¬ng tr×nh v« nghiÖm.
+ NÕu b = 0 vµ c = 0 th× ph¬ng tr×nh cã v« sè nghiÖm.
Víi a ≠ 0 ph¬ng tr×nh trë thµnh ph¬ng tr×nh bËc hai cã biÖt sè:
∆ = b2 – 4ac ( hay ∆ ’ = b’2 – ac)
+ NÕu ∆ < 0 (∆ ’ < 0) th× ph¬ng tr×nh v« nghiÖm.
+ NÕu ∆ = 0 (∆ ’ = 0) th× ph¬ng tr×nh cã nghiÖm kÐp : b b' x − 1 = x2 = - = 2a a
+ NÕu ∆ > 0 (∆ ’ > 0) th× ph¬ng tr×nh cã hai nghiÖm ph©n biÖt: x b b' ' b b' ' 1 = − + ∆ − + ∆ = ; x 2a a 2 = − − ∆ − − ∆ = 2a a
D¹ng 3: T×m ®iÒu kiÖn cña tham sè ®Ó ph¬ng tr×nh cã nghiÖm
- XÐt hai trêng hîp cña hÖ sè a:
Trêng hîp 1: a = 0, ta t×m ®îc mét vµi gi¸ trÞ cña m, sau ®ã thay trùc tiÕp
vµo ph¬ng tr×nh råi kÕt luËn víi nh÷ng gi¸ trÞ nµo cña m th× ph¬ng tr×nh cã nghiÖm Trêng hîp 2: a 0
≠ , ph¬ng tr×nh bËc hai mét Èn cã nghiÖm <=> ∆ ≥ 0( ∆' ≥ 0)
D¹ng 4: T×m ®iÒu kiÖn cña tham sè ®Ó ph¬ng tr×nh cã hai nghiÖm ph©n biÖt
Ph¬ng tr×nh bËc hai mét Èn cã hai nghiÖm ph©n biÖt 20 a ≠ 0
<=> ∆ > 0(∆' > 0)
D¹ng 5: T×m ®iÒu kiÖn cña tham sè ®Ó ph¬ng tr×nh cã nghiÖm kÐp a ≠ 0
Ph¬ng tr×nh bËc hai mét Èn cã nghiÖm kÐp <=> ∆ = 0(∆' = 0)
D¹ng 6: T×m ®iÒu kiÖn cña tham sè ®Ó ph¬ng tr×nh v« nghiÖm
- XÐt hai trêng hîp cña hÖ sè a:
Trêng hîp 1: a = 0, ta t×m ®îc mét vµi gi¸ trÞ cña m, sau ®ã thay trùc tiÕp
vµo ph¬ng tr×nh råi kÕt luËn víi nh÷ng gi¸ trÞ nµo cña m th× ph¬ng tr×nh v« nghiÖm Trêng hîp 2: a 0
≠ , ph¬ng tr×nh bËc hai mét Èn v« nghiÖm
<=> ∆ < 0( ∆ ' < 0)
D¹ng 7: Chøng minh ph¬ng tr×nh lu«n cã hai nghiÖm ph©n biÖt
§Ó chøng minh ph¬ng tr×nh lu«n lu«n cã hai nghiÖm ph©n biÖt: a ≠ 0 C¸ch 1: Chøng minh: ac < 0 a ≠ 0
C¸ch 2: Chøng minh: ∆ > 0
Chó ý: Cho tam thøc bËc hai ∆ = 2 am + bm + c a > 0
§Ó chøng minh ∆ > 0,∀m ta cÇn chøng minh 2 ∆ m = b − 4ac < 0
D¹ng 8: T×m ®iÒu kiÖn cña m ®Ó ph¬ng tr×nh cã hai nghiÖm cïng dÊu, tr¸i
dÊu, cã hai nghiÖm d¬ng, cã hai nghiÖm ©m, cã hai nghiÖm d¬ng ph©n biÖt, cã
hai nghiÖm ©m ph©n biÖt, cã hai nghiÖm lµ hai sè ®èi nhau, cã hai nghiÖm lµ
hai sè nghÞch ®¶o cña nhau Cho ph¬ng tr×nh 2
ax + bx + c = 0 ; trong ®ã a, b, c chøa tham sè b S = x + x 1 2 = − a
Theo ®Þnh lÝ Vi - Ðt, ta cã : c P = x x 1 2 = a a ≠ 0 a ≠ 0
a) Ph¬ng tr×nh cã hai nghiÖm cïng dÊu <=> ∆ ≥ 0 hoÆc ∆ ≥ 0 P > 0 ac > 0 a ≠ 0 a ≠ 0
b) Ph¬ng tr×nh cã hai nghiÖm tr¸i dÊu <=> hoÆc P < 0 ac < 0 a ≠ 0 ∆ ≥ 0
c) Ph¬ng tr×nh cã hai nghiÖm d¬ng <=> P > 0 S > 0 21 a ≠ 0 ∆ ≥ 0
d) Ph¬ng tr×nh cã hai nghiÖm ©m <=> P > 0 S < 0 a ≠ 0 ∆ > 0
e) Ph¬ng tr×nh cã hai nghiÖm d¬ng ph©n biÖt <=> P > 0 S > 0 a ≠ 0 ∆ > 0
f) Ph¬ng tr×nh cã hai nghiÖm ©m ph©n biÖt <=> P > 0 S < 0
g) Ph¬ng tr×nh cã hai nghiÖm lµ hai sè ®èi nhau a ≠ 0 <=> ∆ ≥ 0 b
S = x + x 1 2 = − = 0 a
h) Ph¬ng tr×nh cã 2 nghiÖm lµ hai sè nghÞch ®¶o cña nhau a ≠ 0 <=> ∆ ≥ 0 c P = x x 1 2 = = 1 a
D¹ng 9: TÝnh gi¸ trÞ cña biÓu thøc liªn hÖ gi÷a hai nghiÖm
Bíc 1: T×m ®iÒu kiÖn ®Ó ph¬ng tr×nh cã nghiÖm. −b c Bíc 2: TÝnh x1 + x1 = vµ x a 1.x1 = a
Bíc 3: BiÓu thÞ ®îc c¸c biÓu thøc theo x1 + x1 vµ x1.x1 ; sau ®ã thay gi¸ trÞ
cña x1 + x1 vµ x1.x1 vµo ®Ó tÝnh gi¸ trÞ cña biÓu thøc. Chó ý: 2 + 2 = + 2 a b (a b) − 2ab 3 + 3 = + 3 a b (a b) − 3ab(a + b) − 2 = + 2 (a b) (a b) − 4ab + 2 ( a b) = (a + b) + 2 a.b (a,b ≥ 0) 4 + 4 = 2 + 2 2 − 2 2 a b (a b ) 2a b 3 + 3 a b = a a + b b
= ( a + b)(a − ab + b) (a,b ≥ 0) 22
D¹ng 10: T×m ®iÒu kiÖn cña m ®Ó ph¬ng tr×nh cã hai nghiÖm x1, x2 tháa m·n
mét trong c¸c ®iÒu kiÖn sau: 1 1 a) α x + β x + = n 1 2 = γ b) x x c) 2 2 x + x = k x + x = t 1 2 d) 3 3 1 2 , 1 2
. . . . . . . . . . . . . . . . . . .
Bíc 1: T×m ®iÒu kiÖn cña tham sè ®Ó ph¬ng tr×nh cã hai nghiÖm x1, x2. Gi¶i a ≠ 0 hÖ §K: => m = ? ∆ ≥ 0 b S = x + x 1 2 = − a
Bíc 2: Theo hÖ thøc Vi – Ðt, ta cã: c P = x x 1 2 = a
Bíc 3: BiÕn ®æi ®iÒu kiÖn cña ®Ò bµi (lµ mét ®¼ng thøc hoÆc bÊt ®¼ng thøc)
®Ó cã tæng vµ tÝch hai nghiÖm, sau ®ã thay tæng vµ tÝch hai nghiÖm cã ®îc ë
bíc 2 vµo ®iÒu kiÖn võa biÕn ®æi; tõ ®ã gi¶i
ph¬ng tr×nh hoÆc bÊt ph¬ng tr×nh víi biÕn lµ tham sè ®Ó t×m gi¸ trÞ cña tham
sè. TiÕp theo kiÓm tra xem c¸c gi¸ trÞ tham sè t×m ®îc cã tháa m·n hÖ ®iÒu kiÖn ë bíc 1 hay kh«ng ?
HoÆc cã bµi to¸n ta kÕt hîp ®iÒu kiÖn cña ®Ò bµi víi mét hÖ thøc Vi - Ðt ®Ó
t×m hai nghiÖm x1, x2 (gi¶i hÖ ph¬ng tr×nh víi hai Èn lµ x1, x2); sau ®ã ta thay
x1, x2 vµo hÖ thøc Vi – Ðt cßn l¹i ®Ó t×m tham sè.
D¹ng 11: T×m ®iÒu kiÖn ®Ó ph¬ng tr×nh cã mét nghiÖm x = x1. T×m nghiÖm cßn l¹i
Bíc 1: Thay x = x1 vµo ph¬ng tr×nh, ta cã: 2
ax + bx + c = => m 1 1 0 = ?
Bíc 2: §Ó t×m nghiÖm cßn l¹i x2 ta thùc hiÖn theo hai c¸ch:
C¸ch 1: Thay gi¸ trÞ cña m vµo ph¬ng tr×nh ban ®Çu. Tõ ®ã cã ph¬ng tr×nh
bËc hai vµ gi¶i ph¬ng tr×nh nµy ta t×m ®îc x2 C¸ch 2: TÝnh x
x = S − x hoÆc x = P : x 2 nhê ®Þnh lÝ Vi - Ðt: 2 1 2 1
D¹ng 12: T×m ph¬ng tr×nh bËc hai khi biÕt tríc hai nghiÖm sè
Trêng hîp 1: Cho tõng nghiÖm x1, x2 . Ta cã ph¬ng tr×nh víi Èn x lµ :
( x − x )( x − x ) 2
= <=> x − x + x x + x x 1 2 0 ( 1 2 ) 1 2 = 0
Trêng hîp 2: Kh«ng cã x1, x2 riªng
Bíc 1: T×m S = x + x x x 1 2 vµ P = 1 2
Bíc 2: Ph¬ng tr×nh víi Èn x lµ 2
x − Sx + P = 0 .
Ph¬ng tr×nh cã nghiÖm <=> 2 S ≥ 4P
D¹ng 13: LËp ph¬ng tr×nh bËc hai khi biÕt mèi liªn hÖ gi÷a hai nghiÖm cña
ph¬ng tr×nh cÇn lËp víi hai nghiÖm cña ph¬ng tr×nh cho tríc.
Bíc 1: KiÓm tra §K cã nghiÖm cña ph¬ng tr×nh.
Bíc 2: TÝnh tæng vµ tÝch hai nghiÖm cña ph¬ng tr×nh ®· cho b − c x + x = , x .x = 1 2 1 2 a a 23
Bíc 3: TÝnh tæng vµ tÝch hai nghiÖm cña ph¬ng tr×nh cÇn lËp x3 vµ x4 th«ng
qua mèi liªn hÖ víi x1 , x2.
Bíc 4: LËp ph¬ng tr×nh.
D¹ng 14: T×m ®¼ng thøc liªn hÖ gi÷a hai nghiÖm kh«ng phô thuéc vµo tham sè C¸ch 1:
Bíc 1: T×m ®iÒu kiÖn ®Ó ph¬ng tr×nh cã hai nghiÖm x1, x2. a ≠ 0
Gi¶i hÖ ®iÒu kiÖn ∆ ≥ 0 − = b S x x 1 + 2 = a
Bíc 2: TÝnh hÖ thøc Vi - Ðt: = c P x .x 1 2 = a
Bíc 3: Khö tham sè trong hÖ thøc Vi – Ðt, t×m hÖ thøc liªn hÖ gi÷a S vµ
P. §ã lµ hÖ thøc ®éc lËp víi tham sè gi÷a c¸c nghiÖm cña ph¬ng tr×nh. C¸ch 2:
Bíc 1: T×m ®iÒu kiÖn ®Ó ph¬ng tr×nh cã hai nghiÖm x1, x2. a ≠ 0
Gi¶i hÖ ®iÒu kiÖn ∆ ≥ 0
Bíc 2: Gi¶i ph¬ng tr×nh t×m x1, x2.
Bíc 3: T×m hÖ thøc (khö tham sè).
D¹ng 15: T×m gi¸ trÞ lín nhÊt, nhá nhÊt cña tam thøc bËc hai 2 y = ax + bx + c (a ≠ 0) C¸ch 1:
BiÕn ®æi y = kA2(x) + m (m lµ h»ng sè).
k < 0 ⇒ kA2(x) ≤ 0 ⇒ kA2(x) + m ≤ m ⇒y ≤ m
Gi¸ trÞ lín nhÊt cña y b»ng m ®¹t ®îc khi A(x) = 0.
k > 0 ⇒ kA2(x) ≥ 0 ⇒ kA2(x) + m ≥ m ⇒y ≥ m
Gi¸ trÞ nhá nhÊt cña y b»ng m ®¹t ®îc khi A(x) = 0. C¸ch 2:
y = ax2 + bx + c ⇔ ax2 + bx + c – y = 0
+ Bíc 1: TÝnh ∆ hoÆc ∆' .
+ Bíc 2: §Æt ®iÒu kiÖn ∆ ≥ 0 ( ∆' ≥0)
⇒ Gi¶i bÊt ph¬ng tr×nh chøa Èn y.
y ≥ m ⇒Gi¸ trÞ nhá nhÊt cña y b»ng m ®¹t ®îc khi ∆ − b − ' = ∆' = 0 ⇔ b x = = . 2a a
y ≤ m ⇒Gi¸ trÞ lín nhÊt cña y b»ng m ®¹t ®îc khi − b − ' ∆ = ∆' = 0 ⇔ b x = = 2a a
D¹ng 16: T×m gi¸ trÞ lín nhÊt, nhá nhÊt cña biÓu thøc liªn hÖ gi÷a hai nghiÖm
Bíc 1: KiÓm tra sù cã nghiÖm cña ph¬ng tr×nh b − c Bíc 2: TÝnh x + x = , x .x = 1 2 1 2 a a 24
Bíc 3: BiÕn ®æi biÓu thøc liªn hÖ gi÷a hai nghiÖm lµ A(x1; x2) vÒ d¹ng cã chøa x1+ x2 vµ x1.x2
Bíc 4: Thay x1 + x2 vµ x1.x2 vµo biÓu thøc A. Khi ®ã A trë thµnh tam thøc bËc hai Èn lµ tham sè.
Bíc 5: T×m gi¸ trÞ lín nhÊt vµ nhá nhÊt cña A. Chän gi¸ trÞ tham sè thÝch hîp.
D¹ng 17: Chøng minh biÓu thøc liªn hÖ gi÷a hai nghiÖm kh«ng phô thuéc vµo tham sè
Bíc 1: T×m ®iÒu kiÖn cña tham sè ®Ó ph¬ng tr×nh cã hai nghiÖm 1 x ,x2 −b x x 1 + 2 =
Bíc 2: TÝnh hÖ thøc Vi- Ðt: a c x .x 1 2 = a
Bíc 3: TÝnh gi¸ trÞ cña biÓu thøc theo x1+ x2 vµ x1.x2 ; thÊy kÕt qu¶ lµ mét
h»ng sè => BiÓu thøc liªn hÖ gi÷u hai nghiÖm kh«ng phô thuéc vµo tham sè
D¹ng 18: T×m gi¸ trÞ cña tham sè ®Ó hai nghiÖm cña ph¬ng tr×nh tháa m·n
bÊt ®¼ng thøc ®· cho.
D¹ng 19: T×m hai sè khi biÕt tæng vµ tÝch cña chóng u + v = S
NÕu hai sè u vµ v tho¶ m·n
(S2 ≥ 4P). Th× u vµ v lµ nghiÖm cña u.v = P ph¬ng tr×nh x2 - Sx + P = 0 (*)
- NÕu ph¬ng tr×nh (*) cã hai nghiÖm ph©n biÖt 1
x ,x2 . Do x, y cã vai trß nh nhau u = x u = x
nªn cã hai cÆp sè tháa m·n lµ 1 hoÆc 2 v = x 2 v = 1 x
- NÕu phư¬ng tr×nh (*) cã nghiÖp kÐp 1 x = x2 = a => u = v = a
- NÕu phư¬ng tr×nh (*) v« nghiÖm => Kh«ng t×m ®ưîc cÆp gi¸ trÞ (u, v) nµo tháa m·n yªu cÇu ®Ò bµi
D¹ng 20: T×m gi¸ trÞ cña tham sè ®Ó hai ph¬ng tr×nh bËc hai mét Èn cã nghiÖm chung Cho hai ph¬ng tr×nh 2 2
ax + bx + c = 0 (a ≠ 0) vµ a 'x + b'x + c' = 0 (a ' ≠ 0)
Trong ®ã a, b,c,a ', b',c' chøa tham sè m *) C¸ch 1:
Hai ph¬ng tr×nh trªn cã nghiÖm chung khi vµ chØ khi hÖ phư¬ng tr×nh: 2
ax + bx + c = 0 (a ≠ 0) cã nghiÖm 2 a 'x + b'x + c' = 0 (a ' ≠ 0)
Trõ vÕ víi vÕ cña hai phư¬ng tr×nh trong hÖ ta cã phư¬ng tr×nh d¹ng: A(m).x = B(m)
+) NÕu A(m) = 0, tõ ®¼ng thøc nµy ta rót ra mét vµi gi¸ trÞ cña m, sau ®ã
thay trùc tiÕp vµo hai phư¬ng tr×nh → gi¶i hai phư¬ng tr×nh kh«ng chøa
tham sè vµ xÐt xem øng víi gi¸ trÞ m ®ã hai phư¬ng tr×nh cã nghiÖm chung hay kh«ng ? 25 B(m) +) NÕu A(m) ≠ 0 => x =
(chøa tham sè). Thay vµo mét trong A(m) hai
phư¬ng tr×nh ta rót ra mét vµi gi¸ trÞ cña m, sau ®ã thay tõng gi¸ trÞ cña
m vµo hai phư¬ng tr×nh → gi¶i hai phư¬ng tr×nh kh«ng chøa tham sè vµ
xÐt xem øng víi gi¸ trÞ m ®ã hai phư¬ng tr×nh cã nghiÖm chung hay kh«ng ? B(m) +) NÕu A(m) ≠ 0 => x =
(kh«ng chøa tham sè), kÕt luËn ngay A(m)
®©y lµ nghiÖm chung cña hai phư¬ng tr×nh. Thay nghiÖm chung ®ã vµo mét trong hai
phư¬ng tr×nh ta rót ra gi¸ trÞ cña m
KÕt luËn: øng víi gi¸ trÞ m nµo th× hai phư¬ng tr×nh cã nghiÖm chung, nghiÖm chung lµ g× ?
*) C¸ch 2: ChØ thùc hiÖn c¸ch gi¶i nµy ë mét sè bµi to¸n ®¬n gi¶n Tõ hai phư¬ng tr×nh 2 ax + bx + c = 0 => m = A(x) 2
a ' x + b'x + c' = 0 => m = B(x)
Ta cã: A(x) = B(x). Gi¶i phư¬ng tr×nh nµy ta ®îc nghiÖm chung cña hai
phư¬ng tr×nh, sau ®ã thay nghiÖm chung ®ã vµo mét trong hai phư¬ng tr×nh ta t×m
®îc gi¸ trÞ cña tham sè m, nÕu cÇn thiÕt thö l¹i ®Ó kiÓm tra
C¸ch 3: ChØ thùc hiÖn c¸ch gi¶i nµy ë mét sè bµi to¸n ®¬n gi¶n
Tõ mét trong hai ph¬ng tr×nh ta rót m theo x vµ thÕ vµo ph¬ng tr×nh kia, ®îc
ph¬ng tr×nh Èn x; tõ ph¬ng tr×nh nµy ta t×m ®îc nghiÖm chung, sau ®ã t×m m = ?
D¹ng 21: Chøng minh trong hai ph¬ng tr×nh bËc hai mét Èn cã Ýt nhÊt mét ph¬ng tr×nh cã nghiÖm Cho hai ph¬ng tr×nh 2 2
ax + bx + c = 0 (a ≠ 0) vµ a 'x + b'x + c' = 0 (a ' ≠ 0)
Trong ®ã a, b,c,a ', b',c' chøa tham sè
Chøng minh Ýt nhÊt mét trong hai ph¬ng tr×nh trªn cã nghiÖm P h ¬ng p h¸p : C¸ch 1: Gäi 1
∆ ,∆2 lÇn lît lµ biÖt thøc cña hai ph¬ng tr×nh. Ta cÇn chøng minh +) 1 ∆ + ∆2 ≥ 0 => 1
∆ ≥ 0 hoÆc ∆2 ≥ 0 hoÆc 1 ∆ ,∆2 ≥ 0 +) 1 ∆ .∆2 ≤ 0 => 1 ∆ ≥ 0 hoÆc ∆2 ≥ 0
VËy Ýt nhÊt mét trong hai ph¬ng tr×nh trªn cã nghiÖm
C¸ch 2: Chøng minh b»ng ph¶n chøng
Gi¶ sö c¶ hai ph¬ng tr×nh ®Òu v« nghiÖm. Khi ®ã 1 ∆ < 0,∆2 < 0
Ta lËp luËn dÉn ®Õn ®iÒu v« lÝ => ph¶i cã Ýt nhÊt mét trong hai biÖt thøc kh«ng ©m.
VËy cã Ýt nhÊt mét trong hai ph¬ng tr×nh trªn cã nghiÖm
D¹ng 22: T×m gi¸ trÞ cña tham sè ®Ó hai ph¬ng tr×nh t¬ng ®¬ng
- LÝ thuyÕt chung: Hai ph¬ng tr×nh ®îc gäi lµ t¬ng ®¬ng nÕu chóng cã cïng mét tËp nghiÖm
*) D¹ng 22.1: Hai ph¬ng tr×nh bËc nhÊt
T×m nghiÖm cña hai ph¬ng tr×nh theo tham sè vµ cho hai nghiÖm b»ng nhau,
tõ ®ã t×m ®îc gi¸ trÞ cña tham sè ®Ó hai ph¬ng tr×nh t¬ng ®¬ng
*) D¹ng 22.2: Hai ph¬ng tr×nh bËc hai mét Èn XÐt hai trêng hîp 26
Trêng hîp1: Hai ph¬ng tr×nh cã nghiÖm chung
Tríc hÕt t×m gi¸ trÞ cña tham sè ®Ó hai ph¬ng tr×nh cã nghiÖm chung sau
®ã thay gi¸ trÞ cña tham sè vµo hai ph¬ng tr×nh vµ t×m tËp nghiÖm cña
chóng. NÕu tËp nghiÖm b»ng nhau th× hai ph¬ng tr×nh t¬ng ®¬ng => gi¸ trÞ cña tham sè ∆ < 0
Trêng hîp 2: Hai ph¬ng tr×nh cïng v« nghiÖm <=> 1 ∆ 2 < 0 => Gi¸ trÞ cña tham sè
§Æc biÖt: NÕu nhËn thÊy mét trong hai ph¬ng tr×nh cã hai nghiÖm ( 1 ∆ ≥ 0 hoÆc ∆2 ≥ 0 )
=> Hai ph¬ng tr×nh t¬ng ®¬ng khi hai nghiÖm cña ph¬ng
tr×nh nµy còng lµ hai nghiÖm cña ph¬ng tr×nh kia, do ®ã ta cã
thÓ ¸p dông vi - Ðt cho c¶ hai ph¬ng tr×nh vµ t×m tham sè. Cô thÓ ta cã: −b −b' c −c' 1 x + x2 = = ; 1 x x2 = = => m = ? a a' a a'
D¹ng 23: T×m gi¸ trÞ cña tham sè khi biÕt nghiÖm cña ph¬ng tr×nh
23.1: T×m gi¸ trÞ cña tham sè khi biÕt mét nghiÖm cña ph¬ng tr×nh.
Cho ph¬ng tr×nh ax2 + bx + c = 0 (a ≠ 0) cã mét nghiÖm x = x1. C¸ch gi¶i: Bíc1: Thay x = x 2
1 vµo ph¬ng tr×nh ax1 + bx1 + c = 0.
Bíc 2: Gi¶i ph¬ng tr×nh cã Èn lµ tham sè.
23.2: T×m gi¸ trÞ cña tham sè khi biÕt hai nghiÖm cña ph¬ng tr×nh.
Cho ph¬ng tr×nh ax2 + bx + c = 0 (1) (a ≠ 0) cã hai nghiÖm x = x1; x = x2. C¸ch 1:
Bíc 1: Thay x = x1; x = x2 vµo ph¬ng tr×nh (1) ta cã hÖ ph¬ng tr×nh: 2 ax bx c 0 1 + 1 + = 2 ax bx c 0 2 + 2 + =
Bíc 2: Gi¶i hÖ ph¬ng tr×nh cã Èn lµ tham sè. C¸ch 2:
Bíc 1: T×m ®iÒu kiÖn ®Ó ph¬ng tr×nh cã nghiÖm. −b x x 1 + 2 = Bíc 2: Theo Vi - Ðt a c x .x 1 2 = a
Bíc 3: Thay x = x1; x = x2 vµo hÖ vµ gi¶i ta ®îc gi¸ trÞ cña tham sè.
D¹ng 24: X¸c ®Þnh gi¸ trÞ tham sè ®Ó tam thøc bËc hai lu«n lu«n d¬ng hoÆc
lu«n lu«n ©m víi mäi x
Cho tam thøc bËc hai f(x) = 2 ax + bx + c (a ≠ 0) 2 2 2 f(x) = 2 b c ( b ) b −4ac b a( x x ) a x a x ∆ + + = + − = + − a a 2a 2 ( 2a ) 2 4a 4a +) NÕu ∆ < 0 => ( b x ∆ + −
> 0. Khi ®ã f(x) cïng dÊu víi hÖ sè a, ta cã 2a )2 2 4a c¸c trêng hîp sau a > 0 f(x) > 0, x ∀ <=> ∆ < 0 27 a < 0 f(x) < 0, x ∀ <=> ∆ < 0 a > 0 f(x) 0 ≥ , x ∀ <=> ∆ ≤ 0 a < 0 f(x) 0 ≤ , x ∀ <=> ∆ ≤ 0 +) NÕu b 2 ∆ = 0 => f (x) = a(x + ) 2a
=> f(x) cïng dÊu víi hÖ sè a, trõ trêng hîp x = −b 2a Khi x = −b th× f(x) = 0 2a
VII – Gi¶i bµi to¸n b»ng c¸ch lËp ph¬ng tr×nh, lËp hÖ ph¬ng tr×nh. LÝ thuyÕt chung
1. C¸c bíc gi¶i bµi to¸n b»ng c¸ch lËp ph¬ng tr×nh B íc 1: LËp ph¬ng tr×nh.
- Chän Èn sè vµ x¸c ®Þnh ®iÒu kiÖn thÝch hîp cho Èn sè;
- BiÓu diÔn c¸c ®¹i lîng cha biÕt theo Èn vµ c¸c ®¹i lîng ®· biÕt;
- LËp ph¬ng tr×nh biÓu thÞ mèi quan hÖ gi÷a c¸c ®¹i lîng. B íc 2: Gi¶i ph¬ng tr×nh. B íc
3: Tr¶ lêi: KiÓm tra xem trong c¸c nghiÖm cña ph¬ng tr×nh, nghiÖm nµo tho¶
m·n ®iÒu kiÖn cña Èn, nghiÖm nµo kh«ng råi kÕt luËn.
2. C¸c bíc gi¶i bµi to¸n b»ng c¸ch lËp hÖ ph¬ng tr×nh B íc 1: LËp hÖ ph¬ng tr×nh.
- Chän hai Èn sè vµ x¸c ®Þnh ®iÒu kiÖn thÝch hîp cho chóng;
- BiÓu diÔn c¸c ®¹i lîng cha biÕt theo c¸c Èn vµ c¸c ®¹i lîng ®· biÕt;
- LËp hai ph¬ng tr×nh biÓu thÞ mèi quan hÖ gi÷a c¸c ®¹i lîng. B íc 2:
Gi¶i hÖ hai ph¬ng tr×nh nãi trªn . B íc
3: Tr¶ lêi: KiÓm tra xem trong c¸c nghiÖm cña hÖ ph¬ng tr×nh, nghiÖm nµo
tho¶ m·n ®iÒu kiÖn cña Èn, nghiÖm nµo kh«ng råi kÕt luËn.
Ph©n d¹ng bµi tËp chi tiÕt
D¹ng 1: To¸n chuyÓn ®éng - Ba ®¹i lîng: S, v, t S S
- Quan hÖ: S = vt; t = ; v = (dïng c«ng thøc S = v.t tõ ®ã t×m mèi quan hÖ v t gi÷a S , v vµ t) - Chó ý bµi to¸n can« :
Vxu«i dßng = Vthùc + Vníc ; Vngîc dßng = Vthùc – Vníc 28
*) To¸n ®i gÆp nhau cÇn chó ý ®Õn tæng qu·ng ®êng vµ thêi gian b¾t ®Çu khëi hµnh.
*) To¸n ®uæi kÞp nhau chó ý ®Õn vËn tèc h¬n kÐm vµ qu·ng ®êng ®i ®îc cho ®Õn khi ®uæi kÞp nhau
D¹ng 2: To¸n vÒ quan hÖ gi÷a c¸c sè ab = 10a + b abc = 100a + 10b + c
§iÒu kiÖn: 0 < a ≤ 9; 0 ≤ b, c ≤ 9 (a, b, c ∈ Z )
D¹ng 3: To¸n lµm chung, lµm riªng, n¨ng suÊt
*) Bµi to¸n lµm chung, lµm riªng:
+ Qui íc: C¶ c«ng viÖc lµ 1 ®¬n vÞ.
+ T×m trong 1 ®v thêi gian ®èi tîng tham gia bµi to¸n thùc hiÖn ®îc bao nhiªu phÇn c«ng viÖc. 1
+ C«ng thøc: PhÇn c«ng viÖc = Thêi gian
+ Sè lîng c«ng viÖc = Thêi gian . N¨ng suÊt. *) Bµi to¸n n¨ng suÊt:
+ Gåm ba ®¹i lîng: Tæng s¶n phÈm ; n¨ng suÊt; thêi gian
+ Quan hÖ: Tæng s¶n phÈm = N¨ng suÊt . Thêi gian; Tæng s¶n phÈm Tæng s¶n phÈm => Thêi gian = ; N¨ng suÊt = . N¨ng suÊt Thêi gian
D¹ng 4: To¸n diÖn tÝch
D¹ng 5: To¸n cã quan hÖ h×nh häc
D¹ng 6: To¸n cã néi dung lÝ, hãa
D¹ng 7: To¸n d©n sè, to¸n phÇn tr¨m
VIII – C¸c ph¬ng ph¸p ph©n tÝch ®a thøc thµnh nh©n tö
Ph¬ng ph¸p 1: §Æt nh©n tö chung
a) Ph¬ng ph¸p ®Æt nh©n tö chung ®îc dïng khi c¸c h¹ng tö cña ®a thøc cã nh©n tö
chung. Cô thÓ: AB + AC + AD = A(B + C + D)
b) C¸c bíc tiÕn hµnh: B íc 1:
Ph¸t hiÖn nh©n tö chung vµ ®Æt nh©n tö chung ra ngoµi dÊu ngoÆc. B íc
2 : ViÕt c¸c h¹ng tö trong ngoÆc b»ng c¸ch chia tõng h¹ng tö cña ®a thøc cho nh©n tö chung.
Ph¬ng ph¸p 2: Dïng h»ng ®¼ng thøc
a) Ph©n tÝch ®a thøc thµnh nh©n tö b»ng ph¬ng ph¸p dïng h»ng ®¼ng thøc ®îc
dïng khi c¸c h¹ng tö cña ®a thøc cã d¹ng h»ng ®¼ng thøc.
b) C¸c h»ng ®¼ng thøc quan träng 1) a2 + 2ab + b2 = (a + b)2 + + = + 2 a 2 a.b b ( a b) (a,b ≥ 0) 2) a2 - 2ab + b2 = (a - b)2 − + = − 2 a 2 a.b b ( a b) (a,b ≥ 0) 29
3) a2 – b2 = (a + b).(a – b)
4) a − b = ( a + b).( a − b) (a,b ≥ 0)
5) a3 + 3a2b + 3ab2 + b3 = (a + b)3 3 + + + 3 = + 3 a 3a b 3b a b ( a b) (a,b ≥ 0)
6) a3 - 3a2b + 3ab2 - b3 = (a - b)3 3 − + − 3 = − 3 a 3a b 3b a b ( a b) (a,b ≥ 0) 7) 3 + 3 = + 2 − + 2 a b (a b)(a ab b ) + = 3 + 3 a a b b a
b = ( a + b)(a − ab + b) (a,b ≥ 0)
an + bn =(a + b)(an-1 - an-2b + ... - abn-2 + bn-1) víi n lÎ 8) 3 − 3 = − 2 + + 2 a b (a b)(a ab b ) − = 3 − 3 a a b b a
b = ( a − b)(a + ab + b) (a,b ≥ 0)
an - bn = (a - b)(an-1 + an-2b + ... + abn-2 + bn-1).
9) a2 + b2 + c2 + 2ab + 2ac + 2bc = (a + b + c)2 + + + + + = + + 2 a b c 2 ab 2 ac 2 bc ( a b c) (a,b ≥ 0) 2 2 2 2 2
a + b + c + d + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd = (a + b + c + d)
10) Lòy thõa bËc n cña mét nhÞ thøc (nhÞ thøc Niu t¬n) – §èi tîng HSG 0 (a + b) = 1 1 (a + b) = 1a + 1b 2 2 2 (a + b) = 1a + 2ab + 1b 3 3 2 2 3 (a + b) = 1a + 3a b + 3ab + 1b 4 4 3 2 2 3 4
(a + b) = 1a + 4a b + 6a b + 4ab + 1b 5 5 4 3 2 2 3 4 5
(a + b) = 1a + 5a b + 10a b + 10a b + 5ab + 1b
…………………………………………………………
ViÕt tam gi¸c Pa – xcan ®Ó khai triÓn n (a + b) nh sau: 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1
……………………………………….. C¸ch viÕt:
+ Mçi dßng ®Òu b¾t ®Çu b»ng 1 vµ kÕt thóc b»ng 1
+ Mçi sè trªn mét dßng kÓ tõ dßng thø hai ®Òu b»ng sè liÒn trªn
céngvíi sè bªn tr¸i cña sè liÒn trªn.
Ph¬ng ph¸p 3: Nhãm c¸c h¹ng tö
Ph¬ng ph¸p nµy thêng ®îc dïng cho nh÷ng ®a thøc cÇn ph©n tÝch thµnh
nh©n tö cha cã nh©n tö chung hoÆc cha ¸p dông ngay ®îc h»ng ®¼ng thøc mµ sau
khi nhãm c¸c h¹ng tö ®ã hoÆc biÕn ®æi s¬ bé råi nhãm l¹i th× xuÊt hiÖn h»ng ®¼ng
thøc hoÆc cã nh©n tö chung, cô thÓ: B íc 1:
Ph¸t hiÖn nh©n tö chung hoÆc h»ng ®¼ng thøc ë tõng nhãm. B íc
2: Nhãm ®Ó ¸p dông ph¬ng ph¸p h»ng ®¼ng thøc hoÆc ®Æt nh©n tö chung. B íc 3:
§Æt nh©n tö chung cho toµn ®a thøc. 30
Ph¬ng ph¸p 4: T¸ch mét h¹ng tö thµnh nhiÒu h¹ng tö; hoÆc thªm, bít cïng mét h¹ng tö
*) LÝ thuyÕt chung: Ph¬ng ph¸p nµy nh»m biÕn ®æi ®a thøc ®Ó t¹o ra nh÷ng h¹ng
tö thÝch hîp ®Ó nhãm hoÆc sö dông h»ng ®¼ng thøc: *) C ¸c tr êng hîp :
a, Trêng hîp ®a thøc d¹ng ax2 + bx + c ( a, b, c ∈ Z; a, b, c ≠ 0)
TÝnh : ∆ = b2 - 4ac:
- NÕu ∆ = b2 - 4ac < 0: §a thøc kh«ng ph©n tÝch ®îc.
- NÕu ∆ = b2 - 4ac = 0: §a thøc chuyÓn vÒ d¹ng b×nh ph¬ng cña mét nhÞ thøc bËc nhÊt
- NÕu ∆ = b2 - 4ac > 0
+) ∆ = b2 - 4ac = k2 ( k ∈ Q) ®a thøc ph©n tÝch ®îc trong trêng Q.
+) ∆ = b2 - 4ac ≠ k2 ®a thøc ph©n tÝch ®îc trong trêng sè thùc R.
b, Trêng hîp ®a thøc tõ bËc 3 trë lªn:
- NhÈm nghiÖm cña ®a thøc:
+) NÕu tæng c¸c hÖ sè cña c¸c h¹ng tö b»ng 0 ⇒ ®a thøc cã nghiÖm b»ng 1.
+) NÕu tæng c¸c hÖ sè cña c¸c h¹ng tö bËc ch½n b»ng tæng c¸c hÖ sè cña
c¸c h¹ng tö bËc lÎ ⇒ ®a thøc cã nghiÖm b»ng - 1.
- Lu ý ®Þnh lý: " NÕu ®a thøc cã nghiÖm nguyªn th× nghiÖm nguyªn ®ã ph¶i lµ íc p
cña h¹ng tö tù do. NÕu ®a thøc cã nghiÖm h÷u tØ d¹ng
th× p lµ íc cña h¹ng tö q
tù do, q lµ íc d¬ng cña hÖ sè cña h¹ng tö cã bËc cao nhÊt".
- Khi biÕt mét nghiÖm cña ®a thøc ta cã thÓ dïng phÐp chia ®a thøc, hoÆc dïng s¬
®å Hooc – ne ®Ó h¹ bËc cña ®a thøc.
Ph¬ng ph¸p 5: Dïng phÐp chia ®a thøc (nhÈm nghiÖm)
- §a thøc f(x) chia hÕt cho ®a thøc g(x) khi vµ chØ khi: f(x)= g(x).q(x)
(q(x) lµ th¬ng cña phÐp chia)
*) §Æc biÖt : f(x) chia hÕt cho x - a <=> f(a) = 0
Ph¬ng ph¸p 6: Ph¬ng ph¸p ®Æt Èn phô (®æi biÕn)
- Dùa vµo ®Æc ®iÓm cña ®a thøc ®· cho ta ®a vµo 1 hoÆc nhiÒu biÕn míi ®Ó
®a thøc trë thµnh ®¬n gi¶n .Ph¬ng ph¸p nµy thêng ®îc sö dông ®Ó ®a mét ®a thøc
bËc cao vÒ ®a thøc bËc 2 mµ ta cã thÓ ph©n tÝch ®îc dùa vµo t×m nghiÖm cña ®a thøc bËc 2 .
- CÇn ph¸t hiÖn sù gièng nhau cña c¸c biÓu thøc trong ®a thøc ®Ó chän vµ
®Æt Èn phô cho thÝch hîp
Ph¬ng ph¸p 7: Ph¬ng ph¸p hÖ sè bÊt ®Þnh (®ång nhÊt hÖ sè)
Trªn c¬ së bËc cña ®a thøc ph¶i ph©n tÝch, ta x¸c ®Þnh c¸c d¹ng kÕt qu¶,
ph¸ ngoÆc råi ®ång nhÊt hÖ sè vµ gi¶i.
Ph¬ng ph¸p 8: Ph¬ng ph¸p vËn dông ®Þnh lÝ vÒ nghiÖm cña tam thøc bËc hai
- ¸p dông ®Þnh lý: NÕu ®a thøc P = ax2 + bx + c cã nghiÖm x1, x2 th× : P = a(x - x1)(x - x2) 31




