







Preview text:
ThS. TRAÀN THANH YEÂN TOÅNG HÔÏP LYÙ THUYEÁT THPT MOÂN TOAÙN
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên
TỔNG HỢP LÝ THUYẾT THPT MÔN TOÁN 1
Hằng đẳng thức đáng nhớ 2 2 A B 2 A AB 2 2 B
A B 2 A AB 2 2 B 2 2
A B A B A B 3 3 2 2 A B
A B A AB B 3 3 3 2 2 A B
A B A AB B
A B 3 A 2 A B 2 AB 3 3 3 B 3 A B 3 A 2 A B 2 AB 3 3 3 B
A B A B2 2 2 2AB
A B A B 2 4 4 2 2 2 2 2A B
4 4 2 2 2 2 A B A B A B 2 Chia đa thức
Xem ví dụ sau: Chia đa thức 2
x 2x 2 cho đa thức x 1 : 2
x 2x 2 x 1 2 x x x 3 3 x 2 3 x 3 5 Phép chia 2
x 2x 2 cho x 1 được thương x 3 và phần dư là 5 nên ta có: 2 x 2x 2 5 x 3 . x 1 x 1 3 Sơ đồ Hooc-ne
Chia đa thức f x n n a x 1 a x
... a x a cho đa thức x a ta được thương là n n1 1 0 g x n1 n b x 2 b x
... b x b và dư r : n1 n2 1 0 a a a … a a a n n 1 n 2 2 1 0 a b a b ab a b ab a
… b ab a b ab a r ab a n1 n n 2 n 1 n 1 n 3 n 2 n 2 1 2 2 0 1 1 0 0
“Nhân ngang, cộng chéo”
Khi đó ta viết f x x a.g x r .
Chú ý: Nếu x a là một nghiệm của f x thì phần dư r 0 . Khi đó f x x a.g x .
Xem ví dụ sau: Xét đa thức 3 x 2
4x 7x 6 . Do x 2 là một nghiệm của đa thức trên nên ta có sơ đồ Hooc-ne: 1 –4 7 –6 2 1 –2 3 0 Khi đó ta có 3 x 2
x x x 2 4 7 6
2 x 2x 3 . Trang 1
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên 4 Hình học phẳng Định lý Pytago
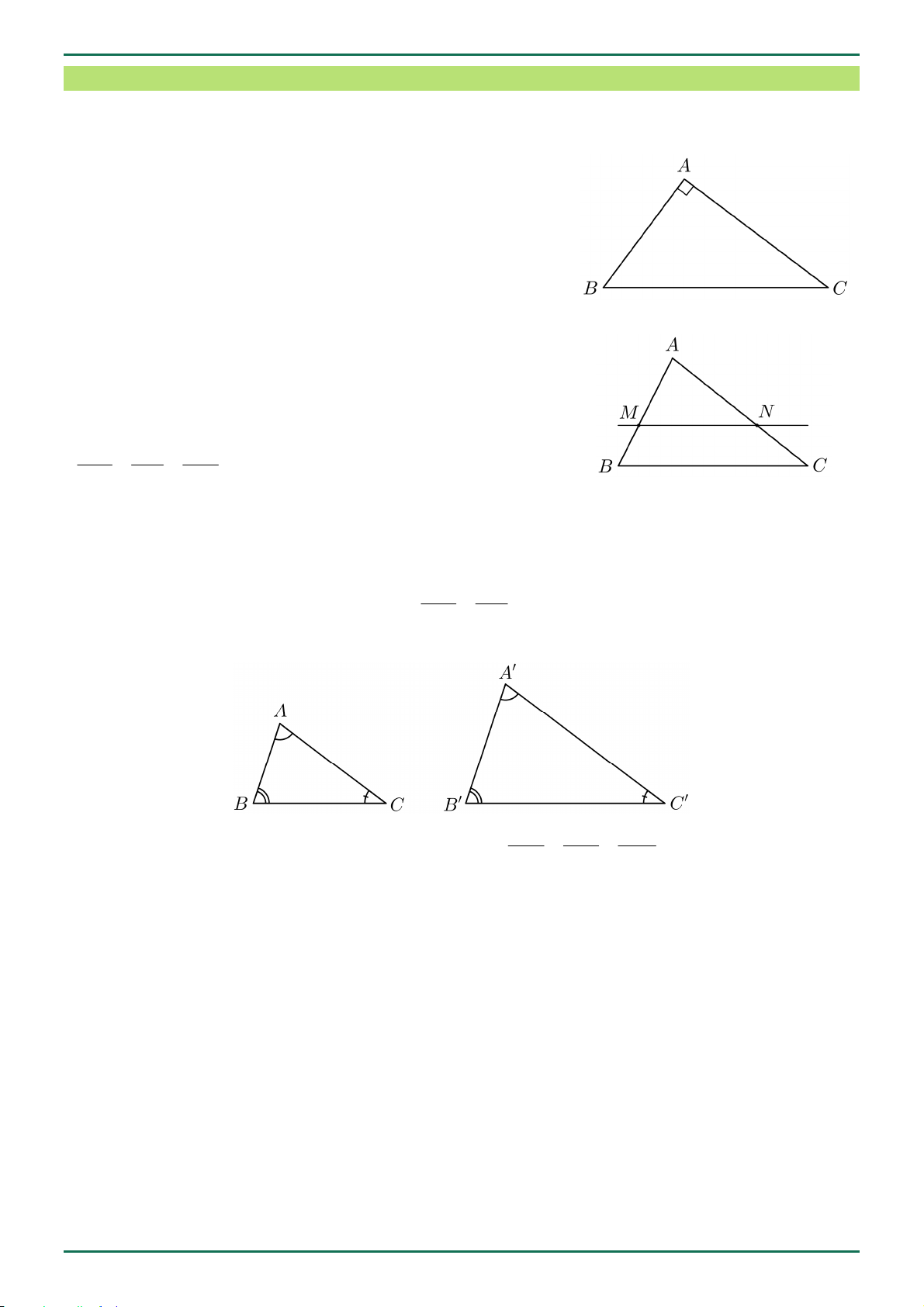
Trong tam giác vuông, bình phương cạnh huyền bằng tổng
bình phương hai cạnh góc vuông: 2 2 2 BC AB AC .
Định lý Talet trong tam giác
Nếu một đường thẳng song song với một cạnh của tam giác
và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những
đoạn thẳng tương ứng tỉ lệ.
Cho tam giác ABC với MN song song BC , khi đó: AM AN MN . AB AC BC
Định lý Talet đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn
thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác. AM AN
Tức là, trong tam giác ABC , nếu ta có tỉ lệ
thì ta suy ra MN BC. AB AC
Tam giác đồng dạng AB BC AC
ABC đồng dạng A B C . A B B C AC
TH1: Nếu 3 cạnh của tam giác này tỉ lệ với 3 cạnh của tam giác kia thì hai tam giác đó đồng dạng (c-c-c).
TH2: Nếu 2 cạnh của tam giác này tỉ lệ với 2 cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh
đó bằng nhau, thì hai tam giác đó đồng dạng (c-g-c).
TH3: Nếu 2 góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng (g-g-g).
Định lí 1: Tỉ số đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
Định lí 2: Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng. Tam giác bằng nhau
Các trường hợp bằng nhau của tam giác : cạnh – cạnh – cạnh, cạnh – góc – cạnh, góc – cạnh – góc,
cạnh huyền – góc nhọn (tam giác vuông).
Các định nghĩa cơ bản trong tam giác
- Đường trung tuyến là đoạn thẳng nối từ đỉnh tới trung điểm của cạnh đối diện. Trang 2
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên
- Đường cao là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện.
- Đường phân giác của một góc chia góc đó thành hai góc có độ lớn bằng nhau.
- Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh bên của tam giác. Độ dài
của nó là bằng một nửa cạnh đáy.
- Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang. Độ
dài của nó là bằng nửa tổng hai đáy.
- Trọng tâm là giao điểm của ba đường trung tuyến.
- Trực tâm là giao điểm của ba đường cao.
- Tâm đường tròn ngoại tiếp là giao điểm của ba đường trung trực.
- Tâm đường tròn nội tiếp là giao điểm của ba đường phân giác trong. Chú ý
Với I là tâm đường tròn nội tiếp tam giác ABC ta có đẳng thức vectơ sau:
BC.IA C . A IB A . B IC 0 . Định lý Menelaus
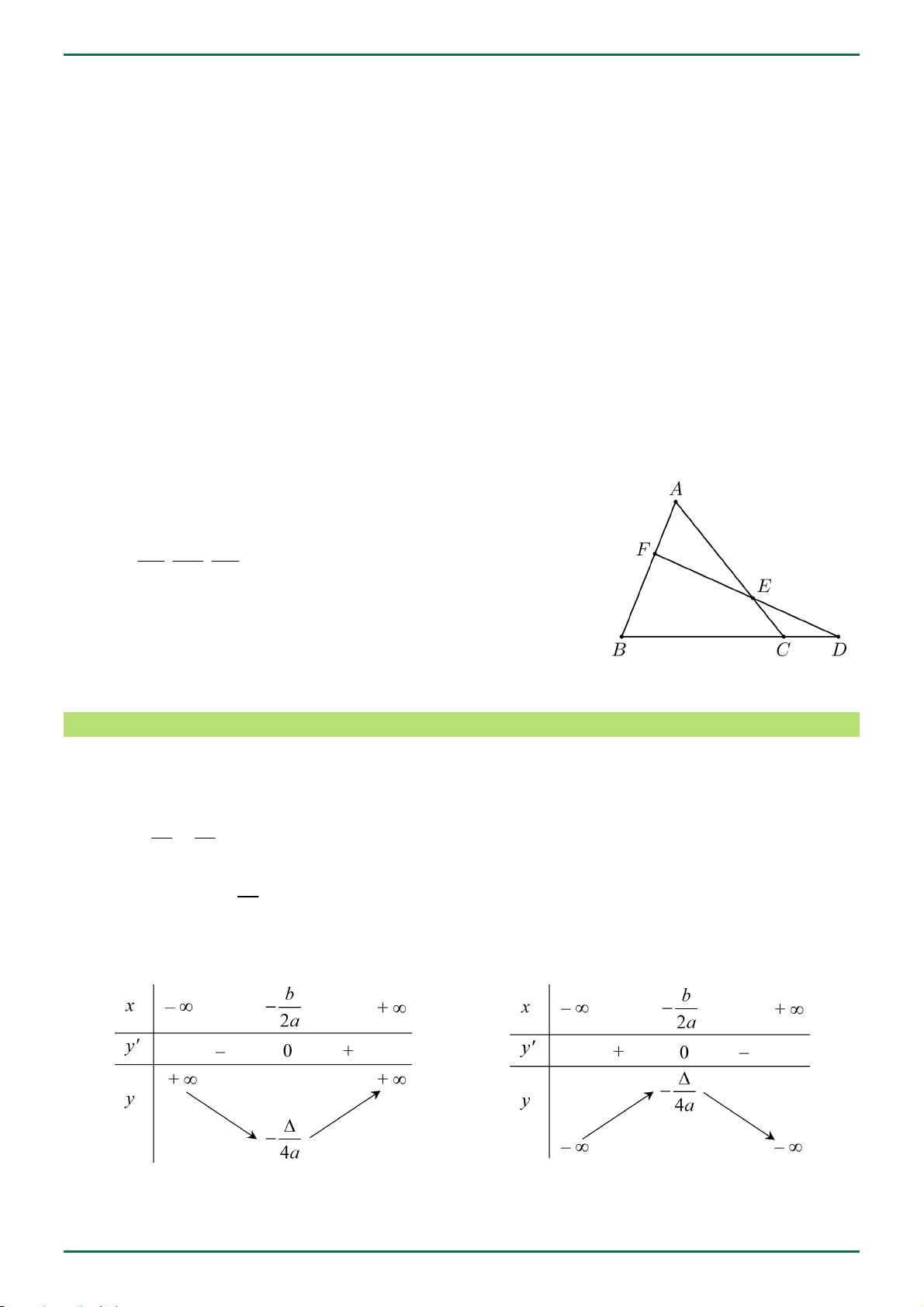
Cho tam giác ABC . Các điểm D, E, F lần lượt nằm trên các
đường thẳng BC, CA, AB . Khi đó D, E, F thẳng hàng khi và FA DB EC chỉ khi . . 1 . FB DC EA LỚP 10 1 Hàm số bậc hai Dạng: y 2
ax bx c a 0 . b Đỉnh: I ; . 2a 4a b
Trục đối xứng: x . 2a Bảng biến thiên: Với a 0 : Với a 0 :
Xét phương trình bậc hai 2
ax bx c 0 a 0 . Trang 3
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên b Ta có: 2 b 4ac ; 2
b ac với b . 2 b b
TH1: 0 0 : Phương trình có 2 nghiệm phân biệt: x x . 2a a b b
TH2: 0 0 : Phương trình có nghiệm kép x x . 2a a
TH3: 0 : Phương trình vô nghiệm.
Xét hàm số bậc hai y 2
ax bx c a 0 . Khi đó: b
Với a 0 : min y x . 4a 2a b
Với a 0 : max y x . 4a 2a 2 Định lí Vi-et
Xét phương trình bậc hai 2
ax bx c 0 a 0 có 2 nghiệm là x , x . Khi đó: 1 2 b c
S x x và P x x 2
ax bx c a x x x x 1 2 1 2 a 1 2 a 0
Phương trình có 2 nghiệm trái dấu ac 0 Phương trình có 2 nghiệm dương P 0 S 0 0 0
Phương trình có 2 nghiệm âm P 0 .
Phương trình có 2 nghiệm cùng dấu . P 0 S 0
Chú ý: Khi cần 2 nghiệm phân biệt thì điều kiện ở trên không có dấu bằng " " . 3
So sánh nghiệm của phương trình bậc hai với các số Cho phương trình bậc hai 2
ax bx c 0 a 0 có 2 nghiệm phân biệt x , x và các số , . 1 2 Khi đó:
x . x 0
x . x 0 1 2 1 2
x x
x x 1 2 1 2 x x 2 x x 2 1 2 1 2
x x x . x 0
x x . a f 0 1 2 1 2
2 1 0 0
x x . a f 0
x x . a f 0 1 2 1 2 S S 0 0 2 2 .
a f 0 .
a f 0
x x
x x 1 2 1 2 .
a f 0 .
a f 0 Trang 4
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên 0 .
a f 0
x x 1 2
f . f 0
x x 1 2 .
a f 0
x x 1 2 S 2 4
Dấu của nhị thức bậc nhất
Cho nhị thức bậc nhất f x ax b a 0 . Khi đó: b x a f x trái dấu với a 0 cùng dấu với a
Dấu của tam thức bậc hai
Cho tam thức bậc hai f x 2
ax bx c a 0 . Khi đó:
TH1: 0 (phương trình có 2 nghiệm phân biệt x x ) 1 2 x x x 1 2 f x
cùng dấu với a 0 trái dấu với a 0 cùng dấu với a
TH2: 0 (phương trình có nghiệm kép) b x 2a f x cùng dấu với a 0 cùng dấu với a
TH3: 0 (phương trình vô nghiệm) x f x cùng dấu với a
Tam thức bậc hai không đổi dấu trên
Cho tam thức bậc hai f x 2
ax bx c a 0 . Khi đó: a 0 a 0
f x 0, x
f x 0, x 0 0 a 0 a 0
f x 0, x
f x 0, x 0 0
f x 0 vô nghiệm f x 0, x
f x 0 vô nghiệm f x 0, x
f x 0 vô nghiệm f x 0, x
f x 0 vô nghiệm f x 0, x
Chú ý: Nếu hệ số a có chứa tham số m ta cần xét trường hợp a 0 trước. 5 Trang 5
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên
Phương trình, bất phương trình chứa ẩn trong dấu giá trị tuyệt đối và dấu căn B 0 A B
A B
A B A B A B A B B 0
A 0 hay B 0
A B
A B 2 A B A B B 0 A 0
A B 0 B 0
A B B 0 A 2 0 A B A 0 A 0
A B B 0
A B B 0 A 2 2 B A B B 0 B 0 B 0 B 0 A B A B A 2 2 0 A B A 0 A B B 0 B 0
A B
A B A B A B B 0 B 0 A B 0 A B 0 A 0 A 0 B 0 B 0
A B 0 B 0
A B 0 B 0 A 0 A 0 A B A B
A B
A B A B A B A B A B
A B
A B A B A B A B 2 A 2
B A B A B 0 A B 2 A 2
B A B A B 0 6
Bất đẳng thức Cauchy a b
Với a, b 0 , ta có:
ab. Dấu " " xảy ra khi và chỉ khi a b . 2
a b c
Mở rộng: Với a, b, c 0 , ta có: 3
abc . Dấu " " xảy ra khi và chỉ khi a b c . 3
Bất đẳng thức Bunhiacopxki 2
Với a, b, x, y , ta có: 2 2 2 2 ax by a b
x y hoặc 2 2 2 2 ax by a b x y .
Dấu " " xảy ra khi và chỉ khi ay bx .
Bất đẳng thức Mincopxki 2 2
Với a, b, c, d , ta có: 2 2 2 2
a b c d a c b d . Trang 6
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên a b
Dấu " " xảy ra khi và chỉ khi . c d 7
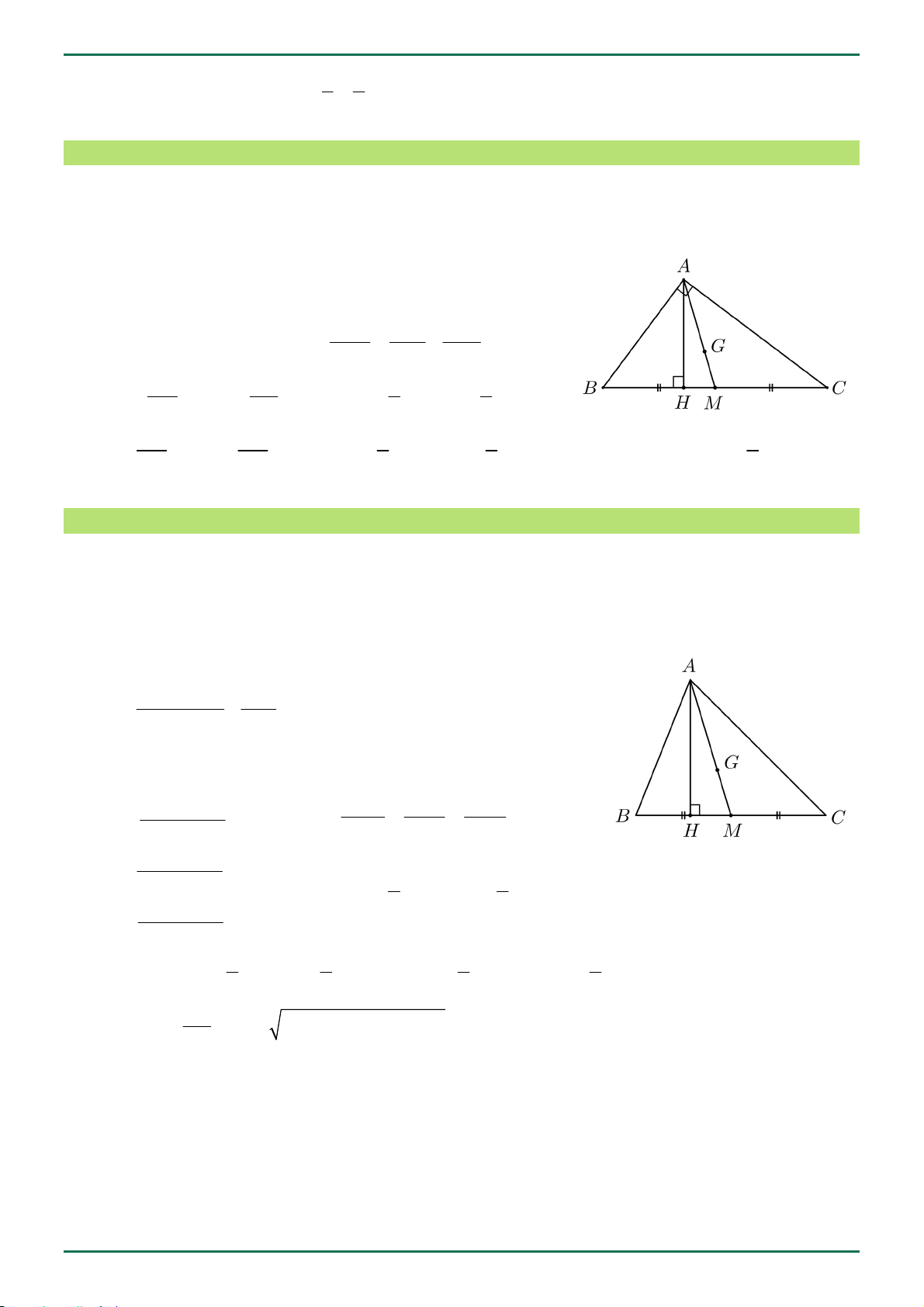
Hệ thức lượng trong tam giác vuông
Cho tam giác ABC vuông tại A , đường cao AH , đường trung tuyến AM , G là trọng tâm tam giác ABC . Khi đó: 2 2 2 BC AB AC A . B AC B . C AH 2
AB BC.BH 2
AC BC.CH 2 AH H . B HC 1 1 1 2 2 2 AH AB AC AC AB 1 1 sin B , cos B , S A . B AC AH.BC BC BC ABC 2 2 AC AB 2 1 1 tan B , cot B AG AM , GM AM
AM BM CM BC AB AC 3 3 2 8
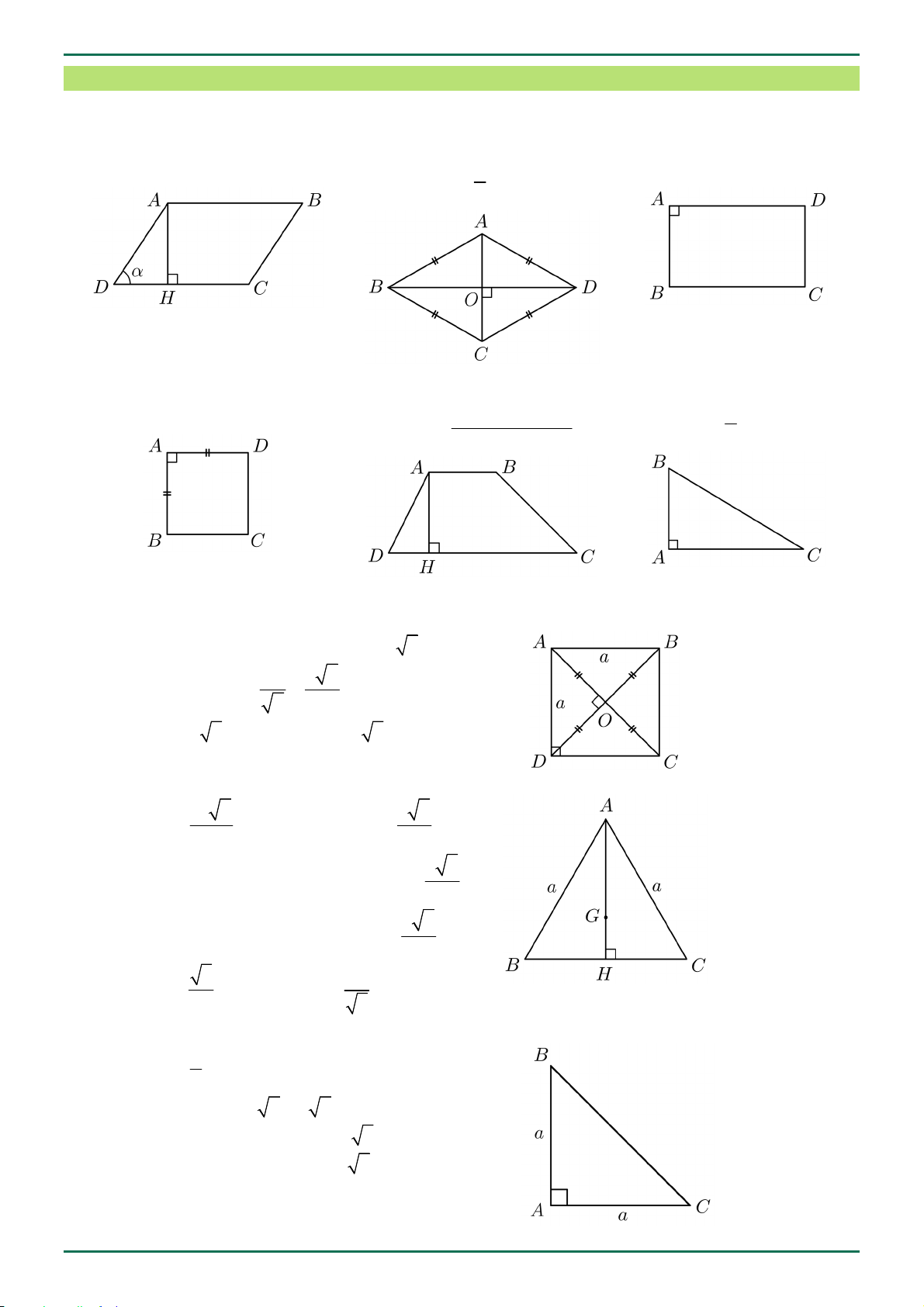
Hệ thức lượng trong tam giác thường
Cho tam giác ABC , AB c, AC b, BC a , đường cao AH , đường trung tuyến AM , G là trọng
tâm tam giác ABC , R là bán kính đường tròn ngoại tiếp, r là bán kính đường tròn nội tiếp, p là nửa chu vi tam giác.
Định lý đường trung tuyến: Định lý cosin: 2 AB 2 2 2 2 2 2 AC BC
a b c 2bc cos A AM 2 4 2 b 2 a 2
c 2ac cos B 2 c 2 a 2
b 2ab cosC
Hệ quả định lý cosin: Định lý sin: 2 b 2 c 2 a a b c cos A 2R 2bc sin A sin B sin C 2 2 2
Tính chất trung tuyến:
a c b cos B 2 1 2ac AG AM , GM AM 2 a 2 b 2 c 3 3 cos C 2ab 1 1 1 1 Diện tích: S AH.BC A . B AC.sin A B .
A BC.sin B C . A . CB sin C ABC 2 2 2 2 abc
pr pp ap b p c . 4R 2 2 2 Chú ý:
a b c cos A 0 A là góc nhọn. 2 2 2
a b c cos A 0 A là góc tù. 2 2 2
a b c cos A 0 A là góc vuông. Trang 7
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên 9
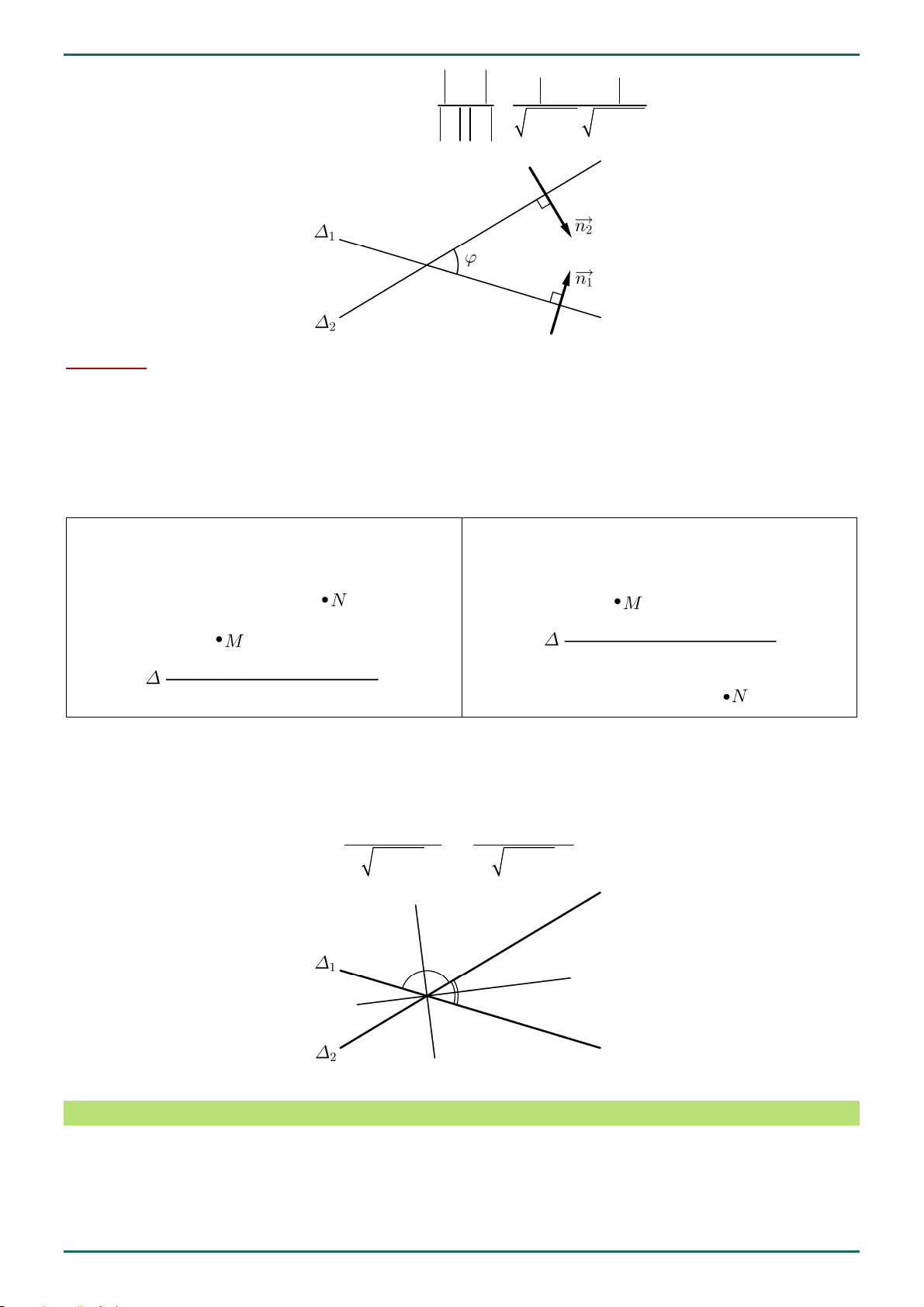
Diện tích các hình thường gặp
Diện tích hình bình hành: Diện tích hình thoi:
Diện tích hình chữ nhật: S
AH .CD AD.CD.sin 1 S AB.BC ABCD S .AC.BD ABCD ABCD 2 Diện tích hình vuông: Diện tích hình thang:
Diện tích tam giác vuông: S 2 AB
AB CD.AH 1 ABCD S S .A . B AC ABCD ABC 2 2 Đặc biệt:
Hình vuông cạnh a Diện tích: 2 S
a . Độ dài đường chéo: a 2 a a 2
OA OB OC OD 2 2
Chéo = Cạnh x 2 ; Cạnh = Chéo / 2
Tam giác đều cạnh a 2 a 3 a 3 Diện tích: S . Đường cao: AH 4 2 a 3
Bán kính đường tròn ngoại tiếp: R AG 3 a 3
Bán kính đường tròn nội tiếp: r HG 6 3 2 Cao = Cạnh x ; Cạnh = Cao x 2 3
Tam giác vuông cân 1 Diện tích: S 2 a . 2
Cạnh huyền: BC AB 2 a 2
Cạnh huyền = Cạnh góc vuông x 2 ;
Cạnh góc vuông = Cạnh huyền / 2 Trang 8
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên 10
Phương trình đường thẳng
Nếu đường thẳng có một VTPT là n ;
a b thì nó có một VTCP là u ; b a .
Nếu đường thẳng có hệ số góc là k thì nó có một VTCP là u 1; k . b
Nếu đường thẳng có một VTCP là u ;
a b thì nó có hệ số góc là k . a VTCP u a;b
x x at
Đường thẳng :
có phương trình tham số 0 : . qua M x ; y
y y bt 0 0 0 0 VTCP u a;b x x y y Đường thẳng : 0 0
có phương trình chính tắc :
a, b 0 . qua M x ; y a b 0 0 0 VTPT n A; B
Đường thẳng :
có phương trình tổng quát : A x x By y 0 . 0 0 qua M x ; y 0 0 0
Đường thẳng qua M x ; y và có hệ số góc k có phương trình đại số : y y k x x . 0 0 0 0 0 x y
Đường thẳng qua M a; 0 , N 0; b với a, b 0 có phương trình đoạn chắn : 1. a b
Khoảng cách từ một điểm đến một đường thẳng
ax by c
Cho điểm M x ; y và đường thẳng : ax by c 0 . Khi đó d M , . 0 0 0 0 0 0 2 a 2 b
Vị trí tương đối của hai đường thẳng
Cho : a x b y c 0 và : a x b y c 0 . 1 1 1 1 2 2 2 2 a b
a x b y c
a) Nếu 1 1 thì cắt hoặc nếu hệ 1 1 1
có nghiệm duy nhất thì cắt . a b 1 2
a x b y c 1 2 2 2 2 2 2 a b c
a x b y c
b) Nếu 1 1 1 thì hoặc nếu hệ 1 1 1
vô nghiệm thì . a b c 1 2
a x b y c 1 2 2 2 2 2 2 2 a b c
a x b y c
c) Nếu 1 1 1 thì hoặc nếu hệ 1 1 1
vô số nghiệm thì . a b c 1 2
a x b y c 1 2 2 2 2 2 2 2
Góc giữa hai đường thẳng
Cho hai đường thẳng: : a x b y c 0 có VTPT n a ;b và 1 1 1 1 1 1 1
: a x b y c 0 có VTPT n a ; b . 2 2 2 2 2 2 2
Góc (với 0 90 ) giữa 2 đường thẳng và được tính bởi: 1 2 Trang 9
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên n .n 1 2 a a b b
cos cos , 1 2 1 2 . 1 2 2 n . n a 2 2 b . a 2 b 1 2 1 1 2 2 Nhận xét:
a) Ta có n n a .a b .b 0 . 1 2 1 2 1 2 1 2
b) Cho : y k x m và : y k x m . Khi đó k .k 1 . 1 1 1 2 2 2 1 2 1 2
Vị trí tương đối của hai điểm đối với một đường thẳng
Cho đường thẳng : ax by c 0 và hai điểm M x ; y , N x ; y
không thuộc . Khi đó: M M N N
Hai điểm M, N nằm cùng phía đối với
Hai điểm M, N nằm khác phía đối với
ax by cax by c 0 .
ax by c ax by c . M M N N 0 M M N N
Phương trình các đường phân giác của các góc tạo bởi hai đường thẳng
Cho hai đường thẳng : a x b y c 0 và : a x b y c 0 cắt nhau. 1 1 1 1 2 2 2 2
Phương trình các đường phân giác của các góc tạo bởi hai đường thẳng và là: 1 2
a x b y c
a x b y c 1 1 1 2 2 2 . 2 a 2 2 b a 2 b 1 1 2 2 11
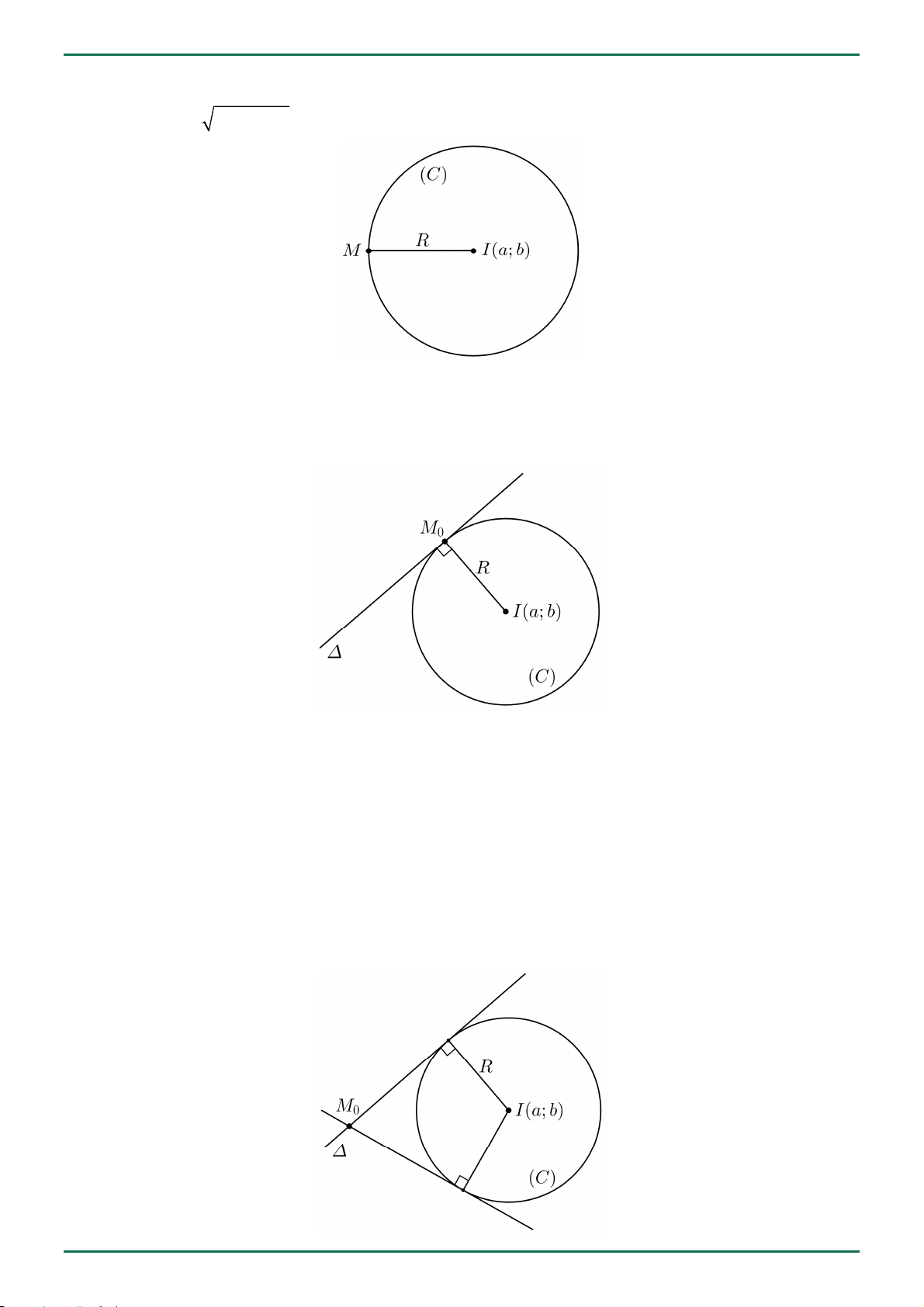
Phương trình đường tròn 2 2
Phương trình đường tròn C có tâm I a; b và bán kính R là: 2 x a y b R . Trang 10
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên Phương trình 2 x 2
y 2ax 2by c 0 với 2 a 2
b c 0 là phương trình đường tròn tâm I a; b và bán kính 2 2 R a b c .
Tiếp tuyến tại điểm
Cho đường tròn C có tâm I a; b và bán kính R . Phương trình tiếp tuyến của C tại điểm
M x ; y C là : a x x x b y y y 0 . 0
0 0 0 0 0 0
Tiếp tuyến qua điểm
Tiếp tuyến của C đi qua M x ; y C . 0 0 0
B1: Viết phương trình đường thẳng đi qua điểm M x ; y có dạng: 0 0 0
y k x – x y kx – y – kx y 0 * 0 0 0 0
B2: Sử dụng điều kiện tiếp xúc d I, R tìm k .
B3: Thay k vào * , ta được phương trình tiếp tuyến cần tìm (thường có 2 phương trình).
Chú ý: Nếu chỉ tìm được 1 nghiệm k thì tiếp tuyến còn lại có phương trình là: x x 0 . M Trang 11
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên 12
Phương trình đường elip
Cho F , F cố định với F F 2c với c 0 . Điểm M E MF MF 2a với a c . 1 2 1 2 1 2
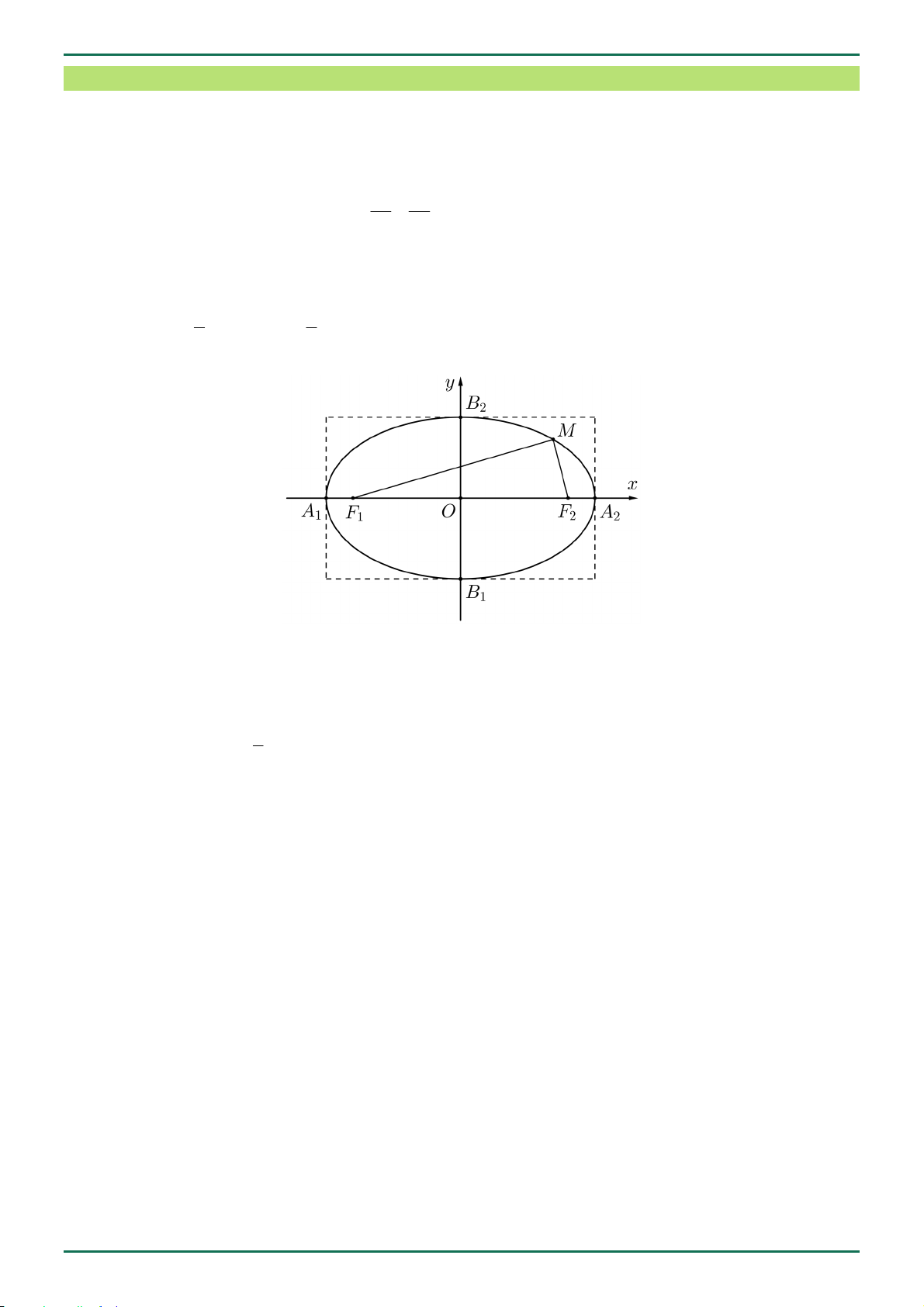
F , F : các tiêu điểm, F F 2c : tiêu cự. 1 2 1 2 2 2 x y
Phương trình chính tắc của elip E : 1 2 2 2
a b 0, b a c . 2 2 a b
Toạ độ các tiêu điểm: F c; 0 , F c; 0 . 1 2
Với M x; y E , MF , MF được gọi là các bán kính qua tiêu của điểm M. 1 2 c c
Ta có MF a x, MF a x . 1 2 a a
Hình dạng của elip
E nhận các trục toạ độ làm các trục đối xứng và gốc toạ độ làm tâm đối xứng.
Toạ độ các đỉnh: A a; 0 , A a; 0 , B 0; b , B 0; b . 1 2 1 2
Độ dài các trục: Trục lớn A A 2a , trục nhỏ B B 2b . 1 2 1 2 c
Tâm sai của E : e 0 e 1 . a
Hình chữ nhật cơ sở: Tạo bởi các đường thẳng x a, y b (ngoại tiếp elip).
Diện tích hình elip: S ab . Trang 12
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên LỚP 11 1 Lượng giác
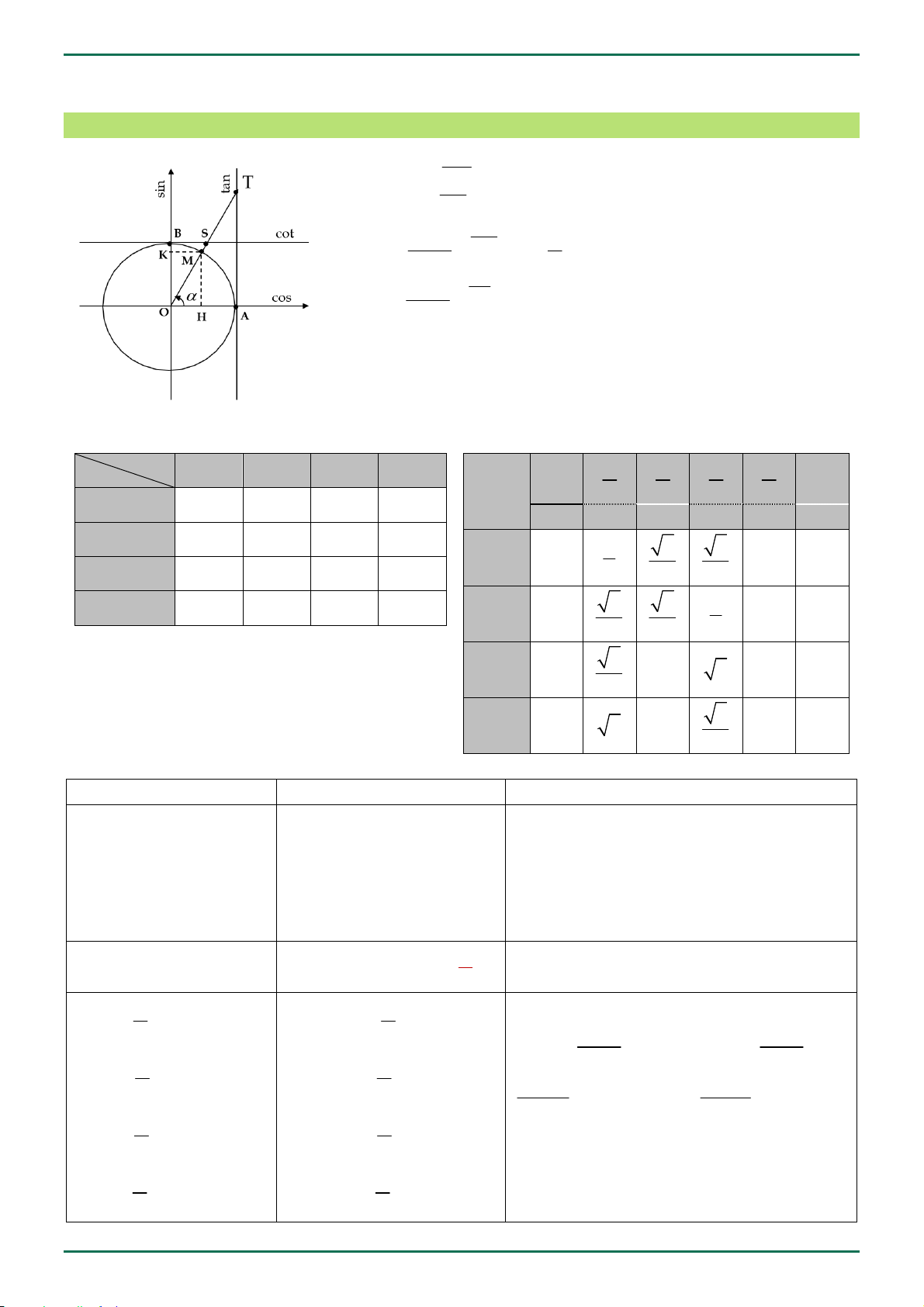
cos x OH , , ta có:
sin y OK 1 cos 1 1 sin 1 sin tan
AT
k sin k2 sin cos 2 cos
cos k2 cos cot
BS k sin
tan k tan
cot k cot
Dấu của các giá trị lượng giác
Giá trị lượng giác của các góc đặc biệt I II III IV 0 sin 6 4 3 2 + + – – 00 300 450 600 900 1800 cos + – – + 1 3 sin 0 2 1 0 tan + – + – 2 2 2 cot + – + – 3 2 1 cos 1 0 –1 2 2 2 3 tan 0 1 3 0 3 3 cot 3 1 0 3
Công thức lượng giác Hai góc đối nhau Hai góc bù nhau
Hai góc hơn kém sin
sin
sin sin
sin sin cos cos
cos cos
cos cos tan
tan
tan tan
tan tan cot
cot
cot cot
cot cot Hai góc phụ nhau Hai góc hơn kém
Công thức lượng giác cơ bản 2 2 2 sin
cos 1 tan.cot 1 sin
cos sin cos 2 2 sin cos tan cot cos sin cos
sin cos sin 1 1 2 2 1 2 tan 1 2 cot 2 cos 2 sin tan
cot tan cot 2 2 cot
tan cot tan 2 2 Trang 13
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên Công thức cộng
Công thức nhân đôi
sin sin cos cos sin sin
2 2sin cos 2 2
sin sin cos cos sin cos
2 cos sin 2 cos 2 1 2sin
cos cos cos sin sin 2 cos 2 2cos 1
cos cos cos sin sin 2ta n tan 2 = tan tan 1 2 tan tan
1 tan tan 2 cot 1 cot 2 tan tan 2 cot tan
1 tan tan
Công thức hạ bậc Công thức nhân ba 3 2 1 cos 2 cos cos
3 4cos 3cos 2 3 sin 3 3sin 4sin 2 1 cos 2 sin 3
3 tan tan 2 tan 3 1 2 3 tan 2 1 cos 2 tan 1 cos 2
Công thức biến đổi tích thành tổng
Công thức biến đổi tổng thành tích 1
cos cos cos cos
cos cos 2 cos cos 2 2 2 1
sin sin cos cos
cos cos 2 sin sin 2 2 2 1
sin cos
sin sin
sin sin 2 sin cos 2 2 2
sin sin 2 cos sin 2 2 x
Công thức tính theo tan
Một số công thức khác 2 x
sin( )
Đặt t tan . Khi đó:
tan tan 2 cos.cos 2 1 t 2t
sin( ) cos x sin x
tan tan 2 1 t 2 1 t cos.cos 2t 2 1 t tan x cot x
sin( ) 2
cot cot 1 t 2t sin.sin sin( )
cot cot sin.sin 1 tan tan 4 1 tan 1 tan tan 4 1 tan Trang 14
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên
sin cos 2.sin 2.cos 4 4
sin cos 2 sin
2 cos 4 4
Hàm số lượng giác
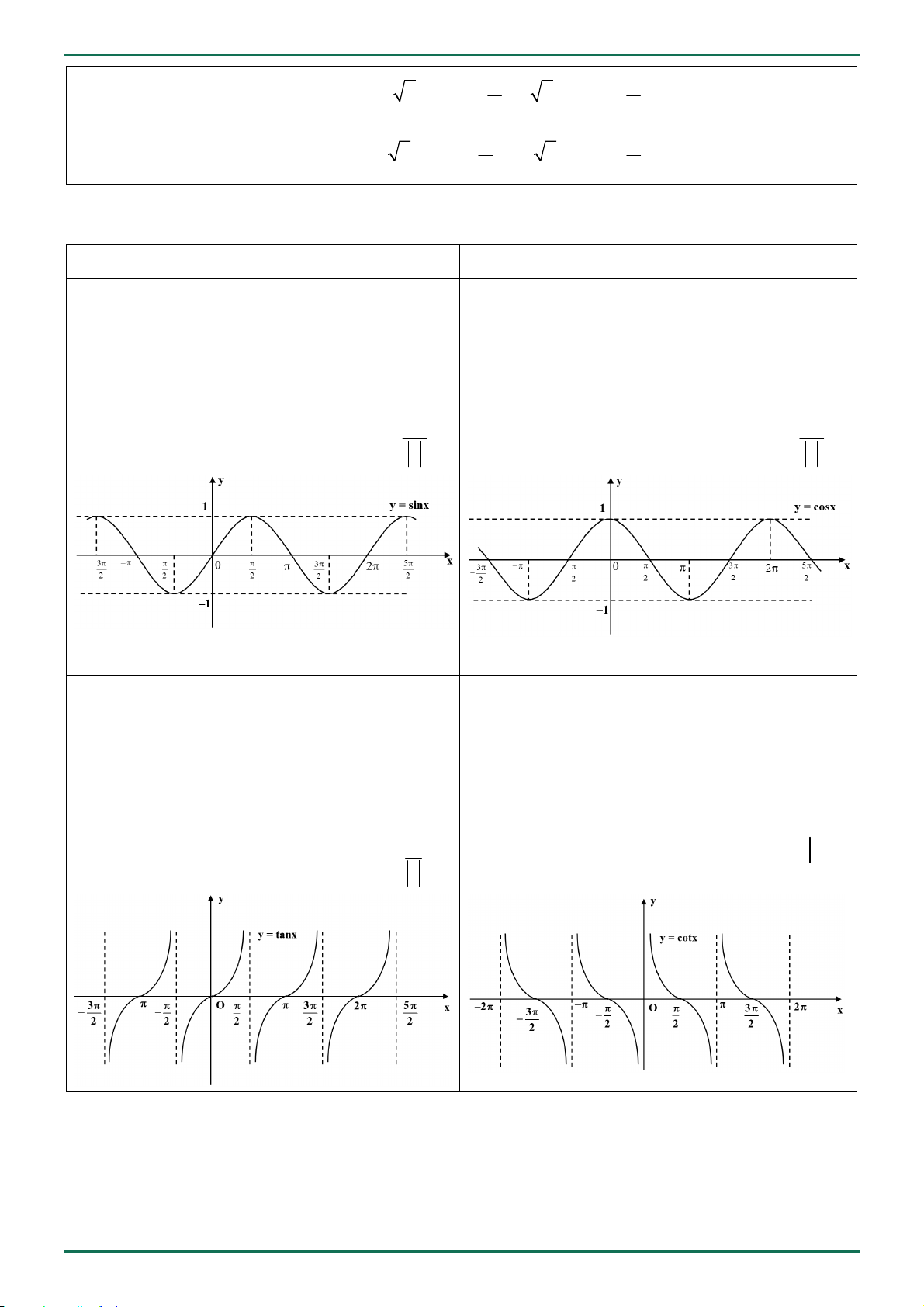
Hàm số y sin x
Hàm số y cos x
- Tập xác định D
- Tập xác định D
- Tập giá trị T 1,1
- Tập giá trị T 1,1 - Là hàm số lẻ - Là hàm số chẵn
- Chu kỳ T 2
- Chu kỳ T 2 0 0 2 2
- Hàm số y sin ax b có chu kỳ T
- Hàm số y cos ax b có chu kỳ T 0 a 0 a
Hàm số y tan x
Hàm số y cot x
- Tập xác định D
\ k : k
- Tập xác định D \ k : k 2
- Tập giá trị T
- Tập giá trị T - Là hàm số lẻ - Là hàm số lẻ
- Chu kỳ T 0
- Chu kỳ T 0
- Hàm số y cot ax b có chu kỳ T 0 - Hàm số y a
tan ax b có chu kỳ T 0 a Chú ý
Cho hàm số y f x có chu kỳ T và hàm số y f x có chu kỳ T . Khi đó hàm số 2 1 1 2
y f (x) f (x) có chu kỳ T là bội chung nhỏ nhất của T và T . 1 2 0 1 2 Trang 15
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên
Phương trình sin x m với m 1 ;1
x k2
sin x m sin x sin k .
x k2
x arcsin m k2
sin x m k .
x arcsin m k2
Phương trình cos x m với m 1 ;1
x k2
cos x m cos x cos k . x k2
x arccos m k2
cos x m k .
x arccos m k2
Phương trình tan x m
tan x tan x k k .
tan x m x arctan m k k .
Phương trình cot x m
cot x cot x k k .
cot x m x arccot m k k . 1
Chú ý: arccot m arctan . m
Một số trường hợp đặc biệt
Với k , ta có:
sin u 0 u k
cosu 0 u k 2
sin u 1 u k2
cosu 1 u k2 2 sin u 1 u k2
cos u 1 u k2 2
tan u 0 sin u 0 u k
cot u 0 cos u 0 u k 2
tan u 1 sin u cos u u k
cot u 1 sin u cosu u k 4 4 tan u 1
sin u cos u u k cot u 1
sin u cos u u k 4 4
Phương trình bậc hai theo một hàm số lượng giác Dạng 2
at bt c 0 ( a 0 ) với t là một hàm số lượng giác nào đó. Chẳng hạn như t là 1
sin x, cos x, tan x, cot x, sin x cos x , sin x , , … sin x
Phương trình bậc nhất đối với sinx và cosx
Dạng a sin x b cos x c với 2 2 a b 0 . Trang 16
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên Điều kiện có nghiệm: 2 2 2
a b c . Cách giải:
Chia hai vế của phương trình cho 2 2
a b , phương trình trở thành: a b c sin x cos x . 2 2 2 2 2 2 a b a b a b a b c Đặt: cos và
sin . Ta được: sin x cos cos x sin . 2 2 a b 2 2 a b 2 2 a b c
Áp dụng công thức cộng, ta được phương trình sin x . 2 2 a b
Bất đẳng thức B.C.S 2 2 2 2 2 2 y . a sin x .
b cos x a b . sin x cos x a b . sin x cos x a Khi đó: 2 2
min y a b và 2 2
max y a b khi hay tan x . a b b
Phương trình thuần nhất bậc hai theo sinx và cosx Dạng 2 2
a sin x b sin x cos x c cos x d (*) với 2 2 2
a b c 0 . Cách giải 1:
TH1: cos x 0 x
k với k . Suy ra 2
sin x 1. Thay vào (*) xem có nghiệm không. 2
TH2: cos x 0 x
k với k . Chia hai vế của phương trình cho 2
cos x để đưa về phương 2 trình theo tan x . Cách giải 2:
Áp dụng công thức hạ bậc và công thức nhân đôi, phương trình thuần nhất bậc hai được chuyển
thành phương trình bậc nhất theo sin 2x và cos 2 . x
Phương trình đối xứng đối với sinx và cosx
Dạng: Phương trình có chứa tích sin x cos x và tổng sin x cos x hoặc hiệu sin x cos x . Cách giải: 2 t 1
Đặt t sin x cos x (điều kiện t 2 ). Suy ra sin x cos x
và đưa phương trình về ẩn t. 2 2 1 t
Đặt t sin x cos x hoặc t cos x sin x (điều kiện t 2 ). Suy ra sin x cos x và đưa 2
phương trình về ẩn t. 2 Quy tắc đếm Quy tắc cộng
Giả sử một công việc có thể được thực hiện theo phương án A hoặc phương án B . Có n cách
thực hiện phương án A và m cách thực hiện phương án B . Khi đó công việc có thể được thực
hiện theo n m cách. Trang 17
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên Quy tắc nhân
Giả sử một công việc bao gồm hai hành động liên tiếp A và B . Hành động A có thể làm theo n
cách. Với mỗi cách thực hiện hành động A thì hành động B có thể làm theo m cách. Khi đó công
việc có thể được thực hiện theo . n m cách. Hoán vị
Cho tập hợp A có n phần tử n 1 . Khi sắp xếp n phần tử này theo một thứ tự, ta được một
hoán vị các phần tử của tập hợp A (gọi tắt là một hoán vị của A ).
Số các hoán vị của một tập hợp có n phần tử là P n! nn 1n 2...1. n Chỉnh hợp
Cho tập hợp A gồm n phần tử và số nguyên k với 1 k n . Khi lấy ra k phần tử của tập hợp
A và sắp xếp chúng theo một thứ tự, ta được một chỉnh hợp chập k của n phần tử của A (gọi
tắt là một chỉnh hợp chập k của A ).
Số các chỉnh hợp chập k của một tập hợp có n phần tử 0 k n là: k n! A
với quy ước 0! 1 và 0 A 1. n n k! n Tổ hợp
Cho tập hợp A có n phần tử và số nguyên k với 1 k n . Mỗi tập con của A có k phần tử được
gọi là một tổ hợp chập k của n phần tử của A (gọi tắt là một tổ hợp chập k của A ).
Số các tổ hợp chập k của một tập hợp có n phần tử 0 k n là: n! k A k n C với quy ước 0 C 1. n
k!n k! k! n
Hai tính chất cơ bản của số k
C : k C n k C và k1 C k C k C . n n n n n n 1 3 Nhị thức Newton n
a bn 0 n 1 n 1
C a C a b ... k nk k C a b ... n n k nk k
C b C a b . n n n n n * k 0
- Số hạng tổng quát thứ k 1 trong khai triển là k nk k T C a b . k 1 n
- Trong cùng một số hạng, số mũ của a và b có tổng bằng n .
- Trong khai triển * có n 1 số hạng.
- Số mũ của a giảm dần từ n đến 0, số mũ của b tăng dần từ 0 đến n .
- Các hệ số của các cặp số hạng cách đều số hạng đầu và cuối thì bằng nhau. 4
Phép thử và không gian mẫu
Phép thử ngẫu nhiên (gọi tắt là phép thử) là một thí nghiệm hay hành động mà: Trang 18
Tổng hợp lý thuyết THPT môn Toán ThS. Trần Thanh Yên
- Kết quả của nó không đoán trước được.
- Có thể xác định được tập hợp tất cả các kết quả có thể xảy ra của phép thử đó.
Phép thử thường được kí hiệu bởi chữ T .
Tập hợp tất cả các kết quả có thể xảy ra của phép thử được gọi là không gian mẫu của phép thử
và được kí hiệu là . Biến cố
Biến cố là một tập con của không gian mẫu.
Mỗi phần tử của biến cố A được gọi là một kết quả thuận lợi cho A .
Trong một phép thử, nếu kết quả của phép thử là một kết quả thuận lợi cho A thì ta nói biến cố A xảy ra.
Biến cố A \A được gọi là biến cố đối của biến cố A .
Biến cố là biến cố chắc chắn, biến cố là biến cố không thể xảy ra. n A
Xác suất của biến cố: P A . n
Nhận xét: 0 P A 1; P 1 và P 0 ; P A 1 P A .
Quy tắc cộng xác suất Biến cố hợp
Cho hai biến cố A và B . Biến cố A B được gọi là hợp của hai biến cố A và B . Biến cố A B
có nghĩa là “ A hoặc B xảy ra”.
Biến cố xung khắc
Hai biến cố A và B được gọi là xung khắc nếu A B .
Đối với hai biến cố xung khắc, nếu biến cố này xảy ra thì biến cố kia không xảy ra. Định lý
Nếu A và B là hai biến cố xung khắc thì P A B P A P B .
Mở rộng, nếu A và B là hai biến cố bất kì thì P A B P A P B ( P . A ) B .
Quy tắc nhân xác suất Biến cố giao
Cho hai biến cố A và B . Biến cố “Cả A và B cùng xảy ra”, kí hiệu là .
A B , được gọi là giao của
hai biến cố A và B .
Biến cố độc lập
Hai biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không
ảnh hưởng tới xác suất xảy ra của biến cố kia. Định lý
Nếu A và B là hai biến cố độc lập thì P AB P A P B . Trang 19