Kế hoạch bài dạy chuyên đề học tập Toán 12 Chân Trời Sáng Tạo

NGUYỄN THÀNH ANH – HUỲNH NGỌC THANH (đồng Chủ biên)
THỌ CHẾ QUỐC ÂN – TRỊNH TUẤN HIỀN – NGUYỄN VƯƠNG HIỂN
VÕ QUỐC HÙNG – THÁI DOÃN HÙNG – TRẦN ĐỨC NGỌC
NGUYỄN TUẤN PHÚ – NGUYỄN THỊ NHƯ QUỲNH
DƯƠNG QUANG THÁI – NGUYỄN MINH TRÍ Kế hoạch bài dạy Chuyên đề học tập TOÁN 12 Lớp
(Hỗ trợ giáo viên thiết kế kế hoạch bài dạy
theo sách giáo khoa Chuyên đề học tập Toán 12 –
Bộ sách Chân trời sáng tạo)
NHÀ XUẤT BẢN GIÁO DỤC VIỆT NAM 1 2 LỜI NÓI ĐẦU
Quý thầy, cô giáo thân mến!
Giáo dục Việt Nam đang chuyển mình từ dạy học định hướng nội dung sang dạy
học định hướng phát triển năng lực học sinh. Từ đó, mục tiêu, nội dung, hình thức,
phương pháp giảng dạy cũng như hoạt động kiểm tra, đánh giá kết quả học tập của học
sinh phải thay đổi. Những thay đổi trên được hướng dẫn khá cụ thể trong Phụ lục IV,
Công văn số 5512/BGDĐT-GDTrH ngày 18 tháng 12 năm 2020 của Bộ Giáo dục và
Đào tạo: “Khung kế hoạch bài dạy” dành cho giáo viên THCS và THPT từ năm học
2021-2022. Trong đó, mỗi hoạt động (Khởi động, Khám phá, Luyện tập, Vận dụng)
bao gồm bốn yếu tố: Mục tiêu, Nội dung, Sản phẩm, Tổ chức thực hiện. Mỗi yếu tố
trong bốn hoạt động đều được hướng dẫn tương đối cụ thể và khác nhau để giáo viên
thuận tiện trong việc soạn bài.
Xuất phát từ nhu cầu thực tiễn, Nhà xuất bản Giáo dục Việt Nam phối hợp với đội
ngũ các chuyên gia, những thầy cô có nhiều kinh nghiệm, năng lực giảng dạy môn
Toán theo định hướng phát triển năng lực học sinh để thực hiện bộ Kế hoạch bài dạy
Chuyên đề học tập Toán lớp 12 (Hỗ trợ giáo viên thiết kế kế hoạch bài dạy theo sách
giáo khoa Chuyên đề học tập Toán 12 – Bộ sách Chân trời sáng tạo) như một gợi ý
nhằm chia sẻ, hỗ trợ thầy cô đang giảng dạy môn Toán 12 cách thức soạn một bài dạy
theo định hướng phát triển năng lực học sinh.
Trong quá trình biên soạn sẽ không thể tránh khỏi sơ suất, rất mong được lắng
nghe các góp ý từ quý thầy, cô để cuốn sách ngày càng hoàn thiện hơn.
Trân trọng cảm ơn quý thầy, cô! CÁC TÁC GIẢ 3 Mục lục
Chuyên đề 1. ỨNG DỤNG TOÁN HỌC GIẢI CÁC BÀI TOÁN TỐI ƯU .................. 5
Bài 1. Bài toán quy hoạch tuyến tính .................................................................................. 5
Bài 2. Vận dụng đạo hàm giải bài toán tối ưu .................................................................. 12
Bài tập cuối chuyên đề 1 .................................................................................................. 19
Chuyên đề 2. ỨNG DỤNG TOÁN HỌC TRONG MỘT SỐ VẤN ĐỀ
LIÊN QUAN ĐẾ TÀI CHÍNH ................................................................ 25
Bài 1. Tiền tệ. Lãi suất ....................................................................................................... 25
Bài 2. Tín dụng. Vay nợ ..................................................................................................... 35
Bài 3. Đầu tư tài chính. Lập kế hoạch tài chính cá nhân ................................................... 41
Bài tập cuối chuyên đề 2 .................................................................................................. 48
Chuyên đề 3. BIẾN NGẪU NHIÊN RỜI RẠC. CÁC SỐ ĐẶC TRƯNG
CỦA BIẾN NGẪU NHIÊN RỜI RẠC .................................................... 54
Bài 1. Biến ngẫu nhiên rời rạc ........................................................................................... 54
Bài 2. Phân bố Bernoulli và phân bố nhị thức ................................................................... 64
Bài tập cuối chuyên đề 3 .................................................................................................. 71 4 Chuyên đề
ỨNG DỤNG TOÁN HỌC 1
GIẢI CÁC BÀI TOÁN TỐI ƯU BÀI TOÁN Bài 1.
QUY HOẠCH TUYẾN TÍNH
Thời gian thực hiện: 3 tiết I. MỤC TIÊU 1. Về kiến thức
– Vận dụng kiến thức về hệ bất phương trình bậc nhất để giải quyết một số bài toán quy hoạch tuyến tính.
– Giải được bài toán quy hoạch tuyến tính (hai biến), vận dụng để giải các bài toán xuất
hiện trong thực tiễn, bao gồm những bài toán tối ưu trong kinh tế. 2. Về năng lực 2.1. Năng lực chung:
– Tự chủ, tự học: Học sinh (HS) tự chuẩn bị bài ở nhà, trả lời được những câu hỏi ở hoạt động Khám phá (HĐKP).
– Giao tiếp, hợp tác: HS hoạt động nhóm, trình bày, thảo luận thông qua việc giải quyết
vấn đề một số bài toán quy hoạch tuyến tính.
2.2. Năng lực Toán học:
– Giải quyết vấn đề toán học: Giải bài toán thực tế về việc hiểu dữ liệu bài toán và HS
thiết lập được biểu thức liên quan đến bài toán tối ưu.
– Tư duy và lập luận toán học: Sử dụng các bước làm và vẽ miền nghiệm tương ứng để
giải các hoạt động Thực hành (HĐTH) và hoạt động Vận dụng (HĐVD). 3. Về phẩm chất
– Chăm chỉ: Có chuẩn bị bài trước ở nhà, chuẩn bị các bước làm của bài toán quy hoạch tuyến tính.
– Trung thực: HS thừa nhận và học tập các kết quả đúng của các bạn thông qua các hoạt
động giải các bài tập Luyện tập, Thực hành, Vận dụng.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với giáo viên: Sách giáo khoa (SGK), sách giáo viên (SGV), kế hoạch bài dạy
(KHBD), ti vi, bài trình chiếu.
2. Đối với học sinh: SGK, máy tính cầm tay, đồ dùng học tập. 5
III. TIẾN TRÌNH DẠY HỌC A. KHỞI ĐỘNG
Hoạt động: Khởi động
a) Mục tiêu: Gợi mở kết nối HS vào bài toán kinh tế thông qua bài toán thực tế về câu
chuyện thương lái thu mua hàng hoá.
b) Nội dung: GV yêu cầu HS đọc yêu cầu ở hoạt động Khởi động (HĐKĐ) và trả lời
câu hỏi: Làm sao biết được thương nhân đó nên mua khối lượng bao nhiêu mỗi loại để thu
được lợi nhuận cao nhất khi bán hết hàng đã thu mua?
c) Sản phẩm: HS làm việc cá nhân hoặc theo nhóm, tìm hiểu bài toán, thể hiện được
suy nghĩ theo cách hiểu và diễn đạt theo quan điểm của mình (không nhất thiết đưa ra đáp án đầy đủ).
d) Tổ chức thực hiện:
 GV chuyển giao nhiệm vụ học tập: GV tổ chức cho mỗi HS quan sát kênh hình trong
SGK và đọc yêu cầu ở HĐKĐ.
 HS thực hiện nhiệm vụ học tập: HS thảo luận, suy nghĩ tìm câu trả lời.
 Báo cáo kết quả hoạt động và thảo luận: HS xung phong phát biểu quan điểm cá nhân.
 Kết luận, nhận định:
– GV nhận xét đánh giá kết quả làm việc của HS (chưa kết luận tính đúng, sai).
– GV dẫn dắt vào HĐKP.
B. KHÁM PHÁ – THỰC HÀNH – VẬN DỤNG
1. Bài toán quy hoạch tuyến tính
Hoạt động 1.1: Khám phá 1
a) Mục tiêu: HS nhớ lại các bước tìm giá trị lớn nhất, nhỏ nhất của một biểu thức dựa
vào miền nghiệm của hệ bất phương trình bậc nhất một ẩn.
b) Nội dung: GV yêu cầu HS làm việc theo nhóm, thảo luận và thực hiện HĐKP 1.
c) Sản phẩm: HS quan sát đồ thị trong đề bài và tuần tự trả lời các câu hỏi:
a) Qua O(0; 0)  F  0 ; Qua B(2; 3)  F  8 .
b) Khi giá trị của F tăng (hoặc giảm) thì tung độ giao điểm của d với trục Oy tăng (hoặc
giảm) theo; Khi đó, phương của đường thẳng d không thay đổi.
c) Với điều kiện 0  F  8 thì đường thẳng d và miền nghiệm  có điểm chung.
d) Ta có: max F  8 tại điểm B (2; 3) và min F  0 tại điểm O (0; 0).  
d) Tổ chức thực hiện:
 GV chuyển giao nhiệm vụ học tập: Nhìn vào hình ảnh đồ thị hàm số và các miền
nghiệm tương ứng, GV yêu cầu HS quan sát và thực hiện HĐKP 1. Nêu nhận xét đúng, sai và giải thích.
 HS thực hiện nhiệm vụ học tập: HS nghiên cứu nội dung hoạt động và quan sát hình
liên quan đến miền nghiệm của hệ bất phương trình bậc nhất ở Hình 1 trong SGK và trả lời
được câu hỏi ở HĐKP 1. 6
 Báo cáo kết quả hoạt động và thảo luận:
– GV gọi hai HS bất kì lên bảng trình bày kết quả của HĐKP 1.
– HS còn lại quan sát, đối chiếu và nhận xét, bổ sung.
 Kết luận, nhận định:
– GV đánh giá, nhận xét sản phẩm của HS với đáp án đúng.
– GV gọi một HS đọc khái niệm bài toán quy hoạch tuyến tính, quy trình tìm giá trị lớn
nhất (nhỏ nhất) của hàm mục tiêu F và phần Chú ý.
– GV hướng dẫn HS tìm hiểu Ví dụ 1, qua đó HS hiểu rõ hơn cách tìm max, min theo quy
trình từng bước tính của bài toán quy hoạch tuyến tính.
Hoạt động 1.2: Khám phá 2
a) Mục tiêu: Giúp HS đối chiếu miền nghiệm của hệ bất phương trình bậc nhất hai ẩn
với đồ thị hàm số ở Hình 3 trong SGK.
b) Nội dung: GV yêu cầu HS làm việc nhóm, đọc đề bài, thảo luận, trình bày lời giải HĐKP 2.
c) Sản phẩm: HS quan sát đồ thị ở Hình 3 trong SGK và tuần tự trả lời các câu hỏi: a) F  5 . A
b) Khi giá trị của F tăng (hoặc giảm) thì tung độ giao điểm của d với trục Oy tăng
(hoặc giảm); Khi đó, phương của đường thẳng d không thay đổi.
c) Nếu F  F thì d và  không có điểm chung; Suy ra min F  5 . A 
d) d và  có điểm chung F  FA = 5; Hàm mục tiêu F  2x  y không đạt giá trị lớn nhất trên  .
d) Tổ chức thực hiện:
 GV chuyển giao nhiệm vụ học tập: Nhìn vào hình ảnh đồ thị hàm số và các miền
nghiệm tương ứng, GV tổ chức cho HS làm việc cá nhận hoặc nhóm, trình bày lời giải của mình ở HĐKP 2.
 HS thực hiện nhiệm vụ học tập: HS hoạt động nhóm, quan sát miền nghiệm của hệ
bất phương trình bậc nhất và trả lời được các câu hỏi.
 Báo cáo kết quả hoạt động và thảo luận:
– GV gọi hai HS bất kì lên bảng trình bày kết quả của HĐKP 2.
– HS còn lại quan sát, đối chiếu và nhận xét, bổ sung.
 Kết luận, nhận định:
– GV nhận xét, đánh giá câu trả lời của HS.
– GV gọi một HS đọc phần Chú ý và quy trình tìm giá trị nhỏ nhất.
– GV hướng dẫn HS tìm hiểu Ví dụ 2, qua đó HS hiểu rõ hơn quy trình tìm giá trị nhỏ
nhất của hàm mục tiêu F.
Hoạt động 1.3: Thực hành
a) Mục tiêu: Bước đầu thực hành thuần thục quy trình giải bài toán quy hoạch tuyến tính. b) Nội dung:
– GV yêu cầu HS tìm max, min của các hàm mục tiêu F ở HĐTH 1 và HĐTH 2. 7
– GV hướng dẫn HS thực hiện vẽ miền nghiệm của hệ bất phương trình bậc nhất hai ẩn
tương ứng đề bài. Tìm được toạ độ giao điểm của các đường thẳng (nếu có). Tính giá trị của
hàm mục tiêu tại các điểm biên giao nhau trên miền nghiệm. So sánh kết quả và trả lời câu hỏi min, max.
c) Sản phẩm: HS hoạt động nhóm, thảo luận và trả lời được: Đối với HĐTH 1:
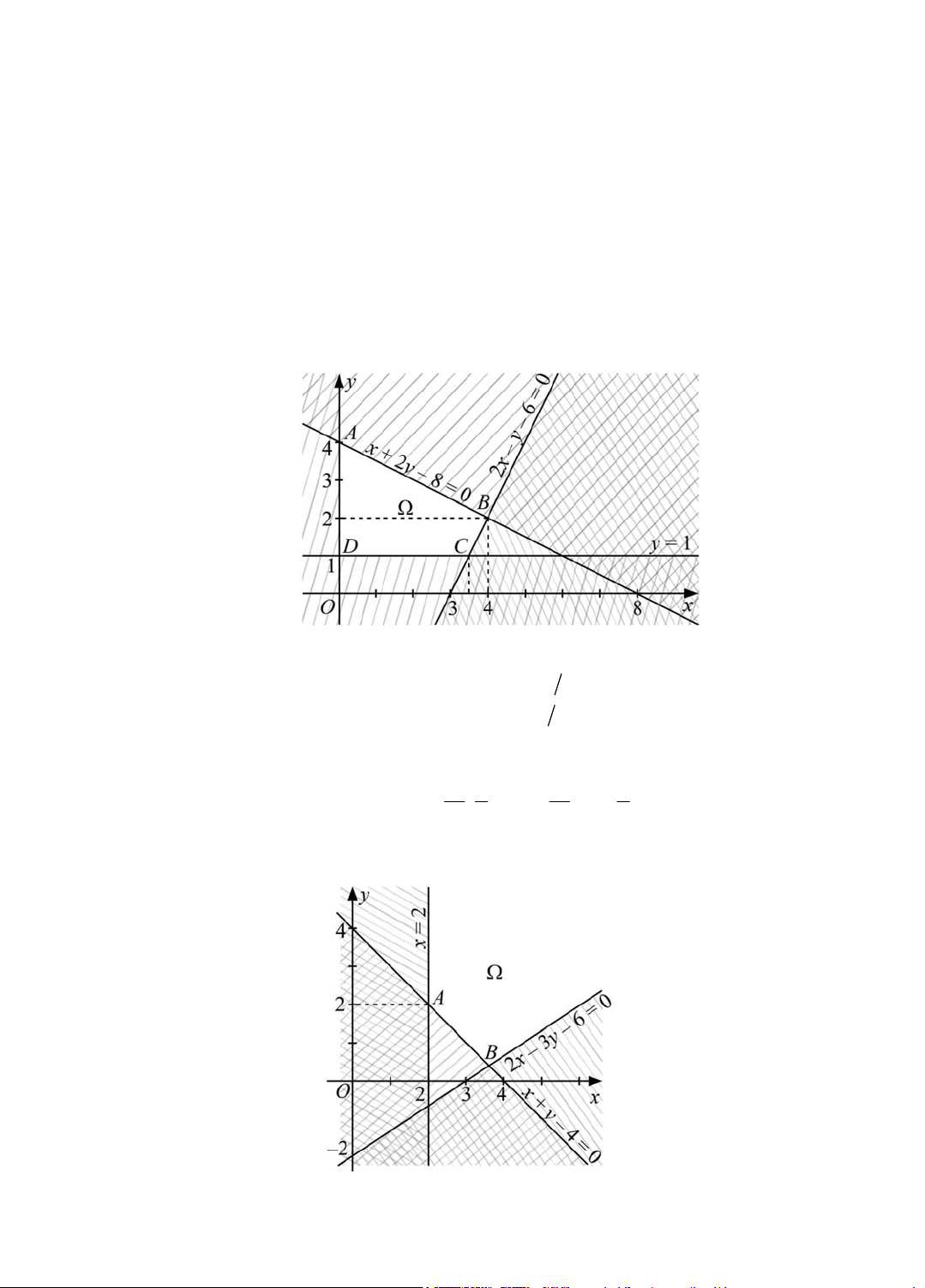
– Tập phương án Ω là miền tứ giác ABCD với: A(0; 4), B(4; 2), C(3,5; 1), D(0; 1).
– Giá trị của biểu thức F tại các đỉnh của Ω: F(0; 4) = 12; F(4; 2) = 22; F(3,5; 1) = 17; F(0; 1) = 3.
– Từ đó, max F = F(4; 2) = 22; min F = F(0; 1) = 3.   Đối vói HĐTH 2:
2x  3y  6 x 18 5
– Toạ độ B là nghiệm của hệ    x  y  4 y  2 5
– Đặt d : 25x 10 y  F  0 . 18 2  18 2
– Ta có F 2; 2  25.2 10.2  70 ; F ;  25 10  94   .  5 5  5 5
– Từ đó min F khi d qua điểm A(2; 2)  F  70 .  8
d) Tổ chức thực hiện:
 GV chuyển giao nhiệm vụ học tập: Chia lớp thành bốn nhóm tương ứng bốn tổ. Các
nhóm tiến hành thảo luận, trình bày lời giải vào bảng phụ.
 HS thực hiện nhiệm vụ học tập:
– Các nhóm trao đổi thống nhất ý kiến viết lời giải vào bảng phụ.
– GV quan sát, theo dõi và hỗ trợ HS khi cần thiết.
 Báo cáo kết quả hoạt động và thảo luận:
– Các nhóm dán bảng phụ lên bảng, đại diện từng nhóm trình bày.
– Các HS chú ý theo dõi đặt ra những câu hỏi để làm sáng tỏ vấn đề.
 Kết luận, nhận định:
– GV nhận xét, đánh giá sản phẩm HS với kết quả đúng.
– Tuyên dương các nhóm hoàn thành tốt nhiệm vụ được giao, giải quyết được bài toán quy hoạch tuyến tính.
Hoạt động 1.4: Vận dụng
a) Mục tiêu: Bước đầu thực hành thuần thục các bước giải bài toán quy hoạch tuyến
tính. Bên cạnh đó, HS nêu được điều kiện ràng buộc của hàm mục tiêu dựa vào miền nghiệm đồ thị có sẵn.
b) Nội dung: GV yêu cầu HS đọc đề bài và nêu các bước thực hiện HĐVD.
c) Sản phẩm: HS trả lời được: Các bước thực hiện HĐVD là giải bài toán quy hoạch
tuyến tính từ đồ thị hàm số với các miền nghiệm trên hình vẽ.
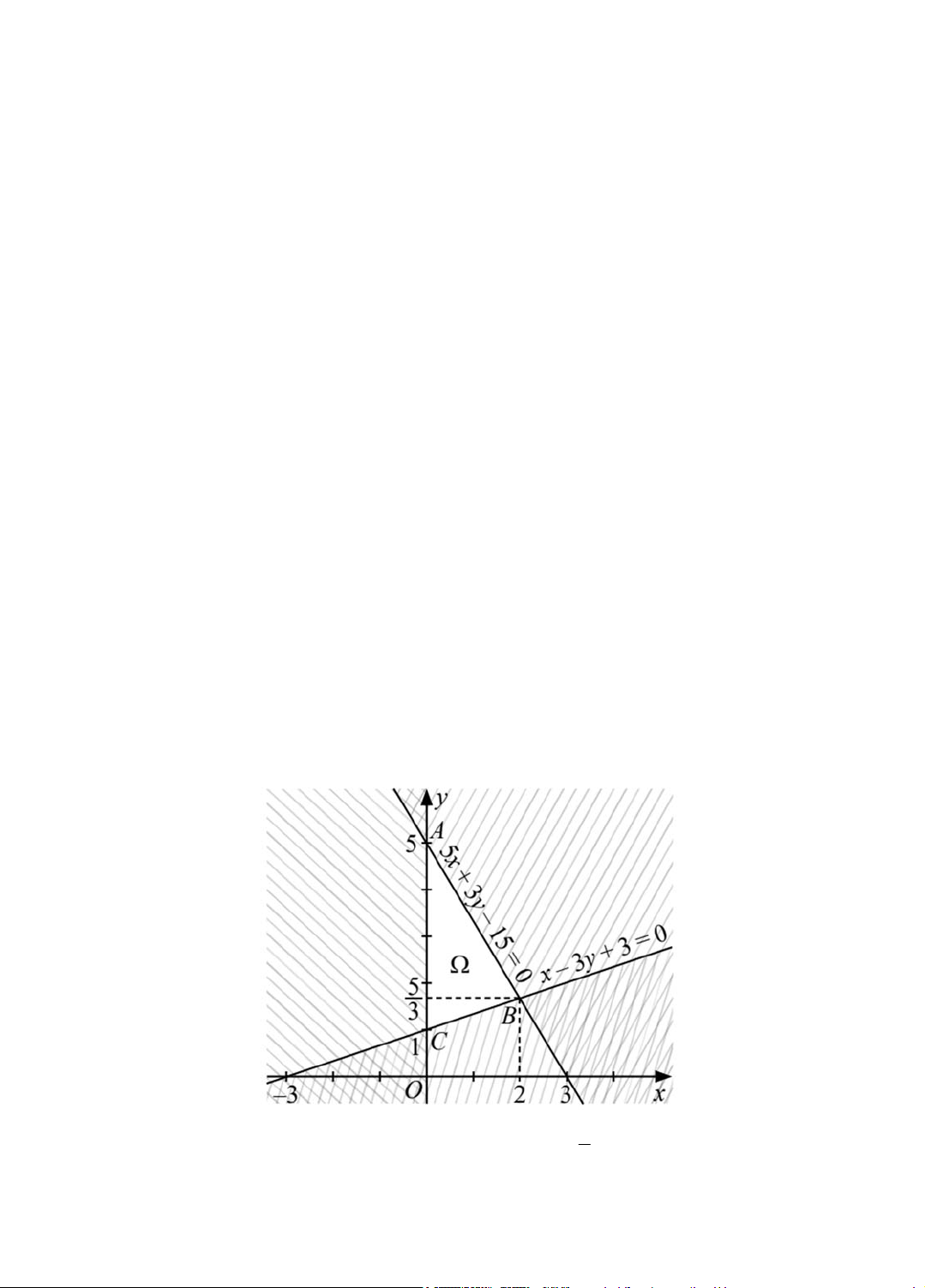
a) F 0; 5  3.0  3.5 15 ; F(4; 1)  3.4  3. 1 15 ;
F(2; 1)  3.2  3.1  9 ; F(0; 2)  3.0  3.2  6 .
Do đó min F  6 tại đỉnh D(0; 2) và max F  15 tại đỉnh A(0; 5), B(4; 1).  
b) Hàm mục tiêu F đạt giá trị lớn nhất trên  tại mọi điểm thuộc đường thẳng (AB):
x + y – 5 = 0, do phương trình đường thẳng d đi qua hai điểm A(0; 5), B(4; 1) khi max F  15 . 
d) Tổ chức thực hiện:
 GV chuyển giao nhiệm vụ học tập: Chia lớp thành bốn nhóm tương ứng bốn tổ.
Các nhóm tiến hành thảo luận, trình bày lời giải vào bảng phụ.
 HS thực hiện nhiệm vụ học tập: Các nhóm trao đổi thống nhất ý kiến viết lời giải vào bảng phụ.
 Báo cáo kết quả hoạt động và thảo luận:
– Các nhóm dán bảng phụ lên bảng, đại diện từng nhóm trình bày.
– Các HS chú ý theo dõi đặt ra những câu hỏi để làm sáng tỏ vấn đề.
 Kết luận, nhận định:
– GV nhận xét, đánh giá sản phẩm của HS với kết quả đúng.
– Các nhóm nỗ lực làm bài hoàn thành tốt nhiệm vụ được giao, giải quyết được bài toán
tìm giá trị lớn nhất, nhỏ nhất của biểu thức đề bài yêu cầu. 9
2. Ứng dụng vào các bài toán thực tế
Hoạt động 2.1: Khám phá 3
a) Mục tiêu: HS biết cách thiết lập hệ bất phương trình với các điều kiện ràng buộc của bài toán.
b) Nội dung: GV yêu cầu HS đọc HĐKP 3 và trả lời câu hỏi trong đề bài.
c) Sản phẩm: HS trình bày được cách thiết lập hệ bất phương trình với các điều kiện
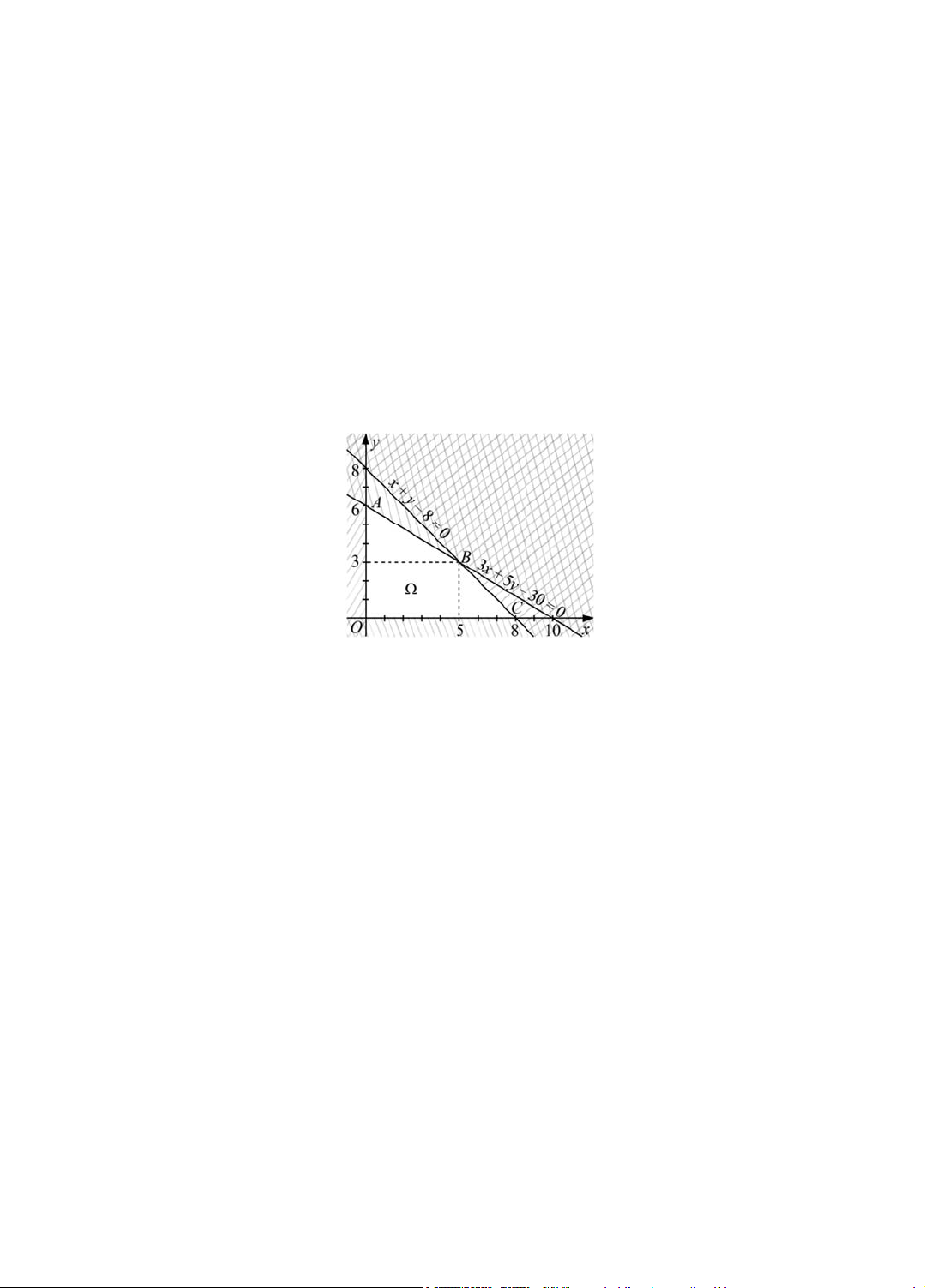
ràng buộc của bài toán. Từ đó HS thực hiện bài toán tối ưu theo yêu cầu. x  y  8 x  y  8 12  
 x  20y 120 3
 x  5y  30
a) Hệ bất phương trình:    x  0  x  0  y  0 y  0 b) x  y  8 
3x  5y  30
Bài toán quy hoạch tuyến tính: F  1,1x 1,5y  max , với ràng buộc  x  0  y  0
Ta có F 0; 0 1,1.0 1,5.0  0 ; F0; 6 1,1.0 1,5.6  9 ;
F 5; 3 1,1.5 1,5.3 10 ; F8; 0 1,1.8 1,5.0  8,8 .
Do đó max F = 10 khi d đi qua điểm B 5; 3 . 
Vậy thương nhân cần mua 5 tấn loại A và 3 tấn loại B thì thu được lợi nhuận cao nhất.
d) Tổ chức thực hiện:
 GV chuyển giao nhiệm vụ học tập: GV yêu cầu HS đọc kĩ đề bài và tìm mối liên hệ
giữa các đại lượng đã biết và hai ẩn số x, y . Sau đó HS thiết lập hệ bất phương trình tương
ứng. Cuối cùng HS giải bài toán quy hoạch tuyến tính trên.
 HS thực hiện nhiệm vụ học tập: HS thực hiện từng câu hỏi của GV.
 Báo cáo kết quả hoạt động và thảo luận: HS trình bày quan điểm cá nhân, giải thích từng câu trả lời.
 Kết luận, nhận định:
– HS giải quyết tốt các vấn đề, qua đó hình dung được cách thiết lập hệ bất phương trình
từ những dữ kiện bài toán thực tế. 10
– GV gọi một HS đọc phần kiến thức về quy trình ba bước để giải bài toán thực tế.
– GV hướng dẫn HS tìm hiểu Ví dụ 3, 4, qua đó HS hiểu rõ hơn cách giải một bài toán
thực tế có mô hình bài toán quy hoạch tuyến tính.
Hoạt động 2.2: Thực hành
a) Mục tiêu: Phát triển kĩ năng giải bài toán thực tế liên quan đến quy hoạch tuyến tính. b) Nội dung:
– GV yêu cầu HS đọc yêu cầu của HĐTH 3 và trả lời câu hỏi như quy trình của HĐKP 3.
– GV yêu cầu HS đọc yêu cầu của HĐTH 4 và trả lời câu hỏi.
c) Sản phẩm: HS hoạt động nhóm, thảo luận và trả lời được: Đối với HĐTH 3: 200
Nhà máy cần sản xuất 200 tấn loại A và
tấn loại B thì thu được lợi nhuận cao nhất. 3 Đối với HĐTH 4:
Cần mua khối lượng 1,8 kg thịt bò loại I và 1,4 kg thịt bò loại II thì chi phí thấp nhất.
d) Tổ chức thực hiện:
 GV chuyển giao nhiệm vụ học tập: GV tổ chức cho mỗi HS đọc HĐTH 3, 4 và trả
lời câu hỏi ở phần nội dung.
 HS thực hiện nhiệm vụ học tập:
– Đối với HĐTH 3: HS thực hiện các bước tính toán tìm ra kết quả.
– Đối với HĐTH 4: HS tiến hành các bước tính toán tương tự.
 Báo cáo kết quả hoạt động và thảo luận: HS lên bảng trình bày theo các bước đã học.
 Kết luận, nhận định:
– GV yêu cầu HS trả lời các câu hỏi ở hai HĐTH ( hoặc xung phong).
– GV mời các HS khác góp ý, nhận xét. C. NHIỆM VỤ
– Xem lại cách tìm giá trị lớn nhất, nhỏ nhất (nếu có) của biểu thức của hàm mục tiêu
trong bài toán quy hoạch tuyến tính.
– Hoàn thành bài tập 1, 2, 3, 4, 5 trong sách giáo khoa.
– Chuẩn bị bài mới “Bài 2. Vận dụng đạo hàm giải bài toán tối ưu”.
IV. KẾ HOẠCH ĐÁNH GIÁ
(GV tự cân đối từng hoạt động để đưa ra phương án đánh giá cho phù hợp)
V. HỒ SƠ DẠY HỌC (Đính kèm các phiếu học tập/bảng kiểm quan sát) 11 VẬN DỤNG ĐẠ Bài 2.
O HÀM GIẢI BÀI TOÁN TỐI ƯU Thờ
i gian thực hiện: 4 tiết I. MỤC TIÊU 1. Về kiến thức
– Vận dụng kiến thức về đạo hàm để giải quyết một số bài toán tối ưu xuất hiện trong
thực tiễn, bao gồm một số bài toán tối ưu trong kinh tế.
– Vận dụng Bất đẳng thức Cauchy (thay vì dùng đạo hàm trong vài trường hợp) để giải
quyết nhanh một số bài toán tối ưu trong thực tiễn.
– Vận dụng kĩ năng đọc hiểu để thiết lập một số biểu thức liên quan đến bài toán tối ưu
xuất hiện trong thực tiễn. 2. Về năng lực 2.1. Năng lực chung:
– Tự chủ và tự học: HS tự chuẩn bị bài ở nhà, trả lời được những câu hỏi ở HĐKP.
– Giao tiếp và hợp tác: HS hoạt động nhóm thông qua việc giải quyết vấn đề một số bài toán tối ưu.
2.2. Năng lực Toán học:
– Giải quyết vấn đề toán học: Giải bài toán thực tế về việc hiểu dữ liệu bài toán và HS
thiết lập được biểu thức liên quan đến bài toán tối ưu.
– Tư duy và lập luận toán học: Sử dụng các bước khảo sát và vẽ bảng biến thiên để giải các HĐTH và HĐVD. 3. Về phẩm chất
– Chăm chỉ: Có chuẩn bị bài trước ở nhà, chuẩn bị các bước làm của bài toán tối ưu bằng đạo hàm.
– Trung thực: HS thừa nhận và học tập các kết quả đúng của các bạn thông qua các hoạt
động giải các bài tập Luyện tập, Thực hành, Vận dụng.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với giáo viên: SGK, SGV, KHBD, ti vi, bài trình chiếu.
2. Đối với học sinh: SGK, máy tính cầm tay, đồ dùng học tập.
III. TIẾN TRÌNH DẠY HỌC A. KHỞI ĐỘNG
Hoạt động: Khởi động
a) Mục tiêu: Gợi mở kết nối HS vào bài toán tối ưu thông qua bài toán thực tế về
phương án đường đi của một người từ A đến B. 12
b) Nội dung: GV yêu cầu HS đọc yêu cầu ở HĐKĐ và trả lời câu hỏi: Nếu người đó
chèo thuyền thẳng từ A đến B thì tốn bao nhiêu thời gian? Có phương án nào tốn ít thời gian hơn không?
c) Sản phẩm: HS nêu được: Thời gian để người đó chèo thẳng từ A đến B là 2 2 300  400 t 
 10 (phút). HS có thể trả lời được hoặc chưa được cách tìm ra phương 50
án tốn ít thời gian hơn.
d) Tổ chức thực hiện:
 GV chuyển giao nhiệm vụ học tập: GV tổ chức cho HS đọc kênh chữ, quan sát hình ở HĐKĐ.
 HS thực hiện nhiệm vụ học tập: Cá nhân HS suy nghĩ tìm câu trả lời.
 Báo cáo kết quả hoạt động và thảo luận: HS xung phong phát biểu quan điểm cá nhân.
 Kết luận, nhận định:
– GV nhận xét, đánh giá kết quả thực hiện của HS (chưa kết luận tính đúng, sai).
– GV dẫn dắt vào HĐKP.
B. KHÁM PHÁ – THỰC HÀNH – VẬN DỤNG
1. Vận dụng đạo hàm giải bài toán tối ưu.
Hoạt động 1.1: Khám phá
a) Mục tiêu: HS nhớ lại các bước tìm giá trị lớn nhất, nhỏ nhất của một biểu thức bằng đạo hàm.
b) Nội dung: GV tổ chức cho HS làm việc độc lập, suy nghĩ trả lời câu hỏi với HĐKP.
c) Sản phẩm: HS đọc dữ liệu đề bài và tuần tự trả lời các câu hỏi a), b), c). a) 2 3
S  x  4hx (dm ) . 500
b) Có thể. Từ giả thiết 2
V  500  x h  h  . 2 x 500 2000 Khi đó 2 2 S  x  4. x  x  . 2 x x
c) Cách 1: Áp dụng BĐT Cauchy, ta được: 1000 1000 1000 1000 2 2 3 S  x    3 x . .  300 (dm2). x x x x 1000  500  Nên 2
min S  300 khi x   x 10  50 ;  . x  3   
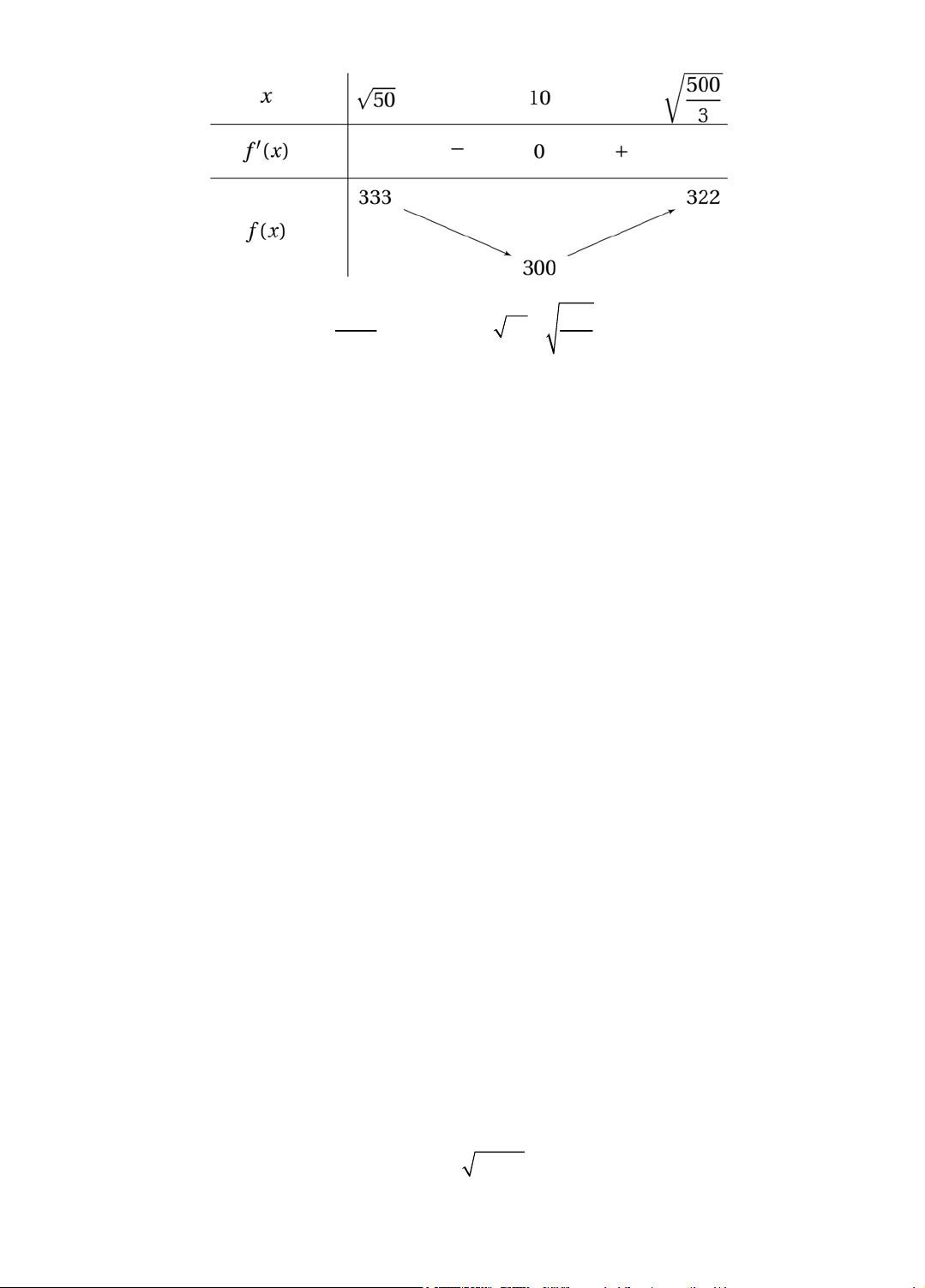
Cách 2: Dùng đạo hàm, khảo sát hàm số và vẽ bảng biến thiên của hàm số: 2000  500  2
S  f (x)  x  , với x  50 ;  . x  3    13 1000  500  Nên 2
min S  300 khi x   x 10  50 ;  . x  3   
d) Tổ chức thực hiện:
 GV chuyển giao nhiệm vụ học tập: Từ các giả thiết trong HĐKP, GV yêu cầu HS
hãy đọc, hiểu, xử lí dữ liệu và thực hiện HĐKP. Nêu kết quả và nhận xét tính đúng, sai và giải thích.
 HS thực hiện nhiệm vụ học tập: HS suy nghĩ, thảo luận trả lời được câu hỏi ở HĐKP.
 Báo cáo kết quả hoạt động và thảo luận:
– HS xung phong trả lời các câu hỏi ở HĐKP.
– GV trao đổi, góp ý cho HS nếu cần.
 Kết luận, nhận định:
– Để giải bài toán tối ưu, ta có thể sử dụng đạo hàm khảo sát và vẽ bảng biến thiên, từ
đó tìm được giá trị tối ưu (giá trị lớn nhất hoặc giá trị nhỏ nhất). Trong vài trường hợp, chúng
ta có thể áp dụng BĐT Cauchy để tìm nhanh được giá trị tối ưu đó.
– GV gọi một HS đọc bốn bước để vận dụng đạo hàm tìm giá trị tối ưu trong SGK.
– GV hướng dẫn HS tìm hiểu Ví dụ 1, 2, qua đó HS hiểu rõ hơn cách tìm max, min bằng
cách vận dụng đạo hàm (hoặc áp dụng BĐT Cauchy).
Hoạt động 1.2: Thực hành
a) Mục tiêu: Bước đầu thực hành thuần thục quy trình vận dụng đạo hàm giải bài toán tối ưu. b) Nội dung:
– GV yêu cầu HS tìm giá trị nhỏ nhất của HĐTH 1, giá trị lớn nhất của HĐTH 2.
– Hãy nêu các bước thực hiện HĐTH 1, 2.
c) Sản phẩm: HS nêu được các bước thực hiện HĐTH 1, 2 là: Lập biểu thức cần tìm
giá trị tối ưu, vận dụng đạo hàm tìm giá trị tối ưu (hoặc có thể dùng BĐT Cauchy tìm giá trị
tối ưu trong vài trường hợp). So sánh kết quả và trả lời câu hỏi. Đối với HĐTH 1:
Tổng độ dài đường ống là: 2
s  f (x)  2 x  4  x  3, x  (0; 3). 14 Bảng biến thiên:
Từ bảng biến thiên trên, ta được tổng độ dài đường ống nhỏ nhất là: 3  2 3 khi 2 3 IM  . 3
Vậy tổng độ dài đường ống nhỏ nhất là khoảng 6,464 km khi điểm I được đặt ở
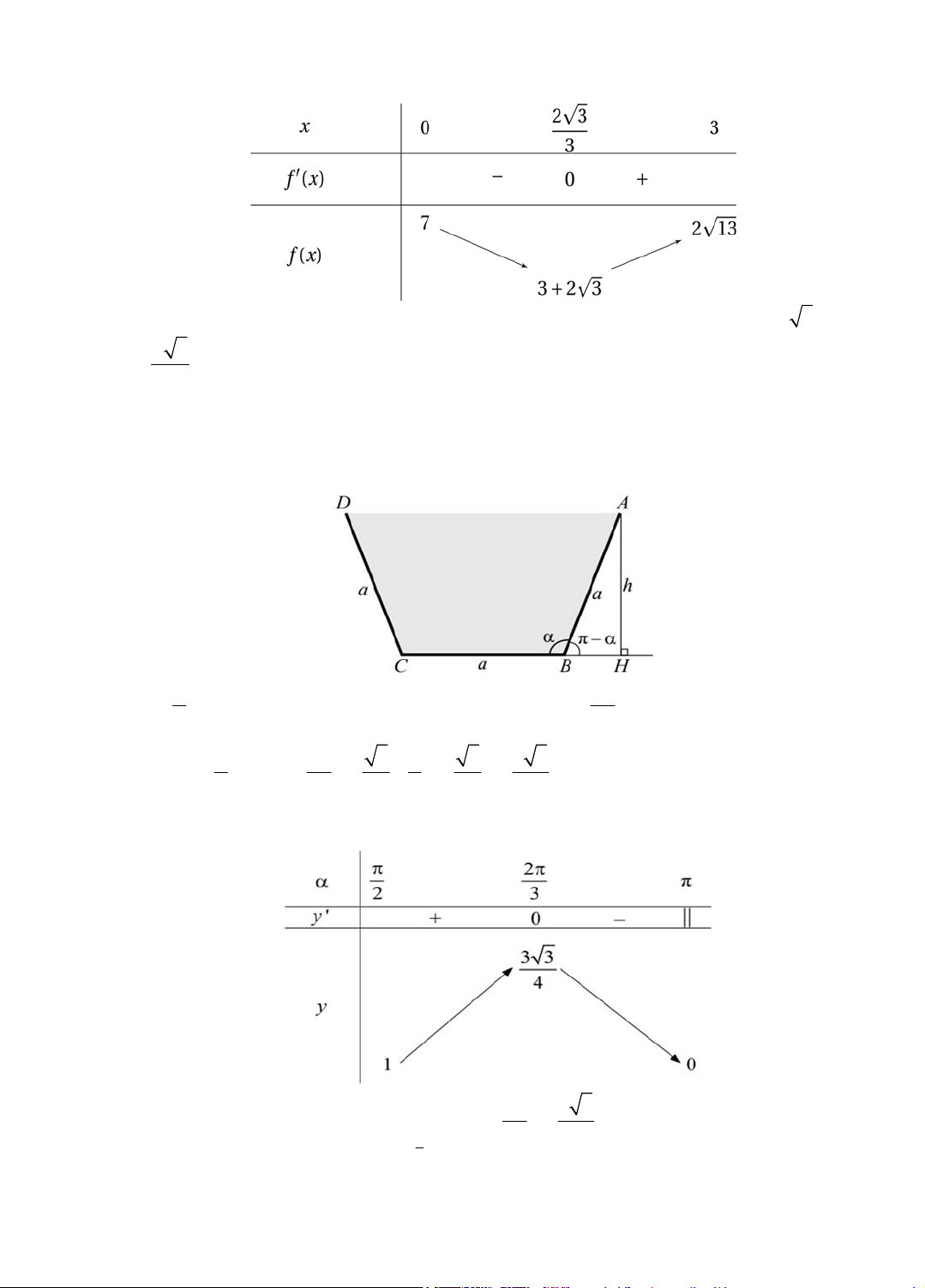
vị trí cách điểm M một khoảng bằng 1,155 km. Đối với HĐTH 2:  2
Do <  <  nên phương trình có nghiệm là  = . 2 3     2  3 1  3  3 3
Ta có y   = 1; y   .       .  2  3 2 2  2    4   Bảng biến thiên:  2  3 3
Từ bảng biến thiên, ta được: max y = y    .    3  4 ;     2  15 2    3a 3
Suy ra giá trị lớn nhất của S là: a2 . y    .  3  4 2 3a 3
Vậy diện tích mặt cắt ngang của máng dẫn nước có giá trị lớn nhất là: 4 2 khi  = . 3
d) Tổ chức thực hiện:
 GV chuyển giao nhiệm vụ học tập: Chia lớp thành bốn nhóm tương ứng bốn tổ. Các
nhóm tiến hành thảo luận, trình bày lời giải vào bảng phụ.
 HS thực hiện nhiệm vụ học tập: Các nhóm trao đổi thống nhất ý kiến viết lời giải vào bảng phụ.
 Báo cáo kết quả hoạt động và thảo luận:
– Các nhóm dán bảng phụ lên bảng, đại diện từng nhóm trình bày.
– Các HS chú ý theo dõi, quan sát, đặt ra những câu hỏi để làm sáng tỏ vấn đề.
 Kết luận, nhận định:
– GV mời một số nhóm HS trình bày kết quả của câu hỏi trong HĐTH.
– Các nhóm còn lại lắng nghe, nhận xét, bổ sung để hoàn thiện bài tập.
– GV nhận xét, đánh giá kết quả thực hiện của HS.
2. Giải bài toán tối ưu trong kinh tế
GV hướng dẫn HS tìm hiểu Ví dụ 3, Ví dụ 4 về một số bài toán tối ưu trong kinh tế mà
ta có thể giải nhờ ứng dụng đạo hàm.
Hoạt động 2.1: Thực hành
a) Mục tiêu: Phát triển kĩ năng giải bài toán tối ưu trong kinh tế. b) Nội dung:
– GV yêu cầu HS đọc yêu cầu của HĐTH 3 và trả lời câu hỏi như quy trình của Ví dụ 3, Ví dụ 4.
– GV yêu cầu HS đọc yêu cầu của HĐTH 4 và trả lời câu hỏi.
c) Sản phẩm: Nội dung trả lời của HS. Đối với HĐTH 3:
a) Chi phí trung bình để sản xuất một sản phẩm là: C(x) 5000 M (x)   0,005x 
 50  x  0 . x x 5000
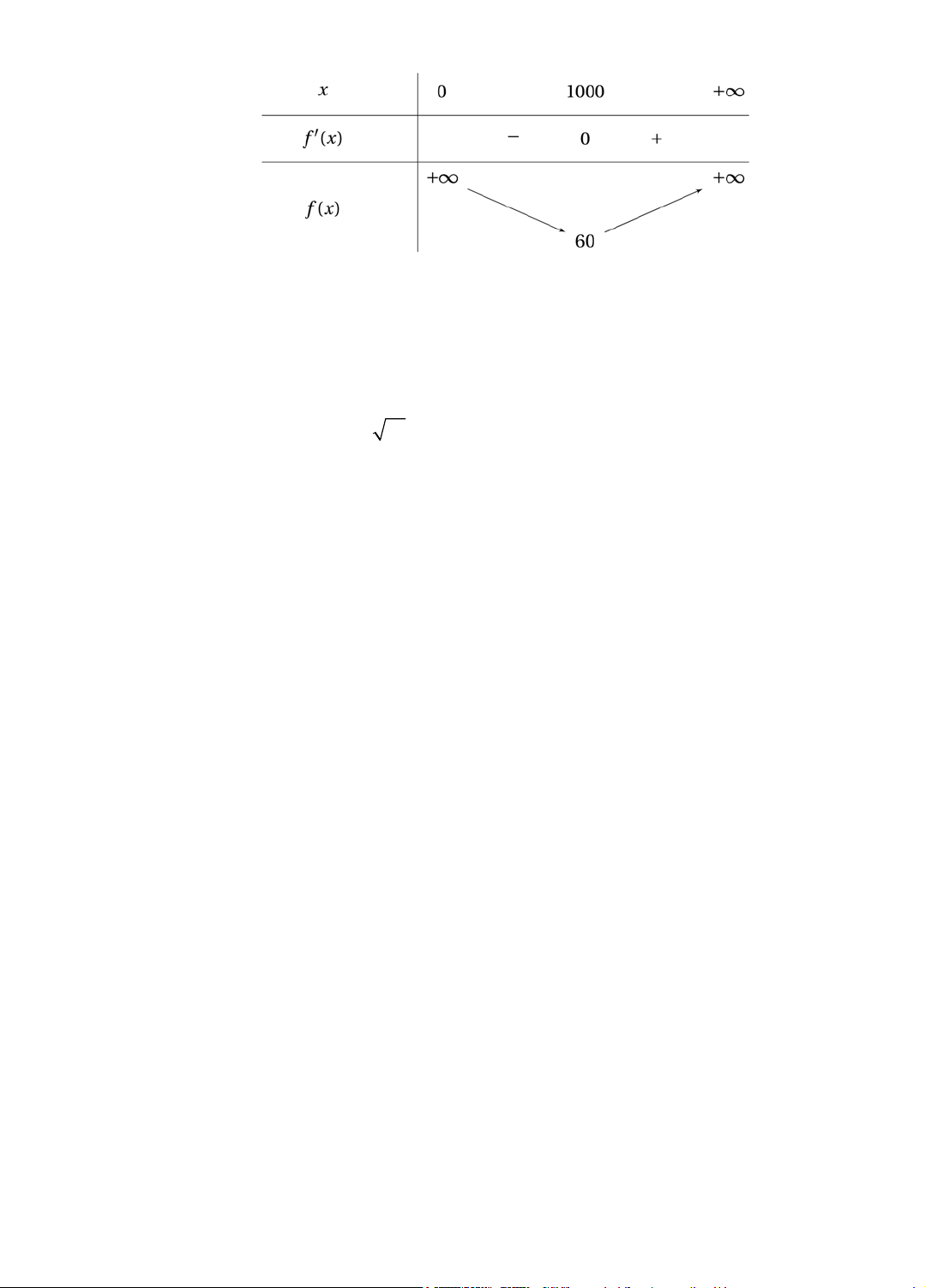
b) Ta có: M '(x)  0,005  . 2 x 2
M '(x)  0  x  1000000  x  1000. 16
Từ bảng biên thiên, để chi phí trung bình thấp nhất, mỗi tháng xưởng cần sản xuất 1 000 sản phẩm. Đối với HĐTH 4:
a) Lợi nhuận (triệu đồng) mà cơ sở A thu được là: 3
L(x)  R(x)  C(x)  1,5x  0,0005x 10 .
b) Ta có: y(0) = −10; y(10 10 )  21,6; y(40) = 18.
Trong mỗi tháng, cơ sở A nhận được lợi nhuận lớn nhất là 21,62 triệu đồng, khi
B đặt 31,62 tạ sản phẩm X.
d) Tổ chức thực hiện:
 GV chuyển giao nhiệm vụ học tập: GV tổ chức cho mỗi HS đọc câu hỏi ở
HĐTH 3, 4 và suy nghĩ trả lời.
 HS thực hiện nhiệm vụ học tập:
– Đối với HĐTH 3: HS thực hiện các bước tính toán tìm ra kết quả.
– Đối với HĐTH 4: HS tiến hành các bước tính toán tương tự.
 Báo cáo kết quả hoạt động và thảo luận:
– HS lên bảng trình bày theo các bước đã học.
– Các HS còn lại lắng nghe, theo dõi và bổ sung.
 Kết luận, nhận định:
– GV nhận xét, đánh giá kết quả thực hiện của HS với kết quả đúng.
– GV tuyên dương, khen thưởng các HS có kết quả tốt, có kĩ năng giải bài toán thực tế
liên quan đến bài toán tối ưu trong kinh tế.
Hoạt động 2.2: Vận dụng
a) Mục tiêu: Giải bài toán tối ưu trong kinh tế (liên quan đến lợi nhuận) bằng cách vận
dụng các kiến thức về đạo hàm, ở đó HS cần lập công thức xác định hàm số từ các dữ kiện của bài toán.
b) Nội dung: GV yêu cầu HS đọc yêu cầu của HĐVD và trả lời câu hỏi.
c) Sản phẩm: HS nêu được:
Tổng số sản phẩm bán ra là (100 + 10x), với đơn giá mỗi sản phẩm là (20 – x)
(nghìn đồng), nên lợi nhuận từ việc bán sản phẩm A là:
L  x  
 x  x 2 100 10 20  10
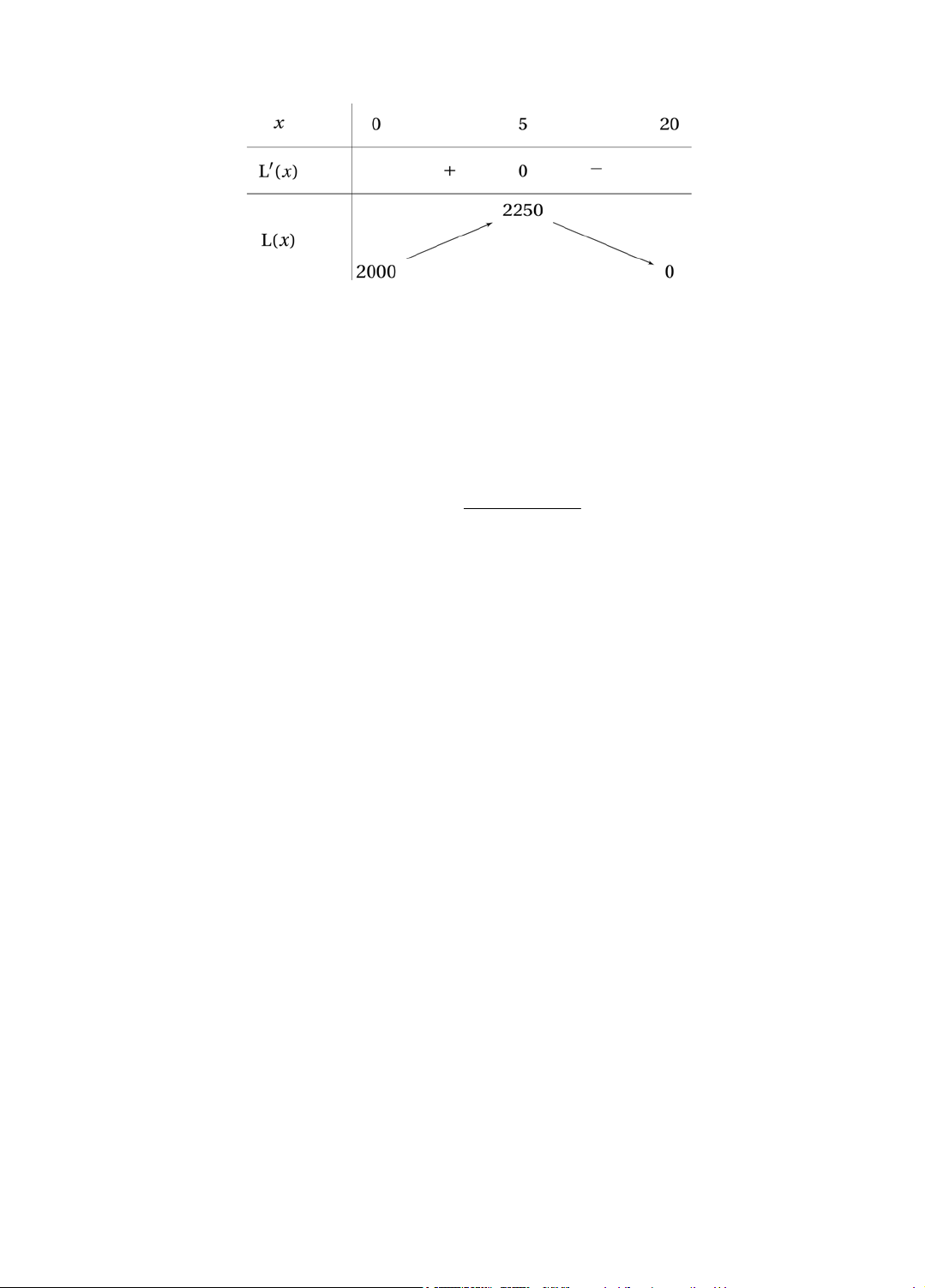
 x 100x  2000 (nghìn đồng). 17 Bảng biến thiên:
Từ bảng biến thiên, nếu cửa hàng giảm giá 5 000 đồng/sản phẩm (tức là bán với
giá 15 000 đồng/sản phẩm), thì sẽ thu được lợi nhuận lớn nhất là 225 000 (đồng).
Nhận xét: Có thể tìm giá trị lớn nhất của L  x 2  10
 x 100x  2000 bằng hai cách khác như sau:
Cách 1: L  x 2
 2250 10(x  5)  2250. Cách 2: Dùng BĐT Cauchy: 2         
 x  x 10 x 20 x L x 10 10 20 10  2250   .  2 
d) Tổ chức thực hiện:
 GV chuyển giao nhiệm vụ học tập: GV hướng dẫn HS đọc HĐVD và trả lời câu hỏi ở phần nội dung.
 HS thực hiện nhiệm vụ học tập: HS làm việc cá nhân hoặc theo nhóm, thảo luận, trình
bày lời giải của mình và nhận xét lời giải của bạn.
 Báo cáo kết quả hoạt động và thảo luận:
– HS lên bảng trình bày theo các bước đã học.
– GV chỉ định ngẫu nhiên hai HS lên trình bày câu trả lời của mình.
 Kết luận, nhận định:
– GV nhận xét, đánh giá kết quả thực hiện của HS với kết quả đúng.
– GV nhận xét kết quả thực hiện bài tập của lớp trong suốt quá trình làm việc. Tuyên
dương, khen thưởng các HS có kết quả tốt. C. NHIỆM VỤ
– Xem lại cách vận dụng đạo hàm tìm giá trị tối ưu của các bài toán thực tế, cách vận
dụng BĐT Cauchy tìm giá trị tối ưu trong vài trường hợp.
– Hoàn thành bài tập 1, 2, 3, 4, 5 trong SGK.
– Chuẩn bị bài mới “Bài tập cuối chuyên đề 1”.
IV. KẾ HOẠCH ĐÁNH GIÁ
(GV tự cân đối từng hoạt động để đưa ra phương án đánh giá cho phù hợp)
V. HỒ SƠ DẠY HỌC (Đính kèm các phiếu học tập/bảng kiểm quan sát) 18
BÀI TẬP CUỐI CHUYÊN ĐỀ 1
Thời gian thực hiện: 3 tiết I. MỤC TIÊU 1. Về kiến thức
– Vận dụng kiến thức của hệ bất phương trình bậc nhất để giải quyết một số bài toán quy hoạch tuyến tính.
– Vận dụng kĩ năng đọc hiểu để thiết lập một số biểu thức liên quan đến bài toán tối ưu
xuất hiện trong thực tiễn, bao gồm những bài toán tối ưu trong kinh tế.
– Vận dụng kiến thức về đạo hàm để giải quyết một số bài toán tối ưu.
– Vận dụng Bất đẳng thức Cauchy (thay vì dùng đạo hàm trong vài trường hợp) để giải
quyết nhanh một số bài toán tối ưu trong thực tiễn.
– Vận dụng kĩ năng đọc hiểu để thiết lập một số biểu thức liên quan đến bài toán tối ưu
xuất hiện trong thực tiễn. 2. Về năng lực 2.1. Năng lực chung:
– Tự chủ, tự học: HS chuẩn bị bài tập cuối Chuyên đề 1 ở nhà.
– Giao tiếp, hợp tác: Phân tích, đánh giá, chủ động thực hiện các hoạt động nhóm.
2.2. Năng lực Toán học:
– Năng lực tư duy và lập luận toán học: Giải bài toán thực tế về việc hiểu dữ liệu bài
toán và HS thiết lập được biểu thức liên quan đến bài toán tối ưu.
– Năng lực mô hình hoá toán học: Sử dụng các kiến thức về bài toán quy hoạch tuyến
tính, đạo hàm để tìm giá trị tối ưu của các bài toán thực tế (Vật lí, Kinh tế, chuyển động, …). 3. Về phẩm chất
– Trung thực: Báo cáo đúng kết quả chuẩn bị bài tập ở nhà.
– Trách nhiệm: Chủ động, tích cực trong thực hiện các nhiệm vụ học tập cá nhân và nhóm.
– Chăm chỉ: Tự nghiên cứu và giải một số bài tập trước ở nhà.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với giáo viên: SGK, SGV, KHBD, ti vi, bài trình chiếu, phiếu học tập, bảng nhóm.
2. Đối với học sinh: SGK, máy tính cầm tay, đồ dùng học tập.
III. TIẾN TRÌNH DẠY HỌC
A. CÂU HỎI TRẮC NGHIỆM
Hoạt động: Câu hỏi thực hành, vận dụng
a) Mục tiêu: Giúp HS củng cố lại một số kiến thức trong Chuyên đề 1 và rèn luyện khả
năng làm bài tập trắc nghiệm. 19
b) Nội dung: HS đọc và thực hiện giải câu hỏi trắc nghiệm.
c) Sản phẩm: HS thực hiện được: 1. C; 2. A; 3. B; 4. C; 5. C.
d) Tổ chức thực hiện:
 GV chuyển giao nhiệm vụ học tập: GV có thể sử dụng phiếu học tập và yêu cầu HS
điền vào chỗ trống trên phiếu, sau đó yêu cầu HS đọc đề và trả lời các câu trắc nghiệm 1, 2, 3, 4, 5, 6 trong SGK.
 HS thực hiện nhiệm vụ học tập: HS hoàn thành các chỗ trống trên phiếu học tập rồi
tiến hành đọc đề và giải các câu trắc nghiệm trong SGK dựa trên các kiến thức đã học.
 Báo cáo kết quả hoạt động và thảo luận: HS thực hiện cá nhân, đứng tại chỗ phát
biểu đáp án. HS khác nhận xét.
 Kết luận, nhận định:
– GV nhận xét, đánh giá bài làm của HS và nêu đáp án đúng.
– GV kết luận, HS cần nắm vững được các lí thuyết về bài toán quy hoạch tuyến tính,
cách vận dụng đạo hàm và BĐT Cauchy trong vài trường hợp để giải quyết bài toán tối ưu.
B. BÀI TẬP TỰ LUẬN
Hoạt động 1: Bài tập quy hoạch tuyến tính.
a) Mục tiêu: Giúp HS củng cố lại các kiến thức về bài toán quy hoạch tuyến tính để
tìm giá trị tối ưu của một số vấn đề liên quan đến thực tiễn.
b) Nội dung: HS hoạt động cá nhân để thực hiện các bài tập tự luận 6, 7, 8, 9 trong SGK.
c) Sản phẩm: Kết quả làm việc của HS.
6. Từ giả thiết, ta có được miền nghiệm và hàm mục tiêu như hình vẽ:  5 
Suy ra min F  15 tại C 0; 
1 ; max F  105 tại B 2;   .    3  20