18 trang 8 lượt tải

Tổng hợp lý thuyết và đề tự luyện Hàm số mũ - Lũy thừa – Logarit môn Toán 11

15

Tổng hợp lý thuyết và đề tự luyện Hàm số mũ - Lũy thừa – Logarit môn Toán 11. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem.

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT) 192 tài liệu

Môn: Toán 11 3.7 K tài liệu

Tác giả:

Profile

Đạt lê

2 ngày trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/18
Hàm số
n
yx
với
n
được gọi là hàm số lũy thừa.
Tập xác định của hàm số
n
yx là:
n
là số nguyên dương

TXĐ:
D
n
là số nguyên âm hoặc số 0

TXĐ:

\0D
n
là số không nguyên

TXĐ:

0;D 
a
yx

0; 
Đồ thị hàm số
yx
luôn đi qua điểm

1;1 .I
Lưu ý: Khi khảo sát hàm số lũy thừa với sỗ mũ cụ thể,
ta phải xét hàm số đó trên toàn bộ tập xác định của nó.
Chẳng hạn:
Hàm số:
3
yx

.x
Hàm số:
4
yx

0.x
Hàm số:
1
3
yx

0.x
ĐỒ THỊ VÀ HÀM SỐ LUỸ THỪA
Tập xác định của hàm số

3
2yx

là
A.

2; 
. B.
. C.

;2
. D.

\2
.
Tập xác định của hàm số

4
2
6yxx
 là
A.

;2 3;D 
. B.

\2;3D 
.
C.
D
. D.

\0D
.
Tìm tập xác định
D
của hàm số

log100
2
2yxx
 .
A.

1; 2 .D 
B.

\1;2.D 
C.

\1;2.D 
D.
D
Tập xác định của hàm số

1
5
1yx
là
A.
1; 
B.

\1
C.

1; 
D.

0; 
Tập xác định của hàm số

1
2
3
32yx x

.
A.

;1 2; 
. B.

\1;2
. C.
. D.

;1 2; 
.
Tập xác định của hàm số

2
2
68yxx
là
A.

2; 4
. B.

;2
. C.

4; 
. D.
D
.
Tìm tập xác định
D
của hàm số

2
2
69yx x

.
A.

\0D
. B.

3;D 
. C.

\3
. D.
.
Tập xác định của hàm số


3
2
2
5
32 3yx x x

là
A.

;\3D 
B.

;1 2; \ 3D 
.
C.

;\1;2D 
. D.

;1 2;D 
.
Tìm tập xác định
D
của hàm số

1
2
3
34 2.yxx x
A.
1; 2 .D 
B.

1; 2 .D 
C.
;2 .D 
D.

1; 2 .D 
Tìm giá trị thực của tham số
m
để hàm số

2
2
yxm
có tập xác định là
.
A.
.m
B.
0.m
C.
0.m
D.
0.m
Có bao nhiêu giá trị nguyên của tham số
m
để hàm số

2
2
32 3yxmx
xác định với mọi
x
?
A. 7. B. 6. C. 4. D. 5.
Có bao nhiêu giá trị nguyên của

2023;2023m
để hàm số

5
2
21yx xm
xác định
với mọi
x
?
A. 4036. B. 2023. C. 2022. D. Vô số
Cho số thực
0, 1aa
. Hàm số
x
ya được gọi là hàm số mũ cơ số
.a
Tập xác định :
D
.
Tập giá trị:

0;T 
do 0
x
ya x
x
ya

0, 1aa
1a
01a
Hàm số luôn đồng biến trên
Hàm số luôn nghịch biến trên
Đồ thị hàm số
x
ya luôn đi qua các điểm

0;1
và

1; a
.
Đồ thị hàm số
x
ya luôn nằm phía trên trục hoành.
Tập xác định của hàm số
25
1
2
x
y



là
A.
. B.

0; 
. C.

\0
. D.
0;
.
Tập xác định của hàm số
1
1
3
x
x
y
là
A.
. B.

0; 
. C.

\1
. D.
0;
.
ĐỒ THỊ VÀ HÀM SỐ MŨ
Trong các hàm số sau, hàm số nào đồng biến trên
?
A.

x
e
fx



. B.

1
x
fx
e



. C.

1
3
x
fx
. D.

3
x
fx
.
Đồ thị hình bên là của hàm số nào?
A.

3.
x
y B.
1
.
2
x
y



C. 3.
x
y D.
1
.
3
x
y



Cho hai hàm số ,
x
ya
x
yb với
,ab
là hai số thực dương
khác 1, lần lượt có đồ thị là

1
C
và

2
C
như hình bên. Mệnh
đề nào dưới đây đúng?
A.
01.ab
B.
01.ba
C.
01.ba
D.
01.ab
Cho
, , abc
là các số thực dương khác 1. Đồ thị hàm số
,
x
ya
,
x
yb
x
yc
được cho trong hình bên. Chọn
khẳng định đúng?
A.
1.cab
B.
1.cab
C.
1.cba
D.
1.cab
Cho hai hàm số
x
ya
và
x
yb
có đồ thị lần lượt là

1
C
và

2
C
như hình vẽ. Đường thẳng
2y
cắt đồ thị

1
C
và

2
C
và trục tung lần lượt tại các điểm
,,ABC
biết
2BC AC
. Khẳng định nào sau đây là đúng?
A.
2
ab
. B.
2
ba
.
C.
2
1ab
. D.
2
1ab
.
Cho
25
x
. Giá trị của biểu thức
12
42
xx
T


bằng
A.
504
5
. B.
104
5
. C.
104
25
. D.
504
25
.
Cho
44 34
xx

. Tính giá trị của biểu thức
11
22 3
12 2
xx
xx
T



.
A.
3
4
T
. B.
3
11
T
. C.
3
11
T 
. D.
3
13
T
.
Cho hàm số

x
x
a
fx
aa
. Ta có

11fx f x
.
Cho hàm số

9
93
x
x
fx
. Tính tổng
12 2022
2023 2023 2023
Sf f f
 

 
 
.
A.
1002S
. B.
3008
3
S
. C.
1003S
. D.
1011S
.
Cho số thực
0, 1aa
. Hàm số log
a
yx được gọi là hàm số logarit cơ số
Hàm số

log
a
yfx
có điều kiện xác định là:

0fx
.
log
a
yx

0, 1aa
1a
01a
Hàm số luôn đồng biến trên

0; 
Hàm số luôn nghịch biến trên

0; 
Đồ thị hàm số log
a
yx
đi qua các điểm

1; 0 , ; 1a
và luôn nằm bên phải trục tung.
Đồ thị hàm số
x
ya
và log
a
yx đối xứng nhau qua đường thẳng
yx
.
.
a
ĐỒ THỊ VÀ HÀM SỐ LÔGARIT
Tìm tập xác định
D
của hàm số

3
log 2 10 1yx
là
A.

5; .D 
B.
9
;
2
D




. C.

5; . D 
D.
9
;
2
D



.
Tập xác định của hàm số

2
log 3 2yx
là:
A.

0;D 
. B.
3
;
2
D




. C.

;0D 
. D.
3
;
2
D




.
Tập xác định của hàm số

2
3
log 4 3yxx
là
A.

;1 3; . 
B.

1; 3 .
C.

;1 .
D.

3; .
Tập xác định của hàm số

2
2
log 3 2yxx
là
A.

1;1D 
. B.

1; 3D 
. C.

3;1D 
. D.

0;1D
.
Tập xác định của

2
ln 5 6yxx
là
A.

;2 3; 
. B.

2;3
. C.

2;3
. D.

;2 3; 
.
Tập xác định của hàm số

log log 3yx x
là
A.

3;
. B.

0;3
. C.
3;
. D.

0;3
.
Tìm tập xác định
D
của hàm số


2
2
2021 2020
log 1 log 4yx x
.
Tìm tập xác định của hàm số
5
1
log
6
y
x
.
A.

;6
B.
C.

0; 
D.

6; 
Tìm tập xác định
D
của hàm số

2
9
log 2yxx
.
A.
1
0;
2
D



. B.

1
;0 ;
2
D




.
C.
1
0;
2
D



D.
1
;0 ;
2
D



.
Tìm tập xác định của hàm số

2 log 3
x
yx
.
A.
0; 
. B.

0;3
. C.

;3
. D.
0;3
.
Có bao nhiêu giá trị nguyên thuộc tập xác định của hàm số

log 6 2

yxx
?
A.
7
. B.
8
. C.
9
. D. Vô số.
A.
D
2;2
\
1
B.
D
1; 2
C.
D
2;1
D.
D
2;2
Tìm tập xác định
D
của hàm số
5
3
log .
2
x
y
x
A.

;2 3;D 
B.

2;3D 
C.

;2 3;D 
D.

\2D 
Tìm tất cả các giá trị thực của tham số
m
để hàm số

2
log 4 1yxxm
có tập xác định là
.
A.
4m 
. B.
0m
. C.
4m 
. D.
3m 
.
Có bao nhiêu giá trị nguyên của tham số
m
để hàm số

2
ln 1 2 3 1ymxmx


có tập
xác định là
?
A. 3. B. 5. C. 4. D. 2.
Có bao nhiêu giá trị nguyên của tham số

10;10m
để hàm số

2
2
log 2yxxm
xác
định với mọi

0; ?x
A. 8. B. 7. C. 9. D. 18.
Tìm tất cả các giá trị của
m
để hàm số

2
ln 2 1yxmxm
xác định với mọi

1; 2x
.
A.
1
3
m 
. B.
3
4
m
. C.
3
4
m
. D.
1
3
m 
.
Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
3
1
log
21
yxm
mx


xác định trên khoảng

2;3
?
A.
1
. B.
2
. C.
4
. D.
3
.
Hàm số nào dưới đây đồng biến trên khoảng

0; 
?
A.
3
logyx
. B.
6
logyx
. C.
3
log
e
yx
. D.
1
4
logyx
.
Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
A.
3
logyx
B.

2
log 1yx C.
4
logyx
D.
3
x
y



Đồ thị hình bên là của hàm số nào?
A.
1
2
log .yx B. 2.
x
y
C. 2.
x
y D.
2
log .yx
Tìm a để hàm số có đồ thị là hình bên.
A.
2a
B.
1
2
a
C.
1
2
a
D.
2a
Cho đồ thị hàm số ,
x
ya log
b
yx (như hình vẽ). Khẳng
định nào sau đây đúng?
A.
01ba
B.
01ab
C.
1a
và
1b
D.
01a
và
01b
Cho hai số
, 0,ab
1, 1.ab
Đồ thị các hàm số
log ,
a
yx log
b
yx được cho trong hình vẽ bên. Mệnh
đề nào sau đây đúng?
A.
10.ab
B.
10.ba
C.
1.ba
D.
1.ab
Cho ba số
,, 0,abc
1, 1, 1.abc
Đồ thị các hàm số
log ,
a
yx log ,
b
yx log
c
yx được cho trong hình vẽ
bên. Mệnh đề nào sau đây đúng?
A.
.abc
B.
.bac
C.
.cba
D.
.cab
log
a
01
a

x
y
1
2
2
O
Cho hàm số log
a
yx và log
b
yx có đồ thị như hình
vẽ bên. Đường thẳng
7x
cắt trục hoành, đồ thị hàm số
log
a
yx và log
b
yx lần lượt tại
,HM
và
.N
Biết
rằng
.HM MN
Mệnh đề nào sau đây là đúng?
A.
7.ab
B.
2
.ab
C.
7
.ab
D.
2.ab
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ
VINCENT TUẤN
ĐỀ SỐ 01
ĐỀ TỰ LUYỆN HÀM SỐ MŨ - LŨY THỪA - LOGARIT
Môn:
Toán 11
Thời gian làm bài: 90 phút (không tính thời gian giao đề)
ĐỀ BÀI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Tập xác định của hàm số
3
2
y x
là
A.
0;
. B.
2;
. C.
. D.
\ 0
.
Câu 2: Tập xác định của hàm số
logy x
là
A.
1;
. B.
0;
. C.
0;
. D.
1;
.
Câu 3: Tập xác định
D
của hàm số
ln 1y x
là
A.
\{1}D
. B.
D
. C.
;1D 
. D.
1;D 
.
Câu 4: Tập xác định của hàm số
2
log 1y x
là
A.
\ 1
. B.
1;
. C.
1;
. D.
;1
.
Câu 5: Hàm số
2022
1y x
có tập xác định là
A.
D
. B.
1;D 
. C.
1;D 
. D.
\ 1D
.
Câu 6: Tập xác định của hàm số
2 lny x
là
A.
2
0;e
. B.
2
;e
. C.
2
;e

. D.
2
;e

.
Câu 7: Tập xác định của hàm số
1
5 12
x
y
là
A.
0;
. B.
\ 0
. C.
. D.
0;
.
Câu 8: Tập xác định của hàm số
2
1
2
log 7 3y x x
là:
A.
8; 7 0;1
. B.
8; 7 0;1
. C.
8; 7 0;1
. D.
8; 7 0;1
.
Câu 9: Tập xác định
D
của hàm số
5
3
3 log 4y x x
là
A.
3;4D
. B.
;4 \ 3D 
. C.
4;D
. D.
;4D 
.
Câu 10: Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
3
log 4 1y x x m
xác định với mọi
x
.
A.
3m
. B.
3m
. C.
3m
. D.
3m
.
Câu 11: Tìm tập xác định của hàm số
ln 3y x x
A.
;3
. B.
0;
. C.
;3
. D.
0;3
.
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ
Câu 12: Tìm tập xác định
D
của hàm số
1
3
3
log 1y x x
.
A.
0;1D
. B.
0;D 
. C.
0;1D
. D.
1;D 
.
Câu 13: Tập xác định của hàm số
2
1
log 1
y
x
là
A.
\ 2
. B.
0;
. C.
0; \ 2
. D.
0; \ 1
.
Câu 14: Tập xác định của hàm số
2019
2021
2021y x
là
A.
2021; 
. B.
\ 2021
. C.
2021;
. D.
;2021
.
Câu 15: Tập xác định D của hàm số
3
1
2
log 1
1
y
x
x
là:
A.
; 3D 
. B.
1;D 
. C.
3; 1D
. D.
0;3D
.
Câu 16: Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
1
1x mx
y e
có tập xác định là
.
A.
2
2
m
m
. B.
2m
. C.
2 2m
. D.
2m
.
Câu 17: Tất cả các giá trị thực của tham số
m
để hàm số
2
log 2 1y x x m
có tập xác định là
.
A.
0m
. B.
0m
. C.
2m
. D.
2m
.
Câu 18: Cho các đồ thị hàm số
, log ,
x c
b
y a y x y x
ở hình vẽ sau đây.
Khẳng định nào sau đây đúng?
A.
0 1 .c a b
B.
0 1 .c a b
C.
0 1.c a b
D.
0 1.c a b
Câu 19: Cho các hàm số
,
x
y a
log ,
b
y x
log
c
y x
có đồ thị như hình vẽ bên. Chọn khẳng định đúng?
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ
A.
b c a
. B.
b a c
. C.
a b c
D.
c b a
.
Câu 20: Cho ba hàm số
2
x
y
,
y x
,
y f x
có đồ thị như hình bên, mệnh đề nào sau đây đúng?
A.
1
2
logy f x x
. B.
lny f x x
. C.
2
logy f x x
. D.
logy f x x
.
Câu 21: Cho
a
,
b
,
c
là ba số thực dương khác
1
. Đồ thị hàm số
x
y a
,
x
y b
,
x
y c
được cho ở hình
vẽ dưới đây. Mệnh nào nào sau đây đúng?
A.
a b c
. B.
b c a
. C.
c a b
. D.
a c b
.
Câu 22: Đường cong trong hình bên là của đồ thị hàm số nào sau đây?
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ
A.
2
logy x
. B.
0,8
x
y
. C.
0,4
logy x
. D.
2
x
y
.
Câu 23: Tìm
a
để đồ thị hàm số
log 0 1
a
y x a
có đồ thị là hình bên.
A.
2a
. B.
1
2
a
. C.
1
2
a
. D.
2a
Câu 24: Cho
, ,a b c
là ba số dương khác
1
. Đồ thị các hàm số
log , log , log
a b c
y x y x y x
như hình vẽ
bên. Mệnh đề nào dưới đây là mệnh đề đúng?
A.
a b c
. B.
b c a
. C.
c a b
. D.
c b a
.
Câu 25: Trong hình vẽ dưới đây có đồ thị của các hàm số
, , log
x x
c
y a y b y x
.
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ
Mệnh đề nào sau đây đúng?
A.
a b c
.
B.
a b c
.
C.
b c a
.
D.
a c b
.
Câu 26: Cho đồ thị hàm số
x
y a
;
x
y b
;
log
c
y x
như hình vẽ. Tìm mối liên hệ của
,a
,b
c
.
A.
c b a
. B.
b a c
. C.
a b c
. D.
c a b
.
Câu 27: Cho
,a b
là các số thực dương khác
1
, đường thẳng
d
song song trục hoành cắt trục tung, đồ thị
hàm số
x
y a
, đồ thị hàm số
x
y b
lần lượt tại
H
,
M
,
N
(như hình bên). Biết
3HM MN
.
Mệnh đề nào sau đây đúng?
A.
4 3a b
. B.
4 3
b a
. C.
3 4
b a
. D.
3 4a b
.
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ
Câu 28: Biết hàm số
2
3
x
a
f x
b
có đồ thị đối xứng với đồ thị hàm số
3
x
y
qua đường thẳng
1x
.
Biết
a
,
b
là các số nguyên. Chọn khẳng định đúng trong các khẳng định sau:
A.
2
9b a
. B.
2
4b a
. C.
2
6b a
. D.
2
b a
.
Câu 29: Đồ thị hàm số
y f x
đối xứng với đồ thị của hàm số
2022
x
y
qua điểm
1;1I
. Giá trị của
biểu thức
2022
1
2 log
2023
f
bằng
A.
2021
. B.
2023
. C.
2020
. D.
2020
.
Câu 30: Đồ thị hàm số
y f x
đối xứng với đồ thị hàm số
0, 1
x
y a a a
qua điểm
1;1I
. Giá trị
của biểu thức
1
2 log
2023
a
f
bằng
A.
2022
. B.
2024
. C.
2023
. D.
2021
.
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho các hàm số
2024
2023
logy x
và
2023
2024
x
y
. Xét tính đúng sai của các khẳng định sau:
a) Hàm số
2024
2023
logy x
có tập giá trị là
.
b) Hàm số
2023
2024
x
y
đồng biến trên
.
c) Đồ thị hàm số
2024
2023
logy x
nằm bên phải trục tung.
d) Đồ thị hàm số
2023
2024
x
y
cắt trục tung.
Câu 2: Cho hàm số
log 0 1
a
y x a
có đồ thị
C
. Xét tính đúng sai của các khẳng định sau:
a) Tập xác định của hàm số là
0;D 
và tập giá trị của hàm số là
T
b) Đồ thị
C
đi qua điểm
1;0
, nằm bên phải trục tung
c) Hàm số đồng biến trên
khi
1.a
d) Đồ thị
C
và đồ thị hàm số
2 log 4
a
y x
đối xứng nhau qua điểm
2;1 .I
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ
Câu 3: Cho hàm số
5
logy x
có đồ thị
C
. Xét tính đúng sai của các khẳn định sau:
a) Tập xác định của hàm số
5
logy x
là
D
.
b) Hàm số đồng biến trên khoảng
1;
.
c) Đồ thị
C
nằm phía trên trục hoành.
d) Đồ thị
C
cắt trục hoành tại điểm có hoành độ bằng 1.
Câu 4: Cho đồ thị hàm số
x
y a
dưới đây. Xét tính đúng sai của các khẳng định sau:
a) Hàm số đã cho nghịch biến trên khoảng
0;1
.
b) Hàm số cho bởi công thức
3 .
x
y
c) Đồ thị hàm số đã cho cắt đường thẳng
1
3
y
tại điểm có hoành độ không âm.
d) Đồ thị hàm số đã cho cắt đường thẳng
1y x
tại điểm có hoành độ dương.
Câu 5: Cho các hàm số
log ,
x
a
y x y a
với
a
là số thực dương khác
1
. Xét tính đúng sai của các
khẳng định sau:
a) Đồ thị hàm số
x
y a
và đồ thị hàm số
log
a
y x
đối xứng nhau qua đường thẳng
y x
.
b) Hàm số
log
a
y x
và hàm số
x
y a
có cùng tập giá trị.
c) Hàm số
x
y a
với
0 1a
nghịch biến trên khoảng
; 
.
d) Đồ thị hàm số
x
y a
với
0a
và
1a
luôn đi qua điểm
;1A a
.
Câu 6: Cho các hàm số
log , log , log
a b c
y x y x y x
với
, ,a b c
là ba số thực dương khác
1
. Xét tính
đúng sai của các khẳng định sau:
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ
a) Đồ thị các hàm số trên đều đi qua điểm
(1;0)A
.
b) Hàm số
log
c
y x
đồng biến trên khoảng
0;
c) Từ đồ thị ta có:
0 1c a b
.
d) Đường thẳng
3y
cắt hai đồ thị
log , log
a b
y x y x
tại các điểm có hoành độ lần lượt là
1 2
;x x
sao cho
2 1
2x x
. Khi đó
3
2
a
b
.
Câu 7: Cho hàm số
x
y a
với
0 1a
. Xét tính đúng sai của các khẳng định sau:
a) Hàm số
x
y a
có tập xác định
0;D 
b) Đồ thị hàm số
x
y a
đi qua điểm
0;1
.
c) Hàm số
x
y a
đồng biến trên
nếu
0 1a
.
d) Hàm số
x
y a
có tập giá trị là
;a 
nếu
1x
và
1a
.
Câu 8: Cho hàm số
2
x
y
. Xét tính đúng sai của các khẳng định sau:
a) Hàm số có tập xác định
D
.
b) Hàm số nghịch biến trên khoảng
; 
c) Đồ thị hàm số đi qua điểm
2;4A
d) Đồ thị hàm số
2
x
y
đối xứng với đồ thị
1
2
x
y
qua trục tung.
Câu 9: Cho hàm số
4
logy x
. Xét tính đúng sai của các khẳng định sau:
a) Hàm số có tập xác định
D
b) Hàm số có tập giá trị
T
c) Hàm số đồng biến trên khoảng
; 
d) Đồ thị hàm số cắt đường thẳng
1y
tại điểm có hoành độ bằng
3
Câu 10: Cho các hàm số
1
2
logy x
và
2
x
y
. Xét tính đúng sai của các khẳng định sau:
a) Có hai hàm số mũ.
b) Đồ thị hàm số
1
2
logy x
đi qua điểm
2; 1M
.
c) Đồ thị hàm số
2
x
y
đi qua điểm
1; 1N
.
d) Hai đồ thị hàm số
2
x
y
và
1
2
logy x
cắt nhau tại 1 điểm.
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ
Câu 11: Cho các hàm số
1
2
logy x
;
2
x
y
;
3
logy x
;
0,5
logy x
và
0,5
x
y
. Xét tính đúng sai
của các khẳng định sau:
a) Hàm số
2
x
y
có tập giá trị là
0;
.
b) Hàm số
3
logy x
có tập giá trị là
.
c) Có hai hàm số có tập giá trị là
.
d) Có hai hàm số có tập giá trị là
0;
.
Câu 12: Cho các hàm số
1
3
logy x
;
x
y
;
lny x
;
0,2
logy x
và
1
2
x
y
. Xét tính đúng sai của
các khẳng định sau:
a) Hàm số
1
2
x
y
nghịch biến trên
.
b) Hàm số
logy x
nghịch biến trên khoảng
0;
.
c) Có ba hàm số nghịch biến trên tập xác định.
d) Có hai hàm số đồng biến trên
0;
.
Câu 13: Cho hàm số
3
log 5 3y x
. Xét tính đúng sai của các khẳng định sau:
a) Tập xác định của hàm số là
0;D 
.
b) Hàm số đồng biến trên
3
;
5

.
c) Đồ thị hàm số đi qua điểm
2;7M
.
d) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f x
trên
4 12
;
5 5
là
2
Câu 14: Cho ba điểm
;log ,
a
A b b
;2log
a
B c c
và
;3log
a
C b b
với
, ,a b c
dương và đều khác 1.
a)
B
là trung điểm của
AC
khi và chỉ khi
0b c
.
b) Ba điểm
, ,A B C
tạo thành tam giác vuông tại
A
khi và chỉ khi
2b c
.
c) Khi ba điểm
, ,A B C
tạo thành tam giác thì có diện tích là
2
.log
a
S c b b
.
d) Khi
B
là trọng tâm của tam giác
OAC
(với
O
là gốc tọa độ) thì giá trị của biểu
thức
2S b c
là bằng 9.
Câu 15: Cho hàm số
2
1
1
1
4 1
x
khi x
y
x
ax khi x
liên tục tại điểm
1x
a) Hàm số
x
y a
nghịch biến trên
; 
.
b)
1
16
x
a
khi
4x
.
c) Đồ thị hàm số
log
a
y x
đi qua điểm
2;1
.
d) Giá trị nhỏ nhất của hàm số
1 1 2x x
y a a
bằng
3
2
.
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ

Tài liệu khác của Toán 11

Preview text:


ĐỒ THỊ VÀ HÀM SỐ LUỸ THỪA Hàm số n
y x với n   được gọi là hàm số lũy thừa.
Tập xác định của hàm số n y x là:
n là số nguyên dương 
TXĐ: D  
n là số nguyên âm hoặc số 0 
TXĐ: D   \  0
n là số không nguyên 
TXĐ: D  0; a y x 0;
Đồ thị hàm số y x 
luôn đi qua điểm I 1;  1 .
Lưu ý: Khi khảo sát hàm số lũy thừa với sỗ mũ cụ thể,
ta phải xét hàm số đó trên toàn bộ tập xác định của nó. Chẳng hạn: Hàm số: 3
y x x . Hàm số: 4 y x   x  0. 1 Hàm số: 3
y x x  0.
Tập xác định của hàm số y   x  3 2 là A. 2; . B.  . C.  ;  2 . D.  \  2 . 
Tập xác định của hàm số y   x x   4 2 6 là
A. D   ;2   3; .
B. D   \  2  ;  3 . C. D   .
D. D   \  0 . 
Tìm tập xác định D của hàm số y   x x   log100 2 2 . A. D   1;  2.
B. D   \ 1;2.
C. D   \ 1  ;  2 . D. D  
Tập xác định của hàm số y   x  15 1 là A. 1; B.  \   1 C. 1; D. 0; 
Tập xác định của hàm số y   x x   1 2 3 3 2 . A .   ;1 2; . B.  \ 1;  2 . C.  . D.   ;1 2;.
Tập xác định của hàm số y  x x   2 2 6 8 là A. 2;4 . B.  ;  2 . C. 4; . D. D   . 
Tìm tập xác định D của hàm số y   2 x x  2 6 9 .
A. D   \   0 .
B. D  3; . C.  \   3 . D.  . 3 
Tập xác định của hàm số y  x x    x   2 2 5 3 2 3 là
A. D   ;   \  3
B. D    ;1  2; \  3 .
C. D   ;
  \ 1;2.
D. D    ;1  2; .
Tìm tập xác định D của hàm số y  x x  1 2 3 3 4  2  x. A. D   1;  2. B. D   1  ;  2 .
C. D   ;  2. D. D   1;  2.
Tìm giá trị thực của tham số m để hàm số     2 2 y x m có tập xác định là .  A . m   .  B. m  0. C. m  0. D. m  0.
Có bao nhiêu giá trị nguyên của tham số m để hàm số y   x mx   2 2 3 2 3 xác định với mọi x   ? A. 7. B. 6. C. 4. D. 5.
Có bao nhiêu giá trị nguyên của m 2
 023;2023 để hàm số y  x x m  5 2 2 1 xác định
với mọi x   ? A. 4036. B. 2023. C. 2022. D. Vô số
ĐỒ THỊ VÀ HÀM SỐ MŨ
Cho số thực a  0, a  1 . Hàm số x
y a được gọi là hàm số mũ cơ số . a
 Tập xác định : D   .
 Tập giá trị: T  0; do x
y a  0 x    x
y a a  0, a   1 a  1 0  a 1
Hàm số luôn đồng biến trên 
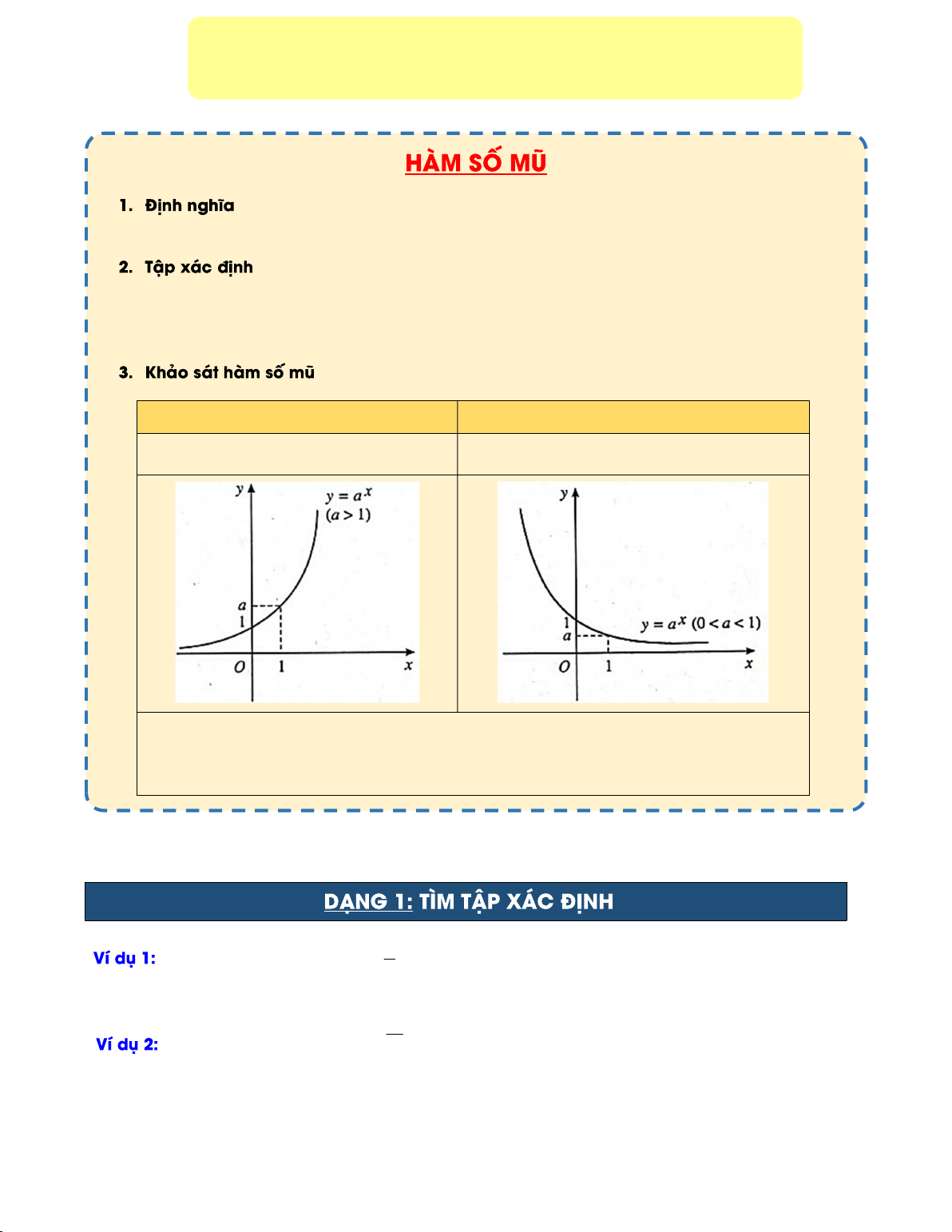
Hàm số luôn nghịch biến trên   Đồ thị hàm số x
y a luôn đi qua các điểm 0;  1 và 1;a .  Đồ thị hàm số x
y a luôn nằm phía trên trục hoành. 2 x5  1 
Tập xác định của hàm số y    là  2  A.  . B. 0;. C.  \   0 . D. 0;  . x 1 
Tập xác định của hàm số x 1 y 3   là A.  . B. 0;. C.  \   1  . D. 0;  .
Trong các hàm số sau, hàm số nào đồng biến trên  ? xx e     
A. f x   . B.   1 x f x  .
C. f x 1  . D.   3x f x  .          e   3 
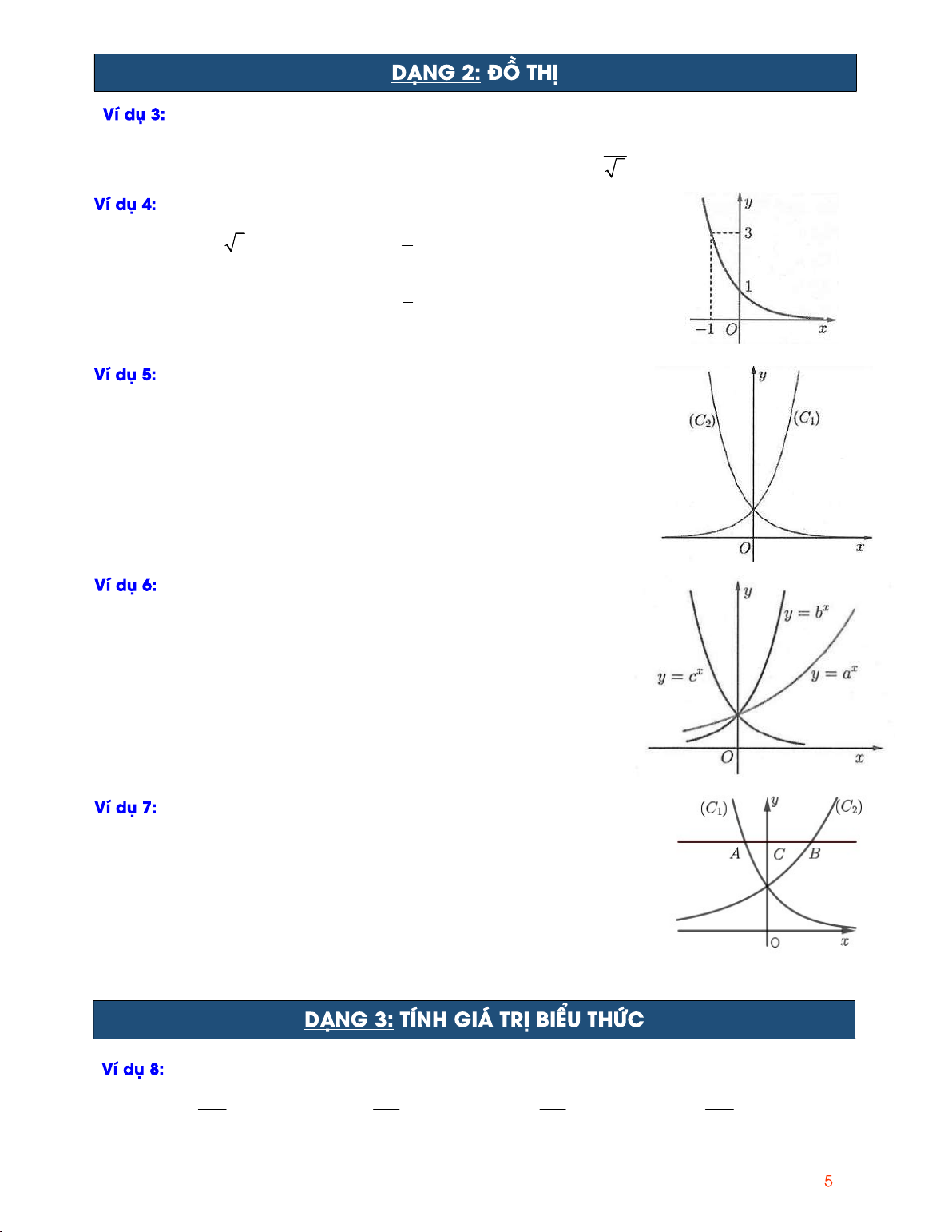
Đồ thị hình bên là của hàm số nào? x x  1 
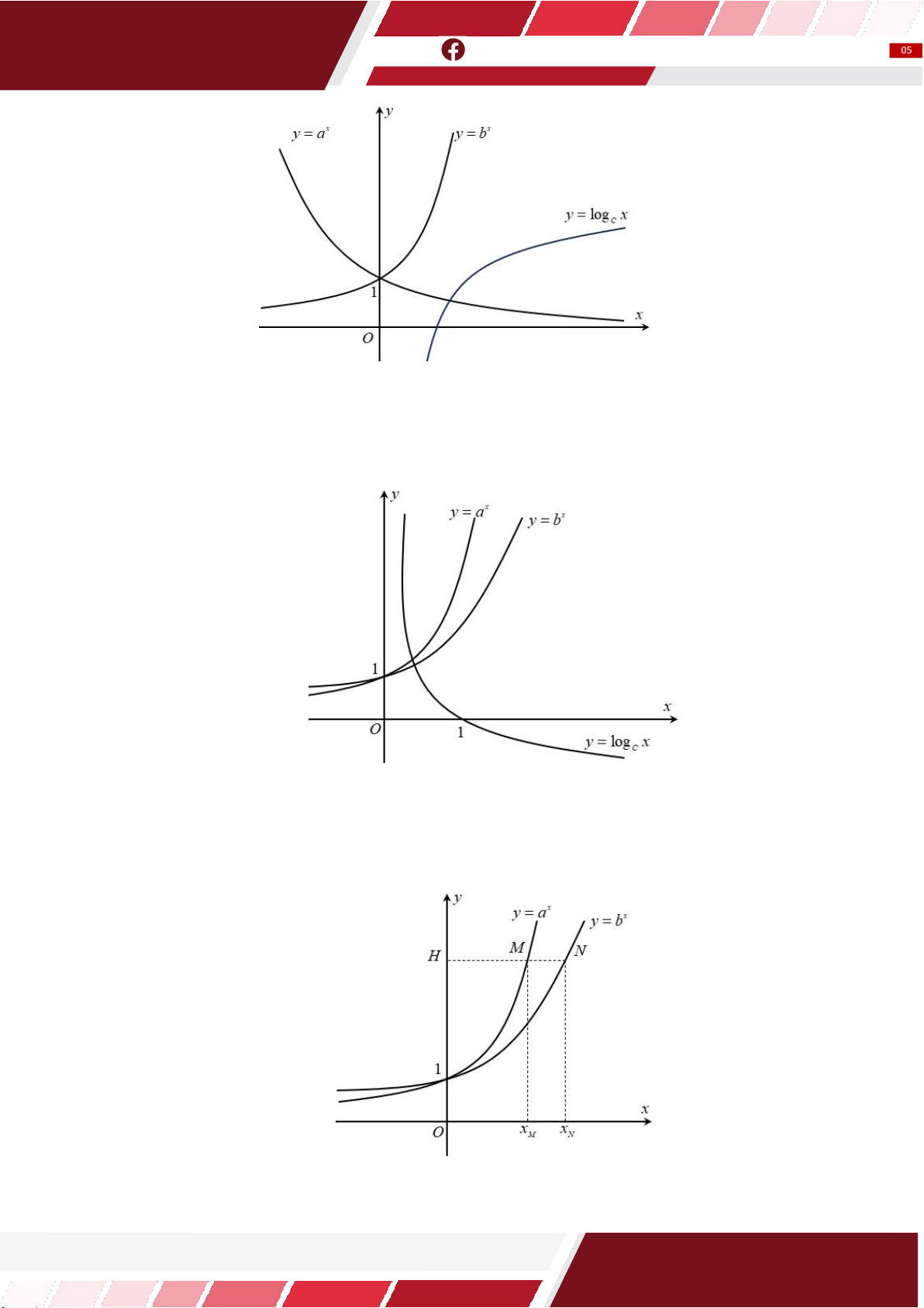
A. y   3 . B. y  .    2   1 xC. 3x y  . D. y  .    3  Cho hai hàm số x y a , x
y b với a,b là hai số thực dương
khác 1, lần lượt có đồ thị là C và C như hình bên. Mệnh 2  1 
đề nào dưới đây đúng?
A. 0  a  1  . b
B. 0  b  1  . a
C. 0  b a 1.
D. 0  a b 1.
Cho a, b, c là các số thực dương khác 1. Đồ thị hàm số x y a , x y b , x
y c được cho trong hình bên. Chọn khẳng định đúng?
A. 1  c a  . b
B. c a b 1.
C. c  1  b  . a
D. c  1  a  . b Cho hai hàm số x y a và x
y b có đồ thị lần lượt là
C và C như hình vẽ. Đường thẳng y  2 cắt đồ thị 2  1 
C và C và trục tung lần lượt tại các điểm , A B,C 2  1 
biết BC  2AC . Khẳng định nào sau đây là đúng? A. 2
a b . B. 2
b a . C. 2 a b  1. D. 2 ab  1.
Cho 2x  5 . Giá trị của biểu thức x 1 2 4 2 x T     bằng 504 104 104 504 A. . B. . C. . D. . 5 5 25 25
2x  2x  3
Cho 4x  4x  34 . Tính giá trị của biểu thức T  . x 1  1 1 2  2 x 3 3 3 3 A. T  . B. T  . C. T   . D. T  . 4 11 11 13 x a
Cho hàm số f x 
. Ta có f x  f 1 x 1. x a a x  1   2   2022 
Cho hàm số f x 9 
. Tính tổng S ff  f . 9x  3        2023   2023   2023  3008 A. S  1002 . B. S  . C. S  1003.
D. S  1011. 3
ĐỒ THỊ VÀ HÀM SỐ LÔGARIT
Cho số thực a  0, a  1 . Hàm số y  log x được gọi là hàm số logarit cơ số . a a
Hàm số y  log f x có điều kiện xác định là: f x  0 . a  
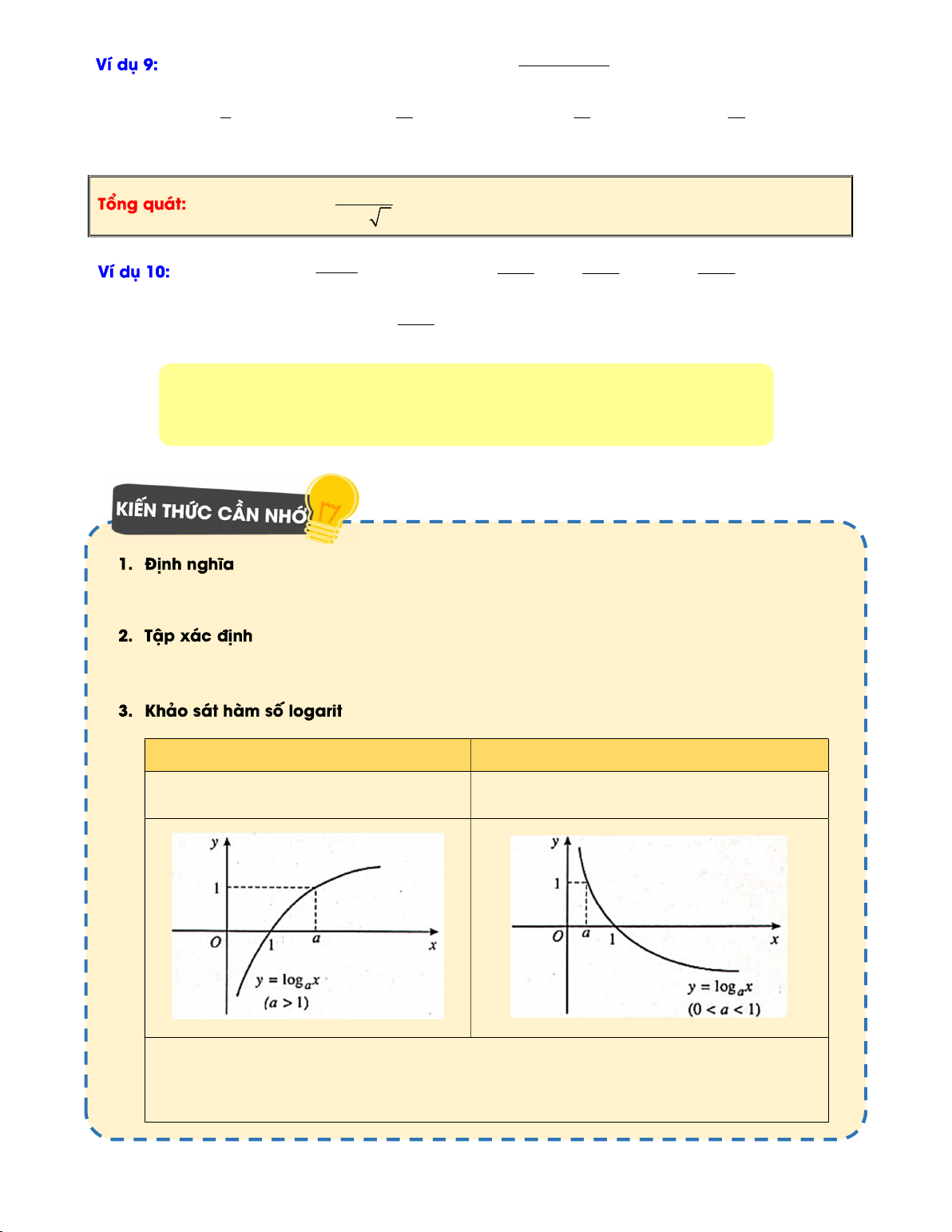
y  log x a  0, a   1 a a  1 0  a 1
Hàm số luôn đồng biến trên 0;
Hàm số luôn nghịch biến trên 0;
 Đồ thị hàm số y  log x 1; 0 , ;
a 1 và luôn nằm bên phải trục tung. a đi qua các điểm      Đồ thị hàm số x
y a và y  log x đối xứng nhau qua đường thẳng y x . a
Tìm tập xác định D của hàm số y  log 2x 10 1 là 3    9  9  A. D   5;  . B. D  ;    .
C. D  5;. D. D  ;    .  2   2 
Tập xác định của hàm số y  log 3 2x là: 2    3   3 
A. D  0; . B. D  ;    .
C. D   ;0   . D. D  ;   .  2   2 
Tập xác định của hàm số y  log  2
x  4x  3 là 3  A.   ;1 3;. B. 1;3. C.   ;1 . D. 3;.
Tập xác định của hàm số y  log  2
3  2x x là 2  A. D   1;   1 . B. D   1  ;3. C. D   3;   1 .
D. D  0;  1 .
Tập xác định của y   2
ln x  5x  6 là
A. ;23; . B. 2;3 . C. 2;3. D.  ;
 2 3;.
Tập xác định của hàm số y  log x  log 3  x là A. 3; . B. 0;  3 . C. 3; . D. 0;3 .
Tìm tập xác định D của hàm số y  log x  2 1  log  2 4  x . 2021 2020 
A. D  2;2 \1
B. D  1;2
C. D  2;1
D. D  2;2 1
Tìm tập xác định của hàm số y  log . 5 6  x A.  ;6   B. C. 0; D. 6;
Tìm tập xác định D của hàm số y  log  2 x  2x . 9   1    A. D  0;  .
B. D    1 ;0  ;    . 2     2   1    C. D  0;  
D. D    1 ;0  ;    .  2  2 
Tìm tập xác định của hàm số  2 x y
 log 3  x . A. 0; . B. 0;3 . C.  ;3   . D. 0;3 .
Có bao nhiêu giá trị nguyên thuộc tập xác định của hàm số y  log 6  x x  2 ?   A. 7 . B. 8 . C. 9 . D. Vô số. x  3
Tìm tập xác định D của hàm số y  log . 5 x  2
A. D   ;  2
  3; B. D   2;  3
C. D   ;  2
  3;
D. D   \  2
Tìm tất cả các giá trị thực của tham số m để hàm số y   2
log x  4x m   1 có tập xác định là  . A . m  4  . B. m  0 . C. m  4  . D. m  3  .
Có bao nhiêu giá trị nguyên của tham số m để hàm số y  m   2 ln
1 x  2m  3 x 1 có tập xác định là  ? A. 3. B. 5. C. 4. D. 2.
Có bao nhiêu giá trị nguyên của tham số m 10
 ;10 để hàm số y  log  2
x  2x m xác 2 
định với mọi x 0;? A. 8. B. 7. C. 9. D. 18.
Tìm tất cả các giá trị của m để hàm số y   2
ln x mx  2m  
1 xác định với mọi x  1;2 . 1 3 3 1 A. m   . B. m  . C. m  .
D. m   . 3 4 4 3
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số 1 y   log
x m xác định trên khoảng 2;3? 3 2m 1 x A. 1. B. 2 . C. 4 . D. 3 .
Hàm số nào dưới đây đồng biến trên khoảng 0;   ?
A. y  log x .
B. y  log x .
C. y  log x .
D. y  log x . 3  e 1 6 3 4
Hàm số nào dưới đây nghịch biến trên tập xác định của nó? x   
A. y  log x B. y  log
x 1 C. y  log x y  2     3  D.  3  4
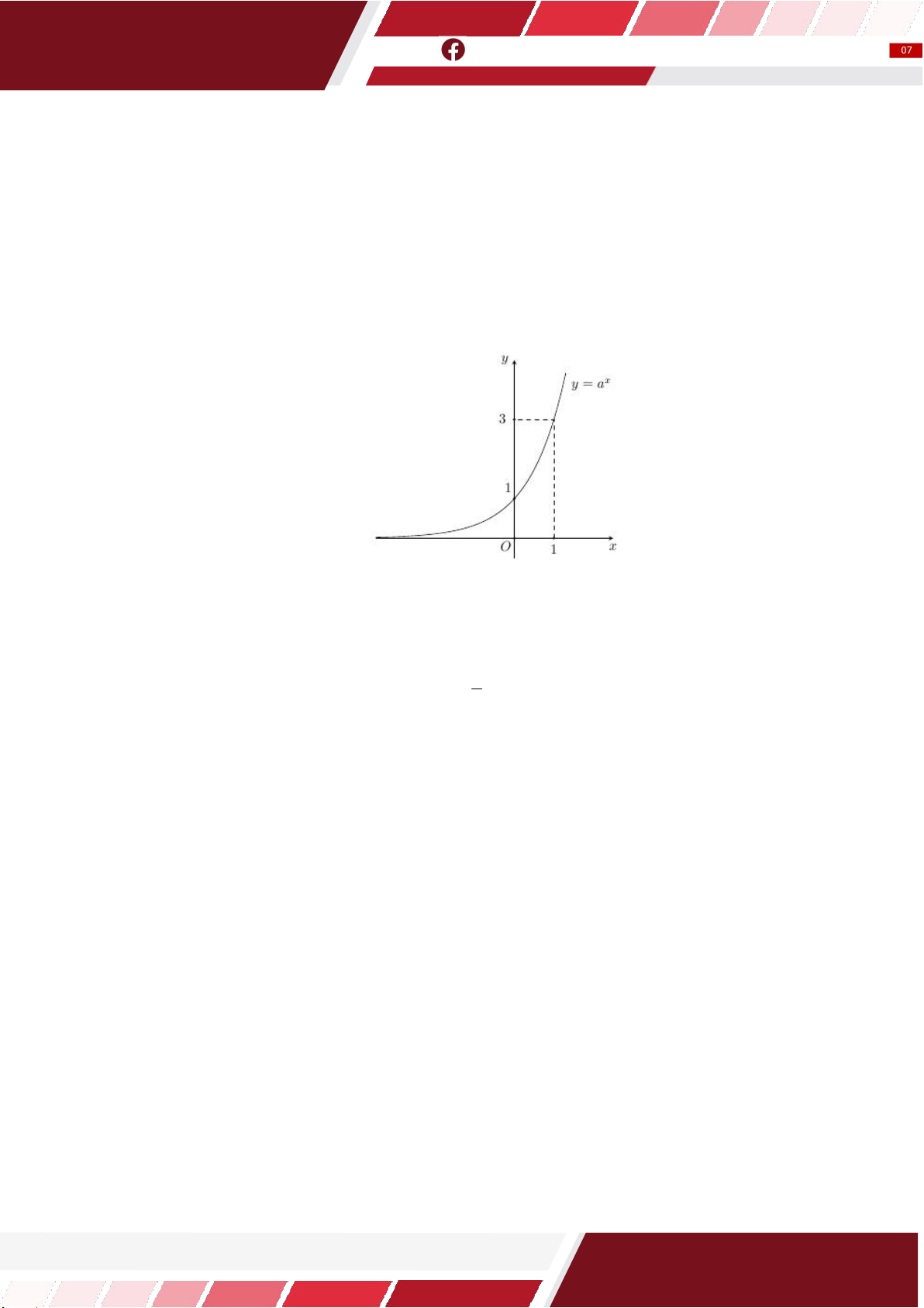
Đồ thị hình bên là của hàm số nào? A. y  log . x B. 2 .x y   1 2 C. 2 .x y D. y  log . x 2 y
Tìm a để hàm số y  log x 0  a  
1 có đồ thị là hình bên. a 1 2
A. a  2 B. a 2 O x 1 1 2
C. a D. a  2 2 Cho đồ thị hàm số x
y a , y  log x (như hình vẽ). Khẳng b
định nào sau đây đúng?
A. 0  b  1  a
B. 0  a  1  b
C. a  1 và b 1
D. 0  a 1 và 0  b  1
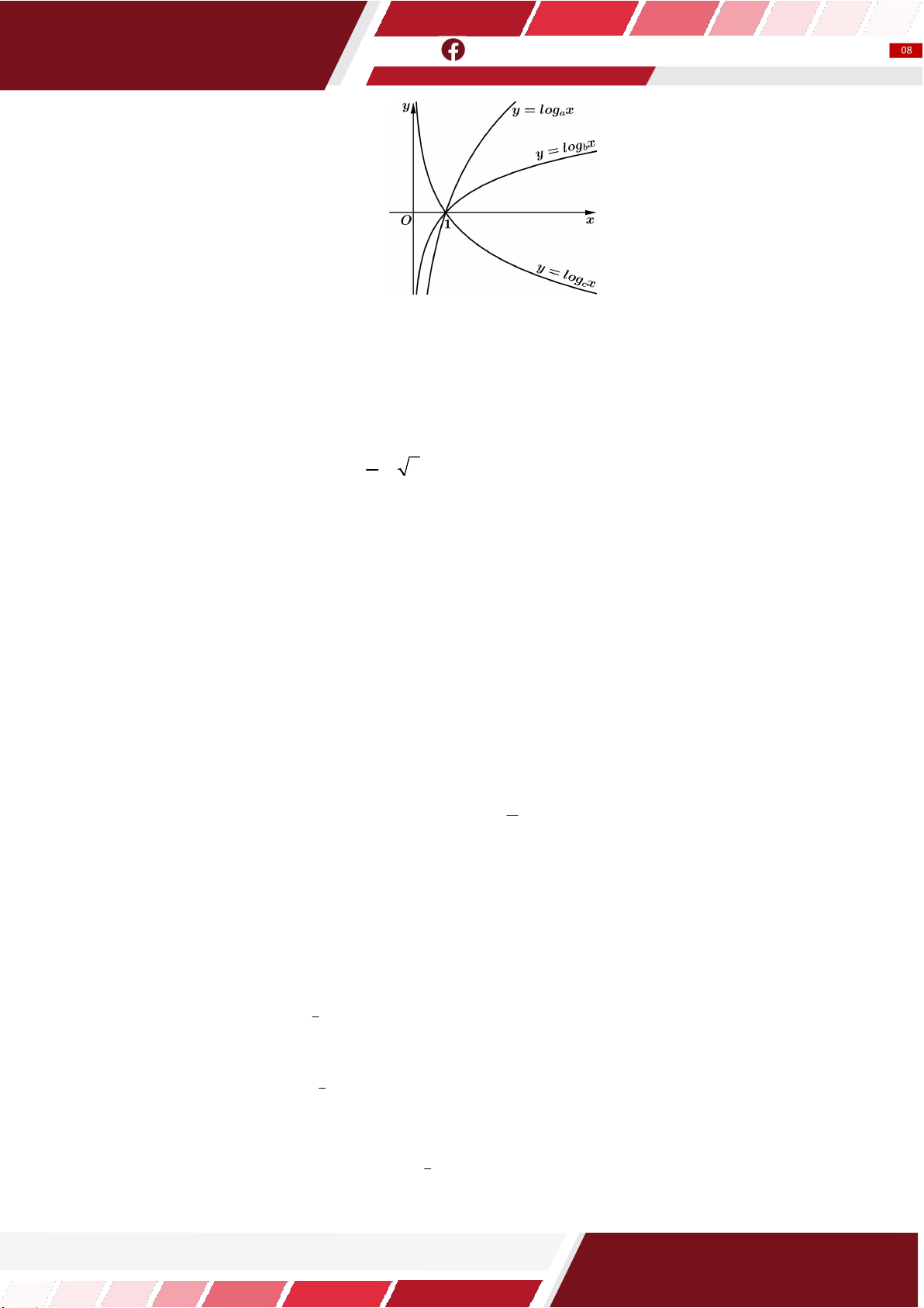
Cho hai số a,b  0, a  1,b  1. Đồ thị các hàm số
y  log x, y  log x được cho trong hình vẽ bên. Mệnh a b đề nào sau đây đúng?
A. 1  a b  0.
B. 1  b a  0.
C. b a 1.
D. a b  1.
Cho ba số a,b, c  0, a  1,b  1,c  1. Đồ thị các hàm số
y  log x, y  log ,
x y  log x được cho trong hình vẽ a b c
bên. Mệnh đề nào sau đây đúng?
A. a b  . c
B. b a  . c
C. c b  . a
D. c a  . b
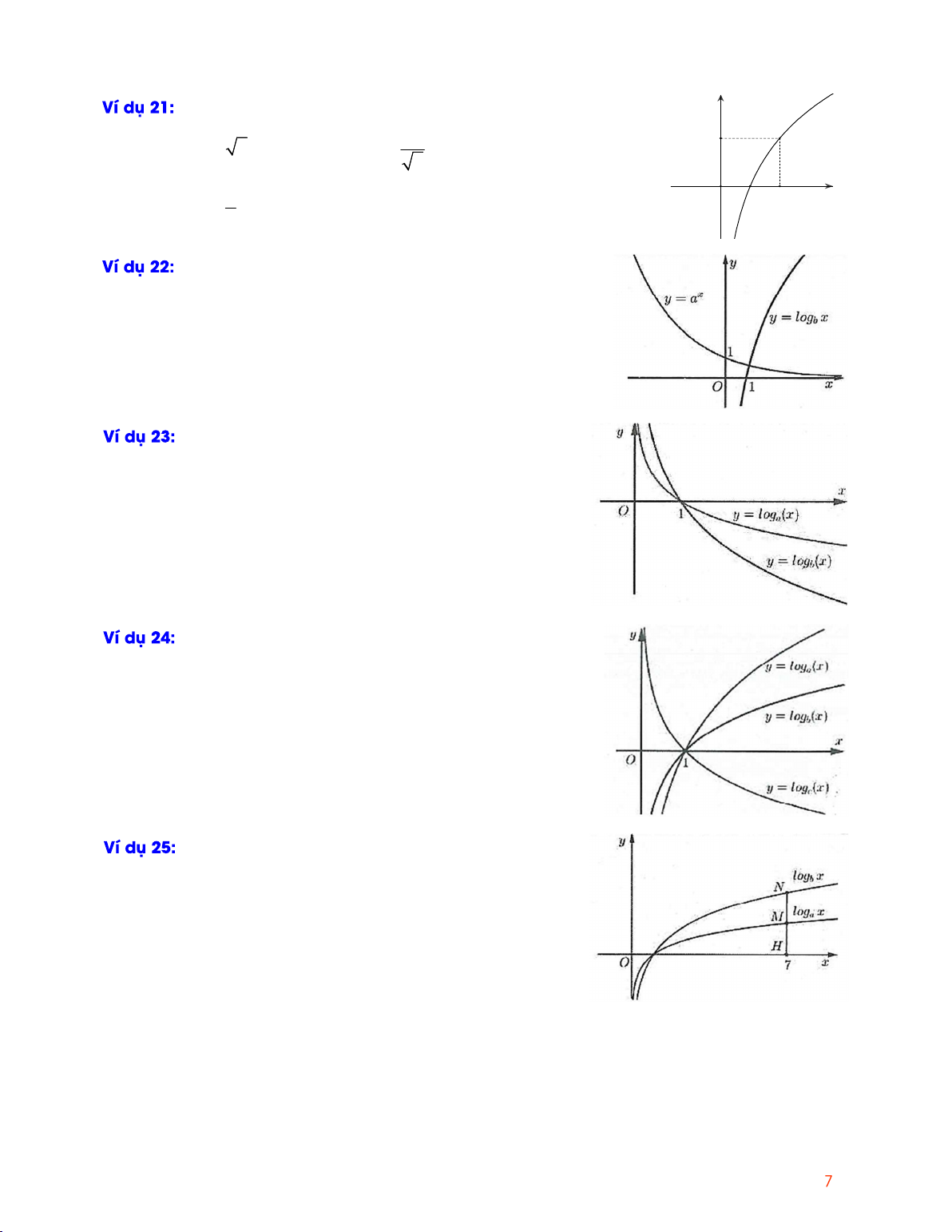
Cho hàm số y  log x và y  log x có đồ thị như hình a b
vẽ bên. Đường thẳng x  7 cắt trục hoành, đồ thị hàm số
y  log x và y  log x lần lượt tại H , M và N. Biết a b
rằng HM MN. Mệnh đề nào sau đây là đúng? A. a  7 . b B. 2 a b . C. 7 a b . D. a  2 . b
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556 VINCENT TUẤN
ĐỀ TỰ LUYỆN HÀM SỐ MŨ - LŨY THỪA - LOGARIT Môn: Toán 11 ĐỀ SỐ 01
Thời gian làm bài: 90 phút (không tính thời gian giao đề) ĐỀ BÀI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án. 3 Câu 1:
Tập xác định của hàm số 2 y x là A. 0; . B. 2; . C.  . D.  \   0 . Câu 2:
Tập xác định của hàm số y  log x là A. 1  ;   . B. 0; . C. 0;   . D. 1; . Câu 3:
Tập xác định D của hàm số y  ln 1 x là A. D   \ {1}. B. D   . C. D  ;  1 .
D. D  1; . Câu 4:
Tập xác định của hàm số y  log x 1 là 2   A.  \   1 . B. 1; . C. 1; . D. ;  1 . Câu 5:
Hàm số y  x  2022 1 có tập xác định là A. D   .
B. D  1; .
C. D  1; . D. D   \   1 . Câu 6:
Tập xác định của hàm số y  2  ln x là A.  2 0;e  2 2  . B.  ;  e  . C.  2  ;  e  . D. e ;  . Câu 7:
Tập xác định của hàm số x1 y 5 1  2 là A. 0;   . B.  \   0 . C.  . D. 0;  . Câu 8:
Tập xác định của hàm số y  log  2
x  7x  3 là: 1  2
A. 8;7  0;1 .
B. 8;7  0;  1 .
C. 8;7  0;1 .
D. 8;7 0;  1 . Câu 9:
Tập xác định D của hàm số y  x  35  log 4  x là 3   A. D  3;4 .
B. D  ;4 \   3 .
C. D  4;  .
D. D  ;4 .
Câu 10: Tìm tất cả các giá trị thực của tham số m để hàm số y  log  2
x  4x m  1 xác định với mọi 3  x   . A. m  3 . B. m  3 . C. m  3 . D. m  3 .
Câu 11: Tìm tập xác định của hàm số y ln 3 xx    A.  ;   3 . B. 0; . C. ;3 . D. 0;3 .
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556 1
Câu 12: Tìm tập xác định D của hàm số 3
y x  log 1 x . 3   A. D  0;  1 .
B. D  0; . C. D  0;  1 .
D. D  1; . 1
Câu 13: Tập xác định của hàm số y  là log x 1 2 A.  \   2 . B. 0; . C. 0; \   2 . D. 0; \   1 .
Câu 14: Tập xác định của hàm số y  x  2019 2021 2021 là A. 2021; . B.  \ 202  1 . C. 2021; . D.  ;  202  1 . 1
Câu 15: Tập xác định D của hàm số y  là: 2x log 1 3 x 1
A. D  ;3 .
B. D  1; .
C. D  3;  1 . D. D  0;3 . 1
Câu 16: Tìm tất cả các giá trị thực của tham số m để hàm số 2 x mx 1 y e   
có tập xác định là  . m  2 A.  . B. m  2 . C. 2  m  2 . D. m  2 . m  2
Câu 17: Tất cả các giá trị thực của tham số m để hàm số y   2
log x  2x m  1 có tập xác định là  . A. m  0 . B. m  0 . C. m  2 . D. m  2 .
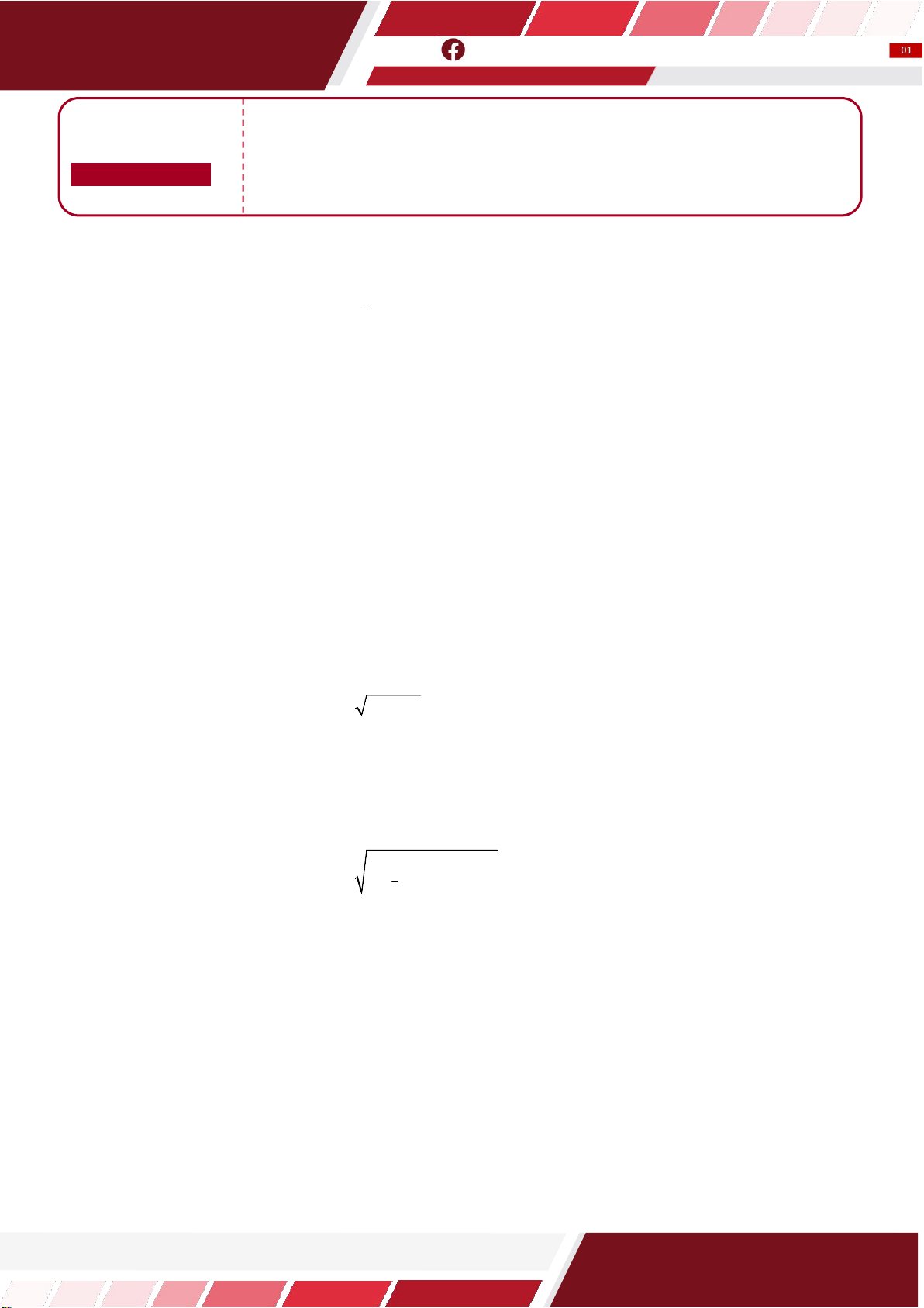
Câu 18: Cho các đồ thị hàm số x
y a , y  log x, c
y x ở hình vẽ sau đây. b
Khẳng định nào sau đây đúng?
A. 0  c  1  a  . b
B. c  0  a  1  . b
C. c  0  a b  1.
D. 0  c a b  1. Câu 19: Cho các hàm số x
y a , y  log x, y  log x có đồ thị như hình vẽ bên. Chọn khẳng định đúng? b c
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
A. b c a .
B. b a c .
C. a b c
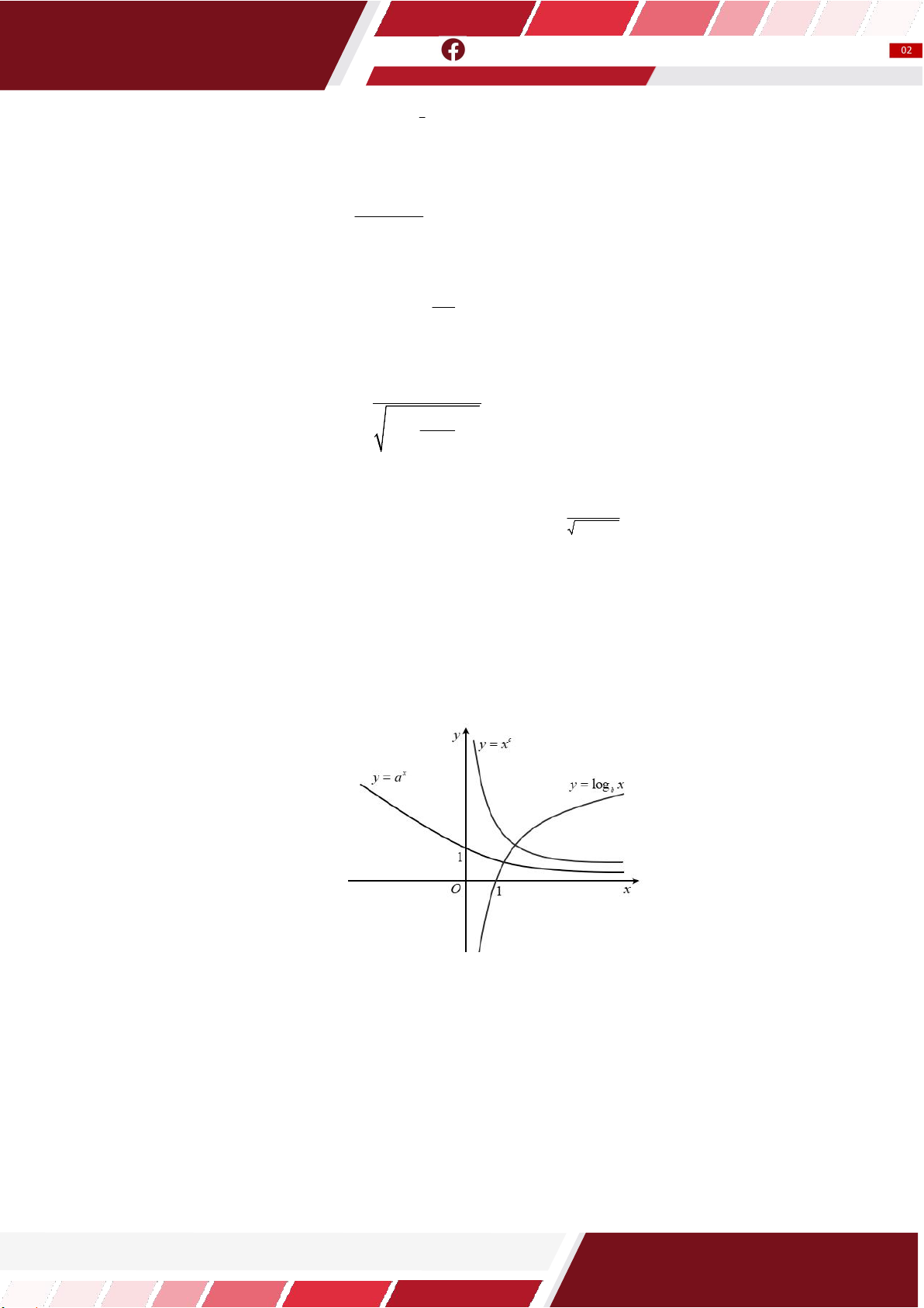
D. c b a . Câu 20: Cho ba hàm số 2x y
, y x , y f x có đồ thị như hình bên, mệnh đề nào sau đây đúng?
A. y f x  log x . B. y f x  ln x .
C. y f x  log x . D. y f x  log x . 1 2 2
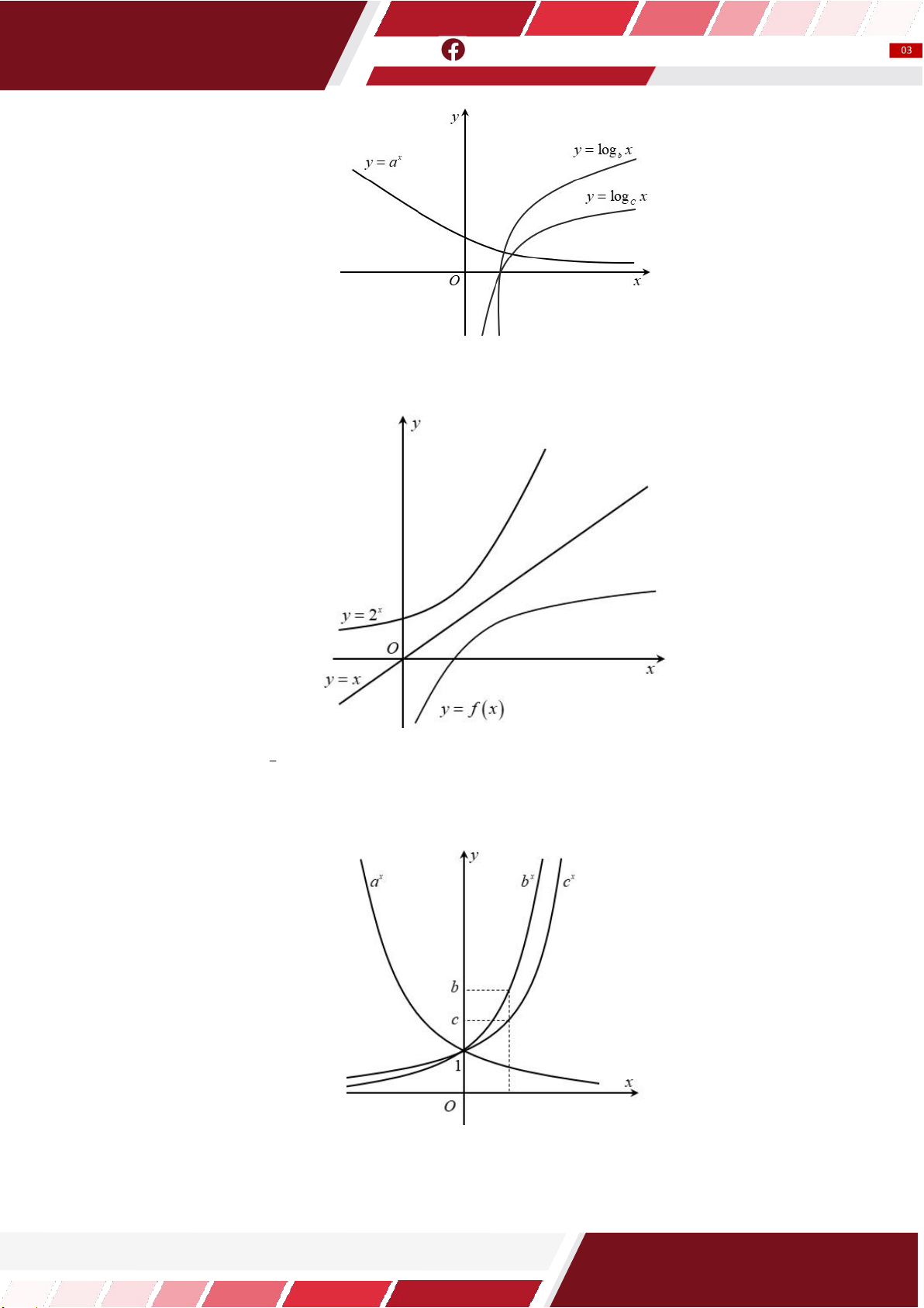
Câu 21: Cho a , b , c là ba số thực dương khác 1. Đồ thị hàm số x y a , x y b , x
y c được cho ở hình
vẽ dưới đây. Mệnh nào nào sau đây đúng?
A. a b c .
B. b c a .
C. c a b .
D. a c b .
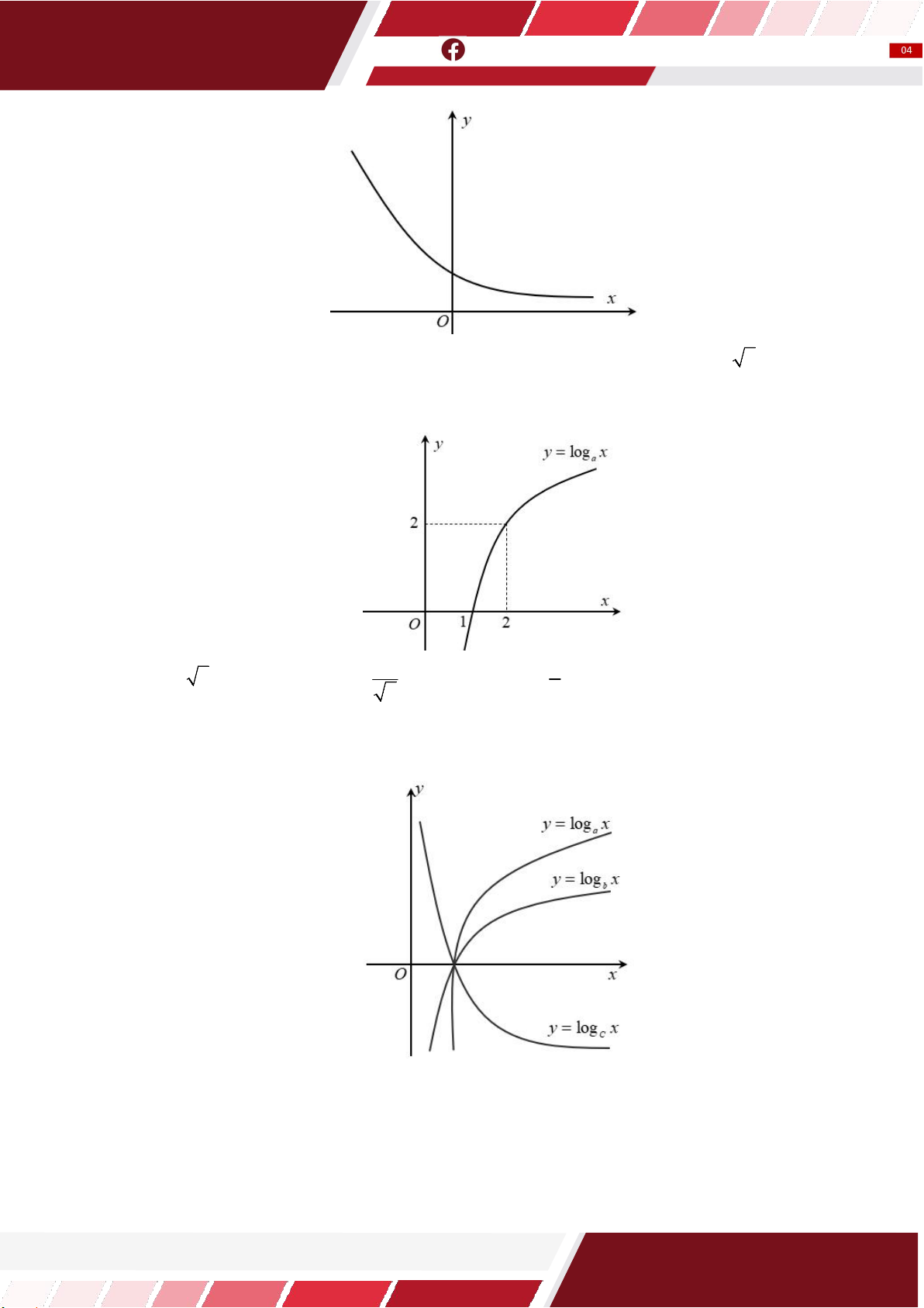
Câu 22: Đường cong trong hình bên là của đồ thị hàm số nào sau đây?
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556 x A. y  log x . B. 0,8x y  . C. y  log x . D. y   2 . 2 0,4
Câu 23: Tìm a để đồ thị hàm số y  log x 0  a  1 có đồ thị là hình bên. a  1 1 A. a  2 . B. a  . C. a  . D. a  2 2 2 Câu 24: Cho a, ,
b c là ba số dương khác 1. Đồ thị các hàm số y  log x, y  log x, y  log x như hình vẽ a b c
bên. Mệnh đề nào dưới đây là mệnh đề đúng?
A. a b c .
B. b c a .
C. c a b .
D. c b a . Câu 25:
Trong hình vẽ dưới đây có đồ thị của các hàm số x y a , x
y b , y  log x c .
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
Mệnh đề nào sau đây đúng?
A. a b c .
B. a b c .
C. b c a .
D. a c b .
Câu 26: Cho đồ thị hàm số x y a ; x
y b ; y  log x như hình vẽ. Tìm mối liên hệ của a, , b c . c
A. c b a .
B. b a c .
C. a b c .
D. c a b .
Câu 27: Cho a,b là các số thực dương khác 1, đường thẳng d song song trục hoành cắt trục tung, đồ thị hàm số x
y a , đồ thị hàm số x
y b lần lượt tại H , M , N (như hình bên). Biết HM  3MN .
Mệnh đề nào sau đây đúng? A. 4a  3b . B. 4 3 b a . C. 3 4 b a . D. 3a  4b .
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556 a
Câu 28: Biết hàm số f x 
có đồ thị đối xứng với đồ thị hàm số 3x y
qua đường thẳng x  1 . 2 b  3x
Biết a , b là các số nguyên. Chọn khẳng định đúng trong các khẳng định sau: A. 2 b  9a . B. 2 b  4a . C. 2 b  6a . D. 2 b a .
Câu 29: Đồ thị hàm số y f x đối xứng với đồ thị của hàm số 2022x y  qua điểm I 1;  1 . Giá trị của  1 
biểu thức f 2  log  bằng 2022   2023 A. 2021. B. 2023 . C. 2020 . D. 2020 .
Câu 30: Đồ thị hàm số y f x đối xứng với đồ thị hàm số x
y a a  0,a  
1 qua điểm I 1;  1 . Giá trị  1 
của biểu thức f 2  log  bằng a   2023  A. 2022 . B. 2024 . C. 2023 . D. 2021.
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.  2023 x  Câu 1:
Cho các hàm số y  log x và y
. Xét tính đúng sai của các khẳng định sau: 2024    2024  2023 a) Hàm số y  log
x có tập giá trị là  . 2024 2023  2023 x  b) Hàm số y    đồng biến trên  .  2024 
c) Đồ thị hàm số y  log
x nằm bên phải trục tung. 2024 2023  2023 x
d) Đồ thị hàm số y    cắt trục tung.  2024  Câu 2:
Cho hàm số y  log x 0  a  
1 có đồ thị C  . Xét tính đúng sai của các khẳng định sau: a
a) Tập xác định của hàm số là D  0; và tập giá trị của hàm số là T  
b) Đồ thị C đi qua điểm 1;0 , nằm bên phải trục tung
c) Hàm số đồng biến trên  khi a  1.
d) Đồ thị C và đồ thị hàm số y  2  log 4  x đối xứng nhau qua điểm I 2;  1 . a
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556 Câu 3:
Cho hàm số y  log x có đồ thị C . Xét tính đúng sai của các khẳn định sau: 5
a) Tập xác định của hàm số y  log x là D   . 5
b) Hàm số đồng biến trên khoảng 1; .
c) Đồ thị C nằm phía trên trục hoành.
d) Đồ thị C cắt trục hoành tại điểm có hoành độ bằng 1. Câu 4: Cho đồ thị hàm số x
y a dưới đây. Xét tính đúng sai của các khẳng định sau:
a) Hàm số đã cho nghịch biến trên khoảng 0;  1 .
b) Hàm số cho bởi công thức 3x y  . 1
c) Đồ thị hàm số đã cho cắt đường thẳng y
tại điểm có hoành độ không âm. 3
d) Đồ thị hàm số đã cho cắt đường thẳng y  x 1 tại điểm có hoành độ dương. Câu 5:
Cho các hàm số y  log x, x
y a với a là số thực dương khác 1 . Xét tính đúng sai của các a khẳng định sau: a) Đồ thị hàm số x
y a và đồ thị hàm số y  log x đối xứng nhau qua đường thẳng y x . a
b) Hàm số y  log x và hàm số x
y a có cùng tập giá trị. a c) Hàm số x
y a với 0  a  1 nghịch biến trên khoảng  ;   . d) Đồ thị hàm số x
y a với a  0 và a  1 luôn đi qua điểm A ; a  1 . Câu 6:
Cho các hàm số y  log x, y  log x, y  log x với a, ,
b c là ba số thực dương khác 1. Xét tính a b c
đúng sai của các khẳng định sau:
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
a) Đồ thị các hàm số trên đều đi qua điểm ( A 1;0) .
b) Hàm số y  log x đồng biến trên khoảng 0;  c
c) Từ đồ thị ta có: 0  c 1  a b .
d) Đường thẳng y  3 cắt hai đồ thị y  log x, y  log x tại các điểm có hoành độ lần lượt là a b a
x ; x sao cho x  2x . Khi đó 3  2 . 1 2 2 1 b Câu 7: Cho hàm số x
y a với 0  a  1. Xét tính đúng sai của các khẳng định sau: a) Hàm số x
y a có tập xác định D  0; b) Đồ thị hàm số x
y a đi qua điểm 0;  1 . c) Hàm số x
y a đồng biến trên  nếu 0  a  1. d) Hàm số x
y a có tập giá trị là a; nếu x  1 và a  1. Câu 8: Cho hàm số 2x y
. Xét tính đúng sai của các khẳng định sau:
a) Hàm số có tập xác định D   .
b) Hàm số nghịch biến trên khoảng  ;  
c) Đồ thị hàm số đi qua điểm A2;4  1 x  d) Đồ thị hàm số 2x y
đối xứng với đồ thị y    qua trục tung.  2  Câu 9:
Cho hàm số y  log x . Xét tính đúng sai của các khẳng định sau: 4
a) Hàm số có tập xác định D  
b) Hàm số có tập giá trị T  
c) Hàm số đồng biến trên khoảng  ;  
d) Đồ thị hàm số cắt đường thẳng y  1 tại điểm có hoành độ bằng 3
Câu 10: Cho các hàm số y  log x và 2x y
. Xét tính đúng sai của các khẳng định sau: 1 2 a) Có hai hàm số mũ.
b) Đồ thị hàm số y  log x đi qua điểm M 2;  1 . 1 2 c) Đồ thị hàm số 2x y
đi qua điểm N 1;  1 . d) Hai đồ thị hàm số 2x y
và y  log x cắt nhau tại 1 điểm. 1 2
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
Câu 11: Cho các hàm số y  log x ; 2x y
; y  log x ; y  log x và 0,5x y  . Xét tính đúng sai 1 3 0,5 2
của các khẳng định sau: a) Hàm số 2x y
có tập giá trị là 0; .
b) Hàm số y  log x có tập giá trị là  . 3
c) Có hai hàm số có tập giá trị là  .
d) Có hai hàm số có tập giá trị là 0; .  1 x
Câu 12: Cho các hàm số y  log x ; x
y   ; y  ln x ; y  log x và y  . Xét tính đúng sai của 1 0,2    2  3 các khẳng định sau:  1 x  a) Hàm số y  
 nghịch biến trên  .  2 
b) Hàm số y  log x
nghịch biến trên khoảng 0; .
c) Có ba hàm số nghịch biến trên tập xác định.
d) Có hai hàm số đồng biến trên 0; .
Câu 13: Cho hàm số y  log 5x  3 . Xét tính đúng sai của các khẳng định sau: 3  
a) Tập xác định của hàm số là D  0; .  3 
b) Hàm số đồng biến trên ;   .  5 
c) Đồ thị hàm số đi qua điểm M 2;7 .  4 12
d) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x trên ;  là 2 5 5   
Câu 14: Cho ba điểm A ;
b log b, B ;
c 2log c và C  ;
b 3log b với a, ,
b c dương và đều khác 1. aaa
a) B là trung điểm của AC khi và chỉ khi b c  0 . b) Ba điểm , A ,
B C tạo thành tam giác vuông tại A khi và chỉ khi b  2c . c) Khi ba điểm , A ,
B C tạo thành tam giác thì có diện tích là S  c b 2 .log b . a
d) Khi B là trọng tâm của tam giác OAC (với O là gốc tọa độ) thì giá trị của biểu
thức S  2b c là bằng 9. 2 1   xkhi x  1
Câu 15: Cho hàm số y   x 1
liên tục tại điểm x  1
ax  4 khi x 1 a) Hàm số x
y a nghịch biến trên  ;   . b) x 1 a  khi x  4  . 16
c) Đồ thị hàm số y  log x đi qua điểm 2;  1 . a
d) Giá trị nhỏ nhất của hàm số x 1  12x y aa bằng 3 . 2
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC
CHINH PHỤC KỲ THI THPT QUỐC GIA 2026
Anh Vincent Tuấn – Luyện Thi Toán 9-10-11-12 0398054556
NẾU HÔM NAY EM CHƯA HỌC GÌ THÌ ĐỪNG NÊN NGỦ Vincent Tuấn
HỌC TOÁN MỖI NGÀY – THÀNH CÔNG MỖI BƯỚC

Tài liệu liên quan: