





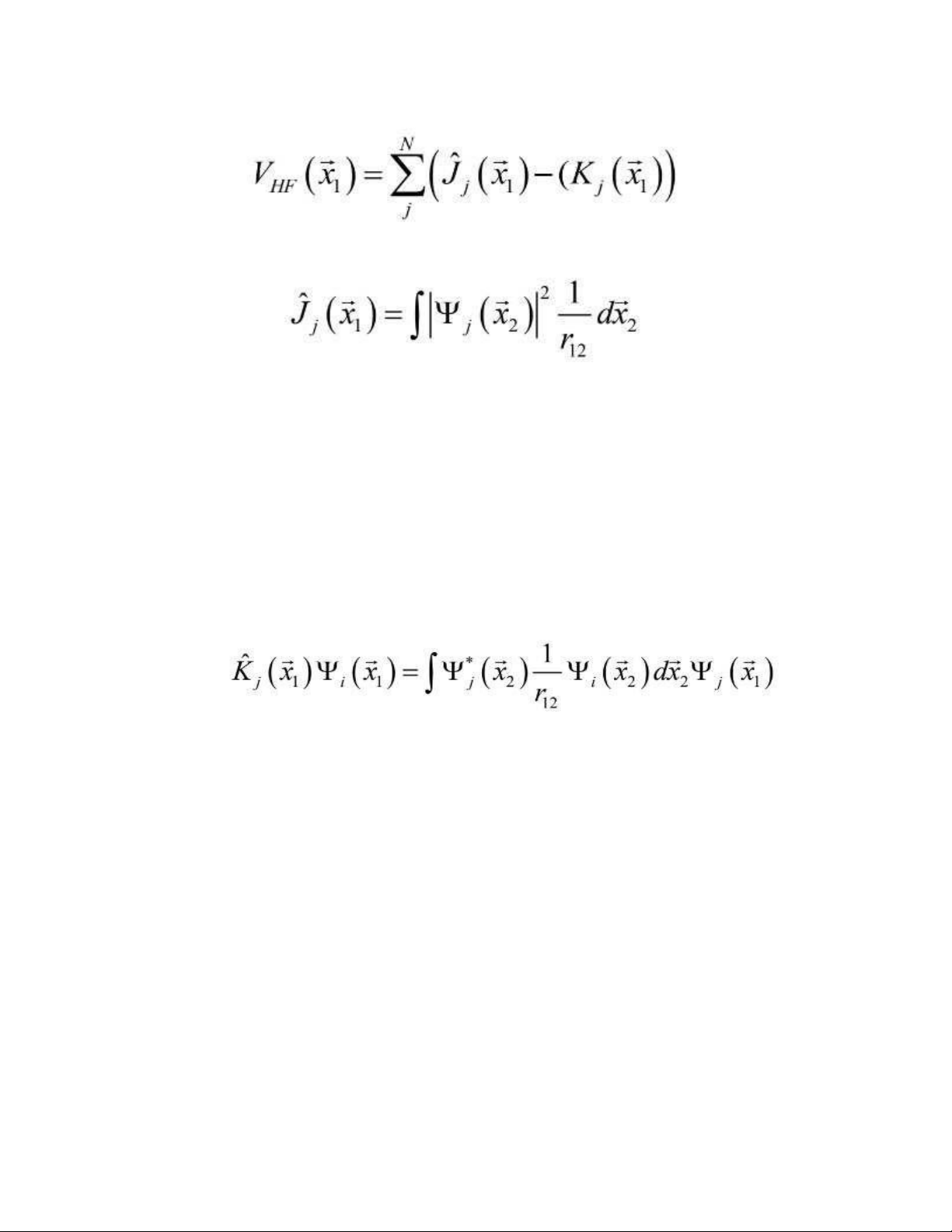

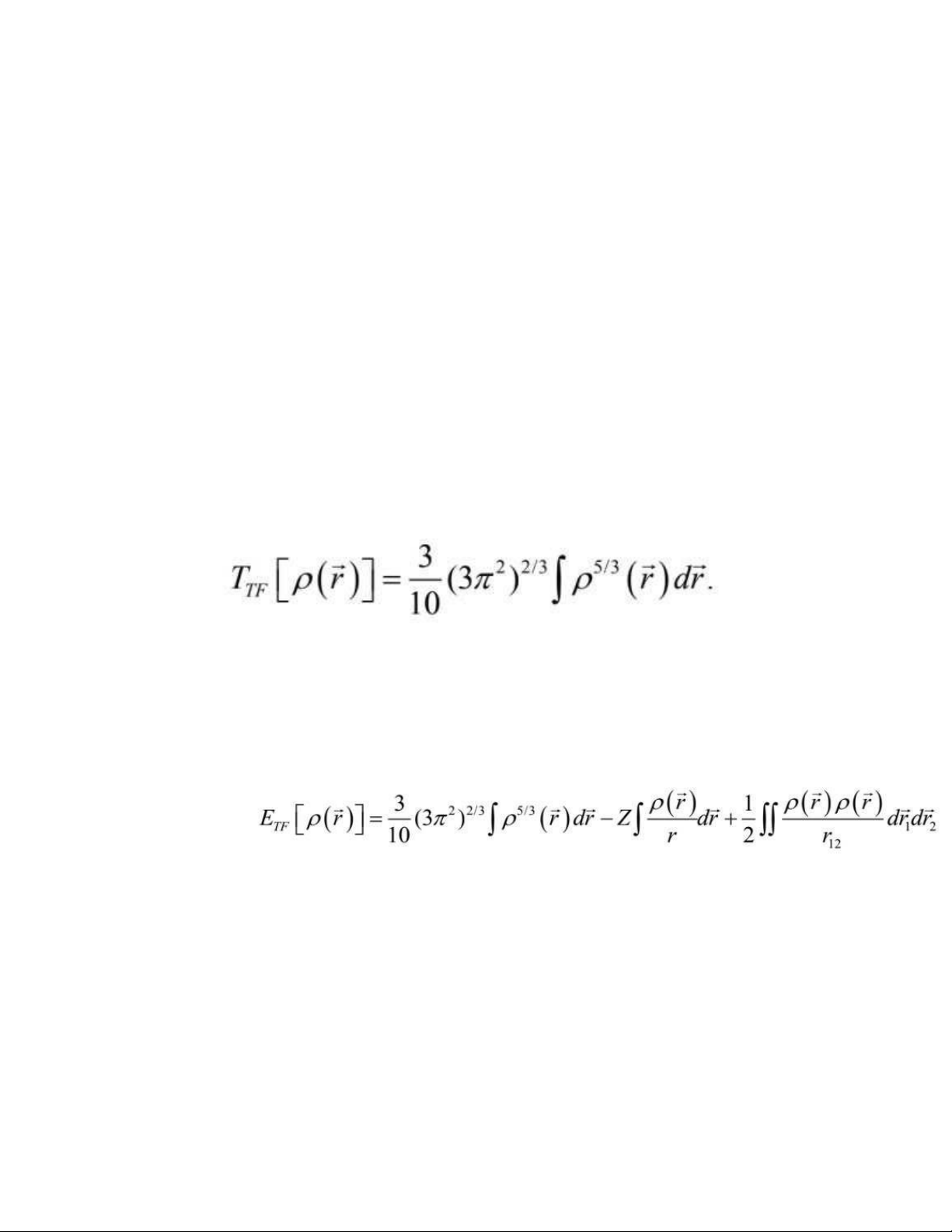


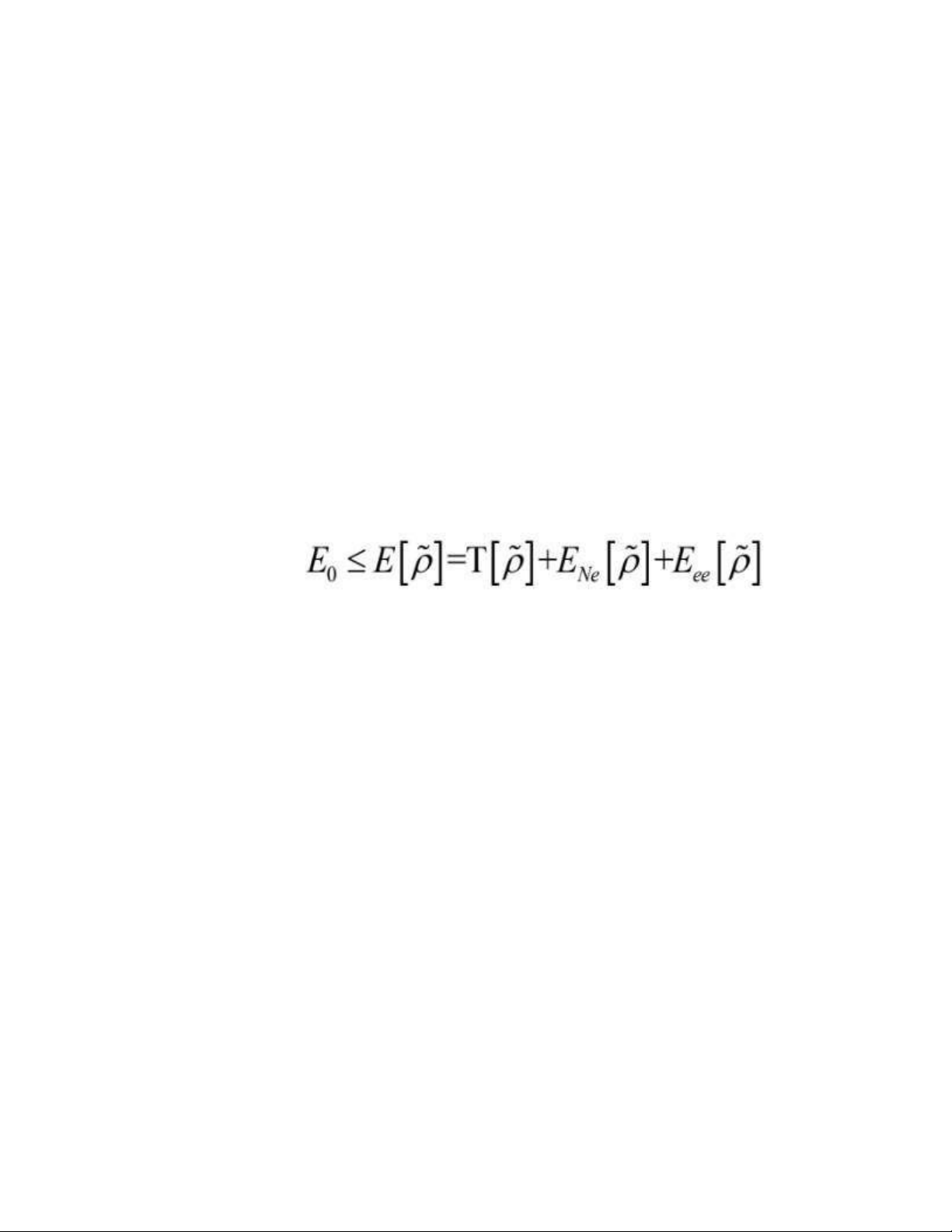

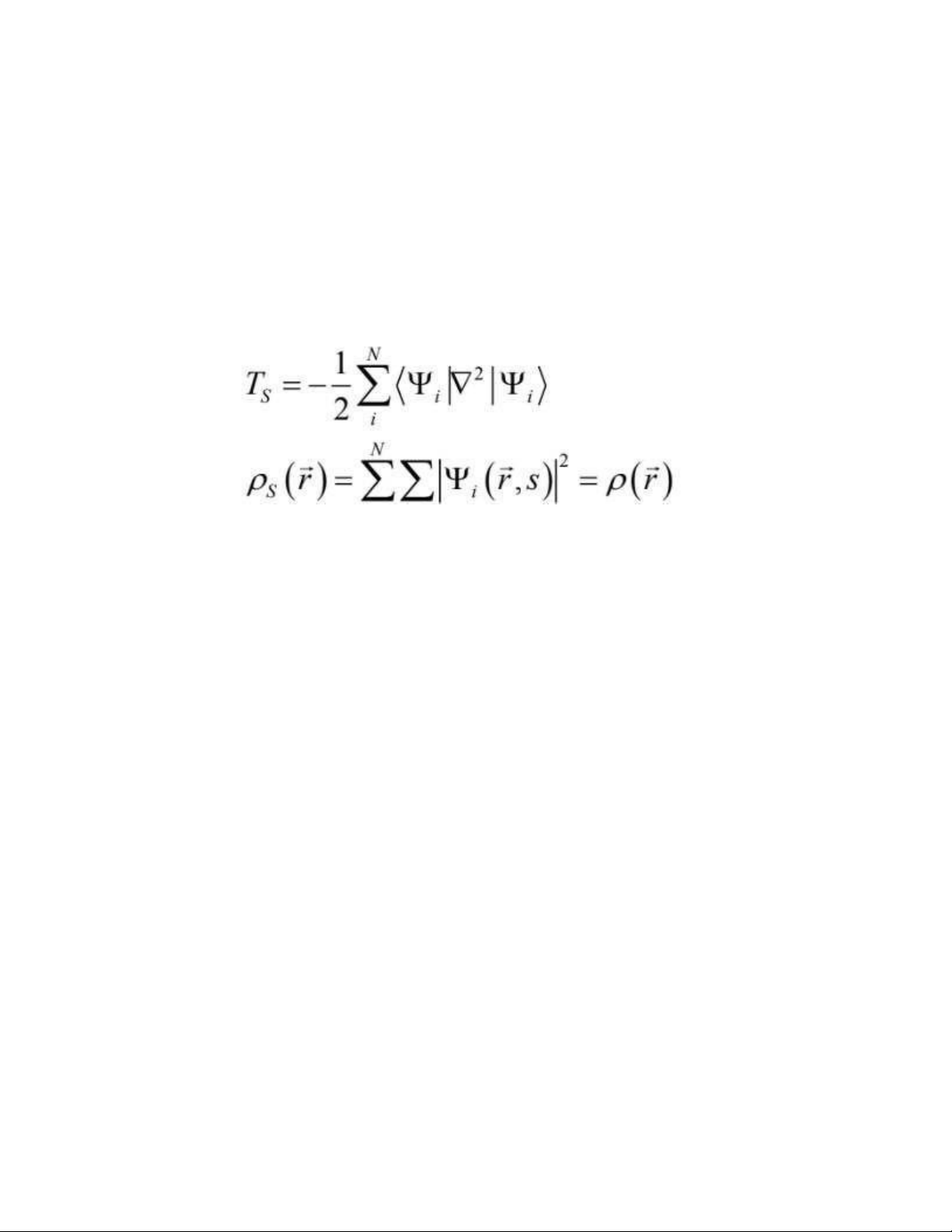



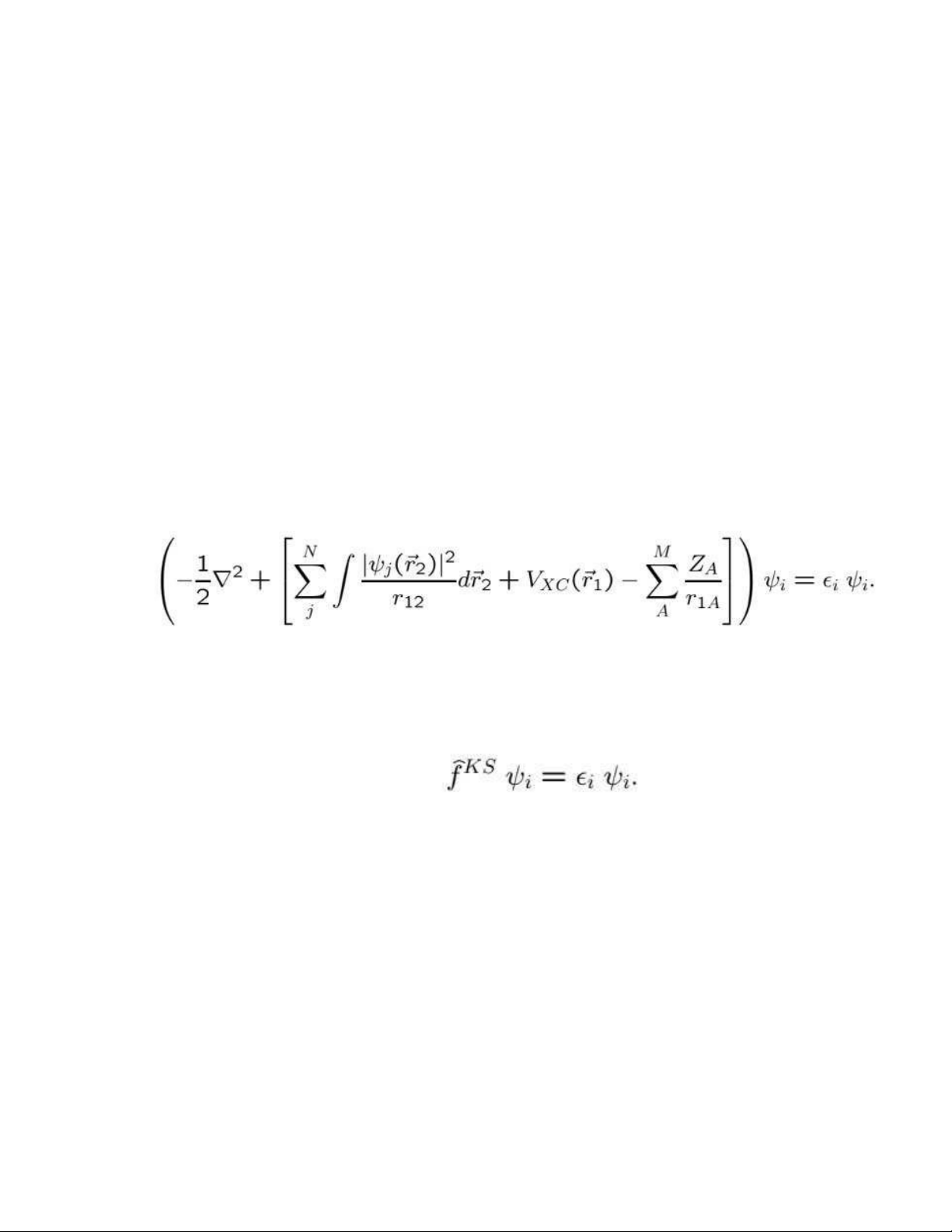

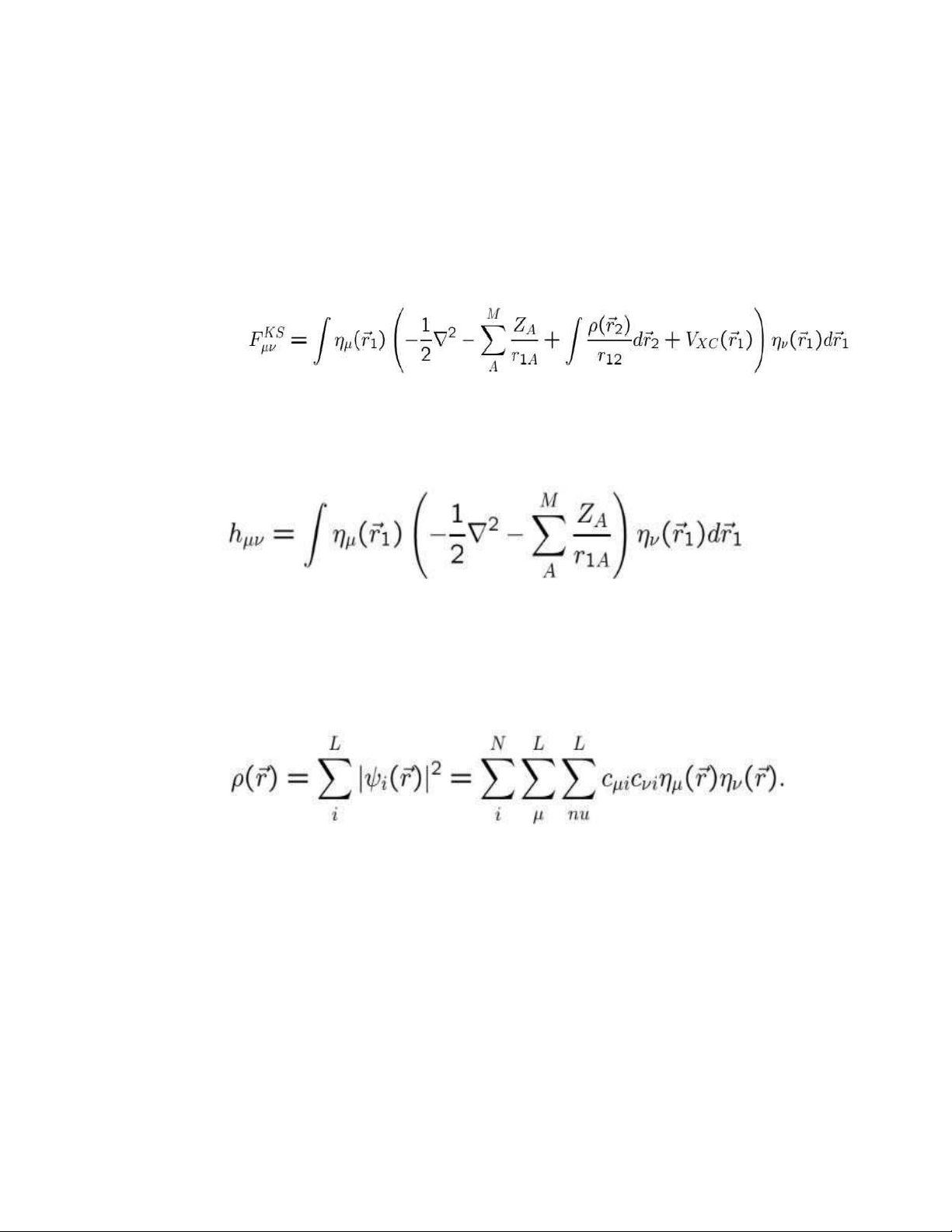
Preview text:
I. Tổng quan lý thuyết phiếm hàm mật độ. 1. Khái niệm
Lý thuyết phiếm hàm mật độ (Density Functional Theory - DFT) là một lý
thuyết trong lĩnh vực lượng tử được sử dụng để mô tả tính chất của hệ electron trong
nguyên tử, phân tử và vật rắn. Thay vì sử dụng hàm sóng, lý thuyết này biểu diễn các
tính chất của hệ N electron qua hàm mật độ electron của toàn bộ hệ. Điều này giúp tính
toán các tính chất vật lý hiệu quả hơn. Lý thuyết phiếm hàm mật độ đã có nhiều đóng
góp quan trọng và được sử dụng rộng rãi trong các lĩnh vực như vật lý chất rắn, hóa
học lượng tử và khoa học vật liệu.
Lý thuyết Phiếm hàm mật độ (Density Functional Theory - DFT) là một công cụ
quan trọng trong lĩnh vực lượng tử và khoa học vật liệu. Dưới đây là một số lý do vì
sao nó được coi là quan trọng: -
Hiệu quả tính toán: DFT cho phép tính toán các tính chất vật lý của hệ
electron một cách hiệu quả hơn so với lý thuyết hàm sóng. Thay vì phải giải phương
trình Schrödinger cho toàn bộ hệ, DFT chỉ cần tính toán hàm mật độ electron. -
Áp dụng rộng rãi: DFT được sử dụng trong nhiều lĩnh vực như vật lý
chất rắn, hóa học lượng tử, thiết kế vật liệu, và nghiên cứu phân tử. Nó giúp dự đoán
tính chất của các hệ phức tạp mà không cần tới các phép đo thực nghiệm. -
Phân tích cấu trúc và tương tác: DFT cho phép phân tích cấu trúc của các
hợp chất và tương tác giữa các electron. Điều này quan trọng trong việc hiểu cơ chế
phản ứng và tính chất của vật liệu. •
Ứng dụng của nó bao gồm từ các nguyên tử, phân tử và chất rắn đến hạt
nhân và các chất lỏng lượng tử và cổ điển. •
Trong hình thức nguyên thủy của mình, lý thuyết phiếm hàm mật độ
cung cấp các tính chất trạng thái cơ bản của một hệ, và mật độ electron đóng vai trò chủ chốt. •
Một ví dụ: hóa học. DFT dự đoán nhiều tính chất phân tử: cấu trúc phân
tử, tần số dao động, năng lượng phân hủy, năng lượng ion hóa, các tính chất điện và từ,
các đường phản ứng, v.v. •
Lý thuyết phiếm hàm mật độ nguyên thủy đã được tổng quát hóa để giải
quyết nhiều tình huống khác nhau: các hệ phân cực spin, các hệ đa thành phần như hạt
nhân và giọt lỗ electron, năng lượng tự do ở nhiệt độ hữu hạn, siêu dẫn với các cơ chế
ghép đôi điện tử, electron tương đối tính, các hiện tượng phụ thuộc thời gian và trạng
thái kích thích, boson, động lực học phân tử, v.v.
1.1. Bài toán hệ nhiều hạt
1.1.1. Phương trình Schrödinger
Mục đích cuối cùng của hầu hết các phép gần đúng trong vật lý chất rắn và hóa
học lượng tử là giải được phương trình Schrödinger phi tương đối không phụ thuộc vào thời gian: (1.1)
Ở đây, 𝐻 ^ H ^ là Hamiltonian cho hệ có chứa 𝑀 M hạt nhân và 𝑁 N electron: (1.2)
Ở đó, A và B là các chỉ số tương ứng với số hạt nhân, trong khi đó i và j là các
chỉ số tương ứng với các electron trong hệ.
Trong biểu thức (1.2), hai số hạng đầu tiên mô tả động năng của các electron và
động năng của các hạt nhân. Ba số hạng cuối là tương tác Coulomb giữa điện tử và hạt
nhân, điện tử với điện tử và hạt nhân với hạt nhân. Tuy nhiên, để giải chính xác phương
trình Schrodinger tương ứng với toán tử này là không khả thi. Trong khuôn khổ của các
phương pháp một điện tử, ba cấp độ gần đúng đã được xem xét để giải phương trình
Schrodinger cho hệ trên bao gồm: (1) gần đúng Born-Oppenheimer, (2)gần đúng một
điện tử, (3) gần đúng trong quá trình giải phương trình một điện tử bằng các phương pháp số.
1.1.2. Gần đúng Born-Oppenheimer
Cấp độ gần đúng này dựa vào việc khối lượng của điện tử nhỏ hơn khối lượng
của hạt nhân rất nhiều: Mi/me cỡ 103đến 104, hệ quả là các hạt nhân chuyển động chậm
hơn rất nhiều so với các electron. Chính vì vậy, động năng của các hạt nhân không
đáng kể so với động năng các điện tử. Ta có thể coi như các điện tử chuyển động trong
trường mà ở đó các hạt nhân bị cố định. Trong phương trình (2), có thể bỏ qua số hạng
động năng của các hạt nhân (số hạng thứ hai), số hạng tương tác Coulomb giữa các hạt
nhân (số hạng cuối cùng) là hằng số và chỉ xem xét đến ba số hạng còn lại: (1.3)
Lời giải của phương trình Schrodinger với toán tử Ĥ là hàm sóng điện tử elec Ψ elec
và năng lượng điện tử E . Tổng năng lượng là tổng của
và thành phần lực đẩy elec Etot Eelec
hạt nhân không đổi E . nuc 1.4 1.5 1.2.
Nguyên lý biến phân cho
trạng thái cơ bản
Khi một hệ đang ở trong trạng thái Ψ, giá trị năng lượng có thể có được cho bởi biểu thức: 1.6
Nguyên lý biến phân phát biểu rằng năng lượng tính toán từ một hàm sóng Ψcho
trước là giới hạn trên đối với năng lượng trạng thái cơ bản thực E0. Cực tiểu hóađối với
phiếm hàm E[Ψ] (liên quan đến tất cả các hàm sóng cho phép của N electron) sẽ cho
chúng ta hàm sóng của trạng thái cơ bản thực và năng lượng E[Ψ]=E0 mà (1.7)
Đối với một hệ N electron và thế năng hạt nhân đã cho Vext, nguyên lý biến
phân xác định một phương pháp để xác định hàm sóng trạng thái cơ bản Ψ , năng 0
lượng trạng thái cơ bản E [N,Vext], và các tính chất cần quan tâm khác. Mặt khác, năng 0
lượng trạng thái cơ bản là một phiếm hàm của số electron N và thế năng hạt nhân Vext: E =E [N, Vext] 0 (1.8)
1.3. Phương pháp xấp xỉ HARTREE – FOCK
Để chuyển bài toán hệ nhiều hạt thành bài toán hệ một hạt, phương pháp Hatree
– Fock giả thiết rằng các điện tử được xem như chiếm các orbital một hạt góp phần tạo
nên hàm sóng của cả hệ. Một điện tử chịu một thế năng hiệu dụng gây bởi tất cả các
điện tử còn lại. Mỗi orbital, theo đó chịu tác động bởi sự có mặt của các điện tử trong các orbital khác.
Các phép gần đúng của phương pháp Hatree – Fock (H – F) chuyển bài toán
hệnhiều hạt thành bài toán một điện tử dựa trên phương pháp biến phân, dựa vào hàm
sóng Ψ0 . Xuất phát điểm của phương pháp H – F là viết một hàm sóng biến phân, được
xây dựng từ các orbital một hạt. Hàm sóng này phải thỏa mãn tính phản đối xứng của
hàm sóng điện tử. Một hàm toán học thỏa mãn các điều kiện trên là định thức Slater
với các yếu tố ma trận là các orbital một điện tử: (1.9)
Gần đúng H – F là phương pháp dựa vào các orbital trực giao Ψ0 được tìm ra
mà cực tiểu hóa năng lượng là hàm đã xác định của Ψ0:
EEF=min(ΨHF⟶N)E[Ψ EF ¿ (1.10)
Các giá trị có thể có của toán tử Hamiltonian với hàm song Ψ EF được cho bởi: (1.12) (1.11)
Xác định sự đóng góp bởi yếu tố động năng và lực hút giữa electron - các hạt nhân và: (1.13) (1.14)
Tất cả là các số nguyên thực, và Jij ≥ Kij ≥0. Jij được gọi là các tích phân
Coulomb, Kij được gọi là các tích phân trao đổi. Trong đó, có một tính chất cần lưu ý là khi Jij= Kij.
Bậc biến phân trong biểu thức năng lượng (1.11) phụ thuộc vào lựa chọn của các
orbital. Cực tiểu hóa hàm phiếm hàm năng lượng với điều kiện chuẩn hóa
Ψ j(x⃗)dx⃗ =δij dẫn tới các phương trình H-F khác nhau ^ f Ψ i=ε ,i= 1,2,…,N iΨ i (1.15)
N phương trình này có sự xuất hiện của các phương trình giá trị riêng, ở đó các
hằng số nhân Lagrangian εi là các giá trị riêng của toán tử ^f .Toán tử Fock ^f là toán
tử một electron hiệu dụng được định nghĩa như sau: 1 M ^f= -2∇2i - A rZiA
Hai thành phần đầu tiên liên quan đến động năng và thế năng bởi tương tác
electron và hạt nhân. V (i) là thế năng H – F, trung bình thế năng tương tác đẩy đối với HF
electron thứ i bởi sự tồn tại N – 1 electron, và nó được cho bởi : (1.17) (1.18) Toán tử
Coulomb ^jđại diện cho nội năng mà một electron ở vị trí ⃗x bởi sự phân phối điện tử 1
trung bình của các electron khác trong orbital spin Ψ .j
Thành phần thứ hai trong phương trình (1.17) là sự đóng góp cho thế năng H –
F. Nó không có sự tương tự cổ điển và nó được xác định thông qua hiệu ứng của
nó khi toán tử tác động lên một quỹ đạo spin: (1.19)
Từ đó, rút ra một vài kết luận như sau: -
Thế năng H – F là phiếm hàm không cục bộ và nó phụ thuộc vào các quỹ
đạo spin. Vì vậy các phương trình H – F phải được giải theo cách tự liên hợp. -
Định lý Koopman (1934) cung cấp một giải thích vật lý về các năng
lượng quỹđạo: nó phát biểu rằng năng lượng quỹ đạo εi là phép gần đúng của âm năng
lượng ion hóa tương ứng với sự dịch chuyển một electron từ quỹ đạo Ψi.
1.4 Phương pháp phiếm hàm mật độ
1.4.1 Mật độ electron
Mật độ electron là đại lượng đóng vai trò chủ đạo trong lý thuyết phiếm hàm
mật độ. Nó được xác định bằng tích phân trên toàn bộ các tọa độ spin của tất cả các
electron và trên tất cả nhưng chỉ một trong những biến không gian (x≡⃗ r⃗,s) (1.20)
ρ(→r¿ r xác định khả năng có thể trong việc tìm kiếm bất kì electron nào trong N
electron bên trong đơn vị thể tích ¿
Một vài tính chất của mật độ electron -
ρ(→r¿ là hàm không âm của chỉ ba biến không gian mà bằng không ở vô
hạn và bằng tổng số electron khi lấy tích phân toàn miền không gian:
ρ(r→∞⃗ ¿=¿0∫ ρ¿¿)dr⃗=N (1.21) -
ρ(→r¿là đại lượng có thể quan sát được và có thể được đo bằng thực
nghiệm, ví dụ như phép đo nhiễu xạ tia X. -
Ở bất kì vị trí nào của một nguyên tử, gradient của ρ(→r¿của một điểm gián đoạn : ⃗
lim ¿riA →0[∇r+2Z A ]ρ(r¿)=0¿¿ (1.22)
Trong đó, Z là điện tích của hạt nhân và ⃗ ⃗
ρ(r¿)¿là trung bình cầu của ρ(r¿).¿ Sự
phân kì hàm mũ tiệm cận cho những khoảng cách rộng từ tất cả các hạt nhân: ⃗
ρ(r¿) exp ¿⌊r⃗ ⌋¿] (1.23)
Ở đó, I là năng lượng ion hóa chính xác
1.4.2. Mô hình Thomas – Fermi
Những phương pháp thông thường sử dụng hàm sóng Ψ là đại lượng chính, vì
hàm sóng Ψ có chứa đầy đủ thông tin của một hệ. Tuy nhiên, hàm sóng Ψ là một đại
lượng rất phức tạp, chúng ta không thể đo đạc, kiểm tra bằng thực nghiệm, và nó phụ
thuộc vào 4N biến, với N là số các electron.
Mô hình Thomas – Fermi: Lý thuyết phiếm hàm mật độ đầu tiên (1927) -
Dựa vào khí electron đồng nhất, người ta đề xuất phiếm hàm dưới đây cho năng lượng động năng: (1.24)
Năng lượng của một nguyên tử thu được cuối cùng dùng công thức cổ điển cho
thế năng hạt nhân – hạt nhân và thế năng tương tác electron – electron: (1.25
Biểu thức năng lượng đã cho là hàm của chỉ mật độ electron.
- Để xác định được mật độ chính xác có trong biểu thức (1.25), người ta sử dụng
nguyên lý biến phân. Họ giả sử rằng trạng thái cơ bản của hệ có liên quan đến mật độ
electron ρ(→r¿ với việc cực tiểu hóa năng lượng dưới điều kiện ràng buộc : ∫ ρ(r⃗¿)dr⃗¿ =N.
1.4.3. Lý thuyết của hohenberg – kohn
Hohenberg và Kohn đã chứng minh hai định lý nổi tiếng vào năm 1964
1.4.3.1. Định lý Hohenberg – Kohn thứ nhất
Định lý Hohenberg – Kohn thứ nhất chỉ ra rằng mật độ electron xác định duy
nhất toán tử Hamiltonian và quyết định toàn bộ tính chất của hệ.
Định lý được phát biểu như sau: Với một hệ bất kỳ gồm các hạt tương tác với
nhau và với trường ngoài thì thế bên ngoài này được xác định duy nhất (sai khác hằng
số cộng) bởi mật độ điện tử ở trạng thái cơ bản của các hạt. Chứng minh:
Giả sử rằng có hai hàm thế năng ngoài V ext ¿) và V 'ext (r⃗)khác nhau bởi nhiều hơn
một hằng số cộng. Ở trạng thái cơ bản của chúng, mỗi hàm đều là hàm của cùng mật độ
điện tử ρ¿). Như vậy chúng ta sẽ có hai toán tử Hamiltonian Ĥ và Ĥ ' sao cho mật độ
trạng thái cơ bản của chúng là như nhau, dù cho các hàm sóng chuẩn hóa Ψ và Ψ ' sẽ
khác nhau. Lấy Ψ 'như là hàm sóng thử cho toán tử Ĥ , ta có: (1.26)
Trong đó E0và E' là năng lượng ở trạng thái cơ bản lần lượt ứng với 0
Hamiltonian Ĥ và Ĥ '. E
Một cách tương tự, lấy hàm sóng Ψ như là hàm thử
0+E'0<E'0+E0 cho trường hợp Ĥ: (1.27)
Lấy tổng phương trình (1.26) và (1.27), chúng ta sẽ thu được . E (mâu
0+E'0<E'0+E0
thuẫn), vì vậy, không thể có hai hàm thế năng ngoài khác nhau mà cho cùng giá trị của
hàm mật độ điện tử đối với trạng thái cơ bản của chúng.
Như vậy, hàm mật độ điện tử ρ¿) xác định số electron, hàm thế năng ngoài ρ¿)
xác định số electron, hàm thế năng ngoài V ext ¿) và tất cả các tính chất của trạng thái cơ
bản, bao gồm: động năng T[ρ] năng lượng thế năng v[ρ¿,và tổng năng lượng E[ρ¿ . Bây
giờ, chúng ta có thể viết lại biểu thức tổng năng lượng như sau: (1.28) (1.29)
Phiến hàm FHK [ρ] là linh hồn của lý thuyết phiếm hàm mật độ. Nếu chúng ta biết
được dạng của phiếm hàm này, chúng ta sẽ giải được phương trình Schrodinger một cách
chính xác. FHK [ρ] có chứa phiếm hàm đối với năng lượng động năng và đối với hiếm hàm
tương tác electron-electron EEE[ρ]. Dạng tường minh của các phiếm hàm này vẫn chưa rõ
ràng. Tuy nhiên, ít nhất chúng ta có thể xác định được phần tương tác cổ điển J[ρ]: (1.30)
Encl [ρ] là phần đóng góp phi cổ điển trong tương tác electron – electron: phần tự
tương tác, trao đổi và tương quan Coulomb.
Dạng tường minh của các phiếm hàm T[ρ] và Encl [ρ] là thử thách lớn của lý
thuyết phiếm hàm mật độ.
1.4.3.2. Định lý Hohenberg – Kohn thứ hai
Định lý thứ 2 được phát biểu như sau: một phiếm hàm phổ dụng với năng lượng
E[ρ¿) có thể được xác định theo mật độ electron. Trạng thái cơ bản chính xác là
giá trị thấp nhất toàn cục của phiếm hàm này. Từ định lý thứ nhất, chúng ta nhận thấy
rằng thế ngoài được xác định duy nhất bởi hàm mật độ. Vì vậy trạng thái cơ bản đầy đủ
của hệ nhiều hạt là phiếm hàm duy nhất theo mật độ điện tử.
Theo nguyên lý biến phân: (1.31)
Mặt khác điều này có nghĩa rằng, đối với bất kì một hàm mật độ điện tử thử nào
~p(r⃗),mà thỏa mãn điều kiện biên cần thiết gồm có ~p(r⃗)≥0,∫ ρ(r⃗1¿)d r⃗=N ¿ và phù hợp
với một vài thế năng ngoài Vext , năng lượng thu được từ phiếm hàm trong phương
trình (1.28) đại diện cho biên trên đối với năng lượng trạng thái cơ bản thực E0. E0 cho
kết quả nếu chỉ mật độ trạng thái cơ bản chính xác được đưa vào phương trình (1.24) Chứng minh:
Chứng minh phương trình (1.31) giúp chúng ta hình thành nguyên lý biến phân
cho hàm sóng. Chúng ta gọi lại bất kì hàm mật độ trạng thái thử mà xác định
Hamiltonian riêng và hàm sóng riêng của nó. Hàm sóng này có thể được lấy như là
hàm sóng thử cho toán tử năng lượng được tạo thành từ hàm thế năng ngoài thực Vext. Vì vậy: (1.32)
Kết luận cho phần này, chúng ta thu được:
- Tất cả các tính chất của một hệ được xác định bởi hàm thế năng ngoài Vext có
thể tìm ra bằng cách sử dụng hàm mật độ trạng thái cơ bản. Cụ thể, năng lượngn trạng
thái cơ bản tương đương với một hàm mật độ được xác định thông qua phiếm hàm:
∫~p(r⃗) V extdr⃗ +FHK[ρ] (1.33)
Phiếm hàm này thu được giá trị nhỏ nhất có liên quan đến tất cả các mật độ điện
tử được cho phép nếu và chỉ nếu mật độ điện tử đầu vào là mật độ điệntử trạng thái cơ
bản thực, ví dụ : ~p(⃗r¿¿ =ρ(r⃗).
Nguyên lý biến phân chỉ được áp dụng cho trạng thái cơ bản. Vì vậy, về cơ bản,
không dễ dàng tính toán các giá trị trong trường hợp hệ ở trạng thái kích thích.
Dạng tường minh của phiếm hàm F [
HK ρ] là thử thách lớn trong lý thuyết phiếm hàm mật độ.
1.4.4. Phương trình kohn – sham
Chúng ta đã biết được năng lượng của trạng thái cơ bản được viết như sau:
E0=minρ→N(F[ρ¿+∫ ρ¿¿)V Ned r⃗) (1.34)
Trong đó, phiếm hàm phổ dụng F[ρ]có chứa các sự đóng góp của năng lượng
động năng, tương tác Coulomb cổ điển và phần phi cổ điển:
F[ρ]=T[ρ]+ J[ρ]+Encl [ρ] (1.35)
Trong các đại lượng trên, chỉ có J[ρ¿ đã xác định. Vấn đề chính là cần tìm được
biểu thức cho hai thành phần còn lại trong phương trình (1.35)
Mô hình Thomas – Fermi cung cấp cho chúng ta một ví dụ của lý thuyết phiếm
hàm mật độ. Tuy nhiên, cách biểu diễn của mô hình này không cho kết quả cao bởi
phép gần đúng đối với trường hợp năng lượng động năng. Để giải quyết bài toán này,
Kohn và Sham đã đề xuất một phương pháp sẽ được trình bày dưới đây vào năm 1965.
Hai tác giả gợi ý rằng, để tính toán năng lượng động năng chính xác của hệ quy chiếu
không tương tác với cùng mật độ điện tử như là hệ thực – hệ tương tác: (1.36)
Ở đó hàm sóng Ψilà những quỹ đạo của hệ không tương tác. Đương nhiên giátrị
của Ts thì không bằng chính xác năng lượng động năng thực của hệ. Kohn và Shamđã
tính toán đến điều đó bằng cách tách phiếm hàm F[ρ]thành các thành phần dưới đây:
F[ρ]=Ts[ρ]+J[ρ]+EXC[ρ] (1.37)
Ở đó, EXC là năng lượng tương quan trao đổi, được xác định thông qua phương trình (1.37) như sau:
EXC[ρ] =(T[ρ]-T S[ρ])+(Eee[ρ¿-J[ρ]) (1.38)
Năng lượng tương quan và trao đổi EXC là phiếm hàm có chứa mọi thứ mà chưa được xác định.
Câu hỏi được đặt ra bây giờ là: chúng ta có thể xác định được các quỹ đạo một
cách duy nhất trong hệ tham chiếu không tương tác bằng cách nào? Mặt khác, chúng ta
xác định thế năng Vs để nó cung cấp cho chúng ta định thức Slater mà đặc trưng cho
mật độ điện tử như trong hệ thực của chúng ta như thế nào? Để giải quyết bài toán này,
chúng ta viết lại công thức tính năng lượng của hệ tương tác với bốn thành phần riêng
rẽ được mô tả như trong phương trình (1.37) (1.39) (1.40)
Thành phần duy nhất chưa tường minh là EXC. Áp dụng nguyên lý biến phân, và
xem xét điều kiện cho hàm sóng Ψi thỏa mãn cực tiểu hóa biểu thức năng lượng:
⟨Ψi/Ψi ⟩=δ12, , kết quả là chúng ta thu được các phương trình Kohn- Sham: (1.41) (1.42)
Để giải được các phương trình trên, cần biết được dạng của phiếm hàm tương
quan trao đổi. Có hai dạng cơ bản được đề xuất cho phiếm hàm này:
- Phiếm hàm mật độ địa phương LDA: chỉ phụ thuộc vào mật độ điện tích
- Phiếm hàm gradient suy rộng GGA: phụ thuộc cả vào mật độ điện tích và gradient của nó.
Các phép gần đúng kể trên sẽ được trình bày ở phần tiếp theo.
1.5. Phiếm hàm tương quan trao đổi.
1.5.1. Gần đúng mật độ địa phương (LDA)
Phép gần đúng LDA là phép gần đúng cơ sở cho tất cả các phiếm hàm tương
quan trao đổi xấp xỉ. Trong LDA, chất rắn được xem xét gần đúng như khí điện tử
đồng nhất. Trong giới hạn đó, hiệu ứng tương quan và trao đổi mang tính cục bộ. Theo
đó, năng lượng tương quan trao đổi là tích phân trên toàn bộ không gian của mật độ
năng lượng tương quan trao đổi tại mỗi điểm trong không gian. Mật độ năng lượng này
được xem là như nhau trong khí điện tử đồng nhất. Ta có: ELDA [
XC ρ¿ = ∫f ¿¿dr⃗)=∫ ρ¿¿)εXC(ρ¿))dr⃗ (1.43)
Ở đó,εXC ¿)) là mật độ năng lượng tương quan trao đổi của khí điện tử đồng nhất.
Đại lượng này có thể được tách thành hai phần riêng biệt là thành phần tương quan và
thành phần trao đổi như sau:
εXC ¿))=εX ¿)) +εC¿)) (1.44)
Phần εX ¿)) đại diện cho năng lượng trao đổi của một electron trong khí điện tử
đồng nhất của một hàm mật độ cụ thể, xuất phát từ công thức được đưa ra bởi Bloch và Dirac vào cuối năm 1920: ε = c − () (1.45) 4 π
Thành phần εc chưa được xác định. Mô phỏng Monte – Carlo lượng tử số có độ
chính xác cao cho khí electron đồng nhất đã được đề xuất (CeperlyAlder, 1980).
Một vài nhận xét về phép gần đúng này:
Cơ sở cho phép gần đúng cục bộ này là mật độ điện tử chất rắn, khoảng tác dụng
của hiệu ứng tương quan và trao đổi khá ngắn. Tuy nhiên, không thể xác minh tính
đúng đắn của nó chỉ bằng sự mở rộng hình thức của một thông số nhỏ nào đó. Ta cần
thử nghiệm tính đúng đắn của nó bằng các ứng dụng thực tế. Ta có thể mong đợi phép
gần đúng này áp dụng tốt nhất với các chất rắn gần với khí điện tử đồng nhất như kim
loại với các điện tử gần tự do và kém nhất đối với các trường hợp không đồng nhất như
các nguyên tử trong đó mật độ tiến về không một cách liên tục tại biên của nguyên tử.
Đối với hệ có xem xét đến sự phân cực spin, hàm năng lượng tương quan trao đổi lúc
này được viết lại như sau: ELSDA [
XC ρα , ρβ ¿¿=∫¿¿)dr⃗ (1.46)
1.5.2 Gần đúng Gradient suy rộng (GGA)
Phép gần đúng GGA cải thiện độ chính xác của phương pháp LDA trong nhiều
trường hợp. Phương pháp này ngày nay có thể đạt được độ chính xác cần thiết để có
thể được áp dụng rộng rãi trong cộng đồng hóa học. Thuật ngữ gradient suy rộng chỉ sự
đa dạng của các phương pháp được sử dụng để thay đổi những lượng tương quan trao
đổi khi gradient lớn để thu được những tính chất mong muốn. Năng lượng tương quan
trao đổi được viết dưới dạng dưới đây: Phiếm hàm tương quan trao đổi trong trường
hợp này là phiếm hàm phụ thuộc không chỉ vào hàm mật độ điện tử với cả spin up và
spin down, còn phụ thuộc vào đạo hàm bậc một của chúng nữa.
ELSDAXC [ρα , ρβ ¿¿=∫¿¿)dr⃗ (1.47)
Phiếm hàm tương quan trao đổi trong trường hợp này là phiếm hàm phụ thuộc
không chỉ vào hàm mật độ điện tử với cả spin up và spin down, còn phụ thuộc vàođạo
hàm bậc một của chúng nữa. -
Các xấp xỉ GGA và hybrid đã giảm sai số của LDA đối với năng lượng
nguyên tử hóa của tập hợp tiêu chuẩn các phân tử nhỏ từ 3-5 lần. Độ chính xác được
cải thiện này đã làm cho DFT trở thành một thành phần quan trọng của hóa học lượng tử. -
Tất cả các hàm hiện tại đều không đủ cho các tình huống mà mật độ
không phải là một hàm biến thiên chậm. Các ví dụ bao gồm (a) tinh thể Wigner; (b)
năng lượng Van der Waals giữa các hệ con không chồng chéo; (c) các đuôi điện tử
biến mất vào chân không gần bề mặt của các hệ điện tử giới hạn. Tuy nhiên, điều này
không có nghĩa là DFT với các xấp xỉ thích hợp không thể xử lý thành công các vấn đề như vậy.
1.6 Bộ máy cơ bản của DFT
1.6.1 Phương pháp LCAO trong các phương trình KS
Nhớ lại thành phần trung tâm của phương pháp Kohn-Sham trong lý thuyết hàm
mật độ, tức là các phương trình KS một điện tử. 1.48
Thuật ngữ trong ngoặc vuông định nghĩa toán tử một điện tử Kohn-Sham và
phương trình (1.48) có thể được viết gọn hơn như sau: 1.49
Hầu hết các ứng dụng trong hoá học của lý thuyết hàm mật độ Kohn-Sham sử
dụng phương pháp mở rộng LCAO của các orbital Kohn-Sham. Trong phương pháp
này, chúng ta giới thiệu một tập hợp các hàm cơ sở được định nghĩa trước {ημ} và mở
rộng tuyến tính các orbital Kohn-Sham như sau: 1.50
Bây giờ, chúng ta chèn phương trình (1.44) vào phương trình (1.43) và thu được
kết quả tương tự như trong trường hợp Hartree-Fock. 1.51
Nếu bây giờ chúng ta nhân phương trình này từ bên trái với một hàm cơ sở tùy ý
ημ và tích phân trên không gian, chúng ta sẽ thu được L phương trình. 1.52
Các tích phân ở cả hai vế của phương trình này xác định một ma trận: (1.53)
là các phần tử của ma trận Kohn-Sham và ma trận chồng chéo, tương ứng. Cả
hai ma trận đều có kích thước L × L. Các phương trình (1.52) có thể được viết lại gọn
gàng dưới dạng một phương trình ma trận
F^ KC C^=^SC^ ϵ^ (1.54)
Do đó, thông qua sự mở rộng LCAO, chúng ta đã chuyển đổi bài toán tối ưu phi
tuyến thành một bài toán tuyến tính, có thể được biểu diễn bằng ngôn ngữ đại số tiêu chuẩn.
Bằng cách mở rộng ^f KS thành các thành phần của nó, các phần tử riêng lẻ của ma trận KS trở thành (1.55)
Hai số hạng đầu tiên mô tả năng lượng động học và tương tác electron-hạt nhân,
và chúng thường được kết hợp thành tích phân một electron. (1.56)
Đối với số hạng thứ ba, chúng ta cần mật độ điện tích , có dạng sau trong sơ đồ LCAO (1.57)
Các hệ số khai triển thường được tập hợp trong ma trận mật độ P^với các phần tử N
Pμv=∑Cμi Cvi (1.58) i




