Tổng hợp ma trận Tài liệu - Thực Chiến – Min Max của hàm hợp | Đại học Sư phạm Hà Nội

Tổng hợp ma trận Tài liệu - Thực Chiến – Min Max của hàm hợp | Đại học Sư phạm Hà Nội với những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống.

32 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Nhập môn lý thuyết ma trận

Trường: Đại học Sư Phạm Hà Nội

Thông tin:

4 trang 2 tháng trước

Tác giả:

Profile Kim Oanh
Câu 1: Cho hàm số
f x , đồ thị hàm số
'y f x là đường cong như hình bên.
Giá trị lớn nhất của hàm số
2 4
g x f x x trên đoạn
3
; 2
2
bằng
A.
0f B.
3 6f
C.
2 4f D.
4 8f
Câu 2: Cho hàm số
,f x đồ thị của hàm số
/
y f x là đường cong như hình vẽ.
Giá trị nhỏ nhất của hàm số
2 1 6
g x f x x trên đoạn
1
;1
2
bằng
A.
1f . B.
1 3f .
C.
1 6f . D.
3 6f .
Câu 3: Cho hàm đa thức bậc bốn ( ),y f x đồ thị hàm số ( )y f x là đường cong
ở hình vẽ bên dưới. Giá trị nhỏ nhất của hàm số
2
1
( ) (2 1) 2 2
2
g x f x x x trên
đoạn
1
;1
2
bằng
A.
1
(1)
2
f B. ( 2) 2.f
C.
1
( 1)
2
f D. (0).f
Câu 4: (ĐỀ THI THPT QG 2017) Cho hàm số = ). Đồ thị của hàm số 𝑦 𝑓(𝑥
𝑦 𝑓 𝑥 = ’( ) như hình bên. Đặt . Mệnh đề nào dưới đây đúng ?
A.
B.
C.
D.
Câu 5: Cho hàm số
y f x liên tục trên có đồ thị
'y f x như hình
vẽ. Hàm số
2
2 1g x f x x đạt giá trị nhỏ nhất trên đoạn
3;3 tại
A. 3.x B. 3.x
C. 0.x D. 1.x
Câu 6: Cho hàm số
y f x . Hàm số
'y f x có bảng biến thiên như hình vẽ
Đặt
2
ln 1g x f x x . Khẳng định nào sau đây là sai ?
A.
2 1g g B.
1 0g g C.
1 2g g D.
3 4g g
2
2
h x f x x
h h h
4 2 2
h h h
2 4 2
h h h
2 2 4
h h h
-2
3
8
3
+∞
0
32
f '(x)
0 1
+∞
-1
x
-∞
5
12
+∞
-9
4
Câu 7: Cho hàm số
y f x có đạo hàm cấp 2 trên . Hàm số '( )y f x có
đồ thị như hình bên. Giá trị lớn nhất của hàm số
sin 3cos
2
x x
y f
trên
đoạn
5
;
6 6
bằng
A.
5
6
f
B.
3
f
C.
0f D.
6
f
Câu 8: Cho hàm số
y f x có đạo hàm liên tục trên và có đồ thị hàm số R
'y f x như hình vẽ bên. Gọi
3 2
1 1
2019
3 2
g x f x x x x . Biết
1 1 0 2g g g g . Với
1;2x thì
g x đạt giá trị nhỏ nhất bằng:
A.
2g B.
1g
C.
1g D.
0g
Câu 9:Cho hàm số bậc ba
y f x có đồ thị là đường cong trong hình bên dưới.
Giá trị lớn nhất của hàm số
2
3 2 2022g x f x x trên đoạn
1
3;
2
bằng
A. B.
2025
21
2022
16
f
C. D.
2024
3
2022
4
f
Câu 10: Cho hàm số
y f x có đồ thị hàm số như hình vẽ. Hàm số
cos cos 6y f x x có giá trị nhỏ nhất trên khoảng ;
2 2
bằng
A B. . 3 0
C. D 1 . 2
Câu 11: Cho hàm số
y f x có bảng biến thiên như sau:
Tìm giá trị lớn nhất của hàm số
sin 3 cos 1 2cos 2 4cos 10y f x x x x
A. B. 2 5 C. 9 D. 2
+
1
00
f '(x)
3
f (x)
+∞
_
-2
x
-
∞
2
+
+∞
-
∞
x
y
2
-1
-1
-3
1
1
O
Câu 12: Cho hàm số
f x có bảng biến thiên như sau:
Tìm tất cả các giá trị của tham số m để bất phương trình
1 1f x m có nghiệm ?
A. 5m B. 2m C. 4m D. 1m
Câu 13: Cho hàm số ( )y f x , hàm số '( )y f x có bảng biến thiên như hình bên. Bất phương trình
2
( ) sin 3f x x m đúng với mọi 0;
2
x
khi và chỉ khi:
A.
1
1
3 2
m f
B.
1 1
3 4 6
m f
C.
1
0
3
m f
D.
1
1
3 2
m f
Câu 14: Cho hàm số
f x có bảng biến thiên như hình vẽ
Tìm điều kiện của tham số m để
2
m f x x với mọi
1;2x
A.
2 4m f B.
1 1m f C.
2 4m f D.
1 1m f
Câu 15: Cho hàm số
f x . Hàm số
'f x có bảng biến thiên như sau:
Điều kiện của tham số m để bất phương trình
2
1
2
f x x m nghiệm đúng với mọi giá trị của
1;2x là
A.
1
1
2
m f B.
2 2m f C.
1
1
2
m f D.
2 2m f
Câu 16: Cho hai hàm số đa thức bậc bốn ( )y f x và ( )y g x có đồ thị như
hình vẽ bên dưới, trong đó đường là đồ thị hàm số đậm hơn ( )y f x . Biết rằng
hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là 3 và cắt nhau tại hai
điểm nữa có hoành độ lần lượt là 1 và . Tìm tập hợp tất cả các giá trị thực của 3
tham số để bất phương trình m ( ) ( )f x g x m nghiệm đúng với mọi [ 3;3]x
A.
12 8 3
;
9

. B.
12 10 3
;
9

C.
12 10 3
;
9

. D.
12 8 3
;
9

.
+∞
+
_
-5
0
0
y'
-4
3
y
1
x
-∞
2
+
+∞
-∞
_
-1 1
0
2
f '(x)
2
f (x)
_
-1
x
-
∞
3
+
+∞
-∞
0
-1
1
f '(x)
3
-1
x
-∞
1
+∞
-
∞
Câu 17: Cho hàm số
( )
y f x
liên tục và có đồ thị như hình vẽ. Gọi
S
là tổng
các giá trị nguyên của tham số
m
sao cho giá trị lớn nhất của hàm số
( ) | ( ) |
g x f x m
trên đoạn
[ 1;3]
nhỏ hơn hoặc bằng
2 505
.
A.
2019
. B.
2018
.
C.
1
. D.
0
.
BẢNG ĐÁP ÁN
1.C 2.A 3.D 4.C 5.A 6.A 7.C 8.A 9.A 10.D
11.B 12.C 13.A 14.D 15.C 16.A 17.A
Câu 1: 0:00 - 7:01 Câu 7: 47:51 - 51:20 Câu 13: 1:15:56 - 1:21:53
Câu 2: 7:02 - 12:45 Câu 8: 51:21 - 54:31 Câu 14: 1:21:55 - 1:25:43
Câu 3: 12:48 - 18:28 Câu 9: 54:33 - 58:44 Câu 15: 1:25:43 - 1:28:51
Câu 4: 18:29 - 27:03 Câu 10: 58:45 - 1:03:03 Câu 16: 1:28:52 - 1:33:20
Câu 5: 27:04 - 33:54 Câu 11: 1:03:04 - 1:10:46 Câu 17: 1:33:21 - 1:45:10
Câu 6: 33:55 - 47:50 Câu 12: 1:10:47 - 1:15:55
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

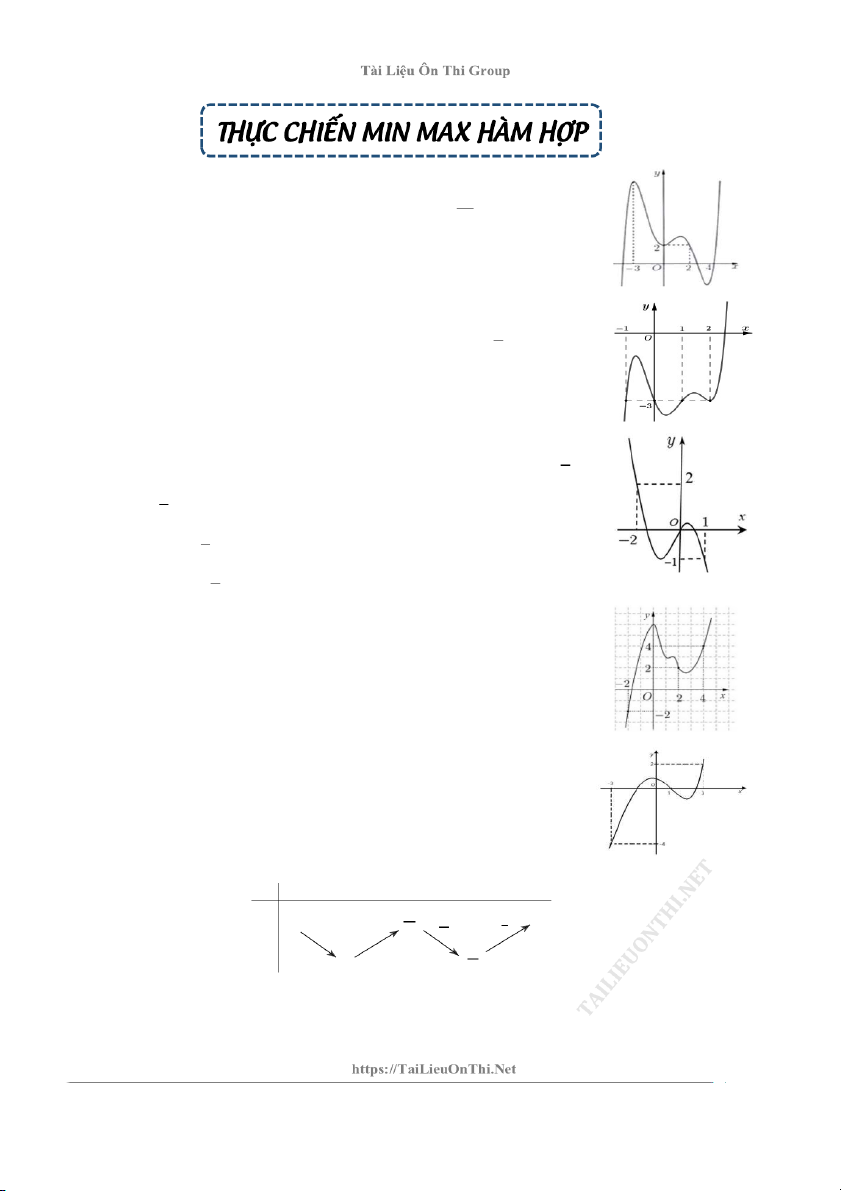
Câu 1: Cho hàm số f x , đồ thị hàm số y  f ' x là đường cong như hình bên. 3 
Giá trị lớn nhất của hàm số g  x  f  2x  4x trên đoạn ; 2  bằng 2    A. f 0 B. f 3 6 C. f 2  4 D. f 4  8
Câu 2: Cho hàm số f x , đồ thị của hàm số / y  f  
x là đường cong như hình vẽ.  1 
Giá trị nhỏ nhất của hàm số g  x  f 2x   1  6x trên đoạn  ;1  bằng 2    A. f   1 . B. f 1 3 . C. f   1  6 . D. f   3  6 .
Câu 3: Cho hàm đa thức bậc bốn y  f (x), đồ thị hàm số y  f (  ) x là đường cong 1
ở hình vẽ bên dưới. Giá trị nhỏ nhất của hàm số 2
g (x )  f (2x  1) 2x  2x  trên 2  1  đoạn  ;1  bằng 2    1 A. f (1)   B. f ( 2  )  2. 2 1 C. f ( 1  )   D. f (0). 2
Câu 4: (ĐỀ THI THPT QG 2017) Cho hàm số 𝑦 = 𝑓( ). Đồ thị của hàm số 𝑥
𝑦 = 𝑓’(𝑥) như hình bên. Đặt h  x   f  x  2 2
 x . Mệnh đề nào dưới đây đúng ? A. h4  h 2    h 2 B. h4  h  2   h  2
C. h2  h4  h   2 D. h2  h  2  h 4
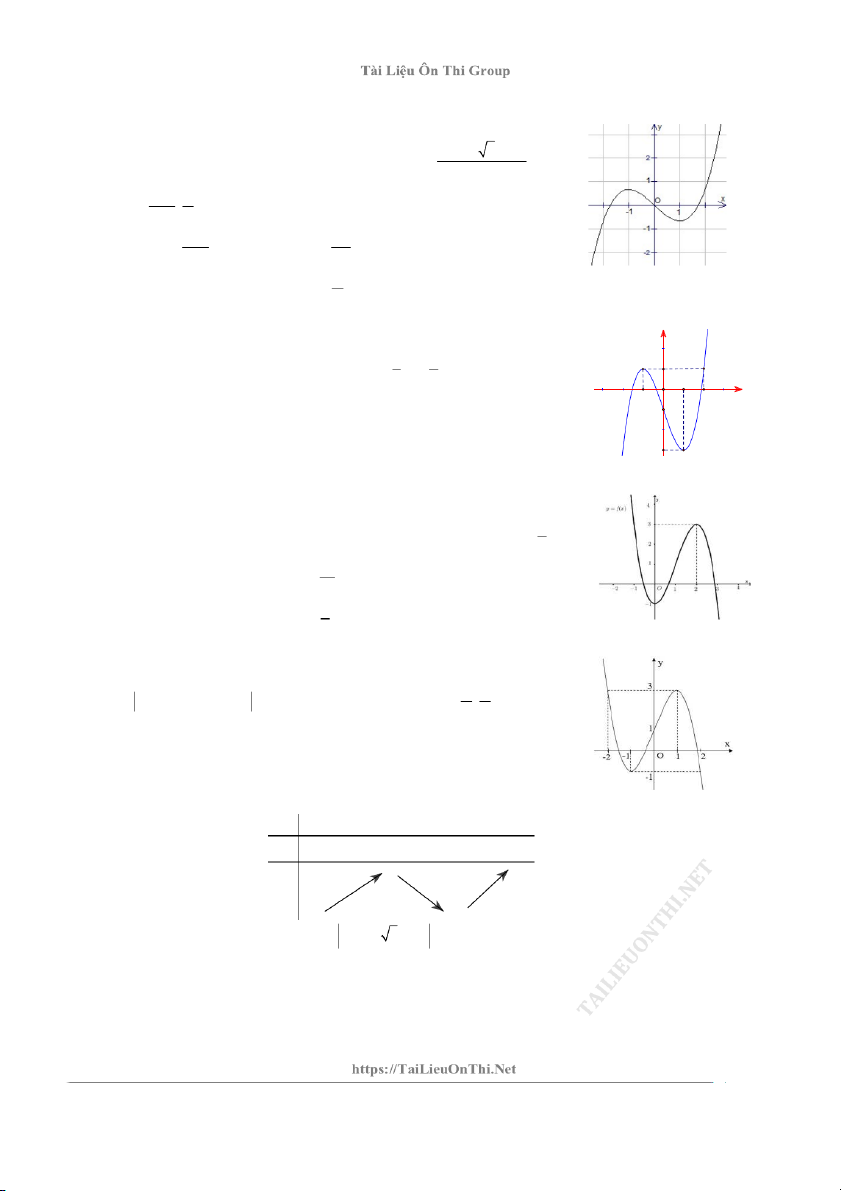
Câu 5: Cho hàm số y  f x liên tục trên  có đồ thị y  f '  x như hình
vẽ. Hàm số g  x  f  x   x  2 2
1 đạt giá trị nhỏ nhất trên đoạn  3  ;  3 tại A. x  3  . B. x  3. C. x  0. D. x 1.
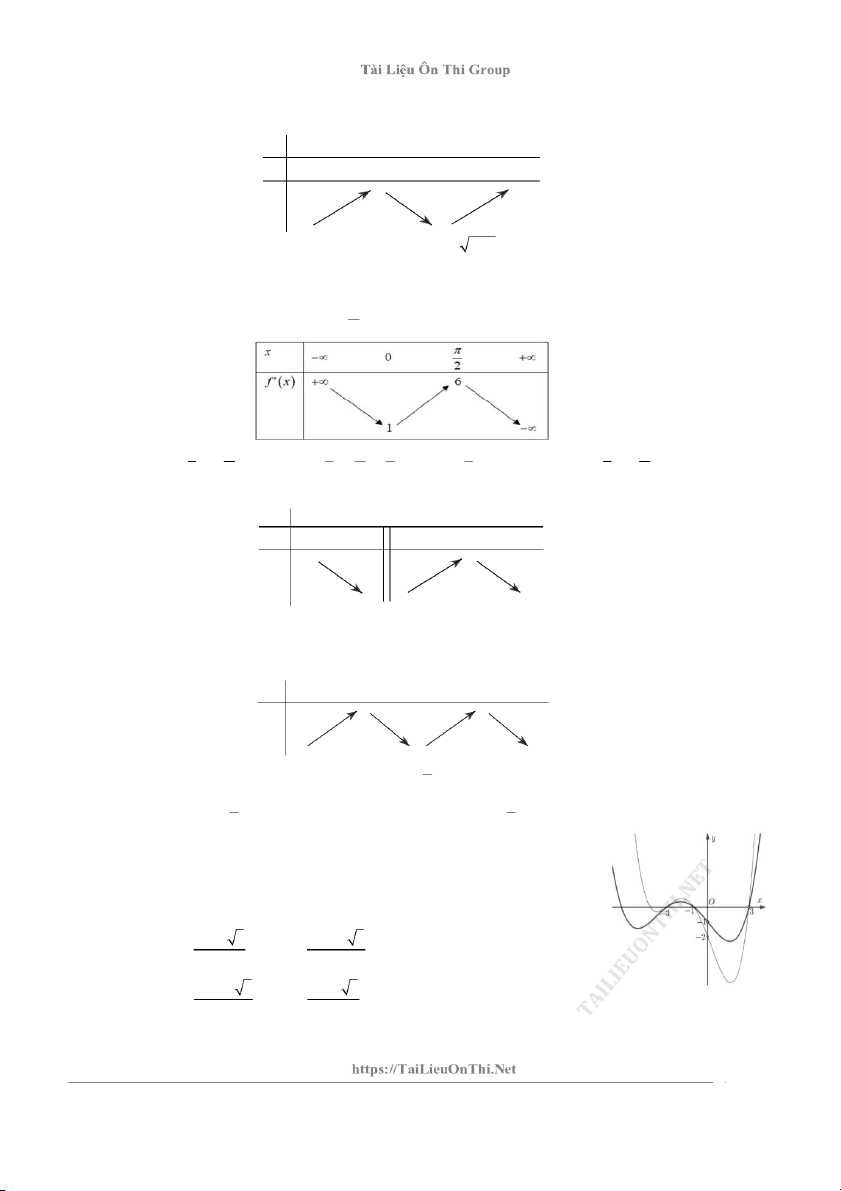
Câu 6: Cho hàm số y  f x. Hàm số y  f ' x có bảng biến thiên như hình vẽ x -∞ -1 0 1 2 3 +∞ f '(x) 5 -2 8 +∞ +∞ 12 3 3 -9 0 4
Đặt g  x  f  x   2 ln x  
1 . Khẳng định nào sau đây là sai ? A. g  2    g   1 B. g  1   g 0  C. g   1  g 2 D. g   3  g 4
Câu 7: Cho hàm số y  f x có đạo hàm cấp 2 trên  . Hàm số y  f '(x) có  sin x  3 cosx 
đồ thị như hình bên. Giá trị lớn nhất của hàm số y  f    trên 2     5   đoạn ;  bằng 6 6     5     A. f  B. f 6       3     C. f 0 D. f  6   
Câu 8: Cho hàm số y  f x có đạo hàm liên tục trên y
R và có đồ thị hàm số 1 1
y  f ' x như hình vẽ bên. Gọi g  x  f  x 3 2
 x  x  x  2019 . Biết 1 3 2 1 x g    1  g   1  g 0  g   2 . Với x 1;  2 thì g 
x đạt giá trị nhỏ nhất bằng: -1 O 2 -1 A. g 2 B. g 1 C. g   1 D. g 0  -3
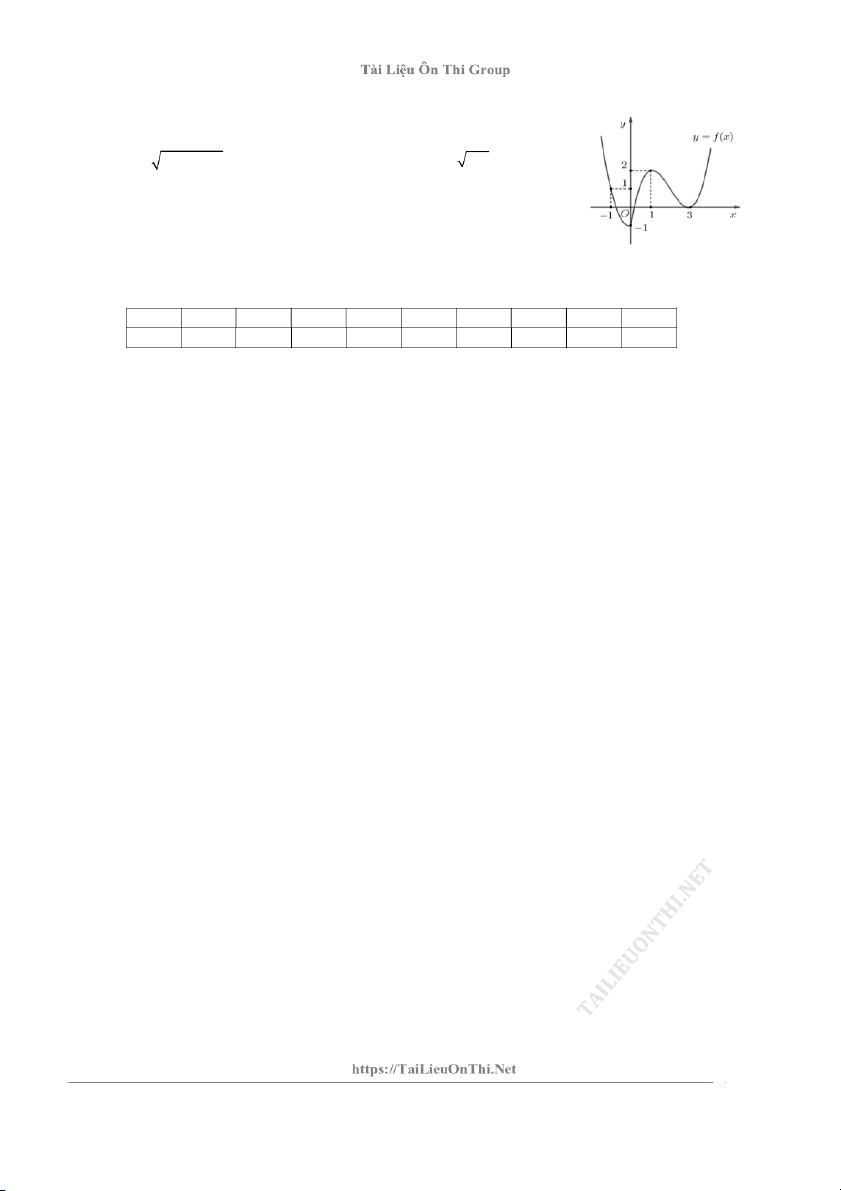
Câu 9:Cho hàm số bậc ba y  f x có đồ thị là đường cong trong hình bên dưới.  1
Giá trị lớn nhất của hàm số  g  x  f  2
x  3x  2  2022 trên đoạn 3;  bằng 2    21 A.2025 B.  f   2022 16   3  C. 2024 D. f  2022  4   
Câu 10: Cho hàm số y  f x  có đồ thị hàm số như hình vẽ. Hàm số    
y  f cos x  cos x  6 có giá trị nhỏ nhất trên khoảng  ;  bằng 2 2    A. 3 B. 0 C. 1 D .2
Câu 11: Cho hàm số y  f x  có bảng biến thiên như sau: x -∞ 1 3 +∞ f '(x) + 0 _ 0 + 2 +∞ f (x) -2 -∞
Tìm giá trị lớn nhất của hàm số y  f  sin x  3cos x  
1  2 cos 2x  4 cos x 10 A. 2 B. 5  C. 9  D. 2
Câu 12: Cho hàm số f x có bảng biến thiên như sau: x -∞ 1 3 +∞ y' + _ 0 0 + 2 +∞ y -5 -4
Tìm tất cả các giá trị của tham số m để bất phương trình f  x 1 1  m có nghiệm ? A. m  5  B. m  2 C. m  4  D. m 1
Câu 13: Cho hàm số y  f (x) , hàm số y  f '(x) có bảng biến thiên như hình bên. Bất phương trình 2   
f (x)  sin x  3m đúng với mọi x  0;  khi và chỉ khi: 2    1     1    1 1 1      A. m  f 1    B. m  f    C. m  f 0 D. m  f 1    3   2     3  4  6 3 3   2  
Câu 14: Cho hàm số f x có bảng biến thiên như hình vẽ x -∞ -1 2 +∞ _ _ f '(x) + 0 2 3 f (x) -∞ -1 1
Tìm điều kiện của tham số m để    2 m
f x  x với mọi x  1; 2 A. m  f 2  4 B. m  f   1 1 C. m  f 2  4 D. m  f   1 1
Câu 15: Cho hàm số f x . Hàm số f ' 
x có bảng biến thiên như sau: x -∞ -1 1 3 +∞ 1 0 f '(x) -∞ -1 -∞ 1
Điều kiện của tham số m để bất phương trình f   2 x 
x  m nghiệm đúng với mọi giá trị của x   1;  2 là 2 A. m  f   1 1  B. m  f 2  2 C. m  f   1 1  D. m  f 2  2 2 2
Câu 16: Cho hai hàm số đa thức bậc bốn y  f (x) và y  g(x) có đồ thị như
hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số y  f (x) . Biết rằng
hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là 3  và cắt nhau tại hai
điểm nữa có hoành độ lần lượt là 1 và 3 . Tìm tập hợp tất cả các giá trị thực của
tham số m để bất phương trình f (x)  g(x)  m nghiệm đúng với mọi x [  3;3]  12 8 3  12 10 3  A.  ;    . B.  ; 9    9    12 10 3  12 8 3  C.  ;    . D.  ; . 9    9  
Câu 17: Cho hàm số y  f (x ) liên tục và có đồ thị như hình vẽ. Gọi S là tổng
các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số
g(x)  | f (x)  m | trên đoạn [ 1
 ;3] nhỏ hơn hoặc bằng 2 505 . A. 2  019 . B. 2018 . C. 1  . D. 0 . BẢNG ĐÁP ÁN 1.C 2.A 3.D 4.C 5.A 6.A 7.C 8.A 9.A 10.D 11.B 12.C 13.A 14.D 15.C 16.A 17.A Câu 1: 0:00 - 7:01 Câu 7: 47:51 - 51:20 Câu 13: 1:15:56 - 1:21:53 Câu 2: 7:02 - 12:45 Câu 8: 51:21 - 54:31 Câu 14: 1:21:55 - 1:25:43 Câu 3: 12:48 - 18:28 Câu 9: 54:33 - 58:44 Câu 15: 1:25:43 - 1:28:51 Câu 4: 18:29 - 27:03 Câu 10: 58:45 - 1:03:03 Câu 16: 1:28:52 - 1:33:20 Câu 5: 27:04 - 33:54 Câu 11: 1:03:04 - 1:10:46 Câu 17: 1:33:21 - 1:45:10 Câu 6: 33:55 - 47:50 Câu 12: 1:10:47 - 1:15:55