TOP 10 đề ôn thi HKI Toán 12 – Trần Đại

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi học kỳ 1 môn Giới Toán 12 năm học 2016 – 2017 .Mời bạn đọc đón xem.

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 12

Môn: Toán 12

Thông tin:

64 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
LUYỆN THI TRẦN ĐẠI
Số 8, ngõ 462 đường Bưởi
ĐIỂM
Mã đề thi
01
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Chuyên đề: Học kỳ I lớp 12
Thời gian làm bài: 90 phút
(50 câu trắc nghiệm)
H và tên h
Câu 1:  th ca hàm s 
A.
42
21y x x
B.
42
21y x x
C.
42
21y x x
D.
42
21y x x
Câu 2: Cho hàm s
 th là
C
. Tìm t m M thuc
C
sao cho tip tuyn ca
 th
C
ti M song song vng thng
( ): 9 2yx
.
A.
(4;3)M
B.
(0; 1), ( 4;3)MM
C.
(0;1)M
D.
(0;1), (4;3)MM
Câu 3: Tìm m  
42
32x x m
có 3 nghim ?
A.
1
4
m
B.
1
4
m
C.
2m 
D.
2m 
Câu 4: Có my loi khu ?
A. 1 B. 3 C. 5 D. 6
Câu 5: Hàm s
t cc tiu ti
A.
2x 
B.
0x
C.
2x
D.
1x
Câu 6: Cho hình chóp
.S ABC
có 
ABC
là tam giác vuông ti
B
,
SA ABC
, gi
,DE
lt là
m ca
SB
và
SC
. Tâm ca mt cu ngoi tip hình chóp
.S ABC
là
A. m
B
B. m
S
C. m
E
D. m
D
Câu 7: Bng bin thiên trong hình bên là bng bin thiên ca hàm s n
A.
32
32y x x x
B.
C.
3
1y x x
D.
3
23y x x
Câu 8: Giá tr ln nht ca hàm s :
32
3 9 35y x x x
n
4;4
lt là
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A. 20 B. 10 C. 40 D. 30
Câu 9: Tìm tt c các giá tr ca m  
32
60x x m
có ba nghim phân bit.
A.
02m
B.
04m
C.
0 32m
D.
08m
Câu 10: Bit
log 2,log 3
aa
bc
 ca
2
3
log
a
ab
c




bng
A.
6
B.
1
3
C.
2
3
D.
5
Câu 11: Tìm tnh ca hàm s
36
2
log 2 1
x
y

A.
1
;
2
D




B.
DR
C.
1
;
2
D




D.
1
;
2
D



Câu 12: Tìm m  hàm s
32
2 3 1 6 2 3y x m x m x
nghch bin trên kho dài l
A.
0m
B.
9m
C.
8m
D.
0m
hoc
8m
Câu 13: Các khong nghch bin ca hàm s
21
1
x
y
x
là :
A.
;2
B.
; 
C.
1; 
D.
;1
và
1; 
Câu 14: Cho hình chóp
.S ABC

ABC
u cnh
2a
, tam giác
SAB
u và
nm trong mt phng vuông góc vi m tích khi chóp
.S ABC
là
A.
3
2
a
V
B.
3
Va
C.
3
3Va
D.
3
3
2
a
V
Câu 15:  th (C):
32
32y x x
p tuyn ca (C) t
0
3x
có
h s góc là
A. 6 B. 9 C. 9 D. 6
Câu 16: Giá tr ln nht ca hàm s
35y x x
là
A.
max 2
D
y
B.
max 2 2
D
y
C.
max 2
D
y
D.
max 1
D
y
Câu 17: Tìm tt c các giá tr ca tham s m 
2
1
x
e x x m
có nghim trên
[0;2]
A.
2
e m e
B.
me
hoc
2
me
C.
me
D.
2
me
Câu 18: m cng thng
23yx
 th hàm s
1
31
x
y
x

m
M
và
N

 m
I
ca
MN
có giá tr bng
A.
1
B.
0
C.
5
6
D.
2
3
Câu 19: Cho hàm s
1
yx
x

. Hàm s c tr?
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A. 0 B. 2 C. 3 D. 1
Câu 20: Mu tr  v trí A ca tnh Qung Bình mun tip cn v  tip t 
thc và thuc phng t n B và t c ngp con
ng t u tr không th n C bu tr có th chèo thuyn
t n v ng t n C vi vn tc 4km/h r n C vi vn tc 6km/h. Bit A
cách B mt khong 5km, B cách C mt khonh v  u tr n xã C
nhanh nht.
5
km
7
km
C
A
B
D
A.
2 2 BD km
B.
4 BD km
C.
2 5 BD km
D.
5 BD km
Câu 21: Cho hình hp ch nht
/ / / /
.ABCD A B C D
có
/
, 2 , 3AB a AD a AA a
. Th tích khi hp ch nht
/ / / /
.ABCD A B C D
là
A.
3
18Va
B.
3
6Va
C.
3
2Va
D.
2
6Va
Câu 22: Tnh D ca hàm s
2
( 1)yx

là
A.
( ; 1] [-1; )
B.
(1; )D
C.
( ;1) (1; )D
D.
\{1}D
Câu 23: Mi gi tit kim
50
tring vào mt ngân hàng vi lãi sut
7%
mt rng nu
không rút tin ra khi ngân hàng thì c sau m tin lãi s c nhp vào vu. Sau
5

mc s tin lãi là
A.
3,5
tring B.
70,128
tring C.
50,7
tring D.
20,128
tring
Câu 24: Giá tr nh nht ca hàm s hàm s
42
24y x x
là
A. 4 B. 2 C. 2 D. 4
Câu 25: Rút gn biu thc
1 2 3 2
.aa

có kt qu là
A.
4
a
B.
4
a
C.
22
a
D.
4 2 2
a
Câu 26: ng tiêm cng c th hàm s
1
2
x
y
x

A.
2y
B.
1x
C.
2x
D.
2x 
Câu 27: Tìm
m
 hàm s
32
2y x x mx
có hai cc tr.
A.
4
3
m
B.
4
3
m
C.
4
3
m
D.
4
3
m
Câu 28: o hàm ca hàm s
12x
ye
là
A.
'
x
ye
B.
12
'
x
ye
C.
12
'2
x
ye
D.
12
'2
x
ye

Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 29: Cho hàm s
42
1y x x
. Kh
A. Hàm s có hai cc tr.
B. Hàm s ng bin trên khong
,0
C. Hàm s nghch bin trên khong
1, 
.
D. Hàm s có mm cc tiu.
Câu 30: Cho hàm s
2
2
1
xx
y
x
. Kh
A. Hàm s nghch bin trên các khong
( ;1)
và
(1; )
.
B. Hàm s ng bin trên các khong
( ;1)
và
(1; )
.
C. Hàm s có tim cng
1y
.
D. Hàm s có tim cn ngang
1x
.
Câu 31: Gii b
2 1 2
34
43
xx
A.
1x
B.
1x
C.
1x
D.
1x
Câu 32: Tìm các giá tr ca tham s m sao cho hàm s
2x
y
xm
ng bin trên khong
(0;1)
A.
0m
B.
12m
C.
2m
D.
0m
hoc
12m
Câu 33: Cho hàm s
1
ln
1
y
x
. Khnh sai?
A.
. ' 1
y
x y e
B.
1
. ' 1
1
xy
x

C.
1
'
1
y
x
D.
. ' 1 0xy
Câu 34: Th tích ca khi tr 
2r cm
và chiu cao
9h cm
là
A.
3
18cm
B.
3
18 cm
C.
3
162 cm
D.
3
36 cm
Câu 35: Hàm s
42
21y x x
ng bin trên kho
A.
( 1;0);(1; ) 
B.
( 1;0);(0;1)
C. ng bin trên R D.
( ; 1);(0;1)
Câu 36: Th tích ca khi l
/ / / /
.ABCD A B C D
có cnh bng
a
là
A.
3Va
B.
1
3
Va
C.
3
1
3
Va
D.
3
Va
Câu 37: Cho kh ng
. ' ' 'ABC A B C

ABC
u cnh
2a
, gi
I
m
BC
, góc gia
'AI
và mt phng
()ABC
bng
0
30
. Th tích ca kh
. ' ' 'ABC A B C
là
A.
3
6a
B.
3
3a
C.
3
3
3
a
D.
3
2
4
a
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 38: Din tích xung quanh cng sinh
10l cm

5r cm
là
A.
2
50cm
B.
2
50 cm
C.
2
25 cm
D.
2
100 cm
Câu 39: Cho hình chóp
.S ABCD
 
ABCD
là hình thoi vi
2 , 3AC a BD a
,
SA ABCD
,
6SA a
. Th tích khi chóp
.S ABCD
là
A.
3
2Va
B.
3
6Va
C.
3
18Va
D.
3
12Va
Câu 40: u kin c  mt phng
()P
tip xúc vi mt cu
( ; )S O r
tm
H
là
A. Mt phng
()P
vuông góc vi bán kính
OH
tm
H
.
B. Mt phng
()P
song song vi bán kính
OH
.
C. Mt phng
()P
vuông góc vi bán kính
OH
tm
O
.
D. Mt phng
()P
vuông góc vi bán kính
OH
.
Câu 41:  th (C):
21
1
x
y
x
. Gm cng tim cn, t m I là
A.
1;2I
B.
1;2I
C.
2; 1I
D.
2;1I
Câu 42:     ng tam giác
/ / /
.ABC A B C
, tam giác
ABC
có
,2AB a AC a
, góc
0
60BAC
,
/
BB a
. Th tích kh
/ / /
.ABC A B C
là
A.
3
Va
B.
3
2
a
V
C.
3
3Va
D.
3
3
2
a
V
Câu 43: Tnh D ca hàm s
y ln(3 1)x
là
A.
1
( ; )
3
D 
B.
1
\{ }
3
D
C.
1
=[ ; )
3
D 
D.
1
( ; )
3
D 
Câu 44: Cho hình chóp tam giác
.S ABC
i
B
, cnh
SA
vuông góc vi m
bit
,2AB a SA a
. Khong cách t
A
n
mp SBC
là
A.
6
3
a
B.
3
3
a
C.
6
6
a
D.
2a
Câu 45: u
.S ABC
có cng
a
, cnh bên hp vi mt góc
0
60
.
Th tích V ca khi chóp
.S ABC
là
A.
3
3
16
a
V
B.
3
12
a
V
C.
3
3
12
a
V
D.
3
3
24
a
V
Câu 46: Cho hình chóp
.S ABCD
 t hình vuông cnh
a
. Các mt phng
( ), ( )SAB SAD
cùng
vuông góc vi mt phng
()ABCD
, cnh bên SC to v  t góc
0
30
. Th tích V ca khi chóp
.S ABCD
là
A.
3
6
9
a
V
B.
3
6
4
a
V
C.
3
3
3
a
V
D.
3
2
4
a
V
Câu 47: Cho hình chu
.S ABC
có tt c các cu bng
4
. Din tích ca mt cu ngoi
tip hình chóp
.S ABC
là
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
12
B.
2
4 r
C.
24
D.
2
4
3
r
Câu 48: Tìm m   th ca hàm s
4 2 4
22y x mx m m
m cc tr to thành mt tam giác
vuông.
A.
1m
B.
3m
C.
3m 
D.
1m 
Câu 49: Hàm s
32
y ax bx cx d
có bng bi
A. H s
0a
B. Hàm s t cc tr
C. Hàm s có giá tr ci bng
2
D. Hàm s có giá tr nh nht bng
3
Câu 50: i vi hàm s
sin2
()
x
f x e
ta có
A.
'3
12
fe



B.
'3
12
fe




C.
3
2
'
12
fe




D.
'
12
fe



LUYỆN THI TRẦN ĐẠI
Số 8, ngõ 462 đường Bưởi
ĐIỂM
Mã đề thi
02
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Chuyên đề: Học kỳ I lớp 12
Thời gian làm bài: 90 phút
(50 câu trắc nghiệm)
H và tên h
Câu 1: Cho hàm s
y f x
có bng bin thiên sau :
Vi giá tr nào c
()f x m
có 3 nghim phân bit
A.
15m
B.
15m
C.
1m
hoc
5m
D.
1m
hoc
5m
Câu 2:  th hàm s y =
2
21
x
x
i xng là :
A.
1
;2
2



B.
11
;
22
I



C. i xng D.
11
;
22
I



1
5
0
x
y
/
y
+
∞
-
∞
+
_
0
2
-
∞
0
+
+
∞
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 3: Cho hàm s
3
1
x
y
x
 th
C
. Chn câu khnh SAI:
A. Tnh
\1DR
B. o hàm
2
4
' 0, 1
( 1)
yx
x
C. ng bin trên
; 1 1;
D. i xng
1; 1I
Câu 4: Cho hàm s
C
. Tip tuyn c th hàm s tm ca
C
vi trc tung

A.
2y
B.
0y
C.
2xy
D.
20xy
Câu 5: Mt hình nón có chiu cao bng a và thit din qua trc là tam giác vuông. Din tích xung quanh ca
hình nón là :
A.
2
22a
B.
2
2
2
a
C.
a
2
2
D.
2
2 a
Câu 6: Cho hàm s
y f x
có bng bin thiên sau :
_
0
0
0
-1
-1
0
x
y
/
y
+
∞
-
∞
+
_
-1
1
+
∞
0
+
+
∞
Vi giá tr nào c
( ) 1f x m
m
A.
1m
B.
1m 
C.
1m 
hoc
2m 
D.
1m 
hoc
2m 
Câu 7: Mng gi ngân hàng kì hn 3 tháng (1 quý) vi lãi sut 0,65% mt
c lãi kép (tt c nh kì). Hi v khách này
sau bao nhiêu quý mi có s tin lãi l tin gu gi ngân hàng?
A. 12 quý B. 24 quý C. 36 quý D. Không th có
Câu 8: Hàm s
()y f x
 th  sau :
2
0
1
2
1
x
y
A.
1
()
2
x
y f x
x

B.
1
()
2
x
y f x
x

C.
1
()
2
x
y f x
x

D.
1
()
2
x
y f x
x

Câu 9: Bng bin thiên sau là ca hàm s nào ?
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
1
x
y
/
y
+
∞
-
∞
_
2
1
-
∞
+
∞
_
A.
21
3
x
y
x
B.
46
2
x
y
x
C.
3
2
x
y
x
D.
5
2
x
y
x
Câu 10: Hình chóp
.S ABC
có tam giác
ABC
vuông ti
A
,
AB AC a
,
I
m ca
SC
, hình
chiu vuông góc ca
S
lên mt phng
ABC
m
H
ca
BC
, mt phng
SAB
to v
góc bng
60
. Khong cách t m
I
n mt phng
SAB
theo
a
là :
A.
3
2
a
B.
3
4
a
C.
3
8
a
D.
3
16
a
Câu 11: Cho hàm s
32
– 3 2y x x
m M thung thng
( ) : 3 – 2d y x
và có tng khong
cách t M tm cc tr c th hàm s (1) nh nht có t là :
A.
42
;
55
M



B.
42
;
55
M




C.
42
;
55
M



D.
42
;
55
M



Câu 12: B
14x x m
có nghim khi :
A.
5m 
B.
5m
C.
5m
D.
5m 
Câu 13: B
2
12
2
3
log 2 log 5
4
xx



có nghim là:
A.
2;1x
B.
; 1 2;x  
C.
; 2 1;x  
D.
1;2x
Câu 14: Ct mt nón tròn xoay bi mt mt phng song song vi trc ca mc phn giao là:
A. mt parabol B. mt elip C. mt hypebol D. mng tròn
Câu 15:  th (C) ca hàm s
6
2
x
y
x
m có t nguyên ?
A. 2 B. 3 C. 6 D. 4
Câu 16: Da vào bng bin thiên ca hàm s, chn câu khnh ĐÚNG ?
A. Hàm s nh ti
3x
B. Hàm s có 2 cc tr
C. Hàm s không có cc tr D. Hàm s có 1 cc tr
Câu 17: Hàm s
4 2 2
25y x m x
t ci ti x = - 2 khi :
A.
2m
,
2m 
B.
2m
C.
2m 
D. Không có giá tr m
Câu 18: Khy là khnh SAI ?
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A. ng tròn xung quanh mt dây cung ca nó luôn to ra mt hình cu
B. ng cao ca nó luôn to ra mt hình nón
C. Quay mt tam giác nhn xung quanh cnh ca nó không th to ra hình nón
D. Quay hình vuông xung quanh cnh ca nó luôn sinh ra hình tr có
,,r h l
bng nhau.
Câu 19:  th hàm s
2
41
1
xx
y
x

m cc tr thuc ng thng
:d y ax b

ab
bng
A. -2 B. -8 C. 2 D. -6
Câu 20: Cho
( 2 1) ( 2 1)
mn

A.
mn
B.
mn
C.
mn
D.
mn
Câu 21: Cho các phát biu sau:

32
3 3 1y x x x


(II) 
32
3 3 1y x x x


( 1,0)I



32
2
x
y
x



32
2
x
y
x
có
2
32
lim 3
2
x
x
x
S các phát biu ĐÚNG là:
A. 2 B. 1 C. 3 D. 4
Câu 22: Giá tr ln nht và giá tr nh nht ca hàm s
2
2lny x x
trên
1
;ee


lt là :
A.
2
1
2
e



và 1 B.
2
2e
và 1 C. 1 và 0 D.  khác
Câu 23: Cho hàm s
42
22y x mx
  th hàm s m cc tr lp thành mt tam
giác vuông cân.
A.
0m
B.
1m
C.
0 1mm
D.  khác
Câu 24: Hình chóp SABC có SB = SC = BC = CA = a . Hai mt (ABC) và (ASC) cùng vuông góc vi (SBC). Th
tích hình chóp là :
A.
3
3
3
a
B.
3
3a
C.
3
3
4
a
D.
3
3
12
a
Câu 25: Cho hàm s
32
1
2 10
3
y x x mx
 hàm s ng bin trên
0;
A. Không có m B.  khác C.
0m
D.
0m
Câu 26: Mt công ty mun thit k  ng sa vi th tích
3
1dm
c thit k bi mt
trong hai mô hình sau: dng hình hp ch nhc dng hình tr c sn xut
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
cùng mt nguyên vt liu. Hi thit k theo mô hình nào s tit kic nguyên vt liu nht? Và thit
k  nào?
A. Hình tr và chiu cao b
B. Hình hp ch nht và cnh bên gp hai ln c
C. Hình tr và chiu cao b
D. Hình hp ch nht và cnh bên bng c
Câu 27: 
22
log ( 3) log ( 1) 3xx
có nghim là:
A.
11x
B.
9x
C.
7x
D.
5x
Câu 28: Cho hàm s
2
2
2
xx
y
x

(1). Tip tuyn v th hàm s (1) và song song vng thng
3 2 0xy
 :
A.
33yx
B.
33yx
;
3 19yx
C.
35yx
D.
35yx
;
33yx
Câu 29: Hình chóp t u có bao nhiêu mt phi xng ?
A. Bn B. Mt C. Ba D. Hai
Câu 30: Tnh ca hàm s
3
(2 )yx
là:
A.
\2D
B.
;2D 
C.
2;D 
D.
;2D 
Câu 31: 
2
4x x m
 m phân bit.
A.
2 2 2m
B.
2 2 2m
C.
2 2 2m
D.
2 2 2m
Câu 32: KhSAI ?
A.
2018 2017
22
11
22
B.
2017 2016
3 1 3 1
C.
2016 2017
2 1 2 1
D.
2 1 3
22
Câu 33: nh a.Mt bên SAB là tam giác u nm trong
mt phng vuông góc v tích khi chóp S.ABCD là:
A.
3
3a
B.
3
3
2
a
C.
3
3
4
a
D.
3
3
6
a
Câu 34: Hàm s
32
1 1 1
3 2 3
y x ax bx
t ci ti x = 1 và giá tr ci tng 2 khi
ab
bng :
A. 2 B. 3 C. 0 D. 1
Câu 35: i xng qua mt phng (P) bing thng d thành chính nó khi và ch khi :
A. d song song vi (P) B. d nm trên (P)
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
C.
()dP
D. d nm trên (P) hoc
()dP
Câu 36:  th hàm s
2
2
23
x
y
xx

có bao nhiêu ng tim cn ?
A. 3 B. 1 C. 2 D. 0
Câu 37: Cho a > 0, a 1. Tìm m ĐÚNG trong các m sau:
A. Tp giá tr ca hàm s y = a
x
là tp R
B. Tnh ca hàm s y = a
x
là khong (0; +)
C. Tnh ca hàm s y =
log
a
x
là R
D. Tp giá tr ca hàm s y =
log
a
x
là tp R
Câu 38: u S.ABC. Chn mnh  khnh ĐÚNG:
A. Hình chóp S.ABC là hình chóp có mu;
B. Hình chóp S.ABC có cng cnh bên;
C. Hình ching tròn ni tip tam giác ABC;
D. Hình chiu S trên (ABC) là trc tâm tam giác ABC;
Câu 39: ng thng
:y x k
c th (C) ca hàm s
3
2
x
y
x
tm phân bit khi và ch
khi:
A. Vi mi
kR
B.
0k
C.
1k
D. Vi mi
0k
Câu 40:  u cnh a. Hình chiu ca A' xung (ABC)
ng tròn ngoi tip tam giác ABC bit AA' hp vt góc
0
60
. Th  là :
A.
3
3a
B.
3
3
2
a
C.
3
3
6
a
D.
3
3
4
a
Câu 41: Hàm s ng bin trên tng khonh ca nó
A.
2y x x
B.
32
1
2 3 2
3
y x x x
C.
21
2
x
y
x
D.
1
2
x
y
x
Câu 42: ng cong (H) :
2
1
x
y
x
. M ĐÚNG ?
A. (H) có tip tuyn song song vi trc tung
B. (H) có tip tuyn song song vi trc hoành
C. Không tn ti tip tuyn ca (H) có h s 
D. Không tn ti tip tuyn ca (H) có h s góc âm
Câu 43: Cho hình chóp
.S ABC
, có
SA
vuông góc mt phng
()ABC
; tam giác
ABC
vuông ti
B
. Bit
2 ; ; 3SA a AB a BC a
a mt cu ngoi tip hình chóp là
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
22a
B.
2a
C.
2a
D.
a
Câu 44: Cho hàm s
2
ln 4y f x x x x
,
'2f
ca hàm s bng bao nhiêu ?
A.
2ln 2
B. 2 C.
ln 2
D. 4
Câu 45:  u cnh a = 4 và bit din tích tam giác
ng 8. Th tích kh là :
A.
23
B.
43
C.
83
D.
16 3
Câu 46: i mt ph
mt cu ngoi tim nào ?
A. m ca SC. B. m A
C. nh S D. Tâm hình vuông ABCD
Câu 47: Hàm s
()y f x
 th  sau :
A.
2
( ) ( 3) 4y f x x x
B.
2
( ) ( 3) 4y f x x x
C.
2
( ) ( 3) 4y f x x x
D.
2
( ) ( 3) 4y f x x x
Câu 48: Mt hình tr có trc
27OO
, ABCD là hình vuông có cnh bnh nng
a hình vuông trùng vi trung m ca
.OO
Th tích ca hình tr bng bao nhiêu ?
A.
50 7
B.
25 7
C.
16 7
D.
25 14
Câu 49: Cho hàm s
2
43
2
xx
y
x
 th (C). Tích các khong cách t mm bt k  th (C)
ng tim cn ca nó bng bao nhiêu ?.
A.
7
2
B.
2
2
C.
72
2
D.
1
2
Câu 50: Nghim c
2
3 2 9 .3 9.2 0
x x x x
là :
A.
2x
B.
0x
C.
2, 0xx
D. Vô nghim
4
2
x
-1
0
y
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
LUYỆN THI TRẦN ĐẠI
Số 8, ngõ 462 đường Bưởi
ĐIỂM
Mã đề thi
03
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Chuyên đề: Học kỳ I lớp 12
Thời gian làm bài: 90 phút
(50 câu trắc nghiệm)
H và tên h
Câu 1: Cho hàm s
32
34y x x
 th ( C ). Tip tuyn vng cong (C), song song vng
thng
( ): 3 5d y x
có 
A.
34yx
B.
35yx
C.
31yx
D.
32yx
Câu 2:  hàm s
32
3 2 1y x mx mx
luôn nghch bin trên R.
A.
3
0
2
m
B.
3
0
2
m
C.
3
0
2
m
D.
3
0
2
m
Câu 3: p tuyn ca (C):
21
2
x
y
x
vuông góc vng thng
1
2
5
yx

trình là:
A.
1
2
5
yx
và
1
22
5
yx
B.
52yx
và
5 22yx
C.
52yx
và
5 22yx
D.
1
2
5
yx
và
1
22
5
yx
Câu 4: Giá tr ln nht ca hàm s
32
3 9 35y x x x
n [-4 ; 4] bng. Ch
A. 40 B. 8 C. 41 D. 15
Câu 5: Trong các khnh sau v hàm s
3 10
9
x
y
x
, hãy tìm kh
A.  th hàm s ch có mt tim cn. B. Hàm s có mm cc tr
C. Hàm s nghch bin trên tng khonh D. Hàm s ng bin trên tng khonh
Câu 6:  hàm s
2 3 2
1
2 3 1
3
y m m x mx x
ng bin trên R
A.
30m
B.
30m
C.
30m
D.
30m
Câu 7: nh m  hàm s
32
1
3 2 3
x mx
y
t cc tiu ti
2x
.
A.
1m 
B.
2m 
C.
1m
D.
2m
Câu 8: Cho t din SABC có SA = 2a, SA
(ABC). Tam giác ABC có AB = a, BC = 2a, CA =
5a
. Din tích mt
cu ngoi tip t din SABC là:
A.
2
9 a
B.
2
18 a
C.
2
27 a
D.
2
36 a
Câu 9: Hàm s
42
21y x x
có bao nhiêu cc tr ?
A. 0 B. 2 C. 1 D. 3
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 10: Hàm s y =
5
1
log
6 x
có tnh là:
A.  B. (- C.  D. R
Câu 11: Tìm các giá tr ca tham s m  hàm s
3
2
15
3
x
y m x mx
m cc tr.
A.
35
2
m
B.
35
2
35
2
m
m
C.
23m
D.
1m
Câu 12: Cho hình lnh bng a; Gi
xq
S
là din tích xung quanh ca hình tr
i tin tích
xq
S
là :
A.
2
a
B.
2
2a
C.
2
3a
D.
2
2
2
a
Câu 13: Nghim c
9 4.3 45 0
xx
là
A.
2x 
B.
1x
C.
3x
D.
2x
Câu 14:  th hàm s
42
2( 2) 2 3y x m x m
ct trc hoành tm phân bit khi
A.
3
2
m 
B.
3
2
1
m
m


C.
3
2
1
m
m

D.
1m 
Câu 15: Cho hàm s:
22
ln(2 )y x e
.
o hàm cp 1 ca hàm s trên là:
A.
2 2 2
42
(2 )
xe
xe
B.
2 2 2
4
(2 )
x
xe
C.
22
4
(2 )
x
xe
D.
2 2 2
(2 )
x
xe
Câu 16: Mt hình hp ch nht ni tip mt ca mt cu
bng:
A.
2 2 2
1
2
abc
B.
2 2 2
abc
C.
2 2 2
2( )abc
D.
2 2 2
3
abc
Câu 17:  th hàm s
1
2
x
y
x
có dng:
A.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
B.
-4 -3 -2 -1 1 2
-2
-1
1
2
3
4
x
y
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
C.
-2 -1 1 2 3 4
-2
-1
1
2
3
4
x
y
D.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
Câu 18: Cho t diu ABCD cnh a; Din tích xung quanh cng tròn ngoi tip
tam giác BCD, chiu cao bng chiu cao ca t din ABCD là:
A.
2
3
2
a
B.
2
2
3
a
C.
2
3
3
a
D.
2
3 a
Câu 19: Nghim ca b
21
39
x
là
A.
3
2
x
B.
2
3
x
C.
3
2
x
D.
2
3
x
Câu 20:  th hàm s
42
2y x x
có dng:
A.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
B.
-4 -3 -2 -1 1 2 3 4
-3
-2
-1
1
2
3
4
5
x
y
C.
-4 -3 -2 -1 1 2 3 4
-3
-2
-1
1
2
3
4
5
x
y
D.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
Câu 21:  th hàm s
32
4 6 1y x x
có dng:
A.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
B.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
C.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
D.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
Câu 22:














Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
3
2a
B.
3
3a
C.
3
1
a
3
D.
3
1
a
2
Câu 23: Cho hàm s
32
3 3 1 1 3
m
y x x m x m C
 hàm s có ci , cc ting
thm ci và cc tiu cùng vi gc t O to thành mt tam giác có din tích bng 4 .
A.
2m 
B.
1m 
C.
1m 
D.
1m
Câu 24: Tp nghim ca b
1
2
log 1x
là
A.
1
;
2




B.
2;
C.
;2
D.
1
;
2




Câu 25:   p tuyn c  th (C):
4
2
9
2
44
x
yx
t  m ca nó vi trc
Ox
có

A.
15( 3)yx
B.
9
4
y 
C.
15( 3)yx
và
15( 3)yx
D.
9
4
y 
và
9
4
y 
Câu 26: Cho hàm s
1
2
x
y
x
. Kh
A. Hàm s ch bin trên R
B. Hàm s ng bin trên khong
;2 2; 
C. Hàm s ng bin trên tng khonh ca nó
D. Hàm s ch bin trên tng khonh ca nó
Câu 27: Cho hàm s
2
()
1
x
yC
x
ng thng
:d y m x
. Vi giá tr nào ca m thì d ct (C) tm
phân bit.
A.
2
2
m
m

B.
22m
C.
22m
D.
2
2
m
m

Câu 28: Vi giá tr nào ca m, n thì hàm s
3
y x mx n
t cc tiu tm
1x 
 th c
m (1;4)?
A. m = 1; n = 2 B. m = 2; n = 3 C. m = 2; n = 1 D. m = 3; n = 2
Câu 29:  t c các cnh bng a; Th  bng:
A.
3
3
4
a
B.
3
3
12
a
C.
3
3
a
D.
3
2
a
Câu 30: 
2
55
1
log log (5 ) 2 0
2
xx
có hai nghim
12
,xx
m bng :
A.
5
25
B. 5 C.
5
5
D.
5
5
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 31: S nghim c
5
5
log ( 2) log (4 6)xx
là
A. 3 B. 1 C. 2 D. 0
Câu 32: Cho hình vuông ABCD cng trung trc ca cc hình tr. K
din tích xung quanh ca hình tr bng:
A.
2
2 a
B.
2
4 a
C.
2
6 a
D.
2
8 a
Câu 33: Bn An mun dán li bên ngoài chic nón lá bng giy màu, bi dài t nh n vành nón
là 0.3m, bán kính ma nón là 0.25m. Tính s giy màu bn An cn dùng?
A.
2
10
xq
Sm
B.
2
20
xq
Sm
C.
2
5
20
xq
Sm
D.
2
3
20
xq
Sm
Câu 34: Mi gi s tin 100 tring vào mt ngân hàng vi lãi sut rng nu không
rút tin ra khi ngân hàng thì c sau m tin s c nhp vào vi ta g
 c s tin 260 trin gi trong khong th
? ( nu trong khong thi gian này không rút tin ra và lãi sui )
A.  B.  C.  D. 
Câu 35: Th tích khi chóp có diu cao h là:
A.
V Bh
B.
1
2
V Bh
C.
2V Bh
D.
1
3
V Bh
Câu 36:  th hàm s
21
1
x
y
x
i xng là:
A. K( 0; 2) B. M( 2; 1) C. I( 1; 2) D. N(1; - 2) ;
Câu 37: 
11
9 13.6 4 0
x x x
có 2 nghim
12
,xx
. Phát bi
A. m vô t B. m nguyên
C.  D. 
Câu 38: g cân ti B vi AC = a bit SA vuông góc v
ABC và SB hp vt góc 60
o
. Tính th tích khi chóp.
A.
3
3
4
a
B.
3
6
24
a
C.
3
3
a
D.
3
2
a
Câu 39: Cho hàm s
21
1
x
y
x
 th ng thng
2y x m
ct (C) tm phân bit A, B
sao cho tam giác OAB ( O là gc t ) có din tích bng
3
khi:
A.
3m
B.
3m 
C.
3m 
D.
2m 
Câu 40:  th hàm s
i xng là:
A. M( 1; - 2) B. I( -1; 0) C. N(- 1; - 2) D. K( -2; 0)
Câu 41:  ng
. ' ' 'ABC A B C
ci
, 2A BC a
'3A B a
. Din
 bng:
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
2
2a
B.
2
9a
C.
2
4
a
D.
2
2
a
Câu 42: Ch u
. ' ' 'ABC A B C
có cng a, mt php vi (ABC) mt góc
0
45
.
Chiu cao c bng:
A.
2a
B.
3
3
a
C.
3
2
a
D.
3a
Câu 43: Cho hàm s
42
11
22
y x x
. Kh
A. Hàm s t ci tm
1x 
, giá tr ci ca hàm s là
11y 
.
B. Hàm s t ci tm
0x
, giá tr ci ca hàm s là
00y
.
C. Hàm s t cc tiu tm
1x 
, giá tr cc tiu ca hàm s là
11y 
.
D. Hàm s t cc tiu tm
0x
, giá tr cc tiu ca hàm s là
00y
.
Câu 44: Tính th tích ca gic, bit gic có hình tr ng kính mt ging là 4m.
A.
3
20Vm
B.
3
18Vm
C.
3
125.7 Vm
D.
3
251.3 Vm
Câu 45: Giá tr ln nht ca hàm s
54yx
n [-1 ; 1 ] bng. Ch
A. 3 B. 0 C. 1 D. 9
Câu 46: u SABC cng a và cnh bên to v (ABC) mt góc 60
0
.Tính
th u SABC .
A.
3
3
12
a
B.
3
3
12
a
C.
3
3
a
D.
3
3
8
a
Câu 47: Nghim c
2
2
log ( 1) 3x 
là
A.
7x 
B.
7x 
C.
22x 
D.
7x
Câu 48: Vi giá tr nào c
42
30x x m
có ba nghim phân bit?
A. m = 0 B. m = 4 C. m = - 4 D. m = -3
Câu 49: Cho hàm s
32
6 9 1y x x x
. Kh
A. Hàm s ch bin trên khong
1;3
B. Hàm s ch bin trên khong
1; 
C. Hàm s ng bin trên khong
1;3
D. Hàm s ng bin trên khong
5;
Câu 50: u cnh a bit SA vuông góc v
hp vt góc 60
o
.Tính th tích khi chóp.
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
3
3
a
B.
3
3
12
a
C.
3
3
8
a
D.
3
3
4
a
LUYỆN THI TRẦN ĐẠI
Số 8, ngõ 462 đường Bưởi
ĐIỂM
Mã đề thi
04
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Chuyên đề: Học kỳ I lớp 12
Thời gian làm bài: 90 phút
(50 câu trắc nghiệm)
H và tên h
Câu 1: Cho hình chóp
.S ABCD

ABCD
ng chéo
23AC a
,
2BD a
và ct
nhau ti
O
, hai mt phng
SAC
và
SBD
cùng vuông góc vi mt phng
ABCD
. Bit khong cách t
m
O
n mt phng
SAB
bng
3
4
a
. Tính th tích
V
ca khi chóp
.S ABCD
.
A.
3
3
3
a
V
B.
3
3
6
a
V
C.
3
2
6
a
V
D.
3
3
12
a
V
Câu 2: S ng tim cn c th hàm s
2
2
21
43
x
y
xx

là:
A. 0 B. 2 C. 3 D. 1
Câu 3: Gi M, N lt là giá tr ln nht và giá tr nh nht ca hàm s
3
3sin 4siny x x
n
;
0
2



. Giá tr ca tng M+N là:
A. 0 B. 2 C. -1 D. 1
Câu 4:  th a hàm s nào ?
-2
-4
O
-3
-1
1
A.
42
33y x x
B.
42
1
33
4
y x x
C.
42
23y x x
D.
42
23y x x
Câu 5: Cho hình chóp tam giác
.S ABC

ABC
u cnh
a
, cnh bên
SA
vuông góc vi
m
SA a
. Tính th tích
V
ca khi chóp
.S ABC
.
A.
3
2
3
Va
B.
3
3
12
a
V
C.
3
3
3
a
V
D.
3
3
4
a
V
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 6: 
22
2x x m
m thc khi:
A.
0m
B.
01m
C.
1m
D.
0m
.
Câu 7: Tt c các giá tr ca tham s m  hàm s y = x
4
+ 2mx
2
+ m
2
+ m m cc tr là:
A. m
1 B. m
0 C. m < 0 D. m > 1
Câu 8: Các khong nghch bin ca hàm s
21
1
x
y
x
là
A. (- 1) và ( B. (- và 
C. (-  D. (-
Câu 9: GTLN ca hàm s y = 2 2sinxcosx là :
A. 1 B. 4 C. 3 D. 0
Câu 10: Gi x
1
, x
2
m cc tr ca hàm s
3 2 2 3
3 3( 1)y x mx m x m m
tha
22
1 2 1 2
7x x x x
khi m bng
A.
0m
B.
9
2
m 
C.
1
2
m 
D.
2m 
Câu 11: Th tích kh có diu cao h là:
A.
1
3
V Bh
B.
1
2
V Bh
C.
2V Bh
D.
V Bh
Câu 12: Hàm s y = x +
4
x
t cc tiu ti:
A. x = 2 B. x = 2 C. x = 0 D. Không tn ti
Câu 13: S m cc tr ca hàm s
32
43y x x x
là:
A. 0 B. 1 C. 2 D. 3
Câu 14: Cho
0a
,
1a
,
,xy
là 2 s  
A.
log
log
log
a
a
a
x
x
yy
B.
log
log
log
a
a
a
x
xy
y

C.
log log log
a a a
x
xy
y

D.
log log log
a a a
x y x y
Câu 15: ng thng
y x m
c  th hàm s
21
1
x
y
x
t  m phân bit A, B tha mãn
22AB
 ca m tha mãn:
A.
1m 
B.
1;7m
C.
1m 
D.
7m
Câu 16: Cho hình chóp t giác
.S ABCD

ABCD
là hình vuông cnh
a
, cnh bên
SA
vuông góc vi
m
2SA a
. Tính th tích
V
ca khi chóp
.S ABCD
.
A.
3
2
6
a
V
B.
3
2
3
a
V
C.
3
2Va
D.
3
2
4
a
V
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 17: Anh Vit mun mua mt ngôi nhà tr giá 500 tria. Bit rng lãi su
vi là 8% my ngay t bây gi s tin ít nht anh Vit phi gi tit kim vào ngân hàng
theo th th  tin mua nhà (kt qu n hàng triu) là:
A. 396 tring B. 395 tring C. 397 tring D. 394 tring
Câu 18: Cho log
23
5 ; log 5ab
. Giá tr ca
6
log 5
tính theo a và b là:
A.
1
ab
B.
ab
ab
C. a + b D.
22
ab
Câu 19:
log 0
a
b
khi.
A.
01
1
a
b

B.
01
01
a
b


hoc
1
1
a
b
C.
1
01
a
b

D.
1
1
a
b
Câu 20: B
2
1
3
log 2 3 0x ax a
có tp nghim là tp s thc R khi:
A.
2a
B.
12a
C.
1a 
D.
1
2
a
a

Câu 21: Cho hình chóp S.ABCD ABCD là hình ch nht, bit AB = 2a; AD = a; Hình chiu ca S 
m H ca cnh AB ; góc to bi SC 
0
45
. Th tích ca khi chóp S.ABCD là:
A.
3
3
a
B.
3
3
2
a
C.
3
22
3
a
D.
3
2
3
a
Câu 22: Gi M và m lt là giá tr ln nht và giá tr nh nht ca hàm s
2
61
3
xx
y

n
6; 7
.
M – m bng bao nhiêu?
A. 6561 B. 6562 C. 6564 D. 6558
Câu 23: Mt hình nón có bán kính mng
3,cm
 ng sinh bng
4cm
. Khi nón gii hn bi
 tích bng bao nhiêu ?
A.
2
3 7 cm
B.
2
12 cm
C.
2
15 cm
D.
2
2 7 cm
Câu 24: Th tích khi chóp có diu cao h là:
A.
V Bh
B.
1
2
V Bh
C.
2V Bh
D.
1
3
V Bh
Câu 25: Mt hình tr có bán kính mng
5,cm
thit din qua trc ca hình tr có din tích bng
2
20 .cm
n tích xung quanh ca hình tr bng bao nhiêu ?
A.
2
40 cm
B.
2
30 cm
C.
2
45 cm
D.
2
15 cm
Câu 26: Cho mt tm nhôm hình vuông ci ta ct 4 góc 4 hình vuông bng nhau và gp
tm nhôm l c mt cái hp không n th tích khi hp ln nht thì cnh hình vuông b ct dài:
A. 8cm B.
48
3
cm C.
8
92
cm D. 24cm
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 27:  th hàm s
2
1
mx m
y
x
ng bin trên tng khonh ca nó khi và ch khi tham s m
tha
A.
0
1
m
m

B.
0
1
m
m
. C.
0
1
m
m

D.
0
1
m
m
Câu 28: 
32
2
x
y
x
CC

A. (-1;1) và (-3;-7) B. (1;1) và (3;7) C. (1;-1) và (3;-7) D. (-1;-1) và (-3;7)
Câu 29: Cho hàm s
42
21y x m x m
 th (C), m là tham sm cc tr A, B, C sao
cho
OA BC
c tm cc tr thuc trc tung khi:
A.
3 3 3m 
B.
0m
hoc
2m
C.
5 5 5m 
. D.
2 2 2m 
Câu 30: Tp nghim ca b
22
2log 1 log 5 1xx
là:
A.
1;3
B.
1;5
C.
3;5
D.
3;3
Câu 31: Nc ca mt khi ch nht u n thì th tích c
A. 4 ln B. 64 ln C. 16 ln D. 192 ln
Câu 32: Cho hình l
. ' ' ' 'ABCD A B C D
có cnh bng
a
. Mnh là tâm ca hình
vuông
ABCD
i tip hình vuông
' ' ' 'A B C D
. Din tích xung quanh ca hình nón

A.
2
3
3
a
B.
2
2
2
a
C.
2
3
2
a
D.
2
6
2
a
Câu 33:  dài 3 cnh là 13, 14, 15. Mt mt cu tâm O, bán kính R = 5 tip xúc vi 3
cnh ca tam giác ABC. Tính khong cách t tâm mt cn mt phng cha tam giác .
A. 4 B. 3 C. 6 D. 5
Câu 34:  th hàm s
1
2
mx
y
xm
ng tim c
1; 2A

A.
22m 
B.
2m 
C.
2m
D.
22m 
Câu 35: Hàm s y = x
4
- 2x
2
+ 1 ng bin trên các khong
A. (--1) và ( 0;1) ; B. (- C. (- D. ∀x ∈ R
Câu 36:  ng
. ' ' 'ABC A B C
có tt c các cnh bng a; Tính th tích
V
ca kh
. ' ' 'ABC A B C
.
A.
3
3
4
a
V
B.
3
3
2
a
V
C.
3
2
a
V
D.
3
2
3
a
V
Câu 37: i ta mun xây mt bn chc dng khi hp ch nht trong mt phòng tm. Bit chiu
dài, chiu rng, chiu cao ca khi ht là 5m, 1m, 2m ( hình v bên). Bit mi viên gch có
chiu dài 20cm, chiu rng 10cm, chiu cao 5cm. Hi ta s dng ít nht bao nhiêu viên g xây
b tích thc ca bn chc? (Gi s  )
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
5m
2m
1dm
1dm
1m
V
H'
V
H
A. 1180 viên; 8820 lít B. 1180 viên; 8800 lít C. 1182 viên; 8820 lít D. 1182 viên; 8800 lít
Câu 38: Cho hình chóp tam giác
.S ABC

ABC
là tam giác vuông ti
,A AB a
2AC a
, cnh bên
SA
vuông góc vi m
SA a
. Tính th tích
V
ca khi chóp
.S ABC
.
A.
3
3
a
V
B.
3
Va
C.
3
2
a
V
D.
3
4
a
V
Câu 39: Hàm s  ng bin trên tnh ca nó ?
A.
2
x
y
B.
1
2
x
y



C.
0.5
y log x
D.
1
2
y log x
Câu 40: Hàm s y = x
3
+ 3x
2
nghch bin trên khong
A. (- B.  C. (-2; 0) D. (0; 2)
Câu 41:  th hàm s
34
25
x
y
x
có tim cn ngang là
A.
4
5
y 
B.
1
5
y 
C.
3
5
y 
D.
3
2
y
Câu 42: Hàm s m cc tr
A.
32
23y x x
B.
42
3y x x
C.
1
1
1
yx
x
D.
1
2
x
y
x
Câu 43: Cho hàm s  th 
A. GTLN ca hàm s an[-1; 2] là 2 B. GTLN ca hàm s n [-1; 2] là 0
1
-2
-1
2
0
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
C. GTLN ca hàm s n [-1; 2] là 4 D. GTLN ca hàm s n [-1; 2] là 1
Câu 44:  th a hàm s nào ?
4
2
-2
1
1
O
-2
A.
21
1
x
y
x
B.
2
1
x
y
x
C.
1
1
x
y
x
D.
2
1
x
y
x
Câu 45:  th a hàm s nào ?
2
1
O
3
-1
1
-1
A.
3
31y x x
B.
32
31y x x
C.
3
31y x x
D.
32
31y x x
Câu 46: Tip tuyn tm cc tiu c th hàm s
32
1
2 3 5
3
y x x x
A. Có h s góc bng
1
B. Có h s 
C. Song song vng thng
1x
D. Song song vi trc hoành
Câu 47: Giá tr ca biu thc
2 3 2 5 4
15 7
log
a
a a a
P
a




bng:
A. 2 B.
12
5
C.
9
5
D. 3
Câu 48: Hàm s y =
2 3 2
1
( ) 2 3 1
3
m m x mx x
ng bin trên R khi và ch khi
A.
30m
B.
30m
C.
30m
D.
30m
Câu 49: 
32
4 16
x
có nghim là:
A.
3
4
x=
B.
4
3
x
C.
3x
D.
5x
Câu 50: Cho hìi B,
AC a
, bit SA vuông góc vi mt
phng thng SC to vi mt phng (ABC) mt góc
0
60
. Bán kính ca mt cu ngoi tip hình
chóp S.ABC bng
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
a
B.
2a
C.
23a
D.
3a
LUYỆN THI TRẦN ĐẠI
Số 8, ngõ 462 đường Bưởi
ĐIỂM
Mã đề thi
05
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Chuyên đề: Học kỳ I lớp 12
Thời gian làm bài: 90 phút
(50 câu trắc nghiệm)
H và tên h
Câu 1: ng thng x = 1 là tim cng c th hàm s 
A.
22
2
x
y
x
B.
1
1
x
y
x
C.
2
1
1
x
y
x
D.
2
2 3 2
2
xx
y
x

Câu 2: Hàm s
32
1
3
y x x mx
ng bin trên khong
(1; )
thì m thuc kho
A.
[3; )
B.
( 1; ) 
C.
( 1;3)
D.
( ;3]
Câu 3: Tnh ca hàm s
1
3
yx
là:
A.
(0; )
B.
C.
1
;
3




D.
\{0}
Câu 4: Có bao nhiêu khu ?
A. 5 B. 3 C. 4 D. 2
Câu 5: Din tích xung quanh ca mng 3 và chiu cao bng 4 là:
A.
30
B.
36
C.
15
D.
12
Câu 6: Mt cái ni ni ta làm dng hình tr không np chiu cao ca ni 60cm, di
là
2
900 cm
. Hi h cn ming kim loi hình ch nht có chiu dài và chiu r làm thân
n
A. Chiu dài
60
cm chiu rng 60cm. B. Chiu dài 65cm chiu rng 60cm.
C. Chiu dài 180cm chiu rng 60cm. D. Chiu dài
30
cm chiu rng 60cm.
Câu 7: Hàm s
2
( ) 4f x x x m
t giá tr ln nht bng:
A. 3 B. 8 C. 3 D. 6
Câu 8: t
33
log 15, log 10ab
. Hãy biu din
3
log 50
theo a và b
A.
2ab
B.
22ab
C.
1ab
D.
2 2 2ab
Câu 9: Hàm s
32
2 9 12 5y x x x
m cc tr?
A. 1 B. 3 C. 2 D. 4
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 10: Cho hàm s
3
31y x x
  th        c   
trình:
3
3 1 0x x m
có ba nghim phân bit là:
A.
22m
B.
22m
C.
13m
D.
13m
Câu 11: Trong các hình ch nhn tích ln nht:
A. Hình vuông có cnh bng 20cm B. Hình ch nht có cnh bng 20cm
C. Hình ch nht có cnh bng 10cm D. Hình vuông có cnh bng 10cm
Câu 12: Hàm s
32
5 3 1y x x x
t cc tr ti:
A.
1
3;
3
xx
B.
1
3;
3
xx
C.
10
0;
3
xx
D.
10
0;
3
xx
Câu 13: S nghim âm c
22
4 6.2 8 0
xx
là
A. 0 B. 3 C. 2 D. 1
Câu 14: Mt mt cu có din tích
2
36 m
. Th tích ca khi cu này bng:
A.
3
36 m
B.
3
4
3
m
C.
3
108 m
D.
3
72 m
Câu 15: Hàm s
32
3 2 1y x mx x
ng bin trên khi và ch khi:
A.
32m 
hoc
32m
B.
3 2 3 2m
C.
3 2 3 2m
D. m > 0
Câu 16: Hàm s
42
1
33
2
y x x
nghch bin trên các khong nào ?
A.
3
0;
2




và
3
;
2





B.
3;0
và
3;
C.
;3
và
0; 3
D.
3;
Câu 17: Khu loi {3;5} là khi:
A. T diu B. u C. L D. Tám mu
Câu 18: Tp nghim ca b
2
5
log 4 1 0x
là:
A.
13
4;
2



B.
13
;
2




C.
13
;
2



D.
4;
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 19: a, chiu cao là 4a . th tích ca khi nón bng:
A.
3
15 a
B.
3
12 a
C.
3
12 a
D.
3
36 a
Câu 20: Bng bia hàm s nào?
A.
2
()
1
x
fx
x
B.
21
()
1
x
fx
x
C.
21
()
1
x
fx
x
D.
1
()
21
x
fx
x
Câu 21: Khi hp ch nhc là a, b  tích ca nó là:
A.
1
3
V abc
B.
1
2
V abc
C.
1
6
V abc
D.
V abc
Câu 22: Vi s thc a > 0. Kh
A.
m
m
n
aa
B.
m
nm
n
aa
C.
m
n
n
aa
D.
m
mn
n
aa
Câu 23: Hàm s
42
21y x x
 th là:
A. B. C. D.
Câu 24: 
2
0.5
log ( 5 6) 1xx
=0 có hai nghim là
12
,xx
. Tính
22
12
xx
A. 15 B. 15 C. 51 D. 51
Câu 25: Cho khi t din ABCD. Lm M nm gim N nm gia C và D; Bng hai mt phng
(CDM) và (ABN), ta chia khi t din khi t di
A. MANC, BCDN, AMND, ABND B. NACB, BCMN, ABND, MBND
C. ABCN, ABND, AMND, MBND D. MANC, BCMN, AMND, MBND
Câu 26:  th hàm s
32
22y x x x
 th (C) . Gi
12
,xx
 m M, N trên (C)
mà tp tuyn ca (C) vuông góc vng th
12
xx
bng :
A.
4
3
B. 1 C.
1
3
D.
4
3
Câu 27:





4 25
5 1 6
x




A.
(0; )
B.
( ; 2)
C.
( ;2)
D.
;2

Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 28: Mt khu rng có tr ng g 4.10
5
mét khi. Bit t ng ca các cây khu r
4% m có bao nhiêu mét khi g ?
A. 2016.10
3
(m
3
) B. 4,8666.10
5
(m
3
) C. 125.10
7
(m
3
) D. 36.10
5
(m
3
)
Câu 29:  th a hàm s nào ?
A.
32
31y x x
B.
3
31y x x
C.
3
31y x x
D.
32
31y x x
Câu 30: Cho hàm s
2
5
1
x
y
x
 th (C). Kh
A. (C) không có tim cng và có mt tim cn ngang
B. (C) không có tim cn
C. (C) không có tim cng và có 2 tim cn ngang
D. (C) có 2 tim cng và 2 tim cn ngang
Câu 31: Bng bia hàm s f(x). Hàm s f(x) ng bin trên khong nào ?
A.
( ;0)
B.
( 1;3)
C. (0;2) D.
(2; )
Câu 32: S m cng cong
32
21y x x x
ng thng y = 1 2x là:
A. 3 B. 0 C. 1 D. 2
Câu 33: Cho khu. Nn và gim chin thì th tích
ca kh:
A. n B. i C. Gin D. Gin
Câu 34: Cho kh u cnh bng a; m trong
mt pho vt góc 30
0
. Khi  tích kh ng:
A.
3
12
a
B.
3
4
a
C.
3
3
4
a
D.
3
3
12
a
Câu 35: S tim cn c th hàm s
1
1
x
y
x
là:
A. 0 B. 1 C. 3 D. 2
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 36: Cho hình chóp t u S.ABCD có cng a và góc gia mng
0
45
. Din
tích ca mt cu ngoi tip hình chóp S.ABCD là:
A.
2
9
4
a
B.
2
4
3
a
C.
2
3
4
a
D.
2
2
3
a
Câu 37: o hàm ca hàm s
log (2 2)
x
y

là:
A.
2
'
(2 2)ln
x
x
y
B.
2 ln 2
'
(2 2)ln
x
x
y
C.
2 ln 2
'
22
x
x
y
D.
2
'
22
x
x
y
Câu 38: Cho t din OABC bit OA, OBt vuông góc vi nhau, bit OA = 3, OB = 4 và th tích khi
t din OABC bng cách t n mt phng (ABC) bng:
A. 3 B.
41
12
C.
144
41
D.
12
41
Câu 39: Gi
,,l h R
l ng sinh, chia hình tr (T). Din tích xung
quanh
xq
S
ca hình tr (T) là:
A.
2
xq
S R h
B.
xq
S Rh
C.
xq
S Rl
D.
2
xq
S Rl
Câu 40: Giá tr ca biu thc:
3
5log 2
32
3 log log 8
bng:
A. 32 B. 25 C. 33 D. 26
Câu 41: Cho hàm s
()y f x
liên tng bin trên khong (a; b). Khnh
 là sai ?
A. Hàm s t giá tr nh nht ti x = a B. Giá tr ln nht ca hàm s bng
()fb
C. Giá tr nh nht ca hàm s bng
(a)f
D. Hàm s t giá tr nh nht ti x = b
Câu 42: Giá tr c hàm s
32
5y x x mx
có cc tr là:
A.
1
3
m
B.
1
3
m
C.
1
3
m
D.
1
3
m
Câu 43: Giá tr c  th hàm s
3 2 2 3
3 3( 1) 4 1y x mx m x m m
m cc tr A, B sao
cho tam giác AOB vuông ti O là:
A.
1; 2mm
B.
2m
C.
1m 
D.
1; 2mm
Câu 44: Giá tr ln nht ca hàm s
2
23f x x x
bng:
A. 2 B. 0 C. 3 D.
2
Câu 45: Trong mt chic hp hình tri ta b vào ba qu bóng Tennis, bit ra hình tr bng
hình tròn ln trên qu bóng và chiu cao ca hình tr bng 3 lng kính qu bóng. Gi
1
S
là tng din
tích ca ba qu bóng,
2
S
là din tích xung quanh ca hình tr. T s din tích
1
2
S
S
là:
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A. 1 B. 2 C. 5 D. 3
Câu 46: Gi R là bán kính, S là din tích và
V
là th tích ca khi cu. Công thsai ?
A.
2
SR
B.
2
4SR
C.
3
4
3
VR
D.
3.V S R
Câu 47: Trong các hàm s sau, hàm s ng bin trên khong (1; 3) ?
A.
3
1
x
y
x
B.
24
2y x x
C.
2
45y x x
D.
2
48
2
xx
y
x

Câu 48: Bng bia hàm s f(x). Hàm s f(x) t cc tiu tm:
A. x = 3 B. x = 2 C. x = 0 D. 
Câu 49: m cc tiu ca hàm s
42
32y x x
là:
A. x = 0
B. 
C.
1, 2xx
D. x = 5
Câu 50: Giá tr ln nht ca hàm s
32
3 9 35y x x x
n [-4; 4] bng:
A. 41 B. 8 C. 40 D. 15
LUYỆN THI TRẦN ĐẠI
Số 8, ngõ 462 đường Bưởi
ĐIỂM
Mã đề thi
06
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Chuyên đề: Học kỳ I lớp 12
Thời gian làm bài: 90 phút
(50 câu trắc nghiệm)
H và tên h
Câu 1: Cho hàm s
y f x
 th  bên. Tp hp tt c các giá tr c 
1f x m
có ba nghim phân bit là:
A.
22m
B.
24m
C.
13m
D.
12m
Câu 2: Tìm s m ln nh hàm s
32
1
4 3 2017
3
y x mx m x
ng bin trên R ?
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
3m
B.
4m
C.
2m
D.
1m
Câu 3: Tng ca giá tr ln nht và giá tr nh nht ca hàm s
2 lnf x x x
n
2;3
bng:
A.
10 2ln2 3ln3
B.
4 2ln2 e
C.
6 3ln3 e
D.
10 2ln2 3ln3 e
Câu 4: Tp nghim ca b
2
0,8 0,8
log log 2 4x x x
là :
A.
; 4 1; 
B.
4;1
C.
; 4 1;2
D.
4;1 2; 
Câu 5: i E, F lm ca SB, SD. T s
.
.
S AEF
S ABCD
V
V
bng:
A.
1
2
B.
3
8
C.
1
8
D.
1
4
Câu 6:  th ca hàm s 
A.
32
31y x x
B.
3
2 3 1y x x
C.
32
2 3 1y x x
D.
3
31y x x
Câu 7: Tp nghim ca b
31
11
39
xx
là :
A.
2; 
B.
;2
C.
; 2 2; 
D.
Câu 8: S ng tim cn c th hàm s
2
3
1
x
y
x
là :
A. 3 B. 1 C. 2 D. 0
Câu 9: Tip tuyn c th hàm s
4
1
y
x
t
1
o
x 

A.
3yx
B.
2yx
C.
2yx
D.
3yx
Câu 10: Tng các nghim c
11
4 6.2 8 0
xx
là:
A. 5 B. 1 C. 6 D. 3
Câu 11: Giá tr ln nht ca hàm s
3 2 2
45
x
f x e x x

n
13
;
22



bng:
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
14
3
2
3
e
B.
13
2
3
2
e
C.
11
4
5
2
e
D.
12
5
4
5
e
Câu 12: Cho hàm s
32
: 3 1C y x x
. Tip tuyn ca (C) song song vng thng
d : y = -3x+6
có

A.
y = -3x+5
B.
y = -3x 2
C.
y = -3x+1
D.
y = -3x-2
Câu 13: t thit dinh
ca hình nón có khong cách t tâm cn mt phng cha thit din là 12cm. Din tích ca thit
din có giá tr bng:
A.
2
200
ABC
S cm
B.
2
300
ABC
S cm
C.
2
400
ABC
S cm
D.
2
500
ABC
S cm
Câu 14: Cho hàm s
y f x
 th  k bên. Khsai?
A. Hàm s nghch bin trên khong
2; 1
B. Hàm s t cc tiu ti
1x 
,
1
CT
y 
C. Hàm s t ci ti
0x
,
0
CĐ
y
D. Hàm s ng bin trên khong
0;
Câu 15: Cho hàm s
4
2
x
y
x
. Khđúng:
A. Hàm s nghch bin trên khong
2;
B. Hàm s ng bin trên trên khong
2;4
C. Hàm s nghch bin trên trên khong
4;
D. Hàm s ng bin trên trên khong
;4
Câu 16: Cho hàm s
3
26y x x
. Khsai?
A. Hàm s t ci ti
1x 
B. Hàm s t cc tiu ti
1x
C. Hàm s ng bin trên khong
;2
D. Hàm s nghch bin trên khong
2;1
Câu 17: u kin ca tham s   ng thng
:5d y x
c  th hàm s
32
2 1 2 3 5y x m x m x
tm phân bit là:
A.
2m
B.
15m
C.
15mm
D.
mR
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 18: Cho hàm s
23
2
x
y
x
 th  ng thng
:2d y x m
c th (C) ti hai
m phân bit A, B sao cho tip tuyn ca (C) ti A, B song song nhau ?
A.
2m 
B.
1m 
C.
0m
D.
1m
Câu 19: Cho hình ch nht ABCD bit
1AB
,
3AD
. Khi quay hình ch nht ABCD xung quanh trc AB
thì cnh CD to nên hình tr tròn xoay. Th tích ca khi tr là:
A.
3
B.
3
C.
D.
3
3
Câu 20:  th  th  th ca hàm s
1
1
x
y
x
?
A.
-2 -1 1 2 3
-3
-2
-1
1
2
x
y
B.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
C.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
D.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
Câu 21: Cho hàm s
32
32y x x mx
. Tp hp tt c các giá tr c hàm s ng bin trên
khong
0;
là:
A.
1m 
B.
0m
C.
2m 
D.
3m 
Câu 22: Gi M và m lt là giá tr ln nht và giá tr nh nht ca hàm s
32
2 3 12 2y x x x
trên
n
1;2
. T s
M
m
bng:
A.
1
2
B.
1
3
C.
3
D.
2
Câu 23: o hàm ca hàm s
log 4yx
là:
A.
4
'
ln10
y
x
B.
1
'
ln10
y
x
C.
1
'
4 ln10
y
x
D.
ln10
'
4
y
x
Câu 24: u cnh a, SA vuông góc vnh bên SC hp v
mt góc
0
30
. Th tích ca khi chóp S.ABC là:
A.
3
3
12
a
B.
3
12
a
C.
3
4
a
D.
3
3
4
a
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 25: i A,
AB a
; Cnh bên SA vuông góc vi mt
a SB và mng
0
45
. Th tích ca khi cu ngoi tip hình chóp S.ABC là:
A.
3
3
8
a
B.
3
3
4
a
C.
3
3
2
a
D.
3
3
16
a
Câu 26: S m c th hàm s
42
32y x x x
ng thng
: 3 2d y x
là:
A. 3 B. 0 C. 1 D. 2
Câu 27: c s h tr t Ngân hàng Chính sách xã h các sinh viên có hoàn
coàn thành vic phí hc tp, mt ba ngân hàng 20 triu
ng vi lãi su bu tính lãi sau khi bn A kt thúc khóa hc. B
hoàn thành khóa hi mng/tháng. Bn A d tính s tr ht n gc ln
lãi sut cho ngân hàng trong 36 tháng. Hi s tin m mi tháng mà bn A phi tr cho ngân hàng là bao
nhiêu?
A.
2
2
1,12 20 0,12
1,12 1 12
m


triu B.
3
3
1,12 36 0,12
1,12 1 12
m


triu
C.
2
2
1,12 36 0,12
1,12 1 12
m


triu D.
3
3
1,12 20 0,12
1,12 1 12
m


triu
Câu 28: Bit
log2 a
,
log3 b
thì
log45
tính theo a và b bng:
A.
21ba
B.
21ba
C.
15b
D.
21ab
Câu 29:   
2
4 .2 2 0
xx
mm
. N      m
12
,xx
thõa mãn
12
4xx
thì m có giá tr bng:
A. 1 B. 2 C. 4 D. 8
Câu 30: Cho hàm s
32
3 1 9y x m x x m
. Giá tr nào c m
cc tr
1
x
,
2
x
tha mãn
12
2xx
:
A.
3m 
B. c A và B. C.
5m
D.
1m
Câu 31: Cho hàm s
y f x
o hàm
34
2
' 1 2f x x x x
. S m cc tr ca hàm s là:
A. 3 B. 2 C. 1 D. 0
Câu 32: i A, B bit
2AD a
,
AB BC a
. Cnh
bên SA vuông góc va SC và mng
0
45
. Th tích ca khi chóp S.ABCD bng:
A.
3
22
3
a
B.
3
2
2
a
C.
3
32
2
a
D.
3
3
2
a
Câu 33:  ng a, mt php vt góc
0
60
. Th
tích ca kh 
A.
3
33
2
a
B.
3
33
8
a
C.
3
33
4
a
D.
3
3
8
a
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 34: Cho
2
1
log
5
x
. Giá tr biu thc
22
4
log 8 log
4
1 log
x
x
P
x
bng:
A.
50
11
B.
10
11
C.
5
7
D.
5
6
Câu 35: nh a; Hai mt bên (SAB) và (SAD) cùng vuông
góc va SC và mng
0
30
. Th tích ca khi cu ngoi tip hình chóp S.ABCD là:
A.
3
86
9
a
B.
3
64 6
27
a
C.
3
86
27
a
D.
3
32
9
a
Câu 36: Tnh ca hàm s
3
2
2
2 3 1y x x
là:
A.
1
1;
2



B.
1
; 1;
2

 


C.
1
; 1 ;
2

 


D.
1
;1
2



Câu 37: Cho hàm s
4 2 4
22y x mx m m
 hàm s m cc tr m cc
tr to thành mt tam giác có din tích bng 1 ?
A.
2m 
B.
1m 
C.
0m
D.
1m
Câu 38: Cho hàm s
3 2 2
1
1
3
y x mx m m x
. Giá tr  hàm s t ci ti
1x
là:
A.
3m
B.
0m
C.
5m
D.
2m
Câu 39: Cho hình chóp t u S.ABCD có các cnh cùng bng a; Bán kính mt cu ngoi tip hình chóp
là:
A.
2a
B.
2
2
a
C.
3a
D.
3
2
a
Câu 40: Giá tr c tip tuyn c th hàm s
32
3 1 1y x mx m x
t    
1x 
m
1;2A
là:
A.
4
5
m
B.
3
4
m
C.
5
8
m
D.
2
3
m 
Câu 41:  u có các cnh bng a; Din tích mt cu ngoi ti là:
A.
2
7 a
B.
2
7
2
a
C.
2
7
3
a
D.
2
7
6
a
Câu 42: nh a, mu và nm trong
mt phng vuông góc vng cách t n mp(SCD) bng:
A.
21
5
a
B.
21
6
a
C.
21
7
a
D.
21
8
a
Câu 43: Cho hàm s
21
:
1
x
Cy
x
m
2;5M
thuc (C). Tip tuyn ca (C) tm M ct trc ta

Ox
,
Oy
lt tm A và B. Din tích ca tam giác OAB bng :
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
112
5
B.
122
3
C.
97
2
D.
121
6
Câu 44:  u cnh a, hình chiu ct phng (ABC)
m ca BC. Bit góc ging
0
60
. Th tích ca kh là:
A.
3
3
4
a
B.
3
33
8
a
C.
3
3
8
a
D.
3
33
4
a
Câu 45: Cho hàm s
. Tng các khong cách bé nht t m M thung
tim cn c th (C) là:
A. 6 B. 9 C. 3 D. 4
Câu 46: Cho hàm s
2
1x
y
xm
. Giá tr nh nht ca hàm s n
0,3
bng
1
4
khi:
Câu 47: S nghim c
log 3 log 9 log 2x x x
là:
A. 1 B. 2 C. Nhi D. 0
Câu 48: Cnh S bi mt phc mt tam giác vuông cân có cnh huyn
bng
2a
. Cho dây cung BC ct phng (SBC) to vi mt phng
cht góc 60
0
n tích tam giác SBC bng:
A.
2
2
9
ABC
a
S
B.
2
2
3
ABC
a
S
C.
2
2
4
ABC
a
S
D.
2
2
ABC
Sa
Câu 49: Cho mt tm nhôm hình ch nht ABCD bit
60AD cm
. Ta gp tm nhôm theo 2 cnh MN và PQ
 v c m khuy
th tích kh ln nht:
A.
40x
B.
30x
C.
45x
D.
20x
Câu 50:  tam giác vuông cân ti A,
2AB a
, SA vuông góc v
gia (SBC) và mng
0
60
. Th tích ca khi chóp S.ABC là:
A.
3
3
2
a
B.
3
3
6
a
C.
3
6
3
a
D.
3
3
3
a
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
LUYỆN THI TRẦN ĐẠI
Số 8, ngõ 462 đường Bưởi
ĐIỂM
Mã đề thi
07
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Chuyên đề: Học ky I lớp 12
Thời gian làm bài: 90 phút
(50 câu trắc nghiệm)
H và tên h
Câu 1: Cho
0a
;
0b
và biu thc
1
1
2
12
2
1
2( ) .( ) . 1 ( )
4
ab
T a b ab
ba




A.
1
3
T
B.
1T
C.
2
3
T
D.
1
2
T
Câu 2: Tp nghim ca b
2 2 2
2 1 2
4 .2 3.2 .2 8 12
x x x
x x x x
là
A.
1; 2 3;S 
B.
2; 1 3;3S
C.
2; 1 2;3S
D.
; 2 2;3S 
Câu 3: Cho
log3 ;log5 .mn

9
log 45
tính theo m, n là:
A.
1
2
n
m
B.
1
n
m
C.
2
2
n
m
D.
1
2
n
m
Câu 4: Tìm các giá tr c b
2
22
log ( 1 ) log ( )x ax a
có nghim?
A.
;1 3;a  
B.
3
; 1 ;
2
a

 



C.
; 1 2;a  
D.
2
; 1 ;
2
a

 



Câu 5: Trong các m sau, mn 
A. Hai khi t din bng nhau nu s nh bng nhau và s mt bng nhau
B. Hai khn bng nhau nu s mt bng nhau
C. Hai khn bng nhau nu có mi xng qua mt phng (P) bin khi này thành khi kia
D. Hai khn bng nhau nu s nh bng nhau
Câu 6: i vào 1 ngân hàng X vi lãi sut
t ln tìm li các giy t c- Role mi
bin rút ht s tic ngân hàng X. Ngân hàng
X tr cho ông Role s tin là 572,y thc s ông Role phi nhn
c s tin là bao nhiêu?
A.
380
24.1,06
 B.
381
24.1,06
 C.
380
25.1,06
 D.
380
24.1,07

Câu 7: Tìm m  sau:
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.  th hàm s
x
ya
vi
01a
m (a;1)
B.
x
ya
vi
1a
là hàm s nghch bin trên
; 
C.  th các hàm s
x
ya
và
1
()
x
y
a
vi
01a
i xng vi nhau qua trc Oy.
D.
x
ya
vi
01a
là hàm s ng bin trên
; 
Câu 8: Tp nghim c
2
3 8.3 15 0
x
x
. Là
A.
2;3S
B.
3
2;log 25S
C.
33
log 5;log 25S
D.
3
3;log 25S
Câu 9: Tp nghim ca b
1
1
1
5 2 5 2
x
x
x
là
A.
; 2 1;1S 
B.
2; 1 1;S 
C.
2; 1 2;S 
D.
; 3 1;2S 
Câu 10: Cho t diu ABCD. Góc ging thng AB và mt phng (BCD) bng:
A.
45
o
B.
1
arccos
3
C.
60
o
D.
1
arccos
3
Câu 11:  th ca hàm s
3
3y x x
t ci t
A. -1 B. 3 C. 0 D. 1
Câu 12: Tìm tt c các giá tr c 
2
44x x x x m
có nghii
mi
0;4x
.
A.
5m
B.
4m
C.
4m
D.
5m
Câu 13: Hãy chn cm t (hoc t n nó vào ch trng tc m 
 cnh ca m mt cn 
A. bng B. nh c bng
C. nh n D. l
Câu 14:  th  th ca hàm s nào:
-3 -2 -1 1 2 3
-1
1
2
3
4
5
6
7
8
9
x
y
A.
42
22y x x
B.
42
22y x x
C.
42
22y x x
D.
42
32y x x
Câu 15:  nht, AB=a, AD=a
3
ng thng SA vuông góc
vng thng SB to vi mp(SAC) góc 30
0
. Tính th tích khi chóp SABCD?
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
3
6
6
a
B.
3
6
2
a
C.
3
6a
D.
3
6
3
a
Câu 16: u cnh bng a . SA vuông góc mp(ABC),
2SA a
. Tính
theo a th tích khi chóp S.ABC.
A.
3
3
8
a
B.
3
3
12
a
C.
3
6
8
a
D.
3
6
12
a
Câu 17: Tìm các giá tr c  th hàm s
2
1
24
x
y
mx x

ng tim cn:
A.
0
1
3
m
m
B.
0
6
1
3
m
m
m
C.
0
6
1
4
m
m
m

D.
0
1
5
m
m
Câu 18: Tp nghim c
2
21
2
log ( 1) log ( 1)xx
là
A.
15
2;
2
S





B.
S 
C.
15
2
S





D.
15
3;
2
S





Câu 19: Cho a>0, b>0 và
22
7a b ab
. Chn m 
A.
3
ln( ) (ln ln )
2
a b a b
B.
1
ln( ) (ln ln )
32
ab
ab

C.
1
3ln( ) (ln ln )
2
a b a b
D.
2(ln ln ) ln(7 )a b ab
Câu 20: Hàm s
2
ln( 2)y x x
có tnh :
A.
2;1
B.
2;1
C.
; 2 1; 
D.
; 2 1; 
Câu 21: Cho hàm s
32
3 5 1y x x x
 th (C). Tip tuyn có h s góc ln nht c
trình là:
A.
21yx
B.
2yx
C.
21yx
D.
22yx
Câu 22:  th hàm s
3
32y x x
 th  th sau:
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
2
-2
B.
4
2
C.
4
2
D.
2
-2
Câu 23:







(ABC)

















n ABCKH theo
A.
3
a3
50
B.
3
3a 3
25
C.
3
3a 2
25
D.
3
3a 3
50
Câu 24: Cho khi chóp SABC có ABC là tam giác vuông cân ti A, AB = a, SA vuông góc vi mp(ABC), SA=a.
Khong cách gia AB và SC là:
A.
2
3
a
B.
2 21
7
a
C.
21
14
a
D.
2
2
a
Câu 25: ng thng (d):
31yx
; c th (C):
32
21y x x
tm A(x
o
; y
o
) thì :
A.
0
2y
B.
0
1y 
C.
0
2y 
D.
0
1y
Câu 26: Giá tr ln nht ca hàm s
5cos cos5y x x
n
;
44




là :
A.
33
B.
43
C.
23
D.
33
2
Câu 27: Cho hàm s
32
;( 0)y ax bx cx d a
. Bi      m phân bit x
1
; x
2
và
12
( ). ( ) 0y x y x
. Chn khnh sau
A.  th hàm s có hai cc tr ni vi trc hoành
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
B.  th hàm s có hai cc tr ni trc hoành
C.  th hàm s có hai cc tr nm phía trên trc hoành
D.  th hàm s t cc tr
Câu 28: Biu thc
5
3
;( 0)T a a a
. Vii dng lu tha vi s u t là:
A.
4
15
a
B.
2
15
a
C.
1
3
a
D.
3
5
a
Câu 29: Th tích ca kh có diB và chiu cao h là:
A.
V Bh
B.
1
2
V Bh
C.
4
3
V Bh
D.
1
3
V Bh
Câu 30: Mt nhà sn xut bt tr em cn thit k bao bì mi cho mt loi sn phm mi ca nhà máy. Bao
c thit k theo dng hình hp ch nht có chinh bng x và
hp có th tích là 1
3
dm
. Nu em là nhân viên thit k, em s thit k   tn ít nhiên liu
nht.
A.
1
2
hx
B.
hx
C.
1
3
hx
D.
1
3
xh
Câu 31: Cho kh u c
(ABC) là trm H ca AC. Góc ging 60
0
.
H
A
C
A'
C'
B
B'
Khong cách t 
A.
3
4
a
B.
3
4
a
C.
2
4
a
D.
3
2
a
Câu 32: Cho khi hp
1 1 1 1
.ABCD A BC D
. Mt phng
1
()A BD
chia khi hp thành hai phn. T s th tích gia
phn có th tích nh vi phn có th tích ln là:
A.
1
3
B.
1
4
C.
1
6
D.
1
5
Câu 33: Cho khi chóp có th tích bng V, khi gim di3 lu cao lên 2 ln
thì th tích khng:
A.
2
3
V
B.
3
2
V
C.
3
V
D.
5
V
Câu 34: Tìm các giá tr c hàm s ng bin trên
32
1 1 3 2 1y m x m x m x
A.
;1m
B.
1;m 
C.
1;m 
D.
;0m
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 35: Kht không phu?
A. Bát diu B. T diu
C. i hai mu D. u
Câu 36: Cho (H) là kh u có tt c các cnh bng a. Th tích ca (H) bng:
A.
3
2
3
a
B.
3
3
2
a
C.
3
3
4
a
D.
3
2
a
Câu 37: Gi M, N l t là giá tr ln nht, giá tr nh nht ca hàm s
42
2 4 5y x x
 n
1;3
ng :
A. 0 B. 135 C. 136 D. 134
Câu 38: Tp nghim c
3
log (3 2 ) 2x
. là
A.
2S 
B.
9S
C.
3S 
D.
4S 
Câu 39: Tìm các giá tr thc ca tham s   th hàm s
42
2 3 4y x mx m
có các cc tr u thuc
các trc to 
A.
1;0;4m
B.
;0 4m 
C.
1;2;3m
D.
4;0;4m
Câu 40: S tim cn c th hàm s
2
2
3
43
xx
y
xx

là
A. 3 B. 4 C. 2 D. 1
Câu 41: Hàm s
4 2 2
( 3) 2 1y x m x m
t cc tr khi và ch khi:
A.
3m 
B.
0m
C.
3m 
D.
3m 
Câu 42: Tp nghim c
2
3
1
( ) 27
3
xx
. Là
A.
2 21 2 21
;
22
S






B.
3 21 3 21
;
22
S






C.
3 21 3 21
;
22
S





D.
2 21 2 21
;
22
S





Câu 43: Hàm s ng bin trên
A.
3
1yx
B.
1
1
y
x
C.
73
3y x x
D.
tan2yx
Câu 44: Chn kh
A.
11
log
log
a
a
bb
B.
log .log log
a b a
b c c
C.
log .log log
b b a
a c c
D.
1
log log
a
a
bb
Câu 45: Tìm các giá tr thc ca tham s   th hàm s:
42
(3 1) 4 3y x m x m
ct trc hoành ti
bm phân bit ?
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
4
;
3




B.
3
;
4




C.
4
;
3




D.
3
;
4




Câu 46: Cho
0a
;
0b
và
a b c

A.
2 2 2
3 3 3
a b c
B.
2 2 2
3 3 3
a b c
C.
2 2 2
3 3 3
a b c
D.
2 2 2
3 3 3
a b c
Câu 47: Tp nghim ca b
2
1
2
1 log (2 ) 0xx
là:
A.
1;0 1;2
B.
1;0 1;2
C.
1
1; 1;2
2



D.
3
1;0 1;
2



Câu 48: Cho kh  tích
3
36cm
m bt kì thuc mt phng (ABCD).
A
D
C
B
A'
D'
C'
B'
M
Th tích ca kh
A.
3
16cm
B.
3
24cm
C.
3
18cm
D.
3
12cm
Câu 49: Bng bin thiên sau là bng bin thiên ca hàm s nào?
x
y’
y




–
–
–1
–1
–1
A.
2
1
x
y
x

B.
2
2
x
y
x

C.
2
1
x
y
x

D.
2
1
x
y
x
Câu 50: Khi hai mu thuc loi:
A. {3, 4} B. {3, 5} C. {5, 3} D. {4, 3}
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
LUYỆN THI TRẦN ĐẠI
Số 8, ngõ 462 đường Bưởi
ĐIỂM
Mã đề thi
08
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Chuyên đề: Học kỳ I lớp 12
Thời gian làm bài: 90 phút
(50 câu trắc nghiệm)
H và tên h
Câu 1: Vi giá tr nào ca tham s m thì hàm s nghch bin trên khong
1; 
.
A.
12m
B.
2; 2mm
C.
2m
D.
2m 
Câu 2: Mt khu rng có tr ng g 5.10
5
mét khi. Bit t ng ca các cây khu r
5% m có bao nhiêu mét khi g ?
A. 6.3814.10
4
(m
3
) B. 25.10
5
(m
3
) C. 6.3814.10
5
(m
3
) D. 6.3814.10
6
(m
3
)
Câu 3: Cho t diu ABCD cnh bng a; Th tích ca hình tr ng tròn ngoi tip tam giác
BCD và có chiu cao bng chiu cao ca t din ABCD là:
A.
3
2
3
a
B.
3
6
4
a
C.
2
3a
D.
3
6
3
a
Câu 4: Cho hàm s f(x) có bng bin thiên hình bên . Hàm s f(x) t cc tiu tm:
A. x = 2 B. x = 3 C. x = 0 D. x 
Câu 5: Cho hình chóp S.ABC có th tích là
3
70 .a
Gi M, N trên SB và SC sao cho
24
;
35
SM SN
SB SC

. Tính th
tích V ca khi t din SAMN.
A.
3
35Va
B.
3
14Va
C.
3
35
2
a
V
D.
3
112
3
a
V
Câu 6:  th k bên là ca hàm s nào trong các hàm s sau ?
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
3
x
y



B.
3
x
y
C.
x
ye
D.
x
e
y



Câu 7: Cho hàm s
1
yx
x

, giá tr nh nht ca hàm s trên
0;
là
A.
9
4
B.
1
2
C. 2 D. 0
Câu 8: Cho hàm s
31
21
x
y
x
. Kh
A.  th hàm s có tim cng là
3
2
x
B.  th hàm s có tim cn ngang là
3
2
y
C.  th hàm s có tim cng là x= 1 D.  th hàm s có tim cn ngang là
1
2
y
Câu 9: o hàm ca hàm s
log (3 3)
x
y

là:
A.
3 ln3
'
(3 3)ln
x
x
y
B.
3 ln3
'
33
x
x
y
C.
3
'
33
x
x
y
D.
3
'
(3 3)ln
x
x
y
Câu 10: Cho tam giác
ABC
vuông ti
B
có
2;AC a BC a
; khi quay tam giác
ABC
quanh cnh góc
vuông
AB
ng gp khúc
ABC
to thành mt hình nón tròn xoay có din tích xung quanh bng:
A.
2
2 a
B.
2
4 a
C.
2
3 a
D.
2
a
Câu 11: B
42
log 7 log 1xx
có tp nghim là :
A.
1;4
B. (-1; 2) C.
5;
D. (-; 1)
Câu 12: Cho hàm s
31
21
x
y
x

. Kh
A.  th hàm s có tim cn ngang là y = 3; B.  th hàm s có tim cng là
1x
;
C.  th hàm s có tim cn ngang là
3
2
y 
D.  th hàm s không có tim cn.
Câu 13: Cho hình chóp S.ABC có th tích bng
3
20a
. Gi M, N lm ca cnh BC, SC. Tính
th tích V ca khi t din BAMN.
A.
3
20
6
a
V
B.
3
20
3
a
V
C.
3
4Va
D.
3
5Va
Câu 14:  th hàm s m cc tr:
A.
42
21y x x
B.
42
21y x x
C.
42
21y x x
D.
42
2 4 1y x x
Câu 15: Vi
01a
và
0b
. Khnh nào sau 
A.
22
2 4 4
log log log
a
aa
b b b
B.
2
2 4 4
log log log
aa
a
b b b
C.
2
2 4 2
log log 6log
aa
a
b b b
D.
2
24
log log log
aa
a
b b b
Câu 16:  th ca mt trong bn hàm s nào?
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
2
2y x x
B.
32
21y x x x
C.
42
2y x x
D.
42
2y x x
Câu 17: Mt công ti b ng s     cho thuê. Bit rng nu cho thuê m   vi giá
ng mt tháng thì m i thuê và c mi lgiá cho thuê m
ng m b b trng. Hi mun có thu nhp cao nhi
cho thuê m vi giá bao nhiêu mt tháng.
A. 220000 B. 2150000 C. 2250000 D. 2300000
Câu 18: Hàm s
42
1
33
2
y x x
nghch bin trên các khong nào ?
A.
;3
và
0; 3
B.
3
;0
2




và
3
;
2





C.
3;
D.
3;0
và
3;
Câu 19:  th hàm s m cc tiu là
42
32y x x
A.
( 1;2)
B.
(1;2)
C.
2
(3; )
3
D.
(0;2)
Câu 20: Cho hàm s
3
31y x x
  th  hình bên. Các giá tr ca m  
trình:
3
31x x m
có ba nghim phân bit là:
A.
13m
B.
22m
C.
13m
D.
22m
Câu 21: Cho
ln 3x
. Giá tr ca biu thc:
2
ln4.log ln10.logxx
bng:
A.
33
B.
3
C.
23
D.
43
Câu 22: Cho hình chóp t giác
S.ABCD
. G t là m ca SA, SB, SC, SD. Khi
 s th tích ca hai khng:
A.
1
2
B.
1
4
C.
1
8
D.
1
16
Câu 23: Cho hàm s
()y f x
liên tn [a; b] và luôn nghch bin trên khong (a; b). Khnh
sai ?
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A. Hàm s t giá tr nh nht ti x = a B. Giá tr nh nht ca hàm s bng
()fb
C. Hàm s t giá tr nh nht ti x = b D. Giá tr ln nht ca hàm s bng
(a)f
Câu 24: Trong các hàm s  ng bin trên ?
A.
1
x
y
e



B.
3
x
y



C.
3
x
y
D.
2
x
y
Câu 25: Cho hàm s
2
5
11
x
y
x

 th (C). Kh
A. (C) không có tim cn
B. (C) không có tim cng và có mt tim cn ngang
C. (C) có 2 tim cng và 2 tim cn ngang
D. (C) không có tim cng và có 2 tim cn ngang
Câu 26: Ta  giao m ca  th hàm s
2
23
2
xx
y
x

và ng thng
1yx
là
A.
2; 3
B.
1;0
C.
2;2
D.
3;1
Câu 27: Cho kh u cnh b tích khi
 ng:
A.
3
4
a
B.
3
12
a
C.
3
3
4
a
D.
3
3
12
a
Câu 28: Cho hàm s y = f(x)= ax
3
+bx
2
+cx+d,a
0 . Khsai ?
A.  th hàm s luôn ct trc hoành B.
lim ( )
x
fx


C.  th hàm s i xng. D. Hàm s luôn có cc tr
Câu 29: Hàm s
32
34y x x mx
ng bin trên trên khong
( ;0)
vi m
A.
3m 
B. m>3 C. m<-3 D.
3m 
Câu 30: Cho
23
log 5 ; log 5ab

6
log 5
tính theo a và b là:
A.
ab
ab
B.
1
ab
C.
22
ab
D. a + b
Câu 31:

32
1
1
3
y x mx x m

m






A, B

22
2
AB
xx
A.
0m
B.
1m 
C.
3m 
D.
2m
Câu 32: Bng bia hàm s f(x). Hàm s f(x) ng bin trên khong nào?
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A. (0;2) B.
( 1;3)
C.
(2; )
D.
( ;0)
Câu 33: Mt hình tr có bán kính mng
5,cm
thit din qua trc ca hình tr có din tích bng
2
80 .cm
n tích xung quanh ca hình tr bng bao nhiêu ?
A.
2
60 cm
B.
2
80 cm
C.
2
45 cm
D.
2
40 cm
Câu 34:  u có các cnh cùng bng a; Din tích mt cu ngoi ti là:
A.
2
7 a
B.
2
7
2
a
C.
2
7
3
a
D.
2
7
6
a
Câu 35: Mt hành lang gia hai nhà có hình dng ca m     i. Hai mt bên
m kính hình ch nht dài 20m, rng 5m. Gi x (mét) là  dài cnh BC. Tìm x sao
cho hình  tr có th tích ln nht.
A.
52
B.
25
C.
10
D.
2
Câu 36: ng cong  th ca hàm s.
A.
42
21y x x
B.
32
31y x x
C.
2
31y x x
D.
3
31y x x
Câu 37: Tnh ca hàm s:
2
2
log (4 )x
là:
A.
( ; 2) (2; ) 
B.
[ 2;2]
C.
( 2;2)
D.
Câu 38: Cho tam giác OAB vuông ti O có
4, 3.OA OB
Quay tam giác OAB quanh cnh OA c mt
hình nón tròn xoay. Din tích toàn phn ca hình nón bng bao nhiêu ?
A.
15
B.
20
C.
24
D.
37
Câu 39: Cho hàm s y =f(x) có
lim ( ) 2
x
fx

và
lim ( ) 2
x
fx

. Phát bi
A.  th hàm s có TCN x = 2 B.  th hàm s 
C.  th hàm s không có TCN D.  th hàm s có 2 TCN
Câu 40: 
32
4 16
x
có nghim là:
A. x = 5 B. x =
4
3
C. x =
3
4
D. x = 3
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 41: Tính th tích V ca khi lt
'6AC a
A.
3
8Va
B.
3
8
3
a
V
C.
3
3
a
V
D.
3
22Va
Câu 42: Mt khi c dài bán kính là
R
. N n thì th tích ca khi cu

A. 4 ln B. 16 ln C. 24 ln D. 8 ln
Câu 43: ng thng x = 1 là tim cng c th hàm s nào s
A.
1
1
x
y
x
B.
22
2
x
y
x
C.
2
1
1
x
y
x
D.
2
2 3 2
2
xx
y
x

Câu 44: Giá tr ln nht ca hàm s
32
3 9 35y x x x
n [-4; 4] bng:
A. 8 B. 15 C. 41 D. 40
Câu 45: Cho khi B, AB = 3, BC = 4. Cnh bên SA vuông góc v
c tích khi chóp bng:
A. 12 B. 20 C. 10 D. 8
Câu 46: Giá tr cc tiu ca hàm s
23
10 15 6y x x x
là
A. -1 B. 110 C. 2 D. 3
Câu 47: Kim t tháp Kêp Ai Cc xây dng vào khoc Công nguyên. Kim t tháp
này là mt khi chóp t u có chiu cao 147 m, c tích ca nó là:
A. 7776300 m
3
B. 3888150 m
3
C. 2592100 m
3
D. 2592100 m
2
Câu 48: Cho hình chóp tam giác O.ABC, có 3 ct vuông góc và
;;OA a OB b OC c
ng cao
OH ca khi chóp bng:
A.
2 2 2
abc
a b a
B.
2 2 2 2 2 2
abc
a b b c a c
C.
abc
ab bc ac
D.
2 2 2 2 2 2
abc
a b b c a c
Câu 49: Hình v  th ca mt trong bn hàm s nào?
A.
2
1
x
y
x
B.
2
1
x
y
x
C.
2
1
x
y
x
D.
2
1
x
y
x
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 50: Cho hình cnh bng
a
, tam giác SAD cân ti S, mt bên
(SAD) vuông góc vi mt th tích khi chóp S.ABCD bng
3
3
3
a
. Tính khong cách h t n mt
phng (SBC).
A.
ha
B.
3
2
a
h
C.
3
3
a
h
D.
2ha
-----------------------------------------------
LUYỆN THI TRẦN ĐẠI
Số 8, ngõ 462 đường Bưởi
ĐIỂM
Mã đề thi
09
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Chuyên đề: Học kỳ I lớp 12
Thời gian làm bài: 90 phút
(50 câu trắc nghiệm)
H và tên h
Câu 1: Cho hình chóp
.S ABCD
có
ABCD
là hình vuông cnh a,
SA
vuông góc vi m
2SA a
.
Th tích ca khi chóp
.S ABCD
là:
A.
3
2a
B.
3
2
3
a
C.
3
2
6
a
D.
3
2
12
a
Câu 2: Cho khi chóp t giác u
.S ABCD
có tt c các cnh bng aa mt bên và mt

A.
60
O
B.
3
C.
30
O
D.
1
3
Câu 3: Cho
2
log 20 a
, giá tr ca
20
log 5
theo a là
A.
1
1
a
a
B.
1
a
a
C.
2a
a
D.
1
1
a
a
Câu 4: Cho hàm s
42
84y x x
. Chn phát bing các phát biu sau
A. Tt c u sai
B. Hàm s có cc tiu
C.  th hàm s ct trc hoành tm phân bit
D. Hàm s t cc tiu ti
0x
Câu 5: ng tim cn ngang ca hàm s
2
21
x
y
x
là
A.
1x
B.
1y
C.
1
2
x 
D.
1
2
y 
Câu 6: Tp nghim c
2
31
3
log log 4 1x x x
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
1;6
B.
C.
2;3
D.
2;6
Câu 7: Hàm s
32
27y x x x
ng bin trên
A.
1
; 1;
3

 


B.
1
;
3




C. D.
1
;1
3



Câu 8: S cc tr ca hàm s
32
3 4 2y x x x
là
A. 0 B. 2 C. 3 D. 1
Câu 9: Rút gn biu thc
31
31
2016 2017 2018 2016
.
a
aa

là
A.
2
1
a
B.
2
a
C.
1
a
D.
a
Câu 10: Cho hàm s
21
1
x
y
x
. Tip tuyn v th hàm s t bng 2 là
A.
11
33
yx
B.
11
33
yx
C.
1
1
3
yx
D.
1
3
yx
Câu 11: S m ci ca hàm s
4
2016yx
là
A. 0 B. 2 C. 1 D. 3
Câu 12: Hàm s
4
2
2 2016
4
x
yx
có giá tr ci là là
A.
0
CD
x
B.
2016
CD
y
C.
2
CD
x
D.
2012
CD
y
Câu 13: Giá tr ca
2
log 3
4A
là
A.
3A
B.
3A
C.
9A
D.
6A
Câu 14: Cho t din
ABCD
. Gi
', 'BC
lt là m ca AB và AC s th tích ca khi
t din
''AB C D
và khi t din
ABCD
bng
A.
1
2
B.
1
4
C.
1
8
D.
1
6
Câu 15: Tp nghim ca b
21
21
2
log 3 6 log 3.2 4.3 1
x x x x
x
là
A.
3
2
log 3;



B.
2
3
;log 3




C.
2
; 3;
3

 


D.
3; 
Câu 16: Cho hàm sô
1
1
x
y
x
. Kt lu
A. Hàm s ng bin trên tng khonh ca nó.
B. Hàm s luôn nghch bin trên
C. Hàm s luôn nghch bin trên tng khonh ca nó.
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
D. Hàm s nghch bin trên khong
; 1 1; 
Câu 17: Cho tam giác
ABC
u cnh bng 4 cm ng cao AH to nên mt hình nón.
Th tích c
A.
3
43
3
cm
B.
3
32 3
3
cm
C.
3
83
3
cm
D.
3
16 3
3
cm
Câu 18: Mt hình tr có bán kính
2r cm
và chiu cao
23h cm
n tích xung quanh ca hình
tr là:
A.
2
43 cm
B.
2
83 cm
C.
2
16 3 cm
D.
2
23 cm
Câu 19: Cho hàm s
32
2 3 3f x x x x
và
0 ab
. Kh ?
A. Hàm s nghch bin trên B.
f a f b
C.
0fb
D.
f a f b
Câu 20: S ng tim cn ca hàm s
2016
21
x
y
x
là
A. 3 B. 2 C. 0 D. 1
Câu 21: Hàm s
42
22y x x
nghch bin trên
A.
;1
B.
1;1
C.
;1
0;1
D.
1;0 1; 
Câu 22: Cho hàm s
32
1
4 5 17
3
y x x x
có hai cc tr
12
,xx
. Hi
12
.xx
là bao nhiêu ?
A. -8 B. 8 C. 5 D. -5
Câu 23: Cho t din
OABC
vi
1OA OB OC cm
và
,,OA OB OC
t vuông góc vi nhau. Din
tích mt cu ngoi tip t din bng
A.
3
4
B.
3
C.
3
4
D.
3
Câu 24: Cho mt tm nhôm hình vuông có cnh bng 12cmi ta ct bn góc hình vuông bng nhau,
ri gp tm nhôm l  c cái hp không np. Tính cnh ca hình vuông b ct sao cho th
tích ca khi hp là ln nht.
12
x
A.
2cm
B.
3cm
C.
4cm
D.
1cm
Câu 25: Mt hình tr i tip trong hai hình vuông ABCD và A’B’C’D’ ca hình lp
nh bng 2a. Th tích ca khi tr 
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
3
2
3
a
B.
3
4a
C.
3
4
3
a
D.
3
2a
Câu 26:  th hàm s
1mx
y
mx
(m là tham s) có d ?
A. Hình 3 B. Hình 4 C. Hình 1 D. Hình 2
Câu 27: Vi giá tr nào ca m hàm s
32
11
33
y x x mx
có hai cc tr
12
,xx
tha mãn
1 2 1 2
20x x x x
A.
3m
B.
2m
C.
4
3
m
D.
3m 
Câu 28: Vi giá tr nào ca m hàm s
3
21y x mx
t cc tiu ti
1x
A.
2
3
m 
B.
3
2
m 
C.
3
2
m
D.
2
3
m
Câu 29: Trong các hàm s i, hàm s nào có bng bin thiên
x

1

'y
- -
y
A.
23
1
x
y
x
B.
23
1
x
y
x
C.
3
1
x
y
x
D.
3
1
x
y
x
Câu 30: Hàm s
32
1
1 2 2
3
y x mx m x m
có ci và cc tiu khi và ch khi
A.
1m 
B. Vi mi m C. Không có giá tr m D.
1m 
Câu 31: S nghim c
2
2 7 5
2016 1
xx
là
A. 2 B. 0 C. 3 D. 1
Câu 32: Tìm tnh ca hàm s
5
31yx

A.
DR
B.
;1D 
C.
\1DR
D.
1;D 
Câu 33: Khnh nào s
A.
2016 2017
2 3 2 3
B.
2016 2017
2 1 2 1
Hình (1) Hình (2) Hình (3) Hình (4)
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
C.
2016 2017
3 2 3 2
D.
2016 2017
3 1 3 1
Câu 34: Trong các hàm s sau, hàm s nào có bng bin thiên
x

-1 0 1

'y
- 0 + 0 - 0 +
y


-3
- 4 - 4
A.
42
33y x x
B.
42
1
33
4
y x x
C.
42
23y x x
D.
42
23y x x
Câu 35: Hình chóp
.S ABC
có
SBC
và
ABC
u cnh a,
3
2
a
SA
ng cách t
S
n mt phng
ABC
bng
A.
a
B.
3
4
a
C.
3
2
a
D.
3
3
a
Câu 36: Cho hàm s
  th (C). Tip tuyn ca (C) song song v ng thng
3 2017yx

A.
32yx
B.
35yx
C.
34yx
D.
33yx
Câu 37: Anh Hùng gi s tin 50 tring vào mt ngân hàng vi lãi sut rng nu anh
Hùng không rút tin ra khi ngân hàng thì c sau m tin lãi s c nhp vào vu. Hi
c s tin là 80 tring.
A.  B.  C.  D. 
Câu 38: Trong các hàm s sau, hàm s nào ch có ci mà không có cc tiu ?
A.
21x
y
x
B.
2
45
2
xx
y
x

C.
42
5y x x
D.
32
3 6 1y x x x
Câu 39: Kh
. ' ' 'ABC A B C
có th tích là
V
, Gi
,,I J K
lm ca
', ', 'AA BB CC
.
 tích ca khi t din
'C IJK
bng
A.
1
6
V
B.
1
4
V
C.
1
5
V
D.
2
5
V
Câu 40: Tp nghim ca b
2016 2016
log log 2 1xx
là
A.
B.
1
;0
2



C.
1;3
D.
;1
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 41: Cho t din
OABC
có
,,OA OB OC
t vuông góc vi nhau và
1, 3OA OB
và
4OC

ng cao
OH
ca hình chóp là
A.
13
12
B.
12
13
C.
14
13
D. 7
Câu 42: Th tích ca khi cu ngoi tip hình l
. ' ' ' 'ABCD A B C D
có cnh bng
23
A.
36
B.
43
C.
32 3
D.
64 6
Câu 43: Cho hình chóp
.S ABC

ABC
u cnh a,
SA
vuông góc va
SB
và mng
60
O
. Tính khong cách gia
AC
và
SB
theo
a
A.
2a
B.
2
2
a
C.
15
5
a
D.
7
7
a
Câu 44: Hàm s nào trong các hàm s  th hàm s 
A.
32
32y x x
B.
C.
42
81y x x
D.
42
22y x x
Câu 45: Cho hình chóp
.S ABC
 
ABC
là tam giác vuông ti A,
SA
vuông góc v  
2, 4, 5AB AC SA
. Mt cnh ca hình chóp
.S ABC
có bán kính
r
bng
A.
5
2
B.
10
3
C.
25
2
D.
5
Câu 46: 
. ' ' ' 'ABCD A B C D

ABCD
là hình vuông cnh a,
13
'
2
a
DD
. Hình chiu
ca
'D
lên
ABCD
m
H
ca
AB
. Th tích kh là
A.
3
2
3
a
B.
3
12a
C.
3
2
3
a
D.
3
2a
Câu 47: Giá tr nh nht ca hàm s
1
1
x
y
x
n
3;5
là
A.
0
B.
1
C.
2
D.
3
2
Câu 48: Mt hp không nc làm t mt mnh các tông theo hình mu. Ht hình vuông
cnh x(cm), chiu cao là h(cm) và có th tích là 500cm
3
 dài cnh ca hình vuông sao cho chic
hc làm ra tn ít nhiên liu nht
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
h
h
h
h
x
x
A. 3cm B. 10cm C. 5cm D. 2cm
Câu 49: Cho hàm s
21
1
x
y
x
. Vi giá tr nào ca tham s a, b ng thng
y ax b
tip xúc
v th (C) tm  bng 5.
A.
3, 11ab
B.
3, 11ab
C.
11, 3ab
D.
11, 3ab
Câu 50:  u cng a, cnh bên bng
3
3
a
. Th tích ca (H)
bng:
A.
3
4
a
B.
3
12
a
C.
3
3
4
a
D.
3
3
12
a
LUYỆN THI TRẦN ĐẠI
Số 8, ngõ 462 đường Bưởi
ĐIỂM
Mã đề thi
10
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Chuyên đề: Học kỳ I lớp 12
Thời gian làm bài: 90 phút
(50 câu trắc nghiệm)
H và tên h
Câu 1: B
3
0
2
x



có tp nghim là:
A.
S
B.
S 
C.
0;S 
D.
0;S 
Câu 2: T l   Vic duy trì mc 1,05%. Theo s liu ca Tng Cc Thng
Kê, dân s ca Vii. Vi t   
thì dân s ca Vit Nam là:
A. i B. i C. i D. i
Câu 3: Tnh ca hàm s
2
1
log
32
x
y
x



là:
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
3
\
2



B. C.
3
;
2




D.
3
1;
2



Câu 4:  th hàm s ng tim cn ngang là
2y 
A.
2
1
x
y
x
B.
1
2y
x

C.
12
3
x
y
x
D.
2
2
2
x
y
x
Câu 5:  trình tip tuyn ca
21
:
2
x
Hy
x
tm vi trc hoành là:
A.
42yx
B.
0y
C.
4 5 2 0xy
D.
42yx
Câu 6: gim huyt áp ca mt b bi công thc
2
0,025 30G x x x

mgx
và
0x
là ling thuc cn tiêm cho b huyt áp gim nhiu nht thì cn tiêm cho bnh
nhân mt ling bng:
A.
40mg
. B.
30mg
. C.
15mg
. D.
20mg
.
Câu 7: Cho a, b  dài hai cnh góc vuông, c  dài cnh huyn ca m
1; 1c b c b
nh nào là đúng.
A.
2
c b c b c b c b
log a log a log a log a
B.
2.
c b c b c b c b
log a log a log a log a

C.
.
c b c b c b c b
log a log a log a log a

D.
2
c b c b c b
log a log a log c b
Câu 8: Cho hàm s
3
4
yx
. Kh
A. Hàm s nghch bin trên B. Hàm s o hàm là
7
4
3
0
4
xx

C.  th hàm s ng tim cn D.  th hàm s 
1;1A
Câu 9: Mt hình tr có din tích toàn phn gn tích xung quanh, th tích ca khi tr ng
bng
16
a hình tr bng bao nhiêu ?
A.
3
22r
B.
4r
C.
22r
D.
2r
Câu 10: Xét hàm s
43yx
n
1;1
. M 
A. Hàm s không có giá tr ln nht và giá tr nh nhn
1;1
.
B. Hàm s có cc tr trên khong
1;1
.
C. Hàm s ng bin
1;1
.
D. Hàm s có giá tr nh nht bng 1 khi
1x
, giá tr ln nht bng
7
khi
1x 
.
Câu 11: Cho hàm s
3
2
yx
. Khng.
A.  th hàm s ng tim cn B.  th hàm s 
C. Hàm s o hàm là
3
2
x
D. Hàm s ng bin trên R
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 12: Cho hàm s
y f x
có bng bin thiên sau:
 th nào th hin hàm s
y f x
?
A.
x
y
1
2
-1
O
-2
A
B.
x
y
1
2
-1
O
4
B
C.
x
y
1
-4
-1
O
-2
C
D.
x
y
1
2
-1
O
-2
D
Câu 13: Cho hàm s
32
y x bx cx d
.
x
y
x
y
x
y
x
y
(I) (II) (III) (IV)
 th nào có th  th biu din hàm s 
A. (III) và (IV). B. (II) và (IV) C. (I) D. (I) và (III)
Câu 14: Cho
0a
,
1a
,
,xy
là 2 s  
A.
log log log
a a a
x y x y
B.
log . log log
a a a
x y x y
y
x
'y
1
2
2
1
0
0
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
C.
log . log .log
a a a
x y x y
D.
log log .log
a a a
x y x y
Câu 15: i ta cn xây mt h ch c vi dng khi hp ch nht không np có th tích bng
3
500
m
3
 là hình ch nht có chiu dài gu r xây h là
500.000
ng/m
2
nh kích thc ca h c sao cho chi phí thuê nhân công thp nht. Tính chi phí 
A. 75 tring B. 74 tring C. 76 tring D. 77 tring
Câu 16:  ng
. ' ' 'ABC A B C
. Gi
M
m
''AC
,
I
m ca
AM
và
'AC

t s th tích ca khi t din
IABC
vi kh 
A.
2
3
. B.
2
9
. C.
4
9
. D.
1
2
.
Câu 17: o hàm ca hàm s
3
2
2
1yx
là:
A.
1
2
2
31xx
B.
1
2
2
3
1
2
x
x
C.
1
2
2
3
1
2
x
D.
2
31xx
Câu 18: Kim t tháp Kê-p Ai cc xây dng vào khoc Công nguyên . Kim t tháp
này là mt t u có chiu cao 147m , c tích ca Kim t tháp bng:
A. 2592100 m
3
B. 2592100 m
2
C. 7776300 m
3
D. 7776300 m
2
Câu 19: Tp nghim ca b
2
22
55
xx
A.
21x
B.
12x
C.
12x
D.
21xx
Câu 20: Cho hàm s
42
1
21
4
y x x
. Hàm s có
A. Mm cm cc tiu
B. Mm cm cc tiu
C. Mm cc tim ci
D. Mm cc tiu và mm ci
Câu 21: Cho hàm s
y f x
nh, liên tc trên và có bng bi
Kh
A. Hàm s t cc tr.
B. Hàm s có giá tr ln nht bng 0 và giá tr nh nht bng
1
.
C. Hàm s t ci ti
0x
t cc tiu ti
1x
.
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
D. Hàm s có giá tr cc tiu bng
1
.
Câu 22: T i xng c th hàm s
3
2
2 3 1
3
x
y x x
là:
A.
1
1;
3



B.
0; 1
C.
3; 1
D.
1
2;
3



Câu 23: Cho hàm s
2
2 .7
xx
fx
. Khnh nh sai ?
A.
2
2
1 log 7 0f x x x
. B.
2
1 ln2 ln7 0f x x x
.
C.
2
7
1 log 2 0f x x x
. D.
2
1 1 log 7 0f x x
.
Câu 24: Trong các m sau, m nào sai.
A. S cnh cn luôn lc bng 6.
B. S nh hoc s mt ca bt k c bng 4.
C. Tn tn có s nh và s mt bng nhau.
D. Tn tn có s cnh bng s mt.
Câu 25: Cho hình chóp S.ABCD. Gi M, N, P, Q theo th t m ca SA, SB, SC, SD. T s th tích
ca hai khi chóp S. MNPQ và S.ABCD bng :
A.
1
2
B.
1
4
C.
1
16
D.
1
8
Câu 26:  th ca ba hàm s
;;
x x x
y a y b y c

A.
bac
B.
c b a
C.
b c a
D.
c a b
Câu 27: Cho a > 0, a 1. T×m mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau:
A. TËp gi¸ trÞ cña hµm sè y = a
x
lµ tËp R
B. TËp x¸c ®Þnh cña hµm sè y = a
x
lµ kho¶ng (0; +)
C. TËp x¸c ®Þnh cña hµm sè y =
log
a
x
lµ tËp R
D. TËp gi¸ trÞ cña hµm sè y =
log
a
x
lµ tËp R
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 28: Vi giá tr nào ca m thì hàm s
sin3 cosy x m x
t cực tiểu tm
3
x
A.
23m 
B.
23m
C.
6m
D.
6m 
Câu 29: Cho hàm s
1
2
x
y
x
 th
C
. Chn phát bi:
A.  th
C
có mm cc tiu.
B.  th
C
ct trc hoành tm có t
1;0
.
C.  th
C
ki xng.
D.  th
C
có mm ci.
Câu 30:  th hình bên là ca hàm s nào?
A.
3
x
y
. B.
1
3
x
y



. C.
1
2
x
y



. D.
2
x
y
.
Câu 31: S n
ghim c
9 2.3 3 0
xx
là
:
A. 1 B. 4 C. 3 D. 2
Câu 32: Cho hàm s
2
yx
, xét các phát biu sau:
I. Tnh
0;D 
.
II. Hàm s ng bin vi mi x thuc tnh.
III. Hàm s m
1;1M
.
IV. Hàm s không có tim cn.
 phát biu đúng là
A. (I) B. (IV) C. (II) D. (III)
Câu 33: Vi giá tr nào ca tham s m thì hàm s
31xm
y
xm

nghch bin trên
(3; )
.
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
1
3
4
m
B.
1
3
4
m
C.
1
3
4
m
D.
1
4
m
Câu 34: p tuyn cng cong
3
: 2 3C y x x
tm
1;2M
là:
A.
31yx
. B.
2yx
. C.
22yx
. D.
1yx
.
Câu 35: Hàm s  th :
A.
32
33y x x x
B.
32
3 3 1y x x x
C.
32
2 3 3y x x x
D.
32
33y x x x
Câu 36: Mi vay ngân hàng vi s tin 20 tring, mi tháng tr ng
và phi chu lãi sut kép ca s ti là 0,4%/tháng. H ht n ?
A. 78 B. 79 C. 80 D. 81
Câu 37: Nhng hình nào không phi là khn là:
A. H1 và H2 B. H2 và H4 C. H1 và H3 D. H3 và H5
Câu 38: Hàm s
42
3 2 1y mx m x m
ch có ci mà không có cc tiu vi m:
A.
03mm
B.
3m
C.
30m
D.
3m 
Câu 39: Hàm s
42
4y x x
ng bin trên:
A. . B.
0;
C.
;0
D.
1;1
Câu 40:  t c các cu bng a ; Th tích ca khi t ding:
A.
3
3
12
a
. B.
3
3
6
a
. C.
3
3
24
a
. D.
3
3
36
a
.
H1
H2
H3
H4
H5
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Câu 41: i AC=2BD=2a và tam giác SAD vuông cân ti S nm trong
mp vuông góc v tích khi chóp là:
A.
3
3
12
a
B.
3
15
24
a
C.
3
5
12
a
D.
3
5
4
a
Câu 42:

2 3 2 3
xx
m



A.
2;m 
B.
2;m 
C.
;5m 
D.
;5m 
Câu 43: §Ó gi¶i bÊt ph¬ng tr×nh: ln
2
1
x
x
> 0 (*), mét häc sinh lËp luËn qua ba bíc nh sau:
Bíc1: §iÒu kiÖn:
2
0
1
x
x
0
1
x
x
(1)
Bíc2: Ta cã ln
2
1
x
x
> 0 ln
2
1
x
x
> ln1
2
1
1
x
x
(2)
Bíc3: (2) 2x > x - 1 x > -1 (3)
KÕt hîp (3) vµ (1) ta ®îc
10
1
x
x
VËy tËp nghiÖm cña bÊt ph¬ng tr×nh lµ: (-1; 0) (1; +)
Hái lËp luËn trªn ®óng hay sai? NÕu sai th× sai tõ bíc nµo?
A. Sai tõ bíc 1 B. Sai tõ bíc 3
C. Sai tõ bíc 2 D. LËp luËn hoµn toµn ®óng
Câu 44: Trong không gian, cho hình ch nht
ABCD
có
1AB
và
2AD
. Gi
, MN
lm
ca
AD
và
BC
. Quay hình ch nhó xung quanh trc
MN
c mt hình tr. Din tích toàn phn
ca hình tr bng:
A.
4
. B.
3
. C.
2
. D.
8
.
Câu 45: Din tích xung quanh ca hình tr ng tròn ngoi tip hình vuông có cnh bng 4 và
ng sinh l = 8 là :.
A.
32
B.
32 2
C.
32 2
D.
32 2
Câu 46: Ct hình tr có bán kính r = 5 và chiu cao
53h
bi mt mt phng song song vi trc và cách
trc 3cm. Hãy tính din tích ca thit dic to nên
A.
3
100 3cm
B.
3
20 3cm
C.
2
80 3cm
D.
2
40 3cm
Câu 47: o hàm ca hàm s :
3
x
y
A.
3
ln3
x
y
B.
' 13
x
y
C.
' 3 .ln3
x
y
D.
1
' .13
x
yx
Câu 48: Cho hình chóp t u có tt c các cu bng a; Tính th tích kh
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
A.
3
2
4
a
B.
3
2
6
a
C.
3
3
12
a
D.
3
3
3
a
Câu 49: Cho hình chóp S.ABCD, M m trên SA mà SM=
1
3
SA s
SMBD
SABD
V
V
bng:
A.
1
2
B. 3 C.
1
3
D. 2
Câu 50: Hàm s ng bin trên tnh ca nó?
A.
0,5
x
y
B.
2
x
y
e



C.
2
x
y
D.
x
e
y



-----------------------------------------------
| 1/64
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
LUYỆN THI TRẦN ĐẠI
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Số 8, ngõ 462 đường Bưởi
Chuyên đề: Học kỳ I lớp 12 ĐIỂM Mã đề thi
Thời gian làm bài: 90 phút 01
(50 câu trắc nghiệm)
Họ và tên học sinh:………………………………………………..
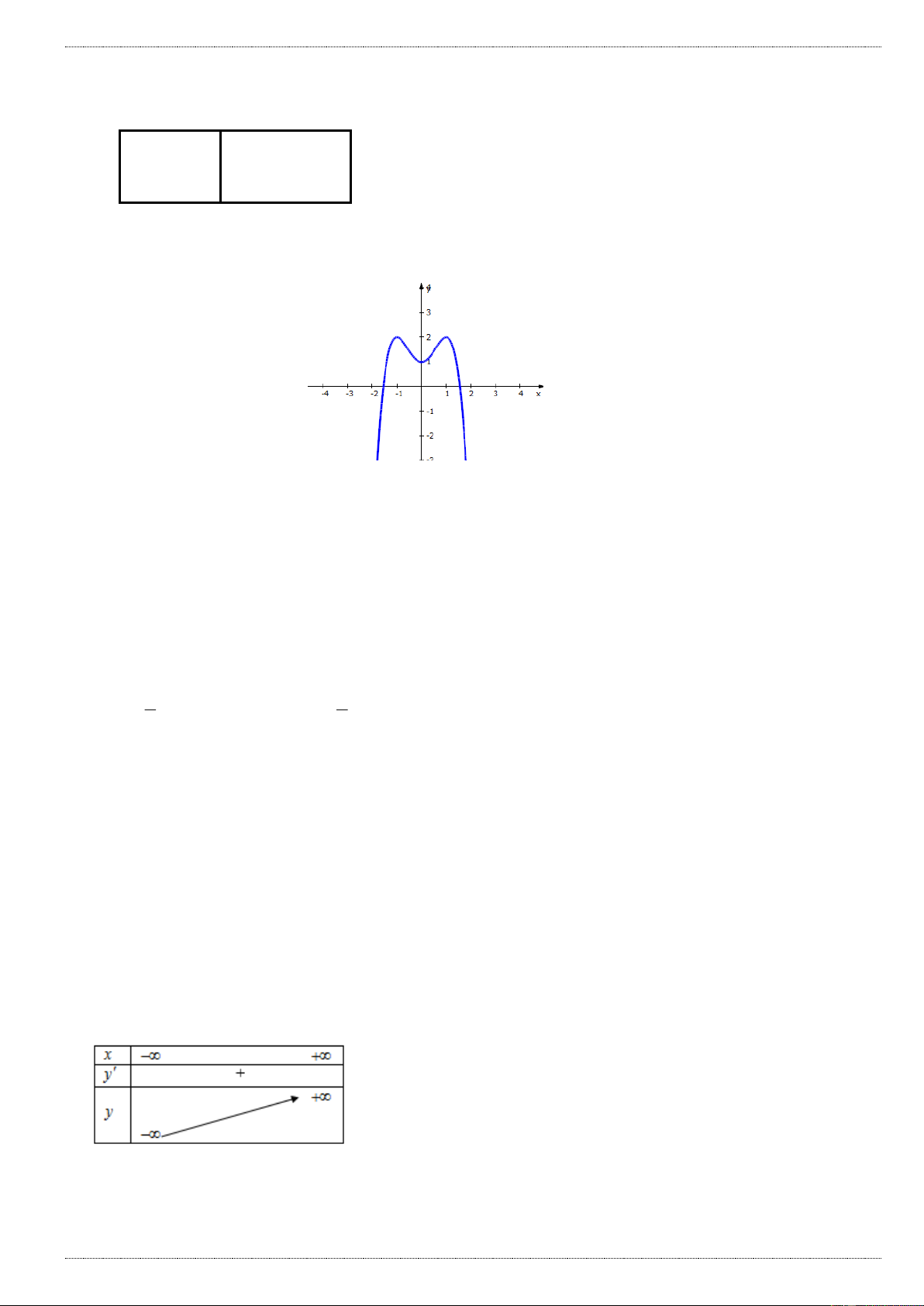
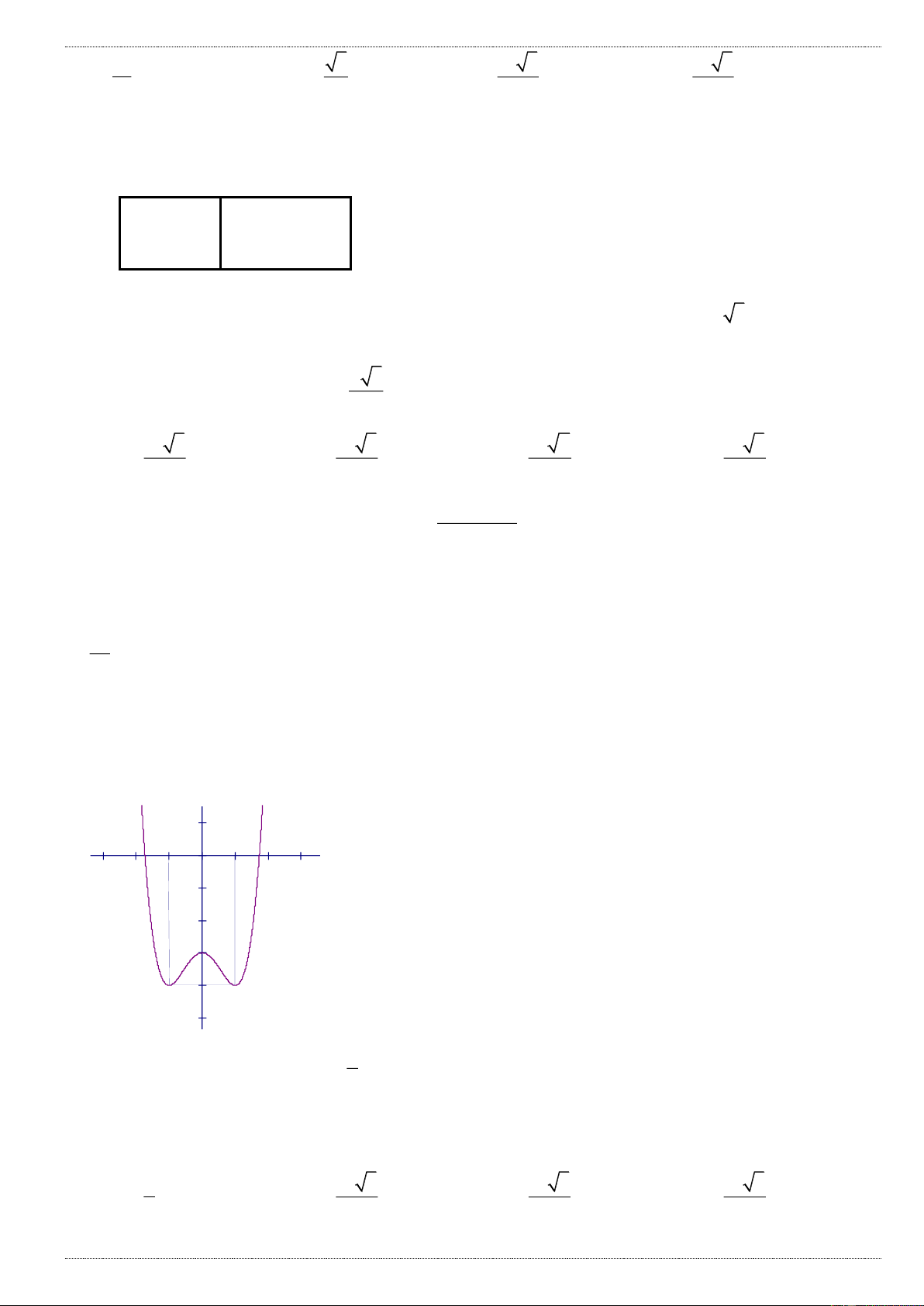
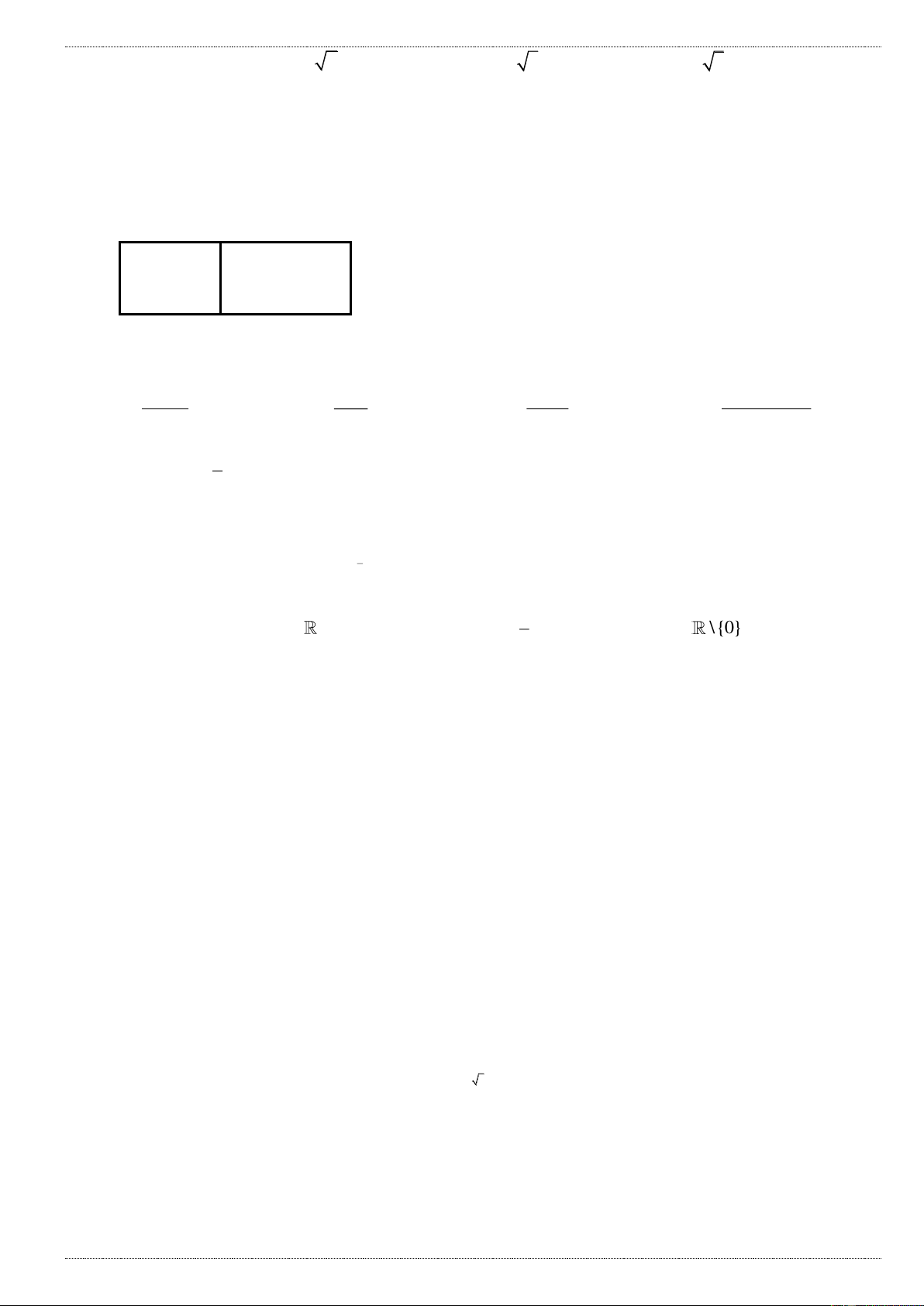
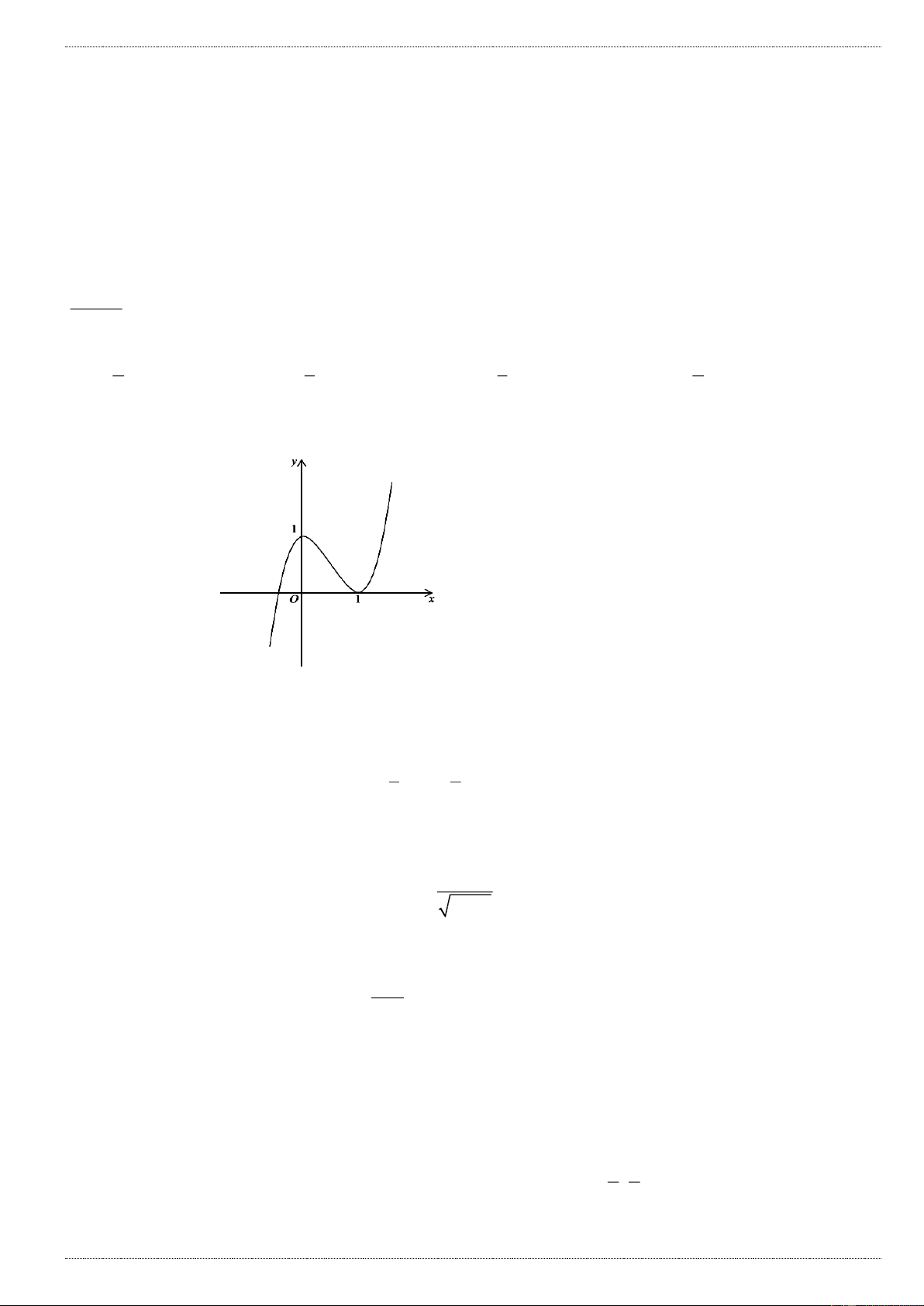
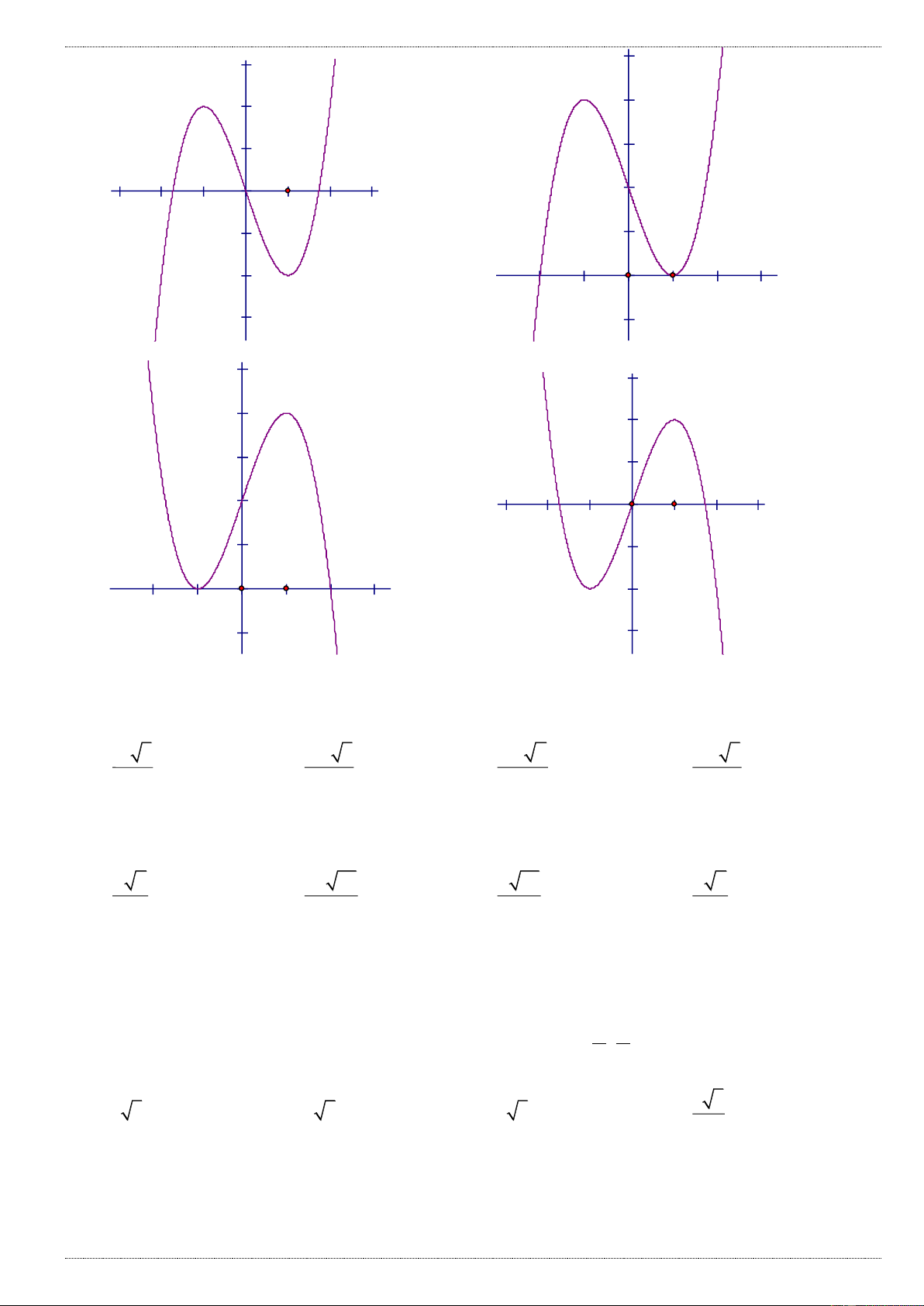
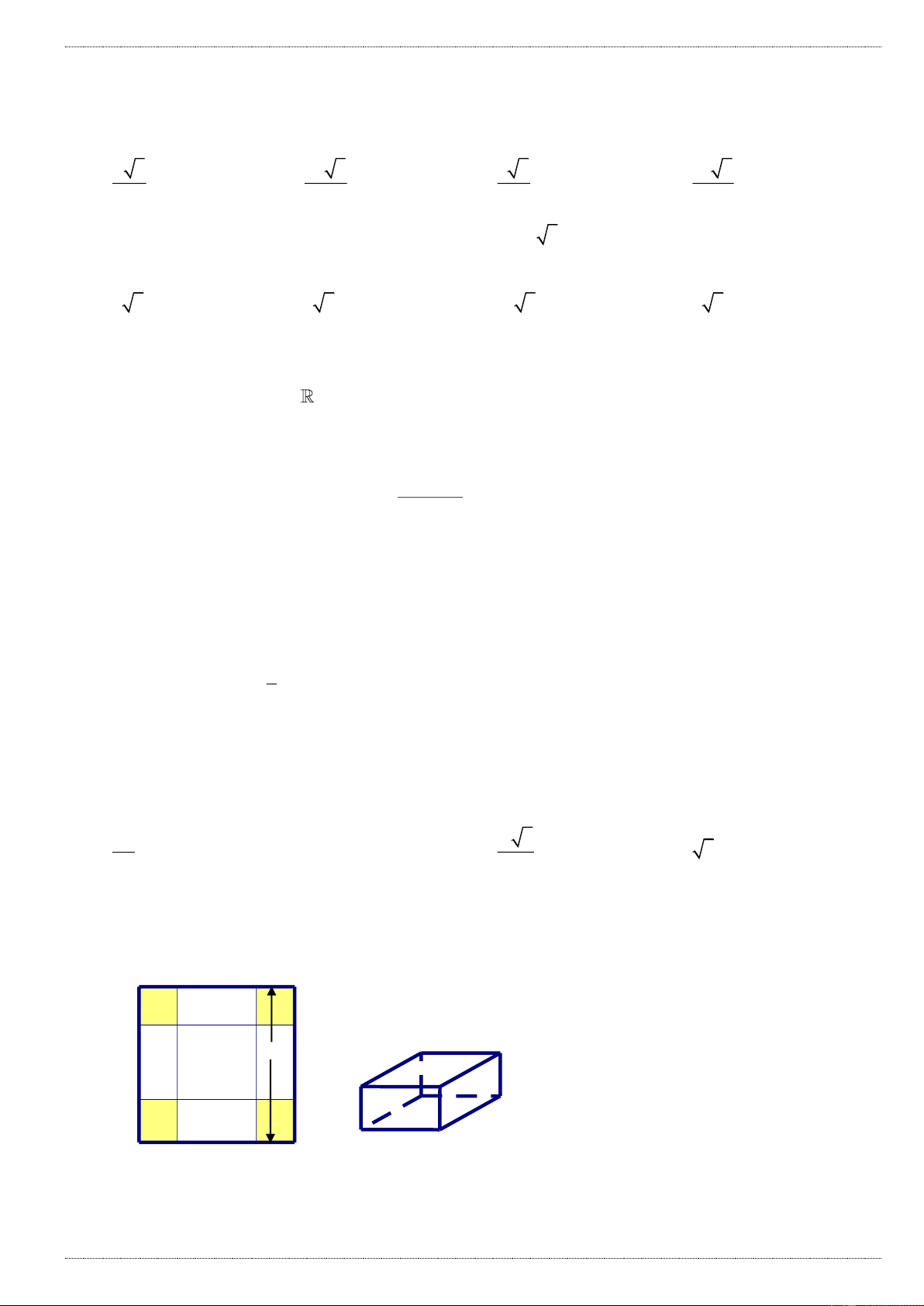
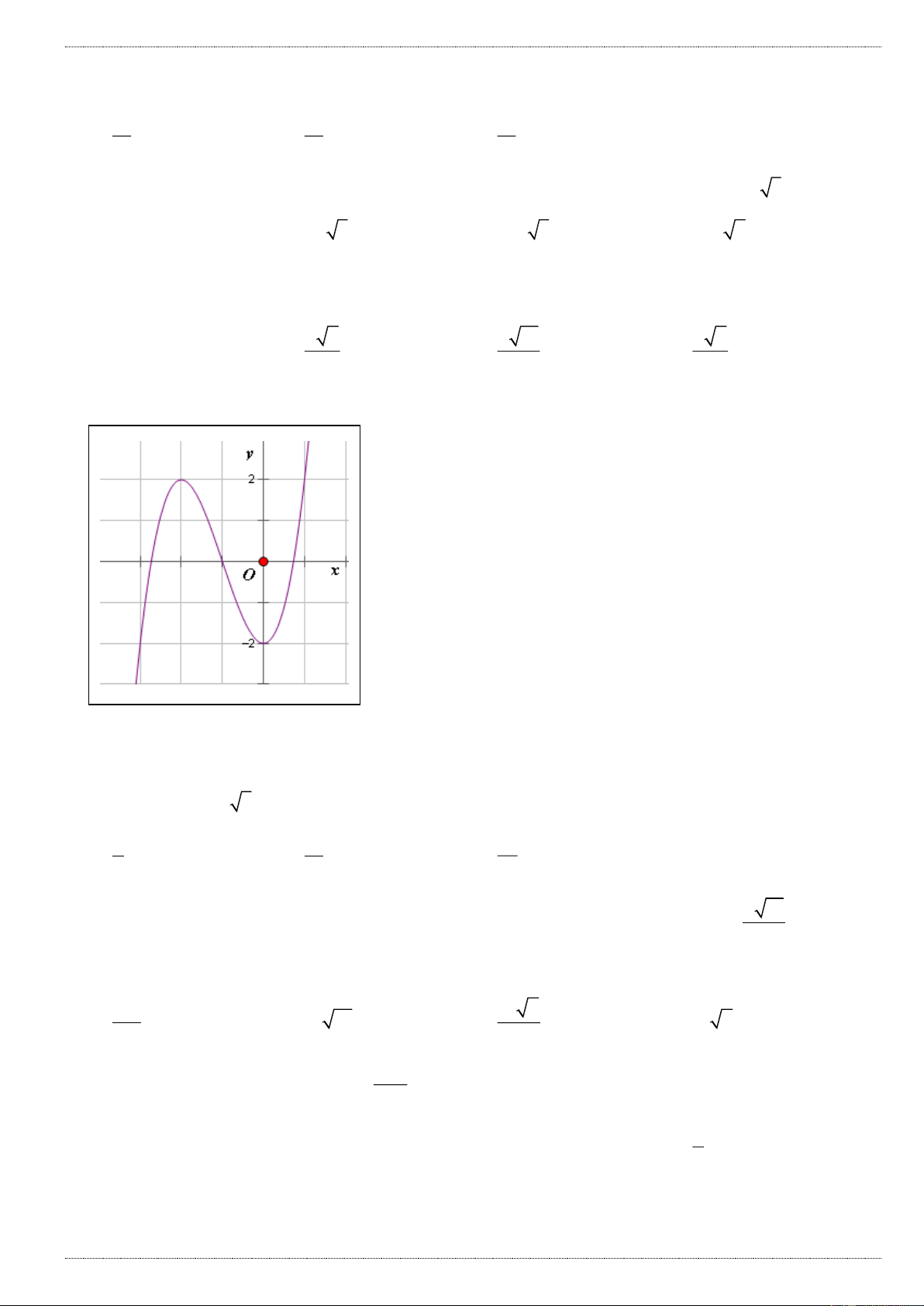
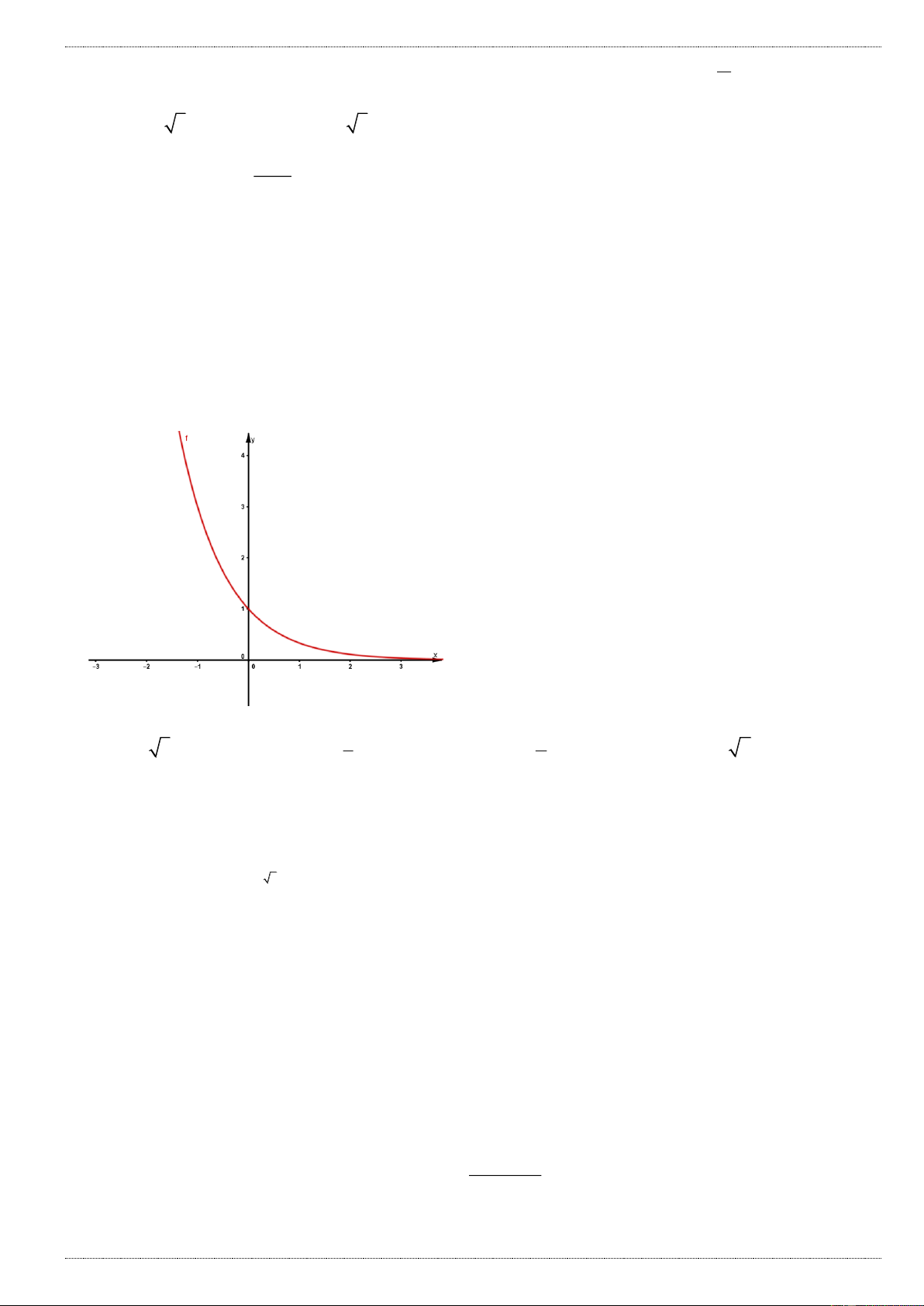
Câu 1: Đường cong trong hình bên là đồ thị của hàm số nào dưới đây: A. 4 2
y x  2x 1 B. 4 2
y  x  2x 1 C. 4 2
y x  2x 1 D. 4 2
y  x  2x 1 Câu 2: Cho hàm số 3 2
y x  3x  2 có đồ thị là C  . Tìm tọa độ điểm M thuộc C  sao cho tiếp tuyến của
đồ thị C  tại M song song với đường thẳng () : y  9x  2 . A. M (4;3) B. M (0; 1  ), M ( 4  ;3) C. M (0;1)
D. M (0;1), M (4;3)
Câu 3: Tìm m để phương trình 4 2
x  3x  2  m có 3 nghiệm ? 1 1 A. m B. m C. m  2  D. m  2  4 4
Câu 4: Có mấy loại khối đa diện đều ? A. 1 B. 3 C. 5 D. 6 Câu 5: Hàm số 3 2
y x  3x  2 đạt cực tiểu tại A. x  2  B. x  0 C. x  2 D. x 1
Câu 6: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , SA   ABC  , gọi , D E lần lượt là
trung điểm của SB và SC . Tâm của mặt cầu ngoại tiếp hình chóp S.ABC là A. điểm B B. điểm S C. điểm E D. điểm D
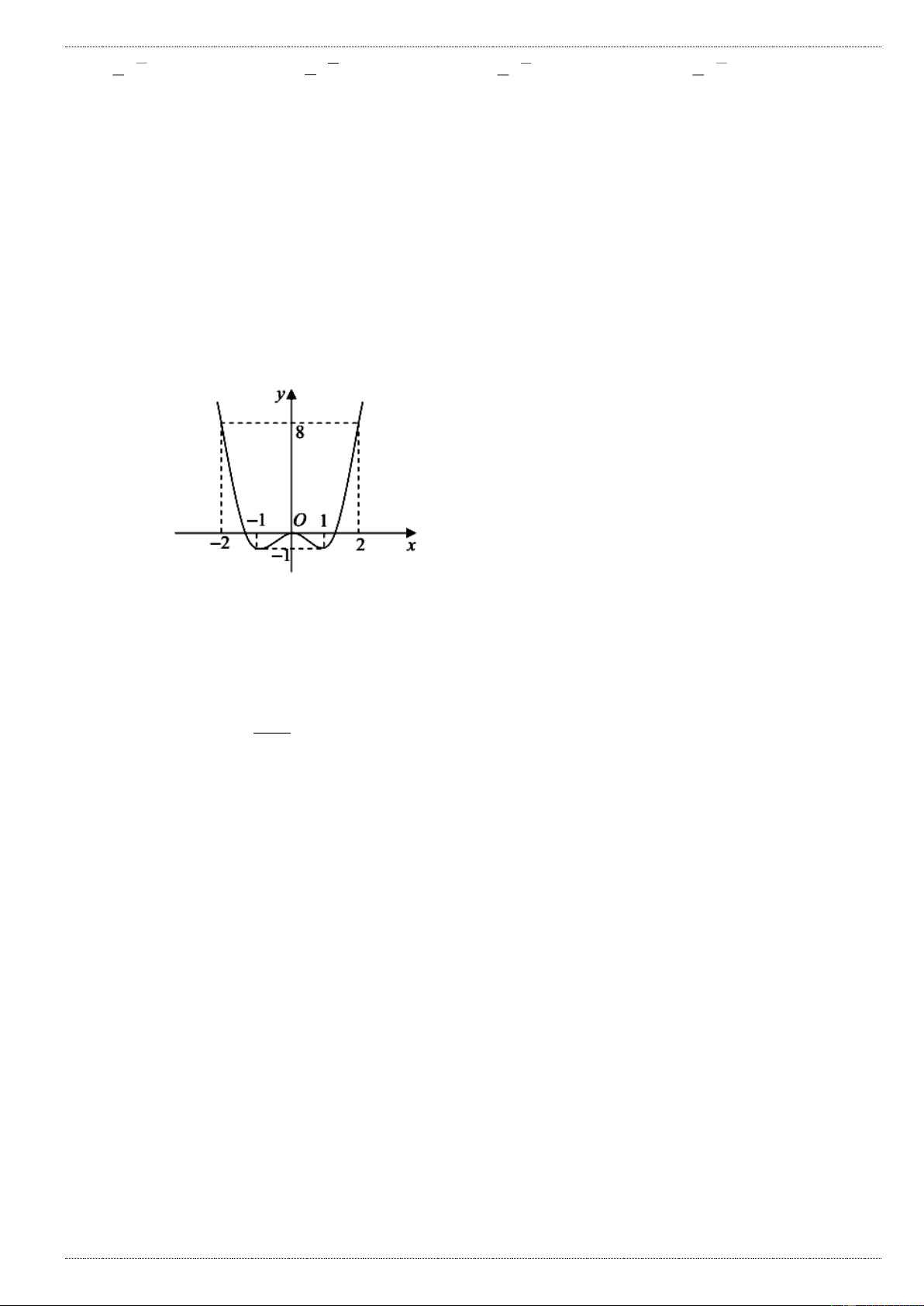
Câu 7: Bảng biến thiên trong hình bên là bảng biến thiên của hàm số nào sau đây? A. 3 2
y x  3x x  2 B. 4 2
y x  2x 1 C. 3
y  x x 1 D. 3
y x  2x  3
Câu 8: Giá trị lớn nhất của hàm số : 3 2
y x  3x  9x  35 trên đoạn  4  ;4lần lượt là
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại A. 20 B. 10 C. 40 D. 30
Câu 9: Tìm tất cả các giá trị của m để phương trình 3 2
x  6x m  0 có ba nghiệm phân biệt.
A. 0  m  2
B. 0  m  4
C. 0  m  32
D. 0  m  8 2 3  a b
Câu 10: Biết log b  2,log c  3 . Khi đó giá trị của log   bằng a a a   c   1 2 A. 6 B. C. D. 5 3 3
Câu 11: Tìm tập xác định của hàm số log  3 6 2 x y   1 2   1   1   1  A. D  ;   
B. D R C. D   ;     D. D   ;     2   2   2 
Câu 12: Tìm m để hàm số 3
y x  m   2 2 3
1 x  6 m  2 x  3nghịch biến trên khoảng có độ dài lớn hơn 3. A. m  0 B. m  9 C. m  8
D. m  0 hoặc m  8 2x 1
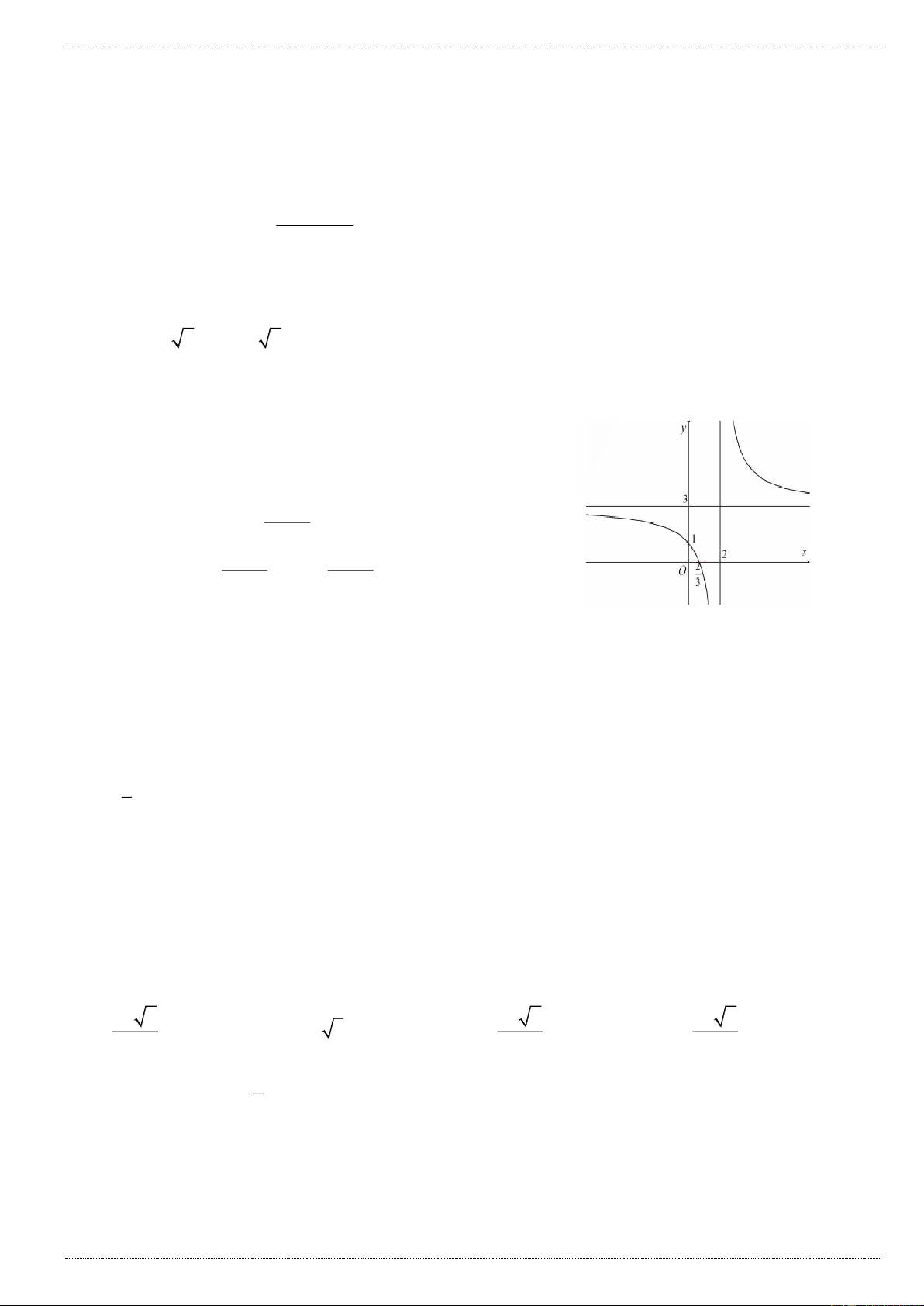
Câu 13: Các khoảng nghịch biến của hàm số y  là : x 1 A.  ;  2 B.  ;   C. 1;  D.   ;1  và 1;
Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a , tam giác SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích khối chóp S.ABC là 3 a 3 3a A. V B. 3 V a C. 3 V  3a D. V  2 2
Câu 15: Cho đồ thị (C): 3 2
y  x  3x  2 . Phương trình tiếp tuyến của (C) tại điểm có hoành độ x  3 có 0 hệ số góc là A. 6 B. 9 C. – 9 D. – 6
Câu 16: Giá trị lớn nhất của hàm số y x  3  5  x là A. max y  2
B. max y  2 2 C. max y  2 D. max y  1 D D D D
Câu 17: Tìm tất cả các giá trị của tham số m để x e  2 x x  
1  m có nghiệm trên [0; 2] A. 2 e
  m e
B. m  e hoặc 2 m e
C. m  e D. 2 m e x 1
Câu 18: Giao điểm của đường thẳng y  2x  3 và đồ thị hàm số y
là điểm M và N . Khi đó hoành 3x 1
độ trung điểm I của MN có giá trị bằng 5 2 A. 1 B. 0 C. D. 6 3 1
Câu 19: Cho hàm số y x
. Hàm số đã cho có bao nhiêu cực trị? x
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại A. 0 B. 2 C. 3 D. 1
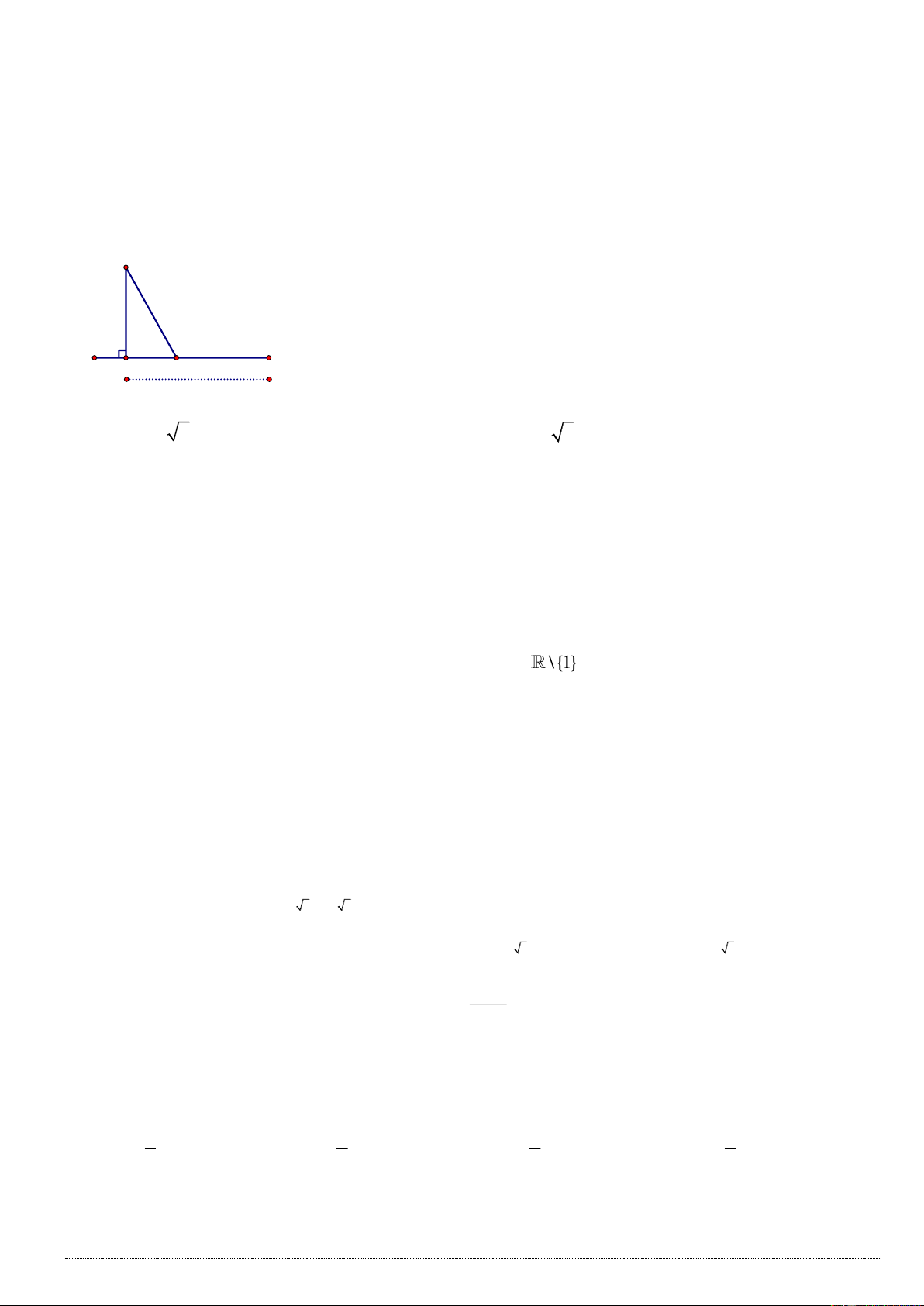
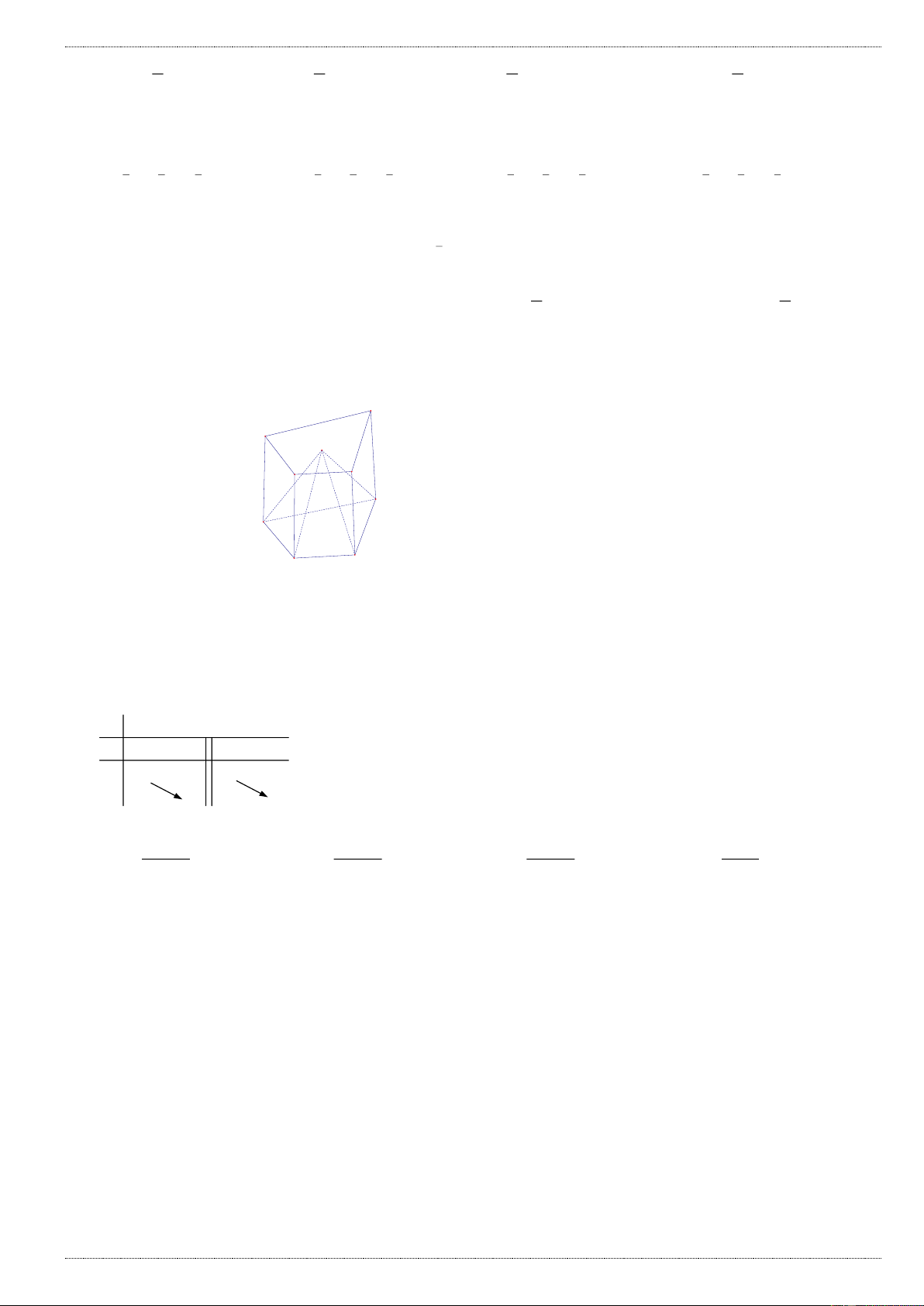
Câu 20: Một đoàn cứu trợ lũ lụt đang ở vị trí A của tỉnh Quảng Bình muốn tiếp cận vị trí C để tiếp tế lương
thực và thuốc phải đi theo con đường từ A đến B và từ B đến C (như hình vẽ). Tuy nhiên do nước ngập con
đường từ A đến B nên đoàn cứu trợ không thể đi đến C bằng xe, nhưng đoàn cứu trợ có thể chèo thuyền
từ A đến vị trí D trên đoạn đường từ B đến C với vận tốc 4km/h rồi đi bộ đến C với vận tốc 6km/h. Biết A
cách B một khoảng 5km, B cách C một khoảng 7km. Xác định vị trí điểm D để đoàn cứu trợ đi đến xã C nhanh nhất. A 5 km C B D 7 km
A. BD  2 2 km
B. BD  4 km
C. BD  2 5 km
D. BD  5 km
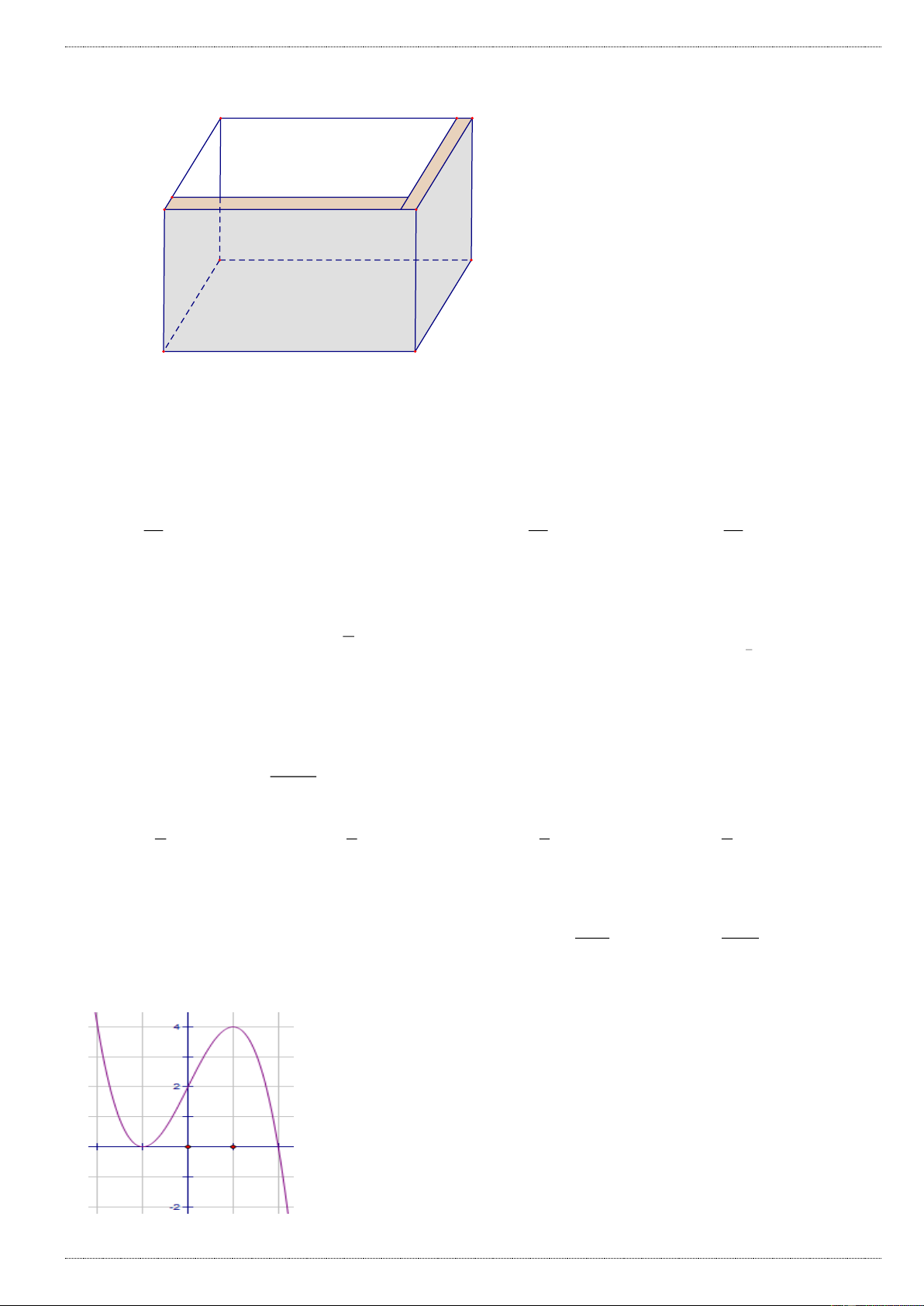
Câu 21: Cho hình hộp chữ nhật / / / / ABC . D A B C D có /
AB a, AD  2a, AA  3a . Thể tích khối hộp chữ nhật / / / / ABC . D A B C D là A. 3 V  18a B. 3 V  6a C. 3 V  2a D. 2 V  6a
Câu 22: Tập xác định D của hàm số 2 y (x 1)   là A. ( ;  1  ][-1; ) 
B. D  (1;  )  C. D  ( ;  1) (1;) D. D  \{1}
Câu 23: Một người gửi tiết kiệm 50 triệu đồng vào một ngân hàng với lãi suất 7% một năm. Biết rằng nếu
không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu. Sau 5 năm
mới rút lãi thì người đó thu được số tiền lãi là A. 3,5 triệu đồng
B. 70,128 triệu đồng
C. 50,7 triệu đồng
D. 20,128 triệu đồng
Câu 24: Giá trị nhỏ nhất của hàm số hàm số 4 2
y x  2x  4 là A. – 4 B. 2 C. −2 D. 4
Câu 25: Rút gọn biểu thức 1 2 3 2 a .a có kết quả là A. 4 aB. 4 a C. 2 2 a D. 4 2 2 a x 1
Câu 26: Đường tiêm cận đứng của đồ thị hàm số y  có phương trình là x  2 A. y  2 B. x 1 C. x  2 D. x  2 
Câu 27: Tìm m để hàm số 3 2
y x  2x mx có hai cực trị. 4 4 4 4 A. m B. m C. m D. m  3 3 3 3
Câu 28: Đạo hàm của hàm số 1 2 x y e   là A. ' x y e B. 1 2 ' x y e   C. 1 2 ' 2 x y e   D. 1 2 ' 2 x y e   
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại Câu 29: Cho hàm số 4 2
y x x 1. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có hai cực trị.
B. Hàm số đồng biến trên khoảng  ,  0
C. Hàm số nghịch biến trên khoảng 1,  .
D. Hàm số có một điểm cực tiểu. 2 x  2x
Câu 30: Cho hàm số y
. Khẳng định nào sau đây đúng. 1 x
A. Hàm số nghịch biến trên các khoảng ( ;1  ) và (1;).
B. Hàm số đồng biến trên các khoảng ( ;1  ) và (1;).
C. Hàm số có tiệm cận đứng y 1.
D. Hàm số có tiệm cận ngang x 1 . 2 x 1  2  x  3   4 
Câu 31: Giải bất phương trình       4   3  A. x  1 B. x  1 C. x  1 D. x 1 x  2
Câu 32: Tìm các giá trị của tham số m sao cho hàm số y
đồng biến trên khoảng (0;1) x m A. m  0
B. 1  m  2 C. m  2
D. m  0 hoặc 1  m  2 1
Câu 33: Cho hàm số y  ln
. Khẳng định nào sao đây là khẳng định sai? 1 x 1 1 A. . '1 y x ye B. . x y '1  C. y '  D. . x y '1  0 x 1 x 1
Câu 34: Thể tích của khối trụ có bán kính đáy r  2cm và chiều cao h  9cm là A. 3 18cm B. 3 18 cm C. 3 162 cm D. 3 36 cm Câu 35: Hàm số 4 2
y x  2x 1 đồng biến trên khoảng nào sau đây: A. ( 1  ;0);(1; )  B. ( 1  ;0);(0;1)
C. Đồng biến trên R D. ( ;  1  );(0;1)
Câu 36: Thể tích của khối lập phương / / / / ABC .
D A B C D có cạnh bằng a là 1 1
A. V  3a
B. V a C. 3 V a D. 3 V a 3 3
Câu 37: Cho khối lăng trụ đứng AB .
C A' B 'C ' có đáy ABC là tam giác đều cạnh 2a , gọi I là trung điểm
BC , góc giữa A' I và mặt phẳng ( ABC) bằng 0
30 . Thể tích của khối lăng trụ AB .
C A' B 'C ' là 3 a 3 3 a 2 A. 3 a 6 B. 3 a 3 C. D. 3 4
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 38: Diện tích xung quanh của hình nón tròn xoay có đường sinh l  10cm , bán kính đáy r  5cm là A. 2 50cm B. 2 50 cm C. 2 25 cm D. 2 100 cm
Câu 39: Cho hình chóp S.ABCD có đáy ABCD là hình thoi với AC  2 ,
a BD  3a , SA   ABCD ,
SA  6a . Thể tích khối chóp S.ABCD là A. 3 V  2a B. 3 V  6a C. 3 V  18a D. 3 V  12a
Câu 40: Điều kiện cần và đủ để mặt phẳng (P) tiếp xúc với mặt cầu S( ;
O r) tại điểm H là
A. Mặt phẳng (P) vuông góc với bán kính OH tại điểm H .
B. Mặt phẳng (P) song song với bán kính OH .
C. Mặt phẳng (P) vuông góc với bán kính OH tại điểm O .
D. Mặt phẳng (P) vuông góc với bán kính OH . 2x 1
Câu 41: Cho đố thị (C): y
. Gọi I là giao điểm của 2 đường tiệm cận, tọa độ điểm I là x 1 A. I 1; 2 B. I  1  ;2
C. I 2;  1 D. I 2;  1
Câu 42: Cho hình lăng trụ đứng tam giác / / / AB .
C A B C , tam giác ABC có AB  ,
a AC  2a , góc 0 BAC  60 , /
BB a . Thể tích khối lăng trụ / / / AB . C A B C là 3 a 3 a 3 A. 3 V a B. V C. 3 V a 3 D. V  2 2
Câu 43: Tập xác định D của hàm số y  ln(3x 1) là 1 1 1 1
A. D  ( ; ) B. D  \ { }
C. D =[ ; ) D. D  ( ;  ) 3 3 3 3
Câu 44: Cho hình chóp tam giác S.ABC có đáy là tam giác vuông tại B , cạnh SA vuông góc với mặt đáy, biết AB  ,
a SA a 2 . Khoảng cách từ A đến mp SBC là 6 3 6 A. a B. a C. a D. a 2 3 3 6
Câu 45: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a , cạnh bên hợp với mặt đáy một góc 0 60 .
Thể tích V của khối chóp S.ABC là 3 3a 3 a 3 3a 3 a 3 A. V B. V C. V D. V  16 12 12 24
Câu 46: Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a . Các mặt phẳng (SAB), (SA ) D cùng
vuông góc với mặt phẳng (ABCD) , cạnh bên SC tạo với đáy một góc 0
30 . Thể tích V của khối chóp S.ABCD là 3 a 6 3 a 6 3 a 3 3 a 2 A. V B. V C. V D. V  9 4 3 4
Câu 47: Cho hình chóp tam giác đều S.ABC có tất cả các cạnh đều bằng 4 . Diện tích của mặt cầu ngoại
tiếp hình chóp S.ABC là
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 4 A. 12 B. 2 4 r C. 24 D. 2  r 3
Câu 48: Tìm m để đồ thị của hàm số 4 2 4
y x  2mx  2m m có ba điểm cực trị tạo thành một tam giác vuông. A. m  1 B. m  3 C. m   3 D. m  1  Câu 49: Hàm số 3 2
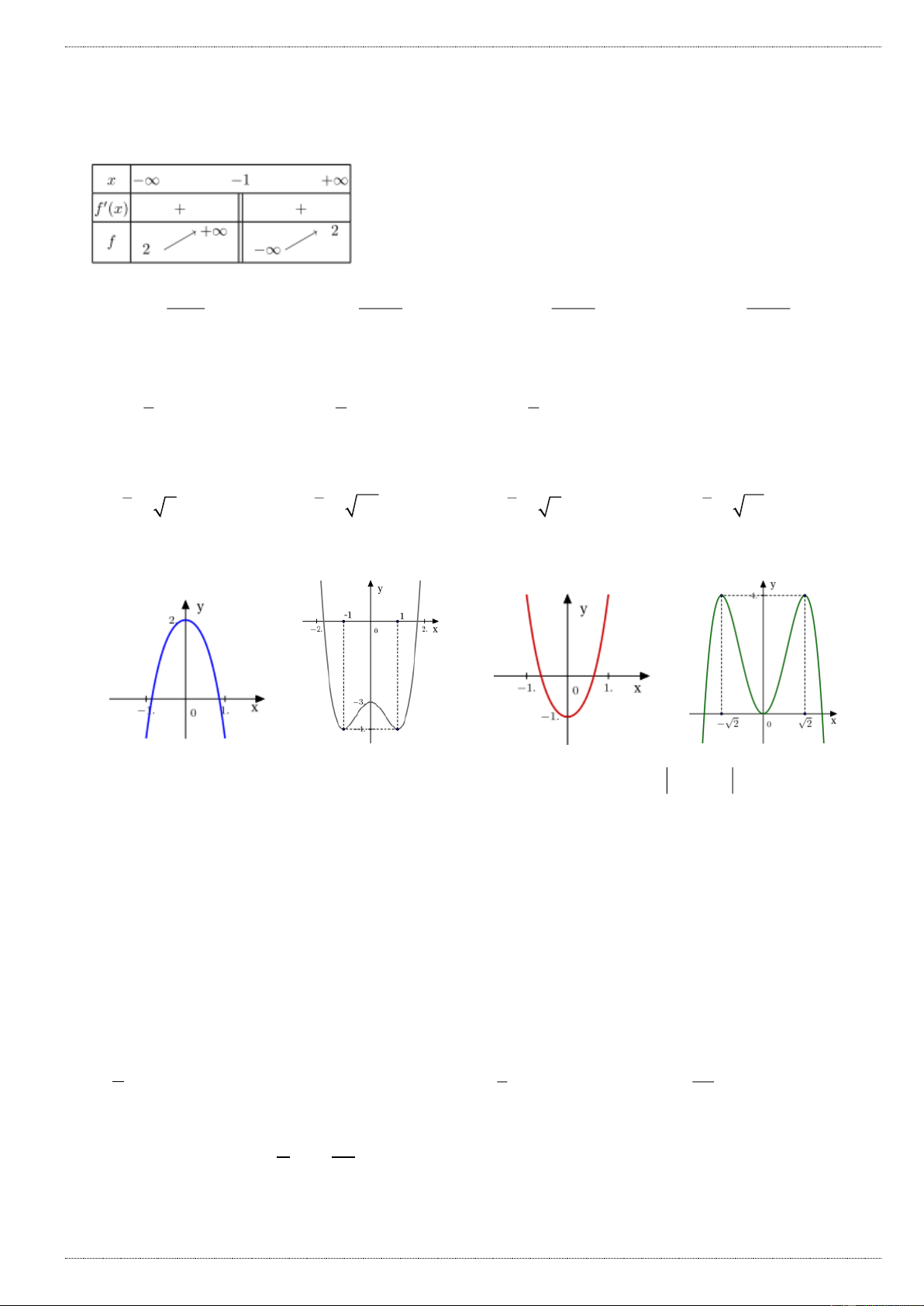
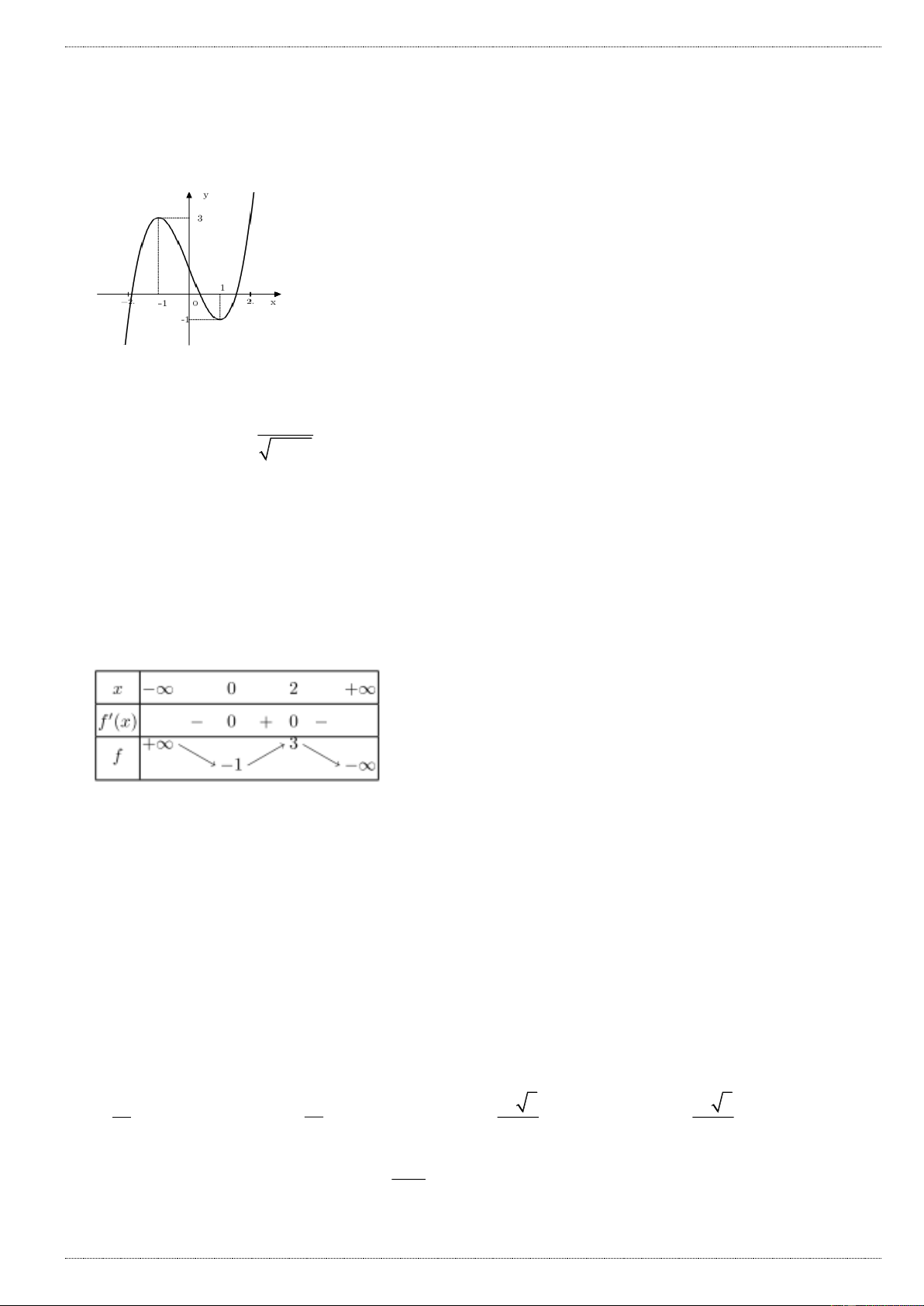
y ax bx cx d có bảng biến thiên như hình bên. Khẳng định nào sau đây đúng?
A. Hệ số a  0
B. Hàm số có đúng một cực trị
C. Hàm số có giá trị cực đại bằng 2
D. Hàm số có giá trị nhỏ nhất bằng 3
Câu 50: Đối với hàm số sin 2 ( ) x f x e ta có       3       A. f '  3e   B. f '   3e   C. 2 f '  e   D. f '  e   12  12  12  12 
LUYỆN THI TRẦN ĐẠI
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Số 8, ngõ 462 đường Bưởi
Chuyên đề: Học kỳ I lớp 12 ĐIỂM Mã đề thi
Thời gian làm bài: 90 phút 02
(50 câu trắc nghiệm)
Họ và tên học sinh:………………………………………………..
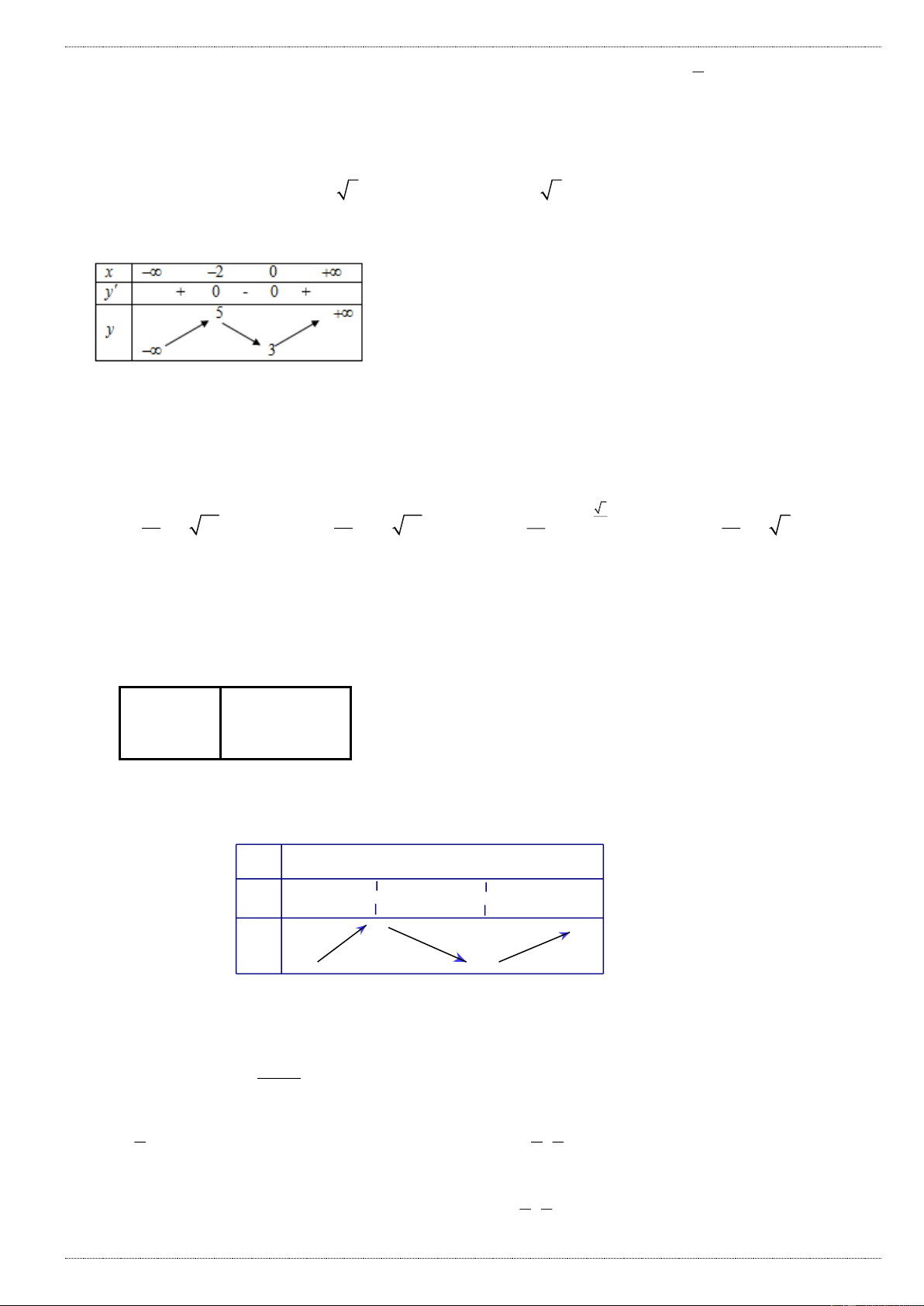
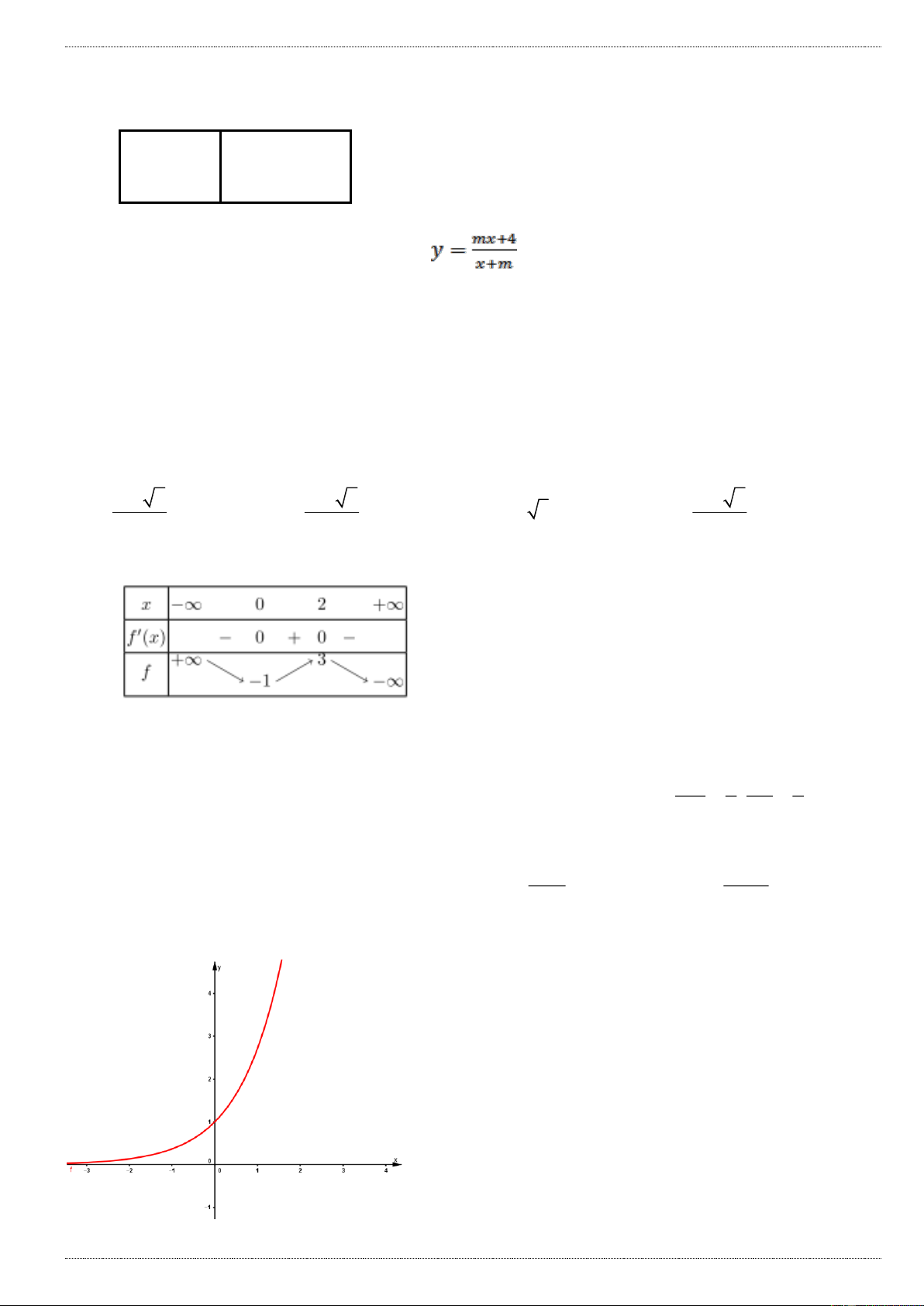
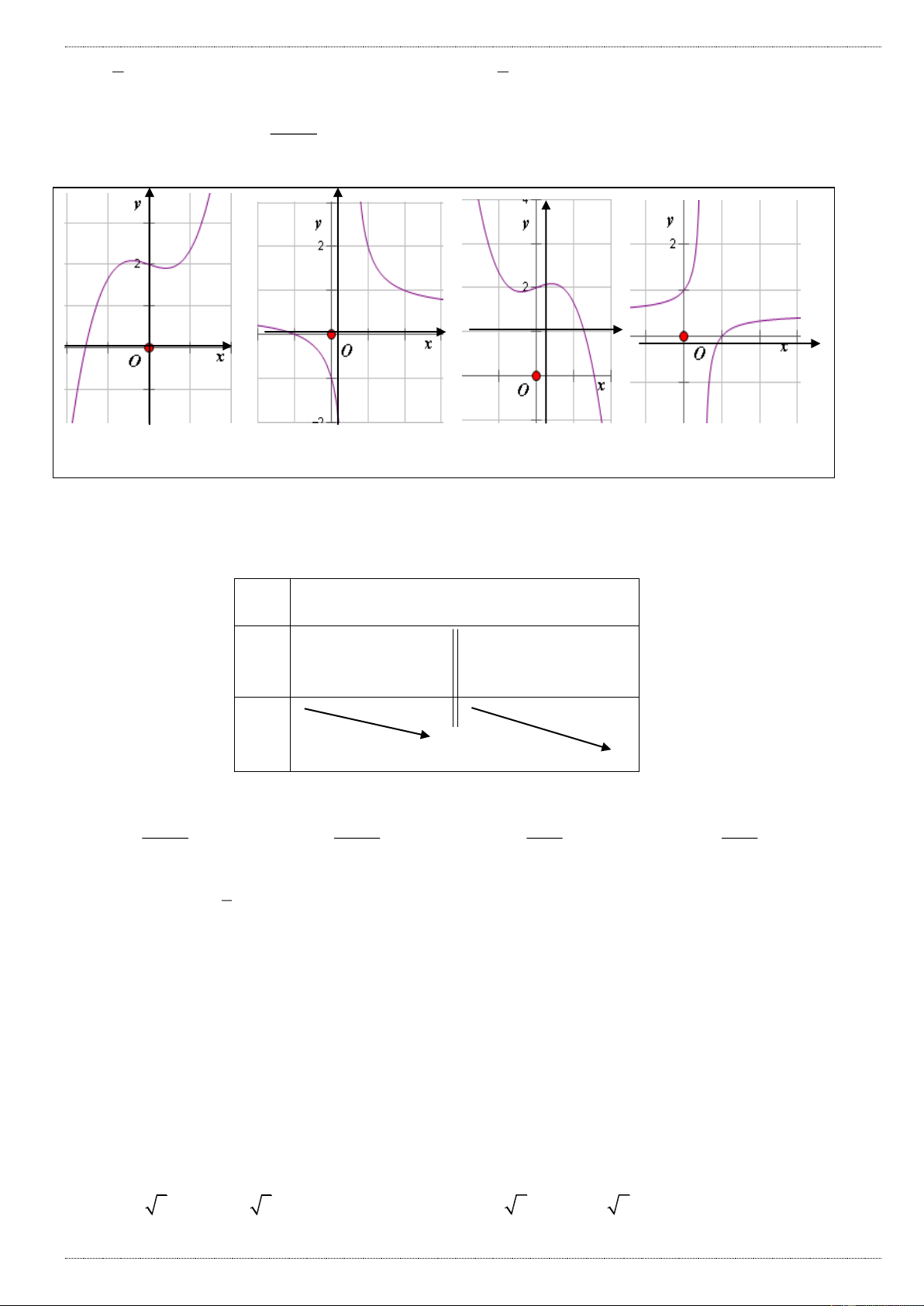
Câu 1: Cho hàm số y f x có bảng biến thiên sau : x - ∞ 0 2 +∞ + 0 _ y / 0 + 5 +∞ y -∞ 1
Với giá trị nào của m thì phương trình f (x)  m có 3 nghiệm phân biệt A. 1 m  5 B. 1 m  5
C. m  1 hoặc m  5
D. m  1 hoặc m  5 x  2
Câu 2: Đồ thị hàm số y = có tâm đối xứng là : 2x 1  1   1 1  A.  ; 2   B. I  ;    2   2 2   1 1 
C. Không có tâm đối xứng D. I ;    2 2 
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại x  3
Câu 3: Cho hàm số y
có đồ thị C  . Chọn câu khẳng định SAI: x 1 4 
A. Tập xác định D R \   1
B. Đạo hàm y '   0, x   1 2 (x 1)
C. Đồng biến trên  ;   1  1;  
D. Tâm đối xứng I 1;  1 Câu 4: Cho hàm số 3 2
y x  3x  2 C  . Tiếp tuyến của đồ thị hàm số tại giao điểm của C  với trục tung có phương trình : A. y  2 B. y  0
C. x y  2
D. x  2y  0
Câu 5: Một hình nón có chiều cao bằng a và thiết diện qua trục là tam giác vuông. Diện tích xung quanh của hình nón là : 2  a 2 A. 2 2 a 2 B. C.  a2 2 D. 2 2 a 2
Câu 6: Cho hàm số y f x có bảng biến thiên sau : x - ∞ -1 0 1 +∞ _ _ 0 y / + 0 0 + +∞ 0 +∞ y -1 -1
Với giá trị nào của m thì phương trình f (x) 1  m có đúng 2 nghiệm A. m  1 B. m  1  C. m  1  hoặc m  2  D. m  1  hoặc m  2 
Câu 7: Một khách hàng có 100 000 000 đồng gửi ngân hàng kì hạn 3 tháng (1 quý) với lãi suất 0,65% một
tháng theo phương thức lãi kép (tức là người đó không rút lãi trong tất cả các quý định kì). Hỏi vị khách này
sau bao nhiêu quý mới có số tiền lãi lớn hơn số tiền gốc ban đầu gửi ngân hàng? A. 12 quý B. 24 quý C. 36 quý D. Không thể có
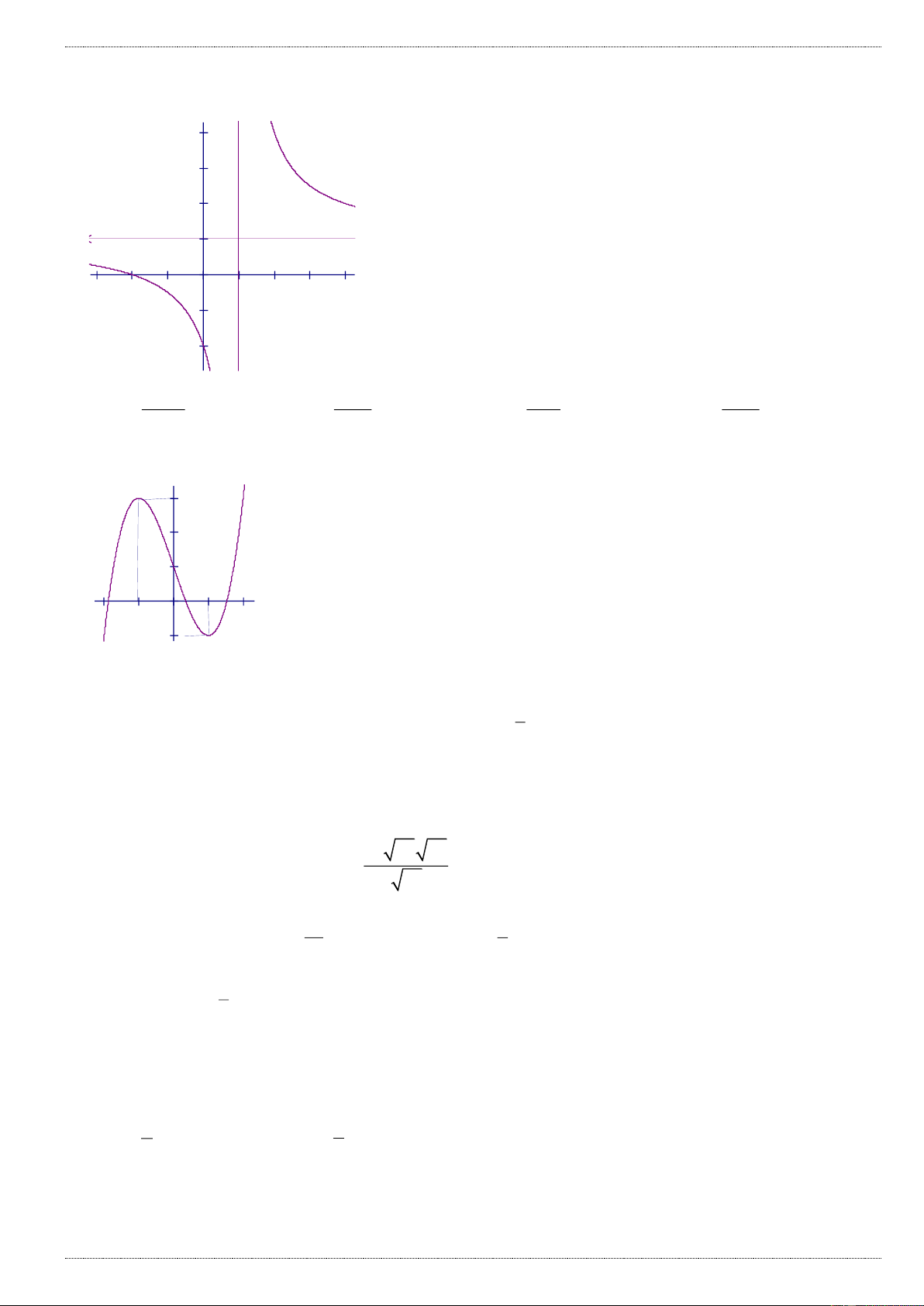
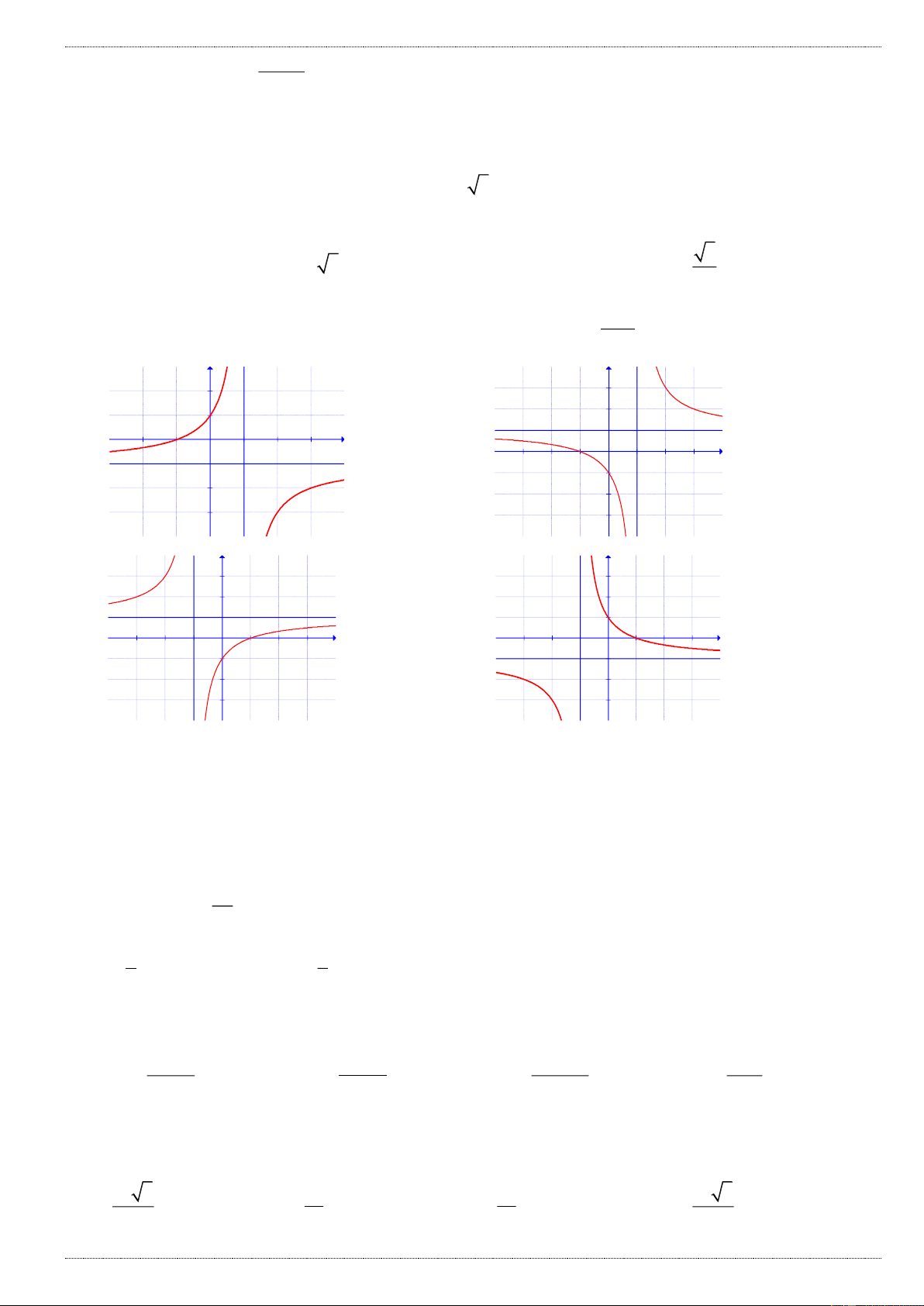
Câu 8: Hàm số y f (x) nào có đồ thị như hình vẽ sau : y 2 1 x 0 1 2 x 1 x 1 x 1 x 1
A. y f (x) 
B. y f (x) 
C. y f (x) 
D. y f (x)  x  2 x  2 x  2 x  2
Câu 9: Bảng biến thiên sau là của hàm số nào ?
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại x - ∞ 2 +∞ _ _ y / 1 +∞ y -∞ 1 2x 1 4x  6 3  x x  5 A. y B. y C. y D. y x  3 x  2 2  x x  2
Câu 10: Hình chóp S.ABC có tam giác ABC vuông tại A , AB AC a , I là trung điểm của SC , hình
chiếu vuông góc của S lên mặt phẳng  ABC  là trung điểm H của BC , mặt phẳng SAB tạo với đáy 1
góc bằng 60 . Khoảng cách từ điểm I đến mặt phẳng SAB theo a là : a 3 a 3 a 3 a 3 A. B. C. D. 2 4 8 16 Câu 11: Cho hàm số 3 2
y x – 3x  2 (1). Điểm M thuộc đường thẳng (d) : y  3x – 2 và có tổng khoảng
cách từ M tới hai điểm cực trị của đồ thị hàm số (1) nhỏ nhất có tọa độ là :  4 2   4 2   4 2   4 2  A. M ;   B. M  ;    C. M  ;   D. M ;     5 5   5 5   5 5   5 5 
Câu 12: Bất phương trình x 1  4  x m có nghiệm khi : A. m   5 B. m  5 C. m  5 D. m   5  3 
Câu 13: Bất phương trình 2 log x x
 2  log 5 có nghiệm là: 1   2  4  2 A. x  2   ;1 B. x  ;    1 2; C. x  ;  2  1; D. x  1  ;2
Câu 14: Cắt mặt nón tròn xoay bởi một mặt phẳng song song với trục của mặt nón ta được phần giao là: A. một parabol B. một elip C. một hypebol
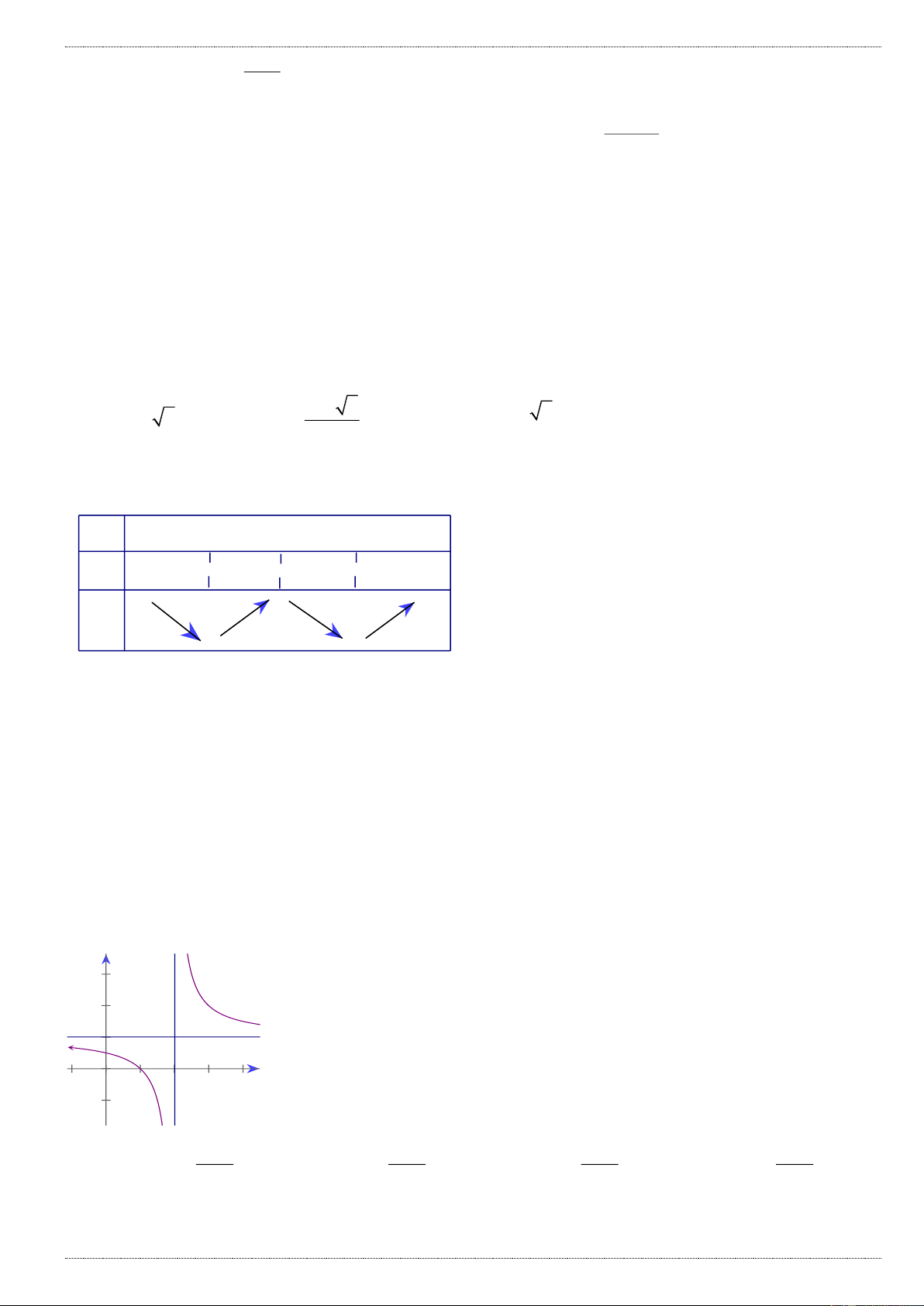
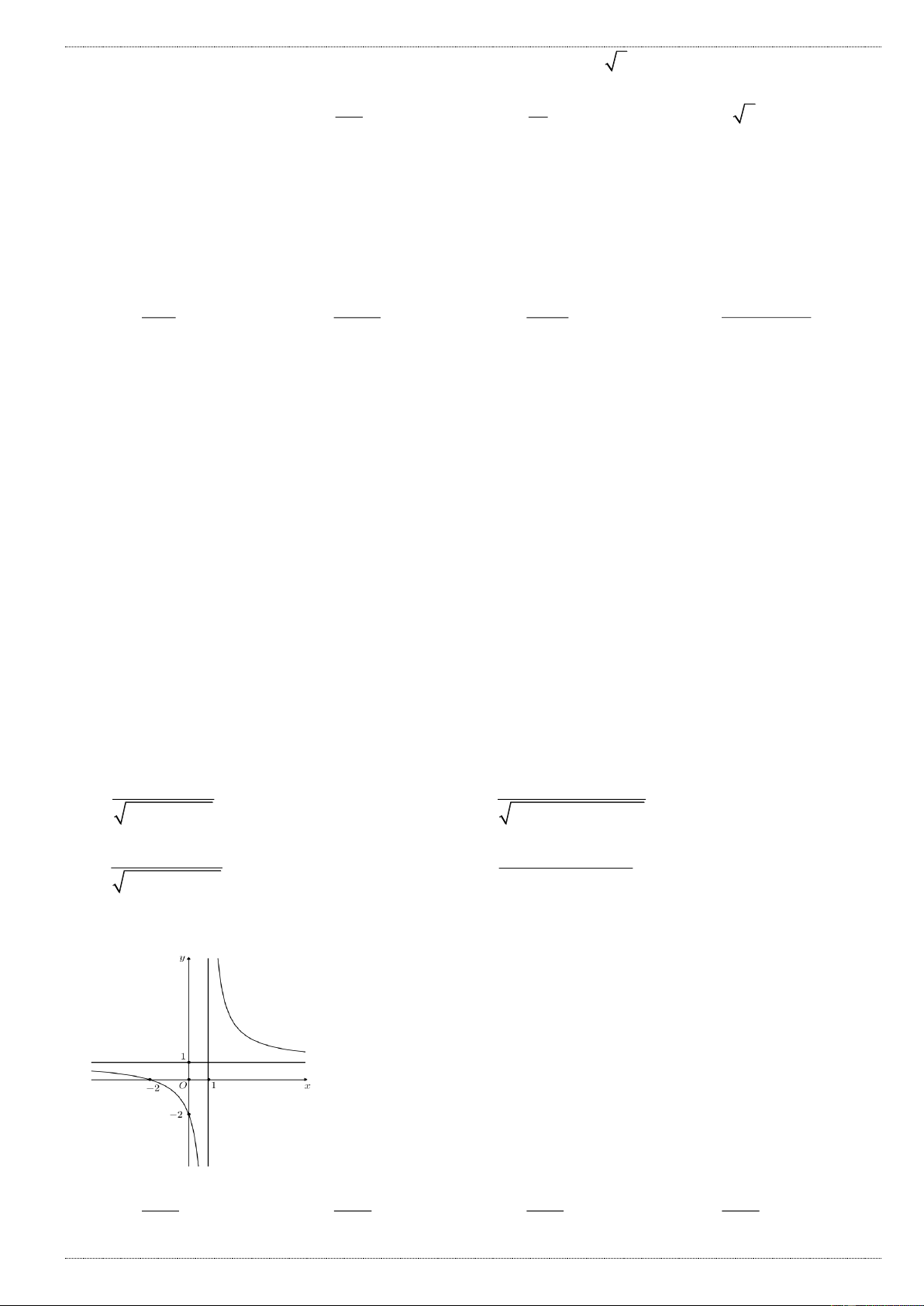
D. một đường tròn x  6
Câu 15: Trên đồ thị (C) của hàm số y
có bao nhiêu điểm có tọa độ nguyên ? x  2 A. 2 B. 3 C. 6 D. 4
Câu 16: Dựa vào bảng biến thiên của hàm số, chọn câu khẳng định ĐÚNG ?
A. Hàm số không xác định tại x  3
B. Hàm số có 2 cực trị
C. Hàm số không có cực trị
D. Hàm số có 1 cực trị Câu 17: Hàm số 4 2 2
y x  2m x  5 đạt cực đại tại x = - 2 khi :
A. m  2 , m  2  B. m  2 C. m  2 
D. Không có giá trị m
Câu 18: Khẳng định nào dưới đây là khẳng định SAI ?
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
A. Quay đường tròn xung quanh một dây cung của nó luôn tạo ra một hình cầu
B. Quay tam giác đều quanh đường cao của nó luôn tạo ra một hình nón
C. Quay một tam giác nhọn xung quanh cạnh của nó không thể tạo ra hình nón
D. Quay hình vuông xung quanh cạnh của nó luôn sinh ra hình trụ có r, , h l bằng nhau. 2 x  4x 1
Câu 19: Đồ thị hàm số y
có hai điểm cực trị thuộc đường thẳng d : y ax b . Khi đó tích ab x 1 bằng A. -2 B. -8 C. 2 D. -6
Câu 20: Cho ( 2 1)m ( 2 1)n    . Khi đó
A. m n
B. m n
C. m n
D. m n
Câu 21: Cho các phát biểu sau: (I) Hàm số 3 2
y x  3x  3x 1 không có cực tri ̣ (II) Hàm số 3 2
y x  3x  3x 1 có điểm uốn là I ( 1  ,0) 3x  2
(III) Đồ thi ̣ hàm số y  có dạng như hình vẽ x  2 3x  2 3x  2 (IV) Hàm số y  có lim  3 x  2 x2 x  2
Số các phát biểu ĐÚNG là: A. 2 B. 1 C. 3 D. 4
Câu 22: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y x  2 ln x trên 1 e  ;e   lần lượt là : 2  1  A.  2   và 1 B. 2 e  2 và 1 C. 1 và 0 D. Đáp số khác  e Câu 23: Cho hàm số 4 2
y x  2mx  2 . Xác định m để đồ thị hàm số có ba điểm cực trị lập thành một tam giác vuông cân. A. m  0 B. m  1
C. m  0  m 1 D. Đáp số khác
Câu 24: Hình chóp SABC có SB = SC = BC = CA = a . Hai mặt (ABC) và (ASC) cùng vuông góc với (SBC). Thể tích hình chóp là : 3 a 3 3 a 3 3 a 3 A. B. 3 a 3 C. D. 3 4 12 1 Câu 25: Cho hàm số 3 2 y
x  2x mx 10 . Xác định m để hàm số đồng biến trên 0;   3 A. Không có m B. Đáp số khác C. m  0 D. m  0
Câu 26: Một công ty muốn thiết kế bao bì để đựng sữa với thể tích 3
1dm . Bao bì được thiết kế bởi một
trong hai mô hình sau: dạng hình hộp chữ nhật có đáy là hình vuông hoặc dạng hình trụ và được sản xuất
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
cùng một nguyên vật liệu. Hỏi thiết kế theo mô hình nào sẽ tiết kiệm được nguyên vật liệu nhất? Và thiết
kế mô hình đó theo kích thước như thế nào?
A. Hình trụ và chiều cao bằng bán kính đáy
B. Hình hộp chữ nhật và cạnh bên gấp hai lần cạnh đáy
C. Hình trụ và chiều cao bằng đường kính đáy
D. Hình hộp chữ nhật và cạnh bên bằng cạnh đáy
Câu 27: Phương trình log (x  3)  log (x 1)  3 có nghiệm là: 2 2 A. x  11 B. x  9 C. x  7 D. x  5 2 x x  2
Câu 28: Cho hàm số y
(1). Tiếp tuyến với đồ thị hàm số (1) và song song với đường thẳng x  2
3x y  2  0 có phương trình : A. y  3  x  3 B. y  3
x  3; y  3  x 19 C. y  3  x  5 D. y  3
x  5; y  3  x  3
Câu 29: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng ? A. Bốn B. Một C. Ba D. Hai
Câu 30: Tập xác định của hàm số 3
y  (2  x) là: D  \   2
B. D   ;  2
C. D  2;
D. D   ;  2 A.
Câu 31: Cho phương trình 2
x  4  x m . Xác định m để phương trình có hai nghiệm phân biệt.
A. 2  m  2 2
B. 2  m  2 2
C. 2  m  2 2
D. 2  m  2 2
Câu 32: Khẳng định nào sau đây SAI ? 2018 2017  2   2  2017 2016 A. 1   1      B.  3   1   3   1 2 2     2016 2017 C.   2   1   2   1 D. 2 1 3 2  2
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a.Mặt bên SAB là tam giác đều nằm trong
mặt phẳng vuông góc với đáy (ABCD). Thể tích khối chóp S.ABCD là: 3 a 3 3 a 3 3 a 3 A. 3 a 3 B. C. D. 2 4 6 1 1 1 Câu 34: Hàm số 3 2 y   x ax bx
đạt cực đại tại x = 1 và giá trị cực đại tại điểm đó bằng 2 khi 3 2 3
a b bằng : A. 2 B. 3 C. 0 D. 1
Câu 35: Phép đối xứng qua mặt phẳng (P) biến đường thẳng d thành chính nó khi và chỉ khi :
A. d song song với (P)
B. d nằm trên (P)
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
C. d  (P)
D. d nằm trên (P) hoặc d  (P) 2x
Câu 36: Đồ thị hàm số y
có bao nhiêu đường tiệm cận ? 2 x  2x  3 A. 3 B. 1 C. 2 D. 0
Câu 37: Cho a > 0, a  1. Tìm mệnh đề ĐÚNG trong các mệnh đề sau:
A. Tập giá trị của hàm số y = ax là tập R
B. Tập xác định của hàm số y = ax là khoảng (0; +)
C. Tập xác định của hàm số y = log x là R a
D. Tập giá trị của hàm số y = log x là tập R a
Câu 38: Cho hình chóp tam giác đều S.ABC. Chọn mệnh đề khẳng định ĐÚNG:
A. Hình chóp S.ABC là hình chóp có mặt đáy là tam giác đều;
B. Hình chóp S.ABC có cạnh đáy bằng cạnh bên;
C. Hình chiếu S trên (ABC) là tâm đường tròn nội tiếp tam giác ABC;
D. Hình chiếu S trên (ABC) là trực tâm tam giác ABC; x  3
Câu 39: Đường thẳng  : y  x k cắt đồ thị (C) của hàm số y
tại hai điểm phân biệt khi và chỉ x  2 khi:
A. Với mọi k R B. k  0 C. k 1
D. Với mọi k  0
Câu 40: Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh a. Hình chiếu của A' xuống (ABC)
là tâm O đường tròn ngoại tiếp tam giác ABC biết AA' hợp với đáy ABC một góc 0
60 . Thể tích lăng trụ là : 3 a 3 3 a 3 3 a 3 A. 3 a 3 B. C. D. 2 6 4
Câu 41: Hàm số nào sau đây đồng biến trên từng khoảng xác định của nó 1
A. y  2  x x B. 3 2 y  
x  2x  3x  2 3 2x 1 x 1 C. y D. y x  2 2  x x  2
Câu 42: Cho đường cong (H) : y
. Mệnh đề nào sau đây là ĐÚNG ? x 1
A. (H) có tiếp tuyến song song với trục tung
B. (H) có tiếp tuyến song song với trục hoành
C. Không tồn tại tiếp tuyến của (H) có hệ số góc dương
D. Không tồn tại tiếp tuyến của (H) có hệ số góc âm
Câu 43: Cho hình chóp S.ABC , có SA vuông góc mặt phẳng (ABC) ; tam giác ABC vuông tại B . Biết SA  2 ; a AB  ;
a BC a 3 . Khi đó bán kính R của mặt cầu ngoại tiếp hình chóp là
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại A. 2a 2 B. a 2 C. 2a D. a
Câu 44: Cho hàm số y f x  x  2
ln 4x x  , f '2 của hàm số bằng bao nhiêu ? A. 2 ln 2 B. 2 C. ln 2 D. 4
Câu 45: Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác đều cạnh a = 4 và biết diện tích tam giác
A’BC bằng 8. Thể tích khối lăng trụ là : A. 2 3 B. 4 3 C. 8 3 D. 16 3
Câu 46: Cho hình chóp S.ABCD có đáy ABCD là hình vuông , SA vuông góc với mặt phẳng đáy. Khi đó tâm
mặt cầu ngoại tiếp hình chóp là điểm nào ?
A. Trung điểm của SC. B. Điểm A C. Đỉnh S
D. Tâm hình vuông ABCD
Câu 47: Hàm số y f (x) nào có đồ thị như hình vẽ sau : y 4 2 x -1 0 A. 2
y f (x)  x(x  3)  4 B. 2
y f (x)  x(x  3)  4 C. 2
y f (x)  x(x  3)  4 D. 2
y f (x)  x(x  3)  4
Câu 48: Một hình trụ có trục OO  2 7 , ABCD là hình vuông có cạnh bằng 8 có đỉnh nằm trên hai đường
tròn đáy sao cho tâm của hình vuông trùng với trung điểm của OO . Thể tích của hình trụ bằng bao nhiêu ? A. 50 7 B. 25 7 C. 16 7 D. 25 14 2
x  4x  3
Câu 49: Cho hàm số y
có đồ thị (C). Tích các khoảng cách từ một điểm bất kỳ trên đồ thị (C) x  2
đến các đường tiệm cận của nó bằng bao nhiêu ?. 7 2 7 2 1 A. B. C. D. 2 2 2 2
Câu 50: Nghiệm của phương trình: 2 3 x
2x 9.3x 9.2x     0 là : A. x  2 B. x  0
C. x  2, x  0 D. Vô nghiệm
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
LUYỆN THI TRẦN ĐẠI
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Số 8, ngõ 462 đường Bưởi
Chuyên đề: Học kỳ I lớp 12 ĐIỂM Mã đề thi
Thời gian làm bài: 90 phút 03
(50 câu trắc nghiệm)
Họ và tên học sinh:……………………………………………….. Câu 1: Cho hàm số 3 2
y x  3x  4 có đồ thị ( C ). Tiếp tuyến với đường cong (C), song song với đường
thẳng (d) : y  3
x  5 có phương trình là: A. y  3  x  4 B. y  3  x  5 C. y  3  x 1 D. y  3  x  2
Câu 2: Tìm m để hàm số 3 2 y  3
x  2mx mx 1 luôn nghịch biến trên R. 3 3 3 3
A.   m  0
B.   m  0
C.   m  0
D.   m  0 2 2 2 2 2x 1 1
Câu 3: Phương trình tiếp tuyến của (C): y
vuông góc với đường thẳng y   x  2 có phương x  2 5 trình là: 1 1
A. y   x  2 và y   x  22
B. y  5x  2 và y  5x  22 5 5 1 1
C. y  5x  2 và y  5x  22
D. y   x  2 và y   x  22 5 5
Câu 4: Giá trị lớn nhất của hàm số 3 2
y x  3x  9x  35 trên đoạn [-4 ; 4] bằng. Chọn 1 câu đúng. A. 40 B. 8 C. – 41 D. 15 3x 10
Câu 5: Trong các khẳng định sau về hàm số y
, hãy tìm khẳng định đúng? x  9
A. Đồ thị hàm số chỉ có một tiệm cận.
B. Hàm số có một điểm cực trị
C. Hàm số nghịch biến trên từng khoảng xác định D. Hàm số đồng biến trên từng khoảng xác định 1
Câu 6: Tìm m để hàm số y   2 m m 3 2
x  2mx  3x 1 luôn đồng biến trên R 3 A. 3   m  0 B. 3   m  0 C. 3   m  0 D. 3   m  0 3 2 x mx 1
Câu 7: Định m để hàm số y  
 đạt cực tiểu tại x  2 . 3 2 3 A. m  1  B. m  2  C. m  1 D. m  2
Câu 8: Cho tứ diện SABC có SA = 2a, SA  (ABC). Tam giác ABC có AB = a, BC = 2a, CA = a 5 . Diện tích mặt
cầu ngoại tiếp tứ diện SABC là: A. 2 9 a B. 2 18 a C. 2 27 a D. 2 36 a Câu 9: Hàm số 4 2
y x  2x 1 có bao nhiêu cực trị ? A. 0 B. 2 C. 1 D. 3
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 1
Câu 10: Hàm số y = log có tập xác định là: 5 6  x A. (0; +∞) B. (-∞; 6) C. (6; +∞) D. R 3 x
Câu 11: Tìm các giá trị của tham số m để hàm số y   m   2
1 x mx  5 có 2 điểm cực trị. 3  3  5 m  3  5 A. 2 m B.
C. 2  m  3 D. m  1 2  3  5 m   2
Câu 12: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a; Gọi S là diện tích xung quanh của hình trụ xq
có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A’B’C’D’. Diện tích S là : xq 2  a 2 A. 2 a B. 2  a 2 C. 2  a 3 D. 2
Câu 13: Nghiệm của phương trình 9x 4.3x
 45  0 là A. x  2  B. x 1 C. x  3 D. x  2
Câu 14: Đồ thị hàm số 4 2
y  x  2(m  2)x  2m  3 cắt trục hoành tại 4 điểm phân biệt khi  3  3 3 m   m A. m   B.  2 C.  2 D. m  1  2 m  1  m  1 
Câu 15: Cho hàm số: 2 2
y  ln(2x e ) . Đạo hàm cấp 1 của hàm số trên là: 4x  2e 4x 4x x A. B. C. D. 2 2 2 (2x e ) 2 2 2 (2x e ) 2 2 (2x e ) 2 2 2 (2x e )
Câu 16: Một hình hộp chữ nhật nội tiếp mặt cầu và có ba kích thước là a,b,c. Khi đó bán kính R của mặt cầu bằng: 1 2 2 2
a b c A. 2 2 2
a b c B. 2 2 2
a b c C. 2 2 2
2(a b c ) D. 2 3 x 1
Câu 17: Đồ thị hàm số y  có dạng: 2x y y 3 4 2 3 1 2 x 1 -3 -2 -1 1 2 3 x -1 -4 -3 -2 -1 1 2 -2 -1 -3 -2 A. B.
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại y y 4 3 3 2 2 1 x 1 -3 -2 -1 1 2 3 x -1 -2 -1 1 2 3 4 -1 -2 -2 -3 C. D.
Câu 18: Cho tứ diện đều ABCD cạnh a; Diện tích xung quanh của hình nón có đáy là đường tròn ngoại tiếp
tam giác BCD, chiều cao bằng chiều cao của tứ diện ABCD là: 3 2 3 A. 2  a B. 2  a C. 2  a D. 2 3 a 2 3 3
Câu 19: Nghiệm của bất phương trình 2x 1 3   9 là 3 2 3 2 A. x B. x C. x D. x  2 3 2 3
Câu 20: Đồ thị hàm số 4 2
y  x x  2 có dạng: y y 5 3 4 2 3 1 2 x 1 -3 -2 -1 1 2 3 x -1 -4 -3 -2 -1 1 2 3 4 -1 -2 -2 -3 A. B. -3 y y 5 3 4 2 3 1 2 x 1 x -3 -2 -1 1 2 3 -4 -3 -2 -1 1 2 3 4 -1 -1 -2 -2 -3 C. -3 D.
Câu 21: Đồ thị hàm số 3 2
y  4x  6x 1 có dạng: y y 3 3 2 2 1 1 x x -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -2 -2 -3 -3 A. B. y y 3 3 2 2 1 1 x x -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -2 -2 -3 -3 C. D.
Câu 22: Khối chóp S.ABCD có đáy là hình vuông cạnh a và chiều cao SA bằng a; Thể ti ́ch khối chóp S.ABCD bằng:
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 1 1 A. 3 2a B. 3 3a C. 3 a D. 3 a 3 2 Câu 23: Cho hàm số 3 2
y x  3x  31 mx 1 3m C
.Tìm m để hàm số có cực đại , cực tiểu , đồng m
thời các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam giác có diện tích bằng 4 . A. m  2  B. m  1  C. m  1  D. m  1
Câu 24: Tập nghiệm của bất phương trình log x  1 là 1 2  1   1  A. ;    B. 2;  C.  ;  2 D. ;     2   2  4 x 9
Câu 25: Phương trình tiếp tuyến của đồ thị (C): 2 y
 2x  tại giao điểm của nó với trục Ox có 4 4 phương trình là: 9
A. y  15(x  3) B. y   4 9 9
C. y  15(x  3) và y  1  5(x  3)
D. y   và y   4 4 x 1
Câu 26: Cho hàm số y
. Khẳng định nào sau đây đúng: 2  x
A. Hàm số đã cho nghịch biến trên R
B. Hàm số đã cho đồng biến trên khoảng  ;  22;
C. Hàm số đã cho đồng biến trên từng khoảng xác định của nó
D. Hàm số đã cho nghịch biến trên từng khoảng xác định của nó x  2
Câu 27: Cho hàm số y
(C) và đường thẳng d : y m x . Với giá trị nào của m thì d cắt (C) tại 2 điểm x 1 phân biệt. m  2  m  2  A. B. 2   m  2 C. 2   m  2 D.  m  2 m  2
Câu 28: Với giá trị nào của m, n thì hàm số 3
y  x mx n đạt cực tiểu tại điểm x  1
 và đồ thị của nó đi qua điểm (1;4)?
A. m = 1; n = 2
B. m = 2; n = 3
C. m = 2; n = 1
D. m = 3; n = 2
Câu 29: Cho lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a; Thể tích lăng trụ bằng: 3 a 3 3 3 a 3 a A. B. 3 a C. D. 4 12 3 2 1
Câu 30: Phương trình 2 log x
log (5x)  2  0 có hai nghiệm x , x . Khi đó tích hai nghiệm bằng : 5 5 2 1 2 5 5 5 A. B. 5 C. D. 25 5 5
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 31: Số nghiệm của phương trình log (x  2)  log (4x  6) là 5 5 A. 3 B. 1 C. 2 D. 0
Câu 32: Cho hình vuông ABCD cạnh 2a quay quanh đường trung trực của cạnh AB thì được hình trụ. Khi đó,
diện tích xung quanh của hình trụ bằng: A. 2 2 a B. 2 4 a C. 2 6 a D. 2 8 a
Câu 33: Bạn An muốn dán lại bên ngoài chiếc nón lá bằng giấy màu, biết độ dài từ đỉnh nón đến vành nón
là 0.3m, bán kính mặt đáy của nón là 0.25m. Tính số giấy màu bạn An cần dùng?   5 3 A. 2 Sm B. 2 Sm C. 2 Sm D. 2 Sm xq 10 xq 20 xq 20 xq 20
Câu 34: Một người gửi số tiền 100 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền sẽ được nhập vào vốn ban đầu ( người ta gọi đó là lãi
kép). Để người đó lãnh được số tiền 260 triệu thì người đó cần gửi trong khoảng thời gian bao nhiêu năm
? ( nếu trong khoảng thời gian này không rút tiền ra và lãi suất không thay đổi ) A. 12 năm B. 13 năm C. 14 năm D. 15 năm
Câu 35: Thể tích khối chóp có diện tích đáy B và chiều cao h là: 1 1
A. V Bh B. V Bh
C. V  2Bh D. V Bh 2 3 2x 1
Câu 36: Đồ thị hàm số y  có tâm đối xứng là: x 1 A. K( 0; 2) B. M( 2; 1) C. I( 1; 2) D. N(1; - 2) ;
Câu 37: Phương trình x 1  x x 1 9 13.6 4   
 0 có 2 nghiệm x , x . Phát biểu nào sao đây đúng 1 2
A. Phương trình có 2 nghiệm vô tỉ
B. Phương trình có 2 nghiệm nguyên
C. Phương trình có 1 nghiệm dương
D. Phương trình có 2 nghiệm dương
Câu 38: Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B với AC = a biết SA vuông góc với đáy
ABC và SB hợp với đáy một góc 60o. Tính thể tích khối chóp. 3 a 3 6 3 a 3 a A. B. 3 a C. D. 4 24 3 2 2x 1
Câu 39: Cho hàm số y
có đồ thị (C). Đường thẳng y  2
x m cắt (C) tại hai điểm phân biệt A, B x 1
sao cho tam giác OAB ( O là gốc tọa độ ) có diện tích bằng 3 khi: A. m  3 B. m  3  C. m  3  D. m  2 
Câu 40: Đồ thị hàm số 3 2
y x  3x  4 có tâm đối xứng là: A. M( 1; - 2) B. I( -1; 0) C. N(- 1; - 2) D. K( -2; 0)
Câu 41: Cho lăng trụ đứng AB .
C A' B 'C ' có đáy là tam giác vuông cân tại ,
A BC a 2 A' B  3a . Diện
tích đáy của lăng trụ bằng:
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 2 a 2 a 2 2a B. 2 9a C. D. A. 4 2
Câu 42: Cho lăng trụ đều AB .
C A' B 'C ' có cạnh đáy bằng a, mặt phẳng (A’BC) hợp với (ABC) một góc 0 45 .
Chiều cao của lăng trụ bằng: a 3 a 3 2a B. C. D. 3a A. 3 2 1 1 Câu 43: Cho hàm số 4 2 y   x x
. Khẳng định nào sau đây đúng: 2 2
A. Hàm số đạt cực đại tại điểm x  1
 , giá trị cực đại của hàm số là y   1  1 .
B. Hàm số đạt cực đại tại điểm x  0 , giá trị cực đại của hàm số là y 0  0 .
C. Hàm số đạt cực tiểu tại điểm x  1
 , giá trị cực tiểu của hàm số là y   1  1 .
D. Hàm số đạt cực tiểu tại điểm x  0 , giá trị cực tiểu của hàm số là y 0  0 .
Câu 44: Tính thể tích của giếng nước, biết giếng nước có hình trụ và sâu 20m, đường kính mặt giếng là 4m. A. 3 V  20 m B. 3 V  18 m C. 3 V  125.7 m D. 3 V  251.3 m
Câu 45: Giá trị lớn nhất của hàm số y  5  4x trên đoạn [-1 ; 1 ] bằng. Chọn 1 câu đúng. A. 3 B. 0 C. 1 D. 9
Câu 46: Cho hình chóp tam giác đều SABC cạnh đáy bằng a và cạnh bên tạo với đáy (ABC) một góc 600.Tính
thể tích chóp đều SABC . 3 a 3 3 3 a 3 a 3 A. B. 3 a C. D. 12 12 3 8
Câu 47: Nghiệm của phương trình 2
log (x 1)  3 là 2 A. x   7 B. x   7 C. x  2 2 D. x  7
Câu 48: Với giá trị nào của m thì phương trình 4 2
x  3x m  0 có ba nghiệm phân biệt? A. m = 0 B. m = 4 C. m = - 4 D. m = -3 Câu 49: Cho hàm số 3 2
y x  6x  9x 1. Khẳng định nào sau đây đúng:
A. Hàm số đã cho nghịch biến trên khoảng 1;3
B. Hàm số đã cho nghịch biến trên khoảng 1;
C. Hàm số đã cho đồng biến trên khoảng 1;3
D. Hàm số đã cho đồng biến trên khoảng 5;
Câu 50: Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a biết SA vuông góc với đáy ABC và (SBC)
hợp với đáy (ABC) một góc 60o.Tính thể tích khối chóp.
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 3 a 3 3 a 3 3 a 3 A. B. 3 a C. D. 3 12 8 4
LUYỆN THI TRẦN ĐẠI
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Số 8, ngõ 462 đường Bưởi
Chuyên đề: Học kỳ I lớp 12 ĐIỂM Mã đề thi
Thời gian làm bài: 90 phút 04
(50 câu trắc nghiệm)
Họ và tên học sinh:………………………………………………..
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình thoi , hai đường chéo AC  2a 3 , BD  2a và cắt
nhau tại O , hai mặt phẳng SAC  và SBD cùng vuông góc với mặt phẳng  ABCD . Biết khoảng cách từ a 3
điểm O đến mặt phẳng SAB bằng
. Tính thể tích V của khối chóp S.ABCD . 4 3 a 3 3 a 3 3 a 2 3 a 3 A. V B. V C. V D. V  3 6 6 12 2 2x 1
Câu 2: Số đường tiệm cận của đồ thị hàm số y  là: 2 x  4x  3 A. 0 B. 2 C. 3 D. 1
Câu 3: Gọi M, N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3
y  3sin x  4sin x trên đoạn  ;  0 
 . Giá trị của tổng M+N là:  2  A. 0 B. 2 C. -1 D. 1
Câu 4: Đồ thị sau đây là của hàm số nào ? -1 1 O -2 -3 -4 1 A. 4 2
y x  3x  3 B. 4 2 y   x  3x  3 C. 4 2
y x  2x  3 D. 4 2
y x  2x  3 4
Câu 5: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a , cạnh bên SA vuông góc với
mặt đáy và SA a . Tính thể tích V của khối chóp S.ABC . 2 3 a 3 3 a 3 3 a 3 A. 3 V a B. V C. V D. V  3 12 3 4
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 6: Phương trình 2 2
x x  2  m có đúng 6 nghiệm thực khi: A. m  0
B. 0  m  1 C. m  1 D. m  0 .
Câu 7: Tất cả các giá trị của tham số m để hàm số y = x4 + 2mx2 + m2 + m có ba điểm cực trị là: A. m  1 B. m  0 C. m < 0 D. m > 1 2x 1
Câu 8: Các khoảng nghịch biến của hàm số y  là x 1
A. (-∞; – 1) và (–1; +∞) ;
B. (-∞; 1) và (1; +∞)
C. (-∞; – 1) và (1; +∞) D. (-∞; +∞)
Câu 9: GTLN của hàm số y = 2 – 2sinxcosx là : A. 1 B. 4 C. 3 D. 0
Câu 10: Gọi x1, x2 là hai điểm cực trị của hàm số 3 2 2 3
y x  3mx  3(m 1)x m m thỏa 2 2
x x x x  7 1 2 1 2 khi m bằng 9 1 A. m  0 B. m   C. m   D. m  2  2 2
Câu 11: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: 1 1 A. V Bh B. V Bh
C. V  2Bh
D. V Bh 3 2 4
Câu 12: Hàm số y = x + + 3 đạt cực tiểu tại: x A. x = –2 B. x = 2 C. x = 0 D. Không tồn tại
Câu 13: Số điểm cực trị của hàm số 3 2
y x x  4x  3 là: A. 0 B. 1 C. 2 D. 3
Câu 14: Cho a  0 , a  1, x, y là 2 số dương. Tìm mệnh đề đúng: x log x x A. log aB. x y a   log log a a y log y log y a a x C. log
 log x  log y D. log x y x y a   log log a a a y a a 2x 1
Câu 15: Đường thẳng y x m cắt đồ thị hàm số y
tại hai điểm phân biệt A, B thỏa mãn x 1
AB  2 2 .Khi đó giá trị của m thỏa mãn: A. m  1 
B. m 1;7 C. m  1  D. m  7
Câu 16: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với
mặt đáy và SA a 2 . Tính thể tích V của khối chóp S.ABCD . 3 a 2 3 a 2 3 a 2 A. V B. V C. 3 V a 2 D. V  6 3 4
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 17: Anh Việt muốn mua một ngôi nhà trị giá 500 triệu đồng sau 3 năm nữa. Biết rằng lãi suất hàng năm
vẫn không đổi là 8% một năm. Vậy ngay từ bây giờ số tiền ít nhất anh Việt phải gửi tiết kiệm vào ngân hàng
theo thể thức lãi kép để có đủ tiền mua nhà (kết quả làm tròn đến hàng triệu) là: A. 396 triệu đồng B. 395 triệu đồng C. 397 triệu đồng D. 394 triệu đồng
Câu 18: Cho log 5  ;
a log 5  b . Giá trị của log 5 tính theo a và b là: 2 3 6 1 ab A. B. C. a + b D. 2 2 a b a b a b
Câu 19: log b  0 khi. a 0  a 1 0  a 1 a  1 A. B.  hoặc  b   1 0  b 1 b   1 a 1 a  1 C. D.  0  b 1 b   1
Câu 20: Bất phương trình log  2
x  2ax a  3  0 có tập nghiệm là tập số thực R khi: 1  3 a  1 A. a  2 B. 1   a  2 C. a  1  D.  a  2
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, biết AB = 2a; AD = a; Hình chiếu của S lên đáy
là trung điểm H của cạnh AB ; góc tạo bởi SC và đáy là 0
45 . Thể tích của khối chóp S.ABCD là: 3 a 3 a 3 3 2a 2 3 2a A. B. C. D. 3 2 3 3 2
Câu 22: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 6 1 3x x y    trên đoạn 6; 7 .
Khi đó, M – m bằng bao nhiêu? A. 6561 B. 6562 C. 6564 D. 6558
Câu 23: Một hình nón có bán kính mặt đáy bằng 3 ,
cm độ dài đường sinh bằng 4 cm . Khối nón giới hạn bởi
hình nón đó có thể tích bằng bao nhiêu ? A. 2 3 7 cm B. 2 12 cm C. 2 15 cm D. 2 2 7 cm
Câu 24: Thể tích khối chóp có diện tích đáy B và chiều cao h là: 1 1
A. V Bh B. V Bh
C. V  2Bh D. V Bh 2 3
Câu 25: Một hình trụ có bán kính mặt đáy bằng 5 ,
cm thiết diện qua trục của hình trụ có diện tích bằng 2
20 cm . Khi đó diện tích xung quanh của hình trụ bằng bao nhiêu ? A. 2 40 cm B. 2 30 cm C. 2 45 cm D. 2 15 cm
Câu 26: Cho một tấm nhôm hình vuông cạnh 48cm . Người ta cắt ở 4 góc 4 hình vuông bằng nhau và gập
tấm nhôm lại để được một cái hộp không nắp. Để thể tích khối hộp lớn nhất thì cạnh hình vuông bị cắt dài: 48 8 A. 8cm B. cm C. cm D. 24cm 3 92
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 2 mx m
Câu 27: Đồ thị hàm số y
đồng biến trên từng khoảng xác định của nó khi và chỉ khi tham số m x 1 thỏa m  0 m  0 m  0 m  0 A. B.  . C. D.  m  1  m  1 m  1  m  1 3x  2
Câu 28: Cho hàm số y
có đồ thị (C). Những điểm trên (C), tại đó tiếp tuyến có hệ số góc bằng 4 có x  2 tọa độ là: A. (-1;1) và (-3;-7) B. (1;1) và (3;7) C. (1;-1) và (3;-7) D. (-1;-1) và (-3;7) Câu 29: Cho hàm số 4
y x  m   2 2
1 x m có đồ thị (C), m là tham số. (C) có ba điểm cực trị A, B, C sao
cho OA BC ; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung khi:
A. m  3  3 3
B. m  0 hoặc m  2
C. m  5  5 5 .
D. m  2  2 2
Câu 30: Tập nghiệm của bất phương trình 2log x 1  log 5  x 1 là: 2   2   A. 1;  3 B. 1;5 C. 3;  5 D.  3  ;  3
Câu 31: Nếu ba kích thước của một khối chữ nhật đều tăng lên 4 lần thì thể tích của nó tăng lên: A. 4 lần B. 64 lần C. 16 lần D. 192 lần
Câu 32: Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng a . Một hình nón có đỉnh là tâm của hình
vuông ABCD và có đường tròn đáy ngoại tiếp hình vuông A' B 'C ' D ' . Diện tích xung quanh của hình nón đó là: 2  a 3 2  a 2 2  a 3 2  a 6 A. B. C. D. 3 2 2 2
Câu 33: Cho tam giác ABC có độ dài 3 cạnh là 13, 14, 15. Một mặt cầu tâm O, bán kính R = 5 tiếp xúc với 3
cạnh của tam giác ABC. Tính khoảng cách từ tâm mặt cầu đến mặt phẳng chứa tam giác . A. 4 B. 3 C. 6 D. 5 mx 1
Câu 34: Đồ thị hàm số y
có đường tiệm cận đứng đi qua A1; 2 . Khi đó: 2x m
A. m  2  2 B. m  2  C. m  2
D. m  2  2
Câu 35: Hàm số y = x4 - 2x2 + 1 đồng biến trên các khoảng
A. (-∞; -1) và ( 0;1) ;
B. (-1; 0) và ( 1; +∞)
C. (-1; 0) và (1; +∞) , D. ∀x ∈ R
Câu 36: Cho hình lăng trụ đứng AB .
C A' B 'C ' có tất cả các cạnh bằng a; Tính thể tích V của khối lăng trụ AB .
C A' B 'C ' . 3 a 3 3 a 3 3 a 3 a 2 A. V B. V C. V D. V  4 2 2 3
Câu 37: Người ta muốn xây một bồn chứa nước dạng khối hộp chữ nhật trong một phòng tắm. Biết chiều
dài, chiều rộng, chiều cao của khối hộp đó lần lượt là 5m, 1m, 2m ( hình vẽ bên). Biết mỗi viên gạch có
chiều dài 20cm, chiều rộng 10cm, chiều cao 5cm. Hỏi người ta sử dụng ít nhất bao nhiêu viên gạch để xây
bồn đó và thể tích thực của bồn chứa bao nhiêu lít nước? (Giả sử lượng xi măng và cát không đáng kể )
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 1dm VH' 1dm VH 2m 1m 5m
A. 1180 viên; 8820 lít
B. 1180 viên; 8800 lít
C. 1182 viên; 8820 lít
D. 1182 viên; 8800 lít
Câu 38: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại ,
A AB a AC  2a , cạnh bên
SA vuông góc với mặt đáy và SA a . Tính thể tích V của khối chóp S.ABC . 3 a 3 a 3 a A. V B. 3 V a C. V D. V  3 2 4
Câu 39: Hàm số nào sau đây là hàm số đồng biến trên tập xác định của nó ? x  1  A. 2x y
B. y   
C. y log x
D. y log x  2  0.5 1 2
Câu 40: Hàm số y = x3 + 3x2 nghịch biến trên khoảng A. (-∞; 2) B. (0; +∞) C. (-2; 0) D. (0; 2) 3x  4
Câu 41: Đồ thị hàm số y  có tiệm cận ngang là 2x  5 4 1 3 3 A. y   B. y   C. y   D. y  5 5 5 2
Câu 42: Hàm số nào dưới đây không có điểm cực trị 1 x 1 A. 3 2
y  2x x  3 B. 4 2
y x x  3
C. y x 1 D. y x 1 x  2
Câu 43: Cho hàm số y = f(x) có đồ thị như hình vẽ A. GTL -2 N củ - a 1 hàm 0 số trên 1 đọan[- 2 1; 2] là 2
B. GTLN của hàm số trên đoạn [-1; 2] là 0
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
C. GTLN của hàm số trên đoạn [-1; 2] là 4
D. GTLN của hàm số trên đoạn [-1; 2] là 1
Câu 44: Đồ thị sau đây là của hàm số nào ? 4 2 1 -2 O 1 -2 2x 1 x  2 x 1 x  2 A. y B. y C. y D. y x 1 x 1 x 1 1 x
Câu 45: Đồ thị sau đây là của hàm số nào ? 3 2 1 -1 1 O -1 A. 3
y x  3x 1 B. 3 2
y  x  3x 1 C. 3
y x  3x 1 D. 3 2
y  x  3x 1 1
Câu 46: Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số 3 2 y
x  2x  3x  5 3
A. Có hệ số góc bằng 1 
B. Có hệ số góc dương
C. Song song với đường thẳng x 1
D. Song song với trục hoành 2 3 2 5 4  a a a
Câu 47: Giá trị của biểu thức P  log   bằng: a  15 7  a   12 9 A. 2 B. C. D. 3 5 5 1 Câu 48: Hàm số y = 2 3 2
(m m)x  2mx  3x 1 đồng biến trên R khi và chỉ khi 3 A. 3   m  0 B. 3   m  0 C. 3   m  0 D. 3   m  0
Câu 49: Phương trình 3x2 4 16 có nghiệm là: 3 4 A. x = B. x C. x  3 D. x  5 4 3
Câu 50: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AC a , biết SA vuông góc với mặt
phẳng (ABC), đường thẳng SC tạo với mặt phẳng (ABC) một góc 0
60 . Bán kính của mặt cầu ngoại tiếp hình chóp S.ABC bằng
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại A. a B. a 2 C. 2a 3 D. a 3
LUYỆN THI TRẦN ĐẠI
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Số 8, ngõ 462 đường Bưởi
Chuyên đề: Học kỳ I lớp 12 ĐIỂM Mã đề thi
Thời gian làm bài: 90 phút 05
(50 câu trắc nghiệm)
Họ và tên học sinh:………………………………………………..
Câu 1: Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số nào sao đây? 2x  2 1 x 2 1 x 2 2x  3x  2 A. y B. y C. y D. y x  2 1 x 1 x 2  x 1 Câu 2: Hàm số 3 2 y
x x mx đồng biến trên khoảng (1; ) thì m thuộc khoảng nào sau đây: 3 A. [3; )  B. ( 1  ; )  C. ( 1  ;3) D. ( ;  3] 1 
Câu 3: Tập xác định của hàm số 3 y x là:  1  A. (0; ) B. C.  ;    D. \ {0}  3 
Câu 4: Có bao nhiêu khối đa diện đều ? A. 5 B. 3 C. 4 D. 2
Câu 5: Diện tích xung quanh của một hình nón có bán kính đáy bằng 3 và chiều cao bằng 4 là: A. 30 B. 36 C. 15 D. 12
Câu 6: Một cái nồi nấu nước người ta làm dạng hình trụ không nắp chiều cao của nồi 60cm, diện tích đáy là 2
900 cm . Hỏi họ cần miếng kim loại hình chữ nhật có chiều dài và chiều rộng là bao nhiêu để làm thân nồi đó
A. Chiều dài 60 cm chiều rộng 60cm.
B. Chiều dài 65cm chiều rộng 60cm.
C. Chiều dài 180cm chiều rộng 60cm.
D. Chiều dài 30 cm chiều rộng 60cm. Câu 7: Hàm số 2
f (x)  x  4x m đạt giá trị lớn nhất bằng 10 trên đoạn [−1; 3] khi m bằng: A. 3 B. −8 C. −3 D. −6
Câu 8: Đặt a  log 15, b  log 10 . Hãy biểu diễn log 50 theo a và b 3 3 3
A. a b  2
B. 2a  2b
C. a b 1
D. 2a  2b  2 Câu 9: Hàm số 3 2
y  2x  9x 12x  5 có bao nhiêu điểm cực trị? A. 1 B. 3 C. 2 D. 4
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại Câu 10: Cho hàm số 3
y x  3x 1 có đồ thị như hình dưới đây. Các giá trị của m để phương trình: 3
x  3x 1 m  0 có ba nghiệm phân biệt là: A. 2   m  2 B. 2   m  2 C. 1   m  3 D. 1   m  3
Câu 11: Trong các hình chữ nhật có chu vi là 40cm. Hình nào sau đây có diện tích lớn nhất:
A. Hình vuông có cạnh bằng 20cm
B. Hình chữ nhật có cạnh bằng 20cm
C. Hình chữ nhật có cạnh bằng 10cm
D. Hình vuông có cạnh bằng 10cm Câu 12: Hàm số 3 2
y x  5x  3x 1 đạt cực trị tại: 1 1 10 10 A. x  3;  x  
B. x  3; x
C. x  0; x
D. x  0; x   3 3 3 3 2 2
Câu 13: Số nghiệm âm của phương trình: 4x 6.2x   8  0 là A. 0 B. 3 C. 2 D. 1
Câu 14: Một mặt cầu có diện tích 2
36 m . Thể tích của khối cầu này bằng: 4 A. 3 36 m B. 3  m C. 3 108 m D. 3 72 m 3 Câu 15: Hàm số 3 2
y  3x mx  2x 1 đồng biến trên khi và chỉ khi:
A. m  3 2 hoặc m  3 2
B. 3 2  m  3 2
C. 3 2  m  3 2 D. m > 0 1 Câu 16: Hàm số 4 2 y
x  3x  3 nghịch biến trên các khoảng nào ? 2  3   3  A.  0;     và  ;     
B.  3 ;0 và  3 ;  2   2  
C. ; 3 và0; 3 D.  3 ; 
Câu 17: Khối đa diện đều loại {3;5} là khối: A. Tứ diện đều
B. Hai mươi mặt đều C. Lập phương D. Tám mặt đều
Câu 18: Tập nghiệm của bất phương trình log
x  4 1  0 là: 2   5  13   13  13  A. 4;   B. ;    C. ;    D. 4;   2   2   2 
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 19: Cho hình nón có bán kính đáy là 3a, chiều cao là 4a . thể tích của khối nón bằng: A. 3 15 a B. 3 12 a C. 3 12 a D. 3 36 a
Câu 20: Bảng biến thiên dưới đây là của hàm số nào? x  2 2x 1 2x 1 x 1
A. f (x) 
B. f (x) 
C. f (x) 
D. f (x)  1 x x 1 x 1 2x 1
Câu 21: Khối hộp chữ nhật có ba kích thước là a, b và c; Khi đó thể tích của nó là: 1 1 1
A. V abc B. V abc
C. V abc
D. V abc 3 2 6
Câu 22: Với số thực a > 0. Khẳng định nào sau đây là đúng ? m m m m A. n m aa B. n m n a a C. n n aa D. m n n a a Câu 23: Hàm số 4 2
y x  2x 1 có đồ thị là: A. B. C. D.
Câu 24: Cho phương trình 2 log
(x  5x  6) 1=0 có hai nghiệm là x , x . Tính 2 2 x x 0.5 1 2 1 2 A. −15 B. 15 C. −51 D. 51
Câu 25: Cho khối tứ diện ABCD. Lấy điểm M nằm giữa A và B, điểm N nằm giữa C và D; Bằng hai mặt phẳng
(CDM) và (ABN), ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây ?
A. MANC, BCDN, AMND, ABND
B. NACB, BCMN, ABND, MBND
C. ABCN, ABND, AMND, MBND
D. MANC, BCMN, AMND, MBND
Câu 26: Cho đồ thị hàm số 3 2
y x  2x  2x có đồ thị (C) . Gọi x , x là hoành độ các điểm M, N trên (C) 1 2
mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = −x + 2017 . Khi đó x x bằng : 1 2 4 1 4 A. B. −1 C. D. 3 3 3  4 x 25
Câu 27: Bất phương trình    có tập nghiệm là:  5  16 (0; )  (;2) ( ;  2)  ;  2   A. B. C. D.
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 28: Một khu rừng có trữ lượng gỗ 4.105 mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là
4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ ? A. 2016.103(m3) B. 4,8666.105(m3) C. 125.107(m3) D. 36.105(m3)
Câu 29: Đồ thị dưới đây là của hàm số nào ? A. 3 2
y  x  3x 1 B. 3
y x  3x 1 C. 3
y x  3x 1 D. 3 2
y  x  3x 1 5x
Câu 30: Cho hàm số y
có đồ thị (C). Khẳng định nào sau đây là đúng ? 2 x 1
A. (C) không có tiệm cận đứng và có một tiệm cận ngang
B. (C) không có tiệm cận
C. (C) không có tiệm cận đứng và có 2 tiệm cận ngang
D. (C) có 2 tiệm cận đứng và 2 tiệm cận ngang
Câu 31: Bảng biến thiên dưới đây là của hàm số f(x). Hàm số f(x) đồng biến trên khoảng nào ? A. ( ;  0) B. ( 1  ;3) C. (0;2) D. (2; ) 
Câu 32: Số giao điểm của đường cong 3 2
y x  2x x 1 và đường thẳng y = 1 – 2x là: A. 3 B. 0 C. 1 D. 2
Câu 33: Cho khối chóp tam giác đều. Nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi 4 lần thì thể tích của khối chóp đó sẽ:
A. Tăng lên hai lần B. Không thay đổi
C. Giảm đi hai lần D. Giảm đi ba lần
Câu 34: Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a; Đường chéo AC’ nằm trong
mặt phẳng (AA’C’C) tạo với đáy (ABC) một góc 300. Khi đó thể tích khối lăng trụ đó bằng: 3 a 3 a 3 a 3 3 a 3 A. B. C. D. 12 4 4 12 1 x
Câu 35: Số tiệm cận của đồ thị hàm số y  là: 1 x A. 0 B. 1 C. 3 D. 2
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 36: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa mặt bên và đáy bằng 0 45 . Diện
tích của mặt cầu ngoại tiếp hình chóp S.ABCD là: 2 9 a 2 4 a 2 3 a 2 2 a A. B. C. D. 4 3 4 3
Câu 37: Đạo hàm của hàm số  log (2x y  2)  là: 2x 2x ln 2 2x ln 2 2x A. y '  B. y '  C. y '  D. y '  (2x  2) ln  (2x  2) ln  2x  2 2x  2
Câu 38: Cho tứ diện OABC biết OA, OB, OC đôi một vuông góc với nhau, biết OA = 3, OB = 4 và thể tích khối
tứ diện OABC bằng 6. Khi đó khoảng cách từ O đến mặt phẳng (ABC) bằng: 41 144 12 A. 3 B. C. D. 12 41 41
Câu 39: Gọi l, ,
h R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ (T). Diện tích xung
quanh S của hình trụ (T) là: xq A. 2 S   R h
B. S   Rh
C. S   Rl
D. S  2 Rl xq xq xq xq
Câu 40: Giá trị của biểu thức: 5log 2 3 3  log log 8 bằng: 3  2  A. 32 B. 25 C. 33 D. 26
Câu 41: Cho hàm số y f (x) liên tục trên đoạn [a; b] và luôn đồng biến trên khoảng (a; b). Khẳng định
nào sao đây là sai ?
A. Hàm số đạt giá trị nhỏ nhất tại x = a
B. Giá trị lớn nhất của hàm số bằng f ( ) b
C. Giá trị nhỏ nhất của hàm số bằng f (a)
D. Hàm số đạt giá trị nhỏ nhất tại x = b
Câu 42: Giá trị của m để hàm số 3 2
y x x mx  5 có cực trị là: 1 1 1 1 A. m B. m C. m D. m  3 3 3 3
Câu 43: Giá trị của m để đồ thị hàm số 3 2 2 3
y x  3mx  3(m 1)x m  4m 1 có hai điểm cực trị A, B sao
cho tam giác AOB vuông tại O là:
A. m  1; m  2  B. m  2 C. m  1  D. m  1  ;m  2
Câu 44: Giá trị lớn nhất của hàm số f x 2
 x  2x  3 bằng: A. 2 B. 0 C. 3 D. 2
Câu 45: Trong một chiếc hộp hình trụ, người ta bỏ vào ba quả bóng Tennis, biết rằng đáy của hình trụ bằng
hình tròn lớn trên quả bóng và chiều cao của hình trụ bằng 3 lần đường kính quả bóng. Gọi S là tổng diện 1 S
tích của ba quả bóng, S là diện tích xung quanh của hình trụ. Tỉ số diện tích 1 là: 2 S2
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại A. 1 B. 2 C. 5 D. 3
Câu 46: Gọi R là bán kính, S là diện tích và V là thể tích của khối cầu. Công thức nào sau đây là sai ? 4 A. 2 S   R B. 2 S  4 R C. 3 V   R
D. 3V S.R 3
Câu 47: Trong các hàm số sau, hàm số nào đồng biến trên khoảng (1; 3) ? x  3 2 x  4x  8 A. y B. 2 4
y  2x x C. 2
y x  4x  5 D. y x 1 x  2
Câu 48: Bảng biến thiên dưới đây là của hàm số f(x). Hàm số f(x) đạt cực tiểu tại điểm: A. x = 3 B. x = 2 C. x = 0 D. x = −1
Câu 49: Các điểm cực tiểu của hàm số 4 2
y x  3x  2 là: A. x = 0 B. x = −1
C. x  1, x  2 D. x = 5
Câu 50: Giá trị lớn nhất của hàm số 3 2
y x  3x  9x  35 trên đoạn [-4; 4] bằng: A. 41 B. 8 C. 40 D. 15
LUYỆN THI TRẦN ĐẠI
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Số 8, ngõ 462 đường Bưởi
Chuyên đề: Học kỳ I lớp 12 ĐIỂM Mã đề thi
Thời gian làm bài: 90 phút 06
(50 câu trắc nghiệm)
Họ và tên học sinh:………………………………………………..
Câu 1: Cho hàm số y f x có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị của m để phương trình
f x  m 1 có ba nghiệm phân biệt là: A. 2   m  2 B. 2   m  4 C. 1   m  3 D. 1   m  2 1
Câu 2: Tìm số m lớn nhất để hàm số 3 2 y
x mx  4m  3 x  2017 đồng biến trên R ? 3
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại A. m  3 B. m  4 C. m  2 D. m  1
Câu 3: Tổng của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x  x 2  ln x trên đoạn 2;3 bằng:
A. 10  2ln 2 3ln 3
B. 4  2ln 2  e
C. 6  3ln 3  e
D. 10  2ln 2 3ln 3  e
Câu 4: Tập nghiệm của bất phương trình log  2 x x  log 2  x  4 là : 0,8  0,8   A.  ;  4  1; B.  4   ;1 C.  ;  4  1;2 D.  4   ;1  2; 
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi E, F lần lượt là trung điểm của SB, SD. Tỉ số VS.AEF bằng: VS.ABCD 1 3 1 1 A. B. C. D. 2 8 8 4
Câu 6: Đường cong hình bên là đồ thị của hàm số nào sau đây: A. 3 2
y x  3x 1 B. 3
y  2x  3x 1 C. 3 2
y  2x  3x 1 D. 3
y x  3x 1 3x x 1   1   1 
Câu 7: Tập nghiệm của bất phương trình      là :  3   9  A.  2;   B.  ;  2   C.  ;  2   2  ; D. x  3
Câu 8: Số đường tiệm cận của đồ thị hàm số y  là : 2 x 1 A. 3 B. 1 C. 2 D. 0 4
Câu 9: Tiếp tuyến của đồ thị hàm số y
tại điểm có hoành độ x  1  có phương trình là: x 1 o
A. y  x  3
B. y  x  2
C. y  x  2
D. y  x  3
Câu 10: Tổng các nghiệm của phương x 1  x 1 4 6.2   8  0 là: A. 5 B. 1 C. 6 D. 3 1 3
Câu 11: Giá trị lớn nhất của hàm số f x 3x2  e  2
4x  5x trên đoạn ;   bằng:  2 2
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 14 2 13 3 11 5 12 4 A. 3 e B. 2 e C. 4 e D. 5 e 3 2 2 5
Câu 12: Cho hàm số C  3 2
: y x  3x 1 . Tiếp tuyến của (C) song song với đường thẳng d : y = -3 x+ 6 có phương trình là: A. y = -3x+ 5 B. y = -3x 2 C. y = -3x+1 D. y = -3x- 2
Câu 13: Cho hình nón tròn xoay có đường cao h = 20cm, bán kính đáy r = 25cm. Một thiết diện đi qua đỉnh
của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12cm. Diện tích của thiết diện có giá trị bằng: A. 2 S  200cm B. 2 S  300cm C. 2 S  400cm D. 2 S  500cm ABC ABC ABC ABC
Câu 14: Cho hàm số y f x có đồ thị như hình vẽ kề bên. Khẳng định nào sau đây là sai?
A. Hàm số nghịch biến trên khoảng  2  ;  1
B. Hàm số đạt cực tiểu tại x  1  , y  1  CT
C. Hàm số đạt cực đại tại x  0 , y  0
D. Hàm số đồng biến trên khoảng 0; CĐ x  4
Câu 15: Cho hàm số y
. Khẳng định nào sau đây là đúng: x  2
A. Hàm số nghịch biến trên khoảng 2; 
B. Hàm số đồng biến trên trên khoảng 2;4
C. Hàm số nghịch biến trên trên khoảng 4; 
D. Hàm số đồng biến trên trên khoảng  ;  4 Câu 16: Cho hàm số 3
y  2x  6x . Khẳng định nào sau đây là sai?
A. Hàm số đạt cực đại tại x  1 
B. Hàm số đạt cực tiểu tại x 1
C. Hàm số đồng biến trên khoảng  ;  2  
D. Hàm số nghịch biến trên khoảng  2   ;1
Câu 17: Điều kiện của tham số m để đường thẳng d  : y x  5 cắt đồ thị hàm số 3
y x  m   2 2
1 x  2m  3 x  5 tại ba điểm phân biệt là: A. m  2 B. 1 m  5
C. m 1 m  5 D. m  R
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 2x  3
Câu 18: Cho hàm số y
có đồ thị (C). Tìm m để đường thẳng d  : y  2x m cắt đồ thị (C) tại hai x  2
điểm phân biệt A, B sao cho tiếp tuyến của (C) tại A, B song song nhau ? A. m  2  B. m  1  C. m  0 D. m  1
Câu 19: Cho hình chữ nhật ABCD biết AB  1, AD  3 . Khi quay hình chữ nhật ABCD xung quanh trục AB
thì cạnh CD tạo nên hình trụ tròn xoay. Thể tích của khối trụ là: 3 A. 3 B.  3 C. D.  3 x 1
Câu 20: Trong các đồ thị dưới đây, đồ thị nào là đồ thị của hàm số y  ? 1 x y y 2 3 2 1 x 1 -2 -1 1 2 3 x -3 -2 -1 1 2 3 -1 -1 -2 -2 -3 -3 A. B. y y 3 3 2 2 1 1 x x -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -2 -2 -3 -3 C. D. Câu 21: Cho hàm số 3 2
y x  3x mx  2 . Tập hợp tất cả các giá trị của m để hàm số đã cho đồng biến trên khoảng 0; là: A. m  1  B. m  0 C. m  2  D. m  3 
Câu 22: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y  2x  3x 12x  2 trên M đoạn  1  ;2. Tỉ số bằng: m 1 1 A. B. C. 3  D. 2 2 3
Câu 23: Đạo hàm của hàm số y  log 4x là: 4 1 1 ln10 A. y '  B. y '  C. y '  D. y '  x ln10 x ln10 4x ln10 4x
Câu 24: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Cạnh bên SC hợp với đáy một góc 0
30 . Thể tích của khối chóp S.ABC là: 3 a 3 3 a 3 a 3 a 3 A. B. C. D. 12 12 4 4
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 25: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, AB a ; Cạnh bên SA vuông góc với mặt
đáy. Góc giữa SB và mặt đáy bằng 0
45 . Thể tích của khối cầu ngoại tiếp hình chóp S.ABC là: 3 3 3 3 A. 3  a B. 3  a C. 3  a D. 3  a 8 4 2 16
Câu 26: Số giao điểm của đồ thị hàm số 4 2
y x x  3x  2 và đường thẳng d  : y  3x  2 là: A. 3 B. 0 C. 1 D. 2
Câu 27: Được sự hỗ trợ từ Ngân hàng Chính sách xã hội địa phương, nhằm giúp đỡ các sinh viên có hoàn
cảnh khó khăn hoàn thành việc đóng học phí học tập, một bạn sinh viên A đã vay của ngân hàng 20 triệu
đồng với lãi suất 12%/năm, và ngân hàng chỉ bắt đầu tính lãi sau khi bạn A kết thúc khóa học. Bạn A đã
hoàn thành khóa học và đi làm với mức lương là 5,5 triệu đồng/tháng. Bạn A dự tính sẽ trả hết nợ gốc lẫn
lãi suất cho ngân hàng trong 36 tháng. Hỏi số tiền m mỗi tháng mà bạn A phải trả cho ngân hàng là bao nhiêu? 2 1,12  20  0,12 3 1,12  36  0,12 A. m   triệu B. m  triệu 2 1,12   1 12  3 1,12   1 12 2 1,12  36  0,12 3 1,12  20  0,12 C. m   triệu D. m  triệu 2 1,12   1 12  3 1,12   1 12
Câu 28: Biết log 2  a , log 3  b thì log 45 tính theo a và b bằng:
A. 2b a 1
B. 2b a 1 C. 15b
D. a  2b 1
Câu 29: Cho phương trình x x2 4  . m 2
 2m  0 . Nếu phương trình này có hai nghiệm x , x thõa mãn 1 2
x x  4 thì m có giá trị bằng: 1 2 A. 1 B. 2 C. 4 D. 8 Câu 30: Cho hàm số 3
y x  m   2 3
1 x  9x m . Giá trị nào của m sau đây thì hàm số đã cho có hai điểm
cực trị x , x thỏa mãn x x  2 : 1 2 1 2 A. m  3  B. cả A và B. C. m  5 D. m  1 3 4
Câu 31: Cho hàm số y f x có đạo hàm f x 2 '
x x  
1  x  2 . Số điểm cực trị của hàm số là: A. 3 B. 2 C. 1 D. 0
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B biết AD  2a , AB BC a . Cạnh
bên SA vuông góc với đáy, góc giữa SC và mặt đáy bằng 0
45 . Thể tích của khối chóp S.ABCD bằng: 3 2a 2 3 a 2 3 3a 2 3 a 3 A. B. C. D. 3 2 2 2
Câu 33: Cho lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng a, mặt phẳng (A’BC) hợp với đáy một góc 0 60 . Thể
tích của khối lăng trụ ABC.A’B’C’ là: 3 3 3a 3 3 3a 3 3 3a 3 a 3 A. B. C. D. 2 8 4 8
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại x log 8x  log 2   1 2
Câu 34: Cho log x  . Giá trị biểu thức 4 P  bằng: 2 5 1 log x 4 50 10 5 5 A. B. C. D. 11 11 7 6
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; Hai mặt bên (SAB) và (SAD) cùng vuông
góc với đáy. Góc giữa SC và mặt đáy bằng 0
30 . Thể tích của khối cầu ngoại tiếp hình chóp S.ABCD là: 8 6 64 6 8 6 32 A. 3  a B. 3  a C. 3  a D. 3  a 9 27 27 9
Câu 36: Tập xác định của hàm số y   x x  3 2 2 2 3 1 là:  1   1     1  A. 1  ;   B.  ;  1;    C.    1 ; 1  ;    D. ;1    2   2   2   2  Câu 37: Cho hàm số 4 2 4
y x  2mx  2m m . Tìm m để hàm số đã cho có ba điểm cực trị và các điểm cực
trị tạo thành một tam giác có diện tích bằng 1 ? A. m  2  B. m  1  C. m  0 D. m  1 1 Câu 38: Cho hàm số 3 2 y
x mx   2 m m  
1 x . Giá trị m để hàm số đạt cực đại tại x 1 là: 3 A. m  3 B. m  0 C. m  5 D. m  2
Câu 39: Cho hình chóp tứ giác đều S.ABCD có các cạnh cùng bằng a; Bán kính mặt cầu ngoại tiếp hình chóp là: a 2 a 3 A. a 2 B. C. a 3 D. 2 2
Câu 40: Giá trị của m để tiếp tuyến của đồ thị hàm số 3 2
y x  3mx  m  
1 x 1tại điểm có hoành độ x  1
 đi qua điểm A1;2 là: 4 3 5 2 A. m B. m C. m D. m   5 4 8 3
Câu 41: Cho hình lăng trụ tam giác đều có các cạnh bằng a; Diện tích mặt cầu ngoại tiếp hình lăng trụ là: 2 7 a 2 7 a 2 7 a A. 2 7 a B. C. D. 2 3 6
Câu 42: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên (SAB) là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy. Khoảng cách từ A đến mp(SCD) bằng: a 21 a 21 a 21 a 21 A. B. C. D. 5 6 7 8 x
Câu 43: Cho hàm số C  2 1 : y
và điểm M 2;5 thuộc (C). Tiếp tuyến của (C) tại điểm M cắt trục tọa x 1
độ Ox , Oy lần lượt tại điểm A và B. Diện tích của tam giác OAB bằng :
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 112 122 97 121 A. B. C. D. 5 3 2 6
Câu 44: Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, hình chiếu của A’ lên mặt phẳng (ABC)
là trung điểm của BC. Biết góc giữa AA’ và mặt đáy bẳng 0
60 . Thể tích của khối lăng trụ là: 3 3 3 3 3 3 A. 3 a B. 3 a C. 3 a D. 3 a 4 8 8 4 x
Câu 45: Cho hàm số C  4 3 : y
. Tổng các khoảng cách bé nhất từ điểm M thuộc (C) đến hai đường x  3
tiệm cận của đồ thị (C) là: A. 6 B. 9 C. 3 D. 4 x 1 1
Câu 46: Cho hàm số y
. Giá trị nhỏ nhất của hàm số trên đoạn 0,  3 bằng  khi: 2 x m 4
Câu 47: Số nghiệm của phương trình log  x  3  log  x  9  log  x  2 là: A. 1 B. 2 C. Nhiều hơn 2 D. 0
Câu 48: Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền
bằng a 2 . Cho dây cung BC của đường tròn đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phẳng
chứa đáy hình nón một góc 600. Khi đó, diện tích tam giác SBC bằng: 2 a 2 2 a 2 2 a 2 A. SB. SC. SD. 2 Sa 2 ABC 9 ABC 3 ABC 4 ABC
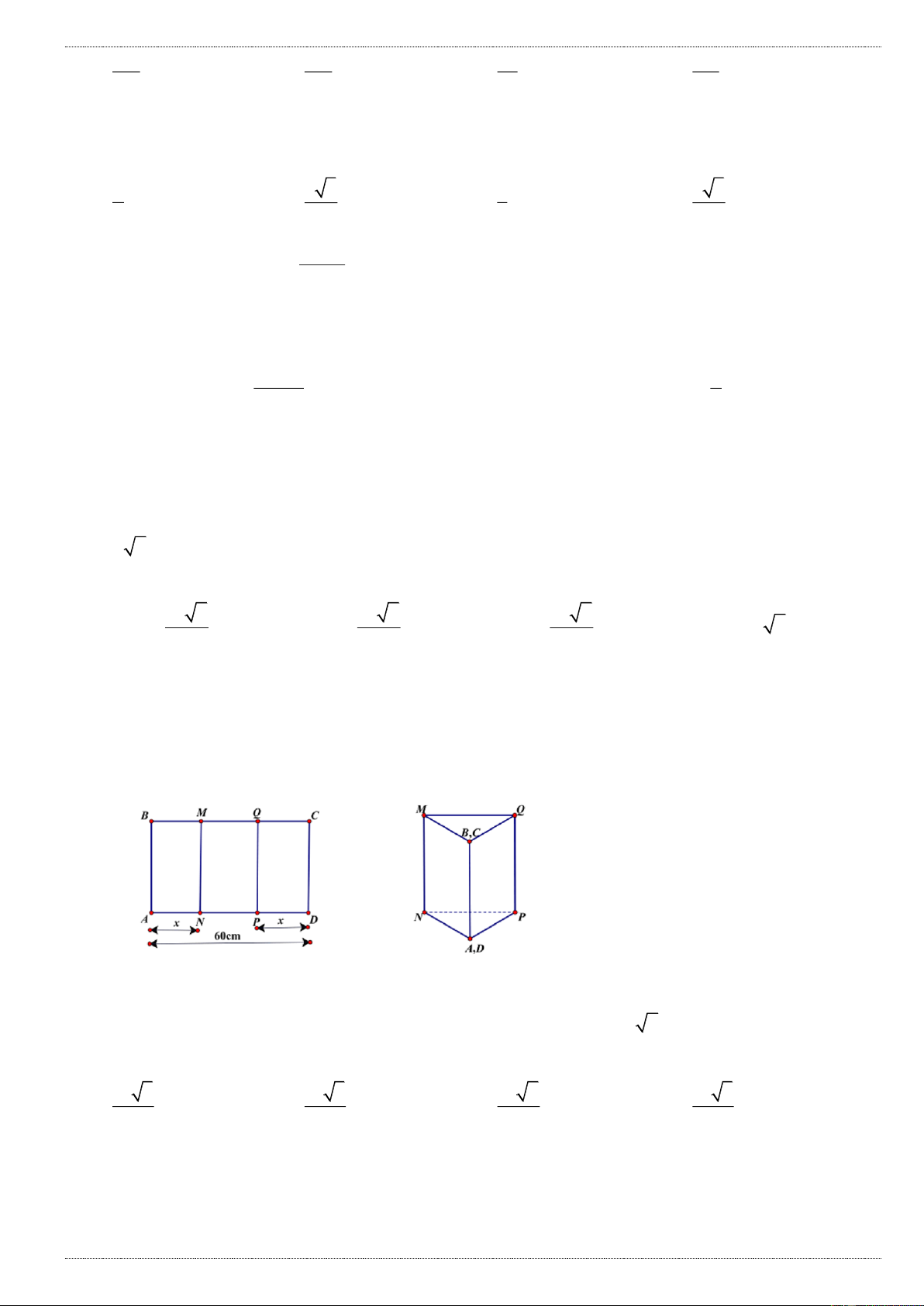
Câu 49: Cho một tấm nhôm hình chữ nhật ABCD biết AD  60cm . Ta gập tấm nhôm theo 2 cạnh MN và PQ
vào phía trong đến khi AB và DC trùng nhau như hình vẽ, để được một hình lăng trụ khuyết 2 đáy. Tìm x để
thể tích khối lăng trụ lớn nhất: A. x  40 B. x  30 C. x  45 D. x  20
Câu 50: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, AB a 2 , SA vuông góc với đáy. Góc
giữa (SBC) và mặt đáy bằng 0
60 . Thể tích của khối chóp S.ABC là: 3 a 3 3 a 3 3 a 6 3 a 3 A. B. C. D. 2 6 3 3
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
LUYỆN THI TRẦN ĐẠI
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Số 8, ngõ 462 đường Bưởi
Chuyên đề: Học ky I lớp 12 ĐIỂM Mã đề thi
Thời gian làm bài: 90 phút 07
(50 câu trắc nghiệm)
Họ và tên học sinh:……………………………………………….. 1 1 2    1 a b
Câu 1: Cho a  0 ; b  0 và biểu thức 1 2 2
T  2(a b) .(ab) . 1   (  )  . Khi đó: 4 b a   1 2 1 A. T B. T  1 C. T D. T  3 3 2 2 2 2
Câu 2: Tập nghiệm của bất phương trình 2 x 1  x 2 4  .2  3.2  .2x x x x  8x 12 là A. S   1  ; 2 3;
B. S   2;  1   3;3
C. S   2;  1   2;3
D. S   ;   2  2;3 Câu 3: Cho log 3  ; m log 5  .
n Khi đó log 45 tính theo m, n là: 9 n n n n A. 1 B. 1 C. 2  D. 1 2m m 2m 2m
Câu 4: Tìm các giá trị của a để bất phương trình 2
log ( 1 x )  log (ax a) có nghiệm? 2 2  
A. a   ;1   3;
B. a    3 ; 1   ;     2     C. a   ;    1   2;
D. a    2 ; 1   ;     2  
Câu 5: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai khối tứ diện bằng nhau nếu số đỉnh bằng nhau và số mặt bằng nhau
B. Hai khối đa diện bằng nhau nếu số mặt bằng nhau
C. Hai khối đa diện bằng nhau nếu có một phép đối xứng qua mặt phẳng (P) biến khối này thành khối kia
D. Hai khối đa diện bằng nhau nếu số đỉnh bằng nhau
Câu 6: Vào năm 1626, ông Michle bán gia tài của mình được 24 đô la và gửi vào 1 ngân hàng X với lãi suất
6% / năm. Đến năm 2007, trong một lần tìm lại các giấy tờ của gia đình mình, cháu ông Michle- Role mới
biết điều đó và muốn rút hết số tiền mà ông mình là Michle đã gửi vào lúc trước ở ngân hàng X. Ngân hàng
X trả cho ông Role số tiền là 572,64 đô la. Ông Role không đồng ý. Như vậy thực sự ông Role phải nhận
được số tiền là bao nhiêu? A. 380 24.1, 06 (đô la) B. 381 24.1, 06 (đô la) C. 380 25.1, 06 (đô la) D. 380 24.1, 07 (đô la)
Câu 7: Tìm mệnh đề đúng trong các mệnh đề sau:
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
A. Đồ thị hàm số x
y a với 0  a  1 luôn đi qua điểm (a;1) B. x
y a với a 1 là hàm số nghịch biến trên  ;   1
C. Đồ thị các hàm số x y a và  ( )x y
với 0  a  1, đối xứng với nhau qua trục Oy. a D. x
y a với 0  a  1 là hàm số đồng biến trên  ;   x
Câu 8: Tập nghiệm của phương trình x 2 3  8.3 15  0 . Là
A. S  2;  3
B. S  2;log 25
C. S  log 5;log 25 D. S  3;log 25 3  3 3  3  xx
Câu 9: Tập nghiệm của bất phương trình     1 1 x 1 5 2 5 2     là
A. S   ;  2   1   ;1 B. S   2  ;  1 1; C. S   2  ;  1 2; 
D. S   ;    3   1  ;2
Câu 10: Cho tứ diện đều ABCD. Góc giữa đường thẳng AB và mặt phẳng (BCD) bằng: 1 1 A. 45o B. arccos C. 60o D. arccos 3 3
Câu 11: Đồ thị của hàm số 3
y x  3x đạt cực đại tại điểm có hoành độ A. -1 B. 3 C. 0 D. 1
Câu 12: Tìm tất cả các giá trị của m để bt phương trình 2
x  4  x
4x x m có nghiệm đúng với
mọi x 0;4 . A. m  5 B. m  4 C. m  4 D. m  5
Câu 13: Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống ta được mệnh đề đúng:
“Số cạnh của một hình đa diện luôn …………..…… số mặt của hình đa diện ấy.” A. bằng
B. nhỏ hơn hoặc bằng C. nhỏ hơn D. lớn hơn
Câu 14: Đồ thị hình bên là đồ thị của hàm số nào: y 9 8 7 6 5 4 3 2 1 x -3 -2 -1 1 2 3 -1 A. 4 2
y x  2x  2 B. 4 2
y x  2x  2 C. 4 2
y x  2x  2 D. 4 2
y x  3x  2
Câu 15: Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, AB=a, AD=a 3 . Đường thẳng SA vuông góc
với đáy. Đường thẳng SB tạo với mp(SAC) góc 300. Tính thể tích khối chóp SABCD?
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 3 a 6 3 a 6 3 a 6 A. B. C. 3 a 6 D. 6 2 3
Câu 16: Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a . SA vuông góc mp(ABC), SA a 2 . Tính
theo a thể tích khối chóp S.ABC. 3 a 3 3 a 3 3 a 6 3 a 6 A. B. C. D. 8 12 8 12 x 1
Câu 17: Tìm các giá trị của m để đồ thị hàm số y
có ba đường tiệm cận: 2 mx  2x  4     m  0 m  0 m  0      m 0  A.  1 B.m  6
C. m  6 D.  1 m   m      3 1  1  5 m  m   3  4
Câu 18: Tập nghiệm của phương trình 2
log (x 1)  log (x 1) là 2 1 2  1 5  1   5   1 5  A. S  2;  B. S   C. S    S  3;   D. 2    2    2  
Câu 19: Cho a>0, b>0 và 2 2
a b  7ab . Chọn mệnh đề đúng. 3 a b 1
A. ln(a b)  (ln a  ln b) B. ln( )  (ln a  ln b) 2 3 2 1
C. 3ln(a b)  (ln a  ln b)
D. 2(ln a  ln ) b  ln(7a ) b 2 Câu 20: Hàm số 2
y  ln(x x  2) có tập xác định : A.  2   ;1 B.  2  ;  1 C.  ;  2  1; D.  ;  2  1; Câu 21: Cho hàm số 3 2
y  x  3x  5x 1có đồ thị (C). Tiếp tuyến có hệ số góc lớn nhất của (C), có phương trình là:
A. y  2x 1 B. y  2  x C. y  2  x 1
D. y  2x  2
Câu 22: Đồ thị hàm số 3
y x  3x  2 là đồ thị nào trong các đồ thị sau:
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 4 2 2 -2 A. B. 4 2 2 -2 C. D.
Câu 23: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và SA  (ABC) , SA= 2a. Gọi H, K lần lượt là hình
chiếu vuông góc của điểm lần lượt lên cạnh SB, SC. Ti ́nh thể ti ́ch khối đa diện ABCKH theo 3 a 3 3 3a 3 3 3a 2 3 3a 3 A. B. C. D. 50 25 25 50
Câu 24: Cho khối chóp SABC có ABC là tam giác vuông cân tại A, AB = a, SA vuông góc với mp(ABC), SA=a.
Khoảng cách giữa AB và SC là: a 2 2a 21 a 21 a 2 A. B. C. D. 3 7 14 2
Câu 25: Đường thẳng (d): y  3
x 1; cắt đồ thị (C): 3 2
y x  2x 1 tại điểm A(xo; yo) thì : A. y  2 B. y  1  C. y  2  D. y  1 0 0 0 0    
Câu 26: Giá trị lớn nhất của hàm số y  5cos x  cos5x trên đoạn  ;   là :  4 4  3 3 A. 3 3 B. 4 3 C. 2 3 D. 2 Câu 27: Cho hàm số 3 2
y ax bx cx d;(a  0) . Biết đạo hàm y’ có hai nghiệm phân biệt x1; x2 và
y(x ).y(x )  0 . Chọn khẳng định đúng trong các khẳng định sau 1 2
A. Đồ thị hàm số có hai cực trị nằm khác phía đối với trục hoành
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
B. Đồ thị hàm số có hai cực trị nằm phía dưới trục hoành
C. Đồ thị hàm số có hai cực trị nằm phía trên trục hoành
D. Đồ thị hàm số có đúng một cực trị Câu 28: Biểu thức 5 3 T
a a ; (a  0) . Viết dưới dạng luỹ thừa với số mũ hữu tỉ là: 4 2 1 3 A. 15 a B. 15 a C. 3 a D. 5 a
Câu 29: Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là: 1 4 1
A. V Bh B. V Bh C. V Bh D. V Bh 2 3 3
Câu 30: Một nhà sản xuất bột trẻ em cần thiết kế bao bì mới cho một loại sản phẩm mới của nhà máy. Bao
bì đó được thiết kế theo dạng hình hộp chữ nhật có chiều cao h, có đáy là hình vuông có cạnh bằng x và hộp có thể tích là 1 3
dm . Nếu em là nhân viên thiết kế, em sẽ thiết kế như thế nào để tốn ít nhiên liệu nhất. 1 1 1 A. h x
B. h x C. h x
D. x h 2 3 3
Câu 31: Cho khối lăng trụ ABC.A’B’C’ có đáy là tam giác vuông cân, BA = BC = a. Hình chiếu của A’ trên
(ABC) là trung điểm H của AC. Góc giữa mp(ABA’) và mp(ABC) bằng 600. A' B' C' A B H C
Khoảng cách từ C đến (ABB’A’) là: a 3 3a a 2 a 3 A. B. C. D. 4 4 4 2
Câu 32: Cho khối hộp ABC .
D A B C D . Mặt phẳng ( A BD) chia khối hộp thành hai phần. Tỉ số thể tích giữa 1 1 1 1 1
phần có thể tích nhỏ với phần có thể tích lớn là: 1 1 1 1 A. B. C. D. 3 4 6 5
Câu 33: Cho khối chóp có thể tích bằng V, khi giảm diện tích đa giác đáy 3 lần và tăng chiều cao lên 2 lần
thì thể tích khối chóp lúc đó bằng: 2V 3V V V A. B. C. D. 3 2 3 5
Câu 34: Tìm các giá trị của m để hàm số sau đồng biến trên
y  m   3
x  m   2 1
1 x  3m  2 x 1 m   ;1 m  1; 
C. m 1; D. m  ;  0 A. B.
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 35: Khối đa diện đều nào sau đây có mặt không phải là tam giác đều? A. Bát diện đều B. Tứ diện đều
C. Mười hai mặt đều
D. Hai mươi mặt đều
Câu 36: Cho (H) là khối lăng trụ tam giác đều có tất cả các cạnh bằng a. Thể tích của (H) bằng: 3 a 2 3 a 3 3 a 3 3 a A. D. 3 B. 2 C. 4 2
Câu 37: Gọi M, N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 4 2
y  2x  4x  5 trên đoạn  1  ;  3 . Khi đó M + N bằng : A. 0 B. 135 C. 136 D. 134
Câu 38: Tập nghiệm của phương trình log (3  2x)  2 . là 3
A. S    2 S    9
C. S    3 S    4 B. D.
Câu 39: Tìm các giá trị thực của tham số m để đồ thị hàm số 4 2
y x  2mx  3m  4 có các cực trị đều thuộc các trục toạ độ A. m  1  ;0;  4 m  ;  0  4
C. m 1; 2;  3 m  4  ;0;  4 B. D. 2 x  3x
Câu 40: Số tiệm cận của đồ thị hàm số y  là 2 x  4x  3 A. 3 B. 4 C. 2 D. 1 Câu 41: Hàm số 4 2 2
y  x  (m  3)x  2m 1có đúng một cực trị khi và chỉ khi: A. m  3  B. m  0 C. m  3  D. m  3  2 1
Câu 42: Tập nghiệm của phương trình  x 3 ( ) x  27 . Là 3 2  21 2  21 3 21 3 21 A. S   ;  B. S   ;   2 2    2 2    3   21 3   21   2   21 2  21  C. S   ;  D. S   ;   2 2    2 2  
Câu 43: Hàm số nào đồng biến trên 1 A. 3 y  x 1     B. y C. 7 3 y x 3x y tan 2x x 1 D.
Câu 44: Chọn khẳng định đúng. 1 1 A. log  log .
b log c  log c C. log .
a log c  log c
log b  log b a b log b a b a b b a D. 1 a a B. a
Câu 45: Tìm các giá trị thực của tham số m để đồ thị hàm số: 4 2
y x  (3m 1)x  4m  3 cắt trục hoành tại bốn điểm phân biệt ?
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại  4   3   4   3  A. ;    ;    C. ;    ;     3   4   3   4  B. D.
Câu 46: Cho a  0 ; b  0 và a b c . Khi đó: 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3
A. a b c
B. a b c
C. a b c
D. a b c
Câu 47: Tập nghiệm của bất phương trình 2
1 log (2  x x )  0 là: 1 2  1    A.  1  ;01;2  1  ;0 1;2 1  ;    1;2 D.   3 1; 0  1;   B. C.  2   2 
Câu 48: Cho khối lăng trụ ABCD.A’B’C’D’ thể tích 3
36cm . M là điểm bất kì thuộc mặt phẳng (ABCD). B A M C D B' A' C' D'
Thể tích của khối chóp M.A’B’C’D’ là: A. 3 16cm B. 3 24cm 3 3 C. 18cm D. 12cm
Câu 49: Bảng biến thiên sau là bảng biến thiên của hàm số nào? x  –1  y’ – – –  1 y  –1 x  2 x  2 x  2 x  2 A. y y C. y y x 1 B. x  2 x 1 D. x 1
Câu 50: Khối mười hai mặt đều thuộc loại: A. {3, 4} B. {3, 5} C. {5, 3} D. {4, 3}
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
LUYỆN THI TRẦN ĐẠI
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Số 8, ngõ 462 đường Bưởi
Chuyên đề: Học kỳ I lớp 12 ĐIỂM Mã đề thi
Thời gian làm bài: 90 phút 08
(50 câu trắc nghiệm)
Họ và tên học sinh:………………………………………………..
Câu 1: Với giá trị nào của tham số m thì hàm số
nghịch biến trên khoảng 1; . A. 1  m   2 
B. m  2; m  2  C. m  2 D. m  2 
Câu 2: Một khu rừng có trữ lượng gỗ 5.105 mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là
5% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ ? A. 6.3814.104(m3) B. 25.105(m3) C. 6.3814.105(m3) D. 6.3814.106(m3)
Câu 3: Cho tứ diện đều ABCD cạnh bằng a; Thể tích của hình trụ có đáy là đường tròn ngoại tiếp tam giác
BCD và có chiều cao bằng chiều cao của tứ diện ABCD là: 3  a 2 3  a 6 3  a 6 A. B. C. 2  a 3 D. 3 4 3
Câu 4: Cho hàm số f(x) có bảng biến thiên hình bên . Hàm số f(x) đạt cực tiểu tại điểm: A. x = 2 B. x = 3 C. x = 0 D. x = −1 SM 2 SN 4
Câu 5: Cho hình chóp S.ABC có thể tích là 3
70a . Gọi M, N trên SB và SC sao cho  ;  . Tính thể SB 3 SC 5
tích V của khối tứ diện SAMN. 3 35a 3 112a A. 3 V  35a B. 3 V  14a C. V D. V  2 3
Câu 6: Đồ thị kề bên là của hàm số nào trong các hàm số sau ?
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại xx 3   e A. y       B. 3 x y   C. x y e D. y        1
Câu 7: Cho hàm số y x
, giá trị nhỏ nhất của hàm số trên 0; là x 9 1 A. B. C. 2 D. 0 4 2 3x 1
Câu 8: Cho hàm số y
. Khẳng định nào sau đây đúng? 2x 1 3 3
A. Đồ thị hàm số có tiệm cận đứng là x
B. Đồ thị hàm số có tiệm cận ngang là y  2 2 1
C. Đồ thị hàm số có tiệm cận đứng là x= 1
D. Đồ thị hàm số có tiệm cận ngang là y  2
Câu 9: Đạo hàm của hàm số  log (3x y 3)  là: 3x ln 3 3x ln 3 3x 3x A. y '  B. y '  C. y '  D. y '  (3x  3) ln  3x  3 3x  3 (3x  3) ln 
Câu 10: Cho tam giác ABC vuông tại B có AC  2 ;
a BC a ; khi quay tam giác ABC quanh cạnh góc
vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng: A. 2 2 a B. 2 4 a C. 2 3 a D. 2 a
Câu 11: Bất phương trình : log  x  7  log  x   1 có tập nghiệm là : 4 2 A. 1;4 B. (-1; 2) C. 5; D. (-; 1) 3x 1
Câu 12: Cho hàm số y
. Khẳng định nào sau đây đúng? 2  x 1
A. Đồ thị hàm số có tiệm cận ngang là y = 3;
B. Đồ thị hàm số có tiệm cận đứng là x 1 ; 3
C. Đồ thị hàm số có tiệm cận ngang là y  
D. Đồ thị hàm số không có tiệm cận. 2
Câu 13: Cho hình chóp S.ABC có thể tích bằng 3
20a . Gọi M, N lần lượt là trung điểm của cạnh BC, SC. Tính
thể tích V của khối tứ diện BAMN. 3 20a 3 20a A. V B. V C. 3 V  4a D. 3 V  5a 6 3
Câu 14: Đồ thị hàm số nào sau đây có 3 điểm cực trị: A. 4 2
y x  2x 1 B. 4 2
y x  2x 1 C. 4 2
y  x  2x 1 D. 4 2
y  2x  4x 1
Câu 15: Với 0  a  1 và b  0 . Khẳng định nào sau đây là đúng ? A. 2 4 4
log b  log b  log b B. 2 4 4
log b  log b  log b 2 2 a a a 2 a a a C. 2 4 2
log b  log b  6 log b D. 2 4
log b  log b   log b 2 a a a 2 a a a
Câu 16: Đường cong hình dưới đây là đồ thị của một trong bốn hàm số nào?
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại A. 2
y  x  2x B. 3 2
y x  2x x 1 C. 4 2
y x  2x D. 4 2
y  x  2x
Câu 17: Một công ti bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá
2000000 đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn hộ
100000 đồng một tháng thì có thêm hai căn hộ bị bỏ trống. Hỏi muốn có thu nhập cao nhất, công ti đó phải
cho thuê mỗi căn hộ với giá bao nhiêu một tháng. A. 220000 B. 2150000 C. 2250000 D. 2300000 1 Câu 18: Hàm số 4 2 y
x  3x  3 nghịch biến trên các khoảng nào ? 2  3   3 
A. ; 3 và0; 3 B.   ; 0    và  ;      2   2   C.  3 ; 
D.  3 ;0 và  3 ; 
Câu 19: Đồ thị hàm số có điểm cực tiểu là 4 2
y x  3x  2 2 A. ( 1  ;2) B. (1;2) C. (3; ) D. (0; 2) 3 Câu 20: Cho hàm số 3
y x  3x 1 có đồ thị như hình bên. Các giá trị của m để phương trình: 3
x  3x 1  m có ba nghiệm phân biệt là: A. 1   m  3 B. 2   m  2 C. 1   m  3 D. 2   m  2
Câu 21: Cho ln x  3 . Giá trị của biểu thức: ln 4.log x  ln10.log x bằng: 2 A. 3 3 B. 3 C. 2 3 D. 4 3
Câu 22: Cho hình chóp tứ giác S.ABCD . Gọi A’,B’, C’, D’ theo thứ tự là trung điểm của SA, SB, SC, SD. Khi
đó tỉ số thể tích của hai khối chóp S.ABCD và S.A’B’C’D’ bằng: 1 1 1 1 A. B. C. D. 2 4 8 16
Câu 23: Cho hàm số y f (x) liên tục trên đoạn [a; b] và luôn nghịch biến trên khoảng (a; b). Khẳng định
nào sau đây là sai ?
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
A. Hàm số đạt giá trị nhỏ nhất tại x = a
B. Giá trị nhỏ nhất của hàm số bằng f ( ) b
C. Hàm số đạt giá trị nhỏ nhất tại x = b
D. Giá trị lớn nhất của hàm số bằng f (a)
Câu 24: Trong các hàm số sau đây, hàm số nào đồng biến trên ? xx 1   3   x A. x y   
B. y   
C. y  3
D. y   2  e     x  5
Câu 25: Cho hàm số y
có đồ thị (C). Khẳng định nào sau đây là đúng ? 2 1 x 1
A. (C) không có tiệm cận
B. (C) không có tiệm cận đứng và có một tiệm cận ngang
C. (C) có 2 tiệm cận đứng và 2 tiệm cận ngang
D. (C) không có tiệm cận đứng và có 2 tiệm cận ngang 2 x  2x  3
Câu 26: Tọa độ giao điểm của đồ thị hàm số y
và đường thẳng y x 1 là x  2 A. 2;  3 B.  1  ;0 C. 2; 2 D. 3  ;1
Câu 27: Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a, AA’= A; Khi đó thể tích khối lăng trụ đó bằng: 3 a 3 a 3 a 3 3 a 3 A. B. C. D. 4 12 4 12
Câu 28: Cho hàm số y = f(x)= ax3+bx2+cx+d,a  0 . Khẳng định nào sau đây sai ?
A. Đồ thị hàm số luôn cắt trục hoành
B. lim f (x)   x
C. Đồ thị hàm số luôn có tâm đối xứng.
D. Hàm số luôn có cực trị Câu 29: Hàm số 3 2
y x  3x mx  4 . luôn đồng biến trên trên khoảng ( ;  0) với m A. m  3  B. m>3 C. m<-3 D. m  3 
Câu 30: Cho log 5  ;
a log 5  b . Khi đó log 5 tính theo a và b là: 2 3 6 ab 1 A. B. C. 2 2 a b D. a + b a b a b 1
Câu 31: Cho hàm số 3 2 y
x mx x m 1. Tìm m để hàm số có 2 cực tri ̣ tại A, B thỏa 2 2 xx  2 3 A B A. m  0 B. m  1  C. m  3  D. m  2
Câu 32: Bảng biến thiên dưới đây là của hàm số f(x). Hàm số f(x) đồng biến trên khoảng nào?
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại A. (0;2) B. ( 1  ;3) C. (2; )  D. ( ;  0)
Câu 33: Một hình trụ có bán kính mặt đáy bằng 5 ,
cm thiết diện qua trục của hình trụ có diện tích bằng 2
80 cm . Khi đó diện tích xung quanh của hình trụ bằng bao nhiêu ? A. 2 60 cm B. 2 80 cm C. 2 45 cm D. 2 40 cm
Câu 34: Cho hình lăng trụ tam giác đều có các cạnh cùng bằng a; Diện tích mặt cầu ngoại tiếp lăng trụ là: 2 7 a 2 7 a 2 7 a A. 2 7 a B. C. D. 2 3 6
Câu 35: Một hành lang giữa hai nhà có hình dạng của một lăng trụ đứng như hình dưới. Hai mặt bên
ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20m, rộng 5m. Gọi x (mét) là độ dài cạnh BC. Tìm x sao
cho hình lăng trụ có thể tích lớn nhất. A. 5 2 B. 2 5 C. 10 D. 2
Câu 36: Đường cong trong hình bên là đồ thị của hàm số. A. 4 2
y x  2x 1 B. 3 2
y  x  3x 1 C. 2
y  x  3x 1 D. 3
y x  3x 1
Câu 37: Tập xác định của hàm số: 2 log (4  x ) là: 2 A. ( ;  2  ) (2; )  B. [  2; 2] C. ( 2  ;2) D.
Câu 38: Cho tam giác OAB vuông tại O có OA  4,OB  3. Quay tam giác OAB quanh cạnh OA thu được một
hình nón tròn xoay. Diện tích toàn phần của hình nón bằng bao nhiêu ? A. 15 B. 20 C. 24 D. 3 7
Câu 39: Cho hàm số y =f(x) có lim f (x)  2 và lim f (x)  2 . Phát biểu nào sau đây đúng: x x
A. Đồ thị hàm số có TCN x = 2
B. Đồ thị hàm số có đúng 1 TCN
C. Đồ thị hàm số không có TCN
D. Đồ thị hàm số có 2 TCN
Câu 40: Phương trình 3x2 4 16 có nghiệm là: 4 3 A. x = 5 B. x = C. x = D. x = 3 3 4
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 41: Tính thể tích V của khối lập phương ABCDA’B’C’D’ biết AC '  a 6 3 8a 3 a A. 3 V  8a B. V C. V D. 3 V  2 2a 3 3
Câu 42: Một khối cầu có độ dài bán kính là R . Nếu độ dài bán kính tăng lên 2 lần thì thể tích của khối cầu tăng lên là: A. 4 lần B. 16 lần C. 24 lần D. 8 lần
Câu 43: Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số nào sao đây? 1 x 2x  2 2 1 x 2 2x  3x  2 A. y B. y C. y D. y  1 x x  2 1 x 2  x
Câu 44: Giá trị lớn nhất của hàm số 3 2
y x  3x  9x  35 trên đoạn [-4; 4] bằng: A. 8 B. 15 C. 41 D. 40
Câu 45: Cho khối chóp S.ABC có đáy là tam giác vuông tại B, AB = 3, BC = 4. Cạnh bên SA vuông góc với đáy,
cạnh bên SA = 5. Khi đó thể tích khối chóp bằng: A. 12 B. 20 C. 10 D. 8
Câu 46: Giá trị cực tiểu của hàm số 2 3
y  10 15x  6x x là A. -1 B. 110 C. 2 D. 3
Câu 47: Kim tự tháp Kêốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự tháp
này là một khối chóp tứ giác đều có chiều cao 147 m, cạnh đáy dài 230 m. Thế tích của nó là: A. 7776300 m3 B. 3888150 m3 C. 2592100 m3 D. 2592100 m2
Câu 48: Cho hình chóp tam giác O.ABC, có 3 cạnh đôi một vuông góc và OA  ; a OB  ;
b OC c .Đường cao OH của khối chóp bằng: abc abc A. B. 2 2 2
a b a 2 2 2 2 2 2
a b b c a c abc abc C. D. 2 2 2 2 2 2
ab bc ac
a b b c a c
Câu 49: Hình vẽ dưới đây là đồ thị của một trong bốn hàm số nào? x  2 x  2 x  2 x  2 A. y B. y C. y D. y x 1 x 1 x 1 x 1
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 50: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , tam giác SAD cân tại S, mặt bên 3 3a
(SAD) vuông góc với mặt đáy. Biết thể tích khối chóp S.ABCD bằng
. Tính khoảng cách h từ D đến mặt 3 phẳng (SBC). 3a 3a
A. h a B. h C. h
D. h  2a 2 3
-----------------------------------------------
LUYỆN THI TRẦN ĐẠI
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Số 8, ngõ 462 đường Bưởi
Chuyên đề: Học kỳ I lớp 12 ĐIỂM Mã đề thi
Thời gian làm bài: 90 phút 09
(50 câu trắc nghiệm)
Họ và tên học sinh:………………………………………………..
Câu 1: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy, và SA a 2 .
Thể tích của khối chóp S.ABCD là: 3 a 2 3 a 2 3 a 2 A. 3 a 2 B. C. D. 3 6 12
Câu 2: Cho khối chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a; Khi đó côsin góc giữa mặt bên và mặt đáy là: 1 A. 60O B. 3 C. 30O D. 3
Câu 3: Cho log 20  a , giá trị của log 5 theo a là 2 20 1 a a a  2 1 a A. B. C. D. 1 a a 1 a a 1 Câu 4: Cho hàm số 4 2
y  x  8x  4 . Chọn phát biểu đúng trong các phát biểu sau
A. Tất cả đều sai
B. Hàm số có cực đại nhưng không có cực tiểu
C. Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt
D. Hàm số đạt cực tiểu tại x  0 2  x
Câu 5: Đường tiệm cận ngang của hàm số y  là 2x 1 1 1 A. x 1 B. y 1 C. x   D. y   2 2
Câu 6: Tập nghiệm của phương trình log  2 x x  log x  4  1 3  1   3
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại A. 1;  6 B. C. 2;  3 D.  2  ;  6 Câu 7: Hàm số 3 2
y  x  2x x  7 đồng biến trên  1   1   1  A.  ;  1;    B. ;    C. D. ;1    3   3   3 
Câu 8: Số cực trị của hàm số 3 2
y  x  3x  4x  2 là A. 0 B. 2 C. 3 D. 1   a   3 1 3 1
Câu 9: Rút gọn biểu thức là 2016 2017 2018 2016 a .a 1 1 A. B. 2 a C. D. a 2 a a 2x 1
Câu 10: Cho hàm số y
. Tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng 2 là x 1 1 1 1 1 1 1 A. y x B. y x C. y x 1 D. y x 3 3 3 3 3 3
Câu 11: Số điểm cực đại của hàm số 4
y  x  2016 là A. 0 B. 2 C. 1 D. 3 4 x Câu 12: Hàm số 2 y
 2x  2016 có giá trị cực đại là là 4 A. x  0 B. y  2016 C. x  2 D. y  2012 CD CD CD CD
Câu 13: Giá trị của log 3 2 A  4 là A. A  3 B. A  3 C. A  9 D. A  6
Câu 14: Cho tứ diện ABCD . Gọi B ',C ' lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối
tứ diện AB 'C ' D và khối tứ diện ABCD bằng 1 1 1 1 A. B. C. D. 2 4 8 6
Câu 15: Tập nghiệm của bất phương trình log  2x 1 3   6x  log
3.2x  4.3x x 1 là 2  1   2      2  A. log 3; B.  ;  log 3 C.  ;   3;    D. 3; 3  2  3  2   3  1 x
Câu 16: Cho hàm sô y
. Kết luận nào sau đây đúng? x 1
A. Hàm số luôn đồng biến trên từng khoảng xác định của nó.
B. Hàm số luôn nghịch biến trên
C. Hàm số luôn nghịch biến trên từng khoảng xác định của nó.
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
D. Hàm số nghịch biến trên khoảng  ;    1   1  ;
Câu 17: Cho tam giác ABC đều cạnh bằng 4 cm quay xung quanh đường cao AH tạo nên một hình nón.
Thể tích của hình nón đó là: 4 3 32 3 8 3 16 3 A.   3 cm B.   3 cm C.   3 cm D.   3 cm  3 3 3 3
Câu 18: Một hình trụ có bán kính r  2cm và chiều cao h  2 3 cm . Khi đó diện tích xung quanh của hình trụ là: A.   2 4 3 cm B.   2 8 3 cm C.   2 16 3 cm D.   2 2 3 cm
Câu 19: Cho hàm số f x 3 2  2
x  3x  3x và 0  a b. Khẳng định nào sau đây sai ?
A. Hàm số nghịch biến trên
B. f a  f b
C. f b  0
D. f a  f bx  2016
Câu 20: Số đường tiệm cận của hàm số y  là 2x 1 A. 3 B. 2 C. 0 D. 1 Câu 21: Hàm số 4 2
y x  2x  2 nghịch biến trên A.  ;    1 B.  1   ;1 C.  ;    1  0  ;1 D.  1  ;0 1; 1 Câu 22: Cho hàm số 3 2 y  
x  4x  5x 17 có hai cực trị x , x . Hỏi x .x là bao nhiêu ? 3 1 2 1 2 A. -8 B. 8 C. 5 D. -5
Câu 23: Cho tứ diện OABC với OA OB OC  1cm và O , A O ,
B OC đôi một vuông góc với nhau. Diện
tích mặt cầu ngoại tiếp tứ diện bằng 3  3 A. B. 3 C. D. 3 4 4
Câu 24: Cho một tấm nhôm hình vuông có cạnh bằng 12cm. Người ta cắt ở bốn góc hình vuông bằng nhau,
rồi gập tấm nhôm lại như hình vẽ để được cái hộp không nắp. Tính cạnh của hình vuông bị cắt sao cho thể
tích của khối hộp là lớn nhất. 12 x A. 2cm B. 3cm C. 4cm D. 1cm
Câu 25: Một hình trụ có hai đáy là hai hình tròn nội tiếp trong hai hình vuông ABCD và A’B’C’D’ của hình lập
phương cạnh bằng 2a. Thể tích của khối trụ đó là
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 2 4 A. 3 a B. 3 4a C. 3 a D. 3 2a  3 3 mx 1
Câu 26: Đồ thị hàm số y
(m là tham số) có dạng nào sau đây ? m x A. Hình 3 B. Hình 4 C. Hình 1 D. Hình 2 1 1
Câu 27: Với giá trị nào của m để hàm số 3 2 y x x
mx có hai cực trị x , x thỏa mãn 3 3 1 2
x x  2x x  0 1 2 1 2 4 A. m  3 B. m  2 C. m D. m  3  3
Câu 28: Với giá trị nào c ủ a m để hàm số 3
y x  2mx
1 đạt cực tiểu tại x 1
Hình (1) 2 Hình (2) 3 Hình (3) 3 Hình (4) 2 A. m   B. m   C. m D. m  3 2 2 3
Câu 29: Trong các hàm số bên dưới, hàm số nào có bảng biến thiên x  1  - - y ' y 2x  3 2x  3 x  3 x  3 A. y B. y C. y D. y  1 x x 1 x 1 1 x 1 Câu 30: Hàm số 3 2 y
x mx  1 2mx m  2 có cực đại và cực tiểu khi và chỉ khi 3 A. m  1 
B. Với mọi m
C. Không có giá trị m D. m  1  2
Câu 31: Số nghiệm của phương trình 2 x 7 x5 2016 1 là A. 2 B. 0 C. 3 D. 1 
Câu 32: Tìm tập xác định của hàm số y   x   5 3 1
A. D R
B. D    ;1
C. D R \   1
D. D  1;
Câu 33: Khẳng định nào sau đây là sai? 2016 2017 2016 2017 A. 2  3  2 3 B.  2   1   2   1
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 2016 2017 2016 2017 C. 3 2  3 2 D.  3   1   3   1
Câu 34: Trong các hàm số sau, hàm số nào có bảng biến thiên x  -1 0 1  y ' - 0 + 0 - 0 +   y -3 - 4 - 4 1 A. 4 2
y x  3x  3 B. 4 2 y   x  3x  3 C. 4 2
y x  2x  3 D. 4 2
y x  2x  3 4 a 3
Câu 35: Hình chóp S.ABC có SBC và ABC là tam giác đều cạnh a, SA
. Khi đó khoảng cách từ S 2
đến mặt phẳng  ABC  bằng 3 3 3 A. a B. a C. a D. a 4 2 3 Câu 36: Cho hàm số 3 2
y x  3x  4 có đồ thị (C). Tiếp tuyến của (C) song song với đường thẳng y  3
x  2017 có phương trình là A. y  3  x  2 B. y  3  x  5 C. y  3  x  4 D. y  3  x  3
Câu 37: Anh Hùng gửi số tiền 50 triệu đồng vào một ngân hàng với lãi suất 8,4%/năm. Biết rằng nếu anh
Hùng không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu. Hỏi
sau bao năm anh Hùng lĩnh được số tiền là 80 triệu đồng. A. 7 năm B. 5 năm C. 4 năm D. 6 năm
Câu 38: Trong các hàm số sau, hàm số nào chỉ có cực đại mà không có cực tiểu ? 2x 1 2 4x x  5 A. y B. y C. 4 2
y  x x  5 D. 3 2
y x  3x  6x 1 x x  2
Câu 39: Khối lăng trụ AB .
C A' B 'C ' có thể tích là V , Gọi I , J , K lần lượt là trung điểm của AA', BB ',CC ' .
Khi đó thể tích của khối tứ diện C ' IJK bằng 1 1 1 2 A. V B. V C. V D. V 6 4 5 5
Câu 40: Tập nghiệm của bất phương trình log x  log 2x 1 là 2016 2016    1  A. B.  ;0   C. 1;3 D.  ;    1  2 
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 41: Cho tứ diện OABC có O , A O ,
B OC đôi một vuông góc với nhau và OA  1,OB  3 và OC  4 . Độ
dài đường cao OH của hình chóp là 13 12 14 A. B. C. D. 7 12 13 13
Câu 42: Thể tích của khối cầu ngoại tiếp hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng 2 3 A. 36 B. 4 3 C. 32 3 D. 64 6
Câu 43: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với đáy. Góc giữa SB
và mặt đáy bằng 60O . Tính khoảng cách giữa AC và SB theo a a 2 a 15 a 7 A. 2a B. C. D. 2 5 7
Câu 44: Hàm số nào trong các hàm số bên dưới, có đồ thị hàm số như hình vẽ A. 3 2
y  x  3x  2 B. 3 2
y x  3x  2 C. 4 2
y  x  8x 1 D. 4 2
y x  2x  2
Câu 45: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với đáy và
AB  2, AC  4, SA  5 . Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính r bằng 5 10 25 A. B. C. D. 5 2 3 2 a 13
Câu 46: Cho hình lăng trụ ABC .
D A' B 'C ' D ' có đáy ABCD là hình vuông cạnh a, D ' D  . Hình chiếu 2
của D ' lên  ABCD là trung điểm H của AB . Thể tích khối lăng trụ là 3 2a 3 a 2 A. B. 3 a 12 C. D. 3 a 2 3 3 x 1
Câu 47: Giá trị nhỏ nhất của hàm số y  trên đoạn 3;  5 là x 1 3 A. 0 B. 1 C. 2 D. 2
Câu 48: Một hộp không nắp được làm từ một mảnh các tông theo hình mẫu. Hộp có đáy là một hình vuông
cạnh x(cm), chiều cao là h(cm) và có thể tích là 500cm3. Hãy tìm độ dài cạnh của hình vuông sao cho chiếc
hộp được làm ra tốn ít nhiên liệu nhất
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại h h x h x h A. 3cm B. 10cm C. 5cm D. 2cm 2x 1
Câu 49: Cho hàm số y
. Với giá trị nào của tham số a, b sao cho đường thẳng y ax b tiếp xúc x 1
với đồ thị (C) tại điểm có tung độ bằng 5.
A. a  3,b  1  1 B. a  3  ,b 11
C. a  11,b  3  D. a  1  1,b  3 a 3
Câu 50: Cho hình (H) là lăng trụ đứng tam giác đều cạnh đáy bằng a, cạnh bên bằng . Thể tích của (H) 3 bằng: 3 a 3 a 3 a 3 3 a 3 A. B. C. D. 4 12 4 12
LUYỆN THI TRẦN ĐẠI
ĐỀ ÔN THI HỌC KỲ I MÔN TOÁN
Số 8, ngõ 462 đường Bưởi
Chuyên đề: Học kỳ I lớp 12 ĐIỂM Mã đề thi
Thời gian làm bài: 90 phút 10
(50 câu trắc nghiệm)
Họ và tên học sinh:……………………………………………….. x  3 
Câu 1: Bất phương trình  0   có tập nghiệm là:  2  A. S B. S  
C. S  0;
D. S  0;
Câu 2: Tỉ lệ tăng dân số hàng năm ở Việt Nam được duy trì ở mức 1,05%. Theo số liệu của Tổng Cục Thống
Kê, dân số của Việt Nam năm 2014 là 90.728.900 người. Với tốc độ tăng dân số như thế thì vào năm 2030
thì dân số của Việt Nam là:
A. 106.118.331 người
B. 198.049.810 người
C. 107.232.574 người
D. 107.232.573 người  x 1 
Câu 3: Tập xác định của hàm số y  log   là: 2  3  2x
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 3  3   3  A. \   B. C. ;    D. 1  ;   2  2   2 
Câu 4: Đồ thị hàm số nào sau đây có đường tiệm cận ngang là y  2  2x 1 1 2x 2x A. y B. y  2  C. y D. y x 1 x x  3 2 x  2 x
Câu 5: Phương trình tiếp tuyến của  H  2 1 : y
tại giao điểm với trục hoành là: x  2
A. y  4x  2 B. y  0
C. 4x  5y  2  0 D. y  4  x  2
Câu 6: Độ giảm huyết áp của một bệnh nhân được đo bởi công thức G x 2
 0,025x 30 x  trong đó xmg
và x  0 là liều lượng thuốc cần tiêm cho bệnh nhân. Để huyết áp giảm nhiều nhất thì cần tiêm cho bệnh
nhân một liều lượng bằng: A. 40mg . B. 30mg . C. 15mg . D. 20mg .
Câu 7: Cho a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền của một tam giác vuông, trong đó
c b  1;c b  1. Khi đó khẳng định nào là đúng. A. log a log a  2log a log a B. log a log a  2log . a log a cb cb cb cb cb cb cb cb C. log a log a log . a log a D. log a log a  2log c b cb cb cb cb cb cb cb 3  Câu 8: Cho hàm số 4 y x
. Khẳng định nào sau đây sai? 7 3 
A. Hàm số nghịch biến trên
B. Hàm số có đạo hàm là 4
x x  0 4
C. Đồ thị hàm số có 2 đường tiệm cận
D. Đồ thị hàm số luôn đi qua A1;  1
Câu 9: Một hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh, thể tích của khối trụ tương ứng
bằng 16 . Khi đó bán kính mặt đáy của hình trụ bằng bao nhiêu ? A. 3 r  2 2 B. r  4 C. r  2 2 D. r  2
Câu 10: Xét hàm số y  4  3x trên đoạn  1  
;1 . Mệnh đề nào sau đây đúng?
A. Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn  1   ;1 .
B. Hàm số có cực trị trên khoảng  1   ;1 .
C. Hàm số đồng biến trên đoạn  1   ;1 .
D. Hàm số có giá trị nhỏ nhất bằng 1 khi x 1 , giá trị lớn nhất bằng 7 khi x  1  . 3 Câu 11: Cho hàm số 2
y x . Khẳng định nào sau đây đúng.
A. Đồ thị hàm số có 2 đường tiệm cận
B. Đồ thị hàm số luôn đi qua A(1;1) 3
C. Hàm số có đạo hàm là x
D. Hàm số đồng biến trên R 2
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 12: Cho hàm số y f x có bảng biến thiên sau: x 1 1 y ' 0 0 y 2 2
Đồ thị nào thể hiện hàm số y f x ? y y A B 2 4 x 1 2 -1 O x -2 -1 O 1 A. B. y C y x -1 1 D O 2 -2 x -1 -4 O 1 -2 C. D. Câu 13: Cho hàm số 3 2
y x bx cx d . y y y y x x x x (I) (II) (III) (IV)
Các đồ thị nào có thể là đồ thị biểu diễn hàm số đã cho? A. (III) và (IV). B. (II) và (IV) C. (I) D. (I) và (III)
Câu 14: Cho a  0 , a  1, x, y là 2 số dương. Tìm mệnh đề đúng:
A. log  x y  log x  log y B. log x y x y a  .  log log a a a a a
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại C. log  . x y  log . x log y D. log x y x y a   log .log a a a a a
Câu 15: Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng 500 3
m . Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là 500.000 3
đồng/m2. Hãy xác định kích thước của hồ nước sao cho chi phí thuê nhân công thấp nhất. Tính chi phí đó. A. 75 triệu đồng B. 74 triệu đồng C. 76 triệu đồng D. 77 triệu đồng
Câu 16: Cho lăng trụ đứng AB .
C A' B 'C ' . Gọi M là trung điểm A'C ' , I là giao điểm của AM và A'C . Khi đó
tỉ số thể tích của khối tứ diện IABC với khối lăng trụ đã cho là: 2 2 4 1 A. . B. . C. . D. . 3 9 9 2
Câu 17: Đạo hàm của hàm số y   x  3 2 2 1 là: 3x 3
A. x x  1 2 2 3 1 B. x  1 2 2 1
C. x  1 2 2 1 D. x  2 3 x   1 2 2
Câu 18: Kim tự tháp Kê-ốp ở Ai cập được xây dựng vào khoảng 2500 năm trước Công nguyên . Kim tự tháp
này là một tứ giác đều có chiều cao 147m , cạnh đáy dài 230 m. Khi đó thể tích của Kim tự tháp bằng: A. 2592100 m 3 B. 2592100 m 2 C. 7776300 m 3 D. 7776300 m 2 2 x x  2   2 
Câu 19: Tập nghiệm của bất phương trình       5   5  A. 2   x  1  B. 1 x  2 C. 1   x  2 D. x  2   x 1 1 Câu 20: Cho hàm số 4 2 y
x  2x 1. Hàm số có 4
A. Một điểm cực đại và không có điểm cực tiểu
B. Một điểm cực đại và hai điểm cực tiểu
C. Một điểm cực tiểu và hai điểm cực đại
D. Một điểm cực tiểu và một điểm cực đại
Câu 21: Cho hàm số y f x xác định, liên tục trên và có bảng biến thiên như sau:
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1  .
C. Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x 1 .
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
D. Hàm số có giá trị cực tiểu bằng 1. 3 x
Câu 22: Tọa độ tâm đối xứng của đồ thị hàm số 2 y
 2x  3x 1 là: 3  1   1  A. 1;   B. 0;   1 C. 3;  1  D. 2;     3   3 
Câu 23: Cho hàm số   2 2 .7 x x f x
. Khẳng định nào sau đây là khẳng định sai ?
A. f x 2
1  x x log 7  0 .
B. f x 2
1  x ln 2  x ln 7  0 . 2
C. f x 2
1  x log 2  x  0 .
D. f x  1  1 x log 7  0. 7 2
Câu 24: Trong các mệnh đề sau, mệnh đề nào sai.
A. Số cạnh của hình đa diện luôn lớn hơn hoặc bằng 6.
B. Số đỉnh hoặc số mặt của bất kỳ hình đa diện nào cũng lớn hơn hoặc bằng 4.
C. Tồn tại hình đa diện có số đỉnh và số mặt bằng nhau.
D. Tồn tại hình đa diện có số cạnh bằng số mặt.
Câu 25: Cho hình chóp S.ABCD. Gọi M, N, P, Q theo thứ tự là trung điểm của SA, SB, SC, SD. Tỉ số thể tích
của hai khối chóp S. MNPQ và S.ABCD bằng : 1 1 1 1 A. B. C. D. 2 4 16 8
Câu 26: Cho đồ thị của ba hàm số x  ; x  ; x y a y
b y c như hình vẽ. Khi đó
A. b a c
B. c b a
C. b c a
D. c a b
Câu 27: Cho a > 0, a  1. T×m mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau:
A. TËp gi¸ trÞ cña hµm sè y = ax lµ tËp R
B. TËp x¸c ®Þnh cña hµm sè y = ax lµ kho¶ng (0; +)
C. TËp x¸c ®Þnh cña hµm sè y = log x lµ tËp R a
D. TËp gi¸ trÞ cña hµm sè y = log x lµ tËp R a
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 28: Với giá trị nào của m thì hàm số y  sin 3x mcos x đạt cực tiểu tại điểm x  3 A. m  2  3 B. m  2 3 C. m  6 D. m  6  1 x
Câu 29: Cho hàm số y
có đồ thị C  . Chọn phát biểu đúng: x  2
A. Đồ thị C  có một điểm cực tiểu.
B. Đồ thị C  cắt trục hoành tại điểm có tọa độ 1;0 .
C. Đồ thị C  không có tâm đối xứng.
D. Đồ thị C  có một điểm cực đại.
Câu 30: Đồ thị hình bên là của hàm số nào? x x x  1   1  x
A. y   3 .
B. y    .
C. y    .
D. y   2 .  3   2 
Câu 31: Số nghiệm của phương trình 9x 2.3x  3  0 là: A. 1 B. 4 C. 3 D. 2 Câu 32: Cho hàm số 2 y x , xét các phát biểu sau:
I. Tập xác định D  0; .
II. Hàm số luôn đồng biến với mọi x thuộc tập xác định.
III. Hàm số luôn đi qua điểm M 1  ;1 .
IV. Hàm số không có tiệm cận.
Khi đó số phát biểu đúng là A. (I) B. (IV) C. (II) D. (III) x  3m 1
Câu 33: Với giá trị nào của tham số m thì hàm số y
nghịch biến trên (3; ) . x m
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 1 1 1 1 A. m  3 B. m  3 C. m  3 D. m  4 4 4 4
Câu 34: Phương trình tiếp tuyến của đường cong C 3
: y x  2x  3 tại điểm M 1; 2 là:
A. y  3x 1 .
B. y  2  x .
C. y  2x  2 .
D. y x 1.
Câu 35: Hàm số nào sau đây có đồ thị như hình vẽ: A. 3 2
y x  3x  3x B. 3 2
y  x  3x  3x 1 C. 3 2 y  2
x  3x  3x D. 3 2
y  x  3x  3x
Câu 36: Một người vay ngân hàng với số tiền 20 triệu đồng, mỗi tháng trả góp cho ngân hàng 300.000 đồng
và phải chịu lãi suất kép của số tiền chưa trả là 0,4%/tháng. Hỏi sau bao nhiêu tháng người đó trả hết nợ ? A. 78 B. 79 C. 80 D. 81
Câu 37: Những hình nào không phải là khối đa diện là: H1 H2 H3 H4 H5 A. H1 và H2 B. H2 và H4 C. H1 và H3 D. H3 và H5 Câu 38: Hàm số 4
y mx  m   2
3 x  2m 1 chỉ có cực đại mà không có cực tiểu với m:
A. m  0  m  3 B. m  3 C. 3   m  0 D. m  3  Câu 39: Hàm số 4 2
y x x  4 đồng biến trên: A. . B. 0;  C.  ;  0 D.  1   ;1
Câu 40: Cho lăng trụ đứng ABC.A’B’C’có tất cả các cạnh đều bằng a ; Thể tích của khối tứ diện A’.ABC bằng: 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 12 6 24 36
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại
Câu 41: Cho hình chóp S.ABCD đáy là hình thoi với AC=2BD=2a và tam giác SAD vuông cân tại S nằm trong
mp vuông góc với đáy.Thể tích khối chóp là: 3 3a 3 15a 3 5a 3 5a A. B. C. D. 12 24 12 4 x x
Câu 42: Phương trình 2  3  2  3  m có nghiệm khi:
A. m 2;
B. m 2;
C. m  ;5  
D. m  ;5   2x
Câu 43: §Ó gi¶i bÊt ph¬ng tr×nh: ln
> 0 (*), mét häc sinh lËp luËn qua ba bíc nh sau: x 1 2xx  0 Bíc1: §iÒu kiÖn:  0   (1) x 1 x 1 2x 2x 2x Bíc2: Ta cã ln > 0  ln > ln1  1 (2) x 1 x 1 x 1
Bíc3: (2)  2x > x - 1  x > -1 (3)  1   x  0
KÕt hîp (3) vµ (1) ta ®îc  x 1
VËy tËp nghiÖm cña bÊt ph¬ng tr×nh lµ: (-1; 0)  (1; +)
Hái lËp luËn trªn ®óng hay sai? NÕu sai th× sai tõ bíc nµo? A. Sai tõ bíc 1 B. Sai tõ bíc 3 C. Sai tõ bíc 2
D. LËp luËn hoµn toµn ®óng
Câu 44: Trong không gian, cho hình chữ nhật ABCD có AB  1 và AD  2 . Gọi M , N lần lượt là trung điểm
của AD và BC . Quay hình chữ nhật đó xung quanh trục MN , ta được một hình trụ. Diện tích toàn phần của hình trụ bằng: A. 4 . B. 3 . C. 2 . D. 8 .
Câu 45: Diện tích xung quanh của hình trụ có đáy là đường tròn ngoại tiếp hình vuông có cạnh bằng 4 và đường sinh l = 8 là :. A. 32 B. 32 2 C. 32 2 D. 32 2
Câu 46: Cắt hình trụ có bán kính r = 5 và chiều cao h  5 3 bởi một mặt phẳng song song với trục và cách
trục 3cm. Hãy tính diện tích của thiết diện được tạo nên A. 3 100 3 cm B. 3 20 3cm C. 2 80 3 cm D. 2 40 3 cm
Câu 47: Tính đạo hàm của hàm số : 3x y  3x A. y B. ' 13x y C. ' 3 . x y  ln 3 D. 1 ' .13x y x   ln 3
Câu 48: Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a; Tính thể tích khối chóp đều đó.
GV: Trần Đại Tel, Zalo, Facebook: 0979877188
Bộ đề ôn thi học kỳ I – Luyện thi Trần Đại 3 a 2 3 a 2 3 a 3 3 a 3 A. B. C. D. 4 6 12 3 1 V
Câu 49: Cho hình chóp S.ABCD, M là điểm trên SA mà SM= SA. Khi đó tỉ số SMBD bằng: 3 VSABD 1 1 A. B. 3 C. D. 2 2 3
Câu 50: Hàm số nào sau đây đồng biến trên tập xác định của nó? xx 2  xe A. x y  0, 5
B. y   
C. y   2
D. y     e    
-----------------------------------------------
GV: Trần Đại Tel, Zalo, Facebook: 0979877188