TOP 10 đề tuyển sinh toán 10 năm 2020 tập 4 (có lời giải)

Tổng hợp TOP 10 đề tuyển sinh toán 10 năm 2020 tập 4 (có lời giải) rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.

112 56 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Trang 1

SỞ GIÁO DỤC VÀ ĐÀO TẠO

LONG AN

ĐỀ CHÍNH THỨC

(Đề thi gồm có 01 trang)

ĐỀ THI TUYỂN SINH 10 NĂM HỌC 2019 - 2020

Môn thi: TOÁN (Công Lập)

Ngày Thi: 05 – 06 - 2019

Thời gian:120 phút (không kể thời gian phát đề)

Câu 1: (2,0 điểm)

1. Rút gọn các biểu thức:

9 45 3 5K   

2. Rút gọn các biểu thức:

x x x







(với

0x 

)

3. Giải phương trình:

4 4 3xx  

Câu 2: (2,0 điểm)

Trong mặt phẳng tọa độ

Oxy

,cho Parabol

 

2P : y x

và đường thẳng

 

24d : y x

1.Vẽ Parabol

 

và đường thẳng

 

trên cùng một mặt phẳng tọa độ

Oxy

2.Tìm tọa độ giao điểm của Parabol

 

và đường thẳng

 

bằng phép tính.

3.Viết phương trình đường thẳng

 

d' : y ax b

. Biết rằng

 

song song với

 

và

 

và

đi qua điểm

 

23N;

Câu 3: (2,0 điểm)

1.Giải phương trình:

7 10 0xx  

(không giải trực tiếp bằng máy tính cầm tay)

2.Giải hệ phương trình:











(không giảitrực tiếp bằng máy tính cầm tay)

3.Cho phương trình (ẩn

)

60x x m  

a)Tìm giá trị

để phương trình có hai nghiệm phân biệt

x ,x

b)Tìm giá trị

để phương trình có hai nghiệm phân biệt

x ,x

thỏa mãn điều kiện

12xx

Câu 4: (4,0 điểm)

1. Cho tam giác

ABC

vuông tại

có đường cao

, biết

5AB cm ;

3BH cm

. Tính

AH,AC

và

sinCAH

2.Cho đường tròn

 

O,R

, đường kính

. Kẻ tiếp tuyến

với đường tròn

 

O,R

và lấy

trên tiếp tuyến đó điểm

sao cho

AP R

, từ

kẻ tiếp tuyến thứ hai tiếp xúc với đường tròn

 

O,R

tại

a) Chứng minh tứ giác

APMO

nội tiếp được đường tròn.

b) Chứng minh

song song

c) Biết đường thẳng vuông góc với

tại

cắt

tại

cắt

tại

cắt

tại

cắt

tại

. Chứng minh ba điểm

K,I,J

thẳng hàng.

----HẾT----

Giám thị không giải thích gì thêm

Họ và tên thí sinh ---------------------------------- Số báo danh:-------------------------

Chữ kí giám thị 1:---------------------------------- Chữ kí giám thị 2:------------------

Trang 2

LỜI GIẢI

1. Rút gọn các biểu thức:

9 45 3 5K   

2. Rút gọn các biểu thức:

x x x







(với

0x 

)

3. Giải phương trình:

4 4 3xx  

Lời giải

9 45 3 5 3 3 5 3 5 3K       

     

2 2 2

x . x x x

x x x

Q x x x

x x x x

  



        



4 4 3xx  

  

4 4 9

4 5 0

1 5 0

   

   

   













Vy

 

S 1; 5

Câu 1:

Trong mặt phẳng tọa độ

Oxy

,cho Parabol

 

2P : y x

và đường thẳng

 

24d : y x

1.Vẽ Parabol

 

và đường thẳng

 

trên cùng một mặt phẳng tọa độ

Oxy

2.Tìm tọa độ giao điểm của Parabol

 

và đường thẳng

 

bằng phép tính.

3.Viết phương trình đường thẳng

 

d' : y ax b

. Biết rằng

 

song song với

 

và

 

và

đi qua điểm

 

23N;

Lời giải

1. Học sinh t vẽ hình.

2. Phương trình hoành độ giao điểm là

   



          



  



2 2 2

x 1 y 2

2x 2x 4 2x 2x 4 0 x x 2 0

x 2 y 8

Vy tọa độ giao điểm là

   

1;2 , 2;8

3. Vì

 

song song với

 

nên











Vì

 

và đi qua điểm

 

23N;

nên











Thay vào

 

ta có

3 2.2 1bb    

(TMĐK

4b 

Vy phương trình

 

' : 2 1.d y x

Câu 2:

1.Giải phương trình:

7 10 0xx  

(không giải trực tiếp bằng máy tính cầm tay)

Trang 3

2.Giải hệ phương trình:











(không giảitrực tiếp bằng máy tính cầm tay)

3.Cho phương trình (ẩn

)

60x x m  

a)Tìm giá trị

để phương trình có hai nghiệm phân biệt

x ,x

b)Tìm giá trị

để phương trình có hai nghiệm phân biệt

x ,x

thỏa mãn điều kiện

12xx

Lời giải

  

x 7x 10 0

Ta có

 

4 7 4 1 10 9 0b ac . .       

Phương trình có hai nghiệm phân biệt:

    

  

    

  

2 5 3 6 2

1 1 1

x y x x

x y y x y

   

  



  

     

  

Vy

(x;y) (2; 1)

60x x m  

    

' b' ac 9 m

Để phương trình có 2 nghiệm phân biệt thì

      ' 0 9 m 0 m 9

b)p dng Viet ta có











x x 6

x x m

  

 

     

     

   

    

1 2 1 2 1 2

1 2 1 2

x x 12 x x x x 12

x x 2 x x 4

x x 4x x 4

36 4m 4 m 8(tm)

Vy

m8

Câu 3:

1. Cho tam giác

ABC

vuông tại

có đường cao

, biết

5AB cm ;

3BH cm

. Tính

AH,AC

và

sinCAH

2.Cho đường tròn

 

O,R

, đường kính

. Kẻ tiếp tuyến

với đường tròn

 

O,R

và lấy

trên tiếp tuyến đó điểm

sao cho

AP R

, từ

kẻ tiếp tuyến thứ hai tiếp xúc với đường tròn

 

O,R

tại

a) Chứng minh tứ giác

APMO

nội tiếp được đường tròn.

b) Chứng minh

song song

c) Biết đường thẳng vuông góc với

tại

cắt

tại

cắt

tại

cắt

tại

cắt

tại

. Chứng minh ba điểm

K,I,J

thẳng hàng.

Lời giải

Trang 4

p dng Pitago vào tam giác vuông

ABH

2 2 2

2 2 2 2 2

5 3 16 4

AB AH BH

AH AB BH AH (cm)



       

    

BH.BC AB BH.13 5 BH (cm)

p dng hệ thức lượng vào tam giác vuông

ABC

 

AH BH.CH CH cm

   

Do đó

 

16 25

BC BH CH cm    

p dng Pitago vào tam giác vuông

ABC

16 25 400

3 3 9

AC CH.BC

AC cm )

   



16 20 4

3 3 5

sinCAH

  

a)Xét tứ giác

APMO

có

    

0 0 0

PAO PMO 90 90 180 APMO

nội tiếp đường tròn đường kính

b) Chứng minh

BM // OP

BM AM

(góc nội tiếp chắn nửa đườn

tròn) (1)

PA,PM

là hai tiếp tuyến xuất phát từ

P PO AM

(2)

Từ (1),(2)

BM // OP

c) Tam giác

ANB

có

là đường cao

đồng thời là đường trung tuyến nên

ANB



cân tại

suy ra

cũng là phân giác

hay

ANO ONB

Lại có

ANO PAN

(so le trong,

PA // NO

)

ONB NOP

(so le trong,

PO // BM

)

Suy ra

ANO ONB

PNOA

nội tiếp

đường tròn đường kính

90PNO PAON  

là hình chữ nht.

K

là trung điểm

và

3cm

5cm

Trang 5

Ta có

JOP

có

ON,PM

là các đường cao cắt nhau tại

I

là trc tâm

JOP



 

3JI OP

Mặt khác

PNMO

là hình thang nội tiếp đường tròn đường kính

PNMO

là hình thang cân

NPO MOP

hay

JPO JOP

Do đó

JPO



cân tại

có

là trung tuyến

JK

cũng là đường cao

 

4JK OP

Từ

   

34, K,I,J

thẳng hàng.

SỞ GIÁO DỤC VÀ ĐÀO TẠO

NAM ĐỊNH

ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT

NĂM HỌC 2019 – 2020

Môn thi: TOÁN

Thời gian làm bài: 120 phút

Phần 1: Trắc nghiệm (2,0 điểm)

Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm

Câu 1. Tìm tất cả các giá trị của m để hàm số y = (1 – m)x + m + 1 đồng biến trên R

A. m > 1 B. m < 1 C. m < -1 D. m > -1

Câu 2. Phương trình

x 2x 1 0  

có 2 nghiệm

x ; x

. Tính

xx

x x 2

x x 1

x x 2  

x x 1  

Câu 3. Cho điểm M(x

; y

) thuộc đồ thị hàm số y = -3x

. Biết x

= - 2. Tính y

A. y

= 6 B. y

= -6 C. y

= -12 D. y

= 12

Câu 4. Hệ phương trình

x y 2

3x y 1











có bao nhiêu nghiệm ?

A. 0 B. 1 C. 2 D. Vô số

Câu 5. Với các số a, b thoả mãn a < 0, b < 0 thì biểu thức

a ab

bằng

ab

Câu 6. Cho ∆ABC vuông tại A có AB = 3cm, AC = 4cm. Tính độ dài đường cao AH của ∆ABC

AH cm



AH cm



AH cm



AH cm



Câu 7. Cho đường tròn (O; 2cm) và (O’; 3cm). biết OO’ = 6cm. Số tiếp tuyến chung của 2 đường tròn là

A. 1 B. 2 C. 3 D. 4

Câu 8. Một quả bóng hình cầu có đường kính 4cm. Thể tích quả bóng là

cm

256

cm

256

Phần 2: Tự luận (8,0 điểm)

Câu 1. (1,5 điểm)

1) Rút gọn biểu thức

A 3 2 2 3 2 2   

2) Chứng minh rằng

 

2 1 6

. a 3 1

a 3 a 3



   









Với

0, 9aa

Câu 2. (1,5 điểm) Cho phương trình x

– (m – 2)x - 6 = 0 (1) (với m là tham số)

1) Giải phương trình (1) với m = 0

2) Chứng minh rằng với mọi giá trị của m phương trình luôn có 2 nghiệm phân biệt

3) Gọi x

, x

là 2 nghiệm của phương trình . Tìm các giá trị của m để

2 1 2 1

x x x (m 2)x 16   

ĐỀ CHÍNH THỨC

Trang 6

Câu 3. (1,0 điểm) Giải hệ phương trình

x xy y 7 0

x xy 2y 4(x 1)



   





   





Câu 4. (2,5 điểm) Qua điểm A năm ngoài đường tròn (O) vẽ 2 tiếp tuyến AB, AC của đường tròn (B, C là

các tiếp điểm. Gọi E là trung điểm của đoạn AC, F là giao điểm thứ hai của EB với (O)

1) Chứng minh tứ giác ABOC là tứ giác nội tiếp và ∆CEF  ∆BEC

2) Gọi K là giao điểm thứ hai của AF với đường tròn (O). Chứng minh BF.CK = BK.CF

3) Chứng minh AE là tiếp tuyến của đường tròn ngoại tiếp ∆ABF

Câu 5. (1,5 điểm) Xét các số x, y, z thay đổi thoả mãn x

+ y

+ z

– 3xyz = 2.

Tìm giá trị nhỏ nhất của biểu thức

2 2 2 2

P (x y z) 4(x y z xy yz zx)

        

----------------------------Hết----------------------------

HƯỚNG DẪN GIẢI ĐỀ THI VÀO 10 TỈNH NAM ĐỊNH 2019 -2020

I/ Trắc nghiệm

Câu

Đáp án

II/ Tự luận

Câu 1:

A 3 2 2 3 2 2 2 2. 2.1 1 2 2. 2.1 1         

( 2 1) ( 2 1) 2 1 2 1

2 1 2 1 2

       

     

2) Với

0, 9aa

Ta có:

   

2 1 6 2( a 3) ( a 3) 6

VT . a 3 . a 3

a 3 a 3 ( a 3)

2 a 6 a 3 6 a 3

1 VP

a 3 a 3



   



     





  



    

   



Vy

 

2 1 6

. a 3 1

a 3 a 3



   









Với

0, 9aa

Câu 2:

1/ Với m = 0 ta có phương trình:

x 1 7

x 2x 6 0

x 1 7



  

  



  







Vy khi m =0 phương trình có hai nghiệm phân biệt

x 1 7  

và

x 1 7  

2/ Ta có

(m 2) 4.1.( 6) (m 2) 24 0        

với mọi m.

Vy phương trình luôn có hai nghiệm phân biẹt với mọi m.

3) Phương trình luôn có hai nghiệm phân biẹt với mọi m.

Theo Vi-ét ta có:

x x m 2

x x 6

  









Ta có :

2 1 2 1

x x x (m 2)x 16   

Trang 7

2 2 2

2 1 2 1 2 1 2 1 2 1 1 2

1 2 1 2

x x x (x x )x 16 x x x x x x 16

(x x ) 2x x 16 0 (m 2) 2.( 6) 16 0

m 2 2 m 4

(m 2) 4

m 2 2 m 0

         

          

  



    



   



Vy khi m = 0, m = 4 thì phương trình có 2 nghiệm phân biệt thỏa mãn:

2 1 2 1

x x x (m 2)x 16   

Câu 3:

x xy y 7 0 (1)

x xy 2y 4(x 1) (2)



   





   





Ta có:

(2) x xy 2y 4x 4 0     

(x 4x 4) xy 2y 0

(x 2) y(x 2) 0

     

    

x 2 0 x 2

(x 2)(x 2 y) 0

x 2 y 0 x 2 y

  



      



    



+ Thay x = 2 vào phương trình (1) ta được: 4 – 2y + y – 7 = 0  y = -3

+ Thay x = 2 – y vào phương trình (1) ta được :

(2 y) (2 y)y y 7 0

4 4y y 2y y y 7 0

2y 5y 3 0

     

       

   

Phương trình

2y 5y 3 0  

có

( 5) 4.2.( 3) 49 0, 7        

Ta có:

5 7 5 7 1

y 3;y

4 4 2



    

y 3 x 2 3 1

1 1 5

y x 2

2 2 2

      

      

Vy hệ phương trình có nghiệm (x; y)

( 1; 3), (2; 3), ;





   









Bài 4:

1) Chứng minh tứ giác ABOC là tứ giác nội tiếp và ∆CEF  ∆BEC

Có AB, AC là các tiếp tuyến của đường tròn (O) , B và C là ác tiếp điểm

AB OB, AC OC ABO 90 , ACO 90    

Tứ giác ABOC có

0 0 0

ABO ACO 90 90 180   

nên tứ giác ABOC nội tiếp đường tròn

+ Đường tròn (O) có:

EBC

là góc nội tiếp chắn cung CF

Trang 8

ECF

là góc tạo bởi tia tiếp tuyến AC và dây cung CF

EBC ECF

(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung CF)

Xét ∆CEF và ∆BEC có

BEC

là góc chung

EBC ECF

(chứng minh trên)

 ∆CEF  ∆BEC (g . g)

2) Chứng minh BF.CK = BK.CF

Xét ∆ABF và ∆AKB có

BAK

là góc chung

ABF AKB

(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BF)

 ∆ABF  ∆AKB (g . g)

BF AF

(1)

BK AB



Chứng minh tương t ta có:

∆ACF  ∆AKC (g . g) 

CF AF

(2)

CK AC



Mà AB = AC (t/c 2 tiếp tuyến cắt nhau của (O)) (3)

Từ (1), (2) và (3) 

BF CF

BF.CK BK.CF

BK CK

   

3) Chứng minh AE là tiếp tuyến của đường tròn ngoại tiếp ∆ABF

Có ∆ECF  ∆EBC (Chứng minh câu a)

EC EF

EC EB.EF

EB EC

   

Mà EC = EA (gt)

EA EF

EA EB.EF

EB EA

   

Xét ∆BEA  ∆AEF có:

EA EF

EB EA



AEB

là góc chung

 ∆BEA  ∆AEF (c.g.c)

EAF EBA

( hai góc tương ứng) hay

EAF ABF

Trên nửa mặt phẳng bờ AB có chưa điểm E, kẻ tia Ax là tiếp tuyến của đường tròn ngoại tiếp

ABF

EAF xAF

(Cùng bằng

ABF

)  tia AE trùng với tia Ax

 AE là tiếp tuyến của đường tròn ngoại tiếp ∆ABF

Câu 5:

Ta có:

x³ + y³ + z³ - 3xyz = (x + y)³ - 3xy(x - y) + z³ - 3xyz = 2

 [(x + y)³ + z³] - 3xy(x + y +z ) = 2

 (x + y + z)³ - 3z(x + y)(x + y + z) - 3xy(x – y - z) = 2

 (x + y + z)[(x + y + z)² - 3z(x + y) - 3xy] = 2

 (x + y + z)(x² + y² + z² + 2xy + 2xz + 2yz - 3xz - 3yz - 3xy) = 2

 (x + y + z)(x² + y² + z² - xy - xz - yz) = 2

 x² + y² + z² - xy - xz – yz ≠ 0

Chứng minh: x² + y² + z² - xy - xz – yz ≥ 0 với mọi x, y, z

 x² + y² + z² - xy - xz – yz > 0  x + y + z

Đặt x + y + z = t (t > 0)  x² + y² + z² - xy - xz – yz



khi đó ta có

Trang 9

2 2 2 2

1 t 8 t 8

P (x y z) 4(x y z xy yz zx) 2 2

2 2 t 2 t



              





p dng BĐT Cô si ta có:

2 2 .2 2t

  

(dấu bằng xảy ra  t = 2)

2t 2 2t. 8

  

(dấu bằng xảy ra  t = 2)

 P ≥ 8 – 2 = 6. Tồn tại x = y = 1, z = 0 thì P = 6

Vy giá trị nhỏ nhất của P là 6

ĐỀ THI TUYỂN SINH VÀO LỚP 10 TỈNH NGHỆ AN NĂM HỌC 2019 - 2020

Câu 1: (2 điểm) Rút gọn biểu thức sau:

 

12 2 5 3 60.A   

4 6 9

x x x







với 0 < x < 3.

Câu 2: (2,5 điểm)

1) Xác định hàm số bc nhất y = ax + b, biết rằng đồ thị hàm số đi qua điểm M(1; -1) và N(2; 1).

2) Cho phương trình:

2 3 0    x mx m m

(1), với m là tham số.

a) Giải phương trình (1) với m = 4.

b) Tìm các giá trị của m để phương trình (1) có hai nghiệm

,xx

và biểu thức:

1 2 1 2

P x x x x  

đạt giá trị nhỏ nhất.

Câu 3: (1,5 điểm)

Tình cảm gia đình có sức mạnh phi trường. Bạn Vì Quyết Chiến - Cu bé 13 tuổi qua

thương nhớ em trai của mình đã vượt qua một quãng đường dài 180km từ Sơn La đến bệnh viện

Nhi Trung ương Hà Nội để thăm em. Sau khi đi bằng xe đạp 7 giờ, bạn ấy được lên xe khách và

đi tiếp 1 giờ 30 phút nữa thì đến nơi. Biết vn tốc của xe khách lớn hơn vn tốc của xe đạp là

35km/h. Tính vn tốc xe đạp của bạn Chiến.

Câu 4: (3,0 điểm)

Cho đường tròn (O) có hai đường kính AB và MN vuông góc với nhau. Trên tia đối của tia

MA lấy điểm C khác điểm M. Kẻ MH vuông góc với BC (H thuộc BC).

a) Chứng minh BOMH là tứ giác nội tiếp.

b) MB cắt OH tại E. Chứng minh ME.MH = BE.HC.

c) Gọi giao điểm của đường tròn (O) với đường tròn ngoại tiếp ∆MHC là K. Chứng minh 3

điểm C, K, E thẳng hàng.

Câu 5: (1,0 điểm) Giải phương trình:

5 27 25 5 1 4.x x x x     

HƯỚNG DẪN LÀM BÀI

Câu 1:

 

12 2 5 3 60 36 2 15 2 15 36 6A        

b) Với 0 < x < 3 thì

33xx  

   

 

3 2 3

4 6 9 2 2

. . . 2

3 3 3

x x x

x x x x x

x x x



  

  

     

  



Câu 2:

1) Vì đồ thị hàm số đi qua điểm M(1; -1) nên

1ab  

đồ thị hàm số đi qua điểm N(2; 1) nên

21ab

Trang 10

Yêu cầu bài toán



2 1 3

a b a

a b b

   







   



Vy hàm số phải tìm là y = 2x - 3.

2) a) Với m = 4, phương trình (1) trở thành:

8 15 0xx  

. Có

10  

Phương trình có hai nghệm phân biệt

3; 5;xx

b) Ta có: ∆' =

 

2 2 2

1. 3 3 3m m m m m m m         

Phương trình (1) có hai nghiệm

,xx

khi ∆'



3 0 3mm    

Với

3m

, theo định lí Vi-ét ta có:

x x m

x x m m







  



Theo bài ra:

1 2 1 2 1 2 1 2

()P x x x x x x x x     

p đng định lí Vi-ét ta được:

3 2 3 3 ( 3) 3P m m m m m m m         

Vì

3m

nên

( 3) 0mm

, suy ra

3P 

. Dấu " = " xảy ra khi m = 3.

Vy giá trị nhỏ nhất của P là 3 khi m = 3.

Bài 3:

Đổi 1 giờ 30 phút = 1,5 giờ.

Gọi vn tốc xe đạp của bạn Chiến là

(km/h,

0x 

)

Vn tốc của ô tô là

35x 

(km/h)

Quãng đường bạn Chiến đi bằng xe đạp là:

(km)

Quãng đường bạn Chiến đi bằng ô tô là:

1,5( 35)x 

(km)

Do tổng quãng đường bạn Chiến đi là 180km nên ta có phương trình:

7 1,5( 35) 180xx  

7 1,5 52,2 180 8,5 127,5 15x x x x       

(thỏa mãn)

Vy bạn Chiến đi bằng xe đạp với vn tốc là 15 km/h.

Bài 4:

a) Ta có:

90MOB 

(do AB



MN) và

90MHB 

(do MH



BC)

Suy ra:

0 0 0

90 90 180MOB MHB   



Tứ giác BOMH nội tiếp.

b) ∆OMB vuông cân tại O nên

OBM OMB

(1)

Tứ giác BOMH nội tiếp nên

OBM OHM

(cùng chắn cung OM)

và

OMB OHB

(cùng chắn cung OB) (2)

Từ (1) và (2) suy ra:

OHM OHB



HO là tia phân giác của

MHB

ME MH

BE HB



(3)

p dng hệ thức lượng trong ∆BMC vuông tại M có MH là

đường cao ta có:

HM HC

HM HC HB

HB HM

  

(4)

Từ (3) và (4) suy ra:

 

5 . .

ME HC

ME HM BE HC

BE HM

  

(đpcm)

c) Vì

90MHC 

(do MH



BC) nên đường tròn ngoại tiếp ∆MHC có đường kính là MC

90MKC

(góc nội tiếp chắn nửa đường tròn)

MN là đường kính của đường tròn (O) nên

90MKN 

(góc nội tiếp chắn nửa đường tròn)

180MKC MKN  



3 điểm C, K, N thẳng hàng (*)

∆MHC  ∆BMC (g.g)

HC MC

MH BM



. Mà MB = BN (do ∆MBN cân tại B)

Trang 11



HC MC

HM BN



, kết hợp với

ME HC

BE HM



(theo (5) )

Suy ra:

MC ME

BN BE



. Mà

90EBN EMC



∆MCE  ∆BNE (c.g.c)

MEC BEN

, mà

180MEC BEC

(do 3 điểm M, E, B thẳng hàng)

180BEC BEN  



3 điểm C, E, N thẳng hàng (**)

Từ (*) và (**) suy ra 4 điểm C, K, E, N thẳng hàng



3 điểm C, K, E thẳng hàng (đpcm)

Câu 5: ĐKXĐ:

2x 

Ta có:

2 2 2

5 27 25 5 1 4

5 27 25 4 25 25 10 ( 1)( 4)

4 2 4 10 1)(x 4)

2 2 5 ( 1)( 4) (1)

x x x x

x x x x x x

x x x

x x x x

     

      

         

    

     

Cách 1:

(1)

  

2 4 4 13 26 0x x x x     

Giải ra được:

15x 

(loại);

15x 

(nhn);

13 3 65





(nhn);

13 3 65





(loại)

Cách 2:

(1)

 

5 2 2 2 2 3 2x x x x x x        

(2)

Đặt

2; 2 ( 0; 0)a x x b x a b      

Lúc đó, phương trình (2) trở thành:

5 2 3ab a b

  





        







2 5 3 0 2 3 0

a ab b a b a b

(*)

- Với a = b thì

1 5( )

2 2 2 4

1 5( )

x ktm

x x x x x

x tm





       









- Với 2a = 3b thì

13 3 65

()

2 2 3 2 4 13 26 0

13 3 65

()

x tm

x x x x x

x ktm









        











Vy phương trình đã cho có hai nghiệm:

15x 

và

13 3 65





TUYỂN SINH VÀO 10 NINH BÌNH NĂM HỌC 2019-2020

Câu 1: a) Rút gọn biêu thức

2 18A 

b) Giải hệ phương trình

2 3.











c) Tìm tọa độ giao điểm của hai đường thẳng

   

: 3 và : 2 3d y x d y x    

Trang 12

Câu 2: 1. Rút gọn biểu thức

  





(với

0, 9xx

2. Cho phương trình

 

5 2 0 1x x m   

với

là tham số.

a) Giải phương trình (1) khi

6m 

b) Tìm tất cả các giá trị của

để phương trình (1) có hai nghiệm

, xx

sao cho biểu thức

 

1 2 1 2

8S x x x x  

đạt giá trịNINH lớn nhất.

Câu 3: Bác Bình gửi tiết kiệm

100

triệu đồng vào ngân hàng A, kì hạn một năm. Cùng ngày, bác

gửi tiết kiệm 150 triệu đồng vào ngân hàng B, kì hạn một năm, với lãi suất cao hơn lãi suất

của ngân hàng A là 1% / năm. Biết sau đúng 1 năm kể từ ngày gửi tiền. Bác Bình nhn được

tổng sổ tiền lãi là

16.5

triệu đồng từ hai khoản tiền gửi tiết kiệm nêu trên. Hỏi lãi suất tiền

gửi tiết kiệm kì hạn một năm của ngân hàng A là bao nhiêu phần trăm?

Câu 4: 1. Cho đờng tròn tâm

một điểm

nằm ngoài đường tròn. Từ

kẻ đường thẳng đi

qua tâm

, cắt đường tròn tại hai điểm

, AB

(

nằm giữa

và

). Kẻ đường thẳng thứ

hai đi qua

, cắt đường tròn tại hai điểm phân biệt

, CD

(

nằm giữa

và

khác

). Đường thẳng vuông góc với

tại

cắt đường thẳng

tại

, đường thẳng

cắt đường tròn tại điểm thứ hai là

a. Chứng minh tứ giác

AMNC

là tứ giác nội tiếp.

b. Chứng minh

vuông góc với

2. Trên một khúc sông với 2 bờ song song với nhau, có một chiếc đò d định chèo qua sông

từ vị trí

ở bở bên này sang vị trí

ở bờ bên kia, đường thẳng

vuông góc với các bờ

sông. Do bị dòng nước đẩy xiên nên chiếc đò đã cp bờ bên kia tại vị tri

cách

mội

khoảng bằng 30 m. Biết khúc sông rộng

150

m, hỏi dòng nước đã đẩy chiếc đò lệch đi một

góc có số đo bằng bao nhiêu? (kết quả làm tròn đến giây).

Câu 5: 1. Tìm tất cả các số nguyên tố

sao cho tổng các ước nguyên dương của

là một số

chính phương.

2. Cho

, , x y z

là các số thc dương thỏa mãn

2019x y z  

. Tìm giá trị nhỏ nhất của

biểu thức

2 2 2

x y z

x yz y zx z xy

  

  

LỜI GIẢI

Câu 1

2 18 2 2.3 2 3 2 4 2      A

3 2 5 5 1 1

2 3 2 3 2.1 3 1

    

   

  

   

       

   

x y x x x

x y x y y y

Vy hệ phương trình có nghiệm duy nhất là

( ) ( )

; 1; 1xy =-

c) Tọa độ giao điểm của hai đường thằng

   

: 3 và : 2 3d y x d y x    

là nghiệm của hệ

phương trình

3 3 3

2 3 3 2

132

     

       



   

  

   



   

y x y x y x

y x x

yxx

Vy tọa độ giao điểm của hai đường thằng

   

: 3 và : 2 3d y x d y x    

là

( ) ( )

; 2; 1xy =-

Câu 2

  





Trang 13

 

  

 

     

  

3 3 3

3 3 3 3 3 3

3 3 9 6

3 3 3 3



  

     

   









   

x x x

x x x x x x

x x x x

Vy

1P

2. Cho phương trình

 

5 2 0 1x x m   

a) Khi

6m 

phương trình (1) trở thành

5 4 0   xx

có

1 5 4 0     a b c

nên có hai

nghiệm là

1; 4     

Vy, khi

6m 

thì tp nghiệm của phương trình đã cho là

 

4; 1  S

 

5 2 0 1x x m   

Ta có

 

5 4 2 33 4     mm

Phương trình (1) có hai nghiệm

;xx

khi và chỉ khi

0 33 4 0

      mm

p dng định lí Vi ét cho phương trình (1) ta có

  









x x m

Theo đề ra ta có

 

1 2 1 2

8  S x x x x

 

   

1 1 2

1 2 1 2

5 4 2

17 4

   



   





x x x x x

Ta có

4 33 17 4 17 33 50

       m m m

Vy giá trị lớn nhất của

50S

. Dấu “=” xảy ra khi

m

Câu 3

Gọi lãi suất gửi tiết kiệm kì hạn một năm của ngân hàng A là

/ năm. (

0x

)

Thì lãi suất gửi tiết kiệm kì hạn một năm của ngân hàng B là

 

1%x

/ năm.

Tiền lãi bác Bình nhn được sau 1 năm gửi vào ngân hàng A là :

100 %x

(triệu đồng)

Tiền lãi bác Bình nhn được sau 1 năm gửi vào ngân hàng B là :

 

150 1 %x

(triệu đồng)

Tổng số tiền lãi bác Bình nhn được từ hai khoản tiết kiệm trên là

16,5

triệu đồng nên ta có

phương trình :

 

100 % 150 1 % 16,5  xx

100 150 150 1650

250 1500

   



6x

(thỏa mãn )

Vy lãi suất tiền gửi tiết kiệm kì hạn một năm của

ngân hàng A là

Câu 4

Trang 14

150m

30m

a. Chứng minh tứ giác

AMNC

là tứ giác nội tiếp.

Ta có

90  MN AB NMA

ACB

là góc nội tiếp chắn nửa đường tròn nên

90ACB

 

90  ACB NMA



Tứ giác

AMNC

là tứ giác nội tiếp (tứ giác có góc ngoài tại một đỉnh bằng góc trong tại

đỉnh đối diện)

b. Chứng minh

vuông góc với

Ta có tứ giác

AMNC

là tứ giác nội tiếp (chứng minh trên)

CNA CMA

(hai góc nội tiếp cùng chắn cung

)

Hay

BNE BMD

(1)

Xét đường tròn

 

ta có :

BNE

là góc có đỉnh nằm ngoài đường tròn chắn cung

và

 

  BNE BE ACññ

(2)

DMB

là góc có đỉnh nằm ngoài đường tròn chắn cung

và

 

  DMB BD ACññ

(3)

Từ (1), (2) và (3) suy ra

ssBE BDññ

BD BE

(hai cung bằng nhau căng hai dây bằng nhau)

 B

nằm trên đường trung trc của

(4)

Lại có

90ADB AEB

(các góc nội tiếp chắn nửa đường tròn

 

)

Xét

ADB

và

AEB

ta có :

90ADB AEB

(chứng minh trên)

chung

BD BE

(chứng minh trên)

Do đó

  ADB AEB

(ch-cgv)

AD AE

(hai cạnh tương ứng)

 A

nằm trên đường trung trc của

(5)

Từ (4) và (5) suy ra

là đường trung trc của

AB DE

hay

MB DE

(đpcm)

Ta có hình vẽ :

Ta có

 AB BC ABC

vuông tại

Do đó

150

tan 5 78 41'24"

    

ACB ACB

Vy dòng nước đã đẩy chiếc đò đi lệch một góc có số đo bằng

0 0 0

90 78 41'24" 1118'36"

Câu 5

Ta có

là số nguyên tố (

p

)

 p

là số có các ước dương là

1; ;pp

Theo đề bài ta có tổng các ước nguyên dương của

là một số chính phương

Trang 15

 

2 2 *

1 ( )

4 4 4 4

4 2 1 3

    

   

   

   

p p k k

k p p

  

2 2 1 2 2 1 3     k p k p

(*)

Ta có

, 2 2 1 0; 2 2 1 2 2 1         k p k p k p k p

2 2 1 1 2 2 2 1 (

(*)

2 2 1 3 2 2 2 0 (

     

  

  

  

     

  

k p k p k

k p k p p

thoûa maõn)

khoâng thoûa maõn)

Vy không có số nguyên tố

nào thỏa mãn đề bài

Ta chứng minh bất đẳng thức

 

2 2 2

a b c

x y z x y z



  



với

a,b,c,x,y,z 0

p dng bất đẳng thức Bu – nhi – a - cốp – xki cho ba bộ số

a b c

; x , ; y , ; z

x y z



   



   



   



ta có

 

     

2 2 2

a b c a b c

x y z x y z

x y z





   





        



   









   





 

a b c

. x . y . z a b c

x y z



     





 

2 2 2

a b c

x y z x y z



   



(*)

Dấu “=” xảy khi khi

a b c

x y z



p dng bất đẳng thức Cô si ta có

y z z x x y

yz ; zx ; xy

2 2 2

  

  

2 2 2

x y z

y z z x x y

x y z

2 2 2

   

  

2 2 2

2x 2y 2z

2x y z x 2y z x y 2z

  

     

2 2 2

x y z

2x y z x 2y z x y 2z



  



     



p dng bất đẳng thức (*) ta có

 

x y z

x y z 2019

4 x y z 2 2



  



Dấu “=” xảy ra khi

x y z 673  

Vy giá trị nhỏ nhất của biểu thức

2019

T

khi

x y z 673  

Trang 16

TUYỂN SINH VÀO 10 BẮC NINH NĂM HỌC 2019-2020

I. TRẮC NGHIỆM (3,0 điểm) Chọn phương án trả lời đúng trong các câu sau:

Câu 1: Khi

7x =

biểu thức

21x +-

có giá trị là

. B.

. C.

. D.

Lời giải

Chọn: D

Thay

7x 

(thỏa mãn) vào biểu thức

21x 

ta tính được biểu thức có giá trị bằng

7 2 1







Câu 2: Trong các hàm số sau, hàm số nào đồng biến trên ?

1yx=-

. B.

23yx=-

. C.

( )

12yx=-

. D.

26yx= - +

Lời giải

Chọn: B

Hàm số

23yx

đồng biến trên .

Câu 3: Số nghiệm của phương trình

3 2 0xx- + =

là

. B.

. C.

. D.

Lời giải

Chọn: D

Đặt

( 0)t x t

. Khi đó phương trình tương đương

3 2 0tt  

Ta thấy

1-3 2 0

. Nên phương trình có hai nghiệm

1t 

(thỏa mãn);

2t 

(thỏa mãn).

Khi đó

  

















Câu 4: Cho hàm số

( )

0y ax a=¹

. Điểm

( )

1;2M

thuộc đồ thị hàm số khi

2a =

. B.

a =

. C.

2a =-

. D.

a =

Lời giải

Chọn

Vì

(1;2)M

thuộc đồ thị hàm số

( 0)y ax a

nên ta có

2 .1 2aa  

(thỏa mãn).

Câu 5: Từ điểm

nằm bên ngoài đường tròn

( )

kẻ hai tiếp tuyến

,AB AC

tới đường tròn (

,BC

là các tiếp điểm). Kẻ đường kính

. Biết

30BAC =

, số đo của cung nhỏ

là

30°

. B.

60°

. C.

120°

. D.

150°

Lời giải

Chọn: A.

Trang 17

Từ giả thiết ta suy ra tứ giác nội tiếp nên

30BAC COK  

, mà

COK 

sđ

nên

Số đo cung nhỏ

là

30

Câu 6: Cho tam giác

ABC

vuông tại

. Gọi

là chân đường cao hạ từ đỉnh

xuống cạnh

Biết

12A H cm=

. Độ dài đoạn

là

6 cm

. B.

8 cm

. C.

4 3 cm

. D.

12 cm

Lời giải

Chọn: B

Theo đề bài ta có:

HC HB

  

. Áp

dng hệ thức lượng trong tam giác ABC vuông

tại A có đường cao AH ta có

. 12 .3

AH BH HC BH BH

BH BH

  

   

 

3. 3.2 6

2 6 8 cm

HC HB

BC HB HC

   

     

II. TỰ LUẬN (7,0 điểm)

Câu 7: Cho biểu thức

( ) ( )

( )( )

+ + -

với

0x ³

1x ¹

b) Tìm

là số chính phương để

2019A

là số nguyên.

Lời giải

( ) ( )

1 1 3 1

)

x x x

+ + - - -

2 1 2 1 3 1

x x x x x

+ + + - + - -

( )( )

2 2 1

1 2 1

2 3 1 2 1

x x x

- + -

= = =

- - +

( )

2019 2 2 3

6057

2019 4038

= = -

2019A

là số nguyên khi và chỉ khi

1x +

là ước nguyên dương của

6057

gồm:

1;3;9;673,2019;6057

1 1 0xx+ = Û =

, thỏa mãn.

ABOC

a) Rút gọn biểu thức

Trang 18

1 3 4xx+ = Û =

, thỏa mãn.

1 9 64xx+ = Û =

, thỏa mãn.

1 673 451584xx+ = Û =

, thỏa mãn.

1 2019 4072324xx+ = Û =

, thỏa mãn.

1 6057 36675136xx+ = Û =

, thỏa mãn.

Câu 8: An đếm số bài kiểm tra một tiết đạt điểm

và điểm

của mình thấynhiều hơn

bài.

Tổng số điểm của tất cả các bài kiểm tra đạt điểm

và điểm

đó là

160

. Hỏi An được

bao nhiêu bài điểm

và bao nhiêu bài điểm

Lời giải

Gọi số bài điểm

và điểm

của An đạt được lần lượt là

,xy

(bài)

( )

,xyÎ ¥

Theo giả thiết

16xy+>

Vì tổng số điểm của tất cả các bài kiểm tra đó là

160

nên

9 10 160xy+=

Ta có

( )

160

160 9 10 9

x y x y x y= + ³ + Þ + £

xy+Î¥

và

160

xy< + £

nên

17xy+=

Ta có hệ

( )

17 10

9 10 160 7

9 17 10 160

x y x

x y y

ìì

ïï

+ = =

ïï

ÛÛ

í í í

ï ï ï

+ = =

- + =

ï ï ï

îî

(thỏa mãn).

Vy An được

bài điểm

và

bài điểm

Câu 9: Cho đường tròn

( )

, hai điểm

,AB

nằm trên

( )

sao cho

90ºAOB =

. Điểm

nằm trên

cung lớn

sao cho

AC BC>

và tam giác

ABC

có ba góc đều nhọn. Các đường cao

,A I BK

của tam giác

ABC

cắt nhau tại điểm

cắt

( )

tại điểm

(khác điểm

);

cắt

( )

tại điểm

(khác điểm

);

cắt

tại điểm

. Chứng minh rằng:

a) Tứ giác

CIHK

nội tiếp một đường tròn.

là đường kính của đường tròn

( )

song song với

Lời giải

a)Ta có

90º 90º 180º

HK KC

HKC HIC

HI IC

Þ + = + =

Do đó,

CIHK

là tứ giác nội tiếp.

b) Do tứ giác

CIHK

nội tiếp nên

sđ sđ

45º

ICK BHI BM AN= = = +

sđ sđ 90BM AN   

Suy ra,

sđ sđ sđ sđ()

90 90 180º

MN AB BM AN= + +

= ° + ° =

hay

là đường kính của

( )

Trang 19

c) Do

là đường kính của

( )

nên

,MA DN NB DM^^

. Do đó,

là trc tâm tam

giác

DMN

hay

DH MN^

,IK

cùng nhìn

dưới góc

90º

nên tứ giác

ABIK

nội tiếp.

Suy ra,

sđ sđCAI CBK CM CN C= Þ = Þ

là điểm chính giữa của cung

MN CO MNÞ^

Vì

AC BC>

nên

ABCD

không cân tại

do đó

,,C O H

không thẳng hàng. Từ đó suy

/ /CO DH

Câu 10: a) Cho phương trình

2 2 1 0x mx m- - - =

( )

với

là tham số. Tìm

để phương trình

( )

có hai nghiệm phân biệt

,xx

sao cho

1 2 1 2

3 2 1x x x x m+ + + = +

b) Cho hai số thc không âm

,ab

thỏa mãn

2ab+=

. Tìm giá trị lớn nhất, giá trị nhỏ

nhất của biểu thức

Lời giải

( )

2 1 1m m mD¢= + + = +

Phương trình

( )

có hai nghiệm phân biệt khi và chỉ khi

01mD¢> Û ¹ -

p dng ĐL Vi-ét ta có

1 2 1 2

2 ; . 2 1x x m x x m+ = = - -

Ta có

2 2 2 2 1m m m+ - = +

(

ĐK

01m££

(*)

)

( )

2 1 2 2 1 2 1 0m m mÛ - + - - - - =

( )

2 1 2 1

2 1 0

2 1 2 2 1

Û - - - =

+ - +

( )

2 1 1 0

2 1 2 2 1

1 0 2

2 1 2 2 1

m t m

æö

Û - - - = Û

èø

+ - +

- - =

+ - +

Vì

2 1 1,mm+ ³ "

thỏa mãn

01m££

21m

Þ£

. Do đó,

( ) ( )

2 0 2VT VP<=

hay

( )

vô

nghiệm.

Vy giá trị cần tìm là

m =

b) Ta có

( )

3 3 3 3

4 1 3 3 3a b a b ab+ + = + + + ³ +

. Dấu bằng xảy ra khi và chỉ khi

1ab==

Vì

10ab +>

nên

( )

ab ab

= ³ =

Do đó, giá trị nhỏ nhất của biểu thức

là

đạt được khi

1ab==

+) Vì

2ab

nên Suy ra

 

3 3 2 2

4 2 4 2 2 4a b a b      

Mặt khác

1 do 1 1

  



. Suy ra

2 2 4



  



Dấu bằng xảy ra khi và chỉ khi

2; 2.ab

Trang 20

( )

; 0; 2 ; 2;0

a b a b

Û = Ú =

Giá trị lớn nhất của biểu thức

là

4 2 2

đạt được khi

( )

; 0; 2 ; 2;0a b a b= Ú =

---------------Hết---------------

SỞ GIÁO DỤC VÀ ĐÀO TẠO

NINH THUẬN

(Đề chính thức)

KỲ THI TUYỂN SINH LỚP 10 THPT

NĂM HỌC 2019 - 2020

Khóa ngày : 01/6/2019

Môn thi: TOÁN

Thời gian làm bài: 120 phút (không kể thời gian phát đề)

ĐỀ

(Đề thị này gồm một trang)

Bài 1. (2,0 điểm): Giải bất phương trình và hệ phương trình sau:

7 – 2 4 3xx

; b)











Bài 2. (2,0 điểm) : Cho Parabol

 

:2P y x

và đường thẳng

 

: 3 2d y x

a) Vẽ đồ thị (P) trên hệ trc tọa độ

Oxy

;

b) Tìm tọa độ giao điểm của (P) và (d).

Bài 3. (2,0 điểm)

a) Rút gọn biểu thức :

1 1 1

2 1 1

a a a

  



  

  



  

với

0a 

và

1a 

b) Chứng minh rằng phương trình :

(2 1) 2 4 0x m x m    

luôn có hai nghiệm phân biệt

,xx

Tìm giá trị nhỏ nhất của biểu thức

A x x

Bài 4. (2,0 điểm) : Cho



ABC vuông tại C nội tiếp trong đường tròn tâm O, đường kính AB = 2R,

60ABC 

. Gọi H là chân đường cao hạ từ C xuống AB, K là trung điểm đoạn thẳng AC. Tiếp tuyến

tại B của đường tròn tâm O cắt AC kéo dài tại điểm D.

a) Chứng minh tứ giác CHOK nội tiếp trong một đường tròn

b) Chứng minh rằng AC.AD= 4R

c) Tính theo R diện tích của phần tam giác ABD nằm ngoài hình tròn tâm O.

-----------------------HẾT-----------------------

HƯỚNG DẪN

Bài 1. (2,0 điểm):

7 – 2 4

3xx xx   

Trang 21

Vy nghiệm của bất phương trình là x >

3 1 6 2 2 7 7 1 1

2 5 2 5 2 5 1 2. 5 2

x y x y x x x

x y x y x y y y

      

    

   

    

         

    

Vy, nghiệm của hệ phương trình là

   

; 1; 2xy

Bài 2. (2,0 điểm)

a) Vẽ đồ thị hàm số

2yx

Bảng giá trị :

-2

-1

2yx

Đồ thị hàm số

2yx

là một đường cong đi qua các điểm:

         

2;8 , 1;2 , 0;0 , 1;2 , 2;8

Đồ thị như hình vẽ :

b) Phương trình hoành độ giao điểm của (P) và (d) :

2 3 22 – 3 – 2 0x x x x  

(

Ta có



= (-3)

– 4.2.(-2) = 25 > 0



5



Phương trình (*) có hai nghiệm :





hoặc

2x 

Khi





thì y =











ta được giao điểm

;









Khi x = 2 thì y =

 

2. 2 8

ta được giao điểm

 

2;8

Vy giao điểm của (P) và (d) là

;









và

 

2;8

Bài 3. (2,0 điểm)

a) Rút gọn :

1 1 1

2 1 1

a a a

  



  

  



  

với a > 0 và a



   

  

  













= -2

Vy P = -2

b) Ta có



’ =

   

1 2 4 2 1 2 4 4 5m m m m m m m          

Trang 22

 

4 4 1mm  

 

21m

> 0 với mọi m



Phương trình luôn có hai nghiệm phân biệt

,xx

với mọi m

Theo định lí vi-ét ta có :

2( 1)

. 2 4

x x m

  









Theo đề bài ta có :

 

1 2 1 2 1 2

2A x x x x x x    



       

2 2 2

4 1 2 2 4 4 8 4 4 8 2 2.2 .3 3 3 2 3 3A m m m m m m m m               





Vy giá trị nhỏ nhất của A bằng 3 khi m =

Bài 4. (2,0 điểm)

a) Chứng minh tứ giác CHOK nội tiếp trong một đường tròn

Vì K là trung điểm của dây cung AC nên OK





90CKO 

Xét tứ giác CHOK có :

90CKO 

(cmt)

90CHO 

(vì CH



AB)

Vì

0 0 0

90 90 180CKO CHO   

nên tứ giác CHOK nội tiếp

b) Chứng minh rằng AC.AD= 4R

Xét



ACB và



ABD có :

90ACB ABD

BAD

là góc chung

Vy



ACB





ABD (g-g)



AC AB

AB AD





AC.AD = AB

= (2R)

= 4R

(đpcm)

c) Tính theo R diện tích của phần tam giác ABD nằm ngoài hình tròn tâm O.

Gọi S là diện tích của phần tam giác ABD nằm ngoài hình tròn tâm O

Khi đó :

ABD ABC vp

S S S S



  

Ta có : OB = OC = bk,

60ABC 





OBC là tam giác đều



OB = OC = BC = R và

60BOC 

Lại có CH





H là trung điểm OB



BH =



AH =

Trong



CHB vuông tại H có :

2 2 2

CH BH BC



2 2 2

CH BC HB R    

Trang 23

Vì CH // BD (cùng vuông góc với AB) nên

.CH 2 3

AH CH AB R

AB BD AH

    

Khi đó :

1 1 2 3 2 3

. .2 .

2 2 3 3

ABD

S AB BD R



  

1 1 3 3

. . .2

2 2 2 2

ABC

S CH AB R



  

2 2 2 2

. .60 1 1 3 3

. . .

360 2 6 2 2 6 4

vp qBOC BOC

R R R R R

S S S OB CH R



  

       

Vy diện tích phần tam giác ABD nằm ngoài hình tròn tâm O là :

ABD ABC vp

S S S S



  

 

2 2 2 2

10 3

2 3 3 3

3 2 6 4 12

R R R R







   





(đvdt)

………………………………

SỞ GIÁO DỤC VÀ ĐÀO TẠO

PHÚ THỌ

KỲ THI TUYỂN SINH LỚP 10

TRUNG HỌC PHỔ THÔNG NĂM HỌC 2019-2020

MÔN: TOÁN

Đề thi có 02 trang

Thời gian làm bài: 120 phút (không kể thời gian giao đề)

Thí sinh làm bài (cả phần trắc nghiệm khách quan và phần tự luận) vào tờ giấy thi

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)

Câu 1. Tìm x biết

4.x 

2.x 

4.x 

8.x 

16.x 

Câu 2. Hàm số nào dưới đây đồng biến trên ?

yx

2.yx

2 1.yx

3 1.yx  

Câu 3. Điểm nào dưới đây thuộc đường thẳng

35yx

(3; 5).M 

(1; 2).N 

(1;3).P

(3;1).Q

Câu 4. Hệ phương trình

3 2 4











có nghiệm là

( ; ) ( 2;5).xy

( ; ) (5; 2).xy 

( ; ) (2;5).xy

( ; ) (5;2).xy

Câu 5. Giá trị của hàm số

yx

tại

2x 

bằng

1.

Câu 6. Biết Parabol

yx

cắt đường thẳng

34yx  

tại hai điểm phân biệt có hoành độ là

 

1 2 1 2

;.x x x x

Giá trị

23T x x

bằng

5.

10.

10.

Câu 7. Cho tam giác ABC vuông tại A. Khẳng định nào dưới đây đúng?

tan .



tan .



tan .



tan .



ĐỀ CHÍNH THỨC

Trang 24

Câu 8. Cho tứ giác ABCD nội tiếp đường tròn

đường kính AC. Biết

55 ,DBC 

số đo

ACD

bằng

30 .

40 .

45 .

35 .

Câu 9. Cho tam giác ABC vuông cân tại A có

AB a

. Bán kính đường tròn ngoại tiếp tam

giác ABC bằng

2.a

Câu 10. Từ một tấm tôn hình chữ nht có chiều dài

bằng 2 (m), chiều rộng bằng 1 (m) gò thành mặt xung

quanh của một hình tr có chiều cao 1 (m), (hai cạnh

chiều rộng của hình chữ nht sau khi gò trùng khít

nhau). Thể tích của hình tr đó bằng

(m ).



(m ).



2 (m ).



4 (m ).



PHẦN II. TỰ LUẬN (7,5 điểm)

Câu 1 (1,5 điểm). Lớp 9A và lớp 9B của một trường THCS d định làm 90 chiếc đèn ông sao để

tặng các em thiếu nhi nhân dịp Tết Trung Thu. Nếu lớp 9A làm trong

ngày và lớp 9B làm trong

ngày thì được

chiếc đèn; nếu lớp 9A làm trong

ngày và lớp 9B làm trong

ngày thì được

chiếc đèn. Biết rằng số đèn từng lớp làm được trong mỗi ngày là như nhau, hỏi nếu cả hai lớp

cùng làm thì hết bao nhiêu ngày để hoàn thành công việc đã d định ?

Câu 2 (2,0 điểm). Cho phương trình

30x mx  

(m là tham số).

a) Giải phương trình với

2.m 

b) C/minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của

c) Gọi

,xx

là hai nghiệm của phương trình. Tìm m để

( 6)( 6) 2019.xx  

Câu 3 (3,0 điểm). Cho tam giác

ABC

vuông tại A có đường cao

 

.AD D BC

Gọi

là trung

điểm của

;AC

kẻ

vuông góc với

tại

a) Chứng minh tứ giác

ABDH

nội tiếp. Tìm tâm đường tròn ngoại tiếp tứ giác

.ABDH

b) Chứng minh tam giác

BDH

đồng dạng với tam giác

.BIC

c) Chứng minh

. . . .

AB HD AH BD AD BH

Câu 4 (1,0 điểm). Giải hệ phương trình sau

















  







.......................Hết.....................

Trang 25

ĐÁP ÁN MÔN TOÁN

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)

Câu 1

Câu 2

Câu 3

Câu 4

Câu 5

Câu 6

Câu 7

Câu 8

Câu 9

Câu 10

PHẦN II. TỰ LUẬN (7,5 điểm)

Câu 1 (1,5 điểm). Lớp 9A và lớp 9B của một trường THCS d định làm 90 chiếc đèn ông sao để

tặng các em thiếu nhi nhân dịp Tết Trung Thu. Nếu lớp 9A làm trong

ngày và lớp 9B làm trong

ngày thì được

chiếc đèn; nếu lớp 9A làm trong

ngày và lớp 9B làm trong

ngày thì được

chiếc đèn. Biết rằng số đèn từng lớp làm được trong mỗi ngày là như nhau, hỏi nếu cả hai lớp

cùng làm thì hết bao nhiêu ngày để hoàn thành công việc đã d định ?

HD:

Gọi số đèn mà lớp 9A, lớp 9B làm được trong 1 ngày lần lượt là

, ( , )x y x y 

Theo bài ra ta có hệ phương trình

2 23

2 22











Giải hệ phương trình trên ta thu được











Suy ra trong một ngày cả 2 lớp làm được

8 7 15

chiếc đèn.

Vy nếu cả 2 lớp cùng làm thì hết



ngày sẽ xong công việc đã d định.

Câu 2 (2,0 điểm). Cho phương trình

30x mx  

(m là tham số).

a) Giải phương trình với

2.m 

b) C/minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của

c) Gọi

,xx

là hai nghiệm của phương trình. Tìm m để

( 6)( 6) 2019.xx  

HD:

a) Với

2m 

, phương trình đã cho trở thành

  

2 3 0 3 1 0x x x x      













Vy phương trình có tp nghiệm

 

1;3 .S 

Phương trình đã cho có

12m  

Vì

12 0mm    

nên phương trình luôn có hai nghiệm phân biệt với mọi

Gọi

,xx

là hai nghiệm của phương trình. Tìm m để

( 6)( 6) 2019.xx  

Theo định lí Vi-ét ta có

. 3.

x x m











Ta có

1 2 1 2 1 2

( 6)( 6) 2019 . 6( ) 36 2019.x x x x x x       

Suy ra:

3 6 36 2019 6 1986 331.m m m       

Câu 3 (3,0 điểm). Cho tam giác

ABC

vuông tại A có đường cao

 

.AD D BC

Gọi

là trung

điểm của

;AC

kẻ

vuông góc với

tại

a) Chứng minh tứ giác

ABDH

nội tiếp. Tìm tâm đường tròn ngoại tiếp tứ giác

.ABDH

b) Chứng minh tam giác

BDH

đồng dạng với tam giác

.BIC

Trang 26

c) Chứng minh

. . . .

AB HD AH BD AD BH

HD:

Ta có

90 ; 90 .ADB AHB   

Suy ra

,HD

cùng nhìn đoạn

dưới một góc vuông. Vy tứ giác

ABDH

nội tiếp

đường tròn đường kính

.AB

Đường tròn ngoại tiếp tứ giác

ABDH

có tâm là trung điểm của

b) Xét

BDH

và

BIC

có:

;HBD CBI

DHB DAB

(do tứ giác

ABDH

nội tiếp);

DAB ICB

(cùng ph

DAC

Suy ra

.DHB ICB

Suy ra

BDH BIC

(g.g).

c) Theo phần b) ta có

HD IC AC

BH BC BC



Mặt khác áp dng hệ thức lượng trong tam giác vuông

ABC

ta có

..AD BC AB AC

hay

AC AD

BC AB



Do đó

HD AD

BH AB



hay

 

. . 1 .

AB HD AD BH

Ta có

AHB IAB

(g.g) nên

AH AI

BH AB



Mặt khác

ADB CAB

(g.g) nên

AD AC AI

BD AB AB



Suy ra

2AH AD

BH BD



hay

 

. . 2 .

AH BD AD BH

Từ

 

và

 

ta có

. . . .

AB HD AH BD AD BH

Câu 4 (1,0 điểm). Giải hệ phương trình sau

















  







HD:

a) ĐKXĐ: x



- 1; y



Hệ phương trình đã cho tương đương với hệ phương trình:

Trang 27

1 1 1 1



   

   















   



    

  











Đặt





;





Hệ phương trình đã cho trở thành:

a b a

a b b

  







   



+ Với a = 1 ta có:

1 ( 1) 1 1

1 1 1

1 1 0 ( / )

x x x

x x x x t m

  

   

  

      

+ Với b = 3 ta có:

1 ( 1) 1 3.( 1)

1 1 1

1 3 3 4 4 0 2 ( / )

y y y

y y y y y y t m

  

   

  

          

Vy hệ phương trình đã cho có nghiệm duy nhất (x; y) =(0; 2)

……….Hết……….

QUẢNG NAM (Đề chung)

Câu 1. (2,0 điểm)

a) Rút gọn biểu thức

 

12 2 1

A    



b) Cho biểu thức

1 2 1

x x x x

  





với

0x 

và

1x 

. Rút gọn biểu thức

và

tìm

để

8B 

Câu 2. (2,0 điểm)

Trong mặt phẳng tọa độ

Oxy

, cho parabol

):(P y x

a) Vẽ parabol

( .)P

b) Hai điểm

, AB

thuộc

( .)P

có hoành độ lần lượt là

2; 1.

Viết phương trình đường thẳng

đi qua hai điểm

và

Câu 3. (2,0 điểm)

a) Giải phương trình

2 8 0xx  

b) Cho phương trình

()2 1 1 0x m x m    

(

là tham số). Tìm giá trị nguyên của

để

phương trình đã cho có hai nghiệm phân biệt

;xx

sao cho biểu thức

.xx





có giá trị nguyên.

Trang 28

Câu 4. (3,5 điểm)

Cho hình vuông

ABCD

có cạnh bằng

6.cm

Điểm

nằm trên cạnh

sao cho

2DN cm

là điểm nằm trên tia đối của tia

sao cho

BP DN

a) Chứng minh

ABP ADN  

và tứ giác

ANCP

nội tiếp đường tròn.

b) Tính độ dài đường tròn ngoại tiếp tứ giác

ANCP

c) Trên cạnh

, lấy điểm

sao cho

45MAN  

. Chứng minh

MP MN

và tính diện tích

tam giác

.AMN

Câu 5. (0,5 điểm)

Cho hai số thc

, xy

thỏa mãn

3; 3.xy

Tìm giá trị nhỏ nhất của biểu thức

21 3T x y



   





LỜI GIẢI THAM KHẢO

Câu 1. (2,0 điểm)

a) Rút gọn biểu thức

 

12 2 1

A    



b) Cho biểu thức

1 2 1

x x x x

  





với

0x 

và

1x 

. Rút gọn biểu thức

và tìm

để

8B 

Lời giải

 

12 2 1

2 3 2 1

( 3 2)( 3 2)

2 3 2 1 3 2

   





   



    



1 2 1

( 1) ( 1)( 1) ( 1)

1 2 1

( 1)( 1)

2 2 2( 1)( 1) 2

( 1)( 1) ( 1)( 1)

x x x x

x x x x x x

x x x

x x x x x x x

  





  

   

   





  



   

2 1 1

8 8 ( )

B x x TMĐK

      

Trang 29

Câu 2. (2,0 điểm)

Trong mặt phẳng tọa độ

Oxy

, cho parabol

):(P y x

c) Vẽ parabol

( .)P

d) Hai điểm

, AB

thuộc

( .)P

có hoành độ lần lượt là

2; 1.

Viết phương trình đường thẳng

đi qua hai điểm

và

Lời giải

(2;2); ( 1; )

AB

Gọi phương trình đường thẳng cần tìm là:

axyb

Vì

(2;2); ( 1; )

AB

thuộc đường thẳng

axyb

nên:

2 2 2 2 2

2 2 2 4 4 2

a b a b a

a b a b b





    

  



  

   

       

  

  





Vy đường thẳng cần tìm là:

22yx

Câu 3. (2,0 điểm)

a) Giải phương trình

2 8 0xx  

b) Cho phương trình

()2 1 1 0x m x m    

(

là tham số). Tìm giá trị nguyên của

để

phương trình đã cho có hai nghiệm phân biệt

;xx

sao cho biểu thức

.xx





có giá trị nguyên.

Lời giải

a) Đặt

0,xt

phương trình trở thành

2 8 0 (1)tt   

' 1 1.( 8) 9 0     



' 9 3  

Phương trình (1) có hai nghiệm phân biệt:

' ' 1 3 ' ' 1 3

2( ); 4( )

t TM t KTM

         

      

Với

2t 

, ta có:

22xx   

Vy phương trình có tp nghiệm:

 

2; 2S 

()2 1 1 0x m x m    

 

2 2 2 2

2 1 ( 1) 4 4 4 1 3 4 3 3( 0m m m m m m m m               



Phương trình đã cho có hai nghiệm phân biệt với mọi m.

Trang 30

Theo hệ thức Vi et ta có:

x x m



    







  





Theo đề ta có

x x m







Để P có giá trị nguyên thì

1 2 1 4 1 2 1 (2 1)(2 1) 2 2 1m m m m m m m         

2 2 1 2 1mm    

Ư(2)

 

1; 2  

2 1 1 0m m Z    

2 1 1 1m m Z      

2 1 2

m m Z    

2 1 2

m m Z



     

Vy

 

0; 1m

thì phương trình đã cho có hai nghiệm phân biệt

;xx

sao cho biểu thức

.xx





có giá trị nguyên.

Câu 4. (3,5 điểm)

Cho hình vuông

ABCD

có cạnh bằng

6.cm

Điểm

nằm trên cạnh

sao cho

2DN cm

là

điểm nằm trên tia đối của tia

sao cho

BP DN

a) Chứng minh

ABP ADN  

và tứ giác

ANCP

nội tiếp đường tròn.

b) Tính độ dài đường tròn ngoại tiếp tứ giác

ANCP

c) Trên cạnh

, lấy điểm

sao cho

45MAN  

. Chứng minh

MP MN

và tính diện tích

tam giác

.AMN

Lời giải

a) Xét

ABP

và

ADN

, có:

( ); ( 90 ); ( 2 )AB AD gt ABP ADN BP DN cm    



( . . )ABP ADN c g c  

ABP ADN APB AND    



Tứ giác

ANCP

nội tiếp đường tròn.

b) Gọi O là tâm đường tròn ngoại tiếp tứ giác

ANCP

Tứ giác ANCP nội tiếp, có

90NCP 

Trang 31



là đường kính của đường tròn

()O

và

90NAP 



2NP AN AP AN  

(1)

ADN

vuông tai

, nên:

2 2 2 2

6 2 2 10AN AD DN    

(2)

Từ (1) và (2) suy ra:

2.2 10 4 5NP 

(cm)



Bán kính đường tròn ngoại tiếp tứ giác

ANCP

là

2 5 ( )cm

Độ dài đường tròn ngoại tiếp tứ giác ANCP là:

2 2 .2 5 4 5CR

  

  

(cm)

c) Ta có

1 2 3 1 3

90 45A A A A A     

Mà

AA

nên

45AA

45MAP

Xét

MAN

và

MAP

, có:

AM: cạnh chung;

( 45 )MAN MAP

;

AN AP

Do đó

MAN MAP  

(c.g,c)

MN MP

Ta có

;;AN AP MN MP ON OP   

AM NP

tại O.

. 2 5.4 5

( . ) . . 5( )

PO PN

POM PCN g g PM PC PO PN PM cm

       #

3( )BM cm

2 2 2 2

6 3 45 3 5( )AM AB BM cm     

. . .3 5.2 5 15( )

ANM

S AM NO cm  

Câu 5. (0,5 điểm)

Cho hai số thc

, xy

thỏa mãn

3; 3.xy

Tìm giá trị nhỏ nhất của biểu thức

21 3T x y



   





Lời giải

21 3 62 3 21 7 2

21 3

3 3 3 3

3 21 7 62 2

2 14 62 2 80

3 3 3 3

T x y x y y

y x x y

y x y

         



          





Dấu

“”

xảy ra













Vy giá trị nhỏ nhất của

là 80 khi x = 3; y =3.

Trang 32

SỞ GIÁO DỤC VÀ ĐÀO TẠO KÌ THI TUYỂN SINH VÀO LỚP 10 PTTH

QUẢNG NGÃI NĂM HỌC 2019 – 2020

Ngày thi: 05/6/2019

Môn thi: TOÁN

(Đề thi có 01 trang) Thời gian: 120 phút , không kể phát đề

Bài 1. (1,0 điểm)

a) Cho biểu thức

16 25 4A.  

So sánh A với

b) Giải hệ phương trình:

2 11

  









Bài 2. (2,5 điểm)

1. Cho Parabol

 

P : y x

và đường thẳng

 

2d : y x

a) Vẽ

   

P và d

trên cùng một mặt phẳng tọa độ

Oxy

b) Viết phương trình đường thẳng

 

song song với

 

và tiếp xúc với

 

2. Cho phương trình

40x x m  

(m là tham số)

a) Biết phương trình có một nghiệm bằng

1

. Tính nghiệm còn lại.

b) Xác định m để phương trình có hai nghiệm

x ,x

thỏa mãn

  

3 1 3 1 4xx  

Bài 3. (2,0 điểm)

Một đội công nhân đặt kế hoạch sản xuất 250 sản phẩm. Trong 4 ngày đầu, họ thc hiện đúng kế

hoạch. Mỗi ngày sau đó, họ đều vượt mức 5 sản phẩm nên đã hoàn thành công việc sớm hơn 1 ngày so

với d định. Hỏi theo kế hoạch, mỗi ngày đội công nhân đó làm được bao nhiêu sản phẩm? Biết rằng

năng suất làm việc của mỗi công nhân là như nhau.

Bài 4. (3,5 điểm)

Cho tam giác nhọn ABC (AB<AC), đường cao AH, nội tiếp đường tròn (O). Gọi D và E thứ t là hình

chiếu vuông góc của H lên AB và AC.

a) Chứng minh các tứ giác AEHD và BDEC nội tiếp được đường tròn.

b) Vẽ đường kính AF của đường tròn (O). Chứng minh

BC AB.BD AC.CE

và AF

vuông góc với DE.

c) Gọi O’ là tâm đường tròn ngoại tiếp tam giác BDE. Chứng minh O’ là trung điểm của HF.

d) Tính bán kính đường trò (O’) biết

8 6 10BC cm, DE cm, AF cm.  

Bài 5. (1,0 điểm)

----------------------- HẾT-----------------------

Ghi chú: Cán bộ coi thi không giải thích gì thêm.

HƯỚNG DẪN

Bài 1. (1,0 điểm)

a) Cho biểu thức

16 25 4A.  

So sánh A với

ĐỀ CHÍNH THỨC

Cho hình vuông ABCD. Gọi

là diện tích phần giao

của hai nửa đường tròn đường kính AB và AD.

là diện tích

phần còn lại của hình vuông nằm ngoài hai nửa đường trong nói

trên (như hình vẽ bên).Tính

Trang 33

16 25 4 4 5 2 1 2A        

. Vy

2A 

b) Giải hệ phương trình:

2 11

  









5 3 6 2 2

2 11 5 2 5 7

x y x x x

x y x y y y

     

   

  

   

        

   

Bài 2. (2,5 điểm)

1. Cho Parabol

 

P : y x

và đường thẳng

 

2d : y x

a) Vẽ

   

P và d

trên cùng một mặt phẳng tọa độ

Oxy

b) Viết phương trình đường thẳng

 

song song với

 

và tiếp xúc với

 

P : y x

3

2

1

9

4

1

4

9

 

2d : y x

 

0 2 0 2x y : ;    

 

0 2 2 0y x : ;  

b) Phương trình đường thẳng

 

có dạng

y ax b

 

2 1 2d : y x a ; b     

Phương trình hoành độ giao điểm của

   

P và d'

là

 

0x x b x x b *      

 

có

14b  

   

P và d'

tiếp xúc nhau khi PT

 

có nghiệm kép

0 1 4 0

bb       

(nhn).

-2

-4

-6

-8

-10

-5

Trang 34

Vy PT đường thẳng

 

d' là : y x

2. Cho phương trình

40x x m  

(m là tham số)

a) Biết phương trình có một nghiệm bằng

1

. Tính nghiệm còn lại.

b) Xác định m để phương trình có hai nghiệm

x ,x

thỏa mãn

  

3 1 3 1 4xx  

a) PT

40x x m  

có một nghiệm bằng

1

0 1 4 0 5a b c m m          

Nghiệm còn lại của PT là



     

b) ĐK

 

2 0 4' m m      

p dng định lí Vi et ta có:

4xx

x x m











    

 

1 2 1 2 1 2

3 1 3 1 4 9 3 1 4

9 3 4 1 4 1

x x x x x x

m . m tm

       

      

Vy

1m 

là giá trị cần tìm.

Bài 3. (2,0 điểm)

Một đội công nhân đặt kế hoạch sản xuất 250 sản phẩm. Trong 4 ngày đầu, họ thc hiện đúng kế

hoạch. Mỗi ngày sau đó, họ đều vượt mức 5 sản phẩm nên đã hoàn thành công việc sớm hơn 1 ngày so

với d định. Hỏi theo kế hoạch, mỗi ngày đội công nhân đó làm được bao nhiêu sản phẩm? Biết rằng

năng suất làm việc của mỗi công nhân là như nhau.

Gọi số sản phẩm mỗi ngày đội công nhân đó làm theo kế hoạch là x(sp).ĐK

0x ;x Z

Khi đó, số sản phẩm mỗi ngày đội công nhân đó làm trong thc tế là

 

5x sp

Thời gian hoàn thành công việc theo kế hoạch là

250

(ngày)

Số sản phẩm làm được trong 4 ngày đầu là:

 

4x sp

Số sản phẩm còn lại phải làm là

 

250 4x sp

Thời gian làm

 

250 4x sp

còn lại là

250 4





(ngày).

Theo bài toán ta có PT:

250 250 4



  



Giải PT này ta được:

25x 

(nhn)

50x 

(loại)

Vy số sản phẩm mỗi ngày đội công nhân đó làm theo kế hoạch là 25 sản phẩm.

Gợi ý hai bài hình

Bài 4. (3,5 điểm)

Cho tam giác nhọn ABC (AB<AC), đường cao AH, nội tiếp đường tròn (O). Gọi D và E thứ t là hình

chiếu vuông góc của H lên AB và AC.

a) Chứng minh các tứ giác AEHD và BDEC nội tiếp được đường tròn.

b) Vẽ đường kính AF của đường tròn (O). Chứng minh

BC AB.BD AC.CE

và AF

vuông góc với DE.

c) Gọi O’ là tâm đường tròn ngoại tiếp tam giác BDE. Chứng minh O’ là trung điểm của HF.

d) Tính bán kính đường trò (O’) biết

8 6 10BC cm, DE cm, AF cm.  

Trang 35

a) Tứ giác AEHD có

0 0 0

90 90 180ADH AEH    

Tứ giác AEHD nội tiếp được

đường tròn đường kính AH.

Tứ giác AEHD (cmt)

 

1ADE AHE

(cùng chắn

). Dễ thấy

 

2ACH AHE

(cùng

ph

HAE

Từ (1) và (2) suy ra

ADE ACH

nên tứ giác BDEC nội tiếp được đường tròn.

b) p dng hệ thức lượng trong hai tam giác vuông AHB và AHC ta có:

BH AB.BD BH AB.BD

HB AC.CE HB AC.CE

  

Do đó

BC BH HC AB.BD AC.CE   

Nối FB, FC. Gọi I là giao điểm của AF và DE.

Ta có

ADE ACH

(cmt) và

AFB ACH

(cùng chắn

) suy ra

ADE AFB

nên tứ

giác BDIF nội tiếp được đường tròn

0 0 0 0 0

180 180 180 90 90DIF DBF DIF DBF        

. Vy

AF DE

c) Gọi M,N,O’’ lần lượt là trung điểm của BD,EC,HF.

- Ta chứng minh được MO’’ và NO’’ lần lượt là đường trung bình của các hình thang BDHF và

CEHF

 

3MO''/ / DH

và

 

4NO''/ / EH

- Vì tứ giác BDEC nội tiếp mà

là tâm đường tròn ngoại tiếp tam giác BDE suy ra

cũng là

tâm đường tròn ngoại tiếp tứ giác BDEC

O'

thuộc đường trung trc của BD . Suy ra MO’ là

trung trc của BD do đó

MO' BD

lại có

DH BD

 

5MO'/ / DH

Tương t ta có

 

6NO'/ / EH

- Từ (3) và (5) suy ra MO’’ và MO’ là hai tia trùng nhau

- Từ (4) và (6) suy ra NO’’ và NO’ là hai tia trùng nhau

Do đó O’ trùng O”. Mà O’’ là trung điểm của HF nên O’ cũng là trung điểm của HF.

O''

Trang 36

d) - Trong

ABC

ta có

10 5

BC BC

AF SinA

SinA AF

    

- Trong

ADE

ta có

 

AH AH , cm

SinA

   

- Vì O’ và O lần lượt là trung điểm của HF và AF nên OO’ là đường trung bình của tam giác

AHF

 

3 75

AH ,

OO'= , cm  

- Gọi K là giao điểm của OO’ và BC dễ thấy

OO' BC

tại trung điểm K của BC. p dng

định lí Pytago vào tam giác vuông OKC ta tính được

 

2 2 2 2

5 4 3OK OC KC cm    

- Ta có

 

3 75 3 0 75KO' OO' OK , , cm    

- p dng định lí Pytago vào tam giác vuông O’KC ta tính được

 

2 2 2 2

265

0 75 4

O'C O' K KC , cm    

Vy bán kính đường trò (O’) là

 

265

Bài 5. (1,0 điểm)

Gọi a là cạnh hình vuông ABCD. Ta cm được:

360 2 2 4 4 2









   



     

   

   

2 2 2

1 3 4

1 1 1

4 4 2 4 4 2 2 4 2

a a a

S S S

  

     

       

     

     

Cho hình vuông

ABCD

. Gọi

là diện tích phần giao

của hai nửa đường tròn đường kính

và

là diện

tích phần còn lại của hình vuông nằm ngoài hai nửa

đường trong nói trên (

như hình vẽ bên).

Tính

Trang 37

1 1 3

2 2 4 2 2 2 4



   

    

   

   

Do đó

2 4 2

2 2 4



























SỞ GIÁO DỤC VÀ ĐÀO TẠO

TỈNH QUẢNG NINH

KỲ THI TUYỂN SINH LỚP 10 THPT NĂM 2019

Môn thi: Toán (Dành cho mọi thí sinh)

Thời gian làm bài: 120 phút, không kể thời gian giao đề

(Đề thi này có 01 trang)

Câu 1. (2,0 điểm )

1. Thc hiện phép tính:

4392 

2. Rút gọn các biểu thức:

228

)a( 

, với

2 > a

3. Tìm tọa độ giao điểm của đồ thị hàm số

xy 

và đồ thị hàm số

2- 3x y 

Câu 2. (2,0 điểm )

Cho phương trình:

012

 mxx

, với m là tham số.

1. Giải phương trình với m = 1

2. Tìm giá trị của m để phương trình đã cho hai nghiệm phân biệt

và

thỏa mãn:

).mm(xxxx

46 

Câu 3. (2,0 điểm ) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:

Hai người thợ cùng làm một công việc trong 9 ngày thì xong. Mỗi ngày, lượng công việc

của người thợ thứ hai làm được nhiều gấp ba lần lượng công việc của người thợ thứ nhất. Hỏi

nếu làm một mình thì mỗi người làm xong công việc đó trong bao nhiêu ngày

Câu 4. (3,5 điểm )

Cho đường tròn (O; R), hai đường kính AB và CD vuông goác với nhau. Gọi E là điểm

thuộc cung nhỏ BC ( E không trùng với B và C), tiếp tuyến của đường tròn (O; R) tại E cắt

đường thẳng AB tại I. Gọi F là giao điểm của DE và AB, K là điểm thuộc đường thẳng IE sao

cho KF vuông góc với AB.

a. Chứng minh tứ giác OKEF nội tiếp.

b. Chứng minh









c. Chứng minh 



d. Gọi M là giao điểm của OK với CF, tính tan 



khi 







Câu 5. (0,5 điểm )

ĐỀ THI CHÍNH THỨC

Trang 38

Cho x, y, z là các số thc dương thỏa mãn x+ y + z ≤1. Tìm giá trị nhỏ nhất của biểu

thức

zxyzxy

zyx









222

--------------------Hết--------------------

Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.

Họ và tên thí sinh: …………………………………………Số báo danh………………….

Chữ ký của cán bộ coi thi 1:……………….Chữ ký của cán bộ coi thi 1:…………………

SỞ GIÁO DỤC VÀ ĐÀO TẠO

TỈNH QUẢNG NINH

HƯỚNG DẪN CHẤM THI TUYỂN SINH

LỚP 10 THPT NĂM 2019

Môn thi: Toán (Dành cho mọi thí sinh)

(Hướng dẫn này có 02 trang)

Câu

Sơ lược lời giải

Điểm

Câu 1

(2,0đ)

023324392  ..

0,5



󰇛 󰇜









󰇛 󰇜



0,25



󰇛

 

󰇜



󰇛

 

󰇜

 



 



 

0,5

Hoành độ giao điểm của đồ thị hai hàm số đã cho là nghiệm của PT: 



 

Giải được hai nghiệm: 









0,25

Từ đó tìm được hai giao điểm có tọa độ là: (1; 1) và (2; 4)

0,25

Câu 2

(2,0đ)

Với m = 1 PT có dạng: 



 

0,5



󰇛

 

󰇜











0,5

Để PT hai nghiệm phân biệt thì 

0,25

Theo hệ thức Vi-ét có







 













  

0,25













 









󰇛

 



󰇜





   

0,25

Suy ra m = -1 nhn; m = 2 (loai)

0,25

Câu 3

(2,0đ)

Gọi x (ngày), y (ngày) lần lượt là thời gian hoàn thành công việc một mình của

người thứ nhất và người thứ hai, 󰇛󰇜



󰇜

0,5

Do hai người cùng làm trong 9 ngày thì xong công việc nên:

















(1)

Trong cùng một ngày người thứ hai làm được nhiều gấp ba lần người thứ nhất nên











(2)

0,5

Từ (1) và (2) giải hệ tìm được x=36; y =12 (thỏa mãn).

0,5

Vy nếu làm một mình xong công việc người thứ nhất làm hết 36 ngày, người thứ

hai làm hết 12 ngày.

0,5

ĐỀ THI CHÍNH THỨC

Trang 39

Câu 4

(3,5đ)

Vẽ đúng hình ý a cho 0,25 điểm

Có 























 hay tứ giác

OKEF nội tiếp

0,25

Vì tứ giác OKEF nội tiếp nên









󰵎 󰉷

󰇛



󰇜











Vy 







0,5

Xét 󰵎  và 󰵎  ta có 



 











Suy ra 󰵎 󰉰󰉗󰉵 󰵎 

















0,5

Kẻ MN vuông góc CD tại N

Ta có 



















󰵎 󰵎 



󰊀󰉝

󰉨󰉻󰉨󰉻 













0,25

Mặt khác ta có 







 󰵎 󰉗

Ta có 󰵎 󰉗



  󰇛



- 1) R

Do đó 







󰇛



󰇜





Suy ra 

















0,25

Câu 5

(0,5đ)

Ta có

 







zyx

zxyzxy

nên

6051

2017



 zxyzxy

0,25

p dng BĐT

 

111

















zyx

, ta có:

 

111

222

111

222





















































zxyzxyzxyzxy

zyx

)zxyzxyzyx(

zxyzxyzxyzxy

zyx

)zxyzxy()zxyzxy()zyx(

Hay

222









zxyzxy

zyx

Từ đó ta có:

606060519

201721

222















zxyzxyzxyzxy

zyx









 











   





  

  

6060 P

Vy GTNN của P là 6060 khi và chỉ khi

 zyx







0,25

Trang 40

Lưu ý:

1. Đây chỉ là sơ lược lời giải của bài toán, bài làm phải chặt chẽ đủ các bước mới cho

điểm tối đa.

2. Nếu làm cách khác mà vẫn ra đáp án đúng thì vẫn cho điểm tối đa của ý đó

3. Bài hình không vẽ hình không chấm cả bài.

SỞ GIÁO DỤC VÀ ĐÀO TẠO

LÀO CAI

KỲ THI TUYỂN SINH LỚP 10

TRUNG HỌC PHỔ THÔNG NĂM 2019

MÔN THI : TOÁN KHÔNG CHUYÊN

Thời gian : 120 phút (không tính thời gian giao đề)

Bài 1. (1,0 điểm) Tính giá trị của các biểu thức sau:

43

. b)

 

5 6 5

Bài 2: (1,5 điểm) Cho biểu thức

2x 2x 1 1

x 1 x 1



  





với

x 0;x 1

a) Rút gọn biểu thức H

b) Tìm tất cả các giá trị của x để

x H 0

Bài 3. (2,5 điểm)

1) Cho đường thẳng (d):

y x 1

và parabol (P):

y 3x

a) Tìm tọa độ A thuộc parabol (P) biết điểm A có hoành độ

x1

b) Tìm b để đường thẳng (d) và đường thẳng (d’):

y x b



cắt nhau tại một điểm trên trc

hoành.

2) a) Giải hệ phương trình

x y 5

2x y 1











b) Tìm tham số a để hệ phương trình

x y a

7x 2y 5a 1







  



. Có nghiệm duy nhất

 

x;y

thỏa mãn

y 2x

Bài 4. (2,0 điểm)

a) Giải phương trình:

x 3x 2 0  

b) Tìm các giá trị của tham số m để phương trình

x 2(m 1)x m 0   

có hai nghiệm phân

biệt

x ,x

thỏa mãn hệ thức

 

1 2 1 2

x x 6m x 2x   

Bài 5. (3,0 điểm)

Cho đường tròn (O), điểm M nằm ngoài đường tròn (O). kẻ hai tiếp tuyến MB, MC (B và C là

các tiếp điểm) với đường tròn. Trên cung lớn BC lấy điểm A sao cho AB < AC. Từ điểm M kẻ đường

thẳng song song với AB, đường thẳng này cắt đường tròn (O) tại D và E (MD < ME),cắt BC tại F, cắt

ĐỀ CHÍNH THỨC

Trang 41

AC tại I.

a) Chứng minh tứ giác MBOC nội tiếp.

b) Chứng minh

FD.FE FB.FC;FI FE FD.FE  

c) Đường thẳng OI cắt đường tròn (O) tại P và Q (P thuộc cung nhỏ AB). Đường thẳng QF cắt

đường tròn (O) tại K (K khác Q). Chứng minh 3 điểm P, K, M thẳng hàng.

--- HẾT ---

Họ và tên thí sinh:

SBD:

Phòng thi số:

HƯỚNG DẪN GIẢI

Bài 1:

4 3 2 3 5   

 

5 6 5 5 6 5 5 6 5 6        

Bài 2:

 

  

2x x 1

2x 2x 1 1 1 1

x 1 x 1 x 1

x 1 x 1 x 1 x 1



     

  

   

  

2x 1 1 2x 1 1

x 1 x 1 x 1 x 1

x 1 x 1

     



   



b) Theo đề bài ta có

x H 0 x 2 x 2 x 4       

Kết hợp điều kiện

x 0;x 1

ta có

0 x 4;x 1  

Vy với

0 x 4;x 1  

thì

x H 0

Bài 3:

1) a) Điểm A có hoành độ

x1

và thuộc P nên thay

x1

vào P ta được :

 

y 3. 1 3  

 

A 1;3

b)Gọi

 

B x ;0

là điểm thuộc trc hoành và là giao điểm của hai đường thẳng d, d’. ta có

 

B x ;0

thuộc d

 

x 1 B 1;0   

Lại có:

 

B 1;0 d' 0 .1 b b

      

2) a)

x y 5 3x 6 x 2

2x y 1 y 5 x y 3

   

  



  

    

  

Vy hệ pt có nghiệm duy nhất:

   

x;y 2;3

b)Hệ phương trình có







hệ pt

 

x y a 1

7x 2y 5a 1 2

  



  



có nghiệm duy nhất với mọi a.

Trang 42

Theo đề bài ta có hệ pt có nghiệm duy nhất thỏa mãn

y 2x

Thay

y 2x

vào (1) ta được:

x 2x a x a y 2a       

Thay

x a;y 2a   

vào (2) ta được:

   

7 a 2 2a 5a 1    

7a 4a 5a 1     

8a 1  



Vy



thỏa mãn bài toán

Bài 4:

x 3x 2 0  

Phương trình có dạng

a b c 0  

. Khí đó pt có hai nghiệm phân biệt

x 1;x 2

Vy tp nghiệm của phương trình là:

 

S 1;2

x 2(m 1)x m 0   

Ta có:

 

' m 1 m     



m 2m 1 m 1 2m     

Phương trình có hai nghiệm phân biệt

x ,x

' 0 1 2m 0 m

       

Theo vi-ét ta có:

 

x x 2 m 1

x x m



  







Theo đề bài ta có:

 

1 2 1 2

x x 6m x 2x   

 

1 2 1 2 1 2

x x 4x x 6m x 2x     

 

4 m 1 4m 6m x 2x     

2m 4 x 2x    

Khi đó kết hợp với

 

x x 2 m 1  

ta có hệ pt:

 

x m 2 x m 2

3x 4m 6

x x 2 m 1

x x 2m 2

x 2x 2m 4

x 2m 2 m 2 x m



   







  





  

   

  

   





    





Thay

x m 2

















vào

x x m

ta được:

4 2 1 4 1 4

m 2 . m m m m 0 m m 0

m 12

3 3 9 3 9 3







   

         

   





   



(tm)

Vy

m 0;m 12  

thỏa mãn yêu cầu đề bài.

Bài 5:

Trang 43

a) Do Mb,Mc là hai tiếp tuyến của đường tròn (O) nên

OBM OCM 90

Xét tứ giác MBOC có:

OBM OCM 180

suy ra tứ giác MBOC là tứ giác nội tiếp.

b) Xét tam giác FBD và tam giác FEC có:

 

BFD EFC dd

FDB FCE

( hai góc nội tiếp cùng chắn cung BE)

   

FB FD

FBD FEC g g FD.FE FB.FC 1

FE FC

       

Ta có AB// ME suy ra

BAC DIC

Mà

BAC MBC

(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BC)

DIC MBC MBF CIF   

Xét tam giác FBM và tam giác FIC có:

BFM IFC

(đđ)

 

MBF CIF cmt

   

FB FM

FBM FIC g g FI.FM FB.FC 2

FI FC

       

Từ (1) và (2)

 

FI.FM FD.FE 3

c) Xét tam giác FDK và tam giác FQE có:

KFD EFQ

(đđ)

FKD FEQ

( hai góc nội tiếp cùng chắn cung DQ)

 

FKD FEQ g g   

 

FK FD

FD.FE FK.FQ 4

FE FQ

   

Từ (3) và (4)

FM FK

FI.FM FK.FQ

FQ FI

   

Xét tam giác FMQ và tam giác FKI có:

 

FM FK

cmt

FQ FI



MFQ KFI

 

FMQ FKI c g c FMQ FKI      

Trang 44

Suy ra tứ giác KIQM là tứ giác nội tiếp

MQK MIQ

(hai góc nội tiếp cùng chắn cung MQ)

Ta có

MBF CIF MBC MIF  

suy ra tứ giác MBIC là tứ giác nội tiếp

Mà MOBC là tứ giác nội tiếp nên M, B, O, I, C cùng thuộc 1 đường tròn.

Ta có

OBM 90

suy ra OM là đường kính của đường tròn đi qua 5 điểm M, B, O, I, C.

Suy ra

OIM 90

(góc nội tiếp chắn nửa đường tròn)

IM OI MIQ 90   

MKQ MIQ 90  

Lại có

QKP 90

(góc nội tiếp chắn nửa đường tròn)

Từ đó ta có:

MKP MKQ QKP 180  

Vy 3 điểm P, K, M thẳng hàng.

Bấm Tải xuống để xem toàn bộ.

| 1/44

| | Tải xuống

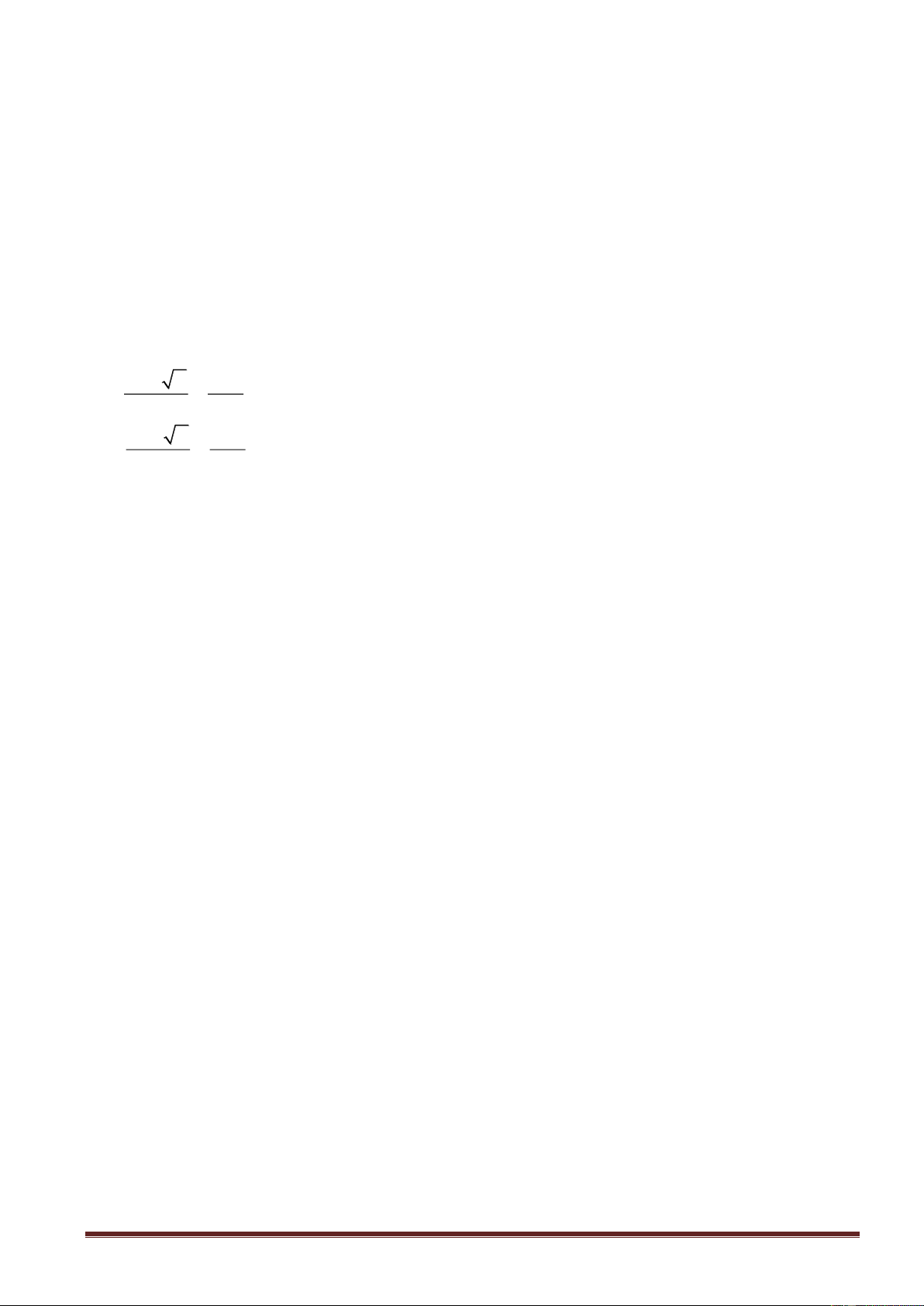
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH 10 NĂM HỌC 2019 - 2020 LONG AN
Môn thi: TOÁN (Công Lập) Ngày Thi: 05 – 06 - 2019 ĐỀ CHÍNH THỨC
Thời gian:120 phút (không kể thời gian phát đề)
(Đề thi gồm có 01 trang) Câu 1: (2,0 điểm)
1. Rút gọn các biểu thức: K  9  45  3 5 x  x  x
2. Rút gọn các biểu thức: 4 2 Q   (với x  0 ) x  2 x
3. Giải phương trình: 2
x  4x  4  3 Câu 2: (2,0 điểm)
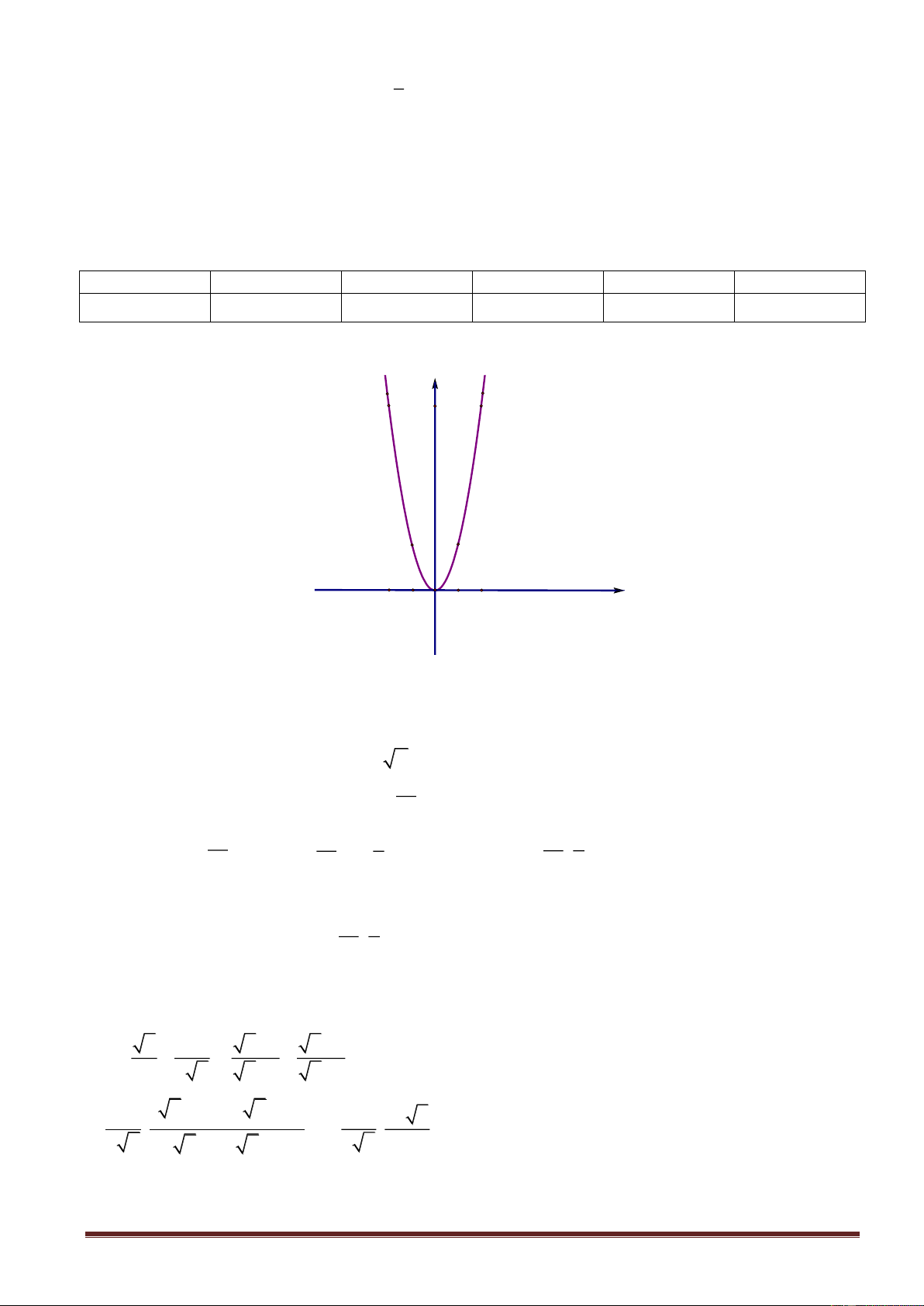
Trong mặt phẳng tọa độ Oxy ,cho Parabol  P 2
: y  2x và đường thẳng d  : y  2x  4
1.Vẽ Parabol P và đường thẳng d  trên cùng một mặt phẳng tọa độ Oxy .
2.Tìm tọa độ giao điểm của Parabol P và đường thẳng d  bằng phép tính.
3.Viết phương trình đường thẳng d '  : y  ax  b . Biết rằng d '  song song với d  và d và 1 
đi qua điểm N 2;3 . Câu 3: (2,0 điểm) 1.Giải phương trình: 2
x  7x 10  0 (không giải trực tiếp bằng máy tính cầm tay)
2x  y  5
2.Giải hệ phương trình: 
(không giảitrực tiếp bằng máy tính cầm tay) x  y  1
3.Cho phương trình (ẩn x ) 2
x  6x  m  0
a)Tìm giá trị m để phương trình có hai nghiệm phân biệt x ,x . 1 2
b)Tìm giá trị m để phương trình có hai nghiệm phân biệt x ,x thỏa mãn điều kiện 1 2 2 2
x  x  12 . 1 2 Câu 4: (4,0 điểm)
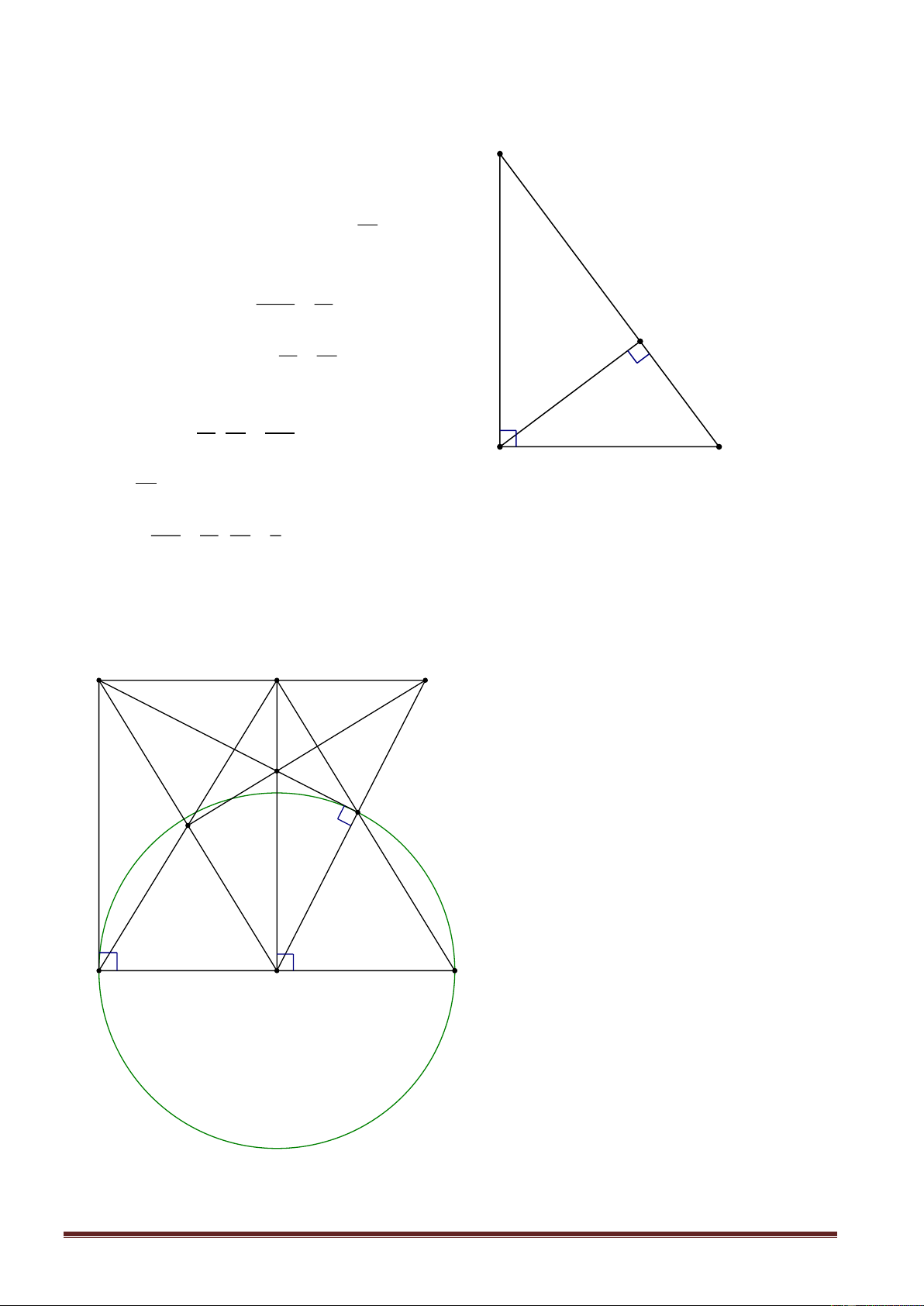
1. Cho tam giác ABC vuông tại A có đường cao AH , biết AB  5cm ; BH  3cm . Tính
AH , AC và sin CAH .
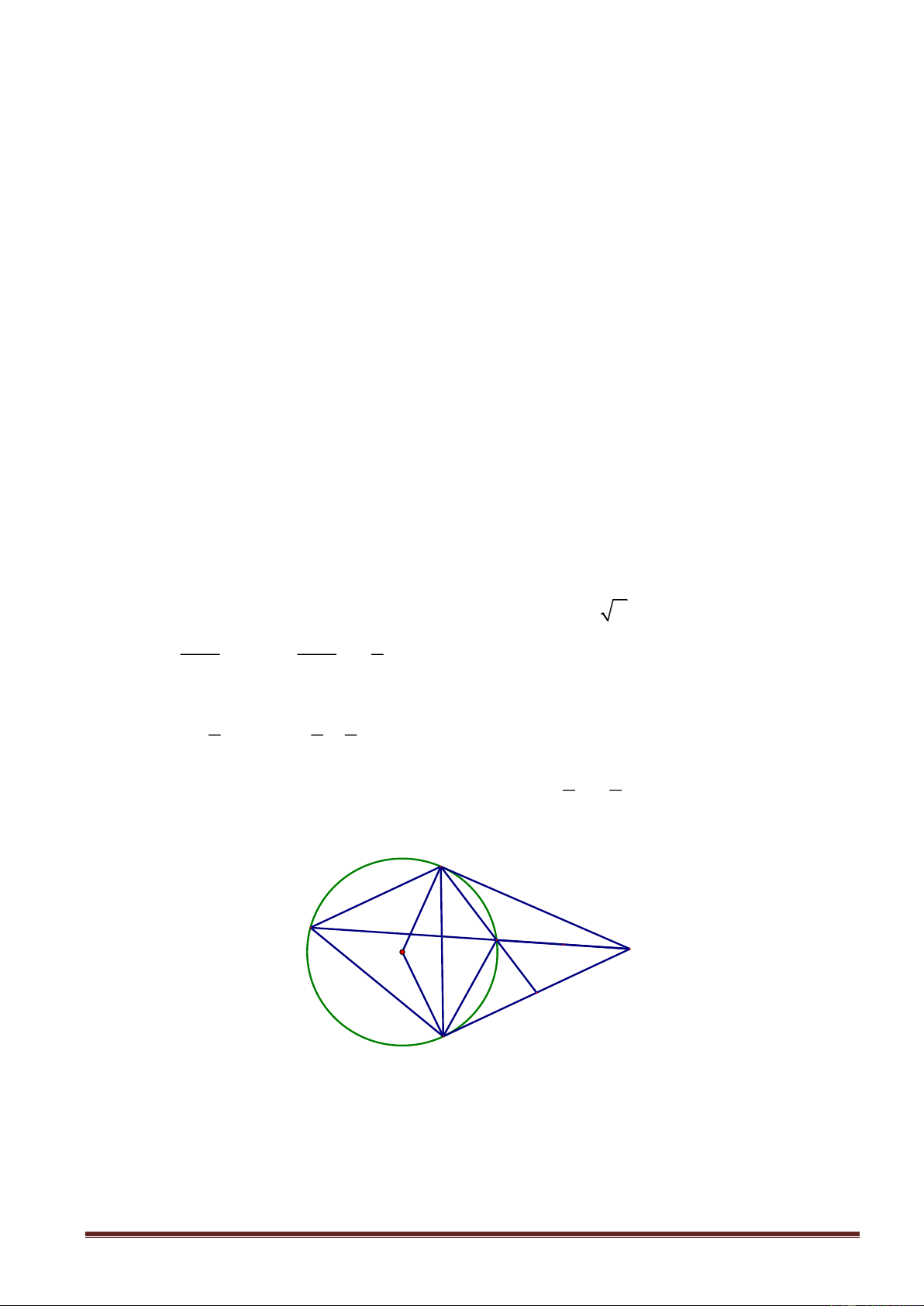
2.Cho đường tròn O,R , đường kính AB . Kẻ tiếp tuyến Ax với đường tròn O,R và lấy
trên tiếp tuyến đó điểm P sao cho AP  R , từ P kẻ tiếp tuyến thứ hai tiếp xúc với đường tròn
O,R tại M .
a) Chứng minh tứ giác APMO nội tiếp được đường tròn.
b) Chứng minh BM song song OP .
c) Biết đường thẳng vuông góc với AB tại O cắt BM tại N , AN cắt OB tại K , PM
cắt ON tại I , PN cắt OM tại J . Chứng minh ba điểm K ,I ,J thẳng hàng. ----HẾT----
Giám thị không giải thích gì thêm
Họ và tên thí sinh ----------------------------------
Số báo danh:-------------------------
Chữ kí giám thị 1:----------------------------------
Chữ kí giám thị 2:------------------ Trang 1 LỜI GIẢI
1. Rút gọn các biểu thức: K  9  45  3 5 x  x  x
2. Rút gọn các biểu thức: 4 2 Q   (với x  0 ) x  2 x
3. Giải phương trình: 2
x  4x  4  3 Lời giải
1. K  9  45  3 5  3  3 5  3 5  3 .    x  x  x
 x 2. x 2 x x 2 4 2  2. Q    
 x  2  x  2  2 x . x  2 x x  2 x 3. 2
x  4x  4  3 2
 x  4x  4  9 2
 x  4x  5  0  x   1  x  5  0 x   1  x  5 Vậy S 1;  5 Câu 1:
Trong mặt phẳng tọa độ Oxy ,cho Parabol  P 2
: y  2x và đường thẳng d  : y  2x  4
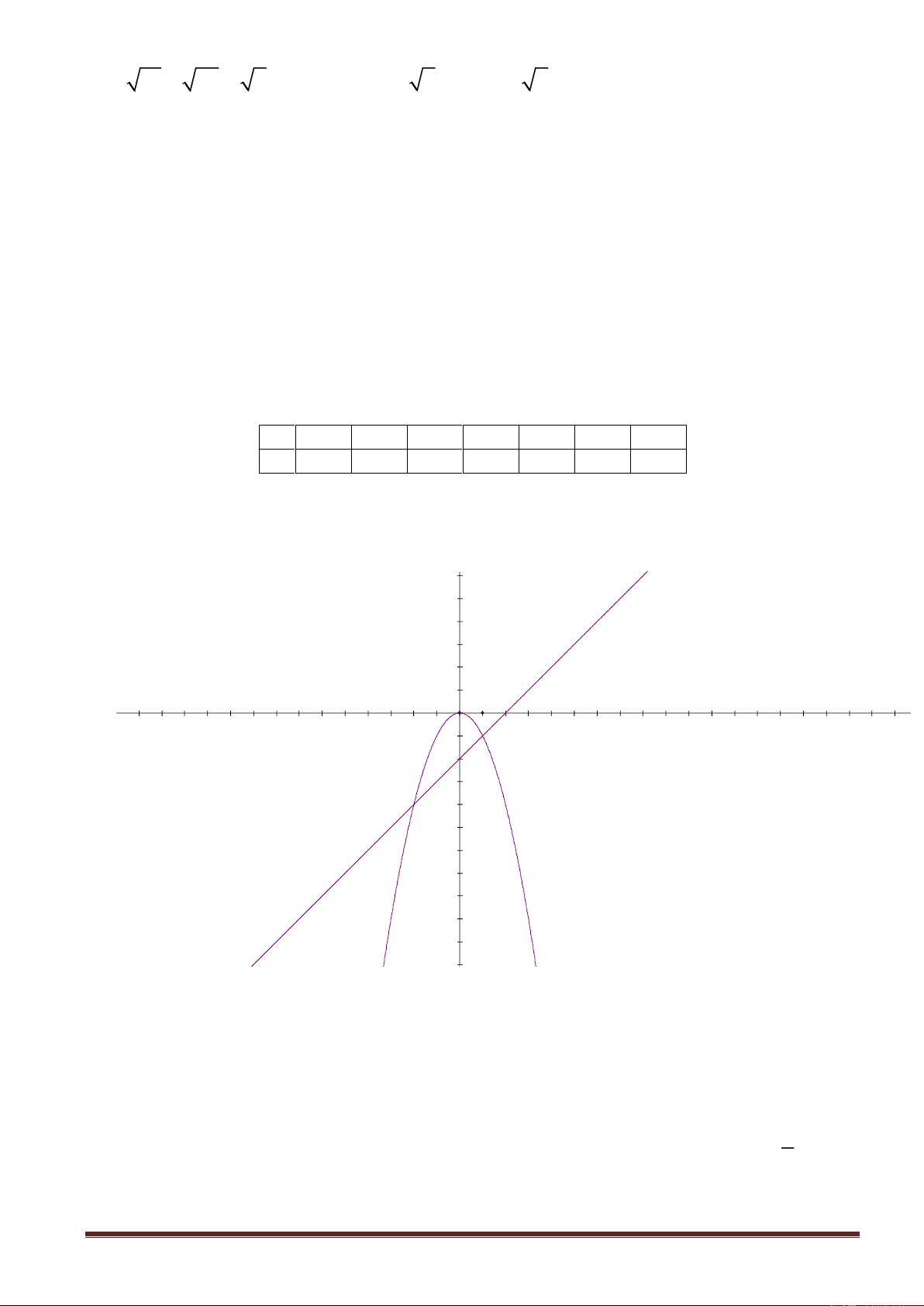
1.Vẽ Parabol P và đường thẳng d  trên cùng một mặt phẳng tọa độ Oxy .
2.Tìm tọa độ giao điểm của Parabol P và đường thẳng d  bằng phép tính.
3.Viết phương trình đường thẳng d '  : y  ax  b . Biết rằng d '  song song với d  và d và 1 
đi qua điểm N 2;3 . Lời giải
1. Học sinh tự vẽ hình.
2. Phương trình hoành độ giao điểm là x  1 y  2 2 2x  2x  4  2 2x  2x  4  0  2 x  x  2  0   x  2  y  8
Vậy tọa độ giao điểm là  1  ;2,2;8 . a  2
3. Vì d ' song song với d  nên  . b  4 x  2
Vì d '  và đi qua điểm N 2;3 nên  .  y  3
Thay vào d ' ta có 3  2.2  b  b  1  (TMĐK b  4 ).
Vậy phương trình d ' : y  2x 1. Câu 2: 1.Giải phương trình: 2
x  7x 10  0 (không giải trực tiếp bằng máy tính cầm tay) Trang 2
2x  y  5
2.Giải hệ phương trình: 
(không giảitrực tiếp bằng máy tính cầm tay) x  y  1
3.Cho phương trình (ẩn x ) 2
x  6x  m  0
a)Tìm giá trị m để phương trình có hai nghiệm phân biệt x ,x . 1 2
b)Tìm giá trị m để phương trình có hai nghiệm phân biệt x ,x thỏa mãn điều kiện 1 2 2 2
x  x  12 . 1 2 Lời giải 1. 2 x  7x 10  0
Ta có   b  ac   2 2 4 7  4 1 . 1 . 0  9  0
Phương trình có hai nghiệm phân biệt: b   7   x    5 1 2a 2 b   7   x    2 2 2a 2
2x  y  5 3  x  6 x  2 2.      x  y  1 y  1 x y  1
Vậy (x;y)  (2;1) . 3. 2
x  6x  m  0 a)   2 '
b'  ac  9  m .
Để phương trình có 2 nghiệm phân biệt thì '  0 9 m  0 m 9 x  x  6 1 2 b)Áp dụng Viet ta có  x x   m 1 2 2 x  2 x  12  x x x x 12 1 2   1 2    1 2    x  x  2  x x 4 1 2   1 2 2   x  x 4x x 4 1 2 2   1 2
 36 4m  4  m  8(tm) Vậy m  8 . Câu 3:
1. Cho tam giác ABC vuông tại A có đường cao AH , biết AB  5cm ; BH  3cm . Tính
AH , AC và sin CAH .
2.Cho đường tròn O,R , đường kính AB . Kẻ tiếp tuyến Ax với đường tròn O,R và lấy
trên tiếp tuyến đó điểm P sao cho AP  R , từ P kẻ tiếp tuyến thứ hai tiếp xúc với đường tròn
O,R tại M .
a) Chứng minh tứ giác APMO nội tiếp được đường tròn.
b) Chứng minh BM song song OP .
c) Biết đường thẳng vuông góc với AB tại O cắt BM tại N , AN cắt OB tại K , PM
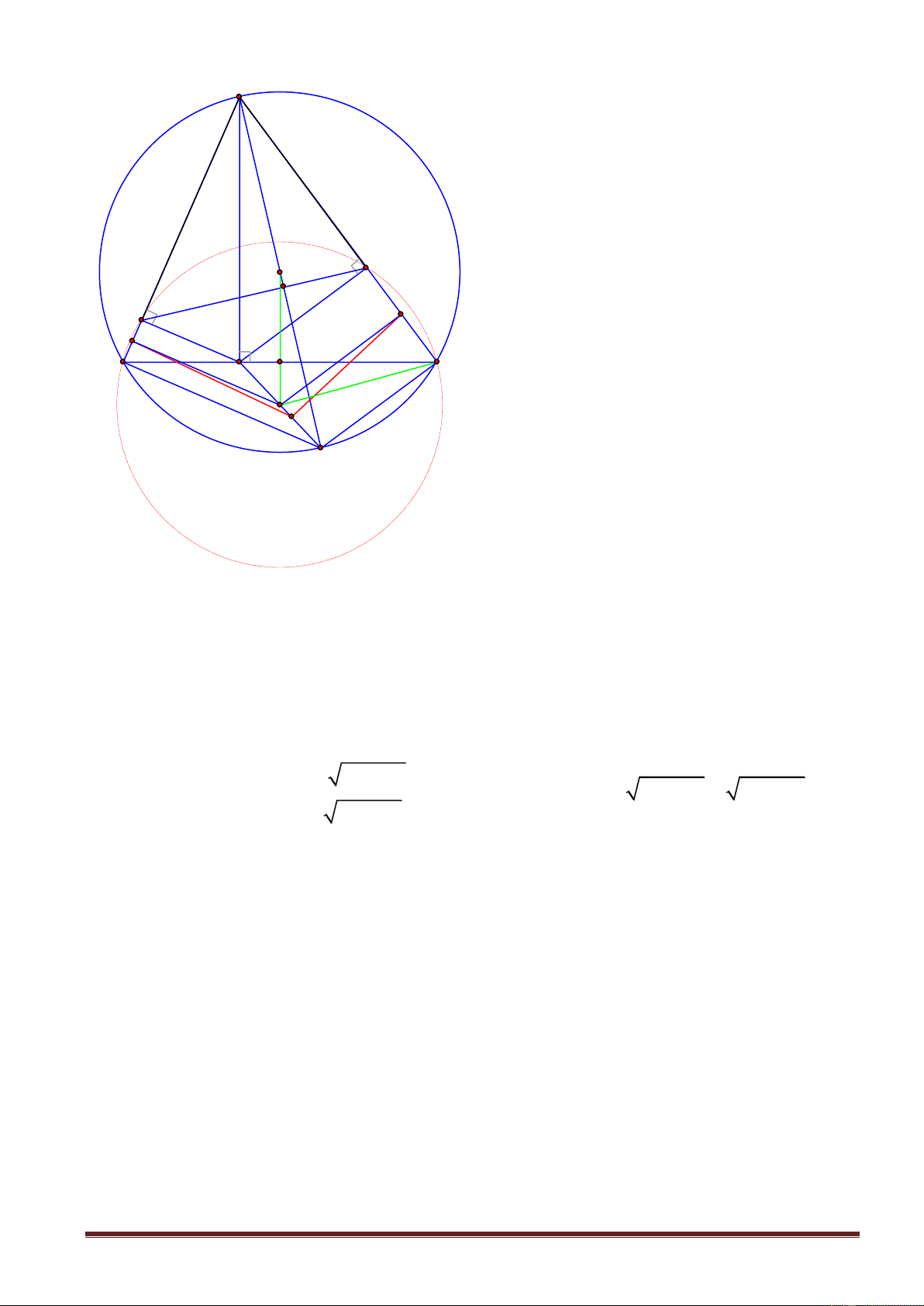
cắt ON tại I , PN cắt OM tại J . Chứng minh ba điểm K ,I ,J thẳng hàng. Lời giải Trang 3 1.
Áp dụng Pitago vào tam giác vuông ABH C 2 2 2
AB  AH  BH 2 2 2 2 2
 AH  AB  BH  5  3 16  AH  4( cm ) BH .BC  25 2 AB  BH.13  2 5  BH  (cm) . 13
Áp dụng hệ thức lượng vào tam giác vuông ABC 2 AH 16 2
AH  BH .CH  CH   cm BH 3 H Do đó 16 25
BC  BH  CH  3   cm 3 3 3cm
Áp dụng Pitago vào tam giác vuông ABC 16 25 400 2
AC  CH .BC    3 3 9 B 20 5cm A  AC  cm ) 3 CH 16 20 4 sin CAH   :  CA 3 3 5 2. P N J
a)Xét tứ giác APMO có   0  0  0 PAO PMO 90 90 180  APMO
nội tiếp đường tròn đường kính PO . I
b) Chứng minh BM // OP
BM  AM (góc nội tiếp chắn nửa đườn M tròn) (1) K
PA,PM là hai tiếp tuyến xuất phát từ
P  PO  AM (2)
Từ (1),(2)  BM // OP
c) Tam giác ANB có NO là đường cao
đồng thời là đường trung tuyến nên ANB A B cân tại N O
suy ra NO cũng là phân giác
hay ANO  ONB
Lại có ANO  PAN (so le trong, PA // NO )
ONB  NOP (so le trong, PO // BM )
Suy ra ANO  ONB  PNOA nội tiếp
đường tròn đường kính PO 0
 PNO  90  PAON là hình chữ nhật.
 K là trung điểm POvà AN Trang 4
Ta có JOP có ON ,PM là các đường cao cắt nhau tại I
 I là trực tâm JOP  JI  OP3
Mặt khác PNMOlà hình thang nội tiếp đường tròn đường kính PO
 PNMO là hình thang cân
 NPO  MOP hay  JPO  JOP
Do đó JPOcân tại J có JK là trung tuyến  JK cũng là đường cao
 JK  OP4
Từ 3 ,4  K,I ,J thẳng hàng.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT NAM ĐỊNH
NĂM HỌC 2019 – 2020 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
Phần 1: Trắc nghiệm (2,0 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm
Câu 1. Tìm tất cả các giá trị của m để hàm số y = (1 – m)x + m + 1 đồng biến trên R A. m > 1 B. m < 1 C. m < -1 D. m > -1
Câu 2. Phương trình 2
x  2x 1  0 có 2 nghiệm x ; x . Tính x  x 1 2 1 2 A. x  x  2 B. x  x  1 C. x  x  2  D. x  x  1  1 2 1 2 1 2 1 2
Câu 3. Cho điểm M(xM; yM) thuộc đồ thị hàm số y = -3x2 . Biết xM = - 2. Tính yM A. yM = 6 B. yM = -6 C. yM = -12 D. yM = 12 x  y  2
Câu 4. Hệ phương trình  có bao nhiêu nghiệm ? 3x   y 1 A. 0 B. 1 C. 2 D. Vô số
Câu 5. Với các số a, b thoả mãn a < 0, b < 0 thì biểu thức a ab bằng A. 2  a b B. 3  a b C. 2 a b D. 3  a b
Câu 6. Cho ∆ABC vuông tại A có AB = 3cm, AC = 4cm. Tính độ dài đường cao AH của ∆ABC 12 5 12 7 A. AH  cm B. AH  cm C. AH  cm D. AH  cm 7 2 5 2
Câu 7. Cho đường tròn (O; 2cm) và (O’; 3cm). biết OO’ = 6cm. Số tiếp tuyến chung của 2 đường tròn là A. 1 B. 2 C. 3 D. 4
Câu 8. Một quả bóng hình cầu có đường kính 4cm. Thể tích quả bóng là 32 32 256 256 A. 3  cm B. 3 cm C. 3  cm D. 3 cm 3 3 3 3
Phần 2: Tự luận (8,0 điểm) Câu 1. (1,5 điểm)
1) Rút gọn biểu thức A  3  2 2  3  2 2  2 1 6  2) Chứng minh rằng   . 
  a  3 1 Với a  0, a  9  a  3 a  3 a  9 
Câu 2. (1,5 điểm) Cho phương trình x2 – (m – 2)x - 6 = 0 (1) (với m là tham số)
1) Giải phương trình (1) với m = 0
2) Chứng minh rằng với mọi giá trị của m phương trình luôn có 2 nghiệm phân biệt 3) Gọi x    
1, x2 là 2 nghiệm của phương trình . Tìm các giá trị của m để 2 x x x (m 2)x 16 2 1 2 1 Trang 5 2
x  xy  y  7  0
Câu 3. (1,0 điểm) Giải hệ phương trình  2
x  xy  2y  4(x 1)
Câu 4. (2,5 điểm) Qua điểm A năm ngoài đường tròn (O) vẽ 2 tiếp tuyến AB, AC của đường tròn (B, C là
các tiếp điểm. Gọi E là trung điểm của đoạn AC, F là giao điểm thứ hai của EB với (O)
1) Chứng minh tứ giác ABOC là tứ giác nội tiếp và ∆CEF  ∆BEC
2) Gọi K là giao điểm thứ hai của AF với đường tròn (O). Chứng minh BF.CK = BK.CF
3) Chứng minh AE là tiếp tuyến của đường tròn ngoại tiếp ∆ABF
Câu 5. (1,5 điểm) Xét các số x, y, z thay đổi thoả mãn x3 + y3 + z3 – 3xyz = 2. 1
Tìm giá trị nhỏ nhất của biểu thức 2 2 2 2 P 
(x  y  z)  4(x  y  z  xy yz zx) 2
----------------------------Hết----------------------------
HƯỚNG DẪN GIẢI ĐỀ THI VÀO 10 TỈNH NAM ĐỊNH 2019 -2020 I/ Trắc nghiệm Câu 1 2 3 4 5 6 7 8 Đáp án B A C B D C D A II/ Tự luận Câu 1:
1) A  3  2 2  3  2 2  2  2. 2.11  2  2. 2.11 2 2
 ( 2 1)  ( 2 1)  2 1  2 1  2 1 2 1  2 
2) Với a  0, a  9 Ta có:  2 1 6       
   2( a 3) ( a 3)  6  VT . a 3   .    a  3  a  3 a  3 a  9  ( a  3)   2 a  6  a  3  6 a  3    1  VP a  3 a  3   Vậy 2 1 6   . 
  a  3 1 Với a  0, a  9  a  3 a  3 a  9  Câu 2: x  1   7
1/ Với m = 0 ta có phương trình: 2 x  2x  6  0   x  1   7
Vậy khi m =0 phương trình có hai nghiệm phân biệt x  1   7 và x  1   7 2/ Ta có 2 2   (m  2)  4.1.( 6
 )  (m 2)  24  0 với mọi m.
Vậy phương trình luôn có hai nghiệm phân biẹt với mọi m.
3) Phương trình luôn có hai nghiệm phân biẹt với mọi m. x  x  m  2 Theo Vi-ét ta có: 1 2  x x  6   1 2 Ta có : 2
x  x x  (m  2)x  16 2 1 2 1 Trang 6 2 2 2
 x  x x  (x  x )x 16  x  x x  x  x x 16 2 1 2 1 2 1 2 1 2 1 1 2 2 2
 (x  x )  2x x 16  0  (m  2)  2.( 6)  16  0 1 2 1 2 m  2  2 m  4 2  (m  2)  4     m  2  2  m  0
Vậy khi m = 0, m = 4 thì phương trình có 2 nghiệm phân biệt thỏa mãn: 2
x  x x  (m  2)x  16 2 1 2 1 Câu 3: 2
x  xy  y  7  0 (1)  2
x  xy  2y  4(x 1) (2) Ta có: 2
(2)  x  xy  2y  4x  4  0 2
 (x  4x  4)  xy 2 y  0 2
 (x 2)  y(x  2)  0 x  2  0 x  2
 (x  2)(x  2  y)  0     x  2  y  0 x  2  y
+ Thay x = 2 vào phương trình (1) ta được: 4 – 2y + y – 7 = 0  y = -3
+ Thay x = 2 – y vào phương trình (1) ta được : 2
(2  y)  (2  y)y  y  7  0 2 2
 4  4y  y  2y  y  y  7  0 2  2y  5y  3  0 Phương trình 2 2y  5y  3  0 có 2   ( 5  )  4.2.( 3  )  49  0,   7 5  7 5  7 1 Ta có: y   3; y    1 2 4 4 2
 y  3  x  2  3  1  1 1 5
 y    x  2   2 2 2   5 1 
Vậy hệ phương trình có nghiệm (x; y)  (1; 3), (2;  3), ;      2 2  Bài 4: B K F A O H E x C
1) Chứng minh tứ giác ABOC là tứ giác nội tiếp và ∆CEF  ∆BEC
Có AB, AC là các tiếp tuyến của đường tròn (O) , B và C là ác tiếp điểm 0 0
AB  OB, AC  OC  ABO  90 , ACO  90 Tứ giác ABOC có 0 0 0
ABO  ACO  90  90  180 nên tứ giác ABOC nội tiếp đường tròn + Đường tròn (O) có:
EBC là góc nội tiếp chắn cung CF Trang 7
ECF là góc tạo bởi tia tiếp tuyến AC và dây cung CF
 EBC  ECF (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung CF) Xét ∆CEF và ∆BEC có BEC là góc chung
EBC  ECF (chứng minh trên)
 ∆CEF  ∆BEC (g . g)
2) Chứng minh BF.CK = BK.CF
Xét ∆ABF và ∆AKB có BAK là góc chung
ABF  AKB (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BF)  BF AF ∆ABF  ∆AKB (g . g)   (1) BK AB
Chứng minh tương tự ta có: CF AF ∆ACF  ∆AKC (g . g)   (2) CK AC
Mà AB = AC (t/c 2 tiếp tuyến cắt nhau của (O)) (3) BF CF Từ (1), (2) và (3)     BF.CK  BK.CF BK CK
3) Chứng minh AE là tiếp tuyến của đường tròn ngoại tiếp ∆ABF
Có ∆ECF  ∆EBC (Chứng minh câu a) EC EF 2    EC  EB.EF EB EC EA EF Mà EC = EA (gt) 2  EA  EB.EF   EB EA Xét ∆BEA  ∆AEF có: EA EF  EB EA AEB là góc chung
 ∆BEA  ∆AEF (c.g.c)  EAF  EBA ( hai góc tương ứng) hay EAF  ABF
Trên nửa mặt phẳng bờ AB có chưa điểm E, kẻ tia Ax là tiếp tuyến của đường tròn ngoại tiếp
ABF  EAF  xAF (Cùng bằng ABF)  tia AE trùng với tia Ax
 AE là tiếp tuyến của đường tròn ngoại tiếp ∆ABF Câu 5: Ta có:
x³ + y³ + z³ - 3xyz = (x + y)³ - 3xy(x - y) + z³ - 3xyz = 2
 [(x + y)³ + z³] - 3xy(x + y +z ) = 2
 (x + y + z)³ - 3z(x + y)(x + y + z) - 3xy(x – y - z) = 2
 (x + y + z)[(x + y + z)² - 3z(x + y) - 3xy] = 2
 (x + y + z)(x² + y² + z² + 2xy + 2xz + 2yz - 3xz - 3yz - 3xy) = 2
 (x + y + z)(x² + y² + z² - xy - xz - yz) = 2
 x² + y² + z² - xy - xz – yz ≠ 0
Chứng minh: x² + y² + z² - xy - xz – yz ≥ 0 với mọi x, y, z
 x² + y² + z² - xy - xz – yz > 0  x + y + z t
Đặt x + y + z = t (t > 0)  x² + y² + z² - xy - xz – yz  khi đó ta có 2 Trang 8 2 2 1 t 8  t  8 2 2 2 2 P 
(x  y  z)  4(x  y  z  xy yz zx) 
    2   2 2 2 t 2 t   2 2
Áp dụng BĐT Cô si ta có: t t  2  2
.2  2t (dấu bằng xảy ra  t = 2) 2 2 8 8 2t 
 2 2t.  8 (dấu bằng xảy ra  t = 2) t t
 P ≥ 8 – 2 = 6. Tồn tại x = y = 1, z = 0 thì P = 6
Vậy giá trị nhỏ nhất của P là 6
ĐỀ THI TUYỂN SINH VÀO LỚP 10 TỈNH NGHỆ AN NĂM HỌC 2019 - 2020
Câu 1: (2 điểm) Rút gọn biểu thức sau:
a) A   12  2 5 3  60. 2 4x x  6x  9 b) B  . với 0 < x < 3. x  3 x
Câu 2: (2,5 điểm)
1) Xác định hàm số bậc nhất y = ax + b, biết rằng đồ thị hàm số đi qua điểm M(1; -1) và N(2; 1). 2) Cho phương trình: 2 2
x  2mx  m  m  3  0 (1), với m là tham số.
a) Giải phương trình (1) với m = 4.
b) Tìm các giá trị của m để phương trình (1) có hai nghiệm x , x và biểu thức: 1 2
P  x x  x  x đạt giá trị nhỏ nhất. 1 2 1 2
Câu 3: (1,5 điểm)
Tình cảm gia đình có sức mạnh phi trường. Bạn Vì Quyết Chiến - Cậu bé 13 tuổi qua
thương nhớ em trai của mình đã vượt qua một quãng đường dài 180km từ Sơn La đến bệnh viện
Nhi Trung ương Hà Nội để thăm em. Sau khi đi bằng xe đạp 7 giờ, bạn ấy được lên xe khách và
đi tiếp 1 giờ 30 phút nữa thì đến nơi. Biết vận tốc của xe khách lớn hơn vận tốc của xe đạp là
35km/h. Tính vận tốc xe đạp của bạn Chiến.
Câu 4: (3,0 điểm)
Cho đường tròn (O) có hai đường kính AB và MN vuông góc với nhau. Trên tia đối của tia
MA lấy điểm C khác điểm M. Kẻ MH vuông góc với BC (H thuộc BC).
a) Chứng minh BOMH là tứ giác nội tiếp.
b) MB cắt OH tại E. Chứng minh ME.MH = BE.HC.
c) Gọi giao điểm của đường tròn (O) với đường tròn ngoại tiếp ∆MHC là K. Chứng minh 3
điểm C, K, E thẳng hàng.
Câu 5: (1,0 điểm) Giải phương trình: 2 2
5x  27x  25  5 x 1  x  4.
HƯỚNG DẪN LÀM BÀI Câu 1:
a) A   12  2 5 3  60  36  2 15  2 15  36  6
b) Với 0 < x < 3 thì x  3  3 x 4x x  6x  9 2 x x 32 2 2  x x  3 2  x 3  x B  .  .  .   2     x 3 x x 3 x 3 x x 3 x x Câu 2:
1) Vì đồ thị hàm số đi qua điểm M(1; -1) nên a b  1 
đồ thị hàm số đi qua điểm N(2; 1) nên 2a  b 1 Trang 9
a  b   a  Yêu cầu bài toán  1 2    2a  b 1 b   3 
Vậy hàm số phải tìm là y = 2x - 3.
2) a) Với m = 4, phương trình (1) trở thành: 2
x  8x 15  0 . Có  1  0
Phương trình có hai nghệm phân biệt x  3; x  5; 1 2
b) Ta có: ∆' = m2   2 m  m   2 2 1.
3  m  m  m  3  m  3 .
Phương trình (1) có hai nghiệm x , x khi ∆'  0  m  3  0  m  3 1 2
x  x  2m 1 2
Với m  3 , theo định lí Vi-ét ta có:  2
x .x  m  m  3  1 2
Theo bài ra: P  x x  x  x  x x  (x  x ) 1 2 1 2 1 2 1 2
Áp đụng định lí Vi-ét ta được: 2 2
P  m  m  3  2m  m  3m  3  ( m m  3)  3
Vì m  3 nên m(m  3)  0 , suy ra P  3. Dấu " = " xảy ra khi m = 3.
Vậy giá trị nhỏ nhất của P là 3 khi m = 3. Bài 3:
Đổi 1 giờ 30 phút = 1,5 giờ.
Gọi vận tốc xe đạp của bạn Chiến là x (km/h, x  0 )
Vận tốc của ô tô là x  35(km/h)
Quãng đường bạn Chiến đi bằng xe đạp là: 7x (km)
Quãng đường bạn Chiến đi bằng ô tô là: 1,5(x  35) (km)
Do tổng quãng đường bạn Chiến đi là 180km nên ta có phương trình:
7x 1,5(x  35)  180  7x 1,5x  52, 2  180  8,5x  127,5  x  15 (thỏa mãn)
Vậy bạn Chiến đi bằng xe đạp với vận tốc là 15 km/h. Bài 4: a) Ta có: 0
MOB  90 (do AB  MN) và 0
MHB  90 (do MH  BC) C Suy ra: 0 0 0
MOB  MHB  90  90  180
Tứ giác BOMH nội tiếp. M H
b) ∆OMB vuông cân tại O nên OBM  OMB (1) K
Tứ giác BOMH nội tiếp nên OBM  OHM (cùng chắn cung OM) E
và OMB  OHB (cùng chắn cung OB) (2)
Từ (1) và (2) suy ra: OHM  OHB A B O ME MH
 HO là tia phân giác của MHB   (3) BE HB
Áp dụng hệ thức lượng trong ∆BMC vuông tại M có MH là HM HC đường cao ta có: 2 N
HM  HC.HB   (4) HB HM ME HC Từ (3) và (4) suy ra: 
5  ME.HM  BE.HC (đpcm) BE HM c) Vì 0
MHC  90 (do MH  BC) nên đường tròn ngoại tiếp ∆MHC có đường kính là MC 0
 MKC  90 (góc nội tiếp chắn nửa đường tròn)
MN là đường kính của đường tròn (O) nên 0
MKN  90 (góc nội tiếp chắn nửa đường tròn) 0
 MKC  MKN 180
3 điểm C, K, N thẳng hàng (*) HC MC ∆MHC ∽ ∆BMC (g.g)  
. Mà MB = BN (do ∆MBN cân tại B) MH BM Trang 10  HC MC  , kết hợp với ME HC  (theo (5) ) HM BN BE HM MC ME Suy ra:  . Mà 0
EBN  EMC  90  ∆MCE ∽ ∆BNE (c.g.c) BN BE
 MEC  BEN , mà 0
MEC  BEC  180 (do 3 điểm M, E, B thẳng hàng) 0
 BEC  BEN 180
 3 điểm C, E, N thẳng hàng (**)
Từ (*) và (**) suy ra 4 điểm C, K, E, N thẳng hàng
3 điểm C, K, E thẳng hàng (đpcm)
Câu 5: ĐKXĐ: x  2 Ta có: 2 2
5x  27x  25  5 x 1  x  4 2 2
 5x  27x  25  5 x 1  x  4 2 2 2
 5x  27x  25  x  4  25x  25 10 (x 1)(x  4) 2 2
4x  2x  4  10 x 1)(x  4) 2 2
 2x  x  2  5 (x 1)(x  4) (1) Cách 1: (1)   2
x  x   2 2
4 4x 13x  26  0 Giải ra được:       x  1 5 (loại); x  1 5 (nhận); 13 3 65 x (nhận); 13 3 65 x (loại) 8 8 Cách 2: (1) 
 2x  x x    2 5 2 2
2 x  x  2  3 x  2 (2) Đặt 2 a 
x  x  2; b 
x  2 (a  0; b  0)
Lúc đó, phương trình (2) trở thành: a b 2 2  2 a  ab  2 2 5
3b  0  a  b2a  3b 
5ab  2a  3b  0   (*) 2a  3b
x 1 5(k ) tm - Với a = b thì 2 2
x  x  2 
x  2  x  2x  4   x 1 5( ) tm  13  3 65 x  (tm) 8 - Với 2a = 3b thì 2 2
2 x  x  2  3 x  2  4x 13x  26  0    13  3 65 x  (ktm)  8 13  3 65
Vậy phương trình đã cho có hai nghiệm: x 1 5 và x  . 8
TUYỂN SINH VÀO 10 NINH BÌNH NĂM HỌC 2019-2020 Câu 1:
a) Rút gọn biêu thức A  2  18 . 3
 x  y  2
b) Giải hệ phương trình 
2x  y  3.
c) Tìm tọa độ giao điểm của hai đường thẳng d : y  x  3 và d : y  2  x  3 . 1   2 Trang 11 x x Câu 2: 1. Rút gọn biểu thức 3 6 P   
(với x  0, x  9 ). x  3 x  3 x  9 2. Cho phương trình 2
x  5x  m  2  0  
1 với m là tham số.
a) Giải phương trình (1) khi m  6.
b) Tìm tất cả các giá trị của m để phương trình (1) có hai nghiệm x , x sao cho biểu thức 1 2
S   x  x 2  8x x đạt giá trịNINH lớn nhất. 1 2 1 2 Câu 3:
Bác Bình gửi tiết kiệm 100 triệu đồng vào ngân hàng A, kì hạn một năm. Cùng ngày, bác
gửi tiết kiệm 150 triệu đồng vào ngân hàng B, kì hạn một năm, với lãi suất cao hơn lãi suất
của ngân hàng A là 1% / năm. Biết sau đúng 1 năm kể từ ngày gửi tiền. Bác Bình nhận được
tổng sổ tiền lãi là 16.5 triệu đồng từ hai khoản tiền gửi tiết kiệm nêu trên. Hỏi lãi suất tiền
gửi tiết kiệm kì hạn một năm của ngân hàng A là bao nhiêu phần trăm? Câu 4:
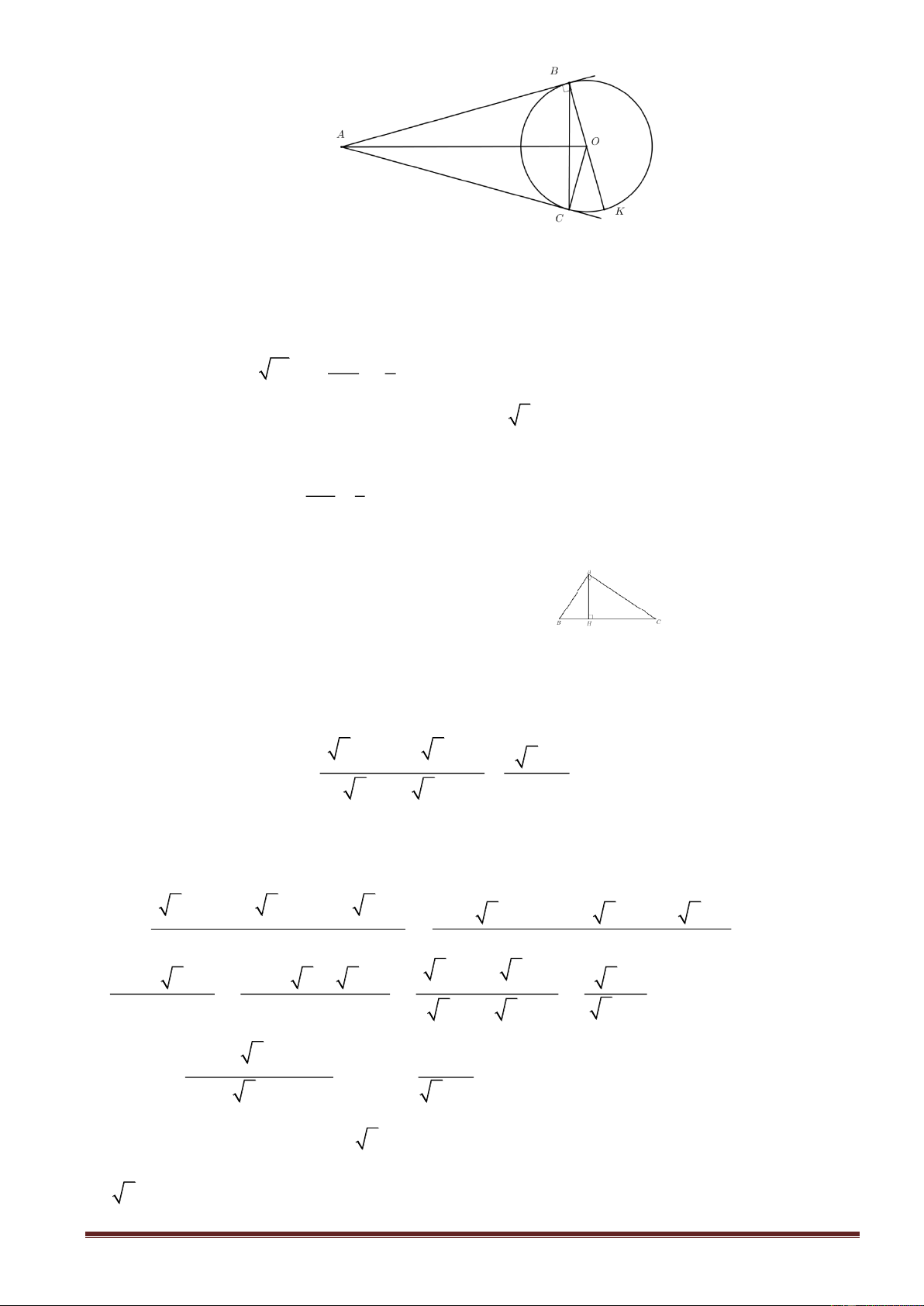
1. Cho đựờng tròn tâm O một điểm M nằm ngoài đường tròn. Từ M kẻ đường thẳng đi
qua tâm O , cắt đường tròn tại hai điểm ,
A B ( A nằm giữa M và B ). Kẻ đường thẳng thứ
hai đi qua M , cắt đường tròn tại hai điểm phân biệt C, D ( C nằm giữa M và D , C khác
A ). Đường thẳng vuông góc với MA tại M cắt đường thẳng BC tại N , đường thẳng NA
cắt đường tròn tại điểm thứ hai là E . a.
Chứng minh tứ giác AMNC là tứ giác nội tiếp.
b. Chứng minh DE vuông góc với MB .
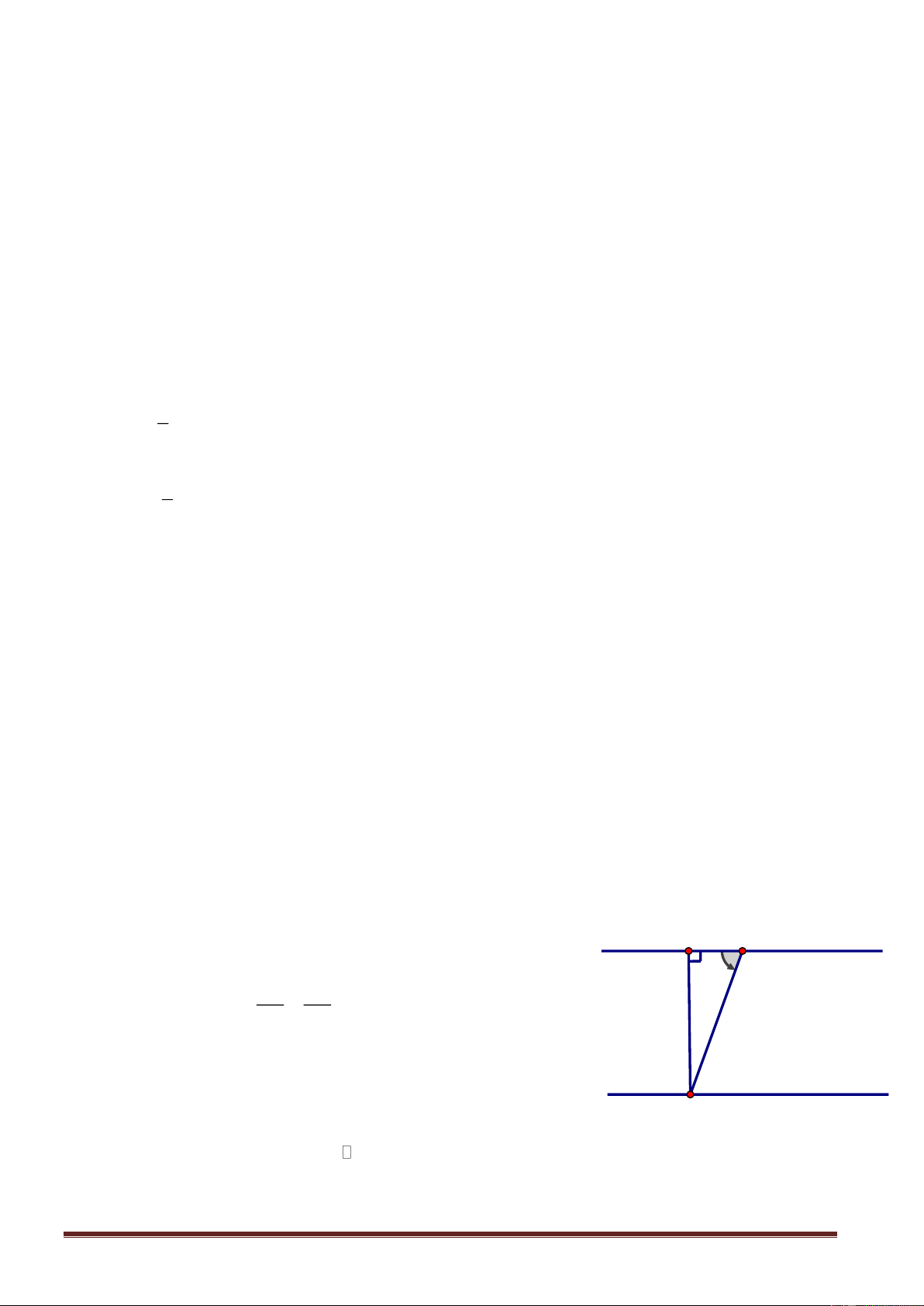
2. Trên một khúc sông với 2 bờ song song với nhau, có một chiếc đò dự định chèo qua sông
từ vị trí A ở bở bên này sang vị trí B ở bờ bên kia, đường thẳng AB vuông góc với các bờ
sông. Do bị dòng nước đẩy xiên nên chiếc đò đã cập bờ bên kia tại vị tri C cách B mội
khoảng bằng 30 m. Biết khúc sông rộng 150 m, hỏi dòng nước đã đẩy chiếc đò lệch đi một
góc có số đo bằng bao nhiêu? (kết quả làm tròn đến giây).
Câu 5: 1. Tìm tất cả các số nguyên tố p sao cho tổng các ước nguyên dương của 2 p là một số chính phương. 2. Cho ,
x y, z là các số thực dương thỏa mãn x  y  z  2019 . Tìm giá trị nhỏ nhất của 2 2 2 biểu thức x y z T    . x  yz y  zx z  xy LỜI GIẢI Câu 1 a) 2 A  2  18  2  2.3  2  3 2  4 2 3
 x  y  2 5  x  5 x  1 x  1 b)       
2x  y  3
2x  y  3 2.1 y  3 y  1 
Vậy hệ phương trình có nghiệm duy nhất là (x;y)= (1;- ) 1
c) Tọa độ giao điểm của hai đường thằng d : y  x  3 và d : y  2
 x  3 là nghiệm của hệ 1   2 phương trình y  x  3 y  x  3 y  x  3 x  2       y   2  x  3 x  3  2  x  3 x  2 y  1 
Vậy tọa độ giao điểm của hai đường thằng d : y  x 3 và d : y  2  x  3 là 1   2 (x;y)= (2;- ) 1 Câu 2 x 3 6 x 1. P    x  3 x  3 x  9 Trang 12 x  x  3 3 x  3 6  x   
x  3 x  3  x  3 x  3  x  3 x  3
x  3 x  3 x  9  6 x  
x  3 x  3 x 
 x 3 x 3 9 
  x   x     x   x   1 3 3 3 3 Vậy P  1 2. Cho phương trình 2
x  5x  m  2  0   1
a) Khi m  6 phương trình (1) trở thành 2
x  5x  4  0 có a b  c 1 5 4  0 nên có hai c nghiệm là x  1  ; x    4  1 2 a
Vậy, khi m  6thì tập nghiệm của phương trình đã cho là S   4  ;  1 b) 2
x  5x  m  2  0   1 Ta có 2
  5  4m  2  33 4m 33
Phương trình (1) có hai nghiệm x ; x khi và chỉ khi   0  33  4m  0  m  1 2 4
x  x  5
Áp dụng định lí Vi ét cho phương trình (1) ta có 1 2 
x .x  m  2  1 2
Theo đề ra ta có S  x  x 2 8x x 1 2 1 2 2 2
 x  2x x  x  8x x 1 1 2 2 1 2
 x  x  4x x 1 2 2 1 2   5
 2  4m  2 17  4m 33 Ta có m 
 4m  33  17  4m  17  33  50 4 33
Vậy giá trị lớn nhất của S  50 . Dấu “=” xảy ra khi m  4 Câu 3
Gọi lãi suất gửi tiết kiệm kì hạn một năm của ngân hàng A là % x / năm. ( x  0 )
Thì lãi suất gửi tiết kiệm kì hạn một năm của ngân hàng B là  x   1 % / năm.
Tiền lãi bác Bình nhận được sau 1 năm gửi vào ngân hàng A là : 100 % x (triệu đồng)
Tiền lãi bác Bình nhận được sau 1 năm gửi vào ngân hàng B là : 150x   1 % (triệu đồng)
Tổng số tiền lãi bác Bình nhận được từ hai khoản tiết kiệm trên là 16,5 triệu đồng nên ta có
phương trình : 100x% 150x   1 %  16,5
100x 150x 150 1650  250x 1500
 x  6 (thỏa mãn ) N
Vậy lãi suất tiền gửi tiết kiệm kì hạn một năm của D ngân hàng A là 6% C Câu 4 1. B M A O Trang 13 E
a. Chứng minh tứ giác AMNC là tứ giác nội tiếp. Ta có 0
MN  AB  NMA  90
ACB là góc nội tiếp chắn nửa đường tròn nên 0 ACB  90
 ACB  NMA 0  90 
Tứ giác AMNC là tứ giác nội tiếp (tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện)
b. Chứng minh DE vuông góc với MB .
Ta có tứ giác AMNC là tứ giác nội tiếp (chứng minh trên)
 CNA  CMA (hai góc nội tiếp cùng chắn cung AC )
Hay BNE  BMD (1)
Xét đường tròn O ta có :
BNE là góc có đỉnh nằm ngoài đường tròn chắn cung AC và BE 1
 BNE  sñBE sñAC (2) 2
DMB là góc có đỉnh nằm ngoài đường tròn chắn cung AC và BD 1
 DMB  sñBD sñAC (3) 2
Từ (1), (2) và (3) suy ra sñBE  sñBD
 BD  BE (hai cung bằng nhau căng hai dây bằng nhau)
 B nằm trên đường trung trực của DE (4) Lại có 0
ADB  AEB  90 (các góc nội tiếp chắn nửa đường tròn O )
Xét ADB và AEB ta có : 0
ADB  AEB  90 (chứng minh trên) AB chung
BD  BE (chứng minh trên)
Do đó ADB  AEB (ch-cgv)
 AD  AE (hai cạnh tương ứng)
 Anằm trên đường trung trực của DE (5)
Từ (4) và (5) suy ra AB là đường trung trực của DE
 AB  DE hay MB  DE (đpcm) 2.
B 30m C Ta có hình vẽ :
Ta có AB  BC  ABC vuông tại B Do đó AB 150 0 tan ACB  
 5  ACB  78 41'24" 150m BC 30
Vậy dòng nước đã đẩy chiếc đò đi lệch một góc có số đo bằng 0 0 0
90  78 41' 24"  11 18 '36" Câu 5 A 1.
Ta có p là số nguyên tố ( * p  ) 2
 p là số có các ước dương là 2 1; ; p p
Theo đề bài ta có tổng các ước nguyên dương của p là một số chính phương Trang 14 2 2 *
1 p  p  k (k  ) 2 2
 4k  4  4 p  4 p
 4k  2 p  2 2 1  3
 4k  2 p  2 2 1  3
 2k  2p  
1 2k  2 p   1  3 (*) Ta có * k, p 
 2k  2 p 1  0; 2k  2 p 1 2k  2 p 1
2k  2 p 1 1
2k  2 p  2
k 1 (thoûa maõn) (*)      
2k  2 p 1  3
2k  2 p  2
 p  0 (khoâng thoûa maõn)
Vậy không có số nguyên tố p nào thỏa mãn đề bài 2. a b c    2 2 2 2 a b c
Ta chứng minh bất đẳng thức    với a,b,c, x, y,z  0 x y z x  y  z
Áp dụng bất đẳng thức Bu – nhi – a - cốp – xki cho ba bộ số  a   b   c  ; x ,    ; y , ; z      x  y    z  2 2 2   2 2 2       2 2 2 a b c a b  c    ta có    x  y  z            
  x    y    z   x y z    x  y    z       2  a b c    . x  . y 
. z   a  b  c2   x y z   a b c    2 2 2 2 a b c     (*) x y z x  y  z a b c Dấu “=” xảy khi khi   x y z y  z z  x x  y
Áp dụng bất đẳng thức Cô si ta có yz  ; zx  ; xy  2 2 2 2 2 2 x y z  T    y  z z  x x  y x  y  z  2 2 2 2 2 2 2x 2y 2z    2x  y  z x  2y  z x  y  2z 2 2 2  x y z   2   
 2x  y  z x  2y  z x  y  2z 
Áp dụng bất đẳng thức (*) ta có    2 x y z x  y  z 2019 T  2   4x  y  z 2 2
Dấu “=” xảy ra khi x  y  z  673
Vậy giá trị nhỏ nhất của biểu thức 2019 T  khi x  y  z  673 2 Trang 15
TUYỂN SINH VÀO 10 BẮC NINH NĂM HỌC 2019-2020
I. TRẮC NGHIỆM (3,0 điểm) Chọn phương án trả lời đúng trong các câu sau: Câu 1:
Khi x = 7 biểu thức 4 có giá trị là x + 2 - 1 1 4 4 A. . B. . C. . D. 2 . 2 8 3 Lời giải Chọn: D
Thay x  7 (thỏa mãn) vào biểu thức 4
ta tính được biểu thức có giá trị bằng x  2 1 4 4   2 . 7  2 1 3 1 Câu 2:
Trong các hàm số sau, hàm số nào đồng biến trên ? A. y = 1 - x . B. y = 2x - 3 .
C.y = (1 - 2)x .
D.y = - 2x + 6 . Lời giải Chọn: B
Hàm số y  2x  3 đồng biến trên . Câu 3:
Số nghiệm của phương trình 4 2
x - 3x + 2 = 0 là A.1 . B. 2 . C. 3 . D. 4 . Lời giải Chọn: D Đặt 2
t  x (t  0) . Khi đó phương trình tương đương 2
t  3t  2  0 .
Ta thấy 1-3 2  0 . Nên phương trình có hai nghiệm t 1 (thỏa mãn); t  2 (thỏa mãn). 2 x 1 x  1  Khi đó     2 x  2  x   2 Câu 4: Cho hàm số 2
y = ax (a ¹ ) 0 . Điểm M (1; )
2 thuộc đồ thị hàm số khi 1 1 A.a = 2 . B.a = . C.a = - 2 . D.a = . 2 4 Lời giải
Chọn A .
Vì M (1;2) thuộc đồ thị hàm số 2
y  ax (a  0) nên ta có 2 2  .1 a
 a  2 (thỏa mãn). Câu 5:
Từ điểm A nằm bên ngoài đường tròn (O) kẻ hai tiếp tuyến A B,A C tới đường tròn (B,C
là các tiếp điểm). Kẻ đường kính BK . Biết ·
B A C = 30o , số đo của cung nhỏ CK là A. 30° . B. 60° . C.120° . D.150° . Lời giải Chọn: A. Trang 16
Từ giả thiết ta suy ra tứ giác ABOC nội tiếp nên BAC  COK  30 , mà COK  sđ CK nên
Số đo cung nhỏ CK là 30 . Câu 6:
Cho tam giác A BC vuông tại A . Gọi H là chân đường cao hạ từ đỉnh A xuống cạnh B C . Biết HB 1 A H = 12cm , =
. Độ dài đoạn BC là HC 3 A. 6 cm . B. 8 cm . C. 4 3 cm . D.12 cm . Lời giải Chọn: B
Theo đề bài ta có: HB 1
  HC  3HB . Áp HC 3
dụng hệ thức lượng trong tam giác ABC vuông
tại A có đường cao AH ta có 2
AH  BH .HC  12  BH .3BH 2
 BH  4  BH  2
 HC  3.HB  3.2  6
 BC  HB  HC  2  6  8 cm
II. TỰ LUẬN (7,0 điểm) 2 2 ( x + ) 1 + ( x - ) 1 3 x + 1 Câu 7:
Cho biểu thức A = -
với x ³ 0 , x ¹ 1 . ( x - )( x + ) x - 1 1 1 a) Rút gọn biểu thức A .
b) Tìm x là số chính phương để 2019A là số nguyên. Lời giải 2 2 ( x + ) 1 + ( x - ) 1 - 3 x - 1
x + 2 x + 1 + x - 2 x + 1 - 3 x - 1 a) A = = x - 1 x - 1 x - 1 2 x - 1 2x - 3 x + 1 2x - 2 x - x + 1 ( )( ) 2 x - 1 = = = = . x - 1 x - 1 ( x - ) 1 ( x + ) 1 x + 1 2019(2 x + 2 - 3) 6057 2019A = = 4038 - . x + 1 x + 1 b)
2019A là số nguyên khi và chỉ khi x + 1 là ước nguyên dương của 6057 gồm: 1; 3; 9; 673, 2019; 6057 .
+) x + 1 = 1 Û x = 0 , thỏa mãn. Trang 17
+) x + 1 = 3 Û x = 4 , thỏa mãn.
+) x + 1 = 9 Û x = 64 , thỏa mãn.
+) x + 1 = 673 Û x = 451584 , thỏa mãn.
+) x + 1 = 2019 Û x = 4072324 , thỏa mãn.
+) x + 1 = 6057 Û x = 36675136 , thỏa mãn. Câu 8:
An đếm số bài kiểm tra một tiết đạt điểm 9 và điểm 10 của mình thấynhiều hơn16 bài.
Tổng số điểm của tất cả các bài kiểm tra đạt điểm 9 và điểm 10 đó là 160 . Hỏi An được
bao nhiêu bài điểm 9 và bao nhiêu bài điểm 10 ? Lời giải
Gọi số bài điểm 9 và điểm 10 của An đạt được lần lượt là x, y (bài)(x,y Î ¥ ).
Theo giả thiết x + y > 16 .
Vì tổng số điểm của tất cả các bài kiểm tra đó là 160 nên 9x + 10y = 160 . Ta có = x + y ³ (x + y) 160 160 9 10 9 Þ x + y £ . 9 160
Do x + y Î ¥ và 16 < x + y £
nên x + y = 17 . 9 ìï x + y = 17 ìï x = 17- y ìï x = 10 Ta có hệ ï ï ï í Û í Û í (thỏa mãn).
ï 9x + 10y = 160 ï 9 ïî
ï (17 - y )+ 10y = 160 ï y = 7 ï ï î î
Vậy An được 10 bài điểm 9 và 7 bài điểm 10 . · Câu 9:
Cho đường tròn (O), hai điểm A,B nằm trên (O) sao cho A OB = 90º . Điểm C nằm trên
cung lớn A B sao cho AC > BC và tam giác A BC có ba góc đều nhọn. Các đường cao
A I , B K của tam giác A BC cắt nhau tại điểm H . B K cắt (O ) tại điểmN (khác điểmB );
A I cắt (O ) tại điểmM (khác điểm A ); NA cắt MB tại điểmD . Chứng minh rằng:
a) Tứ giác CIHK nội tiếp một đường tròn.
b) MN là đường kính của đường tròn (O ).
c) OC song song với DH . Lời giải C a)Ta có ìï HK ^ KC ï · · í
Þ HKC + HIC = 90º + 90º = 180º . ï HI ^ IC ï N î O
Do đó,CIHK là tứ giác nội tiếp. K
b) Do tứ giác CIHK nội tiếp nên M I · · 1 ¼ 1 ¼ H
45º = ICK = BHI = sđBM + sđA N . A 2 2 B
 sđBM  sđAN  90 . ¼ » ¼ ¼
Suy ra, sđMN = sđA B + (sđBM + sđA N ) hay = 90° + 90° = 180º
MN là đường kính của (O ). D Trang 18
c) Do MN là đường kính của (O ) nên MA ^ DN , NB ^ DM . Do đó, H là trực tâm tam
giác DMN hay DH ^ MN .
Do I , K cùng nhìn A B dưới góc 90º nên tứ giác A BIK nội tiếp. · · ¼ »
Suy ra, CA I = CBK Þ sđCM = sđCN Þ C là điểm chính giữa của cung
MN Þ CO ^ MN .
Vì AC > BC nên DA BC không cân tại C do đó C ,O, H không thẳng hàng. Từ đó suy
ra CO / / DH .
Câu 10: a) Cho phương trình 2
x - 2mx - 2m - 1 = 0 ( )
1 với m là tham số. Tìm m để phương trình ( )
1 có hai nghiệm phân biệt x , x sao cho x + x +
3 + x x = 2m + 1 . 1 2 1 2 1 2
b) Cho hai số thực không âm a,b thỏa mãn 2 2
a + b = 2 . Tìm giá trị lớn nhất, giá trị nhỏ 3 3 nhất của biểu thức a + b + 4 M = . ab + 1 Lời giải a) D ¢= m + m + = (m + )2 2 2 1 1 . Phương trình ( )
1 có hai nghiệm phân biệt khi và chỉ khi D¢> 0 Û m ¹ - 1.
Áp dụng ĐL Vi-ét ta có x + x = 2m;x .x = - 2m - 1. 1 2 1 2 Ta có 2m +
2 - 2m = 2m + 1 ( ĐK 0 £ m £ 1 (*) ) 2m - 1 2m - 1 Û 2m - 1 +
2 - 2m - 1 - (2m - ) 1 = 0 Û - - (2m - ) 1 = 0 2m + 1 2 - 2m + 1 é 1 m ê = æ ö ê (t / m ( ) * ) Û ( ç ÷ m - ) 1 1 2 2 1 ç - - 1÷= 0 Û ê ç ÷ ç ÷ è + - + ø ê 1 1 2m 1 2 2m 1 - - 1 = 0 ê (2) êë 2m + 1 2 - 2m + 1 1
Vì 2m + 1 ³ 1, " m thỏa mãn 0 £ m £ 1 Þ £ 1 . Do đó, VT ( ) 2 < 0 = V P ( ) 2 hay (2)vô 2m + 1 nghiệm.
Vậy giá trị cần tìm là 1 m = . 2 b) Ta có 3 3 a + b + = ( 3 3 4 a + b + )
1 + 3 ³ 3ab + 3 . Dấu bằng xảy ra khi và chỉ khi a = b = 1 . 3 3 3(ab a b + + + ) 1 4
Vì ab + 1 > 0 nên M = ³ = 3 . ab + 1 ab + 1
Do đó, giá trị nhỏ nhất của biểu thứcM là 3 đạt được khi a = b = 1. +) Vì 2 2
a  b  2 nên a  2; b  2. Suy ra 3 3 a  b    2 2 4
2 a  b   4  2 2  4 . 3 3   Mặt khác 1  a b 4
1 do ab 1  1. Suy ra M   2 2  4 . ab 1 ab 1
Dấu bằng xảy ra khi và chỉ khi Trang 19 2 2 ìïa + b = 2 ï í
Û (a;b)= (0; 2)Ú(a;b)= ( 2; ) 0 . ï ab = 0 ïî
Giá trị lớn nhất của biểu thức M là 4  2 2 đạt được khi (a;b)= (0; 2)Ú(a;b)= ( 2;0)
---------------Hết---------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT NINH THUẬN NĂM HỌC 2019 - 2020
Khóa ngày : 01/6/2019
(Đề chính thức) Môn thi: TOÁN
Thời gian làm bài: 120 phút (không kể thời gian phát đề) ĐỀ
(Đề thị này gồm một trang)
Bài 1. (2,0 điểm): Giải bất phương trình và hệ phương trình sau:
3x  y  1
a) 7x – 2  4x  3; b) 
x  2y  5
Bài 2. (2,0 điểm) : Cho Parabol  P 2
: y  2x và đường thẳng d  : y  3x  2.
a) Vẽ đồ thị (P) trên hệ trục tọa độ Oxy ;
b) Tìm tọa độ giao điểm của (P) và (d). Bài 3. (2,0 điểm)      a) Rút gọn biểu thức : a 1 a 1 a 1 P        
 với a  0 và a 1. 2 2 a a 1 a 1   
b) Chứng minh rằng phương trình : 2
x  (2m 1)x  2m  4  0 luôn có hai nghiệm phân biệt x , x . 1 2
Tìm giá trị nhỏ nhất của biểu thức 2 2
A  x  x . 1 2
Bài 4. (2,0 điểm) : Cho  ABC vuông tại C nội tiếp trong đường tròn tâm O, đường kính AB = 2R, 0
ABC  60 . Gọi H là chân đường cao hạ từ C xuống AB, K là trung điểm đoạn thẳng AC. Tiếp tuyến
tại B của đường tròn tâm O cắt AC kéo dài tại điểm D.
a) Chứng minh tứ giác CHOK nội tiếp trong một đường tròn
b) Chứng minh rằng AC.AD= 4R2.
c) Tính theo R diện tích của phần tam giác ABD nằm ngoài hình tròn tâm O.
-----------------------HẾT----------------------- HƯỚNG DẪN Bài 1. (2,0 điểm): a) 7x – 2  4 5
x  3  3x  5  x  . 3 Trang 20
Vậy nghiệm của bất phương trình là x > 5 3 3
 x  y  1
6x  2y  2 7x  7 x 1 x 1 b)         
x  2y  5
x  2y  5
x  2y  5 1   2.y  5 y  2 
Vậy, nghiệm của hệ phương trình là  ; x y  1; 2  . Bài 2. (2,0 điểm) a) Vẽ đồ thị hàm số 2 y  2x Bảng giá trị : x -2 -1 0 1 2 2 y  2x 8 2 0 2 8 Đồ thị hàm số 2
y  2x là một đường cong đi qua các điểm:  2  ;8, 1
 ;2,0;0,1;2,2;8 Đồ thị như hình vẽ : y x O
b) Phương trình hoành độ giao điểm của (P) và (d) : 2 2
2x  3x  22x – 3x – 2  0 ( *)
Ta có  = (-3)2 – 4.2.(-2) = 25 > 0    5   1
Phương trình (*) có hai nghiệm : x  hoặc x  2 2 1 2  1   1    Khi x  thì y = 2.    ta được giao điểm 1 1 ;   2  2  2  2 2  Khi x = 2 thì y =  2 2. 2
 8 ta được giao điểm 2;8   
Vậy giao điểm của (P) và (d) là 1 1 ;   và 2;8  2 2  Bài 3. (2,0 điểm) a) Rút gọn :  a 1   a 1 a 1  P        
 với a > 0 và a  1 2 2 a a 1 a 1   
  a  2   a  a 2 1 1 1    a 1 4 a . =  . = -2 2 a
 a  1 a  1 2 a a 1 Vậy P = -2 2
b) Ta có  ’ = m     m   2 2 1 2
4  m  2m 1 2m  4  m  4m  5 Trang 21 =  2
m  4m  4 1 = m  2 2 1> 0 với mọi m
 Phương trình luôn có hai nghiệm phân biệt x , x với mọi m 1 2
x  x  2(m 1)
Theo định lí vi-ét ta có : 1 2 
x .x  2m  4  1 2
Theo đề bài ta có : A  x  x  x  x 2 2 2  2x x 1 2 1 2 1 2  2 2 2
A  m     m   2
 m  m   m    m 2 4 1 2 2 4 4 8 4 4 8 2  2.2 .
m 3  3  3  2m  3  3  3  m
Vậy giá trị nhỏ nhất của A bằng 3 khi m = 3 2 Bài 4. (2,0 điểm) D C K 600 A B O H
a) Chứng minh tứ giác CHOK nội tiếp trong một đường tròn
Vì K là trung điểm của dây cung AC nên OK  AC  0 CKO  90 Xét tứ giác CHOK có : 0 CKO  90 (cmt) 0
CHO  90 (vì CH  AB) Vì 0 0 0
CKO  CHO  90  90  180 nên tứ giác CHOK nội tiếp
b) Chứng minh rằng AC.AD= 4R2.
Xét  ACB và  ABD có : 0
ACB  ABD  90 BAD là góc chung
Vậy  ACB ∽  ABD (g-g)  AC AB 
 AC.AD = AB2 = (2R)2 = 4R2 (đpcm) AB AD
c) Tính theo R diện tích của phần tam giác ABD nằm ngoài hình tròn tâm O.
Gọi S là diện tích của phần tam giác ABD nằm ngoài hình tròn tâm O
Khi đó : S  S  S  S A  BD A  BC vp Ta có : OB = OC = bk, 0
ABC  60   OBC là tam giác đều  OB = OC = BC = R và 0 BOC  60 R 3R
Lại có CH  AB  H là trung điểm OB  BH =  AH = 2 2 2 R R 3
Trong  CHB vuông tại H có : 2 2 2
CH  BH  BC  2 2 2 CH  BC  HB  R   4 2 Trang 22 R 3 2 . R
Vì CH // BD (cùng vuông góc với AB) nên AH CH A . B CH 2R 3 2   BD    AB BD AH 3R 3 2 Khi đó : 2 1 1 2R 3 2R 3 S  . AB BD  .2 . R   ABD 2 2 3 3 2 1 1 R 3 R 3 S  CH.AB  . .2R   ABC 2 2 2 2 2 2 2 2 .  R .60 1 R  1 R 3 R  R 3 S  S  S   .O . B CH   . R   vp qBOC BO  C 360 2 6 2 2 6 4
Vậy diện tích phần tam giác ABD nằm ngoài hình tròn tâm O là : 2 2 2 2 2    R   R R R R 10 3 2 3 3 3  S  S  S  S =       (đvdt) A  BD A  BC vp   3 2 6 4 12  
………………………………
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 PHÚ THỌ
TRUNG HỌC PHỔ THÔNG NĂM HỌC 2019-2020 MÔN: TOÁN ĐỀ CHÍNH THỨC
Đề thi có 02 trang
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Thí sinh làm bài (cả phần trắc nghiệm khách quan và phần tự luận) vào tờ giấy thi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)
Câu 1. Tìm x biết x  4. A. x  2. B. x  4. C. x  8. D. x 16.
Câu 2. Hàm số nào dưới đây đồng biến trên ? 1 A. y   . x B. y  2 . x
y  x  D. y  3x 1. 2 C. 2 1.
Câu 3. Điểm nào dưới đây thuộc đường thẳng y  3x  5 ? A. M (3; 5  ). B. N(1; 2  ). C. ( P 1;3). D. Q(3;1).
2x  y  1
Câu 4. Hệ phương trình  có nghiệm là 3
 x  2y  4 A. ( ; x y)  ( 2  ;5). B. ( ; x y)  (5; 2  ). C. ( ; x y)  (2;5). D. ( ; x y)  (5;2). 1
Câu 5. Giá trị của hàm số 2 y  x tại x  2  bằng 2 A. 1.  B. 4. C. 2. D. 1. Câu 6. Biết Parabol 2
y  x cắt đường thẳng y  3
 x  4 tại hai điểm phân biệt có hoành độ là x ; x
x  x . Giá trị T  2x  3x bằng 1 2  1 2  1 2 A. 5.  B. 10.  C. 5. D. 10.
Câu 7. Cho tam giác ABC vuông tại A. Khẳng định nào dưới đây đúng? AC AB AB AC A. tan C  . B. tan C  . C. tan C  . D. tan C  . BC AC BC AB Trang 23
Câu 8. Cho tứ giác ABCD nội tiếp đường tròn B
đường kính AC. Biết DBC  55 ,  số đo ACD 55o bằng A. 30 .  B. 40 .  C. 45 .  D. 35 .  A C D
Câu 9. Cho tam giác ABC vuông cân tại A có AB  a . Bán kính đường tròn ngoại tiếp tam giác ABC bằng a 2 A. . a B. 2 . a C. . D. a 2. 2
Câu 10. Từ một tấm tôn hình chữ nhật có chiều dài
bằng 2 (m), chiều rộng bằng 1 (m) gò thành mặt xung
quanh của một hình trụ có chiều cao 1 (m), (hai cạnh
chiều rộng của hình chữ nhật sau khi gò trùng khít
nhau). Thể tích của hình trụ đó bằng 1 1 A. 3 (m ).    B. 3 (m ). D. 3 4 (m ). 2 C. 3 2 (m ).
PHẦN II. TỰ LUẬN (7,5 điểm)
Câu 1 (1,5 điểm). Lớp 9A và lớp 9B của một trường THCS dự định làm 90 chiếc đèn ông sao để
tặng các em thiếu nhi nhân dịp Tết Trung Thu. Nếu lớp 9A làm trong 2 ngày và lớp 9B làm trong
1 ngày thì được 23 chiếc đèn; nếu lớp 9A làm trong 1 ngày và lớp 9B làm trong 2 ngày thì được
22 chiếc đèn. Biết rằng số đèn từng lớp làm được trong mỗi ngày là như nhau, hỏi nếu cả hai lớp
cùng làm thì hết bao nhiêu ngày để hoàn thành công việc đã dự định ?
Câu 2 (2,0 điểm). Cho phương trình 2
x  mx  3  0 (m là tham số).
a) Giải phương trình với m  2.
b) C/minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của . m
c) Gọi x , x là hai nghiệm của phương trình. Tìm m để (x  6)(x  6)  2019. 1 2 1 2
Câu 3 (3,0 điểm). Cho tam giác ABC vuông tại A có đường cao AD  D  BC . Gọi I là trung
điểm của AC; kẻ AH vuông góc với BI tại H.
a) Chứng minh tứ giác ABDH nội tiếp. Tìm tâm đường tròn ngoại tiếp tứ giác ABDH.
b) Chứng minh tam giác BDH đồng dạng với tam giác BI . C c) Chứng minh 1 .
AB HD  AH .BD  . AD BH . 2
Câu 4 (1,0 điểm). Giải hệ phương trình sau 2 2  x y   4
x 1 y 1  x  2 y  2    y  . x
 x 1 y 1
.......................Hết..................... Trang 24 ĐÁP ÁN MÔN TOÁN
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm) Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 D C B A C A B D C A
PHẦN II. TỰ LUẬN (7,5 điểm)
Câu 1 (1,5 điểm). Lớp 9A và lớp 9B của một trường THCS dự định làm 90 chiếc đèn ông sao để
tặng các em thiếu nhi nhân dịp Tết Trung Thu. Nếu lớp 9A làm trong 2 ngày và lớp 9B làm trong
1 ngày thì được 23 chiếc đèn; nếu lớp 9A làm trong 1 ngày và lớp 9B làm trong 2 ngày thì được
22 chiếc đèn. Biết rằng số đèn từng lớp làm được trong mỗi ngày là như nhau, hỏi nếu cả hai lớp
cùng làm thì hết bao nhiêu ngày để hoàn thành công việc đã dự định ? HD:
Gọi số đèn mà lớp 9A, lớp 9B làm được trong 1 ngày lần lượt là x, y (x, y  ) .
2x  y  23
Theo bài ra ta có hệ phương trình  .
x  2y  22 x  8
Giải hệ phương trình trên ta thu được  . y  7
Suy ra trong một ngày cả 2 lớp làm được 8  7 15 chiếc đèn.
Vậy nếu cả 2 lớp cùng làm thì hết 90  6 ngày sẽ xong công việc đã dự định. 15
Câu 2 (2,0 điểm). Cho phương trình 2
x  mx  3  0 (m là tham số).
a) Giải phương trình với m  2.
b) C/minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của . m
c) Gọi x , x là hai nghiệm của phương trình. Tìm m để (x  6)(x  6)  2019. 1 2 1 2 HD:
a) Với m  2 , phương trình đã cho trở thành 2
x  2x  3  0   x  3 x   1  0 x  3  .  x  1 
Vậy phương trình có tập nghiệm S   1  ;  3 . b) Phương trình đã cho có 2   m 12 . Vì 2
  m 12  0 m
 nên phương trình luôn có hai nghiệm phân biệt với mọi . m
c) Gọi x , x là hai nghiệm của phương trình. Tìm m để (x  6)(x  6)  2019. 1 2 1 2
x  x  m
Theo định lí Vi-ét ta có 1 2 x .x  3.   1 2
Ta có (x  6)(x  6)  2019  x .x  6(x  x )  36  2019. 1 2 1 2 1 2 Suy ra: 3
  6m36  2019  6m 1986  m  331.
Câu 3 (3,0 điểm). Cho tam giác ABC vuông tại A có đường cao AD  D  BC . Gọi I là trung
điểm của AC; kẻ AH vuông góc với BI tại H.
a) Chứng minh tứ giác ABDH nội tiếp. Tìm tâm đường tròn ngoại tiếp tứ giác ABDH.
b) Chứng minh tam giác BDH đồng dạng với tam giác BI . C Trang 25 c) Chứng minh 1 .
AB HD  AH .BD  . AD BH . 2 HD: A I H B D C     a) Ta có ADB 90 ; AHB 90 .
Suy ra H , D cùng nhìn đoạn AB dưới một góc vuông. Vậy tứ giác ABDH nội tiếp
đường tròn đường kính . AB
Đường tròn ngoại tiếp tứ giác ABDH có tâm là trung điểm của AB . b) Xét B  DH và B  IC có:
+) HBD  CBI ;
+) DHB  DAB (do tứ giác ABDH nội tiếp); DAB  ICB (cùng phụ DAC ).
Suy ra DHB  IC . B Suy ra B  DH B  IC (g.g).
c) Theo phần b) ta có HD IC AC   . BH BC 2BC
Mặt khác áp dụng hệ thức lượng trong tam giác vuông ABC ta có AC AD A . D BC  A . B AC hay  . BC AB Do đó HD AD  1 hay A . B HD  A . D BH   1 . BH 2 AB 2 AH AI Ta có A  HB I  AB (g.g) nên  . BH AB Mặt khác AD AC 2 AI A  DB C  AB (g.g) nên   . BD AB AB 2 AH AD 1 Suy ra  hay AH .BD  . AD BH 2. BH BD 2 Từ   1 1 và 2 ta có .
AB HD  AH .BD  . AD BH . 2
Câu 4 (1,0 điểm). Giải hệ phương trình sau 2 2  x y   4
x 1 y 1  x  2 y  2    y  . x
 x 1 y 1 HD:
a) ĐKXĐ: x  - 1; y  1
Hệ phương trình đã cho tương đương với hệ phương trình: Trang 26 2 2       1 1 x 1 1 y 1 1   x   y   4 4      x  1 y 1 x 1 y 1     x  1  1 y 1 1 1  1      y  x x   y   2    x 1 y 1  x  1   y 1  1 Đặt 1 x   a ; y   b x  1 y  1
Hệ phương trình đã cho trở thành: a  b  4 a  1    a  b  2  b   3 + Với a = 1 ta có: 1 x(x 1) 1 x 1 x   1   x 1 x 1 x 1 2
 x  x 1  x 1  x  0 (t / m) + Với b = 3 ta có: 1 y( y 1) 1 3.( y 1) y   3   y 1 y 1 y 1 2 2
 y  y 1  3y  3  y  4y  4  0  y  2 (t / m)
Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) =(0; 2)
……….Hết………. QUẢNG NAM (Đề chung)
Câu 1. (2,0 điểm)
a) Rút gọn biểu thức A     2 1 12 2 1  3  2 x b) Cho biểu thức 1 2 1 B   
với x  0 và x 1. Rút gọn biểu thức B và x  x x 1 x  x
tìm x để B  8.
Câu 2. (2,0 điểm) 1
Trong mặt phẳng tọa độ Oxy , cho parabol 2 (P) : y  x . 2 a) Vẽ parabol (P). b) Hai điểm ,
A B thuộc (P). có hoành độ lần lượt là 2; 1. Viết phương trình đường thẳng
đi qua hai điểm A và . B
Câu 3. (2,0 điểm) a) Giải phương trình 4 2
x  2x  8  0 . b) Cho phương trình 2 2 x  (2m  )
1 x  m 1  0 ( m là tham số). Tìm giá trị nguyên của m để
phương trình đã cho có hai nghiệm phân biệt x .x
x ; x sao cho biểu thức 1 2 P  có giá trị nguyên. 1 2 x  x 1 2 Trang 27
Câu 4. (3,5 điểm)
Cho hình vuông ABCD có cạnh bằng 6 .
cm Điểm N nằm trên cạnh CD sao cho DN  2cm,
P là điểm nằm trên tia đối của tia BC sao cho BP  DN . a) Chứng minh A  BP  A
 DN và tứ giác ANCP nội tiếp đường tròn.
b) Tính độ dài đường tròn ngoại tiếp tứ giác ANCP .
c) Trên cạnh BC , lấy điểm M sao cho MAN  45 . Chứng minh MP  MN và tính diện tích tam giác AMN.
Câu 5. (0,5 điểm)
Cho hai số thực x, y thỏa mãn x  3; y  3.    
Tìm giá trị nhỏ nhất của biểu thức 1 1 T  21 x   3 y       y   x  LỜI GIẢI THAM KHẢO
Câu 1. (2,0 điểm)
a) Rút gọn biểu thức A     2 1 12 2 1  3  2 b) Cho biểu thức 1 2 x 1 B   
với x  0 và x 1. Rút gọn biểu thức B và tìm x để x  x x 1 x  x B  8. Lời giải A     2 1 12 2 1  3 2 3  2 A  2 3  2 1  ( 3  2)( 3  2)  2 3  2 1 3  2  3 1 1 2 x 1 B    x  x x 1 x  x 1 2 x 1 B    x ( x 1)
( x 1)( x 1) x ( x 1) x 1 2x  x 1 B 
x ( x 1)( x 1) 2x  2
2( x 1)( x 1) 2 B   
x ( x 1)( x 1)
x ( x 1)( x 1) x 2 1 1 B  8 
 8  x   x  (TMĐK) x 4 6 Trang 28
Câu 2. (2,0 điểm)
Trong mặt phẳng tọa độ 1 Oxy , cho parabol 2 (P) : y  x . 2 c) Vẽ parabol (P). d) Hai điểm ,
A B thuộc (P). có hoành độ lần lượt là 2; 1. Viết phương trình đường thẳng
đi qua hai điểm A và . B Lời giải 1 ( A 2; 2); B( 1  ; ) 2
Gọi phương trình đường thẳng cần tìm là: y  ax  b 1 Vì ( A 2; 2); B( 1
 ; ) thuộc đường thẳng y  ax  b nên: 2
2a  b  2 
2a  b  2
2a  b  2 a  2 1       a  b  1  
a  2b  2 
2a  4b  4  b   2  2
Vậy đường thẳng cần tìm là: y  2x  2
Câu 3. (2,0 điểm) a) Giải phương trình 4 2
x  2x  8  0 . b) Cho phương trình 2 2 x  (2m  )
1 x  m 1  0 ( m là tham số). Tìm giá trị nguyên của m để
phương trình đã cho có hai nghiệm phân biệt x .x
x ; x sao cho biểu thức 1 2 P  có giá trị nguyên. 1 2 x  x 1 2 Lời giải a) Đặt 2
x  t  0, phương trình trở thành 2
t  2t  8  0 (1) 2  ' 1 1.( 8  )  9  0   '  9  3
Phương trình (1) có hai nghiệm phân biệt: b  '  ' 1 3 b '  ' 1 3 t    2(TM );t    4(KTM ) 1 2 a 1 a 1
Với t  2, ta có: x  2  x   2
Vậy phương trình có tập nghiệm: S   2; 2 b) 2 2 x  (2m  )
1 x  m 1  0    m 2 2 2 2 2 2
1  (m 1)  4m  4m  4  m 1  3m  4m  3  3( 0 m 
 Phương trình đã cho có hai nghiệm phân biệt với mọi m. Trang 29  b x  x    2m 1  1 2  a
Theo hệ thức Vi et ta có:  c 2
x .x   m 1 1 2  a 2  Theo đề ta có x .x m 1 1 2 P   x  x 2m 1 1 2
Để P có giá trị nguyên thì 2 2
m 1 2m 1  4m 1 2m 1  (2m 1)(2m 1)  2 2m 1
 2 2m1 2m1Ư(2)  1  ;  2
+ 2m 1  1  m  0 Z + 2m 1  1   m  1   Z 1
+ 2m 1  2  m   Z 2 3  + 2m 1  2   m   Z 2 Vậy x .x m 0;  
1 thì phương trình đã cho có hai nghiệm phân biệt x ; x sao cho biểu thức 1 2 P  1 2 x  x 1 2 có giá trị nguyên.
Câu 4. (3,5 điểm)
Cho hình vuông ABCD có cạnh bằng 6 .
cm Điểm N nằm trên cạnh CD sao cho DN  2cm, P là
điểm nằm trên tia đối của tia BC sao cho BP  DN . a) Chứng minh A  BP  A
 DN và tứ giác ANCP nội tiếp đường tròn.
b) Tính độ dài đường tròn ngoại tiếp tứ giác ANCP .
c) Trên cạnh BC , lấy điểm M sao cho MAN  45 . Chứng minh MP  MN và tính diện tích tam giác AMN. Lời giải a) Xét ABP  và A  DN , có: 0
AB  AD(gt); ABP  ADN ( 90 ); BP  DN ( 2c ) m  A  BP  A  DN( . c g.c) P A  BP  A
 DN  APB  AND
 Tứ giác ANCP nội tiếp đường tròn. 4 A B 3
b) Gọi O là tâm đường tròn ngoại tiếp tứ giác ANCP 2 1 O
Tứ giác ANCP nội tiếp, có 0 NCP  90 M Trang 30 D N C
 NP là đường kính của đường tròn (O) và 0 NAP  90  2 2 NP 
AN  AP  2AN (1) A
 DN vuông tai D , nên: 2 2 2 2 AN 
AD  DN  6  2  2 10 (2)
Từ (1) và (2) suy ra: NP  2.2 10  4 5 (cm)
Bán kính đường tròn ngoại tiếp tứ giác ANCP là 2 5 (cm)
Độ dài đường tròn ngoại tiếp tứ giác ANCP là: C  2 R  2.2 5  4 5 (cm) c) Ta có 0 0
A  A  A  90  A  A  45 1 2 3 1 3
Mà A  A nên 0 A  A  45 0  MAP  45 1 4 4 3 Xét M  AN và M  AP , có: AM: cạnh chung; 0
MAN  MAP( 45 ) ; AN  AP Do đó M  AN  M
 AP (c.g,c)  MN  MP Ta có AN  ; AP MN  M ;
P ON  OP  AM  NP tại O. . PO PN 2 5.4 5 POM  # PC 
N (g.g)  PM .PC  . PO PN  PM    5(cm) PC 8
 BM  3(cm) 2 2 2 2 AM  AB  BM  6  3  45  3 5(cm) 1 1 2 S
 .AM.NO  .3 5.2 5 15(cm ) ANM 2 2
Câu 5. (0,5 điểm)
Cho hai số thực x, y thỏa mãn x  3; y  3.    
Tìm giá trị nhỏ nhất của biểu thức 1 1 T  21 x   3 y       y   x  Lời giải 21 3 x 62 3 21 7 2 T  21x   3y    x    y  y y x 3 3 x y 3 3
 x 3   21 7  62 2     y  x 
y  2 14  62  2  80    
 3 x   y 3  3 3 x  3
Dấu “” xảy ra    y  3
Vậy giá trị nhỏ nhất của T là 80 khi x = 3; y =3. Trang 31
SỞ GIÁO DỤC VÀ ĐÀO TẠO KÌ THI TUYỂN SINH VÀO LỚP 10 PTTH
QUẢNG NGÃI NĂM HỌC 2019 – 2020 Ngày thi: 05/6/2019 ĐỀ CHÍNH THỨC Môn thi: TOÁN
(Đề thi có 01 trang) Thời gian: 120 phút , không kể phát đề
Bài 1. (1,0 điểm)
a) Cho biểu thức A  16  25  4. So sánh A với 2 x  y  5 
b) Giải hệ phương trình: 
2x  y 11
Bài 2. (2,5 điểm) 1. Cho Parabol   2
P : y  x và đường thẳng d  : y  x  2
a) Vẽ  P và d  trên cùng một mặt phẳng tọa độ Oxy .
b) Viết phương trình đường thẳng d '  song song với d  và tiếp xúc với  P . 2. Cho phương trình 2
x  4x  m  0 (m là tham số)
a) Biết phương trình có một nghiệm bằng 1
 . Tính nghiệm còn lại.
b) Xác định m để phương trình có hai nghiệm x ,x thỏa mãn 3x 1 3x 1  4 1  2  1 2
Bài 3. (2,0 điểm)
Một đội công nhân đặt kế hoạch sản xuất 250 sản phẩm. Trong 4 ngày đầu, họ thực hiện đúng kế
hoạch. Mỗi ngày sau đó, họ đều vượt mức 5 sản phẩm nên đã hoàn thành công việc sớm hơn 1 ngày so
với dự định. Hỏi theo kế hoạch, mỗi ngày đội công nhân đó làm được bao nhiêu sản phẩm? Biết rằng
năng suất làm việc của mỗi công nhân là như nhau.
Bài 4. (3,5 điểm)
Cho tam giác nhọn ABC (AB), đường cao AH, nội tiếp đường tròn (O). Gọi D và E thứ tự là hình
chiếu vuông góc của H lên AB và AC.
a) Chứng minh các tứ giác AEHD và BDEC nội tiếp được đường tròn.
b) Vẽ đường kính AF của đường tròn (O). Chứng minh BC  AB.BD  AC.CE và AF vuông góc với DE.
c) Gọi O’ là tâm đường tròn ngoại tiếp tam giác BDE. Chứng minh O’ là trung điểm của HF.
d) Tính bán kính đường trò (O’) biết BC  8cm, DE  6cm, AF  10cm.
Bài 5. (1,0 điểm) B C
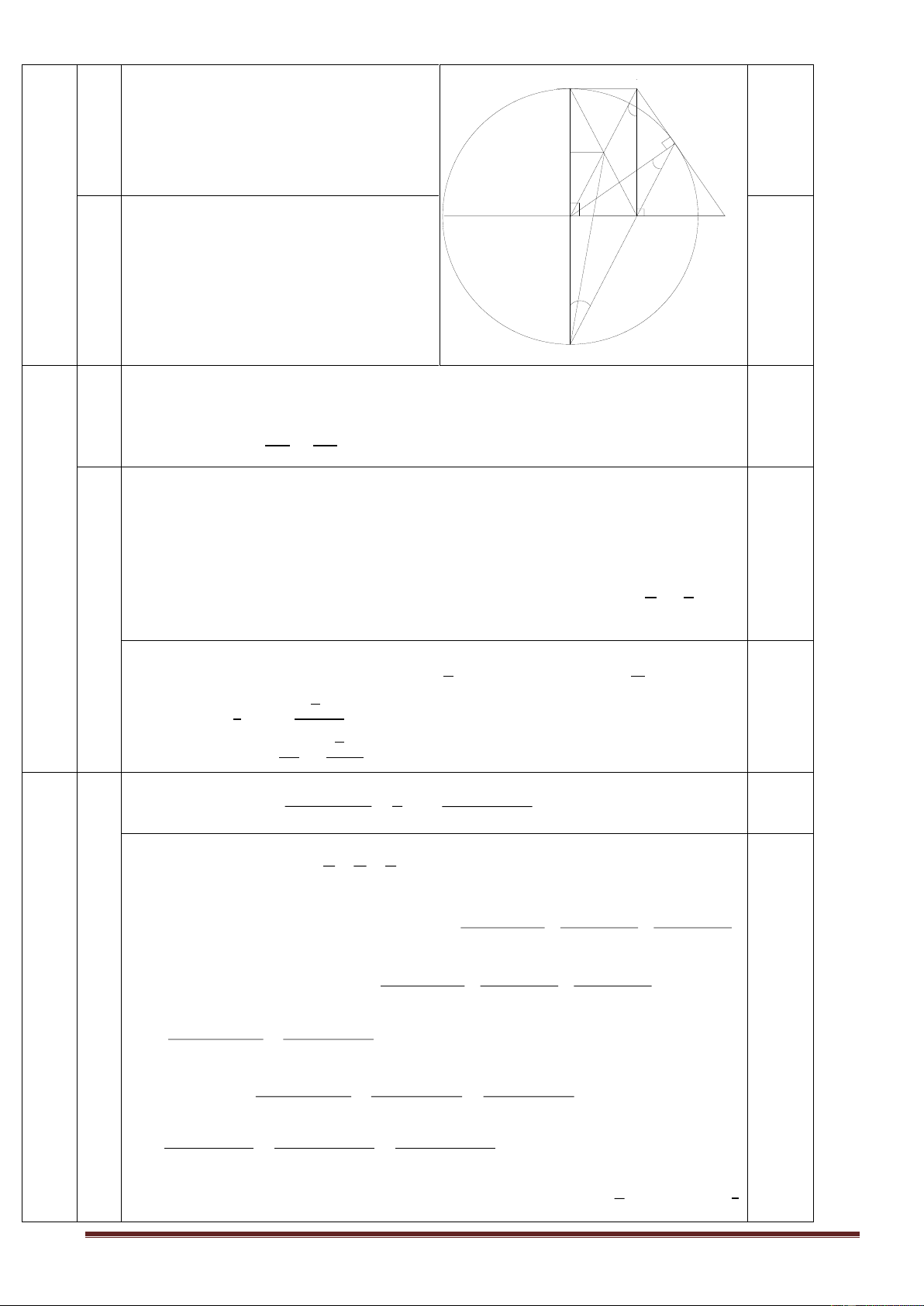
Cho hình vuông ABCD. Gọi S là diện tích phần giao 1
của hai nửa đường tròn đường kính AB và AD. S là diện tích S2 2
phần còn lại của hình vuông nằm ngoài hai nửa đường trong nói S S1
trên (như hình vẽ bên).Tính 1 S2
----------------------- HẾT----------------------- A D
Ghi chú: Cán bộ coi thi không giải thích gì thêm. HƯỚNG DẪN
Bài 1. (1,0 điểm)
a) Cho biểu thức A  16  25  4. So sánh A với 2 Trang 32
A  16  25  4  4  5  2 1  2 . Vậy A  2 x  y  5 
b) Giải hệ phương trình: 
2x  y 11 x  y  5  3  x  6 x  2 x  2       
2x  y 11 x  y  5  2  y  5  y  7
Bài 2. (2,5 điểm) 1. Cho Parabol   2
P : y  x và đường thẳng d  : y  x  2
a) Vẽ  P và d  trên cùng một mặt phẳng tọa độ Oxy .
b) Viết phương trình đường thẳng d '  song song với d  và tiếp xúc với  P . a)   2 P : y  x x 3  2  1  0 1 2 3 y 9  4  1  0 1  4  9 
d  : y  x  2
x  0  y  2  : 0; 2  
y  0  x  2 : 2;0 6 4 2 -10 -5 5 10 15 -2 -4 -6 -8 -10
b) Phương trình đường thẳng d '  có dạng y  ax  b
d'//d: y  x2 a 1;b  2
Phương trình hoành độ giao điểm của  Pvàd'  là 2 2
x  x  b  x  x  b  0 *
PT *  có   1 4b.  1
Pvàd'  tiếp xúc nhau khi PT *  có nghiệm kép    0  1 4b  0  b  (nhận). 4 Trang 33
Vậy PT đường thẳng d'  1
là : y  x  4 2. Cho phương trình 2
x  4x  m  0 (m là tham số)
a) Biết phương trình có một nghiệm bằng 1
 . Tính nghiệm còn lại.
b) Xác định m để phương trình có hai nghiệm x ,x thỏa mãn 3x 1 3x 1  4 1  2  1 2 a) PT 2
x  4x  m  0 có một nghiệm bằng 1
  a  b  c  0 1 4  m  0  m  5  . c m 5 
Nghiệm còn lại của PT là       5 a 1 1
b) ĐK '   2 2
 m  0  m  4 x  x  4
Áp dụng định lí Vi et ta có: 1 2  x x  m  1 2
3x 1 3x 1  4  9x x  3 x  x 1 4 1  2  1 2  1 2  9m  3 4
.  1  4  m    1 tm Vậy m  1
 là giá trị cần tìm.
Bài 3. (2,0 điểm)
Một đội công nhân đặt kế hoạch sản xuất 250 sản phẩm. Trong 4 ngày đầu, họ thực hiện đúng kế
hoạch. Mỗi ngày sau đó, họ đều vượt mức 5 sản phẩm nên đã hoàn thành công việc sớm hơn 1 ngày so
với dự định. Hỏi theo kế hoạch, mỗi ngày đội công nhân đó làm được bao nhiêu sản phẩm? Biết rằng
năng suất làm việc của mỗi công nhân là như nhau.
Gọi số sản phẩm mỗi ngày đội công nhân đó làm theo kế hoạch là x(sp).ĐK x  0; x  Z
Khi đó, số sản phẩm mỗi ngày đội công nhân đó làm trong thực tế là x  5sp 250
Thời gian hoàn thành công việc theo kế hoạch là (ngày) x
Số sản phẩm làm được trong 4 ngày đầu là: 4xsp
Số sản phẩm còn lại phải làm là 250  4xsp 250  4x
Thời gian làm 250  4xsp còn lại là x  (ngày). 5 250 250  4x Theo bài toán ta có PT:  4  1 x x  5
Giải PT này ta được: x  25 (nhận) 1 x  50  (loại) 2
Vậy số sản phẩm mỗi ngày đội công nhân đó làm theo kế hoạch là 25 sản phẩm.
Gợi ý hai bài hình
Bài 4. (3,5 điểm)
Cho tam giác nhọn ABC (AB), đường cao AH, nội tiếp đường tròn (O). Gọi D và E thứ tự là hình
chiếu vuông góc của H lên AB và AC.
a) Chứng minh các tứ giác AEHD và BDEC nội tiếp được đường tròn.
b) Vẽ đường kính AF của đường tròn (O). Chứng minh BC  AB.BD  AC.CE và AF vuông góc với DE.
c) Gọi O’ là tâm đường tròn ngoại tiếp tam giác BDE. Chứng minh O’ là trung điểm của HF.
d) Tính bán kính đường trò (O’) biết BC  8cm, DE  6cm, AF  10cm. Trang 34 A E O I N D M B K H C O' O'' F 0 0 0
a) Tứ giác AEHD có ADH  AEH  90  90  180  Tứ giác AEHD nội tiếp được
đường tròn đường kính AH.
Tứ giác AEHD (cmt) ADE  AHE  
1 (cùng chắn AE ). Dễ thấy ACH  AHE 2 (cùng phụ HAE ).
Từ (1) và (2) suy ra ADE  ACH nên tứ giác BDEC nội tiếp được đường tròn.
b) Áp dụng hệ thức lượng trong hai tam giác vuông AHB và AHC ta có: 2
BH  AB.BD  BH 
AB.BD Do đó BC  BH  HC  AB.BD  AC.CE 2
HB  AC.CE  HB  AC.CE
Nối FB, FC. Gọi I là giao điểm của AF và DE.
Ta có ADE  ACH (cmt) và AFB  ACH (cùng chắn AB ) suy ra ADE  AFB nên tứ
giác BDIF nội tiếp được đường tròn 0 0 0 0 0
 DIF  DBF 180  DIF 180  DBF 180  90  90 . Vậy AF  DE
c) Gọi M,N,O’’ lần lượt là trung điểm của BD,EC,HF.
- Ta chứng minh được MO’’ và NO’’ lần lượt là đường trung bình của các hình thang BDHF và
CEHF  MO''/ / DH 3và  NO''/ / EH 4
- Vì tứ giác BDEC nội tiếp mà O' là tâm đường tròn ngoại tiếp tam giác BDE suy ra O' cũng là
tâm đường tròn ngoại tiếp tứ giác BDEC  O' thuộc đường trung trực của BD . Suy ra MO’ là
trung trực của BD do đó
MO'  BD lại có DH  BD  MO'/ / DH 5 .
Tương tự ta có NO'/ / EH 6
- Từ (3) và (5) suy ra MO’’ và MO’ là hai tia trùng nhau
- Từ (4) và (6) suy ra NO’’ và NO’ là hai tia trùng nhau
Do đó O’ trùng O”. Mà O’’ là trung điểm của HF nên O’ cũng là trung điểm của HF. Trang 35 BC BC 8 4 d) - Trong ABC  ta có
 AF  SinA    SinA AF 10 5 DE 6 - Trong A  DE ta có
 AH  AH   7 5 , cm SinA 4 5
- Vì O’ và O lần lượt là trung điểm của HF và AF nên OO’ là đường trung bình của tam giác AH 7 5 , AHF  OO'=   3 7 , 5cm 2 2
- Gọi K là giao điểm của OO’ và BC dễ thấy OO'  BC tại trung điểm K của BC. Áp dụng
định lí Pytago vào tam giác vuông OKC ta tính được 2 2 2 2
OK  OC  KC  5  4  3cm
- Ta có KO'  OO'  OK  3,75  3  0,75cm
- Áp dụng định lí Pytago vào tam giác vuông O’KC ta tính được 265 2 2 2 2
O' C  O' K  KC  0,75  4  cm 4 265
Vậy bán kính đường trò (O’) là cm 4
Bài 5. (1,0 điểm) B C
Cho hình vuông ABCD. Gọi S là diện tích phần giao 1
của hai nửa đường tròn đường kính AB và AD. S là diện S2 2
tích phần còn lại của hình vuông nằm ngoài hai nửa S
đường trong nói trên (như hình vẽ bên).Tính S 1 1 S2 A D B C S3 S2 S S 4 1 A D
Gọi a là cạnh hình vuông ABCD. Ta cm được: 2
 a  . 90 . 2   2  2  1  a  a   1  S  S      3 4     360 2  2  4  4 2  2 2 2 a   1  a   1  a   1 
S  S  S       1 3 4       4  4 2  4  4 2  2  4 2  Trang 36 2 2 1 a   1  a  3   2 S  a     2     2 2  4 2  2  2 4  2 a   1     S 2  4 2    2 Do đó 1   2 S a  3   6   2    2  2 4 
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT NĂM 2019 TỈNH QUẢNG NINH
Môn thi: Toán (Dành cho mọi thí sinh)
Thời gian làm bài: 120 phút, không kể thời gian giao đề ĐỀ THI CHÍNH THỨC
(Đề thi này có 01 trang)
Câu 1. (2,0 điểm )
1. Thực hiện phép tính: 2 9  3 4 . 28( a  2 2 )
2. Rút gọn các biểu thức: , với 2 > a . 7
3. Tìm tọa độ giao điểm của đồ thị hàm số 2
y  x và đồ thị hàm số y  - 3x 2
Câu 2. (2,0 điểm ) Cho phương trình: 2
x  2x  m  1  0 , với m là tham số.
1. Giải phương trình với m = 1
2. Tìm giá trị của m để phương trình đã cho hai nghiệm phân biệt x và x thỏa mãn: 1 2
x3  x3  6x x  (
4 m  m2 ). 1 2 1 2
Câu 3. (2,0 điểm ) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Hai người thợ cùng làm một công việc trong 9 ngày thì xong. Mỗi ngày, lượng công việc
của người thợ thứ hai làm được nhiều gấp ba lần lượng công việc của người thợ thứ nhất. Hỏi
nếu làm một mình thì mỗi người làm xong công việc đó trong bao nhiêu ngày
Câu 4. (3,5 điểm )
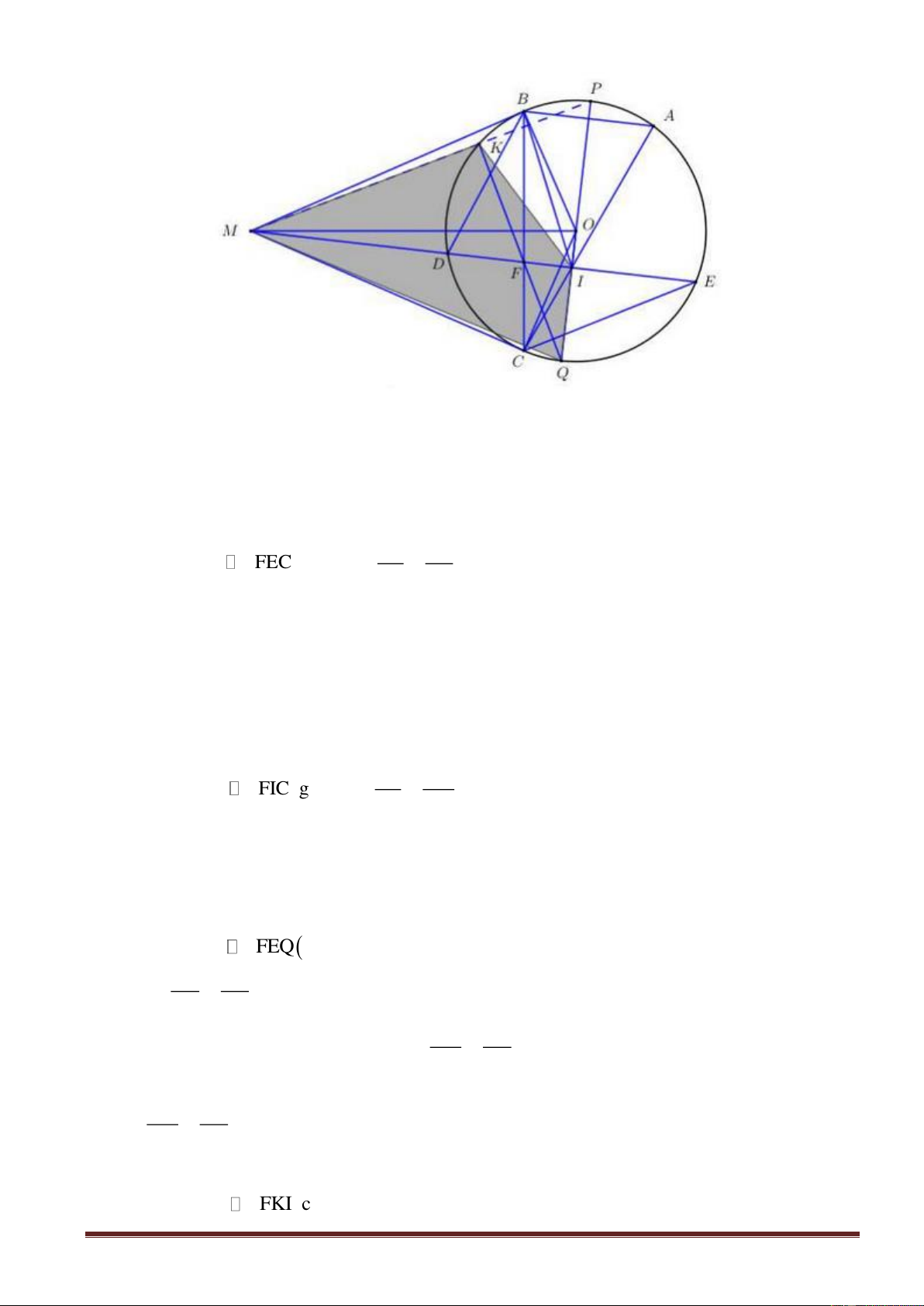
Cho đường tròn (O; R), hai đường kính AB và CD vuông goác với nhau. Gọi E là điểm
thuộc cung nhỏ BC ( E không trùng với B và C), tiếp tuyến của đường tròn (O; R) tại E cắt
đường thẳng AB tại I. Gọi F là giao điểm của DE và AB, K là điểm thuộc đường thẳng IE sao cho KF vuông góc với AB.
a. Chứng minh tứ giác OKEF nội tiếp.
b. Chứng minh 𝑂𝐾𝐹 ̂ = 𝑂𝐷𝐹 ̂ .
c. Chứng minh 𝐷𝐸. 𝐷𝐹 = 2𝑅2
d. Gọi M là giao điểm của OK với CF, tính tan 𝑀𝐷𝐶 ̂ khi 𝐸𝐼𝐵 ̂ = 450
Câu 5. (0,5 điểm ) Trang 37
Cho x, y, z là các số thực dương thỏa mãn x+ y + z ≤1. Tìm giá trị nhỏ nhất của biểu thức 1 1 P  
x 2  y 2  z 2
xy  yz  zx
--------------------Hết--------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: …………………………………………Số báo danh………………….
Chữ ký của cán bộ coi thi 1:……………….Chữ ký của cán bộ coi thi 1:…………………
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM THI TUYỂN SINH TỈNH QUẢNG NINH
LỚP 10 THPT NĂM 2019
Môn thi: Toán (Dành cho mọi thí sinh) ĐỀ THI CHÍNH THỨC
(Hướng dẫn này có 02 trang) Câu Ý
Sơ lược lời giải Điểm 1 2 9  3 4  2 3 .  3.2  0 0,5 0,25 28 (𝑎 − 2)2 √ 2 = √4 (𝑎 − 2)2 Câu 1 7 (2,0đ)
= 2. |(𝑎 − 2)| = 2 (𝑎 − 2). Do 𝑎 > 2 nên 𝑎 − 2 > 0 ⇒ |𝑎 − 2| = 𝑎 − 2 0,5
Hoành độ giao điểm của đồ thị hai hàm số đã cho là nghiệm của PT: 𝑥2 = 3𝑥 − 2 0,25 3
Giải được hai nghiệm: 𝑥1 = 1; 𝑥2 = 2 0,25
Từ đó tìm được hai giao điểm có tọa độ là: (1; 1) và (2; 4) 0,25
Với m = 1 PT có dạng: 𝑥2 + 2𝑥 = 0 0,5 1
𝑥(𝑥 + 2) = 0 ⇔ 𝑥1 = 0; 𝑥2 = −2 0,5 Để Câu 2
PT hai nghiệm phân biệt thì ∆> 0 ⇔ 𝑚 < 2 0,25 (2,0đ) 𝑥 Theo hệ thức Vi 0,25 -ét có { 1 + 𝑥2 = −2 2 𝑥1. 𝑥2 = 𝑚 − 1 𝑥3 3
1 +𝑥2 − 6𝑥1𝑥2 = 4(𝑚 − 𝑚2) ⇔ ⋯ ⇔ 𝑚2 − 𝑚 − 2 = 0 0,25
Suy ra m = -1 nhận; m = 2 (loai) 0,25
Gọi x (ngày), y (ngày) lần lượt là thời gian hoàn thành công việc một mình của 0,5
người thứ nhất và người thứ hai, (𝑥, 𝑦 ) ∈ 𝑁∗)
Do hai người cùng làm trong 9 ngày thì xong công việc nên: 1 + 1 = 1 (1) 𝑥 𝑦 9 0,5 2
Trong cùng một ngày người thứ hai làm được nhiều gấp ba lần người thứ nhất nên Câu 3 1 (2,0đ) = 3 (2) 𝑦 𝑥
Từ (1) và (2) giải hệ tìm được x=36; y =12 (thỏa mãn). 0,5
Vậy nếu làm một mình xong công việc người thứ nhất làm hết 36 ngày, người thứ 0,5 hai làm hết 12 ngày. Trang 38
Vẽ đúng hình ý a cho 0,25 điểm C K 0,25
Có 𝐶ó 𝐾𝐹 ⊥ 𝑂𝐹 nên 𝐾𝐹𝑂 ̂ = 900 0,25 a
và 𝐼𝐸 ⊥ 𝑂𝐸 nên 𝐾𝐸𝑂 ̂ = 900 0,25 E M Suy ra 𝐾𝐹𝑂 ̂ = 𝐾𝐸𝑂 ̂ , hay tứ giác N 0,25 Câu 4 OKEF nội tiếp (3,5đ)
Vì tứ giác OKEF nội tiếp nên 0,5 O B I F 𝑂𝐾𝐹 ̂ = 𝑂𝐸𝐹 ̂
△ 𝑂𝐸𝐷 cân ở 𝑂 (𝑂𝐸 = 𝑂𝐷) nên 0,5 b 𝑂𝐷𝐹 ̂ = 𝑂𝐸𝐷 ̂ Vậy 𝑂𝐾𝐹 ̂ = 𝑂𝐷𝐹 ̂ D
Xét △ 𝑂𝐹𝐷 và △ 𝐸𝐶𝐷 ta có 𝐸𝐷𝐶 ̂ chung, 𝐶𝐸𝐷 ̂ = 𝐹𝑂𝐷 ̂ = 900 0,5 c
Suy ra △ 𝑂𝐹𝐷 đồng dạng với △ 𝐸𝐶𝐷 𝑂𝐷 𝐹𝐷 ⇒ =
⇒ 𝑅 .2𝑅 = 𝐹𝐷. 𝐸𝐷 ℎay 𝐹𝐷. 𝐸𝐷 = 2𝑅2 𝐸𝐷 𝐶𝐷 0,5
Kẻ MN vuông góc CD tại N Ta có 𝑂𝐾𝐹 ̂ = 𝑂𝐷𝐹 ̂ , 𝐾𝐹𝑂 ̂ = 𝐷𝑂𝐹
̂ = 900 ⇒ △ 𝐾𝐹𝑂 =△ 𝐷𝑂𝐹
⇒ 𝐾𝐹 = 𝐷𝑂 = 𝑂𝐶 = 𝑅 0,25
Có 𝐾𝐹 ⊥ 𝐴𝐵, 𝐶𝑂 ⊥ 𝐴𝐵 ⇒ 𝐾𝐹 ∥ 𝑂𝐶 ⇒ 𝐶𝐾𝐹𝑂 là hình chữ nhật ⇒ 𝑀 là trung 𝑅 3
điểm của 𝐶𝐹 ⇒ 𝑁 là trung điểm của 𝑂𝐶 ⇒ 𝐷𝑁 = 𝑂𝐷 + 𝑂𝑁 = 𝑅 + = 𝑅 2 2 d
Mặt khác ta có 𝐸𝐼𝐵
̂ = 450 nên △ 𝐹𝐾𝐼 vuông cân tại 𝐹 ⇒ 𝐹𝐼 = 𝐹𝐾 = 𝑅
Ta có △ 𝐸𝑂𝐼 vuông cân tại 𝐸 ⇒ 𝑂𝐼 = 𝑅√2 ⇒ 𝑂𝐹 = 𝑂𝐼 − 𝐹𝐼 = ( √2 - 1) R 0,25
Do đó 𝑀𝑁 = 1 𝐹𝑂 = ( √2 − 1) 𝑅 2 2 Suy ra tan 𝑀𝐷𝐶 ̂ = 𝑀𝑁 = √2 − 1 𝐷𝑁 3
x  y  z3 1 2017 0,25
Ta có xy  yz  zx   nên  6051 3 3
xy  yz  zx  1 1 1 
Áp dụng BĐT x  y  z    9   , ta có:  x y z     2 2 2
( x  y  z )  ( xy  yz  zx )  ( xy  yz  zx  1 1 1 )    9  2 2 2 
 x  y  z
xy  yz  zx
xy  yz  zx    2 2 2 1 1 1 Câu 5
 ( x  y  z  2xy  2yz  2zx )    9  2 2 2  (0,5đ)
x  y  z
xy  yz  zx xy  yz   zx  0,25 1 2 Hay   9 2 2 2
x  y  z
xy  yz  zx 1 2 2017 Từ đó ta có: P     9  6051 6060 2 2 2
x  y  z
xy  yz  zx
xy  yz  zx 1 21 2017 𝑃 = + + ≥ 9 + 6051 = 6060 𝑥2 + 𝑦2+𝑧2 𝑥𝑦 + 𝑦𝑧 + 𝑧𝑥 𝑥𝑦 + 𝑦𝑧 + 𝑧𝑥  1
P  6060. Vậy GTNN của P là 6060 khi và chỉ khi x  y  z  𝑥 = 𝑦 = 𝑧 = 1 3 3 Trang 39 Lưu ý:
1. Đây chỉ là sơ lược lời giải của bài toán, bài làm phải chặt chẽ đủ các bước mới cho điểm tối đa.
2. Nếu làm cách khác mà vẫn ra đáp án đúng thì vẫn cho điểm tối đa của ý đó
3. Bài hình không vẽ hình không chấm cả bài.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 LÀO CAI
TRUNG HỌC PHỔ THÔNG NĂM 2019
MÔN THI : TOÁN KHÔNG CHUYÊN ĐỀ CHÍNH THỨC Thời gian
: 120 phút (không tính thời gian giao đề)
Bài 1. (1,0 điểm) Tính giá trị của các biểu thức sau: a) 4  3 . b)    2 5 6 5 2 2x  2x 1 1
Bài 2: (1,5 điểm) Cho biểu thức H    với x  0; x  1 2 x 1 x 1 x 1 a) Rút gọn biểu thức H
b) Tìm tất cả các giá trị của x để x  H  0
Bài 3. (2,5 điểm)
1) Cho đường thẳng (d): y  x 1 và parabol (P): 2 y  3x
a) Tìm tọa độ A thuộc parabol (P) biết điểm A có hoành độ x  1  1
b) Tìm b để đường thẳng (d) và đường thẳng (d’): y 
x  b cắt nhau tại một điểm trên trục 2 hoành. x  y  5
2) a) Giải hệ phương trình  2x  y 1  x  y  a
b) Tìm tham số a để hệ phương trình 
. Có nghiệm duy nhất x; y thỏa mãn 7x  2y  5a 1 y  2x
Bài 4. (2,0 điểm) a) Giải phương trình: 2 x  3x  2  0
b) Tìm các giá trị của tham số m để phương trình 2 2
x  2(m 1)x  m  0 có hai nghiệm phân
biệt x , x thỏa mãn hệ thức x  x  6m  x  2x . 1 2 2 1 2 1 2
Bài 5. (3,0 điểm)
Cho đường tròn (O), điểm M nằm ngoài đường tròn (O). kẻ hai tiếp tuyến MB, MC (B và C là
các tiếp điểm) với đường tròn. Trên cung lớn BC lấy điểm A sao cho AB < AC. Từ điểm M kẻ đường
thẳng song song với AB, đường thẳng này cắt đường tròn (O) tại D và E (MD < ME),cắt BC tại F, cắt Trang 40 AC tại I.
a) Chứng minh tứ giác MBOC nội tiếp.
b) Chứng minh FD.FE  FB.FC;FI  FE  FD.FE
c) Đường thẳng OI cắt đường tròn (O) tại P và Q (P thuộc cung nhỏ AB). Đường thẳng QF cắt
đường tròn (O) tại K (K khác Q). Chứng minh 3 điểm P, K, M thẳng hàng. --- HẾT --- Họ và tên thí sinh: SBD: Phòng thi số: HƯỚNG DẪN GIẢI Bài 1: a) 4  3  2  3  5 b)    2 5 6 5
 5  6  5  5  6  5  6 Bài 2: 2 2x  2x 1 1 2x x   1 1 1 a) H       2 x 1 x 1 x 1 x   1 x   1 x 1 x 1 2x 1 1 2x 1 1       x 1 x 1 x 1
 x  1 x  1 x 1 x 1
b) Theo đề bài ta có
x  H  0  x  2  x  2  x  4
Kết hợp điều kiện x  0; x  1 ta có 0  x  4; x  1
Vậy với 0  x  4; x  1 thì x  H  0 Bài 3:
1) a) Điểm A có hoành độ x  1
 và thuộc P nên thay x  1
 vào P ta được :   2 y 3. 1  3  A 1  ;3
b)Gọi Bx ;0 là điểm thuộc trục hoành và là giao điểm của hai đường thẳng d, d’. ta có B  Bx ;0 thuộc d  x  1   B 1;0 B   B  Lại có:   1 1 B 1;0  d '  0  .1  b  b   2 2 x  y  5 3  x  6 x  2 2) a)      2x  y  1 y  5  x y  3
Vậy hệ pt có nghiệm duy nhất: x; y  2;3 1 1  x  y  a   1 b)Hệ phương trình có   
có nghiệm duy nhất với mọi a. 7  hệ pt 2 7x  2y  5a    1 2 Trang 41
Theo đề bài ta có hệ pt có nghiệm duy nhất thỏa mãn y  2x
Thay y  2x vào (1) ta được: x  2x  a  x  a  y  2a  Thay x  a; y  2  a vào (2) ta được: 1 7 a    2 2  a  5a 1  7  a  4a 5a  1   8  a  1   a  8 1
Vậy a  thỏa mãn bài toán 8 Bài 4: a) 2 x  3x  2  0
Phương trình có dạng a  b  c  0 . Khí đó pt có hai nghiệm phân biệt x  1; x  2 . 1 2
Vậy tập nghiệm của phương trình là: S  1;  2 b) 2 2 x  2(m 1)x  m  0 Ta có:        2 2 ' m 1   m  2 2
 m  2m 1 m  1 2m 1
Phương trình có hai nghiệm phân biệt x , x   '  0  1 2m  0  m  1 2 2 x  x  2 m 1 1 2   Theo vi-ét ta có:  2 x x  m  1 2 Theo đề bài ta có:
x  x 2  6m  x  2x  x  x  4x x  6m  x  2x 1 2 2 1 2 1 2 1 2 1 2  4m  2 2
1  4m  6m  x  2x  2  m  4  x  2x 1 2 1 2
Khi đó kết hợp với x  x  2 m 1 ta có hệ pt: 1 2    4  4 x  m  2 x  m  2  x  x  2 m 1  3x  4m  6     1 2   2 2 2 3 3        x  2x  2  m  4 x  x  2m  2 4 2   1 2 1 2 x 2m 2 m 2      x  m 1 1  3  3  4 x  m  2  2  3 Thay  vào 2 x x  m ta được: 2 1 2  x  m 1  3  4  2 1  4  1 4   m  0 2 2 m  2 . m  m  m  m  0  m m   0       (tm)  3  3 9 3  9 3  m  12  Vậy m  0;m  12
 thỏa mãn yêu cầu đề bài. Bài 5: Trang 42
a) Do Mb,Mc là hai tiếp tuyến của đường tròn (O) nên 0 OBM  OCM  90 Xét tứ giác MBOC có: 0
OBM  OCM  180 suy ra tứ giác MBOC là tứ giác nội tiếp.
b) Xét tam giác FBD và tam giác FEC có: BFD  EFCdd
FDB  FCE ( hai góc nội tiếp cùng chắn cung BE)       FB FD FBD FEC g g    FD.FE  FB.FC  1 FE FC
Ta có AB// ME suy ra BAC  DIC
Mà BAC  MBC (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BC)
 DIC  MBC  MBF  CIF
Xét tam giác FBM và tam giác FIC có: BFM  IFC (đđ) MBF  CIFcmt       FB FM FBM FIC g g    FI.FM  FB.FC2 FI FC
Từ (1) và (2)  FI.FM  FD.FE3
c) Xét tam giác FDK và tam giác FQE có: KFD  EFQ (đđ)
FKD  FEQ ( hai góc nội tiếp cùng chắn cung DQ)  F  KD F  EQg  g FK FD    FD.FE  FK.FQ4 FE FQ FM FK
Từ (3) và (4)  FI.FM  FK.FQ   FQ FI
Xét tam giác FMQ và tam giác FKI có: FM FK  cmt FQ FI MFQ  KFI  F  MQ F
 KIc  g  c  FMQ  FKI Trang 43
Suy ra tứ giác KIQM là tứ giác nội tiếp
 MQK  MIQ (hai góc nội tiếp cùng chắn cung MQ)
Ta có MBF  CIF  MBC  MIF suy ra tứ giác MBIC là tứ giác nội tiếp
Mà MOBC là tứ giác nội tiếp nên M, B, O, I, C cùng thuộc 1 đường tròn. Ta có 0
OBM  90 suy ra OM là đường kính của đường tròn đi qua 5 điểm M, B, O, I, C. Suy ra 0
OIM  90 (góc nội tiếp chắn nửa đường tròn) 0  IM  OI  MIQ  90 0  MKQ  MIQ  90 Lại có 0
QKP  90 (góc nội tiếp chắn nửa đường tròn) Từ đó ta có: 0 MKP  MKQ  QKP  180
Vậy 3 điểm P, K, M thẳng hàng. Trang 44

TOP 10 đề tuyển sinh toán 10 năm 2020 tập 4 (có lời giải)

Thông tin :

Tài liệu liên quan:

Đề thi thử Toán vào lớp 10 lần 2 năm 2024 – 2025 phòng GD&ĐT Nghĩa Đàn – Nghệ An

Đề thi thử Toán vào lớp 10 lần 2 năm 2024 – 2025 phòng GD&ĐT Quốc Oai – Hà Nội

Đề thi vào 10 môn Toán năm 2023 - 2024 sở GD&ĐT Long An

Đề thi vào 10 môn Toán năm 2023 - 2024 sở GD&ĐT Cao Bằng

Đề thi vào 10 môn Toán năm 2023 - 2024 sở GD&ĐT Bình Phước