

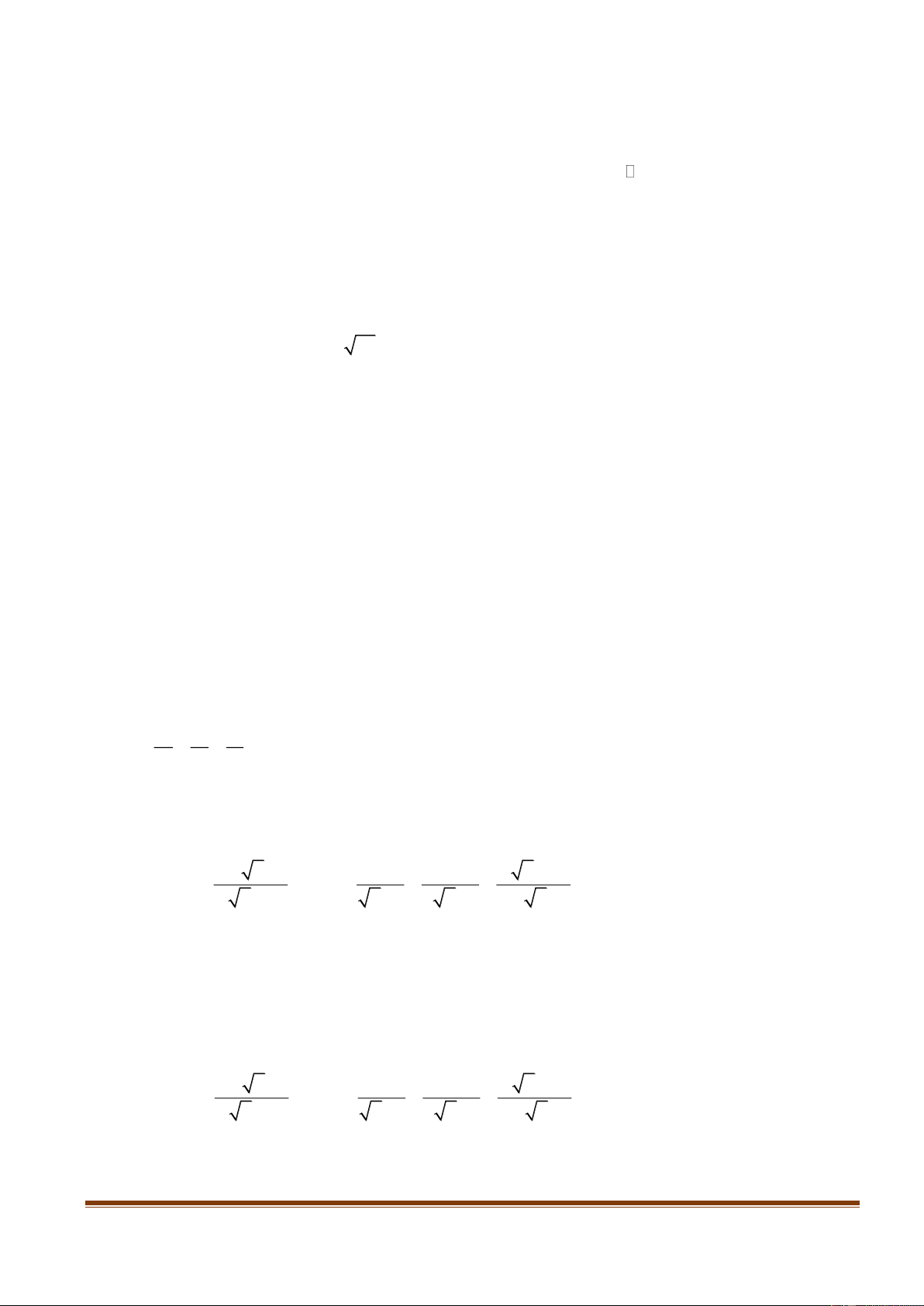









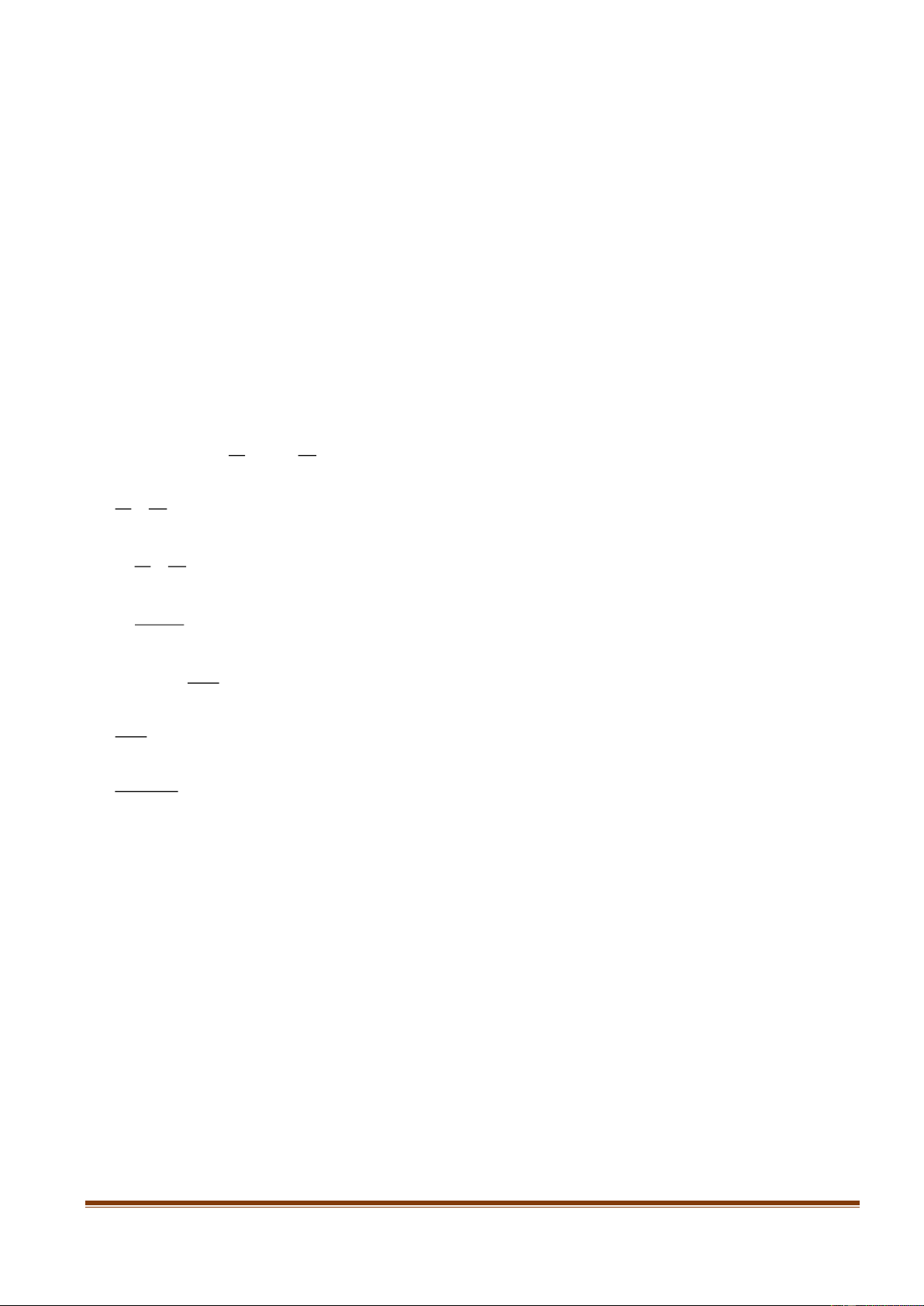















Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO TÂY NINH KỲ THI TUYỂN SINH VÀO LỚP 10 NĂM HỌC 2019-2020
Ngày thi: 01 tháng 6 năm 2019
Môn thi: TOÁN ( không chuyên)
Thời gian làm bài: 120 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
(Đề có 01 trang, thí sinh không phải chép đề vào giấy thi) Câu 1: (1,0 điểm)
Tính giá trị biểu thức T 4 25 9 Câu 2: (1,0 điểm)
Tìm m để đồ thị hàm số y m 2 (2 1)x đi qua điểm ( A 1; 5) . Câu 3: (1,0 điểm) Giải phương trình 2
x x 6 0. Câu 4: (1,0 điểm)
Vẽ đồ thị của hàm số 2 y x . Câu 5: (1,0 điểm)
Tìm tọa độ giao điểm của đường thẳng d : y 2x 1và đường thẳng d : y x 3. 1 2 Câu 6: (1,0 điểm)
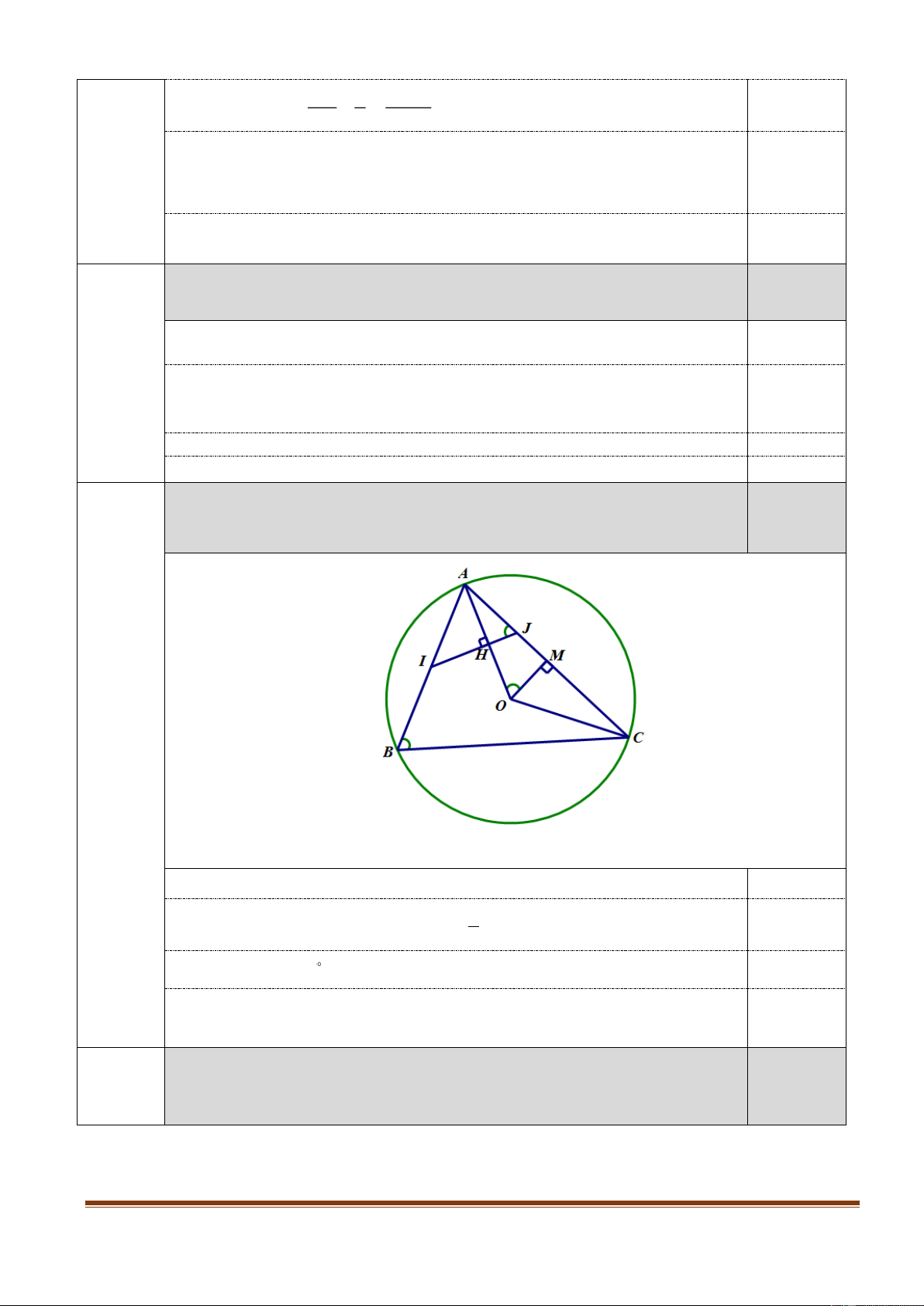
Cho tam giác ABC vuông cân tại A có đường trung tuyến BM ( M thuộc cạnh AC ). Biết
AB 2a . Tính theo a độ dài AC , AM và BM . Câu 7: (1,0 điểm)
Hai ô tô khởi hành cùng một lúc từ A đến B . Vận tốc của ô tô thứ nhất lớn hơn vận tốc của ô 1
tô thứ hai là 10 km/h nên ô tô thứ nhất đến B trước ô tô thứ hai giờ. Tính vận tốc mỗi ô tô biết 2
quãng đường AB dài 150 km. Câu 8: (1,0 điểm)
Tìm các giá trị nguyên của m để phương trình 2
x 4x m1 0 có hai nghiệm phân biệt x1 và x thỏa 3 x 3 x 100 2 1 2 Câu 9: (1,0 điểm)
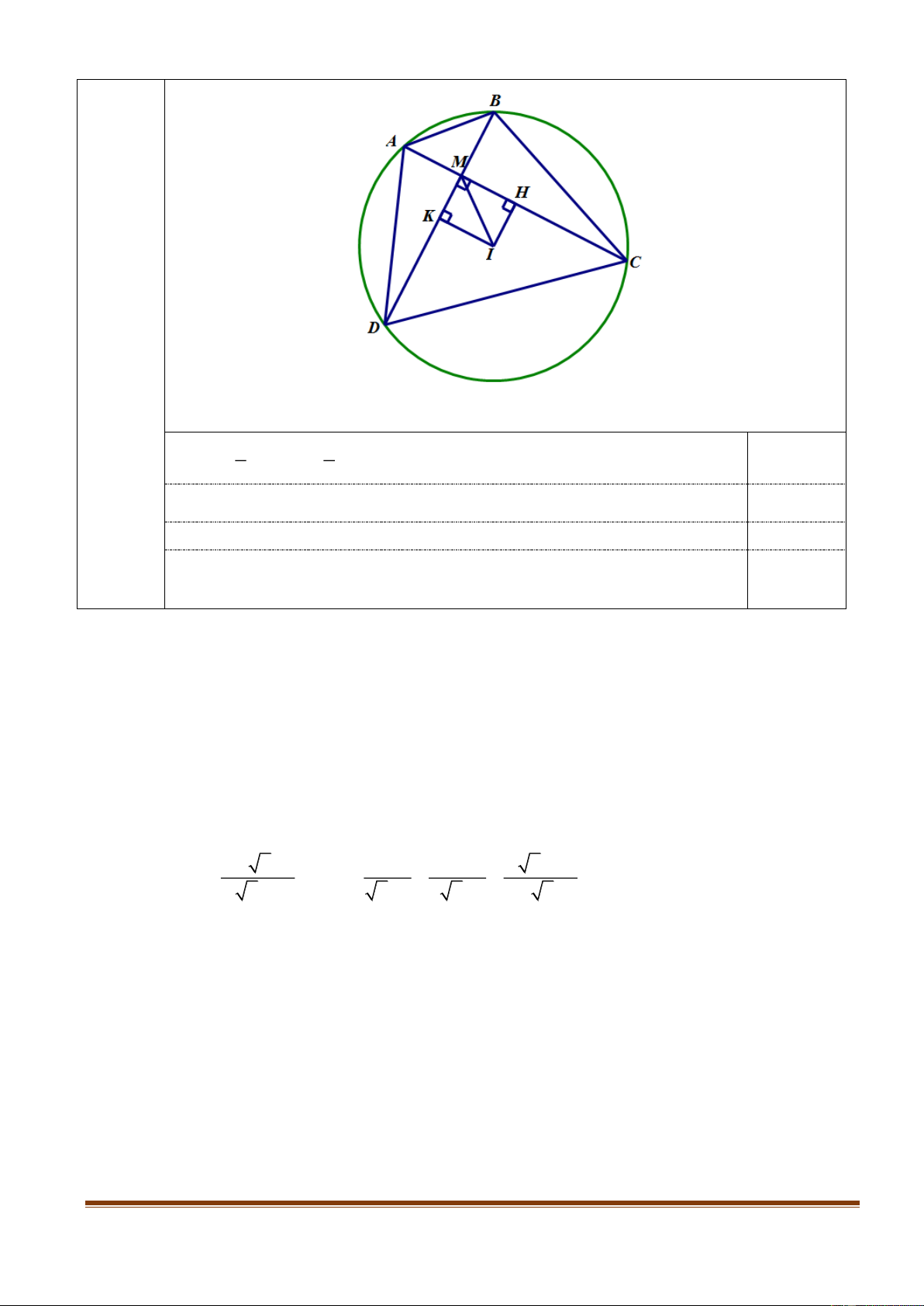
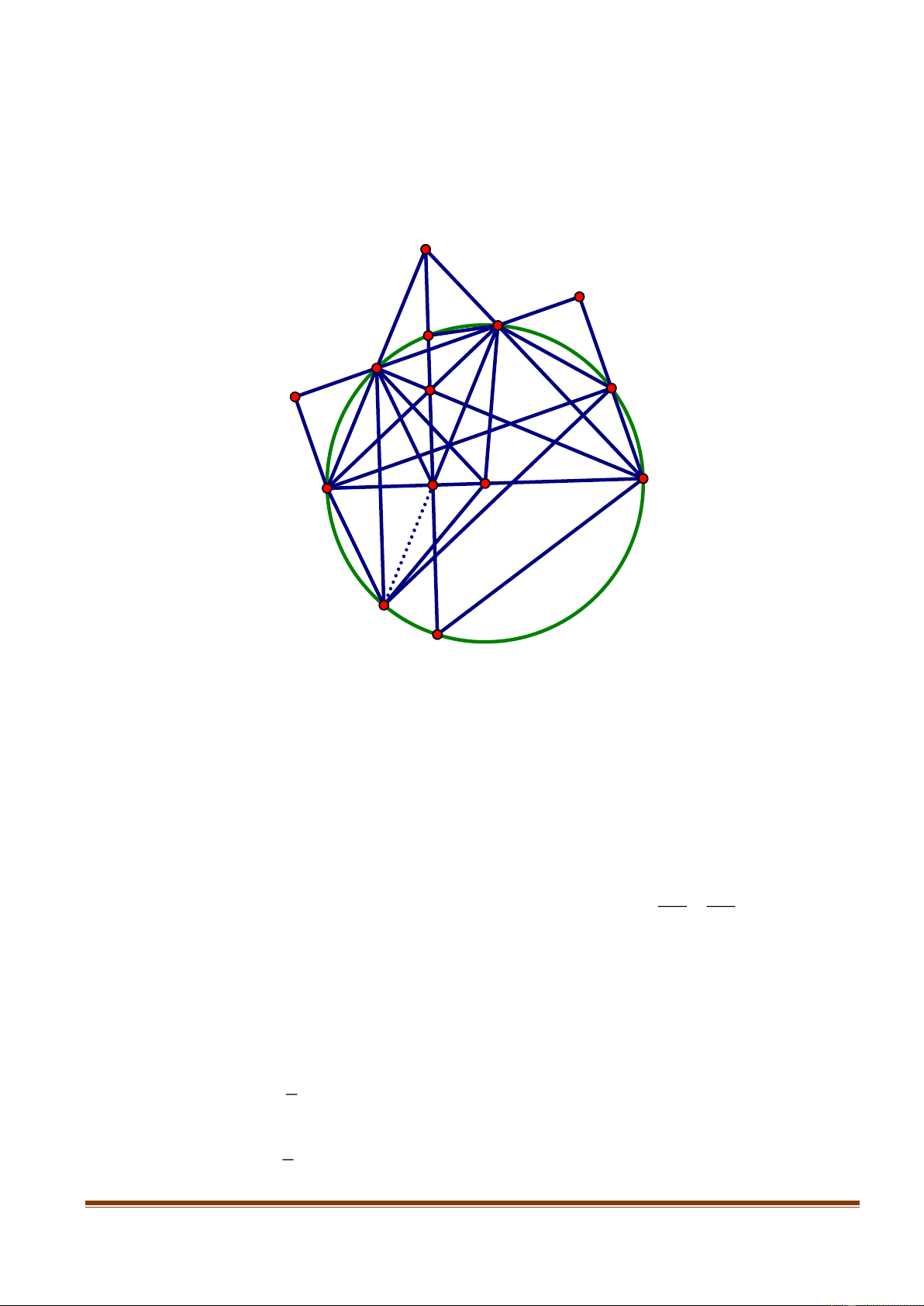
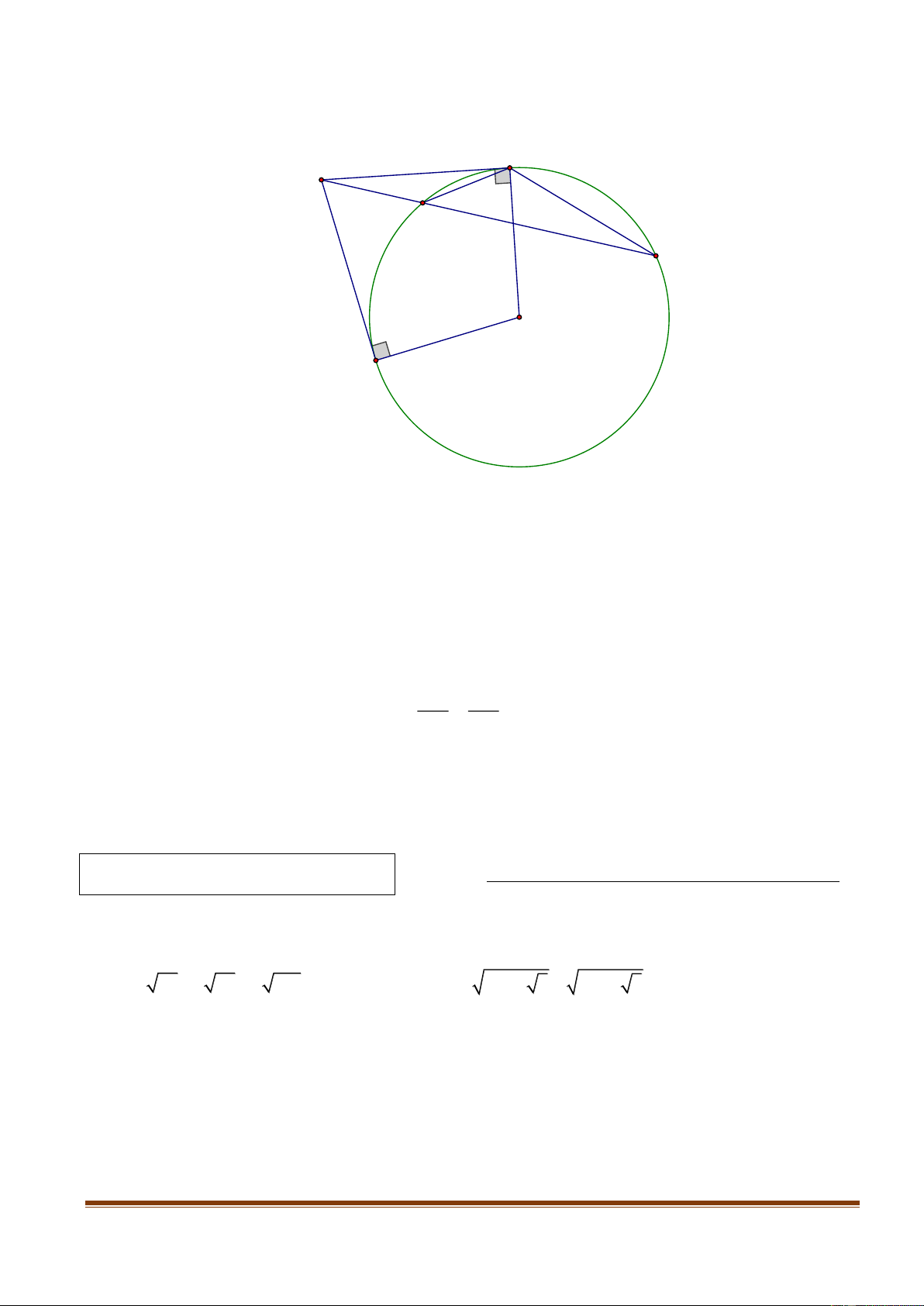
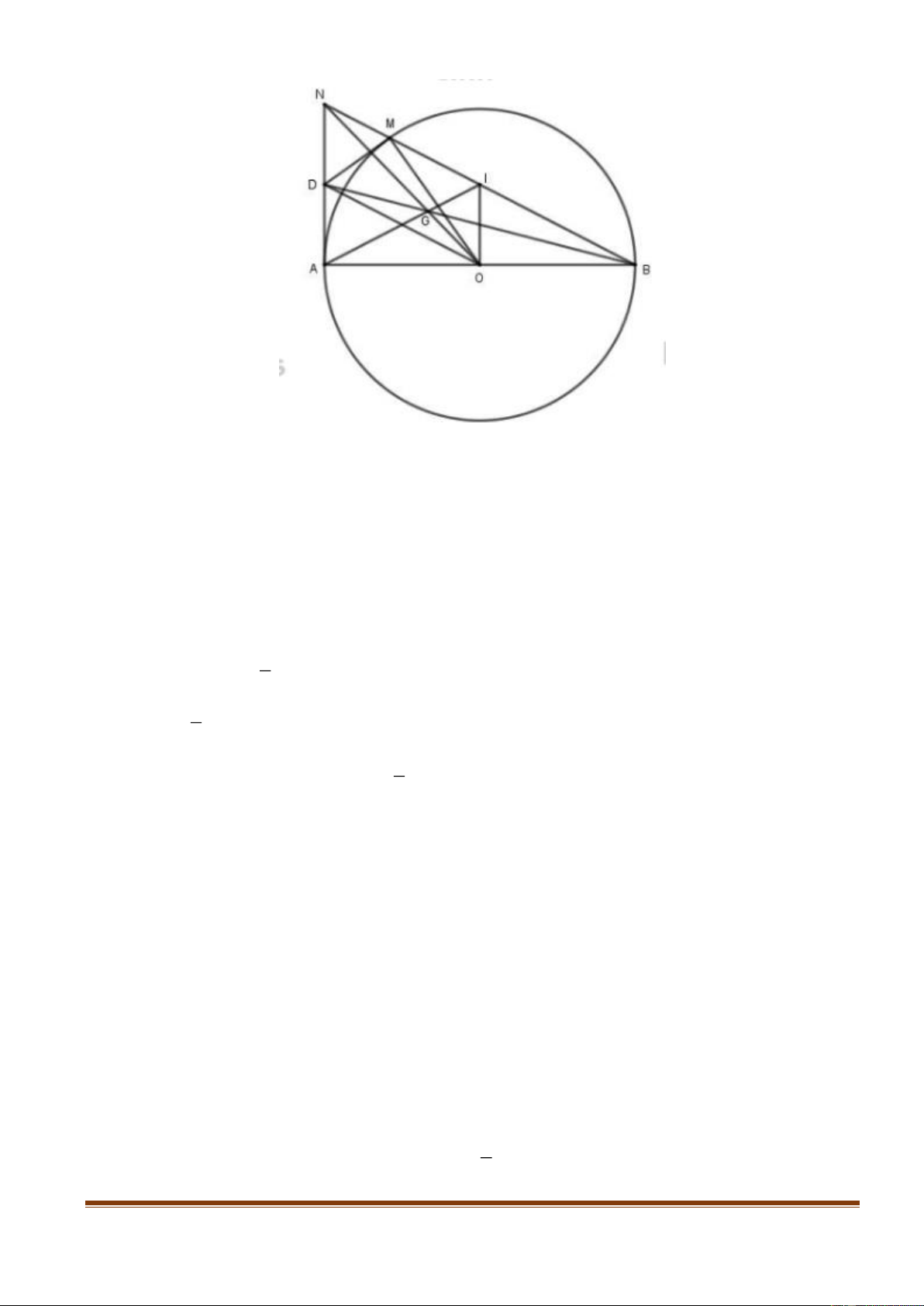
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O . Gọi I là trung điểm AB .
Đường thẳng qua I vuông góc AO và cắt AC tại J . Chứng minh: B,C, J và I cùng thuộc một đường tròn. Câu 10: (1,0 điểm)
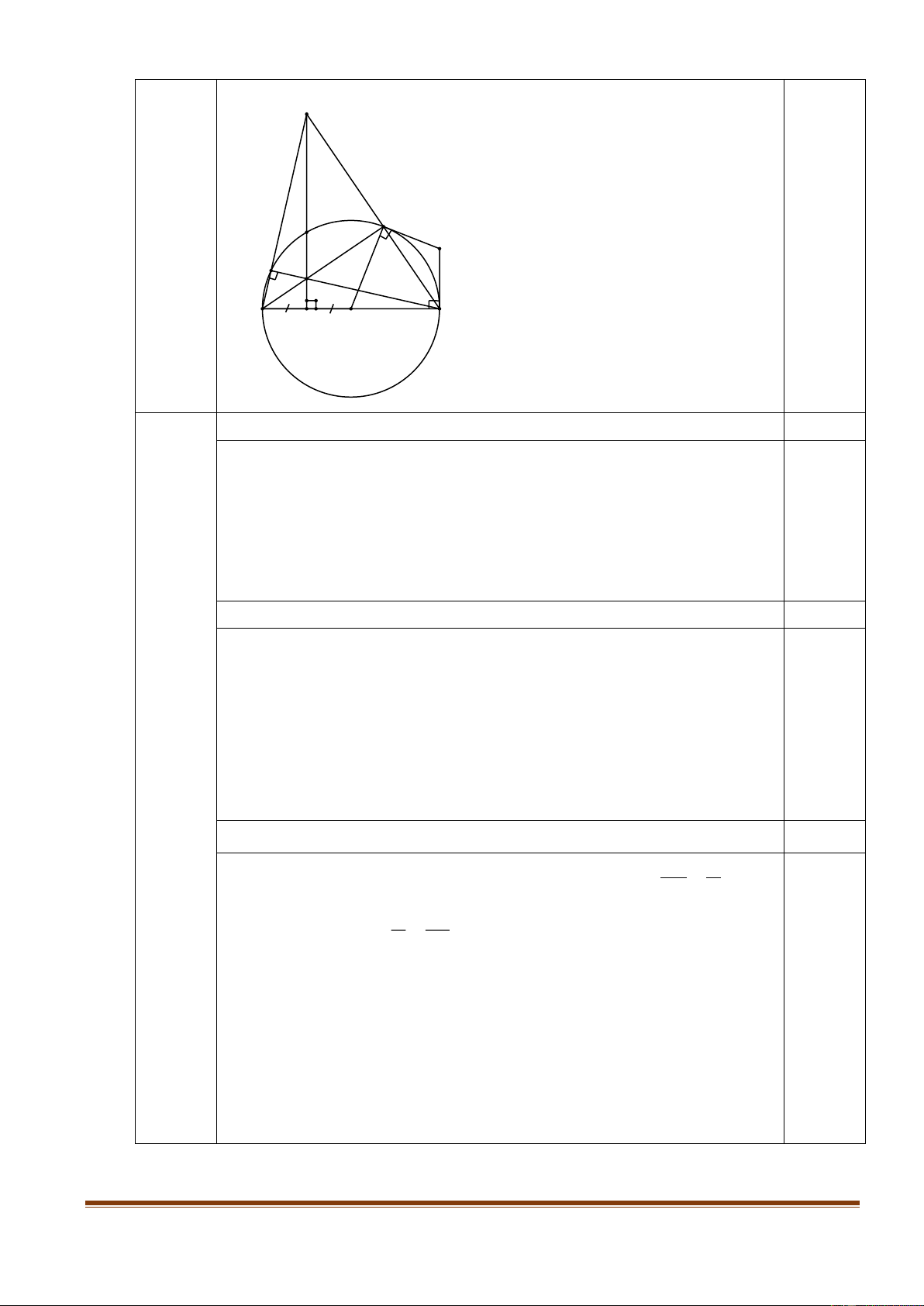
Cho đường tròn (C) có tâm I và có bán kính R 2a . Xét điểm M thay đổi sao cho IM a .
Hai dây AC, BD đi qua M và vuông góc với nhau. ( ,
A B, C, D thuộc (C) ). Tìm giá trị lớn nhất của
diện tích tứ giác ABCD. ---Hết---
Họ và tên thí sinh:...................................................................................Số báo danh:............................
Chữ kí của giám thị 1:.............................................Chữ kí của giám thị 2:............................................. Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO TÂY NINH
KỲ THI TUYỂN SINH VÀO LỚP 10 NĂM HỌC 2019-2020
HƯỚNG DẪN CHẤM THI
Môn thi: TOÁN ( không chuyên)
(Bản hướng dẫn này có 04 trang)
A. Hướng dẫn chung
1. Nếu thí sinh làm bài theo cách riêng nhưng đáp ứng được yêu cầu cơ bản như trong
hướng dẫn chấm thi vẫn cho điểm đúng như hướng dẫn chấm qui định.
2. Việc chi tiết hóa điểm số (nếu có) so với biểu điểm phải bảo đảm không sai lệch với
hướng dẫn chấm, thống nhất trong toàn tổ và được lãnh đạo Hội đồng chấm thi phê duyệt.
3. Sau khi cộng điểm toàn bài được làm tròn đến 0,25 điểm.
B. Đáp án và thang điểm Câu
Nội dung cần đạt Điểm
Tính giá trị biểu thức T 4 25 9 1,0 điểm 4 2 0,25 1 25 5 0,25 9 3 0,25 Vậy T 4 0,25
Tìm m để đồ thị hàm số y m 2 (2 1)x đi qua điểm ( A 1; 5) . 1,0 điểm A1;
5 thuộc đồ thị hàm số y m 2 2
1 x suy ra 5 2m1 0,25 2 2m 4 0,25 m 2 0,25
Vậy m 2 là giá trị cần tìm. 0,25 Giải phương trình 2
x x 6 0. 1,0 điểm 2
b 4ac 0,25 3 25 0,25
Vậy phương trình đã cho có hai nghiệm là x 2 0,25 x 3 0,25
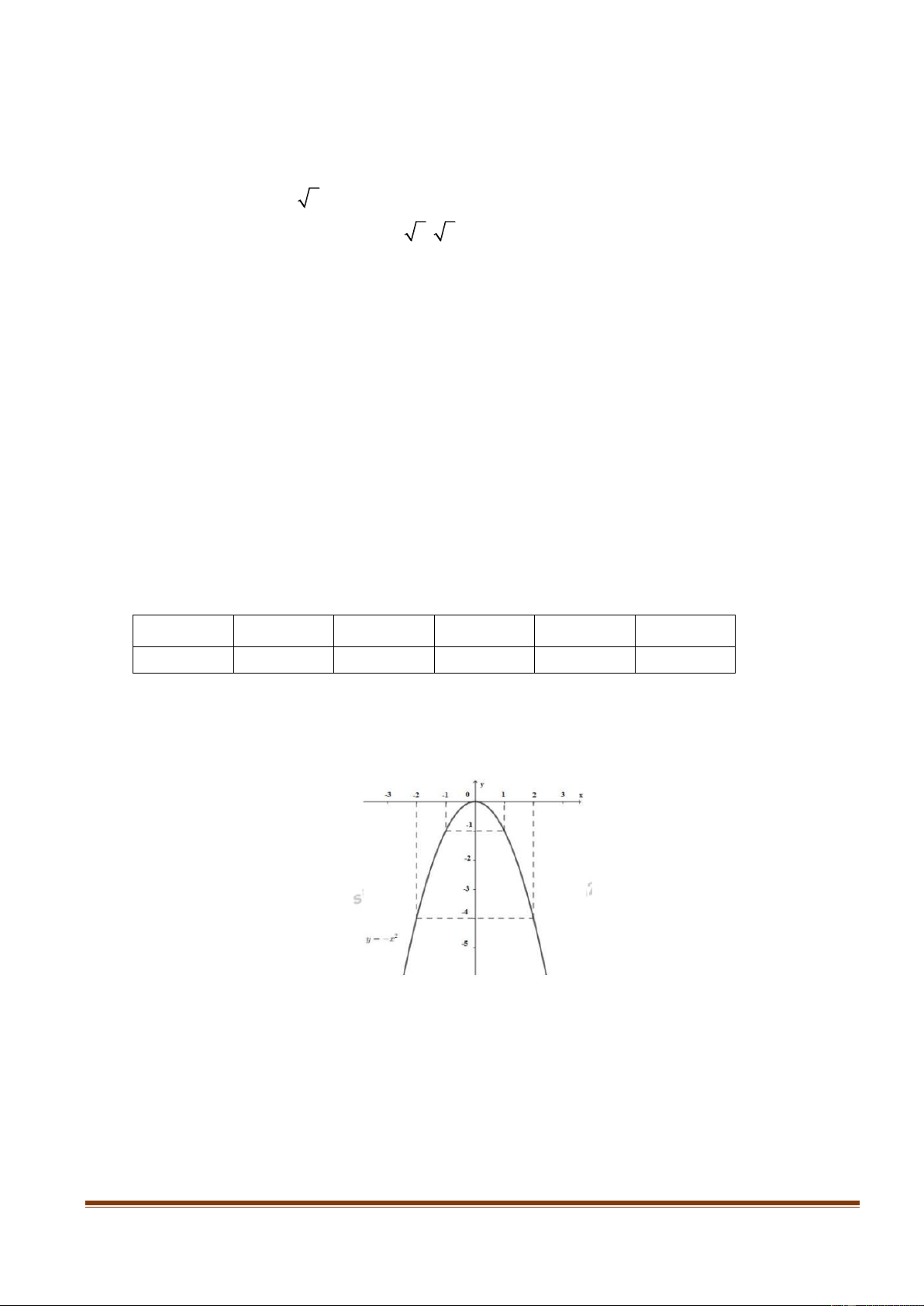
Vẽ đồ thị của hàm số 2 y x 1,0 điể . m
Bảng sau cho một số giá trị tương ứng của x và y x 2 1 0 1 2 4 2 y x 4 1 0 1 4 0,5
(nếu đúng 3 cặp ;
x y thì được 0,25 điểm) Vẽ đồ thị: 0,5 Trang 2
(nếu vẽ qua đúng 3 điểm thì được 0,25 điểm)
Tìm tọa độ giao điểm của đường thẳng d : y 2x 1và đường thẳng 1 1,0 điểm
d : y x 3 . 2
Phương trình hoành độ giao điểm của d và d là 2x1 x3 0,25 1 2 5 x 2 0,25
Với x 2 tìm được y 5 0,25
Vậy tọa độ giao điểm của d và d là 2; 5 . 1 2 0,25
Cho tam giác ABC vuông cân tại A có đường trung tuyến BM ( M thuộc 1,0 điể cạnh m
AC ). Biết AB 2a . Tính theo a độ dài AC , AM và BM . 6
AC AB 2a 0,25 AC AM a 0,25 2 2 2 2
BM AB AM 0,25 BM 5a 0,25
Hai ô tô khởi hành cùng một lúc từ A đến B . Vận tốc của ô tô thứ nhất lớn
hơn vận tốc của ô tô thứ hai là 10 km/h nên ô tô thứ nhất đến B trước ô tô 1,0 điểm 1
thứ hai giờ. Tính vận tốc mỗi ô tô biết quãng đường AB dài 150 km. 7 2
Gọi xkm/h là vận tốc ô tô thứ nhất. Điều kiện x 10 0,25
Khi đó vận tốc ô tô thứ hai là x 10km/h 0,25 Trang 3 150 1 150 Từ giả thiết ta có x 2 x 10 x 60 2
x 10x 3000 0 x 50 0,25
Do x 10 nên nhận x 60.
Vậy vận tốc của ô tô thứ nhất là 60 km/h và vận tốc của ô tô thứ hai là 0,25 50 km/h
Tìm các giá trị nguyên của m để phương trình 2
x 4x m1 0 có hai 1,0 điể nghiệm phân biệt m x và x thỏa 3 x 3 x 100 1 2 1 2
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi 0,25 0 m 3 8
x x 4; x .x m1. 1 2 1 2 3 0,25 Ta có 3 3
x x 100 x x
3x x x x 100 m 4 1 2 1 2 1 2 1 2
Kết hợp với điều kiện m 3 ta được 4 m 3 0,25
Vậy các giá trị nguyên của m cần tìm là 3 ; 2 ; 1 ;0;1;2 0,25
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O . Gọi I là
trung điểm AB . Đường thẳng qua I vuông góc AO và cắt AC tại J . 1,0 điểm
Chứng minh: B,C, J và I cùng thuộc một đường tròn. 9
Gọi M là trung điểm AC ; H là giao điểm của IJ và AO
Ta có AOC 2ABC ( góc ở tâm và góc chắn cung) 0,25 1
Tam giác OAC cân tại O nên AOM
AOC ABC AOM 1 0,25 2
Mặt khác AJI 90 OAM AOM 2 0,25 Từ
1 và 2 suy ra IBC AJI . Vậy bốn điểm , B ,
C J và I cùng thuộc 0,25 một đường tròn.
Cho đường tròn (C) có tâm I và có bán kính R 2a . Xét điểm M thay 10
đổi sao cho IM a . Hai dây AC, BD đi qua M và vuông góc với nhau. 1,0 điểm ( ,
A B, C, D thuộc (C) ). Tìm giá trị lớn nhất của diện tích tứ giác ABCD. Trang 4
Đặt H,K lần lượt là trung điểm của AC và BD , S
là diện tích tứ giác ABCD . ABCD 1 1 S A . C BD AC BD . 0,25 ABCD 2 2 2 4 2 2
AC BD 2 2
AH BK 2 2 2 2 4
4 R IH R IK . 0,25 Do 2 2 2
IH IK IM nên 2 2 2
AC BD 28a . 0,25 2 S
7a khi AC BD . ABCD 0,25
Vậy giá trị lớn nhất của diện tích tứ giác ABCD là 2 7a . ---Hết---
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT NĂM HỌC 2019-2020 THÁI BÌNH Môn: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài 120 phút (không kể thời gian giao đề)
Câu 1. (2,0 điểm) x x 1 1 x 2 x 1 Cho A và B
với x 0 , x 1. x 1 x 1 x x 1 x x 1
a).Tính giá trị của biếu thức A khi x 2 .
b).Rút gọn biểu thức B .
c).Tìm x sao cho C .
A B nhận giá trị là số nguyên.
Câu 2. (2,0 điểm)
4x y 3
a).Giải hệ phương trình
(không sử dụng máy tính cầm tay).
2x y 1
b).Một mảnh vườn hình chữ nhật có diện tích 2
150 m . Biết rằng, chiều dài mảnh vườn hơn
chiều rộng mảnh vườn là 5 m . Tính chiều rộng mảnh vườn. Trang 5
Câu 3. (2,0 điểm)
Cho hàm số y m 4 x m 4 ( m là tham số)
a).Tìm m để hàm số đã cho là hàm số bậc nhất đồng biến trên .
b).Chứng minh rằng với mọi giá trị của m thì đồ thị hàm số đã cho luôn cắt parabol P 2
: y x tại hai điểm phân biệt. Gọi x , x là hoành độ các giao điểm, tìm m sao cho 1 2 x x 1 x x 1 18 . 1 1 2 2
c).Gọi đồ thị hàm số đã cho là đường thẳng d . Chứng minh khoảng cách từ điểm O 0;0
đến d không lớn hơn 65 .
Câu 4. (3,5 điểm)
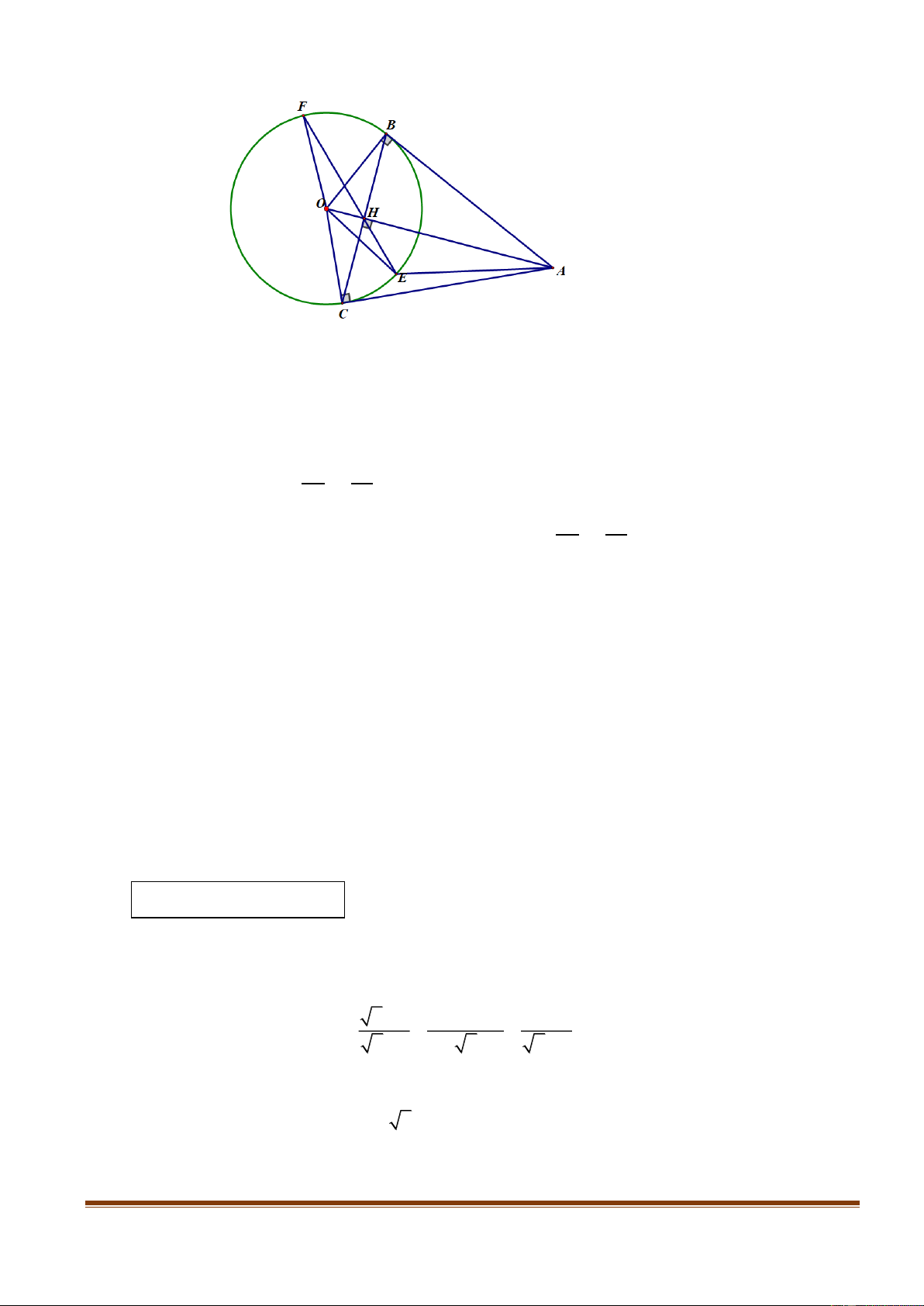
Cho đường tròn tâm O đường kính AB . Kẻ dây cung CD vuông góc với AB tại H ( H
nằm giữa A và O , H khác A và O ). Lấy điểm G thuộc CH ( G khác C và H ), tia
AG cắt đường tròn tại E khác A .
a).Chứng minh tứ giác BEGH là tứ giác nội tiếp.
b).Gọi K là giao điểm của hai đường thẳng BE và CD . Chứng minh: K . C KD K . E KB .
c).Đoạn thẳng AK cắt đường tròn O tại F khác A . Chứng minh G là tâm đường tròn
nội tiếp tam giác HEF .
d).Gọi M , N lần lượt là hình chiếu vuông góc của A và B lên đường thẳng EF . Chứng
minh HE H F MN .
Câu 5. Cho a , b , c là các số thực dương thỏa mãn a b c ab bc ac 6 . Chứng minh rằng: 3 3 3
a b c 3. b c a Hướng dẫn giải
Câu 1. (2,0 điểm) x x 1 1 x 2 x 1 Cho A và B
với x 0 , x 1. x 1 x 1 x x 1 x x 1
a).Tính giá trị của biếu thức A khi x 2 .
b).Rút gọn biểu thức B .
c).Tìm x sao cho C .
A B nhận giá trị là số nguyên. Lời giải x x 1 1 x 2 x 1 Cho A và B
với x 0 , x 1. x 1 x 1 x x 1 x x 1
a).Tính giá trị của biếu thức A khi x 2 . Trang 6 x x
x x x 3 1 1 1 x 1 Có A x 1 x 1 x 1
Khi x 2 A 2 2 1.
b).Rút gọn biểu thức B .
c).Tìm x sao cho C .
A B nhận giá trị là số nguyên. 1 x 2 x 1 Có B x 1 x x 1 x x 1 x
x 1 x 2 x 1 x 1 x x x B x
1 x x 1
x 1x x 1 x x 1 3 x 1 x x 1 Có C . A B . 1 x 1 x x 1 x 1 x 1
Có x 1 1, x 0 , x 1.
C nhận giá trị là số nguyên
x 1 1 x 0 (nhận).
Câu 2. (2,0 điểm)
4x y 3
a).Giải hệ phương trình
(không sử dụng máy tính cầm tay).
2x y 1
b).Một mảnh vườn hình chữ nhật có diện tích 2
150 m . Biết rằng, chiều dài mảnh vườn hơn
chiều rộng mảnh vườn là 5 m . Tính chiều rộng mảnh vườn. Lời giải
4x y 3
a).Giải hệ phương trình
(không sử dụng máy tính cầm tay).
2x y 1 2 x 4x y 3 6x 4 3 Có .
2x y 1 2x y 1 1 y 3 2 1 Vậy nghiệm của hệ là ; 3 3
b).Một mảnh vườn hình chữ nhật có diện tích 2
150 m . Biết rằng, chiều dài mảnh vườn hơn
chiều rộng mảnh vườn là 5 m . Tính chiều rộng mảnh vườn.
Gọi x , y lần lượt là chiều dài, chiều rộng của mảnh vườn, điều kiện x 0 y 0 , x y . Trang 7 x y 5 x y 5 Có xy 150 y y 5 150 1
y 10 nhaän 2
1 y 5y 150 0 . y 1 5 loaïi
Vậy chiều rộng mảnh vườn là 10m
Câu 3. (2,0 điểm)
Cho hàm số y m 4 x m 4 ( m là tham số)
a).Tìm m để hàm số đã cho là hàm số bậc nhất đồng biến trên .
b).Chứng minh rằng với mọi giá trị của m thì đồ thị hàm số đã cho luôn cắt parabol P 2
: y x tại hai điểm phân biệt. Gọi x , x là hoành độ các giao điểm, tìm m sao cho 1 2 x x 1 x x 1 18 . 1 1 2 2
c).Gọi đồ thị hàm số đã cho là đường thẳng d . Chứng minh khoảng cách từ điểm O 0;0
đến d không lớn hơn 65 . Lời giải
a).Tìm m để hàm số đã cho là hàm số bậc nhất đồng biến trên .
y m 4 x m 4 đồng biến trên
m4 0 m 4.
Vậy m 4 thì hàm số đồng biến trên .
b).Chứng minh rằng với mọi giá trị của m thì đồ thị hàm số đã cho luôn cắt parabol P 2
: y x tại hai điểm phân biệt. Gọi x , x là hoành độ các giao điểm, tìm m sao cho 1 2 x x 1 x
x 1 18 . 1 1 2 2
d: y m4 x m 4, P 2
: y x .
Phương trình hoành độ giao điểm của d , P : 2
x m 4 x m 4 2
x m
4 x m 4 0 1 , Có a 1 0 2 2
Có m m 2 4 4
4 m 4m 32 m 2 28 0, m a 0 Do có 0, m
Suy ra d cắt luôn cắt P tại hai điểm phân biệt .
Có x x 1 x x 1 18 2 2
x x x x 18 0 1 2 1 2 1 1 2 2 Trang 8
x x m 4
x x 2 2x x x x 18 0 , mà 1 2 1 2 1 2 1 2
x x m 4 1 2 m m 2 4 2m 4 m 4 18 0 2
m 7m10 0 m 5 m 2 5 0 . m 2
Vậy m 5, m 2 thỏa yêu cầu bài
c).Gọi đồ thị hàm số đã cho là đường thẳng d . Chứng minh khoảng cách từ điểm
O 0;0 đến d không lớn hơn 65 . m 4
d : y m 4 x m 4 cắt trục Ox , Oy lần lượt ở A ; 0
và B0;m 4 . m 4
*Trường hơp 1: Xét m 4 0 m 4, thì d :y 8, d song song trục Ox , d cắt trục
Oy tại B0; 8
Có khoảng cách từ O đến đường thẳng d là OB 8
Gọi H là hình chiếu của O lên đường thẳng d . O
AB vuông tại O có OH AB, Có OH.AB O . AOB 2 m 4 1 1 1 2 1 m4 1 2 2 2 OH OA OB 2
m 42 m 42 m4 m42 2 OH m 42 1 m42 Giả sử OH 65 2 OH 65 2 m m 2 8 16
65 m 8m 17 m4 65 2 1 2
64m 528m1089 0 2 2
8m 2.16.8m 33 0 m 2 8 33 0 (sai) Vậy OH 65 .
Câu 4. (3,5 điểm)
Cho đường tròn tâm O đường kính AB . Kẻ dây cung CD vuông góc với AB tại H ( H
nằm giữa A và O , H khác A và O ). Lấy điểm G thuộc CH ( G khác C và H ), tia
AG cắt đường tròn tại E khác A .
a).Chứng minh tứ giác BEGH là tứ giác nội tiếp.
b).Gọi K là giao điểm của hai đường thẳng BE và CD . Chứng minh: K . C KD K . E KB . Trang 9
c).Đoạn thẳng AK cắt đường tròn O tại F khác A . Chứng minh G là tâm đường tròn nội tiếp tam giác HEF .
d).Gọi M , N lần lượt là hình chiếu vuông góc của A và B lên đường thẳng EF . Chứng
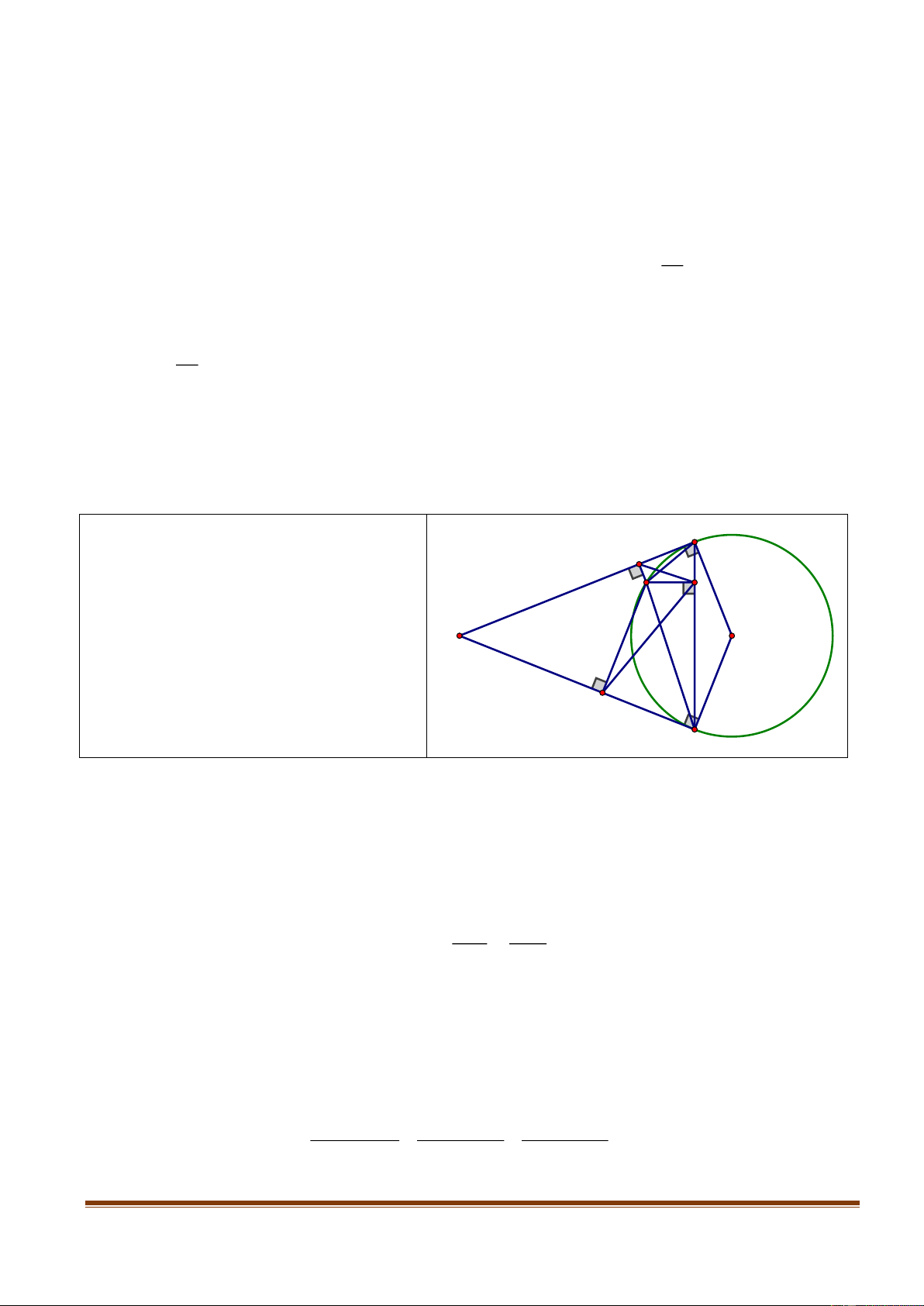
minh HE H F MN . K N E C F T M G O B A H Q D Lời giải
a).Chứng minh tứ giác BEGH là tứ giác nội tiếp.
Có BHG BEG 90 BHG BEG 180 .
Tứ giác BEGH nội tiếp đường tròn đường kính BG .
b).Gọi K là giao điểm của hai đường thẳng BE và CD . Chứng minh: K . C KD K . E KB . KE KC
Có KEC KDB , EKC DKB (góc chung) K EC ∽ K DB KD KB K . C KD K . E KB
c).Đoạn thẳng AK cắt đường tròn O tại F khác A . Chứng minh G là tâm đường tròn
nội tiếp tam giác HEF . K
AB có ba đường cao AE , BF , KH đồng qui tại G . Suy ra G là trực tâm của K AB .
Có GHE GBE 1 sñGE (trong đường tròn BEGH ) 2
Có GBE GAF 1 sñEF (trong đường tròn O ) 2 Trang 10
Có GAF GHF 1 sñEG (tứ giác AFGH nội tiếp đường tròn đường kính AG ) 2
Suy ra GHE GHF HG là tia phân giác của EHF .
Tương tự EG là tia phân giác của FEG .
EHF có hai tia phân giác HG và EG cắt nhau tại G . Suy ra G là tâm đường tròn nội tiếp EHF .
d).Gọi M , N lần lượt là hình chiếu vuông góc của A và B lên đường thẳng EF .
Chứng minh HE H F MN .
Gọi Q là giao điểm của tia EH và đường tròn O .
Có EOB 2EFB sñEB , 2EFB EFO (do FG là tia phân giác của EFH )
EOB EFH Tứ giác EFHO nội tiếp đường tròn.
FOH FEH 1 sñEQ 1 FOQ FOH 1 FOQ. 2 2 2
OH là tia phân giác của FOQ
OFH,OQH có OH chung, OF OQ, FOH QOH
OFH OQH HF HQ
Do đó HE HF HE HQ EQ .
Có AMN MNT NTA
90 . Suy ra AMNT là hình chữ nhật, nên AT MN .
Suy ra AQ FA ET AE // QT , mà AETQ nội tiếp đường tròn O .
AETQ là hình thang cân EQ AT MN
Vậy HE H F MN .
Câu 5. Cho a , b , c là các số thực dương thỏa mãn a b c ab bc ac 6 . Chứng minh rằng: 3 3 3
a b c 3. b c a Lời giải 3 3 3 Đặ a b c t P . b c a
Có a , b , c là các số thực dương, theo bất đẳng thức AM-GM có: Trang 11 3 a ab 2 2a b 3 b 3 3 3 a b c bc 2 2b . P 2 a 2 b 2 2
c ab bc ac , mà c b c a 3 c ac 2 2c a
a b c ab bc ac 6 . P 2 a 2 b 2 2
c a b c 6 . 2 2 2 Có a
b b c a c 0 2 a 2 b 2 2
c 2ab bc ca
2 2 2 2 3 a b c a b c . 2 2 Suy ra P
abc abc6. 3 Có 2 2 2
ab bc ca a b c 2 3 ab bc ac a b c . 1
Do đó 6 a b c ab bc ac a b c a b c2 3 1
a b c2 a b c 6 0. a b c 3, a b c2 9. 3 2 Suy ra P
.9 3 6 3. Dấu đẳng thức xảy ra khi a b c . 3 3 3 3 a b c Vậy 3. b c a
UBND TỈNH THÁI NGUYÊN
THI TUYỂN SINH VÀO LỚP 10 THPT
SỞ GIÁO DỤC VÀ ĐÀO TẠO Năm học 2019 – 2020 MÔN: TOÁN
Thời gian làm bài 120 phút không kể thời gian giao đề
( Đề thi gồm 01 trang, 10 câu, mỗi câu 01 điểm )
Câu 1. Chứng minh A = 2 A
2 5 6 ( 5 1) 2018 là một số nguyên a 1 b 2 b 1
Câu 2. Rút gọn biểu thức P với a < 1 và b > 1 2 b 1 a 2a 1
Câu 3. Tìm các giá trị của m 1 để hàm số y = (2m – 1) x2 đạt giá trị lớn nhất bằng 0 2 tại x = 0. Trang 12
Câu 4. Cho hàm số y = ax + b với a 0. Xác định các hệ số a, b biết đồ thị hàm số
song song với đường thẳng y = 2x + 2019 và cắt trục tung tại điểm có tung độ là 2020.
Câu 5. Một địa phương cấy 10ha giống lúa loại I và 8ha giống lúa loại II. Sau một mùa
vụ, địa phương đó thu hoạch và tính toán sản lượng thấy:
+ Tổng sản lượng của hai giống lúa thu về là 139 tấn;
+ Sản lượng thu về từ 4ha giống lúa loại I nhiều hơn sản lượng thu về từ 3ha giống lúa loại II là 6 tấn.
Hãy tính năng suất lúa trung bình ( đơn vị: tấn/ ha) của mỗi loại giống lúa.
Câu 6. Cho phương trình
x2 – 4x + m – 1 = 0. Tìm m để phương trình có hai nghiệm x 2 2
1, x2 thỏa mãn x1 + x2 -10x1x2 = 2020.
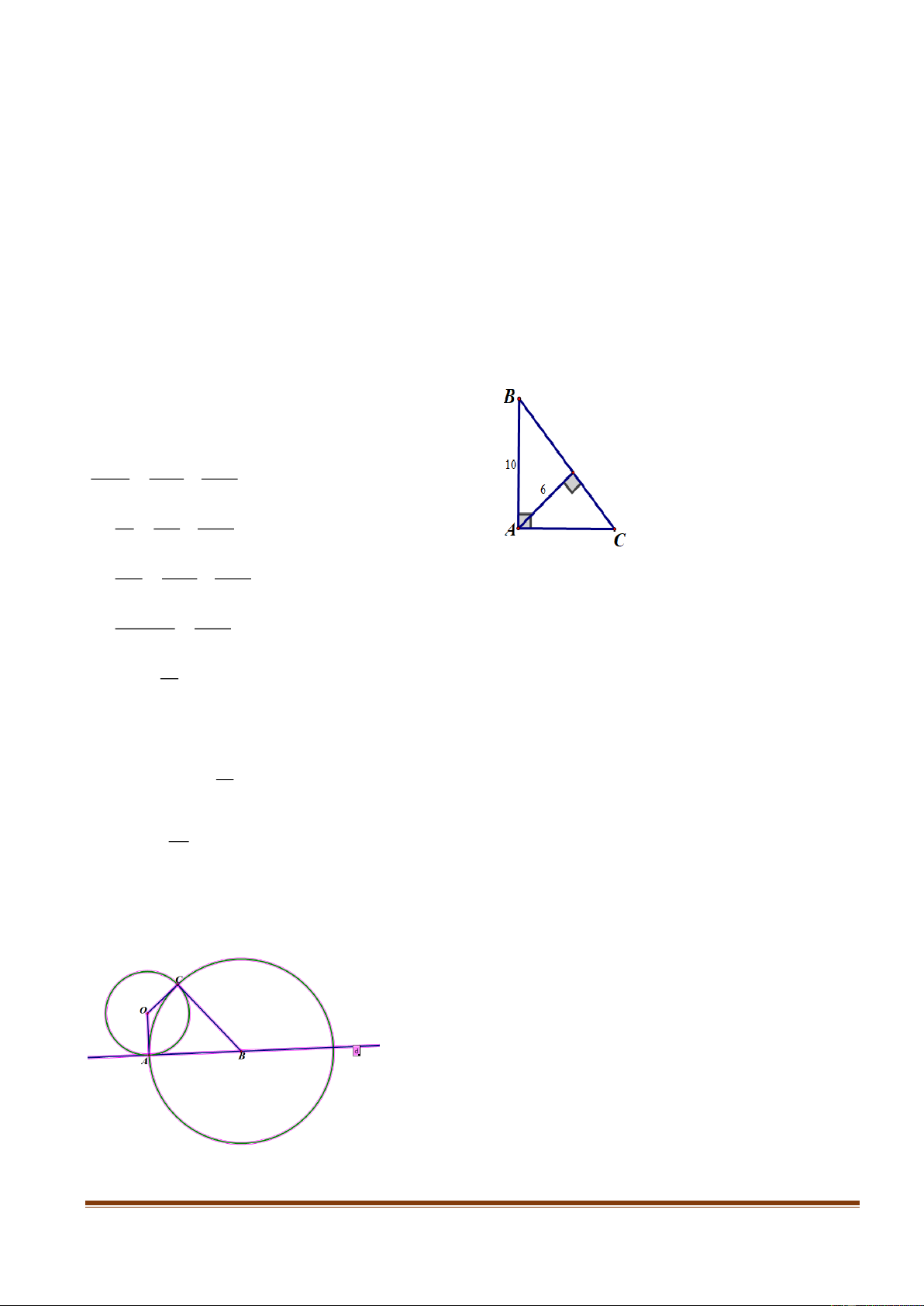
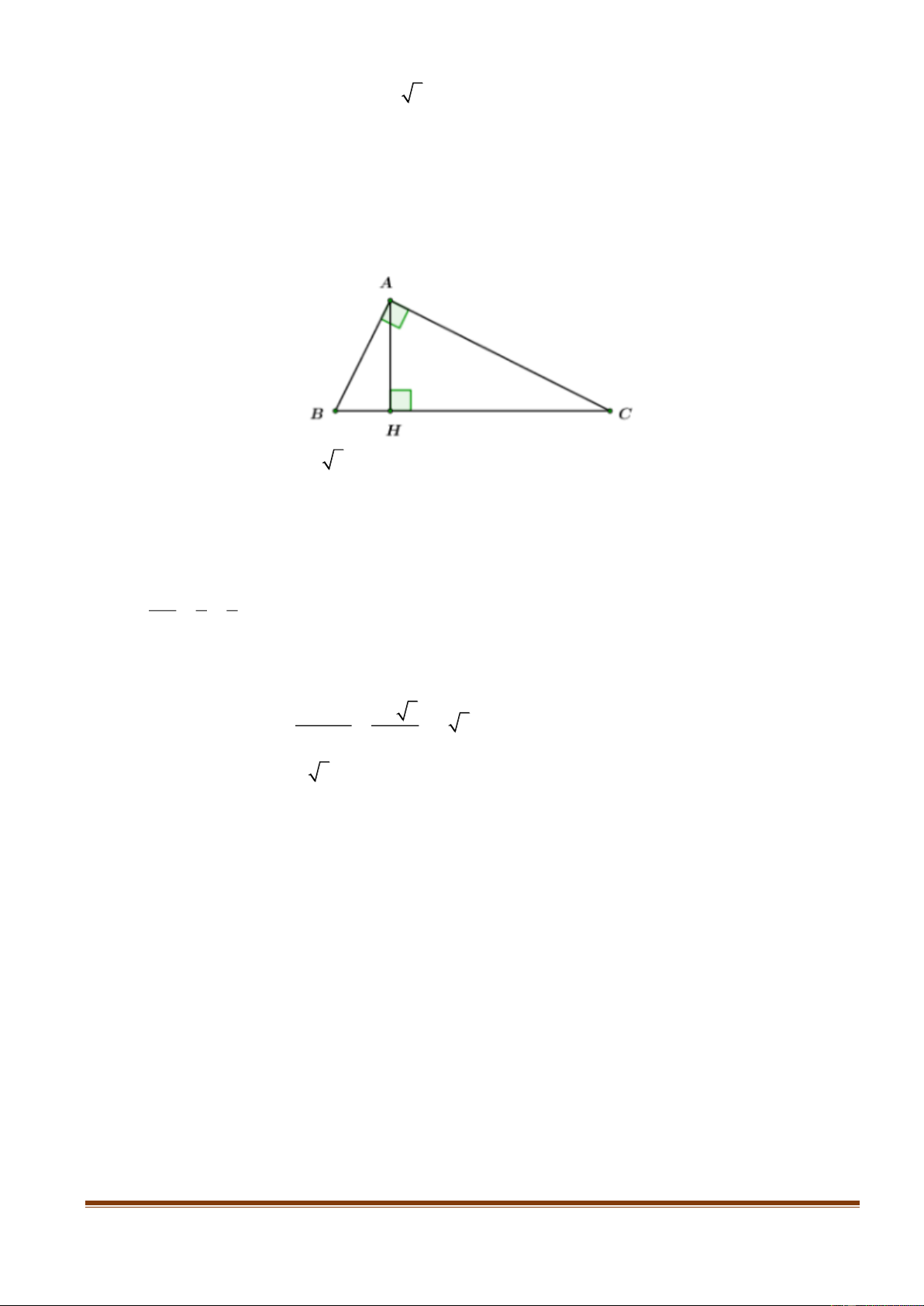
Câu 7. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 10cm, AH = 6cm,
Tính độ dài các cạnh AC, BC của tam giác ABC.
Câu 8. Cho đường tròn (O). Đường thẳng d tiếp xúc với đường tròn ( O) tại A. Trên d
lấy một điểm B( B khác A), vẽ đường tròn (B, BA) cắt đường tròn ( O) tại điểm C ( C
khác A). Chứng minh BClà tiếp tuyến của (O).
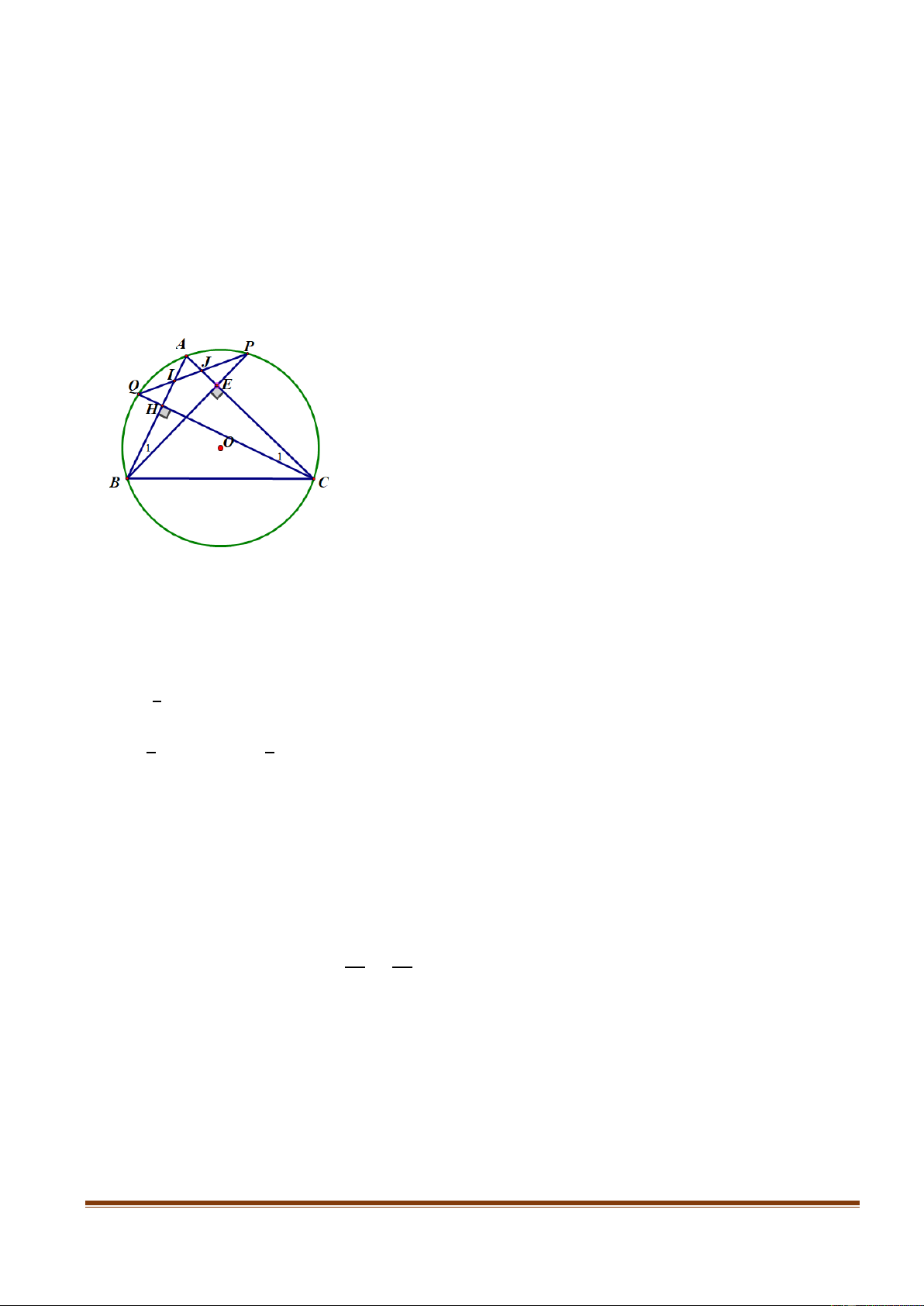
Câu 9. Cho tam giác ABC( AB< AC) có ba góc nhọn nội tiếp đường tròn (O). Lấy các
điểm P, Q lần lượt thuộc các cung nhỏ AC, AB sao cho BP vuông góc với AC, CQ
vuông góc với AB. Gọi I, J lần lượt là giao điểm của PQ với AB và AC. Chứng minh IJ.AC = AI.CB.
Câu 10. Từ điểm A nằm ngoài đường tròn ( O) kẻ các tiếp tuyến AB, AC đến đường
tròn ( B, C là tiếp điểm ). Gọi H là giao điểm của OA và BC. a. Chứng minh OB2 = OH. OA
b. EF là một dây cung của (O) đi qua H sao cho A, E, F không thẳng hàng. Chứng
minh bốn điểm A, E, O, F nằm trên cùng một đường tròn. ----Hết--- ĐÁP ÁN Câu 1. Chứng minh 2 2 2 A 25 5 1 6 ( 5 5 1 1 ) 2 2 0 0 1 1 8 8 5 1 5 1 2018 2020
Vậy A là một số nguyên Câu 2. Trang 13 a 1 b 2 b 1 P 2 b 1 a 2a 1 b a 2 1 1
b 1 a 2 1 b 1 a 1 . b 1 a 1 a 1 b 1 . b 1 1 a 1 ( do a < 1 và b > 1)
Câu 3. Hàm số y = (2m – 1) x2 đạt giá trị lớn nhất tại x = 0. 1
Khi 2m – 1 < 0 ↔ m < 2
Câu 4. ( d): y = ax + b ( a 0) song song với (∆): y = 2x + 2019 → a = 2 (1) b 2019
+ (d) cắt Oy tại điểm có tung độ 2020 → b = 2020 (2)
Từ (1), (2) ta có: y = 2x + 2020 Câu 5.
Gọi năng suất lúa trung bình của loại I là x ( 0 < x < 139)
Gọi năng suất lúa trung bình của loại II là y (0 < y < 139)
Theo bài ra ta có hệ phương trình 10𝑥 + 8𝑦 = 139 𝑥 = 7,5 {
4𝑥 − 3𝑦 = 6 ↔ { 𝑦 = 8
Vậy năng suất lúa trung bình của loại I là: 7,5 (tấn / ha)
Vậy năng suất lúa trung bình của loại II là: 8 (tấn / ha)
Câu 6. Cho phương trình
x2 – 4x + m – 1 = 0. Tìm m để phương trình có hai nghiệm x 2 2
1, x2 thỏa mãn x1 + x2 -10x1x2 = 2020. ∆’ = 4-m-1 = 3-m
+ PT có 2 nghiệm ↔ ∆’ ≥ 0 ↔ 3-m ≥ 0 ↔ m ≤ 3 𝑥 + Theo viet { 1 + 𝑥2 = 4 𝑥1𝑥2 = 𝑚 + 1 (1) Trang 14 Mà: x 2 2 1 + x2 -10x1x2 = 2020
↔ (x1 + x2 )2 - 12 x1x2 -2020 = 0 (2)
Thế (1) vào (2) ↔ 16 - 12(m+1) – 2020 = 0 ↔ -12m - 2016 = 0 ↔ m = -168 ( t/m) Câu 7. Ta có: 1 1 1 2 2 2 AH AB AC 1 1 1 2 2 2 6 10 AC 1 1 1 2 36 100 AC 64 1 2 36.100 AC 15 AC (cm) 2 Ta có: AH.BC = AB.AC 15 6.BC = 10. 2 25 BC = (cm) 2 Câu 8.
Theo bài ra ta có AB là tiếp tuyến của đường tròn (O) → AB OA (1) Trang 15
Xét hai tam giác ∆OAB và ∆OCB có: OA = OC
BA = BC → ∆OAB = ∆OCB ( c.c.c) (2) OB chung
Từ (1), (2) suy ra 𝑂𝐴𝐵 ̂ = 𝑂𝐶𝐵 ̂ (=900) hay 𝑂𝐶𝐵 ̂ =900 nên BC OC
Vậy BClà tiếp tuyến của (O) Câu 9.
Tứ giác HECB nội tiếp đường tròn ( vì 2 đỉnh liên tiếp nhìn 1 cạnh cố định dưới góc vuông) → 𝐵1 ̂ = 𝐶1
̂ ( Nội tiếp chắn cung HE) → AP AQ 1 𝐴𝐶𝐵 ̂ = AB 2 1 1 𝐴𝐼𝑃
̂ = ( AP BQ ) = AB (vì AP AQ ) 2 2 → 𝐴𝐶𝐵 ̂ = 𝐴𝐼𝑃 ̂
Xét tam giác ∆AIJ và ∆ ACB Có 𝐴̂ chung 𝐴𝐶𝐵 ̂ = 𝐴𝐼𝑃 ̂ (cmt) 𝐴𝐼 𝐼𝐽
Vậy ∆AIJ và ∆ ACB (g.g) → = → IJ.AC = AI.CB 𝐴𝐶 𝐶𝐵 Câu 10. Trang 16 a. Xét tam giác ∆OBA và ∆OHB có: 𝑂 ̂ chung 𝐻 ̂ = 𝐵̂ = 900 → ∆ 𝑂𝐵 𝑂𝐴 OBA ~ ∆OHB → = → OB2 = OH. OA 𝑂𝐻 𝑂𝐵 𝑂𝐴
b. theo cmt: OB2 = OH. OA → OE2 = OH. OA → 𝑂𝐸 = lại có: 𝐻𝑂𝐸 ̂ = 𝐴𝑂𝐸 ̂ 𝑂𝐻 𝑂𝐸
→∆OEH ~ ∆OAE →𝑂𝐴𝐸 ̂ = 𝑂𝐸𝐹 ̂ ( 1)
Vì ∆OEF cân nên: 𝑂𝐹𝐸 ̂ = 𝑂𝐸𝐹 ̂ (2)
Từ (1), (2) suy ra: 𝑂𝐴𝐸 ̂ = 𝑂𝐹𝐸
̂ ( hai đỉnh liên tiếp bằng nhau cùng nhìn dưới
cạnh cố định OE) → Tứ giác OEAF nội tiếp đường tròn
Vậy bốn điểm A, E, O, F nằm trên cùng một đường tròn
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀOLỚP 10 THPT THANH HÓA NĂM HỌC 2019 - 2020
------------------------- Môn Toán : Lớp 10 ĐỀ CHÍNH THỨC
(Thời gian làm bài: 120 phút) --------------------------- Bài 1. (2 điể x 2 5 1
m) Cho biểu thức: A
với x 0; x 4. x 3 x x 6 x 2
1. Rút gọn A
2. Tìm giá trị của cảu A khi x 6 4 2 Trang 17 Bài 2. (2 điểm)
1. Cho đường thẳng d : y ax+b . Tìm a, b để đường thẳng (d) song song với đường
thẳng d ' : y 5x+6 và đi qua điểm A2;3 3
x 2y 11
2. Giải hệ phương trình
x 2y 5 Bài 3: ( 2 điểm) 1. Giải phương trình 2
x 4x 3 0 2. Cho phương trình: 2
x 2m
1 x 2m 5 0 với m là tham số.Chứng minh rằng
phương trình luôn có hai nghiệm phân biệt x1, x2 với mọi m. Tìm m để các nghiệm đó thỏa mãn hệ thức 2
x 2mx x 2m 3 x 2mx x 2m 3 19. 1 1 2 2 2 2 1
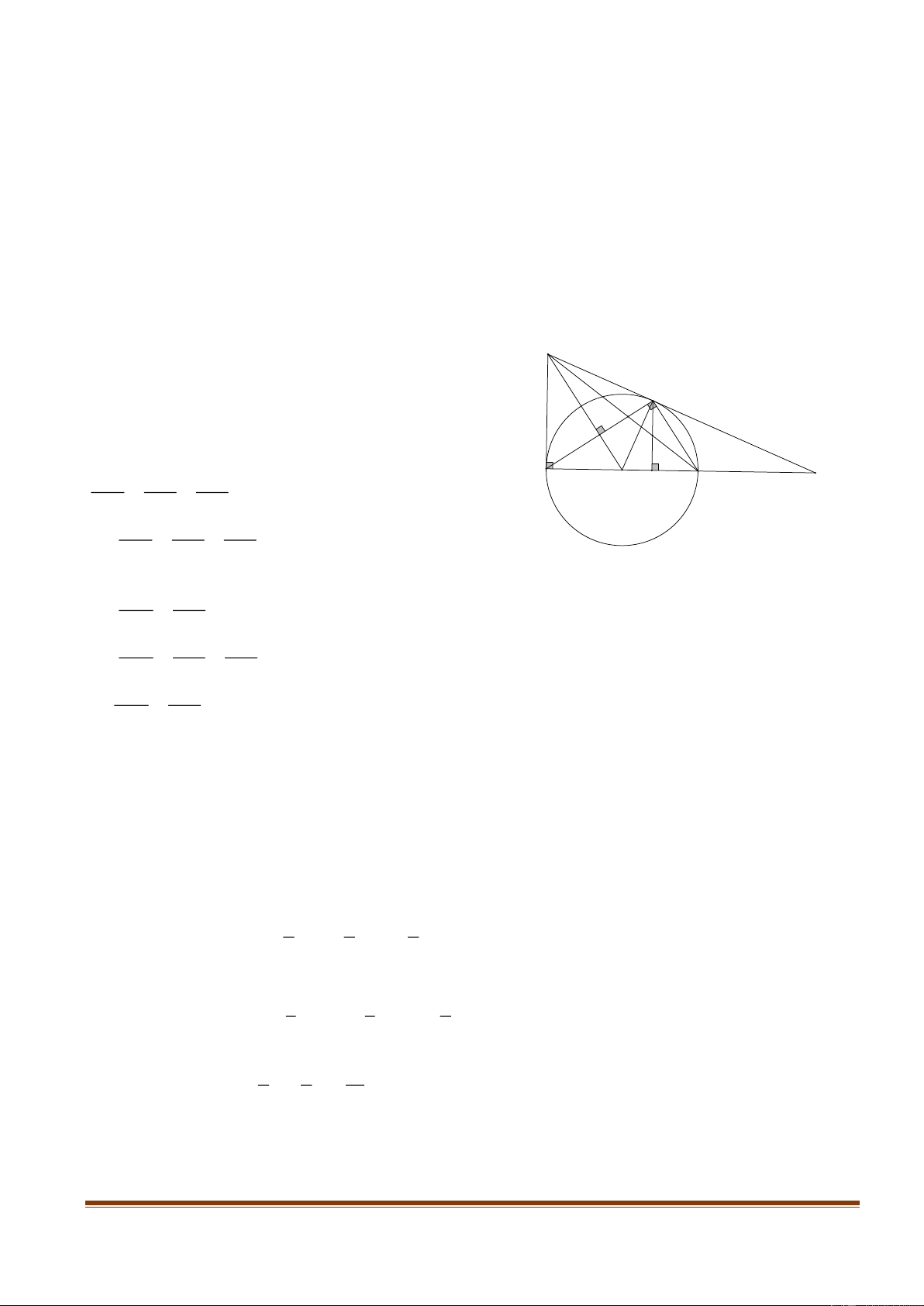
Bài 4. (3,0 điểm) Từ một điểm A nằm ngoài đường tròn tâm O bán kính R, kẻ các tiếp tuyến
AB, AC với đường tròn ( B, C là các tiếp điểm). Trê cung nhỏ BC lấy một điểm M bất kỳ khác
B và C. Gọi I,K,P lần lượt là hình chiếu vuông góc của M trên các đường thẳng AB, AC, BC
1) Chứng minh AIMK là tứ giác nội tiếp;
2) Chứng minh MPK MBC
3) Xác định vị trí điểm M trên cung nhỏ BC để tích MI .MK.MP đạt giá trị nhỏ nhât..
Bài 5. (1,0 điểm) Cho các số thực a, b, c thỏa mãn abc 1, Chứng minh rằng: ab bc ca 1 4 a 4 b 4 ab b 4 c 4 bc c 4 a ca ------Hết------- Lời giải Câu I.
1. Rút gọn biểu thức A với với x 0; x 4. x 2 5 1 A x 3
x 3 x 2 x 2
x 4 5 x 3
x 3 x 2 x x 12
x 3 x 2 Trang 18 x 4 x 2 2.
Tìm giá trị của cảu A khi x 6 4 2 x 2 6 4 2 2 2 tmđk 2 24 2 2
x 2 2 thay vào A ta đc: A 2 2 1 2 2 2
Vậy với x 6 4 2 thì A 1 2 Bài 2. (2 điểm)
1. Cho đường thẳng d : y ax+b . Tìm a, b để đường thẳng (d) song song với đường
thẳng d ' : y 5x+6 và đi qua điểm A2;3 a 5
Vì d / / d ' nên b 6
Vì (d) đi qua A2;3 nên ta có: 3 5.2+b b 7
Vậy a 5; b 7
ta có d : y 5x 7 3
x 2y 11
2. Giải hệ phương trình
x 2y 5 3
x 2y 11 x 3 2x 6 y 1 Bài 3: ( 2 điểm) 1. Giải phương trình 2
x 4x 3 0
PT có : a b c 1 4 3 0 nên PT có hai nghiệm: x 1; x 3 1 2 2 2
2. Ta có: m m 2 ' 1 2
5 m 4m 6 m
2 2 0 m nên phương
trình luôn có hai nghiệm phân biệt x1, x2 với mọi m 2 2
Có : x 2m
1 x 2m 5 0 x 2mx 2m 3 2 2x
Vì x1, x2 là các nghiệm của PT (1) nên ta có: 2
x 2mx 2m 3 2 2x 2 ; x
2mx 2m 3 2 2x thay vào (*) ta đc: 1 1 1 2 2 2 2
x 2mx x 2m 3 x 2mx x 2m 3 19 1 1 2 2 2 2 1
2 2x x 2 2x x 19 1 2 2 1 Trang 19 2x x 6 x x x x 15 1 2 2 1 2 1 2
x x 2 m 1 1 2 Theo Vi-et có thay vào ta đc: x x 2m 5 1 2 m 0 m 2 8 1 12m 1 2m 5 15 2
8m 26m 0 m 13 4 m 0 Vây: m 13 4
Bài 4. (3,0 điểm) Từ một điểm A nằm ngoài đường tròn tâm O bán kính R, kẻ các tiếp tuyến
AB, AC với đường tròn ( B, C là các tiếp điểm). Trên cung nhỏ BC lấy một điểm M bất kỳ
khác B và C. Gọi I,K,P lần lượt là hình chiếu vuông góc của M trên các đường thẳng AB, AC, BC
1. Chứng minh AIMK là tứ giác nội B tiếp; I Có: 90o AIM AKM nên tứ giác M P AIMK nội tiếp.
2. Chứng minh MPK MBC . A O
TT câu a ta cm đc tứ giác KCPM nội tiếp.
Suy ra: MCK MPK ( hai góc nt cùng K chắn cung MK) (1) C
Mà MCK PBM ( góc tạo bởi tia tiếp tuyến và dây và góc nt cùng chắn cung MC của (O)) (2)
Từ (1) và (2) suy ra MPK MBP hay MPK MBC
1) Xác định vị trí điểm M trên cung nhỏ BC để tích MI .MK.MPđạt giá trị nhỏ nhât.. IM MP
Chứng minh được IMP ∽ PMK nên: MP MK MI MK 2
MP MI MK MP 3 . . . MP
Để MI .MK.MPlớn nhất khi chỉ khi MP lớn nhất, nên M là điểm chính giữa cung nhỏ BC
Bài 5. (1,0 điểm) Cho các số thực a, b, c thỏa mãn abc 1, Chứng minh rằng: ab bc ca 1 4 a 4 b 4 ab b 4 c 4 bc c 4 a ca Trang 20 ab ab 1 Ta có: 4 4 2 2 a b ab a b 4 4 a b ab ab 2 a 2 b 2 ab a 2 b 1 bc 1 ca 1 Tương tự có: ; 4 b 4 c 2 bc b 2 c 1 4 c 4 a 2 ca c 2 a 1 1 1 1 Suy ra VT 2 a 2 b 2 1 b 2 c 2 1 c 2 a 1 Đặt 2 a 3 2 x b 3 2 y c 3 ; '
z ta có: xyz 1 ( do abc 1) 1 1 1 Suy ra: VT 3 x 3 y 3 1 y 3 z 3 1 z 3 x 1 Dễ cm đc 3 3 x
y xy x y VT 1 1 1 xy x y 1 y z y
z 1 zxz x 1 z x y VT xy z x y z xy z y
z x zxyz x y z x y VT 1
x y z
x y z
zx y z
Vậy VT 1 Dấu “_” xảy ra khi a b c
SỜ GIÁO DỤC VÀ ĐẠO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT NĂM 2019 – 2020 THỪA THIÊN HUẾ
Khóa ngày 02 tháng 6 năm 2019
ĐỀ THI CHÍNH THỨC Môn thi: TOÁN
Thời gian làm bài: 120 phút ( không kể thời gian giao đề) Câu 1: (1,5 điểm)
a) Tìm giá trị của x sao cho biểu thức A x 1 có giá trị dương.
b) Đưa thừa số ra ngoài dấu căn, tính giá trị biểu thức 2 2 2
B 2 2 .5 3 3 .5 4 4 .5 2 1 a a 1 a
c) Rút gọn biểu thức C a
với a 0 và a 1 . 1 a 1 a
Câu 2: (1,5 điểm)
4x y 7
a) Không sử dụng máy tính cầm tay, giải hệ phương trình
x 3y 5
b) Cho đường thẳng d : y ax b . Tìm giá trị của a và b sao cho đường thẳng d đi qua điểm A0;
1 và song song với đường thẳng : y x 2019 .
Câu 3: (1,0 điểm) Hưởng ứng Ngày Chủ nhật xanh do UBND tỉnh phát động với chủ đề “Hãy hành
động để Thừa Thiên Huế thêm Xanh, Sạch, Sáng”, một trường THCS đã cử học sinh của hai lớp 9A và 35
9B cùng tham gia làm tổng vệ sinh một con đường, sau
giờ thì làm xong công việc. Nếu làm riêng 12
từng lớp thì thời gian học sinh lớp 9A làm xong công việc ít hơn thời gian học sinh lớp 9B là 2 giờ.
Hỏi nếu mỗi lớp làm riêng thì sau bao nhiêu giờ sẽ làm xong công việc?
Câu 4: (2,0 điểm) Cho phương trình: 2
x m 2 2
2 x m 4m 0 1 (với x là ẩn số). Trang 21
a) Giải phương trình 1 khi m 1 .
b) Chứng minh rằng phương trình
1 luôn có hai nghiệm phân biệt với mọi giá trị của m.
c) Tìm các giá trị của m để phương trình
1 có hai nghiệm phân biệt x , x thỏa mãn điều kiện 1 2 3 3 x x . 2 1 x x 1 2
Câu 5: (3,0 điểm) Cho đường tròn tâm O đường kính AB. Trên đường tròn O lấy điểm C không
trùng B sao cho AC BC . Các tiếp tuyến của đường tròn O tại A và tại C cắt nhau tại D. Gọi H là
hình chiếu vuông góc của C trên AB, E là giao điểm của hai đường thẳng OD và AC.
a) Chứng minh OECH là tứ giác nội tiếp.
b) Gọi F là giao điểm của hai đường thẳng CD và AB. Chứng minh 2BCF CFB 90 .
c) Gọi M là giao điểm của hai đường thẳng BD và CH. Chứng minh hai đường thẳng EM và AB song song với nhau.
Câu 6: (1,0 điểm) Một chiếc cốc thủy tinh có dạng hình trụ chứa đầy nước, có chiều cao bằng 6cm ,
bán kính đáy bằng 1cm . Người ta thả từ từ lần lượt vào cốc nước một viên bi hình cầu và một vật có
dạng hình nón đều bằng thủy tinh (vừa khít như hình vẽ) thì thấy nước trong chiếc cốc tràn ra ngoài.
Tính thể tích của lượng nước còn lại trong chiếc cốc (biết rằng đường kính của viên bi, đường kính của
đáy hình nón và đường kính của đáy cốc nước xem như bằng nhau; bỏ qua bề dày của lớp vỏ thủy tinh).
……………Hết……………
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên thí sinh:………………………………Số báo danh:……………………. ĐÁP ÁN Câu 1: (1,5 điểm)
a) A x 1
Ta có A có giá trị dương A 0 x 1 0 x 1
Vậy x 1 thì A có giá trị dương b) 2 2 2
B 2 2 .5 3 3 .5 4 4 .5 2 2 2
2 2 .5 3 3 .5 4 4 .5 2.2 5 3.3 5 4.4 5
4 5 9 5 16 5 11 5 Vậy B = 11 5 c)
ĐKXĐ: a 0; a 1 2 2
1 a1 a a 1 a a 1 a 1 a C a a . 1 a 1 a 1 a
1 a 1 a
a a a 2 1 1 . a a 2 1 1 2 . 1 a 1 a a 2 2 1 1 . 1 1 a
Vậy với a 0; a 1 thì B = 1
Câu 2: (1,5 điểm) Trang 22
4x y 7 1 2x 3y 21 1 3x 26 x 2 x 2 a)
x 3y 5
x 3y 5 y 4x 7 y 4.2 7 y 1
Vậy hệ phương trình có nghiệm duy nhất là: ; x y 2; 1 a 1
b) Ta có d // b 2019
d : y x b (b 2019)
Đường thẳng d : y x b (b 2019) đi qua điểm (
A 0; 1) nên thay x 0; y 1 vào phương trình
đường thẳng d ta được 1
0 b b 1 (TM)
Vậy a 1; b 1
Câu 3: (1,0 điểm) 35
Gọi thời gian lớp 9A làm một mình xong công việc là x (giờ) x 12
Gọi thời gian lớp 9B làm một mình xong công việc là y (giờ) y 2 1
Mỗi giờ lớp 9A làm được phần công việc là: (công việc) x 1
Mỗi giờ lớp 9B làm được phần công việc là: (công việc) y 1 1
Mỗi giờ lớp cả hai ớp 9A, 9B làm được phần công việc là: (công việc) x y 35
Theo đề bài, hai lớp cùng làm chung công việc trong
giờ thì xong công việc nên ta có phương 12 1 1 35 1 1 12 trình: 1: (1) x y 12 x y 35
Nếu làm riêng từng lớp thì thời gian học sinh lớp 9A làm xong công việc ít hơn thời gian lớp 9B là 2
giờ nên ta có phương trình: y x 2 (2)
Thế phương trình (2) vào phương trình (1) ta được: 1 1 12 (1)
35(x 2) 35x 12x(x 2) x x 2 35 2
35x 70 35x 12x 24x 2 12x 46x 70 0 2
12x 60x+14x 70 0
12x(x 5) 14(x 5) 0
(x 5)(12x 14) 0 x 5 (tm) x 5 0 7 12 x 14 0
x (Ktm) 6
Vậy nếu làm một mình thì lớp 9A làm xong công việc trong 5 giờ, lớp 9B làm xong công việc trong 5 2 7 giờ
Câu 4: (2,0 điểm) Phương trình: 2
x m 2 2
2 x m 4m 0 1
Thay m 1 vào phương trình (1) ta được pương trình: 2 2
x 2x 3 0 x 3x x 3 0
x(x 3) (x 3) 0 Trang 23
(x 3)(x 1) 0 x 3 0 x 3 x 1 0 x 1
Vậy với m 1 thì tập nghiệm của phương trình là: S 1 ; 3 b) 2
x m 2 2
2 x m 4m 0 1 CÓ 2 2 2 2
' (m 2) m 4m m 4m 4 m 4m 4 0 m Vậy phương trình
1 luôn có hai nghiệm phân biệt với mọi giá trị của m. c) Phương trình
1 luôn có hai nghiệm phân biệt x , x với mọi giá trị của m. 1 2
x x 2( m 2) 2 m 4
Áp dụng hệ thức Vi-ét ta có: 1 2 2
x .x m 4m 1 2
Phương trình có hai nghiệm x 0; x 0 khi x x 0 2
m 4m 0 m 0 và m 4 1 2 1 2 3 3 Theo đề bài ta có: x x 2 1 x x 1 2 3 3
x x 0 x x 0 m 0;m 4 1 2 1 2 x x 1 2 1 1
3 x x 0 2 1 x x 1 2 x x 2 1 3
x x 0 2 1 x x 1 2 3 x x 1 0 2 1 x x 1 2 3
1 0( Do x x x x 0) 1 2 2 1 x x 1 2 3 2
1 0 m 4m 3 0 2 m 4m 2
m 3m m 3 0 m(m 3) (m 3) m 3(tm)
(m 3)(m 1) 0 m 1(tm)
Vậy m 1; m 3 là các giá trị thỏa mãn bài toán. Câu 5: (3,0 điểm) a)
DC DA (tính chất hai tiếp tuyến cắt nhau) O
A OC (bán kính)
Do đó OD là đường trung trực của đoạn thẳng AC OD AC
Tứ giác OECH có CEO CHO 90 90 180
Tứ giác OECH là tứ giác nội tiếp.
b) Xét O có: BCF BAC (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BC) (1)
HCB BAC (Cùng phụ CBA ) (2) Trang 24
Từ (1) và (2) suy ra BCF HCB CB là tia phân giác của HCF (*)
HCF 2.BCF C
HF vuông tại H nên HCF CFB 90 hay 2.BCF CFB 90
c) Gọi K là giao điểm của DB và AC.
Xét O ta có: ABC ACD (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn AC ) (3) Ta có A
CH vuông tại H có ACH 90 CAH D ABC
vuông tại C có CBA 90 CAB
ACH ABC (Cùng phụ CAH ) (4) C
Từ (3) và (4) suy ra ACH ACD E K M
CA là tia phân giác trong của tam giác B CD (**)
Theo tính chất tia phân giác trong B CD ta có: A H KM BM CM O B F KD BD CD KM BM CM
(Do DC DA ) KD BD AD
Mặt khác ta có: CH / / AD (cùng vuông góc AB ) HM BM (Định lý Ta lét) AD BD HM BM CM AD BD AD HM CM AD AD HM CM
Mà CE AE (Do OD là đường trung trực của AB) nên ME là đường trung bình của C AH
ME / /AH hay ME / /AB
Câu 6: (1,0 điểm)
Chiều cao hình trụ là: h 6 cm t
Thể tích hình trụ là: V = 2 3 .1 .6 6 cm t
Bán kính hình cầu và hình trụ là: r = 1cm 4 4 4 Thể tích hình cầu là: 3 3 V
r .1 cm c 3 3 3 3
Chiều cao hình nón là: h h 2r 6 2.1 4 cm t 1 1 4 Thể tích hình nón là: 2 2 V
r .h .1 .4 cm n n 3 3 3 3
Thể tích lượng nước còn trong chiếc cốc là: 4 4 10
V V V V 6 cm t n c 3 3 3 3 Trang 25
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT TRÀ VINH
NĂM HỌC 2019 – 2020 MÔN THI: TOÁN ĐỀ CHÍNH THỨC
Thời gian: 120 phút (không kể thời gian phát đề)
I. PHẦN CHUNG DÀNH CHO TẤT CẢ CÁC THÍ SINH (7,0 ĐIỂM) Câu 1: (3,0 điểm)
1. Rút gọn biểu thức: A 20 45 3 80 3
x 4y 5
2. Giải hệ phương trình:
6x 7 y 8 3. Giải phương trình: 2
x x 12 0 Câu 2: (2,0 điểm)
Cho hai hàm số y x 3
có đồ thị lần lượt là d và 2 y 2x và P
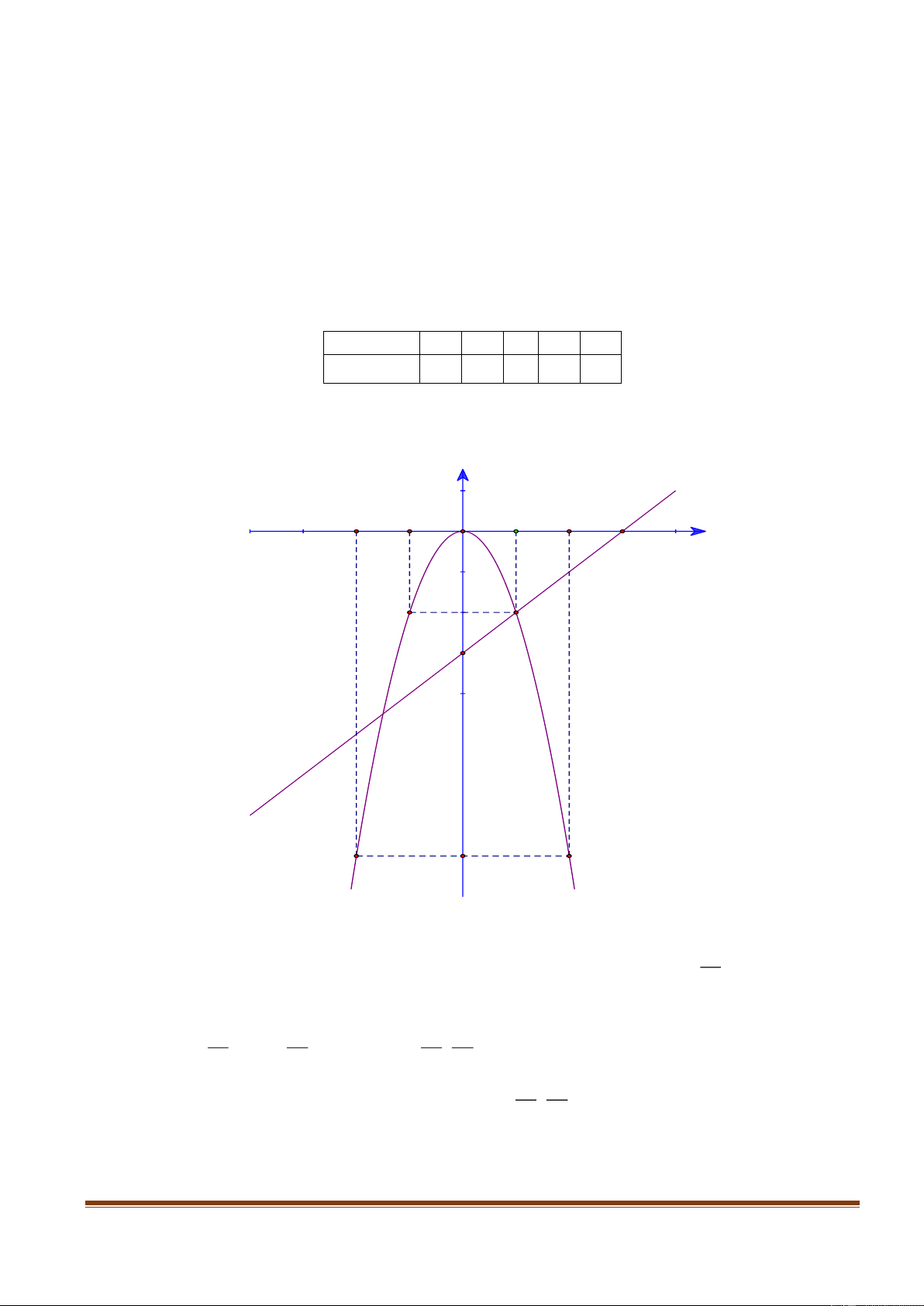
1. Vẽ d và P trên cùng hệ trục tọa độ Oxy
2. Tìm tọa độ giao điểm của d và P bằng phép toán Câu 3: (2,0 điểm) Cho phương trình 2
x x 3m 11 0
1 (với m là tham số)
1. Với giá trị nào của m thì phương trình 1 có nghiệm kép
2. Tìm m để phương trình
1 có hai nghiệm phân biệt x , x sao cho 2017x 2018x 2019 1 2 1 2
II. PHẦN TỰ CHỌN (3,0 ĐIỂM)
Thí sinh chọn một trong hai đề sau đây: Đề 1: Câu 4: (3,0 điểm)
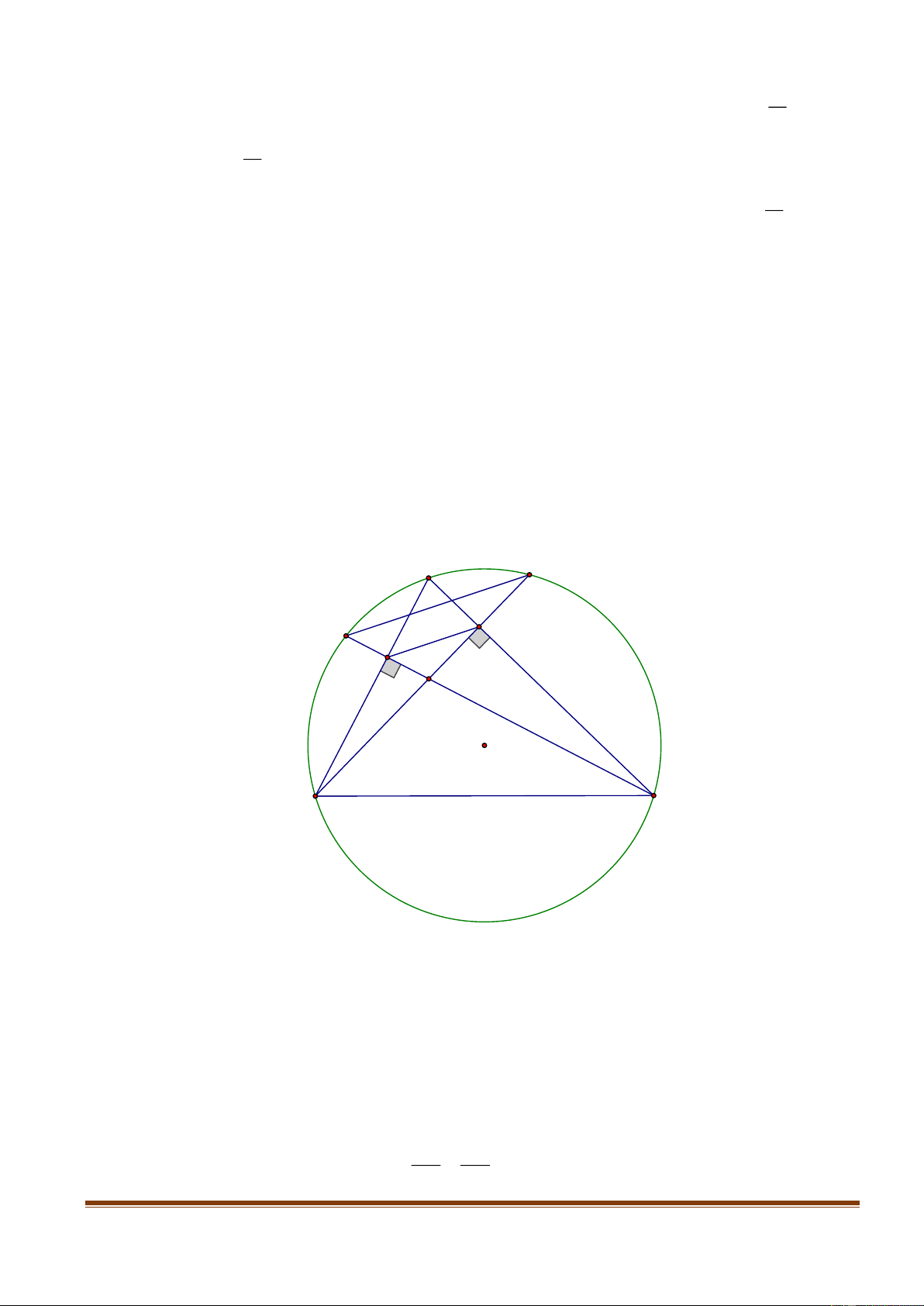
Cho tam giác ABC có ba góc đều nhọn nội tiếp đường tròn tâm O , hai đường cao BD và
CE cắt đường tròn tâm O theo thứ tự tại P và Q P , B Q C
1. Chứng minh tứ giác BCDE nội tiếp đường tròn
2. Gọi H là giao điểm của BD và CE . Chứng minh .
HB HP HC.HQ Đề 2: Câu 5: (3,0 điểm)
Cho đường tròn tâm O . Từ điểm M nằm ngoài đường tròn tâm O vẽ các tiếp tuyến MA , MB
với O ( A , B là hai tiếp điểm). Vẽ cát tuyến MCD không đi qua tâm O , C nằm giữa M và D .
1. Chứng minh tứ giác MAOB nội tiếp đường tròn 2. Chứng minh 2
MA MC.MD …….HẾT…… HƯỚNG DẪN GIẢI
I. PHẦN CHUNG DÀNH CHO TẤT CẢ CÁC THÍ SINH (7,0 ĐIỂM) Câu 1: (3,0 điểm)
1. A 20 45 3 80 2 5 3 5 12 5 11 5 3
x 4y 5
6x 8y 10 y 2 2.
6x 7 y 8
6x 7 y 8 x 1
Vậy hệ phương trình có nghiệm là (1; 2) Trang 26 x x 3 3. 2
x x 12 0 (x 3)(x 4) 3 0 0 x 4 0 x 4
Vậy tập nghiệm của phương trình là: S 3; 4 Câu 2: (2,0 điểm)
Cho hai hàm số y x 3
có đồ thị lần lượt là d và 2 y 2x
và P
1. Vẽ d và P trên cùng hệ trục tọa độ Oxy .
Đồ thị của hàm số y x 3 là đường thẳng đi qua hai điểm 0; 3 và 3;0
Bảng giá trị của hàm số 2 y 2 x là: x 2 1 0 1 2 2 y 2 x 8 2 0 2 8 Đồ thị hàm số 2 y 2
x là Parabol đi qua các điểm 2 ; 8 ; 1 ; 2 ; 0;0 ; 2; 8 ; 1; 2 nhận
Oy làm trục đối xứng. y y = x - 3 -2 -1 O 1 2 3 x -2 -3 -8 y = -2x2
2. Xét phương trình hoành độ giao điểm của P và d là: 2 x 3 2 x 2
2x x 3 0 (*) Vì phương trình 3
(*) có hệ số a b c 0 nên có 2 nghiệm là x 1; x 1 2 2
Với x 1 y 2, ta có điểm A1; 2 Với 3 x 9 y ta có điểm 3 9 B ; 2 2 2 2 Vậy 3 9
d giao P tại hai điểm là A1; 2 và B ; 2 2 Câu 3: (2,0 điểm) Cho phương trình 2
x x 3m 11 0
1 (với m là tham số) Trang 27 a 0 1 0
1. Để phương trình 15 1 có nghiệm kép thì m 0 1
4(3m 11) 45 12m 0 4 Vậy với 15 m
thỏa mãn yêu cầu đề bài. 4 a 0 1 0
2. Để phương trình 15
1 có hai nghiệm phân biệt x , x thì m 1 2 0 45 12m 0 4 x x 1
Theo hệ thức Vi-et ta có: 1 2
x .x 3m 11 1 2
Mà theo đề bài ta có 2017x 2018x 2019 nên ta có hệ phương trình: 1 2 x x 1 x 1 1 2 1
2017x 2018x 2019 x 2 1 2 2 Thay giá trị x 1
, x 2 vào x .x 3m 11 ta được m 3 (thỏa mãn). 1 2 1 2
Vậy m 3 thỏa mãn điều kiện đề bài.
II. PHẦN TỰ CHỌN (3 ĐIỂM)
Thí sinh chọn một trong hai đề sau đây: Đề 1: Câu 4: (3,0 điểm) A P Q D E H O B C
1. Chứng minh tứ giác BCDE nội tiếp đường tròn Xét ABC
có: BD AC , CE AB (gt) BDC BEC 90
Xét tứ giác BCDE có: BDC BEC 90 (cmt) nên hai đỉnh D , E kề nhau cùng nhìn cạnh
BC dưới các góc vuông.
Do đó: BCDE là tứ giác nội tiếp.
2. Gọi H là giao điểm của BD và CE . Chứng minh .
HB HP HC.HQ
Xét đường tròn O có: QPB QCB (hai góc cùng chắn cung BQ ). Lại có: HP HQ H PQ ∽ H CB (g.g) nên H .
P HB HC.HQ HC HB Trang 28 Đề 2: Câu 5: (3,0 điểm) A M C D O B
1. Chứng minh tứ giác MAOB nội tiếp đường tròn.
Vì MA , MB là hai tiếp tuyến của O nên MA AO , MB OB (gt) MAO MBO 90
Xét tứ giác MAOB có: MAO MBO 90 90 180
Mà hai góc ở vị trí đối nhau nên tứ giác MAOB là tứ giác nội tiếp. 2. Chứng minh 2
MA MC.MD
Xét O có: MAC ADC (góc tạo bởi tiếp tuyến và dây cung ; góc nội tiếp cùng chắn cung AC ) MA MC Lại có: M AC ∽ M DA (g.g) nên 2 MA M . D MC MD MA
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYÊN SINH LỚP 10 THPT VĨNH LONG
NĂM HỌC 2019 – 2020 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút (không kể thời gian giao đề) Bài 1. (1.0 điểm)
Tính giá trị biểu thức
a) A 2 48 3 75 2 108
b) B 19 8 3 19 8 3
Bài 2. (2.0 điểm) Giải các phương trình và hệ phương trình sau: a) 2
2x 3x 2 0 b) 2 5x 2x 0
2x y 7 c) 4 2
x 4x 5 0 d) 3
x y 27 Bài 3. (2.0 điểm)
Trong mặt phẳng tọa độ Oxy, cho hàm số 2
y x có đồ thị (P).
a) Vẽ đồ thị (P). Trang 29
b) Tìm giá trị của m để đường thẳng (d): y 2x 3m (với m là tham số) cắt (P) tại hai điểm
phân biệt có hoành độ là x , x thỏa mãn 2
x x x 3m 2x 6. 1 2 2 1 1 2 Bài 4. (1.0 điểm)
Một công ty vận tải dự định dùng loại xe lớn để vận chuyển 20 tấn hàng hóa theo một hợp đồng.
Nhưng khi vào việc, công ty không còn xe lớn nên phải thay bằng những xe nhỏ. Mỗi xe nhỏ vận
chuyển được khối lượng ít hơn 1 lần so với mỗi xe lên theo dự định. Để đảm bảo thời gian đã hợp
đồng, công ty phải dùng một số lượng xe nhiều hơn số xe dự định là 1 xe. Hỏi mỗi xe nhỏ vận chuyển
bao nhiêu tấn hàng hóa? (Biết các xe cùng loại thi có khối lượng vận chuyển như nhau). Bài 5. (1.0 điểm)
Cho tam giác ABC có AB 4 c ,
m AC 4 3c ,
m BC 8c . m
a) Chứng minh tam giác ABC vuông.
b) Tính số đo B, C và độ dài đường cao AH của tam giác ABC. Bài 6. (2.5 điểm)
Cho đường tròn (O) đường kính AB và điểm M bất kì thuộc đường tròn sao cho MA MB M A .
Kẻ tiếp tuyến tại A của đường tròn, tiếp tuyến này cắt tia BM ở N. Tiếp tuyến của đường tròn tại M cắt CN ở D.
a) Chứng minh bốn điểm A, D, M, O cùng thuộc một đường tròn.
b) Chứng minh OD song song BM.
c) Qua O kẻ đường thẳng vuông góc với AB và cắt đường thẳng BM tại I. Gọi giao điểm
của AI và BD là G. Chứng minh ba điểm N, G, O thẳng hàng. Bài 7. (0.5 điểm) Cho ,
x y là các số thực dương thỏa x y 1. 1
Tìm giá trị nhỏ nhất của biểu thức 2 2
A 2x y x 1. x ...HẾT... Trang 30
HƯỚNG DẪN GIẢI ĐỀ THI VÀO 10 –MÔN TOÁN – VĨNH LONG Bài 1. (1.0 điểm)
Tính giá trị biểu thức
a) A 2 48 3 75 2 108
b) B 19 8 3 19 8 3 Lời giải a)
A 2 48 3 75 2 108 2 2 2 A 2 4 3 . 3 5 .3 2 6 .3
A 2.4. 3 3.5 3 2.6 3
A 8 3 15 3 12 3 Câu 1.
A (8 15 12) 3 11 3 Vậy A 11 3. b)
B 19 8 3 19 8 3 2 2 2 2
B 4 2.4. 3 ( 3) 4 2.4. 3 ( 3) 2 2
B (4 3) (4 3) B | 4 3 | | 4 3 |
B 4 3 4 3
(4 3 0; 4 3 0) B 8 Vậy B 8.
Bài 2. (2.0 điểm) Giải các phương trình và hệ phương trình sau: a) 2
2x 3x 2 0 b) 2 5x 2x 0
2x y 7 c) 4 2
x 4x 5 0 d) 3
x y 27 Lời giải a) 2 2
2x 3x 2 0 2x 4x x 2 0 2x(x 2) (x 2) 0 1 2x 1 0 x (2x 1)(x 2) 0 2 x 2 0 x 2 1
Vậy phương trình có tập nghiệm là S ; 2. 2 x 0 x 0 b) 2
5x 2x 0 x(5x 2) 0 2 5x 2 0 x 5 2
Vậy phương trình có tập nghiệm là S 0; . 5 Trang 31 c) Đặt 2
t x (t 0) t 1 (ktm)
Khi đó phương trình trở thành: 2
t 4t 5 0 (t 1)(t 5) 0 t 5 (tm) Với 2
t 5 x 5 x 5
Vậy phương trình có tập nghiệm là S 5; 5.
2x y 7 5 x 20 x 4 x 4 d) 3x y 27
2x y 7 2.4 y 7 y 15
Vậy hệ đã cho có nghiệm (x; y) là (4;15) Bài 3: (2.0 điểm)
Trong mặt phẳng tọa độ Oxy, cho hàm số 2
y x có đồ thị (P).
a) Vẽ đồ thị (P).
b) Tìm giá trị của m để đường thẳng (d): y 2x 3m (với m là tham số) cắt (P) tại hai điểm
phân biệt có hoành độ là x , x thỏa mãn 2
x x x 3m 2x 6. 1 2 2 1 1 2 Lời giải a)
Bảng giá trị của hàm số 2 y x . x 2 1 0 1 2 y 4 1 0 1 4
Vẽ đường cong đi qua các điểm có tọa độ 2 ; 4 , 1 ; 1 ,0,0,1; 1 ; 2; 4
ta được parabol (P): 2 y x . b)
Xét phương trình hoành độ giao điểm của đường thẳng (d) và parabol (P), ta có 2 2
x 2x 3m x 2x 3m 0 (*) Phương trình (*) có 2 ' 1 1.( 3 ) m 1 3m Trang 32
Để đường thẳng (d) cắt (P) tại hai điểm phân biệt có hoành độ là x , x thì phương trình (*) có hai 1 2 a 0 1 0(luon dung) 1
nghiệm phân biệt x , x m 1 2 ' 0 1 3m 0 3 x x 2
Theo hệ thức Vi-ét ta có: 1 2 x x 3 m 1 2 Theo bài ra ta có: 2
x x x 3m 2x 6 1 2 2 1
x x x 3mx 2x x 6 1 2 2 2 1 2 3
mx 3mx 2( 3 ) m 6 2 2 6m 6 m 1(tm) Vậy
m 1 là giá trị cần tìm. Câu 4. (1.0 điểm)
Một công ty vận tải dự định dùng loại xe lớn để vận chuyển 20 tấn hàng hóa theo một hợp đồng.
Nhưng khi vào việc, công ty không còn xe lớn nên phải thay bằng những xe nhỏ. Mỗi xe nhỏ vận
chuyển được khối lượng ít hơn 1 lần so với mỗi xe lên theo dự định. Để đảm bảo thời gian đã hợp
đồng, công ty phải dùng một số lượng xe nhiều hơn số xe dự định là 1 xe. Hỏi mỗi xe nhỏ vận chuyển
bao nhiêu tấn hàng hóa? (Biết các xe cùng loại thi có khối lượng vận chuyển như nhau). Lời giải
Gọi số tấn hàng hóa mỗi xe nhỏ vận chuyển được là: x (tấn) (x >0)
Mỗi xe lớn vận chuyển được số tấn hàng là: x+1 (tấn) Khi đó số 20
xe nhỏ dự định phải dùng để chở hết 20 tấn hàng hóa là: (xe). x 20
Số xe lớn dự định phải dùng để chở hết 20 tấn hàng hóa là: (xe) x 1
Vì thực tế số xe nhỏ phải dùng nhiều hơn dự định là 1 xe.
Nên ta có phương trình: 20 20 1 x x 1 Giải phương trình: 20 20 1 1 1 20 1 x x 1 x x 1 1 1 1 x 1 x 1 x x 1 20 x(x 1) 20 1 1
x(x 1) 20 x(x 1) 20 2
x x 20 0 (x 5)(x 4) 0 x 5 0 x 5 (ktm) x 4 0 x 4(tm)
Vậy mỗi xe nhỏ vận chuyển được 4 tấn hàng hóa. Bài 5. (1.0 điểm) Trang 33
Cho tam giác ABC có AB 4 c ,
m AC 4 3c ,
m BC 8c . m
a) Chứng minh tam giác ABC vuông.
b) Tính số đo B, C và độ dài đường cao AH của tam giác ABC. Lời giải a) Ta có: 2 2 2 2 2 2
AB 4 16; AC (4 3) 48; BC 8 64 2 2 2
AB AC 16 48 64 BC ABC
vuông tại A (định lý Pitago đảo). b)
Áp dụng tỉ số lượng giác của góc nhọn trong ABC ta có: AB 4 1 cos B B 60 BC 8 2 C 180 B A 180 60 90 30
Áp dụng hệ thức lượng trong ABC
vuông tại A và có đường cao AH ta có: . AB AC 4.4 3 AH .BC . AB AC AH 2 3 cm BC 8 Vậy B 60,C 30 , AH 2 3 c . m Bài 6. (2.5 điểm)
Cho đường tròn (O) đường kính AB và điểm M bất kì thuộc đường tròn sao cho MA MB M A .
Kẻ tiếp tuyến tại A của đường tròn, tiếp tuyến này cắt tia BM ở N. Tiếp tuyến của đường tròn tại M cắt CN ở D.
a) Chứng minh bốn điểm A, D, M, O cùng thuộc một đường tròn.
b) Chứng minh OD song song BM.
c) Qua O kẻ đường thẳng vuông góc với AB và cắt đường thẳng BM tại I. Gọi giao điểm
của AI và BD là G. Chứng minh ba điểm N, G, O thẳng hàng. Lời giải Trang 34 a) Ta có:
OM MD (tính chất tiếp tuyến) OMD 90
OA AD (tính chất tiếp tuyến) OAD 90 Xét tứ giác OMD4 có: OMD OAD 90 90 180
Mà hai góc này ở vị trí đối diện
Nên tứ giác OMDA nội tiếp Hay bốn điểm ,
A D, M , O cùng thuộc một đường tròn.
b) Xét (O) ta có: OD là tia phân giác trong góc M
OA (tính chất hai tiếp tuyến cắt nhau) 1 M OD AO D AOM (1) 2 1 Mà M BA M
OA (góc nội tiếp và góc ở tâm củng chắn cung MA) (2) 2 1
Từ (1) và (2) suy ra AOD ABM MOA 2
Mà hai góc này ở vị trí đồng vị nên OD / /BM (đpcm).
c) Vì OI AB, AN AB OI / / AN
Mà O là trung điểm của AB OI là đường trung bình của tam giác ABN
I là trung điểm của BN AI là trung tuyến của tam giác ABN.
Lại có OD / /BM (cmt), mà O là trung điểm của AB OD là đường trung bình của tam giác ABN
D là trung điểm của AN BD là trung tuyến của tam giác ABN.
Mà NO là trung tuyến của tam giác ABC.
Mặt khác ta lại có: AI BD { } G
Do đó AI, BD, NO đồng qui tại G là trọng tâm của tam giác ABN.
Suy ra N , G, O thẳng hàng. Bài 7. (0.5 điểm) Cho ,
x y là các số thực dương thỏa x y 1. 1
Tìm giá trị nhỏ nhất của biểu thức 2 2
A 2x y x 1. x Trang 35 Lời giải
Ta có: x y 1 y 1 x thay vào A ta được: 1 1 2 2 2 2
A 2x y x
1 2x (1 x) x 1 x x 1 1 2 2x 2 x 2x 2 1 x
1 x 2x x x x 2 1 1 1 1 1 1 2 x x 4x x 4x 4 x 4 2 x 4 2 1 Dễ thấy x 0, x 2 1 1
Áp dụng bất đẳng thức Cô-si ta có 4x 2 4 . x 4 x x 2 1 1 1 1 15 Suy ra x 4x 0 4 2 x 4 4 4 1
Dấu "=" xảy ra khi x 2 15 1 Vậy A khi x . min 4 2
SỞ GD&ĐT VĨNH PHÚC
KỲ THI TUYỂN SINH LỚP 10 THPT NĂM HỌC 2019 – 2020 ĐỀ THI MÔN: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút, không kể thời gian giao đề
I. PHẦN TRẮC NGHIỆM (2,0 điểm)
Trong các câu sau, mỗi câu chỉ có một lựa chọn đúng. Em hãy ghi vào bài làm chữ cái in hoa đứng trước
lựa chọn đúng (Ví dụ: Câu 1 nếu chọn A là đúng thì viết 1.A).
Câu 1. Cho khối hộp chữ nhật có chiều dài 3m, chiều rộng 2m và cao 1m. Thể tích của khối hộp đã cho bằng A. 3m3 B. 6m3 C. 2m3 D. 12m3
Câu 2. Biểu thức P =
5 ( 10 - 40) có giá trị bằng A. P = - 5 10 B. P = - 5 6 C. P = - 5 30 D. P = - 5 2
Câu 3. Tổng các nghiệm của phương trình 2
x - 6x + 1 = 0 bằng A. 6 B. -3 C. 3 D. -6 Trang 36
Câu 4. Tìm tất cả các giá trị của x để biểu thức P = x - 2 xác định. A. x < 2 B. x > 2 C. x ³ 2 D. x £ 2
II. PHẦN TỰ LUẬN (8,0 điểm) ìï x - 2y = 3 Câu 5 (1,0 điể ï
m). Giải hệ phương trình í ï x + y = 6 ïî Câu 6 (2,0 điể 1
m). Cho parabol (P ) 2 : y =
x và đường thẳng (d) : y = - x + m (x là ẩn, m tham 2 số).
a) Tìm tọa độ giao điểm của parabol (P ) với đường thẳng (d ) khi m = 4 .
b) Tìm tất cả các giá trị của tham số m để đường thẳng (d ) cắt parabol (P ) tại hai điểm phân
biệt A (x ;y , B x ;y thỏa mãn x x + y y = 5. 1 1 ) ( 2 2) 1 2 1 2
Câu 7 (1,0 điểm). Người thứ nhất đi đoạn đường từ địa điểm A đến địa điểm B cách nhau 78km. Sau khi
người thứ nhất đi được 1 giờ thì người thứ hai đi theo chiều ngược lại vẫn trên đoạn đường đó từ B về A.
Hai người gặp nhau ở địa điểm C cách B một quãng đường 36km. Tính vận tốc của mỗi người, biết rằng
vận tốc của người thứ hai lớn hơn vận tốc của người thứ nhất là 4km/h và vận tốc của mỗi người trong
suốt đoạn đường là không thay đổi.
Câu 8 (3,0 điểm). Cho tam giác nhọn ABC nội tiếp đường tròn (O). Gọi M là một điểm di động trên
cung nhỏ BC của đường tròn (O) (M không trùng với B, C). Gọi H, K, D theo thứ tự là chân các đường
vuông góc kẻ từ M đến các đường thẳng AB, AC, BC.
a) Chứng minh tứ giác AHMK nội tiếp đường tròn.
b) Chứng minh MH .MC = MK .MB.
c) Tìm vị trí của điểm M để DH + DK lớn nhất.
Câu 9 (1,0 điểm). Cho ba số thực dương a, b, c. Chứng minh:
2 + 6a + 3b + 6 2bc 16 ³
2a + b + 2 2bc
2b + 2(a + c)2 2 + 3 -------Hết------
Cán bộ coi thi không giải thích gì thêm.
HƯỚNG DẪN GIẢI.
I. PHẦN TRẮC NGHIỆM. (Mỗi câu đúng được 0,5 điểm) Trang 37 Câu 1 2 3 4 Đáp án B D A C
II. PHẦN TỰ LUẬN. ìï x - 2y = 3 Câu 5 (1,0 điể ï
m). Giải hệ phương trình í ï x + y = 6 ïî Lời giải ìï x - 2y = 3 ìï 3y = 3 ìï y = 1 ï ï ï í Û í Û í ï x + y = 6 ï x = 6 - y ï x = 5 ïî ïî ïî
Vậy, hệ phương trình đã cho có nghiệm duy nhất (x ,y)= (5, ) 1 Câu 6 (2,0 điể 1
m). Cho parabol (P ) 2 : y =
x và đường thẳng (d) : y = - x + m (x là ẩn, m tham 2 số).
a) Tìm tọa độ giao điểm của parabol (P ) với đường thẳng (d ) khi m = 4 .
b) Tìm tất cả các giá trị của tham số m để đường thẳng (d ) cắt parabol (P ) tại hai điểm phân
biệt A (x ;y , B x ;y thỏa mãn x x + y y = 5. 1 1 ) ( 2 2) 1 2 1 2 Lời giải
a. Khi m = 4, đường thẳng (d) có dạng: y = - x + 4 .
Xét phương trình hoành độ 1
giao điểm của (d) và (P): 2 2
x = - x + 4 Û x + 2x - 8 = 0 (1) 2 PT (1) có D¢= 1 + 8 = 9 Þ D¢= 3 x é = - 1- 3 = - 4
PT (1) có hai nghiệm phân biệt : ê 1 x ê = - 1+ 3 = 2 ê 2 ë 1
Với x = - 4 Þ y = .(- 4)2 = 8 1 1 2 1
Với x = 2 Þ y = .( )2 2 = 2 2 2 2 Trang 38
Vậy, khi m = 4 thì đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt có tọa độ lần lượt là (- 4;8) và (2; ) 2
b. Xét phương trình hoành độ 1
giao điểm của (d) và (P): 2 2
x = - x + m Û x + 2x - 2m = 0 (2) 2
PT (2) có D ¢= 1 + 2m
Để (d) cắt (P) tại hai điểm phân biệt thì PT (2) phải có hai nghiệm phân biệt. 1
hay D ¢= 1 + 2m > 0 Û m > - (*) 2
Với ĐK (*) , gọi x ;x là hai nghiệm của PT (2). 1 2 ìï x + x = - 2 ï
Áp dụng định lí Viets, ta có : 1 2 í (3) ï x x = - 2m ï 1 2 î
Với x = x Þ y = - x + m 1 1 1
Với x = x Þ y = - x + m 2 2 2
Xét biểu thức : x x + y y = 5 Û x x + - x + m - x + m = 5 1 2 1 2 1 2 ( 1 )( 2 )
Û x x + x x - m (x + x ) 2
+ m = 5 Û 2x x - m (x + x ) 2 + m = 5 (4) 1 2 1 2 1 2 1 2 1 2
Thay (3) vào (4), ta được :
ém= 1+ 6 (t / m (*)) ( ê 2 - 2 ) m - ( m - ) 2 2
2 + m = 5 Û m - 2m- 5 = 0 Û ê m ê = 1- 6 (Loaïi) ë Vậy, với m= 1+
6 thì yêu cầu bài toán được thỏa mãn.
Câu 7 (1,0 điểm). Người thứ nhất đi đoạn đường từ địa điểm A đến địa điểm B cách nhau 78km. Sau khi
người thứ nhất đi được 1 giờ thì người thứ hai đi theo chiều ngược lại vẫn trên đoạn đường đó từ B về A.
Hai người gặp nhau ở địa điểm C cách B một quãng đường 36km. Tính vận tốc của mỗi người, biết rằng
vận tốc của người thứ hai lớn hơn vận tốc của người thứ nhất là 4km/h và vận tốc của mỗi người trong
suốt đoạn đường là không thay đổi. Lời giải
Gọi vận tốc của người thứ nhất là x (km/ )
h (Đk: x > 0)
Khi đó, vận tốc của người thứ hai là x + 4(km/ ) h 78- 36 42
Thời gian người thứ nhất đi từ A đến C là: = (giôø ) x x Trang 39 36
Thời gian người thứ hai đi từ B đến C là: (giôø ) x + 4
Do người thứ nhất đi trước người thứ hai 1 giờ, nên khi hai người gặp nhau tại C thì ta có phương trình: 42 36 - = 1 (1) x x + 4
Giải phương trình (1) và kết hợp với ĐK x > 0, ta được: x = 14 (km/ ) h
Vậy, vận tốc của người thứ nhất là 14 (km/h) và vận tốc của người thứ hai là 14 + 4 = 18 (km/h)
Câu 8 (3,0 điểm). Cho tam giác nhọn ABC nội tiếp đường tròn (O). Gọi M là một điểm di động trên
cung nhỏ BC của đường tròn (O) (M không trùng với B, C). Gọi H, K, D theo thứ tự là chân các đường
vuông góc kẻ từ M đến các đường thẳng AB, AC, BC.
a) Chứng minh tứ giác AHMK nội tiếp đường tròn.
b) Chứng minh MH .MC = MK .MB.
c) Tìm vị trí của điểm M để DH + DK lớn nhất. Lời giải
Câu 9 (1,0 điểm). Cho ba số thực dương a, b, c. Chứng minh:
2 + 6a + 3b + 6 2bc 16 ³
2a + b + 2 2bc
2b + 2(a + c)2 2 + 3 Lời giải
SỞ GD&ĐT VĨNH PHÚC
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN NĂM HỌC 2019 – 2020
Dành cho thí sinh thi chuyên Toán và chuyên Tin ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút, không kể thời gian giao đề Câu 1 (4,0 điểm) a) Giải phương trình 2 x - x- 2 2
2 x - 2x + 2 - 1= 0 1 3 10 b) Giải phương trình + = 2 2x - x + 2 1 2x - x + 2 3 2x - x + 7 Trang 40
ìïï 2 x+ 3y+ 2- 3 y = x+ 2
c) Giải hệ phương trình í ïï 2 y + xy + 2 x = 4y + î 1 Câu 2 (1,5 điểm)
a) Tìm tất cả các số nguyên , x y thỏa mãn 2 x - xy- x- 2 9 3 24 2y + y + 28= 0
b) Tìm tất cả các số nguyên dương , p ,
m n thỏa mãn m 2 p + = 5 2 1
n , trong đó p là số nguyên tố.
Câu 3 (1,0 điểm). Cho các số nguyên dương , a ,
b c thỏa mãn abc ³ 1. Chứng minh rằng: a + b + c ³ 3 b+ ac c + ab a+ 2 bc
Câu 4 (3,0 điểm). Cho tam giác nhọn ABC có AB < AC. Đường tròn tâm I nội tiếp tam giác ABC tiếp xúc
với các cạnh BC, CA, AB lần lượt tại các điểm D, E, F. Gọi M là trung điểm của đoạn thẳng BC, gọi N là
giao điểm của hai đường thẳng ID và EF. Qua N kẻ đường thẳng song song với BC cắt hai đường thẳng
AB, AC lần lượt tại các điểm Q, P. Qua điểm A kẻ đường thẳng song song với BC cắt đường thẳng EF tại điểm K.
a) Chứng minh các tứ giác INQF, INEP nội tiếp đường tròn và tam giác IPQ cân. · ·
b) Chứng minh IAM = FKI .
c) Chứng minh hai đường thẳng IM, DK vuông góc với nhau.
Câu 5 (0,5 điểm). Bạn Bình có 19 viên bi màu xanh, 21 viên bi màu đỏ và 23 viên bi màu vàng. Bình
thực hiện một trò chơi theo quy tắc sau: Mỗi lần Bình chọn 2 viên bi có màu khác nhau, rồi sơn chúng bởi
màu thứ ba (Ví dụ: Nếu Bình chọn 2 viên bi gồm 1 viên bi màu xanh và 1 viên bi màu đỏ thì Bình sơn 2
viên bi này thành màu vàng). Hỏi sau một số hữu hạn lần thực hiện trò chơi theo quy tắc trên, bạn Bình
có thể thu được tất cả các viên bi cùng một màu hay không ? Tại sao ?
------Hết------
Cán bộ coi thi không giải thích gì thêm.
SỞ GD&ĐT VĨNH PHÚC
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN NĂM HỌC 2019 – 2020 ĐỀ THI MÔN: TOÁN ĐỀ CHÍNH THỨC
Dành cho tất cả các thí sinh.
Thời gian làm bài: 120 phút, không kể thời gian giao đề Trang 41 æ ö ç 2 1 x(3- ÷ x x )
Câu 1 (2,0 điểm). Cho biểu thức P = ç ÷ + ç ÷ ÷. ç9- è x 3+ x ÷ ø x - 2
a) Rút gọn biểu thức P. 1
b) Tìm tất cả các số thực x để P = - 3
Câu 2 (2,0 điểm). Cho phương trình 2 x - ( 2 m+ )
1 x + m- 4 = 0 (1) ( x là ẩn, m là tham số).
a) Giải phương trình (1) khi m= - 2
b) Tìm m để phương trình (1) có hai nghiệm phân biệt x , x thỏa mãn điều kiện 1 2 2 x + 2 x - 3x x = 25. 1 2 1 2 Câu 3 (2,0 điểm). a) Giải phương trình 2
4x + 3x + 3 = 4x x + 3 + 2 2x - 1 ìï 3 2x + 2 3x y = ï 5
b) Giải hệ phương trình í ïï 3 y + 2 6xy = î 7
Câu 4 (3,0 điểm). Cho nửa đường tròn tâm O đường kính AB = 2R. Gọi K là điểm chính giữa cung AB,
M là điểm di động trên cung AK (M không trùng với A và K). Lấy điểm N thuộc đoạn thẳng BM sao cho
AM = BN. Gọi D là giao điểm của hai đường thẳng AM và OK. ·
a) Chứng minh MK là đường phân giác của góc DMB . · ·
b) Chứng minh AMK = BNK .
c) Chứng minh rằng khi điểm M di động trên cung AK thì đường thẳng vuông góc với BM tại N
luôn đi qua một điểm E cố định. Xác định vị trí của M để đường thẳng DE song song với đường thẳng AB.
Câu 5 (1,0 điểm). Cho , a ,
b c là các số thực dương thỏa mãn (a+ ) b (b+ ) c (c+ ) a = 8. Tìm giá trị 1 1 1 1
nhỏ nhất của biểu thức P = + + + 3 abc a+ 2b b + 2c c + 2a
------Hết------
Cán bộ coi thi không giải thích gì thêm. Trang 42
TUYỂN SINH VÀO 10 SƠN LA NĂM HỌC 2019-2020 Bài 1.(3,0 điểm)
a) Giải phương trình 3(x + 2) = x +36 4x 3y 1
b) Giải hệ phương trình
x 3y 2 x 2
c) Rút gọn biểu thức P . x 4
(với x 0 và x 4 ) x 2 x 2 Bài 2.(1,5 điểm)
Trong kỳ thi tuyển sinh vào lớp 10 năm học 2019 – 2020, số thí sinh vào trường THPT chuyên 2 bằng
số thí sinh thi vào trường PTDT Nội trú. Biết rằng tổng số phòng thi của cả hai trường 3
là 80 phòng thi và mỗi phòng thi có đúng 24 thí sinh. Hỏi số thí sinh vào mỗi trường bằng bao nhiêu? Bài 3. (1,5 điểm) Cho parabol (P) 2
y x và đường thẳng 2
y 2(m 1)x m 2m (m là tham số, m ).
a) Xác định tất cả các giá trị của m để đường thẳng (d) đi qua điểm I (1; 3).
b) Tìm m để parabol (P) cắt đường thẳng (d) tại hai điểm phân biệt A, B. Gọi x , x là 1 2
hoành độ hai điểm A, B; tìm m sao cho 2 2
x x 6x x 2020 . 1 2 1 2 Bài 4. (3,0 điểm)
Cho đường tròn (O) đường kính AB = 2R và C là một điểm nằm trên đường tròn sao cho CA >
CB. Gọi I là trung điểm của OA, vẽ đường thẳng d vuông góc với AB tại I, d cắt tia BC tại M
và cắt đoạn AC tại P, AM cắt đường tròn (O) tại điểm thứ hai K.
a) Chứng minh tứ giác BCPI nội tiếp được trong một đường tròn.
b) Chứng minh ba điểm B, P, K thẳng hàng.
c) Các tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại Q, biết BC = R. Tính độ dài BK
và diện tích tứ giác QAIM theo R. Bài 5. (1,0 điểm) Giải phương trình 3 x x 3 x
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM Bài Đáp án Điểm a)(1,0 điểm) 3(x + 2) = x + 36 3x + 6 = x + 36 0,25 2x = 30 0,25 Trang 43 x = 15 0,25
Vậy phương trình đã cho có 1 nghiệm x =15 0,25 b) (1,0 điểm) 4x 3y 1 3x 3 x 1 Bài 1
x 3y 2
x 3y 2 1 3y 2 0,5 (3,0 x 1 x 1 x 1 điểm)
Vậy hệ đã cho có nghiệm duy nhất 3 y 3 y 1 y 1 0,5 b) (1,0 điểm) x 2 P . x 4
(với x 0 và x 4 ) x 2 x 2 x x 2 2 x 2 0,5 P x x
2 x 2 x 2 x 2 . 4
x 2 x 2 x 4 . x 4 x 4 0,5 x 4 Bài 2
Gọi số thí sinh vào trường THPT Chuyên và số thí sinh vào trường 0,25 (1,5
PTDT Nội trú lần lượt là x , y (thí sinh) (điều kiện x > 0, y > 0)
điểm) Vì số thí sinh vào trường THPT Chuyên bằng 2 số thí sinh vào 3
trường PTDT Nội trú nên ta có: 2 0,25 x y (1) 3
Vì tổng số phòng thi của cả hai trường là 80 phòng thi và mỗi
phòng thi có đúng 24 thí sinh nên tổng số thí sinh của cả hai trường là: 0,25 24.80 = 1920 (thí sinh)
Do đó ta có phương trình; x + y = 1920 (2)
Từ (1) và (2) ta có hệ phương trình 2 2 2 x y x y x y y 1152 3 3 0,25 3 2 5 x 768 x y 1920 y y 1920 y 1920 3 3
Đối chiếu điều kiện ta thấy x = 768; y = 1152 đều thỏa mãn. 0,25
Vậy số thí sinh vào trường THPT Chuyên và số thí sinh vào trường 0,25
PTDT Nội trú lần lượt là 768 thí sinh , 1152 thí sinh. 3 a)(0,5 điểm) Để đường thẳng (d) 2
y 2(m 1)x m 2m đi qua điểm I (1;3) thì x
= 1; y = 3 thỏa mãn phương trình đường thẳng (d) nên ta có: Trang 44 2
3 2(m 1).1 m 2m 2
m 2m 2m 2 3 0,25 2
m 4m 5 0 2
m 1 4m 4 0 m 1 m 1 4 m 1 0 m 1 m 5 Bài 3 0 (1,5 m 1 0 điểm) m 5 0 0,25 m 1 m 5
Vậy với m = 1 hoặc m = - 5 thì đường thẳng (d) đi qua điểm I(1;3) 3 b) (1,0 điểm) (P) 2 y x và (d) 2
y 2(m 1)x m 2m (m 1)
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình: 2 2
x 2(m 1)x m 2m (1) 0,25 2 2
x 2(m 1)x (m 2m) 0 ' 2 2 2
(m 1) m 2m 2m 1 0 với mọi m
Phương trình (1) luôn có hai nghiệm phân biệt với mọi m
x x 2 m 1 0,25 1 2
Khi đó theo hệ thức Vi-ét (2) 2
x x (m 2m) 1 2 Theo bài ra, ta có: 2 2 x x 6x x 2020 1 2 1 2
x x 2 2x x 6x x 2020 1 2 1 2 1 2
x x 2 4x x 2020(3) 1 2 1 2 0,25 Thay (2) vào (3) ta có: 2(m 1)2 2
4(m 2m) 2020 2 2
4m 4m 4 4m 8m 2020 12m 2016 m 168
Vậy m = 168 thỏa mãn bài. 0,25 Vẽ hình đúng cho câu a 0,25 Trang 45 M Bài 4 (3,5 điểm) C P Q K P A I B O 4.1 a (0,75 điểm) Xét (O) có 0
ACB 90 (Góc nội tiếp chắn nửa đường tròn) nên 0 0,25 PCB 90 0,25
Ta có: d AB tại I; Pd nên PI AB tại I => 0 PIB 90 Xét tứ giác BCPI có: 0 PCB 90 0 và PIB 90 (cmt)
Do đó tứ giác BCPI nội tiếp được đường tròn. 0,25 4.1 b (1,0 điểm) Xét M
AB có MI AB tại I(gt); AC BM tại C ( 0 ACB 90 )
Mà MI AC
P nên P là trực tâm của M AB (1) 0,25 Lại có: 0
AKB 90 (Góc nội tiếp chắn nửa đường tròn) 0,25
BK AK tại K hay BK AM tại K
BK là đường cao của M AB (2) 0,25
Từ (1) và (2) suy ra BK đi qua P hay 3 điểm B, P, K thẳng hàng. 0,25 4.1 c (1,0 điểm)
Có OA = R mà I là trung điểm của AO nên OA R AI O I 2 2 R 3R BI = OB + IO = R 2 2 Xét B
OC có OB = OC = BC = R nên B
OC là tam giác đều. 0,25 Do đó 0 OBC 60 hay 0 ABC 60 Xét ABC có : 0
ACB 90 (Góc nội tiếp chắn nửa đường tròn) Nên 0
ABC CAB 90 mà 0 ABC 60 nên 0 0 0
CAB 90 60 30 hay 0 PAI 30 Xét 0 A I :
P AIP 90 ( d A ;
B P d ) nên: Trang 46 R R 3 R 3 0
PI AI. tan PAI . tan 30 . 2 2 3 6 Xét ABK và BI P có ABK chung; 0
AKB PIB 90 Do đó A BK BI P (g.g) BK BI
(các cạnh tương ứng tỉ lệ) hay BK AK AK PI BI PI 2 2 BK AK BK AK BK AK 3R 3 9 1 3R 3 0,25 2 2 4 12 6 6 2 2 2 2 2 2 2 BK AK BK AK AB 4R 12R Do đó: 9 1 9 1 7 7 7 4 12 4 12 3 3 189R Suy ra: BK = (đơn vị độ dài) 7 MI BK Có A IM A B K (g.g)
(các cạnh tương ứng tỉ lệ) AI AK BK BI MI BI Mà (cmt) nên AK PI AI PI R 3R . 0,25 AI.BI 3R 6 3 3 2 2 R MI . PI 3.R 4 3 2 6
Từ Q kẻ QH IM tại H. Dễ dàng chứng minh được tứ giác QHIB là hình vuông. Suy ra QH = BI Ta có : AI.MI QH.MI MI S S S .( AI QH ) AMQI AMI QMI 2 2 2 0,25 2 MI AB 3 3R 3 3R
.( AI BI ) MI. .R (đvdt) 2 2 2 2 3 x x 3 x
Điều kiện 0 x 9 0,25
Bình phương hai vế phương trình đã cho, ta được: 2
3 x x .( 3 x) 0,25 3 2
x 3.x x 3 Trang 47 2 3 3 1 1 1 1 3 2 x 3.x . 3. . x 3 3 3 3 3 3 1 10 10 3 Bài 5 x 0,25 3 3 3 9 (1,0 điểm) 1 10 3 3 x 3 9 10 3 3 3 x (thỏa mãn điều kiện) 9 3 0,25 10 3 3
Vậy phương trình đã cho có 1 nghiệm 3 x 9 3
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT AN GIANG Khóa ngày 03/6/2019 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
(Đề thi gồm có 01 trang)
(Không kể thời gian phát đề) Bài 1. (3,0 điểm)
Giải các phương trình và hệ phương trình sau đây: x a) 3x 3 b) 2
x 6x 5 0 3
2x y 2 2 c)
2 2x y 2 2 2 Bài 2. (1,5 điểm)
Cho hàm số có đồ thị là Parabol P : 2
y 0, 25x .
a) Vẽ đồ thị P của hàm số đã cho.
b) Qua điểm A0;
1 vẽ đường thẳng song song với trục hoành Ox cắt P tại
hai điểm E và F . Viết tọa độ của E và F . Bài 3. (2,0 điểm)
Cho phương trình bậc hai 2
x m 2 x 2m 0 (∗) ( m là tham số)
a) Chứ ng minh rằng phương trình (∗) luôn có nghiêm với moi số m .
b) Tìm các giá trị của m để phương trình (∗) có hai nghiệm x ; x thỏa mãn 1 2 2 x x 1 2 1 1 x . x 1 2 Bài 4. (2,5 điểm)
Cho tam giác ABC vuông tại A có AB 4c ,
m AC 3cm . Lấy điêm ̉ D thuộc cạnh
AB AB AD . Đường tròn O đường kính BD cắt CB tại E , kéo dài CD cắt
đường tròn O tại F . Trang 48
a) Chứng minh rằng ACED là tứ giác nội tiếp.
b) Biết BF 3cm . Tính BC và diện tích tam giác BFC .
c) Kéo dài AF cắt đường tròn O tại điểm G . Chứng minh rằng BA là tia
phân giác của góc CBG . Hội Âm Bài 5. (1,0 điểm) họa nhạc
Trường A tiến hành khảo sát 1500 học sinh về
sự yêu thích hội hoạ, thể thao, âm nhạc và các
yêu thích khác. Mỗi học sinh chỉ chọn một yêu
thích. Biết số học sinh yêu thích hội họa chiếm tỉ lê Yêu
̣ 20% so với số học sinh khảo sát. thích Thể khác thao
Số học sinh yêu thích thể thao hơn số học
sinh yêu thích âm nhạc là 30 học sinh; số học
sinh yêu thích thể thao và hội họa bằng với số học sinh yêu thích âm nhạc và yêu thích khác.
a) Tính số học sinh yêu thích hội họa.
b) Hỏi tổng số học sinh yêu thích thể thao và âm nhạc là bao nhiêu? -------Hết--------
Số báo danh: . . . . . . . . . . . . . . . . . . . Phòng thi:. . . . . . . HƯỚNG DẪN CHẤM Bài Nội dung gợi ý Điểm x x 3x 3 3x 3 3 3 1 x 3x 3 0,5 x 3 3
(Làm mất căn ở mẫu hoặc đưa 3 về ax b ) Bài 4x 3 1a 4x 4 3x 3 (hay 3 ) 1,0đ 3 3 3 x 4 4x 3. 3
Vậy phương trình có nghiệm 3 x 3 0,5 4 là x 4
Vậy phương trình có nghiệm là 3 x 4 Bài 2
x 6x 5 0 1b Biệt thức Delta 2
b ac 2 4 36 20 56 ' 3 5 14 0,5 1,0đ
Phương trình có nghiệm là b 6 2 14 x 3 14 1 2a 2 0,5 b 6 2 14 x 3 14 2 2a 2 Trang 49
2x y 2 2
2x y 2 2
Tính được x hay y; 0,5 đ Bài
2 2x y 2 2 2 3 2x 3 2 1c
Làm mất x hay y của một 1,0 1,0đ
x y x 1 2 2 2 x 1 phương trình 0,25đ x 1
2 y 2 2 y 2 2 y 0, 25x Bảng giá trị : x 4 2 0 2 4 2 1,0 Bài y 0, 25x 4 1 0 1 4 2a Đồ thị hình vẽ bên 1,0đ
Bảng giá trị cho ít nhất ba cặp tọa độ đúng 0,5 đ
Hệ trục 0,25đ, Parabol 0,25đ Bài 2b
Tọa độ điểm E 2 ; 1 ; F 2;
1 . ( mỗi tọa độ viết đúng 0,25đ) 0,5 0,5đ 2
x m 2 x 2m 0 (*) 0,25 Bài
Biệt thức m 2 2 4.2m 3a 2 2
m 4m 4 8m m 4m 4 0,25
1,0đ Do m 2 2 0 với mọi m
Viết thành tổng bình phương
nên phương trình luôn có nghiệm với mọi 0,25đ m 0,5
Ta có x x m 2; x x 2m ( hoặc x ; m x 2 ) 0,25 1 2 1 2 1 2 2 x x 2 x x 1 2 1 2 1 1 1 1 x . x x . x 1 2 1 2 0,25 2 m 2 2 x x 1 2 1 1 m 0 1 2m x . x 1 2 2 m 2 Bài 1 1 1 1 m 0 m m 3b 0,25 1,0đ 2 2 2 0 m 4m 4 m 1 2 m 2 2 Từ trên ta được 2
m m 0 m 0 ; 4 4 m m
4m 4 0 m 1 khi đó 2 0,25 2
2m 2 m 1 Vậy m 1 thỏa đề bài m Vậy m 1 thỏa đề bài C C Bài 4 E E Trang 50 A B D O A B D O F G 0,5
(Hình vẽ cho câu a; 0,5đ)
Chứng minh rằng ACED là tứ giác nội tiếp. 0,25 Bài 0
CAD 90 (giả thiết 4a 0
CED 90 (góc nội tiếp chắn nửa đường tròn) 0,25
0,75đ Bốn điểm C, D, ,
A E cùng nằm trên đường tròn đường kính CD 0,25
Vậy tứ giác ACED là tứ giác nội tiếp.
Biết BF 3cm . Tính BC và diện tích tam giác BFC . ABCvuông tại A : 2 2 2 2 2
BC AB AC 4 3 25 0,25 Bài BC 5 4b
BFC vuông tại F : 2 2 2 2 2
CF BC BF 5 3 16 0,75đ 0,25 CF 4 1 1 2 S
.BF.CF .3.4 6 (cm ) 0,25 BFC 2 2
Tứ giác ACBF nội tiếp đường tròn ( do 0
CAB CFB 90 ) 0,25 Bài
nên ABC AFC (cùng chắn cung AC ) 4c
Mà ABG AFC (cùng bù với DFG )
0,5đ ABC ABG 0,25
Vậy BA là tia phân giác của CBG Bài
Số học sinh yêu thích hội họa chiếm 20% số học sinh toàn trường nên số học 0,5 5a
sinh yêu thích hội họa là học sinh 0,5đ 1500.20% 300
Gọi số học sinh yêu thích thể thao, âm nhạc và yêu thích khác lần lượt là a; ; b c
Ta có a b c 300 1500 a b c 1200 (1)
Số học sinh yêu thích thể thao và hội họa bằng với số học sinh yêu thích âm
nhạc và yêu thích khác nên a 300 b c (2) 0,25
Số học sinh yêu thích thể thao hơn số học sinh yêu thích âm nhạc là 30 nên ta
được a b 30 (3) Bài
(Tìm các mối quan hệ giữa các biến) 5b
Thay (2) vào phương trình (1) ta được a a 300 1200 a 450
0,5đ Thay vào phương trình (3) b 420
Vậy tổng số học sinh yêu thích thể thao và âm nhạc là a b 870
(học sinh có thể lập hệ phương trình rồi giải bằng máy tính) 0,25 Trang 51
Học sinh làm cách khác đúng vẫn cho điểm tối đa
Giám khảo họp thống nhất cách chấm trước khi chấm Trang 52




