
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
KIỂM TRA HỌC KÌ I LỚP 12
TRƯỜNG THPT
MARIE-CURIE-HÀ-NỘI
NĂM HỌC: 2020-2021
THỜI GIAN: 90 PHÚT
Câu 1. Cho hàm số
ax b
y
xc
+
=
−
có đồ thị như hình vẽ
Khi đó tổng
abc
++
bằng
A.
3
. B.
0
. C.
2−
. D.
2
.
Câu 2. Tâm đối xứng của đồ thị hàm số
31
2
x
y
x
−
=
+
là điểm có tọa độ nào sau đây?
A.
( )
2;3
−
. B.
( )
3; 2−
. C.
( )
2; 1−
. D.
( )
1; 2−
.
Câu 3. Cho hàm số
( )
y fx=
. Chọn mệnh đề sai trong các mệnh đề sau:
A.
0
xx=
là điểm cực tiểu của hàm số thì hàm số có giá trị cực tiểu là
( )
0
fx
.
B. Hàm số đạt cực trị tai điểm
0
xx=
thì
(
)
0
0
fx
′
=
.
C. Hàm số đạt cực đại tại điểm
0
xx=
thì
( )
fx
′
đổi dấu từ dương sang âm khi qua
0
x
.
D. Nếu hàm số đơn điệu trên
thì hàm số không có cực trị.
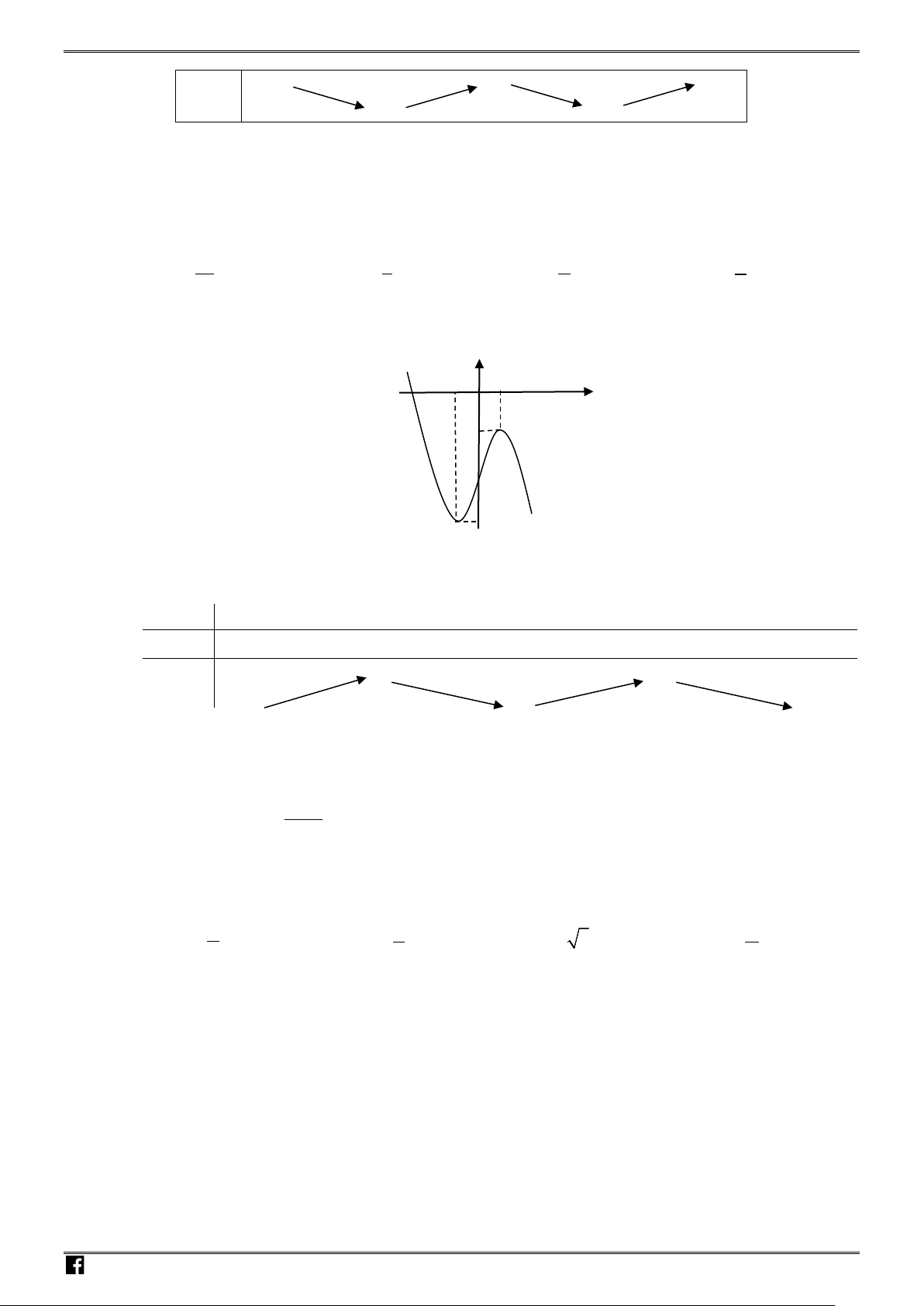
Câu 4: Cho hàm số
( )
y fx=
có bảng biến thiên như sau :
Khẳng định nào sau đây là Đúng ?
A. Hàm số đồng biến trên khoảng
( )
0; +∞
.
B. Hàm số đồng biến trên khoảng
( )
1; 2
.
0
0

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
C. Hàm số nghịch biến trên khoảng
( )
0; 4
.
D. Hàm số đồng biến trên khoảng
( )
;0−∞
.
Câu 5: Cho hàm số
4
yx
x
= +
với
( )
0;x∈ +∞
. Khẳng định nào sau đây là Đúng ?
A. Hàm số đạt giá trị nhỏ nhất tại
2x =
và không có giá trị lớn nhất trên khoảng
( )
0; +∞
.
B. Hàm số có giá trị lớn nhất và nhỏ nhất trên khoảng
( )
0; +∞
.
C. Hàm số đạt giá trị lớn nhất tại
2x =
và không có giá trị nhỏ nhất trên khoảng
(
)
0; +∞
.
D. Hàm số không giá trị nhỏ nhất và không có giá trị lớn nhất trên khoảng
( )
0; +∞
.
Câu 6: Cho các số dương
a
,
b
thỏa mãn
1a
≠
;
11
log log
23
aa
>
và
22
35
bb>
. Kết luận nào sau đây là
Đúng ?
A.
1a >
,
1b >
. B.
01
a<<
,
1b >
. C.
1a >
,
01b<<
. D.
01
a<<
,
01
b<<
.
Câu 7: Giá trị nhỏ nhất của hàm số
52yx= −
trên đoạn
[ ]
1; 2
là:
A.
3
. B.
1
. C.
2
D.
0.
Câu 8: Hàm số nào sau đây nghịch biến trên
A.
25yx
= +
. B.
3
2 21yx x= +−
. C.
25
1
x
y
x
+
=
+
.
D.
sin 4y xx= −
.
Câu 9: Biểu diễn biểu thức
( )
2
3
:0= >
A aaa a
dưới dạng lũy thừa với số mũ hữu tỉ ta được kết quả:
A.
3
4
=Aa
. B.
4
3
−
=Aa
. C.
2
3
=Aa
. D.
3
4
−
=Aa
.
Câu 10: Cho hình lập phương cạnh
a
. Khối cầu nội tiếp hình lập phương này có thể tích bằng
A.
3
3
π
2
a
. B.
3
4
π
3
a
. C.
3
4π
a
. D.
3
1
π
6
a
Câu 11: Cho hàm số
( )
y fx=
. Hàm số
( )
y fx
′
=
có đồ thị như hình vẽ
Số điểm cực trị của hàm số
( )
y fx=
là
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 12: Khối đa diện nào sau đây có tất cả các mặt là ngũ giác đều
A. Khối mười hai mặt đều. B. Khối bát diện đều.
C. Khối hai mươi mặt đều. D. Khối tứ diện đều.
Câu 13: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật tâm
,O SA
vuông góc với mặt phẳng
()ABCD
. Khối cầu ngoại tiếp hình chóp
.S ABCD
có bán kính bằng:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
1
2
SC
. B.
SA
. C.
1
2
AB
. D.
OA
.
Câu 14: Cho hàm số
()
y fx=
liên tục trên
và có đạo hàm
3
( ) 2 ( 1)(3 )y fx xx x
′′
= = +−
. Hàm số đồng
biến trên khoảng nào sau đây?
A.
( )
;1I −∞ −
. B.
( )
;0I −∞
. C.
( )
3;D = +∞
. D.
( )
1; 3I
−
.
Câu 15: Cho hình chóp đều
.,S ABCD O
là giao điểm của
,AC BD
. Thể tích khối chóp
.
S ABCD
được
tính bằng công thức:
A.
2
.V SO AB=
. B.
2
1
.
3
V SO AB=
. C.
2
1
.
3
V SA AB=
. D.
1
..
6
V SO AB AD=
.
Câu 16: Nếu tăng cạnh của một khối lập phương lên hai lần thì thể tích khối lập phương tăng lên.
A.
4
lần. B.
2
lần. C.
8
lần. D.
6
lần.
Câu 17: Cho hình chóp
.S ABC
đáy là tam giác
ABC
vuông cân tại
B
,
2AC a=
.
SA
vuông góc với
mặt phẳng
ABC
và
3SA a=
. Thể tích khối chóp
SABC
tính theo
a
bằng:
A.
3
1
3
a
. B.
3
2a
. C.
3
a
. D.
3
2
3
a
.
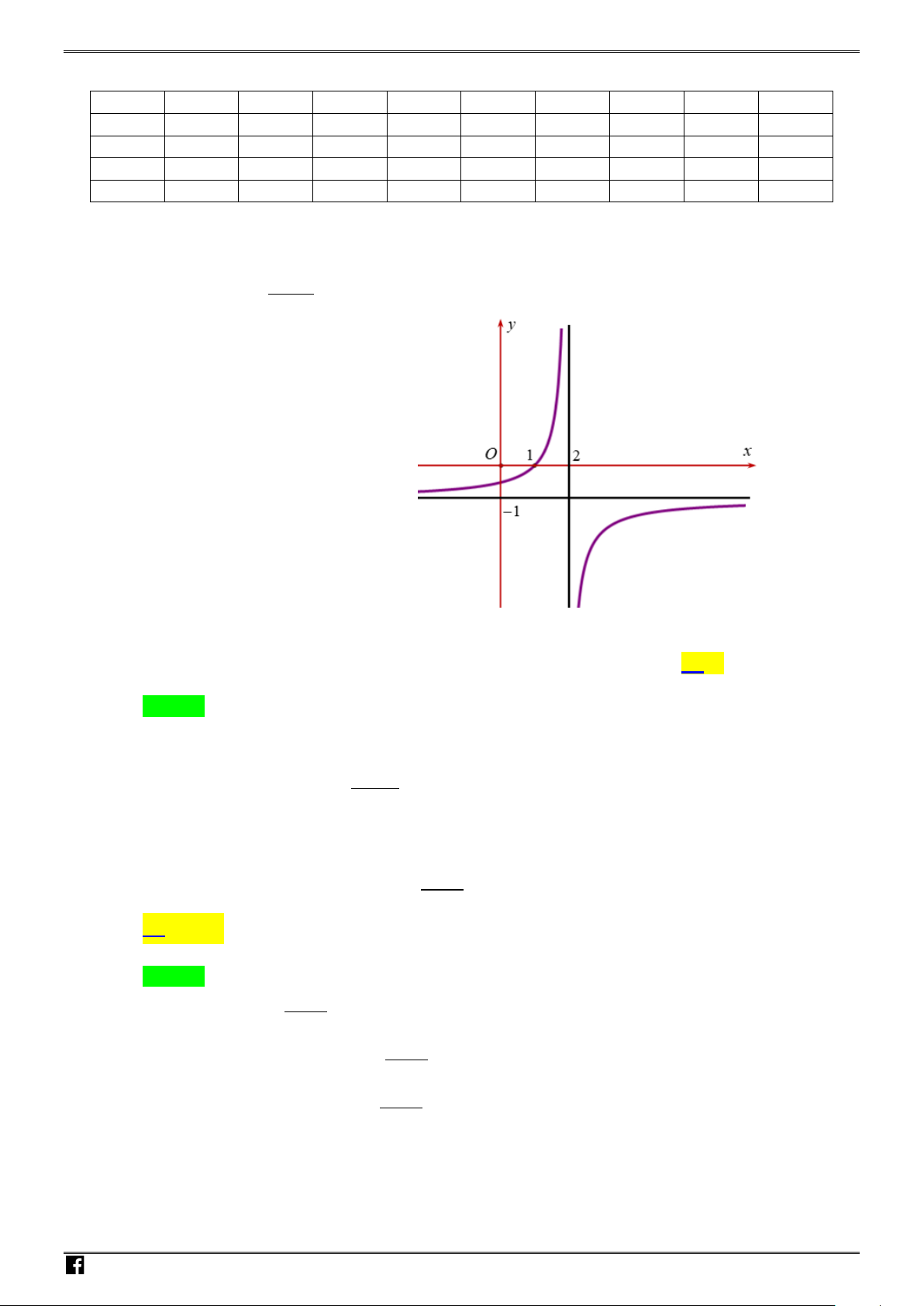
Câu 18: Hình vẽ bên là đồ thị của hàm số nào sau đây?
A.
42
22yx x
=−− +
. B.
42
2yx x=++
.
C.
42
2y xx=−+ +
. D.
2
22yx x=−+ +
.
Câu 19 : Cho hàm số
32
21y x xx
. Phương trình tiếp tuyến của đồ thị hàm số tại điểm có
hoành độ
0
2x
là:
A.
37yx
. B.
47yx
.
C.
37yx
. D.
35yx
.
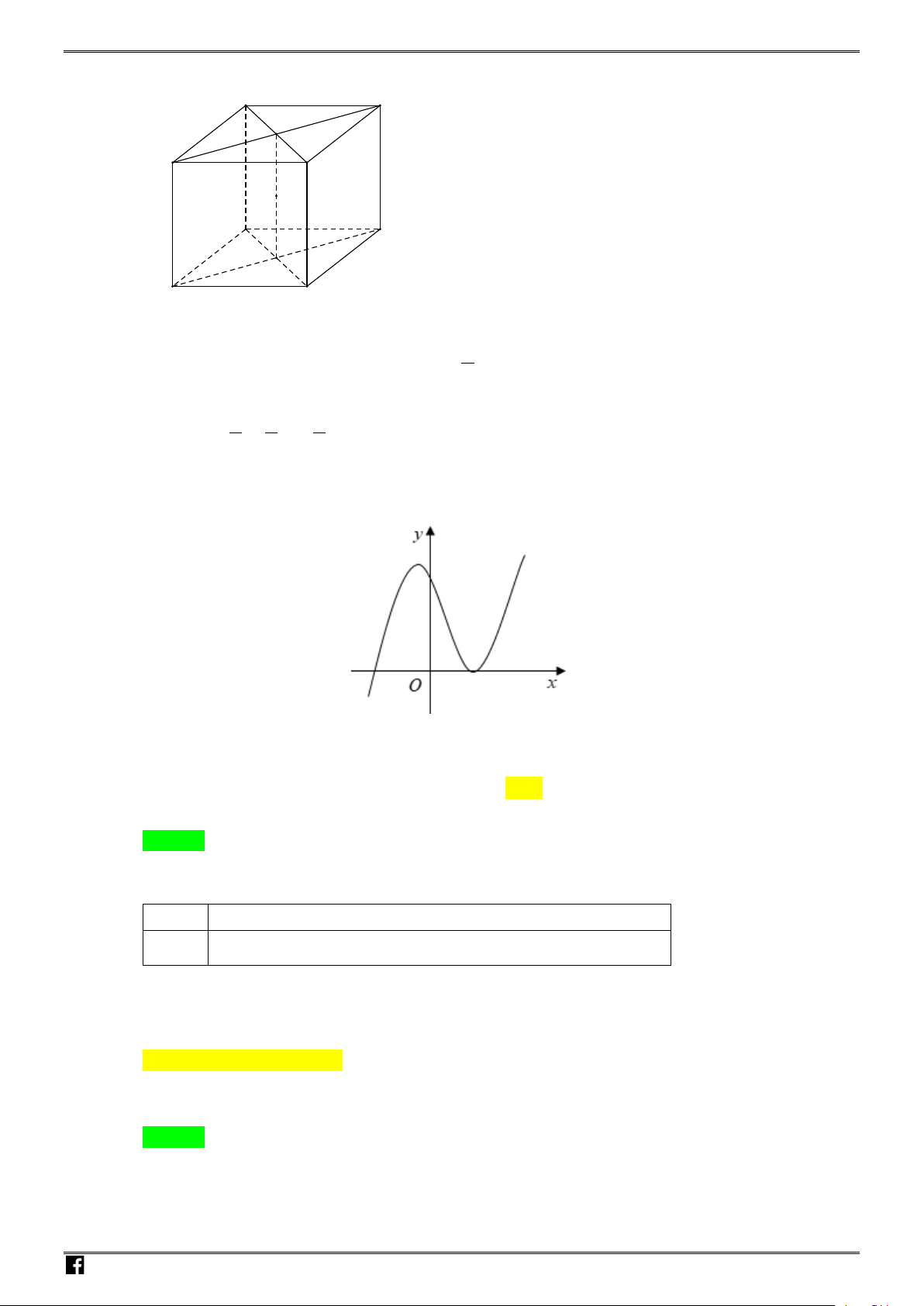
Câu 20: Cho hàm số
y fx
có đồ thị như hình vẽ.
Số nghiệm thực của phương trình
2fx
là:
A.
4
. B.
3
. C.
2
. D.
6.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 21: Cho các số thực dương
a
và
,1ba
. Rút gọn biểu thức
4 2 log
a
b
Ta
A.
42
T ab
. B.
24
T ab
. C.
2
T ab
. D.
43
T ab
.
Câu 22: Cho khối chóp
12
. .....
n
S AA A
. Khẳng định nào sau đây đúng?
A. Khối chóp
12
. .....
n
S AA A
có
2n
cạnh. B. Khối chóp
12
. .....
n
S AA A
có
2n
mặt.
C. Khối chóp
12
. .....
n
S AA A
có
n
đỉnh. D. Khối chóp
12
. .....
n
S AA A
có
n
mặt.
Câu 23: Đạo hàm của hàm số
2
ln 2 1yx
là
A.
2
' 4 .ln 2 1yxx
. B.
2
1
'
21
y
x
. C.
2
2
'
21
x
y
x
. D.
2
4
'
21
x
y
x
.
Câu 24: Hàm số nào sau đây không có cực trị?
A.
2
31yx x
. B.
4
3yx
. C.
21
2
x
y
x
. D.
32
31
yx x
.
Câu 25. Với
,,Rlh
lần lượt là bán kính đáy, độ dài đường sinh và chiều cao của hình nón
( )
N
. Khẳng
định nào sau đây đúng?
A.
2
()
1
3
N
V Rl
π
=
B.
2
()N
V Rh
π
=
. C.
( )
2
xq N
S Rl
π
=
. D.
222
lhR= +
.
Câu 26. Tập xác định của hàm số
(
)
1
2
2
2
yx x
= −
là
A.
( ) ( )
;0 2;D = −∞ ∪ +∞
.B.
(
] [
)
;0 2;D = −∞ ∪ +∞
.C.
( )
0; 2
D =
. D.
{ }
\ 0; 2D =
.
Câu 27. Cho hàm số
x
ya=
với
1a
>
. Mệnh đề nào sau đây sai?
A. Hàm số có tập giá trị
( )
0; +∞
. B. Đồ thị hàm số luôn đi qua điểm
( )
0;1
.
C. Hàm số đồng biến trên
. D. Đồ thị hàm số luôn có tiệm cận đứng.
Câu 28: Đường thẳng
2yx= +
là đường tiệm cận ngang của đồ thị hàm số nào sau đây?
A.
2
32
=
+
y
x
. B.
2
23
2
−
=
+
x
y
x
. C.
2
21
( 1)(3 )
+−
=
+−
xx
y
xx
. D.
2
1
21
+
=
+
x
y
x
.
Câu 29: Cho
a
là số thực dương,
1a ≠
. Mệnh đề nào sau đây là đúng?
A.
log 1
a
a=
. B.
log 0=
a
a
. C.
log 2
=
a
a
. D.
2
log 2=
a
a
.
Câu 30: Điều kiện của tham số
m
để phương trình
1
5 30
x
m
+
− +=
có nghiệm là
A.
m ∈
. B.
3≥m
. C.
3
>m
. D.
3<m
.
Câu 31: Cho
x
là số thực dương thỏa mãn
3
log 2x =
. Giá trị của biểu thức
P =
22
33
3
log log log
3
x
xx
−+
bằng:
A.
4
. B.
3−
. C.
2−
. D.
3
.
Câu 32: Cho hàm số
2
cosy x xm=++
(
m
là tham số). Với giá trị nào của
m
thì
0;
4
min 4y
π
=
?
A.
3
m =
. B.
3
4
m =
. C.
5
2
m =
. D.
0m =
.
Câu 33: Cho hàm số
2 31mx m
y
xm
+−
=
+
(
m
là tham số). Điều kiện của tham số
m
để hàm số đồng biến
trên khoảng
( )
;2−∞
là:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
1
1
2
m<<
. B.
1
2
2
m−≤ ≤
. C.
1
2
m ≤
. D.
2m ≤−
.
Câu 34: Cho
,,abc
là ba số thực khác
0
thỏa mãn
2 5 10
ab c
−
= =
. Giá trị biểu thức
ab bc ac++
bằng
A.
1
−
. B.
0
. C.
1
. D.
3
.
Câu 35: Cho lăng trụ
.ABC A B C
′′′
có cạnh bên bằng
2a
, đáy
ABC
là tam giác vuông tại
A
,
,3AB a AC a= =
. Hình chiếu vuông góc của
A
′
lên
( )
ABC
trùng với trung điểm của
BC
.
Khoảng cách giữa
BB
′
và
AC
theo
a
bằng
A.
2 39
13
a
. B.
13
4
a
. C.
39
13
a
. D.
13
13
a
.
Câu 36: Cho tứ diện đều
ABCD
có cạnh bằng
3a
. Hình nón
( )
N
có đỉnh
A
và đường tròn đáy là
đường tròn ngoại tiếp tam giác
BCD
. Diện tích xung quanh của hình nón
( )
N
bằng:
A.
2
63a
π
. B.
2
33a
π
. C.
2
3 a
π
. D.
2
6
a
π
.
Câu 37: Số điểm cực trị của hàm số
(
)
2
22
x
yx x e= −+
là
A. 2. B. 0. C. 3. D. 1.
Câu 38: Cho lăng trụ đứng
..ABC A B C
′′′
Gọi
M
là trung điểm
.AC
′′
Tỉ số thể tích của khối tứ diện
B ABM
′
với khối lăng trụ
.ABC A B C
′′′
là
A.
1
12
. B.
1
2
. C.
1
4
. D.
1
6
.
Câu 39: Đồ thị hàm số
42
y ax bx c=++
có điểm cực đại là
(
)
0; 3
A −
và một điểm cực tiểu là
(
)
1; 5 .
B −−
Khi đó tổng
abc++
bằng
A.
1−
. B. 7. C.
5−
. D. 3.
Câu 40: Giá trị của tham số
m
để bất phương trình
( )
2 14xmxm−− −≤ −
có nghiệm là:
A.
3m ≤
. B.
2m ≥
. C.
0m ≥
. D.
2m <
.
Câu 41: Một người gửi số tiền 100 triệu đồng vào ngân hang theo thể thức lãi kép với lãi suất là
8%
năm.
Giả sử lãi suất hằng năm không thay đổi thì số tiền lãi người đó nhận được sau thời gian 10 năm
gần nhất với kết quả nào sau đây?
A.
110,683
triệu. B.
116,253
triệu. C.
114,295
triệu. D.
115,892
triệu.
Câu 42: Cho biết
22
log 5 ;log 3 .ab= =
Tính giá trị của
25
log 108
theo
a
và
.b
A.
25
3
log 108
2
ab+
=
. B.
25
2
log 108
3ab
=
+
. C.
25
2
log 108
3
a
b
+
=
. D.
25
23
log 108
2
b
a
+
=
.
Câu 43. Cho lăng trụ đứng
.'' ' 'ABCD A B C D
có đáy là hình thoi
ABCD
cạnh
a
, góc
ABC
bằng
60
o
.
Đường chéo
'AC
tạo với mặt phẳng
()ABCD
một góc
30
o
. Thể tích khối lăng trụ
.'' ' 'ABCD A B C D
tính theo
a
bằng:
A.
3
1
4
a
. B.
3
1
6
a
. C.
3
1
2
a
. D.
3
3
2
a
.
Câu 44. Tập tất cả các giá trị của tham số m để đồ thị hàm số
( )
32
1
12
3
y xx m x= ++ − +
có hai điểm
cực trị nằm bên trái trục tung là:
A.
( )
;1−∞
. B.
( )
1; 2
. C.
( )
;2−∞
. D.
( )
1; +∞
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 45. Cho tứ diện
ABCD
đều cạnh
a
.
,,
MNP
lần lượt là trọng tâm các tam giác
,,ABC ABD ACD
.
Thể tích của khối tứ diện
AMNP
tính theo
a
bằng:
A.
3
2
108
a
. B.
3
2
144
a
. C.
3
22
81
a
. D.
3
2
162
a
.
Câu 46. Một tấm kim loại hình chữ nhật có kích thước 30cm x 80cm. Người ta gò tấm kim loại này thành
mặt xung quanh của một khối trụ có chiều cao 30cm. Thể tích khối trụ được tạo thành bằng:
A.
(
)
3
24000
cm
π
B.
( )
3
48000 cm
π
C.
( )
3
12000 cm
π
D.
(
)
3
48000
cm
π
Câu 47. Tập các giá trị của tham số m để phương trình
42
2 3 10xxm
− − +=
có 2 nghiệm phân biệt
là:
A.
{ }
+∞ ∪(1; ) 0
B.
{ }
+∞ ∪
1
;0
3
C.
+∞(0; )
D.
+∞
(1; )
Câu 48. Tất cả các giá trị thực của tham số m để đồ thị hàm số
2
1
2 34
x
y
x mx m
+
=
+ ++
có đúng một
đường tiệm cận đứng là:
A.
[ 1; 4]m
∈−
B.
{ 1; 4; 5}m ∈−
C.
( 1; 4)m ∈−
D.
{ 5; 1; 4}m∈− −
Câu 49. Cho hàm số
32
1
21 1
3
y x mx m x
(
m
là tham số ). Có bao nhiêu giá trị nguyên của
tham số
m
để hàm số đồng biến trên
.
A.
3
. B.
0
. C.
1
. D. Vô số.
Câu 50. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
H
là trung điểm
AB
,
SH
vuông góc
với mặt phẳng
ABCD
. Biết
13
2
a
SC
, khoảng cách từ
A
đến mặt phẳng
SCD
tính
theo
a
.
A.
2
2
a
. B.
2a
. C.
6
3
a
. D.
2
a
.
80cm
30cm
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
BẢNG ĐÁP ÁN
1.D
2.A
3.B
4.B
5.A
6.A
7.B
8.D
9.B
10.D
11.C
12.A
13.A
14.A
15.B
16.C
17.C
18.A
19.A
20.A
21.A
22.A
23.D
24.C
25.D
26.A
27.D
28.C
29.C
30.C
31.B
32.A
33.D
34.B
35.A
36.B
37.B
38.D
39.C
40.B
41.D
42.D
43.A
44.B
45.D
46.D
47.B
48.D
49.C
50.C
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Cho hàm số
ax b
y
xc
+
=
−
có đồ thị như hình vẽ
Khi đó tổng
abc
++
bằng
A.
3
. B.
0
. C.
2−
. D.
2
.
Lời giải
Chọn D
Ta có
2x =
và
1y = −
lần lượt là đường tiệm cận đứng và đường tiệm cận ngang nên
2c =
và
1a = −
.
Khi đó hàm số có dạng
2
xb
y
x
−+
=
−
.
Lại có đồ thị hàm số đi qua điểm
( )
1; 0
suy ra
1b
=
.
Do đó
112 2abc+ + =−++ =
.
Câu 2. Tâm đối xứng của đồ thị hàm số
31
2
x
y
x
−
=
+
là điểm có tọa độ nào sau đây?
A.
( )
2;3−
. B.
( )
3; 2−
. C.
( )
2; 1−
. D.
( )
1; 2−
.
Lời giải
Chọn A
Đồ thị hàm số
31
2
x
y
x
−
=
+
nhận giao của hai tiệm cận làm tâm đối xứng.
Tiệm cận đứng
2x = −
vì
2
31
lim
2
x
x
x
−
→−
−
= +∞
+
Tiệm cận ngang
3y
=
vì
31
lim 3
2
x
x
x
→+∞
−
=
+
Do đó đồ thị hàm số nhận
( )
2;3I −
làm tâm đối xứng.
Câu 3. Cho hàm số
( )
y fx=
. Chọn mệnh đề sai trong các mệnh đề sau:
A.
0
xx=
là điểm cực tiểu của hàm số thì hàm số có giá trị cực tiểu là
( )
0
fx
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
B. Hàm số đạt cực trị tai điểm
0
xx=
thì
( )
0
0fx
′
=
.
C. Hàm số đạt cực đại tại điểm
0
xx=
thì
( )
fx
′
đổi dấu từ dương sang âm khi qua
0
x
.
D. Nếu hàm số đơn điệu trên
thì hàm số không có cực trị.
Lời giải
Chọn B
Hàm số đạt cực trị tại các điểm thuộc tập xác định mà ở đó không tồn tại đạo hàm hoặc
( )
0
0fx
′
=
.
Câu 4: Cho hàm số
( )
y fx=
có bảng biến thiên như sau :
Khẳng định nào sau đây là Đúng ?
A. Hàm số đồng biến trên khoảng
( )
0; +∞
.
B. Hàm số đồng biến trên khoảng
(
)
1; 2
.
C. Hàm số nghịch biến trên khoảng
( )
0; 4
.
D. Hàm số đồng biến trên khoảng
( )
;0−∞
.
Lời giải
Chọn B
Hàm số đồng biến trên khoảng
( )
0;3
nên hàm số đồng biến trên khoảng
( )
1; 2
.
Câu 5: Cho hàm số
4
yx
x
= +
với
( )
0;
x∈ +∞
. Khẳng định nào sau đây là Đúng ?
A. Hàm số đạt giá trị nhỏ nhất tại
2x
=
và không có giá trị lớn nhất trên khoảng
( )
0; +∞
.
B. Hàm số có giá trị lớn nhất và nhỏ nhất trên khoảng
( )
0; +∞
.
C. Hàm số đạt giá trị lớn nhất tại
2x =
và không có giá trị nhỏ nhất trên khoảng
( )
0; +∞
.
D. Hàm số không giá trị nhỏ nhất và không có giá trị lớn nhất trên khoảng
( )
0; +∞
.
Lời giải
Chọn A
44
2. 4
yx x
xx
=+≥ =
Dấu bằng xảy ra khi :
4
x
x
=
2
42xx⇔ =⇔=
vì
( )
0;x ∈ +∞
.
Vậy hàm số đạt giá trị nhỏ nhất tại
2x =
và không có giá trị lớn nhất trên khoảng
( )
0; +∞
.
0
0

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 6: Cho các số dương
a
,
b
thỏa mãn
1a
≠
;
11
log log
23
aa
>
và
22
35
bb
>
. Kết luận nào sau đây là
Đúng ?
A.
1
a >
,
1b >
. B.
01a<<
,
1
b
>
. C.
1a >
,
01b<<
. D.
01a<<
,
01b
<<
.
Lời giải
Chọn A
11
log log
23
aa
>
1
a⇒>
;
22
35
1bb b
> ⇒>
.
Câu 1. Câu 7: Giá trị nhỏ nhất của hàm số
52yx
= −
trên đoạn
[ ]
1; 2
là:
A.
3
. B.
1
. C.
2
D.
0.
Lời giải
Chọn B
Ta có
5
;
2
D
= −∞
do đó hàm số liên tục trên đoạn
[ ]
1; 2
.
Mặt khác:
[ ]
1
' 0, 1; 2
52
yx
x
−
= < ∀∈
−
( ) ( )
1 3; 2 1yy= =
nên giá trị nhỏ nhất của hàm số trên
[ ]
1; 2
bằng 1. Chọn B.
Câu 2. Câu 8: Hàm số nào sau đây nghịch biến trên
A.
25
yx= +
. B.
3
2 21yx x= +−
. C.
25
1
x
y
x
+
=
+
.
D.
sin 4y xx
= −
.
Lời giải
Chọn D
Ta có
sin 4 ; XD :y x xT D=−=
và có
' cos 4 0,yx x
= − < ∀∈
nên hàm số nghịch biến trên
.
Câu 9: Biểu diễn biểu thức
( )
2
3
:0= >A aaa a
dưới dạng lũy thừa với số mũ hữu tỉ ta được kết quả:
A.
3
4
=Aa
. B.
4
3
−
=Aa
. C.
2
3
=Aa
. D.
3
4
−
=Aa
.
Lời giải
Chọn B
Ta có
12
1
4
63
2
3
22
.
−
= = =
aa a
Aa
aa
.
Câu 10: Cho hình lập phương cạnh
a
. Khối cầu nội tiếp hình lập phương này có thể tích bằng
A.
3
3
π
2
a
. B.
3
4
π
3
a
. C.
3
4πa
. D.
3
1
π
6
a
Lời giải
Chọn D
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
O
là tâm mặt cầu nội tiếp,
2
a
r OI
= =
Suy ra
3
3
4 π
π
32 6
a
Va
= =
.
Câu 11: Cho hàm số
( )
y fx=
. Hàm số
(
)
y fx
′
=
có đồ thị như hình vẽ
Số điểm cực trị của hàm số
( )
y fx=
là
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn C
Bảng xét dấu
x
ab−∞ +∞
( )
fx
′
00−+ +
Suy ra hàm số
( )
y fx=
có
1
cực trị
Câu 12: Khối đa diện nào sau đây có tất cả các mặt là ngũ giác đều
A. Khối mười hai mặt đều. B. Khối bát diện đều.
C. Khối hai mươi mặt đều. D. Khối tứ diện đều.
Lời giải
Chọn A
Lý thuyết
O
I
I'
D
A
C
B
B'
C'
A'
D'

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 13: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật tâm
,
O SA
vuông góc với mặt phẳng
()ABCD
. Khối cầu ngoại tiếp hình chóp
.S ABCD
có bán kính bằng:
A.
1
2
SC
. B.
SA
. C.
1
2
AB
. D.
OA
.
Lời giải
Chọn A
Gọi
I
là trung điểm của
SC
. Tam giác
SAC
vuông tại
A
, tam giác
SBC
vuông tại
B
, tam
giác
SCD
vuông tại
D
,
IA IB IC ID IS
⇒== = =⇒
I
là tâm của mặt cầu ngoại tiếp hình
chóp
.S ABCD
.
1
2
R SC⇒=
.
Câu 14: Cho hàm số
()
y fx=
liên tục trên
và có đạo hàm
3
( ) 2 ( 1)(3 )y fx xx x
′′
= = +−
. Hàm số đồng
biến trên khoảng nào sau đây?
A.
( )
;1I −∞ −
. B.
( )
;0
I −∞
. C.
( )
3;D = +∞
. D.
( )
1; 3I −
.
Lời giải
Chọn A
0
01
3
x
yx
x
=
′
=⇔=−
=
.
Câu 15: Cho hình chóp đều
.,S ABCD O
là giao điểm của
,AC BD
. Thể tích khối chóp
.S ABCD
được
tính bằng công thức:
A.
2
.V SO AB=
. B.
2
1
.
3
V SO AB=
. C.
2
1
.
3
V SA AB=
. D.
1
..
6
V SO AB AD=
.
Lời giải
Chọn B
S
B
C
D
A
I
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Tam giác
SAC
có
,SA SC OA OC SO AC= =⇒⊥
.
Tam giác
SBD
có
,SB SD OB OD SO BD= = ⇒⊥
.
()SO ABCD⇒⊥
.
Tứ giác
ABCD
có
AB BC CD DA
= = =
, mà
SA SB SC SD ABCD= = = ⇒
là hình vuông
2
ABCD
S AB
⇒=
.
Vậy
2
.
1
.
3
S ABCD
V SO AB=
.
Câu 16: Nếu tăng cạnh của một khối lập phương lên hai lần thì thể tích khối lập phương tăng lên.
A.
4
lần. B.
2
lần. C.
8
lần. D.
6
lần.
Lời giải
Chọn C
Giả sử độ dài cạnh hình lập phương bằng
a
và có thể tích là
V
, độ dài cạnh hình lập
phương sau khi tăng bằng
2a
và có thể tích là
1
V
. Khi đó
( )
3
3
1
2 88V a aV= = =
.
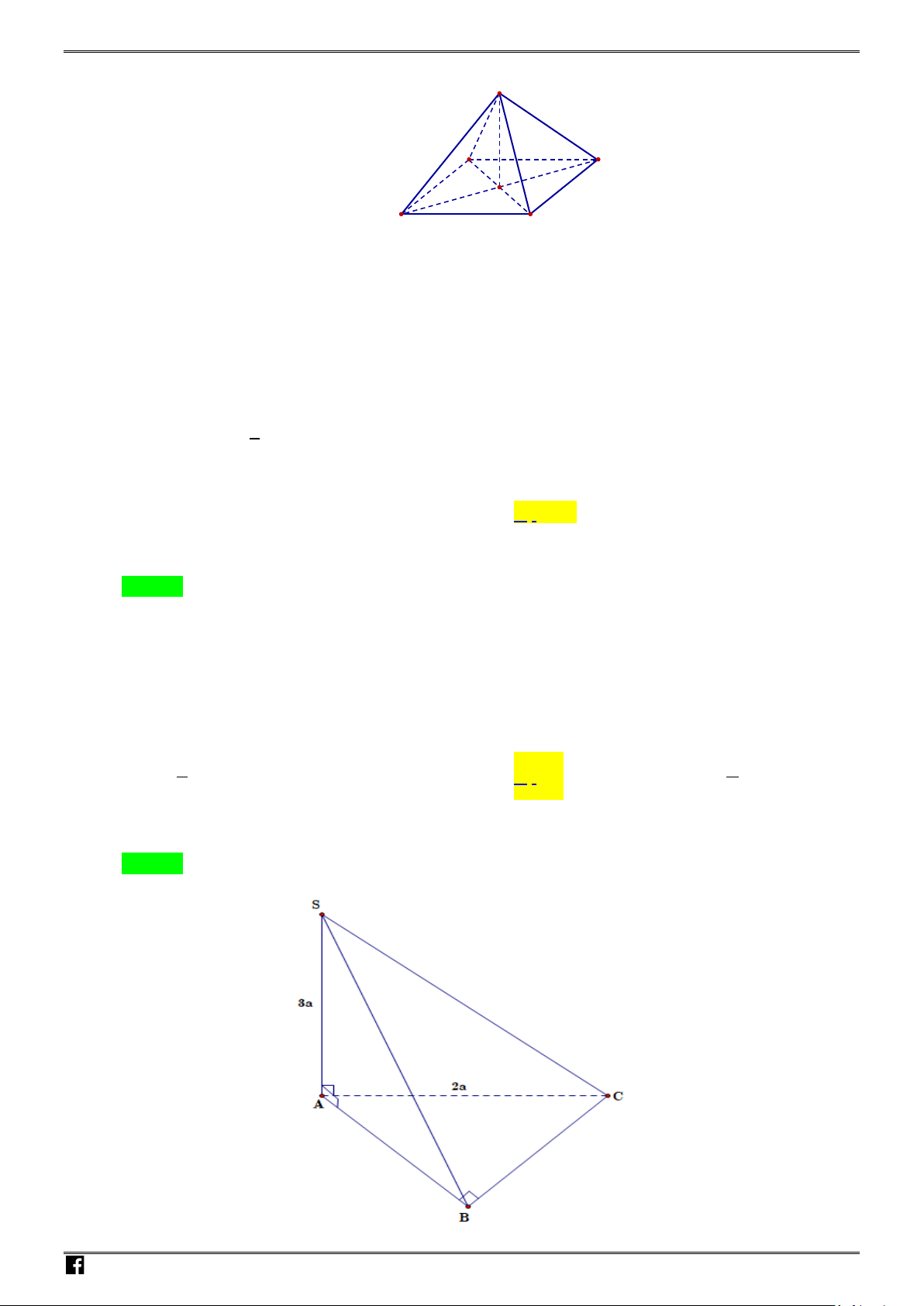
Câu 17: Cho hình chóp
.S ABC
đáy là tam giác
ABC
vuông cân tại
B
,
2AC a=
.
SA
vuông góc với
mặt phẳng
ABC
và
3SA a=
. Thể tích khối chóp
SABC
tính theo
a
bằng:
A.
3
1
3
a
. B.
3
2a
. C.
3
a
. D.
3
2
3
a
.
Lời giải
Chọn C
S
A
B
C
D
O

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
ABC
∆
vuông cân tại
B
nên
2AB BC a= =
2
1
.
2
ABC
S AB BC a
∆
⇒= =
.
3
1
.
3
ABC
V SA S a
∆
⇒= =
.
Câu 18: Hình vẽ bên là đồ thị của hàm số nào sau đây?
A.
42
22
yx x
=−− +
. B.
42
2
yx x=++
.
C.
42
2y xx
=−+ +
. D.
2
22yx x=−+ +
.
Lời giải
Chọn A
Ta có
lim
x
y
→±∞
= −∞
nên loại phương án
B
Quan sát đồ thị ta thấy hàm số chỉ có
1
điểm cực trị nên ta loại phương án
C
Phương án
D
không thỏa mãn vì hàm số
2
22yx x=−+ +
có tọa độ đỉnh là
( )
1; 3
.
Câu 19 : Cho hàm số
32
21
y x xx
. Phương trình tiếp tuyến của đồ thị hàm số tại điểm có
hoành độ
0
2x
là:
A.
37yx
. B.
47yx
.
C.
37yx
. D.
35yx
.
Lời giải
Chọn A
2
3 41y xx
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
0
2
x
là
222
yy x y
3 21yx
37yx
.
Câu 20: Cho hàm số
y fx
có đồ thị như hình vẽ.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Số nghiệm thực của phương trình
2
fx
là:
A.
4
. B.
3
. C.
2
. D.
6.
Lời giải
Chọn A
Ta có:
2
2
2
fx
fx
fx
Từ đồ thị hàm số ta thấy đường thẳng
2
y
cắt đồ thị hàm số đã cho tại 3 điểm.
Đường thẳng
2y
cắt đồ thị hàm số đã cho tại 1 điểm.
Do đó phương trình
2fx
có 4 nghiệm phân biệt.
Câu 21: Cho các số thực dương
a
và
,1
ba
. Rút gọn biểu thức
4 2 log
a
b
Ta
A.
42
T ab
. B.
24
T ab
. C.
2
T ab
. D.
43
T ab
.
Lời giải
Chọn D
2
4 2 log log
4 42
.
aa
bb
T a a a ab
.
Câu 22: Cho khối chóp
12
. .....
n
S AA A
. Khẳng định nào sau đây đúng?
A. Khối chóp
12
. .....
n
S AA A
có
2n
cạnh. B. Khối chóp
12
. .....
n
S AA A
có
2n
mặt.
C. Khối chóp
12
. .....
n
S AA A
có
n
đỉnh. D. Khối chóp
12
. .....
n
S AA A
có
n
mặt.
Lời giải
Chọn A
Câu 23: Đạo hàm của hàm số
2
ln 2 1yx
là
A.
2
' 4 .ln 2 1yxx
. B.
2
1
'
21
y
x
. C.
2
2
'
21
x
y
x
. D.
2
4
'
21
x
y
x
.
Lời giải
Chọn D
Ta có
2
2
22
21
4
ln 2 1
2121
x
x
yx
xx
.
Câu 24: Hàm số nào sau đây không có cực trị?
A.
2
31yx x
. B.
4
3yx
. C.
21
2
x
y
x
. D.
32
31yx x
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn C
Câu 25. Với
,,Rlh
lần lượt là bán kính đáy, độ dài đường sinh và chiều cao của hình nón
( )
N
. Khẳng
định nào sau đây đúng?
A.
2
()
1
3
N
V Rl
π
=
B.
2
()N
V Rh
π
=
. C.
(
)
2
xq N
S Rl
π
=
. D.
222
lhR
= +
.
Lời giải
Chọn D
Ta có
222
lhR= +
.
Câu 26. Tập xác định của hàm số
(
)
1
2
2
2
yx x= −
là
A.
( ) ( )
;0 2;D = −∞ ∪ +∞
.B.
(
] [
)
;0 2;D = −∞ ∪ +∞
.C.
( )
0; 2D =
. D.
{ }
\ 0; 2D =
.
Lời giải
Chọn A
Điều kiện xác định
( ) ( )
2
2 0 ;0 2;xx x− > ⇔ ∈ −∞ ∪ +∞
.
Vậy tập xác định của hàm số là
( ) ( )
;0 2;D = −∞ ∪ +∞
.
Câu 27. Cho hàm số
x
ya=
với
1a >
. Mệnh đề nào sau đây sai?
A. Hàm số có tập giá trị
( )
0; +∞
. B. Đồ thị hàm số luôn đi qua điểm
( )
0;1
.
C. Hàm số đồng biến trên
. D. Đồ thị hàm số luôn có tiệm cận đứng.
Lời giải
Chọn D
Đồ thị hàm số
x
ya=
không có tiệm cận đứng.
Câu 28: Đường thẳng
2yx
= +
là đường tiệm cận ngang của đồ thị hàm số nào sau đây?
A.
2
32
=
+
y
x
. B.
2
23
2
−
=
+
x
y
x
. C.
2
21
( 1)(3 )
+−
=
+−
xx
y
xx
. D.
2
1
21
+
=
+
x
y
x
.
Lời giải
Chọn C
Hàm số
2
21
( 1)(3 )
+−
=
+−
xx
y
xx
có tập xác định hàm số là
{ }
\ 1; 3−
.
Ta có
2
21
lim 2
( 1)(3 )
→+∞
+−
= −
+−
x
xx
xx
. Do đó tiệm cận ngang của đồ thị hàm số
2
21
( 1)(3 )
+−
=
+−
xx
y
xx
là
2y
= −
hay
20y +=
.
Câu 29: Cho
a
là số thực dương,
1a ≠
. Mệnh đề nào sau đây là đúng?
A.
log 1
a
a=
. B.
log 0=
a
a
. C.
log 2=
a
a
. D.
2
log 2=
a
a
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn C
Ta có
1
2
log log 2log 2
= = =
a
a
a
aa a
.
Câu 30: Điều kiện của tham số
m
để phương trình
1
5 30
x
m
+
− +=
có nghiệm là
A.
m ∈
. B.
3≥m
. C.
3>m
. D.
3<m
.
Lời giải
Chọn C
Ta có
11
5 30 5 3
xx
mm
++
− +=⇔ = −
phương trình có nghiệm khi
30 3mm−>⇔ >
.
Câu 31: Cho
x
là số thực dương thỏa mãn
3
log 2
x =
. Giá trị của biểu thức
P =
22
33
3
log log log
3
x
xx−+
bằng:
A.
4
. B.
3−
. C.
2−
. D.
3
.
Lời giải
Chọn B
Ta có
( ) ( )
22
2
3 33 3 3
log 4log log 1 log 3log 1 2 3.2 1 3P x xx x x= − + −= − −= − −=−
.
Câu 32: Cho hàm số
2
cosy x xm=++
(
m
là tham số). Với giá trị nào của
m
thì
0;
4
min 4y
π
=
?
A.
3m =
. B.
3
4
m =
. C.
5
2
m =
. D.
0m =
.
Lời giải
Chọn A
Ta có
0cos in1 2 s 1 sin 2 ,
y xx x x
′
=− =− ≥ ∀∈
.
Suy ra hàm số đã cho đồng biến trên đoạn
0;
4
π
.
Do đó
( )
0;
4
min 0 1 4 3yy m m
π
= =+=⇔=
.
Câu 33: Cho hàm số
2 31mx m
y
xm
+−
=
+
(
m
là tham số). Điều kiện của tham số
m
để hàm số đồng biến
trên khoảng
( )
;2−∞
là:
A.
1
1
2
m<<
. B.
1
2
2
m−≤ ≤
. C.
1
2
m ≤
. D.
2m ≤−
.
Lời giải
Chọn D

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Hàm số đồng biến trên khoảng
( )
;2−∞
( )
0
;2
y
m
′
>
⇔
− ∉ −∞
.
2
1
2 3 10
2
2
1
2
2
m
mm
m
m
m
m
<
− +>
⇔ ⇔ ⇔ ≤−
>
−≥
≤−
.
Câu 34: Cho
,,abc
là ba số thực khác
0
thỏa mãn
2 5 10
ab c−
= =
. Giá trị biểu thức
ab bc ac++
bằng
A.
1−
. B.
0
. C.
1
. D.
3
.
Lời giải
Chọn B
Đặt
2 5 10 0
ab c
t
−
= = = >
. Ta có
11 1
2 ,5 ,10
ab c
tt t
−
= = =
.
Nhận xét:
11 1
11 1
2.5 10 . 0
ab c
t t t ab bc ac
ab c
−
= ⇒ = ⇔+=−⇔ + + =
.
Câu 35: Cho lăng trụ
.ABC A B C
′′′
có cạnh bên bằng
2a
, đáy
ABC
là tam giác vuông tại
A
,
,3AB a AC a
= =
. Hình chiếu vuông góc của
A
′
lên
( )
ABC
trùng với trung điểm của
BC
.
Khoảng cách giữa
BB
′
và
AC
theo
a
bằng
A.
2 39
13
a
. B.
13
4
a
. C.
39
13
a
. D.
13
13
a
.
Lời giải
Chọn A
Gọi
H
là trung điểm của
BC
. Khi đó
( )
A H ABC
′
⊥
.
Ta có
BB
′
song song
( )
ACC A
′′
.
Khi đó
( ) ( )
( )
( )
( )
( )
( )
, , , 2,d BB AC d BB ACC A d B ACC A d H ACC A
′ ′ ′′ ′′ ′′
= = =
Gọi
,IK
lần lượt là hình chiếu vuông góc của
H
lên
AC
và
AI
′
Ta có
AC HI⊥
và
( )
AC A H AC A IH AC HK
′′
⊥ ⇒⊥ ⇒⊥
. Vậy
( )
HK ACC A
′′
⊥
hay
( )
( )
,d H ACC A HK
′′
=
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
2
22 2
1 3 13
,4
22 2 2
a aa
HI AB A I AA AI a
′′
= = = −= − =
, khi đó
22
22
13
3
44
aa
AH AI HI a
′′
= − = −=
.
Khi đó
.3
. 39
2
13
13
2
a
a
HI A H a
HK
AI
a
′
= = =
′
. Vậy
( )
2 39
,
13
a
d BB AC
′
=
.
Câu 36: Cho tứ diện đều
ABCD
có cạnh bằng
3a
. Hình nón
( )
N
có đỉnh
A
và đường tròn đáy là
đường tròn ngoại tiếp tam giác
BCD
. Diện tích xung quanh của hình nón
(
)
N
bằng:
A.
2
63
a
π
. B.
2
33a
π
. C.
2
3 a
π
. D.
2
6 a
π
.
Lời giải
Chọn B
Gọi
I
là trung điểm của
CD
,
:2G BI BG GI
∈=
. Khi đó
( )
AG BCD⊥
và
G
là tâm đường
tròn ngoại tiếp tam giác
BCD
.
Ta có
2 23 3
.3
3 32
a
BG BI a= = =
. Khi đó
2
. . . 3.3 3 3
xq
S BG AB a a a
ππ π
= = =
.
Câu 37: Số điểm cực trị của hàm số
( )
2
22
x
yx x e= −+
là
A. 2. B. 0. C. 3. D. 1.
Lời giải
Chọn B
Ta có
2
..
x
y xe
′
=
0 0.yx
′
=⇔=
Bảng biến thiên
x
−∞
0
+∞
y
′
+
0
+

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
y
0
+∞
Vậy hàm số không có cực trị.
Câu 38: Cho lăng trụ đứng
..ABC A B C
′′′
Gọi
M
là trung điểm
.AC
′′
Tỉ số thể tích của khối tứ diện
B ABM
′
với khối lăng trụ
.ABC A B C
′′′
là
A.
1
12
. B.
1
2
. C.
1
4
. D.
1
6
.
Lời giải
Chọn D
Gọi
N
là trung điểm
.AC
Do đó
1
.
2
ABN ABC
SS
=
Vì
(
)
//MN ABB
′
nên
..
.
M ABB N ABB
VV
′′
=
Ta có
..
1 11 1 1
.. ... .. .
3 32 6 6
B ABN ABN ABC ABC ABC A B C
V BB S BB S BB S V
′ ′′′
′′ ′
= = = =
Vậy
.
1
.
6
B ABM
ABC A B C
V
V
′
′′′
=
Câu 39: Đồ thị hàm số
42
y ax bx c=++
có điểm cực đại là
( )
0; 3A −
và một điểm cực tiểu là
(
)
1; 5 .B −−
Khi đó tổng
abc++
bằng
A.
1−
. B. 7. C.
5−
. D. 3.
Lời giải
Chọn C
Vì
,A
B
thuộc đồ thị hàm số nên ta có
3 (1)
.
5 (2)
c
abc
−=
−= ++
3
4 2.y ax bx
′
= +
Vì
B
là điểm cực tiểu nên
( )
1 0 4 2 0 (3).y ab
′
− = ⇔− − =
Từ (1), (2), (3) ta có
2
4.
3
a
b
c
=
= −
= −

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vậy
5.abc++=−
Câu 40: Giá trị của tham số
m
để bất phương trình
( )
2 14xmxm
−− −≤ −
có nghiệm là:
A.
3m ≤
. B.
2m ≥
. C.
0m
≥
. D.
2m
<
.
Lời giải
Chọn B
Đặt
( )
( )
( )
23
10 1 4 1 4 0t x t t mt m t mt m= − ≥ ⇒ −− ≤ − ⇔ − + + − ≤
[
)
( )
33
0;
44
min
11
tt tt
m m ft
tt
+∞
−+ −+
⇔ ≤⇒≥ =
++
Ta có:
( )
( )
( )
(
)
23
32
2
31 1 4
' 0 2 3 50 1
1
t t tt
ft t t t
t
− + − +−
= = ⇔ + −= ⇔=
+
.
Xét bảng biến thiên:
Vậy để bất phương trình trên có nghiệm thì
2.
m ≥
Câu 41: Một người gửi số tiền 100 triệu đồng vào ngân hang theo thể thức lãi kép với lãi suất là
8%
năm.
Giả sử lãi suất hằng năm không thay đổi thì số tiền lãi người đó nhận được sau thời gian 10 năm
gần nhất với kết quả nào sau đây?
A.
110,683
triệu. B.
116,253
triệu. C.
114,295
triệu. D.
115,892
triệu.
Lời giải
Chọn D
Theo công thức lãi kép ta có
( )
1
n
TA r= +
trong đó
T
là số tiền cả gốc lẫn lãi khi lấy về
A
là
số tiền ban đầu
r
là lãi suất và
n
là số kỳ hạn.
Khi đó số tiền lãi người đó nhận được sau thời gian 10 năm là:
( )
10
100 1 8% 100 115,892+−
triệu đồng.
Câu 42: Cho biết
22
log 5 ;log 3 .ab= =
Tính giá trị của
25
log 108
theo
a
và
.
b
A.
25
3
log 108
2
ab+
=
. B.
25
2
log 108
3
ab
=
+
. C.
25
2
log 108
3
a
b
+
=
. D.
25
23
log 108
2
b
a
+
=
.
Lời giải
Chọn D
Ta có:
3
3
22
25
2
22
log 4.3 2 3log 3
23
log 4.3 .
log 5 2 log 5 2
b
a
+
+
= = =
Câu 43. Cho lăng trụ đứng
.'' ' 'ABCD A B C D
có đáy là hình thoi
ABCD
cạnh
a
, góc
ABC
bằng
60
o
.
Đường chéo
'AC
tạo với mặt phẳng
()ABCD
một góc
30
o
. Thể tích khối lăng trụ
.'' ' 'ABCD A B C D
tính theo
a
bằng:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
1
4
a
. B.
3
1
6
a
. C.
3
1
2
a
. D.
3
3
2
a
.
Lời giải
Chọn A
Hình thoi ABCD có góc
ABC
bằng
60
o
ABC⇒∆
đều
3
,3
2
a
AC a OD BD a⇒= = ⇒=
0
',( ) ' 30AC ABCD A CA
= =
'3
tan ' '
3
AA a
A CA AA
AC
=⇒=
2
3
.''' '
11 3
. . .. 3
22 2
1
.'
2
ABCD
ABCD A B C D ABCD
a
S AC BD a a
V S AA a
= = =
= =
Câu 44. Tập tất cả các giá trị của tham số m để đồ thị hàm số
( )
32
1
12
3
y xx m x
= ++ − +
có hai điểm
cực trị nằm bên trái trục tung là:
A.
(
)
;1−∞
. B.
( )
1; 2
. C.
(
)
;2
−∞
. D.
( )
1; +∞
.
Lời giải
Chọn B
( )
2
2
' 2 10
'1 1 2
y x xm
mm
= + + −=
∆= − − =− +
Đồ thị hàm số có 2 điểm cực trị nằm bên trái trục tung
⇔
phương trình có 2 nghiệm phân biệt âm

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
12
12
'0
20
. 10
20
20
1
12
xx
xx m
m
m
m
∆>
⇔ + =−<
= −>
−+>
⇔−<
>
⇔< <
Vậy
( )
1; 2m∈
.
Câu 45. Cho tứ diện
ABCD
đều cạnh
a
.
,,MNP
lần lượt là trọng tâm các tam giác
,,ABC ABD ACD
.
Thể tích của khối tứ diện
AMNP
tính theo
a
bằng:
A.
3
2
108
a
. B.
3
2
144
a
. C.
3
22
81
a
. D.
3
2
162
a
.
Lời giải
Chọn D
Tam giác
BCD
đều
3 23 3
.
2 32 3
a aa
DE DH⇒= ⇒ = =
( )
( )
22
2
,,
23
6
3
1 11 1 1 3
. . . . ..
2 2 2 2 2 2 2 16
1 16 3 2
. ..
3 3 3 16 48
EFK
E FK D BC
AKFE EFK
a
AH AD DH
DE a a
S d FK d BC
aa a
V AH S
∆
= −=
= = = =
⇒= = =
Mà
2
3
AM AN AP
AE AK AF
= = =
Lại có
8
..
27
AMNP
AEKF
V
AM AN AP
V AE AK AF
= =

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 23
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
3
3
8 8 22
..
27 27 48 162
AMNP AEKF
a
VV a⇒= = =
Câu 46. Một tấm kim loại hình chữ nhật có kích thước 30cm x 80cm. Người ta gò tấm kim loại này thành
mặt xung quanh của một khối trụ có chiều cao 30cm. Thể tích khối trụ được tạo thành bằng:
A.
( )
3
24000
cm
π
B.
( )
3
48000 cm
π
C.
( )
3
12000 cm
π
D.
( )
3
48000
cm
π
Lời giải
Chọn D
+ Gọi R là bán kính hình trụ, h là chiều cao hình trụ.
Ta có h = 30cm;
Chu vi đường tròn đáy
2 80
40
C R cm
R
π
π
= =
⇔=
+ Thể tích
( )
2
23
40 48000
. . .30V B h R h cm
ππ
ππ
= = = =
Câu 47. Tập các giá trị của tham số m để phương trình
42
2 3 10xxm− − +=
có 2 nghiệm phân biệt
là:
A.
{ }
+∞ ∪(1; ) 0
B.
{ }
+∞ ∪
1
;0
3
C.
+∞
(0; )
D.
+∞(1; )
Lời giải
Chọn B
Cách 1: Ta có:
42
42
2 3 10
3 21
xxm
mx x
− − +=
⇔=−+
Số nghiệm phương trình là số giao điểm của đồ thị
42
21yx x=−+
với đường thẳng
( )
= ≡3 , / /,
d y m d Ox
Xét
42
21yx x=−+
{ }
3
' 4 4 0 0; 1yxx x= − =⇔∈ ±
Bảng biến thiên:
80cm
30cm

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 24
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Qua đồ thị ta thấy đường thẳng
3 / /,y m Ox= ≡
cắt đồ thị tại 2 điểm phân biệt khi
{ }
{ }
1
3 (1;)0 (;)0
3
mm
∞∞
∈+∪ ⇔∈ +∪
Cách 2: Đặt
( )
2
0txt= ≥
Phương trình
( )
42
2 3 1 01xxm
− − +=
trở thành
( )
2
2 3 1 02t tm− − +=
Để pt (1) có 2 nghiệm x thì pt (2) có duy nhất 1 nghiệm
0
t >
TH1: pt (2) có 2 nghiệm trái dấu
12
0
tt<<
.0ac⇒<
1
3 10
3
mm
⇔− + < ⇔ >
TH2: pt(2) có nghiệm kép dương
( )
10
0
'0 1 3 1 0 0
0
20
a
mm
S
≠
≠
⇔ ∆= ⇔ −− + = ⇒ =
>
>
Vậy
{ }
1
(; ) 0
3
m
∞
∈ +∪
Câu 48. Tất cả các giá trị thực của tham số m để đồ thị hàm số
2
1
2 34
x
y
x mx m
+
=
+ ++
có đúng một
đường tiệm cận đứng là:
A.
[ 1; 4]m ∈−
B.
{ 1; 4; 5}m ∈−
C.
( 1; 4)m ∈−
D.
{ 5; 1; 4}m ∈− −
Lời giải
Chọn D
Để đồ thị f(x) có tiệm cận đứng thì
( )
0
lim
xx
fx
→
= ∞
Theo bài thì nghĩa là nghiệm của mẫu sau khi rút gọn.
Từ đó đồ thị có một tiệm cận đứng khi:
TH1: phương trình
2
2 3 40x mx m+ + +=
có nghiệm kép
x
-∞
+∞
-1
0
1
y’
y
0
0
0
+
+
-
-
+∞
+∞
1
0
0

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 25
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
{ }
2
' 0 3 4 0 1; 4
mm m
⇒∆ = ⇔ − − = ⇔ ∈ −
TH2: phương trình
2
2 3 40x mx m+ + +=
có 2 nghiệm phân biệt trong đó có một nghiệm -1
( )
10
f⇒ −=
( ) ( ) ( )
2
1 0 1 2 1 3 40 5f mm m⇒ − = ⇔− + − + + = ⇔ =−
Thử lại với
5m = −
thì phương trình có 2 nghiệm
{ }
1;11x ∈−
(thỏa mãn)
Vậy
{ 5; 1; 4}m
∈− −
.
Câu 49. Cho hàm số
32
1
21 1
3
y x mx m x
(
m
là tham số ). Có bao nhiêu giá trị nguyên của
tham số
m
để hàm số đồng biến trên
.
A.
3
. B.
0
. C.
1
. D. Vô số.
Lời giải
Chọn C
Ta có:
2
2 21y x mx m
.
Hàm số
32
1
21 1
3
y x mx m x
đồng biến trên
0,yx
.
2
2 2 1 0,x mx m x
2
10
0
1
'0
2 10
a
m
mm
.
Vậy có
1
giá trị nguyên của tham số
m
để hàm số đồng biến trên
.
Câu 50. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
H
là trung điểm
AB
,
SH
vuông góc
với mặt phẳng
ABCD
. Biết
13
2
a
SC
, khoảng cách từ
A
đến mặt phẳng
SCD
tính
theo
a
.
A.
2
2
a
. B.
2a
. C.
6
3
a
. D.
2
a
.
Lời giải
Chọn A
Gọi
M
là trung điểm
CD
, kẻ
,HK SM K SM
ta có:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 26
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
// // , ,AH CD AH SCD d A SCD d H SCD
.
HM CD
CD HK
SH CD
.
Mà
HK SM HK SCD
,,d H SCD d H SCD HK
.
Tam giác
BHC
vuông tại
B
, nên:
2
2 22
5
4
a
HC BH BC
.
2 2 22
2SH ABCD SH HC SH SC HC a
.
Tam giác
SHM
vuông tại
H
và
HK
là đường cao nên:
2 2 22
1 113 6
3
2
a
HK
HK SH HM a
.
Vậy
6
,
3
a
d A SCD
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
KIỂM TRA HỌC KÌ I LỚP 12
TRƯỜNG THPT HK1-L12-NGUYỄN-BỈNH-KHIÊM – HÀ NỘI
NĂM HỌC:2020-2021
THỜI GIAN: 90 phút
Câu 1: Cho hình lăng trụ đứng có diện tích đáy là
2
3a
, độ dài cạnh bên bằng
3a
. Thể tích khối lăng trụ
này bằng
A.
3
6a
. B.
3
18a
. C.
3
9a
. D.
3
3a
.
Câu 2: Thể tích
V
của khối nón có bán kính đáy
R
và độ dài đường cao
h
được tính theo công thức
nào dưới đây ?
A.
2
1
3
V Rh=
. B.
2
3
V Rh
π
=
. C.
3
4
3
V Rh
π
=
. D.
2
4
3
V Rh
π
=
.
Câu 3: Tính bán kính
r
của mặt cầu có diện tích là
( )
3
16 S cm
π
=
.
A.
( )
3
12 r cm=
. B.
( )
2 r cm=
. C.
( )
12 r cm=
. D.
(
)
3
r cm
=
.
Câu 4: Tập xác định của hàm số
5
( 2)yx
= −
là
A.
( )
;2
D = −∞
. B.
( )
2;D = +∞
. C.
{
}
\2
D
=
. D.
(
]
;2D = −∞
.
Câu 5: Tìm tọa độ giao điểm
I
của đồ thị hàm số
3
43y xx=−+
với đường thẳng
2yx= −
.
A.
(
)
2; 2
I
. B.
( )
1;1
I
. C.
(
)
2;1D
=
. D.
( )
1; 1I −
.
Câu 6: Cho hàm số
32
(,,, )y ax bx cx d a b c d= + ++ ∈
có đồ thị như hình vẽ bên. Mệnh đề nào dưới
đây sai?
A. Giá trị cực đại của hàm số là
1−
. B. Hàm số đạt cực đại tại
1x = −
.
C. Hàm số đạt cực tiểu tại
1x =
. D. Giá trị cực tiểu của hàm số là
0
.
Câu 7: Tìm nghiệm của phương trình
2
log (1 ) 3x−=
.
A.
7x = −
. B.
5x
=
. C.
3x =
. D.
5x = −
.
Câu 8: Bảng biến thiên dưới đây là của hàm số nào?
x
−∞
1−
0
1
+∞
'y
−
0
+
0
−
0
+
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
y
+∞
3−
+∞
4−
4−
A.
42
23yx x=+−
. B.
42
23
yx x
=−−
.
C.
42
23yx x=−+ −
. D.
42
23yx x=++
.
Câu 9: Giải phương trình
6 12
4 32
xx−−
=
.
A.
17
12
x =
. B.
1
8
x =
. C.
4
3
x =
. D.
3
4
x =
.
Câu 10: Cho hàm số
(
)
y fx=
có đồ thị như hình vẽ bên. Phương trình
( )
6fx= −
có số nghiệm là:
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 11: Cho hàm số
(
)
y fx=
có bảng biến thiên như sau:
x
−∞
1−
0
1
+∞
'y
+
−
+
−
y
2
2
−∞
1
−∞
Hàm số
( )
y fx=
đồng biến trên khoảng nào dưới đây?
A.
(
)
0;1
. B.
(
)
0;3
. C.
( )
;0−∞
. D.
( )
1;1−
.
Câu 12: Đồ thị hàm số
2
1
x
y
x
−
=
+
có đường tiệm cận ngang là
A.
1x =
. B.
1y
=
. C.
1y
= −
. D.
1x = −
.
Câu 13: Trong các hàm số sau đây, hàm số nào nghịch biến trên
?
A.
1
2
x
y
−
=
B.
2
x
y
e
=
C.
( )
3
x
y =
D.
3
x
y
π
=
Câu 14: Cho hình chóp
.S ABCD
có tất cả các cạnh bên và cạnh đáy đều bằng nhau và
ABCD
là hình
vuông. Góc giữa đường thẳng
SB
và mặt phẳng đáy là góc giữa cặp đường thẳng nào sau đây?
6−
y
x
2−
4−
1
−
1

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
( )
,SB BD
. B.
(
)
,SB AB
. C.
( )
,SB SC
. D.
( )
,SB AC
.
Câu 15: Tìm giá trị cực đại của hàm số
42
43yx x=−+
.
A.
3
CĐ
y =
B.
1
CĐ
y = −
. C.
6
C
Đ
y
= −
. D.
8
CĐ
y =
.
Câu 16: Đạo hàm của hàm số
( )
( )
2
log 1fx x
= +
là
A.
(
)
2
2
1
x
fx
x
′
=
+
. B.
( )
( )
2
2
1 log
x
fx
xe
′
=
+
.
C.
( )
( )
2
1
1 ln10
fx
x
′
=
+
. D.
( )
( )
2
2
1 ln10
x
fx
x
′
=
+
.
Câu 17: Giải bất phương trình
21
1
1
3
9
x
x
−
−
>
là
A.
3
5
x <
. B.
5
3
x >
. C.
3
5
x >
. D.
5
3
x <
.
Câu 18: Với các số thực dương
,ab
bất kì. Mệnh đề nào đúng?
A.
3
2 22
21
log 1 log log
3
a
ab
b
=++
. B.
3
2 22
2
log 1 3log log
a
ab
b
=++
.
C.
3
2 22
2
log 1 3log log
a
ab
b
=+−
. D.
3
2 22
21
log 1 log log
3
a
ab
b
=+−
.
Câu 19: Cho
,,abc
là ba số thực dương và khác 1. Hàm số
log , log , log
abc
y xy xy x= = =
có đồ thị như
hình vẽ bên. Mệnh đề nào sau đây đúng?
A.
acb>>
. B.
cab>>
. C.
bca>>
. D.
abc>>

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 20: Tổng của giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
32
21fx x x=−+ −
trên đoạn
[
]
1; 2
−
là:
A.
23
27
−
. B.
1
. C.
2−
. D.
32
27
−
.
Câu 21: Cho khối chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
,a SA
vuông góc với mặt phẳng đáy và
SA a=
. Tính thể tích khối chóp.
A.
3
3
24
a
. B.
3
3
4
a
. C.
3
3
12
a
. D.
3
3
6
a
.
Câu 22: Cho hàm số
(
)
=y fx
có đồ thị như hình vẽ dưới đây. Tìm
m
để phương trình
( )
=fx m
có
bốn nghiệm phân biệt.
A.
1>−m
. B.
10−≤ <m
. C.
10−< ≤m
. D.
10−< <m
.
Câu 23: Cho khối nón có độ dài đường sinh bằng
10
và diện tích xung quanh bằng
60
π
. Thể tích khối
nón đã cho bằng
A.
288
π
. B.
96
π
. C.
360
π
. D.
120
π
.
Câu 24: Cho tam giác
ABC
vuông tại
A
có độ dài cạnh
3, 4= =AB a AC a
. Quay tam giác
ABC
quanh
cạnh
AB
. Thể tích của khối nón tròn xoay được tạo thành là
A.
3
12
π
a
. B.
3
36
π
a
. C.
3
100
3
π
a
. D.
3
16
π
a
.
Câu 25: Hàm số nào sau đây đồng biến trên từng khoảng xác định của nó?
A.
3 10
57
x
y
x
+
=
+
. B.
1
53
x
y
x
−+
=
−
. C.
8
3
x
y
x
−−
=
+
. D.
35
1
x
y
x
+
=
+
.
Câu 26: Cho tứ diện đều
ABCD
cạnh bằng
2
a
. Tính thể tích của khối tứ diện đó.
A.
3
22
3
a
V =
. B.
3
42
3
a
V
=
. C.
3
43
3
a
V =
. D.
3
23
3
a
V
=
.
Câu 27: Tìm tập xác định của hàm số
3
3
log
2
x
y
x
−
=
+
.
A.
{ }
\2D = −
. B.
( )
2;3D = −
.
C.
(
] [
)
; 2 3;D = −∞ − ∪ +∞
. D.
( ) ( )
; 2 3;D = −∞ − ∪ +∞
.
Câu 28: Cho
11<≠a
. Giá trị của biểu thức
(
)
3
22
log .=
a
P aa
là
A.
8
3
. B.
7
3
. C.
7
2
. D.
4
.
x
y
-
2
2
-1
-1
O
1

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 29: Nghiệm của bất phương trình
11
9 36.3 3 0
xx−−
− +≥
là
A.
13≤≤x
. B.
1
2
≤
≥
x
x
. C.
12≤≤x
. D.
1
3
≤
≥
x
x
.
Câu 30: Gọi
,
Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
(
)
1
2
+
= −
x
fx e
trên đoạn
0; 3
. Tính
Mm−
.
A.
2
4+−ee
. B.
4
−ee
. C.
4
4−−ee
. D.
4
+ee
.
Câu 31: Tập xác định của hàm số
1
4
3 log 2
yx x
là
A.
2;
D
. B.
3;
D
.
C.
2;3D
. D.
2; \ 3D
.
Câu 32: Cho đồ thị hàm số
3
32yx x
là
C
. Phương trình tiếp tuyến của đồ thị
C
tại
2;0M
là
A.
9 18
yx
. B.
9 22yx
. C.
9 18yx
. D.
9 18
yx
.
Câu 33: Bất phương trình
2
log 4 4x
có bao nhiêu nghiệm nguyên?
A. Vô số. B.
2
. C.
1
. D.
3
.
Câu 34: Diện tích toàn phần của một khối lập phương là
3
54cm
. Tính thể tích của khối lập phương.
A.
3
27cm
. B.
3
81cm
. C.
3
9cm
. D.
3
36cm
.
Câu 35: Cho hình lăng trụ đứng
.ABCD A B C D
′′′′
có đáy là hình vuông cạnh bằng
6
, đường chéo
AB
′
của mặt bên
(
)
ABB A
′′
có độ dài bằng
10
. Tính thể tích
V
của khối lăng trụ
.ABCD A B C D
′′′′
A.
384V =
. B.
180V =
. C.
380V =
. D.
288V
=
.
Câu 36: Cho tứ diện
ABCD
có
ABC
là tam giác vuông cân tại
C
và nằm trong mặt phẳng vuông góc
với mặt phẳng
( )
ABD
, tam giác
ABD
là tam giác đều và có cạnh bằng
a
. Tính thể tích
V
của
khối của khối tứ diện
ABCD
.
A.
3
3
8
a
. B.
3
3
3
a
. C.
3
2
8
a
. D.
3
3
24
a
.
Câu 37: Cho hàm số
()fx
có bảng biến thiên như hình vẽ:
tìm số nghiệm thuộc
;
2
π
π
−
của phương trình
( )
3sin 5 1fx+=
A.
0
. B.
2
. C.
3
D.
1.
Câu 38: Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình bên. Trong các giá trị
,,,abcd
có bao
nhiêu giá trị âm.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 39: Tìm tất cả các giá trị của
m
để hàm số
16mx
y
xm
+
=
+
nghịch biến trên khoảng
( )
0;10
.
A.
[ ]
4;0m∈−
. B.
( )
4; 4
m∈−
. C.
(
]
(
)
; 10 4;m
∈ −∞ − ∪ +∞
. D.
[
)
0; 4
m∈
Câu 40: Cho khối lăng trụ
.'' ' '
ABCD A B C D
có thể tích bằng
24
, đáy
ABCD
là hình vuông tâm
O
. Thể
tích của khối chóp
'.A BCO
bằng
A.
1
. B.
4.
C.
3.
D.
2.
Câu 41: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
B
và
( )
SA ABC⊥
. Tính thể tích khối cầu
ngoại tiếp chóp
.S ABC
theo
a
biết
2
SC a
=
.
A.
3
24 a
π
. B.
3
4
3
a
π
C.
3
8
3
a
π
D.
3
24
3
a
π
.
Câu 42: Cho hàm số
(
)
y fx
=
liên tục trên từng khoảng
{ }
\1
và có bảng biến thiên như sau:
Đồ thị hàm số
1
2 () 7
y
fx
=
−
có bao nhiêu đường tiệm cận đứng.
A.
1
. B.
4.
C.
0.
D.
2.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 43: Một người gửi tiết kiệm ngân hàng
20
triệu với lãi suất không đổi là
7,2%
/năm và tiền lãi hàng
tháng được nhập vào vốn. Hỏi sau ít nhất bao nhiêu năm người đó thu về được tổng số tiền lớn
hơn
345
triệu đồng?
A.
33
năm B.
41
năm C.
50
năm D.
10
năm
Câu 44: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật
AD a
=
,
3AB a=
. Cạnh bên
SA
vuông góc với đáy và
2SA a=
. Tính khoảng cách
d
từ điểm
C
đến mặt phẳng
( )
SBD
.
A.
2
5
a
d =
B.
57
19
a
d =
C.
2 57
19
a
d
=
D.
5
2
a
d =
Câu 45: Có bao nhiêu giá trị nguyên thuộc
( )
0;5
của tham số
m
để phương trình
1
4 .2 2 1 0
xx
mm
+
− + −=
có hai nghiệm phân biệt trong đó có đúng một nghiệm dương?
A.
2
B.
0
C.
1
D.
3
Câu 46: Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
sao cho giá trị lớn nhất của hàm số
42
1 19
30 20
42
y x x xm= − + +−
trên đoạn
[ ]
0; 2
không vượt quá
20
. Tổng các phần tử của
S
bằng:
A.
300
B.
105
C.
195−
D.
210
Câu 47: Cho hàm số
( )
32
3fx x x= −
. Có bao nhiêu giá trị nguyên của
m
để đồ thị hàm số
( )
( )
gx f x m= +
cắt trục hoành tại
4
điểm phân biệt?
A.
2
B.
0
C.
4
D.
3
Câu 48: Cho hàm số
( )
y fx=
xác định trên
và có đạo hàm
( )
fx
′
thỏa mãn
( )
( )( ) ( )
1 2 2018
f x x x gx
′
=−+ +
trong đó
(
)
0,gx x
< ∀∈
. Hàm số
( )
1 2018 2019yf x x= −+ +
đồng biến trên khoảng nào?
A.
( )
1; +∞
B.
( )
0;3
C.
( )
3; +∞
D.
( )
;3−∞
Câu 49: Cho phương trình
( )
( )
2
2
33
log 3 log 3 2 2 1 0x m xmm
+ + − −=
. Gọi
S
là tập hợp tất cả các số tự
nhiên
m
mà phương trình có hai nghiệm phân biệt
12
,xx
thỏa
12
10
3
xx+<
. Số phần tử của
S
là
A.
1
. B.
0
. C.
10
. D. Vô số.
Câu 50: Cho hình chóp
.S ABCD
có
ABCD
là hình bình hành.
, ,,M N PQ
lần lượt là trung điểm của
,,,SA SB SC SD
. Gọi
12
,VV
lần lượt là thể tích của khối chóp
.S MNPQ
và khối chóp
.S ABCD
.
Tính tỉ số
2
1
V
V
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
16
. B.
8
. C.
2
. D.
4
.
BẢNG ĐÁP ÁN
1.C
2.B
3.B
4.B
5.D
6.A
7.A
8.B
9.A
10.D
11.A
12.B
13.B
14.A
15.A
16.D
17.B
18.B
19.B
20.B
21.C
22.D
23.B
24.D
25.C
26.A
27.B
28.A
29.B
30.B
31.D
32.A
33.D
34.A
35.D
36.D
37.B
38
39
40.D
41.B
42.D
43.B
44.C
45.D
46.B
47.D
48.B
49.D
50.B
HƯỚNG DẪN GIẢI
Câu 1: Cho hình lăng trụ đứng có diện tích đáy là
2
3a
, độ dài cạnh bên bằng
3a
. Thể tích khối lăng trụ
này bằng
A.
3
6a
. B.
3
18a
. C.
3
9a
. D.
3
3a
.
Lời giải
Chọn C.
Thể tích khối lăng trụ là
23
3 .3 9V aa a= =
.
Câu 2: Thể tích
V
của khối nón có bán kính đáy
R
và độ dài đường cao
h
được tính theo công thức
nào dưới đây ?
A.
2
1
3
V Rh=
. B.
2
3
V Rh
π
=
. C.
3
4
3
V Rh
π
=
. D.
2
4
3
V Rh
π
=
.
Lời giải
Chọn B.
Câu 3: Tính bán kính
r
của mặt cầu có diện tích là
( )
3
16 S cm
π
=
.
A.
( )
3
12
r cm=
. B.
( )
2 r cm=
. C.
( )
12 r cm
=
. D.
( )
3 r cm=
.
Lời giải
Chọn B.
Ta có
22
4 16 2 4 2
mc
Srrr r
ππ
= = =⇔ =⇔=
.
Câu 4: Tập xác định của hàm số
5
( 2)
yx= −
là
A.
( )
;2D
= −∞
. B.
( )
2;D = +∞
. C.
{ }
\2D =
. D.
(
]
;2D = −∞
.
Lời giải
Chọn B.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
5 2 0 2.xx∉⇒−>⇔>
Câu 5: Tìm tọa độ giao điểm
I
của đồ thị hàm số
3
43y xx=−+
với đường thẳng
2yx= −
.
A.
( )
2; 2I
. B.
( )
1;1I
. C.
( )
2;1D =
. D.
( )
1; 1I −
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm
33
4 3 2 4 2 20 1 1x xx x x x y− +=−⇔− ++=⇔=⇒=−
.
Câu 6: Cho hàm số
32
(,,, )y ax bx cx d a b c d
= + ++ ∈
có đồ thị như hình vẽ bên. Mệnh đề nào dưới
đây sai?
A. Giá trị cực đại của hàm số là
1−
. B. Hàm số đạt cực đại tại
1x = −
.
C. Hàm số đạt cực tiểu tại
1x =
. D. Giá trị cực tiểu của hàm số là
0
.
Lời giải
Chọn A
Câu 7: Tìm nghiệm của phương trình
2
log (1 ) 3x
−=
.
A.
7x = −
. B.
5x =
. C.
3
x =
. D.
5x = −
.
Lời giải
Chọn A
Điều kiện:
10 1
xx−>⇔<
.
Ta có:
( )
2
log 1 3x−=
3
12x⇔− =
7x
⇔=−
(nhận).
Vậy phương trình có nghiệm
7x = −
.
Câu 8: Bảng biến thiên dưới đây là của hàm số nào?
x
−∞
1−
0
1
+∞
'y
−
0
+
0
−
0
+
y
+∞
3−
+∞
4
−
4−
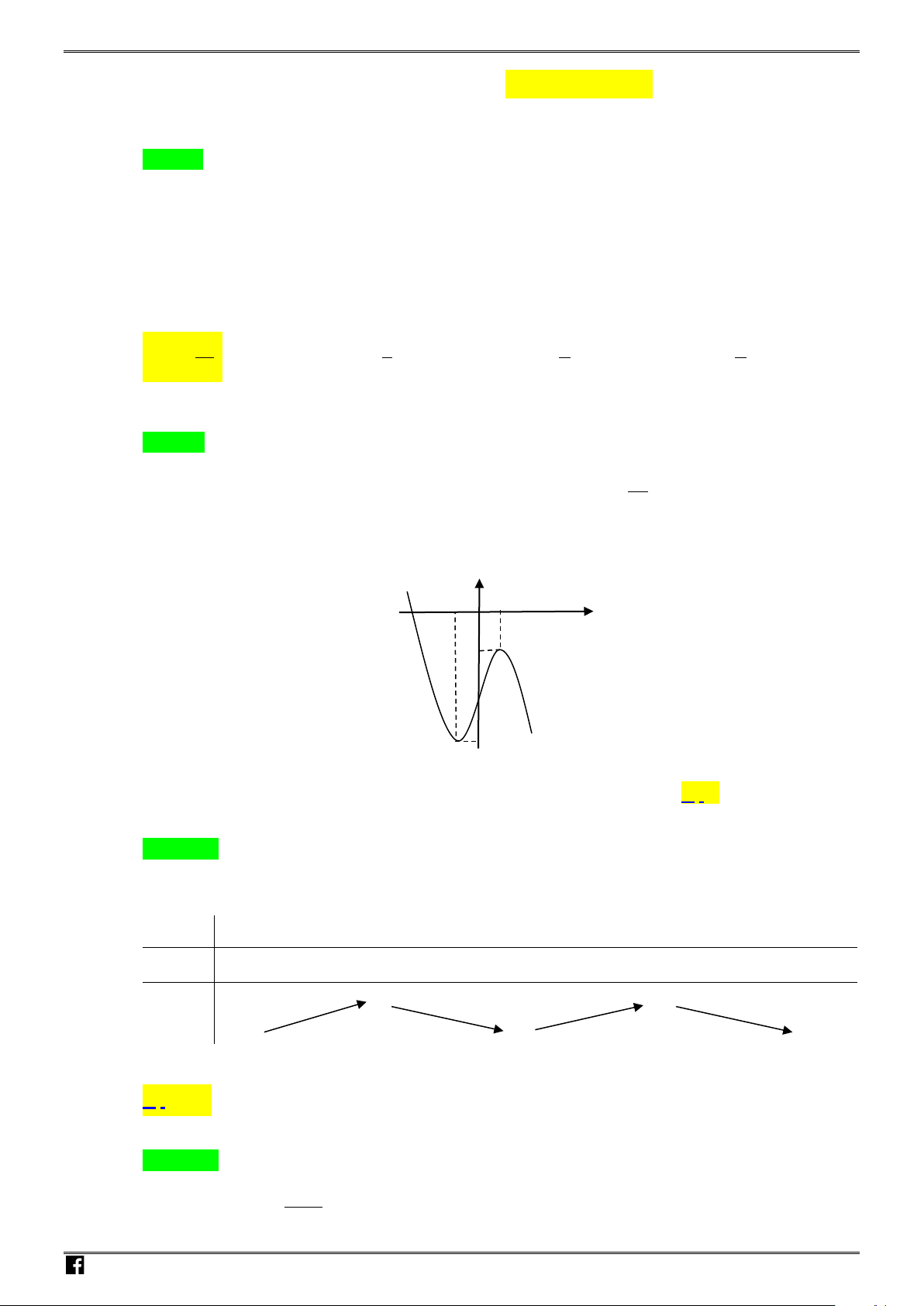
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
42
23yx x=+−
. B.
42
23
yx x
=−−
.
C.
42
23yx x=−+ −
. D.
42
23
yx x=++
.
Lời giải
Chọn B
Dựa vào BBT nhận thấy:
+
lim 0
x
ya
→+∞
= +∞ ⇒ >
nên loại C.
+ Hàm số có 3 điểm cực trị, ta có:
.0ab<
nên loại A, D.
Câu 9: Giải phương trình
6 12
4 32
xx
−−
=
.
A.
17
12
x =
. B.
1
8
x =
. C.
4
3
x =
. D.
3
4
x
=
.
Lời giải
Chọn A
Ta có:
6 12
4 32
xx−−
=
2 12 5 10
22
xx−−
⇔=
2 12 5 10xx⇔ −=−
17
.
12
x⇔=
Câu 10: Cho hàm số
( )
y fx=
có đồ thị như hình vẽ bên. Phương trình
( )
6fx= −
có số nghiệm là:
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn D .
Câu 11: Cho hàm số
(
)
y fx=
có bảng biến thiên như sau:
x
−∞
1−
0
1
+∞
'y
+
−
+
−
y
2
2
−∞
1
−∞
Hàm số
( )
y fx=
đồng biến trên khoảng nào dưới đây?
A.
( )
0;1
. B.
( )
0;3
. C.
( )
;0−∞
. D.
( )
1;1
−
.
Lời giải
Chọn A .
Câu 12: Đồ thị hàm số
2
1
x
y
x
−
=
+
có đường tiệm cận ngang là
6−
y
x
2−
4−
1−
1

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
1x =
. B.
1y =
. C.
1y = −
. D.
1x = −
.
Lời giải
Chọn B .
Đường tiệm cận ngang có phương trình
2
lim 1.
1
x
x
y
x
→∞
−
= =
+
Câu 13: Trong các hàm số sau đây, hàm số nào nghịch biến trên
?
A.
1
2
x
y
−
=
B.
2
x
y
e
=
C.
( )
3
x
y =
D.
3
x
y
π
=
Lời giải
Chọn B .
Hàm số mũ
2
x
y
e
=
có cơ số
2
1
e
<
nên hàm số nghịch biến trên
.
Câu 14: Cho hình chóp
.
S ABCD
có tất cả các cạnh bên và cạnh đáy đều bằng nhau và
ABCD
là hình
vuông. Góc giữa đường thẳng
SB
và mặt phẳng đáy là góc giữa cặp đường thẳng nào sau đây?
A.
( )
,SB BD
. B.
( )
,
SB AB
. C.
( )
,SB SC
. D.
( )
,SB AC
.
Lời giải
Chọn A .
Gọi
O AC BD= ∩
ta có
( )
SO ABC D⊥
nên hình chiếu của
SB
lên mặt phẳng
( )
ABCD
là
OB
, do đó góc giữa đường thẳng
SB
và mặt phẳng đáy là góc giữa cặp đường thẳng
SB
và
BD
.
Câu 15: Tìm giá trị cực đại của hàm số
42
43yx x=−+
.
A.
3
CĐ
y =
B.
1
CĐ
y = −
. C.
6
CĐ
y = −
. D.
8
C
Đ
y =
.
Lời giải
Chọn A .
TXĐ:
.
Cách 1 :
Ta có :
( )
32
4 84 2y x x xx
′
= −= −
, khi đó
0
0
2
2
x
y
x
x
=
′
= ⇔
=
= −
Mặt khác:
2
12 8yx
′′
= −
.
Ta có
( )
0 80y
′′
=−<
nên
0x =
là điểm cực đại và
( )
03
CĐ
yy= =
( )
2 16 0y
′′
±=>
nên
2, 2xx= = −
là các điểm cực tiểu.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Cách 2 :
Nhận xét : Hàm số
42
43yx x
=−+
có
1, 4ab= = −
nên
.0ab<
nên hàm số có ba điểm cực trị
và đạt cực đại tại
03
CĐ
xy=⇒=
.
Câu 16: Đạo hàm của hàm số
( )
( )
2
log 1
fx x
= +
là
A.
( )
2
2
1
x
fx
x
′
=
+
. B.
( )
( )
2
2
1 log
x
fx
xe
′
=
+
.
C.
(
)
(
)
2
1
1 ln10
fx
x
′
=
+
. D.
( )
( )
2
2
1 ln10
x
fx
x
′
=
+
.
Lời giải
Chọn D
Áp dụng công thức đạo hàm hàm số logarit, ta có:
( )
( )
2
2
1 ln10
x
fx
x
′
=
+
.
Câu 17: Giải bất phương trình
21
1
1
3
9
x
x
−
−
>
là
A.
3
5
x <
. B.
5
3
x >
. C.
3
5
x >
. D.
5
3
x <
.
Lời giải
Chọn B
Ta có:
( )
21
22 1
11
13
3 3 3 142
95
x
x
xx
x xx
−
−−
−−
> ⇔ > ⇔ − >− + ⇔ >
.
Câu 18: Với các số thực dương
,ab
bất kì. Mệnh đề nào đúng?
A.
3
2 22
21
log 1 log log
3
a
ab
b
=++
. B.
3
2 22
2
log 1 3log log
a
ab
b
=++
.
C.
3
2 22
2
log 1 3log log
a
ab
b
=+−
. D.
3
2 22
21
log 1 log log
3
a
ab
b
=+−
.
Lời giải
Chọn B
Ta có:
( )
3
3
2 22 2 22
2
log log 2 log log 1 3log log
a
a b ab
b
=+ +=+ +
.
Câu 19: Cho
,,abc
là ba số thực dương và khác 1. Hàm số
log , log , log
abc
y xy xy x= = =
có đồ thị như
hình vẽ bên. Mệnh đề nào sau đây đúng?
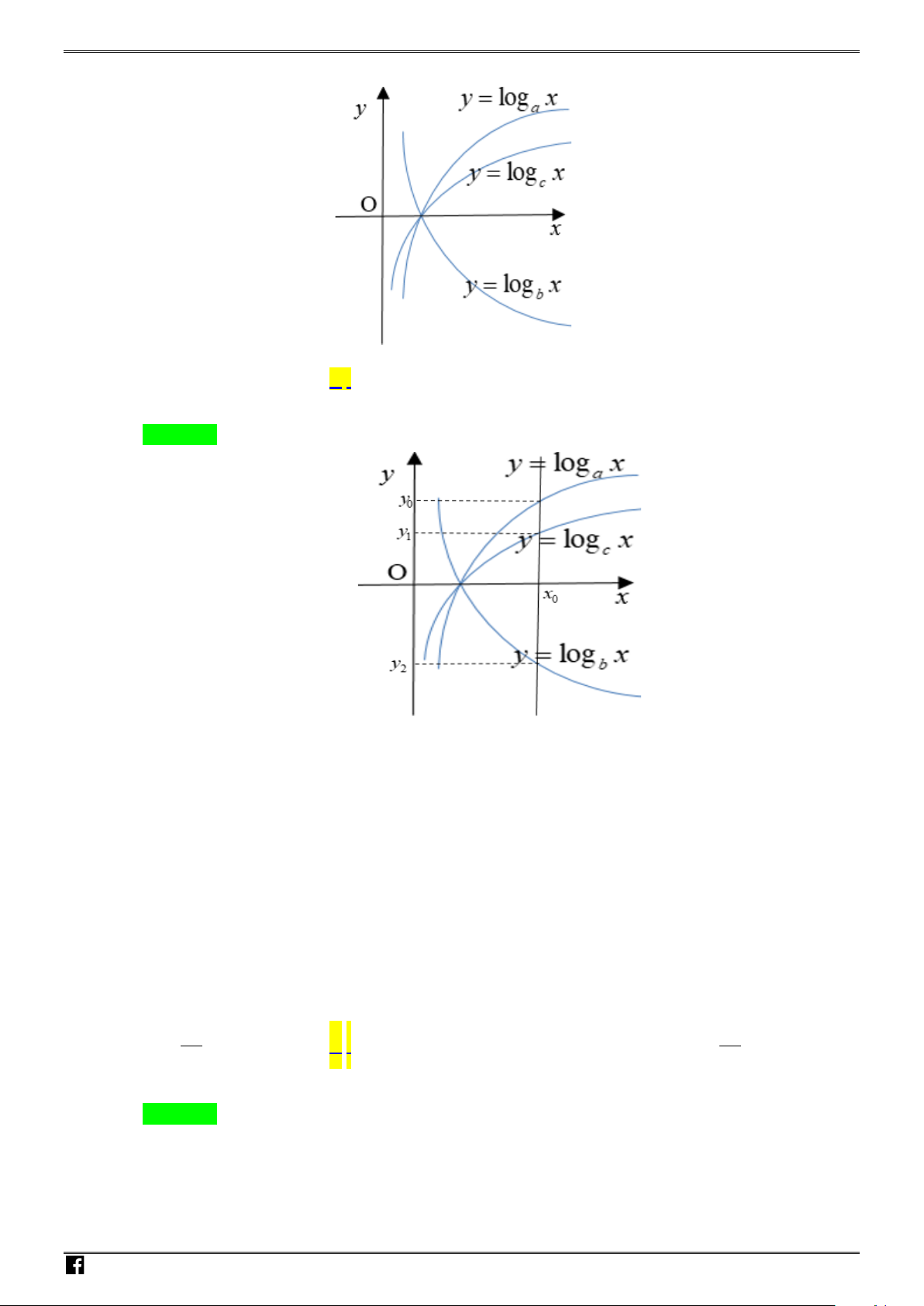
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
acb>>
. B.
cab
>>
. C.
bca>>
. D. .
abc>>
Lời giải
Chọn B .
+) Xét đường thẳng
0
0xx= >
cắt các đồ thị như hình vẽ.
+) Dựa vào đồ thị hàm số
log
b
yx=
=> hàm nghịch biến
01b⇒<<
Các hàm số
log , log
ca
y xy x= =
là hàm đồng biến
,1
ac⇒>
Mặt khác
0
1
1 00 0 0
log , log
y
y
ca
y xy x x c a= = ⇒= =
mà
10
y y ca< ⇒>
Vậy
cab⇒>>
Câu 20: Tổng của giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
32
21fx x x=−+ −
trên đoạn
[
]
1; 2
−
là:
A.
23
27
−
. B.
1
. C.
2−
. D.
32
27
−
.
Lời giải
Chọn B .
+) Ta có
( )
32
21fx x x=−+ −
liên tục trên
[ ]
1; 2−
1
y

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
+)
(
)
( )
( )
22
0 1; 2
' 34 340
4
1; 2
3
x
fx xx xx
x
= ∈−
=−+⇒−+=⇔
= ∈−
+) Tính:
(
) (
) (
)
45
01; ;12;21
3 27
ff ff
=− = −= =−
+) GTLN là 2, GTNN là -1 nên tổng =1
Câu 21: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
,
a SA
vuông góc với mặt phẳng đáy
và
SA a=
. Tính thể tích khối chóp.
A.
3
3
24
a
. B.
3
3
4
a
. C.
3
3
12
a
. D.
3
3
6
a
.
Lời giải
Chọn C .
+) Diện tích tam giác
ABC
là:
2
13
. .sin
24
ABC
a
S AB AC A= =
+) Thể tích khối trụ là
3
13
..
3 12
ABC
a
V SA S= =
Câu 22: Cho hàm số
( )
=y fx
có đồ thị như hình vẽ dưới đây. Tìm
m
để phương trình
(
)
=fx m
có
bốn nghiệm phân biệt.
A.
1>−m
. B.
10−≤ <m
. C.
10−< ≤m
. D.
10−< <m
.
Lời giải
x
y
-
2
2
-1
-1
O
1

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn D
Nhìn vào đồ thị ta thấy đồ thị
=ym
cắt đồ thị
( )
=y fx
tại bốn điểm phân biệt khi
10−< <m
.
Từ đó suy ra phương trình
( )
=fx m
có bốn nghiệm phân biệt khi
10
−< <m
.
Câu 23: Cho khối nón có độ dài đường sinh bằng
10
và diện tích xung quanh bằng
60
π
. Thể tích khối
nón đã cho bằng
A.
288
π
. B.
96
π
. C.
360
π
. D.
120
π
.
Lời giải
Chọn B
Ta có diện tích xung quanh của hình nón là
π
rl
với
r
là bán kính đáy và
l
là độ dài đường
sinh.
Từ đó suy ra
60 10 6
ππ π
= = ⇒=rl r r
, do đó chiều cao của khối nón là
22
8= −=h lr
. Khi
đó thể tích cần tìm là
22
11
8.6 96
33
ππ π
= =hr
.
Câu 24: Cho tam giác
ABC
vuông tại
A
có độ dài cạnh
3, 4= =AB a AC a
. Quay tam giác
ABC
quanh
cạnh
AB
. Thể tích của khối nón tròn xoay được tạo thành là
A.
3
12
π
a
. B.
3
36
π
a
. C.
3
100
3
π
a
. D.
3
16
π
a
.
Lời giải
Chọn D
Khối nón tròn xoay được tạo thành có chiều cao là
3a
và bán kính đáy
4a
. Thể tích cần tính
bằng
( )
2
3
1
4 .3 16
3
ππ
=aa a
.
Câu 25: Hàm số nào sau đây đồng biến trên từng khoảng xác định của nó?
A.
3 10
57
x
y
x
+
=
+
. B.
1
53
x
y
x
−+
=
−
. C.
8
3
x
y
x
−−
=
+
. D.
35
1
x
y
x
+
=
+
.
Lời giải
Chọn C
Xét hàm số
8
3
x
y
x
−−
=
+
.
Tập xác định
{ }
\3D = −
.
Ta có
( )
2
5
0,
3
y xD
x
′
= > ∀∈
+
.
Vậy hàm số trên đồng biến trên từng khoảng xác định của nó.
Câu 26: Cho tứ diện đều
ABCD
cạnh bằng
2a
. Tính thể tích của khối tứ diện đó.
A.
3
22
3
a
V =
. B.
3
42
3
a
V =
. C.
3
43
3
a
V =
. D.
3
23
3
a
V =
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn A
Gọi
G
là trọng tâm tam giác
BCD
.
Do
ABCD
là tứ diện đều nên
( )
AG BCD⊥
.
Ta có
2 22323
.
3 32 3
aa
BG BI
= = =
.
Suy ra
(
)
2
2
22
23 26
2
33
aa
AG AB BG a
= −= − =
.
Lại có
( )
2
2
23
3
4
BCD
a
Sa= =
.
Vậy
3
2
1 1 262 2
. . 3.
3 3 33
ABCD BCD
aa
V S AG a= = =
.
Câu 27: Tìm tập xác định của hàm số
3
3
log
2
x
y
x
−
=
+
.
A.
{
}
\2D
= −
. B.
( )
2;3D = −
.
C.
(
] [
)
; 2 3;D = −∞ − ∪ +∞
. D.
( ) ( )
; 2 3;D = −∞ − ∪ +∞
.
Lời giải
Chọn B
Hàm số đã cho xác định khi và chỉ khi
3
02 3
2
x
x
x
−
> ⇔− < <
+
.
Vậy tập xác định là
( )
2;3D = −
.
Câu 28: Cho
11<≠a
. Giá trị của biểu thức
(
)
3
22
log .=
a
P aa
là
A.
8
3
. B.
7
3
. C.
7
2
. D.
4
.
Lời giải
Chọn B
A
B
C
D
G
I

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Với
01a<≠
thì
(
)
(
)
33
22 8
8
log log
3
aa
P aa a= = =
Câu 29: Nghiệm của bất phương trình
11
9 36.3 3 0
xx−−
− +≥
là
A.
13
≤≤
x
. B.
1
2
≤
≥
x
x
. C.
12≤≤x
. D.
1
3
≤
≥
x
x
.
Lời giải
Chọn B
Đặt
3
x
t =
, thì bất phương trình đã cho viết lại thành
2
12
30
99
t
t− +≥
2
12 27 0tt
⇔− + ≥
9
3
t
t
≥
⇔
≤
39
33
x
x
≥
⇔
≤
2
1
x
x
≥
⇔
≤
Vậy
2
1
x
x
≥
≤
thì
x
là nghiệm của bấ tphương trình trên.
Câu 30: Gọi
,Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
(
)
1
2
+
= −
x
fx e
trên đoạn
0; 3
. Tính
Mm−
.
A.
2
4+−ee
. B.
4
−ee
. C.
4
4
−−ee
. D.
4
+ee
.
Lời giải
Chọn B
Ta có
( )
1
'0
x
fx e
+
= >
với mọi
x
thuộc đoạn
[ ]
0,3
, và
( )
fx
là hàm liên tục, do đó là hàm số
đồng biến trên
[ ]
0,3
.
Khi đó giá trị lớn nhất
( )
4
32Mf e= = −
.
Giá trị nhỏ nhất
( )
1
0 22mf e e= = −=−
.
Vậy
4
.Mme e−=−
Câu 31 : Tập xác định của hàm số
1
4
3 log 2yx x
là

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2;D
. B.
3;D
.
C.
2;3D
. D.
2; \ 3D
.
Lời giải
Chọn D
Điều kiện xác định
30 3
20 2
xx
xx
.
Tập xác định:
2; \ 3D
.
Câu 32: Cho đồ thị hàm số
3
32yx x
là
C
. Phương trình tiếp tuyến của đồ thị
C
tại
2;0M
là
A.
9 18yx
. B.
9 22yx
. C.
9 18yx
. D.
9 18yx
.
Lời giải
Chọn A
Ta có:
2
33yx
Phương trình tiếp tuyến của đồ thị hàm số tại điểm
2;0M
là:
2 20yy x
92yx
9 18yx
Câu 33: Bất phương trình
2
log 4 4x
có bao nhiêu nghiệm nguyên?
A. Vô số. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn D
Điều kiện:
0x
.
2
0
log 4 4 0 4
4 16
x
xx
x
.
Mà
1; 2; 3xx
.
Vậy có 3 giá trị nguyên là nghiệm của bất phương trình.
Câu 34: Diện tích toàn phần của một khối lập phương là
3
54cm
. Tính thể tích của khối lập phương .
A.
3
27cm
. B.
3
81cm
. C.
3
9cm
. D.
3
36cm
.
Lời giải
Chọn A
Gọi
x
là cạnh của hình lập phương
32 3
54 6. 54 3
tp
S cm x cm x cm= ⇔ = ⇒=
Vậy thể tích của khối lập phương là:
3
27V cm=
.
Câu 35: Cho hình lăng trụ đứng
.ABCD A B C D
′′′′
có đáy là hình vuông cạnh bằng
6
, đường chéo
AB
′
của mặt bên
( )
ABB A
′′
có độ dài bằng
10
. Tính thể tích
V
của khối lăng trụ
.ABCD A B C D
′′′′
A.
384V =
. B.
180V =
. C.
380V =
. D.
288V
=
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn D
22
100 36 8BB AB AB
′′
= − = −=
.
Vậy thể tích cần tìm là :
.
. 8.36 288
ABCD A B C D ABCD
V S BB
′′′′
′
= = =
.
Câu 36: Cho tứ diện
ABCD
có
ABC
là tam giác vuông cân tại
C
và nằm trong mặt phẳng vuông góc
với mặt phẳng
( )
ABD
, tam giác
ABD
là tam giác đều và có cạnh bằng
a
. Tính thể tích
V
của khối của khối tứ diện
ABCD
.
A.
3
3
8
a
. B.
3
3
3
a
. C.
3
2
8
a
. D.
3
3
24
a
.
Lời giải
Chọn D
Gọi
E
là trung điểm
AB
( ) ( )
( )
ABC ABD
CE AB
CE ABD
⊥
⊥
⇒⊥
Trong tam giác
CAB
:
1
22
a
CE AB= =
.
Vậy thể tích
V
cần tìm:
23
1 1 33
. . ..
3 3 2 4 24
ABCD ABD
aa a
V CE S= = =
.
Câu 37: Cho hàm số
()fx
có bảng biến thiên như hình vẽ:
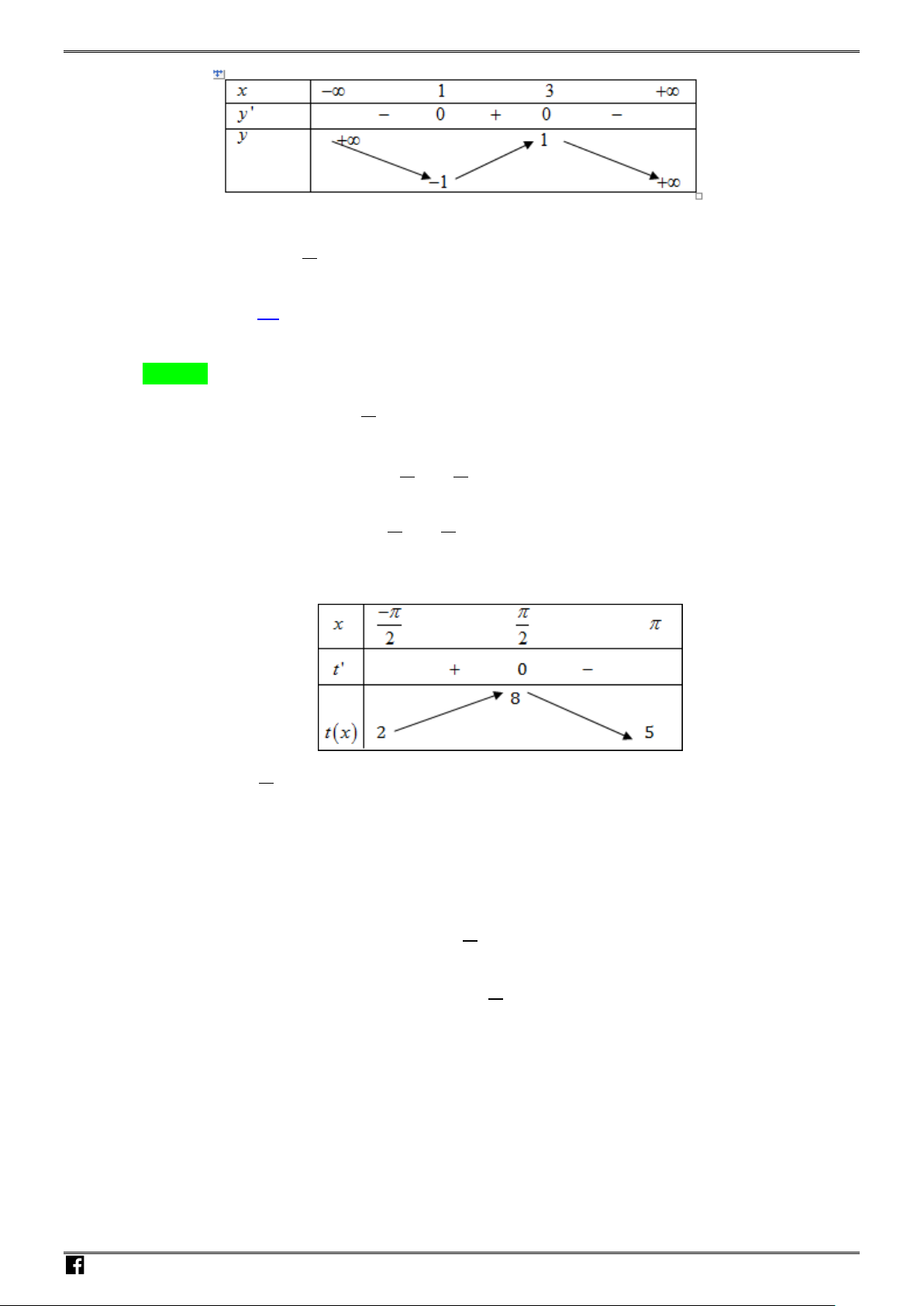
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
tìm số nghiệm thuộc
;
2
π
π
−
của phương trình
( )
3sin 5 1fx+=
A.
0
. B.
2
. C.
3
D.
1.
Lời giải
Chọn B.
Xét
( )
3sin 5tx x= +
trên
;
2
π
π
−
. Có
' 3cos
tx=
Ta có
;
22
' 0 cos 0
;
22
x
tx
x
ππ
π
ππ
π
=− ∈−
=⇔=⇔
= ∈−
Bảng biến thiên của
( )
tx
Vậy với
;
2
x
π
π
∈−
thì
[ ]
2;8
t ∈
Dựa vào đồ thị hàm số ta có
( )
3
1
1
t
ft
ta
=
= ⇔
= <
Dựa vào bảng biến thiên của
( )
tx
ta có:
Với
3
t =
tương ứng có hai nghiệm
;
2
x
π
π
∈−
Với
ta=
không có nghiệm thuộc khoảng
;
2
π
π
−
Chọn đáp án B.
Câu 38: Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình bên. Trong các giá trị
,,,abcd
có bao
nhiêu giá trị âm.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2
. B.
1
. C.
4
.
D.
3
.
Lời giải
Chọn A.
Đồ thị có hướng đi xuống nên
0a
<
Giao của đồ thị với trục tung tại điểm có tung độ âm nên
0d <
Gọi
12
,xx
lần lượt là hai điểm cực trị của hàm số.
Do
12
0xx <
nên
.0
ac
<
nên
0c >
.
Hơn nữa
12
0xx+>
nên
0 0.
3
b
b
a
−
>⇒>
Vậy có hai hệ số âm. Chọn A.
Câu 39: Tìm tất cả các giá trị của
m
để hàm số
16mx
y
xm
+
=
+
nghịch biến trên khoảng
(
)
0;10
.
A.
[ ]
4;0m ∈−
. B.
( )
4; 4m∈−
. C.
(
]
( )
; 10 4;m ∈ −∞ − ∪ +∞
. D.
[
)
0; 4m∈
Lời giải
Chọn D.
{ }
XD : \
TD m= −
. Ta có
( )
2
2
16
'
m
y
xm
−
=
+
Để hàm số nghịch biến trên
( )
0;10
( )
2
44
16 0
04
0
0;10
10
m
m
m
m
m
m
−< <
−<
⇔ ⇔ ⇔≤ <
≥
−∉
≤−
.
Câu 40: Cho khối lăng trụ
.'' ' 'ABCD A B C D
có thể tích bằng
24
, đáy
ABCD
là hình vuông tâm
O
. Thể
tích của khối chóp
'.A BCO
bằng
A.
1
. B.
4.
C.
3.
D.
2.
Lời giải
Chọn D
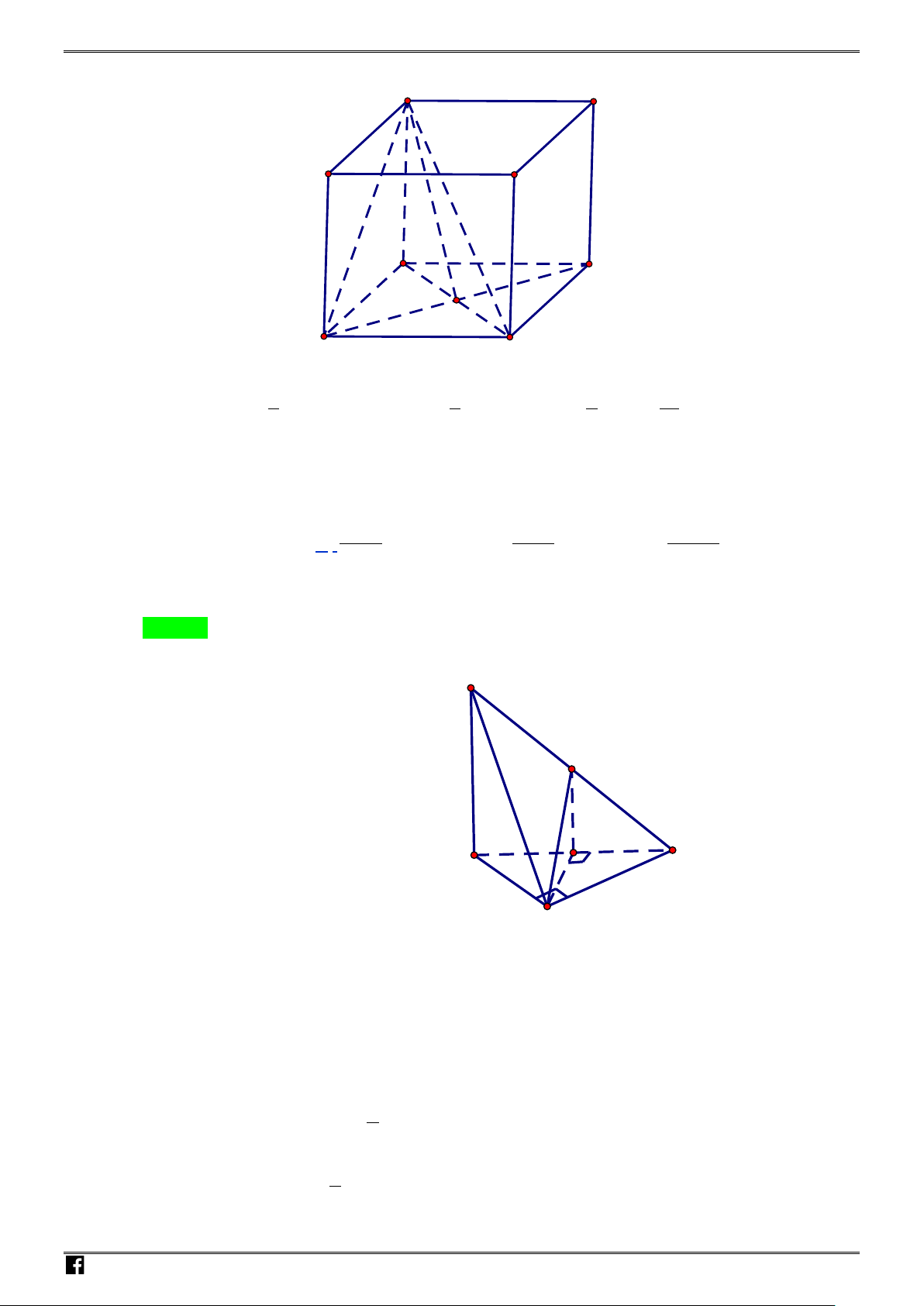
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
( )
( )
( )
( )
'. . ' ' ' '
1 1 11
', . ', . 2
3 3 4 12
A BCO BCO ABCD ABCD A B C D
V d A BC O S d A ABCD S V
∆
= = = =
Câu 41: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
B
và
( )
SA ABC⊥
. Tính thể tích khối cầu
ngoại tiếp chóp
.S ABC
theo
a
biết
2SC a=
.
A .
3
24 a
π
. B.
3
4
3
a
π
C.
3
8
3
a
π
D.
3
24
3
a
π
.
Lời giải
Chọn B.
Gọi
M
là tâm đường tròn ngoại tiếp đáy, do đáy là
ABC∆
vuông tại
B
nên
M
là trung điểm
của
.AC
Từ
M
dựng đường thẳng vuông góc với mặt phẳng
( )
ABC
cắt
SC
tại
I
. Ta có
I
là trung
điểm của
SC
và là tâm của mặt cầu ngoại tiếp hình chóp.
.
Suy ra bán kính mặt cầu:
1
.
2
R SC a= =
Thể tích mặt cầu là:
3
4
.
3
Va
π
=
O
B'
C'
D'
C
A
D
B
A'
I
M
A
C
B
S
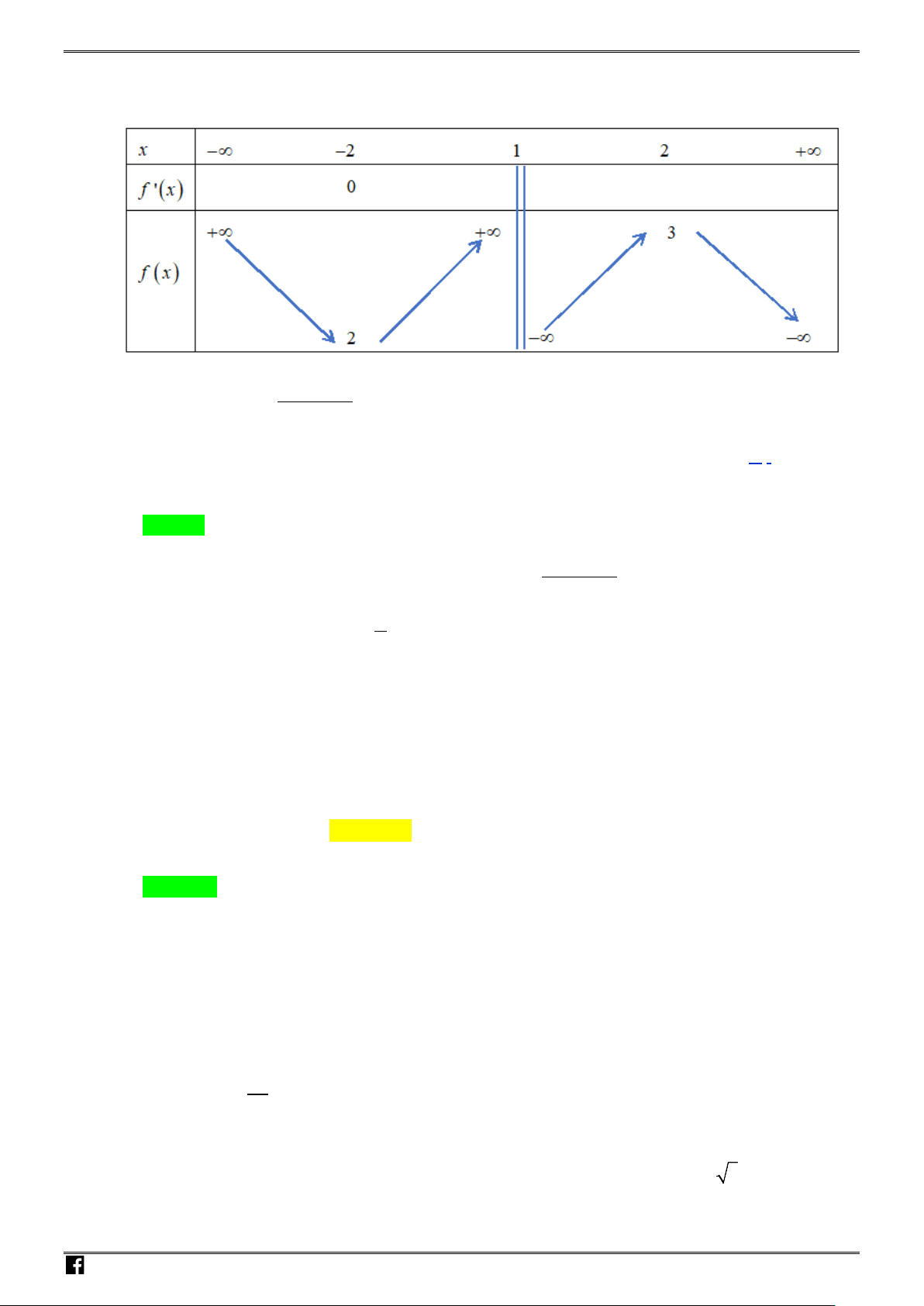
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 23
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 42: Cho hàm số
( )
y fx=
liên tục trên từng khoảng
{ }
\1
và có bảng biến thiên như sau:
Đồ thị hàm số
1
2 () 7
y
fx
=
−
có bao nhiêu đường tiệm cận đứng.
A.
1
. B.
4.
C.
0.
D.
2.
Lời giải
Chọn D
Ta có số đường tiệm cận đứng của đồ thị hàm số
1
2 () 7
y
fx
=
−
bằng số nghiệm của phương
trình:
7
2 () 7 0 () .
2
fx fx−=⇔ =
Từ đồ thị hàm số suy ra phương trình trên có hai nghiệm phân biệt. Do đó đồ thị hàm số có hai
đường tiệm cận đứng.
Câu 43: Một người gửi tiết kiệm ngân hàng
20
triệu với lãi suất không đổi là
7,2%
/năm và tiền lãi hàng
tháng được nhập vào vốn. Hỏi sau ít nhất bao nhiêu năm người đó thu về được tổng số tiền lớn
hơn
345
triệu đồng?
A.
33
năm B.
41
năm C.
50
năm D.
10
năm
Lời giải
Chọn B .
Gọi
n
S
là số tiền người đó nhận được sau
n
kì hạn,
A
là số tiền ban đầu gởi vào,
%
r
là lãi
suất.
Ta có công thức của Bài toán lãi kép như sau:
(
)
.1 %
n
n
SA r= +
Đối với bài toán trên, để có được đúng
345
triệu đồng thì phải sau số năm gởi là
n
, được tính
như sau :
( )
66
345.10 20.10 . 1 7,2%
n
= +
1,072
69
log 40,96
4
n⇒= ≈
Như vậy để nhận được số tiền lớn hơn
345
triệu đồng thì phải gửi ít nhất
41
năm.
Câu 44: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật
AD a
=
,
3AB a=
. Cạnh bên
SA
vuông góc với đáy và
2SA a=
. Tính khoảng cách
d
từ điểm
C
đến mặt phẳng
( )
SBD
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 24
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2
5
a
d =
B.
57
19
a
d =
C.
2 57
19
a
d =
D.
5
2
a
d =
Lời giải
Chọn C .
Trong
( )
ABCD
, kẻ
AK BD
⊥
tại
K
.
Tron
SAK∆
, gọi
AH
là đường cao.
Ta có
( )
( )
,
BD AK
BD SA SA ABCD
⊥
⊥⊥
suy ra
( ) ( ) ( )
BD SAK SBD SAK⊥⇒⊥
Mà
AH
lại vuông góc với giao tuyến
SK
( ) ( )
( )
,AH SBD d A SBD AH⇒⊥ ⇒ =
Ta có
22 2
222
1 11
111
AH SA AK
AK AB AD
= +
= +
22 2 2
1 11 1
AH SA AB AD
⇒ =++
2 22 2
1 111
43AH a a a
⇒ = ++
2 22 2
1 111
43AH a a a
⇒ = ++
( )
( )
( )
( )
2
2
12 2 57 2 57
,,
19 19 19
aa a
AH AH d C SBD d A SBD⇒ = ⇒= ⇒ = =
Câu 45: Có bao nhiêu giá trị nguyên thuộc
( )
0;5
của tham số
m
để phương trình
1
4 .2 2 1 0
xx
mm
+
− + −=
có hai nghiệm phân biệt trong đó có đúng một nghiệm dương?
A.
2
B.
0
C.
1
D.
3
Lời giải

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 25
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn D .
Với
( )
1
4 .2 2 1 0, 1
xx
mm
+
− + −=
Đặt
( )
2, 0
x
tt= >
Ta có phương trình sau:
2
2 2 10t mt m− + −=
(
)( )
1 2 10t tm⇔− − +=
1
21
t
tm
=
⇔
= −
Gọi
12
,xx
là hai nghiệm của pt
( )
1
, theo yêu cầu ta phải có
12
1 2 12
0 2 12 1
xx
x x tt≤ < ⇔ ≤< ⇔ ≤<
, như vậy ta đã có
1
1t =
Suy ra để thỏa yêu cầu thì
2
2 11tm
= −>
1m⇔>
Điều kiện
( )
0;5
m∈⇒
có
3
giá trị
m
nguyên là
1, 2, 3m =
thỏa yêu cầu.
Câu 46: Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
sao cho giá trị lớn nhất của hàm số
42
1 19
30 20
42
y x x xm= − + +−
trên đoạn
[ ]
0; 2
không vượt quá
20
. Tổng các phần tử của
S
bằng:
A.
300
B.
105
C.
195−
D.
210
Lời giải
Chọn B.
Đặt hàm số
(
)
42
1 19
30 20
42
gx x x x= − +−
. Xét hàm số này trên đoạn
[
]
0; 2
.
Ta có:
( ) ( )
( )
( )
( )
3
5
19 30 0 3
2
xl
gx x x gx x l
xn
= −
′′
=− +⇒ =⇔=
=
( ) ( )
0 20 ; 2 6gg⇒=− =
( ) (
)
0 20 ; 2 6y my m⇒ =−+ =+
[ ]
{ }
0;2
2 14 26
max max 20 , 6 20 2 14 14 0 14
2
x
m
y mm m m
∈
−+
= − + + = ≤ ⇔ − ≤ ⇔≤ ≤
( do
{ }
max ,
2
ab ab
ab
++−
=
)
{ }
{ }
0,1, 2,3,....,14 0,1,2,3,....,14 105mS m⇒ ∈ ⇒ = ⇒∑ =
.
Câu 47: Cho hàm số
( )
32
3fx x x= −
. Có bao nhiêu giá trị nguyên của
m
để đồ thị hàm số
( )
( )
gx f x m= +
cắt trục hoành tại
4
điểm phân biệt?
A.
2
B.
0
C.
4
D.
3
Lời giải
Chọn D .

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 26
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Xét hàm số
( ) ( ) ( )
32 2
0
3 36 0
2
x
fx x x fx x x fx
x
=
′′
=−⇒=−⇒=⇒
=
.
Ta có bảng biến thiên:
Ta suy ra bbt của hàm số:
( )
y fx=
Xét phương trình
( )
fx m= −
Để đồ thị hàm số
( )
( )
gx f x m= +
cắt trục hoành tại
4
điểm phân biệt
( )
fx m⇔=−
có 4
nghiệm.
{
}
4 0 0 4 1, 2, 3m mm
⇒− <− < ⇔ < < ⇒ ∈
Vậy có 3 giá trị thỏa đk đề bài.
Câu 48: Cho hàm số
( )
y fx=
xác định trên
và có đạo hàm
( )
fx
′
thỏa mãn
( ) ( )( ) ( )
1 2 2018f x x x gx
′
=−+ +
trong đó
( )
0,gx x
< ∀∈
. Hàm số
( )
1 2018 2019yf x x= −+ +
đồng biến trên khoảng nào?
A.
( )
1; +∞
B.
( )
0;3
C.
( )
3; +∞
D.
( )
;3−∞
Lời giải
Chọn B .
Xét hàm số
( ) ( ) ( )
1 2018 2019 1 2018 1 4037yfx x fx x= −+ + = −− −+
xác định trên
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 27
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Đặt
( )
1
t x tx=−⇒
nghịch biến
x∀∈
(
)
2018 4037y ft t⇒= − +
(
) (
)
(
)
(
)
2018 1 2
y f t t t gt
′′
= − =−+
( do
( ) ( )
( )
(
)
1 2 2018f t t t gt
′
=−+ +
)
Để
( )
1 2018 2019yf x x= −+ +
đồng biến
( )
2018 4037y ft t⇒= − +
nghịch biến
( )( ) ( )
120y t t gt
′
⇔=− + ≤
. Do
(
)
(
)
0,g t t gt< ∀∈
( )( ) ( ) ( )( )
12012021y tt gt tt t
′
⇒ = − + ≤⇔ − + ≥⇔−≤≤
[ ]
2 1 1 0 3 0;3x xx⇔−≤− ≤⇔ ≤ ≤ ⇒ ∈
.
Câu 49: Cho phương trình
( ) ( )
2
2
33
log 3 log 3 2 2 1 0x m xmm+ + − −=
. Gọi
S
là tập hợp tất cả các số tự
nhiên
m
mà phương trình có hai nghiệm phân biệt
12
,xx
thỏa
12
10
3
xx+<
. Số phần tử của
S
là
A.
1
. B.
0
. C.
10
. D. Vô số.
Lời giải
Chọn D
Điều kiện:
0x >
. Phương trình đã cho tương đương với phương trình
(
) ( ) ( )
2
2
33
log 3 1 log 2 2 1 0 1
x m xm m+ + + − −=
.
Đặt
3
log ,xt=
phương trình
( )
1
trở thành
( )
22
3 2 10 2t mt m m
+ + + −=
.
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình
( )
2
có hai nghiệm phân
biệt
2
0 4 40 2mm m⇔∆>⇔ − +>⇔ ≠
.
Với
2
m
≠
thì
(
)
2
có hai nghiệm phân biệt
1
1tm=−−
và
2
21tm=−+
. Khi đó,
(
)
1
có hai
nghiệm phân biệt
1
1
3
m
x
−−
=
và
21
2
3
m
x
−+
=
.
Do đó,
1 21
12
10 10
33
33
mm
xx
−− − +
+< ⇔ + <
22
3 3 10 0
mm− −+
⇔ + −<
2
9.3 3 10 0
mm−−
⇔ + −<
10
31 0 0
9
m
mm
−
⇔− < < ⇔− < ⇔ >
Vậy có vô số số tự nhiên
m
thỏa mãn đề bài.
Câu 50: Cho hình chóp
.
S ABCD
có
ABCD
là hình bình hành.
, ,,M N PQ
lần lượt là trung điểm của
,,,SA SB SC SD
. Gọi
12
,VV
lần lượt là thể tích của khối chóp
.S MNPQ
và khối chóp
.S ABCD
.
Tính tỉ số
2
1
V
V
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 28
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
16
. B.
8
. C.
2
. D.
4
.
Lời giải
Chọn B
Do các tứ giác
ABCD
và
MNPQ
là những hình bình hành nên ta có
.
2
1.
2
.. 8
2
S ABC
S MNP
V
V
SA SB SC
V V SM SN SP
= = =
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
KIỂM TRA HỌC KÌ I LỚP 12
TRƯỜNG THPT PHAN ĐÌNH PHÙNG HÀ NỘI
NĂM HỌC:2020-2021
THỜI GIAN: 90 PHÚT
Câu 1. Cho đường thẳng
∆
, xét đường thẳng
l
cắt đường thẳng
∆
tại O tạo thành góc
α
( )
0 90
α
°< < °
. Khi
l
quay quanh
∆
ta được
A. Một mặt nón tròn xoay. B. Một hình nón tròn xoay.
C. Một hình trụ tròn xoay. D. Một mặt trụ tròn xoay.
Câu 2. Khối cầu có bánh kính R có thể tích bằng?
A.
2
4
3
R
π
. B.
3
2
R
π
. C.
3
4 R
π
. D.
3
4
3
R
π
.
Câu 3. Số nghiệm của phương trình
7 10
x
−=
là
A. 3. B. 2. C. 0. D. 1.
Câu 4. Điểm cực đại
0
x
của hàm số
42
27yx x
là
A.
0
1x
= −
. B.
0
1x =
. C.
0
0x =
. D.
0
3x =
.
Câu 5. Giá trị
x
để biểu thức
5
2
1x
có nghĩa là
A.
{ }
\1
x∀∈ ±
. B.
( ) ( )
; 1 1;x∀ ∈ −∞ − ∪ +∞
.
C.
(
)
1;1x∀∈−
. D.
(
] [
)
;1 1;x∀ ∈ −∞ ∪ +∞
.
Câu 6. Số nghiệm của phương trình
2
2020 2020
log 2 logxx
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 7. Khối cầu
( )
1
S
có thể tích bằng
3
108m
và có bán kính gấp
3
lần bán kính khối cầu
( )
2
S
. Thể
tích của khối cầu
( )
2
S
bằng
A.
3
12m
. B.
3
4m
. C.
3
36m
. D.
3
8m
.
Câu 8. Một khối trụ có chiều cao bằng
2
, thể tích bằng
18
π
. Bán kính đáy của khối trụ bằng
A.
33
. B.
6
. C.
9
. D.
3
.
Câu 9. Cho
,, 0abc>
và
,1
ab≠
. Trong các khẳng định sau, khẳng định nào sai ?
A.
log
a
b
ab=
. B.
log 1 0
a
=
.
C.
log 1
b
b =
. D.
( )
log log log
a aa
bc b c
+= +
.
Câu 10. Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ dưới đây?
A.
3
3yxx=−+
. B.
3
32
yxx=−+ +
. C.
3
32yx x=−+
. D.
3
31yx x=−+
.
Câu 11. Đạo hàm của hàm số
7
x
y =
là.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
7 .ln 7
x
y
′
=
. B.
1
7
x
y
−
′
=
. C.
7
ln 7
x
y
′
=
. D.
1
.7
x
yx
−
′
=
.
Câu 12. Cho hàm số
(
)
y fx
=
có bảng biến thiên như hình sau
Khẳng định nào dưới đây sai?
A. Hàm số nghịch biến trên
( )
1; 0−
. B. Hàm số nghịch biến trên
( )
1; +∞
.
C. Hàm số đồng biến trên
(
)
2;3
. D. Hàm số đồng biến trên
( )
;1
−∞ −
Câu 13. Số nghiệm của phương trình
2
44
33
xx−− −
=
là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 14. Cho khối nón tròn xoay có chiều cao bằng
a
và bán kính đáy bằng
3
a
. Thể tích của khối nón
bằng
A.
3
2
3
a
π
. B.
3
4
3
a
π
. C.
3
a
π
. D.
3
3 a
π
.
Câu 15. Cho
0, 1aa
>≠
. Khi đó
3
log
a
a
có giá trị bằng
A.
3
. B.
3−
. C.
1
3
. D.
1
3
−
.
Câu 16. Biết rằng hàm số
( )
32
39fx x x x=−−
đạt giá trị nhỏ nhất trên đoạn
[ ]
0;5
tại
0
x
. Khẳng định
nào sau đây đúng?
A.
0
3
x =
. B.
0
5x =
. C.
0
1x
= −
D.
0
0x =
Câu 17. Cho hình chóp tam giác đều
SABC
có chiều cao bằng
a
, cạnh đáy
AB a=
. Thể tích của khối
chóp
SABC
bằng
A.
3
12
a
. B.
3
4
a
. C.
3
3
4
a
. D.
3
3
12
a
.
Câu 18. Tập xác định của hàm số
2
1
logy
x
=
là
A.
D =
. B.
{
}
\0D =
. C.
( )
0;D = +∞
.
D.
[
)
0;D = +∞
.
Câu 19. Giá trị lớn nhất của hàm số
4
1
y
x
=
+
trên doạn
[ ]
1; 2
bằng
A.
8
3
. B.
2
3
. C.
4
3
. D.
2
.
Câu 20. Tổng số đường tiện cận của đồ thị hàm số
1
21
x
y
x
−
=
+
bằng
A.
3
. B.
0
. C.
2
. D.
1
.
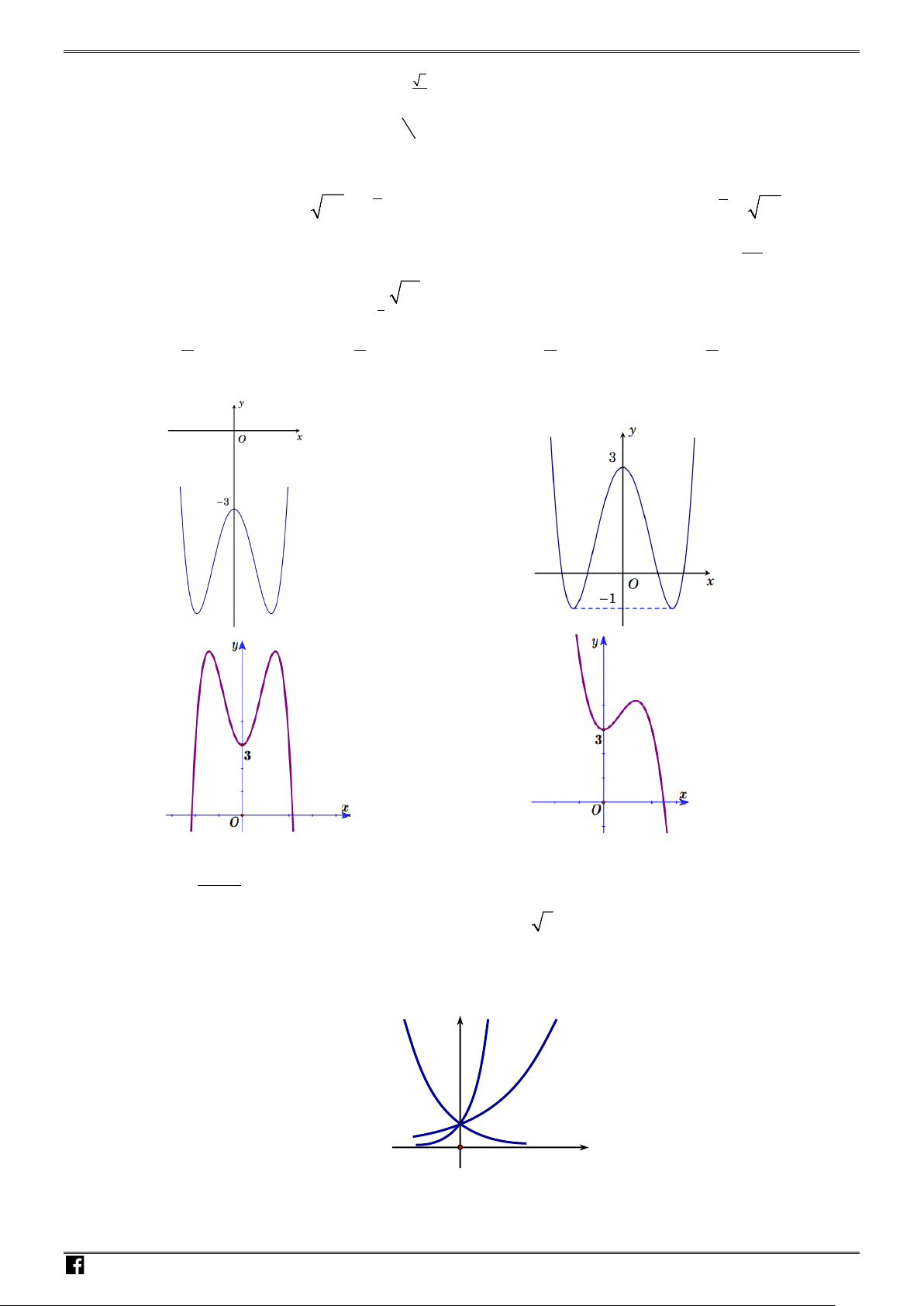
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 21. Tập xác định của hàm số
( )
5
2
1yx= +
là
A.
D =
. B.
D
=
{ }
1−
. C.
( )
1;D = − +∞
. D.
( )
0;D = +∞
.
Câu 22. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
;, :
m
n
m
n
a mn a a
∀∈ ∀ ∈ =
. B.
{ }
\0; , :
m
n
m
n
a mn a a∀∈ ∀ ∈ =
.
C.
0
:1aa∀∈ =
. D.
{ }
1
\0, :
n
n
a na
a
−
∀∈ ∀∈ =
.
Câu 23. Cho
0, 1aa>≠
, giá trị của
7
5
1
log
a
a
bằng
A.
5
7
−
. B.
5
7
. C.
7
5
−
. D.
7
5
.
Câu 24. Đồ thị hàm số
42
43
yx x=−+
là hình nào trong số các hình vẽ dưới đây?
A. . B. .
C. . D. .
Câu 25. Trong các hàm số sau, hàm số nào đồng biến trên
?
A.
21
3
x
y
x
−
=
+
. B.
3
7 19yx x=+−
. C.
3
2 4 25
yx x= −+
. D.
42
2
yx x
= +
.
Câu 26. Cho khối hộp
.ABCD A B C D
′′′′
có thể tích bằng
3
3a
,
AB BC CA a= = =
. Độ dài đường cao
của khối hộp đã cho bằng
A.
2
a
. B.
3a
. C.
4a
. D.
a
.
Câu 27. Cho đồ thị ba hàm số
,,
xxx
yaybyc= = =
như hình vẽ bên dưới . Kết luận nào sau đây đúng?
A.
01c ba< << <
. B.
01a cb< << <
. C.
01a bc< << <
. D.
01c ab<<< <
.
O
x
y
1
x
ya=
x
yb=
x
yc=

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 28. Cho phương trình
(
)
2
21
2
2
log 3log log 2 *+ +=x xx
. Nếu đặt
2
log=tx
thì phương trình
( )
*
trở thành phương trình nào trong số các phương trình cho dưới đây?
A.
2
10+−=tt
. B.
2
2 10+−=
tt
. C.
2
10++=tt
. D.
2
2 10++=tt
.
Câu 29. Trong các biều thức sau, biểu thức nào không có nghĩa?
A.
( )
2
2
−
−
. B.
2021
0
−
. C.
4
3
. D.
0
1
5
.
Câu 30. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số
32
34=−+yx x
bằng
A.
4
. B.
25
. C.
22
. D.
2
.
Câu 31. Cho hàm số
3
4
yx
−
=
. Trong các khẳng định sau, khẳng định nào sai?
A. Hàm số luôn nghịch biến trên
.
B. Hàm số không có điểm cực trị.
C. Đồ thị hàm số đi qua điểm
( )
1;1
A
.
D. Đồ thị hàm số có tiệm cậng ngang và tiệm cận đứng.
Câu 32. Cho hàm số
1
2
x
y
x
−
=
−
. Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên mỗi khoảng xác định.
B. Hàm số đồng biến trên
.
C. Hàm số nghịch biến trên mỗi khoảng xác định.
D. Hàm số đồng biến trên
.
Câu 33. Cho hình nón có bán kính đáy bằng
r
, chiều cao bằng
h
, độ dài đường sinh bằng
l
. Khẳng
định nào sau đây đúng?
A.
22
2lhr= +
. B.
22
h rl= +
. C.
22
l rh= +
. D.
22
l rh= −
.
Câu 34. Cho hàm số
2
1
1
x
y
x
+
=
−
. Số đường tiệm cận ngang của đồ thị hàm số là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 35. Cắt mặt cầu
( )
S
bằng một mặt phẳng cách tâm một khoảng bằng
4cm
ta được thiết diện là
đường tròn có bán kính bằng
3cm
. Bán kính của mặt cầu
(
)
S
bằng
A.
25
cm
. B.
7cm
. C.
12cm
. D.
5cm
.
Câu 36. Biết phương trình
( )
2
22
5 24 49 10 24
xx−−
+=−
có hai nghiệm
(
)
12 1 2
;xx x x
<
. Khi đó giá trị
của
12
xx−
bằng
A.
2
. B.
2−
. C.
1−
. D.
4−
.
Câu 37. Cho hình chữ nhật ABCD có cạnh
6, 4
AB AD= =
quay quanh AB ta được hình trụ có diện tích
xung quanh và diện tích toàn phần lần lượt là
12
,
SS
. Chọn khẳng định đúng.
A.
1
2
2
3
S
S
=
. B.
1
2
3
2
S
S
=
. C.
1
2
3
5
S
S
=
. D.
1
2
5
3
S
S
=
.
Câu 38. Cho hàm số
( )
y fx=
liên tục trên
và có đồ thị như hình vẽ dưới đây. Giá trị lớn nhất và giá
trị nhỏ nhất của hàm số
( )
y fx=
trên đoạn
3
;2
2
có tổng bằng

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
. B.
2−
. C.
4
. D.
3−
.
Câu 39. Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O. Biết
,2
AB a BC a
= =
và
( )
3
,
2
SO ABCD SO a⊥=
. Gọi M, N lần lượt là trung điểm của BC, SD. Mặt phẳng
( )
AMN
cắt
SC tại E. Thể tích V của khối đa diện lồi SABEN bằng
A.
3
5
12
a
V =
. B.
3
3
a
V
=
. C.
3
7
12
a
V =
. D.
3
2
a
V =
.
Câu 40. Cho hàm số
( )
42
11y mx m x m= + − +−
. Tìm tất cả các giá trị của tham số
m
để hàm số chỉ có
một điểm cực trị là
A.
01m<<
. B.
01m≤≤
. C.
0
1
m
m
<
>
. D.
0
1
m
m
≥
≤
.
Câu 41. Cho hàm số
1
log
b
y
x
=
đồng biến trên khoảng
( )
0; +∞
và hàm số
2
log
a
y
x
=
nghịch biến trên
khoảng
( )
0; +∞
. Khẳng định nào sau đây đúng?.
A.
1
ba
<<
. B.
01ba< <<
. C.
01ba<<<
. D.
01ab< <<
Câu 42. Lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác cân tại
, 2, 120 ,A AB BAC= = °
góc giữa
AC
′
và
( )
ABC
bằng
60 .°
Diện tích mặt cầu ngoại tiếp hình chóp
.C ABB A
′′
bằng.
A.
28
π
. B.
7
π
. C.
6
π
. D.
24
π
.
Câu 43. Tổng bình phương các nghiệm của phương trình
( )
22
22
9 3 .3 2 2 0
xx
xx+ − − +=
bằng
A.
3
log 2
. B.
3
log 2
. C.
0
. D.
3
log 4
.
Câu 44. Một hình trụ có bán kính đáy bằng
r
, chiều cao bằng
3r
. Trên hai đường tròn đáy của hình
trụ lần lượt lấy hai điểm
,MN
sao cho góc giữa đường thẳng
MN
và trục
OO
′
bằng
o
30
.
Khoảng cách
d
giữa đường thẳng
MN
và trục của hình trụ là
A.
3
4
r
d =
. B.
3dr=
. C.
3
2
r
d =
. D.
3
3
r
d =
.
Câu 45. Tập hợp tất cả các giá trị của
m
để biểu thức
( )
( )( )
22
5
log 2 3 2 1fx xx xx m
= −+ −−−
xác
định với mọi
( )
2;x ∈ − +∞
A.
( )
;2−∞ −
. B.
( )
;1−∞ −
. C.
(
]
;3−∞ −
. D.
(
]
;2−∞ −
.
Câu 46. Cho hàm số
( )
1
,, , 0
ax
y abc b
bx c
−
= ∈≠
+
có đồ thị như hình vẽ sau

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Mệnh đề nào dưới đây sai?
A.
2abc++=
. B.
0abc−+=
C.
0abc++=
. D.
2
abc
= −
.
Câu 47. Cho hình nón đỉnh
S
có chiều cao bằng bán kính đáy và bằng
a
. Mặt phẳng
( )
P
đi qua đỉnh
S
và cách tâm đáy một khoảng bằng
5
a
,
( )
P
cắt đường tròn đáy của hình nón tại
A
và
B
.
Độ dài dây cung
AB
bằng
A.
3a
. B.
4
5
a
. C.
3
2
a
. D.
2
5
a
Câu 48. Cho
n
là số nguyên dương thỏa mãn
22
3
22 2
2 2 2 22
11
11 1
log 2022 2 log 2022 3 log 2022 log 2022 2017 1008 log 2022
n
nn
nn n
n
++
++ +
+ + +…+ = ⋅ ⋅
Khi đó
n
thuộc khoảng nào trong các khoảng cho dưới đây?
A.
(2020;2023)
. B.
(2015;2018)
. C.
(2017;2019)
. D.
(2018;2020)
.
Câu 49. Cho khối chóp
.S ABC
có tam giác
ABC
vuông tại
B
,
2AC =
,
1AB =
. Tam giác
SAC
nhọn.
Gọi
I
là trung điểm
AC
, biết
()SI ABC⊥
và diện tích mặt cầu ngoại tiếp hình chóp
.S ABC
bằng
25
4
π
. Gọi
12
,SS
lần lượt là diện tích các mặt cầu ngoại tiếp tứ diện
SABI
và
SBCI
. Khi
đó tổng
12
SS+
bằng
A.
22
3
π
. B.
40
3
π
. C.
112
3
π
. D.
35
6
π
.
Câu 50. Cho phương trình
( )
( )
32
22
log 5 6 log 3 1
m
mx mx x x
+
− +−= − −
, với
m
là tham số. Số các giá
trị
x
nghiệm đúng phương trình đã cho với mọi
1m >−
là
A.
2
. B. vô số. C.
0
. D.
1
.
----HẾT---

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
BẢNG ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
D
D
C
A
C
B
D
D
B
A
C
B
C
C
A
D
B
D
C
C
D
A
B
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
A
B
B
B
A
A
C
B
D
B
C
A
D
D
B
A
D
C
A
C
A
B
B
D
Câu 1. Cho đường thẳng
∆
, xét đường thẳng
l
cắt đường thẳng
∆
tại O tạo thành góc
α
( )
0 90
α
°< < °
. Khi
l
quay quanh
∆
ta được
A. Một mặt nón tròn xoay. B. Một hình nón tròn xoay.
C. Một hình trụ tròn xoay. D. Một mặt trụ tròn xoay.
Lời giải
Chọn A
Câu 2. Khối cầu có bánh kính R có thể tích bằng?
A.
2
4
3
R
π
. B.
3
2 R
π
. C.
3
4 R
π
. D.
3
4
3
R
π
.
Lời giải
Chọn D
Câu 3. Số nghiệm của phương trình
7 10
x
−=
là
A. 3. B. 2. C. 0. D. 1.
Lời giải
Chọn D
7 10 0
x
x−= ⇔ =
.
Số nghiệm của phương trình là 1.
Câu 4. Điểm cực đại
0
x
của hàm số
42
27
yx x
là
A.
0
1x = −
. B.
0
1x =
. C.
0
0x =
. D.
0
3x =
.
Lời giải
Chọn C
Ta có
3
44yxx
0
0
1
x
y
x
.
Bảng xét dấu
y
Từ bảng xét dấu
y
ta thấy hàm số có điểm cực đại là
0
0x
.
Câu 5. Giá trị
x
để biểu thức
5
2
1x
có nghĩa là
A.
{ }
\1x∀∈ ±
. B.
( ) ( )
; 1 1;x∀ ∈ −∞ − ∪ +∞
.
C.
( )
1;1x∀∈−
. D.
(
] [
)
;1 1;x∀ ∈ −∞ ∪ +∞
.
Lời giải
Chọn A.
Điều kiện:
2
1 0 1.xx
Vậy điều kiện xác định của hàm số là
{ }
\1x∀∈ ±
.
Câu 6. Số nghiệm của phương trình
2
2020 2020
log 2 logxx
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn C
Điều kiện:
2
0
x
x
.
2
2020 2020
log 2 logxx
2
2xx
2
1
x tm
x tm
Vậy phương trình có 2 nghiệm.
Câu 7. Khối cầu
( )
1
S
có thể tích bằng
3
108m
và có bán kính gấp
3
lần bán kính khối cầu
(
)
2
S
. Thể
tích của khối cầu
( )
2
S
bằng
A.
3
12m
. B.
3
4m
. C.
3
36m
. D.
3
8m
.
Lời giải
Chọn B
Ta có
1
3
33
11 2
4 33
108 3
3
S
Vr r r
π
ππ
= = ⇒= ⇒=
.
Từ đó suy ra
2
33
2
4 43
4
33
S
Vr m
ππ
π
= = =
.
Câu 8. Một khối trụ có chiều cao bằng
2
, thể tích bằng
18
π
. Bán kính đáy của khối trụ bằng
A.
33
. B.
6
. C.
9
. D.
3
.
Lời giải
Chọn D
Ta có
22
18 9 3V hr r r
ππ
= = ⇒ =⇒=
.
Câu 9. Cho
,, 0abc>
và
,1
ab≠
. Trong các khẳng định sau, khẳng định nào sai ?
A.
log
a
b
ab
=
. B.
log 1 0
a
=
.
C.
log 1
b
b =
. D.
( )
log log log
a aa
bc b c+= +
.
Lời giải
Chọn D
Ta có công thức đúng là
log log log
a bc
bc a= +
.
Câu 10. Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ dưới đây?
A.
3
3
yxx=−+
. B.
3
32yxx
=−+ +
. C.
3
32yx x=−+
. D.
3
31yx x=−+
.
Lời giải
Chọn B
Dựa vào đồ thị, ta thấy đây là dạng đồ thị của hàm bậc ba với hệ số
0a <
, nên loại phương án
C, D.
Khi
0x =
thì
2y =
nên loại phương án A, chọn phương án B.
Câu 11. Đạo hàm của hàm số
7
x
y =
là.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
7 .ln 7
x
y
′
=
. B.
1
7
x
y
−
′
=
. C.
7
ln 7
x
y
′
=
. D.
1
.7
x
yx
−
′
=
.
Lời giải
Chọn A
7 7 .ln 7
xx
yy
′
=⇒=
.
Câu 12. Cho hàm số
(
)
y fx=
có bảng biến thiên như hình sau
Khẳng định nào dưới đây sai?
A. Hàm số nghịch biến trên
( )
1; 0−
. B. Hàm số nghịch biến trên
( )
1; +∞
.
C. Hàm số đồng biến trên
( )
2;3
. D. Hàm số đồng biến trên
( )
;1
−∞ −
Lời giải
Chọn C
Dựa vào bảng biến thiên, ta thấy hàm số nghịch biến trên
( )
2;3
nên phương án C sai.
Câu 13. Số nghiệm của phương trình
2
44
33
xx−− −
=
là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn B
Ta có
2
44 2 2
0
3 3 44 0
2
xx
x
xx xx
x
−− −
=
= ⇔−−=−⇔−=⇔
=
.
Vậy phương trình đã cho có 2 nghiệm.
Câu 14. Cho khối nón tròn xoay có chiều cao bằng
a
và bán kính đáy bằng
3
a
. Thể tích của khối nón
bằng
A.
3
2
3
a
π
. B.
3
4
3
a
π
. C.
3
a
π
. D.
3
3 a
π
.
Lời giải
Chọn C
Thể tích khối nón là
( )
2
23
11
.3
33
V Rh a a a
ππ π
= = =
.
Câu 15. Cho
0, 1aa>≠
. Khi đó
3
log
a
a
có giá trị bằng
A.
3
. B.
3−
. C.
1
3
. D.
1
3
−
.
Lời giải
Chọn C
Ta có
3
11
log log
33
a
a
aa= =
.
Câu 16. Biết rằng hàm số
( )
32
39
fx x x x=−−
đạt giá trị nhỏ nhất trên đoạn
[ ]
0;5
tại
0
x
. Khẳng định
nào sau đây đúng?
A.
0
3x =
. B.
0
5x =
. C.
0
1
x = −
D.
0
0x =
Lời giải
Chọn A
Ta có
( )
32
39fx x x x=−−
là hàm liên tục trên
[ ]
0;5

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
và
(
)
( )
[ ]
[ ]
2
1 0;5
3 6 9; 0
3 0;5
x
fx x x fx
x
=−∉
′′
= −− =⇔
= ∈
( ) ( ) ( )
0 0; 5 5; 3 27.fff
= = = −
Vậy giá trị nhỏ nhất của hàm số bằng
27−
đạt được tại
0
3x =
.
Câu 17. Cho hình chóp tam giác đều
SABC
có chiều cao bằng
a
, cạnh đáy
AB a=
. Thể tích của khối
chóp
SABC
bằng
A.
3
12
a
. B.
3
4
a
. C.
3
3
4
a
. D.
3
3
12
a
.
Lời giải
Chọn D
Diện tích đáy
2
3
4
ABC
a
S =
. Chiều cao
ha=
Vậy thể tích khối chóp bằng
3
13
..
3 12
ABC
a
V hS= =
Câu 18. Tập xác định của hàm số
2
1
logy
x
=
là
A.
D =
. B.
{ }
\0D =
. C.
(
)
0;D
= +∞
. D.
[
)
0;
D
= +∞
.
Lời giải
Chọn C
Ta có
1
00x
x
>⇔>
. Vậy
( )
0;D = +∞
.
Câu 19. Giá trị lớn nhất của hàm số
4
1
y
x
=
+
trên doạn
[ ]
1; 2
bằng
A.
8
3
. B.
2
3
. C.
4
3
. D.
2
.
Lời giải
Chọn D
Ta có hàm số liên tục trên đoạn
[ ]
1; 2
và
( )
2
4
0
1
y
x
′
=−<
+
trên
[ ]
1; 2
. Vậy
[ ]
( )
1;2
max 1 2yy= =
.
Câu 20. Tổng số đường tiện cận của đồ thị hàm số
1
21
x
y
x
−
=
+
bằng
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn C
Ta có
1
lim
2
x
y
→±∞
= −
. Suy ra đường thẳng
1
2
y = −
là tiệm cận ngang của đồ thị hàm số.
11
22
lim , lim
xx
yy
+−
→− →−
= +∞ = −∞
. Suy ra đường thẳng
1
2
x = −
là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tổng hai đường tiệm cận.
Câu 21. Tập xác định của hàm số
( )
5
2
1yx= +
là
A.
D =
. B.
D =
{ }
1−
. C.
( )
1;D = − +∞
. D.
( )
0;D = +∞
.
Lời giải
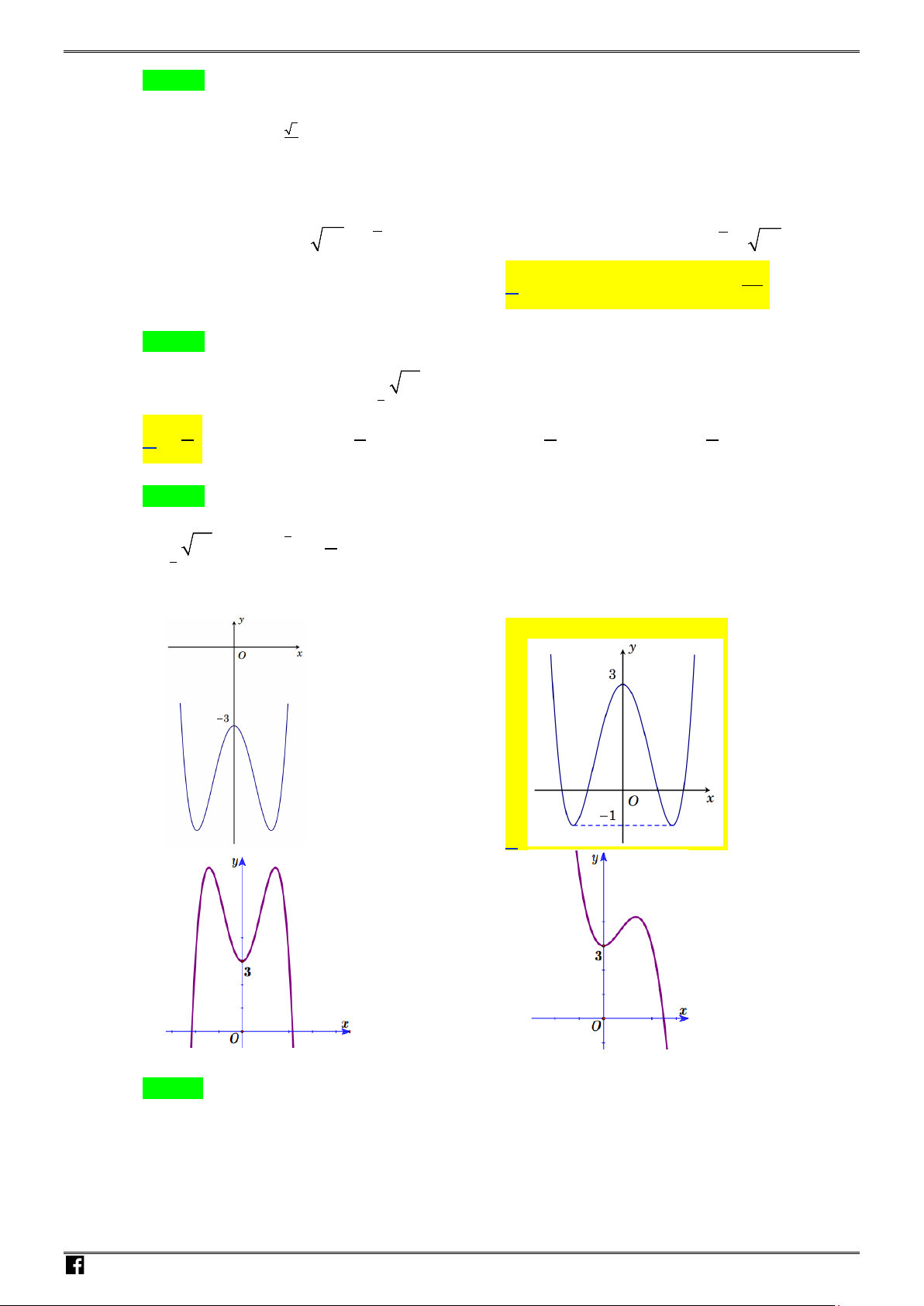
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn C
Ta có hàm số
yx
α
=
với
α
không nguyên xác định khi
0x >
.
Hàm số
( )
5
2
1yx= +
xác định khi
10 1xx+ > ⇔ >−
.
Vậy xác định của hàm số
( )
1;
D = − +∞
.
Câu 22. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
;, :
m
n
m
n
a mn a a∀∈ ∀ ∈ =
. B.
{ }
\0; , :
m
n
m
n
a mn a a∀∈ ∀ ∈ =
.
C.
0
:1aa∀∈ =
. D.
{ }
1
\0, :
n
n
a na
a
−
∀∈ ∀∈ =
.
Lời giải
Chọn D
Câu 23. Cho
0, 1
aa
>≠
, giá trị của
7
5
1
log
a
a
bằng
A.
5
7
−
. B.
5
7
. C.
7
5
−
. D.
7
5
.
Lời giải
Chọn A
1
5
7
5
7
1
5
log log
7
a
a
aa
−
= = −
.
Câu 24. Đồ thị hàm số
42
43
yx x=−+
là hình nào trong số các hình vẽ dưới đây?
A. . B. .
C. . D. .
Lời giải
Chọn B
Tập xác định
D =
.
lim ; lim
xx
yy
→−∞ →+∞
= +∞ = +∞
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
3
48
yxx
′
= −
,
0
0
2
x
y
x
=
′
= ⇔
= ±
.
Bảng biến thiên:
Dựa vào bảng biến thiên suy ra đồ thị hình B.
Câu 25. Trong các hàm số sau, hàm số nào đồng biến trên
?
A.
21
3
x
y
x
−
=
+
. B.
3
7 19
yx x=+−
. C.
3
2 4 25yx x= −+
. D.
42
2yx x= +
.
Lời giải
Chọn B
Hàm số
3
7 19yx x
=+−
có
2
3 70yx x
′
= + > ∀∈
, suy ra hàm số đồng biến trên
.
Câu 26. Cho khối hộp
.ABCD A B C D
′′′′
có thể tích bằng
3
3
a
,
AB BC CA a= = =
. Độ dài đường cao
của khối hộp đã cho bằng
A.
2a
. B.
3a
. C.
4
a
. D.
a
.
Lời giải
Chọn A
Tam giác
ABC
đều cạnh
a
, suy ra
22
33
2 2.
42
ABCD ABC
aa
SS= = =
.
Gọi
h
độ dài đường cao của khối hộp. Thể tích khối hộp là
.2
ABCD
ABCD
V
VS h h a
S
= ⇒= =
.
Câu 27. Cho đồ thị ba hàm số
,,
xxx
yaybyc= = =
như hình vẽ bên dưới . Kết luận nào sau đây đúng?
A.
01c ba< << <
. B.
01a cb
< <<<
. C.
01a bc< << <
. D.
01c ab<<< <
.
Lời giải
Chọn A
Đồ thị hàm số
x
yc=
nghịch biến, suy ra
01c<<
.
O
x
y
1
x
ya=
x
yb=
x
yc=

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Đồ thị hàm số
x
ya=
và
x
yb=
đồng biến, suy ra
1a >
và
1
b
>
.
Với
1x =
ta thấy
ab>
. Suy ra
01c ba< << <
. Do đó đáp án đúng là A.
Câu 28. Cho phương trình
( )
2
21
2
2
log 3log log 2 *+ +=x xx
. Nếu đặt
2
log=tx
thì phương trình
( )
*
trở
thành phương trình nào trong số các phương trình cho dưới đây?
A.
2
10+−=tt
. B.
2
2 10
+−=
tt
. C.
2
10++=tt
. D.
2
2 10++=tt
.
Lời giải
Chọn B
Ta có:
( )
22
2 22 22
* 4 log 3log log 2 0 2log log 1 0⇔+−−=⇔+−=x xx xx
.
Nếu đặt
2
log
=tx
thì phương trình
( )
*
trở thành phương trình:
2
2 10+−=tt
.
Câu 29. Trong các biều thức sau, biểu thức nào không có nghĩa?
A.
( )
2
2
−
−
. B.
2021
0
−
. C.
4
3
. D.
0
1
5
.
Lời giải
Chọn B
Biểu thức không có nghĩa là
2021
0
−
do
α
a
(với
α
nguyên âm) xác định khi
0
≠
a
.
Câu 30. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số
32
34=−+yx x
bằng
A.
4
. B.
25
. C.
22
. D.
2
.
Lời giải
Chọn B
Tập xác định:
= D
.
Ta có:
2
04
3 6; 0
20
=⇒=
′′
=−=⇒
=⇒=
xy
y x xy
xy
.
Suy ra hai điểm cực trị của đồ thị hàm số đã cho là:
( ) ( )
0; 4 , 2; 0AB
.
Khi đó:
( )
2
2
2 4 25= +− =AB
.
Câu 31. Cho hàm số
3
4
yx
−
=
. Trong các khẳng định sau, khẳng định nào sai?
A. Hàm số luôn nghịch biến trên
.
B. Hàm số không có điểm cực trị.
C. Đồ thị hàm số đi qua điểm
( )
1;1A
.
D. Đồ thị hàm số có tiệm cậng ngang và tiệm cận đứng.
Lời giải
Chọn A
Câu 32. Cho hàm số
1
2
x
y
x
−
=
−
. Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên mỗi khoảng xác định.
B. Hàm số đồng biến trên
.
C. Hàm số nghịch biến trên mỗi khoảng xác định.
D. Hàm số đồng biến trên
.
Lời giải
Chọn A
Tập xác định:
{ }
\2D =
.
Ta có
11
22
xx
y
xx
−−
= =
− −+
( )
2
1
0
2
y
x
′
⇒= >
−+
,
xD∀∈

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 33. Cho hình nón có bán kính đáy bằng
r
, chiều cao bằng
h
, độ dài đường sinh bằng
l
. Khẳng
định nào sau đây đúng?
A.
22
2lhr= +
. B.
22
h rl= +
. C.
22
l rh
= +
. D.
22
l rh
= −
.
Lời giải
Chọn C
Câu 34. Cho hàm số
2
1
1
x
y
x
+
=
−
. Số đường tiệm cận ngang của đồ thị hàm số là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn B
Ta có
2
2
1
1
1
lim lim 1
1
1
1
xx
x
x
x
x
→+∞ →+∞
+
+
= =
−
−
;
2
2
1
1
1
lim lim 1
1
1
1
xx
x
x
x
x
→−∞ →−∞
+
+
= = −
−
−−
, suy ra đường tiệm
cận ngang của đồ thị hàm số là
1; 1yy= = −
.
Câu 35. Cắt mặt cầu
( )
S
bằng một mặt phẳng cách tâm một khoảng bằng
4
cm
ta được thiết diện là đường
tròn có bán kính bằng
3
cm
. Bán kính của mặt cầu
( )
S
bằng
A.
25cm
. B.
7cm
. C.
12cm
. D.
5
cm
.
Lời giải
Chọn D
Ta có bán kính mặt cầu
( )
S
bằng
2 2 22
43 5r dR= + = +=
.
Câu 36. Biết phương trình
( )
2
22
5 24 49 10 24
xx
−−
+=−
có hai nghiệm
( )
12 1 2
;xx x x<
. Khi đó giá trị của
12
xx−
bằng
A.
2
. B.
2−
. C.
1−
. D.
4−
.
Lời giải
Chọn B
Ta có
( ) ( ) ( ) ( )
22
22 22 2
5 24 25 2.5. 24 24 5 24 5 24
xx xx
−− −−
+=−+⇔+=−
( ) ( )
2
22 2
22
0
5 24 5 24 2 2 2 2 0
2
xx
x
xx xx
x
−− −
=
⇔+ =+ ⇔−−=−⇔−=⇔
=
Vậy
12
02 2xx− =−=−
.
Câu 37. Cho hình chữ nhật ABCD có cạnh
6, 4AB AD
= =
quay quanh AB ta được hình trụ có diện tích
xung quanh và diện tích toàn phần lần lượt là
12
,SS
. Chọn khẳng định đúng.
A.
1
2
2
3
S
S
=
. B.
1
2
3
2
S
S
=
. C.
1
2
3
5
S
S
=
. D.
1
2
5
3
S
S
=
.
Lời giải
Chọn C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có:
4, 6AD AB= =
.
Vậy
1
22
2
2 . . 2 .4.6 3
2 . . 2 2 .4.6 2 4 5
S
AD AB
S AD AB AD
ππ
π π ππ
= = =
++
.
Câu 38. Cho hàm số
( )
y fx=
liên tục trên
và có đồ thị như hình vẽ dưới đây. Giá trị lớn nhất và giá
trị nhỏ nhất của hàm số
( )
y fx=
trên đoạn
3
;2
2
có tổng bằng
A.
3
. B.
2−
. C.
4
. D.
3−
.
Lời giải
Chọn A
Dựa vào đồ thị hàm
( )
y fx=
ta vẽ được đồ thị hàm
( )
y fx=
như sau:
Dựa vào đồ thị hàm
( )
y fx=
ta có
3
3
;2
;2
2
2
max 3, min 0yy
= =
.
Câu 39. Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O. Biết
,2AB a BC a= =
và
( )
3
,
2
SO ABCD SO a⊥=
. Gọi M, N lần lượt là trung điểm của BC, SD. Mặt phẳng
( )
AMN
cắt
SC tại E. Thể tích V của khối đa diện lồi SABEN bằng
A.
3
5
12
a
V =
. B.
3
3
a
V =
. C.
3
7
12
a
V =
. D.
3
2
a
V =
.
Lời giải
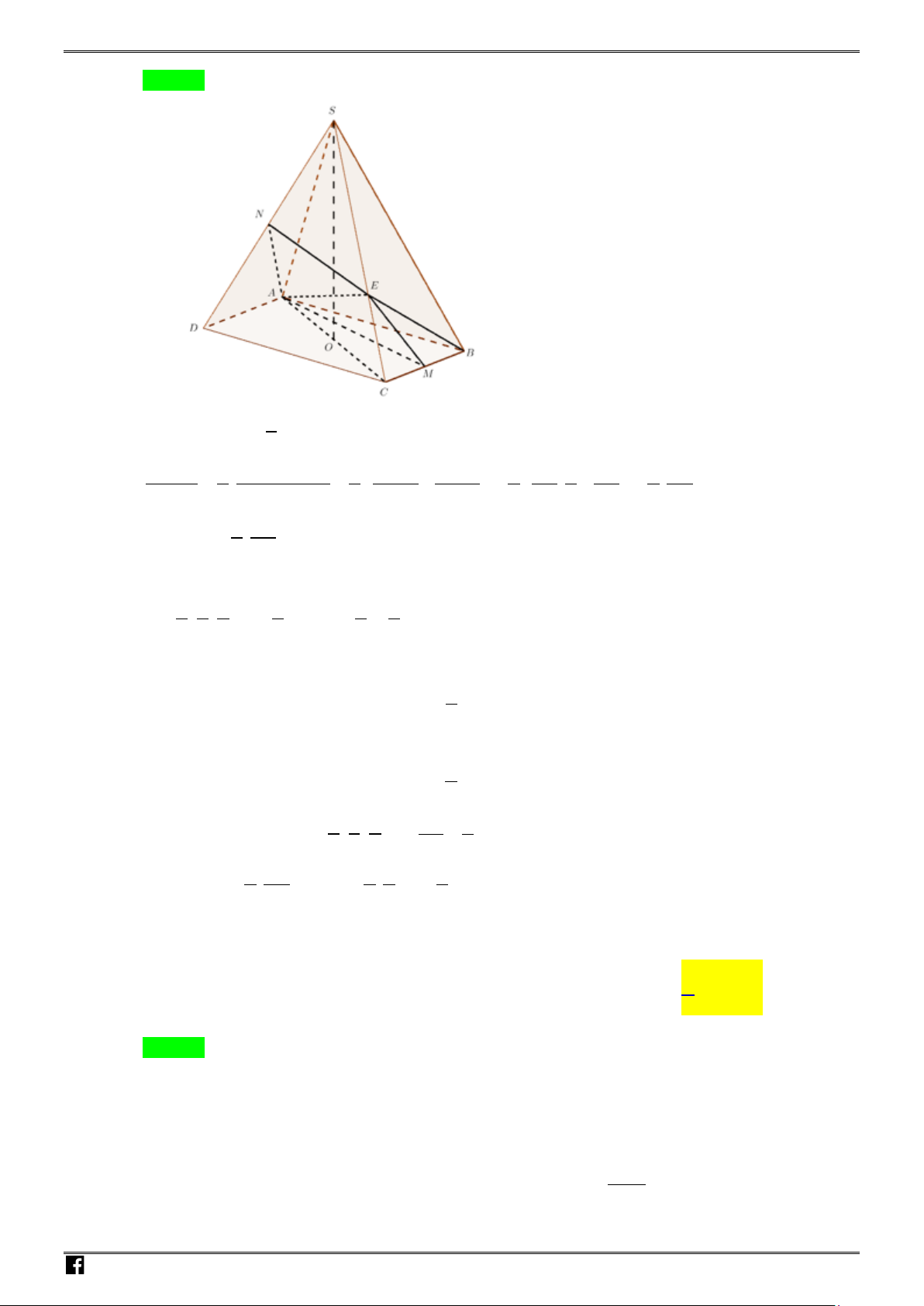
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn D
Ta có:
3
.
1
..
3
S ABCD
V AB BC SO a= =
.
. . ..
1 1 11 3
. ..
2 2 22 4
SABEN SAEN SAEB SAEN SAEB
S ABCD S ACD S ACD S ACB
V VV V V
SE SE SE
V V V V SC SC SC
+
= = + = +=
.
.
3
..
4
SABEN S ABCD
SE
VV
SC
⇒=
.
Chọn hệ trục tọa độ với
( ) ( ) ( ) ( ) ( )
0;0;0 , 1; 0; 0 , 0; 2;0 , 1; 2;0 , 0;1; 0
B AC DM
333 1 1 3
; ; , ;1; 0 , ;1;
424 2 2 2
N OS
. Khi đó, ta có:
Phương trình mặt phẳng
(
)
:3 3 5 3 0
AMN x y z+ − −=
.
Phương trình đường thẳng
( )
1
2
:2
3
2
xt
SC y t
zt
= −
= +
= −
( )
151
;;
632
E SC AMN
⇒= ∩ =
2
3
SE
SC
⇒=
.
Vậy
33
.
3 32 1
. . ..
4 43 2
SABEN S ABCD
SE
V V aa
SC
= = =
.
Câu 40. Cho hàm số
( )
42
11y mx m x m= + − +−
. Tìm tất cả các giá trị của tham số
m
để hàm số chỉ có
một điểm cực trị là
A.
01m<<
. B.
01m≤≤
. C.
0
1
m
m
<
>
. D.
0
1
m
m
≥
≤
.
Lời giải
Chọn D
+) TH1: Nếu
0m =
thì hàm số trở thành
2
1yx=−+
là parabol nên có một điểm cực đại. Suy
ra
0m =
thỏa mãn.
+) TH2: Nếu
0m ≠
thì hàm số là hàm bậc bốn trùng phương.
Ta có:
( )
( )
( )
32
2
0
'4 2 1 22 1 0
1
*
2
x
y mx m x x mx m
m
x
m
=
= + − = +−=⇔
−
=
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Để đồ thị hàm số có một điểm cực trị thì phương trình
( )
*
phải vô nghiệm học có nghiệm kép
0x =
0
1
0
1
2
m
m
m
m
<
−
⇔ ≤⇔
≥
.
Kết hợp hai trường hợp trên ta được
0
1
m
m
≥
≤
.
Câu 41. Cho hàm số
1
log
b
y
x
=
đồng biến trên khoảng
( )
0; +∞
và hàm số
2
log
a
y
x
=
nghịch biến trên
khoảng
(
)
0; +∞
. Khẳng định nào sau đây đúng?.
A.
1
ba<<
. B.
01ba< <<
. C.
01ba<<<
. D.
01ab< <<
Lời giải
Chọn B
Do hàm số
1
log log
bb
yx
x
= = −
đồng biến trên khoảng
( )
0; +∞
nên hàm số
log
b
yx
=
sẽ
nghịch biến trên khoảng
( )
0; +∞
, suy ra
01b<<
.
Do hàm số
2
log log 2 log
a aa
yx
x
= = −
nghịch biến trên khoảng
(
)
0; +∞
nên hàm số
log
a
yx=
sẽ đồng biến trên khoảng
( )
0; +∞
, suy ra
1a >
.
Vậy
01ba< <<
.
Câu 42. Lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác cân tại
, 2, 120 ,A AB BAC= = °
góc giữa
AC
′
và
( )
ABC
bằng
60 .°
Diện tích mặt cầu ngoại tiếp hình chóp
.C ABB A
′′
bằng.
A.
28
π
. B.
7
π
. C.
6
π
. D.
24
π
.
Lời giải
Chọn A
Gọi
K
là tâm đường tròn ngoại tiếp
, ABC O∆
là tâm hình chữ nhật
ABCD
Gọi
1
d
là đường thẳng đi qua
O
và vuông góc với
( )
;ABCD
2
d
là đường thẳng đi qua
K
và
vuông góc với
( )
ABC
.
Ta có:
12
ddI∩=
nên
I
là tâm mặt cầu.
Mà
( )
( )
, 60A C ABC A CA
′′
= = °
.
Trong tam giác
A CA
′
vuông tại
1
2 3 3.
2
A AA IK OJ AA
′′
⇒ = ⇒= = =
K
M
J
O
'
C
'B
'A
C
B
A
2
d
1
d
I

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
22
1.2.2.sin120 3; 2 2 2.2.cos120 2 3.
ABC
S BC
= °= = + − °=
. . 2.2.2 3
2
4
43
ABC
AB AC BC
AK
S
⇒= = =
22
7.IA AK KI R⇒= + = =
Suy ra:
2
4 28 .
SR
ππ
= =
Câu 43. Tổng bình phương các nghiệm của phương trình
( )
22
22
9 3 .3 2 2 0
xx
xx+ − − +=
bằng
A.
3
log 2
. B.
3
log 2
. C.
0
. D.
3
log 4
.
Lời giải
Chọn D
Đặt
( )
2
31
x
tt= ≥
, phương trình trở thành
( )
22 2
3 2 20t x tx+ − − +=
( )
1
Ta xem
( )
1
là phương trình bậc 2 ẩn
t
Ta có
( ) ( ) ( )
22
2 2 42 2 42 2
3 4 2 2 6 98 8 2 1 1x x xx x xx x∆= − − − + = − + + − = + + = +
.
Suy ra
(
) ( )
( ) (
)
2
22
1
2
22
2
2
31
2
2
31
1
2
xx
t
xx
tx
− −+ +
= =
− −− +
= =−+
Với
2
2
1 33
2 3 2 log 2 log 2
x
t xx=⇔ =⇔ = ⇔=±
.
Với
2 22
2
13 1tx xx=−+⇔ =−+
( )
2
.
Nhận xét
(
)
( )
2
2
2
2
1
1
31
0
11
11
x
VT
VT
x
VP VP
x
≥
=
=
⇒ ⇔ ⇔=
≤=
− +=
.
Vậy phương trình đã cho có 3 nghiệm là
3
log 2 ; 0xx=±=
. Vậy tổng bình phương các
nghiệm của phương trình bằng
33 3
log 2 log 2 0 log 4
+ +=
.
Câu 44. Một hình trụ có bán kính đáy bằng
r
, chiều cao bằng
3r
. Trên hai đường tròn đáy của hình
trụ lần lượt lấy hai điểm
,
MN
sao cho góc giữa đường thẳng
MN
và trục
OO
′
bằng
o
30
.
Khoảng cách
d
giữa đường thẳng
MN
và trục của hình trụ là
A.
3
4
r
d =
. B.
3dr=
. C.
3
2
r
d =
. D.
3
3
r
d =
.
Lời giải
Chọn C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Kẻ
//MK OO
′
với
(
)
KO
′
∈
.
Ta có
//MK OO
′
, nên
( ) ( )
o
, , 30MN OO MN MK NMK
′
= = =
.
Ta có
//OO MK
′
, nên
( )
//OO MNK
′
, suy ra
( ) ( )
(
)
,,d OO MN d OO MNK
′′
=
Kẻ
O H MK H
′
⊥⇒
là trung điểm của
MK
và
( ) ( )
,
O H MNK d OO MN O H
′ ′′
⊥⇒ =
.
Tam giác
MNK
vuông tại
K ⇒
oo
.tan30 3.tan30AM MK r r= = =
.
Tam giác
O KN
′
đều cạnh bằng
r
, đường cao
OH
′
, suy ra
3
2
r
OH
′
=
.
Câu 45. Tập hợp tất cả các giá trị của
m
để biểu thức
(
)
( )( )
22
5
log 2 3 2 1fx xx xx m
= −+ −−−
xác
định với mọi
( )
2;x ∈ − +∞
A.
( )
;2−∞ −
. B.
(
)
;1−∞ −
. C.
(
]
;3−∞ −
. D.
(
]
;2
−∞ −
.
Lời giải
Chọn A
Ta có
( )
( )( )
22
3
log 2 3 2 1fx xx xx m
= −+ −−−
xác định với mọi
( )
2;x ∈ − +∞
( )( )
( )
22
2 3 2 1 0, 2;xx xx m x⇔ −+ −−− >∀∈−+∞
( )
2
2 1 0, 2;xx m x⇔ − − − > ∀ ∈ − +∞
( vì
( )
2
2 3 0, 2;xx x− + > ∀ ∈ − +∞
).
( ) ( )
2
2 1 , 2;m x x gx x⇔ < − − = ∀ ∈ − +∞
.
Ta có
(
)
2 20 1gx x x
′
= −=⇔=
.
Lập bảng biến thiên, ta thấy
( )
( ) ( )
2;
min 1 2gx g
− +∞
= = −
. Vậy
2m <−
.
Câu 46. Cho hàm số
( )
1
,, , 0
ax
y abc b
bx c
−
= ∈≠
+
có đồ thị như hình vẽ sau

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Mệnh đề nào dưới đây sai?
A.
2abc++=
. B.
0abc−+=
C.
0abc++=
. D.
2
abc
= −
.
Lời giải
Chọn C
Ta có tiệm cận ngang của đồ thị hàm số là
22
a
x ab
b
= =⇒=
và tiệm cận đứng của đồ thị hàm
số là
1
c
x cb
b
=−=⇒=−
.
Suy ra hàm số
21bx
y
bx b
−
=
−
mà điểm
( )
0;1A
thuộc đồ thị hàm số nên
2 .0 1 1
1 11
.0
b
b
bb b
−−
= ⇔= ⇔ =
−−
nên
2; 1ac= = −
. Vậy
2
abc++=
.
Câu 47. Cho hình nón đỉnh
S
có chiều cao bằng bán kính đáy và bằng
a
. Mặt phẳng
( )
P
đi qua đỉnh
S
và cách tâm đáy một khoảng bằng
5
a
,
( )
P
cắt đường tròn đáy của hình nón tại
A
và
B
. Độ
dài dây cung
AB
bằng
A.
3a
. B.
4
5
a
. C.
3
2
a
. D.
2
5
a
Lời giải
Chọn A
Gọi
H
là trung điểm của dây cung
AB
ta có
OH AB⊥
mà
SO AB⊥
( )
AB SOH⇒⊥
( ) (
)
SAB SOH⇒⊥
theo giao tuyến SH.
Kẻ
(
)
OK SH OK SAB⊥⇒⊥
hay
( )
( )
,
5
a
OK d O SAB= =
.
Ta có
222222
1 1 1 51 1
2
a
OH
OK SO OH a a OH
=+⇔=+⇔=
.
Do đó
2
22 2
22 2 3
4
a
AB AH OA OH a a= = − = −=
.
Câu 48. Cho
n
là số nguyên dương thỏa mãn
22
3
22 2
2 2 2 22
11
11 1
log 2022 2 log 2022 3 log 2022 log 2022 2017 1008 log 2022
n
nn
nn n
n
++
++ +
+ + +…+ = ⋅ ⋅
K
B
A
H
O
S

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Khi đó
n
thuộc khoảng nào trong các khoảng cho dưới đây?
A.
(2020;2023)
. B.
(2015;2018)
. C.
(2017;2019)
. D.
(2018;2020)
.
Lời giải
Chọn B
Ta có
22
3
22 2
2 2 2 22
11
11 1
log 2022 2 log 2022 3 log 2022 log 2022 2017 1008 lo
g 2022
n
nn
nn n
n
++
++ +
+ + +…+ = ⋅ ⋅
2 22 2 2
33 22
11
3
11 1
log 2022 2 log 2022 3 log 2022 log 2022 2017 1008 log 2022
nnn n n
n
+++ + +
⇔ + + +…+ = ⋅ ⋅
(
)
22
2233
1
33
1
2 3 log 2022 2017 1008 log 20221
nn
n
++
⇔ + + +…+ = ⋅ ⋅
2
333 3 2
2 3 2017 01 1 08
n
⇔ + + +…+ = ⋅
( )
2
2
2
20 7
1
2
1 1008
nn
⇔=
+
⋅
(
)
22
2
2
2016
. 1 .2017
22
n
n
⇔ +=
2016n⇔=
.
Vậy
(2015;2018)
2016
n = ∈
Câu 49. Cho khối chóp
.S ABC
có tam giác
ABC
vuông tại
B
,
2AC =
,
1AB =
. Tam giác
SAC
nhọn.
Gọi
I
là trung điểm
AC
, biết
()
SI ABC
⊥
và diện tích mặt cầu ngoại tiếp hình chóp
.S ABC
bằng
25
4
π
. Gọi
12
,SS
lần lượt là diện tích các mặt cầu ngoại tiếp tứ diện
SABI
và
SBCI
. Khi
đó tổng
12
SS+
bằng
A.
22
3
π
. B.
40
3
π
. C.
112
3
π
. D.
35
6
π
.
Lời giải
Chọn B
Gọi
12
,,OO O
lần lượt là tâm và
12
,,RR R
tương ứng là bán kính của các mặt cầu ngoại tiếp các
hình chóp
. ,. ,.S ABC S ABI S BCI
.
Diện tích mặt cầu ngoại tiếp hình chóp
.S ABC
bằng
25
4
π
nên
2
25 5
4
44
RR
π
π
= ⇒=
.
ABC∆
vuông tại
B
nên
SI
là trục của đường tròn ngoại tiếp
ABC∆
. Do đó,
O SI∈
và
O
là
tâm đường tròn ngoại tiếp
SAC∆
. Vì
SAC∆
nhọn nên
O
thuộc đoạn
SI
. Suy ra
2
22 2
55
12
44
SI OS OI R OC IC
= + =+ − =+ −=
.
Ta có
22
3BC AC AB= −=
và
13
24
ABI BCI ABC
SS S= = =
.
Gọi
,
JK
lần lượt là tâm của các đường tròn ngoại tiếp
ABI∆
và
BCI∆
. Khi đó,
.. 1
4
3
ABI
IA AB BI
IJ
S
= =
và
..
1
4
BCI
IC CB BI
IK
S
= =
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Dựng các đường thẳng
12
,∆∆
lần lượt đi qua
,JK
và vuông góc với
( )
ABC
. Khi đó,
11
O
∈∆
và
22
O
∈∆
. Gọi
H
là trung điểm của
SI
thì
12
,
HIJO HIKO
là các hình chữ nhật. Suy ra
2
2 22 2 2
11
14
1
3
3
R O I IJ IH
= = + = +=
và
2 2 2 2 22
22
11 2R O I IK IH= = + =+=
.
Vậy
( )
22
12 1 2
4 40
4 42
33
SS RR
π
ππ
+= + = +=
.
Câu 50. Cho phương trình
( )
( )
32
22
log 5 6 log 3 1
m
mx mx x x
+
− + −= − −
, với
m
là tham số. Số các giá
trị
x
nghiệm đúng phương trình đã cho với mọi
1m >−
là
A.
2
. B.vô số. C.
0
. D.
1
.
Lời giải
Chọn D
Điều kiện cần:
Giá trị
x
nghiệm đúng phương trình đã cho với mọi
1m >−
thì cũng nghiệm đúng phương
trình với
0m =
. Lúc này phương trình trở thành
( )
(
)
22
log 6 log 3 1
xx−= − −
( )
2
2
16
16 16
2
5
6 13
6 3 1 6 . 12
x
xx
x
x
xx
x x xx
≤<
≤< ≤<
=
⇔ ⇔ ⇔⇔
=
−+ − =
− =− − − −=
.
Điều kiện đủ:
+) Thay
2
x =
vào phương trình ta được
( )
22
log 12 2 log 2
m
m
+
− +=
. Với
1m =
thì đẳng thức
sai. Vậy
2x =
không thỏa mãn đề bài.
+) Thay
5x =
vào phương trình ta được
22
log 1 log 1
m+
=
(luôn đúng với mọi
1
m >−
).
Tóm lại, có duy nhất một giá trị
x
nghiệm đúng phương trình đã cho với mọi
1m >−
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
ĐỀ THI HỌC KỲ 1 – NĂM HỌC 2020 – 2021
SỞ GD & ĐT ĐÀ NẴNG
Môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề)
Câu 1: Hàm số nào sau đây có tối đa
3
điểm cực trị.
A.
( )
32
, ,,,y ax bx cx d a b c d= + ++ ∈
. B.
( )
, ,,,
ax b
y abcd
cx d
+
= ∈
+
.
C.
( )
2
, ,,y ax bx c a b c= ++ ∈
. D.
( )
42
, ,,y ax bx c a b c=++ ∈
.
Câu 2: Cho hình chóp
.
S ABC
đáy là tam giác
ABC
vuông cân tại
B
,
SA
vuông góc với mặt phẳng
đáy và
4SA a=
,
6AC a=
. Thể tích khối chóp
SABC
bằng:
A.
3
12a
. B.
3
48a
. C.
3
24a
. D.
3
16a
.
Câu 3: Cho hình chóp
.S ABCD
đáy là hình vuông cạnh
2a
,
SA
vuông góc với mặt phẳng đáy và
3SA a=
. Thể tích khối chóp
SABCD
bằng:
A.
3
32a
. B.
3
3a
. C.
3
6
a
. D.
3
2a
.
Câu 4: Cho hàm số
32
y ax bx cx d
,,,abcd
có đồ thị như hình vẽ bên. Có bao nhiêu số
dương trong các số
,,,abcd
?
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 5: Với
,ab
là hai số thực dương tùy ý,
a
khác
1
thì
7
4
log ab
bằng
A.
log
a
b
. B.
7 log
a
b
. C.
1 7 log
a
b
. D.
7 log
a
b
.
Câu 6: Với số thực a dương, khác 1 và các số thực
,
αβ
bất kì thì ta có
A.
a aa
αβ α β
+
= −
. B.
( )
aa
β
αβ α
+
=
. C.
a aa
αβ α β
+
= +
. D.
.a aa
αβ α β
+
=
.
Câu 7: Nếu đặt
5
x
t
thì phương trình
21 1
5 5 250
xx
trở thành
A.
2
25 1250 0tt
B.
2
5 1250 0tt
.
C.
2
5 250 0tt
D.
2
25 250 0tt
Câu 8: Nghiệm của phương trình
2
log 3x
là
A.
6x =
B.
5
x =
. C.
9x =
. D.
8x =
.
Câu 9: Tiệm cận ngang của đồ thị hàm số
2
x
y
x
là đường thẳng
A.
0y =
B.
1y = −
. C.
1
2
y
=
. D.
2y =
.
Câu 10: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
3yx x= −
. B.
3
3
yxx
=−+
.
C.
3
3yx x= +
. D.
3
3yxx=−−
.
Câu 11: Giao điểm hai đường tiệm cận của đồ thị hàm số
2
3
x
y
x
+
=
−
là điểm
A.
( )
3; 2G −
. B.
( )
1; 3F
. C.
( )
2;3H −
. D.
( )
3;1E
.
Câu 12: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3
41xx m− + +=
có 3 nghiệm phân
biệt
A. 5. B. 17. C. 7. D. 15.
Câu 13: Trung điểm các cạnh của một tứ diện đều là các đỉnh của một hình
A. bát diện đều. B. chóp đều. C. lăng trụ đều. D. lục giác đều.
Câu 14: Giá trị lớn nhất của hàm số
3
31yx x
trên đoạn
2; 2
là
A.
1
. B.
2
. C.
2
. D.
3
.
Câu 15: Khối lăng trụ tam giác đều có cạnh đáy bằng 1m và cạnh bên bằng 12m thì có thể tích là
A.
3
12 m
. B.
3
3m
. C.
3
3 3m
. D.
3
6m
.
Câu 16: Phương trình
(
)
3
log 1 2
x +=
có nghiệm là
A.
5
x
=
. B.
10
x =
. C.
7x =
. D.
8x
=
.
Câu 17: Một khu rừng có trữ lượng gỗ là
33
5.10 .m
Biết tốc độ sinh trưởng của các cây ở khu rừng đó là
4%
mỗi năm. Hỏi sau 6 năm, khu rừng đó sẽ có mét khối gỗ gần với giá trị nào nhất sau đây?
A.
( )
3
657966 m
. B.
( )
3
729990 m
. C.
( )
3
632660 m
. D.
( )
3
608326 m
.
Câu 18: Hàm số
32
37yx x=−+ −
đạt cực tiểu tại điểm
A.
7x
= −
. B.
0x =
. C.
3x = −
. D.
2x =
.
Câu 19: Cho hàm số
( )
y fx=
có bảng xét dấu đạo hàm như sau
Hàm số đã cho:
A. Nghịch biến trên khoảng
( )
0; +∞
. B. Đồng biến trên khoảng
( )
;3−∞ −
.
B. Đồng biến trên khoảng
( )
3; 0−
. C. Nghịch biến trên khoảng
( )
3; 3−
.
Câu 20: Giá trị của
31 31
:
ππ
+−
bằng

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
23
π
. B.
π
. C.
2
π
. D.
4
π
.
Câu 21: Tọa độ giao điểm của đồ thị hàm số
42
23yx x=−−
với trục hoành.
A.
(
)
3; 60
và
( )
3; 60−
. B.
( )
3;0−
và
( )
3;0
.C.
( )
0; 3−
. D.
( )
1; 0−
và
( )
1; 0
.
Câu 22: Cho khối tứ diện
ABCD
và gọi
M
là trung điểm của đoạn thẳng
AB
. Khi đó mặt phẳng
( )
P
chứa đường cạnh
CM
, song song với
BD
chia khối tứ diện
ABCD
thành
A. Hai khối chóp tứ giác B. Hai khối tứ diện.
C. Một khối tứ diện và một khối lăng trụ. D. Một khối tứ diện và một khối chóp tứ giác
Câu 23: Có tất cả bao nhiêu loại khối đa diện đều.
A.
4
. B.
5
. C.
6
. D.
7
.
Câu 24: Giá trị lớn nhất của hàm số
3
1
x
y
x
−
=
+
trên
[
]
0;50
là
A.
1
−
. B.
0
. C.
3−
. D.
47
51
.
Câu 25: Tập nghiệm của phương trình
32
x
là
A.
. B.
2
3
. C.
3
log 2
. D.
2
log 3
.
Câu 26: Tìm đạo hàm của hàm số
3
log
yx
trên khoảng
0;
A.
ln 3yx
. B.
1
y
x
. C.
1
ln 3
y
x
. D.
ln 3
y
x
.
Câu 27: Số giao điểm của đồ thị hàm số
42
2yx x
và đường thẳng
1y
là
A.
3
. B.
4
. C.
0
. D.
2
.
Câu 28: Hàm số
4
9= −yx
A. Đồng biến trên khoảng
( )
0; +∞
. B. Nghịch biến trên khoảng
( )
;3
−∞
.
C. Đồng biến trên khoảng
( )
;0−∞
. D. Nghịch biến trên khoảng
( )
3;+∞
.
Câu 29: Điểm cực đại của đồ thị hàm số
42
64=−−
yx x
là:
A.
( )
3; 13−
P
. B.
( )
0; 4−N
. C.
( )
3; 23Q
. D.
( )
0;0M
.
Câu 30: Diện tích xung quanh của hình nón có độ đường sinh
3l =
và có bán kính đáy
2r =
là
A.
12
π
. B.
24
π
. C.
18
π
. D.
6
π
.
Câu 31: Thể tích của khối chóp có diện tích đáy
2
6mS
=
và chiều cao
3mh =
bằng
A.
3
6m
. B.
3
12m
. C.
3
18m
. D.
3
4m
.
Câu 32: Tiếp tuyến của đồ thị hàm số
32
32yx x
=+−
tại điểm có hoành độ bằng
2
là đường thẳng đi
qua điểm
A.
( )
3; 42
K
. B.
( )
4;38L
. C.
( )
1; 72H
. D.
( )
0; 2G −
.
Câu 33: Tìm đạo hàm của hàm số
( )
1
e
yx= −
trên khoảng
( )
1; +∞
.
A.
( )
1
1
e
y ex
+
′
= −
. B.
( )( )
11
e
ye x
′
=−−
. C.
( )
1
1
e
y ex
−
′
= −
. D.
( )
1
e
yx
′
= −
.
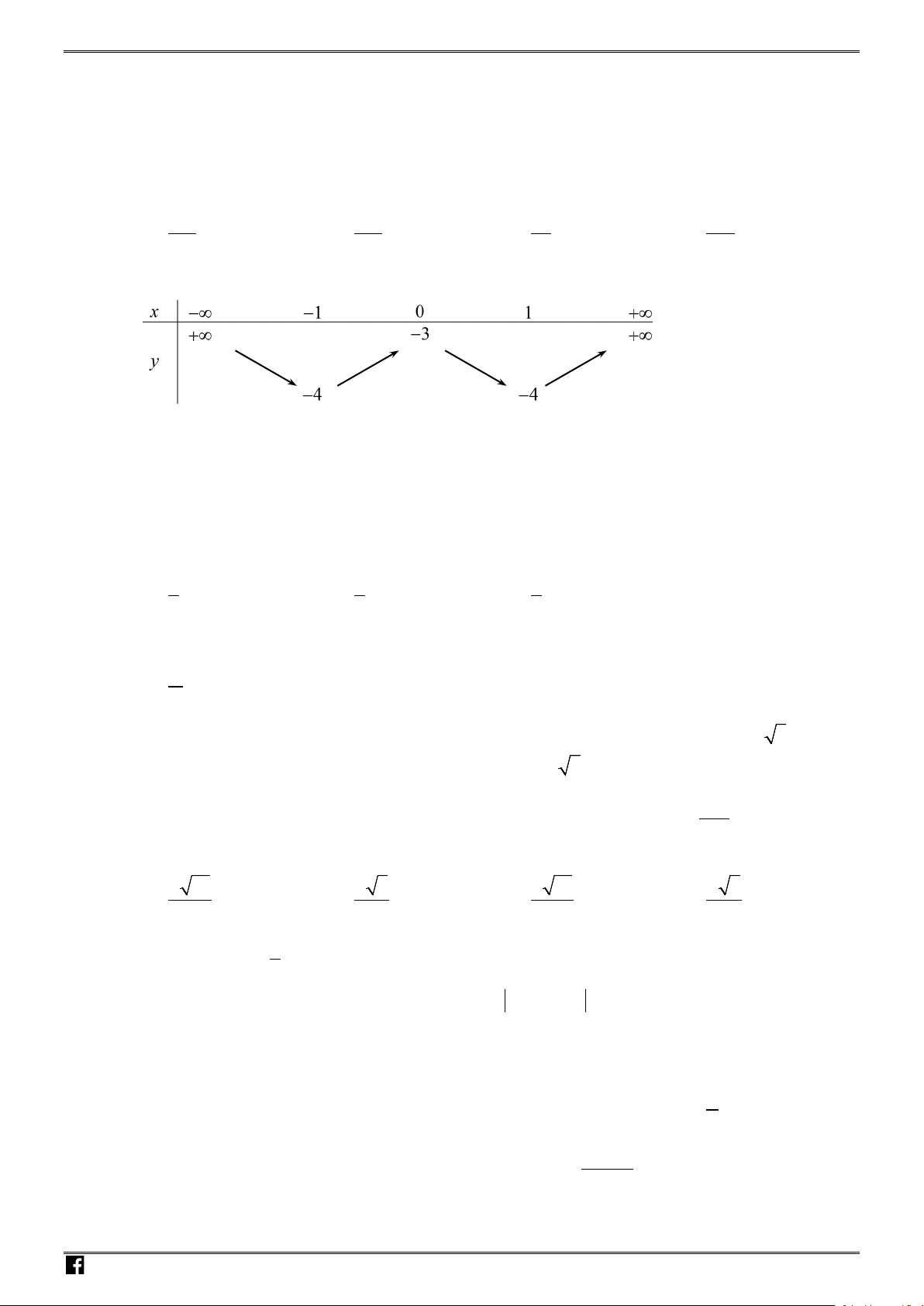
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 34: Tập xác định của hàm số
3
x
y =
là
A.
. B.
( )
0;+∞
. C.
[
)
0;+∞
. D.
{ }
\0
.
Câu 35: Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
và
AC
′
tạo với mặt phẳng
đáy một góc
0
60
. Thể tích khối lăng trụ
.
ABC A B C
′′′
bằng
A.
3
3
2
a
. B.
3
3
4
a
. C.
3
4
a
. D.
3
3
8
a
.
Câu 36: Tìm hàm số
42
y ax bx c=++
có bảng biến thiên như hình vẽ bên
A.
42
23yx x=−−
. B.
42
23yx x=+−
.
C.
42
23yx x=−+ +
. D.
42
23yx x=−+ −
Câu 37: Số cạnh của khối mười hai mặt đều là
A.
12
. B.
20
. C.
30
. D.
16
.
Câu 38: Khối nón có chiều cao
h
, độ dài đường sinh
l
, bán kính đáy
r
thì có thể tích bằng
A.
2
1
3
rh
π
. B.
1
3
rh
π
. C.
2
1
3
rl
π
. D.
2
rh
π
.
Câu 39: Với
a
và
b
là các số thực dương, khác 1 và
α
là số thực bất kỳ thì
log
a
b
α
bằng
A.
1
log
a
b
α
. B.
log
a
b
α
−
. C.
log
b
a
α
−
. D.
log
a
b
α
.
Câu 40: Thể tích của khối hộp chữ nhật
.ABCD A B C D
′′′′
có
AA a
′
=
,
2AB a=
và
5
AC a=
bằng
A.
3
6a
. B.
3
15a
. C.
3
25a
. D.
3
2a
.
Câu 41: Nếu khối lăng trụ đều
.ABC A B C
′′′
có cạnh đáy bằng
a
và thể tích bằng
2
3
4
a
thì khoảng cách
giữa hai đường thẳng
AB
và
AC
′
là
A.
15
3
a
. B.
3
5
a
. C.
15
5
a
. D.
5
3
a
.
Câu 42: Cho hàm số
( )
32
1
2 91
3
yxm x x
= −− −+
, với
m
là tham số. Gọi
1
x
,
2
x
là các điểm cực trị của
hàm số đã cho thì giá trị nhỏ nhất của biểu thức
12
9 25xx−
là
A.
15
. B.
90
. C.
450
. D.
45
.
Câu 43: Gía trị của biểu thức
23
2020! 2020!
log (2020!) log (2020!)−
bằng :
A.
0
. B.
1
. C.
2020!
. D.
2
3
.
Câu 44: Đặt
3
log 2a =
, khi đó
72
log 768
được biểu diễn dưới dạng
2
ma n
pa
+
+
, với
,,mn p
là các số nguyên.
Giá trị
23
mn p++
bằng:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
12.
B.
36.
C.
10.
D.
73.
Câu 45: Người ta cần xây một hồ chứa nước dạng hình hộp chứ nhật không nắp cao
1, 5
m
và có chiều dài
gấp đôi chiều rộng ( minh họa như hình vẽ bên ). Nếu tổng diện tích bốn mặt xung quanh của hồ
là
2
18
m
thì dung tích của hồ là
A.
3
48m
. B.
3
18
m
. C.
3
12
m
. D.
3
5m
.
Câu 46: Cho
0, 0ab>>
thỏa mãn
4 25
4
log log log
4
ba
ab
−
= =
. Giá trị của
66
log 4 2 log
2
a
bb
+−
bằng
A.
4
. B.
6
. C.
2
. D.
1
.
Câu 47: Cho hàm số bậc bốn
()y fx=
và hàm số bậc hai
()y gx=
có đồ thị cắt nhau tại điểm
0
x
như
hình vẽ bên, trong đó đường đậm hơn là đồ thị của hàm số
( ).y fx
=
Xét hàm số
() ().(),
hx f x gx
=
tìm mệnh đề đúng.
A.
(
)
0
'0hx =
. B.
( )
0
'0hx >
.
C.
( )
0
'0hx<
. D.
( ) ( ) ( )
0 00
' ' .'hx f x gx=
.
Câu 48: Có bao nhiêu giá trị nguyên thuộc khoảng
( 30;30)−
của tham số
m
để mọi tiếp tuyến của đồ thị
hàm số
32
(2 3) 1y x mx m x=− + −−
đều có hệ số góc dương?
A.
1
. B.
59
. C.
0
. D.
58
.
Câu 49: Cho hàm số
( )
y fx=
có
( )
0,fx x
′
> ∀∈
. Có bao nhiêu giá trị nguyên của
x
để
( )
( )
2
22f x fx>
A.
23
. B.
20
. C.
21
. D.
22
.
Câu 50: Cho khối chóp
.S ABC
có thể tích
3
24 cm
. Gọi
B
′
là trung điểm của
AB
và
C
′
là điểm trên cạnh
AC
sao cho
3AC CC
′′
=
( minh họa như hình vẽ)
1,5m
x
y
x
0
y=g(x)
y=f(x)
O

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Thể tích của khối chóp
.
S AB C
′′
bằng
A.
3
8 cm
. B.
3
6 cm
. C.
3
2 cm
. D.
3
9 cm
.
A
C
B
S
B'
C'
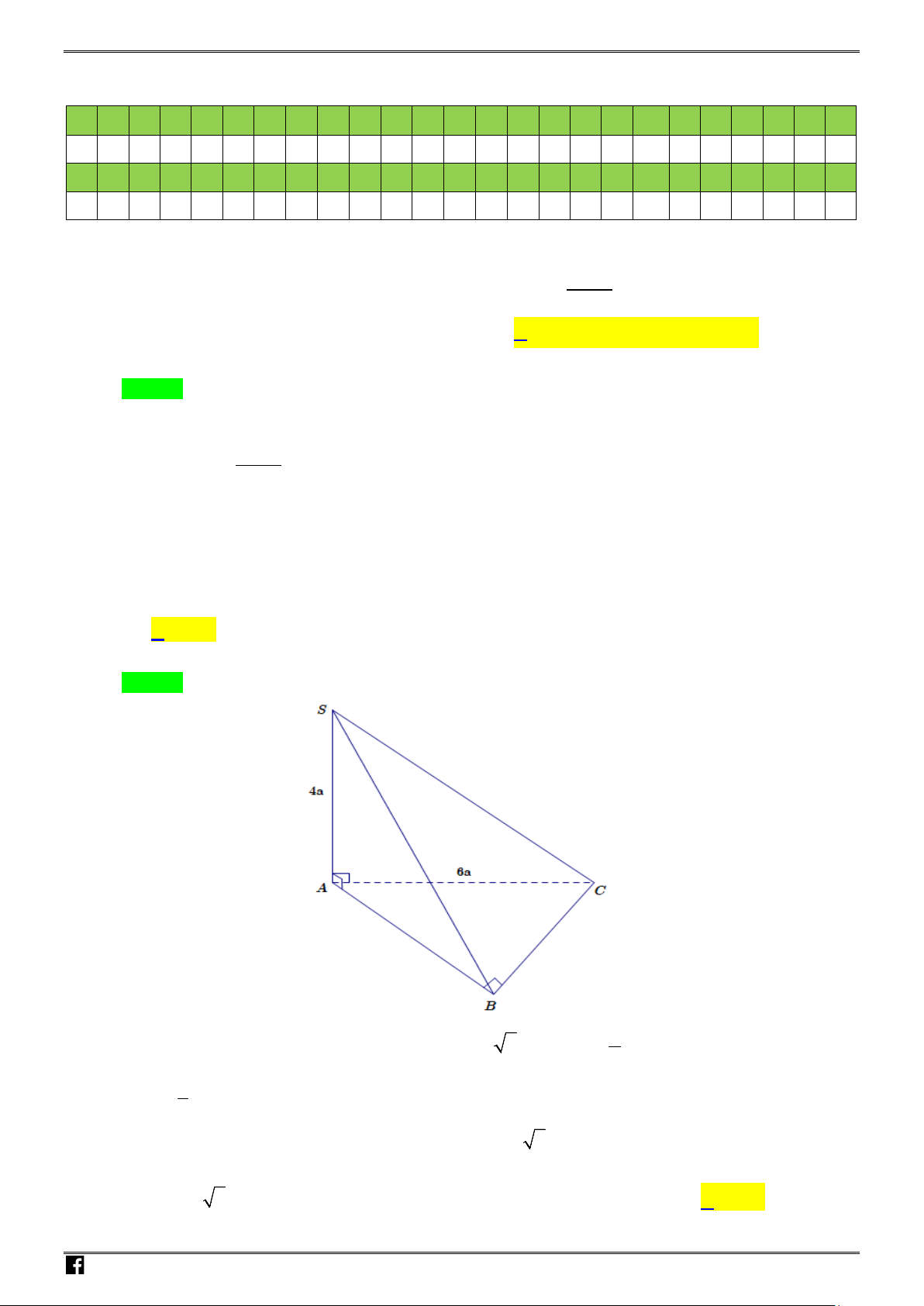
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
BẢNG ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
A
D
B
D
D
A
D
B
A
D
A
A
D
C
D
C
B
B
C
B
D
B
D
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
C
D
A
B
D
A
A
C
A
B
A
C
A
D
D
C
B
B
B
C
C
C
C
C
D
Câu 1: Hàm số nào sau đây có tối đa
3
điểm cực trị.
A.
( )
32
, ,,,y ax bx cx d a b c d= + ++ ∈
. B.
( )
, ,,,
ax b
y abcd
cx d
+
= ∈
+
.
C.
( )
2
, ,,y ax bx c a b c= ++ ∈
. D.
( )
42
, ,,y ax bx c a b c=++ ∈
.
Lời giải
Chọn D
Ta có
( )
32
, ,,,y ax bx cx d a b c d= + ++ ∈
có tối đa
2
cực trị.
Hàm số
( )
, ,,,
ax b
y abcd
cx d
+
= ∈
+
không có cực trị.
Hàm số
( )
2
, ,,y ax bx c a b c= ++ ∈
có tối đa
1
cực trị.
Hàm số
( )
42
, ,,y ax bx c a b c=++ ∈
có tối đa
3
cực trị.
Câu 2: Cho hình chóp
.S ABC
đáy là tam giác
ABC
vuông cân tại
B
,
SA
vuông góc với mặt phẳng
đáy và
4SA a
=
,
6AC a=
. Thể tích khối chóp
SABC
bằng:
A.
3
12a
. B.
3
48
a
. C.
3
24a
. D.
3
16a
.
Lời giải
Chọn A
Ta có
ABC∆
vuông cân tại
B
nên
32AB BC a= =
2
1
.9
2
ABC
S AB BC a
∆
⇒= =
.
3
1
. 12
3
ABC
V SA S a
∆
⇒= =
.
Câu 3: Cho hình chóp
.S ABCD
đáy là hình vuông cạnh
2a
,
SA
vuông góc với mặt phẳng đáy và
3SA a=
. Thể tích khối chóp
SABCD
bằng:
A.
3
32a
. B.
3
3a
. C.
3
6a
. D.
3
2a
.
Lời giải
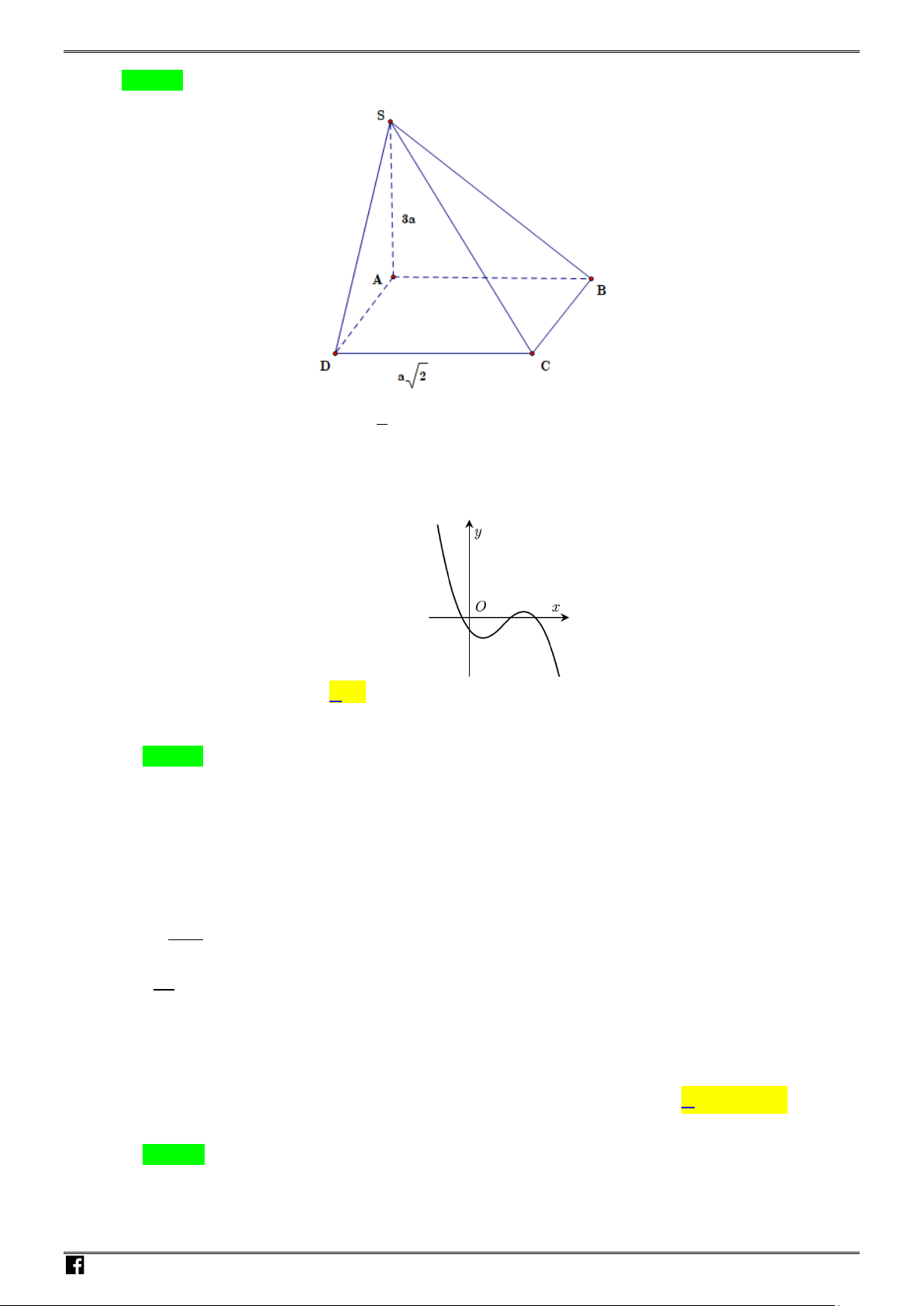
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn D
Ta có
2
2
ABCD
Sa=
3
1
.2
3
ABCD
V SA S a⇒= =
.
Câu 4: Cho hàm số
32
y ax bx cx d
,,,abcd
có đồ thị như hình vẽ bên. Có bao nhiêu số
dương trong các số
,,,
abcd
?
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Từ đồ thị hàm số đã cho ta có:
0a
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ am nên
0d
.
Hoành độ hai điểm cực trị là nghiệm của phương trình
2
32y x ax bx c
các giá trị này
đều dương nên ta có:
2
0
2.3
0
3
b
a
c
a
0
0
b
c
Như vậy trong bốn số
,,,abcd
chỉ có một số dương là số
b
.
Câu 5: Với
,ab
là hai số thực dương tùy ý,
a
khác
1
thì
7
4
log ab
bằng
A.
log
a
b
. B.
7 log
a
b
. C.
1 7 log
a
b
. D.
7 log
a
b
.
Lời giải
Chọn D
Ta có:
7
log
a
ab
7log log
aa
ab
7 log
a
b

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 6: Với số thực a dương, khác 1 và các số thực
,
αβ
bất kì thì ta có
A.
a aa
αβ α β
+
= −
. B.
(
)
aa
β
αβ α
+
=
. C.
a aa
αβ α β
+
= +
. D.
.a aa
αβ α β
+
=
.
Lời giải
Chọn D
Câu 7: Nếu đặt
5
x
t
thì phương trình
21 1
5 5 250
xx
trở thành
A.
2
25 1250 0tt+− =
. B.
2
5 1250 0tt++ =
.
C.
2
5 250 0tt+− =
D.
2
25 250 0
tt+− =
Lời giải
Chọn A
21 1
5 5 250
xx
2
1
. 5 5.5 250 0
5
xx
2
1
5 250 0
5
tt
2
25 1250 0tt
.
Câu 8: Nghiệm của phương trình
2
log 3x
là
A.
6x =
B.
5x
=
. C.
9x =
. D.
8x =
.
Lời giải
Chọn D
Điều kiện:
0x
.
3
2
log 3 2 8x x x tm
.
Vậy phương trình có nghiệm là
8
x
.
Câu 9: Tiệm cận ngang của đồ thị hàm số
2
x
y
x
là đường thẳng
A.
0y =
B.
1y
= −
. C.
1
2
y =
. D.
2y =
.
Lời giải
Chọn B
Ta có
lim 1 1
x
yy
là đường tiệm cận ngang của đồ thị hàm số.
Câu 10: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
3yx x= −
. B.
3
3yx x=−+
.
C.
3
3yx x= +
. D.
3
3yxx=−−
.
Lời giải
Chọn A

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta thấy khoảng ngoài cùng bên tay phải của đồ thị đi lên
0a⇒>
, Loại đáp án B,D.
Và đồ thị có 2 điểm cực trị nên loại đáp án A.
Câu 11: Giao điểm hai đường tiệm cận của đồ thị hàm số
2
3
x
y
x
+
=
−
là điểm
A.
(
)
3; 2G
−
. B.
( )
1; 3F
. C.
( )
2;3H −
. D.
( )
3;1E
.
Lời giải
Chọn D
Đồ thị hàm số đã cho có tiệm cận đứng
3x
=
, tiệm cận ngang
1
y =
.
Giao điểm 2 đường tiệm cận của đồ thị hàm số là điểm
( )
3;1
.
Câu 12: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3
41xx m
− + +=
có 3 nghiệm phân
biệt
A. 5. B. 17. C. 7. D. 15.
Lời giải
Chọn A
3
41xx m− + +=
Đặt
3
() 4 1y fx x x= =−+ +
(*)
22
23
3
' 3 40 3 40
23
3
x
yx x
x
= −
=− +=⇔− +=⇔
=
BBT:
Dựa vào bảng biến thiên:
(*) có 3 nghiệm phân biệt
16 16
33
11
33
m
−
⇔ +< < +
24m≈− < <
mà
{ }
1; 0;1; 2; 3mm∈ ⇒ ∈−
Câu 13: Trung điểm các cạnh của một tứ diện đều là các đỉnh của một hình
A. bát diện đều. B. chóp đều. C. lăng trụ đều. D. lục giác đều.
Lời giải
Chọn A
Dễ thấy có 6 đỉnh và tính đối xứng nên đáp án là bát diện đều.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 14: Giá trị lớn nhất của hàm số
3
31yx x
trên đoạn
2; 2
là
A.
1
. B.
2
. C.
2
. D.
3
.
Lời giải
Chọn D
Ta có
2
1
3 30
1
x
yx
x
.
Khi đó
21y
,
13y
,
11y
,
23y
.
Từ đó suy ra giá trị lớn nhất cần tìm là
3
.
Câu 15: Khối lăng trụ tam giác đều có cạnh đáy bằng 1m và cạnh bên bằng 12m thì có thể tích là
A.
3
12 m
. B.
3
3m
. C.
3
3 3m
. D.
3
6m
.
Lời giải
Chọn C
Ta có diện tích tam giác đều cạnh
a
là
2
3
4
a
suy ra diện tích đáy là
2
3
m
4
.
Do đó thể tích cần tìm bằng
3
3
12. 3 3 m
4
Bh
.
Câu 16: Phương trình
( )
3
log 1 2x +=
có nghiệm là
A.
5x =
. B.
10x =
. C.
7
x =
. D.
8x =
.
Lời giải
Chọn D .
( )
2
3
log 1 2 1 3 8.xxx+ = ⇔ += ⇔ =
Câu 17: Một khu rừng có trữ lượng gỗ là
33
5.10 .m
Biết tốc độ sinh trưởng của các cây ở khu rừng đó là
4%
mỗi năm. Hỏi sau 6 năm, khu rừng đó sẽ có mét khối gỗ gần với giá trị nào nhất sau đây?
A.
( )
3
657966 m
. B.
( )
3
729990 m
. C.
( )
3
632660 m
. D.
( )
3
608326 m
.
Lời giải
Chọn C
Sau 6 năm, khu rừng đó sẽ có mét khối gỗ là
( )
(
)
6
33
6
5.10 . 1 0,04 632660Pm= +≈
.
Câu 18: Hàm số
32
37yx x=−+ −
đạt cực tiểu tại điểm
A.
7x = −
. B.
0x
=
. C.
3x
= −
. D.
2x =
.
Lời giải
Chọn B
Ta có
32 2
0
37 36 0 .
2
x
y x x y x xy
x
=
′′
=−+ −⇒=− +⇒=⇔
=
( ) ( )
6 6 0 6; 2 6.yx y y
′′ ′′ ′′
=− +⇒ = =−
Vậy hàm số đạt cực tiểu tại
0.x =
Câu 19: Cho hàm số
( )
y fx=
có bảng xét dấu đạo hàm như sau

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Hàm số đã cho:
A. Nghịch biến trên khoảng
( )
0; +∞
. B. Đồng biến trên khoảng
( )
;3−∞ −
.
B. Đồng biến trên khoảng
( )
3; 0−
. C. Nghịch biến trên khoảng
( )
3; 3
−
.
Lời giải
Chọn B
Từ bảng xét dấu
y
′
ta có
( )
0, ; 3yx
′
> ∀ ∈ −∞ −
nên hàm số đồng biến trên khoảng
( )
;3−∞ −
.
Câu 20: Giá trị của
31 31
:
ππ
+−
bằng
A.
23
π
. B.
π
. C.
2
π
. D.
4
π
.
Lời giải
Chọn C
( )
31 31
31 31 2
:
ππ π π
+− −
+−
= =
.
Câu 21: Tọa độ giao điểm của đồ thị hàm số
42
23yx x=−−
với trục hoành.
A.
( )
3; 60
và
( )
3; 60−
. B.
( )
3;0
−
và
( )
3;0
.C.
( )
0; 3−
. D.
( )
1; 0−
và
( )
1; 0
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm
2
42
2
1
2 30 3
3
x
xx x
x
= −
− −=⇔ ⇔ =±
=
.
Vậy tọa độ giao điểm là
( )
3;0−
và
( )
3;0
.
Câu 22: Cho khối tứ diện
ABCD
và gọi
M
là trung điểm của đoạn thẳng
AB
. Khi đó mặt phẳng
( )
P
chứa đường cạnh
CM
, song song với
BD
chia khối tứ diện
ABCD
thành
A. Hai khối chóp tứ giác B. Hai khối tứ diện.
C. Một khối tứ diện và một khối lăng trụ. D. Một khối tứ diện và một khối chóp tứ giác
Lời giải
Chọn D
Kẻ
MO
song song với
BD
Suy ra mặt phẳng
( )
P
chứa đường cạnh
CM
, song song với BD là mặt phẳng
( )
COM

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Mặt phẳng
(
)
COM
chia tứ diện thành một khối tứ diện A.MOC và một khối chóp tứ giác
C.BMOD.
Câu 23: Có tất cả bao nhiêu loại khối đa diện đều.
A.
4
. B.
5
. C.
6
. D.
7
.
Lời giải
Chọn B
Ta có 5 loại khối đa diện đều
{ } { } { } { } { }
3;3 , 4;3 , 3;4 , 5;3 , 3;5
.
Câu 24: Giá trị lớn nhất của hàm số
3
1
x
y
x
−
=
+
trên
[ ]
0;50
là
A.
1−
. B.
0
. C.
3−
. D.
47
51
.
Lời giải
Chọn D
Ta có
(
)
2
4
1
y
x
′
=
+
.
0y
′
=
( )
2
4
0
1x
⇔=
+
( vô nghiệm)
( )
03
03
01
y
−
= = −
+
;
( )
50 3 47
50
50 1 51
y
−
= =
+
Vậy giá trị lớn nhất của hàm số là
47
51
.
Câu 25: Tập nghiệm của phương trình
32
x
là
A.
. B.
2
3
. C.
3
log 2
. D.
2
log 3
.
Lời giải
Chọn C
Ta có
3
3 2 log 2
x
x
.
Câu 26: Tìm đạo hàm của hàm số
3
logyx
trên khoảng
0;
A.
ln 3yx
. B.
1
y
x
. C.
1
ln 3
y
x
. D.
ln 3
y
x
.
Lời giải
Chọn C
Ta có
3
1
log
ln 3
yx
x
.
Câu 27: Số giao điểm của đồ thị hàm số
42
2yx x
và đường thẳng
1y
là
A.
3
. B.
4
. C.
0
. D.
2
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm
2
42 42 2
2 1 2 10 1 0xx xx x
2
10 1 1x xx
hai đồ thị có hai giao điểm.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 28: Hàm số
4
9= −yx
A. Đồng biến trên khoảng
( )
0; +∞
. B. Nghịch biến trên khoảng
(
)
;3
−∞
.
C. Đồng biến trên khoảng
(
)
;0
−∞
. D. Nghịch biến trên khoảng
(
)
3;
+∞
.
Lời giải
Chọn A
Xét hàm số
4
9= −yx
ta có:
Tập xác định:
=
D
3
4yx
′
=
.
00yx
′
=⇔=
Bảng biến thiên:
Suy ra hàm số đồng biến trên khoảng
( )
0; +∞
, nghịch biến trên khoảng
( )
;0−∞
.
Vậy chọn A.
Câu 29: Điểm cực đại của đồ thị hàm số
42
64
=−−yx x
là:
A.
(
)
3; 13−
P
. B.
( )
0; 4−N
. C.
( )
3; 23Q
. D.
( )
0;0M
.
Lời giải
Chọn B
Xét hàm số
42
64
=−−yx x
ta có:
Tập xác định:
= D
3
04
4 12 ; 0
3 13
=⇒=−
′′
=−=⇔
=± ⇒=−
xy
y x xy
xy
Bảng biến thiên:
Suy ra điểm cực đại của đồ thị hàm số đã cho là:
( )
0; 4−N
.
Câu 30: Diện tích xung quanh của hình nón có độ đường sinh
3l =
và có bán kính đáy
2
r =
là
A.
12
π
. B.
24
π
. C.
18
π
. D.
6
π
.
Lời giải
Chọn D

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
.2.3 6
xq
S rl
ππ π
= = =
.
Câu 31: Thể tích của khối chóp có diện tích đáy
2
6m
S =
và chiều cao
3mh =
bằng
A.
3
6m
. B.
3
12m
. C.
3
18m
. D.
3
4m
.
Lời giải
Chọn A
Thể tích của khối chóp là
3
11
. .6.3 6m
33
V Sh= = =
.
Câu 32: Tiếp tuyến của đồ thị hàm số
32
32yx x=+−
tại điểm có hoành độ bằng
2
là đường thẳng đi
qua điểm
A.
( )
3; 42K
. B.
(
)
4;38L
. C.
( )
1; 72H
. D.
( )
0; 2
G
−
.
Lời giải
Chọn A
Ta có
( )
2
3 6 2 24y x xy
′′
= +⇒ =
và
( )
2 18y
=
.
Phương trình tiếp tuyến tại điểm có hoành độ bằng
2
là
( )
24 2 18yx= −+
hay
24 30
yx= −
.
Đưởng thẳng tiếp tuyến đi qua điểm
( )
3; 42K
.
Câu 33: Tìm đạo hàm của hàm số
( )
1
e
yx= −
trên khoảng
( )
1; +∞
.
A.
( )
1
1
e
y ex
+
′
= −
. B.
( )(
)
11
e
ye x
′
=−−
. C.
( )
1
1
e
y ex
−
′
= −
. D.
( )
1
e
yx
′
= −
.
Lời giải
Chọn C
Ta có
( )
( )
( ) ( ) ( )
11
1 .1.1 1
ee e
y x e x x ex
−−
′
′
′
= − = − −= −
.
Câu 34: Tập xác định của hàm số
3
x
y
=
là
A.
. B.
( )
0;+∞
. C.
[
)
0;+∞
. D.
{ }
\0
.
Lời giải
Chọn A.
Theo định nghĩa, tập xác định của hàm số mũ là
D =
.
Câu 35: Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
và
AC
′
tạo với mặt
phẳng đáy một góc
0
60
. Thể tích khối lăng trụ
.ABC A B C
′′′
bằng
A.
3
3
2
a
. B.
3
3
4
a
. C.
3
4
a
. D.
3
3
8
a
.
Lời giải
Chọn B
R
h
l

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có :
0
tan .tan 60 3
AA
A CA AA AC a
AC
′
′′
=⇔= =
23
.
33
. .3
44
ABC A B C d
aa
V Sh a
′′′
⇒== =
.
Câu 36: Tìm hàm số
42
y ax bx c=++
có bảng biến thiên như hình vẽ bên
A.
42
23yx x=−−
. B.
42
23yx x=+−
.
C.
42
23yx x=−+ +
. D.
42
23yx x=−+ −
Lời giải
Chọn A
Nhận xét : Dựa vào chiều biến thiên ta thấy
0a
>
, đồ thị hàm số có 3 điểm cực trị nên
00ab b<⇒<
. Kiểm tra đáp án A.
42 3
23 44
yx x y x x
′
= − −⇒ = −
.
3
03
04 40
14
xy
y xx
xy
=⇒=−
′
=⇔ −=⇔
=±⇒ =−
Chọn đáp án A.
Câu 37: Số cạnh của khối mười hai mặt đều là
A.
12
B.
20
C.
30
D.
16
Lời giải
Chọn C
Câu 38: Khối nón có chiều cao
h
, độ dài đường sinh
l
, bán kính đáy
r
thì có thể tích bằng
A.
2
1
3
rh
π
. B.
1
3
rh
π
. C.
2
1
3
rl
π
. D.
2
rh
π
.
Lời giải
Chọn A
Câu 39: Với
a
và
b
là các số thực dương, khác 1 và
α
là số thực bất kỳ thì
log
a
b
α
bằng
A.
1
log
a
b
α
. B.
log
a
b
α
−
. C.
log
b
a
α
−
. D.
log
a
b
α
.
Lời giải
Chọn D
Theo quy tắc tính logarit thì
log log
aa
bb
α
α
=
.
a
a
a
B
C
A'
C'
B'
A
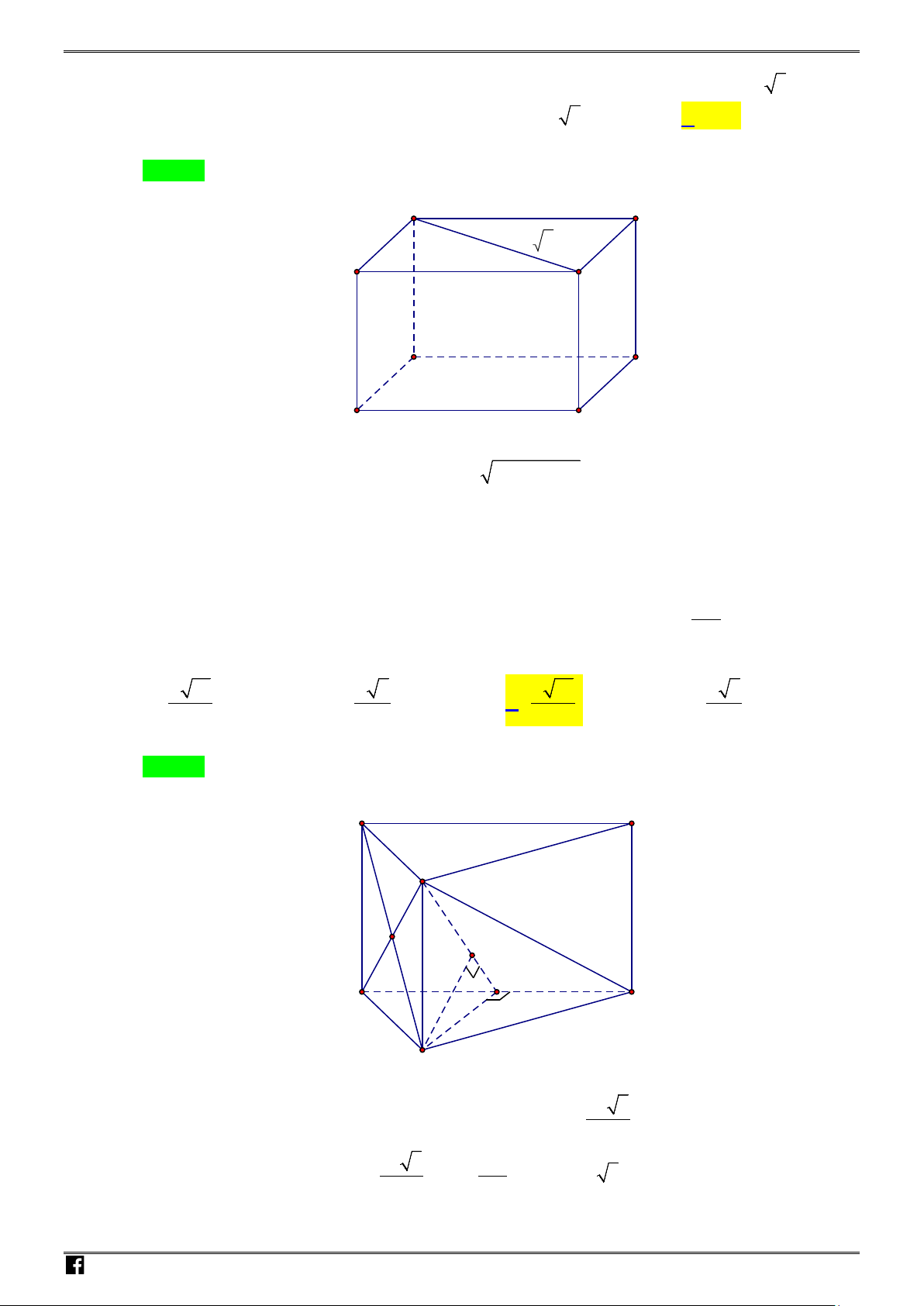
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 40: Thể tích của khối hộp chữ nhật
.ABCD A B C D
′′′′
có
AA a
′
=
,
2AB a=
và
5AC a
=
bằng
A.
3
6a
. B.
3
15a
. C.
3
25a
. D.
3
2a
.
Lời giải
Chọn D
Xét tam giác
ABC
vuông tại
A
ta có:
22
BC AC AB a= −=
.
Ta có:
2
.2
ABCD
S AB BC a= =
.
23
.
. .2 2
ABCD A B C D ABCD
V AA S a a a
′′′′
′
= = =
.
Vậy
3
.
2
ABCD A B C D
Va
′′′′
=
.
Câu 41: Nếu khối lăng trụ đều
.
ABC A B C
′′′
có cạnh đáy bằng
a
và thể tích bằng
2
3
4
a
thì khoảng cách
giữa hai đường thẳng
AB
và
AC
′
là
A.
15
3
a
. B.
3
5
a
. C.
15
5
a
. D.
5
3
a
.
Lời giải
Chọn C
Theo đề bài,
ABC∆
là tam giác đều cạnh
a
suy ra
2
3
4
ABC
a
S
∆
=
.
Ta có
23
.
33
.. 3
44
ABC A B C ABC
aa
V S CC CC CC a
′′′
∆
′′′
= ⇔ =⇔=
.
Mặc khác
//AB A B
′′
( )
//AB CA B
′′
⇒
.
2a
a
a
5
D
C
B
C'
A'
B'
D'
A
D
I
C
B
C'
B'
A'
A
H

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Do đó
( ) ( )
( )
( )
( )
,, ,
d AB AC d AB CAB d A CAB
′ ′′ ′′
= =
. (1)
Gọi
I
là tâm hình chữ nhật
ACC A
′′
. Suy ra
I
là trung điểm
AC
′
(
)
(
)
( )
( )
,,d A CA B d C CA B
′′ ′ ′′
⇒=
. (2)
Kẻ
,CD AB D AB
′ ′′ ′′
⊥∈
. Kẻ
,C H CD H CD
′
⊥∈
.
Khi đó
( )
( )
,'d C CA B C H
′ ′′
=
. (3)
ABC
′′′
∆
cũng là tam giác đều cạnh
a
do đó
3
2
a
CD
′
=
.
Khi đó
22
22
3
3.
. 15
2
'
5
3
3
4
a
a
CCCD a
CH
CC CD
aa
′′
= = =
′′
+
+
. (4)
Từ (1), (2), (3), (4) ta có
( )
15
,
5
a
d AB A C
′
=
.
Câu 42: Cho hàm số
( )
32
1
2 91
3
yxm x x= −− −+
, với
m
là tham số. Gọi
1
x
,
2
x
là các điểm cực trị của
hàm số đã cho thì giá trị nhỏ nhất của biểu thức
12
9 25xx−
là
A.
15
. B.
90
. C.
450
. D.
45
.
Lời giải
Chọn B
Ta có
( )
2
2 29yx m x
′
=− −−
.
Vì
( )
1. 9 0−<
nên
0
y
′
=
luôn có 2 nghiệm phân biệt
1
x
,
2
x
và cũng là 2 điểm cực trị của hàm
số.
Nhận xét:
12
9 25xx−
không đổi giá trị khi
12
0xx<<
hay
21
0xx<<
.
Giả sử
21
0xx<<
. Khi đó
( )
2
1
2 29
xm m= −+ − +
,
( )
2
2
2 29xm m= −− − +
và
( )
( )
( )
( )
22
12
9 25 9. 2 2 9 25 2 2 9xx m m m m− = −+ − + − −− − +
( )
( )
2
34 2 9 16 2 0mm= − +− − >
.
Suy ra
12
9 25xx−
( ) ( )
2
2
34 2 9 16 2 34 9 16m m tt= − +− − = +−
với
2tm= −
.
Xét hàm số
( )
2
34 9 16ft t t= +−
.
Ta có:
( )
2
8
34. 16 0
5
9
t
ft t
t
′
= − = ⇔=
+
.
Lập bảng biến thiên, ta thấy được:
( )
8
max 90
5
ft f
= =
. Với
8 8 18
2
5 55
tm m= ⇔ −= ⇔ =
.
Vậy
12
9 25xx−
đạt giá trị lớn nhất bằng
90
khi
18
5
m
=
.
Câu 43: Gía trị của biểu thức
23
2020! 2020!
log (2020!) log (2020!)−
bằng :
A.
0
. B.
1
. C.
2020!
. D.
2
3
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn B
Ta có :
23
2020! 2020!
log (2020!) log (2020!) 2 3 1.
− =−=−
Câu 44: Đặt
3
log 2a =
, khi đó
72
log 768
được biểu diễn dưới dạng
2
ma n
pa
+
+
, với
,,mn p
là các số nguyên.
Giá trị
23
mn p++
bằng :
A.
12.
B.
36.
C.
10.
D.
73.
Lời giải
Chọn B
Ta có:
( ) ( )
5
72 72 72
32 32
3 23
23
32 1 5 1 5 1
log 768 log .72 1 log 2 1 1
3 log 72 log 72 log 72
log 2 .3 log 2 .3
5 1 5 1 81
11 .
2
32 323232
3
aa
a aaa
a
= =+−=+−=+ −
+
=+−=+−=
+ +++
+
Vậy
23
8, 1, 3 36.m n p mn p= = =⇒+ + =
Câu 45: Người ta cần xây một hồ chứa nước dạng hình hộp chứ nhật không nắp cao
1, 5
m
và có chiều dài
gấp đôi chiều rộng ( minh họa như hình vẽ bên ). Nếu tổng diện tích bốn mặt xung quanh của hồ
là
2
18m
thì dung tích của hồ là
A.
3
48m
. B.
3
18m
. C.
3
12m
. D.
3
5m
.
Lời giải
Chọn C
Đặt chiều dài rộng cao của hình hộp chữ nhật như hình vẽ :
Theo đó ta có :
( )
3
2.1,5. 2.1,5.2 18 2( ) 2.4.1,5 12 .a a a mV m
+ = ⇔= ⇒= =
Câu 46: Cho
0, 0ab>>
thỏa mãn
4 25
4
log log log
4
ba
ab
−
= =
. Giá trị của
66
log 4 2 log
2
a
bb
+−
bằng
A.
4
. B.
6
. C.
2
. D.
1
.
Lời giải
1,5m
2a
a
1,5m

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn C
Theo đề:
4 25
4
4
log log log 25
4
4 4.10
t
t
t
a
ba
a b tb
ba
=
−
= = =⇔=
−=
.
Ta được:
2
22 2
4 4.10 4.25 4 4.10 4. 4 0 2 2 2
55 5
tt t
t tt t
ba
− = ⇔ − = ⇔ + − = ⇔ =−+
.
Suy ra:
( )
2
2
2
2 2 2 12 8 2
5
t
a
b
= =−+ = −
.
Từ đó:
( )
6 66 6 6
log 4 2 log log 4 2 log 6 4 2 4 2 log 6 2
22
aa
bb
b
+ − = + = −+ = =
.
Câu 47: Cho hàm số bậc bốn
()y fx=
và hàm số bậc hai
()y gx=
có đồ thị cắt nhau tại điểm
0
x
như
hình vẽ bên, trong đó đường đậm hơn là đồ thị của hàm số
( ).
y fx=
Xét hàm số
() ().(),hx f x gx=
tìm mệnh đề đúng.
A.
( )
0
'0hx =
. B.
( )
0
'0hx >
.
C.
( )
0
'0hx <
. D.
( ) ( ) ( )
0 00
' ' .'
hx f x gx=
.
Lời giải
Chọn C
x
y
x
0
y=g(x)
y=f(x)
O

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có:
(
)
( ) ( ) ( )
0 00 0 0
'( ) ' . . 'hx fxgx fxgx= +
. Từ đồ thị ta nhận thấy
( )
( )
0
0
0
0
fx
gx
>
>
(giao điểm
M
của hai đồ thị hàm số nằm phía trên trục hoành) và
( )
(
)
0
0
'0
'0
fx
gx
<
<
(
,AB
là các điểm cực tiểu của
hai đồ thị hàm số nên đạo hàm đổi dấu từ âm sang dương). Suy ra
( )
0
'0hx <
.
Câu 48: Có bao nhiêu giá trị nguyên thuộc khoảng
( 30;30)
−
của tham số
m
để mọi tiếp tuyến của đồ thị
hàm số
32
(2 3) 1y x mx m x=− + −−
đều có hệ số góc dương?
A.
1
. B.
59
. C.
0
. D.
58
.
Lời giải
Chọn C
Yêu cầu bài toán
2
' 0, 3 2 2 3 0,y x mx m
xx⇔
∈> −+ ∈−>∀⇔ ∀
(
)
2
2
'0
6 90 3 0
30
mm m
∆<
⇔ ⇔ − +>⇔ − <
>
(vô lý).
Vậy không có giá trị nào của tham số
m
thỏa mãn yêu cầu bài toán.
Câu 49: Cho hàm số
( )
y fx=
có
(
)
0,fx x
′
> ∀∈
. Có bao nhiêu giá trị nguyên của
x
để
(
)
(
)
2
22f x fx
>
A.
23
. B.
20
. C.
21
. D.
22
.
Lời giải
Chọn C
Vì
( )
0,fx x
′
> ∀∈
nên hàm số
( )
y fx=
đồng biến trên
( )
( )
22
22 22 0 22f x fx x x x⇒ > ⇔ > ⇔<<
Vì
x
∈
nên
{ }
1;2;...;21x ∈
. Vậy có
21
giá trị nguyên của
x
thỏa ycbt.
Câu 50: Cho khối chóp
.
S ABC
có thể tích
3
24 cm
. Gọi
B
′
là trung điểm của
AB
và
C
′
là điểm trên
cạnh
AC
sao cho
3AC CC
′′
=
( minh họa như hình vẽ)
Thể tích của khối chóp
.S AB C
′′
bằng
A
C
B
S
B'
C'

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
8
cm
. B.
3
6
cm
. C.
3
2 cm
. D.
3
9 cm
.
Lời giải
Chọn D
Cách 1 :
..
..
13 3
..
24 8
S ABC ASBC
S ABC A SBC
VV
AB AC
V V AB AC
′′ ′′
′′
= == = =
3
..
33
.24 9
88
cm
S AB C S ABC
VV
′′
⇒= ==
Cách 2 :
Ta có
(
)
( )
( )
(
)
.
.
1
1
,.
. .sin
13 3
3
2
..
11
24 8
, . . .sin
32
AB C
S AB C AB C
S ABC ABC
ABC
d A ABC S
AB AC A
VS
AB AC
V S AB AC
d A ABC S AB AC A
′′
∆
′′ ′′
∆
∆
∆
′′
′′
= = = = = =
3
..
33
.24 9
88
cm
S AB C S ABC
VV
′′
⇒= ==
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
KIỂM TRA HỌC KÌ I LỚP 12
SỞ GD&ĐT BẠC LIÊU
NĂM HỌC: 2020-2021
THỜI GIAN: 90 phút
Câu 1: Cho khối chóp
.S ABC
có
( )
SA ABC⊥
, tam giác
ABC
vuông cân tại
, 4, 3A BC a SA a= =
.
Tính thể tích khối chóp đã cho
A.
3
43
3
a
V =
. B.
3
23
3
a
V =
. C.
3
43
Va
=
. D.
3
23Va=
.
Câu 2: Tìm giá trị của tham số
m
để đồ thị hàm số
( )
42
37y x mx= −− −
đi qua điểm
( )
2;1A −
.
A.
1m = −
. B.
5
m
=
. C.
0
m
=
. D.
1m =
.
Câu 3: Gọi
1
x
và
2
x
là hai nghiệm của phương trình
9 12.3 27 0
xx
− +=
. Tính
12
P xx
=
.
A.
27
P
=
. B.
3P
=
. C.
2P =
. D.
12P =
.
Câu 4: Cho phương trình
( )
2
3
3
log 2 log 9 5 0
+ −=xx
. Nếu đặt
3
log=tx
ta được phương trình nào sau
đây?
A.
2
4 2 50+ −=tt
. B.
2
2 2 10+ −=tt
. C.
2
4 2 10+ −=tt
. D.
2
2 2 50+ −=tt
.
Câu 5: Hàm số
42
81=−+ −yx x
nghịch biến trên khoảng nào dưới đây?
A.
( )
2;0−
. B.
( )
0;1
. C.
( )
1; +∞
. D.
( )
;2−∞ −
.
Câu 6: Cho hàm số
(
) ( )
32
0
= + ++ ≠f x ax bx cx d a
có đồ thị như hình vẽ bên dưới.
Mệnh đề nào sau đây đúng?
A.
0, 0><
ad
. B.
0, 0<>ad
. C.
0, 0<<ad
. D.
0, 0>>ad
.
Câu 7: Đồ thị hàm số
32
3 24yx x x=−+ + −
cắt trục tung tại điểm
A.
( )
1; 0Q
. B.
( )
4;0N −
. C.
(
)
0;1
P
. D.
( )
0; 4M
−
.
Câu 8: Tính
( ) ( )
2020 2020
ln 2 2 3 ln 3 2 2S = + +−
A.
0S =
. B.
2020S =
. C.
2
2020S =
. D.
1S =
.
Câu 9: Cho hàm số
( )
y fx=
liên tục và có bảng biến thiên trên đoạn
[ ]
1; 3−
như hình vẽ bên dưới

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Khẳng định nào sau đây đúng?
A.
[
]
( )
1;3
max 4fx
−
=
. B.
[ ]
( )
1;3
max 3fx
−
=
. C.
[
]
(
)
1;3
max 5
fx
−
=
. D.
[
]
(
)
1;3
max 0
fx
−
=
.
Câu 10: Đạo hàm của hàm số
3 2020
x
y
= −
là
A.
3
ln
x
y
x
′
=
. B.
1
.ln 3
y
x
′
=
. C.
1
.3
x
yx
−
′
=
. D.
3 .ln 3
x
y
′
=
.
Câu 11: Có bao nhiêu loại khối đa diện đều?
A.
2
. B.
5
. C. vô số. D.
4
.
Câu 12: Hàm số nào dưới đây có dạng đồ thị như đường cong trong hình vẽ bên dưới?
A.
32
1y xx=−+ −
. B.
42
1yx x=−−
. C.
32
1yx x=−−
. D.
42
1y xx
=−+ −
.
Câu 13: Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
A. 2. B. 3. C. 1. D. 4.
Câu 14: Với
a
là số thực dương tùy ý,
( )
2
2
log a
bằng
A.
2
2log a
. B.
2
2 log
a+
. C.
2
18log a
. D.
2
3log a
.
Câu 15: Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
,
AB
′
tạo với mặt phẳng
( )
ABC
một góc
0
30
. Thể tích của khối lăng trụ
.ABC A B C
′′′
bằng
A.
3
3
4
a
. B.
3
12
a
. C.
3
2
a
. D.
3
4
a
.
Câu 16: Cho khối tứ diện
ABCD
, gọi
M
là trung điểm
AB
. Mặt phẳng
( )
MCD
chia khối tứ diện đã
cho thành hai khối tứ diện:
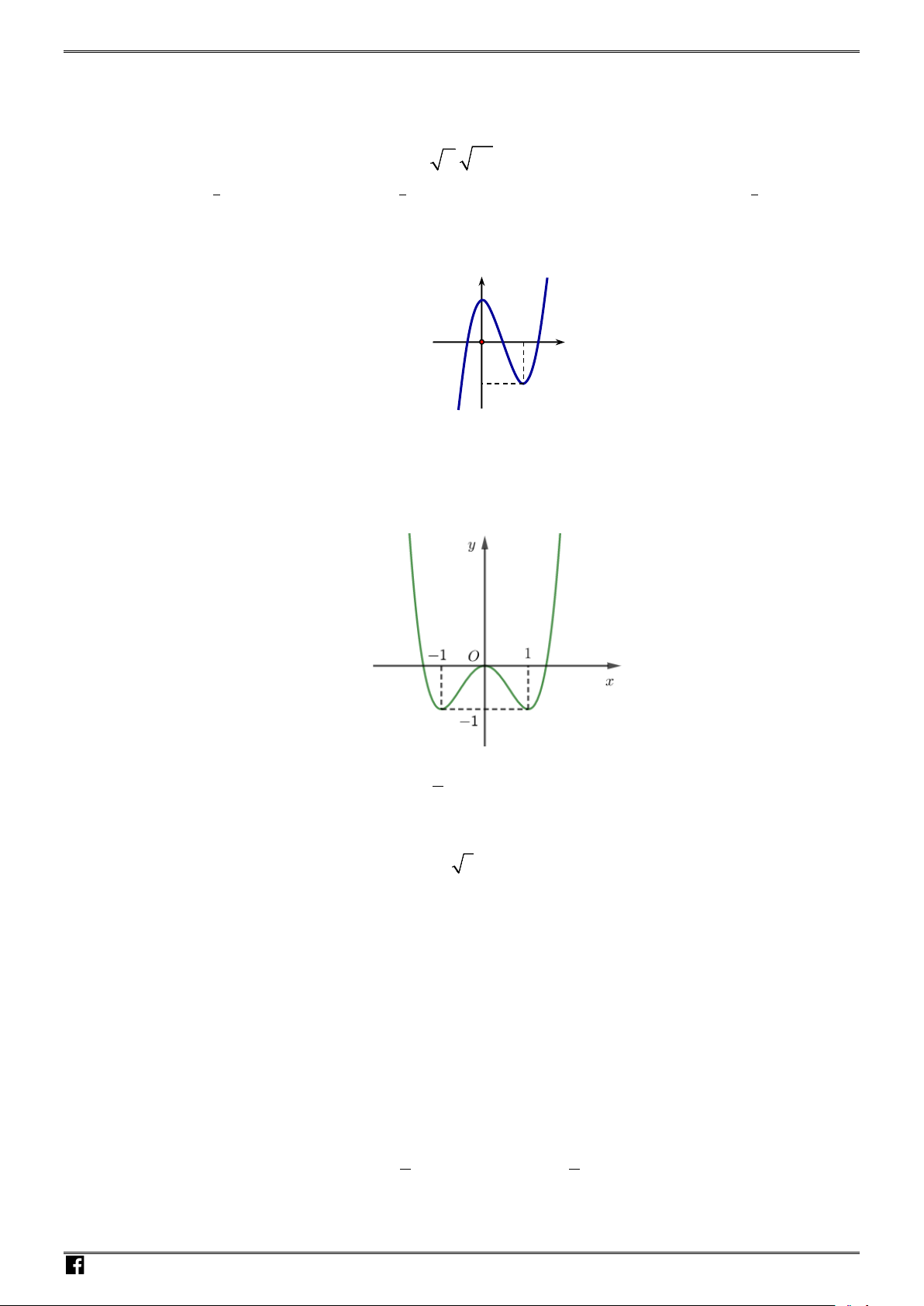
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
MACD
và
MBAC
. B.
MBCD
và
MACD
.
C.
AMCD
và
ABCD
. D.
BMCD
và
BACD
.
Câu 17: Cho số thực dương
a
. Biểu thức
2
3
.
P aa
=
được viết dưới dạng lũy số với số mũ hữu tỉ là
A.
1
2
Pa=
. B.
7
6
Pa
=
. C.
2
Pa=
. D.
5
6
Pa=
.
Câu 18: Cho hàm số
( )
y fx
=
liên tục trên
và có đồ thị như hình bên dưới
Tìm khoảng đồng biến của hàm số
( )
y fx=
.
A.
( )
2;+∞
. B.
( )
2;− +∞
. C.
( )
;2−∞
. D.
( )
0;2
.
Câu 19: Cho hàm số
(
)
y fx=
có đồ thị như hình vẽ bên.
Số nghiệm của phương trình
( )
1
3
fx= −
là
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 20: Cho hình nón
( )
N
có chiều cao bằng
23a
và đường sinh tạo với mặt phẳng chứa đường tròn
đáy một góc bằng
60°
. Tính diện tích xung quanh của hình nón
( )
N
.
A.
2
4 a
π
. B.
2
8 a
π
. C.
2
a
π
. D.
2
16 a
π
Câu 21: Theo thống kê, trong năm
2019
diện tích nuôi tôm công nghệ cao của tỉnh Bạc liêu là
( )
1001 ha
. Biết rằng diện tích nuôi tôm công nghệ cao mỗi năm tăng
5,3%
so với diện của năm liền trước.
Kể từ sau năm
2019
, năm nào dưới đây là năm đầu tiên tỉnh Bạc Liêu có diện tích nuôi tôm công
nghệ cao đạt trên
( )
1700 ha
?
A. Năm
2031
. B. Năm
2050
. C. Năm
2030
. D. Năm
2029
Câu 22: Phương trình
2020 1
x
m
có nghiệm khi
A.
1m ≥
. B.
0m >
. C.
1m >
. D.
m∈
.
Câu 23: Cho khối trụ có bán kính đáy bằng
r
và chiều cao bằng
h
. Thể tích của khối trụ đó là:
A.
2
V rh
π
=
. B.
2
1
3
V rh
π
=
. C.
2
1
3
V rh
π
=
. D.
2
V hr
π
=
.
Câu 24: Thể tích khối lăng trụ có diện tích đáy bằng
2
3a
và chiều cao bằng
2a
là:
A.
3
a
. B.
3
6a
. C.
3
2a
. D.
3
4a
.
O
x
y
2
2
−
2
1

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 25: Cho khối nón
( )
N
có bán kính đường tròn đáy
3ra=
và chiều cao
4ha=
. Tính thể tích khối
nón đã cho.
A.
3
36Va=
. B.
3
12
Va
=
. C.
3
12Va
π
=
. D.
3
36
Va
π
=
.
Câu 26: Tìm tất cả các giá trị thực của
m
để hàm số
( )
42
2 6 2020yx m x=+− −
có ba điểm cực trị.
A.
3m <
. B.
3m
>
. C.
3m ≤
. D.
3m
≥
.
Câu 27: Cho hàm số
( )
y fx
=
liên tục trên
và có đạo hàm
2
1yx
′
=−−
, x∀∈
. Khẳng định nào sau
đây là đúng?
A.
( )
(
)
22ff−=
. B.
( ) ( )
10ff>
.
C.
(
) (
)
0 2020
ff>
. D.
( )
( )
2020 2020
ff−<
.
Câu 28: Cho hàm số
22
1
x
y
x
−
=
+
có đồ thị
( )
C
. Gọi
A
,
B
là giao điểm của đồ thị
(
)
C
với đường thẳng
(
)
: 2 10dy x
= +
. Tính độ dài đoạn
AB
.
A.
10
. B. 10. C. 5. D.
5
.
Câu 29: Cho hàm số
( )
y fx
=
lien tục trên R và có bảng xét dấu
( )
fx
′
như sau:
Số điểm cực đại của hàm số
(
)
y fx=
là
A. 2. B. 3. C. 0. D. 1.
Câu 30: Hàm số
21
2020
x
y
x
−
=
+
có bao nhiêu điểm cực trị?
A. 0. B. 1. C. 2. D. vô số.
Câu 31: Phương trình đường tiệm cận ngang của đồ thị hàm số
32
23
x
y
x
−
=
−
là
A.
2
3
x =
. B.
3
2
y
=
. C.
3
2
x =
. D.
2
3
y =
.
Câu 32: Giá trị nhỏ nhất của hàm số
3
2 30yx x= −
trên đoạn
[ ]
1; 20
.
A.
44−
. B.
25 5−
. C.
20 5−
. D.
100−
.
Câu 33: Tập xác định hàm số
( )
9
2yx
−
= −
là.
A.
( )
;2D = −∞
. B.
{ }
\2D = −
. C.
{ }
\2D =
. D.
( )
2;D = +∞
.
Câu 34: Tính thể tích
V
của khối chóp có đáy là hình vuông cạnh bằng 2, chiều cao bằng 6.
A.
4V =
. B.
24V =
. C.
12V =
. D.
8V =
.
Câu 35: Một khối cầu có đường kính
4
cm thì có thể tích bằng
A.
( )
3
256
3
cm
π
. B.
( )
3
16 cm
π
. C.
( )
3
64 cm
π
. D.
( )
3
32
3
cm
π
Câu 36: Cho hình chữ nhật
ABCD
. Khi quay đường gấp khúc
ABCD
xung quanh cạnh
AD
ta được
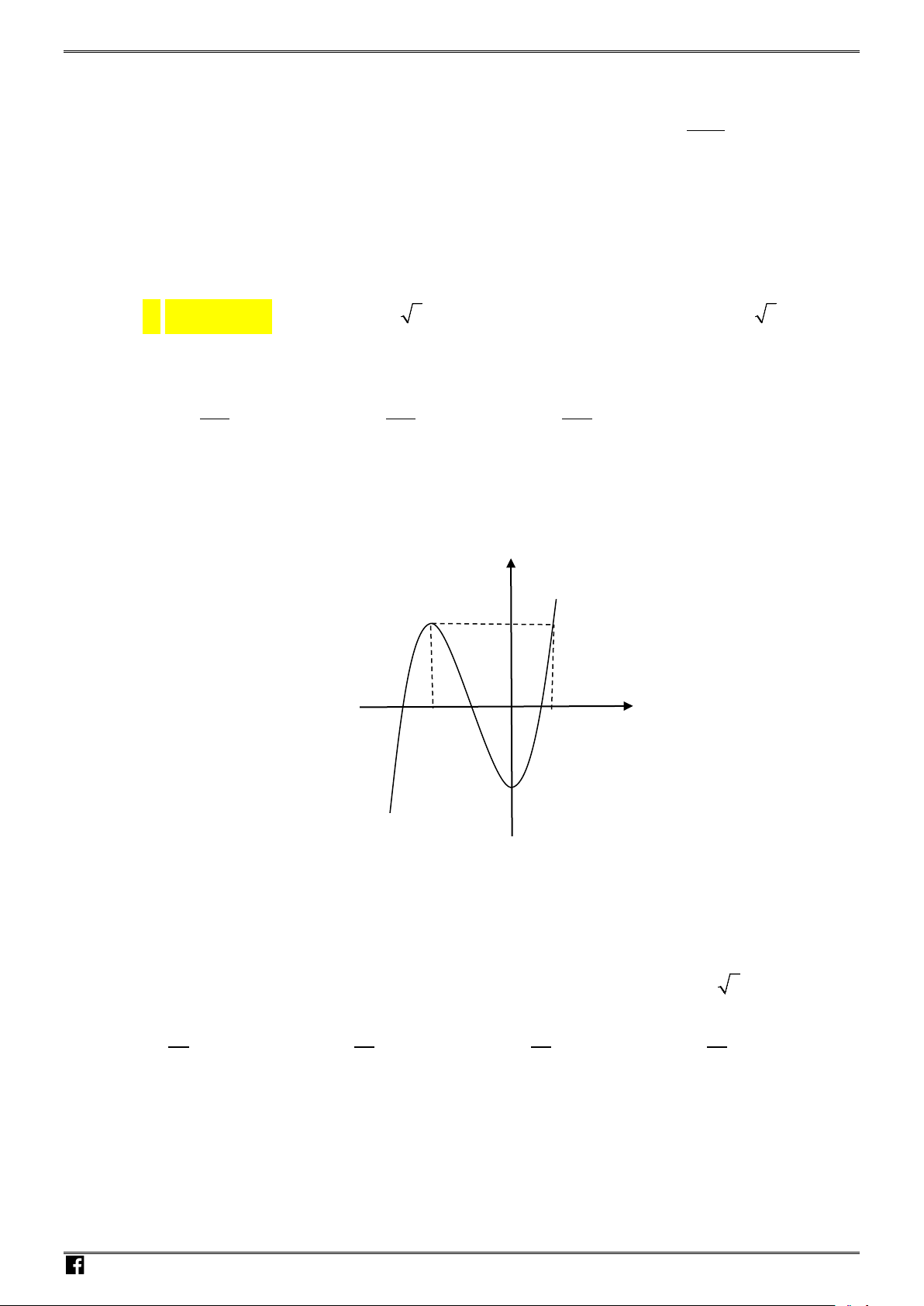
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A. Một mặt cầu. B. Một hình lăng trụ. C. Một hình trụ. D. Một hình nón.
Câu 37: Gọi
,
Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
1
x
y
x
−
=
+
trên đoạn
[ ]
0; 2
.
Tính
Mm
+
.
A.
0
. B.
2
−
. C.
3−
. D.
2
.
Câu 38: Cho hình nón có đỉnh
S
, đáy là tâm
O
và độ dài đường sinh bằng
8cm
. Mặt phẳng
( )
α
đi qua
đỉnh
S
, cắt đường tròn đáy tại hai điểm
M
và
N
sao cho
30MSN = °
. Tính diện tích thiết diện
được tạo bởi
( )
α
và hình nón đã cho.
A.
( )
2
16S cm=
. B.
(
)
2
16 3
S cm=
. C.
( )
2
32S cm=
. D.
(
)
2
32 3
S cm=
.
Câu 39: Một hình trụ có thiết diện qua trục là hình vuông cạnh
a
. Tính thể tích
V
của khối trụ tương
ứng hình trụ đó.
A.
3
4
a
V
π
=
. B.
3
12
a
V
π
=
. C.
3
3
a
V
π
=
. D.
3
Va= π
.
Câu 40: Phương trình
(
)
3
log 4 0
x −=
có nghiệm là
A.
6x
=
. B.
5x =
. C.
4
x =
. D.
1x =
.
Câu 41: Cho hàm số
( )
y fx=
xác định trên
và hàm số
( )
y fx
′
=
có đồ thị như hình vẽ bên dưới.
Hỏi hàm số
( )
fx
ye=
có bao nhiêu điểm cực trị ?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 42: Cho hàm số
( )
322 3
331 ,y x mx m x m m=− + − −−
với
m
là tham số. Gọi
,AB
là hai điểm cực
trị của đồ thị hàm số và
( )
2; 2 .I −
Gọi
S
là tập hợp các giá trị thực của tham số
m
sao cho ba
điểm
,,I AB
tạo thành một tam giác nội tiếp đường tròn có bán kính bằng
5.
Tính tổng các
phần tử của
.S
A.
20
17
. B.
3
17
. C.
4
17
. D.
15
17
.
Câu 43: Gọi
S
là tập hợp tất cả giá trị nguyên của tham số m để hàm số
( )
( )
32 2
3 4 2020fx x x mm x=−+ − +
đồng biến trên
( )
0; 4
. Tính tổng T tất cả phần tử của tập
S
.
A.
8T =
. B.
2T =
. C.
3T =
. D.
6T =
.
2−
y
3−
2−
1−
O
1
2
x
2
( )
'y fx
=
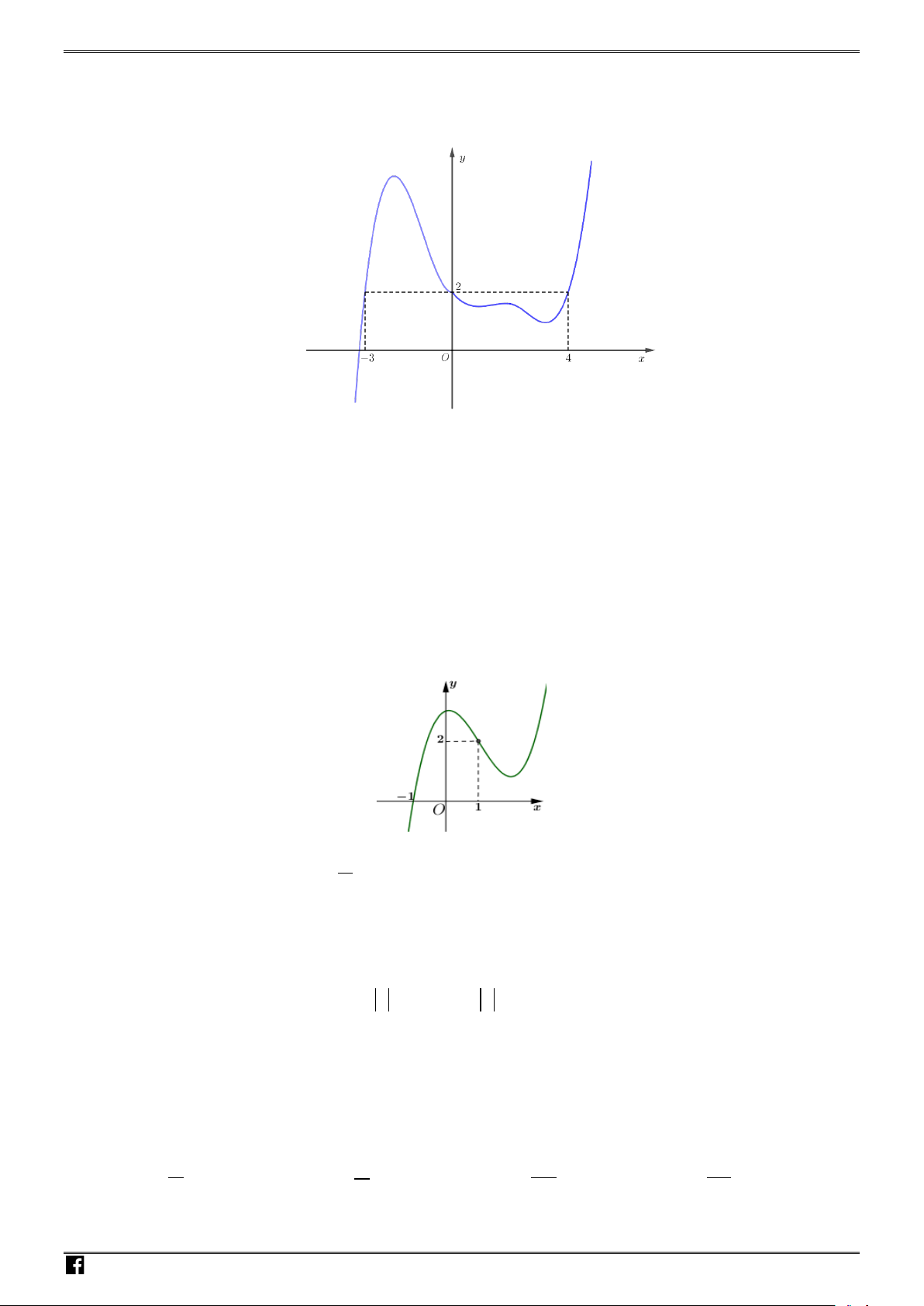
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 44: Cho hàm số
( )
fx
liên tục trên
. Hàm số
( )
y fx
′
=
có đồ thị như hình bên dưới.
Hỏi hàm số
(
)
( )
22
326gx f x x x x= −−+
nghịch biến trên khoảng nào dưới đây?
A.
( )
0; 4
. B.
( )
1; 0−
. C.
( )
;0−∞
. D.
( )
0;1
.
Câu 45: Cho phương trình
( )
( )
2
0,5 2
log 6 log 3 2 0m x xx+ + −− =
(m là tham số). Có bao nhiêu giá trị
nguyên dương của m để phương trình có nghiệm thực?
A.
23
. B.
15
. C.
17
. D.
18
.
Câu 46: Cho hàm số
( )
fx
là hàm đa thức bậc ba có đồ thị như hình vẽ bên dưới
Số nghiệm thuộc đoạn
;2
2
π
π
−
của phương trình
(
)
cos 1 cosfx x−=
là
A.
2
. B.
1
. C.
3
. D.
5
.
Câu 47: Cho hàm số
( )
3 22
32= =− +−y fx x x m m
. Gọi
S
là tập hợp tất cả các giá trị nguyên của
tham số
m
thoả mãn
[ ]
( )
[ ]
( )
3;1
3;1
3max 2min 112
−
−
+≤
fx fx
. Số phần tử của
S
bằng
A.
11
. B.
9
. C.
12
. D.
10
.
Câu 48: Cho khối chóp
.S ABCD
có thể tích là
V
và đáy là hình bình hành. Gọi
M
là trung điểm của
cạnh
SA
,
N
là điểm trên đoạn
SB
sao cho
2SN NB=
;
( )
α
là mặt phẳng đi qua các điểm
,MN
và cắt các cạnh
,SC SD
lần lượt tại các điểm
,KQ
. Tính giá trị lớn nhất của thể tích khối chóp
.S MNKQ
theo
V
.
A.
3
V
. B.
2
V
. C.
2
3
V
. D.
3
4
V
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 49: Cho khối trụ
( )
T
, đáy thứ nhất có tâm
O
, đáy thứ hai có tâm
O
′
. Mặt phẳng
(
)
P
song song với
trục
OO
′
và cắt khối trụ theo thiết diện là hình chữ nhật
ABCD
(
AB
thuộc đáy thứ nhất,
CD
thuộc đáy thứ hai) sao cho
120AOB = °
. Gọi
1
V
là thể tích khối lăng trụ
.
OAB O DC
′
,
2
V
là thể
tích phần còn lại. Tính tỉ số
1
2
V
V
.
A.
1
2
43
3
V
V
π
−
=
. B.
1
2
3
43
V
V
π
=
−
. C.
1
2
43
3
V
V
π
+
=
. D.
1
2
3
43
V
V
π
=
+
.
Câu 50: Cho phương trình
(
) (
)
2
22
log 2 3log 2 2 3 0
x
xx m
−− −+ −=
. Hỏi có tất cả bao nhiêu giá trị
nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm thực phân biệt ?
A.
8
. B. Vô số. C.
648
. D.
656
.
-----HẾT-----

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
BẢNG ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
D
C
C
A
D
D
A
C
D
B
B
B
A
D
B
B
A
D
B
C
C
A
B
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
C
D
A
A
B
C
C
D
D
C
B
A
A
B
D
A
D
D
C
C
A
A
B
D
Câu 1: Cho khối chóp
.S ABC
có
( )
SA ABC⊥
, tam giác
ABC
vuông cân tại
, 4, 3A BC a SA a
= =
.
Tính thể tích khối chóp đã cho
A.
3
43
3
a
V
=
. B.
3
23
3
a
V =
. C.
3
43Va=
. D.
3
23
Va=
.
Lời giải
Chọn A.
Vì
(
)
SA ABC⊥
nên
SA
là đường cao của hình chóp.
Tam giác
ABC
vuông cân tại
, 4 22
2
BC
A BC a AB AC a
=⇒== =
.
( )
3
2
1 1 1 1 43
. . . . . 3. 2 2
3 32 6 3
ABC
a
V SA S SA AB AC a a⇒= = = =
Câu 2: Tìm giá trị của tham số
m
để đồ thị hàm số
( )
42
37y x mx= −− −
đi qua điểm
( )
2;1A −
.
A.
1m = −
. B.
5m =
. C.
0
m =
. D.
1m
=
.
Lời giải
Chọn D.
Đồ thị hàm số
(
)
42
37y x mx= −− −
đi qua điểm
( )
2;1
A −
nên tọa độ điểm
A
phải thỏa mãn
phương trình hàm số
⇒
( ) ( )( )
42
1 2 3 2 74 4 1m mm=−−− −−⇔ =⇔=
.
Câu 3: Gọi
1
x
và
2
x
là hai nghiệm của phương trình
9 12.3 27 0
xx
− +=
. Tính
12
P xx=
.
A.
27P =
. B.
3P =
. C.
2P =
. D.
12P =
.
Lời giải
Chọn C.
Phương trình:
33 1
9 12.3 27 0
2
39
x
xx
x
x
x
= =
− +=⇔ ⇔
=
=
.
12
1.2 2
P xx⇒= = =
.
Câu 4: Cho phương trình
( )
2
3
3
log 2 log 9 5 0
+ −=xx
. Nếu đặt
3
log=tx
ta được phương trình nào sau
đây?
A.
2
4 2 50+ −=tt
. B.
2
2 2 10+ −=tt
. C.
2
4 2 10+ −=tt
. D.
2
2 2 50+ −=tt
.
A
S
B
C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn C
Ta có:
( )
22
3 33
3
log 2 log 9 5 0 4log 2log 1 0+ −= ⇔ + −=x x xx
.
Đặt
3
log=tx
ta được phương trình:
2
4 2 10
+ −=
tt
.
Câu 5: Hàm số
42
81
=−+ −yx x
nghịch biến trên khoảng nào dưới đây?
A.
( )
2;0−
. B.
( )
0;1
. C.
( )
1; +∞
. D.
(
)
;2−∞ −
.
Lời giải
Chọn A
Xét hàm số
42
81
=−+ −yx x
ta có:
Tập xác định:
=
D
3
0
4 16 ; 0
2
=
′′
=−+ =⇔
= ±
x
y x xy
x
Bảng xét dấu của
′
y
:
x
0
0
0
0
y
2−
2
Suy ra hàm số nghịch biến trên khoảng
( )
2;0−
.
Câu 6: Cho hàm số
( ) ( )
32
0= + ++ ≠f x ax bx cx d a
có đồ thị như hình vẽ bên dưới.
Mệnh đề nào sau đây đúng?
A.
0, 0><ad
. B.
0, 0<>ad
. C.
0, 0<<ad
. D.
0, 0>>ad
.
Lời giải
Chọn D
Dựa vào đồ thị hàm số
( )
fx
ta có:
0>a
.
Mặt khác, đồ thị hàm số
( )
fx
cắt trục tung tại điểm có tung độ dương nên
0>d
.
Vậy
0, 0>>ad
.
Câu 7: Đồ thị hàm số
32
3 24yx x x=−+ + −
cắt trục tung tại điểm
A.
( )
1; 0Q
. B.
( )
4;0N −
. C.
(
)
0;1P
. D.
( )
0; 4M −
.
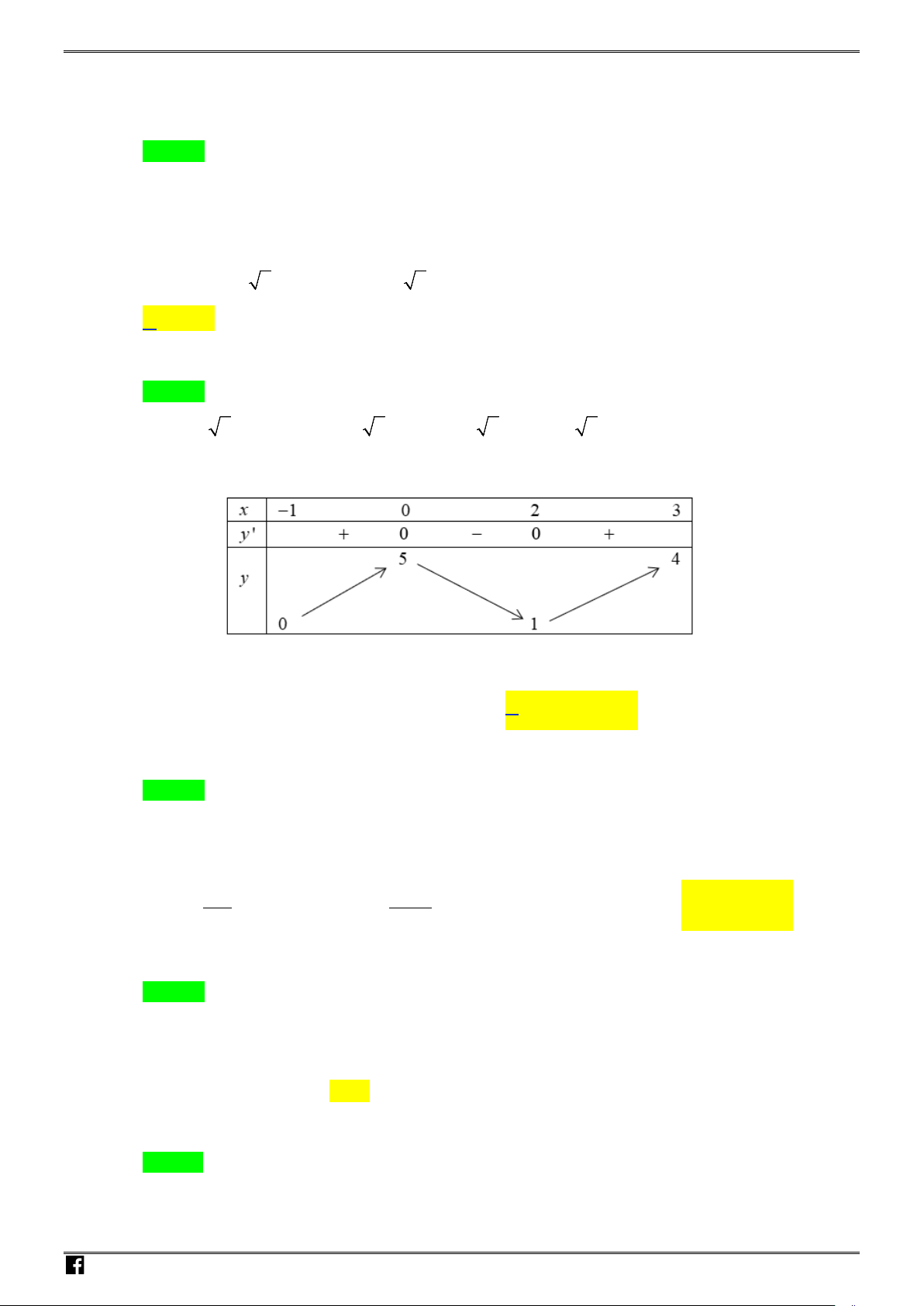
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn D
Giao trục tung
04xy=⇒=−
Vậy đồ thị cắt trục tung tại điểm
( )
0; 4M −
.
Câu 8: Tính
( ) ( )
2020 2020
ln 2 2 3 ln 3 2 2S = + +−
A.
0
S =
. B.
2020S
=
. C.
2
2020S =
. D.
1S =
.
Lời giải
Chọn A
( )
(
)
(
)
(
)
2020
2020 2020
2020
ln 2 2 3 ln 3 2 2 ln 2 2 3 3 2 2 ln1 0
S
= + +− = +− = =
.
Câu 9: Cho hàm số
(
)
y fx=
liên tục và có bảng biến thiên trên đoạn
[ ]
1; 3
−
như hình vẽ bên dưới
Khẳng định nào sau đây đúng?
A.
[ ]
( )
1;3
max 4fx
−
=
. B.
[ ]
( )
1;3
max 3fx
−
=
. C.
[ ]
( )
1;3
max 5fx
−
=
. D.
[ ]
( )
1;3
max 0fx
−
=
.
Lời giải
Chọn C
Câu 10: Đạo hàm của hàm số
3 2020
x
y = −
là
A.
3
ln
x
y
x
′
=
. B.
1
.ln 3
y
x
′
=
. C.
1
.3
x
yx
−
′
=
. D.
3 .ln 3
x
y
′
=
.
Lời giải
Chọn D
3 2020 3 .ln3
xx
yy
′
=− ⇒=
.
Câu 11: Có bao nhiêu loại khối đa diện đều?
A.
2
. B.
5
. C. vô số. D.
4
.
Lời giải
Chọn B
Có 5 loại khối đa diện đều là: Tứ diện đều, Khối lập phương, Bát diện đều, Mười hai mặt đều,
Hai mươi mặt đều.
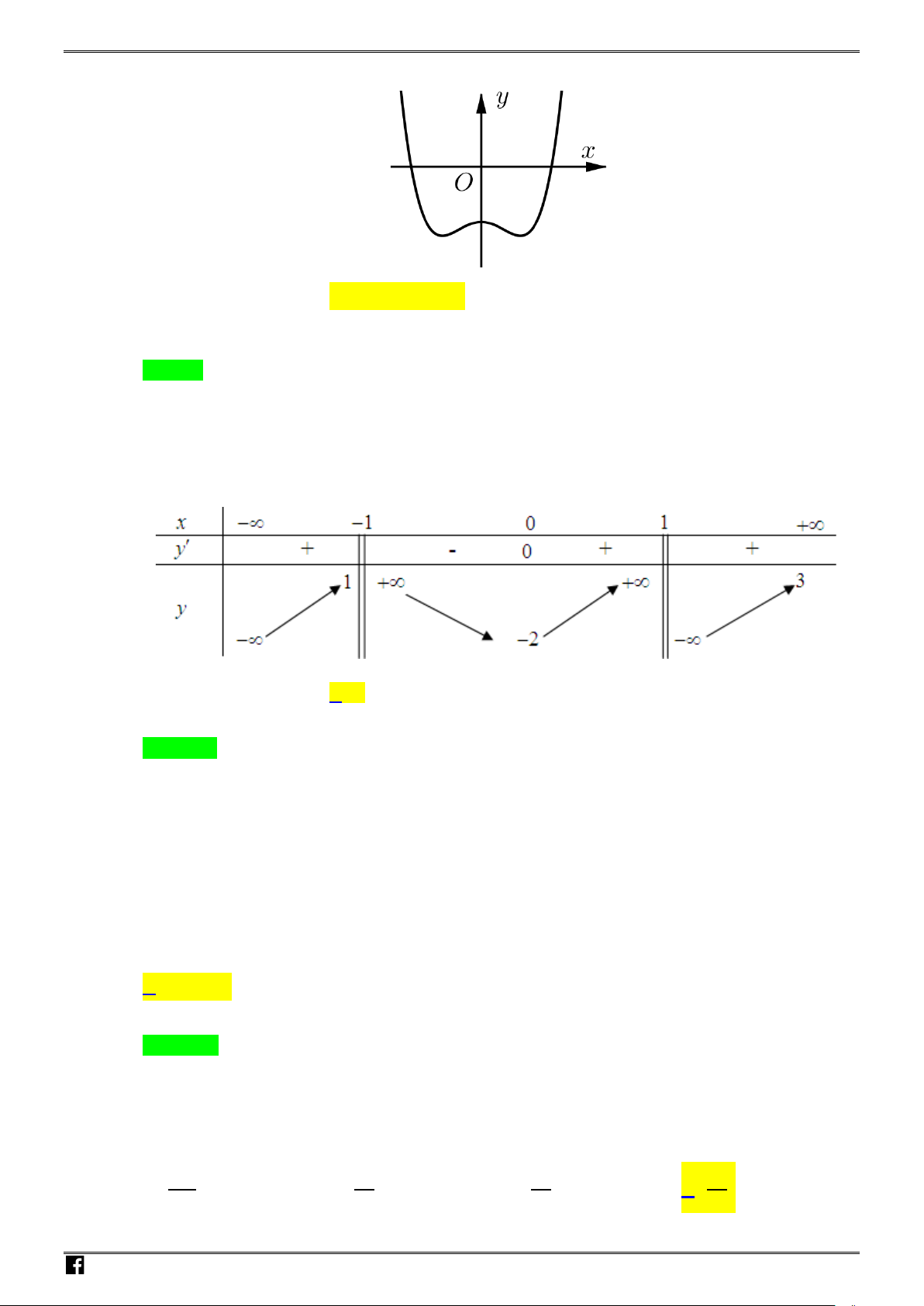
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 12: Hàm số nào dưới đây có dạng đồ thị như đường cong trong hình vẽ bên dưới?
A.
32
1
y xx=−+ −
. B.
42
1yx x=−−
. C.
32
1yx x=−−
. D.
42
1
y xx=−+ −
.
Lời giải
Chọn B
Dựa vào hình dáng đồ thị suy ra đồ thị là đồ thị của hàm số bậc bốn có hệ số
0a >
Câu 13: Cho hàm số
( )
y fx
=
có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
A. 2. B. 3. C. 1. D. 4.
Lời giải
Chọn B .
Ta có
1
lim
x
y
+
→−
= +∞
,
1
lim
x
y
−
→
= +∞
,
1
lim
x
y
+
→
= −∞
.
Suy ra đồ thị hàm số có hai tiệm cận đứng là
1x = −
và
1x =
.
Ta lại có
lim 3
x
y
→+∞
=
.
Suy ra đồ thị hàm số có tiệm cận ngang là
3y =
.
Vậy đồ thị hàm số có 3 tiệm cận.
Câu 14: Với
a
là số thực dương tùy ý,
( )
2
2
log a
bằng
A.
2
2log a
. B.
2
2 log a+
. C.
2
18log a
. D.
2
3log a
.
Lời giải
Chọn A .
Ta có
( )
2
22
log 2logaa=
.
Câu 15: Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
,
AB
′
tạo với mặt phẳng
( )
ABC
một góc
30°
. Thể tích của khối lăng trụ
.ABC A B C
′′′
bằng
A.
3
3
4
a
. B.
3
12
a
. C.
3
2
a
. D.
3
4
a
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn D .
Góc giữa
AB
′
và mặt phẳng
( )
ABC
là
A BA
′
nên ta có
30
A BA
′
= °
.
Khối lăng trụ có chiều cao là
3
.tan 30
3
a
h AA a
′
= = °=
.
Vì khối lăng trụ có đáy là tam giác đều cạnh
a
nên diện tích đáy là
2
3
4
a
B =
.
Vậy thể tích của khối lăng trụ là
23
33
43 4
aa a
V Bh= = =
.
Câu 16: Cho khối tứ diện
ABCD
, gọi
M
là trung điểm
AB
. Mặt phẳng
(
)
MCD
chia khối tứ diện đã
cho thành hai khối tứ diện:
A.
MACD
và
MBAC
. B.
MBCD
và
MACD
.
C.
AMCD
và
ABCD
. D.
BMCD
và
BACD
.
Lời giải
Chọn B
Mặt phẳng
( )
MCD
chia khối tứ diện
ABCD
thành hai khối tứ diện
MBCD
và
MACD
.
Câu 17: Cho số thực dương
a
. Biểu thức
2
3
.P aa=
được viết dưới dạng lũy số với số mũ hữu tỉ là
A'
B'
C'
B
C
A
M
B
C
D
A

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
1
2
Pa=
. B.
7
6
Pa=
. C.
2
Pa=
. D.
5
6
Pa=
.
Lời giải
Chọn B
Ta có
2127
1
2
3
3 23 6
2
..P a a aa a a
+
= = = =
.
Câu 18: Cho hàm số
( )
y fx
=
liên tục trên
và có đồ thị như hình bên dưới
Tìm khoảng đồng biến của hàm số
( )
y fx=
.
A.
( )
2;+∞
. B.
( )
2;− +∞
. C.
( )
;2
−∞
. D.
( )
0;2
.
Lời giải
Chọn A
Từ đồ thị ta suy ra khoảng đồng biến của hàm số
(
)
y fx=
là
(
)
2;+∞
.
Câu 19: Cho hàm số
( )
y fx=
có đồ thị như hình vẽ bên.
Số nghiệm của phương trình
( )
1
3
fx= −
là
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn D
O
x
y
2
2−
2
1

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Dựa vào đồ thị ta thấy đường thẳng
1
3
y
= −
cắt đồ thị hàm
( )
y fx=
tại ba điểm phân biệt.
Câu 20: Cho hình nón
( )
N
có chiều cao bằng
23a
và đường sinh tạo với mặt phẳng chứa đường tròn
đáy một góc bằng
60°
. Tính diện tích xung quanh của hình nón
(
)
N
.
A.
2
4 a
π
. B.
2
8 a
π
. C.
2
a
π
. D.
2
16 a
π
Lời giải
Chọn B
Từ giả thiết ta có góc giữa đường sinh và mặt đáy là góc
60ABH = °
.
Trong tam giác
ABH
vuông tại
H
ta có:
0
0
1
.cot 60 2 3. 2
3
2
2 3. 4
sin 60
3
r AH a a
AH
l aa
= = =
= = =
Diện tích xung quanh của hình nón là:
2
.2 .4 8
xq
S rl a a a
ππ π
= = =
.
Câu 21: Theo thống kê, trong năm
2019
diện tích nuôi tôm công nghệ cao của tỉnh Bạc liêu là
( )
1001 ha
. Biết rằng diện tích nuôi tôm công nghệ cao mỗi năm tăng
5,3%
so với diện của năm liền trước.
Kể từ sau năm
2019
, năm nào dưới đây là năm đầu tiên tỉnh Bạc Liêu có diện tích nuôi tôm công
nghệ cao đạt trên
( )
1700 ha
?
A. Năm
2031
. B. Năm
2050
. C. Năm
2030
. D. Năm
2029
Lời giải
Chọn C
Diện tích nuôi tôm sau
n
năm là:
(
)
1001. 1 5.3%
n
n
T = +
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có:
( )
( )
1 5,3%
1700
1001. 1 5,3% 1700 log 10,25553046 11
1001
n
n
Tn n
+
= + > ⇔> = ⇒=
.
Vậy thêm 11 năm sau thì diện tích nuôi tôm công nghệ cao của tỉnh Bạc Liêu sẽ đạt trên
( )
1700 ha
, nghĩa là vào năm
2030
thì diện tích nuôi tôm công nghệ cao của tỉnh Bạc Liêu sẽ
đạt trên
( )
1700 ha
.
Câu 22: Phương trình
2020 1
x
m
có nghiệm khi
A.
1m ≥
. B.
0m >
. C.
1m >
. D.
m
∈
.
Lời giải
Chọn C
Phương trình
2020 1
x
m
có nghiệm khi
1 0 1.mm
Câu 23: Cho khối trụ có bán kính đáy bằng
r
và chiều cao bằng
h
. Thể tích của khối trụ đó là:
A.
2
V rh
π
=
. B.
2
1
3
V rh
π
=
. C.
2
1
3
V rh
π
=
. D.
2
V hr
π
=
.
Lời giải
Chọn A
Câu 24: Thể tích khối lăng trụ có diện tích đáy bằng
2
3a
và chiều cao bằng
2a
là:
A.
3
a
. B.
3
6a
. C.
3
2a
. D.
3
4a
.
Lời giải
Chọn B
Thể tích khối lăng trụ là
23
. 3 .2 6
V Sh a a a
.
Câu 25: Cho khối nón
(
)
N
có bán kính đường tròn đáy
3ra=
và chiều cao
4ha=
. Tính thể tích khối
nón đã cho.
A.
3
36Va=
. B.
3
12Va=
. C.
3
12
Va
π
=
. D.
3
36Va
π
=
.
Lời giải
Chọn C.
Ta có:
2
1
3
V rh
π
=
( )
2
1
3 .4
3
aa
π
=
3
12 a
π
=
.
Câu 26: Tìm tất cả các giá trị thực của
m
để hàm số
( )
42
2 6 2020yx m x=+− −
có ba điểm cực trị.
A.
3m
<
. B.
3m >
. C.
3m ≤
. D.
3m ≥
.
Lời giải
Chọn A .
Hàm số
(
)
42
2 6 2020yx m x
=+− −
có ba điểm cực trị khi và chỉ khi:
( )
1. 2 6 0m −<
3m⇔<
.
Câu 27: Cho hàm số
( )
y fx=
liên tục trên
và có đạo hàm
2
1yx
′
=−−
, x∀∈
. Khẳng định nào sau
đây là đúng?
A.
( ) ( )
22ff−=
. B.
( ) ( )
10ff>
.
C.
( ) ( )
0 2020ff>
. D.
( ) ( )
2020 2020ff−<
.
Lời giải
Chọn C .
Ta có:
2
1yx
′
=−−
( )
2
1 0,xx=− + < ∀∈
⇒
hàm số
( )
fx
nghịch biến trên
( ) (
)
0 2020ff⇒>
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 28: Cho hàm số
22
1
x
y
x
−
=
+
có đồ thị
(
)
C
. Gọi
A
,
B
là giao điểm của đồ thị
(
)
C
với đường thẳng
( )
: 2 10
dy x
= +
. Tính độ dài đoạn
AB
.
A.
10
. B. 10. C. 5. D.
5
.
Lời giải
Chọn D
Hoành độ giao điểm
A
,
B
của hai đồ thị là nghiệm phương trình
( )
2
22
2 10
1
5 60 1
2
3
x
x
x
x x dkx
x
x
−
= +
+
⇔ + + = ≠−
= −
⇔
= −
Vậy
( ) ( )
2; 6 , 3; 4 5A B AB− −⇒=
Câu 29: Cho hàm số
( )
y fx=
lien tục trên R và có bảng xét dấu
( )
fx
′
như sau:
Số điểm cực đại của hàm số
( )
y fx=
là
A. 2. B. 3. C. 0. D. 1.
Lời giải
Chọn A
Vì hàm số
( )
y fx=
liên tục trên R và có dấu
( )
fx
′
đổi từ + sang – hai lần, nên hàm số có hai
cực đại.
Câu 30: hàm số
21
2020
x
y
x
−
=
+
có bao nhiêu điểm cực trị?
A. 0. B. 1. C. 2. D. vô số.
Lời giải
Chọn A
Câu 31: Phương trình đường tiệm cận ngang của đồ thị hàm số
32
23
x
y
x
−
=
−
là
A.
2
3
x =
. B.
3
2
y =
. C.
3
2
x =
. D.
2
3
y =
.
Lời giải
Chọn B

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
3 23
lim lim
2 32
xx
x
y
x
→±∞ →±∞
−
= =
−
. Vậy
3
2
y =
là
3
2
y
=
là đường tiệm cận ngang của đồ thị hàm
số.
Câu 32: Giá trị nhỏ nhất của hàm số
3
2 30
yx x= −
trên đoạn
[ ]
1; 20
.
A.
44−
. B.
25 5
−
. C.
20 5
−
. D.
100−
.
Lời giải
Chọn C
Ta có
2
6 30yx
′
= −
Khi đó
(
)
( )
5
0
5
xn
y
xl
=
′
= ⇔
= −
Ta có
( ) (
)
(
)
1 28; 20 15400; 5 20 5
yy y
=−= =−
.
Vậy
[ ]
1;20
min 20 5y = −
.
Câu 33: Tập xác định hàm số
( )
9
2yx
−
= −
là.
A.
( )
;2D = −∞
. B.
{ }
\2D = −
. C.
{ }
\2D =
. D.
(
)
2;D = +∞
.
Lời giải
Chọn C
Hàm số xác định khi
20 2
xx
−≠⇔≠
Vậy
{ }
\2D =
.
Câu 34: Tính thể tích
V
của khối chóp có đáy là hình vuông cạnh bằng 2, chiều cao bằng 6.
A.
4V =
. B.
24
V =
. C.
12V =
. D.
8V =
.
Lời giải
Chọn D
Thể tích
V
của khối chóp có đáy là hình vuông cạnh bằng 2, chiều cao bằng 6 bằng:
V
2
1
.2 .6
3
=
8=
Câu 35: Một khối cầu có đường kính
4
cm thì có thể tích bằng
A.
( )
3
256
3
cm
π
. B.
( )
3
16 cm
π
. C.
( )
3
64 cm
π
. D.
( )
3
32
3
cm
π
Lời giải
Chọn D
( )
33
33
4 4 4 4 4 32
.8
3 32 32 3 3
d
V R cm
π
ππ π π
= = = = =
.
Câu 36: Cho hình chữ nhật
ABCD
. Khi quay đường gấp khúc
ABCD
xung quanh cạnh
AD
ta được
A. Một mặt cầu. B. Một hình lăng trụ. C. Một hình trụ. D. Một hình nón.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn C
.
Câu 37: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
1
x
y
x
−
=
+
trên đoạn
[ ]
0; 2
.
Tính
Mm+
.
A.
0
. B.
2
−
. C.
3−
. D.
2
.
Lời giải
Chọn B
Hàm số xác định và liên tục trên đoạn
[ ]
0; 2
.
Đạo hàm
( )
[ ]
2
3
0, 0; 2
1
yx
x
= > ∀∈
+
nên hàm số luôn tăng trên đoạn
[ ]
0; 2
.
Suy ra
[ ]
(
)
0;2
max 2 0
x
M yy
∈
= = =
và
[ ]
( )
0;2
min 0 2
x
m yy
∈
= = = −
.
Vậy
2Mm+=−
.
Câu 38: Cho hình nón có đỉnh
S
, đáy là tâm
O
và độ dài đường sinh bằng
8cm
. Mặt phẳng
( )
α
đi qua
đỉnh
S
, cắt đường tròn đáy tại hai điểm
M
và
N
sao cho
30MSN = °
. Tính diện tích thiết diện
được tạo bởi
( )
α
và hình nón đã cho.
A.
( )
2
16S cm=
. B.
(
)
2
16 3S cm=
. C.
( )
2
32
S cm
=
. D.
( )
2
32 3S cm=
.
Lời giải
Chọn A

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Xét tam giác
MSN
và áp dụng công thức diện tích
(
)
2
11
. . .sin .8.8.sin30 16
22
MSN
S SM SN MSN cm
∆
= = °=
Câu 39: Một hình trụ có thiết diện qua trục là hình vuông cạnh
a
. Tính thể tích
V
của khối trụ tương
ứng hình trụ đó.
A.
3
4
a
V
π
=
. B.
3
12
a
V
π
=
. C.
3
3
a
V
π
=
. D.
3
Va= π
.
Lời giải
Chọn A
Thiết diện qua trục là hình vuông nên
2
2
ha
h Ra
a
R
=
= = ⇔
=
.
Thể tích khối trụ cần tìm
2
3
2
..
24
aa
V hR a
π
=π=π =
.
Câu 40: Phương trình
( )
3
log 4 0x
−=
có nghiệm là
A.
6x =
. B.
5
x =
. C.
4x =
. D.
1
x =
.
Lời giải
Chọn B.
Ta có:
(
)
3
log 4 0 4 1 5.x xx
− =⇔−=⇔=
Câu 41: Cho hàm số
(
)
y fx
=
xác định trên
và hàm số
( )
y fx
′
=
có đồ thị như hình vẽ bên dưới.
Hỏi hàm số
( )
fx
ye=
có bao nhiêu điểm cực trị ?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn D.
2−
y
3−
2−
1−
O
1
2
x
2
( )
'y fx=

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có:
( )
( )
( )
( )
( )
( )
( )
3; 2
;0 0 0 1
0;1
fx fx
x
y fxe y fxe fx x
x
∈− −
′′ ′ ′ ′
= =⇔ =⇔ =⇔=−
∈
Vậy hàm số có 3 cực trị.
Câu 42: Cho hàm số
( )
322 3
331 ,y x mx m x m m=− + − −−
với
m
là tham số. Gọi
,AB
là hai điểm cực
trị của đồ thị hàm số và
( )
2; 2 .I
−
Gọi
S
là tập hợp các giá trị thực của tham số
m
sao cho ba
điểm
,,I AB
tạo thành một tam giác nội tiếp đường tròn có bán kính bằng
5.
Tính tổng các
phần tử của
.S
A.
20
17
. B.
3
17
. C.
4
17
. D.
15
17
.
Lời giải
Chọn A.
Ta có:
(
)
22
1 42
3 6 3 1; 0
1 42
xm y m
y x mx m y
xm y m
= +⇒ =− −
′′
=−+ − =⇔
= −⇒ =− +
(
)
1; 4 2
Am m
⇒ +− −
là điểm cực tiểu,
(
)
1; 4 2
Bm m−− +
là điểm cực đại của đồ thị hàm số.
Dễ thấy
25 2AB R= =
nên đường tròn ngoại tiếp tam giác
IAB
có tâm chính là trung điểm
AB
hay tam giác
IAB
vuông tại
.I
Có
( ) ( )
1 ;4 , 3 ; 4 4IA m m IB m m= − = − −+
nên
( )( )
( )
1
. 0 1 3 4 44 0
3
17
m
IA IB IA IB m m m m
m
=
⊥ ⇔ = ⇔ − − + −+ = ⇔
=
Vậy tổng các giá trị của
m
là
3 20
1.
17 17
+=
Câu 43: Gọi
S
là tập hợp tất cả giá trị nguyên của tham số m để hàm số
( )
( )
32 2
3 4 2020fx x x mm x=−+ − +
đồng biến trên
(
)
0; 4
. Tính tổng T tất cả phần tử của tập
S
.
A.
8T =
. B.
2T
=
. C.
3T =
. D.
6T =
.
Lời giải
Chọn D
Ta có:
( )
22
3 64fx x x mm
′
= −+ −
Hàm số
( )
y fx=
đồng biến trên
( ) ( ) (
)
0; 4 0, 0; 4fx x
′
⇔ ≥ ∀∈
( )
( ) ( )
22
22
3 6 4 0, 0; 4
4 3 6 , 0; 4 *
x x mm x
m m x xx
⇔ − + − ≥ ∀∈
⇔ − ≤ − ∀∈
Hàm số
( )
2
36gx x x= −
có bảng biến thiên trên
( )
0; 4
như sau:
x
0
1
4
( )
gx
′
−
0
+

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
( )
gx
24
0
3−
Do đó,
( )
[ ]
2
* 4 3 1; 3mm m⇔ − ≤− ⇔ ∈
Do
{
}
1; 2; 3 6mA T
∈⇒= ⇒=
.
Câu 44: Cho hàm số
( )
fx
liên tục trên
. Hàm số
( )
y fx
′
=
có đồ thị như hình bên dưới.
Hỏi hàm số
( )
( )
22
326gx f x x x x= −−+
nghịch biến trên khoảng nào dưới đây?
A.
( )
0; 4
. B.
( )
1; 0−
. C.
( )
;0−∞
. D.
( )
0;1
.
Lời giải
Chọn D
Ta có:
(
) ( )
(
)
( )
( )
22
23 3 4623 3 2gx x fx x x x fx x
′′ ′
=− −−+=− −−
.
( )
( )
2
2
2
2
3
2 30
2
2 30
3 3( )
0 3, 0
32
30
1, 4
34
x
x
x
x x VN
gx x x
fx x
xx
xx
xx
−=
=
−=
−=−
′
=⇔ ⇔ ⇔= =
′
−=
−=
=−=
−=
.
Bảng xét dấu của
( )
'gx
:
x
−∞
1−
0
3
2
3
4
+∞
( )
gx
′
−
0
+
0
−
0
+
0
−
0
+
Do đó hàm số
( )
y gx=
nghịch biến trên các khoảng
( ) ( )
3
; 1 , 0; , 3; 4
2
−∞ −
.
⇒
Hàm số
( )
y gx=
nghịch biến trên
( )
0;1
.
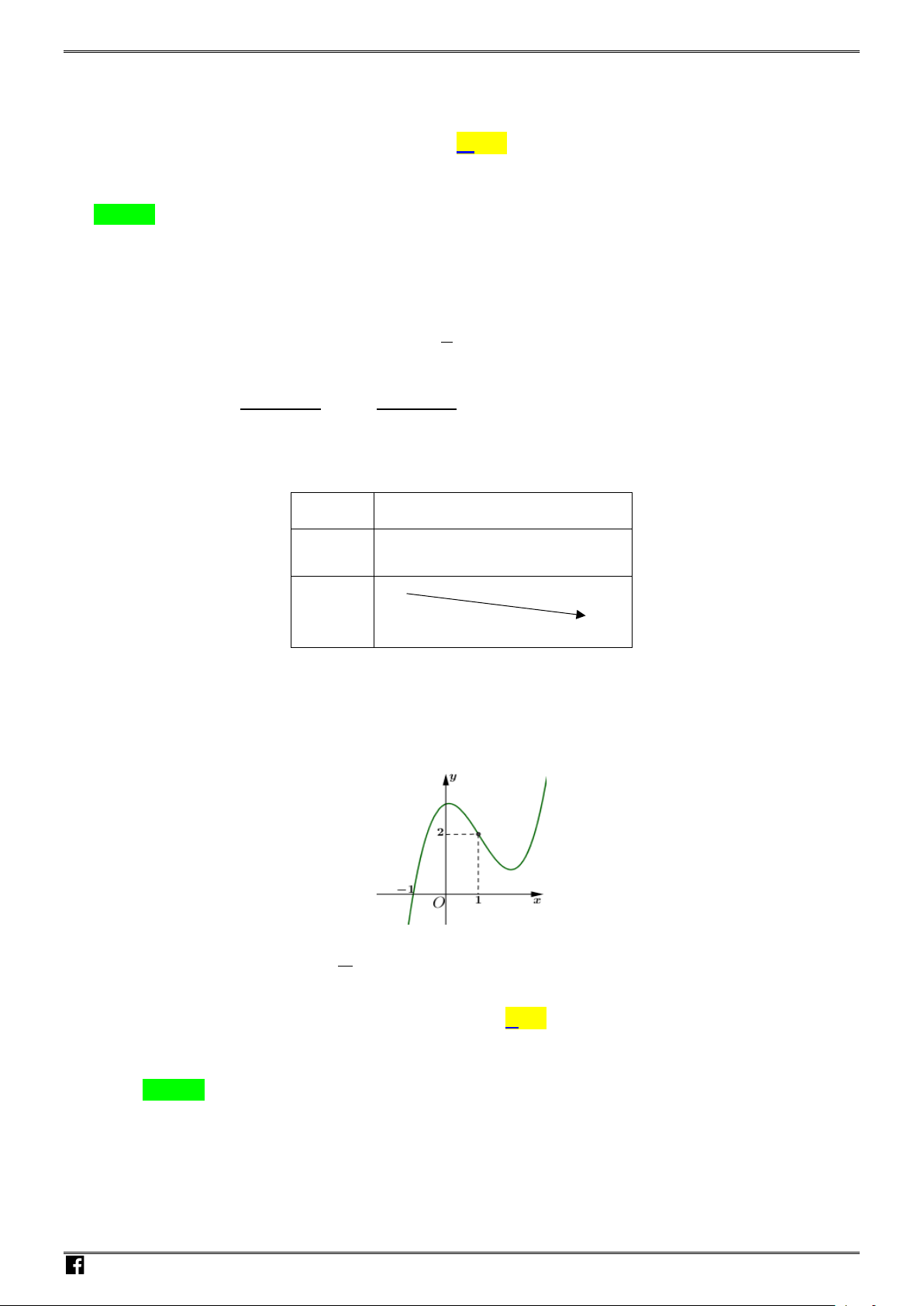
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 45: Cho phương trình
( )
(
)
2
0,5 2
log 6 log 3 2 0
m x xx+ + −− =
(m là tham số). Có bao nhiêu giá trị
nguyên dương của m để phương trình có nghiệm thực?
A.
23
. B.
15
. C.
17
. D.
18
.
Lời giải
Chọn C
Ta có:
(
)
( )
( )
2
0,5 2
log 6 log 3 2 0 *
m x xx+ + −− =
Điều kiện xác định:
2
31
60
1
32 0
6
x
mx
xx
xm
−< <
+>
⇔
−−>
>−
Khi đó,
( )
22
2
2
32 32
* log 0 1 8 3
66
xx xx
xx m
mx mx
−− −−
⇔ = ⇔ = ⇔− − + =
++
Hàm số
( )
2
83gx x x=−− +
có bảng biến thiên trên
( )
3;1−
như sau:
x
3−
1
(
)
gx
′
−
( )
gx
18
6−
Do đó, phương trình đã cho có nghiệm thực khi:
6 18m−< <
Do
{ }
1;2;...;17mm
+
∈ ⇒∈
.
Câu 46: Cho hàm số
( )
fx
là hàm đa thức bậc ba có đồ thị như hình vẽ bên dưới
Số nghiệm thuộc đoạn
;2
2
π
π
−
của phương trình
(
)
cos 1 cos
fx x−=
là
A.
2
. B.
1
. C.
3
. D.
5
.
Lời giải
Chọn C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 23
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Đặt
cos 1
tx= −
. Vì
[ ]
; 2 2;0
2
xt
π
π
∈− ⇒ ∈−
Khi đó ta có:
(
) ( )
[ ]
(
)
[ ]
cos 1 cos 1, 2; 0 1, 2; 0
f x x ft t t fx x x− = ⇔ = + ∈− ⇔ = + ∈−
Đồ thị của hàm số
(
)
y fx=
và
1yx= +
được thể hiện như hình vẽ.
Do
[ ]
( )
2;0 1t ft t∈− ⇒ = +
có nghiệm
1t = −
.
Suy ra
cos 1 1 cos 1 cos 0 ,
2
t x x x x kk
π
π
= −⇔−= −⇔ = ⇔ = + ∈
.
Vì
{ }
3
; 2 2 1 1; 0;1
2 22 2
x k kk
π ππ
π ππ
−−
∈ ⇔ ≤ + ≤ ⇔− ≤ ≤ ⇔ = −
.
Vậy phương trình
( )
cos 1 cosfx x−=
có 3 nghiệm trên
;2 .
2
π
π
−
Câu 47: Cho hàm số
( )
3 22
32= =− +−y fx x x m m
. Gọi
S
là tập hợp tất cả các giá trị nguyên của
tham số
m
thoả mãn
[ ]
( )
[
]
( )
3;1
3;1
3max 2min 112
−
−
+≤
fx fx
. Số phần tử của
S
bằng
A.
11
. B.
9
. C.
12
. D.
10
.
Lời giải
Chọn A
Ta có
( )
2
36
′
= −fx x x
, nên lập được bảng biến thiên
Suy ra
Từ đây ta có
[ ]
( )
[ ]
( )
( ) ( )
22
3;1
3;1
3max 2min 112 3. 2 2. 2 4 112
−
−
+ ≤ ⇔ − + − −≤fx fx m m m m
2
2 24 0 4 6⇔ − − ≤ ⇔− ≤ ≤mm m
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 24
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vậy có 11 giá trị nguyên của tham số
m
.
Câu 48: Cho khối chóp
.
S ABCD
có thể tích là
V
và đáy là hình bình hành. Gọi
M
là trung điểm của
cạnh
SA
,
N
là điểm trên đoạn
SB
sao cho
2SN NB=
;
( )
α
là mặt phẳng đi qua các điểm
,
MN
và cắt các cạnh
,SC SD
lần lượt tại các điểm
,KQ
. Tính giá trị lớn nhất của thể tích khối chóp
.S MNKQ
theo
V
.
A.
3
V
. B.
2
V
. C.
2
3
V
. D.
3
4
V
.
Lời giải
Chọn A
Gọi
( ) ( )
∩=SAC SBD SO
,
( ) { }
α
∩=SO I
; đặt
=
SK
x
SC
,
01≤≤x
Do SO là trung tuyến chung của 2 tam giác SAC và SBD nên ta có
2.
+= =+
SA SC SO SB SD
SM SK SI SN SQ
,
từ đây suy ra
1 11 2 2
,,
22 2
+
= =+= =
+
SC SD x SQ x
SK x SQ x x SD x
.
Lại do đáy là hình bình hành nên ta có
2
.
.
12
. ..
2 36
S MNKQ
S ABCD
V
SM SK SQ SN x x
V SA SC SD SB x
+
= +=
+
.
Khảo sát sự biến thiên của hàm số
( )
2
2
36
xx
fx
x
+
=
+
,
01≤≤
x
ta thấy giá trị lớn nhất bằng
1
3
khi
1=x
.
Câu 49: Cho khối trụ
( )
T
, đáy thứ nhất có tâm
O
, đáy thứ hai có tâm
O
′
. Mặt phẳng
( )
P
song song với
trục
OO
′
và cắt khối trụ theo thiết diện là hình chữ nhật
ABCD
(
AB
thuộc đáy thứ nhất,
CD
thuộc đáy thứ hai) sao cho
120AOB = °
. Gọi
1
V
là thể tích khối lăng trụ
.OAB O DC
′
,
2
V
là thể
tích phần còn lại. Tính tỉ số
1
2
V
V
.
A.
1
2
43
3
V
V
π
−
=
. B.
1
2
3
43
V
V
π
=
−
. C.
1
2
43
3
V
V
π
+
=
. D.
1
2
3
43
V
V
π
=
+
.
Lời giải
Chọn B

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 25
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Gọi
,
Rh
lần lượt là bán kính đáy và chiều cao của khối trụ. Khi đó,
2
0
11 3
. .sin . .sin120
2 24
OAB
R
S OA OB AOB R R= = =
.
Thể tích khối trụ là
2
V Rh
π
=
.
Ta có
2
1
3
.
4
OAB
Rh
VS h= =
và
( )
2
2
2
21
43
3
44
Rh
Rh
V V V Rh
π
π
−
=−= − =
.
Vậy
1
2
3
43
V
V
π
=
−
.
Câu 50: Cho phương trình
( ) ( )
2
22
log 2 3log 2 2 3 0
x
xx m
−− −+ −=
. Hỏi có tất cả bao nhiêu giá trị
nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm thực phân biệt ?
A.
8
. B.Vô số. C.
648
. D.
657
.
Lời giải
Chọn D
Xét phương trình
( )
1
.
Điều kiện:
( )
3
2
20
log do 0
30
x
x
x
x mm
m
>
−>
⇔
≥>
−≥
.
Với điều kiện trên,
( )
( ) ( )
2
22
log 2 3log 2 2 0
30
1
x
xx
m
−=
− − +=
⇔
−
( )
( )
2
2
3
log 2 2 6
log 2 1 4 .
3 log
x
xx
xx
mxm
−= =
−=⇔=
= =
⇔
Phương trình
( )
1
có hai nghiệm phân biệt
3
46
3
log 2
09
4 log 6 3 3
m
m
mm
≤
<≤
⇔⇔
≤ < ≤<
Do
*
m∈
nên
⇒
{1; 2; ; 9}
{81;82;83; ;728}
m
m
∈…
∈…
.
( )
( )
2
22
log 2 3log 2 2 3 0
x
xx m
−− −+ −=

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 26
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vậy có tất cả
( )
9 728 81 1 657+ −+=
giá trị
m
nguyên dương thỏa mãn đề bài.
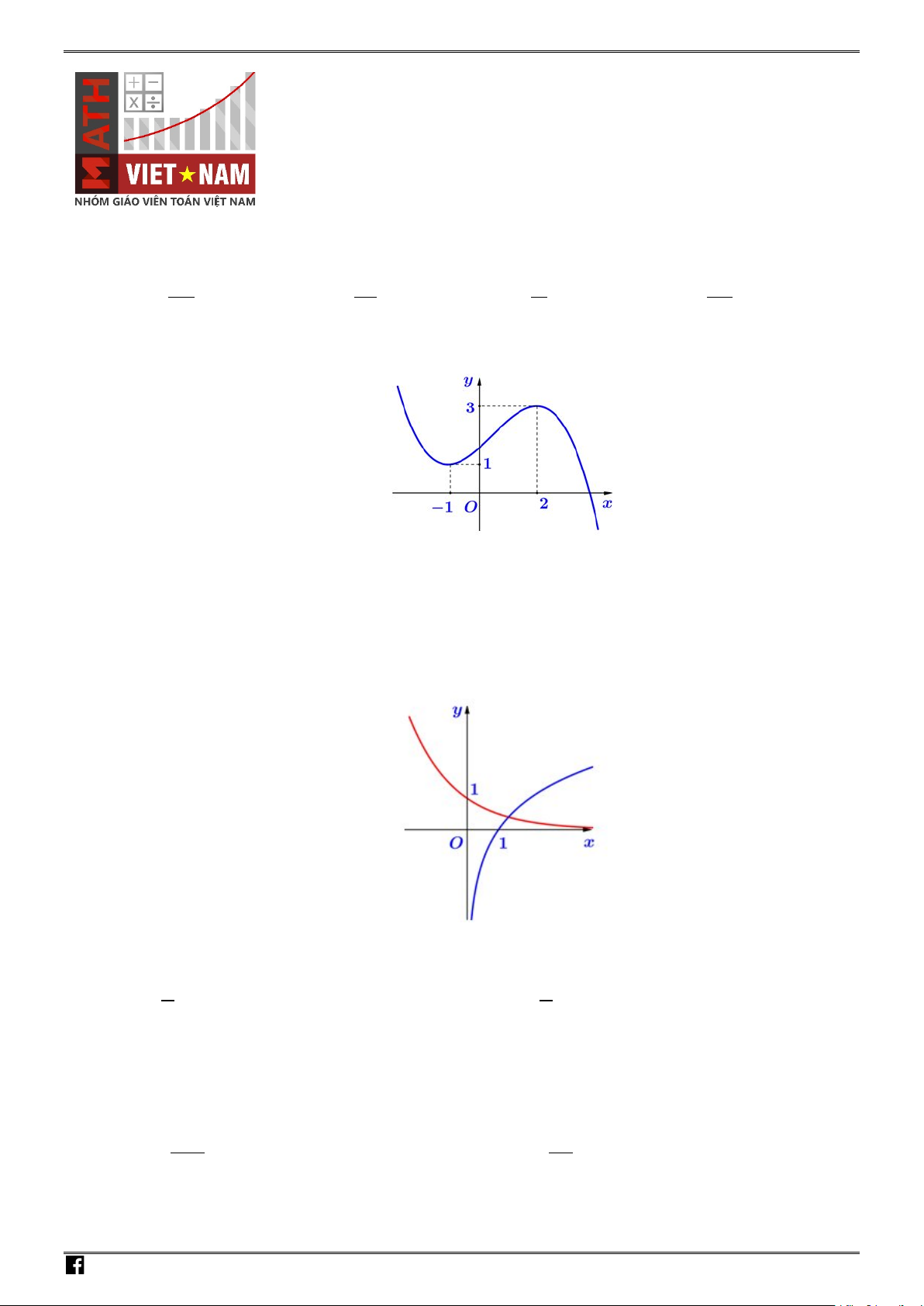
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
KIỂM TRA HỌC KÌ I LỚP 12
SỞ GD&ĐT BÌNH THUẬN
NĂM HỌC: 2020-2021
THỜI GIAN: 90 phút
Câu 1: Cho khối chóp có thể tích
V
và chiều cao
h
. Khi đó diện tích đáy của khối chóp bằng
A.
3
h
V
. B.
3
V
h
. C.
V
h
. D.
3V
h
.
Câu 2: Cho hàm số
()y fx
có đồ thị như hình bên. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
( 1; 2)
.
B. Hàm số đồng biến trên khoảng
(0; 2)
.
C. Hàm số đồng biến trên khoảng
(0; )
.
D. Hàm số nghịch biến trên khoảng
( ; 0)
.
Câu 3: Cho đồ thị các hàm số
, log
x
b
y ay x
như hình vẽ bên. Mệnh đề nào sau đây đúng?
A.
01ba
. B.
1 ba
. C.
01ab
. D.
01ab
.
Câu 4: Thể tích khối trụ tròn xoay có bán kính đáy
R
và chiều cao
h
bằng
A.
2
1
3
Rh
B.
2
Rh
. C.
2
1
.
3
Rh
D.
2
.Rh
Câu 5: Hình nón
N
có đường tròn đáy bán kính
R
và độ dài đường sinh là
.l
N
có diện tích toàn
phần là
A.
.Rl
π
B.
2
2 Rl R
ππ
+
. C.
2
Rl R
ππ
+
. D.
2
22Rl R
ππ
+
.
Câu 6: Thể tích khối lăng trụ có diện tích đáy
B
và chiều cao
2h
là
A.
2
3
Bh
B.
2Bh
. C.
3
Bh
. D.
Bh
.
Câu 7: Khối lập phương cạnh
3a
có thể tích bằng
A.
3
9a
. B.
3
27a
. C.
2
9a
. D.
3
3a
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 8: Hàm số nào sau đây nghịch biến trên khoảng
( )
0; +∞
?
A.
1
2
x
y
=
. B.
21
logyx
+
=
. C.
2
logyx=
. D.
3
x
y =
.
Câu 9: Cho hàm số
(
)
y fx=
có bảng biến thiên như sau:
Khẳng định nào sau đây sai?
A. Hàm số đồng biến trên khoảng
( )
2;5
.
B. Hàm số đồng biến trên khoảng
( )
0; +∞
.
C. Hàm số đồng biến trên các khoảng
( )
;1−∞ −
và
( )
2; +∞
.
D. Hàm số nghịch biến trên khoảng
(
)
1; 2
−
.
Câu 10: Cho hàm số
1
4
yx
−
=
. Khẳng định nào sau đây sai?
A. Đồ thị hàm số không có điểm cực trị. B. Hàm số nghịch biến trên
.
C. Đồ thị hàm số đi qua điểm
( )
1;1A
. D. Đồ thị hàm số có hai đường tiệm cận.
Câu 11: Cho
a
là số thực dương. Biểu thức
2
3
5
3
aa
viết dưới dạng lũy thữa với số mũ hữu tỉ là
A.
1
a
−
. B.
10
3
a
. C.
19
5
a
. D.
7
3
a
.
Câu 12: Phương trình tiếp tuyến của đồ thị hàm số
( )
32
31fx x x=−+
tại điểm
( )
4;17M
là
A.
24 113yx= +
. B.
24 113yx= −
.
C.
24 79yx= −
. D.
24 79yx= +
.
Câu 13: Giá trị nhỏ nhất của hàm số
42
1
2
4
y xx= −−
trên đoạn
[ ]
2; 4
bằng?
A.
37
4
. B.
2−
. C.
3−
. D.
46
.
Câu 14: Cho
a
là số thực dương khác 1 thỏa
log 2 3
a
=
. Khẳng định nào sau đây đúng?
A.
2
3a =
. B.
3
2a
=
. C.
23
a
=
. D.
32
a
=
.
Câu 15: Cho
,xy
là hai số thực dương và
,mn
là hai số thực tùy ý. Đẳng thức nào sau đây sai?
A.
( ) ( )
mn
nm
xx=
. B.
( )
3
3
mm
xx=
. C.
( )
.
n
nn
xy x y=
. D.
m n mn
xx x
+
=
.
Câu 16: Tiệm cận ngang của đồ thị hàm số
21
3
x
y
x
có phương trình là
A.
2y
. B.
1
3
y
. C.
3y
. D.
2x
.
Câu 17: Cho
,,abc
là các số thực dương khác
1
thỏa
log 6
a
b
,
log 3
c
b
. Khi đó
log
a
c
bằng

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2
. B.
9
. C.
1
2
. D.
3
.
Câu 18: Cho hình trụ
T
có bán kính đáy
5R
, chiều cao
3
h
. Diện tích xung quanh của
T
là
A.
55
. B.
75
. C.
15
. D.
30
.
Câu 19: Giá trị cực đại của hàm số
32
1
31
3
y xx x
= +−+
bằng
A.
3
−
. B.
2
3
−
. C.
1
. D.
10
.
Câu 20: Cho hàm số
( )
y fx=
có đồ thị như hình bên. Số nghiệm của phương trình
( )
2 30
fx−=
là
A.
0
. B.
3
. C.
4
. D.
2
.
Câu 21: Hàm số nào sau đây có đồ thị như hình bên?
A.
32
31yx x=++
. B.
42
31yx x=−+
. C.
42
32
yx x=++
. D.
32
32yx x=−+
.
Câu 22: Tập hợp tất cả giá trị của tham số
m
để hàm số
( )
2
1
1
mx
fx
x
−
=
+
có giá trị lớn nhất trên đoạn
[ ]
0;1
bằng
4
là
A.
{ }
3; 1−−
. B.
. C.
{ }
3; 2
. D.
{ }
3; 3−
.
Câu 23: Cho hình chóp
.S ABC
. Gọi
,AB
′′
lần lượt là trung điểm của
SA
và
SB
. Khi đó tỉ số thể tích
của hai khối chóp
.SABC
′′
và
.S ABC
bằng
A.
1
4
. B.
1
8
. C.
1
2
. D.
1
3
.
Câu 24: Cho hàm số
( )
( )
ln 1
x
fx e= +
. Khi đó
( )
ln 2
f
′′
bằng
A.
9
2
−
. B.
2
9
. C.
2
9
−
. D.
9
2
.
Câu 25: Cho hình nón
( )
N
có độ dài đường sinh bằng
5
và bán kính đáy bằng
3
.
( )
N
có chiều cao bằng
A.
4
. B.
2
. C.
3
. D.
5
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 26: Thể tích của khối nón
( )
N
có bán kính đáy
Ra=
và chiều cao
3ha=
là
A.
2
3 a
π
. B.
3
2
a
π
. C.
3
a
π
. D.
3
3 a
π
.
Câu 27: Cho hàm số
( )
y fx=
, biết
( )
fx
′
có đồ thị như hình bên dưới.
Khẳng định nào sau đây sai?
A. Hàm số
( )
fx
đạt cực đại tại điểm
3x =
.
B. Hàm số
( )
fx
đạt cực tiểu tại các điểm
4
x
= −
và
6x =
.
C. Hàm số
( )
fx
có
4
điểm cực trị.
D. Hàm số
( )
fx
có
3
điểm cực trị.
Câu 28: Tập xác định
D
của hàm số
( )
10
2
2yx x
−
= −
là
A.
{ }
\0D =
. B.
{ }
\2D =
. C.
{ }
\ 0;2D =
. D.
D
=
.
Câu 29: Hàm số
2
4yx= −
đồng biến trên khoảng nào dưới đây?
A.
(
)
0; 2
. B.
(
)
1;1−
. C.
( )
2;0−
. D.
( )
2; 2−
.
Câu 30: Biết tiếp tuyến của đồ thị hàm số
1
2
x
y
x
+
=
−
song song với đường thẳng
31
yx=−+
có phương
trình
y ax b= +
. Khi đó giá trị
ab−
bằng
A.
4
. B.
16−
. C.
4−
. D.
16
.
Câu 31: Cho hàm số
( )
y fx=
có bảng biến thiên như hình bên. Khẳng định nào sau đây sai?
A. Giá trị nhỏ nhất của
( )
fx
trên
bằng
2−
.
B. Phương trình
(
)
0fx
=
có
3
nghiệm phân biệt.
C. Đồ thị của hàm số
( )
fx
không có tiệm cận.
D. Giá trị nhỏ nhất của
( )
fx
trên đoạn
[ ]
2; 4
bằng
( )
4f
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 32: Cho hàm số
( )
y fx=
có bảng biến thiên như hình bên. Đồ thị của hàm số
(
)
y fx=
có bao
nhiêu đường tiệm cận đứng và tiệm cận ngang?
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 33: Giá trị nhỏ nhất của tham số
m
để hàm số
2
1
mx
y
xm
−
=
−+
đồng biến trên khoảng
( )
;1−∞ −
là
A.
1
2
m =
. B.
1
m =
. C.
3
m = −
. D.
0m
=
.
Câu 34: Cho lăng trụ đứng
.
′′′
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
và
′
= =AA AB a
. Thể
tích khối lăng trụ
.
′′′
ABC A B C
bằng
A.
3
6
a
. B.
3
2
a
. C.
3
a
. D.
3
3
a
.
Câu 35: Cho hàm số
( )
=y fx
và
( )
′
fx
có bảng xét dấu như hình bên. Số điểm cực trị của hàm số
( )
fx
là
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 36: Biết rằng
( )
0; 2A
và
(
)
1;1−
B
là hai trong ba điểm cực trị của đồ thị hàm số
( ) ( )
42
, ,,=++ ∈f x ax bx c a b c
. Khi đó giá trị của
( )
2f
bằng
A.
10
. B.
65
. C.
226
. D.
1
.
Câu 37: Cho lặng trụ đứng
.'' 'ABC A B C
có đáy là tam giác vuông tại
A
,
=AB a
,
0
30=ACB
, góc giữa
hai mặt phẳng
( )
''BA C
và
( )
'''ABC
bằng
0
45
. Gọi
( )
T
là hình trụ ngoại tiếp lăng trụ
.'' 'ABC A B C
. Thể tích của khối trụ sinh bởi
( )
T
là
A.
3
a
π
. B.
3
6
a
π
. C.
3
3
a
π
. D.
3
2 a
π
.
Câu 38: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
A
và
D
,
3=AB a
,
= =AD CD a
,
SA
vuông góc với mặt phẳng
( )
ABCD
. Nếu góc giữa đường thẳng
SD
và mặt phẳng
( )
ABCD
bằng
0
60
thì khối chóp
.S ABCD
có thể tích bằng
A.
3
23
3
a
. B.
3
3
3
a
. C.
3
23a
. D.
3
3
2
a
.
Câu 39: Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho phương trình
3
30x xm− −=
có
3 nghiệm phân biệt trong đó có
2
nghiệm dương. Khẳng định nào sau đây đúng?
A.
( )
0; 2S =
. B.
{ }
2; 2S = −
. C.
( )
2; 2S = −
. D.
( )
2;0S = −
.
Câu 40: Diện tích xung quanh của của hình nón ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng
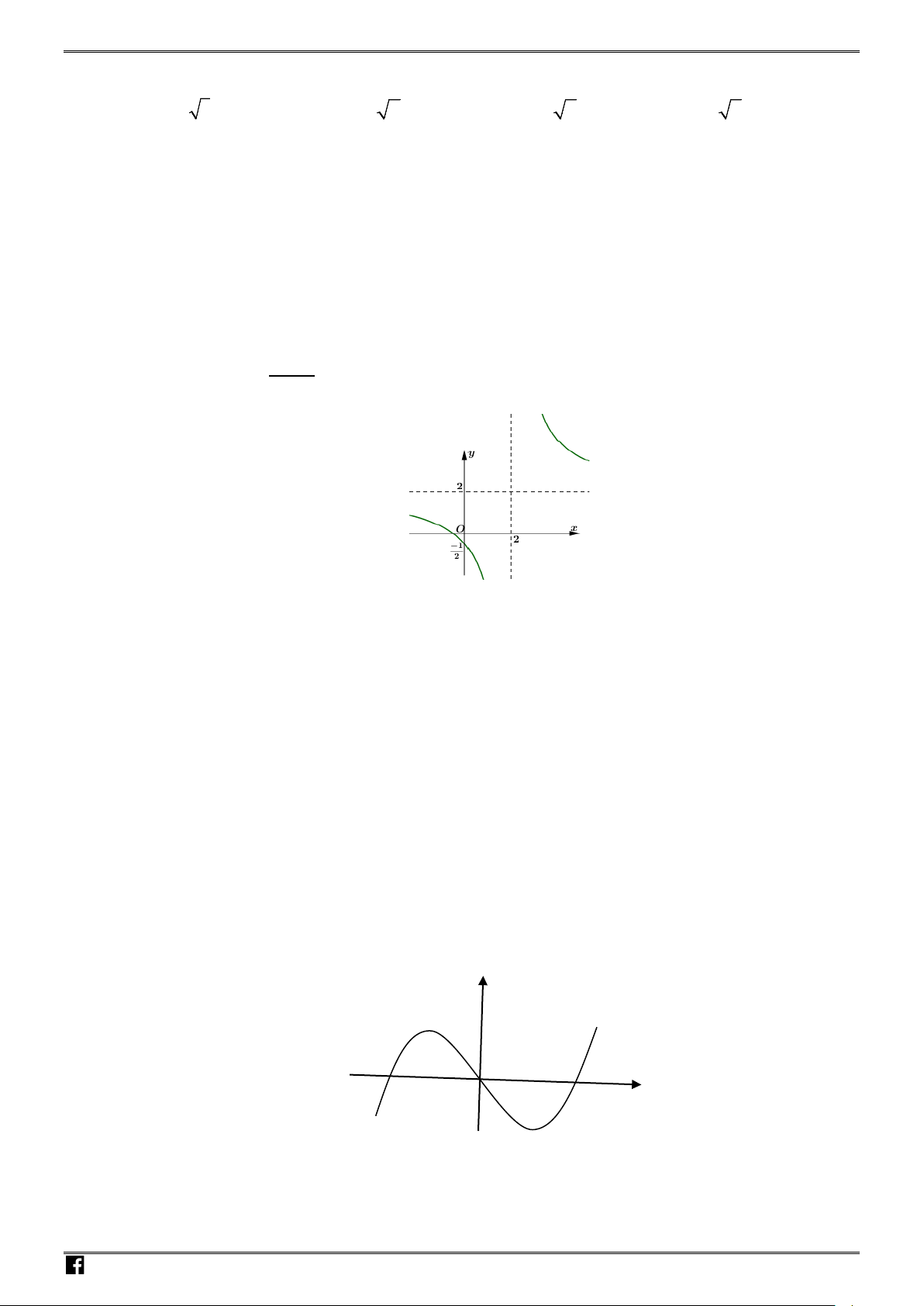
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
2
là
A.
23
π
. B.
42
π
. C.
22
π
. D.
2
π
.
Câu 41: Cho hình hộp chữ nhật
.
ABCD A B C D
′′′′
có
,2AB a AD a
= =
, góc giữa hai mặt phẳng
( )
ABC D
′′
và
(
)
ABCD
bằng
0
45
. Khối hộp
.ABCD A B C D
′′′′
có thể tích bằng
A.
3
4a
. B.
3
2a
. C.
3
8a
. D.
3
6a
.
Câu 42: Cho hình nón
( )
N
có thiết diện qua trục là tam giác vuông cân có diện tích bằng
9
. Khối nón
sinh bởi
( )
N
có thể tích bằng
A.
6
π
. B.
3
π
. C.
9
π
. D.
π
.
Câu 43: Cho hàm số
1
ax
y
bx c
+
=
+
có đồ thị như hình vẽ dưới
Giá trị của
abc++
bằng
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 44: Cắt hình trụ
( )
T
bởi một mặt phẳng qua trục của nó được thiết diện là hình vuông cạnh
2a
.
Diện tích toàn phần của
( )
T
là:
A.
2
2 a
π
. B.
2
4 a
π
. C.
2
8
a
π
. D.
2
6 a
π
Câu 45: Xét các số thực dương
,ab
thoả mãn
22
20
ab+=
. Khẳng định nào sau đây đúng?
A. Giá trị nhỏ nhất của
log ab
bằng
0
. B. Giá trị lớn nhất của
log
ab
bằng
0
.
C. Giá trị nhỏ nhất của
log ab
bằng
1
. D. Giá trị lớn nhất của
log ab
bằng
1
.
Câu 46: Cho hàm số
( )
,y fx=
biết
( )
'
fx
liên tục trên
và có đồ thị như hình bên. Hàm số
( )
( )
2
4 2020gx f x= −+
đồng biến trên khoảng nào sau đây?
A.
( )
2;0−
. B.
( )
0; 2
. C.
( )
2; +∞
. D.
( )
1; 2
.
y
O
3−
3
( )
'fx
x
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 47: Cho lăng trụ đứng
.'' '
ABC A B C
có đáy là tam giác đều cạnh
.a
Gọi
,MN
lần lượt là trung
điểm của
''AB
và
'CC
. Nếu
AM
và
'AN
vuông góc với nhau thì khối lăng trụ
.'' 'ABC A B C
có thể tích bằng
A.
3
6
8
a
. B.
3
6
2
a
. C.
3
6
4
a
. D.
3
6
24
a
.
Câu 48: Cắt hình trụ
( )
T
có bán kính đáy
R
và chiều cao
h
thỏa
2 3.Rh+=
Thể tích
( )
T
có giá trị lớn
nhất bằng
A.
2
π
. B.
3
π
. C.
π
. D.
4
π
.
Câu 49: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật,
BC a=
. Mặt bên
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với mặt phẳng đáy. Góc giữa đường thẳng
SC
và mặt phẳng
( )
ABCD
bằng
0
30
. Thể tích khối chóp
.S ABCD
bằng
A.
3
3a
. B.
3
3
3
a
. C.
3
3
12
a
. D.
3
3
6
a
.
Câu 50: Cho khối lăng trụ
.ABC A B C
′′′
có thể tích bằng
a
. Gọi
M
là trung điểm của
.AB
Nếu tam giác
MB C
′′
có diện tích bằng
b
thì khoảng cách từ
C
đến mặt phẳng
( )
MB C
′′
bằng
A.
2
a
b
. B.
a
b
. C.
2
b
a
. D.
6
a
b
.
N
'C
'
B
'A
C
B
A
M
K
H
O

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
ĐỀ THI HỌC KỲ 1 – NĂM HỌC 2020 – 2021
SỞ GD & ĐT BÌNH THUẬN
Môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề)
BẢNG ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
1.D
2.B
3.C
4.D
5.C
6.B
7.B
8.A
9.B
10.B
11.D
12.C
13.B
14.B
15.B
16.A
17.A
18.D
19.D
20.D
21.D
22.D
23.A
24.B
25.A
26.C
27.C
28.C
29.C
30.B
31.A
32.D
33.D
34.A
35.A
36.A
37.A
38.A
39.D
40.C
41.A
42.C
43.A
44.D
45.D
46.D
47.A
48.C
49.C
50.A
Câu 1: Cho khối chóp có thể tích
V
và chiều cao
h
. Khi đó diện tích đáy của khối chóp bằng
A.
3
h
V
. B.
3
V
h
. C.
V
h
. D.
3V
h
.
Lời giải
Chọn D
Câu 2: Cho hàm số
()y fx
có đồ thị như hình bên. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
( 1; 2)
.
B. Hàm số đồng biến trên khoảng
(0; 2)
.
C. Hàm số đồng biến trên khoảng
(0; )
.
D. Hàm số nghịch biến trên khoảng
( ; 0)
.
Lời giải
Chọn B
Câu 3: Cho đồ thị các hàm số
, log
x
b
y ay x
như hình vẽ bên. Mệnh đề nào sau đây đúng?
A.
01ba
. B.
1 ba
. C.
01ab
. D.
01ab
.
Lời giải
Chọn C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Dựa vào đồ thị ta có:
x
ya
là hàm nghịch biến nên
01a
.
log
b
yx
là hàm đồng biến nên
1b
.
Câu 4: Thể tích khối trụ tròn xoay có bán kính đáy
R
và chiều cao
h
bằng
A.
2
1
3
Rh
B.
2
Rh
. C.
2
1
.
3
Rh
D.
2
.Rh
Lời giải
Chọn D
Câu 5: Hình nón
N
có đường tròn đáy bán kính
R
và độ dài đường sinh là
.l
N
có diện tích toàn
phần là
A.
.Rl
π
B.
2
2 Rl R
ππ
+
. C.
2
Rl R
ππ
+
. D.
2
22Rl R
ππ
+
.
Lời giải
Chọn C
Câu 6: Thể tích khối lăng trụ có diện tích đáy
B
và chiều cao
2h
là
A.
2
3
Bh
B.
2Bh
. C.
3
Bh
. D.
Bh
.
Lời giải
Chọn B
Câu 7: Khối lập phương cạnh
3a
có thể tích bằng
A.
3
9a
. B.
3
27
a
. C.
2
9a
. D.
3
3a
.
Lời giải
Chọn B .
Thể tích khối lập phương cần tìm là
( )
3
3
3 27Va a= =
.
Câu 8: Hàm số nào sau đây nghịch biến trên khoảng
( )
0; +∞
?
A.
1
2
x
y
=
. B.
21
logyx
+
=
. C.
2
logyx=
. D.
3
x
y =
.
Lời giải
Chọn A .
Vì
1
01
2
<<
nên hàm số
1
2
x
y
=
nghịch biến trên khoảng
( )
0; +∞
.
Câu 9: Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Khẳng định nào sau đây sai?
A. Hàm số đồng biến trên khoảng
( )
2;5
.
B. Hàm số đồng biến trên khoảng
( )
0; +∞
.
C. Hàm số đồng biến trên các khoảng
( )
;1−∞ −
và
( )
2; +∞
.
D. Hàm số nghịch biến trên khoảng
( )
1; 2−
.
Lời giải

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn B
Câu 10: Cho hàm số
1
4
yx
−
=
. Khẳng định nào sau đây sai?
A. Đồ thị hàm số không có điểm cực trị. B. Hàm số nghịch biến trên
.
C. Đồ thị hàm số đi qua điểm
( )
1;1
A
. D. Đồ thị hàm số có hai đường tiệm cận.
Lời giải
Chọn B
Ta có hàm số
1
4
yx
−
=
xác định khi
0x >
do đó hàm số không thể nghịch biến trên
.
Câu 11: Cho
a
là số thực dương. Biểu thức
2
3
5
3
aa
viết dưới dạng lũy thữa với số mũ hữu tỉ là
A.
1
a
−
. B.
10
3
a
. C.
19
5
a
. D.
7
3
a
.
Lời giải
Chọn D
Ta có
2 25 7
3
5
3 33 3
.a a aa a= =
.
Câu 12: Phương trình tiếp tuyến của đồ thị hàm số
( )
32
31fx x x=−+
tại điểm
( )
4;17M
là
A.
24 113yx= +
. B.
24 113yx= −
.
C.
24 79yx= −
. D.
24 79yx= +
.
Lời giải
Chọn C
Ta có
(
)
2
36fx x x
′
= −
(
)
4 24f
′
⇒=
. Phương trình tiếp tuyến tại
( )
4;17M
là
( )
24 4 17 24 79yx x= −+= −
Câu 13: Giá trị nhỏ nhất của hàm số
42
1
2
4
y xx= −−
trên đoạn
[ ]
2; 4
bằng?
A.
37
4
. B.
2
−
. C.
3−
. D.
46
.
Lời giải
Chọn B
Hàm số xác định và liên tục trên
[ ]
2; 4
.
Đạo hàm
3
'2yx x
= −
.
Cho
( )
( )
( )
3
0
'0 2 0 2
2
x
loai
y x x x loai
loai
x
=
=⇔−=⇔=
= −
Tính giá trị
( )
22y = −
và
( )
4 46
y =
.
Vậy giá trị nhỏ nhất của hàm số là
2−
.
Câu 14: Cho
a
là số thực dương khác 1 thỏa
log 2 3
a
=
. Khẳng định nào sau đây đúng?
A.
2
3a =
. B.
3
2a =
. C.
23
a
=
. D.
32
a
=
.
Lời giải
Chọn B
Ta có:
33
log 2 3 2 2.
a
aa=⇔= ⇔ =
Câu 15: Cho
,xy
là hai số thực dương và
,mn
là hai số thực tùy ý. Đẳng thức nào sau đây sai?
A.
( ) ( )
mn
nm
xx=
. B.
( )
3
3
mm
xx=
. C.
( )
.
n
nn
xy x y=
. D.
m n mn
xx x
+
=
.
Chọn B

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu B sai vì vế phải
( )
3
3mm
xx=
.
Câu 16: Tiệm cận ngang của đồ thị hàm số
21
3
x
y
x
có phương trình là
A.
2
y
. B.
1
3
y
. C.
3y
. D.
2x
.
Lời giải
Chọn A
Ta có
1
1
2
2
21
lim lim lim 2
33
3
1
1
xx x
x
x
x
x
x
x
x
x
.
Hàm số có tiệm cận ngang
2
y
.
Câu 17: Cho
,,abc
là các số thực dương khác
1
thỏa
log 6
a
b
,
log 3
c
b
. Khi đó
log
a
c
bằng
A.
2
. B.
9
. C.
1
2
. D.
3
.
Lời giải
Chọn A
Ta có
11
log log .log log . 6. 2
log 3
a ab a
c
cbcb
b
.
Câu 18: Cho hình trụ
T
có bán kính đáy
5
R
, chiều cao
3h
. Diện tích xung quanh của
T
là
A.
55
. B.
75
. C.
15
. D.
30
.
Lời giải
Chọn D
Diện tích xung quanh của khối trụ là
2 . 2 .5.3 30S Rh
.
Câu 19: Giá trị cực đại của hàm số
32
1
31
3
y xx x
= +−+
bằng
A.
3−
. B.
2
3
−
. C.
1
. D.
10
.
Lời giải:
Chọn D.
Ta có
2
23yx x
′
=+−
;
2
1
0 23
3
x
y xx
x
=
′
=⇔ + −⇔
= −
.
Bảng biến thiên
Dựa vào bảng biến thiên, ta có giá trị cực đại của hàm số bằng
10
.
Câu 20: Cho hàm số
( )
y fx=
có đồ thị như hình bên. Số nghiệm của phương trình
( )
2 30fx−=
là

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
0
. B.
3
. C.
4
. D.
2
.
Lời giải:
Chọn D.
Ta có
( ) ( )
3
2 30
2
fx fx−=⇔ =
.
Dựa vào đồ thị, nhận thấy đường thẳng
3
2
y
=
và đồ thị hàm số
(
)
fx
có hai điểm chung, do đó
phương trình đã cho có 2 nghiệm.
Câu 21: Hàm số nào sau đây có đồ thị như hình bên?
A.
32
31yx x=++
. B.
42
31
yx x=−+
. C.
42
32yx x=++
. D.
32
32yx x=−+
.
Lời giải:
Chọn D.
Dựa vào dáng điệu đồ thị và các đáp án, nhận thấy đây là đồ thị hàm số bậc ba, đồ thị cắt trục
tung tại điểm có tung độ bằng
2
nên chọn đáp án D.
Câu 22: Tập hợp tất cả giá trị của tham số
m
để hàm số
( )
2
1
1
mx
fx
x
−
=
+
có giá trị lớn nhất trên đoạn
[ ]
0;1
bằng
4
là
A.
{ }
3; 1−−
. B.
. C.
{ }
3; 2
. D.
{
}
3; 3−
.
Lời giải
Chọn D.
Ta có :
( )
2
1
1
mx
fx
x
−
=
+
liên tục trên
[
]
0;1
.
( )
( )
[ ]
( )
2
2
1
0, 0;1
1
m
f x x fx
x
+
′
= > ∀∈ ⇒
+
đồng biến trên
[
]
0;1
.
Khi đó :
[ ]
(
) ( )
2
0;1
1
1 43
2
m
max f x f m
−
= = =⇒=±
.
Câu 23: Cho hình chóp
.S ABC
. Gọi
,AB
′′
lần lượt là trung điểm của
SA
và
SB
. Khi đó tỉ số thể tích
của hai khối chóp
.SABC
′′
và
.S ABC
bằng
A.
1
4
. B.
1
8
. C.
1
2
. D.
1
3
.
Lời giải

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn A.
Áp dụng công thức tỉ số thể tích của khối chóp khi
,AB
′′
lần lượt là trung điểm của
SA
và
SB
,
ta có:
.
.
11 1
. . . .1
22 4
S ABC
S ABC
V
SA SB SC
V SA SB SC
′′
′′
= = =
.
Câu 24: Cho hàm số
( )
( )
ln 1
x
fx e= +
. Khi đó
( )
ln 2f
′′
bằng
A.
9
2
−
. B.
2
9
. C.
2
9
−
. D.
9
2
.
Lời giải
Chọn B.
Ta có:
(
)
( )
(
)
( )
1
ln 1
11
x
x
x
xx
e
e
fx e f x
ee
′
+
′
= +⇒ = =
++
.
( )
( ) ( ) ( )
(
)
( )
(
) (
)
2 22
.1 1. .1.
1 11
x x x x x x xx
x
x xx
e e e e e e ee
e
fx
e ee
′′
+− + +−
′′
⇒= = =
+ ++
.
( )
( )
( )
ln 2
22
ln 2
22
ln 2
9
21
1
e
f
e
′′
⇒= ==
+
+
.
Câu 25: Cho hình nón
( )
N
có độ dài đường sinh bằng
5
và bán kính đáy bằng
3
.
( )
N
có chiều cao bằng
A.
4
. B.
2
. C.
3
. D.
5
.
Lời giải
Chọn A
Chiều cao của
( )
N
là
22
25 9 4h lr= − = −=
.
Câu 26: Thể tích của khối nón
( )
N
có bán kính đáy
Ra=
và chiều cao
3ha=
là
A.
2
3 a
π
. B.
3
2 a
π
. C.
3
a
π
. D.
3
3 a
π
.
Lời giải
Chọn C
Thể tích của khối nón
( )
N
là
223
11
.3
33
V Rh a a a
πππ
= = =
.
Câu 27: Cho hàm số
( )
y fx
=
, biết
(
)
fx
′
có đồ thị như hình bên dưới.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Khẳng định nào sau đây sai?
A. Hàm số
( )
fx
đạt cực đại tại điểm
3x =
.
B. Hàm số
(
)
fx
đạt cực tiểu tại các điểm
4x = −
và
6x =
.
C. Hàm số
( )
fx
có
4
điểm cực trị.
D. Hàm số
( )
fx
có
3
điểm cực trị.
Lời giải
Chọn C
Từ đồ thị hàm số
( )
fx
′
ta thấy
( )
fx
′
chỉ đổi dấu
3
lần nên hàm số
( )
fx
có
3
điểm cực trị.
Câu 28: Tập xác định
D
của hàm số
( )
10
2
2yx x
−
= −
là
A.
{
}
\0D
=
. B.
{ }
\2D =
. C.
{ }
\ 0;2D =
. D.
D
=
.
Lời giải
Chọn C .
Điều kiện xác định :
2
0
20
2
x
xx
x
≠
− ≠⇔
≠
. Vậy tập xác định của hàm số là
{
}
\ 0; 2D =
.
Câu 29: Hàm số
2
4yx= −
đồng biến trên khoảng nào dưới đây?
A.
( )
0; 2
. B.
( )
1;1−
. C.
( )
2;0−
. D.
( )
2; 2−
.
Lời giải
Chọn C .
Tập xác định của hàm số là
[ ]
2; 2D = −
.
Có
2
4
x
y
x
−
′
=
−
,
00yx
′
=⇔=
.
Bảng biến thiên của hàm số

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vậy hàm số đồng biến trên
( )
2;0−
Câu 30: Biết tiếp tuyến của đồ thị hàm số
1
2
x
y
x
+
=
−
song song với đường thẳng
31yx
=−+
có phương
trình
y ax b= +
. Khi đó giá trị
ab−
bằng
A.
4
. B.
16
−
. C.
4−
. D.
16
.
Lời giải
Chọn B .
Giả sử tiếp điểm có hoành độ
( )
00
2xx≠
.
Có
( )
2
3
2
y
x
−
′
=
−
, theo giả thiết ta có
(
)
( )
0
0
2
0
0
1
3
33
3
2
x
yx
x
x
=
−
′
=−⇔ =−⇔
=
−
.
+ Với
0
1x =
ta có
0
2
y = −
, khi đó phương trình tiếp tuyến với đồ thị tại
( )
1; 2−
là:
( )
3 12 31y x yx=− −−⇔ =− +
( loại do trùng với đường thẳng đã cho ).
+ Với
0
3x
=
ta có
0
4y =
, khi đó phương trình tiếp tuyến với đồ thị tại
( )
3; 4
là:
( )
3 3 4 3 13y x yx=− − +⇔ =− +
, suy ra
3, 13ab=−=
nên
16ab−=−
.
Câu 31: Cho hàm số
( )
y fx=
có bảng biến thiên như hình bên. Khẳng định nào sau đây sai?
A. Giá trị nhỏ nhất của
( )
fx
trên
bằng
2
−
.
B. Phương trình
( )
0fx=
có
3
nghiệm phân biệt.
C. Đồ thị của hàm số
( )
fx
không có tiệm cận.
D. Giá trị nhỏ nhất của
( )
fx
trên đoạn
[ ]
2; 4
bằng
( )
4f
.
Lời giải
Chọn A
Dựa vào bảng biến thiên ta thấy hàm số
( )
lim
x
fx
→+∞
= −∞
nên hàm số không có giá trị nhỏ nhất
trên
.
Câu 32: Cho hàm số
( )
y fx=
có bảng biến thiên như hình bên. Đồ thị của hàm số
( )
y fx=
có bao
nhiêu đường tiệm cận đứng và tiệm cận ngang?
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn D
Dựa vào bảng biến thiên ta thấy hàm số
( )
1
lim
x
fx
+
→−
= +∞
,
( )
2
lim 1, 2
x
fx x x
±
→
= ±∞ ⇒ = − =
là
tiêm cận đứng,
(
)
lim 1 1
x
fx y
→+∞
=−⇒ =−
là tiệm cận ngang.
Câu 33: Giá trị nhỏ nhất của tham số
m
để hàm số
2
1
mx
y
xm
−
=
−+
đồng biến trên khoảng
( )
;1−∞ −
là
A.
1
2
m
=
. B.
1m
=
. C.
3m = −
. D.
0m =
.
Lời giải
Chọn D
Tập xác định
{ }
\1Dm
= −
Ta có
( )
2
2
2
1
mm
y
xm
− ++
′
=
−+
Hàm số đồng biến trên khoảng
( )
;1−∞ −
( )
(
)
2
1212
20
0, ; 1
11 0
1 ;1
mm
mm
yx
mm
m
−< < −< <
− + +>
′
⇔ > ∀ ∈ −∞ − ⇔ ⇔ ⇔
− ≥− ≥
− ∉ −∞ −
02m⇔≤ <
.
Vậy giá trị nhỏ nhất của tham số
0m =
.
Câu 34: Cho lăng trụ đứng
.
′′′
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
và
′
= =
AA AB a
. Thể
tích khối lăng trụ
.
′′′
ABC A B C
bằng
A.
3
6
a
. B.
3
2
a
. C.
3
a
. D.
3
3
a
.
Lời giải
Chọn A
A
C
B
′
A
′
B
′
C
Ta có:
3
.
1 11
. . ..
3 32 6
′′′
∆
′′
= = =
ABC A B C ABC
a
V S AA AB AC AA
.
Câu 35: Cho hàm số
( )
=y fx
và
( )
′
fx
có bảng xét dấu như hình bên. Số điểm cực trị của hàm số
( )
fx
là
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải
Chọn A
Bảng biến thiên:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
x
()fx
()fx
1
0
0
0
1
3
4
0
Dựa vào bảng biến thiên, hàm số đã cho có ba điểm cực trị.
Câu 36: Biết rằng
(
)
0; 2A
và
( )
1;1−B
là hai trong ba điểm cực trị của đồ thị hàm số
( )
( )
42
, ,,=++ ∈f x ax bx c a b c
. Khi đó giá trị của
( )
2f
bằng
A.
10
. B.
65
. C.
226
. D.
1
.
Lời giải
Chọn A
Ta có:
( )
3
42
′
= +f x ax bx
Do
( )
0; 2
A
và
(
)
1;1−B
là hai trong ba điểm cực trị của đồ thị hàm số
( ) ( )
42
, ,,=++ ∈f x ax bx c a b c
nên ta có:
21
420 2
12
= =
−− =⇔ =−
++= =
ca
ab b
abc c
.
Suy ra:
( ) ( )
42
2 2 2 10= − +⇒ =fx x x f
.
Câu 37: Cho lặng trụ đứng
.'' 'ABC A B C
có đáy là tam giác vuông tại
A
,
=AB a
,
0
30=ACB
, góc giữa
hai mặt phẳng
( )
''BA C
và
( )
'''A BC
bằng
0
45
. Gọi
( )
T
là hình trụ ngoại tiếp lăng trụ
.'' 'ABC A B C
. Thể tích của khối trụ sinh bởi
( )
T
là
A.
3
a
π
. B.
3
6
a
π
. C.
3
3
a
π
. D.
3
2 a
π
.
Lời giải
Chọn A
Gọi
,rh
lần lượt là bán kính, chiều cao của
( )
T
.
Tam giác
ABC
vuông tại
A
0
sin sin
22 2
30
= = = =⇒
AB a
BC
C
ra
.
( )
'
'
''
''
'' ''
''
'
'
⇒
⊥
⊥
⇒⊥
⊥
ACB
BB A A A
C
B
A
B
C
A
BA
A
C
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
( ) ( )
( )
(
)
'' ''' ''
' ' ', '
'' ''',''
''
''
∩=
⊂
⊥ ⇒
⊂ ⊥
A
BAC ABC AC
BA BA C BA
BA
ACABC B
C
A
( ) ( )
( )
0
'' '', ''' 45= =BA B BA C A B C
.
⇒
Tam giác
''ABB
vuông cân tại
'
B
' '' '⇒ = = =⇒= =BB A B AB a h BB a
.
Vậy thể tích của khối trụ sinh bởi
( )
T
là
23
= =rh aV
ππ
.
Câu 38: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
A
và
D
,
3
=AB a
,
= =AD CD a
,
SA
vuông góc với mặt phẳng
(
)
ABCD
. Nếu góc giữa đường thẳng
SD
và mặt phẳng
(
)
ABCD
bằng
0
60
thì khối chóp
.
S ABCD
có thể tích bằng
A.
3
23
3
a
. B.
3
3
3
a
. C.
3
23a
. D.
3
3
2
a
.
Lời giải
Chọn A
Ta có:
( )
( )
0
, 60= =SDA SD ABCD
.
Tam giác
SAD
vuông tại
A
0
tan .tan 60 3
. SDAA aS AD a=
= =⇒
.
( ) ( )
2
11
. 3 .2
22
ABCD
S AB CD AD a a a a= + = +=
.
Từ đó:
3
2
.
1 1 23
. 3.2
33 3
S ABCD ABCD
a
V SA S a a= = =
(đvtt).
Câu 39: Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho phương trình
3
30x xm
− −=
có
3 nghiệm phân biệt trong đó có
2
nghiệm dương. Khẳng định nào sau đây đúng?
A.
( )
0; 2S
=
. B.
{ }
2; 2
S = −
. C.
( )
2; 2S
= −
. D.
( )
2;0S
= −
.
Lời giải
Chọn D
Ta có:
33
30 3xxm xxm− −=⇔ − =
. Xét hàm số
( )
3
3gx x x= −
trên
.
( )
( )
22
' 3 33 1gx x x
= −= −
.
( )
1'0gx x= =
±⇔
.
Bảng biến thiên:
Dựa vào bảng biến thiên, yêu cầu bài toán
( )
;02 20mm⇔<∈−−< ⇔
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 40: Diện tích xung quanh của của hình nón ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng
2
là
A.
23
π
. B.
42
π
. C.
22
π
. D.
2
π
.
Lời giải
Chọn C
Giả sử hình chóp nội tiếp hình nón là
.S ABCD
.
Khi đó
22
. . . .2 2 2
22
xq
AC
S SA
ππ π
= = =
.
Câu 41: Cho hình hộp chữ nhật
.
ABCD A B C D
′′′′
có
,2AB a AD a
= =
, góc giữa hai mặt phẳng
( )
ABC D
′′
và
( )
ABCD
bằng
0
45
. Khối hộp
.ABCD A B C D
′′′′
có thể tích bằng
A.
3
4a
. B.
3
2a
. C.
3
8a
. D.
3
6
a
.
Lời giải
Chọn A
Ta có
( )
DC ADDA DC AD
′′ ′′ ′′ ′
⊥ ⇒⊥
và
AD DC
′′ ′′
⊥
.
Khi đó
(
) ( )
(
)
0
, 45ABC D ABCD AD A
′′ ′′
= =
. Vậy
AD A
′′
∆
vuông cân tại
A
′
nên
2AA AD a
′
= =
Vậy
3
.
. . .2 .2 4
ABCD A B C D
V AB AD AA a a a a
′′′′
′
= = =
.
Câu 42: Cho hình nón
( )
N
có thiết diện qua trục là tam giác vuông cân có diện tích bằng
9
. Khối nón
sinh bởi
( )
N
có thể tích bằng
A.
6
π
. B.
3
π
. C.
9
π
. D.
π
.
Lời giải
Chọn C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Giả sử thiết diện là tam giác vuông cân
SAB
. Gọi bán kính của hình nón
( )
N
là
r
.
Do
1
9 .2 9 3
2
SAB
S rr r
∆
=⇔ =⇒=
.
Vậy thể tích sinh bởi
( )
N
:
23
11
. . .3 9
33
V rr
π ππ
= = =
.
Câu 43: Cho hàm số
1ax
y
bx c
+
=
+
có đồ thị như hình vẽ dưới
Giá trị của
abc++
bằng
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn A
Đặt thị cắt
Oy
tại điểm có toạ độ
1
0;
2
−
11
2
2
yc
c
⇒=−=⇒=−
.
Đồ thị có tiệm cận đứng
21
c
xb
b
−
== ⇒=
.
Đồ thị có tiệm cận ngang
22
a
ya
b
==⇒=
.
Vậy
2121abc+ + =−++ =
.
Câu 44: Cắt hình trụ
( )
T
bởi một mặt phẳng qua trục của nó được thiết diện là hình vuông cạnh
2a
.
Diện tích toàn phần của
( )
T
là:
A.
2
2 a
π
. B.
2
4 a
π
. C.
2
8 a
π
. D.
2
6 a
π
Lời giải
Chọn D
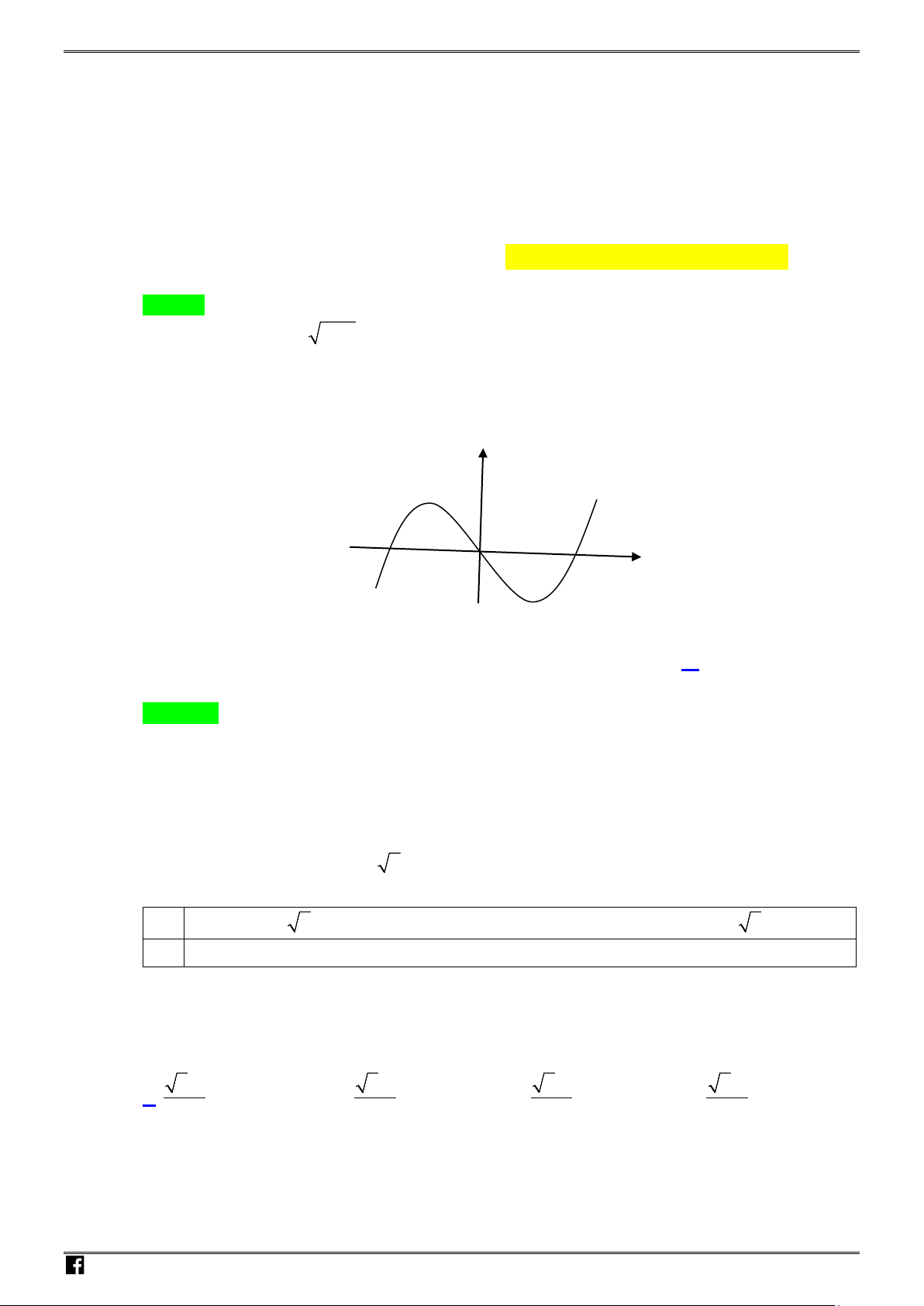
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Diện tích toàn phần của hình trụ
( )
T
bằng:
2
tp xq day
SS S= +
.
Vì thiết diện là hình vuông nên ta có:
,2R ah a= =
Vậy ta có
2 22
2 2 2 2 . .2 2 6 .
tp xq day
S S S Rh R a a a a
ππ π ππ
=+= + = +=
Câu 45: Xét các số thực dương
,ab
thoả mãn
22
20
ab+=
. Khẳng định nào sau đây đúng?
A. Giá trị nhỏ nhất của
log
ab
bằng
0
. B. Giá trị lớn nhất của
log ab
bằng
0
.
C. Giá trị nhỏ nhất của
log ab
bằng
1
. D. Giá trị lớn nhất của
log
ab
bằng
1
.
Lời giải
Chọn D
Ta có
2 2 22
20 2 2 10 1 loga b a b ab ab ab= + ≥ = ⇔ ≥ ⇔≥
.
Vậy giá trị lớn nhất của
log ab
bằng
1
.
Câu 46: Cho hàm số
( )
,y fx=
biết
( )
'fx
liên tục trên
và có đồ thị như hình bên. Hàm số
( )
( )
2
4 2020gx f x= −+
đồng biến trên khoảng nào sau đây?
A.
( )
2;0−
. B.
( )
0; 2
. C.
( )
2; +∞
. D.
(
)
1; 2
.
Lời giải
Chọn D .
Xét hàm số
( )
2
4 2020y fx= −+
. Ta có
( )
2
' 2 ' 4.y xf x= −
2
2
2
0
0
1
43
'0
2
40
7
43
x
x
x
x
y
x
x
x
x
=
=
= ±
−=−
=⇒⇒
= ±
−=
= ±
−=
Bảng xét dấu:
x
−∞
7−
2−
1−
0
1
2
7
+∞
'y
−
+
−
+
−
+
−
+
Từ bảng xét dấu ta có hàm số đồng biến trên khoảng
( )
1; 2
Câu 47: Cho lăng trụ đứng
.'' 'ABC A B C
có đáy là tam giác đều cạnh
.a
Gọi
,MN
lần lượt là trung
điểm của
''AB
và
'CC
. Nếu
AM
và
'AN
vuông góc với nhau thì khối lăng trụ
.'' 'ABC A B C
có thể tích bằng
A.
3
6
8
a
. B.
3
6
2
a
. C.
3
6
4
a
. D.
3
6
24
a
.
y
O
3−
3
( )
'fx
x

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn A
Gọi
H
là trung điểm của
'' ' ''AC BH AC
⇒⊥
.
Mặc khác
( )
' '''AA A B C⊥
nên suy ra
( )
' ' ' ''BH AA BH AACC⊥⇒ ⊥
Lấy
K
là trung điểm của
( )
' // ' ' ' ' .A H MK B H MK AA C C MK A N⇒ ⇒⊥ ⇒⊥
Mà
( )
' ' '.A N AM A N AMK A M AK⊥⇒ ⊥ ⇒ ⊥
Đặt
( )
'0AA x x= >
.
Xét tam giác
( )
2
22
22
'' '
4
' '' ' 1
'' '
4
44
a
AO AK AO a
AOK AC N AO
AC AN a
xx
aa
∆ ∆ ⇒ = ⇒ = ⇒⇒ =
++
Mặc khác trong tam giác
'A AK
ta có:
( )
2
2
.
4
'2
16
a
x
AO
a
x
=
+
.
Từ
( )
1
và
( )
2
ta được
2
4
22
22
.
4
4
4
16 4
a
x
aa
x
ax
xa
= ⇒=
++
.
Vậy
3
2
.'''
4
36
..
48
4
ABC A B C
aa
Va= =
Câu 48: Cắt hình trụ
( )
T
có bán kính đáy
R
và chiều cao
h
thỏa
2 3.Rh+=
Thể tích
( )
T
có giá trị lớn
nhất bằng
A.
2
π
. B.
3
π
. C.
π
. D.
4
π
.
Lời giải
Chọn C .
Ta có:
( )
( )
22
32
T
V Rh R R
ππ
= = −
. Để
( )
T
V
max thì
(
)
( )
2 32
max
max
32 2 3R R RR
π
− ⇒− +
Xét hàm số
32
23y RR=−+
có
2
0
' 6 6;' 0 .
1
R
y R Ry
R
=
=−+ =⇔
=
Suy ra
max
y
khi
( )
11 .
T
RhV
π
=⇒=⇒ =
N
'
C
'B
'A
C
B
A
M
K
H
O
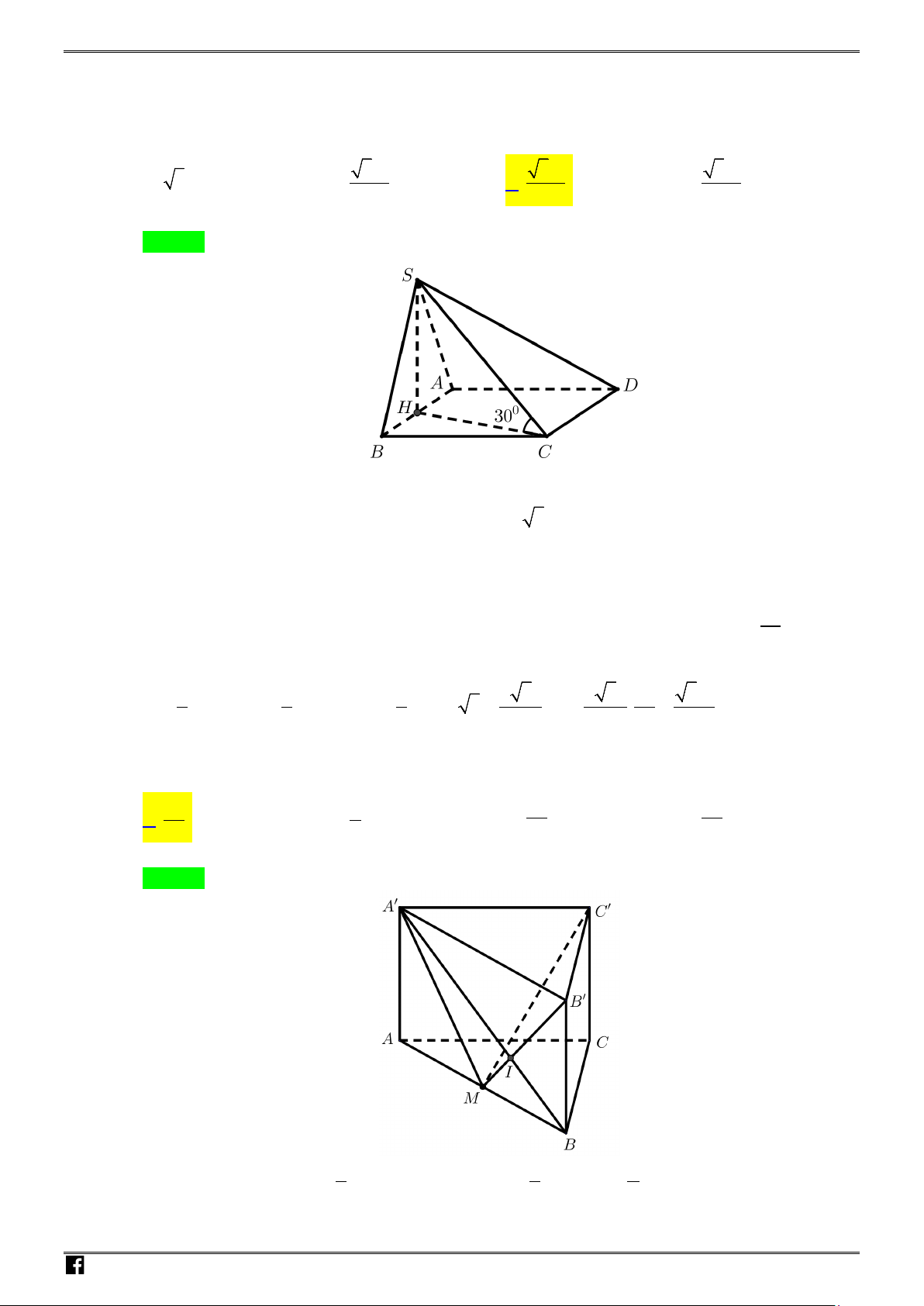
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 23
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 49: Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật,
BC a=
. Mặt bên
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với mặt phẳng đáy. Góc giữa đường thẳng
SC
và mặt phẳng
( )
ABCD
bằng
0
30
. Thể tích khối chóp
.S ABCD
bằng
A.
3
3a
. B.
3
3
3
a
. C.
3
3
12
a
. D.
3
3
6
a
.
Lời giải
Chọn C
Đặt
(
)
20AB x x= >
. Gọi
H
là trung điểm của
AB
.
Do
SAB
là tam giác đều nên
SH AB⊥
và
3SH x=
.
Mặt khác,
( ) ( )
SAB ABCD⊥
nên
( )
SH ABCD⊥
. Do đó,
( )
( )
0
, 30SCH SC ABCD= =
.
Suy ra
0
cot 30 3HC SH x
= =
.
Do tam giác
HBC
vuông tại
B
nên
( )
2
2
2 2 2 22 2
3
8
a
HC HB BC x x a x= + ⇔ =+⇔=
.
Thể tích khối chóp
.S ABCD
là
23
2
1 1 1 23 23 3
. . . . .2 . . 3 . .
3 3 3 3 3 8 12
ABCD
a aa a
V S SH AB BC SH x a x x
= = = = = =
.
Câu 50: Cho khối lăng trụ
.ABC A B C
′′′
có thể tích bằng
a
. Gọi
M
là trung điểm của
.AB
Nếu tam giác
MB C
′′
có diện tích bằng
b
thì khoảng cách từ
C
đến mặt phẳng
( )
MB C
′′
bằng
A.
2
a
b
. B.
a
b
. C.
2
b
a
. D.
6
a
b
.
Lời giải
Chọn A
Ta có
( )
( )
.. .
11
.,
3 33
A MBC M ABC ABC ABC ABC
a
V V S d M ABC V
′ ′′ ′′′ ′′′ ′′′
′′′
= = = =
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 24
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Mặt khác,
( )
( )
( )
( )
( )
.
.
3
1
., , 1
3
A MB C
A MB C MB C
MB C
V
a
V S d A MB C d A MB C
Sb
′ ′′
′ ′′ ′′
′′
′ ′′ ′ ′′
= ⇒==
Ta lại có,
( ) ( )
( )
( )
( )
( )
, ,2// //BC BC BC MBC d C MBC d B MBC
′′ ′′ ′′ ′′
⇒⇒ =
Gọi
I
là giao điểm của
AB
′
và
MB
′
. Ta có
( )
( )
( )
( )
( )
11 1
, ,3
22 2
//
IB MB
AB A B IB IA d B MB C d A MB C
IA A B
′′ ′ ′′ ′ ′′
⇒ = =⇒= ⇒ =
′ ′′
Từ
( )
( )
1,2
và
( )
3
ta có
( )
(
)
,
2
a
d C MB C
b
′′
=
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
SỞ AN GIANG
ĐỀ THI HỌC KÌ I - NĂM HỌC 2020 - 2021
Môn: TOÁN – LỚP 12
Thời gian: 90 phút (Không kể thời gian phát đề)
Câu 1: Tìm tất cả các giá trị của tham số
m
đề hàm số
xm
y
xm
đồng biến trên từng khoảng xác
định.
A.
0m ≤
B.
0m <
. C.
0
m
>
. D.
0
m
≥
.
Câu 2: Cho hàm số
y fx
có bảng xét dấu đạo hàm như hình vẽ. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
1; 3
. B. Hàm số đồng biến trên khoảng
2;1
.
C. Hàm số đồng biến trên khoảng
;2
. D. Hàm số nghịch biến trên khoảng
1;
.
Câu 3: Tìm điểm cực tiểu của đồ thị hàm số
32
3yxx
A.
( )
0;0
. B.
( )
2;3
. C.
( )
1; 4−
. D.
( )
1; 2
.
Câu 4: Tổng tất cả các nghiệm của phương trình
2
2 54
24
xx++
=
là
A.
5
2
. B.
5
2
−
. C.
1
−
. D.
1
.
Câu 5: Đường cong ở hình vẽ bên dưới là đồ thị của một trong bốn hàm
số dưới đây. Hàm số đó là hàm số nào?
A.
3
32yx x=−+
. B.
3
32yx x=−+ +
.
C.
3
32yx x=++
. D.
3
32
yxx=−− +
.
Câu 6: Cho ba số dương
,,
abc
và
1a ≠
. Tìm mệnh đề đúng
A.
log
c
a
cb a b=⇔=
. B.
log
c
a
bc=
. C.
log
a
b
ab=
. D.
log 0
a
a =
.
Câu 7: Đồ thị hình vẽ bên là đồ thị của hàm số
21
1
+
=
+
x
y
x
. Tìm tất cả các giá trị
m
để phương trình
21
21
1
+
= −
+
x
m
x
có hai nghiệm phân biệt.
A.
0,5 1,5≤≤m
. B.
02<<m
. C.
0,5 1,5<<m
. D.
02≤≤m
.
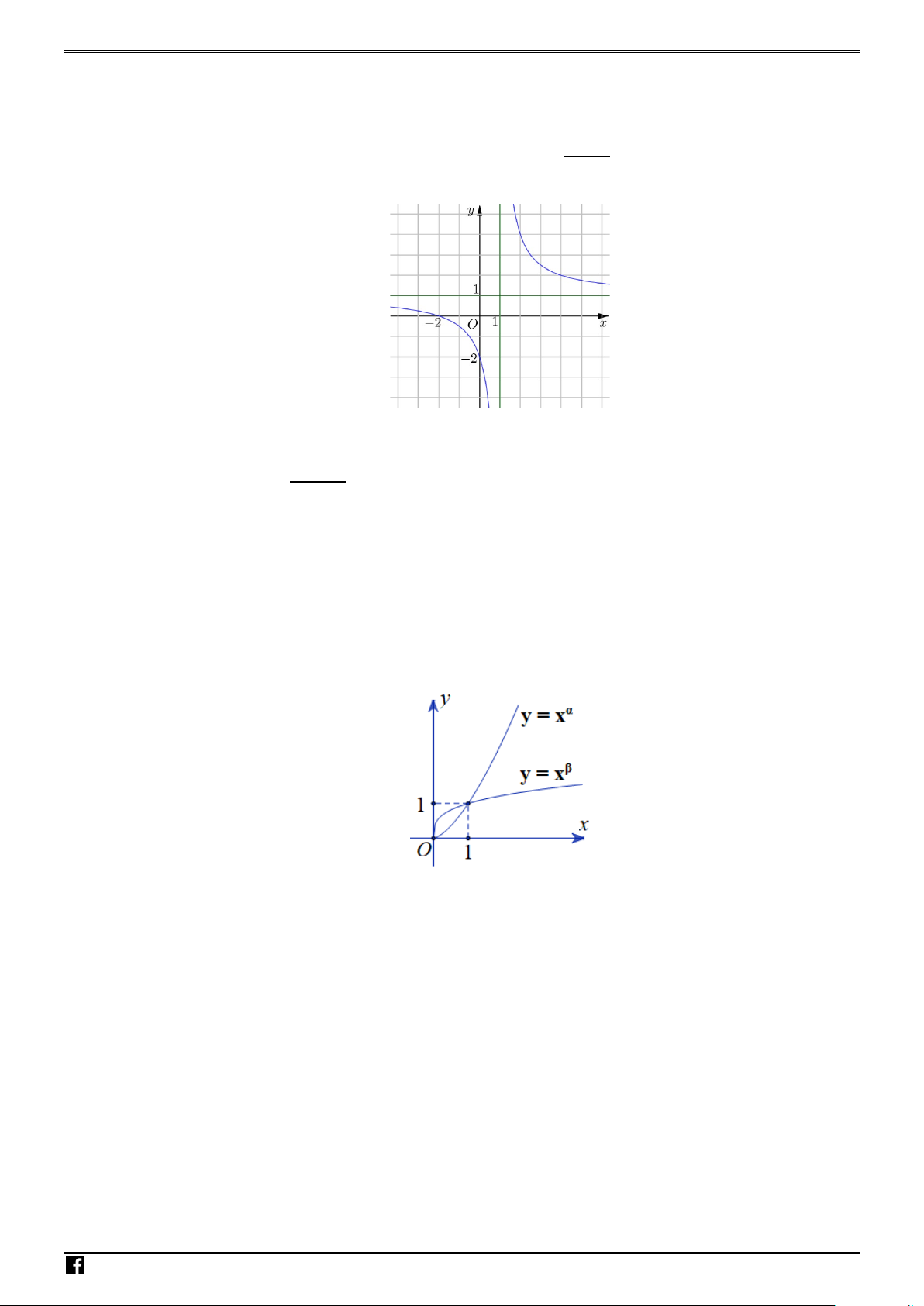
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 8: Nghiệm của phương trình
2
3 27
+
=
x
là
A.
1=x
. B.
1
= −
x
. C.
2=x
. D.
2
= −
x
.
Câu 9: Đường cong ở hình vẽ bên là đồ thị của hàm số
1
+
=
−
ax b
y
cx
với
;;
abc
là các số thực. Tính
=++S abc
.
A.
5=S
. B.
4=S
. C.
2=S
. D.
3=S
.
Câu 10: Đồ thị hàm số
2
1
2
x
y
xx
+
=
+
có bao nhiêu đường tiệm cận?
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 11: Cho
log 2
a
b =
,
log 3
a
c =
. Tính
( )
23
log .
a
P bc
=
.
A.
31P =
. B.
30P =
. C.
13P =
. D.
12P
=
.
Câu 12: Đồ thị hàm số
yx
α
=
,
yx
β
=
trên khoảng
( )
0; +∞
như hình vẽ dưới đây. Mệnh đề nào sau
đây đúng?
A.
01
βα
< <<
. B.
01
βα
< <<
. C.
01
αβ
< <<
. D.
01
αβ
< <<
.
Câu 13: Cho hai số dương
,ab
và
,
αβ
∈
. Mệnh đề nào dưới đây sai?
A. Nếu
1
a <
thì
aa
αβ
αβ
< ⇔<
. B. Nếu
1
b >
thì
bb
αβ
αβ
> ⇔>
.
C.
( )
..ab a b
α
αα
=
. D.
( )
.
aa
β
α αβ
=
.
Câu 14: Cho hàm số
42
21yx x=−+ −
có đồ thị như hình vẽ bên dưới. Tìm
m
để phương trình
42
2 10x xm− + +=
có bốn nghiệm phân biệt.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
1; 0
mm<− =
. B.
10m
−≤ ≤
. C.
1m ≤−
. D.
10
m−< <
.
Câu 15: Cho
2
log 5 a=
. Tính
4
log 1250
theo
a
.
A.
14a+
. B.
0,5 2a+
. C.
0,5 4a+
. D.
12a+
.
Câu 16: Rút gọn
( )
12
2 22 122
.Pa aa
+
−−
= −
với
0a >
ta được.
A.
2
1a
P
a
+
=
. B.
2
1 a
P
a
−
=
. C.
1
Paa
−
= +
. D.
1
Paa
−
= −
.
Câu 17: Đồ thị hai hàm số
x
ya
=
;
log
b
yx=
được cho bởi hình vẽ bên.
A.
01ab
< <<
. B.
01a<<
và
01
b
<<
.
C.
01ba< <<
. D.
1a
>
và
1b >
.
Câu 18: Số nghiệm của phương trình
( ) ( ) ( )
ln 1 ln 3 ln 7xx x++ + = +
là.
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 19: Cho hàm số
32
11
2
32
yx xx=+−
. Gọi
,MN
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
hàm số trên đoạn
[
]
1; 2−
. Tính
MN−
.
A.
10
3
. B.
13
6
. C.
7
6
−
. D.
2
3
.
Câu 20: Tiệm cận đứng của đồ thị hàm số
2
4
2
yx
x
= −
−
có phương trình
A.
2x =
. B.
2x = −
. C.
1y =
. D.
1y = −
.
Câu 21: Cho hàm số
24
4y xx= −
. Số điểm cực trị của hàm số đã cho là
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 22: Cho hàm số
42
2y mx x m= ++
, tìm tất cả các giá trị của tham số
m
để đồ thị hàm số đã cho
có điểm chung với trục hoành.
A.
10m−≤ ≤
. B.
1 1; 0mm−≤ ≤ ≠
. C.
10m
−< <
. D.
01m≤≤
.
Câu 23: Nghiệm của phương trình
( )
3
log 2 1 2x −=
là
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
. B.
5
. C.
9
2
. D.
7
2
.
Câu 24: Cho hàm số
32
21
32
xx
yx=+−+
. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên
( )
0;1
. B. Hàm số đồng biến trên
(
)
2;
− +∞
.
C. Hàm số đồng biến trên
( )
2;1−
. D. Hàm số nghịch biến trên
( )
;2
−∞ −
.
Câu 25: Cho
2a
π
=
;
1
2
b
−π
=
;
2
2c
π
=
. Mệnh đề nào sau đây đúng.
A.
abc≤≤
. B.
bac<<
. C.
cab<≤
. D.
bca<≤
Câu 26: Mỗi hình sau gồm một số hữu hạn các đa giác, tìm hình không phải hình đa diên.
A. B. C. D.
Câu 27: Thể tích khối trụ có bán kính đáy bằng 5 và chiều cao bằng 3 là
A.
25
π
. B.
30π
. C.
75
π
. D.
15π
.
Câu 28: Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có ba kích thước là :
1; 2; 3
là
A.
6
π
. B.
4
π
. C.
8
π
. D.
2
π
.
Câu 29: Một hộp đựng thực phẩm có dạng hình hộp chữ nhật có ba kích thước
1dm;1,2dm;1,5dm
.
Diện
tích toàn phần của hình hộp là
A.
2
4,5 dm
. B.
2
6 dm
. C.
2
4, 2 dm
. D.
2
9 dm
.
Câu 30: Một hình nón có bán kính đường tròn đáy bằng
R
, đường sinh
l
. Tỉ số diện tích xung
quang và
diện tích đáy hình nón bằng
A.
l
R
. B.
2l
R
. C.
R
l
. D.
2R
l
.
Câu 31: Thể tích khối lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3 là
A.
27 3
4
. B.
93
2
. C.
93
4
. D.
27 3
4
.
Câu 32: Thể tích khối chóp tứ giác có diện tích đáy
2
4a
, chiều cao
2a
bằng
A.
3
4
3
a
. B.
3
2
3
a
. C.
3
8
3
a
. D.
3
3
a
.
Câu 33: Tìm độ dài cạnh hình lập phương nội tiếp trong một mặt cầu bán kính
1R =
A.
3
3
B.
23
3
. C.
22
. D.
2
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 34: Số nghiệm của phương trình
( )
( )
2
31
3
log 4 log 2 3 0xx x+ + +=
là
A.
1
. B.
3
. C.
0
. D.
2
.
Câu 35: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
a
, cạnh bên
SA
vuông góc với đáy.
Tính thể tích của khối chóp
.
S ABC
biết
2SB a=
.
A.
3
4
a
. B.
3
3
4
a
. C.
3
2
a
. D.
3
3
2
a
.
Câu 36: Có bao nhiêu số nguyên của
m
để phương trình
2
22
log (2 ) 2log 4 2 1xm x x x m+− =−− −
có
hai nghiệm thực phân biệt.
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 37: Có bao nhiêu giá trị m nguyên thuộc đoạn
[ ]
2020;2020−
để phương trình
( ) ( )
log 2log 1mx x= +
có nghiệm duy nhất?
A.
2020
. B.
4040
. C.
4042
. D.
2021
.
Câu 38: Tập xác định của hàm số
( )
2
1yx= −
là tập hợp nào?
A.
[
)
1;
+∞
. B.
. C.
( )
1; +∞
. D.
{
}
\1
.
Câu 39: Hình chóp đều
.S ABC
có cạnh đáy bằng
a
, các cạnh bên bằng
2a
. Gọi
M
là trung điểm
SB
, điểm
N
thuộc
SC
sao cho
2NS NC=
. Tính thể tích khối đa diện
ABCMN
.
A.
3
11
18
a
. B.
3
11
16
a
. C.
3
11
36
a
. D.
3
11
24
a
.
Câu 40: Một sợi dây chuyền có chiều dài
28m
được cắt thành hai đoạn, đoạn có chiều dài
( )
lm
để
làm thành một hình vuông và đoạn
(
)
28
lm−
tạo thành hình tròn. Biết tổng diện tích hình
tròn và hình vuông nhỏ nhất. Hỏi số
l
gần nhất với số nào sau đây?
A.
11, 8m
. B.
12,9m
. C.
7,8m
. D.
15, 7m
.
Câu 41: Cho hàm số
( )
y fx=
, hàm số
( )
'y fx
=
liên tục trên
và có đồ thị như hình vẽ bên. Bất
phương trình
(
)
fx x m<+
(m là tham số) nghiệm đúng với mọi
( )
0; 2x∈
khi và chỉ khi
A.
( )
0mf
>
. B.
( )
0mf
≥
. C.
( )
22mf>−
. D.
(
)
22mf≥−
.
Câu 42: Cho khối tứ diện
.ABCD
Lấy điểm
M
nằm giữa
A
và
,B
điểm
N
nằm giữa
C
và
.D
Mặt
phẳng
( )
CDM
và
( )
ABN
chia khối tứ diện đó thành bốn khối tứ diện nào sau đây?
A.
; ;;NACB BC MN ABND MBND
. B.
;;;
MANC BCMN AMND MBND
.
C.
;;;MANC BCDN AMND ABND
. D.
;; ;ABCN ABND AMND MBND
.
Câu 43: Cho hàm số
( )
y fx=
liên tục trên nửa khoảng
[
)
1; 2−
, có bảng biến thiên như hình vẽ.
Khẳng định nào sau đây là SAI?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A. Đồ thị hàm số không đi qua điểm
( )
2;5
.
B. Hàm số đồng biến trên khoảng
( )
0;1
.
C.
[
)
1;2
min 2y
−
=
.
D.
[
)
1;2
max 5y
−
=
.
Câu 44: Cho phương trình
( ) ( )
3
13
8 8. 0,5 3.2 125 24. 0,5
xx
xx++
+ +=−
. Đặt
22
xx
t
−
= +
, phương trình đã
cho trở thành phương trình nào dưới đây?
A.
3
8 125 0t −=
. B.
3
8 3 12 0tt−− =
. C.
32
8 3 10 0t tt+ −− =
. D.
3
8 36 0tt+− =
.
Câu 45: Cho hình nón có chiều cao
2R
và bán kính đáy
R
.Xét hình trụ nội tiếp hình nón sao cho
thể tích khối trụ lớn nhất
.
Khi đó bán kính đáy của khối trụ là
A.
3
R
. B.
2
3
R
. C.
3
4
R
. D.
2
R
.
Câu 46:
Tìm tất cả các giá trị của tham số
m
để đồ thị
( )
m
C
của hàm số
3 23
32y x mx m=−+ −
có hai
điểm cực trị
;MN
sao cho đường thẳng
MN
vuông góc với đường thẳng
( )
: 2.dy x= −
A.
1
.
2
m = ±
B.
11
;.
42
mm=−=
C.
11
;.
24
mm=−=
D.
1
.
4
m = ±
Câu 47: Một người gửi tiết kiệm
100
triệu đồng không rút lãi, thời hạn
5
năm. Ngân hàng A nhận
tiền gửi lãi suất
1, 2%
tháng, Ngân hàng B nhận tiền gửi lãi suất
%r
năm. Tìm
r
nhỏ nhất
để người gửi vào ngân hàng B có lợi hơn ngân hàng A.
A.
16,39%.r =
B.
13,31%.r =
C.
15,39%.r =
D.
12,24%.r =
Câu 48:
Cho hình chóp
.,S ABCD
có đáy
ABCD
là hình vuông,
SA
vuông góc với mặt phẳng đáy,
cho biết
.SA AB a= =
Tính khoảng cách từ
B
đến mặt phẳng
( )
SCD
theo
a
.
A.
2
.
2
a
B.
2.a
C.
3.a
D.
3
.
3
a
Câu 49: Tính thể tích khối chóp
.S ABCD
, biết đáy hình chóp là hình vuông cạnh
,a SA
vuông góc
với mặt đáy,
SD
tạo với mặt phẳng
SAB
một góc
0
30
.
A.
3
3a
. B.
3
6
3
a
. C.
3
6
9
a
. D.
3
3
3
a
.
Câu 50: Cho hình nón tròn xoay có bán kính đường tròn đáy
r
, chiều cao
h
và đường sinh
l
. Ký
hiệu
V
là thể tích khối nón
;
tp xq
SS
lần lượt là diện tích toàn phần, diện tích xung quanh của
hình nón. Tìm mệnh đề SAI trong các mệnh đề sau?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2
xq
S rl
. B.
2
1
3
V rh
. C.
2
tp
S rl r
. D.
222
lrh
BẢNG ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT
1.B
2.B
3.A
4.B
5.B
6.C
7.C
8.A
9.B
10.C
11.C
12.B
13.A
14.D
15.B
16.D
17.C
18.D
19.A
20.A
21.A
22.A
23.C
24.A
25.A
26.D
27.C
28.C
29.D
30.A
31.A
32.C
33.B
34.A
35.A
36.C
37.D
38.C
39.A
40.C
41.D
42.B
43.D
44.A
45.B
46.A
47.C
48.A
49.D
50.A
Câu 1: Tìm tất cả các giá trị của tham số
m
đề hàm số
xm
y
xm
đồng biến trên từng khoảng xác
định.
A.
0m ≤
B.
0m <
. C.
0m >
. D.
0m ≥
.
Lời giải
Chọn B.
Để hàm số đồng biến trên từng khoảng xác định
0y
với mọi
x
thuộc khoảng xác định.
2
2
0
m
xm
với mọi
x
thuộc khoảng xác định.
0m
.
Câu 2: Cho hàm số
y fx
có bảng xét dấu đạo hàm như hình vẽ. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
1; 3
.
B. Hàm số đồng biến trên khoảng
2;1
.
C. Hàm số đồng biến trên khoảng
;2
.
D. Hàm số nghịch biến trên khoảng
1;
.
Lời giải
Chọn B.
Từ bảng xét dấu đạo hàm số đồng biến trên các khoảng:
2;1,1;3
.
Hàm số nghịch biến trên các khoảng:
; 2 , 3;
.
Vậy mệnh đề B đúng.
Câu 3: Tìm điểm cực tiểu của đồ thị hàm số
32
3yxx
A.
( )
0;0
. B.
( )
2;3
. C.
( )
1; 4−
. D.
( )
1; 2
.
Lời giải
Chọn A.
Ta có
2
36y xx
0
0
2
x
y
x
Bảng biến thiên:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Từ bảng biến thiên ta thấy điểm cực tiểu của đồ thị hàm số là
0;0
.
Câu 4: Tổng tất cả các nghiệm của phương trình
2
2 54
24
xx++
=
là
A.
5
2
. B.
5
2
−
. C.
1−
. D.
1
.
Lời giải
Chọn B
Ta có
2
2 54 2 2
1
2
1
2 42 5422 520
2
2
xx
x
xx xx
x
++
= −
=⇔ + +=⇔ + +=⇔
= −
.
Tồng các nghiệm là
12
5
2
xx+=−
.
Câu 5: Đường cong ở hình vẽ bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó
là hàm số nào?
A.
3
32yx x
=−+
. B.
3
32yx x
=−+ +
. C.
3
32yx x
=++
. D.
3
32yxx=−− +
.
Lời giải
Chọn B
Vì
( )
lim 0
x
fx a
→+∞
= −∞ ⇒ <
, nên
,AC
loại.
Đồ thị hàm số có hai điểm cực trị nằm về hai phía trục tung, nên chọn
B
Câu 6: Cho ba số dương
,,abc
và
1a ≠
. Tìm mệnh đề đúng
A.
log
c
a
cb a b=⇔=
. B.
log
c
a
bc=
. C.
log
a
b
ab
=
. D.
log 0
a
a =
.
Lời giải
Chọn C
Ta có
log
a
b
ab=

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 7: Đồ thị hình vẽ bên là đồ thị của hàm số
21
1
+
=
+
x
y
x
. Tìm tất cả các giá trị
m
để phương trình
21
21
1
+
= −
+
x
m
x
có hai nghiệm phân biệt.
A.
0,5 1,5≤≤m
. B.
02<<m
. C.
0,5 1,5<<m
. D.
02≤≤m
.
Lời giải
Chọn C
Ta có:
21 1
21
12
21 1
1
12
+
≥−
+
+
=
+
+
− <−
+
x
khi x
x
x
x
x
khi x
x
.
Từ đó, ta có đồ thị hàm số
21
1
+
=
+
x
y
x
như sau:
Dựa vào đồ thị trên, phương trình
21
21
1
+
= −
+
x
m
x
có hai nghiệm phân biệt
13
02 12 12 3
22
⇔ < −< ⇔< < ⇔ < <m mm
.
Câu 8: Nghiệm của phương trình
2
3 27
+
=
x
là
A.
1=x
. B.
1= −x
. C.
2=x
. D.
2= −x
.
Lời giải

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn A
Ta có:
2 23
3 27 3 3 1
++
= ⇔ = ⇔=
xx
x
.
Câu 9: Đường cong ở hình vẽ bên là đồ thị của hàm số
1
+
=
−
ax b
y
cx
với
;;abc
là các số thực. Tính
=++S abc
.
A.
5=S
. B.
4=S
. C.
2=S
. D.
3=S
.
Lời giải
Chọn B
Ta có đồ thị hàm số
1
+
=
−
ax b
y
cx
có tiệm cận đứng là
1
=
x
c
, tiệm cận ngang là
=
a
y
c
.
Dựa vào hình vẽ, ta thấy đồ thị hàm số có tiệm cận đứng là
1
=x
, tiệm cận ngang là
1=y
và cắt trục tung tại điểm có tung độ
2−
.
Suy ra:
1
1
1
12
1
2
=
=
= ⇔=
=
−=−
c
a
a
b
c
c
b
. Vậy
121 4=++=S
.
Câu 10: Đồ thị hàm số
2
1
2
x
y
xx
+
=
+
có bao nhiêu đường tiệm cận?
A.
2
. B.
1
. C.
3
. D.
0
.
Lời giải
Chọn C
Ta có
lim y lim y 0
xx→+∞ →−∞
= =
.
Suy ra đồ thị hàm số có đường tiệm cận ngang là
0y =
.
Lại có
0
lim y
x
+
→
= +∞
,
0
lim y
x
−
→
= −∞
,
( )
2
lim y
x
+
→−
= +∞
,
( )
2
lim y
x
−
→−
= −∞
.
Suy ra đồ thị hàm số có hai đường tiệm cận đứng là
0x =
và
2x = −
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vậy hàm số đã cho có ba đường tiệm cận.
Câu 11: Cho
log 2
a
b =
,
log 3
a
c
=
. Tính
( )
23
log .
a
P bc
=
.
A.
31P =
. B.
30P
=
. C.
13P =
. D.
12P =
.
Lời giải
Chọn C
Ta có
( )
23
log . 2log 3log 2.2 3.3 13
a aa
P bc b c= = + =+=
.
Câu 12: Đồ thị hàm số
yx
α
=
,
yx
β
=
trên khoảng
( )
0; +∞
như hình vẽ dưới đây. Mệnh đề nào sau
đây đúng?
A.
01
βα
< <<
. B.
01
βα
< <<
. C.
01
αβ
< <<
. D.
01
αβ
< <<
.
Lời giải
Chọn B
Dựa vào đồ thị ta có
01
β
<<
và
1
α
>
.
Từ đó suy ra
01
βα
< <<
.
Câu 13: Cho hai số dương
,ab
và
,
αβ
∈
. Mệnh đề nào dưới đây sai?
A. Nếu
1a <
thì
aa
αβ
αβ
< ⇔<
. B. Nếu
1b >
thì
bb
αβ
αβ
> ⇔>
.
C.
( )
..ab a b
α
αα
=
. D.
( )
.
aa
β
α αβ
=
.
Lời giải
Chọn A
Nếu
01a<<
thì hàm số
x
ya=
nghịch biến trên
. Do đó,
aa
αβ
αβ
< ⇔>
.
Câu 14: Cho hàm số
42
21
yx x=−+ −
có đồ thị như hình vẽ bên dưới. Tìm
m
để phương trình
42
2 10x xm− + +=
có bốn nghiệm phân biệt.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
1; 0mm<− =
. B.
10m−≤ ≤
. C.
1
m ≤−
. D.
10m−< <
.
Lời giải
Chọn D
Ta có
( )
42 42
2 10 2 1x xm x x m− + + = ⇔− + − = ∗
.
Số nghiệm của phương trình
( )
∗
bằng số điểm chung của đồ thị hàm số
42
21yx x=−+ −
và đường thẳng
ym=
.
Dựa vào đồ thị, suy ra phương trình
( )
∗
có bốn nghiệm phân biệt khi và chỉ khi
10m
−< <
.
Câu 15: Cho
2
log 5 a=
. Tính
4
log 1250
theo
a
.
A.
14a
+
. B.
0,5 2a
+
. C.
0,5 4a+
. D.
12a+
.
Lời giải
Chọn B
Ta có
( )
( ) (
)
2
4
4 22
2
11
log 1250 log 2.5 log 2 4log 5 1 4 0,5 2
22
aa
= = + =+=+
.
Câu 16: Rút gọn
( )
12
2 22 122
.Pa aa
+
−−
= −
với
0a >
ta được.
A.
2
1a
P
a
+
=
. B.
2
1 a
P
a
−
=
. C.
1
Paa
−
= +
. D.
1
Paa
−
= −
.
Hướng dẫn giải
Chọn D.
( )
( )
12 12
2 22 122 2 122 22 122 222122 22122 1 1
. ..P a a a a a a a a a aa
++
−− −− −− + −− −− −
=− = − = −=−
.
Câu 17: Đồ thị hai hàm số
x
ya
=
;
log
b
yx=
được cho bởi hình vẽ bên.
A.
01ab< <<
. B.
01a<<
và
01b<<
.
C.
01ba< <<
. D.
1a >
và
1b >
.
x
ya=
x
y
O
1
1
log
b
yx=

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Hướng dẫn giải
Chọn C.
Đồ thị hàm số
x
ya
=
đồng biến trên
nên
1a >
Đồ thị hàm số
log
b
yx
=
nghịch biến trên
( )
0; +∞
nên
01b<<
Do đó:
01ba< <<
Câu 18: Số nghiệm của phương trình
( ) ( ) ( )
ln 1 ln 3 ln 7xx x++ + = +
là.
A.
2
. B.
3
. C.
0
. D.
1
.
Hướng dẫn giải
Chọn D.
Điều kiện
10
30 1
70
x
xx
x
+>
+ > ⇔ >−
+>
.
Ta có phương trình
( )( ) ( )
22
1
ln 1 3 ln 7 4 3 7 3 4 0
4
x
x x x xx x xx
x
=
+ += +⇒++=+⇒+−=⇒
= −
Kết hợp với điều kiện ta có nghiệm của phương trình
1x =
Vậy số nghiệm của phương trình là 1.
Câu 19: Cho hàm số
32
11
2
32
yx xx=+−
. Gọi
,
MN
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
hàm số trên đoạn
[ ]
1; 2
−
. Tính
MN−
.
A.
10
3
. B.
13
6
. C.
7
6
−
. D.
2
3
.
Lời giải
Chọn A
Ta có:
2
'2yxx
= +−
,
[ ]
[ ]
1; 2
12 ;
1
0
2
'
x
y
x
=
= ⇔
= −
∉−
∈−
.
( )
13
1
6
y −=
,
( )
7
1
6
y = −
,
( )
2
2
3
y =
.
Suy ra
13
6
M =
và
7
6
N = −
. Vậy
13 7 20 10
6 6 63
MN
− = −− = =
.
Câu 20: Tiệm cận đứng của đồ thị hàm số
2
4
2
yx
x
= −
−
có phương trình
A.
2x =
. B.
2x = −
. C.
1y =
. D.
1y = −
.
Lời giải
Chọn A

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
2
22
4
lim lim
2
xx
yx
x
−−
→→
= − = +∞
−
,
2
22
4
lim lim
2
xx
yx
x
++
→→
= − = −∞
−
2x⇒=
là tiệm cận đứng của đồ thị hàm số đã cho.
Câu 21: Cho hàm số
24
4y xx= −
. Số điểm cực trị của hàm số đã cho là
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn A
( )
32
'8 4 42
y xx x x=−= −
,
2
'0 0
2
x
yx
x
= −
=⇔=
=
.
2
'' 8 12yx= −
.
( )
'' 2 16 0 2yx− =− <⇒=−
là điểm cực đại của hàm số.
( )
'' 0 8 0 0yx=>⇒=
là điểm cực tiểu của hàm số.
( )
'' 2 16 0 2yx=− <⇒=
là điểm cực đại của hàm số.
Vậy hàm số có 3 điểm cực trị.
Câu 22: Cho hàm số
42
2y mx x m= ++
, tìm tất cả các giá trị của tham số
m
để đồ thị hàm số đã cho
có điểm chung với trục hoành.
A.
10m−≤ ≤
. B.
1 1; 0mm
−≤ ≤ ≠
. C.
10
m
−< <
. D.
01
m≤≤
.
Lời giải
Chọn A.
Xét phương trình hoành độ giao điểm của đồ thị với trục hoành
42
20mx x m
+ +=
.
Đặt
2
,0t xt= ≥
ta được phương trình
2
2
2
20
1
t
mt t m m
t
−
++=⇔=
+
.
Đồ thị hàm số đã cho có điểm chung với trục hoành khi và chỉ khi phương trình (*) có
nghiệm
0t ≥
.
Xét hàm số
( )
2
2
1
t
ft
t
−
=
+
trên
[
)
0;
+∞
, có
( )
( )
2
2
2
22
1
t
ft
t
−
′
=
+
, trên trên
[
)
0; +∞
:
( )
01
ft t
′
= ⇔=
.
Bảng biến thiên
Suy ra điều kiện của tham số
m
là
10m−≤ ≤
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 23: Nghiệm của phương trình
( )
3
log 2 1 2
x −=
là
A.
3
. B.
5
. C.
9
2
. D.
7
2
.
Lời giải
Chọn C.
Ta có
( )
3
3
9
log212 212
2
x xx− = ⇔ −= ⇔ =
.
Câu 24: Cho hàm số
32
21
32
xx
yx
=+−+
. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên
( )
0;1
. B. Hàm số đồng biến trên
( )
2;− +∞
.
C. Hàm số đồng biến trên
( )
2;1−
. D. Hàm số nghịch biến trên
( )
;2
−∞ −
.
Lời giải
Chọn A.
Tập xác định của hàm số đã cho là
.
Có
2
1
2, 0
2
x
yxx y
x
=
′′
= +− =⇔
= −
Suy ra: Hàm số đồng biến trên các khoảng
( )
;2−∞ −
và
( )
1; +∞
.
Hàm số nghịch biến trên khoảng
( )
2;1−
do đó cũng nghịch biến trên
( ) ( )
0;1 2;1⊂−
Câu 25: Cho
2a
π
=
;
1
2
b
−π
=
;
2
2c
π
=
. Mệnh đề nào sau đây đúng.
A.
abc≤≤
. B.
bac<<
. C.
cab
<≤
. D.
bca<≤
Giải
Chọn A.
Ta có:
2
22a
π
π
= =
.
( )
2
1
22
2
b
−π
π
π
= = =
.
2
2c
π
=
.
Vậy
abc= =
.
Câu 26: Mỗi hình sau gồm một số hữu hạn các đa giác, tìm hình không phải hình đa diên.
A. B. C. D.
Giải:
Chọn D

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Có một cạnh là cạnh chung của 3 mặt.
Câu 27: Thể tích khối trụ có bán kính đáy bằng 5 và chiều cao bằng 3 là
A.
25π
. B.
30π
. C.
75π
. D.
15π
.
Giải:
Chọn C
Ta có:
22
5 3 75V Rh . .
=π=π =π
Câu 28: Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có ba kích thước là :
1; 2; 3
là
A.
6
π
. B.
4
π
. C.
8
π
. D.
2
π
.
Lời giải
Chọn C.
Bán kính mặt cầu ngoại tiếp khối hộp chữ nhật là
( )
2
222 22
11
12 3 2
22
R abc= ++= ++ =
Diện tích mặt cầu là
( )
2
2
4 428SR
ππ π
= = =
.
Câu 29: Một hộp đựng thực phẩm có dạng hình hộp chữ nhật có ba kích thước
1dm;1,2dm;1,5dm
.
Diện tích toàn phần của hình hộp là
A.
2
4,5 dm
. B.
2
6 dm
. C.
2
4, 2 dm
. D.
2
9 dm
.
Lời giải
Chọn D.
Diện tích toàn phần của hình hộp là
( )
2
2 1.1,2 1.1,5 1,2.1,5 9 dmS = ++ =
.
Câu 30: Một hình nón có bán kính đường tròn đáy bằng
R
, đường sinh
l
. Tỉ số diện tích xung
quang và
diện tích đáy hình nón bằng
A.
l
R
. B.
2l
R
. C.
R
l
. D.
2R
l
.
Lời giải
Chọn A.
Diện tích xung quang
1
S Rl
π
=
.
Diện tích đường tròn đáy
2
2
SR
π
=
.
Ta có
1
2
S
l
SR
=
.
Câu 31: Thể tích khối lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3 là
A.
27 3
4
. B.
93
2
. C.
93
4
. D.
27 3
4
.
Lời giải
I
D
'
C
'
B
'
A
'
C
D
B
A

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn A
Thể tích khối lăng trụ là
2
.
3 3 27 3
. 3.
44
ABC A B C ABC
V AA S
′′′
′
= = =
.
Câu 32: Thể tích khối chóp tứ giác có diện tích đáy
2
4a
, chiều cao
2a
bằng
A.
3
4
3
a
. B.
3
2
3
a
. C.
3
8
3
a
. D.
3
3
a
.
Lời giải
Chọn C
Thể tích khối chóp là
3
2
18
.2 .4
33
a
V aa= =
.
Câu 33: Tìm độ dài cạnh hình lập phương nội tiếp trong một mặt cầu bán kính
1R =
A.
3
3
B.
23
3
. C.
22
. D.
2
.
Lời giải
Chọn B
Hình lập phương nội tiếp hình cầu bán kính
R
có cạnh bằng
2 23
3
3
R
=
.
Câu 34: Số nghiệm của phương trình
( )
( )
2
31
3
log 4 log 2 3 0
xx x+ + +=
là
A.
1
. B.
3
. C.
0
. D.
2
.
Lời giải
Chọn A
Điều kiện:
0x >
.
Phương trình đã cho tương đương với:
( )
( )
( )
( )
2 22
33 3 3
log 4 log 2 3 0 log 4 log 2 3 4 2 3xx x xx x xxx+ − +=⇔ + = +⇔+ = +
2
1
2 30
3
x
xx
x
=
⇔ + −=⇔
= −
. Kết hợp với điều kiện suy ra phương trình có nghiệm
1x =
.
C'
B'
A'
C
B
A
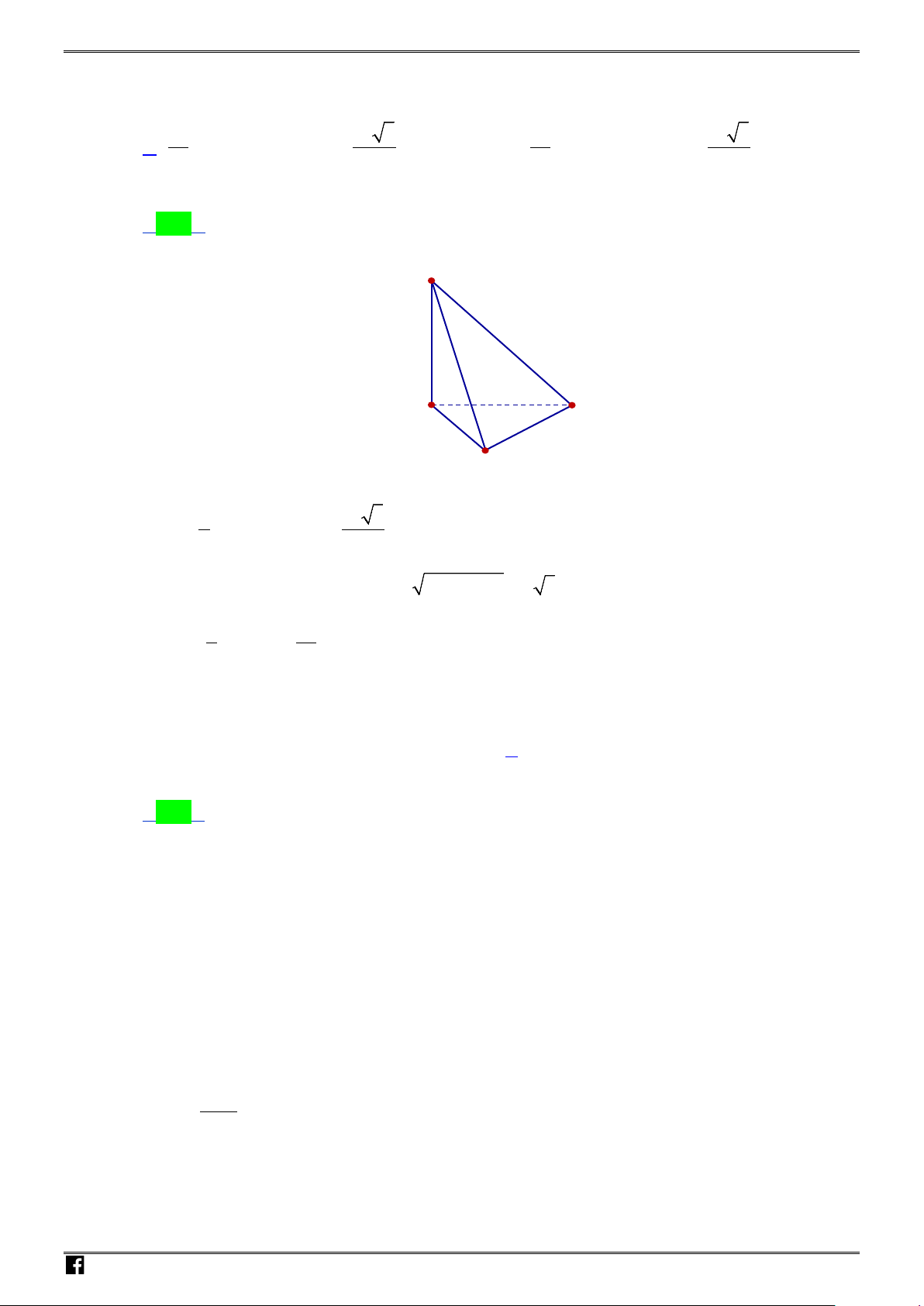
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 35: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
a
, cạnh bên
SA
vuông góc với đáy.
Tính thể tích của khối chóp
.
S ABC
biết
2SB a=
.
A.
3
4
a
. B.
3
3
4
a
. C.
3
2
a
. D.
3
3
2
a
.
Lời giải
Chọn A
2
0
13
. .sin 60
24
ABC
a
S AB AC
= =
.
Tam giác
SAB
vuông tại
A
:
22
3SA SB AB a= −=
.
3
.
1
.
34
S ABC ABC
a
V SA S= =
.
Câu 36: Có bao nhiêu số nguyên của
m
để phương trình
2
22
log (2 ) 2log 4 2 1xm x x x m
+− =−− −
có
hai nghiệm thực phân biệt.
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Chọn C
Điều kiện:
0
0
2 ()
x
m
m x gx
>
⇒≤
>− =
.
Phương trình đã cho tương đương với:
( ) ( ) ( )
2 2 22
2 22 2
log 2 1 4 2 log log 4 2 4 2 logxm xmx x xm xm xx+ ++ + = + ⇔ + + + = +
2
(4 2 ) ( ).f x m fx⇔ +=
Xét hàm số
2
( ) logft t t= +
trên khoảng
(0; ).+∞
1
( ) 1 0 (0; )
ln 2
ft t
t
′
= + > ∀ ∈ +∞ ⇒
hàm số
()ft
đồng biến trên khoảng
(0; )+∞
.
Khi đó
22
42 42x mx x x m+ =⇔−=
.
Đồ thị hàm số
2
() 4hx x x= −
là parabol có đỉnh
(2; 4).I −
S
A
B
C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Phương trình
2
42x xm−=
có hai nghiệm phân biệt khi và chỉ khi
42 0 2 0mm
−< < ⇔−< <
. Kết hợp với điều kiện
0m ≤
ta được
20m−< <
. Vì
1mm∈⇒ =−
.
Câu 37: Có bao nhiêu giá trị m nguyên thuộc đoạn
[ ]
2020;2020−
để phương trình
( ) ( )
log 2log 1mx x= +
có nghiệm duy nhất?
A.
2020
. B.
4040
. C.
4042
. D.
2021
.
Lời giải
Điều kiện:
1
0
x
mx
>−
>
. Khi đó, PT
( ) ( ) ( )
2
2
1 2 10 2mx x x m x⇔ = + ⇔ + − +=
Xét:
2
4mm
∆= −
Trường hợp 1:
{ }
0 0; 4
m∆= ⇔ ∈
Với
0m =
, phương trình
(
)
2
có nghiệm là
1x = −
(không thỏa yêu cầu).
Với
4m =
, phương trình
( )
2
có nghiệm là
1x =
(thỏa yêu cầu)
Trường hợp 2:
( ) (
)
0 ;0 4;m∆ > ⇔ ∈ −∞ ∪ +∞
, phương trình
(
)
2
có 2 nghiệm
( )
12 1 2
,
xx x x<
với
12
12
2
.1
xx m
xx
+=−
=
.
Khi đó, YCBT
( )( )
1 2 1 2 12 1 2
1 1 1 0 10 0x x x x xx x x m⇔ ≤−< ⇒ + +≤⇔ + + +≤⇔ ≤
Do
( ) (
)
;0 4;m ∈ −∞ ∪ +∞
nên
{ }
2020; 2019;...; 1
m∈− − −
Vậy có 2021 giá trị m cần tìm.
Câu 38: Tập xác định của hàm số
( )
2
1yx= −
là tập hợp nào?
A.
[
)
1; +∞
. B.
. C.
( )
1; +∞
. D.
{ }
\1
.
Lời giải
Hàm số
( )
2
1yx= −
xác định khi
10 1xx−> ⇔ >
.
Vậy tập xác định của hàm số
( )
2
1yx= −
là:
( )
1;D = +∞
Câu 39: Hình chóp đều
.S ABC
có cạnh đáy bằng
a
, các cạnh bên bằng
2a
. Gọi
M
là trung điểm
SB
, điểm
N
thuộc
SC
sao cho
2NS NC=
. Tính thể tích khối đa diện
ABCMN
.
A.
3
11
18
a
. B.
3
11
16
a
. C.
3
11
36
a
. D.
3
11
24
a
.
Lời giải

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có:
22222 2 2
4 4 1 33
9 99 3
a
SO SA AO SA AI SA AB BC= −= − = − + =
Diện tích tam giác
ABC
:
2
13
. .sin
24
ABC
a
S AB AC BAC
∆
= =
23
.
1 1 33 3 11
. ..
3 3 3 4 12
S ABC ABC
aa a
V SO S
∆
⇒= = =
Xét tỉ số:
( )
( )
( )
( )
..
..
1
1
., .
. . .sin
12 1
3
2
..
11
23 3
. , . . . .sin
32
SMN
S AMN A SMN SMN
S ABC A SBC SBC
SBC
d A SMN S
SM SN MSN
VV S
SM SN
V V S SB SC
d A SBC S SB SC BSC
∆
∆
∆
∆
= = = = = = =
Do đó:
33
.
2 2 11 11
.
3 3 12 18
ABCMN S ABC
aa
VV
= = =
.
Câu 40: Một sợi dây chuyền có chiều dài
28m
được cắt thành hai đoạn, đoạn có chiều dài
( )
lm
để
làm thành một hình vuông và đoạn
( )
28 lm−
tạo thành hình tròn. Biết tổng diện tích hình
tròn và hình vuông nhỏ nhất. Hỏi số
l
gần nhất với số nào sau đây?
A.
11, 8m
. B.
12,9m
. C.
7,8m
. D.
15, 7m
.
Lời giải
Chọn C.
Cạnh hình vuông là
,
4
l
bán kính hình tròn là
( )
1
28
2
l
π
−
.
Tổng diện tích
( ) ( ) ( ) ( )
2
2
1 11
28 ' 28
16 4 8 2
l
Sl l S l l
ππ
=+ −⇒ =− −
.
Do đó
( )
112
'0
4
Sl l
π
=⇒=
Lập bảng biến thiên ta thấy
S
đạt giá trị nhỏ nhất bằng
196 112
,
44
l
ππ
=
+
Câu 41: Cho hàm số
( )
y fx=
, hàm số
( )
'y fx=
liên tục trên
và có đồ thị như hình vẽ bên. Bất
phương trình
( )
fx x m<+
(m là tham số) nghiệm đúng với mọi
( )
0; 2x∈
khi và chỉ khi

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
(
)
0mf
>
. B.
( )
0mf≥
. C.
( )
22mf>−
. D.
(
)
22mf≥−
.
Lời giải
Chọn D.
Bất phương trình:
( ) ( )
fx x m fx x m
<+ ⇔ −<
Xét hàm số
(
) ( )
gx f x x= −
trên
( )
0; 2
có
( ) ( )
' ' 1.gx f x= −
Ta thấy
(
) ( )
' 1, 0; 2fx x> ∀∈
hay
( ) ( )
' 1 0, 0; 2fx x−> ∀∈
( ) ( )
' 0, 0; 2gx x⇒ > ∀∈
nên hàm số
( )
gx
đồng biến trên
( )
0; 2
( ) ( ) ( ) ( ) ( ) ( )
0 2 0 22g gx g f f x x f⇒<<⇔<−<−
.
Do đó bất phương trình
( )
fx x m
−<
nghiệm đúng với mọi
( ) ( ) ( )
0; 2 2 2 2x mg f∈ ⇔≥ = −
Câu 42: Cho khối tứ diện
.
ABCD
Lấy điểm
M
nằm giữa
A
và
,B
điểm
N
nằm giữa
C
và
.D
Mặt
phẳng
( )
CDM
và
( )
ABN
chia khối tứ diện đó thành bốn khối tứ diện nào sau đây?
A.
; ;;NACB BCMN ABND MBN D
. B.
;;;MANC BCMN AMND MBND
.
C.
;;;MANC BCDN AMND ABND
. D.
;; ;ABCN ABND AMND MBND
.
Lời giải
Chọn B.
Nhìn vào hình vẽ ta thấy
MN
là giao tuyến của hai mặt phẳng
( )
MCD
và
( )
,
NAB
khi đó
ta thấy tứ diện đã cho được chia thành bốn tứ diện
,,,.
ACMN AMND BMNC BMND
Câu 43: Cho hàm số
( )
y fx=
liên tục trên nửa khoảng
[
)
1; 2−
, có bảng biến thiên như hình vẽ.
Khẳng định nào sau đây là SAI?
A. Đồ thị hàm số không đi qua điểm
( )
2;5
.
N
D
C
B
A
M
x
y
1
1−

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
B. Hàm số đồng biến trên khoảng
( )
0;1
.
C.
[
)
1;2
min 2y
−
=
.
D.
[
)
1;2
max 5y
−
=
.
Lời giải
Chọn D.
Không tồn tại
[
)
1;2
max 5y
−
=
.
Câu 44: Cho phương trình
( ) ( )
3
13
8 8. 0,5 3.2 125 24. 0,5
xx
xx++
+ +=−
. Đặt
22
xx
t
−
= +
, phương trình đã
cho trở thành phương trình nào dưới đây?
A.
3
8 125 0t −=
. B.
3
8 3 12 0tt−− =
. C.
32
8 3 10 0t tt+ −− =
. D.
3
8 36 0tt+− =
.
Lời giải
Chọn A.
Ta có:
( ) ( )
3
13 3
3
8 24
8 8. 0,5 3.2 125 24. 0,5 8.2 24.2 125
22
xx
x x xx
xx
++
+ + =− ⇔ ++ =−
3
3
3
1 1 11
8. 2 24. 2 125 0 8 2 3. 2
2 2 22
x x xx
x x xx
⇔ + + + −=⇔ + − +
1
24 2 125
2
x
x
+ +=
3
1
8 2 125 0
2
x
x
⇔ + −=
1
24 2 125
2
x
x
+ +=
Đặt
( )
3
3
3
1
22 2 22
2
xx x xx
x
tt
−−
=+⇒ + =+ =
. Phương trình đã cho trở thành:
3
8 125 0t −=
Câu 45: Cho hình nón có chiều cao
2R
và bán kính đáy
R
.Xét hình trụ nội tiếp hình nón sao cho
thể tích khối trụ lớn nhất
.
Khi đó bán kính đáy của khối trụ là
A.
3
R
. B.
2
3
R
. C.
3
4
R
. D.
2
R
.
Lời giải
Chọn B.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 23
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Gọi
r
bán kính đáy,
h
là chiều cao của hình trụ. Hai tam giác
SO M
′
và
SOA
đồng dạng
21 1
1. 1.
22 2 2
O M SO R h h r h h
rR
OA SO R R R R
′′
−
⇒ == =−⇒=−⇒=−
.
Thể tích khối trụ bằng:
2
2
2
h
V rh R h
ππ
= = −
.
Áp dụng bất đẳng thức côsi ta có:
3
2
3
8
22
2 3 27
hh
RRh
hR
Rh
−+−+
−≤ =
3
8
27
R
V
π
⇒≤
.
Dấu “=” xảy ra khi
22
2 33
h RR
R hh r
− =⇒= ⇒=
.
Câu 46:
Tìm tất cả các giá trị của tham số
m
để đồ thị
( )
m
C
của hàm số
3 23
32y x mx m=−+ −
có hai
điểm cực trị
;MN
sao cho đường thẳng
MN
vuông góc với đường thẳng
(
)
: 2.
dy x= −
A.
1
.
2
m = ±
B.
11
;.
42
mm
=−=
C.
11
;.
24
mm=−=
D.
1
.
4
m = ±
Lời giải
Chọn A
( )
3
0
' 3 6 ; ' 0 0
2
x
y x mx y m
xm
=
=−+ =⇔ ≠
=
(
) ( )
( )
33 3
0; 2 ; 2 ;2 2 ;4M m N mm MN mm− ⇒=
Suy ra hệ số góc của đường thẳng
MN
là
2
2km=
Vì đường thẳng
MN
vuông góc với đường thẳng
( )
:2dy x= −
Nên:
( )
2
1
2 21 .
2
mm− =−⇔ =±
Câu 47: Một người gửi tiết kiệm
100
triệu đồng không rút lãi, thời hạn
5
năm. Ngân hàng A nhận
tiền gửi lãi suất
1, 2%
tháng, Ngân hàng B nhận tiền gửi lãi suất
%r
năm. Tìm
r
nhỏ nhất
để người gửi vào ngân hàng B có lợi hơn ngân hàng A.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 24
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
16,39%.r
=
B.
13,31%.r =
C.
15,39%.r =
D.
12,24%.r =
Lời giải
Chọn C
Số tiền nhận được khi gửi ngân hàng A trong 5 năm là:
(
)
60
100. 1 1, 2%
A
m
= +
( triệu đồng)
Số tiền nhận được khi gửi ngân hàng B trong 5 năm là:
( )
5
100. 1 %
B
mr= +
( triệu đồng)
YCBT
( ) ( ) ( )
5 60 12
1 % 1 1,2% 1 1,2% 1 15,389%
BA
mm r r⇔ > ⇔+ >+ ⇔>+ −≈
Suy ra giá trị nhỏ nhất của
r
là
15,39%.
Câu 48:
Cho hình chóp
.,S ABCD
có đáy
ABCD
là hình vuông,
SA
vuông góc với mặt phẳng đáy,
cho biết
.SA AB a= =
Tính khoảng cách từ
B
đến mặt phẳng
( )
SCD
theo
a
.
A.
2
.
2
a
B.
2.a
C.
3.a
D.
3
.
3
a
Lời giải
Chọn A
Ta có
( ) ( )
( )
( )
( )
// // , ,AB CD AB SCD d B SCD d A SCD⇒⇒=
.
Ta có
SA AB AD a= = =
suy ra
SAD∆
vuông cân tại
.A
Gọi
H
là trung điểm của
SD
ta có:
( )
.
AH SD
AH SCD
AH CD
⊥
⇒⊥
⊥
Do đó
( )
( )
22
11 2
,.
22 2
a
d A SCD AH SD SA AD== = +=
Câu 49: Tính thể tích khối chóp
.S ABCD
, biết đáy hình chóp là hình vuông cạnh
,a SA
vuông góc
với mặt đáy,
SD
tạo với mặt phẳng
SAB
một góc
0
30
.
H
C
A
D
B
S
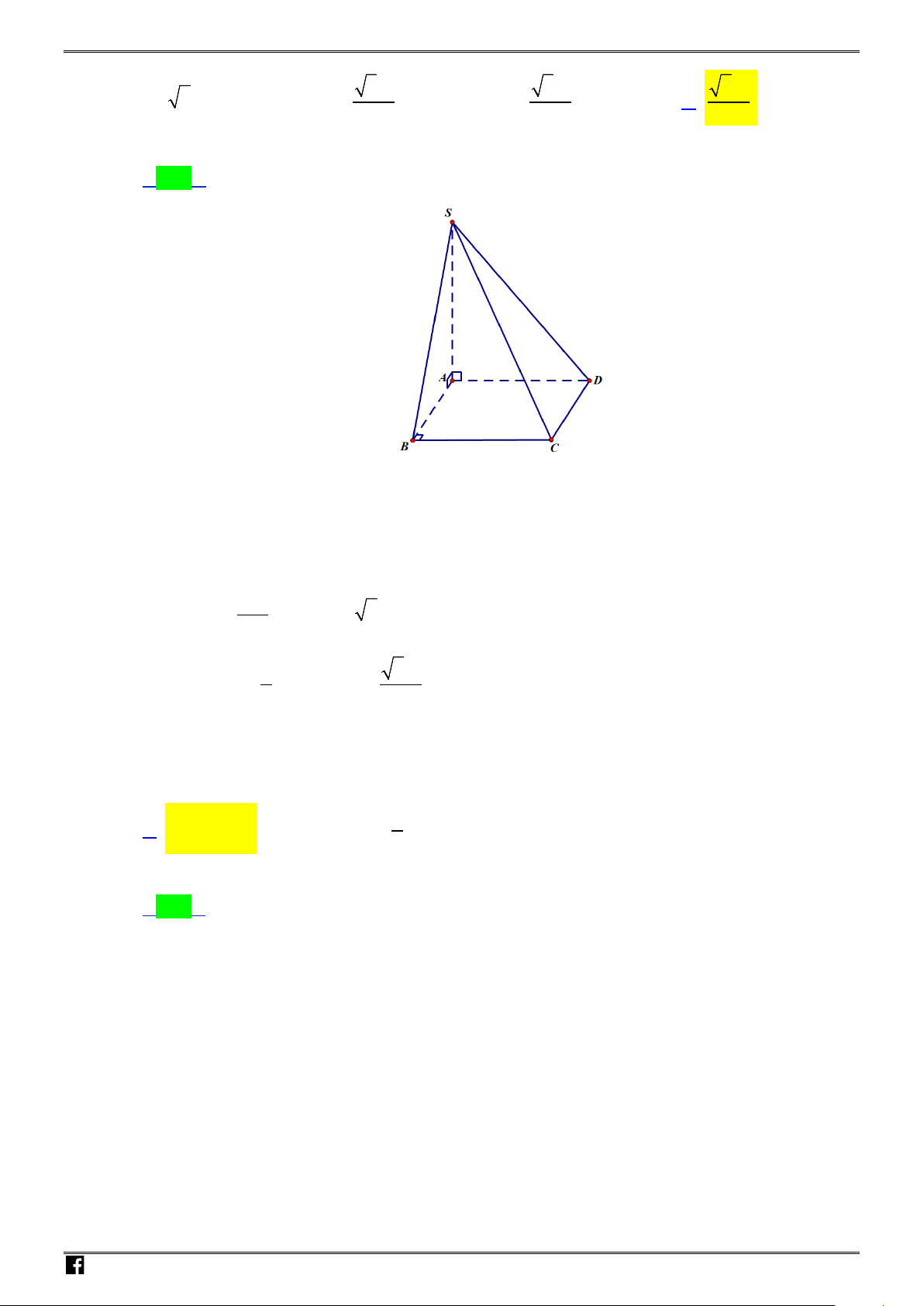
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 25
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
3a
. B.
3
6
3
a
. C.
3
6
9
a
. D.
3
3
3
a
.
Lời giải
Chọn D
Ta có:
0
, , 30
SA AD
AD SA B SD SAB SD SA DSA DSA
AD AB
.
tan 3
AD
DSA SA a
SA
.
Vậy
3
.
13
.
33
S ABCD ABCD
a
V SAS
.
Câu 50: Cho hình nón tròn xoay có bán kính đường tròn đáy
r
, chiều cao
h
và đường sinh
l
. Ký
hiệu
V
là thể tích khối nón
;
tp xq
SS
lần lượt là diện tích toàn phần, diện tích xung quanh của
hình nón. Tìm mệnh đề SAI trong các mệnh đề sau?
A.
2
xq
S rl
. B.
2
1
3
V rh
. C.
2
tp
S rl r
. D.
222
lrh
.
Lời giải
Chọn A
Lý thuyết.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
CHUYÊN CHU VĂN AN – LẠNG SƠN
ĐỀ THI HỌC KÌ I - NĂM HỌC 2020 - 2021
Môn: TOÁN – LỚP 12
Thời gian: 90 phút (Không kể thời gian phát đề)
Câu 1: Cho hình nón có bán kính đáy bằng
a
và độ dài đường sinh bằng
2a
. Diện tích xung quanh
của hình nón đó bằng
A.
2
4.
a
π
B.
2
3 a
π
. C.
2
2
a
π
. D.
2
a
π
.
Câu 2: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
32
1y xx
=−+ −
. B.
42
21yx x=−−
. C.
42
21yx x=−+ −
. D.
32
1yx x=−−
.
Câu 3: Thể tích
V
của khối trụ có bán kính đáy
R
và độ dài đường sinh được tính theo công thức
nào dưới đây?
A.
2
V Rl
π
=
. B.
2
4
3
V Rl
π
=
. C.
3
4
3
V Rl
π
=
. D.
2
1
3
V Rl=
.
Câu 4: Lăng trụ đều là lăng trụ
A. có đáy là tam giác đề và các cạnh bên vuông góc với đáy.
B. Đứng và có đáy là đa giác đều.
C. Có đáy là tam giác đều và các cạnh bên bằng nhau.
D. Có tất cả các cạnh bên bằng nhau.
Câu 5: Hàm số nào dưới đây có đồ thị như trong hình vẽ?
A.
3
31yx x=−+ +
. B.
42
21yx x=−+ +
. C.
42
21yx x=−+
. D.
3
31yx x
=−+
.
Câu 6: Cho a là số thực dương khác 1. Giá trị của biểu thức
2
3
Pa a=
bằng
A.
3
a
. B.
2
3
a
. C.
7
6
a
. D.
5
6
a
.
Câu 7: Khối tứ diện đều thuộc loại khối đa diện nào dưới đây?
A.
{ }
5;3
. B.
{ }
3;3
. C.
{ }
3; 4
. D.
{ }
4;3
.
Câu 8: Cho khối chóp có thể tích là
3
3
6
a
và diện tích mặt đáy là
2
3
8
a
. Khi đó chiều cao của khối
chóp đó là
A.
4
3
a
. B.
3
2
a
. C.
2a
. D.
4a
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 9: Cho hàm số
( )
y fx=
xác định trên đoạn
3; 5
−
và có bảng biến thiên như hình vẽ
Khẳng định nào sau đây là đúng?
A.
)
3; 5
min 2y
−
= −
. B.
)
3; 5
min 2y
−
=
. C.
)
3; 5
min 2 5y
−
=
. D.
)
3; 5
min 0y
−
=
.
Câu 10: Tìm tập nghiệm của phương trình
( )
2
3
log 2 3 1xx++ =
.
A.
1
0;
2
−
. B.
1
0;
2
. C.
1
2
−
. D.
{ }
0
.
Câu 11: Cho hàm số
(
)
y fx
=
có
( )
2
lim 1
x
fx
−
→
= −
và
( )
2
lim
x
fx
+
→
= +∞
. Mệnh đề nào dưới đây đúng?
A. Đường thẳng
2y = −
là tiệm cận ngang của đồ thị hàm số đã cho.
B. Đường thẳng
2x = −
là tiệm cận đứng của đồ thị hàm số đã cho.
C. Đường thẳng
2y =
là tiệm cận ngang của đồ thị hàm số đã cho.
D. Đường thẳng
2x =
là tiệm cận đứng của đồ thị hàm số đã cho.
Câu 12: Cho hàm số
(
)
y fx=
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào sau đây?
A.
( )
1; 0−
. B.
( )
0;1
. C.
( )
;0−∞
. D.
( )
0;3
.
Câu 13: Cho khối lăng trụ đứng
111
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh
2BC a
=
,
1
3AB a
=
. Thể tích khối lăng trụ
111
.ABC A B C
là:
A.
3
2
3
a
. B.
3
2a
. C.
3
6a
. D.
3
2a
.
Câu 14: Cho hàm số
( )
y fx=
. Đồ thị hàm số
( )
y fx
′
=
như hình vẽ bên dưới.
Đồ thị hàm số
(
)
y fx=
có bao nhiêu điểm cực trị?
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 15: Diện tích mặt cầu có bán kính
3
2
a
bằng

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2
3aπ . B.
2
3 aπ
. C.
2
4 aπ
. D.
2
3
2
aπ
.
Câu 16: Tìm đạo hàm của hàm số
2
2
3
xx
y
−
=
A.
(
)
2
2
3 . 2 2 .ln 3
xx
yx
−
′
= −
. B.
2
2
3
ln 3
xx
y
−
′
=
.
C.
2
2
3 .ln 3
xx
y
−
′
=
D.
( )
2
2
3 22
ln 3
xx
x
y
−
−
′
=
.
Câu 17: Khối lăng trụ có đáy là hình vuông cạnh
a
, đường cao bằng
3a
có thể tích bằng
A.
3
3
3
a
. B.
3
3a
. C.
3
23a
. D.
3
3
6
a
.
Câu 18: Cho hàm số
(
)
fx
xác định trên
R
và có đồ thị hàm số
( )
y = fx
′
là đường cong trong hình
bên.
Mệnh đề nào sau đây đúng?
A. Hàm số
( )
fx
đồng biến trên khoảng
( )
2;1−
.
B. Hàm số
( )
fx
nghịch biến trên khoảng
(
)
1;1
−
.
C. Hàm số
( )
fx
nghịch biến trên khoảng
( )
0; 2
.
D. Hàm số
( )
fx
đồng biến trên khoảng
( )
1; 2
.
Câu 19: Cho hình nón có diện tích xung quanh bằng
2
5 a
π
và bán kính đáy bằng
a
. Tính độ dài
đường sinh của hình nón đã cho.
A.
3a
. B.
5a
. C.
5a
. D.
32a
.
Câu 20: Tìm số đường tiệm cận đứng của đồ thị hàm số
2
2
34
16
xx
y
x
−−
=
−
.
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 21: Cho
b
là số thực dương khác
1
. Tính
1
2
2
log .
b
P bb
=
.
A.
1
4
P
=
. B.
3
2
P =
. C.
1P =
. D.
5
2
P =
.
Câu 22: Cho hàm số
( ) ( )
42
,,f x ax bx c a b c=++ ∈
. Đồ thị hàm số
( )
y fx=
như hình vẽ bên.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Số nghiệm của phương trình
( )
4 30
fx+=
là
A.
2
. B.
0
. C.
4
. D.
3
.
Câu 23: Giá trị nhỏ nhất của hàm số
( )
2
4
1
xx
fx
x
++
=
+
trên đoạn
[ ]
0; 2
bằng:
A.
3
. B.
10
3
. C.
4
. D.
5
−
.
Câu 24: Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Hàm số đạt cực tiểu tại điểm nào trong các điểm sau đây?
A.
4x =
. B.
2x =
. C.
3x =
. D.
2x = −
.
Câu 25: Nghiệm của phương trình
1
3 27
x
−
=
là
A.
4x =
. B.
9x =
. C.
10x =
. D.
3x =
.
Câu 26: Đồ thị có hình vẽ bên là của hàm số nào trong các hàm số sau đây?
A.
ln
yx=
. B.
x
ye
−
=
. C.
log 1yx= +
. D.
yx=
.
Câu 27: Cho
,ab
là hai số thực dương thỏa mãn
32
32ab
=
. Giá trị của
22
3log 2 logab+
bằng
A.
32
. B.
4
. C.
5
. D.
2
.
Câu 28: Cho hình lập phương
.ABCD A B C D
′′′′
cạnh
a
. Gọi
S
là diện tích xung quanh của hình nón
sinh bởi đoạn
AC
′
khi quay quan trục
AA
′
. Diện tích
S
là
A.
2
a
π
. B.
2
2
a
π
. C.
2
3a
π
. D.
2
6a
π
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 29: Cho hình chóp
.S ABC
có
A
′
,
B
′
,
C
′
lần lượt là trung điểm của
SA
,
SB
,
SC
. Tỷ số
.
.
S ABC
S ABC
V
V
′′′
bằng bao nhiêu
A.
1
4
. B.
1
6
. C.
1
8
. D.
8
.
Câu 30: Nghiệm của phương trình
4 6.2 8 0
xx
− +=
là
A.
0; 2xx= =
B.
1; 2
xx
= =
. C.
1x =
. D.
2
x
=
.
Câu 31: Cho khối chóp
.S ABC
có đáy là tam giác
ABC
đều cạnh bằng
a
. Hai mặt phẳng
SAB
và
SAC
cùng vuông góc với đáy. Tính thể tích khối chóp
.
S ABC
biết
SM
hợp với đáy góc
60
, với
M
là trung điểm BC.
A.
3
3
4
a
. B.
3
3
8
a
. C.
3
6
24
a
. D.
3
6
8
a
.
Câu 32: Cho khối trụ có thiết diện qua trục là hình vuông cạnh
a
. Thể tích khối trụ là
A.
3
a
. B.
3
3
a
. C.
3
12
a
. D.
3
4
a
.
Câu 33: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
. Biết
3AB cm
,
32BC cm
. Thể tích khối lăng trụ đã cho là:
A.
3
27
8
cm
. B.
3
27
4
cm
. C.
3
27 cm
. D.
3
27
2
cm
.
Câu 34: Số nghiệm của phương trình
( )
( )
2
31
3
log 4 log 2 3 0xx x+ + +=
là
A.
1
. B.
3
. C.
0
. D.
2
.
Câu 35: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
a
, cạnh bên
SA
vuông góc với đáy.
Tính thể tích của khối chóp
.S ABC
biết
2SB a=
.
A.
3
4
a
. B.
3
3
4
a
. C.
3
2
a
. D.
3
3
2
a
.
Câu 36: Có bao nhiêu số nguyên của
m
để phương trình
2
22
log (2 ) 2log 4 2 1xm x x x m+− =−− −
có
hai nghiệm thực phân biệt.
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 37: Cho hình hộp đứng
.ABCD A B C D
′′′′
có các cạnh
0
3
2 , , 60
2
a
AB AD a AA BAD
′
= = = =
. Gọi
M
và
N
lần lượt là trung điểm các cạnh của
AD
và
AB
. Tính thể tích
ABDNM
′′′
bằng
A.
3
8
a
. B.
3
3
4
a
. C.
3
5
48
a
. D.
3
24
a
.
Câu 38: Cho hàm số
( )
32
1
4 3 2017
3
y x mx m x= − + −+
. Tìm giá trị lớn nhất của tham số thực
m
để hàm số đã cho đồng biến trên
A.
4m =
. B.
3m =
. C.
1m =
. D.
2m =
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 39: Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh
22AC =
. Biết
AC
′
tạo với mặt phẳng
( )
ABC
một góc
0
60
và
4AC
′
=
.Thể tích khối
chóp
.B ACC A
′′
bằng
A.
16
3
. B.
8
3
. C.
83
3
. D.
16 3
3
.
Câu 40: Khối chóp
.S ABCD
có đáy là hình vuông cạnh bằng
2a
, chân đường cao trùng với trung
điểm
H
của
AB
, mặt bên
( )
SCD
tạo với mặt đáy một góc
0
30
. Gọi
M
là trung điểm của
SC
. Thể tích khối chóp
.H BCM
là
A.
3
2
3
a
. B.
3
3
8
a
. C.
3
3
9
a
. D.
3
6
3
a
.
Câu 41: Cho hàm số
( )
42
21 1y mx m x=−+ +
. Tìm tất cả các giá trị của
m
để hàm số có một điểm cực
đại
A.
1
0
2
m−≤ <
. B.
1
2
m
≤−
. C.
1
0
2
m−≤ ≤
. D.
1
2
m ≥−
.
Câu 42: Gọi
,
Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
54yx= −
trên đoạn
[
]
1;1
−
. Khi đó
Mm
−
bằng
A.
9
. B.
3
. C.
1
. D.
2
.
Câu 43: Cho hàm số
( )
y fx=
liên tục trên
có đồ thị như hình vẽ. Đồ thị của hàm số
( ) ( )
2
gx f x=
có bao nhiêu điểm cực đại, bao nhiêu điểm cực tiểu?
A.
2
điểm cực đại, 3 điểm cực tiểu. B.
3
điểm cực đại, 2 điểm cực tiểu.
C.
1
điểm cực đại, 3 điểm cực tiểu. D.
2
điểm cực đại, 2 điểm cực tiểu.
Câu 44: Cho hàm số
bx c
y
xa
−
=
−
(
0a ≠
và
,, )
abc∈
có đồ thị như hình bên. Khẳng định nào sau
đây đúng?
O
y
x

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
0, 0, 0
a b c ab
> < −<
. B.
0, 0, 0
abcab
> > −<
.
C.
0, 0, 0a b c ab< > −<
. D.
0, 0, 0abcab< < −>
.
Câu 45: Cho hình trụ có hai đáy là hai hình tròn
( )
O
và
( )
'O
, chiều cao
2
R
và bán kính đáy
.R
Một mặt phẳng
( )
α
đi qua trung điểm của
'OO
và tạo với
'OO
một góc
0
30 .
Hỏi
(
)
α
cắt
đường tròn đáy theo một dây cung có độ dài bằng bao nhiêu?
A.
2
3
R
. B.
2
3
R
. C.
22
3
R
. D.
4
33
R
.
Câu 46: Cho hàm số
21
1
x
y
x
−
=
+
có đồ thị
(
)
C
và đường thẳng
: 23dy x= −
. Đường thẳng
d
cắt
( )
C
tại hai điểm
A
và
B
. Khoảng cách giữa
A
và
B
là
A.
2
5
. B.
25
5
. C.
5
2
. D.
55
2
.
Câu 47: Cho hình hộp đứng
.ABCD A B C D
′′′′
có đáy là hình thoi,
0
60BAD =
,
2AA AB a
′
= =
. Gọi
,JI
lần lượt là giao điểm của các đường chéo của các hình
ABCD
′′′′
và
A D DA
′′
;
,KL
lần
lượt là trung điểm các cạnh
,AB BC
. Thể tích của khối chóp
IJKL
bằng
A.
3
3
24
a
. B.
3
3
4
a
. C.
3
3
32
a
. D.
3
3
12
a
.
Câu 48: Tìm tất cả các giá trị thực của tham số
m
để phương trình
( )
2
4 2 .6 3 .9 0
xx x
mm− +− =
có hai
nghiệm phân biệt.
A.
0m >
. B.
3m = ±
. C.
3
m ≥
. D.
3m
>
.
Câu 49: Một người gửi 100 triệu đồng vào ngân hàng với kì hạn 3 tháng (1 quý), lãi suất
6%
một
quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó lại gửi thêm 100 triệu đồng với hình
thức và lãi suất như trên. Hỏi sau 1 năm tính từ lần gửi đầu tiên người đó nhận được số tiền
gần với kết quả nào nhất?
A.
236,6
triệu đồng. B.
243,5
triệu đồng
C.
238,6
triệu đồng D.
224,7
triệu đồng
Câu 50: Cho hàm số
()y fx=
liên tục trên
và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị của
tham số
m
để phương trình
(cos ) 2 1fx m=−+
có nghiệm thuộc khoảng
0;
2
π
là
A.
( )
0;1
. B.
( )
1;1−
. C.
(
]
0;1
. D.
(
]
1;1−
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
BẢNG ĐÁP ÁN
1.C
2.B
3.A
4.B
5.D
6.C
7.B
8.D
9.A
10.B
11.D
12.A
13.B
14.C
15.B
16.A
17.B
18.C
19.B
20.C
21.D
22.A
23.A
24.A
25.A
26.D
27.C
28.C
29.C
30.B
31.B
32.D
33.D
34.A
35.A
36.C
37.B
38.B
39.D
40.C
41.C
42.D
43.A
44.B
45.C
46.D
47.B
48.D
49.C
50.A
Câu 1: Cho hình nón có bán kính đáy bằng
a
và độ dài đường sinh bằng
2a
. Diện tích xung quanh
của hình nón đó bằng
A.
2
4.a
π
B.
2
3
a
π
. C.
2
2
a
π
. D.
2
a
π
.
Lời giải
Chọn C.
Diện tích xung quanh là
2
. .2 2 .S rl a a a
Câu 2: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
32
1
y xx=−+ −
. B.
42
21yx x=−−
. C.
42
21yx x=−+ −
. D.
32
1yx x
=−−
.
Lời giải
Chọn B.
Từ hình dáng đồ thị ta thấy hàm số có dạng
42
y ax bx c
loại A và D.
Ta có
lim
x
y
loại C.
Vậy chọn B.
Câu 3: Thể tích
V
của khối trụ có bán kính đáy
R
và độ dài đường sinh được tính theo công thức
nào dưới đây?
A.
2
V Rl
π
=
. B.
2
4
3
V Rl
π
=
. C.
3
4
3
V Rl
π
=
. D.
2
1
3
V Rl=
.
Lời giải
Chọn A.
Thể tích khối trụ là
22
.V Rh Rl
Câu 4: Lăng trụ đều là lăng trụ
A. có đáy là tam giác đề và các cạnh bên vuông góc với đáy.
B. Đứng và có đáy là đa giác đều.
C. Có đáy là tam giác đều và các cạnh bên bằng nhau.
D. Có tất cả các cạnh bên bằng nhau.
Lời giải
Chọn B
Câu 5: Hàm số nào dưới đây có đồ thị như trong hình vẽ?
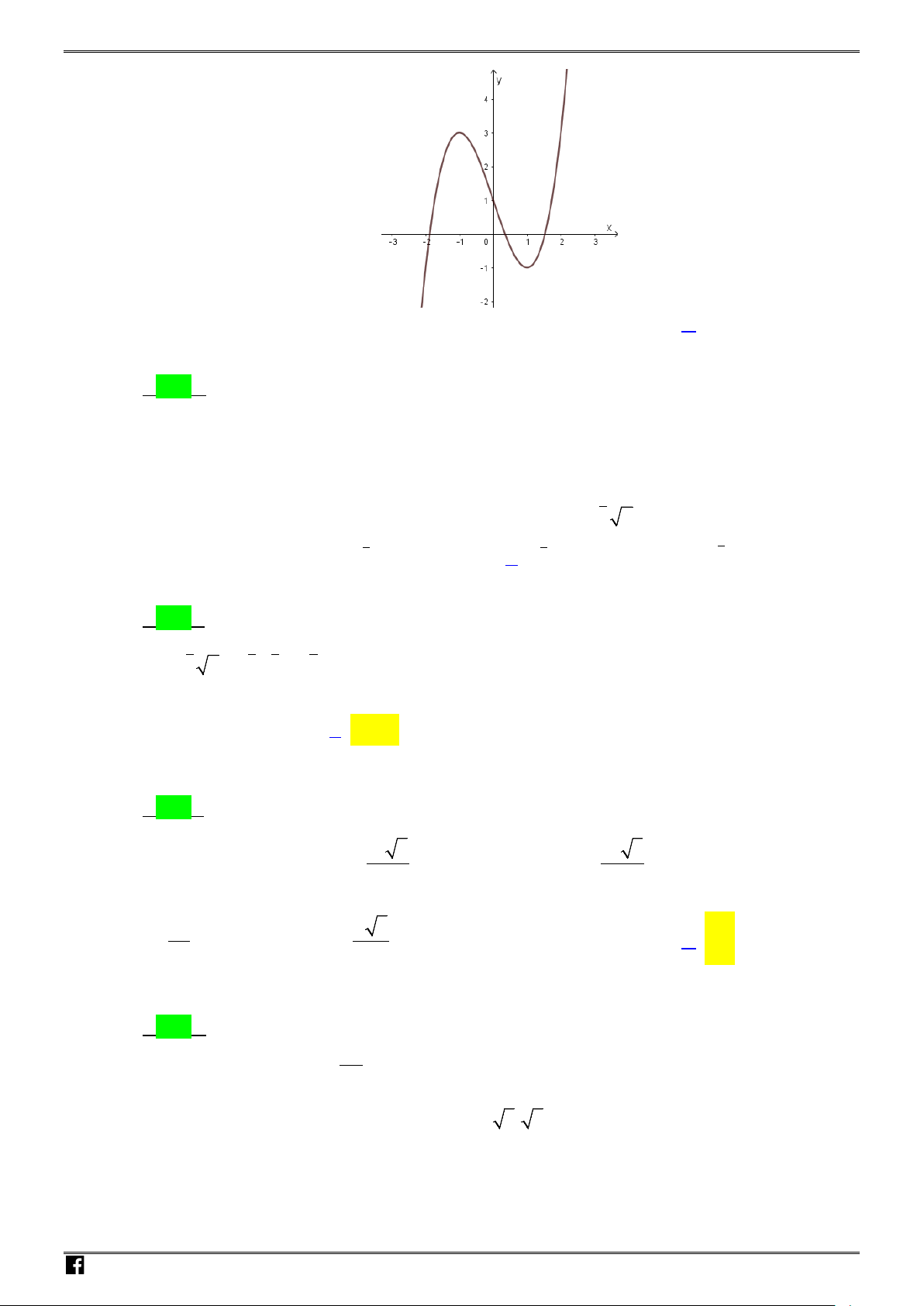
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
31yx x=−+ +
. B.
42
21
yx x=−+ +
. C.
42
21
yx x=−+
. D.
3
31yx x=−+
.
Lời giải
Chọn D
Vì đồ thị có 2 điểm cực trị nên loại B, C
Vì
lim
x→+∞
= +∞
nên chọn D.
Câu 6: Cho a là số thực dương khác 1. Giá trị của biểu thức
2
3
Pa a=
bằng
A.
3
a
. B.
2
3
a
. C.
7
6
a
. D.
5
6
a
.
Lời giải
Chọn C
227
1
336
2
.P a a aa a= = =
.
Câu 7: Khối tứ diện đều thuộc loại khối đa diện nào dưới đây?
A.
{ }
5;3
. B.
{ }
3;3
. C.
{ }
3; 4
. D.
{ }
4;3
.
Lời giải
Chọn B
Câu 8: Cho khối chóp có thể tích là
3
3
6
a
và diện tích mặt đáy là
2
3
8
a
. Khi đó chiều cao của khối
chóp đó là
A.
4
3
a
. B.
3
2
a
. C.
2a
. D.
4
a
.
Lời giải
Chọn D
Chiều cao khối chóp
3
4
V
ha
S
= =
.
Câu 9: Cho hàm số
( )
y fx=
xác định trên đoạn
3; 5
−
và có bảng biến thiên như hình vẽ
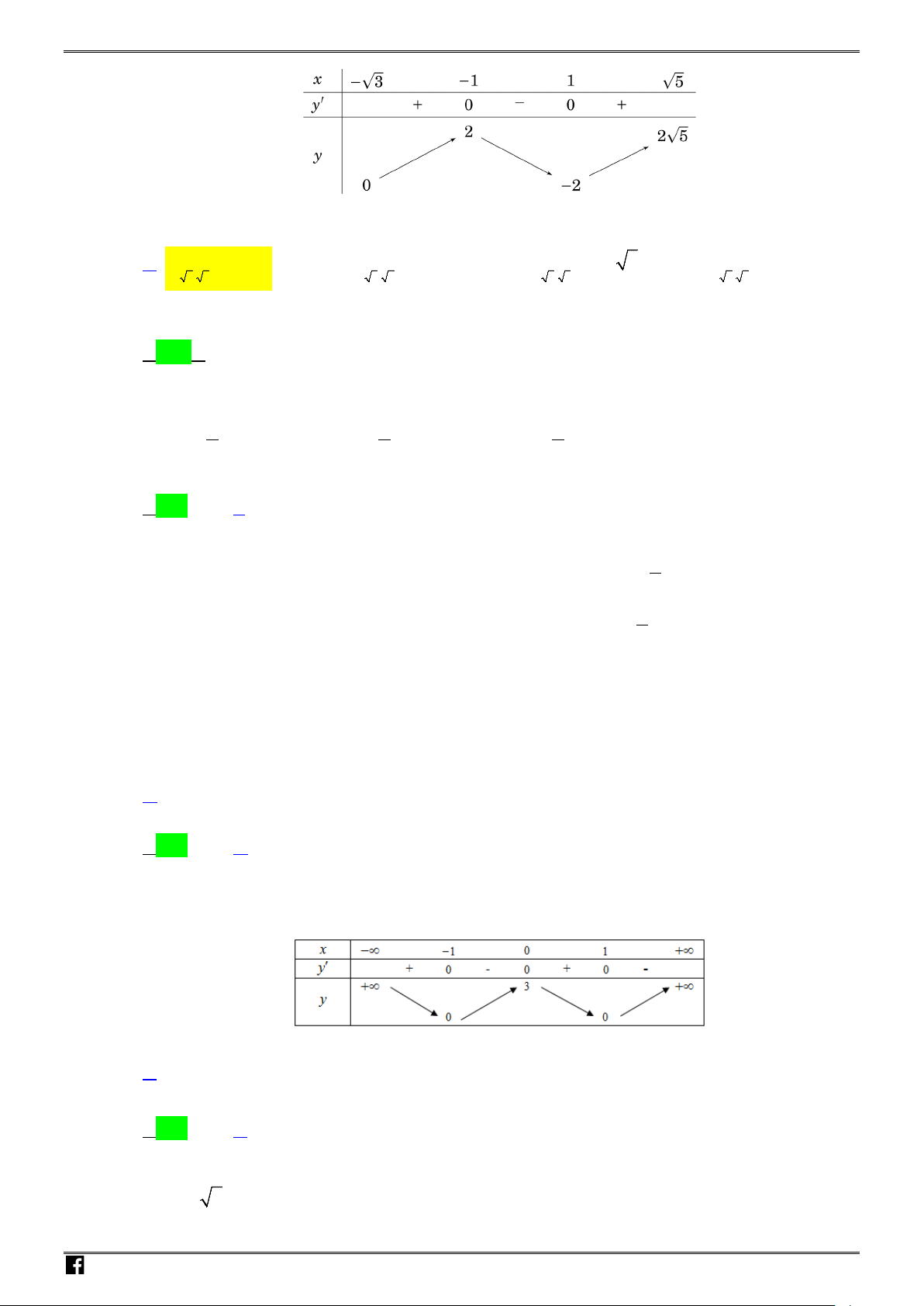
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Khẳng định nào sau đây là đúng?
A.
)
3; 5
min 2
y
−
= −
. B.
)
3; 5
min 2y
−
=
. C.
)
3; 5
min 2 5y
−
=
. D.
)
3; 5
min 0y
−
=
.
Lời giải
Chọn A
Câu 10: Tìm tập nghiệm của phương trình
( )
2
3
log 2 3 1xx++ =
.
A.
1
0;
2
−
. B.
1
0;
2
. C.
1
2
−
. D.
{
}
0
.
Lời giải
Chọn B.
Ta có
( )
2 22
3
0
log2312332 0
1
2
x
xx xx xx
x
=
++ =⇔ ++=⇔ +=⇔
= −
.
Tìm tập nghiệm của phương trình
( )
2
3
log 2 3 1xx++ =
là
1
0;
2
−
.
Câu 11: Cho hàm số
(
)
y fx=
có
(
)
2
lim 1
x
fx
−
→
= −
và
( )
2
lim
x
fx
+
→
= +∞
. Mệnh đề nào dưới đây đúng?
A. Đường thẳng
2y = −
là tiệm cận ngang của đồ thị hàm số đã cho.
B. Đường thẳng
2x = −
là tiệm cận đứng của đồ thị hàm số đã cho.
C. Đường thẳng
2y =
là tiệm cận ngang của đồ thị hàm số đã cho.
D. Đường thẳng
2x =
là tiệm cận đứng của đồ thị hàm số đã cho.
Lời giải
Chọn D.
Ta có
( )
2
lim 2
x
fx x
+
→
= +∞ ⇒ =
là đường tiệm cận đứng của đồ thị hàm số.
Câu 12: Cho hàm số
( )
y fx
=
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào sau đây?
A.
( )
1; 0−
. B.
( )
0;1
. C.
( )
;0−∞
. D.
( )
0;3
.
Lời giải
Chọn A.
Câu 13: Cho khối lăng trụ đứng
111
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh
2BC a=
,
1
3AB a=
. Thể tích khối lăng trụ
111
.ABC A B C
là:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
2
3
a
. B.
3
2a
. C.
3
6a
. D.
3
2a
.
Lời giải
Chọn B
Ta có
2
1
.
22
ABC
a
AB AC a S AB AC==⇒= =
và
22
11
22AA A B AB a= −=
.
Thể tích khối lăng trụ là
3
1
.2
ABC
V S AA a= =
Câu 14: Cho hàm số
( )
y fx=
. Đồ thị hàm số
( )
y fx
′
=
như hình vẽ bên dưới.
Đồ thị hàm số
( )
y fx=
có bao nhiêu điểm cực trị?
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn C
( )
01fx x
′
=⇔=±
.
Bảng xét dấu
( )
fx
′
Vậy hàm số
( )
y fx
=
không có điểm cực trị.
Câu 15: Diện tích mặt cầu có bán kính
3
2
a
bằng
A.
2
3aπ
. B.
2
3 aπ
. C.
2
4 aπ
. D.
2
3
2
aπ
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn B
Diện tích mặt cầu là
2
22
3
44.3
4
a
SR a
=π=π =π
Câu 16: Tìm đạo hàm của hàm số
2
2
3
xx
y
−
=
A.
( )
2
2
3 . 2 2 .ln 3
xx
yx
−
′
= −
. B.
2
2
3
ln 3
xx
y
−
′
=
.
C.
2
2
3 .ln 3
xx
y
−
′
=
D.
( )
2
2
3 22
ln 3
xx
x
y
−
−
′
=
.
Lời giải.
Chọn A.
TXĐ:
R
D =
.
Ta có
( )
2
2
3 . 2 2 .ln 3
xx
yx
−
′
= −
.
Câu 17: Khối lăng trụ có đáy là hình vuông cạnh
a
, đường cao bằng
3a
có thể tích bằng
A.
3
3
3
a
. B.
3
3a
. C.
3
23
a
. D.
3
3
6
a
.
Chọn B.
Ta có
23
. .3 3
LT
V Sh a a a= = =
.
Câu 18: Cho hàm số
( )
fx
xác định trên
R
và có đồ thị hàm số
( )
y = fx
′
là đường cong
trong hình bên.
Mệnh đề nào sau đây đúng?
A. Hàm số
( )
fx
đồng biến trên khoảng
( )
2;1−
.
B. Hàm số
( )
fx
nghịch biến trên khoảng
( )
1;1−
.
C. Hàm số
( )
fx
nghịch biến trên khoảng
( )
0; 2
.
D. Hàm số
( )
fx
đồng biến trên khoảng
( )
1; 2
.
Lời giải.
Chọn C.
Căn cứ vào đồ thị hàm số
( )
y = <0fx
′
,
( )
0; 2x∀∈
.Suy ra hàm số
( )
y = fx
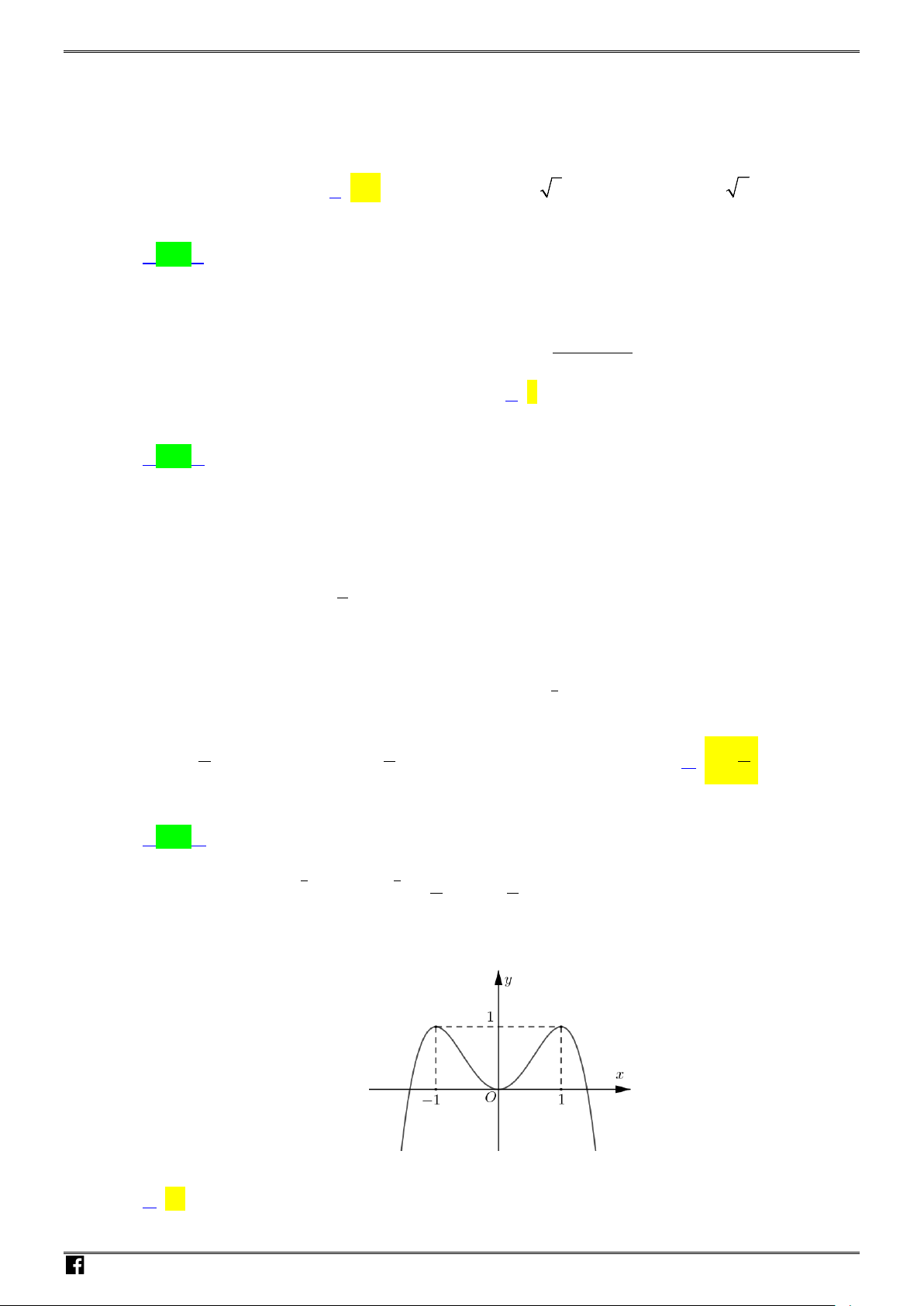
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
nghịch biến trên khoảng
( )
0; 2
.
Câu 19: Cho hình nón có diện tích xung quanh bằng
2
5
a
π
và bán kính đáy bằng
a
. Tính độ dài
đường sinh của hình nón đã cho.
A.
3a
. B.
5a
. C.
5
a
. D.
32a
.
Lời giải
Chọn B
Ta có
2
.. 5 5
xq
S rl a l a l a
ππ π
= = = ⇔=
.
Câu 20: Tìm số đường tiệm cận đứng của đồ thị hàm số
2
2
34
16
xx
y
x
−−
=
−
.
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn C
Ta có
( )
4
lim
x
y
+
→−
= −∞
,
( )
4
lim
x
y
−
→−
= +∞
.
Suy ra
4x = −
là đường tiệm cận đứng của đồ thị hàm số đã cho.
Ta lại có
44
5
lim lim
8
xx
yy
+−
→→
= =
.
Suy ra
4x =
không là đường tiệm cận đứng của đồ thị hàm số đã cho.
Câu 21: Cho
b
là số thực dương khác
1
. Tính
1
2
2
log .
b
P bb
=
.
A.
1
4
P =
. B.
3
2
P =
. C.
1
P =
. D.
5
2
P =
.
Lời giải
Chọn D
Ta có
15
2
22
55
log . log log
22
b bb
P bb b b
= = = =
.
Câu 22: Cho hàm số
( )
( )
42
,,f x ax bx c a b c
=++ ∈
. Đồ thị hàm số
( )
y fx=
như hình vẽ bên.
Số nghiệm của phương trình
(
)
4 30
fx+=
là
A.
2
. B.
0
. C.
4
. D.
3
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn A.
Ta có
(
)
( )
3
4 30
4
fx fx
+=⇔ =−
.
Số nghiệm của phương trình
( )
4 30fx+=
là số giao điểm của đồ thị hàm số
( )
y fx=
và
đường thẳng
3
4
y
= −
.
Dựa vào đồ thị nhận thấy phương trình
( )
4 30fx+=
có nghiệm
2
.
Câu 23: Giá trị nhỏ nhất của hàm số
( )
2
4
1
xx
fx
x
++
=
+
trên đoạn
[ ]
0; 2
bằng:
A.
3
. B.
10
3
. C.
4
. D.
5−
.
Lời giải
Chọn A.
Tập xác định
{ }
\1D
= −
.
Ta có
( )
2
44
11
xx
fx x
xx
++
= = +
++
.
Khi đó
( )
( )
2
4
1
1
fx
x
′
= −
+
.
Cho
( )
( )
( )
[ ]
[ ]
2
2
1 0;2
4
01 0 1 4
3 0; 2
1
x
fx x
x
x
= ∈
′
= ⇔− = ⇔ + = ⇔
=−∉
+
.
Ta có
( )
04f =
;
( )
13f =
;
( )
10
2
3
f =
.
Vậy
[ ]
( )
0;2
3Min f x =
tại
1x =
.
Câu 24: Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Hàm số đạt cực tiểu tại điểm nào trong các điểm sau đây?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
4
x
=
. B.
2x =
. C.
3x =
. D.
2x = −
.
Lời giải
Chọn A.
Hàm số đạt cực tiểu tại điểm nào trong các điểm
2x = −
.
Câu 25: Nghiệm của phương trình
1
3 27
x−
=
là
A.
4x =
. B.
9x =
. C.
10x =
. D.
3
x =
.
Lời giải
Chọn A
Ta có:
1
33
3 27 1 log 27 1 log 27 4
x
xx
−
= ⇔ −= ⇔ =+ =
Câu 26: Đồ thị có hình vẽ bên là của hàm số nào trong các hàm số sau đây?
A.
lnyx
=
. B.
x
ye
−
=
. C.
log 1
yx= +
. D.
yx
=
.
Lời giải
Chọn D
Dựa vào hình vẽ, đồ thị hàm số đi qua 2 điểm
( )
0;0
O
và
( )
1;1A
.
Câu 27: Cho
,ab
là hai số thực dương thỏa mãn
32
32
ab =
. Giá trị của
22
3log 2 logab+
bằng
A.
32
. B.
4
. C.
5
. D.
2
.
Lời giải
Chọn C
Ta có:
( )
3 2 32
2 22 2 2 2
3log 2log log log log log 32 5
a b a b ab+ =+= ==
Câu 28: Cho hình lập phương
.ABCD A B C D
′′′′
cạnh
a
. Gọi
S
là diện tích xung quanh của hình nón
sinh bởi đoạn
AC
′
khi quay quan trục
AA
′
. Diện tích
S
là
A.
2
a
π
. B.
2
2a
π
. C.
2
3a
π
. D.
2
6a
π
.
Lời giải
Chọn C
Quay
AC
′
quanh cạnh
AA
′
ta được hình nón có bán kính đáy
2R AC a
′
= =
và chiều
cao
'h AA a= =
( )
2
22 2
23
l hR a a a⇒= + = + =
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vậy
2
.3 3
S Rl a a a
ππ π
= = =
.
Câu 29: Cho hình chóp
.S ABC
có
A
′
,
B
′
,
C
′
lần lượt là trung điểm của
SA
,
SB
,
SC
. Tỷ số
.
.
S ABC
S ABC
V
V
′′′
bằng bao nhiêu
A.
1
4
. B.
1
6
. C.
1
8
. D.
8
.
Lời giải
Chọn C
Ta có
.
.
111 1
. . ..
222 8
S ABC
S ABC
V
SA SB SC
V SA SB SC
′′′
′′′
= = =
.
Câu 30: Nghiệm của phương trình
4 6.2 8 0
xx
− +=
là
A.
0; 2
xx
= =
B.
1; 2xx= =
. C.
1x =
. D.
2
x
=
.
Lời giải
Chọn B
Đặt
2, 0
x
tt= >
Phương trình
2
2 22
6 8 0 1; 2
4
24
x
x
t
tt xx
t
= =
⇔ − +=⇔ ⇒ ⇔= =
=
=
.
Câu 31: Cho khối chóp
.
S ABC
có đáy là tam giác
ABC
đều cạnh bằng
a
. Hai mặt phẳng
SAB
và
SAC
cùng vuông góc với đáy. Tính thể tích khối chóp
.S ABC
biết
SM
hợp với đáy góc
60
, với
M
là trung điểm BC.
A.
3
3
4
a
. B.
3
3
8
a
. C.
3
6
24
a
. D.
3
6
8
a
.
Lời giải
Chọn B.
Ta có:
SAB ABC
SAC ABC SA ABC
SAB SAC SA
.
; 60SM ABC SMA
.
Tam giác
ABC
đều cạnh
a
,
M
là trung điểm
BC

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
3
2
a
AM
.tan 60
SA AM
33
.3
22
aa
.
.
1
.
3
S ABC ABC
V S SA
2
1 33
.
34 2
aa
3
3
8
a
.
Câu 32: Cho khối trụ có thiết diện qua trục là hình vuông cạnh
a
. Thể tích khối trụ là
A.
3
a
. B.
3
3
a
. C.
3
12
a
. D.
3
4
a
.
Lời giải
Chọn D.
Thiết diện qua trục là hình vuông cạnh
a
2h ra
2
a
r
.
2
3
2
..
24
aa
V rh a
.
Câu 33: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
. Biết
3AB cm
,
32BC cm
. Thể tích khối lăng trụ đã cho là:
A.
3
27
8
cm
. B.
3
27
4
cm
. C.
3
27 cm
. D.
3
27
2
cm
.
Lời giải
Chọn D.
Tam giác
ABC
vuông cân tại
B
3AB BC
.
22
CC BC BC
2
2
32 3 3
.
.
1
..
2
ABC A B C
V AB BC CC
1
3.3.3
2
3
27
2
cm
.
Câu 34: Số nghiệm của phương trình
( )
( )
2
31
3
log 4 log 2 3 0
xx x+ + +=
là
A.
1
. B.
3
. C.
0
. D.
2
.
Lời giải
Chọn A
Điều kiện:
0x >
.
Phương trình đã cho tương đương với:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
(
)
(
)
( )
(
)
2 22
33 3 3
log 4 log 2 3 0 log 4 log 2 3 4 2 3
xx x xx x xxx
+ − +=⇔ + = +⇔+ = +
2
1
2 30
3
x
xx
x
=
⇔ + −=⇔
= −
. Kết hợp với điều kiện suy ra phương trình có nghiệm
1x =
.
Câu 35: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
a
, cạnh bên
SA
vuông góc với đáy.
Tính thể tích của khối chóp
.
S ABC
biết
2SB a=
.
A.
3
4
a
. B.
3
3
4
a
. C.
3
2
a
. D.
3
3
2
a
.
Lời giải
Chọn A
2
0
13
. .sin 60
24
ABC
a
S AB AC
= =
.
Tam giác
SAB
vuông tại
A
:
22
3SA SB AB a= −=
.
3
.
1
.
34
S ABC ABC
a
V SA S= =
.
Câu 36: Có bao nhiêu số nguyên của
m
để phương trình
2
22
log (2 ) 2log 4 2 1xm x x x m+− =−− −
có
hai nghiệm thực phân biệt.
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Chọn C
Điều kiện:
0
0
2 ()
x
m
m x gx
>
⇒≤
>− =
.
Phương trình đã cho tương đương với:
( ) ( ) ( )
2 2 22
2 22 2
log 2 1 4 2 log log 4 2 4 2 logxm xmx x xm xm xx+ ++ + = + ⇔ + + + = +
2
(4 2 ) ( ).f x m fx⇔ +=
Xét hàm số
2
( ) logft t t= +
trên khoảng
(0; ).+∞
S
A
B
C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
1
( ) 1 0 (0; )
ln 2
ft t
t
′
= + > ∀ ∈ +∞ ⇒
hàm số
()ft
đồng biến trên khoảng
(0; )+∞
.
Khi đó
22
42 42x mx x x m+ =⇔−=
.
Đồ thị hàm số
2
() 4
hx x x= −
là parabol có đỉnh
(2; 4).I −
Phương trình
2
42
x xm−=
có hai nghiệm phân biệt khi và chỉ khi
42 0 2 0mm−< < ⇔−< <
. Kết hợp với điều kiện
0m ≤
ta được
20m−< <
. Vì
1mm∈⇒ =−
.
Câu 37: Cho hình hộp đứng
.ABCD A B C D
′′′′
có các cạnh
0
3
2 , , 60
2
a
AB AD a AA BAD
′
= = = =
.
Gọi
M
và
N
lần lượt là trung điểm các cạnh của
AD
và
AB
. Tính thể tích
ABDNM
′′′
bằng
A.
3
8
a
. B.
3
3
4
a
. C.
3
5
48
a
. D.
3
24
a
.
Lời giải
Chọn B
Xét tam giác
ABD
có
2 , 60AB AD a BAD= = = °
ABD⇒∆
đều và
2BD AB a
= =
.
Kẻ
BE MN⊥
tại
E
và
DF MN⊥
tại
F
. Dễ thấy, tứ giác
BDFE
là hình chữ nhật.
+ Thể tích khối lăng trụ
.BB E DD F
′′
là
3
1
3
.
4
DD F
a
V S BD
′
= =
.
+ Thể tích khối chóp
.D DMF
′
là
3
2
1
.
3 16
DMF
a
V S DD
′
= =
.
+ Thể tích khối chóp
.A AMN
′
là
3
3
1
.
38
AMN
a
V S AA
′
= =
.
+ Thể tích khối
BDD B MN
′′
là
3
41 2
5
2
8
a
VV V=−=
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
+ Thể tích khối lăng trụ
.ABD A B D
′′′
là
3
5
3
.
2
ABD
a
V S AA
′
= =
.
Vậy thể tích khối
ABDNM
′′′
là
3
543
3
4
a
VVVV=−−=
.
Câu 38: Cho hàm số
(
)
32
1
4 3 2017
3
y x mx m x= − + −+
. Tìm giá trị lớn nhất của tham số thực
m
để hàm số đã cho đồng biến trên
A.
4m =
. B.
3m =
. C.
1m =
. D.
2m =
.
Lời giải
Chọn B
TXĐ:
D
=
.
Ta có:
( )
2
2 43y x mx m
′
=−+−
.
Hàm số đồng biến trên
khi chỉ khi
0,yx
′
≥∈
0
0
a >
⇔
′
∆≤
2
4 30 1 3mm m⇔ − +≤ ⇔≤ ≤
.
Giá trị
m
lớn nhất là 3.
Câu 39: Cho lăng trụ tam giác
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh
22AC =
. Biết
AC
′
tạo với mặt phẳng
( )
ABC
một góc
0
60
và
4AC
′
=
.Thể tích khối
chóp
.B ACC A
′′
bằng
A.
16
3
. B.
8
3
. C.
83
3
. D.
16 3
3
.
Lời giải
Chọn D

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Gọi
H
là hình chiếu vuông góc của
C
′
trên mặt phẳng
( )
'ABC C H⇒
là chiều cao của
lăng trụ.
⇒
Góc giữa
'AC
và mặt phẳng
(
)
ABC
là
60C AH
′
= °
.
Xét tam giác
AHC
′
vuông tại
H
có:
3
.sin 60 4. 2 3
2
C H AC
′′
= °= =
Diện tích tam giác
ABC
là
1
.4
2
ABC
S AB AC= =
Thể tích lăng trụ là
.
. 83
ABC A B C ABC
V S CH
′′′
′
= =
Mặt khác, ta có:
.
.
11
.
33
ABC A B C
B ABC ABC
V CHS V
′′′
′′′ ′′′
′
= =
.
Vậy
..
..
2 2 16 3
.8 3
3 33
ABC A B C ABC A B C
B ACCA B ABC
V VV V
′′′ ′′′
′′ ′ ′ ′
= −= ==
.
Câu 40: Khối chóp
.S ABCD
có đáy là hình vuông cạnh bằng
2a
, chân đường cao trùng với trung
điểm
H
của
AB
, mặt bên
( )
SCD
tạo với mặt đáy một góc
0
30
. Gọi
M
là trung điểm của
SC
. Thể tích khối chóp
.
H BCM
là
A.
3
2
3
a
. B.
3
3
8
a
. C.
3
3
9
a
. D.
3
6
3
a
.
Lời giải
Chọn C
Ta có
.
...
.
1 11
2 28
M HBC
M HBC S HBC S ABCD
S HBC
V
MC
V VV
V SC
==⇒= =
.
Gọi
K
là trung điểm của
CD
. Khi đó
( ) ( )
( )
0
, 30SCD ABCD SKH= =
.
Ta có
( )
3
2
0
..
2 11 2 3
.tan 30 . . 2 .
83 9
33
H BCM M HBC
a aa
SH HK V V a= =⇒== =
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 23
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 41: Cho hàm số
( )
42
21 1y mx m x=−+ +
. Tìm tất cả các giá trị của
m
để hàm số có một điểm cực
đại
A.
1
0
2
m−≤ <
. B.
1
2
m ≤−
. C.
1
0
2
m−≤ ≤
. D.
1
2
m ≥−
.
Lời giải
Chọn C
Ta có
( )
(
)
32
2
0
4 22 1 2 2 2 1; 0
2 21
x
y mx m x x mx m y
mx m
=
′′
= − + = −− =⇔
= +
*
0m =
ta có
2
1yx=−+
. Vậy hàm số đạt cực đại tại
0x =
.
*
0
m ≠
để hàm số có một điểm cực đại khi
0
1
0
2 10
2
m
m
m
<
⇔− ≤ <
+≥
.
Vậy
1
0
2
m−≤ ≤
thì hàm số có một điểm cực đại.
Câu 42: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
54yx= −
trên đoạn
[
]
1;1
−
. Khi đó
Mm
−
bằng
A.
9
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn D
Ta có
2
0
54
y
x
′
=−<
−
trên
[
]
1;1−
. Vậy
( ) ( )
1 3, 1 1M y my= −= = =
Khi đó
31 2Mm− =−=
.
Câu 43: Cho hàm số
( )
y fx=
liên tục trên
có đồ thị như hình vẽ. Đồ thị của hàm số
( ) ( )
2
gx f x=
có bao nhiêu điểm cực đại, bao nhiêu điểm cực tiểu?
A.
2
điểm cực đại, 3 điểm cực tiểu. B.
3
điểm cực đại, 2 điểm cực tiểu.
C.
1
điểm cực đại, 3 điểm cực tiểu. D.
2
điểm cực đại, 2 điểm cực tiểu.
Lời giải
Chọn A.
O
3
1
x
y

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 24
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có:
( ) ( )
( )
( )
0
0.5
' 2 ' ;' 0 1
2
3
x
x
gx fx fx gx x
x
x
=
=
= =⇔=
=
=
.
Ta có bảng biến thiên
Vậy của hàm số
( ) ( )
2
gx f x=
có 2 điểm cực đại, 3 điểm cực tiểu.
Câu 44: Cho hàm số
bx c
y
xa
−
=
−
(
0a ≠
và
,, )abc∈
có đồ thị như hình bên. Khẳng định nào sau
đây đúng?
A.
0, 0, 0
a b c ab> < −<
. B.
0, 0, 0
abcab> > −<
.
C.
0, 0, 0a b c ab< > −<
. D.
0, 0, 0abcab< < −>
.
Lời giải
Chọn B
Vì hàm số
bx c
y
xa
−
=
−
nghịch biến trên tập xác định nên
0 0.ab c c ab− +<⇔− <
Mặc khác tiệm cận đứng
xa
=
nằm bên phải trục tung nên
0.a >
Câu 45: Cho hình trụ có hai đáy là hai hình tròn
( )
O
và
( )
'O
, chiều cao
2R
và bán kính đáy
.R
Một mặt phẳng
( )
α
đi qua trung điểm của
'OO
và tạo với
'OO
một góc
0
30 .
Hỏi
( )
α
cắt
đường tròn đáy theo một dây cung có độ dài bằng bao nhiêu?
A.
2
3
R
. B.
2
3
R
. C.
22
3
R
. D.
4
33
R
.
Lời giải
Chọn C.
O
y
x

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 25
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Gọi
M
là trung điểm
'.OO
Gọi
,AB
là giao điểm của mặt phẳng
(
)
α
và đường tròn
( )
O
và
H
là hình chiếu của
O
trên
( )
.AB AB MHO⇒⊥
Trong mặt phẳng
( )
MHO
kẻ
( )
,OK MH K MH⊥∈
khi đó góc giữa
'OO
và mặt phẳng
( )
α
là góc
0
30 .OMK =
Xét tam giác vuông
MHO
ta có
00
3
.tan 30 .tan 30 .
3
R
HO OM R= = =
Xét tam giác vuông
AHO
ta có
2
222
2
.
3
3
RR
AH OA OH R= − = −=
Do
H
là trung điểm của
AB
nên
22
.
3
R
AB =
Câu 46: Cho hàm số
21
1
x
y
x
−
=
+
có đồ thị
( )
C
và đường thẳng
: 23dy x
= −
. Đường thẳng
d
cắt
( )
C
tại hai điểm
A
và
B
. Khoảng cách giữa
A
và
B
là
A.
2
5
. B.
25
5
. C.
5
2
. D.
55
2
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm của
( )
C
và
d
là
21
23
1
x
x
x
−
= −
+
( )( )
2123 1x xx⇔ −= − +
(do
1x = −
không là nghiệm của phương trình)
2
2
2 3 20
1
2
x
xx
x
=
⇔ − −=⇔
= −
.
Đường thẳng
d
cắt
( )
C
tại hai điểm
( )
2;1A
và
1
;4
2
B
−−
.
K
M
B
H
D
C
'O
O
A

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 26
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Khoảng cách giữa
A
và
B
là
( )
2
2
1 55
2 41
22
AB
= − − +−− =
.
Câu 47: Cho hình hộp đứng
.ABCD A B C D
′′′′
có đáy là hình thoi,
0
60BAD =
,
2AA AB a
′
= =
. Gọi
,
JI
lần lượt là giao điểm của các đường chéo của các hình
ABCD
′′′′
và
A D DA
′′
;
,KL
lần
lượt là trung điểm các cạnh
,AB BC
. Thể tích của khối chóp
IJKL
bằng
A.
3
3
24
a
. B.
3
3
4
a
. C.
3
3
32
a
. D.
3
3
12
a
.
Lời giải
Chọn B
Ta có
( )
( )
( )
( ) ( ) ( )
,do //
do
LK BD LK AC AC BD
LK BDD B L KJ BDD B
LK BB BB ABCD
⊥⊥
′′ ′′
⇒⊥ ⇒ ⊥
′′
⊥⊥
theo giao
tuyến
JM
(với
M LK BD
= ∩
)
( )
1
ABD∆
đều nên
2BD a=
và
1
42
a
BM BD= =
. Trên cạnh
BB
′
lấy điểm
G
sao cho
2
a
BG =
.
Ta có
(
)( )
. ......
DG MJ DB BG MB BB B J DB MB DB BB DB B J BG MB BG BB BG B J
′′ ′ ′ ′ ′
=+ ++=+++++
( )
. 2. 0 2. 0 .2 0 0 2
22
aa
DG MJ a a a a DG JM⇒ = +− ++ +=⇒ ⊥
Từ
( )
1
và
( )
2
suy ra
( )
DG LK J⊥
. Gọi
H DG JM= ∩
. Tứ giác
BMHG
nội tiếp nên

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 27
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
( )
22 2
2
3
.2
.. 6
2
..
17
2
2
a
a
DM DB DM DB a
DH DG DM DB DH
DG
DB BG
a
a
= ⇒= = = =
+
+
.
Đường thẳng
DI
cắt
( )
LKJ
tại
A
′
và
I
là trung điểm của
DA
′
nên
( )
( )
(
)
(
)
1 13
,,
22
17
a
d I LKJ d D LKJ DH= = =
.
JML∆
vuông tại
M
nên
( )
2
22
2 2 2 2 2 22
3
17
(2 )
4 4 42
a
KL AO a
JM JL ML A K A A AK a a
′′
= − = − = + − = +− =
.
Thể tích của khối chóp
IJKL
là
( )
( )
( )
( )
3
1 11 11 17 3 3
., . .., .. .3.
3 32 32 2 4
17
LKJ
a aa
V S d I L KJ JM KL d I LKJ a= = = =
.
Câu 48: Tìm tất cả các giá trị thực của tham số
m
để phương trình
(
)
2
4 2 .6 3 .9 0
xx x
mm
− +− =
có hai
nghiệm phân biệt.
A.
0m >
. B.
3m = ±
. C.
3m ≥
. D.
3m >
.
Lời giải
Chọn D
Phương trình đã cho tương đương với
( )
2
2
22
2. 3 0
33
xx
mm
− + −=
.
Đặt
( )
2
,0
3
x
tt
= >
. Phương trình đã cho trở thành
( )
( )
22
2. 3 0t mt m− + −= ∗
.
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình
( )
∗
có hai nghiệm
dương phân biệt
2
0 30
0 20 3
0
30
S mm
P
m
′
∆> >
>⇔ > ⇔>
>
−>
.
Câu 49: Một người gửi 100 triệu đồng vào ngân hàng với kì hạn 3 tháng (1 quý), lãi suất
6%
một
quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó lại gửi thêm 100 triệu đồng với hình
thức và lãi suất như trên. Hỏi sau 1 năm tính từ lần gửi đầu tiên người đó nhận được số tiền
gần với kết quả nào nhất?
A.
236,6
triệu đồng. B.
243,5
triệu đồng
C.
238,6
triệu đồng D.
224,7
triệu đồng
Lời giải
Chọn C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 28
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Số tiền người đó nhận được sau đúng 6 tháng là:
2
8
1
6
10 1
100
T
= +
Số tiền người đó nhận được sau 1 năm là:
( )
2
8
21
6
10 1 238,6
100
TT
=++=
triệu đồng.
Câu 50: Cho hàm số
()y fx
=
liên tục trên
và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị của
tham số
m
để phương trình
(cos ) 2 1fx m=−+
có nghiệm thuộc khoảng
0;
2
π
là
A.
( )
0;1
. B.
( )
1;1−
. C.
(
]
0;1
. D.
(
]
1;1−
.
Lời giải
Chọn A
Đặt
( )
cos , 0;1x tt= ∈
.
Phương trình đã cho có nghiệm thuộc khoảng
0;
2
π
⇔
phương trình
() 2 1ft m=−+
có
nghiệm thuộc khoảng
(0;1)
. Dựa vào đồ thị trên suy ra
1 2 11 1 0mm
− <− + < ⇔ > >
.
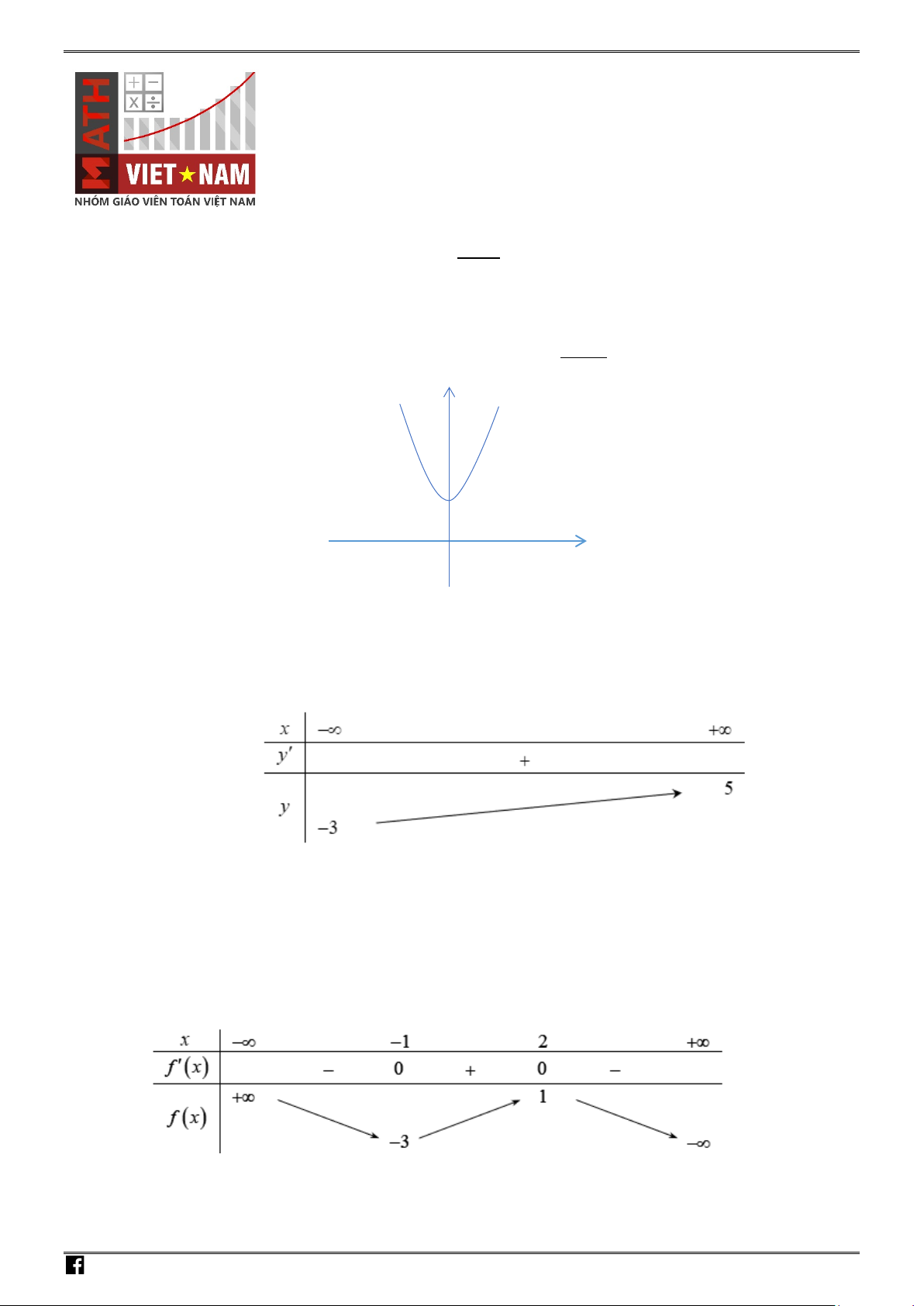
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
ĐỀ THI HỌC KỲ 1 – NĂM HỌC 2020 – 2021
SỞ GD & ĐT NAM ĐỊNH
Môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề)
Câu 1: Tìm tiệm cận đứng của đồ thị hàm số
31
2
x
y
x
−
=
+
.
A.
2
y
= −
. B.
2x = −
. C.
3x
=
. D.
2
x =
.
Câu 2: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
1
yx= +
. B.
42
21yx x=++
. C.
32
2
x
y
x
+
=
+
. D.
42
21yx x=−+
.
Câu 3: Cho hình nón có bán kính đáy
2r =
và độ dài đường sinh
4l =
.Diện tích xung quanh
của hình nón đã cho bằng:
A.
3
π
. B.
16
π
. C.
9
π
. D.
8
π
.
Câu 4: Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Số đường tiệm cận ngang của đồ thị hàm số
( )
y fx=
là
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 5: Cho khối lăng trụ
.ABCD A B C D
′′′′
có chiều cao
9h =
. Đáy
ABCD
là hình vuông có cạnh bằng
2
. Thể tích của khối lăng trụ đã cho bằng
A.
18
. B.
36
. C.
6
. D.
12
.
Câu 6: Cho hàm số
( )
fx
có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
2; +∞
. B.
( )
1;− +∞
. C.
( )
;2−∞
. D.
( )
1; 2−
.
Câu 7: Cho
a
là số thực dương và
,
mn
là các số thực tùy ý . Khẳng định nào dưới đây đúng?
x
O
y
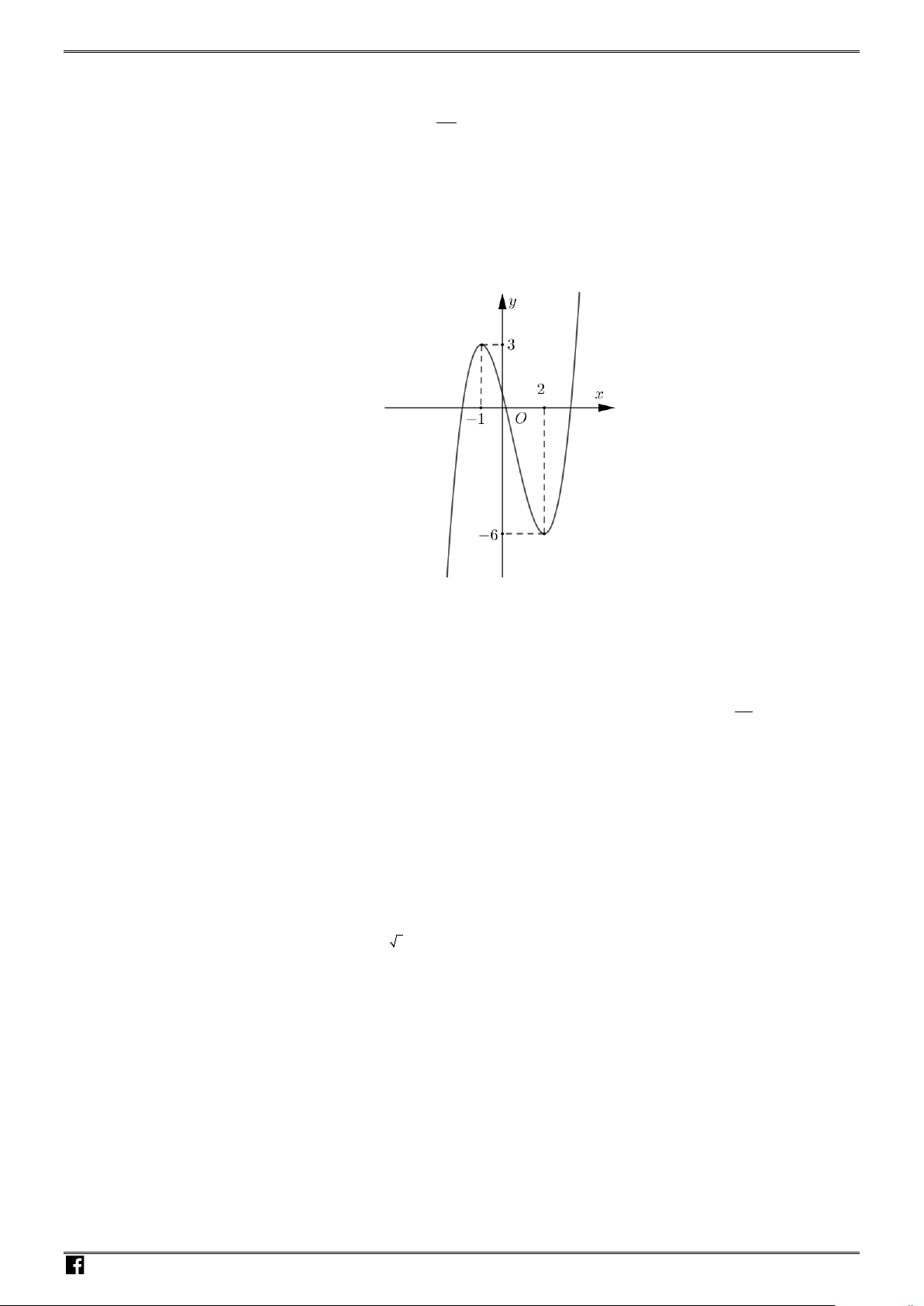
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
m n mn
aaa
+
+=
. B.
.
.
m n mn
aa a
=
. C.
m n mn
aaa+=
. D.
.
m n mn
aa a
+
=
.
Câu 8: Tập nghiệm của bất phương trình
1
5
25
x
là
A.
(
)
1;
− +∞
. B.
( )
5; +∞
. C.
( )
2;− +∞
. D.
( )
2; +∞
.
Câu 9: Cho khối trụ có bán kính đáy
6r
và chiều cao
2h
. Thể tích của khối trụ đã cho bằng
A.
24
π
. B.
72
π
. C.
18
π
. D.
36
π
.
Câu 10: Cho hàm số bậc ba
32
y ax bx cx d= + ++
có đồ thị là đường cong trong hình bên. Hàm số đã cho
đạt cực đại tại điểm nào dưới đây?
A.
3x =
. B.
1x = −
. C.
6x = −
. D.
2x =
.
Câu 11: Cho khối chóp có diện tích đáy
12
B =
và chiều cao
6h =
. Thể tích của khối chóp đã cho bằng
A.
6
. B.
72
. C.
36
. D.
24
.
Câu 12: Nghiệm của phương trình
( )
3
log 2 1 2x
−=
là
A.
10x =
. B.
5x =
. C.
4x =
. D.
11
2
x =
.
Câu 13: Cho khối lập phương có cạnh bằng
5
. Thể tích của khối lập phương đã cho bằng
A.
125
. B.
50
. C.
15
. D.
25
.
Câu 14: Tập xác định của hàm số
2
yx
−
=
là
A.
( ;4)−∞
. B.
\ {0}
. C.
. D.
[0; )
+∞
.
Câu 15: Cho hình trụ có bán kính đáy
3r =
và độ dài đường sinh
1l =
. Diện tích xung quanh của hình
trụ đã cho bằng
A.
6
π
. B.
3
π
. C.
9
π
. D.
24
π
.
Câu 16: Tập xác định của hàm số
2
logyx=
là
A.
( )
0; +∞
. B.
{ }
\0
. C.
[
)
0; +∞
. D.
.
Câu 17: Cho hàm số
(
)
fx
có bảng biến thiên như sau

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Giá trị cực tiểu của hàm số đã cho bằng
A.
1−
. B.
0
. C.
1
. D.
2
.
Câu 18: Cho khối nón có bán kính đáy là
1r =
và chiều cao
3h =
. Thể tích của khối nón đã cho bằng
A.
π
. B.
22
π
. C.
3
π
. D.
22
3
π
.
Câu 19: Nghiệm của phương trình
1
24
x
+
=
là
A.
0x =
. B.
1x =
. C.
1x = −
. D.
2
x =
.
Câu 20: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
B
,
,3AB a SA a= =
và
SA
vuông góc với
mặt phẳng đáy ( tham khảo hình vẽ bên). Góc giữa
SB
và mặt phẳng đáy bằng
A.
0
45
. B.
0
60
. C.
0
30
. D.
0
90
.
Câu 21: Cắt hình nón đỉnh
S
bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân
có cạnh huyền bằng
2
. Thể tích của khối nón tạo nên bởi hình nón đã cho bằng
A.
2
3
π
. B.
π
. C.
4
3
π
. D.
3
π
.
Câu 22: Cho
a
là số thực dương,
1a ≠
và
4
log
a
Pa
=
. Mệnh đề nào dưới đây đúng?
A.
4P =
. B.
2P =
. C.
8P =
. D.
6P =
.
Câu 23: Cho khối chóp
.
S ABCD
có đáy là hình vuông cạnh
a
.
SA
vuông góc với mặt phẳng đáy và tam
giác
SAC
là tam giác cân (tham khảo hình vẽ bên). Tính thể tích
V
của khối chóp đã cho.
A.
3
2
3
a
V =
. B.
3
2Va=
. C.
3
3
a
V =
. D.
3
Va=
.
Câu 24: Tính đạo hàm của hàm số
1
3
x
y
−
=
.
A.
1
'
3
x
y
−
=
. B.
1
' 3 .ln 3
x
y
−
= −
. C.
1
' 3 .ln 3
x
y
−
=
. D.
1
'3
x
y
−
= −
.
Câu 25: Cho lăng trụ tam giác đều
.'' 'ABC A B C
có cạnh đáy bằng
a
và cạnh bên bằng
4a
(tham khảo
hình vẽ bên). Thể tích khối lăng trụ đã cho là

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
Va
=
. B.
3
3Va=
. C.
3
32V a=
. D.
3
3
3
a
V =
.
Câu 26: Hàm số nào sau đây đồng biến trên khoảng
( )
;
−∞ + ∞
.
A.
5
2
x
y
x
+
=
−
. B.
3
3yx x= +
. C.
2
3
x
y
x
−
=
+
. D.
3
3yxx=−−
Câu 27: Cắt hình trụ bởi một mặt phẳng đi qua trục được thiết diện là một hình vuông có diện tích bằng
4
.Thể tích của khối trụ tạo nên hình trụ đã cho bằng
A.
22
π
. B.
2
3
π
. C.
2
π
. D.
8
π
.
Câu 28: Tập nghiệm của bất phương trình
1
3
log 1 1x
là
A.
0;6
. B.
1;6
. C.
6;
. D.
;6
.
Câu 29: Số giao điểm của đồ thị hàm số
3
yx x
và trục hoành là
A.
2
. B.
0
. C.
3
. D.
1
.
Câu 30: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
5AC a
,
2BC a
,
3AA a
(tham khảo hình bên). Khoảng cách từ
C
đến mặt phẳng
A BC
bằng
A.
3
2
a
. B.
3a
. C.
3
2
a
. D.
3
4
a
.
Câu 31: Cho hàm số
( )
y fx=
liên tục trên
và có bảng xét dấu của
( )
'fx
như sau
Số điểm cực trị của hàm số đã cho là
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 32: Giá trị nhỏ nhất của hàm số
3
31yx x=−+
trên đoạn
[ ]
0; 2
là
A.
2−
. B.
1−
. C.
1
. D.
3
.
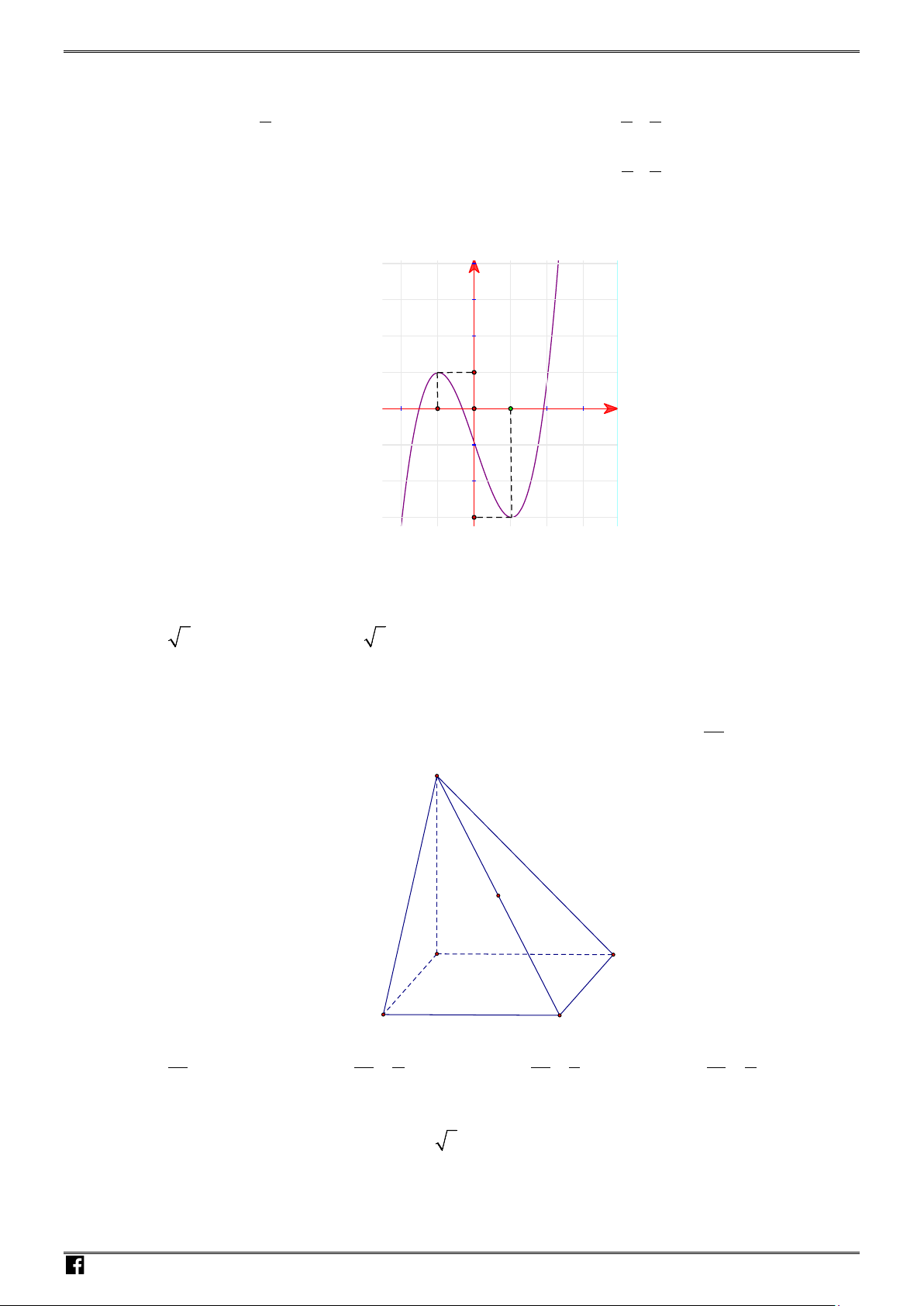
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 33: Cho
,ab
là hai số thực dương và
a
khác
1
. Khẳng định nào sau đây đúng?
A.
( )
6
1
log log
6
a
a
ab b
=
. B.
( )
6
11
log log
66
a
a
ab b
= +
.
C.
(
)
6
log 6 6log
a
a
ab b= +
. D.
( )
6
11
log log
56
a
a
ab b= +
.
Câu 34: Cho hàm số bậc ba
( )
y fx=
có đồ thị là đường cong hình bên. Số nghiệm thực của phương
trình
( )
2fx= −
là
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 35: Tổng tất cả các nghiệm của phương trình
2
33
28
xx x−− −
=
bằng
A.
3
. B.
23
. C.
3−
. D.
0
.
Câu 36: Cho khối chóp
.
S ABCD
có đáy là hình bình hành. Gọi
M
là trung điểm của
SC
. Mặt phẳng
qua
AM
và song song với
BD
chia khối chóp thành hai phần, trong đó phần chứa đỉnh
S
có
thể tích
1
V
, phần còn lại có thể tích
2
V
(tham khảo hình vẽ bên). Tính tỉ số
1
2
V
V
.
A.
1
2
1
V
V
=
. B.
1
2
1
2
V
V
=
. C.
1
2
1
3
V
V
=
. D.
1
2
2
7
V
V
=
.
Câu 37: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh bằng
2
. Các điểm
,MN
lần lượt là trung
điểm của các cạnh
BC
và
CD
,
5SA =
và vuông góc với đáy (tham khảo hình vẽ). Khoảng
cách giữa hai đường thẳng
SN
và
DM
bằng
x
y
1
-3
-1
-1
O
1
M
C
D
A
B
S

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
10
10
. B.
5
10
. C.
10
2
. D.
10
5
.
Câu 38: Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh bằng
2
. Tam giác
SAB
đều, tam giác
SCD
vuông cân tại
S
(tham khảo hình vẽ). Tính thể tích
V
của khối chóp đã cho
A.
83
3
V =
. B.
23
3
V =
. C.
23V =
. D.
43
3
V =
.
Câu 39: Cho hình nón có chiều cao bằng
4
thiết diện qua đỉnh hình nón và cắt hình nón theo một thiết
diện là tam giác vuông có diện tích bằng
32
. Thể tích của khối nón được giới hạn bởi hình nón
đã cho bằng
A.
64
3
π
. B.
64
π
. C.
32
π
. D.
192
π
.
Câu 40: Biết rằng tập nghiệm của bất phương trình
(
) ( )
3 5 3 5 3.2
xx
x
+ +− <
là khoảng
( )
;ab
, hãy
tính
S ba= −
.
A.
4S =
. B.
2S =
. C.
1
S
=
. D.
3S =
.
Câu 41: Có bao nhiêu giá trị nguyên của tham số
[ ]
2020;2020m ∈−
để hàm số
21
3
7
9
x
xm
+
+
đồng biến trên
khoảng
( )
3; ?+∞
A.
8
. B.
2015
. C.
9
. D.
2014
.
Câu 42: Cho hàm số
4ax b
y
cx b
+−
=
+
có đồ thị là đường cong trong hình bên. Mệnh để nào dưới đây đúng?
A.
0,0 4, 0
a bc< << <
. B.
0, 0, 0abc
>><
.
C.
0, 4, 0abc>><
. D.
0,0 4, 0a bc> << <
.
Câu 43: Cho hàm số
( )
fx
có đạo hàm trên
R
. Đồ thị hàm số
( )
'y fx=
trên đoạn
[ ]
2; 2−
là đường cong
trong hình bên. Mệnh đề nào sau đây đúng?
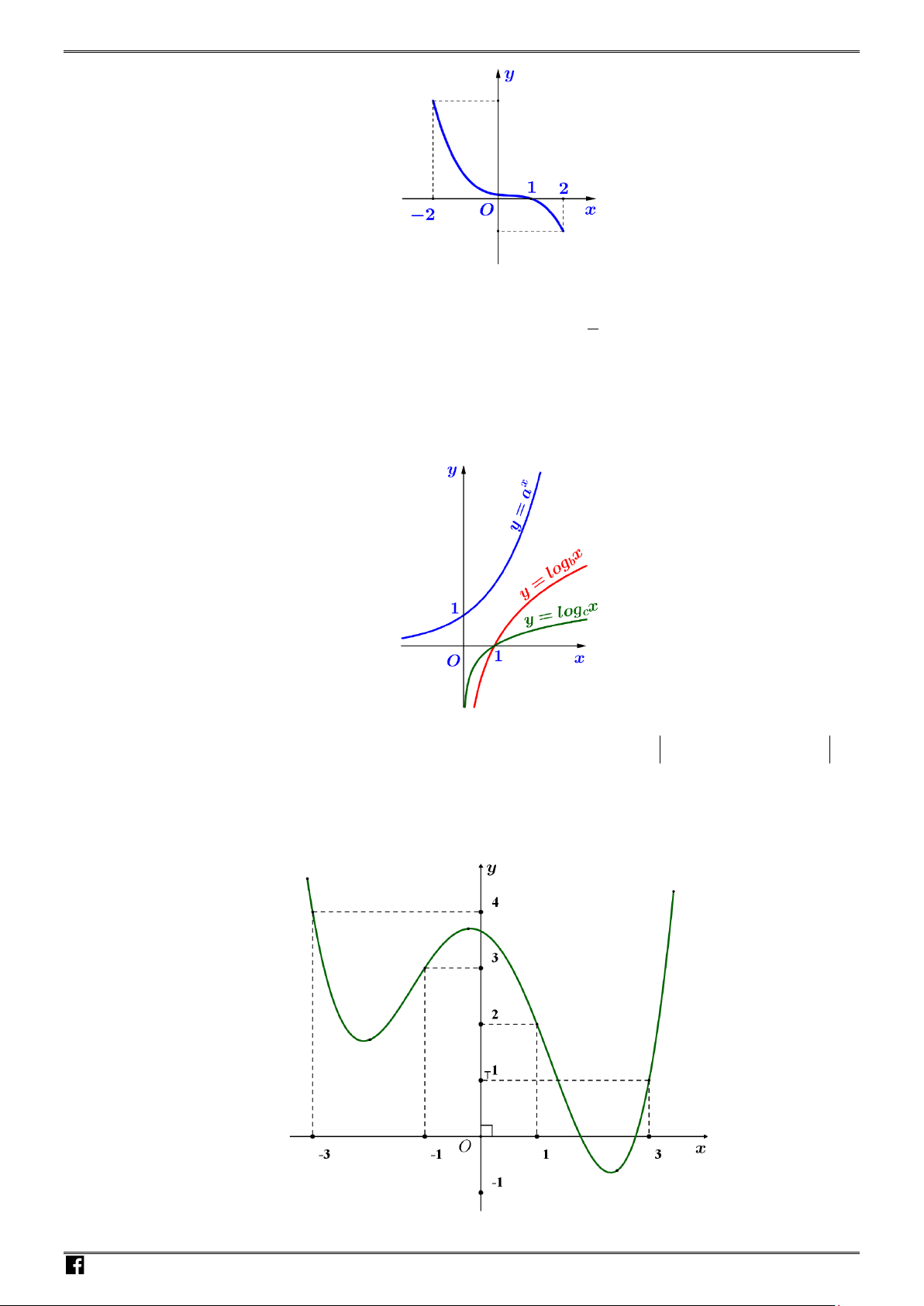
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
[ ]
( ) ( )
2;2
max 2fx f
−
= −
. B.
[ ]
( ) ( )
2;2
max 2fx f
−
=
. C.
[ ]
( ) ( )
2;2
min 1fx f
−
=
. D.
[ ]
( ) ( )
2;2
max 1fx f
−
=
.
Câu 44: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
32
1
16 10
3
y x mx x= − ++
đồng biến trên
khoảng
(
)
;−∞ +∞
A.
9
. B.
10
. C.
8
. D.
7
.
Câu 45: Cho
,,
abc
là ba số thực dương và khác 1. Đồ thị các hàm số
, log , log
x
bc
y a y xy x= = =
được
cho trong hình bên. Mệnh đề nào sau đây đúng?
A.
bac<<
. B.
abc
<<
. C.
bca<<
. D.
cba<<
.
Câu 46: Có bao nhiêu giá trị nguyên dương của tham số
m
đề hàm số
32
9 ( 8)y x x m xm=− ++ −
có
năm điểm cực trị?
A.
13
. B.
15
. C.
14
. D. Vô số.
Câu 47: Cho hàm số bậc năm
(
)
fx
. Hàm số
( )
y fx
′
=
có đồ thị là đường cong trong hình bên.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Hàm số
( )
( )
( )
2
72 1gx f x x
= − +−
đồng biến trên khoảng nào dưới đây?
A.
(
)
2;0−
. B.
( )
3; 1−−
. C.
( )
3; +∞
. D.
( )
2;3
.
Câu 48: Cho bất phương trình
2
2
2
22
22
2
10
33
3
x xm
x xm
− −+
− +−
+>
, với
m
là tham số thực. Có bao nhiêu giá tri
nguyên của
m
để bất phương trình đã cho nghiệm đúng với mọi
[0; 2]?x ∈
A.
9
. B.
10
. C.
11
. D.
15
.
Câu 49: Cho khối hộp
.ABCD A B C D
′′′′
có
22AA AB AD
′
= =
,
0
90
BAD
=
,
0
60BAA
′
=
,
0
120DAA
′
=
,
6
AC
′
=
. Tính thể tích
V
của khối hộp đã cho.
A.
2V =
. B.
23
V
=
. C.
2
2
V
=
. D.
22
V =
.
Câu 50: Cho hàm số
( )
32
3y fx x x= = −
có đồ thị là đường cong trong hình bên dưới. Phương trình
( )
( )
( )
(
)
2
4
4
21
f fx
f x fx
−
= −
++
có bao nhiêu nghiệm ?
A.
4
. B.
6
. C.
3
. D.
7
.
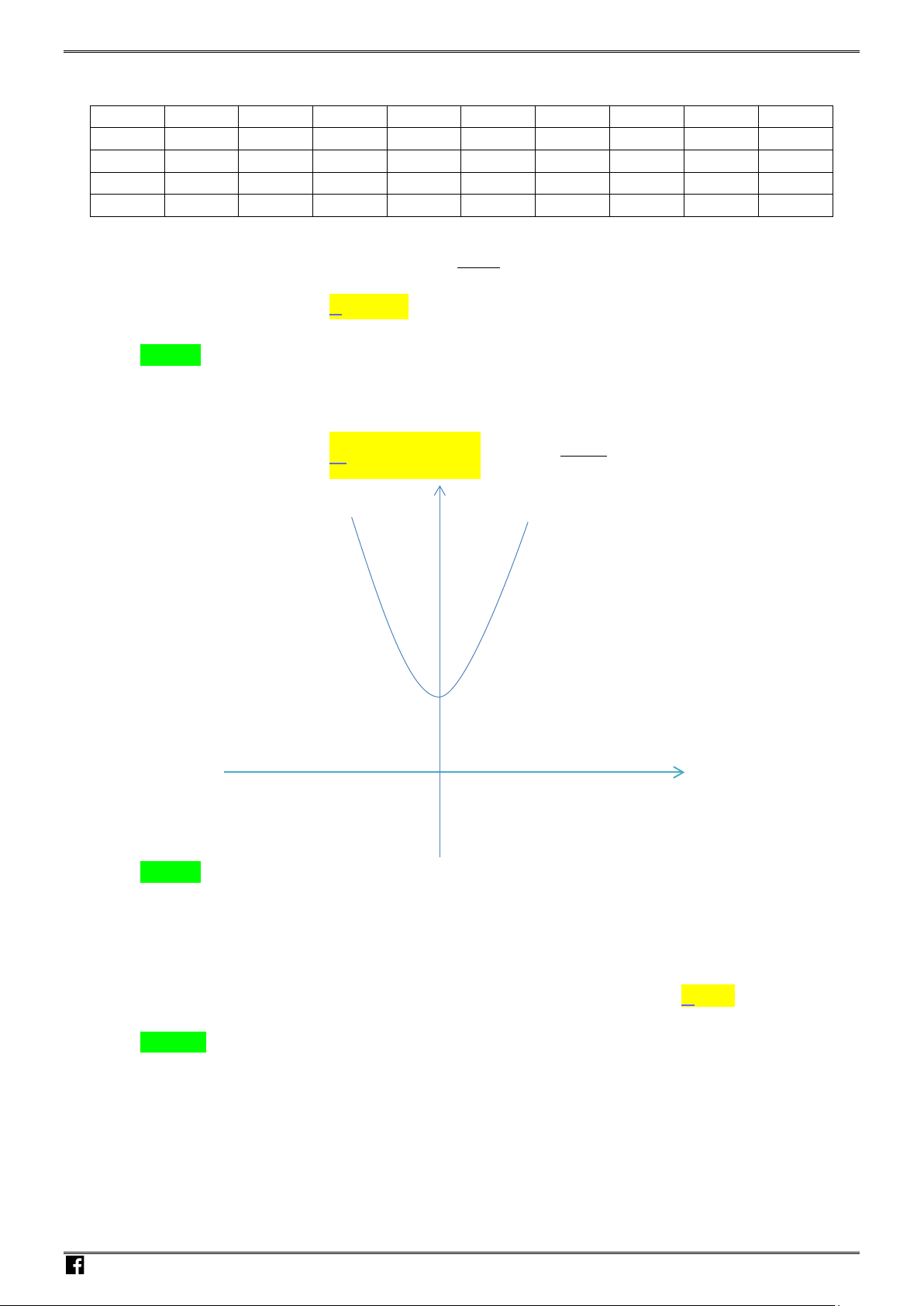
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
BẢNG ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
1.B
2.B
3.D
4.C
5.B
6.A
7.D
8.C
9.B
10.B
11.D
12.B
13.A
14.B
15.A
16.A
17.C
18.A
19.B
20.B
21.D
22.C
23.A
24.B
25.B
26.B
27.C
28.B
29.C
30.A
31.C
32.B
33.B
34.C
35.D
36.B
37.A
38.B
39.B
40.B
41.A
42.D
43.D
44.A
45.A
46.C
47.D
48.D
49.A
50.D
Câu 1: Tìm tiệm cận đứng của đồ thị hàm số
31
2
x
y
x
−
=
+
.
A.
2
y
= −
. B.
2x
= −
. C.
3x =
. D.
2x =
.
Lời giải
Chọn B
Ta có
( )
2
lim
x
y
+
→−
= −∞
,
( )
2
lim
x
y
−
→−
= +∞
. Nên
2x = −
là tiệm cận đứng của đồ thị hàm số.
Câu 2: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
1
yx
= +
. B.
42
21yx x
=++
. C.
32
2
x
y
x
+
=
+
. D.
42
21yx x=−+
.
Chọn B
Căn cứ vào đồ thị hàm số ta loại các đáp án
,
AC
.
Loại đáp án
D
vì
.0ab<
hàm số có 3 cực trị.
Câu 3: Cho hình nón có bán kính đáy
2r =
và độ dài đường sinh
4l =
.Diện tích xung quanh
của hình nón đã cho bằng:
A.
3
π
. B.
16
π
. C.
9
π
. D.
8
π
.
Lời giải
Chọn D.
Ta có
..
xq
S rl
π
=
.2.4 8
ππ
= =
.
Câu 4: Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
x
O
y

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Số đường tiệm cận ngang của đồ thị hàm số
( )
y fx=
là
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn C
Ta có
lim 3
x
y
→−∞
= −
nên
3y = −
là tiệm cận ngang.
Ta có
lim 5
x
y
→+∞
=
nên
5y =
là tiệm cận ngang.
Vậy số đường tiệm cận ngang của đồ thị hàm số
( )
y fx=
là
2
.
Câu 5: Cho khối lăng trụ
.ABCD A B C D
′′′′
có chiều cao
9h =
. Đáy
ABCD
là hình vuông có cạnh bằng
2
. Thể tích của khối lăng trụ đã cho bằng
A.
18
. B.
36
. C.
6
. D.
12
.
Lời giải
Chọn B
Thể tích của khối lăng trụ đã cho là
2
9.2 36V = =
.
Câu 6: Cho hàm số
( )
fx
có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
2; +∞
. B.
(
)
1;− +∞
. C.
( )
;2−∞
. D.
( )
1; 2
−
.
Lời giải
Chọn A
Câu 7: Cho
a
là số thực dương và
,mn
là các số thực tùy ý . Khẳng định nào dưới đây đúng?
A.
m n mn
aaa
+
+=
. B.
.
.
m n mn
aa a
=
. C.
m n mn
aaa+=
. D.
.
m n mn
aa a
+
=
.
Lời giải
Chọn D
Câu 8: Tập nghiệm của bất phương trình
1
5
25
x
là
A.
( )
1;− +∞
. B.
( )
5; +∞
. C.
( )
2;− +∞
. D.
( )
2; +∞
.
Lời giải
Chọn C
2
1
5 5 5 2 2;
25
xx
xx
.
Vậy tập nghiệm bất phương trình là
2;S
.
Câu 9: Cho khối trụ có bán kính đáy
6r
và chiều cao
2h
. Thể tích của khối trụ đã cho bằng

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
24
π
. B.
72
π
. C.
18
π
. D.
36
π
.
Lời giải
Chọn B
22
6 .2 72 .V rh
Câu 10: Cho hàm số bậc ba
32
y ax bx cx d= + ++
có đồ thị là đường cong trong hình bên. Hàm số đã cho
đạt cực đại tại điểm nào dưới đây?
A.
3
x
=
. B.
1x = −
. C.
6x = −
. D.
2x =
.
Lời giải
Chọn B
Dựa vào đồ thị nhận thấy hàm số đạt cực đại tại điểm
1
x = −
.
Câu 11: Cho khối chóp có diện tích đáy
12B
=
và chiều cao
6h =
. Thể tích của khối chóp đã cho bằng
A.
6
. B.
72
. C.
36
. D.
24
.
Lời giải
Chọn D
Thể tích của khối chóp đã cho bằng
11
.12.6 24
33
V Bh
= = =
.
Câu 12: Nghiệm của phương trình
( )
3
log 2 1 2x
−=
là
A.
10x =
. B.
5x =
. C.
4x =
. D.
11
2
x =
.
Lời giải
Chọn B
Ta có
( )
2
3
log212 213 5x xx− = ⇔ −= ⇔ =
.
Vậy nghiệm của phương trình là
5
x =
.
Câu 13: Cho khối lập phương có cạnh bằng
5
. Thể tích của khối lập phương đã cho bằng
A.
125
. B.
50
. C.
15
. D.
25
.
Lời giải
Chọn A
Thể tích của khối lập phương đã cho là
33
5 125Va= = =
.
Câu 14: Tập xác định của hàm số
2
yx
−
=
là
A.
( ;4)−∞
. B.
\ {0}
. C.
. D.
[0; )+∞
.
Lời giải
Chọn B
Hàm số a
2
yx
có mũ là số nguyên âm nên có tập xác định là
\ {0}
.
Câu 15: Cho hình trụ có bán kính đáy
3r =
và độ dài đường sinh
1l =
. Diện tích xung quanh của hình
trụ đã cho bằng

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
6
π
. B.
3
π
. C.
9
π
. D.
24
π
.
Lời giải
Chọn A
Chiều cao của hình trụ là
1
hl
= =
.
Diện tích xung quanh của hình trụ là
2 2 .3.1 6
xq
S rh
ππ π
= = =
.
Câu 16: Tập xác định của hàm số
2
log
yx=
là
A.
( )
0;
+∞
. B.
{ }
\0
. C.
[
)
0; +∞
. D.
.
Lời giải
Chọn A
Điều kiện xác định của hàm số là
0x >
, vậy tập xác định của hàm số là
( )
0;D = +∞
.
Câu 17: Cho hàm số
( )
fx
có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng
A.
1−
. B.
0
. C.
1
. D.
2
.
Lời giải
Chọn C .
Dự vào bảng biến thiên , hàm số đạt cực tiểu tại
0x =
và
( )
01
CT
yy= =
Câu 18: Cho khối nón có bán kính đáy là
1r =
và chiều cao
3
h =
. Thể tích của khối nón đã cho bằng
A.
π
. B.
22
π
. C.
3
π
. D.
22
3
π
.
Lời giải
Chọn A .
Thể tích của khối nón bằng
2
11
.1.3
33
V rh
π ππ
= = =
.
Câu 19: Nghiệm của phương trình
1
24
x+
=
là
A.
0x =
. B.
1x =
. C.
1x = −
. D.
2x =
.
Lời giải
Chọn B
1 12
2422 12 1
xx
xx
++
= ⇔ = ⇔ += ⇔ =
.
Câu 20: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
B
,
,3AB a SA a= =
và
SA
vuông góc với
mặt phẳng đáy ( tham khảo hình vẽ bên). Góc giữa
SB
và mặt phẳng đáy bằng

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
0
45
. B.
0
60
. C.
0
30
. D.
0
90
.
Lời giải
Chọn B
Ta có
( ) (
)
( )
;SA ABC SA ABC SBA
⊥⇒ =
.
0
3
tan 3 60
SA a
SBA SBA
AB a
== =⇒=
.
Câu 21: Cắt hình nón đỉnh
S
bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân
có cạnh huyền bằng
2
. Thể tích của khối nón tạo nên bởi hình nón đã cho bằng
A.
2
3
π
. B.
π
. C.
4
3
π
. D.
3
π
.
Lời giải
Chọn D
Thiết diện đi qua trục là tam giác vuông cân tại đỉnh có cạnh huyền bằng 2
( )
2
2
22 2lrl⇒ = ⇔=
và
1r =
.
Khi đó ta có
222
211 1hlr h= − = −=⇒ =
.
Thể tích của khối nón là
2
1
33
V rh
π
π
= =
.
Câu 22: Cho
a
là số thực dương,
1a
≠
và
4
log
a
Pa=
. Mệnh đề nào dưới đây đúng?
A.
4
P =
. B.
2
P =
. C.
8P =
. D.
6P =
.
Lời giải
Chọn C.
Với
a
là số thực dương và
1a ≠
, ta có:
1
2
4 4
4
log log 8
1
2
log
a
a
a
P a
a a= = = =
.
Câu 23: Cho khối chóp
.
S ABCD
có đáy là hình vuông cạnh
a
.
SA
vuông góc với mặt phẳng đáy và tam
giác
SAC
là tam giác cân (tham khảo hình vẽ bên). Tính thể tích
V
của khối chóp đã cho.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
2
3
a
V
=
. B.
3
2Va=
. C.
3
3
a
V
=
. D.
3
Va=
.
Lời giải
Chọn A.
Vì
SA AC⊥
nên
SAC∆
là tam giác cân tại
A
, do đó:
22
2
SA AC AB BC a== +=
.
Thể tích
V
của khối chóp đã cho:
3
2
11 2
. . . 2.
33 3
ABCD
a
V SA S a a= = =
.
Câu 24: Tính đạo hàm của hàm số
1
3
x
y
−
=
.
A.
1
'
3
x
y
−
=
. B.
1
' 3 .ln 3
x
y
−
= −
. C.
1
' 3 .ln 3
x
y
−
=
. D.
1
'3
x
y
−
= −
.
Lời giải
Chọn B.
11
' 3 .ln 3.(1 )' 3 .ln 3
xx
yx
−−
= −=−
.
Câu 25: Cho lăng trụ tam giác đều
.'' 'ABC A B C
có cạnh đáy bằng
a
và cạnh bên bằng
4a
(tham khảo
hình vẽ bên). Thể tích khối lăng trụ đã cho là
A.
3
Va=
. B.
3
3
Va=
. C.
3
32V a=
. D.
3
3
3
a
V =
.
Lời giải
Chọn B
Thể tích khối lăng trụ đã cho là:
2
3
3
.4 3
4
a
V aa= =
.
Câu 26: Hàm số nào sau đây đồng biến trên khoảng
( )
;−∞ + ∞
.
A.
5
2
x
y
x
+
=
−
. B.
3
3yx x= +
. C.
2
3
x
y
x
−
=
+
. D.
3
3yxx=−−
.
Lời giải
Chọn B
Hàm số đồng biến trên khoảng
( )
;−∞ + ∞
. Nên loại A và C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có:
32
3 ' 3 3 0,yx x y x x= + ⇒ = + > ∀∈
.
Câu 27: Cắt hình trụ bởi một mặt phẳng đi qua trục được thiết diện là một hình vuông có diện tích bằng
4
.Thể tích của khối trụ tạo nên hình trụ đã cho bằng
A.
22
π
. B.
2
3
π
. C.
2
π
. D.
8
π
.
Lời giải
Chọn C
Thiếu diện là hình vuông
ABCD
Ta có:
2
42
ABCD
Sa a= =⇔=
suy ra bán kính đáy :
1r =
.
Thể tích khối trụ đã cho bằng :
2
2V rh
ππ
= =
.
Câu 28: Tập nghiệm của bất phương trình
1
3
log 1 1x
là
A.
0;6
. B.
1;6
. C.
6;
. D.
;6
.
Lời giải
Chọn B .
Ta có:
1
5
log 1 1x
1
10
1
1
5
x
x
1
6
x
x
.
Vậy tập nghiệm của bất phương trình là
1;6
.
Câu 29: Số giao điểm của đồ thị hàm số
3
yx x
và trục hoành là
A.
2
. B.
0
. C.
3
. D.
1
.
Lời giải
Chọn C .
Xét phương trình hoành độ giao điểm của đồ thị hàm số
3
yx x
với trục hoành ta có:
3
0xx
0
1
x
x
.
Vậy số giao điểm của đồ thị hàm số
3
yx x
với trục hoành là
3
.
Câu 30: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
5AC a
,
2BC a
,
3AA a
(tham khảo hình bên). Khoảng cách từ
C
đến mặt phẳng
A BC
bằng

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
2
a
. B.
3a
. C.
3
2
a
. D.
3
4
a
.
Lời giải
Chọn A .
Ta có:
BC A A
BC AB
BC A AB
.
Kẻ
AM A B
AM A BC
;
d A A BC AM
mà
;;
d C A BC d A A BC
.
Ta có:
22
AB AC BC
a
.
Xét tam giác
A AB
vuông tại
A
ta có:
22
.A A AB
AM
A A AB
22
3. 3
2
3
aa a
aa
3
;
2
a
d C A BC
.
Câu 31: Cho hàm số
(
)
y fx=
liên tục trên
và có bảng xét dấu của
( )
'fx
như sau
Số điểm cực trị của hàm số đã cho là
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn C
Hàm số có hai điểm cực trị là
2x = −
và
1x =
.
Câu 32: Giá trị nhỏ nhất của hàm số
3
31yx x=−+
trên đoạn
[ ]
0; 2
là
A.
2−
. B.
1−
. C.
1
. D.
3
.
Lời giải
Chọn B
Hàm số xác định và liên tục trên
[ ]
0; 2
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Đạo hàm
2
'3 3
yx
= −
.
Cho
( )
(
)
2
1
'0 3 30
1
nhan
x
yx
loai
x
=
=⇔ −=⇔
= −
Tính giá trị:
( )
01y
=
,
( )
23y =
và
( )
11y
= −
Vậy giá trị nhỏ nhất của hàm số là
1
−
.
Câu 33: Cho
,ab
là hai số thực dương và
a
khác
1
. Khẳng định nào sau đây đúng?
A.
( )
6
1
log log
6
a
a
ab b=
. B.
( )
6
11
log log
66
a
a
ab b
= +
.
C.
( )
6
log 6 6log
a
a
ab b= +
. D.
( )
6
11
log log
56
a
a
ab b= +
.
Chọn B
Ta có:
( )
( ) ( )
6
1 1 11
log log log log log
6 6 66
a aa a
a
ab ab a b b
= = +=+
.
Câu 34: Cho hàm số bậc ba
( )
y fx=
có đồ thị là đường cong hình bên. Số nghiệm thực của phương
trình
( )
2
fx
= −
là
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn C
Nhìn vào đồ thị ta thấy đồ thị
2y = −
cắt đồ thị
( )
y fx=
tại ba điểm phân biệt. Từ đó suy ra
phương trình có ba nghiệm.
Câu 35: Tổng tất cả các nghiệm của phương trình
2
33
28
xx x−− −
=
bằng
A.
3
. B.
23
. C.
3−
. D.
0
.
Lời giải
Chọn D
Ta có
22
33 33 3 2 2
2 8 2 2 33 3 3 3
xx x xx x
x x xx x
−− − −− −
= ⇔ = ⇔ − −=− ⇔ =⇔ =±
.
Từ đó suy ra tổng các nghiệm bằng
0
.
Câu 36: Cho khối chóp
.
S ABCD
có đáy là hình bình hành. Gọi
M
là trung điểm của
SC
. Mặt phẳng
qua
AM
và song song với
BD
chia khối chóp thành hai phần, trong đó phần chứa đỉnh
S
có
thể tích
1
V
, phần còn lại có thể tích
2
V
(tham khảo hình vẽ bên). Tính tỉ số
1
2
V
V
.
x
y
1
-3
-1
-1
O
1

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
1
2
1
V
V
=
. B.
1
2
1
2
V
V
=
. C.
1
2
1
3
V
V
=
. D.
1
2
2
7
V
V
=
.
Lời giải
Chọn B
Gọi
O
là tâm của hình bình hành của
ABCD
,
G
là trọng tâm
SAO
∆
. Qua
G
dựng
NP
song
song với
BD
. Do đó
2
3
SN SG SP
SB SO SD
= = =
.
Từ đó suy ra
1.S ANMP
VV
=
và
2.
NMP ABCD
VV=
.
Ta có
. . ..
21 1
32 3
S ANM S ABC S ABC S ABC
SN SM
V V VV
SB SC
=⋅ =⋅=
và
. . ..
21 1
32 3
S AMP S ACD S ACD S ACD
SM SP
V V VV
SC SD
=⋅ =⋅=
.
Do đó
( )
. . . .. .
11
33
S ANMP S ANM S AMP S ABC S ACD S ABCD
V V V VV V=+= + =
.
Suy ra
..
2
3
NMP ABCD S ABCD
VV=
.
Vậy
1
2
1
2
V
V
=
.
Câu 37: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh bằng
2
. Các điểm
,MN
lần lượt là trung
điểm của các cạnh
BC
và
CD
,
5SA =
và vuông góc với đáy (tham khảo hình vẽ). Khoảng
cách giữa hai đường thẳng
SN
và
DM
bằng
M
C
D
A
B
S
P
N
G
O
M
C
D
A
B
S

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
10
10
. B.
5
10
. C.
10
2
. D.
10
5
.
Lời giải
Chọn A
Gọi
E
là trung điểm của
,, ,MC I J O
lần lượt là giao điểm của
AC
với
,NE DM
và
BD
Khi đó
DM
song song với
(
)
SEN
và
NE
là đường trung bình của
DMC∆
,
J
là trọng tâm của
BDC∆
.
Vậy
(
) (
)
( )
( )
(
)
( )
(
)
1
, ,, ,
5
d SN DM d DM SEN d J SEN d A SEN= = =
.
Ta có
AN DM AN NE⊥ ⇒⊥
, gọi
K
là hình chiếu vuông góc của
A
lên
SN
, khi đó
( )
( )
,d A SEN AK=
.
Mặt khác:
222
22 2
1 1 1 2 10
5
52
AN AD DN AK
AK SA AN
= + =⇒ = + =⇒=
.
Vậy
( ) ( )
( )
1 1 10
,,
5 5 10
d SN DM d A SEN AK= = =
.
Câu 38: Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh bằng
2
. Tam giác
SAB
đều, tam giác
SCD
vuông cân tại
S
(tham khảo hình vẽ). Tính thể tích
V
của khối chóp đã cho
A.
83
3
V =
. B.
23
3
V =
. C.
23V =
. D.
43
3
V =
.
Lời giải
Chọn B
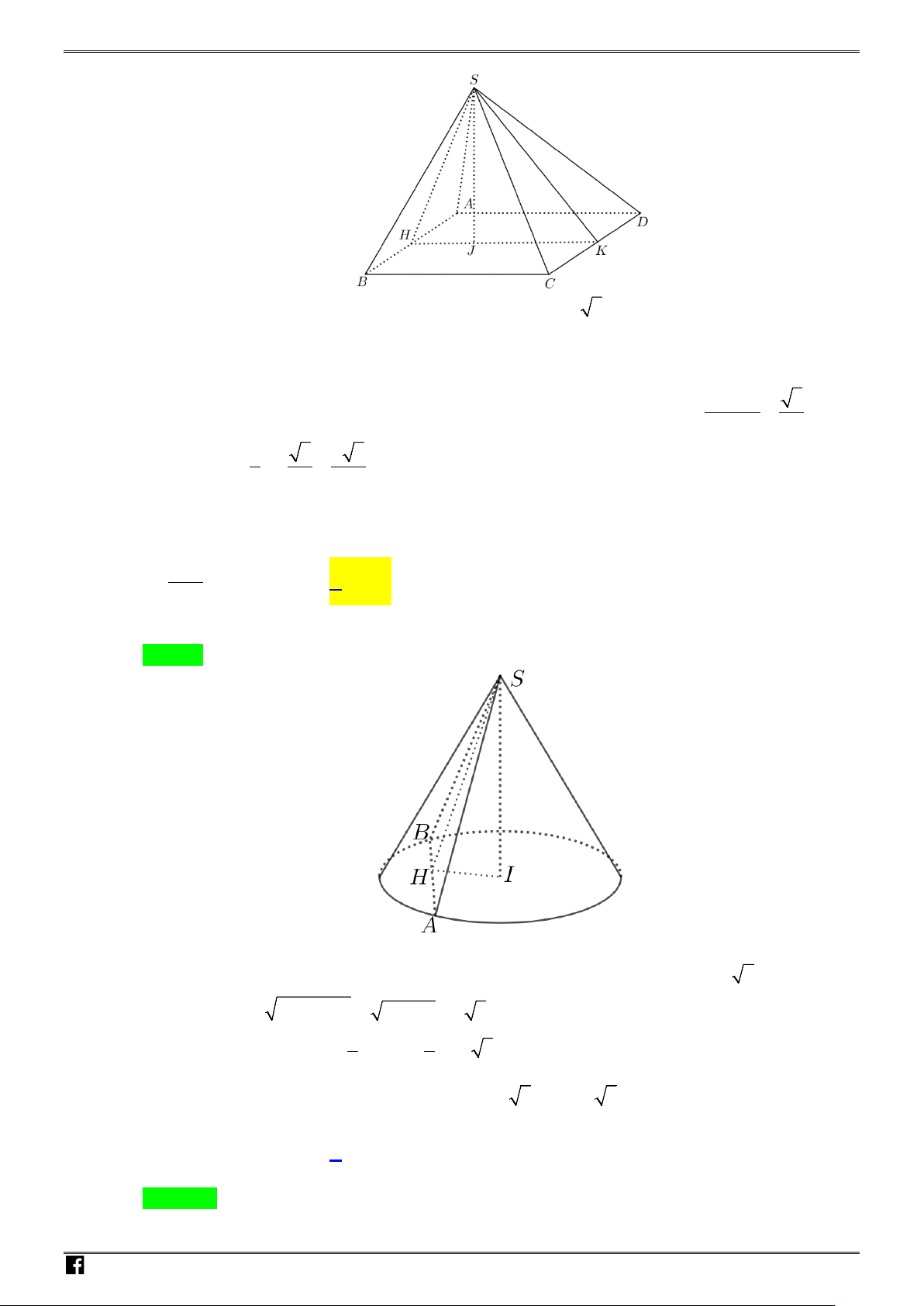
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Gọi
,HK
lần lượt là trung điểm của
,
AB CD
, ta có
3, 1SH SK= =
Khi đó
2 22
HK SH SK= +
, vậy
SHK∆
vuông tại
S
Ta có
(
)
,DCD HK C SK CD SHK⊥ ⊥⇒⊥
hay
( ) ( )
ABCD SHK⊥
.
Gọi
J
là hình chiếu vuông góc của
S
lên
HK
thì
( )
SJ ABCD⊥
và
.3
2
SH SK
SJ
HK
= =
.
Vậy
2
.
1 3 23
.2 .
32 3
S ABCD
V
= =
.
Câu 39: Cho hình nón có chiều cao bằng
4
thiết diện qua đỉnh hình nón và cắt hình nón theo một thiết
diện là tam giác vuông có diện tích bằng
32
. Thể tích của khối nón được giới hạn bởi hình nón
đã cho bằng
A.
64
3
π
. B.
64
π
. C.
32
π
. D.
192
π
.
Lời giải
Chọn B
Giả sử thiết diện là tam giác vuông cân
SAB
, chiều cao
h SI=
và bán kính
r IA=
.
Gọi
H
là trung điểm của
AB
. Do
32 . 32 4 2 8
SAB
S SH HA SH HA SA
∆
=⇔ =⇔ = = ⇒=
.
Khi đó
22
64 16 4 3r IA SA SI== − = −=
.
Vậy thể tích khối nón:
( )
2
2
11
. . . 4 3 4 64
33
V rh
ππ π
= = =
.
Câu 40: Biết rằng tập nghiệm của bất phương trình
( ) ( )
3 5 3 5 3.2
xx
x
+ +− <
là khoảng
( )
;ab
, hãy
tính
S ba= −
.
A.
4S =
. B.
2S =
. C.
1S =
. D.
3S =
.
Lời giải
Chọn B .
Chia cả hai vế cho
2
x
và có nhận xét:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
35 35 35 1
33
22 2
35
2
xx x
x
+− +
+ <⇒ + <
+
Đặt ẩn phụ
( )
35
0
2
x
tt
+
= >
2
1 35 35
3 3 10 1 1
22
t tt t x
t
−+
⇒+ < ⇔ − +< ⇔ << ⇒−< <
.
Vậy
( )
1 12S ba= − = −− =
.
Câu 41: Có bao nhiêu giá trị nguyên của tham số
[ ]
2020;2020m ∈−
để hàm số
21
3
7
9
x
xm
+
+
đồng biến trên
khoảng
( )
3; ?+∞
A.
8
. B.
2015
. C.
9
. D.
2014
.
Lời giải
Chọn A .
Ta có:
( )
21 21
33
2
7 3 21 7 7
' . .ln
9 99
3
xx
xm xm
m
yy
xm
++
++
−
= ⇒=
+
.
Để hàm số đồng biến trên khoảng
(
)
3; +∞
thì
( )
(
)
21
3
22
3 21 7 7 3 21
' . .ln 0 0 7
99
33
x
xm
mm
ym
xm xm
+
+
−−
= >⇔ <⇒ <
++
Mặc khác:
30 3xm x m
+ ≠ ⇔ ≠−
. Mà
( )
3; 3 3 1x mm∈ +∞ ⇒− ≤ ⇔ ≥−
.
Vậy
1 7.m
−≤ <
Câu 42: Cho hàm số
4ax b
y
cx b
+−
=
+
có đồ thị là đường cong trong hình bên. Mệnh để nào dưới đây đúng?
A.
0,0 4, 0a bc< << <
. B.
0, 0, 0abc>><
.
C.
0, 4, 0abc>><
. D.
0,0 4, 0a bc
> << <
.
Lời giải
Chọn D .
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên
4
00 4
b
b
b
−
>⇒<<
Tiệm cận đứng của đồ thị hàm số nằm bên phải trục tung nên
0
b
b
c
−
>⇒
và
c
trái dấu suy ra
0c <
Tiệm cận ngang của đồ thị hàm số nằm phía trục hoành nên
0
a
c
<⇒
a
và
c
trái dấu suy ra
0a >
O
y
x
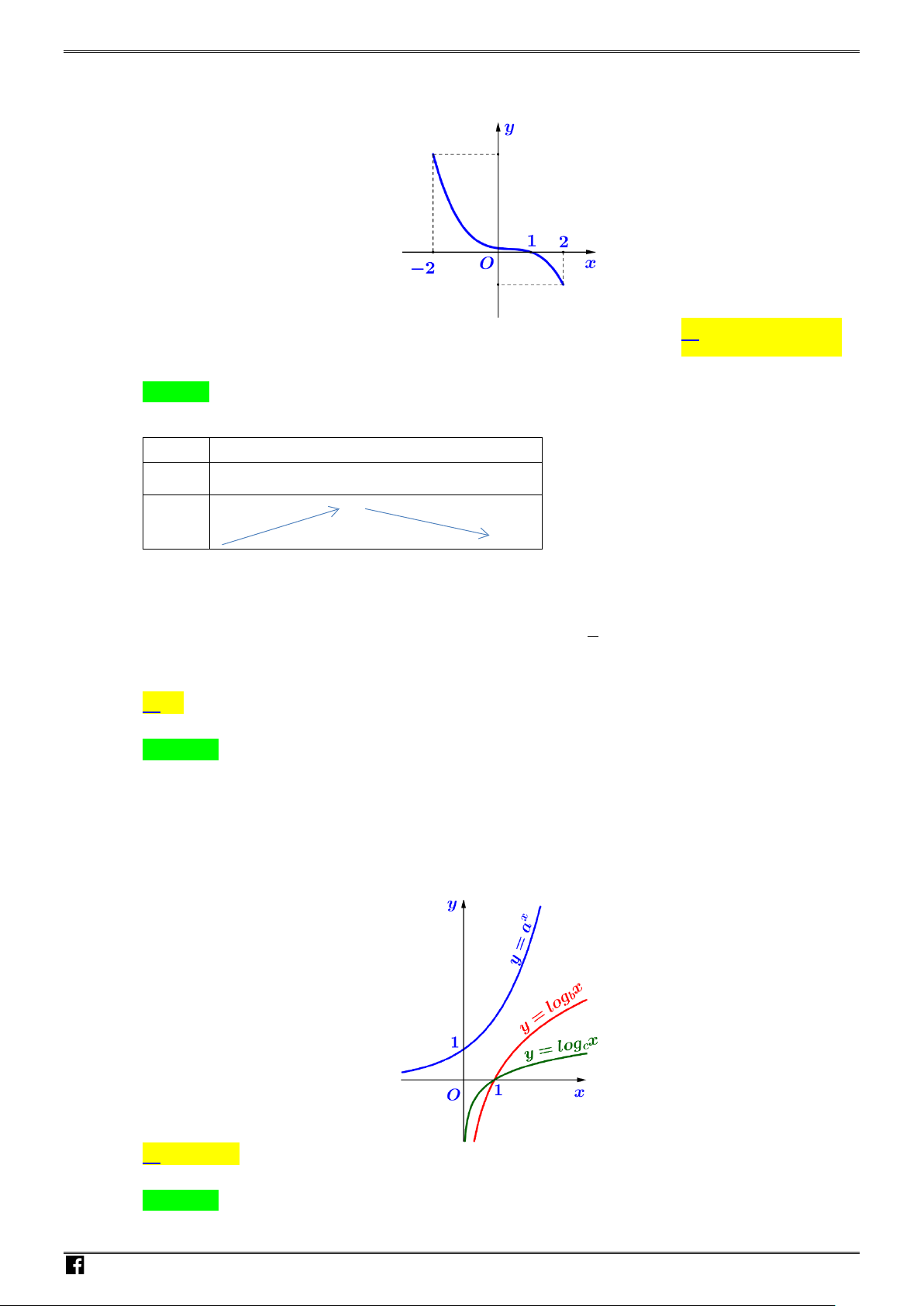
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 43: Cho hàm số
(
)
fx
có đạo hàm trên
. Đồ thị hàm số
( )
'y fx=
trên đoạn
[ ]
2; 2−
là đường cong
trong hình bên. Mệnh đề nào sau đây đúng?
A.
[ ]
( ) ( )
2;2
max 2fx f
−
= −
. B.
[ ]
( )
( )
2;2
max 2fx f
−
=
. C.
[ ]
( ) ( )
2;2
min 1fx f
−
=
. D.
[ ]
( ) ( )
2;2
max 1fx f
−
=
.
Lời giải
Chọn D
Dựa vào đồ hị hàm số
( )
'y fx
=
ta có bảng biến thiên.
x
2−
1
2
( )
'fx
+
0
−
( )
fx
[ ]
( ) ( )
2;2
max 1fx f
−
⇒=
.
Câu 44: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
32
1
16 10
3
y x mx x
= − ++
đồng biến trên
khoảng
(
)
;−∞ +∞
A.
9
. B.
10
. C.
8
. D.
7
.
Lời giải
Chọn A .
Ta có
2
' 2 16y x mx=−+
.
Hàm số đồng biến trên
( )
2
; '0, '0 160y xR m−∞ +∞ ⇔ ≥ ∀ ∈ ⇔ ∆ ≤ ⇔ − ≤
44m⇔− ≤ ≤
. Vậy có 9 giá trị nguyên của tham số
m
.
Câu 45: Cho
,,abc
là ba số thực dương và khác 1. Đồ thị các hàm số
, log , log
x
bc
y a y xy x= = =
được
cho trong hình bên. Mệnh đề nào sau đây đúng?
A.
bac<<
. B.
abc<<
. C.
bca<<
. D.
cba<<
.
Lời giải
Chọn A.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 23
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vẽ đồ thị hàm số
log
a
yx=
đối xứng với đồ thị
x
ya=
qua đường thẳng
.yx=
Kẻ đường thẳng
1y
=
cắt đồ thị
log
b
yx=
tại điểm có hoành độ
1
xb=
và cắt đồ thị
log
a
yx=
tại điểm có hoành độ
2
,xa=
đồ thị hàm số
log
c
yx=
tại điểm có hoành độ
3
xc
=
.
Dựa vào đồ thị ta thấy
123
x x x bac
< < ⇔<<
.
Câu 46: Có bao nhiêu giá trị nguyên dương của tham số
m
đề hàm số
32
9 ( 8)y x x m xm=− ++ −
có
năm điểm cực trị?
A.
13
. B.
15
. C.
14
. D. Vô số.
Lời giải
Chọn C
Để hàm số có 5 cực trị thì phương trình
( )
32
9 ( 8) 0, 1x x m xm− + + −=
có 3 nghiệm phân biệt.
Ta có
( )
32 2
2
1
9 ( 8) 0 ( 1) 8 0
8 0. (2)
x
x x m xm x x xm
x xm
=
− + + −=⇔ − − + =⇔
− +=
.
Để (1) có 3 nghiệm phân biệt thì (2) có 2 nghiệm khác 1
0 64 4 0 16
18 0 7 7
mm
mm m
∆> − > <
⇔ ⇔⇔
−+ ≠ ≠
≠
.
Vây có 14 giá tri nguyên dương thỏa yêu cầu.
Câu 47: Cho hàm số bậc năm
( )
fx
. Hàm số
( )
y fx
′
=
có đồ thị là đường cong trong hình bên.
Hàm số
( ) ( ) ( )
2
72 1gx f x x= − +−
đồng biến trên khoảng nào dưới đây?
A.
( )
2;0−
. B.
( )
3; 1−−
. C.
( )
3; +∞
. D.
( )
2;3
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 24
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn D
Ta có
(
)
( )
( )
2
72 1
gx f x x= − +−
( ) ( ) ( )
2 72 2 1gx f x x
′′
⇒ =− −+−
.
Hàm số
( ) ( ) ( )
2
72 1gx f x x
= − +−
đồng biến khi và chỉ khi
( ) ( ) ( ) ( )
0 2 72 2 1 0 72 1gx fxx fxx
′′ ′
≥⇔− − + − ≥⇔ − ≤−
(1).
Đặt
75
72 1 1
22
tt
t xx
−−
= − ⇒ −= −=
. Suy ra
( )
( )
15
1:
22
ft t
′
≤− +
.
Từ đồ thị suy ra
3 1 372 1 4 5
1 3 172 3 2 3
t xx
t xx
− ≤ ≤− − ≤ − ≤− ≤ ≤
⇔⇔
≤≤ ≤ − ≤ ≤ ≤
.
Câu 48: Cho bất phương trình
2
2
2
22
22
2
10
33
3
x xm
x xm
− −+
− +−
+>
, với
m
là tham số thực. Có bao nhiêu giá tri
nguyên của
m
để bất phương trình đã cho nghiệm đúng với mọi
[0; 2]?x∈
A.
9
. B.
10
. C.
11
. D.
15
.
Lời giải
Chọn D
Điều kiện
2
2
20
2 20
x xm
x xm
− +≥
− + −≠
Ta có
2
2
2
22
22
2
10
33
3
x xm
x xm
− −+
− +−
+>
2
2
2
22
22
2
10
33
3
x xm
x xm
− +−
−
− +−
⇔ +>
2
2
2
22
22
2
1 10
3
3
3
x xm
x xm
− +−
− +−
⇔ +>
.
Đặt
2
2
22 2 1
2
22
x xm
t
t
x xm
− +−
=⇒=
− +−
. Điều kiện
0t ≠
.
Ta được bất phương trình
( )
11
10 1 10
33 3 2
33 3
t
t
tt
−
+> ⇔ +>
.
Xét hàm số
( ) ( )
11
2
1 11 1
3 .ln 3 .ln 3. 0, 0
3 33
tt
tt
ft f t t
t
−
′
= + ⇒ = + < ∀≠
Hàm số
( )
1
1
3
3
t
t
ft
= +
nghịch biến trên mỗi khoảng
( )
;0−∞
và
(
)
0; +∞
.
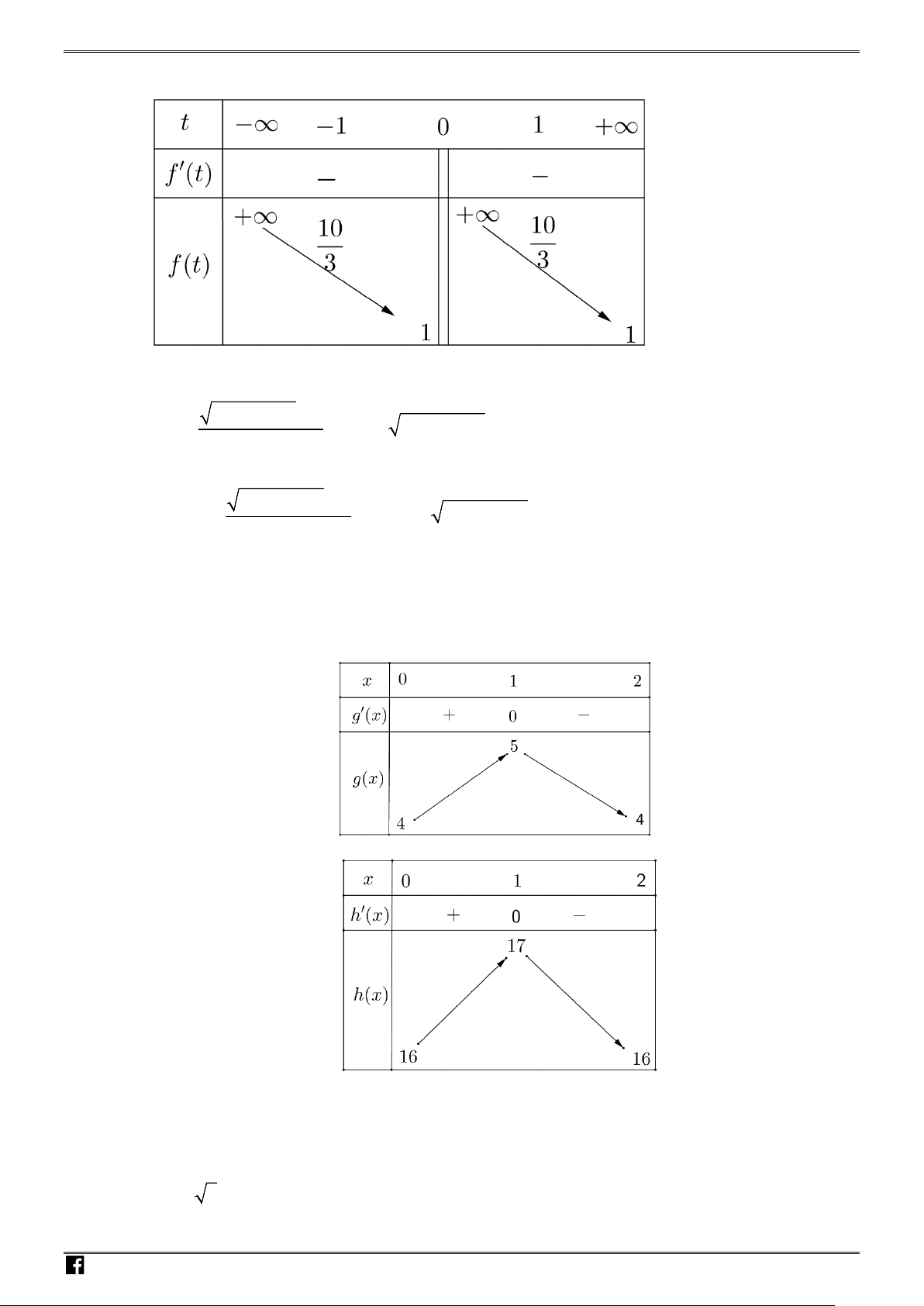
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 25
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Bảng biến thiên
+) Với
0t
<
ta có
(
) (
) (
)
2 11
ft f t
⇔ > ⇔ <−
.
Suy ra
2
2
22
1 20
2
x xm
x xm
− +−
<− ⇔ − + <
(vô nghiệm)
+) Với
0t >
ta có
( )
(
) ( )
2 10 1ft f t⇔ > ⇔ <<
.
Suy ra
2
22
22
0 1 2 2 4 4 2 16
2
x xm
x xm x xm
− +−
< <⇔< − + <⇔< − + <
.
Yêu cầu bài toán
[ ] [ ]
22
22
2 4 24
, 0; 2 , 0; 2
2 16 2 16
x xm m x x
xx
x xm m x x
− + > >− + +
⇔ ∀∈ ⇔ ∀∈
− + < <− + +
.
Xét hàm số
( ) ( )
22
2 4; 2 16gx xxhxxx=−+ + =−+ +
với mọi
[ ]
0; 2x
∈
.
Bảng biến thiên
Từ đó suy ra
5 16m<<
, vì
m
nguyên nên
{ }
6;7;8;...;15m∈
.
Vậy có 10 giá trị nguyên của tham số
m
thỏa mãn.
Câu 49: Cho khối hộp
.ABCD A B C D
′′′′
có
22AA AB AD
′
= =
,
0
90BAD =
,
0
60BAA
′
=
,
0
120DAA
′
=
,
6AC
′
=
. Tính thể tích
V
của khối hộp đã cho.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 26
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2V =
. B.
23V =
. C.
2
2
V =
. D.
22
V
=
.
Lời giải
Chọn A
Đặt
(
)
,0x AB AD x= = >
thì
2AA x
′
=
. Áp dụng định lý côsin trong tam giác
ABA
′
, ta có
2 2 2 02 2 2
1
2 . .cos60 4 2. .2 . 3
2
A B AB AA AB AA x x x x x
′ ′′
= + − =+− =
.
Suy ra
22 2
AA AB A B
′′
= +
. Do đó tam giác
ABA
′
vuông tại
B
hay
AB BA
′
⊥
.
Mà
AB BC⊥
(do
AB AD⊥
) nên
( )
AB BCD A
′′
⊥
. Vì vậy,
..
2 2.3 2 .
ABA DCD A A BC A BC
V V V AB S
′′ ′ ′
= = =
.
Mặt khác,
( )
2
22
1
..
2
A BC
S BC BA BC BA
′
′′
= −
mà
( )
02
. . . . .2 .cos120 0BC BA AD AA AB AD AA AD AB x x x
′′ ′
= − = − = −=−
nên
( )
2
2
22 2
12
.3
22
A BC
x
S xx x
′
= −− =
.
Do đó,
2
3
2
2. 2
2
x
Vx x
= =
.
Theo quy tắc hình hộp,
AC AB AD AA
′′
=++
. Suy ra
( )
2222
2. . .
AC AB AD AA AB AD AD AA AA AB
′ ′ ′′
=+++ + +
.
22 2
11
6 4 20 .2. 2.. 1
22
x x x x x xx x
⇒= + + + − + ⇒=
.
Vậy thể tích của khối hộp đã cho là
2V =
.
Câu 50: Cho hàm số
( )
32
3y fx x x= = −
có đồ thị là đường cong trong hình bên dưới. Phương trình
( )
( )
( ) ( )
2
4
4
21
f fx
f x fx
−
= −
++
có bao nhiêu nghiệm ?
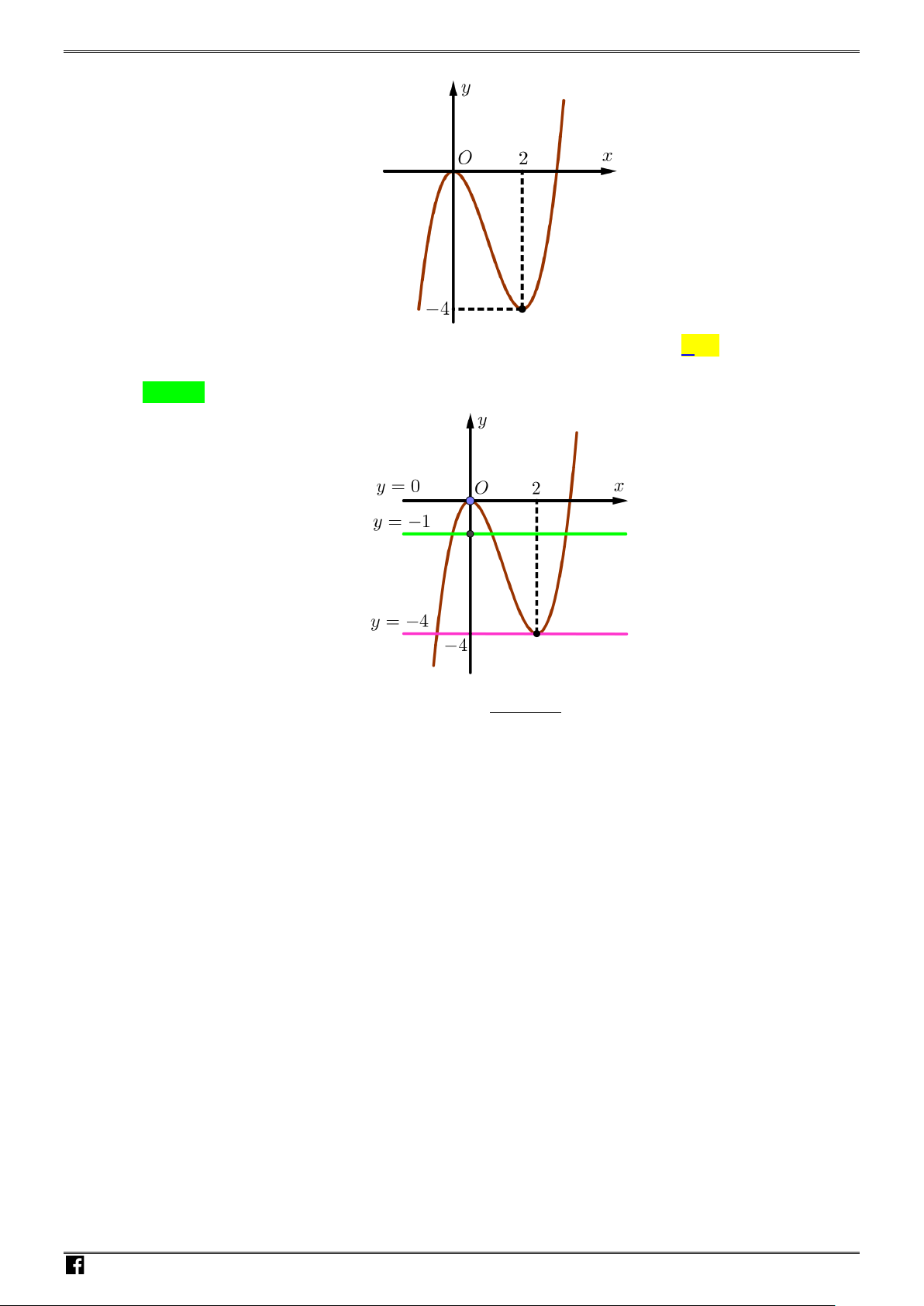
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 27
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
4
. B.
6
. C.
3
. D.
7
.
Lời giải
Chọn D
Đặt
( )
fx t=
. Phương trình đã cho trở thành
( )
2
4
4
21
ft
tt
−
= −
++
( )
32 2
3 4 42 1t t tt⇔ − − =− ++
(do
2
2 1 0,tt t++≠ ∀
)
32
0
5 40 1
4
t
ttt t
t
=
⇔+ +=⇔=−
= −
.
Do đó, phương trình đã cho tương đương với
( ) ( )
( ) (
)
( ) ( )
01
12
43
fx
fx
fx
=
= −
= −
.
Dựa vào đồ thị của hàm số
( )
y fx=
, ta có số nghiệm của các phương trình
( ) ( ) ( )
1,2,3
lần lượt
là
2, 3, 2
và các nghiệm đó không trùng nhau. Vậy số nghiệm của phương trình đã cho là
2327
++=
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
TRƯỜNG THPT LOMONOXỐP
ĐỀ THI HỌC KÌ I - NĂM HỌC 2020 - 2021
Môn: TOÁN – LỚP 12
Thời gian: 90 phút (Không kể thời gian phát đề)
Câu 1: Cho hàm số
( )
fx
liên tục trên
và có bảng biến thiên như sau:
Giá trị cực đại của hàm số là
A.
26−
. B.
6
. C.
3
. D.
1−
.
Câu 2: Cho hàm số
( )
42
2 2020fx x x=−+
. Khẳng định nào dưới đây sai?
A. Hàm số đồng biến trên khoảng
( )
;1−∞ −
.
B. Hàm số đồng biến trên khoảng
( )
1;+∞
.
C. Hàm số có ba điểm cực trị.
D. Đồ thị hàm số luôn nằm phía trên trục hoành.
Câu 3: Đồ thị hình bên dưới là của hàm số nào?
A.
42
21yx x=+−
. B.
42
21yx x=−+ −
. C.
42
21yx x=−−
. D.
42
21yx x=−+ +
.
Câu 4: Một khối chóp có thể tích bằng
3
1000cm
và diện tích đáy bằng
3
100cm
. Chiều cao của khối
chóp đó bằng
A.
25cm
. B.
15cm
. C.
20cm
. D.
30cm
.
Câu 5: Cho
5
ln 2, log 8ab= =
. Khẳng định nào sau đây đúng?
A.
36
ln 200
a ab
b
+
=
. B.
63
ln 200
a ab
b
+
=
.
C.
6
ln 200
3
a ab
b
+
=
. D.
3
ln 200
6
a ab
b
+
=
.
Câu 6: Phép vị tự tỉ số
3k =
biến khối lăng trụ có thể tích
V
thành khối lăng trụ có thể tích bằng
A.
27V
. B.
3V
. C.
12V
. D.
9V
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 7: Tính đạo hàm của hàm số
3
x
y =
?
A.
1
.3
x
yx
−
′
=
. B.
3
ln 3
x
y
′
=
. C.
3 ln 3
x
y
′
=
. D.
3 ln 3
x
y
x
′
=
.
Câu 8: Phương trình
29
28
x−
=
có nghiệm là:
A.
2
x =
. B.
8x =
. C.
4
x
=
. D.
6x =
.
Câu 9: Thể tích khối lăng trụ có diện tích đáy là
S
, chiều cao
h
là:
A.
1
.
2
Sh
. B.
3
Sh
. C.
1
3
Sh
. D.
Sh
.
Câu 10: Một khối cầu có thể tích bằng
288
π
.Tính diện tích của mặt cầu có cùng bán kính?
A.
144
π
. B.
216
π
. C.
180
π
. D.
108
π
.
Câu 11: Có bao nhiêu giá trị nguyên của tham số m để phương trình
3
3 10xx m−+=
có đúng
ba nghiệm phân biệt?
A.
2
. B.
1
. C.
3
. D.
5
.
Câu 12: Một khối trụ có chiều cao bằng
h
,bán kính đáy bằng
R
thì có thể tích bằng
A.
3
hR
π
. B.
3
1
3
hR
π
. C.
2
hR
π
. D.
2
1
3
hR
π
.
Câu 13: Cho số thực a thỏa mãn điều kiện
( ) ( )
21
53
22aa
−−
− <−
. Mệnh đề nào sau đúng?
A.
23a<<
. B.
1a >
. C.
01a<<
. D.
3a >
.
Câu 14: Gọi
12
,xx
là nghiệm của phương trình
21
3 7.3 2 0
xx+
− +=
. Tính tích
12
?
xx
A.
12 3
log 2
xx = −
. B.
12
7
3
xx
=
. C.
12 2
log 3
xx =
. D.
12
2
3
xx
=
.
Câu 15: Phương trình
( )
3
log 2 1 2x +=
có nghiệm là
A.
4
x =
. B.
6x =
. C.
2x =
. D.
8x =
.
Câu 16: Cho hàm số
3
2
2
23
33
x
y xx= − ++
. Tọa độ điểm cực tiểu của đồ thị hàm số là
A.
( )
1; 2
. B.
2
3;
3
. C.
( )
2;1
. D.
2
;3
3
.
Câu 17: Trong không gian, một tam giác đều có bao nhiêu mặt phẳng đối xứng?
A. 1. B. 2. C. 3. D. 4.
Câu 18: Hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
14
, cạnh bên bằng
2 14
. Bán kính của
mặt cầu ngoại tiếp hình chóp đó bằng:
A. 2. B. 6. C. 4. D. 8.
Câu 19: Cho hàm số có bảng biến thiên như hình sau

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại
3x =
.
B. Hàm số nghịch biến trên
( )
1;1−
.
C. Đồ thị hàm số có hai đường tiệm cận.
D. Hàm số có giá trị nhỏ nhất bằng
2
.
Câu 20: Đồ thị hàm số
3
1
x
y
x
=
+
có bao nhiêu đường tiệm cận?
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 21: Trong các hàm số sau, hàm số nào nghịch biến trên
?
A.
2
3
x
y
−
=
. B.
1
2
log
yx=
. C.
5
x
y =
. D.
3
x
e
y
=
.
Câu 22: Một hình trụ có diện tích xung quanh bằng
30π
, bán kính đáy bằng
3
. Tính chiều cao h của
hình trụ?
A.
10h
=
. B.
10
3
h =
. C.
5
3
h =
. D.
5h =
.
Câu 23: Hệ số góc của tiếp tuyến với đồ thị hàm số
y ln x=
tại điểm
( )
10M;
bằng
A.
0
. B.
2−
. C.
1−
. D.
1
.
Câu 24: Phương trình
( )
3
2 1 54log x x+=−
có tất cả bao nhiêu nghiệm?
A.
1
nghiệm. B.
3
nghiệm. C.
2
nghiệm. D. vô nghiệm.
Câu 25: Đồ thị sau là của hàm số nào?
A.
= −
32
3yx x
. B.
= +
3
3yx x
. C.
= +
32
3yx x
. D.
= −
3
3yx x
.
Câu 26: Với phương trình
21
5 16.5 3 0
xx+
− +=
, nếu đặt
5
x
t =
ta được phương trình nào dưới đây?
A.
− +=
2
5 16 3 0tt
. B.
− +=
2
16
5 30
5
tt
. C.
− +=
2
16
30
5
tt
. D.
− +=
2
16 3 0tt
.
Câu 27: Biết thể tích khối lăng trụ
.'' 'ABC A B C
bằng 30. Tính thể tích
V
của khối chóp
'.A ABC
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
15V =
. B.
20V =
. C.
10V =
. D.
5
V
=
.
Câu 28: Cho hàm số
( )
y fx=
liên tục trên
và có đồ thị như hình vẽ. Khoảng nghịch biến của
hàm số là:
A.
( )
4;0−
B.
( )
0; 2
C.
( )
;3−∞
D.
( )
3; +∞
Lời giải
Câu 29: Tổng các giá trị của tham số
m
sao cho đường thẳng
6
y xm= +
tiếp xúc với đồ thị hàm số
3
32yx x=++
bằng:
A.
4
B.
8−
C.
4−
D.
8
Lời giải
Câu 30: Điểm
M
thuộc mặt cầu tâm
,I
bán kính
R
khi và chỉ khi
A.
2IM R
=
B.
IM R=
C.
IM R>
D.
IM R<
Lời giải
Câu 31: Hàm số nào sau đây có đồ thị như hình bên?
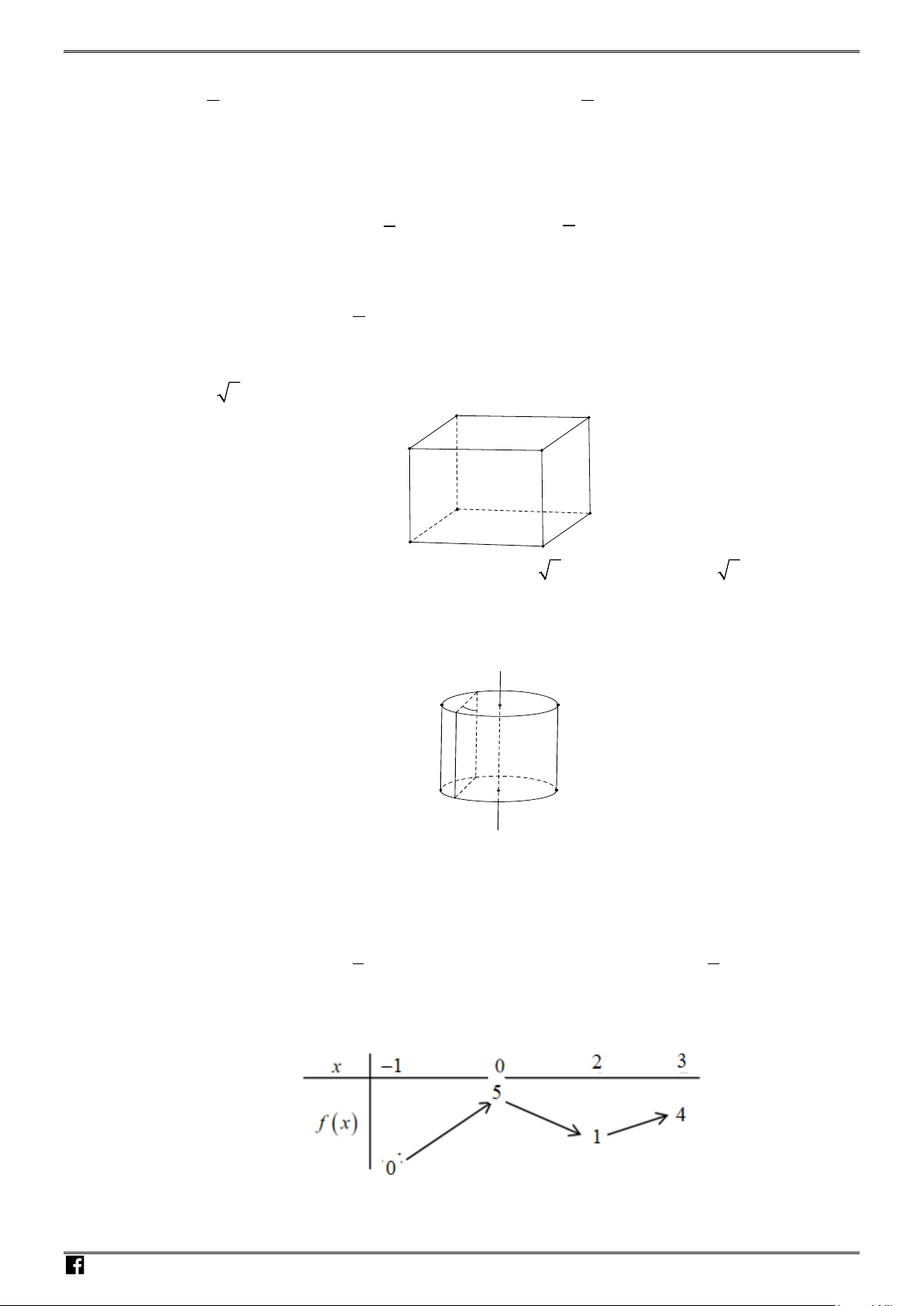
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
1
2
x
y
=
. B.
2
x
y = −
. C.
1
2
x
y
= −
. D.
2
x
y =
.
Câu 32: Tính thể tích
V
của khối chóp
.S ABC
có
SA a=
và
( )
SA ABC
⊥
, biết
ABC
là tam giác
vuông cân tại
B
,
3AB a=
.
A.
3
9Va=
. B.
3
9
2
Va=
. C.
3
3
2
Va=
. D.
3
3
Va
=
.
Câu 33: Tổng các giá trị nghiệm của phương trình
2
22
log 3log 2 0xx− +=
bằng
A.
2
. B.
3
2
. C.
3
. D.
6
.
Câu 34: Cho hình hộp chữ nhật có đáy là hình vuông, cạnh bên bằng
a
và diện tích xung quanh
bằng
2
42a
. Tính thể tích khối hộp theo
a
.
A.
3
3a
. B.
3
2a
. C.
3
32
a
. D.
3
22a
.
Câu 35: Một hình trụ có đường cao
25cm
và bán kính đáy bằng
10cm
. Mặt phẳng
(
)
P
song song và
cách trục của hình trụ
8cm
. Diện tích thiết diện của hình trụ cắt bởi mặt phẳng
( )
P
bằng
A.
2
300 cm
. B.
2
200 cm
. C.
2
150 cm
. D.
2
250 cm
.
Câu 36: Cho khối chóp
.S ABC
có thể tích bằng
16
. Gọi
,,MNP
lần lượt là trung điểm của các cạnh
,,SA SB SC
. Thể tích khối chóp
.S MNP
bằng
A.
2
. B.
1
8
. C.
8
. D.
1
2
.
Câu 37: Hàm số
y fx
liên tục trên
1; 3
và có bảng biến thiên sau:
Giá trị nhỏ nhất của hàm số trên đoạn
1; 3
là:
P

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
4
. B.
0
. C.
1
. D.
1
.
Câu 38: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, tam giác
SAB
cân tại
S
và
nằm trong mặt phẳng vuông góc với đáy,
2SA a
. Tính theo
a
thể tích
V
của khối chóp
.
S ABCD
.
A.
3
15
12
a
. B.
3
15
6
a
. C.
3
2a
. D.
3
2
3
a
.
Câu 39: Cho là các số dương khác. Khẳng định nào sau đây là sai?
A.
1
log
log
a
b
b
a
. B.
log .log log
ab a
bc c
.
C.
log log
c
aa
bc b
. D.
log log .log
a aa
bc b c
.
Câu 40: Phép đối xứng qua mặt phẳng
( )
P
biến đường thẳng d thành chính nó khi và chỉ khi
A.
d
song song với
( )
P
.
B.
d
nằm trên
(
)
P
hoặc
d
vuông góc với
( )
P
.
C.
d
vuông góc
( )
P
.
D.
d
nằm trên
(
)
P
.
Câu 41: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
21
1
x
fx
x
+
=
−
trên đoạn
[
]
2; 4 .
Khi đó
Mm−
bằng
A.
4
. B.
2−
. C.
8
. D.
2
.
Câu 42: Hình nào sau đây không có mặt cầu ngoại tiếp?
A. Lăng trụ xiên. B. Hình hộp chữ nhật. C. Hình chóp đều. D. Hình lập phương.
Câu 43: Cho hình chóp đều
.S ABC
có đáy là tam giác đều cạnh
6cm
, góc giữa mặt bên và mặt đáy
là
0
45
. Thể tích
V
của khối chóp
.S ABC
là
A.
3
12
cm
. B.
3
36
cm
. C.
3
9cm
. D.
3
27
cm
.
Câu 44: Gọi
P
là tích tất cả các nghiệm của phương trình
( )
(
)
22
75
log 3 2 log 3xx xx− += −
. Tính
giá trị của
P
.
A. 3. B.
5−
. C.
33
. D.
23−
.
Câu 45: Với
,,abx
là các số dương thỏa mãn
222
log 3log 5logxab= +
. Mệnh đề nào sau đây đúng
A.
12
35
x ab=
. B.
35
x ab=
. C.
35xab= +
. D.
35
xa b= +
.
Câu 46: Hình bát diện đều có tất cả bao nhiêu cạnh?
A. 20. B. 12. C. 14. D. 8.
Câu 47: Cho hàm số
( )
y fx=
liên tục trên
và có bảng biến thiên như sau:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Số nghiệm của phương trình
( )
2020 2021 0fx
+=
là
A. 3. B. 0. C. 1. D. 2.
Câu 48: Đồ thị sau là của hàm số nào?
A.
23
1
x
y
x
+
=
−
. B.
2
1
x
y
x
+
=
+
. C.
1
1
x
y
x
−
=
+
. D.
21
1
x
y
x
+
=
+
.
Câu 49: Thiết diện qua trục của một hình trụ là hình vuông cạnh bằng 4. Tính thể tích
V
của khối
trụ?
A.
24V
π
=
. B.
64V
π
=
. C.
16V
π
=
. D.
4
V
π
=
.
Câu 50: Cho số thực dương
1a ≠
thỏa mãn
2
5
m
n
aa=
. Tính
m
n
=
?
A.
2
5
. B.
5
. C.
5
2
. D.
2
.
----------HẾT----------
HƯỚNG DẪN GIẢI CHI TIẾT
ĐỀ THI HỌC KÌ I - NĂM HỌC 2020 - 2021
Câu 1: Cho hàm số
(
)
fx
liên tục trên
và có bảng biến thiên như sau:
Giá trị cực đại của hàm số là
A.
26−
. B.
6
. C.
3
. D.
1−
.
x
– ∞
-1
3
+ ∞
y'
–
0
+
0
–
y
+ ∞
0
5
– ∞

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn B
Dựa vào bảng biến thiên ta thấy
6
CÐ
y =
.
Câu 2: Cho hàm số
( )
42
2 2020fx x x=−+
. Khẳng định nào dưới đây sai?
A. Hàm số đồng biến trên khoảng
( )
;1−∞ −
.
B. Hàm số đồng biến trên khoảng
( )
1;+∞
.
C. Hàm số có ba điểm cực trị.
D. Đồ thị hàm số luôn nằm phía trên trục hoành.
Lời giải
Chọn A
Tập xác định
D
=
.
33
1 2019
4 4 ; 0 4 4 0 1 2019
0 2020
xy
yxxy xx x y
xy
=⇒=
′′
= − = ⇔ − = ⇔ =−⇒ =
=⇒=
.
Bảng biến thiên
Hàm số nghịch biến trên
( )
;1
−∞ −
nên phương án A sai.
Câu 3: Đồ thị hình bên dưới là của hàm số nào?
A.
42
21yx x=+−
. B.
42
21yx x=−+ −
. C.
42
21yx x=−−
. D.
42
21yx x=−+ +
.
Lời giải
Chọn B
Đây là dạng đồ thị của hàm trùng phương, khi
x → ±∞
,
y → +∞
nên
0a >
. Loại phương
án B, D.
Đồ thị hàm số có 3 điểm cực trị nên
.0ab<
mà
00ab>⇒<
. Loại phương án A, chọn
phương án C.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 4: Một khối chóp có thể tích bằng
3
1000
cm
và diện tích đáy bằng
3
100
cm
. Chiều cao của khối
chóp đó bằng
A.
25cm
. B.
15cm
. C.
20cm
. D.
30
cm
.
Lời giải
Chọn D
Ta có thể tích khối chóp
1 3 3000
. 30
3 100
V
V S h h cm
S
= ⇒= = =
.
Câu 5: Cho
5
ln 2, log 8ab= =
. Khẳng định nào sau đây đúng?
A.
36
ln 200
a ab
b
+
=
. B.
63
ln 200
a ab
b
+
=
.
C.
6
ln 200
3
a ab
b
+
=
. D.
3
ln 200
6
a ab
b
+
=
.
Lời giải
Chọn B
Ta có
5
ln 8 2 2
log 8 ln 5
ln 5 ln 5
aa
b
b
= = =⇒=
.
Vậy
(
)
32
6 63
ln 200 ln 2 .5 3ln 2 2ln 5 3
a a ab
a
bb
+
= = + =+=
.
Câu 6: Phép vị tự tỉ số
3k =
biến khối lăng trụ có thể tích
V
thành khối lăng trụ có thể tích bằng
A.
27V
. B.
3V
. C.
12V
. D.
9V
.
Lời giải
Chọn A
Phép vị tự tỉ số
3k =
biến khối lăng trụ thành khối lăng trụ đồng dạng với nó và có thể
tích bằng
3
3 27VV=
.
Câu 7: Tính đạo hàm của hàm số
3
x
y =
?
A.
1
.3
x
yx
−
′
=
. B.
3
ln 3
x
y
′
=
. C.
3 ln 3
x
y
′
=
. D.
3 ln 3
x
y
x
′
=
.
Lời giải
Chọn D.
Ta có
3 3 ln 3
xx
yy
′
=⇒=
.
Câu 8: Phương trình
29
28
x−
=
có nghiệm là:
A.
2x =
. B.
8x =
. C.
4x =
. D.
6x =
.
Lời giải
Chọn D.
Ta có
29 29 3
2 8 2 2 2 93 6
xx
xx
−−
=⇔ = ⇔ −=⇔=
.
Câu 9: Thể tích khối lăng trụ có diện tích đáy là
S
, chiều cao
h
là:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
1
.
2
Sh
. B.
3Sh
. C.
1
3
Sh
. D.
Sh
.
Lời giải
Chọn D.
Câu 10: Một khối cầu có thể tích bằng
288
π
.Tính diện tích của mặt cầu có cùng bán kính?
A.
144
π
. B.
216
π
. C.
180
π
. D.
108
π
.
Lời giải.
Chọn A.
Ta có:
3
4
288
3
C
VR
ππ
= =
6R⇒=
.
Vậy
2
4 144 .
C
SR
ππ
= =
Câu 11: Có bao nhiêu giá trị nguyên của tham số m để phương trình
3
3 10xx m−+=
có đúng
ba nghiệm phân biệt?
A.
2
. B.
1
. C.
3
. D.
5
.
Lời giải
Chọn C.
Ta có
( )
3
3 10xx m−+=∗
Đặt
3
3 10
yx x=−+
,
2
3 30yx
′
= −=
1, 12.
1, 8.
xy
xy
=−=
⇔
= =
Ta có BBT sau:
Căn cứ vào BBT để
( )
∗
có ba nghiệm phân biệt
⇔
8 12m<<
.
Mà
mZ∈
nên
9,10,11m =
. Vậy có ba giá trị nguyên của
m
thỏa mãn ycbt.
Câu 12: Một khối trụ có chiều cao bằng
h
,bán kính đáy bằng
R
thì có thể tích bằng
A.
3
hR
π
. B.
3
1
3
hR
π
. C.
2
hR
π
. D.
2
1
3
hR
π
.
Lời giải.
Chọn C.
Câu 13: Cho số thực a thỏa mãn điều kiện
( ) ( )
21
53
22aa
−−
− <−
. Mệnh đề nào sau đúng?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
23a<<
. B.
1a
>
. C.
01a<<
. D.
3a >
.
Lời giải
Chọn D.
Ta có:
(
) ( )
21
53
22aa
−−
− <−
, mà
21
53
−−
<
21 3aa⇒ −>⇔ >
.
Câu 14: Gọi
12
,xx
là nghiệm của phương trình
21
3 7.3 2 0
xx+
− +=
. Tính tích
12
?xx
A.
12 3
log 2
xx = −
. B.
12
7
3
xx =
. C.
12 2
log 3xx =
. D.
12
2
3
xx =
.
Lời giải
Chọn A.
21
3 7.3 2 0
xx+
− +=
( )
2
3. 3 7.3 2 0
xx
⇔ − +=
3
32
log 2
1
1
3
3
x
x
x
x
=
=
⇔⇔
= −
=
.
Do đó
12 3
log 2.xx = −
Câu 15: Phương trình
( )
3
log 2 1 2
x
+=
có nghiệm là
A.
4x =
. B.
6x =
. C.
2
x
=
. D.
8x =
.
Lời giải
Chọn A.
Điều kiện:
1
2
x
−
>
.
( )
3
log 2 1 2
x +=
2 19x⇔ +=
(
)
4x tm⇔=
.
Vậy phương trình có nghiệm
4.x =
Câu 16: Cho hàm số
3
2
2
23
33
x
y xx
=− ++
. Tọa độ điểm cực tiểu của đồ thị hàm số là
A.
( )
1; 2
. B.
2
3;
3
. C.
( )
2;1
. D.
2
;3
3
.
Lời giải
Chọn B

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
3
2
2
2
23
33
3
' 4 30
1
x
y xx
x
yx x
x
=− ++
=
= − +=⇔
=
'' 2 4yx= −
(
)
'' 3 2 0y
=>⇒
Hàm số đạt cực tiểu tại
3
x
=
.
3
2
3 22
3 2.(3) 3.3
3 33
CT CT
xy=⇒ = − + +=
.
Vậy tọa độ điểm cực tiểu của đồ thị hàm số là
2
3;
3
.
Câu 17: Trong không gian, một tam giác đều có bao nhiêu mặt phẳng đối xứng?
A. 1. B. 2. C. 3. D.
4.
Lời giải
Chọn D
Trong không gian, với tam giác đều bất kì ABC có bốn mặt phẳng đối xứng. Đó là ba mặt
phẳng trung trực của ba cạnh và mặt phẳng chứa
ABC∆
.
Câu 18: Hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
14
, cạnh bên bằng
2 14
. Bán kính của
mặt cầu ngoại tiếp hình chóp đó bằng:
A. 2. B. 6. C. 4. D.
8.
Lời giải
Chọn C
Gọi H là tâm hình vuông ABCD
(
)
SH ABCD
⇔⊥
.
( )
22
2
2
14. 2
7
22
7
2 14
4
2. 2.7
AC
AH
SH SA AH
SA
R
SH
= = =
= −=
= = =
Câu 19: Cho hàm số có bảng biến thiên như hình sau

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại
3
x =
.
B. Hàm số nghịch biến trên
( )
1;1−
.
C. Đồ thị hàm số có hai đường tiệm cận.
D. Hàm số có giá trị nhỏ nhất bằng
2
.
Lời giải
Chọn C.
lim 2 2
x
yy
→−∞
=⇒=
là tiệm cận ngang của đồ thị hàm số.
0
lim 0
x
yx
−
→
= −∞ ⇒ =
là tiệm cận đứng của đồ thị hàm số.
Câu 20: Đồ thị hàm số
3
1
x
y
x
=
+
có bao nhiêu đường tiệm cận?
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Chọn A.
lim 3 3
x
yy
→±∞
=⇒=
là tiệm cận ngang của đồ thị hàm số.
( ) ( )
11
lim , lim 1
xx
y yx
+−
→− →−
= −∞ = +∞ ⇒ = −
là tiệm cận đứng của đồ thị hàm số.
Câu 21: Trong các hàm số sau, hàm số nào nghịch biến trên
?
A.
2
3
x
y
−
=
. B.
1
2
logyx=
. C.
5
x
y =
. D.
3
x
e
y
=
.
Lời giải
Chọn D.
Hàm số
3
x
e
y
=
có
01
3
e
<<
nên hàm số nào nghịch biến trên
.
Câu 22: Một hình trụ có diện tích xung quanh bằng
30π
, bán kính đáy bằng
3
. Tính chiều cao h của
hình trụ?
A.
10h =
. B.
10
3
h =
. C.
5
3
h =
. D.
5
h =
.
Lời giải
Chọn D.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
2 2 3 30 5
xq
S rl . .l l= π = π = π⇒ =
.
Do hình trụ có
5
hl h
=⇒=
Câu 23: Hệ số góc của tiếp tuyến với đồ thị hàm số
y ln x=
tại điểm
(
)
10
M;
bằng
A.
0
. B.
2−
. C.
1−
. D.
1
.
Lời giải
Chọn D.
Ta có
1
y ln x y'
x
= ⇒=
.
Hệ số góc của tiếp tuyến với đồ thị hàm số
y ln x=
tại điểm
(
)
10M;
bằng
( )
1
11
1
y' = =
.
Câu 24: Phương trình
( )
3
2 1 54log x x
+=−
có tất cả bao nhiêu nghiệm?
A.
1
nghiệm. B.
3
nghiệm. C.
2
nghiệm. D. vô nghiệm.
Lời giải
Chọn A.
Điều kiện:
1
2
x >−
.
Ta có:
54
1
2 1 3 2 1 243
81
x
x
x x.
−
+= ⇔ +=
.
Nhận thấy
1x =
là nghiệm phương trình.
Hàm số
21yx= +
có
20y' = >
nên hàm số đồng biến trên
1
2
;
− +∞
.
Hàm số
1
243
81
x
y.
=
có
1
1
81
a
= <
nên hàm số nghịch biến trên
1
2
;
− +∞
.
Vậy phương trình
1
2 1 243
81
x
x.
+=
có tối đa 1 nghiệm.
Nên phương trình
( )
3
2 1 54log x x
+=−
có 1 nghiệm
1x =
.
Câu 25: Đồ thị sau là của hàm số nào?
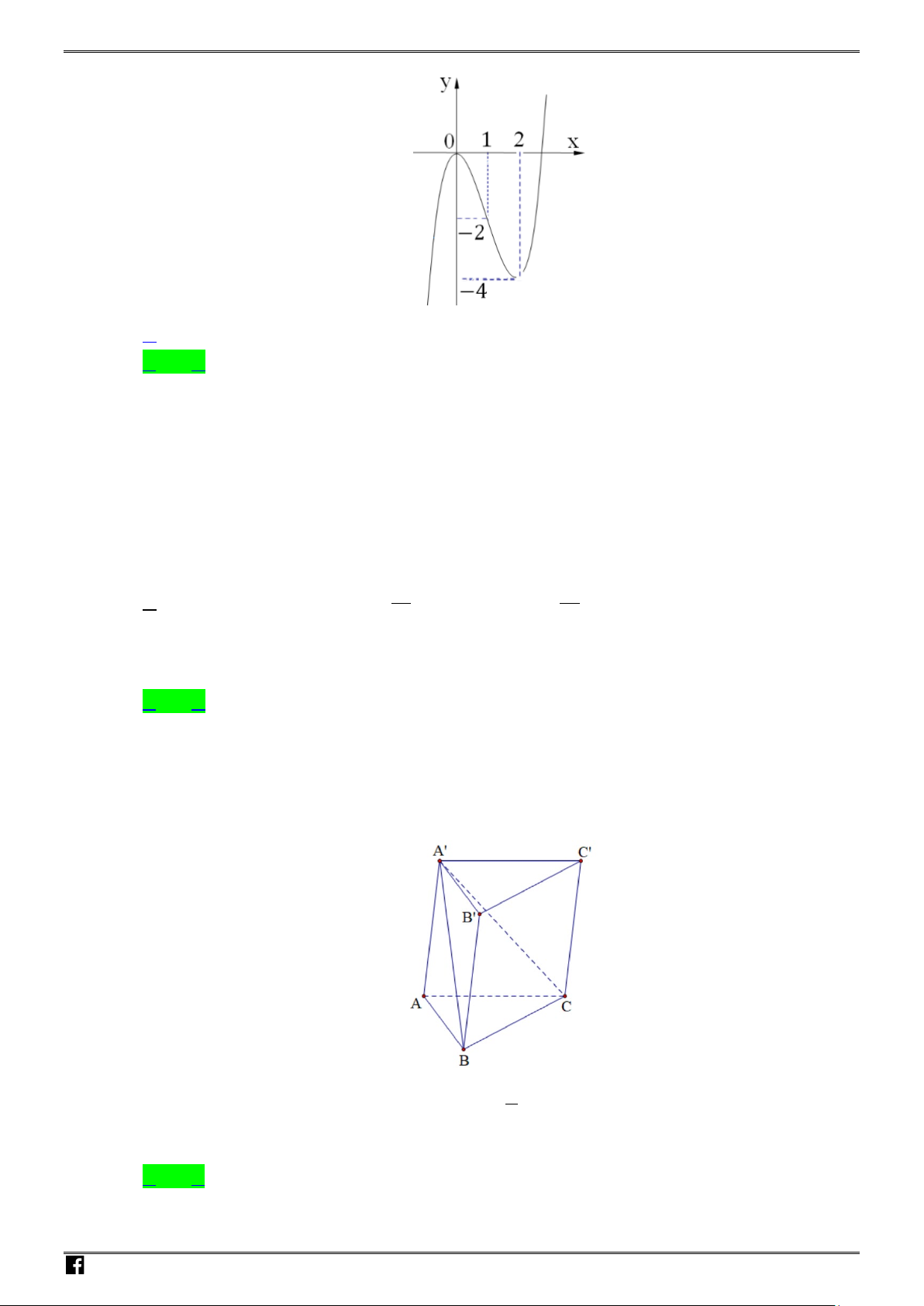
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
= −
32
3
yx x
. B.
= +
3
3yx x
. C.
= +
32
3yx x
. D.
= −
3
3yx x
.
Chọn A
= −
32
3yx x
2
'3 6yxx= −
2
00
'0 3 6 0
24
xy
y xx
xy
=⇒=
=⇔ −=⇔
=⇒=−
.
Câu 26: Với phương trình
21
5 16.5 3 0
xx+
− +=
, nếu đặt
5
x
t
=
ta được phương trình nào dưới đây?
A.
− +=
2
5 16 3 0tt
. B.
− +=
2
16
5 30
5
tt
. C.
− +=
2
16
30
5
tt
. D.
− +=
2
16 3 0tt
.
Lời giải
Chọn A
21
5 16.5 3 0
xx+
− +=
2
5.5 16.5 3 0
xx
⇔ − +=
. Đặt
5, 0
x
tt= >
.
Phương trình trở thành:
− +=
2
5 16 3 0tt
.
Câu 27: Biết thể tích khối lăng trụ
.'' 'ABC A B C
bằng 30. Tính thể tích
V
của khối chóp
'.A ABC
.
A.
15V =
. B.
20
V =
. C.
10V =
. D.
5V
=
.
Lời giải
Chọn C
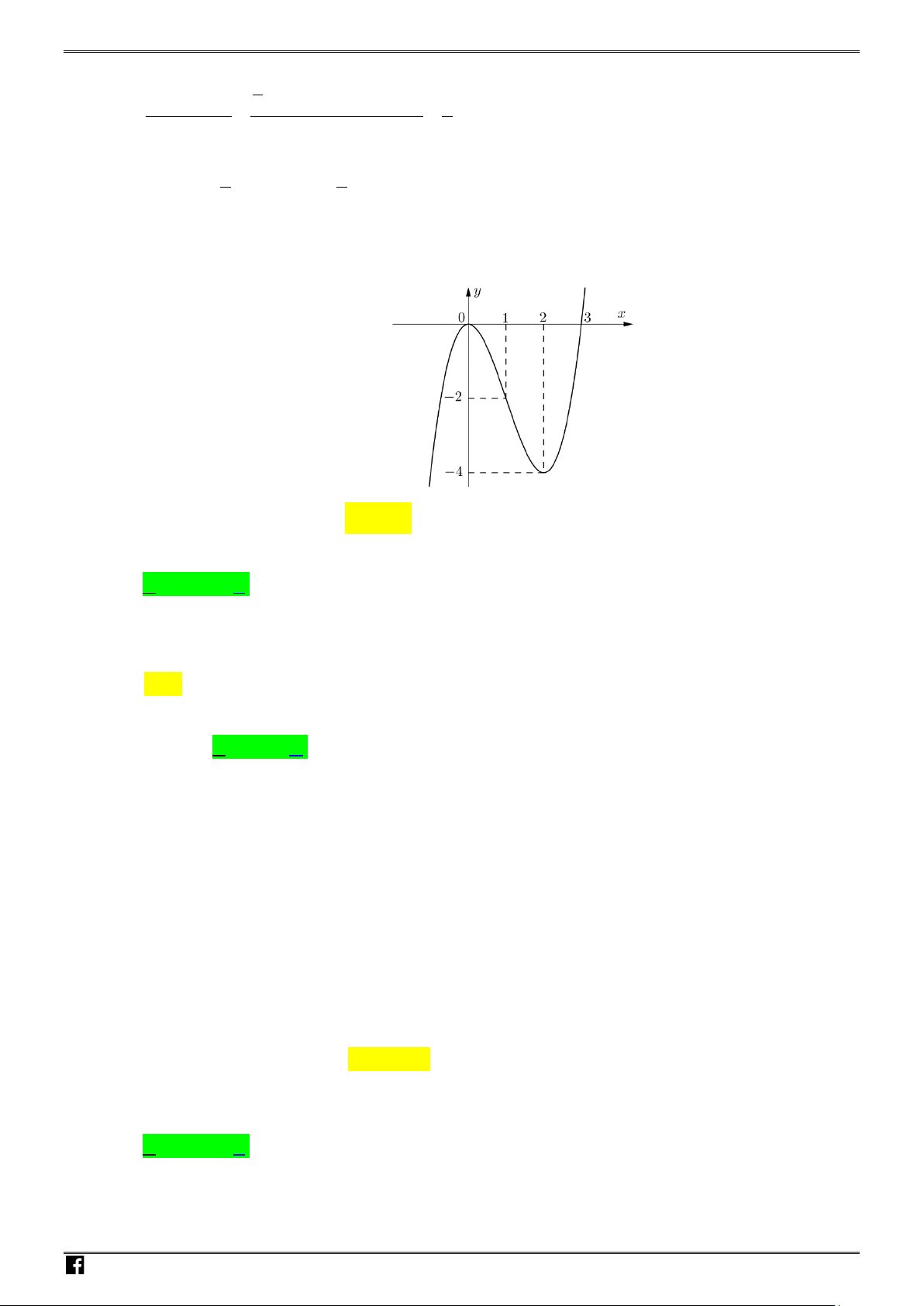
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
( )
( )
( )
( )
'.
.'''
1
', .
1
3
3
', .
ABC
A ABC
ABC A B C
ABC
d A ABC S
V
V
d A ABC S
∆
∆
= =
.
'. . ' ' '
11
30 10
33
A ABC ABC A B C
VV= = =
.
Câu 28: Cho hàm số
(
)
y fx
=
liên tục trên
và có đồ thị như hình vẽ. Khoảng nghịch biến của
hàm số là:
A.
( )
4;0
−
B.
( )
0; 2
C.
( )
;3−∞
D.
( )
3; +∞
Lời giải
Chọn B.
Câu 29: Tổng các giá trị của tham số
m
sao cho đường thẳng
6
y xm
= +
tiếp xúc với đồ thị hàm số
3
32yx x=++
bằng:
A.
4
B.
8−
C.
4−
D.
8
Lời giải
Chọn A.
Xét
( )
1
6fx xm
= +
,
( )
3
2
32
fx x x=++
Đường thẳng
6y xm= +
tiếp xúc với đồ thị hàm số
3
32yx x=++
( ) ( )
( ) ( )
2
12
3
3
12
''
1
3 36
32
3 26
fx fx
x
x
mx x
fx fx
x x xm
=
= ±
+=
⇔⇔ ⇔
=−+
=
+ += +
Với
1x =
thì
0m =
Với
1x = −
thì
4m =
Câu 30: Điểm
M
thuộc mặt cầu tâm
,I
bán kính
R
khi và chỉ khi
A.
2IM R=
B.
IM R=
C.
IM R>
D.
IM R<
Lời giải
Chọn B.
Câu 31: Hàm số nào sau đây có đồ thị như hình bên?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
1
2
x
y
=
. B.
2
x
y = −
. C.
1
2
x
y
= −
. D.
2
x
y =
.
Lời giải
Chọn B
Đồ thị là hàm số nghịch biến nên đáp án C, D loại.
Lại có
lim
x
y
→+∞
= −∞
nên chọn B.
Câu 32: Tính thể tích
V
của khối chóp
.S ABC
có
SA a=
và
(
)
SA ABC
⊥
, biết
ABC
là tam giác
vuông cân tại
B
,
3
AB a=
.
A.
3
9Va=
. B.
3
9
2
Va=
. C.
3
3
2
Va=
. D.
3
3Va=
.
Lời giải
Chọn C
Ta có
ABC
là tam giác vuông cân tại
B
,
3AB a=
nên
3BC AB a= =
.
Do đó diện tích tam giác
ABC
bằng
2
.9
22
AB BC a
S = =
.
Suy ra thể tích khối chóp
.S ABC
là
2
3
19 3
..
322
a
Va a= =
.
Câu 33: Tổng các giá trị nghiệm của phương trình
2
22
log 3log 2 0xx− +=
bằng
A.
2
. B.
3
2
. C.
3
. D.
6
.
Lời giải
Chọn D
Điều kiện:
0x >
.
Phương trình
( )
( )
2
2
22
2
log 1 2
log 3log 2 0
log 2 4
x x TM
xx
x x TM
=⇔=
− +=⇔
=⇔=
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Do đó tổng các nghiệm của phương trình là 6.
Câu 34: Cho hình hộp chữ nhật có đáy là hình vuông, cạnh bên bằng
a
và diện tích xung quanh
bằng
2
42a
. Tính thể tích khối hộp theo
a
.
A.
3
3a
. B.
3
2a
. C.
3
32a
. D.
3
22a
.
Lời giải
Chọn B
Đặt cạnh đáy hình vuông là
0x >
. Khi đó diện tích xung quanh của hình hộp là
4
xq
S
xa=
.
Theo đề bài ta có
2 2 22
42 42 24 2
xq ð
a x a xaS xaa
S⇔ = ⇒= ⇒ = ==
.
Thể tích khối hộp là
23
.2 2V aa a= =
.
Câu 35: Một hình trụ có đường cao
25cm
và bán kính đáy bằng
10cm
. Mặt phẳng
( )
P
song song và
cách trục của hình trụ
8cm
. Diện tích thiết diện của hình trụ cắt bởi mặt phẳng
( )
P
bằng
A.
2
300 cm
. B.
2
200 cm
. C.
2
150 cm
. D.
2
250 cm
.
Lời giải
Chọn A
Theo đề bài mặt phẳng
( )
P
song song với trục
OO
′
và cách trục của hình trụ
8cm
do đó
( )
( )
( )
(
)
;8;88d OO ABCD d O ABCD OI
′
=⇔ =⇔=
.
Ta có
2 2 2 22
25; 10 10 8 36h OO AD r OA AI OA OI
′
= = = = =⇒ = − = −=
P

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
6 2 12AI AB AI⇒=⇒ = =
.
Vậy diện tích của thiết diện là
2
. 25.12 300
ABCD
S AB AD cm
= = =
.
Câu 36: Cho khối chóp
.S ABC
có thể tích bằng
16
. Gọi
,,
MNP
lần lượt là trung điểm của các cạnh
,,SA SB SC
. Thể tích khối chóp
.S MNP
bằng
A.
2
. B.
1
8
. C.
8
. D.
1
2
.
Lời giải
Chọn A
Ta có
111 1 1 1
. . . . . .16 2
222 8 8 8
SMNP
SMNP SABC
SABC
V
SM SN SP
VV
V SA SB SC
= = =⇒= ==
.
Câu 37: Hàm số
y fx
liên tục trên
1; 3
và có bảng biến thiên sau:
Giá trị nhỏ nhất của hàm số trên đoạn
1; 3
là:
A.
4
. B.
0
. C.
1
. D.
1
.
Lời giải
Chọn B
Từ bảng biến thiên của hàm số
y fx
trên đoạn
1; 3
ta có
1;3
min 0fx
.
Câu 38: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, tam giác
SAB
cân tại
S
và
nằm trong mặt phẳng vuông góc với đáy,
2SA a
. Tính theo
a
thể tích
V
của khối chóp
.S ABCD
.
A.
3
15
12
a
. B.
3
15
6
a
. C.
3
2a
. D.
3
2
3
a
.
Lời giải
P
M
N
A
C
B
S
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn B
Gọi
H
là trung điểm
AB
, vì tam giác
SAB
cân tại
S
và nằm trong mặt phẳng vuông góc
với đáy nên
SH ABCD
.
SAH
vuông tại
2
2
15
22
AH a
H SH SA
.
Thể tích khối chóp
.S ABCD
:
3
1 15
.
36
ABCD
a
V SH S
.
Câu 39: Cho là các số dương khác. Khẳng định nào sau đây là sai?
A.
1
log
log
a
b
b
a
. B.
log .log log
ab a
bc c
.
C.
log log
c
aa
bc b
. D.
log log .log
a aa
bc b c
.
Lời giải
Chọn D
Câu 40: Phép đối xứng qua mặt phẳng
(
)
P
biến đường thẳng d thành chính nó khi và chỉ khi
A.
d
song song với
( )
P
.
B.
d
nằm trên
(
)
P
hoặc
d
vuông góc với
(
)
P
.
C.
d
vuông góc
( )
P
.
D.
d
nằm trên
( )
P
.
Lời giải
Chọn C.
Câu 41: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
21
1
x
fx
x
+
=
−
trên đoạn
[ ]
2; 4 .
Khi đó
Mm−
bằng
A.
4
. B.
2−
. C.
8
. D.
2
.
Lời giải
Chọn D.
Hàm số
21
1
x
y
x
+
=
−
có
( )
2
3
'0
1
y
x
−
= <
−
nên hàm số nghịch biến trên
( )
;1−∞
và
( )
1; +∞
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vì hàm số đã cho liên tục và xác định trên
[ ]
2; 4
nên ta có GTLN và GTNN lần lượt là
( )
25f =
và
( )
4 3.f =
Khi đó
5; 3 5 3 2.
M m Mm= =⇒ − =−=
Câu 42: Hình nào sau đây không có mặt cầu ngoại tiếp?
A. Lăng trụ xiên. B. Hình hộp chữ nhật. C. Hình chóp đều. D. Hình lập phương.
Lời giải
Chọn A.
Câu 43: Cho hình chóp đều
.S ABC
có đáy là tam giác đều cạnh
6cm
, góc giữa mặt bên và mặt đáy
là
0
45
. Thể tích
V
của khối chóp
.S ABC
là
A.
3
12cm
. B.
3
36cm
. C.
3
9cm
. D.
3
27
cm
.
Lời giải
Chọn C
Ta có
( )
( )
( )
( )
,
,
BC SBC ABC
SM SBC SM BC
AM SBC AM BC
= ∩
⊂⊥
⊂⊥
, suy ra góc giữa
()SBC
và
( )
ABC
là góc
0
45SMO∠=
Khi đó tam giác
SMO
vuông cân tại nên
13
.6 3
3. 2
SO OM= = =
Vậy thể tích khối chóp
.S ABC
là
23
1 13
. . . 3. .6 9
3 34
ABC
V SO S cm= = =
Câu 44: Gọi
P
là tích tất cả các nghiệm của phương trình
( ) ( )
22
75
log 3 2 log 3xx xx− += −
. Tính
giá trị của
P
.
A. 3. B.
5−
. C.
33
. D.
23
−
.
Lời giải
Chọn B
Điều kiện
2
30xx−>
Đặt
( ) ( )
22
75
log 3 2 log 3xx xxt− += − =
O
S
G
H
A
M
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
2
2
3 27
35
t
t
xx
xx
− +=
⇒
−=
51
7 5 2 5 2 7 2. 1
77
tt
tt t t
− =⇔ += ⇔ + =
(1)
Ta thấy
(
)
51
2.
77
tt
ft
= +
là hàm số nghịch biến trên
nên phương trình (1) có tối đa
một nghiệm trên
Mà phương trình có dạng
(
)
(
)
1ft f
=
2
1 3 50t xx⇔=⇔ − −=
Vậy tích các nghiệm là
5−
Câu 45: Với
,,abx
là các số dương thỏa mãn
222
log 3log 5logxab= +
. Mệnh đề nào sau đây đúng
A.
12
35
x ab=
. B.
35
x ab=
. C.
35xab= +
. D.
35
xa b= +
.
Lời giải
Chọn B
Ta có
3 5 35
2 2 22 2 2
log 3log 5log log log logx a b a b ab= + =+=
35
x ab⇒=
Câu 46: Hình bát diện đều có tất cả bao nhiêu cạnh?
A. 20. B. 12. C. 14. D. 8.
Lời giải
Chọn B
Hình bát diện đều có tất cả 12 cạnh.
Câu 47: Cho hàm số
(
)
y fx=
liên tục trên
và có bảng biến thiên như sau:
Số nghiệm của phương trình
( )
2020 2021 0fx+=
là
A. 3. B. 0. C. 1. D. 2.
Lời giải
Chọn C
x
– ∞
-1
3
+ ∞
y'
–
0
+
0
–
y
+ ∞
0
5
– ∞

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 – GIẢI ĐỀ THI HK1
https://www.facebook.com/groups/toanvd.vdc
Trang 23
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
phương trình
( ) ( )
2021
2020 2021 0
2020
fx fx
−
+=⇔ =
. Đây là phương trình hoành độ giao
điểm giữa hai đồ thị
(
)
y fx=
và
2021
2020
y
−
=
. Dựa và BBT suy ra đường thẳng
2021
2020
y
−
=
cắt đồ thị
(
)
y fx=
tại 1 điểm nên phương trình
( )
2020 2021 0fx+=
có 1 nghiệm.
Câu 48: Đồ thị sau là của hàm số nào?
A.
23
1
x
y
x
+
=
−
. B.
2
1
x
y
x
+
=
+
. C.
1
1
x
y
x
−
=
+
. D.
21
1
x
y
x
+
=
+
.
Lời giải
Chọn D
Dựa vào đồ thị ta có tiệm cận đứng là
1x = −
và tiệm cận ngang
2
y
=
. Chỉ câu D.
21
1
x
y
x
+
=
+
thỏa. Các câu còn lại không thỏa.
Câu 49: Thiết diện qua trục của một hình trụ là hình vuông cạnh bằng 4. Tính thể tích
V
của khối
trụ?
A.
24V
π
=
. B.
64V
π
=
. C.
16V
π
=
. D.
4V
π
=
.
Lời giải
Chọn C
Thiết diện qua trục là hình vuông nên hình trụ có
22
4
2 4 .2 .4 16
2
h
h R V Rh
R
ππ π
=
= =⇒ ⇒= = =
=
.
Câu 50: Cho số thực dương
1a ≠
thỏa mãn
2
5
m
n
aa=
. Tính
m
n
=
?
A.
2
5
. B.
5
. C.
5
2
. D.
2
.
Lời giải
Chọn C
Ta có
22
55
25
52
n
m
n
m
nm
aa a a
mn
= ⇔ =⇒=⇒=
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
SỞ GIÁO DỤC & ĐÀO TẠO VĨNH LONG
KIỂM TRA HỌC KỲ 1 - LỚP 12
NĂM HỌC:2020-2021
THỜI GIAN: 90 PHÚT
Câu 1: Cho hàm số
()
y fx
=
có đạo hàm trên khoảng
K
. Mệnh đề nào dưới đây đúng?
A. Nếu
() 0fx
′
<
với mọi
x
thuộc
K
thì hàm số
()fx
đồng biến trên
K
.
B. Nếu
() 0fx
′
≤
với mọi
x
thuộc
K
thì hàm số
()fx
đồng biến trên
K
.
C. Nếu
() 0fx
′
≥
với mọi
x
thuộc
K
thì hàm số
()
fx
đồng biến trên
K
.
D. Nếu
() 0fx
′
>
với mọi
x
thuộc
K
thì hàm số
()fx
đồng biến trên
K
.
Câu 2: Cho hàm số
()y fx=
có bảng biến thiên như hình bên. Hàm số nghịch biến trên khoảng nào
dưới đây?
A.
( 2;0)−
. B.
(1; 3)
−
. C.
(0; )+∞
. D.
( ; 2)−∞ −
.
Câu 3: Hàm số nào sau đây không có điểm cực trị?
A.
42
25yx x=−+ −
. B.
3
6 2019yx x=+−
.
C.
4
1
6
4
yx
=−+
. D.
42
25yx x=+−
.
Câu 4: Cho hàm số
()y fx=
có đồ thị như hình vẽ dưới đây.
Giá trị cực đại của hàm số bằng
A.
2−
. B.
0
. C.
1−
. D.
1
.
Câu 5: Hàm số
()y fx
=
liên tục trên đoạn
[ 1; 3]−
và có bảng biến thiên như sau.
Gọi
M
là giá trị lớn nhất của hàm số
()y fx=
trên đoạn
[ 1; 3]−
. Khẳng định nào sau đây là
khẳng định đúng?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
( 1)Mf= −
. B.
(3)Mf=
. C.
(2)
Mf
=
. D.
(0)
Mf
=
.
Câu 6: Nếu hàm số
()y fx
=
thỏa mãn
1
lim ( )
x
fx
−
→
= −∞
thì đồ thị hàm số
()
y fx
=
có đường tiệm cận
đứng là đường thẳng có phương trình
A.
1x =
. B.
1y =
. C.
1x = −
. D.
1y = −
.
Câu 7: Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
A.
3
3yx x= −
. B.
3
31
yx x=−+ +
. C.
3
33
yx x=−+
. D.
3
31yx x=−+
.
Câu 8: Biết rằng đường thẳng
45yx= +
cắt đồ thị hàm số
3
21yx x
=++
tại điểm duy nhất, kí hiệu
( )
00
;xy
là tọa độ của điểm đó. Tìm
0
y
.
A.
0
10y =
. B.
0
13y =
. C.
0
11y =
. D.
0
12y =
.
Câu 9: Tìm tất cả giá trị của tham số
m
để hàm số
32
21y x x mx=+ −+
đồng biến trên
.
A.
4
3
m <−
. B.
4
3
m >−
. C.
4
3
m ≥−
. D.
4
3
m ≤−
.
Câu 10: Điểm cực tiểu của đồ thị hàm số
32
55y xx x=−+ + −
là điểm nào?
A.
( 1; 8)−−
. B.
(0; 5)−
. C.
5 40
;
3 27
. D.
(1; 0)
.
Câu 11: Gọi
m
là giá trị nhỏ nhất của hàm số
4
yx
x
= +
trên khoảng
(0; )+∞
. Tìm
m
.
A.
4m =
. B.
2m =
. C.
1m =
. D.
3m =
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 12: Tập hợp các giá trị
m
để đồ thị hàm số
2
62
2
mx x
y
x
+−
=
+
có tiệm
cận đứng là
A.
7
2
. B.
. C.
7
2
−
. D.
7
2
.
Câu 13: Đồ thị sau đây là của hàm số
3
31yx x=−+
. Với giá trị nào của
m
thì phương trình
3
30
x xm
− −=
có 3 nghiệm phân biệt?
A.
22
m
−< <
. B.
13m
−< <
. C.
22
m
−≤ <
. D.
23m−< <
.
Câu 14: Biết rằng tập tất cả các giá trị thực của tham số
m
để hàm số
32
1
( 1) ( 3) 2020
3
y xmxmx m= −− −− +
đồng biến trên khoảng
( 3; 1)
−−
và
(0;3)
là đoạn
[;]
T ab
=
. Tính
22
ab+
A.
22
13
ab+=
. B.
22
8ab+=
. C.
22
10ab
+=
. D.
22
5
ab
+=
.
Câu 15: Tìm
m
để bất phương trình
4
1
xm
x
+≥
−
có nghiệm trên khoảng
( ;1)−∞
.
A.
1m
≤−
. B.
3m ≤
. C.
3m
≤−
. D.
5
m ≤
.
Câu 16: Tiếp tuyến của đường cong
21
( ):
1
x
Cy
x
+
=
−
tại điểm
(2;5)M
cắt các trục tọa độ
,Ox Oy
lần lượt
tại
A
và
B
. Tính diện tích tam giác
OAB
.
A.
121
6
. B.
121
6
−
. C.
121
3
. D.
121
3
−
.
Câu 17: Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
( 6;5)
−
sao cho phương trình
2cos 2 4sin 2 0x xm+ −=
vô nghiệm.
A.
3
. B.
2
. C.
5
. D.
4
.
Câu 18: Cho hàm số
()y fx=
có bảng biến thiên như sau

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Gọi
S
là tập hợp các số nguyên dương
m
để bất phương trình
( )
22
() 2 2f x mx x m≥ −+
có
nghiệm thuộc đoạn
[0;3]
. Số phần tử của tập
S
là
A. Vô số. B.
10
. C.
9
. D.
0
.
Câu 19: Tính
( )
5
2
0,75
1
0, 25
16
P
−
−
= +
.
A.
80P =
. B.
20P =
. C.
40
P =
. D.
10
P =
.
Câu 20: Cho
,
xy
là hai số thực dương và
,mn
là hai số thực tùy ý. Đẳng thức nào sau đây là \bf sai?
A.
()
n nn
xy x y=
. B.
()
m n mn
x y xy
+
=
. C.
( )
()
n
m mn
xx=
. D.
m n mn
xx x
+
⋅=
.
Câu 21: Với
,
ab
là hai số thực dương tùy ý,
23
log( )ab
bằng
A.
11
log log
23
ab+
. B.
2log 3logab
⋅
. C.
2log logab
+
. D.
2log 3log
ab+
.
Câu 22: Phương trình
32
x
=
có nghiệm là
A.
2
log 3x =
. B.
3
2x
=
. C.
3
log 2x =
. D.
2
3
x
=
.
Câu 23: Cho
α
là một số thực dương. Viết
2
3
αα
⋅
dưới dạng lũy thừa với số mũ hữu tỷ.
A.
7
6
α
. B.
7
3
α
. C.
5
3
α
. D.
1
3
α
.
Câu 24: Tập xác định
của hàm số
1
3
( 1)
yx
= +
là
A.
( )
;1= −∞ −
. B.
=
. C.
{ 1}
= −
. D.
( )
1;= − +∞
.
Câu 25: Đặt
2
log 5 a=
, khi đó
25
log 16
bằng
A.
2
a
. B.
2a
. C.
1
2
a
. D.
1
2
a
.
Câu 26: Tìm đạo hàm của hàm số
2
log (2 1)
yx= +
.
A.
2
21x
y
′
=
+
. B.
1
21x
y
′
=
+
.
C.
1
(2 1) ln 2x
y =
+
′
. D.
2
(2 1) ln 2x
y =
+
′
.
Câu 27: Hàm số nào sau đây đồng biến trên
?
A.
2
logyx=
. B.
1
1
x
y
x
−
=
+
. C.
3
x
y =
. D.
42
24yx x
=++
.
Câu 28: Phương trình
22
1
42 3
xx xx− −+
+=
có nghiệm là
A.
1
2
x
x
=
=
. B.
1
1
x
x
= −
=
. C.
0
2
x
x
=
=
. D.
0
1
x
x
=
=
.
Câu 29: Gọi
T
là tổng các nghiệm của phương trình
2
13
3
log 5log 4 0xx
− +=
. Tính
T
.
A.
84T =
. B.
4T =
. C.
5T =
. D.
5T
= −
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 30: Một khu rừng có trữ lượng gỗ
5
4 10×
3
m
. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là
4%
mỗi năm. Hỏi sau
5
năm, khu rừng đó sẽ có khoảng bao nhiêu
3
m
gỗ?
A.
5
4,8666 10⋅
3
m
. B.
7
125 10⋅
3
m
.
C.
3
2016 10⋅
3
m
. D.
5
35 10⋅
3
m
.
Câu 31: Đặt
2
log 3a =
,
5
log 3b =
. Nếu biểu diễn
6
()
log 45
()
a m nb
ba p
+
=
+
với
,,
mnp∈
thì
mnp++
bằng
A.
3
. B.
4
. C.
6
. D.
3−
.
Câu 32:
Biết hàm số
2
()
3
x
a
fx
b
=
⋅
có đồ thị đối xứng với đồ thị hàm số
3
x
y =
qua đường thẳng
1x = −
. Biết
a
,
b
là các số nguyên. Chọn khẳng định đúng trong các khẳng định sau.
A.
2
ba
=
. B.
2
9
ba=
. C.
2
6ba
=
. D.
2
4ba=
.
Câu 33: Anh
X
muốn mua một chiếc xe máy Yamaha Exciter
150
i giá
47500000
đồng của cửa hàng
Phú Tài nhưng vì chưa đủ tiền nên anh
X
đã quyết định mua theo hình thức như sau: trả trước
25
triệu đồng và trả góp trong
12
tháng, với lãi suất là
0,6% /
tháng. Hỏi mỗi tháng, anh
X
sẽ
phải trả cho cửa hàng Phú Tài số tiền là bao nhiêu? (qui tròn đến hàng đơn vị).
A.
1948927
đồng. B.
1948000
đồng. C.
2014545
đồng. D.
2014546
đồng.
Câu 34: Phương trình
2
2 28
23
x xx
− +−
=
có một nghiệm dạng
log 4
a
xb= −
với
a
,
b
là các số nguyên dương
thuộc khoảng
(1; 5)
. Khi đó,
2ab
+
bằng
A.
6
. B.
14
. C.
9
. D.
7
.
Câu 35: Một khối hộp chữ nhật có bao nhiêu đỉnh?
A.
12
. B.
8
. C.
10
. D.
6
.
Câu 36: Đa diện đều loại
{ }
5,3
có tên gọi nào dưới đây?
A. Tứ diện đều. B. Lập phương.
C. Hai mươi mặt đều. D. Mười hai mặt đều.
Câu 37: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Biết cạnh bên
2SA a=
và vuông
góc với mặt đáy. Tính thể tích khối chóp
.S ABCD
.
A.
3
4
3
a
. B.
3
2a
. C.
3
3
a
. D.
3
2
3
a
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 38: Cho hình chóp
.S ABCD
đáy là hình chữ nhật
2AD a=
,
AB a=
( 0)a >
, có
()SAB
và
()
SAD
vuông góc đáy và góc
SC
và đáy bằng
30
°
. Thể tích khối chóp là
A.
3
2
3
a
. B.
3
2 15
9
a
. C.
3
3
6
a
. D.
3
3
3
a
.
Câu 39: Khối bát diện đều có bao nhiêu cạnh?
A.
12
. B.
10
. C.
8
. D.
9
.
Câu 40: Hãy chọn mệnh đề đúng.
A. Số đỉnh và số mặt trong một hình đa diện luôn bằng nhau.
B. Tồn tại hình đa diện có số đỉnh và số mặt bằng nhau.
C. Tồn tại hình đa diện có số cạnh bằng số mặt.
D. Tồn tại hình đa diện có số đỉnh bằng số cạnh.
Câu 41: Có tất cả bao nhiêu khối đa diện đều?
A.
7
. B.
4
. C.
5
. D.
6
.
Câu 42: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
A.
2
. B.
3
. C.
4
. D.
5
.
Câu 43: Lăng trụ tam giác
.ABC A B C
′′′
có thể tích bằng
V
. Khi đó thể tích khối chóp
.A BCC B
′′
bằng
A.
2
V
. B.
3
4
V
. C.
2
3
V
. D.
3
V
.
Câu 44: Cho khối lăng trụ
.ABC A B C
′′′
có đáy là tam giác vuông tại
B
, biết
AB a
=
,
3BC a=
và thể
tích của khối lăng trụ bằng
3
6
2
a
. Chiều cao của lăng trụ là
A.
3
2
a
. B.
2
2
a
. C.
3a
. D.
2a
.
Câu 45: Hình tạo bởi
6
đỉnh là
6
trung điểm của các cạnh một tứ diện đều có bao nhiêu mặt phẳng đối
xứng?
A.
6
. B.
3
. C.
4
. D.
9
.
Câu 46: Cho khối chóp
.S ABC
có thể tích bằng
16
. Gọi
,,MNP
lần lượt là trung điểm của các cạnh
,,SA SB SC
. Tính thể tích
V
của khối tứ diện
AMNP
.
A.
8V =
. B.
14V
=
. C.
12V =
. D.
2V =
.
Câu 47: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA a=
và
SA
vuông góc với
đáy. Gọi
M
là trung điểm của
SB
,
N
thuộc cạnh
SD
sao cho
2SN ND=
. Tính thể tích
V
của
khối tứ diện
ACMN
.
A.
3
1
12
Va=
. B.
3
1
6
Va=
. C.
3
1
8
Va=
. D.
3
1
36
Va
=
.
Câu 48: Cho khối lăng trụ
.
ABC A B C
′′′
có thể tích bằng
3
a
. Gọi
,MN
lần lượt là trung điểm của
AB
′′
và
CC
′
. Tính thể tích khối chóp
ABMN
.
A.
3
2
3
a
. B.
3
3a
. C.
3
3
a
. D.
3
3
2
a
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 49: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
. Biết
AC a=
,
2
a
BC =
,
3
2
a
SA =
và cạnh
SA
vuông góc với mặt phẳng đáy. Khoảng cách từ
A
đến mặt phẳng
()SBC
bằng
A.
6a
. B.
6
4
a
. C.
3
2
a
. D.
6
2
a
.
Câu 50: Từ một tấm bìa hình vuông
ABCD
có cạnh bằng
5
dm, người ta cắt bỏ bốn tam giác bằng nhau
AMB
,
BNC
,
CPD
,
DQA
. Với phần còn lại, người ta gắp lên và ghép lại để thành hình chóp tứ
giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất?
A.
32
2
. B.
5
2
. C.
22
. D.
52
2
.
BẢNG ĐÁP ÁN
1.D
2.A
3.B
4.C
5.D
6.A
7.D
8.B
9.D
10.A
11.A
12.D
13.A
14.D
15.C
16.A
17.A
18.C
19.C
20.B
21.D
22.C
23.A
24.D
25.A
26.D
27.C
28.D
29.A
30.A
31.B
32.B
33.A
34.D
35.B
36.D
37.D
38.B
39.A
40.B
41.C
42.C
43.C
44.D
45.D
46.D
47.A
48.C
49.B
50.C
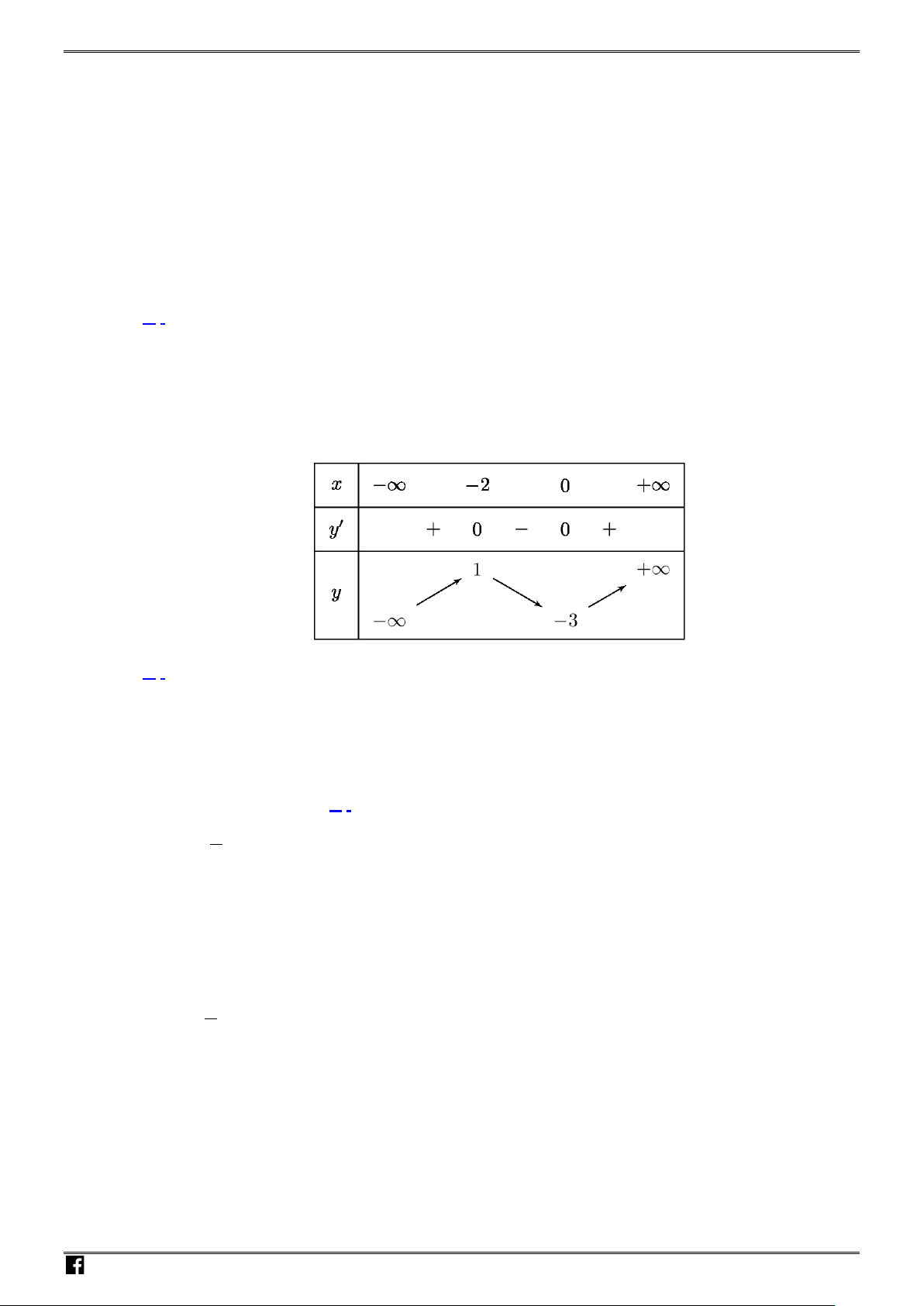
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
SỞ GIÁO DỤC & ĐÀO TẠO VĨNH LONG
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA HỌC KÌ 1, NĂM HỌC 2020-2021
Môn thi: TOÁN 12- Thời gian làm bài: 90 phút;
Câu 1: Cho hàm số
()y fx
=
có đạo hàm trên khoảng
K
. Mệnh đề nào dưới đây đúng?
A. Nếu
() 0fx
′
<
với mọi
x
thuộc
K
thì hàm số
()fx
đồng biến trên
K
.
B. Nếu
() 0fx
′
≤
với mọi
x
thuộc
K
thì hàm số
()fx
đồng biến trên
K
.
C. Nếu
() 0fx
′
≥
với mọi
x
thuộc
K
thì hàm số
()
fx
đồng biến trên
K
.
D. Nếu
() 0fx
′
>
với mọi
x
thuộc
K
thì hàm số
()fx
đồng biến trên
K
.
Lời giải
Theo lý thuyết ta có: Nếu
() 0fx
′
>
với mọi
x
thuộc
K
thì hàm số
()fx
đồng biến trên
K
.
Câu 2: Cho hàm số
()y fx
=
có bảng biến thiên như hình bên. Hàm số nghịch biến trên khoảng nào
dưới đây?
A.
( 2;0)−
. B.
(1; 3)−
. C.
(0; )+∞
. D.
( ; 2)−∞ −
.
Lời giải
Từ bảng biến thiên dễ thấy hàm số nghịch biến trên khoảng
( 2;0)
−
.
Câu 3: Hàm số nào sau đây không có điểm cực trị?
A.
42
25yx x=−+ −
. B.
3
6 2019yx x=+−
.
C.
4
1
6
4
yx
=−+
. D.
42
25yx x=+−
.
Lời giải
-)
42
21yx x=−+ −
có
0ab⋅<
, nên hàm số có
3
cực trị.
-)
3
6 2019yx x=+−
có
2
3 6 0,yx x
′
= + > ∀∈
, nên hàm số không có cực trị.
-)
4
1
6
4
yx=−+
có
0ab⋅=
, nên hàm số có
1
cực trị.
-)
42
25yx x=+−
có
0ab⋅>
, nên hàm số có
1
cực trị.
Câu 4: Cho hàm số
()y fx=
có đồ thị như hình vẽ dưới đây.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Giá trị cực đại của hàm số bằng
A.
2−
. B.
0
. C.
1−
. D.
1
.
Lời giải
Dựa vào đồ thị hàm số ta suy ra giá trị cực đại bằng
1−
.
Câu 5: Hàm số
()y fx=
liên tục trên đoạn
[ 1; 3]−
và có bảng biến thiên như sau.
Gọi
M
là giá trị lớn nhất của hàm số
()y fx=
trên đoạn
[ 1; 3]−
. Khẳng định nào sau đây là
khẳng định đúng?
A.
( 1)Mf= −
. B.
(3)Mf
=
. C.
(2)Mf=
. D.
(0)Mf=
.
Lời giải
Dựa vào bảng biến thiên ta có
(0) 5Mf= =
.
Câu 6: Nếu hàm số
()
y fx=
thỏa mãn
1
lim ( )
x
fx
−
→
= −∞
thì đồ thị hàm số
()y fx
=
có đường tiệm cận
đứng là đường thẳng có phương trình
A.
1x =
. B.
1
y =
. C.
1x = −
. D.
1
y = −
.
Lời giải
Ta có
1
lim ( )
x
fx
−
→
= −∞
nên
1x =
là một tiệm cận đứng của đồ thị
()y fx=
.
Câu 7: Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
3yx x= −
. B.
3
31yx x=−+ +
. C.
3
33yx x=−+
. D.
3
31yx x=−+
.
Lời giải
Gọi hàm số cần tìm
32
y ax bx cx d= + ++
.
Ta có
2
32y ax bx c
′
= ++
.
Từ đồ thị suy ra
( 1) 3 3 1
(1) 1 1 0
(0) 1 1 3
( 1) 0 3 2 0 1.
y abcd a
y abcd b
yd c
y a bc d
− = −+−+ = =
=− +++ =− =
⇒⇒
= = = −
′
−= − += =
Vậy
3
31yx x=−+
.
Câu 8: Biết rằng đường thẳng
45yx= +
cắt đồ thị hàm số
3
21
yx x=++
tại điểm duy nhất, kí hiệu
( )
00
;xy
là tọa độ của điểm đó. Tìm
0
y
.
A.
0
10y =
. B.
0
13y =
. C.
0
11y =
. D.
0
12y =
.
Lời giải
Ta có
0
x
là nghiệm của phương trình hoành độ giao điểm
33
2 1 4 5 2 4 0 2.
xx x xx x+ += + ⇔ − − = ⇔ =
Với
0
2x =
thì
0
4 2 5 13y =⋅+=
.
Vậy
0
13y
=
.
Câu 9: Tìm tất cả giá trị của tham số
m
để hàm số
32
21y x x mx=+ −+
đồng biến trên
.
A.
4
3
m <−
. B.
4
3
m >−
. C.
4
3
m ≥−
. D.
4
3
m ≤−
.
Lời giải
Ta có:
2
34y x xm
′
= +−
.
Để hàm số
32
21y x x mx=+ −+
đồng biến trên
thì
2
3 4 0,x xm x+ − ≥ ∀∈
.
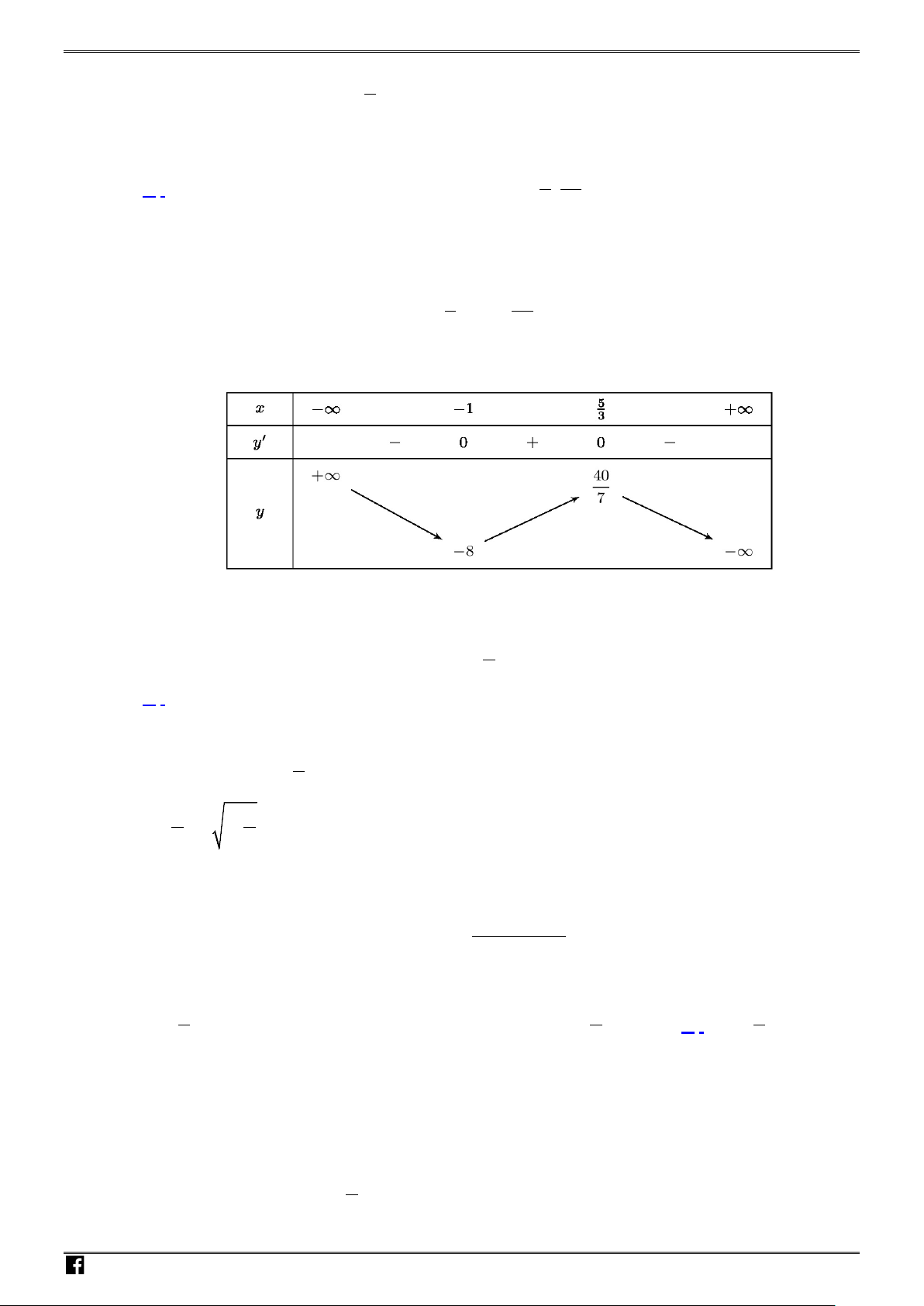
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Hay
4
43 0
3
mm
′
∆ = + ≤ ⇔ ≤−
.
Câu 10: Điểm cực tiểu của đồ thị hàm số
32
55y xx x=−+ + −
là điểm nào?
A.
( 1; 8)−−
. B.
(0; 5)
−
. C.
5 40
;
3 27
. D.
(1; 0)
.
Lời giải
Ta có
2
3 25y xx
′
=− ++
,
18
0
5 40
3 27
xy
y
xy
=−⇒ =−
′
= ⇔
=⇒=
.
Ta có bảng biến thiên
Vậy đồ thị hàm số có điểm cực tiểu là
(
)
1; 8
−−
.
Câu 11: Gọi
m
là giá trị nhỏ nhất của hàm số
4
yx
x
= +
trên khoảng
(0; )+∞
. Tìm
m
.
A.
4m
=
. B.
2m =
. C.
1m
=
. D.
3m
=
.
Lời giải
Với
(0; )x
∈ +∞
thì
4
(0; )
x
∈ +∞
, theo bất đẳng thức Cô-si cho hai số dương ta có
44
2 4.xx
xx
+≥ ⋅=
Dấu đẳng thức xảy ra khi
2x =
. Vậy giá trị nhỏ nhất của hàm số trên
(0; )+∞
là
4
.
Câu 12: Tập hợp các giá trị
m
để đồ thị hàm số
2
62
2
mx x
y
x
+−
=
+
có tiệm
cận đứng là
A.
7
2
. B.
. C.
7
2
−
. D.
7
2
.
Lời giải
Đồ thị hàm số có tiệm cận đứng khi và chỉ khi phương trình
2
6 20
mx x+ −=
không có nghiệm
2x = −
.
Khi đó
7
4 14 0 .
2
mm− ≠⇔ ≠

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vậy tập hợp các giá trị
m
cần tìm là
7
2
.
Câu 13: Đồ thị sau đây là của hàm số
3
31yx x
=−+
. Với giá trị nào của
m
thì phương trình
3
30x xm− −=
có 3 nghiệm phân biệt?
A.
22m−< <
. B.
13m−< <
. C.
22m−≤ <
. D.
23m−< <
.
Lời giải
Ta có
33
3 0 31 1xxm xx m−−=⇔−+=+
. Phương trình có ba nghiệm phân biệt
⇔
Đường
thẳng
1ym
= +
cắt đồ thị hàm số
3
31yx x=−+
tại ba điểm phân biệt
1 13 2 2mm⇔− < + < ⇔− < <
.
Câu 14: Biết rằng tập tất cả các giá trị thực của tham số
m
để hàm số
32
1
( 1) ( 3) 2020
3
y xmxmx m= −− −− +
đồng biến trên khoảng
( 3; 1)−−
và
(0;3)
là đoạn
[;]T ab
=
. Tính
22
ab
+
A.
22
13
ab+=
. B.
22
8ab
+=
. C.
22
10
ab
+=
. D.
22
5ab+=
.
Lời giải
Tập xác đinh
=
.
2
2( 1) ( 3)
yx m xm
′
=− −−−
.
-) Hàm số đã cho đồng biến trên
(0;3)
tức là
0, (0;3)yx
′
≥ ∀∈
2
23
, (0;3)
21
xx
mx
x
++
⇔ ≥ ∀∈
+
.
Xét
2
23
()
21
xx
fx
x
++
=
+
trên
(0;3)
.
Ta có
2
2
2 24
()
(2 1)
xx
fx
x
+−
′
=
+
.
1
() 0
2(lo?i).
x
fx
x
=
′
= ⇔
= −
Ta có bảng biến thiên.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Từ bảng biến thiên suy ra
( ) (0;3) 2fx mx m≥ ∀∈ ⇔ ≤
.\hfill (1)
-) Hàm số đã cho đồng biến trên
( 3; 1)
−−
tức là
0, ( 3; 1)
yx
′
≤ ∀∈− −
2
23
, ( 3; 1)
21
xx
mx
x
++
⇔ ≥ ∀∈− −
+
.
Xét
2
23
()
21
xx
fx
x
++
=
+
trên
( 3; 1)−−
.
Ta có
2
2
2 24
()
(2 1)
xx
fx
x
+−
′
=
+
.
1(lo?i)
() 0
2.
x
fx
x
=
′
= ⇔
= −
Ta có bảng biến thiên.
Từ bảng biến thiên suy ra
( ) , ( 3; 1) 1
fx m x m≤ ∀ ∈ − − ⇔ ≥−
. \hfill (2)
Kết hợp
(1)
và
(2)
ta được
12m−≤ ≤
hay
[ 1; 2]m∈−
.
Suy ra
1, 2ab=−=
. Khi đó
22
5ab+=
.
Câu 15: Tìm
m
để bất phương trình
4
1
xm
x
+≥
−
có nghiệm trên khoảng
( ;1)−∞
.
A.
1m ≤−
. B.
3m ≤
. C.
3m ≤−
. D.
5m ≤
.
Lời giải
Xét hàm số
4
()
1
fx x
x
= +
−
trên khoảng
( ;1)−∞
.
Ta có
2
3 ( ;1)
4
1 , 0
1 ( ;1)
( 1)
x
yy
x
x
= ∉ −∞
′′
=−=⇔
= − ∈ −∞
−
Bảng biến thiên

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vậy
4
1
xm
x
+≥
−
, có nghiệm
( ;1)
4
( ;1) max 3
1
x
x mx m
x
∈ −∞
∈−∞⇔≤ + ⇔≤−
−
.
Câu 16: Tiếp tuyến của đường cong
21
( ):
1
x
Cy
x
+
=
−
tại điểm
(2;5)M
cắt các trục tọa độ
,Ox Oy
lần lượt
tại
A
và
B
. Tính diện tích tam giác
OAB
.
A.
121
6
. B.
121
6
−
. C.
121
3
. D.
121
3
−
.
Lời giải
Ta có
2
3
,1
( 1)
yx
x
−
′
= ∀≠
−
.
Hệ số góc tiếp tuyến của đồ thị hàm số tại
M
là
(2) 3ky
′
= = −
.
Phương trình tiếp tuyến của đồ thị hàm số tại
M
là
3 11yx=−+
.
Tiếp tuyến cắt các trục tọa độ tại
11
; 0 , (0;11)
3
AB
, do đó diện tích tam giác
OAB
là
1 11 121
11 .
23 6
S =⋅⋅=
Câu 17: Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
( 6;5)
−
sao cho phương trình
2cos 2 4sin 2 0x xm+ −=
vô nghiệm.
A.
3
. B.
2
. C.
5
. D.
4
.
Lời giải
Ta có
2
2cos2 4sin 2 0 4sin 4sin 2 2xxm xxm+−=⇔− ++=
.
Đặt
[ ]
sin , 1;1t xt= ∈−
. Ta có hàm số
2
4 42y tt=− ++
, có hoành độ đỉnh
1
2
t =
.
Bảng biến thiên

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Để phương trình có nghiệm thì
32
6 2 3 32
2
mm
− ≤ ≤ ⇔− ≤ ≤
. Suy ra điều kiện phương
trình vô nghiệm, kết hợp với điều kiện
( 6;5)m∈−
, ta có
6 32
32
5.
2
m
m
− < ≤−
≤<
Mà
{ }
5; 3; 4mm∈ ⇒ ∈−
.
Câu 18: Cho hàm số
()
y fx=
có bảng biến thiên như sau
Gọi
S
là tập hợp các số nguyên dương
m
để bất phương trình
(
)
22
() 2 2
f x mx x m≥ −+
có
nghiệm thuộc đoạn
[0;3]
. Số phần tử của tập
S
là
A. Vô số. B.
10
. C.
9
. D.
0
.
Lời giải
Bất phương trình đã cho tương đương với
42
()
22
fx
m
xx
≥
−+
.
Từ bảng biến thiên ta thấy
5 () 9fx≤≤
với mọi
[0;3]x∈
.
Xét hàm số
42
() 2 2gx x x=−+
với
[0;3]x ∈
ta có
3
() 4 4gx x x
′
= −
,
0
() 0
1.
x
gx
x
=
′
= ⇔
=
Ta lại có
(0) 2
g
=
,
(1) 1g =
,
(3) 65g
=
. Từ đó suy ra
1 ( ) 65gx≤≤
với mọi
[0;3]x∈
.
Xét hàm số
()
()
()
fx
hx
gx
=
,
[0;3]
x∈
. Từ đó ta có đánh giá
5
() 9
65
hx≤≤
với mọi
[0;3]x∈
.
Từ đó suy ra
[0;3]
5
min ( )
65
x
hx
∈
=
khi
3x =
;
[0;3]
max ( ) 9
x
hx
∈
=
khi
1x =
.
Vậy bất phương trình đã cho có nghiệm thuộc đoạn
[0;3]
khi và chỉ khi
9m ≤
.
Vì
m
nguyên dương nên có tất cả
9
giá trị thỏa đề bài.
Câu 19: Tính
( )
5
2
0,75
1
0, 25
16
P
−
−
= +
.
A.
80P =
. B.
20P =
. C.
40P =
. D.
10P =
.
Lời giải
Ta có:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
( )
( ) ( )
5
5
2
2
0,75
0,75
4 2 35
1
0,25 2 2 2 2 40
16
P
−
−−
−
−−
= + = + =+=
.
Câu 20: Cho
,
xy
là hai số thực dương và
,mn
là hai số thực tùy ý. Đẳng thức nào sau đây là \bf sai?
A.
()
n nn
xy x y=
. B.
()
m n mn
x y xy
+
=
. C.
( )
()
n
m mn
xx=
. D.
m n mn
xx x
+
⋅=
.
Lời giải
Đẳng thức sai là
()
m n mn
x y xy
+
=
.
Câu 21: Với
,ab
là hai số thực dương tùy ý,
23
log( )
ab
bằng
A.
11
log log
23
ab
+
. B.
2log 3logab
⋅
. C.
2log logab+
. D.
2log 3logab+
.
Lời giải
Ta có
23 2 3
log( ) log log 2log 3logab a b a b=+= +
.
Câu 22: Phương trình
32
x
=
có nghiệm là
A.
2
log 3x =
. B.
3
2
x =
. C.
3
log 2x =
. D.
2
3
x
=
.
Lời giải
Ta có
3
3 2 log 2
x
x=⇔=
.
Câu 23: Cho
α
là một số thực dương. Viết
2
3
αα
⋅
dưới dạng lũy thừa với số mũ hữu tỷ.
A.
7
6
α
. B.
7
3
α
. C.
5
3
α
. D.
1
3
α
.
Lời giải
Ta có
7
22
1
3 36
2
.
α α αα α
⋅ =⋅=
Câu 24: Tập xác định
của hàm số
1
3
( 1)yx= +
là
A.
( )
;1= −∞ −
. B.
=
. C.
{ 1}= −
. D.
( )
1;= − +∞
.
Lời giải
Hàm số luỹ thừa
1
3
( 1)yx= +
có số mũ bằng
1
3
∉
.
Do đó điều kiện xác định của hàm số là
1 0 1.
xx+ > ⇔ >−
Suy ra tập xác định của hàm số là
( )
1; .= − +∞
Câu 25: Đặt
2
log 5 a=
, khi đó
25
log 16
bằng
A.
2
a
. B.
2a
. C.
1
2a
. D.
1
2
a
.
Lời giải
Ta có
2
4
25 5
5
2
22
log 16 log 2 2log 2 .
log 5 a
= = = =

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 26: Tìm đạo hàm của hàm số
2
log (2 1)yx
= +
.
A.
2
21
x
y
′
=
+
. B.
1
21x
y
′
=
+
.
C.
1
(2 1) ln 2x
y =
+
′
. D.
2
(2 1) ln 2
x
y =
+
′
.
Lời giải
Ta có
(
)
(
)
21
2
2 1 ln 2 (2 1)ln 2x
y
x
x
′
+
= =
′
++
.
Câu 27: Hàm số nào sau đây đồng biến trên
?
A.
2
logyx=
. B.
1
1
x
y
x
−
=
+
. C.
3
x
y =
. D.
42
24yx x=++
.
Lời giải
Dễ thấy hàm số
3
x
y =
đồng biến trên
.
Câu 28: Phương trình
22
1
42 3
xx xx− −+
+=
có nghiệm là
A.
1
2
x
x
=
=
. B.
1
1
x
x
= −
=
. C.
0
2
x
x
=
=
. D.
0
1
x
x
=
=
.
Lời giải
Ta có
22 2 2
1 2( )
4 2 3 2 22 3 0
xx xx xx xx
− −+ − −
+ =⇔ +⋅ −=
2
2
21
2 3, (l)
xx
xx
−
−
=
⇔
= −
0
1.
x
x
=
⇔
=
Câu 29: Gọi
T
là tổng các nghiệm của phương trình
2
13
3
log 5log 4 0xx− +=
. Tính
T
.
A.
84T =
. B.
4T =
. C.
5T =
. D.
5T = −
.
Lời giải
Điều kiện xác định
0x >
. Ta có
2
13
3
log 5log 4 0xx− +=
2
33
log 5log 4 0xx⇔ − +=
3
4
3
3
log 1
log 4
3.
x
x
x
x
=
=
⇔⇔
=
=
Vậy
4
3 3 84T =+=
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 30: Một khu rừng có trữ lượng gỗ
5
4 10×
3
m
. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là
4%
mỗi năm. Hỏi sau
5
năm, khu rừng đó sẽ có khoảng bao nhiêu
3
m
gỗ?
A.
5
4,8666 10⋅
3
m
. B.
7
125 10⋅
3
m
.
C.
3
2016 10⋅
3
m
. D.
5
35 10⋅
3
m
.
Lời giải
Gọi trữ lượng gỗ ban đầu là
0
V
, tốc độ sinh trưởng hàng năm của rừng là
%r
. Ta có
Sau
1
năm, trữ lượng gỗ là
10 00
(1 )V V rV V r= +⋅ = +
.
Sau
2
năm, trữ lượng gỗ là
2
21 11 0
(1 ) (1 )
V V rV V r V r= +⋅ = + = +
.
Tổng quát, sau
n
năm trữ lượng gỗ là
0
(1 )
n
n
VV r= +
.
Áp dụng công thức ta có trữ lượng gỗ sau
5
năm trong bài toán là
( )
5
55
5
4 10 1 4% 4,8666 10V =⋅+≈ ⋅
3
m
.
Câu 31: Đặt
2
log 3a =
,
5
log 3
b =
. Nếu biểu diễn
6
()
log 45
()
a m nb
ba p
+
=
+
với
,,mnp
∈
thì
mnp++
bằng
A.
3
. B.
4
. C.
6
. D.
3−
.
Lời giải
Ta có
2 2 22
6
22 2
23 2
2
log 45 log (5 9) log 5 2log 3
log 45
log 6 log (2 3) 1 log 3
2
log 3 log 5 2log 3
1 log 3 1
2 (1 2 )
.
( 1)
a
a
b
a
a ab a b
ab b b a
⋅+
= = =
⋅+
+
⋅+
= =
++
++
= =
++
Theo đề bài
6
()(12)()
log 45
() (1)()
a m nb a b a m nb
ba p ba ba p
+++
= ⇔=
+ ++
suy ra
1m =
,
2n =
,
1p =
. Vậy
4.mnp++ =
Câu 32:
Biết hàm số
2
()
3
x
a
fx
b
=
⋅
có đồ thị đối xứng với đồ thị hàm số
3
x
y
=
qua đường thẳng
1x = −
. Biết
a
,
b
là các số nguyên. Chọn khẳng định đúng trong các khẳng định sau.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2
ba=
. B.
2
9ba
=
. C.
2
6ba=
. D.
2
4ba=
.
Lời giải
Lấy
(0;1)M
thuộc đồ thị hàm số
3
x
y
=
.
Khi đó
M
′
đối xứng với
M
qua đường thẳng
1x = −
có tọa độ là
( 2;1)M
′
−
.
Theo giả thiết
M
′
thuộc đồ thị hàm số
2
2 22
() 1 9.
33
x
aa
fx b a
bb
−
= ⇒= ⇔ =
⋅⋅
Câu 33: Anh
X
muốn mua một chiếc xe máy Yamaha Exciter
150
i giá
47500000
đồng của cửa hàng
Phú Tài nhưng vì chưa đủ tiền nên anh
X
đã quyết định mua theo hình thức như sau: trả trước
25
triệu đồng và trả góp trong
12
tháng, với lãi suất là
0,6% /
tháng. Hỏi mỗi tháng, anh
X
sẽ
phải trả cho cửa hàng Phú Tài số tiền là bao nhiêu? (qui tròn đến hàng đơn vị).
A.
1948927
đồng. B.
1948000
đồng. C.
2014545
đồng. D.
2014546
đồng.
Lời giải
Số tiền anh
X
trả góp trong
12
tháng là:
47,5 25 22,5−=
triệu đồng.
Gọi
1 0,6%q
= +
thì sau
12
tháng giá trị số tiền nợ cửa hàng anh phải trả là:
12
22,5 q⋅
.
Giả sử mỗi tháng anh
X
trả số tiền
m
(triệu đồng) để trả hết sau
12
tháng thì tổng số tiền anh
X
đã trả tính theo lãi suất là:
12
1
1
q
m
q
−
⋅
−
.
Anh
X
trả hết nợ đúng hạn khi
12
12
1
22,5 1,948926902.
1
q
qm m
q
−
⋅ =⋅ ⇔=
−
Vậy mỗi tháng anh
X
phải trả số tiền
1948927
đồng.
Câu 34: Phương trình
2
2 28
23
x xx− +−
=
có một nghiệm dạng
log 4
a
xb= −
với
a
,
b
là các số nguyên dương
thuộc khoảng
(1; 5)
. Khi đó,
2ab+
bằng
A.
6
. B.
14
. C.
9
. D.
7
.
Lời giải
Ta có

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
2
2 28 2
3
3
3
2 3 ( 2)log 2 2 8
2
( 2)log 2 ( 2)( 4)
log 2 4.
x xx
x xx
x
x xx
x
− +−
= ⇔− =+−
=
⇔ − =− +⇔
= −
Suy ra
3a =
,
2b =
. Do đó,
27ab+=
.
Câu 35: Một khối hộp chữ nhật có bao nhiêu đỉnh?
A.
12
. B.
8
. C.
10
. D.
6
.
Lời giải
Một khối hộp chữ nhật có
8
đỉnh.
Câu 36: Đa diện đều loại
{
}
5,3
có tên gọi nào dưới đây?
A. Tứ diện đều. B. Lập phương.
C. Hai mươi mặt đều. D. Mười hai mặt đều.
Lời giải
Khối đa diện đều loại
{ }
5,3
là khối mười hai mặt đều.
Câu 37: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Biết cạnh bên
2SA a=
và vuông
góc với mặt đáy. Tính thể tích khối chóp
.
S ABCD
.
A.
3
4
3
a
. B.
3
2a
. C.
3
3
a
. D.
3
2
3
a
.
Lời giải
Gọi
V
là thể tích khối chóp
.S ABCD
. Khi đó:
3
1 12
2.
3 33
a
V SA AB AD a a a= ⋅ ⋅ = ⋅ ⋅⋅=
Câu 38: Cho hình chóp
.S ABCD
đáy là hình chữ nhật
2AD a
=
,
AB a=
( 0)a >
, có
()
SAB
và
()SAD
vuông góc đáy và góc
SC
và đáy bằng
30
°
. Thể tích khối chóp là
A.
3
2
3
a
. B.
3
2 15
9
a
. C.
3
3
6
a
. D.
3
3
3
a
.
Lời giải
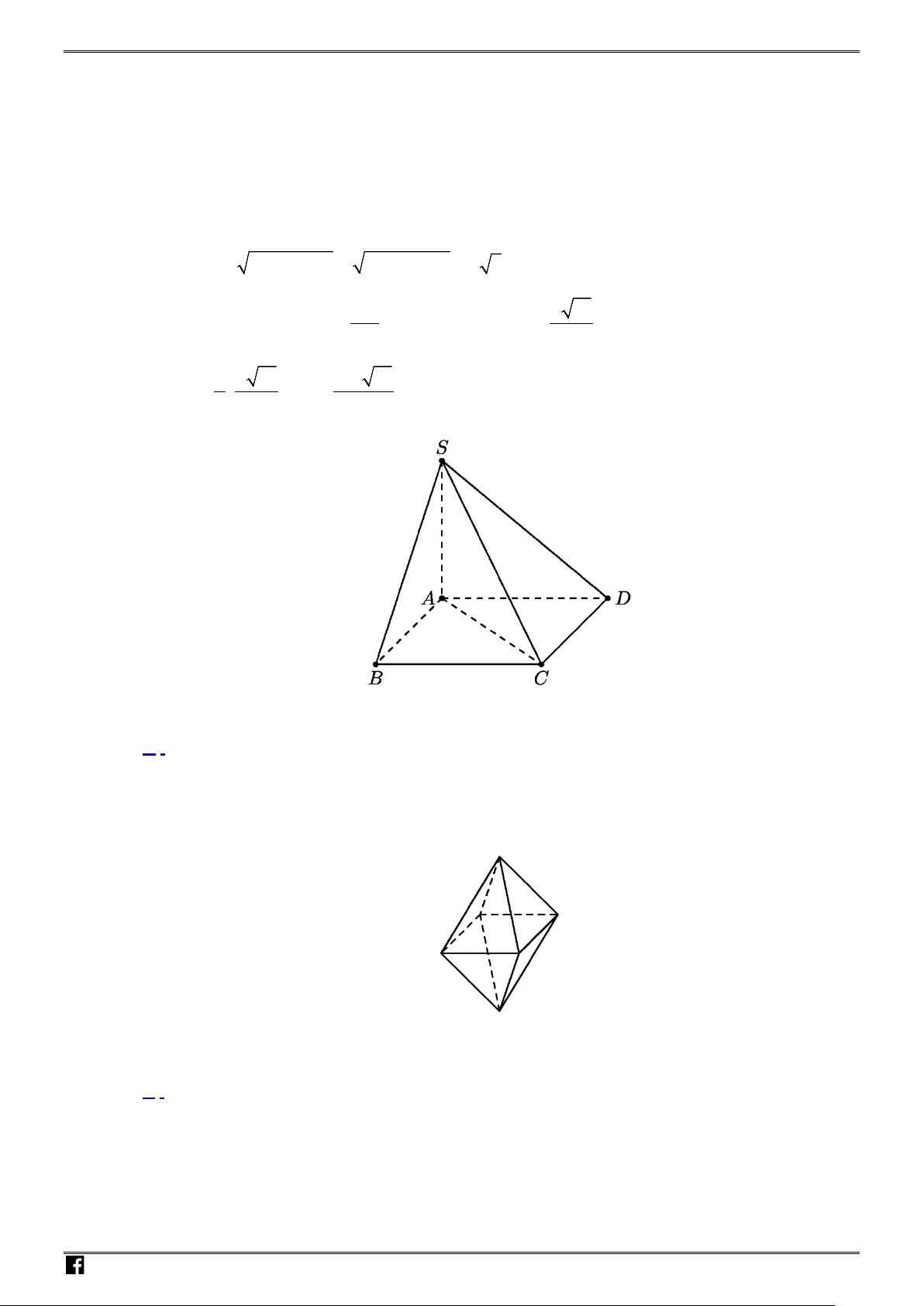
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Từ
( )( )
()() ()
( )( )
SAB ABCD
SAD ABCD SA ABCD
SAB SAD SA
⊥
⊥ ⇒⊥
∩=
.
Suy ra
AC
là hình chiếu vuông góc của
SC
lên
()ABCD
. Hay
(,( ))(, ) 30SC ABCD SC AC SCA
°
= = =
.
Ta có
22 22
5.AC AB BC AB AD a= += +=
Trong
SAC
có
15
tan tan 30 .
3
SA a
SCA SA AC
AC
°
= ⇒= ⋅ =
3
2
.
1 15 2 15
2.
33 9
S ABCD
aa
Va=⋅ ⋅=
Câu 39: Khối bát diện đều có bao nhiêu cạnh?
A.
12
. B.
10
. C.
8
. D.
9
.
Lời giải
Theo hình vẽ, khối bát diện đều có
12
cạnh.
Câu 40: Hãy chọn mệnh đề đúng.
A. Số đỉnh và số mặt trong một hình đa diện luôn bằng nhau.
B. Tồn tại hình đa diện có số đỉnh và số mặt bằng nhau.
C. Tồn tại hình đa diện có số cạnh bằng số mặt.
D. Tồn tại hình đa diện có số đỉnh bằng số cạnh.
Lời giải
Hình tứ diện có số đỉnh và số mặt đều bằng
4
.
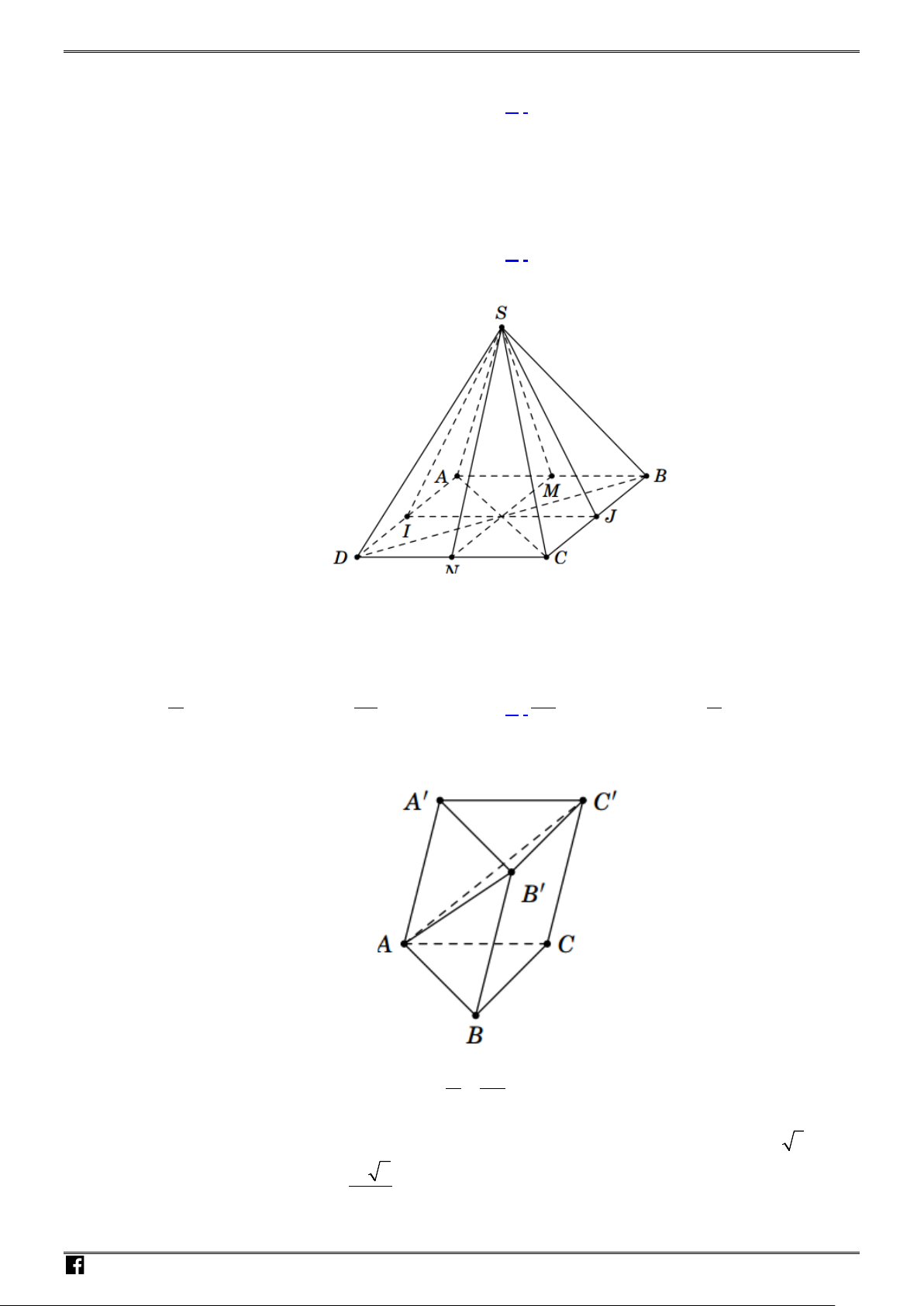
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 41: Có tất cả bao nhiêu khối đa diện đều?
A.
7
. B.
4
. C.
5
. D.
6
.
Lời giải
Có
5
khối đa diện đều là khối tứ diện đều, khối lập phương, khối bát diện đều, khối mười hai
mặt đều và khối hai mươi mặt đều.
Câu 42: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Hình chóp tứ giác đều
.S ABCD
có bốn mặt phẳng đối xứng là
()SAC
,
()SBD
,
()SMN
và
()SIJ
với
, ,,MNIJ
lần lượt là trung điểm
AB
,
CD
,
AD
,
BC
.
Câu 43: Lăng trụ tam giác
.ABC A B C
′′′
có thể tích bằng
V
. Khi đó thể tích khối chóp
.A BCC B
′′
bằng
A.
2
V
. B.
3
4
V
. C.
2
3
V
. D.
3
V
.
Lời giải
Ta có
. ..
2
33
A BCC B ABC A B C A A B C
VV
V V VV
′′ ′′′ ′′′
= − =−=
.
Câu 44: Cho khối lăng trụ
.ABC A B C
′′′
có đáy là tam giác vuông tại
B
, biết
AB a=
,
3BC a=
và thể
tích của khối lăng trụ bằng
3
6
2
a
. Chiều cao của lăng trụ là
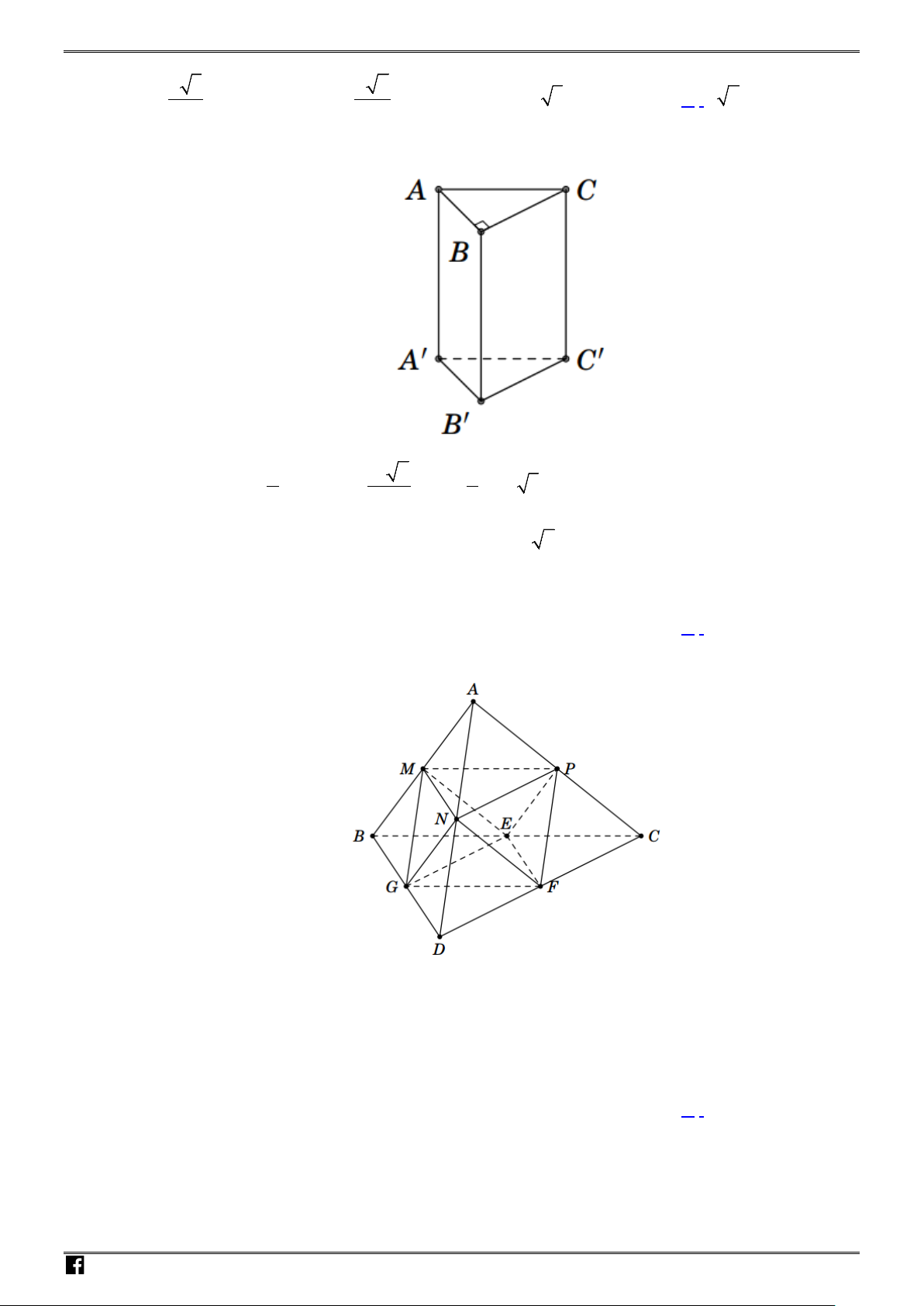
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 23
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
2
a
. B.
2
2
a
. C.
3a
. D.
2a
.
Lời giải
3
.
1 61
3
2 22
ABC A B C
a
V AA BA BC AA a a
′′′
′′
= ⋅ ⋅ ⇔ = ⋅ ⋅⋅
.
Vậy đường cao của lăng trụ
.ABC A B C
′′′
là
2
AA a
′
=
.
Câu 45: Hình tạo bởi
6
đỉnh là
6
trung điểm của các cạnh một tứ diện đều có bao nhiêu mặt phẳng đối
xứng?
A.
6
. B.
3
. C.
4
. D.
9
.
Lời giải
Hình tạo bởi
6
đỉnh là
6
trung điểm của các cạnh một tứ diện đều là một bát diện đều, có
9
mặt phẳng đối xứng.
Câu 46: Cho khối chóp
.S ABC
có thể tích bằng
16
. Gọi
,,MNP
lần lượt là trung điểm của các cạnh
,,SA SB SC
. Tính thể tích
V
của khối tứ diện
AMNP
.
A.
8V =
. B.
14V =
. C.
12V =
. D.
2V =
.
Lời giải
Vì
M
là trung điểm của
SA
nên
( ) ( )
d ,( ) d ,( )A MNP S MNP=
nên
.S MNP
VV=
.
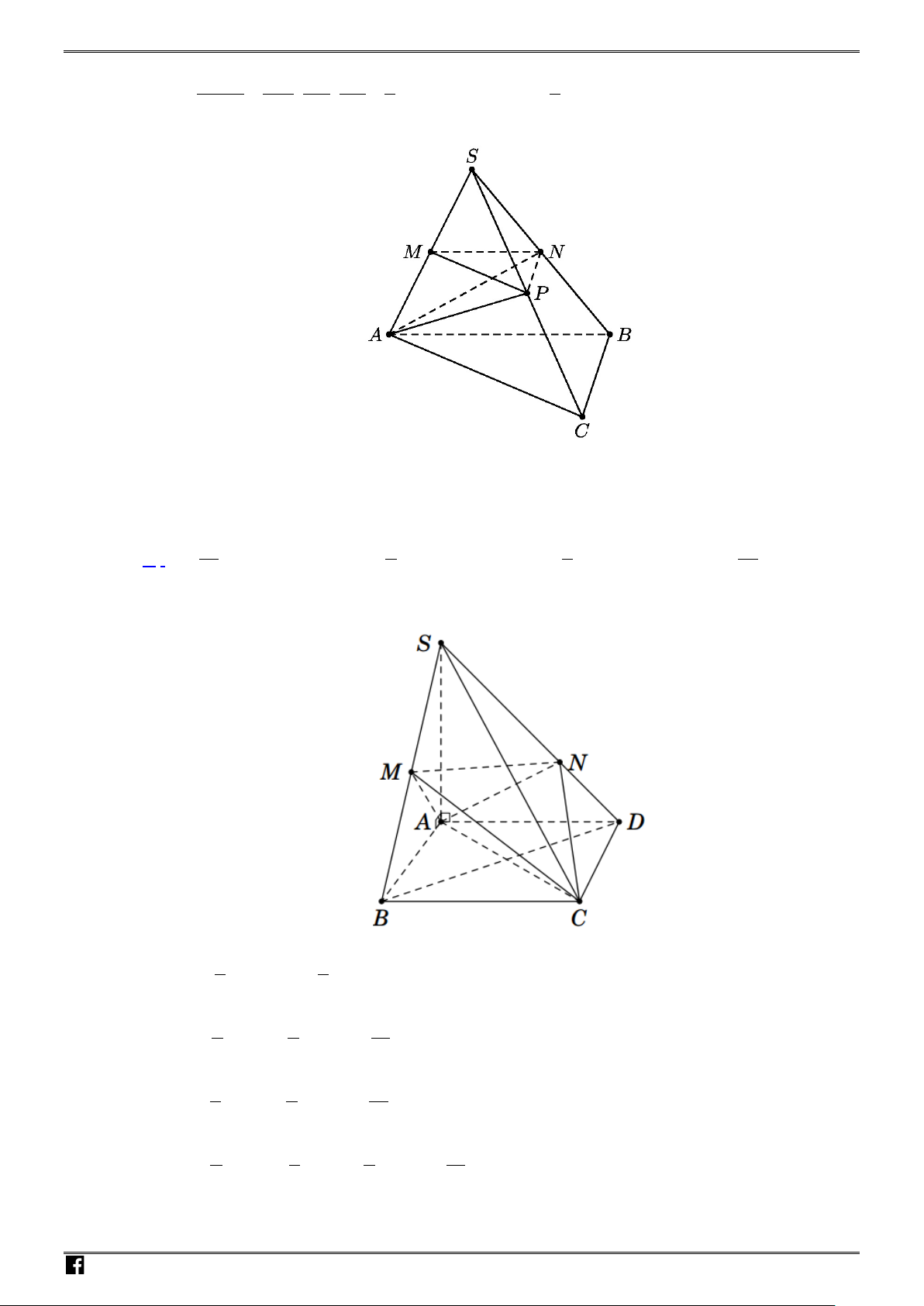
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 24
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lại có
.
.
1
8
S MNP
S ABC
V
SM SN SP
V SA SB SC
= ⋅⋅=
suy ra
..
1
2.
8
S MNP S ABC
VV V= = =
Câu 47: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA a
=
và
SA
vuông góc với
đáy. Gọi
M
là trung điểm của
SB
,
N
thuộc cạnh
SD
sao cho
2SN ND=
. Tính thể tích
V
của
khối tứ diện
ACMN
.
A.
3
1
12
Va
=
. B.
3
1
6
Va=
. C.
3
1
8
Va=
. D.
3
1
36
Va
=
.
Lời giải
3
.
11
33
S ABCD ABCD
V SA S a=⋅=
.
3
...
11 1
2 4 12
M ABC S ABC S ABCD
V VV a= = =
.
3
...
11 1
3 6 18
N ACD S ACD S ABCD
VVV a= = =
.
3
. . ..
2 11 1
3 3 6 18
N SAM D SAM D SAB S ABCD
V V VV a= = = =
.
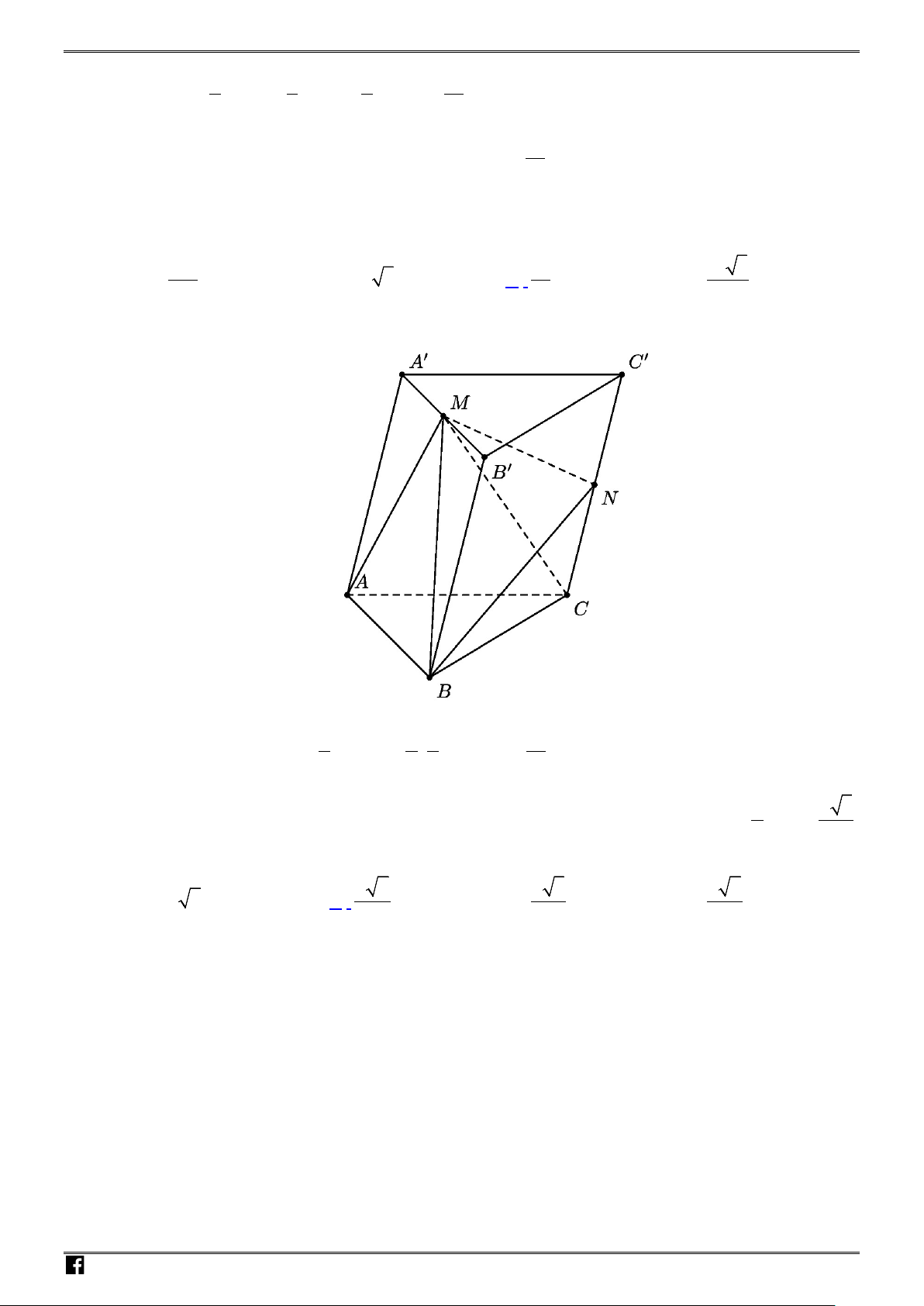
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 25
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
3
. . ..
211 1
3 3 6 18
C SMN C SMD C SBD S ABCD
V VVV a
= = = =
.
3
. ....
1
12
ACMN S ABCD M ABC N ACD N SAM C SMN
VV VVVV a
= −−−−=
.
Câu 48: Cho khối lăng trụ
.ABC A B C
′′′
có thể tích bằng
3
a
. Gọi
,
MN
lần lượt là trung điểm của
AB
′′
và
CC
′
. Tính thể tích khối chóp
ABMN
.
A.
3
2
3
a
. B.
3
3a
. C.
3
3
a
. D.
3
3
2
a
.
Lời giải
Ta có
3
.. .
1 12
2 23 3
ABMN C ABM C ABB A ABC A B C
a
VV V V
′′ ′′ ′
===⋅=
.
Câu 49: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
. Biết
AC a=
,
2
a
BC =
,
3
2
a
SA =
và cạnh
SA
vuông góc với mặt phẳng đáy. Khoảng cách từ
A
đến mặt phẳng
()SBC
bằng
A.
6a
. B.
6
4
a
. C.
3
2
a
. D.
6
2
a
.
Lời giải

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 26
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Kẻ
AH SB⊥
tại
H
. Ta dễ dàng chứng minh được
()
AH SBC⊥
nên
d( ,( ))
A SBC AH
=
.
Xét tam giác vuông
SAB
vuông tại
A
, có
22 2
1 11 6
4
a
AH
AH SA AB
=+ ⇒=
.
Câu 50: Từ một tấm bìa hình vuông
ABCD
có cạnh bằng
5
dm, người ta cắt bỏ bốn tam giác bằng nhau
AMB
,
BNC
,
CPD
,
DQA
. Với phần còn lại, người ta gắp lên và ghép lại để thành hình chóp tứ
giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất?
A.
32
2
. B.
5
2
. C.
22
. D.
52
2
.
Lời giải
Đặt
2MN x=
. Suy ra
FO x=
,
52
2
FC CO FO x=−= −
.
Do đó, đường cao
CO
của hình chóp
.C MNPQ
có độ dài là
2
2
5 2 25
52
22
xx x
− −= −
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 27
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Suy ra thể tích khối chóp là
2
4
5
4
1 25
(2 ) 5 2
32
1 4 52 52 52 52 25
4 52
3 44442
52
25
14
2
4.
35
52
Vx x
xxxx x
= −
=⋅⋅ ⋅⋅⋅⋅⋅−
≤ ⋅⋅
V
lớn nhất khi và chỉ khi
25 5 2
52 22
24
x xx
− = ⇔=
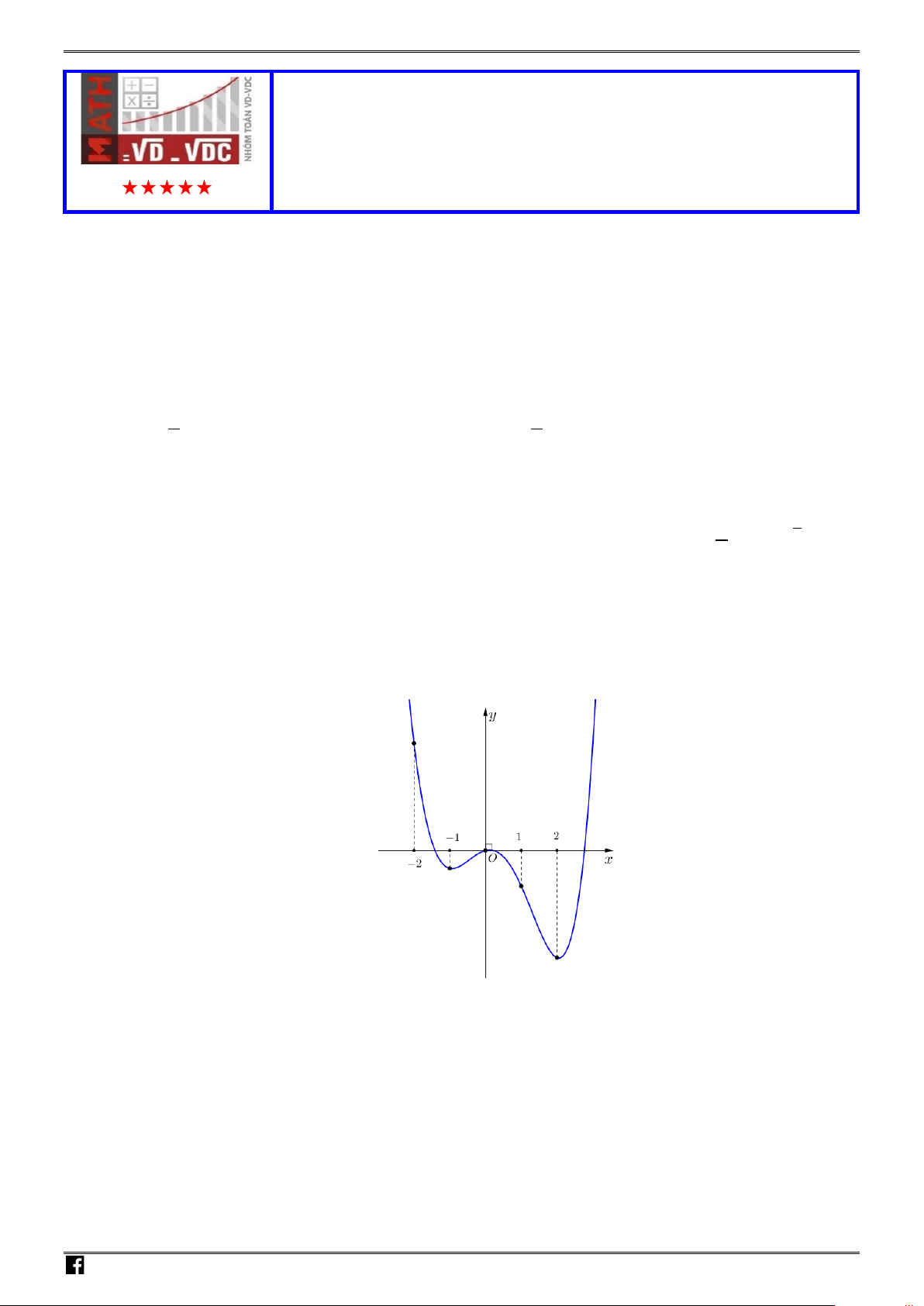
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
ĐỀ THI CUỐI HỌC KỲ 1 – NĂM HỌC 2020 – 2021
TRƯỜNG THPT CHUYÊN ĐẠI HỌC VINH
Môn: Toán
Thời gian:90 phút (Không kể thời gian phát đề)
Câu 1. Giả sử
,ab
là các số thực dương tuỳ ý thoả mãn
23 4
4.
ab =
Mệnh đề nào sau đây đúng?
A.
22
2log 3log 8.ab+=
B.
22
2log 3log 8.ab−=
C.
22
2log 3log 4.ab+=
D.
22
2log 3log 4.
ab−=
Câu 2. Diện tích của mặt cầu có đường kính
AB a=
là
A.
3
4
.
3
a
π
B.
2
.a
π
C.
3
1
.
6
a
π
D.
2
4.a
π
Câu 3. Giả sử
a
,
b
và
α
là các số thực tùy ý
( )
0, 0ab>>
. Mệnh đề nào sau đây đúng?
A.
( )
ab a b
α
αα
= +
. B.
( )
ab a b
α
αα
=
. C.
( )
ab a b
α
αα
+=+
. D.
1
a
ab
b
α
α
α
=
.
Câu 4. Phương trình
( )
log 1 2x +=
có nghiệm là:
A.
11
. B.
9
. C.
101
. D.
99
.
Câu 5. Cho hàm số
(
)
y fx
=
có đồ thị như hình vẽ.
Hàm số đã cho đồng biến trên khoảng
A.
( )
0;1
. B.
( )
2; 1−−
. C.
( )
1; 0−
. D.
( )
1; 2
.
Câu 6. Trong không gian
Oxyz
cho
2 34u jik= −−
. Tọa độ của
u
là:
A.
( )
3; 2; 4−
. B.
( )
2; 3; 4−−
. C.
(
)
3; 2; 4−−
. D.
( )
3;2;4−
.
Câu 7. Khối lăng trụ có
8
đỉnh thì có bao nhiêu mặt?
A.
8
. B.
4
. C.
6
. D.
10
.
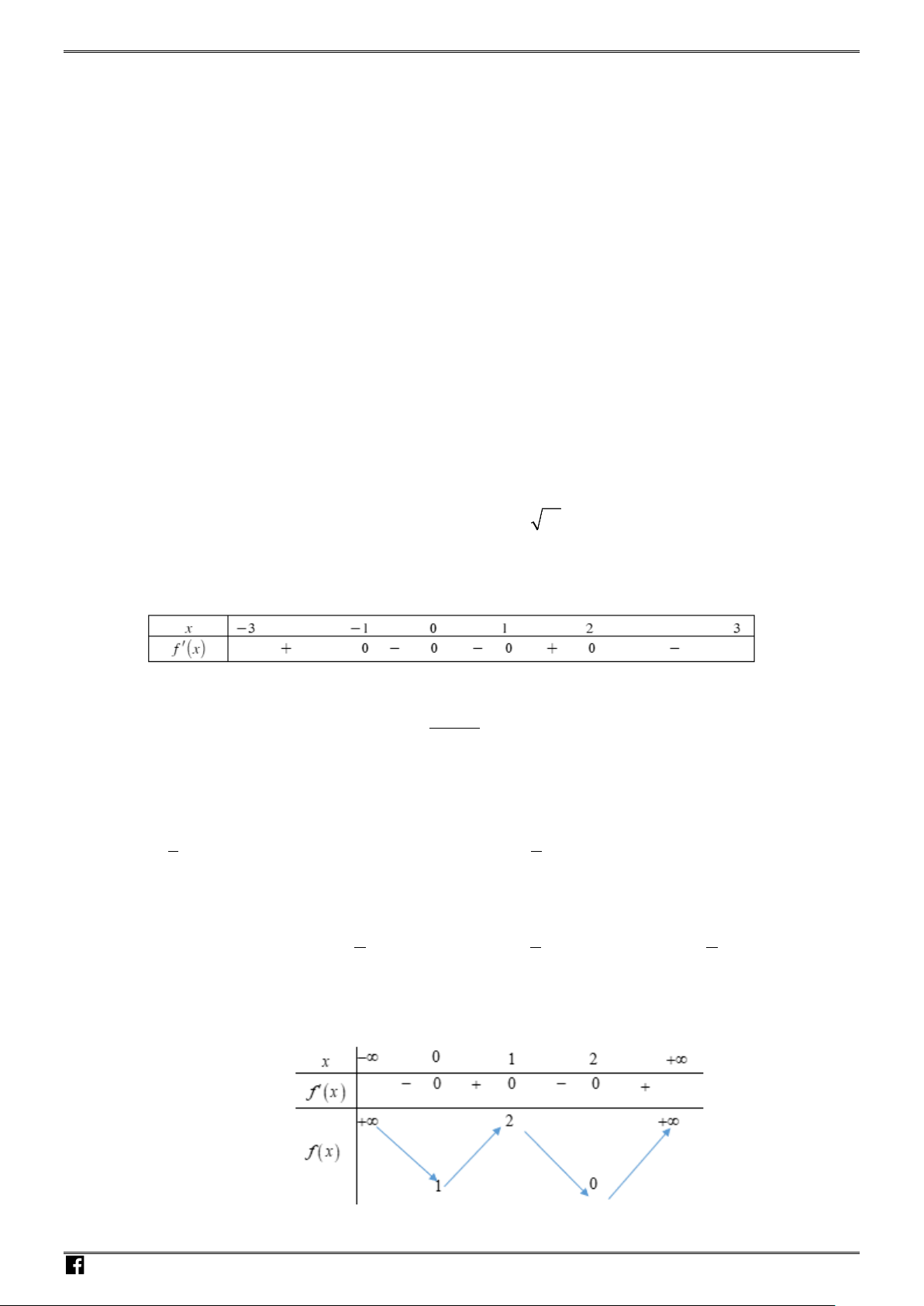
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 8. Biết rằng đường cong ở hình bên là đồ thị của một trong các hàm số dưới đây, đó là hàm số
nào?
A.
32
36yxx x=−+ −
. B.
32
2yx x= −
. C.
32
2yx x
=−+
. D.
32
56yx x x=−+
.
Câu 9. Mỗi mặt của hình bát diện đều là
A. Tam giác đều. B. Hình vuông. C. Bát giác đều. D. Ngũ giác đều.
Câu 10. Trong không gian, khoảng cách từ điểm
1; 2; 3M
đến gốc tọa độ bằng
#A.
2.
B.
3
. C.
14
. D.
1
.
Câu 11. Cho hàm số
y fx
liên tục trên
3;3
và có bảng xét dấy đạo hàm như hình bên. Hàm số đã
cho có bao nhiêu điểm cực trị thuộc khoảng
3;3
.
#A.
4
. B.
2
. C.
1
. D.
3
.
Câu 12. Tiệm cận đứng của đồ thị hàm số
22
1
x
y
x
là
#A.
1.
x
B.
1.y
C.
1x
D.
2y
Câu 13. Khối nón có bán kính đáy, đường cao, đường sinh lần lượt là
,,
rhl
thì có thể tích bằng
A.
22
1
()
3
l hh
π
−
. B.
2
rh
π
. C.
2
1
3
rl
π
. D.
rl
π
.
Câu 14. Thể tích của khối chóp
OABC
có
,,
OA OB OC
đôi một vuông góc bằng
A.
..
OAOB OC
. B.
1
..
2
OAOB OC
. C.
1
..
3
OAOB OC
. D.
1
..
6
OAOB OC
.
Câu 15. Cho hàm số
()y fx=
liên tục trên
và có bảng biến thiên như hình bên. Phương trình
() 2 0fx
−=
có bao nhiêu nghiệm?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2
. B.
3
. C.
1
. D.
4
Câu 16. Tập nghiệm của bất phương trình
2
39
x+
>
là
A.
(
)
1;+∞
. B.
( )
0;+∞
. C.
( )
;0−∞
. D.
(
)
;1−∞
.
Câu 17. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng
(
)
ABCD
. Góc giữa
SB
và
( )
ABCD
bằng
45°
. Thể tích khối chóp
.S ABCD
bằng
A.
3
2
3
a
. B.
3
a
. C.
3
2a
. D.
3
1
3
a
.
Câu 18. Biết rằng
α
;
β
là các số thực thỏa mãn
( ) ( )
2 2 2 82 2
βα β α β
−−
+= +
. Giá trị của
2
αβ
+
bằng
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 19. Diện tích xung quanh của hình trụ có thiết diện qua trục là hình vuông cạnh a bằng:
A.
2
2 a
π
. B.
2
3
2
a
π
. C.
2
a
π
. D.
2
3 a
π
.
Câu 20. Đạo hàm của hàm số
( )
31
31
x
x
fx
−
=
+
là:
A.
( )
( )
2
2
' .3 ln 3
31
x
x
fx= −
+
. B.
(
)
( )
2
2
' .3
31
x
x
fx= −
+
.
C.
( )
( )
3
2
' .3 ln 3
31
x
x
fx=
+
. D.
( )
(
)
2
2
' .3 ln 3
31
x
x
fx
=
+
.
Câu 21. Cho hàm số
( )
y fx=
có đạo hàm
(
)
( )
22
' 1,y fx xx x= = − ∀∈
. Hàm số
( )
yfx= −
đồng
biến trên khoảng nào
A.
( )
2; +∞
. B.
( )
0; 2
. C.
( )
1;1−
. D.
(
)
;1−∞ −
.
Câu 22. Trong không gian
Oxyz
, góc giữa hai véctơ
(
)
1;1; 2
u
và
( )
1; 2;1v
−
bằng
A.
60
. B.
30
. C.
150
. D.
120
.
Câu 23. Đồ thị hàm số
3
3
4
32
xx
y
xx
−
=
−−
có bao nhiêu đường tiệm cận ?
A. 4. B. 3. C. 1. D. 2.
Câu 24. Cho hàm số
( )
y fx=
có đạo hàm trên
và có bảng biến thiên như hình vẽ. Hàm số
( )
12yf x= −
đạt cực tiểu tại
A.
1
2
x = −
. B.
1
2
x =
. C.
1x =
. D.
0x =

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 25. Cho hàm số
1
()
1
x
fx
x
+
=
−
. Biết rằng đường cong ở hình sau là đồ thị của một trong các hàm số
dưới đây, đó là hàm số nào?
A.
( )
1yfx= −−
. B.
( )
1y fx= −
. C.
( )
1yf x= −
. D.
( )
1y fx= +
.
Câu 26. Cho hàm số
( )
y fx=
có đạo hàm trên
là
( )
( )( )
23
34fx x xx x
′
=−−
, hàm số đã cho có
điểm cực đại là :
A.
0x =
. B.
3
x =
. C.
2x = −
. D.
2x =
.
Câu 27. Cho hình chóp
SABC
có đáy
ABC
là tam giác vuông tại
B
,
SA
vuông góc với
( )
ABC
.
Tâm mặt cầu ngoại tiếp hình chóp
.S ABC
là:
A. Trung điểm của
SB
. B. Trung điểm của
AC
.
C. Trung điểm của
SC
. D. Trung điểm của
SA
.
Câu 28. Cho hình hộp chữ nhật
.ABCD A B C D
′′′′
có
1, 2AB AD AA
′
= = =
. Bán kính mặt cầu ngoại tiếp
tứ diện
AB CD
′′
bằng
A.
5
. B.
3
. C.
3
2
. D.
5
2
.
Câu 29. Thể tích khối lăng trụ tứ giác đều
.ABCD A B C D
′′′′
có
2AC AA a
′
= =
là
A.
3
4a
. B.
3
2a
. C.
3
2a
. D.
3
22
a
.
Câu 30. Gọi
,mM
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số
( )
2
4 sinfx x x
π
= +
trên
đoạn
[ ]
1; 2−
. Giá trị của
mM
+
bằng
A.
0
. B.
4
. C.
2−
. D.
4−
.
Câu 31. Cho hàm số
(
)
fx
có đồ thị như hình vẽ bên. Hàm số
( )
32y fx=−−
nghịch biến trên khoảng

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
(
)
2; 4
. B.
( )
;1−∞
. C.
( )
0;3
. D.
( )
3; +∞
.
Câu 32. Biết rằng phương trình
2
22
log 7log 9 0xx− +=
có hai nghiệm là
12
,xx
. Giá trị của
12
xx
là
A.
64
. B.
512
. C.
128
. D.
9
.
Câu 33. Cho khối lăng trụ tam giác
.'' 'ABC A B C
có thể tích là
V
. Tính thể tích khối chóp
. ''B ACC A
là
A.
1
2
V
. B.
3
4
V
. C.
1
3
V
. D.
2
3
V
.
Câu 34. Có bao nhiêu cặp số thực dương
( )
;ab
thỏa mãn
2
log a
là số nguyên dương,
24
log 1 logab= +
và
2 3 11
2ab+<
?
A.
8
. B.
6
. C.
7
. D.
5
.
Câu 35. Trong không gian, cho các điểm
( )
1; 3;1
A −
,
( )
1;1;1B
. Đường thẳng
AB
cắt mặt phẳng
( )
Oyz
tại điểm
M
. Độ dài của
OM
bằng
A.
5
. B.
2
. C.
10
. D.
13
.
Câu 36. Cho khối trụ
( )
T
có thiết diện qua trục là hình vuông. Mặt cầu
( )
S
có bán kính bằng
2
chứa
hai đường tròn đáy của khối trụ
( )
T
. Thể tích khối trụ
( )
T
bằng
A.
2
π
. B.
2
π
. C.
3
π
. D.
π
.
Câu 37. Có bao nhiêu số nguyên âm
a
để phương trình
11
4
9 33 9
xx
xx a+ =+−+
−−
có 2 nghiệm thực
phân biệt?
A.
4
. B. Vô số.C.
5
. D.
7
Câu 38. Một nguồn âm đẳng hướng phát ra từ điểm
O
. Mức cường độ tại điểm
M
cách điểm
O
một
khoảng
R
được tính bởi công thức
2
log
M
k
L
R
=
(Ben), với
0k >
là hằng số. Biết điểm
O
thuộc
đoạn thẳng
AB
và mức cường độ âm tại
A
và
B
lần lượt là
4,3(Ben)
A
L =
và
5(Ben)
B
L =
.
Mức cường độ âm tại trung điểm của
AB
bằng ( Làm tròn đến hai chữ số thập phân)
A.
( )
4,58 Ben
. B.
( )
5, 42 Ben
. C.
( )
4,65 Ben
. D.
( )
9, 40 Ben
.
Câu 39. Hỏi có bao nhiêu số nguyên dương
m
để bất phương trình
( )
2
2
2
log log 32x xm+≥
nghiệm
đúng với mọi
( )
0; 2x∈
?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
13
. B.
8
C.
9
. D.
12
Câu 40. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác cân tại
0
, , 120A AB a BAC= =
, tam giác
SAB
đều và nằm trong mặt phẳng vuông góc với mặt đáy
( )
ABC
. Thể tích của khối chóp
.S ABC
bằng
A.
3
8
a
. B.
3
3
a
. C.
3
3
2
a
. D.
3
2
a
.
Câu 41. Cho
( )
fx
mà hàm số
( )
'y fx=
có bảng biến thiên như hình vẽ bên.
Tất cả các giá trị của tham số
m
để bất phương trình
( )
23
1
3
m x fx x+< +
nghiệm đúng với mọi
( )
0;3x ∈
là
A.
(
)
2
1
3
mf<−
. B.
( )
3mf≤
. C.
( )
0
mf≤
. D.
( )
0mf<
.
Câu 42. Trong không gian
Oxyz
, cho tam giác
ABC
có
( ) ( )
(
)
2;1;1 , 1; 2;1 , 1;1; 2ABC
. Độ dài đường
cao kẻ từ
A
của tam giác
ABC
bằng
A.
6
2
. B.
2
. C.
3
2
. D.
3
Câu 43. Cho hàm số
( )
fx
có bảng xét dấu đạo hàm như hình bên dưới.
Hàm số
(
)
2
1yf x= −
nghịch biến trên khoảng
A.
( )
2; 3−−
. B.
( )
3;2
. C.
( )
2; +∞
. D.
( )
1;1−
.
Câu 44. Cho hàm số
( )
y fx=
. Hàm số
( )
y fx
′
=
có bảng biến thiên như hình vẽ.
Hỏi hàm số
( ) ( )
2
yx f x x= −
có bao nhiêu cực trị ?
A.
1
. B.
2
. C.
0
. D.
3
.
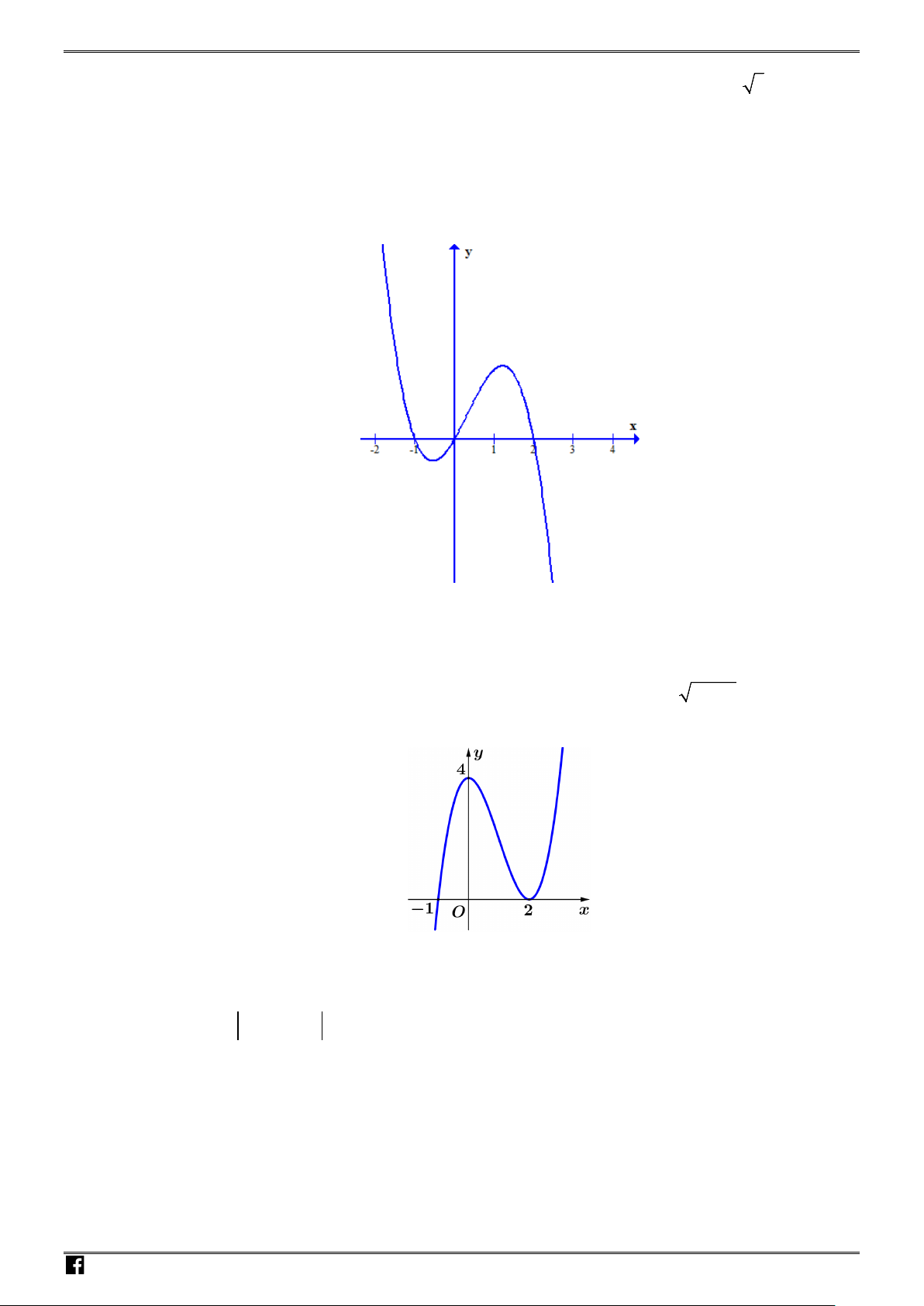
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 45. Cho hình lăng trụ đứng
.
ABC A B C
′′′
có đáy ABC là tam giác vuông tại B,
3AB a=
,
2AC a=
, đường thẳng
BC
′
tạo với mặt phẳng
( )
ACC A
′′
một góc
0
30
. Diện tích của mặt cầu ngoại tiếp
hình lăng trụ đã cho bằng
A.
2
3 a
π
. B.
2
6
a
π
. C.
2
4 a
π
. D.
2
24 a
π
.
Câu 46. Cho hàm số đa thức bậc bốn
()fx
. Đồ thị hàm số
( )
32yf x
′
= −
được cho như hình sau:
Hàm số
()
y fx=
nghịch biến trên khoảng
A.
( )
;1
−∞ −
. B.
(
)
5; +∞
. C.
(
)
1;1−
. D.
( )
1; 5
.
Câu 47. Cho hàm số
( )
y fx=
có đồ thị như hình bên. Phương trình
( )
2 1 631fx x+− + =
có bao
nhiêu nghiệm?
A.
4.
B.
3.
C.
5.
D.
6.
Câu 48. Cho hàm số
432
()f x ax bx cx dx e= + + ++
(
0ae <
). Đồ thị hàm số
()y fx
′
=
như hình bên.
Hàm số
2
4 ()y fx x= −
có bao nhiêu điểm cực tiểu

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
. B.
5
. C.
4
. D.
2
.
Câu 49. Xét các số thực dương
,xy
thỏa mãn
( )
( )
2
22
2
22
4 4 log 4x y xy
xy
+++ + = −
. Khi
4xy
+
đạt
giá trị nhỏ nhất,
x
y
bằng
A.
1
2
. B.
2
. C.
1
4
. D.
4
.
Câu 50. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
,ABaSBa= =
và
(
)
SB ABCD⊥
.
Gọi
M
là trung điểm của
SD
. Biết rằng góc giữa hai mặt phẳng
( )
ACM
và
( )
SAD
bằng
60
°
.
Thể tích khối chóp
.S BCD
bằng
A.
3
3
3
a
. B.
3
2
a
. C.
3
6
a
. D.
3
3
a
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
HƯỚNG DẪN GIẢI ĐỀ THI CUỐI HỌC KỲ 1
NĂM HỌC 2020 – 2021
TRƯỜNG THPT CHUYÊN ĐẠI HỌC VINH
Môn: Toán
Thời gian:90 phút (Không kể thời gian phát đề)
BẢNG ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
B
B
D
C
C
C
D
A
C
D
C
A
D
B
B
D
A
C
D
C
D
D
B
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
C
C
A
B
B
C
D
D
A
B
A
B
C
A
C
A
B
D
B
A
A
A
B
C
Câu 1. Giả sử
,ab
là các số thực dương tuỳ ý thoả mãn
23 4
4.ab =
Mệnh đề nào sau đây đúng?
A.
22
2log 3log 8.
ab+=
B.
22
2log 3log 8.ab−=
C.
22
2log 3log 4.ab+=
D.
22
2log 3log 4.
ab−=
Lời giải
Chọn A
Ta có
( ) ( )
23 4 23 4
2 2 22
4 log log 4 2log 3log 8ab ab a b=⇔ = ⇔+=
.
Câu 2. Diện tích của mặt cầu có đường kính
AB a=
là
A.
3
4
.
3
a
π
B.
2
.
a
π
C.
3
1
.
6
a
π
D.
2
4.a
π
Lời giải
Chọn B
Bán kính
22
AB a
R = =
.
Diện tích mặt cầu
22
4
S Ra
ππ
= =
.
Câu 3. Giả sử
a
,
b
và
α
là các số thực tùy ý
( )
0, 0ab>>
. Mệnh đề nào sau đây đúng?
A.
(
)
ab a b
α
αα
= +
. B.
( )
ab a b
α
αα
=
. C.
(
)
ab a b
α
αα
+=+
. D.
1
a
ab
b
α
α
α
=
.
Lời giải
Chọn B
Câu 4. Phương trình
( )
log 1 2x +=
có nghiệm là:
A.
11
. B.
9
. C.
101
. D.
99
.
Lời giải

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn D
(
)
2
10
1
log 1 2 99
99
1 10
x
x
xx
x
x
+>
>−
+ =⇔ ⇔ ⇔=
=
+=
.
Vậy phương trình đã cho có nghiệm
99x =
.
Câu 5. Cho hàm số
(
)
y fx
=
có đồ thị như hình vẽ.
Hàm số đã cho đồng biến trên khoảng
A.
( )
0;1
. B.
( )
2; 1−−
. C.
(
)
1; 0−
. D.
( )
1; 2
.
Lời giải
Chọn C
Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên các khoảng
( )
1; 0−
và
( )
2; +∞
.
Câu 6. Trong không gian
Oxyz
cho
2 34u jik= −−
. Tọa độ của
u
là:
A.
( )
3; 2; 4−
. B.
( )
2; 3; 4−−
. C.
( )
3; 2; 4−−
. D.
( )
3;2;4−
.
Lời giải
Chọn C
( )
2 3 4 3; 2; 4u jik u= −− ⇔=− −
.
Câu 7. Khối lăng trụ có
8
đỉnh thì có bao nhiêu mặt?
A.
8
. B.
4
. C.
6
. D.
10
.
Lời giải
Chọn C
Khối lăng trụ có
8
đỉnh là khối lăng trụ có đáy là tứ giác
⇒
Khối lăng trụ có
8
đỉnh có
6
mặt
(
4
mặt bên và
2
mặt đáy).
Câu 8. Biết rằng đường cong ở hình bên là đồ thị của một trong các hàm số dưới đây, đó là hàm số nào?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
32
36yxx x=−+ −
. B.
32
2yx x= −
. C.
32
2yx x=−+
. D.
32
56yx x x=−+
.
Lời giải
Chọn D
Đây là đồ thị hàm số bậc ba
32
y ax bx cx d
= + ++
, với hệ số
0a >⇒
Loại đáp án A, C.
Đồ thị cắt trục hoành tại điểm
( )
3; 0 ⇒
Chọn đáp án D.
Câu 9. Mỗi mặt của hình bát diện đều là
A. Tam giác đều. B. Hình vuông. C. Bát giác đều. D. Ngũ giác đều.
Lời giải
Chọn A
Câu 10. Trong không gian, khoảng cách từ điểm
1; 2; 3M
đến gốc tọa độ bằng
#A.
2.
B.
3
. C.
14
. D.
1
.
Lời giải
Chọn C
2
22
1 2 3 14OM
.
Câu 11. Cho hàm số
y fx
liên tục trên
3;3
và có bảng xét dấy đạo hàm như hình bên. Hàm số đã
cho có bao nhiêu điểm cực trị thuộc khoảng
3;3
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
#A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn D
Ta có
1
0
0
1
2
x
x
fx
x
x
fx
đổi dấu tại các điểm
1; 1; 2x xx
hàm số có 3 điểm cực trị trpng khoảng
3;3
.
Câu 12. Tiệm cận đứng của đồ thị hàm số
22
1
x
y
x
là
#A.
1.x
B.
1.
y
C.
1x
D.
2y
Lời giải
Chọn C
Ta có
11
lim ; lim
xx
yy
nên đồ thị hàm số có tiệm cận đứng là
1x
.
Câu 13. Khối nón có bán kính đáy, đường cao, đường sinh lần lượt là
,,
rhl
thì có thể tích bằng
A.
22
1
()
3
l hh
π
−
. B.
2
rh
π
. C.
2
1
3
rl
π
. D.
rl
π
.
Lời giải
Chọn A
2 22
11
( ).
33
V rh l h h
ππ
= = −
Áp dụng công thức tính thể tích khối nón, ta có:
Câu 14. Thể tích của khối chóp
OABC
có
,,OA OB OC
đôi một vuông góc bằng
A.
..OAOB OC
. B.
1
..
2
OAOB OC
. C.
1
..
3
OAOB OC
. D.
1
..
6
OAOB OC
.
Lời giải
Chọn D
1 11 1
. . . ...
3 32 6
OBC
V OA S OA OB OC OA OB OC
∆
= = =
Câu 15. Cho hàm số
()y fx=
liên tục trên
và có bảng biến thiên như hình bên. Phương trình
() 2 0fx−=
có bao nhiêu nghiệm?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2
. B.
3
. C.
1
. D.
4
Lời giải
Chọn B
() 2 0 () 2fx fx−=⇔ =
Số nghiệm của phương trình
() 2 0fx−=
là số hoành độ giao điểm của đồ thị hàm số
()
y fx=
và đường thẳng
2y
=
.
Dựa vào bảng biến thiên ta có phương trình
() 2 0fx−=
có ba nghiệm.
Câu 16. Tập nghiệm của bất phương trình
2
39
x+
>
là
A.
( )
1;+∞
. B.
( )
0;+∞
. C.
( )
;0−∞
. D.
( )
;1−∞
.
Lời giải
Chọn B.
Ta có:
2
39
x+
>
22
33
x
+
>
22x⇔+>
0x⇔>
.
Vậy tập nghiệm của bất phương trình là
( )
0;+∞
.
Câu 17. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng
(
)
ABCD
. Góc giữa
SB
và
( )
ABCD
bằng
45°
. Thể tích khối chóp
.S ABCD
bằng
A.
3
2
3
a
. B.
3
a
. C.
3
2a
. D.
3
1
3
a
.
Lời giải
Chọn D.
Ta có:
( )
( )
; 45SB ABCD SBA= = °
SAB⇒∆
vuông cân tại
A
SA AB a⇒= =
.
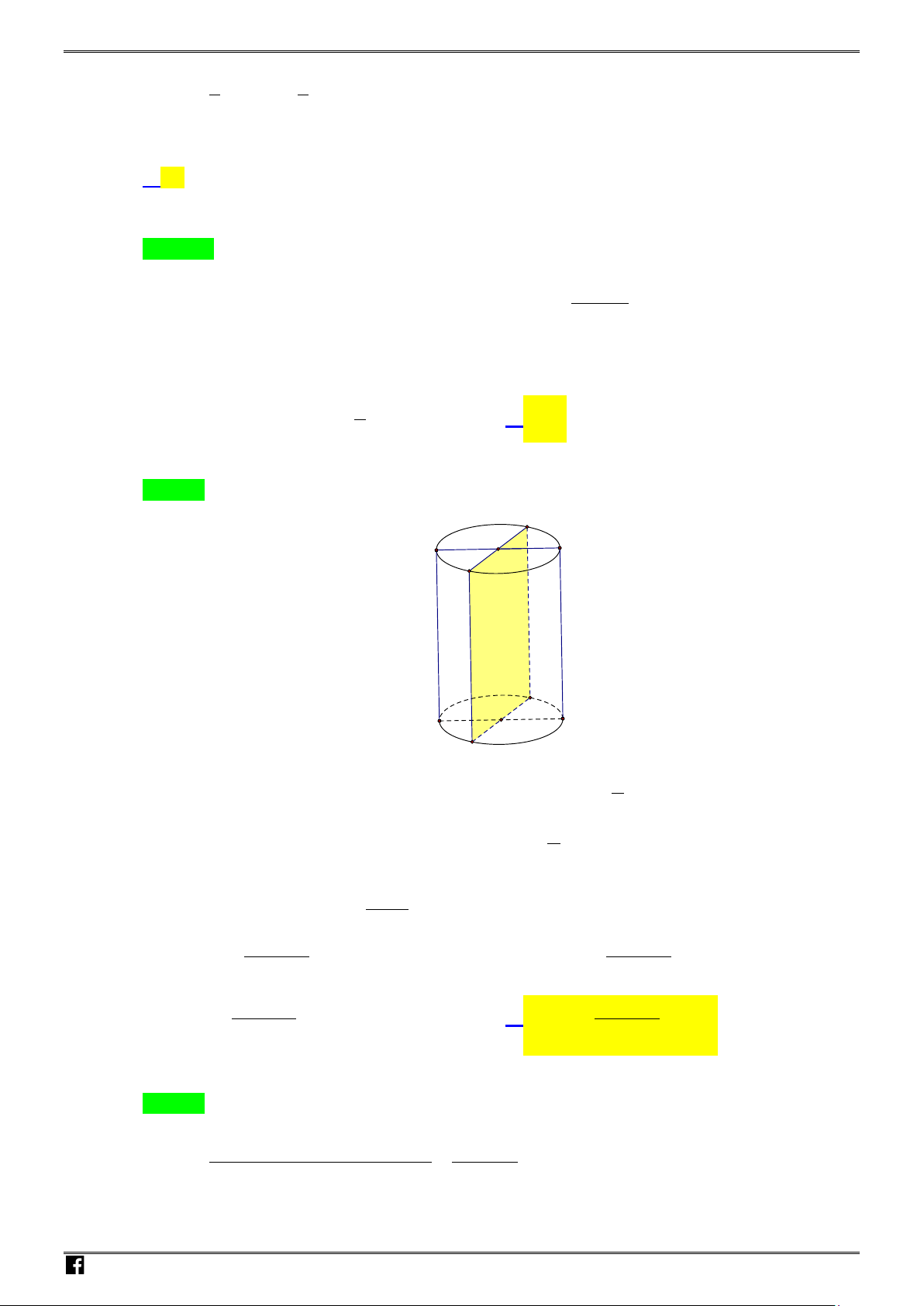
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
2
1
.
3
SABCD
V SA AB=
3
1
3
a
=
.
Câu 18. Biết rằng
α
;
β
là các số thực thỏa mãn
(
) (
)
2 2 2 82 2
βα β α β
−−
+= +
. Giá trị của
2
αβ
+
bằng
A.
3
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn#A.
Ta có:
( )
(
)
2 2 2 82 2
βα β α β
−−
+= +
( )
22
22 2 8
2
αβ
βα β
αβ
+
+
⇔ +=
2 .2 8
β αβ
+
⇔=
23
22
αβ
+
⇔=
23
αβ
⇔+ =
.
Câu 19. Diện tích xung quanh của hình trụ có thiết diện qua trục là hình vuông cạnh a bằng:
A.
2
2
a
π
. B.
2
3
2
a
π
. C.
2
a
π
. D.
2
3 a
π
.
Lời giải
Chọn C
Thiết diện qua trục là
ABCD
hình vuông cạnh a nên ta có
2
a
r =
và
ha=
.
Diện tích xung quang của hình trụ là
2
2 2.
2
xq
a
S rh a a
ππ π
= = =
Câu 20. Đạo hàm của hàm số
( )
31
31
x
x
fx
−
=
+
là:
A.
( )
( )
2
2
' .3 ln 3
31
x
x
fx= −
+
. B.
( )
( )
2
2
' .3
31
x
x
fx= −
+
.
C.
( )
( )
3
2
' .3 ln 3
31
x
x
fx=
+
. D.
( )
( )
2
2
' .3 ln 3
31
x
x
fx=
+
.
Lời giải
Chọn D
( )
( ) ( )
( ) ( )
22
3 ln 3 3 1 3 ln 3 3 1
2
' 3 .ln 3
31 31
xx xx
x
xx
fx
+− −
= =
++
B
A
C
O'
O
D

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 21. Cho hàm số
( )
y fx=
có đạo hàm
( )
( )
22
' 1,y fx xx x
= = − ∀∈
. Hàm số
(
)
yfx
= −
đồng
biến trên khoảng nào
A.
( )
2; +∞
. B.
(
)
0; 2
. C.
( )
1;1−
. D.
( )
;1−∞ −
.
Lời giải
Chọn C
Ta có:
(
)
0
'0
1
x
fx
x
=
= ⇔
= ±
( )
' '( )yfx y f x= −⇒ =− −
Hàm số
(
)
yfx
= −
đồng biến khi và chỉ khi
( )
'( ) 0 ' 0fx f x− −<⇔ − <
1 11 1xx⇔− <− < ⇔ > >−
Câu 22. Trong không gian
Oxyz
, góc giữa hai véctơ
( )
1;1; 2
u
và
( )
1; 2;1v −
bằng
A.
60
. B.
30
. C.
150
. D.
120
.
Lời giải
Chọn D.
( )
( ) (
)
( ) ( )
( )
0
22
22 22
1.1 1. 2 2. 1
. 31
cos , , 120
62
.
1 1 2.1 2 1
uv
uv uv
uv
+ −+ −
= = =−=−⇒ =
+ + +− +−
.
Câu 23. Đồ thị hàm số
3
3
4
32
xx
y
xx
−
=
−−
có bao nhiêu đường tiệm cận ?
A. 4. B. 3. C. 1. D. 2.
Lời giải
Chọn D.
( )
( )
( )
( )
2
32
32
2
22
42
32 21
2 21
x xx
xx xx
y
xx xx
x xx
−+
−+
= = =
−− ++
− ++
Ta có:
3
2
1
lim lim 1
21
1
x
x
x
y
xx
→±∞
→±∞
+
= = ⇒
++
Đồ thị hàm số đã cho có một tiệm cận ngang là
1y =
( )
( )
( )
( )
2
1
1
2
lim lim
1
x
x
xx
y
x
+
+
→−
→−
+
= = −∞ ⇒
+
Đồ thị hàm số đã cho có một tiệm cận đứng là
1x = −
Vậy đồ thị có hai đường tiệm cận.
Câu 24. Cho hàm số
( )
y fx=
có đạo hàm trên
và có bảng biến thiên như hình vẽ. Hàm số
( )
12yf x= −
đạt cực tiểu tại

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
1
2
x
= −
. B.
1
2
x
=
. C.
1x =
. D.
0x =
Lời giải
Chọn B.
(
) ( ) ( )
1
12 1
1
2 12 0 2 12 0 12 0
2
12 2
1
2
x
x
gxfx fx x x
x
x
=
−=−
′′ ′
=− −=⇔⇒− −=⇔−=⇔=
−=
= −
Ta có bảng biến thiên
Ta xét dấu bằng cách thay số
Với
(
) ( )
2 2 2 30
xg f
′′
=⇒ =− −<
Với
33 1
20
44 2
xg f
′′
=⇒ =− −>
Với
11 1
20
44 2
xg f
′′
=⇒=− <
Với
( ) ( )
1 1 230
xg f
′′
=−⇒ − =− >
Vậy hàm số
( )
12
yf x= −
đạt cực tiểu tại
1
2
x =
.
Câu 25. Cho hàm số
1
()
1
x
fx
x
+
=
−
. Biết rằng đường cong ở hình sau là đồ thị của một trong các hàm số
dưới đây, đó là hàm số nào?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
( )
1yfx= −−
. B.
( )
1y fx= −
. C.
( )
1
yf x= −
. D.
( )
1y fx= +
.
Lời giải
Chọn C
Ta có theo đồ thị đề bài thì đồ thị hàm số có đồ thị hàm số có tiệm cận đứng là đường thẳng
0x =
, tiệm cận ngang là đường thẳng
1y =
, cắt trục hoành tại điểm
( )
2;0
.
Xét các đáp án:
( )
11
1
11 2
xx
fx
xx
−−+ −
−− = =
−−− −−
. Đồ thị hàm số có tiệm cận đứng là đường thẳng
2x = −
, không
thỏa mãn. Loại#A.
( )
11
1
11 2
xx
fx
xx
−+
−= =
−− −
, đồ thị hàm số có tiệm cận đứng là đường thẳng
2
x =
, không thỏa
mãn. Loại B.
( )
11 2
1
11
xx
fx
xx
++ +
+= =
+−
đồ thị hàm số có tiệm cận đứng là đường thẳng
0x =
, tiệm cận ngang
là đường thẳng
1
y =
, cắt trục hoành tại điểm
( )
2;0A −
, không thỏa mãn. Loại D.
( )
11 2
1
11
xx
fx
xx
−+ −+
−= =
−− −
, đồ thị hàm số có tiệm cận đứng là đường thẳng
0x =
, tiệm cận
ngang là đường thẳng
1
y =
, cắt trục hoành tại điểm
( )
2;0A
, thỏa mãn.
Vậy chọn đáp án C.
Câu 26. Cho hàm số
( )
y fx=
có đạo hàm trên
là
( )
( )( )
23
34fx x xx x
′
=−−
, hàm số đã cho có
điểm cực đại là :
A.
0x =
. B.
3x =
. C.
2x = −
. D.
2x =
.
Lời giải
Chọn D
Ta có
( )
( )( ) ( ) ( )
23 2 2
0
3
0340340
2
2
x
x
fx xxxx xxxx
x
x
=
=
′
=⇔− −=⇔− −=⇔
=
= −
.
Bảng xét dấu của
()fx
′
là:
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vậy hàm số đạt cực đại tại điểm
2x =
.
Câu 27. Cho hình chóp
SABC
có đáy
ABC
là tam giác vuông tại
B
,
SA
vuông góc với
( )
ABC
. Tâm
mặt cầu ngoại tiếp hình chóp
.S ABC
là:
A. Trung điểm của
SB
. B. Trung điểm của
AC
.
C. Trung điểm của
SC
. D. Trung điểm của
SA
.
Lời giải
Chọn C
Vì
() ,SA ABC SA AC SA BC⊥ ⇒⊥ ⊥
.
Ta có :
( )
( )
,
BC BA
BC SA
BC SAB
AB SA SAB
AB SA
⊥
⊥
⇒⊥
⊂
∩
.
Mà
( )
SB SAB⊂
nên
SB BC⊥
.
Xét tam giác
SBC
vuông tại
B
nên ba điểm
,,SBC
cùng thuộc mặt cầu tâm
I
đường kính
SC
(với
I
là trung điểm của
SC
).
Xét tam giác
SAC
vuông tại
A
nên ba điểm
,,S AC
cùng thuộc mặt cầu tâm
I
đường kính
SC
(với
I
là trung điểm của
SC
).
Vậy bốn điểm
,,,S ABC
cùng thuộc mặt cầu tâm
I
đường kính
SC
(với
I
là trung điểm của
SC
).
I
A
C
B
S

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 28. Cho hình hộp chữ nhật
.ABCD A B C D
′′′′
có
1, 2AB AD AA
′
= = =
. Bán kính mặt cầu ngoại tiếp
tứ diện
AB CD
′′
bằng
A.
5
. B.
3
. C.
3
2
. D.
5
2
.
Lời giải
Chọn C
Chọn hệ trục tọa độ
Oxyz
thỏa mãn
OB
′
≡
,
A
′
thuộc tia
Ox
,
C
′
thuộc tia
Oy
và
B
thuộc tia
Oz
(như hình vẽ)
Khi đó
( ) ( ) ( )
( )
0;0;0 , 1; 0;2 , 0; 2; 2 , 1;2; 0
B AC D
′′
.
Gọi phương trình mặt cầu ngoại tiếp
AB CD
′′
dạng
( )
2 22
: 2 2 2z 0
S x y z ax by c d+ + + + + +=
.
Do
( )
S
đi qua
, ,,AB CD
′′
nên ta có
1
0
2
24 5
1
44 8
1
24 5
0
d
a
a cd
b
b cd
c
a bd
d
=
= −
+ +=−
= −
⇔
+ +=−
= −
+ +=−
=
Vậy bán kính mặt cầu ngoại tiếp tứ diện
AB CD
′′
là
2
22
13
11
22
r
= ++ =
.
Câu 29. Thể tích khối lăng trụ tứ giác đều
.ABCD A B C D
′′′′
có
2AC AA a
′
= =
là
A.
3
4a
. B.
3
2a
. C.
3
2a
. D.
3
22a
.
Lời giải
Chọn A
Trong tam giác vuông
ABC
ta có
22 2
2AB BC AC AB BC a+ = ⇒==
.
Vậy
3
.
. . 2. 2.2 4
ABCD A B C D
V AB BC AA a a a a
′′′′
′
= = =
.
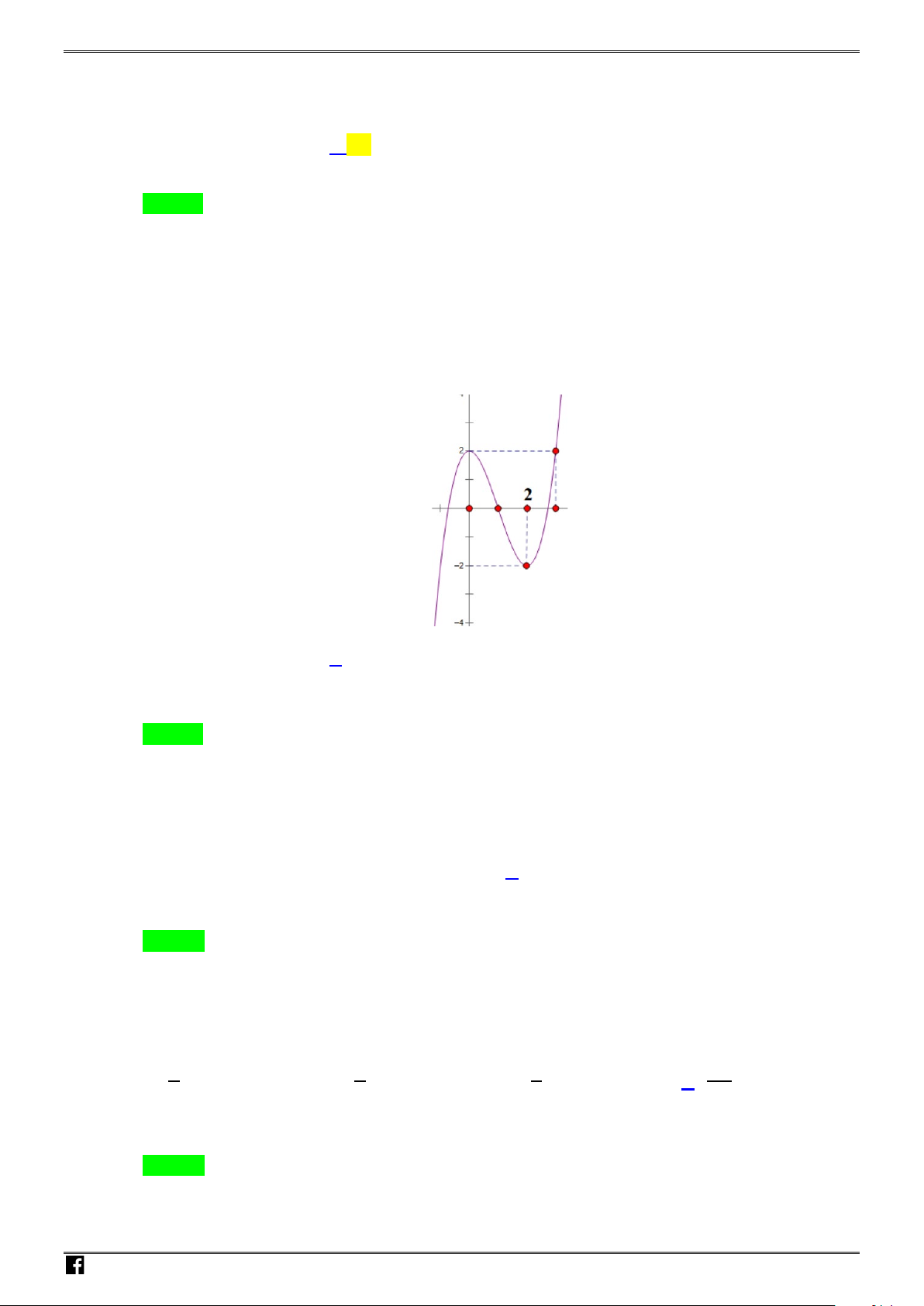
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 30. Gọi
,mM
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số
( )
2
4 sinfx x x
π
= +
trên đoạn
[ ]
1; 2−
. Giá trị của
mM+
bằng
A.
0
. B.
4
. C.
2−
. D.
4−
.
Lời giải
Chọn B
Ta có
( )
4 2 sin .cos 4 sin 2fx x x x
ππ π π π
′
=+=+
Do
( )
[ ]
1 sin 2 1 0 1; 2x fx x
π
′
− ≤ ≤ ⇒ > ∀∈−
.
Vậy
(
) ( ) ( ) ( )
22
1 2 4 sin 8 sin 2 4
mM f f
ππ
+ = − + =−+ − ++ =
.
Câu 31. Cho hàm số
( )
fx
có đồ thị như hình vẽ bên. Hàm số
( )
32y fx=−−
nghịch biến trên khoảng
A.
(
)
2; 4
. B.
( )
;1−∞
. C.
( )
0;3
. D.
(
)
3;
+∞
.
Lời giải
Chọn B
Ta có:
( )
(
)
22
' 3 20 20
20
x
y fx fx
x
−>
′′
=− − <⇔ − >⇔
−<
4
2
x
x
>
⇔
<
Câu 32. Biết rằng phương trình
2
22
log 7log 9 0
xx− +=
có hai nghiệm là
12
,xx
. Giá trị của
12
xx
là
A.
64
. B.
512
. C.
128
. D.
9
.
Lời giải
Chọn C
Ta có:
( )
7
12 2 2 12 2 1 2 2
log log log log 7 2A xx A xx x x A= ⇒ = = + =⇔=
Câu 33. Cho khối lăng trụ tam giác
.'' 'ABC A B C
có thể tích là
V
. Tính thể tích khối chóp
. ''
B ACC A
là
A.
1
2
V
. B.
3
4
V
. C.
1
3
V
. D.
2
3
V
.
Lời giải
Chọn D
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có:
.''' ''' .'''
12
.
3 3 33
BABC ABC ABCABC
V VV
V hS V V= =⇒ =−=
Câu 34. Có bao nhiêu cặp số thực dương
( )
;ab
thỏa mãn
2
log a
là số nguyên dương,
24
log 1 logab
= +
và
2 3 11
2ab+<
?
A.
8
. B.
6
. C.
7
. D.
5
.
Lời giải
Chọn D
Ta có
2
log a
là số nguyên dương nên
2
m
a
=
với
m∈
và
0m >
.
Lại có
( )
( )
2
2 4 24 2 2 2 2
1
log 1 log log log 4 log log 4 log 4 log
2
a b a b a b ba=+⇔= ⇔= ⇔ =
Khi đó
2
2
4
4
a
ba b
= ⇔=
Ta lại có
{ }
66
2 3 11 2 11 2 11
2 2 2 0 0 50,37 2;4;8;1;32
64 64
aa
ab a a a a+<⇔+<⇔+−<⇒<< ⇒∈
Tương ứng mỗi giá trị nguyên dương
a
ta có một giá trị dương
b
.
Vậy có cặp giá trị
(
)
;ab
thỏa mãn yêu cầu đề bài.
Câu 35. Trong không gian, cho các điểm
(
)
1; 3;1A −
,
( )
1;1;1B
. Đường thẳng
AB
cắt mặt phẳng
( )
Oyz
tại điểm
M
. Độ dài của
OM
bằng
A.
5
. B.
2
. C.
10
. D.
13
.
Lời giải
Chọn A
Gọi
( )
M AB Oyz= ∩
.
Ta có
( )
2; 2;0AB = −
⇒
phương trình đường thẳng
( )
12
: 3 2 1 2;3 2;1
1
xt
AB y t M t t
z
=−+
= − ⇒ −+ −
=
.
Khi đó
( ) ( ) ( )
1
1 2 0 0; 2;1 0; 2;1
2
M Oyz t t M OM∈ ⇒− + = ⇔ = ⇒ ⇒ =
.
Vậy
5OM =
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 36. Cho khối trụ
( )
T
có thiết diện qua trục là hình vuông. Mặt cầu
( )
S
có bán kính bằng
2
chứa
hai đường tròn đáy của khối trụ
( )
T
. Thể tích khối trụ
( )
T
bằng
A.
2
π
. B.
2
π
. C.
3
π
. D.
π
.
Lời giải
Chọn B
Gọi
,
hr
lần lượt là chiều cao và bán kính đáy của khối trụ
( )
T
và
R
là bán kính mặt cầu
( )
S
.
Ta có thiết diện qua trục của khối trụ là hình vuông nên
2hr=
.
Lại có mặt cầu chứa hai đáy của khối trụ nên ta suy ra khối trụ nội tiếp mặt cầu.
Khi đó
2
22 22 2
2 11
2
h
rR rR r r
+ = ⇔ = ⇔ =⇒=
(vì
0r
>
)
2h⇒=
.
Vậy thể tích khối trụ bằng
2
2V rh
ππ
= =
.
Câu 37. Có bao nhiêu số nguyên âm
a
để phương trình
11
4
9 33 9
xx
xx a+ =+−+
−−
có 2 nghiệm thực
phân biệt?
A.
4
. B. Vô số.C.
5
. D.
7
Lời giải
Chọn A
Điều kiện:
1
9 30
2
3 90
2
x
x
x
x
−≠
≠
⇔
−≠
≠
Ta có:
11 11
44
9 33 9 9 33 9
xx xx
xx a xx a
+ =+ − +⇔ + −− − =
−− −−
Xét hàm số:
( )
11
4
9 33 9
xx
fx x x= + −− −
−−
( )
11
2 4 khi 4
9 33 9
11
4 khi 4
9 33 9
xx
xx
xx
y fx
x
+ −+ ≥
−−
⇒= =
+− <
−−
( )
( )
( )
( ) (
)
( )
22
22
9 ln 9 3 ln 3
2 khi 4
93 39
1
0, ; 2
2
9 ln 9 3 ln 3
khi 4
93 39
xx
xx
xx
xx
x
fx fx x
x
− − −≥
−−
′′
= ⇒ < ∀≠
−− <
−−
.
Suy ra hàm số
( )
fx
nghịch biến trên mỗi khoảng xác định.
Bảng biến thiên của hàm số

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 23
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Từ bảng biến thiên của hàm số,ta thấy để phương trình đã cho có 2 nghiệm phân biệt thì
40
9
a ≥−
. Vì
a
nguyên âm nên
{
}
40
0 4;3;2;1
9
aa
<≤− ⇒∈−−−−
.
Câu 38. Một nguồn âm đẳng hướng phát ra từ điểm
O
. Mức cường độ tại điểm
M
cách điểm
O
một
khoảng
R
được tính bởi công thức
2
log
M
k
L
R
=
(Ben), với
0k >
là hằng số. Biết điểm
O
thuộc
đoạn thẳng
AB
và mức cường độ âm tại
A
và
B
lần lượt là
4,3(Ben)
A
L =
và
5(Ben)
B
L
=
.
Mức cường độ âm tại trung điểm của
AB
bằng ( Làm tròn đến hai chữ số thập phân)
A.
( )
4,58 Ben
. B.
(
)
5, 42 Ben
. C.
( )
4,65 Ben
. D.
( )
9, 40 Ben
.
Lời giải
Chọn B
Gọi
I
là trung điểm của đoạn
AB
.
Ta có
22
log 10
10
A
A
L
A
L
kk k
L OA
OA OA
= ⇒ = ⇒=
.
22
log 10
10
A
A
L
B
L
kk k
L OB
OB OB
= ⇒ = ⇒=
.
22
log 10
10
A
A
L
I
L
kk k
L OI
OI OI
= ⇒ = ⇒=
Vì
BA
L L OA OB>⇒ >
( )
1 1 1 11 1
22 2
10 10 10 10 10 10
I AB I AB
L LL L LL
k kk
OI OA OB
⇒=−⇒= − ⇒= −
( )
11 1
2log 5, 42 Ben
2
10 10
AB
I
LL
L
⇒=− − ≈
.
Câu 39. Hỏi có bao nhiêu số nguyên dương
m
để bất phương trình
( )
2
2
2
log log 32x xm+≥
nghiệm đúng
với mọi
( )
0; 2x∈
?
A.
13
. B.
8
C.
9
. D.
12

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 24
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn C
Điều kiện:
0x >
Ta có:
(
) (
)
22 2
2 2 2 22
2
log log 32 log 2 5 log log 2log 10x xm x xm x x m+ ≥⇔ + + ≥⇔ + +≥
(
)
1
.
Đặt
(
)
( )
2
log ; 0; 2 ;1
t xx t= ∈ ⇒ ∈ −∞
.
Ta được bất phương trình:
2
2 10tt m++≥
( )
2
.
Bất phương trình
( )
1
nghiệm đúng với mọi
( )
0; 2x
∈
khi và chỉ khi bất phương trình
( )
2
nghiệm đúng với mọi
( )
;1
t
∈ −∞
.
Xét hàm số
( )
2
2 10ft t t=++
.
Bảng biến thiên của hàm số
Từ bảng biến thiên ta thấy, bất phương trình
( ) ( )
, ;1ft m t≥ ∀ ∈ −∞
thì
( )
min 9ft m m≥⇒≤
.
Vì
m
nguyên dương nên
{ }
1; 2;3; 4;5;6;7;8;9m∈
.
Câu 40. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác cân tại
0
, , 120A AB a BAC= =
, tam giác
SAB
đều và nằm trong mặt phẳng vuông góc với mặt đáy
( )
ABC
. Thể tích của khối chóp
.S ABC
bằng
A.
3
8
a
. B.
3
3
a
. C.
3
3
2
a
. D.
3
2
a
.
Lời giải
Chọn A

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 25
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Gọi
H
là trung điểm của cạnh
AB
thì
SH AB
⊥
.
Ta có:
(
) (
)
( ) ( )
( )
( )
,
SAB ABC AB
SAB ABC SH ABC
SH SAB SH AB
∩=
⊥ ⇒⊥
⊂⊥
.
Do tam giác
SAB
là tam giác đều cạnh
a
nên đường cao
3
2
a
SH
=
.
Thể tích của khối chóp
.S ABC
bằng:
3
00
.
1 1 1 1 31
. . . .sin120 . . .sin120
3 3 2 32 2 8
S ABC ABC
aa
V SH S SH AB AC a a
∆
= = = =
.
Câu 41. Cho
( )
fx
mà hàm số
( )
'y fx=
có bảng biến thiên như hình vẽ bên.
Tất cả các giá trị của tham số
m
để bất phương trình
( )
23
1
3
m x fx x+< +
nghiệm đúng với mọi
( )
0;3x ∈
là
A.
( )
2
1
3
mf<−
. B.
( )
3mf≤
. C.
( )
0mf≤
. D.
( )
0mf<
.
Lời giải
Chọn C
Ta có:
( )
23
1
3
m x fx x+< +
( )
32
1
3
m fx x x⇔< + −
với mọi
( )
0;3
x∈
.
Xét hàm số
( ) ( )
32
1
3
gx f x x x= +−
trên
[ ]
0;3
, có
( ) ( )
2
'' 2gx f x x x= +−
.
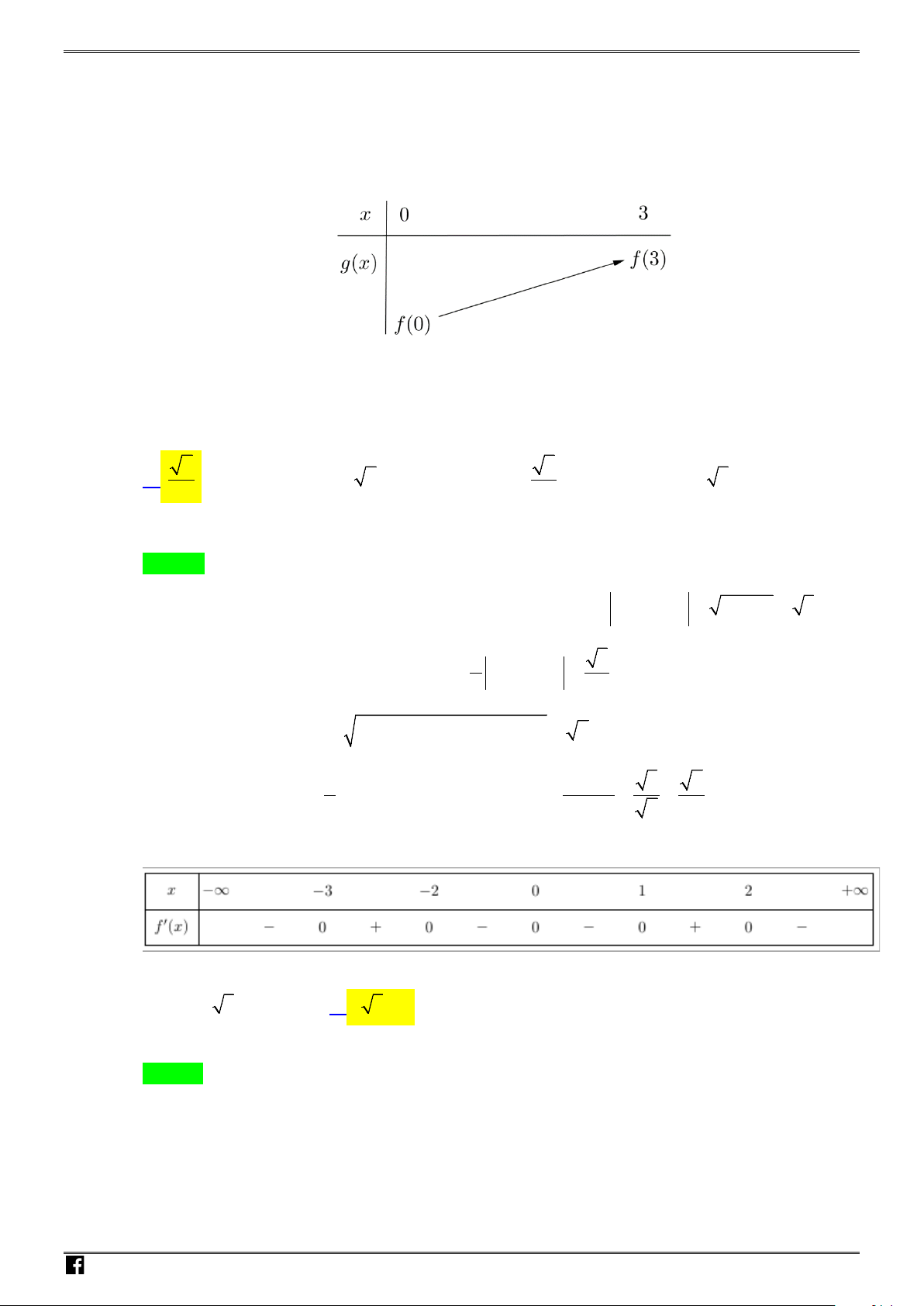
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 26
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
( ) ( )
2
'0'2gx f x xx≥⇔ ≥ −
[ ]
0;3
x
∀∈
.
Theo bảng biến thiên
( )
'1fx>
,
[ ]
0;3x∀∈
, mà
2
2 1,xx x− ≤ ∀∈
( )
[ ]
2
' 2 , 0;3fx xx x⇒ > − ∀∈
nên ta có bảng biến thiên của
(
)
gx
trên
[ ]
0;3
:
Từ bảng biến thiên ta có
( ) ( ) ( )
, 0;3 0m gx x m f< ∀∈ ⇔ ≤
.
Câu 42. Trong không gian
Oxyz
, cho tam giác
ABC
có
( ) ( ) ( )
2;1;1 , 1; 2;1 , 1;1; 2ABC
. Độ dài đường cao
kẻ từ
A
của tam giác
ABC
bằng
A.
6
2
. B.
2
. C.
3
2
. D.
3
Lời giải
Chọn A
Ta có:
(
) ( ) ( )
1;1; 0 , 1; 0;1 , 1;1;1 , 1 1 1 3AB AC AB AC AB AC
=− =− ⇒ = ⇒ = ++=
Diện tích của tam giác
ABC
bằng:
13
,
22
ABC
S AB AC
∆
= =
Độ dài cạnh
BC
là:
( ) (
) ( )
222
11 12 21 2BC = − +− + − =
Mặt khác ta có:
( ) ( )
2
1 36
., . ,
22
2
ABC
ABC
S
S d A BC BC d A BC
BC
∆
∆
= ⇒===
.
Câu 43. Cho hàm số
( )
fx
có bảng xét dấu đạo hàm như hình bên dưới.
Hàm số
( )
2
1yf x= −
nghịch biến trên khoảng
A.
( )
2; 3−−
. B.
( )
3;2
. C.
( )
2; +∞
. D.
( )
1;1−
.
Lời giải
Chọn B
Ta có
( )
2
21y xf x
′′
=−−
.
Xét
( ) (
)
22
21 0 1 0xf x xf x
′′
− − <⇔ − >
.
TH1:
( )
( )
2
0
1 01
x
fx
>
′
−>
.
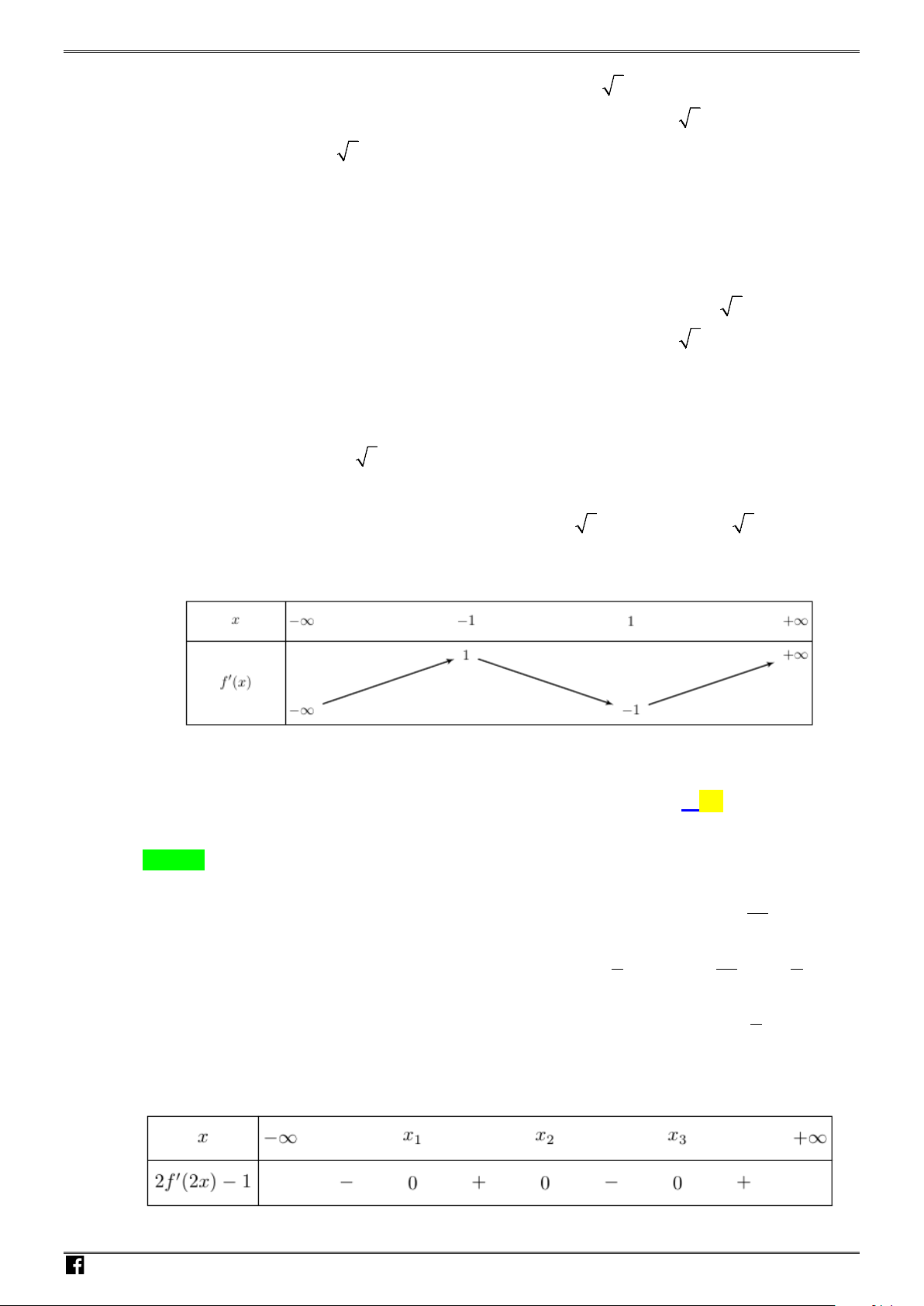
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 27
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Từ giả thiết ta có
( )
22
22
31 2 3 4 3 2
1
11 2 1 0
23
xx x
xx
x
− < − <− < < < <
⇔ ⇔⇔
<− < −< <
− < <−
.
Kết hợp với
0x >
suy ra
32
x<<
.
TH2:
( )
(
)
2
0
1 02
x
fx
<
′
−<
.
Từ giả thiết ta có
( )
22
22
22
22
2
2
13 4
21 0 1 3 1 3
2
01 1 0 1
31
01
12 1
10
x
x
xx
xxx
xx
x
x
xx
x
>
<−
− <− >
−<− < < < < <
⇔ ⇔⇔
<− < < <
− < <−
<<
− > <−
−< <
.
Kết hợp với
0x <
suy ra
2
31
10
x
x
x
<−
− < <−
−< <
.
Từ đó suy ra
( )
2
1yf x= −
nghịch biến trên
( )
;2−∞ −
,
( )
3; 1
−−
,
( )
1; 0−
và
( )
3;2
.
Câu 44. Cho hàm số
( )
y fx=
. Hàm số
( )
y fx
′
=
có bảng biến thiên như hình vẽ.
Hỏi hàm số
( ) ( )
2yx f x x= −
có bao nhiêu cực trị ?
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn D
Ta có
( ) ( )
22 1yx f x
′′
= −
. Khi đó
( ) ( )
11
22
33
1
2
1 11
02
2 22
1
2
xxx
yx f x x x x
xxx
−
= <
−
′′
=⇔ =⇔= <<
= >
.
Từ giả thiết ta có bảng thiên của
( ) ( )
22 1yx f x
′′
= −
như sau

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 28
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Do đó hàm số
( )
2yfxx= −
có ba cực trị.
Câu 45. Cho hình lăng trụ đứng
.
ABC A B C
′′′
có đáy ABC là tam giác vuông tại B,
3AB a=
,
2AC a=
, đường thẳng
BC
′
tạo với mặt phẳng
(
)
ACC A
′′
một góc
0
30
. Diện tích của mặt cầu ngoại tiếp
hình lăng trụ đã cho bằng
A.
2
3 a
π
. B.
2
6 a
π
. C.
2
4 a
π
. D.
2
24 a
π
.
Lời giải
Chọn B
Gọi
O
và
O
′
lần lượt là trung điểm của
AC
và
AC
′′
. Khi đó,
OO
′
là trục của các đường tròn
ngoại tiếp hai đáy ABC và
ABC
′′′
của lăng trụ đứng
.ABC A B C
′′′
. Gọi
I
là trung điểm
OO
′
ta
có:
I A IB IC IA IB IC R
′′′
= = = = = =
hay I chính là tâm của mặt cầu ngoại tiếp hình lăng trụ đã
cho.
Ta có:
( ) ( )
0
;( ) ; 30BC ACC A BC MC BC M
′ ′′ ′ ′ ′
∠ =∠ =∠=
.
Xét tam giác ABC vuông tại B có:
2
2 2 2222
1 1 1 11 4 3
33 2
a
BM
BM BA BC a a a
= + = += ⇒ =
.
Xét tam giác
BMC
′
vuông tại M có:
0
3
2
3
1
sin 30
2
a
BM
BC a
′
= = =
.
Xét tam giác
BCC
′
vuông tại C có:
2 2 22
32CC BC BC a a a
′′
= − = −=
.
Xét tam giác
IOA
vuông tại O có:
2
22 2
26
22
aa
R IO OA a
= + = +=
.
Diện tích mặt cầu ngoại tiếp hình lăng trụ đã cho bằng

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 29
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
2
22
6
44 6
2
a
SR a
ππ π
= = =
.
Câu 46. Cho hàm số đa thức bậc bốn
()fx
. Đồ thị hàm số
( )
32yf x
′
= −
được cho như hình sau:
Hàm số
()
y fx=
nghịch biến trên khoảng
A.
( )
;1
−∞ −
. B.
( )
5; +∞
. C.
( )
1;1−
. D.
( )
1; 5
.
Lời giải
Chọn A
Đặt
32tx= −
. Ta có bảng xét dấu của
( )
32fx
′
−
được mô tả lại như sau:
Từ đó suy ra bảng xét dấu của
()ft
′
:
Vậy hàm số
()y fx=
nghịch biến trên các khoảng
( )
;1
−∞ −
và
( )
3; 5
.
Câu 47. Cho hàm số
( )
y fx=
có đồ thị như hình bên. Phương trình
( )
2 1631fx x+− + =
có bao nhiêu
nghiệm?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 30
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
4.
B.
3.
C.
5.
D.
6.
Lời giải
Chọn A
Xét phương trình
( )
2 1631fx x+− + =
, đặt
1
1 6 3,
2
tx x x= + − + ≥−
Có
3
1 ;0 1
63
t tx
x
′′
=− =⇔=
+
Bảng biến thiên
Dựa vào bảng biến thiên, ta có
1t <−
: phương trình
0
t =
vô nghiệm.
1
,1
2
tt>=−
: phương trình
0t =
có
1
nghiệm.
1
1
2
t−<<
: phương trình
0t =
có
2
nghiệm.
Khi đó phương trình
( )
2 1631fx x+− + =
trở thành
( )
1
2
ft=
có ba nghiệm
( )
1
1; 0t ∈− ⇒
phương trình đã cho có
2
nghiệm
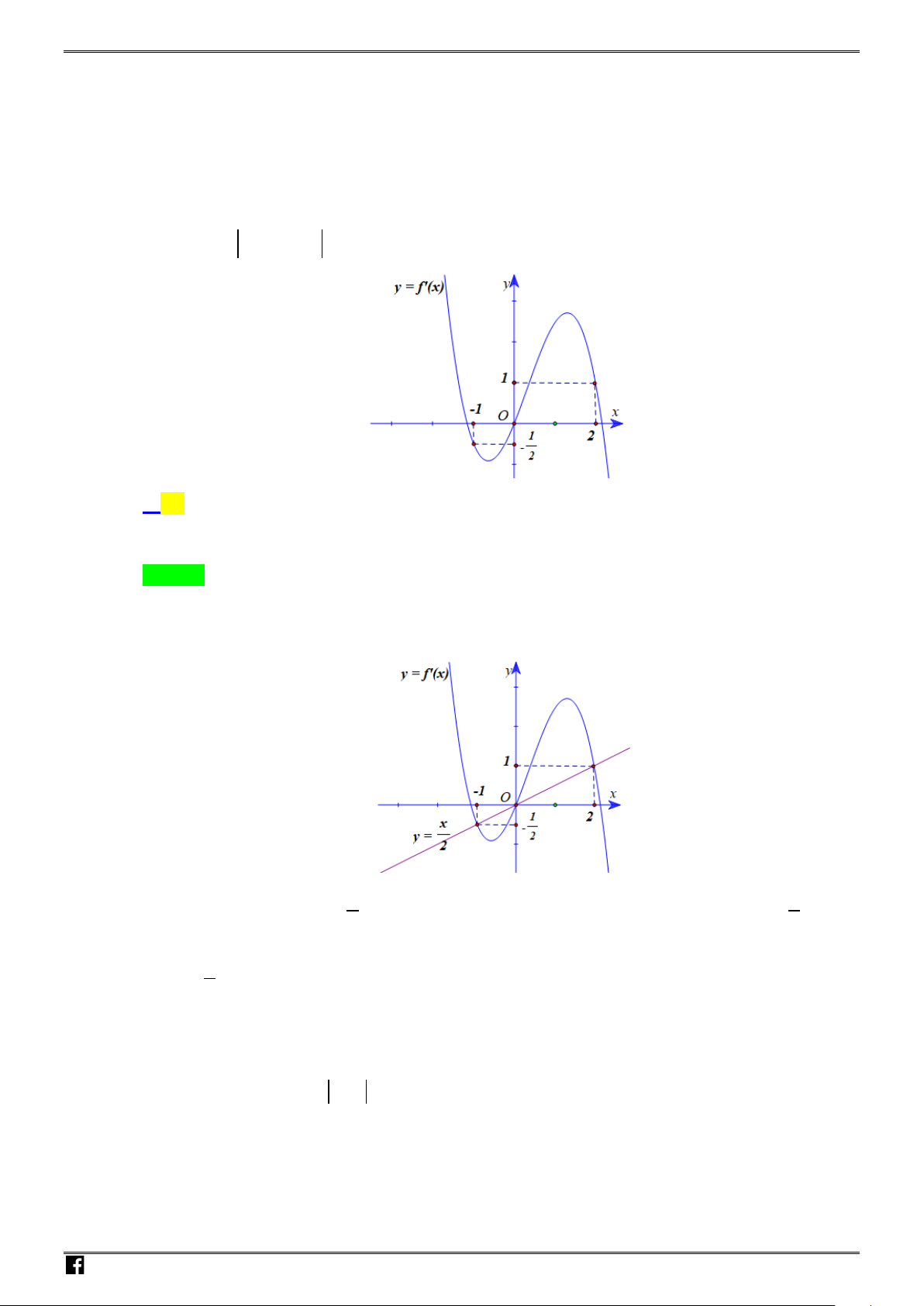
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 31
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
(
)
2
1; 2
∈⇒
t
phương trình đã cho có
1
nghiệm
(
)
3
2;t ∈ +∞ ⇒
phương trình đã cho có
1
nghiệm
Vậy phương trình đã cho có
4
nghiệm.
Câu 48. Cho hàm số
432
()f x ax bx cx dx e= + + ++
(
0ae <
). Đồ thị hàm số
()y fx
′
=
như hình bên.
Hàm số
2
4 ()
y fx x= −
có bao nhiêu điểm cực tiểu
A.
3
. B.
5
. C.
4
. D.
2
.
Lời giải
Chọn A
Đặt
2
() 4 ()gx f x x= −
. Ta có
( )
() 4 () 2 22 ()gx fx x fx x
′′ ′
= −= −
.
Ta có
() 0 ()
2
x
gx f x
′′
=⇔=
. Dựa vào đồ thị hàm số
()y fx
′
=
và đường thẳng
2
x
y =
suy ra
1
() 0
2
2
x
x
fx x
x
= −
′
=⇔=
=
.
Theo hình vẽ ta có
0a <
, mà
00ae e<⇒>
suy ra
(0) 4 (0) 4 0gfe= = >
.
Bảng biến thiên của
()y gx=
như sau:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 32
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Dựa vào đồ thị
()
y gx=
suy ra hàm số
2
4 ()y fx x= −
có 3 điểm cực tiểu.
Câu 49. Xét các số thực dương
,xy
thỏa mãn
( )
( )
2
22
2
22
4 4 log 4x y xy
xy
+++ + = −
. Khi
4xy+
đạt
giá trị nhỏ nhất,
x
y
bằng
A.
1
2
. B.
2
. C.
1
4
. D.
4
.
Lời giải
Chọn B
Ta có:
( )
( )
( )
( )
( )
22 2
22
22
2
22
4 4 log 4 4 8 16 log 4
xy
x y xy x y xy xy
x y xy
+
+++ + = − ⇔ + − ++ = −
.
( ) ( )
( ) ( )
2
2
22
2 log 2 log
x y x y xy xy⇔ + + += +
.
Xét hàm số
( )
( ) ( )
2
, 0 2 1 0, 0ft t tt f t t t ft
′
= + >⇒ = +> ∀>⇒
đồng biến trên
( )
0; +∞
do đó:
( ) ( ) ( ) ( )
2 2*f x y f xy x y xy+ = ⇔ +=
.
Nhận xét
( )
24 4= +≥ ⇒ ≥xy x y xy xy
( )
2 +=x y xy
Đặt
44Px y xP y=+ ⇔=−
thay vào (*) ta có:
(
) ( )
24 4PyyyPy
−+= −
( ) ( )
2
4 6 2 0 **y Py P
⇔ −+ + =
.
Xét bài toán phương trình (**) phải có nghiệm
Ta có
( )
2
2
18
6 32 0 20 36 0
2
P
P P PP
P
≥
∆= + − ≥⇔ − + ≥⇔
≤
.
Lại có
4 4 16=+ ≥ ⇒≥P x y xy P
Vậy
4xy+
đạt giá trị nhỏ nhất bằng
18
khi
( )
2
6
2
3
4 18
x y xy
x
x
y
y
xy
+=
=
⇒ ⇒=
=
+=
.
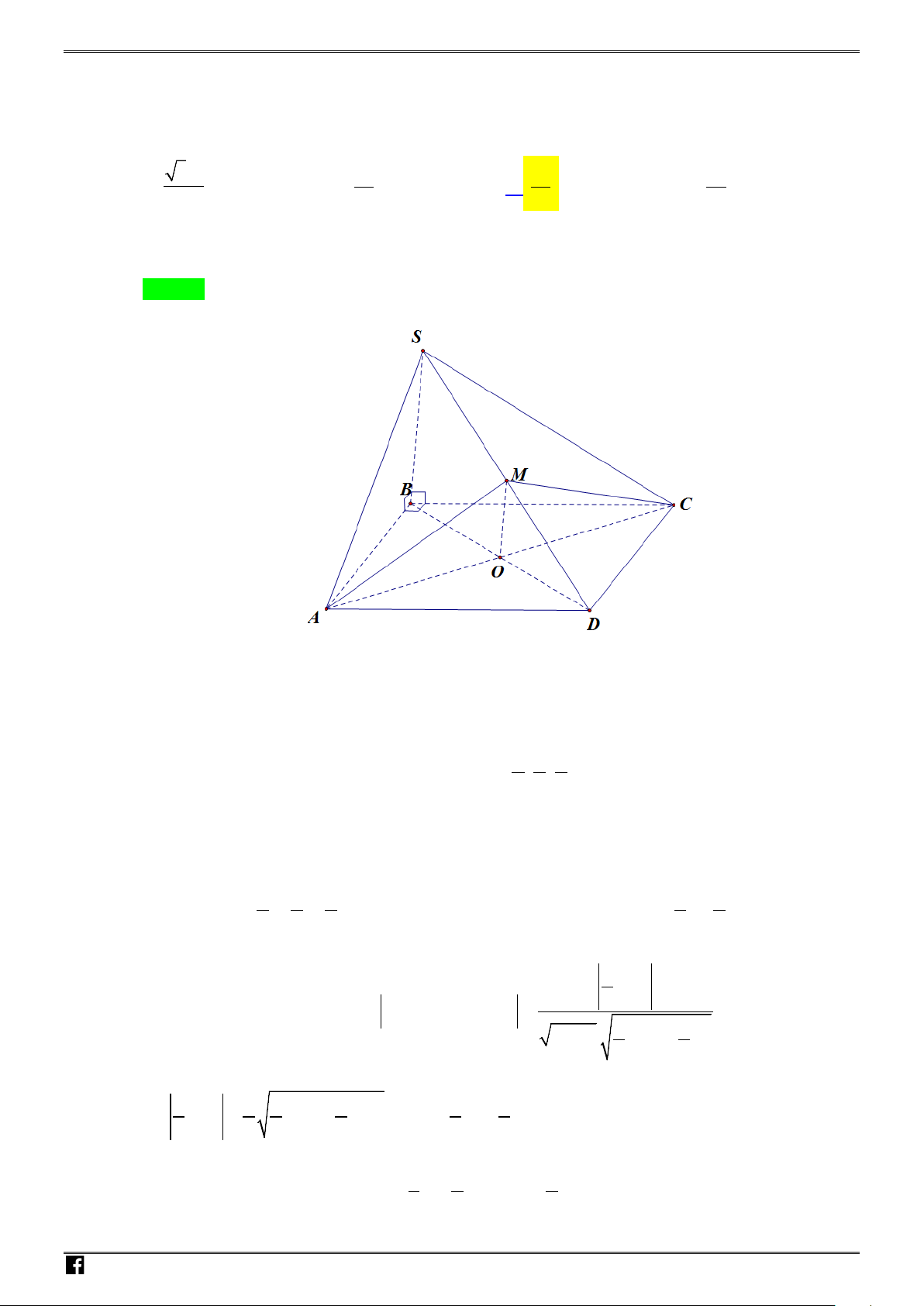
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 33
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 50. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
,ABaSBa= =
và
( )
SB ABCD⊥
.
Gọi
M
là trung điểm của
SD
. Biết rằng góc giữa hai mặt phẳng
(
)
ACM
và
( )
SAD
bằng
60
°
.
Thể tích khối chóp
.S BCD
bằng
A.
3
3
3
a
. B.
3
2
a
. C.
3
6
a
. D.
3
3
a
.
Lời giải:
Chọn C
Đặt
AD x
=
.
Chọn hệ trục tọa độ sao cho
( )
0;0;0 , ; ;≡ ≡≡≡B O Ox BA Oy BC Oz BS
khi đó
( ) ( ) ( ) ( )
;0;0 , 0;0; , 0; ;0 ; ;0 , ; ;
222
⇒
axa
Aa S a C x Dax M
.
Ta có:
( ) ( )
( )
(
)
;0; ; 0; ;0 , ;0;
SAD
SA a a AD x n SA AD ax ax
=− = ⇒= =
.
Lại có:
( )
( )
2
11
; ; ; a; ;0 , ; ;0
222 2 2
CAM
axa
MA AC x n MA AC ax a
= −− =− ⇒ = =−
.
Khi đó:
( ) ( )
( )
( ) ( )
( )
22
22 22 4
1
2
cos ; cos , cos 60
11
2.
44
°
= = =
+
SAD CAM
ax
SAD CAM n n
ax ax a
.
22 44 62 2 2 2
1 11 1 1 1
2 22 2 2 2
ax ax ax x x a x a⇔ = + ⇔ = + ⇒=
.
Thể tích khối chóp
.S BCD
là:
3
11 1
. ., .
32 6
V SB AB AD a= =
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 34
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
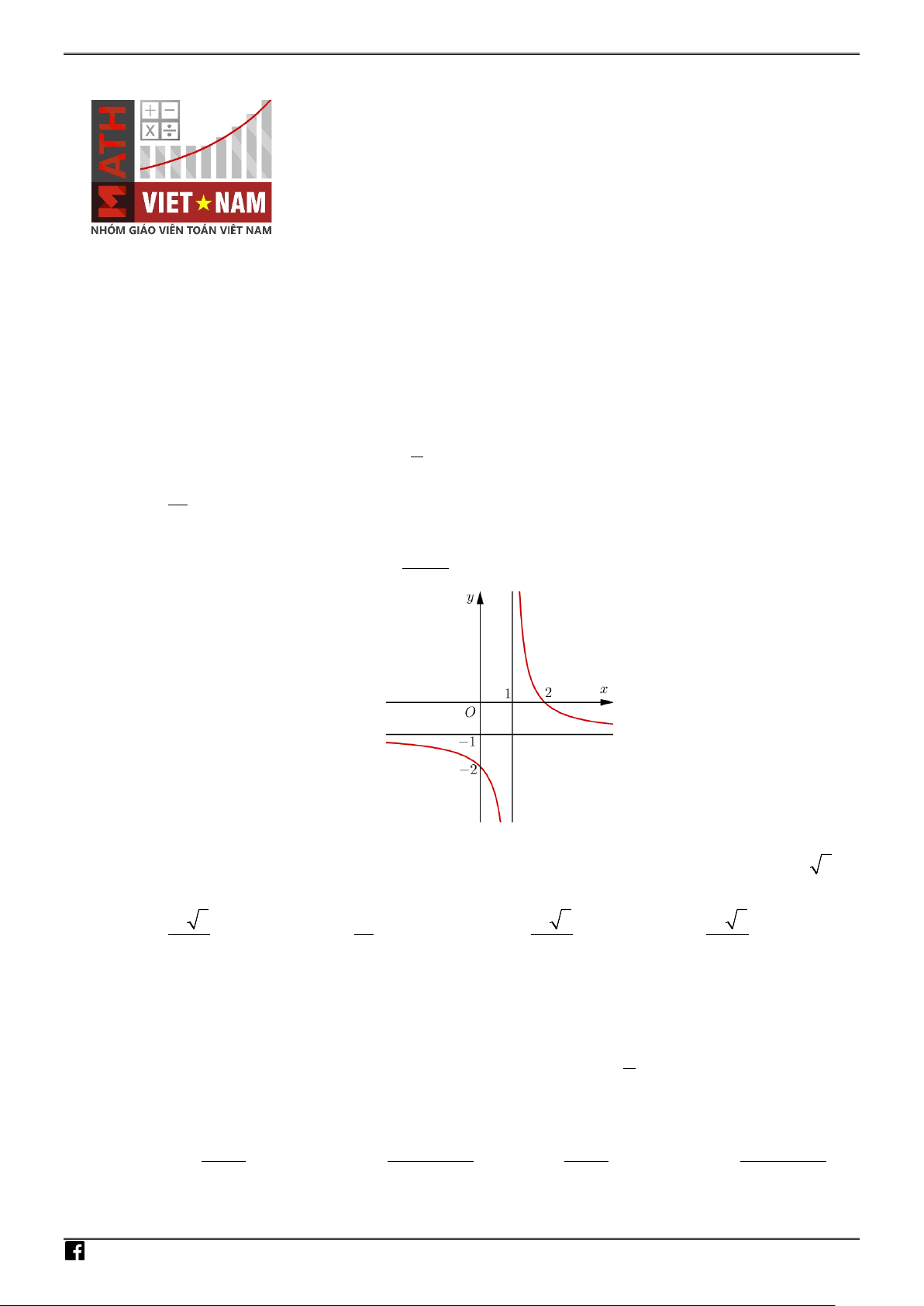
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
KIỂM TRA GIỮA KÌ I LỚP 12
TRƯỜNG THPT VŨNG TÀU
NĂM HỌC:2021-2022
THỜI GIAN: 90 PHÚT
Câu 1. Phương trình
4 6.2 16 0
xx
− −=
có bao nhiêu nghiệm
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 2. Cho hình nón có bán kính đáy
r
và độ dài đường sinh
l
. Khi đó diện tích xung quanh của hình
nón được tính theo công thức
A.
2
xq
S rl
π
=
. B.
xq
S rl
π
=
. C.
3
xq
Sr
π
=
. D.
2
4
xq
Sr
π
=
.
Câu 3. Giá trị nhỏ nhất của hàm số
4
yx
x
= +
trên khoảng
(
)
0;
+∞
bằng
A.
17
2
. B.
4−
. C.
5
. D.
4
.
Câu 4. Đồ thị hình bên là của hàm số
(
)
2
,
ax
y ab
xb
+
= ∈
+
. Khi đó tổng
ab+
bằng
A.
2−
. B.
1
−
. C.
0
. D.
1
.
Câu 5. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
A
với
AB a=
. Cạnh bên
3SA a=
và
SA
vuông góc với mặt phẳng đáy. Thể tích khối chóp
.
S ABC
bằng
A.
3
3
2
a
. B.
3
4
a
. C.
3
3
3
a
. D.
3
3
6
a
.
Câu 6. Cho các số thực dương
a
,
b
với
1a ≠
. Khẳng định nào sau đây đúng?
A.
( )
2
log 2 log
aa
ab b
= +
. B.
( )
2
log 1 log
aa
ab b
= +
.
C.
( )
2
log 1 2 log
aa
ab b= +
. D.
( )
2
1
log log
2
aa
ab b= +
.
Câu 7. Tính đạo hàm của hàm số
( )
3
log 2 1yx= +
.
A.
2
21
y
x
′
=
+
. B.
( )
2
2 1 ln 3
y
x
′
=
+
. C.
1
21
y
x
′
=
+
. D.
( )
1
2 1 ln 3
y
x
′
=
+
.
Câu 8. Hàm số
42
23yx x=−−
đạt cực trị tại các điểm
1
x
,
2
x
,
3
x
. Tính
123
Sxx x=++
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2−
. B.
0
. C.
1−
. D.
2
.
Câu 9. Cho hàm số
31
2
x
y
x
−
=
−
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên các khoảng
( )
;2−∞
và
( )
2; +∞
.
B. Hàm số đồng biến trên
{ }
2\
.
C. Hàm số nghịch biến trên các khoảng
( )
;2−∞
và
( )
2; +∞
.
D. Hàm số nghịch biến trên
{ }
2\
.
Câu 10. Tính thể tích của một hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao lần lượt là
3
m
,
1m
,
3m
.
A.
3
9m
. B.
3
3
m
. C.
3
9
2
m
. D.
3
7 m
.
Câu 11. Cho hàm số
(
)
y fx=
xác định trên
{ }
\1−
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình sau
Tìm tập hợp tất cả các giá trị của tham số
m
để phương trình
( )
fx m=
có đúng 3 nghiệm thực
phân biệt.
A.
[
)
4; 2
−
. B.
(
]
4; 2−
. C.
(
)
4; 2
−
. D.
(
]
;2−∞
.
Câu 12. Cho hàm số
( )
y fx=
xác định và có đạo hàm trên trên
{ }
\ 2;1−
và có bảng biến thiên như
sau
Số đường tiệm cận của đồ thị hàm số là
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 13. Tìm tập xác định
D
của hàm số
( )
31yx
π
= −
.
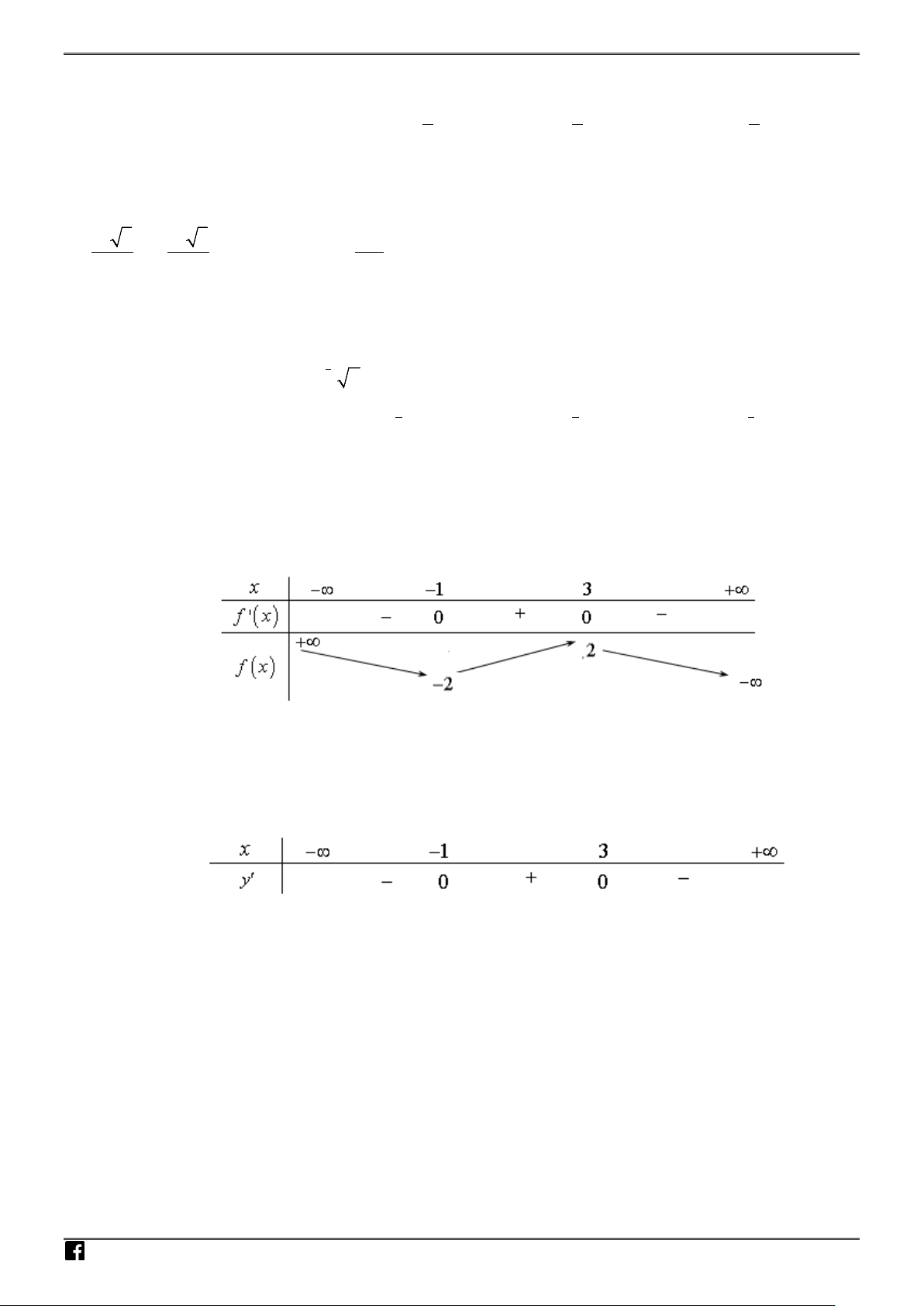
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
D =
. B.
1
\
3
D
=
. C.
1
;
3
D
= +∞
. D.
1
;
3
D
= +∞
.
Câu 14. Cho hình lăng trụ đứng
D. ' ' ' 'ABC A B C D
có đáy là hình vuông cạnh
a
, cạnh bên bằng
2a
. Thể tích của khối lăng trụ
D. ' ' ' 'ABC A B C D
là
A.
3
3
2
a
. B.
3
3
6
a
. C.
3
2a
3
. D.
3
2a
.
Câu 15. Tổng tất cả các nghiệm của phương trình
2
4x 5
28
x −+
=
là
A.
2
−
. B.
4
−
. C.
2
. D.
4
.
Câu 16. Rút gọn biểu thức
1
6
3
.Pa a=
, với
0a
>
ta được
A.
2
Pa=
. B.
2
9
Pa=
. C.
1
2
Pa=
. D.
1
8
Pa=
.
Câu 17. Phương trình
( )
4
log 1 3x −=
có nghiệm
A.
65x =
. B.
82x =
. C.
63x =
. D.
80x =
.
Câu 18. Cho hàm số
( )
y fx=
liên tục trên
và có bảng biến thiên
Hàm số đã cho đồng biến trên khoảng
A.
( )
3; +∞
. B.
(
)
1; 3
−
. C.
( )
2; 2−
. D.
( )
;1−∞ −
.
Câu 19. Cho hàm số
( )
y fx=
liên tục trên
và có bảng xét dấu đạo hàm được cho ở hình dưới
Hỏi hàm số đã cho có bao nhiêu điểm cực trị
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 20. Hàm số nào trong các hàm số dưới đây có đồ thị như hình vẽ bên?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
42
2yx x=−+
. B.
3
32yx x=−+
. C.
3
2y xx
=− −+
. D.
3
2yx= +
.
Câu 21. Khối đa diện đều loại
{ }
4;3
có bao nhiêu mặt?
A.
20
. B.
12
. C.
6
. D.
4
.
Câu 22. Cho khối chóp
.
S ABC
có thể tích bằng 6. Gọi
,
MN
lần lượt là trung điểm các cạnh
,SB SC
. Thể
tích
V
của khối chóp
.S AMN
là
A.
3V
=
. B.
4V =
. C.
3
2
V =
. D.
9
2
V =
.
Câu 23. Cắt mặt cầu
(
)
S
bằng một mặt phẳng cách tâm mặt cầu một khoảng bằng
4
cm
ta được thiết diện
là một đường tròn có bán kính bằng
4cm
. Bán kính của mặt cầu
( )
S
là
A.
10cm
. B.
7cm
. C.
12cm
. D.
5cm
.
Câu 24. Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài
2a
. Thể tích của khối
nón bằng?
A.
3
3
6
a
π
. B.
3
3a
π
. C.
3
3
3
a
π
. D.
3
3
12
a
π
.
Câu 25. Gọi
,Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
32
32yx x=−+ +
trên
[ ]
0;3
.
Giá trị của
Mm+
bằng?
A. 6. B. 8. C. 10. D. 4.
Câu 26. Trong các hàm số sau, hàm số nào đồng biến trên
?
A.
2
3
x
y
=
. B.
2
3
x
y
=
. C.
( )
0,99
x
y =
. D.
( )
23
x
y = −
.
Câu 27. Cho hình chóp đều
.S ABC
có độ dài cạnh đáy là
2a
, cạnh bên tạo với mặt đáy một góc
60°
.
Tính thể tích khối chóp
.S ABC
?
A.
3
23
3
a
. B.
3
3
3
a
. C.
3
3
6
a
. D.
3
23a
.
Câu 28. Số giao điểm của đồ thị hàm số
3
43yx x=−+
và đường thẳng
3yx= +
là
A.
1
. B.
3
. C.
2
. D.
0
.
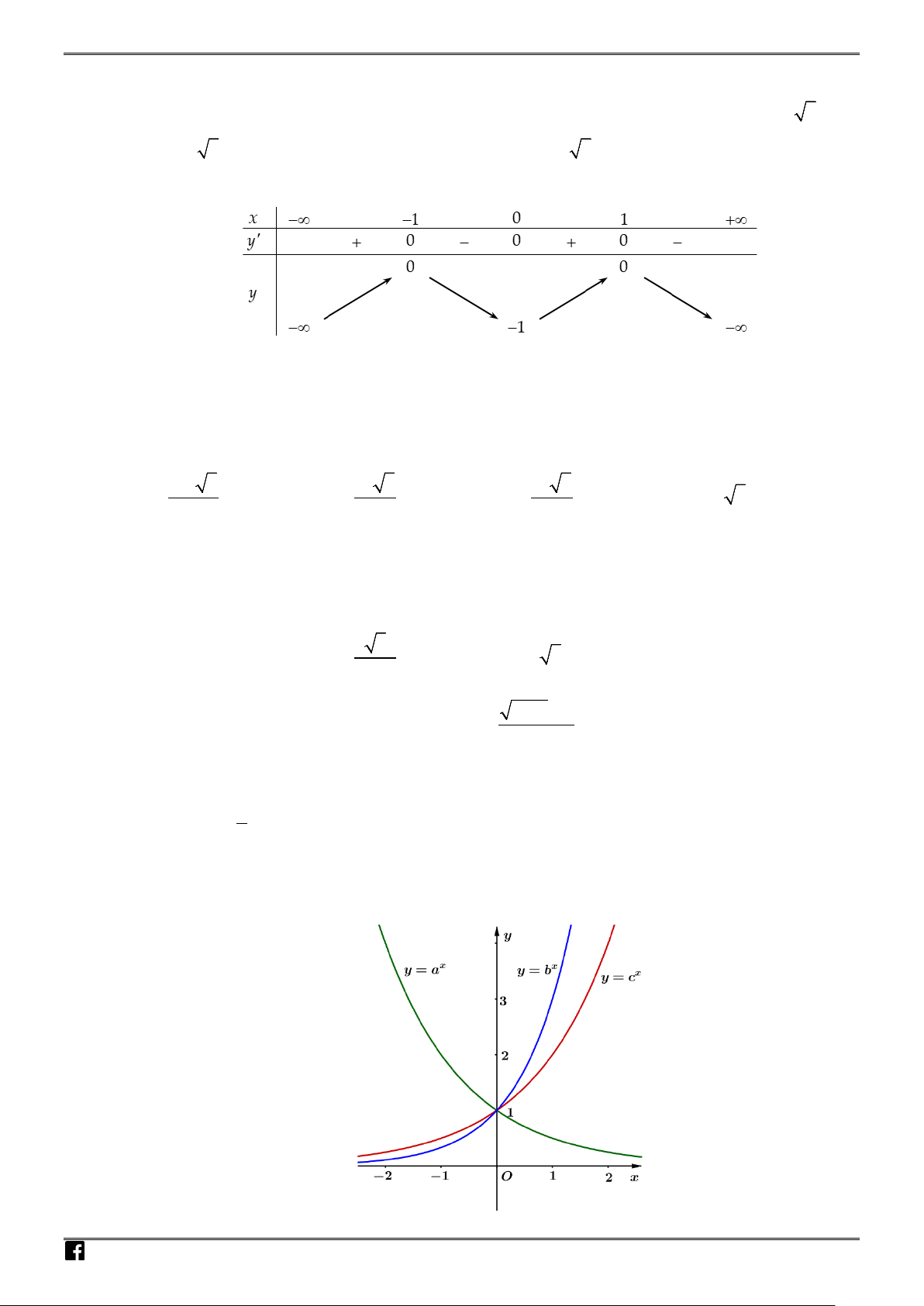
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 29. Tính diện tích xung quanh của hình trụ biết hình trụ có bán kính đáy
a
và đường cao
3a
.
A.
3
3a
π
. B.
3
2 a
π
. C.
3
23a
π
. D.
3
a
π
.
Câu 30. Hàm số nào trong các hàm số dưới đây có bảng biến thiên như sau?
A.
42
31yx x=−−
. B.
42
21yx x=−+
. C.
42
21yx x=−+ −
. D.
3
31yxx=−+ −
.
Câu 31. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có góc giữa hai mặt phẳng
( )
A BC
′
và
( )
ABC
bằng
60°
và
AB a=
. Khi đó thể tích của khối đa diện
ABCC B
′′
bằng
A.
3
33
8
a
. B.
3
3
8
a
. C.
3
3
4
a
. D.
3
3a
.
Câu 32. Cho hình chóp
.S ABCD
có đáy là hình chữ nhật
3, 4AB a AD a= =
. Cạnh bên
SA
vuông góc
với mặt đáy,
SC
tạo với mặt phẳng đáy một góc
60°
. Tính bán kính của mặt cầu ngoại tiếp hình
chóp
.S ABCD
theo
a
.
A.
10a
. B.
53
2
a
. C.
53a
. D.
5a
.
Câu 33. Số đường tiệm cận đứng của đồ thị hàm số
2
93x
y
xx
+−
=
+
là
A.
2
. B.
4
. C.
1
. D.
3
.
Câu 34. Hàm số
( )
322
1
11
3
y x mx m m x= − + −+ +
đạt cực đại tại điểm
1x =
khi
A.
2
m = −
. B.
1
m = −
. C.
2m
=
. D.
1m =
.
Câu 35. Cho đồ thị của ba hàm số
x
ya=
,
x
yb
=
,
x
yc=
như hình vẽ bên. Khẳng định nào sau đây đúng?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
bca>>
. B.
bac
>>
. C.
cab>>
. D.
cb a>>
.
Câu 36. Có bao nhiêu số nguyên
m
để đồ thị hàm số
(
)
(
)
42
16
y m x mx m
= − +− +
có đúng một điểm
cực trị?
A.
6
. B.
1
. C.
4
. D.
5
.
Câu 37. Cho hàm số
( )
y fx=
liên tục trên
và có đồ thị như hình vẽ dưới.
Gọi
M
,
m
theo thứ tự là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( )
2y fx= −
trên đoạn
[
]
1;5
. Tổng
Mm+
bằng
A.
8
. B.
7
. C.
9
. D.
1
.
Câu 38. Một người gửi
50
triệu đồng vào một ngân hàng theo hình thức lãi kép với lãi suất
6%
/ năm.
Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn
100
triệu đồng bao gồm cả
gốc và lãi? Giả sử trong suốt thời gian gửi lãi suất không đổi và người đó không rút tiền ra.
A.
12
năm. B.
14
năm. C.
13
năm. D.
11
năm.
Câu 39. Cho hình trụ có bán kính đáy bằng
.a
Cắt hình trụ bởi một mặt phẳng
( )
P
song song với trục
của hình trụ và cách trục của hình trụ một khoảng bằng
2
a
ta được thiết diện là một hình vuông.
Thể tích khối trụ bằng
A.
3
3 a
π
. B.
3
3a
π
. C.
3
3
4
a
π
. D.
3
a
π
.
Câu 40. Số giá trị nguyên của
m
để hàm số
3
3
mx
y
xm
−+
=
−
nghịch biến trên từng khoảng xác định là.
A.
2
. B.
5
. C.
3
. D.
7
.
Câu 41. Cho hàm số
( )
y fx=
có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của
m
để phương trình
( )
0fx m−=
có 8 nghiệm phân biệt?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
62
m
−< <
. B.
16m<<
. C.
03m<<
. D.
02m<<
.
Câu 42. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2,
a
mặt phẳng
( )
SAB
vuông góc với mặt
phẳng đáy. Tính thể tích khối chóp
.S ABCD
theo
a
biết
,3SA a SB a= =
.
A.
3
23a
. B.
3
43
3
a
. C.
3
4
3
a
. D.
3
23
3
a
.
Câu 43. Biết rằng phương trình
( )
2
2
13
9
4log 9 log 8 0
27
x
x
+ −=
có hai nghiệm phân biệt
12
,xx
. Tính
12
P xx=
.
A.
4
3
−
.
B.
2
3
. C.
2
9
. D.
6
3
−
.
Câu 44. Người ta thả một viên bi hình cầu với bán kính
3cm
vào một cái ly dạng hình trụ đang chứa
nước. Người ta thấy viên bi chìm xuống đáy ly và chiều cao của nước dâng lên
1cm
. Biết rằng
chiều cao của nước trong ly ban đầu là
7,5
cm
. Tính thể tích
V
của khối nước ban đầu trong ly
(kết quả làm tròn đến hàng phần trăm).
A.
3
1272,35cm
.
B.
3
636,17cm
. C.
3
282,74cm
. D.
3
848,23cm
.
Câu 45. Cho hình chóp tứ giác đều
.S ABCD
. Gọi
M
là điểm đối xứng của
C
qua
D
,
N
là trung điểm
của
.SC
Mặt phẳng
( )
BMN
chia khối chóp
.S ABCD
thành hai phần. Tỉ số thể tích giữa hai
phần (phần lớn trên phần bé) bằng
A.
7
3
.
B.
5
4
. C.
7
5
. D.
6
5
.
Câu 46. Cho hàm số
( )
y fx=
có đạo hàm trên
và có đồ thị là đường cong như hình vẽ bên. Đặt
( ) ( )
gx f f x=
. Tìm số nghiệm của phương trình
( )
0
gx
′
=
.
x
y
2
4
3
2
1
O
-
4
2
6−
3−
O
y
x

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
8
. B.
6
. C.
2
. D.
4
.
Câu 47. Cho hình lăng trụ tam giác
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
A
và
AB a=
,
3AC a=
. Tính thể tích khối lăng trụ
.ABC A B C
′′′
biết
2AA AB AC a
′′′
= = =
.
A.
3
3a
. B.
3
3
2
a
. C.
3
2
a
. D.
3
3
3
a
.
Câu 48. Có bao nhiêu giá trị của tham số
m
để phương trình
( )
2
9 2 13 8 0
xx
m mm− + +−=
có hai nghiệm
1
x
,
2
x
thỏa mãn
12
2xx+=
?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 49. Biết
a
b
(trong đó
a
b
tối giản và
*
,
ab
∈
) là giá trị của tham số
m
để hàm số
(
)
32 2
2 3 6 3 1 2020y x mx m x= − − −+
có hai điểm cực trị
12
,xx
thỏa mãn
( )
12 1 2
21xx x x+ +=
.
Tính
2Pa b= +
.
A.
6
. B.
5
. C.
8
. D.
7
.
Câu 50. Cho các số thực dương
,xy
thỏa mãn
3
1
log 3 3 4
3
y
xy x y
x xy
−
= ++ −
+
. Giá trị nhỏ nhất của biểu
thức
Pxy= +
bằng
A.
43 4
9
+
. B.
43 4
9
−
. C.
43 4
3
+
. D.
43 4
3
−
.
HẾT

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
ĐỀ THI HỌC KÌ 1 – NĂM HỌC 2020 – 2021
THPT VŨNG TÀU
Môn: Toán
Thời gian:90 phút (Không kể thời gian phát đề)
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14
15 16 17 18 19
20 21 22 23 24
25
B B D A D A B B C A C C D D D C B B A D C C D C B
26 27
28 29
30 31 32 33 34
35 36 37 38 39
40 41 42 43 44
45 46 47 48 49
50
A A B C C C D C C A A B A B B D D D D C B B B C D
Câu 1. Phương trình
4 6.2 16 0
xx
− −=
có bao nhiêu nghiệm
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Phương trình
2
28
4 6.2 16 0 2 6.2 16 0 2 8 3
2 2( )
x
xx xx x
x
x
l
=
− −=⇔ − −=⇔ ⇔=⇔=
= −
.
Vậy phương trình có nghiệm
3
x =
Câu 2. Cho hình nón có bán kính đáy
r
và độ dài đường sinh
l
. Khi đó diện tích xung quanh của hình
nón được tính theo công thức
A.
2
xq
S rl
π
=
. B.
xq
S rl
π
=
. C.
3
xq
Sr
π
=
. D.
2
4
xq
Sr
π
=
.
Lời giải
Chọn B
Ta có xung quanh của hình nón được tính theo công thức
xq
S rl
π
=
.
Câu 3. Giá trị nhỏ nhất của hàm số
4
yx
x
= +
trên khoảng
( )
0; +∞
bằng
A.
17
2
. B.
4−
. C.
5
. D.
4
.
Lời giải
Chọn D
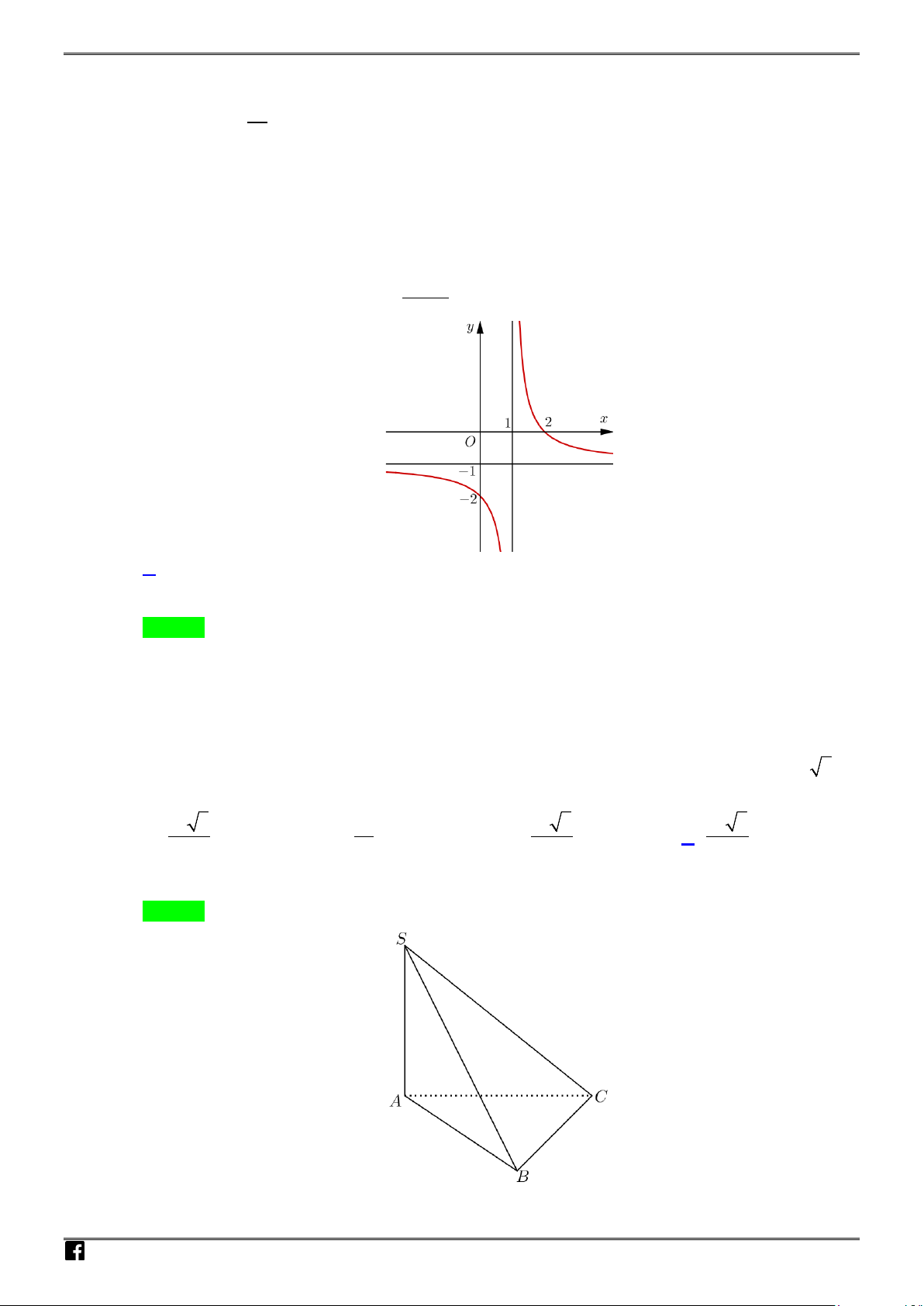
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
2
2
4
1;0 4 2
y yx x
x
′′
=− =⇔ =⇔=±
. Do
( )
0;x ∈ +∞
nên
2x =
Ta có:
( )
0
lim ; 2 4;lim
x
x
yy y
+
→+∞
→
= +∞ = = +∞
.
Vậy
(
)
0;
min 4
y
+∞
=
.
Câu 4. Đồ thị hình bên là của hàm số
( )
2
,
ax
y ab
xb
+
= ∈
+
. Khi đó tổng
ab
+
bằng
A.
2−
. B.
1
−
. C.
0
. D.
1
.
Lời giải
Chọn A
* Đồ thị có đường tiệm cận đứng
1x =
. Suy ra
1b = −
.
* Đồ thị có đường tiệm cận ngang
1y = −
. Suy ra
1a = −
.
Vậy
2ab+=−
.
Câu 5. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
A
với
AB a=
. Cạnh bên
3SA a=
và
SA
vuông góc với mặt phẳng đáy. Thể tích khối chóp
.
S ABC
bằng
A.
3
3
2
a
. B.
3
4
a
. C.
3
3
3
a
. D.
3
3
6
a
.
Lời giải
Chọn D

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
3
.
11 11 3
. . . . . ... 3
32 32 6
S ABC
a
V AB AC S A a a a
= = =
.
Câu 6. Cho các số thực dương
a
,
b
với
1a ≠
. Khẳng định nào sau đây đúng?
A.
( )
2
log 2 log
aa
ab b= +
. B.
( )
2
log 1 log
aa
ab b= +
.
C.
( )
2
log 1 2 log
aa
ab b= +
. D.
(
)
2
1
log log
2
aa
ab b
= +
.
Lời giải
Chọn A
Ta có:
( )
22
log log log 2 log
a aa a
ab a b b= +=+
.
Câu 7. Tính đạo hàm của hàm số
(
)
3
log 2 1yx
= +
.
A.
2
21
y
x
′
=
+
. B.
( )
2
2 1 ln 3
y
x
′
=
+
. C.
1
21
y
x
′
=
+
. D.
( )
1
2 1 ln 3
y
x
′
=
+
.
Lời giải
Chọn B
1
;.
2
D
= − +∞
Ta có:
( )
2
2 1 ln 3
y
x
′
=
+
.
Câu 8. Hàm số
42
23yx x=−−
đạt cực trị tại các điểm
1
x
,
2
x
,
3
x
. Tính
123
Sxx x=++
.
A.
2
−
. B.
0
. C.
1−
. D.
2
.
Lời giải
Chọn B
42
23yx x=−−
TXĐ:
D =
3
44
yxx
′
= −
3
0
04 40
1
x
y xx
x
=
′
=⇔ −=⇔
= ±
Vậy
101 0S =−+ + =
.
Câu 9. Cho hàm số
31
2
x
y
x
−
=
−
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên các khoảng
( )
;2−∞
và
( )
2; +∞
.
B. Hàm số đồng biến trên
{
}
2\
.
C. Hàm số nghịch biến trên các khoảng
( )
;2
−∞
và
( )
2; +∞
.
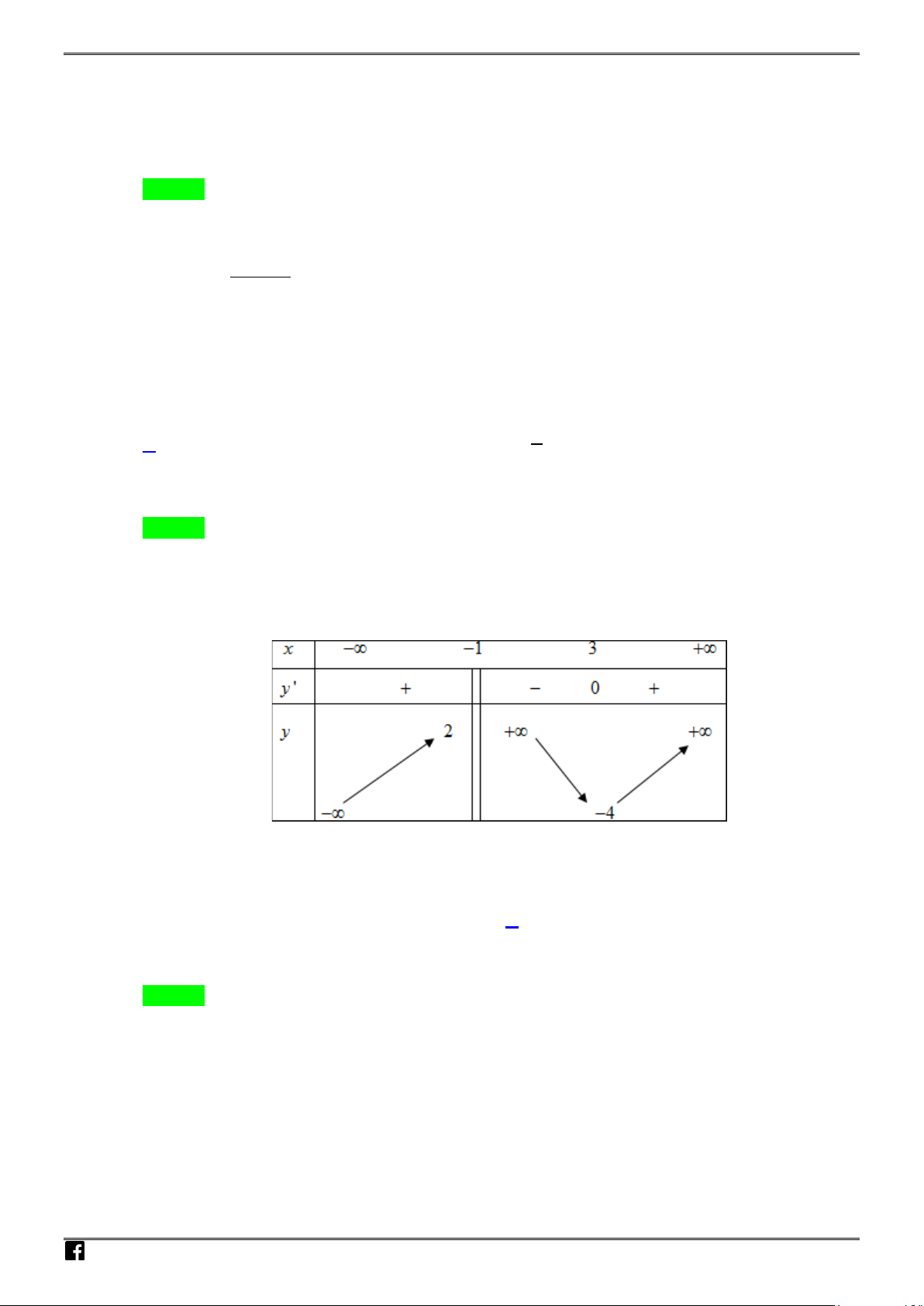
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
D. Hàm số nghịch biến trên
{ }
2\
.
Lời giải
Chọn C
{ }
\ 2.
D =
Ta có:
( )
2
5
0
2
y
x
−
′
= <
−
,
2
x
∀≠
Vậy hàm số nghịch biến trên các khoảng
( )
;2−∞
và
( )
2; +∞
.
Câu 10. Tính thể tích của một hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao lần lượt là
3m
,
1m
,
3
m
.
A.
3
9m
. B.
3
3
m
. C.
3
9
2
m
. D.
3
7 m
.
Lời giải
Chọn A
Ta có:
3
3.1.3 9Vm
= =
.
Câu 11. Cho hàm số
( )
y fx=
xác định trên
{ }
\1−
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình sau
Tìm tập hợp tất cả các giá trị của tham số
m
để phương trình
(
)
fx m=
có đúng 3 nghiệm thực
phân biệt.
A.
[
)
4; 2−
. B.
(
]
4; 2−
. C.
(
)
4; 2−
. D.
(
]
;2
−∞
.
Lời giải
Chọn C
Số nghiệm của phương trình
( )
fx m=
là số giao điểm của đồ thị hàm số
( )
y fx=
và
ym=
Vậy để phương trình có 3 nghiệm phân biệt thì
42m−< <
Câu 12. Cho hàm số
( )
y fx=
xác định và có đạo hàm trên trên
{ }
\ 2;1−
và có bảng biến thiên như
sau
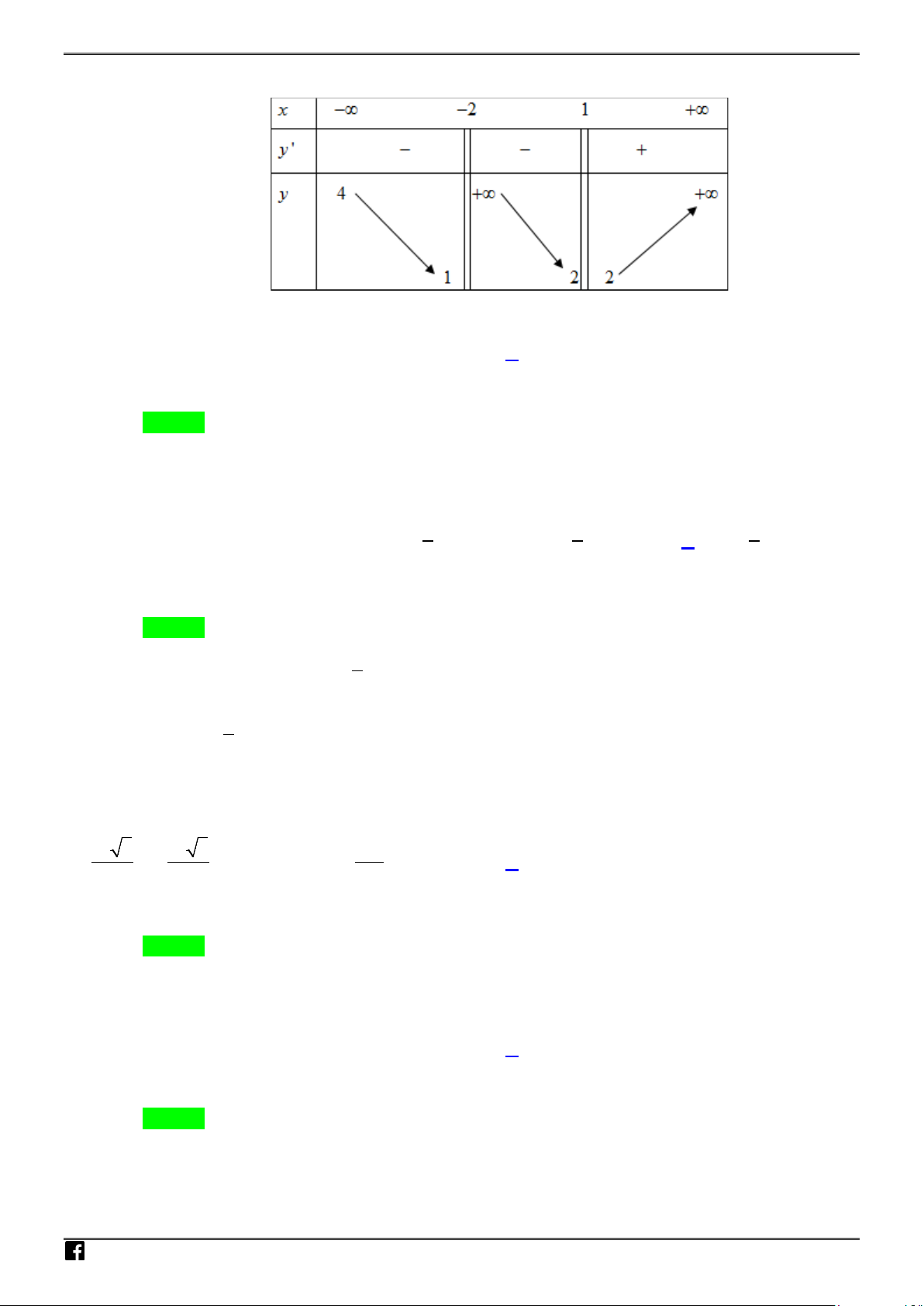
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Số đường tiệm cận của đồ thị hàm số là
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn C
Đồ thị hàm số có một đường tiệm cận ngang là
4y =
và một đường tiệm cận đứng
2x = −
Câu 13. Tìm tập xác định
D
của hàm số
(
)
31yx
π
= −
.
A.
D
=
. B.
1
\
3
D
=
. C.
1
;
3
D
= +∞
. D.
1
;
3
D
= +∞
.
Lời giải
Chọn D
Điều kiện:
1
3 10
3
xx−> ⇔ >
.
Vậy
1
;
3
D
= +∞
Câu 14. Cho hình lăng trụ đứng
D. ' ' ' 'ABC A B C D
có đáy là hình vuông cạnh
a
, cạnh bên bằng
2a
. Thể tích của khối lăng trụ
D. ' ' ' 'ABC A B C D
là
A.
3
3
2
a
. B.
3
3
6
a
. C.
3
2a
3
. D.
3
2a
.
Lời giải
Chọn D
Ta có
2
DABC
Sa=
, đường cao
2ah =
. Vậy thể tích khối lăng trụ là
3
D
.S 2a
ABC
Vh= =
Câu 15. Tổng tất cả các nghiệm của phương trình
2
4x 5
28
x −+
=
là
A.
2−
. B.
4−
. C.
2
. D.
4
.
Lời giải
Chọn D
Ta có
2
4x 5 2 2
2 8 4x 5 3 4x 2 0
x
xx
−+
=⇔−+=⇔−+=
Vậy tổng các nghiệm của phương trình là
4.
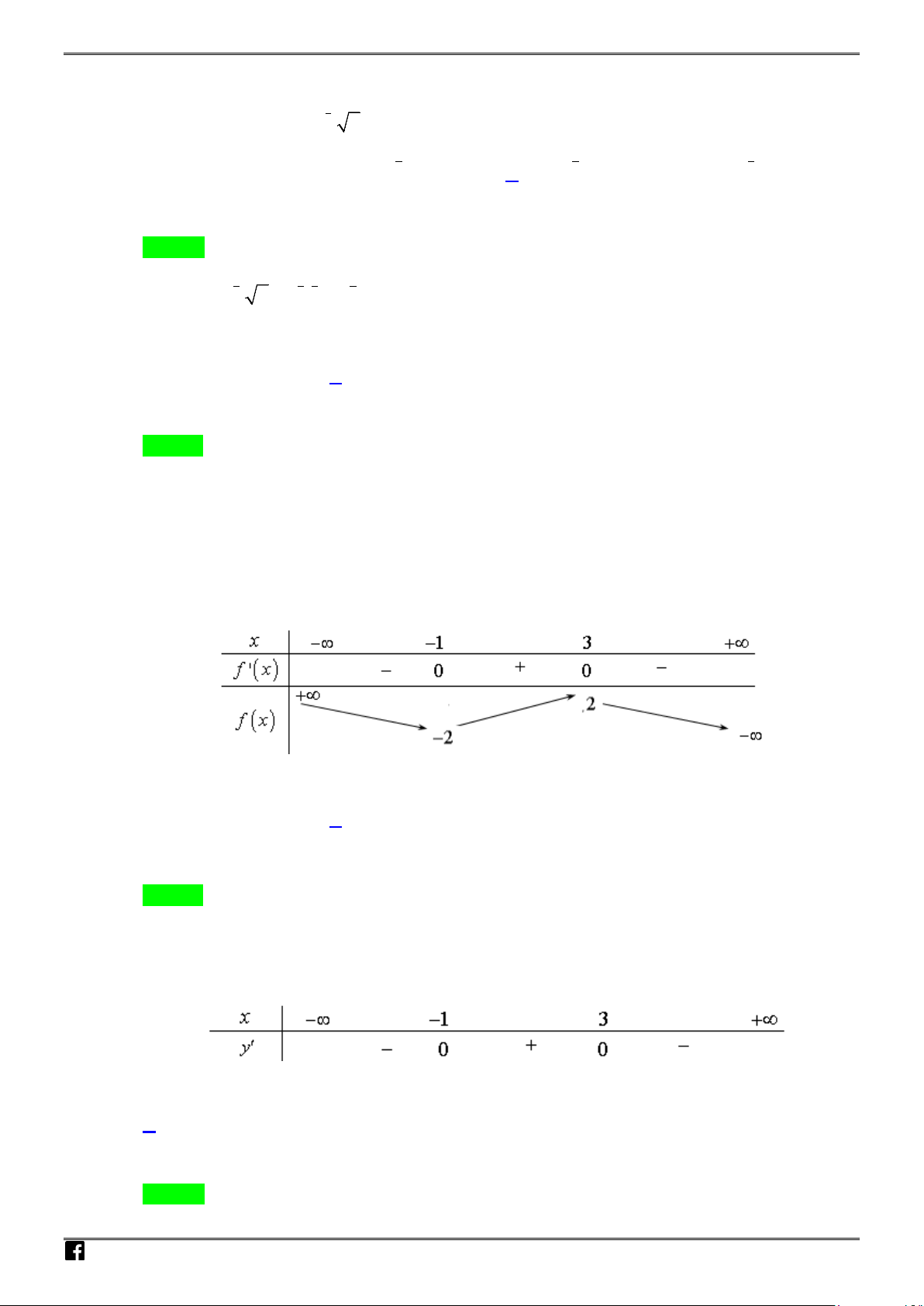
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 16. Rút gọn biểu thức
1
6
3
.Pa a=
, với
0a >
ta được
A.
2
Pa=
. B.
2
9
Pa
=
. C.
1
2
Pa=
. D.
1
8
Pa=
.
Lời giải
Chọn C
Ta có
1 11
1
6
3 36
2
.Pa aa a
+
= = =
.
Câu 17. Phương trình
( )
4
log 1 3x −=
có nghiệm
A.
65x =
. B.
82x =
. C.
63x =
. D.
80x =
.
Lời giải
Chọn B
Điều kiện:
1
x >
Ta có
( )
3
4
log 1 3 1 4 81 82xx x− = ⇔ −= = ⇔ =
(TM).
Vậy phương trình có nghiệm
82x =
Câu 18. Cho hàm số
( )
y fx=
liên tục trên
và có bảng biến thiên
Hàm số đã cho đồng biến trên khoảng
A.
( )
3; +∞
. B.
(
)
1; 3
−
. C.
( )
2; 2−
. D.
( )
;1−∞ −
.
Lời giải
Chọn B
Dựa vào đồ thị ta thấy hàm số đồng biến trên
(
)
1; 3
−
.
Câu 19. Cho hàm số
(
)
y fx=
liên tục trên
và có bảng xét dấu đạo hàm được cho ở hình dưới
Hỏi hàm số đã cho có bao nhiêu điểm cực trị
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn A
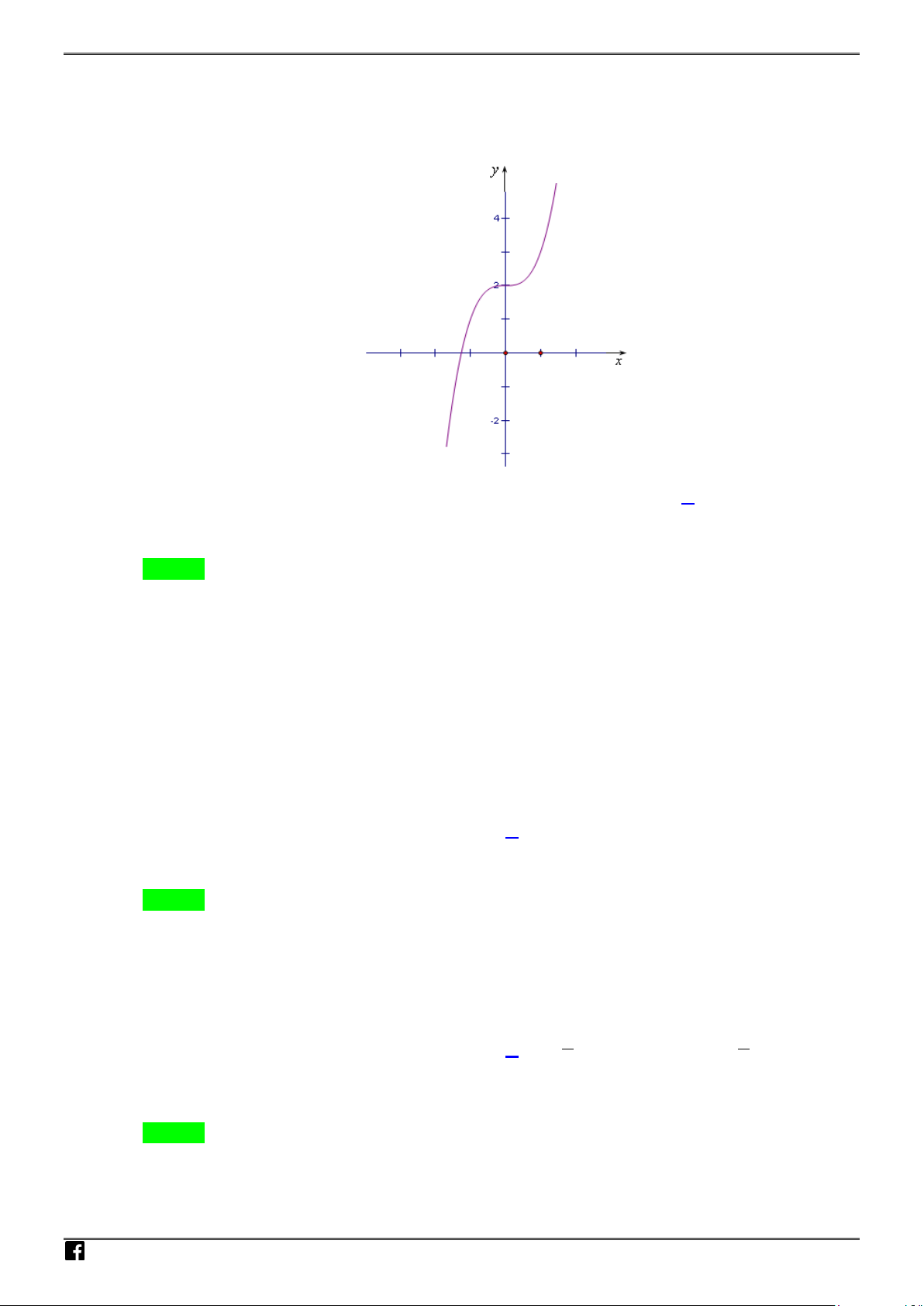
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Hàm số đạt cực đại tại
3x =
và đạt cực tiểu tại
1x = −
nên hàm số có 2 điểm cực trị
Câu 20. Hàm số nào trong các hàm số dưới đây có đồ thị như hình vẽ bên?
A.
42
2yx x=−+
. B.
3
32yx x=−+
. C.
3
2y xx=− −+
. D.
3
2
yx= +
.
Lời giải
Chọn D
Dựa vào đồ thị ta thấy:
Hình bên là đồ thị hàm số bậc ba nên đáp án A loại.
Đồ thị không có cực trị nên đáp án B loại.
Đồ thị có
'0 0yx=⇔=
nên đáp án D là đáp án đúng
Đáp án C có phương trình
'0y =
vô nghiệm nên loại.
Câu 21. Khối đa diện đều loại
{ }
4;3
có bao nhiêu mặt?
A.
20
. B.
12
. C.
6
. D.
4
.
Lời giải
Chọn C
Khối đa diện đều loại
{ }
4;3
là hình lập phương có 6 mặt.
Câu 22. Cho khối chóp
.S ABC
có thể tích bằng 6. Gọi
,MN
lần lượt là trung điểm các cạnh
,SB SC
. Thể
tích
V
của khối chóp
.S AMN
là
A.
3V =
. B.
4V =
. C.
3
2
V =
. D.
9
2
V =
.
Lời giải
Chọn C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
.
..
.
.1 1 3
.
.4 4 2
S AMN
S AMN S ABC
S ABC
V
SM SN
VV
V SB SC
= =⇒= =
Câu 23. Cắt mặt cầu
( )
S
bằng một mặt phẳng cách tâm mặt cầu một khoảng bằng
4
cm
ta được thiết diện
là một đường tròn có bán kính bằng
4cm
. Bán kính của mặt cầu
(
)
S
là
A.
10cm
. B.
7cm
. C.
12cm
. D.
5cm
.
Lời giải
Chọn D
Bán kính mặt cầu
( )
2 2 22
34 5 .R IH AH cm= + = +=
Câu 24. Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài
2a
. Thể tích của khối
nón bằng?
A.
3
3
6
a
π
. B.
3
3a
π
. C.
3
3
3
a
π
. D.
3
3
12
a
π
.
Lời giải
Chọn C
P
R
A
I
H

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Thiết diện qua trục là tam giác đều cạnh
2a
nên bán kính đường tròn đáy
1
.2
2
r aa= =
và chiều cao
(
)
2
2
23h a aa= −=
.
Vậy thể tích
3
2
13
33
a
V rh
π
π
= =
.
Câu 25. Gọi
,Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
32
32yx x=−+ +
trên
[ ]
0;3
.
Giá trị của
Mm+
bằng?
A. 6. B. 8. C. 10. D. 4.
Lời giải
Chọn B
[
]
[ ]
32
2
32
2 0;3
'3 60
0 0;3
yxx
x
y xx
x
=−+ +
= ∈
=−+=⇔
= ∈
( ) ( ) ( )
3 2; 0 2; 2 6yyy= = =
[ ]
[ ]
0;3
0;3
max 6
min 2
My
my
= =
= =
Vậy
628
Mm+ =+=
.
Câu 26. Trong các hàm số sau, hàm số nào đồng biến trên
?
A.
2
3
x
y
=
. B.
2
3
x
y
=
. C.
( )
0,99
x
y =
. D.
( )
23
x
y = −
.
Lời giải
Chọn A
Hàm số
x
ya=
đồng biến khi
1a >
.
Ta có:
2
1
3
>
nên
2
3
x
y
=
đồng biến trên
.
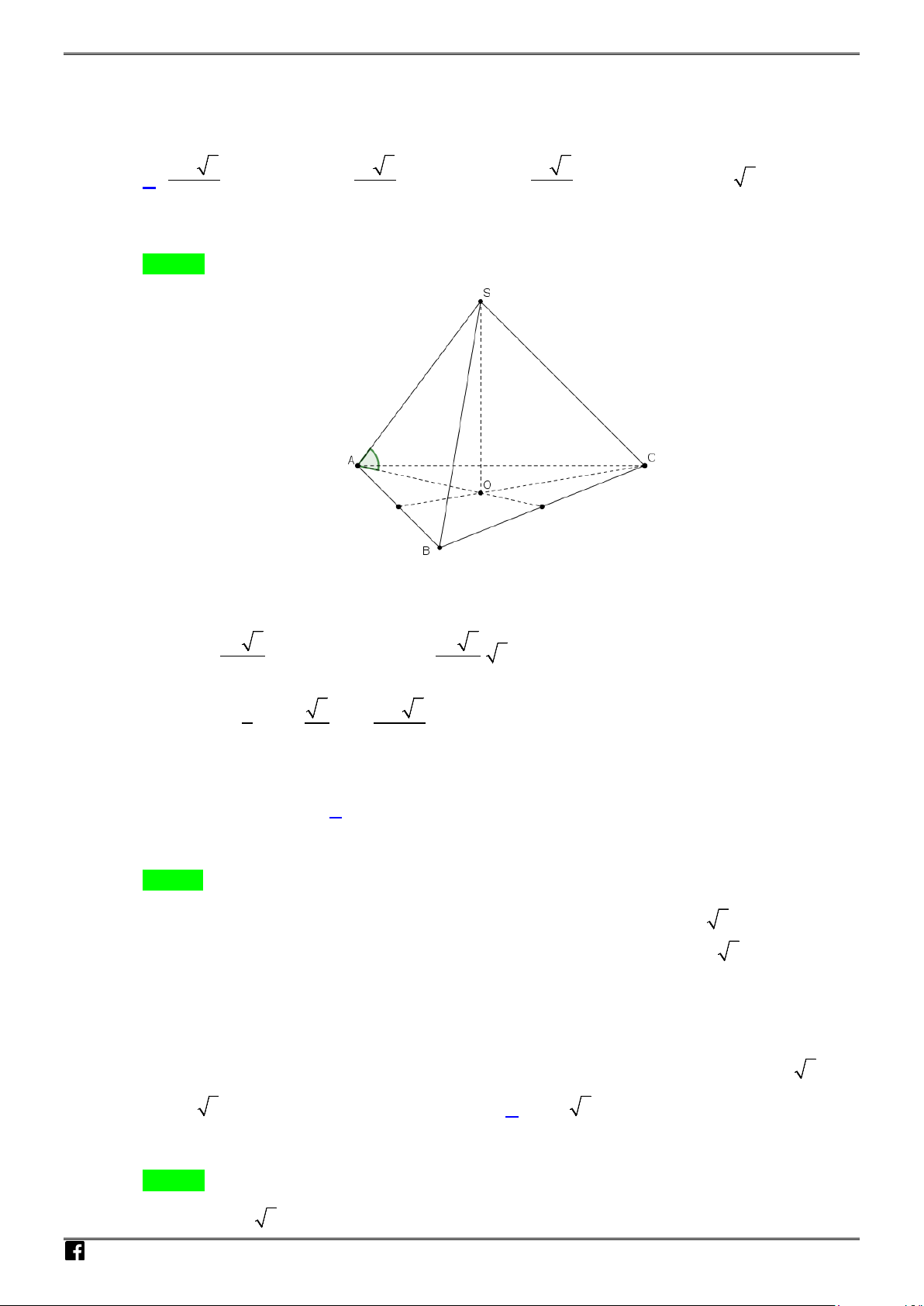
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 27. Cho hình chóp đều
.S ABC
có độ dài cạnh đáy là
2a
, cạnh bên tạo với mặt đáy một góc
60
°
.
Tính thể tích khối chóp
.S ABC
?
A.
3
23
3
a
. B.
3
3
3
a
. C.
3
3
6
a
. D.
3
23a
.
Lời giải
Chọn A
Ta có
( )
(
)
( )
, , 60
SA ABC SA AO SAO= = = °
.
Mà
23 23
.tan 60 . 3 2
33
aa
AO SO AO a= ⇒ = °= =
.
Nên
( )
3
2
.
1 3 23
. 2 .2
34 3
S ABC
a
V aa= =
.
Câu 28. Số giao điểm của đồ thị hàm số
3
43yx x=−+
và đường thẳng
3yx= +
là
A.
1
. B.
3
. C.
2
. D.
0
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm:
33
5
43 3 50 5
0
x
xx x xx x
x
=
− +=+⇔ − =⇔ =−
=
.
Phương trình có 3 nghiệm nên số giao điểm là 3.
Câu 29. Tính diện tích xung quanh của hình trụ biết hình trụ có bán kính đáy
a
và đường cao
3a
.
A.
3
3a
π
. B.
3
2 a
π
. C.
3
23a
π
. D.
3
a
π
.
Lời giải
Chọn C
Ta có
3,hla ra= = =
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Nên
2
xq
2 2.32 3S rl a a a
ππ π
= = =
.
Câu 30. Hàm số nào trong các hàm số dưới đây có bảng biến thiên như sau?
A.
42
31yx x=−−
. B.
42
21
yx x=−+
. C.
42
21yx x=−+ −
. D.
3
31yxx=−+ −
.
Lời giải
Chọn C
Dựa vào bảng biến thiên, ta thấy đây là bảng biến thiên của hàm trùng phương.
lim
x
y
→±∞
= −∞
nên
0a
<
. Vậy đây là bảng biến thiên của hàm số
42
21yx x=−+ −
.
Câu 31. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có góc giữa hai mặt phẳng
(
)
A BC
′
và
( )
ABC
bằng
60°
và
AB a=
. Khi đó thể tích của khối đa diện
ABCC B
′′
bằng
A.
3
33
8
a
. B.
3
3
8
a
. C.
3
3
4
a
. D.
3
3a
.
Lời giải
Chọn C
Gọi
I
là trung điểm
BC
. Khi đó
( ) ( )
( )
, 60A BC ABC A IA
′′
= = °
.
Do đó
33
.tan 60 . 3
22
aa
AA AI
′
= °= =
.
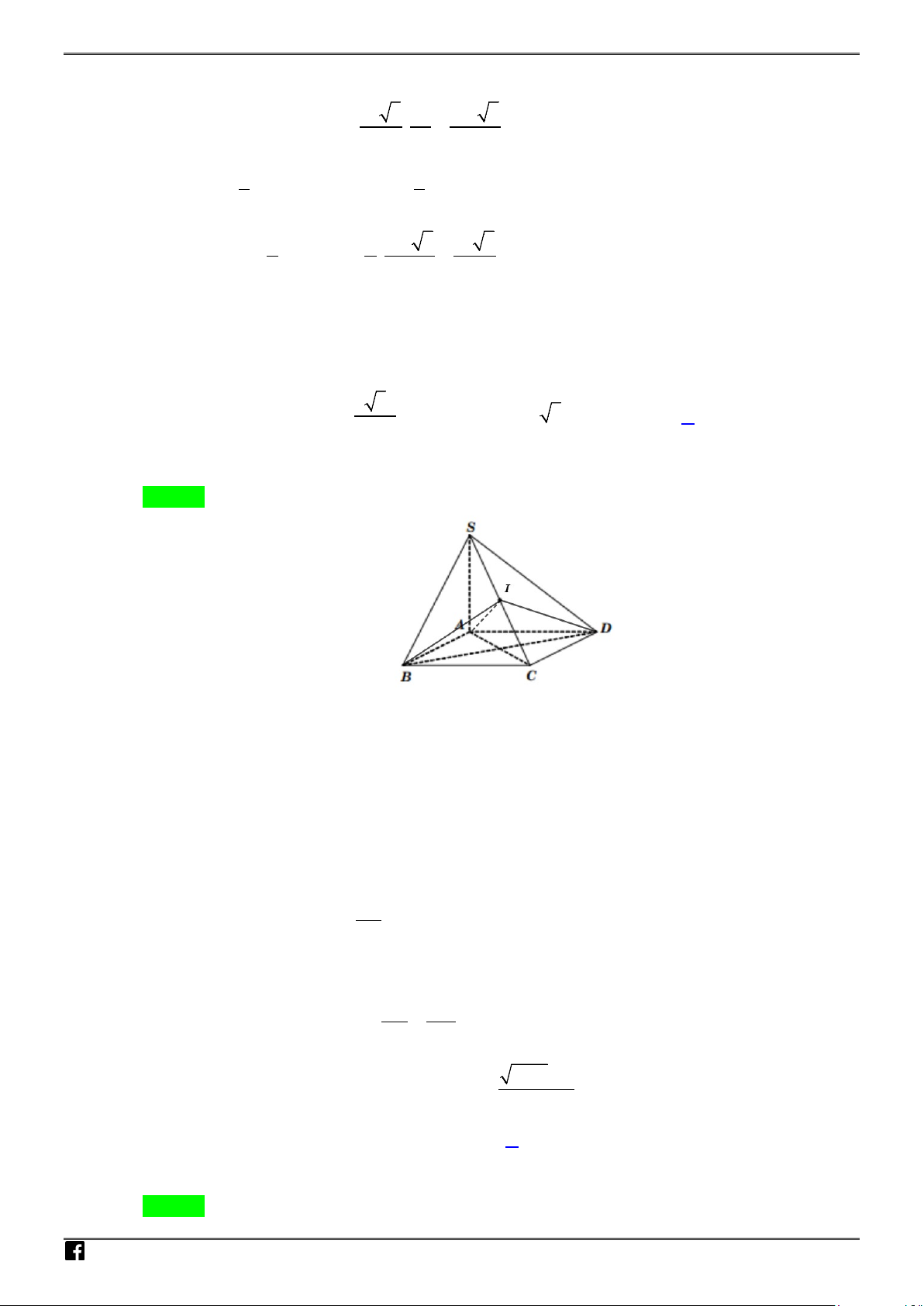
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
23
.
33 3 3
..
42 8
ABC A B C ABC
a aa
V S AA
′′′
′
= = =
.
Mà
. ..
11
.
33
A ABC ABC A ABC ABC A B C
V S AA V V
′ ′ ′′′
∆
′
= ⇒=
Do đó
33
.
2 23 3 3
.
3 38 4
ABCB C ABC A B C
aa
VV
′′ ′′′
= = =
.
Câu 32. Cho hình chóp
.S ABCD
có đáy là hình chữ nhật
3, 4AB a AD a
= =
. Cạnh bên
SA
vuông góc
với mặt đáy,
SC
tạo với mặt phẳng đáy một góc
60°
. Tính bán kính của mặt cầu ngoại tiếp hình
chóp
.S ABCD
theo
a
.
A.
10
a
. B.
53
2
a
. C.
53a
. D.
5a
.
Lời giải
Chọn D
Ta có
( )
( )
( )
, , 60SC ABCD SC CA SCA= = = °
.
Vì
ABCD
là hình chữ nhật có
3, 4 5AB a AD a AC a= =⇒=
.
Gọi
I
là trung điểm SC.
Ta chứng minh được các tam giác
,,
SAC SBC SDC
∆∆
là các tam giác vuông với cạnh huyền là
SC
.
2
SC
IS IC IA IB ID⇒= === =
.
Do đó
I
là tâm mặt cầu ngoại tiếp chóp
.S ABCD
.
Bán kính mặt cầu khi đó là
10
5
22
SC a
Ra= = =
.
Câu 33. Số đường tiệm cận đứng của đồ thị hàm số
2
93x
y
xx
+−
=
+
là
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
( )
(
)
( )
( )
( )
2
99
93 1
1 93 1 93
x
x
y
xx
xxx xx
+−
+−
= = =
+
+ ++ + ++
Do đó
( )
1
lim
x
y
+
→−
= +∞
nên đồ thị hàm số có đường tiệm cận đứng
1x = −
.
Câu 34. Hàm số
( )
322
1
11
3
y x mx m m x= − + −+ +
đạt cực đại tại điểm
1
x
=
khi
A.
2
m = −
. B.
1m = −
. C.
2m
=
. D.
1m =
.
Lời giải
Chọn C
Ta có
22
21y x mx m m
′
= − + −+
và
22y xm
′′
= −
.
Hàm số đạt cực đại tại điểm
( )
( )
2
10
12 10
12
22 0
10
y
mm m
xm
m
y
′
=
− + − +=
=⇔ ⇔ ⇔=
′′
−<
<
.
Câu 35. Cho đồ thị của ba hàm số
x
ya=
,
x
yb=
,
x
yc=
như hình vẽ bên. Khẳng định nào sau đây đúng?
A.
bca>>
. B.
bac>>
. C.
cab>>
. D.
cb a>>
.
Lời giải
Chọn A
+) Từ đồ thị hàm số
x
ya=
ta thấy hàm số này nghịch biến trên
1a⇒<
.
+) Từ đồ thị hàm số
x
yb=
và
x
yc=
ta thấy hai hàm số này đồng biến trên
b⇒
,
1c >
.
+) Mặt khác, với
0x
>
thì
0
11
x
xx
b bb
b c bc
c cc
> ⇔ >= ⇔ >⇔ >
(do
b
,
0c >
).
Vậy
bca>>
.
Câu 36. Có bao nhiêu số nguyên
m
để đồ thị hàm số
( ) ( )
42
16y m x mx m= − +− +
có đúng một điểm
cực trị?
A.
6
. B.
1
. C.
4
. D.
5
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn A
Ta có:
( ) ( ) ( )
32
41 26 221 6
y mx mxxmx m
′
= − + − = − +−
.
( )
( )
2
0
0
2 1 6 0 1
x
y
mx m
=
′
= ⇔
− +− =
.
Hàm số đã cho có đúng một cực trị
⇔
0y
′
=
có đúng một nghiệm
( )( )
1 60mm⇔ − −≤
16m⇔≤ ≤
.
Do
m∈
nên
{ }
1;2;3;4;5;6
m∈
.
Vậy có
6
giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Cách khác: Hàm số
42
y ax bx c=++
có đúng một điểm cực trị
( )( )
. 0 16 0 1 6ab m m m⇔ ≥⇔ − − ≥⇔≤ ≤
.
Do
m
∈
nên
{ }
1;2;3;4;5;6m∈
.
Vậy có
6
giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 37. Cho hàm số
( )
y fx=
liên tục trên
và có đồ thị như hình vẽ dưới.
Gọi
M
,
m
theo thứ tự là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( )
2y fx= −
trên đoạn
[ ]
1;5
. Tổng
Mm+
bằng
A.
8
. B.
7
. C.
9
. D.
1
.
Lời giải
Chọn B
Đặt
2tx= −
. Do
[ ]
1;5x ∈
nên
[ ]
1;3t ∈−
.
Khi đó
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( )
y ft=
trên đoạn
[ ]
1;3−
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 23
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Dựa vào đồ thị ta có:
5M =
,
2m =
.
Vậy
7
Mm+=
.
Câu 38. Một người gửi
50
triệu đồng vào một ngân hàng theo hình thức lãi kép với lãi suất
6%
/ năm.
Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn
100
triệu đồng bao gồm cả
gốc và lãi? Giả sử trong suốt thời gian gửi lãi suất không đổi và người đó không rút tiền ra.
A.
12
năm. B.
14
năm. C.
13
năm. D.
11
năm.
Lời giải
Chọn A
Áp dụng công thức lãi kép
( )
1
n
CA r= +
với
50A =
,
100C >
,
6% 0,06
r = =
ta được:
(
)
1,06
50 1 0,06 100 1,06 2 log 2 11,90
n
n
n+ > ⇔ >⇔> ≈
.
Vậy sau ít nhất
12
năm người đó nhận được số tiền nhiều hơn
100
triệu đồng bao gồm cả gốc
và lãi.
Câu 39. Cho hình trụ có bán kính đáy bằng
.a
Cắt hình trụ bởi một mặt phẳng
(
)
P
song song với trục
của hình trụ và cách trục của hình trụ một khoảng bằng
2
a
ta được thiết diện là một hình vuông.
Thể tích khối trụ bằng
A.
3
3 a
π
. B.
3
3a
π
. C.
3
3
4
a
π
. D.
3
a
π
.
Lời giải
Chọn B
Gọi hình vuông thiết diện là
ABCD
và tâm
O
là tâm đường tròn
đáy của hình trụ.
Gọi
H
là trung điểm của
,AB
ta có
2
2 22
3
3.
2 22
a aa
OH AH OA AH a AB a
=⇒ = − = − = ⇒=
Chiều cao của khối trụ chính la độ dài cạnh của hình vuông bằng
3.ha=
Thể tích của khối trụ là:
22 3
.3 3V rh a a a
ππ π
= = =
D
H
C
B
A
'O
O
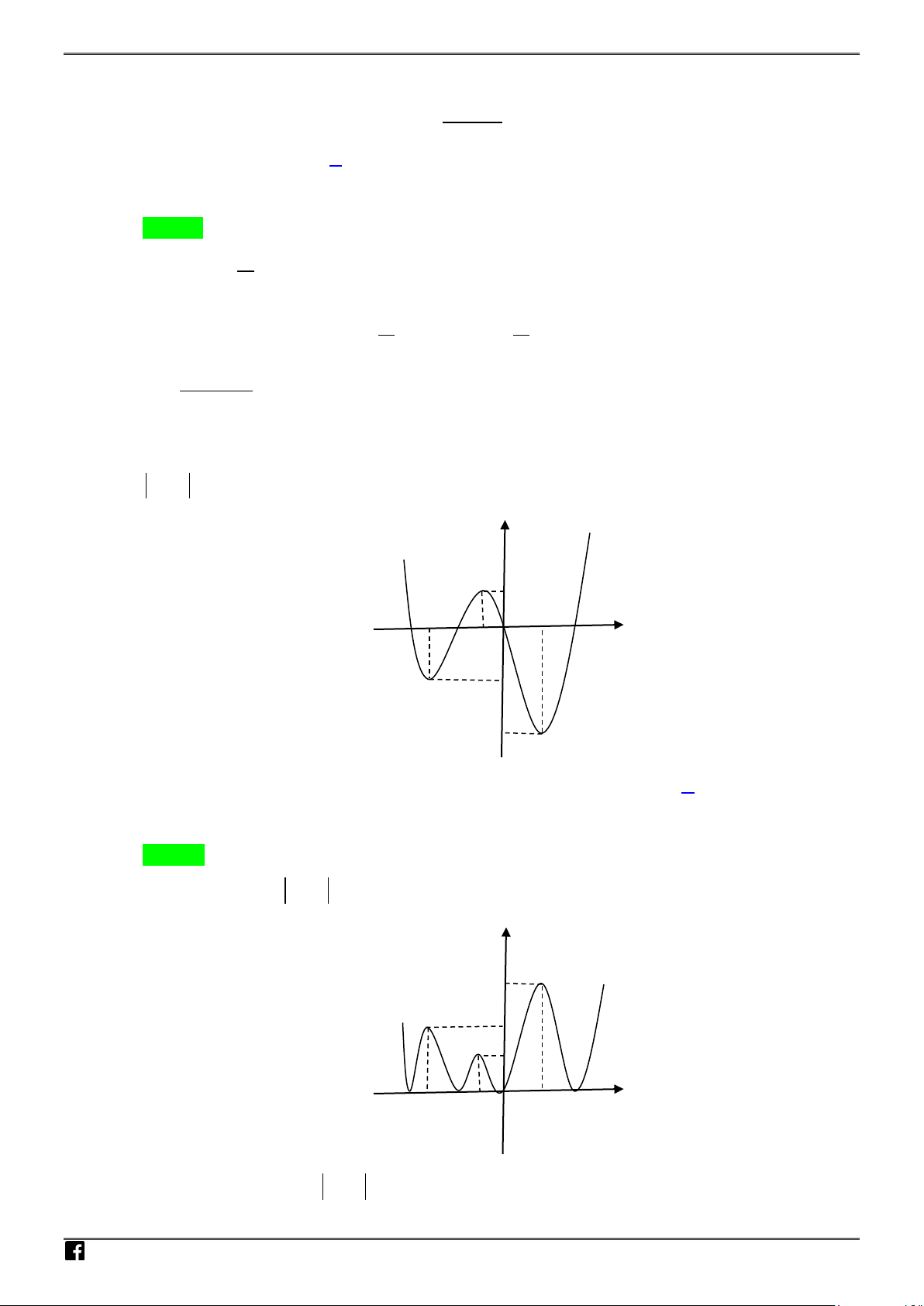
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 24
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 40. Số giá trị nguyên của
m
để hàm số
3
3
mx
y
xm
−+
=
−
nghịch biến trên từng khoảng xác định là.
A.
2
. B.
5
. C.
3
. D.
7
.
Lời giải
Chọn B
ĐKXĐ:
3
m
x
≠
.
Xét 2 khoảng
;
3
m
x
∈ −∞
và
;
3
m
x
∈ +∞
. Để hàm số nghịch biến
( )
2
2
2
9
' 0 9 0 3 3.
3
m
y mm
xm
−
= <⇒ −<⇒−< <
−
Câu 41. Cho hàm số
( )
y fx=
có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của
m
để phương trình
( )
0fx m
−=
có 8 nghiệm phân biệt?
A.
62
m−< <
. B.
16m<<
. C.
03m<<
. D.
02m<<
.
Lời giải
Chọn D
Đồ thị hàm số
( )
y fx=
:
Suy ra để phương trình
( )
0fx m−=
có 8 nghiệm phân biệt thì
0 2.m<<
2
6
3
O
y
x
2
6−
3−
O
y
x

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 25
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 42. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2,
a
mặt phẳng
(
)
SAB
vuông góc với mặt
phẳng đáy. Tính thể tích khối chóp
.S ABCD
theo
a
biết
,3SA a SB a= =
.
A.
3
23
a
. B.
3
43
3
a
. C.
3
4
3
a
. D.
3
23
3
a
.
Lời giải
Chọn D
Dễ dàng ta chứng minh được
SAB∆
vuông tại
S
.
Mà
( ) (
) ( ) ( )
SAB ABCD SH ABCD H AB
⊥ ⇒⊥ ∈
Ta có:
( )
2
222 2
1 1 1 11 1 3
2
3
AH a
AH SA SB AH a
a
=+⇒ =+ ⇒=
Thể tích khối chóp
( )
3
2
.
1 1 3 23
. . . .2 .
3 32 3
S ABCD ABCD
a
V AH S a a= = =
Câu 43. Biết rằng phương trình
( )
2
2
13
9
4log 9 log 8 0
27
x
x
+ −=
có hai nghiệm phân biệt
12
,xx
. Tính
12
P xx=
.
A.
4
3
−
.
B.
2
3
. C.
2
9
. D.
6
3
−
.
Lời giải
Chọn D
Điều kiện
0x >
.
Ta có
( )
( )
2
2
2
13 3 3
9
4log 9 log 8 0 log 2 2log 11 0
27
x
x xx
+ −=⇔ + + − =
3
26
3 3 12
7
3
3
log 1
log 6log 7 0 3
log 7
3
x
x
x x P xx
x
x
−
−
=
=
⇔ + −=⇔ ⇔ ⇒ = =
= −
=
.
Câu 44. Người ta thả một viên bi hình cầu với bán kính
3cm
vào một cái ly dạng hình trụ đang chứa
nước. Người ta thấy viên bi chìm xuống đáy ly và chiều cao của nước dâng lên
1cm
. Biết rằng
a
2a
H
D
C
B
A
S
3a

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 26
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
chiều cao của nước trong ly ban đầu là
7,5cm
. Tính thể tích
V
của khối nước ban đầu trong ly
(kết quả làm tròn đến hàng phần trăm).
A.
3
1272,35
cm
.
B.
3
636,17
cm
. C.
3
282,74cm
. D.
3
848,23cm
.
Lời giải
Chọn D
Gọi bán kính đáy của ly là
( )
r cm
, suy ra thể tích nước ban đầu trong cốc là:
( )
23
.7,5V r cm
π
=
Sau khi thả viên bi thì thể tích của nước trong cốc là:
( )
23
1
.8,5V r cm
π
=
Thể tích của viên bi là:
( )
33
2
4
.3 36
3
V cm
ππ
= =
Ta có:
( )
22 2
21
.8,5 .7,5 36 36 6V V V r r r r cm
ππ π
= − ⇔ − = ⇔ = ⇒=
.
Vậy thể tích nước ban đầu trong cốc là
( )
23
.6 .7,5 848,23V cm
π
= =
.
Câu 45. Cho hình chóp tứ giác đều
.S ABCD
. Gọi
M
là điểm đối xứng của
C
qua
D
,
N
là trung điểm
của
.SC
Mặt phẳng
( )
BMN
chia khối chóp
.S ABCD
thành hai phần. Tỉ số thể tích giữa hai
phần (phần lớn trên phần bé) bằng
A.
7
3
.
B.
5
4
. C.
7
5
. D.
6
5
.
Lời giải
Chọn C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 27
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Đặt
.S ABCD
VV=
.
Gọi
J
là giao điểm của
MN
và
SD
suy ra
J
là trọng tâm của tam giác
SCM
.
Gọi
I
là giao điểm của
BM
và
AD
suy ra
I
trung điểm của
AD
.
Khi đó, mặt phẳng
( )
BMN
chia khối chóp
.S ABCD
thành hai khối đa diện
.S BN JI
và
NJDCBI
có thể tích lần lượt là
1
V
và
2
V
.
Vì
MBC ABCD
SS=
và
1
4
MID ABCD
SS=
nên
.
1
2
N MBC
VV=
và
.
1
12
J MID
VV=
.
Suy ra
2. .
5
12
N MBC J MID
VV V V= −=
. Do đó,
12
7
12
V VV V=−=
.
Vậy
1
2
7
5
V
V
=
.
Câu 46. Cho hàm số
( )
y fx=
có đạo hàm trên
và có đồ thị là đường cong như hình vẽ bên. Đặt
( ) ( )
gx f f x=
. Tìm số nghiệm của phương trình
( )
0gx
′
=
.
I
J
N
O
C
A
D
B
S
M
x
y
2
4
3
2
1
O
-
4

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 28
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
8
. B.
6
. C.
2
. D.
4
.
Lời giải
Chọn B
Ta có
( )
(
) (
)
.gx f xf fx
′ ′′
=
. Khi đó
( )
( ) ( )
( ) ( )
0 1
0
0 2
fx
gx
f fx
′
=
′
= ⇔
′
=
Vì hàm số có hai cực trị nên phương trình
( )
1
có 2 nghiệm phân biệt.
Xét
( )
( )
( ) ( )
0
2
2;3
fx
fx a
=
⇔
= ∈
Phương trình
( )
0fx
=
có 3 nghiệm phân biệt.
Phương trình
( ) ( )
2;3fx a= ∈
có 1 nghiệm.
Vậy phương trình
( )
0gx
′
=
có 6 nghiệm phân biệt.
Câu 47. Cho hình lăng trụ tam giác
.
ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
A
và
AB a=
,
3AC a=
. Tính thể tích khối lăng trụ
.ABC A B C
′′′
biết
2
AA AB AC a
′′′
= = =
.
A.
3
3a
. B.
3
3
2
a
. C.
3
2
a
. D.
3
3
3
a
.
Lời giải
Chọn B
Gọi
H
là chân đường cao hạ từ
A
′
xuống đáy
( )
ABC
.
Vì
AA AB AC
′′′
= =
và tam giác
ABC
vuông tại
A
nên
H
là trung điểm
BC
Ta có
2
3
2
BC
AH a A H A A AH a
′′
==⇒ = −=
.
Thể tích khối lăng trụ là
3
.
13
. 3. . 3
22
ABC A B C ABC
a
V AHS a aa
′′′
′
= = =
.
H
C
B
A
C'
B'
A'

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 29
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 48. Có bao nhiêu giá trị của tham số
m
để phương trình
( )
2
9 2 13 8 0
xx
m mm− + +−=
có hai nghiệm
1
x
,
2
x
thỏa mãn
12
2xx
+=
?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Đặt
3, 0
x
tt= >
. Khi đó phương trình đã cho trở thành
(
) ( )
22
2 1 8 0 *t m tm m− ++−=
Phương trình đã cho có hai nghiệm
1
x
,
2
x
khi và chỉ khi phương trình
(
)
*
có hai nghiệm dương
1
t
,
2
t
(
)
( )
( )
2
2
2
2
1 80
0 10 1 0
1
0 2 1 0 1 0 0 hay 8
10
0
80
80
m mm
m
S m m mm
P
mm
mm
+− − ≥
′
∆≥ + ≥
⇔ >⇔ +> ⇔ +> ⇔− ≤< >
>
−>
−>
.
Khi đó
1 2 12
2
12
. 2 .2 2 2 4
x x xx
tt
+
= = = =
.
Suy ra
( )
( )
22
4 2 5
8 4 8 40
4 2 5
mn
mm mm
ml
= +
− =⇔ − −=⇔
= −
.
Vậy có một giá trị của tham số
m
thỏa đề.
Câu 49. Biết
a
b
(trong đó
a
b
tối giản và
*
,ab∈
) là giá trị của tham số
m
để hàm số
( )
32 2
2 3 6 3 1 2020y x mx m x= − − −+
có hai điểm cực trị
12
,xx
thỏa mãn
( )
12 1 2
21
xx x x
+ +=
.
Tính
2Pa b
= +
.
A.
6
. B.
5
. C.
8
. D.
7
.
Lời giải
Chọn C
Xét hàm số
( )
32 2
2 3 6 3 1 2020y x mx m x= − − −+
, ta có
( )
22
6 6 63 1y x mx m
′
=−− −
22
0 3 10y x mx m
′
= ⇔ − − +=
( )
1
Hàm số có hai điểm cực trị
12
,xx
khi và chỉ khi phương trình
( )
1
có hai nghiệm phân biệt
( )
( )
2
2
43 1 0mm⇔∆= − − − + >
2
2
13 4 0
13
mm⇔ − > ⇔ <−
hoặc
2
13
m >
.
Khi đó, theo định lí Viet, ta có
12
2
12
. 31
xx m
xx m
+=
=−+
.
Theo giả thiết,
( )
12 1 2
21xx x x+ +=
nên
22
3 12 1 3 2 0m m mm− ++=⇔− +=

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 30
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
0m⇔=
(loại) hoặc
2
3
m =
(chọn).
Suy ra
2, 3ab= =
. Vậy
28
Pa b=+=
.
Câu 50. Cho các số thực dương
,xy
thỏa mãn
3
1
log 3 3 4
3
y
xy x y
x xy
−
= ++ −
+
. Giá trị nhỏ nhất của biểu
thức
Pxy= +
bằng
A.
43 4
9
+
. B.
43 4
9
−
. C.
43 4
3
+
. D.
43 4
3
−
.
Lời giải
Chọn D
Vì
,0xy
>
nên
1
0
3
y
x xy
−
>
+
;0 1xy
⇔> <<
.
Theo giả thiết, ta có
(
) ( ) ( )
( )
3 33
1
log 3 3 4 3 1 log 3 1 3 log 3
3
y
xy x y y y x xy x xy
x xy
−
= ++ −⇔ − + − = + + +
+
( )
*
Xét hàm số
( )
3
logft t t= +
trên khoảng
( )
0; +∞
ta có
( )
( )
1
1 0, 0;
.ln 3
ft t
t
′
= + > ∀ ∈ +∞
.
Do đó, hàm số
( )
ft
đồng biến trên khoảng
( )
0; +∞
.
Từ
( )
*
ta có
( ) ( )
31 3f y f x xy−= +
( ) ( ) ( )
31 3 31 1 3yxxy yx y⇔ −=+ ⇔ −= +
( )
**
Để ý rằng
1
3
y = −
không phải là nghiệm của
( )
**
nên
( )
31
13
y
x
y
−
=
+
.
Do đó,
(
)
31
13
y
Pxy y
y
−
=+= +
+
Ta có
( )
( )
2
12
1
31
Py
y
−
′
= +
+
;
( ) ( )
2
23 1
0 3 1 12
3
Py y y
±−
′
=⇔ + = ⇔=
.
Vì
( )
0;1y
∈
nên
23 1
3
y
−
=
. Suy ra
23 3
3
x
−
=
.
Khi đó
min
23 1 43 4
33
PP
−−
= =
.
HẾT

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
ĐỀ THI HỌC KÌ I SGD TỈNH BẮC NINH
NĂM HỌC 2020 - 2021
Môn: TOÁN - Lớp: 12
Thời gian: 90 phút (Không kể thời gian phát đề)
Câu 1. Khối chóp có diện tích đáy bằng
2
a
, chiều cao bằng
a
có thể tích bằng
A.
3
2a
. B.
3
a
. C.
3
1
3
a
. D.
3
2
3
a
.
Câu 2. Cho hàm số
( )
y fx
=
có bảng biến thiên như hình sau:
Hàm số trên đạt cực đại tại
A.
2x = −
. B.
3x =
. C.
2x =
. D.
0x =
.
Câu 3. Cho khối lăng trụ đứng
.
ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
B
, cạnh
AB a=
,
2BC a=
,
3
AA a
′
=
. Thể tích khối lăng trụ đã cho là
A.
3
a
B.
3
3a
. C.
3
2a
. D.
3
6a
.
Câu 4. Khối hộp chữ nhật có ba kích thước lần lượt là
1;2;3
có thể tích bằng
A.
2
. B.
4
. C.
8
. D.
6
.
Câu 5. Giá trị nhỏ nhất của hàm số
43yx= −
trên đoạn
[ ]
0;1
bằng
A.
2
. B.
1
. C.
0
. D.
4
.
Câu 6. Tập xác định
D
của hàm số
( )
2
3yx
−
= −
là
A.
( )
0;D
= +∞
. B.
( )
3;D = +∞
. C.
D =
. D.
{ }
\3D
=
.
Câu 12. Một hình nón tròn xoay có bán kính đáy
3r
, chiều cao
1h
thì có độ dài đường sinh bằng
A.
13+
. B.
2
. C.
2
. D.
4
.
Câu 13. Đồ thị hàm số
2
32
yxx
và trục hoành có bao nhiêu điểm chung?
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 14. Hàm số nào sau đây nghịch biến trên
;
?
A.
21yx=−+
. B.
yx=
. C.
2yx=−+
. D.
5yx= −
.
Câu 15. Cho hình lập phương có cạnh bằng
2
. Tổng diện tích các mặt của hình lập phương đã cho bằng
A.
16
. B.
12
. C.
4
. D.
24
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 16. Quay hình vuông
ABCD
có cạnh bằng
1
xung quanh đường thẳng
AB
ta thu được khối trụ tròn
xoay có chiều cao bằng bao nhiêu?
A.
1
. B.
1
2
. C.
2
2
. D.
2
.
Câu 17. Cho hàm số
21
3
x
y
x
−
=
+
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên mỗi khoảng
( )
(
)
; 3 , 3;
−∞ +∞
.
B. Hàm số đồng biến trên mỗi khoảng
11
;,;
22
−∞ +∞
.
C. Hàm số đồng biến trên mỗi khoảng
( ) ( )
; 3 , 3;−∞ − − +∞
.
D. Hàm số đồng biến trên
.
Câu 18. Hàm số
ln
yx=
có đạo hàm là
A.
1
ln
y
xx
′
=
. B.
1y
′
=
. C.
1
y
x
′
=
. D.
yx
′
=
.
Câu 19. Cho hai số dương
a
và
, 1, 1ba b≠≠
. Trong các khẳng định sau, khẳng định nào sai
A.
log 1
a
a =
. B.
log
b
a
ab=
. C.
log
b
a
ab=
. D.
log 1 0
a
=
.
Câu 20. Cho hàm số
yx
α
=
với
0,x
α
>∈
có đạo hàm được tính bởi công thức
A.
1
yx
α
α
−
′
=
. B.
1
yx
α
−
′
=
. C.
1
lnyx x
α
α
−
′
=
. D.
( )
1
yx
α
α
′
= −
.
Câu 21. Phương trình
( ) ( )
55
log 2 1 log 2xx−= −
có bao nhiêu nghiệm?
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 22. Tập nghiệm của bất phương trình
2
log 3
x <
là
A.
( )
8; +∞
. B.
( )
;8−∞
. C.
( )
0;8
. D.
( )
0;6
.
Câu 23. Phương trình
1
28
x
+
=
có nghiệm là
A.
3x =
. B.
4x
=
. C.
1x =
. D.
2
x =
.
Câu 24. Tập xác định
D
của hàm số
2
3
log
yx=
là
A.
( )
0;D = +∞
. B.
( )
;0D = −∞
. C.
D =
. D.
{ }
\0D =
.
Câu 25. Cho hàm số
( )
fx
có đạo hàm
( )
2 1,
fx x x
′
= − ∀∈
. Hỏi
( )
fx
có bao nhiêu điểm cực trị?
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 26. Đường tiệm cận ngang của đồ thị hàm số
1
3
x
y
x
−−
=
+
cắt đường thẳng
2021yx
=
tại điểm có tung
độ bằng
A.
1
−
. B.
2−
. C.
0
. D.
1
2021
−
.
Câu 27. Bất phương trình
3 81
x
<
có tập nghiệm là
A.
( )
;4−∞
. B.
{ }
4
. C.
( )
4; +∞
. D.
( )
;27−∞
.
Câu 28. Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
1
x
y
x
−
=
+
là

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 29. Điểm cực tiểu của hàm số
32
3x 1
yx
=−+ −
là:
A.
1x = −
. B.
3
x
=
. C.
2x =
. D.
0x
=
.
Câu 30. Giá trị của biểu thức
2
3
log 4 log 9P = +
là
A.
6
. B.
7
. C.
8
. D.
4
.
Câu 31. Hình chóp tứ giác có số cạnh là:
A.
6
. B.
7
. C.
8
. D.
4
.
Câu 32. Cho mặt cầu có bán kính bằng
2
a
. Đường kính của mặt cầu đó bằng
A.
a
. B.
3
2
a
. C.
3a
. D.
2a
.
Câu 33. Hình nào sau đây không phải là hình đa diện đều?
A. Hình lập phương. B. Hình bát diện đều.
C. Hình chóp tứ giác đều. D. Hình tứ diện đều.
Câu 34. Điểm nào sau đây thuộc đồ thị hàm số
3
3yx x
= −
?
A.
( )
3; 0N
. B.
( )
1; 2M −
. C.
( )
2;14Q
. D.
( )
1; 4P −−
.
Câu 37. Ông
A
gửi
200
triệu đồng vào một ngân hàng theo hình thức lãi kép,với lãi suất là
6,5%
một
năm và lãi suất không đổi trong suốt thời gian gửi. Sau
5
năm, số tiền lãi (làm tròn đến hàng
triệu) của ông bằng bao nhiêu?
A.
80
triệu đồng. B.
65
triệu đồng. C.
74
triệu đồng. D.
274
triệu đồng.
Câu 38. Cho khối chóp đều
.S ABCD
có thể tích bằng
42
3
,cạnh đáy
2AB =
.Góc giữa cạnh bên
SA
và mặt phẳng
(
)
ABCD
có giá trị bằng
A.
0
45
. B.
0
60
. C.
0
135
. D.
0
30
.
Câu 39. Biết rằng có hai giá trị
12
,mm
của tham số
m
để đường thẳng
:dy m x= −
và đồ thị hàm số
1
x
y
x
=
−
có đúng một điểm chung. Khẳng định nào sau đây đúng?
A.
( )
12
10; 1mm+ ∈− −
. B.
( )
12
7;12mm+∈
. C.
12
9
1;
2
mm
+ ∈−
. D.
12
9
;7
2
mm
+∈
.
Câu 40. Tập nghiệm của bất phương trình
9 2.3 3
xx
+≤
là
A.
[ ]
3;1−
. B.
(
]
;0−∞
. C.
[ ]
1; 0−
. D.
( )
;0−∞
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 41. Tập hợp tất cả các giá trị của tham số
m
để hàm số
(
)
32 2
21y x x m xm=+ ++ −
đồng biến trên
khoảng
( )
;−∞ +∞
là
A.
(
]
;3−∞
. B.
( )
;3−∞
. C.
1
;
3
+∞
. D.
1
;
3
+∞
.
Câu 42. Cho khối chóp
.
S ABC
có thể tích bằng
12.
Gọi
M
và
N
lần lượt là trung điểm của
,.SB SC
Thể tích của khối chóp
.S AMN
bằng
A.
8
. B.
3
. C.
9
. D.
6
.
Câu 43. Cho
a
và
b
là hai số thực dương thỏa mãn
2
log
43
ab
b
. Giá trị của
2
ab
bằng
A.
2
. B.
4
. C.
6
. D.
3
.
Câu 47. Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
3
và cạnh bên bằng
x
, với
1
x >
. Gọi
V
là thể tích khối cầu xác định bởi mặt cầu ngoại tiếp hình chóp
.S ABC
. Giá trị nhỏ nhất của
V
thuộc khoảng nào sau đây?
A.
(
)
7;3
π
. B.
( )
0;1
. C.
( )
1; 5
. D.
( )
5; 7
.
Câu 48. Cho hàm số đa thức bậc ba
( )
y fx=
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
tham số
m
để phương trình
(
)
24
21
9 81
fx m m= −
có 8 nghiệm phân biệt?
A.
9
. B.
8
. C.
6
. D.
3
.
Câu 49. Cho khối tứ diện
ABCD
có thể tích bằng
3
. Trên các mặt phẳng
(
)
BCD
,
( )
ACD
,
( )
ABD
,
( )
ABC
lần lượt lấy các điểm
111 1
,,,ABCD
sao cho các đường thẳng
1
AA
,
1
BB
,
1
CC
,
1
DD
đôi
một song song với nhau. Thể tích khối tứ diện
111 1
ABCD
bằng
A.
8
. B.
9
. C.
6
. D.
12
.
Câu 50. Cho hàm số
( )
fx
xác định và có đạo hàm trên
. Hàm số
( )
fx
′
có bảng biến thiên như sau:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Hàm số
( ) ( )
( )
( )
( )
( )
53
14
4 2021
53
gx fx fx fx= − ++
luôn nghịch biến trên khoảng nào sau
đây?
A.
( )
;5−∞
. B.
( )
;1−∞
. C.
( )
1;− +∞
. D.
( )
;−∞ +∞
.
-------------------------------------- HẾT --------------------------------------
SỞ GIÁO DỤC TỈNH BẮC NINH
HƯỚNG DẪN GIẢI CHI TIẾT
ĐỀ THI HỌC KÌ I - NĂM HỌC 2020 - 2021
BẢNG ĐÁP ÁN
0
∞
∞
+
1
f'(x)
x
1
5
∞
∞
+

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
A
B
B
D
C
D
D
C
B
C
D
A
D
A
C
C
B
A
A
C
D
D
B
A
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
B
D
A
C
A
C
B
B
A
C
A
C
B
C
B
D
B
A
A
C
C
B
B
B
LỜI GIẢI CHI TIẾT
Câu 1. Khối chóp có diện tích đáy bằng
2
a
, chiều cao bằng
a
có thể tích bằng
A.
3
2
a
. B.
3
a
. C.
3
1
3
a
. D.
3
2
3
a
.
Lời giải
Chọn C
Thể tích khối chóp là
23
11
..
33
V aa a= =
.
Câu 2. Cho hàm số
( )
y fx=
có bảng biến thiên như hình sau:
Hàm số trên đạt cực đại tại
A.
2x = −
. B.
3x =
. C.
2x =
. D.
0x =
.
Lời giải
Chọn A
Nhìn vào bảng biến thiên hàm số đạt cực đại tại
2x = −
.
Câu 3. Cho khối lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
B
, cạnh
AB a=
,
2BC a
=
,
3AA a
′
=
. Thể tích khối lăng trụ đã cho là
A.
3
a
B.
3
3a
. C.
3
2a
. D.
3
6a
.
Lời giải
Chọn B
Thể tích khối lăng trụ đứng
.ABC A B C
′′′
là
3
11
. . . 3 . .2 3
22
ABC
V AA S AA BA BC a a a a
∆
′′
= = = =
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 4. Khối hộp chữ nhật có ba kích thước lần lượt là
1;2;3
có thể tích bằng
A.
2
. B.
4
. C.
8
. D.
6
.
Lời giải
Chọn D
Thể tích khối hộp chữ nhật là
1.2.3 6V = =
.
Câu 5. Giá trị nhỏ nhất của hàm số
43yx= −
trên đoạn
[ ]
0;1
bằng
A.
2
. B.
1
. C.
0
. D.
4
.
Lời giải
Chọn B
Tập xác định
4
;
3
D
= −∞
.
Ta có
34
0,
3
24 3
yx
x
−
′
= < ∀<
−
.
Mà
( ) ( )
0 2, 1 1yy= =
nên
[ ]
0;1
min 1y =
khi
1
x
=
.
Câu 6. Tập xác định
D
của hàm số
( )
2
3yx
−
= −
là
A.
( )
0;D = +∞
. B.
( )
3;D = +∞
. C.
D
=
. D.
{ }
\3D
=
.
Lời giải
Chọn D
Hàm số
( )
2
3yx
−
= −
xác định
30 3xx⇔−≠⇔ ≠
.
Vậy
{ }
\3D =
.
Câu 7. Phương trình đường tiệm cận đứng của đồ thị hàm số
21
2
x
y
x
−
=
+
là:
A.
2y = −
. B.
2x =
. C.
2x = −
. D.
2y =
.
Lời giải
Chọn C
{ }
\2D
= −
.
Ta có
( ) ( )
( ) ( )
22
22
21
lim lim
2
21
lim lim
2
xx
xx
x
y
x
x
y
x
++
−−
→− →−
→− →−
−
= = −∞
+
−
= = +∞
+
Nên
2x = −
là đường tiệm cận đứng của đồ thị hàm số đã cho.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 8. Một hình trụ tròn xoay có bán kính đáy
2r
=
, chiều cao
5h
=
thì có diện tích xung quanh bằng
A.
10
π
. B.
50
π
. C.
4
π
. D.
20
π
.
Lời giải
Chọn D
Ta có
5
hl= =
nên
xq
2 2 .2.5 20S rl
ππ π
= = =
.
Câu 9. Giá trị lớn nhất của hàm số
42
21yx x=−+ +
trên đoạn
[ ]
2;5−
bằng
A.
1−
. B.
7−
. C.
5
. D.
2
.
Lời giải
Chọn D
Hàm số
42
21yx x
=−+ +
xác định và liên tục trên đoạn
[ ]
2;5−
.
[ ]
[ ]
[ ]
33
1 2;5
44;0 440 12;5
0 2;5
x
y xxy xx x
x
= ∈−
′′
=−+ =⇔−+=⇔=−∈−
= ∈−
.
Khi đó,
(
) (
) (
) (
) (
)
2 7; 1 2; 0 1; 1 2; 5 574y y yyy−=− −= = = =−
.
Vậy
[ ]
2;5
max 2y
−
=
.
Câu 10. Mặt cầu có bán kính
3r =
thì có diện tích bằng
A.
9
π
. B.
108
π
. C.
36
π
. D.
27
π
.
Lời giải
Chọn C
Ta có
22
4 4 .3 36
mc
Sr
ππ π
= = =
.
Câu 11. Cho
,ab
là các số thực dương;
,
là các số thực tùy ý. Khẳng đinh nào sau đây sai?
A.
a
a
a
α
αβ
β
−
=
. B.
( )
aa
β
β
αα
=
. C.
.aa a
α β αβ
+
=
. D.
( )
ab a b
α
αα
=
.
Lời giải
Chọn B
Khẳng định B sai.
Câu 12. Một hình nón tròn xoay có bán kính đáy
3r
, chiều cao
1h
thì có độ dài đường sinh bằng
A.
13+
. B.
2
. C.
2
. D.
4
.
Lời giải
Chọn C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
2 22 22
2l hr l hr
.
Câu 13. Đồ thị hàm số
2
32
yxx
và trục hoành có bao nhiêu điểm chung?
A.
0
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn D
Xét phương trình hoành độ giao điểm
2
1
3 20
2
3
x
xx
x
.
Vậy số điểm chung của hai đồ thị là 2.
Câu 14. Hàm số nào sau đây nghịch biến trên
;
?
A.
21yx=−+
. B.
yx=
. C.
2yx
=−+
. D.
5yx= −
.
Lời giải
Chọn A
Hàm số bậc nhất
0y ax b a
nghịch biến trên khoảng
;
0
a
.
Do đó ta chọn đáp án#A.
Câu 15. Cho hình lập phương có cạnh bằng
2
. Tổng diện tích các mặt của hình lập phương đã cho bằng
A.
16
. B.
12
. C.
4
. D.
24
.
Lời giải
Chọn D
Hình lập phương có 6 mặt là hình vuông có các cạnh bằng nhau.
Do đó tổng diện tích các mặt là
2
2 .6 24S
.
Câu 16. Quay hình vuông
ABCD
có cạnh bằng
1
xung quanh đường thẳng
AB
ta thu được khối trụ tròn
xoay có chiều cao bằng bao nhiêu?
A.
1
. B.
1
2
. C.
2
2
. D.
2
.
Lời giải
Chọn A

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có chiều cao
1h AB= =
.
Câu 17. Cho hàm số
21
3
x
y
x
−
=
+
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên mỗi khoảng
( ) ( )
; 3 , 3;−∞ +∞
.
B. Hàm số đồng biến trên mỗi khoảng
11
;,;
22
−∞ +∞
.
C. Hàm số đồng biến trên mỗi khoảng
( )
( )
; 3 , 3;−∞ − − +∞
.
D. Hàm số đồng biến trên
.
Lời giải
Chọn C
TXĐ:
{ }
\3D = −
.
Ta có
(
)
2
7
0,
3
y xD
x
′
= > ∀∈
+
.
Vậy hàm số đồng biến trên mỗi khoảng
( )
;3−∞ −
và
( )
3;− +∞
.
Câu 18. Hàm số
lnyx=
có đạo hàm là
A.
1
ln
y
xx
′
=
. B.
1y
′
=
. C.
1
y
x
′
=
. D.
yx
′
=
.
Lời giải
Chọn C
Câu 19. Cho hai số dương
a
và
, 1, 1
ba b≠≠
. Trong các khẳng định sau, khẳng định nào sai
A.
log 1
a
a =
. B.
log
b
a
ab
=
. C.
log
b
a
ab=
. D.
log 1 0
a
=
.
Lời giải
Chọn B
Sai vì
log
a
b
ab=
Câu 20. Cho hàm số
yx
α
=
với
0,x
α
>∈
có đạo hàm được tính bởi công thức
A.
1
yx
α
α
−
′
=
. B.
1
yx
α
−
′
=
. C.
1
ln
yx x
α
α
−
′
=
. D.
( )
1yx
α
α
′
= −
.
Lời giải
Chọn A
Câu 21. Phương trình
( ) ( )
55
log 2 1 log 2xx−= −
có bao nhiêu nghiệm?
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn A
Điều kiện xác định:
2 10
1
2
20
2
x
x
x
−>
⇔ <<
−>
.
Phương trình khi đó tương đương với
2 12 3 3 1x xx x−= − ⇔ = ⇔ =
(thỏa mãn). Vậy phương
trình đã cho có đúng 1 nghiệm.
Câu 22. Tập nghiệm của bất phương trình
2
log 3
x <
là
A.
( )
8; +∞
. B.
( )
;8−∞
. C.
( )
0;8
. D.
( )
0;6
.
Lời giải
Chọn C
Ta có
3
2
log 3 0 2 0 8xx x<⇔<< ⇔<<
.Vậy tập nghiệm của bất phương trình là
( )
0;8
.
Câu 23. Phương trình
1
28
x
+
=
có nghiệm là
A.
3x =
. B.
4x =
. C.
1x =
. D.
2x =
.
Lời giải
Chọn D
Ta có
1
2 8 13 2
x
xx
+
= ⇔ += ⇔ =
vậy phương trình có một nghiệm duy nhất là
2x =
.
Câu 24. Tập xác định
D
của hàm số
2
3
logyx=
là
A.
( )
0;D = +∞
. B.
( )
;0
D = −∞
. C.
D
=
. D.
{ }
\0D =
.
Lời giải
Chọn D
Điều kiện xác định:
2
00xx>⇔≠
. Vậy tập xác định của hàm số là
{ }
\0D =
.
Câu 25. Cho hàm số
( )
fx
có đạo hàm
( )
2 1,fx x x
′
= − ∀∈
. Hỏi
( )
fx
có bao nhiêu điểm cực trị?
A.
3
. B.
1
. C.
0
. D.
2
.
Lời giải
Chọn B
Ta có
( )
1
0 2 10
2
fx x x
′
= ⇔ −= ⇔ =
, suy ra
( )
fx
′
đổi dấu một lần khi
x
đi qua giá trị
1
2
x =
nên hàm số
( )
fx
có 1 điểm cực trị.
Câu 26. Đường tiệm cận ngang của đồ thị hàm số
1
3
x
y
x
−−
=
+
cắt đường thẳng
2021
yx=
tại điểm có tung
độ bằng
A.
1−
. B.
2−
. C.
0
. D.
1
2021
−
.
Lời giải
Chọn A

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
1
1
lim lim 1
3
1
xx
x
y
x
→+∞ →+∞
−−
= = −
+
và
1
1
lim lim 1
3
1
xx
x
y
x
→−∞ →−∞
−−
= = −
+
1y
⇒=−
là đường tiệm cận ngang của ĐTHS
Đường tiệm cận ngang
1
y
= −
cắt đường thẳng
2021yx=
tại điểm có tung độ bằng
1−
.
Câu 27. Bất phương trình
3 81
x
<
có tập nghiệm là
A.
( )
;4−∞
. B.
{ }
4
. C.
( )
4; +∞
. D.
( )
;27−∞
.
Lời giải
Chọn A
Ta có
4
3 81 3 3 4
xx
x< ⇔ < ⇔<
.
Tập nghiệm của bất phương trình
3 81
x
<
là
( )
;4−∞
.
Câu 28. Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
1
x
y
x
−
=
+
là
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Chọn B
Tập xác định
D =
. Đồ thị hàm số không có tiệm cận đứng.
Ta có
2
2
11
lim lim 0
1
1
xx
x
x
y
x
→+∞ →+∞
−
= =
+
và
2
2
11
lim lim 0
1
1
xx
x
x
y
x
→−∞ →−∞
−
= =
+
0y⇒=
là đường tiệm cận ngang của ĐTHS.
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
1
x
y
x
−
=
+
là
1
.
Câu 29. Điểm cực tiểu của hàm số
32
3x 1yx=−+ −
là:
A.
1x = −
. B.
3x =
. C.
2x =
. D.
0x =
.
Lời giải
Chọn D
TXD:
D =
Ta có
2
0
' 3x 6x ' 0
2
x
yy
x
=
=− + ⇒=⇔
=
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Khi đó
( )
(
)
0 60
66
2 60
y
yx
y
′′
= >
′′
=− +⇒
′′
=−<
Câu 12: Vậy hàm số đạt cực tiểu tại
0x =
Câu 30. Giá trị của biểu thức
2
3
log 4 log 9P = +
là
A.
6
. B.
7
. C.
8
. D.
4
.
Lời giải
Chọn A
Ta có
22
2 23
3
log 4 log 9 log 2 2log 3 6.P =+=+ =
Câu 31. Hình chóp tứ giác có số cạnh là:
A.
6
. B.
7
. C.
8
. D.
4
.
Lời giải
Chọn C
Hình chóp tứ giác có
4
cạnh đáy và
4
cạnh bên, nên có tổng số cạnh là
8
.
Câu 32. Cho mặt cầu có bán kính bằng
2
a
. Đường kính của mặt cầu đó bằng
A.
a
. B.
3
2
a
. C.
3a
. D.
2
a
.
Lời giải
Chọn A
Đường kính
2 2.
2
a
dr a= = =
.
Câu 33. Hình nào sau đây không phải là hình đa diện đều?
A. Hình lập phương. B. Hình bát diện đều.
C. Hình chóp tứ giác đều. D. Hình tứ diện đều.
Lời giải
Chọn C
Câu 34. Điểm nào sau đây thuộc đồ thị hàm số
3
3yx x= −
?
A.
( )
3; 0N
. B.
( )
1; 2M −
. C.
( )
2;14Q
. D.
( )
1; 4P −−
.
Lời giải
Chọn B
Thế
1x =
vào
3
3yx x= −
, ta được
3
1 3.1 2y =−=−
.
Nên
( )
1; 2M −
thuộc đồ thị hàm số
3
3yx x= −
.
Câu 35. Biết rằng hình bên là đồ thị của một trong bốn hàm số cho ở các đáp án
,,,ABCD
.Hỏi đó là

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
hàm số nào?
A.
42
2yx x=−+
. B.
42
241y xx
=−+ +
. C.
42
1
1
2
y xx=− −+
. D.
42
21yx x=−+
.
Lời giải
Chọn B
Ta thấy đồ thị đi qua
(
)
0;1
nên loại A
Loại đáp án C vì
.0ab
>
Ta loại đáp án D do hệ số
0a >
.
Câu 36. Cho mặt cầu
(
)
S
tâm
I
và bán kính
10r =
.Cho mặt phẳng
(
)
P
,biết rằng khoảng cách từ điểm
I
đến mặt phẳng
( )
P
bằng
8
. Khẳng định nào sau đây đúng?
A. Mặt cầu
( )
S
cắt mặt phẳng
(
)
P
theo giao tuyến là đường tròn có bán kính bằng
6
.
B. Mặt cầu
(
)
S
tiếp xúc với mặt phẳng
( )
P
tại một điểm.
C. Mặt cầu
( )
S
và mặt phẳng
( )
P
không có điểm chung.
D. Mặt cầu
( )
S
cắt mặt phẳng
( )
P
theo giao tuyến là đường tròn có bán kính bằng
12
.
Lời giải
Chọn A
Ta có
( )
( )
, 8 10= <dI P
, nên mặt cầu
( )
S
cắt mặt phẳng
( )
P
theo giao tuyến là đường tròn có
bán kính bằng
2 2 22
10 8 6r Rd= − = −=
.
Câu 37. Ông
A
gửi
200
triệu đồng vào một ngân hàng theo hình thức lãi kép,với lãi suất là
6,5%
một
năm và lãi suất không đổi trong suốt thời gian gửi. Sau
5
năm, số tiền lãi (làm tròn đến hàng
triệu) của ông bằng bao nhiêu?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
80
triệu đồng. B.
65
triệu đồng. C.
74
triệu đồng. D.
274
triệu đồng.
Lời giải
Chọn C
Số tiền lãi sau
5
năm của ông
A
là
( )
5
200. 1 6,5% 200 74+ −≈
(triệu).
Câu 38. Cho khối chóp đều
.S ABCD
có thể tích bằng
42
3
,cạnh đáy
2AB =
.Góc giữa cạnh bên
SA
và mặt phẳng
(
)
ABCD
có giá trị bằng
A.
0
45
. B.
0
60
. C.
0
135
. D.
0
30
.
Lời giải
Chọn A
Ta có
4
ABCD
S =
3
2
V
h
S
⇒= =
.
Ta có
( )
( )
( )
;SO ABCD SA ABCD SAO
⊥⇒ =
.
0
2
tan 1 45
2
SO
SAO SAO
AO
===⇒=
.
Câu 39. Biết rằng có hai giá trị
12
,mm
của tham số
m
để đường thẳng
:dy m x= −
và đồ thị hàm số
1
x
y
x
=
−
có đúng một điểm chung. Khẳng định nào sau đây đúng?
A.
( )
12
10; 1mm+ ∈− −
. B.
( )
12
7;12mm+∈
. C.
12
9
1;
2
mm
+ ∈−
. D.
12
9
;7
2
mm
+∈
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm:
1
−=
−
x
mx
x
( )( 1)⇔ − −=m xx x
( do
1
=x
không là nghiệm của phương trình).
(
)
2
0 1.⇔ − +=x mx m

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Đường thẳng
:dy m x
= −
và đồ thị hàm số
1
x
y
x
=
−
có một điểm chung khi và chỉ khi phương
trình (1) có nghiệm duy nhất
2
0
0 40
4
=
⇔∆= ⇔ − = ⇔
=
m
mm
m
.
Vậy
12
9
4 1;
2
+ = ∈−
mm
.
Câu 40. Tập nghiệm của bất phương trình
9 2.3 3
xx
+≤
là
A.
[ ]
3;1−
. B.
(
]
;0−∞
. C.
[ ]
1; 0−
. D.
( )
;0−∞
.
Lời giải
Chọn B
Ta có
2
9 2.3 3 3 2.3 3 0 3 3 1 0+ ≤ ⇔ + − ≤ ⇔− ≤ ≤ ⇔ ≤
xx xx x
x
.
Câu 41. Tập hợp tất cả các giá trị của tham số
m
để hàm số
( )
32 2
21y x x m xm=+ ++ −
đồng biến trên
khoảng
( )
;
−∞ +∞
là
A.
(
]
;3−∞
. B.
( )
;3−∞
. C.
1
;
3
+∞
. D.
1
;
3
+∞
.
Lời giải
Chọn C
Hàm số đồng biến trên
khi và chỉ khi
2
' 3 4 1 0,= + + + ≥ ∀∈
y x xm x
( )
2
30
1
' 2 3. 1 0
3
= >
⇔ ⇔≥
∆= − + ≤
a
m
m
.
Câu 42. Cho khối chóp
.
S ABC
có thể tích bằng
12.
Gọi
M
và
N
lần lượt là trung điểm của
,.SB SC
Thể tích của khối chóp
.S AMN
bằng
A.
8
. B.
3
. C.
9
. D.
6
.
Lời giải
Chọn B
Ta có
.
..
.
11 1 1 1
. . 1. . .12 3.
22 4 4 4
S AMN
S AMN S ABC
S ABC
V
SA SM SN
VV
V SA SB SC
= ==⇒= ==
N
M
A
C
B
S

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 43. Cho
a
và
b
là hai số thực dương thỏa mãn
2
log
43
ab
b
. Giá trị của
2
ab
bằng
A.
2
. B.
4
. C.
6
. D.
3
.
Lời giải
Chọn D
Ta có
( )
( )
( )
( ) ( )
2
2
2 22
log
log 2log log
2
4 3 2 32 32 3
ab
ab ab ab
b bbb=⇔ =⇔=⇔=
Khi đó
( )
2
22 2
3 33ab b ab b ab=⇔ =⇔=
.
Câu 44. Cho hàm số
(
)
2
3
xm
fx
x
+
=
−
(với
m
là tham số). Giá trị của
m
để
[ ]
( )
[ ]
( )
1;2
1;2
max min 8fx fx
−
−
+=
là
A.
4
5
m =
. B.
46
5
m = −
. C.
12m = −
. D.
18
5
m =
.
Lời giải
Chọn B
Ta có
( )
2
1
4
m
f
−
−=
và
(
)
24fm=−−
Khi đó
[ ]
( )
[ ]
( )
1;2
1;2
2 46
max min 8 4 8 5 46 0
45
m
fx fx m m m
−
−
−
+ =⇒ −−=⇔−−=⇔=−
.
Câu 45. Cho khối nón tròn xoay, biết rằng thiết diện của khối nón cắt bởi mặt phẳng đi qua trục là một
tam giác đều có cạnh bằng
a
. Thể tích khối nón tròn xoay đã cho bằng
A.
3
3
24
a
π
. B.
3
1
8
a
π
. C.
3
1
24
a
π
. D.
3
3
8
a
π
.
Lời giải
Chọn A
Thiết diện qua trục là tam giác đều cạnh
22
3
2
2
2
la
la
a
a h lR
a
Ra
R
=
=
⇒ ⇔ ⇒= − =
=
=
.
Vậy thể tích khối nón là
2
23
1 1 33
.
3 3 2 2 24
aa
V Rh a
ππ π
= = =
.
Câu 46. Có tất cả bao nhiêu giá trị nguyên dương nhỏ hơn
2020
của tham số
m
để phương trình
( ) ( )
log 2 log 1mx x= +
có nghiệm thực?
A.
2016
. B.
2019
. C.
2017
. D.
2015
.
Lời giải
Chọn A
Phương trình
( )
( )
( )
( )
2
2
1
1
log 2log 1
2 11
1
x
x
mx x
mx x x
mx x
>−
>−
= +⇔ ⇔
=++
= +
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Nhận thấy
0x =
không là nghiệm của phương trình
( )
1
. Do đó
(
)
1
12xm
x
⇔++=
.
Xét hàm số
(
)
( )
2
11
21fx x f x
xx
′
=+ +⇒ =−
;
(
)
( )
1
0
1
xl
fx
x
= −
′
= ⇔
=
Từ bảng biến thiên, phương trình đã cho có ngiệm khi
0m <
hoặc
4m ≥
.
Vì
m
nguyên dương nhỏ hơn
2020
[
) { }
4;2020 4;5;6;...;2019mm⇒∈ ⇒∈
.
Câu 47. Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
3
và cạnh bên bằng
x
, với
1x >
. Gọi
V
là thể tích khối cầu xác định bởi mặt cầu ngoại tiếp hình chóp
.
S ABC
. Giá trị nhỏ nhất của
V
thuộc khoảng nào sau đây?
A.
( )
7;3
π
. B.
( )
0;1
. C.
( )
1; 5
. D.
( )
5; 7
.
Lời giải
Chọn C
Gọi
M
là trung điểm của
BC
,
G
là trong tâm tam giác
( )
ABC SG ABC⇒⊥
.
Trong mặt phẳng
( )
SAM
, đường trung trực của đoạn
SA
cắt
SG
tại
I IA IB IC IS⇒===
là
tâm mặt cầu ngoại tiếp khối chóp
.
S ABC
.
2
32
;11
23
AM AG AM SG x= = =⇒= −
K
I
G
M
A
S
B
C

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Hai tam giác
SKI
và
SGA
đông dạng
22
22 2
2
.
121 21
x
SI SK x x
SI x R
SA SG
xx x
⇒ = ⇒ = = ⇒=
−− −
.
Thể tích khối cầu:
( )
6
3
22
41
36
11
x
VR
xx
ππ
= =
−−
Đặt
( )
3
2 22 62 642
1 1 1 331
t x xt x t t t t
= −⇒=+⇒=+=+++
( )
3
3
6 642
3
33
22
3 3 1 31 1 1
3 2. . 8
11
x ttt
tt t t
t tt t t
xx
+++
= = + ++ = + ≥ =
−−
.
Dấu “=” xảy ra khi
12tx=⇒=
.
Do đó, giá trị nhỏ nhất của thể tích khối chóp
.S ABC
là
4
3
V
π
=
.
Câu 48. Cho hàm số đa thức bậc ba
( )
y fx=
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
tham số
m
để phương trình
(
)
24
21
9 81
fx m m= −
có 8 nghiệm phân biệt?
A.
9
. B.
8
. C.
6
. D.
3
.
Lời giải
Chọn C
Từ đồ thị hàm số
( )
y fx=
, ta có đồ thị hàm số
( )
y fx=
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Điều kiện:.
Dựa vào đồ thị hàm số
(
)
y fx=
, suy ra phương trình
(
)
24
21
9 81
fx m m
= −
có 8 nghiệm phân
biệt khi
24
21
01
9 81
mm<− <
2
24
2
42
21
32
0 18
0
9 81
92 9
3 21
18 81 0
m
m
mm
m
m
mm
<
<<
−>
⇔ ⇔⇔
>−
>−
+ −>
3 2 1 32
32 3 2 1
m
m
−< <
− < <− −
{
}
4; 3; 2; 2;3; 4m⇒ ∈− − −
.
Câu 49. Cho khối tứ diện
ABCD
có thể tích bằng
3
. Trên các mặt phẳng
( )
BCD
,
( )
ACD
,
( )
ABD
,
( )
ABC
lần lượt lấy các điểm
111 1
,,,ABCD
sao cho các đường thẳng
1
AA
,
1
BB
,
1
CC
,
1
DD
đôi
một song song với nhau. Thể tích khối tứ diện
111 1
ABCD
bằng
A.
8
. B.
9
. C.
6
. D.
12
.
Lời giải
Chọn B
Cách của thầy Đặng Minh Trường (cách trắc nghiệm)

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Giả sử
1
A
là trọng tâm tam giác
BCD
;
11 1
BB CC DD= =
(thỏa mãn các giả thiết của bài toán và
được minh họa như hình vẽ trên).
Vì
11 1
BB CC DD= =
và các đường thẳng
1
AA
,
1
BB
,
1
CC
,
1
DD
đôi một song song với nhau nên
111
.BCD B C D
là lăng trụ
Ta có
( )
( )
( )
( )
111 1
111
.
11
1
1 11 1
1
,.
1
3
1
3
,.
3
BCD
A BCD
ABCD
BCD
d A BCD S
V
AA FA
V DD FD
d A BCD S
∆
∆
= = = =
( Vì
( )
( )
( )
( )
111
1
1
1 11 1
,
;
,
BCD B C D
d A BCD
AA
SS
DD
d A BCD
∆∆
= =
)
Do đó
111 1
.
39
A B C D A BCD
VV= =
.
Câu 50. Cho hàm số
( )
fx
xác định và có đạo hàm trên
. Hàm số
( )
fx
′
có bảng biến thiên như sau:
A
1
G
F
E
B
D
C
C
1
D
1
B
1
A

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Hàm số
( ) ( )
( )
( )
( )
( )
53
14
4 2021
53
gx fx fx fx= − ++
luôn nghịch biến trên khoảng nào sau
đây?
A.
( )
;5−∞
. B.
( )
;1−∞
. C.
( )
1;− +∞
. D.
(
)
;
−∞ +∞
.
Lời giải
Chọn B
( ) ( ) ( )
( )
( )
( )
(
)
( ) ( )
( )
(
)
2
42 2
44 2gx f x fx fx f x fx
′′ ′
= − += −
Từ bảng biến thiên ta thấy
( ) ( ) (
)
;1 0 0x f x gx
′′
∀ ∈ −∞ ⇒ ≤ ⇒ ≤
Vậy hàm số
( )
gx
luôn nghịch biến trên
( )
;1−∞
.
--------------------------- HẾT ---------------------------
0
∞
∞
+
1
f'(x)
x
1
5
∞
∞
+

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
THPT HỒNG LĨNH HÀ TĨNH
ĐỀ THI HỌC KÌ I - NĂM HỌC 2020 - 2021
Môn: TOÁN – LỚP 12
Thời gian: 90 phút (Không kể thời gian phát đề)
Câu 1: Số đỉnh của một khối lăng trụ tam giác là?
A.
9
. B.
3
. C.
6
. D.
12
.
Câu 2: Đạo hàm của hàm số
4
yx=
là
A.
3
'4yx=
. B.
'0
y
=
. C.
2
'4yx=
. D.
'4yx
=
.
Câu 3: Cho hàm số
( )
y fx=
xác định, liên tục trên
và có bảng biến thiên sau
−∞
0
1
+∞
||
0
0
+∞
−∞
1−
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị lớn nhất bằng
0
và giá trị nhỏ nhất bằng
1−
.
B. Hàm số có đúng một cực trị.
C. Hàm số có giá trị cực tiểu bằng 1.
D. Hàm số đạt cực đại tại
0x
=
và đạt cực tiểu tại
1x =
.
Câu 4:
( )
3
1
1
lim
x
xx
→−
−−
bằng
A. -1. B. 3. C. -3. D. 1.
Câu 5: Cho khối lăng trụ có diện tích đáy
6B =
và chiều cao
3h =
. Thể tích của khối lăng trụ đã cho
bằng
A.
18
. B.
54
. C.
36
. D.
2
.
Câu 6: Cho hàm số
( )
fx
có bảng biến thiên sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
2;0−
. B.
( )
1; 3
. C.
( )
;2−∞ −
. D.
( )
0; +∞
.
Câu 7: Xét phép thử ngẫu nhiên có không gian mẫu
Ω
. Gọi
( )
PA
là xác suất của biến cố A liên quan
đến phép thử. Khẳng định nào sau đây là khẳng định đúng?
A.
( ) ( )
PA nA=
. B.
( ) ( ) ( )
.PA nAn= Ω
.
x
y
′
+
−
+
y
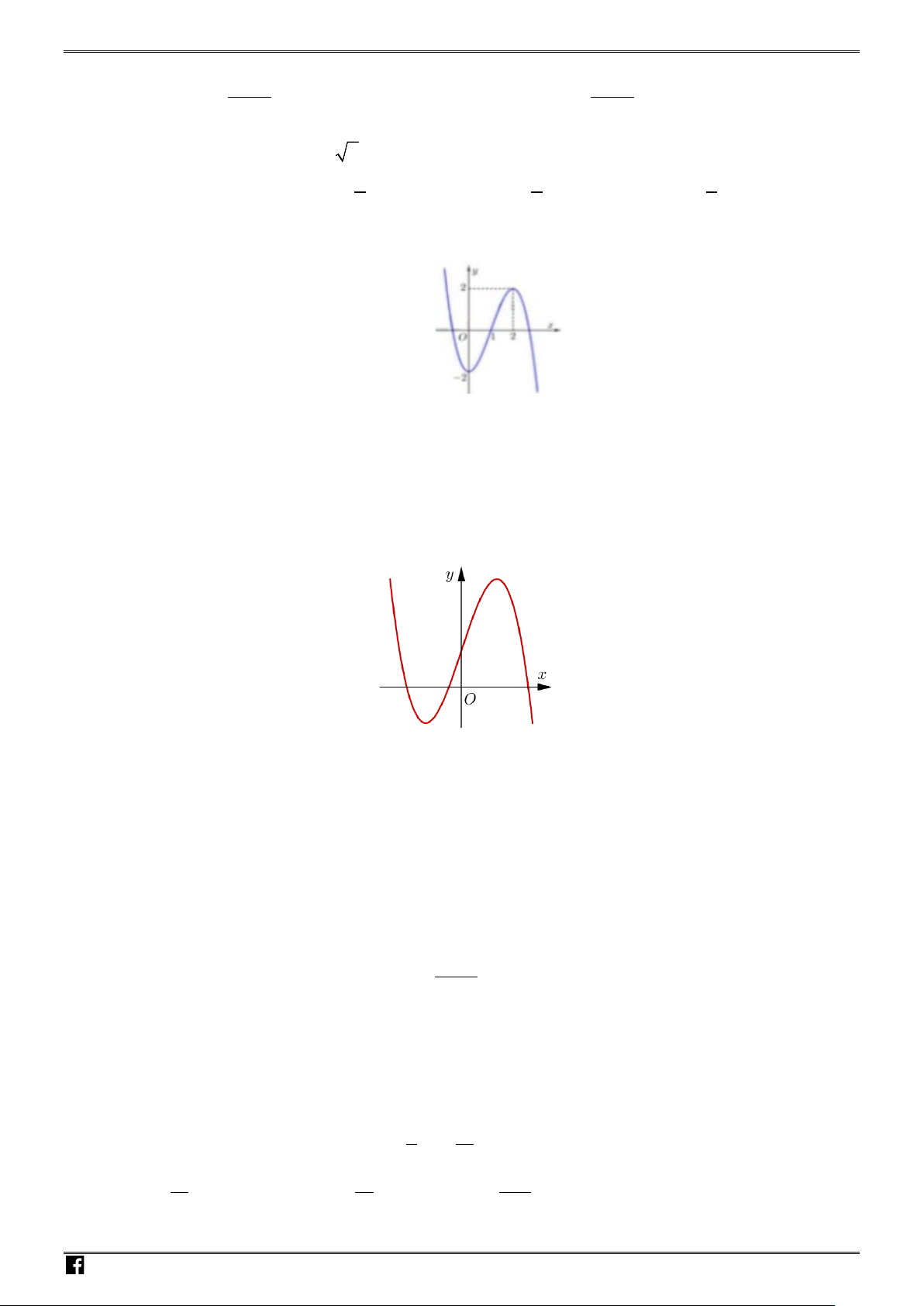
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
C.
(
)
( )
(
)
n
PA
nA
Ω
=
. D.
( )
(
)
(
)
nA
PA
n
=
Ω
.
Câu 8: Đạo hàm của hàm số
yx=
tại điểm
9x =
bằng:
A. 0. B.
1
2
. C.
1
6
. D.
1
3
.
Câu 9: Cho hàm số
y fx
xác định, liên tục trên
và có đồ thị như hình vẽ sau
Hàm số
y fx
đồng biến trên những khoảng nào dưới đây
A.
( )
;0−∞
. B.
( )
0; 2
. C.
( )
2; +∞
. D.
( )
2; 2−
.
Câu 10: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng
A.
1
. B.
2
. C.
4
. D.
5
.
Câu 11: Đồ thị của hàm số nào dưới đậy có dạng đường cong như hình vẽ sau
A.
42
21yx x
=−+
. B.
42
21yx x=−+ +
. C.
3
31yx x=−+
. D.
3
31yx x=−+ +
.
Câu 12: Cho hàm số
( )
y fx=
có
(
)
lim 1
x
fx
→+∞
=
và
( )
lim 1
x
fx
→−∞
= −
. Khẳng định nào sau đây là khẳng
định đúng?
A. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường
1x =
và
1x = −
.
B. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường
1y =
và
1
y = −
.
C. Hàm số đã cho có hai đường tiệm cận ngang là các đường
1
x =
và
1x
= −
.
D. Đồ thị hàm số đã cho không có tiệm cận ngang .
Câu 13: Tiệm cận ngang của đồ thị hàm số
31
1
x
y
x
−
=
−
là
A.
3y = −
. B.
3y =
. C.
1x
=
. D.
1x = −
.
Câu 14: Số cách xếp
5
học sinh thành một hàng dọc ?
A.
20
. B.
5
5
. C.
5!
. D.
5
.
Câu 15: Cho một cấp số cộng
( )
n
u
có
1
1 11
;
33
ud
= =
. Số hạng thứ hai của cấp số cộng là:
A.
11
9
. B.
10
3
. C.
10
3
−
.
D.
4
.
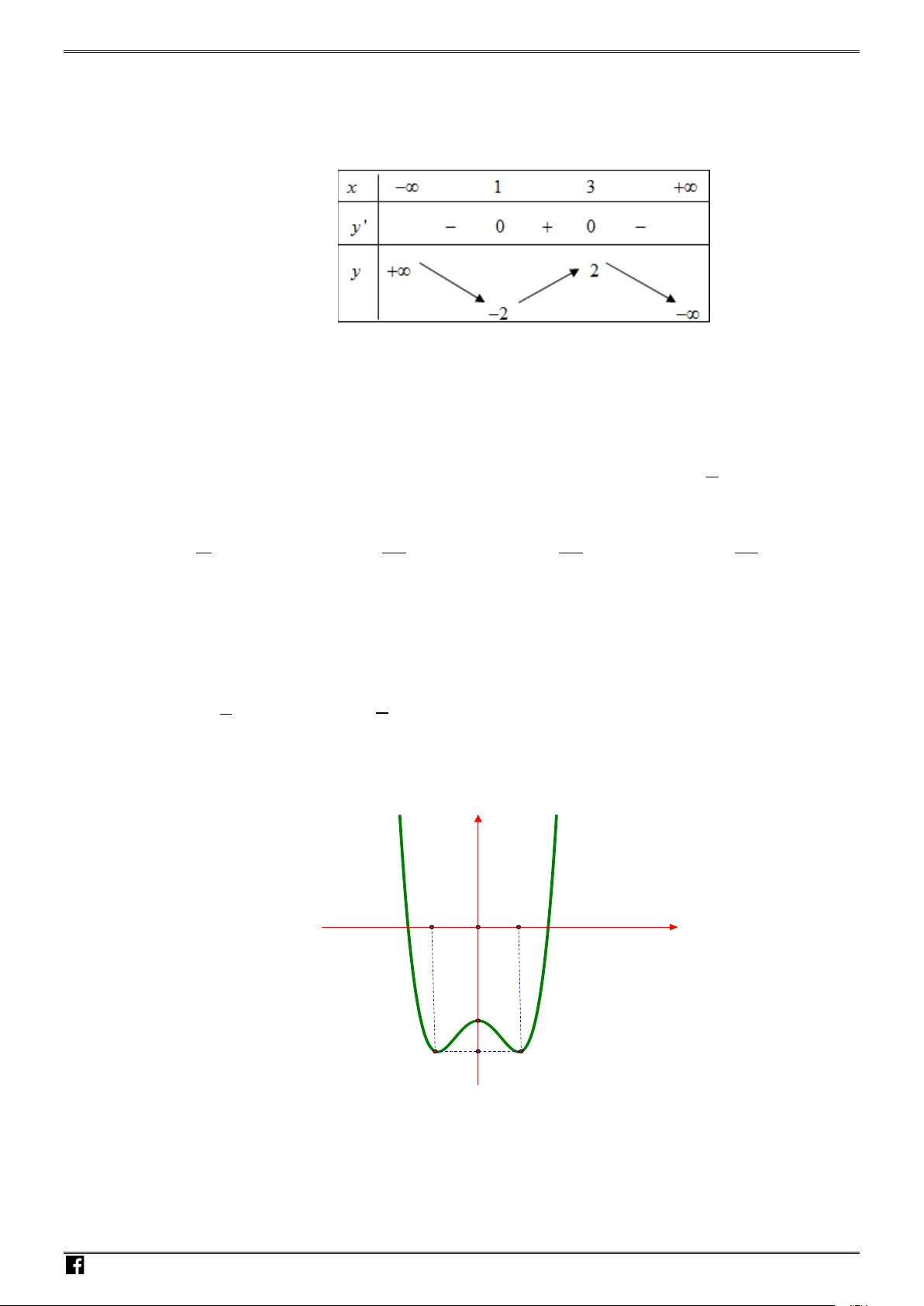
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 16: Cho hàm số
3
3xyx= −
có đồ thị
( )
C
. Số giao điểm của
( )
C
và trục hoành là:
A.
1
. B.
3
. C.
0
.
D.
2
.
Câu 17: Cho hàm số
( )
y fx=
có bảng biến thiên như sau
Giá trị cực đại của hàm số
(
)
y fx=
bằng
A.
2
−
. B.
1
. C.
3
.
D.
2
.
Câu 18: Cho cấp số nhân
( )
n
u
với
1
2u
=
và
2
8u =
.Công bội của cấp số nhân đã cho bằng
A.
6
. B.
4
. C.
6−
. D.
1
2
.
Câu 19: Chiều cao của khối chóp có diện tích đáy bằng
B
và thể tích bằng
V
là
A.
=
V
h
B
. B.
6
=
V
h
B
. C.
2
=
V
h
B
. D.
3
=
V
h
B
.
Câu 20: Từ các chữ số
1, 2, 3, 4
lập được bao nhiêu số có
3
chữ số ?
A.
12
. B.
81
. C.
24
. D.
64
.
Câu 21: Hàm số
4
21yx
= +
đồng biến trên khoảng nào dưới đây?
A.
1
;
2
−∞ −
. B.
1
;
2
− +∞
. C.
( )
0;
+∞
. D.
( )
;0−∞
.
Câu 22: Cho hàm số
( )
fx
có đồ thị như hình vẽ
Tất cả giá trị của tham số m để phương trình
( )
fx m=
có 4 nghiệm phân biệt là?
A.
4m >−
. B.
43m− < <−
. C.
43m− < ≤−
. D.
43m− ≤ ≤−
.
Câu 23: Cho khối chóp có đáy hình vuông cạnh
a
và chiều cao
2a
. Thể tích của khối chóp đã cho bằng
x
y
-3
O
1
-4
-1
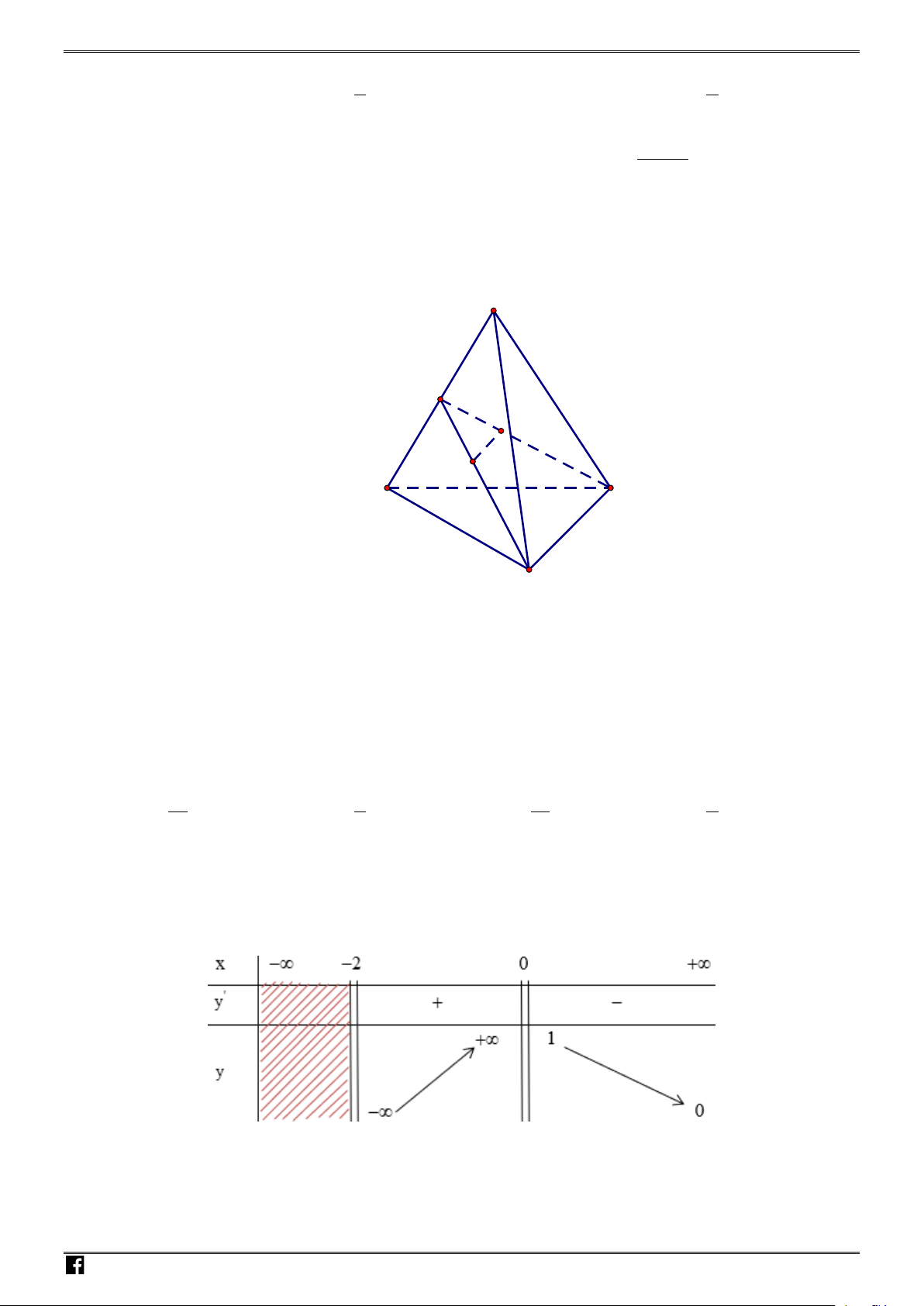
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
2a
. B.
3
4
3
a
. C.
3
4a
. D.
3
2
3
a
.
Câu 24: Có bao nhiêu giá trị nguyên của tham số
(
]
0; 20m∈
để hàm số
2
3
x
y
xm
+
=
+
đồng biến trên khoảng
( )
;6−∞ −
?
A.
2
. B.
4
. C.
20
. D.
21
.
Câu 25. Cho khối chóp
ABCD
. Gọi
G
và
E
lần lượt là trọng tâm các tam giác
ABD
và
ABC
.
Khẳng định nào sau đây đúng?
A. Đường thẳng
GE
song song với đường thẳng
CD
.
B. Đường thẳng
GE
cắt đường thẳng
CD
.
C. Đường thẳng
GE
và đường thẳng
AD
cắt nhau.
D. Đường thẳng
GE
và đường thẳng
CD
chéo nhau.
Câu 26. Gieo ngẫu nhiên hai con súc sắc cân đối đồng chất. Xác suất để tổng số chấm xuất hiện trên hai
con súc sắc đó bằng
7
là
A.
7
12
. B.
1
2
. C.
1
12
. D.
1
6
.
Câu 27: Cho hình lập phương
.ABCD A B C D
′′′′
cạnh
a
. Góc giữa
BD
′′
và
AD
′
bằng
A.
0
60
. B.
0
90
. C.
0
45
. D.
0
120
.
Câu 28: Cho hàm số
( )
y fx=
có bảng biến thiên như hình vẽ bên dưới.
Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận đứng?
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 29: Cho khối lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông cân tại
A
, biết
AB a=
và
2AA a
′
=
. Thể tích của khối lăng trụ đã cho bằng
E
G
C
D
B
A

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
3
a
. B.
3
3
a
. C.
3
2a
. D.
3
3a
.
Câu 30: Thể tích
V
của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
là
A.
3
3
12
a
V =
. B.
3
3
4
a
V
=
. C.
3
3
6
a
V
=
. D.
3
3
2
a
.
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với đáy,
AB a=
,
2
AD a
=
. Góc giữa SB và đáy bằng
0
45
. Thể tích khối chóp S.ABCD bằng
A.
3
2
3
a
. B.
3
3
a
. C.
3
2
6
a
. D.
3
2
3
a
.
Câu 32: Cho hàm số
()
fx
có đạo hàm
( )
2
() 2 ,
f x xx x
′
= − ∀∈
. Số điểm cực trị của hàm số đã cho là
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 33: Đồ thị của hàm số
32
3 91yx x x
=− −+
có hai điểm cực trị
A
và
B
. Điểm nào dưới đây thuộc
đường thẳng
AB
?
A.
( )
1; 0P
. B.
( )
1; 10N −
. C.
( )
0; 1M −
. D.
( )
1;10Q −
.
Câu 34: Bảng biến thiên sau đây là của hàm số nào trong các hàm số sau?
A.
1
2
x
y
x
+
=
−
. B.
3
2
x
y
x
+
=
+
. C.
1
22
x
y
x
−
=
+
. D.
21
2
x
y
x
+
=
−
.
Câu 35: Cho hàm số
32
21yx x x= − ++
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số nghịch biến trên khoảng
( )
1; +∞
. B. Hàm số nghịch biến trên khoảng
1
;
3
−∞
.
C. Hàm số đồng biến trên khoảng
1
;1
3
. D. Hàm số đồng biến trên khoảng
( )
1; +∞
.
Câu 36: Giá trị nhỏ nhất của hàm số
32
3yx x= +
trên đoạn
[
]
4; 1−−
bằng
A.
0
. B.
16−
. C.
23−
. D.
4
.
Câu 37: Cho hàm số
( )
y fx
=
xác định và liên tục trên
. Hàm số
( )
'y fx
=
có đồ thị như hình dưới.
Hàm số
( ) ( )
2y gx f x= = −
đồng biến trên khoảng nào dưới đây ?
y = f '
x
( )
4
1
-1
O
y
x
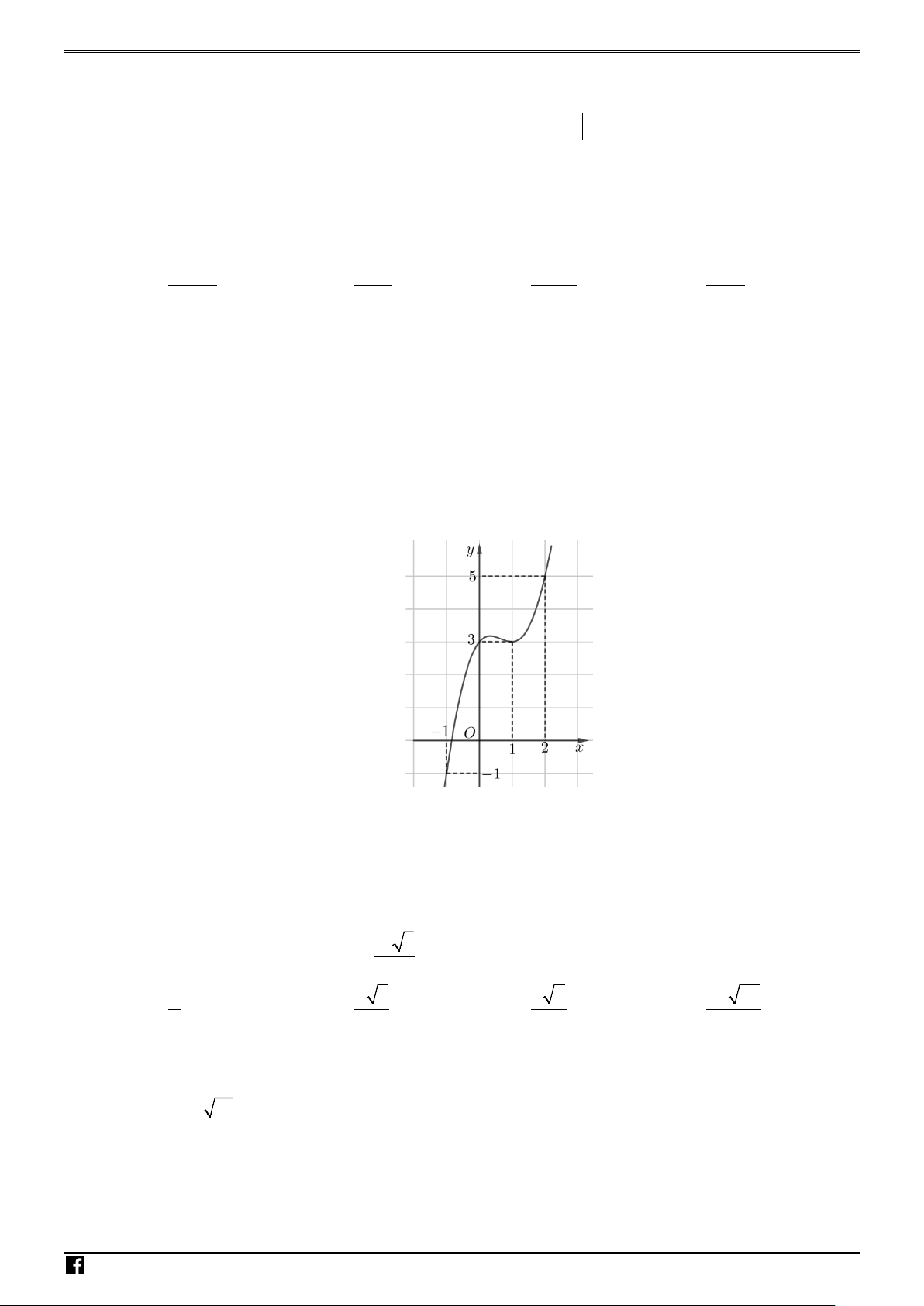
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
( ; 2).
−∞ −
B.
(3; ).+∞
C.
(1; 3).
D.
(2; )+∞
Câu 38: Gọi
m
là tham số thực để giá trị lớn nhất của hàm số
2
24
y x xm
= + +−
trên đoạn
[ ]
2;1−
đạt
giá trị nhỏ nhất. Giá trị của
m
là
A.
1
. B.
3
. C.
5
. D.
4
.
Câu 39: Gọi
S
là tập hợp các số tự nhiên có 6 chữ số được lập từ tập
{ }
0;1;2;3;...;9A =
. Chọn ngẫu
nhiên một số từ tập
S
. Tính xác suất để chọn được số tự nhiên có tích các chữ số bằng 1400.
A.
1
37500
. B.
1
1500
. C.
7
15000
. D.
7
5000
.
Câu 40: Anh Thường dự định dùng hết
2
4m
kính để làm một bể cá bằng kính có dạng hình hộp chữ
nhật không nắp, có chiều dài gấp đôi chiều rộng ( các mối ghép có kích thước không đáng kể).
Bể cá có dung tích lớn nhất bằng bao nhiêu ( kết quả làm tròn đến hàng phần trăm)?.
A.
3
1, 50 m
. B.
3
1,33m
. C.
3
1, 61 m
. D.
3
0,73m
.
Câu 41: Cho hàm số
( )
y fx=
có đạo hàm và liên tục trên
.
Biết rằng đồ thị hàm số
( )
'y fx=
như
dưới đây.
Xét hàm số
( ) ( )
2
gx f x x x= −−
trên
.
Khẳng định nào sau đây là khẳng định sai?
A.
( ) ( )
11gg−<
. B.
( ) ( )
12gg<
.
C.
( ) ( )
21gg<
. D.
( )
( )
( ) ( )
( )
1; 2Min g x Min g g= −
.
Câu 42: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a SA
vuông góc với đáy. Biết thể
tích khối chóp
.S ABCD
bằng
3
3
3
a
. Khoảng cách từ điểm
D
đến mặt phẳng
( )
SBC
bằng.
A.
2
a
. B.
3
2
a
. C.
2
2
a
. D.
2 39
13
a
.
Câu 43: Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác cân có
3AC BC a= =
. Đường thẳng
AC
′
tạo với đáy một góc
60°
. Trên cạnh
AC
′
lấy điểm
M
sao cho
2A M MC
′
=
, biết rằng
31AB a
′
=
(tham khảo hình dưới đây). Khoảng cách từ điểm
M
đến mặt phẳng
( )
ABB A
′′
là
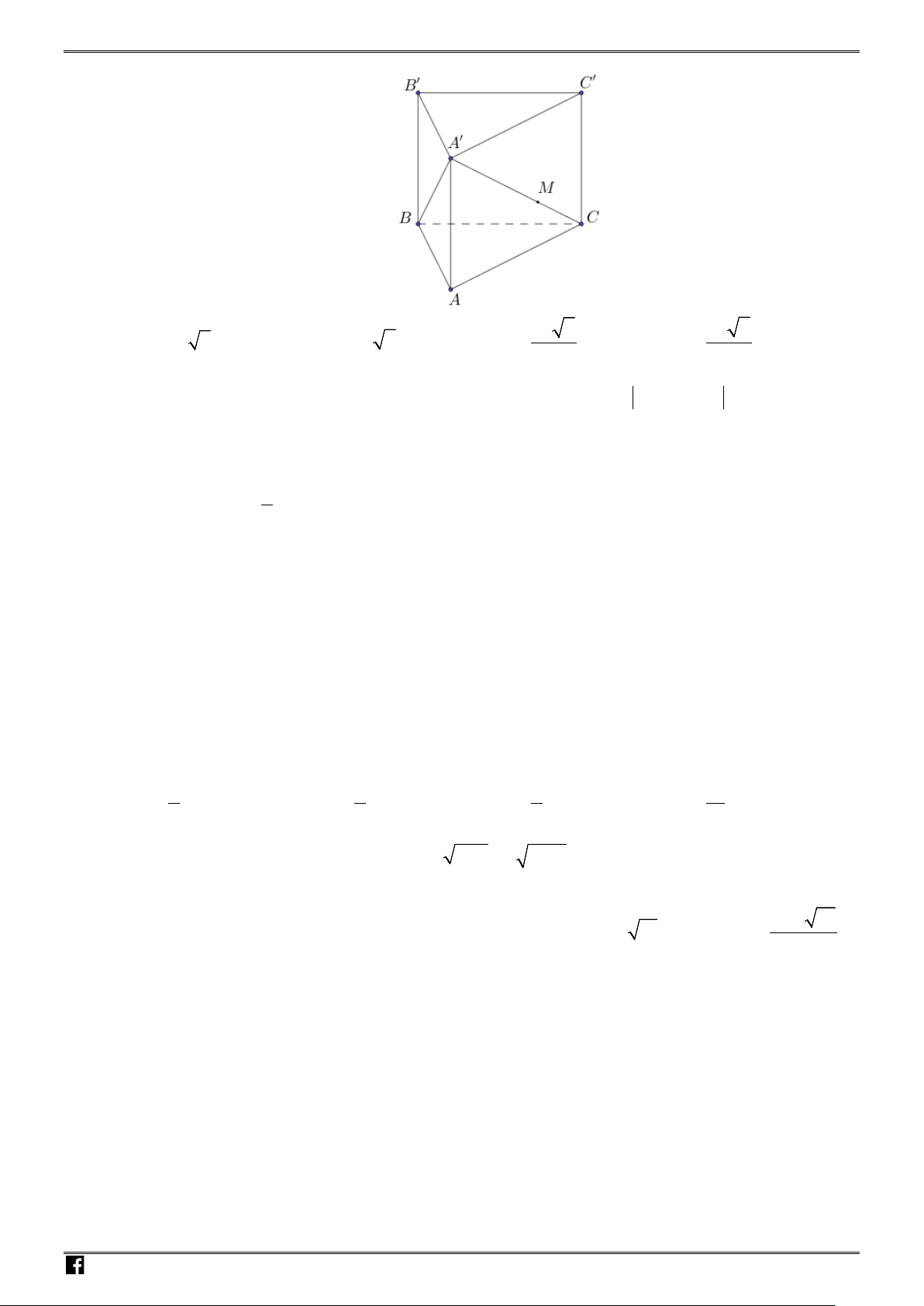
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
22a
. B.
32
a
. C.
42
3
a
. D.
32
4
a
.
Câu 44: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
sin cos 4sin 2x x xm−+ =
có
nghiệm thực ?
A.
7
. B.
5
. C.
6
. D.
8
.
Câu 45: Cho hàm số
322
1
( 1) 1
3
y x mx m m x= − + −− +
. Có bao nhiêu giá trị nguyên của tham số thực
m
để hàm số đạt cực trị tại
12
,xx
thỏa mãn
22
12
2 3 50
x mx m m
+ − + −≤
.
A. 9 B. 3 C. 7 D. 4
Câu 46: Cho hàm số
32
3yx x= −
. Có bao nhiêu số nguyên
( )
10;10b ∈−
để có đúng một tiếp tuyến của
(C) đi qua điểm
( )
0;Bb
?
A. 9 B. 2 C. 17 D. 16
Câu 47: Cho hình lập phương
.'' ' 'ABCD A B C D
có cạnh bằng
a
. Gọi
O
là tâm hình vuông
ABCD
.
S
là điểm đối xứng với
O
qua
'CD
. Thể tích của khối đa diện
''''ABCDSA B C D
bằng:
A.
3
5
4
a
. B.
3
7
6
a
. C.
3
7
5
a
. D.
3
13
11
a
.
Câu 48: Cho các số thực
,xy
thỏa mãn
3 13 2xx y y
− += +−
. Giá trị nhỏ nhất của biểu thức
Pxy= +
.
A.
min 63P = −
. B.
min 91
P = −
. C.
min 9 3 15P = +
. D.
9 3 21
min
2
P
+
=
.
Câu 49: Cho hàm số
( )
y fx
=
có đạo hàm
( ) ( )
( )( )
2020
22
3 2021 2 ,
xx
fx x x x x
ππ
′
= − − + − ∀∈
. Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
để hàm số
( )
2
8y fx xm= −+
có đúng 3 điểm cực
trị
1
x
,
2
x
,
3
x
thỏa mãn
223
1 23
50
xxx++=
. Khi đó tổng các phần tử của
S
bằng
A.
17
. B.
33
. C.
35
. D.
51
.
Câu 50: Cho hàm số
( )
y fx=
có bảng biến thiên như sau
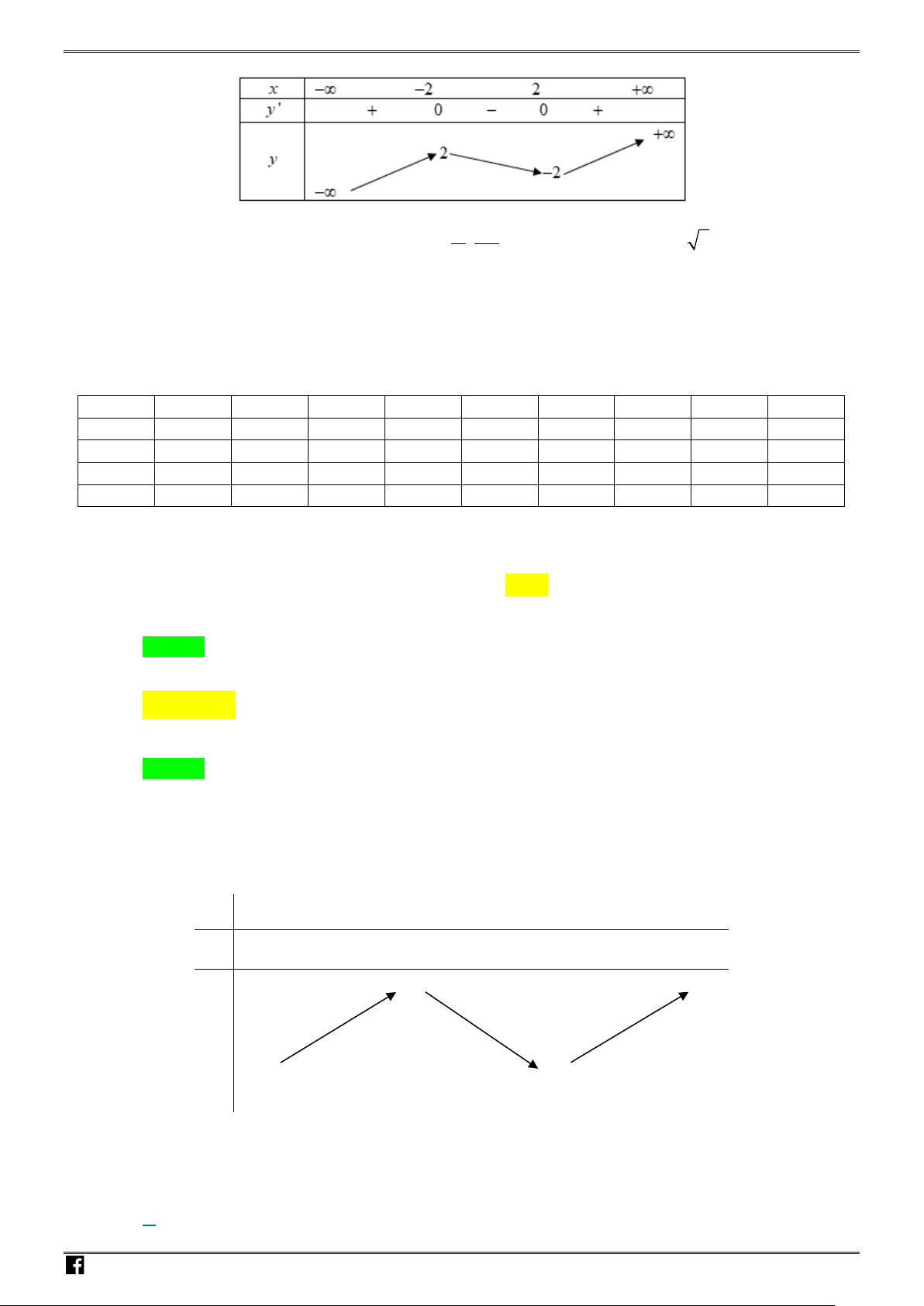
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Biết
(
)
00f =
, số nghiệm thuộc đoạn
7
;
63
ππ
−
có phương trình
( )
( )
3 sin cos 1ff x x+=
là
A.
4
. B.
3
. C.
2
. D.
5
.
BẢNG ĐÁP ÁN
1.C
2.A
3.D
4.B
5.A
6.C
7.D
8.C
9.B
10.C
11.D
12.B
13.A
14.C
15.D
16.B
17.D
18.B
19.D
20.D
21.C
22.B
23.D
24.A
25.A
26.D
27.A
28.A
29.A
30.B
31.A
32.D
33.B
34.A
35.D
36.B
37.B
38.B
39.B
40D
41.B
42.B
43.C
44.A
45.B
46.C
47.B
48.D
49.A
50.B
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Số đỉnh của một khối lăng trụ tam giác là?
A.
9
. B.
3
. C.
6
. D.
12
.
Lời giải
Chọn C
Câu 2: Đạo hàm của hàm số
4
yx
=
là
A.
3
'4yx=
. B.
'0
y =
. C.
2
'4yx=
. D.
'4yx=
.
Lời giải
Chọn A
Ta có:
(
)
'
1
.
nn
x nx
−
=
nên
3
'4yx
=
.
Câu 3: Cho hàm số
( )
y fx=
xác định, liên tục trên
và có bảng biến thiên sau
−∞
0
1
+∞
||
0
0
+∞
−∞
1−
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị lớn nhất bằng
0
và giá trị nhỏ nhất bằng
1−
.
B. Hàm số có đúng một cực trị.
C. Hàm số có giá trị cực tiểu bằng 1.
D. Hàm số đạt cực đại tại
0x =
và đạt cực tiểu tại
1x =
.
x
y
′
+
−
+
y

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
ChọnD .
Câu 4:
( )
3
1
1
lim
x
xx
→−
−−
bằng
B. -1. B. 3. C. -3. D. 1.
Lời giải
ChọnB .
( )
( )
(
)
3
3
1
1 11 13
lim
x
xx
→−
− − = −− −− =
.
Câu5: Cho khối lăng trụ có diện tích đáy
6B =
và chiều cao
3h =
. Thể tích của khối lăng trụ đã cho
bằng
A.
18
. B.
54
. C.
36
. D.
2
.
Lời giải
Chọn A
Ta có
6.3 18V Bh= = =
(đvtt).
Câu 6: Cho hàm số
( )
fx
có bảng biến thiên sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
2;0−
. B.
( )
1; 3
. C.
( )
;2−∞ −
. D.
( )
0; +∞
.
Lời giải
Chọn C
Hàm số đã cho nghịch biến trên khoảng
( )
;2−∞ −
.
Câu 7: Xét phép thử ngẫu nhiên có không gian mẫu
Ω
. Gọi
( )
PA
là xác suất của biến cố A liên quan
đến phép thử. Khẳng định nào sau đây là khẳng định đúng?
A.
( ) ( )
PA nA=
. B.
( ) ( ) ( )
.PA nAn= Ω
.
C.
( )
( )
( )
n
PA
nA
Ω
=
. D.
( )
( )
( )
nA
PA
n
=
Ω
.
Lời giải
Chọn D
Câu 8: Đạo hàm của hàm số
yx=
tại điểm
9x =
bằng:
A. 0. B.
1
2
. C.
1
6
. D.
1
3
.
Lời giải
Chọn C
Ta có:
( )
11
' '9
6
2
y xy y
x
= ⇒= ⇒ =
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 9: Cho hàm số
y fx
xác định, liên tục trên
và có đồ thị như hình vẽ sau
Hàm số
y fx
đồng biến trên những khoảng nào dưới đây
A.
(
)
;0−∞
. B.
( )
0; 2
. C.
( )
2;
+∞
. D.
( )
2; 2−
.
Lời giải
Chọn B
Từ đô thị hàm số ta thấy hàm số đồng biến trên khoảng
0;2
.
Câu 10: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng
A.
1
. B.
2
. C.
4
. D.
5
.
Lời giải
Chọn C
Hình chóp tứ giác đều có
4
mặt phẳng đối xứng.
Câu 11: Đồ thị của hàm số nào dưới đậy có dạng đường cong như hình vẽ sau
A.
42
21yx x=−+
. B.
42
21yx x=−+ +
. C.
3
31yx x=−+
. D.
3
31yx x=−+ +
.
Lời giải
Chọn D
Đồ thị hàm số dạng
32
y ax bx cx d= + ++
có hai điểm cực trị và
0a <
. Chon D.
Câu 12: Cho hàm số
( )
y fx=
có
( )
lim 1
x
fx
→+∞
=
và
( )
lim 1
x
fx
→−∞
= −
. Khẳng định nào sau đây là khẳng
định đúng?
A. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường
1x =
và
1x = −
.
B. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường
1y =
và
1y = −
.
C. Hàm số đã cho có hai đường tiệm cận ngang là các đường
1x =
và
1x = −
.
D. Đồ thị hàm số đã cho không có tiệm cận ngang .
Lời giải

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn B
Ta có
( )
lim 1
x
fx
→+∞
=
và
( )
lim 1
x
fx
→−∞
= −
. Vậy đồ thị hàm số đã cho có hai đường tiệm cận ngang
là các đường
1
y =
và
1y = −
.
Câu 13: Tiệm cận ngang của đồ thị hàm số
31
1
x
y
x
−
=
−
là
A.
3
y
= −
. B.
3y =
. C.
1x
=
. D.
1x = −
.
Lời giải
Chọn A
Ta có:
lim lim 3
xx
yy
→+∞ →−∞
= = −
Từ đây ta suy ra
3y = −
là tiệm cận ngang của đồ thị hàm số đã cho .
Câu 14: Số cách xếp
5
học sinh thành một hàng dọc ?
A.
20
. B.
5
5
. C.
5!
. D.
5
.
Lời giải
Chọn C
Câu 15: Cho một cấp số cộng
( )
n
u
có
1
1 11
;
33
ud= =
. Số hạng thứ hai của cấp số cộng là:
A.
11
9
. B.
10
3
. C.
10
3
−
.
D.
4
.
Lời giải
Chọn D.
Ta có
21
1 11
4
33
uud= +=+ =
.
Câu 16: Cho hàm số
3
3xyx= −
có đồ thị
( )
C
. Số giao điểm của
( )
C
và trục hoành là:
A.
1
. B.
3
. C.
0
.
D.
2
.
Lời giải
Chọn B.
Phương trình hoành độ giao điểm của
( )
C
và trục hoành là:
3
0
30
3
x
xx
x
=
−=⇔
= ±
Vậy số giao điểm của
( )
C
và trục hoành là 3.
Câu 17: Cho hàm số
( )
y fx=
có bảng biến thiên như sau
Giá trị cực đại của hàm số
( )
y fx=
bằng

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2−
. B.
1
. C.
3
.
D.
2
.
Lời giải
Chọn D.
Câu 18: Cho cấp số nhân
(
)
n
u
với
1
2u =
và
2
8u =
.Công bội của cấp số nhân đã cho bằng
A.
6
. B.
4
. C.
6
−
. D.
1
2
.
Lời giải
Chọn B
21
1
88
8 .8 4
2
u uq q
u
=⇔ =⇔= ==
.
Câu 19: Chiều cao của khối chóp có diện tích đáy bằng
B
và thể tích bằng
V
là
A.
=
V
h
B
. B.
6
=
V
h
B
. C.
2
=
V
h
B
. D.
3
=
V
h
B
.
Lời giải
Chọn D
Ta có: thể tích khối chóp có diện tích đáy bằng
B
và chiều cao bằng
h
là
13
.
3
V
V Bh h
B
= ⇒=
Từ đây ta chọn D.
Câu 20: Từ các chữ số
1, 2, 3, 4
lập được bao nhiêu số có
3
chữ số ?
A.
12
. B.
81
. C.
24
. D.
64
.
Lời giải
Chọn D
Gọi số có
3
chữ số là
abc
ta có :
Chữ số
a
có
4
cách chọn.
Chữ số
b
có
4
cách chọn
Chữ số
c
có
4
cách chọn
Theo quy tắc nhân ta có :
4.4.4 64
=
số thỏa mãn bài ra.
Từ đây ta chọn đáp án D.
Câu 21: Hàm số
4
21yx= +
đồng biến trên khoảng nào dưới đây?
A.
1
;
2
−∞ −
. B.
1
;
2
− +∞
. C.
( )
0;
+∞
. D.
( )
;0−∞
.
Lời giải
Chọn C
Ta có:
'3
80 0yx x= =⇔=
.
'
0, 0yx> ∀>
nên hàm số đồng biến trên
( )
0; +∞
.
Câu 22: Cho hàm số
( )
fx
có đồ thị như hình vẽ

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Tất cả giá trị của tham số m để phương trình
( )
fx m=
có 4 nghiệm phân biệt là?
A.
4m >−
. B.
43m− < <−
. C.
43m− < ≤−
. D.
43m
− ≤ ≤−
.
Lời giải
Chọn B
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số
( )
fx
và đường thẳng
ym=
.
Nhìn vào đồ thị ta có
43m− < <−
.
Câu 23: Cho khối chóp có đáy hình vuông cạnh
a
và chiều cao
2a
. Thể tích của khối chóp đã cho bằng
A.
3
2a
. B.
3
4
3
a
. C.
3
4a
. D.
3
2
3
a
.
Lời giải
Chọn D
Thể tích hình chóp có đáy hình vuông và chiều cao là :
23
12
. .2 .
33
V aa a= =
Câu 24: Có bao nhiêu giá trị nguyên của tham số
(
]
0; 20m ∈
để hàm số
2
3
x
y
xm
+
=
+
đồng biến trên khoảng
( )
;6−∞ −
?
A.
2
. B.
4
. C.
20
. D.
21
.
Lời giải
Chọn A
Tập xác định :
{ }
\3Dm= −
.Khi đó :
( )
2
32
' ,.
3
m
y xD
xm
−
= ∀∈
+
Để hàm số
2
3
x
y
xm
+
=
+
đồng biến trên
( )
;6−∞ −
thì
( )
' 0, ; 6yx> ∀ ∈ −∞ −
.
( )
2
3 20
2
2.
3
3 ;6
3
36
m
m
m
m
m
−>
>
⇔ ⇔ ⇔<≤
− ∉ −∞ −
− ≥−
Kết hợp
(
]
0; 20m ∈
ta được
1
.
2
m
m
=
=
Vậy có 2 giá trị nguyên của
m
thỏa.
x
y
-3
O
1
-4
-1

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 25. Cho khối chóp
ABCD
. Gọi
G
và
E
lần lượt là trọng tâm các tam giác
ABD
và
ABC
.
Khẳng định nào sau đây đúng?
A. Đường thẳng
GE
song song với đường thẳng
CD
.
B. Đường thẳng
GE
cắt đường thẳng
CD
.
C. Đường thẳng
GE
và đường thẳng
AD
cắt nhau.
D. Đường thẳng
GE
và đường thẳng
CD
chéo nhau.
Lời giải
Chọn A
Gọi
M
là trung điểm của cạnh
AB
.
Trong mặt phẳng
MCD
, ta có:
1
3
ME MG
MC MD
//CDGE
.
Vậy đường thẳng
GE
song song với đường thẳng
CD
.
Câu 26. Gieo ngẫu nhiên hai con súc sắc cân đối đồng chất. Xác suất để tổng số chấm xuất hiện trên hai
con súc sắc đó bằng
7
là
E
G
C
D
B
A
M
E
G
C
D
B
A
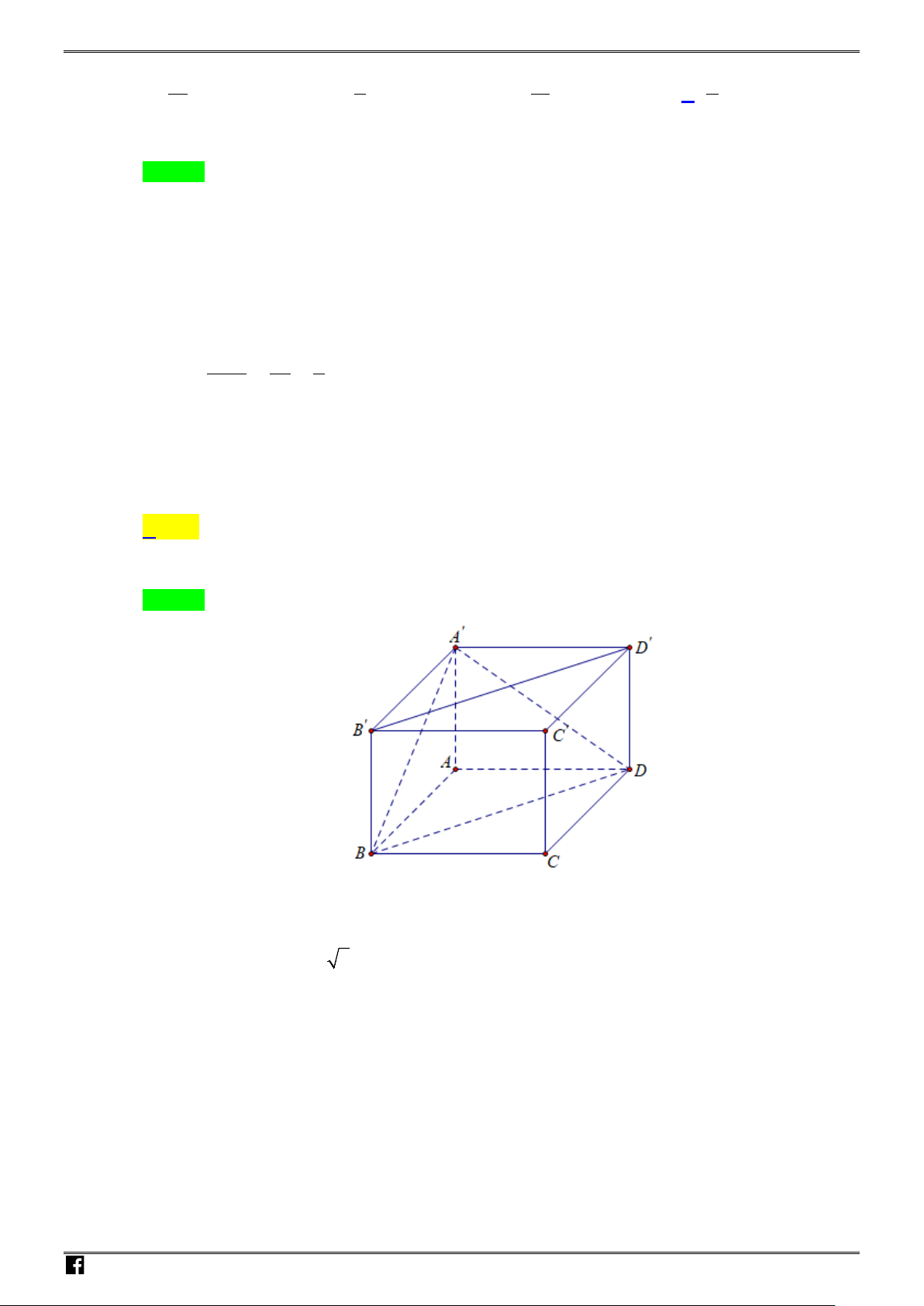
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
7
12
. B.
1
2
. C.
1
12
. D.
1
6
.
Lời giải
Chọn D
Ta có:
2
6 36n
.
:A
“Tổng số chấm xuất hiện trên hai con súc sắc bằng
7
”
1;6 ; 6;1 ; 2;5 ; 5; 2 ; 3; 4 ; 4;3A
,
6nA
.
nA
PA
n
6
36
1
6
.
Câu 27: Cho hình lập phương
.ABCD A B C D
′′′′
cạnh
a
. Góc giữa
BD
′′
và
AD
′
bằng
A.
0
60
. B.
0
90
. C.
0
45
. D.
0
120
.
Lời giải
Chọn A
Vì
//B D BD
′′
, suy ra
( )
( )
;;BD AD BD AD
′′ ′ ′
=
.
Mà
2AB BD AD a
′′
= = = ⇒
tam giác
A BD
′
đều
( )
0
; 60BD A D
′
⇒=
.
Vậy
( )
0
; 60BD AD
′′ ′
=
.
Câu 28: Cho hàm số
( )
y fx=
có bảng biến thiên như hình vẽ bên dưới.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận đứng?
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn A
Từ bảng biến thiên ta thấy
( )
( )
2
lim
x
fx
+
→−
= −∞
và
( )
0
lim
x
fx
−
→
= +∞
, suy ra đồ thị hàm số có hai
đường tiệm cận đứng là
2x = −
và
0x =
.
Câu 29: Cho khối lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông cân tại
A
, biết
AB a=
và
2AA a
′
=
. Thể tích của khối lăng trụ đã cho bằng
A.
3
a
. B.
3
3
a
. C.
3
2a
. D.
3
3a
.
Lời giải
Chọn A
Diện tích đáy
2
2
1
22
ABC
a
S AB= =
.
Thể tích khối lăng trụ
.ABC A B C
′′′
là
2
3
. 2.
2
ABC
a
V AA S a a
′
= = =
.
Câu 30: Thể tích
V
của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
là
A.
3
3
12
a
V =
. B.
3
3
4
a
V =
. C.
3
3
6
a
V =
. D.
3
3
2
a
.
Lời giải
Chọn B
C'
B'
A
C
B
A'

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 17
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Diện tích đáy
22
.3 3
44
ABC
AB a
S = =
.
Thể tích khối lăng trụ
.ABC A B C
′′′
là
23
33
..
44
ABC
aa
V AA S a
′
= = =
.
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với đáy,
AB a=
,
2
AD a=
. Góc giữa SB và đáy bằng
0
45
. Thể tích khối chóp S.ABCD bằng
A.
3
2
3
a
. B.
3
3
a
. C.
3
2
6
a
. D.
3
2
3
a
.
Lời giải
Chọn A.
Ta có:
( ) (
)
0
;( ) ; 45SB ABCD SB AB SBA∠ =∠ =∠=
;
0
.tan 45SA AB a= =
.
Thể tích khối chóp S.ABCD bằng:
3
.
1 1 12
. . . . . ...2
3 3 33
S ABCD ABCD
a
V SA S SA AB AD a a a
= = = =
.
Câu 32: Cho hàm số
()fx
có đạo hàm
( )
2
() 2 ,f x xx x
′
= − ∀∈
. Số điểm cực trị của hàm số đã cho là
A.
2
. B.
3
. C.
0
. D.
1
.
C'
B'
A
C
B
A'
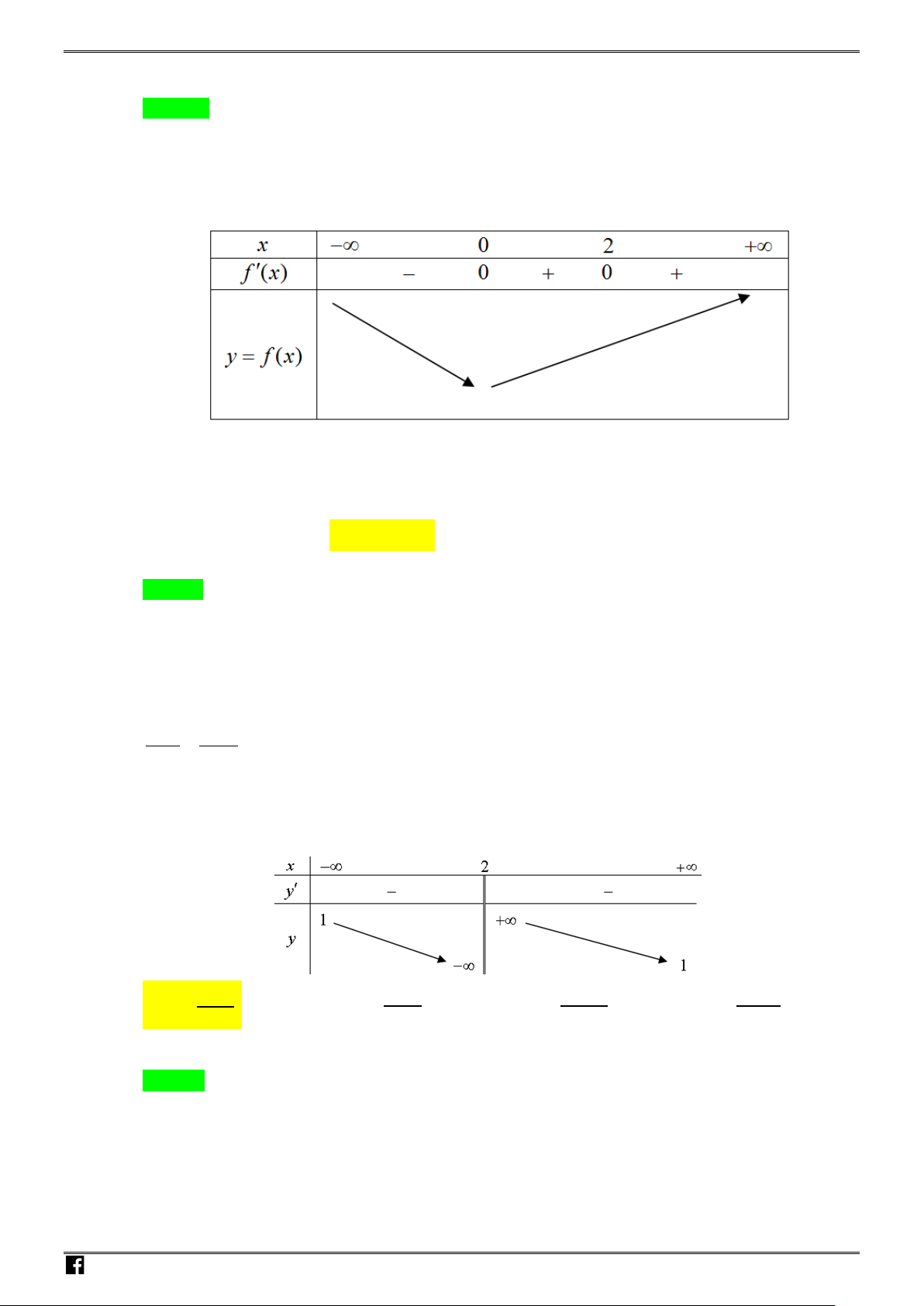
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 18
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn D.
Ta có:
( )
2
0
() 0 2 0
2
x
f x xx
x
=
′
=⇔ −=⇔
=
(Với
0x =
là nghiệm đơn và
2x =
là nghiệm kép).
Bảng biến thiên của hàm số
()fx
:
Vậy hàm số có 1 điểm cực trị.
Câu 33: Đồ thị của hàm số
32
3 91yx x x
=− −+
có hai điểm cực trị
A
và
B
. Điểm nào dưới đây thuộc
đường thẳng
AB
?
A.
( )
1; 0P
. B.
( )
1; 10N −
. C.
( )
0; 1M
−
. D.
( )
1;10Q −
.
Lời giải
Chọn B
Ta có:
2
1
3 6 90
3
x
y' x x
x
= −
= − −=⇔
=
Hai cực trị đó là:
( )
16A;−
và
(
)
3 26B;−
.
Phương trình đường thẳng
AB
là:
( )
16
8 1 6 8 20
4 32
xy
x y xy
+−
= ⇔− + = − ⇔ + + =
−
.
Vậy điểm
( )
1; 10N −
thuộc Phương trình đường thẳng
AB
.
Câu 34: Bảng biến thiên sau đây là của hàm số nào trong các hàm số sau?
A.
1
2
x
y
x
+
=
−
. B.
3
2
x
y
x
+
=
+
. C.
1
22
x
y
x
−
=
+
. D.
21
2
x
y
x
+
=
−
.
Lời giải
Chọn A
Ta có: Hàm số có tiệm cận đứng là đường thẳng
2x =
nên đáp án B, C loại
Hàm số có tiệm cận ngang là đường thẳng
1
y =
nên đáp án A đúng.
Câu 35: Cho hàm số
32
21yx x x= − ++
. Khẳng định nào sau đây là khẳng định đúng?

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 19
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A. Hàm số nghịch biến trên khoảng
( )
1; +∞
. B. Hàm số nghịch biến trên khoảng
1
;
3
−∞
.
C. Hàm số đồng biến trên khoảng
1
;1
3
. D. Hàm số đồng biến trên khoảng
( )
1; +∞
.
Lời giải
Chọn D
Ta có
2
3 41yxx
′
= −+
.
1
0
1
3
x
y
x
=
′
= ⇔
=
.
Bảng biến thiên
Dựa vào bảng biến thiên, suy ra hàm số đồng biến trên
( )
1; +∞
.
Câu 36: Giá trị nhỏ nhất của hàm số
32
3yx x= +
trên đoạn
[ ]
4; 1−−
bằng
A.
0
. B.
16−
. C.
23−
. D.
4
.
Lời giải
Chọn B
Đạo hàm
2
36yxx
′
= +
.
[ ]
[ ]
0 4; 1
0
2 4; 1
x
y
x
= ∉− −
′
= ⇔
=− ∈− −
.
( ) ( )
( )
4 16; 1 2; 2 4y yy
−=− −= −=
.
Vậy
[ ]
(
)
4; 1
min 4 16
yy
−−
= −=−
.
Câu 37: Cho hàm số
( )
y fx=
xác định và liên tục trên
. Hàm số
( )
'y fx=
có đồ thị như hình dưới.
Hàm số
( ) ( )
2y gx f x= = −
đồng biến trên khoảng nào dưới đây ?
y = f '
x
( )
4
1
-1
O
y
x

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 20
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
( ; 2).
−∞ −
B.
(3; ).+∞
C.
(1; 3).
D.
(2; )+∞
Lời giải
Chọn B
Ta có
( )
(
)
' '2gx f x=−−
.
Do đó,
( ) (
)
21 3
' 0 '2 0
12421
xx
gx f x
xx
− <− >
>⇔ − <⇔ ⇔
<−< −<<
Suy ra hàm số
( )
gx
đồng
biến trên khoảng
(3; ).
+∞
Câu 38: Gọi
m
là tham số thực để giá trị lớn nhất của hàm số
2
24y x xm= + +−
trên đoạn
[
]
2;1
−
đạt
giá trị nhỏ nhất. Giá trị của
m
là
A.
1
. B.
3
. C.
5
. D.
4
.
Lời giải
Chọn B
Xét hàm số
(
)
2
24fx x xm= + +−
trên đoạn
[ ]
2;1−
.
Ta có
( )
( )
' 2 2; ' 0 1
fx x fx x= + =⇔=−
.
( ) ( )
2 4; ( 1) 5; 1 1f mf mf m−= − −= − = −
.
Suy ra
[
]
(
)
[
]
( )
2;1 2 ;1
1; 5
Max f x m Min f x m
−−
=−=−
[ ]
( )
2;1
2 64
322
2
m
Max f x m
−
−+
⇒ = = −+≥
Vậy
[ ]
( )
2;1
Max f x
−
nhỏ nhất bằng 2 khi
3
m
=
.
Câu 39: Gọi
S
là tập hợp các số tự nhiên có 6 chữ số được lập từ tập
{
}
0;1;2;3;...;9A =
. Chọn ngẫu
nhiên một số từ tập
S
. Tính xác suất để chọn được số tự nhiên có tích các chữ số bằng 1400.
A.
1
37500
. B.
1
1500
. C.
7
15000
. D.
7
5000
.
Lời giải
Chọn B.
Số phần tử của khoog gian mẫu:
( )
5
9.10n Ω=
.
Gọi
A
là biến cố thỏa mãn bài toán.
Ta có
32
1400 2 .5 .7 2.2.2.5.5.7 1.1.8.5.5.7 1.2.4.5.5.7= = = =
,do đó để tích các chữ số bằng
1400
thì số đó được lập trong các trường hợp sau:
Trường hợp 1: Số được lập có ba chữ số 2, hai chữ sô 5 và một chữ số 7, có
6!
60
3!2!
=
( số) .
Trường hợp 2: Số được lập có hai chữ số 1, hai chữ sô 5 và hai chữ số 7, 8 có
6!
180
2!2!
=
( số).
Trường hợp 3: Số được lập có một chữ số 1, một chữ số 2, một chữ số 4, hai chữ sô 5 và chữ
số 7 có
6!
360
2!
=
( số).
( )
60 180 360 600nA
⇒ =++ =

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 21
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
(
)
( )
(
)
5
600 1
9.10 1500
nA
PA
n
⇒===
Ω
.
Câu 40: Anh Thường dự định dùng hết
2
4m
kính để làm một bể cá bằng kính có dạng hình hộp chữ
nhật không nắp, có chiều dài gấp đôi chiều rộng ( các mối ghép có kích thước không đáng kể).
Bể cá có dung tích lớn nhất bằng bao nhiêu ( kết quả làm tròn đến hàng phần trăm)?.
A.
3
1, 50 m
. B.
3
1,33m
. C.
3
1, 61 m
. D.
3
0,73m
.
Lời giải
Chọn D.
Gọi
,2 ,x xy
lần lượt là chiều dài, rộng, cao của bể cá dựng được
3
0,
2
xy
<<
.
.Thể tích bể cá bằng
2
2
V xy=
.
Theo giả thiết, Anh Thường dùng hết
2
4m
, nên ta có
( )
22
2 2 23
2 22
2 2 4 4 3 2 2. 2
3 33
xx
xy x xy xy x y V x x x
xx
−−
+ + =⇔ + =⇒= ⇒= = −
( )
02x<<
.
Xét hàm số
( )
( ) ( )
32
6
2 23; 0
3
fx xx fx xfx x
′′
= − ⇒ =− =⇔=
.
Bảng biến thiên của
(
)
fx
.
Từ bảng biến thiên, suy ra thể tích lớn nhất bằng
3
86
0,73m
27
≈
.
y
2x
x
C
D'
C'
B'
A'
D
B
A
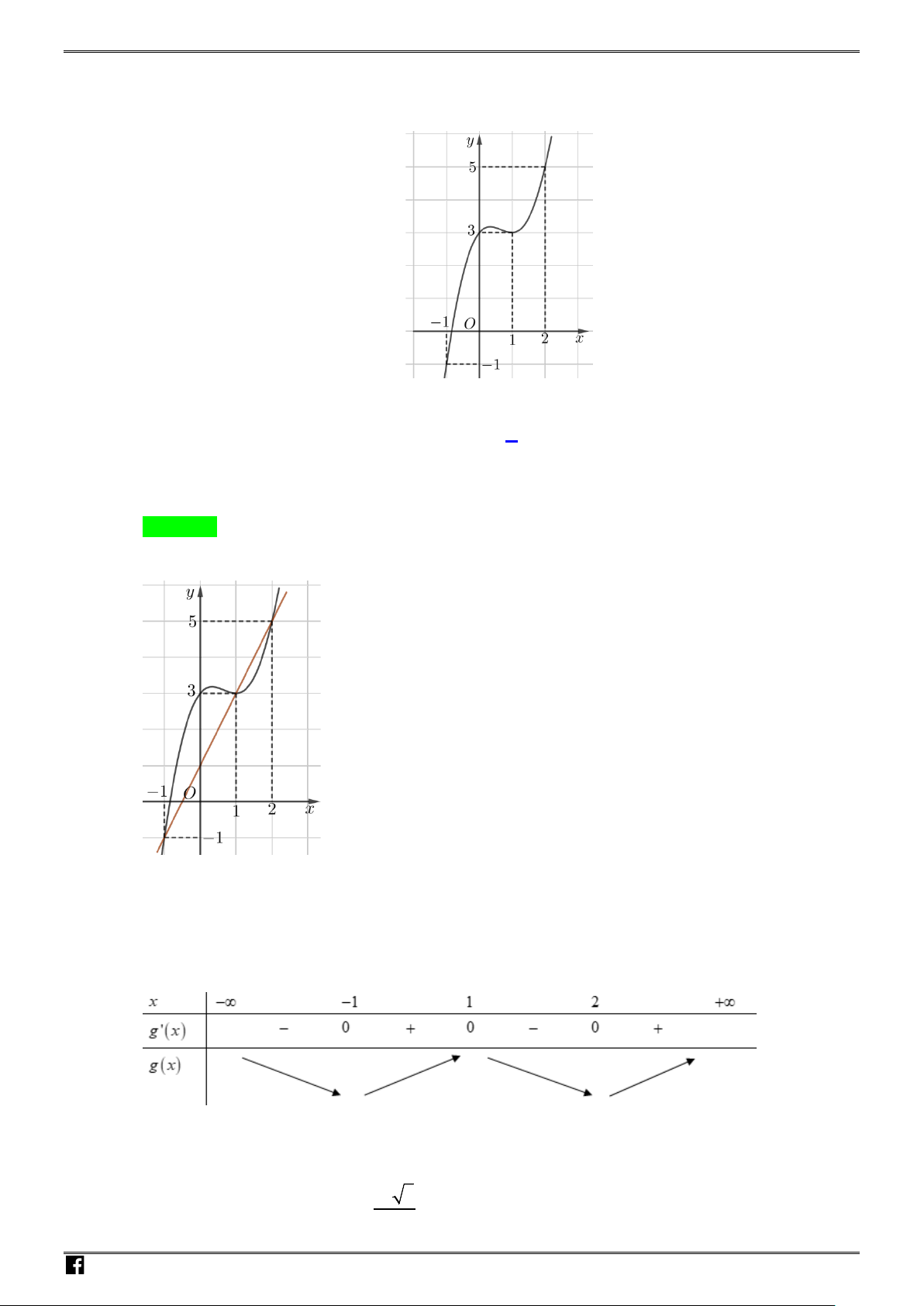
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 22
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 41: Cho hàm số
(
)
y fx
=
có đạo hàm và liên tục trên
.
Biết rằng đồ thị hàm số
( )
'
y fx
=
như
dưới đây.
Xét hàm số
( ) ( )
2
gx f x x x
= −−
trên
.
Khẳng định nào sau đây là khẳng định sai?
A.
( ) ( )
11gg−<
. B.
( )
(
)
12gg
<
.
C.
( ) ( )
21gg
<
. D.
( )
( )
( ) ( )
( )
1; 2Min g x Min g g= −
.
Lời giải
Chọn B .
Ta có:
( )
( )
' ' 21
gx f x x= −−
. Ta vẽ thêm đường thẳng
( ): 2 1dy x
= +
Khi đó:
( ) ( )
1
' 0 ' 21 1
2
x
gx f x x x
x
= −
= ⇔ = +⇔ =
=
.
Bảng biến thiên hàm số
( )
'gx
là
Từ bảng biến thiên, dễ thấy
( ) ( )
21gg<
nên B sai.
Câu 42: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a SA
vuông góc với đáy. Biết thể
tích khối chóp
.S ABCD
bằng
3
3
3
a
. Khoảng cách từ điểm
D
đến mặt phẳng
( )
SBC
bằng.
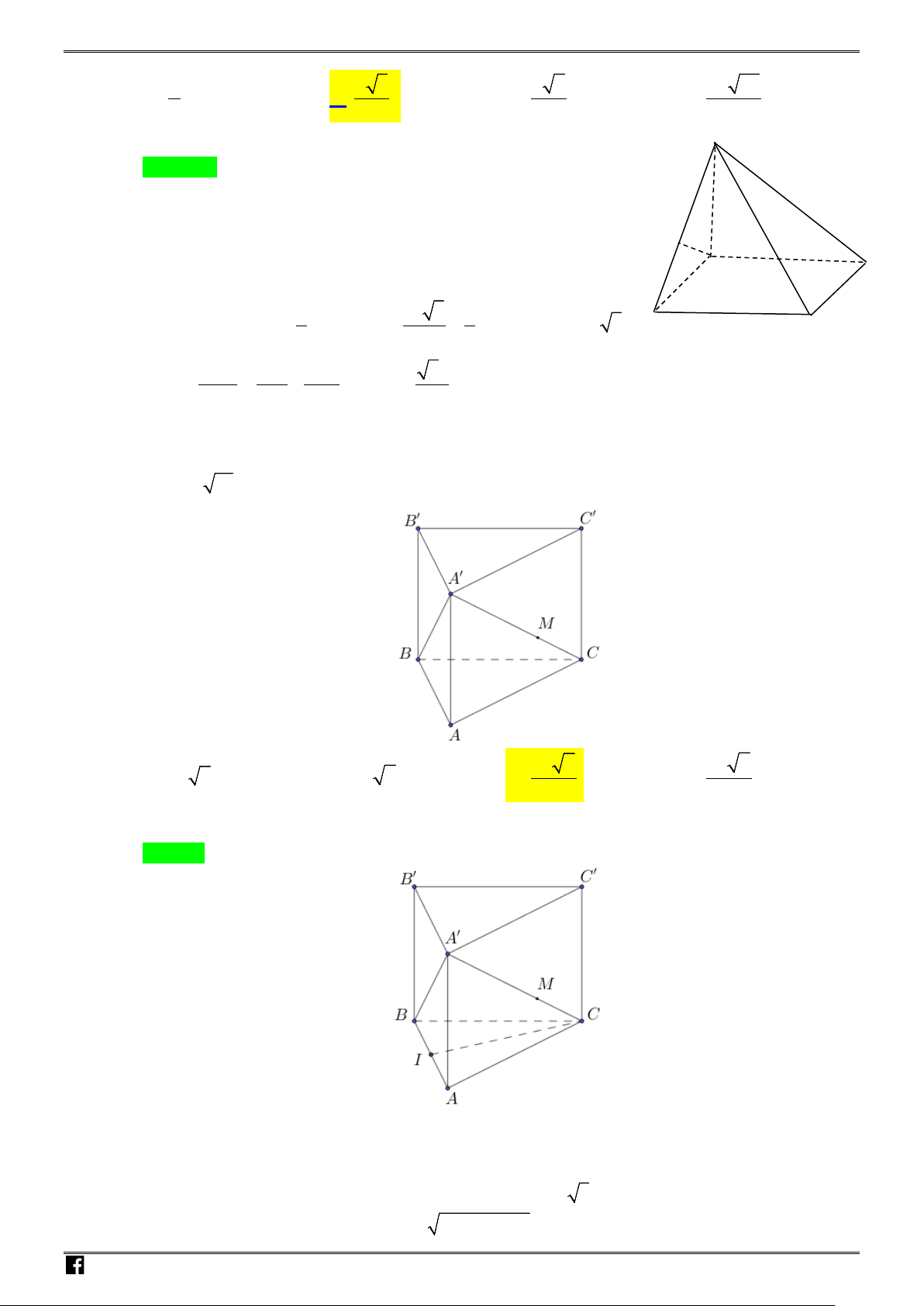
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 23
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
2
a
. B.
3
2
a
. C.
2
2
a
. D.
2 39
13
a
.
Lời giải
Chọn B .
Kẻ
( )
.AH SB H SB⊥∈
Dễ dàng ta chứng minh được
( )
AH SBC⊥
( )
( )
(
)
(
)
, ,.d D SBC d A SBC AH⇒==
Mặc khác:
3
2
.
1 31
. . . 3.
3 33
S ABCD ABCD
a
V SA S SA a SA a= ⇔ = ⇔=
Suy ra
22 2
1 11 3
.
2
a
AH
AH SA AB
=+ ⇔=
Câu 43: Cho hình lăng trụ đứng
.
ABC A B C
′′′
có đáy là tam giác cân có
3AC BC a= =
. Đường thẳng
AC
′
tạo với đáy một góc
60°
. Trên cạnh
AC
′
lấy điểm
M
sao cho
2A M MC
′
=
, biết rằng
31AB a
′
=
(tham khảo hình dưới đây). Khoảng cách từ điểm
M
đến mặt phẳng
( )
ABB A
′′
là
A.
22a
. B.
32a
. C.
42
3
a
. D.
32
4
a
.
Lời giải
Chọn C
Ta có
.ABC A B C
′′′
là lăng trụ đứng
( )
AA ABC
′
⇒⊥
.
Mà
( ) ( )
( )
, 60A C ABC C A C ABC A CA
′ ′′
∩=⇒ ==°
.
Tam giác
A AC
′
vuông tại
.tan 3 3A AA AC A CA a
′′
⇒= =
.
Tam giác
A AB
′
vuông tại
22
2A AB AB AA a
′′
⇒= − =
.
D
C
B
A
S
H

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 24
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Gọi
I
là trung điểm của
AB
, vì tam giác
CAB
cân tại
C CI AB⇒⊥
.
Ta có
( ) ( )
( ) ( )
( )
( ) ( )
( )
,
,
ABB A ABC
ABB A ABC AB CI ABB A d C ABB A CI
CI ABC CI AB
′′
⊥
′′ ′′ ′′
∩ = ⇒⊥ ⇒ =
⊂⊥
.
Tam giác
CAI
vuông tại
22
22I CI AC AI a⇒= − =
, (vì
1
2
AI AB a
= =
).
Lại có
( )
MC ABB A A
′′ ′
∩=
và
( )
( )
( )
( )
2 2 42
,,
3 33
a
MA CA d M ABB A d C ABB A
′ ′ ′′ ′′
=⇒= =
.
Vậy
( )
( )
42
,
3
a
d M ABB A
′′
=
.
Câu 44: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
sin cos 4sin 2x x xm−+ =
có
nghiệm thực ?
A.
7
. B.
5
. C.
6
. D.
8
.
Lời giải
Chọn A
Đặt
sin cos 2 sin
4
t xx x
π
=−= −
,
0; 2t
∈
2
sin 2 1xt
⇒=−
.
Phương trình đã cho trở thành
( )
22
41 4 4
t t m tt m+ − = ⇔− + + =
.
Xét hàm số
( )
2
44ft t t=− ++
, với
0; 2t
∈
.
Bảng biến thiên
Dựa vào bảng biến thiên, suy ra phương trình
( )
m ft=
có nghiệm trên
0; 2
khi và chỉ khi
65
42 .
16
m−+ ≤ ≤
Vì
m∈
nên
{ }
2; 1;0;1; 2;3; 4m∈− −
.
Vậy có
7
giá trị nguyên của tham số
m
thỏa mãn yêu cầu bài toán.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 25
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 45: Cho hàm số
322
1
( 1) 1
3
y x mx m m x
= − + −− +
. Có bao nhiêu giá trị nguyên của tham số thực
m
để hàm số đạt cực trị tại
12
,xx
thỏa mãn
22
12
2 3 50x mx m m+ − + −≤
.
A. 9 B. 3 C. 7 D. 4
Lời giải.
Chọn B.
Ta có
22
0 2 10
y x mx m m
′
= ⇔ − + − −=
. Điều kiện 2 cực trị là
10 1mm
′
∆ = + > ⇔ >−
.
Theo hệ thức Viet có
12
2
12
2
1
xx m
xx m m
+=
= −−
Theo bài ra
22
12
2 3 50x mx m m
+ − + −≤
( )
( )
22 2
1 1 12
22
12
2 1 2 2 4 2 40
2 20 .2 2 20 2
x mx m m mx mx m m
mxx mm mmmm m
⇔ − + − − + + − + −≤
⇔ + − + −≤⇔ − + −≤⇔ ≤
Kết hợp với
{
}
1 1 2 0;1; 2
m mm>− ⇒− < ≤ ⇒ ∈
, vậy có 3 giá trị nguyên
m
.
Câu 46: Cho hàm số
32
3yx x= −
. Có bao nhiêu số nguyên
( )
10;10b ∈−
để có đúng một tiếp tuyến của
(C) đi qua điểm
( )
0;Bb
?
A. 9 B. 2 C. 17 D. 16
Lời giải.
Chọn C.
Đường thẳng d có hệ số góc k đi qua điểm
( )
0;Bb
có dạng
( 0)y k x b kx b= − += +
.
Điều kiện tiếp xúc của đường cong (C) và đường thẳng d là
32
32 32 32
2
3
3 6 3 2 3 ()
36
kx b x x
x x b x x b x x fx
kx x
+= −
⇒ − += − ⇒=− + =
= −
.
Đồ thị hàm số
()fx
như hình vẽ.
Qua
( )
0;Bb
có đúng 1 tiếp tuyến cần có
1
0
b
b
>
<
.
Kết hợp
( )
10;10b∈−
thu được 17 giá trị nguyên b.
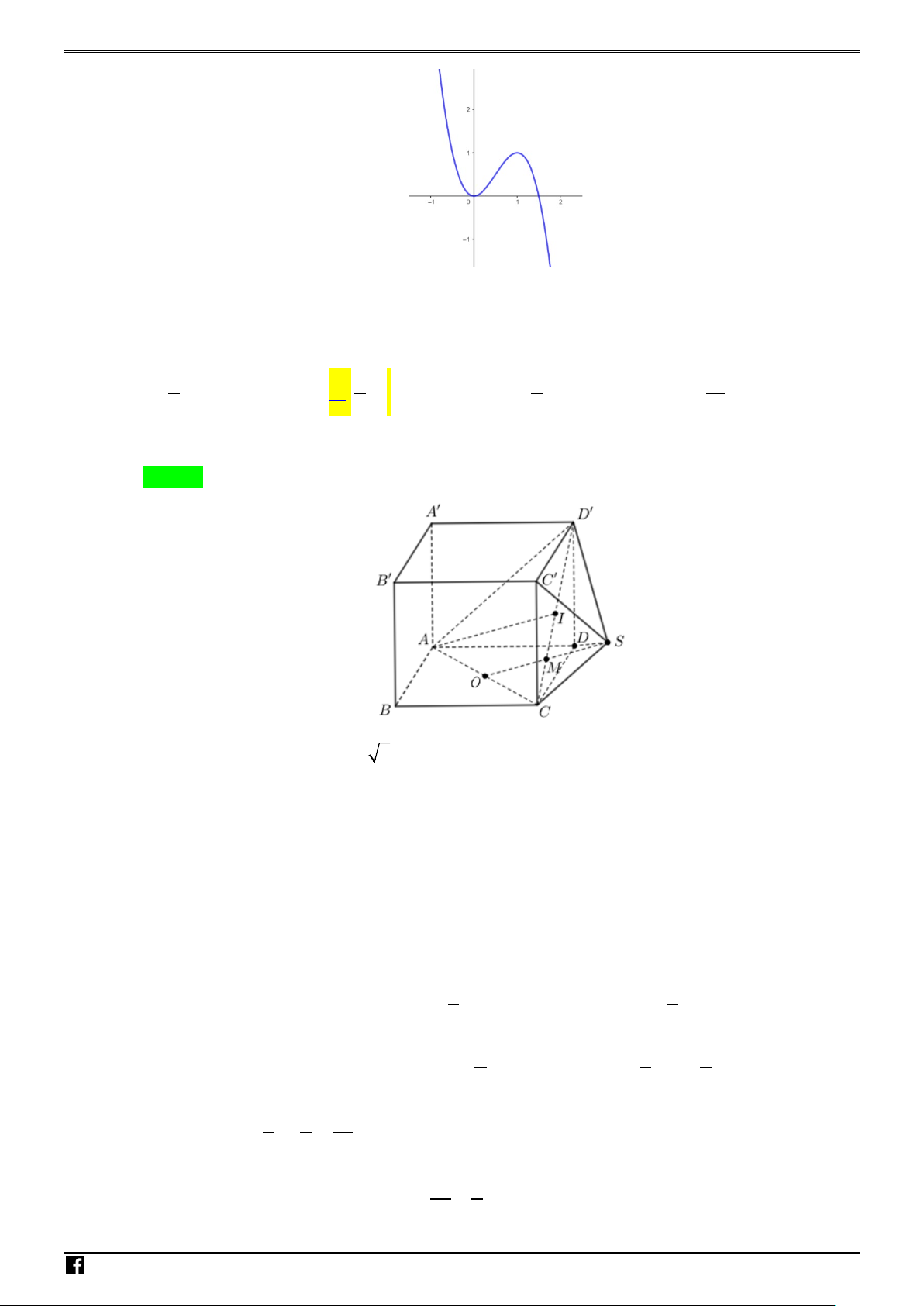
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 26
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 47: Cho hình lập phương
.'' ' '
ABCD A B C D
có cạnh bằng
a
. Gọi
O
là tâm hình vuông
ABCD
.
S
là điểm đối xứng với
O
qua
'CD
. Thể tích của khối đa diện
''''
ABCDSA B C D
bằng:
A.
3
5
4
a
. B.
3
7
6
a
. C.
3
7
5
a
. D.
3
13
11
a
.
Lời giải
Chọn B
Dễ thấy
' '2 '= = = ⇒∆AC CD AD a D AC
đều.
Gọi
I
là trung điểm
''
⇒⊥CD AI D C
. Gọi
M
là trung điểm
'IC
.
Suy ra
OM
là đường trung bình của tam giác
// '⇒ ⇒⊥AIC OM AI OM CD
.
Mà
S
là điểm đối xứng của
O
qua
⇒MM
là trung điểm
SO
.
Vì
IOCS
là hình bình hành nên
// // '// 'CS IO AD BC
hay
( )
''S BCC B∈
.
Ta có
( )
'''' .'''' . ''
1= +
ABCDSA B C D ABCD A B C D S CC D D
V VV
.
Có
( )
3
.''' '
2
=
ABCD A B C D
Va
và
( )
(
)
( )
( )
2
. '' ''
11
. ; '' . ; ''
33
= =
S CC D D CC D D
V S d S CC D D a d S CC D D
.
Mà
( )
( )
(
)
( )
( )
( )
11
; '' ; '' ; ''
2 22
= = = =
a
d S CC D D d O CC D D d A CC D D AD
.
Nên
( )
3
2
. ''
1
. 3
326
= =
S CC D D
aa
Va
.
Từ
( ) ( ) ( )
3
33
''''
7
1,2,3
66
⇒ =+=
ABCDSA B C D
a
V aa
.

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 27
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 48: Cho các số thực
,
xy
thỏa mãn
3 13 2xx y y
− += +−
. Giá trị nhỏ nhất của biểu thức
Pxy= +
.
A.
min 63P = −
. B.
min 91
P = −
. C.
min 9 3 15P = +
. D.
9 3 21
min
2
P
+
=
.
Lời giải
Chọn D
Ta chứng minh bất đẳng thức phụ:
,, 0+ ≥ +∀ ≥A B A B AB
.
Thật vậy:
, 2 20
+ ≥ + ⇔++ ≥+⇔ ≥A B AB AB AB AB AB
(luôn đúng với mọi
,0≥AB
).
Đẳng thức xảy ra khi
0
0
=
=
A
B
.
Ta có điều kiện:
1
2
≥−
≥−
x
y
.
Theo giả thiết:
313 2 313 2− += + − ⇔ + = ++ +x x y y xy x y
.
Áp dụng bất đẳng thức trên, ta có:
( )
3 13 2 3 1 2 3 3 3 3Pxy x y x y xy P= + = ++ + = ++ + ≥ + + = +
.
Như vậy
(
)
2
0
9 3 21
33
93
2
≥
+
≥ +⇔ ⇔ ≥
≥+
P
PP P
PP
. Dấu "=" xảy ra khi
1
2
= −
= −
x
y
.
Với
11 3 21
1 13 2
2
+
=−⇒ −= + ⇒ =
x y yy
;
Với
13 3 21
2 23 1
2
+
=−⇒ − = +⇒ =y x xx
.
Vậy
9 3 21
min
2
+
=P
.
Câu 49: Cho hàm số
( )
y fx=
có đạo hàm
( ) ( )
( )( )
2020
22
3 2021 2 ,
xx
fx x x x x
ππ
′
= − − + − ∀∈
. Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
để hàm số
( )
2
8y fx xm= −+
có đúng 3 điểm cực
trị
1
x
,
2
x
,
3
x
thỏa mãn
223
1 23
50
xxx++=
. Khi đó tổng các phần tử của
S
bằng
A.
17
. B.
33
. C.
35
. D.
51
.
Lời giải
Chọn A
Đặt
(
) ( )( )
( )( )
2020
2 22
8 2 8 3 2021 2
tt
t x xm ft x t t t
ππ
′
= − +⇒ = − − − + −
.
Để hàm số có cực trị thì
( )
0ft
′
=
có nghiệm đơn

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 28
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
(
)
2020
30t
−≥
,
2
2
1 8083
2021 0
24
tt t
ππ π
−+ = − + >
,
t∀∈
Do đó
( )
(
) ( )
(
)
2
2
22
4
2 80
0
20
8 2 8 0 *
x
x
ft
tt
x xm x xm
=
−=
′
=⇔⇔
−=
−+ − −+ =
Xét
(
)
*
ta có
( )
(
)
2
2
8 0 1
8 2 0 2
x xm
x xm
− +=
− + −=
Không mất tính tổng quát, ta giả sử
3
4x =
Suy ra
( )
222 22
123 12
50 34 **xxx xx++=⇔+=
Trường hợp 1.
( )
1
có 2 nghiệm
1
x
,
2
x
và
( )
2
vô nghiệm hoặc có nghiệm kép
Khi đó
( )
( )
( )
1
2
16 0
16
18
16 2 0
m
m
m
m
′
∆= −>
<
⇔
′
≥
∆= − − ≤
(vô lý) nên loại trường hợp này.
Trường hợp 2.
( )
2
có 2 nghiệm
1
x
,
2
x
và
( )
1
có nghiệm kép
Khi đó
( )
( )
( )
1
2
16 0
16
18
16 2 0
m
m
m
m
′
∆= −≤
≥
⇔
′
<
∆= − − >
( ) ( ) ( )
2
2
1 2 12
** 2 34 8 2. 2 34 17x x xx m m⇔ + − = ⇔− −= ⇔=
(nhận)
Vậy
17S =
.
Câu 50: Cho hàm số
( )
y fx=
có bảng biến thiên như sau
Biết
( )
00
f =
, số nghiệm thuộc đoạn
7
;
63
ππ
−
có phương trình
( )
( )
3 sin cos 1ff x x+=
là
A.
4
. B.
3
. C.
2
. D.
5
.
Lời giải
Chọn B
Đặt
7
3 sin cos , ;
63
t x xx
ππ
= + ∀∈−
0 3 cos sin 0 sin 0 ,
33
t x x x x kk
ππ
π
′
⇒=⇔ − =⇔ − =⇔= + ∈

NHÓM GIÁO VIÊN TOÁN VIỆT NAM TỔ 5 - ĐỀ THI HK1 - NĂM 2021-2022
https://www.facebook.com/groups/toanvd.vdc
Trang 29
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vì
7
;
63
x
ππ
∈−
nên ta được
3
x
π
=
và
4
3
x
π
=
Bảng biến thiên của
t
như sau :
Vậy phương trình
( )
( )
3 sin cos 1ff x x+=
có 3 nghiệm thuộc
7
;
33
ππ
−
.
1y =
Bấm Tải xuống để xem toàn bộ.




