














































Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 1 x2 y2 z2
Bài 1: (1 điểm) Tìm số xyz biết: , và x – y + z = 4 4 9 25 2 b2 2 b2
Bài 2: (1 điểm) Biết a ab 25 ;c
9 ; a2 ac c2 16 3 3 c 2 b c
và a 0; c ≠ 0; a ≠ -c. Chứng minh rằng: . a a c Bài 3: (2,5 điểm0
a/ Tìm giá trị của m để đa thức sau là đa thức bậc 3 theo biến x:
f (x) = (m2- 25) x4+ (20 + 4m) x3 + 7 x2 - 9
b/ Tìm giá trị nhỏ nhất của đa thức g(x) = 16 x4 - 72 x2 + 90.
Bài 4: (2 điểm) Tìm số chia và số dư biết rằng số bị chia bằng 112 và thương bằng 5.
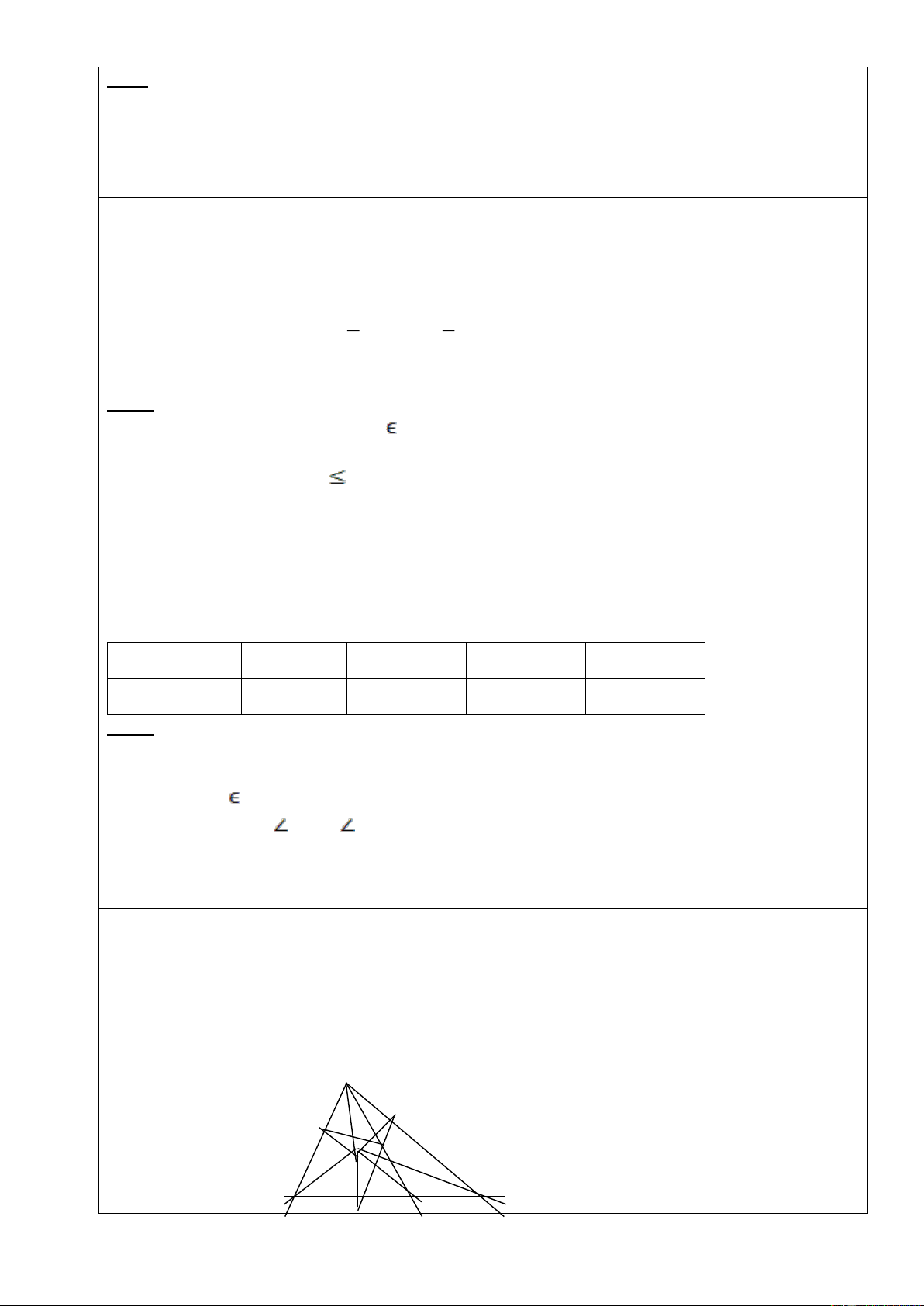
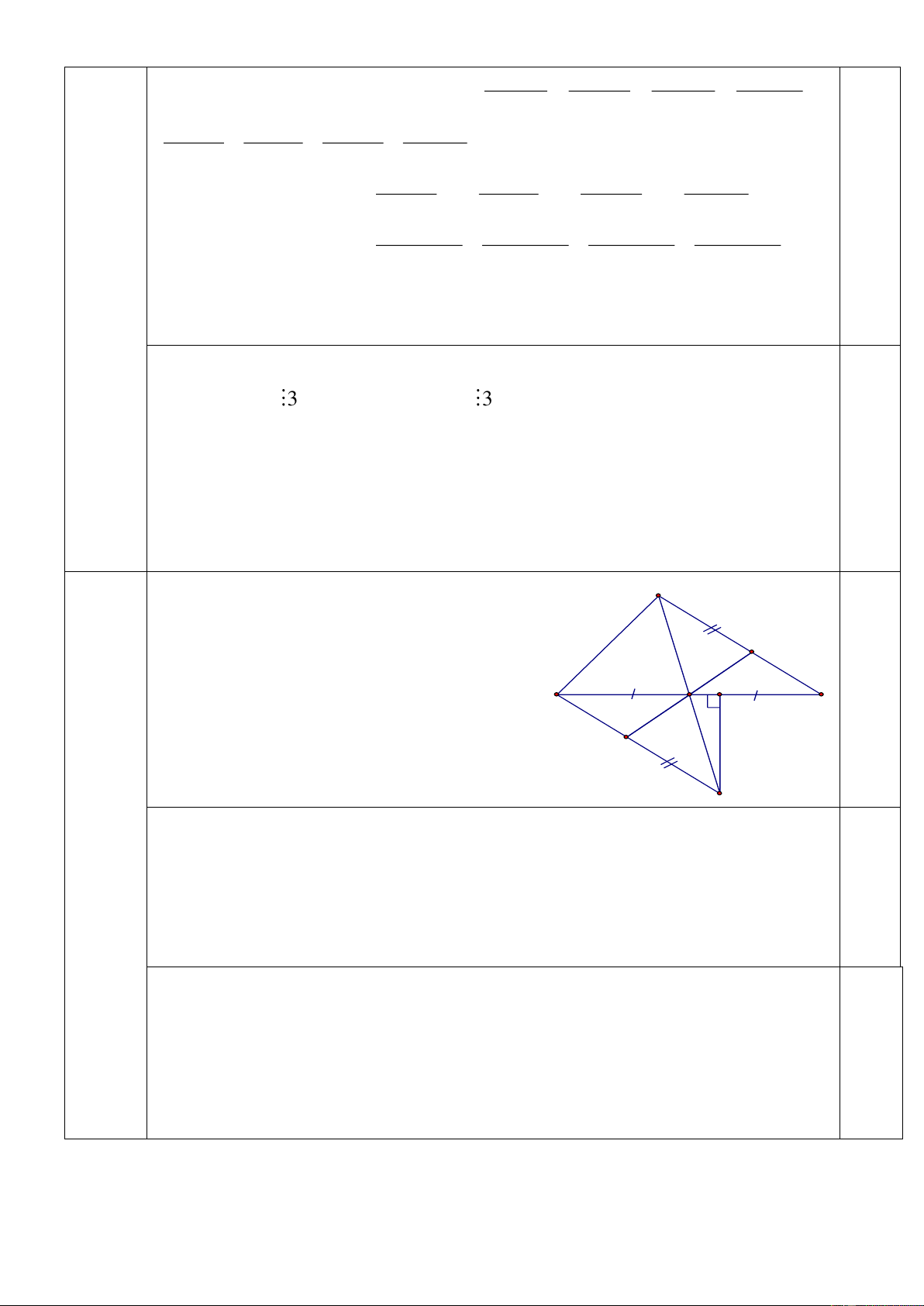
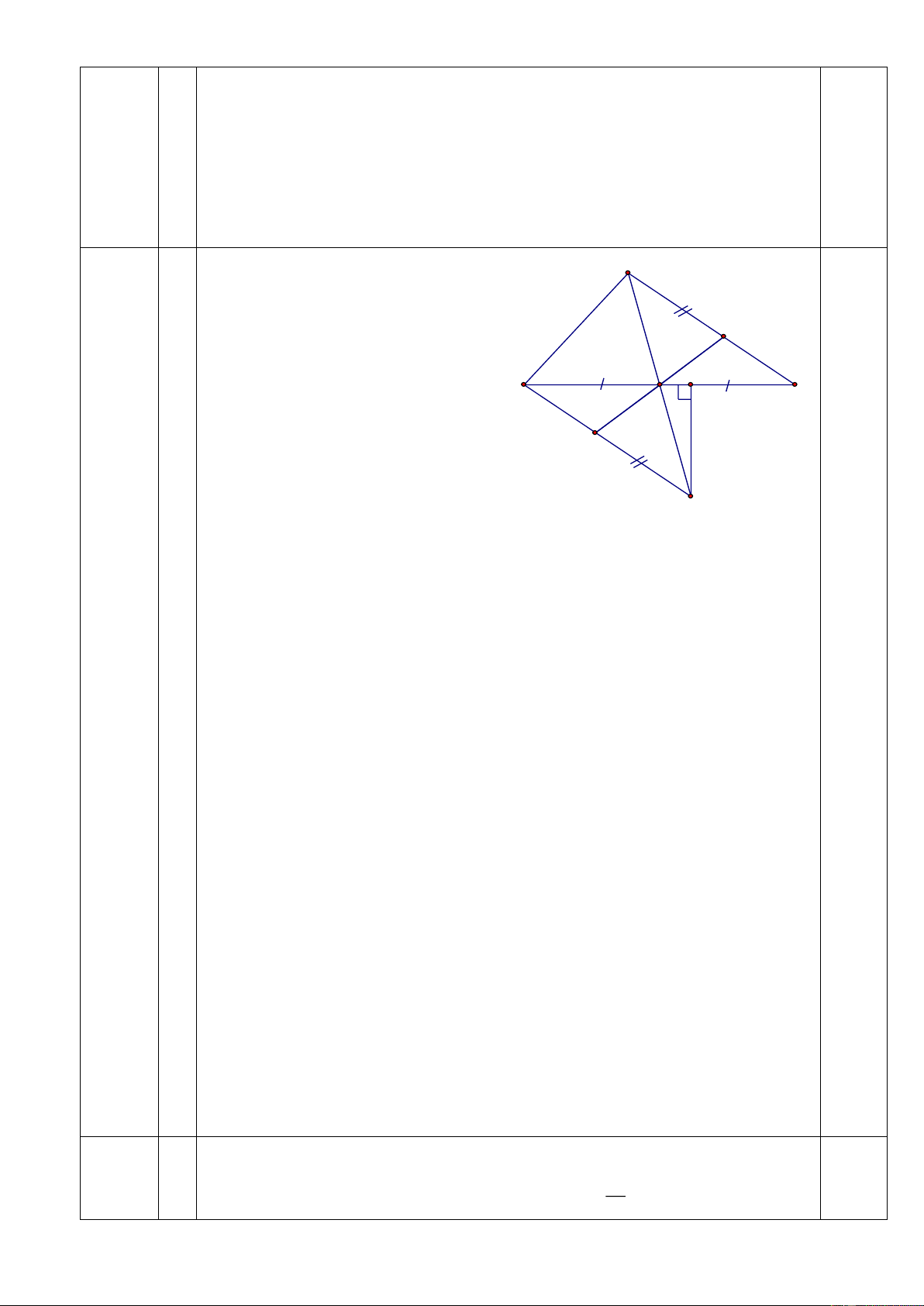
Bài 5: (3 điểm) Cho tam giác ABC có ba góc nhọn, AB < AC < BC. Các tia phân giác của
góc A và góc C cắt nhau tại O. Gọi F là hình chiếu của O trên BC; H là hình chiếu của O
trên AC. Lấy điểm I trên đoạn FC sao cho FI = AH. Gọi K là giao điểm của FH và AI.
a/ Chứng minh tam giác FCH cân và AK = KI.
b/ Chứng minh ba điểm B, O, K thẳng hàng.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 1 Bài 1: (1điểm) x2 y2 z2 0,5đ x y z
và x, y, z N, x ≠ 0 0,25đ 4 9 25 2 3 5 0,25đ x y z x y z 4 1 2 3 5 2 3 5 4
x = 2; y = 3; z = 5. Vậy xyz = 235 Bài 2: (1,5 điểm) 2 b 0,5đ 2 b2 Ta có: 2 c 2 a ac 2 c a ab (vì 9 + 16 = 25) 0,25đ 3 3 0,25đ Suy ra: 2c2= a(b – c) c 2 b c (vì a ≠ 0; c ≠ 0) 0,5đ a c c 2 b c c 2 b c b c
(vì a ≠ -c nên a + c ≠ 0) a c a c a c Trang 1 Bài 3: (2,5điểm) 0,5đ
a/ (1 điểm) f(x) = ( m2- 25)x4 + (20 + 4m)x3 + 7x2 - 9 là đa thức bậc 3 0,25đ
biến x khi: m2 - 25 = 0 và 20 + 4m ≠ 0 0,25đ m = 5 và m ≠ -5
Vậy m = 5 thì f(x) là đa thức bậc 3 biến x.
b/ (1,5 điểm) g(x) = 16 x4 - 72 x2 + 90 =(4x2 )2 - 2.4 x2.9 + 92 + 9 0,25đ g(x) = (4x2 – 9)2 + 9 0,25đ
Với mọi giá trị của x ta có: = (4x2 – 9)2 ≥ 0 g(x) = (4x2 – 9)2 + 9 ≥ 9.
Giá trị nhỏ nhất của g(x) là 9 0,25đ
Khi và chỉ khi (4x2 – 9)2 = 0 0,25đ 9 3
4x2 - 9 = 0 4x2 = 9 x2 = x = . 4 2 0,5đ Bài 4: (2 điểm)
Gọi số chia là a và số dư là r (a, r N*; a > r) 0,5đ Ta có: * 112 = 5a + r 5a < 112 a 22 (1)
*a > r 5a + r < 5a + a 112 < 6a 0,5đ a > 112 : 6 a ≥ 19 (2)
Từ (1) và (2) a = 19; 20; 21; 22 lập bảng số: a 19 20 21 22 0,5đ r = 112 – 5a 17 12 7 2 Bài 5: (3 điểm)
a/ (1,5 điểm) - Chứng minh CHO = CFO (cạnh huyền – góc nhọn) 0,25đ
suy ra: CH = CF. Kết luận FCH cân tại C. 0,25đ
-Vẽ IG //AC (G FH). Chứng minh FIG cân tại I. 0,25đ
- Suy ra: AH = IG, và IGK = AHK. 0,25đ
- Chứng minh AHK = IGK (g-c-g). 0,25đ - Suy ra AK = KI.. 0,25đ b/ (1,5 điểm)
Vẽ OE AB tại E. Tương tự câu a ta có: AEH, BEF thứ tự cân tại A, B. Suy ra: BE = BF và AE = AH. 0,5đ
BA = BE + EA = BF + AH = BF + FI = BI. Suy ra: ABI cân tại B. 0,5đ
Mà BO là phân giác góc B, và BK là đường trung tuyến của ABI nên: B, O, K là ba điểm thẳng hàng. 0,5đ A E H K O G Trang 2 B F I C
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 2 Câu 1: ( 2 điểm)
Thực hiện phép tính : 2 1 1 1 a- . 6 .
3 1 : ( 1 3 3 3 3 2 2 3
. . 2003 1 3 4 b- 2 3 2 5 . 5 12 Câu 2: ( 2 điểm) 2 a a 3 a- Tìm số nguyên a để là số nguyên a 1
b- Tìm số nguyên x,y sao cho x - 2xy + y = 0 Câu 3: ( 2 điểm) a c
a- Chứng minh rằng nếu a + c = 2b và 2bd = c (b+d) thì với b,d khác 0 b d
b- Cần bao nhiêu số hạng của tổng S = 1+2+3+… để được một số có ba chữ số giống nhau . Câu 4: ( 3 điểm)
Cho tam giác ABC có góc B bằng 450 , góc C bằng 1200. Trên tia đối của tia CB lấy
điểm D sao cho CD = 2CB . Tính góc ADE Câu 5: ( 1điểm)
Tìm mọi số nguyên tố thoả mãn : x2 - 2y2 =1 Trang 3
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 2 CÂU HƯỚNG DẪN CHẤM ĐIỂM 1.a
Thực hiện theo từng bước đúng kết quả -2 cho điểm tối đa 1Điểm 1.b
Thực hiện theo từng bước đúng kết quả 14,4 cho điểm tối đa 1Điểm 2.a 2 a a 3 a(a ) 1 3 3 0,25 Ta có : = a a 1 a 1 a 1 2 a a 3 3 vì a là số nguyên nên là số nguyên khi là số a a 1 1
nguyên hay a+1 là ước của 3 do đó ta có bảng sau : 0,25 a+1 -3 -1 1 3 a -4 -2 0 2 0,25 2 a a Vậy với a 3 , 4 , 0 , 2 2 thì là số nguyên a 1 0,25 2.b Từ : x-2xy+y=0 Hay (1-2y)(2x-1) = -1 0,25
Vì x,y là các số nguyên nên (1-2y)và (2x-1) là các số nguyên
do đó ta có các trường hợp sau : 1 2y 1 x 0 2x 1 1 y 0 0,25 1 2y 1 x Hoặc 1 0,25 2x 1 1 y 1
Vậy có 2 cặp số x, y như trên thoả mãn điều kiện đầu bài 0,25 3.a
Vì a+c=2b nên từ 2bd = c (b+d) Ta có: (a+c)d=c(b+d) 0,5 a c Hay ad=bc Suy ra ( ĐPCM) b d 0,5 3.b
Giả sử số có 3 chữ số là aaa =111.a ( a là chữ số khác 0)
Gọi số số hạng của tổng là n , ta có : n(n ) 1 11 a 1 a . 37 . 3 Hay n(n+1) =2.3.37.a 2 0,25
Vậy n(n+1) chia hết cho 37 , mà 37 là số nguyên tố và Trang 4
n+1<74 ( Nếu n = 74 không thoả mãn ) Do đó n=37 hoặc n+1 = 37 0,25 n n
Nếu n=37 thì n+1 = 38 lúc đó ( ) 1 703 không thoả mãn 2 n n
Nếu n+1=37 thì n = 36 lúc đó ( ) 1 666 thoả mãn 2
Vậy số số hạng của tổng là 36 0,5 4 A H B C D
Kẻ DH Vuông góc với AC vì ACD =600 do đó CDH = 300 0,5 CD Nên CH = CH = BC 2
Tam giác BCH cân tại C CBH = 300 ABH = 150 0,5
Mà BAH = 150 nên tam giác AHB cân tại H
Do đó tam giác AHD vuông cân tại H Vậy ADB = 1,0 450+300=750 1,0 5
Từ : x2-2y2=1suy ra x2-1=2y2 0,25
Nếu x chia hết cho 3 vì x nguyên tố nên x=3 lúc đó y= 2 0,25 nguyên tố thoả mãn
Nếu x không chia hết cho 3 thì x2-1 chia hết cho 3 do đó 2y2
chia hết cho 3 Mà(2;3)=1 nên y chia hết cho 3 khi đó x2=19 không thoả mãn 0,25
Vậy cặp số (x,y) duy nhất tìm được thoả mãn điều kiện đầu bài là (2;3) 0,25 Trang 5
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 3 Bài 1:(4 điểm) a) Thực hiện phép tính: 12 5 6 2 10 3 5 2 2 .3 4 .9 5 .7 25 .49 A 2 .36 8 .3 125.73 9 3 2 4 5 5 .14
b) Chứng minh rằng : Với mọi số nguyên dương n thì : n2 n2 3
2 3n 2n chia hết cho 10 Bài 2:(4 điểm) Tìm x biết: 1 4 x 3,2 2 a. 3 5 5 x 1 x 1 1
b. x 7 x 7 0 Bài 3: (4 điểm) 2 3 1
a) Số A được chia thành 3 số tỉ lệ theo : : . Biết rằng tổng các bình phương của ba 5 4 6
số đó bằng 24309. Tìm số A. a c 2 2 a c a b) Cho . Chứng minh rằng: c b 2 2 b c b Bài 4: (4 điểm)
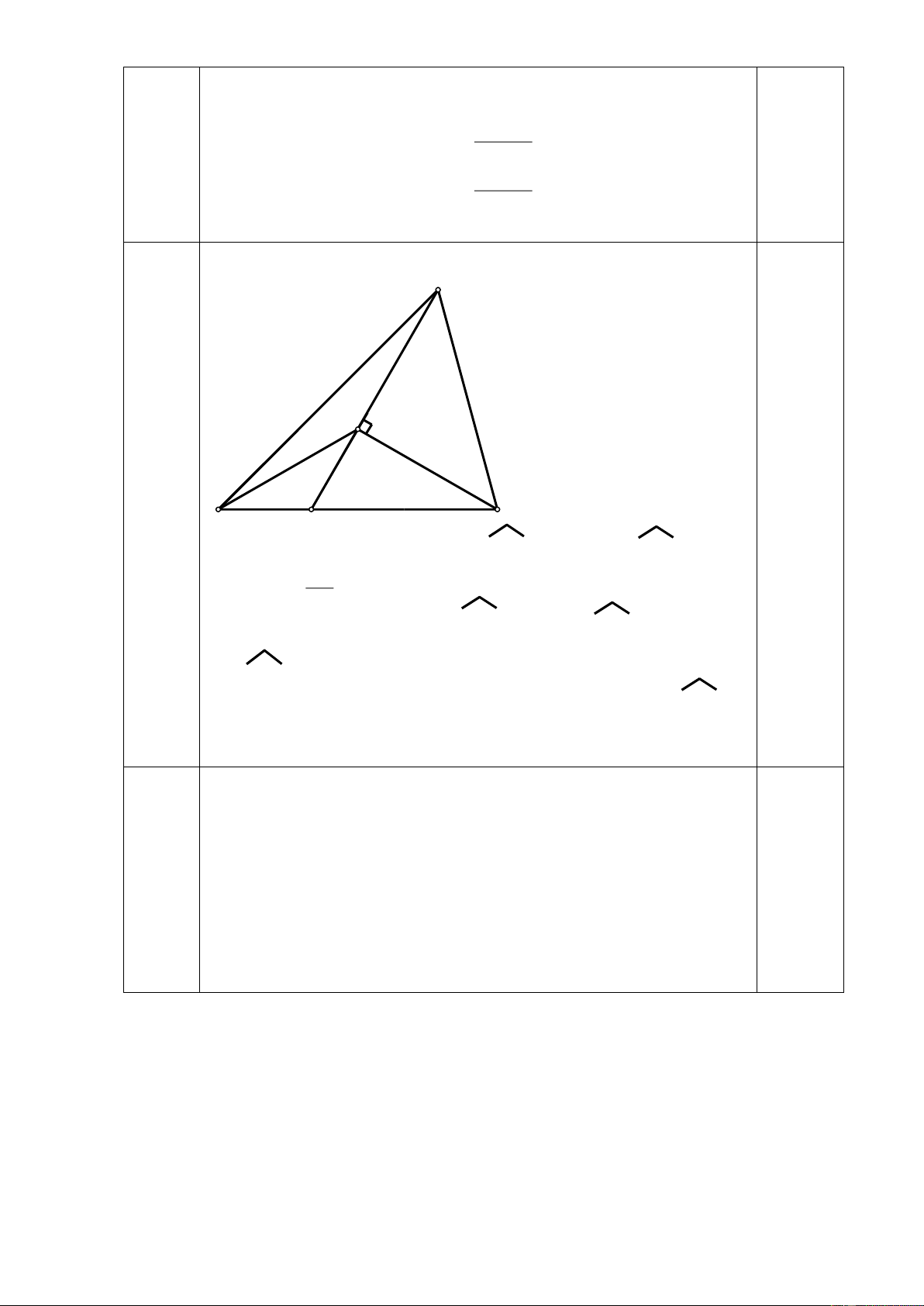
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của của tia MA lấy điểm E sao
cho ME = MA. Chứng minh rằng: a) AC = EB và AC // BE
b) Gọi I là một điểm trên AC ; K là một điểm trên EB sao cho AI = EK . Chứng
minh ba điểm I , M , K thẳng hàng
c) Từ E kẻ EH BC H BC . Biết HBE = 50o ; MEB =25o .
Tính HEM và BME Bài 5: (4 điểm)
Cho tam giác ABC cân tại A có 0
A 20 , vẽ tam giác đều DBC (D nằm trong tam giác
ABC). Tia phân giác của góc ABD cắt AC tại M. Chứng minh: Trang 6
a) Tia AD là phân giác của góc BAC b) AM = BC
……………………………… Hết ………………………………
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 3 Bài 1:(4 điểm): Đáp án Thang điểm a) (2 điểm) 10 12 5 6 2 10 3 5 2 12 5 12 4 10 3 4 2 .3 4 .9 5 .7 25 .49 2 .3 2 .3 5 .7 5 .7 A 0,5 điể m 2 .36 8 .3 125.73 12 6 12 5 9 3 9 3 3 9 3 2 4 5 5 .14 2 .3 2 .3 5 .7 5 .2 .7 12 4 2 .3 .3 10 3 1 5 .7 . 1 7 0,5 điểm 12 5 2 .3 .3 9 3 1 5 .7 . 3 1 2 0,5 điểm 12 4 10 3 2 .3 .2 5 .7 . 6 0,5 điể 12 5 9 3 m 2 .3 .4 5 .7 .9 1 10 7 6 3 2 b) (2 điểm)
3 n + 2 - Với mọi số nguyên dương n ta có: 0,5 điểm n2 n2 n n n2 n n2 n 3
2 3 2 = 3 3 2 2 1 điểm = n 2 n 2 3 (3 1) 2 (2 1) 0,5 điểm n n n n 1
= 3 10 2 5 3 10 2 10 = 10( 3n -2n) n2 n2 n n Vậy 3
2 3 2 10 với mọi n là số nguyên dương. Bài 2:(4 điểm) Đáp án Thang điểm a) (2 điểm) 0,5 điểm 0,5 điểm Trang 7 1 4 0,5 điểm x 2 1 4 16 2 3, 2 x 3 5 5 3 5 5 5 1 4 14 x 0,5 điểm 3 5 5 1 x 2 1 3 x 2 1 3 x 2 0,5 điểm 3 0,5 điểm 1 7 x2 3 3 1 5 x 2 3 3 0,5 điểm b) (2 điểm) x x
x 7 1 x 7 11 0 x 0,5 điể x 7 1 1
x 710 0 m x x 7 1 1
x 710 0 x 1 x 7 0 10 1 ( x 7) 0 x 7 0 x 7 10 ( x 7 ) 1 x 8 Bài 3: (4 điểm) Đáp án Thang điểm a) (2,5 điểm)
Gọi a, b, c là ba số được chia ra từ số A. 0,5 điểm Theo đề 2 3 1 bài ta có: a : b : c = : : (1) 5 4 6 0,5 điể và a2 +b2 +c2 = 24309 (2) m a b c k Từ (1) = k 2 3 a k;b k;c 2 3 1 5 4 6 5 4 6 0,5 điểm Do đó (2) 4 9 1 2 k ( ) 24309 25 16 36 k = 180 và k = 180 0,5 điểm
+ Với k =180, ta được: a = 72; b = 135; c = 30.
Khi đó ta có số A = a + b + c = 237. 0,5 điểm + Với k = 180 , ta được: a = 72 ; b = 135 ; c = 30 Khi đó ta có só A = 72 +( 135 ) + ( 30 ) = 237 . b) (1,5 điể m) Trang 8 a c 0,5 điểm Từ suy ra 2 c . a b c b 2 2 2 0,5 điểm a c a . a b khi đó 2 2 2 b c b . a b 0,5 điểm
a(a b) a =
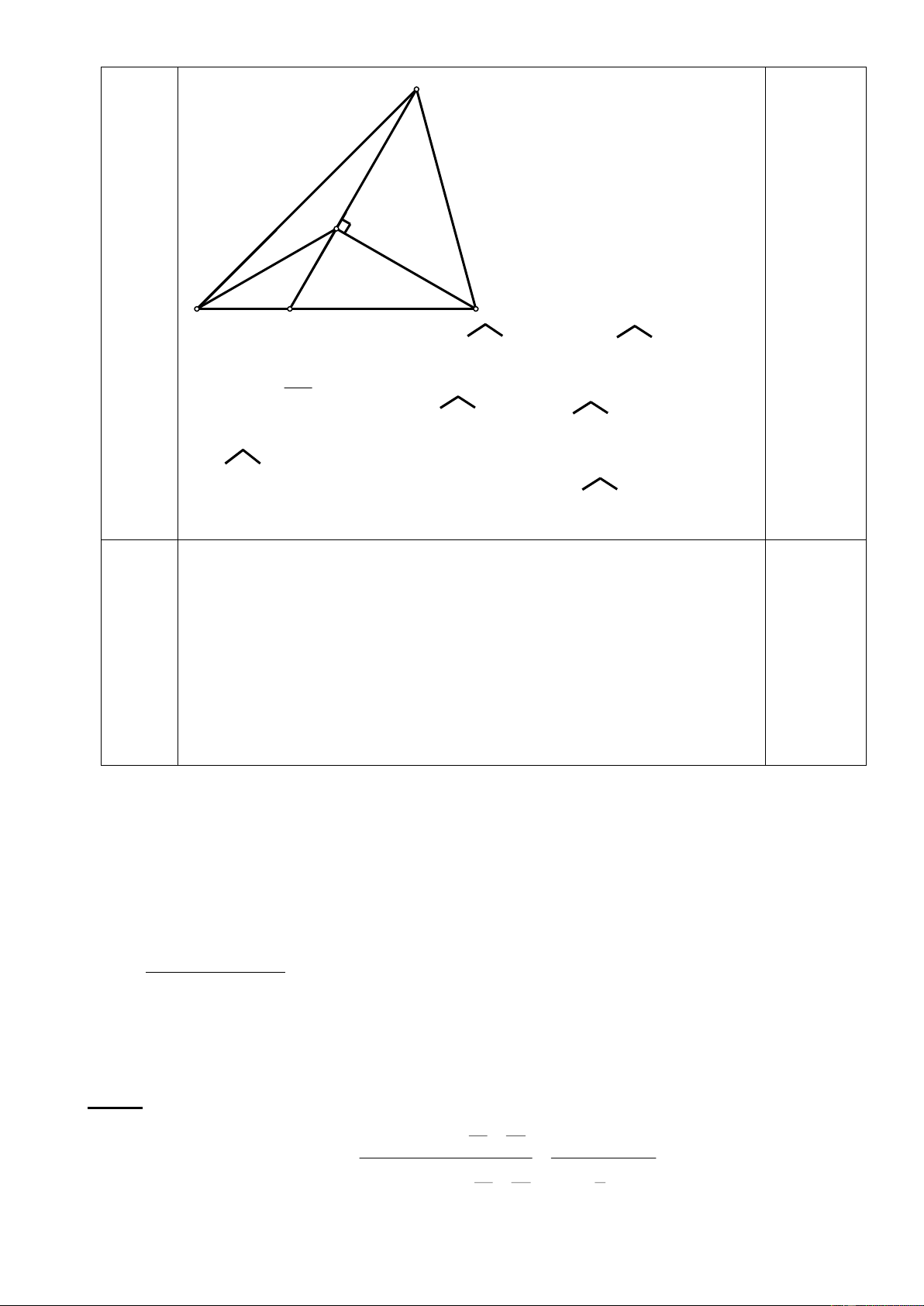
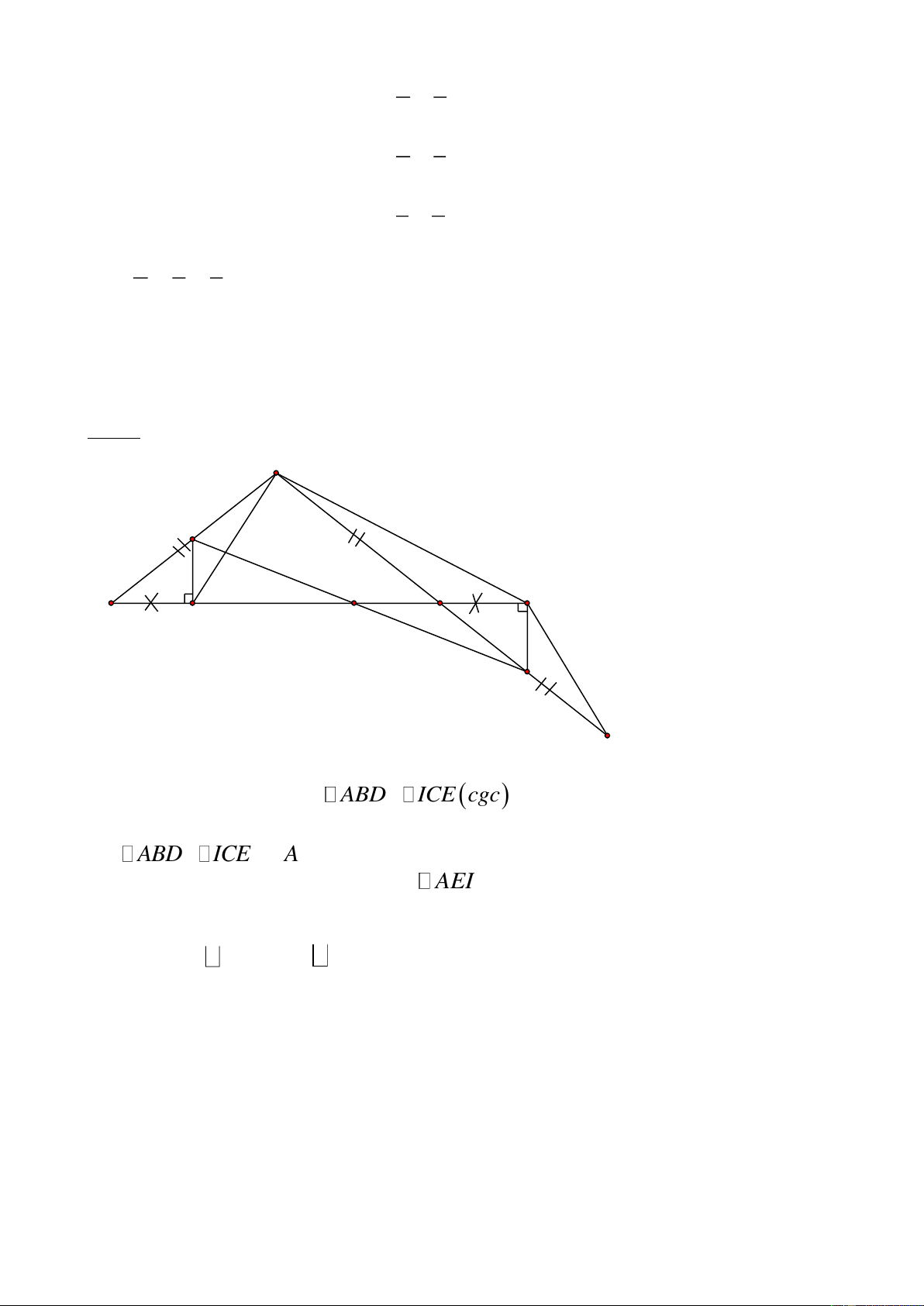
b(a b) b Bài 4: (4 điểm) Đáp án Thang điểm Vẽ hình 0,5 điểm A I M B C H K E
a/ (1điểm) Xét A
MC và EMB có : AM = EM (gt )
AMC = EMB (đối đỉnh ) BM = MC (gt ) Nên : A
MC = EMB (c.g.c ) 0,5 điểm AC = EB Vì A
MC = EMB MAC = MEB
(2 góc có vị trí so le trong được tạo bởi đường thẳng AC và EB cắt đường thẳng AE ) Suy ra AC // BE . 0,5 điểm b/ (1 điểm ) Xét AM I và EMK có : AM = EM (gt )
MAI = MEK ( vì A MC E MB ) AI = EK (gt ) Nên AM I EM K ( c.g.c ) 0,5 điểm
Suy ra AMI = EMK
Mà AMI + IME = 180o ( tính chất hai góc kề bù ) EMK + IME = 180o
Ba điểm I;M;K thẳng hàng 0,5 điểm c/ (1,5 điểm )
Trong tam giác vuông BHE ( H = 90o ) có HBE = 50o
HBE = 90o - HBE = 90o - 50o =40o 0,5 điểm
HEM = HEB - MEB = 40o - 25o = 15o 0,5 điểm Trang 9
BME là góc ngoài tại đỉnh M của H EM
Nên BME = HEM + MHE = 15o + 90o = 105o
( định lý góc ngoài của tam giác ) 0,5 điểm Bài 5: (4 điểm) A 200 M D B C -Vẽ hình
a) Chứng minh ADB = ADC (c.c.c) 1 điểm
suy ra DAB DAC 0,5 điểm Do đó 0 0 DAB 20 : 2 10 0,5 điểm b) ABC cân tại A, mà 0 A 20 (gt) nên 0 0 0
ABC (180 20 ) : 2 80 ABC đều nên 0 DBC 60 0,5 điểm
Tia BD nằm giữa hai tia BA và BC suy ra 0 0 0
ABD 80 60 20 .
Tia BM là phân giác của góc ABD nên 0 ABM 10 0,5 điểm
Xét tam giác ABM và BAD có: AB cạnh chung ; 0 0
BAM ABD 20 ; ABM DAB 10
Vậy: ABM = BAD (g.c.g)
suy ra AM = BD, mà BD = BC (gt) nên AM = BC 0,5 điểm
Lưu ý: Nếu học sinh làm theo cách khác đúng vẫn đạt điểm tối đa.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Trang 10 ĐỀ 4 Câu 1: ( 2 điểm)
Thực hiện phép tính : 2 1 1 1 a. . 6 .
3 1 : ( 1 3 3 3 3 2 2 3
. . 2003 1 3 4 b. 2 3 2 5 . 5 12 Câu 2: ( 2 điểm) 2 a a a. Tìm số nguyên a để 3 là số nguyên a 1
b. Tìm số nguyên x, y sao cho x- 2xy + y = 0 Câu 3 : ( 2 điểm)
a. Chứng minh rằng nếu a + c = 2b và 2bd = c(b + d) thì a c với b, d khác 0 b d
b. Cần bao nhiêu số hạng của tổng S = 1 + 2 + 3 +… để được một số có ba chữ số giống nhau . Câu 4 : ( 3 điểm)
Cho tam giác ABC có góc B bằng 450 , góc C bằng 1200. Trên tia đối của tia CB lấy
điểm D sao cho CD = 2CB . Tính góc ADE Câu 5 : ( 1điểm)
Tìm mọi số nguyên tố thoả mãn : x2- 2y2 = 1
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 4 CÂU HƯỚNG DẪN CHẤM ĐIỂM 1.a
Thực hiện theo từng bước đúng kết quả -2 cho điểm tối đa 1Điểm 1.b
Thực hiện theo từng bước đúng kết quả 14,4 cho điểm tối đa 1Điểm Trang 11 2.a 2 a a 3 a(a ) 1 3 3 0,25 Ta có : = a a 1 a 1 a 1 2 a a 3 3 vì a là số nguyên nên là số nguyên khi là số a a 1 1
nguyên hay a+1 là ước của 3 do đó ta có bảng sau : 0,25 a+1 -3 -1 1 3 a -4 -2 0 2 0,25 2 a a Vậy với a 3 , 4 , 0 , 2 2 thì là số nguyên a 1 0,25 2.b Từ : x- 2xy + y = 0 Hay (1- 2y)(2x - 1) = -1 0,25
Vì x,y là các số nguyên nên (1 - 2y)và (2x - 1) là các số nguyên
do đó ta có các trường hợp sau : 1 2y 1 x 0 2x 1 1 y 0 0,25 1 2y 1 x Hoặc 1 0,25 2x 1 1 y 1
Vậy có 2 cặp số x, y như trên thoả mãn điều kiện đầu bài 0,25 3.a
Vì a + c = 2b nên từ 2bd = c(b + d) Ta có: (a + c)d =c(b + d) 0,5 a c Hay ad = bc Suy ra ( ĐPCM) b d 0,5 3.b
Giả sử số có 3 chữ số là aaa =111.a ( a là chữ số khác 0)
Gọi số số hạng của tổng là n , ta có : n(n ) 1 11 a 1 a . 37 . 3 Hay n(n + 1) =2.3.37.a 2 0,25
Vậy n(n+1) chia hết cho 37 , mà 37 là số nguyên tố và n + 1 < 74
( Nếu n = 74 không thoả mãn ) 0,25
Do đó n=37 hoặc n + 1 = 37 n n
Nếu n =37 thì n + 1 = 38 lúc đó ( ) 1 703 không thoả mãn 2 n n
Nếu n + 1=37 thì n = 36 lúc đó ( ) 1 666 thoả mãn 2 0,5
Vậy số số hạng của tổng là 36 4 Trang 12 A 0,5 H 0,5 B C D 1,0
Kẻ DH Vuông góc với AC vì ACD =600 do đó CDH = 300 CD Nên CH = CH = BC 1,0 2
Tam giác BCH cân tại C CBH = 300 ABH = 150
Mà BAH = 150 nên tam giác AHB cân tại H
Do đó tam giác AHD vuông cân tại H Vậy ADB = 450 + 300 =750 5
Từ : x2- 2y2 =1suy ra x2- 1 = 2y2 0,25
Nếu x chia hết cho 3 vì x nguyên tố nên x = 3 lúc đó y = 2 0,25 nguyên tố thoả mãn
Nếu x không chia hết cho 3 thì x2-1 chia hết cho 3 do đó 2y2 chia
hết cho 3 Mà(2;3) =1 nên y chia hết cho 3 khi đó x2 =19 không thoả mãn 0,25
Vậy cặp số (x,y) duy nhất tìm được thoả mãn điều kiện đầu bài là (2;3) 0,25
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 5 Câu 1: (1,5 điểm) 3 3 0,375 0,3 1,5 1 0,75 a. Thực hiện phép tính: 11 12 5 5 5 0 ,265 0,5 2,5 1,25 11 12 3 Trang 13
b. So sánh: 50 26 1 và 168 . Câu 2: (4,0 điểm)
a. Tìm x biết: x 2 3 2x 2x 1 b. Tìm ;
x y Z biết: xy 2x y 5
c. Tìm x; y; z biết: 2x = 3y; 4y = 5z và 4x - 3y + 5z = 7 Câu 3: (1,5 điểm)
a. Tìm đa thức bậc hai biết f(x) - f(x-1) = x. Từ đó áp dụng tính tổng S = 1+2+3+ ....+ n. 2bz 3cy 3cx az ay 2bx x y z b. Cho Chứng minh: . a 2b 3c a 2b 3c Câu 4: (3,0 điểm) Cho tam giác ABC ( 90o BAC
), đường cao AH. Gọi E; F lần lượt là điểm đối xứng
của H qua AB; AC, đường thẳng EF cắt AB; AC lần lượt tại M và N. Chứng minh rằng: a. AE = AF;
b. HA là phân giác của MHN ; c. CM // EH; BN // FH. Hết./.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 5 Câu Ý Nội dung Điểm a. 0,5 3 3 3 3 3 3 3 0.25 điể m A = 8 10 11 12 2 3 4 53 5 5 5 5 5 5 100 10 11 12 2 3 4 A= 1 1 1 1 1 1 1 165 132 120 110 3 3 8 10 11 12 2 3 4 3( ) 3 Câu 1 1320 53 1 1 1 1 1 1 53 66 60 55 1,5 5 5 5 5( ) 0.25 điểm 100 10 11 12 2 3 4 100 660 263 263 3. 3. 3 3 3945 3 1881 1320 1320 53 49 5 17491225 5 5948 5 29740 5. 100 660 3300 b. 1
Ta có: 50 > 49 = 4; 26 > 25 = 5 0.5 điểm 0,5
Vậy: 50 26 1 7 5 1 13 169 168 a. 1
Nếu x >2 ta có: x - 2 + 2x - 3 = 2x + 1 x = 6 0.25 điểm 3 0.25 Câu 2
Nếu x 2 ta có: 2 - x + 2x - 3 = 2x + 1 x = - 2 loại 4 điể 2 m 0.25 3 4
Nếu x< ta có: 2 - x + 3 - 2x = 2x + 1 x = 2 5 Trang 14 4 0.25 Vậy: x = 6 ; x = 5 b. 1.5
Ta có: xy + 2x - y = 5 x(y+2) - (y+2) = 3 0. 5 điểm
(y+2)(x-1) = 3.1 =1.3 = (-1).(-3) = (-3).(-1) 0. 5 y + 2 3 1 -1 -3 0.5 x - 1 1 3 -3 -1 X 2 4 -2 0 Y 1 -1 -3 -5
c. 1.5 Từ: 2x= 3y; 4y = 5z 8x = 12y = 15z 0. 5 điểm x y z 4x 3y 5z 4x 3y 5z 7 = 12 1 1 1 1 1 1 1 1 1 7 0.5 8 12 15 2 4 3 2 4 3 12 0. 5 1 3 1 1 4 x = 12. = ; y = 12. = 1; z = 12. 8 2 12 15 5
a. 0.5 Đa thức bậc hai cần tìm có dạng: 2
f x ax bx c (a 0). điểm
Ta có : f x a x 2 1
1 b x 1 c . 1 0.25 2a 1 a 2
f x f x
1 2ax a b x b a 0 1 b 2 1 1
Vậy đa thức cần tìm là: f x 2
x x c (c là hằng số tùy ý). 2 2 Áp dụng:
+ Với x = 1 ta có : 1 f 1 f 0. 0.25
+ Với x = 2 ta có : 1 f 2 f 1 . Câu 3
…………………………………. 1.5
+ Với x = n ta có : n f n f n 1 . điểm 2 n n n n S = 1+2+3+…+n = 1
f n f 0 =
c c . 2 2 2 b. 1 2bz 3cy 3cx az ay 2bx điể m a 2b 3c 2abz 3acy 6bcx 2abz 3acy 6bcx 0.5 2 2 2 a 4b 9c
2abz 3acy 6bcx 2abz 3acy 6bcx 0 2 2 2
a 4b 9c 0.25 z y 2bz - 3cy = 0 (1) 3c 2b 0.25 x z x y z 3cx - az = 0 (2); Từ (1) và (2) suy ra: a 3c a 2b 3c Trang 15 Câu 4 Hình 0.25 3 điể F m vẽ 0. 5 đ A N M E B C H a. 1
Vì AB là trung trực của EH nên ta có: AE = AH (1) 0.25
điểm Vì AC là trung trực của HF nên ta có: AH = AF (2) 0.25
Từ (1) và (2) suy ra: AE = AF 0. 5 b. 1 Vì M
AB nên MB là phân giác EMH MB là phân giác 0.25 điểm
ngoài góc M của tam giác MNH 0.25 Vì N
AC nên NC là phân giác FNH NC là phân giác
ngoài góc N của tam giác MNH 0.25
Do MB; NC cắt nhau tại A nên HA là phân giác trong góc H 0.25
của tam giác HMN hay HA là phân giác của MHN . c. 1
Ta có AH BC (gt) mà HM là phân giác MHN HB là phân 0.25
điểm giác ngoài góc H của tam giác HMN 0.25
MB là phân giác ngoài góc M của tam giác HMN (cmt) NB
là phân giác trong góc N của tam giác HMN 0.25
BN AC ( Hai đường phân giác của hai góc kề bù thì vuông
góc với nhau). BN // HF ( cùng vuông góc với AC)
Chứng minh tương tự ta có: EH // CM
Lưu ý: Học sinh làm cách khác đúng thì vẫn cho điểm tối đa.
Học sinh không vẽ hình hoặc vẽ hình sai thì không chấm bài hình. Trang 16
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 6
Bài 1: Thực hiện phép tính (6 điểm). a. 3 2 5 9 : . ; 4 3 9 4 1 1 1 45 1 1 1 b. ; 19 2 3 4 15 9 20 9 . 5 4 .9 . 4 3 8 . c. . 10 19 29 6 5 2 . .6 7 2 . 27 . Bài 2: (6 điểm)
a. Tìm x, biết: 2(x-1) – 3(2x+2) – 4(2x+3) = 16; 1 21
b. Tìm x, biết: 3 : 2x 1 = 2 22 2x y 3y 2z c. Tìm x, y, z biết: và x + z = 2y. 5 15 a c
Bài 3: (1,5 điểm) Cho tỉ lệ thức . b d
Chứng minh rằng : (a+2c)(b+d) = (a+c)(b+2d).
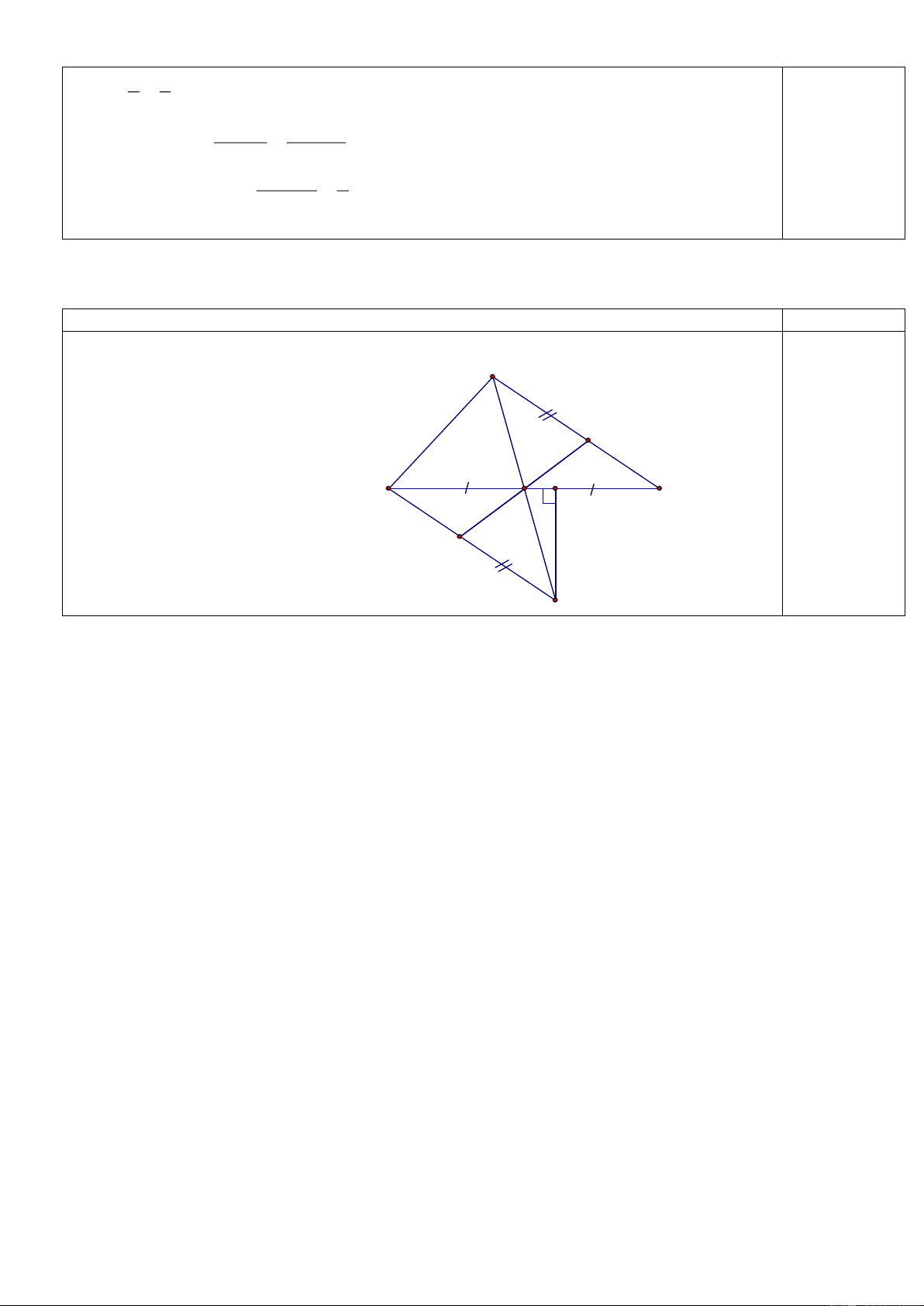
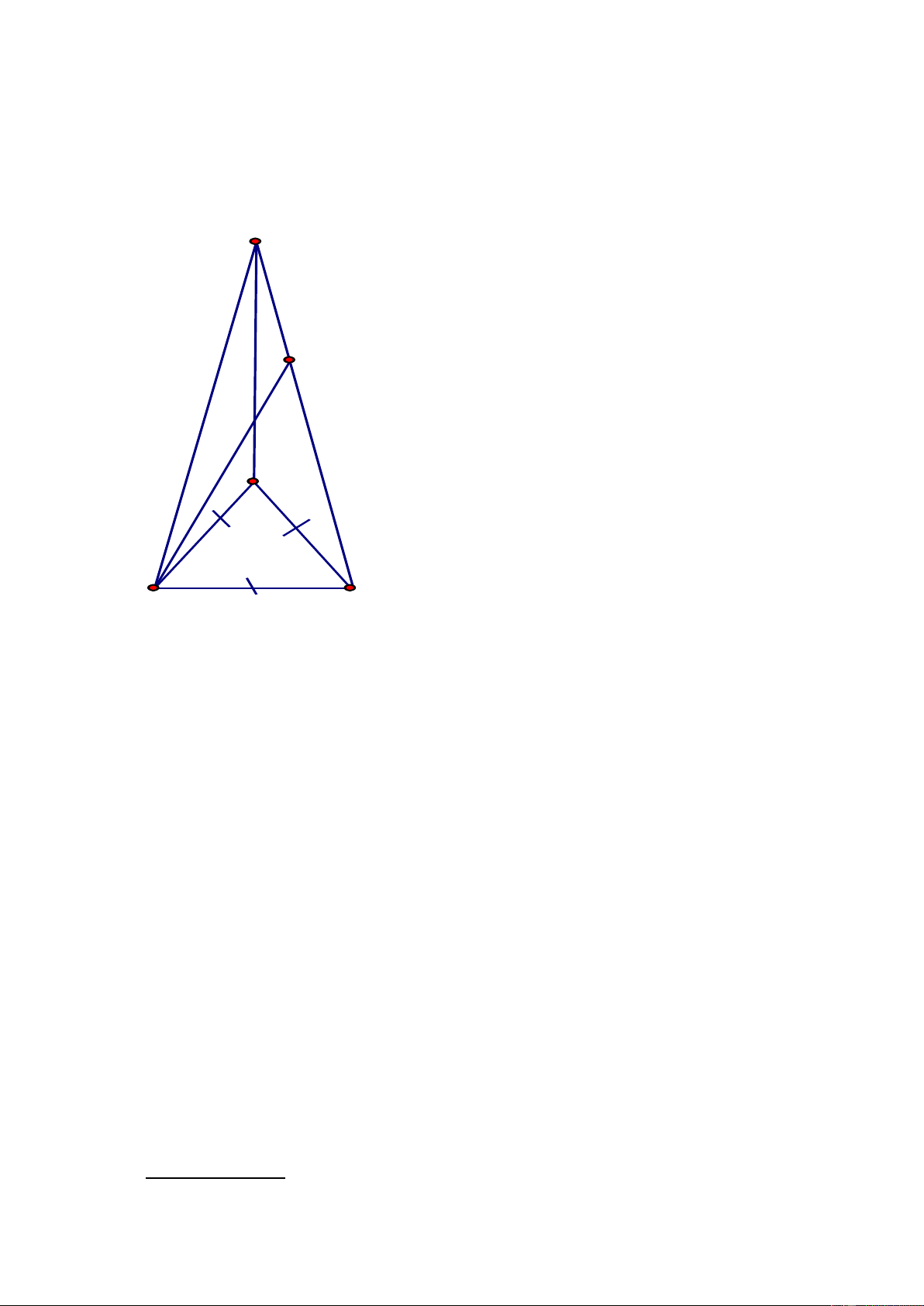
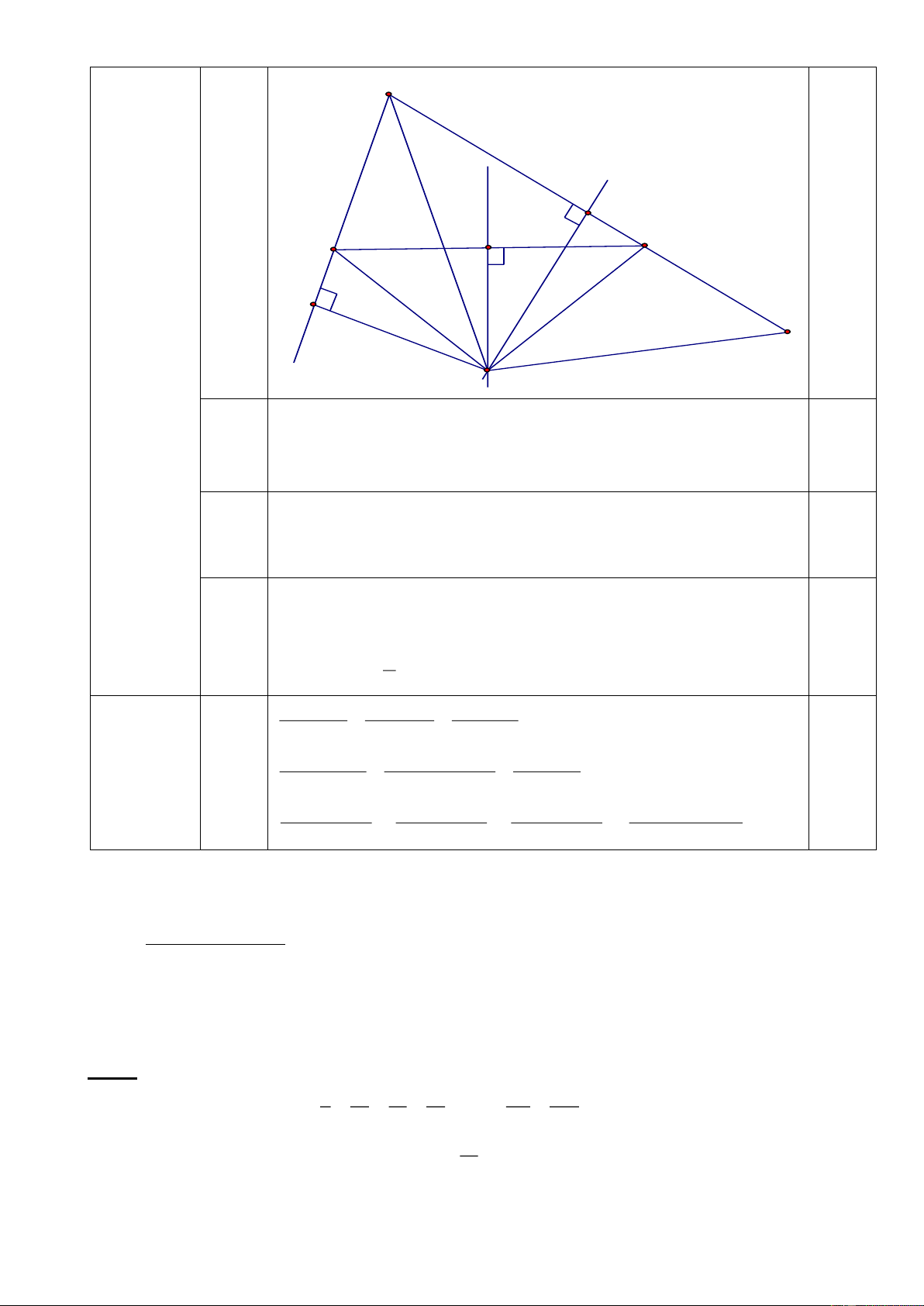
Bài 4: (4,5 điểm) Cho tam giác ABC vuông tại A; K là trung điểm của BC. Trên tia đối
của tia KA lấy D , sao cho KD = KA. a. Chứng minh: CD // AB.
b. Gọi H là trung điểm của AC; BH cắt AD tại M; DH cắt BC tại N .
Chứng minh rằng: ABH = CDH.
c. Chứng minh: HMN cân.
Bài 5: (2 điểm): Chứng minh rằng số có dạng abcabc luôn chia hết cho 11. Hết
Họ và tên học sinh:.............................................................; SBD:............................
Học sinh trường:......................................................................................................... Trang 17
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 6
Bài 1: Thực hiện phép tính (6 điểm). Giải: a. 3 2 5 9 : . 4 3 9 4 3 2 5 9 3 1 9 0,75đ : : 4 3 9 4 4 9 4 3 9 9 36 0,75đ = . 9 4 1 4 4 1 1 1 45 1 1 1 b. 19 2 3 4 1 1 1 45 1 1 1 45 1 19 2 3 4 19 1 1 1,0đ 2 1 4 3 45 26 19 = 1 1,0đ 19 19 19 15 9 20 9 . 5 4 .9 . 4 3 8 . c. 10 19 29 6 5 2 . .6 7 2 . 27 . 15 9 20 9 . 5 4 .9 . 4 3 8 . 15 . 2 9 . 2 2 20 9 . 3 2 . 5 3 . 2 3 . 2 . = 01đ 10 19 29 6 5 2 . .6 7 2 . 27 . 10 19 19 29 6 . 3 2 . 5 2 . 3 . 2 . 7 3 . 229 3 . 18 2 . 5 32 01đ 229 3 . 18 3 . 5 7 10 9 1 = 0,5đ 15 7 8 Bài 2: (6 điểm) Giải:
a. Tìm x, biết: 2(x-1) – 3(2x+2) – 4(2x+3) = 16.
2x – 2 – 6x – 6 – 8x – 12 = 16 0,25đ -12x – 20 = 16 0,25đ -12x = 16 + 20 = 36 0,50đ x = 36 : (-12) = -3 0,50đ 1 21
b. Tìm x, biết: 3 : 2x 1 = 2 22 1
Nếu x . Ta có: (vì nếu x = ½ thì 2x – 1 = 0) 0,25đ 2 Trang 18 1 21 3 : 2x 1 = 2 22 7 21 : (2x – 1) = 0,25đ 2 22 7 21 7 22 11 2x – 1 = : = . 0,25đ 2 22 2 21 3 11 14 2x = + 1 = 0,25đ 3 3 14 7 1 x = : 2 = > 0,25đ 3 3 2 1 Nếu x . Ta có: 0,25đ 2 1 21 3 : 2x 1 = 2 22 7 21 : (1 - 2x) = 0,25đ 2 22 11 8 -2x = - 1 = 0,25đ 3 3 8 4 1 x = : (-2) = 0,25đ 3 3 2 7 4 Vậy x = hoặc x = 0,25đ 3 3 2x y 3y 2z c. Tìm x, y, z biết : và x + z = 2y 5 15 Từ x + z = 2y ta có:
x – 2y + z = 0 hay 2x – 4y + 2z = 0 hay 2x – y – 3y + 2z = 0 0,25đ hay 2x – y = 3y – 2z 0,25đ 2x y 3y 2z Vậy nếu:
thì: 2x – y = 3y – 2z = 0 (vì 5 15). 0,25đ 5 15 1
Từ 2x – y = 0 suy ra: x = y 0,25đ 2 1
Từ 3y – 2z = 0 và x + z = 2y. x + z + y – 2z = 0 hay y + y – z = 0 0,25đ 2 3 2 1
hay y - z = 0 hay y = z. suy ra: x = z. 0,25đ 2 3 3 1 2
Vậy các giá trị x, y, z cần tìm là: {x = z; y = z ; với z R } 3 3 0,5đ 1 3
hoặc {x = y; y R; z = y} hoặc {x R; y = 2x; z = 3x} 2 2 a c
Bài 3: (1,5 điểm) Cho tỉ lệ thức . b d
Chứng minh rằng : (a+2c)(b+d) = (a+c)(b+2d)
Ta có: (a+2c)(b+d) = (a+c)(b+2d)
ab + ad + 2cb + 2cd = ab + 2ad + cb + 2cd 0,75đ a c cb = ad suy ra: 0,75đ b d Trang 19
Bài 4: (4,5 điểm) Cho tam giác ABC vuông tại A; K là trung điểm của BC. Trên tia đối
của tia KA lấy D , sao cho KD = KA. a. Chứng minh: CD // AB.
b. Gọi H là trung điểm của AC; BH cắt AD tại M; DH cắt BC tại N .
Chứng minh rằng: ABH = CDH.
c. Chứng minh: HMN cân. Giải: B D K M N A C H
a/ Chứng minh CD song song với AB.
Xét 2 tam giác: ABK và DCK có: 0,25đ BK = CK (gt) A K ˆ B D K ˆ C (đối đỉnh) 0,25đ AK = DK (gt) 0,25đ ABK = DCK (c-g-c) 0,25đ K C ˆ D K B ˆ D ; mà 0 C B ˆ A B C ˆ A 90 0 D C ˆ A B C ˆ A D C ˆ B 90 0,25đ D C ˆ A 900 C A ˆ B
AB // CD (AB AC và CD AC). 0,25đ
b. Chứng minh rằng: ABH = CDH
Xét 2 tam giác vuông: ABH và CDH có: 0,25đ BA = CD (do ABK = DCK) AH = CH (gt) 0,25đ ABH = CDH (c-g-c) 0,50đ
c. Chứng minh: HMN cân.
Xét 2 tam giác vuông: ABC và CDA có: 0,25đ AB = CD; D C ˆ A 900 C A ˆ B
; AC cạnh chung: ABC = CDA (c-g-c) Cˆ A B D A ˆ C 0,25đ mà: AH = CH (gt) và A H ˆ M C H ˆ N (vì ABH = CDH) 0,50đ AMH = CNH (g-c-g) 0,50đ
MH = NH. Vậy HMN cân tại H 0,50đ
Bài 5: (2 điểm): Chứng minh rằng số có dạng abcabc luôn chia hết cho 11. Giải:
Ta có: abcabc = a.105 + b.104 + c.103 + a.102 + b.10 + c 0,25đ
= a.102(103 + 1) + b.10(103 + 1) + c(103 + 1) 0,50đ
= (103 + 1)( a.102 + b.10 + c) 0,50đ Trang 20
= (1000 + 1)( a.102 + b.10 + c) = 1001( a.102 + b.10 + c) 0,25đ
= 11.91( a.102 + b.10 + c) 11 0,25đ Vậy abcabc 11 0,25đ
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 7
Câu 1. (4,0 điểm) 2 2 1 1 0, 4 0,25 2012 1) M = 9 11 3 5 : 7 7 1 2013 1,4 1 0,875 0, 7 9 11 6 2) Tìm x, biết: 2 x x 1 2 x 2 .
Câu 2. (5,0 điểm)
a b c
b c a
c a b
1) Cho a, b, c là ba số thực khác 0, thoả mãn điều kiện: . Hãy c a b b a c
tính giá trị của biểu thức B 1 1 1 . a c b
2) Ba lớp 7A, 7B, 7C cùng mua một số gói tăm từ thiện, lúc đầu số gói tăm dự định chia
cho ba lớp tỉ lệ với 5:6:7 nhưng sau đó chia theo tỉ lệ 4:5:6 nên có một lớp nhận nhiều hơn
dự định 4 gói. Tính tổng số gói tăm mà ba lớp đã mua.
Câu 3. (4,0 điểm)
1) Tìm giá trị nhỏ nhất của biểu thức A = 2x 2 2x 2013 với x là số nguyên.
2) Tìm nghiệm nguyên dương của phương trình x y z xyz .
Câu 4. (6,0 điểm)
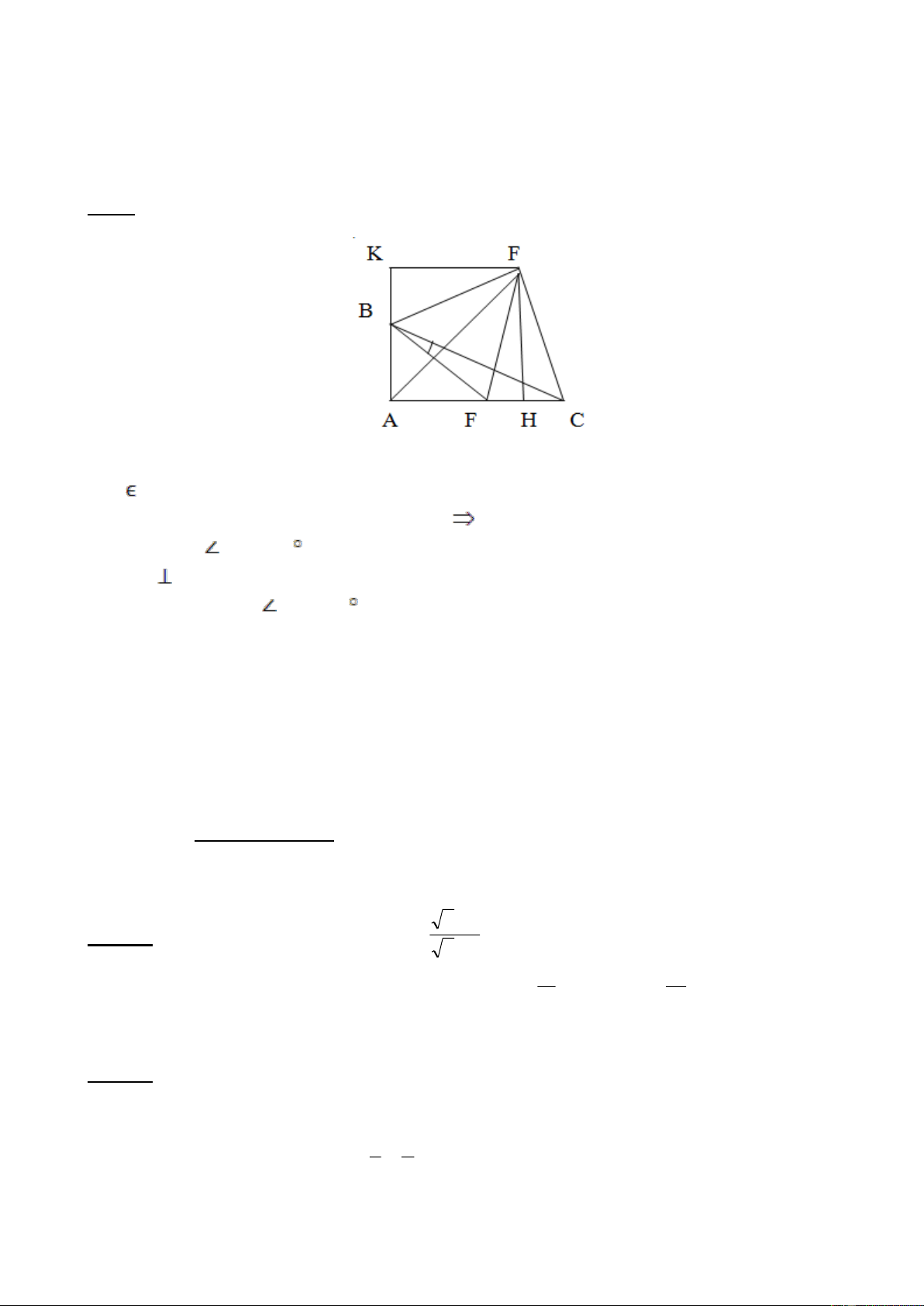
Cho xAy =600 có tia phân giác Az . Từ điểm B trên Ax kẻ BH vuông góc với Ay tại H, kẻ
BK vuông góc với Az và Bt song song với Ay, Bt cắt Az tại C. Từ C kẻ CM
vuông góc với Ay tại M . Chứng minh :
a ) K là trung điểm của AC.
b ) KMC là tam giác đều.
c) Cho BK = 2cm. Tính các cạnh AKM.
Câu 5. (1,0 điểm) a b c
Cho ba số dương 0 a b c 1 chứng minh rằng: 2 bc 1 ac 1 ab 1
--------------Hết----------------
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: .................................................................Số báo danh:....................... Trang 21
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 7 Câu Nội dung Điểm 2 2 1 1 0, 4 0,25 2012 1) Ta có: 9 11 3 5 M : 7 7 1 2013 1, 4 1 0,875 0, 7 9 11 6 2 2 2 1 1 1 0.5đ 2012 5 9 11 3 4 5 : 7 7 7 7 7 7 2013 5 9 11 6 8 10 1 1 1 1 1 1 2 5 9 11 3 4 5 2012 : Câu 1 1 1 1 7 1 1 1 2013 7 0.5đ (4 điểm)
5 9 11 2 3 4 5 2 2 2012 : 0 7 7 2013 KL:…….. 0.5đ 0.5đ 2) vì 2
x x 1 0 nên (1) => 2 2
x x 1 x 2 hay x 1 2 0.5đ
+) Nếu x 1 thì (*) = > x -1 = 2 => x = 3 0.5đ
+) Nếu x <1 thì (*) = > x -1 = -2 => x = -1 KL:…………. 0.5đ 0.5đ 1) +Nếu a+b+c 0 0.25đ
Theo tính chất dãy tỉ số bằng nhau ,ta có: 0.25đ
a b c
b c a
c a b
0.25đ
= a b c b c a c a b = 1 c a b
a b c 0.25đ mà a b c b c a c a b 1 1 1 = 2 c a b Câu 2 => a b b c c a =2 (5 điểm) c a b b a c
b a c a b c Vậy B = 1 1 1 ( )( )( ) =8 a c b a c b +Nếu a+b+c = 0
Theo tính chất dãy tỉ số bằng nhau ,ta có: 0.25đ
a b c
b c a
c a b
0.25đ
= a b c b c a c a b = 0 c a b
a b c 0.25đ Trang 22 mà a b c b c a c a b 0.25đ 1 1 1 = 1 c a b => a b b c c a =1 c a b b a c
b a c a b c Vậy B = 1 1 1 ( )( )( ) =1 a c b a c b
2) Gọi tổng số gói tăm 3 lớp cùng mua là x ( x là số tự nhiên khác 0)
Số gói tăm dự định chia chia cho 3 lớp 7A, 7B, 7C lúc đầu lần lượt là: a, 0,5 đ b, c a b c
a b c x 5x 6x x 7x Ta có: a ;b ;c (1) 0,5đ 5 6 7 18 18 18 18 3 18
Số gói tăm sau đó chia cho 3 lớp lần lượt là a’, b’, c’, ta có: 0,25đ , , , , , , a b c
a b c x 4x 5x x 6x , , , a ;b ;c (2) 4 5 6 15 15 15 15 3 15 0,5đ
So sánh (1) và (2) ta có: a > a’; b=b’; c < c’ nên lớp 7C nhận nhiều hơn lúc đầu 0,5đ Vây: c’ – 6x 7x x c = 4 hay 4 4 x 360 0,5đ 15 18 90
Vậy số gói tăm 3 lớp đã mua là 360 gói. 0,25đ
1) Ta có: A 2x 2 2x 2013 2x 2 2013 2x 0,5đ
2x 2 2013 2x 2011 2013 0,5đ
Dấu “=” xảy ra khi (2x 2)(2013 2x) 0 1 x 2 KL:…….. 0,5đ 0,5đ
2) Vì x,y,z nguyên dương nên ta giả sử 1 x y z 1 1 1 1 1 1 3 0,25đ Câu 3 Theo bài ra 1 = + + + + = 0,5đ yz yx zx 2 x 2 x 2 x 2 x (4 điểm) => x 2 3 => x = 1 Thay vào đầ
u bài ta có 1 y z yz => y – yz + 1 + z = 0
=> y(1-z) - ( 1- z) + 2 =0 => (y-1) (z - 1) = 2
TH1: y -1 = 1 => y =2 và z -1 = 2 => z =3
TH2: y -1 = 2 => y =3 và z -1 = 1 => z =2
Vậy có hai cặp nghiệp nguyên thỏa mãn (1,2,3); (1,3,2) 0,5đ 0,25đ 0,25đ 0,25đ V ẽ h ình , GT _ KL Câu 4 (6 điểm) 0,25đ Trang 23
a, ABC cân tại B do CAB ACB( MAC) và BK là đường cao BK là đườ ng trung tuyến 1đ
K là trung điểm của AC 1đ
b, ABH = BAK ( cạnh huyền + góc nhọn ) 1
BH = AK ( hai cạnh t. ư ) mà AK = AC 0,5đ 2 0,25đ 1 BH = AC 2 1 0,25đ
Ta có : BH = CM ( t/c cặp đoạn chắn ) mà CK = BH = AC CM = CK 2
MKC là tam giác cân ( 1 ) 0,25đ
Mặt khác : MCB = 900 và ACB = 300 MCK = 600 (2) 0,5đ
Từ (1) và (2) MKC là tam giác đều
c) Vì ABK vuông tại K mà góc KAB = 300 => AB = 2BK =2.2 = 4cm 0,25đ
Vì ABK vuông tại K nên theo Pitago ta có: 0,25đ AK = 2 2
AB BK 16 4 12 1 Mà KC = AC => KC = AK = 12 0,25đ 2
KCM đều => KC = KM = 12 0,25đ Theo phần b) AB = BC = 4 AH = BK = 2 0,25đ
HM = BC ( HBCM là hình chữ nhật) => AM = AH + HM = 6 0,5đ 0,25đ Câu 5
Vì 0 a b c 1 nên: (1 điểm) 1 1 c c
(a 1)(b 1) 0 ab 1 a b (1) ab 1 a b ab 1 a b Tương tự a a b b : (2) ; (3) 0,25đ bc 1 b c ac 1 a c Do đó: a b c a b c (4) 0,25đ bc 1 ac 1 ab 1 b c a c a b a b c 2a 2b 2c
2(a b c) Mà 0,25đ 2 (5) b c a c a b
a b c
a b c
a b c
a b c a b c Từ (4) và (5) suy ra: 2 (đpcm) bc 1 ac 1 ab 1 0,25đ
Lưu ý: - Các tổ cần nghiên cứu kỹ hướng dẫn trước khi chấm.
- Học sinh làm bài các cách khác nhau mà đúng thì vẫn cho điểm tối đa.
- Bài hình không có hình vẽ thì không chấm.
- Tổng điểm của bài cho điểm lẻ đến 0,25đ ( ví dụ : 13,25đ , 14,5đ, 26,75đ).
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 8 Trang 24 Câu 1: (4,5 điểm). 4 2 2 3 3 2
a) Tính giá trị của biểu thức A : : 7 5 3 7 5 3 1
b) Tính giá trị của biểu thức B = 2x2 – 3x + 1 với x . 2 x y y z
c) Tìm 3 số x, y, z biết rằng:
; và x + y + z = - 110. 3 7 2 5
Câu 2: (4,5 điểm).
a) Tìm tập hợp các số nguyên x, biết rằng: 5 5 1 31 1 4 : 2
7 x 3 :3,2 4,5.1 : 21 9 18 5 45 2 b) T×m x, biÕt: 1 1 1 1 1 x x x x ... x x 11 2 6 12 20 110
c) Tính giá trị của biểu thức:C = 2x5 – 5y3 + 2015 tại x, y thỏa mãn:
x 1 + (y + 2)20 = 0
Câu 3: (3,5 điểm).
a) Tìm số tự nhiên có ba chữ số, biết rằng số đó là bội của 18 và các chữ số của nó tỉ lệ theo 1: 2: 3.
b) Tìm tất cả các số tự nhiên a, b sao cho : 2a + 37 = b 45 + b - 45. Câu 4: (6,0 điểm)
Cho tam giác ABC có ba góc nhọn (AB < AC). Vẽ về phía ngoài tam giác ABC các
tam giác đều ABD và ACE. Gọi I là giao của CD và BE, K là giao của AB và DC.
a) Chứng minh rằng: ADC = ABE.
b) Chứng minh rằng: DIB = 600.
c) Gọi M và N lần lượt là trung điểm của CD và BE. Chứng minh rằng AMN đều.
d) Chứng minh rằng IA là phân giác của góc DIE. Câu 5: (1,5 điểm)
Cho 20 số nguyên khác 0 : a , … , a 1, a2, a3 20 có các tính chất sau: * a1 là số dương.
* Tổng của ba số viết liền nhau bất kì là một số dương.
* Tổng của 20 số đó là số âm.
Chứng minh rằng : a1.a14 + a14a12 < a1.a12.
.............. Hết.............
Giám thị xem thi không giải thích gì thêm!
Họ và tên thí sinh::........................................... SBD........................................
Giám thị 1:.................................................... Giám thị 2:..............................
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 8 Nội dung Điểm Trang 25 4 2 2 3 3 2 A : : 7 5 3 7 5 3 4 2 3 3 2 0,75 đ a = : (1,5) 7 5 7 5 3 0,5đ 4 3 2 3 2 2 : 0: 0 7 7 5 5 3 3 0,25đ Vậy : A = 0 1 1 1 0,75 đ Vì x nên x = hoặc x = - 2 2 2 1 1 1 0,25đ CÂU 1 Với x = thì: A = 2.( )2 – 3. + 1 = 0 (4,5đ) b 2 2 2 (1,5) 1 1 1 Với x = - thì: A = 2.(- )2 – 3.(- ) + 1 = 3 0,25đ 2 2 2 1 1 0,25đ Vậy : A=0 với x = và A=3 với x = - 2 2 x y x y y z y z x y z 0,5đ Từ ; . Suy ra 3 7 6 14 2 5 14 35 6 14 35
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: c (1,5) x y z x y z 110 0,5đ 6 14 35 6 14 = -2 35 55 0,25đ
Suy ra x = -2.6 = -12; y = -2.14 = -28; z = -2.35 = - 70. 0,25đ
Vậy:x = -12; y = -28; z = - 70. 5 5 41 18 0,5đ 2) Ta có: 4 : 2 7 . 7 2 7 5 9 18 9 41 Lạicó: a 1 31 1 16 5 9 76 43 38 2 43 2 2 0,5đ (1,5) 3 :3,2 4,5.1 : 21 . . : 1 . . 5 45
2 5 16 2 45 2 5 43 5 43 5 0,5đ 2 Do đó: - 5 < x <
mà x Z nên x {-4; -3; -2; -1} 5
a) NhËn xÐt: VÕ tr¸i cña ®¼ng thøc lu«n 0 nªn vÕ ph¶i 0 0,75đ CÂU 2 suy ra 11x 0 hay x 0. (4,5đ) víi x 0 ta cã: 1 1 1 1 1 x
x x x ... x 11x 2 6 12 20 110 0,75đ b (2,0) 1 1 1 1 1
x x x x ... x 11x 0,25đ 2 6 12 20 110 1 10 0,25đ suy ra x = 1- = (TM) 11 11 10 Vậy:x = 11 Trang 26
1) Do x 1 ≥ 0; (y + 2)20 ≥ 0 x 1 + (y + 2)20 ≥ 0 với mọi x, y. 0,25 đ
Kết hợp x 1 + (y + 2)20 = 0 suy ra x 1 = 0 và (y + 2)20 = 0 0,25đ c x = 1; y = - 2.
(1,0) Giá trị của biểu thức :C=2x5 – 5y3 + 2015 tại x = 1; y = - 2 0,25 đ
là:C=2.15 – 5.(-2)3 + 2015 = 2 + 40 + 2015 = 2057 0,25đ Vậy C=2057
Gọi a, b, c là các chữ số của số có ba chữ số cần tìm. Không mất tính tổng quát,
giả sử a b c 9. 0,25 đ
Ta có 1 a + b + c 27 .
Mặt khác số cần tìm là bội của 18 nên là bội của 9,
do đó a + b + c = 9 hoặc a + b + c = 18 hoặc a + b + c = 27. 0,5 đ a b c
a b c a Theo đề bài ta có: ; 0,25 đ (1,5) 1 2 3 6
Như vậy a + b + c chia hết cho 6, nên a + b + c = 18. 0,25 đ
Từ đó suy ra a = 3, b = 6, c = 9.
Do số phải tìm là bội của 18 nên chữ số hàng đơn vị chẵn, 0,25 đ CÂU 3
vì vậy hai số cần tìm là: 396; 936. (3,5đ)
Nhận xét: Với x ≥ 0 thì x + x = 2x 0,5 đ
Với x < 0 thì x + x = 0. Do đó x + x luôn là số chẵn với xZ.
Áp dụng nhận xét trên thì b 45 + b – 45 là số chẵn với b Z. 0,25 đ b 0,25 đ
Suy ra 2a + 37 là số chẵn 2a lẻ a = 0 . (2,0) 0,25 đ
Khi đó b 45 + b – 45 = 38 0,25 đ
+ Nếu b < 45, ta có - (b – 45) + b – 45 = 38 0 = 38 (loại) 0,25 đ
+ Nếu b ≥ 45 , ta có 2(b – 45) = 38 b – 45 = 19 b = 64 (TM) 0,25 đ vậy (a; b) = (0; 64) E A D a K (1,0) I CÂU 4 C (6,0đ) B 0,75 đ 0,25 đ
Ta có: AD = AB; DAC BAE và AC = AE
Suy ra ADC = ABE (c.g.c) 0,5 đ
Từ ADC = ABE (câu a) ABE ADC , b 0,5 đ (1,5) mà BKI AKD(đối đỉnh). 0,5 đ
Khi đó xét BIK và DAK suy ra BIK DAK = 600 (đpcm) c Trang 27 (1,5) E A D N J K M I C B 0,5 đ 0,5 đ
Từ ADC = ABE (câu a) CM = EN và ACM AEN 0,5 đ
ACM = AEN (c.g.c) AM = AN và CAM EAN
MAN CAE = 600. Do đó AMN đều. d
Trên tia ID lấy điểm J sao cho IJ = IB BIJ đều BJ = BI và JBI DBA (2,0)
= 600 suy ra IBA JBD , kết hợp BA = BD
IBA = JBD (c.g.c) AIB DJB = 1200 mà BID = 600
DIA = 600. Từ đó suy ra IA là phân giác của góc DIE
Ta có : a1 + (a2 + a3 + a4) + … + (a11 + a12 + a13) + a14 + (a15 + a16 + a17) + (a18 +
a19 + a20) < 0 ; a1 > 0 ; a2 + a3 + a4 > 0 ; … ; a11 + a12 + a13 > 0 ; a15 + a16 + a17 > 0,5 đ 0 ; a CÂU 5
18 + a19 + a20 > 0 => a14 < 0. Cũng như vậ 0,5 đ (1,5đ) (1,5) y : (a
1 + a2 + a3) + … + (a10 + a11 + a12) + (a13 + a14) + (a15 + a16 +
a17) + (a18 + a19 + a20) < 0 => a13 + a14 < 0.
Mặt khác, a12 + a13 + a14 > 0 => a12 > 0. 0,25 đ
Từ các điều kiện a1 > 0 ; a12 > 0 ; a14 < 0 => a1.a14 + a14a12 < a1.a12 (đpcm). 0,25 đ Chú ý:
+)Nếu HS làm theo cách khác đúng vẫn cho điểm tối đa.
+)Nếu HS thiếu đáp số trừ 0,25 điểm.
+)Câu 2a);3a) Nếu thiếu 1 giá trị trừ 0,1 điểm.
+)Câu 2b);3b) Không kiểm tra điều kiện trừ 0,1 điểm.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 9
Câu 1. (4,0 điểm) 2 3 193 33 7 11 1931 9
a) Thực hiện phép tính: A . : . . 193 386 17 34 1931 3862 25 2 b) Rút gọn :
B = (-5)0 + (-5)1 + (-5)2 + (-5)3 + … + (-5)2016 + (-5)2017. Câu 2 (4,0 điểm). 12a 15b 20c 12a 15b 20c a) Tìm a, b, c biết và a + b + c = 48. 7 9 11
b) Một công trường dự định phân chia số đất cho ba đội I, II, III tỉ lệ với 7; 6; 5. Nhưng
sau đó vì số người của các đội thay đổi nên đã chia lại tỉ lệ với 6; 5; 4. Như vậy có một đội làm
nhiều hơn so với dự định là 6m3 đất. Tính tổng số đất đã phân chia cho các đội. Câu 3 (4,5 điểm). | x 2017 | 2018
a)Tìm giá trị nhỏ nhất của biểu thức: C = . | x 2017 | 2019 Trang 28 2 3 8 15 n 1 b) Chứng tỏ rằng S = ...
không là số tự nhiênvới mọi n N, n > 2. 2 4 9 16 n
c) Tìm tất cả các cặp số nguyên x, y sao cho: x - 2xy + y = 0. Câu 4 (5,5 điểm).
Cho tam giác cân ABC, AB = AC. Trên cạnh BC lấy điểm D, trên tia đối của CB lấy điểm E
sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB và AC lần lượt ở M và N. Chứng minh rằng: a) DM = EN.
b) Đường thẳng BC cắt MN tại điểm I là trung điểm của MN.
c) Đường thẳng vuông gócvới MN tại I luôn luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC. Câu 5 (2,5 điểm).
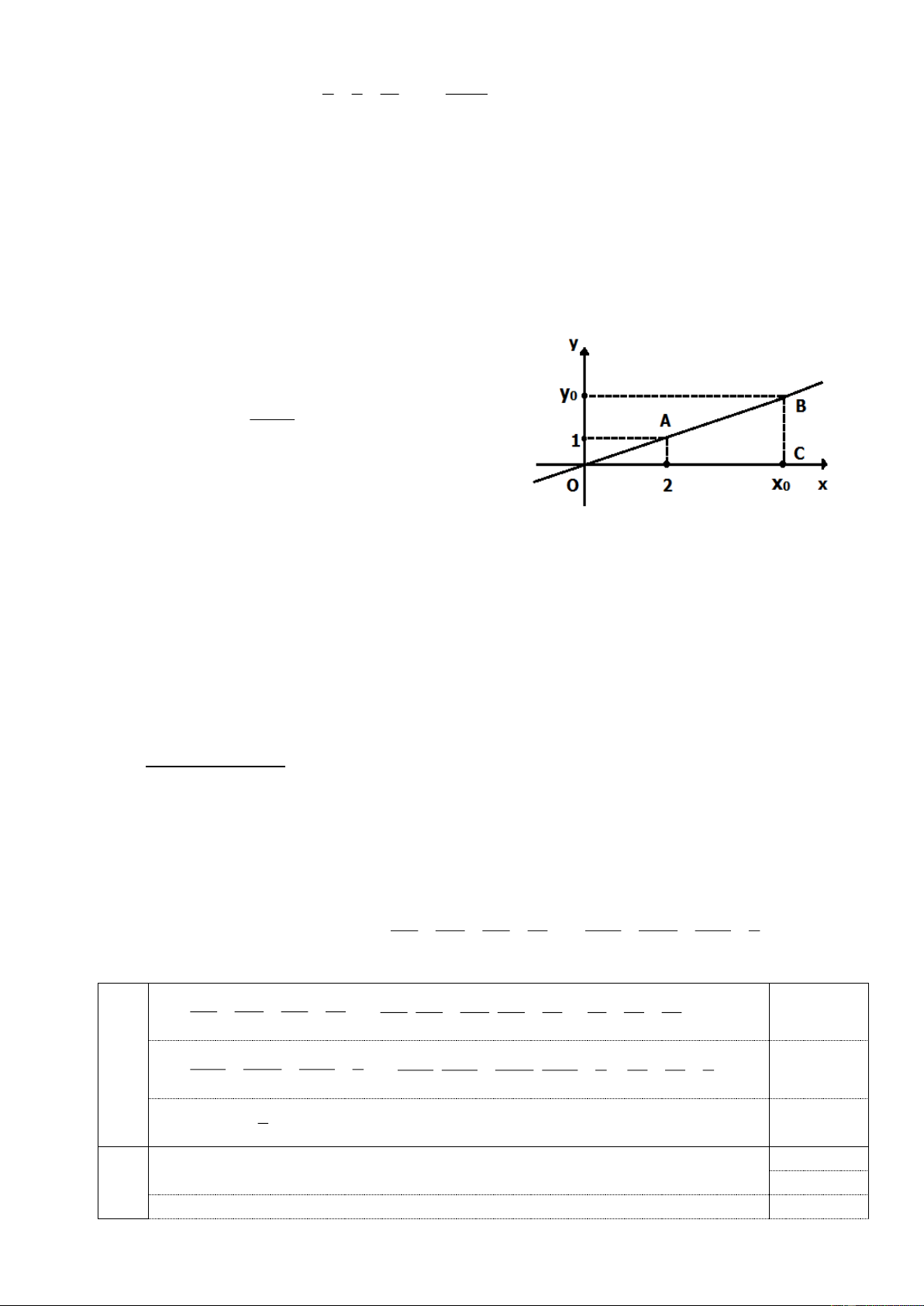
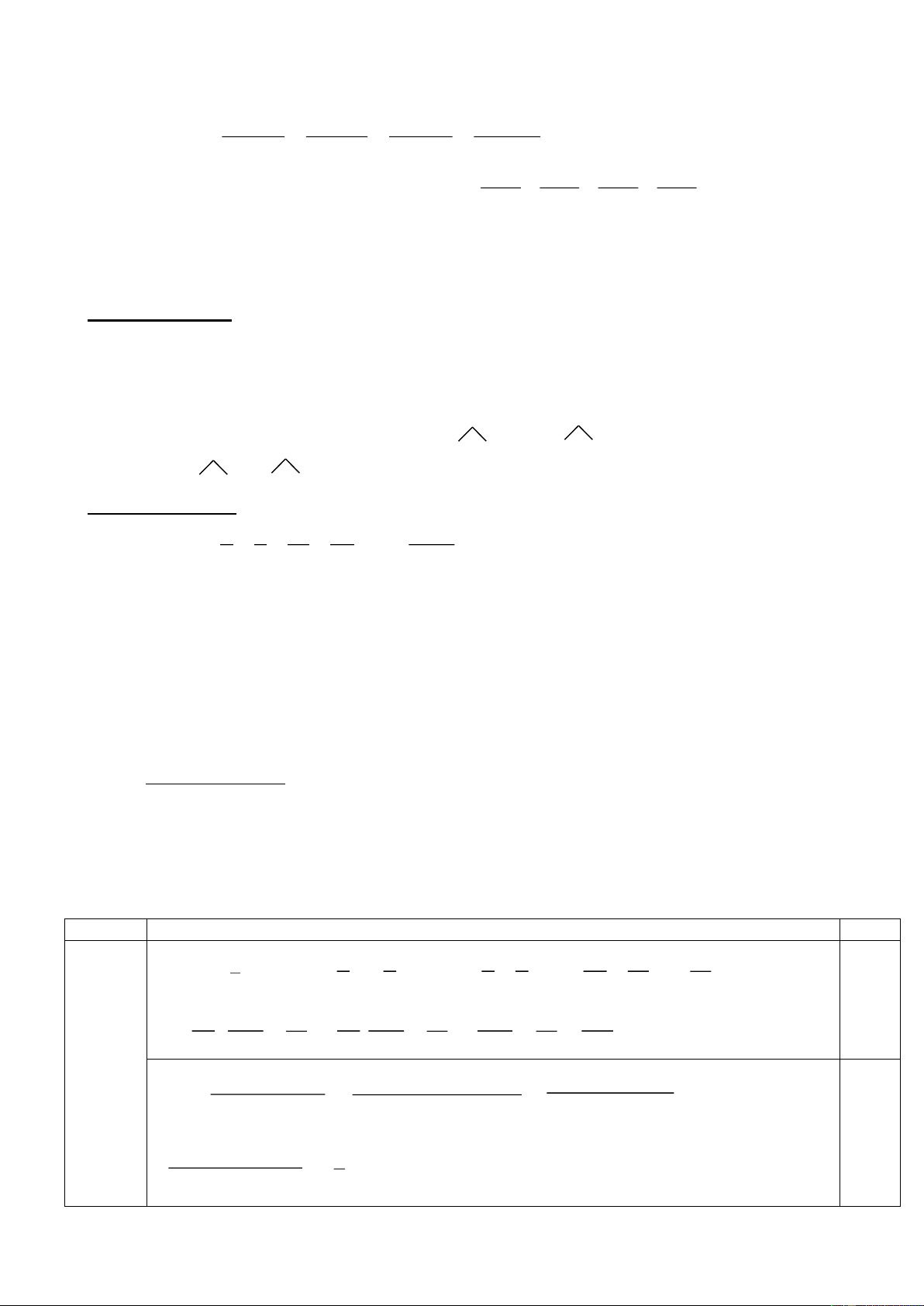
Trong hình bên, đường thẳng OA là đồ thị của hàm số y = f(x) = ax. y 2 a) Tính tỉ số 0 . x 4 0
b) Giả sử x0 = 5. Tính diện tích tam giác OBC
-------------------------------------------------------------
Cán bộ coi thi không giải thích gì thêm – SBD: ……………
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 9
Câu 1. (4,0 điểm) 2 3 193 33 7 11 1931 9
a) Thực hiện phép tính: A . : . . 193 386 17 34 1931 3862 25 2 b) Rút gọn :
B = (-5)0 + (-5)1 + (-5)2 + (-5)3 + … + (-5)49 + (-5)50. 2 3 193 33 2 193 3 193 33 2 3 33 . = . . = = 1 0,75 193 386 17 34 193 17 386 17 34 17 34 34 a 7 11 1931 9 7 1931 11 1931 9 7 11 9 . = . . = = 5 0,75 1931 3862 25 2 1931 25 3862 25 2 25 50 2 1 A = 1 : 5 = 0,5 5
(-5)B = (-5)1 + (-5)2 + (-5)3 + … + (-5)2016 + (-5)2017+ (-5)2018. 0,5 b
B = (-5)0 + (-5)1 + (-5)2 + (-5)3 + … + (-5)2016 + (-5)2017.
Do đó: (-5)B – B = (-6)B = (-5)2018 - 1 0,75 Trang 29 2018 ( 5 ) 1 2018 1 5 Vậy B = = 0,75 4 4 Câu 2 (4,0 điểm). 12a 15b 20c 12a 15b 20c a) Tìm a, b, c biết và a + b + c = 48. 7 9 11
b) Một công trường dự định phân chia số đất cho ba đội I, II, III tỉ lệ với 7; 6; 5. Nhưng
sau đó vì số người của các đội thay đổi nên đã chia lại tỉ lệ với 6; 5; 4. Như vậy có một đội làm
nhiều hơn so với dự định là 6m3 đất. Tính tổng số đất đã phân chia cho các đội.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: 12a 15b 20c 12a 15b 20c
12a 15b 20c 12a 15b 20c = 0 0,25 7 9 11 27 12a 15b 0 1 2a 15b 7
12a 15b 20c a b c 20c 12a 1 1 1 0,5 0 20c 12a 9 12 15 20 và a + b + c = 48 a
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: a b c a b c 48 = = 24 0,5 1 1 1 1 1 1 1 12 15 20 12 15 20 5 a 240 a b 20 240 b c 16 240 c 12 1 1 1 0,5 12 15 20 Vậy a = 20; b = 16; c = 12. 0,25
Gọi tổng số đất đã phân chia cho các đội là x (m3) ĐK: x > 0. 0,25
Số đất dự định chia cho ba đội I, II, III lần lượt là a, b, c (m3) ĐK: a,b,c > 0. a b c
a b c x x x 5x 0,25 Ta có: 7 6 a ; b ; c (1) 7 6 5 18 18 18 18 18
Số đất sau đó chia cho ba đội I, II, III lần lượt là a’, b’, c’ (m3) ĐK: a’,b’,c’ > 0. b a ' b ' c '
a ' b ' c ' x x x 4x 0,25 Ta có: 6 5 a ' ; b ' ; c ' (2) 6 5 4 15 15 15 15 15
So sánh (1) và (2) ta có: a < a’; b = b’ ; c > c’ nên đội I nhận nhiều hơn lúc đầu. 0,25 x 6x x Vì a – a’ = 6 hay 7 = 6 4 x 360 0,25 18 15 90
Vậy tổng số đất đã phân chia cho các đội là 360m3 đất. 0,25 Câu 3 (4,5 điểm). | x 2017 | 2018
a) Tìm giá trị nhỏ nhất của biểu thức: C = . | x 2017 | 2019 2 3 8 15 n 1 b) Chứng tỏ rằng S = ...
không là số nguyên với mọi n Z, n > 2. 2 4 9 16 n
c) Tìm số nguyên x, y sao cho: x - 2xy + y = 0. | x 2017 | 2018
x2017 20191 1 a C = = = 1 0,5 | x 2017 | 2019 | x 2017 | 2019 | x 2017 | 2019
Biểu thức C đạt giá trị nhỏ nhất khi | x 2017 | 2
019 có giá trị nhỏ nhất 0,25 Trang 30
Mà | x 2017 | ≥ 0 nên | x 2017 | 2 019 ≥ 2019. 0,25 2018 0,25
Dấu “=” xảy ra khi x = 2017 C = . 2019 2018 0,25
Vậy giá trị nhỏ nhất của C là khi x = 2017. 2019 2 3 8 15 n 1 2 2 2 2 2 1 3 1 4 1 n 1 S = ... = ... 2 4 9 16 n 2 2 2 2 2 3 4 n 1 1 1 1 = 1 1 1 ...1 2 2 2 2 2 3 4 n 0,25 1 1 1 1 = (111 ... 1) ... 2 2 2 2 2 3 4 n 1 1 1 1 = (n 1) ... 2 2 2 2 2 3 4 n b S < n – 1 (1) 0,25 1 1 1 1 1 1 1 1 Nhận xét: < ; < ; < ; …; < 2 2 1.2 2 3 2.3 2 4 3.4 2 n (n 1).n 0,25 1 1 1 1 1 1 1 ... < + + + … + 1 = 1– 1 < 1. 2 2 2 2 2 3 4 n 1.2 2.3 3.4 (n 1).n n 1 1 1 1 1 1 1 1 ...
>-1 (n 1) ...
> (n–1)–1= n – 2. 0,25 2 2 2 2 2 3 4 n 2 2 2 2 2 3 4 n S > n – 2 (2) 0,25
Từ (1) và (2) suy ra n – 2 < S < n – 1 hay S không là số nguyên. 0,25 Ta có: x - 2xy + y = 0. x(1 – y) + y = 0 0,5
(1 – y) + x(1 – y) = 1 (1 + x)(1 – y) = 1 Ta có: 1 = 1.1 = (-1).(-1) 0,25 c Ta có bảng: 1 + x 1 -1 1 – y 1 -1 0,5 x 0 -2 y 0 2 abccjh Vậy (x;y) {(0;0);(-2;2)} 0,25 Câu 4 (5,5 điểm).
Cho tam giác cân ABC, AB = AC. Trên cạnh BC lấy điểm D, trên tia đối của CB lấy điểm E
sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB và AC lần lượt ở M và N. Chứng minh rằng: a) DM = EN.
b) Đường thẳng BC cắt MN tại điểm I là trung điểm của MN.
c) Đường thẳng vuông gócvới MN tại I luôn luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC. Vẽ GT ∆ABC hình; AB = AC 0,25 Ghi BD = CE Trang 31 GT- MD BC; NE BC KL BC MN = {I} KL a) DM = EN
b) Đường thẳng BC cắt MN tại điểm I là trung điểm của MN
c) Đường thẳng vuông gócvới MN tại I luôn luôn đi qua một điểm
cố định khi D thay đổi trên cạnh BC 0,5 ∆MDB = ∆NEC (g.c.g) 0,75 a
DM = EN (cặp cạnh tương ứng) 0,25
MB = NC (cặp cạnh tương ứng) Ta có: ∆MDI vuông tại D: 0
DMI MID 90 (tổng hai góc nhọn trong tam giác vuông) 0,5 ∆NEI vuông tại E: 0
ENI NIE 90 (tổng hai góc nhọn trong tam giác vuông) b
Mà MID NIE (đối đỉnh) nên DMI = ENI ∆MDI = ∆NEI (g.c.g) 0,75
IM = IN (cặp cạnh tương ứng) 0,25
VậyBC cắt MN tại điểm I là trung điểm của MN 0,25
Gọi H là chân đường vuông góc kẻ từ A xuống BC. 0,25
∆AHB = ∆AHC (cạnh huyền.cạnh góc vuông) 0,25
HAB HAC (cặp góc tương ứng)
Gọi O là giao điểm của AH với đường thẳng vuông góc với MN kẻ từ I. 0,25 ∆OAB = ∆OAC (c.g.c)
OBA OCA (cặp góc tương ứng) (1) 0,25 c
OC = OB (cặp cạnh tương ứng) ∆OIM = ∆OIN (c.g.c) 0,25
OM = ON (cặp cạnh tương ứng) ∆OBM = ∆OCN (c.c.c) 0,25
OBM OCN (cặp góc tương ứng) (2)
Từ (1) và (2) suy ra OCA OCN =900, do đó OC AC. 0,25 Vậy điểm O cố định. 0,25 Câu 5 (2,5 điểm).
Trong hình bên, đường thẳng OA là đồ thị của hàm số y = f(x) = ax. y 2 a) Tính tỉ số 0 . x 4 0
b) Giả sử x0 = 5. Tính diện tích tam giác OBC
Điểm A thuộc đồ thị hàm số y = ax nên tọa độ (2;1) của A phải thỏa mãn hàm a 0,25 số y = ax. Trang 32 Do đó, 1 = a.2 1 1 a =
. Vậy hàm số được cho bởi công thức y = x. 0,25 2 2
Hai điểm A và B thuộc đồ thị hàm số nên hoành độ và tung độ của chúng tỉ 0,25 lệ thuận với nhau. y 1 2 y 2 Suy ra 0 0
(theo tính chất của dãy tỉ số bằng nhau) 0,5 x 2 4 x 4 0 0 y 2 1 Vậy 0 = . 0,25 x 4 2 0 1 5 Nếu x0 = 5 thì y0 = x0 = = 2,5. 0,25 2 2
Diện tích tam giác OBC là: b 1 Áp dụng công thức S = (a.h) ta có: 2 0,75 1 SOBC = . 5. 2,5 = 6,25. 2
*Lưu ý. Học sinh có cách giải khác đúng vẫn cho điểm tối đa.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 10 Câu 1: (4,0 điểm). 1 1 1
a) Tính giá trị biểu thức A = 2 5 , 3 : 4 2 +7,5 3 6 7 4 2 9 2.8 .27 4.6
b) Rút gọn biểu thức B = 7 7 7 4 2 .6 2 .40.9
c) T×m ®a thøc M biÕt r»ng : M 2 x xy 2 2 5 2
6x 9xy y . Tính giá trị của 2018 2020
M khi x, y thỏa mãn 2x 5 3y 4 0 .
Câu 2(4,0 điểm): Tìm x biết 15 3 6 1 a) x x 12 7 5 2 1 1 1 1 49 b) .... 1.3 3.5 5.7
(2x 1)(2x 1) 99
c) Tìm x, y nguyên biết 2xy – x – y = 2 Câu 3(6,0 điểm): Trang 33
a) Tìm hai số nguyên dương x và y biết rằng tổng, hiệu và tích của chúng lần lượt tỉ lệ nghịch với 35; 210;12. x y z t b) Cho
y z t
z t x
t x y
x y z chøng minh r»ng biÓu thøc x y y z z t t x P cã gi¸ trÞ z t t x x y y z nguyªn.
c) Cho a,b,c,d Z thỏa mãn 3 3
a b 3 3
2 c 8d .Chứng minh a + b + c + d chia hết cho 3 Câu 4(5,0 điểm):
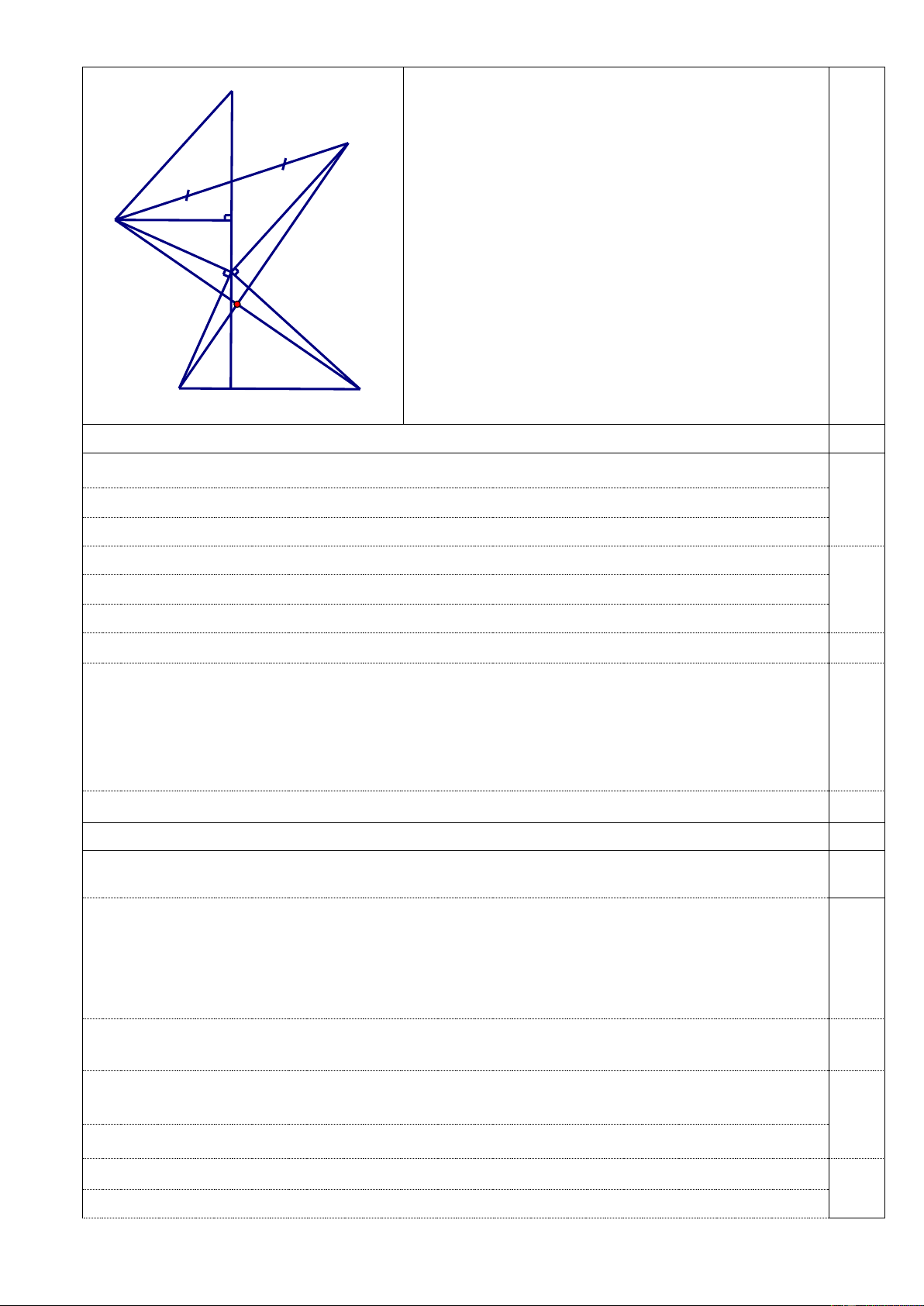
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của của tia MA lấy điểm E sao
cho ME = MA. Chứng minh rằng: a) AC = EB và AC // BE
b) Gọi I là một điểm trên AC ; K là một điểm trên EB sao cho AI = EK . Chứng minh ba
điểm I , M , K thẳng hàng
c) Từ E kẻ EH BC H BC . Biết HBE = 50o ; MEB = 25o . Tính HEM và BME Câu 5 (1,0 điểm): 3 8 15 24 2499 Cho B = ...
. Chứng tỏ B không phải là số nguyên. 4 9 16 25 2500
.................................... Hết ......................................
Họ và tên thí sinh: ........................................................ Số báo danh: ....................
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 10 Câu Nội dung Điểm 0.5 1 1 1 7 7 25 15 15 a) A = 2 5 , 3 : 4 2 +7,5 = : + 3 6 7 3 2 6 7 2 35 85 35 4 2 49 15 157 = : 15 = . 15 = + = 6 42 2 6 85 2 17 2 34 0.5 1 4 2 13 6 11 9 4 2 9 2. 3 2 . 3 3 2 9 9 1.0 (4.0đ) 2.8 .27 4.6 2 .2 .3 2 .3 2 .3 b) B = = = 7 7 7 4 2 .6 2 .40.9 14 7 10 8 2 .2 .3 2 .2 .5.3 4 7 7 7 7 3 2 2 .3 2 .3 .5 11 6 2 .3 . 2 3 2 3 2 = = 10 7 2 .3 . 4 2 3.5 3 0.5 Trang 34 c) M 2 x xy 2 2 2 2
x xy y M x xy y 2 5 2 6 9 6 9 5x 2xy 2 2 2 2 2
M 6x 9xy y 5x 2xy x 11xy y 0.5 2x 5 2018 0 Ta cã :
2x 52018 3y 42020 0 0.25 3y 4 2020 0 0.25 Mµ 2018 2020
x 2018 y 2020 2 5 3 4 0 2x 5 3y 4 0 5 2x 5 2018 x 0 0.25 2 . Thay vào ta đượ c y 2020 4 3 4 0 y 3 2 2 5 5 4 4 25 110 16 1159 0.25 M = + 11. . - = - - = 2 2 3 3 4 3 9 36 15 3 6 1 0.5đ a) x x 6 5 3 1 x x 12 7 5 2 5 4 7 2 6 5 13 130 130 ( )x 49 13 x
x , Vậy x 0.5đ 5 4 14 20 14 343 343 1 1 1 1 49 b) .... 1.3 3.5 5.7
(2x 1)(2x 1) 99 1 1 1 1 1 1 1 49 2 1 ... 0.25 (4.0đ) 2 3 3 5 5 2x 1 2x 1 99 1 1 49 1 98 1 1 1 1 0.75 2 2x 1 99 2x 1 99 2x 1 99
2x + 1 = 99 2x = 98 x = 49. Vậy x = 49 0.5
c) 2xy – x – y = 2 4xy - 2x - 2y = 4 2x(2y - 1) - 2y +1 = 5 (2y -1) ( 2x -1) = 5 0.75
HS xét 4 trường hợp tìm ra ( x,y) = 1;3;3; 1; 2 ;0;0; 2 Vậy ( x,y) = 1;3;3; 1; 2 ;0;0; 2 0.75
a) Do tổng, hiệu và tích của x và y lần lượt tỉ lệ nghịch với 35; 210; 12.
Ta có ( x + y).35 = ( x - y) .210 = 12. xy 0,5 x y x y x y x y x y
Từ ( x + y).35 = ( x - y) .210 2 2 0,5 210 35 210 35 245 175 3 (6.0đ) x y 7 y x
thay vào đẳng thức ( x + y).35 = 12. xy ta được 7 5 5 0,5
y2- 5y = 0 y(y – 5) = 0 y 0; 5 mà y > 0 nên y = 5 0,5 Với y = 5 thì x = 7. Trang 35 b) x y z t
y z t
z t x
t x y
x y z
y z t
z t x
t x y
x y z x y z t 0,75 y z t z t x t x y x y z 1 1 1 1 x y z t 0,5 x y z t z t x y t x y z x y z t x y z t
Nếu x + y + z + t = 0 thì P = - 4 0,75
Nếu x + y + z + t 0 thì x = y = z = t P = 4 Vậy P nguyên c) Ta có 3 3
a b 3 3 c 3 3 3 3 3 3 2 8d
a b c d 3c 15d Mà 3 3 3c 15d 3 nên 3 3 3 3
a b c d 3 (1) 0.75
Dư trong phép chia a cho 3 là 0; 1
suy ra dư trong phép chia a3 cho 3 cũng là 0; 1 hay 3
a a m d3 o 0.5 Tương tự ta có 3
b b mod3 ; 3
c c m d3 o ; 3
d d m d3 o 3 3 3 3
a b c d a b c d mod3 (2) 0.75
Từ (1) và (2) suy ra a + b + c + d chia hết cho 3 Vẽ hình ; ghi GT-KL A 0,5 I M B C H K 4 (5,0đ) E a) X a) Xét A
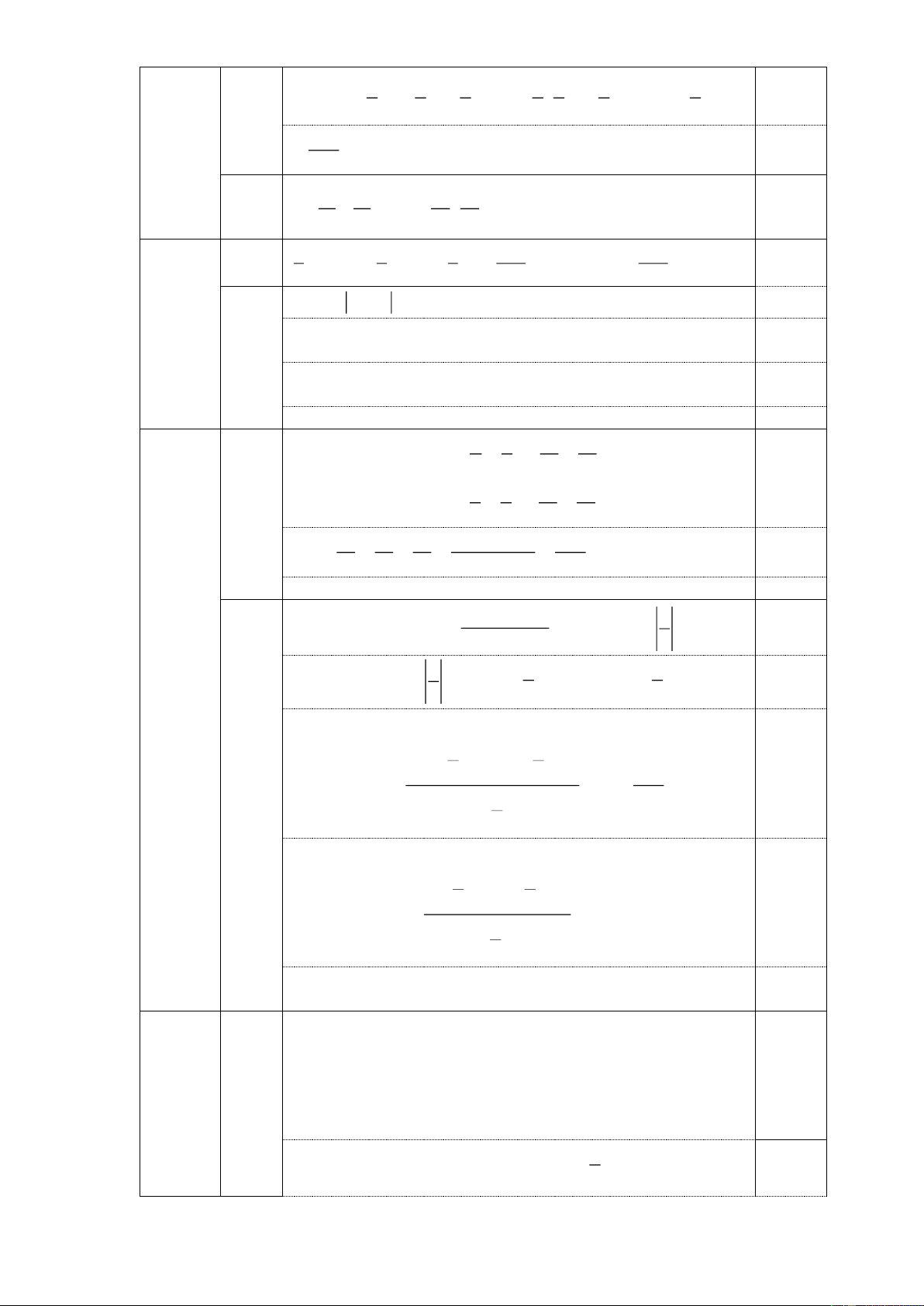
MC và EMB có : AM = EM (gt )
AMC = EMB (đối đỉnh ) BM = MC (gt )
= EMB (c.g.c ) AC = EB ( Hai cạnh tương ứng) AMC 1,0 Vì A
MC = EMB MAC = MEB nà 2 góc này ở vị trí so le trong Suy ra AC // BE . 0,5 b) Xét AM I và EMK có : AM = EM (gt )
MAI = MEK ( vì A MC E MB ) AI = EK (gt ) Nên AM I EM
K ( c.g.c ) AMI = EMK 1,0 Mà
AMI + IME = 180o ( tính chất hai góc kề bù )
EMK + IME = 180o Ba điểm I;M;K thẳng hàng 0,5 Trang 36
c) Trong tam giác vuông BHE ( H = 90o ) có HBE = 50o
HBE = 90o - HBE = 90o - 50o = 40o HEM = HEB - MEB = 40o - 25o =15o 1,0
BME là góc ngoài tại đỉnh M của H EM
BME = HEM + MHE =15o + 90o = 105o 0,5 3 8 15 24 2499 b) Ta có: B = ... 4 9 16 25 2500 3 8 15 24 2499 B= 49 1 1 1 1 ...1 4 9 16 25 2500 1 1 1 1 1 B= 49 - ... = 49 - M 2 2 2 2 2 2 3 4 5 50 1 1 1 1 1 5 Trong đó M = ... 2 2 2 2 2 (1,0đ) 2 3 4 5 50 0.5 1 1 1 Áp dụng tính chất < < (𝑛+1)𝑛 𝑛2 (𝑛−1)𝑛 1 1 1 1 1 1 1 1 1 1 Ta có: ( + + + + ⋯ + ) < ( + + + + ⋯ + ) 22 32 42 52 502 2.1 3.2 4.3 5.4 50.49 1 1 1 1 1 1 1 1 1 1
M < 1 − + − + − + − + ⋯ + − =1- < 1 2 2 3 3 4 4 5 49 50 50 Ta lại có: 1 1 1 1 1 1 1 1 1 1 1 1 1 M > + + + + ⋯ + = − + − + − + ⋯ + − 2.3 3.4 4.5 5.6 50.51 2 3 3 4 4 5 50 51 1 1 49 M > − = > 0 2 51 101
Từ đó suy ra 0< M <1 B = 49- M không phải là một số nguyên. 0.5 Chú ý:
1. Thí sinh có thể làm bài bằng cách khác, nếu đúng vẫn được điểm tối đa.
2. Nếu thí sinh chứng minh bài hình mà không vẽ hình thì không chấm điểm bài hình.
3. Chấm và cho điểm từng phần, điểm của toàn bài là tổng các điểm thành phần không làm tròn.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 11
Bài 1: (3,5 điểm) Thực hiện phép tính: 3 4 7 4 7 7 a) : : 7 11 11 7 11 11 1 1 1 1 1 b) ... 99.97 97.95 95.93 5.3 3.1 Trang 37
Bài 2: (3,5 điểm) Tìm x; y; z biết:
a) 2009 – x 2009 = x 2008 b) x 2008 2 2 1 y
x y z 0 5
Bài 3: (3 điểm)
Tìm 3 số a; b; c biết: 3a 2b 2c 5a 5b 3c và a + b + c = – 50 5 3 2
Bài 4: (7 điểm)
Cho tam giác ABC cân (AB = AC ; góc A tù). Trên cạnh BC lấy điểm D, trên tia đối của CB
lấy điểm E sao cho BD = CE. Trên tia đối của CA lấy điểm I sao cho CI = CA.
Câu 1: Chứng minh: a) A BD I CE b) AB + AC < AD + AE
Câu 2: Từ D và E kẻ các đường thẳng cùng vuông góc với BC cắt AB; AI theo thứ tự tại M; N. Chứng minh BM = CN.
Câu 3: Chứng minh rằng chu vi tam giác ABC nhỏ hơn chu vi tam giác AMN. Bài 5 (3 điểm):
Tìm các số tự nhiên a; b sao cho (2008.a + 3.b + 1).(2008a + 2008.a + b) = 225
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 11 Bài 1: 3 điểm
Câu a: 1 điểm (kết quả = 0). Câu b: 2 điểm 1 1 1 1 1 ... 99.97 97.95 95.93 5.3 3.1 Trang 38 1 1 1 1 1 ... 99.97 1.3 3.5 5.7 95.97 1 1 1 1 1 1 1 1 1 1 ... 99.97 2 3 3 5 5 7 95 97 1 1 1 1 99.97 2 97 1 48 99.97 97 4751 99.97 Bài 2: 3,5 điểm Câu a: 2 điểm
- Nếu x 2009 2009 – x + 2009 = x 2.2009 = 2x x = 2009
- Nếu x < 2009 2009 – 2009 + x = x 0 = 0
Vậy với x < 2009 đều thoả mãn.
- Kết luận : với x 2009 thì 2009 x 2009 x Hoặc cách 2:
2009 x 2009 x
2009 x x 2009
x 2009 x 2009 x 2009 Câu b: 1,5 điểm 1 x 2 ; y 9 ; z 2 5 10 Bài 3: 2,5 điểm 3a 2b 2c 5a 5b 3c 5 3 2 15a 10b 6c 15a 10b 6c 25 9 4
áp dụng tính chất dãy tỉ số bằng nhau có: 15a 10b 6c 15a 10b 6c
15a 10b 6c 15a 10b 6c 0 25 9 4 38 Trang 39 a b 2 3 15
a 10b 0 3 a 2b a c
6c 15a 0 2c 5a 2 5 10b 6c 0 5b 3c c b 5 3 a b c Vậy 2 3 5 a 10
áp dụng tính chất dãy tỉ số bằng nhau b 15 c 25 Bài 4: 7 điểm A M O B C E D N I
Câu 1: mỗi câu cho 1,5 điểm
Câu a: Chứng minh ABD ICE cgc
Câu b: có AB + AC = AI
Vì ABD ICE AD EI (2 cạnh tương ứng)
áp dụng bất đẳng thức tam giác trong AEI có:
AE + EI > AI hay AE + AD > AB + AC Câu 2: 1,5 điểm Chứng minh vBDM = vCEN (gcg) BM = CN Câu 3: 2,5 điểm
Vì BM = CN AB + AC = AM + AN (1) có BD = CE (gt) BC = DE
Gọi giao điểm của MN với BC là O ta có: Trang 40 MO OD
MO NO OD OE NO OE MN DE
MN BC 2
Từ (1) và (2) chu vi ABC nhỏ hơn chu vi AMN Bài 5: 2 điểm
Theo đề bài 2008a + 3b + 1 và 2008a + 2008a + b là 2 số lẻ.
Nếu a 0 2008a + 2008a là số chẵn
để 2008a + 2008a + b lẻ b lẻ
Nếu b lẻ 3b + 1 chẵn do đó
2008a + 3b + 1 chẵn (không thoả mãn) Vậy a = 0
Với a = 0 (3b + 1)(b + 1) = 225
Vì b N (3b + 1)(b + 1) = 3.75 = 5. 45 = 9.25
3b + 1 không chia hết cho 3 và 3b + 1 > b + 1 3 b 1 25 b 8 b 1 9 Vậy a = 0 ; b = 8.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 12 Bài 1: Tính Trang 41 2 3 3 3 1 3 1 2 a) A = 5 2 : 5 4 4 2 2010 2009 0 2 4 1 7 1 8 b) B = 2 : 2 4 11 25 22 2 4
Bài 2 : Tìm x biết 1 1 a) 1 : x 4 b) 2x 1 x 4 5 5 Bài 3:
a) Tìm a , b , c Biết: 3a = 2b ; 4b = 5c và - a - b + c = - 52 . 2 2x 5x 3 3
b) Tính giá trị của biểu thức C = tại x 2x 1 2 Bài 4:
Bốn con Ngựa ăn hết một xe cỏ trong một ngày , một con Dê ăn hết một xe cỏ trong
sáu ngày , hai con Cừu trong 24 ngày ăn hết hai xe cỏ . Hỏi chỉ ba con (Ngựa , Dê và Cừu)
ăn hết hai xe cỏ trong mấy ngày ?
Bài 5:
Cho tam giác ABC (AB > AC ) , M là trung điểm của BC . Đường thẳng vuông góc với
tia phân giác của góc A tại M cắt cạnh AB , AC lần lượt tại E và F . Chứng minh : a) EH = HF b)
2BME ACB B . 2 FE 2 2 c)
AH AE . 4 d) BE = CF .
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 12 Câu ý Nội dung Điểm Trang 42 3 3 3 9 3 1 9 4 1 1 2 2 A 3 : 3 9 27 0, 5 a 4 4 2 4 3 2 2 (0,75) 1 35 0,25 (1,5đ) 2 2009 2010 b 8 4 7 1 2 = 11 0 0,75 (0,75) 2 6 11 11 2 2 a 1 6 1 2 6 1 : x 4 : x x (0,5) 5 5 5 5 2 6 0,5 ...
2x 1 4 x (1) 0,25 2 (1,5 đ)
* Với 2x – 1 0 từ (1) ta có 2x – 1 = x + 4 b 0,25
x = 5 thoả mãn điều kiện 2x – 1 0 (1,0)
* Với 2x – 1 < 0 thì từ (1) ta có 1 – 2x = x + 4 x = -
1 thoả mãn điều kiện 2x – 0,25 1 < 0 Đáp số : x1 = 5 ; x2 = -1 0,25 a b a b Giải : Từ 3a = 2b . 2 3 10 15 0,25 b c b c a Từ 4b = 5c 5 4 15 12 (0,75) a b c
c a b 52 4 0,25 10 15 12 12 10 15 1 3 a = 40 ; b = 60 ; c = 48 0,25 2 2x 5x 3 3 Biểu thức C = tại x 2x 1 2 3 3 3 Vì x x ; x 1 2 0,25 2 2 2 3 (1,5đ) Thay x
1= -3/2 vào biểu thức C ta được 2 3 3 2 5 3 2 2 15 0,25 C = b 3 4 (0,75) 2 1 2
Thay x2 = 3/2 vào biểu thức C ta được 2 3 3 2 5 3 2 2 0,25 C = 0 3 2 1 2
Vậy khi x1 = -3/2 thì C = -15/4 khi x2 = 3/2 thì C = 0 4 Giải : (2đ)
Vì bốn con ngựa cùng ăn hết xe cỏ trong 1 ngày ,
do đó một con ngựa ăn hết một xe cỏ trong 4 ngày . 0,5
Một con dê ăn hết một xe cỏ trong 6 ngày .
Hai con cừu ăn hết hai xe cỏ trong 24 ngày nên một
con cừu ăn hết một xe cỏ trong 12 ngày . 1
Trong một ngày : một con ngựa ăn hết (xe cỏ ) 0,5 4 Trang 43 1 một con dê ăn hết (xe cỏ ) 6 1 Một con cừu ăn hết (xe cỏ ) 12 . 1 1 1 1
Cả ba con ăn hết : (xe cỏ) 4 6 12 2 0,5
Cả ba con ăn hết 1 xe cỏ trong 2 ngày nên ăn hết 2 xe cỏ 0,5 trong 4 ngày Vẽ hình đúng A (0,5) E 0,5 1 B M C H D F a C/m được AE H AF
H (g-c-g) Suy ra EH = HF (đpcm) 0,75 (0,75) Từ AE H AF
H Suy ra E F 1 5 Xét C
MF có ACB là góc ngoài suy ra CMF ACB F ( 3,5đ) b
BME có E là góc ngoài suy ra BME E B 0,75 (0,75) 1 1
vậy CMF BME ( ACB F ) (E B) 1
hay 2BME ACB B (đpcm).
Áp dụng định lí Pytago vào tam giác vuông AFH : 2 c FE ta có HF2 + HA2 = AF2 hay 2 2 AH AE 0,5 (0,5) 4 (đpcm) C/m A HE A
HF(g c g) Suy ra AE = AF và E F 0,25 1
Từ C vẽ CD // AB ( D EF ) 0,25 C/m được B ME C
MD(g c g) BE CD (1) d E CDF 0,25 (1,0) và có (cặp góc đồng vị) 1
do do đó CDF F C
DF cân CF = CD ( 2) 0,25
Từ (1) và (2) suy ra BE = CF
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 13 Trang 44 Bài 1:(4 điểm) a/ Tính: 3 3 3 1 1 1 A= 4 11 13 2 3 4 5 5 5 5 5 5 7 11 13 4 6 8
b/ Cho 3 số x,y,z là 3 số khác 0 thỏa mãn điều kiện:
y z x
z x y
x y z x y z
Hãy tính giá trị biểu thức: x y z B = 1 1 1 . y z x Bài 2 : (4điểm) 1 2 a/ Tìm x,y,z biết: 2 x y
x xz 0 2 3
b/ CMR: Với mọi n nguyên dương thì n2 n2 3 2
3n 2n chia hết cho 10. Bài 3 : (4 điểm)
Một bản thảo cuốn sách dày 555 trang được giao cho 3 người đánh máy. Để đánh
máy một trang người thứ nhất cần 5 phút, người thứ 2 cần 4 phút, người thứ 3 cần 6 phút.
Hỏi mỗi người đánh máy được bao nhiêu trang bản thảo, biết rằng cả 3 người cùng nhau
làm từ đầu đến khi đánh máy xong. Bài 4 : (6 điểm)
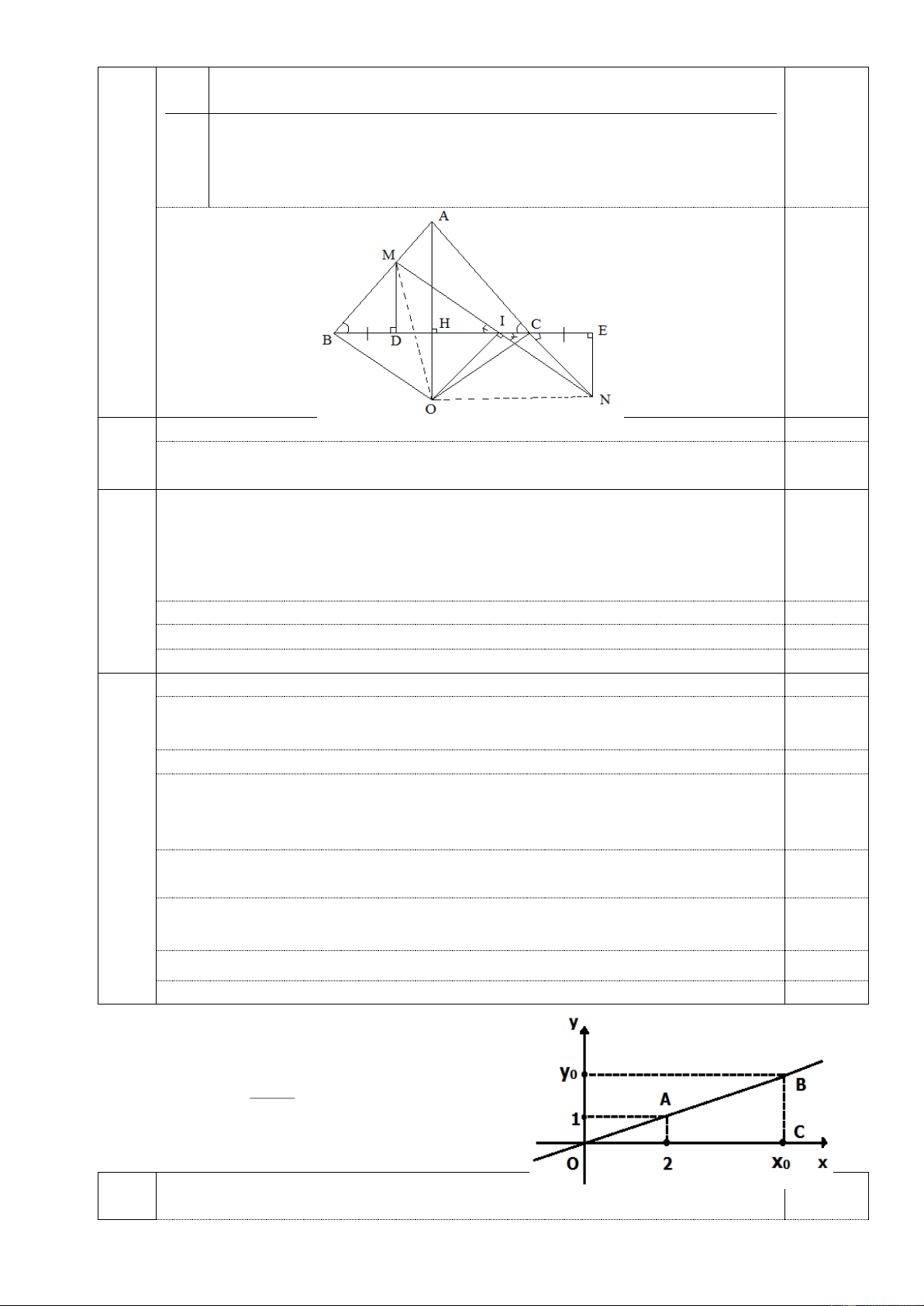
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E
sao cho ME=MA. Chứng minh rằng: a/ AC=EB và AC // BE
b/ Gọi I là một điểm trên AC, K là một điểm trên EB sao cho : AI=EK. Chứng minh: I, M, K thẳng hàng.
c/ Từ E kẻ EH BC (H BC). Biết góc HBE bằng 500; góc MEB bằng 250, tính
các góc HEM và BME ? Bài 5 : (2điểm) Tìm x, y N biết:
y x 2 2 36 8 2010
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 13 Trang 45 Bài ý Nội dung Điểm a 3 3 3 1 1 1 1 1 1 3 1 1 1 3 135 x 4 11 13 2 3 4 4 11 13 2 3 4 4 11 x 13 x 2 1 + = + 2 5 5 5 5 5 5 1 1 1 5 1 1 1 5 129 x 5 5 7 11 13 4 6 8
7 11 13 2 2 3 4 7 11 x 13 x 4 điểm 3 135 x 7 11 x 13 x 2 189 2 189x5 172x2 1289 = x + = = = 4 11 x 13 x 5 129 x 5 172 5 172x5 860 b
y z x
z x y
x y z y z z x x y 0,5 Ta có: 1 1 1 x y z x y z y z z x x y
2 x y z 2 0,5 x y z
x y z x y z
x y y z z x 0,5 B 1 1 1 . . y z x y z x 0,5
x y z x y z . . 2.2.2 8 z y x Vậy B=8 a 1 2 2 x y
x xz 0 2 3 2 0,25
Áp dụng tính chất A 0 1 1 1 x 0 x 0 x 2 2 2 1,5 2 2 2 y 0
y 0 y 4 điểm 3 3 3 2 x x z x xz 0 0 1
z x 2 0,25
Vậy x = 1/2; y = -2/3; z = -1/2 n n n n n n n n b Ta có: 2 2 3 2 3 2 = 2 2 (3 3 ) (2 2 ) 0,75 0,5 n 2 n 2 3 3 1 2 2 1 n n
3 .10 2 .5 = 10.(3n – 2n-1) 0,5
Vì 10.(3n – 2n-1) chia hết cho 10 với mọi n nguyên dương 0,25
Suy ra điều phải chứng minh.
Gọi số trang người thứ nhất, người thứ 2, người thứ 3 đánh máy được theo thứ tự 0,5 là x,y,z. 3
Trong cùng một thời gian, số trang sách mỗi người đánh được tỉ lệ nghịch với
thời gian cần thiết để đánh xong 1 trang; tức là số trang 3 người đánh tỉ lệ nghịch 1,0 với 5; 4; 6. 4điể Do đó ta có: 1 1 1
x : y: z : : 12 :15:10 . m 5 4 6 0,75
Theo tính chất dãy tỉ số bằng nhau, ta có: x y z
x y z 555 15 0,75 12 15 10 12 15 10 37 0,75
x 180; y 225; z 150 .
Vậy số trang sách của người thứ nhất, thứ hai, thứ ba đánh được lần lượt là: 180, 0,25 Trang 46 225, 150 . A a (2 điểm) Xét A
MC và EMB có : AM = EM (gt ) I 4
góc AMC bằng góc EMB (đối đỉnh ) BM = MC (gt ) M B C 0,75 Nên : A
MC = EMB (c.g.c ) H 0,25 AC = EB Vì A
MC = EMB K 0,5
=> Góc MAC bằng góc MEB
(2 góc có vị trí so le trong được tạo E
bởi đường thẳng AC và EB cắt đường thẳng AE ) 0,5 b Suy ra AC // BE . (2 điểm) Xét AM I và EMK có : AM = EM (gt ) 6 điểm
MAI = MEK ( vì AMC EMB ) 0,5 AI = EK (gt ) 0,5 Nên AMI EMK ( c.g.c )
Suy ra AMI = EMK 0,5
Mà AMI + IME = 180o ( tính chất hai góc kề bù ) c 0,5 EMK + IME = 180o
Ba điểm I;M;K thẳng hàng (1,5 điểm ) 0,5 0,5
Trong tam giác vuông BHE ( H = 90o ) có HBE = 50o
HBE = 90o - HBE = 90o - 50o =40o (1.0đ) 0,5
HEM = HEB - MEB = 40o - 25o = 15o
BME là góc ngoài tại đỉnh M của H EM
Nên BME = HEM + MHE = 15o + 90o = 105o
( định lý góc ngoài của tam giác ) 0,25 Ta có:
y x 2 2 36 8 2010
y x 2 2 8 2010 36 . 5 36 0,25 Vì 2 y 0 8x 20102 2
36 (x 2010) 8 Trang 47 Vì 2
0 (x 2010) và x N , x 2
2010 là số chính phương nên 2
(x 2010) 4 hoặc 2
(x 2010) 1 hoặc 2 (x 2010) 0 . 0,5 x 2012 2 điể m + Với 2 (x 2010) 4 x 2010 2 x 2008 y 2 2 y 4 0,25 y 2 (loai) 0,25 + Với 2 2
(x 2010) 1 y 36 8 28 (loại) y 6 + Với 2
(x 2010) 0 x 2010 và 2 y 36 0,25 y 6 (loai) 0,25 Vậy ( ,
x y) (2012; 2); (2008; 2); (2010; 6).
Chú ý : Nếu học sinh làm theo cách khác đúng vẫn chấm điểm tối đa. Trang 48
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 14 Câu1. (2,0 điểm) a) Tìm x biết: 2016 0
3x 3 2x ( 1 ) 3x 2017 1 1 1 1 b) Cho B = 1+
(1 2) (1 2 3)
(1 2 3 4) ....
(1 2 3 ... x) 2 3 4 x
Tìm số nguyên dương x để B = 115. Câu 2. (2,0 điểm) y z 1 x z 2 x y 3 1
a) Cho x, y, z là các số thực thỏa mãn . x y z
x y z
Tính giá trị của biểu thức: A = 2016.x + y2017 + z2017.
b) Cho x, y, z là các số thực thỏa mãn: 2x = 3y = 5z và x 2 y = 5.
Tìm giá trị lớn nhất của 3x – 2z. Câu 3. (2,0 điểm) 2016x 2016
a) Tìm giá trị nguyên của x để biểu thức M = có giá trị nhỏ nhất. 3x 2
b) Cho đa thức f(x) = 2016.x4 – 32(25.k + 2).x2 + k2 – 100 (với k là số thực dương cho trước). Biết
đa thức f(x) có đúng ba nghiệm phân biệt a, b, c (với a < b < c). Tính hiệu của a – c.
Câu 4. (2,5 điểm) Cho đoạn thẳng BC cố định, M là trung điểm của đoạn thẳng BC. Vẽ góc CBx sao cho 0
CBx 45 , trên tia Bx lấy điểm A sao cho độ dài đoạn thẳng BM và BA tỉ lệ với 1 và 2 . Lấy
điểm D bất kì thuộc đoạn thẳng BM. Gọi H và I lần lượt là hình chiếu của B và C trên đường thẳng AD.
Đường thẳng AM cắt CI tại N. Chứng minh rằng: a) DN vuông góc với AC.
b) BH2 + CI2 có giá trị không đổi khi D di chuyển trên đoạn thẳng BM.
c) Tia phân giác của góc HIC luôn đi qua một điểm cố định. Câu 5. (1,5 điểm)
a) Tìm các số nguyên tố p thỏa mãn 2
2 p p là số nguyên tố.
b) Trong một bảng ô vuông gồm có 5x5 ô vuông, người ta viết vào mỗi ô vuông chỉ một trong 3
số 1; 0 hoặc -1. Chứng minh rằng trong các tổng của 5 số theo mỗi cột, mỗi hàng, mỗi đường chéo phải
có ít nhất hai tổng số bằng nhau.
--------------Hết----------------
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ....................................................SBD:..............Phòng thi................. Trang 49
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 14 Câu
Nội dung cần đạt Điểm a) 2016 0
3x 3 2x ( 1 ) 3x 2017
3x 3 2x 1 3x 1 (*) Điề 1
u kiện để x thỏa mãn bài toán là 3x 1 0 x 3 Khi đó 1 0,25 x
2x 1 0 nên (*) trở thành 2
3x 3 2x 1 3x 1 3x 3 x (điều kiện x 0 ) 0,25 3
Nếu x 1 ta có 3x – 3 = x nên x = (thỏa mãn) 0,25 2 3 0,25
Nếu 0 x 1 ta có 3 - 3x = x nên x = (thỏa mãn) 4 3 3
Vậy x ; 2 4
1 2.3 1 3.4 1 4.5
1 x(x 1) b) B = 1+ .... = 1
2 2 3 2 4 2 x 2 (2đ) 3 4 x 1 1 = 1+ ...
2 3 4 ... (x 1) 0,25 2 2 2 2
1 x(x 3) = 0,25 2 2 x x 0,25 Từ đó B = 115 khi 1 (
3) 115 x(x 3) 460 2 2 0,25
Mà x là số nguyên dương nên x và x + 3 là ước dương của 460 nên x = 20. Vậy x = 20
a) Áp dụng tính chất dãy tỉ số bằng nhau ta có: y z 1 x z 2 x y 3 1 = = = =2 x y z
x y z 0, 5 x 1 0, 5 y 2 0, 5 z 3 x+y+z = 0,5 = 2 0,25 2 x y z (2đ) 1 5 5 0,25 x = ; y = ; z = - 2 6 6 0,25 Khi đó ta có 2016.x + y 1
2017 + z2017 = 2016. +0 = 1008 2 0,25 y z 1 x z 2 x y 3 1
Vậy với x,y,z là các số thực thỏa mãn x y z
x y z
thì giá trị của biểu thức 2016.x + y2017 + z2017 là 1008 x 2 y x 2 y 0,25 b) Ta có , 3y = 5z. 3 4 1 0,25 Trang 50 B H D M I N A C
Nếu x-2y = 5 x= -15, y = -10, z = -6. Khi đó 3x - 2z = -45 + 12 = -33 0,25
Nếu x-2y = -5 x= 15, y = 10, z = 6 Khi đó 3x - 2z = 45 - 12 = 33 0,25
Vậy giá trị lớn nhất của 3x – 2z là 33 2016x 2016
672(3x 2) 2016 1344 3360 0,25 a) M 672 3x 2 3x 2 3x 2 3360 M nhỏ nhất lớn nhất 3x 2 0,25 3360
Xét 3x 2 0 thì 0 (1) 3x 2 3360
Xét 3x 2 0 thì 0 0,25 3x 2 3360 0,25
lớn nhất khi 3x+2 nhỏ nhất 3x 2
Mà x nguyên, 3x+2 dương và 3x+2 chia 3 dư 2 nên 3x+2 = 2 nên x 0 3 3360 (2đ) Khi đó: 3360 = 1680 (2) 3x 2 3.0 2 3360 So sánh (1) và (2) thì
có giá trị lớn nhất bằng 1680 3x 2 Vậy M 1008 x 0 min
b) Ta thấy đa thức f(x) nếu có nghiệm x = a ( a khác 0) thì x = -a cũng là một nghiệm
của f(x), nên đa thức f(x) có 2m nghiệm 0,25
Mà đa thức f(x) có đúng ba nghiệm phân biệt nên một trong ba nghiệm sẽ bằng 0. Thay
x = 0 vào đa thức đã cho ta được: 0,25
k2 – 100 = 0 nên k = 10 (vì k dương). 0,25
Với k = 10 ta có f(x) = 2016.x4 – 8064. x2 = 2016x2. (x2 – 4) 0,25
Từ đó f(x) sẽ có 3 nghiệm phân biệt là a = -2; b = 0 và c = 2 nên a – c = - 4
a) Từ M kẻ tia My vuông góc với BC và cắt tia Bx tại A’ .
Tam giác BMA’ vuông cân tại M nên MB: BA’ = 1: 2 0,75
Suy ra A A ' nên AM vuông góc với BC
Tam giác ADC có AM và CI là đường cao nên N là trực tâm của tam giác ADC
Suy ra DN vuông góc với AC 4
b) Ta có AMB = AMC (c- g- c) nên AB = AC và góc ACB = 450 0,25
(2,5) Tam giác ABC vuông cân tại A và có 0 B AH A
CI 90 C AH
H, I là hình chiếu của B và C trên AD nên H = I = 900 0,25
Suy ra AIC = BHA (c.h – g.n) BH = AI
BH2 + CI2 = BH2 + AH2 = AB2 (không đổi) . 0,25
c) BHM = AIM HM = MI và BMH = IMA
mà IMA + BMI = 900 BMH + BMI = 900 0,5 Trang 51
HMI vuông cân HIM = 450 0,5
mà : HIC = 900 HIM =MIC= 450
IM là tia phân giác HIC.
Vậy tia phân giác của HIC luôn đi qua điểm cố định M. Với p = 2 thì 2
2 p p = 4+4 = 8 không là số nguyên tố 0,25 Với p = 3 thì 2
2 p p = 8+9 = 17 là số nguyên tố
Với p > 3 thì p là số nguyên tố nên p lẻ nên p 2k 1 2 2 2(mod 3) 0,25 và 2 p 2
p 1(mod 3) nên 2 p 3 5 Mà 2
2 p p > 3 nên 2
2 p p là hợp số. 0,25 (1,5) Vậy với p = 3 thì 2
2 p p là số nguyên tố
Ta có 5 cột, 5 hàng và 2 đường chéo nên sẽ có 12 tổng. 0,25
Mỗi ô vuông chỉ một trong 3 số 1; 0 hoặc -1 nên mỗi tổng chỉ nhận các giá trị từ -5 đến 0,25
5. Ta có 11 số nguyên từ -5 đến 5 là -5; -4; …; 0; 1; …;5.
Vậy theo nguyên lí Dirichle phải có ít nhất hai tổng số bằng nhau (đpcm). 0,25
Chú ý: - Học sinh giải theo cách khác, nếu đúng vẫn cho điểm tối đa tương ứng.
- Câu 4, nếu học sinh không vẽ hình hoặc vẽ sai hình phần nào thì không chấm phần đó.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 15
Bài 1: (1,5 điểm): So sánh hợp lý: 200 1000 1 1 a) và b) (-32)27 và (-18)39 16 2
Bài 2: (1,5 điểm): Tìm x biết:
a) (2x-1)4 = 16 b) (2x+1)4 = (2x+1)6 c) x 3 8 20 Trang 52
Bài 3: (1,5 điểm): Tìm các số x, y, z biết :
a) (3x - 5)2006 +(y2 - 1)2008 + (x - z) 2100 = 0 x y z b)
và x2 + y2 + z2 = 116 2 3 4 Bài 4: (1,5 điểm):
Cho đa thức : A = 11x4y3z2 + 20x2yz - (4xy2z - 10x2yz + 3x4y3z2) - (2008xyz2 + 8x4y3z2)
a) Xác định bậc của A.
b) Tính giá trị của A nếu 15x - 2y = 1004z. Bài 5: (1 điểm): Chứng minh rằng: x y z t M
có giá trị không phải là số tự nhiên. x, y, z, t * N ). x y z x y t y z t x z t
Bài 6: (3 điểm):
Cho tam giác ABC vuông cân tại A, M là trung điểm BC. Lấy điểm D bất kì thuộc cạnh BC. H
và I thứ tự là hình chiếu của B và C xuống đường thẳng AD. Đường thẳng AM cắt CI tại N. Chứng minh rằng: a) BH = AI.
b) BH2 + CI2 có giá trị không đổi.
c) Đường thẳng DN vuông góc với AC.
d) IM là phân giác của góc HIC.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 15 Bài 1: (1,5 điểm): 200 . 4 200 800 1000 1 1 1 1 a) Cách 1: = > 16 2 2 2 200 200 . 5 200 1000 1 1 1 1 Cách 2: > = (0,75điểm) 16 32 2 2 b) 3227 = 5 27
(2 ) = 2135 < 2156 = 24.39 = 1639 < 1839 (0, 5điểm)
-3227 > -1839 (-32)27 > (-18)39 (0,25điểm) Trang 53 Bài 2: (1,5 điểm):
a) (2x-1)4 = 16 . Tìm đúng x =1,5 ; x = -0,5 (0,5điểm)
b) (2x+1)4 = (2x+1)6. Tìm đúng x = -0,5 ; x = 0; x = -15 (0,5điểm)
c) x 3 8 20 x 3 8 20 ; x 3 8 20
x 3 8 20 x 3 28 x = 25; x = - 31 (0,25điểm) x 3 8 20 x 3 12
: vô nghiệm (0,25điểm) Bài 3: (1,5 điểm):
a) (3x - 5)2006 +(y2 - 1)2008 + (x - z) 2100 = 0
(3x - 5)2006 = 0; (y2 - 1)2008 = 0; (x - z) 2100 = 0 (0,25điểm) 5
3x - 5 = 0; y2 - 1 = 0 ; x - z = 0 x = z = ;y = -1;y = 1 (0,5điểm) 3 x y z b)
và x2 + y2 + z2 = 116 2 3 4 2 2 2 2 2 2 x y z x y z 116 Từ giả thiết 4 (0,25điểm) 4 9 16 4 9 16 29
Tìm đúng: (x = 4; y = 6; z = 8 ); (x = - 4; y = - 6; z = - 8 ) (0,5điểm) Bài 4: (1,5 điểm):
a/ A = 30x2yz - 4xy2z - 2008xyz2 A có bậc 4 (0,5điểm)
b/ A = 2xyz( 15x - 2y - 1004z ) A = 0 nếu 15x - 2y = 1004z (0,725điểm) Bài 5: (1 điểm): Ta có: x x x (0,25điểm) x y z t x y z x y y y y x y z t x y t x y z z z (0,25điểm) x y z t y z t z t t t t x y z t x z t z t x y z t x y z t M ( ) ( ) (0,25điểm) x y z t x y x y z t z t
hay: 1 < M < 2 . Vậy M có giá trị không phải là số tự nhiên (0,25điểm)
Bài 6: (3 điểm):
a. AIC = BHA BH = AI (0,5điểm)
b. BH2 + CI2 = BH2 + AH2 = AB2 (0,75điểm)
c. AM, CI là 2 đường cao cắt nhau tại N N là trực tâm DN AC (0,75điểm)
d. BHM = AIM HM = MI và BMH = IMA (0,25điểm)
mà : IMA + BMI = 900 BMH + BMI = 900 (0,25điểm)
HMI vuông cân HIM = 450 (0,25điểm)
mà : HIC = 900 HIM =MIC= 450 IM là phân giác HIC (0,25điểm) B H D M I N A C Trang 54
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 16 3 2 x x 03y 1
Bài 1: (1,5 điểm) Cho A biết x
; y là số nguyên âm lớn nhất 2 x y 2 x 16 y 25 z 9 9 x 11 x
Bài 2: (2 điểm) Cho và 2.Tìm x+y+z 9 16 25 7 9 Bài 3: (1,5 điểm)
Tìm x, y Z biết 2xy+3x = 4 16 - 72 + 90. Trang 55
Bài 4: (2 điểm) Cho đa thức: P = 3x3 + 4x2 - 8x+1
a/ Chứng minh rằng x= 1 là nghiệm của đa thức.
b/ Tính giá trị của P biết x2+x-3 = 0
Bài 5: (3 điểm) Cho tam giác ABC có vuông tại A(ABcho AE = AB. Tia phân giác của góc BAC cắt đường trung trực của CE tại F. a/ Chứng minh tam giác BFC
b/ Biết góc ACB bằng 300.Chứng minh tam giác BFE đều.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 16 Bài1: (1,5 điểm) + Tìm được: x = ; y = -1 (0,5đ)
+ Với x = - ; y = -1 A = - (0,5đ) + Với x = ; y = -1 A= - (0,5đ) Bài 2: (2 điểm) + Từ +
= 2 (2 – x)( + ) = 0 x = 2 (0,75đ) + Thay x = 2 = = = = = 2. (1đ) + x + y + z = 100 (0,25đ) Bài 3: (2 điểm)
+ Biến đổi được: x(2y + 3) = 4 (0,5đ)
+ Chỉ ra được x, y Z x Ư(4) và 2y + 3 lẻ (0,5đ) + Lập bảng. (1đ) x -4 -2 -1 1 2 4 2y + 3 -1 -2 -4 4 2 1 y -2 loại loại loại loại -1 Bài 4: (2 điểm).
a) Chỉ được; a + b + c + d = 0 đpcm. (0,5đ)
(hoặc tính được P(1) = 0 đpcm). b) + Rút được: + x = 3 (1) (0,25đ)
+ Biến đổi được P = (3 + 3 ) + ( + x) – 9x + 1 = 3x( + x) + ( + x) – 9x + 1 (1đ)
+ Thay (1) vào: P = 9x + 3 – 9x + 1 = 4(0,25đ)
(Học sinh có thể giải đúng bằng cách khác vẫn cho điểm) Trang 56 Bài 5: (2,5 điểm)
+ Hình vẽ (phục vụ được câu 1): (0,25đ)
a) Chỉ ra được F là giao điểm 2 trung trực của BEC (0,5đ)
F trung trực BC BFC cân (0,5đ)
(học sinh có thể chứng minh: FC = FE; FB = FE đpcm).
b) + Tính được EBC = 15 . (0,5đ)
+ Hạ FK AB FKB = FHC (ch + cgv) (0,75đ)
BFC vuông cân FBC = 45 . (0,25đ) + Kết luận BFE đều. (0,25đ)
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) x
Bµi 1 : Cho biÓu thøc A = 1 . x 1
a. TÝnh gi¸ trÞ cña A t¹i x = 16 vµ x = 25 . 9 9
b. T×m gi¸ trÞ cña x ®Ó A =5.
Bµi 2 : T×m tØ lÖ ba c¹nh cña mét tam gi¸c biÕt r»ng nÕu
céng lÇn l-ît ®é dµi tõng hai ®-êng cao cña tam gi¸c ®ã th×
tØ lÖ c¸c kÕt qu¶ lµ :5 : 7 : 8. a c
Bài 3: (1,5 điểm) Cho tỉ lệ thức . b d
Chứng minh rằng : (a+2c)(b+d) = (a+c)(b+2d). Trang 57
Bài 4: (4,5 điểm) Cho tam giác ABC vuông tại A; K là trung điểm của BC. Trên tia đối
của tia KA lấy D , sao cho KD = KA. a. Chứng minh: CD // AB.
b. Gọi H là trung điểm của AC; BH cắt AD tại M; DH cắt BC tại N .
Chứng minh rằng: ABH = CDH.
c. Chứng minh: HMN cân.
Câu 5. (1,0 điểm) a b c
a. Cho ba số dương 0 a b c 1 chứng minh rằng: 2 bc 1 ac 1 ab 1
b. Cho a, b, c lµ ba c¹nh cña mét tam gi¸c. Chøng minh r»ng:
2(ab + bc + ca) > a2 + b2 + c2. 14 x
Câu 6. T×m gi¸ trÞ nhá nhÊt cña biÓu thøc: P =
; x Z . 4 x
Khi ®ã x nhËn gi¸ trÞ nguyªn nµo?
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 17
Bài 1: Thực hiện phép tính (6 điểm). Giải: a. 3 2 5 9 : . 4 3 9 4 3 2 5 9 3 1 9 0,75đ : : 4 3 9 4 4 9 4 3 9 9 36 0,75đ = . 9 4 1 4 4 1 1 1 45 1 1 1 b. 19 2 3 4 1 1 1 45 1 1 1 45 1 19 2 3 4 19 1 1 1,0đ 2 1 4 3 45 26 19 = 1 1,0đ 19 19 19 15 9 20 9 . 5 4 .9 . 4 3 8 . c. 10 19 29 6 5 2 . .6 7 2 . 27 . 15 9 20 9 . 5 4 .9 . 4 3 8 . 15 . 2 9 . 2 2 20 9 . 3 2 . 5 3 . 2 3 . 2 . = 01đ 10 19 29 6 5 2 . .6 7 2 . 27 . 10 19 19 29 6 . 3 2 . 5 2 . 3 . 2 . 7 3 . Trang 58 229 3 . 18 2 . 5 32 01đ 229 3 . 18 3 . 5 7 10 9 1 = 0,5đ 15 7 8 Bài 2: (6 điểm) Giải:
a. Tìm x, biết: 2(x-1) – 3(2x+2) – 4(2x+3) = 16.
2x – 2 – 6x – 6 – 8x – 12 = 16 0,25đ -12x – 20 = 16 0,25đ -12x = 16 + 20 = 36 0,50đ x = 36 : (-12) = -3 0,50đ 1 21
b. Tìm x, biết: 3 : 2x 1 = 2 22 1
Nếu x . Ta có: (vì nếu x = ½ thì 2x – 1 = 0) 0,25đ 2 1 21 3 : 2x 1 = 2 22 7 21 : (2x – 1) = 0,25đ 2 22 7 21 7 22 11 2x – 1 = : = . 0,25đ 2 22 2 21 3 11 14 2x = + 1 = 0,25đ 3 3 14 7 1 x = : 2 = > 0,25đ 3 3 2 1 Nếu x . Ta có: 0,25đ 2 1 21 3 : 2x 1 = 2 22 7 21 : (1 - 2x) = 0,25đ 2 22 11 8 -2x = - 1 = 0,25đ 3 3 8 4 1 x = : (-2) = 0,25đ 3 3 2 7 4 Vậy x = hoặc x = 0,25đ 3 3 2x y 3y 2z c. Tìm x, y, z biết : và x + z = 2y 5 15 Từ x + z = 2y ta có:
x – 2y + z = 0 hay 2x – 4y + 2z = 0 hay 2x – y – 3y + 2z = 0 0,25đ hay 2x – y = 3y – 2z 0,25đ 2x y 3y 2z Vậy nếu:
thì: 2x – y = 3y – 2z = 0 (vì 5 15). 0,25đ 5 15 1
Từ 2x – y = 0 suy ra: x = y 0,25đ 2 Trang 59 1
Từ 3y – 2z = 0 và x + z = 2y. x + z + y – 2z = 0 hay y + y – z = 0 0,25đ 2 3 2 1
hay y - z = 0 hay y = z. suy ra: x = z. 0,25đ 2 3 3 1 2
Vậy các giá trị x, y, z cần tìm là: {x = z; y = z ; với z R } 3 3 0,5đ 1 3
hoặc {x = y; y R; z = y} hoặc {x R; y = 2x; z = 3x} 2 2 a c
Bài 3: (1,5 điểm) Cho tỉ lệ thức . b d
Chứng minh rằng : (a+2c)(b+d) = (a+c)(b+2d)
Ta có: (a+2c)(b+d) = (a+c)(b+2d)
ab + ad + 2cb + 2cd = ab + 2ad + cb + 2cd 0,75đ a c cb = ad suy ra: 0,75đ b d
Bài 4: (4,5 điểm) Cho tam giác ABC vuông tại A; K là trung điểm của BC. Trên tia đối
của tia KA lấy D , sao cho KD = KA. a. Chứng minh: CD // AB.
b. Gọi H là trung điểm của AC; BH cắt AD tại M; DH cắt BC tại N .
Chứng minh rằng: ABH = CDH.
c. Chứng minh: HMN cân. Giải: B D K M N A C H
a/ Chứng minh CD song song với AB.
Xét 2 tam giác: ABK và DCK có: 0,25đ BK = CK (gt) A K ˆ B D K ˆ C (đối đỉnh) 0,25đ AK = DK (gt) 0,25đ ABK = DCK (c-g-c) 0,25đ K C ˆ D K B ˆ D ; mà 0 C B ˆ A B C ˆ A 90 0 D C ˆ A B C ˆ A D C ˆ B 90 0,25đ D C ˆ A 900 C A ˆ B
AB // CD (AB AC và CD AC). 0,25đ
b. Chứng minh rằng: ABH = CDH
Xét 2 tam giác vuông: ABH và CDH có: 0,25đ BA = CD (do ABK = DCK) AH = CH (gt) 0,25đ ABH = CDH (c-g-c) 0,50đ Trang 60
c. Chứng minh: HMN cân.
Xét 2 tam giác vuông: ABC và CDA có: AB = CD; D C ˆ A 900 C A ˆ B
; AC cạnh chung: ABC = CDA (c- 0,25đ g-c) Cˆ A B D A ˆ C 0,25đ mà: AH = CH (gt) và A H ˆ M C H ˆ N (vì ABH = CDH) 0,50đ AMH = CNH (g-c-g) 0,50đ
MH = NH. Vậy HMN cân tại H 0,50đ
Bài 5: (2 điểm): Chứng minh rằng số có dạng abcabc luôn chia hết cho 11. Giải:
Ta có: abcabc = a.105 + b.104 + c.103 + a.102 + b.10 + c 0,25đ
= a.102(103 + 1) + b.10(103 + 1) + c(103 + 1) 0,50đ
= (103 + 1)( a.102 + b.10 + c) 0,50đ
= (1000 + 1)( a.102 + b.10 + c) = 1001( a.102 + b.10 + c) 0,25đ
= 11.91( a.102 + b.10 + c) 11 0,25đ Vậy abcabc 11 0,25đ Hết
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
Bài 1: (6,0 điểm). Tính: 1 1 1 a) A = 4.( )3 - 2.( )2 + 3.( ) + 1 2 2 2 1 1 1 1 1 1 1 b) B : 1 :1 : 1 :1 : 1 : ... : 1 . 2 2 3 4 5 6 100 6 5 9 4 9 . 6 1 . 20 c) C = 4 12 11 8 .3 6
Bài 2: (4,0 điểm). x y a) Tìm x,y Biết = và x.y = 112 4 7
b) Chứng minh rằng: Nếu a, b, c là các số khác 0 thoả mãn: ab ac bc ba ca cb a b c thì 2 3 4 3 5 15
Bài 3: (4,0 điểm).
a) Tìm giá trị nhỏ nhất của biểu thức: P 2013 x 2014 x . Trang 61
b) Tìm số có 3 chữ số biết rằng số đó chia hết cho 36 và các chữ số của nó tỷ lệ với 1 ; 2 ; 3.
Bài 4: (4,0 điểm).
Cho tam giác ABC cân tại A ( 0
B C 40 ). Kẻ phân giác BD ( D AC ). Trên tia AB lấy điểm M sao cho AM = BC. a) Chứng minh BD + AD = BC b) Tính AMC
Bài 5: (2,0 điểm).
Tìm các số a,b,c nguyên dương thoả mãn a 3 +3a 2 +5 = 5b và a + 3 = 5c
-------------------------------
Họ và tên thí sinh:.............................................Số báo danh: ................................
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 18 Bài
Phương pháp-Kết quả Điểm Bài 1 1 1 1 a) A = 4.( )3 - 2.( )2 + 3.( ) + 1 ( 6 điểm) 2 2 2 1 1 3 0.5 đ = 4.( ) - 2. +1 8 4 2 1 1 3 = - +1 0.5 đ 2 2 2 3 = - 2 0.5 đ 3 Vậy A = - 2 0.5 đ b) 1 1 1 1 1 1 1 B : 1 :1 : 1 :1 : 1 : ... : 1 2 2 3 4 5 6 100 1 3 4 5 6 7 101 0.5đ : : : : : : ... : 2 2 3 4 5 6 100 (có 50 thừa số âm ) 1 2 3 4 5 6 100 . . . . . ..... 2 3 4 5 6 7 101 0.5đ . 1 ..... 6 . 5 . 4 . 3 . 2 . 1 00 1 0.5 đ 1 ..... 7 . 6 . 5 . 4 . 3 . 2 01 101 Vậy 1 0.5 đ B 101 c) C = 6 5 9 4 9 . 6 1 . 20 4 12 11 8 .3 6 0,5đ Trang 62 = 2 6 2 .3 5 2 9 9 3 2 3 . .2 .3.5 2 4 3 12 11 11 .3 2 .3 0,5 đ 12 10 12 10 2 3 . 2 3 . 5 . = 12 12 11 11 2 3 . 2 3 . 0,5 đ 212 3 . 10 1 5 211 3 . 11 1 3 . 2 0,5 đ . 2 6 4 4 . 3 5 5 5 Bài 2 x y 2 x . x y 122 (4 điểm) a) Ta có = = = 4 7 16 4.7 28 0.5 đ 16 112 . x2 = = 64 28 0.5 đ x = 8 hoặc x = -8 8 y Nếu x = 8 = y = 14 0.5 đ 4 7 8 y 0.5 đ Nếu x = - 8 = y = - 14 4 7 b) Ta có: ab ac bc ba ca cb 2 3 4
ab ac bc ba ca cb 2 3 4 (
2 ab bc ca) 9 0.5 đ
ab bc ca 5 , 4
ab bc ca ab ac bc 5 , 4 2 5 , 2
ab bc ca bc ba ca 0.5 đ 5 , 4 3 5 , 1
ab bc ca ca cb ab 5 , 4 4 5 , 0 0.5 đ ab ac bc Do đó: 5 , 0 5 , 1 5 , 2 0.5 đ 5 , 1 ab 5 , 0 ac 3 b c
(a, b, c ) 0 5 , 1 bc 5 , 2 ac 5 a 3b a b c
5a 3b c . 3 5 15 Bài 3
a) Áp dụng BĐT a b a b (4 điểm)
Dấu “ =” xảy ra khi và chỉ khi a,b cùng dấu
(HS không làm phần này vẫn cho điểm tối đa) 0.5 đ Trang 63
Ta có P = 2013 x 2014 x = x 2013 2014 x 0.5 đ
P x 2013 2014 x 1 1 0.5 đ
Dấu “ =” xảy ra khi và chỉ khi (x-2013) và (2014-x) cùng dấu 0.5 đ Hay 2013 x 2014
Vậy minP = 1 khi và chỉ khi 2013 x 2014
b) Gọi ba chữ số của số phải tìm là a, b,c ta có : a b c 0.5 đ
áp dụng tính chất dãy tỉ số bằng nhau ta được 1 2 3 a b c a b c = (*) 1 2 3 6 0.5 đ
Do số phải tìm chia hết cho 36 nên số đó chia hết cho 9 suy ra a+b+c chia hết cho 9
Mà a, b, c là các chữ số có ít nhất một chữ số khác 0 nên a+b +c chỉ có thể nhận
một trong ba giá trị : 9; 18;27 a b c
a b c
Nếu a+b +c = 9 Từ (*) ta có =
=> a= 9/6 (không thoả mãn vì 1 2 3 6 a là chữ số)
Nếu a+b +c = 18 kết hợp (*) ta có a =3 ; b = 6; c = 9 vì số phải tìm chia hết cho 36 0.5 đ
nên chữ số hàng đơn vị chẵn ta có số 396; hoặc 936
Nếu a +b + c = 27 từ (*) => a=27/6 (loại) 0.5 đ
Thử lại ta thấy cả hai số 396 và 936 đều thoả mãn
Vậy số phải tìm là 936 và 396 . Bài 4 A (4 điểm) D E B F C M
a) Từ D kẻ DE//BC, trên BC lấy điểm F sao cho N BD = BF (1)
Chứng minh được DE = BE (tam giác BED cân) 0.5 đ
Do tam giác AED cân nên AD =AE suy ra BE = CD 0.5 đ Vậy DE = CD 0.5 đ Tam giác BDF cân có 0 DBF 20 nên 0 0
BFD 80 DFC 100 suy ra 0
DFC EAD 100 Vậy tam giác DFC có 0 FDC 40
Chứng minh được AD E FC D (g. .
c g) AD CF (2)
Từ (1) và (2) suy ra đpcm. 0.5 đ
b) Dựng tam giác đều AMN sao cho N và C ở cùng một phía so với AB. 0.5 đ 0.5 đ Vì 0
AC chung; BC AN ( AM ); ACB CAN 40 Trang 64 B AC NC A Suy ra AC = CN = AB
vậy MC là trung trực của AN 0.5 đ 1 0.5 đ Nên 0 AMC AMN 30 2 Bài 5
Do a Z + => 5b = a3 + 3a2 + 5 > a + 3 = 5c (2 điểm) => 5b > 5c => b>c 0.5 đ => 5b 5c
=> (a3 + 3a2 + 5) ( a+3) => a2 (a+3) + 5 a + 3
Mà a2 (a+3) a + 3 [do (a+3) (a+3)] 0.5 đ => 5 a + 3 => a + 3 Ư (5)
=> a+ 3 { 1 ; 5 } (1) 0.5 đ
Do a Z+ => a + 3 4 (2) Từ (1) và (2)
=> a + 3 = 5 => a = 5 – 3 =2
=> 23 + 3 . 22 + 5 = 55 25 = 5b 52 = 5b b = 2 0.5 đ
2 + 3 = 5c 5 = 5c 5 = 5c c = 1 Vậy : a = 2 b = 2 c = 1
Ghi chú: Đáp án chỉ là sơ lược từng bước giải và cách cho điểm từng phần của mỗi
bài. Bài làm của học sinh yêu cầu phải chi tiết, lập luận chặt chẽ, hình vẽ sai không chấm điểm. Nếu HS
giải cách khác đúng thì chấm điểm từng phần tương ứng.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 19
Câu 1.(4 điểm) 12 5 6 2 10 3 5 2 2 .3 4 .9 5 .7 25 .49 A a) Thực hiện phép tính: 2 .36 8 .3 125.73 9 3 2 4 5 5 .14 b) Tính 100 99 98 2 S 2
2 2 .... 2 2 1 2 3 2019 c) Chứng tỏ: ... 0,75 2 3 2019 3 3 3 3
Câu 2.(4 điểm)
a) Cho a, b, c là ba số thực khác 0, thoả mãn : a b c
b c a
c a b và a+b+c 0 c a b b a c
Hãy tính giá trị của biểu thức: B 1 1 1 . a c b Trang 65
b)Ba lớp 7A, 7B, 7C cùng mua một số gói tăm từ thiện, lúc đầu số gói tăm dự định chia cho ba lớp
tỉ lệ với 5,6,7 nhưng sau đó chia theo tỉ lệ 4,5,6 nên có một lớp nhận nhiều hơn dự định 4 gói. Tính
tổng số gói tăm mà ba lớp đã mua.
2017x 2018y 2019z
d) Cho ba số x,y, z tỉ lệ với 3,4,5. Tính P
2017x 2018y 2019z
Câu 3:(4 điểm) 5z 6 y 6x 4z 4 y 5x a) Tìm x, y, z biết: và 3x – 2y + 5z = 96. 4 5 6
b) Chứng minh rằng: 3x+1 + 3x+2 + 3x+3 +……+ 3x+100 chia hết cho 120 (với x N) Câu 4.(6 điểm)
Cho tam giác ABC có AB < AC. Trên tia đối của tia CA lấy điểm D sao cho
CD = AB. Gọi P,Q là trung điểm của AD, BC, và I là giao điểm các đường vuông góc với AD và BC tại P và Q.
a) Chứng minh ∆AIB = ∆DIC
b) Chứng minh AI là tia phân giác của góc BAC. 1
c) Kẻ IE vuông góc với AB, chứng minh AE AD . 2
Câu 5.(2 điểm) Cho biết xyz=1 x y z Tính giá trị A = xy x 1 yz y 1 xz z 1
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 19 Câu Phần Nội dung Điểm a 12 5 6 2 10 3 5 2 2 .3 4 .9 5 .7 25 .49 2đ A 6 3 Câu 1
2 .3 8 .3 125.7 9 3 2 4 5 5 .14 (4 điểm) 10 12 5 12 4 10 3 4 2 .3 2 .3 5 .7 5 .7 0,5 12 6 12 5 9 3 9 3 3 2 .3 2 .3 5 .7 5 .2 .7 12 4 2 .3 .3 10 3 1 5 .7 .1 7 0,5 12 5 2 .3 .3 9 3 1 5 .7 . 3 1 2 1 12 4 10 3 2 .3 .2 5 .7 . 6 1 10 7 12 5 9 3 2 .3 .4 5 .7 .9 6 3 2 b
S =(-3)0+(-3)1 + (-3)2+(-3)3+...+ (-3)2015. 0.5 2đ
-3S = (-3).[(-3)0+(-3)1+(-3)2 + ....+(-3)2015]
= (-3)1+ (-3)2+ ....+(-3)2016] 0.5
-3S – S = [(-3)1 + (-3)2+...+(-3)2016]-(3)0-(-3)1-...-(-3)2015. -4S = (-3)2016 -1. 0.5 0.5 Trang 66 2016 ( 3 ) 1 2016 2016 3 1 1 3 S = 4 = 4 4 +Vì a+b+c 0 a
Theo tính chất dãy tỉ số bằng nhau ,ta có: 2đ
a b c
b c a
c a b = a b c b c a c a b = 1
a b c 0.5 c a b
a b c
b c a
c a b mà 1 1 1 = 2 Câu 2 0.5 c a b ( 4 điểm )
=> a b b c c a =2 c a b 0.5 Vậy B = b a c b a c a b c 1 1 1 ( )( )( ) =8 a c b a c b 0.5 b
Gọi tổng số gói tăm 3 lớp cùng mua là x ( x là số tự nhiên khác 0) 2đ
Số gói tăm dự định chia cho 3 lớp 7A, 7B, 7C lúc đầu lần lượt là: a, b, c Ta có: a b c a b c x 5x 6x x 7x a ; b ;c (1) 1 5 6 7 18 18 18 18 3 18
Số gói tăm sau đó chia cho 3 lớp lần lượt là a’, b’, c’, ta có: , , , , , , a b c
a b c x 4x 5x x 6x , , , a ;b ;c (2) 4 5 6 15 15 15 15 3 15
So sánh (1) và (2) ta có: a > a’; b=b’; c < c’ nên lớp 7C nhận nhiều 0,5 hơn lúc đầu Vây: c’ – 6x 7x x c = 4 hay 4 4 x 360 15 18 90
Vậy số gói tăm 3 lớp đã mua là 360 gói. 0.5 5z 6 y 6x 4z 4 y 5x a Từ 4 5 6 2đ 20z 24 y 30x 20z 24 y 30x 0.5 => Câu 3 16 25 36 (4 điểm) =>10z = 12y = 15x 0.5 0.5 x y z 3x 2 y 5z => => và 3x – 2y + 5z = 96 0.5 4 5 6 12 10 30
Giải ra ta được x = 12; y = 15; z = 18 b
3x+1 + 3x+2 + 3x+3 +…… + 3x+100 2đ
= (3x+1 + 3x+2 + 3x+3 + 3x+4) + (3x+5 + 3x+6 + 3x+7 + 3x+8)+…+ (3x+97 + 3x+98 + 3x+99 + 3x+100) 1
= 3x(3+32+33+34) + 3x+4(3+32+33+34) +…+3x+96(3+32+33+34)
= 3x.120 + 3x+4.120 +…+3x+96.120 0.5
= 120(3x + 3x+4 +…+3x+96) 120 (đpcm) 0.5 Trang 67 A P C B 0,5 Câu 4 E (6 điểm ) D I a Ta có IB = IC, IA = ID 1 2đ Lại có AB = CD (gt) 0,5
Do đó ∆AIB = ∆DIC (c.c.c) 0,5 b CM: DAI = D 0,5 1,5đ
∆AIB = ∆DIC (câu a), suy ra BAI = D 0,5 Do đó DAI = BAI. 0,5
Vậy AI là tia phân giác của góc BAC c
Kẻ IE AB, ta có ∆AIE = ∆AIP 0,5 => AE = AP 0,5 2đ
Mà AP = ½ AD (vì P là trung điểm AD) 0,5 1 0,5 Suy ra AE AD 2 Câu 5 x y z ( 2 điể m ) xy x 1 yz y 1 xz z 1 1 xz xyz z = 1 2
xyz xz z
xyz xyz xz xz z 1 xz xyz z xyz xz 1 1 1 xz z z 1 xz xz z 1 xyz xz 1
Lưu ý .Học sinh có cách giải khác đúng vẫn cho điểm tối đa.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 20 Bài 1. (4,0 điểm) 1 2 3 4 99 100
Cho biểu thức : C ..... 2 3 4 99 100 3 3 3 3 3 3 3
Chứng minh rằng : C < 16 Trang 68
Bài 2. (5,0 điểm)
Câu 1: Tìm x, y, z biết : 3x = 4y = 5z – 3x - 4y và 2x + y = z - 38 2 2 a + b ab
Câu 2: Cho tỉ lệ thức =
với a, b, c, d ≠ 0 và c ≠ - d 2 2 c + d cd a c a d Chứng minh rằng : = hoặc = b d b c Bài 3. (3,0 điểm)
Câu 1 : Chứng minh rằng với mọi n nguyên dương ta luôn có n + 3 n + 2 n + 1 n 4 + 4 - 4 - 4 chia hết cho 300 27 - 2x Câu 2 : Cho Q =
. Tìm các số nguyên x để Q có giá trị nguyên ? 12 - x
Bài 4. (3,0 điểm). Tìm giá trị lớn nhất của biểu thức sau 2 2
H = 3x - 2y - 4y - 6x - xy - 24 Bài 5. (5,0 điểm).
Cho Δ ABC nhọn.Trên nửa mặt phẳng bờ AB không chứa điểm C dựng đoạn thẳng AD vuông
góc với AB và AD = AB.Trên nửa mặt phẳng bờ AC không chứa điểm B dựng đoạn thẳng AE
vuông góc với AC và AE = AC.
1) Chứng minh rằng BE = CD .
2) Gọi M là trung điểm của DE, tia MA cắt BC tại H.Chứng minh MA BC
3) Nếu AB = c, AC = b, BC = a. Hãy tính độ dài đoạn thẳng HC theo a, b, c ? ----- Hết -----
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 20 1 2 3 4 99 100
Bài 1. (4,0 điểm) Cho biểu thức : C ..... 2 3 4 99 100 3 3 3 3 3 3 3
Chứng minh rằng : C < 16 Đáp án Điểm 1 2 3 4 99 100 2 3 4 99 100
Biến đổi: 3C 3. ..... 1 ..... 2 3 4 99 100 2 3 98 99 3 3 3 3 3 3 3 3 3 3 3 0,25 Ta có 2 3 4 99 100 1 2 3 4 99 100
3C C 1 ..... ..... 2 3 98 99 2 3 4 99 100 3 3 3 3 3 3 3 3 3 3 3 2 3 4 99 100 1 2 3 4 99 100 4C 1 .... ..... 2 3 98 99 2 3 4 99 100 3 3 3 3 3 3 3 3 3 3 3 0,25 Trang 69 2 1 3 2 4 3 100 99 100 0,25 4C 1 .... 2 2 3 3 99 99 100 3 3 3 3 3 3 3 3 3 1 1 1 1 100 0,25 4C 1 .... 2 3 99 100 3 3 3 3 3 Đặ 1 1 1 1 t D 1 .... 2 3 99 3 3 3 3 1 1 1 1 1 1 1 0,25
Ta có: 3D 3. 1 .... 3 1 .... 2 3 99 2 98 3 3 3 3 3 3 3 Khi đó 1 1 1 1 1 1 1
: 3D D 3 1 .... 1 .... 2 98 2 3 99 3 3 3 3 3 3 3 1 1 1 1 1 1 1
4D 3 1 .... 1 .... 2 98 2 3 99 3 3 3 3 3 3 3 0,25 1 1 1 1 1 1 1
4D 3 1 1 ... 2 2 98 98 99 3 3 3 3 3 3 3 0,25 1 4D 3 99 3 0,25 1 1 Suy ra D = . 3 - 99 4 3 0,25 3 1 D = - 99 4 4.3 0,25 3 1 100
Nên ta có 4C 99 100 4 4.3 3 0,25 3 1 100 4C 99 100 4 4.3 3 0,25 1 3 1 100 C . 99 100 4 4 4.3 3 0,25 3 1 25 C 2 99 100 16 4 .3 3 0,25 3 1 25 C - + 2 99 100 16 4 .3 3 0,25 1 25 3 1 25 3 3 Ta có > 0 nên < . Vậy C < 2 99 100 4 .3 3 2 99 100 0,25 16 4 .3 3 16 16 Bài 2. (5,0 điểm)
Câu 1: (2,5 điểm)
Tìm x, y, z biết : 3x = 4y = 5z – 3x - 4y và 2x + y = z – 38 Trang 70 Đáp án Điểm
Ta có : 2x + y = z – 38 nên 2x + y – z = – 38 0,25
+ Vì 3x = 4y = 5z – 3x – 4y nên 3x = 5z – 3x – 3x 0,25
3x = 5z – 6x 9x = 5z x z x z = = (1) 0,25 5 9 20 36 x y x y + Vì 3x = 4y = = (2) 0,25 4 3 20 15 x y z Từ (1) và (2) suy ra = 0,25 20 15 36
Áp dụng tính chất của dãy tỉ số bằng nhau ta có : x y z 2x + y - z -38 0,25 = = = - 2 20 15 36 2.20 + 15 - 36 19 x Do đó :
= - 2 x = (-2) . 20 = - 40 0,25 20 y
= - 2 y = (-2) . 15 = - 30 0,25 15 z
= - 2 z = (-2) . 36 = - 72 0,25 36
Vậy x = -40 ; y = -30 ; z = - 72 0,25
Câu 2: (2,5 điểm) a 2 b2 ab a c a d Cho
với a, b, c, d 0; c - d . Chứng minh rằng hoặc c 2 d 2 cd b d b c Đáp án Điểm 2 2 a + b ab 2 2 a + b 2ab Ta có: = nên = 2 2 c + d cd 2 2 c + d 2cd
Áp dụng tính chất của dãy tỉ số bằng nhau ta có 0,25 2 2 2 2 2 2 a + b 2ab a + b + 2ab a + b - 2ab = = 2 2 2 2 2 2 c + d 2cd c + d + 2cd c + d - 2cd
2a + ab + 2b + ab 2a - ab + 2b - ab a + b2 a - b2 = = 0,25 2 c + cd + 2 d + cd
2c - cd + 2d - cd c + d2 c - d2 2 2 a + b a - b a + b a - b a + b b - a Suy ra hoặc 0,25 c + d c - d c + d c - d c + d c - d a + b a - b + Với
thì a + b. c - d = a - b.c + d 0,25 c + d c - d
ac - ad +bc – bd = ac + ad –bc - bd 0,25 Trang 71 a c ad = bc = 0,25 b d a + b b - a + Với
thì a + b . c - d = b - a . c + d 0,25 c + d c - d
ac - ad +bc – bd = bc + bd –ac - ad 0,25 a d ac = bd = 0,25 b c 2 2 a + b ab a c a d Vậy nếu =
với a, b, c, d 0; c - d thì = hoặc = 0,25 2 2 c + d cd b d b c Bài 3. (3,0 điểm)
Câu 1: (1,0 điểm) Chứng minh rằng với mọi n nguyên dương ta luôn có n + 3 n + 2 n + 1 n 4 + 4 - 4 - 4 chia hết cho 300 Đáp án Điểm
Với mọi n nguyên dương, ta có n + 3 n + 2 n + 1 n 4 + 4 - 4 - 4 = n 3 2 4 .(4 + 4 - 4 - 1) 0,25 n n
= 4 .(64 + 16 - 4 - 1) = 4 .75 0,25 n - 1 n - 1 = 4 . 4 . 75 = 300 . 4 0,25 Mà n - 1 300 . 4
chia hết cho 300 ( với mọi n nguyên dương ) 0,25 n + 3 n + 2 n + 1 n Nên 4 + 4 - 4
- 4 chia hết cho 300 ( với mọi n nguyên dương ) 27 - 2x
Câu 2: (2,0 điểm) Cho Q =
. Tìm các số nguyên x để Q có giá trị nguyên ? 12 - x Đáp án Điểm
Điều kiện : x Z ; x ≠ 12 27 - 2x 2.(12 - x) + 3 3 0,25 Biến đổi Q = = = 2 + 12 - x 12 - x 12 - x
Ta có 2 Z ; x Z ; x ≠ 12 3 0,25
nên Q có giá trị nguyên khi và chỉ khi có giá trị nguyên 12 x 3 Mà
có giá trị nguyên khi và chỉ khi 12 x Ư(3) 12 x 0,25 Ư(3) = -3; -1; 1; 3
+ Nếu 12 - x = - 3 thì x = 15 (thỏa mãn điều kiện) 0,25
+ Nếu 12 - x = -1 thì x = 13 (thỏa mãn điều kiện) 0,25
+ Nếu 12 - x = 1 thì x = 11 (thỏa mãn điều kiện) 0,25
+ Nếu 12 - x = 3 thì x = 9 (thỏa mãn điều kiện) 0,25 Trang 72
Vậy Q có giá trị nguyên khi và chỉ khi x 9; 11; 13; 1 5 0,25
Bài 4. (3,0 điểm). Tìm giá trị lớn nhất của biểu thức sau : 2 2
H = 3x - 2y - 4y - 6x - xy - 24 . Đáp án Điểm 2 2
Ta có H = 3x - 2y - 4y - 6x - xy - 24 2 2 2 2
= 3x - 2y - 4.2y - 3x - xy - 24 3x - 2y - 4.3x - 2y - xy - 24 0,25 2 = - 3. 3x - 2y - xy - 24 2 = - 3. 3x - 2y + xy - 24 Ta có 2 3. 3x - 2y
0 với mọi giá trị của x, y 0,25
xy - 24 0 với mọi giá trị của x, y Do đó 2 3. 3x - 2y
+ xy - 24 0 với mọi giá trị của x, y 0,25 Nên 2 - 3. 3x - 2y + xy - 24 0
với mọi giá trị của x, y 0,25
Hay H ≤ 0 với mọi giá trị của x, y
Dấu ‘‘ = ’’ xảy ra khi và chỉ khi 3x - 2y 0 0,25 và xy - 24 0 (1) x y
+ Với 3x - 2y = 0 thì 3x = 2y = 0,25 2 3 x y Đặ 0,25 t =
= k . Khi đó x = 2k ; y = 3k 2 3
Thay x = 2k và y = 3k vào (1) ta được 2k . 3k - 24 = 0 0,25 6k2 = 24
k2 = 4 k = 2 hoặc k = -2 0,25
+ Với k = 2 thì x = 2.2 = 4 0,25 y = 3.2 = 6
+ Với k = - 2 thì x = 2.(-2) = - 4 0,25 y = 3.(-2) = - 6
Vậy giá trị lớn nhất của biểu thức H là 0 khi và chỉ khi x = 4; y = 6 0,25 hoặc x = - 4; y = - 6 Bài 5. (5,0 điểm). Trang 73 N E M D F
- Nếu hình vẽ sai thì không chấm cả bài hình
- Nếu câu trước làm sai thì HS vẫn có thể sử A
dụng kết quả câu trước để làm câu sau. I K C B H
1) (1,5 điểm ). Chứng minh : BE = CD .
+ Ta có DAC DAB BAC ( Vì tia AB nằm giữa 2 tia AD và AC ) 0,25 Mà 0
BAD 90 (Vì AB AD tại A ) Nên 0 DAC 90 BAC (1)
+ Ta có BAE CAE BAC ( Vì tia AC nằm giữa 2 tia AB và AE ) 0,25 Mà 0
CAE 90 (Vì AE AC tại A ) Nên 0 BAE 90 BAC (2)
Từ (1) và (2) suy ra BAE DAC 0,25
Xét ∆ ABE và ∆ ADC có : AB = AD (GT) 0,50
BAE DAC (chứng minh trên) AE = AC (GT)
Do đó ∆ABE = ∆ ADC (c – g - c)
BE = CD ( vì là hai cạnh tương ứng) 0,25
2) (2,5 điểm). Chứng minh: MA BC
+ Trên tia đối của tia MA lấy điểm N sao cho M là trung điểm của AN
Từ D kẻ DF vuông góc với MA tại F
Xét ∆ MAE và ∆ MDN có :
MN = MA (Vì M là trung điểm của AN ) 0,25
AME DMN (chứng minh trên)
ME = MD (Vì M là trung điểm của DE )
Do đó ∆ MAE = ∆ MND (c – g - c)
Suy ra AE = DN ( vì là hai cạnh tương ứng ) 0,25
và NDM MEA ( vì là hai góc tương ứng )
Mà NDM và MEA ở vị trí so le trong của hai đường thẳng AE và DN
Nên AE // DN ( dấu hiệu nhận biết hai đường thẳng song song ) 0,25 Suy ra 0
ADN DAE 180 (Vì là hai góc trong cùng phía ) (3) + Ta lại có 0
DAE +DAB + BAC + EAC = 360 0,25 Hay 0
DAE + BAC = 180 (Vì 0 DAB EAC 90 ) (4) Trang 74
Từ (3) và (4) ADN = BAC
+ Ta có AE = DN (chứng minh trên) và AE = AC (GT) Nên AC = DN 0,25
Xét ∆ ABC và ∆ DAN có : AB = AD (GT )
ADN = BAC (chứng minh trên)
AC = DN (chứng minh trên) 0,25
Do đó ∆ ABC = ∆ DAN (c – g - c)
Suy ra DNA = ACB ( vì là hai góc tương ứng ) hay DNF = ACB Ta có 0
DAF + BAD + BAH = 180 (Vì ba điểm F, A, H thẳng hàng) Hay 0 DAF + BAH = 90 ( Vì 0 BAD 90 ) (5) 0,25
Trong ∆ ADF vuông tại F có : 0
FDA + DAF = 90 ( Vì là hai góc phụ nhau ) (6)
Từ (5) và (6) FDA = BAH
+ Ta có ADN = NDF + FDA ( Vì tia DF nằm giữa 2 tia DA và DN )
BAC = HAC + BAH ( Vì tia AH nằm giữa 2 tia AB và AC ) 0,25
Mà ADN = BAC và FDA = BAH (chứng minh trên) Nên NDF = HAC
Xét ∆ AHC và ∆ DFN có :
NDF = HAC (chứng minh trên)
AC = DN (chứng minh trên) 0,25
DNF = ACB (chứng minh trên)
Do đó ∆ AHC = ∆ DFN (g - c - g)
Suy ra DFN = AHC ( vì là hai góc tương ứng ) Mà 0
DFN = 90 (Vì DE MA tại F ) nên 0 AHC 90 0,25
Suy ra MA BC tại H (đpcm)
3).(1,0 điểm). Nếu AB = c, AC = b, BC = a. Hãy tính độ dài đoạn thẳng HC theo a, b, c
+ MA BC tại H (chứng minh trên) nên ∆ AHB vuông tại H 0,25 ∆ AHC vuông tại H
Đặt HC = x HB = a - x ( Vì H nằm giữa B và C )
+ Áp dụng định lý Py-ta-go cho 2 tam giác vuông AHB và AHC ta có: 0,25 AH2 = AB2 - BH2 và AH2 = AC2 - CH2
AB2 - BH2 = AC2 - CH2 c2 - (a - x)2 = b2 - x2 0,25 2 2 2
a b c 0,25
Từ đó tìm được HC = x = 2a
Chú ý: Học sinh giải theo cách khác mà đúng thì vẫn cho điểm tương ứng với từng câu, từng bài
theo hướng dẫn trên./. Trang 75




