TOP 20 đề kiểm tra 1 tiết chương IV – chương giới hạn giải tích môn Toán lớp 11 (có đáp án)

TOP 20 đề kiểm tra 1 tiết chương IV – chương giới hạn giải tích môn Toán lớp 11 có đáp án. Mỗi đề bao gồm cả phần trắc nghiệm và tự luận. Nội dung gồm giới hạn dãy số, giới hạn của hàm số, hàm số liên tục. Bộ đề kiểm tra được viết dưới dạng PDF gồm 42 trang. Các bạn xem và tải về ở bên dưới.

50 25 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 5: Giới hạn. Hàm số liên tục (KNTT)

Môn: Toán 11

Thông tin:

42 trang 8 tháng trước

Tác giả:

Profile Thùy Dương (H)
! Trang!1!
ĐỀ 1
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I. TRẮC NGHIỆM KHÁCH QUAN(6đ)
Câu 1: Kết quả của là
A. B. C. D. 0
Câu 2: lim(-3n
3
+ 5n - 2) bằng
A. -3 B. C. D. 3
Câu 3: bằng
A. 1 B. C. D. -2
Câu 4: bằng
A. 0 B. C. 4 D.
Câu 5: bằng
A. B. 0 C. 10 D. 15
Câu 6: bằng
A. 2 B. C. D. 0
Câu 7: bằng
A. B. 2 C. D.
Câu 8: bằng
A. B. C. – 2 D. 2
Câu 9: bằng
A. B. C. 3 D. 0
Câu 10: bằng
A. 0 B. C. D.
Câu 11: bằng
A. B. 3 C. 0 D.
++
+-
2
2
325
lim
78
nn
nn
3
7
+¥
5
8
-
+¥
-¥
3 4.7
lim
3.7 2
nn
n
+
-
1
3
4
3
+¥
1
4
( )
32
0
lim 4 10
x
xx
®
++
+¥
2
21
lim
2
x
x
x
-
®
+
-
-¥
+¥
2
2
1
231
lim
1
x
xx
x
®-
++
-
1
2
-¥
+¥
3
lim( 2x 3 4)
x
x
®-¥
-+-
-¥
+¥
®+¥
-+
-
2
2
351
lim
2
x
xx
x
-¥
+¥
®-¥
+-
+
2
3
21
lim
21
x
xx
x
+¥
-¥
1
2
®+¥
-+
+
3
2
351
lim
2
x
xx
x
+¥
-¥
! Trang!2!
Câu 12: bằng
A. 6 B. -3 C. D.
Câu 13: Cho hàm số , hàm số liên tục trên
A. B. C. D.
Câu 14: Hàm số liên tục tại x = 1 khi
A. a = 1 B. Không có a thỏa mãn. C. a = 0 D. a = -1
Câu 15: Phương trình 2x
3
– 6x +1 = 0 có số nghiệm thuộc là
A. 1 B. 2 C. 3 D. Vô nghiệm.
II. PHẦN TỰ LUẬN(4đ)
Câu 16: a, Tính giới hạn
b, Tính giới hạn .
Câu 17: a,
b,
c,
Câu 18: Chứng minh rằng phương trình 4x
4
+ 2x
2
– x – 3 = 0 có ít nhất hai nghiệm
thuộc (-1;1).
Câu 19: Định m để hàm số liên tục tại x = 2.
*** Hết***
( )
®+¥
æö
-+
ç÷
ç÷
+
èø
2
3
3
2
lim 3 1
.1
x
xx
xx
+¥
3
2
2 1 nêu x > 1
()
3
nêu x 1
2
x
fx
x
-
ì
ï
=
í
-
£
ï
î
!
(;1)(1;)-¥ È +¥
(;1)-¥
(1; )+¥
( )
( )
( )
2
2 x 1
x +x-1 x 1
ax
fx
ì
+³
ï
=
í
<
ï
î
[ ]
2; 2-
-+
-+
3
3
21
lim
23
nn
nn
13
lim
2 4.3
n
nn
-
+
®
-+
-
2
2
32
lim
2
x
xx
x
®-¥
--
-+-
32
32
21
lim
452
x
xx
xxx
(
)
®+¥
++-
2
lim 3
x
xx x
2
7 10
nêu x 2
()
2
2 1 nêu x 2
xx
fx
x
m
ì
-+
¹
ï
=
-
í
ï
-- =
î
! Trang!3!
ĐÁP ÁN
I. PHẦN TRẮC NGHIỆM
Câu
1
2
3
4
5
6
7
Đáp án
A
C
C
D
C
B
A
8
9
10
11
12
13
14
15
B
C
A
A
A
A
D
C
II. PHẦN TỰ LUẬN:
Câu
Nội dung
Thang
điểm
16a
0,5
16b
0,5
17a
0,5
17b
0,5
17c
0,25
0,25
18
Đặt f(x) = 4x
4
+ 2x
2
– x – 3 = 0, hàm số này liên tục trên R
+, Xét khoảng (-1;0)
Ta có f(-1) = 4, f(0) = -3
Do f(-1).f(0) < 0 nên phương trình có ít nhất 1 nghiệm trong
khoảng (-1;0).
+ Xét khoảng (0;1)
Ta có f(0) = -3, f(1) = 4.
0,25
-+
-+
-+
== =
-+ -+
-+
3
3
323
33
23
3
21 2 1
1
21 1
lim lim lim
13
2
2323
2
nn
nn
nnn
nn nn
nn
n
13 1
1
13 1
33
lim lim lim
2 4.3
2 4.3 4
2
4
3
3
n
n
nn
nn n
nn
n
-
-
-
===-
-
+
æö
+
ç÷
èø
( )( )
( )
2
22 2
21
32
lim lim lim 1 2 1 1
22
xx x
xx
xx
x
xx
®® ®
--
-+
==-=-=
--
®-¥
--
=
-+-
32
32
21
lim 2
452
x
xx
xxx
(
)
(
)
(
)
®+¥ ®+¥
®+¥ ®+¥
®+¥
++- +++
++- =
+++
++- +
==
+++ +++
+
==
+++
22
2
2
22
22
33
lim 3 lim
3
33
lim lim
33
3
1
1
lim
2
13
11
xx
xx
x
xx x xx x
xx x
xx x
xx x x
xx x xx x
x
xx
! Trang!4!
Do f(0).f(1)< 0 nên phương trình có ít nhất một nghiệm trong
khoảng (0;1).
Vậy phương trình có ít nhất hai nghiệm thuộc khoảng (-1;1).
0,25
19
Ta có: f(2) = -2a - 1
Hàm số f(x) liên tục tại x = 2
Vậy a = 1 thì f(x) liên tục tại x = 2.
www.thuvienhoclieu.com
ĐỀ 2
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
A. TRẮC NGHIỆM: ( 0,5điểm/1câu x 6câu = 3 điểm)
Câu 1: Giới hạn của hàm số sau đây bằng bao nhiêu: (với k nguyên dương)
A. + B. 0 C. 14 D. k
Câu 2: Giới hạn của hàm số sau đây bằng bao nhiêu:
A. 0 B. 1 C. 2 D.+
Câu 3: Giới hạn của hàm số sau đây bằng bao nhiêu:
A. 0 B. - C. 1 D. 2
Câu 4: cho hàm số: Trong các mệnh đề sau, tìm mệnh đề sai?
A. B.
C. D. Không tồn tại giới hạn của hàm số f(x) khi x tiến
tới 1.
Câu 5: Cho các hàm số: (I) y = sinx ; (II) y = cosx ; (III) y = tanx ; (IV) y = cotx
Trong các hàm số sau hàm số nào liên tục trên .
A. (I) và (II) B. (III) và IV) C. (I) và (III) D. (I), (II), (III) và (IV)
2
22
22
7 10
lim ( ) lim
2
( 2)( 5)
lim lim( 5 ) 3
2
xx
xx
xx
fx
x
xx
x
x
®®
®®
-+
=
-
--
==-=-
-
2
lim ( ) (2)
x
fx f
®
Û=
321 22 1aaaÛ- =- - Û- =- Û =
lim
k
x
x
®+¥
¥
2
2
2
22
lim
( 2)
x
xx
x
®
-+
-
¥
2
lim ( 2 )
x
xxx
®+¥
+-
¥
2
21
1
()
1
1
x
khi x
x
fx
xx
khi x
x
-
ì
³
ï
ï
=
í
-
ï
<
ï
-
î
1
lim ( ) 1
x
fx
-
®
=
1
lim ( ) 1
x
fx
+
®
=
1
lim ( ) 1
x
fx
®
=
!
! Trang!5!
Câu 6: Cho hàm số f(x) chưa xác định tại x = 0: . Để f(x) liên tục tại x =
0, phải gán cho f(0) giá trị bằng bao nhiêu?
A. -3 B. -2 C. -1 D. 0
B. TỰ LUẬN: (7 điểm)
Bài 1: ( 3 điểm) Tính giới hạn của các hàm số sau:
Bài 2: ( 2 điểm) Tìm m để hàm số liên tục tai x
0
= 3.
Bài 3: ( 2 điểm) Chứng minh rằng phương trình:
có ít nhất một nghiệm thuộc khoảng .
luôn có nghiệm với mọi giá trị của tham số m.
..................................................Hết............................................................
(Cán bộ coi thi không giải thích gì thêm)
ĐÁP ÁN ĐỀ KIỂM TRA 45’ TRẮC NGHIỆM: ( 0,5điểm/1câu x 6câu = 3 điểm)
1A
2D
3C
4D
5A
6B
A. TỰ LUẬN: (7 điểm)
Bài
Đáp án
Thang điểm
1(3đ)
1đ
1đ
0,5đ
0,5đ
2(2đ)
+/ TXĐ:
+/
0,5đ
0,5đ
0,5đ
2
2
()
xx
fx
x
-
=
2
2
22
2 4 1 7 10 2
) lim b) lim c)lim
121 2
xx x
xxx x
a
xxx x
®®+¥ ®
--+ --
+++-
( )
ì
-+
¹
ï
=
-
í
ï
-=
î
2
22
3116
3
3
3
xx
khi x
fx
x
mxkhix
53
)10ax x+-=
( )
0;1
) osx os2x 0bc mc+=
2
2 4 2.2 4
)lim 0
121
x
x
a
x
®
--
==
++
2
2
2
2
11
1
11
)lim lim
11
21 2
2
xx
xx
xx
b
xx
xx
®+¥ ®+¥
-+
-+
==
++
++
( ) ( )
( )
( )
( )
( )
22
22
7 10 2 . 7 10 2
7 10 2
c) lim lim
2
2 7 10 2
7x-14 7 7
lim lim
4
7 10 2
2 7 10 2
xx
xx
xx
x
x
xx
x
xx
®®
®®
-- -+
--
=
-
--+
===
-+
--+
( )
0
3Dx==Î!!
( )
( )( )
®® ®
--
-+
== =
--
2
33 3
3 3x 2
3116
lim lim lim 7
33
xx x
x
xx
fx
xx
! Trang!6!
+/
+/ Do đó:
Vậy: với hàm số liên tục tại x
0
= 3
0,5đ
3(2đ)
+/ Đặt: , liên tục trên liên tục trên
+/ Có:
đpcm
0,5đ
0,5đ
+/ Đặt: liên tục trên liên tục
trên
+/ Có:
đpcm
0,5đ
0,5đ
Học sinh giải cách khác mà đúng vẫn cho điểm tối đa.
www.thuvienhoclieu.com
ĐỀ 3
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I.Phần trắc nghiệm:(4điểm).
Câu 1: Biết giới hạn . Khi đó giá trị của a là.
A. 1 B. 2 C. 3 D. a=2 hoặc a= -
2.
Câu 2: Tính giới hạn ta được kết quả là:
A. - B. C. 0 D. 2
Câu 3: Tính giới hạn ta được kết quả là:
A. – 3 B. 1 C. 3 D. – 2
Câu 4: Tìm a để giới hạn .
A. a=3 B.a = 5 C.a >1 D. a < 1.
Câu 5: Tìm giới hạn ta được kết quả là:
A. B. 1 C. -2 D.
3
( )
=-
2
39fm
-= Û =±
2
97 4mm
=±4m
()fx
53
)10ax x+-=
( )
53
1fx x x=+-
( )
fx
!
Þ
( )
fx
[ ]
0;1
( )
( )
( ) ( ) ( )
( )
00
01
0. 1 1 0 0;1: 0
11
f
ff x fx
f
=-
ì
ï
Þ=-<Þ$Î =Þ
í
=
ï
î
) ox os2x 0bc mc+=
( ) ( )
ox os 2x ffx c mc x=+ Þ
!
Þ
( )
fx
3
;
44
pp
éù
êú
ëû
( )
00
2
42
31 3
.0;:0
442 44
32
42
f
ff x fx
f
p
pp pp
p
ì
æö
=
ï
ç÷
ïè ø
æöæ ö æ ö
Þ=-<Þ$Î =
í
ç÷ç ÷ ç ÷
èøè ø è ø
æö
ï
=-
ç÷
ï
èø
î
Þ
22
2
23
lim 4
1
an n
n
++
=
+
1
21
lim
1
x
x
x
+
®
-+
-
¥
+¥
2
1
43
lim
1
x
xx
x
®
-+
-
2
lim ( 3 5 )
x
x x ax
®-¥
- + + = +¥
3
lim( 2 2)nn+-
+¥
! Trang!7!
Câu 6: Tìm giới hạn:
ta được kết quả là:
A. -1 B. + C. - D. 2
Câu7. Biết giới hạn .Tìm a?
A.a= -2 B. C. D.
Câu 8: Tìm a để giới hạn =4 :
A. -20 B. 20 C. 2 D. 4
Tự luận: (6đ)
Câu 1
.
Câu 2.Chứng minh phương trình : có ít nhất 2 nghiệm trên khoảng (0;3).
Câu 3: Tìm m để hàm số liên tục tại .
Câu 4:
-Gọi C là nữa đường tròn đường kính AB=2R.
- là đường gồm hai nữa đường tròn đường kính
-Gọi là đường gồm bốn nữa đường tròn đường kính
- là đường gồm 2
n
nữa đường tròn đường kính
Gọi là diện tích hình phẳng giới hạn bởi và đoạn thẳng
AB và .Tính giới hạn lim .
………………Hết………………..
Đáp án
1
2
3
4
5
6
7
8
D
A
D
A
A
B
B
A
Câu
Hướng dẫn
Điểm
1a(1đ)
0,5x0,25
x0,25
1b(1đ)
0,5 x 0,5
2
32
lim
1
x
xx
x
®+¥
-+
-
¥
¥
21
lim 5
3
x
x
ax
®-¥
+
=
-
2
5
a =-
5
2
a =-
2
3
a =
1
.5 2.3
lim
45
nn
nn
a
+
+
-
2
2
2
2
73 3 1
. lim .lim . lim ( 4 3 2 )
232
xx
xnn
abcxxx
xn
®®+¥
+- + -
+--
-+
3
520xx-+=
2
2
23 3
23 2
()
3
26
2
xx
khi x
x
fx
m khi x
ì
--
¹
ï
ï
-
=
í
ï
-=
ï
î
3
2
x =
1
C
2
AB
2
C
,...
4
AB
n
C
,...
2
n
AB
n
S
n
C
12
...
nn
uSS S=+++
n
u
22 2
73 2 1 1
lim lim lim
26
( 2)( 7 3) 7 3
xx x
xx
x
xx x
®® ®
+- -
===
-
-++ ++
2
2
2
2
31
1
31 1
lim lim
2
32 3
3
nn
nn
n
n
+-
+-
==
+
+
! Trang!8!
1c(1đ)
0,25x4
2(1đ)
Câu 2.Chứng minh phương trình : có ít nhất 2 nghiệm trên
khoảng (0;3).
Xét hàm số f(x)= liên tục trên [0;3]
f(0)=2, f(1)=-2, f(3)=14 (0.5)
Ta thấy : f(0).f(1)=-4<0 ,f(1).f(3)=-28<0 (0.25)
Do đó pt đã cho có ít nhất 2 nghiệm trên khoảng (0;3). (0.25)
0.5x0,25
x0,25.
Câu 3
(1đ)
Câu 3: Tìm m để hàm số liên tục tại .
.
f(x) liên tục tại
khi và chỉ khi :
.
0,25x2
0,25x2
Câu 4
(1đ)
Ta có:
0,25
0,25
0,25x2
www.thuvienhoclieu.com
ĐỀ 4
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I.Phần trắc nghiệm:(4 điểm).
Câu 1: Biết giới hạn . Khi đó giá trị của a là.
A. 4 B. 2 C. hoặc D. a=2 hoặc a=
-2.
Câu 2: Tính giới hạn ta được kết quả là:
22
2
22
2
3
1
434 3 1
lim ( 4 3 2 ) lim lim lim
4
13
432 432
42
xxxx
xx x x
x
xx x
xx x xx x
xx
®+¥ ®+¥ ®+¥ ®+¥
-
+-- -
+-- = = = =
+-+ +-+
+- +
3
520xx-+=
3
52xx-+
2
2
23 3
23 2
()
3
26
2
xx
khi x
x
fx
m khi x
ì
--
¹
ï
ï
-
=
í
ï
-=
ï
î
3
2
x =
2
2
33 3
22 2
23(23)(1) 53
lim lim lim( 1) , ( ) 2 6
23 23 2 2
xx x
xx x x
xfm
xx
®® ®
-- - +
==+==-
--
3
2
x =
2
5 17
26
22
mm=-Û=±
222 2
123
222 2
2
222
, , ,..., .
248 2
111 1
... ( ... )
248 2 2482
111 1 1
lim lim ( .... ) lim 1
248 2 2
n
n
n
nn
n
n
n
RRR R
SS S S
RRR R
uR
uR R R
ppp p
ppp p
p
ppp
=== =
=++++= ++++
éù
æö
=++++=-=
êú
ç÷
èø
êú
ëû
22
2
223
lim 4
1
an n
n
++
=
+
2a =
2a =-
1
21
lim
1
x
x
x
+
®
+
-
! Trang!9!
A. - B. C. 0 D. 2
Câu 3: Tính giới hạn ta được kết quả là:
A. – 3 B. 1 C. 2 D. – 2
Câu 4: Tìm a để giới hạn .
A. a=1 B.a <-1 C.a= -1 D. a =5
Câu 5: Tìm giới hạn ta được kết quả là:
A. B. 1 C. D.
3
Câu 6: Tìm giới hạn:
ta được kết quả là:
A. -1 B. + C. - D. 2
Câu7. Biết giới hạn .Tìm a?
A.a= -1 B. C. D.
Câu 8: Tìm a để giới hạn =4 :
A. 2 B. 25 C. 4 D. 100.
II.Tự luận: (6đ)
Câu 1
Câu 2.Chứng minh phương trình : có ít nhất 2 nghiệm trên khoảng (-
1;3).
Câu 3: Tìm m để hàm số liên tục tại .
Câu 4:
-Gọi C là nữa đường tròn đường kính AB=2R.
- là đường gồm hai nữa đường tròn đường kính
-Gọi là đường gồm bốn nữa đường tròn đường kính
- là đường gồm 2
n
nữa đường tròn đường kính
Gọi là diện tích hình phẳng giới hạn bởi và đoạn thẳng
AB và .Tính giới hạn lim .
…………………..Hết…………………..
Đáp án:
1
2
3
4
5
6
7
8
C
B
C
B
C
C
D
D
¥
+¥
2
1
43
lim
1
x
xx
x
®-
++
+
2
lim ( 3 5 )
x
x x ax
®+¥
- + + = -¥
3
lim ( 2 2)nn-+ -
+¥
-¥
2
32
lim
31
x
xx
x
®+¥
-+ +
-
¥
¥
31
lim 5
3
x
x
ax
®-¥
+
=
-
5a =
5
3
a =-
3
5
a =-
2
.5 2.3
lim
45
nn
nn
a
+
+
+
2
2
2
3
63 2 3 1
. lim .lim . lim ( 9 3 3 )
32
xx
xnn
ab cxxx
xn
®®-¥
+- + -
+-+
--+
3
2520xx--=
2
2
34 4
34 3
()
4
26
3
xx
khi x
x
fx
m khi x
ì
--
¹
ï
ï
-
=
í
ï
-=
ï
î
4
3
x =
1
C
2
AB
2
C
,...
4
AB
n
C
,...
2
n
AB
n
S
n
C
12
...
nn
uSS S=+++
n
u
! Trang!10!
Câu
Hướng dẫn
Điểm
1a(1đ)
0,5x0,25
x0,25
1b(1đ)
.
0,5 x 0,5
1c(1đ)
0,25x4
2(1đ)
Câu 2.Chứng minh phương trình : có ít nhất 2 nghiệm
trên khoảng (-1;3).
Xét hàm số f(x)= liên tục trên [-1;3]
f(-1)=2, f(0)= -2, f(3)=37 (0.5)
Ta thấy : f(-1).f(0)= -4<0 ,f(0).f(3)= - 74<0 (0.25)
Do đó pt đã cho có ít nhất 2 nghiệm trên khoảng (-1;3). (0.25)
0.5x0,25
x0,25.
Câu 3
(1đ)
Câu 3: Tìm m để hàm số liên tục tại .
.
f(x) liên tục tại
khi và chỉ khi :
.
0,25x2
0,25x2
Câu 4
(1đ)
Ta có:
0,25
0,25
0,25x2
33 3
63 3 1 1
lim lim lim
36
(3)( 63) 63
xx x
xx
x
xx x
®® ®
+- -
===
-
-++ ++
2
2
2
2
31
2
231
lim lim 2
2
2
1
nn
nn
n
n
+-
+-
==-
-+
-+
22
2
22
2
3
1
939 3 1
lim ( 9 3 3 ) lim lim lim
6
13
933 933
93
xxxx
xx x x
x
xx x
xx x xx x
xx
®-¥ ®-¥ ®-¥ ®-¥
-
+-- -
+-+ = = = =-
æö
+-- +--
-+-+
ç÷
èø
3
2520xx--=
3
252xx--
2
2
34 4
34 3
()
4
26
3
xx
khi x
x
fx
m khi x
ì
--
¹
ï
ï
-
=
í
ï
-=
ï
î
4
3
x =
2
2
44 4
33 3
3 4 (3 4)( 1) 7 4
lim lim lim( 1) , ( ) 2 6
34 34 3 3
xx x
xx x x
xfm
xx
®® ®
-- - +
==+==-
--
4
3
x =
2
75
26
3
6
mm=-Û=±
222 2
123
222 2
2
222
, , ,..., .
248 2
111 1
... ( ... )
248 2 2482
111 1 1
lim lim ( .... ) lim 1
248 2 2
n
n
n
nn
n
n
n
RRR R
SS S S
RRR R
uR
uR R R
ppp p
ppp p
p
ppp
=== =
=++++= ++++
éù
æö
=++++=-=
êú
ç÷
èø
êú
ëû
! Trang!11!
www.thuvienhoclieu.com
ĐỀ 5
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
Câu 1.
Tổng của cấp số nhân lùi vô hạn là
A.
1
B.
C.
-1
D.
Câu 2.
Dãy số nào sau đây có giới hạn là ?
A.
B.
C.
D.
Câu 3.
Cho một hàm số xác định trên khoảng (a;b). Khẳng định nào sau đây là
đúng ?
A.
Nếu hàm số liên tục trên đoạn và thì phương trình
có nghiệm trong khoảng .
B.
Nếu phương trình có nghiệm trong khoảng thì hàm số liên
tục trên khoảng
C.
Nếu liên tục trên đoạn thì pt có nghiệm trên
khoảng .
D.
Nếu thì phương trình có ít nhất một nghiệm trong khoảng
.
Câu 4.
Giới hạn (a/b tối giản) có a+b bằng
A.
21
B.
11
C.
19
D.
51
Câu 5.
bằng :
A.
không tồn tại
B.
1
C.
D.
2
Câu 6.
Tính :
A.
B.
C.
D.
Câu 7.
Hàm số nào trong các hàm sau có giới hạn tại điểm x=2 ?
A.
B.
C.
D.
Câu 8.
Dãy số nào sau đây có giới hạn bằng 0?
A.
B.
C.
D.
Câu 9.
bằng:
A.
-
B.
C.
D.
11 1 1 1
, , , ..., ,...
2 4 8 16 2
n
æö
-- -
ç÷
èø
1
2
1
3
-
+¥
23
34
n
unn=-
2
3
221
4
n
nn
u
n
+-
=
+
2
2
2
n
nn
u
n
-
=
-
2
3 13
n
un n=-
().() 0fa fb<
[ ]
; ; f(a).f(b)=0ab
2
53 3
lim
2(3 2)
nna
nb
+
=
+
1 3 5 ... (2 1)
lim
2(2 3)
n
nn
+++ + -
-
1
4
2
lim ( 2 3 4 )
x
xx x
®+¥
-+-
3
21
-
+
+¥
21-
-¥
1
()
1
fx
x
=
+
1
()
2
fx
x
=
-
2
2
()
4
x
fx
x
=
-
13
()
2
fx
x
=
-
6
5
n
æö
ç÷
èø
2
3
n
æö
-
ç÷
èø
3
3
1
nn
n
-
+
2
4nn-
23
2
1
2
lim
523
x
xx
xx
®
-
-+
1
5
-¥
1
6
2
5
! Trang!12!
Câu 10.
Hàm số Giá trị m để f(x) liên tục tại x=1 là:
A.
B.
C.
m=1
D.
m=0
Câu 11.
Trong các dãy số sau, dãy số nào có giới hạn hữu hạn?
A.
B.
C.
D.
Câu 12.
Hàm số nào sau đây liên tục tại x=2 ?
A.
B.
C.
D.
Câu 13.
Tính Khi đó đặt P=a+b có:
A.
6
B.
7
C.
5
D.
10
Câu 14.
Phương trình có mấy nghiệm ?
A.
4
B.
3
C.
5
D.
1
Câu 15.
Cho hàm số: để f(x) liên tục tại điêm x
0
= 2 thì a bằng ?
A.
4
B.
6
C.
8
D.
Không có giá
trị a
Câu 16.
Trong các hàm số sau hàm số nào liên tục trên R ?
A.
B.
C.
D.
y= tan3x
Câu 17.
Tính :
A.
-2
B.
C.
3
D.
Câu 18.
Tính :
A.
1
B.
0
C.
D.
3/2
Câu 19.
Giới hạn
bằng: A. 3/2
B. 3
C. -3/2
D. Không tồn tại.
Câu 20.
Dãy số nào sau đây có giới hạn khác 0?
A.
B.
C.
D.
Câu 21.
Giới hạn bằng:
A.
-2
B.
3
C.
-5
D.
5
Câu 22.
; (a;b nguyên). Khi đó a+b bằng:
A.
9
B.
19
C.
8
D.
21
2
32
(x>1)
1
()
1
(x 1)
4
x
x
fx
mm
ì
+-
ï
ï
-
=
í
ï
++ £
ï
î
{ }
0;1m Î
{ }
0; 1m Î-
2.5 12
32
n
n
n
u
-
=
-
1
6
3
n
n
n
u
æö
=+
ç÷
èø
43
4
32
24
n
nn
u
nn
-+
=
-+ -
3
2
233
5
n
nn
u
n
-+
=
-+
2
261
()
2
xx
fx
x
++
=
+
1
()
2
x
fx
x
+
=
-
2
1
()
2
xx
fx
x
++
=
-
2
2
32
()
4
xx
fx
x
--
=
-
2
3
26
lim
3
x
x
ab
x
®
-
=
-
54 2
32540xx xx-++-=
3
8
( 2)
()
2
2 4 ( 2)
x
x
fx
x
ax
ì
-
¹
ï
=
-
í
ï
-=
î
3
1 cos
x
y
x
-
=
-
3
2
21
2
xx
y
x
-+
=
+
32
256
1
xx
y
x
-+
=
+
2
34
lim
23
x
x
xx
+
®
+
--
1
3 3.5
lim
25
nn
n+
+
-
3
5
-
2
1
31
lim
1
x
x
x
®
-
-
2
2
21
34
n
n
+
+
2
3
5
n
æö
ç÷
èø
3
3
nn+
2
4
3n +
2
34
lim
1
x
xxx
x
®-¥
++
+
43
4
522
lim
16 9 5
x
xx a
xx b
®+¥
++
=
++
! Trang!13!
Câu 23.
bằng:
A.
17/2
B.
C.
D.
Câu 24.
bằng:
A.
8/3
B.
10/3
C.
3
D.
1
Câu 25.
Tính :
A.
-3/2
B.
0
C.
5/2
D.
3/2
HẾT
Đáp án
01. - - - ~ 08. - / - - 15. - - = - 22. ; - - -
02. - - - ~ 09. - - = - 16. - / - - 23. - - - ~
03. ; - - - 10. - / - - 17. - - - ~ 24. - - - ~
04. - / - - 11. - - = - 18. - - = - 25. ; - - -
05. - - = - 12. ; - - - 19. - - - ~
06. - / - - 13. - / - - 20. ; - - -
07. ; - - - 14. - / - - 21. - - = -
2
18 1 5
lim
27
x
xx
x
®+¥
+- +
-
+¥
23
3
32
2
2
91 2
lim
33
nn
n
+- +
-
(
)
2
lim 3nnn--
! Trang!14!
www.thuvienhoclieu.com
ĐỀ 6
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
A. PHẦN TRẮC NGHIỆM .(7điểm)
Câu 1. Với k là số nguyên dương. Tìm giới hạn .
A. . B. . C. 0. D. .
Câu 2. Giới hạn nào sau đây bằng 0 ?
A. lim . B. lim . C. lim . D. lim
Câu 3. Tính .
A. -1. B. 1. C.
D.
Câu 4. Tính .
A. 1. B.
C. . D. .
Câu 5. Biết . Tìm a.
A. 8. B. 9. C. 5.
D. 4.
Câu 6.
Cho hàm số có đồ thị như hình vẽ
.Mệnh đề nào sau đây sai ?
A. Hàm số gián đoạn tại .
B. .
C. .
D. .
Câu 7. Cho hàm số xác định trên khoảng K chứa điểm 0 và .
Khẳng định nào dưới đây đúng ?
A.
B.
C.
D.
Câu 8. Tìm .
A.
.
B.
.
C. . D. -1.
Câu 9. Hàm số nào dưới đây không có giới hạn tại điểm ?
1
lim
k
x
x
®+¥
+¥
-¥
1
k
2
nn1
2n 1
-+
-
2
2
n3n2
nn
-+
+
3
3
n2n1
n2n
+-
-
2
3
2n 3n
n3n
-
+
1
1
lim
2
x
x
x
®
+
+
1
.
2
2
.
3
2
2
2
lim
2
x
x
x
®
-
-
1
.
22
1
2
2
1
1
lim 4
1
x
ax
x
®
-
=
+
( )
yfx=
1x =
( )
lim 1
x
fx
®+¥
=
( )
1
lim
x
fx
+
®
= -¥
( ) ( )
3
lim 3
x
fx f
®
=
8
6
4
2
2
4
6
8
15
10
5
5
10
15
O
1
1
()fx
() 1fx x+£
0
lim ( ) 0.
x
fx
®
=
0
lim ( ) 1.
x
fx
®
=
0
lim ( ) 1.
x
fx
®
=-
0
lim ( ) .
x
fx
®
= +¥
5 2.3
lim
4 2.5
nn
nn
+
-
+¥
1
1
2
-
0x =
! Trang!15!
A. . B.
C.
D.
Câu 10. Cho hàm số . Khẳng định nào sau đây đúng ?
A. Hàm số chỉ có giới hạn bên phải tại điểm .
B. Hàm số có giới hạn bên trái và giới hạn bên phải tại điểm .
C. Hàm số có giới hạn tại điểm .
D. Hàm số chỉ có giới hạn bên trái tại điểm
Câu 11. Tính
A. +
.
B. . C.1 . D. .
Câu 12. Cho hàm số f(x) xác định trên [a; b]. Mệnh đề nào sau đây đúng ?
A. Nếu hàm số f(x) liên tục, tăng trên [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0
không có nghiệm trong khoảng (a; b).
B. Nếu hàm số f(x) liên tục trên [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0
không có nghiệm trong khoảng (a; b).
C. Nếu phương trình f(x) = 0 có nghiệm trong khoảng (a; b) thì hàm số f(x) phải liên
tục
trên (a; b).
D. Nếu f(a).f(b) < 0 thì phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (a;
b).
Câu 13. Khẳng định nào sau đây sai ?
A. Hàm số liên tục trên tập R.
B. Hàm số được xác định bởi liên tục tại .
C. Hàm số liên tục .
D. Hàm số liên tục trên .
Câu 14. Cho hàm số xác định trên khoảng K chứa a . Khẳng định nào sau đây
đúng ?
A. Hàm số không liên tục tại điểm thì không tồn tại
B. Nếu thì liên tục tại .
C. Nếu thì liên tục tại .
D. Hàm số có giới hạn bên trái và bên phải tại điểm thì liên tục tại .
B. PHẦN TỰ LUẬN (3 điểm ).
Câu 1. Tính các giới hạn sau :
a. ; b. .
()fx x=
1
() .fx
x
=
1
() .fx
x
=
1
() .
1
fx
x
=
-
1
()
3
fx
x
=
-
3x =
3x =
3x =
3.x =
2
2 5 8 ... 3 1
lim .
23
n
n
n
®+¥
+++ + -
+
¥
3
2
3
4
() 3 1fx x=+
()fx
1 khi 0
()
0 khi 0
xx
fx
x
+³
ì
=
í
<
î
0x =
1
()fx
x
=
0x"¹
()fx x=
[
)
0; +¥
( )
fx
xa=
( )
lim .
xa
fx
®
( )
lim
xa
fx a
®
=
( )
fx
xa=
( ) ( )
lim
xa
fx fa
®
=
( )
fx
xa=
xa=
xa=
2
2
4
lim
2
x
x
x
®
-
-
2
2
2
lim
1
nn
nn
-
++
! Trang!16!
Câu 2 . Tìm m để hàm số liên tục tại .
Câu 3. Từ độ 63m của một tòa nhà người ta thả một quả bóng làm bằng cao su
xuống mặt đất .Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng độ cao
mà quả bóng đạt được ngay trước đó .Tính độ dài hành trình của quả bóng từ thời
điểm ban đầu cho đến khi nó nằm yên trên mặt đất .
www.thuvienhoclieu.com
ĐỀ 7
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
Câu 1 :
Giới hạn của hàm số sau đây bằng bao nhiêu:
A.
5a
4
B.
3a
4
C.
2a
2
D.
4a
3
Câu 2 :
Tính
A.
1
B.
-1/2
C.
-2
D.
3/2
Câu 3 :
Khẳng định nào sau đây là đúng?
A.
B.
C.
D.
Câu 4 :
Trong các giới hạn sau, giới hạn nào không tồn tại
A.
B.
C.
D.
Câu 5 :
Tính
A.
1
B.
2
C.
0
D.
3
Câu 6 :
Phương pháp nào sau đây thường được sử dụng để khử dạng giới hạn vô định của phân thức
A.
Phân tích tử và mẫu thành nhân tử rồi rút gọn
B.
Nhân biểu thức liên hợp
C.
Chia cả tử và mẫu cho biến số có bậc thấp
nhất
D.
Sử dụng định nghĩa
Câu 7 :
Hàm số có bao nhiêu điểm gián đoạn
A.
1
B.
3
C.
2
D.
4
Câu 8 :
Tính
A.
B.
2
C.
D.
-2
Câu 9 :
Với k là số nguyên dương. Kết quả của giới hạn là
A.
x
B.
C.
0
D.
Câu 10 :
Tính
A.
2
B.
1
C.
1/2
D.
-1/2
( )
2
6
khi 3
3
2 khi 3
xx
x
fx
x
xm x
ì
--
¹
ï
=
-
í
ï
+=
î
3x =
1
10
44
lim
xa
xa
xa
®
-
-
1
1
lim
2
x
x
x
®
+
-
lim ( ) ( ) lim ( ) lim ( )
ooo
xx xx xx
fx gx fx gx
®®®
+= +
lim ( ) ( ) lim [ ( ) ( )]
oo
xx xx
fx gx fx gx
®®
+= +
lim ( ) ( ) lim [ ( ) ( )]
oo
xx xx
fx gx fx gx
®®
+= +
lim ( ) ( ) lim ( ) lim ( )
ooo
xx xx xx
fx gx fx gx
®®®
+= +
1
1
lim
2
x
x
x
®-
+
-+
1
1
lim
2
x
x
x
®
+
-
1
1
lim
2
x
x
x
®
+
-
1
1
lim
2
x
x
x
®-
+
+
2
lim
2
x
xx
xx
®+¥
-+
42
5
10 9
x
y
xx
+
=
-+
22
lim ( 4 )
x
xx x
®-¥
+- +
1
2
-
1
2
lim
k
x
x
®+¥
2
1
1
lim
1
x
x
x
®
-
-
! Trang!17!
Câu 11 :
Tính
A.
-8
B.
8
C.
-6
D.
6
Câu 12 :
Khẳng định nào sau đây là đúng?
A.
B.
C.
D.
Câu 13 :
Giới hạn nào dưới đây có kết quả bằng 3
A.
B.
C.
D.
Cả ba hàm số trên
Câu 14 :
Tính
A.
B.
2
C.
D.
1
Câu 15 :
Giới hạn của hàm số nào dưới đây có kết quả bằng 1?
A.
B.
C.
D.
Câu 16 :
Một học sinh bảo rằng phương trình x
4
-x-2=0 (1), có nghiệm , nằm trong khoảng (0;2)
Và lập luận như sau, Hỏi phần lập luận đó sai ở bước nào?
A.
B.
hàm số liên tục trên
C.
nên (1) có ít nhất một nghiệm
nên (1) có ít nhất một nghiệm
D.
Vậy (1) có ít nhất 2 nghiệm , nằm trong khoảng (0;2)
Câu 17 :
Tính
A.
-1
B.
1
C.
-2
D.
2
Câu 18 :
Cho hàm số với giá trị nào của m thì hàm số sau liên tục tại x=2
A.
m=1/2
B.
m=1/8
C.
m=1/16
D.
m=1/4
Câu 19 :
Hàm số chỉ gián đoạn tại các điểm
A.
x=1
B.
x=-2
C.
Đáp án khác
D.
x=-2 và x=1
Câu 20 :
Cho hàm số . Khẳng định nào sau đây là đúng
A.
Hàm số chỉ có giới hạn trái tại điểm
B.
Hàm số chỉ có giới hạn phải tại điểm
C.
Hàm số có giới hạn tại điểm
D.
Hàm số có giới hạn trái và giới hạn phải bằng nhau
Câu 21 :
Tính
A.
0
B.
2
C.
3
D.
1
Câu 22 :
Cho phương trình msin2x + sinx – cosx =0 (1), m là tham số. Mệnh đề nào sau đây đúng?
I. Trong khoảng , phương trình (1) không có nghiệm nào cả
3
1
lim 7
x
xx
®-
+
333
lim ( ) ( ) lim ( ) lim ( )
ooo
xx xx xx
fx gx fx gx
®®®
+= +
3
3
lim ( ) ( ) lim [ ( ) ( )]
oo
xx xx
fx gx fx gx
®®
+= +
3
33
lim ( ) ( ) lim ( ) lim ( )
ooo
xx xx xx
fx gx fx gx
®®®
+= +
333
lim ( ) ( ) lim [ ( ) ( )]
oo
xx xx
fx gx fx fx
®®
+= +
1
3
lim
2
x
x
x
®
-
1
3
lim
2
x
x
x
®
-
-
1
3
lim
2
x
x
x
®
-
-
2
2
2
lim
2
x
x
x
®-
+
-
1
22
-
2
1
32
lim
1
x
xx
x
®-
++
-
2
1
43
lim
1
x
xx
x
®-
++
+
2
1
32
lim
1
x
xx
x
®-
++
+
2
1
32
lim
1
x
xx
x
®-
++
-
1
x
2
x
(2) 12 0, (0) 2 0, (1) 2 0ff f=> =-< =-<
4
() 2fx x x=--
!
(2) (0) 24 0ff=- <
1
(0; 2)x Î
(2) (1) 24 0ff=- <
2
(1;2)x Î
1
x
2
x
0
1
lim 1
x
x
x
®
æö
-
ç÷
èø
2
22
2
4
2
x
khi x
x
y
m khi x
ì
+-
¹
ï
-
=
í
ï
=
î
3
25
32
x
y
xx
+
=
-+
1
()
2
fx
x
=
-
3
4
1
lim
(2 1)( 3)
x
xx
xx
®
-
--
;
22
pp
æö
-
ç÷
èø
! Trang!18!
II.- Trong khoảng , phương trình (1) có nghiệm
III. x = 0 là một nghiệm của (1).
A.
Chỉ I
B.
Chỉ II và III
C.
Chỉ I và III
D.
Chỉ II
Câu 23 :
Xác định
A.
B.
1
C.
D.
-1
Câu 24 :
Hàm nào trong các hàm sau có giới hạn tại điểm
A.
B.
C.
D.
Câu 25 :
Kết quả của giới hạn (với k nguyên dương) là
A.
x
B.
0
C.
D.
www.thuvienhoclieu.com
ĐỀ 8
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I. Trắc nghiệm
Câu 1: Giới hạn của hàm số sau đây bằng bao nhiêu:
A. 0 B. 1 C. + D. 2
Câu 2: Kết quả của
là
A. 2 B. 1 C. D.
Câu 3: Kết quả của bằng bao nhiêu?
A. 0 B. 1 C. + D. 2
Câu 4: Kết quả của
là
A. 1 B. .
.
C. -1 D.
Câu 5: Kết quả của
là
A. -8 B. 6 C. -6 D. 8
Câu 6: Cho hàm số: để f(x) liên tục trên R thì a bằng?
A. -2 B. 4 C. 2 D. 1
Câu 7: Dãy số nào sau đây có giới hạn bằng ?
A. B. C. D.
Câu 8: Tổng của một cấp số nhân này là?
;
22
pp
æö
-
ç÷
èø
2
(1)
32
lim
1
x
xx
x
-
®-
++
+
1
()
2
fx
x
=
-
1
()
2
fx
x
=
-
1
()
2
fx
x
=
-
1
()
2
fx
x
=
-
1
lim
k
x
x
®-¥
2
lim ( 2 )
x
xxx
®+¥
++
¥
2
1
22
lim
1
x
x
x
®
-
-
1
2
1
2
-
2
2
231
lim
42
nn
nn
+-
--
¥
(1)
32
lim
1
x
x
x
-
®-
+
+
2
2
lim 5
x
xx
®
-
2
ax 3 1
()
11
khi x
fx
x x khi x
-³
ì
=
í
+- <
î
1
3
2
2
2
53
n
nn
u
nn
-
=
+
2
2
12
53
n
n
u
nn
-
=
+
2
2
72
53
n
n
u
nn
-
=
+
2
12
53
n
n
u
nn
-
=
+
( )
n1
n
1
111
, , ,..., ,...
3 9 27 3
+
-
-
! Trang!19!
A. B. C. D. 4
Câu 9: Cho hàm số . Xét phương trình: . Trong các mệnh
đề sau, tìm mệnh đề sai?
A. (1) có nghiệm trên khoảng (-1; 1) B. (1) có nghiệm trên khoảng (0; 1)
C. Vô nghiệm D. (1) có nghiệm trên R
Câu 10: Kết quả của là
A.
B. C. -3
D.
II. Tự luận
-----------------------------------------------
Câu 1: Tính các giới hạn sau:
a) b) c)
Câu 2: Xét tính liên tục của hàm số sau tại điểm :
.
Câu 3: Chứng minh rằng phương trình sau luôn có nghiệm với mọi m:
----------- HẾT ----------
www.thuvienhoclieu.com
ĐỀ 9
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I. Phần Trắc Nghiệm:
Câu 1. Giới hạn bằng bao nhiêu?
A.2 B. 0 C. D.
Câu 2. Giới hạn bằng bao nhiêu?
A.1 B. -1 C.0 D.
Câu 3. Giới hạn bằng bao nhiêu?
A.1 B. 2 C.
D.
Câu 4. Giới hạn bằng bao nhiêu?
A. B. C. D.
1
4
1
2
3
4
( ) ( )
0 1fx=
+-
-
42.2 6.7
lim
83.7
nn
nn
0
1
5
2
1
23
lim
4
x
x
x
®
-+
-
32
3
326
lim
3
x
xx x
x
®-
+++
+
(
)
2
lim 9 2 3
x
xxx
®+¥
+-
2x =
2
213
2
2
()
4
2
3
x
khi x
x
fx
khi x
ì
+-
¹
ï
ï
-
=
í
ï
=
ï
î
( )
( )
2
3240mm x++ - +=
(
)
2
lim 4 2nn n+-
1
4
-¥
32
1
64
lim
1
x
xx x
x
®
+-+
-
+¥
2
4
lim
9
x
x
x
®+¥
+
-
-¥
+¥
(
)
2
lim 9 5
x
xxx
®-¥
+-
5
4
5
2
+¥
-¥
! Trang!20!
Câu 5. Tổng Có giá trị là:
A. B. C. D.
Câu 6. Giới hạn bằng bao nhiêu?
A. -35 B. 1 C. 5 D.
-5
Câu 7. Giới hạn bằng bao nhiêu?
A.
B. C. D.
Câu 8. Giới hạn bằng bao nhiêu?
A. 8. B.
C. 4 D.
Câu 9.
A.-4 B. -3 C.-2 D. 2
Câu 10.
A. B. - C.0 D.
II. Phần Tự Luận:
Câu 1(2 đ):Tính giới hạn của các hàm số sau:
a) b)
Câu 2(2 đ): Xét tính liên tục của hàm số sau trên tập số thực R.
Câu 3(1 đ): Chứng minh phương trình sau có ít nhất một nghiệm :
...
3
1
...
3
1
3
1
2
++++=
n
S
3
1
2
1
9
1
4
1
nn
nn
72
7.52
lim
+
-
2
1
42
lim
1
x
x
x
+
®-
+
-
1
2
-¥
+¥
2
7
3
2
0
41 16
lim
42
x
xx
x
®
+- +
+-
20000
2499
20000
4999
( ) ( )
3
3
1
22 1
,lim
31
x
x x khi x
fx fx
x x khi x
-
®
ì
-³
ï
=
í
-<
ï
î
( ) ( )
2
1
23
1
1
,lim
1
1
8
x
x
khi x
x
fx fx
khi x
-
®
ì
-+
¹
ï
ï
-
=
í
ï
=
ï
î
1
8
1
8
+¥
2
lim ( 2 )
x
xxx
®+¥
--
2
1
32
lim
1
x
x
x
®
+-
-
2
34
...... ... 1
()
1
5...................... ... 1
xx
khi x
fx
x
khi x
ì
+-
¹
ï
=
-
í
ï
=
î
32
32510xxx+--=
! Trang!21!
www.thuvienhoclieu.com
ĐỀ 10
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I.Phần Trắc Nghiệm:
Câu 1. Giới hạn bằng bao nhiêu?
A.1 B. 2 C.
D.
Câu 2. Giới hạn bằng bao nhiêu?
A.2 B. 0 C. D.
Câu 3. Giới hạn bằng bao nhiêu?
A.1 B. -1 C.0 D.
Câu 4. Giới hạn bằng bao nhiêu?
A.
B. C. D.
Câu 5. Giới hạn bằng bao nhiêu?
A. B. C. D.
Câu 6. Giới hạn bằng bao nhiêu?
A.1 B.3 C.
-3
D.-1
Câu 7. Giới hạn bằng bao nhiêu?
A. 8. B.
C. 4 D.
Câu 8. Tổng Có giá trị là:
A. - B. C.1 D. -
Câu 9.
A.11 B. 7 C.-1 D. -13
Câu 10.
A.-1 B. 0 C.-2 D.+
2
4
lim
9
x
x
x
®+¥
+
-
-¥
+¥
(
)
2
lim 4 2nn n+-
1
4
-¥
32
1
64
lim
1
x
xx x
x
®
+-+
-
+¥
2
1
42
lim
1
x
x
x
+
®-
+
-
1
2
-¥
+¥
2
7
(
)
2
lim 9 5
x
xxx
®-¥
+-
5
4
5
2
+¥
-¥
n
n
21
32
lim
-
+
3
2
0
41 16
lim
42
x
xx
x
®
+- +
+-
20000
2499
20000
4999
...
2
)1(
...
8
1
)
4
1
(
2
1
1
+
-
+++-+=
+
n
n
S
3
1
3
1
3
2
( ) ( )
2
2
31 2
,lim
53 2
x
x x khi x
fx fx
x khi x
-
®
ì
-+ <
=
í
-³
î
( ) ( )
2
1
1
1
,lim
1
22 1
x
x
khi x
fx fx
x
x khi x
-
®
ì
-
<
ï
=
-
í
ï
-³
î
¥
! Trang!22!
II. Phần Tự Luận:
Câu 1(2 đ):Tính giới hạn của các hàm số sau:
a) b)
Câu 2(2 đ): Xét tính liên tục của hàm số sau trên tập số thực R.
Câu 3(1 đ): Chứng minh phương trình sau có ít nhất một nghiệm :
2
lim ( 2 )
x
xxx
®+¥
--
2
1
32
lim
1
x
x
x
®
+-
-
2
34
...... ... 1
()
1
5...................... ... 1
xx
khi x
fx
x
khi x
ì
+-
¹
ï
=
-
í
ï
=
î
32
32510xxx+--=
! Trang!23!
www.thuvienhoclieu.com
ĐỀ 11
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I.Phần Trắc Nghiệm:
Câu 1. Giới hạn bằng bao nhiêu?
A. 2 B. 0 C. D.
Câu 2. Giới hạn bằng bao nhiêu?
A.1 B. -1 C. 0 D.
Câu 3. Giới hạn bằng bao nhiêu?
A.1 B. 2 C.
D.
Câu 4. Giới hạn bằng bao nhiêu?
A. B. C. D.
Câu 5. Giới hạn bằng bao nhiêu?
A.
B. C. 0,666 D. 0
Câu 6. Tổng Có giá trị là:
B. - B. C.-1 D. -
Câu 7. Giới hạn bằng bao nhiêu?
A .-1 B.
1
C. D. -
Câu 8. Giới hạn bằng bao nhiêu?
A. 8. B.
C.
D. 4
Câu 9.
A.-4 B. -3 C.-2 D. 2
(
)
2
lim 4 8 2nnn+-
1
4
-¥
3
1
264
lim
1
x
xx
x
®
-+
-
+¥
2
7
lim
9
x
x
x
®+¥
-
-
-¥
+¥
(
)
2
lim 9 16 2
x
xxx
®-¥
+-
5
4
5
2
+¥
-¥
2
2
2
473
lim
4
x
x
x
®-
--
-
19
30
2
3
...
2
)1(
...)
8
1
(
4
1
2
1
+
-
++-++-=
n
n
S
3
1
2
1
4
1
nn
n
32.3
13
lim
-
+
3
1
3
1
3
2
0
14 6 1
lim
11
x
xx
x
®
-+ -
+-
20000
4999
20000
2499
( ) ( )
3
3
1
22 1
,lim
31
x
x x khi x
fx fx
x x khi x
-
®
ì
-³
ï
=
í
-<
ï
î
! Trang!24!
Câu 10.
A. B. - C.0 D.
II. Phần Tự Luận:
Câu 1(2 đ):Tính giới hạn của các hàm số sau:
a) b)
Câu 2(2 đ): Xét tính liên tục của hàm số sau trên tập số thực R.
Câu 3(1 đ): Chứng minh phương trình sau có ít nhất một nghiệm : x
5
- 5x
3
+ 4x -1 = 0
( ) ( )
2
1
23
1
1
,lim
1
1
8
x
x
khi x
x
fx fx
khi x
-
®
ì
-+
¹
ï
ï
-
=
í
ï
=
ï
î
1
8
1
8
+¥
)5(lim
2
xxx
x
--
-¥®
x
x
x
2
191
lim
0
-+
®
( )
2
23
khi 1
1
1
1
8
x
x
x
yfx
khi x
ì
-+
¹
ï
ï
-
==
í
ï
=
ï
î
! Trang!25!
-----------------Hết-----------------
www.thuvienhoclieu.com
ĐỀ 12
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I. Phần Trắc Nghiệm:
Câu 1. Giới hạn bằng bao nhiêu?
A. B. C. D.
Câu 2. Giới hạn bằng bao nhiêu?
A. 2 B. 0 C. D.
Câu 3. Giới hạn bằng bao nhiêu?
A.1 B. 2 C.
D.
Câu 4. Giới hạn bằng bao nhiêu?
A.1 B. -1 C. 0 D.
Câu 5. Giới hạn bằng bao nhiêu?
A.
B. C. 0,666 D. 0
Câu 6. Tổng Có giá trị là:
A. B. C. D.
Câu 7. Giới hạn bằng bao nhiêu?
A. 8. B.
C.
D. 4
Câu 8. Giới hạn bằng bao nhiêu?
A .- B. -
1
C. D.
Câu 9.
A.11 B. 7 C.-1 D. -13
(
)
2
lim 9 16 2
x
xxx
®-¥
+-
5
4
5
2
+¥
-¥
(
)
2
lim 4 8 2nnn+-
1
4
-¥
2
7
lim
9
x
x
x
®+¥
-
-
-¥
+¥
3
1
264
lim
1
x
xx
x
®
-+
-
+¥
2
2
2
473
lim
4
x
x
x
®-
--
-
19
30
2
3
...
3
1
...
3
1
3
1
2
++++=
n
S
3
1
2
1
9
1
4
1
3
2
0
14 6 1
lim
11
x
xx
x
®
-+ -
+-
20000
4999
20000
2499
13.22
13
lim
+-
-
nn
n
2
1
2
1
2
3
( ) ( )
2
2
31 2
,lim
53 2
x
x x khi x
fx fx
x khi x
-
®
ì
-+ <
=
í
-³
î
! Trang!26!
Câu 10.
A.-1 B. 0 C.-2 D.+
II. Phần Tự Luận:
Câu 1(2 đ):Tính giới hạn của các hàm số sau:
a) b)
Câu 2(2 đ): Xét tính liên tục của hàm số sau trên tập số thực R.
Câu 3(1 đ): Chứng minh phương trình sau có ít nhất một nghiệm : x
5
- 5x
3
+ 4x -1 = 0
( ) ( )
2
1
1
1
,lim
1
22 1
x
x
khi x
fx fx
x
x khi x
-
®
ì
-
<
ï
=
-
í
ï
-³
î
¥
)5(lim
2
xxx
x
--
-¥®
x
x
x
2
191
lim
0
-+
®
( )
2
23
khi 1
1
1
1
8
x
x
x
yfx
khi x
ì
-+
¹
ï
ï
-
==
í
ï
=
ï
î
! Trang!27!
www.thuvienhoclieu.com
ĐỀ 13
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I.PHẦN TRẮC NGHIỆM: (7đ)
Câu 1: Trong các giới hạn sau giới hạn nào có giá trị hữu hạn
Câu
2:
Giới
hạn bằng
A.
Câu 3: Giới hạn bằng
A.
Câu 4 :Giới hạn bằng
A.
Câu 5: Tìm
A. B. C. D.
Câu 6: Giới hạn bằng
A.
Câu 7: Giới hạn bằng
A.
Câu 8: Giới hạn bằng
A.
Câu 9: Giới hạn . giá trị của a là:
A.
Câu 10: Giới hạn bằng
A.
1
1
lim
3
5
1
+
+
-®
x
x
x
1.
5
3
.
3
5
.0 DCB
)73.2(2
6.232
lim
1
11
+
++
-
++
nn
nnn
0.18..2 DCB ¥+
1..
5
1
.
5
1
DCB ¥-
-
22
41
lim
23
x
xx x
x
®-¥
-- +
+
1
2
+¥
1
2
-
-¥
2
2
0
11
lim
x
xxx
x
++-+
®
0..1.
2
1
DCB ¥---
xxx
x
x
++
+
-¥®
2
253
20172
lim
1.
8
1
.2.1 -- DCB
1
1
lim
2
7
1
-
+
-®
x
x
x
1.
2
7
.
2
7
.0 DCB
-
(
)
62017lim
2
=+++
-¥®
xaxx
x
6.12.12.6 -- DCB
22
2
2)2(
lim
ax
axax
ax
-
+++
-®
a
a
DaCaBa
2
2
.1..1
-
+-
20172
32
lim.
43
201749
lim.
12
20172
lim.
42
20172
lim.
2
4
4
4
2
3
4
5
--
-
+
+
--
-
--
-
n
n
D
n
n
C
n
n
B
n
n
A
! Trang!28!
Câu 11: Cho hàm số . Khi đó bằng
A.
Câu 12: Giới hạn bằng
A.
Câu 13: Cho hàm số . Khi đó bằng
A. không tồn tại.
Câu 14: Giới hạn bằng
A.
Câu 15: Giới hạn bằng
A.
Câu 16: Cho hàm số . Khi đó giá trị tham số m để
liên tục tại x=4 là:
A.
Câu 17: Cho hàm số . Khi đó giá trị m để liên tục tại
x=0 là:
A.
Câu 18: Cho hàm số . Khi đó có tính chất:
A.liên tục trên các khoảng nhưng không liên tục tại x= -1
B .liên tục tại x= -1
C. liên tục tại mọi điểm
D. liên tục tại x= -1; x=4; x=0
ï
ï
î
ï
ï
í
ì
=
¹
-
+-+
=
1;
8
1
1;
1
322
)(
2
x
x
x
xx
xf
)(lim
1
xf
x®
0.1.
8
1
.
8
1
DCB
-
1169
344
lim
4
24
1
-+
+-
-®
xx
xxx
x
¥+.
3
2
.
4
6
.
8
1
DCB
ï
î
ï
í
ì
³-
<
-
+-
=
1;35
1;
1
34
)(
2
xkhix
xkhi
x
xx
xf
)(lim
1
xf
x®
.4.2.2 DCB -
x
aax
x
33
0
)(
lim
+-
®
2222
3.7.2. aDaCaBa
x
x
x
1
4
3
2
lim
0
-
+
®
3.
2
1
.3.
4
3
-DCB
ï
î
ï
í
ì
=+
¹
-
+-+
=
4;32
4;
4
512
)(
xm
x
x
xx
xf
)(xf
2
5
.
6
11
.
24
17
.
6
1
DCB
--
ï
ï
î
ï
ï
í
ì
=-
¹
-+
=
0;
4
5
2
0;
24
)(
xm
x
x
x
xf
)(xf
1.2.
4
3
.3 DCB
î
í
ì
-=+
-¹+
=
1;20172
1;32
)(
2
xx
xx
xf
)(xf
( ) ( )
+¥--¥- ;11; va
! Trang!29!
Câu 19: Cho hàm số . Xét phương trình: f(x) = 0 (1) trong các
mệnh đề sau, mệnh đề nào đúng?
A. (1) Vô nghiệm B. (1) có nghiệm trên khoảng (1; 2)
C. (1) có 5 nghiệm trên R D. (1) có ít nhất một nghiệm dương
Câu 20: Cho một hàm số . Mệnh đề nào sau đây là đúng:
A. Nếu liên tục trên đoạn thì phương trình không có
nghiệm trên khoảng .
B. Nếu thì phương trình có ít nhất một nghiệm trong khoảng
.
C. Nếu phương trình có nghiệm trong khoảng thì hàm số phải liên
tục trên khoảng
D. Nếu hàm số liên tục, tăng trên đoạn và thì phương trình
không có nghiệm trong khoảng .
II.PHẦN TỰ LUẬN (3đ)
Xét tính liên tục của hàm số tại điểm .
………………………..HẾT………………………………………………
ĐÁP ÁN PHẦN TỰ LUẬN
NỘI DUNG
ĐIỂM
0,25x2
0,25x2
Vì
0,25x2
f(-1)=-3/2
0,5
Vì nên f(x) liên tục tại x=-1
0,5x2
223)(
3
-+= xxxf
()fx
()fx
[;]; (). () 0ab f a f b >
() 0fx=
(;)ab
().() 0fa fb<
() 0fx=
(;)ab
() 0fx=
(;)ab
()fx
(;)ab
()fx
[;]ab
().() 0fa fb>
() 0fx=
(;)ab
ï
ï
î
ï
ï
í
ì
-³--
-<
-
+
=
1
2
1
1
1
1
)(
2
2
3
xkhix
xkhi
x
x
xf
1
0
-=x
2
3
)
1
1
(lim)(lim
2
11
-
=
-
+-
=
--
-®-®
x
xx
xf
xx
2
3
)
2
1
(lim)(lim
2
11
-
=--=
++
-®-®
xxf
xx
2
3
)(lim)(lim)(lim
1
11
-
=Þ=
-®
-®-®
+-
xfxfxf
x
xx
2
3
)1()(lim
1
-
=-=
-®
fxf
x
! Trang!30!
www.thuvienhoclieu.com
ĐỀ 14
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I) PHẦN TRẮC NGHIỆM (8 điểm - mỗi câu 0.4 điểm)
Câu 1: Trong bốn giới hạn sau đây, giới hạn nào bằng 2?
A. . B. . C. . D.
.
Câu 2: Trong bốn giới hạn sau đây, giới hạn nào bằng 0?
A. B. .
C. . D. .
Câu 3: Chọn kết quả đúng trong các kết quả sau: bằng:
A. 0. B. . C. . D. 1.
Câu 4: Chọn kết quả đúng trong các kết quả sau: bằng:
A. . B. 1. C. . D. 0.
Câu 5: Giả sử và (L, M ). Khẳng định nào sau đây sai?
A. . B. .
C. . D. .
Câu 6: Chọn kết quả đúng trong các kết quả sau: bằng:
A. 2. B. . C. 1. D. .
Câu 7: Chọn mệnh đề sai trong các mệnh đề sau:
A. Hàm số liên tục trên toàn bộ tập . B. Hàm số liên tục trên
toàn bộ tập .
C. Hàm số liên tục trên toàn bộ tập . D. Hàm số liên
tục trên tập .
Câu 8: Chọn kết quả đúng trong các kết quả sau: bằng:
A. B. 2. C. . D. .
Câu 9: Cho hàm số . Tìm khẳng định đúng trong các khẳng định sau:
A. Hàm số f liên tục tại mọi điểm .
( )
3
lim 4 10
x
x
®
-
2
1
1
lim
21
x
x
x
®
-
+
2
2
1
lim
21
x
x
xx
®+¥
-
++
( )
2
2
lim 3 1
x
xx
®
+-
(
)
22
lim 2 2 3 1nn n-+- +
( )
( )
( )
3
32
51 4
lim
12
nnn
nn
++-
+-
2016
2017
3 si nn
lim
1
n
n
+
+
2
2
23
lim
nn
n
-+ -
-¥
1-
3
32
2
21
lim
21
x
xx
x
®-¥
++
+
2
2
2
2
-
( )
0
lim
xx
fx L
®
=
( )
0
lim
xx
gx M
®
=
Î !
( ) ( )
0
lim . .
xx
fxgx LM
®
éù=
ëû
( )
0
3
3
lim
xx
fx L
®
=
( ) ( )
0
lim
xx
fx gx L M
®
é+ù=+
ëû
( )
0
lim
xx
fx L
®
=
2
21
lim
2
x
x
x
®
-
+
5
4
3
4
sinyx=
!
35
1
x
y
x
+
=
+
!
2
4
1
x
y
x
-
=
+
!
32
257yx x x=+ -+
!
2
2
(3)
253
lim
(3)
x
xx
x
+
®-
+-
+
1
2
-¥
+¥
( )
4
2
khi x 0, x -1
3 khi x 1
1 khi 0
xx
xx
fx
x
ì
+
¹¹
ï
+
ï
ï
==-
í
ï
=
ï
ï
î
x Î !
! Trang!31!
B. Hàm số f liên tục tại mọi điểm trừ điểm x = -1.
C. Hàm số f liên tục tại mọi điểm trừ các điểm x thuộc .
D. Hàm số f liên tục tại mọi điểm trừ điểm x = 0.
Câu 10: Cho hàm số Với giá trị nào của thì hàm số liên tục tại x = 2
A. a = 2. B. a = 4. C. a = -2. D. a = 1.
Câu 11: Chọn kết quả đúng trong các kết quả sau: bằng:
A. 0. B. -1. C. 1. D. 4.
Câu 12: Chọn kết quả đúng trong các kết quả sau: bằng:
A. 0. B. 1. C. 2. D. .
Câu 13: Cho . Giá trị của S bằng:
A. . B. . C. . D. 1.
Câu 14: Cho hàm số . Kết quả nào sau đây là đúng?
A. B. C. . D.
.
Câu 15: Cho phương trình : x
5
– 3x
4
+ 5x – 2 = 0. Các mệnh đề sau mệnh đề nào đúng
A. Phương trình vô nghiệm trong khoảng ( -2 ; 5)
B. Phương trình có ít nhất 3 nghiệm nằm trong khoảng ( -2 ; 5).
C. Phương trình đúng 2 nghiệm nằm trong khoảng ( -2 ; 5)
D. Phương trình có đúng 1 nghiệm nằm trong khoảng ( -2 ; 5)
Câu 16: Chọn kết quả đúng trong các kết quả sau: bằng:
A. . B. 1. C. 0. D. .
Câu 17: Chọn kết quả đúng trong các kết quả sau: bằng:
A. . B. . C. . D. .
Câu 18: Chọn kết quả đúng trong các kết quả sau: bằng:
A. . B. . C. 0. D. .
Câu 19: Chọn kết quả đúng trong các kết quả sau: bằng.
A. . B. . C. 1. D. .
Câu 20: Chọn kết quả đúng trong các kết quả sau: bằng:
A. 5. B. . C. -5. D. .
[ ]
1; 0-
( )
2
4
khi x 2
2
khi x = 2
x
fx
x
a
ì
-
¹
ï
=
-
í
ï
î
a
42
lim
4 2.3
nn
nn
+
-
1
lim
n
n
+
+¥
( )
1
1
11
... ...
39 3
n
n
S
+
-
=-++ +
3
4
1
2
1
4
( )
2 1 khi 1
2 khi 1
xx
fx
x
-<
ì
=
í
³
î
( )
1
lim 2
x
fx
®
=
( ) ( )
11
lim lim
xx
fx fx
+-
®®
=
( )
1
lim 3
x
fx
-
®
=
( )
1
lim 2
x
fx
+
®
=
2
2
1 4 4 ... 4
lim
1 3 3 ... 3
n
n
++ + +
++ + +
4
3
+¥
2
2
325
lim
27
n
xx
x
®+¥
-+-
-
3
2
1
2
3
2
-
5
7
2
2
434
lim
96
x
xxx
xxx
®-¥
+-
+-
1-
-¥
3
2
2
2
1
43
lim
45
x
xx
xx
®
-+
+-
2
3
1
3
-
1
2
2
3
lim 8
x
x
®
-
38-
3
! Trang!32!
II) PHẦN TỰ LUẬN (2 điểm - mỗi câu 1 điểm)
Câu 1. (1đ) Tính giới hạn:
Câu 2. (1đ) Cho 3 số thực a,b,c khác không và thỏa . Chứng minh
rằng phương trình có nghiệm thuộc khoảng
------ HẾT ------
www.thuvienhoclieu.com
ĐỀ 15
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I/TRẮC NGHIỆM(6đ): Chọn câu trả lời đúng
Câu 1. Tổng của cấp số nhân lùi vô hạn là
A. 1 B. C. -1 D.
Câu 2. Dãy số nào sau đây có giới hạn là ?
A. B. C. D.
Câu 3. Cho một hàm số xác định trên khoảng (a;b). Khẳng định nào sau đây là đúng ?
A. Nếu hàm số liên tục trên đoạn và thì phương trình có nghiệm
trong khoảng .
B. Nếu phương trình có nghiệm trong khoảng thì hàm số liên tục trên khoảng
C. Nếu liên tục trên đoạn thì pt có nghiệm trên khoảng .
D. Nếu thì phương trình có ít nhất một nghiệm trong khoảng .
Câu 4. Giới hạn (a/b tối giản) có a+b bằng
A. 21 B. 11 C. 19 D. 51
Câu 5. bằng :
A. không tồn tại B. 1 C. D. 2
Câu 6. Tính : A. B. C. D.
Câu 7. Hàm số nào trong các hàm sau có giới hạn tại điểm x=2 ?
A. B. C. D.
Câu 8. Dãy số nào sau đây có giới hạn bằng 0?
A. B. C. D.
2
1
235
lim
1
x
xx
x
®
+-
-
3470abc++=
2
0ax bx c++=
( )
0;1
11 1 1 1
, , , ..., ,...
2 4 8 16 2
n
æö
-- -
ç÷
èø
1
2
1
3
-
+¥
23
34
n
unn=-
2
3
221
4
n
nn
u
n
+-
=
+
2
2
2
n
nn
u
n
-
=
-
2
3 13
n
un n=-
().() 0fa fb<
[ ]
; ; f(a).f(b)=0ab
2
53 3
lim
2(3 2)
nna
nb
+
=
+
1 3 5 ... (2 1)
lim
2(2 3)
n
nn
+++ + -
-
1
4
2
lim ( 2 3 4 )
x
xx x
®+¥
-+-
3
21
-
+
+¥
21-
-¥
1
()
1
fx
x
=
+
1
()
2
fx
x
=
-
2
2
()
4
x
fx
x
=
-
13
()
2
fx
x
=
-
6
5
n
æö
ç÷
èø
2
3
n
æö
-
ç÷
èø
3
3
1
nn
n
-
+
2
4nn-
! Trang!33!
Câu 9. bằng: A. - B. C. D.
Câu 10. Hàm số Giá trị m để f(x) liên tục tại x=1 là:
A. B. C. m=1 D. m=0
Câu 11. Trong các dãy số sau, dãy số nào có giới hạn hữu hạn?
A. B. C. D.
Câu 12. Hàm số nào sau đây liên tục tại x=2 ?
A. B. C. D.
Câu 13. Tính Khi đó đặt P=a+b ta có P = : A. 6 B. 7 C. 5 D. 10
Câu 14.
Phương trình có mấy nghiệm ?
A. 4 B. 3 C. 5 D. 1
Câu 15. Cho hàm số: để f(x) liên tục tại điêm x
0
= 2 thì a bằng ?
A. 4 B. 6 C. 8 D. Không có giá trị a
II/TỰ LUẬN (4đ):
Câu 1 (2đ) :a/ Tính giới hạn:
b/ Tính giới hạn:
Câu 2 (2đ) : a) Tìm m để hàm số liên tục tại .
b) Chứng minh phương trình sau luôn có nghiệm với mọi giá trị của m:
23
2
1
2
lim
523
x
xx
xx
®
-
-+
1
5
-¥
1
6
2
5
2
32
(x>1)
1
()
1
(x 1)
4
x
x
fx
mm
ì
+-
ï
ï
-
=
í
ï
++ £
ï
î
{ }
0;1m Î
{ }
0; 1m Î-
2.5 12
32
n
n
n
u
-
=
-
1
6
3
n
n
n
u
æö
=+
ç÷
èø
43
4
32
24
n
nn
u
nn
-+
=
-+ -
3
2
233
5
n
nn
u
n
-+
=
-+
2
261
()
2
xx
fx
x
++
=
+
1
()
2
x
fx
x
+
=
-
2
1
()
2
xx
fx
x
++
=
-
2
2
32
()
4
xx
fx
x
--
=
-
2
3
26
lim
3
x
x
ab
x
®
-
=
-
54 2
32540xx xx-++-=
3
8
( 2)
()
2
2 4 ( 2)
x
x
fx
x
ax
ì
-
¹
ï
=
-
í
ï
-=
î
3
1
32 21
lim
1
x
xx
x
®
-- -
-
3
3
2
2
32( 31)6
lim ;
4
x
xxx
x
®
+-+-
-
ì
++
ï
¹-
=
í
+
ï
=-
î
xx
, x
fx
x
mx x
2
2
32
2
()
2
3, 2
2=-x
2016
2 ( 1) ( 2) 2x-3=0mx x--+
! Trang!34!
www.thuvienhoclieu.com
ĐỀ 16
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I/TRẮC NGHIỆM(6đ): Chọn câu trả lời đúng
Câu 1. Trong các hàm số sau hàm số nào liên tục trên R ?
A. B. C. D. y= tan3x
Câu 2. Tính : A. -2 B. C. 3 D.
Câu 3. Tính : A. 1 B. 0 C. D. 3/2
Câu 4. Giới hạn
bằng: A. 3/2
B. 3
C. -3/2
D. Không tồn tại.
Câu 5. Dãy số nào sau đây có giới hạn khác 0?
A. B. C. D.
Câu 6. Giới hạn bằng: A. -2 B. 3 C. -5 D. 5
Câu 7. ; (a;b nguyên). Khi đó a+b bằng:
A. 9 B. 19 C. 8 D. 21
Câu 8. bằng: A. 17/2 B. C. D.
Câu 9. bằng: A. 8/3 B. 10/3 C. 3 D. 1
Câu 10. Tính : A. -3/2 B. 0 C. 5/2 D. 3/2
Câu 11. bằng :
A. 1 B. không tồn tại C. 2 D.
Câu 12. Dãy số nào sau đây có giới hạn bằng 0?
A. B. C. D.
Câu 13. Tổng của cấp số nhân lùi vô hạn là
A. -1 B. C. 1 D.
Câu 14. Cho một hàm số xác định trên khoảng (a;b). Khẳng định nào sau đây là đúng ?
A. Nếu thì phương trình có ít nhất một nghiệm trong khoảng .
3
1 cos
x
y
x
-
=
-
3
2
21
2
xx
y
x
-+
=
+
32
256
1
xx
y
x
-+
=
+
2
34
lim
23
x
x
xx
+
®
+
--
1
3 3.5
lim
25
nn
n+
+
-
3
5
-
2
1
31
lim
1
x
x
x
®
-
-
2
2
21
34
n
n
+
+
2
3
5
n
æö
ç÷
èø
3
3
nn+
2
4
3n +
2
34
lim
1
x
xxx
x
®-¥
++
+
43
4
522
lim
16 9 5
x
xx a
xx b
®+¥
++
=
++
2
18 1 5
lim
27
x
xx
x
®+¥
+- +
-
+¥
23
3
32
2
2
91 2
lim
33
nn
n
+- +
-
(
)
2
lim 3nnn--
1 3 5 ... (2 1)
lim
2(2 3)
n
nn
+++ + -
-
1
4
3
3
1
nn
n
-
+
2
3
n
æö
-
ç÷
èø
6
5
n
æö
ç÷
èø
2
4nn-
11 1 1 1
, , , ..., ,...
2 4 8 16 2
n
æö
-- -
ç÷
èø
1
3
-
1
2
! Trang!35!
B. Nếu phương trình có nghiệm trong khoảng thì hàm số liên tục trên khoảng
C. Nếu liên tục trên đoạn thì pt có nghiệm trên khoảng .
D. Nếu hàm số liên tục trên đoạn và thì phương trình có nghiệm
trong khoảng .
Câu 15. Cho hàm số: để f(x) liên tục tại điêm x
0
= 2 thì a bằng ?
A. 6 B. 8 C. 4 D. Không có giá trị a
II/TỰ LUẬN (4đ):
Câu 1 (2đ) :a/ Tính giới hạn:
b/ Tính giới hạn:
Câu 2 (2đ) : a) Tìm m để hàm số liên tục tại .
b) Chứng minh phương trình sau luôn có nghiệm với mọi giá trị của m :
www.thuvienhoclieu.com
ĐỀ 17
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I/TRẮC NGHIỆM(6đ): Chọn câu trả lời đúng
Câu 1. Tính : A. B. C. D.
Câu 2. bằng: A. 3 B. 10/3 C. 8/3 D. 1
Câu 3. Dãy số nào sau đây có giới hạn bằng 0?
A. B. C. D.
Câu 4. Cho một hàm số xác định trên khoảng (a;b). Khẳng định nào sau đây là đúng ?
A. Nếu phương trình có nghiệm trong khoảng thì hàm số liên tục trên khoảng
B. Nếu liên tục trên đoạn thì pt có nghiệm trên khoảng .
C. Nếu hàm số liên tục trên đoạn và thì phương trình có nghiệm
trong khoảng .
D. Nếu thì phương trình có ít nhất một nghiệm trong khoảng .
Câu 5.
Phương trình có mấy nghiệm ?
A. 4 B. 1 C. 3 D. 5
Câu 6. bằng: A. 17/2 B. C. D.
[ ]
; ; f(a).f(b)=0ab
().() 0fa fb<
3
8
( 2)
()
2
2 4 ( 2)
x
x
fx
x
ax
ì
-
¹
ï
=
-
í
ï
-=
î
3
1
731
lim
1
x
xx
x
®
+- +
-
3
3
2
2
6( 3) 6
lim ;
4
x
xxx
x
®
+---
-
ì
--
ï
¹-
=
í
+
ï
=-
î
xx
, x
fx
x
mx x
2
310
2
()
2
2, 2
2x =-
( )
22
2 4 ( 1) 2 - 1=0+-+mx x
2
lim ( 2 3 4 )
x
xx x
®+¥
-+-
3
21
-
+
+¥
21-
-¥
2
91 2
lim
33
nn
n
+- +
-
6
5
n
æö
ç÷
èø
2
3
n
æö
-
ç÷
èø
3
3
1
nn
n
-
+
2
4nn-
[ ]
; ; f(a).f(b)=0ab
().() 0fa fb<
54 2
32540xx xx-++-=
2
18 1 5
lim
27
x
xx
x
®+¥
+- +
-
32
2
23
3
+¥
! Trang!36!
Câu 7. Trong các dãy số sau, dãy số nào có giới hạn hữu hạn?
A. B. C. D.
Câu 8. Tính Khi đó đặt P=a+b có: A.7 B. 10 C. 5 D. 6
Câu 9. Dãy số nào sau đây có giới hạn là ?
A. B. C. D.
Câu 10. bằng : A. không tồn tại B. 2 C. D.
1
Câu 11. Tổng của cấp số nhân lùi vô hạn là
A. B. C. 1 D. -1
Câu 12. Tính : A. 3/2 B. 0 C. -3/2 D. 5/2
Câu 13. bằng: A. B. C. - D.
Câu 14. Giới hạn (a/b tối giản) có a+b bằng
A. 11 B. 19 C. 21 D. 51
Câu 15. Hàm số Giá trị m để f(x) liên tục tại x=1 là:
A. m=1 B. C. m=0 D.
II/TỰ LUẬN (4đ):
Câu 1 (2đ) :a/ Tính giới hạn:
b/ Tính giới hạn:
Câu 2 (2đ) : a) Tìm m để hàm số liên tục tại .
b) Chứng minh phương trình sau có ít nhất 2 nghiệm trên (-3;3):
2.5 12
32
n
n
n
u
-
=
-
43
4
32
24
n
nn
u
nn
-+
=
-+ -
1
6
3
n
n
n
u
æö
=+
ç÷
èø
3
2
233
5
n
nn
u
n
-+
=
-+
2
3
26
lim
3
x
x
ab
x
®
-
=
-
+¥
2
3
221
4
n
nn
u
n
+-
=
+
23
34
n
unn=-
2
3 13
n
un n=-
2
2
2
n
nn
u
n
-
=
-
1 3 5 ... (2 1)
lim
2(2 3)
n
nn
+++ + -
-
1
4
11 1 1 1
, , , ..., ,...
2 4 8 16 2
n
æö
-- -
ç÷
èø
1
2
1
3
-
(
)
2
lim 3nnn--
23
2
1
2
lim
523
x
xx
xx
®
-
-+
-¥
2
5
1
5
1
6
2
53 3
lim
2(3 2)
nna
nb
+
=
+
2
32
(x>1)
1
()
1
(x 1)
4
x
x
fx
mm
ì
+-
ï
ï
-
=
í
ï
++ £
ï
î
{ }
0; 1m Î-
{ }
0;1m Î
3
2
1
54 32
lim
1
x
xx
x
®
-- -
-
3
3
2
2
6(2 5 3) 6
lim ;
4
x
xxx
x
®
+---
-
ì
+-
ï
¹-
=
í
+
ï
=-
î
xx
, x
fx
x
mx x
2
2
2
2
()
2
,2
2x =-
432
995440xxxx-++-=
! Trang!37!
www.thuvienhoclieu.com
ĐỀ 18
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
Câu 1: Cho . Khi đó giá trị của a là:
A. -14 B. -30 C. 30 D. 14
Câu 2: Tính giới hạn ta được kết quả là:
A. - B. C. 0 D. 2
Câu 3: Tính giới hạn ta được kết quả là:
A. – 3 B. 1 C. 3 D. – 2
Câu 4: Tính giới hạn ta được kết quả là:
A. 3 B. - C. + D. 0
Câu 5: Tìm giới hạn ta được kết quả:
A. B. 2 C. 3 D. -
Câu 6: Tìm giới hạn ta được kết quả là:
A. 4 B. + C. - D. -1
Câu 7: Cho phương trình 2x
4
– 5x
2
+ x + 1 = 0 (1). Mệnh đề nào đúng trong các mệnh đề sau:
A. Phương trình (1) có ít nhất hai nghiệm thuộc khoảng (0; 2).
B. Phương trình (1) không có nghiệm trong khoảng (-2; 0).
C. Phương trình (1) không có nghiệm trong khoảng ( -1; 1).
D. Phương trình (1) chỉ có một nghiệm trong khoảng (-2; 1).
Câu 8: Tìm giới hạn ta được kết quả :
A. + B. - C. -1 D. 1
Câu 9: Tìm giá trị đúng của S = ta được kết quả là
A. B. 2 C. D.
Câu 10: Tìm giới hạn ta được kết quả là:
A. + B. C. -1 D. -
Câu 11: Tính giới hạn với ta được kết quả là:
A. ab B. a – b C. b – a D.
Câu 12: Để hàm số liên tục tại điểm x = 2 thì giá trị của a là:
A. 1 B. 2 C. 5 D. -3
2
1
lim( ax 5 ) 5
x
xx
®
++-=
1
21
lim
1
x
x
x
+
®
-+
-
¥
+¥
2
1
43
lim
1
x
xx
x
®
-+
-
52
lim (7 5 7)
x
xxx
®-¥
+-+
¥
¥
2
lim( 3 2 1)nn--+
+¥
¥
5
2
221
lim
1
nn
n
+-
+
¥
¥
5 2.3
lim
45
nn
nn
+
-
¥
¥
111 1
2(1 ... ...)
248 2
n
+++++ +
2
1
2
22
2
2 5 8 ... 3 1
lim
23
n
n
+++ + -
+
¥
3
4
¥
lim
1
ab
x
xx
x
®+¥
-
-
*
,abÎ •
a
b
2
232
2
()
2
ax 1 2
xx
khi x
fx
x
khi x
ì
--
>
ï
=
-
í
ï
+£
î
! Trang!38!
Tự luận: (4đ)
1. Tính: a,
b,
.
2. Tìm a để hàm số liên tục tại điểm x = 0 .
www.thuvienhoclieu.com
ĐỀ 19
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I-Trắc nghiệm (3đ).
1.Kết quả của là:
A) B) C) D) 2
2.Kết quả của là :
A) B) C) D)
3.Tổng có kết quả là:
A) B) C) D)
4. kết quả của giới hạn là:
A) 3 B) -3 C) -1 D) 11
5.Cho M = Khi đó:
A. M = B. M = - C. M = +∞ D. M = -
6.kết quả của giới hạn là:
A) B) C) D)
II-Tự luận (7đ).
Câu 2(4 đ):Tính giới hạn của các hàm số sau:
a) b)
Câu 3(2 đ): Xét tính liên tục của hàm số sau trên tập số thực R.
3
2
52
lim
25
x
xx x
x
®
-+
-
3
0
11
lim
x
xx
x
®
+- -
42
0
()
7
20
4
x
khi x
x
fx
a khi x
ì
+-
¹
ï
ï
=
í
ï
-=
ï
î
1
2
1
2
-
0
n
nn
32
14
lim
2
+
+-
4
3
-
4
3
2
3
2
3
-
...
3
1
...13
3
++++=
-n
S
27
2
27
4
9
2
9
4
23
23
lim
2
2
3
+-
--
®
xx
xx
x
12
lim
2
2
1
--
-
®
xx
xx
x
2
1
3
1
2
1
x
x
x
2
191
lim
0
-+
®
3
2
4
9
-
3
2
-
4
9
2
lim ( 2 )
x
xxx
®+¥
--
2
1
32
lim
1
x
x
x
®
+-
-
! Trang!39!
Câu 4(1 đ): Chứng minh phương trình sau có ít nhất một nghiệm :
www.thuvienhoclieu.com
ĐỀ 20
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
I-Trắc nghiệm (3đ).Khoanh tròn vào đáp án đúng.
1.Kết quả của là:
A) 0 B) C) D) 2
2.Kết quả của là :
A) B) C) D)
3.Tổng có kết quả là:
A) B) C) D)
4. kết quả của giới hạn là:
A) 11 B) -3 C) -11 D) 3
5.Cho M = Khi đó:
A. M = B. M = - C. M = +∞ D. M = -
6.kết quả của giới hạn là:
A) B) C) D)
II-Tự luận (7đ).
Câu 2(4 đ):Tính giới hạn của các hàm số sau:
a) b)
Câu 3(2 đ): Xét tính liên tục của hàm số sau trên tập số thực R.
2
34
...... ... 1
()
1
5...................... ... 1
xx
khi x
fx
x
khi x
ì
+-
¹
ï
=
-
í
ï
=
î
32
32510xxx+--=
1
2
-
1
2
n
nn
32
14
lim
2
+
+-
4
3
-
4
3
2
3
-
2
3
...
3
1
...13
3
++++=
-n
S
9
2
27
4
27
2
9
4
23
23
lim
2
2
3
+-
--
®
xx
xx
x
12
lim
2
2
1
--
-
®
xx
xx
x
2
1
2
1
3
1
x
x
x
2
191
lim
0
-+
®
3
2
4
9
-
4
9
3
2
-
2
lim ( 2 )
x
xxx
®+¥
+-
2
2
53
lim
2
x
x
x
®
+-
-
! Trang!40!
Câu 4(1 đ): Chứng minh phương trình sau có ít nhất một nghiệm :
www.thuvienhoclieu.com
ĐỀ 21
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV
Thời gian: 45 phút
Câu 1: Cho . Khi đó giá trị của a là:
A. -6 B. -10 C. 10 D. 6
Câu 2: Cho hàm số . Tính giới hạn của hàm số tại x =2 ta
được kết quả là:
A. 2 B. 1 C. Không tồn tại D. -2
Câu 3: Tính giới hạn ta được kết quả là:
A. - B. C. 0 D. 2
Câu 4: : Đồ thị hàm số ở hình bên là đồ thị của
hàm số nào ?
A.
B.
C.
D.
Câu 5: Tính được kết quả là:
A. B. a
C. a - 1 D. a + 1
Câu 6: Tính giới hạn ta được kết quả là:
A. – 3 B. 1 C. 3 D. – 2
Câu 7: Tính giới hạn ta được kết quả là:
A. 3 B. - C. + D. 0
Câu 8: Tìm giới hạn ta được kết quả:
A. B. 2 C. 3 D. -
2
34
..... ... 1
()
1
5........ ... 1
xx
khi x
fx
x
khi x
ì
--
¹-
ï
=
+
í
ï
-=-
î
32
210xxx+--=
2
lim ( ax 5 ) 5
x
xx
®+¥
++-=
3
3
22
()
32
x x khi x
fx
x x khi x
ì
-³
ï
=
í
-<
ï
î
1
21
lim
1
x
x
x
+
®
-+
-
¥
+¥
41
21
x
y
x
+
=
+
3
1
23
2
yx x=-+
42
1
22
2
yxx=-+
2
32yx x=-+
2
22
(1)
lim
x
xaxa
xa
®+¥
-+ +
-
1
2
a
a
-
2
1
43
lim
1
x
xx
x
®
-+
-
52
lim (7 5 7)
x
xxx
®+¥
+-+
¥
¥
2
lim( 3 2 1)nn--+
+¥
¥
! Trang!41!
Câu 9: Tìm giới hạn ta được kết quả là:
A. 4 B. + C. - D. -1
Câu 10: Cho phương trình 2x
4
– 5x
2
+ x + 1 = 0 (1). Mệnh đề nào đúng trong các
mệnh đề sau:
A. Phương trình (1) có ít nhất hai nghiệm thuộc khoảng (0; 2).
B. Phương trình (1) không có nghiệm trong khoảng (-2; 0).
C. Phương trình (1) không có nghiệm trong khoảng ( -1; 1).
D. Phương trình (1) chỉ có một nghiệm trong khoảng (-2; 1).
Câu 11: Cho hàm số f(x) xác định trên [a; b]. Trong các mệnh đề sau mệnh đề nào
đúng?
A. Nếu hàm số f(x) liên tục, tăng trên [a; b] và f(a).f(b) > 0 thì phương trình f(x) =
0 không có nghiệm trong khoảng (a; b).
B. Nếu hàm số f(x) liên tục trên [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0
không có nghiệm trong khoảng (a; b).
C. Nếu phương trình f(x) = 0 có nghiệm trong khoảng (a; b) thì hàm số f(x) phải
liên tục
trên (a; b).
D. Nếu f(a).f(b) < 0 thì phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng
(a; b).
Câu 12: Tìm giới hạn ta được kết quả:
A. - B. 3 C. D. +
Câu 13: Tìm giới hạn ta được kết quả :
A. + B. - C. -1 D. 1
Câu 14: Tìm giá trị đúng của S = ta được kết quả là
A. B. 2 C. D.
Câu 15: Tìm giới hạn ta được kết quả là:
A. + B. C. -1 D. -
Câu 16: Tính giới hạn với ta được kết quả là:
A. ab B. a – b C. b – a D.
Câu 17: Để hàm số liên tục tại điểm x = 0 thì giá trị
của a là:
A. 1 B. 3 C. 2 D. 1
5
2
221
lim
1
nn
n
+-
+
¥
¥
32
3
322
lim
1
nn
n
-+
+
¥
1
2
¥
5 2.3
lim
45
nn
nn
+
-
¥
¥
111 1
2(1 ... ...)
248 2
n
+++++ +
2
1
2
22
2
2 5 8 ... 3 1
lim
23
n
n
+++ + -
+
¥
3
4
¥
lim
1
ab
x
xx
x
®+¥
-
-
*
,abÎ •
a
b
42
0
()
7
20
4
x
khi x
x
fx
a khi x
ì
+-
¹
ï
ï
=
í
ï
-=
ï
î
! Trang!42!
Câu 18: Tính giới hạn ta được kết quả là:
A. 2 B. -5 C. D. 0
Câu 19: Hàm số có tính chất:
A. liên tục tại x = 2 và x = 0.
B. liên tục tại x = 2 nhưng không liên tục tại x = 0.
C. liên tục tại mọi điểm.
D. Liên tục tại x = 1, x = 3, x = 0.
Câu 20: Để hàm số liên tục tại điểm x = 2 thì giá trị của
a là:
A. 1 B. 2 C. 5 D. -3
4
75
5
lim
5
x
x
xx
®+¥
-
+
2
5
2
50
()
15 0
x khi x
fx
khi x
ì
¹
=
í
-=
î
2
232
2
()
2
ax 1 2
xx
khi x
fx
x
khi x
ì
--
>
ï
=
-
í
ï
+£
î
| 1/42
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ 1
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút
I. TRẮC NGHIỆM KHÁCH QUAN(6đ) 2 3n + 2n + 5
Câu 1: Kết quả của lim là 2 7n + n - 8 3 A. B. +¥ 5 C. - D. 0 7 8
Câu 2: lim(-3n3 + 5n - 2) bằng A. -3 B. +¥ C. -¥ D. 3 3n + 4.7n Câu 3: lim bằng 3.7n - 2 1 4 A. 1 B. C. D. -2 3 3 x +1 - 2 Câu 4: lim bằng x®3 x - 3 A. 0 B. +¥ 1 C. 4 D. 4 Câu 5: lim ( 3 2
x + 4x + 10)bằng x®0 A. +¥ B. 0 C. 10 D. 15 2x +1 Câu 6: lim bằng x 2- ® x - 2 A. 2 B. -¥ C. +¥ D. 0 2 2x + 3x +1 Câu 7: lim bằng 2 x 1 ®- x -1 1 A. B. 2 C. -¥ D. +¥ 2 Câu 8: 3 lim( 2 - x + 3x - 4) bằng x®-¥ A. -¥ B. +¥ C. – 2 D. 2 2 3x - 5x + 1 Câu 9: lim bằng x®+¥ 2 x - 2 A. -¥ B. +¥ C. 3 D. 0 2 x + 2x -1 Câu 10: lim bằng x®-¥ 3 2x + 1 A. 0 B. +¥ C. -¥ 1 D. 2 3 3x - 5x + 1 Câu 11: lim bằng x®+¥ 2 x + 2 A. +¥ B. 3 C. 0 D. -¥ Trang 1 æ 2 ö Câu 12: lim ç ÷ 2 x x x ç 3 1 3 3 ÷( - + ) bằng ®+¥ è . x x + 1 ø A. 6 B. -3 C. +¥ 3 D. 2 ì2x -1 nêu x > 1 ï
Câu 13: Cho hàm số f (x) = í 3 - x , hàm số liên tục trên nêu x £ 1 ïî 2 A. ! B. ( ; -¥ 1) È (1;+¥) C. ( ; -¥ 1) D. (1;+¥) ìax + 2 (x ³ ï )1
Câu 14: Hàm số f ( x) = í
liên tục tại x = 1 khi 2 ïx +x-1 î (x < )1 A. a = 1 B. Không có a thỏa mãn. C. a = 0 D. a = -1
Câu 15: Phương trình 2x3 – 6x +1 = 0 có số nghiệm thuộc [ 2; - 2] là A. 1 B. 2 C. 3 D. Vô nghiệm.
II. PHẦN TỰ LUẬN(4đ) 3 n - 2n + 1
Câu 16: a, Tính giới hạn lim 3 2n - n + 3 1- 3n b, Tính giới hạn lim . 2n + 4.3n 2 x - 3x + 2 Câu 17: a, lim x®2 x - 2 3 2x - 2 x -1 b, lim x®-¥ 3 x - 2 4x + 5x - 2 c, 2 lim
x + x + 3 - x x®+¥ ( )
Câu 18: Chứng minh rằng phương trình 4x4 + 2x2 – x – 3 = 0 có ít nhất hai nghiệm thuộc (-1;1). 2 ì x -7x +10 ï nêu x ¹ 2
Câu 19: Định m để hàm số liên tục f (x) = í x - 2 tại x = 2. ïî 2-m-1 nêu x = 2 *** Hết*** Trang 2 ĐÁP ÁN
I. PHẦN TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 Đáp án A C C D C B A 8 9 10 11 12 13 14 15 B C A A A A D C II. PHẦN TỰ LUẬN: Câu Nội dung Thang điểm 3 n - 2n + 1 2 1 3 1 - + n - 2n + 3 2 3 1 1 n n n 16a lim = lim = lim = 3 3 0,5 2n - n + 3 2n - n + 3 2 - 1 + 3 2 3 2 3 n n n 1- 3n 1 - n 1 1- 3 n n 1 3 3 16b lim = lim = lim = - n n n n n 0,5 2 + 4.3 2 - 4.3 æ 2 ö 4 + n 4 3 ç ÷ è 3 ø 2 x - 3x + 2 (x - 2)(x - )1 17a lim = lim = lim (x - ) 1 = 2 -1 = 1 0,5 x®2 x®2 x®2 x - 2 x - 2 3 2x - 2 x - 1 17b lim = 2 3 2 0,5
x®-¥ x - 4x + 5x - 2 2 2
x + x + 3 - x x + x + 3 + x 2 lim
x + x + 3 - x = lim x®+¥ ( ) ( )( ) x®+¥ 2
x + x + 3 + x 2 2
x + x + 3 - x x + = = 3 lim lim 0,25 17c x®+¥ 2 x®+¥ x + x + 3 + 2 x
x + x + 3 + x 3 1 + 1 = lim x = x®+¥ 1 3 2 1 + + +1 0,25 x x
Đặt f(x) = 4x4 + 2x2 – x – 3 = 0, hàm số này liên tục trên R +, Xét khoảng (-1;0) Ta có f(-1) = 4, f(0) = -3
Do f(-1).f(0) < 0 nên phương trình có ít nhất 1 nghiệm trong 18 khoảng (-1;0). 0,25 + Xét khoảng (0;1) Ta có f(0) = -3, f(1) = 4. Trang 3
Do f(0).f(1)< 0 nên phương trình có ít nhất một nghiệm trong khoảng (0;1). 0,25
Vậy phương trình có ít nhất hai nghiệm thuộc khoảng (-1;1). Ta có: f(2) = -2a - 1 2 x - 7x +10 lim f (x) = lim x®2 x®2 x - 2 19 (x - 2)(x - 5) = lim = lim(x - 5) = 3 - x®2 x®2 x - 2
Hàm số f(x) liên tục tại x = 2
Û lim f (x) = f (2) Û 3 - = 2 - a -1 Û 2 - = -2a Û a =1 x®2
Vậy a = 1 thì f(x) liên tục tại x = 2. www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 2
A. TRẮC NGHIỆM: ( 0,5điểm/1câu x 6câu = 3 điểm)
Câu 1: Giới hạn của hàm số sau đây bằng bao nhiêu: lim k
x (với k nguyên dương) x®+¥ A. + ¥ B. 0 C. 14 D. k 2
Câu 2: Giới hạn của hàm số sau đây bằng bao nhiêu: x - 2x + 2 lim 2 x®2 (x - 2) A. 0 B. 1 C. 2 D.+ ¥
Câu 3: Giới hạn của hàm số sau đây bằng bao nhiêu: 2
lim ( x + 2x - x) x®+¥ A. 0 B. - ¥ C. 1 D. 2
ì2x -1 khi x ³1 ï Câu 4: cho hàm số: ï x f (x) = í
Trong các mệnh đề sau, tìm mệnh đề sai? 2 x - x ï khi x < 1 ïî x -1 A. lim f (x) =1 B. lim f (x) =1 x 1- ® x 1+ ® C. lim f (x) =1
D. Không tồn tại giới hạn của hàm số f(x) khi x tiến x 1 ® tới 1.
Câu 5: Cho các hàm số: (I) y = sinx ; (II) y = cosx ; (III) y = tanx ; (IV) y = cotx
Trong các hàm số sau hàm số nào liên tục trên ! . A. (I) và (II) B. (III) và IV) C. (I) và (III) D. (I), (II), (III) và (IV) Trang 4 2
Câu 6: Cho hàm số f(x) chưa xác định tại x = 0: x - 2x f (x) =
. Để f(x) liên tục tại x = x
0, phải gán cho f(0) giá trị bằng bao nhiêu? A. -3 B. -2 C. -1 D. 0
B. TỰ LUẬN: (7 điểm)
Bài 1: ( 3 điểm) Tính giới hạn của các hàm số sau: 2 2x - 4 x - x +1 7x -10 - 2 a) lim b) lim c) lim 2 x®2 x®+¥ x®2 x +1 2x + x +1 x - 2 ì 2 3x -11x + 6 ï khi x ¹
Bài 2: ( 2 điểm) Tìm m để hàm số f (x) = 3 í x - 3
liên tục tai x0 = 3. ïî 2 m - 2 x khi x = 3
Bài 3: ( 2 điểm) Chứng minh rằng phương trình: 5 3
a)x + x -1 = 0 có ít nhất một nghiệm thuộc khoảng (0; ) 1 . b) osx c + m os
c 2x = 0 luôn có nghiệm với mọi giá trị của tham số m.
..................................................Hết............................................................
(Cán bộ coi thi không giải thích gì thêm)
ĐÁP ÁN ĐỀ KIỂM TRA 45’ TRẮC NGHIỆM: ( 0,5điểm/1câu x 6câu = 3 điểm) 1A 2D 3C 4D 5A 6B
A. TỰ LUẬN: (7 điểm) Bài Đáp án Thang điểm 2x - 4 2.2 - 4 a) lim = = 0 1đ x®2 x +1 2 +1 1 1 2 1- + 2 x - x +1 1 ) lim = lim x x b = 2 1đ
x®+¥ 2x + x +1 x®+¥ 1 1 2 2 + + 2 1(3đ) x x x - -
( 7x-10 -2).( 7x-10 +2 7 10 2 ) 0,5đ c) lim = lim x®2 x®2 x - 2
(x - 2)( 7x-10 + 2) 7x-14 7 7 = lim = lim =
x®2 ( x - 2)( 7x -10 + 2) x®2 7x -10 + 2 4 0,5đ +/ TXĐ: D = ! ( = Î 0 x 3 ! ) 0,5đ 2 3x -11x + 6 x - 3 3x - 2
2(2đ) +/ lim f (x) ( )( ) = lim = lim = 7 0,5đ x®3 x®3 x® x - 3 3 x - 3 0,5đ Trang 5 +/ f ( ) = 2 3 m - 9 0,5đ +/ Do đó: 2
m - 9 = 7 Û m = ±4
Vậy: với m = ±4 hàm số f ( )
x liên tục tại x0 = 3 5 3
a)x + x -1 = 0 +/ Đặt: f (x) 5 3
= x + x -1, f (x)liên tục trên ! Þ f (x)liên tục trên 0,5đ [0; ]1 +/ Có: ì f ï (0) = 1 - í Þ f (0). f ( ) 1 = 1 - < 0 Þ $ Î = Þ 0 x (0; ) 1 : f ( 0 x ) 0 đpcm 0,5đ ï f î ( ) 1 = 1 b) ox c + m os c 2x = 0
3(2đ) +/ Đặt: f ( x) = ox c + m os
c 2x Þ f ( x) liên tục trên ! Þ f ( x)liên tục 0,5đ ép p trên 3 ù ; ê ú ë 4 4 û +/ Có: ì æ p ö 2 ï f = ç ÷ ï è 4 ø 2 æ p ö æ 3p ö 1 æ p 3p ö í Þ f . f = - < 0 Þ $ Î = ç ÷ ç ÷ 0 x ; : f ç ÷ ( 0x) 0 0,5đ ï æ 3p ö 2 è 4 ø è 4 ø 2 è 4 4 ø f = - ï ç ÷ î è 4 ø 2 Þ đpcm
Học sinh giải cách khác mà đúng vẫn cho điểm tối đa. www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 3
I.Phần trắc nghiệm:(4điểm). 2 2 Câu 1: Biết giới hạn a n + 2n + 3 lim
= 4 . Khi đó giá trị của a là. 2 n +1 A. 1 B. 2 C. 3 D. a=2 hoặc a= - 2. Câu 2: Tính giới hạn 2 - x +1 lim ta được kết quả là: x 1+ ® x -1 A. - ¥ B. +¥ C. 0 D. 2 2 Câu 3: Tính giới hạn x - 4x + 3 lim ta được kết quả là: x 1 ® x -1 A. – 3 B. 1 C. 3 D. – 2
Câu 4: Tìm a để giới hạn 2
lim ( x - 3x + 5 + ax) = +¥ . x®-¥ A. a=3 B.a = 5 C.a >1 D. a < 1. Câu 5: Tìm giới hạn 3
lim(n + 2n - 2) ta được kết quả là: A. +¥ B. 1 C. -2 D. 3 Trang 6 Câu 6: Tìm giới hạn: 2 x - 3x + 2 lim x®+¥ ta được kết quả là: x -1 A. -1 B. + ¥ C. - ¥ D. 2 Câu7. Biết giới hạn 2x +1 lim = 5 .Tìm a? x®-¥ 3 - ax A.a= -2 B. 2 5 2 a = - C. a = - D. a = 5 2 3 n n
Câu 8: Tìm a để giới hạn .5 a + 2.3 lim =4 : n n 1 4 - 5 + A. -20 B. 20 C. 2 D. 4 Tự luận: (6đ) 2 Câu 1 x + 7 - 3 n + 3n -1 2 . a lim . b lim .
c lim ( 4x + x - 3 - 2x) 2 . x®2 x - 2 3n + 2 x®+¥
Câu 2.Chứng minh phương trình : 3
x - 5x + 2 = 0 có ít nhất 2 nghiệm trên khoảng (0;3). 2 ì2x - x - 3 3 khi x ¹ ï
Câu 3: Tìm m để hàm số ï 2x -3 2 3 f (x) = í
liên tục tại x = . 3 ï 2 2 2m - 6 khi x = ïî 2 Câu 4:
-Gọi C là nữa đường tròn đường kính AB=2R. - AB
C là đường gồm hai nữa đường tròn đường kính 1 2 -Gọi AB
C là đường gồm bốn nữa đường tròn đường kính ,... 2 4 - AB
C là đường gồm 2n nữa đường tròn đường kính ,... n 2n
Gọi S là diện tích hình phẳng giới hạn bởi C và đoạn thẳng n n
AB và u = S + S +...+ S .Tính giới hạn lim u . n 1 2 n n
………………Hết……………….. Đáp án 1 2 3 4 5 6 7 8 D A D A A B B A Câu Hướng dẫn Điểm 1a(1đ) x + 7 - 3 x - 2 1 1 0,5x0,25 lim = lim =lim = x®2 x®2 x®2 x - 2
(x - 2)( x + 7 + 3) x + 7 + 3 6 x0,25 1b(1đ) 3 1 0,5 x 0,5 2 1+ - 2 n + 3n -1 1 lim = lim n n = 2 3n + 2 2 3 3 + 2 n Trang 7 1c(1đ) 3 0,25x4 2 2 1-
4x + x - 3- 4x x - 3 1 2 lim ( 4 + - 3 - 2 ) = lim = lim = lim x x x x = x®+¥ x®+¥ 2 x®+¥ 2
4x + x - 3 + 2x 4x + x - 3 + 2 x x ®+¥ 1 3 4 4 + - + 2 2 x x 2(1đ)
Câu 2.Chứng minh phương trình : 3
x - 5x + 2 = 0 có ít nhất 2 nghiệm trên khoảng (0;3). Xét hàm số f(x)= 3
x - 5x + 2 liên tục trên [0;3]
f(0)=2, f(1)=-2, f(3)=14 (0.5) 0.5x0,25
Ta thấy : f(0).f(1)=-4<0 ,f(1).f(3)=-28<0 (0.25) x0,25.
Do đó pt đã cho có ít nhất 2 nghiệm trên khoảng (0;3). (0.25) Câu 3 2 ì2x - x -3 3 khi x ¹ ïï 3 (1đ)
Câu 3: Tìm m để hàm số 2x - 3 2 f (x) = í
liên tục tại x = . 3 ï 2 2 2m - 6 khi x = ïî 2 2 2x - x - 3 (2x - 3)(x +1) 5 3 2 lim = lim = lim(x +1) = , f ( ) = 2m - 6 3 3 3 . 0,25x2 x® 2x - 3 x® 2x - 3 x® 2 2 2 2 2 f(x) liên tục tại 3 x = 0,25x2 5 17 khi và chỉ khi : 2
= 2m - 6 Û m = ± . 2 2 2 Câu 4 Ta có: 2 2 2 2 p R p R p R p R (1đ) S = , S = , S = ,..., S = . 1 2 3 n 0,25 2 4 8 2n 2 2 2 2 p R p R p R p R 1 1 1 1 0,25 2 u = + + + ...+ = p R ( + + + ...+ ) n 2 4 8 2n 2 4 8 2n 1 1 1 1 é æ 1 n ù 2 2 ö 2
lim u = limp R ( + + + ....+ ) l = imp R 1 ê - ç ÷ ú = p R n n 0,25x2 2 4 8 2 ê è 2 ø ë úû www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 4
I.Phần trắc nghiệm:(4 điểm). 2 2 Câu 1: Biết giới hạn 2a n + 2n + 3 lim
= 4 . Khi đó giá trị của a là. 2 n +1 A. 4
B. 2 C.a = 2 hoặca = - 2 D. a=2 hoặc a= -2. Câu 2: Tính giới hạn 2x +1 lim ta được kết quả là: x 1+ ® x -1 Trang 8 A. - ¥ B. +¥ C. 0 D. 2 2 Câu 3: Tính giới hạn x + 4x + 3 lim ta được kết quả là: x 1 ®- x +1 A. – 3 B. 1 C. 2 D. – 2
Câu 4: Tìm a để giới hạn 2
lim ( x - 3x + 5 + ax) = -¥ . x®+¥ A. a=1 B.a <-1 C.a= -1 D. a =5 Câu 5: Tìm giới hạn 3
lim (-n + 2n - 2) ta được kết quả là: A. +¥ B. 1 C. -¥ D. 3 Câu 6: Tìm giới hạn: 2 -x + 3x + 2 lim x®+¥ ta được kết quả là: 3x -1 A. -1 B. + ¥ C. - ¥ D. 2 Câu7. Biết giới hạn 3x +1 lim = 5 .Tìm a? x®-¥ 3 - ax A.a= -1 B. 3 a = 5 5 C. a = - D. a = - 3 5 n n
Câu 8: Tìm a để giới hạn .5 a + 2.3 lim =4 : n n+2 4 + 5 A. 2 B. 25 C. 4 D. 100. II.Tự luận: (6đ) 2 Câu 1 x + 6 - 3 2n + 3n -1 2 . a lim . b lim .
c lim ( 9x + x - 3 + 3x) 2 x®3 x - 3 -n + 2 x®-¥
Câu 2.Chứng minh phương trình : 3
2x - 5x - 2 = 0 có ít nhất 2 nghiệm trên khoảng (- 1;3). 2 ì3x - x - 4 4 khi x ¹ ï
Câu 3: Tìm m để hàm số ï 3x - 4 3 4 f (x) =
liên tục tại x = . í 4 ï 3 2 2m - 6 khi x = ïî 3 Câu 4:
-Gọi C là nữa đường tròn đường kính AB=2R. - AB
C là đường gồm hai nữa đường tròn đường kính 1 2 -Gọi AB
C là đường gồm bốn nữa đường tròn đường kính ,... 2 4 - AB
C là đường gồm 2n nữa đường tròn đường kính ,... n 2n
Gọi S là diện tích hình phẳng giới hạn bởi C và đoạn thẳng n n
AB và u = S + S +...+ S .Tính giới hạn lim u . n 1 2 n n
…………………..Hết………………….. Đáp án: 1 2 3 4 5 6 7 8 C B C B C C D D Trang 9 Câu Hướng dẫn Điểm 1a(1đ) x + 6 - 3 x - 3 1 1 0,5x0,25 lim = lim =lim = x®3 x®3 x®3 x - 3
(x - 3)( x + 6 + 3) x + 6 + 3 6 x0,25 1b(1đ) 3 1 0,5 x 0,5 2 2 + - 2 2n + 3n -1 lim = lim n n = 2 - . 2 -n + 2 2 1 - + 2 n 1c(1đ) 3 0,25x4 2 2 1-
9x + x - 3- 9x x - 3 1 2 lim ( 9 + - 3 + 3 ) = lim = lim = lim x x x x = - x®-¥ x®-¥ 2 x®-¥ 2
9x + x - 3 - 3x 9x + x - 3 - 3 x x ®-¥ æ 1 3 ö 6 -ç 9+ - +3÷ 2 x x è ø 2(1đ)
Câu 2.Chứng minh phương trình : 3
2x - 5x - 2 = 0 có ít nhất 2 nghiệm trên khoảng (-1;3). Xét hàm số f(x)= 3
2x - 5x - 2 liên tục trên [-1;3]
f(-1)=2, f(0)= -2, f(3)=37 (0.5) 0.5x0,25
Ta thấy : f(-1).f(0)= -4<0 ,f(0).f(3)= - 74<0 (0.25) x0,25.
Do đó pt đã cho có ít nhất 2 nghiệm trên khoảng (-1;3). (0.25) Câu 3 2 ì3x - x - 4 4 khi x ¹ ïï - 4 (1đ)
Câu 3: Tìm m để hàm số 3x 4 3 f (x) = í
liên tục tại x = . 4 ï 3 2 2m - 6 khi x = ïî 3 2 3x - x - 4 (3x - 4)(x +1) 7 4 2 lim = lim = lim(x +1) = , f ( ) = 2m - 6 4 4 4 . 0,25x2 x® 3x - 4 x® 3x - 4 x® 3 3 3 3 3 f(x) liên tục tại 4 x = 7 5 0,25x2 khi và chỉ khi : 2
= 2m - 6 Û m = ± . 3 3 6 Câu 4 Ta có: 2 2 2 2 p R p R p R p R (1đ) S = , S = , S = ,..., S = . 1 2 3 n 0,25 2 4 8 2n 2 2 2 2 p R p R p R p R 1 1 1 1 0,25 2 u = + + + ...+ = p R ( + + + ...+ ) n 2 4 8 2n 2 4 8 2n 1 1 1 1 é æ 1 n ù 2 2 ö 2
lim u = limp R ( + + + ....+ ) l = imp R 1 ê - ç ÷ ú = p R n n 0,25x2 2 4 8 2 ê è 2 ø ë úû Trang 10 www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 5 1 1 1 1 1 n æ ö
Câu 1. Tổng của cấp số nhân lùi vô hạn - , , - , ..., - ,... là ç ÷ 2 4 8 16 è 2 ø 1 1 A. 1 B. C. -1 D. - 2 3
Câu 2. Dãy số nào sau đây có giới hạn là +¥ ? 2 + - 2 - 2n 2n 1 n 2n A. 2 3
u = 3n - 4n B. u = C. u = D. 2
u = 3n -13n n n 3 n + 4 n 2 - n n
Câu 3. Cho một hàm số
xác định trên khoảng (a;b). Khẳng định nào sau đây là đúng ? A. Nếu hàm số liên tục trên đoạn
và f (a). f (b) < 0 thì phương trình có nghiệm trong khoảng .
B. Nếu phương trình có nghiệm trong khoảng thì hàm số liên tục trên khoảng C. Nếu liên tục trên đoạn [ ;
a b]; f(a).f(b)=0 thì pt có nghiệm trên khoảng . D. Nếu thì phương trình
có ít nhất một nghiệm trong khoảng . 2 5 3n + n a 3
Câu 4. Giới hạn lim =
(a/b tối giản) có a+b bằng 2(3n + 2) b A. 21 B. 11 C. 19 D. 51 1+ 3 + 5 + ...+ (2n -1) Câu 5. lim bằng : 2n(2n - 3) 1 A. không tồn tại B. 1 C. D. 2 4 3 - Câu 6. Tính 2
lim ( 2x - 3x + 4 - x) : A. B. +¥ C. 2 -1 D. x®+¥ 2 +1 -¥
Câu 7. Hàm số nào trong các hàm sau có giới hạn tại điểm x=2 ? 1 1 2x 13
A. f (x) =
B. f (x) =
C. f (x) =
D. f (x) = x +1 x - 2 2 x - 4 x - 2
Câu 8. Dãy số nào sau đây có giới hạn bằng 0? n n 3 - æ 6 ö æ 2 ö n 3n A. B. - C. D. 2 ç ÷ ç ÷ n - 4n è 5 ø è 3 ø n +1 2 3 2x - x 1 Câu 9. lim bằng: A. - B. -¥ 1 C. D. 2 x 1 ® 5x - 2x + 3 5 6 2 5 Trang 11 ì x + 3 - 2 ï (x>1) ï - Câu 10. Hàm số x 1 f (x) = í
Giá trị m để f(x) liên tục tại x=1 là: 1 ï 2 m + m + (x £ 1) ïî 4 A. m Î{0; } 1 B. m Î{0;- } 1 C. m=1 D. m=0
Câu 11. Trong các dãy số sau, dãy số nào có giới hạn hữu hạn? n - n 4 3 - + 2.5 12 n 3n 2 n æ 1 ö A. u = B. u = 6 + C. u = D. n ç ÷ 3n - 2 n è 3 ø n 4 -n + 2n - 4 3 2n - 3n + 3 u = n 2 -n + 5
Câu 12. Hàm số nào sau đây liên tục tại x=2 ? 2 x +1 2 2x + 6x +1 x + x +1
A. f (x) =
B. f (x) =
C. f (x) = D. x + 2 x - 2 x - 2 2 3x - x - 2 f (x) = 2 x - 4 2 2x - 6 Câu 13. Tính lim
= a b Khi đó đặt P=a+b có: A. 6 B. 7 C. 5 D. 10 x® 3 x - 3
Câu 14. Phương trình 5 4 2
x - 3x + 2x + 5x - 4 = 0 có mấy nghiệm ? A. 4 B. 3 C. 5 D. 1 3 ì x -8 ï (x ¹ 2)
Câu 15. Cho hàm số: f (x) = í x - 2
để f(x) liên tục tại điêm x0 = 2 thì a bằng ? ïî2a -4 (x = 2) A. 4 B. 6 C. 8 D. Không có giá trị a
Câu 16. Trong các hàm số sau hàm số nào liên tục trên R ? x - 3 3 - + 3 2 2x - 5x + 6 x 2x 1 A. y = B. y = C. y = D. y= tan3x 1- cos x 2 x + 2 x +1 3 x + 4 Câu 17. Tính lim : A. -2 B. C. 3 D. x 2+ ® x - 2 3 - x 3n + 3.5n 3 Câu 18. Tính lim - n 1 +
: A. 1 B. 0 C. D. 3/2 2 - 5 5 3 x -1
Câu 19. Giới hạn lim bằng: A. 3/2 B. 3 C. -3/2 D. Không tồn tại. 2 x 1 ® x -1
Câu 20. Dãy số nào sau đây có giới hạn khác 0? 2 + 2n 3 4 2n 1 æ 3 ö A. B. C. D. 2 ç ÷ 3n + 4 è 5 ø 3 n + n 2 n + 3 2
3 x + 4x + x
Câu 21. Giới hạn lim
bằng: A. -2 B. 3 C. -5 D. 5 x®-¥ x +1 4 3 5x + 2x + 2 a Câu 22. lim =
; (a;b nguyên). Khi đó a+b bằng: 4 x®+¥ 16x + 9x + 5 b A. 9 B. 19 C. 8 D. 21 Trang 12 2 18x +1 - x + 5 Câu 23. lim bằng: A. 17/2 B. +¥ 2 3 C. D. x®+¥ 2x - 7 3 3 2 2 2 9n +1 - n + 2 Câu 24. lim bằng: A. 8/3 B. 10/3 C. 3 D. 1 3n - 3 ( 2 lim
n - 3n - n) Câu 25. Tính : A. -3/2 B. 0 C. 5/2 D. 3/2 HẾT Đáp án 01. - - - ~ 08. - / - - 15. - - = - 22. ; - - - 02. - - - ~ 09. - - = - 16. - / - - 23. - - - ~ 03. ; - - - 10. - / - - 17. - - - ~ 24. - - - ~ 04. - / - - 11. - - = - 18. - - = - 25. ; - - - 05. - - = - 12. ; - - - 19. - - - ~ 06. - / - - 13. - / - - 20. ; - - - 07. ; - - - 14. - / - - 21. - - = - Trang 13 www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 6
A. PHẦN TRẮC NGHIỆM .(7điểm)
Câu 1. Với k là số nguyên dương. Tìm giới hạn 1 lim . k x®+¥ x A. +¥ . B. -¥ . C. 0. D. 1 . k
Câu 2. Giới hạn nào sau đây bằng 0 ? 2 2 3 2
A. lim n - n +1 . B. lim n - 3n + 2 .
C. lim n + 2n -1 . D. lim 2n - 3n 2n -1 2 n + n 3 n - 2n 3 n + 3n Câu 3. Tính x +1 lim . x 1 ® x + 2 A. -1. B. 1. C. 1 2 . D. . 2 3 Câu 4. Tính x - 2 lim . 2 x® 2 x - 2 A. 1. B. 1 1 . C. . D. 2 . 2 2 2 Câu 5. Biết ax -1 lim = 4 . Tìm a. x 1 ® x +1 A. 8. B. 9. C. 5. D. 4. Câu 6.
Cho hàm số y = f (x) có đồ thị như hình vẽ 8 6
.Mệnh đề nào sau đây sai ? 4
A. Hàm số gián đoạn tại x =1. 2
B. lim f (x) =1. 1 x®+¥ 15 10 5 5 10 15 O 1
C. lim f (x) = -¥. 2 x 1+ ® 4
D. lim f (x) = f (3) . x®3 6 8
Câu 7. Cho hàm số f (x) xác định trên khoảng K chứa điểm 0 và f (x) +1 £ x .
Khẳng định nào dưới đây đúng ?
A. lim f (x) = 0. B. lim f (x) =1.
C. lim f (x) = 1. -
D. lim f (x) = + . ¥ x®0 x®0 x®0 x®0 n n Câu 8. Tìm 5 + 2.3 lim . 4n - 2.5n A. +¥ 1 . B. 1. C. - . D. -1. 2
Câu 9. Hàm số nào dưới đây không có giới hạn tại điểm x = 0 ? Trang 14 A. f (x) = 1 x . B. f (x) = 1 . C. f (x) = 1 . D. f (x) = . x x x -1 Câu 10. Cho hàm số 1 f (x) =
. Khẳng định nào sau đây đúng ? 3 - x
A. Hàm số chỉ có giới hạn bên phải tại điểm x = 3.
B. Hàm số có giới hạn bên trái và giới hạn bên phải tại điểm x = 3.
C. Hàm số có giới hạn tại điểm x = 3.
D. Hàm số chỉ có giới hạn bên trái tại điểm x = 3. Câu 11. Tính 2 + 5 + 8 + ...+ 3n -1 lim . 2 n®+¥ 2n + 3 A. + ¥ 3 3 . B. . C.1 . D. . 2 4
Câu 12. Cho hàm số f(x) xác định trên [a; b]. Mệnh đề nào sau đây đúng ?
A. Nếu hàm số f(x) liên tục, tăng trên [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0
không có nghiệm trong khoảng (a; b).
B. Nếu hàm số f(x) liên tục trên [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0
không có nghiệm trong khoảng (a; b).
C. Nếu phương trình f(x) = 0 có nghiệm trong khoảng (a; b) thì hàm số f(x) phải liên tục trên (a; b).
D. Nếu f(a).f(b) < 0 thì phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (a; b).
Câu 13. Khẳng định nào sau đây sai ?
A. Hàm số f (x) = 3x +1 liên tục trên tập R.
ìx +1 khi x ³ 0
B. Hàm số f (x) được xác định bởi f (x) = í
liên tục tại x = 0 . î0 khi x < 0 C. Hàm số 1
f (x) = liên tục x " ¹ 0. x
D. Hàm số f (x) = x liên tục trên[0;+¥) .
Câu 14. Cho hàm số f (x) xác định trên khoảng K chứa a . Khẳng định nào sau đây đúng ?
A. Hàm số không liên tục tại điểm x = a thì không tồn tại lim f (x). x®a
B. Nếu lim f (x) = a thì f (x) liên tục tại x = a. x®a
C. Nếu lim f (x) = f (a) thì f (x) liên tục tại x = a. x®a
D. Hàm số có giới hạn bên trái và bên phải tại điểm x = a thì liên tục tại x = a .
B. PHẦN TỰ LUẬN (3 điểm ).
Câu 1. Tính các giới hạn sau : 2 2 a. x - 4 2n - n lim ; b. lim . x®2 x - 2 2 n + n +1 Trang 15 2 ì x - x - 6
Câu 2 . Tìm m để hàm số ï ¹ f ( x) khi x 3 = í x -3
liên tục tại x = 3. ïî2x + m khi x = 3
Câu 3. Từ độ 63m của một tòa nhà người ta thả một quả bóng làm bằng cao su
xuống mặt đất .Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng 1 độ cao 10
mà quả bóng đạt được ngay trước đó .Tính độ dài hành trình của quả bóng từ thời
điểm ban đầu cho đến khi nó nằm yên trên mặt đất . www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 7 Câu 1 : 4 4 x - a
Giới hạn của hàm số sau đây bằng bao nhiêu: lim x®a x - a A. 5a4 B. 3a4 C. 2a2 D. 4a3 Câu 2 : x +1 Tính lim x 1 ® x - 2 A. 1 B. -1/2 C. -2 D. 3/2
Câu 3 : Khẳng định nào sau đây là đúng?
A. lim f (x) + g(x) = lim f (x) + lim g(x)
B. lim f (x) + g(x) = lim [f (x) + g(x)] x® ® ® o x x o x x o x x® ® o x x o x
C. lim f (x) + g(x) = lim [f (x) + g(x)]
D. lim f (x) + g(x) = lim f (x) + lim g(x) x® ® ® ® ® o x x o x x o x x o x x o x
Câu 4 : Trong các giới hạn sau, giới hạn nào không tồn tại x +1 x +1 x +1 x +1 A. lim B. lim C. lim D. lim x 1 ®- -x + 2 x 1 ® 2 - x x 1 ® x - 2 x 1 ®- 2 + x Câu 5 : x x Tính lim 2
x®+¥ x - x + 2 A. 1 B. 2 C. 0 D. 3
Câu 6 : Phương pháp nào sau đây thường được sử dụng để khử dạng giới hạn vô định của phân thức
A. Phân tích tử và mẫu thành nhân tử rồi rút gọn
B. Nhân biểu thức liên hợp
C. Chia cả tử và mẫu cho biến số có bậc thấp
D. Sử dụng định nghĩa nhất Câu 7 : x + 5 Hàm số y =
có bao nhiêu điểm gián đoạn 4 2 x -10x + 9 A. 1 B. 3 C. 2 D. 4 Câu 8 : Tính 2 2
lim ( x + x - 4 + x ) x®-¥ 1 - 1 A. B. 2 C. D. -2 2 2
Câu 9 : Với k là số nguyên dương. Kết quả của giới hạn lim k x là x®+¥ A. x B. C. 0 D. Câu 10 : x -1 Tính lim 2 x 1 ® x -1 A. 2 B. 1 C. 1/2 D. -1/2 Trang 16 Câu 11 : Tính 3 lim x + 7x x 1 ®- A. -8 B. 8 C. -6 D. 6
Câu 12 : Khẳng định nào sau đây là đúng? A. 3 3 3
lim f (x) + g(x) = lim f (x) + lim g(x) B. 3
lim f (x) + g(x) = 3 lim [f (x) + g(x)] x® ® ® x®x x®x o x x o x x o x o o C. 3
lim f (x) + g(x) = 3 lim f (x) + 3 lim g(x) D. 3 3 3
lim f (x) + g(x) = lim [ f (x) + f (x)] x® ® ® o x x o x x o x x® ® o x x o x
Câu 13 : Giới hạn nào dưới đây có kết quả bằng 3 3x 3 - x 3 - x A. lim B. lim C. lim
D. Cả ba hàm số trên x 1 ® x - 2 x 1 ® x - 2 x 1 ® 2 - x Câu 14 : x + 2 Tính lim 2 x®- 2 x - 2 1 - A. B. 2 C. D. 1 2 2
Câu 15 : Giới hạn của hàm số nào dưới đây có kết quả bằng 1? 2 x + 3x + 2 2 x + 4x + 3 2 x + 3x + 2 2 x + 3x + 2 A. lim B. lim C. lim D. lim x 1 ®- x -1 x 1 ®- x +1 x 1 ®- x +1 x 1 ®- 1- x
Câu 16 : Một học sinh bảo rằng phương trình x4-x-2=0 (1), có nghiệm x , x nằm trong khoảng (0;2) 1 2
Và lập luận như sau, Hỏi phần lập luận đó sai ở bước nào?
A. f (2) = 12 > 0, f (0) = 2 - < 0, f (1) = 2 - < 0 B. hàm số 4
f (x) = x - x - 2 liên tục trên ! f (2) f (0) = 24 -
< 0 nên (1) có ít nhất một nghiệm x Î (0;2) C. 1 f (2) f (1) = 24 -
< 0 nên (1) có ít nhất một nghiệm x Î (1;2) 2
D. Vậy (1) có ít nhất 2 nghiệm x , x nằm trong khoảng (0;2) 1 2 Câu 17 : æ 1 ö Tính lim x 1- ç ÷ x®0 è x ø A. -1 B. 1 C. -2 D. 2 Câu 18 : ì x + 2 - 2 ï khi x ¹ 2 Cho hàm số 2 y = x - 4 í
với giá trị nào của m thì hàm số sau liên tục tại x=2 ïm khi x = 2 î A. m=1/2 B. m=1/8 C. m=1/16 D. m=1/4 Câu 19 : 2x + 5 Hàm số y =
chỉ gián đoạn tại các điểm 3 x - 3x + 2 A. x=1 B. x=-2 C. Đáp án khác D. x=-2 và x=1 Câu 20 : 1
Cho hàm số f (x) =
. Khẳng định nào sau đây là đúng 2 - x
A. Hàm số chỉ có giới hạn trái tại điểm
B. Hàm số chỉ có giới hạn phải tại điểm
C. Hàm số có giới hạn tại điểm
D. Hàm số có giới hạn trái và giới hạn phải bằng nhau Câu 21 : 3 x - x Tính lim 4 x 1
® (2x -1)(x - 3) A. 0 B. 2 C. 3 D. 1
Câu 22 : Cho phương trình msin2x + sinx – cosx =0 (1), m là tham số. Mệnh đề nào sau đây đúng? æ p p ö I. Trong khoảng - ;
, phương trình (1) không có nghiệm nào cả ç ÷ è 2 2 ø Trang 17 æ p p ö II.- Trong khoảng - ;
, phương trình (1) có nghiệm ç ÷ è 2 2 ø
III. x = 0 là một nghiệm của (1). A. Chỉ I B. Chỉ II và III C. Chỉ I và III D. Chỉ II Câu 23 : 2 x + 3x + 2 Xác định lim x ( 1)- ® - x +1 A. B. 1 C. D. -1
Câu 24 : Hàm nào trong các hàm sau có giới hạn tại điểm 1 1 1 1
A. f (x) =
B. f (x) =
C. f (x) =
D. f (x) = x - 2 x - 2 x - 2 2 - x Câu 25 : 1
Kết quả của giới hạn lim
(với k nguyên dương) là k x®-¥ x A. x B. 0 C. D. www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 8 I. Trắc nghiệm
Câu 1: Giới hạn của hàm số sau đây bằng bao nhiêu: 2
lim ( x + 2x + x) x®+¥ A. 0 B. 1 C. + ¥ D. 2
Câu 2: Kết quả của 2x - 2 lim là 2 x 1 ® x -1 A. 2 B. 1 C. 1 D. 1 - 2 2 2
Câu 3: Kết quả của 2n + 3n -1 lim bằng bao nhiêu? 2 n - 4n - 2 A. 0 B. 1 C. + ¥ D. 2
Câu 4: Kết quả của 3x + 2 lim là x ( 1)- ® - x +1 A. 1 B. . . C. -1 D.
Câu 5: Kết quả của 2 lim x - 5x là x®2 A. -8 B. 6 C. -6 D. 8 ìax - 3 khi x ³ 1
Câu 6: Cho hàm số: f (x) = í
để f(x) liên tục trên R thì a bằng? 2
îx + x -1 khi x < 1 A. -2 B. 4 C. 2 D. 1
Câu 7: Dãy số nào sau đây có giới hạn bằng 1 ? 3 2 2 2 A. n - 2n 1- 2n 7n - 2 1- 2n u = B. u = C. u = D. u = n 2 5n + 3n n 2 5n + 3n n 2 5n + 3n n 2 5n + 3n + 1 1 1 (- )n 1 1
Câu 8: Tổng của một cấp số nhân này ,- , ,..., ,... là? n 3 9 27 3 Trang 18 A. 1 B. 1 C. 3 D. 4 4 2 4 Câu 9: Cho hàm số 5
f (x) = x + x -1. Xét phương trình: f ( x) = 0 ( ) 1 . Trong các mệnh
đề sau, tìm mệnh đề sai?
A. (1) có nghiệm trên khoảng (-1; 1)
B. (1) có nghiệm trên khoảng (0; 1) C. Vô nghiệm
D. (1) có nghiệm trên R 4 + 2.2n - 6.7n
Câu 10: Kết quả của lim là 8n - 3.7n 1 A. 0 B. C. -3 D. 2 5 II. Tự luận
-----------------------------------------------
Câu 1: Tính các giới hạn sau: 3 2 a) 2 - x + 3
x + 3x + 2x + 6 lim b) lim c) + - ®+¥ ( 2 lim 9x 2x 3x x ) x 1 ® x - 4 x 3 ®- x + 3
Câu 2: Xét tính liên tục của hàm số sau tại điểm x = 2 : 2 ì 2x +1 -3 ï khi x ¹ 2 ï x - 2 f (x) = í . ï 4 khi x = 2 ïî 3
Câu 3: Chứng minh rằng phương trình sau luôn có nghiệm với mọi m: ( 2
m + m + 3)(x - 2) + 4 = 0 ----------- HẾT ---------- www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 9
I. Phần Trắc Nghiệm: Câu 1. Giới hạn ( 2 lim
4n + n - 2n) bằng bao nhiêu? A.2 B. 0 C. 1 D. -¥ 4 3 2 Câu 2. Giới hạn
x + x - 6x + 4 lim bằng bao nhiêu? x 1 ® x -1 A.1 B. -1 C.0 D. +¥ 2 Câu 3. Giới hạn x + 4 lim bằng bao nhiêu? x®+¥ x - 9 A.1 B. 2 C. -¥ D. +¥ Câu 4. Giới hạn + - ®-¥ ( 2 lim 9x 5x x x ) bằng bao nhiêu? A. 5 B. 5 C. +¥ D. -¥ 4 2 Trang 19 Câu 5. Tổng 1 1 1 S = + + ... + + ... Có giá trị là: 3 32 3n A. 1 B. 1 C. 1 D. 1 3 2 9 4 n n Câu 6. Giới hạn 2 - 7 . 5 lim bằng bao nhiêu? n n 2 + 7 A. -35 B. 1 C. 5 D. -5 Câu 7. Giới hạn 4x + 2 lim bằng bao nhiêu? + 2 x 1 ®- x -1 A. 1 B. -¥ C. +¥ D. 2 2 7 3 + - + Câu 8. Giới hạn 4x 1 1 6x lim bằng bao nhiêu? x®0 2 x + 4 - 2 A. 8. B. 20000 C. 4 D. 20000 2499 4999 3
ìï2x - 2x khi x ³1
Câu 9. f ( x) = í , lim f ( x) 3 1 ïîx - 3x khi x < 1 x - ® A.-4 B. -3 C.-2 D. 2 ì2 - x + 3 ï khi x ¹ 1 2 ï Câu 10. f ( x) x -1 = í , lim f ( x) x 1 1 - ® ï khi x = 1 ïî8 1 1 A. B. - C.0 D. +¥ 8 8
II. Phần Tự Luận:
Câu 1(2 đ):Tính giới hạn của các hàm số sau: 2 x + 3 - 2 2
a) lim ( x - 2x - x) b) lim x®+¥ x 1 ® x -1
Câu 2(2 đ): Xét tính liên tục của hàm số sau trên tập số thực R. 2 ì x + 3x - 4 ï ......k ... hi x ¹ 1 f (x) = í - x 1 5...................... ïî k ... hi x = 1
Câu 3(1 đ): Chứng minh phương trình sau có ít nhất một nghiệm : 3 2
3x + 2x - 5x -1 = 0 Trang 20 www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 10
I.Phần Trắc Nghiệm: 2 Câu 1. Giới hạn x + 4 lim bằng bao nhiêu? x®+¥ x - 9 A.1 B. 2 C. -¥ D. +¥ Câu 2. Giới hạn ( 2 lim
4n + n - 2n) bằng bao nhiêu? A.2 B. 0 C. 1 D. -¥ 4 3 2 Câu 3. Giới hạn
x + x - 6x + 4 lim bằng bao nhiêu? x 1 ® x -1 A.1 B. -1 C.0 D. +¥ Câu 4. Giới hạn 4x + 2 lim bằng bao nhiêu? + 2 x 1 ®- x -1 A. 1 B. -¥ C. +¥ D. 2 2 7 Câu 5. Giới hạn + - ®-¥ ( 2 lim 9x 5x x x ) bằng bao nhiêu? A. 5 B. 5 C. +¥ D. -¥ 4 2 n Câu 6. Giới hạn 2 + 3 lim bằng bao nhiêu? n 1- 2 A.1 B.3 C.-3 D.-1 3 + - + Câu 7. Giới hạn 4x 1 1 6x lim bằng bao nhiêu? x®0 2 x + 4 - 2 A. 8. B. 20000 C. 4 D. 20000 2499 4999 n 1 + Câu 8. Tổng 1 1 1 (- ) 1 S = + (- ) + + ... + + ... Có giá trị là: 2 4 8 2n A. - 1 B. 1 C.1 D. - 2 3 3 3 2
ìx - 3x +1 khi x < 2
Câu 9. f ( x) = í , lim f ( x) 2 5 î x - 3 khi x ³ 2 x - ® A.11 B. 7 C.-1 D. -13 2 ì x -1 ï khi x < 1
Câu 10. f ( x) = í 1- x , lim f ( x) x 1- ® ï î 2x - 2 khi x ³ 1 A.-1 B. 0 C.-2 D.+ ¥ Trang 21
II. Phần Tự Luận:
Câu 1(2 đ):Tính giới hạn của các hàm số sau: 2 x + 3 - 2 2
a) lim ( x - 2x - x) b) lim x®+¥ x 1 ® x -1
Câu 2(2 đ): Xét tính liên tục của hàm số sau trên tập số thực R. 2 ì x + 3x - 4 ï ......k ... hi x ¹ 1 f (x) = í - x 1 5...................... ïî k ... hi x = 1
Câu 3(1 đ): Chứng minh phương trình sau có ít nhất một nghiệm : 3 2
3x + 2x - 5x -1 = 0 Trang 22 www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 11 I.Phần Trắc Nghiệm: Câu 1. Giới hạn ( 2 lim
4n + 8n - 2n) bằng bao nhiêu? A. 2 B. 0 C. 1 D. -¥ 4 3 Câu 2. Giới hạn 2x - 6x + 4 lim bằng bao nhiêu? x 1 ® x -1 A.1 B. -1 C. 0 D. +¥ 2 Câu 3. Giới hạn 7 - x lim bằng bao nhiêu? x®+¥ x - 9 A.1 B. 2 C. -¥ D. +¥ Câu 4. Giới hạn + - ®-¥ ( 2 lim 9x 16x 2x x ) bằng bao nhiêu? A. 5 B. 5 C. +¥ D. -¥ 4 2 2 Câu 5. Giới hạn 4x - 7 - 3 lim bằng bao nhiêu? 2 x 2 ®- x - 4 A. 19 B. 2 C. 0,666 D. 0 30 3 n Câu 6. Tổng 1 1 1 (- ) 1 S = - + + (- ) + ... + + ... Có giá trị là: 2 4 8 2n B. - 1 B. 1 C.-1 D. - 1 3 2 4 n Câu 7. Giới hạn 3 +1 lim bằng bao nhiêu? n n 2 . 3 - 3 A .-1 B. 1 1 1 C. D. - 3 3 3 - + - Câu 8. Giới hạn 1 4x 6x 1 lim bằng bao nhiêu? x®0 2 x +1 -1 A. 8. B. 20000 C. 20000 D. 4 4999 2499 3
ìï2x - 2x khi x ³1
Câu 9. f ( x) = í , lim f ( x) 3 1 ïîx - 3x khi x < 1 x - ® A.-4 B. -3 C.-2 D. 2 Trang 23 ì2 - x + 3 ï khi x ¹ 1 2 ï Câu 10. f ( x) x -1 = í , lim f ( x) x 1 1 - ® ï khi x = 1 ïî8 1 1 A. B. - C.0 D. +¥ 8 8
II. Phần Tự Luận:
Câu 1(2 đ):Tính giới hạn của các hàm số sau: 1+ 9x -1 a) lim ( 2
x - 5x - x) b)lim x®-¥ x®0 2x
Câu 2(2 đ): Xét tính liên tục của hàm số sau trên tập số thực R. ì2 - x + 3 ï khi x ¹ 1 ï
y = f ( x) 2 x -1 = í 1 ï khi x = 1 ïî8
Câu 3(1 đ): Chứng minh phương trình sau có ít nhất một nghiệm : x5- 5x3 + 4x -1 = 0 Trang 24
-----------------Hết----------------- www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 12 I. Phần Trắc Nghiệm: Câu 1. Giới hạn + - ®-¥ ( 2 lim 9x 16x 2x x ) bằng bao nhiêu? A. 5 B. 5 C. +¥ D. -¥ 4 2 Câu 2. Giới hạn ( 2 lim
4n + 8n - 2n) bằng bao nhiêu? A. 2 B. 0 C. 1 D. -¥ 4 2 Câu 3. Giới hạn 7 - x lim bằng bao nhiêu? x®+¥ x - 9 A.1 B. 2 C. -¥ D. +¥ 3 Câu 4. Giới hạn 2x - 6x + 4 lim bằng bao nhiêu? x 1 ® x -1 A.1 B. -1 C. 0 D. +¥ 2 Câu 5. Giới hạn 4x - 7 - 3 lim bằng bao nhiêu? 2 x 2 ®- x - 4 A. 19 B. 2 C. 0,666 D. 0 30 3 Câu 6. Tổng 1 1 1 S = + + ... + + ... Có giá trị là: 3 32 3n A. 1 B. 1 C. 1 D. 1 3 2 9 4 3 - + - Câu 7. Giới hạn 1 4x 6x 1 lim bằng bao nhiêu? x®0 2 x +1 -1 A. 8. B. 20000 C. 20000 D. 4 4999 2499 n Câu 8. Giới hạn 3 -1 lim bằng bao nhiêu? 2n - 3 . 2 n +1 A .- 1 B. - 1 3 1 C. D. 2 2 2 2
ìx - 3x +1 khi x < 2
Câu 9. f ( x) = í , lim f ( x) 2 5 î x - 3 khi x ³ 2 x - ® A.11 B. 7 C.-1 D. -13 Trang 25 2 ì x -1 ï khi x < 1
Câu 10. f ( x) = í 1- x , lim f ( x) x 1- ® ï î 2x - 2 khi x ³ 1 A.-1 B. 0 C.-2 D.+ ¥
II. Phần Tự Luận:
Câu 1(2 đ):Tính giới hạn của các hàm số sau: 1+ 9x -1 a) lim ( 2
x - 5x - x) b)lim x®-¥ x®0 2x
Câu 2(2 đ): Xét tính liên tục của hàm số sau trên tập số thực R. ì2 - x + 3 ï khi x ¹ 1 ï
y = f ( x) 2 x -1 = í 1 ï khi x = 1 ïî8
Câu 3(1 đ): Chứng minh phương trình sau có ít nhất một nghiệm : x5- 5x3 + 4x -1 = 0 Trang 26 www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 13
I.PHẦN TRẮC NGHIỆM: (7đ)
Câu 1: Trong các giới hạn sau giới hạn nào có giá trị hữu hạn 2 5 n - 2017 2 3 n - 2017 49 4 n + 2017 2 4 n - 3 Câu . A lim . B lim C.lim . D lim 4 2 4 2 2: - 2n - 4 - 2n -1 3 + 4n - 2n - 2017 Giới 5 hạn x + 1 lim bằng 3 x® 1 - x + 1 A. 5 3 0 . B C. D 1 . 3 5 n 1 + n n 1 + + + Câu 3: Giới hạn 2 3 6 . 2 lim bằng 2n ( 3 . 2 n 1 - + 7) A. 2 . B + ¥ C 18 . D 0 . 3 Câu 4 :Giới hạn 2n + sin 2n lim bằng 3 2017 -10n A. 1 -1 . B C. - ¥ D 1 . 5 5 2 2 Câu 5: Tìm
x - x - 4x +1 lim x®-¥ 2x + 3 A. 1 B. +¥ C. 1 - D. -¥ 2 2 2 Câu 6: Giới hạn
x +1 - x + x +1 lim bằng 2 x®0 x A. 1 - . B -1 C. - ¥ D 0 . 2 2 + Câu 7: Giới hạn x 2017 lim bằng x®-¥ 3x + x2 25 + x A. 1 1 . B - 2 C. . D -1 8 7 Câu 8: Giới hạn x +1 lim bằng 2 x® 1 - x -1 A. - 7 7 0 . B C. D 1 . 2 2
Câu 9: Giới hạn lim ( 2
x + ax + 2017 + x)= 6 . giá trị của a là: x®-¥ A. 6 B 12 . C. -12 . D - 6 2 Câu 10: Giới hạn x + (a + ) 2 x + 2a lim bằng 2 2 x®-a x - a A. a - 2 a -1 B a . C a . + 1 D. 2a Trang 27
ì 2x + 2 - x + 3 ;x ¹1 2 Câu 11: Cho hàm số ïï f (x) = í x -1
. Khi đó lim f (x) bằng ï1 x 1 ® ï ; x = 1 î8 A. 1 -1 . B C 1 . D 0 . 8 8 4 2 Câu 12: Giới hạn
4x - 4x + 3x lim bằng x® 1 - 9 4 x +16x -1 A. 1 6 2 . B C. . D + ¥ 8 4 3 ì 2
x - 4x + 3 ;khi x <1 Câu 13: Cho hàm số ï f (x) = í x -1
. Khi đó lim f (x) bằng ï x 1 ® î5x - 3 ; khi x ³ 1 A. 2 . B - 2 C 4 . . D không tồn tại. 3 3 Câu 14: Giới hạn
(x - a) + a lim bằng x®0 x A. 2 2 2 2 a B 2 . a C 7 . a D 3 . a 3 2 + Câu 15: Giới hạn x lim bằng x®0 1 4 - x A. 3 1 B 3 . C. . D - 3 4 2 ì 2x +1 - x + 5 Câu 16: Cho hàm số ï ; x ¹ f (x) = 4 í x - 4
. Khi đó giá trị tham số m để f (x) ïî2m + 3 ; x = 4 liên tục tại x=4 là: A. 1 -17 -11 5 . B C. . D 6 24 6 2
ì x + 4 - 2 ;x ¹ 0 Câu 17: Cho hàm số ïï f (x) = í x
. Khi đó giá trị m để f (x) liên tục tại ï 5 ï2m - ; x = 0 î 4 x=0 là: A. 3 3 . B C 2 . D 1 . 4 ì2 2 x + ; 3 x ¹ - Câu 18: Cho hàm số 1 f (x) = í
. Khi đó f (x) có tính chất: î2x + 2017 ; x = -1
A.liên tục trên các khoảng (- ¥;- ) 1 va(- ;
1 +¥) nhưng không liên tục tại x= -1 B .liên tục tại x= -1
C. liên tục tại mọi điểm
D. liên tục tại x= -1; x=4; x=0 Trang 28
Câu 19: Cho hàm số f (x) = 3 3
x + 2x - 2 . Xét phương trình: f(x) = 0 (1) trong các
mệnh đề sau, mệnh đề nào đúng? A. (1) Vô nghiệm
B. (1) có nghiệm trên khoảng (1; 2) C. (1) có 5 nghiệm trên R
D. (1) có ít nhất một nghiệm dương
Câu 20: Cho một hàm số f (x) . Mệnh đề nào sau đây là đúng:
A. Nếu f (x) liên tục trên đoạn [ ;
a b]; f (a). f (b) > 0 thì phương trình f (x) = 0 không có nghiệm trên khoảng ( ; a b) .
B. Nếu f (a). f (b) < 0 thì phương trình f (x) = 0 có ít nhất một nghiệm trong khoảng ( ; a b) .
C. Nếu phương trình f (x) = 0 có nghiệm trong khoảng ( ;
a b) thì hàm số f (x) phải liên tục trên khoảng ( ; a b)
D. Nếu hàm số f (x) liên tục, tăng trên đoạn [ ;
a b] và f (a). f (b) > 0 thì phương trình
f (x) = 0 không có nghiệm trong khoảng ( ; a b).
II.PHẦN TỰ LUẬN (3đ) ì 3
x +1 khi x < -1
Xét tính liên tục của hàm số ïï 2 x = 1 -
f (x) = í x -1 tại điểm 0 . ï 2 1 ï- x - khi x ³ -1 î 2
………………………..HẾT………………………………………………
ĐÁP ÁN PHẦN TỰ LUẬN NỘI DUNG ĐIỂM 2 x - x +1 - 3 0,25x2
lim f (x) = lim ( ) = x® 1- - x® 1- - x -1 2 - 2 1 3
lim f (x) = lim (-x - ) = 0,25x2 x® 1+ - x® 1+ - 2 2 Vì - 3
lim f (x) = lim f (x) Þ lim f (x) = 0,25x2 x® 1 - - x® 1 - + x® 1 - 2 f(-1)=-3/2 0,5 Vì - 3
lim f (x) = f (- ) 1 =
nên f(x) liên tục tại x=-1 0,5x2 x® 1 - 2 Trang 29 www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 14
I) PHẦN TRẮC NGHIỆM (8 điểm - mỗi câu 0.4 điểm)
Câu 1: Trong bốn giới hạn sau đây, giới hạn nào bằng 2? 2 2 A. x -1 x -1 lim(4x -10) . B. lim . C. lim . D. x®3 x 1 ® 2x +1 2
x®+¥ 2x + x + 1 lim( 2 3x + x - ) 1 . x®2
Câu 2: Trong bốn giới hạn sau đây, giới hạn nào bằng 0? (5n + ) 1 ( 3 n + n - 4) A. ( 2 2 lim
n - 2n + 2 - 3n +1) B. lim . ( 3n + ) 2 1 n - 2 2016 2016 C. 5n - 3n -1 3n + sinn lim . D. lim . 2 n + 2n -1 2017 n +1 2 -n + 2n - 3
Câu 3: Chọn kết quả đúng trong các kết quả sau: lim bằng: 2 n A. 0. B. -¥ . C. 1 - . D. 1. 3 3 2 x + 2x +1
Câu 4: Chọn kết quả đúng trong các kết quả sau: lim bằng: x®-¥ 2 2x +1 A. 2 . B. 1. C. 2 - . D. 0. 2 2
Câu 5: Giả sử lim f ( x) = L và lim g ( x) = M (L, M Î! ). Khẳng định nào sau đây sai? x® ® 0 x x 0 x A. lim é f
ë ( x).g ( x)ù = . L M . B. 3 3 lim f x = L . û ( ) x® ® 0 x x 0 x C. lim é f
ë ( x) + g ( x)ù = L + M .
D. lim f x = L . û ( ) x® ® 0 x x 0 x 2x -1
Câu 6: Chọn kết quả đúng trong các kết quả sau: lim bằng: x®2 x + 2 A. 2. B. 5 . C. 1. D. 3 . 4 4
Câu 7: Chọn mệnh đề sai trong các mệnh đề sau: A. Hàm số 3x + 5
y = sin x liên tục trên toàn bộ tập ! . B. Hàm số y = liên tục trên x +1 toàn bộ tập ! . C. Hàm số 4 - x y =
liên tục trên toàn bộ tập ! . D. Hàm số 3 2
y = x + 2x - 5x + 7 liên 2 x +1 tục trên tập ! . 2 2x + 5x - 3
Câu 8: Chọn kết quả đúng trong các kết quả sau: lim bằng: + 2 x®( 3 - ) (x + 3) A. 1 B. 2. C. -¥ . D. +¥ . 2 4
ì x + x khi x ¹ 0, x ¹ -1 ï 2 x + x ïï
Câu 9: Cho hàm số f ( x) = 3 khi x í = 1 -
. Tìm khẳng định đúng trong các khẳng định sau: 1 ï khi x = 0 ï ïî
A. Hàm số f liên tục tại mọi điểm xÎ! . Trang 30
B. Hàm số f liên tục tại mọi điểm trừ điểm x = -1.
C. Hàm số f liên tục tại mọi điểm trừ các điểm x thuộc [ 1; - 0] .
D. Hàm số f liên tục tại mọi điểm trừ điểm x = 0. 2 ì x - 4 ï khi x ¹ 2
Câu 10: Cho hàm số f ( x) = í x - 2
Với giá trị nào của a thì hàm số liên tục tại x = 2 ïîa khi x = 2 A. a = 2. B. a = 4. C. a = -2. D. a = 1. 4n + 2n
Câu 11: Chọn kết quả đúng trong các kết quả sau: lim bằng: 4n - 2.3n A. 0. B. -1. C. 1. D. 4. 1+ n
Câu 12: Chọn kết quả đúng trong các kết quả sau: lim bằng: n A. 0. B. 1. C. 2. D. +¥ . + 1 1 (- )n 1 1
Câu 13: Cho S = - + ... +
+ ... . Giá trị của S bằng: 3 9 3n A. 3 . B. 1 . C. 1 . D. 1. 4 2 4 ì x - x <
Câu 14: Cho hàm số f ( x) 2 1 khi 1 = í
. Kết quả nào sau đây là đúng? î2 khi x ³1
A. lim f (x) = 2
B. lim f (x) = lim f (x) C. lim f (x) = 3 . D. x 1 ® x 1+ x 1- ® ® x 1- ®
lim f ( x) = 2 . x 1+ ®
Câu 15: Cho phương trình : x5 – 3x4 + 5x – 2 = 0. Các mệnh đề sau mệnh đề nào đúng
A. Phương trình vô nghiệm trong khoảng ( -2 ; 5)
B. Phương trình có ít nhất 3 nghiệm nằm trong khoảng ( -2 ; 5).
C. Phương trình đúng 2 nghiệm nằm trong khoảng ( -2 ; 5)
D. Phương trình có đúng 1 nghiệm nằm trong khoảng ( -2 ; 5) 2 1+ 4 + 4 + ... + 4n
Câu 16: Chọn kết quả đúng trong các kết quả sau: lim bằng: 2 1+ 3 + 3 + ... + 3n A. 4 . B. 1. C. 0. D. +¥ . 3 2 3 - x + 2x - 5
Câu 17: Chọn kết quả đúng trong các kết quả sau: lim bằng: 2 n®+¥ 2x - 7 A. 3 . B. 1 . C. 3 - . D. 5 . 2 2 2 7 2
4x + 3x - 4x
Câu 18: Chọn kết quả đúng trong các kết quả sau: lim bằng: x®-¥ 2
9x + 6x - x A. 3 1 - . B. -¥ . C. 0. D. . 2 2 x - 4x + 3
Câu 19: Chọn kết quả đúng trong các kết quả sau: lim bằng. 2 x 1 ® x + 4x - 5 A. 2 . B. 1 - . C. 1. D. 1 . 3 3 2
Câu 20: Chọn kết quả đúng trong các kết quả sau: 2 lim x - 8 bằng: x® 3 A. 5. B. 3 - 8 . C. -5. D. 3 . Trang 31
II) PHẦN TỰ LUẬN (2 điểm - mỗi câu 1 điểm) 2 2x + 3x - 5
Câu 1. (1đ) Tính giới hạn: lim x 1 ® x -1
Câu 2. (1đ) Cho 3 số thực a,b,c khác không và thỏa 3a + 4b + 7c = 0 . Chứng minh rằng phương trình 2
ax + bx + c = 0 có nghiệm thuộc khoảng (0; ) 1
------ HẾT ------ www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 15
I/TRẮC NGHIỆM(6đ): Chọn câu trả lời đúng 1 1 1 1 1 n æ ö
Câu 1. Tổng của cấp số nhân lùi vô hạn - , , - , ..., - ,... là ç ÷ 2 4 8 16 è 2 ø 1 1 A. 1 B. C. -1 D. - 2 3
Câu 2. Dãy số nào sau đây có giới hạn là +¥ ? 2 2n + 2n -1 2 n - 2n A. 2 3
u = 3n - 4n B. u = C. u = D. 2
u = 3n -13n n n 3 n + 4 n 2 - n n
Câu 3. Cho một hàm số
xác định trên khoảng (a;b). Khẳng định nào sau đây là đúng ? A. Nếu hàm số liên tục trên đoạn
và f (a). f (b) < 0 thì phương trình có nghiệm trong khoảng .
B. Nếu phương trình có nghiệm trong khoảng thì hàm số liên tục trên khoảng C. Nếu liên tục trên đoạn [ ;
a b]; f(a).f(b)=0 thì pt có nghiệm trên khoảng . D. Nếu thì phương trình
có ít nhất một nghiệm trong khoảng . 2 5 3n + n a 3
Câu 4. Giới hạn lim =
(a/b tối giản) có a+b bằng 2(3n + 2) b A. 21 B. 11 C. 19 D. 51 1+ 3 + 5 + ...+ (2n -1) Câu 5. lim bằng : 2n(2n - 3) 1 A. không tồn tại B. 1 C. D. 2 4 3 - Câu 6. Tính 2
lim ( 2x - 3x + 4 - x) : A. B. +¥ C. 2 -1 D. -¥ x®+¥ 2 +1
Câu 7. Hàm số nào trong các hàm sau có giới hạn tại điểm x=2 ? 1 1 2x 13
A. f (x) =
B. f (x) =
C. f (x) =
D. f (x) = x +1 x - 2 2 x - 4 x - 2
Câu 8. Dãy số nào sau đây có giới hạn bằng 0? 6 n æ ö 2 n æ ö 3 n - 3n A. B. - C. D. 2 n - 4n ç ÷ ç ÷ è 5 ø è 3 ø n +1 Trang 32 2 3 2x - x 1 Câu 9. lim bằng: A. - B. -¥ 1 C. D. 2 x 1 ® 5x - 2x + 3 5 6 2 5 ì x + 3 - 2 ï (x>1) ï - Câu 10. Hàm số x 1 f (x) = í
Giá trị m để f(x) liên tục tại x=1 là: 1 ï 2 m + m + (x £ 1) ïî 4 A. m Î{0; } 1 B. m Î{0; - } 1 C. m=1 D. m=0
Câu 11. Trong các dãy số sau, dãy số nào có giới hạn hữu hạn? 2.5n -12 4 3 n - 3n + 2 3 2n - 3n + 3 n æ 1 n ö A. u = B. u = 6 + C. u = D. u = n ç ÷ 3n - 2 n è 3 ø n 4 -n + 2n - 4 n 2 -n + 5
Câu 12. Hàm số nào sau đây liên tục tại x=2 ? 2 2x + 6x +1 x +1 2 x + x +1
A. f (x) =
B. f (x) =
C. f (x) = D. x + 2 x - 2 x - 2 2 3x - x - 2 f (x) = 2 x - 4 2 2x - 6 Câu 13. Tính lim
= a b Khi đó đặt P=a+b ta có P = : A. 6 B. 7 C. 5 D. 10 x® 3 x - 3
Câu 14. Phương trình 5 4 2
x - 3x + 2x + 5x - 4 = 0 có mấy nghiệm ? A. 4 B. 3 C. 5 D. 1 3 ì x -8 ï (x ¹ 2)
Câu 15. Cho hàm số: f (x) = í x - 2
để f(x) liên tục tại điêm x0 = 2 thì a bằng ? ïî2a -4 (x = 2) A. 4 B. 6 C. 8
D. Không có giá trị a II/TỰ LUẬN (4đ): 3 3x - 2 - 2x -1
Câu 1 (2đ) :a/ Tính giới hạn: lim x 1 ® 1- x 3 3
3x + 2(x - 3x +1) - 6 b/ Tính giới hạn: lim ; 2 x®2 x - 4 ì x2 + 3x + ï 2 , x ¹ -2
Câu 2 (2đ) : a) Tìm m để hàm số f (x) = í
liên tục tại x = 2 - . x + 2 ïî3mx2, x = -2
b) Chứng minh phương trình sau luôn có nghiệm với mọi giá trị của m: 2016 2m(x -1) (x - 2) + 2x-3=0 Trang 33 www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 16
I/TRẮC NGHIỆM(6đ): Chọn câu trả lời đúng
Câu 1. Trong các hàm số sau hàm số nào liên tục trên R ? x - 3 3 x - 2x +1 3 2 2x - 5x + 6 A. y = B. y = C. y = D. y= tan3x 1- cos x 2 x + 2 x +1 3 x + 4 Câu 2. Tính lim : A. -2 B. C. 3 D. x 2+ ® x - 2 3 - x 3n + 3.5n 3 Câu 3. Tính lim - n 1 + :
A. 1 B. 0 C. D. 3/2 2 - 5 5 3 x -1
Câu 4. Giới hạn lim bằng: A. 3/2 B. 3 C. -3/2 D. Không tồn tại. 2 x 1 ® x -1
Câu 5. Dãy số nào sau đây có giới hạn khác 0? 2 2n +1 2 3 n æ ö 3 4 A. B. C. D. 2 ç ÷ 3n + 4 è 5 ø 3 n + n 2 n + 3 2
3 x + 4x + x
Câu 6. Giới hạn lim bằng: A. -2 B. 3 C. -5 D. 5 x®-¥ x +1 4 3 5x + 2x + 2 a Câu 7. lim =
; (a;b nguyên). Khi đó a+b bằng: 4 x®+¥ 16x + 9x + 5 b A. 9 B. 19 C. 8 D. 21 2 18x +1 - x + 5 Câu 8. lim bằng: A. 17/2 B. +¥ 2 3 C. D. x®+¥ 2x - 7 3 3 2 2 2 9n +1 - n + 2 Câu 9. lim bằng: A. 8/3 B. 10/3 C. 3 D. 1 3n - 3 ( 2 lim
n - 3n - n) Câu 10. Tính : A. -3/2 B. 0 C. 5/2 D. 3/2 1+ 3 + 5 + ...+ (2n -1) Câu 11. lim bằng : 2n(2n - 3) 1 A. 1 B. không tồn tại C. 2 D. 4
Câu 12. Dãy số nào sau đây có giới hạn bằng 0? 3 n - 3n 2 n æ ö 6 n æ ö A. B. - C. D. 2 n - 4n ç ÷ ç ÷ n +1 è 3 ø è 5 ø 1 1 1 1 1 n æ ö
Câu 13. Tổng của cấp số nhân lùi vô hạn - , , - , ..., - ,... là ç ÷ 2 4 8 16 è 2 ø 1 A. -1 B. - 1 C. 1 D. 3 2
Câu 14. Cho một hàm số
xác định trên khoảng (a;b). Khẳng định nào sau đây là đúng ? A. Nếu thì phương trình
có ít nhất một nghiệm trong khoảng . Trang 34
B. Nếu phương trình có nghiệm trong khoảng thì hàm số liên tục trên khoảng C. Nếu liên tục trên đoạn [ ;
a b]; f(a).f(b)=0 thì pt có nghiệm trên khoảng . D. Nếu hàm số liên tục trên đoạn
và f (a). f (b) < 0 thì phương trình có nghiệm trong khoảng . 3 ì x -8 ï (x ¹ 2)
Câu 15. Cho hàm số: f (x) = í x - 2
để f(x) liên tục tại điêm x0 = 2 thì a bằng ? ïî2a -4 (x = 2) A. 6 B. 8 C. 4
D. Không có giá trị a II/TỰ LUẬN (4đ): 3 x + 7 - 3x +1
Câu 1 (2đ) :a/ Tính giới hạn: lim x 1 ® x -1 3 3
x + 6(x - x - 3) - 6 b/ Tính giới hạn: lim ; 2 x®2 x - 4 ì x2 - 3x - ï 10 , x ¹ -2
Câu 2 (2đ) : a) Tìm m để hàm số f (x) = í
liên tục tại x = 2 - . x + 2 ïî2mx , x = -2
b) Chứng minh phương trình sau luôn có nghiệm với mọi giá trị của m : ( m + ) 2 2 2
4 (x -1) + 2x - 1=0 www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 17
I/TRẮC NGHIỆM(6đ): Chọn câu trả lời đúng 3 - Câu 1. Tính 2
lim ( 2x - 3x + 4 - x) : A. B. +¥ C. 2 -1 D. -¥ x®+¥ 2 +1 2 9n +1 - n + 2 Câu 2. lim bằng: A. 3 B. 10/3 C. 8/3 D. 1 3n - 3
Câu 3. Dãy số nào sau đây có giới hạn bằng 0? 6 n æ ö 2 n æ ö 3 n - 3n A. B. - C. D. 2 n - 4n ç ÷ ç ÷ è 5 ø è 3 ø n +1
Câu 4. Cho một hàm số
xác định trên khoảng (a;b). Khẳng định nào sau đây là đúng ?
A. Nếu phương trình có nghiệm trong khoảng thì hàm số liên tục trên khoảng B. Nếu liên tục trên đoạn [ ;
a b]; f(a).f(b)=0 thì pt có nghiệm trên khoảng . C. Nếu hàm số liên tục trên đoạn
và f (a). f (b) < 0 thì phương trình có nghiệm trong khoảng . D. Nếu thì phương trình
có ít nhất một nghiệm trong khoảng .
Câu 5. Phương trình 5 4 2
x - 3x + 2x + 5x - 4 = 0 có mấy nghiệm ? A. 4
B. 1 C. 3 D. 5 2 18x +1 - x + 5 3 2 2 3 Câu 6. lim bằng: A. 17/2 B. C. D. +¥ x®+¥ 2x - 7 2 3 Trang 35
Câu 7. Trong các dãy số sau, dãy số nào có giới hạn hữu hạn? 2.5n -12 4 3 n - 3n + 2 3 2n - 3n + 3 n æ 1 n ö A. u = B. u = C. u = 6 + D. u = n ç ÷ 3n - 2 n 4 -n + 2n - 4 n è 3 ø n 2 -n + 5 2 2x - 6 Câu 8. Tính lim
= a b Khi đó đặt P=a+b có: A.7 B. 10 C. 5 D. 6 x® 3 x - 3
Câu 9. Dãy số nào sau đây có giới hạn là +¥ ? 2 2n + 2n -1 2 n - 2n A. u = B. 2 3
u = 3n - 4n C. 2
u = 3n -13n D. u = n 3 n + 4 n n n 2 - n 1+ 3 + 5 + ...+ (2n -1) 1 Câu 10. lim
bằng : A. không tồn tại B. 2 C. D. 2n(2n - 3) 4 1 1 1 1 1 1 n æ ö
Câu 11. Tổng của cấp số nhân lùi vô hạn - , , - , ..., - ,... là ç ÷ 2 4 8 16 è 2 ø 1 1 A. B. - C. 1 D. -1 2 3 ( 2 lim
n - 3n - n) Câu 12. Tính : A. 3/2 B. 0 C. -3/2 D. 5/2 2 3 2x - x 1 1 Câu 13. lim bằng: A. -¥ 2
B. C. - D. 2 x 1 ® 5x - 2x + 3 5 5 6 2 5 3n + n a 3
Câu 14. Giới hạn lim =
(a/b tối giản) có a+b bằng 2(3n + 2) b A. 11 B. 19 C. 21 D. 51 ì x + 3 - 2 ï (x>1) ï - Câu 15. Hàm số x 1 f (x) = í
Giá trị m để f(x) liên tục tại x=1 là: 1 ï 2 m + m + (x £ 1) ïî 4 A. m=1 B. m Î{0; - } 1 C. m=0 D. m Î{0; } 1 II/TỰ LUẬN (4đ):
3 5x - 4 - 3x - 2
Câu 1 (2đ) :a/ Tính giới hạn: lim 2 x 1 ® x -1 3 3
x + 6(2x - 5x - 3) - 6 b/ Tính giới hạn: lim ; 2 x®2 4 - x ì x2 + x - ï 2 , x ¹ -2
Câu 2 (2đ) : a) Tìm m để hàm số f (x) = í
liên tục tại x = 2 - . x + 2 ïîmx2, x = -2
b) Chứng minh phương trình sau có ít nhất 2 nghiệm trên (-3;3): 4 3 2
9x - 9x + 5x + 4x - 4 = 0 Trang 36 www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 18 Câu 1: Cho 2
lim( x + ax + 5 - x) = 5 . Khi đó giá trị của a là: x 1 ® A. -14 B. -30 C. 30 D. 14 2 - x +1
Câu 2: Tính giới hạn lim ta được kết quả là: x 1+ ® x -1 A. - ¥ B. +¥ C. 0 D. 2 2 x - 4x + 3
Câu 3: Tính giới hạn lim ta được kết quả là: x 1 ® x -1 A. – 3 B. 1 C. 3 D. – 2
Câu 4: Tính giới hạn 5 2
lim (7x + 5x - x + 7) ta được kết quả là: x®-¥ A. 3 B. - ¥ C. + ¥ D. 0
Câu 5: Tìm giới hạn 2 lim( 3
- n - 2n +1) ta được kết quả: A. +¥ B. 2 C. 3 D. - ¥ 5 2n + 2n -1
Câu 6: Tìm giới hạn lim ta được kết quả là: 2 n +1 A. 4 B. + ¥ C. - ¥ D. -1
Câu 7: Cho phương trình 2x4 – 5x2 + x + 1 = 0 (1). Mệnh đề nào đúng trong các mệnh đề sau:
A. Phương trình (1) có ít nhất hai nghiệm thuộc khoảng (0; 2).
B. Phương trình (1) không có nghiệm trong khoảng (-2; 0).
C. Phương trình (1) không có nghiệm trong khoảng ( -1; 1).
D. Phương trình (1) chỉ có một nghiệm trong khoảng (-2; 1). 5n + 2.3n
Câu 8: Tìm giới hạn lim ta được kết quả : 4n - 5n A. + ¥ B. - ¥ C. -1 D. 1 1 1 1 1
Câu 9: Tìm giá trị đúng của S = 2(1+ + + + ...+
+ ...) ta được kết quả là 2 4 8 2n 1 A. 2 B. 2 C. D. 2 2 2 2 + 5 + 8 + ...+ 3n -1
Câu 10: Tìm giới hạn lim ta được kết quả là: 2 2n + 3 A. + ¥ 3 B. C. -1 D. - ¥ 4 a b x - x
Câu 11: Tính giới hạn lim với *
a,b Î • ta được kết quả là: x®+¥ 1- x a A. ab B. a – b C. b – a D. b 2 ì 2x - 3x - 2 ï khi x > 2
Câu 12: Để hàm số f (x) = í x - 2
liên tục tại điểm x = 2 thì giá trị của a là: ïîax +1 khi x £ 2 A. 1 B. 2 C. 5 D. -3 Trang 37 Tự luận: (4đ) 3
x - 5x + 2x 3 x +1 - 1- x 1. Tính: a, lim b, lim x®2 2x - 5 x®0 x . ì x + 4 - 2 ï khi x ¹ 0 ï
2. Tìm a để hàm số ( ) x f x = í
liên tục tại điểm x = 0 . 7 ï2a - khi x = 0 ïî 4 www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 19 I-Trắc nghiệm (3đ). 3 2n - 2n + 3 1.Kết quả của lim là: 3 1+ 4n 1 1 A) B) - C) 0 D) 2 2 2 4n2 - n +1 2.Kết quả của lim là : 2 + n 3 A) 4 - B) 4 C) 2 D) 2 - 3 3 3 3 1
3.Tổng S = 3 +1+ ... + + ...có kết quả là: 3n-3 27 27 9 9 A) B) C) D) 2 4 2 4 2 x - x -
4. kết quả của giới hạn 3 2 lim là: 2
x®3 x - 3x + 2 A) 3 B) -3 C) -1 D) 11 2 x - x 5.Cho M = lim Khi đó: x 1 ® 2 2 x - x -1 1 1 A. M = 1 B. M = - C. M = +∞ D. M = - 2 3 2 + -
6.kết quả của giới hạn 1 9x 1 lim là: x®0 2x A) 3 B) 9 - C) 3 - D) 9 2 4 2 4 II-Tự luận (7đ).
Câu 2(4 đ):Tính giới hạn của các hàm số sau: 2 x + 3 - 2 2
a) lim ( x - 2x - x) b) lim x®+¥ x 1 ® x -1
Câu 3(2 đ): Xét tính liên tục của hàm số sau trên tập số thực R. Trang 38 2 ì x + 3x - 4 ï ......k ... hi x ¹ 1 f (x) = í - x 1 5...................... ïî k ... hi x = 1
Câu 4(1 đ): Chứng minh phương trình sau có ít nhất một nghiệm : 3 2
3x + 2x - 5x -1 = 0 www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 20
I-Trắc nghiệm (3đ).Khoanh tròn vào đáp án đúng. 3 2n - 2n + 3 1.Kết quả của lim là: 3 1+ 4n 1 A) 0 B) - 1 C) D) 2 2 2 4n2 - n +1 2.Kết quả của lim là : 2 + n 3 4 2 A) - 4 B) C) - 2 D) 3 3 3 3 3.Tổng 1 S = 3 +1+ ... + + ...có kết quả là: 3n-3 A) 9 B) 27 C) 27 D) 9 2 4 2 4 3 2 x - x - 2
4. kết quả của giới hạn lim là: 2
x®3 x - 3x + 2 A) 11 B) -3 C) -11 D) 3 2 x - x 5.Cho M = lim Khi đó: x 1 ® 2 2 x - x -1 1 1 1 A. M = B. M = - C. M = +∞ D. M = - 2 2 3 1+ 9x -1
6.kết quả của giới hạn lim là: x®0 2x 3 9 9 3 A) B) - C) D) - 2 4 4 2 II-Tự luận (7đ).
Câu 2(4 đ):Tính giới hạn của các hàm số sau: 2 x + 5 - 3 2
a) lim ( x + 2x - x) b) lim x®+¥ x®2 x - 2
Câu 3(2 đ): Xét tính liên tục của hàm số sau trên tập số thực R. Trang 39 2 ì x - 3x - 4 ï .....k ... hi x ¹ 1 - f (x) = í + x 1 ïî 5........ - k ... hi x = 1 - 3 2
Câu 4(1 đ): Chứng minh phương trình sau có ít nhất một nghiệm : x + 2x - x -1 = 0 www.thuvienhoclieu.com
ĐỀ KIỂM TRA THỬ 1 TIẾT CHƯƠNG IV Thời gian: 45 phút ĐỀ 21 Câu 1: Cho 2
lim ( x + ax + 5 - x) = 5 . Khi đó giá trị của a là: x®+¥ A. -6 B. -10 C. 10 D. 6 3
ìï2x - x khi x ³ 2
Câu 2: Cho hàm số f (x) = í
. Tính giới hạn của hàm số tại x =2 ta 3
ïîx - 3x khi x < 2 được kết quả là: A. 2 B. 1 C. Không tồn tại D. -2
Câu 3: Tính giới hạn 2 - x +1 lim ta được kết quả là: x 1+ ® x -1 A. - ¥ B. +¥ C. 0 D. 2
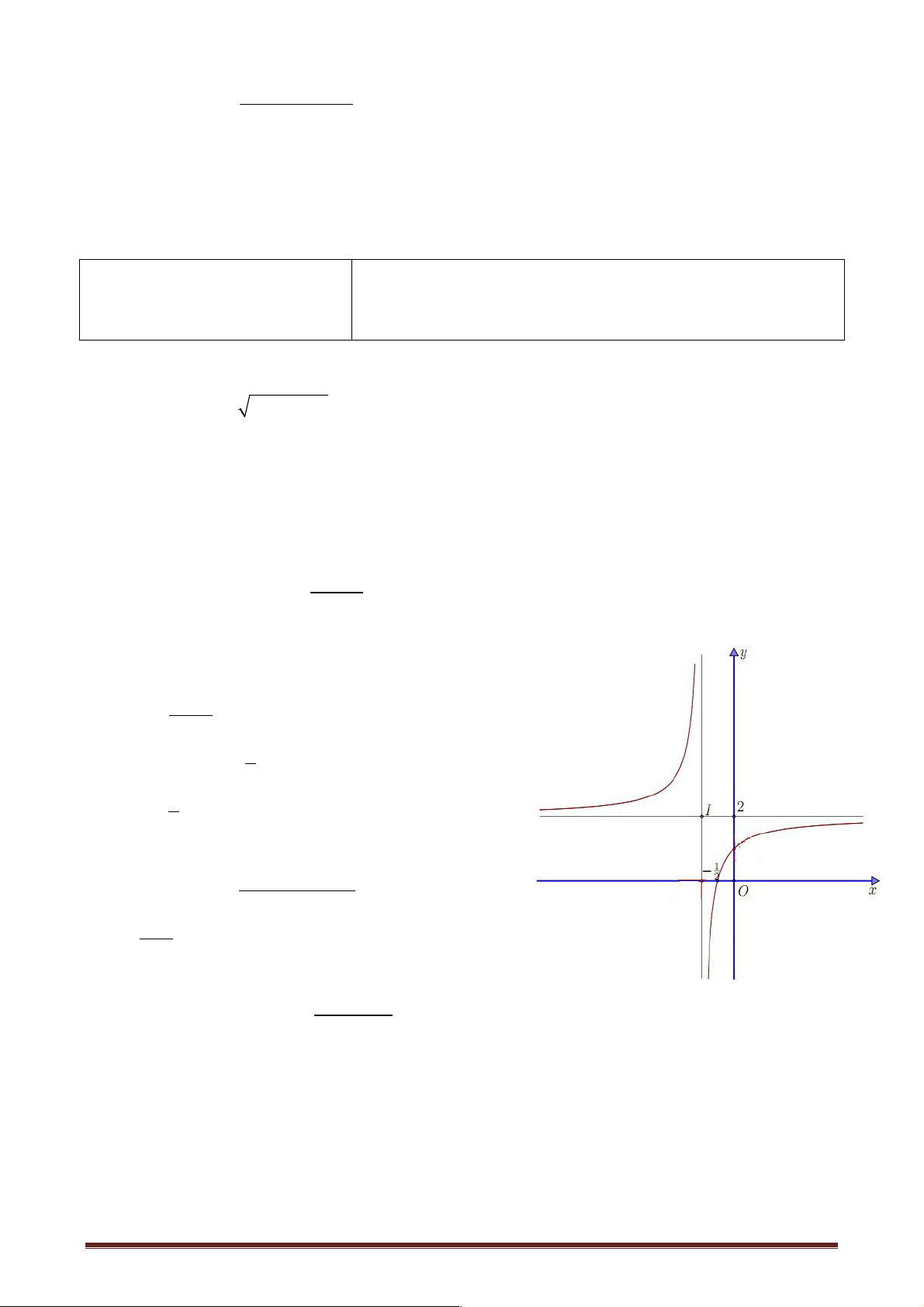
Câu 4: : Đồ thị hàm số ở hình bên là đồ thị của hàm số nào ? A. 4x +1 y = 2x +1 B. 1 3
y = 2x - 3x + 2 C. 1 4 2 y = x 2 - x + 2 2 D. 2
y = x - 3x + 2 2 Câu 5: Tính
x - (a +1)x + a lim được kết quả là: 2 2 x®+¥ x - a A. a -1 B. a 2a C. a - 1 D. a + 1 2
Câu 6: Tính giới hạn x - 4x + 3 lim ta được kết quả là: x 1 ® x -1 A. – 3 B. 1 C. 3 D. – 2
Câu 7: Tính giới hạn 5 2
lim (7x + 5x - x + 7) ta được kết quả là: x®+¥ A. 3 B. - ¥ C. + ¥ D. 0
Câu 8: Tìm giới hạn 2 lim( 3
- n - 2n +1) ta được kết quả: A. +¥ B. 2 C. 3 D. - ¥ Trang 40 5
Câu 9: Tìm giới hạn 2n + 2n -1 lim ta được kết quả là: 2 n +1 A. 4 B. + ¥ C. - ¥ D. -1
Câu 10: Cho phương trình 2x4 – 5x2 + x + 1 = 0 (1). Mệnh đề nào đúng trong các mệnh đề sau:
A. Phương trình (1) có ít nhất hai nghiệm thuộc khoảng (0; 2).
B. Phương trình (1) không có nghiệm trong khoảng (-2; 0).
C. Phương trình (1) không có nghiệm trong khoảng ( -1; 1).
D. Phương trình (1) chỉ có một nghiệm trong khoảng (-2; 1).
Câu 11: Cho hàm số f(x) xác định trên [a; b]. Trong các mệnh đề sau mệnh đề nào đúng?
A. Nếu hàm số f(x) liên tục, tăng trên [a; b] và f(a).f(b) > 0 thì phương trình f(x) =
0 không có nghiệm trong khoảng (a; b).
B. Nếu hàm số f(x) liên tục trên [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0
không có nghiệm trong khoảng (a; b).
C. Nếu phương trình f(x) = 0 có nghiệm trong khoảng (a; b) thì hàm số f(x) phải liên tục trên (a; b).
D. Nếu f(a).f(b) < 0 thì phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (a; b). 3 2
Câu 12: Tìm giới hạn 3n - 2n + 2 lim ta được kết quả: 3 n +1 A. - ¥ B. 3 C. 1 D. + ¥ 2 n n
Câu 13: Tìm giới hạn 5 + 2.3 lim ta được kết quả : 4n - 5n A. + ¥ B. - ¥ C. -1 D. 1
Câu 14: Tìm giá trị đúng của S = 1 1 1 1 2(1+ + + + ...+
+ ...) ta được kết quả là 2 4 8 2n A. 1 2 B. 2 C. D. 2 2 2
Câu 15: Tìm giới hạn 2 + 5 + 8 + ...+ 3n -1 lim ta được kết quả là: 2 2n + 3 A. + ¥ B. 3 C. -1 D. - ¥ 4 a b
Câu 16: Tính giới hạn x - x lim với *
a,b Î • ta được kết quả là: x®+¥ 1- x A. ab B. a – b C. b – a D. a b ì x + 4 - 2 ï khi x ¹ 0
Câu 17: Để hàm số ï ( ) x f x = í
liên tục tại điểm x = 0 thì giá trị 7 ï2a - khi x = 0 ïî 4 của a là: A. 1 B. 3 C. 2 D. 1 Trang 41 4
Câu 18: Tính giới hạn x - 5 lim ta được kết quả là: 7 5
x®+¥ x + 5x A. 2 B. -5 C. 2 D. 0 5 2 ì ¹ Câu 19: Hàm số 5x khi x 0 f (x) = í có tính chất: î 15 - khi x = 0
A. liên tục tại x = 2 và x = 0.
B. liên tục tại x = 2 nhưng không liên tục tại x = 0.
C. liên tục tại mọi điểm.
D. Liên tục tại x = 1, x = 3, x = 0. 2 ì 2x - 3x - 2
Câu 20: Để hàm số ï khi x > 2 f (x) = í x - 2
liên tục tại điểm x = 2 thì giá trị của ïîax +1 khi x £ 2 a là: A. 1 B. 2 C. 5 D. -3 Trang 42