TOP 3 Đề thi thử Tuyển Sinh vào 10 môn Toán Quận 6 Tp. HCM năm học 2024-2025 (có đáp án)

SỞ GIÁO DỤC VÀ ĐẠO TẠO
ĐỀ THAM KHẢO TUYỂN SINH 10 THPT THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC: 2024 - 2025 QUẬN 6 (ĐỀ 1) MÔN THI: TOÁN
(đề thi gồm 02 trang) 2 −x x
Câu 1: (1,5 điểm) Cho hàm số y =
có đồ thị là parabol (P) và hàm số y = − 2 có đồ thị 4 2 là đường thẳng (D).
a) Vẽ đồ thị (P) và (D) trên cùng một hệ trục toạ độ.
b) Tìm toạ độ các giao điểm của (P) và (D) bằng phép tính.
Câu 2: (1,0 điểm) Cho phương trình: 2
2x + 7x − 5 = 0 có 2 nghiệm x và x . Không giải 1 2
phương trình, hãy tính giá trị biểu thức: P = (3x − 5x 3x − 5x . 1 2 ) ( 2 1 )
Câu 3: (0,75 điểm) Một vật rơi tự do từ độ cao so với mặt đất là 120 mét. Bỏ qua sức cản
không khí, quãng đường chuyển động s (mét) của vật rơi sau thời gian t được biểu diễn gần đúng bởi công thức: 2
s = 5t , trong đó t là thời gian tính bằng giây.
a) Sau 3 giây vật này cách mặt đất bao nhiêu mét?
b) Sau bao lâu kể từ khi bắt đầu rơi thì vật này chạm mặt đất? (Làm tròn kết quả đến chữ số hàng đơn vị).
Câu 4: (0,75 điểm) Trong tuần, mỗi ngày Nam chỉ chơi một môn thể thao. Nam chạy ba
ngày một tuần nhưng không bao giờ chạy trong hai ngày liên tiếp. Vào thứ Hai, anh ta chơi
bóng bàn và hai ngày sau đó anh ta chơi bóng đá. Nam còn đi bơi và chơi cầu lông, nhưng
không bao giờ Nam chơi cầu lông sau ngày anh ta chạy hoặc bơi. Hỏi ngày nào trong tuần Nam đi bơi?
Câu 5: (1.0 điểm) Bạn Nam gửi ngân hàng 20 triệu đồng, kì hạn 1 năm với lãi suất kép. Sau
1 năm, tổng số tiền Nam có trong ngân hàng là 21 triệu đồng. Hỏi sau 2 năm số tiền trong
ngân hàng của Nam là bao nhiêu? Biết lãi suất ngân hàng không đổi và Nam không rút tiền lãi sau năm thứ nhất. Trang 1
Câu 6: (1,0 điểm) Một vật có khối lượng 279g và có thể tích 37ml là hợp kim của sắt và
kẽm. Tính xem trong đó có bao nhiêu gam sắt và bao nhiêu gam kẽm? Biết khối lượng riêng
của sắt là 7800kg/m3 và khối lượng riêng của kẽm là 7000kg/m3.
Câu 7: (1,0 điểm) Các ống hút nhựa
thường khó phân hủy và gây hại cho môi
trường. Mỗi ngày có 60 triệu ống hút thải
ra môi trường gây hậu quả nghiêm trọng.
Ngày nay người ta chủ động sản xuất các
loại ống hút dễ phân hủy. Tại tỉnh Đồng Tháp có cơ sở chuyên sản xuất ống hút “thân thiện
với môi trường” xuất khẩu ra thị trường thế giới và được nhiều nước ưa chuộng. Ống hút
được làm từ bột gạo, các màu chiết xuất từ củ dền, lá dứa, bông sen, bông điên điển, .
Một ống hút hình trụ, đường kính 12 mm, bề dày ống 2 mm, chiều dài ống 180 mm.
Em hãy tính xem để sản xuất mỗi ống thì thể tích bột gạo được sử dụng là bao nhiêu.
(Biết thể tích hình trụ: 2 V
.R .h với R là bán kính đáy và h là chiều cao; kết quả làm tròn
đến chữ số thập phân thứ 2 với   3,14 )
Câu 8: (3,0 điểm) Cho đường tròn (O; R) và điểm A ở ngoài (O) với OA = 2R. Đoạn thẳng
OA cắt đường tròn (O) tại D, Gọi H là trung điểm của OD, đường thẳng vuông góc với OA tại H cắt (O) tại M.
a) Chứng minh: AM là tiếp tuyến của (O).
b) Qua A vẽ cát tuyến ABC đến đường tròn (O) (B; C  (O), B nằm giữa A và C).
Chứng minh: AH.AO = AB.AC = AM2 và đường thẳng MH chứa tia phân giác của BHC
c) Tiếp tuyến tại B và C của (O) cắt nhau tại T. Chứng minh: ba điểm M, H, T thẳng hàng. HẾT Trang 2
SỞ GIÁO DỤC VÀ ĐẠO TẠO
ĐỀ THAM KHẢO TUYỂN SINH 10 THPT THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC: 2024 - 2025 QUẬN 6 (ĐỀ 2) MÔN THI: TOÁN
(đề thi gồm 04 trang)
Bài 1: (1, 5 điểm) Cho parabol (𝑃): 𝑦 = 𝑥2 và đường thẳng (𝑑): 𝑦 = 𝑥 + 2.
a) Vẽ (𝑃) và (𝑑) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (𝑃) và (𝑑) bằng phép tính.
Bài 2: (1,0 điểm). Cho phương trình: 𝑥2 − 𝑥 − 12 = 0 có hai nghiệm x ; x . 1 2
Không giải phương trình, hãy tính giá trị của biểu thức: 2 2 2 2 A = x + x − x x . 1 2 1 2
Bài 3: (0,75 điểm). Để ước tính chiều cao tối đa của trẻ em khi đạt đến độ trưởng thành,
hoàn toàn có thể dựa vào chiều cao của bố mẹ. Cách tính chiều cao của con theo bố mẹ được
các chuyên gia đánh giá cao bởi thực tế, sự di truyền các thế hệ có ảnh hưởng nhất định đến
chiều cao của trẻ. Ta có công thức tính như sau: C = (B + M + 13A) : 2 .
Trong đó: C là chiều cao của người con ( ) cm
B là chiều cao của người bố ( ) cm
M là chiều cao của người mẹ ( ) cm
A = 1 khi người con có giới tính là Nam
A = −1 khi người con có giới tính là Nữ
a) Em hãy dùng công thức trên để tìm chiều cao tối đa của bạn Nam (giới tính là nam) biết
Ba của bạn Nam có chiều cao là 175 cm và Mẹ của bạn Nam có chiều cao là 168 cm.
b) Bạn Hương (giới tính là nữ) có chiều cao là 164 cm. Em hãy tính xem chiều cao tối đa của
Mẹ bạn Hương khi biết chiều cao của Ba bạn Hương là 180 cm.
Bài 4 (0,75 điểm) Nhân ngày quốc tế phụ nữ 8/3. Một cửa hàng bán quà lưu niệm bán đồng
giá 50 000 đồng một món và có chương trình giảm giá 15% cho một món hàng và nếu khách
hàng mua 5 món trở lên thì từ món thứ 5 trở đi khách hàng chỉ phải trả 70% giá đã giảm. Đặc Trang 3
biệt, nếu khách hàng mua trên 10 món thì cũng được khuyến mãi như trên và chỉ phải trả
80% tổng số tiền trên hóa đơn.
a/ Cô Mai đến cửa hàng và mua tổng cộng 10 món hàng. Em hãy tính xem cô Mai phải trả bao nhiêu tiền? .
b/ Cùng thời điểm ấy chị Lan cũng đến mua hàng. Khi ra quầy tính tiền chị Lan đã trả tổng số
tiền là 397 800 đồng. Em hãy tính xem chị Lan đã mua bao nhiêu món hàng?
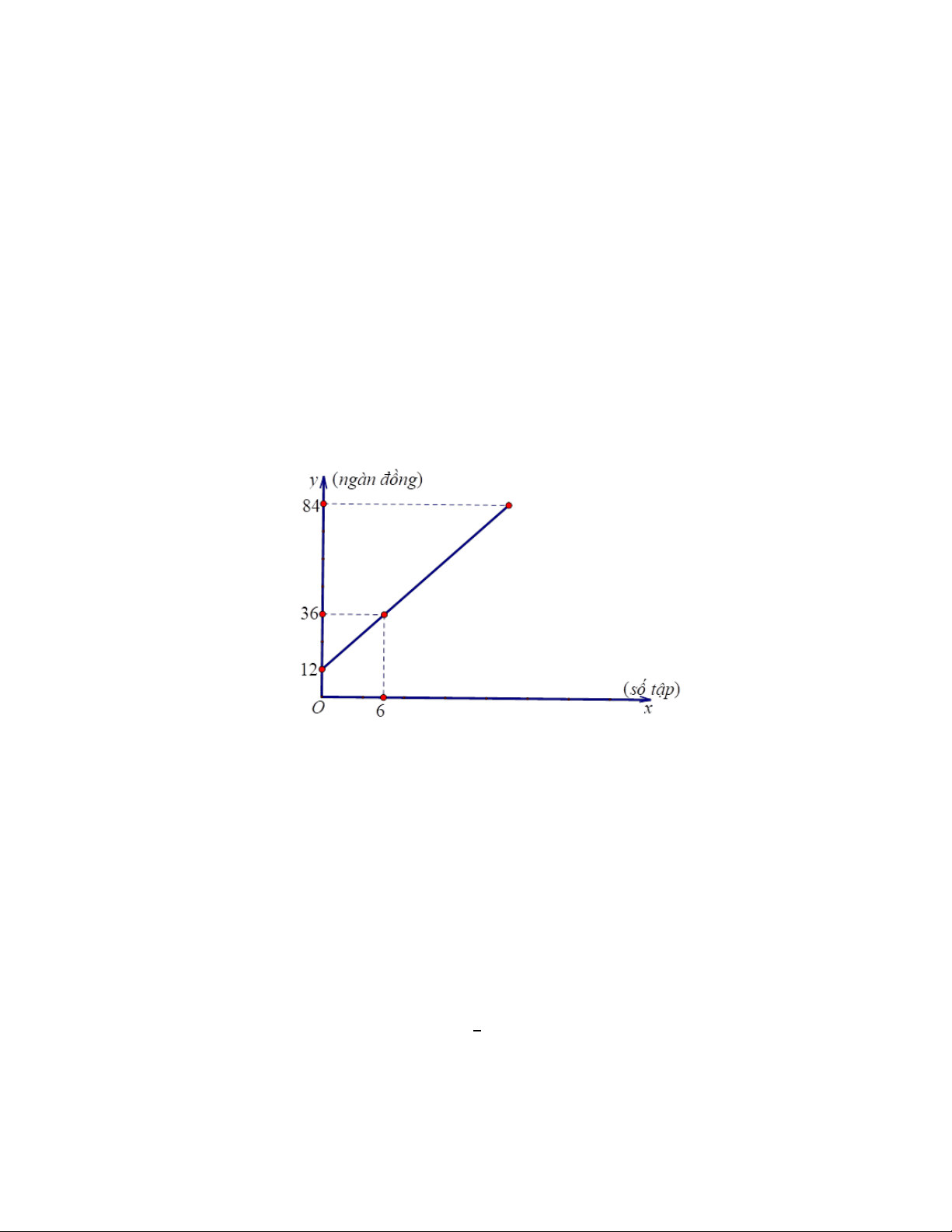
Bài 5. (1,0 điểm) Bạn Mai đi xe buýt đến cửa hàng để mua x quyển tập, giá mỗi quyển tập là
a (đồng), gọi b (đồng) là chi phí đi xe buýt cả đi lẫn về. Biết rằng mối liên hệ giữa tổng số
tiền bạn Mai phải sử dụng là y (đồng) khi đi mua x quyển tập của cửa hàng đó là hàm số bậc
nhất y = ax + b và có đồ thị như hình bên:
a) Hãy xác định các hệ số a và b.
b) Nếu tổng số tiền bạn C sử dụng để mua tập là 84 ngàn (đồng) (không mua gì khác)
thì bạn C mua được bao nhiêu quyển tập?
Bài 6. (1,0 điểm) Một quả dưa hấu không hạt ruột đỏ dạng hình cầu có đường kính 25 cm và phần vỏ dày 2 cm.
a) Coi phần ruột màu đỏ cũng có dạng hình cầu và đặc. Thể tích phần ruột màu đỏ chiếm bao
nhiêu phần trăm thể tích quả dưa hấu? (Kết quả làm tròn tới chữ số thập phân thứ hai). 4
Cho biết công thức tính thể tích hình cầu là 𝑉 = 𝜋𝑅3, với 𝑅 là bán kính hình cầu. 3 Trang 4 2 cm 25 cm
b) Người ta ép phần ruột màu đỏ của quả dưa hấu trên thì thể tích nước ép thu được bằng 80%
thể tích phần ruột. Nước ép dưa hấu được đựng trong một một ly thủy tinh, phần lòng trong dạng
hình trụ có chiều cao 10 cm và đường kính đáy lòng trong là 5 cm. Mỗi ly chỉ chứa 70% nước ép
dưa hấu. Hỏi dùng nước ép của một quả dưa hấu nói trên thì đủ nguyên liệu làm ra bao nhiêu ly
nước ép dưa hấu?
(Cho biết công thức tính thể tích hình trụ là 𝑉 = 𝜋𝑟2ℎ, trong đó 𝑟 là bán kính đáy hình trụ, ℎ là chiều cao).
Bài 7. (1,0 điểm) Tổng chi phí của một doanh nghiệp sản xuất áo sơ mi là 410 triệu đồng/tháng.
Giá bán của mỗi chiếc áo sơ mi là 350 nghìn đồng. Hỏi trung bình mỗi tháng doanh nghiệp phải
bán được ít nhất bao nhiêu chiếc áo sơ mi để thu được lợi nhuận ít nhất là 1,38 tỉ đồng sau 1 năm?
Bài 8. (3,0 điểm)
Cho đường tròn tâm O, đường kính AB, dây CD vuông góc với AB tại F. Gọi M là một điểm
thuộc cung nhỏ BC (M khác B, M khác C), hai đường thẳng AM và CD cắt nhau tại E
a) Chứng minh tứ giác BMEF nội tiếp
b) Chứng minh tia MA là phân giác của góc CMD và 2
AC = AE.AM
c) Gọi I là giao điểm của hai đường thẳng MD và AB, N là giao điểm của hai đường thẳng AM
và BC. Chứng minh tâm đường tròn ngoại tiếp tam giác CEN nằm trên đường thẳng CI ---- HẾT----- Trang 5
SỞ GIÁO DỤC VÀ ĐẠO TẠO
ĐỀ THAM KHẢO TUYỂN SINH 10 THPT THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC: 2024 - 2025 QUẬN 6 (ĐỀ 3) MÔN THI: TOÁN
(đề thi gồm 03 trang)
Câu 1 (1,5 điểm).
Cho parabol (P): y = x2 và đường thẳng (d): y = x + 2.
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 2 (1,0 điểm).
Cho phương trình: 2x2 – x – 3 = 0 có 2 nghiệm là x1, x2.
Không giải phương trình, hãy tính giá trị của biểu thức 2 2 2 2 A = x + x − x x + 2023 1 2 1 2 .
Câu 3 (1,0 điểm).
Tại một vòng xoay ngã tư, người ta cần làm các bồn trồng hoa như hình 1. Em hãy tính phần
diện tích của 1 bồn hoa ở hình 2 (phần được tô đậm). Biết rằng bán kính của vòng tròn lớn là
7m, vòng tròn nhỏ là 3m và góc ở tâm là 60o h
Câu 4 (0,75 điểm). HÌNH 1 HÌNH 2
Ông Ba có một miếng đất hình chữ nhật có chiều dài là 20m, chiều rộng 5m. Ông dự định
làm hàng rào xung quanh miếng đất với tổng chi phí là 2 000 000đ gồm tiền công và tiền mua vật liệu.
a) Gọi y (đồng) là chi phí tiền công, x (đồng) là giá tiền mỗi mét vật liệu. Lập hàm số của y theo x
b) Nếu giá tiền mỗi mét vật liệu là 30 000đ. Hỏi chi phí tiền công là bao nhiêu?
Câu 5 (0,75 điểm).
Sau buổi tổng kết, lớp 9A đi ăn kem ở một quán gần trường. Do quán mới khai trương nên có
khuyến mãi, bắt đầu từ ly thứ 10 giá mỗi ly kem giảm 10 000 đồng so với giá ban đầu. Lớp
9A mua 40 ly kem, khi tính tiền chủ cửa hàng thấy lớp mua nhiều nên giảm thêm 20% số Trang 6
tiền trên hóa đơn, vì vậy số tiền lớp 9A chỉ phải trả là 712 000 đồng. Hỏi giá của mỗi ly kem ban đầu là bao nhiêu?
Câu 6 (1,0 điểm).
Một hãng sản xuất rượu vang đã đặt hàng một công ty sản xuất thủy
tinh một kiểu ly có phần đựng rượu cao 6cm, đường kính miệng ly là
6cm. Biết rằng để tạo thành một cái ly là sự kết hợp gồm thành ly là
một hình trụ cao 3cm, phần đáy ly là một nửa khối cầu có đường kính
bằng với đường kính của miệng ly.
a/ Hãy tính thể tích rượu được chứa tối đa khi đổ vào ly? Cho biết: V  trụ = 2
r h với r là bán kính đáy; h là chiều cao hình trụ. V 4 cầu = 3 R 
với R là bán kính hình cầu. 3
b/ Ông A cần chuẩn bị một số chai rượu vang, lượng rượu trong mỗi
chai là 0,85 lít. Biết rằng trong bữa tiệc có 12 người (bao gồm luôn
ông A), mỗi người uống 4 ly rượu, lượng rượu được rót bằng 60% thể
tích của ly. Ông A cần chuẩn bị ít nhất bao nhiêu chai rượu vang?
Câu 7 (1,0 điểm). Để 5
tham gia thi đấu cầu lông đánh đôi nam nữ, thầy Thể dục chọn số nam của lớp kết hợp 6 10 với
số nữ của lớp để bắt cặp thi đấu. Sau khi bắt cặp xong trong lớp còn 6 cổ động viên. 11
Hỏi lớp có bao nhiêu học sinh?
Câu 8 (3,0 điểm).
Cho nửa đường tròn ( )
O , đường kính BC . Trên nửa đường tròn ( )
O , lấy hai điểm A và D (theo thứ tự , B , A ,
D C ). Tia BA và CD cắt nhau tại S , đoạn thẳng AC cắt BD tại . H
a) Chứng minh SH ⊥ BC tại E và tứ giác HECD nội tiếp.
b) Gọi T là trung điểm SH , tia AT cắt SC tại I , DE cắt HC tại K . Chứng minh:
TAH = KDC . Từ đó suy ra C . K CA = C . D CI
c) Đường trung trực cả đoạn thẳng AK cắt BH tại Q . Chứng minh I  AK cân và ba
điểm A,O,Qthẳng hàng. ---- HẾT ---- Trang 7
CÁC CÂU XÁC SUẤT THỐNG KÊ – ĐÁP ÁN QUẬN 6
Bài 1: Một túi chứa 3 viên bi màu xanh và một số viên bi màu đỏ có cùng kích thước và khối
lượng. Bạn An lấy ra ngẫu nhiên một viên bi. Biết rằng xác suất lấy ra viên bi màu xanh là
0,6. Hỏi trong túi có bao nhiêu viên bi màu đỏ?
Bài 2: Một hộp có 25 thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4; 5;…..; 25;
hai thẻ khác nhau thì ghi số khác nhau.
Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a/ “Số xuất hiện trên thẻ được rút ra là số chia hết cho 5”;
b/ “Số xuất hiện trên thẻ được rút ra là số có hai chữ số”;
c/ “Số xuất hiện trên thẻ được rút ra là số có hai chữ số và tổng các chữ số bằng 5”.
Bài 3: Bạn An đến một hội chợ được tổ chức gần nhà trong dịp tết Nguyên Đán. Bạn tham
gia trò chơi ném bi. Đích đến là một bảng có 25 ô như hình
vẽ. Cách tính điểm như sau: 5 3 3 3 5 3 – 2 – 1 – 2 3
*Ném ra ngoài bảng trừ 5 điểm 3 – 1 5 – 1 3
*Ném vào một trong 25 ô điểm tính được ghi như hình bên. 3 – 2 – 1 – 2 3
*Nếu sau 10 lần ném mà : 5 3 3 3 5
- Đạt 50 điểm thì nhận được phần quà trị giá 500 000 đồng.
- Đạt từ 30 điểm đến 49 điểm thì nhận được phần quà trị giá 300 000 đồng.
- Đạt từ 15 điểm đến 29 điểm thì nhận được phần quà trị giá 50 000 đồng
- Dưới 15 điểm không có quà.
a. Trong 9 lần ném bi, bạn An ném được 5 lần vào ô điểm 5, một lần ra ngoài bảng, 2 lần
vào ô điểm 3, một lần ô điểm – 1. Tính số điểm bạn An nhận được sau 9 lần ném.
b. Hỏi bạn An có cơ hội nhận phần quà trị giá 300 000 không? Nếu có thì bạn An phải ném
vào ô nào? Tính xác xuất để bạn An nhận đươc phần quà đó. Trang 8 Đáp án Bài 1:
Tổng số viên bi trong túi: 3 : 0,6 = 5 viên
Số viên bi màu đỏ: 5 – 3 = 2 viên Bài 2
a/ Có 5 kết quả thuận lợi cho biến cố “ Số xuất hiện trên thẻ được rút ra là số chia hết cho
5” là 5; 10; 15; 20; 25.
Xác suất của biến cố đó là 5 1 = . 25 5
b/ Có 16 kết quả thuận lợi cho biến cố“ Số xuất hiện trên thẻ được rút ra là số có hai chữ số” là 10; 11; 12; ….; 24; 25.
Xác suất của biến cố đó là 16 . 25
c/ Có 2 kết quả thuận lợi cho biến cố “ Số xuất hiện trên thẻ được rút ra là số có hai chữ số
và tổng các chữ số bằng 5” là 14; 23.
Xác suất của biến cố đó là 2 25
Bài 3 : a. Tổng số điểm bạn An đạt được sau 9 lần ném:
5.5 – 5 + 2.3 + ( – 1 ) = 25 điểm
b. Vì để nhận được phần quà trị giá 300 000 đồng bạn An phải đạt từ 30 điểm đến 49 điểm
sau 10 lần ném, mà 30 – 25 = 5 điểm nên bạn An vẫn còn cơ hội để nhận quà.
Do An đã ném 9 lần nên để nhận quà bạn chỉ còn 1 lần ném và phải ném vào ô điểm 5
Có 5 khả năng ném vào ô điểm 5 trên tổng số 26 khả năng (gồm 25 ô trong bảng và 1 khả năng ném ra ngoài ) 5
Nên xác suất để bạn An nhận phần quà trị giá 300 000 đồng là 26 Trang 9