PHÒNG GD-ĐT QUẬN TÂN PHÚ
ĐỀ ĐỀ NGHỊ TUYỂN SINH 10
TRƯỜNG THCS ĐẶNG TRẦN CÔN
Năm học: 2024–2025
MÔN: TOÁN – LỚP: 9 Thời gian: 120 phút
(không kể thời gian phát đề)
Câu 1. Cho (P) y = 2 :
x và đường thẳng (d) : y = x + 2 .
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 2. Cho phương trình 2
2x + 6x − 1 = 0 có hai nghiệm x , x . Không giải phương trình. 1 2
Tính giá trị của biểu thức P = (x − 2
x ) − x − x 1 2 1 2
Câu 3. Quy tắc sau đây cho ta cách tính ngày cuối cùng của tháng hai trong năm 20ab là thứ mấy ?
- Lấy ab chia cho 12 được thương là x , dư là y
- Lấy y chia cho 4 được thương là z - Tính M x y z
- Lấy M chia 7 được dư r Nếu r 0đó là thứ 3 Nếu r 1đó là thứ 4 … Nếu r 5 đó là chủ nhật Nếu r 6 đó là thứ hai
Em hãy dùng quy tắc trên tính xem ngày cuối cùng của tháng hai trong năm 2025 là thứ mấy ?
Câu 4. Bến xe Miền Đông mới được thiết kế theo mô hình Transit Oriented
Development (viết tắt là TOD) – là mô hình định hướng phát triển giao thông
công cộng làm cơ sở quy hoạch phát triển của đô thị, lấy giao thông làm điểm tập
trung dân cư để từ đó hình thành hệ thống giao
thông phân tán, mô hình này rất phát triển trên
thế giới. Một xe ô tô chở khách đi từ bến xe
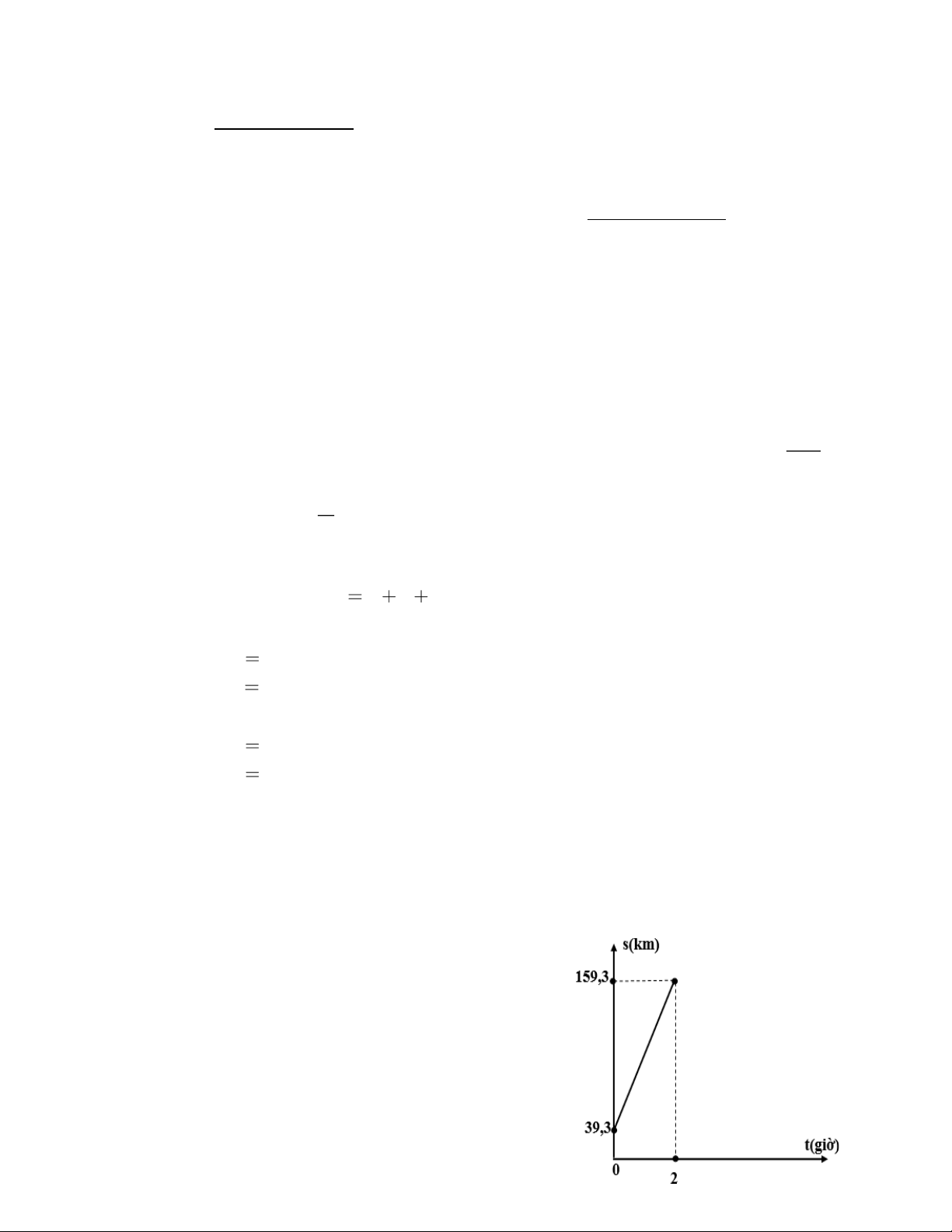
Miền Đông mới hướng về Miền Trung. Gọi s
(km) là quãng đường đi được của xe cách Trung
tâm Thành phố Hồ Chí Minh và t (giờ) là thời Trang 1
gian xe chạy được cho bởi hàm số bậc nhất s = at + b và có đồ thị như hình:
a) Xác định các hệ số a và b của hàm số trên.
b) Sau 4 giờ, xe đã cách trung tâm Thành phố Hồ Chí Minh bao nhiêu km; biết
xe có ghé nghỉ ngơi tại trạm dừng chân 30 phút
Câu 5. Bà Tám mua 10 thùng nước ngọt, mỗi thùng có 24 lon với tổng số tiền 2 triệu và
bán lẻ mỗi lon với giá 10 000 đồng.
a) Hỏi khi bán hết 10 thùng nước ngọt đó thì bà Tám lãi được bao nhiêu phần trăm so với giá gốc?
b) Để lời được ít nhất 200 000 đồng so với giá vốn thì bà Tám cần giảm giá nhiều
nhất bao nhiêu phần trăm? (làm tròn đến chữ số thập phân thứ nhất)
Câu 6. Một tháp đồng hồ có phần dưới có dạng hình hộp chữ nhật, đáy là hình vuông có
cạnh dài 5m , chiều cao của hình hộp chữ nhật là 12 m . Phần trên của tháp có
dạng hình chóp đều, các mặt bên là các tam giác cân chung đỉnh (hình vẽ). Mỗi
cạnh bên của hình chóp dài 8 m .
a) Tính theo mét chiều cao của tháp đồng hồ? (làm tròn đến chữ số thập phân thứ nhất).
b) Cho biết thể tích của hình hộp chữ nhật được tính theo công thức V S.h ,
trong đó S là diện tích mặt đáy, h là chiều cao của hình hộp chữ nhật. Thể 1
tích của hình chóp được tính theo công thức V
S.h , trong đó S là diện 3
tích mặt đáy, h là chiều cao của hình chóp. Tính thể tích của tháp đồng hồ
này? (Làm tròn đến hàng đơn vị).
Câu 7. Một người mua hai loại mặt hàng A và B. Nếu tăng giá mặt hàng A thêm 10% và
mặt hàng B thêm 20% thì ngườ đó phải trả 232 000 đồng. Nhưng nếu giảm giá cả hai mặt Trang 2
hàng là 10% thì người đó phải trả tất cả là 180 000 đồng. Tính giá tiền mỗi mặt hàng lúc đầu?
Câu 8. Từ một điểm A ở bên ngoài đường tròn O , vẽ tiếp tuyến A , B AC với đường tròn O ( ,
B C là các tiếp điểm). Đoạn thẳng OA cắt đường tròn (O) và BC lần lượt tại I
và H. Vẽ đường kính CD của O , AD cắt O tại E (E khác D ).
c) Chứng minh tam giác DEC vuông và tứ giác AEHC nội tiếp.
d) BE cắt AO tại F. Chứng minh F là trung điểm của AH .
e) Tia IO cắt đường tròn (O) tại L. Chứng minh IH.LA = I . A LH . --- Hết --- Trang 3
PHÒNG GD-ĐT QUẬN TÂN PHÚ
ĐỀ ĐỀ NGHỊ TUYỂN SINH 10
TRƯỜNG THCS ĐỒNG KHỞI
Năm học: 2024–2025
MÔN: TOÁN – LỚP: 9 Thời gian: 120 phút
(không kể thời gian phát đề) Bài 1. (1,5điểm) −1 Cho parabol (𝑃): 𝑦 =
𝑥2 và đường thẳng (𝑑): 𝑦 = 3𝑥 + 4. 2
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Bài 2. (1 điểm)
Cho phương trình −2𝑥2 − 5𝑥 + 4 = 0 có hai nghiệm x1, x2. 2x 2x
Không giải phương trình, hãy tính giá trị của biểu thức M = ( x − x )2 1 2 + + 1 2 x x 2 1 Bài 3. (0,75 điểm)
Để ước tính chiều cao tối đa của trẻ em khi đạt đến độ trưởng thành, hoàn toàn có thể dựa vào
chiều cao của bố mẹ. Cách tính chiều cao của con theo bố mẹ được các chuyên gia đánh giá cao bởi thực
tế, sự di truyền các thế hệ có ảnh hưởng nhất định đến chiều cao của trẻ.
Ta có công thức tính như sau: C = (B + M + 13A) : 2 . Trong đó:
C là chiều cao của người con (cm)
B là chiều cao của người bố (cm); M là chiều cao của người mẹ (cm)
A = 1 khi người con là Nam ; A = -1 khi người con là Nữ
a) Em hãy dùng công thức trên để tìm chiều cao tối đa của bạn Nam (giới tính là nam) biết ba của
bạn Nam có chiều cao là 175cm và mẹ của bạn Nam có chiều cao là 168cm.
b) Bạn Hương (giới tính là nữ) có chiều cao là 164cm. Em hãy tính xem chiều cao tối đa của mẹ
bạn Hương khi biết chiều cao của ba bạn Hương là 180cm. Bài 4. (0,75 điểm)
Do các hoạt động công nghiệp thiếu kiểm soát của con người làm cho nhiệt độ trái đất tăng dần
một cách rất đáng lo ngại. Các nhà khoa học đã đưa ra công thức dự báo nhiệt độ trung bình trên bề mặt
trái đất như sau: T = at + b. Trong đó, T là nhiệt độ trung bình của bề mặt trái đất tính theo độ C; t là số Trang 4
năm kể từ năm 1950. Từ năm 1950 nhiệt độ trái đất là 150C và sau 30 năm khảo sát các nhà khoa học đã
thấy nhiệt độ trái đất đã tăng 0,60C.
a) Em hãy xác định hệ số a và b.
b) Nhiệt độ trên trái đất ngày càng nóng đã làm băng tan ở các cực nhanh hơn, làm cho mực nước
biển dâng cao dẫn đến hiện tượng biển lấn – nước biển xâm nhập sâu vào trong đất liền dẫn đến tình trạng
các vùng đất quanh biển, ven sông nhiễm mặn ngày càng nhiều và còn thiếu cả nước ngọt cho sản xuất và
sinh hoạt. Các nhà khoa học đã thống kê được rằng nếu trái đất nóng lên 10C thì mực nước biển sẽ tăng 2
mm, em hãy tính xem vào năm nào thì mực nước biển dâng lên 15 mm? Bài 5. (1 điểm)
Một cửa hàng mở chương trình khuyến mãi như sau: Nếu mua sản phẩm thứ nhất nguyên giá thì
sản phẩm thứ 2 được giảm 10 nghìn đồng, sản phẩm thứ 3 được giảm 10%. Từ sản phẩm thứ 4 trở đi
khách hàng chỉ phải trả 80% giá niêm yết.
a) Bạn An đến mua 13 sản phẩm và phải trả 1298 nghìn đồng. Hỏi giá bán 1 sản phẩm khi chưa giảm là bao nhiêu?
b) Khi chủ của hàng nhập vào 100 sản phẩm và chỉ bán được 80 sản phẩm thì khi bán xong chủ
cửa hàng lời hay lỗ bao nhiêu %? Biết giá vốn 1 sản phẩm và 60 nghìn đồng. Bài 6. (1 điểm)
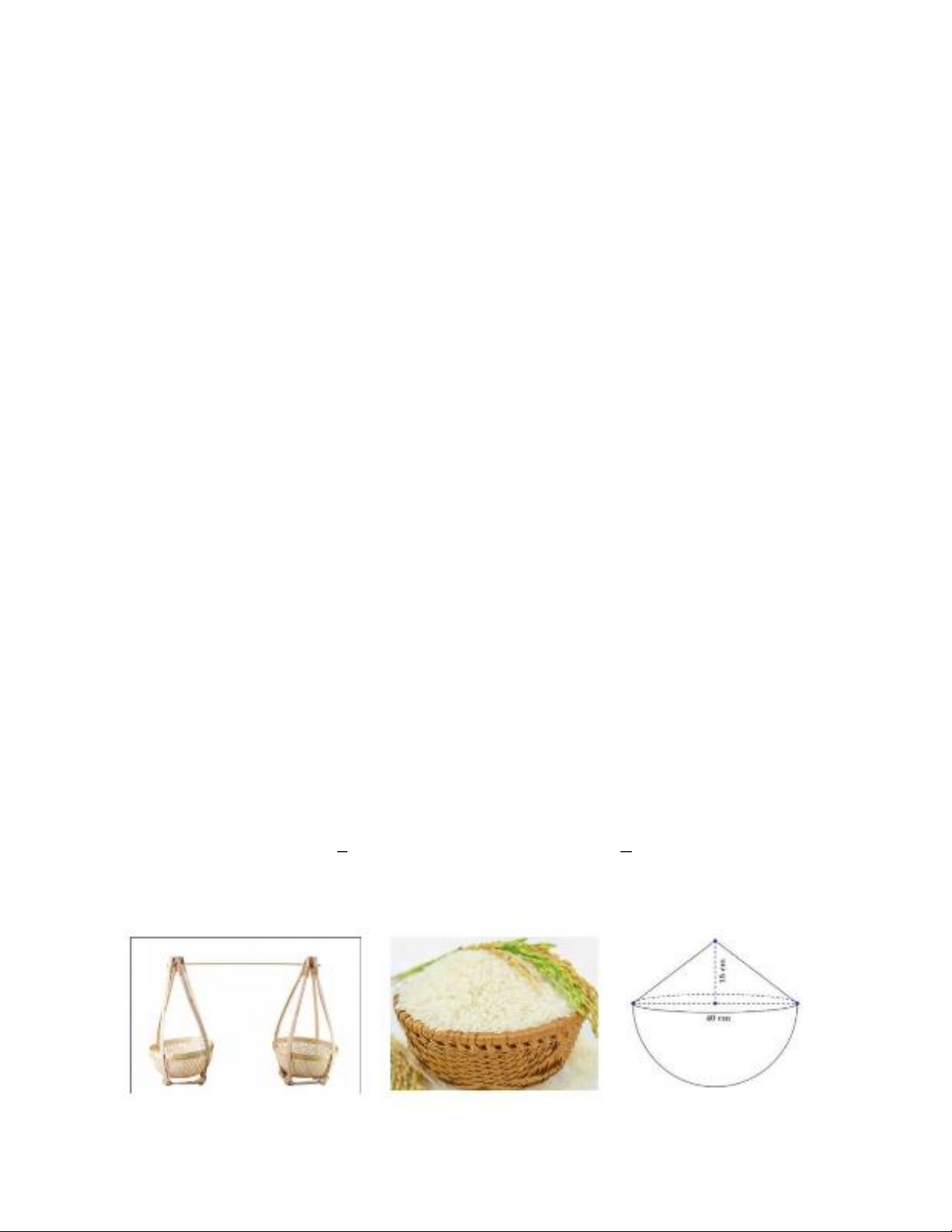
Một người nông dân gánh một quang gánh gồm 2 thúng gạo có kích thước và chứa lượng gạo hai
bên như nhau. Một thúng gạo là nửa hình cầu có đường kính là 40 cm và để có thể đem được nhiều gạo
hơn, người dân mới đổ đầy gạo vào thúng và vun gạo lên trên thành một hình nón có chiều cao 15cm.
a) Tính lượng gạo trong 1 thúng của quang gánh (làm tròn đến chữ số thập phân thứ nhất)
b) Người nông dân dùng lon sữa bò có dạng hình trụ có bán kính đáy 4cm, chiều cao bằng 10cm để đong
gạo vào thúng. Mỗi lần đong được lượng gạo bằng 95% thể tích lon. Hỏi người nông dân cần đong ít nhất
bao nhiêu lon gạo để đủ gạo cho quang gánh như trên. 1 4
(Biết thể tích hình nón 2
V = .3,14.R .h ; thể tích hình cầu 3 V =
.3,14.R ; thể tích hình trụ 3 3 Trang 5 2
V = 3,14.R .h ) Bài 7. (1 điểm)
Trong kho của một công ty xuất khẩu nông sản, có 2500 bao gạo và ngô, mỗi bao gạo nặng 20 kg,
mỗi bao ngô nặng 15kg. Do thời tiết ẩm ướt, nên 15% số bao ngô đã bị hỏng không thể xuất khẩu. Biết
giá xuất khẩu 20000 đồng/kg gạo và 15000 đồng/kg ngô và công ty thu về được 582500000 đồng. Hỏi
ban đầu có bao nhiêu bao gạo? Bài 8. (3 điểm)
Cho  ABC có ba góc nhọn (AB < AC), nội tiếp (O). Tiếp tuyến tại A của (O) cắt đường thẳng BC
tại S. Gọi I là hình chiếu của O lên BC.
a) Chứng minh: tứ giác SAOI nội tiếp
b) Gọi H và D lần lượt là chân đường vuông góc kẻ từ điểm A đến các đường thẳng SO và SC.
Chứng minh: OAH = IAD
c) Vẽ đường cao CE của ABC. Gọi Q là trung điểm của đoạn thẳng BE. Đường thẳng QD cắt đường
thẳng AH tại K. Chứng minh: BQ.BA = BD.BI và CK // SO --- Hết --- Trang 6 UBND QUẬN TÂN PHÚ
ĐỀ TUYỂN SINH LỚP 10
TRƯỜNG THCS HOÀNG DIỆU
NĂM HỌC: 2024 – 2025 Môn: Toán Thời gian: 120 phút
ĐỀ THAM KHẢO TUYỂN SINH 10
Câu 1: (2 điểm) 1
Cho parabol (P) ∶ y = − x2 và đường thẳng (d): y = −2x + 2 2
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ Oxy.
b) Tìm tọa độ giao điểm của (P), (d) bằng phép toán.
Câu 2: (1 điểm)
Cho phương trình x2 − 3x − 4 = 0 có 2 nghiệm x1, x2. Không giải phương trình hãy tính: 3𝑥 2𝑥 A = 1 + 2𝑥2 + 1 + 𝑥2 𝑥1 𝑥2
Câu 3: (0,75 điểm)
Một bánh xe lăn vòng trên một dốc nghiêng theo C
một đường thẳng. Bánh xe lăn đúng 150 vòng từ điểm B đến điể B
m A. Chiều cao của dốc nghiêng là
BH = 50m, góc nghiêng của dốc BAH ̂ = 15° (tam 50m giác ABH vuông tại H) a/ Tính độ A H
dài AB của con dốc (làm tròn đến hàng đơn vị)
b/ Khoảng cách từ tâm C của bánh xe đến đường thẳng AB. (làm tròn đến cm)
Câu 4: (1 điểm)
Một xí nghiệp đầu tư sản xuất viết máy với số vốn ban đầu là 72 triệu đồng
để mua trang thiết bị. Mỗi cây viết sản xuất ra với chi phí là 30 000 đồng.
a/ Viết hàm số y (triệu đồng) là tổng chi phí bỏ ra để sản xuất ra x cây
viết máy. (tính cả vốn ban đầu)
b/ Xí nghiệp bán ra thị trường mỗi cây viết máy giá 50 000 đồng.
i/ Để hoà vốn thì cần bán bao nhiêu cây viết máy?
ii/ Muốn lời mỗi tháng 10 triệu đồng và cần hoàn vốn trong 1 năm thì
mỗi tháng phải bán bao nhiêu cây viết máy.
Câu 5: (1 điểm) Một cửa hàng lấy ở đại lý phân phối 100 hộp kẹo trái
cây 6 vị với giá 35 000 đồng/1 hộp. Đợt đầu cửa hàng bán với giá 80
000 đồng/1 hộp và bán được 40 hộp. Đợt thứ hai cửa hàng khuyến mãi
giảm giá 20%(so với giá đợt đầu) và bán hết số còn lại. Hỏi sau khi Trang 7
bán hết số hộp kẹo này cửa hàng lãi bao nhiêu % theo giá mua? (Làm tròn 1 chữ số thập phân)
Câu 6: (0,75 điểm) Một nhà kính trồng rau sạch có dạng nửa hình
trụ đường kính đáy là 30m, chiều dài là 45m. Người ta dùng
màng nhà kính Politiv – Israel để bao quanh phần diện tích xung
quanh nửa hình trụ và hai nửa đáy hình trụ.
a/ Tính diện tích phần màng cần cho nhà trồng rau trên.
Biết hao phí khi thi công là khoảng 10% diện tích màng. (làm
tròn đến hàng đơn vị)
b/ Tính chi phí cần có để mua màng làm nhà kính trên biết
rằng màng có khổ rộng 2,2m và dài 100m có giá 13 000 30m 45m
đồng/m2(chỉ bán theo cuộn).
Câu 7: (1 điểm) Hai phân xưởng A và B có tất cả 64 công nhân cùng sản xuất một mặt
hàng. Xưởng A trung bình mỗi người làm ra 30 sản phẩm 1 ngày, xưởng b trung bình
mổi người làm được 28 sản phẩm mỗi ngày. Biết hai xưởng 1 ngày làm ra tổng cộng
1860 sản phẩm, tìm số công nhân của mỗi xưởng.
Câu 8: (2,5 điểm) Cho đường tròn (O) và điểm A ở ngoài đường tròn. Vẽ tiếp tuyến AM,
AN. Gọi H là giao điểm của MN và OA. Kẻ dây BC của (O) sao cho BC đi qua H và BC
⊥ OM (C thuộc cung nhỏ MN). Đường thẳng AC cắt (O) tại điểm thứ hai là D. Gọi I là
trung điểm CD và F là giao điểm của MN và CD.
a/ Chứng minh tứ giác AMOI nội tiếp đường tròn và xác định tâm K.
b/ Chứng minh CHIN nội tiếp và FI . FA = FC . FD.
c/ Kẻ KE ⊥ AM tại E. Chứng minh E, H, D thẳng hàng. Hết.
CÁC CÂU XÁC SUẤT THỐNG KÊ – ĐÁP ÁN TÂN PHÚ
Câu 1. Tung một đồng tiền ba lần
a) Mô tả không gian mẫu
b) Xác định các biến cố sau và tính xác suất các biến cố đó
A: “ Có ít nhất một lần xuất hiện mặt S”
B: “ Mặt N xuất hiện ít nhất hai lần” Giải. Trang 8
a) Ta có:  = SSS,SSN,SNS,SNN,NSN,NSS,NNS,NN  N n()=8 b) Ta có:
A = SSS,SSN,SNS,SNN,NSN,NSS,NN  S => n(A)=7 B = NNS,NSN,SNN,NN  N => n(B)=4 = 7 P(A) 8 = 4 = 1 P(B) 8 2
Câu 2. Có 3 thị trấn A, B, C. Có 5 con đường để đi từ A đến B, có 3 con đường để đi từ B đến C. Có
bao nhiêu cách chọn một con đường để đi từ A, qua B rồi đến C? Giải
Số cách đi từ A đến B: 5 cách
Số cách đi từ B đến C: 3 cách
Số cách đi từ A đến C: 5.3 = 15 cách
Câu 3. Một chiếc hộp chứa 40 quả bóng cùng hình dạng và kích thước. Các quả bóng
được ghi số lần lượt từ 1 đến 40; hai quả bóng khác nhau thì ghi hai số khác nhau.
Lấy ngẫu nhiên 1 quả bóng trong hộp. Tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên quả bóng lớn hơn 30”.
b) “Số xuất hiện trên quả bóng là số chẵn nhỏ hơn 30”. Giải
a) “Số xuất hiện trên quả bóng lớn hơn 30”. Trang 9
A: “Số xuất hiện trên quả bóng lớn hơn 30”
Có 10 quả bóng có ghi số lớn hơn 30 (từ 31 đến 40) nên xác suất của biến cố A là: 10 1 𝑃(𝐴) = = 40 4
b) “Số xuất hiện trên quả bóng là số chẵn nhỏ hơn 30”.
B: “Số xuất hiện trên quả bóng là số chẵn nhỏ hơn 30”
Có 29 quả bóng có ghi số nhỏ hơn 30 (từ 1 đến 29), trong 29 số này có 14 số chẵn ( các
số 2, 4, 8, …, 28) nên xác suất của biến cố B là: 14 7 𝑃(𝐵) = = 40 20 Trang 10