




























































































































Preview text:
UBND TỈNH HẢI DƯƠNG KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2020 – 2021 MÔN THI: TOÁN Ngày thi: 27/01/2021 ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút, không kể thời gian giao đề
(Đề thi gồm 05 câu, 01 trang) Câu 1. (2,0 điểm) 2 2 x y x y x y
1. Rút gọn biểu thức A . với x > y > 0. 2 2 2 2 x y x y
x y x y x y
2. Cho a, b, c là các số thực khác 0 thỏa mãn: 1 1 1
| a b c 2020 | 2020(ab bc ca) abc 0 . Tính P . 2021 2021 2021 a b c Câu 2. (2,0 điểm) 2 3x 17x 27 1
1. Giải phương trình : 4x 9 2 x 2 1 y 1 9 1 2 x xy x
2. Giải hệ phương trình: 4 y 2
x xy 4 x Câu 3. (2,0 điểm)
1. Tìm các số nguyên x, y thỏa mãn đẳng thức: 2x2 + y2 + 3xy + 3x + 2y + 3 = 0.
2. Cho a, b, c là các số nguyên thỏa mãn : (a - b)(b - c)(c - a) = a + b + c.
Chứng minh a + b + c chia hết cho 27. Câu 4. (3,0 điểm)
1. Cho đường tròn (O; R) và một điểm A nằm ngoài đường tròn (O; R). Qua A lần lượt kẻ
các tiếp tuyến AB, AC đến với đường tròn (O; R) (B, C là các tiếp điểm). Lấy điểm D
thuộc đường tròn (O; R) sao cho BD song song với AO, đường thẳng AD cắt đường tròn
(O; R) tại điểm thứ hai là E. Gọi M là trung điểm của AC.
a) Chứng minh ME là tiếp tuyến của đường tròn (O; R).
b) Từ D kẻ tiếp tuyến với đường tròn (O; R), tiếp tuyến này cắt ME tại T. Gọi r1, r2,
r3 lần lượt là bán kính các đường tròn nội tiếp của ΔOME, ΔOTE, ΔOMT. Chứng minh
khi A thay đổi thì r1 + r2 + r3 luôn không đổi.
2. Cho tam giác ABC có ba góc nhon. Chứng minh sin2A + sin2B + sin2C > 2.
Câu 5. (1,0 điểm) Cho x, y, z là các số thực dương thỏa mãn: 2xy + 5yz + 6zx = 18xyz.
Tìm giá trị nhỏ nhất của biểu thức: 16xy 25 yz 81zx P . y 2x 4z y x 4z
…………………….. HẾT …………………………. Trang 1
ĐÁP ÁN THAM KHẢO – HẢI DƯƠNG (2020 – 2021) Câu 1. 1) Ta có: 2 2 x y x y x y P . 2 2 x y x y
x y ( x y x y ) x y 2 2 x y x y x y . 2 2 x y x y
x y x y x y 2 2
x y ( x y x y )
x y ( x y x y ) x y . 2 2 2 2
( x y ) ( x y ) x y 2 2
x y.2 x y x y .
(x y) (x y)
x y. x y 2 2 2.(x y ) 2 y 2 2 x y y
2) Có | a b c 2020 | 2020(ab bc ca) abc 0
Mà | a b c 2020 | 0, 2020(ab bc ca) abc 0
a b c 2020 0 Do đó:
2020(ab bc ca) abc 0 Ta có:
| a b c 2020 | 2020(ab bc ca) abc 0
| a b c 2020 | 0, 2020(ab bc ca) abc 0
a b c 2020 0
2020(ab bc ca) abc 0
(a b c)(ab bc ca) abc 0 2 2 2 2 2 2
a b b a b c c b a c c a 3abc abc 0 2 2 2 2 2 2
a b b a b c c b a c c a abc abc 0 2 (a b 2 2 2 2 2
b a b c abc) (c b a c c a abc) 0 2 2
b(a ab bc ca) c(bc a ca ab) 0 2
(b c)(a ab bc ca) 0
(a b)(b c)(c a) 0 b c a b a c
Trong 3 số a, b, c có hai số đối nhau Trang 2
Không làm mất tính tổng quát, giả sử b c
a b c a 2020 1 1 1 1 1 1 1 Vậy: P 2021 2021 2021 2021 2021 2021 2021 a b c 2020 b b 2020 Câu 2.
1) Điều kiện xác định: 9 x , x 2 4 Cách 1: 2 3x 17x 27 1 4x 9 2 x 2 1
(4x 9)(2 x 2 1) 2
3x 17x 27 4(x 2) 1 2
3x 17x 27 2 x 2 1 Ta có: 2
3x 17x 26 2 x 2 2 2 2
(3x 17x 26) (2 x 2) 2 2
(x 3) (9x 48x 76) 0 x 3 2
9x 48x 76 0 KL: Vì 2
9x 48x 76 0 (vô nghiệm) nên x=3 là nghiệm của phương trình. Cách 2: 2 3x 17x 27 1 4x 9 2 x 2 1 2
3x 6x 11x 22 5 1 4(x 2) 1 2 x 2 1
3(x 2) 11(x 2) 5 1 4(x 2) 1 2 x 2 1
Đặt x 2 t ( t 0 ) 2
x t 2 2 2 2
3(t 2).t 11t 5 1 2 4t 1 2t 1 2 2 2
3(t 2).t 11t 5 1 1 (t )
(2t 1)(2t 1) 2t 1 2 4 2 2
3t 6t 11t 5 2t 1 4 2
3t 5t 2t 4 0 3 2
(t 1)(3t 3t 2t 4) 0 t 1 3 2
3t 3t 2t 4 0 t 1
Với t 1 x 3 KL: x=3 Trang 3
2) Điều kiện: x, y 0 1 9 𝑥 + 𝑦 + = (1) Hệ tương đương: { 𝑦 𝑥 4 4𝑦 𝑥 + 𝑦 − = (2) 𝑥 𝑥2
Lấy (1) trừ (2) ta được: 1 4 9 4 y 4 y 5 1 x y 2 2
0 x 5xy 4y 0 (x 4y)(x y) 0 2 2 y x x x x x y x 4y 8
Với x y , thay vào (1) ta được: 2x
0 x y 2 x 5 1
Với x 4 y , thay vào (1) ta được: 5y
0 y x 2 4 y 2 1 1 Vậy ( ; x y) (2; 2) ( 2 ; 2) (2; ) ( 2 ; ) 2 2 Câu 3. 1) Cách 1: 2 2 2 2
2x y 3xy 3x 2 y 2 0 2x 2xy 2x xy y y x y 1 1
(x y 1)(2x y 1) 1
x y 1 1 x 2
2x y 1 1 y 4 x y 1 1 x 2
2x y 1 1 y 2 KL: (x;y)=(2;-4)=(-2;2) Cách 2: 2 2 2 2
2x y 3xy 3x 2 y 2 0 y (3x 12) y 2x 3x 2 0 2 x 4
Để phương trình có nghiệm nguyên thi 2
x 4 là số chính phương, ta đặt: 2
n 4 k ( k ) 2
(n 2)(n 2) k Ta có bảng sau: x + k 1 4 -4 -1 2 -2 x - k 4 1 -1 -4 2 -2 x -5/2 (loại) 5/2 (loại) -5/2 (loại) 5/2 (loại) 2 -2 y -4 2 KL: (x;y)=(2;-4)=(-2;2) 2)
TH1: Nếu a, b, c có cùng số dư khi chia cho 3 Trang 4 a b 3 b
c 3 a b c 3.3.3 27 c a 3
TH2: Nếu a, b, c khác số dư khi chia cho 3 a b c 3
Mà (a b)(b c)(c a) không chia hết cho 3 (vô lí)
Trong 3 số a, b, c tồn tại ít nhất 2 số có cùng số dư khi chia cho 3
Tổng a+b+c không chia hết cho 3 (1) (a )
b (b c)(c a) 3 (Mâu thuẫn với (1)) Loại TH1 đúng
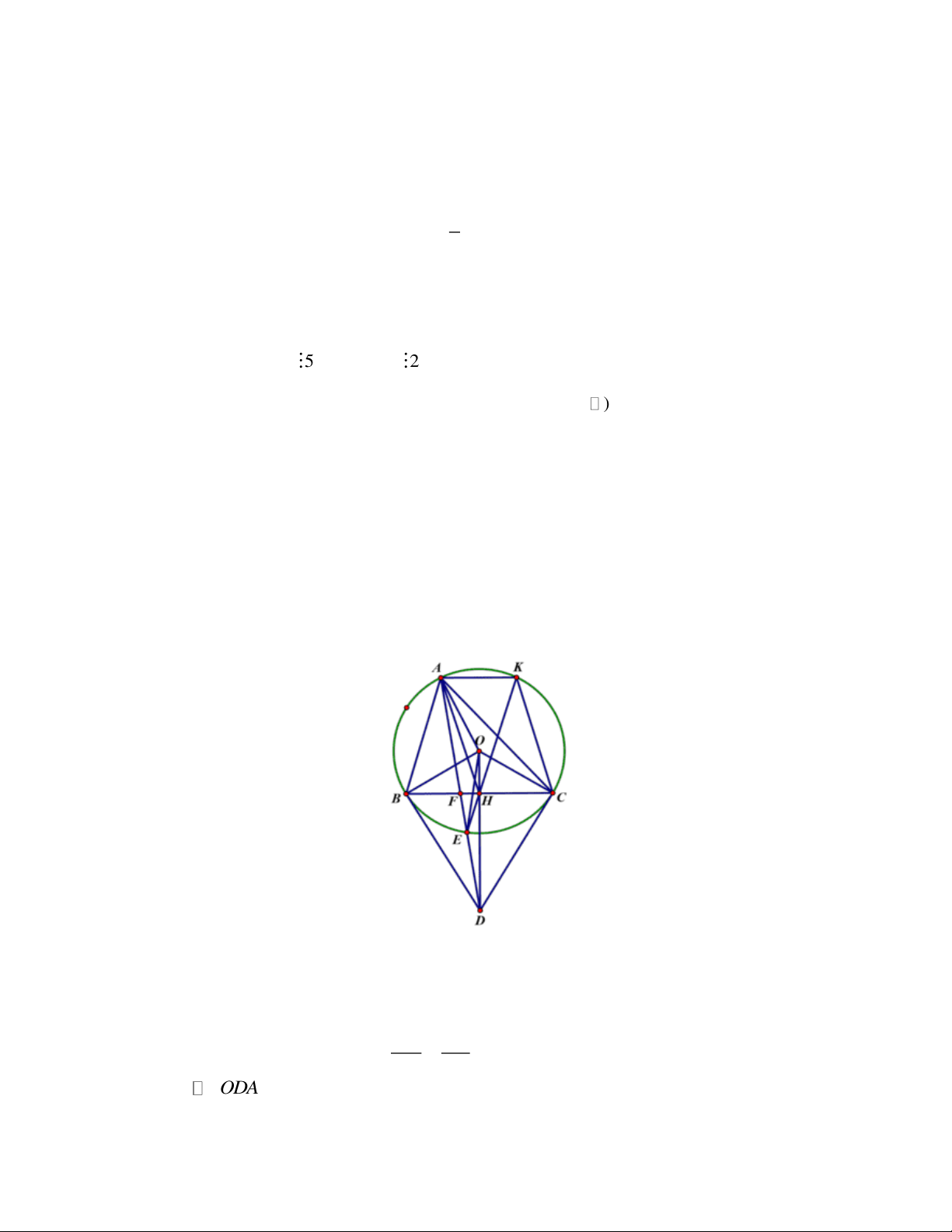
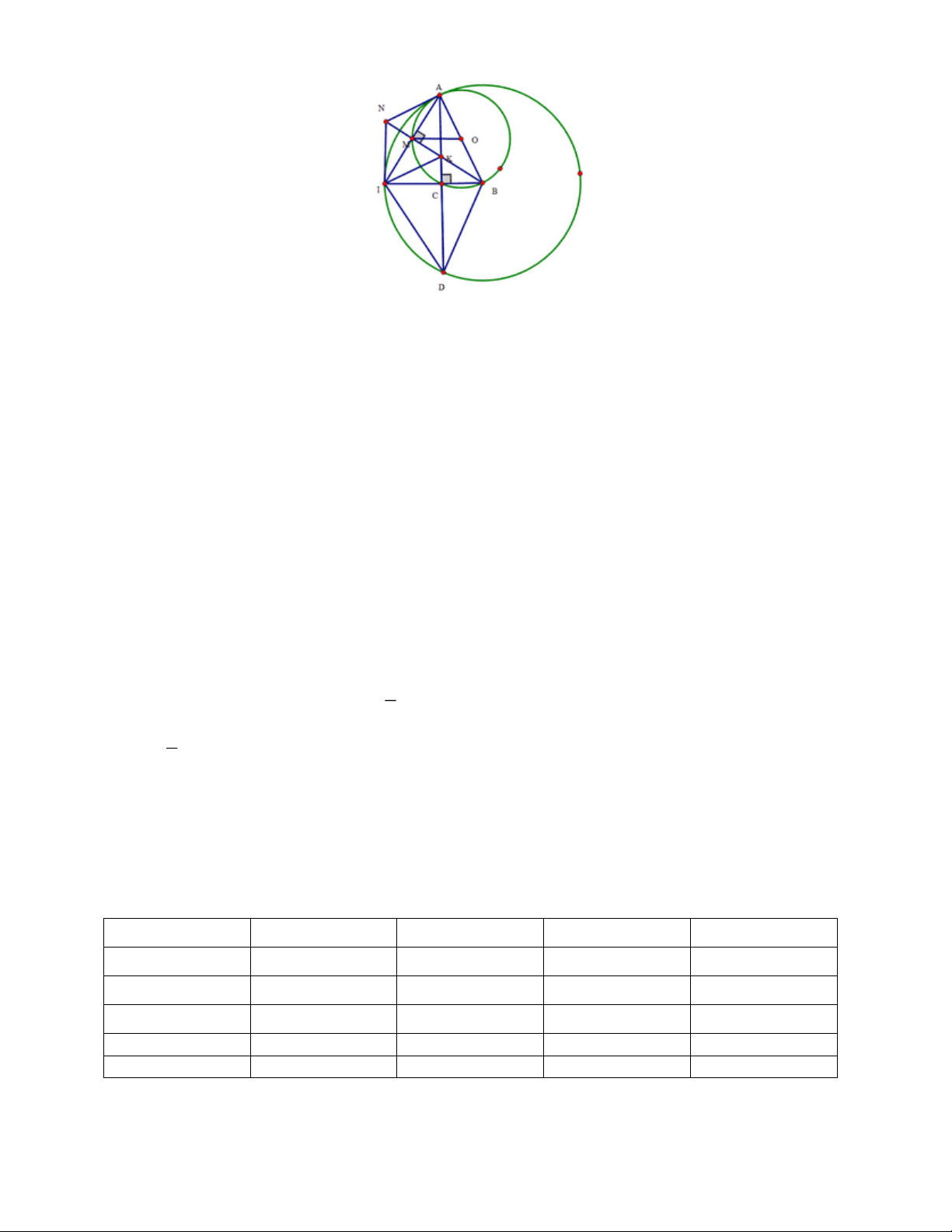
Vậy a b c 27 Câu 4. 1)
a)Vì BD//AO OBD BOA (1)
Có AOC BOA (2)
Từ (1) và (2) suy ra: AOC OBD (3)
Lại có: ABC AOC (4) (cung chắn cung AC)
Từ (3), (4) suy ra: OBD ABC Mặt khác: 0 0
ABC CBO 90 OBD CBO 90
Suy ra tam giác CBD vuông tại B
Do đó CD là đường kính của (O) 0
CED 90 A EC vuông tại C
Có M là trung điểm của AC nên EM=MC Trang 5
Dễ dàng chứng minh M EO M CO (c.g.c) 0
MEO MCO 90 ME là tiếp tuyến của (O). b) Đang cập nhật….. 2) Ta có: 1 os2A c 1 os2B c 2 2 2 2
sin A sin B sin C 1 os c C 2 2 cos2A+cos2B 2 2 2 os c C 2 os(A c +B).cos(A-B)- os c C 2 2 2 osC c
.cos(A-B)-cos C 2 osC c .cos(A-B)-cosC 2 osC c
.cos(A-B) cos(A+B) 2 2 cos . A cos . B cos C
Vì tam giác có ba góc nhọn nên cosA, cosB, cosC đều có giá trị dương nên os . A cos . B cosC > 0. Do đó: 2 2cos . A cos .
B cosC đpcm Câu 5. a b c
a b c2 2 2 2 Ta chứng minh: k q n k q n Ấp dụng B.C.S: a b c
a b c2 2 2 2 k q n
k q n a b c ( ) ( ) ( )
k 2 q 2 r 2 a b c2 2 2 2 k q n a b c
a b c2 2 2 2 k q r
k q n a b r
a b c Dấu “=” xảy ra k q r k q n Áp dụng: 2 2 2 16xy 25 yz 81zx 4 5 9 P . y 2x 4z y x 4z 1 2 4 1 1 4 x y y z z x 2 2 (4 5 9) 18 P 18 5 6 2
5 yz 6xz 2xy x y z xyz 1 2 4 1 x y x 2 4 1
MinP 18 5 y 1 y z z 1 1 4 9 z x Trang 6
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI HỌC SINH GIỎI LỚP 9 CẤP THÀNH PHỐ
THÀNH PHỐ HỒ CHÍ MINH
KHÓA THI NGÀY 17.3.2021 Môn thi: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 120 phút
(Đề thi gồm 01 trang)
(Không kể thời gian phát đề)
Bài 1. (3 điểm)
Cho hai số a, b thỏa mãn điều kiện a-b=1
Tính giá trị của biểu thức: 4 3 2 2 3 2 4
P a 4ab 3a b a b 3a b b
Bài 2. (3 điểm) Giải phương trình: 2 2
x (2 x) 3(1 x) 5
Bài 3. (4 điểm)
Cho tam giác ABC vuông tại A có đường phân giác trong BD ( D AC ). Đường tròn (BCD) cắt
cạnh AB tại E. Chứng minh AE+AB=BC.
Bài 4. (3 điểm)
Cho bốn số thực a, b, c, d thỏa điều kiện 2 2 2 2
a b c d 4 . Chứng minh bất đẳng thức:
(a 2)(b 2) cd
Bài 5. (4 điểm)
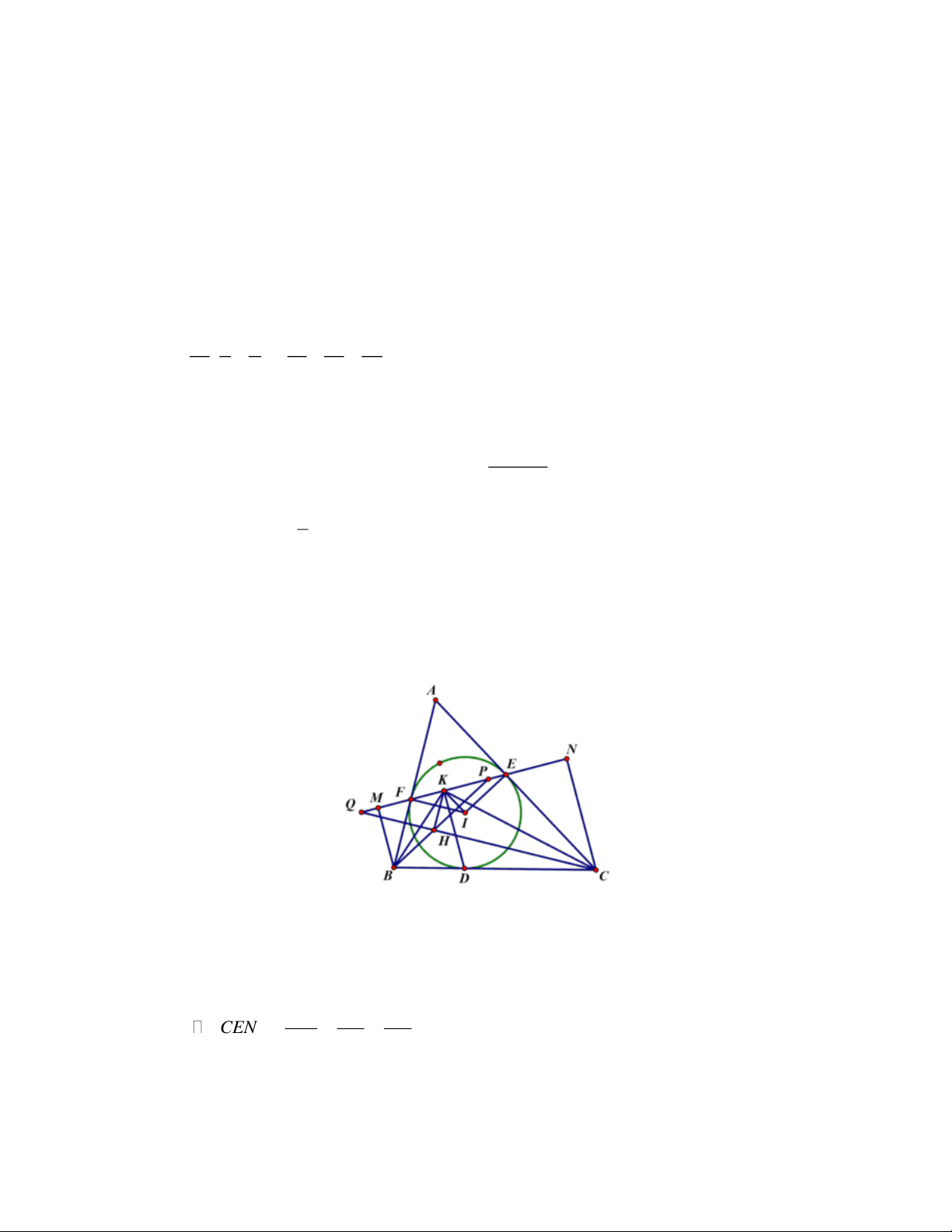
Cho tứ giác ABCD (AB không song song với CD) nội tiếp đường tròn (O) và M là điểm chính
giữa của cung nhỏ AB. Các dây MC, MD cắt AB lần lượt tại các điểm F, E.
a) Chứng minh tứ giác CDEF nội tiếp.
b) Gọi I là giao điểm của MC và MD. Gọi J là giao điểm của MD và AC.
Chứng minh: IJ song song với AB.
c) Đường thẳng IJ cắt AD, BC, CD lần lượt tại các điểm P, Q, K. Chứng minh: KP.KQ=KI.KJ
Bài 6. (3 điểm) Cho phương trình 2
x +ax+b=0 (1) với a, b là các tham số nguyên. Giả sử phương trình (1) có một nghiệm là 2 3 . a) Tìm a, b. Trang 7
b) Chứng minh rằng A 2021 2021 2 3 (2 3)
là một số nguyên và A chia hết cho 4. HẾT
ĐÁP ÁN THAM KHẢO – HỒ CHÍ MINH (2020 – 2021) Trang 8 Trang 9 Trang 10 Trang 11 Trang 12
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THCS CẤP TỈNH HƯNG YÊN
NĂM HỌC 2020 – 2021 Môn thi: Toán ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút, không kể thời gian giao đề Câu 1. (4,0 điểm) 2 2021
(2x 6x 3) 3 5
a) Tính giá trị của biểu thức 2 2020
B (10x 30x 11) khi x 5 4 3
x 3x x 1 2
b) Tìm các cặp số nguyên (x;y) thỏa mãn 2
x (2 y 3)x y 1 0 Câu 2. (4,0 điểm) a) Giải phương trình 2
x x 4 2 x 1(1 ) x
b) Trên mặt phẳng tọa độ Oxy, cho hai điểm M, N là hai điểm phân biệt di động lần lượt trên
trục hoành và trục tung sao cho đường thẳng MN luôn đi qua điểm cố định I(1;2). Tìm giá 1 1
trị nhỏ nhất của biểu thức P . 2 2 OM ON Câu 3. (4,0 điểm) 3 3
x y 65
a) Giải hệ phương trình 2 2
x y xy 20
b) Một nhóm học sinh được giao sắp xếp 810 quyển sách vào tủ ở thư viện trong một thời
gian nhất định. Khi bắt đầu làm việc, nhóm được bổ sung thêm học sinh nên mỗi giờ
nhóm sắp xếp nhiều hơn dự định 110 quyển sách. Vì vậy không những hoàn thành trước
dự định 1 giờ 30 phút mà còn vượt mức được giao 60 quyển sách. Hỏi số quyển sách mỗi
giờ nhóm dự định sắp xếp là bao nhiêu? Câu 4. (2,0 điểm)
Cho tam giác ABC có ba góc nhọn. Chứng minh rằng: A .
B sin C B .
C sin A C .
A sin B ( AB BC C )
A (sin A sin B sin C) Câu 5. (4,0 điểm)
Cho đường tròn (O;R) có hai đường kính AB và CD vuông góc với nhau. Lấy E là điểm bất kỳ
nằm trên cung nhỏ AD (E không trùng với A và D). Đường thẳng EC cắt OA tại M, đường thẳng EB cắt OD tại N.
a) Chứng minh rằng: AM.ED= 2 .OM.AE OM ON
b) Xác định vị trí của điểm E để tổng
đạt giá trị nhỏ nhất AM DN Câu 6. (2,0 điểm) 3
Cho các số dương a, b, c thỏa mãn điều kiện a b c . Tìm giá trị nhỏ nhất của biểu thức: 2 1 1 1 1 1 1 P (3
)(3 )(3 ) . a b b c c a
…………HẾT………… Trang 13
Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
Cán bộ coi thi không giải thích gì thêm.
ĐÁP ÁN THAM KHẢO – HƯNG YÊN (2020 – 2021) Câu 1. 3 5 a) Ta có: 2 2 x
(2x 3) 5 x 3x 1 0 2 Lại có: 2 2
10x 30x 11 10(x 3x 1) 1 1 2 2
2x 6x 3 2(x 3x 1) 1 1 5 4 3 3 2
x 3x x 1 x (x 3x 1) 1 1 Suy ra: B=0 b) Ta có: 2 2
x (2 y 3)x y 1 0 x 3x 1 y(2x 1) (1) Vì x
nên 2x 1 0 , do vậy: 2 x 3x 1 x 7 11 (1) y y 2x 1 2 4 4(2x 1) 11
4y (2x 7) (2) 2x 1
Vì x, y là các số nguyên nên 4y và 2x-7 cũng là số nguyên.
Do vậy, từ (2) suy ra 11 (2x 1) 2x 1Ư(11) 2x 1 1 1,1 , 11 1 x 6 , 1 ,0, 5 Thay x 6 , 1 ,0,
5 vào phương trình (1) ta được:
;x y 6 ; 5 ;( 1 ; 5 );(0;1);(5;1 ) (thỏa mãn (x;y) nguyên) Vậy ; x y 6 ; 5 ;( 1 ; 5 );(0;1);(5;1 ) . Câu 2.
a. Điều kiện x 1 Ta có: 2
x x 4 2 x 1(1 x) 2
x 2x x 1 x 1 2(x x 1) 3 0 2
(x x 1) 2(x x 1) 3 0
Đặt x x 1 y (Điều kiện y 1) Trang 14 Suy ra 2
y 2 y 3 0 . Giải ra ta được y=-1, y=3 Với y=-1 (loại) Với y=3. Thay số ta có: x x 1 3
x 1 3 x 1 x 3 2
x 1 9 6x x 1 x 3
x 2,x 5 x 2
Kết luận: Phương trình có nghiệm x=2
b. Đặt m x , n y , ,
m n 0; m 1; n 2 (1). m n
Gọi đường thẳng đi qua 3 điểm M, I, N có dạng y ax+b , a 0
am b 0
a b 2 b n 1 2
2m n mn 1(2) m n 1 2 1 1 2 1 2 2 1 ( ) 5 ( ) 2 2 m n m n m n 1 1 1 1 1 1 5( ) P 2 2 2 2 m n m n 5 2 1 Đẳng thức xảy ra khi
. Kết hợp (2) suy ra: m=5, n=2,5 (thỏa mãn (1)) m n 1
Vậy giá trị nhỏ nhất của P là . 5 Câu 3. 3 3
x y 65
a) Hệ phương trình tương đương: 2 2 3
x y 3xy 60 Suy ra: 3 3 2 2
x y 3x y 3xy 125 x y 5 Dễ dàng suy ra: xy=4 Trang 15 x y 5 x 4 x 1 Suy ra: hoặc xy 4 y 1 y 4
Vậy hệ phương trình có 2 nghiệm: (4;1), (1;4)
b) Gọi số quyển sách mỗi giờ nhóm dự định sắp xếp là: x quyển ( * x N )
Số quyển sách mỗi giờ thực tế sắp xếp là: x+110 (quyển) 810
Thời gian dự định để sắp xếp 810 quyển sách là: (h) x
Tổng số quyển sách đã được sắp xếp trong thực tế là: 810+60=870 (quyển) 870
Thời gian thực tế để sắp xếp 870 quyển sách là: (h) x 110
Do công việc hoàn thành trước dự định 1 giờ 30 phút nên ta có phương trình: 810 870 1,5 x x 110
Suy ra: x=180 (thỏa mãn) hoặc x=-330 (loại).
Vậy số quyển sách mỗi giờ nhóm dự đinh sắp xếp là180 quyển. Câu 4. A C H B
Kẻ đường cao AH của tam giác ABC. Ta có: AB AB A . B AC A . B AC.BC A . B AC.BC sin C AH AH AH .BC 2SABC AC . AB AC.BC Đặt
k (k>0) AB k sinC 2SABC
Tương tự, suy ra: AC k sin ;
B BC k sin A Trang 16 AB sin C
BC sin A CAsin B 2 2 2
k sin C k sin A k sin B
k(sin A sin B sin C) Lại có:
( AB BC C )
A (sin A sin B sin C)
(k sin A k sin B k sin C)(sin A sin B sin C)
k (sin A sin B sin C) Từ đó suy ra:
AB sin C BC sin A CAsin B (AB BC C )
A (sin A sin B sin C) Câu 5. C O M A B N E D
a) Xét COM và CED, ta có: 0
COM CED 90 , ECD chung. CO OM C OM C ED (1) CE ED
Do AB, CD là 2 đường kính vuông góc với nhau nên: 0
CEA CAB 45 Xét A MC và E CAcó: 0
CEA CAB 45 , ACE chung. AC AM AM C EAC . CE AE Mà AC 2CO (Do A
COvuông cân tại O) AM 2CO 2OM Kết hợp với (1) suy ra: AE CE ED Trang 17
AM.ED 2OM.AE (ĐPCM)
b) Tương tự câu a), ta có: ED 2OM EA 2ON (2), (3) AE AM DE DN OM ON 1
Nhân theo về của (2) và (3), suy ra: . AM DN 2 OM ON OM ON Ta có: 2 . 2 AM DN AM DN OM ON ED EA
Dấu “=” xảy ra khi và chỉ khi:
ED EA , E là điểm chính giữa cung AM DN 2EA 2ED nhỏ AD. OM ON GTNN của
là 2 , đạt khi E là điểm chính giữa cung nhỏ AD. AM DN
Vậy E là điểm chính giữa cung nhỏ AD (thỏa mãn bài toán). 1 1 1 1 1 1 Câu 6. Đặt ; x
y; z x, y, z 0 . a b b c c a
Do đó: P (3 x)(3 y)(3 z) 27 3(xy yz zx) 9(x y z) xyz
Áp dụng bất đẳng thức Cauchy ta có: 3 3 3
P 27 9 (xyz) 27 xyz xyz (*) 1 1 1 1 1 1 8 Mà: xyz ( )( )( ) a b b c c a abc 3 1 8 Mặt khác: 3 3
a b c 3 abc abc 64 xyz 64 2 2 abc
Từ (*) suy ra: P 343 1
Dấu “=” xảy ra khi và chỉ khi: a b c 2 1
Vậy MinP=343, dấu “=” xảy ra khi a b c . 2 Trang 18
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI KHÁNH HÒA NĂM HỌC 2020 - 2021 Môn: Toán – Lớp: 9 ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút Ngày: 3/12/2020
(Đề thi gồm: 01 trang) Câu 1. (4,0 điểm) a) Rút gọn 3
A 3 2 2 7 5 2 . b) Cho các số thực ,
x y, z thỏa mãn x y z 3 và 2 2 2
x y z xy yz zx . Tính giá trị của biểu thức 2020 2020 2020 B x y z xyz . Câu 2. (4,0 điểm) a) Cho đa thức 2
f (x) x bx c biết rằng f (x) chia cho x 4 dư 3, chia cho x 1 dư 8. Tìm b, c .
2x x 2x x 2 3 3 3 x b) Giải phương trình: 0 x . 1 Câu 3. (5,0 điểm) a b 2 2 2
a) Chứng minh rằng a b
2ab với mọi số thực a,b . 2
b) Cho các số thực dương a,b, c thỏa mãn điều kiện abc 1. Tìm giá trị lớn nhất của biểu thức 1 1 1 P 2 2 2 2 2 2 a 2b 3 b 2c 3 c 2a . 3 Câu 4. (5, 0 điểm)
Cho hình vuông ABCD . Điểm I thay đổi trên đường chéo BD (điểm I khác B và D ). Gọi
M , N theo thứ tự là chân đường vuông góc kẻ từ I đến AB và AD .
a) Chứng minh rằng IM IN không đổi.
b) Đường thẳng d đi qua I và vuông góc với MN . Chứng minh đường thẳng d luôn đi qua một điểm cố định.
c) Xác định vị trí điểm I để tam giác CMN có diện tích nhỏ nhất. Câu 5. (3,5 diểm) 2 a b 1 a 1
a) Tìm tất cả các cặp số nguyên dương (a, b) sao cho: a và 1
b là các số nguyên. 1
b) Trên bản đồ có 2021 đồng xu. Hai bạn An và Bình thực hiện một số trò chơi bằng cách đi lần
lượt như sau: mỗi người, đến lượt của mình sẽ lấy đi một số các đồng xu sao cho nó là ước của số
các đồng xu hiện có trên bàn. Người lấy đồng xu lượt cuối cùng là thua. Nếu An đi trước, Bình sẽ
dùng chiến thuật như thế nào để chiến thắng? -----HẾT------ Trang 19
ĐÁP ÁN THAM KHẢO – KHÁNH HÒA (2020 – 2021) Câu 1. a) Ta có 3
A 3 2 2 7 5 2 = 2 3 3 2 1 2 1 2 1 2 1 2
x y z xy yz zx x y2 y z2 z x2 2 2 2 0 b)
x y z
Mà x y z 3 nên x y z 1 do đó 2020 2020 2020 B 1 1 1 1 4 Câu 2.
a) Số dư của đa thức f (x) cho x a là f (a) ta có 2 f ( 4 ) 3 ( 4
) 4b c 3 b 4 2 f (1) 8 1
b c 8 c 3
Vậy b 4; c 3 b) ĐKXĐ: x 1 Ta có 2
x x 2 x x 2 3 3 3 x 0 4 3 2
x 4x 2x 12x 9 0
x 3x 2 1 0 x 3(TM ) x 1 (TM ) Vậy x 1 ; 3 Câu 3. a b 2 2 2 a) a b
2ab với mọi số thực a,b 2 a b 2 2 2 2 Xét a b
a b 0 đúng với mọi số thực a,b (1) 2
a b2 ab ab2 2
0 đúng với mọi số thực a,b (2) 2 Trang 20 a b 2 2 2
Từ (1) và ( 2) ta có a b 2ab 2
b) Áp dụng bất đẳng thức Cô-si ta có 2 2
a b 2ab và 2 b 1 2 . b Suy ra 2 2
a 2b 3 2(ab b 1) và ta có 1 1 2 2 a 2b 3 2(ab b 1) Tương tự 1 1 1 1 ; 2 2 b 2c 3 2(bc c 1) 2 2 c 2a 3 2(ac a 1)
Đặt vế trái của BĐT cần chứng minh là A , ta có 1 1 1 1 A
2 ab b 1 bc c 1 ac a 1 1 1 ab b 1 ab b 1 1 ( vì abc 1)
2 ab b 1 b 1 ab 1 ab b 2 ab b 1 2
Đẵng thức xảy ra khi và chỉ khi a b c 1
Vậy giá trị lớn nhất của 2 P là
khi a b c 1 2 Câu 4.
a) Kéo dài MI cắt DC tại F ; Kéo dài NI cắt BC tại E Trang 21
Xét tứ giác MIEB có 0
B M E 90 nên tứ giác MIEB là hình chữ nhật
Mà BI là đường phân giác nên hình chữ nhật MIEB là hình vuông
Tương tự tứ giác NDFI là hình vuông
Ta có IM IN AM BE (do tứ giác ANIM là hình chữ nhật)
AM BM ( Do MIEB là hình vuông) = AB ( không đổi)
b) Kéo dài CI cắt MN tại K ta có NI M CE I ( . c g.c) xét 0
KIN NIK ICE CIE 90 Hay 0
IKN 90 nên CI MN theo tiên đề ơ clit đường thẳng d và đường thẳng CI
trùng nhau nên đường thẳng d đi qua điểm C cố định c) S S S S S S S
(Do các tam giác đó cùng cạnh đáy và CMN MCI ICN MIC NID ICN MIB chiều cao) 2 2 2 AB AB AM .AN AB
AM AN 2 2 (AM AN) S S CMN 2 AMN 2 4 2 8 2 2 2 AB AB 3AB 2 8 8 2
Giá trị diện tích nhỏ nhất 3AB C MN là
khi AM AN hay điểm I là trung điểm 8 cạnh BD Câu 5. a) Từ giả thiết ta có: 2
a b 1 a 1 2 2
a b 1 b 1 a b 2 2
1 a 1 b 1 a 1 b 1
a 1 b 1 2
a 1 a 1 a
1 b 1 2 b 1 Vì * b
b 11 b2, 3 TH1: 2 b
a a 2 2 2 1 1 2 a
1 3 a 1 3 a 1 vì * a a 2 TH2: 2 b a a 2 3 3 1 1 3 a
1 4 a 1 4 a 1 vì * a a 1; 3
Vậy a,b
1,3;2,2;3,3
b) Ta có nhận xét: Các số lẻ chỉ có các ước lẻ nên với mọi cách trừ đi một ước của số
đó luôn được một số chẵn (có thể bằng 0). Trang 22
Vậy ta có chiến thuật của Bình như sau. Sau lần lấy đi đồng xu đầu tiên của An trên bàn
còn lại một số chẵn đồng xu. Vậy Bình cần lấy đi một ước lẻ của số đồng xu ấy để đưa
số xu còn lại về lẻ. Khi đó An chỉ có thể để lại số chẵn đồng xu trên bàn. Cứ làm như
vậy An phải là người lấy đi các đồng xu cuối cùng (lấy hết số xu khi số đồng xu lớn
hơn 1 hoặc lấy đồng xu cuối cùng).
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9 KON TUM
NĂM HỌC 2020 – 2021 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) Ngày thi: 20/3/202. Bài 1.
a) Tính giá trị của biểu thức 4 2 4 2 P 15 4 14 4 2 4 2
b) Cho hàm số y f x 2 ( )
m 3m 5 x m 2 (m là tham số). Đồ thị của nó là đường
thẳng . Xác định các giá trị của m để đường thẳng cắt trục Ox tại A, cắt trục Oy tại B
(A và B khác O) sao cho OB=3OA. Bài 2.
a) Cho a, b là các số nguyên thỏa mãn 2 2 2 2
(2 a b )(a b) 4ab (1 ab) Chứng minh rằng 1 ab M là một số nguyên. 2 2
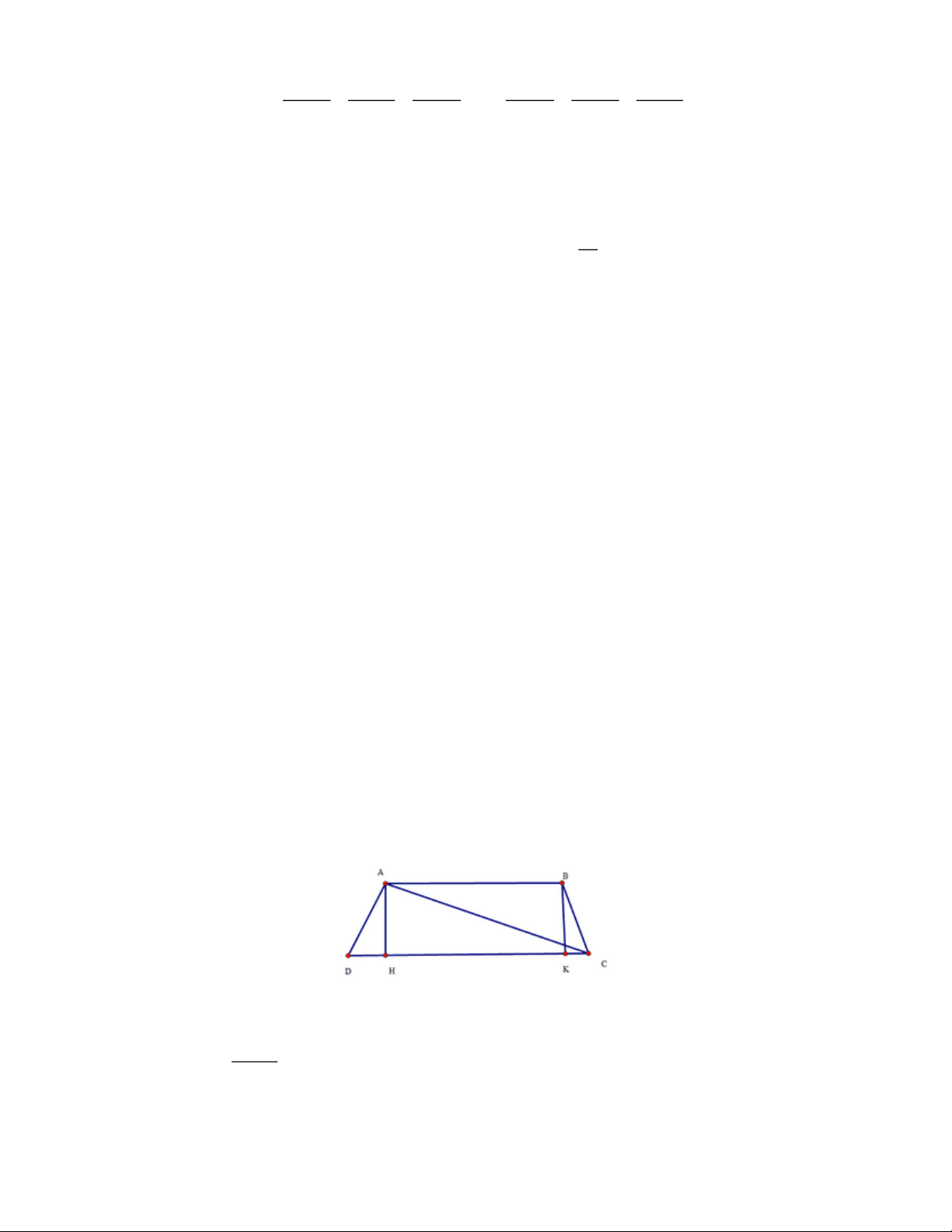
a b ab b) Cho hình thang ABCD có 0
A D 90 ; AB=7cm; BC=10cm; DC=13cm. Gọi M là
trung điểm của BC, đường trung trực của đoạn BC cắt đường thẳng AD tại N. Tính độ dài đoạn MN. Bài 3:
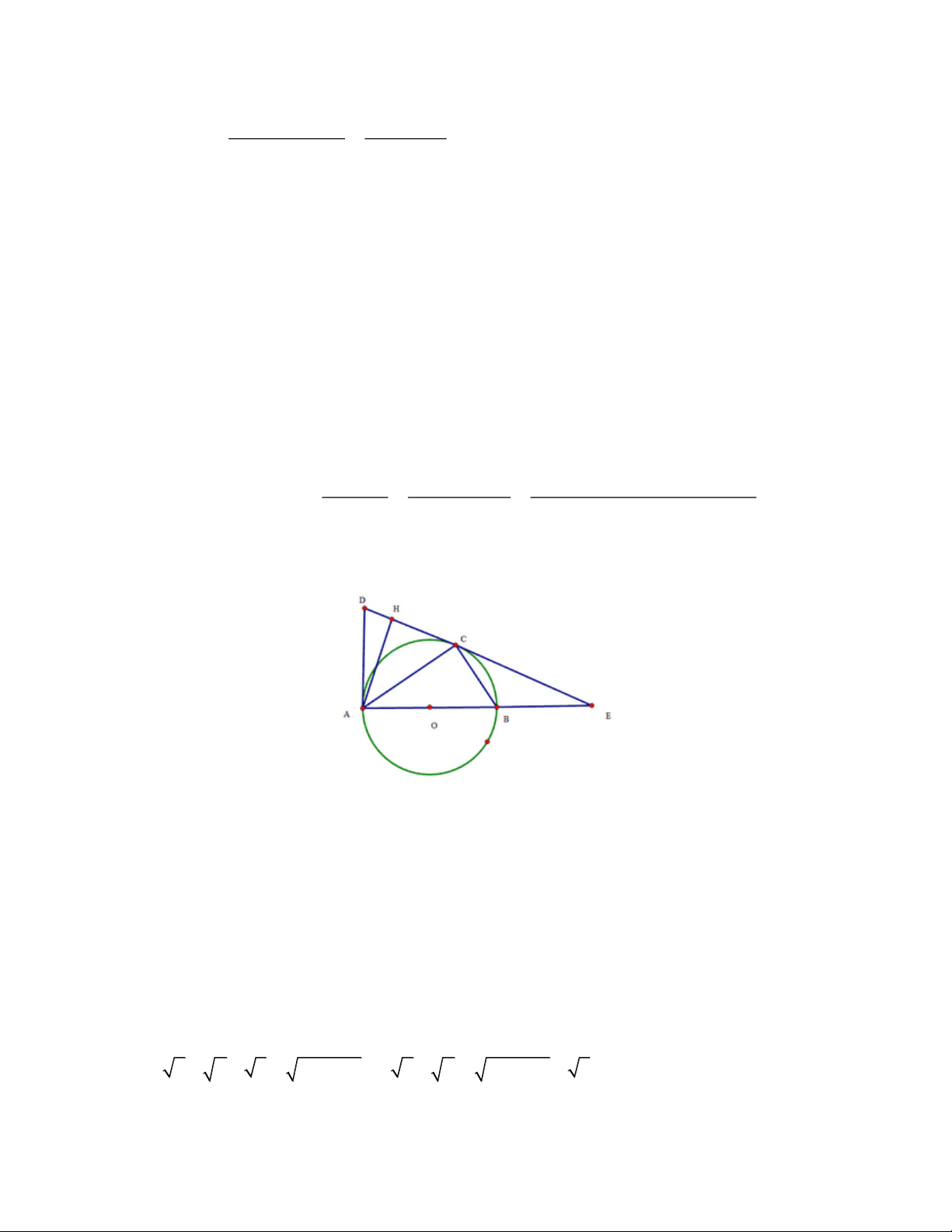
Trên đường thẳng d lấy ba điểm A, B, C theo thứ tự đó thỏa mãn AB = 36 cm, AC
= 60 cm. Đường tròn (O) đi qua điểm B và C có tâm O không nằm trên đường thẳng AC.
Kẻ hai tiếp tuyến AM, AN với đường tròn (O) (M, N là các tiếp điểm). Đường thẳng BC
cắt MN tại K, đường thẳng AO cắt MN tại H và đường tròn (O) tại các điểm P, Q (P nằm giữa A và Q).
a) Tính độ dài đoạn AK.
b) Gọi D là trung điểm của HQ, qua H kẻ đường thẳng vuông góc MD cắt đường thẳng
MP tại E. Chứng minh rẳng P là trung điểm của ME. Bài 4. a) Giải phương trình 2
10 x 5 x 124 25x
b) Cho x, y là các số thực thỏa mãn x y 1 và 2 2
x 3y 2xy 2(x y) 1 0
Tìm giá trị nhỏ nhất của biểu thức 2
M y 2x 11 ------HẾT------ Trang 23
ĐÁP ÁN THAM KHẢO – KON TUM (2020 – 2021) Bài 1. a) 4 2 4 2 P 15 4 14 4 2 4 2 2 ( 4 2 4 2 ) 2 (2 2 7) 4 2 4 2 8 2 2 2 2 7 2 2 2 2 1 2 2 7 1 7
b) y f x 2
m 3m 5 x m 2 () m 2 () Ox=A A ; 0 2
m 3m 5
() Oy=B B 0;m 2 Vì ,
A B O m 2 3 m 2 m 1 2
OB 3OA m 2
m 3m 5 3 2 m 3m 5 m 2 Vậy m=1; m=2 Câu 2. a) Ta có: 2 2 2 2
(2 a b )(a b) 4ab (1 ab)
a b2 2 2
2(ab 1) (a b) (1 ab) 0 4 2 2
(a b) 2(a b) (1 ab) (1 ab) 0 2 2
(a b) (1 ab) 0
a b 1 ab 1 ab 1 ab Suy ra: M
1 ab a b 2
(a b) ab 1 ab ab
Vì a, b là số nguyên nên M cũng là số nguyên (đpcm) Trang 24 b) Bài 3.
a) Gọi I là trung điểm của BC suy ra IO BC AB AN
Dễ dàng chứng minh: ABN đồng dạng với A NC (g.g) 2 A . B AC AN AN AC A
NO vuông tại N, đường cao NH nên 2
AH.AO AN A .
B AC AH.AO AH AK A
HK đồng dạng với A IO (g.g)
AI.AK AH.AO (2) AI AO A . B AC 36.60
Từ (1) và (2) suy ra: AI.AK A . B AC AK 45 AI 48 Trang 25 ME MH b) Ta có: M HE Q DM (g.g) MQ DQ MP MH MH PM H M QH (g.g) MQ QH 2DQ MP ME
ME 2MP P là trung điểm của ME. MQ 2MQ Bài 4.
a) Điều kiện x 5 2
10 x 5 x 124 2 x 2
x 24x 144 x 510 x 5 25 0
x 12 x 5 52 2 0
x 12 x 5 5x 12 x 5 5 0
x x 5 7x x 5 17 0
x x 5 7 0 x 9
x x5170 x14 Vậy x=9, x=14 b) Ta có: 2 2
x 3y 2xy 2 x y 1 0 2 2 2
x 2xy y 4y 2x y 1 0 2
x y 2 x y 2 1 4y 0
x y 2 1 2 y2 0
x 3y
1 x y 1 0
x 3y 1 0 (vì x y 1)
x 3y 1
M y x
y y y 2 2 2 2 11 2 3 1 11 3 4 4
Vậy MinM=4. Dấu “=” xảy ra khi và chỉ khi x=-8, y=-3 Trang 26
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 9 LAI CHÂU
NĂM HỌC 2020 – 2021 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) Ngày thi: 11/4/2021 x x x x
Bài 1. Cho biểu thức 2 3 2 A 1 : x 1 x 5 x 6 x 2 3 x a) Rút gọn biểu thức A b) So sánh A với 5 2 Bài 2. a) Chứng minh rằng 43 17
2021.(43 17 ) 2020 chia hết cho 5. b) Giải phương trình 2
(x 3)(x 1) (x 1) 2 0 Bài 3. 1) Cho phương trình 2
x 2(m 1)x 2m 10 0
a) Tìm m để phương trình có nghiệm.
b) Giả sử phương trình có hai nghiệm x1, x2.
Tìm giá trị nhỏ nhất của biểu thức 2 2
P x x 8x x 1 2 1 2 2 2
2) Giải hệ phương trình x xy 2 y 0 2
xy 3y x 3
Bài 4. Cho đường tròn (O;R) có đường kính AB cố định. Trên tia đối của tia AB lấy điểm
C sao cho AC = R. Qua C kẻ đường thẳng d vuông góc với CA. Lấy điểm M bất kỳ trên
đường tròn (O) không trùng với A, B. Tia BM cắt đường thẳng d tại P. Tia CM cắt đường
tròn (O) tại điểm thứ hai là N, tia PA cắt đường tròn (O) tại điểm thứ hai là Q.
a) Chứng minh tứ giác ACPM nội tiếp.
b) Chứng minh rằng PC song song với NQ.
c) Chứng minh rằng trọng tâm G của tam giác CMB luôn nằm trên một đường tròn cố
định khi M thay đổi trên đường tròn (O). Trang 27
Bài 5. Cho x, y, z là ba số thực dương thỏa mãn x+y+z=2. 2 2 2
Tìm giá trị nhỏ nhất của biểu thức x y z P y z z x x y -----HẾT------
ĐÁP ÁN THAM KHẢO – LAI CHÂU (2020 – 2021) Bài 1. a) 5 x 2 5 7 x 1 b) Ta có: A
0 (Vì 7 x 1>0, 2( x 1) >0) 2 x 1 2 2( x 1) 5 Suy ra: A 2 Bài 2. a) Ta có 43 40 3 4 10 3 43 43 .43 (43 ) .43
Do 433 có tận cùng là chữ số 7 nên 434 có tận cùng là chữ số 1 hay 4340 có tận cùng là chữ số 1
Mà 433 có tận cùng là chữ số 7. Vậy 4340.433 có tận cùng là chữ số 7 hay 433 có tận cùng là chữ số 7. Ta có 17 4 4 17 (17 ) .17
Vì 174 có tận cùng là 1 nên 4 4
(17 ) cũng có tận cùng là 1 hay 1716 có tận cùng là 1 Do đó: 17 17 có tận cùng là 7
Hai số 4343 và 1717 có chữ số tận cùng giống nhau nên 43 17
43 17 có chữ số tận cùng là 0. Do đó 43 17 43 17 chia hết cho 5 Lúc đó 43 17
2021.(43 17 ) 2020 chia hết cho 5.
b) Phương trình đã cho tương đương với: Trang 28 2 2
x 2x 3
x 2x 3 0 2 2
x 2x 3 x 2x 3 6 0 2 2
( x 2x 3 3)( x 2x 3 2) 0 2
x 2x 3 2 0 (vì 2
x 2x 3 3 0 ) x 1 2 Bài 3. m 3
1) Để phương trình có nghiệm: ' 2
m 9 0 m 3 2) Ta có:
P x x 2 2 2
6x x 4(m 1) 6(2m 10) (2m 5) 36 36 1 2 1 2 5
KL: MinP=36, P nhỏ nhất khi 2m 5 0 m 2
𝑥2 + 𝑥𝑦 − 2𝑦2 = 0 (1) 2) Hệ phương trình: {
𝑥𝑦 + 3𝑦2 + 𝑥 = 3 (2) x y Từ (1) suy ra: 2 2
(x y ) y(x y) 0 (x y)(x 2 y) 0 x 2 y 3
Với x = y, thay vào (2) ta được: 2
4x x 3 0 x 1; x 1 2 4 3 3
Khi đó: (x;y)=(-1; -1)= ( ; ) 4 4
Với x = -2y, thay vào (2) ta được: 2
y 2y 3 0 y 1 ; y 3 1 2
Khi đó: (x;y) = (2; -1) = (-6; 3) 3 3
Vậy hệ có 4 nghiệm: (x;y) = (-1; -1) = ( ; ) = (2; -1) = (-6; 3) 4 4 Bài 4. Trang 29
a) AB là đường kính của (O) ( M (O) ) AMB là góc nội tiếp chắn nửa đường tròn 0 0
AMB 90 AMP 90 0
AMP ACP 90
Suy ra tứ giác ACPM nội tiếp đường tròn.
b) Có AMNQ là tứ giác nội tiếp nên MNQ PAM (góc trong tại một đỉnh và góc ngoài tại đỉnh đối diện) (1)
AMPC là tứ giác nội tiếp nên PCM PAM (hai góc nột tiếp cùng chắn cung PM) (2)
Từ (1) và (2) suy ra: MNQ PCM
Hai góc ở vị trí so le nhau nên PC//NQ
c) Gọi D là trung điểm BC, là điểm cố định. Qua G kẻ đường thẳng song song MO cắt AB tại I 2
G là trọng tâm tam giác BCM nên G đoạn MD và MG MD 3
Do GI / /MO nên theo định lí Ta – lét cho tam giác DMO ta có: OI MG 2 2 I đoạn MO và
OI .OD OD MD 3 3
Mà O, D là hai điểm cố định nên I cố định. GI DG 1 1 R
Do GI / /MO nên theo định lí Ta – lét ta có:
IG MO MO DM 3 3 3 R
G luôn cách điểm I cố định một khoảng không đổi. 3 R
Khi M di động, điểm G luôn nằm trên đường tròn tâm I, bán kính 3 2 2 2 x y z x y z x y z
Bài 5. Áp dụng bất đẳng thức Cô – si ta có: 2 . x y z 4 y z 4 y z 4 2 y z x 2 z x y Tương tự: y z z , x 4 x y 4 y z z x x y
x y y 2
Do đó: P x y z ( ) 1 4 4 4 2 2 2
MinP = 1. Dấu “=” xảy ra khi: x y z 3 Trang 30
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LÂM ĐỒNG
LỚP 9 THCS NĂM HỌC 2020 – 2021 ĐỀ CHÍNH THỨC Môn thi: TOÁN (Đề thi có 01 trang)
Thời gian làm bài: 150 phút Ngày thi: 05/03/2021
Câu 1. (2,0 điểm)
Phân tích đa thức thành nhân tử 3 3 3
(x 1) (1 2x) (x 2) .
Câu 2. (2,0 điểm) Chứng minh 2
n 4n 5 không chia hết cho 8 với mọi n là số lẻ.
Câu 3. (2,0 điểm)
Cho hình thang cân ABCD (AB//CD) có đường chéo vuông góc với cạnh bên.
Biết AB = 7cm, DC = 25cm. Tính chu vi của hình thang.
x(y 2) y 14
Câu 4. (2,0 điểm)
Giải hệ phương trình 3 2
x 3x 3x y 1
Câu 5. (2,0 điểm)
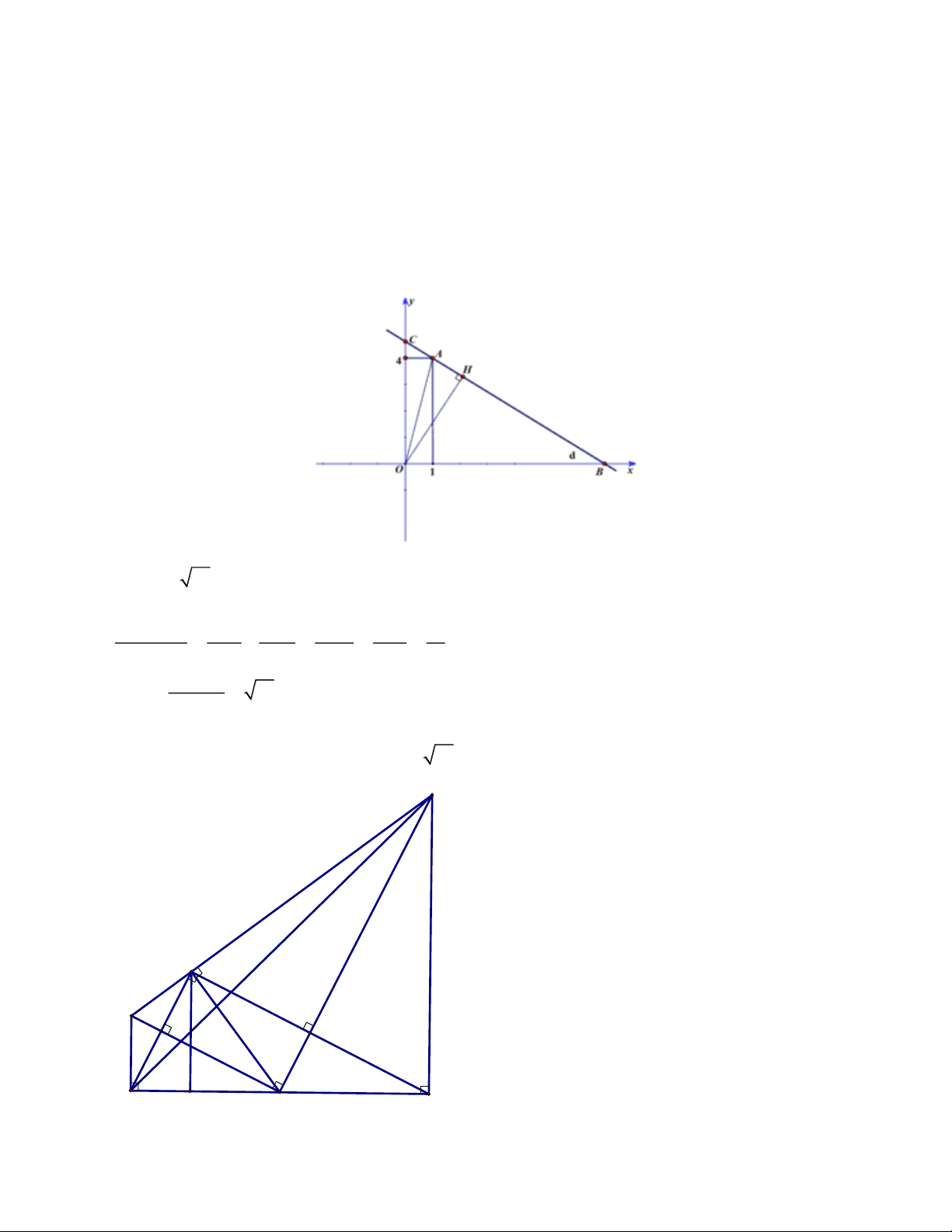
Cột ăng ten dài 12 mét được dựng trên mái của một
ngôi nhà và có các dây cáp neo từ ăng ten xuống mặt đất.
Dây cáp AD được neo từ đỉnh của ăng ten xuống cọc D
Dưới mặt đất như hình vẽ (A, B, C nằm trên một đường
thẳng vuông góc với CD). Một kỹ sư đã đặt máy và đo được 0 CBD 30 , 0
ADB 18 . Tính độ dài dây neo AD. Biết 0 sin18 0,31 ; 0 cos18 0, 95 .
Câu 6. (1,5 điểm)
Lấy điểm C trên nửa đường tròn đường kính AB sao cho AC
lớn hơn BC. Tiếp tuyến của nửa đường tròn tại C cắt tiếp
tuyến tại A ở D và cắt AB ở E. Gọi H là hình chiếu của A
trên DC. Chứng minh DC.CE = CH.DE.
Câu 7. (1,5 điểm)
Cho một tam giác có độ dài ba cạnh là x, y, z thảo mãn: x y z
x y z . Chứng minh tam giác đó là tam giác cân.
Câu 8. (1,5 điểm)
Trên quãng đường AB dài 6 km, cùng một thời điểm người thứ nhất đi từ A
đến B và người thứ hai đi từ B đến A. Sau khi gặp nhau người thứ nhất đi tiếp
nửa giờ thì đến B và người thứ hai đi tiếp hai giờ thì đến A. Biết vận tốc hai người
không thay đổi trên suốt chặng đường. Tính vận tốc mỗi người.
Câu 9. (1,5 điểm)
Lấy điểm B nằm trên nửa đường tròn đường kính AD (B khác A và D). Trên cung
DB lấy điểm C (C khác B và D). Gọi E là giao điểm của AC và BD, F là giao S S
điểm của hai đường thẳng AB và CD. Chứng minh DAC ABCD 1 S S EAD FAD
Câu 10. (1,5 điểm)
Cho ba số thực x, y, z dương. Chứng minh: Trang 31 x y z x y z 2 y 2z z 2x x 2 y y 2x z 2 y x 2z
Câu 11. (1,0 điểm)
Cho hình bình hành ABCD có góc A là góc tù. Kẻ AM vuông góc với DC tại
M (M nằm giữa D và C) và AN vuông góc với BC tại N (N nằm giữa B và C).
Kẻ DI vuông góc với đường thẳng MN tại I và BK vuông góc với đường thẳng
MN tại K. Chứng minh MI bằng NK.
Câu 12. (1,5 điểm)
Cho một dãy các số tự nhiên liên tiếp bắt đầu từ 1. Người ta xóa đi một số thì 7
trung bình cộng của các số còn lại bằng 35 . Tìm số bị xóa 17 ---HẾT---
ĐÁP ÁN THAM KHẢO – LÂM ĐỒNG (2020 – 2021) Câu 1.
Đặt a=x+1; b=1-2x; c=x-2. Thấy a+b+c=0. Ta có: 3 3 3 3 3 3
P (x 1) (1 2x) (x 2) a b c Suy ra: 3 3 3 3 3
P a b c (a b) c 3ab(a b) 2 2
(a b c) (a b) (a b)c c 3ab(a b) 3
ab(c) 3abc
3(x 1)(1 2x)(x 2) Câu 2. Với n=2k+1, ta có: 2 2 (
A n) n 4n 5 (2k 1) 4(2k 1) 5 4k(k 1) 8(k 1) 2
Biểu thức A(n) bằng tổng của ba hạng tử, trong đó hai hạng tử đầu chia hết cho 8, duy chỉcó hạng
tử 2 không chia hết cho 8.
Vậy A(n) không chia hết cho 8 Câu 3.
Kẻ AH và BK lần lượt vuông góc với CD. Ta có: HK=AB=7cm, DH=DK 25 7
DH KC 9cm 2 Trang 32 Trong A
DC vuông tại A có DH=9cm, HC=16cm 2
AH DH.DC 9.16 144 AH 12cm
( AB DC).AH (7 25).12 Suy ra: S 192 2 cm ABCD 2 2 Câu 4. Ta có:
x(y 2) y 14
x(y 2) y 14 3 2 3 2
x 3x 3x y 1 y 1
x 3x 3x Thay y 3 2 3 2 x( 1
x 3x 3x) 2x 1 x 3x 3x 14 x 3 y 10
. Hệ có 2 nghiệm: (x;y)=(-3;-10)=(1;6) x 1 y 6 Câu 5. Có 0 0 0 0
CDB 90 CBD 90 30 60 AC 12 12 Xét A
DC vuông tại C: D 12,27 0 0 0 0 0 0 sin ADC sin(60 18 ) sin 60 . o c s18 o c s60 .sin18 Câu 6. DC.CE = CH.DE.
Hai tiếp tuyến tại A và C cắt nhau tại H nên AD=DC.
Ta có: DC.CE CH .DE DC.(DE DC) CH .DE 0 2
DC.DE DC CH.DE 0 2
DE(DC CH ) DC 0 2
DE.DH DC 0 2 2
AD DC 0 đpcm Câu 7. Ta có: x y z
x y z x y
x y z z Trang 33
x y 2 xy x y z z 2 z(x y z)
xy z(x y z) 2
xy zy zx z
y(x z) z(x z) x z
y z Suy ra đpcm Câu 8.
Gọi v1, v2 là vận tốc 2 người tương ứng xuất phát từ A, B; t là thời gian từ lúc xuất phát đến khi 2 người gặp nhau
Ta có: 6 = v1(t + 0,5); 6= v2(t + 2) (1) 6 = 0,5 v1 + 2v2 (2) 6 6 6 6 6 6
Từ (1) suy ra: t = t 0,5 2 0,5 2 1,5 (3) v v v v v v 1 2 1 2 2 1
Giải hệ gồm (2) và (3) suy ra: v1 = 4, v2 = 2
Kết luận: v1 = 4 km/h, v2 = 2 km/h
Câu 9. Đang cập nhật….. Câu 10. x y z x y z 2 y 2z z 2x x 2 y y 2x z 2 y x 2z x y z x y z 2 y 2z z 2x x 2 y y 2x z 2 y x 2z
Áp dụng bất đẳng thức Bunhia ta có: x y z x
y z y z x z x y
x y z2 2 2 2
y 2z z 2x x 2y x y z
x y z2 (vì 2 2 2
x y z xy yz zx ) (1) y z z x x y
xy yz zx 1 2 2 2 3 z y z Tương tự: 1 x 2 y z 2 y x (2) 2z
Cộng hai vế của (1) và (2) suy ra điều phải chứng minh.
Câu 11. Đang cập nhật….. Câu 12. Trang 34
Giả sử có n số tự nhiên liên tiếp từ 1 đến n:
2 3 4 ... n
(2 n)(n 1) 2 n
- Nếu xóa số 1 thì trung bình cộng của các số còn lại là: n 1 2(n 1) 2
1 2 3 ... (n 1) n(n 1) n
- Nếu xóa số n thì trung bình cộng của các số còn lại là: n 1 2(n 1) 2 n 7 n 2 14 14 Ta có: 35 68 n 70 2 17 2 17 17
Do n là số tự nhiên nên n = 69 hoặc n = 70 7
Nếu n = 70 thì tổng của 69 số còn lại là 35 .69 (loại) 17 7
Nếu n = 69 thì tổng của 69 số còn lại là 35 .68 2408 (t/m) 17
Số bị xóa là (1+2+3+…+69)-2408=7 Trang 35
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH TỈNH LẠNG SƠN
LỚP 9 NĂM HỌC 2020 – 2021
Môn thi: Toán lớp 9 THCS
Thời gian: 150 phút (không kể thời gian giao đề)
Ngày thi: 18/3/2021 Bài 1: (4 điểm) Cho biểu thức: 𝑥+𝑦+2𝑥𝑦
𝑃 = (√𝑥−√𝑦 − √𝑥+√𝑦) : (1 +
) với 𝑥 ≥ 0; 𝑦 ≥ 0; 𝑥𝑦 ≠ 1. 1+√𝑥𝑦 1−√𝑥𝑦 1−𝑥𝑦
a) Rút gọn biểu thức 𝑃.
b) Tính giá trị của 𝑃 với 𝑦 = 9 + 4√5. Bài 2: (4 điểm)
Cho phương trình 𝑚𝑥2 + 2(𝑚 − 2)𝑥 + 𝑚 − 3 = 0 ( 𝑚 là tham số).
a) Tìm tất cả các giá trị của tham số 𝑚 để phương trình có hai nghiệm trái dấu.
b)Tìm tất cả các giá trị của tham số 𝑚 để phương trình có hai nghiệm 𝑥1, 𝑥2 thỏa mãn: 1 1 + = 2. 𝑥2 2 1 𝑥2 Bài 3: (4 điểm)
𝑥𝑦 + 𝑥 + 𝑦 = 𝑥2 − 2𝑦2
a) Giải hệ phương trình {
𝑥√2𝑦 − 𝑦√𝑥 − 1 = 2𝑥 − 2𝑦
b) Tìm tất cả các số nguyên dương 𝑥, 𝑦, 𝑧 thỏa mãn phương trình
𝑥6 + 𝑦6 + 15𝑦4 + 𝑧3 + 75𝑦2 = 3𝑥2𝑦2𝑧 + 15𝑥2𝑧 − 125
Bài 𝟒: (𝟔 điểm )
Cho tam giác đều 𝐴𝐵𝐶 nội tiếp đường tròn (𝑂; 𝑅). Gọi 𝐻 là một điểm di động trên đoạn thẳng
𝑂𝐴 ( 𝐻 khác 𝑂 và 𝐻𝐴 > 𝐻𝑂 ). Đường thẳng đi qua 𝐻 và vuông góc với 𝑂𝐴 cắt cung nhỏ 𝐴𝐵 tại Trang 36
𝑀. Gọi 𝐾 là hình chiếu vuông góc của 𝑀 trên 𝑂𝐵. a) Chứng minh 𝐵𝑀𝐾 ̂ = 𝑀𝐴𝐵 ̂ .
b) Các tiếp tuyến của (𝑂; 𝑅) tại 𝐴 và 𝐵 cắt tiếp tuyến tại 𝑀 của (𝑂; 𝑅) lần luợt tại 𝐷 và 𝐸.
𝑂𝐷, 𝑂𝐸 cắt 𝐴𝐵 lần lượt tại 𝐹 và 𝐺. Chứng minh rằng 𝑂𝐸. 𝑂𝐺 = 𝑂𝐹. 𝑂𝐷
c) Tìm vị trí điểm 𝐻 để chu vi tam giác 𝑀𝐴𝐵 đạt giá trị lớn nhất. Bài 5: (2 điểm) 1 1
a) Cho 𝑎, 𝑏, 𝑐 là các số thực dương thoả mãn 1 + + = 6. 𝑎2 𝑏2 𝑐2 𝑏2𝑐2 𝑐2𝑎2 𝑎2𝑏2
Tìm giá trị nhỏ nhất của biểu thức 𝑄 = + + . 𝑎(𝑏2+𝑐2) 𝑏(𝑐2+𝑎2) 𝑐(𝑎2+𝑏2)
b) Cho mỗi điểm trên mặt phẳng được tô bởi một trong hai màu xanh hoặc đỏ. Chứng
minh rằng tồn tại một tam giác mà ba đỉnh và trọng tâm cùng màu.
- - - - - - - - - - - - -HẾT - - - - - - - - - - - - -
ĐÁP ÁN THAM KHẢO – LẠNG SƠN (2020 – 2021) Bài 1. x y x y
x y 2xy a) P : 1 1 xy 1 xy 1 xy ( x
y )(1 xy ) ( x y )(1 xy ) 1 xy . (1 xy )(1 xy )
1 x y xy x x y
y y x x x y y y x 1 xy . 1 xy
1 x y xy 2 x y 2 y 2 y (x 1) 2 y
1 x y xy
(x 1)( y 1) y 1 b) Với 2
y 9 4 5 4 2.2. 5 5 (2 5) . Ta được: 2 (2 5) 2 (2 5) 2 (2 5) 1 P 9 4 5 1 10 4 5 2 5( 5 2) 5 Bài 2.
a) Điều kiện để phương trình có hai nghiệm trái dấu là: m 0 m 0 2 2
' 0 m 4m 4 m 3m 0 x x 0 m 3 1 2 0 m 0 m 3
b) Để phương trình có 2 nghiệm phân biệt thì: ' 0 m 4 Trang 37 1 1
2 x x 2.x .x x x
2x x 2.x .x 2 2 2 2 2 2 2 2 2 1 2 1 2 1 2 1 2 1 2 x x 1 2 2 m 2 m 3
Áp dụng Viet ta có: x x ; x x 1 2 1 2 m m 4 m 22 2 m 3 (m 3) 2. 2. 2 2 m m m
m 1 (thỏa mãn) Bài 3.
a) Điều kiện: x 1; y 0 Ta có: 2 2
xy x y x 2 y 2 2
xy x y x y
(x y)(y 1) (x y)(x y)
y 1 x y (vì x+y 1)
x 2y 1
Thay vào phương trình thứ hai của hệ ta được:
2x x 1 (x 1) x 1 4x 2(x 1)
2x (x 1) x 1 2x 2
x 1 2x 1 0
x 1 2 0 (Vì x 1 2) x 5 Vậy (x;y)=(5;2) b) Đặt 2 2
x a, y b (a,b>0)
Phương trình tương đương với: 3 3 2 3
a b 15b z 75b 3abz 15az 125 3 3 3
a z b 125 15b(b 5) 3az(b 5) 0 3 3
a z b 5 2
b 5b 25 15b(b 5) 3az(b 5) 0 3 3
a z b 5 2
b 10b 25 3az 0
a z b 53 3 3
3az b 5 0
a z b 53 3 3
3az b 5
Vì a, b, z nguyên dương nên: 3 3 3 3
a z b 3 3 3 5
3 a z b 5 3az b 5 Dấu “=” xảy ra khi:
a z b 5 Trang 38 x 3 2 2
x y 5
(x y)(x y) 5 2 2
x z y 5 y 2 2 2 x z z x z 9 Vậy (x;y;z)=(3;2;9) Bài 4.
a) Gọi N là giao điểm của MK và (O).
MN OK là trung điển của MN B
MN cân tại B BMK BNM MAB
BMK MAB b) Ta có: 0
OD AM OFG 90 MAB 0
MEO 90 MOE 1 Mà MOE
MOB MAB OFG MEO 2 Xét O FG và O
ED có O chung, OFG MEO OF G O ED(g.g) OF OG
OF.OD OE.OG OE OD Trang 39 Bài 5. 1 1 2 2 1 1 a b a) Đặt 1 x , y , z , ta có: a b c 2 2 2 2 x y 1 1 a b 2 2 a b 2 2 1 b c 2 2 1 a c Tương tự: 2 2 2 2 y z b , c 2 2 2 2 z x a c 2 2 2 x y z x y z Ta được: Q 2 2 2 2 2 2 2 2 2 2 2 2 y z z x x y
x( y z )
y(z x ) z(x y ) Và 2 2 2
x y z 6
Áp dụng bấy đẳng thức Cô – si, ta có: 3 2 2 2 2 2 1 1
2x y z y z 2 2 2 2 2 2 2
x( y z )
. 2x ( y z )( y z ) 4 2 2 2 3 2 2 x x 2 2 x( y z ) 4 2 2 2 2 2 y y z z Tương tự: ; 2 2 2 2
y(z x ) 4 2 z(x y ) 4 2 2 2 2 x y z 6 3 2 Suy ra: Q 4 2 4 2 4 2 4 2 4 3 2 1 Vậy MinQ
, dấu “=” xảy ra khi và chỉ khi: a b c 4 2
b) Lấy 5 điểm tùy ý sao cho không có ba điểm nào thẳng hàng trên mặt phẳng.
Khi đó vì chỉ dùng có hai màu để tô các đỉnh nên theo nguyên lí Dirichlet phải tồn tại ba điểm cùng màu.
Giả sử ba điểm đó là ba điểm A, B, C cùng có màu đỏ. Như vậy ta có tam giác ABC với ba đỉnh màu đỏ.
Gọi G là trọng tâm tam giác ABC, chỉ có 2 trường hợp xảy ra:
- Nếu G là màu đỏ, khi đó A, B, C, G có cùng màu đỏ và bài toán được chứng minh.
- Nếu G có màu xanh. Kéo dài GA, GB, GC các đoạn AA’=3GA, BB’=3GB, CC’=3GC. Khi đó nếu M, N,
P tương ứng là các trung điểm của BC, CA, AB thì AA’=3GA=6GM AA’=2AM. Tương tự BB’=2BN,
CC’=2CP. Do đó các tam giác A’BC, B’CA, C’AB tương ứng nhận A, B, C là trọng tâm. Mặt khác, tam Trang 40
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THCS CẤP TỈNH LÀO CAI
NĂM HỌC 2020 – 2021 Môn: Toán
Thời gian: 150 phút (Không kể thời gian giao đề) ĐỀ CHÍNH THỨC Ngày thi 16/03/2021
(Đề thi gồm 01 trang, 05 câu)
giác ABC và A’B’C’ có cùng trọng tâm G. Có 2 trường hợp xảy ra:
TH1: Nếu A’, B’, C’ cùng màu xanh. Khi đó, tam giác A’B’C’ và trọng tâm G có cùng màu xanh
TH2: Nếu ít nhất một trong các điểm A’, B’, C’ có màu điểm. Không mất tính tổng quát giả sử A’ màu đỏ.
Khi đó tam giác A’BC và trọng tâm có màu đỏ. Vậy trong mọi khả năng luôn tồn tại một tam giác mà ba
đỉnh và trọng tâm màu đỏ Câu 1 (4,0 điểm). 3 x 2 x 9x x 1 3 x 1
Cho biểu thức P ( ) : , x 1 3x 2 x 3x x 2 7x 7 x
(x 0, x 1) .
a) Rút gọn biểu thức P .
b) Tìm x sao cho P nhận giá trị là một số nguyên. Câu 2 (6,0 điểm). a) Cho phương trình 2
x 2(m 1)x 2m 5 0 , ( x là ẩn,m là tham số). Tìm m để
phương trình có hai nghiệm phân biệt x 1, x2 thỏa mãn x x 2 2 . 1 2
b) Lúc 7 giờ sáng một người đi xe đạp từ địa điểm A đến địa điểm B với khoảng cách là Trang 41 18 km . Sau khi đi đượ 1 c
quãng đường do xe bị hỏng nên người đó phải dừng lại sửa mất 20 3
phút rồi đi tiếp trên đoạn đường còn lại với vận tốc kém vận tốc lúc đầu là 8 km/h . Khi đến B
người đónghỉ lại 30 phút rồi trở về A với vận tốc bằng một nửa vận tốc đi trên 1 quãng đường 3
AB đầu tiên. Biết người đó trở về A lúc 10 giờ 20 phút sáng cùng ngày. Hỏi xe đạp hỏng lúc mấy giờ? 2 2
(x 1) y xy y 1
c) Giải hệ phương trình 3
2y x y 1
Câu 3 (6,0 điểm). Cho tam giác ABC nhọn có AB < AC . Gọi D là trung điểm của BC . Hai
đường cao BE và CF cắt nhau tại H . Đường tròn tâm O ngoại tiếp BDF và đường tròn tâm O’
ngoại tiếp CDE cắt nhau tại I ( I khác D ), EF cắt BC tại K . Chứng minh
a) Tứ giác AEIF nội tiếp.
b) Tam giác DCA đồng dạng với tam giác DIC .
c) Ba đường thẳng BE,CF,KI đồng quy. Câu 4 (2 điểm). 1 1 1
Cho 3 số thực dương a,b,c thỏa mãn:
1. Tìm giá trị nhỏ nhất của 2 2 2 a b c 2 2 2 2 2 2 a b b c a c biểu thức P . 2 2 2 2 2 2
c(a b )
a(b c )
b(a c )
Câu 5 (2,0 điểm). Giải phương trình nghiệm nguyên: 4 3 2 2
y 2 y y 2 y x x 0
-----------------------HẾT-----------------------
Thí sinh không được sử dụng máy tính cầm tay!
Chữ ký của giám thị số 1:………………........... Chữ ký của giám thị số 2:………………..
ĐÁP ÁN THAM KHẢO – LÀO CAI (2020 – 2021) Câu 1 (4,0 điểm). a) Ta có: 3 x 2 9x x 1 3 x 1 P ( ) : x 1 3 x 2
( x 1)(3 x 2) 7x 7 x
3 x (3 x 2) 2( x 1) 9x
x 1 7 x ( x 1) .
( x 1)(3 x 2) 3 x 1 3 x 1 7 x . x 2 3 x 1 7 x 3 x 2 b) Ta có: Trang 42 7 x x
0, x 1 x 0 P 0 3 x 2 7 x 7 14 7 P 3 x 2 3 3(3 x 2) 3 7
0 P , x 0, x 1 3
P nhận giá trị là một số nguyên P 1; 2 1 1 P 1 x
x (thỏa mãn) 2 4 P 2
x 4 x 16 (thỏa mãn) Vậy 1
x ;16 thì P nhận giá trị là một số nguyên. 4 Câu 2 (6,0 điểm). a) ' 2
(m 2) 2 0, m
. Phương trình luôn có 2 nghiệm phân biệt.
x x 2(m 1)
Áp dụng định lí Vi-et: 1 2 x x 2m 5 1 2 x x 2 2 1 2 2
(x x ) 8 1 2 2
(x x ) 4x x 8 1 2 1 2 2
m 4m 4 0 m 2 1 1 1 b) Đổi 20 phút = (h), 30 phút =
(h), 10 giờ 20 phút = 10 (h) 3 2 3
Gọi vận tốc xe đạp đi trên 1/3 quãng đường AB đầu tiên là x(km / h)(x 8)
Vận tốc xe đạp đi trên 2/3 quãng đường còn lại là x - 8 (km/h)
Vận tốc xe đạp đi từ B về A là 0,5x (km/h)
Tổng thời gian xe đi từ A đến B rồi quay về A là: 1 1 1 5 10 7 . 3 3 2 2
Theo đề bài ta có phương trình: 6 12 18 5 x x 8 0, 5x 2 x 24 28 x 5
Kết hợp với điều kiện được: x =24 (km/h) 6 1
Thời gian xe đi 1/3 quãng đường AB đầu tiên là (h) 24 4
Vậy xe đạp hỏng lúc 7 giờ 15 phút.
c) Hệ phương trình đã cho tương đương: Trang 43 2 2
(x 1) (x 1)y y 1 3
(x 1) y 2y
Nhân vế với vế của 2 phương trình ta được: 3 3 3
(x 1) y 2 y x 1 y
Thay vào phương trình đầu tiên ta được: 2
y 1 y 1
Với y=1, thay số suy ra x=0
Với y=-1, thay số suy ra x=-2
Vậy hệ phương trình đã cho có nghiệm: ( ; x y) (0;1),( 2 ; 1 ) Câu 3 (6,0 điểm). A F I O' H O K M D a) 0
IDC IEC 180 (tứ giác CDIE nội tiếp) 0
IDC IDB 180 (hai góc kề bù) 0
IDB IFB 180 (tứ giác BDIF nội tiếp) 0
IEC IFB 180 0
AEI AFI 180 Tứ giác AEIF nội tiếp. b) Ta có:
AIF AEF (tứ giác AEIF nội tiếp)
ABC AEF (tứ giác BCEF nội tiếp) 0
ABC FID 180 (tứ giác BDIF nội tiếp) 0
AIF FID 180
Ba điểm A,I,D thẳng hàng.
BEC vuông tại E,D là trung điểm của BC DB DC DE
DEC DCE ( CDE cân tại D ).
Mà DEC DIC (tứ giác CDIE nội tiếp) DCE DIC Trang 44
DCA và DIC có ADC chung và DCE DIC nên DCA DIC (g.g) c) Do DCA
DIC (g.g) nên DCI DAC
Mặt khác: DAC IFE (tứ giác AEIF nội tiếp)
DCI IFE
Nên tứ giác CIFK nội tiếp
KFC KIC
Ta lại có: KFB ACD (tứ giác BCEF nội tiếp)
KFB CID( ACD) 0
KID BFC 90
KI AD (1)
Tứ giác AEHF nội tiếp đường tròn đường kính AH
Tứ giác AEIF nội tiếp nên I thuộc đường tròn đường kính AH
HI AD (2)
Từ (1) và (2) suy ra ba điểm K,H,I thẳng hàng
Vậy ba đường thẳng BE,CF,KI đồng quy tại H . Câu 4 (2 điểm). 1 1 1 Ta có: P 1 1 1 1 1 1 c( ) a( ) b( ) 2 2 2 2 2 2 b a c b c a Đặt: 1 1 1 x , y , z
thì: x, y, z 0 và 2 2 2
x y z 1 a b c 2 2 2 z x y z x y P 2 2 2 2 2 2 2 2 2 x y y z z x z(1 z ) x(1 x ) y(1 y )
Áp dụng bất đẳng thức Côsi cho 3 số dương ta có: 2 2 2 1
1 2x 1 x 1 x 2 2 2 2 2 2 3 x (1 x )
.2x (1 x )(1 x ) .( ) 2 2 3 4 2 2 2
x (1 x ) 27 2 2
x(1 x ) 3 3 2 x 3 3 2 .x 2 x(1 x ) 2 2 2 Tương tự: y 3 3 z 3 3 2 .y , 2 .z 2 y(1 y ) 2 2 z(1 z ) 2 3 3 3 3 Suy ra: 2 2 2 P
.(x y z ) 2 2
Dấu “=” xảy ra khi và chỉ khi: 1
x y z
hay a b c 3 3 Câu 5 (2,0 điểm). Ta có: 4 3 2 2
y 2 y y 2 y x x 0 2 2 2
(y y 1) x x 1 (*) Trang 45 Nếu x > 0 thì 2 2 2
x x x 1 (x 1) suy ra 2
x x 1 không là số chính phương nên không tồn
tại số nguyên x,y thỏa mãn (*). Nếu x <-1 thì 2 2 2
(x 1) x x 1 x suy ra 2
x x 1 không là số chính phương nên không tồn
tại số nguyên x,y thỏa mãn (*). y 2 y 1
Nếu x =-1 hoặc x = 0 thì từ (*) suy ra 2
y y 1 1 y 0 y 1
Vậy phương trình có nghiệm nguyên: ( ; x y) ( 1 ; 2 ),( 1 ; 1 ),( 1 ;0),( 1 ;1),(0; 2 ),(0; 1 ),(0;0),(0;1 )
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI NAM ĐỊNH NĂM HỌC 2020 - 2021
Môn: Toán – Lớp: 9 ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút
(Đề thi gồm: 01 trang) Câu 1: (3,0 điểm) a 4 1) Cho 3
P 7 4 3 (a 3) a 3a 1 :
1 với a 0;a 1;a 4 3( a 2 Rút gọn biểu thức P. 1
2) Tìm tất cả các số thực x, y, z thỏa mãn điều kiện 2 x 2 y x 3 z y (z 17) 2 Câu 2. (5,0 điểm) 1) Giải phương trình 3 3 3
6x 2x 7 6x 2x 22 4 2x 7 2 2
xy 3x 2y
2) Giải hệ phương trình 2 2
x y y 2 x Câu 3. (3,0 điểm)
1) Tính tổng tất cả các số nguyên x thỏa mãn 2
x x a 0 với a là số nguyên tố.
2) Tìm tất cả các nghiệm nguyên dương của phương trình 2 2
(x y) y 3x z 1 Trang 46
Câu 4. (7,0 điểm) Trên đường tròn (O) lấy ba điểm A, B,C sao cho tam giác ABC nhọn. Gọi AD,
BE, CF là các đường cao của tam giác ABC; đường thẳng EF cắt đường thẳng BC tại P . QuaD kẻ
đường thẳng song song với đường thẳng EF cắt đường thẳng AC và AB lần lượt tại Q và R, M là trung điểm của BC .
1) Chứng minh tứ giác BQCR là tứ giác nội tiếp.
2) Chứng minh hai tam giác EPM và DEM đồng dạng.
3) Giả sử BC là dây cung cố định không đi qua tâm O, A di động trên cung lớn BC của đường
tròn (O). Chứng minh đường tròn ngoại tiếp tam giác PQR luôn đi qua một điểm cố định. Câu 5. (2,0 điểm)
1) Cho 2021 số tự nhiên từ 4 đến 2024 trên bảng, mỗi lần thay một hoặc một vài số bởi tổng các
chữ số của nó cho đến khi trên bảng chỉ còn lại các số từ 1 đến 9. Hỏi cuối cùng, trên bảng có bao
nhiêu số 3, bao nhiêu số 7?
2) Cho các số thực dương x, y, z thỏa mãn 3 3 3
x y z 24 . Tìm giá trị nhỏ nhất của biểu thức 2
xyz 2(x y z) 8 M
xy yz zx
xy yz zx 1 ------------Hết------------
Họ và tên thí sinh:.............................. Số báo danh:...........................Ký tên:...................................
Họ, tên và chữ ký của GT 1:.................................Họ, tên và chữ ký của GT 2:................................
ĐÁP ÁN THAM KHẢO – NAM ĐỊNH (2020 – 2021) Câu 1. 1) Ta có: 7 4 3 2 3
3 (a 3) a 3a 1 a 1 a 4 a 1 1 3( a 2) 3 a 1
Suy ra: P 2 3 ( a 1) : 5 3 3 x 0
2) Điều kiện: y x 0 hay 0 x y z z y 0 1
2 x 2 y x 3 z y (z 17) 2
4 x 4 y x 6 z y z 17
4 x 4 y x 6 z y z y 9 y x 4 x 4 2 2 2
( z y 3) ( y x 2) ( x 2) 0 x 2
y x 2
z y 3 Trang 47 x 4
y 8 (thỏa mãn) z 17 Kết luận: x=4, y=8, z=17 Câu 2. 1) Điều kiện: 7 3 x 2 Đặt 3
t 2x 7 ( t 0 )
Phương trình đã cho trở thành: 2
(6x 4)t 3(t 7) 2x 22 2
3t 2(3x 2)t 2x 1 0 t 2x 1 t 1/3
TH1: t 2x 1. Ta có: 3
2x 7 2x 1 2x 1 0 3 2
x 2x 2x 3 0 1 x 2 2
(x 1)(x x 3) 0 1 13 x 2 x 1 31 TH2: t=1/3 ta có 3 3
2x 7 1/ 3 x 9
Vậy phương trình có 3 nghiệm: 1 13 31 x , x 1, 3 x 2 9
2) Nếu x = 0 tính được y = 0
Nếu y = 0 tính được x = 0
Do đó ta được (x; y) = (0;0) là một nghiệm của hệ phương trình đã cho. 2 x xy 3 2 y
Với x và y khác 0. Hệ tương đương: 2 y xy 2 x 2 2
ab 3a 2 Đặt: x y a ,b . Ta được: y x
ab b 2 Giải hệ trên suy ra: ( ; a b) (1; 1 ) ( 2 / 3; 6 ) TH1: với a =1; b = -1 Trang 48 2 x 1 y x 1 2 y 1 y 1 x TH 2: với a=-2/3; b=-6 2 x 2 / 3 2 3 x 9 y 3 2 y 3 6 y 2 3 x 2
Kết luận: vậy hệ phương trình đã cho có ba nghiệm là (0;0), (-1;1), 3 3 ( 9; 2 3) 3 Câu 3.
1) Từ giả thiết suy ra 2
a x x hay a x(x 1) mà x và x+1 là hai số nguyên liên tiếp nên
x(x 1) là số chẵn, do đó a là số chẵn.
Mặt khác a là số nguyên tố nên a = 2 x 1 Khi đó ta được: 2
x x 2 0 x 2
KL: tổng tất cả các số nguyên x thỏa mãn là 1- 2 = -1 2) Ta có: 2 2 2 2
(x y) y 3x z 1 (x y) 3x y 1 z (*)
Mà 3x y 1>0 với mọi x, y nguyên dương 2 2
z (x y) (1) Ta lại có: 2 2 2 2
(x y 2) z (x y 2) (x y) 3x y 1 2 2
(x y) 4(x y) 4 (x y) 3x y 1
x 3y 5 0 Nên 2 2
(x y 2) z (2) Từ (1) và (2) suy ra: 2 2
(x y 1) z Thay vào (*) ta được: 2 2
(x y) 3x y 1 (x y 1) x y 2 Khi đó z=2y+3
Vậy tất cả các nghiệm nguyên dương (x; y; z) của phương trình có dạng (k + 2;k;2k + 3)
với k là số nguyên dương. Câu 4. Trang 49
1) Chứng minh tứ giác BCEF là tứ giác nội tiếp.
Suy ra AFE BCQ
Chỉ ra AFE BRQ
Suy ra BRQ BCQ
Chỉ ra tứ giác BQCR nội tiếp
2) Chỉ ra tam giác ECM cân tại M
Chứng minh được EMD 2ACB
Tứ giác BCEF; ACDF nội tiếp nên AFE ACB BFD Suy ra 0
EMD 2ACB AFE BFD EMD DFE 180
Chỉ ra tứ giác DMEF nội tiếp, suy ra BDF PEM
Mà BDF BAC MDE nên MDE PEM . Suy ra tam giác EPM và DEM đồng dạng
3) Do tứ giác DMEF nội tiếp, suy ra PFD EMD PD ED
Mà PDF EDM nên tam giác PFD đồng dạng với tam giác EMD suy ra DF MD
Do RFD ACB AFE FRD nên tam giác FDR cân tại D suy ra FD=DR
Chứng minh tương tự tam giác DEQ cân tại D nên DE=DQ . PD DQ Ta có: FD=DR;DE=DQ suy ra DR MD
Chỉ ra hai tam giác PDR và QDM đồng dạng, suy ra PRQ PMQ
Chỉ ra tứ giác PRMQ nội tiếp nên đường tròn ngoại tiếp tam giác PQR đi qua điểm M cố định Câu 5.
Một số chia cho 9 dư k thì tổng các chữ số của nó chia 9 cũng dư k
Do đó sau khi thay đủ số lần, mà mỗi lần thay một hoặc một vài số bởi tổng các chữ số của nó thì
cuối cùng trên bảng chỉ còn lại các số dư k tương ứng của các số đã cho.
Các số chia 9 dư 3 trong dãy từ 4 đến 2024 là: 12; 21; 30; … ; 2019 2019 12 Dãy số trên có
1 224 (số), do đó trên bảng có 224 số 3 9
Các số chia 9 dư 7 trong dãy từ 4 đến 2024 là: 7; 16; 25; … ; 2023. Trang 50
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9 NGHỆ AN NĂM HỌC 2020 - 2021
Môn thi: TOÁN – BẢNG A ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) 2023 7 Dãy số trên có
1 225 (số), do đó trên bảng có 225 số 7 9
Vậy cuối cùng trên bảng có 224 số 3, có 225 số 7. Câu 6. Ta có 3 3 3
x 8 8 2 x .8.8 12x hay 3
x 16 12x Tương tự 3
y 16 12 y , 3
z 16 12z
Cộng vế ba bất đẳng thức trên ta được 3 3 3
12(x y z) x y z 48 72 x y z 6 Có 3 3 3 3 3 3 3
24 x y z 3 x .y .z 3xyz xyz 8 Ta lại có: 3 3 3 2 2 2
24 3xyz x y z 3xyz (x y z)(x y z xy yz zx) 2 2 2
6(x y z xy yz zx) 2 2 2 2
8 xyz 2(x y z xy yz zx) 2((x y z) 3(xy yz zx)) 2
xyz 2(x y z) 8 6(xy yz zx) 2 2
8 6(xy yz zx) xyz 2(x y z) 8 2.6 80
0 xy yz zx 2
8 6(xy yz zx) 8 8 8 Có: M 6 f (t)
xy yz zx
xy yz zx 1 t t 1
Với t xy yz ;
zx 0 t 12 Khi đó 8 8 236 f (t) 6 6 t(t 1) 12(12 1) 39
Kết luận: giá trị nhỏ nhất của biểu thức M là 236/39 khi x = y = z = 2. Câu 1 (3,0 điểm).
a) Tìm tất cả các giá trị nguyên của a để 2
A a 4a 2021 là một số chính phương.
b) Cho đa thức P(xvới các hệ số nguyên thỏa mãn P(2019).P(2020)2021.
Chứng minh rằng đa thức P(x2022 không có nghiệm nguyên. Câu 2 (6,5 điểm). a) Giải phương trình 2 3
x 5x 2 2 x 1 x 3 2 2 2
y y(x x 1) x x
b) Giải hệ phương trình 2 3 2
y(x 1) x x 2
Câu 3 (1,5 điểm). Cho ba số thực không âm a,b,c thỏa mãn ab bc ca1. Tìm giá trị 2 2 2
nhỏ nhất của biểu thức a b c 3 P
a b c abc Trang 51
Câu 4 (6,0 điểm). Cho tam giác nhọn ABC có D,E,F lần lượt là chân các đường cao kẻ từ
ba đỉnh A,B,C của tam giác. Gọi H là trực tâm tam giác ABC và K là trung điểm của HC.
a) Chứng minh rằng 4 điểm E,K,D,F cùng thuộc một đường tròn.
b) Đường thẳng đi qua K song song với BC cắt DF tại M. Trên tia DE lấy điểm P S MF
sao cho MAP BAC . Chứng minh rằng AMF
(Trong đó SAMF, SAMP lần S MP AMP
lượt là diện tích các tam giác AMF và AMP). Câu 5 (3,0 điểm).
a) Cho hình thoi ABCD có ABa. Gọi R1,R2 lần lượt là bán kính đường tròn ngoại
tiếp của các tam giác ABC và ABD. Chứng minh rằng R R a 2 . 1 2
b) Cho đa giác đều có 2021 đỉnh, sao cho mỗi đỉnh của đa giác đó chỉ được tô bằng
một trong hai màu xanh hoặc đỏ. Chứng minh rằng tồn tại 3 đỉnh của đa giác đã cho là các
đỉnh của một tam giác cân mà các đỉnh đó được tô cùng một màu.
……………Hết……………
Họ và tên thí sinh………………………………… Số báo danh……………………
Chú ý: Thí sinh không được phép sử dụng máy tính bỏ túi.
ĐÁP ÁN THAM KHẢO – NGHỆ AN BẢNG A (2020 – 2021) Câu 1.
a) Ta có a2 4a 2021y2 a 22 2 170y2
2017 y2 a 22 y a 2y a 22017
Do 2017 là số nguyên tố nên ta có các trường hợp sau xảy ra
y a 2 2017 y 1009 TH1:
y a 2 1 a 1010
y a 2 2017 y 1009 TH2:
y a 2 1 a 1006
y a 2 1 y 1009 TH3:
y a 2 2017 a 1006
y a 2 1 y 1009 TH4:
y a 2 2017 a 1010
Vậy có 2 giá trị nguyên của a thỏa mãn yêu cầu bài toán là a 1010 và a 1006. Trang 52
b) Giả sử đa thức P(x)-2022 có nghiệm nguyên x-a, khi đó:
P(x) 2022 (x a).Q(x) P(x) 2022 (x a).Q(x) (Với Q(x) là đa thức hệ số nguyên) Khi đó:
P(2019) 2022 (2019 a).Q(2019)
P(2020) 2022 (2020 a).Q(2020) Mà:
P(2019).P(2020) 2021
2022(2019a).Q(2019)2022 (2020a).Q(2020) 2021 2
2022 2022(2019 a).Q(2019) (2020 a).Q(2020) (*)
(2019 a)(2020 a)Q(2019).Q(2020) 2021
Do 2019a2020a là hai số tự nhiên liên tiếp, suy ra vế trái của (*) là số chẵn.
Vậy không tồn tại a để đẳng thức (*) xảy ra. Hay đa thức P x2022 không có nghiệm nguyên Câu 2.
a) Điều kiện: x 1
Phương trình đã cho tương đương với 2 3
x 5x 2 2 x 1 x 3 0 3 2
x 1( x 1 2) ( x 3 2) x 6x 5 0 x 5 x 5 x 1.
(x 1)(x 5) 0 2 3 3 x 1 2
(x 3) 2 x 3 4 x 1 1 (x 5)( x 1) 0 2 3 3 x 1 2
(x 3) 2 x 3 4 x 5 x 1 1 Do x 1, x 1 2 3 3 x 1 2
(x 3) 2 x 3 4 Vậy: x=5 b) Ta có: 2 2 2 2 2
y y(x x 1) x x ( y 1) (x x 1)( y 1) 0 y 1 2
(y 1)(y x x) 0 2
y x x 3 + Với y= x 3
-1, thay vào phương trình thức 2 và giải ta được: y 1 + Với 2
y x x , thay vào phương trình thứ 2 ta được: Trang 53 2 2 3 2 4 3 2
(x x)(x 1) x x 2 x 2x 2x x 2 0 1 5 x 2 1 5 1 5 Khi đó, hệ có nghiệm x x : 2 , 2 y 1 y 1 1 5 1 5 3
Vậy hệ có nghiệm: x 3 x x , 2 , 2 y 1 y 1 y 1 Câu 3. Ta có: 2 2 2 2 2 2
a b c 3 a b c 3(ab bc ca)
(a b)(b c) (c a)(a b) (b c)(c a)
a b c abc (a b c)(ab bc ca) abc
(a b)(b c)(c a) Khi đó suy ra: 1 1 1 P a b b c c a
Theo nguyên lí Dirichlet trong ba số thực a,b,c luôn tồn tại hai số 1 hoặc 1
Giả sử hai số đó là a và b. Khi đó: (1 a)(1 b) 0 a b ab 1
Lại có: ab bc ca 1 1 ab c(a b) 0 ab 1
Từ đó suy ra: 0 a b ab 1 2 Ta lại có: 2 1 a b a b
a (a b)
a(a b)
a(a b)
(a b)
(a b) a b 2 2 c a
(c a)(a b) a 1 a 1 a 1/ a 2 Tương tự: 1 b(a b) a b b c 2 2 Từ đó ta có: 1 1 1 1 (a b) P
2(a b) a b b c c a a b 2
Đặt a b x,0 x 2 . Khi đó: 2 2 3 2 2 1 x 2 4x x
(x 1) (2 x) 5x 5
(x 1) (2 x) 5 P 2x x 2 2x 2x 2 2x 2
Vậy minP 5/2 đạt được khi và chỉ khi a 1;b 1;c 0 và các hoán vị. Câu 4. Trang 54
a) +) Do EK là trung tuyến của tam giác vuông EHC KE KC KEC ECK
EKF KCE KEC 2ECK (1)
+) Do tứ giác nội tiếp HDCE ECK EDH
+) Do tứ giác nội tiếp FECB ECK EBH
+) Do tứ giác nội tiếp FBDH FBH FDH
Từ đó suy ra: FDE FDH EDH 2EDH 2ECK (2)
Từ (1) và (2) suy ra FDE EKF . Do đó: tứ giác FDKE nội tiếp hay 4 điểm F,D,K,E cùng thuộc một đường tròn.
b) Gọi N là giao điểm của MK và DE Ta có:
MN / /BC BDN MNE (3)
ABDE là tứ giác nội tiếp nên 0
BDE BAE 180 (4) Từ (3) và (4) suy ra: 0
MNP MAP 180
Do đó: MNPA là tứ giác nội tiếp nên AMP ANP (5) Lại có: 0 0 A MD A ND( .
c g.c) AMD AND 180 AMD 180 AND (6)
Từ (5) và (6) suy ra: AMP AMF
Gọi h1, h2 lần lượt là độ cao kẻ từ đỉnh F, P của các tam giác AMF và AMP. 1 1 1 Ta có: S
.h .MA .(MF.sin).MA . Tương tự: S .M . A M . P sin AMF 1 2 2 AMP 2 Từ đó suy ra: S MF AMF S MP AMP Câu 5. a) Trang 55
Gọi M là trung điểm của cạnh AB. Đường trung trực của đoạn AB cắt các đường AC và BD lần
lượt tại I, J. Khi đó I, J lần lượt là tâm đường tròn ngoại tiếp của các tam giác ABD và ABC. MA MJ MA MJ Dễ thấy: M AI M
JB(g.g) AI JB R R 2 1 2 2 2 2 2 2 2 MA MJ MA JB MB R MB 1 2 2 2 2 2 R R R R R 2 1 2 1 1 2 2 2 2 MA MB a a 1 1 2 2 2 2 R R 4R 4R 2 1 2 1 2 2 2 2 Khi đó: a a a a 1 R R 2 2 1 2 4R 4R 2R R 2 2 1 1 2 2 Do đó: a
R R 2 R R 2 a 2 1 2 1 2 2
Dấu “=” xảy ra khi R1=R2 hay tứ giác ABCD là hình vuông. b)
Do đa giác đã cho là đa giác đều nên đa giác đó nội tiếp đường tròn tâm O.
Do 2021 là số lẻ nên tồn tại 2 đỉnh kề nhau tô cùng màu. Giả sử 2 đỉnh đó là A và B và cùng được tô màu đỏ.
Cũng do đa giác đã cho đều và có số đỉnh lẻ nên tồn tại đỉnh M của đa giác nằm trên trung trực đoạn AB M ABcân.
Ta xét hai khả năng xảy ra:
+) Khả năng 1: Nếu tô màu đỏ đpcm.
+) Khả năng 2: Nếu M tô màu xanh.
Gọi E,F là các đỉnh kề của A và B có: EA AB BF EF//AB E
M F cân tại M. Khi đó: Trang 56 Nếu E,F màu xanh thì EF M
cân và thỏa mãn bài toán
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9 NGHỆ AN NĂM HỌC 2020 - 2021
Môn thi: TOÁN – BẢNG B ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề)
Nếu một trong hai đỉnh E,F màu đỏ, giả sử E màu đỏ thì EAB
thỏa mãn yêu cầu bài toán
Vậy luôn tồn tại 3 đỉnh của đa giác đều đã cho lập nên một tam giác cân có các đỉnh cùng màu Câu 1 (3,0 điểm).
a) Tìm tất cả các cặp số nguyên (x;y) thỏa mãn 2 2
x y 6x 8 .
b) Chứng minh rằng với mọi số tự nhiên * n N thì 3
n 5n chia hết cho 6. Câu 2 (6,5 điểm).
a) Giải phương trình x 6 6 x x 1 Trang 57 3 3
x 5x y 5y
b) Giải hệ phương trình 4 2
x y 2
Câu 3 (1,5 điểm). Cho ba số thực dương x, y, z thỏa mãn điều kiện 2 2
x y z 3xy . 3 3 Chứng minh rằng x y x y 7 . y z x z 16z 8
Câu 4 (6,0 điểm). Cho tam giác nhọn ABC có D,E,F lần lượt là chân các đường cao kẻ từ
ba đỉnh A,B,C của tam giác. Gọi H là trực tâm tam giác ABC và K là trung điểm của HC.
a) Chứng minh rằng 4 điểm E, K, D, F cùng thuộc một đường tròn.
b) Đường thẳng đi qua K song song với BC cắt DF tại M. Trên tia DE lấy điểm P sao
cho MAP BAC . Chứng minh rằng MA là phân giác FMP Câu 5 (3,0 điểm).
a) Cho hình thoi ABCD có ABa. Gọi R1,R2 lần lượt là bán kính đường tròn ngoại
tiếp của các tam giác ABC và ABD. Chứng minh rằng 1 1 4 . 2 2 2 R R a 1 2
b) Cho đa giác đều có 2021 đỉnh, sao cho mỗi đỉnh của đa giác đó chỉ được tô bằng
một trong hai màu xanh hoặc đỏ. Chứng minh rằng tồn tại 3 đỉnh của đa giác đã cho là các
đỉnh của một tam giác cân mà các đỉnh đó được tô cùng một màu.
……………Hết……………
Họ và tên thí sinh………………………………… Số báo danh……………………
Chú ý: Thí sinh không được phép sử dụng máy tính bỏ túi.
ĐÁP ÁN THAM KHẢO – NGHỆ AN BẢNG B (2020 – 2021) Câu 1. a) Ta có 2 2 2 2
x y 6x 8 (x 6x 9) y 17 2 2
(x 3) y 17 (x 3 y)(x 3 y) 17
Do 17 là số nguyên tố nên ta có các trường hợp sau:
x 3 y 17 y 12 TH1:
x 3 y 1 a 8
x 3 y 17 y 6 TH2:
x 3 y 1 a 8 Trang 58
x 3 y 1 y 12 TH3:
x 3 y 17 a 8
x 3 y 1 y 6 TH4:
x 3 y 17 a 8
Vậy các cặp số nguyên (x;y thỏa mãn yêu cầu bài toán là (12; 8 ),( 6 ;8),(12;8),( 6 ; 8 ) b) Ta có: 3 3
n 5n (n n) 6n n(n 1)(n 1) 6n
Do n(n 1)(n 1) là tích của ba số tự nhiên liên tiếp (
n n 1)(n 1) 6
Mà 6n 6 , từ đó suy ra: n n n n 3 ( 1)( 1) 6 6 (n 5 ) n 6 Câu 2.
a) Điều kiện: 1 x 6
Phương trình đã cho tương đương với x 6 x 1 6 x 0
(x 5) ( x 1 2) (1 6 x) 0 1 1 (x 5)(1 ) 0 x 1 2 1 6 x x 5 1 1 Do 1 0, x 1;6 x 1 2 1 6 x Vậy: x=5 b) Ta có: 3 3
x x y y 3 3 5 5
x y 5 x y 0
x y 2 2
x xy y 5 0 x y Do 2 2
x xy y 5 0, x , y
Với x=y, thay vào phương trình thứ hai của hệ ta được: 4 2 x x 2 x 2 2 0 1 x 2 0 2 x 1 vì 2 x 2 0, x x 1
x 1 x 1
Vậy hệ phương trình đã cho có nghiệm: ,
y 1 y 1 Câu 3. Ta có: 2 2
3xy x y z 2xy z xy z Suy ra: 3 3 2 2 x y
(x y)(x y xy)
(x y)xy x y (1) 16z 16z 16z 16 2 2 2 2 x y x y (x y) (x y) 4 (2) y z x z xy xz xy yz
2xy z(x y)
xy(2 x y) 2 x y Trang 59 Từ (1) và (2) ta có: 4 x y P x y 2 16 4 x y 2 1 4 x y 2 1 1 7 P 2 . 1 x y 2 16 8 x y 2 16 8 8 8 Vậy 7 MinP
x y 3, z 9 8 Câu 4.
a) +) Do EK là trung tuyến của tam giác vuông EHC KE KC KEC ECK
EKF KCE KEC 2ECK (1)
+) Do tứ giác nội tiếp HDCE ECK EDH
+) Do tứ giác nội tiếp FECB ECK EBH
+) Do tứ giác nội tiếp FBDH FBH FDH
Từ đó suy ra: FDE FDH EDH 2EDH 2ECK (2)
Từ (1) và (2) suy ra FDE EKF . Do đó: tứ giác FDKE nội tiếp hay 4 điểm F,D,K,E cùng thuộc một đường tròn.
b) Gọi N là giao điểm của MK và DE Ta có:
MN / /BC BDN MNE (3)
ABDE là tứ giác nội tiếp nên 0
BDE BAE 180 (4) Từ (3) và (4) suy ra: 0
MNP MAP 180
Do đó: MNPA là tứ giác nội tiếp nên AMP ANP (5) Lại có: 0 0 A MD A ND( .
c g.c) AMD AND 180 AMD 180 AND (6)
Từ (5) và (6) suy ra: AMP AMF
Do đó MA là phân giác của FMP Trang 60 Câu 5. a)
Gọi M là trung điểm của cạnh AB. Đường trung trực của đoạn AB cắt các đường AC và BD lần
lượt tại I, J. Khi đó I, J lần lượt là tâm đường tròn ngoại tiếp của các tam giác ABD và ABC. MA MJ MA MJ Dễ thấy: M AI M
JB(g.g) AI JB R R 2 1 2 2 2 2 2 2 2 MA MJ MA JB MB R MB 1 2 2 2 2 2 R R R R R 2 1 2 1 1 2 2 2 2 MA MB a a 1 1 2 2 2 2 R R 4R 4R 2 1 2 1 1 1 4 2 2 2 R R a 1 2 b)
Do đa giác đã cho là đa giác đều nên đa giác đó nội tiếp đường tròn tâm O.
Do 2021 là số lẻ nên tồn tại 2 đỉnh kề nhau tô cùng màu. Giả sử 2 đỉnh đó là A và B và cùng được tô màu đỏ.
Cũng do đa giác đã cho đều và có số đỉnh lẻ nên tồn tại đỉnh M của đa giác nằm trên trung trực đoạn AB M ABcân.
Ta xét hai khả năng xảy ra:
+) Khả năng 1: Nếu tô màu đỏ đpcm.
+) Khả năng 2: Nếu M tô màu xanh.
Gọi E,F là các đỉnh kề của A và B có: EA AB BF EF//AB E
M F cân tại M. Khi đó: Nếu E,F màu xanh thì EF M
cân và thỏa mãn bài toán
Nếu một trong hai đỉnh E,F màu đỏ, giả sử E màu đỏ thì EAB
thỏa mãn yêu cầu bài toán Trang 61
Vậy luôn tồn tại 3 đỉnh của đa giác đều đã cho lập nên một tam giác cân có các đỉnh cùng màu
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS TỈNH NINH BÌNH NĂM HỌC 2020 - 2021 Môn: TOÁN
ĐỀ THI CHÍNH THỨC Ngày thi: 09/03/2021
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Đề thi gồm 05 câu, trong 01 trang
Họ và tên thí sinh……................................... Số báo danh:........................................................
Họ và tên, chữ ký: Giám thị thứ nhất:..........................................................................................
Giám thị thứ hai:..........................................................................................
Câu 1 (5,0 điểm) Trang 62
1. Cho phương trình: x2 −2(m+1)x + 4m − m2 = 0 (1) (x là ẩn, m là tham số).
a) Tìm m để phương trình (1) có hai nghiệm dương phân biệt.
b) Giả sử x1, x2 là hai nghiệm của phương trình (1). Tìm giá trị nhỏ nhất của biểu thức
A x x 1 2
x 2021 y 4042
2. Giải hệ phương trình
2021 x y 4042
Câu 2 (5,0 điểm) 1. Cho đa thức 2
f (x) x +ax b(a,b ) thỏa mãn f(1)=1 và f(0)>0
a) Chứng minh phương trình f (x)= x có hai nghiệm phân biệt.
b) Tìm số nghiệm của phương trình f(f(x))=x .
2. Cho hai số thực dương x,y thỏa mãn xy =1. Chứng minh 1 1 2 3 x y x y
Câu 3 (7,0 điểm) Cho đường tròn tâm O bán kính R . Dây cung BC cố định, không đi qua tâm O.
Trên tia đối của tia BC lấy điểm A (A khác B ). Từ A kẻ hai tiếp tuyến AM và AN với đường tròn
(O) (M và N là các tiếp điểm). Gọi I,H lần lượt là trung điểm của BC và MN, BC cắt MN tại K .
1. Chứng minh bốn điểm O,M,N,I cùng thuộc một đường tròn và HK là tia phân giác của BHC
2. Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau ở E. Chứng minh M,N,E thẳng hàng.
3. Đường thẳng ∆ qua điểm M và vuông góc với đường thẳng ON, cắt đường tròn (O) tại
điểm thứ hai là P . Xác định vị trí của điểm A trên tia đối của tia BC để tứ giác AMPN là hình bình hành.
Câu 4 (3,0 điểm)
1. Tìm các số nguyên x,y thoả mãn: x2 −5x + 7= 3y
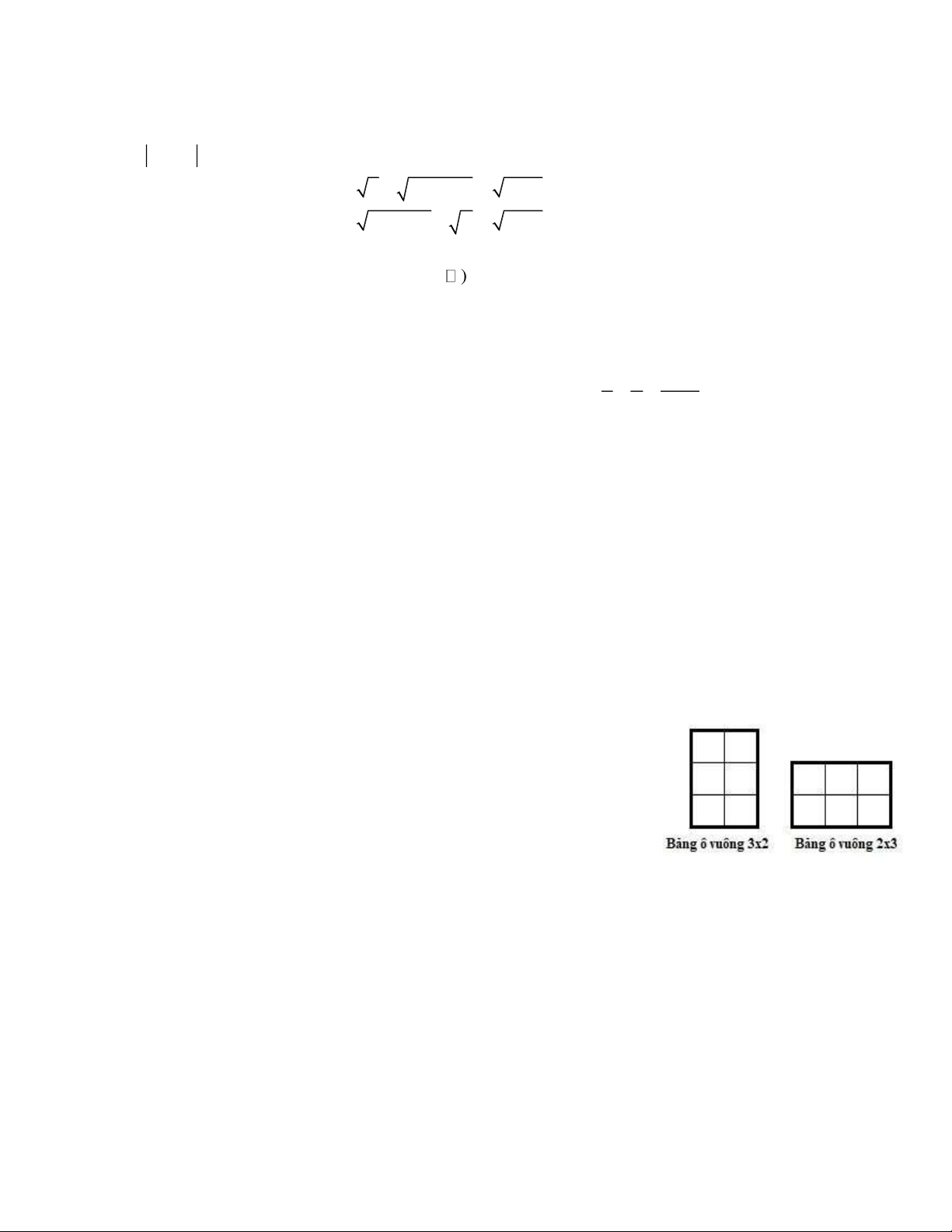
2. Cho một bảng ô vuông m×n (gồm m dòng và n cột). Cho quy
tắc tô màu bảng ô vuông như sau: Mỗi ô vuông đơn vị được tô bằng
màu đỏ hoặc màu xanh sao cho bất kì bảng ô vuông 2×3 hoặc 3×2 nào
cũng có đúng hai ô được tô màu đỏ.
a) Hãy chỉ ra một cách tô màu theo quy tắc trên cho bảng ô vuông
4×6 (Điền chữ Đ vào ô được tô màu đỏ, chữ X vào ô được tô màu xanh).
b) Người ta đã tô bảng ô vuông 2021 2022× theo quy tắc trên. Hỏi bảng ô vuông này có bao
nhiêu ô được tô màu đỏ?
………………HẾT………………
ĐÁP ÁN THAM KHẢO – NINH BÌNH (2020 – 2021) Câu 1. 1. Trang 63 1 1 a. Ta có: ' 2 2
(m 1) (4m m ) 2m 2m 1 2(m ) 0, m 2 2
Nên phương trình luôn có hai nghiệm phân biệt với ∀m ∈
Do đó phương trình có hai nghiệm dương phân biệt: S 0 2(m 1) 0 m 1 0 m 4 2 P 0
4m m 0 0 m 4
b. Theo chứng minh trên phương trình đã cho luôn có hai nghiệm phân biệt x1, x2 với m
x x 2(m 1) 1 2 và 2
x x 4m m 1 2 Ta có: 2
A x x (x x ) (x x ) 4x x 1 2 1 2 1 2 1 2 2 2 2 2
4(m 1) 4(4m m ) 8m 8m 4 2(2m 1) 2 2
Dấu bằng xảy ra khi và chỉ khi m=1/2
Vậy giá trị nhỏ nhất của biểu thức A bằng 2 khi m=1/2 0 x 2021 b. Điều kiện: 0 y 2021
Cách 1: Áp dụng bất đẳng thức Cauchy-Schwarz có 2
4042 ( x 2021 y ) 2(x 2021 y)
x y 0 (1)
Đẳng thức xảy ra khi và chỉ khi x 2021 y x 2021 y
Áp dụng bất đẳng thức Cauchy-Schwarz có 2
4042 ( y 2021 x) 2( y 2021 x)
x y 0 (2)
Đẳng thức xảy ra khi và chỉ khi y 2021 x y 2021 x Từ (1) và (2) suy ra x=y
Từ đó suy ra x=y=2021/2 (thỏa mãn)
Hệ phương trình đã cho có một nghiệm x y 2021 2021 ; ; 2 2
Cách 2: Từ 2 phương trình của hệ ta có: x 2021 y
y 2021 x
x 2021 x y 2021 y (*) Xét phương trình (*):
+ Nếu x>y thì 2021 x 2021 y VT VP (mâu thuẫn)
+ Nếu x+ Nếu x = y . Hệ phương trình đã cho trở thành: x y x y
x 2021 x 4042
2 x(2021 x) 2021 Trang 64 2021 x x y 2 (thỏa mãn) 2 (2x 2021) 0 2021 y 2
Hệ phương trình đã cho có một nghiệm 2021 2021 ( ; x y) ( ; ) 2 2
Cách 3: Từ 2 phương trình của hệ ta có: x 2021 y
y 2021 x
( x y) ( 2021 y 2021 x) 0 x y
( x y) 0
2021 y 2021 x (Vì ;
x y (2021;2021) không phải là nghiệm của hệ phương trình đã cho nên nếu hệ phương trình có nghiệm ;
x y thì 2021 y 2021 x 0 ) x y
( x y)(1 ) 0
2021 y 2021 x x y x y (Vì 1 0 )
2021 y 2021 x
Hệ phương trình đã cho trở thành: 2021 x x y 2 (thỏa mãn)
x 2021 x 4042 2021 y 2
Hệ phương trình đã cho có một nghiệm 2021 2021 ( ; x y) ( ; ) 2 2 Câu 2. 1. f (1) 1 1
a b 1 a b a)Vì 2
f (x) x +ax+b nên ta có f (0) 3 b 3 b 3 2 2
f (x) x x +ax+b x x - (b-1)x+b=0 (*) Ta có 1+ (
b 1) b 0 nên phương trình (*) có 2 nghiệm x 1; x b 1 2
Mà b>3 nên x x 1 2
Do đó phương trình f (x)=x có hai nghiệm phân biệt b) 2 2
f ( f (x)) x f (x) af (x) b x f (x) bf (x) b x 0 2 2 2
f (x) x bf (x) bx x bx b x 0
f (x) x f (x) x b 1 0
f x x 2 ( )
x (b 1)x 1 0
f (x) x 0 2
x (b 1)x 1 0 Trang 65
Phương trình f (x) x (1) có 2 nghiệm phân biệt là 1 và b Phương trình 2
x (b 1)x 1 0 (2) có (b 1)(b 3) 0 (vì b>3)
Nên phương trình (2) có hai nghiệm phân biệt.
Ta lại có x =1; x = b không là nghiệm của phương trình (2)
Vậy phương trình f( (f x))=x có 4 nghiệm phân biệt. 2. Ta có: 1 1 2 xy xy 2 2 x y x y 2 x y x y x y x y x y x y 2 2 x y
Áp dụng bất đẳng thức AM x y x y -GM ta có: xy 1 (1) 2 2
Tương tự áp dụng bất đẳng thức AM-GM ta có: x y 2 x y 2 2 . 2 (2) 2 x y 2 x y 1 1 2 Từ (1) và (2) suy ra
3 . Đẳng thức xảy ra khi x=y=1. x y x y Câu 3.
1. Ta có: AM OM (tính chất tiếp tuyến) A MO vuông tại M
⇒ Ba điểm A,M,O cùng thuộc đường tròn đường kính AO (1)
Chứng minh tương tự suy ra: ba điểm A,N,O cùng thuộc đường tròn đường kính AO (2)
Mặt khác ta có: I là trung điểm của BC (giả thiết)
⇒ OI ⊥ BC ( Quan hệ vuông góc giữa đường kính và dây cung)
⇒ ΔAIO vuông tại I ⇒ Ba điểm A,I,O cùng thuộc đường tròn đường kính AO (3)
Từ (1), (2) và (3) suy ra: 4 điểm O, M, N, I cùng thuộc 1 đường tròn.
*) Ta có: OM=ON (=R) ⇒ O∈ đường trung trực của MN (4)
AM = AN ( tính chất hai tiếp tuyến cắt nhau) ⇒ A∈ đường trung trực của MN (5)
HM = HN(gt) ⇒ H∈ đường trung trực của MN (6)
Từ (4), (5) và (6) suy ra O,H,A thẳng hàng và OA là đường trung trực của MN
Xét Δ ANO vuông tại N có NH⊥AO (OA là đường trung trực của MN ) ⇒ 2
AN AH.AO ( Hệ thức lượng trong tam giác vuông) (*) Trang 66 Chứng minh AB AN A BN A
NC(g.g ) 2 AN . AB AC (**) AN NC Từ (*) và (**) suy ra: AB AO .
AB AC AH.AO AH AC A BH A OC( .
c g.c) AHB ACO (7)
⇒Tứ giác BHOC nội tiếp CHO CBO
Mà BCO CBO nên BCO CHO (8)
Từ (7) và (8) suy ra: AHB CHO KHB CHK ( phụ với hai góc bằng nhau)
HK là tia phân giác của góc BHC 2. MO NP
Cách 1: Tứ giác AMPN là hình bình hành thì suy ra NO MP
Suy ra O vừa là trực tâm vừa là tâm đường tròn ngoại tiếp tam giác MNP M
NP là tam giác đều.
Do bán kính đường tròn ngoại tiếp tam giác MNP bằng R nên MP R 3 AN
Xét tam giác vuông ANO ta có 2 2 AO
AN NO 2R
⇒ A là giao điểm của đường tròn (O;2R) với tia đối của tia BC
Khi A là giao điểm của đường tròn (O; 2R) với tia đối của tia BC, chứng minh tứ giác AMPN là hình bình hành
Vậy A là giao điểm của đường tròn (O; 2R) với tia đối của tia BC thì tứ giác AMPN là hình bình hành
Cách 2: Tứ giác AMPN là hình bình hành ⇒ AP đi qua trung điểm H của MN
⇒ Tứ giác AMPN là hình thoi (hình bình hành có hai đường chéo vuông góc)
⇒ A,H,O,P thẳng hàng và MAP MPA MOA Xét (O; R) có MPA
(hệ quả góc nội tiếp) 2 MOA MAO
MAO 30o (ΔAMO vuông tại M ) 2 AO MO
( cạnh đối diện với góc 300 trong tam giác vuông) ⇒ OA = 2R 2
Khi A là giao điểm của đường tròn với (O;2R) với tia đối của tia BC, ta chứng minh được tứ giác AMPN là hình bình hành.
Vậy A là giao điểm của đường tròn với (O; 2R) với tia đối của tia BC thì tứ giác AMPN là hình bình hành. Câu 4:
1. Tìm các số nguyên x,y thoả mãn: x2 −5x + 7= 3y (*) Nếu y 0 ta có: 2 2
x 5x 7 1 x 5x 6 0 2 x 3
Do x nguyên nên ta có x 2; 3
Lần lượt thay giá trị của x vào phương trình (*) tìm được ( ;
x y) (2;0);(3;0 ) Trang 67 x 1
+ Nếu y = 1 thì phương trình (*) trở thành: 2
x 5x 7 3 x 4 ( ;
x y) (1;1);(4;1
) thỏa mãn phương trình (*)
+ Nếu y≥2 thì 3y 9
Cách 1: Ta xét VT (*) theo các trường hợp số dư của x khi chia cho 3 - Nếu x=3k ( k ) thì 2 2
x 5x 7 9k 15k 7 không chia hết cho 3 - Nếu x=3k+1 ( k ) thì 2 2 2
x 5x 7 (3k 1) 5(3k 1) 7 9k 9k 3 không chia hết cho 9 nên
phương trình (*) vô nghiệm
- Nếu x=3k+2 ( k ) thì 2 2 2
x 5x 7 (3k 2) 5(3k 2) 7 9k 3k 3 không chia hết cho 3
nên phương trình (*) vô nghiệm
Cách 2: Ta có 2 5 7 3y x x 2 5 7 3y x x 0 (1)
Coi phương trình (1) là phương trình bậc hai ẩn x, tham số y có: y y 1 25 4(7 3 ) 3(4.3 1) Vì y 1 (4.3
1) không chia hết cho 3 nên phải là số chính phương
Với y nguyên, y ≥ 2 phương trình (1) là phương trình bậc hai có hệ số nguyên mà Δ không phải là số
chính phương nên phương trình (1) không có nghiệm nguyên Vậy ( ;
x y) (2;0);(3;0);(1;1);(4;1 ) .
2.a).Chỉ ra 1 cách tô đúng. Trang 68 b)
Chia bảng ô vuông ban đầu thành hai bảng ô vuông 2019×2022 và 2x2202 ( xem hình vẽ minh họa)
Bảng ô vuông 2019×2022 được chia thành 2022 2019
680403 bảng ô vuông 3×2 2 3
Trong bảng ô vuông 2019×2022 có 680403.2=1360806 ô được tô màu đỏ
Bảng ô vuông 2×2022 được chia thành 2 2022
674 bảng ô vuông 2×3. 2 3
Trong bảng ô vuông 2×2022 có 674.2=1348 ô được tô màu đỏ.
Bảng ô vuông ban đầu có: 1360806+1348 =1362154 ô được tô màu đỏ. Trang 69
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI PHÚ THỌ NĂM HỌC 2020 - 2021
Môn: Toán – Lớp: 9 ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút
(Đề thi gồm: 01 trang)
I. PHẦN TRẮC NGHIỆM
x 1 2 x 2 Câu 1.
Cho biểu thức : P
, khẳng định nào dưới đây đúng ? x 2 1
A. P 1 khi 2 x 3 .
B. P 1 khi x 3. C. P 1 khi x 3.
D. P 1 khi x 3. Câu 2.
Cho x , y là các số thực thoả mãn đẳng thức: 2 x x 2 1
y 1 y 1. Giá trị của biểu thức 3 3
A x y bằng: A. 3 . B. 1. C. 0 . D. 2 . Câu 3.
Có bao nhiêu giá trị của tham số m để hai đường thẳng d y 2 ( ) : m 1 x 4 và (d )
: y 3x m 2 song song với nhau? A. 1. B. 2 . C. 0 . D. Vô số. Câu 4.
Trên mặt phẳng toạ độ Oxy cho M ;
x y với x , y thoả mãn hệ phương trình:
x y 110m
x y 5 11m
Tìm giá trị của m để điểm M d : y x 1. 3 3 3 6 A. m . B. m . C. m . D. m . 2 2 11 11
mx y 1 Câu 5.
Có bao nhiêu giá trị của m để hệ phương trình: có nghiệm duy nhất
x y m
thoả mãn đẳng thức x y 2 y? A. 0 . B. 1. C. 2 . D. 3 . 1 Câu 6. Cho Parabol P 2 : y
x và điểm I 0;
1 . Biết đường thẳng d qua I với 4
hệ số góc luôn cắt P tại hai điểm phân biệt A , B . Độ dài nhỏ nhất của AB là : A. 4 . B. 3 3 . C. 4 2 . D. 3 2 . 3 x 2x 7 Câu 7. Cho phương trình: 2
x 2x 1. Gọi S là tích tất cả các nghiệm của 3 x 2x 3
phương trình. Giá trị của S là : Trang 70 A. 2 . B. 2 . C. 1. D. 1. Câu 8.
Có bao nhiêu giá trị của tham số a khác 0 để một trong các nghiệm của phương trình 2
x 8x 4a 0 gấp đôi một trong các nghiệm của phương trình 2
x x 4a 0 ? A. 0 . B. 2 . C. 1. D. 3 . Câu 9.
Cho tam giác ABC , trung tuyến AM . Các tia phân giác của các góc AMB , AMC
cắt các cạnh AB , AC theo thứ tự tại D và E . Biết BC 8cm , AM 6cm . Độ dài đoạn thẳng DE bằng A. 5cm . B. 4, 5cm . C. 5, 2cm . D. 4,8cm .
Câu 10. Cho tam giác ABC đều cạnh 4a . Gọi M , N , P là các điểm
di động trên các cạnh AB , AC , CA sao cho AM BN CP (như
hình vẽ bên). Giá trị nhỏ nhất của diện tích tam giác MNP là 2 a 3 A. . B. 2 2a 3 . 4 2 a 3 C. 2 a 3 . D. . 8
Câu 11. Cho hình hộp chữ nhật ABC . D A B C D
có thể tích bằng 3
48cm . Gọi E , E lần lượt là trung điểm của các cạnh CD , C D
. Thể tích của lăng trụ AB . E A B E bằng: A. 3 12cm . B. 3 24cm . C. 3 36cm . D. 3 16cm .
Câu 12. Cho hình vuông ABCD . Gọi M , N lần lượt là trung điểm của BC , CD . Giá trị của cos AMN là: 10 5 3 5 A. . B. . C. . D. . 10 3 2 5
Câu 13. Cho hình vuông ABCD cạnh a . Gọi I là điểm nằm trong hình vuông sao cho
ABI BAI 15 . Giá trị của IC ID bằng: 7a 5a 5a A. . B. . C. . D. 2a . 3 3 2
Câu 14. Cho tam giác ABC vuông tại A , gọi r , R lần lượt là bán kính đường tròn nội r
tiếp, ngoại tiếp tam giác ABC . Biết AB 3cm , AC 4cm . Tỉ số bằng: R 1 2 2 3 A. . B. . C. . D. . 2 5 3 5 Trang 71
Câu 15. Cho tam giác ABC nội tiếp đường tròn O , các
đường cao AH , BH , CH cắt đường tròn O theo thứ tự ở D 1 2 3 AD BE CF , E , F . Tính
. Ta được kết quả là: AH BH CH 1 2 3 9 A. . B. 4 . 2 13 7 C. . D. . 3 2
Câu 16. Từ danh sách giới thiệu giáo viên tham gia làm đề thi chọn học sinh giỏi lớp 9 môn
Toán, trong đó có 6 giáo viên nam và 4 giáo viên nữ, thầy Hồng phụ trách muốn chọn 3 giáo
viên tham gia làm đề thi. Có bao nhiêu cách chọn nếu trong 3 giáo viên đó có ít nhất một giáo viên nữ? A. 100 . B. 21 . C. 19 . D. 52 . II. PHẦN TỰ LUẬN Câu 1. (3,0 điểm).
a) Tìm các nghiệm nguyên của phương trình: 2 2
(x y 3) ( y 2) y 2
b) Có bao nhiêu số tự nhiên n không vượt quá 2021 sao cho 2
n 2021 chia hết cho 30 Câu 2. (3,5 điểm).
a) Giả sử x , x , x là ba nghiệm của phương trình: 3 2
x 4x 2x 4 0 . Đặt 1 2 3 n n n
S x x x n 1 2 3
Chứng minh rằng S là số nguyên với mọi n nguyên dương. n
x 2(x 3) y y(x 2) 1
b) Giải hệ phương trình: 2
x (y 1)(2x y 5) x 16 Câu 3.
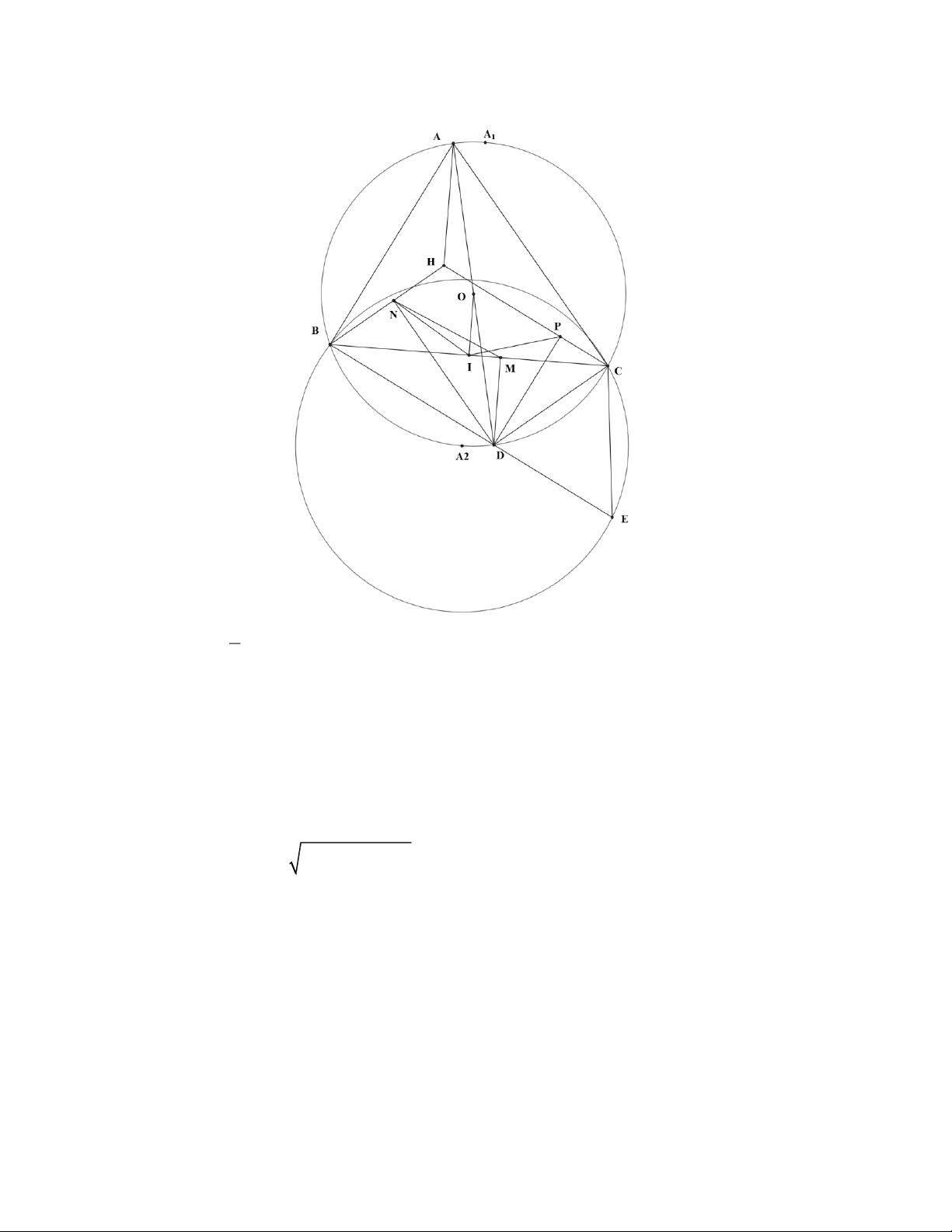
(4,0 điểm). Cho đường tròn O và một dây cung BC cố định không là đường
kính. Xét điểm A thay đổi trên O sao cho A không trùng với B ,C . Gọi H là trực tâm tam
giác ABC , I là trung điểm BC .
a) Chứng minh rằng AH 2OI
b) Gọi D là điểm đối xứng với A qua O , M , N , P lần lượt là hình chiếu vuông góc của
D lên BC , BH , CH . Chứng minh rằng đường tròn ngoại tiếp tam giác MNP luôn đi qua một điểm cố định.
c) Tìm vị trí của điểm A để HA HB HC lớn nhất. Câu 4.
(1,5 điểm). Cho a , b , c là ba số nguyên dương thoả mãn a b c 2021. Tìm
giá trị nhỏ nhất của biểu thức: a b c P(a, , b c) b e c a a b Trang 72 ------HẾT------
ĐÁP ÁN THAM KHẢO – PHÚ THỌ (2020 – 2021)
I. PHẦN TRẮC NGHIỆM
BẢNG ĐÁP ÁN PHẦN TRẮC NGHIỆM Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 B C A D B A D C Câu 9 Câu 10 Câu 11 Câu 12 Câu 13 Câu 14 Câu 15 Câu 16 D C B A D B B A
🕮☞ HƯỚNG DẪN GIẢI CHI TIẾT ☜🕮 II. PHẦN TỰ LUẬN Câu 1. 2 2
a) Phương trình: (x y 3) ( y 2) ( y 2) 0 2 2
x 2(y 3)x 2y 11y 15 0 (*) Ta có: 2 2 2
(y 3) 2y 11y 15 y 5y 6 x
Từ yêu cầu bài toán thì phương trình (*) phải có nghiệm x hay 0 x Vậy 0 2
y 5y 6 0 2 y 3
Mà y Z y 2; 3
Với y 2 x 1
Với y 3 x 0
Vậy phương trình có nghiệm: ( ,
x y) (1;2);(0;3 ) .
b) Có bao nhiêu số tự nhiên n không vượt quá 2021 sao cho 2
n 2021 chia hết cho 30 Ta có: 2 2
n 2021 n n (2021 n) Chứng minh được 2
n n chia hết cho 6. Chứng minh được 2
n n chia hết cho 5 Từ đó ta có: 2
n n chia hết cho 30 Do đó 2 n 202 1 30 (2021 ) n : 30 (201011 )
n 30 (n 11) 30
Do n là số tự nhiên không vượt quá 2021 nên 0 n 2021 n 11 30 11
n 11 2032
n 1130;60;...;201 0 Trang 73
n19;49;....;199 9
Như vậy ta có 67 số tự nhiên n thoả mãn đề bài. Câu 2.
a) Giả sử x , x , x là ba nghiệm của phương trình: 3 2
x 4x 2x 4 0 . Đặt 1 2 3 n n n
S x x x . Chứng minh rằng S , là số nguyên với mọi n nguyên dương. n 1 2 3 n Ta có: 2 2
x 4x 2x 4 0 x 3 (
2) x 2x 2 0 Giải phương trình 3 3
x 4x 2x 4 0 ta được ba nghiệm x 1 3 ; x 1 3 ; x 2 1 2 3 n n n
(1 3)n (1 3)n S x x x 2n . n 1 2 3
Để chứng minh S là số nguyên với mọi n nguyên dương ta đi chứng minh n
T (1 3)n (1 3)n là số nguyên với mọi n nguyên dương. n
Ta đi chứng minh T , bằng quy nạp. n
Ta có: T (1 3) (1 3) 2 ; 2 2
T (1 3) (1 3) 8 tức là T ,T 1 2 1 2
Giả sử T Z, k
n 1. Ta đi chứng minh T Z , thật vậy: n n2 n2 n2 T (1 3) (1 3) n2 n 1 n 1 n 1 n 1
(1 3) (1 3) (1 3) (1 3) (1 3) (1 3) (1 3) (1 3) m 1 n 1 (1 3)
(1 3) (1 3) (1 3) (1 3)n (1 3)n (1 3)(1 3) 2T 2T n 1 n Vì T ,T nên T n n 1 n2
Theo nguyên lý quy nap T
với mọi n nguyên dương. Vậy S là số nguyên với mọi n n n nguyên dương. y 0
b) Điều kiện: x 2
Đặt x 2 a ; y b ; a,b 0
Phương trình thứ nhất trở thành a 2 a
1 b ab 1
a b 2 a ab
1 0 a b (vì 2
a ab 1 0 ) a b x 2
y y x 2
Thay y x 2 vào phương trình 2 ta được x 1 2
2x 5x 7 0 7 x 2 Trang 74
Kết hợp điều kiện ta được x 1 y 3
Vậy nghiệm của hệ phương trình là: ; x y 1;3 . Câu 3.
a) Chứng minh rằng AH 2OI .
Kẻ đường kính AD của đường tròn O , ta có
ACD 90 , mà BH AC , suy ra BH // DC
Tương tự, CH // DB . Do đó tứ giác BHCD là hình bình hành.
Suy ra BC , HD cắt nhau tại trung điểm mỗi
đường, hay I là trung điểm của HD .
Trong tam giác DAH ta có OI là đường trung
bình nên AH 2OI (điều phải chứng minh).
b) Gọi D là điểm đối xứng với A qua O ; M , N
, P lần lượt là hình chiếu vuông góc cùn D lên
BC , BH , CH . Chứng minh rằng đường tròn
ngoại tiếp tam giác MNP luôn đi qua một điểm cố định.
Tứ giác HNDP nội tiếp đường tròn đường kính HD nên NIP 2NDP 2180 BHC
Tứ giác BNMD nội tiếp đường tròn đường kính BD nên NMD 180 NBD BHC .
Tứ giác CPMD nội tiếp đường tròn đường kính CD nên PMD 180 PCD BHC .
Từ đó ta có NMP 360 NMD PMD 360 2BHC
Như vậy NIP NMP , suy ra tử giác NIMP nội tiếp được một đường tròn hay đường tròn
ngoại tiếp tam giác MNP luôn đi qua một điểm cố định I là trung điểm của BC (điều phải chứng minh).
c) Tìm vị trí điểm A để HA HB HC lớn nhất.
Trên tia đối của tia DB lấy điểm E sao cho DE DC 1 1 Ta có: BEC
180CDE 180BAC 2 2 Trang 75
Trường hợp 1: A thuộc cung lớn BC 1 Vì BEC
180BAC nên E thuộc cung tròn cố định dựng trên đoạn thẳng BC, nằm 2
khác phía với A đối với đường thẳng BC . Có HA 2OI
không đổi, nên HA HB HC lớn nhất khi và chỉ khi
HB HC BD DC BD DE BE lớn nhất BE lớn nhất khi và chỉ khi BE là đường
kính của đường tròn chứa cung tròn đó.
Khi đó DI BC , tương ứng cũng có AI BC tức là A là điểm chính giữa cung lớn BC .
Gọi A , A lần lượt là điểm chính giữa cung lớn BC và cung nhỏ BC . 1 2
Ta có: HB HC
BC 2A I 2 2
khi A A là điểm chính giữa cung lớn BC . 2 1
Trường hợp 2: A thuộc cung nhỏ BC Trang 76
Chứng minh tương tự ta có HA HB HC lớn nhất khi và chỉ khi điểm A là điểm chính giữa cung nhỏ BC .
Ta có: HB HC
BC 2A I 2 2
khi A A là điểm chính giữa cung lớn BC . 2 1
Ta có: A I A I nên khi A là điểm chính giữa cung nhỏ BC thì HA HB HC lớn nhất. 2 1 Câu 4.
Ta đi chứng minh với a, ,
b c 673,674,674 , ta được P 673 1348 673, 674,1347 là 1348 1347
giá trị nhỏ nhất của P a, , b c .
Vì chỉ có hữu hạn bộ số nguyên dương a , b , c thỏa mãn a b c 1021 nên tồn tại một bộ
a ,b ,c nguyên dương để P P a ,b ,c là giá trị nhỏ nhất của Pa, ,bc không mất 0 0 0 0 0 0 0 tính tổng quát.
Giả sử a b c . 0 0 0
Ta đi chứng minh c a 1. 0 0
Thật vậy, giả sử c a 2 0 0
Xét bộ a a 1; b b ; c c 1. 1 0 1 0 1 0 Khi đó ta có: Trang 77 a b c P
P a , b , c 1 1 1 1 1 1 1 b c c a a b 1 1 1 1 1 1 Ta có: a 1 c 1 a c 0 0 0 0 P P 1 0 b c 1 a 1 b b c a b 0 1 0 0 0 0 b 0 1 1
a b c 0 0 0
0 b c b c 1 a b a b 1 0 0 0 0 0 0 0 0
Điều này trái với cách trọn bộ a ,b ,c 0 0 0
Như vậy a b c a 1. 0 0 0 0
Kết hợp với điều kiện a b c 2021 ta được a ,b ,c 673,674,674 0 0 0 0 0 0
Từ đó ta có giá trị nhỏ nhất của 673 1348 P a, , b c là P
đạt được khi một trong ba số 0 1348 1347
a , b , c bằng 673, hai số còn lại bằng 674 . Trang 78
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH TỈNH PHÚ YÊN
LỚP 9 THCS, NĂM HỌC 2020 - 2021 Môn thi: TOÁN ĐỀ CHÍNH THỨC Ngày thi: 30/3/2021
Thời gian: 150 phút (không kể thời gian giao đề) -----------
Câu 1.(5,00 điểm) a) Chứng minh rằng: 3 3
5 2 13 5 2 13 1 b) Biết đa thức 4 3 2
x 4x 6 px 4qx r chia hết cho đa thức 3 2
x 3x 9x 3 . Tính giá
trị biểu thức ( p q)r
Câu 2.( 3,50 điểm) Giải hệ phương trình: xy 5 5
2 2x y xy 10
2x y xy 4 xy
Câu 3.(2,50 điểm) Tìm nghiệm nguyên của phương trình: 2 2
2x 5y 13
Câu 4.(3,00 điểm) Cho tam giác nhọn ABC nội tiếp đường tròn (O). Tiếp tuyến tại B và C cắt
nhau ở D. Gọi E, F lần lượt là giao điểm của DA với (O) và DA với BC; H là giao điểm của OD với BC.
a) Chứng minh tam giác OAH đồng dạng với tam giác ODA.
b) Đường thẳng qua A song song với BC cắt (O) tại K (khác A). Chứng minh rằng E, H, K thẳng hàng
Câu 5.(3,00 điểm) Tìm giá trị lớn nhất của biểu thức: 1 1 1 1 1 1 3 3
P x y với x 0, y 0, ( ) 2 2 xy x y x xy y
Câu 6.( 3,00 điểm) Cho tam giác ABC nhọn, có H là trực tâm, (I) là đường tròn nội tiếp. Gọi D,
E, F lần lượt là tiếp điểm của (I) với BC, CA, AB. Gọi K là hình chiếu vuông góc của D trên EF.
a) Chứng minh rằng FKB EKC .
b) Gọi P, Q lần lượt là giao điểm của HB, HC với EF.
Chứng minh đẳng thức: EK.FP = FK .EQ.
c) Chứng minh rằng KD là phân giác của HKI . ---------Hết---------
Thí sinh không sử dụng tài liệu. Giám thị không giải thích gì thêm
Họ và tên thí sinh:………………………………………;Số báo danh:…………………….....…
Chữ kí giám thị 1:……….………………..;Chữ kí giám thị 2:………..………………………... Trang 79
ĐÁP ÁN THAM KHẢO – PHÚ YÊN (2020 – 2021) Câu 1. a) Ta thấy: 3 3 3
A 10 9( 5 2 13 5 2 13 ) 10 9A 2
(A 1)(A A 10) 0 1 39 Vì 2
A A 10 ( A )
0 nên suy ra A1 0 A 1 2 4 b) Giả sử: 4 3 3 2
x 4x 6 px 4qx r (x a)(x 3x 9x 3) 4 3 2
x (a 3)x (3a 9)x (9a 3) 3a 4 a 3 a 1
6 p 3a 9 p 2
Đồng nhất các hệ số cùng bậc hai vế, ta được: 4q 9a 3 q 3 r 3a r 3
Suy ra ( p q)r 15 Câu 2:
Điều kiện: xy 0, 2x y xy 0
Đặt: u xy , v 2x y xy (u,v 0) u 5 5
Hệ phương trình đã cho trở thành: 2 v 10 v 4 u Từ phương trình 10 4u 10 v 4 suy ra: v . u u u 5 u 5u Suy ra: 5
5 u 5 v 2 2 v 2 4u 10 xy 5 xy 5
Ta được hệ phương trình:
2x y xy 2
2x y 7 Trang 80 x 1 xy 5 xy 5 y 5
2x y xy 2
2x y 7 x 5/ 2 y 2
Vậy hệ phương trình có 2 nghiệm là: 5 (1;5) , ( ; 2) 2 Câu 3: Ta có: 2 2 2x 5y 13 2 2
2(x 1) 5(3 y ) Do (2, 5) 1 nên 2 (x 1) 5 và 2 (3 y ) 2 Đặt: 2
x 1 5k và 2
3 y 2l . Ta có: 10k 10l k l (k,l ) 2
x 5k 1 0 k 1/ 5 Do đó:
k l 1 2
y 3 2l 0 l 3 / 2
Vậy: x 2, y 1
Phương trình có các nghiệm nguyên: ( 2 ; 1 ),( 2 ;1),(2; 1 ),(2;1) Câu 4: a)
Theo tính chất tiếp tuyến thì BC OD
Áp dụng HTL vào tam giác vuông OCD, với CH là đường cao ta có: OA OD 2 2
OC OH.OD OA OH.OD OH OA O AH O DA Trang 81
b) Từ câu a) ta có: OHA ODA OEA (1) OAEH nội tiếp
EHD EAO OAD (2)
Từ (1) và (2) suy ra: EHD OHA (3) Dễ thấy A BH K
CH (c.g.c) HA HK hay A
KH cân tại H (4)
Vì OH BC , AK//BC OH AK (5)
Từ (4) và (5) suy ra OH là phân giác của AHK hay OHA OHK (6)
Kết hợp (3) và (6) suy ra EHD OHK Suy ra 0
EHO OHK EHO EHD 180 hay 3 điểm E, H, K thẳng hàng Câu 5: Giả thiết: 1 1 1 1 1 1 2 2 ( )
x y x xy y (Do x 0, y 0 ) 2 2 xy x y x xy y Do đó: 3 3 2 2 2
P x y (x y)(x xy y ) (x y) 2 Thấy (x y) 2 2 2
x y x xy y (x y) 3xy và xy 4 3 Suy ra 2 2
x y (x y)
(x y) (x y)(x y) 4 0 4 Hay 2
0 x y 4 (x y) 16
Vậy Max P=16. Dấu “=” xảy ra khi x=y=2 Câu 6:
a) Gọi M, N theo thứ tự là hình chiếu của B, C lên EF.
Khi đó: BFM AFE AEF CEN BM BF BD B FM CE N CN CE CD
Mặt khác: BM / /DK / /CN nên theo định lí Thales ta có: Trang 82 BD MK BM MK B MK CNK
(c.g.c) FKB EKC CD NK CN NK
b) Dễ chứng minh được BFP CEQ , FBP ECQ (cùng phụ BAC ) Do đó: FB FP BFP C EQ (c.g.c) (1) EC EQ
Theo a) FKB EKC . Kết hợp BFK CEK B FK C EK (g.g) FB FK Suy ra (2) EC EK
Từ (1) và (2) suy ra FP FK
EK.FP FK.EQ (đpcm) EQ EK FP FK FP FK KP EK FK EK FK EF c) Theo b): (3) EQ EK EQ EK KQ QK PK QK PK QP
Hơn nữa, do IE / /HP , IF / /HQ , IE IF nên IEF HPQ IFE HQP Do đó IE EF I EF HQP (g.g) = (4) HQ QP
Từ (3) và (4) ta có EK IE I KE H
KQ (c.g.c) IKE HKQ QK HQ Suy ra 0 0
IKD 90 IKE 90 HKQ HKD hay hay KD là phân giác của IKH Trang 83
SỞ GD&ĐT QUẢNG BÌNH
KỲ THI CHỌN HSG TỈNH NĂM HỌC 2020-2021 ĐỀ CHÍNH THỨC
Khóa ngày 08 tháng 12 năm 2020 Môn thi: TOÁN LỚP 9 THCS
Thời gian: 150 phút (không kể thời gian giao đề)
SỐ BÁO DANH:……………
Đề gồm có 01 trang và 05 câu
Câu 1 (2,0 điểm). x 2 11 x 3 x 2 1 1
a. Rút gọn biểu thức A : (với x 2 , x 7 ) x 2 3 7 x
x 3 x 2 2 x 2
b. Giải phương trình x 4 x 4 x 4 x 4 4
Câu 2 (2,0 điểm).
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y ax b (a 0) đi qua điểm A(1;4)
và cắt các tia Ox, Oy lần lượt tại B và C (khác O)
a. Viết phương trình đường thẳng (d) sao cho biểu thức OA+OB+OC đạt giá trị nhỏ nhất O . B OC
b. Tính giá trị lớn nhất của biểu thức P BC
Câu 3 (3,0 điểm).
Trong mặt phẳng, cho hai điểm B, C cố định với BC=2a (a>0) và A thay đổi sao cho tam
giác ABC vuông tại A. Gọi M là trung điểm của BC, đường thẳng đi qua A vuông góc với
AM cắt các đường phân giác của các góc AMB, AMC lần lượt tại P, Q. Gọi D là giao điểm
của MP với AB và E là giao điểm của MQ với AC.
a. Giả sử AC=2AB, tính số đo góc BQC 3 PD MP b. Chứng minh rằng QE MQ
c. Tính giá trị nhỏ nhất của tổng diện tích hai tam giác ACQ và ABP theo a
Câu 4 (1,0 điểm).
Cho a, b, c là các số thực dương thỏa mãn a b c 2 a b b c c a
( a 1 ( b 1 ( c 1 Chứng minh rằng 4 a b b c c a b c a
Câu 5 (2,0 điểm). Trang 84
a. Số nguyên dương n được gọi là số điều hòa nếu tổng các bình phương của các ước
dương của nó (kể cả 1 và n) bằng 2
(n 3) . Chứng minh rằng nếu pq (với p, q là các số
nguyên tố khác nhau) là số điều hòa thì pq+2 là số chính phương.
b. Tìm tất cả các cặp số nguyên dương (x;y) thỏa mãn 3 3 2 2
x y x y 42xy ------------HẾT-----------
ĐÁP ÁN THAM KHẢO – QUẢNG BÌNH (2020 – 2021) Câu 1.
a. Đặt x 2 t (t 0,t 3) 2
x t 2 2 2
Khi đó: t t 9 3t 1 1 t(3 t) t 9 3t 1 t 3 A : : 2 2 2 2
t 3 9 t t 3t t 9 t t 3t 3 t 2(t 2) 3 x 2 Vậy A 2( x 2 2)
b. Điều kiện x 4
Ta có: x 4 x 4 x 4 x 4 4
x 4 4 x 4 4 x 4 4 x 4 4 4 2 2
( x 4 2) ( x 4 2) 4
x 4 2 x 4 2 4 Nhận xét: x 4 2 x 4 2 x 4 2 x 4 2 4
Đẳng thức xảy ra khi: x 4 22 x 4 0 2 x 4 0 (Do x 4 2 0 )
x 4 2 x 8
Kết hợp với điều kiện suy ra nghiệm của phương trình là 4 x 8 Câu 2.
a) Do (d) đi qua A nên a+b=4 (d) : y ax+4-a a 4 a 4 0 Ta có: B ; 0
, C(0;4 a) theo bài ra thì a a 0 a 4a 0 a 4 OB
, OC 4 a a
Ta có OA+OB+OC nhỏ nhất khi OB+OC nhỏ nhất (Vì OA không đổi) a 4 4 4 OB OC 4 a 5 (a) 5 2 .(a) 9 a a a 4
OA+OB+OC nhỏ nhất bằng 9 17 khi và chỉ khi a
a 2 (Do a<0) a
Vậy phương trình đường thẳng (d) là: y 2 x 6 Trang 85 b)
Theo câu a), với a<0 đường thẳng (d) cắt tia Ox, Oy lần lượt tại B, C (khác O) và đi qua điểm A(1;4) OA 17
Gọi H là hình chiếu vuông góc của O trên đường thẳng (d), ta có: 2 BC 1 1 1 1 1 2 2 2 2 2 2 OB .OC OB OC OH OA 17 O . B OC P 17 BC
Đẳng thức xảy ra khi và chỉ khi H A hay d OA
Vậy giá trị lớn nhất của biểu thức P là 17 Câu 3: Q A P E D B C Trang 86
a) Ta có: MA=MC và ME là phân giác của góc AMC nên ME là đường trung trực của đoạn AC 0
QA QC,QEC 90
Vì MQ là đường trung trực của đoạn AC và AM AQ nên MC QC
Xét hai tam giác vuông ABC và ECQ có: ACB EQC (cùng phụ góc QCE ) và AB=EC (Vì 2EC=AC=2AB) A BC E
CQ CQ CB hay tam giác BCQ vuông cân tại C, do đó 0 BQC 45
b) Ta có MP, MQ là các đường phân giác của các góc AM ,
B AMC nên MP MQ
Tương tự chứng minh câu a ta được AD MP, AE MQ
Áp dụng hệ thức trong tam giác vuông, ta có: 2 2 P .
D PM PA ,Q . E QM QA 2 PD QM .PA Suy ra (1) 2 QE PM .QA 2 PA PM Tương tự: 2 2 P .
A PQ PM ,Q . A QP QM (2) 2 QA QM 3 PD MP Từ (1), (2) ta được: (đpcm) QE MQ
c) Vì MQ là trung trực của đoạn AC và MP là trung trực của đoạn AB suy ra:
CQ=QA, BP=AP và BCQP là hình thang vuông 2 Do đó: (BP CQ).BC P . Q BC BC 2 S 2a (*) BCQP 2 2 2 Kẻ AH.BC AM .BC
AH vuông góc BC thì 2 S a (**) ABC 2 2 Từ (*) và (**) suy ra: 2 2 2 S S S S
2a a a ABP ACQ BCQP ABC
Đẳng thức xảy ra khi và chỉ khi H M , khi đó khi tam giác ABC vuông cân tại A
Vậy giá trị nhỏ nhất của tổng diện tích hai tam giác ACQ và ABP là 2 a Câu 4: b c a a b c Ta có: (1) a b b c c a a b b c c a b c a a b c Thật vậy, xét: a b b c c a a b b c c a
b a c b a c 0
Ta chứng minh bất đẳng thức sau: Với x, ylà các số thực và a, b là các số dương ta có: 2 2 2 x y (x y) (*) a b a b Thật vậy: 2 2 2 2
* (a b)(bx ay ) ab(x y) (ay bx) 0 (BĐT đúng)
Áp dụng bất đẳng thức (*) ta có:
a 2 b c
a b 2 b c 2 c a 2 1 1 1 2 2 2 1 b c a 2 b c c a a b Trang 87
a 2 b 2 c 2 1 1 1 1 c a b (2) b c a 2 b c c a a b Từ (1) và (2) suy ra: a 2 1 b 2 1 c 2 1 1 b c c a a b b c a 4 b c c a a b 2 2 2 a b b c c a ( a 1) ( b 1) ( c 1) 4 a b b c c a b c a Câu 5:
a) Ta có pq có các ước dương là 1, p, q, pq
Vì pq là số điều hòa nên ta có 2 2 2 2
1 p q ( pq) ( pq 3) 2 2 2
p q 6 pq 8 ( p q) 4( pq 2)
Vì 4 là số chính phương nên từ đẳng thức trên suy ra pq+2 cũng là số chính phương (đpcm)
b) Gọi d=(x,y) là ước chung lớn nhất của x và y Suy ra: x=da, y=db với *
d, a,b ,a,b 1 Ta có: 3 3 2 2
x y x y 42xy 3 3 3 2 2 2
d (a b ) d (a b 42ab) 2 2 2 2
d(a b)(a ab b ) a b 42ab 2 2
(da db 1)(a ab b ) 43ab
Đặt c=da+db-1, (c ) Ta viết lại: 2 2
a c abc b c 43ab Từ đó suy ra 2 (ab) ca và 2
a cb b c và a c Do đó: * (a )
b c c ma , b m 2 2
m(a ab b ) 43 2 2
a ab b 43 2 2
a ab b 1 2 2
a ab b 43 TH1: 2 2
a ab b 1, khi đó ab a b2 1 0
Suy ra a b 1 d 22 . Do vậy (x, y) (22, 22) TH2: 2 2
a ab b 43
Do tính đối xứng của x, y. Giả sử x y a b Do đó 2 2 2
43 a ab b ab b b 1, 2,3, 4,5, 6
Thay b=1 thì a=7 và d=1 suy ra (x,y)=(1,7),(7,1)
Thay b=2,3,4,5 thì không tồn tại số nguyên dương a thỏa mãn
Thay b=6 thì a=7 và d=43/13 (không thỏa mãn)
Thử lại, ta có các cặp giá trị cần tìm là (x,y)=(22,22),(1,7),(7,1) Trang 88
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI HỌC SINH GIỎI LỚP 9 CẤP TỈNH QUẢNG NAM NĂM HỌC 2020 - 2021 Môn thi : Toán
Thời gian: 150 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC Ngày thi : 10/4/2021
(Đề thi có 01 trang)
Câu 1. (4,0 điểm)
a) Rút gọn các biểu thức sau: 3 3 4(4 3) 4(4 3) 2 3 12 2 3 12 3 3 27 27
A 13 30 4 9 4 2 ; B 2 2
b) Tìm giá trị của tham số m để phương trình (x 1) 2x 1 mx m 0 có hai nghiệm phân biệt.
Câu 2. (4,0 điểm)
a) Giải phương trình: 4 3 2x 3x 1 4 x 1 2 2
x y xy 4y 1 0
b) Giải hệ phương trình: 2 2 3
x y(x y) 10y 3 0
Câu 3. (2,5 điểm)
Cho hình vuông ABCD có tâm O và cạnh bằng 6cm, điểm M nằm trên cạnh BC.
a) Khi BM=2cm, hạ OK vuông góc với AM tại K. Tính độ dài đoạn thẳng OK.
b) Khi điểm M thay đổi trên cạnh BC (M không trùng với B và C), điểm N thay đổi trên cạnh CD sao cho 0
MAN 45 , E là giao điểm của AN và BD. Chứng minh tam giác AEM vuông
cân và đường thẳng MN luôn tiếp xúc với một đường tròn cố định.
Câu 4. (4,5 điểm)
Cho hai đường tròn (O;R) và (O’;r) tiếp xúc ngoài tại A (R>r). Dựng lần lượt hai tiếp
tuyến OB, O’C của hai đường tròn (O’;r), (O;R) sao cho hai tiếp điểm B, C nằm cùng phía đối với
đường thẳng OO’. Từ B vẽ đường thẳng vuông góc với OO’ cắt O’C tại K, từ C vẽ đường thẳng
vuông góc với OO’ căt OB tại H.
a) Gọi D là giao điểm của OB và O’C. Chứng minh DO.BO’=CO.DO’ và DA là tia phân giác của góc ' ODO .
b) Đường thẳng AH cắt đường tròn (O;R) tại E (E khác A). Chứng minh tứ giác OABE nội tiếp đường tròn.
c) Đường thẳng AK cắt đường tròn (O’,r) tại F (F khác A), L là giao điểm của BC và EF.
Chứng minh BF song song với CE và 3 điểm A, D, L thẳng hàng. Trang 89 Câu 5. (5,0 điểm)
a) Tìm tất cả các cặp số nguyên (x;y) thỏa mãn đẳng thức: 3 3 2 2
x y 3x 3y 3xy 6x 0
b) Cho ba số thực dương x, y, z thỏa mãn xyz=1. Tìm giá trị lớn nhất của biểu thức: 1 1 1 A x 2 yz y 2zx z 2xy
---------- HẾT ----------
Họ và tên thí sinh: ……………………………… Phòng thi: ……… Số báo danh: …….......
ĐÁP ÁN THAM KHẢO – QUẢNG NAM (2020 – 2021) Câu 1. a) Ta có: 2
A 13 30 4 (2 2 1)
13 30 3 2 2 13 30( 2 1) 43 30 2 5 3 2 3 4(4 3) 4(4 3) 2 3 12 2 3 12 3 3 Đặ 27 27 t a , b 2 2 4 3 Suy ra: 3 3
a b 2 3 , ab 3 3 3 3 3
a b 2 3 (a ) b 3a ( b a )
b 2 3 (a )
b (4 3)(a ) b 2 3 3
(a b) 4(a b) 3(a b) 2 3 0 (a b 2) (a b)(a b 2) 3 0
a b 2 (Vì a>0, b>0) Vậy B=2 b) Điề 1 u kiện: x 2 x 1
Phương trình tương đương: (x 1)( 2x 1 ) m 0
2x 1 m Với x=1 (t/m) m 0
Với 2x 1 m 2 m 1 x 2 m 0 m 0
Suy ra phương trình đã cho có hai nghiệm phân biệt khi: 2 m 1 1 m 1 2 Câu 2. 3 2x 0 a) Điề 3 u kiện: x 4 4 x 0 2
Phương trình tương đương với: 4 3 2x 4 x 3x 1 (*)
Do 3 2x 4 x 0 vô nghiệm nên (*) tương đương với phương trình: Trang 90 x
x x x 3x 1 0 4(3 1) (3 1) 3 2 4
3 2x 4 x 4 1
Với 3x 1 0 x (t/m) 3 x 3 Với
3 2x 4 x 4 11 (t/m) x 9 1 11
Vậy phương trình đã cho có 3 nghiệm x , x , x 3 3 9
b) Hệ phương trình tương đương với: 2 2 2
x y xy 4y 1 0 (
x 1) y(x y) 4 y (*) 2 2 2 2 3
x y(x y) 10y 3 0 3
(x 1) y(x y) 1 0y
- Nhận xét y=0, hệ không thỏa mãn. 2
x 1 (x y) 4 y
- Khi y 0 : Hệ phương trình (*) tương đương với hệ (**) 2 x 1 2 3.
(x y) 10 y 2
a b 4 Đặ x 1 t
a, x y b , khi đó hệ (**) có dạng: y 2 3
a b 10 a 2 a 3
+ Giải hệ trên ta được: , b 2 b 1 2 x 1 a 2 2 + y ( ; x y) (1; 1 ) ( 3 ; 5 ) b 2 x y 2 2 x 1 a 3 3 3 17 5 17 3 17 5 17 + y ( ; x y) ( ; ) ( ; ) b 1 2 2 2 2 x y 1 Vậy hệ có 4 nghiệm: 3 17 5 17 3 17 5 17 ( ; x y) (1; 1 ) ( 3 ; 5 ) = ( ; ) ( ; ) 2 2 2 2 Câu 3. a) Trang 91
- Gọi Q là giao điểm của AM và BD, P là trung điểm của MC. Suy ra OP / / AM
- Trong tam giác OBP có MB=MP và MQ / /OP . Suy ra Q là trung điểm của OB. 6 2 3 2 1 1 1 5
Ta có: BD 6 2 OQ , 2 2 2 4 2 OK OA OQ 18 3 2 OK 5 b) + 0
MAN MBE 45 . Suy ra tứ giác ABME nội tiếp Mà 0 ABM 90 nên 0
AEM 90 . Vậy tam giác AEM vuông cân tại E
+ Gọi F là giao điểm của AM và BD. Tương tự suy ra 0 AFN 90
+ Gọi I là giao điểm của EM và FN, H là giao điểm của AI và MN. Suy ra AH vuông góc với MN
+ Xét hai tam giác vuông ABM và AHM có: AM chung + AMB AE ,
B AEB AMH (vì tứ giác MNEF nội tiếp). Do đó AMB AMH
Suy ra hai tam giác vuông ABM và AHM bằng nhau.
Suy ra AH AB 6cm
Do đó MN luôn cách A một khoảng cách bằng 6 cm
Suy ra MN luôn tiếp xúc với đường tròn tâm A, bán kính bằng 6 cm Câu 4. Trang 92
a) Xét hai tam giác và ODC O’DB có: ' ODC O DB
+ Tứ giác OO’BC nội tiếp đường tròn đường kính OO’ nên ' DOC DO B DO CO
Suy ra hai tam giác ODC và '
O DB đồng dạng, do đó ' ' D . O BO C . O DO ' ' DO BO DO CO AO Ta có:
. Suy ra DA là tia phân giác của góc ' ODO ' ' ' DO BO AO b) + '
OCH OO C (Cùng phụ góc ' O CH ) + '
OBC OO C (Cùng chắn cung OC ) OC OB OA OB
Suy ra OCH OBC . Suy ra hai tam giác OCH, OBC đồng dạng OH OC OH OA
OAH OBA hay OEA OBA
Vậy tứ giác OABE nội tiếp trong đường tròn. c) 0 ' 0 ' 0
EOB EAB 180 OAE O AB 180 OBA O BA 90 Mà ' 0 OBO 90 nên '
OE / /O B . Tương tự '
O F / /OC . Suy ra ' EOC BO F
Lại có: Hai tam giác EOC và BO’F là hai tam giác cân. Suy ra ' ECO BFO Hơn nữa '
OE / /O B nên BF / /EC LC EC OE OA OC DC ' ' ' LB BF O B O A O B DB
Suy ra DL là tia phân giác của góc BDC . Suy ra A, D, L thẳng hàng. Câu 5.
a) Phương trình tương đương: 3 3 2 2
x y 3x 3y 3xy 6x 0 3 2 3 2
(x 3x 3x 1) ( y 3y 3y 1) 3xy 3x 3y 0 3 3
(x 1) ( y 1) 3(x 1)( y 1) 3 0
(x 1) (y 1)3 3(x 1)(y 1)(x 1) (y 1)3(x 1)( y 1) 3 0
Đặt a (x 1) ( y 1),b (x 1)( y 1) . Ta có: 3 3
a 3ab 3b 3 0 a 3 3b(a 1) Suy ra 3 3
a 3 (a 1) 4 (a 1) 4 (a 1) + Với 32 a 1 4 a 5 b (loại) 3 Trang 93 + Với 11 a 1 1 a 2 b (loại) 3 + Với 1
a 1 2 a 1 b 3
+ Với a 1 1 a 0 b 1 ;
x y 0;0 2 ;2
+ Với a 1 4 a 3 b 2 ;
x y 0;3 1;2 + Với a 1 2 a 3
b 5. Không tồn tại (x;y) 1 1 1 x y z b) Ta có A 2 2 2 x 2 yz y 2zx z 2xy x 2 y 2 z 2 x x 1 1 2 2
x 2 (x 1) 1 2x 1 (1 ) 2 x 2 2x 1 2 2x 1 Tương tự: y 1 1 z 1 1 (1 ) , (1 ) 2 y 2 2 2 y 1 2 z 2 2 2z 1 3 1 1 1 1 Suy ra: A 2
2 2x 1 2 y 1 2z 1 Đặt a b c x , y , x , (a, , b c 0) b c a 1 1 1 b c a 2x 1 2 y 1 2z 1 2a b 2b c 2c a 2 2 2 2 b c a
(a b c) 2 2 2 2 2 2 2ab b 2bc c 2ca a
2ab b 2bc c 2ca a 3 1 Suy ra A
.1 1. Dấu “=” xảy ra khi a=b=c hay x=y=z=1 2 2
Vậy giá trị lớn nhất của A bằng 1. Trang 94
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 9
QUẢNG NGÃI NĂM HỌC 2020 - 2021 Ngày thi: 11/3/2021 ĐỀ CHÍNH THỨC Môn: Toán
Thời gian làm bài: 150 phút
Bài 1: (4,0 điểm)
a) (1,5 điểm) Tìm số nguyên dương n lớn nhất để 27 2021 4 4 4n A là số chính phương.
b) (1,5 điểm) Tìm các số nguyên x, y thỏa mãn đẳng thức: 3 2
xy y 4 y x 6 . 2 2
c) (1,0 điểm) Số nhà bạn An là số có hai chữ số ab biết ab a 1 b 1 . Tìm số nhà bạn An.
Bài 2: (4,0 điểm)
a) (2,0 điểm) Giải phương trình: 3
5 4x x 7 3 . 2 2
x y xy 1 2x
b) (2,0 điểm) Giải hệ phương trình: . x
x y2 2
x 2 2y Bài 3: (4,0 điểm)
a) (2,0 điểm) Cho các số dương a, b thỏa mãn: 2 2
a b 2021 a 2021 b .
Chứng minh rằng: a2 + b2 = 2021.
b) (2,0 điểm) Tìm giá trị nhỏ nhất của P 1 xy ; trong đó x, y là các số thực thỏa mãn điều kiện: 2021 2021 1010 1010 x
y 2x y . Trang 95 Bài 4: (7,0 điểm)
a) (1,5 điểm) Cho tam giác ABC và điểm M nằm trong tam giác. Từ M kẻ tia MD
song song với AB (với D thuộc BC), tia ME song song với BC (với E thuộc AC) và tia
MF song song với AC (với F thuộc AB). Chứng minh rằng: 3S S . ( S : diện tích EF D ABC ABC tam giác ABC, S
: diện tích tam giác DEF). DEF
b) (5,5 điểm) Từ điểm P kẻ hai tiếp tuyến PA, PB với đường tròn (O;R); A, B là tiếp
điểm. Gọi H là chân đường vuông góc hạ từ A đến đường kính BC của đường tròn.
i) Chứng minh rằng PC cắt AH tại trung điểm của AH.
ii) Cho OP = a. Tính độ dài AH theo R và a.
iii) Đường thẳng d đi qua P sao cho khoảng cách từ O đến đường thẳng d bằng R
2 , đường thẳng vuông góc với PO tại O cắt tia PB tại M. Xác định vị trí của điểm P trên
đường thẳng d để diện tích tam giác POM nhỏ nhất.
Bài 5: (1,0 điểm) Trên công trường có những thanh sắt dài 7,4 m. Người ta muốn cắt các
thanh sắt đó thành các đoạn dài 0,7 m và 0,5 m để sử dụng.
a)(0,5 điểm) Em hãy nêu phương án cắt mà không phải hàn nối các đoạn sắt cần dùng.
b)(0,5 điểm) Muốn có 1000 đoạn sắt 0,7 m và 2000 đoạn sắt 0,5 m. Ta phải dùng ít nhất
bao nhiêu thanh sắt 7,4 m nêu trên? HẾT
Ghi chú: Cán bộ coi thi không giải thích gì thêm.
ĐÁP ÁN THAM KHẢO – QUẢNG NGÃI (2020 – 2021) Bài 1. 2 a) 27 2021 n A 27 1994 n27 4 4 4 2 1 4 4 Vì A và 2 27 2
là số chính phương nên 1994 27 1 4 4n là số chính phương Ta có: n n n 2 1994 27 27 27 1 4 4 4 2 Mà 1994 27 1 4 4n
là số chính phương nên ta có: 1994 n27 n27 2 n27 3987 1 4 4 (2 1) 2 2 n 4014
Vớ n = 4014 thì A 2 27 2021 4014 27 4014 4 4 4 2 2 là số chính phương Vậy n=4014 b) Ta có: 3 2
xy y 4xy 6 3 2
xy 4xy y 6 0 xy 2 y 4 2 y 4 10 0 xy 1 2 y 4 10 Vì 2
y 4 0 , 10=1.10=2.5 Suy ra: xy 1 1 TH1: (loại) 2 y 4 10 Trang 96 xy 1 10 TH2: (loại) 2 y 4 1 xy 1 2 TH3: ( ; x y) (1;1) ( 1 ; 1 ) 2 y 4 5 xy 1 5 TH4: ( ; x y) (4;1) ( 4 ; 1 ) 2 y 4 2 Vậy ( ; x y) (1;1) ( 1 ; 1 ) (4;1) ( 4 ; 1 ) c) Ta có: 2 2
ab (a 1) (b 1) 2 2 .1
a 0 b (a 1) (b 1) 2 2
10a b a 2a 1 b 2b 1 2 2
a 12a 1 b 3b 1 0
Do 1 a 9 nên ta có bảng sau: a 1 2 3 4 5 6 7 8 9 b Loại 6 Loại Loại Loại Loại Loại Loại Loại Suy ra a=2, b=6.
Kết luận: Số nhà là 26 Bài 2. a) Điều kiện: 5 x 4
Phương trình tương đương: 3 5 4x 1 x 7 2 0 4 4x x 1 0 2 3 3 5 4x 1
(x 7) 2 x 7 4 1 4 (x 1) 0 2 3 3
(x 7) 2 x 7 4 5 4x 1 x 1 1 4 0(*) 2 3 3
(x 7) 2 x 7 4 5 4x 1
Phương trình (*) vô nghiệm.
Vậy phương trình có nghiệm duy nhất x=1 b) Từ phương trình 2 2 2 2
x y xy 1 2x 2x 2 y 2xy 2 4x Khi đó ta có:
x x x y
x xy x x x y2 3 2 2 ( ) 2 2 2 4
2x y 3 0 x(x y 1)(x y 3) 0
Xét x=0 thế vào phương trình 2 2
x y xy 1 2x ta được: 2
y 1 0 (vô nghiệm) Trang 97
Xét x y 1 0 y 1 x , thế vào phương trình 2 2
x y xy 1 2x ta được:
x 1 y 0 2
x 3x 2 0
x 2 y 1
Xét x y 3 0 y x 3 , thế vào phương trình 2 2
x y xy 1 2x ta được: 2
x x 10 0 (vô nghiệm)
Vậy hệ có nghiệm: (x;y)=(1;0)=(2;-1) Bài 3. a) Từ giả thiết 2 2
a 2021b 2021 a b 2 2 2 2 2 2 2 2
a (2021 b )
(2021 a ) b a b 2021 a b 2021 2 2 2 2 a 2021 b 2021 a b a 2021 b 2021 a b 1 1 2 2
a b 202 1 0 2 2
a 2021 b
2021 a b 2 2
a b 2021 0 2 2
a b 2021 b) Từ giả thiết ta có:
+ Nếu x 0 y 0; y 0 x 0
+ Nếu x, y 0 thì: 2021 2021 1010 1010 x y 2x y 2021 2021 x y 2 1010 1010 x y 1010 1010 x y . x . y 2 (*) y x 1010 x 1 Đặt t 0 thì: 2 (*) xt . y
2 xt 2t y 0 y t Có ' 1 xy
Để phương trình có nghiệm thì '
1 xy 0 xy 1
Nên giá trị nhỏ nhất của P là 0. Dấu “=” xảy ra khi xy=1 Bài 4. a) Trang 98
Từ D, E, F lần lượt vẽ các đường thẳng song song với MF, MD và ME cắt AB, BC và AC lần lượt tại P, Q, O. 2 S AF
Ta có FR / /BC nên AF R A BC AFR S AB ABC b) Trang 99 Bài 5.
a) Phương án: cắt mỗi thanh thành 2 đoạn 0,7 m và 0,5 m Trang 100 b) Trang 101 Trang 102
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THCS NĂM 2021 TỈNH QUẢNG NINH
Môn thi: TOÁN – Bảng A Ngày thi: 20/03/2021 ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 150 phút, không kể thời gian giao đề
(Đề thi này có 01 trang) x x x
Câu 1: (3,0 điểm). Cho biểu thức 5 1 2 1 2 1 A với x 0 và x 2 x 1 x x 2 x 1.
a. Rút gọn biểu thức A; A
b. Tìm giá trị của x để
nhận giá trị nguyên. 2
Câu 2: (5,0 điểm). 2 2
x y 10
1. Giải hệ phương trình: . 2 2
x y xy 5x 5y 32 2. Giải phương trình: 2
x 5x 4 x 114 0.
Câu 3: (3,0 điểm). Cho các số nguyên dương x, y thỏa mãn: 3 2
x 9y 9x 6y 1. x a. Chứng minh 2
x là phân số tối giản; 9
b. Tìm tất cả các cặp số ; x y .
Câu 4: (7,0 điểm). Cho nửa đường tròn tâm O, đường kính AB. Trên nửa mặt phẳng bờ
AB chứa nửa đường tròn (O) vẽ tia tiếp tuyến Ax với nửa đường tròn. Trên tia Ax lấy
điểm C bất kì (C khác A), đường thẳng BC cắt nửa đường tròn (O) tại điểm D (D khác B).
Gọi H là hình chiếu của A trên OC, đường thẳng DH cắt AB ở E.
a. Chứng minh tứ giác OBDH nội tiếp; b. Chứng minh 2 EA E . O EB; HE c. Tính tỉ số . HB
Câu 5: (2,0 điểm). Cho các số thực dương x, y thỏa mãn 1 x
1. Tìm giá trị nhỏ nhất y 2 2 của biểu thức x 2xy 2y P . 2 xy y
………………… Hết ………………..
- Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
- Giám thị không giải thích gì thêm.
Họ và tên thí sinh: ………………………………………… Số báo danh: ……………….
Chữ kí giám thị 1:……………………….…. Chữ kí giám thị 2:………………………………… Trang 103
ĐÁP ÁN THAM KHẢO – QUẢNG NINH (2020 – 2021) Câu 1. a)
5 x 1 x 12 x 1 x 22 x 1 A
x 2 x 1 7x 5 x 2 7 x 2
x 2 x 1 x 2 b) 12 12 1 A 7 A A 7 . Có x 2 2 0 6 vậy mà x 2 x 2 2 2 3 2 A 1 hoặc 2 hoặc 3 2 A 4 *) 1 x (thỏa mãn) 2 25 A *)
2 x 4 (thỏa mãn) 2 A *)
3 x 100 (thỏa mãn) 2 Câu 2. 1) 2 2 2 x y 10
x y 2xy 10 2 2
x y xy 5x 5y 32 x y xy 5 32
x y2 10 xy
x y2 10 2 xy x y 4 2 2 xy 3
x y x y 10 5 32 3 x y 64 2 Giải được: , x y 1; 3 hoặc ; x y 3; 1 . Trang 104 2) ĐK: x 1 2
x 5x 4 x 1 14 0 2
x 6x
9 x 1 4 x 1 4 0
x x 2 2 3 1 2 0 Vì x 2
3 0, dấu đẳng thức khi x 3 x 2 1 2
0, dấu đẳng thức khi x 3
Vậy: x x 2 2 3 1 2
0 x 3 (thỏa mãn đk). Câu 3. 3 2
a) x 9y 9x 6y 1 x x y 2 2 9 3 1 2 x d x d Giả sử UCLN 2 ; x x 9 d 9 d 2 2 x 9 d x 9 d
d 1 hoặc 3 hoặc 9 x d 2 x 2 x 2 9 d 2 hay 3y 1
d 3y
1 d nhưng 3y 1 không chia 2 x 9 d x
hết cho 3, cho 9 nên d 1 2 x tối giản 9 2 2
b) Ta có x x y 2 2 9 3
1 là số chính phương, UCLN ; x x
9 1 x 9 là số chính phương. Giả sử 2 2
x 9 k kN
k xk x 9 k x và k x là ước của 9 k x 9 k 5
Vì k x k x k x 1 x 4
Với x 4 y 3. KL: ( ; x ) y 4; 3 Trang 105 Câu 4. C D H A E O B a) Chỉ ra 0
CHA CDA 90 tứ giác AHDC nội tiếp HDB HAC
AOC vuông tại A, AH OC AOH HAC
HDB HOA Tứ giác BDHO nội tiếp S
b) EHO và EBD có: E chung; EOH EDB EHO EBD EO ED E .
O EB EH.ED (1) EH EB
Tứ giác AHDC nội tiếp ADH ACH
AOC vuông tại A, AH OC ACH HAO EDA EAH S
EAH và EDA có E chung, EAH EDA EAH EDA EH EA 2 EA E . H ED (2) EA ED Từ (1) và (2) 2 EA E . O EB
c) Tứ giác OBDH nội tiếp OHB ODB và DHC DBO
OBD cân tại O ODB OBD OHB DHC OHB OHE Trang 106 HE OE
HEB có HO là phân giác HB OB 2 2 Có: EA E .
O EB R E O E . O EO R 2 2 2 OE 1 R 2 .
REO EO EO . REO 2 R 3 .
REO R 3.EO . OB 3 HE 1 Vậy HB 3 Câu 5. 1 x x 1 1 x 2 y y y 4 2 x x 2 2 2 2 2
x 2xy 2y y y 2 x t 2t 2 1 P . Đặt t P 0 t 2 xy y x y t với 1 4 1 y 5 16 5 11 P t t 5 3 1 4 t 1 t 1 4 t 1 t 1 5 t 1 5 16t 1 5 16t 1 5 16 5 1 2 . 8, dấu “=” khi t 1 t 5 t 1 5 t 1 5 t 1 4 11 1 t 11 1
, dấu “=” khi t 5 P
, dấu “=” khi x y 1 ; ;2 5 4 4 4 2 5
Vậy giá trị nhỏ nhất của P là tại x y 1 ; ;2 4 2 Trang 107
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH SÓC TRĂNG
Năm học 2020 – 2021 ĐỀ CHÍNH THỨC
Môn: Toán – Lớp 9
(Thời gian làm bài 150 phút, không kể phát đề)
Đề thi này có 02 trang Bài 1: (4,0 điểm) Cho biểu thức 1 x 1 x 2021 x 1 P x 1 x 2021
x 2022 x 2021 x 1 2021 x
a) Rút gọn biểu thức P.
b) Tìm giá trị của x để P=2021. Bài 2: (4,0 điểm)
a) Cho số tự nhiên n 11...122...25(số n gồm có 2021 chữ số 1, 2022 chữ số 2 và 1 2021 2022
chữ số 5 ở hàng đơn vị). Chứng minh rằng n là một số chính phương.
b) Tìm giá trị nhỏ nhất của biểu thức 2 2
T 10x 4 y 16x 12 y 12xy 2031 Bài 3: (4,0 điểm)
a) Cho x1, x2 là hai nghiệm của phương trình: 2 2
x (m 1)x m m 1 0 . Tìm m để 3 3 biểu thức x x 1 2 P
đạt giá trị lớn nhất. x x 2 1
b) Nhân dịp tết Nguyên đán Tân Sửu. Một nhà hàng phân phối bánh kẹo đã chuẩn
bị một số giỏ quà để tặng cho các cửa hàng. Tất cả các giỏ quà được đưa vào kho chứa
hàng và họ dự định sẽ gửi tất cả giỏ quà đi trong 4 ngày. Ngày thứ nhất, họ vào kho và lấy 1 ra
số giỏ quà, sau đó để lại 3 giỏ. Ngày thứ hai, họ tiếp tục vào kho và lấy ra 1 số giỏ 7 3
quà, đồng thời lấy thêm 4 giỏ nữa. Ngày thứ ba, họ lấy ra 1 số giỏ quà từ kho hàng và lấy 2
thêm 1 giỏ quà nữa. Cuối cùng còn 42 giỏ quà. Hỏi trong mỗi ngày, họ đã lấy ra bao nhiêu giỏ quà? Bài 4: (4,0 điểm)
Cho tam giác ABC. Dựng ba tam giác cân ABP, ACQ, BCR lần lượt có AB, AC,
BC là cạnh đáy; PAB ACQ ACR ; hai tam giác ABP, ACQ nằm về phía ngoài tam giác
ABC; tam giác BCR nằm trên cùng nửa mặt phẳng có bờ chứa cạnh BC với tam giác ABC. Trang 108
a) Chứng minh ba tam giác sau đồng dạng với nhau: A BC, P BR, Q RC
b) Một đường thẳng đi qua điểm P và cắt AR, RQ, AQ theo thứ tự tại E, K, G. Chứng minh 2
EP EK.EG Bài 5: (4,0 điểm)
Cho điểm M nằm ngoài đường tròn (O;R). Qua M lần lượt vẽ các tiếp tuyến MA,
MB (A, B là tiếp điểm) và cát tuyến MDC (MDlà tam giác nhọn.
a) Qua O vẽ đường thẳng vuông góc với OM, cắt các tia MA, MB lần lượt tại I, J.
Tìm giá trị nhỏ nhất của diện tích tam giác MIJ theo R.
b) Gọi E, F lần lượt là chân đường cao kẻ từ A và B của tam giác ABC. Qua M kẻ
đường thẳng d song song với EF, d cắt các tia CA, CB lần lượt tại K, L. Chứng minh bốn
điểm A, B, L, K cùng nằm trên một đường tròn và trung điểm N của EF nằm trên MC. -----HẾT----- Trang 109
ĐÁP ÁN THAM KHẢO – SÓC TRĂNG (2020 – 2021) Bài 1.
a) Điều kiện: x 0; x 1 1 x 1 x 2021 x 1 P x 1 x 2021
x 2022 x 2021 x 1 2021 x
x 1 x 202 11
x 202 1 x 202 1 x 1 x x 1 1 x 2021 x 1 x 202 1
x 1 x 202 1 x 1 x 202 1 x x
x 202 1 x 202 1 2020 2020 . x 2021
x 1 x 202 1
x 2020 x 202 0 x 1
x 2020 x 2020 1 5 b) P 2021
2021 x x 1 0 x x 1 2 1 5
Kết hợp điều kiện xác định: x 2 Bài 2. a) 20212
n 11...122...2 5 11...11.10 22...22.10 5 2021 2022 2021 2022 2021 2021 1 2(2021 1 ) 20212 20212 10 1 10 1 10 10 2.10 25 2021 2 n .10 2. .10 5 9 9 9 2 2(2021 1 ) 2021 1 2021 1 10 10.10 25 10 5 2 3 Vì 2021 1 (10
5) 3 nên n là số chính phương. b) Đang cập nhật…… Bài 3. 2 a) Thấy 1 3 2
ac m m 2 m 0, m
nên phương trình luôn có 2 nghiệm trái dấu. 2 4 3 x 1 Đặt 1 t
(với t>0) P t mang giá trị âm và A lớn nhất khi -A đạt giá trị nhỏ nhất. x t 2 1
P t 2 A 2 MaxP=-2 t
Dấu “=” xảy ra khi và chỉ khi t=1 3 x x 1 1 1 1
x x 0 (m 1) 0 m 1 1 2 x x 2 2
b) Gọi số giỏ quà đãchuẩn bị là x (giỏ) ( * x , x 7 )
Số giỏ quà lấy trong ngày 1 là (x/7-3) (giỏ) Trang 110
Số giỏ quà còn lại là x-x/7+3=6x/7+3 (giỏ) 1 6x 2x
Số giỏ quà lấy trong ngày 2 là: 3 4 5 (giỏ) 3 7 7
Số giỏ còn lại là 4x/7-2 (giỏ) 1 4x 2x
Số quả lấy trong ngày 3 là: 2 1 (giỏ) 2 7 7
Số giỏ còn lại là 2x/7-2 (giỏ)
Theo đề bài: 2x/7-2=42 x=154 (giỏ)
Vậy ngày 1 lấy 19 giỏ, ngày 2 lấy 49 giỏ, ngày 3 lấy 44 giỏ Bài 4.
a) Ta có: PBA CBR PBR ABC PB BR Lại có:
ABC PBR (c.g.c) AB BC
Chứng minh tương tự: ABC QRC
Suy ra điều phải chứng minh
b) Từ a) suy ra: ABR APB BPR APB BAC Do đó: 0
APR PAQ QPB 2APB 180 EG EA PR / / AQ
(Hệ quả định lí Ta let) EP ER EP EA
Chứng minh tương tự: QR / / AP EK ER EG EP 2 EP E . G EK EP EK Trang 111 Bài 5. 1 a) S .M . O IJ M . O OI O . A MI . R MI IJ M 2 2 2 S .
R OM OI . R 2M .
O OI R 2S I M J MIJ 2
S R 2S 0 S 2R I M J I M J I M J Vậy 2 S 2R min
b) Tứ giác ABEF nội tiếp nên ABE EFC
Mà AKL EFC (so le trong) AKL ABE
Do đó tứ giác ABLK nội tiếp
Dễ dàng chứng minh được M là trung điểm của KL EF / /KL
Gọi P là giao điểm của CM và EF. Khi đó P là trung điểm của È
Mà N là trung điểm của EF
N P đpcm Trang 112
SỞ GD&ĐT SƠN LA
KỲ THI CHỌN HỌC SINH GIỎI THCS CẤP TỈNH NĂM HỌC 2020 - 2021 ĐỀ CHÍNH THỨC Môn thi: Toán Ngày thi: 14/3/2021 (Đề thi có 01 trang)
Thời gian làm bài: 150 phút, không kể thời gian phát đề 2 x x 1 3 11 x x 3
Câu 1 (4,0 điểm). Cho hai biểu thức A và B x 3 x 3 9 x x 1
với ( x 0; x 9 ) 2 2
a) Tính giá trị của B tại x 5(45 2021) 5(45 2021) b) Rút gọn A.
c) Tìm tất cả các số nguyên x để P = A.B nhận giá trị nguyên
Câu 2 (4,0 điểm). Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y (2m 1)x 2m
và Parabol (P): y = x2 (m là tham số)
a) Tìm tọa độ các giao điểm của (d) và (P) khi m = 2 .
b) Tìm m để (d) và (P) cắt nhau tại hai điểm phân biệt có hoành độ x1, x2 sao cho biểu thức 2 2
E x x x x đạt giá trị nhỏ nhất. 1 2 1 2
Câu 3 (4,0 điểm). 2 2
y 2xy 8x 6x 1
a) Giải hệ phương trình 2 3 2
y x 8x x 1
b) Tìm nghiệm nguyên của phương trình 2 2
x 2 y 2xy 3y 4 0
Câu 4 (6,0 điểm). Cho tam giác ABC có góc A tù. Vẽ đường tròn (O) đường kính AB và
đường tròn (O’) đường kính AC . Đường thẳng AB cắt đường tròn (O’) tại điểm thứ hai là
D, đường thẳng AC cắt đường tròn (O) tại điểm thứ hai là E .
a) Chứng minh bốn điểm B,C,D,E cùng nằm trên một đường tròn.
b) Gọi F là giao điểm thứ hai của hai đường tròn (O) và (O’) ( F khác A). Chứng
minh ba điểmB, F, C thẳng hàng và FA là phân giác của góc EFD.
c) Gọi H là giao điểm của AB và EF. Chứng minh BH.AD AH.BD 1 1 1
Câu 5 (2,0 điểm). Cho 3 số thực dương a, b, c thỏa mãn 1. Tìm giá trị nhỏ 2 2 2 a b c 2 2 2 2 2 2 b c c a a b
nhất của biểu thức P 2 2 2 2 2 2
a(b c )
b(c a )
c(a b )
-------------Hết------------- Trang 113
Thí sinh không sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:……………………………………………..Số báo danh: …………...
ĐÁP ÁN THAM KHẢO – SƠN LA (2020 – 2021) Câu 1. a) Ta có: 2 2 x 5(45 2021) 5(45 2021)
2(5 2021) 2(45 2021) 5(45 2021)(45 2021) 9 x 3 9 3
Thay x = 9 vào biểu thức B ta được: B 0 x 1 9 1 b) Ta có: 2 x x 1 3 11 x A x 3 x 3 9 x
2 x ( x 3) ( x 1)( x 3) 11 x 3
( x 3)( x 3)
2x 6 x x 3 x
x 3 11 x 3
( x 3)( x 3) 3x 9 x 3 x
( x 3)( x 3) x 3
(với x 0, x 9 ) 3 x x 3 3 x 3 c) Ta có: P . A B . 3 x 3 x 1 x 1 x 1 3 P là số nguyên
là số nguyên 3 ( x 1) x 1
Hay ( x 1) Ư(3) = 1 ; 3 x0; 4 Câu 2.
a) Khi m = 2 đường thẳng (d) có dạng: y = 5x + 4
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình: x 1 2 2
x 5x 4 x 5x 4 x 4
Với x 1 y 1, x 4 y 16
Vậy tọa độ giao điểm của (d) và (P) là: (1;1) ; (4;16)
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình: 2 2
x (2m 1)x 2m x (2m 1)x 2m 0 Trang 114 m 2 2 1 1
+ (P) và (d) cắt nhau tại hai điểm phân biệt khi: 0 m 2
x x 2m 1
+ Áp dụng hệ thức Vi-ét, ta có: 1 2 x x 2m 1 2 Do đó: 2 2 2 2
E x x x x (2m 1) 3.2m 4m 2m 1 1 2 1 2 2 1 3 3 2m Với mọi m 2 4 4 Min E=3/4 khi m=1/4 Câu 3.
𝑦2 − 2𝑥𝑦 = 8𝑥2 − 6𝑥 + 1 (1) a) Ta có: {
𝑦2 = 𝑥3 + 8𝑥2 − 𝑥 + 1 (2)
Cộng 2 vế của phương trình (1) với x2 ta được: 2 2 2
y 2xy x 9x 6x 1 2 2
(x y) (3x 1)
(x y 3x 1)(x y 3x 1) 0
(1 2x y)(4x y 1) 0 1
2x y 0
y 1 2x
4x y 1 0
y 4x 1
+ Trường hợp 1: y 1 2x thế vào phương trình (2) ta được 2 3 2
(1 2x) (x 8x x 1) 3 2
x 4x 3x 0 x 0 x 1 x 3
Tìm được nghiệm (x;y) là (0;1),( 1 ;3),( 3 ;7)
+ Trường hợp 2: y 4x 1 thế vào phương trình (2) ta được 2 3 2
(4x 1) x 8x x 1 x 0 3 2
x 8x 7x 0 x 1 x 7
Tìm được nghiệm (x;y) là (0; 1 ),(1;3),(7;27)
Vậy hệ phương trình có tập nghiệm là: S (0;1),( 1 ;3),( 3 ;7),(0; 1 ),(1;3),(7;2 7)
b) Biến đổi phương trình: 2 2 2 2 2
x 2 y 2xy 3y 4 0 (x 2xy y ) y 3y 4 0 Trang 115 2
(x y) (y 1)( y 4) 0 2
(y 1)( y 4) (x y) 0 4 y 1
Vì y nguyên nên y 4 ; 3 ; 2 ; 1 ;0; 1
Suy ra các cặp (x; y) nguyên thỏa mãn phương trình là: (4; 4 );( 1 ;1);(5; 3 );(1; 3 );(2;0);( 2 ;0) Câu 4. a) Dễ dàng suy ra: 0 AEB 90 và 0 ADC 90
Suy ra bốn điểm B, C, D, E cùng nằm trên một đường tròn đường kính BC. b) Có 0
AFB=AFC 90 (Góc nội tiếp chắn nửa đường tròn) suy ra 0
AFB AFC 180
Suy ra ba điểm B, F, C thẳng hàng
AFE ABE (Cùng chắn AE ) và AFD ACD (Cùng chắn AD )
Mà ECD EBD (cùng chắn DE của tứ giác BCDE nội tiếp)
Suy ra: AFE AFD , do đó FA là phân giác của góc EFD
Dễ dàng chứng minh được EA AH EH
là phân giác của tam giác DHE và suy ra (1) AD ED
Xét tam giác HED có EA là phân giác trong của tam giác. Mặt khác BE EA nên BE là
phân giác ngoài của tam giác HED BH EH
EB là phân giác ngoài của tam giác DHE suy ra (2) BD ED
Từ (1) và (2) ta có: AH BH
AH.BD BH.AD AD BD Câu 5. 1 1 1 Ta có: P 1 1 1 1 1 1 a( ) b( ) c( ) 2 2 2 2 2 2 c b c a a b Trang 116 Đặt 1 1 1
x, y, z thì 2 2 2
x y z 1 và 0 x, y, z 1 a b c 2 2 2 x y z x y x P 2 2 2 2 2 2 2 2 2 y z z x x y x(1 x ) y(1 y ) x(1 x )
Áp dụng bất đẳng thức Côsi cho 3 số dương ta có: 2 2 2 1
1 2x 1 x 1 x 4 2 2 2 2 2 2 3 x (1 x )
.2x (1 x )(1 x ) ( ) 2 2 3 27 2 2 x 3 3 2 2
x(1 x ) x 2 3 3 x(1 x ) 2 2 2 Tương tự: y 3 3 z 3 3 2 y , 2 z 2 y(1 y ) 2 2 z(1 z ) 2 3 3 3 3 Suy ra: 2 2 2 P
(x y z ) 2 2 Dấu “=” xảy ra khi: 1
x y z
a b c 3 3 3 3
Vậy giá trị nhỏ nhất của P là
. Dấu “=” xảy ra khi a b c 3 2 Trang 117
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS NĂM HỌC 2020 – 2021 THÁI BÌNH Môn: Toán
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Câu 1. (3,0 điểm) 1 1 3 Cho a 3 3 3 9 a) Chứng minh rằng: 2
9a 2 3a 3 0
b) Tính giá trị biểu thức: 2 4
S 3 3a 27a 16a 8
Câu 2. (3,0 điểm) Cho biểu thức 4 3 2
P(x) x +ax bx cx d thỏa mãn P(1)=5, P(3)=13, P(5)=29.
Tính giá trị của biểu thức T=P(-4) + 21.P(6)
Câu 3. (4,0 điểm) a) Giải phương trình: 2 3
(1 2x) x 1 2x 7x 1 0 2 2
(x y) y x 4y 0
b) Giải hệ phương trình: 2 2
y(x y) 2x 2x 13y
Câu 4. (2,0 điểm)
Cho a, b, c là các số thực dương thỏa mãn: 2 2 2 2
a b c (a b c) 4 ab 1 bc 1 ca 1 Chứng minh rằng: 3 2 2 2 (a b) (b c) (c a)
Câu 5. (3,0 điểm)
Cho hình vuông ABCD có O là giao điểm của hai đường chéo AC và BD. Gọi M là
trung điểm của AB. Trên đoạn thẳng BC lấy điểm N (N khác B, NBqua A song song với MN cắt DC tại H. Chứng minh 2 AB 2 .
NB DH và tính góc NOH .
Câu 6. (3,0 điểm)
Cho đường tròn (O;R) và điểm E cố định, biết OE=a (0tùy ý không phải là đường kính của đường tròn (O). Các tiếp tuyến của đường tròn (O) tại
A và tại B cắt nhau ở M. Gọi K là hình chiếu vuông góc của M trên đường thẳng OE.
a) Chứng minh rằng điểm K luôn cố định khi dây AB thay đổi.
b) Tìm giá trị nhỏ nhất của diện tích tứ giác OAMB theo a và R.
Câu 7. (2,0 điểm) Trang 118
Tìm các cặp số tự nhiên (m;n) thỏa mãn: m 2
3 n 5n 7 -----HẾT-----
ĐÁP ÁN THAM KHẢO – THÁI BÌNH (2020 – 2021) Câu 1. 2 1 1 3 3 a) Ta có: 2
9a 2 3a 3 3a 3 3 2 1 1 3 1 1 3 1 1 3 Thay a 3 ta được: 3 3 0 3 3 9 3 3 9 3 3 2 3 2a 3 1 4a 4a b) Theo a) ta có: 2 2 4
9a 2a 3 3 0 a a 9 27 2 1 4a 4a
27a 16a 8 27.
16a 8 2a 32 4 27 2
9a 2 3a 3 3 3 3 2 2 4 2
S 3 3a 27a 16a 8 3 3a 2a 3 4 3 Câu 2. Xét đa thức 2
f (x) Ax Bx C thỏa mãn P(1)=5, P(3)=13, P(5)=29.
Thay các giá trị tương ứng f(1)=5, f(3)=13, f(5)=29 ta tìm được: A=1, B=0, C=4 2
f (x) x 4
Q(x) P(x) f (x) là đa thức bậc 4 vớ hệ số cao nhất bằng 1 và nhận 1, 3, 5 làm nghiệm
Q(x) (x 1)(x 3)(x 5)(x m)
P(4) Q( 4 ) f ( 4 ) 3 15( 4
m) 20 1280 315m
21P(6) 21Q(6) 21 f (6) 2370 315m T P( 4
) 21P(6) 4010 Câu 3. a) 2 3
(1 2x) x 1 2x 7x 1 0 2 3
(1 2x) x 1 2x 7x 1 2 2 3 2
(1 2x) (x 1) (2x 7x 1) 2
48x 32x 18x 0 x 0 x 3/4
Thay ngược lại phương trình ban đầu: x=0 (t/m), x = -3/4 (loại)
Vậy phương trình có nghiệm x=0 2 2
(x y) y x 4y 0 b) 2 2
y(x y) 2x 2x 13y Trang 119 2
x x 2x2y 4 2 2
x 2xy 2 y x 4 y 0 y y
x y2 2
2x 2x 13y 2 2 x x x y 2. 13 y 2 x x
a 2b 4 Đặt a
,b x y ( ; a b) ( 2 ;3) (18; 7 ) 2 y b 2a 13 0 Với ( ; a b) ( 2
;3) . Thay số và rút ra vô nghiệm Với ( ; a b) (18; 7
) . Thay số và rút ra vô nghiệm
Vậy hệ đã cho vô nghiệm Câu 4.
Từ giả thiết ta suy ra: 2 2 2
a b c ab bc ca 2 Câu 5. BM BN 1 Ta có: B MN D HA (g.g)
BM.DA BN.DA .A .
B DA BN.DH DH DA 2 2 AB 2 . NB DH NB MB Lại có: N . B HD M . B AD AD HD Trang 120 AD OD A OD O MB (g.g) O . D OB A . D MB OB MB NB OD N . B HD O . B OD OB HD Mà 0
NBO ODH 45 O HD N OB (c.g.c)
NOB OHD Mà 0
NOB NOH HOD 180 0
NOH OHD HOD 180 0
ODH OHD HOD 180 Suy ra: 0
NOH ODH 45 Vậy 0 NOH 45 Câu 6. a) Có 0
OKM OAM 90 Tứ giác OAKM nội tiếp AKO AMO Mà 0
AMO AOM 90 OAE AOM AMO OAE
OAE AKG OE OA
Dễ dàng chứng minh O AE O KA (g.g) 2
OE.OK R OA OK
Suy ra K cố định vì OE, R cố định. b) S 2S A . O AM AOBM AOM 4 AO S
min khi và chỉ khi AM min. Mà 2 2 2
M OM AO AO (vì 2
AO OH .OM ) AOBM 2 OH
Do đó AMmin OH max OH=OE H E 4 4 AO R 2 2 AM AO R min 2 2 OE a 4 R 2 S R R AOBM 2 a Trang 121
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9 THÁI NGUYÊN
NĂM HỌC 2020 – 2021 Môn: TOÁN ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) x x x x x
Bài 1. a) Cho biểu thức 2 4 2 1 2 1 P : x x 8 x 1 x 1 x 3 x 2
Chứng minh rằng giá trị của biểu thức P không phụ thuộc vào x (với x 0; x 1; x ; x 4 )
b) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = ax – 4 ( a 0) và hai điểm A(0;-
2), B(6;0). Tìm các giá trị của a để đường thẳng (d) cắt hai trục tọa độ Ox, Oy lần lượt tại
hai điểm M, N sao cho S S OAB OMN
Bài 2. a) Tìm nghiệm nguyên dương x, y của phương trình 2 2
x y 6x 4 y 4 0
b) Chứng minh rằng với mọi số tự nhiên n thì (2020n2 + 2) không phải là lập phương của một số tự nhiên.
c) Tìm các cặp số nguyên tố (p;q) thỏa mãn: 2 3 3
3 pq p q 3 p 3
Bài 3. Cho tam giác nhọn ABC nội tiếp đường tròn (O). Trên cung nhỏ AC của đường
tròn (O) lấy hai điểm M, N sao cho MN song song với AC và AMđiểm của BM và AC. Trên cung nhỏ BC của đường tròn (O) lấy điểm Q sao cho PQ
vuông góc với BC. Gọi R là giao điểm của AC và QN; F là giao điểm của AQ và BN.
a) Chứng minh rằng các điểm B, P, Q, R cùng thuộc một đường tròn.
b) Chứng minh rằng BR vuông góc với AQ.
c) Chứng minh rằng AFB BPQ ABR
Bài 4. Có n vận động viên tham gia một giải thi đấu cầu lông theo thể thức loại trực tiếp,
nghĩa là vận động viên thua sẽ bị loại ngay (không có trận đấu hòa). Theo thể lệ cuộc thi,
hai vận động viên chỉ có thể được thi đấu với nhau nếu chênh lệch giữa số trận đã thi đấu
của họ không quá 1. Biết rẳng, cuối cùng chỉ có đúng một vận động viên vô địch, các vận Trang 122
động viên khác đều bị loại. Tìm n nhỏ nhất sao cho vận động viên vô địch thắng được đúng 10 trận đấu.
Bài 5. Cho các số tự nhiên a, b thỏa mãn 2 2
(4a 2b 4ab 12a 8b 2020) chia hết cho 3.
Chứng minh rằng (a-b) chia hết cho 3. ------HẾT------
ĐÁP ÁN THAM KHẢO – THÁI NGUYÊN (2020 – 2021) Bài 1. a) Ta có: 2 x 2 x 4 ( x 1) x 2 1 P :
( x 2)(x 2 x 4)
( x 1)( x 1) x 1
( x 1)( x 2) 1 x 1 x 3 : x 2 x 1
( x 1)( x 2)
x 1 x 1 x 2 ( x 1)( x 2) .
( x 1)( x 2) x 3 x 3 x3 1 1
b) A(0;-2) nên AO=2, B(6;0) nên OB=6. S . . OA OB 6 OAB 2 (d): y=ax-4 (a 0) 4 4
d Ox=M M( ; 0) OM a a
d Oy=N N (0; 4 ) ON 4 1 8 S .OM.ON OMN 2 a 8 S S 6 OMN OAB a 4 a 3 Bài 2. 2 2
a) Phương trình có dạng 2 2
x y 6x 4y 4 0 x 3
y 2 17 Trang 123 Ta có bảng: x-3 1 -1 -1 1 4 -4 4 -4 y+2 4 -4 4 -4 1 -1 -1 1 x 4 2 2 4 7 -1 7 -1 y 2 -6 2 -6 -1 -3 -3 -1
Các giá trị x, y ở bảng trên là giá trị của x, y b) Đang cập nhật…. c) 2 3 3
3 pq p q 3 p 3
Hai số p, q không thể cùng là số lẻ. Nếu p=q 3 3 3
3p p 4 p 3 p p 3 0 2
p(1 p ) 3 p 3 (loại) 2 1 p 1 p q
Do đó trong 2 số p, q thì phải có 1 số lẻ, 1 số chẵn 2
3pq p và 3 3
q 3 p 3là số lẻ p 2 2 3
6q 2 q 27 q 5 Vậy (p;q)=(2;5) Bài 3.
a) Tứ giác BMNQ nội tiếp nên 0
BMN BQN 180 Trang 124
b) Gọi PQ giao BC tại D, AQ giao BR tại E, ta có: c) Ta có:
Bài 4. Đang cập nhật….. Bài 5. Ta có: 2 2
(4a 2b 4ab 12a 8b 2020) 3 2 2 2
(4a 4ab b ) 12a (b 8b 16) 2004 3 2 2
(2a b) 12a (b 4) 2004 3 Vì 2 2
(12a 2004) 3 (2a ) b (b 4) 3 2
(2a b) 3 Suy ra:
(2a b) 3 (2a b 3 ) b 3 2 (b 4) 3 Vậy: (a ) b 3 Trang 125
SỞ GIÁO DỤC & ĐÀO TẠO
KÌ THI CHỌN HSG MÔN VĂN HÓA CẤP TỈNH THANH HÓA NĂM HỌC 2020-2021
Môn thi: TOÁN – Lớp 9 THCS ĐỀCHÍNH THỨC
Ngày thi: 16 tháng 12 năm 2020
Thời gian: 150 phút (khô ng kể thời gian giao đề)
( Đề gồm có 05 câu, gồm 01 trang)
Câu I: (4,0 điểm)
x 3 x 3 x x 2 9 x
1.Rút gọn biểu thức P 1 :
với x 0; x 4; x 9 x 9 x 2 3 x x x 6
2. Cho a, b,c là các số thực đôi một khác nhau thỏa mãn 3 3 3 a 1 3 ; a b 1 3 ;
b c 1 3c .
Tính giá trị biểu thức: 2 2 2
Q a b c
Câu II: ( 4,0 điểm) 1. Giải phương trình: 3 2
x x x 2 4 15 2
4 5(x 2) x 4 2 2
x xy y 4y 1 0
2. Giải hệ phương trình: 2
(x 1)(x y 2) y
Câu III: ( 4,0 điểm)
1. Tìm tất cả các cặp số nguyên dương (x,y) thỏa mãn phương trình: x 2 2
2 x 9 y 12 y 19
2. Cho x,y là hai số nguyên dương thỏa mãn 2 2
x y 58 chia hết cho xy. 2 2 x y 58 Chứng minh: chia hết cho 12. xy
Câu IV: ( 6,0 điểm).
Cho đường tròn (I. r) có hai bán kính IE, IF vuông góc với nhau. Kẻ hai tiếp tuyến với
đường tròn(I) tại E và F, cắt nhau tại A. Trên tia đối của tia EA lấy điểm B sao cho EB >
r, quaB kẻ tiếp tuyến thứ hai với đường tròn (I). D là tiếp điểm, BD cắt tia AF tại C. Gọi K
là giao điểm của AI với FD.
1) Chứng minh hai tam giác IAB và FAK đồng dạng. Trang 126
2) Qua A kẻ đường thẳng vuông góc với BC, cắt FD tại P. Gọi M là trung điểm của
AB, MI cắt AC tại Q. Chứng minh tam giác APQ là tam giác cân.
3)Xác định vị trí của điểm B để chu vi tam giác AMQ đạt giá trị nhỏ nhất. Tính giá
trị nhỏ nhất đó theo r
Câu V: ( 2,0 điểm)
Cho các số thực dương x, y, z thỏa mãn 2 2
x y 4xyz 2(xy yz zx) . Tính giá trị
lớn nhất của biểu thức P x(1 y)(1 z) Hết
Thí sinh không được sử dụng tài liệu, giám thị không giải thích thêm.
Họ và tên thí sinh:…………………………………………………………….
ĐÁP ÁN THAM KHẢO – THANH HÓA (2020 – 2021) Câu I.
1) Với điều kiện , ta có:
x 3 x 3 x x 2 9 x P 1 : x 3 x 2 3 x
( x 3)( x 2) 2 x ( x 3)
(3 x)(3 x) ( x 2) 9 x 1 :
( x 3)( x 3)
( x 2)( x 3)
x 2 x 3 ( x 2)(3 x) x 9 x x 4 x 4 9 x 1 : 3 x
( x 2)( x 3) ( x 2)(3 x ) ( x 2)(3 x ) 3
x x 9 x x 4 x 4 9 x
x 4( x 2)( x 3) 4 : 3 x
( x 2)( x 3)
( x 2)( x 3) 3
( x 2)( x 3) 3 . 2 3 x ( x 2) x 2 Vậy 3 P x 2 2. Từ giả thiết 3 3 3 a 1 3 ; a b 1 3 ;
b c 1 3c , ta có: 3 3
a b 3(a b)
𝑎2 + 𝑎𝑏 + 𝑏2 = 3 (1) 3 3 b
c 3(b c) {𝑏2 + 𝑏𝑐 + 𝑐2 = 3 (2) 3 3
c a 3(c a)
𝑐2 + 𝑐𝑎 + 𝑎2 = 3 (3) Từ (1) và (2) suy ra: 2 2
a c ab bc 0 (a c)(a b c) 0 a b c 0
Cộng (1); (2) ;(3) vế với vế ta có: Trang 127 2 2 2
2a 2b 2c ab bc ca 9 2 2 2
4(a b c ) 2ab 2bc 2ca 18 2 2 2 2
3(a b c ) (a b c) 18 2 2 2
3(a b c ) 0 18 Vậy Q=6 Câu II.
1) Phương trình tương đương: 2 2 4
15x(x x 2) 4 5(x 2) x 4 1 7 7 Vì 2 2 4
x x 2 x
0; x 2 0; x 4 0 với mọi x 2 4 4 Suy ra x >0
Chia cả hai vế của phương trình cho x2 ta được: 2 1 2 15 x 1 4 x x x 4 x 2 x Đặt 2 t x
, với x>0 suy ra t 2 2 x Phương trình: 2
15(t 1) 4 5t t 4 2
4 5t t 4 20t 5t 15 0
4 t 2t 4 55(t 3) 0 2 4 5t(t 9)
4 5t(t 3)
5(t 3) 0 (t 3) 5 0 2 2 t 4 5 t 4 5
TH1: t=3 (t/m t 2 2 ) 2 x 1 2 x
3 x 3x 2 0 (t/m) x x 2 4 5t(t 3) TH2: 5 0 2 t 4 5 4 5t(t 3) Vì t 2 2 0 Vô nghiệm 2 t 4 5
Vậy phương trình đã cho có hai nghiệm : x=1; x=2 2 2 2
x xy y 4y 1 0
x 1 y(x y) 4y 2) Ta có: 2 2
(x 1)(x y 2) y (
x 1)(x y 2) y
Với y = 0, phương trình thứ nhất vô nghiệm nên hpt vô nghiệm.
Với y 0 , chia từng vế của mỗi phương trình cho y ta được. Trang 128 2
x 1 (x y 2) 2 y Hệ phương trình 2 x 1
x y 2 1 y 2 Đặt x 1 ,
m x y 2 2 hệ phương trình trở thành: y m n 2 m 1 . m n 1 n 1 2 2 x 1 y x 1 2 1 y x 1 Suy ra: y x 1
(x 1)(x 2) 0
x y 2 1 x 2 x 1 x 2
Vậy nghiệm của hệ phương trình là: và y 2 y 5 Câu III. 1) Ta có: x x x y y
x y 2 2 2 2 2 9 12 19 2 3 2 15
+) Nếu x lẻ thì x=2k+1 ( k ) x 2 2k 1 2 k 2 2 2 x 2
x (3 1) .2x 2x (mod 3) . Mà 2 x 0;1(mod 3) k 2
2.4 .x 0;2(mod3) Mặt khác: 2
(3y 2) 1(mod 3)
Vậy x không thể là số lẻ +) Nếu x chẵn thì x=2k ( * k )
Ta có phương trình: 2k 2 2
2 .4 (3 2) 15 (2k.2 3 2)(2k y k y
.2k 3y 2) 15 (*) Vì * k, y
nên 2k.2 3 2 2k k y
.2k 3y 2 và 2k.2k 3y 2 0 nên 2k.2k 3y 2 0 k k Do đó (*) 2 .2k 3y 2 15 k y hoặc 2 .2 3 2 5
2k.2k 3y 2 1
2k.2k 3y 2 3 k k Trườ 2 .2k 3y 2 15 2 .2k 8 ng hợp 1: (vô nghiệm)
2k.2k 3y 2 1 y 3 k 2k.2k 4 k 1 x 2 Trườ 2 .2k 3y 2 5 ng hợp 2:
2k.2k 3y 2 3 y 1 y 1 y 1
Vậy nghiệm nguyên dương của phương trình là (x;y)=(2;1) 2 2 k 3 2) Đặ x y 58 t * 2 2 k , k
kxy x y 58 . Ta chứng minh k 12 xy k 4
+ Nếu trong hai số x,y có một số chí hết cho 3.
Do vai trò x, y bình đẳng , giả sử x 3 xy 3 Ta có: 2 2 2 2 2 2
x y 58 xy x y 58 3 y 1 3 y 2(mod 3)
Vô lí vì y2 là số chính phương
Vì vậy cả x, y đều không chia hết cho 3 mà 3 là nguyên tố. Trang 129 2 2 2 2
(xy,3) 1; x 1(mod3); y 1(mod3) x y 58 111 0(mod3) 2 2 2 2
x y 58 3 kxy x y 58 mà (xy,3) 1 k 3 (1)
+ Nếu trong hai số x, y có một số chia hết cho 2.
Do vai trò x, y như nhau, không mất tính tổng quát giả sử x 2 xy 2 Ta có: 2 2 2 2
x y 58 xy x y 58 2 mà 2
x 2,58 2 y 2 xy 4 2 2
x y 58 4 vô lí vì x 4, y 4do x 2, y 2mà 58 không chia hết cho 4.
Vì vây cả x, y đều không chia hết cho 2.
x, y đều lẻ x -1, x +1, y -1, y +1 đều chia hết cho 2. 2
x 1 (x 1)(x 1) và 2
y 1 (y 1)(y 1) đều chia hết cho 4 2 2 2 2 2 2
x y 58 x 1 y 1 60 4 kxy y 58 4
Mà (xy,4) = 1 do x, y lẻ k 4
Từ (1) và (2) kết hợp với (3, 4) 1 k 12 (đpcm) Câu IV.
1) Theo tính chất hai tiếp tuyến cắt nhau, ta có: CD CE C DF cân tại C Trang 130 0 0 180 C 180 C 0 CFD
AFK 180 CFK (1) 2 2
Tứ giác AEIF có ba góc vuông nên là hình chữ nhật > Hình chữ nhật AEIF có IE= IF nên là hình vuông. Suy ra 0
IAB FAK 45 0 ABC 180 C 0 0 0
AIB 180 (IAB ABI ) 180 (45 ) (2) 2 2
Từ (1) và (2) suy ra: ABI AFK kết hợp IAB AFK I AB F AK (g.g) IA FA IA EA 2) Vì I AB F AK nên
( vì FA = EA). Đẳng thức này kết hợp AB AK AB AK
với điều kiện IAE chung, suy ra A KB A EI (c.g.c) AEI
vuông cân tại E nên AK
B vuông tại K. Suy ra đường trung tuyến KM cũng là
đường cao nên KM AB
Ta có: KM AB, IE AB, AC AB KM / /IE / / AC
ID BC, AP BC ID / / AP
Áp dụng định lí Talet và hệ quả Talet, kết hợp ID = IE. ID KI ME IE AP AQ AP KA MA AQ
APQ cân tại A
3) Đặt ME = x, PQ = y với x>0, y>0 ME EI MEI IFQ (g.g) 2
xy r (1) IF FQ Chu vi AMQ là: 2 2 C
AM AQ MQ AM AQ AMQ 2 2 2
2r (x y) (x y ) 2r(x y) 2r
Áp dụng bất đẳng thức cosi cho hai số thực dương x, y ta có: 2 2 2 2 2 2 C
2r (x y) (x y ) 2r(x y) 2r 2r 2 xy 2 x y 2r.2 xy 2r (2) AMQ
Từ (1) và (2) suy ra: C (4 2 2)r AMQ
Dấu (=) xảy ra khi x = y = r hay EB = 3r.
Vậy khi EB = 3r thì chu vi tam giác AMQ nhỏ nhất. Giá trị nhỏ nhất bằng (4 2 2)r Câu V. 2 ( y z) 2
+ Ta có: P x 1 ( y z) 4 p
2(y z) 4
+ Từ giả thiết ta suy ra được: 2 2
x ( y z) 2x( y z) (1 x)4 yz + Nhận thấy 2 2 2
x ( y z) 2x( y z) (x y z) 0 nên x 1 + Vì vậy: 2 2
x ( y z) 2x( y z) (1 x)4 yz (1 x)( y z) 2 2 2
x 2x(y z) x(y z) x 2(y z) (y z)
x (y z)2 (y z) Trang 131
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THỪA THIÊN HUẾ
LỚP 9 THCS_NĂM HỌC 2020 – 2021 MÔN TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài 150 phút (không kể thời gian giao đề) (Đề gồm 01 trang)
+ Suy ra P y z y z 2 4 ( ) 2
Đặt: 2 y z t , ta có:
x (y z)2 (y z) x 0
2 (y z) 0 0 t 2 (*) y z 0 4 Khi đó ta có 6 3t t t t 81 27 3
4P (2 t)t 12P (6 3t).t.t.t P 4 16 64 3
Dấu “=” xảy ra khi 6 3t t t (t/m (*)) 2 y z Vậy 27 3 3 1 maxP=
khi và chỉ khi 2 ( y x)
x ; y z 64 2 4 4
x (y z)
2(y z)
Bài 1. (4,0 điểm) 3 2 2 2
x 3x (x 4) x 1 4 a) Cho P(x) , với 2 3
x 1, x 2, x
. Hãy tìm các giá trị của x 3 2 2 2
x 3x (x 4) x 1 4 3
để biểu thức P(x)=0. (Không sử dụng máy tính cầm tay). b) Cho biểu thức x 2 x 1 x 1 Q :
( x 0, x 1). Chứng tỏ rằng x x 1 x x 1 1 x 2
0Bài 2. (4,0 điểm) a) Giải phương trình: 2
x 5 3 x 1
x x 2 4 x 2
b) Tìm nghiệm nguyên (x nguyên, y nguyên) của hệ phương trình sau 2 2 3 3 3
(2x 1) ( y 1) 2. (2x 1)( y 1) 4 3 2
y 4 18 16x 48x 48x
Bài 3. (3,0 điểm) Cho phương trình: 2
x (2m 1)x (m 1) 0 (1). (x là ẩn, m là tham số) Trang 132
a) Giải phương trình (1) khi m=0.
b) Tìm các giá trị của m để phương trình (1) có hai nghiệm âm phân biệt.
c) Gọi x1, x2 là hai nghiệm phân biệt của phương trình (1). Tìm các giá trị của m để biểu thức: 1 1 1 K
đạt giá trị nhỏ nhất. 2 2 x x x x 1 2 1 2
Bài 4. (3,5 điểm) Cho tam giác nhọn ABC (AB0
A 60 nội tiếp đường trong (O;R). Hai
đường cao BE, CF cắt nhau tại H. Gọi I là giao điểm hai đường thẳng EF và CB. Đường thẳng AI
cắt đường tròn (O) tại điểm thứ hai là M.
a) Tính độ dài cạnh BC theo R.
b) Chứng minh tứ giác AMFE nội tiếp được trong một đường tròn.
c) Kéo dài MH cắt đường tròn (O) tại K. Tính AB.CK + AC.BK theo R.
Bài 5. (3,5 điểm) Cho tam giác ABC cân (AB=AC) nội tiếp đường tròn (O). M là điểm bất kỳ
trên dây BC. Vẽ đường tròn (D) qua M và tiếp xúc với AB tại B; vẽ đường tròn E qua M và tiếp
xúc với AC tại C. Gọi N là giao điểm thứ hai của hai đường tròn (D) và (E).
a) Chứng minh tứ giác ABNC nội tiếp. b) Chứng minh AM.AN=AC2
c) Khi điểm M thay đổi trên BC thì trung điểm I của đoạn DE chạy trên đường nào?
Bài 6. (2,0 điểm) Cho biểu thức: 2 2
E x 3x y xy 2025 . Với giá trị nào của x, y thì E đạt
giá trị nhỏ nhất? Tính giá trị nhỏ nhất đó? -----HẾT-----
Họ và tên thí sinh:…………………………………Số báo danh:………………………………….
Họ và tên GT1:…………………………………….Họ và tên GT2:……………………………….
ĐÁP ÁN THAM KHẢO - THỪA THIÊN HUẾ (2020 – 2021) Bài 1.
a) Với điều kiện của x đã cho, ta phân tích tử và mẫu thành nhân tử được:
x 2. x 1. x 1.x 2x 2 x 1
P(x) x2. x1. x1.x2x2 x1
x 2. x 1
P(x) x2. x1
P(x) 0 x 1 (thỏa mãn)
b) Với điều kiện của x đã cho, ta có: Trang 133 x 2 x 1 x 1 Q : x x 1 x x 1 1 x 2 x x x 1 2 x x 1 2 x
1 x x 1
x 1x x 1 x 1x x . 1 x 1 2 x 2 1
x 21x x 1 2 x x 1 2
Do x 0, x 1 x x 1 0 0 B 0 x x 1 2 2 x 2 x Xét Q 2 2 x x 1 x x 1
Do x 0, x 1 nên 2
x 2 x 0 Q 2 0 Q 2 Vậy 0Bài 2.
a) Đặt a x 1,b x 2 2
b 2 5 3a ab 4b 2
b ab 4b 3a 3 0
(b a 1)(b 3) 0 b a 1 b 3
Với b a x b a 2 2 2 1 2
1 2 a 2a 1 2
a a 2a 2 a 1 2
x a 2a 1 2
Với b 3 3 x 2 x 7 Kết luận: x=2, x=7 b) Đặt 3 3
a 2x 1,b
y 1 thì phương trình thứ nhất của hệ có dạng: 2 2
a b 2ab a b y 2x 2
Thay vào phương trình thứ hai của hệ ta được: Trang 134 2 x 4 4 3 2
1 2x 2 18 16x 48x 48x 4 3 2
16x 48x 48x 18x 0
x 0 y 2 3 2 16
x 48x 48x 18 0 Ta có: 4 3 2 x x x x x 2 16 48 48 18 0 2
3 8x 12x 6 0 (không có nghiệm nguyên) Vậy (x;y)=(0;-2) Bài 3.
a) Khi m=0, phương trình có dạng: 1 5 2
x x 1 0 x 2
b) Điều kiện để có 2 nghiệm âm phân biệt: 1 0 a 0 0 2m 2 1 4 m 1 0 2 2 m P 0 (m 1) 0 2
S 0 2m1 0
c) Điều kiện phương trình có nghiệm: 2 2
(2m 1) 4(m 1) 4m 8m 5 0 m
Teo Vi-et: x x 2m 1; x x (m 1) 1 2 1 2 x x 2 2 x x 4m 5m 2 1 2 1 2 K 2 2 2 x x m 2m 1 1 2 K. 2 m 2m 2
1 4m 5m 2 K 4 2
m 2K 5 m K 2 0 7
Điề kiện: 4K 7 0 K m 4 7 1 Suy ra MinK
. Dấu “=” xảy ra khi m 4 3 1 Vậy m 3 Bài 4. Trang 135 1
a) Góc BAC chắn cung BC nên BAC
BOC (Mối liên hệ góc ở tâm và góc nội tiếp) 2 0 0
BOC 2.60 120
Mà tam giác BOC cân tại O, ON là đường trung tuyến đồng thời là đường cao, đường phân giác R 3 0 BN .
OB sin BON R sin 60 2
BC 2BN R 3
b) Tứ giác BFCE là tứ giác nội tiếp vì 0
BFC BEC 90 IFB ICE Ta dễ dàng chứng minh IF IB IF B I CE (g.g) I . B IC IF.IE (1) IC IE
Tứ giác BCAM nội tiếp (O) nên ICA BMA IB IM
Dễ dàng chứng minh I MB I CA (g.g) I . B IC I . A IM (2) IA IC IF IM
Từ (1) và (2) suy ra: IF.IE I . A IM IA IE IF IM Mà I MF I
EA vì có I chung,
IFA IAE IA IE
Vậy tứ giác AMFE nội tiếp được trong một đường tròn.
c) Hướng dẫn: Chứng minh A . B CK A . C BK B . C AK Bài 5. Trang 136
a) Ta có MAC MNC , MBA BNM (góc tạo bởi tia tiếp tuyến với dây cung và góc nội tiếp cùng chắn một cung) Suy ra 0
MCA MBA MNC BNM BNC BAC MCA MBA BAC 180
Do đó tứ giác ABNC nội tiếp
b) Ta có ABC ACB (vì tam giác ABC cân tại A)
Mà MNC ACB MNC ABC
Mặt khác: ANC ABC (hai góc nội tiếp cùng chắn cung AC)
Do đó: MNC ANC
Nên hai tia NA, NM trung nhau hay M, A, N thẳng hàng. Mà A CM A
NC (g.g) vì có CAM chung, ACM ANC AM AC 2
AC AM.AN AC AN Trang 137
c) Vẽ đường kính AK của đường tròn. Ta có: 0
ABK ACK 90 (góc nội tiếp chắn nửa đường tròn), 0
ABD 90 (đường tròn (D) tiếp xúc AB tại B) Suy ra B, D, K thẳng hàng.
Tương tự: C, E, K thẳng hàng. Do đó: AB = AC, OB = OC.
Suy ra A, O thuộc đường trung trực của BC AO BC BK CK BK CK K
BC cân tại K (BK=CK) KBC KCB D
BM cân tại D (DB=DM) DBM DMB E
MC cân tại E (EC=EM) ECM EMC
Do đó KBC EMC, KCB DMB KB / /EM , KC / /DM
Mà I là trung điểm của DE nên I là trung điểm của MK. Gọi J là giao điểm của AK và BC. J
MK vuông tại J có IJ là đường trung tuyến JI KI
JK cố định nên I thuộc đường thẳng cố định là đường trung trực của đoạn thẳng JK
Vậy I chạy trên đường trung trực của JK Bài 6. Ta có 2 2
E x 4x 1 y 2 y 1 xy 2 y x 2 2022
x 22 y 2
1 x 2 y 1 2022 2
x 2 x 1 y y 1 3 2 2. 2 . . 1 y 2 1 2022 2 4 4 2 1 3
(x 2) (y 1) y 2 1 2022 2022 2 4
MinE 2022 . Dấu “=” xảy ra khi và chỉ khi: x = 2, y = -1 Trang 138
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN TỈNH TIỀN GIANG
TRUNG HỌC CƠ SỞ, NĂM HỌC 2020 – 2021 Môn: Toán
Thời gian: 150 phút (không kể thời gian giao đề)
ĐỀ THI CHÍNH THỨC Ngày thi: 26/02/2021
(Đề thi có 02 trang, gồm 5 bài)
Bài 1 (4 điểm)
1) Tính giá trị của biểu thức: A x x x 2021 3 2 2 5 2 2020 3 5 2 17 5 38 với x 5 14 6 5
2) Tìm sáu số nguyên tố liên tiếp mà có tổng là một số nguyên tố.
Bài 2 (6 điểm)
1) Cho x, y là các số dương thỏa 18 2
1. Tìm giá trị nhỏ nhất của biểu thức P=x+y. x y 2) Giải phương trình 2 2
7(x x 1) 5(x x 1)
3) Cho hàm số y=f(x) với f(x) là một biểu thức đại số xác định với mọi x . Biết rằng 2 3
(x 1) f (2 x) (x x 4) f (2 x) x 1. Tính giá trị của biểu thức f(5).
Bài 3 (4 điểm)
1) Trong mặt phẳng tọa độ Oxy, cho Parabol (P): 1 2 y
x . Đường thẳng : y=m cắt (P) 4
tại hai điểm phân biệt A, B. M là điểm tùy ý trên trục Ox. Tìm m để tam giác MAB có diện tích bằng 2021.
2) Một cung thủ bắn hơn 11 lần vào bia và đều trúng vào các vòng 8 điểm, 9 điểm, 10
điểm. Biết tổng số điểm cung thủ đạt được sau các lần bắn là 100 điểm. Hỏi cung thủ đã
bắn bao nhiêu lần và mỗi vòng trúng bao nhiêu mũi tên?
Bài 4 (2 điểm)
Cho a, b, c là ba số thực khác không thỏa mãn a+b+c=2021 và 1 1 1 1 . a b c 2021
Chứng minh một trong ba số a, b, c phải có một số bằng 2021. Trang 139
Bài 5 (4 điểm) Cho tam giác ABC có 0 0
BAC 120 , ABC 45 nội tiếp đường tròn tâm O và AC a 2 .
Các đường cao AN, BP và CQ của tam giác ABC cắt nhau tại H (P thuộc AC, Q thuộc AB và N thuộc BC).
a) Tính bán kính đường tròn (O) theo a và tính độ dài cạnh BC.
b) Chứng minh 5 điểm A, Q, C, O, N cùng thuộc một đường tròn và tính góc NQO .
c) HB, HC cắt (O) tại E, F. Chứng minh tứ giác OEHF nội tiếp đường tròn (C) và tính bán kính đường tròn (C).
--------------------------------------------------HẾT---------------------------------------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:………………………………………..Số báo danh:…………………... Trang 140
ĐÁP ÁN THAM KHẢO – TIỀN GIANG (2020 – 2021) Bài 1. 523 3
. 5 2 5 2 5 2 1 1) Ta có: x 5 3 52 5 3 5 3 2021 1 Do đó: A 27
2) Gọi p là số nguyên tố nhỏ nhất trong 6 số
Nếu p chẵn thì p=2. Do đó 6 số là: 2,3,5,7,11,13. Tổng bằng 41, là số nguyên tố (thỏa mãn)
Nếu p lẻ thì p=3. Do đó 6 số là: 3,5,7,11,13,17. Tổng bằng 56, không là số nguyên tố (loại)
Vậy 6 số cần tìm là: 2,3,5,7,11,13 Bài 2. 1) Ta có: 2 2 2 18 2 18 2 18 2 32 1 x y x y x y x y
x y 32 18 2
Vậy MinP=32. Dấu “=” xảy ra khi và chỉ khi: x y
2) Điều kiện x 1 2 2
7(x x 1) 5(x x 1)
7x x 1x x 1 2
5(x x 1)
x x 17
x x 1 5(x x 1) 0
x x 1 1
2 x 1 2x 0
x x 1 6
x 1 x 0 6
x 1 x 0 (vì x
x 1 >1 do x 1)
x 6 x 1 2
x 36x 1 2
x 36x 36 0
x 1812 2 (t/m)
Vậy nghiệm phương trình là x 18 12 2 3) 2 3
(x 1) f (2 x) (x x 4) f (2 x) x 1 (1)
Thay x=3 vào (1) ta được: 4 f
1 16 f 5 28 (2)
Thay x=-3 vào (1) ta được: 10 f 1 2 f 5 2 6 (3) Trang 141
Từ (2) và (3) suy ra f 16 5 7 Bài 3.
1) Ta dễ dàng suy ra tam giác MAB có (
A 2 m; m), B(2 m; m) , h=m 1 1 S . . h AB . .4 m m 2021 MAB 2 2 2 2021 3 m 2 2
2) Gọi x, y, z lần lượt là số lần bắn đzúng vào các vòng 8, 9, 10 điểm ( *
x, y, z )
x y z 11 Ta có: 8
x 9y 10z 100
Rõ ràng 8x 8 y 8z 8x 9 y 10z 100 x y z 12
Suy ra x y z 12 Do đó:
x y z 12
y 2z 4 y 4 2z 8
x 9y 10z 100
y 1 4 2z 1 z 1, 5 z 1
Vậy z 1, y 2, x 9 Bài 4.
Từ giả thiết suy ra: 1 1 1 1 a b c
a b c 1 1 1 1 0 a b c
a b c a b a b 0 ab
c(a b c)
a b c
a b c ab 0
a b 2
ca cb c ab 0
a bb cc a 0 a b 0
b c 0 c a 0
Nếu a b 0 c 2021 a b 2021
Nếu b c 0 a 2021 b c 2021
Nếu c a 0 b 2021 c a 2021 Suy ra đpcm Trang 142 Bài 5. a) Dễ dàng suy ra 0 0
AOC 2ABC 2.45 90
Xét tam giác AOC vuông cân tại O có 0
AOC 90 và AC a 2 OA a R a Dễ dàng suy ra 0
BOC BOA AOC 2BCA 2CAB 120
Xét tam giác BOC cân tại O và 0 BOC 120 0 BC 2. .
R sin 60 R 3 b) Có 0 0 0
AQO 90 , AOC 90 ,CON 90 . Suy ra 5 điểm 5 điểm A, Q, C, O, N cùng thuộc một đường tròn đường kính AC.
Xét đường tròn đường kính AC, dễ dàng nhận thấy 0
NQA NCA 15 (cùng chắn cung AN)
Xét đường tròn đường kính AC, dễ dàng nhận thấy 0
OQC OAC 45 (cùng chắn cung CO) Suy ra 0 0 0 0
NQO AQC NQA OQC 90 15 45 30 Trang 143
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 CẤP TỈNH TRÀ VINH
NĂM HỌC: 2020 – 2021 MÔN THI: TOÁN ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian phát đề) Câu 1. (4.0 điểm) x x x x Cho biểu thức 2 3 3 2 2 M : 1 x 3 x 3 x 9 x 3 1. Rút gọn M 2. Tìm x để 1 M . 2 Câu 2. (2.0 điểm)
Cho a+b+c=0. Tính giá trị của biểu thức 3 3 2 2
N a b c(a b ) abc Câu 3. (3.0 điểm)
x 4y 5
Giải hệ phương trình
2 x 2y x y 1 7 Câu 4. (3.0 điểm) Giải phương trình 2
(x 4)(x 1) 3 x 5x 2 6 Câu 5. (2.0 điểm) 1 1 1
Cho ba số dương x, y, z thỏa mãn
2 . Tìm giá trị lớn nhất của 1 x 1 y 1 z biểu thức P=xyz. Câu 6. (4.0 điểm)
Cho tam giác ABC vuông ở A, đường cao AH. Gọi I, K theo thứ tự là hình chiếu
của H trên AB, AC. Đặt AB=c, AC=b.
1. Tính AH, AI, AK theo b, c. 3 BI c 2. Chứng minh 3 CK b Câu 7. (2.0 điểm)
Từ một điểm A ở ngoài đường tròn tâm O, kẻ hai tiếp tuyến AB và AC với B, C là
các tiếp điểm. Trên đoạn OB lấy điểm N sao cho BN=2ON. Đường trung trực của đoạn
thẳng CN cắt OA tại M. Tính tỉ số AM . AO .…..HẾT…… Trang 144
ĐÁP ÁN THAM KHẢO – TRÀ VINH (2020 – 2021) Câu 1.
1) Điều kiện x 0, x 9
2 x x 3 x x 3 3x 3
x 3 2 x 2 M : x 9 x 3
2x 6 x x 3 x 3x 3 x 1 : x 9 x 3 3
x 3 x 1 : x 9 x 3 3 x 1 x 3 . x 9 x 1 3 x 3 1 3 1 2) M
x 3 6 x 9 2 x 3 2 Câu 2. 3 3
N a b c 2 2 a b 3 3 2 2
abc a b a c b c abc 3 2
a a c 3 2 b b c 2
abc a a c 2
b b c abc 2 a b 2
b a abc
aba b c 0
(vì a b c 0 a c b
,b c a ) Câu 3.
x 4y 5
x 5 4y
2 x 2y x y 1 7
2 x 2y x y 1 7
Suy ra: 2 x 2 y x y 1 7
2 5 4y 2y 5 4y y 1 7
2 5 2y 6 5y 7 (*) 5 23 47
Nếu y thì: (*) 2(
5 2y) (6 5y) 7 y x 2 9 9 5 6 Nếu y
thì: (*) 25 2y 6 5y 0 y 4 x 21 2 5 Trang 145 6 Nếu y thì:
y y 16 19 (*) 2 5 2 6 5 7 y x 5 9 9 47 23 19 16 Vậy Hệ có nghiệm ; x y ; 21;4 ; 9 9 9 9 Câu 4. 2
(x 4)(x 1) 3 x 5x 2 6 2 2
x 5x 4 3 x 5x 2 6 2
x 5x 2 4 2
x 5x 2 1 Suy ra 2
x 5x 2 4 (thỏa mãn) 2
x 5x 2 4 2
x 5x 14 0 x 2 x 7 KL: x=2; x= -7 Câu 5. 1 1 1 y z yz Ta có: 1 1 2 1 x 1 y 1 z 1 y 1 z (1 y)(1 z) 1 zx 1 xy Tương tự : 2 , 2 1 y
(1 x)(1 z) 1 z (1 x)(1 y) 1
Nhân ba bất đẳng thức cùng chiều trên với nhau ta được: xyz 8 1 1
Suy ra giá trị lớn nhất của P là . Dấy “=” xảy ra khi và chỉ khi x y z 8 2 Câu 6. Trang 146 Câu 7.
Gọi K là trung điểm của BN. Ta có OA là trung trực của đoạn BC. Do M thuộc OA nên MB=MC
Do M thuộc trung trực của CN nên MC=MN. Suy ra MB=MN
Do đó M thuộc trung trực của BN, suy ra MK BN
Vì OB BA (tính chất tiếp tuyến) MK / / AB AM BK 1
Xét tam giác OBA, theo tính chất Ta-let ta có: AO BO 3 Trang 147
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THCS NĂM 2021 TỈNH TUYÊN QUANG Môn thi: TOÁN
Thời gian làm bài: 150 phút, không kể thời gian giao đề ĐỀ THI CHÍNH THỨC
(Đề thi này có 01 trang) Câu 1. (5.0 điểm ) a)Rút gọn biểu thức : 1 1 1 1 S = + + + ...... + 2 2 2 2 1 + 2.1 3 + 2.3 5 + 2.5 2021 + 2.2021
b)Cho a;b > 0 thỏa mãn : a + 1 +
2b = 6 .Chứng minh : a + b ³ 11
Câu 2. (5.0 điểm )Giải các phương trình và hệ phương trình sau : a) 4 2 x - 5x + 6 = 0 2
ìï x + xy- 2x- y + 1= 0 ï b)í
ïï 2x+ y- 1- x+ 2= 0 î Câu 3. (5 điểm )
Cho tam giác nhọn ABC (AB < AC)nội tiếp đường tròn (O) và ngoại tiếp đường tròn (I) .Gọi D
là tiếp điểm của BC với đường tròn (I); AI cắt lại đường tròn (O)tại điểm M ¹ A ; MD cắt lại
đường tròn (O)tại Q ¹ M ; AP là đường kính của đường tròn (O).Chứng minh rằng
a) D MBQ đồng dạng với tam giác MDB b) 2 MI = M . Q MD
c)Ba điểm P; I;Q thẳng hàng Câu 4. (3,0 điểm )
a)Tìm tất cả các số nguyên x + x thỏa 2 1 A = Î Z 3x + 1 p- 1 2 - 1 b)Chứng minh rằng : 3 2
- 1 chia hết cho 2 p - 1 với mọi số nguyên tố p > 3
Câu 5. (2,0 điểm)
Có hai chiếc máy in thẻ đặc biệt A và B có thể in ra những tấm thẻ có chứa các bộ số có dạng ( ;
a b)trong đó a là mã số của thẻ; b là mã số của người dùng thẻ đó ( trên mỗi thẻ có đúng 1 bộ số
.Khi đưa thẻ có chứa bộ số ( ;
a b)vào máy in A máy sẽ in ra thẻ có bộ số (6 ; a b + ) 5 và trả lại thẻ
có bộ số (a,b)ban đầu ; khi đưa hai thẻ có bộ số ( ;
a b) và (b, c) vào máy in B máy sẽ in ra thẻ có bộ số (6 ;
a c) và trả lại 2 thẻ có bộ số ( ;
a b)và (b, c)ban đầu .Hỏi từ thẻ có bộ số (22, ) 12 ban đầu ; hai máy in ;
A B có thể in ra thẻ có bộ số (1975;30 ) 4 hay không ?Vì sao . -----HẾT----- Trang 148
ĐÁP ÁN THAM KHẢO – TUYÊN QUANG (2020 – 2021) Câu 1:
a) Ta có công thức tổng quát : ( n + )2 2 1 + 2 ( . 2n + ) 1 = (2n + ) 1 (2n + ) 3
Và nhận thấy (2n + ) 3 - (2n + ) 1 = 2 1 1 1 2 1 æ 1 1 ö Þ = = . = ç ÷ - ç ÷ ç ÷ (2n + )2 1 + 2(2n + ) 1 (2n + ) 1 (2n + ) 3 2 (2n + ) 1 (2n + ) 3 2 è2n + 1 2n + 3ø Áp dụng ta có : 2 1 + 2.1 = 1.3 ; 2 3 + 2.3 = 3.5 ; 2 5 + 2.5 = 5.7 ,…….; 2 2021 + 2.2021 = 2021.2023 Vậy 1 1 1 1 1 S = + + + ....... + + 1.3 3.5 5.7 2019.2021 2021.2023 1 æ 1 1 1 1 1 1 1 1 1 ö 1 ç = - + - + - + ....... ÷ + - + - ç ÷ 2 ç è 3 3 5 5 7 2019 2021 2021 2023÷ ø 1 æ 1 ö 1011 = 1 ç ÷ - ç ÷= 2 ç è 2023÷ ø 2023
b)Bất đẳng thức cần chứng minh Û a + 1+ b ³ 12
Theo bđt Cô Si ta được : (a + ) 1 + 4 ³ 4 a + 1
Và b + 8 ³ 2 8b = 4 2b
Cộng lại ta có : (a + )
1 + b + 12 ³ 4( a + 1 + 2b)= 4.6 = 24 Þ a + b ³ 11 Câu 2: a)Giải phương trình : 4 2 x - 5x + 6 = 0 Đặt 2
t = x (t ³ ) 2
0 Þ t - 5t + 6 = 0 Û (t - ) 2 (t - ) 3 = 0 t é = 2 Û ê Û x = ± 2;± 3 t ê = 3 ë
Kết luận : x = ± 2;± 3 là các nghiệm của phương trình
b)Giải hệ phương trình : Trang 149 2
ìï x + xy - 2x - y + 1 = 0( ) 1 ï í
ïï 2x + y - 1- x + 2 = 0(2) ïî
Xét phương trình ( )Û (x - )2 1 1 + y(x - ) 1 = 0 Û (x - ) 1 (x + y - ) 1 = 0 x é = 1 Û ê x ê = 1- y ë Xét x = 1 Þ
y + 1 + 1 = 0 ( thay vào (2)) ( vô nghiệm )
Xét x = 1- y thay vào (2) ta được : 1- y + y + 1 = 0 ìï - y - 1³ 0 ìï y £ - 1 ï ï Û
1- y = - y - 1 Û í Û í Û y = - 3 2 2
ï 1- y = y + 2y + 1 ï y + 3y = 0 ïî ïî
Khi y = - 3 Þ x = 4 Kết luận :( ; x y)= (4;- )
3 là nghiệm của hệ phương trình Câu 3: A Q I O B C D P M Trang 150
a)Ta có AI là phân giác góc ·
BAC Þ MB = MC ( M là điểm chính giữa cung nhỏ BC ) Do đó · ·
DBM = BQM ( 2 góc nội tiếp chắn hai cung bằng nhau ) Vậy MB MD D BMD đồng dạng 2 DQMB Þ = Þ MB = M . D MQ MQ MB b)Ta chứng minh : · · MBI = MIB Ta có : · · ·
MIB = IBA + IAB và · ·
IBA = CBI ( BI là phân giác · ABC ) Và · · · · · · ·
IAB = CAM = MBC Þ MIB = CBI + MBC = MBI vậy nên tam giác MIB cân ở M Vậy nên 2 MI = M . D MQ · · · · ·
c)Ta có : AQI = AQM - IQM = 180° - ACM - IQM Lại có · ·
ID / /OM Þ DIM = AMO ( so le trong ) MI MQ Và 2 MI = M . D MQ Þ =
Þ DMIQ đồng dạng DMDI (c g c ) · ·
. . ) Þ IQM = DIM MD MI Và cũng có : · 1 · 1 · ACM = AOM = (180°- 2AMO) · = 90° - AMO 2 2 · · ·
Thay vào ta có AQI = 180° - 90° + AMO - AMO = 90° (1)
Mặt khác AP là đường kính của đường tròn (O) · Þ AQP = 90° (2)
Từ (1) và (2) ta được ba điểm P; I;Q thẳng hàng ( đpcm ) Câu 4:
a)Tìm tất cả các số nguyên x + x thỏa 2 1 A = Î Z 3x + 1 2x + 1 Ta có : A = Î Z Þ (2x + ) 1 (3 M x + )
1 ( vì tử và mẫu đều là số nguyên ) 3x + 1 Þ 3(2x + ) 1 (3 M x + ) 1 Þ 2(3x + ) 1 + 1 (3 M x + ) 1 Þ 1 (3 M x + ) 1 3 é x + 1 = 1 Þ ê
Þ x = 0 ( thử lại thấy thỏa mãn ) 3 ê x + 1 = - 1 ë
b)Ta chứng minh : p- 1 2 - 1 (3 M p)
Ta có (2; p)= 1( vì p nguyên tố p > 3 ) nên p- 1 2
º 1 (mod p ) ( đlý Ferrmat nhỏ ) Trang 151 Vậy p- 1 2 - 1 p M
Và p lẻ nên p = 2m + 1( vì p nguyên tố p > 3 ) Nên p- 1 2m m - = - = - ( M - ) p- 1 2 1 2 1 4 1 4 1 Þ 2 - 1 3 M p- 1 Mặt khác - p- 2 1 (3; p)= 1 nên 1 2 - 1 (3 M p)Þ p M 3 p- 1 p- 1 Vậy 2 - 1 2 - 1 p M Þ = . p b ( b Z + Î ) 3 3 p- 1 2 - 1 Do đó b 3 2 - 1 2 pb 1 (2p ) 1b (2p = - = - M - ) 1 ( đpcm ) Trang 152
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THCS CẤP TỈNH VĨNH LONG
NĂM HỌC 2020 – 2021 ĐỀ CHÍNH THỨC Môn: TOÁN
Thời gian: 150 phút (không kể thời gian giao đề) Ngày thi: 14/3/2021
Bài 1. (4.0 điểm) a) Cho biểu thức 1 2 x 2 x P : 1
với x 0, x 1. x 1 x x x x 1 x 1
Rút gọn biểu thức P b) Rút gọn biểu thức 2 A 4 2 3 6 2 5 5 3 Bài 2. (4.0 điểm) 2
xy 3y x 3
a) Giải hệ phương trình 2 2
x xy 2y 0 4 8 b) Giải phương trình 2 x 4x 9 x x Bài 3. (2.0 điểm) Tìm m để phương trình 2
x 2(m 1)x 4m 0 (x là ẩn, m là tham số) có hai nghiệm x1, x2 thảo mãn 3 2 3 2
x x x x . 1 1 2 2 Bài 4. (2.5 điểm)
a) Cho ba số nguyên dương a, b, c thỏa mãn 3 3 3
a b c chia hết cho 14. Chứng minh rằng
tích abc cũng chia hết cho 14.
b) Tìm nghiệm nguyên của phương trình 2 2
x 3y 2xy 2x 10 y 4 0 . Bài 5. (3.0 điểm)
Cho đường tròn (O;R) và M là trung điểm của dây AB của đường tròn (AB<2R). Trên tia đối
của tia AB lấy điểm D sao cho AD=AM. Vẽ dây AC với C là điểm thuộc cung lớn AB. Trên đoạn
thẳng AC lấy hai điểm G và Q sao cho AG=GQ=QC. Gọi N là giao điểm của BQ và CM.
a) Chứng minh rằng ba điểm D, G, N thẳng hàng.
b) Gọi P là giao điểm của MG và CD. Biết 0
BAC 90 . Chứng minh tứ giác PGNQ là hình thoi. Bài 6. (2.5 điểm)
Cho đường tròn (O) và hai điểm A, B nằm trên đường tròn sao cho 0
AOB 90 . Điểm C nằm
trên cung lớn AB sao cho AC>BC và tam giác ABC có ba góc đều nhọn. Các đường cao AI, BK của
tam giác ABC cắt nhau ở H. BK cắt (O) ở N (N khác điểm B), AI cắt (O) ở M (M khác điểm A), hai
đường thẳng NA và MB cắt nhau ở D. Chứng minh rằng:
a) Tứ giác AHBD nội tiếp được đường tròn. b) OC song song với DH. Bài 7. (2.0 điểm)
Cho bốn số thực dương a, b, x, y thỏa mãn a+b=4ab. Chứng minh rằng: a b 2 2 2 a b a b 1 a) x y x b) y 2 2 4b 1 4a 1 2 Trang 153 ---HẾT---
Lưu ý: Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
ĐÁP ÁN THAM KHẢO – VĨNH LONG (2020 – 2021) Bài 1. a) P tương đương: 1 2 x x 2 x 1 P : x 1
(x 1)( x 1) x 1 x 1 2 x x 1 .
(x 1)( x 1) x 2 x 1 1 x 1 2( 5 3) b) 2 2 A ( 3 1) ( 5 1) 2
A 3 1 5 1 5 3 A 2 5 Bài 2. x y
a) Phương trình thứ hai tương đương: 2 2
(x y ) y(x y) 0 (x y)(x 2 y) 0 x 2 y
Với x=y, thay vào phương trình thứ nhất của hệ ta được: x= -1 hoặc x=3/4
Với x = -2y, thay vào phương trình thứ nhất của hệ ta được: y 1 x 2 2
y 2 y 3 0
y 3 x 6 3 3
Vậy hệ đã cho có 4 nghiệm: ( ; x y) ( 1 ; 1 ) ( ; ) (2; 1 ) ( 6 ;3) 4 4
b) Điều kiện: x 0 4 2 2 2
Phương trình tương đương với: 2 x 4
4(x ) 4 9 2
(x ) 4(x ) 5 0 2 x x x x 2 t 5
Đặt x =t, phương trình trở thành: 2
t 4t 5 0 x t 1 5 33
Với t=5, thay vào ta tìm được: x 2
Với t=-1, thay vào ta tìm được: x=-2, x=1 5 33
Vậy phương trình có 4 nghiệm: x , x=-2, x=1 2 Bài 3.
Điều kiện để phương trình có hai nghiệm là: ' 2
(m 1) 0 (luôn đúng). Do đó phương trình luôn có 2 nghiệm x1, x2 Ta có: 3 2 3 2
x x x x 1 1 2 2 Trang 154 3 3 2 2
x x x x 0 1 2 1 2 2 2
(x x )(x x x x x x ) 0 1 2 1 1 2 2 1 2 x x 0 1 2 2 2
x x x x x x 0 1 1 2 2 1 2
2x 2(m 1) 1
TH1: x x m 1 1 2 2 x 4m 1 TH2: 2 2
x x x x x x 0 1 1 2 2 1 2
(x x ) x x (x x ) 0 2(m1)2 2 2
4m 2(m 1) 0 4m 2m 2 0 (Vô 1 2 1 2 1 2 nghiệm) Vậy m=1 Bài 4.
a) Nhận xét: Với x nguyên dương ta có 3 x 0,1(mod 2) và 3 x 1 ,0,1(mod 7)
Nếu cả ba số a, b, c đều không chia hết cho 2 thì 3 3 3
a b c 1(mod 2)
Điều này trái với giả thiết 3 3 3
a b c 14 , do đó phải có một số chia hết cho 2 hay abc 2
Nếu cả ba số a, b, c đều không chia hết cho 7 thì 3 3 3
a b c 3 , 1 ,1,3(mod 7)
Điều này trái với giả thiết 3 3 3
a b c 14 , do đó phải có một số chia hết cho 7 hay abc 7 Vậy abc chia hết cho 14 b) Ta có: 2 2
x 3y 2xy 2x 10 y 4 0 2 2 2
x 2x(y 1) (y 1) (4y 8y 4) 7
(3y x 1)(y x 3) 7
Vì 7 là số nguyên tố nên ta có các trường hợp sau: 3
y x 1 7 3
y x 1 7 3
y x 1 1 3
y x 1 1 ; ; ;
y x 3 1 y x 3 1 y x 3 7 y x 3 7 Kết luận: ( ; x y) ( 3 ;1) (1; 3 ) (7; 3 ) Bài 5. a) Hướng dẫn:
- Chứng minh G là trọng tâm của tam giác MCD. - Chứng minh NC=NQ. Trang 155
Suy ra DN là trung tuyến của tam giác MCD Suy ra D, G, N thẳng hàng. b) Hướng dẫn:
- Chứng minh tam giác MCD cân tại C.
- Chứng minh P là trung điểm của DC.
- Chứng minh 2 đường chéo của tứ giác PGNQ là đường trung trực của nhau.
Suy ra tứ giác PGNQ là hình thoi. Bài 6. a) Có 0 0 0
HK KC, HI IC HKC HIC 90 90 180
Tứ giác AHBD nội tiếp được đường tròn
b) Dễ dàng chứng minh được MN là đường kính của (O) MA DN, NB DN
Do đó H là trực tâm D
MN hay DH MN
Do I, K cùng nhìn AB dưới góc 450 nên tứ giác ABIK nội tiếp CAI CBR
Do đó C là điểm chính giữa của cung MN CO MN
Vì AC>BC nên tam giác ABC không cân tại C Vậy CO//DH Bài 7. a) Ta có: a b a b2 2 2 x y x y a y b x a b2 2 2 xy x y
(a y b x)(x y) xy a b2 2 2 2 2 2 2 2 2 2 2
a xy a y b x b xy a xy 2abxy b xy 2 2 2 2
a y b x 2abxy 2
(ay bx) 0 1
b) Ta có: 4ab a b 2 ab ab 4 Áp dụng phần a) ta có: Trang 156
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9 VĨNH PHÚC
NĂM HỌC 2020 – 2021 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) 2 2 2 a b a b (a b) 1 1 1 2 2 2 2 4b 1 4a 1 4ab a 4ba b
4ab(a b) (a b) 4ab 1 2 1
Dấu “=” xảy ra khi: a b 2 2 x 1 3
x 3 4x 4
Bài 1. Cho biểu thức P . 2
2x 2 x 1 2x 2 5
a) Tìm điều kiện xác định của P
b) Chứng minh rằng khi P xác định thì giá trị của P không phụ thuộc vào x
Bài 2. a) Cho x, y, z là ba số thỏa mãn xyz = 1 và 1 1 1
x y z x y z
Tính giá trị của biểu thức P 9 x 2020 y 2021 1 1 z 1
b) Trong mặt phẳng tọa độ Oxy, đường thẳng (d) có phương trình y = ax + b cắt
các trục tọa độ Ox, Oy lần lượt tại A, B sao cho diện tích tam giác OAB bằng 2 và tổng
OA + OB đạt giá trị nhỏ nhất. Viết phương trình đường thẳng (d). m 3 5 3m mx 3
Bài 3. a) Cho phương trình
(m là tham số). Tìm m để phương 2 x 1 x 2 x x 2 trình vô nghiệm 3 2 2
x 2y x y 2xy
b) Giải hệ phương trình 2 3 3
2 x 2y 1 y 14 x 2
Bài 4. a) Cho tam giác ABC vuông tại A, có D là chân đường phân giác trong của góc A,
H là chân đường vuông góc hạ từ A (D, H thuộc BC), BD = 6 cm, CD = 8 cm. Tính độ dài CH.
b) Tứ giác ABCD có đường tròn đường kính AD tiếp xúc với BC và đường tròn
đường kính BC tiếp xúc với AD. Chứng minh rằng ACD BAC .
c) Cho tam giác ABC vuông tại A (ABphân giác của CAH cắt CH tại K, gọi M là trung điểm của AC, MK cắt AH tại N. Chứng
minh rằng AK song song với BN. a b c
Bài 5. a) Cho các số thực dương a, b, c. Chứng minh rằng 4 2 . b c c a a b
b) Anh A vào làm ở công ty X với mức lương ban đầu là 10 triệu đồng/tháng. Nếu
hoàn thành tốt nhiệm vụ thì cứ sau 6 tháng làm việc, lương của anh sẽ được tăng them
20% so với mức lương mà anh đang hưởng tại thời điểm đó. Hỏi bắt đầu từ tháng thứ mấy Trang 157
kể từ khi vào làm việc tại công ty X, tiền lương mỗi tháng của anh Anhiều hơn 20 triệu
đồng (Biết rằng trong suốt thời gian làm ở công ty X, anh A luôn hoàn thành tốt nhiệm vụ). ------HẾT------
ĐÁP ÁN THAM KHẢO – VĨNH PHÚC (2020 – 2021) Bài 1.
a) Điều kiện xác định: x 1 b) Ta có: 2 2 (x 1) 3
(x 3)(x 1) 4x 4 P . 2
2(x 1)(x 1) x 1 2(x 1)(x 1) 5 2 2 2
x 2x 1 3 x 2x 3 4x 4 . 2 2(x 1) 5 2 7.4.(x 1) 2 2(x 1).5 14 5
Suy ra điều phải chứng minh. Bài 2. a) Ta có: 1 1 1
xy yz zx
xy yz zx
x y z
xy yz zx x y z xyz 1
Thấy: (x 1)( y 1)(z 1) (xy x y 1)(z 1) 1 xy xz yz x y z 1 0 Suy ra: x=y=z=1 Thay vào P ta được: P=0 b b) Ta có: OA , OB b a 1 2 S 2 .O .
A OB 2 O .
A OB 4 b 4 a OAB 2
OA OB 2 O . A OB 2 4 4
Min(OA+OB)=4. Dấu “=” xảy ra b 1 khi OA=OB
b b ( 1) 0 a 1 a a Với a 1 2
b 4 b 2
Vậy phương trình (d): y=x+2; y=x-2; y=-x+2; y=-x-2 Bài 3.
a) Phương trình tương đương với:
(m 3)(x 2) (5 3m)(x 1) mx 3 ( 2
3m)x m 14 Trang 158 2 3m 0
Để phương trình vô nghiệm thì: 2 m m 14 0 3 Vậy 2 m 3
b) Điều kiện xác định: 2 x 2 y 1 Ta có: 3 2 2 2
x 2 y x y 2xy (x y)(x 2 y) 0 x=y (t/m), 2
x 2 y (loại) Với x=y, ta có: 3 2 3 2
x 6x 12 8 0 (x 14) 6(x 2x 1) 0 Đặt: 2
x 2x 1 a 0, x 2 b 3 2 2 2 3 3 2
2a b 6a b 8
a 6b a 12ba 6a 0 Suy ra: 3 3 2 3 3 2
b 6a b 2a
b 6a b 2a
a 0 x y 2 1 Bài 4. a)
AD là đường phân giác của góc A DB AB 6 3
AB AC DC AC 8 4 9 Mà 2 2 2 2 2 2
BC AB BC 14
AC AC AC 11, 22 16
Áp dụng hệ thức lượng trong ABC có: 2
AC CH.BC 125, 44 CH.14 CH 8,96 b) c) Trang 159 Xét A
NC có phân giác AK, trung tuyến NM, đường cao AH đồng quy tại K A NCđều NM AC 0
A A 60 1 2 0
A 30 A A 3 1 2
Lại có: AB AC, NM AC AB / / NM A N 1 2 0
N N 30 (1) 1 2 Xét A
MK vuông tại M có 0 0
A 30 K 60 (2) 2 1 Từ (1) và (2) suy ra: 0
BNM K 60 AK / /BN 1 Bài 5.
a) Đặt: x=b+c, y=c+a, z=a+b (x,y,z>0). Ta được: y z x z x y x y z a , b , c 2 2 2 a b 4c
y z x
z x y
4(x y z) Ta có: b c c a a b 2x 2 y 2z y z z x 2(x y) 3 2x 2 y z y x z 2x z 2 y 1
3 2. 2 2 3 2
2x 2y 2x z 2y z 2 x y
Dấu “=” xảy ra khi: x y z
z 2x 2x 2 y z . Khi đó c 0 (vô lí vì c>0) 2 z 2 y
Vậy dấu “=” không xảy ra nên a b 4c 2 b c c a a b
b) Sử dụng công thức lãi kép (1 )N T A r
với A là số tiền ban đầu, N là số kì hạn, r là lãi suất và
T là số tiền có được sau N kì hạn.
Gọi N là số lần tăng lương của anh A đến khi lương nhiều hơn 20 triệu, khi đó:
10(1 20%)N 20 1,2N T 2 N 4
Vậy sau 4 lần tăng lương hay sau 4.6=24 tháng thì đến tháng thứ 25 anh A sẽ có mức lương 20 triệu Trang 160
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THCS TỈNH YÊN BÁI
NĂM HỌC 2020 – 2021 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) Ngày thi: 12/03/2021
Câu 1. (4,0 điểm)
1) Tính giá trị của biểu thức A x x 2021 5 7 1 , biết 4 2 3 4 2 3 x 12 2 3 3 x (1 x) 1 x 1 x
2) Cho biểu thức B : x x 1 x 1 x 1 x
Với x 0; x 1. Chứng minh rằng 1 M x B 0 2
Câu 2. (4,0 điểm) 1) Giải phương trình: 2
x 4 2020 x 3 2020 x 7x 12
x 3y 5xy
2) Giải hệ phương trình: 2 2 2
x y 5xy
Câu 3. (6,0 điểm)
Cho tam giác ABC vuông tại C, nội tiếp đường trong tâm (O) (CA>CB). Lấy M là điểm
chính giữa của cung nhỏ AC. Các đường thẳng AM và BC cắt nhau tại I, các đường thẳng AC và BM cắt nhau tại K. 1) Chứng minh ABI
cân và tứ giác MICK nội tiếp.
2) Đường thẳng BM cắt tiếp tuyến tại A của (O) tại N. Chứng minh đường thẳng
NI là tiếp tuyến của (B;BA) và NI MO
3) Đường tròn ngoại tiếp tam giác BIK cắt đường tròn (B;BA) tại D (D không
trùng với I). Chứng minh rằng 3 điểm A, C, D thẳng hàng.
Câu 4. (4,0 điểm) Trang 161
1) Tìm các số nguyên x, y thỏa mãn 4 2
x y 4 y 1
2) Tìm tất cả các số nguyên dương n sao cho hai số n+50 và n-11 đều là lập phương
của hai số nguyên dương nào đó.
Câu 5. (2,0 điểm)
Cho x, y, z là các số thực dương thỏa mãn 2 2 2
x y z 1 x y z
Tìm giá trị nhỏ nhất của biểu thức P 2 2 2 2 2 2 y z z x x y ------HẾT------
ĐÁP ÁN THAM KHẢO – YÊN BÁI (2020 – 2021) Câu 1. 2 2 3 1 3 1 3 1 3 1
1) Biến đổi x ta được: 3 1 3 1 x 1 2 3 2 3 2 3 2021 2021 Suy ra: A 5 7 x x 5 7 1 11 1 1 2) Rút gọn B: 2 x (1 x) B : (x x 1
x )(x 1 2 x ) 1 x 2 x (1 x) 2 : (1 x) 1 x x x1
Từ đó thay B vào biểu thức của M dễ dàng suy ra điều phải chứng minh Câu 2.
1) Điều kiện x 3
Phương trình tương đương với: 2020 x 3 1
x 3 x 4 1 x 3 1 0 x 2 2
x 4 1 2020 x 2021 4
Kêt hợp điều kiện thì cả 2 giá trị của x đều thỏa mãn Kết luận: x 2 ; 2 x 2021 4
2) Đáp số: x y 2 1 1 ( ; ) 0; 0 ; (1; ) 5 5 2 Câu 3. Trang 162
1) M là chính giữa của AC AM MC B B (góc nội tiếp chắn 2 cung bằng nhau) 1 2 Ta có 0
BMA 90 (góc nội tiếp chắn nửa đường tròn) Xét BAI
có BM là đường cao đồng thời là đường phân giác nên BAI cân tại B Xét tứ giác MICK ta có: 0 0 0
IMK KCI 90 90 180
Mà IMK và KCI là hai góc nhọn đối nhau
Vậy tứ giác MICK nội tiếp 2) Ta có BAI
cân tại I BA BI I (B, B ) A (1) Xét N
IAcó NM là đường cao đồng thời là đường trung tuyến N IAcân tại N
NAI NIA
Mà AIB BAI (Vì BAI cân) 0
NIA AIB NAI IAB 90 (Vì BA NA do NA là tiếp tuyến)
BI IN (2)
Từ (1) và (2) suy ra: NI là tiếp tuyến của (B;BA)
Ta lại có: NI BC, AC BC NI AC , mà AC MO (dễ dàng chứng minh) NI MO 1
3) Xét đường tròn (B;BA) ta có IDA
IBA (góc nội tiếp và góc ở tâm) 2 1 IBN
IBA IDA IBN 2
Mà IBN IDK (góc nội tiếp cùng chắn cung IK)
IDA IDK Hai tia DA và DK phải trùng nhau (mà A, K, C thẳng hàng) hay ba điểm A, C, D thẳng hàng Câu 4. 1) Ta có: 4 2
x y 4 y 1 4 2 2 2
x (y 2) 3 (x y 2)(x y 2) 3 Ta có bảng sau: 2 x y 2 -3 -1 1 3 2 x y 2 1 3 -3 -1 2 x y -1 1 3 5 2 x y -1 1 -5 -3 x Vô nghiệm 1 Vô nghiệm 1 y 0 0 -4 -4 Trang 163
Vậy nghiệm: (x;y)=(1;0)=(-1;0)=(1;-4)=(-1;-4)
2) Gọi n+50=x3 ; n-11=y3 (x3 > y3 nên x>y>0), ta có: (n+50)-(n-11)= x3- y3
⇔ 61.1= x3- y3= (x-y)(x2+xy+y2) ⇒ x-y=1 và x2+xy+y2=61
Giải ra ta được: y=5, x=6 Suy ra: n=166. Câu 5. 2 x x x Ta có: 2 2 2 2 y z 1 x x(1 x ) Đặt: 2
A x(1 x ) 2 2 2 2
2A 2x (1 x )(1 x ) 3 2 2 2
2x 1 x 1 x 8 Theo AM - GM: 2 2A 3 27 2 A 3 3 x 3 3 2 x 2 2 y z 2 Tương tự: y 3 3 z 3 3 2 2 y , z 2 2 2 2 z x 2 x y 2 3 3 3 3 Suy ra: P hay MinP= 2 2 Dấu “=” xảy ra khi: 1
x y z 3
Kính thưa các thầy cô:
Trên đây là ĐÁP ÁN THAM KHẢO, do đó không tránh được những nhầm lẫn nên nếu có
nhầm lẫn rất mong quý thầy cô thông cảm.
Quý thầy cô có thể chia sẻ tài liệu tới bạn bè, người thân nhưng kính mong các thầy cô
không chia sẻ lên internet.
Chúc quý thầy cô may mắn trong công việc.
Trân trọng cảm ơn quý thầy cô. Trang 164




