






















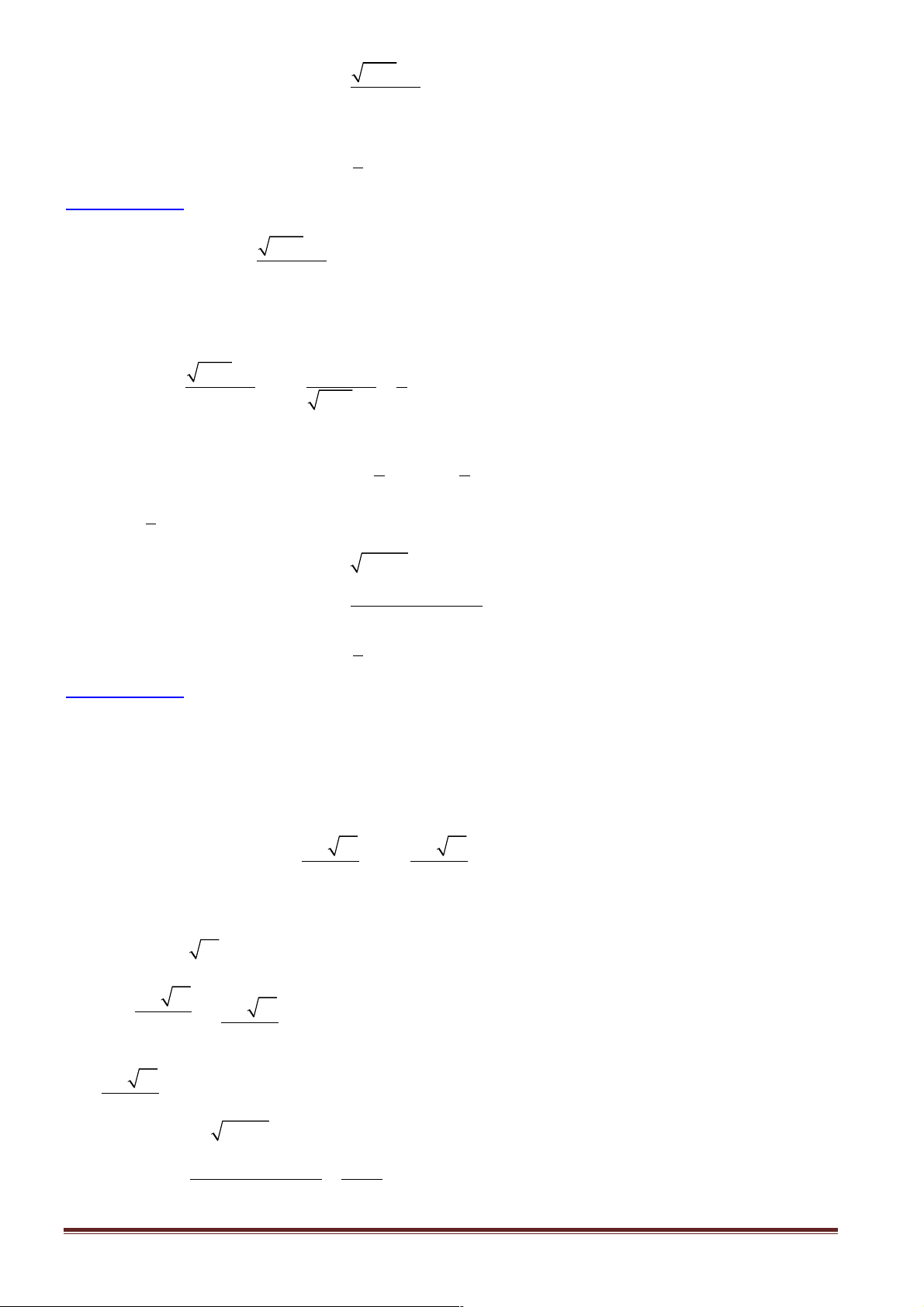

Preview text:
BÀI TẬP TRẮC NGHIỆM HÀM SỐ LIÊN TỤC
A – LÝ THUYẾT VÀ PHƯƠNG PHÁP
1. Hàm số liên tục tại một điểm: y = f(x) liên tục tại x0 Û lim f (x) = f (x ) 0 x® 0 x
• Để xét tính liên tục của hàm số y = f(x) tại điểm x0 ta thực hiện các bước: B1: Tính f(x0).
B2: Tính lim f (x) (trong nhiều trường hợp ta cần tính lim f (x) , lim f (x) ) x® + - 0 x x® x® 0 x 0 x
B3: So sánh lim f (x) với f(x0) và rút ra kết luận. x® 0 x
2. Hàm số liên tục trên một khoảng: y = f(x) liên tục tại mọi điểm thuộc khoảng đó.
3. Hàm số liên tục trên một đoạn [a; b]: y = f(x) liên tục trên (a; b) và
lim f (x) = f (a), lim f (x) = f (b) + - x®a x®b
• Hàm số đa thức liên tục trên R.
• Hàm số phân thức, các hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
Giả sử y = f(x), y = g(x) liên tục tại điểm x0. Khi đó:
• Các hàm số y = f(x) + g(x), y = f(x) – g(x), y = f(x).g(x) liên tục tại x0. f (x) • Hàm số y =
liên tục tại x0 nếu g(x0) ¹ 0. g(x)
4. Nếu y = f(x) liên tục trên [a; b] và f(a). f(b)< 0 thì tồn tại ít nhất một số c Î (a; b): f(c) = 0.
Nói cách khác: Nếu y = f(x) liên tục trên [a; b] và f(a). f(b)< 0 thì phương trình f(x) = 0 có ít nhất một nghiệm cÎ (a; b).
Mở rộng: Nếu y = f(x) liên tục trên [a; b]. Đặt m = min f (x) , M = max f (x) . Khi đó với mọi T Î (m; M) luôn tồn [a;b] [a;b]
tại ít nhất một số c Î (a; b): f(c) = T. B – BÀI TẬP
DẠNG 1: TÍNH LIÊN TỤC CỦA HÀM SỐ TẠI MỘT ĐIỂM Phương pháp:
• Tìm giới hạn của hàm số y = f (x) khi x ® x và tính f (x ) 0 0
• Nếu tồn tại lim f (x) thì ta so sánh lim f (x) với f (x ). x® x® 0 0 x 0 x Chú ý:
1. Nếu hàm số liên tục tại x thì trước hết hàm số phải xác định tại điểm đó 0
2. lim f (x) = l Û lim f (x) = lim f (x) = l . + - x® 0 x x®x x® 0 0 x
ì f (x) khi x ¹ x 3. Hàm số 0 y = í
liên tục tại x = x Û lim f (x) = k . k khi x = î x 0 x®x 0 0
ì f (x) khi x ³ x 4. Hàm số 1 0 f (x) = í
liên tục tại điểm x = x khi và chỉ khi
f (x) khi x < î x 0 2 0
lim f (x) = lim f (x) = f (x ) . + 1 - 2 1 0 x®x x® 0 0 x Chú ý:
ì f (x) khi x ¹ x • Hàm số 0 y = í
liên tục tại x = x khi và chỉ khi k khi x = î x 0 0
lim f (x) = k . x® 0 x Trang 1
ì f (x) khi x > x • Hàm số 0 y = í
liên tục tại x = x khi và chỉ khi
g(x) khi x £ î x 0 0
lim f (x) = lim g(x) . + - x®x x® 0 0 x 2 x -1
Câu 1. Cho hàm số f ( x) = và f ( ) 2
2 = m - 2với x ¹ 2. Giá trị của m để f ( x) liên tục tại x = 2là: x +1 A. 3 . B. - 3 . C. ± 3 . D. 3 ±
Câu 2. Cho hàm số f ( x) 2
= x - 4 . Chọn câu đúng trong các câu sau:
(I) f ( x) liên tục tại x = 2 .
(II) f ( x) gián đoạn tại x = 2 .
(III) f ( x) liên tục trên đoạn [ 2; - 2].
A. Chỉ (I ) và (III ) . B. Chỉ (I ) .
C. Chỉ (II ) . D. Chỉ (II ) và (III ) 2 ì x +1 ï x ¹ 3; x ¹ 2
Câu 3. Cho hàm số f ( x) 3 = í x - x + 6
. Tìm b để f ( x)liên tục tại x = 3. ï îb + 3 x = 3; b Î ! 2 3 A. 3 . B. - 2 3 3 . C. . D. - . 3 3 x -
Câu 4. Cho hàm số f ( x) 1 =
. Tìm khẳng định đúng trong các khẳng định sau: x -1
(I ) f (x)gián đoạn tại x =1.
(II ) f (x)liên tục tại x =1. ( 1
III ) lim f ( x) = x 1 ® 2 A. Chỉ (I ) . B. Chỉ (I ) .
C. Chỉ (I ) và (III ) . D. Chỉ (II ) và (III ). ì 2x +8 - 2 ï x > 2 -
Câu 5. Cho hàm số f ( x) = í x + 2
. Tìm khẳng định đúng trong các khẳng định sau: ï î0 x = 2 -
(I ) lim f (x) = 0 . x 2+ ®-
(II ) f (x)liên tục tại x = 2. -
(III ) f (x)gián đoạn tại x = 2. -
A. Chỉ (I ) và (III ) .
B. Chỉ (I ) và (II ) . C. Chỉ (I ) . D. Chỉ (I ) ìï - x - £ x £
Câu 6. Cho hàm số f ( x) 2 4 2 2 = í
. Tìm khẳng định đúng trong các khẳng định sau:. 1 ïî x > 2
(I ) f (x)không xác định tại x = 3.
(II ) f (x)liên tục tại x = 2. -
(III ) lim f (x) = 2 x®2 A. Chỉ (I ) .
B. Chỉ (I ) và (II ) .
C. Chỉ (I ) và (III ) .
D. Cả (I ); (II ); (III ) đều sai. Trang 2 ìsin 5x ï x ¹ 0
Câu 7. Cho hàm số f ( x) = í 5x
. Tìm a để f ( x) liên tục tại x = 0. ïîa + 2 x = 0 A. 1. B. 1 - . C. 2 - . D. 2. ( ì x + )2 1 , x > 1 ïï
Câu 8.Cho hàm số f ( x) 2
= íx + 3 , x <1 . Tìm k để f (x) gián đoạn tại x =1. ï 2 k , x = 1 ïî A. k ¹ 2 ± . B. k ¹ 2 . C. k ¹ 2 - . D. k ¹ 1 ± . ì x - 2 ï khi x ¹ 4 ï Câu 9.Cho hàm số x - 4 f (x) = í
. Khẳng định nào sau đây đúng nhất 1 ï khi x = 4 ïî4
A. Hàm số liên tục tại x = 4
B. Hàm số liên tục tại mọi điểm trên tập xác định nhưng gián đoạn tại x = 4
C. Hàm số không liên tục tại x = 4
D. Tất cả đều sai 2 ì x - 3x + 2 ï + 2 khi x >1
Câu 10. Cho hàm số f (x) = í x -1
. Khẳng định nào sau đây đúng nhất ï 2 3
î x + x -1 khi x £ 1
A. Hàm số liên tục tại x = 1
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại x = 1
D. Tất cả đều sai ì p x ï x £
Câu 11. Cho hàm số 3. f ( x) cos khi 1 = í 2
. Khẳng định nào sau đây đúng nhất
ï x -1 khi x >1 î
A. Hàm số liên tục tại tại x = 1và x = 1 - .
B. Hàm số liên tục tại x = 1, không liên tục tại điểm x = 1 - .
C. Hàm số không liên tục tại tại x = 1và x = 1 - .
D. Tất cả đều sai 2x +1 -1
Câu 12. Chọn giá trị f (0) để các hàm số f (x) =
liên tục tại điểm x = 0 . x(x +1) A. 1 B. 2 C. 3 D. 4 3 2x + 8 - 2
Câu 13. Chọn giá trị f (0) để các hàm số f (x) =
liên tục tại điểm x = 0 . 3x + 4 - 2 2 1 A. 1 B. 2 C. D. 9 9 ì x + x + 2 ï khi x > 1 -
Câu 14. Cho hàm số f (x) = í x +1
. Khẳng định nào sau đây đúng nhất
ïî2x +3 khi x £ 1 -
A. Hàm số liên tục tại tại tại x = 1 - 0
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại tại x = 1 - . 0
D. Tất cả đều sai Trang 3 3 ì x +1+ x -1 ï khi x ¹ 0
Câu 15. Cho hàm số 3. f (x) = í x
. Khẳng định nào sau đây đúng nhất ïî2 khi x = 0
A. Hàm số liên tục tại x = 0 0
B. Hàm số liên tục tại mọi điểm như gián đoạn tại x = 0 0
C. Hàm số không liên tục tại x = 0 0
D. Tất cả đều sai 3 ì x -1 ï khi x ¹ 1 ï Câu 16. Cho hàm số x -1 f (x) = í
. Khẳng định nào sau đây đúng nhất 1 ï khi x =1 ïî3
A. Hàm số liên tục tại x = 1
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại tại x = 1
D. Tất cả đều sai 2 ì x - x - 2 ï
+ 2x khi x > 2
Câu 17. Cho hàm số f (x) = í x - 2 ï 2
îx - x + 3 khi x £ 2
. Khẳng định nào sau đây đúng nhất
A. Hàm số liên tục tại x = 2 0
B. Hàm số liên tục tại mọi điẻm
C. Hàm số không liên tục tại x = 2 0
D. Tất cả đều sai
ì x + 2a khi x < 0
Câu 18. Tìm a để các hàm số f ( x) = í
liên tục tại x = 0 2
îx + x +1 khi x ³ 0 1 1 A. B. C. 0 D. 1 2 4 ì 4x +1 -1 ï khi x ¹ 0
Câu 19. Tìm a để các hàm số 2
f (x) = íax + (2a +1)x
liên tục tại x = 0 3 khi ï î x = 0 1 1 1 A. B. C. - D. 1 2 4 6 ì 3x +1 - 2 ï khi x > 1 2 ï Câu x -
20.Tìm a để các hàm số 1 f (x) = í
liên tục tại x = 1 2
ïa(x - 2) khi x £1 ïî x -3 1 1 3 A. B. C. D. 1 2 4 4 Trang 4
DẠNG 2: TÍNH LIÊN TỤC CỦA HÀM SỐ TRÊN TẬP XÁC ĐỊNH Phương pháp:
+ Sử dụng các định lí về tính liên tục của hàm đa thức, lương giác, phân thức hữu tỉ …
+ Nếu hàm số cho dưới dạng nhiều công thức thì ta xét tính liên tục trên mỗi khoảng đã chia và tại các điểm
chia của các khoảng đó.
Câu 1. Tìm khẳng định đúng trong các khẳng định sau: ( 1
I ) f ( x) = liên tục trên ! . 2 x -1 (II ) ( ) sin = x f x
có giới hạn khi x ® 0. x
(III ) f (x) 2
= 9 - x liên tục trên đoạn [ 3; - ]3.
A. Chỉ (I ) và (II ) .
B. Chỉ (II ) và (III ) .
C. Chỉ (II ) .
D. Chỉ (III ) .
Câu 2. Tìm khẳng định đúng trong các khẳng định sau: ( x +
I ) . f ( x) 1 =
liên tục với mọi x ¹ 1. x -1
(II ) . f (x) = sin x liên tục trên ! . ( x
III ) . f ( x) =
liên tục tại x = 1. x
A. Chỉ (I ) đúng.
B. Chỉ (I ) và (II ) .
C. Chỉ (I ) và (III ) .
D. Chỉ (II ) và (III ) . 2
ì x - 3 , x ¹ 3 ï
Câu 3. Cho hàm số f ( x) = í x - 3
. Tìm khẳng định đúng trong các khẳng định sau: ï î2 3 , x = 3
(I ) . f (x) liên tục tại x = 3 .
(II ) . f (x) gián đoạn tại x = 3.
(III ) . f (x) liên tục trên ! .
A. Chỉ (I ) và (II ) .
B. Chỉ (II ) và (III ) .
C. Chỉ (I ) và (III ) .
D. Cả (I ) , (II ) , (III ) đều đúng.
Câu 4. Tìm khẳng định đúng trong các khẳng định sau:
(I ) . f (x) 5 2
= x – x +1 liên tục trên ! . ( 1
II ) . f ( x) =
liên tục trên khoảng ( –1; ) 1 . 2 x -1
(III ) . f (x) = x - 2 liên tục trên đoạn [2;+¥).
A. Chỉ (I ) đúng.
B. Chỉ (I ) và (II ) .
C. Chỉ (II ) và (III ) .
D. Chỉ (I ) và (III ) . ì3- 9 - x ï , 0 < x < 9 ï x ï
Câu 5. Cho hàm số f ( x) = ím , x = 0
. Tìm m để f ( x) liên tục trên [0;+¥) là. ï3 ï , x ³ 9 ïî x Trang 5 1 1 1 A. . B. . C. . D. 1. 3 2 6 2 x +1
Câu 6. Cho hàm số f (x) =
.Khi đó hàm số y = f ( x) liên tục trên các khoảng nào sau đây? 2 x + 5x + 6 A. ( 3; - 2). B. ( 2; - +¥). C. ( ;3 -¥ ) . D. (2;3). 2 ì x - 5x + 6 ï khi x < 2
Câu 7. Cho hàm số f ( x) 3 = í 2x -16
. Khẳng định nào sau đây đúng nhất. ïî 2- x khi x ³ 2
A. Hàm số liên tục trên !
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục trên (2 : +¥)
D. Hàm số gián đoạn tại điểm x = 2 . 3 ì x -1 ï khi x > 1 ï x - Câu 1
8. Cho hàm số f (x) = í
. Khẳng định nào sau đây đúng nhất. 3
ï 1- x + 2 khi x £1 ïî x + 2
A. Hàm số liên tục trên !
B. Hàm số không liên tục trên !
C. Hàm số không liên tục trên (1: +¥)
D. Hàm số gián đoạn tại các điểm x = 1. ìtan x p ï
, x ¹ 0 Ù x ¹ + kp ,k Î!
Câu 9. Cho hàm số f ( x) = í x 2
. Hàm số y = f ( x) liên tục trên các khoảng ïî0 , x = 0 nào sau đây? æ p ö æ p ö æ p p ö A. 0; . B. ; -¥ . C. - ; . D. ( ; -¥ +¥) . ç ÷ ç ÷ ç ÷ è 2 ø è 4 ø è 4 4 ø 2 2
ìïa x , x £ 2,aÎ!
Câu 10. Cho hàm số f ( x) = í
. Giá trị của a để f ( x) liên tục trên ! là: ( ï 2 - î a) 2 x , x > 2 A. 1 và 2 . B. 1 và –1. C. –1 và 2 . D. 1 và –2 . 2 ìx , x ³1 ï 3 ï 2x
Câu 11. Cho hàm số f ( x) = í
, 0 £ x < 1. Tìm khẳng định đúng trong các khẳng định sau: 1+ ï x
ïxsin x , x < 0 î
A. f ( x) liên tục trên ! .
B. f ( x) liên tục trên ! \{ } 0 .
C. f ( x) liên tục trên ! \{ } 1 .
D. f ( x) liên tục trên ! \{0; } 1 . x + 2
Câu 12. Cho hàm số f (x) =
. Khẳng định nào sau đây đúng nhất. 2 x - x - 6
A. Hàm số liên tục trên !
B. TXĐ : D = ! \{3;- }
2 .Ta có hàm số liên tục tại mọi x Î D và hàm số gián đoạn tại x = 2, - x = 3
C. Hàm số liên tục tại x = 2, - x = 3
D. Tất cả đều sai Câu 13. Cho hàm số 2
f (x) = 3x -1 . Khẳng định nào sau đây đúng nhất.
A. Hàm số liên tục trên ! Trang 6 æ 1 ö æ 1 ö
B. Hàm số liên tục tại mọi điểm x Î ; -¥ - È ;+¥ ç ÷ ç ÷ è 3 ø è 3 ø æ 1 ù é 1 ö C. TXĐ : D = ; -¥ È ;+¥ ç ú ê ÷ è 2 û ë 2 ø æ 1 1 ö
D. Hàm số liên tục tại mọi điểm x Î - ; . ç ÷ è 3 3 ø
Câu 14. Cho hàm số f (x) = 2sin x + 3tan 2x . Khẳng định nào sau đây đúng nhất.
A. Hàm số liên tục trên !
B. Hàm số liên tục tại mọi điểm ìp p ü
C. TXĐ : D = ! \ í + k , k Î"ý
D. Hàm số gián đoạn tại các điểm î 2 2 þ p p x = + k ,k Î! 4 2 2 ì x - 3x + 2 ï khi x ¹ 1
Câu 15. Cho hàm số f ( x) = í x -1
. Khẳng định nào sau đây đúng nhất. ï î a khi x = 1
A. Hàm số liên tục trên !
B. Hàm số không liên tục trên !
C. Hàm số không liên tục trên (1: +¥)
D. Hàm số gián đoạn tại các điểm x = 1. ì 2x +1 -1 ï khi x ¹ 0
Câu 16. Cho hàm số f ( x) = í x
. Khẳng định nào sau đây đúng nhất. ïî 0 khi x = 0
A. Hàm số liên tục trên !
B. Hàm số không liên tục trên !
C. Hàm số không liên tục trên (0;+¥)
D. Hàm số gián đoạn tại các điểm x = 0 .
ì2x +1 khi x £ 0 ï Câu 17. Cho hàm số 3
f (x) = í(x -1) khi 0 < x < 2 . Khẳng định nào sau đây đúng nhất. ï
î x -1 khi x ³ 2
A. Hàm số liên tục trên !
B. Hàm số không liên tục trên !
C. Hàm số không liên tục trên (2;+¥)
D. Hàm số gián đoạn tại các điểm x = 2 . 2 ì2
ï x + x +1 khi x £1
Câu 18. Cho hàm số f (x) = í
. Khẳng định nào sau đây đúng nhất. 3
ï x -1 khi x >1 î
A. Hàm số liên tục trên !
B. Hàm số không liên tục trên !
C. Hàm số không liên tục trên (2;+¥)
D. Hàm số gián đoạn tại các điểm x = 1 ± . ì p sin x khi x £ ïï Câu 2
19. Xác định a,b để các hàm số f ( x) = í liên tục trên ï p !
ax + b khi x > ïî 2 ì 2 ì 2 ì 1 ì 2 ïa = ïa = ïa = ïa = A. í p B. í p C. í p D. í p ïîb =1 ïîb = 2 ïîb = 0 ïîb = 0 Trang 7 3 2
ì x - 3x + 2x khi x(x-2) ¹ 0 ï x(x -2) ïï
Câu 20. Xác định a,b để các hàm số f (x) = ía khi x = 2 liên tục trên ! ïb khi x = 0 ï ïî ìa = 10 ìa = 11 ìa = 1 ìa = 12 A. í B. í C. í D. í îb = 1 - îb = 1 - îb = 1 - îb = 1 - 3 ì x - 2 + 2x -1 ï khi x ¹ 1
Câu 21. Tìm m để các hàm số f (x) = í x -1 liên tục trên ! 3
ïî m-2 khi x =1 4 A. m = 1 B. m = C. m = 2 D. m = 0 3 ì x +1 -1 ï khi x > 0
Câu 22. Tìm m để các hàm số f (x) = í x liên tục trên ! ï 2
î2x + 3m +1 khi x £ 0 1 A. m = 1 B. m = - C. m = 2 D. m = 0 6
ì 2x - 4 + 3 khi x ³ 2 ï
Câu 23. Tìm m để các hàm số f (x) = í liên tục trên ! x +1 ï khi x < 2 2
î x - 2mx + 3m + 2 1 A. m = 1 B. m = - C. m = 5 D. m = 0 6 Trang 8
DẠNG 3: ÁP DỤNG TÍNH LIÊN TỤC XÉT SỐ NGHIỆM CỦA PHƯƠNG TRÌNH Phương pháp :
• Để chứng minh phương trình f (x) = 0 có ít nhất một nghiệm trên D, ta chứng minh hàm số y = f (x)
liên tục trên D và có hai số a,b Î D sao cho f (a). f (b) < 0 .
• Để chứng minh phương trình f (x) = 0 có k nghiệm trên D, ta chứng minh hàm số y = f (x) liên tục
trên D và tồn tại k khoảng rời nhau (a ; a ) (i=1,2,…,k) nằm trong D sao cho f (a ). f (a ) < 0 . i i 1 + i i 1 +
Câu 1. Tìm khẳng định đúng trong các khẳng định sau:
I. f ( x) liên tục trên đoạn [ ;
a b] và f (a). f (b) < 0 thì phương trình f ( x) = 0 có nghiệm.
II. f ( x) không liên tục trên [ ;
a b] và f (a). f (b) ³ 0 thì phương trình f ( x) = 0 vô nghiệm. A. Chỉ I đúng. B. Chỉ II đúng.
C. Cả I và II đúng. D. Cả I và II sai.
Câu 2. Tìm khẳng định đúng trong các khẳng định sau:
(I ) f (x) liên tục trên đoạn [ ;ab] và f (a).f (b) > 0 thì tồn tại ít nhất một số cÎ(a;b)sao cho f (c) = 0.
(II ) f (x) liên tục trên đoạn ( ;ab] và trên [ ;bc) nhưng không liên tục ( ;ac) A. Chỉ (I ) .
B. Chỉ (II ) .
C. Cả (I ) và (II ) đúng.
D. Cả (I ) và (II ) sai.
Câu 3. Cho hàm số f ( x) 3 2
= x –1000x + 0,01. Phương trình f (x) = 0 có nghiệm thuộc khoảng nào trong các khoảng sau đây? I. ( 1; - 0) . II. (0; ) 1 . III. (1;2). A. Chỉ I. B. Chỉ I và II. C. Chỉ II. D. Chỉ III.
ĐÁP ÁN VÀ LỜI GIẢI
A – LÝ THUYẾT VÀ PHƯƠNG PHÁP
1. Hàm số liên tục tại một điểm: y = f(x) liên tục tại x0 Û lim f (x) = f (x ) 0 x® 0 x
• Để xét tính liên tục của hàm số y = f(x) tại điểm x0 ta thực hiện các bước: B1: Tính f(x0).
B2: Tính lim f (x) (trong nhiều trường hợp ta cần tính lim f (x) , lim f (x) ) x® + - 0 x x® x® 0 x 0 x
B3: So sánh lim f (x) với f(x0) và rút ra kết luận. x® 0 x
2. Hàm số liên tục trên một khoảng: y = f(x) liên tục tại mọi điểm thuộc khoảng đó.
3. Hàm số liên tục trên một đoạn [a; b]: y = f(x) liên tục trên (a; b) và
lim f (x) = f (a), lim f (x) = f (b) + - x®a x®b
• Hàm số đa thức liên tục trên R.
• Hàm số phân thức, các hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
Giả sử y = f(x), y = g(x) liên tục tại điểm x0. Khi đó:
• Các hàm số y = f(x) + g(x), y = f(x) – g(x), y = f(x).g(x) liên tục tại x0. f (x) • Hàm số y =
liên tục tại x0 nếu g(x0) ¹ 0. g(x)
4. Nếu y = f(x) liên tục trên [a; b] và f(a). f(b)< 0 thì tồn tại ít nhất một số c Î (a; b): f(c) = 0.
Nói cách khác: Nếu y = f(x) liên tục trên [a; b] và f(a). f(b)< 0 thì phương trình f(x) = 0 có ít nhất một nghiệm cÎ (a; b).
Mở rộng: Nếu y = f(x) liên tục trên [a; b]. Đặt m = min f (x) , M = max f (x) . Khi đó với mọi T Î (m; M) luôn tồn [a;b] [a;b]
tại ít nhất một số c Î (a; b): f(c) = T. Trang 9 B – BÀI TẬP
DẠNG 1: TÍNH LIÊN TỤC CỦA HÀM SỐ TẠI MỘT ĐIỂM Phương pháp:
• Tìm giới hạn của hàm số y = f (x) khi x ® x và tính f (x ) 0 0
• Nếu tồn tại lim f (x) thì ta so sánh lim f (x) với f (x ). x® x® 0 0 x 0 x Chú ý:
1. Nếu hàm số liên tục tại x thì trước hết hàm số phải xác định tại điểm đó 0
2. lim f (x) = l Û lim f (x) = lim f (x) = l . + - x® 0 x x®x x® 0 0 x
ì f (x) khi x ¹ x 3. Hàm số 0 y = í
liên tục tại x = x Û lim f (x) = k . k khi x = î x 0 x®x 0 0
ì f (x) khi x ³ x 4. Hàm số 1 0 f (x) = í
liên tục tại điểm x = x khi và chỉ khi
f (x) khi x < î x 0 2 0
lim f (x) = lim f (x) = f (x ) . + 1 - 2 1 0 x®x x® 0 0 x Chú ý:
ì f (x) khi x ¹ x • Hàm số 0 y = í
liên tục tại x = x khi và chỉ khi k khi x = î x 0 0
lim f (x) = k . x® 0 x
ì f (x) khi x > x • Hàm số 0 y = í
liên tục tại x = x khi và chỉ khi
g(x) khi x £ î x 0 0
lim f (x) = lim g(x) . + - x®x x® 0 0 x 2 x -1
Câu 1. Cho hàm số f ( x) = và f ( ) 2
2 = m - 2với x ¹ 2. Giá trị của m để f ( x) liên tục tại x = 2là: x +1 A. 3 . B. - 3 . C. ± 3 . D. 3 ±
Hướng dẫn giải: Chọn C
Hàm số liên tục tại x = 2 Û lim f ( x) = f (2). x®2 2 x -1 Ta có lim = lim(x - ) 1 = 1. x®2 x®2 x +1 ém = 3 Vậy 2 m - 2 = 1 Û ê . êëm = - 3
Câu 2. Cho hàm số f ( x) 2
= x - 4 . Chọn câu đúng trong các câu sau:
(I) f ( x) liên tục tại x = 2 .
(II) f ( x) gián đoạn tại x = 2 .
(III) f ( x) liên tục trên đoạn [ 2; - 2].
A. Chỉ (I ) và (III ) . B. Chỉ (I ) .
C. Chỉ (II ) . D. Chỉ (II ) và (III )
Hướng dẫn giải: Chọn B. Trang 10 Ta có: D = ( ; -¥ 2 - ]È[2;+¥) . lim f ( x) 2 = lim x - 4 = 0 . x®2 x®2 f (2) = 0 .
Vậy hàm số liên tục tại x = 2 . 2 ì x +1 ï x ¹ 3; x ¹ 2
Câu 3. Cho hàm số f ( x) 3 = í x - x + 6
. Tìm b để f ( x)liên tục tại x = 3. ï îb + 3 x = 3; b Î ! 2 3 A. 3 . B. - 2 3 3 . C. . D. - . 3 3
Hướng dẫn giải: Chọn D.
Hàm số liên tục tại x = 3 Û lim f ( x) = f (3). x®3 2 x +1 1 lim = . 3 x®3 x - x + 6 3 f (3) = b + 3 . 1 1 2 - Vậy: b + 3 = Û b = - 3 + = . 3 3 3 x -
Câu 4. Cho hàm số f ( x) 1 =
. Tìm khẳng định đúng trong các khẳng định sau: x -1
(I ) f (x)gián đoạn tại x =1.
(II ) f (x)liên tục tại x =1. ( 1
III ) lim f ( x) = x 1 ® 2 A. Chỉ (I ) . B. Chỉ (I ) .
C. Chỉ (I ) và (III ) . D. Chỉ (II ) và (III ).
Hướng dẫn giải: Chọn C. D = ! \{ } 1 x -1 1 1 lim = lim = x 1 ® x 1 x -1 ® x +1 2
Hàm số không xác định tại x = 1. Nên hàm số gián đoạn tại x = 1.. ì 2x +8 - 2 ï x > 2 -
Câu 5. Cho hàm số f ( x) = í x + 2
. Tìm khẳng định đúng trong các khẳng định sau: ï î0 x = 2 -
(I ) lim f (x) = 0 . x 2+ ®-
(II ) f (x)liên tục tại x = 2. -
(III ) f (x)gián đoạn tại x = 2. -
A. Chỉ (I ) và (III ) .
B. Chỉ (I ) và (II ) . C. Chỉ (I ) . D. Chỉ (I )
Hướng dẫn giải: Chọn B. Trang 11 2x + 8 - 2 2x + 8 - 4 2 x + 2 lim = lim = lim = 0 . x 2+ x 2 x + 2 + ( 2x +8 + 2) x 2 x + 2 + ®- ®- ®- ( 2x+8+2)
Vậy lim f ( x) = f ( 2
- ) nên hàm số liên tục tại x = 2. - . x 2+ ®- ìï - x - £ x £
Câu 6. Cho hàm số f ( x) 2 4 2 2 = í
. Tìm khẳng định đúng trong các khẳng định sau:. 1 ïî x > 2
(I ) f (x)không xác định tại x = 3.
(II ) f (x)liên tục tại x = 2. -
(III ) lim f (x) = 2 x®2 A. Chỉ (I ) .
B. Chỉ (I ) và (II ) .
C. Chỉ (I ) và (III ) .
D. Cả (I ); (II ); (III ) đều sai.
Hướng dẫn giải: Chọn B. D = [ 2; - 2]
f ( x) không xác định tại x = 3. 2
lim 4 - x = 0 ; f ( 2
- ) = 0. Vậy hàm số liên tục tại x = 2. - x 2 ®- lim f ( x) 2
= lim 4 - x = 0 ; lim f (x) =1. Vậy không tồn tại giới hạn của hàm số khi x ® 2.. x 2- x 2- ® ® x 2+ ® ìsin 5x ï x ¹ 0
Câu 7. Cho hàm số f ( x) = í 5x
. Tìm a để f ( x) liên tục tại x = 0. ïîa + 2 x = 0 A. 1. B. 1 - . C. 2 - . D. 2.
Hướng dẫn giải: Chọn B. sin 5x Ta có: lim
=1; f (0) = a + 2 . x®0 5x
Vậy để hàm số liên tục tại x = 0 thì a + 2 = 1 Û a = 1 - . ( ì x + )2 1 , x > 1 ïï
Câu 8.Cho hàm số f ( x) 2
= íx + 3 , x <1 . Tìm k để f (x) gián đoạn tại x =1. ï 2 k , x = 1 ïî A. k ¹ 2 ± . B. k ¹ 2 . C. k ¹ 2 - . D. k ¹ 1 ± .
Hướng dẫn giải: Chọn A. TXĐ: D = ! .
Với x = 1 ta có f ( ) 2 1 = k Với x ¹ 1 ta có
lim f ( x) = lim x + =
lim f ( x) = lim ( x + )2 1 = 4 lim f ( x) = 4 - - ( 2 3) 4 ; suy ra . x 1 ® x 1 ® x 1+ x 1+ ® ® x 1 ®
Vậy để hàm số gián đoạn tại x = 1khi lim f ( x) 2 ¹ k 2
Û k ¹ 4 Û k ¹ 2 ± . x 1 ® ì x - 2 ï khi x ¹ 4 ï Câu 9.Cho hàm số x - 4 f (x) = í
. Khẳng định nào sau đây đúng nhất 1 ï khi x = 4 ïî4
A. Hàm số liên tục tại x = 4 Trang 12
B. Hàm số liên tục tại mọi điểm trên tập xác định nhưng gián đoạn tại x = 4
C. Hàm số không liên tục tại x = 4
D. Tất cả đều sai Hướng dẫn giải:
Chọn C. x - 2 1 1
Ta có : lim f (x) = lim = lim = = f (4) x®4 x®4 x®4 x - 4 x + 2 4
Hàm số liên tục tại điểm x = 4 . 2 ì x - 3x + 2 ï + 2 khi x >1
Câu 10. Cho hàm số f (x) = í x -1
. Khẳng định nào sau đây đúng nhất ï 2 3
î x + x -1 khi x £ 1
A. Hàm số liên tục tại x = 1
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại x = 1
D. Tất cả đều sai Hướng dẫn giải:
Chọn C. é(x -1)(x - 2) ù lim f (x) = lim + 2 = 2 ê ú x 1+ x 1+ ® ® ë x -1 û
lim f (x) = lim x + x - = ¹ f x - - ( 2 3 )1 3 lim ( ) x 1 x 1 x 1+ ® ® ®
Hàm số không liên tục tại x = 1. ì p x ï x £
Câu 11. Cho hàm số 3. f ( x) cos khi 1 = í 2
. Khẳng định nào sau đây đúng nhất
ï x -1 khi x >1 î
A. Hàm số liên tục tại tại x = 1và x = 1 - .
B. Hàm số liên tục tại x = 1, không liên tục tại điểm x = 1 - .
C. Hàm số không liên tục tại tại x = 1và x = 1 - .
D. Tất cả đều sai Hướng dẫn giải: Chọn B.
Hàm số liên tục tại x = 1, không liên tục tại điểm x = 1 - . 2x +1 -1
Câu 12. Chọn giá trị f (0) để các hàm số f (x) =
liên tục tại điểm x = 0 . x(x +1) A. 1 B. 2 C. 3 D. 4 Hướng dẫn giải:
Chọn A. 2x +1 -1 2x
Ta có : lim f (x) = lim = lim =1 x®0 x®0 x®0 x(x +1)
x(x +1)( 2x +1 + ) 1
Vậy ta chọn f (0) = 1 3 2x + 8 - 2
Câu 13. Chọn giá trị f (0) để các hàm số f (x) =
liên tục tại điểm x = 0 . 3x + 4 - 2 2 1 A. 1 B. 2 C. D. 9 9 Hướng dẫn giải:
Chọn C. Trang 13 2( 3x + 4 + 2) 2
Ta có : lim f (x) = lim = x®0 x®0 (3 2 3 x + + x + + ) 9 3 (2 8) 2. 2 8 4 2
Vậy ta chọn f (0) = . 9 ì x + x + 2 ï khi x > 1 -
Câu 14. Cho hàm số f (x) = í x +1
. Khẳng định nào sau đây đúng nhất
ïî2x +3 khi x £ 1 -
A. Hàm số liên tục tại tại tại x = 1 - 0
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại tại x = 1 - . 0
D. Tất cả đều sai Hướng dẫn giải: Chọn C. Ta có: f ( 1
- ) =1 và lim f (x) = lim (2x + 3) =1 x 1- x 1- ®- ®- 2 x + x + 2 x - x - 2 lim f (x) = lim = lim x 1+ x 1+ x + x 1 1 + ®- ®- ®-
(x +1)(x - x + 2) x - 2 3 lim = x 1+ ®- x - x + 2 2
Suy ra lim f (x) ¹ lim f (x) x 1+ x 1- ®- ®-
Vậy hàm số không liên tục tại x = 1 - . 0 3 ì x +1+ x -1 ï khi x ¹ 0
Câu 15. Cho hàm số 3. f (x) = í x
. Khẳng định nào sau đây đúng nhất ïî2 khi x = 0
A. Hàm số liên tục tại x = 0 0
B. Hàm số liên tục tại mọi điểm như gián đoạn tại x = 0 0
C. Hàm số không liên tục tại x = 0 0
D. Tất cả đều sai Hướng dẫn giải: Chọn C. Ta có: f (0) = 2 3 3 x +1+ x -1 æ 1+ x -1 ö lim f (x) = lim = lim ç1+ ÷ x®0 x®0 x®0 ç ÷ x è x ø æ 1 ö = lim 1+ = 2 = f (0) ç ÷ x®0 3 è 1- x -1 + x -1ø
Vậy hàm số liên tục tại x = 0 . 3 ì x -1 ï khi x ¹ 1 ï Câu 16. Cho hàm số x -1 f (x) = í
. Khẳng định nào sau đây đúng nhất 1 ï khi x =1 ïî3
A. Hàm số liên tục tại x = 1
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại tại x = 1
D. Tất cả đều sai
Hướng dẫn giải: Trang 14 Chọn C. 3 x -1 1 1
Ta có : lim f (x) = lim = lim = = f (1) x 1 ® x®4 x®4 3 2 3 x -1 x + x +1 3
Hàm số liên tục tại điểm x = 1. 2 ì x - x - 2 ï
+ 2x khi x > 2
Câu 17. Cho hàm số f (x) = í x - 2 ï 2
îx - x + 3 khi x £ 2
. Khẳng định nào sau đây đúng nhất
A. Hàm số liên tục tại x = 2 0
B. Hàm số liên tục tại mọi điẻm
C. Hàm số không liên tục tại x = 2 0
D. Tất cả đều sai Hướng dẫn giải:
Chọn C. é(x +1)(x - 2) ù
Ta có : lim f (x) = lim + 2x = 4 ê ú x 2+ x 2+ ® ® ë x - 2 û
lim f (x) = lim x - x + = ¹ f x - - ( 2 3) 5 lim ( ) x 2 x 2 x 2+ ® ® ®
Hàm số không liên tục tại x = 2 . 0
ì x + 2a khi x < 0
Câu 18. Tìm a để các hàm số f ( x) = í
liên tục tại x = 0 2
îx + x +1 khi x ³ 0 1 1 A. B. C. 0 D. 1 2 4 Hướng dẫn giải: Chọn A. Ta có : 2
lim f (x) = lim (x + x +1) = 1 x 0+ x 0+ ® ®
lim f (x) = lim (x + 2a) = 2a x 0- x 0- ® ® 1
Suy ra hàm số liên tục tại x = 0 Û a = . 2 ì 4x +1 -1 ï khi x ¹ 0
Câu 19. Tìm a để các hàm số 2
f (x) = íax + (2a +1)x
liên tục tại x = 0 3 khi ï î x = 0 1 1 1 A. B. C. - D. 1 2 4 6 Hướng dẫn giải:
Chọn C. 4x +1 -1
Ta có : lim f (x) = lim x®0
x®0 x (ax + 2a + ) 1 4 2 = lim =
x®0 (ax + 2a + ) 1 ( 4x +1 + ) 1 2a +1 2 1
Hàm số liên tục tại x = 0 Û = 3 Û a = - . 2a +1 6 Trang 15 ì 3x +1 - 2 ï khi x > 1 2 ï Câu x -
20.Tìm a để các hàm số 1 f (x) = í
liên tục tại x = 1 2
ïa(x - 2) khi x £1 ïî x -3 1 1 3 A. B. C. D. 1 2 4 4 Hướng dẫn giải:
Chọn C. 3x +1 - 2 3
Ta có : lim f (x) = lim = + + 2 x 1 ® x 1 ® x -1 8 2 a(x - 2) a lim f (x) = lim = x 1- x 1- ® ® x - 3 2 a 3 3
Suy ra hàm số liên tục tại x = 1 Û = Þ a = . 2 8 4 Trang 16
DẠNG 2: TÍNH LIÊN TỤC CỦA HÀM SỐ TRÊN TẬP XÁC ĐỊNH Phương pháp:
+ Sử dụng các định lí về tính liên tục của hàm đa thức, lương giác, phân thức hữu tỉ …
+ Nếu hàm số cho dưới dạng nhiều công thức thì ta xét tính liên tục trên mỗi khoảng đã chia và tại các điểm
chia của các khoảng đó.
Câu 1. Tìm khẳng định đúng trong các khẳng định sau: ( 1
I ) f ( x) = liên tục trên ! . 2 x -1 (II ) ( ) sin = x f x
có giới hạn khi x ® 0. x
(III ) f (x) 2
= 9 - x liên tục trên đoạn [ 3; - ]3.
A. Chỉ (I ) và (II ) .
B. Chỉ (II ) và (III ) .
C. Chỉ (II ) .
D. Chỉ (III ) .
Hướng dẫn giải: Chọn B.
Dễ thấy kđ (I) sai, Kđ (II) là lí thuyết.
Hàm số: f ( x) 2
= 9 - x liên tục trên khoảng ( 3;
- 3) . Liên tục phải tại 3 và liên tục trái tại 3 - . Nên f ( x) 2
= 9 - x liên tục trên đoạn [ 3; - ]3.
Câu 2. Tìm khẳng định đúng trong các khẳng định sau: ( x +
I ) . f ( x) 1 =
liên tục với mọi x ¹ 1. x -1
(II ) . f (x) = sin x liên tục trên ! . ( x
III ) . f ( x) =
liên tục tại x = 1. x
A. Chỉ (I ) đúng.
B. Chỉ (I ) và (II ) .
C. Chỉ (I ) và (III ) .
D. Chỉ (II ) và (III ) .
Hướng dẫn giải: Chọn D.
Ta có (II ) đúng vì hàm số lượng giác liên tục trên từng khoảng của tập xác định.
ì x , khi x ³ 0 x ïïx
Ta có (III ) đúng vì f ( x) = = í . x
ï- x , khi x < 0 ïî x
Khi đó lim f ( x) = lim f ( x) = f ( ) 1 = 1. x 1+ x 1- ® ® x
Vậy hàm số y = f ( x) =
liên tục tại x = 1. x 2
ì x - 3 , x ¹ 3 ï
Câu 3. Cho hàm số f ( x) = í x - 3
. Tìm khẳng định đúng trong các khẳng định sau: ï î2 3 , x = 3
(I ) . f (x) liên tục tại x = 3 .
(II ) . f (x) gián đoạn tại x = 3.
(III ) . f (x) liên tục trên ! . Trang 17
A. Chỉ (I ) và (II ) .
B. Chỉ (II ) và (III ) .
C. Chỉ (I ) và (III ) .
D. Cả (I ) , (II ) , (III ) đều đúng.
Hướng dẫn giải: Chọn C. 2 x - 3
Với x ¹ 3 ta có hàm số f ( x) =
liên tục trên khoảng ( ; -¥ 3) và ( 3;+¥), ( ) 1 . x - 3 2 x - 3
Với x = 3 ta có f ( 3) = 2 3 và lim f (x) = lim
= 2 3 = f ( 3) nên hàm số liên tục tại x® 3 x® 3 x - 3 x = 3 , (2) Từ ( )
1 và (2) ta có hàm số liên tục trên ! .
Câu 4. Tìm khẳng định đúng trong các khẳng định sau:
(I ) . f (x) 5 2
= x – x +1 liên tục trên ! . ( 1
II ) . f ( x) =
liên tục trên khoảng ( –1; ) 1 . 2 x -1
(III ) . f (x) = x - 2 liên tục trên đoạn [2;+¥).
A. Chỉ (I ) đúng.
B. Chỉ (I ) và (II ) .
C. Chỉ (II ) và (III ) .
D. Chỉ (I ) và (III ) .
Hướng dẫn giải: Chọn D.
Ta có (I ) đúng vì f ( x) 5 2
= x - x +1 là hàm đa thức nên liên tục trên ! .
Ta có (III ) đúng vì f ( x) = x - 2 liên tục trên (2;+¥) và lim f ( x) = f (2) = 0 nên hàm số liên tục trên x 2+ ® [2;+¥). ì3- 9 - x ï , 0 < x < 9 ï x ï
Câu 5. Cho hàm số f ( x) = ím , x = 0
. Tìm m để f ( x) liên tục trên [0;+¥) là. ï3 ï , x ³ 9 ïî x 1 1 1 A. . B. . C. . D. 1. 3 2 6
Hướng dẫn giải: Chọn C.
TXĐ: D = [0;+¥) .
Với x = 0 ta có f (0) = m. 3 - 9 - x 1 1
Ta có lim f ( x) = lim = lim = . x 0+ x 0+ ® ® x x 0+ ® 3 + 9 - x 6 1
Vậy để hàm số liên tục trên [0;+¥) khi lim f ( x) = m Û m = . x 0+ ® 6 2 x +1
Câu 6. Cho hàm số f (x) =
.Khi đó hàm số y = f ( x) liên tục trên các khoảng nào sau đây? 2 x + 5x + 6 A. ( 3; - 2). B. ( 2; - +¥). C. ( ;3 -¥ ) . D. (2;3).
Hướng dẫn giải: Chọn B. ìx ¹ 3 - Hàm số có nghĩa khi 2
x + 5x + 6 ¹ 0 Û í . îx ¹ 2 - Trang 18 2 x +1
Vậy theo định lí ta có hàm số f ( x) = liên tục trên khoảng ( ; -¥ 3 - ) ; ( 3; - 2 - ) và ( 2; - +¥). 2 x + 5x + 6 2 ì x - 5x + 6 ï khi x < 2
Câu 7. Cho hàm số f ( x) 3 = í 2x -16
. Khẳng định nào sau đây đúng nhất. ïî 2- x khi x ³ 2
A. Hàm số liên tục trên !
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục trên (2 : +¥)
D. Hàm số gián đoạn tại điểm x = 2 . Hướng dẫn giải: Chọn D. TXĐ : D = ! \{ } 2 2 x - x + • 5 6
Với x < 2 Þ f (x) = Þ hàm số liên tục 3 2x -16
• Với x > 2 Þ f (x) = 2 - x Þ hàm số liên tục
• Tại x = 2 ta có : f (2) = 0
lim f (x) = lim (2 - x) = 0 ; x 2+ x 2+ ® ® (x - 2)(x - 3) 1 lim f (x) = lim = - ¹ lim f (x) - - 2 x 2 x 2 x - x + x + x 2 2( 2)( 2 4) 24 + ® ® ®
Hàm số không liên tục tại x = 2 . 3 ì x -1 ï khi x > 1 ï x - Câu 1
8. Cho hàm số f (x) = í
. Khẳng định nào sau đây đúng nhất. 3
ï 1- x + 2 khi x £1 ïî x + 2
A. Hàm số liên tục trên !
B. Hàm số không liên tục trên !
C. Hàm số không liên tục trên (1: +¥)
D. Hàm số gián đoạn tại các điểm x = 1. Hướng dẫn giải: Chọn A.
Hàm số xác định với mọi x thuộc ! • 1- x + 2
Với x < 1 Þ f (x) = Þ hàm số liên tục x + 2 3 x - • 1
Với x > 1 Þ f (x) = Þ hàm số liên tục x -1 • 2
Tại x = 1 ta có : f (1) = 3 3 x -1 (x -1)( x +1) 2 lim f (x) = lim = lim = ; x 1+ x 1+ x 1+ ® ® ® 3 2 3 x -1
(x -1)( x + x +1) 3 1- x + 2 2 lim f (x) = lim
= = lim f (x) = f (1) x 2- x 1- x + x 1 2 3 + ® ® ®
Hàm số liên tục tại x = 1.
Vậy hàm số liên tục trên ! . Trang 19 ìtan x p ï
, x ¹ 0 Ù x ¹ + kp ,k Î!
Câu 9. Cho hàm số f ( x) = í x 2
. Hàm số y = f ( x) liên tục trên các khoảng ïî0 , x = 0 nào sau đây? æ p ö æ p ö æ p p ö A. 0; . B. ; -¥ . C. - ; . D. ( ; -¥ +¥) . ç ÷ ç ÷ ç ÷ è 2 ø è 4 ø è 4 4 ø
Hướng dẫn giải: Chọn A. ìp ü
TXĐ: D = ! \ í + kp , k Î"ý . î 2 þ
Với x = 0 ta có f (0) = 0. sin x 1 f ( x) tan x lim = lim = lim .lim
= 1 hay lim f (x) ¹ f (0) . x®0 x®0 x x®0 x®0 x cos x x®0
Vậy hàm số gián đoạn tại x = 0 . 2 2
ìïa x , x £ 2,aÎ!
Câu 10. Cho hàm số f ( x) = í
. Giá trị của a để f ( x) liên tục trên ! là: ( ï 2 - î a) 2 x , x > 2 A. 1 và 2 . B. 1 và –1. C. –1 và 2 . D. 1 và –2 .
Hướng dẫn giải: Chọn D. TXĐ: D = ! .
Với x > 2 ta có hàm số f ( x) 2 2
= a x liên tục trên khoảng ( 2;+¥) .
Với x < 2 ta có hàm số f ( x) = ( - a) 2 2
x liên tục trên khoảng ( ; -¥ 2 ) .
Với x = 2 ta có f ( ) 2 2 = 2a .
lim f ( x) = lim (2 - a) 2
x = 2(2 - a) ; lim f ( x) 2 2 2
= lim a x = 2a . + + - - x® 2 x® 2 x® 2 x® 2 Để hàm số liên tục tại éa = 1
x = 2 Û lim f (x) = lim f (x) = f ( 2 2 Û 2a = 2(2 - a) 2
Û a + a - 2 = 0 Û ê + - ) . x® 2 x® 2 ëa = 2 -
Vậy a = 1hoặc a = 2
- thì hàm số liên tục trên ! . 2 ìx , x ³1 ï 3 ï 2x
Câu 11. Cho hàm số f ( x) = í
, 0 £ x < 1. Tìm khẳng định đúng trong các khẳng định sau: 1+ ï x
ïxsin x , x < 0 î
A. f ( x) liên tục trên ! .
B. f ( x) liên tục trên ! \{ } 0 .
C. f ( x) liên tục trên ! \{ } 1 .
D. f ( x) liên tục trên ! \{0; } 1 .
Hướng dẫn giải: Chọn A. TXĐ: TXĐ: D = ! .
Với x > 1 ta có hàm số f ( x) 2
= x liên tục trên khoảng (1;+¥). ( ) 1 3 2x
Với 0 < x < 1 ta có hàm số f ( x) =
liên tục trên khoảng (0; ) 1 . (2) 1+ x
Với x < 0 ta có f ( x) = x sin x liên tục trên khoảng ( ;0 -¥ ). (3) 3 2x
Với x = 1 ta có f ( )
1 = 1; lim f ( x) 2
= lim x =1; lim f (x) = lim =1 x 1+ x 1+ ® ® x 1- x 1- ® ® 1+ x Trang 20
Suy ra lim f ( x) = 1 = f ( ) 1 . x 1 ®
Vậy hàm số liên tục tại x = 1. 3 2x sin x
Với x = 0 ta có f (0) = 0; lim f ( x) = lim
= 0 ; lim f (x) = lim ( .xsin x) 2 = lim x . lim = 0 x 0+ x 0+ ® ® 1+ x x 0- x 0- ® ® x 0- x 0- ® ® x
suy ra lim f ( x) = 0 = f (0). x®0
Vậy hàm số liên tục tại x = 0 . (4) Từ ( )
1 , (2) , (3) và (4) suy ra hàm số liên tục trên ! . x + 2
Câu 12. Cho hàm số f (x) =
. Khẳng định nào sau đây đúng nhất. 2 x - x - 6
A. Hàm số liên tục trên !
B. TXĐ : D = ! \{3;- }
2 .Ta có hàm số liên tục tại mọi x Î D và hàm số gián đoạn tại x = 2, - x = 3
C. Hàm số liên tục tại x = 2, - x = 3
D. Tất cả đều sai Hướng dẫn giải: Chọn B.
TXĐ : D = ! \{3;- } 2 .
Ta có hàm số liên tục tại mọi x Î D và hàm số gián đoạn tại x = 2, - x = 3 Câu 13. Cho hàm số 2
f (x) = 3x -1 . Khẳng định nào sau đây đúng nhất.
A. Hàm số liên tục trên ! æ 1 ö æ 1 ö
B. Hàm số liên tục tại mọi điểm x Î ; -¥ - È ;+¥ ç ÷ ç ÷ è 3 ø è 3 ø æ 1 ù é 1 ö C. TXĐ : D = ; -¥ È ;+¥ ç ú ê ÷ è 2 û ë 2 ø æ 1 1 ö
D. Hàm số liên tục tại mọi điểm x Î - ; . ç ÷ è 3 3 ø Hướng dẫn giải:
Chọn B. æ 1 ù é 1 ö TXĐ : D = ; -¥ - È ;+¥ ç ú ê ÷ è 3 û ë 3 ø æ 1 ö æ 1 ö
Ta có hàm số liên tục tại mọi điểm x Î ; -¥ - È ;+¥ ç ÷ ç ÷ è 3 ø è 3 ø æ 1 ö 1 lim
f (x) = 0 = f -
Þ hàm số liên tục trái tại x = - ç ÷ - æ 1 ö 3 x è 3 ® - ø ç ÷ è 3 ø æ 1 ö 1
lim f (x) = 0 = f
Þ hàm số liên tục phải tại x = ç ÷ + æ 1 ö 3 x è 3 ® ø ç ÷ è 3 ø æ 1 1 ö
Hàm số gián đoạn tại mọi điểm x Î - ; . ç ÷ è 3 3 ø
Câu 14. Cho hàm số f (x) = 2sin x + 3tan 2x . Khẳng định nào sau đây đúng nhất.
A. Hàm số liên tục trên ! B. Hàm số liên tục tại mọi điểm ìp p ü
C. TXĐ : D = ! \ í + k , k Î"ý
D. Hàm số gián đoạn tại các điểm î 2 2 þ p p x = + k ,k Î! 4 2 Trang 21 Hướng dẫn giải:
Chọn D. ìp p ü
TXĐ : D = ! \ í + k , k Î"ý î 4 2 þ
Ta có hàm số liên tục tại mọi điểm thuộc D và gián đoạn tại các điểm p p x = + k ,k Î! . 4 2 2 ì x - 3x + 2 ï khi x ¹ 1
Câu 15. Cho hàm số f ( x) = í x -1
. Khẳng định nào sau đây đúng nhất. ï î a khi x = 1
A. Hàm số liên tục trên !
B. Hàm số không liên tục trên !
C. Hàm số không liên tục trên (1: +¥)
D. Hàm số gián đoạn tại các điểm x = 1. Hướng dẫn giải: Chọn D.
Hàm số liên tục tại mọi điểm x ¹ 1 và gián đoạn tại x = 1 ì 2x +1 -1 ï khi x ¹ 0
Câu 16. Cho hàm số f ( x) = í x
. Khẳng định nào sau đây đúng nhất. ïî 0 khi x = 0
A. Hàm số liên tục trên !
B. Hàm số không liên tục trên !
C. Hàm số không liên tục trên (0;+¥)
D. Hàm số gián đoạn tại các điểm x = 0 . Hướng dẫn giải: Chọn D.
Hàm số liên tục tại mọi điểm x ¹ 0 và gián đoạn tại x = 0
ì2x +1 khi x £ 0 ï Câu 17. Cho hàm số 3
f (x) = í(x -1) khi 0 < x < 2 . Khẳng định nào sau đây đúng nhất. ï
î x -1 khi x ³ 2
A. Hàm số liên tục trên !
B. Hàm số không liên tục trên !
C. Hàm số không liên tục trên (2;+¥)
D. Hàm số gián đoạn tại các điểm x = 2 . Hướng dẫn giải: Chọn D.
Hàm số liên tục tại mọi điểm x ¹ 2 và gián đoạn tại x = 2 2 ì2
ï x + x +1 khi x £1
Câu 18. Cho hàm số f (x) = í
. Khẳng định nào sau đây đúng nhất. 3
ï x -1 khi x >1 î
A. Hàm số liên tục trên !
B. Hàm số không liên tục trên !
C. Hàm số không liên tục trên (2;+¥)
D. Hàm số gián đoạn tại các điểm x = 1 ± . Hướng dẫn giải: Chọn D.
Hàm số liên tục tại mọi điểm x ¹ 1
± và gián đoạn tại x = 1 ± . ì p sin x khi x £ ïï Câu 2
19. Xác định a,b để các hàm số f ( x) = í liên tục trên ï p !
ax + b khi x > ïî 2 Trang 22 ì 2 ì 2 ì 1 ì 2 ïa = ïa = ïa = ïa = A. í p B. í p C. í p D. í p ïîb =1 ïîb = 2 ïîb = 0 ïîb = 0 Hướng dẫn giải:
Chọn D. ìp a +b =1 ì 2 ïï 2 ïa =
Hàm số liên tục trên ! Û í Û í p ï p - a + b = -1 ïîb = 0 ïî 2 3 2
ì x - 3x + 2x khi x(x-2) ¹ 0 ï x(x -2) ïï
Câu 20. Xác định a,b để các hàm số f (x) = ía khi x = 2 liên tục trên ! ïb khi x = 0 ï ïî ìa = 10 ìa = 11 ìa = 1 ìa = 12 A. í B. í C. í D. í îb = 1 - îb = 1 - îb = 1 - îb = 1 - Hướng dẫn giải:
Chọn C. ìa = 1
Hàm số liên tục trên ! Û í . îb = 1 - 3 ì x - 2 + 2x -1 ï khi x ¹ 1
Câu 21. Tìm m để các hàm số f (x) = í x -1 liên tục trên ! 3
ïî m-2 khi x =1 4 A. m = 1 B. m = C. m = 2 D. m = 0 3 Hướng dẫn giải:
Chọn B. 3 x - 2 + 2x -1
Với x ¹ 1 ta có f (x) =
nên hàm số liên tục trên khoảng ! \{ } 1 x -1
Do đó hàm số liên tục trên ! khi và chỉ khi hàm số liên tục tại x = 1
Ta có: f (1) = 3m - 2 3 x - 2 + 2x -1 lim f (x) = lim x 1 ® x 1 ® x -1 é ù 3 ê x + x - 2 ú = lim 1+ x 1 ® ê ú (x -1) ê ( 2 3 3 2
x - x x - 2 + (x - 2) )ú ë û é 2 x x 2 ù + + = lim 1 ê + ú = 2 x 1 ® 2 3 3 2 ê
x - x x - 2 + (x - 2) ú ë û 4
Nên hàm số liên tục tại x = 1 Û 3m - 2 = 2 Û m = 3 4
Vậy m = là những giá trị cần tìm. 3 Trang 23 ì x +1 -1 ï khi x > 0
Câu 22. Tìm m để các hàm số f (x) = í x liên tục trên ! ï 2
î2x + 3m +1 khi x £ 0 1 A. m = 1 B. m = - C. m = 2 D. m = 0 6 Hướng dẫn giải:
Chọn B. • +1 -1
Với x > 0 ta có ( ) = x f x
nên hàm số liên tục trên (0;+¥) x
• Với x < 0 ta có 2
f (x) = 2x + 3m +1 nên hàm số liên tục trên ( ; -¥ 0) .
Do đó hàm số liên tục trên ! khi và chỉ khi hàm số liên tục tại x = 0
Ta có: f (0) = 3m +1 x +1 -1 1 1 lim f (x) = lim = lim = x 0+ x 0+ x 0+ ® ® ® x x +1 +1 2 lim f (x) = lim
x + m + = m + - - ( 2 2 3 )1 3 1 x®0 x®0 1 1
Do đó hàm số liên tục tại x = 0 Û 3m +1 = Û m = - 2 6 1
Vậy m = - thì hàm số liên tục trên ! . 6
ì 2x - 4 + 3 khi x ³ 2 ï
Câu 23. Tìm m để các hàm số f (x) = í liên tục trên ! x +1 ï khi x < 2 2
î x - 2mx + 3m + 2 1 A. m = 1 B. m = - C. m = 5 D. m = 0 6 Hướng dẫn giải: Chọn C.
Với x > 2 ta có hàm số liên tục
Để hàm số liên tục trên ! thì hàm số phải liên tục trên khoảng ( ;
-¥ 2) và liên tục tại x = 2.
• Hàm số liên tục trên ( ;
-¥ 2) khi và chỉ khi tam thức 2
g(x) = x - 2mx + 3m + 2 ¹ 0, "x £ 2 2
ìD ' = m - 3m - 2 £ 0 3 - 17 3 + 17 TH 1: í Û £ m £
îg(2) = -m + 6 ¹ 0 2 2 2
ìm - 3m - 2 > 0 2
ìïD' = m -3m - 2 > 0 ï TH 2: í Û ím > 2
ïx = m - D ' > 2 î 1 ï 2 D ' < (m - 2) î ì 3 + 17 ïm > 3 + 17 Û í 2 Û < m < 6 2 ïîm < 6 3 - 17 Nên
£ m < 6 (*) thì g(x) ¹ 0, "x £ 2 2
• lim f (x) = lim x - + = + + ( 2 4 3) 3 x®2 x®2 x +1 3 lim f (x) = lim = - - 2 x®2
x®2 x - 2mx + 3m + 2 6 - m Trang 24 3
Hàm số liên tục tại x = 2 Û
= 3 Û m = 5 (thỏa (*)) 6 - m
DẠNG 3: ÁP DỤNG TÍNH LIÊN TỤC XÉT SỐ NGHIỆM CỦA PHƯƠNG TRÌNH Phương pháp :
• Để chứng minh phương trình f (x) = 0 có ít nhất một nghiệm trên D, ta chứng minh hàm số y = f (x)
liên tục trên D và có hai số a,b Î D sao cho f (a). f (b) < 0 .
• Để chứng minh phương trình f (x) = 0 có k nghiệm trên D, ta chứng minh hàm số y = f (x) liên tục
trên D và tồn tại k khoảng rời nhau (a ; a ) (i=1,2,…,k) nằm trong D sao cho f (a ). f (a ) < 0 . i i 1 + i i 1 +
Câu 1. Tìm khẳng định đúng trong các khẳng định sau:
I. f ( x) liên tục trên đoạn [ ;
a b] và f (a). f (b) < 0 thì phương trình f ( x) = 0 có nghiệm.
II. f ( x) không liên tục trên [ ;
a b] và f (a). f (b) ³ 0 thì phương trình f ( x) = 0 vô nghiệm. A. Chỉ I đúng. B. Chỉ II đúng.
C. Cả I và II đúng. D. Cả I và II sai.
Hướng dẫn giải: Chọn A.
Câu 2. Tìm khẳng định đúng trong các khẳng định sau:
(I ) f (x) liên tục trên đoạn [ ;ab] và f (a).f (b) > 0 thì tồn tại ít nhất một số cÎ(a;b)sao cho f (c) = 0.
(II ) f (x) liên tục trên đoạn ( ;ab] và trên [ ;bc) nhưng không liên tục ( ;ac) A. Chỉ (I ) .
B. Chỉ (II ) .
C. Cả (I ) và (II ) đúng.
D. Cả (I ) và (II ) sai.
Hướng dẫn giải: Chọn D. KĐ 1 sai. KĐ 2 sai.
Câu 3. Cho hàm số f ( x) 3 2
= x –1000x + 0,01. Phương trình f (x) = 0 có nghiệm thuộc khoảng nào trong các khoảng sau đây? I. ( 1; - 0) . II. (0; ) 1 . III. (1;2). A. Chỉ I. B. Chỉ I và II. C. Chỉ II. D. Chỉ III.
Hướng dẫn giải: Chọn B. TXĐ: D = ! . Hàm số f ( x) 3 2
= x -1000x + 0,01 liên tục trên ! nên liên tục trên[ 1; - 0], [0; ] 1 và [1;2], ( ) 1 . Ta có f (- ) 1 = 1000 -
,99 ; f (0) = 0,01 suy ra f (- )
1 . f (0) < 0, (2) . Từ ( )
1 và (2) suy ra phương trình f ( x) = 0 có ít nhất một nghiệm trên khoảng ( 1; - 0) .
Ta có f (0) = 0,01; f ( ) 1 = 999 -
,99 suy ra f (0). f ( ) 1 < 0 , (3) . Từ ( )
1 và (3) suy ra phương trình f ( x) = 0 có ít nhất một nghiệm trên khoảng (0; ) 1 . Ta có f ( ) 1 = 999 - ,99 ; f (2) = 39991 - ,99suy ra f ( )
1 . f (2) > 0 , (4) . Từ ( )
1 và (4) ta chưa thể kết luận về nghiệm của phương trình f ( x) = 0 trên khoảng (1;2) . Trang 25




