TOP 8 Bài tập Toán 7 về trường hợp bằng nhau thứ hai của tam giác (có lời giải)
Tổng hợp 5 bài tập môn TOÁN 7 chương 4 về trường hợp bằng nhau thứ hai của tam giác có lời giải chi tiết. Tài liệu được biên soạn dưới dạng file PDF gồm 5 trang giúp bạn nắm vững kiến thức và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem!
Tài liệu liên quan:
Preview text:
1. . TRƯỜNG HỢP BẰNG NHAU THỨ HAI CỦA TAM GIÁC:
CẠNH – GÓC – CẠNH (C.G.C)
I. KIẾN THỨC CƠ BẢN A
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và
góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. AB A' B ' B C A' B B ' ABC
A'B 'C ' . c g.c BC B 'C '
Hệ quả: Nếu hai cạnh góc vuông của tam giác vuông này bằng hai C' B'
cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. II. BÀI TẬP
Bài 1: Cho xOy có Om là tia phân giác, C Om ( C O ). Trên tia Ox lấy điểm A , trên tia
Oy lấy điểm B sao cho OA = OB. Chứng minh:
a) OAC = OBC .
b) OAC = OBC và CA = CB .
Bài 2: Cho tam giác ABC , kẻ AH vuông góc với BC ( H BC ) . Trên tia đối của tia HA,
lấy điểm K sao cho HK = HA. Nối KB, KC. Tìm các cặp tam giác bằng nhau trong hình vẽ. Bài 3: Cho ABC có ˆ
A = 90 , trên cạnh BC lấy điểm E sao cho BE = BA . Tia phân giác góc B cắt AC ở D. a) Chứng minh: A BD = E BD .
b) Chứng minh: DA = DE .
c) Tính số đo BED .
Bài 4: Cho hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng.
a) Chứng minh: AC = DB và AC // DB.
b) Chứng minh: AD = CB và AD // CB. c) Chứng minh: ACB BDA .
d) Vẽ CH ⊥ AB tại H .Trên tia đối của tia OH lấy điểm I sao cho OI = OH . Chứng minh: DI ⊥ AB. Trang 1
Bài 5: Cho tam giác ABC có A = 50 . Vẽ đoạn thẳng AI vuông góc và bằng AB (I và C
khác phía đối với AB). Vẽ đoạn thẳng AK vuông góc và bằng AC (K và B khác phía đối với
AC). Chứng minh rằng: a) IC = BK b) IC ⊥ BK Bài 6: Cho A
BC có ba góc nhọn. Vẽ BD ⊥ AC tại D , CE ⊥ AB tại E . Trên tia đối của tia
BD lấy điểm F sao cho BF = AC , trên tia đối của tia CE lấy điểm G sao cho CG = AB .
Chứng minh: AF = AG và AF ⊥ AG .
Bài 7: Cho góc bẹt xOy có tia phân giác Ot. Trên tia Ot lấy hai điểm A, B ( A nằm giữa O
và B). Lấy điểm C Ox sao cho OC O ,
B lấy điểm DOy sao cho OD O . A
a) Chứng minh AC = BD và AC ⊥ BD
b) Gọi M, N lần lượt là trung điểm của AC và BD. Chứng minh OM ON
c) Tính các góc của tam giác MON
d) Chứng minh AD ⊥ BC
Bài 8: (Tự luyện) Cho tam giác ABC có ba góc nhọn. Vẽ AH ⊥ BC (H BC) . Vẽ HI ⊥ AB
tại I, vẽ HK ⊥ AC tại K. Lấy E, F sao cho I là trung điểm của HE, K là trung điểm của HF,
EF cắt AB, AC lần lượt tại M, N. a) Chứng minh MH ME và chu vi M
HN bằng EF b) Chứng minh AE = AF c) Nếu biết 0
BAC = 60 . Khi đó hãy tính các góc của tam giác AEF
( Chu vi của một tam giác bằng tổng độ dài 3 cạnh của tam giác) Trang 2 HDG
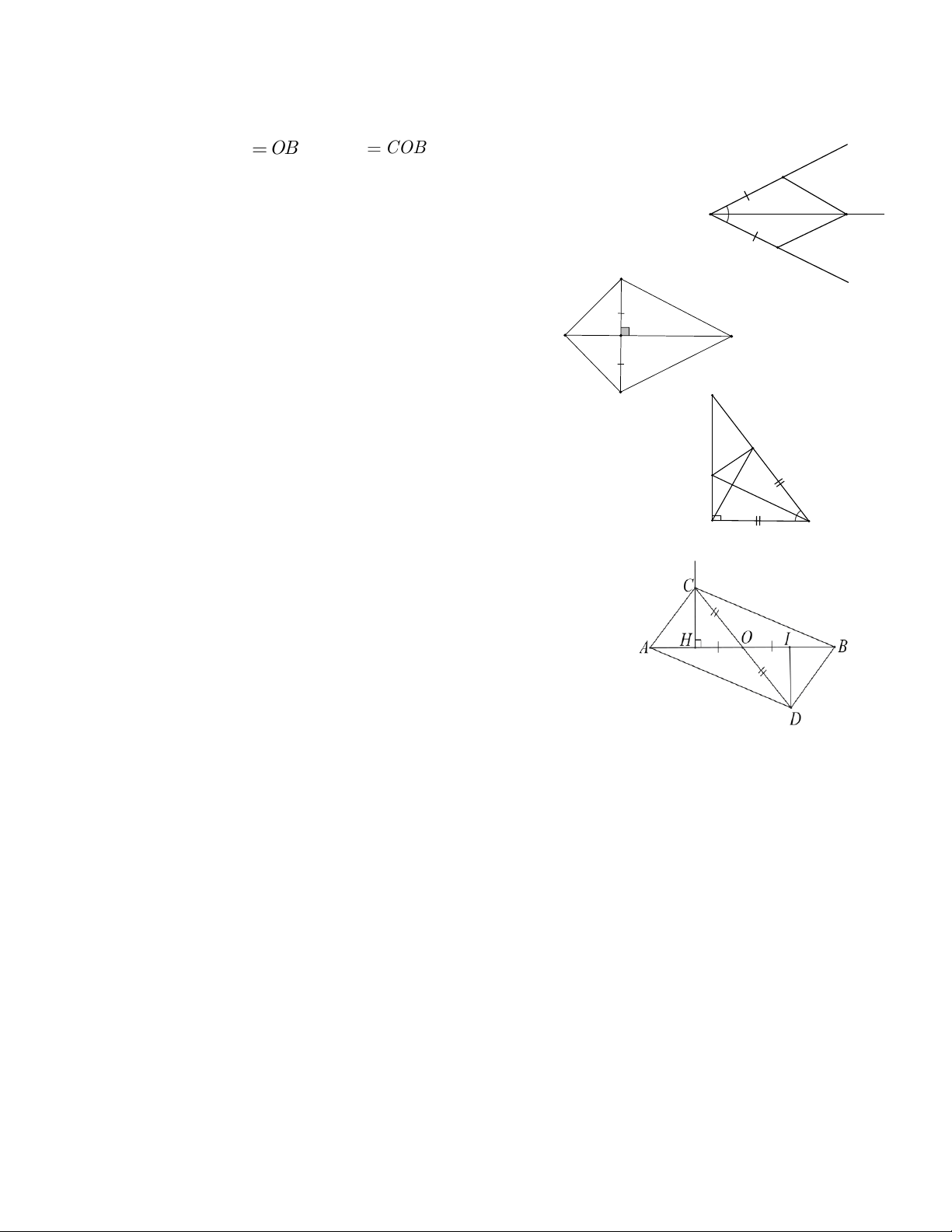
Bài 1: a) Có OA OB ; AOC
COB ; OC là cạnh chung A
OAC = OB ( C . c . g c) O
suy ra OAC = OBC (hai góc tương ứng) C B
suy ra AC = AB ( hai cạnh tương ứng) A Bài 2: A HB = K
HB (c.g.c); A HC = K HC (c.g.c); B H C A BC = K
BC (c.g.c) hoặc (c.c.c) C Bài 3: K
a) ABD = EBD ( . c . g ) c E
b) DA = DE ( Cặp cạnh tương ứng ) D c) A = E = 0
90 ( Cặp góc tương ứng ) A B
Bài 4: a) Chứng minh: AC = DB và AC // DB. * Xét hai tam giác A OC và B OD có: OA = OB (gt)
AOC = BOD (hai góc đối đỉnh) OC = OD (gt) A OC = B OD (c.g.c)
AC = DB.(2 cạnh tương ứng bằng nhau) Vì A OC = B
OD nên OCA = ODB(2 góc tương ứng bằng nhau)
Mà OCA và ODB là hai góc ở vị trí so le trong AC // DB.
b) Chứng minh: AD = CB và AD // CB. * Xét hai tam giác A OD và B OC có: OA = OB (gt)
AOD = BOC (hai góc đối đỉnh) OD = OC (gt) A OD = B OC (c.g.c)
AD = CB(2 cạnh tương ứng bằng nhau). Vì A OD = B
OC nên OCB = ODA (2 góc tương ứng bằng nhau)
Mà OCB và ODA là hai góc ở vị trí so le trong, cát tuyến D C AD // CB. c) Chứng minh: ACB = BDA . Trang 3 Ta có: OCA = ODB (cmt) OCB = ODA (cmt) OCA + OCB = ODB+ ODA ACB = BDA (đpcm)
d) Vẽ CH ⊥ AB tại H .Trên tia đối của tia OH lấy điểm I sao cho OI = OH . Chứng minh: DI ⊥ AB. * Xét hai tam giác HOC và I OD có: OH = OI (gt)
HOC = IOD (hai góc đối đỉnh) OC = OD (gt) HOC = I OD (c.g.c) 0
OID = IHC = 90 hay DI ⊥ AB .
Bài 5: a) IAC = BAK ( 140o = ) K I AC = B
AK (c.g.c) IC = BK .
b) Gọi D là giao điểm của AB và IC, gọi E là giao I
điểm của IC và BK . A Xét A ID và EBD
, ta có AID = EBD (do D E I AC = B
AK) , (đối đỉnh) nên IAD = BED . Do 90o IAD = nên 90o BED =
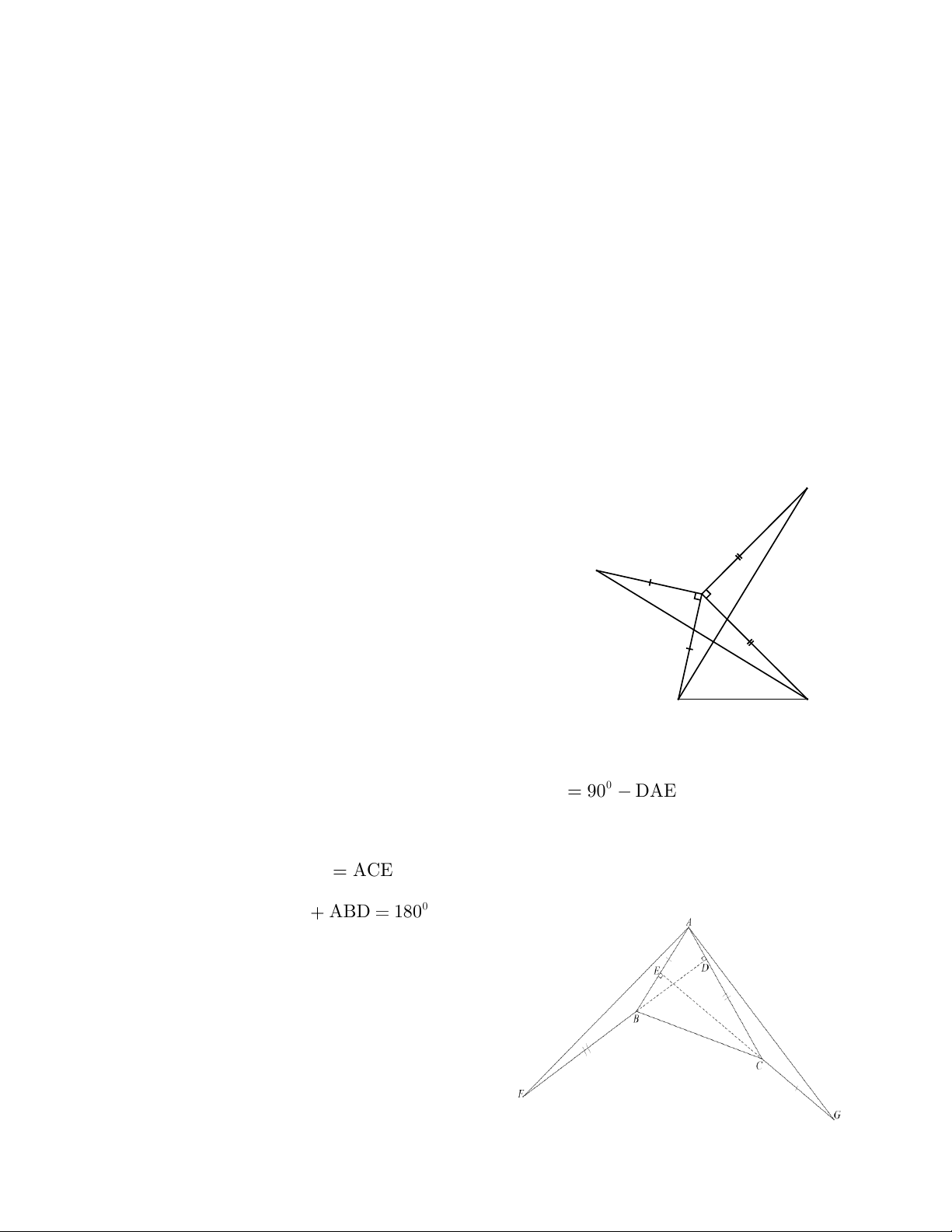
. Vậy IC ⊥ BK . B C Bài 6: Vì A DB vuông tại D nên 0 ABD = 90 − DAB hay 0 ABD 90 DAE ( ) 1 Vì A EC vuông tại E nên 0 ACE = 90 − EAC hay 0 ACE = 90 − EAD (2) Từ ( ) 1 và (2) suy ra ABD ACE Mặt khác, ta lại có 0 FBA ABD 180 0 ACG + ACE = 180 FBA = ACG * Xét hai tam giác F BA và A CG có: FB = AC (gt)
FBA = ACG (theo chứng minh trên) BA = CG (gt) Trang 4 FBA = ACG (c.g.c)
AF = AG (2 cạnh tương ứng bằng nhau).
Vì FBA = ACG nên FAB = AGC (2 góc tương ứng bằng nhau)
Ta có FAG = FAB + BAC + CAG
FAG = AGC+ BAC + CAG = BAC + (AGC + CAG)
= BAC + ACE ( ACE là góc ngoài tại đỉnh C của A CG ) = EAC+ ACE = 90 ( A EC vuông tại E)
Vậy FAG = 90 hay AF ⊥ AG . Bài 7:
a) Vì góc xOy bẹt có Ot là tia phân giác 0
Ot ⊥ xy COA = DOB = 90 Chứng minh A OC = D
OB (c − g −c) DB
AC (2 cạnh tương ứng)
Gọi E là giao điểm của AC và BD. Có 0 EAB EBA OCA OAC 90 AEB vuông tại E AC ⊥ BD b) Vì AOC DOB DBO ACO . Chứng minh O NB = O
MC (c − g −c) OM ON ; và NOB MOC c) NOB
MOC (cmt) từ đó chỉ ra được 0 NOB BOM BOM MOC 90
Gọi P là trung điểm của MN từ đó chỉ ra NOP MOP (c c c) từ đó chỉ ra 0 0 180 NOM 90 0 ONM MON 45 2 2
d) Vận dụng tương tự câu c, gọi Q, T lần lượt là trung điểm của BC và AD, chỉ ra 0 OBC DAO 45 ;DAO A B F 45 Từ đó suy ra 0 BFA
90 hay AD ⊥ BC
Bài 8: a,b tự chứng minh 0 180 FAE 180 120 c) AEF AFE 30 2 2 Trang 5