TOP10 đề ôn tập kiểm tra giữa kỳ 2 Toán 10 có đáp án và lời giải chi tiết

Nhằm giúp các em học sinh lớp 10 tham khảo, chuẩn bị cho kỳ thi khảo sát chất lượng môn Toán 10 giai đoạn giữa học kì 2, xin giới thiệu đến các em tài liệu tuyển chọn 10 đề ôn tập kiểm tra giữa kỳ 2 Toán 10 có đáp án và lời giải chi tiết

82 41 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 10

Môn: Toán 10

Thông tin:

116 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Trang 1/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 1
Mã đề thi
001
Họ và tên :………………………………………...Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Bất phương trình nào sau đây không tương đương với bất phương trình
?
A.
( ) ( )
2
1 5 0xx− +
. B.
( )
5 5 0xx+ −
.
C.
( )
2
50xx− +
. D.
( )
5 5 0xx+ +
.
Câu 2. Nhị thức
( )
26f x x=−
dương trong
A.
( )
3; +
. B.
( )
;3−
. C.
)
3; +
. D.
(
;3−
.
Câu 3. Nếu
22a c b c+ +
thì bất đẳng thức nào sau đây đúng?
A.
22
ab
. B.
22ab
. C.
11
ab
. D.
33ab− −
.
Câu 4. Tam giác
ABC
có các góc
30 , 45BC= =
,
3AB =
. Tính cạnh
AC
.
.
A.
32
2
. B.
6
. C.
26
3
. D.
36
2
.
Câu 5. Tìm điều kiện của bất phương trình
13
2
2
+
+xx
.
A.
0x
. B.
1−x
. C.
2
0
−
x
x
. D.
0
1
−
x
x
.
Câu 6. Đường nào sau đây cắt đường thẳng
có phương trình:
– 4 1 0xy+=
?
A.
23yx=+
. B.
–2 8 0xy+=
. C.
2 – 8 0xy=
. D.
– 4 – 2 0xy+=
.
Câu 7. Nhị thức nào sau đây nhận giá trị dương với mọi
x
nhỏ hơn
2
?
A.
( )
6 – 3=f x x
. B.
( )
4 – 3=f x x
. C.
( )
3 – 6=f x x
. D.
( )
36=+f x x
.
Câu 8. Cho tam giác
ABC
có
10BC =
,
30A =
. Tính bán kính đường tròn ngoại tiếp tam giác
ABC
.
A.
5
. B.
10
3
. C.
10 3
. D.
10
.
Câu 9. Tam giác
ABC
có
75 , 45AB= =
,
2AC =
. Tính cạnh
AB
.
A.
2
2
. B.
6
. C.
6
2
. D.
6
3
.
Câu 10. Số nào dưới đây là nghiệm của bất phương trình
2 1 3x +
?
A.
3x =
. B.
0x =
. C.
1x =
. D.
2x =
.
Câu 11. Đường thẳng
d
vuông góc với đường thẳng
:3 4 12 0xy + − =
có một véctơ chỉ phương
u
là
A.
( )
3;4u =
. B.
( )
4; 3u =−
. C.
( )
3; 4u =−
. D.
( )
3;4u =−
.
Câu 12. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A.
22
2.xy+
B.
2
0.xy+
C.
0.xy+
D.
2
2 3 0.xy+
Câu 13. Tính khoảng cách từ điểm
( )
1; 1M −
đến đường thẳng
( )
:3 4 17 0d x y− − =
A.
2
. B.
7
5
. C.
18
5
. D.
2
5
.
Câu 14. Cho tam thức bậc hai
2
( ) ( 0)f x ax bx c a
. Điều kiện cần và đủ để
( ) 0,f x x
là:
Trang 2/40
A.
0
0
a
. B.
0
0
a
. C.
0
0
a
. D.
0
0
a
.
Câu 15. Số
1x =−
là nghiệm của bất phương trình nào sau đây?
A.
2 1 0x −
. B.
10x −
. C.
30x−
. D.
2 1 0x +
.
Câu 16. Tìm tập nghiệm
S
của bất phương trình
2
4 4 0xx− +
.
A.
\2S =−
. B.
\2S =
. C.
S =
. D.
( )
2;S = +
.
Câu 17. Cho hệ bất phương trình
++
++
−−
01
052
0152
yx
yx
yx
.
Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Điểm
( )
0; 2C −
thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm
( )
0;2D
thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm
( )
0;0O
thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm
( )
1;0B
thuộc miền nghiệm của hệ bất phương trình đã cho.
Câu 18. Viết phương trình tham số của đường thẳng đi qua 2 điểm
( ) ( )
3; 1 ; 6; 2AB−−
.
A.
13
2
xt
yt
= − +
=
. B.
33
1
xt
yt
=+
= − +
. C.
33
1
xt
yt
=+
= − −
. D.
33
6
xt
yt
=+
= − −
.
Câu 19. Với hai số
,xy
dương thoả
36xy =
. Bất đẳng thức nào sau đây đúng?
A.
2
36.
2
xy
xy
+

=


. B. Tất cả đều đúng.
C.
2 12.x y xy+ =
.
D.
22
2 72.x y xy+ =
.
Câu 20. Tìm nghiệm của tam thức bậc hai
( )
2
45f x x x= + −
.
A.
5x =−
;
1x =
. B.
5x =−
;
1x =−
. C.
5x =
;
1x =
. D.
5x =
;
1x =−
.
Câu 21. Trong mặt phẳng
Oxy
, đường thẳng
:3 2 7 0xy − − =
cắt đường thẳng nào sau đây?
A.
1
:3 2 0d x y+=
. B.
4
:6 4 14 0d x y− − =
.
C.
2
:3 2 0d x y−=
. D.
3
: 3 2 7 0d x y− + − =
.
Câu 22. Cho hàm số
( )
y f x=
có tập xác định
( )
D 1;5=−
và đồ thị như hình vẽ. Giá trị nào sau đây là nghiệm
của bất phương trình
( )
f x 0
?
A.
1
2
−
. B.
1
. C.
3
. D.
4
.
Câu 23. Cho hệ bất phương trình
20
2 3 2 0
xy
xy
+ −
− +
. Trong các điểm sau, điểm nào không thuộc miền nghiệm
của hệ bất phương trình?
A.
( )
0;0 .O
B.
( )
1;1 .M
C.
( )
1;1 .N −
D.
( )
1; 1 .P −−
Trang 3/40
Câu 24. Nếu
xa
, với
0a
thì bất đẳng thức nào sau đây luôn đúng?
A.
xa−
. B.
11
xa
. C.
xa− −
. D.
xa
.
Câu 25. Tập nghiệm của bất phương trình
3
1
1
x
x
+
−
là
A.
)
2;1−
. B.
( )
1;1−
. C.
)
3;1−
. D.
)
1;1−
.
Câu 26. Cho
ABC
có
( ) ( ) ( )
1;1 ; 0; 2 ; 4;2A B C−
. Phương trình tổng quát của trung tuyến
BM
A.
3 2 0xy+ − =
. B.
7 7 14 0xy+ + =
.
C.
7 5 10 0xy− + + =
. D.
5 3 1 0xy− + =
.
Câu 27. Cho đường thẳng có phương trình
( )
: 4 3 5 0d x y− + =
. Tính khoảng cách
h
từ điểm
(1, 2)M −
tới
đường thẳng .
A.
1h =
. B.
16h =
. C.
3h =
. D.
7h =
.
Câu 28. Tìm giá trị nhỏ nhất của hàm số
8
2
x
y
x
=+
với
0x
.
A.
16.
B.
8.
C.
4.
D.
2.
Câu 29. Cho hệ bất phương trình
0 (1)
5 0 (2)
xm
x
+
− +
. Hệ đã cho có nghiệm khi và chỉ khi:
A.
5m
. B.
5m
. C.
5m −
. D.
5m −
.
Câu 30. Tập nghiệm của bất phương trình
2018 2018xx− −
là
A.
( )
;2018−
. B.
2018
. C.
( )
2018;+
. D.
.
Câu 31. Cho hình bình hành
ABCD
có
AB a=
,
2BC a=
và
135BAD =
. Diện tích của hình bình hành
ABCD
bằng
A.
2
2a
. B.
2
a
. C.
2
2a
. D.
2
3a
.
Câu 32. Bất phương trình
1 1 2
22x x x
−
−+
có tập nghiệm là
A.
( )
0;2
. B.
\ 2;0;2−
.
C.
( )
2;0−
. D.
; ; ;
3 17 3 17
2 0 2
22
.
Câu 33. Tập nghiệm của bất phương trình
43
1
12
x
x
−
−
−
là
A.
1
;1
2



. B.
1
;1
2


. C.
1
;1
2


. D.
1
;1
2



.
Câu 34. Tam giác
ABC
có
120A =
thì câu nào sau đây đúng
A.
2 2 2
3a b c bc= + +
. B.
2 2 2
a b c bc= + −
.
C.
2 2 2
3a b c bc= + −
. D.
2 2 2
a b c bc= + +
.
Câu 35. Tập xác định của hàm số
2
1
32
1
y x x
x
= + + −
−
là
A.
(
)
;1 2;− +
. B.
( )
1; +
. C.
)
1; +
. D.
(
1;2
.
PHẦN II: TỰ LUẬN
Câu 1. Tìm tập nghiệm của bất phương trình
2
3 2 0xx− +
.
Câu 2. Cho tam giác
ABC
có
5 4 3
sin sin sinA B C
==
và
10a =
. Tính chu vi tam giác đó.
( )
d
Trang 4/40
Câu 3. Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác
ABC
cân tại
( )
1;3A −
. Gọi
D
là một điểm trên
cạnh
AB
sao cho
3AB AD=
và
H
là hình chiếu của
B
trên
CD
. Điểm
13
( ; )
22
M
−
là trung điểm đoạn
.HC
Biết điểm
B
nằm trên đường thẳng
: 7 0d x y+ + =
. Tìm tọa độ điểm C.
Câu 4. Cho ba số thực dương
, , x y z
thỏa mãn điều kiện
3x y z+ + =
. Tìm giá trị lớn nhất của biểu thức
( )
3 3 3
3
3
3
3P x y z x y z= + + + + +
.
------------- HẾT -------------
Trang 5/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 2
Mã đề thi
002
Họ và tên :………………………………………...Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cho 2 điểm
( )
1; 4−A
,
( )
1; 2B
. Viết phương trình tổng quát đường trung trực của đoạn thẳng
AB
.
A.
10−=y
. B.
40−=xy
. C.
10−=x
. D.
10+=y
.
Câu 2. Cho đường thẳng
có phương trình tổng quát:
–2 3 – 1 0xy+=
. Trong những điểm sau, điểm nào
thuộc
?
A.
( )
0; – 3
. B.
( )
3; 0
. C.
( )
1; 1
. D.
( )
–3; 0
.
Câu 3. Bất phương trình
( )
2
2 1 1 0mx m x m+ − + +
có nghiệm khi:
A.
0,25m =
. B.
2m =
. C.
1m =
. D.
0m =
.
Câu 4. Tìm tập nghiệm
S
của bất phương trình
4 16 0x− +
?
A.
)
4;S = +
. B.
( )
4;S = +
. C.
(
;4S = −
. D.
(
;4S = − −
.
Câu 5. Các cặp đường thẳng nào sau đây vuông góc với nhau?
A.
1
3: 20xd y− + =
và
2
1: 2 0.xyd − + =
B.
1
: 2 3 0d x y− + =
và
2
21:4 0.xyd − + =
C.
1
:
12
xt
d
yt
=
= − −
và
2
1:2 – 0.xyd +=
D.
1
: 2 0dx−=
và
2
:
0
.
xt
d
y
=
=
Câu 6. Bất phương trình
3 9 0− + x
có tập nghiệm là
A.
)
3; +
. B.
(
;3−
. C.
( )
3; +
. D.
( )
;3− −
.
Câu 7. Tam giác
ABC
có
60A =
,
10AC =
,
6AB =
. Tính cạnh
BC
A.
2 19
. B.
14
. C.
62
. D.
76
.
Câu 8. Đường thẳng
12 7 5 0− + =xy
không đi qua điểm trong các điểm nào sau?
A.
17
1;
7



. B.
( )
1; 1−−
. C.
( )
1; 1
. D.
5
;0
12

−


.
Câu 9. Tập nghiệm của bất phương trình
2
( 2)(2 1) 2 ( 1)( 3)x x x x x+ − − + − −
là:
A.
(
;1−
. B.
( )
;1−
. C.
1
. D.
.
Câu 10. Cho hệ bất phương trình
+−
−+
045
0132
yx
yx
.
Hỏi khẳng định nào dưới đây là khẳng định sai?
A. Điểm
( )
2;4C −
thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm
( )
3;4D −
thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm
( )
1;4A −
thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm
( )
0;0O
thuộc miền nghiệm của hệ bất phương trình đã cho.
Câu 11. Điểm nào sau đây thuộc miền nghiệm của bất phương trình
2 3 0xy+ −
?
A.
( )
1; 3Q −−
. B.
3
1;
2
M



. C.
( )
1;1N
. D.
3
1;
2
P

−


.
Câu 12. Tập nghiệm của bất phương trình
2
4 2 8 0− + xx
là:
A.
. B. . C.
( )
;2 2−
. D.
\ 2 2
.
Trang 6/40
Câu 13. Tìm nghiệm của nhị thức bậc nhất
( )
36f x x=+
.
A.
3x =−
. B.
3x =
. C.
2x =
. D.
2x =−
.
Câu 14. Tam giác
ABC
có
30B =
.,
, 33BC AB ==
Tính cạnh
AC
A.
1,7
. B.
3
. C.
1,5
. D.
3
.
Câu 15. Mệnh đề nào sau đây sai?
A.
1
20aa
a
+
. B.
2 , 0a b ab a b+
.
C.
11
,0a b a b
ab
. D.
ax
a b x y
by
+ +
.
Câu 16. Cho
( ) ( )
2
0 .f x ax bx c a= + +
Điều kiện để
( )
0, f x x
là
A.
0
.
0
a

B.
0
.
0
a

C.
0
.
0
a

D.
0
.
0
a

Câu 17. Tập xác định của hàm số
2
1
1
+
=
−
x
y
x
là
A.
\1
. B.
( )
;1−
. C.
(
;1−
. D.
( )
1;
.
Câu 18. Trong tam giác
ABC
có:
A.
sina R A=
. B.
2 cosa R A=
. C.
2 sina R A=
. D.
2 tana R A=
.
Câu 19. Cho
( )
24f x x=−
, khẳng định nào sau đây là đúng?
A.
( )
0fx
( )
2;x +
. B.
( )
0fx
( )
;2x − −
C.
( )
0fx
( )
2;x − +
. D.
( )
0fx=
2x = −
.
Câu 20. Với hai số
,xy
dương thoả
36xy =
. Bất đẳng thức nào sau đây đúng?
A. Tất cả đều đúng. B.
22
2 72.x y xy+ =
.
C.
2
36.
2
xy
xy
+

=


.
D.
2 12.x y xy+ =
.
Câu 21. Cho góc
O
30xOy =
. Gọi
A
và
B
là hai điểm di động lần lượt trên
Ox
và
Oy
sao cho
1AB =
. Độ
dài lớn nhất của đoạn
OB
bằng:
A.
22
. B.
2
. C.
1,5
. D.
3
.
Câu 22. Cho hệ bất phương trình
2 5 1 0
2 5 0
10
xy
xy
xy
− −
+ +
+ +
. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ
bất phương trình?
A.
( )
1;0 .M
B.
( )
0; 2 .N −
C.
( )
0;2 .P
D.
( )
0;0 .O
Câu 23. Trong các bất đẳng thức sau, bất đẳng thức nào sai?
A.
22
0 , .a b ab a b+ +
B.
2 2 2
, , , .a b c ab bc ca a b c+ + + +
C.
0; 0ab
, ta có
( )
a b a b
22
2+ +
. D.
11
0ab
ba
.
Câu 24. Cho
3
đường thẳng
( )
1
d
:
3 2 5 0xy− + =
,
( )
2
d
:
2 4 7 0xy+ − =
,
( )
3
d
:
3 4 1 0xy+ − =
. Viết phương
trình đường thẳng
( )
d
đi qua giao điểm của
( )
1
d
,
( )
2
d
và song song với
( )
3
d
.
A.
24 32 53 0xy− − =
. B.
24 32 53 0xy+ − =
.
C.
24 32 53 0xy+ + =
. D.
24 32 53 0xy− + =
.
Trang 7/40
Câu 25. Hệ bất phương trình
2
2
9
0
3 12
7 3 1
0
52
x
xx
xx
x
−
− + −
++
+
−
có nghiệm là:
A.
13x
. B.
3x −
hoặc
1x
.
C.
35x
. D.
13x
.
Câu 26. Khi giải bất phương trình
2
30
1
x
x
−
−
. Một học sinh làm như sau
(I)
22
3 0 3
11
xx
xx
−
−−
(1)
(II)
(1) 2 3( 1)xx −
(2)
(III)
(2) 2 3 3 1x x x −
Vậy bất phương trình có tập nghiệm
( ;1)−
Cách giải trên đúng hay sai? Nếu sau thì
A. Lời giải đúng. B. Sai từ bước
( )
I
.
C. Sai từ bước
( )
II
. D. Sai từ bước
( )
III
.
Câu 27. Tập nghiệm của bất phương trình
1
1
3
x
x
−
−
là
A.
( ) ( )
;3 3;− +
. B.
( )
;3−
.
C.
( )
3;+
. D. .
Câu 28. Xác định
m
để
2
đường thẳng
: 2 3 4 0d x y− + =
và
23
:
14
xt
d
y mt
=−
=−
vuông góc
A.
9
8
m =−
. B.
1
2
m =−
. C.
9
8
m =
. D.
1
2
m =
.
Câu 29. Phương trình:
22
4 2 3 4x x x x+ − = + −
có bao nhiêu nghiệm lớn hơn hoặc bằng
0
:
A.
0
. B.
2.
C.
3
. D.
1.
Câu 30. Cho tam giác
ABC
có
, , BC a CA b AB c= = =
. Mệnh đề nào sau đây là đúng?
A. Nếu
2 2 2
0b c a+ −
thì góc
A
nhọn. B. Nếu
2 2 2
0b c a+ −
thì góc
A
tù.
C. Nếu
2 2 2
0b c a+ −
thì góc
A
nhọn. D. Nếu
2 2 2
0b c a+ −
thì góc
A
vuông.
Câu 31. Đường tròn
( )
C
có tâm là gốc tọa độ
( )
0;0O
và tiếp xúc với đường thẳng
:8 6 100 0xy + + =
. Bán
kính
R
của đường tròn
( )
C
bằng:
A.
8R =
. B.
10R =
. C.
4R =
. D.
6R =
.
Câu 32. Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
2+mx m x
vô nghiệm.
A.
0=m
. B.
2=m
. C.
2=−m
. D.
m
.
Câu 33. Nghiệm của bất phương trình
2 3 1−x
là:
A.
13x
. B.
11− x
. C.
12x
. D.
12− x
.
Câu 34. Giá trị
x
thỏa mãn bất phương trình
2 6 0x− +
là
A.
5x =
. B.
3x =
. C.
4x =
. D.
2x =
.
Câu 35. Tìm tập xác định
D
của hàm số
2
3
.
43
x
y
xx
−
=
−−
A.
D \ 1; 4 .=−
B.
D 4;1 .=−
C.
( )
D 4;1 .=−
D.
( ) ( )
D ;4 1; .= − +
PHẦN II: TỰ LUẬN
Trang 8/40
Câu 1. Tìm các giá trị của m để biểu thức
2
( ) ( 1) 2 7 0f x x m x m x= + + + +
Câu 2. Tam giác
ABC
có các cạnh thỏa mãn hệ thức
( )( )
3a b c a b c ab+ + + − =
. Tìm số đo góc
C
.
Câu 3. Trong mặt phẳng với hệ tọa độ
,Oxy
Cho hình vuông
ABCD
có
( )
2; 2C −
và
( )
; , 0.B a b a
Gọi
điểm
,IK
lần lượt là trung điểm của
DA
và
;DC
điểm
( )
1; 1M −−
là giao của
BI
và
.AK
Tính
P a b=+
.
Câu 4. Cho ba số thực dương
, , x y z
thỏa mãn điều kiện
2x y z+ + =
. Tìm giá trị lớn nhất của biểu thức
P x y y z z x= + + + + +
.
------------- HẾT -------------
Trang 9/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 3
Mã đề thi
003
Họ và tên :………………………………………...Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Nhị thức
32−+x
nhận giá trị dương khi
A.
3
2
−x
. B.
2
3
x
. C.
3
2
x
. D.
2
3
x
.
Câu 2. Cặp số là nghiệm của bất phương trình nào sau đây.
A. . B. . C. . D. .
Câu 3. Cho hệ bất phương trình
−+
+−
−
05
033
0
yx
yx
yx
.
Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Điểm
( )
0;0O
thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm
( )
5;3B
thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm
( )
1; 1C −
thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm
( )
2;2D −
thuộc miền nghiệm của hệ bất phương trình đã cho.
Câu 4. Điều kiện của phương trình là:
A.
2x −
và
1x −
. B. và
1x −
.
C. và
4
3
x
. D.
2, 1xx − −
và
4
3
x
.
Câu 5. Phương trình tham số của đường thẳng đi qua 2 điểm
và
( )
1;5B
là
A.
3
13
xt
yt
=−
= − −
. B.
1
53
xt
yt
=−
=−
. C.
3
13
xt
yt
=+
= − −
. D.
3
13
xt
yt
=+
= − +
.
Câu 6. Trong các khẳng định sau, khẳng định nào đúng với mọi số thực ?
A.
25xx− −
. B. . C. . D. .
Câu 7. Nếu
0ab
,
0.cd
thì bất đẳng thức nào sau đây không đúng?
A.
+ +a c b d
. B.
ac bd
. C.
ab
cd
. D.
ad
bc
.
Câu 8. Cho tam giác
ABC
bất kỳ có
=BC a
,
=AC b
,
=AB c
. Đẳng thức nào sai?
A.
2 2 2
2 cos= + −a b c bc A
. B.
2 2 2
2 cos=++c b a ab C
.
C.
2 2 2
2 cos=+−c b a ab C
. D.
2 2 2
2 cos= + −b a c ac B
.
Câu 9. Cho
( )
2
f x ax bx c= + +
,
( )
0a
và
2
4b ac = −
. Cho biết dấu của
khi
( )
fx
luôn cùng dấu với
hệ số
a
với mọi
x
.
A.
0
. B.
0
. C.
0=
. D.
0
.
Câu 10. Tập nghiệm của bất phương trình
( )( )
2 5 0+ − xx
là
A.
( )
5; 2−−
. B.
)
5;+
.
C.
( ) ( )
; 2 5;− − +
. D.
( )
2;5−
.
( )
3; 2
30xy−
34xy
3 3 0xy− +
3 4 1 0xy− −
1 4 3
2
1
2
x
x
x
x
−
+ − =
+
+
2x −
2x −
x
22
52xx
37xx+ −
52xx
Trang 10/40
Câu 11. Một đường thẳng có bao nhiêu vectơ pháp tuyến?
A. Vô số. B. 2. C. 3. D. 1.
Câu 12. Với hai số
,xy
dương thoả
36xy =
. Bất đẳng thức nào sau đây đúng?
A.
2
36.
2
xy
xy
+

=


. B. Tất cả đều đúng.
C.
2 12.x y xy+ =
.
D.
22
2 72.x y xy+ =
.
Câu 13. Tìm tọa độ giao điểm của đường thẳng
: 4 3 26 0xy − − =
và đường thẳng
:3 4 7 0d x y+ − =
.
A.
( )
5;2
. B. Không có giao điểm.
C.
( )
2; 6−
. D.
( )
5; 2−
.
Câu 14. Tam giác
ABC
có
8, 3, 60a c B= = =
. Độ dài cạnh
b
bằng bao nhiêu ?
A.
61
. B.
49
. C.
7
. D.
97
.
Câu 15. Tập nghiệm của bất phương trình là.
A. . B. . C. . D. .
Câu 16. Xác định vị trí tương đối của 2 đường thẳng:
1
2 ( 3 2)
:
2 ( 3 2)
xt
yt
= + +
= − + −
và
2
3'
:
3 (5 2 6) '
xt
yt
= − +
= − + −
A. Vuông góc. B. Trùng nhau. C. Cắt nhau. D. Song song.
Câu 17. Tam giác
ABC
có
105A =
,
45B =
,
10AC =
. Tính cạnh
AB
.
A.
52
. B.
56
. C.
56
2
. D.
10 2
.
Câu 18. Nhị thức
23−−x
nhận giá trị dương khi và chỉ khi
A.
3
2
−x
. B.
2
3
−x
. C.
3
2
−x
. D.
2
3
−x
.
Câu 19. Tập nghiệm của bất phương trình
( )
5 2 4 0xx− −
là:
A.
8
;
7

−


. B.
8
;
7

− +


. C.
8
;
7

+


. D.
8
;
3

+


.
Câu 20. Tập nghiệm của bất phương trình
2
60− − xx
là:
A.
( ) ( )
; 2 3;− − +
. B.
( ) ( )
; 3 2;− − +
.
C.
( )
3;2−
. D.
( )
2;3−
.
Câu 21. Tập nghiệm của bất phương trình
30xx−
là
A.
1
0;
9



. B.
1
0;
9

+

. C.
0
.
D.
1
;
9

+

.
Câu 22. Nếu
a
,
b
là những số thực và
ab
thì bất đẳng thức nào sau đây luôn đúng?
A.
22
ab
. B.
11
ab
với
0ab
.
C.
b a b−
. D.
ab
.
Câu 23. Cho một hình bình hành
ABCD
có
AB a=
,
BC b=
. Công thức nào dưới đây là công thức tính diện
tích của hình bình hành đó?
A.
22
ab+
. B.
sinab ABC
. C.
ab
. D.
( )
2 ab+
.
Câu 24. Hệ bất phương trình
2
10
0
x
xm
−
−
có nghiệm khi
A.
1m
. B.
1m
. C.
1m =
. D.
1m
.
2
8 16 0xx− +
( )
;4S = −
\4S =
S =
( )
1;4S =
Trang 11/40
Câu 25. Tập nghiệm của bất phương trình
4
0
36
x
x
−
−+
là
A.
( )
2;4
. B.
( )
)
;2 4;− +
.
C.
2;4
. D.
(
2; 4
.
Câu 26. Cho tam giác
ABC
có
( )
1;2A
,
( )
2;3B
,
( )
3; 4C −−
. Diện tích tam giác
ABC
bằng
A.
3
2
. B.
2
. C.
12+
. D.
1
.
Câu 27. Cho
,0ab
. Chứng minh
2
ab
ba
+
. Một học sinh làm như sau
I)
2
ab
ba
+
22
2
ab
ab
+

(1)
II) (1)
2 2 2 2 2
2 2 0 ( ) 0a b ab a b ab a b + + − −
III) vì
( )
2
0ab−
đúng
, 0ab
nên
2
ab
ba
+
Cách làm trên
A. Sai từ I). B. Sai từ II).
C. Sai ở III). D. Cả I), II), III) đúng.
Câu 28. Trong mặt phẳng tọa độ
Oxy
cho điểm
( )
1;2I
và đường thẳng
( )
: 2 5 0d x y+ − =
. Biết rằng có hai
điểm
12
,MM
thuộc
( )
d
sao cho
12
10IM IM==
. Tổng hoành độ của
12
,MM
là :
A.
14
5
B.
2
C.
5
D.
7
5
Câu 29. Cho hai điểm
( ) ( )
1; 4 ; 3;2 .AB−
Viết phương trình tổng quát của đường trung trực của đoạn thẳng
AB
A.
3 8 0xy− + =
. B.
3 8 0xy+ − =
. C.
3 8 0xy− + + =
. D.
3 8 0xy− + =
.
Câu 30. Cho biểu thức
( )
2
4 12
.
4
x
fx
xx
−
=
−
Tập hợp tất cả các giá trị của
x
thỏa mãn bất phương trình
( )
0fx
là
A.
( ) ( )
;0 3;4 .x −
B.
(
( )
0;3 4; .x +
C.
(
)
;0 3;4 .x −
D.
( )
)
;0 3;4 .x −
Câu 31. Tìm tập nghiệm
S
của bất phương trình
2
5 1 3
5
x
x − +
.
A.
5
;
2
S

= − +


. B.
20
;
23
S

= +


. C.
( )
;1S = −
. D.
( )
;2S = −
.
Câu 32. Tập nghiệm
S
của bất phương trình
( 1) 1 0− + xx
là
A.
)
1 1;= − +S
B.
( )
1;= +S
C.
)
1;= − +S
D.
( )
1 1;= − +S
Câu 33. Hệ bất phương trình:
2
56
12
xx
x
+
+
có nghiệm là:
A.
63x− −
. B.
6x −
. C.
21x− −
. D.
10x−
.
Câu 34. Miền nghiệm của hệ bất phương trình
2 3 1 0
5 4 0
xy
xy
+ −
− +
là phần mặt phẳng chứa điểm nào sau đây?
A.
( )
1;4M −
. B.
( )
0;0N
. C.
( )
3;4P −
. D.
( )
2; 4Q −−
.
Câu 35. Cho hình bình hành
ABCD
có
AB a=
,
2BC a=
và
45BAD =
. Diện tích của hình bình hành
ABCD
là
Trang 12/40
A.
2
2a
. B.
2
3a
. C.
2
a
. D.
2
2a
.
PHẦN II: TỰ LUẬN
Câu 1. Tìm tập nghiệm của bất phương trình
( )
2
3 2 6 0xx+ + +
.
Câu 2. Cho tam giác ABC có
,BC a CA b
. Tam giác ABC có diện tích lớn nhất khi góc C bằng:
Câu 3. Trong mặt phẳng với hệ tọa độ
Oxy
, cho đường thẳng đi qua hai điểm
( ) ( )
1;2 , 4;6AB
, tìm tọa độ
điểm
M
trên trục
Oy
sao cho diện tích
MAB
bằng
1
.
Câu 4. Cho a,b,c
a,b,c
là các số thực thuộc đoạn
0;1
. Tìm GTLN của biểu thức
(1 ) (1 ) (1 )P a b b c c a= − + − + −
------------- HẾT -------------
Trang 13/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 4
Mã đề thi
004
Họ và tên :………………………………………...Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Tập nghiệm của bất phương trình
( )
2 1 3 2xx+ −
là
A.
( )
5;+
. B.
( )
;5−
. C.
( )
1; +
. D.
( )
;5− −
.
Câu 2. Bất phương trình
2
2 3 0xx− + +
có tập nghiệm là
A.
( )
1;3−
. B.
1;3−
.
C.
( )
3;1−
. D.
( ) ( )
; 1 3;− − +
.
Câu 3. Phương trình tổng quát của đường thẳng
d
đi qua
O
và song song với đường thẳng
:6 4 1 0xx − + =
là:
A.
3 12 1 0.xy+ − =
B.
6 4 1 0.xy− − =
C.
3 2 0.xy−=
D.
4 6 0.xy+=
Câu 4. Đường thẳng nào sau đây song song với đường thẳng
2 3 1 0xy+ − =
?
A.
4 6 2 0xy− − =
. B.
2 3 1 0xy+ + =
. C.
2 5 0xy− + =
. D.
2 3 3 0xy− + =
.
Câu 5. Đường trung trực của đoạn thẳng
AB
với
( )
3;2A =−
,
( )
3;3B =−
có một vectơ pháp tuyến là:
A.
( )
2
0;1n =
. B.
( )
3
3;5n =−
. C.
( )
4
1;0n =−
. D.
( )
1
6;5n =
.
Câu 6. Cho
( ) ( )
2
0f x ax bx c a= + +
. Điều kiện để
( )
0,f x x
là
A.
0
0
a

. B.
0
0
a

. C.
0
0
a

D.
0
0
a

Câu 7. Cho hệ bất phương trình
+−
−+
0
4
2
3
)1(2
01
32
x
y
x
yx
.
Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Điểm
( )
2;1A
thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm
( )
0;0O
thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm
( )
1;1C
thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm
( )
3;4D
thuộc miền nghiệm của hệ bất phương trình đã cho.
Câu 8. Trong các khẳng định sau, khẳng định nào sau đây đúng?
A.
0
0
ab
ab
cd
cd



. B.
0
0
ab
cd
ab
cd


.
C.
ab
ab
cd
cd

. D.
0
0
ab
cd
ad
bc


.
Câu 9. Nghiệm của bất phương trình
22
22
1
22
x x x x
xx
+ + +
++
là:
A.
2x
. B.
x
. C.
1x
. D.
1x
.
Trang 14/40
Câu 10. Tìm điều kiện của bất phương trình
23
2
63
x
x
x
−
−
−
.
A.
2x
. B.
2x
. C.
2x
. D.
2x
.
Câu 11. Tam giác
ABC
có
150C =
,
3BC =
,
2AC =
. Tính cạnh
AB
A.
1
. B.
13
. C.
10
. D.
3
.
Câu 12. Tính diện tích tam giác
ABC
có ba cạnh là
13, 14, 15.
A.
16 24
. B.
6411
. C.
168.
D.
84.
Câu 13. Phương trình
2
20mx mx− + =
có nghiệm khi và chỉ khi
A.
0m
hoặc
8m
.
B.
0m
hoặc
8m
.
C.
08m
. D.
08m
.
Câu 14. Tập nghiệm của bất phương trình
2
5 4 0xx− + −
là
A.
( ) ( )
;1 4;− +
. B.
(
)
;1 4;− +
. C.
1;4
. D.
( )
1; 4
.
Câu 15. Cho tam giác
ABC
có
2, 2,BC 1.AB AC= = =
Giá trị
cos A
bằng:
A.
7
.
16
B.
7
.
32
C.
7
.
8
D.
0.
Câu 16. Số
3x =
là nghiệm của bất phương trình nào sau đây?
A.
51x−
. B.
3 1 4x +
. C.
4 11xx−
. D.
2 1 3x −
.
Câu 17. Nhị thức nào sau đây nhận giá trị âm với mọi số
x
nhỏ hơn
2
3
−
?
A.
( )
32=+f x x
. B.
( )
3 – 2=−f x x
. C.
( )
23=+f x x
. D.
( )
6 – 4=−f x x
.
Câu 18. Cho
( )
21f x x=+
. Khẳng định nào sau đây là khẳng định sai
A.
( )
0; 0f x x
. B.
( )
1
0;
2
f x x −
.
C.
( )
1
0;
2
f x x
. D.
( )
0; 2f x x
.
Câu 19. Với hai số
,xy
dương thoả
36xy =
. Bất đẳng thức nào sau đây đúng?
A. Tất cả đều đúng. B.
22
2 72.x y xy+ =
.
C.
2
36.
2
xy
xy
+

=


.
D.
2 12.x y xy+ =
.
Câu 20. Tìm tọa độ giao điểm của 2 đường thẳng sau đây:
1
22 2
:
55 5
xt
yt
=+
=+
và
2
12 4 '
:
15 5 '
xt
yt
=+
= − −
A. (2; 5). B. (6; 5). C. (0; 0). D. (−5; 4).
Câu 21. Nghiệm của phương trình:
22
3 2 1x x x x− + − + − =
là:
A.
1; 2 .
B.
0; 1 .
C.
13
.
2
D.
15
.
2
Câu 22. Đường tròn
( )
C
có tâm
( )
2; 2I −−
và tiếp xúc với đường thẳng
:5 12 10 0xy + − =
. Bán kính
R
của đường tròn
( )
C
bằng:
A.
44R =
. B.
7
13
R =
. C.
44
13
R =
. D.
24
13
R =
.
Câu 23. Cho
, , a b c
dương. Bất đẳng thức nào đúng?
A.
1 1 1
( ) 9.abc
abc

+ + + +


B.
1 1 1
( ) 9.abc
abc

+ + + +


Trang 15/40
C.
1 1 1
( ) 3.abc
abc

+ + + +


D.
1 1 1
( ) 3.abc
abc

+ + + +


Câu 24. Tập xác định của hàm số
22
4 25y x x x= − + −
là
A.
5;5−
. B.
(
)
;0 4;− +
.
C.
5;0 4;5−
. D.
( ) ( )
5;0 4;5−
.
Câu 25. Bất phương trình
2
0
21
x
x
−
+
có tập nghiệm là:
A.
1
;2
2

−

. B.
1
;2
2
−



. C.
1
;2
2
−


. D.
1
;2
2
−



.
Câu 26. Cho hai điểm
( )
1;2A −
,
( )
3;1B
và đường thẳng
1
:
2
xt
yt
=+
=+
. Tọa độ điểm
C
thuộc
để tam giác
ACB
cân tại
C
là
A.
7 13
;
66

−


. B.
13 7
;
66



. C.
7 13
;
66

−


. D.
7 13
;
66



.
Câu 27. Cho các số thực
,,abc
. Trong các bất đẳng thức sau, bất đẳng thức nào sai?
A.
( )
2 2 2
a b c a b c+ + +
B.
22
4 1 2 2a b ab b a+ + + +
C.
2 2 2
a b c ab bc ca+ + + +
D.
( )
5 5 2 2
a b a b a b+ +
Câu 28. Tập nào sau đây chứa trong tập nghiệm của phương trình:
30xx+
?
A.
( )
2;10−
. B.
( )
1;10
. C.
( )
4;− +
. D.
( )
3;1−
.
Câu 29. Hình bình hành
ABCD
có
AB a=
,
2BC a=
và
45BAD =
. Khi đó hình bình có diện tích là
A.
2
3a
. B.
2
2a
. C.
2
2a
. D.
2
a
.
Câu 30. Tập nghiệm bất phương trình
2
56
1
−+
−
xx
x
0 là:
A.
( )
;1 2;3−
. B.
(
1;3
. C.
(
)
1;2 3; +
. D.
2;3
.
Câu 31. Cho tam giác
ABC
có
2 2 2
BC AB AC+
. Mệnh đề nào sau đây là đúng?
A.
Â
là góc tù. B.
Â
là góc nhọn.
C.
Â
là góc vuông. D.
Â
là góc nhỏ nhất.
Câu 32. Một học sinh giải phương trình
2
1 13 3 2xx− +
(1) tuần tự như sau
(I)
2
(1) 1 2 13 3xx − +
(2)
(II)
22
(2) (1 2 ) 13 3xx − +
, với
1
2
x
(3)
(III)
2
(3) 4 12 0xx − −
, với
1
2
x
(4)
(IV)
(4) 2x
Lý luận trên nếu sai, thì sai từ bước nào?
A. (III). B. (IV). C. Lý luận đúng. D. (II).
Câu 33. Miền nghiệm của hệ bất phương trình
39
3
28
6
xy
xy
yx
y
+
−
−
là phần mặt phẳng chứa điểm
A.
( )
8;4
. B.
( )
0;0
. C.
( )
2;1
. D.
( )
1; 2
.
Câu 34. Tính góc tạo bởi giữa hai đường thẳng
1
: 3 0d x y+=
và
2
1: 00.xd +=
Trang 16/40
A.
o
90 .
B.
o
30 .
C.
o
45 .
D.
o
60 .
Câu 35. Hệ phương trình
2 1 0
3
x
xm
−
−
vô nghiệm khi và chỉ khi
A.
5
2
m −
. B.
5
2
m −
. C.
5
2
m −
. D.
7
2
m
.
PHẦN II: TỰ LUẬN
Câu 1. Giải bất phương trình
( )
( )
2
5 2 2 .x x x+ +
Câu 2. Trong cuộc thi giải trí toán học tổ chức nhân dịp hoạt động chào mừng Ngày nhà giáo Việt Nam có
một trò chơi như sau: Người ta thiết kế hai đường ray tạo với nhau một góc
0
30
như hình vẽ dưới đây. Trên
các đường thẳng
Ox
và
Oy
người ta để hai vật nặng cùng trọng lượng. Buộc hai vật thể với nhau bằng một
thanh cứng
1AB m=
sao cho mỗi vật đều có thể chuyển động được trên hai đường ray. Nối hai vật bằng một
sợi giây vòng qua một cột có gốc tại
O
. Người tham dự cuộc thi sẽ đứng tại vị trí điểm
B
để kéo vật thể
chuyển động trên
Oy
. Người thắng cuộc sẽ là người kéo được vật thể ra xa nhất so với điểm gốc
O
. Hãy
dùng kiến thức toán học để tính toán vị trí xa nhất mà người tham dự cuộc thi có thể đạt được.
Câu 3. Trong mặt phẳng tạo độ Oxy cho hai điểm A(1;2), B(4;3). Tính tổng tất cả các hoành độ của điểm M
thuộc trục Ox sao cho
0
45AMB =
.
Câu 4. Gọi
,Mm
lần lượt là GTLN và GTNN của hàm số
2
2017 2019
()
2018
x
f x x
trên tập xác định
của nó. Tìm số phần tử của tập hợp
*
[ ; ]mM
?
------------- HẾT -------------
O
B
A
Trang 17/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 5
Mã đề thi
005
Họ và tên :………………………………………...Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cho đường thẳng
có phương trình tổng quát:
–2 3 – 1 0xy+=
. Vectơ nào sau đây không là vectơ
chỉ phương của
?
A.
( )
2; 3
. B.
( )
–3; – 2
. C.
2
1;
3



. D.
( )
3; 2
.
Câu 2. Cho mệnh đề ”Hai bất phương trình tương đương là hai bất phương trình …”. Hãy chọn một kết quả
trong bốn kết quả sau điền tiếp vào dấu "…" để được một mệnh đề đúng.
A. có hai tập nghiệm khác nhau.
B. có một tập nghiệm là con của tập nghiệm kia.
C. có tập nghiệm khác
.
D. có cùng tập nghiệm.
Câu 3. Cho hai số thực
,ab
tùy ý. Mệnh đề nào sau đây là đúng?
A.
a b a b+ = +
. B.
a b a b+ +
. C.
a b a b+ +
. D.
a b a b+ +
.
Câu 4. Số
2−
thuộc tập nghiệm của bất phương trình nào ?
A.
3 1 0−x
. B.
3 2 0+x
. C.
2 1 0− − x
. D.
4 5 0−x
.
Câu 5. Cho nhị thức bậc nhất
( )
f x ax b=+
( )
0a
. Chọn kết quả sai trong các kết quả sau.
A.
( )
fx
có giá trị bằng
0
khi
b
x
a
=−
.
B.
( )
fx
có giá trị cùng dấu với hệ số
a
khi
x
lấy các giá trị trong khoảng
;
b
a

− +


.
C.
( )
fx
có giá trị trái dấu với hệ số
a
khi
x
lấy các giá trị trong khoảng
;
b
a

− −


.
D.
( )
fx
có giá trị cùng dấu với hệ số
a
khi
x
lấy các giá trị trong khoảng
( )
;− +
.
Câu 6. Phương trình đường thẳng đi qua
(1;2)N
và song song với đường thẳng
2 3 12 0xy+ − =
là.
A.
4 6 1 0xy+ + =
. B.
2 3 8 0xy− − =
. C.
2 3 8 0xy+ − =
. D.
2 3 8 0xy+ + =
.
Câu 7. Cho hai điểm
( ) ( )
4; 1 , 1; 4AB−−
. Viết phương trình tổng quát đường trung trực đoạn
AB
.
A.
0xy+=
. B.
0xy−=
. C.
1xy−=
. D.
1xy+=
.
Câu 8. Cho bất phương trình
2 5 0xy− +
có tập nghiệm là
S
.Mệnh đề nào sau đây là đúng?
A.
( )
2;2 S−
. B.
( )
2;2 S
. C.
( )
2;4 S−
. D.
( )
1;3 S
.
Câu 9. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho đường thẳng
( )
d
có phương trình
12
3
xt
yt
=−
=+
. Véctơ
nào sau đây là một véctơ chỉ phương của đường thẳng
( )
d
?
A.
( )
1;2u
. B.
( )
2; 1u −
. C.
( )
1;3u
. D.
( )
4;1u −
.
Câu 10. Tam giác
ABC
có
8 cmAB =
,
10 cmBC =
,
6 cmCA =
. Đường trung tuyến
AM
của tam giác đó
có độ dài bằng
A.
4 cm
. B.
5 cm
. C.
6 cm
. D.
7 cm
.
Câu 11. Tam thức bậc hai
( )
2
12 13f x x x= − −
nhận giá trị không âm khi và chỉ khi
A.
(
)
; 1 13;x − − +
. B.
\ 1;13x −
.
Trang 18/40
C.
1;13x −
. D.
( )
1;13x −
.
Câu 12. Tìm tập nghiệm của bất phương trình
2 2 2x x x+ − + −
.
A.
)
2;+
. B.
. C.
( )
;2−
. D.
2
.
Câu 13. Tính diện tích tam giác có ba cạnh là
9, 10, 11.
A.
44.
B.
30 2.
C.
42.
D.
50 3.
Câu 14. Bất phương trình
2
5 1 3
5
x
x − +
có nghiệm là
A.
5
2
x −
. B.
2x
. C.
20
23
x
. D.
x
.
Câu 15. Cho đường thẳng
: 2 3 0d x y− + =
và điểm
(5; 2).M −
Đối với đường thẳng d, điểm nào dưới đây
nằm cùng một phía đối với điểm
M
?
A.
N(1;6)
. B.
N( 4;0)−
. C.
. D.
(3; 1)N −
.
Câu 16. Tìm điều kiện xác định của bất phương trình
2 6 3 2 2 6xx+ + +
.
A.
3x −
. B. Điều kiện khác. C.
3x −
. D.
3x −
.
Câu 17. Tính diện tích tam giác có ba cạnh lần lượt là
3
,
2
và
1.
A.
3
2
. B.
3
. C.
6
2
. D.
2
2
.
Câu 18. Cặp số
( )
1; –1
là nghiệm của bất phương trình nào sau đây?
A.
– 3 0xy+
. B.
– – 0xy
. C.
3 1 0xy+ +
. D.
– – 3 – 1 0xy
.
Câu 19. Cho tam thức bậc hai
( ) ( )
2
0f x ax bx c a= + +
có biệt thức
2
4b ac = −
. Chọn kết quả sai trong
các kết quả sau.
A. Nếu
0=
thì
( )
.0a f x
với mọi
x
.
B. Nếu
0
thì
( )
fx
cùng dấu với hệ số
a
khi
x
lấy các giá trị trong khoảng
;
b
a

− +


và trái dấu
với hệ số
a
khi
x
lấy các giá trị trong khoảng
;
b
a

− −


.
C. Nếu
0
thì
( )
fx
cùng dấu với hệ số
a
khi
1
xx
hoặc
2
xx
,
( )
fx
trái dấu với hệ số
a
khi
12
x x x
(trong đó
1
x
,
( )
2 1 2
x x x
là hai nghiệm của
( )
fx
).
D. Nếu
0
thì
( )
fx
luôn cùng dấu với hệ số
a
, với mọi
x
.
Câu 20. Cho
,.ab
Mệnh đề nào sau đây đúng?
A.
a b a b+ +
B.
a b a b+ = +
C.
a b a b+ +
D.
a b a b+ +
Câu 21. Viết phương trình tham số của đường thẳng
( )
D
đi qua điểm
2()1;A −
và vuông góc với đường
thẳng
:2 4 0xy − + =
.
A.
12
2
xt
yt
= − +
=−
. B.
12
2
xt
yt
=+
=−
. C.
42
xt
yt
=
= + −
. D.
12
2
xt
yt
= − +
=+
.
Câu 22. Tìm tập nghiệm của bất phương trình
( )
( )
2
1
0
2 5 4
x
x x x
−
− − +
là:
A.
( ) ( )
;2 4; \ 1− +
. B.
( ) ( )
;2 4;− +
.
C.
2;4
. D.
(
)
;2 4;− +
.
Câu 23. Bất phương trình
24xx− +
có tập nghiệm là
A.
)
1;− +
. B. . C.
2−
. D.
6−
.
Trang 19/40
Câu 24. Tập hợp các giá trị
m
để hệ bất phương trình
2 1 3
0
x
xm
−
−
có nghiệm duy nhất là:
A.
2
. B.
)
2;+
. C.
(
;2−
. D.
.
Câu 25. Trong các bất phương trình sau, bất phương trình nào tương đương với bất phương trình
21x
?
A.
2
41x
. B.
2 2 1 2x x x+ + + +
.
C.
2 2 1 2x x x+ − + −
. D.
11
21
33
x
xx
− −
−−
.
Câu 26. Diện tích
S
của tam giác sẽ thỏa mãn hệ thức nào trong hai hệ thức sau đây?
I.
( )( )( )
2
S p p a p b p c= − − −
.
II.
( )( )( )( )
2
16S a b c a b c a b c a b c= + + + − − + − + +
.
A. Chỉ II. B. Cả I và II. C. Không có. D. Chỉ I.
Câu 27. Cho hai đường thẳng song
1
:5 7 4 0d x y− + =
và
2
:5 7 6 0.d x y− + =
Khoảng cách giữa
1
d
và
2
d
là
A.
2
74
. B.
10
74
. C.
4
74
. D.
6
74
.
Câu 28. Trong mặt phẳng
Oxy
, hãy cho biết đường thẳng nào đi qua điểm
( )
2;1A
và song song với đường
thẳng
: 2 3 2 0xy + − =
?
A.
30xy− + =
. B.
4 6 11 0xy+ − =
. C.
2 3 7 0xy− − + =
. D.
3 2 4 0xy− − =
.
Câu 29. Giải bất phương trình:
2
1
21
x
xx
−
−+
.
A.
1x −
hoặc
2x
. B.
1x −
hoặc
2x
.
C.
12x−
. D.
12x−
.
Câu 30. Cho tam giác
ABC
có
3AB =
,
4AC =
,
5BC =
. Bán kính đường tròn nội tiếp tam giác bằng
A.
4
5
. B.
3
4
. C.
1
. D.
8
9
.
Câu 31. Giải bất phương trình
2
2 5 2 4x x x+ + +
được các giá trị
x
thỏa mãn
A.
1x −
hoặc
1x
. B.
11x−
.
C.
1x
. D.
1x
.
Câu 32. Cho
x
,
y
là hai số thực bất kỳ thỏavà
2xy =
. Giá trị nhỏ nhất của
22
A x y=+
.
A.
2
. B.
1
. C.
0
. D.
4
.
Câu 33. Tìm tập nghiệm
S
của bất phương trình
2
40x −
.
A.
( ) ( )
;0 4;S = − +
. B.
( ) ( )
; 2 2;S = − − +
.
C.
( )
2;2S =−
. D.
(
)
; 2 2;S = − − +
.
Câu 34. Bất phương trình
( 2) 5mx−
vô nghiệm khi
A.
2m
. B.
2m
. C.
2m =
. D.
2m
.
Câu 35. Biết rằng giá trị lớn nhất của biểu thức
( )( )
( ) 3 1 1f x x x= + −
với
1
;1
3
x

−


bằng
4
3
. Dấu bằng
xảy ra tại
x
bằng
A.
0
. B.
3
. C.
1
3
. D.
2
3
.
PHẦN II: TỰ LUẬN
Câu 1. Tìm m để biểu thức sau luôn âm
2
( ) 1.= − −f x mx x
Trang 20/40
Câu 2. Cho tam giác
ABC
. Chứng minh rằng
2 1 1 1 1
a a b c
h r r r r
= − = +
Câu 3. Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác
ABC
có đỉnh
( )
4; 1A −
phương trình đường cao
và trung tuyến kẻ từ đỉnh B lần lượt là
2 3 12 0xy− + =
và
2 3 0xy+=
. Xác định tọa độ các đỉnh còn lại của
tam giác
.ABC
Câu 4. Cho
,ab
là số thực dương thỏa mãn
22
2ab+=
. Chứng minh rằng
( )
( )( )
5
22
16 1 1a b ab a b+ + +
.
------------- HẾT -------------
Trang 21/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 6
Mã đề thi
006
Họ và tên :………………………………………...Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cho đường thẳng
: 2 1 0d x y− + =
. Nếu đường thẳng
qua điểm
( )
1; 1M −
và
song song với
d
thì
có phương trình:
A.
2 3 0xy− − =
. B.
2 5 0xy− + =
. C.
2 3 0xy− + =
. D.
2 1 0.xy+ + =
Câu 2. Tập nghiệm của bất phương trình
( ) ( )
6 5 2 10 8x x x x x− + − + −
là
A.
( )
5;S = +
. B.
S =
. C.
S =
. D.
( )
;5S = −
.
Câu 3. Cho tam giác
ABC
có
0
9, 8, 60= = =AB BC ABC
. Tính độ dài đoạn
AC
.
A.
73
. B.
217
. C.
8
D.
113
.
Câu 4. Cho tam thức bậc hai
( )
2
2f x x x=−
. Chọn khẳng định đúng.
A.
( ) ( )
0, 1;f x x +
. B.
( )
0,f x x
.
C.
( )
0,f x x
. D.
( ) ( )
0, 0;2f x x
.
Câu 5. Tính diện tích tam giác có ba cạnh lần lượt là
5
,
12
,
13
.
A.
75
. B.
60
. C.
30
. D.
34
.
Câu 6. Tập nghiệm của bất phương trình
51
33
22
xx
xx
+
+ − + −
là
A.
1
;3
4

−

. B.
1
;3
4


. C.
1
;
4

− +

. D.
1
;3
4

−


.
Câu 7. Cho tam giác
ABC
có
9AB =
,
12AC =
,
15BC =
. Khi đó đường trung tuyến
AM
của tam giác có
độ dài bằng bao nhiêu?
A.
8
. B.
9
. C.
10
. D.
7,5
.
Câu 8. Đường thẳng
43
:
12
xt
d
yt
có véctơ pháp tuyến có tọa độ là:
A.
1;1
. B.
4; 6
. C.
2; 3
. D.
3; 2
.
Câu 9. Hình vẽ nào sau đây biểu diễn miền nghiệm của bất phương trình
2 3 6 0xy− −
(miền không tô đậm
kể cả bờ)?
A. H4 B. H1 C. H2 D. H3
Câu 10. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình
21xy+
?
A.
( )
0;1
. B.
( )
3; 7−
. C.
( )
2;1−
. D.
( )
0;0
.
Câu 11. Bất phương trình sau đây tương đương với bất phương trình
50x +
?
A.
2
( 5) 0xx+
. B.
5( 5) 0xx+ +
.
Trang 22/40
C.
5( 5) 0xx+ −
. D.
2
( 1) ( 5) 0xx− +
.
Câu 12. Nếu
22ab
và
33− −bc
thì bất đẳng thức nào sau đây đúng?
A.
22
ac
. B.
ac
. C.
ac
. D.
33− −ac
.
Câu 13. Khẳng định nào sau đây là khẳng định sai?
A. Bất phương trình
0ax b+
vô nghiệm khi
0a =
và
0b
.
B. Bất phương trình
0ax b+
có tập nghiệm là khi
0a =
và
0b
.
C. Bất phương trình
0ax b+
vô nghiệm khi
0a =
.
D. Bất phương trình bậc nhất một ẩn luôn có nghiệm.
Câu 14. Bất phương trình
0+ax b
có tập nghiệm là khi và chỉ khi
A.
0
0
=
a
b
. B.
0
0
=
a
b
. C.
0
0
=
a
b
. D.
0
0
a
b
.
Câu 15. Tam thức bậc hai nào sau đây luôn dương với mọi
x
?
A.
2
2x 1.x −+
B.
2
8x 192.x −+
C.
2
3x 2.x −+
D.
2
5x 2x 229.− + −
Câu 16. Cho hai số thực
,ab
tùy ý. Mệnh đề nào sau đây là đúng?
A.
a b a b+ +
. B.
a b a b+ = +
. C.
a b a b+ +
. D.
a b a b+ +
.
Câu 17. Tìm điều kiện xác định của bất phương trình
2
5 3 2 4
7
1 2 5 2 5
xx
x x x
−
+ +
+ − −
A.
5
2
x
. B.
5
2
x
. C.
5
2
x
. D.
5
2
x
.
Câu 18. Cho đường thẳng
: 2 1 0xy − + =
. Điểm nào sau đây nằm trên đường thẳng
?
A.
( )
0; 1D −
. B.
( )
1;1A
. C.
1
;2
2
B



. D.
1
;2
2
B

−


.
Câu 19. Phương trình nào sau đây là phương trình đường thẳng đi qua hai điểm
( ) ( )
;0 ; 0; ; , 0A a B b a b
?
A.
1
xy
ab
+=
. B.
0
xy
ab
+=
. C.
ax by ab+=
. D.
1ax by+=
.
Câu 20. Câu nào đúng trong các câu sau?
A. Miền nghiệm của bất phương trình
0x
là nửa mặt phẳng bên phải trục tung kể cả biên (bờ).
B. Miền nghiệm của bất phương trình
2 1 0xy− −
chứa điểm
( )
1;1M −
.
C. Miền nghiệm của bất phương trình
100 400 1 0xy+ +
là nửa mặt phẳng kể cả bờ.
D. Miền nghiệm của bất phương trình
2 1 0xy− −
chứa điểm
( )
0;0O
.
Câu 21. Tập nghiệm của bất phương trình
11
33xx
−+
là
A.
( ) ( )
; 3 3;− − +
.
B.
.
C.
( )
3;+
. D.
(
)
; 3 3;− − +
.
Câu 22. Các nghiệm tự nhiên bé hơn 4 của bất phương trình
2
23 2 16
5
x
x− −
là
A. Một kết quả khác. B.
4; 3; 2; 1;0;1;2;3− − − −
.
C.
35
4
8
x−
. D.
0;1; 2;3}
.
Câu 23. Cho tam giác
ABC
có
(2;6)A
,
(0;3)B
,
(4;0)C
. Phương trình đường cao
AH
của
ABC
là:
A.
3 4 18 0xy− + =
. B.
4 3 10 0xy− + =
. C.
3 4 30 0xy+ − =
. D.
4 3 10 0xy− − =
.
Câu 24. Tập nghiệm của bất phương trình
( )
22
2 2 1 0x x x+ − −
là
A.
( )
5 13
1; 2;
2

−
− +



. B.
9
4; 5;
2

− − −


.
Trang 23/40
C.
22
2; ;1
22
− −
. D.
(
17
; 5 ;5 3
5

− −

.
Câu 25. Gọi
S
là tập nghiệm của bất phương trình
2
12 0xx− −
. Tập nào sau đây không là tập con của
S
.
A.
(
;5− −
. B.
)
0;+
. C.
(
;3− −
. D.
)
5;+
.
Câu 26. Tập hợp các giá trị của m để phương trình
2
1
11
x m m
x
xx
−
− + =
−−
có nghiệm là:
A.
1
;
3

+

.
B.
1
;
3

+


. C.
1
;
3

−


. D.
( )
1; +
.
Câu 27. Tính chu vi tam giác
ABC
biết rằng
6AB =
và
2sin 3sin 4sinA B C==
.
A.
26.
B.
13.
C.
5 26.
D.
10 6.
Câu 28. Cho tam giác
ABC
đều nội tiếp đường tròn bán kính
8R =
. Tính diện tích của tam giác
ABC
.
A.
30
. B.
26
. C.
48 3
. D.
24 3
.
Câu 29. Gọi
1
x
,
2
x
là nghiệm của phương trình
2
4 2 2 1x x x+ − = −
. Tính tổng
12
S x x=+
.
A.
8
3
S =−
. B.
4
3
S =
. C.
4
3
S =−
. D.
8
3
S =
.
Câu 30. Cho
và
1 abc+ + =
. Dùng bất đẳng thức Côsi ta chứng minh được
1 1 1
1 1 1 64
abc
+ + +
. Dấu đẳng thức xảy ra khi và chỉ khi nào:
A.
1.abc= = =
B.
1
.
3
abc= = =
C.
1, 0.a b c
D.
.abc==
Câu 31. Bất phương trình
2 5 3x −
có tập nghiệm là
A.
( )
2;3
. B.
5
2



. C.
0
. D.
1;4
.
Câu 32. Tìm
m
để hệ bất phương trình
( )( )
3 4 0
1
xx
xm
+ −
−
có nghiệm?
A.
2m −
. B.
5m =
. C.
5m
. D.
5m
.
Câu 33. Cho tam giác
ABC
có
( )
1; 1A
,
( )
0; 2B −
,
( )
4; 2C
. Viết phương trình tổng quát của trung tuyến
AM
.
A.
0xy−=
. B.
2 3 0xy+ − =
. C.
2 3 0xy+ − =
. D.
20xy+ − =
.
Câu 34. Tính khoảng cách
d
từ điểm
( )
2;0M
đến đường thẳng
13
24
xt
yt
=+
=−
.
A.
8
5
d =
. B.
2
5
d =
. C.
5
2
d =
. D.
2
5
d =
.
Câu 35. Cho hàm số
4
, ( 1)
1
y x x
x
= +
−
. Giá trị nhỏ nhất của y là:
A.
5
B.
2
. C.
4
. D.
3
.
PHẦN II: TỰ LUẬN
Câu 1. Tìm m để biểu thức sau luôn dương:
( )
22
2 2( 1) 1.+ − + +m x m x
Câu 2. Cho tam giác
ABC
có
2 2 2
5
b c a
m m m+=
. Chứng minh:
2 2 2
sin sin sinB C A+=
.
Trang 24/40
Câu 3. Cho tam giác
ABC
, biết
( )
1;3A
và hai trung tuyến có phương trình là
2 1 0, 1 0x y y− + = − =
. Hãy
lập phương trình tổng quát, tham số của mỗi cạnh
ABC
.
Câu 4. Cho
,ab
là các số thực thuộc đoạn
0;1
. Chứng minh rằng
( )( )( )
8
11
27
a b a b− − +
.
------------- HẾT -------------
Trang 25/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 7
Mã đề thi
007
Họ và tên :………………………………………...Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Miền nghiệm của bất phương trình
( )
5 2 9 2 2 7x x y+ − − +
không chứa điểm nào trong các điểm
sau?
A.
( )
0;0
. B.
( )
2; 1−
. C.
( )
2;1−
. D.
( )
2;3
.
Câu 2. Tìm tọa độ vectơ chỉ phương của đường thẳng song song với trục
Oy
.
A.
(1; 1 .)−
B.
( )
1;0 .
C.
( )
0;1 .
D.
( )
1;1 .
Câu 3. Trong mặt phẳng
Oxy
, đường thẳng
23yx=−
có một véc-tơ pháp tuyến
n
là
A.
( )
2; 1n = − −
. B.
( )
2; 1n =−
. C.
( )
2;1n =
. D.
( )
1;2n =
.
Câu 4. Miền của bất phương trình
21xy+
không chứa điểm nào sau đây?
A.
( )
1;1A
. B.
( )
2;2B
. C.
( )
3;3C
. D.
( )
1; 1D −−
.
Câu 5. Viết phương trình tổng quát của đường thẳng đi qua điểm
( )
0 ; 0O
và song song với đường thẳng có
phương trình
6 4 1 0.xy− + =
A.
3 1 0xy− − =
. B.
3 2 0xy−=
. C.
6 4 1 0xy− − =
. D.
4 6 0xy+=
.
Câu 6. Hỏi cặp số
( )
1; 1−
là nghiệm của bất phương trình nào sau đây?
A.
30+ − xy
. B.
0− − xy
. C.
3 1 0+ + xy
. D.
3 1 0− − − xy
.
Câu 7. Tam giác
ABC
vuông cân tại
A
có
AB AC a==
. Đường trung tuyến
BM
có độ dài là
A.
3
2
a
. B.
2a
. C.
3a
. D.
5
2
a
.
Câu 8. Tam thức bậc hai
( )
2
34f x x x= − −
âm khi.
A.
(
)
; 4 1;x − − +
. B.
(
)
; 1 4;x − − +
.
C.
4;2x −
. D.
( )
1;4−
.
Câu 9. Đường thẳng đi qua điểm
( )
3; 2C −
và có hệ số góc
2
3
k =
có phương trình là
A.
2 3 12 0xy− − =
. B.
2 3 9 0xy− − =
.
C.
3 2 13 0xy− − =
. D.
2 3 0xy+=
.
Câu 10. Cho hàm số
, 0, ,y ax b a a b= +
là tham số. Mệnh đề nào sau đây đúng?
A. Hàm số
y ax b=+
nhận giá trị dương trên
;
b
a

− +


.
B. Hàm số
y ax b=+
nhận giá trị âm trên
;
b
a

− +


.
C. Hàm số
y ax b=+
nhận giá trị âm trên .
D. Hàm số
y ax b=+
nhận giá trị dương trên .
Câu 11. Số nào sau đây là nghiệm của bất phương trình
1
1
33
x
x
xx
−
−
−−
?
A.
1
. B.
0
. C.
3
2
. D.
2
.
Trang 26/40
Câu 12. Cho tam giác
ABC
. Trung tuyến
AM
có độ dài :
A.
2 2 2
22b c a+−
. B.
2 2 2
b c a+−
.
C.
2 2 2
1
22
2
b c a+−
. D.
2 2 2
3 2 2abc−−
.
Câu 13. Tìm mệnh đề đúng?
A.
11
.ab
ab
B.
ab
và
c d ac bd
.
C.
( )
, 0a b ac bc c
. D.
a b ac bc
.
Câu 14. Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của
x
?
A.
32xx+ +
. B.
22
32xx
. C.
23xx
. D.
32xx
.
Câu 15. Cặp số nào sau đây là nghiệm của bất phương trình
( )
–2 – 3x y y+
?
A.
( )
–1; –2
. B.
( )
4;4
. C.
( )
4; –4
. D.
( )
2;1
.
Câu 16. Trong các giá trị sau, giá trị nào không là nghiệm của bất phương trình
2 1 0x +
.
A.
4
3
x
−
=
. B.
1x =
. C.
2x =
. D.
6x =
.
Câu 17. Tìm điều kiện của bất phương trình
23
2
63
x
x
x
−
−
−
.
A.
2x
. B.
2x
. C.
2x
. D.
2x
.
Câu 18. Cho hai số thực
,ab
tùy ý. Mệnh đề nào sau đây là đúng?
A.
a b a b+ = +
. B.
a b a b+ +
. C.
a b a b+ +
. D.
a b a b+ +
.
Câu 19. Cặp bất phương trình nào sau đây không tương đương?
A.
2
( 2) 0xx+
và
20x +
. B.
2
( 2) 0xx+
và
20x +
C.
1xx−
và
(2 1) 1 (2 1)x x x x+ − +
. D.
11
21
33
x
xx
− +
−−
và
2 1 0x −
.
Câu 20. Cho tam giác
ABC
có độ dài ba cạnh là
2AB =
,
3BC =
,
4CA =
. Tính góc
ABC
(chọn kết quả
gần đúng nhất)
A.
104 29
. B.
75 31
. C.
120
. D.
60
.
Câu 21. Tìm tập nghiệm của bất phương trình
22
12 12x x x x− − + −
.
A.
3;4−
. B.
( ) ( )
; 3 4;− − +
.
C.
( )
3;4−
. D.
(
)
; 3 4;− − +
.
Câu 22. Cho tam giác
ABC
có
0
30A =
, góc
0
45B =
. Tìm
?
a
b
h
h
A.
1
2
a
b
h
h
=
. B.
2
a
b
h
h
=
. C.
2
2
a
b
h
h
=
. D.
1
22
a
b
h
h
=
.
Câu 23. Cho
22
1xy+=
, gọi
S x y=+
. Khi đó ta có
A.
2S
. B.
22S−
. C.
11S−
. D.
2S
.
Câu 24. Cho hai điểm
4(1; )A −
và
( )
3;2 .B
Viết phương trình tổng quát của đường thẳng trung trực của đoạn
AB
.
A.
10xy+ − =
. B.
3 1 0xy+ + =
. C.
40xy−+=
. D.
3 1 0xy+ + =
.
Câu 25. Với
x
thuộc tập hợp nào dưới đây thì nhị thức bậc nhất
( ) ( )
2 1 4f x x x= + − +
luôn dương?
A.
2x −
hoặc
2x
. B.
11x−
.
C. Một đáp số khác. D.
2x
.
Trang 27/40
Câu 26. Cho hệ bất phương trình
22
0 (1)
4 1 (2)
xm
x x x
+
− + −
Hệ đã cho có nghiệm khi và chỉ khi:
A.
5.m
B.
–5.m
. C.
5.m
. D.
–5.m
.
Câu 27. Tìm tọa độ vectơ chỉ phương của đường thẳng đi qua hai điểm
( )
3; 2A −
và
( )
1; 4B
A.
( )
2; 1u =
. B.
( )
1; 2u =−
. C.
( )
2; 6u =−
. D.
( )
1; 1u =
.
Câu 28. Cho tam giác
ABC
có
5 , 30BC cm BAC==
. Bán kính đường tròn ngoại tiếp tam giác
ABC
bằng
A.
53
3
cm
. B.
10cm
. C.
53cm
. D.
5cm
.
Câu 29. Trong mặt phẳng
Oxy
, cho đường thẳng
: 4 3 7 0xy + − =
và điểm
( )
1; 2M −
. Phương trình tất cả
các đường thẳng song song với
và cách điểm
M
một khoảng bằng
1
là
A.
4 3 7 0;4 3 3 0x y x y+ − = + + =
. B.
4 3 3 0xy+ − =
.
C.
4 3 7 0;4 3 3 0x y x y+ + = + − =
. D.
4 3 7 0xy+ + =
.
Câu 30. Cho bất phương trình
( )
2
4 1m x m−−
. Với giá trị nào của
m
thì bất phương trình có tập nghiệm
là rỗng?
A.
2
1
m
m
=−
=
. B.
2
1
m
m
=
=
. C.
2m =
. D.
2m =−
.
Câu 31. Tìm tập nghiệm của bất phương trình
( )
( )
2
1
0
2 5 4
x
x x x
−
− − +
.
A.
( ) ( )
;2 4; \ 1− +
. B.
( ) ( )
;2 4;− +
.
C.
2;4
. D.
(
)
;2 4;− +
.
Câu 32. Tập nghiệm của bất phương trình
42
5 4 0xx
là
A.
2; 1 1;2
. B.
2; 1
. C.
1;2
. D.
1;4
.
Câu 33. Nghiệm của bất phương trình
| 3 6 | 3 0xx− −
là:
A.
2x =
. B.
3x =
và
2x =
. C.
3x
. D.
3x =
.
Tập nghiệm của bất phương trình
2006 2006xx− −
là gì?
A.
( )
,2006−
. B.
2006
. C.
. D.
)
2006,+
.
Câu 35. Cho hàm số
1
1
yx
x
=+
−
xác định trên
( )
1; +
. Gọi
m
là giá trị nhỏ nhất của hàm số, giá trị
m
nằm
trong khoảng nào sau đây
A.
( )
4;7
. B.
( )
2;8
. C.
( )
2;3−
. D.
( )
5;+
.
PHẦN II: TỰ LUẬN
Câu 1. Tìm m để biểu thức sau luôn dương
2
( 2) 2( 2) 3+ + + + +m x m x m
Câu 2. Tam giác
ABC
vuông tại
A
, đồng dạng với tam giác
ABC
. Gọi
,,a B C b A C a A B
= = =
và
a
h
là đường cao hạ từ
A
của tam giác
ABC
. Chứng minh rằng:
1 1 1
aa
b b c c
hh
=+


Câu 3. Trong mặt phẳng với hệ tọa độ
,Oxy
cho tam giác
ABC
có
( )
1;3A
và hai đường trung tuyến là
': 2 1 0, ': 1 0.BB x y CC y− + = − =
Xác định tọa độ đỉnh
B
và
.C
Trang 28/40
Câu 4. Với
, , 0abc
thỏa mãn điều kiện:
1.
a b c
bca
+ + =
Chứng minh rằng:
1
b c a
a b c
+ +
------------- HẾT -------------
Trang 29/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 8
Mã đề thi
008
Họ và tên :………………………………………...Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A.
2 5 3 0x y z+ −
. B.
25xy+
. C.
22
2 5 3xy+
. D.
2
2 3 1 0xx+ +
.
Câu 2. Cho hai số thực
,ab
tùy ý. Mệnh đề nào sau đây là đúng?
A.
a b a b+ +
. B.
a b a b+ +
. C.
a b a b+ +
. D.
a b a b+ = +
.
Câu 3. Nếu
ab
và
cd
thì bất đẳng thức nào sau đây luôn đúng?
A.
+ +a c b d
. B.
− −a c b d
. C.
ac bd
. D.
ab
cd
.
Câu 4. Trong các hệ bất phương trình sau, hệ nào là hệ bất phương trình bậc nhất phương trình bậc nhất một
ẩn?
A.
2
2 3 0
2 4 0
xx
x
− −
−
. B.
2 3 7
79
xy
xy
−
+
.
C.
( )
2 1 6 0
7 2 3 5
x
x
− +
−
. D.
( )
2 5 2 1
6 7 0
xx
x
− +
−
.
Câu 5. Cho bất phương trình
( ) ( )
4 1 5 3 2 9x y x− + − −
. Khẳng định nào dưới đây là khẳng định đúng?
A. Điểm
( )
2;5D
thuộc miền nghiệm của bất phương trình đã cho.
B. Điểm
( )
1;1B
thuộc miền nghiệm của bất phương trình đã cho.
C. Điểm
( )
1;1C −
thuộc miền nghiệm của bất phương trình đã cho.
D. Điểm
( )
0;0O
thuộc miền nghiệm của bất phương trình đã cho.
Câu 6. Cặp số
( )
2;3
là nghiệm của bất phương trình nào sau đây?
A.
– 3 7 0xy+
. B.
2 – 3 –1 0xy
. C.
–0xy
. D.
43xy
.
Câu 7. Giải bất phương trình
2 1 0x −
. Kết quả tập nghiệm nào sau đây đúng?
A.
1
;
2
S

= −

. B.
1
;
2
S

= +

.
C.
1
;
2
S

= −


. D.
1
;
2
S

= − +

.
Câu 8. Viết phương trình tổng quát của đường thẳng đi qua điểm
( )
0 ; 0O
và song song với đường thẳng có
phương trình
6 4 1 0.xy− + =
A.
4 6 0xy+=
. B.
3 1 0xy− − =
. C.
3 2 0xy−=
. D.
6 4 1 0xy− − =
.
Câu 9. Cho tam giác
ABC
có độ dài ba cạnh là
2AB =
,
5BC =
,
6CA =
. Tính độ dài đường trung tuyến
MA
, với
M
là trung điểm của
BC
A.
15
2
. B.
55
2
. C.
110
2
. D.
55
.
Câu 10. Cho tam giác
ABC
có
5AB =
;
7BC =
;
8AC =
. Số đo góc
A
bằng
A.
90
. B.
60
. C.
30
. D.
45
.
Câu 11. Cho nhị thức bậc nhất
( )
f x ax b=+
( )
0a
. Chọn kết quả sai trong các kết quả sau.
Trang 30/40
A.
( )
fx
có giá trị bằng
0
khi
b
x
a
=−
.
B.
( )
fx
có giá trị cùng dấu với hệ số
a
khi
x
lấy các giá trị trong khoảng
;
b
a

− +


.
C.
( )
fx
có giá trị trái dấu với hệ số
a
khi
x
lấy các giá trị trong khoảng
;
b
a

− −


.
D.
( )
fx
có giá trị cùng dấu với hệ số
a
khi
x
lấy các giá trị trong khoảng
( )
;− +
.
Câu 12. Bất phương trình
( ) ( )
22
5 5 10xx− + −
có tập nghiệm là
A.
( )
3;S = +
. B.
5
;
2
S

= −

. C.
5
;3
2
S

=



. D.
S =
.
Câu 13. Cho hai điểm
(4;0), (0; 5)AB−
. Phương trình đoạn thẳng AB là
A.
1
54
xy
+=
−
. B.
0
54
xy
+=
−
. C.
0
45
xy
−=
. D.
1
45
xy
+=
−
.
Câu 14. Trong mặt phẳng với hệ tọa độ
Oxy
, cho đường thẳng
1
:
24
xt
yt
= − −
=+
,
( )
t
. Một vectơ chỉ
phương của đường thẳng
là
A.
( )
1; 4u =−
. B.
( )
1;2u =−
. C.
( )
2; 1u =
. D.
( )
4;1u =
.
Câu 15. Cho tam giác
ABC
. Hỏi mệnh đề nào sau đây sai?
A. Đường trung trực của
AB
có
AB
là vectơ pháp tuyến.
B.
BC
là một vectơ pháp tuyến của đường cao
AH
.
C.
BC
là một vectơ chỉ phương của đường thẳng
BC
.
D. Các đường thẳng
,,AB BC CA
đều có hệ số góc.
Câu 16. Cho nhị thức bậc nhất
( )
y f x ax b= = +
,
0a
có bảng xét dấu như sau:
Tìm phát biểu đúng.
A.
30ab+
. B.
0b
. C.
0a
. D.
0ba−
.
Câu 17. Tập nghiệm của bất phương trình
3 2 1 0xy− +
là
A. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng
3 2 1 0xy− + =
(không bao gồm đường
thẳng).
B. Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng
3 2 1 0xy− + =
(bao gồm đường thẳng).
C. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng
3 2 1 0xy− + =
(bao gồm đường thẳng).
D. Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng
3 2 1 0xy− + =
(không bao gồm đường thẳng).
Câu 18. Tìm điều kiện xác định của bất phương trình
11x x x+ − −
là
A.
x
( )
1;1−
. B.
( )
0;1x
. C.
0;1x
. D.
1;1x −
.
Câu 19. Cho tam giác
ABC
có các cạnh
6BC a cm==
,
7AC b cm==
,
5AB c cm==
. Tính
cosB
.
A.
1
cos
15
B =
. B.
1
cos
5
B =
.
C.
5
cos
7
B =
. D.
19
cos
35
B =
.
Câu 20. Cặp số nào sau đây không là nghiệm của bất phương trình
( )
5 2 1 0xy− −
?
A.
( )
–1; 0
. B.
( )
0;1
. C.
( )
1;3
. D.
( )
–1;1
.
Trang 31/40
Câu 21. Cho
ABC
có
BC a=
,
120BAC =
. Bán kính đường tròn ngoại tiếp
ABC
là
A.
3
3
a
R =
. B.
Ra=
. C.
3
2
a
R =
. D.
2
a
R =
.
Câu 22. Tập nghiệm của bất phương trình
2 2 2x x x+ + + +
trên tập số thực là
A.
. B.
( )
;2−
. C.
2
. D.
2;2−
.
Câu 23. Cho tam giác
ABC
có ba cạnh là
6, 8, 10
. Tính bán kính đường tròn nội tiếp tam giác
ABC
.
A.
2
B.
1
. C.
3
. D.
4
Câu 24. Cho bất phương trình
22x m mx+ +
. Khi
1m
tập nghiệm của bất phương trình là:
A.
( )
2;− +
. B.
( )
;2− −
. C.
( )
2;+
. D.
( )
;2−
.
Câu 25. Cho tam giác
ABC
có
( )
1; 1A
,
( )
0; 2−B
,
( )
4; 2C
. Viết phương trình tổng quát của trung tuyến
CM
.
A.
6 5 1 0− − =xy
. B.
5 7 6 0− − =xy
. C.
3 7 26 0+ − =xy
. D.
2 3 14 0+ − =xy
.
Câu 26. Bất phương trình
2 1 4xx+ +
có tập nghiệm là
A.
( )
;1− −
. B.
( ) ( )
; 1 2;− − +
.
C.
( ) ( )
; 2 2;− − +
. D.
( )
2;+
.
Câu 27. Tìm tập nghiệm của bất phương trình
2
2 3 1
0
43
xx
x
−+
−
.
A.
1
;1
2



. B.
13
;1 \
24


.
C.
( )
1
; 1;
2

− +


. D.
( )
13
; 1; \
24
− +


.
Câu 28. Tìm tập nghiệm của bất phương trình:
2
6 9 0xx− +
.
A.
\3
. B.
3
. C.
\0
. D. .
Câu 29. Đường thẳng
:5 3 15xy + =
tạo với các trục tọa độ một tam giác có diện tích bằng bao nhiêu?
A. 5. B. 3. C. 15. D. 7,5.
Câu 30. Tổng các nghiệm nguyên của bất phương trình
( )( )
3 1 0xx+ −
là
A.
5−
. B.
4−
. C.
1
. D.
4
.
Câu 31. Cho các đa thức
( )
( )
2
16 4
4
12
1 1 1
21
x
fx
xx
gx
x x x
−
=−
−−
= + −
−−
tìm các giá trị của
x
để
( )
fx
luôn âm, và
( )
gx
luôn
dương
A.
( )
( )
4; 2 1; .− − +
B.
( ) ( )
( )
2;0 1; 2 2; .− +
C.
( ) ( )
( )
4; 3 0;1 2;2 .− −
D.
( )
( )
3; 2 4; .− +
Câu 32. Nếu
12m
thì số nghiệm của phương trình
2
2 5 6 0x mx m− + − =
là bao nhiêu.
A. Chưa xác định được B. 0.
C. 1. D. 2.
Câu 33. Cho
ABC
có
( )
2; 1 , 4;5 ,( ) ( )3;2A B C−−
. Viết phương trình tổng quát của đường cao
BH
.
A.
3 5 37 0xy+ − =
. B.
3 5 13 0xy− − =
.
C.
5 3 5 0xy− − =
. D.
3 5 20 0xy+ − =
.
Câu 34. Cho
, , 0abc
. Xét các bất đẳng thức sau
Trang 32/40
I)
2
ab
ba
+
II)
3
a b c
b c a
+ +
III)
1 1 1 9
a b c a b c
+ +
++
Bất đẳng thức nào đúng?
A. Chỉ II) đúng. B. Chỉ III) đúng.
C. Cả I), II), III) đúng. D. Chỉ I) đúng.
Câu 35. Hàm số
94
2
y
xx
=+
−
với
02x
đạt giá trị nhỏ nhất tại
a
x
b
=
(
,ab
nguyên dương, phân số
a
b
tối giản). Khi đó
ab+
bằng
A.
7
. B.
9
. C.
13
. D.
11
.
PHẦN II: TỰ LUẬN
Câu 1. Tìm các giá trị nguyên của tham số
m
để
( )
( )
( )
22
3 4 2 2 1 0,f x m x m x x R= − + − +
.
Câu 2. Tam giác
ABC
vuông tại
A
. Gọi
d
là đường phân giác của góc
A
. Chứng minh rằng:
2bc
d
bc
=
+
.
Câu 3. Trong mặt phẳng với hệ tọa độ với
,Oxy
cho tam giác
ABC
biết phương trình cạnh
: 2 5 0,BC x y− = =
phương trình đường trung tuyến
': 2 0BB y −=
và phương trình đường trung tuyến
': 2 2 0.CC x y− − =
Tìm tọa độ các đỉnh của tam giác.
Câu 4. Cho
,,abc
là các số thực dương. Chứng minh rằng:
2 2 2 3 3 3
.a bc b ac c ab a b c+ + + +
------------- HẾT -------------
Trang 33/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 9
Mã đề thi
009
Họ và tên :………………………………………...Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cặp số
( )
;xy
nào sau đây là nghiệm của bất phương trình
4 3 3xy+ −
?
A.
( )
1; 1−−
. B.
( )
1;1−
C.
( )
0; 1−
. D.
( )
4;0−
.
Câu 2. Điểm
( )
2;1A
thuộc miền nghiệm của bất phương trình nào sau đây?
A.
10xy− +
. B.
2 2 0xy− + −
. C.
2 1 0xy− +
. D.
20xy−
.
Câu 3. Điểm
( )
0;0O
thuộc miền nghiệm của bất phương trình nào sau đây?
A.
2 5 2 0xy+ −
. B.
2 2 0xy+ +
. C.
3 2 0xy+ +
. D.
20xy+ +
.
Câu 4. Cho tam giác
ABC
có
0
60 , 10, 6B AB BC= = =
. Tính độ dài cạnh
AC
:
A.
2 19
. B.
62
. C.
14
. D.
76
.
Câu 5. Tìm khẳng định đúng trong các khẳng định sau?
A.
( )
3
3 2 1= + −f x x x
là tam thức bậc hai. B.
( )
42
1= − +f x x x
là tam thức bậc hai.
C.
( )
2
3 2 5= + −f x x x
là tam thức bậc hai. D.
( )
24=−f x x
là tam thức bậc hai.
Câu 6. Số
1x =−
là nghiệm của bất phương trình nào sau đây?
A.
2 1 0x −
. B.
10x −
. C.
30x−
. D.
2 1 0x +
.
Câu 7. Tập xác định của hàm số
1
2
y
x
=
−
là:
A.
)
2;+
. B.
( )
;2−
. C.
( )
2;+
. D.
(
;2−
.
Câu 8. Trong mặt phẳng toạ độ
Oxy
, cho đường thẳng
5
:
32
xt
d
yt
=+
=−
. Hãy chỉ ra một vectơ chỉ phương
u
của đường thẳng đã cho.
A.
( )
5;3u =
. B.
( )
1; 2u =−
. C.
( )
3; 5u =−
. D.
( )
2;1u =
.
Câu 9. Tính diện tích tam giác
ABC
có ba cạnh là
13, 14, 15.
A.
16 24
. B.
84.
C.
6411
. D.
168.
Câu 10. Trong mặt phẳng
,Oxy
đường thẳng đi qua
, nhận
( )
2; 4n =−
làm véctơ pháp tuyến có
phương trình là
A.
40xy+ + =
. B.
2 4 0xy− + − =
.
C.
2 5 0xy− + =
. D.
2 4 0xy− − =
.
Câu 11. Cho bất phương trình
( ) ( )
0f x g x
,
x
. Phép biến đổi nào sau đây là sai ?
A.
( ) ( ) ( ) ( ) ( )
2f x g x f x f x g x +
. B.
( ) ( ) ( ) ( )
22
f x g x f x g x
.
C.
( ) ( ) ( ) ( )
33
f x g x f x g x
. D.
( ) ( ) ( ) ( ) ( )
2
f x g x f x g x g x


.
Câu 12. Phương trình đường thẳng đi qua
(1;2)N
và song song với đường thẳng
2 3 12 0xy+ − =
là.
A.
2 3 8 0xy+ − =
. B.
2 3 8 0xy+ + =
. C.
4 6 1 0xy+ + =
. D.
2 3 8 0xy− − =
.
Câu 13. Cho hệ bất phương trình
Trang 34/40
−+
+−
−
05
033
0
yx
yx
yx
.
Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Điểm
( )
1; 1C −
thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm
( )
2;2D −
thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm
( )
0;0O
thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm
( )
5;3B
thuộc miền nghiệm của hệ bất phương trình đã cho.
Câu 14. Cho
m
. Biểu thức nào sau đây không phải là nhị thức bậc nhất đối với
x
?
A.
( )
2
2018 1= − + +f x x m
. B.
( )
2017 1= + +f x x m
.
C.
( ) ( )
1 2018= + +f x m x
. D.
( )
( )
2
1 2017= + +f x m x
.
Câu 15. Cho tam giác
ABC
có
2 3, 2 2ab==
và
2c =
. Tính độ dài của trung tuyến
AM
.
A. 2. B. 3. C.
3
. D. 5.
Câu 16. Cho hai số thực
,ab
tùy ý. Mệnh đề nào sau đây là đúng?
A.
a b a b+ +
. B.
a b a b+ +
. C.
a b a b+ = +
. D.
a b a b+ +
.
Câu 17. Tìm vectơ pháp tuyến của đường thẳng song song với trục
Oy
.
A.
( )
1;0
. B.
( )
0;1 .
C.
( 1;0 .)−
D.
( )
1;1 .
Câu 18. Tập nghiệm của bất phương trình
2006 2006xx− −
là gì?
A.
( ;2006)−
. B.
{2006}
. C.
. D.
[2006; )+
.
Câu 19. Nếu
0ab
,
0cd
thì bất đẳng thức nào sau đây không đúng?
A.
ac bc
. B.
− −a c b d
.
C.
22
ab
.
D.
ac bd
.
Câu 20. Tập nghiệm của bất phương trình
2 1 3xx− +
là
A.
( )
4;= + S
. B.
( )
4;= − + S
.
C.
( )
;4= −S
. D.
( )
;4= − −S
.
Câu 21. Cho
ABC
có
5, 40 , 60AB A B= = =
. Độ dài
BC
gần nhất với kết quả nào?
A.
3,8.
B.
3,7
. C.
3,5
. D.
3,1
.
Câu 22. Tìm tất cả giá trị của
m
để khoảng cách từ
( )
1;2M −
đến đường thẳng
: 4 0mx y m + − + =
bằng
25
?
A.
2m =
. B.
1
2
m =−
.
C.
2m =−
. D.
1
2;
2
mm= − =
.
Câu 23. Tìm vectơ pháp tuyến của đường thẳng đi qua 2 điểm phân biệt
( )
;0Aa
và
( )
0;Bb
A.
( )
;ba
. B.
( )
;ab
. C.
( )
;ba−
. D.
( )
;ba−
.
Câu 24. Tập hợp nghiệm của bất phương trinh sau:
1 3 5
3
22
x
xx
+
+
+−
là:
A.
12
5
x −
hoặc
22x−
. B.
(
;2−
.
C.
(2; )+
. D.
\{2}
.
Câu 25. Bất phương trình
2
10 16 0xx− +
có tập nghiệm là
A.
( )
8;+
B.
( )
2;8
C.
( )
2;8−
D.
( )
;2−
Trang 35/40
Câu 26. Bất phương trình
2
1
0
4
xx− +
có tập nghiệm là.
A.
1
;
2

− −


. B.
1
;
2

+


C.
1
;
2

−


. D.
1
2



.
Câu 27. Cho bất phương trình:
2
( 2)( 3) 6 (1)m x m m− + + −
. Xét các mệnh đề sau:
I. Nếu
2m
: (1) có nghiệm là
xm
.
II. Nếu
2m
: (1) có nghiệm là
xm
.
III. Nếu
2m =
: (1) vô nghiệm.
Mệnh đề nào đúng?
A. I, II và III. B. Chỉ II. C. I và II. D. Chỉ I.
Câu 28. Hình bình hành
ABCD
có
AB a=
,
2BC a=
và
45BAD =
. Khi đó hình bình có diện tích là
A.
2
2a
. B.
2
2a
. C.
2
a
. D.
2
3a
.
Câu 29. Hệ phương trình
2 1 0
2
x
xm
−
−
có nghiệm khi và chỉ khi
A.
3
2
m −
. B.
3
2
m −
. C.
3
2
m −
. D.
3
2
m −
.
Câu 30. Với
x
thuộc tập hợp nào dưới đây thì
( )
21
2
1
x
fx
x
−
=−
−
luôn dương?
A.
3
, \ 1
4

+


. B.
( )
3
, 3,
4

− +


.
C.
3
,1
4



. D.
( )
1, +
.
Câu 31. Tập nghiệm của bất phương trình
2
0
21
1x
xx
−
++
là:
A.
( ; 1) (1; )− − +
. B.
( )
;1−
.
C.
( ; 1) ( 1;1)− − −
. D.
( )
1;1−
.
Câu 32. Tập nghiệm của hệ bất phương trình
2
7 6 0 (1)
2 1 3 (2)
xx
x
− +
−
là.
A.
( )
1;6
. B.
1;2
. C.
( )
1; 2
. D.
( )
1;6−
.
Câu 33. Trong mặt phẳng
,Oxy
cho ba điểm
( ) ( ) ( )
3;0 , 5;4 , 10;2 .A B C−
Đường thẳng
d
đi qua điểm
C
và
đồng thời cách đều hai điểm
,AB
có phương trình là
A.
2 14 0xy+ − =
hoặc
20y −=
. B.
2 7 0xy− − + =
.
C.
2 18 0xy− + =
. D.
2 6 0xy− + + =
.
Câu 34. Cho các bất đẳng thức:
( )
2
ab
I
ba
+
,
( )
3
a b c
II
bca
+ +
,
( )
1 1 1 9
III
a b c a b c
+ +
++
(với
, , 0abc
). Bất đẳng thức nào trong các bất đẳng thức trên là đúng?
A. chỉ
I
đúng. B. chỉ
II
đúng.
C. chỉ
III
đúng. D.
,,I II III
đều đúng.
Câu 35. Tìm giá trị nhỏ nhất
m
của hàm số
( )
2
1
f x x
x
=+
−
với
1.x
A.
1 2 2m =−
. B.
12m =−
. C.
12m =+
. D.
1 2 2m =+
.
PHẦN II: TỰ LUẬN
Trang 36/40
Câu 1. Tìm m để biểu thức sau luôn âm:
2
( ) ( 4) (2 8) 5= − + − + −g x m x m x m
Câu 2. Tam giác
ABC
vuông tại
A
có các cạnh và góc vuông là
b
và
c
. Lấy một điểm
M
trên cạnh
BC
sao cho
BAM
=
. Chứng minh rằng
cos sin
bc
AM
bc

=
+
.
Câu 3. Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác
ABC
có đỉnh
( )
4; 1A −
phương trình đường cao
và trung tuyến kẻ từ đỉnh B lần lượt là
2 3 12 0xy− + =
và
2 3 0xy+=
. Xác định tọa độ các đỉnh còn lại của
tam giác
.ABC
Câu 4. Với
0x
, tìm giá trị nhỏ nhất của các hàm số sau
2
1
3yx
x
=+
.
------------- HẾT -------------
Trang 37/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 10
Mã đề thi
010
Họ và tên :………………………………………...Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Tìm điều kiện của bất phương trình
12
2
1
x
x
x
−
−
.
A.
1x
. B.
1x
. C.
2x
. D.
2x
.
Câu 2. Phương trình đường thẳng đi qua
(1;2)N
và song song với đường thẳng
2 3 12 0xy+ − =
là.
A.
2 3 8 0xy− − =
. B.
2 3 8 0xy+ − =
. C.
2 3 8 0xy+ + =
. D.
4 6 1 0xy+ + =
.
Câu 3. Cho nhị thức bậc nhất
( )
,0y f x ax b b= = +
có bảng xét dấu sau
Tìm phát biểu đúng.
A.
. B.
30ab+
. C.
0a
. D.
0b
.
Câu 4. Bất phương trình
2 5 3
32
xx−−
có tập nghiệm là
A.
1
;
4

− +


. B.
( )
2;+
. C.
( ) ( )
;1 2;− +
. D.
( )
1; +
.
Câu 5. Cho hai số thực
,ab
tùy ý. Mệnh đề nào sau đây là đúng?
A.
a b a b+ +
. B.
a b a b+ = +
. C.
a b a b+ +
. D.
a b a b+ +
.
Câu 6. Cho hệ bất phương trình
++
++
−−
01
052
0152
yx
yx
yx
.
Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Điểm
( )
0; 2C −
thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm
( )
0;2D
thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm
( )
0;0O
thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm
( )
1;0B
thuộc miền nghiệm của hệ bất phương trình đã cho.
Câu 7. Cặp bất phương trình nào sau đây không tương đương?
A.
1xx−
và
( ) ( )
2 1 1 2 1x x x x+ − +
. B.
11
21
33
x
xx
− +
−−
và
2 1 0.x −
C.
( )
2
20xx+
và
2 0.x +
D.
( )
2
20xx+
và
2 0.x +
Câu 8. Bất phương trình nào sau đây là bậc nhất một ẩn
A.
3 1 2xx−
. B.
2
3 x
x
−
. C.
21xy+
. D.
2 1 0x −=
.
Câu 9. Đường thẳng
12
:
3
xt
d
yt
=+
=−
đi qua điểm nào trong các điểm sau đây?
Trang 38/40
A.
( )
3;5P
. B.
( )
3;2Q
. C.
( )
2; 1M −
. D.
( )
7;0N −
.
Câu 10. Đường thẳng đi qua
( )
1;2A −
, nhận
( )
2; 4n =−
làm vecto pháp tuyến có phương trình là
A.
2 5 0xy− + =
. B.
40xy+ + =
. C.
2 4 0xy− − =
. D.
2 4 0xy− + − =
.
Câu 11. Nếu
,ab
và
c
là các số bất kì và
ab
thì bất đẳng nào sau đây đúng?
A.
22
ab
.
B.
+ +a c b c
. C.
− −c a c b
. D.
ac bc
.
Câu 12. Cho tam giác
ABC
có
3AB =
;
5AC =
và
6BC =
. Giá trị của
cos A
bằng
A.
2
15
. B.
1
15
−
. C.
2
15
−
. D.
1
15
.
Câu 13. Tam thức nào dưới đây luôn dương với mọi giá trị của
x
?
A.
2
2 10−−xx
. B.
2
2 10−+xx
. C.
2
2 10− + +xx
. D.
2
10 2−+xx
.
Câu 14. Tập nghiệm
S
của bất phương trình:
4 16 0.x− +
A.
(
;4 .S = −
B.
( )
4; .S = +
C.
)
4; .S = +
D.
(
; 4 .S = − −
Câu 15. Miền nghiệm của bất phương trình
( ) ( )
3 1 4 2 5 3x y x− + − −
là nửa mặt phẳng chứa điểm
A.
( )
0;0O
. B.
( )
4;2N −
. C.
( )
2;2P −
. D.
( )
5;3Q −
.
Câu 16. Cho đường thẳng
: 2 3 0xy − + =
Véctơ nào sau đây không là véc tơ chỉ phương của
?
A.
( )
4; 2−
. B.
( )
2; 1−−
. C.
( )
2;1
. D.
( )
4;2
.
Câu 17. Tam thức bậc hai
( )
2
37f x x x= − +
A. Không âm với mọi
x
. B. Dương với mọi
x
.
C. Âm với mọi
( )
;0x −
. D. Âm với mọi
x
.
Câu 18. Tam giác
ABC
có
8a
,
3c
,
60B
. Độ dài cạnh
b
bằng bao nhiêu?
A.
61
. B.
49
. C.
97
. D.
7
.
Câu 19. Câu nào đúng trong các câu sau?
A. Miền nghiệm của bất phương trình
2 1 0xy− −
chứa điểm
( )
0;0O
.
B. Miền nghiệm của bất phương trình
0x
là nửa mặt phẳng bên phải trục tung kể cả biên (bờ).
C. Miền nghiệm của bất phương trình
2 1 0xy− −
chứa điểm
( )
1;1M −
.
D. Miền nghiệm của bất phương trình
100 400 1 0xy+ +
là nửa mặt phẳng kể cả bờ.
Câu 20. Cho tam giác
ABC
. Trung tuyến
a
m
được tính theo công thức
A.
2 2 2
2
42
a
b c a
m
+
=−
. B.
2 2 2
2
24
a
b c a
m
+
=+
.
C.
2 2 2
2
24
a
b c a
m
+
=−
. D.
2 2 2
2
24
a
a c b
m
+
=−
.
Câu 21. Phương trình đường thẳng đi qua
( )
1;2N
và song song với đường thẳng
2 3 12 0xy+ − =
là
A.
2 3 8 0xy+ + =
. B.
4 6 1 0xy+ + =
.
C.
2 3 8 0xy− − =
. D.
2 3 8 0xy+ − =
.
Câu 22. Cho bảng xét dấu:
Hàm số có bảng xét dấu như trên là
A.
( )
16 8=−f x x
. B.
( )
2= − −f x x
.
C.
( )
84=−f x x
. D.
( )
24=−f x x
.
Câu 23. Cho tam giác
ABC
có
6a =
,
8b =
,
10c =
. Diện tích
S
của tam giác
ABC
là
A.
30
. B.
48
. C.
24
. D.
12
.
Trang 39/40
Câu 24. Tập nghiệm của bất phương trình
2
4 4 0xx+ +
là
A.
. B.
\2−
. C. . D.
2−
.
Câu 25. Bất phương trình
−31x
có tập nghiệm là
A.
3
. B.
3;4
. C.
( )
2;3
. D.
(
)
− +;2 4;
.
Câu 26. Tìm tập nghiệm của bất phương trình
1
1
33
x
x
xx
−
−
−−
.
A.
( )
;3−
. B.
( )
1; \ 3+
. C.
( )
;1−
. D.
( )
;3 \ 1−
.
Câu 27. Trong tam giác
ABC
, hệ thức nào sau đây sai?
A.
.sin
sin
cA
C
a
=
. B.
2 .sina R A=
. C.
.tanb R B=
. D.
.sin
sin
bA
a
B
=
.
Câu 28. Cho tam giác
ABC
với
1;2 , 0; 3 , 4; 0A B C
. Tính chiều cao tam giác
ABC
ứng với cạnh
BC
A.
1
5
. B.
1
25
. C.
1
5
. D.
3
.
Câu 29. Trong các hình chữ nhật có cùng chi vi thì
A. Hình vuông có diện tích nhỏ nhất.
B. Hình vuông có diện tích lớn nhất.
C. Không xác định được hình có diện tích lớn nhất.
D. Cả A, B, C đều sai.
Câu 30. Tập nghiệm của bất phương trình
2
54x x x− − −
là
A.
( ) ( )
3;1 2 1 2;3− − +
. B.
3;1 2 1 2;3
− − +
.
C.
( )
3;1 2 1 2;3

− − +

. D.
[ 3;3]−
.
Câu 31. Với giá trị nào của
m
thì ba đường thẳng sau đồng quy?
1 2 3
:3 – 4 15 0, : 5 2 –1 0, : – 4 15 0.d x y d x y d mx y+ = + = + =
A.
–5m =
. B.
5m =
. C.
3m =
. D.
–3m =
.
Câu 32. Tìm tập nghiệm của bất phương trình
( )
( )
2
2 4 3 0x x x− + −
?
A.
13x
. B.
3x
. C.
3x
. D.
02x
.
Câu 33. Với
x
thuộc tập nào dưới đây thì
( )
12
21
xx
fx
xx
−+
=−
+−
không âm?
A.
( )
2;− +
. B.
( )
1
2; 1;
2

− − +

.
C.
1
2;
2

−−

. D.
( )
1
; 2 ;1
2

− − −

.
Câu 34. Biết bất phương trình (ẩn
x
):
( 1) 2 3 0m x m− + −
vô nghiệm. Tìm tất cả các giá trị tham số
m
.
A.
1m =
. B.
1m
. C.
3
2
m =
. D.
1m
.
Câu 35. Hàm số
94
2
y
xx
=+
−
với
02x
, đạt giá trị nhỏ nhất tại
a
x
b
=
(
a
,
b
nguyên dương, phân số
a
b
tối giản). Khi đó
ab+
bằng
A.
9
. B.
13
. C.
11
. D.
7
.
PHẦN II: TỰ LUẬN
Câu 1. Tìm giá trị lớn nhất của tham số
m
để
( )
2
2 8 2 0,f x x mx m x R= − + −
.
Câu 2. Cho đoạn thẳng
AB
. Lấy
I
là trung điểm của
AB
và
M
là điểm tùy ý. Chứng minh rằng:
Trang 40/40
a)
2 2 2 2
1
2
2
MA MB MI AB+ = +
. b)
22
1
.
4
MA MB MI AB=−
.
Câu 3. Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác
ABC
có đỉnh
( )
4; 1A −
phương trình đường cao
và trung tuyến kẻ từ đỉnh B lần lượt là
2 3 12 0xy− + =
và
2 3 0xy+=
. Xác định tọa độ các đỉnh còn lại của
tam giác
.ABC
Câu 4. Cho
,,abc
là các số thực dương. Chứng minh rằng
( ) ( ) ( )
2 2 2 2 2 2
1 1 1 6 .a b b c c a abc+ + + + +
------------- HẾT -------------
TOÁN 185 NGUYỄN LỘ TRẠCH
10 ĐỀ ÔN TẬP GIỮA KỲ II - 2021
Đáp án: CHI TIẾT
Họ và tên :………………………………….Lớp:………….......……..………
Lớp 10
Mã đề [001]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
B
A
B
A
C
A
A
D
B
B
A
C
A
D
D
B
A
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
B
A
A
B
C
D
D
C
C
C
C
D
B
D
C
D
B
Mã đề [002]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
D
C
D
A
D
B
A
C
A
C
B
A
D
D
C
D
B
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
A
A
B
B
A
B
D
C
C
A
B
A
B
B
C
D
C
Mã đề [003]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
D
A
B
D
C
A
C
B
B
C
A
B
D
C
C
B
A
A
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
C
D
B
A
B
A
D
D
D
A
C
D
B
A
B
C
C
Mã đề [004]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
C
A
C
B
A
B
A
D
B
D
B
D
B
A
C
D
A
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
A
C
D
C
B
C
A
B
D
B
D
C
A
B
A
D
C
Mã đề [005]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
A
D
B
D
D
C
A
B
B
B
A
D
B
C
D
D
D
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
B
C
A
A
A
A
B
B
A
C
C
C
A
D
B
C
C
Mã đề [006]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
A
B
A
D
C
D
D
C
D
A
B
C
C
A
B
C
B
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
A
C
A
D
B
C
B
B
A
C
D
B
D
A
D
B
A
Mã đề [007]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
D
C
B
D
B
C
D
D
A
A
B
C
C
A
B
A
C
B
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
B
A
B
B
B
D
A
D
A
D
C
C
A
A
D
C
C
Mã đề [008]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
B
A
A
C
A
C
B
C
B
B
D
B
D
A
D
C
A
D
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
B
C
A
D
A
C
B
C
B
A
D
A
B
D
C
C
D
Mã đề [009]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
B
C
B
A
C
D
B
B
B
C
B
A
D
C
C
D
A
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
B
A
D
D
A
A
B
D
A
C
B
A
C
C
A
D
D
Mã đề [010]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
D
B
A
D
C
A
A
A
B
A
B
B
B
C
A
A
B
D
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
D
C
D
C
C
D
D
C
C
A
B
B
C
B
D
A
C
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên :………………………………….Lớp:………….......……..………
Mã đề thi
001
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
B
A
B
A
C
A
A
D
B
B
A
C
A
D
D
B
A
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
B
A
A
B
C
D
D
C
C
C
C
D
B
D
C
D
B
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn B
Ta có .
5 0 5x x
Ta xét các bất phương trình:
.
2
5 0 5x x x
.
5 5 0 5x x x
.
2
1 5 0 5x x x
.
5 5 0 5x x x
Câu 2.
Lời giải
Chọn A.
Theo định lý về dấu của nhị thức bậc nhất, ta có dương với .
2 6f x x
3;x
Câu 3.
Lời giải
Chọn B
Từ giả thiết, ta có
2 2 2 2 .a c b c a b a b
Câu 4.
Lời giải.
Chọn A
.
Ta có: .
.sin .sin 3.sin 30 3. 2
sin sin sin sin sin 45 2
b c c B AB B
AC b
B C C C
Câu 5.
Lời giải
Chọn C
Theo điều kiện để phân thức chứa ẩn ở mẫu có nghĩa ta có: .
2 0
0
x
x
Câu 6.
Lời giải
Chọn A
Ta xét hệ phương trình: Do đó đường thẳng và đường thẳng cắt
11
4 1 0
7
.
2 3 0 1
7
x
x y
x y
y
2 3y x
nhau.
Cách 2 : nhẩm nhanh tỉ số hay không ? ví dụ :
a b
a b
2 8
/ / :
1 4
–2 8 0
B
d x y
Câu 7.
Lời giải
Chọn A
.
2 2 0 3 6 0x x x
Câu 8.
Lời giải
Chọn D.
Trong tam giác ta có: .
ABC
10
2sin
BC
R
A
Câu 9.
Lời giải.
Chọn B
Ta có: .
6
45sin
)4575180sin(.2
sin
sin.
sin
sin.
sinsin
B
CAC
B
Cb
cAB
C
c
B
b
.
Câu 10.
Lời giải
Chọn B
Thay vào bất phương trình ta được: mệnh đề đúng.
0x
2.0 1 3
Câu 11.
Lời giải
Đường thẳng có một véctơ pháp tuyến là .
:3 4 12 0x y
3;4n
Vì nên là một véctơ chỉ phương của .
d
3;4n
d
Câu 12.
Lời giải
Chọn C
Theo định nghĩa thì là bất phương trình bậc nhất hai ẩn. Các bất phương trình còn lại là bất phương
0x y
trình bậc hai.
Câu 13.
Lời giải:
Chọn A
2
2
3.1 4. 1 17
10
; 2
5
3 4
d M d
Câu 14.
Lời giải
Chọn D
, .
2
( ) ( 0)f x ax bx c a= + + ¹
( ) 0,f x x£ " Î
0
0
a
ì
ï
<
ï
Û
í
ï
D £
ï
î
Câu 15.
Lời giải
Chọn D
Thay vào các bất phương trình ta có phương án B đúng.
1x
Câu 16.
Lời giải
Chọn B.
* Bảng xét dấu:
x

2

2
4 4x x
0
* Tập nghiệm của bất phương trình là .
\ 2S
Câu 17.
Lời giải
Chọn A
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy là
0 0
; 0; 2x y
nghiệm của hệ bất phương trình đã cho.
Câu 18.
Lời giải
Chọn C
Ta có . Đường thẳng AB nhận làm vtcp. Suy ra Chọn C
9;3AB
3; 1u
Câu 19.
Lời giải
Chọn.D
Áp dụng bất đẳng thức AM-GM cho 2 số dương x,y ta thấy cả 3 phương án trên đều đúng.
Câu 20.
Lời giải
Chọn A
Ta có ; .
0f x
2
4 5 0x x
5x
1x
Vậy nghiệm của tam thức bậc hai là ; .
2
4 5f x x x
5x
1x
Câu 21.
Lời giải
Chọn A
Ta có .
:3 2 7 0x y
Xét có nên . Tương tự đối với , ssong song với .
3
: 3 2 7 0d x y
3 2
3 2
3
//d
2
d
4
d
Xét có nên song song với .
1
:3 2 0d x y
3 2
3 2
1
d
Câu 22.
Hướng dẫn giải
Chọn B
Ta có hàm số nhận giá trị dương nếu đồ thị của nó nằm về phía trên so với trục . Từ đồ thị ta có:
Ox
. Do đó là một nghiệm của bpt
f x 0 0 x 2
x 1
Câu 23.
Lời giải
Chọn C
Thay lần lượt tọa độ các điểm vào hệ bất phương trình.
Câu 24.
Lời giải
Chọn D
Chọn , thay vào ta có A, B, C đều sai chọn.
1x
2a
D.
Câu 25.
Lời giải
Chọn D.
Ta có: .
3
1
1
x
x
2 2
0
1
x
x
1 1x
Câu 26.
Lời giải:
Chọn C
Gọi là trung điểm của
M
AC
5
2
3
2
M
M
x
y
5 3
;
2 2
M
5 7
; 7;5
2 2
BM
BM n
Phương trình tổng quát của trung tuyến qua là:
BM
0; 2B
7 0 5 2 0 7 5 10 0x y x y
Câu 27.
Lời giải
Chọn C
Ta có:
2
2
16 4
3
9
a a
b
b
Mà
2 2 2 2
7 7a b c c c
Tiêu điểm : và .
1
7;0F
2
7;0F
Ta có : .
1 2
3 3
, . , . 9
1 1
h d F d d F d
Câu 28.
Lời giải
Chọn C
Áp dụng BĐT AM-GM, được .
8 8
2 . 4
2 2
x x
y
x x
Câu 29.
Lời giải
Chọn C
0 (1)
5
5 0 (2)
x m
x m
x
Hệ có nghiệm khi .
5 5m m
Câu 30.
Lời giải
Chọn D
Điều kiện: .
2018 0
2018
2018 0
x
x
x
Thay vào bất phương trình , dễ thấy không phải là nghiệm.
2018x
2018 2018x x
2018x
Vậy bất phương trình vô nghiệm.
Câu 31.
Lời giải
Chọn B.
E
D
A
B
C
Ta có .
45ABC
Gọi kà đường cao của tam giác , khi đó tam giác vuông cân tại .
AE
ABC
AEB
E
Suy ra .
1
2
AE BC
2
2
a
Vậy diện tích hình bình hành là .
ABCD
2
. . 2
2
a
AE BC a
2
a
Câu 32.
Lời giải
Chọn D
ĐK
2;0;2x
Ta có .
2
2
2 4 2 2
1 1 2 2 6 4
0 0
2 2 2 2 2 2
x x x x x
x x
x x x x x x x x x
Lập bảng xét dấu biểu thức . Từ đó suy ra tập nghiệm cần tìm là
2
2 6 4
2 2
x x
x x x
.
);
2
173
()2;0(
2
173
;2 
Câu 33.
Lời giải
Chọn C
Ta có
.
4 3
1
1 2
x
x
2 2
0
1 2
x
x
1
2
2 2 1 2 0
x
x x
1
2
1
1
2
x
x
1
1
2
x
Câu 34.
Lời giải
Chọn D
Ta có .
2 2 2 2 2 2 2
2 .cos 2 .cos120a b c ab A b c ab b c ab
Câu 35.
Lời giải
Chọn B
ĐKXĐ .
2
2 1
3 2 0
1
1
1 0
x x
x x
x
x
x
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Ta có .
2
2
2 03
1
x
x
x
x xf
Bảng xét dấu
Dựa vào bảng xét dấu .
0 1 2f x x
Câu 37.
Lời giải
Ta có .
5 4 3 10 8 6 8 6
sin sin sin sin sin sin sin sin sin
a
A B C A B C A B C
Theo định lý sin trong tam giác ta tính được .
8, 6b c
Chu vi tam giác là .
24a b c
Câu 38.
Lời giải
Gọi là đường thẳng , song song với . Kéo dài .
A
BC
CD N
Gọi là trung điểm tứ giác NAME là hình bình hành.
E
BH
Lấy là trung điểm . Do tam giác cân tại . Dễ chứng minh được là hình chữ nhật.
I
BC
ABC
A
ANBI
Từ đó chứng minh được là trực tâm , Lại có .
E
NBM NE BM
/ /NE AM BM AM
Phương trình đường thẳng đi qua , nhận làm VTPT nên có pt là:
BM
1 3
( ; )
2 2
M
3 9 3
; 1; 3
2 2 2
AM
.
3 5 0x y
Do tọa độ của là nghiệm của hệ .
B BM BC
B
7
( 4; 3)
3 5
x y
B
x y
Do Phương trình đường thẳng đi qua là . Phương trình
3 ( 2;1)AB AD D
CD
,D M
1 0x y
đường thẳng đi qua , vuông góc với là .
BH
B
CD
1 0x y
Mà .
1;0H CD BH H
Lại có là trung điểm
M
(2; 3)HC C
Câu 39.
Lời giải
Áp dụng bất đẳng thức Côsi, ta có
hay .
3
3 3 3
4x x x x x
3
3
3 4x x x
Tương tự: và .
3
3
3 4y y y
3
3
3 4z z z
Suy ra
3 3 3
3
3
3
3 4 12.P x y z x y z x y z
Khi thì
1x y z
12.P
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên :………………………………….Lớp:………….......……..………
Mã đề thi
002
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn D
Ta có
0;6 6 0;1
AB
Gọi là trung điểm . Tọa độ điểm .
I
AB
1; 1I
Đường trung trực của đoạn thẳng đi qua và nhận là vectơ pháp tuyến nên phương trình
AB
I
0;1
AB
u
đường trung trực của đoạn thẳng có dạng: .
AB
0 1 1 0 1 0 x y y
Câu 2.
Lời giải
Chọn C
Ta thay tọa độ điểm vào phương trình đường thẳng: loại A; B thỏa
–2.3 3.0 –1 7
–2.1 3.1–1 0
mãn.
Câu 3.
Lời giải
Chọn D
Với phương trình (bất phương trình có nghiệm).
0m
1 0 1x x
Câu 4.
Lời giải
Chọn A.
Ta có .
4 16 0x
4 16x
4x
Vậy tập nghiệm của bất phương trình là .
4 16 0x
4;S
Câu 5.
Lời giải
Chọn D
1 2 1 2
2
1 1
2 2 2
0 .
. 1
: 2 0 1;0
: : ;0 0;1
0
n
n n d d
u n
d x
x t
d d
y
Câu 6.
Lời giải
Chọn B
Ta có: .
3 9 0 x
3 9 x
3 x
Vậy: Bất phương trình có tập nghiệm là .
3 9 0 x
;3
Câu 7.
Lời giải
Chọn A
Ta có: .
2 2 2 2
1
2 . .cos60 10 6 2.10.6. 2 19
2
BC AB AC AB AC
Câu 8.
Lời giải
Chọn C
Thay tọa độ ở các đáp án vào phương trình đường thẳng: .
12 7 5 0 x y
Với đáp án A: a có thỏa mãn.
12 1 7 1 5 0
Với đáp án B: a có không thỏa mãn.
12.1 7.1 5 10 0
Với đáp án C: a có thỏa mãn.
5
12 7.0 5 0
12
Với đáp án D: a có thỏa mãn.
17
12.1 7. 5 0
7
Câu 9.
Lời giải
Chọn A
.
2
( 2)(2 1) 2 ( 1)( 3) x 1x x x x x
Câu 10.
Lời giải
Chọn C
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy không là
0 0
; 0;0x y
nghiệm của hệ bất phương trình đã cho.
Câu 11.
Lời giải
Chọn B
Tập hợp các điểm biểu diễn nghiệm của bất phương trình là nửa mặt phẳng bờ là đường thẳng
2 3 0x y
và không chứa gốc tọa độ.
2 3 0x y
Từ đó ta có điểm thuộc miền nghiệm của bất phương trình .
3
1;
2
M
2 3 0x y
Câu 12.
Lời giải
Chọn A
Cách 1: ( chọn
2 2
2 2
4 2 8 0 2.2 2. 2 2 0 2 2 0x x x x x
C. ).
Cách 2: Casio: wR1121=p4s2=8==
( nghiệm rỗng).
Câu 13.
Lời giải
Chọn D
.
0 3 6 0f x x
2x
Câu 14.
Lời giải
Chọn D.
Ta có: .
2
2 2 2
3
2 . .cos30 3 3 2.3. 3. 3
2
AC AB BC AB BC
Câu 15.
Lời giải
Chọn C
Theo tính chất của bất đẳng thức và bất đẳng thức Côsi thì A, B, C luôn đúng.
Ta có nếu là sai.
1 1
0b a
a b
Câu 16.
Lời giải
Chọn D
khi và .
0, f x x
0a
0
Câu 17.
Lời giải
Chọn B
ĐK : .
1 0 1x x
Câu 18.
Lời giải
Chọn C
Định lý
trong tam giác.
sin
Câu 19.
Lời giải
Chọn A.
Ta có
A đúng.
0f x
2 4 0x
2x
B sai.
0f x
2 4 0x
2x
C sai
0f x
2 4 0x
2x
D sai.
0f x
2 4 0x
2x
Câu 20.
Lời giải
Chọn.D
Áp dụng bất đẳng thức AM-GM cho 2 số dương x,y ta thấy cả 3 phương án trên đều đúng.
Câu 21.
Lời giải
Chọn B
Xét tam giác có . Với là bán kính đường tròn ngoại tiếp tam giác . Vậy
OAB
2 2 1
sin
AB
R R
O
R
OAB
lớn nhất khi là đường kính của đường tròn ngoại tiếp tam giác .
OB
OB
OAB
Khi đó .
2OB
Câu 22.
Lời giải
Chọn B
Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình.
Với . Bất phương trình thứ nhất và thứ ba sai nên sai.
0;0O
2.0 5.0 1 0
2.0 0 5 0
0 0 1 0
0;0O
Với . Bất phương trình thứ ba sai .
1;0M
2.1 5.0 1 0
2.1 0 5 0
1 0 1 0
Với : Đúng.
0; 3N
2.0 5. 3 1 0
2.0 2 5 0
0 2 1 0
Câu 23.
Lời giải
Chọn A
2
2 2 2
2 2 2
3 3
, , +2a + + = + 0.
2 4 4 2 4
b b b b b
a b a b ab a a
Câu 24.
Lời giải
Chọn B.
Tọa độ giao điểm của và là nghiệm của hệ
M
1
d
2
d
.
3 2 5
2 4 7
x y
x y
3
8
31
16
x
y
3 31
;
8 16
M
Phương trình đường thẳng song song với qua có dạng
3
d
3 31
;
8 16
M
: .
3 31
3 4 0
8 16
x y
53
3 4 0
8
x y
24 32 53 0x y
Câu 25.
Lời giải
Chọn D
Xét bất phương trình: .
2
2
9
0
3 12
x
x x
Bảng xét dấu:
x

3
3

Vế trái
0
0
Vậy nghiệm bất phương trình là: .
1
3;3S
Xét bất pt: .
7 3 1
0
5 2
x x
x
2 14 (3 1)( 5)
0
2( 5)
x x x
x
2
3 12 9
0
2 5
x x
x
Bảng xét dấu:
x

1
3
5

Vế trái
0
0
Vậy nghiệm của bất phương trình là:
.
2
1;3 5;S 
Vậy nghiệm của hệ bất phương trình là: .
1 2
1;3S S S
Câu 26.
Lời giải
Chọn C
Sai từ bước vì phép biến đổi đã làm thay đổi điều kiện của bpt và khi nhân hai veed của bpt với mà
II
1x
chưa biết biểu thức này âm hay dương hay bằng không.
Câu 27.
Lời giải
Chọn C.
Điều kiện: .
3 0 3x x
Ta có: .
1 1 3
1 0
3 3 3
x x x
x x x
2
0 3 0
3
x
x
3x
Vậy tập nghiệm của bất phương trình đã cho là .
3;S
Câu 28.
Lời giải
Chọn A
có VTPT là suy ra VTCP của là .
: 2 3 4 0d x y
2; 3n
d
3;2
d
u
suy ra là VTCP của . Để vuông góc với thì
2 3
:
1 4
x t
d
y mt
3; 4m
d
u
d
d
d
.
9
. 0 9 8 0
8
d d
u u m m
Câu 29.
Lời giải
Chọn B
Điều kiện:
2 2x
2 2
4 2 3 4x x x x
2 2 3 1 2 0x x x x
2
2
1
2 2 1 3
3
x
x x x x
Giải và kết hợp điều kiện được ba nghiệm thỏa mãn là: .
12 504
2; 0;
18
x x x
Câu 30.
Lời giải
Chọn A
Áp dụng định lí cô sin ta có: .
2 2 2 2 2 2
2 cos 2 cosa b c bc A bc A b c a
Suy ra: Nếu nên nhọn.
2 2 2
0 cos 0b c a A
A
Câu 31.
Lời giải
Chọn B
100
; 10.
64 36
R d O
Câu 32.
Lời giải
Chọn B
2 2mx m x m x m
TH1: bất phương trình vô nghiệm.
2 0 2m m
TH2: bất phương trình có nghiệm .
2 0 2m m
2
m
x
m
TH3: bất phương trình có nghiệm .
2 0 2m m
2
m
x
m
KL: giá trị cần tìm .
2m
Câu 33.
Lời giải
Chọn C
Cách 1: Tính chất
0f x m m f x m m
.
2 3 1 1 2 3 1 1 2x x x
Cách 2: .
2
2 2
2 3 1 2 3 1 4 12 8 0 3 2 0 1 2 x x x x x x x
Câu 34.
Lời giải
Chọn D.
Ta có .
2 6 0x
3x
Câu 35.
Lời giải
Chọn C
Hàm số xác định khi và chỉ khi
2
4 3 0.x x
Phương trình Bảng xét dấu:
2
1
4 3 0 1 4 0 .
4
x
x x x x
x
Dựa vào bảng xét dấu, ta thấy
2
4 3 0 4;1 .x x x
Vậy tập xác định của hàm số là
4;1 .D
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Áp dụng bất đẳng thức Côsi, ta có
; và .
4
4
3
.
3 2
x y
x y
4
4
3
.
3 2
y z
y z
4
4
3
.
3 2
z x
z x
Suy ra
4 4 4
. . . 2 4.
3 3 3
x y y z z x x y z
Do đó Khi thì
2 3.P x y y z z x
2
3
x y z
2 3.P
Câu 37.
Lời giải
Ta có :
2
1 0
0
0,
0
1 4 2 7 0
a
f x x
m m
.
2
6 27 0 3 9m m m
Câu 38.
Lời giải
Ta có .
3a b c a b c ab
2
2
3a b c ab
2 2 2
c a b ab
Mặt khác .
2 2 2
cos
2
a b c
C
ab
1
2 2
ab
ab
60C
Câu 39.
Lời giải
Gọi là trung điểm của . khi đó là hình bình hành // .
J
AB
AJCK
AK
CJ
Gọi là trung điểm của
CJ BM N
N
.BM
Chứng minh được từ đó suy ra tam giác tam giác cân tại .
AK BI
BMC
C
Ta có
3; 1 10MC MC
10CM CB AB
Trong tam giác vuông có
ABM
là giao của hai đường tròn
2 2 2
5
. . . 2 2
2
AB BM BI BM AB AI BM AB BM
B
và Tọa độ điểm thỏa mãn:
; 10C
;2 2 .M
B
2 2
2 2
2 2 10
1;1
1 1 8
x y
B
x y
2.a b
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên :………………………………….Lớp:………….......……..………
Mã đề thi
003
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn D
.
2
3 2 0 3 2
3
x x x
Câu 2.
Lời giải
Chọn A
Ta có nên đáp án B đúng.
3.3 2 7 0
Câu 3.
Lời giải
Chọn B
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy là nghiệm
0 0
; 5;3x y
của hệ.
Câu 4.
Lời giải
Chọn D
Điều kiện xác định của phương trình là .
2 0
4 3 0
1 0
x
x
x
2
4
3
1
x
x
x
Câu 5.
Lời giải
là một vecto chỉ phương của đường thẳng .
2;6 1; 3AB u
AB
Phương trình tham số của đường thẳng đi qua điểm và nhận là một vecto chỉ
AB
3; 1A
1; 3u
phương là: , .
3
1 3
x t
y t
t
Câu 6.
Lời giải
Chọn A
*) Do:
5 2x x
. Tức là khẳng định A chỉ đúng khi .
3 0 0x x
0x
*) Do:
2 2
5 2x x
. Tức là khẳng định B chỉ đúng khi .
2
3 0 0x x
0x
*) Do:
3 7x x
. Tức là khẳng định C chỉ đúng khi .
2x
2x
*) Do: đúng với .
2 5x x
0 3x
x
Câu 7.
Lời giải
Chọn C
, luôn đúng.
a c b d
ac bd
Ta có: đúng.
0
ac bd
ac bd a d
bc bc b
b
c
c
a d
b c
Câu 8.
Lời giải
Chọn B
Theo định lí hàm số cosin, nên C sai.
2 2 2
2 cos c b a ab C
Câu 9.
Lời giải
Chọn B.
* Theo định lý về dấu của tam thức bậc hai thì luôn cùng dấu với hệ số với mọi khi .
f x
a
x
0
Câu 10.
Lời giải
Chọn C
Ta có .
2
2 5 0
5
x
x x
x
Câu 11.
Lời giải
Chọn A
Đường thẳng có vô số vectơ pháp tuyến và vô số vectơ chỉ phương.
Câu 12.
Lời giải
Chọn.D
Áp dụng bất đẳng thức AM-GM cho 2 số dương x,y ta thấy cả 3 phương án trên đều đúng.
Câu 13.
Lời giải
Chọn D
Tọa độ giao điểm của đường thẳng và đường thẳng là nghiệm của hệ
: 4 3 26 0x y
:3 4 7 0d x y
phương trình: .
4 3 26 0 5
3 4 7 0 2
x y x
x y y
Câu 14.
Lời giải
8
3
60
°
A
B
C
Áp dụng định lý cosin cho tam giác
ABC
Ta có
2 2 2
2 cosb a c ac B
2 2
8 3 2.8.3.cos60 49 7.b
Câu 15.
Lời giải
Chọn C
2
2
8 16 0 4 0x x x
Điều này không thể xảy ra nên bất phương trình vô nghiệm
Câu 16.
Lời giải
Chọn B
Giải hệ: . Ta được hệ vô số nghiệm.
2 3 2 3
2 3 2 3 5 2 6
t t
t t
Vậy .
1
2
Câu 17.
Lời giải.
Chọn A
Ta có: .
25
45sin
30sin.10
sin
sin.
sin
sin.
sinsin
B
CAC
B
Cb
cAB
C
c
B
b
Câu 18.
Lời giải
Chọn A
.
3
2 3 0 2 3
2
x x x
Câu 19.
Lời giải
Chọn C.
8
5 2 4 0 7 8 .
7
x x x x
Vậy bất phương trình đã cho có tập nghiệm là: .
8
; .
7
S

Câu 20.
Lời giải
Chọn D
Ta có: ( chọn
2
6 0 2 3x x x
C. ).
Câu 21.
Lời giải
Chọn B
Điều kiện .
0x
Bất phương trình tương đương với
2 2
0
3 9 9 0
1
9
x
x x x x x x
x
Kết hợp điều kiện, ta được tập nghiệm của bất phương trình .
1
0 ;
9
S

Câu 22.
Lời giải
Chọn A.
+Ta có , hay ta có A đúng.
2 2
a b a b
,a b
+ Chọn , ta có B, C, D sai chỉ có A đúng.
1
2
a
4b
Câu 23.
Lời giải
Chọn B
.
2
ABCD ABC
S S
1
2. . . sin
2
AB BC ABC
sinab ABC
Câu 24.
Lời giải
Chọn A
Ta có .
2
1 0x
1 1x
.
3 0x
x m
Do đó hệ có nghiệm khi .
1m
Câu 25.
Lời giải
Chọn D.
Điều kiện .
3 6 0x
2x
Xét .
4 0 4x x
Và .
3 6 0 2x x
Bảng xét dấu:
x

2
4

4 x
| 0
3 6x
0 |
Vế trái
|| 0
Vậy tập nghiệm của bất phương trình đã cho là .
2;4S
Câu 26.
Lời giải
Chọn D.
Đường thẳng đi qua và nhận làm VTCP nên
AB
1;2A
1;1AB
:1 1 1 2 0AB x y
.
1 0x y
Khoảng cách từ điểm đến đường thẳng là: .
3; 4C
AB
2 2
3 4 1
, 2
1 1
d C AB
Vậy diện tích tam giác bằng: .
ABC
2 2
1 1
. , . 1 1 . 2 1
2 2
ABC
S AB d C AB
Câu 27.
Lời giải
Chọn D
Câu 28.
Lời giải
Chọn A
Gọi
;5 2M x x d
Ta có :
2 2
10 1 5 2 2 10IM x x
1
2
2
0
5 14 0
14
5
M
M
x
x x
x
Vậy:
1 2
14
5
M M
x x
Câu 29.
Lời giải:
Chọn C
Gọi là trung điểm
M
AB
2; 2M
2; 6AB
1; 3n
Phương trình tổng quát của đường trung trực của đoạn thẳng
AB
1 2 3 2 0 3 8 0x y x y
Câu 30.
Lời giải
Chọn D
Ta có
2
4 12 4 12
.
4 4
x x
f x
x x x x
Phương trình và
4 12 0 3; 0x x x
4 0 4.x x
Bảng xét dấu
Dựa vào bảng xét dấu, suy ra
0 ;0 3;4 .f x x 
Câu 31.
Lời giải
Chọn B
Ta có .
2
5 1 3
5
x
x
25 5 2 15x x
23 20x
20
23
x
Câu 32.
Lời giải
Chọn A
ĐKXĐ: (1)
1 0 1 x x
Lập bảng xét dấu ta dễ dàng suy ra kết quả.
Vậy tập nghiệm của bất phương trình . Chọn A
1 1; S
Cách 2: Xét 2 trường hợp x =1 và x khác 1.
Câu 33.
Lời giải
Chọn B
Cách 1: .
2
5 6
1 2
x x
x
2
5 6 0
1 0
x x
x
Bảng xét dấu chung :
x

6
1

2
5 6x x
0
0
1x
0
Vậy
6x
Cách 2: Dùng MTCT: .
2
5 6
1 2
x x
x
2
5 6 0
1
x x
x
6; 1
1
x x
x
6x
Câu 34.
Lời giải
Chọn C
Bằng cách thay lần lượt tọa độ của các điểm , , , vào hệ bất phương trình. Tại điểm ta
M
N
P
Q
3;4P
được:
đúng. Do vậy điểm thuộc miền nghiệm của hệ đã cho.
2. 3 3.4 1 0
5 0
15 0
5. 3 4 4 0
3;4P
Câu 35.
Lời giải
Chọn C
Ta có: nên .
AD BC
2a
2.
ABCD ABD
S S
1
2. . .sin
2
AB AD BAD
2
a
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Biểu thức
P
được viết lại dưới dạng
1P b c a b c bc
Xét hàm số với .
1f x b c x b c bc
0;1x
Do là hàm số bậc nhất trên đoạn nên ta có
f x
0;1
( ) max{ (0), (1)}, [0;1]f x f f x
Lại có
(0) (1 )(1 ) 1 1, , [0;1]f b c bc b c b c
và
(1) 1 1, , [0;1]f bc b c
Do đó
( ) 1, [0;1] ( ) 1f x x f a
Đẳng thức xảy ra chẳng hạn tại
1, 0, [0;1]a b c
Vậy .
max 1P
Câu 37.
Lời giải
.
2
3 2 6 0 3 2x x x
Câu 38.
Lời giải
Diện tích tam giác . Do đó diện tích tam giác đạt giá trị lớn nhất bằng
1 1
. sin .
2 2
ABC
S CB CA ACB a b= £
ABC
đạt được khi .
1
,
2
ab
sin 1 90ACB ACB
o
= Þ =
Câu 39.
Lời giải
Gọi . Phương trình đường thẳng .
0;M a Oy
: 4 3 2 0AB x y
Ta có: .
3 2 3 2
1 1
. . ; .5.
2 2 5 2
MAB
a a
S AB d M AB
Do đó: . Vậy hoặc .
0
1 3 2 2
4
3
MAB
a
S a
a
0;0M
4
0;
3
M
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên :………………………………….Lớp:………….......……..………
Mã đề thi
004
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn C.
2 1 3 2 5 5 1.x x x x
Vậy bất phương trình đã cho có tập nghiệm là: .
1; .S 
Câu 2.
Lời giải
Chọn A
Ta có:
2
2 3 0 1 3x x x
Câu 3.
Lời giải
Chọn C
0;0
0;0
6.0 4
: 6 4 0 1
|
.0 0
| : 6 4 1 0
0.
d
d
d x
O
O
c c
x c c
d x x

Vậy
: 6 4 0 : 3 2 0.d x y d x y
Câu 4.
Lời giải
Chọn B
Xét
: 2 3 1 0
2 3
: 2 3 1 0
2
1
3
|| .
1
A
A
d
d
d
x y
y
d
x
Để ý rằng một đường thẳng song song với sẽ có dạng Do đó kiểm tra
2 3 1 0x y
12 3 0 .x y c c
chỉ thấy có đáp án A thỏa mãn, các đáp án còn lại không thỏa mãn.
Câu 5.
Lời giải
Chọn A
Gọi là trung trực đoạn AB, ta có:
d
0;1
0;1 .
d
AB
n AB
d AB

Câu 6.
Lời giải
Chọn B.
khi và .
0, f x x
0a
0
Câu 7.
Lời giải
Chọn A
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy là nghiệm
0 0
; 2;1x y
của hệ bất phương trình đã cho.
Câu 8.
Lời giải
Chọn D
Dựa vào đáp án, ta có nhận xét sau:
Chưa đủ dữ kiện để so sánh A sai.
0
0
1 1
0
0
a b
a b
c d
d c
,
a b
c d

Chưa đủ dữ kiện để so sánh B sai.
0
0
1 1
0
0
a b
a b
c d
d c
,
a b
c d

C sai vì chưa thiếu điều kiện
a b
a b
c d
c d

, , , .a b c d
D đúng.
1
0
1
0
1
a
a b
a d a d
b
c d d
b c b c
c
Câu 9.
Lời giải
Chọn B
.
2 2
2 2
1
1 0
2 2
x x x x
S
x x
Câu 10.
Lời giải
Chọn D.
Điều kiện: .
6 3 0x
2x
Câu 11.
Lời giải
Chọn B.
Ta có: .
2
2 2 2
3
2 .B .cos150 2 3 2.2. 3. 13
2
AB AC BC AC C
Câu 12.
Lời giải
Chọn D.
Nữa chu vi: .
13 14 15
21.
2
p
Diện tích: .
( 13)( 14)( 15) 84.S p p p p
Câu 13.
Lời giải
Chọn B
Phương trình vô nghiệm.
0 2 0m
có nghiệm khi và chỉ
2
0 2 0m mx mx
.
2
2
0
0 8 0 8 0
8
m
m m m m
m
So với điều kiện ta có hoặc
.
0m
8m
Câu 14.
Lời giải
Chọn A
Ta có .
2
5
4
1
4 0xx
x
x
f x
Bảng xét dấu
Dựa vào bảng xét dấu .
1
0
4
x
f x
x
Câu 15.
Lời giải
Chọn C
Theo định lý cosin ta có:
2 2 2 2 2 2
2 2 1 7
cosA .
2 . 2.2.2 8
AC AB BC
AB AC
Câu 16.
Lời giải
Chọn D
Thay vào các bất phương trình ta có phương án D đúng.
3x
Câu 17.
Lời giải
Chọn A
.
2
3 2 3 2 0
3
x x x
Câu 18.
Lời giải
Chọn C
Ta có .Vậy là sai.
0f x
2 1 0x
1
2
x
1
0;
2
f x x
Câu 19.
Lời giải
Chọn.D
Áp dụng bất đẳng thức AM-GM cho 2 số dương x,y ta thấy cả 3 phương án trên đều đúng.
Câu 20.
Lời giải
Chọn C
Giải hệ: .
22 2 12 4 0
55 5 12 4 0
t t y
t t x
Vậy tọa độ giao điểm của và là .
1
2
0;0
Câu 21.
Lời giải
Chọn D
Điều kiện:
1 2x
Ta có
2 2
3 2 1x x x x
2 2 2
3 1 2 2 2x x x x x x
2 2
2 2 2 0x x x x
2
2 1x x
2
1 0x x
1 5
2
x
Câu 22.
Lời giải
Chọn C
10 24 10
44
; .
13
25 144
R d I
Câu 23.
Lời giải
Chọn B
C đúng vì và , nhân vế theo vế ta chọn C .
3
3a b c abc
3
1 1 1 1
3
a b c abc
Câu 24.
Lời giải
Chọn C.
ĐKXĐ .
2
2
4 0 4 0 5 0
5 5 4 5
25 0
x x x x x
x x
x
Câu 25.
Lời giải
Chọn A
.
2
2
0
1
2 1
2
x
x
x
x
Câu 26.
Lời giải
Chọn B
1
: (1 ;2 )
2
x t
C C t t
y t
2 2 2
2
t 2 t 2 1CA CB t t
1 7 13
;
6 6 6
t C
Câu 27.
Lời giải
Chọn D
Chọn thay vào ta có vô lí.
0, 1a b
5 5 2 2
a b a b a b
1 0
Câu 28.
Hướng dẫn giải
Chọn B
Ta có:
0 0
3 0
3 0 3
x x
x x
x x
Vậy: .
3; \ 0S 
Câu 29.
Lời giải
Chọn D
a
2
45
°
a
a
2
D
C
B
A
Ta có: .
2
1
2 2. . . .sin 45
2
ABCD ABD
S S AB AD a
Câu 30.
Lời giải
Chọn C
Bảng xét dấu:
Vậy tập nghiệm của bất phương trình là: .
1;2 3;S 
Câu 31.
Lời giải.
Chọn A
Theo giả thiết ta có hay
2 2 2
BC AB AC
2 2 2
0AB AC BC
2 2 2
o o
cos 0 90 180 .
2 .
AB AC BC
A A
AB AC
Câu 32.
Lời giải
Chọn B
Sai từ bước vì .
IV
2
6
4 12 0
2
x
x x
x
Câu 33.
Lời giải
Chọn A
Thay tọa độ điểm , , vào bất phương trình thứ nhất của hệ không thỏa mãn
1;2
0;0
2;1
Câu 34.
Lời giải
Chọn D
1 2
1
2
;
1
2
1 0
1
2
1 3. 1 0
1
: 3 0 1; 3
cos
: 0 0 1;0
d d
d x y
d
n
x n

60 .
Câu 35.
Lời giải
Chọn C
1
2 1 0
2
3
3
x
x
x m
x m
Hệ vô nghiệm thì .
1 5
3
2 2
m m
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Tập xác định
2019; 2019
é ù
= -
ê ú
ë û
D
Dễ thấy là hàm số lẻ trên . Thêm nữa, .
( )f x
D
( ) 0, 0; 2019
é ù
³ " Î
ê ú
ë û
f x x
Do đó,
2019; 2019 0; 2019
2019; 2019 0; 2019
( ) ( )
( ) ( )
é ù é ù
-
ê ú ê ú
ë û ë û
é ù é ù
-
ê ú ê ú
ë û ë û
ì
= =
ï
ï
ï
ï
í
ï
= = -
ï
ï
ï
î
M Max f x Max f x
m Min f x Max f x
Ta có
( )
( ) ( )
( )
( )
( )
2
2
2
2 2
2 2
2
2017 2019
( ) 2017 2017 2019
2018 2018
2017 1 . 2017 2019
2018
2018
2017 2019
2018
æ ö
+ -
÷
ç
÷
ç
= = + -
÷
ç
÷
ç
÷
ç
è ø
£ + + -
= + -
x x
f x x x
x
x
x x
( )
2 2
2017 2019
2018
( ) 2018
2018 2
æ ö
+ + -
÷
ç
÷
ç
Þ £ =
÷
ç
÷
ç
÷
÷
ç
è ø
x x
f x
Đẳng thức xảy ra
( )
2
2 2
2017 2019
1
2018 0; 2019
2017
2017 2019
ì
ï
-
ï
ï
=
ï
é ù
Û Û = Î
í
ê ú
ë û
ï
ï
ï
= + -
ï
î
x
x
x x
Từ đó suy ra
2019; 2019 0; 2019
2019; 2019 0; 2019
( ) ( ) 2018
( ) ( ) 2018
é ù é ù
-
ê ú ê ú
ë û ë û
é ù é ù
-
ê ú ê ú
ë û ë û
ì
ï
= = =
ï
ï
ï
í
ï
= = - = -
ï
ï
ï
î
M Max f x Max f x
m Min f x Max f x
Vậy .
[ ]
( )
( )
( )
* *
; 2018; 2018 44
é ù
Ç = Ç - =
ê ú
ë û
n m M n
Câu 37.
Lời giải
Bất phương trình
2 2 2 2
5 2 2 5 2 4 5 4 0x x x x x x x x
Xét phương trình
2
1
5 4 0 1 4 0 .
4
x
x x x x
x
Lập bảng xét dấu
Dựa vào bảng xét dấu, ta thấy
2
5 4 0 ;1 4; .x x x
Câu 38.
Lời giải
+ Đặt . Khi đó theo định lý cosin ta có:
; ( , 0)OB x OA y x y
2 2 2 0 2 2
2 cos30 3AB x y xy x y xy
Do đó ta có hệ thức:
2 2
3 1x y xy
Xét phương trình bậc hai:
2 2
3 1 0y xy x
Phương trình có nghiệm khi
y
2 2
3 4( 1) 0 0 2x x x
Vậy học vị trí xa nhất mà học sinh có thể đạt được cách một khoảng là
O
2m
Câu 39.
Lời giải
. Vậy I(3;1) hoặc I(2;4).
3
2 2 2 2
1
( 1) ( 2) ( 4) ( 3)
2
( 1)( 4) ( 2)( 3) 0
. 0
4
x
AI BI
y
x y x y
x
x x y y
AI BI
y
Với I(3;1) thì (C): , suy ra nên M ( 1;0) hoặc M(5;0).
2 2
( 3) ( 1) 5x y
( )M Ox C
Với I (2;4) thì (C) . Nhận thấy (C) không giao Ox. Vậy không có điểm M thỏa mãn.
2 2
( 2) ( 4) 5x y
Kết luận có hai điểm M thỏa mãn yêu cầu bài toán M ( 1;0) hoặc M(5;0).
Vậy tổng các hoành độ của điểm M là 6.
Giả sử đã tìm được điểm M thuộc trục Ox
thỏa mãn . Gọi I (x; y) là tâm đường
0
45AMB
tròn (C) ngoại tiếp tam giác ABM. Do ,
0
45AMB
suy ra ( Góc ở tâm gấp hai lần góc
0
90AIB
nội tiếp chắn cùng cung AB). Khi đó
I
M
A
B
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên :………………………………….Lớp:………….......……..………
Mã đề thi
005
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn A
mà . Vậy chỉ có C không thỏa mãn.
–2 3 –1 0 2; 3x y n
1 1
2
. 0 ,
3
n u u u u
Câu 2.
Lời giải
Chọn D
Câu 3.
Lời giải
Chọn B
Đáp án A sai khi
1; 1.a b
Đáp án B và D sai khi
0.a b
Xét : luôn đúng với mọi số thực .
2 2 2 2
2 2a b a b a ab b a ab b ab ab
,a b
Vậy,chọn
B.
Câu 4.
Lời giải
Chọn D
thỏa nên là nghiệm của bất phương trình .
2
4 2 5 0
4 5 0 x
Câu 5.
Lời giải
Chọn D
Theo quy tắc xét dấu nhị thức bậc nhất thì đáp án C sai.
Câu 6.
Lời giải
Chọn C
Phương trình đường thẳng cần tìm là .
2( 1) 3( 2) 0 2 3 8 0x y x y
Câu 7.
Lời giải
Chọn A
Đường trung trực AB nhận véc-tơ làm vectơ pháp tuyến và đi qua trung điểm
1
3; 3 1;1
3
AB
của AB nên có phương trình: .
5 5
;
2 2
I
5 5
0 0
2 2
x y x y
Câu 8.
Lời giải
Chọn B
Thay tọa độ các điểm vào bất phương trình ta thấy .
2;2 S
Câu 9.
Lời giải
Chọn B
Véc-tơ chỉ phương của đường thẳng là véc-tơ vì véc-tơ này cùng phương với véc-tơ
d
2; 1u
2;1v
Câu 10.
Lời giải
Chọn B
Cách 1: Áp dụng công thức tính độ dài đường trung tuyến ta có
.
2 2 2
2
2 4
AB AC BC
AM
2 2 2
6 8 10
2 4
25
5 cmAM
Cách 2: Do nên tam giác vuông tại .
2 2 2
AB AC BC
ABC
1
2
AM BC
5 cm
Câu 11.
Lời giải
Chọn A
.
2
1
0 12 13 0
13
x
f x x x
x
Câu 12.
Lời giải
Chọn D
2 2 2 *x x x
Điều kiện: .
2x
Bất phương trình .
* 2x
Kết hợp với điều kiện, tập nghiệm của bất phương trình là:
2
Câu 13.
Lời giải
Chọn B
Nửa chu vi:
9 10 11
15.
2
p
Diện tích:
( 9)( 10)( 11) 30 2.S p p p p
Câu 14.
Lời giải
Chọn C
.
2
5 1 3
5
x
x
25 5 2 15x x
23 20x
20
23
x
Câu 15.
Lời giải
Chọn D
Thay tọa độ của M vào vế trái của d, ta được
2.5 ( 2) 3 15 0.
Điểm N sẽ nằm cùng phía đối với M so với đường thẳng d nếu thay tọa độ của N vào vế trái của d được kết
quả là một số dương.
Do đó ta chọn được
(3; 1).N
Câu 16.
Lời giải
Chọn D
Bất phương trình xác định .
2 6 0 3x x
Câu 17.
Lời giải
Chọn D
Nửa chu vi của tam giác là: .
3 2 1
2
p
Diện tích tam giác là: .
2
3 2 1
2
S p p p p
Câu 18.
Lời giải
Chọn C
. Thay .
, 3 1f x y x y
1, 1 1 3 1 1 0f
Câu 19.
Lời giải
Chọn B
Câu 20.
Lời giải
Chọn C
Câu 21.
Lời giải
Chọn A
Ta có VTCP của
: 2; 1D u
Vậy PTTS của đưởng thẳng
1 2
:
2
x t
D
y t
Câu 22.
Lời giải
Chọn A
Điều kiện: .
1; 2; 4x x x
Vậy .
;2 4; \ 1x  
Câu 23.
Lời giải
Chọn A
2 2 2 2
2 4 2 4 2 4 0
6 2 2 0 1
x x x x x x
x x
Câu 24.
Lời giải
Chọn A
Hệ BPT . Hệ có nghiệm duy nhất .
2x
x m
2m
Câu 25.
Lời giải
Chọn B
Ta có .
1
2 1
2
x x
Xét bất phương trình
2
2 0
1
2 2 1 2 .
1
2 1
2
2
x
x
x x x x
x
x
Vậy bất phương trình .
2 1x
2 2 1 2 x x x
Câu 26.
Lời giải
Chọn B
Ta có: I. đúng vì là công thức Hê-rông tính diện tích tam giác.
Khi đó:
2
. . .
2 2 2 2
a b c a b c a b c a b c
S
. Do đó II. đúng
2
16S a b c a b c a b c a b c
Câu 27.
Lời giải
Chọn A
Cách 1: Tự luận.
Gọi . Cho , suy ra .
M d
5 3x y
5; 3M
.
1 2 2
2
2
5. 5 7 3 6
2
; ,
74
5 7
d d d d M d
Cách 2: Trắc nghiệm.
.
1 2
1 2
2 2 2
2
4 6
2
;
74
5 7
c c
d d d
a b
Câu 28.
Lời giải
Chọn C
Đường thẳng nào đi qua điểm và song song với đường thẳng
2;1A
: 2 3 2 0x y
Có dạng: .
2 2 3 1 0 2 3 7 0x y x y
Câu 29.
Lời giải
Chọn C
2 2 2
2 2 4 4 2 6
1 1 0 0
2 1 2 1 2 1 2 1
x x x x x x x x
x x x x x x x x
.
1 2x
Câu 30.
Lời giải
Chọn C
Vì nên tam giác vuông tại .
2 2 2
AB AC BC
ABC
A
Do đó bán kính đường tròn nội tiếp .
1
.
3.4
2
1
1
3 4 5
2
AB AC
S
r
p
AB AC BC
Câu 31.
Lời giải
Chọn A
Vì với mọi nên ta có
2
2 4 0x x
x
2
2
2
2 5 2 4
2 5 2 4
2 5 2 4
x x x
x x x
x x x
.
2
2
1 0
4 9 0
x
x x
luoân ñuùng
2
1
1 0
1
x
x
x
Vậy hoặc .
1x
1x
Câu 32.
Lời giải
Chọn D
Áp dụng bất đẳng thức Cô – si cho hai số không âm và . Ta có:
2
x
2
y
. Đẳng thức xảy ra .
2
2 2 2 2
2 2 4A x y x y xy
2x y
Câu 33.
Lời giải
Chọn B
.
2
4 0 2 2 0 ; 2 2;x x x x  
Câu 34.
Lời giải
Chọn C
Để bất phương trình vô nghiệm .
2 0 2m m
Câu 35.
Lời giải
Chọn C
Ta có:
1
;1 (3 1) 0, 1 0
3
x x x
Áp dụng BĐT Cô-si cho hai số dương ta có
3 1 ; 3 3x x
2
(3 1) (3 3 ) 1
3 1 3 3 , ;1
2 3
1
3 1 3 3 4 , ;1
3
4 1
( ) (3 1)(1 ) , ;1
3 3
x x
x x x
x x x
f x x x x
Dấu “=” xảy ra khi và chỉ khi
1
3 1 3 3
3
x x x
Cách 2: Giá trị lớn nhất của biểu thức với bằng
( ) 3 1 1f x x x
1
;1
3
x
4
3
2
4 1 1
3 1 1 3 2 0 ( )
3 3 3
x x x x x tm
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Ta có .
5
2 2 3 2 2 3
2 3 3a b a ab b a ab a b b
Áp dụng bất đẳng thức CôSi, ta có
;
2 2 2 2
2 2 2 4a ab b ab a b ab
.
3 2 2 3 3 2 2 3 2 2
3 3 2 3 3 4 1 1a ab a b b a ab a b b ab b a
Suy ra .
2 2 3 2 2 3 2 2
2 3 3 16 1 1a ab b a ab a b b ab a b
Do đó .
5
2 2
16 1 1a b ab a b
Đẳng thức xảy ra khi và chỉ khi .
1a b
Câu 37.
Lời giải
Với , ta có không thỏa mãn.
0m
( ) 1 0 1:f x x x
Với , yêu cầu Câu toán
0m
2
1 0,mx x x
0
0 0
1
0
1
0 1 4 0
4
4
m
a m
m
m
m
Vậy với thì biểu thức luôn âm.
1
0
4
m
f x
Câu 38.
Lời giải
Ta có .
2 1 1 1 1 2
( ) ( ) ( )
a a b c a a a b c
S S S S S
a p p a p b p c
h r r r r h r r r r
Câu 39.
Lời giải
Định hướng:
- Tọa độ điểm
B BH BM
- Viết phương trình đường thẳng đi qua và vuông góc với .
AC
A
BH
Suy ra tọa độ
M AC BM C
Gọi lần lượt là đường cao và trung tuyến kẻ từ
,
BH BM
.
B
Tọa độ điểm là nghiệm của hệ phương trình
B
2 3 12 0
3;2
2 3 0
x y
B
x y
Đường thẳng đi qua và vuông góc với nên có phương trình
AC
A
BH
3 2 10 0.
x y
Tọa độ điểm là nghiệm của hệ phương trình
M
2 3 0
6; 4
3 2 10 0
x y
M
x y
Do là trung điểm suy ra tọa độ điểm
M
AC
8; 7
C
Vậy .
3;2 , 8; 7B C
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên :………………………………….Lớp:………….......……..………
Mã đề thi
006
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn A
có véc tơ pháp tuyến là .
D
1; 2n
qua và nên .
d
1; 1M
//d D
: 1 1 2 1 0 2 3 0d x y x y
Câu 2.
Lời giải
Chọn B
TXĐ: .
D
Ta có
6 5 2 10 8 0 5x x x x x x
S
Câu 3.
Lời giải
Chọn A
Ta có:
2 2 2 2 2
1
2 . .cos 8 9 2.9.8. 73 73
2
 AC AB BC AB BC ABC AC
Câu 4.
Lời giải
Chọn D
và .
0
0
2
x
f x
x
1 0a
Bảng xét dấu:
Do đó: .
0, 0;2f x x
Câu 5.
Lời giải
Chọn C
Nửa chu vi của tam giác là:
5 12 13
15
2
p
Diện tích của tam giác là:
.
5 12 13 15 15 5 15 12 15 13 30S p p p p
Câu 6.
Lời giải
Chọn D
Ta có: .
5 1
3 3
2 2
x x
x x
3 0 3
3
1
3
5 1 1
4 1
4
2 2 4
x x
x
x
x x
x
x
Vậy tập nghiệm của bất phương trình đã cho là .
1
;3
4
Câu 7.
Lời giải
Chọn D
Áp dụng công thức tính độ dài đường trung tuyến của ta có:
AM
ABC
.
2 2 2 2 2 2
2
2 2 9 12 15
225 15
7,5
4 4 4 2
AB AC BC
AM AM
Câu 8.
Lời giải
Chọn C
d có véctơ chỉ phương nên véctơ pháp tuyến có tọa độ .
( )
3;2u =
( )
2; 3-
Câu 9.
Lời giải
Chọn D
Đường thẳng đi qua hai điểm nên loại đáp án H2 và H4.
2 3 6 0x y
0; 2 , 3;0
Mặt khác không thỏa mãn nên chọn hình H3.
0;0O
2 3 6 0x y
Câu 10.
Lời giải
Chọn A
Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào không thỏa bất phương trình trên.
Câu 11.
Lời giải
Chọn B
.
5 0x
5x
.
5( 5) 0x x
5 0
5 0
x
x
5x
Vậy .
5 0x
5( 5) 0x x
Câu 12.
Lời giải
Chọn C
.
2 2
3 3
a b a b
a c
b c b c
Câu 13.
Lời giải
Chọn C
Vì ( đúng ).
0 1 0 1 0x
x
Câu 14.
Lời giải
Chọn A
Bất phương trình có tập nghiệm là khi và chỉ khi .
0 ax b
0
0
a
b
Câu 15.
Lời giải
Chọn B
Câu 16.
Lời giải
Chọn C
Đáp án A sai khi
1; 1.a b
Đáp án B và D sai khi
0.a b
Xét : luôn đúng với mọi số thực .
2 2 2 2
2 2a b a b a ab b a ab b ab ab
,a b
Vậy,chọn
B.
Câu 17.
Lời giải
Chọn B
ĐK: .
5
2 5 0
2
x x
Câu 18.
Lời giải
Chọn C
Thay tọa độ điểm vào đường thẳng ta được .
1
;2
2
B
: 2 1 0x y
1
2. 2 1 0
2
---HẾT---
Câu 19.
Lời giải
Chọn A
Phương trình đường thẳng theo đoạn chắn .
AB
1
x y
a b
Câu 20.
Lời giải
Chọn C
Câu 21.
Lời giải
Chọn A
ĐK
3 0 3
3
3 0 3
x x
x
x x
1 1 1 1 3 3 6
0 0 0
3 3 3 3 3 3 3 3
3
3 3 0
3
x x
x x x x x x x x
x
x x
x
Vậy .
; 3 3;S  
Câu 22.
Lời giải
Chọn D
Ta có
2 8 35
23 2 16 7
5 5 8
x
x x x
Câu 23.
Lời giải
Chọn B
Viết phương trình đường thẳng đường cao : điểm đi qua vectơ pháp tuyến
AH
2; 6A
4; 3n
: 4 2 3 6 0 4 3 10 0AH x y x y
Câu 24.
Lời giải
Chọn C
Do nên bất phương trình tương đương với:
2
2 1 0x
2
2
2
2 1
2 0
1
2 1 0
2
x
x x
x
x
.
2 1
2
2
2
2
2
2
1
2
2
2
x
x
x
x
x
Vậy, tập nghiệm của bất phương trình là .
2 2
2 2 1 0x x x
2 2
2; ;1
2 2
Câu 25.
Lời giải
Chọn B
.
2
12 0x x
; 3 4;x 
Bất phương trình có tập nghiệm .
; 3 4;S 
Ta có .
0; S
Câu 26.
Lời giải
Chọn B
ĐK
1 0 1x x
2 3 1
1 1 2 2 3 1
2
1 1
x m m m
x x x m m x m x
x x
Vì
3 1 1
1 1 2 3 1 1 3
2 3
m
x m m m
Vậy .
1
;
3
m

Câu 27.
Lời giải
Chọn A
Ta có .
6
8
3
sin sin sin
sin
4
AB AC AC
AC
C B B
B
Và .
8
12
2
sin sin sin
sin
3
BC AC BC
BC
A B A
A
Chu vi tam giác .
26C AB BC CA
Câu 28.
Lời giải
Chọn C
Tam giác đều cạnh có bán kính đường tròn ngoại tiếp .
ABC
a
3
3
a
R
. Diện tích tam giác đều bằng .
8R
8 3a
2
3 64.3 3
48 3
4 4
a
Câu 29.
Lời giải
Chọn D
Điều kiện: .
2
4 2 0x x
2 6
2 6
x
x
Ta có .
2
4 2 2 1x x x
2 2
4 2 4 4 1x x x x
2
3 8 3 0x x
Áp dụng định lí Vi-et ta có .
1 2
8
3
b
S x x
a
Câu 30.
Lời giải
Chọn B
Cách 1: Thử chọn dễ thấy C là đáp án thỏa mãn.
Cách 2: Giải chi tiết:
Xét
1 1 1 1 1 1 1
1VT
a b c ab bc ca abc
Áp dụng BĐT Cauchy cho các số dương trên ta có
; và
3
1 1 1 3
a b c
abc
2
3
1 1 1 3
ab bc ca
abc
3
1
3 27
a b c
abc
Suy ra
1 9 27 27 64VT
Dấu bằng xảy ra khi và chỉ khi .
1
3
a b c
Câu 31.
Lời giải
Chọn D
.
2 5 3 3 2 5 3 2 8 1 4
x x x x
Câu 32.
Lời giải
Chọn A
Ta có
3 4 0 3;4
1 1
x x m
x m x m
bất phương trình có nghiệm khi .
1 3 2m m
Câu 33.
Lời giải
Chọn D
Ta có là trung điểm nên tọa độ điểm .
M
BC
2; 0
M
. Đường thẳng đi qua nhận là véc tơ pháp tuyến có phương
1; 1
AM
1;1
AM
n
AM
M
1;1
AM
n
trình tổng quát: .
: 2 0 : 2 0
AM x y AM x y
Câu 34.
Lời giải
Chọn B
có véc tơ pháp tuyến và đi qua điểm .
4;3n
1;2
Suy ra .
: 4 1 3 2 0 4 3 10 0x y x y
.
2 2
4.2 3.0 10
2
;
5
4 3
d M
Câu 35.
Lời giải
Chọn A
Ta có .
4
1 1
1
y x
x
Do nên theo bất đẳng thức Cô -si cho hai số
1x
4
1;
1
x
x
Ta có: \
4 4 4
1 2 1. 4 1 1 5 5 1
1 1 1
x x x y x
x x x
Dấu “=” xảy ra khi và chỉ khi
4
1 1 2 3
1
x x x
x
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Do nên
, 0;1a b
1 0;1 0; 0.a b a b
Áp dụng bất đẳng thức CôSi cho ba số không âm, ta có
.
3
1 1
1 1
3
a b a b
a b a b
8
1 1
27
a b a b
Đẳng thức xảy ra khi và chỉ khi
1 1
1
1
3
a b
a b
b a b
Câu 37.
Lời giải
Yêu cầu Câu toán
2 2
2 2( 1) 1 0,m x m x x
2 2
2 2
2
( 1) 2 0
0
1
( 1) 2 0 2 1
2
0
2 0
m m
m m m m
a
m
Vậy thỏa mãn.
1
2
m
Câu 38.
Lời giải
Ta có
2 2 2 2 2 2 2 2 2
2 2 2
2 2 2
5 5
4 4 4
b c a
a c b a b c b c a
m m m
2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 10 10 5 9 9 9 0a c b a b c b c a a b c
.
2 2 2
a b c
Áp dụng định lí sin trong tam giác ta có .
ABC
2
sin sinB sinC
a b c
R
A
Khi đó ta có .
2 2 2
2 2 2 2 2 2
2 sin 2 sinB 2 sinC sin sin sina b c R A R R A B C
Câu 39.
Lời giải
*)Ta thấy điểm không thuộc hai đường trung tuyến .
A
: 2 1 0, : 1 0BE x y CD y
.
: 2 1; : 1BE x y CD y
.
2 1; ; ;1B BE B a a C CD C b
là trung điểm của .
D
AB
3
;
2
a
D a
Mà .
3
1 1 3; 1
2
a
D DC a B
là trung điểm của .
E
AC
1
;2
2
b
E
.
1
2.2 1 0 5 5;1
2
b
E BE b C
*) Ta có: ⇒ vecto chỉ phương của đường thẳng là: .
4; 4 4 1;1AB
AB
1;1
AB
u
Vecto pháp tuyến .
1; 1
AB
n
Phương trình tham số của đường thẳng .
1
:
3
x t
AB
y t
Phương trình tổng quát của đường thẳng .
:1 1 1 3 0 2 0AB x y x y
*) Ta có: ⇒ .
8;2 2 4;1BC
4;1 ; 1; 4
BC BC
u n
Phương trình tham số của đường thẳng .
3 4
:
1
x t
BC
y t
Phương trình tổng quát của đường thẳng .
:1 3 4 1 0 4 1 0BC x y x y
*) Ta có: .
4; 2 2 2; 1AC
2; 1 ; 1;2
AC AC
u n
Phương trình tham số của đường thẳng .
1 2
:
3
x t
AC
y t
Phương trình tổng quát của đường thẳng .
:1 1 2 3 0 2 7 0AC x y x y
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên :………………………………….Lớp:………….......……..………
Mã đề thi
007
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn D
Ta có .
5 2 9 2 2 7 3 2 6 0x x y x y
Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào không thỏa bất phương trình trên.
Câu 2.
Lời giải
Chọn C
Vectơ cơ sở của trục là
Oy
0;1 .
Câu 3.
Lời giải
Chọn B
Ta có: .
2 3 2 3 0y x x y
Nên đường thẳng đã cho có véc-tơ pháp tuyến là
2; 1n
Câu 4.
Lời giải
ChọnB
Thử vào dễ thấy rằng không thỏa mãn bất phương trình nên đáp án là
1; 1D
B.
Câu 5.
Lời giải
Chọn B
Đường thẳng đi qua và song song với đường thẳng có dạng:
0
;
o
M x y
: 0d ax by c
.
0 0
0 ( 0)
o o
a x x b y y ax by
Nên đường thẳng đi qua điểm và song song với đường thẳng có phương trình là
0 ; 0O
6 4 1 0x y
.
3 2 0x y
Câu 6.
Lời giải
Chọn C
• Xét đáp án A:
Thay , vào bất phương trình , ta được: ( Vô lý). Vậy cặp số
1x
1y
3 0 x y
1 1 3 0 3 0
không là nghiệm của bất phương trình . Loại
1; 1
3 0 x y
• Xét đáp án B:
Thay , vào bất phương trình , ta được: ( Vô lý). Vậy cặp số
1x
1y
0 x y
1 1 0 0 0
1; 1
không là nghiệm của bất phương trình . Loại
0 x y
• Xét đáp án C:
Thay , vào bất phương trình , ta được: ( Luôn đúng). Vậy cặp
1x
1y
3 1 0 x y
1 3. 1 1 0 1 0
số là nghiệm của bất phương trình . Chọn C
1; 1
3 1 0 x y
• Xét đáp án D:
Thay , vào bất phương trình , ta được: ( Vô lý). Vậy cặp số
1x
1y
3 1 0 x y
1 3. 1 1 0 1 0
không là nghiệm của bất phương trình . Loại
1; 1
3 1 0 x y
Câu 7.
Lời giải
Chọn D
a
M
C
B
A
.
2
2 2 2
5
4 2
a a
BM AB AM a
Câu 8.
Lời giải
Chọn D
Ta có .
2
3 4 0 1 4x x x
Câu 9.
Lời giải
Chọn A
Phương trình hệ số góc: .
0 0
y k x x y
2
3 2
3
y x
2 3 12 0x y
Câu 10.
Lời giải
Chọn A
Câu 11.
Lời giải
Chọn B
Thay các giá trị vào bất phương trình thì ta có là nghiệm.
3
2;1;0;
2
x
0x
Câu 12.
Lời giải
Chọn C
Theo công thức tính độ dài đường trung tuyến .
2 2 2
2
2
4
b c a
AM
Câu 13.
Lời giải
Chọn C
Tính chất của bất đẳng thức.
Câu 14.
Lời giải
Chọn A
Ta có .
3 2 3 2x x
Câu 15.
Lời giải
Chọn B
.
–2 – 3 2 3 3x y y x y
Thay giá trị từng cặp điểm vào, ta chọn đáp án.
D.
Câu 16.
Lời giải
ChọnD
Ta có .
1
2 1 0
2
x x
Do đó
không là nghiệm của bất phương trình.
4
3
x
Câu 17.
Lời giải
Chọn C
Điều kiện: .
6 3 0x
2x
Câu 18.
Lời giải
Chọn B
Đáp án A sai khi
1; 1.a b
Đáp án B và D sai khi
0.a b
Xét : luôn đúng với mọi số thực .
2 2 2 2
2 2a b a b a ab b a ab b ab ab
,a b
Vậy,chọn
B.
Câu 19.
Lời giải
Chọn B
Đáp án A: Do nên nhân vào hai vế cùng biểu thức ta được bất phương trình tương đương.
1x
2 1 0x
Đáp án B: Hai bất phương trình có cùng tập nghiệm là .
1
( ; )
2
S 
Đáp án C: Hai bất phương trình có cùng tập nghiệm là .
( ; 2)S 
Đáp án D: Bất phương trình: ,
2
1
( 2) 0 ( 2;0) (0; )x x S 
Bất phương trình:
2
2 0 ( 2; )x S 
Tập nghiệm hai bất phương trình khác nhau nên chúng không tương đương.
Câu 20.
Lời giải
Chọn A
Áp dụng định lý cosin trong tam giác ta có:
2 2 2
cos
2. .
BA BC AC
ABC
BA BC
.
2 2 2
2 3 4 3 1
cos
2.2.3 12 4
ABC
Suy ra góc .
104 29ABC
Câu 21.
Lời giải
Chọn B
Bất phương trình tương đương với .
2
12 0x x
; 3 4;x  
Câu 22.
Lời giải
Chọn B
Ta có:
1 1
. . . .
2 2
a
ABC a b
b
h
b
S a h b h
h a
Mặt khác: .
2
sin
2
2
1
sin sin sin
2
a
b
h
a b b B
A B a A h
Câu 23.
Lời giải
Chọn B
Ta có: .
2 2
1 2x y xy
2 1xy
Mặt khác: .
2
2 2 2
2 2S x y x xy y
2 2S
Câu 24.
Lời giải
Chọn D
Ta có: , trung điểm của là .
2;6AB
AB
2; 1I
Đường trung trực của đoạn qua và nhận làm vectơ pháp tuyến có phương trình:
AB
2; 1I
2;6AB
.
2 2 6 1 0 2 6 2 0 3 1 0x y x y x y
Câu 25.
Lời giải
Chọn A
.
2 1 4 0x x
2 1 4x x
4 0
4 0
2 1 4
2 1 4
x
x
x x
x x
4
4
2
2
x
x
x
x
4
4 2
2
x
x
x
Vậy .
, 2 2,x  
Câu 26.
Lời giải
Chọn D
Giải ta được: .
2
5x
Giải ta được: .
1
x m
Hệ có nghiệm .
5 5m m
Câu 27.
Lời giải
Chọn A
Có
4; 2 2 2; 1AB
của đường thẳng là .
vtcp
AB
2; 1u
Câu 28.
Lời giải
Chọn D
Áp dụng định lý sin ta có .
5
2 5
2.sin 30
sin
BC
R R
BAC
Câu 29.
Lời giải
Chọn C
Phương trình đường thẳng có dạng: .
d
4 3 0, 7x y m m
Ta có: .
7
4 6
; 1 1 2 5
3
5
m
m
d M d m
m
Vậy phương trình đường thẳng là
d
4 3 7 0;4 3 3 0x y x y
Câu 30.
Lời giải
Chọn C
Bất phương trình có tập nghiệm là rỗng khi .
2
0
1
4
0
m
m
2m
Câu 31.
Lời giải
Chọn A
Điều kiện: .
1; 2; 4x x x
Bảng xét dấu
Vậy .
;2 4; \ 1x  
Câu 32.
Lời giải
Chọn A
4 2
5 4 0xx - + <
( )( )
2 2
1 4 0x xÛ - - <
2 1
1 2
x
x
é
- < <-
ê
Û
ê
< <
ë
Câu 33.
Lời giải.
Chọn D
ĐKXĐ:
3 0 3.x x
3 6 0 2( )
| 3 6 | 3 0 | 3 6 | 3 0
3 0 3( ).
x x L
x x x x
x x TM
Câu 34.
Lời giải
Chọn C
Điều kiện: .
2006 0
2006 0
x
x
2006
2006
x
x
2006x
Thay vào bất phương trình, ta được: (sai).
2006x
2006 2006 2006 2006
0 0
Vậy bất phương trình vô nghiệm.
Câu 35.
Lời giải
Chọn C
1
1 1
1
y x
x
Cauchy cho 2 số dương ta có:
1
1,
1
x
x
1
1
1
11
1 .
1
xx
xx
Suy ra
2
1
1 1
1
x
x
Vậy khi và chỉ khi
min
2y
1
1 2
1
x x
x
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Ta có:
1 2
a b c b
b c a a
Tương tự:
1 2
1 2
b c
c b
c a
a c
Cộng từng vế các bất đẳng thức trên, ta có đpcm.
Bình luận: Lời giải trên là sự kết nối giữa giả thiết và đpcm. Để ý quan sát ta thấy nếu như cứ nhân 2 số
hạng ở biểu thức điều kiện rồi lấy căn thì ta được một số hạng ở biểu thức cần chứng minh. Chính điều này là
xuất phát điểm của Lời giải như trên.
Câu 37.
Lời giải
Với , tam thức bậc hai trở thành : luôn đúng với mọi .
2m
1 0
x
Với , yêu cầu Câu toán
2m
2
( 2) 2( 2) 3 0,m x m x m x
2
0 2 0 2 0
2
0 ( 2) ( 2)( 3) 0 2 0
a m m
m
m m m m
Kết hợp hai trường hợp ta được là giá trị cần tìm.
2m
Câu 38.
Lời giải
Ta có .
2 2 2 2 2
1 1 1 1 1 1 1 1 1 1 1
a a a a a
b b c c k b k c k b c k h k h h h h
Câu 39.
Lời giải
G
B'
C'
A
B
C
Do nên tọa độ của có dạng
'B BB
B
2 1; .b b
Vì là trung điểm của nên
'C
AB
3
' ; .
2
b
C b
Mặt khác, nên ta được: hay
' 'C CC
3
1 0 1
2
b
b
3; 1 .B
Tương tự, là trung điểm của
'B
AC
1
' ;2
2
c
B
Mặt khác nên hay
' 'B BB
1
2.2 1 0 5
2
c
c
5;1 .C
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên :………………………………….Lớp:………….......……..………
Mã đề thi
008
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn B
Câu 2.
Lời giải
Chọn A
Đáp án A sai khi
1; 1.a b
Đáp án B và D sai khi
0.a b
Xét : luôn đúng với mọi số thực .
2 2 2 2
2 2a b a b a ab b a ab b ab ab
,a b
Vậy,chọn
B.
Câu 3.
Lời giải
Chọn A
và (Tính chất cộng 2 vế của 2 bất đẳng thức cùng chiều).
a b
c d
a c b d
Câu 4.
Lời giải
Chọn C
Câu 5.
Lời giải
Chọn A
Lần lượt thay toạ độ điểm ở mỗi phương án vào bất phương trình đã cho, ta thấy là nghiệm
0 0
; 2;5x y
của bất phương trình đã cho.
Câu 6.
Lời giải
Chọn C
. Thay .
,f x y x y
2,3 2 3 1 0f
.
Câu 7.
Lời giải
Chọn B
.
1
2 1 0
2
x x
Câu 8.
Lời giải
Chọn C
Đường thẳng đi qua và song song với đường thẳng có dạng:
0
;
o
M x y
: 0d ax by c
.
0 0
0 ( 0)
o o
a x x b y y ax by
Nên đường thẳng đi qua điểm và song song với đường thẳng có phương trình là
0 ; 0O
6 4 1 0x y
.
3 2 0x y
Câu 9.
Lời giải
Chọn B
Áp dụng công thức tình độ dài trung tuyến ta có:
2 2 2
2 4
AB AC BC
MA
2 2 2
2 6 5 55
2 4 2
Câu 10.
Lời giải
Chọn B
Ta có ; ; .
5AB
7BC
8AC
Từ đó suy ra .
2 2 2 2 2 2
8 5 7 1
cos 60
2 . 2.8.5 2
AC AB BC
A A
AB AC
Câu 11.
Lời giải
Chọn D
Theo quy tắc xét dấu nhị thức bậc nhất thì đáp án C sai.
Câu 12.
Lời giải
Chọn B
Bất phương trình cho .
2 2
2 5 5 2 5 5 10x x x x
5
4 5 10
2
x x
Câu 13.
Lời giải
Chọn D
Ta có phương trình đoạn chắn .
1
4 5
x y
Câu 14.
Lời giải
Chọn A
Câu 15.
Lời giải
Chọn D
Sai. Vì nếu có một trong ba đường thẳng song song hay trùng với thì không có hệ số góc.
, ,AB BC CA
'y Oy
Câu 16.
Lời giải
Chọn C
Ta có: Theo định lí về dấu của nhị thức bậc nhất.
Câu 17.
Lời giải
Chọn A
Quan sát đồ thị hàm số ta có, nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng
3 2 1 0x y
(không bao gồm đường thẳng).
Câu 18.
Lời giải
Chọn D
Điều kiện xác định của bất phương trình là
1 1x x x
1 0
1 0
x
x
1;1x
Câu 19.
Lời giải
Chọn B
Ta có: .
2 2 2
cos
2
a c b
B
ac
2 2 2
6 5 7 1
2.6.5 5
Câu 20.
Lời giải
Chọn C
Ta thế từng cặp từ đáp án vào, nhận thấy đáp án B không thoả vì .
;x y
5.1 2 3 1 1 0
Câu 21.
Lời giải
Chọn A
Theo định lý trong tam giác ta có .
sin
2
sin
BC
R
BAC
1 3
.
2 sin120 3
a a
R
Câu 22.
Lời giải
Chọn D
2 2 2x x x
2
2
x
x
2;2x
Câu 23.
Lời giải
Chọn A
Do nên tam giác vuông và có hai cạnh góc vuông là .
2 2 2
6 8 10
ABC
6, 8
Diện tích tam giác là .
ABC
1
.6.8 24
2
S
Gọi là bán kính đường tròn nội tiếp tam giác.
r
Ta có: .
24
2
6 8 10
2
S
r
p
Câu 24.
Lời giải
Chọn C
Ta có ( vì )
2 2x m mx
1 2 2m x m
2x
1 0m
Câu 25.
Lời giải
Chọn B
Ta có là trung điểm nên tọa độ điểm .
M
AB
1 1
;
2 2
M
. Đường thẳng đi qua nhận là véc tơ pháp tuyến có
7 5
;
2 2
CM
5; 7
CM
n
CM
C
5; 7
CM
n
phương trình tổng quát: .
:5 4 7 2 0 : 5 7 6 0 CM x y CM x y
Câu 26.
Lời giải
Chọn C
.
1 1
2 2 4 2
2
2 1 4
2
1 1
2 2 4 2
x x
x x x
x
x x
x
x x
x x x
Câu 27.
Lời giải
Chọn B
Điều kiện: .
3
4
x
Với điều kiện trên thì BPT đã cho tương đương .
2
1
2 3 1 0 1
2
x x x
Kết hợp với điều kiện thì tập nghiệm của BPT là .
1 3
;1 \
2 4
S
Câu 28.
Lời giải
Chọn A
Ta có .
2
2
6 9 0 3 0 3x x x x
Câu 29.
Lời giải
Chọn D
Gọi là giao điểm của và , là giao điểm của và .
A
Ox
B
Oy
Ta có: , , .
3;0A
0;5B
3OA
5OB
15
2
OAB
S
Câu 30.
Lời giải
Chọn A
Ta có .
3 1 0 3;1x x x
Do nên .
x
3; 2; 1;0;1x
Vậy tổng các nghiệm nguyên của bất phương trình là .
3 1 0x x
5
Câu 31.
Lời giải
Chọn B
ĐK: .
3; 1; 2; 4; 0x x x x x
2
16 4
4 0
12
x
x x
2
2
16 4 4 4 48
0
12
x x x
x x
2
4 16
0
4 3
x
x x
4
0
3
x
x
3
4
x
x
1 1 1
0
2 1x x x
1 2 1 2
0
2 1
x x x x x x
x x x
2
2
0
2 1
x
x x x
2 0
1 2 2
x
x x
Vậy
2;0 1; 2 2;x 
Câu 32.
Lời giải
Chọn D
có nghiệm khi và chỉ
2
2 5 6 0x mx m
2
2
' 0 5 6 0 ;2 3;
3
m
m m m
m
 
Vì nên nên phương trình có 2 nghiệm phân biệt.
1 2 1;2 ;2 3;m m  
' 0
Câu 33.
Lời giải
Chọn C
Đường cao đi qua và vuông góc với
BH
4;5B
5;3AC
Vậy PTTQ là :
5 4 3 5 0 5 3 5 0x y x y
Câu 34.
Lời giải
Chọn C
Dễ thấy I) và III) đúng.
Lại có .Vậy III) cũng đúng.
3
3
1 1 1 1
3. .3. 9a b c abc
a b c abc
1 1 1 9
a b c a b c
Câu 35.
Lời giải
Chọn D
Ta có
9
2
9 4 9 2 9 13 25
2
2 2 .2
2 2 2 2 2 2
x
x
x x x x
Dấu bằng xảy ra khi (thỏa) . Vậy .
9
2
2 6
2
2 5
x
x
x
x x
6; 5a b
11a b
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Áp dụng bất đẳng thức CôSi, ta có
.
2 2 2 2 2 2
, ,
2 2 2
b c a c b a
a bc a b ac b c ba c
Suy ra
(1)
2 2 2 2 2 2
2 2 2
.
2
a b b a a c c a b c c b
a bc b ac c ab
Tiếp tục áp dụng bất đẳng thức CôSi, ta có
3 3 3 3 3 3 3 3 3
2 2 2
3 3 3 3 3 3 3 3 3
2 2 2
, , ,
3 3 3
, ,
3 3 3
a a b b b a a a c
a b b a a c
c c a b b a c c b
c a b c c b
Suy ra (2)
2 2 2 2 2 2 3 3 3
2 .a b b a a c c b b c c b a b c
Từ (1) và (2),suy ra
2 2 2 3 3 3
.a bc b ac c ab a b c
Đẳng thức xảy ra khi và chỉ khi
a b c
Câu 37.
Lời giải
Trường hợp 1:
2
4 0 2m m
-Với:
ta có
, thoả mãn
2m
1f x
0,f x x
-Với:
ta có
, không thoả mãn
2m
8 1f x x
0,f x x
Trường hợp 2:
2
4 0 2m m
Khi đó:
2 2
3 4 2 2 1 0,f x m x m x x
.
2
'
2
2;2
0
4 0
1;2
0
1;2
4 4 8 0
m
a
m
m
m
m m
Từ các trường hợp trên và
ta được
.
m
1;0;1;2m
Vậy
.
1;0;1;2m
Câu 38.
Lời giải
Ta có:
1 1 1
sin 45 sin 45
2 2 2
ABC ABD ACD
S S S bc dc db
1 2
( )sin 45 ( )
2
bc
bc d b c d b c d
b c
Câu 39.
Lời giải
M
G
B'
C'
A
B
C
Do nên tọa độ điểm là nghiệm của hệ: , ta được
'B BB BC
B
2 0 1
2 5 0 2
y x
x y y
1;2 .B
Tượng tự, , ta được
'C CC BC
3;4 .C
Gọi là giao điểm của và , khi đó
G
'BB
'CC
2;2 .G
Gọi là trung điểm của , suy ra và
M
BC
3;1M
1;1 .GM
Do là trọng tâm tam giác nên thỏa mãn:
G
ABC
;A x y
, ta được
1 3. 1
4
3
0
3 3.1
x
x
AM GM
y
y
4;0 .A
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên :………………………………….Lớp:………….......……..………
Mã đề thi
009
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn B
Thay tọa độ các điểm vào bpt thì thỏa mãn. Các cặp khác không thỏa mãn.
1; 1
Câu 2.
Lời giải
Chọn C
Ta có .
2.2 1 1 4 0
Câu 3.
Lời giải
Chọn B
Thay toạ độ điểm vào từng đáp án. Nhận thấy chỉ có mỗi đáp án D là thoả .
0;0O
2 0
Câu 4.
Lời giải
Chọn A
Ta có .
2 2 2
2 . .cos 76AC AB BC AB BC B
2 19AC
Câu 5.
Lời giải
Chọn C
Theo lý thuyết về dấu tam thức bậc hai.
Câu 6.
Lời giải
Chọn D
Thay vào các bất phương trình ta có phương án B đúng.
1x
Câu 7.
Lời giải
Chọn B
Điều kiện:
2 0 2.x x
Tập xác định:
;2 .D 
Câu 8.
Lời giải
Chọn B
Câu 9.
Lời giải
Chọn B
Nữa chu vi: .
13 14 15
21.
2
p
Diện tích: .
( 13)( 14)( 15) 84.S p p p p
Câu 10.
Lời giải
Chọn C
Đường thẳng đi qua , nhận làm véc tơ pháp tuyến có phương trình:
1;2A
2; 4n
2( 1) 4( 2) 0 2 4 10 0 2 5 0x y x y x y
Câu 11.
Lời giải
Chọn B
Ta có phương án A sai vì còn các phương án còn lại đúng theo tính chất về các phép biến
0,f x g x x
đổi bất phương trình.
Câu 12.
Lời giải
Chọn A
Phương trình đường thẳng cần tìm là .
2( 1) 3( 2) 0 2 3 8 0x y x y
Câu 13.
Lời giải
Chọn D
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy là nghiệm
0 0
; 5;3x y
của hệ.
Câu 14.
Lời giải
Chọn C
Chọn thì không phải là nhị thức bậc nhất.
1m
1 2018 2018f x m x
Câu 15.
Lời giải
Chọn C
.
2 2 2
2
8 4 12
3 3
2 4 2 4
b c a
AM AM
Câu 16.
Lời giải
Chọn D
Đáp án A sai khi
1; 1.a b
Đáp án B và D sai khi
0.a b
Xét : luôn đúng với mọi số thực .
2 2 2 2
2 2a b a b a ab b a ab b ab ab
,a b
Vậy,chọn
B.
Câu 17.
Lời giải
Chọn A
VTCP của đường thẳng song song với trục là nên VTPT là
Oy
0;1
1;0
Câu 18.
Lời giải
Chọn C
Bất phương trình xác định khi vô lý nên bất phương trình vô nghiệm.
2006 0
2006 0
x
x
2006x
0 0
Câu 19.
Lời giải
Chọn B
không đúng vì trừ 2 bất đẳng thức cùng chiều thi không được kết quả đúng.
a c b d
Ví dụ: nhưng .
7 8; 5 1
7 5 2 7 8 1
Câu 20.
Lời giải
Chọn A
2 1 3x x
4x
.
Câu 21.
Lời giải
Chọn D
180 40 60 80 .C
Áp đụng định lý sin vào :
ABC
5
.sin .sin 40 3,26.
sin sin sin sin80
AB BC AB
BC A
C A C
Câu 22.
Lời giải
Chọn D
2 2
2
2 2 2 2
2 4 6 2
; 2 5
1 1
2
5 1 3 5 5 6 9 2 3 2 0
1
2
m m m
d M
m m
m
m m m m m m m
m
Câu 23.
Lời giải
Chọn A
Ta có nên vtpt của của đường thẳng là
;AB a b
AB
;b a
Câu 24.
Lời giải
Chọn A
2
1 3 5 1 3 5 5 12
3 3 0 0
2 2 2 2 4
x x x
x x x x x
Đặt: .
2
5 12
4
x
f x
x
Bảng xét dấu:
x

12
5
2
2

5 12x
- + + +
0
2
4x
+ + - +
0
0
f x
- + - +
0
Kết luận: hoặc .
12
5
x
2 2x
Câu 25.
Lời giải
Chọn B
Ta có .
2
10 16 0 2 8 0 2 8x x x x x
Câu 26.
Lời giải
Chọn D
Ta có
2
1 1
1 4. 0 0
4 4
x x
.
2
1 1
0
4 2
x x x
Câu 27.
Lời giải
Chọn A
Ta có
.
2
( 2)( 3) 6 m x m m
2 3 2 3m x m m
Nếu :
2m
1 3 3 .x m x m
Nếu :
2m
1 3 3 .x m x m
Nếu : (vô lý). PT vô nghiệm.
2m
1 0 0
Câu 28.
Lời giải
Chọn C
a
2
45
°
a
a
2
D
C
B
A
Ta có: .
2
1
2 2. . . .sin 45
2
ABCD ABD
S S AB AD a
Câu 29.
Lời giải
Chọn B
.
2 1 0
2
x
x m
1
2
2
x
x m
1
2
2
m
3
2
m
Câu 30.
Lời giải
Chọn A
Ta có .
2 1
2 0
1
x
x
2 1
2
1
x
x
2 1
2
1
2 1
2
1
x
x
x
x
1
0
1
4 3
0
1
x
x
x
1
3
1
4
x
x
Tập .
3
, \ 1
4
x

Câu 31.
Lời giải
Chọn C
Ta có . Do đó bất phương trình
2
2
2 1 1 0, 1x x x x
2
2
1
1 0 1
0 0
1 1
2 1
1
1
x
x
x
x x
x
x
x x
Vậy tập nghiệm của bất phương trình là: .
; 1 1;1S 
Câu 32.
Lời giải
Chọn C
Từ
(1) 1 6x
Từ
(2) 3 2 1 3 1 2x x
Khi đó nghiệm của hệ bất phương trình là .
1;2x
Câu 33.
Lời giải
Chọn A
Đường thẳng đi qua điểm có dạng . (Với )
d
C
10 2 0 10 2 0a x b y ax by a b
2 2
0a b
Ta có
2 2 2 2
.3 10 2 7 2
; ;
a a b a b
d A d
a b a b
2 2 2 2
. 5 .4 10 2
15 2
;
a b a b
a b
d B d
a b a b
A; ; 7 2 15 2d d d B d a b a b
2
0
a b
a
Vậy hoặc .
d
2 14 0x y
2 0y
Câu 34.
Lời giải
Chọn D
Ta có: đúng; đúng;
2 . 2
a b a b
I
b a b a
3
3 . . 3
a b c a b c
II
b c a b c a
đúng.
3
3
1 1 1 1
3
3
a b c abc
a b c abc
1 1 1
9a b c
a b c
1 1 1 9
a b c a b c
III
Câu 35.
Lời giải
Chọn D
Ta có .
2 2 2
1 1 2 1 . 1 2 2 1
1 1 1
f x x x x
x x x
Dấu bằng xảy ra khi và chỉ khi .
2
2
1
1 2
1 2
1
1
1
x
x
x
x
x
x
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Áp dụng bất đẳng thức CôSi, ta có
.
2 2 2
3
3
1 1 1 1 1 3
3 3 3 3 . . 3
2 2 2 2 4
y x x x
x x x x x
Dấu “=” xảy ra khi và chỉ khi .
2 3
3
1 1 1
3
2 6
6
x x x
x
Vậy giá trị nhỏ nhất của là , khi .
y
3
3
3.
4
3
1
6
x
Câu 37.
Lời giải
Với , ta có : đúng với mọi .
4m
( ) -1 0g x
x
Với , yêu cầu Câu toán
4m
2
( 4) (2 8) 5 0,m x m x m x
2
0 4 0 4
4
0 ( 4) ( 4)( 5) 0 4 0
a m m
m
m m m m
Kết hợp hai trường hợp ta được .
4m
Câu 38.
Lời giải
Ta có
ABC MAB MAC
S S S
1 1 1
. .sin . .sin 90
2 2 2
bc AM c AM b
sin cosbc AM c b
Vậy .
cos sin
bc
AM
b c
Câu 39.
Lời giải
Định hướng:
- Tọa độ điểm
B BH BM
- Viết phương trình đường thẳng đi qua và vuông góc với .
AC
A
BH
Suy ra tọa độ
M AC BM C
Gọi lần lượt là đường cao và trung tuyến kẻ từ
,
BH BM
.
B
Tọa độ điểm là nghiệm của hệ phương trình
B
2 3 12 0
3;2
2 3 0
x y
B
x y
Đường thẳng đi qua và vuông góc với nên có phương trình
AC
A
BH
3 2 10 0.
x y
Tọa độ điểm là nghiệm của hệ phương trình
M
2 3 0
6; 4
3 2 10 0
x y
M
x y
Do là trung điểm suy ra tọa độ điểm
M
AC
8; 7
C
Vậy .
3;2 , 8; 7B C
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên :………………………………….Lớp:………….......……..………
Mã đề thi
010
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn D
Điều kiện xác định của bất phương trình .
2 0 2
2
1 0 1
x x
x
x x
Câu 2.
Lời giải
Chọn B
Phương trình đường thẳng cần tìm là .
2( 1) 3( 2) 0 2 3 8 0x y x y
Câu 3.
Lời giải
Chọn A
Theo bảng xét dấu, ta có: .
2 0
b
a
Mà .
0 0 0a b b a
Câu 4.
Lời giải
ChọnA
tương đương với suy ra . Đáp ánA.
2 5 3
3 2
x x
1
0
6
x
1x
Câu 5.
Lời giải
Chọn C
Đáp án A sai khi
1; 1.a b
Đáp án B và D sai khi
0.a b
Xét : luôn đúng với mọi số thực .
2 2 2 2
2 2a b a b a ab b a ab b ab ab
,a b
Vậy,chọn
B.
Câu 6.
Lời giải
Chọn A
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy là
0 0
; 0; 2x y
nghiệm của hệ bất phương trình đã cho.
Câu 7.
Lời giải
Chọn A
Dễ thấy không là nghiệm của bất pt nhưng nó lại là nghiệm của bất pt
1x
1x x
. Do đó hai bất pt không tương đương.
2 1 1 2 1x x x x
Câu 8.
Lời giải
Chọn A
Câu 9.
Lời giải
Chọn B
Thay tọa độ các điểm vào phương trình ta thấy .
3;2Q d
Câu 10.
Lời giải
Chọn A
Đường thẳng đi qua , nhận làm vecto pháp tuyến có phương trình là
1;2A
2; 4n
.
2 1 4 2 0 2 4 10 0 2 5 0x y x y x y
Câu 11.
Lời giải
Chọn B
(Tính chất cộng 1 số cho 2 vế của bất đẳng thức).
a b
a c b c
Câu 12.
Lời giải
Chọn B
Ta có .
2 2 2 2 2 2
3 5 6 1
cos
2. . 2.3.5 15
AB AC BC
A
AB AC
Câu 13.
Lời giải
Chọn B
Câu 14.
Lời giải
Chọn C
Ta có:
4 16 0. 16 4 4 4; .x x x x 
Câu 15.
Lời giải
Chọn A
.
3 1 4 2 5 3 2 4 8 0 2 4 0x y x x y x y
Thay lần lượt tọa độ các điểm vào hệ bất phương trình, tọa độ điểm nào thỏa mãn hệ bất phương trình thì
điểm đó thuộc miền nghiệm của bất phương trình đã cho.
Câu 16.
Lời giải
Chọn A
Do véc tơ chỉ phương của là véc tơ khác véc tơ không và cùng phương với
: 2 3 0x y
2;1u
Suy ra: không là véc tơ chỉ phương của do không cùng phương với
4; 2
2;1u
Câu 17.
Lời giải
Chọn B
Dễ thấy . Vậy .
9 28 19 0
0,f x x
Câu 18.
Lời giải
Chọn D
.
2 2 2
2 cosb a c ac B
2 2
8 3 2.8.3cos60
49
7b
Câu 19.
Lời giải
Chọn D
Câu 20.
Lời giải
Chọn C
Theo công thức độ dài đường trung tuyến.
Câu 21.
Lời giải
Chọn D
Phương trình đường thẳng cần tìm là .
2 1 3 2 0 2 3 8 0x y x y
Câu 22.
Lời giải
Chọn C
Dựa vào bảng xét dấu ta thấy là nghiệm của nên ta loại các đáp án A, B,
2x
f x
Vậy đáp án đúng là
Câu 23.
Lời giải
Chọn C
Nửa chu vi tam giác là: .
6 8 10
12
2
p
.
( )( )( )S p p a p b p c
12(12 6)(12 8)(12 10) 24
Câu 24.
Lời giải
Chọn D
Ta có.
2
2
4 4 0 2 0x x x
Mà , .
2
2 0x
x
Do đó BPT .
2
2 0 2 0 2x x x
Câu 25.
Lời giải
Chọn D
.
3 1 2
3 1
3 1 4
x x
x
x x
Câu 26.
Lời giải
Chọn C
Điều kiện: .
3 0 3x x
BPT đã cho tương đương với .
1 1x x
1 1x x
1 0 1x x
Vậy tập nghiệm của BPT là .
;1
Câu 27.
Lời giải
Chọn C
Theo định lí hàm số sin ta có:
2
sin sinB sinC
a b c
R
A
Suy ra:
+ .
.sin
sin sinB sin
a b b A
a
A B
+ .
.sin
sin
sin sinC
a c c A
C
A a
+ .
2 2 .sin
sin
a
R a R A
A
+ .
2 sin tan
sinB 2 2cosB
b b b
R R B R B
Câu 28.
Lời giải
Chọn A
Phương trình cạnh .
: 1 : 3 4 12 0
4 3
x y
BC BC x y+ = Û + - =
Độ dài đường cao ứng với cạnh là .
BC
( )
3.1 4.2 12
1
,
5 5
AH d A BC
+ -
= = =
Câu 29.
Lời giải
Chọn B
Ý nghĩa hình học của bất đẳng thức Cô si.
Câu 30.
Lời giải
Chọn B
2
5 4x x x
2
4 0
4 5 4
x
x x x x
2
2
4
2 1 0
9 0
x
x x
x
4
1 2
1 2
3 3
x
x
x
x
.
3;1 2 1 2;3x
Câu 31.
Lời giải
Chọn C
Giao điểm của và là nghiệm của hệ .
1
d
2
d
3 – 4 15 0
5 2 –1 0
1
3
x y
y
x
x y
Vậy cắt tại .
1
d
2
d
1;3A
Để ba đường thẳng đồng quy thì phải đi qua điểm thỏa phương trình
1 2 3
, ,d d d
3
d
A
A
3
d
4.3 15 0 3.m m
Câu 32.
Lời giải
Chọn B
Ta có , .
2 2
2 4 ( 1) 3 0x x x
x
Do đó
2
2 4 3 0x x x
3 0x
3x
Câu 33.
Lời giải
Chọn D
Ta có .
3 2 1
1 2
2 1 2 1
x
x x
f x
x x x x
Lập bảng xét dấu biểu thức
f x
Từ đó suy ra .
1
0 ; 2 ;1
2
f x x

Câu 34.
Lời giải
Chọn A
Bất phương trình (ẩn ): vô nghiệm .
x
( 1) 2 3 0m x m
1 0
1
2 3 0
m
m
m
Câu 35.
Lời giải
Chọn C
Ta có
.
9 4 9 25 4 25 25
2
2 4 2 4 2
y x x
x x x x
9 25 4 25 25
2 . 2 . 2
4 2 4 2
x x
x x
75
2
Dấu “ ” xảy ra .
9 25
4
4 25
2
2 4
0 2
x
x
x
x
x
6
5
x
Vậy ; .
0;2
75
min
2
y
6
5
x
6a
5b
11a b
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Áp dụng bất đẳng thức CôSi, ta có
2 2 2 2 2 2
1 2 2 ,1 2 2 ,1 2 2a a a b b b c c c
Suy ra
2 2 2 2 2 2 2 2 2
1 1 1 2 .a b b c c a a b b c c a
Tiếp tục áp dụng bất đẳng thức CôSi,ta có
2 2 2 3 2 2 2
3 . . 3 .a b b c c a a b b c c a abc
Suy ra
3 3 3 3 3 3 3 3 3
2 2 2
, ,
3 3 3
a a b b b c c c a
a b b c c a
Đẳng thức xảy ra khi và chỉ khi .
1a b c
Câu 37.
Lời giải
2
2 8 0,f x x mx m x R
' 2
0 2 8 0 4 2m m m
Vậy giá trị lớn nhất của tham số cần tìm là
m
2m
Câu 38.
Lời giải
a) Trong thì là trung tuyến nên áp dụng công thức độ dài trung tuyến ta có
MAB
MI
.
2 2 2
2
2 2 4
MA MB AB
MI
2
2 2 2
2
2
AB
MI MA MB
2
2 2 2
2
2
AB
MA MB MI
b) .
2
. ( ).( ) ( ) ( ) .MA MB MI IA MI IB MI MI IA IB IA IB
Do là trung điểm của nên thay vào biểu thức ta được
I
AB
1 1
0; ;
2 2
IA IB IA AB IB AB
. Điều phải chứng minh.
2 2 2
1 1 1
. ( ) .0 .
2 2 4
MA MB MI MI AB AB MI AB
Câu 39.
Lời giải
Định hướng:
- Tọa độ điểm
B BH BM
- Viết phương trình đường thẳng đi qua và vuông góc với .
AC
A
BH
Suy ra tọa độ
M AC BM C
Gọi lần lượt là đường cao và trung tuyến kẻ từ
,
BH BM
.
B
Tọa độ điểm là nghiệm của hệ phương trình
B
2 3 12 0
3;2
2 3 0
x y
B
x y
Đường thẳng đi qua và vuông góc với nên có phương trình
AC
A
BH
3 2 10 0.
x y
Tọa độ điểm là nghiệm của hệ phương trình
M
2 3 0
6; 4
3 2 10 0
x y
M
x y
Do là trung điểm suy ra tọa độ điểm
M
AC
8; 7
C
Vậy .
3;2 , 8; 7B C
| 1/116
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 1 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 001
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Bất phương trình nào sau đây không tương đương với bất phương trình x + 5  0 ? 2 A. ( x − )
1 ( x + 5)  0 .
B. x + 5 ( x − 5)  0 . C. 2
−x ( x + 5)  0 .
D. x + 5 ( x + 5)  0 .
Câu 2. Nhị thức f ( x ) = 2x − 6 dương trong
A. (3; +  ) .
B. ( −;3) .
C. 3; +  ) .
D. ( −; 3 .
Câu 3. Nếu a + 2c b + 2c thì bất đẳng thức nào sau đây đúng? 1 1 A. 2 2 ab .
B. 2a  2b . C. .
D. − 3a  − 3b . a b
Câu 4. Tam giác ABC có các góc B = 30, C = 45 , AB = 3 . Tính cạnh AC . . 3 2 2 6 3 6 A. . B. 6 . C. . D. . 2 3 2 1 3
Câu 5. Tìm điều kiện của bất phương trình  2 + . x x + 2 x  −2 x  0
A. x  0 .
B. x  −1. C.  . D.  . x  0  x  −1 
Câu 6. Đường nào sau đây cắt đường thẳng  có phương trình: x – 4 y + 1 = 0 ?
A. y = 2 x + 3 .
B. –2x + 8 y = 0 .
C. 2 x – 8 y = 0 .
D. – x + 4 y – 2 = 0 .
Câu 7. Nhị thức nào sau đây nhận giá trị dương với mọi x nhỏ hơn 2 ?
A. f ( x ) = 6 – 3x .
B. f ( x ) = 4 – 3x .
C. f ( x ) = 3x – 6 .
D. f ( x ) = 3x + 6 .
Câu 8. Cho tam giác ABC có BC = 10 , A = 30 . Tính bán kính đường tròn ngoại tiếp tam giác ABC . 10 A. 5 . B. . C. 10 3 . D. 10 . 3
Câu 9. Tam giác ABC có A = 75, B = 45 , AC = 2 . Tính cạnh AB . 2 6 6 A. . B. 6 . C. . D. . 2 2 3
Câu 10. Số nào dưới đây là nghiệm của bất phương trình 2x +1  3 ?
A. x = 3 .
B. x = 0 .
C. x = 1 .
D. x = 2 .
Câu 11. Đường thẳng d vuông góc với đường thẳng  : 3x + 4 y − 12 = 0 có một véctơ chỉ phương u là
A. u = (3; 4) . B. u = (4; 3 − ) . C. u = (3; 4 − ) .
D. u = (−3; 4) .
Câu 12. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? A. 2 2
x + y  2. B. 2
x + y  0.
C. x + y  0. D. 2 2x + 3 y  0.
Câu 13. Tính khoảng cách từ điểm M (1; −1) đến đường thẳng ( d ) : 3x − 4 y −17 = 0 7 18 2 A. 2 . B. . C. . D. . 5 5 5
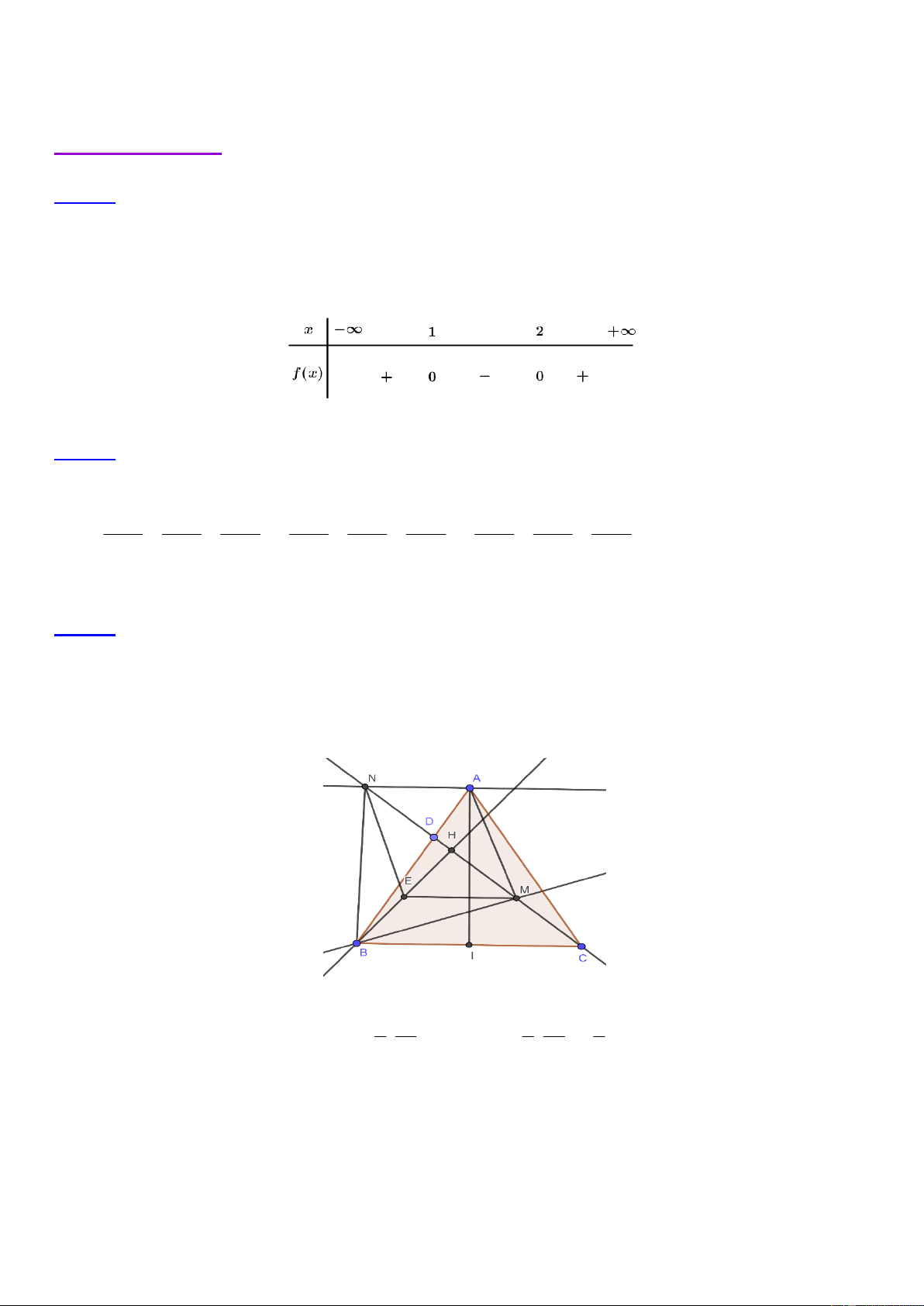
Câu 14. Cho tam thức bậc hai 2 f (x) ax bx c (a
0) . Điều kiện cần và đủ để f (x ) 0, x là: Trang 1/40 a 0 a 0 a 0 a 0 A. . B. . C. . D. . 0 0 0 0
Câu 15. Số x = 1
− là nghiệm của bất phương trình nào sau đây?
A. 2x −1  0 .
B. x −1  0 .
C. 3 − x  0 .
D. 2x +1  0 .
Câu 16. Tìm tập nghiệm S của bất phương trình 2
x − 4 x + 4  0 . A. S = \ −  2 . B. S = \   2 . C. S = .
D. S = ( 2; + ) .
Câu 17. Cho hệ bất phương trình
2x − 5 y − 1  0 
 2x + y + 5  0 . 
x + y + 1  0
Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Điểm C (0; −2) thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm D (0; 2) thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm O (0; 0) thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm B (1; 0) thuộc miền nghiệm của hệ bất phương trình đã cho.
Câu 18. Viết phương trình tham số của đường thẳng đi qua 2 điểm A (3; −1); B (6; −2) . x = −1+ 3tx = 3 + 3tx = 3 + 3tx = 3 + 3t A.  . B.  . C.  . D.  . y = 2ty = −1 + ty = −1 − ty = −6 − t
Câu 19. Với hai số x, y dương thoả xy = 36 . Bất đẳng thức nào sau đây đúng? 2  x + y A. xy = 36.   .
B. Tất cả đều đúng.  2 
x + y  2 xy = 12. D. 2 2
x + y  2xy = 72. . C. .
Câu 20. Tìm nghiệm của tam thức bậc hai f ( x ) 2
= x + 4x − 5 . A. x = 5 − ; x = 1 . B. x = 5 − ; x = 1 − .
C. x = 5 ; x = 1 .
D. x = 5 ; x = 1 − .
Câu 21. Trong mặt phẳng Oxy , đường thẳng  : 3x − 2 y − 7 = 0 cắt đường thẳng nào sau đây?
A. d : 3x + 2 y = 0 .
B. d : 6x − 4 y −14 = 0 . 1 4
C. d : 3x − 2 y = 0 .
D. d : −3x + 2 y − 7 = 0 . 2 3
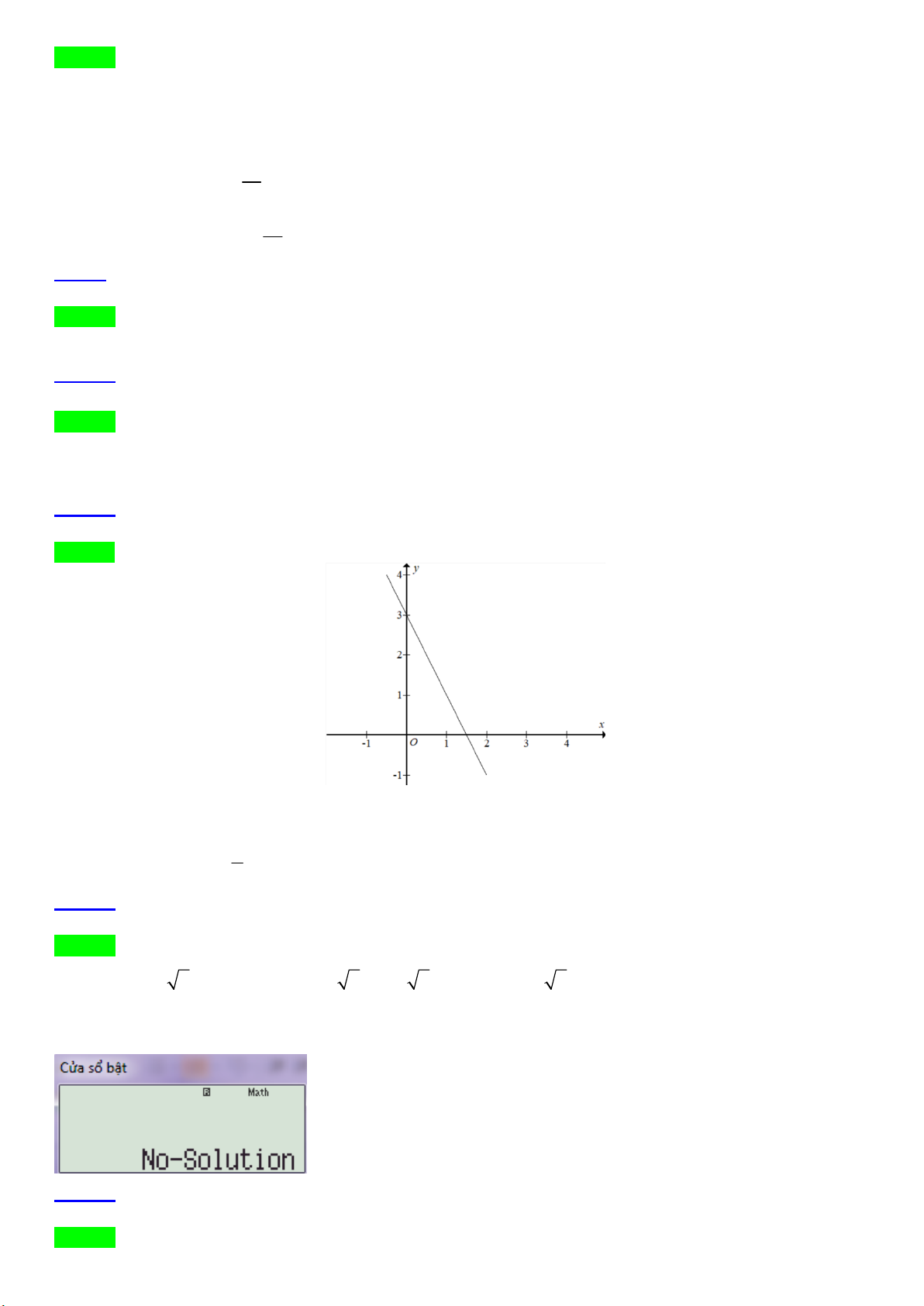
Câu 22. Cho hàm số y = f ( x ) có tập xác định D = ( −1;5) và đồ thị như hình vẽ. Giá trị nào sau đây là nghiệm
của bất phương trình f ( x )  0 ? 1 A. − . B. 1 . C. 3 . D. 4 . 2
x + y − 2  0
Câu 23. Cho hệ bất phương trình 
. Trong các điểm sau, điểm nào không thuộc miền nghiệm
2x − 3 y + 2  0 
của hệ bất phương trình?
A. O (0; 0).
B. M (1;1).
C. N ( −1;1).
D. P ( −1; −1). Trang 2/40
Câu 24. Nếu x a , với a  0 thì bất đẳng thức nào sau đây luôn đúng? 1 1
A. x  −a . B.  .
C. − x  −a .
D. x a . x a x +
Câu 25. Tập nghiệm của bất phương trình 3  1 là 1 − x A. −2;1) . B. ( −1;1) . C. −3;1) . D. −1;1) . Câu 26. Cho ABC
có A (1;1); B (0; −2); C (4; 2) . Phương trình tổng quát của trung tuyến BM
A. 3x + y − 2 = 0 .
B. 7 x + 7 y + 14 = 0 .
C. −7 x + 5 y + 10 = 0 .
D. 5x − 3 y + 1 = 0 .
Câu 27. Cho đường thẳng có phương trình ( d ) : 4x − 3 y + 5 = 0 . Tính khoảng cách h từ điểm M (1, −2) tới
đường thẳng ( d ) .
A. h = 1 .
B. h = 16 .
C. h = 3 .
D. h = 7 . x 8
Câu 28. Tìm giá trị nhỏ nhất của hàm số y =
+ với x  0 . 2 x A. 16. B. 8. C. 4. D. 2. x + m
Câu 29. Cho hệ bất phương trình  0 (1) − x + 5 
. Hệ đã cho có nghiệm khi và chỉ khi: 0 (2)
A. m  5 .
B. m  5 .
C. m  −5 .
D. m  −5 .
Câu 30. Tập nghiệm của bất phương trình x − 2018  2018 − x là
A. ( −; 2018) . B.   2018 .
C. ( 2018; + ) . D.  .
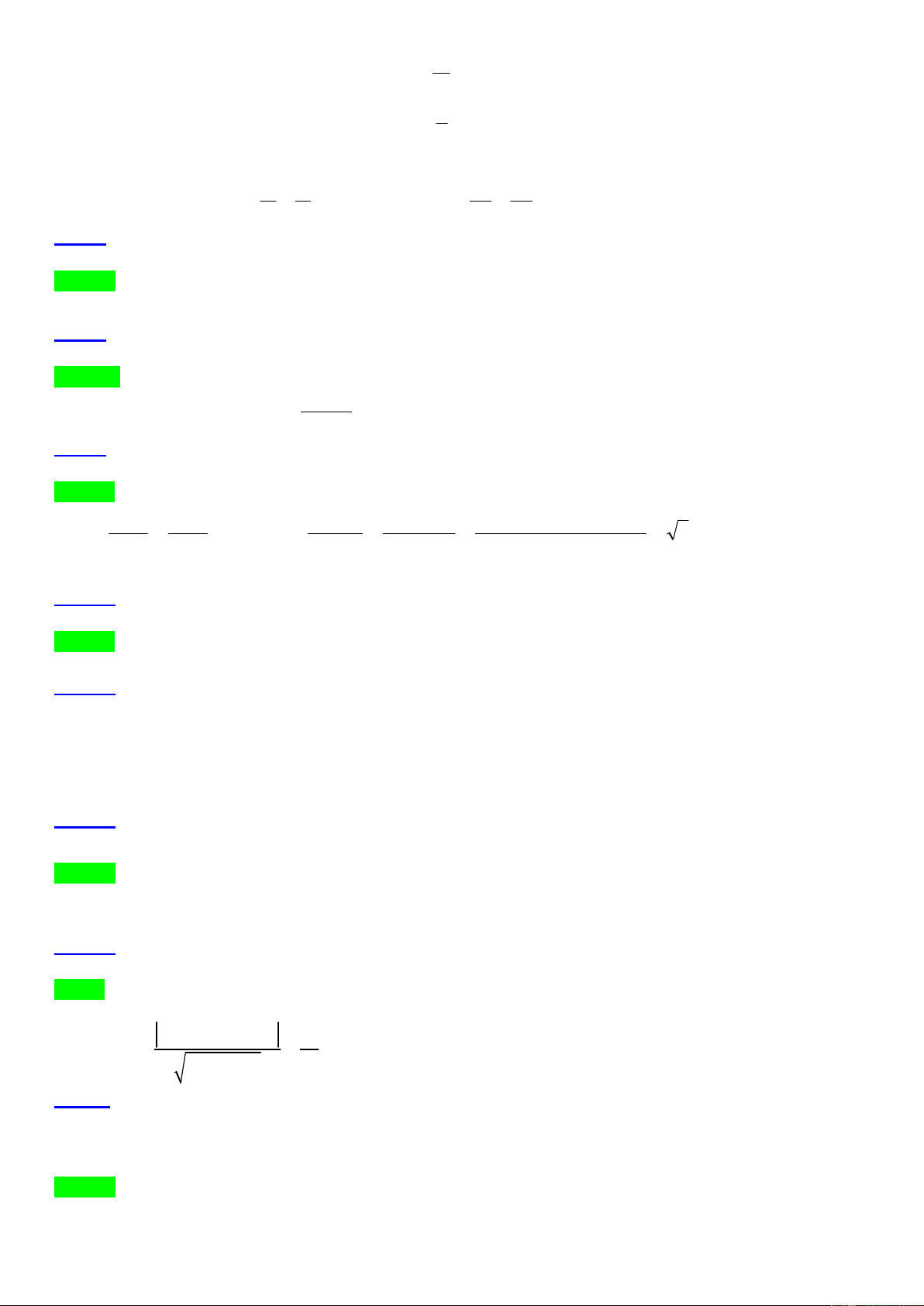
Câu 31. Cho hình bình hành ABCD có AB = a , BC = a 2 và BAD = 135 . Diện tích của hình bình hành ABCD bằng A. 2 2a . B. 2 a . C. 2 a 2 . D. 2 a 3 .
Câu 32. Bất phương trình 1 1 2 − 
có tập nghiệm là x − 2 x x + 2 A. (0; 2) . B. \ −2; 0;  2 . 3 17 3 17 C. ( −2; 0) . D. 2; 0;2 ; . 2 2 x −
Câu 33. Tập nghiệm của bất phương trình 4 3  −1 là 1 − 2 x  1   1   1   1  A. ;1   . B. ;1   . C. ;1  . D. ;1 .     2   2   2   2 
Câu 34. Tam giác ABC có A = 120 thì câu nào sau đây đúng A. 2 2 2
a = b + c + 3bc . B. 2 2 2
a = b + c − bc . C. 2 2 2
a = b + c − 3bc . D. 2 2 2
a = b + c + bc . 1
Câu 35. Tập xác định của hàm số 2 y = x + 3x + 2 − là x −1 A. ( −;  1  2; + ) . B. (1; + ) .
C. 1; + ) . D. (1; 2 . PHẦN II: TỰ LUẬN
Câu 1. Tìm tập nghiệm của bất phương trình 2
x − 3x + 2  0 . 5 4 3
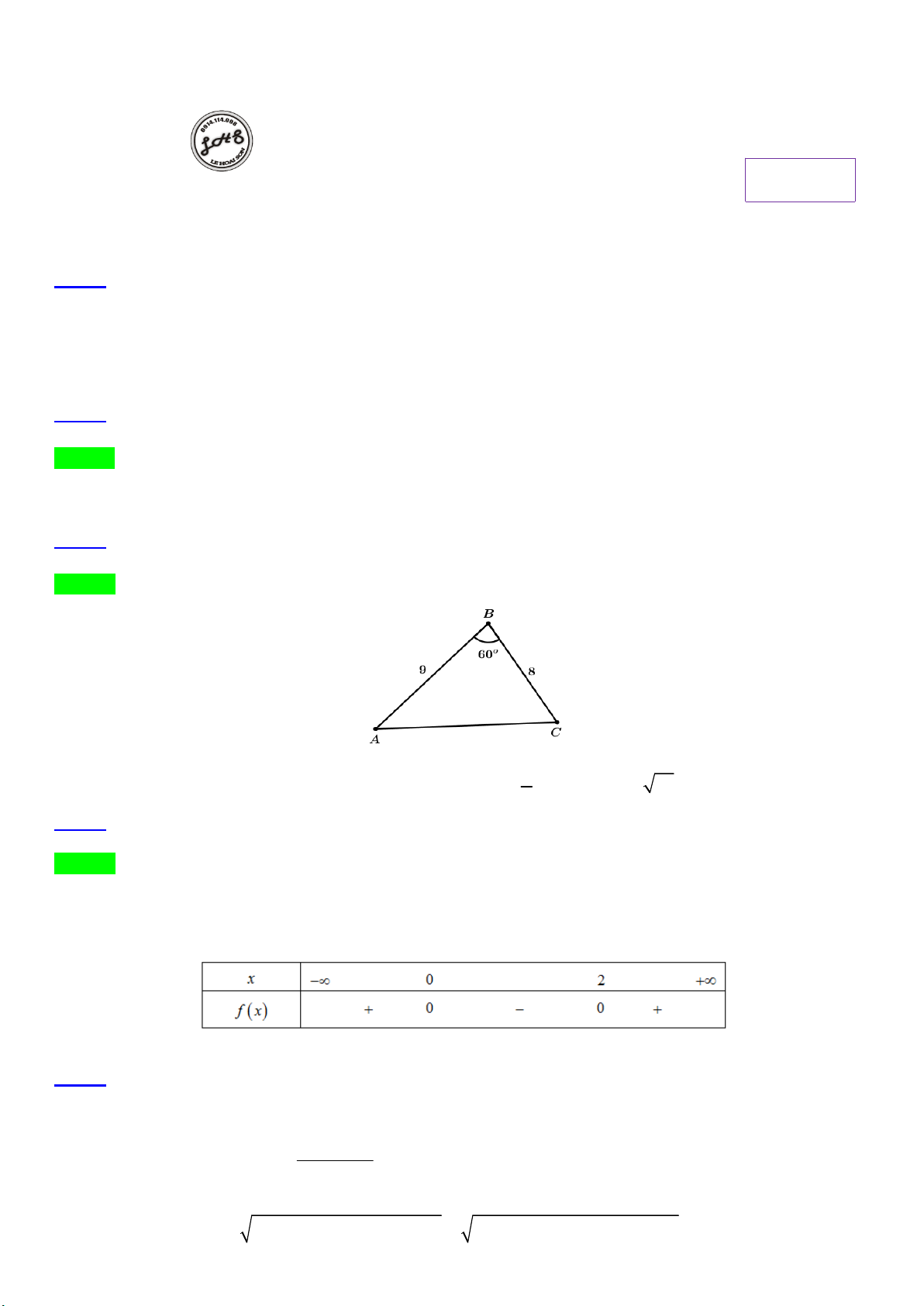
Câu 2. Cho tam giác ABC có = =
và a = 10 . Tính chu vi tam giác đó. sin A sin B sin C Trang 3/40
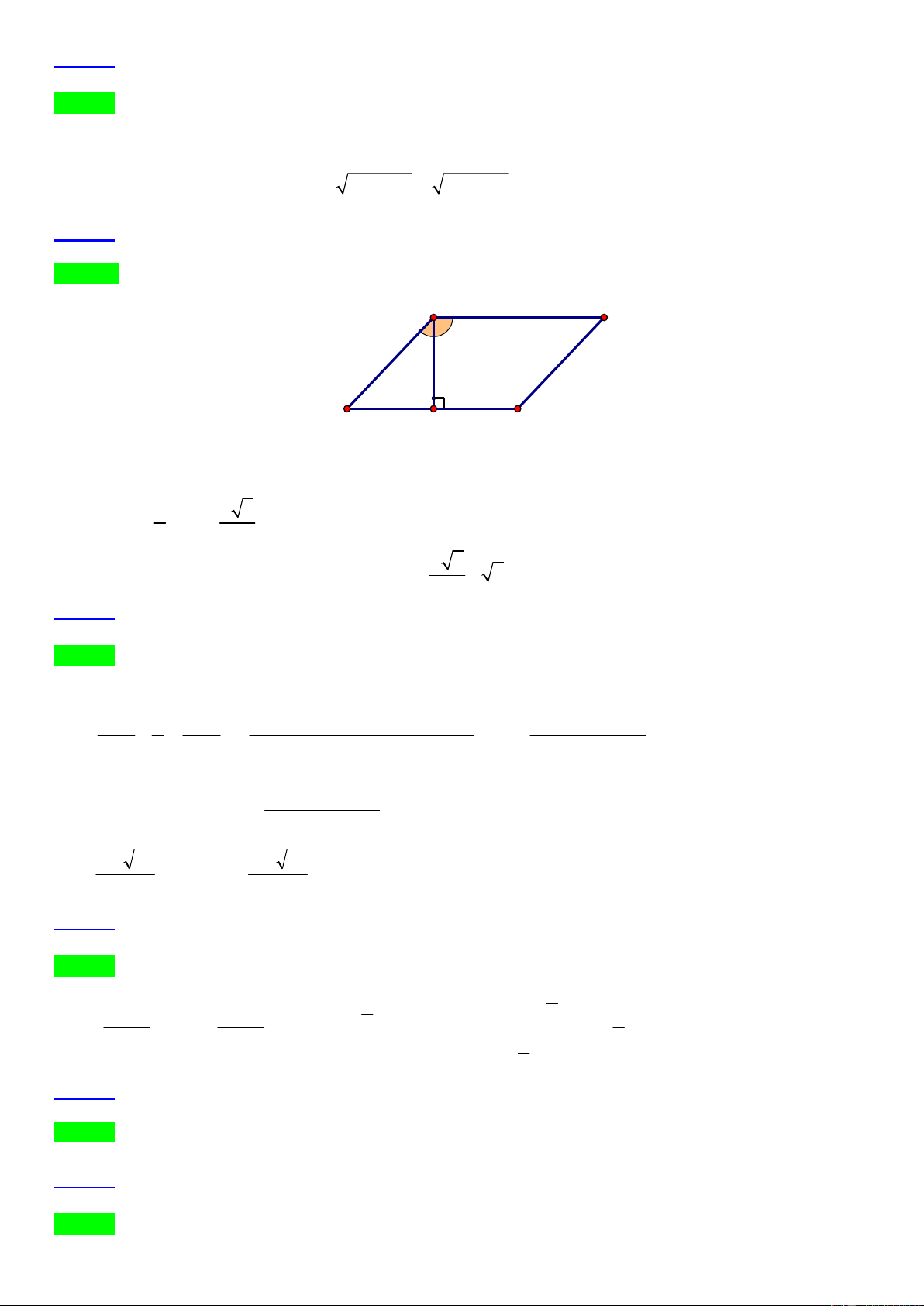
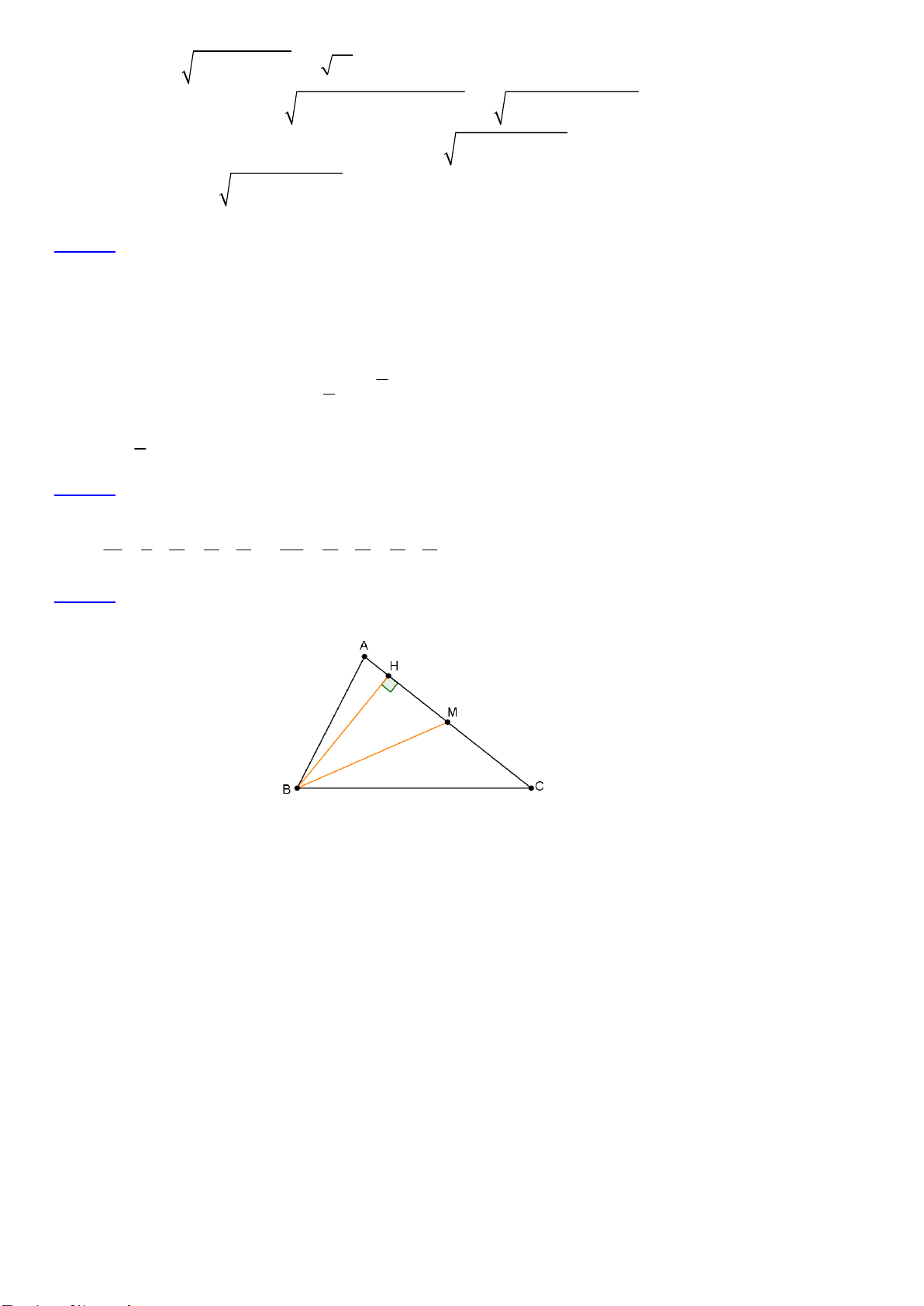
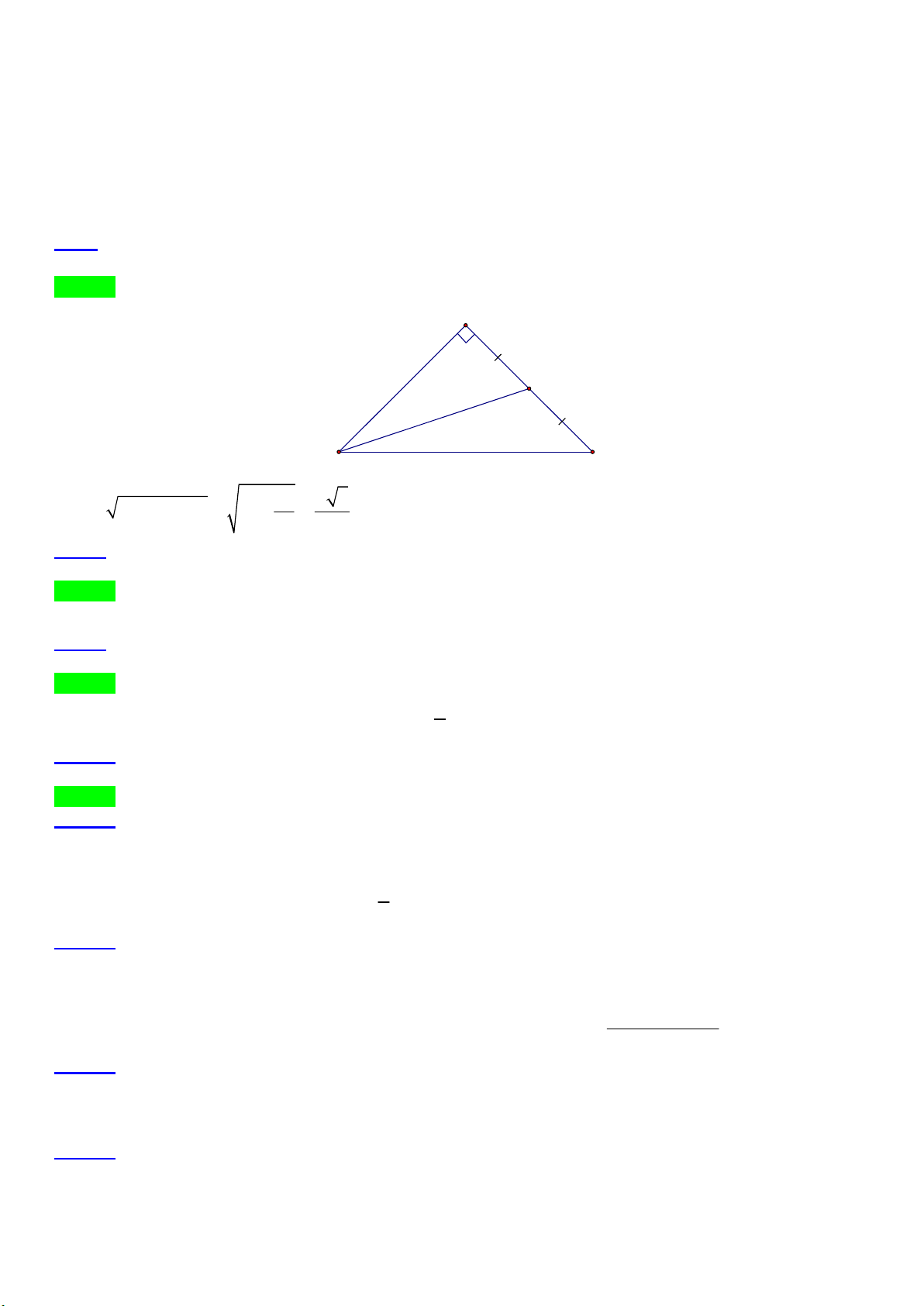
Câu 3. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC cân tại A ( −1; 3) . Gọi D là một điểm trên 1 −3
cạnh AB sao cho AB = 3AD và H là hình chiếu của B trên CD . Điểm M ( ;
) là trung điểm đoạn HC. 2 2
Biết điểm B nằm trên đường thẳng d : x + y + 7 = 0 . Tìm tọa độ điểm C.
Câu 4. Cho ba số thực dương x, y, z thỏa mãn điều kiện x + y + z = 3 . Tìm giá trị lớn nhất của biểu thức 3 3 3
P = x + y + z + ( 3 3 3 3 x + y + z ) .
------------- HẾT ------------- Trang 4/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 2 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 002
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cho 2 điểm A (1; −4) , B (1; 2) . Viết phương trình tổng quát đường trung trực của đoạn thẳng AB .
A. y − 1 = 0 .
B. x − 4 y = 0 .
C. x −1 = 0 .
D. y + 1 = 0 .
Câu 2. Cho đường thẳng  có phương trình tổng quát: –2 x + 3 y – 1 = 0 . Trong những điểm sau, điểm nào thuộc  ? A. (0; – 3) . B. (3; 0) . C. (1; 1) . D. ( –3; 0) .
Câu 3. Bất phương trình 2
mx + ( 2m −1) x + m + 1  0 có nghiệm khi:
A. m = 0, 25 .
B. m = 2 .
C. m = 1.
D. m = 0 .
Câu 4. Tìm tập nghiệm S của bất phương trình 4
− x +16  0 ?
A. S = 4; +  ) .
B. S = ( 4; +  ) .
C. S = ( −; 4 .
D. S = ( −; − 4 .
Câu 5. Các cặp đường thẳng nào sau đây vuông góc với nhau?
A. d : 2x − y + 3 = 0 và d : x − 2 y +1 = 0.
B. d : 2x − y + 3 = 0 và d : 4x − 2 y +1 = 0. 1 2 1 2 x = tx = t C. d : 
và d : 2x + y – 1 = 0.
D. d : x − 2 = 0 và d :  . 1 y = −1 − 2t  2 1 2 y = 0 
Câu 6. Bất phương trình 3
− x + 9  0 có tập nghiệm là
A. 3; +  ) .
B. ( −; 3 .
C. (3; +  ) . D. ( −; − 3) .
Câu 7. Tam giác ABC có A = 60 , AC = 10 , AB = 6 . Tính cạnh BC A. 2 19 . B. 14 . C. 6 2 . D. 76 .
Câu 8. Đường thẳng 12 x − 7 y + 5 = 0 không đi qua điểm trong các điểm nào sau?  17   5  A. 1 ;   .
B. ( −1; −1) . C. (1; 1) . D. − ; 0   .  7   12 
Câu 9. Tập nghiệm của bất phương trình 2
( x + 2)(2 x − 1) − 2  x + ( x − 1)( x − 3) là: A. ( −  ;1 .
B. ( −;1) . C.   1 . D.  .
Câu 10. Cho hệ bất phương trình
2x + 3y −1  0  .
 5x − y + 4  0
Hỏi khẳng định nào dưới đây là khẳng định sai?
A. Điểm C ( −2; 4) thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm D ( −3; 4) thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm A ( −1; 4) thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm O (0; 0) thuộc miền nghiệm của hệ bất phương trình đã cho.
Câu 11. Điểm nào sau đây thuộc miền nghiệm của bất phương trình 2 x + y − 3  0 ?  3   3 
A. Q ( −1; −3) . B. M 1;   .
C. N (1;1) . D. P −1;   .  2   2 
Câu 12. Tập nghiệm của bất phương trình 2
x − 4 2x + 8  0 là: A.  . B. .
C. (−;2 2 ) . D. \ 2 2 . Trang 5/40
Câu 13. Tìm nghiệm của nhị thức bậc nhất f ( x ) = 3x + 6 . A. x = 3 − .
B. x = 3 .
C. x = 2 . D. x = 2 − .
Câu 14. Tam giác ABC có B = 30 ., BC = 3, AB = 3 Tính cạnh AC A. 1, 7 . B. 3 . C. 1, 5 . D. 3 .
Câu 15. Mệnh đề nào sau đây sai? 1 A. a +
 2 a  0 .
B. a + b  2 ab a, b  0 . a 1 1 a x
C. a b  
a,b  0 . D.
a + b x + y . a b b y
Câu 16. Cho f ( x ) 2
= ax + bx + c (a  0). Điều kiện để f ( x)  0, x  là a  0 a  0 a  0 a  0 A.  . B.  . C.  . D.  .   0    0    0    0  2 x + 1
Câu 17. Tập xác định của hàm số y = là 1 − x A. \   1 .
B. ( −;1) . C. ( −  ;1 . D. (1;  ) .
Câu 18. Trong tam giác ABC có:
A. a = R sin A .
B. a = 2R cos A .
C. a = 2R sin A .
D. a = 2R tan A .
Câu 19. Cho f ( x ) = 2x − 4 , khẳng định nào sau đây là đúng?
A. f ( x )  0  x  ( 2; + ) .
B. f ( x )  0  x  ( −; −2)
C. f ( x )  0  x  ( −2; + ) .
D. f ( x ) = 0  x = −2 .
Câu 20. Với hai số x, y dương thoả xy = 36 . Bất đẳng thức nào sau đây đúng?
A. Tất cả đều đúng. B. 2 2
x + y  2xy = 72. . 2  x + y C. xy = 36.   .
x + y  2 xy = 12.  2  D. . Câu 21. Cho góc O
xOy = 30 . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1 . Độ
dài lớn nhất của đoạn OB bằng: A. 2 2 . B. 2 . C. 1, 5 . D. 3 .
2x − 5 y −1  0 
Câu 22. Cho hệ bất phương trình  2x + y + 5  0 . Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ
x + y +1 0  bất phương trình?
A. M (1; 0).
B. N (0; −2).
C. P (0; 2).
D. O (0; 0).
Câu 23. Trong các bất đẳng thức sau, bất đẳng thức nào sai? A. 2 2
a + b + ab  0 a  ,b  . B. 2 2 2
a + b + c ab + bc + ca, a
 ,b,c  . 1 1 C. 2 2
a  0; b  0 , ta có a + b 
2 (a + b ) .
D. a b  0   . b a
Câu 24. Cho 3 đường thẳng ( d : 3x − 2 y + 5 = 0 , ( d
: 2x + 4 y − 7 = 0 , ( d
: 3x + 4 y −1 = 0 . Viết phương 3 ) 2 ) 1 )
trình đường thẳng (d ) đi qua giao điểm của (d , (d và song song với (d . 3 ) 2 ) 1 )
A. 24x − 32 y − 53 = 0 .
B. 24x + 32 y − 53 = 0 .
C. 24x + 32 y + 53 = 0 .
D. 24x − 32 y + 53 = 0 . Trang 6/40 2  x − 9   0 2  − + −
Câu 25. Hệ bất phương trình x 3x 12  có nghiệm là: x + 7 3x + 1 +  0  x − 5 2
A. 1  x  3 . B. x  3
− hoặc x  1 .
C. 3  x  5 .
D. 1  x  3 . x
Câu 26. Khi giải bất phương trình 2
− 3  0 . Một học sinh làm như sau x − 1 2 x 2 x (I) − 3  0   3 (1) x − 1 x − 1
(II) (1)  2 x  3( x − 1) (2)
(III) (2)  2x  3x − 3  x  1
Vậy bất phương trình có tập nghiệm (−;1)
Cách giải trên đúng hay sai? Nếu sau thì
A. Lời giải đúng.
B. Sai từ bước ( I ) .
C. Sai từ bước ( II ) .
D. Sai từ bước ( III ) . x −
Câu 27. Tập nghiệm của bất phương trình 1  1 là x − 3
A. ( − ; 3)  (3; +  ) .
B. ( − ; 3) .
C. (3; +  ) . D. . x = 2 − 3t
Câu 28. Xác định m để 2 đường thẳng d : 2x − 3 y + 4 = 0 và d  :  vuông góc y = 1 − 4mt  9 1 9 1 A. m = − . B. m = − . C. m = . D. m = . 8 2 8 2
Câu 29. Phương trình: 2 2 x +
4 − x = 2 + 3x 4 − x có bao nhiêu nghiệm lớn hơn hoặc bằng 0 : A. 0 . B. 2. C. 3 . D. 1.
Câu 30. Cho tam giác ABC có BC = a, CA = b, AB = c . Mệnh đề nào sau đây là đúng? A. Nếu 2 2 2
b + c − a  0 thì góc A nhọn. B. Nếu 2 2 2
b + c − a  0 thì góc A tù. C. Nếu 2 2 2
b + c − a  0 thì góc A nhọn. D. Nếu 2 2 2
b + c − a  0 thì góc A vuông.
Câu 31. Đường tròn (C ) có tâm là gốc tọa độ O (0; 0) và tiếp xúc với đường thẳng  : 8x + 6 y + 100 = 0 . Bán
kính R của đường tròn (C ) bằng:
A. R = 8 .
B. R = 10 .
C. R = 4 .
D. R = 6 .
Câu 32. Tìm tất cả các giá trị thực của tham số m để bất phương trình mx + m  2x vô nghiệm.
A. m = 0 .
B. m = 2 . C. m = 2 − . D. m  .
Câu 33. Nghiệm của bất phương trình 2 x − 3  1 là:
A. 1  x  3 . B. 1 −  x 1.
C. 1  x  2 . D. 1
−  x  2 .
Câu 34. Giá trị x thỏa mãn bất phương trình 2
− x + 6  0 là
A. x = 5 .
B. x = 3 .
C. x = 4 .
D. x = 2 . 3 − x
Câu 35. Tìm tập xác định D của hàm số y = . 2 4 − 3x − x A. D = \ 1; −  4 . B. D = − 4;  1 .
C. D = ( − 4;1).
D. D = ( − ; 4)  (1; +  ). PHẦN II: TỰ LUẬN Trang 7/40
Câu 1. Tìm các giá trị của m để biểu thức 2
f (x) = x + (m +1)x + 2m + 7  0 x
Câu 2. Tam giác ABC có các cạnh thỏa mãn hệ thức ( a + b + c ) ( a + b − c ) = 3ab . Tìm số đo góc C .
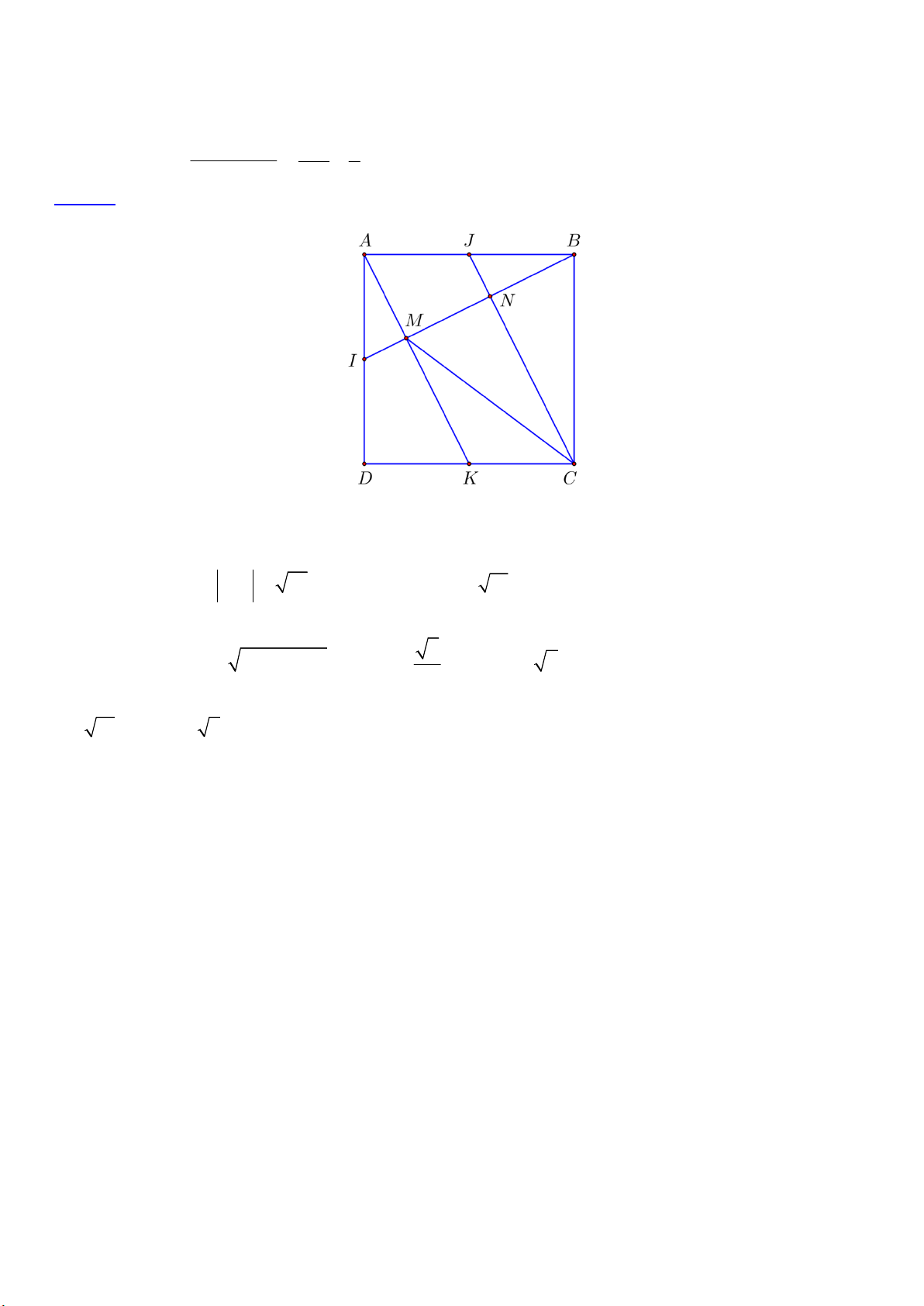
Câu 3. Trong mặt phẳng với hệ tọa độ Oxy, Cho hình vuông ABCD có C ( 2; −2) và B ( a;b ) , a  0. Gọi
điểm I , K lần lượt là trung điểm của DA và DC; điểm M (−1; −1) là giao của BI và AK. Tính P = a + b .
Câu 4. Cho ba số thực dương x, y, z thỏa mãn điều kiện x + y + z = 2 . Tìm giá trị lớn nhất của biểu thức P = x + y + y + z + z + x .
------------- HẾT ------------- Trang 8/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 3 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 003
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Nhị thức −3x + 2 nhận giá trị dương khi 3 2 3 2 A. x  − . B. x  . C. x  . D. x  . 2 3 2 3
Câu 2. Cặp số (3; 2 ) là nghiệm của bất phương trình nào sau đây.
A. 3x − y  0 .
B. 3x  4 y .
C. x − 3 y + 3  0 .
D. 3x − 4 y −1  0 .
Câu 3. Cho hệ bất phương trình
x − y  0 
x − 3y + 3  0 . 
x + y − 5  0
Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Điểm O (0; 0) thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm B (5;3) thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm C (1; −1) thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm D ( −2; 2) thuộc miền nghiệm của hệ bất phương trình đã cho. 1 4 − 3x
Câu 4. Điều kiện của phương trình x + 2 − = là: x + 2 x + 1 A. x  2 − và x  1 − . B. x  2 − và x  1 − . 4 4 C. x  2 − và x  .
D. x  −2, x  −1 và x  . 3 3
Câu 5. Phương trình tham số của đường thẳng đi qua 2 điểm A (3; − 1) và B (1; 5) là x = 3 − tx = 1− tx = 3 + tx = 3 + t A.  . B.  . C.  . D.  . y = −1 − 3ty = 5 − 3ty = −1 − 3ty = −1 + 3t
Câu 6. Trong các khẳng định sau, khẳng định nào đúng với mọi số thực x ?
A. 2 − x  5 − x . B. 2 2
5x  2 x .
C. x + 3  7 − x .
D. 5x  2x .
Câu 7. Nếu a b  0 , c d  0. thì bất đẳng thức nào sau đây không đúng? a b a d
A. a + c b + d .
B. ac bd . C.  . D.  . c d b c
Câu 8. Cho tam giác ABC bất kỳ có BC = a , AC = b , AB = c . Đẳng thức nào sai? A. 2 2 2
a = b + c − 2bc cos A . B. 2 2 2
c = b + a + 2ab cos C . C. 2 2 2
c = b + a − 2ab cos C . D. 2 2 2
b = a + c − 2ac cos B . Câu 9. Cho ( ) 2
f x = ax + bx + c , ( a  0) và 2
 = b − 4ac . Cho biết dấu của  khi f ( x) luôn cùng dấu với
hệ số a với mọi x  . A.   0 . B.   0 . C.  = 0 . D.   0 .
Câu 10. Tập nghiệm của bất phương trình ( x + 2) (5 − x )  0 là
A. ( −5; −2) .
B. 5; + ) .
C. ( −; −2)  (5; + ) . D. ( −2;5) . Trang 9/40
Câu 11. Một đường thẳng có bao nhiêu vectơ pháp tuyến? A. Vô số. B. 2. C. 3. D. 1.
Câu 12. Với hai số x, y dương thoả xy = 36 . Bất đẳng thức nào sau đây đúng? 2  x + y A. xy = 36.   .
B. Tất cả đều đúng.  2 
x + y  2 xy = 12. D. 2 2
x + y  2xy = 72. . C. .
Câu 13. Tìm tọa độ giao điểm của đường thẳng  : 4x − 3 y − 26 = 0 và đường thẳng d : 3x + 4 y − 7 = 0 . A. (5; 2) .
B. Không có giao điểm. C. ( 2; −6) . D. (5; −2) .
Câu 14. Tam giác ABC có a = 8, c = 3, B = 60 . Độ dài cạnh b bằng bao nhiêu ? A. 61 . B. 49 . C. 7 . D. 97 .
Câu 15. Tập nghiệm của bất phương trình 2
x − 8x + 16  0 là.
A. S = ( −; 4) . B. S = \   4 .
C. S =  .
D. S = (1; 4) .
Câu 16. Xác định vị trí tương đối của 2 đường thẳng:
x = 2 + ( 3 + 2)t
x = − 3 + t '  :  và  :  1  2 y = − 2 + ( 3 − 2 )t
y = − 3 + (5 − 2 6)t '  A. Vuông góc. B. Trùng nhau. C. Cắt nhau. D. Song song.
Câu 17. Tam giác ABC có A = 105 , B = 45 , AC = 10 . Tính cạnh AB . 5 6 A. 5 2 . B. 5 6 . C. . D. 10 2 . 2 Câu 18. Nhị thức 2
− x − 3 nhận giá trị dương khi và chỉ khi 3 2 3 2 A. x  − . B. x  − . C. x  − . D. x  − . 2 3 2 3
Câu 19. Tập nghiệm của bất phương trình 5x − 2 (4 − x )  0 là:  8   8   8   8  A. −;   . B. − ; +   . C. ; +   . D. ; +   .  7   7   7   3 
Câu 20. Tập nghiệm của bất phương trình 2
x − x − 6  0 là:
A. ( −; −2)  (3; + ) .
B. ( −; −3)  ( 2; + ) . C. ( −3; 2) . D. ( −2;3) .
Câu 21. Tập nghiệm của bất phương trình x − 3x  0 là  1    1  0;   1 0  ; +   0 ; + A.        . D. 9  . B.  9  . C. 9  .
Câu 22. Nếu a , b là những số thực và a b thì bất đẳng thức nào sau đây luôn đúng? 1 1 A. 2 2
a b . B.
với ab  0 . a b C. b
−  a b .
D. a b .
Câu 23. Cho một hình bình hành ABCD có AB = a , BC = b . Công thức nào dưới đây là công thức tính diện
tích của hình bình hành đó? A. 2 2 a + b .
B. ab sin ABC . C. ab .
D. 2 ( a + b ) . 2 x −1  0
Câu 24. Hệ bất phương trình  có nghiệm khi x − m  0 
A. m  1.
B. m  1.
C. m = 1. D. m  1. Trang 10/40 − x
Câu 25. Tập nghiệm của bất phương trình 4  0 là −3x + 6 A. ( 2 ; 4) .
B. ( − ; 2)  4 ; +  ) .
C. 2 ; 4 . D. ( 2 ; 4 .
Câu 26. Cho tam giác ABC có A (1; 2) , B ( 2;3) , C ( −3; − 4) . Diện tích tam giác ABC bằng 3 A. . B. 2 . C. 1+ 2 . D. 1 . 2 a b
Câu 27. Cho a, b  0 . Chứng minh
+  2 . Một học sinh làm như sau b a a b 2 2 a + b I) +  2   2 (1) b a ab II) (1) 2 2 2 2 2
a + b  2ab a + b − 2ab  0  (a − b)  0 a b
III) vì ( a − b)2  0 đúng a, b  0 nên +  2 b a Cách làm trên A. Sai từ I).
B. Sai từ II).
C. Sai ở III).
D. Cả I), II), III) đúng.
Câu 28. Trong mặt phẳng tọa độ Oxy cho điểm I (1; 2) và đường thẳng ( d ) : 2x + y − 5 = 0 . Biết rằng có hai
điểm M , M thuộc (d ) sao cho IM = IM = 10 . Tổng hoành độ của M , M là : 1 2 1 2 1 2 14 7 A. B. 2 C. 5 D. 5 5
Câu 29. Cho hai điểm A (1; −4); B (3; 2). Viết phương trình tổng quát của đường trung trực của đoạn thẳng AB
A. 3x − y + 8 = 0 .
B. x + 3 y − 8 = 0 .
C. − x + 3 y + 8 = 0 .
D. x − 3 y + 8 = 0 . 4 x − 12
Câu 30. Cho biểu thức f ( x ) =
. Tập hợp tất cả các giá trị của x thỏa mãn bất phương trình f ( x )  0 2 x − 4 x là
A. x  ( − ; 0)  (3; 4).
B. x  (0; 3  ( 4; +  ).
C. x  ( − ; 0  3; 4).
D. x  ( − ; 0)  3; 4). x
Câu 31. Tìm tập nghiệm S của bất phương trình 2 5 x − 1  + 3 . 5  5   20 
A. S = − ; +   . B. S = ; +   .
C. S = ( −;1) .
D. S = ( −; 2) .  2   23 
Câu 32. Tập nghiệm S của bất phương trình (x −1) x + 1  0 là
A. S = −  1  1; + )
B. S = (1; + )
C. S = −1; + )
D. S = −  1  (1; + ) 2 x + 5x  6
Câu 33. Hệ bất phương trình:  có nghiệm là: x + 1  2  A. 6 −  x  3 − . B. x  6 − .
C. −2  x  −1. D. 1
−  x  0 .
2x + 3y −1  0
Câu 34. Miền nghiệm của hệ bất phương trình 
là phần mặt phẳng chứa điểm nào sau đây?
5x − y + 4  0 
A. M ( −1; 4) .
B. N (0; 0) .
C. P ( −3; 4) .
D. Q ( −2; − 4) .
Câu 35. Cho hình bình hành ABCD có AB = a , BC = a 2 và BAD = 45 . Diện tích của hình bình hành ABCD là Trang 11/40 A. 2 a 2 . B. 2 a 3 . C. 2 a . D. 2 2a . PHẦN II: TỰ LUẬN
Câu 1. Tìm tập nghiệm của bất phương trình 2
x + ( 3 + 2 ) x + 6  0 .
Câu 2. Cho tam giác ABC có BC a, CA
b . Tam giác ABC có diện tích lớn nhất khi góc C bằng:
Câu 3. Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng đi qua hai điểm A (1; 2) , B ( 4; 6) , tìm tọa độ
điểm M trên trục Oy sao cho diện tích MAB bằng 1.
Câu 4. Cho a,b,c a, b, c là các số thực thuộc đoạn 0; 
1 . Tìm GTLN của biểu thức
P = a(1 − b) + b(1 − c) + c(1 − a)
------------- HẾT ------------- Trang 12/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 4 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 004
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Tập nghiệm của bất phương trình 2 x +1  3(2 − x ) là A. (5; + ) .
B. ( −;5) . C. (1; + ) .
D. ( −; −5) .
Câu 2. Bất phương trình 2
−x + 2x + 3  0 có tập nghiệm là A. ( −1; 3) . B. −1; 3 . C. ( −3;1) .
D. ( −; −1)  (3; + ) .
Câu 3. Phương trình tổng quát của đường thẳng d đi qua O và song song với đường thẳng  : 6x − 4x +1 = 0 là:
A. 3x + 12 y − 1 = 0.
B. 6x − 4 y −1 = 0.
C. 3x − 2 y = 0.
D. 4x + 6 y = 0.
Câu 4. Đường thẳng nào sau đây song song với đường thẳng 2 x + 3 y −1 = 0 ?
A. 4x − 6 y − 2 = 0 .
B. 2 x + 3 y + 1 = 0 .
C. x − 2 y + 5 = 0 .
D. 2x − 3 y + 3 = 0 .
Câu 5. Đường trung trực của đoạn thẳng AB với A = ( −3; 2) , B = ( −3;3) có một vectơ pháp tuyến là:
A. n = 0;1 .
B. n = −3;5 .
C. n = −1; 0 .
D. n = 6;5 . 1 ( ) 4 ( ) 3 ( ) 2 ( )
Câu 6. Cho f ( x ) 2
= ax + bx + c (a  0) . Điều kiện để f ( x)  0,x  là a  0 a  0 a  0 a  0 A.  . B.  . C. D.   0    0    0    0 
Câu 7. Cho hệ bất phương trình  x y  + − 1  0 2 3  3 y 2(x − ) 1 +  4 .  2  x  0 
Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Điểm A ( 2;1) thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm O (0; 0) thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm C (1;1) thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm D (3; 4) thuộc miền nghiệm của hệ bất phương trình đã cho.
Câu 8. Trong các khẳng định sau, khẳng định nào sau đây đúng? 0  a b a ba b  0 a b A.    . B.    . 0  c dc d c d  0  c da b a ba b  0 a d C.    . D.    . c dc d c d  0  b c 2 2 x + x + 1 x + x
Câu 9. Nghiệm của bất phương trình  là: 2 2 x + 2 x + 2
A. x  2 . B. x  .
C. x  1.
D. x  1 . Trang 13/40 x −
Câu 10. Tìm điều kiện của bất phương trình 2 3  x − 2 . 6 − 3x
A. x  2 .
B. x  2 .
C. x  2 .
D. x  2 .
Câu 11. Tam giác ABC có C = 150 , BC =
3 , AC = 2 . Tính cạnh AB A. 1 . B. 13 . C. 10 . D. 3 .
Câu 12. Tính diện tích tam giác ABC có ba cạnh là 13, 14, 15. A. 16 24 . B. 6411 . C. 168. D. 84.
Câu 13. Phương trình 2
mx − mx + 2 = 0 có nghiệm khi và chỉ khi
A. m  0 hoặc m  8 .
B. m  0 hoặc m  8 .
C. 0  m  8 .
D. 0  m  8 .
Câu 14. Tập nghiệm của bất phương trình 2
−x + 5x − 4  0 là
A. ( −;1)  ( 4; + ) . B. ( −;  1  4; + ) . C. 1; 4 . D. (1; 4 ) .
Câu 15. Cho tam giác ABC có AB = 2, AC = 2, BC = 1. Giá trị cos A bằng: 7 7 7 A. . B. . C. . D. 0. 16 32 8
Câu 16. Số x = 3 là nghiệm của bất phương trình nào sau đây?
A. 5 − x  1.
B. 3x +1  4 .
C. 4x −11  x .
D. 2x −1  3 . 2
Câu 17. Nhị thức nào sau đây nhận giá trị âm với mọi số x nhỏ hơn − ? 3
A. f ( x ) = 3x + 2 .
B. f ( x ) = −3x – 2 .
C. f ( x ) = 2x + 3 .
D. f ( x ) = −6x – 4 .
Câu 18. Cho f ( x ) = 2x + 1 . Khẳng định nào sau đây là khẳng định sai
A. f ( x )  0;x  0 .
B. f ( x ) 1
 0;x  − . 2
C. f ( x ) 1  0;x  .
D. f ( x )  0;x  2 . 2
Câu 19. Với hai số x, y dương thoả xy = 36 . Bất đẳng thức nào sau đây đúng?
A. Tất cả đều đúng. B. 2 2
x + y  2xy = 72. . 2  x + y C. xy = 36.   .
x + y  2 xy = 12.  2  D. .
Câu 20. Tìm tọa độ giao điểm của 2 đường thẳng sau đây: x = 22 + 2tx = 12 + 4t '  :  và  :  1 y = 55 + 5t  2
y = −15 − 5t '  A. (2; 5). B. (6; 5). C. (0; 0). D. (−5; 4).
Câu 21. Nghiệm của phương trình: 2 2 3 − x + x −
2 + x − x = 1 là: 1  3 1  5 A. 1;  2 . B. 0;  1 . C. . D. . 2 2
Câu 22. Đường tròn (C ) có tâm I ( −2; −2) và tiếp xúc với đường thẳng  : 5x + 12 y −10 = 0 . Bán kính R
của đường tròn (C ) bằng: 7 44 24
A. R = 44 . B. R = . C. R = . D. R = . 13 13 13
Câu 23. Cho a, b, c dương. Bất đẳng thức nào đúng?  1 1 1   1 1 1 
A. (a + b + c) + +  9.  
B. (a + b + c) + +  9.   a b c   a b c  Trang 14/40  1 1 1   1 1 1 
C. (a + b + c) + +  3.  
D. (a + b + c) + +  3.   a b c   a b c
Câu 24. Tập xác định của hàm số 2 2 y = x − 4x + 25 − x là
A. −5;5 .
B. ( −; 0  4; + ) .
C. −5; 0  4;5 .
D. ( −5; 0)  ( 4;5) . − x
Câu 25. Bất phương trình 2
 0 có tập nghiệm là: 2 x + 1  1   −1   −1   −1  A. −  ; 2 . B. ; 2 . C. ; 2   . D. ; 2   .    2   2   2   2  x = 1+ t
Câu 26. Cho hai điểm A ( −1; 2) , B (3;1) và đường thẳng  :
. Tọa độ điểm C thuộc  để tam giác y = 2 + t
ACB cân tại C là  7 13   13 7   7 13   7 13  A. ; −   . B. ;   . C. − ;   . D. ;   .  6 6   6 6   6 6   6 6 
Câu 27. Cho các số thực a, ,
b c . Trong các bất đẳng thức sau, bất đẳng thức nào sai? A. 2 2 2
a + b + c a (b + c ) B. 2 2
4a + b + 1  2ab + b + 2a C. 2 2 2
a + b + c ab + bc + ca D. 5 5 2 2
a + b a b ( a + b )
Câu 28. Tập nào sau đây chứa trong tập nghiệm của phương trình: x x + 3  0 ? A. ( −2;10) . B. (1;10) .
C. ( −4; + ) . D. ( −3;1) .
Câu 29. Hình bình hành ABCD có AB = a , BC = a 2 và BAD = 45 . Khi đó hình bình có diện tích là A. 2 a 3 . B. 2 2a . C. 2 a 2 . D. 2 a . 2 x − 5x + 6
Câu 30. Tập nghiệm bất phương trình  0 là: x − 1
A. ( −;1)  2;3 . B. (1;3 .
C. (1; 2  3; + ) . D. 2;3 .
Câu 31. Cho tam giác ABC có 2 2 2
BC AB + AC . Mệnh đề nào sau đây là đúng?
A. Â là góc tù.
B. Â là góc nhọn.
C. Â là góc vuông.
D. Â là góc nhỏ nhất.
Câu 32. Một học sinh giải phương trình 2
1 − 13 + 3x  2 x (1) tuần tự như sau (I) 2
(1)  1− 2x  13 + 3x (2) 1 (II) 2 2
(2)  (1 − 2x)  13 + 3x , với x  (3) 2 1 (III) 2
(3)  x − 4x −12  0 , với x  (4) 2 (IV) (4)  x  2
Lý luận trên nếu sai, thì sai từ bước nào? A. (III). B. (IV).
C. Lý luận đúng. D. (II). 3x + y  9  x y − 3
Câu 33. Miền nghiệm của hệ bất phương trình 
là phần mặt phẳng chứa điểm 2 y  8 − x   y  6  A. (8; 4) . B. (0; 0) . C. ( 2;1) . D. (1; 2 ) .
Câu 34. Tính góc tạo bởi giữa hai đường thẳng d : x + 3 y = 0 và d : x +10 = 0. 1 2 Trang 15/40 A. o 90 . B. o 30 . C. o 45 . D. o 60 . x − 
Câu 35. Hệ phương trình 2 1 0 x − m
vô nghiệm khi và chỉ khi 3 5 5 5 7 A. m  − . B. m  − . C. m  − . D. m  . 2 2 2 2 PHẦN II: TỰ LUẬN
Câu 1. Giải bất phương trình x ( x + )  ( 2 5 2 x + 2).
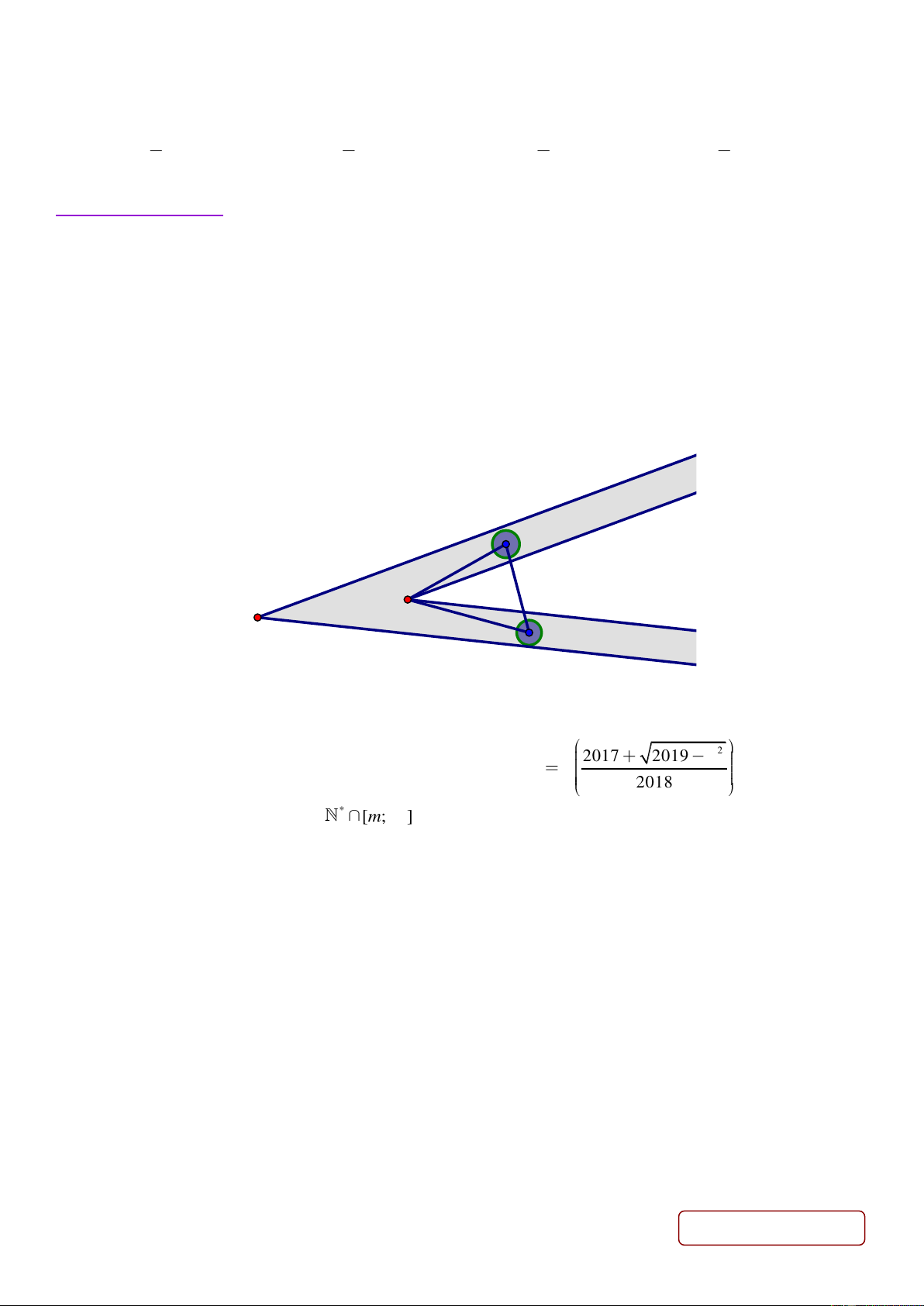
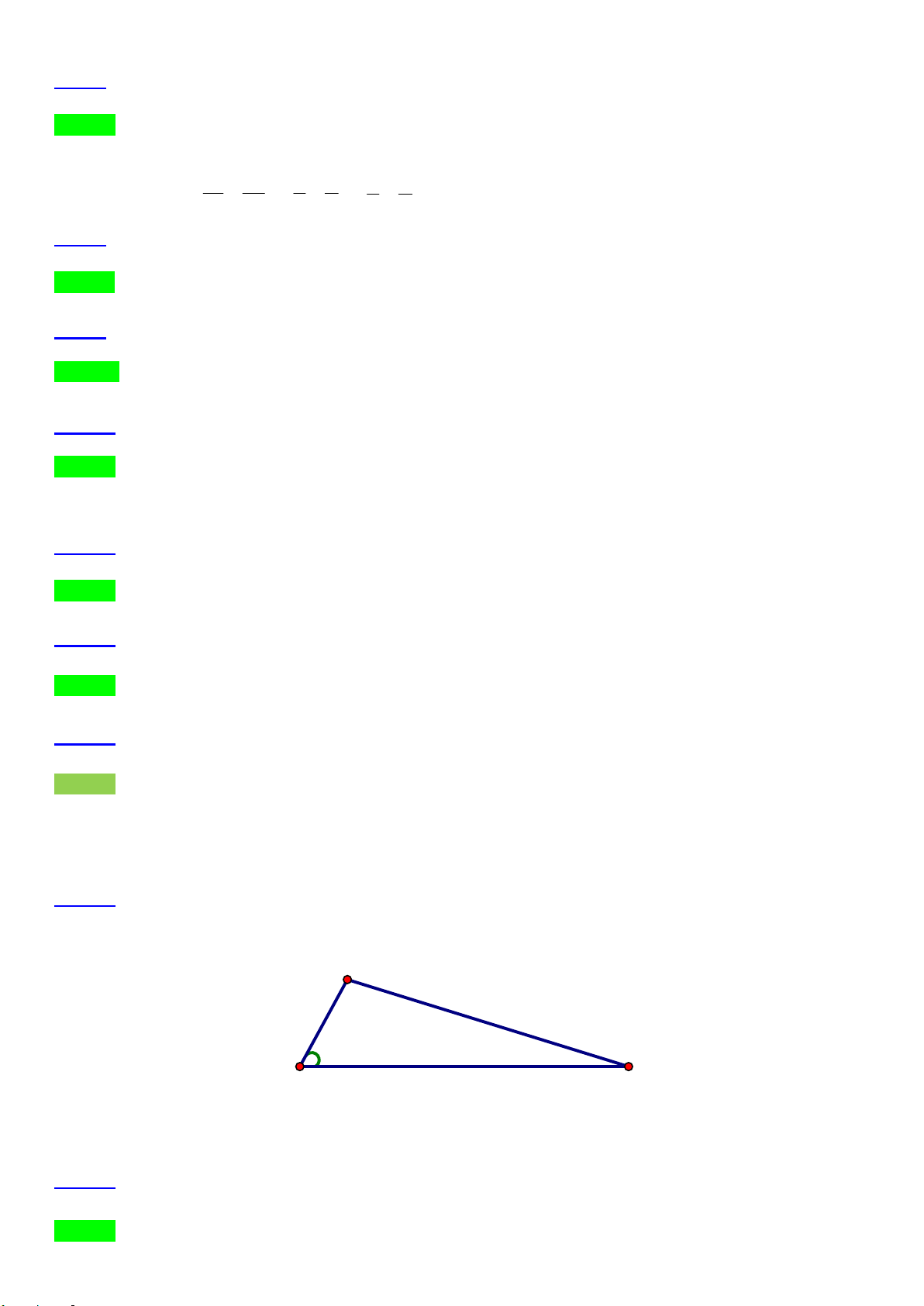
Câu 2. Trong cuộc thi giải trí toán học tổ chức nhân dịp hoạt động chào mừng Ngày nhà giáo Việt Nam có
một trò chơi như sau: Người ta thiết kế hai đường ray tạo với nhau một góc 0
30 như hình vẽ dưới đây. Trên
các đường thẳng Ox và Oy người ta để hai vật nặng cùng trọng lượng. Buộc hai vật thể với nhau bằng một
thanh cứng AB = 1m sao cho mỗi vật đều có thể chuyển động được trên hai đường ray. Nối hai vật bằng một
sợi giây vòng qua một cột có gốc tại O . Người tham dự cuộc thi sẽ đứng tại vị trí điểm B để kéo vật thể
chuyển động trên Oy . Người thắng cuộc sẽ là người kéo được vật thể ra xa nhất so với điểm gốc O . Hãy
dùng kiến thức toán học để tính toán vị trí xa nhất mà người tham dự cuộc thi có thể đạt được. A O B
Câu 3. Trong mặt phẳng tạo độ Oxy cho hai điểm A(1;2), B(4;3). Tính tổng tất cả các hoành độ của điểm M thuộc trục Ox sao cho 0 AMB = 45 . 2 2017 2019 x
Câu 4. Gọi M , m lần lượt là GTLN và GTNN của hàm số f ( x) x trên tập xác định 2018
của nó. Tìm số phần tử của tập hợp * [ ; m M ] ?
------------- HẾT ------------- Trang 16/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 5 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 005
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cho đường thẳng  có phương trình tổng quát: –2 x + 3 y – 1 = 0 . Vectơ nào sau đây không là vectơ
chỉ phương của  ?  2  A. ( 2; 3) .
B. ( –3; – 2) . C. 1;   . D. (3; 2) .  3 
Câu 2. Cho mệnh đề ”Hai bất phương trình tương đương là hai bất phương trình …”. Hãy chọn một kết quả
trong bốn kết quả sau điền tiếp vào dấu "…" để được một mệnh đề đúng.
A. có hai tập nghiệm khác nhau.
B. có một tập nghiệm là con của tập nghiệm kia.
C. có tập nghiệm khác  .
D. có cùng tập nghiệm.
Câu 3. Cho hai số thực a, b tùy ý. Mệnh đề nào sau đây là đúng?
A. a + b = a + b .
B. a + b a + b .
C. a + b a + b .
D. a + b a + b .
Câu 4. Số −2 thuộc tập nghiệm của bất phương trình nào ?
A. 3x −1  0 .
B. 3x + 2  0 . C. 2
− x −1 0 .
D. 4x − 5  0 .
Câu 5. Cho nhị thức bậc nhất f ( x ) = ax + b ( a  0) . Chọn kết quả sai trong các kết quả sau. b
A. f ( x ) có giá trị bằng 0 khi x = − . ab
B. f ( x ) có giá trị cùng dấu với hệ số a khi x lấy các giá trị trong khoảng − ; +    .  a   b
C. f ( x ) có giá trị trái dấu với hệ số a khi x lấy các giá trị trong khoảng −; −   .  a
D. f ( x ) có giá trị cùng dấu với hệ số a khi x lấy các giá trị trong khoảng ( −; +  ) .
Câu 6. Phương trình đường thẳng đi qua N (1; 2) và song song với đường thẳng 2 x + 3 y − 12 = 0 là.
A. 4 x + 6 y + 1 = 0 .
B. 2 x − 3 y − 8 = 0 .
C. 2 x + 3 y − 8 = 0 .
D. 2 x + 3 y + 8 = 0 .
Câu 7. Cho hai điểm A ( 4; −1) , B (1; −4) . Viết phương trình tổng quát đường trung trực đoạn AB .
A. x + y = 0 .
B. x − y = 0 .
C. x − y = 1 .
D. x + y = 1 .
Câu 8. Cho bất phương trình x − 2 y + 5  0 có tập nghiệm là S .Mệnh đề nào sau đây là đúng?
A. ( −2; 2)  S .
B. ( 2; 2)  S .
C. ( −2; 4)  S .
D. (1; 3)  S . x = 1− 2t
Câu 9. Trong mặt phẳng với hệ trục tọa độ Oxy , cho đường thẳng ( d ) có phương trình  . Véctơ y = 3 + t
nào sau đây là một véctơ chỉ phương của đường thẳng (d ) ?
A. u (1; 2) . B. u (2; − ) 1 .
C. u (1;3) . D. u (−4; ) 1 .
Câu 10. Tam giác ABC có AB = 8 cm , BC = 10 cm , CA = 6 cm . Đường trung tuyến AM của tam giác đó có độ dài bằng A. 4 cm . B. 5 cm . C. 6 cm . D. 7 cm .
Câu 11. Tam thức bậc hai f ( x ) 2
= x −12x −13 nhận giá trị không âm khi và chỉ khi
A. x  ( −; −  1  13; + ) . B. x  \ −1;13 . Trang 17/40
C. x  −1;13 .
D. x  ( −1;13) .
Câu 12. Tìm tập nghiệm của bất phương trình x + x − 2  2 + x − 2 .
A. 2; + ) . B.  .
C. ( − ; 2) . D. 2 .
Câu 13. Tính diện tích tam giác có ba cạnh là 9, 10, 11. A. 44. B. 30 2. C. 42. D. 50 3. x
Câu 14. Bất phương trình 2 5 x − 1  + 3 có nghiệm là 5 5 20 A. x  − .
B. x  2 . C. x  .
D. x . 2 23
Câu 15. Cho đường thẳng d : 2 x − y + 3 = 0 và điểm M (5; −2). Đối với đường thẳng d, điểm nào dưới đây
nằm cùng một phía đối với điểm M ? A. N(1;6) . B. N(−4; 0) . C. N(−2; 4) .
D. N (3; −1) .
Câu 16. Tìm điều kiện xác định của bất phương trình 2x + 6  3 + 2 2x + 6 . A. x  3 − .
B. Điều kiện khác. C. x  3 − . D. x  3 − .
Câu 17. Tính diện tích tam giác có ba cạnh lần lượt là 3 , 2 và 1. 3 6 2 A. . B. 3 . C. . D. . 2 2 2
Câu 18. Cặp số (1; –1) là nghiệm của bất phương trình nào sau đây?
A. x + y – 3  0 .
B. – x – y  0 .
C. x + 3 y + 1  0 .
D. – x – 3 y – 1  0 .
Câu 19. Cho tam thức bậc hai f ( x ) 2
= ax + bx + c (a  0) có biệt thức 2
 = b − 4ac . Chọn kết quả sai trong các kết quả sau.
A. Nếu  = 0 thì a. f ( x )  0 với mọi x  . b
B. Nếu   0 thì f ( x ) cùng dấu với hệ số a khi x lấy các giá trị trong khoảng − ; +    và trái dấu  a   b
với hệ số a khi x lấy các giá trị trong khoảng −; −   . a
C. Nếu   0 thì f ( x ) cùng dấu với hệ số a khi x x hoặc x x , f ( x ) trái dấu với hệ số a khi 1 2
x x x (trong đó x , x x x
là hai nghiệm của f ( x ) ). 2 ( 1 2 ) 1 2 1
D. Nếu   0 thì f ( x ) luôn cùng dấu với hệ số a , với mọi x  .
Câu 20. Cho a, b  . Mệnh đề nào sau đây đúng?
A. a + b a + b
B. a + b = a + b
C. a + b a + b
D. a + b a + b
Câu 21. Viết phương trình tham số của đường thẳng ( D ) đi qua điểm ( A 1
− ;2) và vuông góc với đường
thẳng  : 2x − y + 4 = 0 . x = −1+ 2tx = 1 + 2tx = tx = −1+ 2t A.  . B.  . C.  . D.  . y = 2 − ty = 2 − ty = 4 + −2ty = 2 + tx − 1
Câu 22. Tìm tập nghiệm của bất phương trình  ( là: x − 2) ( 0 2 x − 5x + 4)
A. ( −; 2)  ( 4; + ) \   1 .
B. ( −; 2)  ( 4; + ) . C. 2; 4 .
D. ( −; 2  4; + ) .
Câu 23. Bất phương trình x − 2  x + 4 có tập nghiệm là
A. −1; + ) . B. . C. −  2 . D. −  6 . Trang 18/40 2x −1  3
Câu 24. Tập hợp các giá trị m để hệ bất phương trình 
có nghiệm duy nhất là: x − m  0  A.   2 .
B. 2; + ) .
C. ( −; 2 . D.  .
Câu 25. Trong các bất phương trình sau, bất phương trình nào tương đương với bất phương trình 2x  1 ? A. 2 4 x  1 . B. 2x + x + 2  1+ x + 2 . 1 1 C. 2x + x − 2  1+ x − 2 . D. 2 x −  1− . x − 3 x − 3
Câu 26. Diện tích S của tam giác sẽ thỏa mãn hệ thức nào trong hai hệ thức sau đây? I. 2
S = p ( p − a ) ( p − b ) ( p − c ) . II. 2
16S = ( a + b + c ) ( a + b − c ) (a − b + c ) (−a + b + c ) . A. Chỉ II.
B. Cả I và II. C. Không có. D. Chỉ I.
Câu 27. Cho hai đường thẳng song d : 5x − 7 y + 4 = 0 và d : 5x − 7 y + 6 = 0. Khoảng cách giữa d và d là 1 2 1 2 2 10 4 6 A. . B. . C. . D. . 74 74 74 74
Câu 28. Trong mặt phẳng Oxy , hãy cho biết đường thẳng nào đi qua điểm A ( 2;1) và song song với đường
thẳng  : 2x + 3 y − 2 = 0 ?
A. x − y + 3 = 0 .
B. 4x + 6 y − 11 = 0 .
C. −2 x − 3 y + 7 = 0 .
D. 3x − 2 y − 4 = 0 . x
Câu 29. Giải bất phương trình: 2 −  1 . x − 2 x + 1
A. x  −1 hoặc x  2 .
B. x  −1 hoặc x  2 . C. 1
−  x  2 . D. 1
−  x  2 .
Câu 30. Cho tam giác ABC có AB = 3 , AC = 4 , BC = 5 . Bán kính đường tròn nội tiếp tam giác bằng 4 3 8 A. . B. . C. 1 . D. . 5 4 9
Câu 31. Giải bất phương trình 2
2 x + 5  x + 2 x + 4 được các giá trị x thỏa mãn
A. x  −1 hoặc x  1. B. 1 −  x  1.
C. x  1. D. x  1.
Câu 32. Cho x , y là hai số thực bất kỳ thỏavà xy = 2 . Giá trị nhỏ nhất của 2 2
A = x + y . A. 2 . B. 1. C. 0 . D. 4 .
Câu 33. Tìm tập nghiệm S của bất phương trình 2 x − 4  0 .
A. S = ( −; 0)  ( 4; + ) .
B. S = ( −; −2)  ( 2; + ) .
C. S = ( −2; 2) .
D. S = ( −; −2  2; + ) .
Câu 34. Bất phương trình (m − 2) x  5 vô nghiệm khi
A. m  2 .
B. m  2 .
C. m = 2 .
D. m  2 .  1  4
Câu 35. Biết rằng giá trị lớn nhất của biểu thức f ( x) = (3x + 1) (1 − x ) với x  − ;1   bằng . Dấu bằng  3  3
xảy ra tại x bằng 1 2 A. 0 . B. 3 . C. . D. . 3 3 PHẦN II: TỰ LUẬN
Câu 1. Tìm m để biểu thức sau luôn âm 2
f (x) = mx − x −1. Trang 19/40 2 1 1 1 1
Câu 2. Cho tam giác ABC . Chứng minh rằng = − = + h r r r r a a b c
Câu 3. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có đỉnh A ( 4; −1) phương trình đường cao
và trung tuyến kẻ từ đỉnh B lần lượt là 2 x − 3 y + 12 = 0 và 2 x + 3 y = 0 . Xác định tọa độ các đỉnh còn lại của tam giác ABC.
Câu 4. Cho a, b là số thực dương thỏa mãn 2 2
a + b = 2 . Chứng minh rằng
(a + b)5  ab ( 2 + a )( 2 16 1 1 + b ) .
------------- HẾT ------------- Trang 20/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 6 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 006
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cho đường thẳng d : x − 2 y + 1 = 0 . Nếu đường thẳng  qua điểm M (1; −1) và  song song với d
thì  có phương trình:
A. x − 2 y − 3 = 0 .
B. x − 2 y + 5 = 0 .
C. x − 2 y + 3 = 0 .
D. x + 2 y + 1 = 0.
Câu 2. Tập nghiệm của bất phương trình x ( x − 6) + 5 − 2x  10 + x ( x − 8) là
A. S = (5; + ) .
B. S =  . C. S = .
D. S = (−;5) .
Câu 3. Cho tam giác ABC có 0
AB = 9, BC = 8, ABC = 60 . Tính độ dài đoạn AC . A. 73 . B. 217 . C. 8 D. 113 .
Câu 4. Cho tam thức bậc hai f ( x ) 2
= x − 2x . Chọn khẳng định đúng.
A. f ( x )  0, x  (1; + ) .
B. f ( x )  0, x  .
C. f ( x )  0, x  .
D. f ( x )  0, x  (0 ; 2) .
Câu 5. Tính diện tích tam giác có ba cạnh lần lượt là 5 , 12 , 13 . A. 7 5 . B. 60 . C. 30 . D. 34 . x + x
Câu 6. Tập nghiệm của bất phương trình 5
1 + 3 − x  + 3 − x là 2 2  1   1   1   1  A. − ; 3   . B. ; 3   . C. − ; +    . D. − ; 3 .    4   4   4   4 
Câu 7. Cho tam giác ABC có AB = 9 , AC = 12 , BC = 15 . Khi đó đường trung tuyến AM của tam giác có
độ dài bằng bao nhiêu? A. 8 . B. 9 . C. 10 . D. 7, 5 . x 4 3t
Câu 8. Đường thẳng d :
có véctơ pháp tuyến có tọa độ là: y 1 2t A. 1;1 . B. 4; 6 . C. 2; 3 . D. 3; 2 .
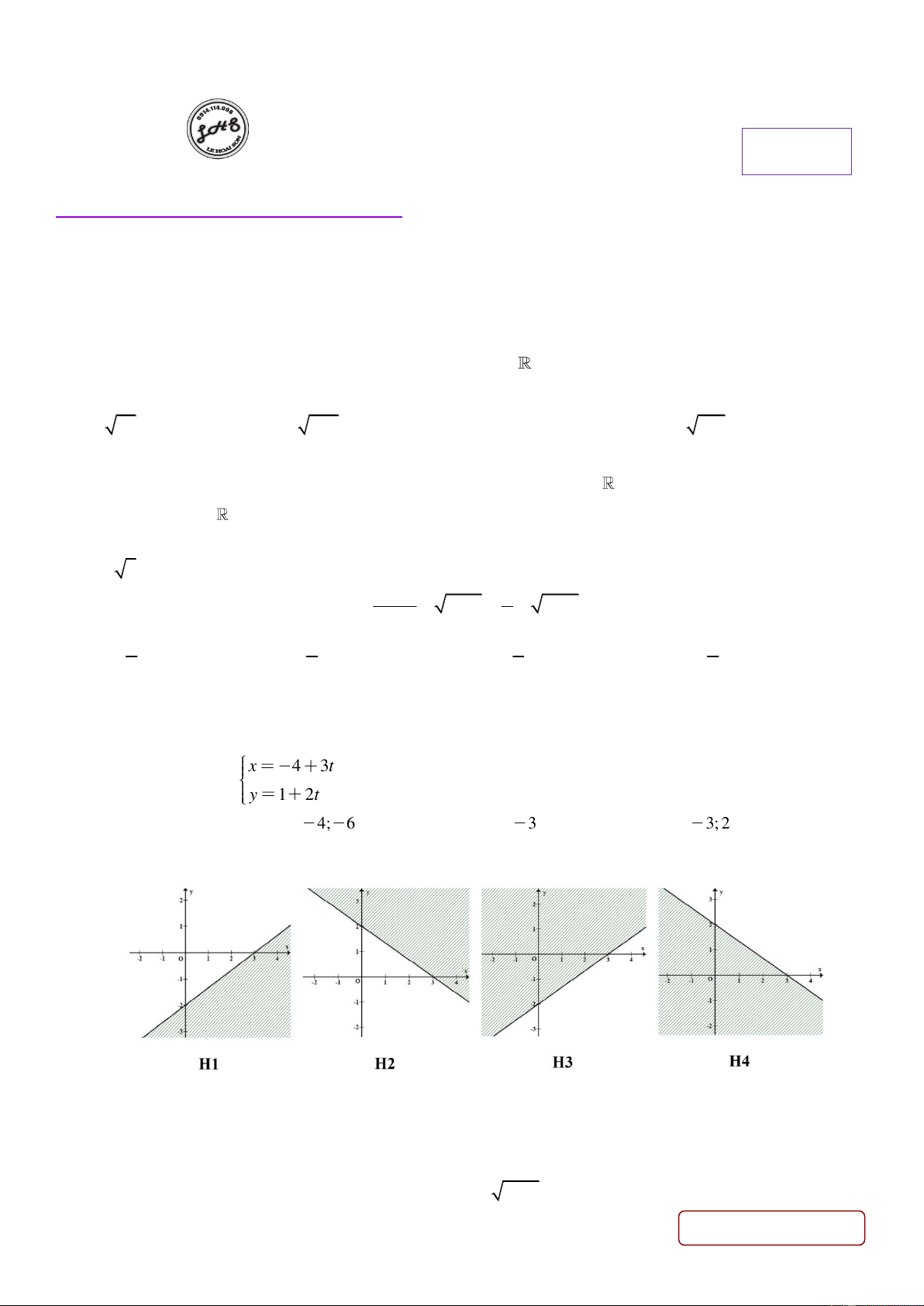
Câu 9. Hình vẽ nào sau đây biểu diễn miền nghiệm của bất phương trình 2x − 3 y − 6  0 (miền không tô đậm kể cả bờ)? A. H4 B. H1 C. H2 D. H3
Câu 10. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 2x + y  1 ? A. ( 0;1) . B. (3; −7) . C. ( −2;1) . D. (0; 0) .
Câu 11. Bất phương trình sau đây tương đương với bất phương trình x + 5  0 ? A. 2
x (x + 5)  0 .
B. x + 5(x + 5)  0 . Trang 21/40
C. x + 5(x − 5)  0 . D. 2
(x −1) (x + 5)  0 .
Câu 12. Nếu 2a  2b và 3 − b  3
− c thì bất đẳng thức nào sau đây đúng? A. 2 2
a c .
B. a c .
C. a c . D. 3 − a  3 − c .
Câu 13. Khẳng định nào sau đây là khẳng định sai?
A. Bất phương trình ax + b  0 vô nghiệm khi a = 0 và b  0 .
B. Bất phương trình ax + b  0 có tập nghiệm là
khi a = 0 và b  0 .
C. Bất phương trình ax + b  0 vô nghiệm khi a = 0 .
D. Bất phương trình bậc nhất một ẩn luôn có nghiệm.
Câu 14. Bất phương trình ax + b  0 có tập nghiệm là khi và chỉ khi a = 0 a = 0 a = 0 a  0 A.  . B.  . C.  . D.  . b  0  b  0  b  0  b  0 
Câu 15. Tam thức bậc hai nào sau đây luôn dương với mọi x  ? A. 2 x − 2x + 1. B. 2 x − 8x +192. C. 2 x − 3x + 2. D. 2 5 − x + 2x − 229.
Câu 16. Cho hai số thực a, b tùy ý. Mệnh đề nào sau đây là đúng?
A. a + b a + b .
B. a + b = a + b .
C. a + b a + b .
D. a + b a + b . 5x 3x − 2 4
Câu 17. Tìm điều kiện xác định của bất phương trình +  7 + 2 x + 1 2 x − 5 2 x − 5 5 5 5 5 A. x  . B. x  . C. x  . D. x  . 2 2 2 2
Câu 18. Cho đường thẳng  : 2x − y + 1 = 0 . Điểm nào sau đây nằm trên đường thẳng  ?  1   1 
A. D (0; −1) .
B. A (1;1) . C. B ; 2   . D. B ; −2   .  2   2 
Câu 19. Phương trình nào sau đây là phương trình đường thẳng đi qua hai điểm A ( a; 0); B (0;b ); a, b  0 ? x y x y A. + = 1. B. + = 0 .
C. ax + by = ab .
D. ax + by = 1. a b a b
Câu 20. Câu nào đúng trong các câu sau?
A. Miền nghiệm của bất phương trình x  0 là nửa mặt phẳng bên phải trục tung kể cả biên (bờ).
B. Miền nghiệm của bất phương trình 2x − y −1  0 chứa điểm M ( −1;1) .
C. Miền nghiệm của bất phương trình 100 x + 400 y + 1  0 là nửa mặt phẳng kể cả bờ.
D. Miền nghiệm của bất phương trình 2x − y −1  0 chứa điểm O (0; 0) .
Câu 21. Tập nghiệm của bất phương trình 1 1  là x − 3 x + 3 A. ( −; −3) (3;+) . B. . C. (3; + ) . D. ( −; −3 3;+) . x
Câu 22. Các nghiệm tự nhiên bé hơn 4 của bất phương trình 2 − 23  2 x − 16 là 5
A. Một kết quả khác.
B. −4; −3; −2; −1; 0;1; 2;3  . 35 C. −  x  4 .
D. 0;1; 2; 3} . 8
Câu 23. Cho tam giác ABC có A(2; 6) , B(0; 3) , C (4; 0) . Phương trình đường cao AH của ABC  là:
A. 3x − 4 y + 18 = 0 .
B. 4 x − 3 y + 10 = 0 .
C. 3x + 4 y − 30 = 0 .
D. 4 x − 3 y − 10 = 0 .
Câu 24. Tập nghiệm của bất phương trình ( 2 x + x − ) 2 2
2 x − 1  0 là  5 − 13   9  A.  −1;   (2; +)  .
B. −4; −5; −  . 2     2  Trang 22/40  2   2  17  C.  −2; −    ;1     .
D. ( −; −5  ; 5      3 . 2 2      5 
Câu 25. Gọi S là tập nghiệm của bất phương trình 2
x − x − 12  0 . Tập nào sau đây không là tập con của S .
A. (−; − 5 .
B. 0; +  ) .
C. (−; − 3 .
D. 5; + ) . x − m m
Câu 26. Tập hợp các giá trị của m để phương trình 2 x −1 + = có nghiệm là: x −1 x −1 1   1   1  A. ; +   . B. ; +   . C. −;   . D. (1; + ) . 3   3   3 
Câu 27. Tính chu vi tam giác ABC biết rằng AB = 6 và 2sin A = 3sin B = 4sin C . A. 26. B. 13. C. 5 26. D. 10 6.
Câu 28. Cho tam giác ABC đều nội tiếp đường tròn bán kính R = 8 . Tính diện tích của tam giác ABC . A. 30 . B. 26 . C. 48 3 . D. 24 3 .
Câu 29. Gọi x , x là nghiệm của phương trình 2
x + 4 x − 2 = 2 x − 1 . Tính tổng S = x + x . 1 2 1 2 8 4 4 8 A. S = − . B. S = . C. S = − . D. S = . 3 3 3 3
Câu 30. Cho a, b, c  0 và a + b + c =1
. Dùng bất đẳng thức Côsi ta chứng minh được  1   1   1  1 + 1 + 1 +  64      
. Dấu đẳng thức xảy ra khi và chỉ khi nào: a   b   c  1
A. a = b = c = 1.
B. a = b = c = . C. a 1, b c 0.
D. a = b = . c 3
Câu 31. Bất phương trình 2x − 5  3 có tập nghiệm là  5  A. ( 2;3) . B.   . C.   0 . D. 1; 4 .  2 
( x + 3)(4 − x)  0
Câu 32. Tìm m để hệ bất phương trình  có nghiệm? x m −1  A. m  2 − .
B. m = 5 .
C. m  5 .
D. m  5 .
Câu 33. Cho tam giác ABC có A (1; 1) , B (0; −2) , C ( 4; 2) . Viết phương trình tổng quát của trung tuyến AM .
A. x − y = 0 .
B. 2 x + y − 3 = 0 .
C. x + 2 y − 3 = 0 .
D. x + y − 2 = 0 . x = 1+ 3t
Câu 34. Tính khoảng cách d từ điểm M ( 2; 0) đến đường thẳng  . y = 2 − 4t  8 2 5 2 A. d = . B. d = . C. d = . D. d = . 5 5 2 5 4
Câu 35. Cho hàm số y = x +
, ( x  1) . Giá trị nhỏ nhất của y là: x − 1 A. 5 B. 2 . C. 4 . D. 3 . PHẦN II: TỰ LUẬN
Câu 1. Tìm m để biểu thức sau luôn dương: ( 2 m + ) 2
2 x − 2(m + 1)x + 1.
Câu 2. Cho tam giác ABC có 2 2 2
m + m = 5m . Chứng minh: 2 2 2
sin B + sin C = sin A . b c a Trang 23/40
Câu 3. Cho tam giác ABC , biết A (1; 3) và hai trung tuyến có phương trình là x − 2 y + 1 = 0, y −1 = 0 . Hãy
lập phương trình tổng quát, tham số của mỗi cạnh ABC  .
Câu 4. Cho a, b là các số thực thuộc đoạn 0; 
1 . Chứng minh rằng ( − a ) ( − b ) ( a + b ) 8 1 1  . 27
------------- HẾT ------------- Trang 24/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 7 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 007
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Miền nghiệm của bất phương trình 5 ( x + 2) − 9  2x − 2 y + 7 không chứa điểm nào trong các điểm sau? A. (0; 0) . B. ( 2; −1) . C. ( −2;1) . D. ( 2; 3) .
Câu 2. Tìm tọa độ vectơ chỉ phương của đường thẳng song song với trục Oy . A. (1; −1). B. (1; 0 ). C. ( 0;1). D. (1;1).
Câu 3. Trong mặt phẳng Oxy , đường thẳng y = 2 x − 3 có một véc-tơ pháp tuyến n là
A. n = (−2; − ) 1 . B. n = (2; − ) 1 . C. n = (2; ) 1 . D. n = (1; 2) .
Câu 4. Miền của bất phương trình 2x + y  1 không chứa điểm nào sau đây?
A. A (1;1) .
B. B ( 2; 2) .
C. C (3;3) .
D. D ( −1; −1) .
Câu 5. Viết phương trình tổng quát của đường thẳng đi qua điểm O (0 ; 0) và song song với đường thẳng có
phương trình 6x − 4 y +1 = 0.
A. 3x − y − 1 = 0 .
B. 3x − 2 y = 0 .
C. 6 x − 4 y − 1 = 0 .
D. 4 x + 6 y = 0 .
Câu 6. Hỏi cặp số (1; −1) là nghiệm của bất phương trình nào sau đây?
A. x + y − 3  0 .
B. − x − y  0 .
C. x + 3 y + 1  0 .
D. − x − 3 y − 1  0 .
Câu 7. Tam giác ABC vuông cân tại A có AB = AC = a . Đường trung tuyến BM có độ dài là 3 a 5 A. a . B. a 2 . C. a 3 . D. . 2 2
Câu 8. Tam thức bậc hai f ( x) 2
= x − 3x − 4 âm khi.
A. x  (−; −4  1; + ) .
B. x  ( −; −  1  4; + ) .
C. x  −4; 2 . D. (−1; 4) . 2
Câu 9. Đường thẳng đi qua điểm C (3; −2) và có hệ số góc k =
có phương trình là 3
A. 2 x − 3 y − 12 = 0 .
B. 2x − 3 y − 9 = 0 .
C. 3x − 2 y − 13 = 0 .
D. 2 x + 3 y = 0 .
Câu 10. Cho hàm số y = ax + b, a  0, a, b là tham số. Mệnh đề nào sau đây đúng? b
A. Hàm số y = ax + b nhận giá trị dương trên − ; +   . a   b
B. Hàm số y = ax + b nhận giá trị âm trên − ; +   . a
C. Hàm số y = ax + b nhận giá trị âm trên .
D. Hàm số y = ax + b nhận giá trị dương trên . 1 − x x − 1
Câu 11. Số nào sau đây là nghiệm của bất phương trình  ? 3 − x 3 − x 3 A. 1 . B. 0 . C. . D. 2 . 2 Trang 25/40
Câu 12. Cho tam giác ABC . Trung tuyến AM có độ dài : A. 2 2 2
2b + 2c − a . B. 2 2 2
b + c − a . 1 C. 2 2 2
2b + 2c − a . D. 2 2 2
3a − 2b − 2c . 2
Câu 13. Tìm mệnh đề đúng? 1 1
A. a b   .
B. a b và c d ac bd . a b
C. a b ac bc, (c  0) .
D. a b ac bc .
Câu 14. Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của x  ?
A. 3 + x  2 + x . B. 2 2
3x  2x .
C. 2x  3x .
D. 3x  2x .
Câu 15. Cặp số nào sau đây là nghiệm của bất phương trình –2 ( x – y ) + y  3 ?
A. ( –1; –2) . B. ( 4; 4) . C. ( 4; –4) . D. ( 2;1) .
Câu 16. Trong các giá trị sau, giá trị nào không là nghiệm của bất phương trình 2x +1  0 . −4 A. x = .
B. x = 1 .
C. x = 2 .
D. x = 6 . 3 x −
Câu 17. Tìm điều kiện của bất phương trình 2 3  x − 2 . 6 − 3x
A. x  2 .
B. x  2 .
C. x  2 .
D. x  2 .
Câu 18. Cho hai số thực a, b tùy ý. Mệnh đề nào sau đây là đúng?
A. a + b = a + b .
B. a + b a + b .
C. a + b a + b .
D. a + b a + b .
Câu 19. Cặp bất phương trình nào sau đây không tương đương? A. 2
x (x + 2)  0 và x + 2  0 . B. 2
x (x + 2)  0 và x + 2  0 1 1
C. x −1  x và (2x +1) x −1  x(2x +1) . D. 2x −1 + 
và 2x −1  0 . x − 3 x − 3
Câu 20. Cho tam giác ABC có độ dài ba cạnh là AB = 2 , BC = 3 , CA = 4 . Tính góc ABC (chọn kết quả gần đúng nhất) A. 104 29   . B. 75 31   . C. 120 . D. 60 .
Câu 21. Tìm tập nghiệm của bất phương trình 2 2
x − x −12  x + 12 − x .
A. −3; 4 .
B. ( −; −3)  ( 4; + ) . C. ( −3; 4) .
D. ( −; −3  4; + ) . h
Câu 22. Cho tam giác ABC có 0 A = 30 , góc 0
B = 45 . Tìm a ? hb h 1 h h 2 h 1 A. a = . B. a = 2 . C. a = . D. a = . h 2 h h 2 hb 2 2 b b b Câu 23. Cho 2 2
x + y = 1, gọi S = x + y . Khi đó ta có
A. S  2 .
B. − 2  S  2 .
C. −1  S  1.
D. S  2 .
Câu 24. Cho hai điểm A(1; −4) và B (3; 2). Viết phương trình tổng quát của đường thẳng trung trực của đoạn AB .
A. x + y −1 = 0 .
B. 3x + y + 1 = 0 .
C. x − y + 4 = 0 .
D. x + 3 y + 1 = 0 .
Câu 25. Với x thuộc tập hợp nào dưới đây thì nhị thức bậc nhất f ( x ) = 2 x + 1 − ( x + 4) luôn dương? A. x  2
− hoặc x  2 . B. 1 −  x 1.
C. Một đáp số khác.
D. x  2 . Trang 26/40
x + m  0 (1)
Câu 26. Cho hệ bất phương trình  2 2
x − x + 4  x − 1 (2) 
Hệ đã cho có nghiệm khi và chỉ khi:
A. m  5.
B. m  –5..
C. m  5. .
D. m  –5. .
Câu 27. Tìm tọa độ vectơ chỉ phương của đường thẳng đi qua hai điểm A ( −3; 2) và B (1; 4) A. u = (2; ) 1 .
B. u = (−1; 2) .
C. u = (−2; 6) . D. u = (1; ) 1 .
Câu 28. Cho tam giác ABC có BC = 5cm, BAC = 30 . Bán kính đường tròn ngoại tiếp tam giác ABC bằng 5 3 A. cm .
B. 10cm .
C. 5 3cm . D. 5cm . 3
Câu 29. Trong mặt phẳng Oxy , cho đường thẳng  : 4 x + 3 y − 7 = 0 và điểm M (1; −2) . Phương trình tất cả
các đường thẳng song song với  và cách điểm M một khoảng bằng 1 là
A. 4x + 3 y − 7 = 0; 4x + 3 y + 3 = 0 .
B. 4x + 3 y − 3 = 0 .
C. 4x + 3 y + 7 = 0; 4x + 3 y − 3 = 0 .
D. 4x + 3 y + 7 = 0 .
Câu 30. Cho bất phương trình ( 2
m − 4) x m −1 . Với giá trị nào của m thì bất phương trình có tập nghiệm là rỗng? m = −2 m = 2 A.  . B.  .
C. m = 2 . D. m = 2 − . m = 1  m = 1  x − 1
Câu 31. Tìm tập nghiệm của bất phương trình  ( . x − 2) ( 0 2 x − 5x + 4)
A. ( −; 2)  ( 4; + ) \   1 .
B. ( −; 2)  ( 4; + ) . C. 2; 4 .
D. ( −; 2  4; + ) .
Câu 32. Tập nghiệm của bất phương trình 4 2 x 5x 4 0 là A. 2; 1 1; 2 . B. 2; 1 . C. 1; 2 . D. 1; 4 .
Câu 33. Nghiệm của bất phương trình | 3x − 6 |
x − 3  0 là:
A. x = 2 .
B. x = 3 và x = 2 .
C. x  3 .
D. x = 3 .
Tập nghiệm của bất phương trình x − 2006 
2006 − x là gì?
A. ( −, 2006) . B.   2006 . C.  .
D. 2006, + ) . 1
Câu 35. Cho hàm số y = x +
xác định trên (1; + ) . Gọi m là giá trị nhỏ nhất của hàm số, giá trị m nằm x − 1
trong khoảng nào sau đây A. ( 4; 7 ) . B. ( 2;8) . C. ( −2;3) . D. (5; + ) . PHẦN II: TỰ LUẬN
Câu 1. Tìm m để biểu thức sau luôn dương 2
(m + 2)x + 2(m + 2)x + m + 3
Câu 2. Tam giác ABC vuông tại A , đồng dạng với tam giác AB C
  . Gọi a = B C
 , b = AC , a = AB và 1 1 1
h  là đường cao hạ từ A của tam giác AB C
  . Chứng minh rằng: = + a   b bc ch h a a
Câu 3. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A (1; 3) và hai đường trung tuyến là
BB ' : x − 2 y + 1 = 0, CC ' : y − 1 = 0. Xác định tọa độ đỉnh B và C. Trang 27/40 a b c b c a
Câu 4. Với a, b, c  0 thỏa mãn điều kiện: + + = 1. Chứng minh rằng: + +  1 b c a a b c
------------- HẾT ------------- Trang 28/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 8 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 008
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. 2x + 5 y − 3z  0 .
B. 2x + y  5 . C. 2 2
2x + 5 y  3 . D. 2
2 x + 3x + 1  0 .
Câu 2. Cho hai số thực a, b tùy ý. Mệnh đề nào sau đây là đúng?
A. a + b a + b .
B. a + b a + b .
C. a + b a + b .
D. a + b = a + b .
Câu 3. Nếu a b và c d thì bất đẳng thức nào sau đây luôn đúng? a b
A. a + c b + d .
B. a − c b − d .
C. ac bd . D.  . c d
Câu 4. Trong các hệ bất phương trình sau, hệ nào là hệ bất phương trình bậc nhất phương trình bậc nhất một ẩn? 2
x − 2x − 3  0
2x − 3y  7 A.  . B.  . 2 x − 4  0  x + 7 y  9 
( 2 −1) x + 6  0
2x − 5  2(1+ x ) C.  . D.  . 7 2  3x − 5  6x − 7  0 
Câu 5. Cho bất phương trình 4 ( x −1) + 5 ( y − 3)  2x − 9 . Khẳng định nào dưới đây là khẳng định đúng?
A. Điểm D ( 2;5) thuộc miền nghiệm của bất phương trình đã cho.
B. Điểm B (1;1) thuộc miền nghiệm của bất phương trình đã cho.
C. Điểm C ( −1;1) thuộc miền nghiệm của bất phương trình đã cho.
D. Điểm O (0; 0) thuộc miền nghiệm của bất phương trình đã cho.
Câu 6. Cặp số ( 2; 3) là nghiệm của bất phương trình nào sau đây?
A. x – 3 y + 7  0 .
B. 2 x – 3 y – 1  0 .
C. x – y  0 .
D. 4 x  3 y .
Câu 7. Giải bất phương trình 2x −1  0 . Kết quả tập nghiệm nào sau đây đúng?  1   1  A. S = − ;   . B. S = ; +    .  2   2   1   1  C. S = − ;   . D. S = − ; +    .  2   2 
Câu 8. Viết phương trình tổng quát của đường thẳng đi qua điểm O (0 ; 0) và song song với đường thẳng có
phương trình 6x − 4 y +1 = 0.
A. 4 x + 6 y = 0 .
B. 3x − y − 1 = 0 .
C. 3x − 2 y = 0 .
D. 6 x − 4 y − 1 = 0 .
Câu 9. Cho tam giác ABC có độ dài ba cạnh là AB = 2 , BC = 5 , CA = 6 . Tính độ dài đường trung tuyến
MA , với M là trung điểm của BC 15 55 110 A. . B. . C. . D. 55 . 2 2 2
Câu 10. Cho tam giác ABC có AB = 5 ; BC = 7 ; AC = 8 . Số đo góc A bằng A. 90 . B. 60 . C. 30 . D. 45 .
Câu 11. Cho nhị thức bậc nhất f ( x ) = ax + b ( a  0) . Chọn kết quả sai trong các kết quả sau. Trang 29/40 b
A. f ( x ) có giá trị bằng 0 khi x = − . ab
B. f ( x ) có giá trị cùng dấu với hệ số a khi x lấy các giá trị trong khoảng − ; +    .  a   b
C. f ( x ) có giá trị trái dấu với hệ số a khi x lấy các giá trị trong khoảng −; −   .  a
D. f ( x ) có giá trị cùng dấu với hệ số a khi x lấy các giá trị trong khoảng ( −; +  ) . 2 2
Câu 12. Bất phương trình ( x − 5 )  ( x + 5 ) −10 có tập nghiệm là  5   5 
A. S = (3; + ) .
B. S =  −;   . C. S =  ; 3    . D. S = . 2   2  
Câu 13. Cho hai điểm A(4; 0), B(0; −5) . Phương trình đoạn thẳng AB là x y x y x y x y A. + = 1. B. + = 0 . C. − = 0 . D. + = 1. −5 4 −5 4 4 5 4 −5
x = −1 − t
Câu 14. Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng  :
, (t  ) . Một vectơ chỉ y = 2 + 4t
phương của đường thẳng  là
A. u = (−1; 4) .
B. u = (−1; 2) . C. u = (2; ) 1 . D. u = (4; ) 1 .
Câu 15. Cho tam giác ABC . Hỏi mệnh đề nào sau đây sai?
A. Đường trung trực của AB có AB là vectơ pháp tuyến.
B. BC là một vectơ pháp tuyến của đường cao AH .
C. BC là một vectơ chỉ phương của đường thẳng BC .
D. Các đường thẳng AB, BC, CA đều có hệ số góc.
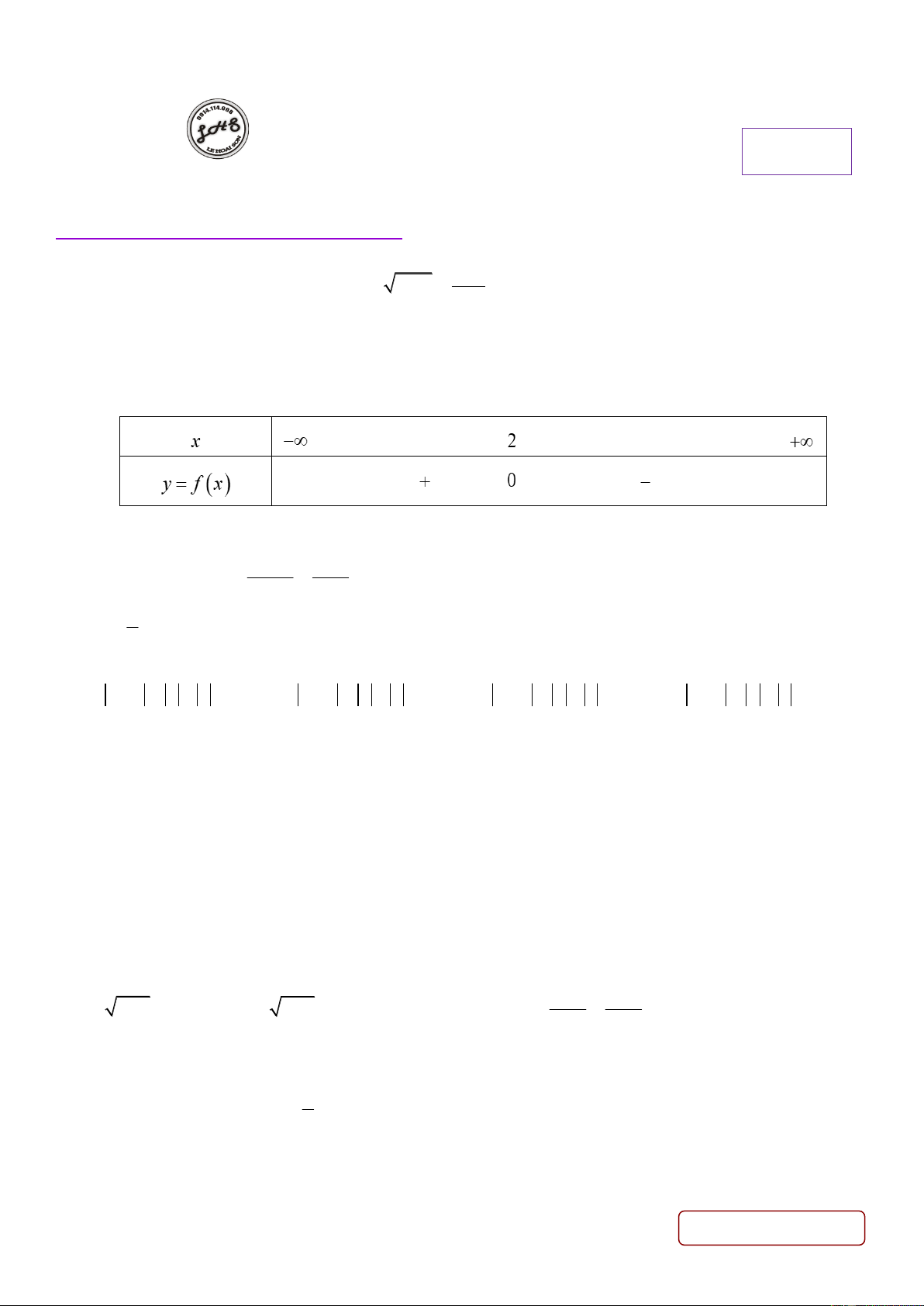
Câu 16. Cho nhị thức bậc nhất y = f ( x ) = ax + b , a  0 có bảng xét dấu như sau: Tìm phát biểu đúng.
A. 3a + b  0 .
B. b  0 .
C. a  0 .
D. b − a  0 .
Câu 17. Tập nghiệm của bất phương trình 3x − 2 y + 1  0 là
A. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng 3x − 2 y + 1 = 0 (không bao gồm đường thẳng).
B. Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng 3x − 2 y + 1 = 0 (bao gồm đường thẳng).
C. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng 3x − 2 y + 1 = 0 (bao gồm đường thẳng).
D. Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng 3x − 2 y + 1 = 0 (không bao gồm đường thẳng).
Câu 18. Tìm điều kiện xác định của bất phương trình 1+ x − 1− x x là
A. x  ( −1;1) .
B. x  (0;1) .
C. x  0;  1 .
D. x  −1;  1 .
Câu 19. Cho tam giác ABC có các cạnh BC = a = 6 cm , AC = b = 7 cm , AB = c = 5 cm . Tính cos B . 1 1 A. cos B = . B. cos B = . 15 5 5 19 C. cos B = . D. cos B = . 7 35
Câu 20. Cặp số nào sau đây không là nghiệm của bất phương trình 5x − 2 ( y −1)  0 ? A. ( –1; 0) . B. ( 0;1) . C. (1; 3) . D. ( –1;1) . Trang 30/40 Câu 21. Cho ABC
có BC = a , BAC = 120 . Bán kính đường tròn ngoại tiếp ABC  là a 3 a 3 a A. R = .
B. R = a . C. R = . D. R = . 3 2 2
Câu 22. Tập nghiệm của bất phương trình x + x + 2  2 +
x + 2 trên tập số thực là A.  .
B. ( −; 2) . C.   2 .
D. −2; 2 .
Câu 23. Cho tam giác ABC có ba cạnh là 6, 8, 10 . Tính bán kính đường tròn nội tiếp tam giác ABC . A. 2 B. 1 . C. 3 . D. 4
Câu 24. Cho bất phương trình x + 2m  2 + mx . Khi m  1 tập nghiệm của bất phương trình là:
A. ( −2; + ) .
B. ( −; −2) .
C. ( 2; + ) .
D. ( −; 2) .
Câu 25. Cho tam giác ABC có A (1; 1) , B (0; −2) , C ( 4; 2) . Viết phương trình tổng quát của trung tuyến CM .
A. 6x − 5 y −1 = 0 .
B. 5x − 7 y − 6 = 0 .
C. 3x + 7 y − 26 = 0 .
D. 2 x + 3 y − 14 = 0 .
Câu 26. Bất phương trình 2 x + 1  x + 4 có tập nghiệm là
A. ( −; −1) .
B. ( −; −1)  ( 2; + ) .
C. ( −; −2)  (2; + ) .
D. ( 2; + ) . 2 2 x − 3x + 1
Câu 27. Tìm tập nghiệm của bất phương trình  0 . 4x − 3  1   1   3  A. ;1   . B. ;1 \     .  2   2   4   1   1   3  C. −;  (1;+   ) . D. −;  
 (1; +) \   .  2   2   4 
Câu 28. Tìm tập nghiệm của bất phương trình: 2
x − 6 x + 9  0 . A. \   3 . B.   3 . C. \   0 . D. .
Câu 29. Đường thẳng  : 5x + 3 y = 15 tạo với các trục tọa độ một tam giác có diện tích bằng bao nhiêu? A. 5. B. 3. C. 15. D. 7,5.
Câu 30. Tổng các nghiệm nguyên của bất phương trình ( x + 3) ( x −1)  0 là A. −5 . B. −4 . C. 1 . D. 4 .  ( ) 16 − 4 x f x = − 4  2  x − x − 12
Câu 31. Cho các đa thức 
tìm các giá trị của x để f ( x ) luôn âm, và g ( x ) luôn g (x) 1 1 1 = + −  x − 2 x − 1 x dương
A. (−4; − 2 )  (1; + ).
B. (− 2;0)  (1; 2 )  (2; + ).
C. ( −4; −3)  (0;1)  ( 2; 2).
D. (−3; 2 )  (4; + ).
Câu 32. Nếu 1  m  2 thì số nghiệm của phương trình 2
x − 2mx + 5m − 6 = 0 là bao nhiêu.
A. Chưa xác định được B. 0. C. 1. D. 2.
Câu 33. Cho  ABC có A(2; −1), B ( 4; 5) , C (−3; 2) . Viết phương trình tổng quát của đường cao BH .
A. 3x + 5 y − 37 = 0 .
B. 3x − 5 y − 13 = 0 .
C. 5x − 3 y − 5 = 0 .
D. 3x + 5 y − 20 = 0 .
Câu 34. Cho a, b, c  0 . Xét các bất đẳng thức sau Trang 31/40 a b a b c 1 1 1 9 I) +  2 II) + +  3 III) + +  b a b c a a b c a + b + c
Bất đẳng thức nào đúng?
A. Chỉ II) đúng.
B. Chỉ III) đúng.
C. Cả I), II), III) đúng.
D. Chỉ I) đúng. 9 4 a a
Câu 35. Hàm số y = +
với 0  x  2 đạt giá trị nhỏ nhất tại x =
( a, b nguyên dương, phân số x 2 − x b b
tối giản). Khi đó a + b bằng A. 7 . B. 9 . C. 13 . D. 11 . PHẦN II: TỰ LUẬN
Câu 1. Tìm các giá trị nguyên của tham số m 2 2
để f ( x ) = 3( 4 − m ) x + 2 ( m − 2) x + 1  0, x R . 2bc
Câu 2. Tam giác ABC vuông tại A . Gọi d là đường phân giác của góc A . Chứng minh rằng: d = . b + c
Câu 3. Trong mặt phẳng với hệ tọa độ với Oxy, cho tam giác ABC biết phương trình cạnh
BC : x − 2 y = 5 = 0, phương trình đường trung tuyến BB ' : y − 2 = 0 và phương trình đường trung tuyến
CC ' : 2 x − y − 2 = 0. Tìm tọa độ các đỉnh của tam giác.
Câu 4. Cho a, b, c là các số thực dương. Chứng minh rằng: 2 2 2 3 3 3 a bc + b ac + c
ab a + b + c .
------------- HẾT ------------- Trang 32/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 9 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 009
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cặp số ( x ; y ) nào sau đây là nghiệm của bất phương trình 4x + 3 y  −3 ?
A. ( −1; −1) . B. ( −1;1) C. (0 ; −1) .
D. ( −4 ; 0) .
Câu 2. Điểm A ( 2;1) thuộc miền nghiệm của bất phương trình nào sau đây?
A. x − y + 1  0 .
B. −2 x + y − 2  0 .
C. 2x − y + 1  0 .
D. x − 2 y  0 .
Câu 3. Điểm O (0; 0) thuộc miền nghiệm của bất phương trình nào sau đây?
A. 2 x + 5 y − 2  0 .
B. 2 x + y + 2  0 .
C. x + 3 y + 2  0 .
D. x + y + 2  0 .
Câu 4. Cho tam giác ABC có 0
B = 60 , AB = 10, BC = 6 . Tính độ dài cạnh AC : A. 2 19 . B. 6 2 . C. 14 . D. 76 .
Câu 5. Tìm khẳng định đúng trong các khẳng định sau?
A. f ( x ) 3
= 3x + 2x −1 là tam thức bậc hai.
B. f ( x ) 4 2
= x − x +1 là tam thức bậc hai.
C. f ( x ) 2
= 3x + 2x − 5 là tam thức bậc hai.
D. f ( x ) = 2x − 4 là tam thức bậc hai.
Câu 6. Số x = 1
− là nghiệm của bất phương trình nào sau đây?
A. 2x −1  0 .
B. x −1  0 .
C. 3 − x  0 .
D. 2x +1  0 . 1
Câu 7. Tập xác định của hàm số y = là: 2 − x
A. 2; + ) .
B. ( −; 2) .
C. ( 2; + ) .
D. ( −; 2 . x = 5 + t
Câu 8. Trong mặt phẳng toạ độ Oxy , cho đường thẳng d : 
. Hãy chỉ ra một vectơ chỉ phương u y = 3 − 2t
của đường thẳng đã cho.
A. u = (5;3) .
B. u = (1; − 2) .
C. u = (3; − 5) . D. u = (2; ) 1 .
Câu 9. Tính diện tích tam giác ABC có ba cạnh là 13, 14, 15. A. 16 24 . B. 84. C. 6411 . D. 168.
Câu 10. Trong mặt phẳng Oxy, đường thẳng đi qua A ( −1; 2) , nhận n = (2; −4) làm véctơ pháp tuyến có phương trình là
A. x + y + 4 = 0 .
B. − x + 2 y − 4 = 0 .
C. x − 2 y + 5 = 0 .
D. x − 2 y − 4 = 0 .
Câu 11. Cho bất phương trình f ( x )  g ( x )  0 , x
  . Phép biến đổi nào sau đây là sai ? 2 2
A. f ( x )  g ( x )  2 f ( x )  f ( x ) + g ( x ) .
B. f ( x )  g ( x )   f ( x )   g ( x )     . 3 3
C. f ( x )  g ( x )   f ( x )   g ( x )     . D.
( )  ( )  ( ) ( )   ( ) 2 f x g x f x g x g x    .
Câu 12. Phương trình đường thẳng đi qua N (1; 2) và song song với đường thẳng 2 x + 3 y − 12 = 0 là.
A. 2 x + 3 y − 8 = 0 .
B. 2 x + 3 y + 8 = 0 .
C. 4 x + 6 y + 1 = 0 .
D. 2 x − 3 y − 8 = 0 .
Câu 13. Cho hệ bất phương trình Trang 33/40
x − y  0 
x − 3 y + 3  0 . 
x + y − 5  0
Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Điểm C (1; −1) thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm D ( −2; 2) thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm O (0; 0) thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm B (5;3) thuộc miền nghiệm của hệ bất phương trình đã cho.
Câu 14. Cho m
. Biểu thức nào sau đây không phải là nhị thức bậc nhất đối với x ?
A. f ( x ) 2
= −2018x + m +1 .
B. f ( x ) = 2017 x + m + 1 .
C. f ( x ) = ( m + 1) x + 2018 .
D. f ( x) = ( 2 m + ) 1 x + 2017 .
Câu 15. Cho tam giác ABC có a = 2 3, b = 2 2 và c = 2 . Tính độ dài của trung tuyến AM . A. 2. B. 3. C. 3 . D. 5.
Câu 16. Cho hai số thực a, b tùy ý. Mệnh đề nào sau đây là đúng?
A. a + b a + b .
B. a + b a + b .
C. a + b = a + b .
D. a + b a + b .
Câu 17. Tìm vectơ pháp tuyến của đường thẳng song song với trục Oy . A. (1; 0 ) . B. ( 0;1). C. (−1; 0). D. (1;1).
Câu 18. Tập nghiệm của bất phương trình x − 2006 
2006 − x là gì?
A. (−; 2006) . B. {2006} . C.  .
D. [2006; +) .
Câu 19. Nếu a b  0 , c d  0 thì bất đẳng thức nào sau đây không đúng?
A. ac bc .
B. a − c b − d . 2 2
C. a b .
D. ac bd .
Câu 20. Tập nghiệm của bất phương trình 2x −1  x + 3 là
A. S = ( 4 ; +  ) .
B. S = ( −4 ; +  ) .
C. S = ( − ; 4) .
D. S = ( − ; − 4) . Câu 21. Cho ABC
có AB = 5, A = 40 ,
B = 60 . Độ dài BC gần nhất với kết quả nào? A. 3,8. B. 3, 7 . C. 3, 5 . D. 3,1 .
Câu 22. Tìm tất cả giá trị của m để khoảng cách từ M ( −1; 2) đến đường thẳng  : mx + y − m + 4 = 0 bằng 2 5 ? 1 A. m = 2  . B. m = − . 2 1 C. m = 2 − .
D. m = −2; m = . 2
Câu 23. Tìm vectơ pháp tuyến của đường thẳng đi qua 2 điểm phân biệt A ( a; 0) và B (0;b)
A. (b; a ) .
B. ( a;b ) .
C. (b; −a ) .
D. ( −b; a ) . x +
Câu 24. Tập hợp nghiệm của bất phương trinh sau: 1 3 5 + 3  là: x + 2 x − 2 12 A. x  − hoặc 2
−  x  2 .
B. ( −; 2 . 5 C. (2; +) . D. \ {2} .
Câu 25. Bất phương trình 2
x − 10 x + 16  0 có tập nghiệm là A. (8; + ) B. ( 2;8) C. ( −2;8)
D. ( −; 2) Trang 34/40 1
Câu 26. Bất phương trình 2 x − x +
 0 có tập nghiệm là. 4  1   1   1  1  A. −; −   . B. ; +   C. −;   . D.   .  2   2   2   2 
Câu 27. Cho bất phương trình: 2
(m − 2)(x + 3)  m + m − 6 (1) . Xét các mệnh đề sau:
I. Nếu m  2 : (1) có nghiệm là x m .
II. Nếu m  2 : (1) có nghiệm là x m .
III. Nếu m = 2 : (1) vô nghiệm.
Mệnh đề nào đúng?
A. I, II và III. B. Chỉ II. C. I và II. D. Chỉ I.
Câu 28. Hình bình hành ABCD có AB = a , BC = a 2 và BAD = 45 . Khi đó hình bình có diện tích là A. 2 2a . B. 2 a 2 . C. 2 a . D. 2 a 3 . 2x −1  0
Câu 29. Hệ phương trình 
có nghiệm khi và chỉ khi x − m  2  3 3 3 3 A. m  − . B. m  − . C. m  − . D. m  − . 2 2 2 2 x −
Câu 30. Với x thuộc tập hợp nào dưới đây thì f ( x) 2 1 = − 2 luôn dương? x − 1  3   3  A. , + \     1 . B. −,  (3, +   ) .  4   4   3  C. ,1   . D. (1, + ) .  4  x − 1
Câu 31. Tập nghiệm của bất phương trình  0 là: 2 x + 2 x + 1
A. (−; −1)  (1; +) .
B. ( −;1) .
C. (−; −1)  (−1;1) . D. ( −1;1) . 2
x − 7x + 6  0 (1)
Câu 32. Tập nghiệm của hệ bất phương trình  là.  2x −1  3 (2)  A. (1; 6 ) . B. 1; 2 . C. (1; 2 ) . D. ( −1; 6) .
Câu 33. Trong mặt phẳng Oxy, cho ba điểm A (3; 0) , B ( −5; 4) , C (10; 2). Đường thẳng d đi qua điểm C và
đồng thời cách đều hai điểm ,
A B có phương trình là
A. x + 2 y − 14 = 0 hoặc y − 2 = 0 .
B. − x − 2 y + 7 = 0 .
C. 2x − y + 18 = 0 .
D. − x + 2 y + 6 = 0 . a b a b c 1 1 1 9
Câu 34. Cho các bất đẳng thức: +  2 ( I ) , + +  3 ( II ) , + +  (III ) (với b a b c a a b c a + b + c
a, b, c  0 ). Bất đẳng thức nào trong các bất đẳng thức trên là đúng?
A. chỉ I đúng.
B. chỉ II đúng.
C. chỉ III đúng.
D. I , II , III đều đúng.
Câu 35. Tìm giá trị nhỏ nhất m của hàm số f ( x ) 2 = x +
với x  1. x − 1
A. m = 1− 2 2 .
B. m = 1− 2 .
C. m = 1+ 2 .
D. m = 1+ 2 2 . PHẦN II: TỰ LUẬN Trang 35/40
Câu 1. Tìm m để biểu thức sau luôn âm: 2
g (x) = (m − 4)x + (2m − 8)x + m − 5
Câu 2. Tam giác ABC vuông tại A có các cạnh và góc vuông là b và c . Lấy một điểm M trên cạnh BC bc
sao cho BAM =  . Chứng minh rằng AM = .
b cos  + c sin 
Câu 3. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có đỉnh A ( 4; −1) phương trình đường cao
và trung tuyến kẻ từ đỉnh B lần lượt là 2 x − 3 y + 12 = 0 và 2 x + 3 y = 0 . Xác định tọa độ các đỉnh còn lại của tam giác ABC. 1
Câu 4. Với x  0 , tìm giá trị nhỏ nhất của các hàm số sau 2 y = 3x + . x
------------- HẾT ------------- Trang 36/40
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 10
Đề ôn tập: SỐ 10 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 010
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN 12 x
Câu 1. Tìm điều kiện của bất phương trình x − 2  . x − 1
A. x  1 .
B. x  1 .
C. x  2 .
D. x  2 .
Câu 2. Phương trình đường thẳng đi qua N (1; 2) và song song với đường thẳng 2 x + 3 y − 12 = 0 là.
A. 2 x − 3 y − 8 = 0 .
B. 2 x + 3 y − 8 = 0 .
C. 2 x + 3 y + 8 = 0 .
D. 4 x + 6 y + 1 = 0 .
Câu 3. Cho nhị thức bậc nhất y = f ( x ) = ax + b, b  0 có bảng xét dấu sau
Tìm phát biểu đúng.
A. b − a  0 .
B. 3a + b  0 .
C. a  0 .
D. b  0 . 2 x − 5 x − 3
Câu 4. Bất phương trình 
có tập nghiệm là 3 2  1  A. − ; +   .
B. ( 2; + ) .
C. ( −;1)  ( 2; + ) . D. (1; + ) .  4 
Câu 5. Cho hai số thực a, b tùy ý. Mệnh đề nào sau đây là đúng?
A. a + b a + b .
B. a + b = a + b .
C. a + b a + b .
D. a + b a + b .
Câu 6. Cho hệ bất phương trình
2x − 5 y − 1  0 
 2x + y + 5  0 . 
x + y + 1  0
Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Điểm C (0; −2) thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm D (0; 2) thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm O (0; 0) thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm B (1; 0) thuộc miền nghiệm của hệ bất phương trình đã cho.
Câu 7. Cặp bất phương trình nào sau đây không tương đương? 1 1
A. x −1  x và (2x + ) 1
x −1  (2x + ) 1 x . B. 2 x − 1 + 
và 2x −1  0. x − 3 x − 3 C. 2
x ( x + 2)  0 và x + 2  0. D. 2
x ( x + 2)  0 và x + 2  0.
Câu 8. Bất phương trình nào sau đây là bậc nhất một ẩn 2
A. 3x  1− 2x . B. − 3  x .
C. 2x + y  1 .
D. 2x −1 = 0 . xx = 1 + 2t
Câu 9. Đường thẳng d : 
đi qua điểm nào trong các điểm sau đây? y = 3 − t  Trang 37/40
A. P (3;5) .
B. Q (3; 2) .
C. M (2; −1) .
D. N ( −7; 0) .
Câu 10. Đường thẳng đi qua A ( −1; 2) , nhận n = ( 2 ; − 4) làm vecto pháp tuyến có phương trình là
A. x − 2 y + 5 = 0 .
B. x + y + 4 = 0 .
C. x − 2 y − 4 = 0 .
D. − x + 2 y − 4 = 0 .
Câu 11. Nếu a, b và c là các số bất kì và a b thì bất đẳng nào sau đây đúng? 2 2
A. a b .
B. a + c b + c .
C. c − a c − b .
D. ac bc .
Câu 12. Cho tam giác ABC có AB = 3 ; AC = 5 và BC = 6 . Giá trị của cos A bằng 2 1 2 1 A. . B. − . C. − . D. . 15 15 15 15
Câu 13. Tam thức nào dưới đây luôn dương với mọi giá trị của x ? A. 2
x − 2 x − 10 . B. 2
x − 2 x + 10 . C. 2
−x + 2x +10 . D. 2
x − 10 x + 2 .
Câu 14. Tập nghiệm S của bất phương trình: 4
− x +16  0.
A. S = ( −; 4.
B. S = ( 4; + ).
C. S = 4; + ).
D. S = ( −; −4.
Câu 15. Miền nghiệm của bất phương trình 3( x −1) + 4 ( y − 2)  5x − 3 là nửa mặt phẳng chứa điểm
A. O (0; 0) .
B. N ( −4; 2) .
C. P ( −2; 2) .
D. Q ( −5;3) .
Câu 16. Cho đường thẳng  : x − 2 y + 3 = 0 Véctơ nào sau đây không là véc tơ chỉ phương của  ? A. ( 4; −2) .
B. (−2; −1) . C. ( 2;1) . D. ( 4; 2) .
Câu 17. Tam thức bậc hai f ( x) 2
= x − 3x + 7
A. Không âm với mọi x .
B. Dương với mọi x .
C. Âm với mọi x  ( −; 0) .
D. Âm với mọi x .
Câu 18. Tam giác ABC có a 8 , c 3 , B
60 . Độ dài cạnh b bằng bao nhiêu? A. 61 . B. 49 . C. 97 . D. 7 .
Câu 19. Câu nào đúng trong các câu sau?
A. Miền nghiệm của bất phương trình 2x − y −1  0 chứa điểm O (0; 0) .
B. Miền nghiệm của bất phương trình x  0 là nửa mặt phẳng bên phải trục tung kể cả biên (bờ).
C. Miền nghiệm của bất phương trình 2x − y −1  0 chứa điểm M ( −1;1) .
D. Miền nghiệm của bất phương trình 100 x + 400 y + 1  0 là nửa mặt phẳng kể cả bờ.
Câu 20. Cho tam giác ABC . Trung tuyến m được tính theo công thức a 2 2 2 b + c a 2 2 2 b + c a A. 2 m = − . B. 2 m = + . a a 4 2 2 4 2 2 2 b + c a 2 2 2 a + c b C. 2 m = − . D. 2 m = − . a a 2 4 2 4
Câu 21. Phương trình đường thẳng đi qua N (1; 2) và song song với đường thẳng 2x + 3 y − 12 = 0 là
A. 2 x + 3 y + 8 = 0 .
B. 4x + 6 y + 1 = 0 .
C. 2 x − 3 y − 8 = 0 .
D. 2 x + 3 y − 8 = 0 .
Câu 22. Cho bảng xét dấu:
Hàm số có bảng xét dấu như trên là
A. f ( x ) = 16x − 8 .
B. f ( x ) = − x − 2 .
C. f ( x ) = 8 − 4x .
D. f ( x ) = 2 − 4x .
Câu 23. Cho tam giác ABC có a = 6 , b = 8 , c = 10 . Diện tích S của tam giác ABC là A. 30 . B. 48 . C. 24 . D. 12 . Trang 38/40
Câu 24. Tập nghiệm của bất phương trình 2
x + 4 x + 4  0 là A.  . B. \ −  2 . C. . D. −  2 .
Câu 25. Bất phương trình x − 3  1 có tập nghiệm là A.   3 . B. 3; 4 . C. (2;3) .
D. ( −;2  4; + ) . 1 − x x − 1
Câu 26. Tìm tập nghiệm của bất phương trình  . 3 − x 3 − x
A. ( −;3) . B. (1; + ) \   3 .
C. ( −;1) .
D. ( −; 3) \   1 .
Câu 27. Trong tam giác ABC , hệ thức nào sau đây sai? c.sin A . b sin A A. sin C = . B. a = 2 .
R sin A . C. b = .
R tan B . D. a = . a sin B
Câu 28. Cho tam giác ABC với A 1;2 , B 0; 3 ,C 4; 0 . Tính chiều cao tam giác ABC ứng với cạnh BC 1 1 1 A. . B. . C. . D. 3 . 5 25 5
Câu 29. Trong các hình chữ nhật có cùng chi vi thì
A. Hình vuông có diện tích nhỏ nhất.
B. Hình vuông có diện tích lớn nhất.
C. Không xác định được hình có diện tích lớn nhất.
D. Cả A, B, C đều sai.
Câu 30. Tập nghiệm của bất phương trình 2
x − x − 5  4 − x là
A. (−3;1 − 2 )  (1 + 2;3) . B. −3;1 − 2   1  + 2;3     .
C. (−3;1 − 2   1  + 2;3   ) . D. [ − 3; 3] .
Câu 31. Với giá trị nào của m thì ba đường thẳng sau đồng quy?
d : 3x – 4 y +15 = 0, d : 5x + 2 y – 1 = 0, d : mx – 4 y +15 = 0. 1 2 3
A. m = –5 .
B. m = 5 .
C. m = 3 .
D. m = –3 .
Câu 32. Tìm tập nghiệm của bất phương trình ( 2
x − 2x + 4)( x − 3)  0 ?
A. 1  x  3 .
B. x  3 .
C. x  3 .
D. 0  x  2 . x − x +
Câu 33. Với x thuộc tập nào dưới đây thì f ( x ) 1 2 = − không âm? x + 2 x − 1  1 
A. ( −2; + ) . B. −2; −  (1;+  )  .  2   1    C. −2; −   . D. ( − − ) 1 ; 2  − ;1   .  2   2 
Câu 34. Biết bất phương trình (ẩn x ): (m − 1) x + 2m − 3  0 vô nghiệm. Tìm tất cả các giá trị tham số m . 3
A. m = 1.
B. m  1. C. m = .
D. m  1. 2 9 4 a a
Câu 35. Hàm số y = +
với 0  x  2 , đạt giá trị nhỏ nhất tại x =
( a , b nguyên dương, phân số x 2 − x b b
tối giản). Khi đó a + b bằng A. 9 . B. 13 . C. 11 . D. 7 . PHẦN II: TỰ LUẬN
Câu 1. Tìm giá trị lớn nhất của tham số m để f ( x ) 2
= x − 2mx + 8 − 2m  0,x R .
Câu 2. Cho đoạn thẳng AB . Lấy I là trung điểm của AB và M là điểm tùy ý. Chứng minh rằng: Trang 39/40 1 1 a) 2 2 2 2
MA + MB = 2MI + AB . b) 2 2 M . A MB = MI − AB . 2 4
Câu 3. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có đỉnh A ( 4; −1) phương trình đường cao
và trung tuyến kẻ từ đỉnh B lần lượt là 2 x − 3 y + 12 = 0 và 2 x + 3 y = 0 . Xác định tọa độ các đỉnh còn lại của tam giác ABC.
Câu 4. Cho a, b, c là các số thực dương. Chứng minh rằng 2 a ( 2 + b ) 2 + b ( 2 + c ) 2 + c ( 2 1 1
1 + a )  6ab . c
------------- HẾT ------------- Trang 40/40
TOÁN 185 NGUYỄN LỘ TRẠCH
10 ĐỀ ÔN TẬP GIỮA KỲ II - 2021 Đáp án: CHI TIẾT
Họ và tên :………………………………….Lớp:………….......……..……… Lớp 10 Mã đề [001] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 B A B A C A A D B B A C A D D B A C 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B A A B C D D C C C C D B D C D B Mã đề [002] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 D C D A D B A C A C B A D D C D B C 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 A A B B A B D C C A B A B B C D C Mã đề [003] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 D A B D C A C B B C A B D C C B A A 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 C D B A B A D D D A C D B A B C C Mã đề [004] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 C A C B A B A D B D B D B A C D A C 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 A C D C B C A B D B D C A B A D C Mã đề [005] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 A D B D D C A B B B A D B C D D D C 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B C A A A A B B A C C C A D B C C Mã đề [006] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 A B A D C D D C D A B C C A B C B C 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 A C A D B C B B A C D B D A D B A Mã đề [007] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 D C B D B C D D A A B C C A B A C B 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B A B B B D A D A D C C A A D C C Mã đề [008] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 B A A C A C B C B B D B D A D C A D 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B C A D A C B C B A D A B D C C D Mã đề [009] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 B C B A C D B B B C B A D C C D A C 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B A D D A A B D A C B A C C A D D Mã đề [010] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 D B A D C A A A B A B B B C A A B D 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 D C D C C D D C C A B B C B D A C
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 001 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 B A B A C A A D B B A C A D D B A C 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B A A B C D D C C C C D B D C D B
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn B
Ta có x  5  0  x  5  .
Ta xét các bất phương trình:  2
x x  5  0  x  5  .
x  5 x  5  0  x  5  . x  2
1  x  5  0  x  5  .
x  5 x  5  0  x  5. Câu 2. Lời giải Chọn A.
Theo định lý về dấu của nhị thức bậc nhất, ta có f x  2x  6 dương với x 3;  . Câu 3. Lời giải Chọn B
Từ giả thiết, ta có a  2c b  2c a b  2a  2 . b Câu 4. Lời giải. Chọn A . b c . c sin B A . B sin B 3.sin 30 3. 2 Ta có:   AC b     . sin B sin C sin C sin C sin 45 2 Câu 5. Lời giải Chọn Cx  2  0
Theo điều kiện để phân thức chứa ẩn ở mẫu có nghĩa ta có:  . x  0 Câu 6. Lời giải Chọn A  11 x  
x  4y 1  0  Ta xét hệ phương trình: 7   
. Do đó đường thẳng  và đường thẳng y  2x  3 cắt
2x y  3  0 1  y    7 nhau. a b 2  8
Cách 2 : nhẩm nhanh tỉ số  hay không ? ví dụ : 
  / /d : –2x  8y  0 ab 1 4 BCâu 7. Lời giải Chọn A
x  2  x  2  0  3  x  6  0 . Câu 8. Lời giải Chọn D. BC
Trong tam giác ABC ta có: R   10 . 2sin A Câu 9. Lời giải. Chọn B b c . b sin C AC.sin C . 2 sin 1 ( 80  75  45 ) Ta có:   AB c     6 . sin B sin C sin B sin B sin 45 . Câu 10. Lời giải Chọn B
Thay x  0 vào bất phương trình ta được: 2.0 1  3 mệnh đề đúng. Câu 11. Lời giải 
Đường thẳng  : 3x  4y 12  0 có một véctơ pháp tuyến là n   3;4. 
Vì d   nên n d
3;4 là một véctơ chỉ phương của . Câu 12. Lời giải Chọn C
Theo định nghĩa thì x y  0 là bất phương trình bậc nhất hai ẩn. Các bất phương trình còn lại là bất phương trình bậc hai. Câu 13. Lời giải: Chọn A   
d M d  3.1 4.  1 17 10 ;    2   2 2 5 3 4 Câu 14. Lời giải Chọn D a ìï < 0 2
f(x) = ax +bx +c (a ¹ 0), f(x) £ 0, "x Î  ï Û . íïD £ 0 ïî Câu 15. Lời giải Chọn D Thay x  1
 vào các bất phương trình ta có phương án B đúng. Câu 16. Lời giải Chọn B. * Bảng xét dấu: x  2  2 x  4x  4  0 
* Tập nghiệm của bất phương trình là S   \  2 . Câu 17. Lời giải Chọn A
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy  x ; y  0; 2  0 0    là
nghiệm của hệ bất phương trình đã cho. Câu 18. Lời giải Chọn C   Ta có AB   9
 ;3 . Đường thẳng AB nhận u  3;  1 làm vtcp. Suy ra Chọn C Câu 19. Lời giải Chọn.D
Áp dụng bất đẳng thức AM-GM cho 2 số dương x,y ta thấy cả 3 phương án trên đều đúng. Câu 20. Lời giải Chọn A
Ta có f x  0  2
x  4x  5  0  x  5  ; x  1.
Vậy nghiệm của tam thức bậc hai f x 2
x  4x  5 là x  5  ; x  1. Câu 21. Lời giải Chọn A
Ta có  : 3x  2y  7  0 . Xét d : 3
x  2y  7  3 2 0 có 
nên //d . Tương tự đối với d , d ssong song với  . 3 3  2  3 2 4 
Xét d : 3x  2y  3 2 0 có 
nên d song song với  . 1 3 2 1 Câu 22. Hướng dẫn giải Chọn B
Ta có hàm số nhận giá trị dương nếu đồ thị của nó nằm về phía trên so với trục Ox . Từ đồ thị ta có:
f x  0  0  x  2 . Do đó x 1 là một nghiệm của bpt Câu 23. Lời giải Chọn C
Thay lần lượt tọa độ các điểm vào hệ bất phương trình. Câu 24. Lời giải Chọn D
Chọn x  1, a  2 thay vào ta có A, B, C đều sai chọn. D. Câu 25. Lời giải Chọn D. x  3 2x  2 Ta có:  1   0  1   x  1. 1 x 1 x Câu 26. Lời giải: Chọn C
Gọi M là trung điểm của AC  5 x   M  2  5 3    M ; 3     2 2 y   M  2
  5 7   BM  ;  nBM     7  ;5  2 2 
Phương trình tổng quát của trung tuyến BM qua B 0; 2   là: 7
 x  0  5 y  2  0  7
x  5y 10  0 Câu 27. Lời giải Chọn C 2
a 16 a  4 Ta có:    2 b   9 b   3 Mà 2 2 2 2
a b c c  7  c  7
Tiêu điểm : F  7;0 F 7;0 2   1   và . 3 3
Ta có : h d F , d .d F , d  .  9 1    2   . 1 1 Câu 28. Lời giải Chọn C x 8 x 8
Áp dụng BĐT AM-GM, được y    2 .  4 . 2 x 2 x Câu 29. Lời giải Chọn C
xm0 (1) 5    5  0 (2) x m x
Hệ có nghiệm khi m  5  m  5  . Câu 30. Lời giải Chọn Dx  2018  0 Điều kiện:   x  2018. 2018  x  0
Thay x  2018 vào bất phương trình x  2018  2018  x , dễ thấy x  2018 không phải là nghiệm.
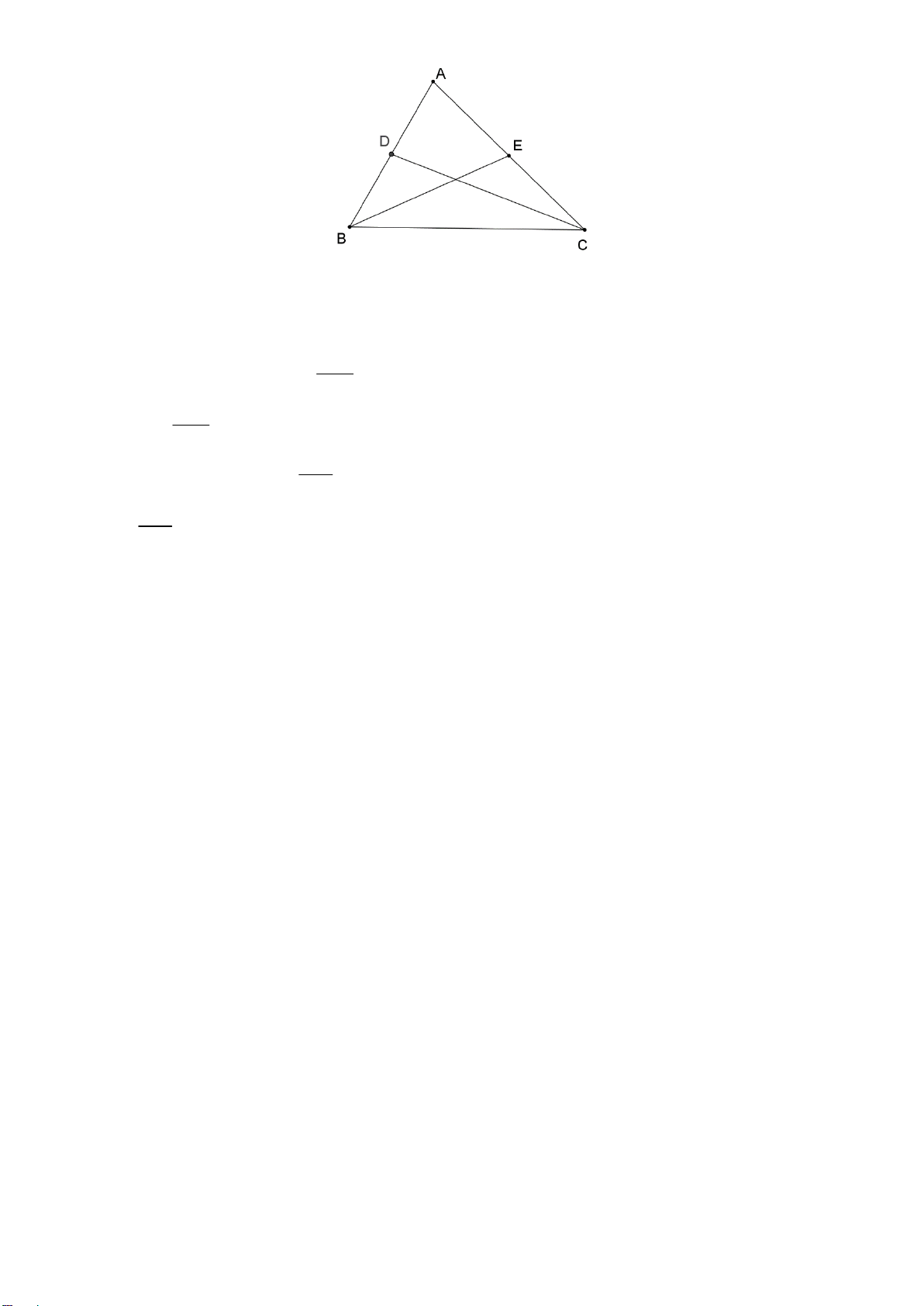
Vậy bất phương trình vô nghiệm. Câu 31. Lời giải Chọn B. A D B E C Ta có  ABC  45 .
Gọi AE kà đường cao của tam giác ABC , khi đó tam giác AEB vuông cân tại E . 1 a Suy ra AE  2 BC  . 2 2 a 2
Vậy diện tích hình bình hành ABCD là AE.BC  .a 2 2  a . 2 Câu 32. Lời giải Chọn D ĐK x  2  ;0;  2 1 1 2
x x     2
x    xx   2 2 4 2 2 2
x  6x  4 Ta có     0   0 . x  2 x x  2
x x  2 x  2
x x  2 x  2 2 2
x  6x  4
Lập bảng xét dấu biểu thức
. Từ đó suy ra tập nghiệm cần tìm là
x x  2 x  2  3  17  3  17  ; 2  ( ; 0 ) 2  ( ;) .  2  2   Câu 33. Lời giải Chọn C   1 1 x  4x  3 x  x   Ta có  1   2 2  0  2  2    1  x 1. 1 2x 1 2x   2x  2 1 2  1 2x  0   x 1 2 Câu 34. Lời giải Chọn D Ta có 2 2 2 2 2 2 2
a b c  2a .
b cos A b c  2a .
b cos120  b c ab . Câu 35. Lời giải Chọn B 2
x  3x  2  0 x  2   x  1  ĐKXĐ     x 1. x 1  0 x 1 PHẦN II: TỰ LUẬN Câu 36. Lời giảix  2
Ta có f x 2
x  3x  2  0  .  x  1 Bảng xét dấu
Dựa vào bảng xét dấu f x  0 1  x  2 . Câu 37. Lời giải 5 4 3 10 8 6 a 8 6 Ta có         . sin A sin B sin C sin A sin B sin C sin A sin B sin C
Theo định lý sin trong tam giác ta tính được b  8,c  6 .
Chu vi tam giác là a b c  24 . Câu 38. Lời giải
Gọi  là đường thẳng A , song song với BC . Kéo dài CD    N .
Gọi E là trung điểm BH  tứ giác NAME là hình bình hành.
Lấy I là trung điểm BC . Do tam giác ABC cân tại A . Dễ chứng minh được ANBI là hình chữ nhật.
Từ đó chứng minh được E là trực tâm N
BM NE BM , Lại có NE / / AM BM AM . 1 3   3 9   3
Phương trình đường thẳng BM đi qua M ( ; ) , nhận AM ;  1; 3   
 làm VTPT nên có pt là: 2 2  2 2  2
x  3y  5  0 . x y  7 
Do B BM BC  tọa độ của B là nghiệm của hệ   B( 4  ; 3  ) .
x  3y  5  
Do AB  3AD D( 2
 ;1)  Phương trình đường thẳng CD đi qua D, M là x y 1  0 . Phương trình
đường thẳng BH đi qua B , vuông góc với CD là x y 1  0 .
Mà H CD BH H  1  ;0 .
Lại có M là trung điểm HC C(2; 3  ) Câu 39. Lời giải
Áp dụng bất đẳng thức Côsi, ta có 3 3 3 3
x x x x  4x hay 3 3
x  3 x  4x . Tương tự: 3 3
y  3 y  4y và 3 3
z  3 z  4z . Suy ra 3 3 3
P x y z   3 3 3 3
x y z   4 x y z 12.
Khi x y z  1 thì P  12.
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 002
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn D 
Ta có AB  0;6  60;  1
Gọi là I trung điểm AB . Tọa độ điểm I 1;  1 . 
Đường trung trực của đoạn thẳng AB đi qua I và nhận u AB
0; 1 là vectơ pháp tuyến nên phương trình
đường trung trực của đoạn thẳng AB có dạng: 0 x  
1  y 1  0  y 1  0 . Câu 2. Lời giải Chọn C
Ta thay tọa độ điểm vào phương trình đường thẳng: –2.3  3.0 –1  7
  loại A; –2.1 3.1–1  0  B thỏa mãn. Câu 3. Lời giải Chọn D
Với m  0 phương trình  x
  1  0  x  1 (bất phương trình có nghiệm). Câu 4. Lời giải Chọn A. Ta có 4  x 16  0  4  x  1  6  x  4 .
Vậy tập nghiệm của bất phương trình 4
x 16  0 là S  4;  . Câu 5. Lời giải Chọn D  
d : x  2  0  n  1;0 1 1       x t
n n  0  d d .   d : d : 
.  u  1;0  n  0;1  2 2   2   1 2 1 2 2 y 0   Câu 6. Lời giải Chọn B Ta có: 3  x  9  0  3  x  9   x  3 . Vậy: Bất phương trình 3
x  9  0 có tập nghiệm là  ;   3 . Câu 7. Lời giải Chọn A 1 Ta có: 2 2 2 2
BC AB AC  2A .
B AC.cos 60  10  6  2.10.6.  2 19 . 2 Câu 8. Lời giải Chọn C
Thay tọa độ ở các đáp án vào phương trình đường thẳng: 12x  7 y  5  0 .
Với đáp án A: a có 12  1  7  1  5  0 thỏa mãn.
Với đáp án B: a có 12.1 7.1 5  10  0 không thỏa mãn.  5 
Với đáp án C: a có 12 
 7.0  5  0 thỏa mãn.    12  17
Với đáp án D: a có 12.1 7.  5  0 thỏa mãn. 7 Câu 9. Lời giải Chọn A 2
(x  2)(2x 1)  2  x  (x 1)(x  3)  x  1. Câu 10. Lời giải Chọn C
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy  x ; y  0;0 0 0    không là
nghiệm của hệ bất phương trình đã cho. Câu 11. Lời giải Chọn B
Tập hợp các điểm biểu diễn nghiệm của bất phương trình 2x y  3  0 là nửa mặt phẳng bờ là đường thẳng
2x y  3  0 và không chứa gốc tọa độ.  3 
Từ đó ta có điểm M 1;
thuộc miền nghiệm của bất phương trình 2x y  3  0 .    2  Câu 12. Lời giải Chọn A 2 2 Cách 1: 2 2
x  4 2x  8  0  x  2.2 2.x  2 2  0  x  2 2  0 ( chọn C. ).
Cách 2: Casio: wR1121=p4s2=8== ( nghiệm rỗng). Câu 13. Lời giải Chọn D
f x  0  3x  6  0  x  2  . Câu 14. Lời giải Chọn D. 2 3 Ta có: 2 2 2
AC AB BC  2A .
B BC.cos 30  3  3  2.3. 3.  3 . 2 Câu 15. Lời giải Chọn C
Theo tính chất của bất đẳng thức và bất đẳng thức Côsi thì A, B, C luôn đúng. 1 1
Ta có nếu b a  0   là sai. a b Câu 16. Lời giải Chọn D
f x  0, x
   khi a  0 và   0 . Câu 17. Lời giải Chọn B
ĐK :1 x  0  x  1. Câu 18. Lời giải Chọn C
Định lý sin trong tam giác. Câu 19. Lời giải Chọn A. Ta có
f x  0  2x  4  0  x  2  A đúng.
f x  0  2x  4  0  x  2   B sai.
f x  0  2x  4  0  x  2  C sai
f x  0  2x  4  0  x  2  D sai. Câu 20. Lời giải Chọn.D
Áp dụng bất đẳng thức AM-GM cho 2 số dương x,y ta thấy cả 3 phương án trên đều đúng. Câu 21. Lời giải Chọn B AB
Xét tam giác OAB có
  R R  . Với R là bán kính đường tròn ngoại tiếp tam giác OAB . Vậy  2 2 1 sin O
OB lớn nhất khi OB là đường kính của đường tròn ngoại tiếp tam giác OAB . Khi đó OB  2 . Câu 22. Lời giải Chọn B
Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình. 2.0  5.0 1  0 
Với O 0;0  2.0  0  5  0 . Bất phương trình thứ nhất và thứ ba sai nên O0;0 sai. 0 01 0  2.1 5.0 1  0 
Với M 1;0  2.1 0  5  0 . Bất phương trình thứ ba sai . 1   01 0  2.0  5. 3   1  0  Với N 0; 3    2.0   2    5  0 : Đúng. 0   2   1 0 Câu 23. Lời giải Chọn A 2 2 2 2 b b 3bb  3b 2 2 2 a
 ,b  ,a b ab a +2a + + = a  +  0.   2 4 4  2  4 Câu 24. Lời giải Chọn B.
Tọa độ giao điểm M của dd2 1  và là nghiệm của hệ  3   3
x  2y  5  x   3 31  8    M  ; .  
2x  4y  7 31   8 16  y   16  3 31
Phương trình đường thẳng  song song với d M  ; 3  qua có dạng    8 16    3  31 53 : 3 x   4 y
 0  3x  4y
 0  24x  32y  53  0 .      8   16  8 Câu 25. Lời giải Chọn D 2 x  9 Xét bất phương trình:  0 . 2
x  3x 12 Bảng xét dấu: x  3  3  Vế trái  0  0 
Vậy nghiệm bất phương trình là:  1 S   3;3 . x  7 3x 1
2x 14  (3x 1)(x  5) 2 3x 12x  9 Xét bất pt:   0   0   0 . x  5 2 2(x  5) 2 x  5 Bảng xét dấu: x  1 3 5  Vế trái  0  0   
Vậy nghiệm của bất phương trình là: S    2 1; 3 5;  .
Vậy nghiệm của hệ bất phương trình là: S    1 S S2 1;3 . Câu 26. Lời giải Chọn C
Sai từ bước II  vì phép biến đổi đã làm thay đổi điều kiện của bpt và khi nhân hai veed của bpt với x 1 mà
chưa biết biểu thức này âm hay dương hay bằng không. Câu 27. Lời giải Chọn C.
Điều kiện: x  3  0  x  3. x 1 x 1 x  3 2 Ta có:  1    0 
 0  x  3  0  x  3 . x  3 x  3 x  3 x  3
Vậy tập nghiệm của bất phương trình đã cho là S  3;  . Câu 28. Lời giải Chọn A  
d :2x 3y  4  0 có VTPT là n  2; 3
  suy ra VTCP của d  là ud  3;2 .  
 x  2 3t d :  suy ra ud   3  ; 4
 m là VTCP của d . Để d vuông góc với d  thì y 1 4mt   9
ud .ud  0  9
  8m  0  m   . 8 Câu 29. Lời giải Chọn B Điều kiện: 2   x  2 2 2
x  4  x  2  3x 4  x  2  x  2  x  3x   1 2  x   0 x  2    
  x    x  x2 1 2 2 1 3 x      3  1  2  504
Giải và kết hợp điều kiện được ba nghiệm thỏa mãn là: x  2; x  0; x  . 18 Câu 30. Lời giải Chọn A
Áp dụng định lí cô sin ta có: 2 2 2
a b c bcA bc  2 2 2 2 cos
2 cos A b c a . Suy ra: Nếu 2 2 2
b c a  0  cos A  0 nên A nhọn. Câu 31. Lời giải Chọn B
R d O  100 ;   10. 64  36 Câu 32. Lời giải Chọn B
mx m  2x  2  mx m
TH1: 2  m  0  m  2 bất phương trình vô nghiệm. m
TH2: 2  m  0  m  2 bất phương trình có nghiệm x  . 2  m m
TH3: 2  m  0  m  2 bất phương trình có nghiệm x  . 2  m
KL: giá trị cần tìm m  2 . Câu 33. Lời giải Chọn C
Cách 1: Tính chất f x  m  m f x  mm  0 2x  3  1  1
  2x  3  1  1  x  2 . Cách 2: 2 2 2
2x  3  1  2x  3  1  4x 12x  8  0  x  3x  2  0  1  x  2 . Câu 34. Lời giải Chọn D. Ta có 2
x  6  0  x  3 . Câu 35. Lời giải Chọn C
Hàm số xác định khi và chỉ khi 2
4  3x x  0. x 1 Phương trình 2
4  3x x  0   x  
1  x  4  0  . Bảng xét dấu:  x   4
Dựa vào bảng xét dấu, ta thấy 2
4  3x x  0  x  4;  1 .
Vậy tập xác định của hàm số là D   4;  1 . PHẦN II: TỰ LUẬN Câu 36. Lời giải
Áp dụng bất đẳng thức Côsi, ta có 4 4 4 x y y z z x   4 4 x y 4 3 .  ;  y z 3 . 
và  z x 3 .  . 3 2 3 2 3 2 4 4 4
Suy ra  x y.   y z.   z x.  x y z  2  4. 3 3 3
Do đó P x y y z z x  2 3. Khi 2
x y z  thì P  2 3. 3 Câu 37. Lời giảia  0 1   0 
Ta có : f x  0, x          0   m   2
1  42m  7  0 2
m  6m  27  0  3   m  9 . Câu 38. Lời giải
Ta có a b ca b c  3ab  a b2 2  c  3ab 2 2 2
c a b ab . 2 2 2
a b c ab Mặt khác cos C  1    C  60 . 2ab 2ab 2 Câu 39. Lời giải
Gọi J là trung điểm của AB . khi đó AJCK là hình bình hành  AK // CJ .
Gọi CJ BM N N là trung điểm của BM .
Chứng minh được AK BI từ đó suy ra tam giác BMC tam giác cân tại C .   Ta có MC 3; 
1  MC  10  CM CB AB  10
Trong tam giác vuông ABM có 2 2 2 5
AB BM .BI BM . AB AI BM .AB
BM  2 2  B là giao của hai đường tròn 2 2 2    x  2 
   y  2 10
C; 10  và M;2 2. Tọa độ điểm B thỏa mãn:   B1;  1   x   2 1   y  2 1  8
a b  2.
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 003
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn D 2 3
x  2  0  3x  2  x  . 3 Câu 2. Lời giải Chọn A
Ta có 3.3  2  7  0 nên đáp án B đúng. Câu 3. Lời giải Chọn B
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy  x ; y  5;3 0 0    là nghiệm của hệ. Câu 4. Lời giải Chọn D   x x    2  0 2    4
Điều kiện xác định của phương trình là 4  3x  0  x  . x 3  1    0 x    1  Câu 5. Lời giải   AB   2
 ;6  u  1; 3 là một vecto chỉ phương của đường thẳng AB . 
Phương trình tham số của đường thẳng AB đi qua điểm A3; 
1 và nhận u  1; 3 là một vecto chỉ x  3  t phương là:  , t   . y  1   3t Câu 6. Lời giải Chọn A
*) Do: 5x  2x  3x  0  x  0 . Tức là khẳng định A chỉ đúng khi x  0 . *) Do: 2 2 5x  2x 2
 3x  0  x  0. Tức là khẳng định B chỉ đúng khi x  0 .
*) Do: x  3  7  x x  2 . Tức là khẳng định C chỉ đúng khi x  2 .
*) Do: 2  x  5  x  0x  3 đúng với x    . Câu 7. Lời giải Chọn C
a c b d , ac bd luôn đúng. ac bd ac bd a d a d Ta có:        đúng. bc  0 bc bc b c b c Câu 8. Lời giải Chọn B
Theo định lí hàm số cosin, 2 2 2
c b a  2ab cosC nên C sai. Câu 9. Lời giải Chọn B.
* Theo định lý về dấu của tam thức bậc hai thì f x luôn cùng dấu với hệ số a với mọi x   khi   0 . Câu 10. Lời giải Chọn Cx  
Ta có  x    x 2 2 5  0  .  x  5 Câu 11. Lời giải Chọn A
Đường thẳng có vô số vectơ pháp tuyến và vô số vectơ chỉ phương. Câu 12. Lời giải Chọn.D
Áp dụng bất đẳng thức AM-GM cho 2 số dương x,y ta thấy cả 3 phương án trên đều đúng. Câu 13. Lời giải Chọn D
Tọa độ giao điểm của đường thẳng  : 4x  3y  26  0 và đường thẳng d : 3x  4y  7  0 là nghiệm của hệ
4x  3y  26  0 x  5 phương trình:    . 3
x  4y  7  0 y  2  Câu 14. Lời giải A 3 60° B C 8
Áp dụng định lý cosin cho tam giác ABC Ta có 2 2 2
b a c  2ac cos B 2 2
 8  3  2.8.3.cos 60  49  b  7. Câu 15. Lời giải Chọn C x x    x  2 2 8 16 0 4  0
Điều này không thể xảy ra nên bất phương trình vô nghiệm Câu 16. Lời giải Chọn B  2  
 3 2t   3t Giải hệ: 
. Ta được hệ vô số nghiệm.  2  
 3 2t   352 6t Vậy    . 1 2 Câu 17. Lời giải. Chọn A b c . b sin C AC.sin C 1 . 0 sin 30 Ta có:   AB c     5 2 . sin B sin C sin B sin B sin 45 Câu 18. Lời giải Chọn A 3 2
x  3  0  2x  3   x   . 2 Câu 19. Lời giải Chọn C.
x    x 8 5 2 4
 0  7x  8  x  . 7  8 
Vậy bất phương trình đã cho có tập nghiệm là: S  ;  . .    7  Câu 20. Lời giải Chọn D Ta có: 2
x x  6  0  2
  x  3 ( chọn C. ). Câu 21. Lời giải Chọn B
Điều kiện x  0 . x  0
Bất phương trình tương đương với 2 2 x 3x x 9x 9x x 0          1 x   9  
Kết hợp điều kiện, ta được tập nghiệm của bất phương trình S    1 0  ;  .   9  Câu 22. Lời giải Chọn A. +Ta có 2 2
a b a b , a
 ,b hay ta có A đúng. 1
+ Chọn a  , b  4
 ta có B, C, D sai chỉ có A đúng. 2 Câu 23. Lời giải Chọn B S  2S 1  2. .A . B BC sin 
ABC absin  ABC . ABCD ABC 2 Câu 24. Lời giải Chọn A Ta có 2 x 1  0  1   x 1.
x  3  0  x m .
Do đó hệ có nghiệm khi m  1. Câu 25. Lời giải Chọn D. Điều kiện 3
x  6  0  x  2 .
Xét 4  x  0  x  4 . Và 3
x  6  0  x  2 . Bảng xét dấu: x  2 4  4  x  |  0  3  x  6  0  |  Vế trái  ||  0 
Vậy tập nghiệm của bất phương trình đã cho là S  2;4. Câu 26. Lời giải Chọn D. 
Đường thẳng AB đi qua A1;2 và nhận AB  1; 
1 làm VTCP nên AB :1 x  
1 1 y  2  0 
x y 1  0 . 3   4 1
Khoảng cách từ điểm C  3
 ; 4 đến đường thẳng AB là: d C, AB   2 . 2 2 1 1 1 1
Vậy diện tích tam giác ABC bằng: SA . B d C AB    ABC  ,  2 2 . 1 1 . 2 1. 2 2 Câu 27. Lời giải Chọn D Câu 28. Lời giải Chọn A Gọi M  ;
x 5  2xd  x  0 M1 Ta có : IM
 x  2    x  2 10 1 5 2 2  10 2 5x 14x 0      14 x M2  5 14 Vậy: x xM1 M2 5 Câu 29. Lời giải: Chọn C
Gọi M là trung điểm ABM 2; 2     AB  2; 6
   n  1; 3  
Phương trình tổng quát của đường trung trực của đoạn thẳng AB 1
 x  2  3 y  2  0  x  3y  8  0 Câu 30. Lời giải Chọn D 4x 12 4x 12
Ta có f x   . 2 x  4x x x  4
Phương trình 4x 12  0  x  3; x  0 và x  4  0  x  4. Bảng xét dấu
Dựa vào bảng xét dấu, suy ra f x  0  x  ;  0 3;4. Câu 31. Lời giải Chọn B 2x Ta có 5x 1 
 3  25x  5  2x 15  23x  20 20  x  . 5 23 Câu 32. Lời giải Chọn A
ĐKXĐ: x 1  0  x  1  (1)
Lập bảng xét dấu ta dễ dàng suy ra kết quả.
Vậy tập nghiệm của bất phương trình S    1 1; . Chọn A
Cách 2: Xét 2 trường hợp x =1 và x khác 1. Câu 33. Lời giải Chọn B 2
x  5x  6 2
x  5x  6  0 Cách 1:    .  x 1 2  x 1  0 Bảng xét dấu chung : x  6  1  2 x  5x  6  0  0  x 1   0  Vậy x  6  2
x  5x  6 2
x  5x  6  0
x   x
Cách 2: Dùng MTCT:     6; 1   x  6  .  x 1  2  x  1  x  1 Câu 34. Lời giải Chọn C
Bằng cách thay lần lượt tọa độ của các điểm M , N , P , Q vào hệ bất phương trình. Tại điểm P  3  ;4 ta được: 2.   3    3.4 1  0 5   0   
đúng. Do vậy điểm P  3
 ;4 thuộc miền nghiệm của hệ đã cho. 5  .   3    4  4  0  1  5  0 Câu 35. Lời giải Chọn C 1
Ta có: AD BC a 2 nên S  2.S  2. A . B A . D sin  BAD 2  a . ABCD ABD 2 PHẦN II: TỰ LUẬN Câu 36. Lời giải
Biểu thức P được viết lại dưới dạng
P  1 b ca b c bc
Xét hàm số f x  1 b cx b c bc với x 0;  1 .
Do f x là hàm số bậc nhất trên đoạn 0;  1 nên ta có
f (x)  max{ f (0), f (1)}, x  [0;1] Lại có
f (0)  b c bc  (1 b)(1 c) 1  1, , b c [0;1] và
f (1)  1 bc  1, , b c [0;1] Do đó
f (x)  1, x
 [0;1]  f (a) 1
Đẳng thức xảy ra chẳng hạn tại a  1,b  0,c [0;1] Vậy max P  1. Câu 37. Lời giải 2
x   3  2 x  6  0   3  x   2 . Câu 38. Lời giải 1 1
Diện tích tam giác S = C . B CAsin  ACB £ .
a b . Do đó diện tích tam giác ABC đạt giá trị lớn nhất bằng ABC 2 2
1 a ,b đạt được khi sin  ACB 1  ACB 90o = Þ = . 2 Câu 39. Lời giải
Gọi M 0;aOy . Phương trình đường thẳng AB : 4x  3y  2  0 . 1 1  a   a  Ta có: S  .A . B d M AB   MAB  ;  3 2 3 2 .5. . 2 2 5 2 a  0  4  Do đó: S 1 3a 2 2        M 0;0 M 0; MAB 4 . Vậy hoặc .    a   3   3
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 004
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn C.
2x 1  32  x  5x  5  x 1.
Vậy bất phương trình đã cho có tập nghiệm là: S  1;.. Câu 2. Lời giải Chọn A Ta có: 2
x  2x  3  0  1   x  3 Câu 3. Lời giải Chọn C O  0;0d O  0;0d     
 .0  c  0  c  0.
d |  : 6x  4x 1  0 d
x x c   c   6.0 4 : 6 4 0 1
Vậy d : 6x  4y  0  d : 3x  2y  0. Câu 4. Lời giải Chọn B
d : 2x  3y 1  0 2 3 1  Xét      d | d .
d : 2x  3y 1  0  2 3 1 AA
Để ý rằng một đường thẳng song song với 2x  3y 1  0 sẽ có dạng 2x  3y c  0 c    1 . Do đó kiểm tra
chỉ thấy có đáp án A thỏa mãn, các đáp án còn lại không thỏa mãn. Câu 5. Lời giải Chọn A  AB  0;  1  
Gọi d là trung trực đoạn AB, ta có:  
n AB  0;  1 . d d AB Câu 6. Lời giải Chọn B.
f x  0, x
   khi a  0 và   0 . Câu 7. Lời giải Chọn A
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy  x ; y  2;1 0 0    là nghiệm
của hệ bất phương trình đã cho. Câu 8. Lời giải Chọn D
Dựa vào đáp án, ta có nhận xét sau: 0  a b 0  a ba b     1
1  Chưa đủ dữ kiện để so sánh ,   A sai. 0  c d 0    c dd ca b  0 a b  0  a b     1 1
Chưa đủ dữ kiện để so sánh ,   B sai. c d  0   0  c dd ca b a b     
C sai vì chưa thiếu điều kiện a, , b c, d. c d c da 1 a b  0 b a d a d       1      D đúng.c d  0 d b c b c 1    c Câu 9. Lời giải Chọn B 2 2 x x 1 x x
 1  0  S   . 2 2 x  2 x  2 Câu 10. Lời giải Chọn D.
Điều kiện: 6  3x  0  x  2 . Câu 11. Lời giải Chọn B. 2  3  Ta có: 2 2  2
AB AC BC  2AC.BC.cos150  2  3  2.2. 3.    13 .  2    Câu 12. Lời giải Chọn D. 13 14 15 Nữa chu vi: p   21. . 2
Diện tích: S p( p 13)( p 14)( p 15)  84.. Câu 13. Lời giải Chọn B
m  0  2  0  Phương trình vô nghiệm. 2
m  0  mx mx  2  0có nghiệm khi và chỉ m
 0  m2 0 2
8m  0  m 8m  0  .  m  8
So với điều kiện ta có m  0 hoặc m  8 . Câu 14. Lời giải Chọn Ax  4
Ta có f x 2
 x  5x  4  0  .  x 1 Bảng xét dấu x
Dựa vào bảng xét dấu f x 1  0  .  x  4 Câu 15. Lời giải Chọn C 2 2 2 2 2 2
AC AB BC 2  2 1 7
Theo định lý cosin ta có: cosA    . 2A . B AC 2.2.2 8 Câu 16. Lời giải Chọn D
Thay x  3 vào các bất phương trình ta có phương án D đúng. Câu 17. Lời giải Chọn A 2
x    3x  2
  3x  2  0 . 3 Câu 18. Lời giải Chọn C
Ta có f x  0  2x 1  1
0  x   .Vậy f x 1  0; x   là sai. 2 2 Câu 19. Lời giải Chọn.D
Áp dụng bất đẳng thức AM-GM cho 2 số dương x,y ta thấy cả 3 phương án trên đều đúng. Câu 20. Lời giải Chọn C
22  2t 12  4t y  0 Giải hệ:    . 5
 5  5t 12  4t x  0
Vậy tọa độ giao điểm của  và  là 0;0 . 1 2 Câu 21. Lời giải Chọn D Điều kiện: 1   x  2 Ta có 2 2
3  x x  2  x x  1 2 2 2
 3 x x 1 2  x x  2 2  x x 2 2
 2  x x  2  x x  2  0 2
 2  x x 1 2
x x 1  0 1 5  x  2 Câu 22. Lời giải Chọn C   
R d I  10 24 10 44 ;   . 25 144 13 Câu 23. Lời giải Chọn B 1 1 1 1 C đúng vì 3
a b c  3 abc và 3    3
, nhân vế theo vế ta chọn C . a b c abc Câu 24. Lời giải Chọn C. 2
x  4x  0
x  4  x  0  5   x  0 ĐKXĐ     .  2 25  x  0  5   x  5 4  x  5 Câu 25. Lời giải Chọn Ax  2 2  x   0   1 . 2x 1 x    2 Câu 26. Lời giải Chọn Bx 1 t C   :
C(1 t;2  t) y  2  t 1  7 13 
CA CB    2  t    2  t  2 2 t 2 t 2
1  t   C ;   6  6 6  Câu 27. Lời giải Chọn D
Chọn a  0,b  1  thay vào 5 5 2 2
a b a b a b ta có 1   0 vô lí. Câu 28. Hướng dẫn giải Chọn B x  0 x  0
Ta có: x x  3  0     x  3  0 x  3  Vậy: S   3  ; \  0 . Câu 29. Lời giải Chọn D B a 2 C a 45° A a 2 D 1 Ta có: 2 S  2S  2. .A . B A .
D sin 45  a . ABCD ABD 2 Câu 30. Lời giải Chọn C Bảng xét dấu:
Vậy tập nghiệm của bất phương trình là: S  1;23; . Câu 31. Lời giải. Chọn A Theo giả thiết ta có 2 2 2
BC AB AC hay 2 2 2
AB AC BC  0 2 2 2
AB AC BC o o  cosA
 0  90  A 180 . 2A . B AC Câu 32. Lời giải Chọn Bx  6
Sai từ bước IV  vì 2
x  4x 12  0  .  x  2  Câu 33. Lời giải Chọn A
Thay tọa độ điểm 1;2 , 0;0 , 2; 
1 vào bất phương trình thứ nhất của hệ không thỏa mãn Câu 34. Lời giải Chọn D  
d : x  3y  0  n  1; 3   1 1
  d d 1 0 1 1 ; 2    cos  
d : x 10  0  n  1;0 1 3. 1 0 2  2 2     60 . Câu 35. Lời giải Chọn C   1 2x 1  0 x   x m 3    2
x m  3 1 5
Hệ vô nghiệm thì m  3   m   . 2 2 PHẦN II: TỰ LUẬN Câu 36. Lời giải
Tập xác định D é 2019; 2019ù = - êë úû
Dễ thấy f (x) là hàm số lẻ trên D . Thêm nữa, f (x) 0, x é0; 2019ù ³ " Î . êë úû Do đó,
ìïM = Max f (x) = Max f (x) ï é 2019; 2019ù é0; 2019ù - ï êë úû êë úû
ïíïm= Min f(x)=- Max f(x) ï é 2019; 2019ù é0; 2019ù ï - ê ïî ë úû êë úû Ta có æ 2 2017 2019 ö ç + - x ÷ x
f (x) = xç ÷ ç ÷= ç ÷ x çè ÷ ( 2 2017 2017 + 2019- 2018 2018 ) ø £ x ( 2017)2 +1 . ( 2017)2 2 +( 2 2019- x 2018 )2 2018 = x + - x 2018 ( 2017 ( 2 2019 )) 2 2018 æç x ( 2 2017 2019 x )ö + + - ÷ Þ f (x) £ ç ÷ ç ÷= 2018 2018 ç 2 ÷ ç ÷ è ø ì 2 ï 2017 2019 ï - ï = x Đẳng thức xảy ra ïí 2017 1 x 2018 é0; 2019ù Û Û = Î ï êë úû ï 2 ïx = 2017+( 2 2019- ïî x ) Từ đó suy ra
ìïM = Max f (x) = Max f (x) = 2018 ï é 2019; 2019ù é0; 2019ù ï - êë úû êë úû
ïíïïm= Min f(x)=- Max f(x)=- 2018 ï é 2019; 2019ù é0; 2019ù - ï ê î ë úû êë úû Vậy n( *  [m M ] * ; n é  2018; 2018ù Ç = Ç - = 44 . ) ( êë úû) Câu 37. Lời giải
Bất phương trình x x     2 x   2 2 2 5 2
2  x  5x  2x  4  x  5x  4  0 x 1 Xét phương trình 2
x  5x  4  0   x  
1  x  4  0  .  x  4 Lập bảng xét dấu
Dựa vào bảng xét dấu, ta thấy 2
x  5x  4  0  x  ;   1 4; . Câu 38. Lời giải + Đặt OB  ;
x OA y(x, y  0) . Khi đó theo định lý cosin ta có: 2 2 2 0 2 2
AB x y  2xy cos30  x y  3xy Do đó ta có hệ thức: 2 2
x y  3xy  1
Xét phương trình bậc hai: 2 2
y  3xy x 1  0
Phương trình có nghiệm y khi 2 2
  3x  4(x 1)  0  0  x  2
Vậy học vị trí xa nhất mà học sinh có thể đạt được cách O một khoảng là 2m Câu 39. Lời giải
Giả sử đã tìm được điểm M thuộc trục Ox thỏa mãn  0
AMB  45 . Gọi I (x; y) là tâm đường
tròn (C) ngoại tiếp tam giác ABM. Do  0 AMB  45 , suy ra  0
AIB  90 ( Góc ở tâm gấp hai lần góc
nội tiếp chắn cùng cung AB). Khi đó B A I M x  3     AI BI  2 2 2 2          y  1 (x 1) ( y 2) (x 4) ( y 3)       
AI.BI  0
(x 1)(x  4)  (y  2)(y  3)  0
x  2 . Vậy I(3;1) hoặc I(2;4).  y  4 Với I(3;1) thì (C): 2 2
(x  3)  ( y 1)  5 , suy ra M Ox  (C) nên M ( 1;0) hoặc M(5;0). Với I (2;4) thì (C) 2 2
(x  2)  ( y  4)  5 . Nhận thấy (C) không giao Ox. Vậy không có điểm M thỏa mãn.
Kết luận có hai điểm M thỏa mãn yêu cầu bài toán M ( 1;0) hoặc M(5;0).
Vậy tổng các hoành độ của điểm M là 6.
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 005
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn A      2 
–2x  3y –1  0  n   2  ; 3 mà .
n u  0  u u , u . Vậy chỉ có C không thỏa mãn.  1 1   3  Câu 2. Lời giải Chọn D Câu 3. Lời giải Chọn B
Đáp án A sai khi a  1;b  1  .
Đáp án B và D sai khi a b  0. Xét : 2 2 2 2
a b a b a  2ab b a  2 ab b ab ab luôn đúng với mọi số thực a,b . Vậy,chọn B. Câu 4. Lời giải Chọn D 2  thỏa 4 2
   5  0 nên là nghiệm của bất phương trình 4x  5  0 . Câu 5. Lời giải Chọn D
Theo quy tắc xét dấu nhị thức bậc nhất thì đáp án C sai. Câu 6. Lời giải Chọn C
Phương trình đường thẳng cần tìm là 2(x 1)  3( y  2)  0  2x  3y  8  0 . Câu 7. Lời giải Chọn A 
Đường trung trực AB nhận véc-tơ 1  AB  3  ; 3    1; 
1 làm vectơ pháp tuyến và đi qua trung điểm 3  5 5   5   5  I ; 
 của AB nên có phương trình: x   y
 0  x y  0     .  2 2   2   2  Câu 8. Lời giải Chọn B
Thay tọa độ các điểm vào bất phương trình ta thấy 2;2 S . Câu 9. Lời giải Chọn B  
Véc-tơ chỉ phương của đường thẳng d  là véc-tơ u 2; 
1 vì véc-tơ này cùng phương với véc-tơ v  2  ;  1 Câu 10. Lời giải Chọn B
Cách 1: Áp dụng công thức tính độ dài đường trung tuyến ta có 2 2 2 AB AC BC 2 2 2 6  8 10 2 AM    
 25  AM  5 cm . 2 4 2 4 1 Cách 2: Do 2 2 2
AB AC BC nên tam giác ABC vuông tại AM BC  5 cm . 2 Câu 11. Lời giải Chọn A    f xx 1 2
 0  x 12x 13  0  .  x 13 Câu 12. Lời giải Chọn D
x x  2  2  x  2 *
Điều kiện: x  2 .
Bất phương trình *  x  2 .
Kết hợp với điều kiện, tập nghiệm của bất phương trình là:   2 Câu 13. Lời giải Chọn B 9 10 11 Nửa chu vi: p   15. 2
Diện tích: S p( p  9)( p 10)( p 11)  30 2. Câu 14. Lời giải Chọn C 2x 20 5x 1 
 3  25x  5  2x 15  23x  20  x  . 5 23 Câu 15. Lời giải Chọn D
Thay tọa độ của M vào vế trái của d, ta được 2.5  ( 2  )  3  15  0.
Điểm N sẽ nằm cùng phía đối với M so với đường thẳng d nếu thay tọa độ của N vào vế trái của d được kết quả là một số dương.
Do đó ta chọn được N (3; 1  ). Câu 16. Lời giải Chọn D
Bất phương trình xác định  2x  6  0  x  3  . Câu 17. Lời giải Chọn D 3  2 1
Nửa chu vi của tam giác là: p  . 2
Diện tích tam giác là: S p p   p  p  2 3 2 1  . 2 Câu 18. Lời giải Chọn C
f x, y  x  3y 1. Thay f 1,  1  1 3 1  1   0 . Câu 19. Lời giải Chọn B Câu 20. Lời giải Chọn C Câu 21. Lời giải Chọn A
Ta có VTCP của D : u  2;  1
x    t
Vậy PTTS của đưởng thẳng D 1 2
: y  2t Câu 22. Lời giải Chọn A
Điều kiện: x  1; x  2; x  4 . Vậy x  ;
 2 4; \  1 . Câu 23. Lời giải Chọn A
x   x   x  2  x  2  x  2  x  2 2 4 2 4 2 4  0
 62x  2  0  x  1 Câu 24. Lời giải Chọn Ax  2 Hệ BPT  
. Hệ có nghiệm duy nhất  m  2 . x m Câu 25. Lời giải Chọn B 1
Ta có 2x  1  x  . 2 x  2  x  2  0  1
Xét bất phương trình 2x x  2  1 x  2     1  x  . 2x  1 x  2  2
Vậy bất phương trình 2x  1  2x x  2  1 x  2 . Câu 26. Lời giải Chọn B
Ta có: I. đúng vì là công thức Hê-rông tính diện tích tam giác.
a b c a b c a b c a b c Khi đó: 2 S  . . . 2 2 2 2 2
 16S  a b ca b ca b ca b c . Do đó II. đúng Câu 27. Lời giải Chọn A Cách 1: Tự luận.
Gọi M d . Cho x  5   y  3  , suy ra M  5  ; 3  .     d  5. 5 7 3 6 2
d ; d d M , d   1 2   2      .   2 2 74 5 7
Cách 2: Trắc nghiệm.   d c c 4 6 2 d ; d    1 2  1 2 . 2 2 a b   2 2 74 5 7 Câu 28. Lời giải Chọn C
Đường thẳng nào đi qua điểm A2; 
1 và song song với đường thẳng  : 2x  3y  2  0
Có dạng: 2 x  2  3 y  
1  0  2x  3y  7  0 . Câu 29. Lời giải Chọn C 2 2 2 x 2
x x  2x  4
x x  4  x x  2 6   1       x x
x  x   1
x  x   0
x  x   0 2 1 2 1 2 1 2 1  1
  x  2 . Câu 30. Lời giải Chọn C Vì 2 2 2
AB AC BC nên tam giác ABC vuông tại A . 1 A .BAC S 3.4
Do đó bán kính đường tròn nội tiếp 2 r     1. p
1 ABAC BC 345 2 Câu 31. Lời giải Chọn A Vì 2
x  2x  4  0 với mọi x   nên ta có 2
2x  5  x  2x  4 2
2x  5  x  2x  4   2
2x  5  x  2x  4 2 x 1 0 x  1    2  x 1  0  . 2 
x  4x  9  0  luoân ñuùng x 1 Vậy x  1  hoặc x  1. Câu 32. Lời giải Chọn D
Áp dụng bất đẳng thức Cô – si cho hai số không âm 2 x và 2 y . Ta có:
A x y x y  xy2 2 2 2 2 2 2
 4 . Đẳng thức xảy ra x y  2 . Câu 33. Lời giải Chọn B 2
x  4  0   x  2 x  2  0  x  ;  2   2; . Câu 34. Lời giải Chọn C
Để bất phương trình vô nghiệm  m  2  0  m  2 . Câu 35. Lời giải Chọn C  1 
Ta có: x   ;1  (3x 1)  0, 1 x  0    3 
Áp dụng BĐT Cô-si cho hai số dương 3x   1 ;3 3x ta có 2        
x    x (3x 1) (3 3x) 1 3 1 3 3  , x    ;1      2   3    
x    x 1 3 1 3 3  4 , x    ;1    3  4  1 
f (x)  (3x 1)(1 x)  , x    ;1   3  3  1
Dấu “=” xảy ra khi và chỉ khi 3x 1  3  3x x  3   4
Cách 2: Giá trị lớn nhất của biểu thức f (x)  3x   1 1 1
x với x   ;1 bằng    3  3 3x   1 1 x 4 1 1 2   3
x  2x   0  x  (tm) 3 3 3 PHẦN II: TỰ LUẬN Câu 36. Lời giải
Ta có a b5   2 2
a ab b  3 2 2 3 2
a  3ab  3a b b  .
Áp dụng bất đẳng thức CôSi, ta có 2 2
a ab b ab 2 2 2 2 2
a b   4 ab ;  3 2
a ab    2 3
a b b    3 2
a ab  2 3
a b b   ab 2  b  2 3 3 2 3 3 4 1 a   1 . Suy ra  2 2
a ab b  3 2 2 3
a ab a b b   ab  2 a   2 2 3 3 16 1 b   1 .
Do đó a b5  ab  2  a  2 16 1 1 b  .
Đẳng thức xảy ra khi và chỉ khi a b  1. Câu 37. Lời giải
Với m  0 , ta có f (x)  x 1  0  x  1  :không thỏa mãn.
Với m  0 , yêu cầu Câu toán 2
mx x 1  0, x      m  0 a  0 m  0  1       1    m  0   0 1 4m  0 m   4       4 1
Vậy với   m  0 thì biểu thức f x luôn âm. 4 Câu 38. Lời giải 2 1 1 1 1 2S S S S S Ta có     
     a p  ( p a)  ( p b)  ( p c) . h r r r r h r r r r a a b c a a a b c Câu 39. Lời giải Định hướng:
- Tọa độ điểm  
B BH BM
- Viết phương trình đường thẳng AC đi qua A và vuông góc với BH .
Suy ra tọa độ M  AC BM C
Gọi BH , BM lần lượt là đường cao và trung tuyến kẻ từ B. 2
x  3y 12  0
Tọa độ điểm B là nghiệm của hệ phương trình   B  3  ;2 2
x  3y  0
Đường thẳng AC đi qua A và vuông góc với BH nên có phương trình 3x  2y 10  0. 2
x  3y  0
Tọa độ điểm M là nghiệm của hệ phương trình   M 6; 4   3
x  2y 10  0
Do M là trung điểm AC suy ra tọa độ điểm C8; 7 Vậy B  3
 ;2,C 8; 7 .
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 006
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn A
D có véc tơ pháp tuyến là n  1; 2   .
d qua M 1; 
1 và d //D nên d : 1 x   1  2 y  
1  0  x  2y  3  0 . Câu 2. Lời giải Chọn B TXĐ: D   .
Ta có x x  6  5  2x 10  xx 8  0x  5  S   Câu 3. Lời giải Chọn A 1 Ta có: 2 2 2
AC AB BC  2A . B BC.cos  2 2
ABC  8  9  2.9.8.  73  AC  73 2 Câu 4. Lời giải Chọn D   f xx 0  0  và a  1  0 .  x  2 Bảng xét dấu:
Do đó: f x  0, x  0;2 . Câu 5. Lời giải Chọn C 5 12 13
Nửa chu vi của tam giác là: p   15 2
Diện tích của tam giác là:
S p p  5 p 12 p 13  1515  515 1215 13  30 . Câu 6. Lời giải Chọn D 3   x  0 x  3 5x 1 x  x  3  1 Ta có:
 3  x   3  x  5x 1 x     1    x  3 . 2 2   4x  1  x   4 2 2    4  1 
Vậy tập nghiệm của bất phương trình đã cho là  ;3 .  4    Câu 7. Lời giải Chọn D
Áp dụng công thức tính độ dài đường trung tuyến AM của ABC ta có: 2 2 2 AB AC  2  BC 2 2 2 9 12  2 15 225 15 2 AM     AM   7,5. 4 4 4 2 Câu 8. Lời giải Chọn C
d có véctơ chỉ phương u =(3;2) nên véctơ pháp tuyến có tọa độ (2;- ) 3 . Câu 9. Lời giải Chọn D
Đường thẳng 2x  3y  6  0 đi qua hai điểm 0; 2
 ,3;0 nên loại đáp án H2 và H4.
Mặt khác O 0;0 không thỏa mãn 2x  3y  6  0 nên chọn hình H3. Câu 10. Lời giải Chọn A
Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào không thỏa bất phương trình trên. Câu 11. Lời giải Chọn B
x  5  0  x  5  . x  5  0
x  5(x  5)  0    x  5  . x  5  0
Vậy x  5  0  x  5(x  5)  0 . Câu 12. Lời giải Chọn C
2a  2b a b   a c .  3  b  3
c b c Câu 13. Lời giải Chọn C Vì 0x    1  0  1   0 ( đúng x  ). Câu 14. Lời giải Chọn Aa  0
Bất phương trình ax b  0 có tập nghiệm là  khi và chỉ khi  . b  0 Câu 15. Lời giải Chọn B Câu 16. Lời giải Chọn C
Đáp án A sai khi a  1;b  1  .
Đáp án B và D sai khi a b  0. Xét : 2 2 2 2
a b a b a  2ab b a  2 ab b ab ab luôn đúng với mọi số thực a,b . Vậy,chọn B. Câu 17. Lời giải Chọn B 5
ĐK: 2x  5  0  x  . 2 Câu 18. Lời giải Chọn C  1 
Thay tọa độ điểm B
; 2 vào đường thẳng  : 2x y 1  1
0 ta được 2.  2 1  0 .    2  2 ---HẾT--- Câu 19. Lời giải Chọn A x y
Phương trình đường thẳng AB theo đoạn chắn   1. a b Câu 20. Lời giải Chọn C Câu 21. Lời giải Chọn Ax  3  0 x  3 ĐK     x  3  x  3  0 x  3  1 1 1 1
x  3  x  3 6     0     x x x x
x  x   0 x  x   0 3 3 3 3 3 3 3 3     
x   x   x 3 3
3  0  x 3 Vậy S   ;  3   3; . Câu 22. Lời giải Chọn D 2x 8 35 Ta có
 23 2x 16  7  x x   5 5 8 Câu 23. Lời giải Chọn B
Viết phương trình đường thẳng đường cao AH : điểm đi qua A2; 6  vectơ pháp tuyến n  4;  3
AH : 4 x  2  3 y  6  0  4x  3y 10  0 Câu 24. Lời giải Chọn C    2 2 x 1
x x  2  0  Do 2
2x 1  0 nên bất phương trình tương đương với:    1 2 2 2x 1  0 x   2  2   x  1   2   2  2   x  x  2     . 2    2  2   x  1 x    2  2  2   2 
Vậy, tập nghiệm của bất phương trình  2 x x   2 2 2x 1  0 là  2  ;   ;1 .  2   2      Câu 25. Lời giải Chọn B 2
x x 12  0  x  ;    3 4;  .
Bất phương trình có tập nghiệm S   ;    3 4;  .
Ta có 0;   S . Câu 26. Lời giải Chọn B
ĐK x 1  0  x  1 x m 2m 3m 1 x 1  
x 1 x m  2m  2x  3m 1  x x 1 x 1 2 3m 1 1 Vì 1  x  1 
 2  3m 1  1  3m   m 2 3  1  Vậy m  ;  .    3  Câu 27. Lời giải Chọn A AB AC 6 AC Ta có     AC  8. sin C sin B 3 sin sin B B 4 BC AC BC 8 Và     BC 12 . sin A sin B sin A 2 sin A 3
Chu vi tam giác C AB BC CA  26 . Câu 28. Lời giải Chọn C a 3
Tam giác ABC đều cạnh a có bán kính đường tròn ngoại tiếp R  . 3 2 a 3 64.3 3
R  8  a  8 3 . Diện tích tam giác đều bằng   48 3 . 4 4 Câu 29. Lời giải Chọn Dx  2   6 Điều kiện: 2
x  4x  2  0   . x  2   6 Ta có 2
x  4x  2  2x 1 2 2
x  4x  2  4x  4x 1 2
 3x  8x  3  0 . b 8
Áp dụng định lí Vi-et ta có S x x    . 1 2 a 3 Câu 30. Lời giải Chọn B
Cách 1: Thử chọn dễ thấy C là đáp án thỏa mãn. Cách 2: Giải chi tiết: 1 1 1 1 1 1 1
Xét VT  1       a b c ab bc ca abc
Áp dụng BĐT Cauchy cho các số dương trên ta có 3 1 1 1 3 1 1 1 3
a b c  1    ;    và abc     3 a b c abc ab bc caabc2 3  3  27
Suy ra VT  1 9  27  27  64 1
Dấu bằng xảy ra khi và chỉ khi a b c  . 3 Câu 31. Lời giải Chọn D
2x  5  3  3  2x  5  3  2  x  8  1 x  4. Câu 32. Lời giải Chọn A
 x  34  x  0 m 3  ;4 Ta có   
x m 1
x m 1
bất phương trình có nghiệm khi m 1  3   m  2  . Câu 33. Lời giải Chọn D
Ta có M là trung điểm BC nên tọa độ điểm M 2; 0 .    AM  1;  1  nAM M n AM 1;  1 AM 1;  1 . Đường thẳng đi qua nhận
là véc tơ pháp tuyến có phương
trình tổng quát: AM : x  2  y  0  AM : x y  2  0. Câu 34. Lời giải Chọn B
 có véc tơ pháp tuyến n  4;3 và đi qua điểm 1;2 .
Suy ra  : 4 x  
1  3 y  2  0  4x  3y 10  0 .  
d M  4.2 3.0 10 2 ;   . 2 2 4  3 5 Câu 35. Lời giải Chọn A 4
Ta có y x 1 1. x 1 Do x  4
1 nên theo bất đẳng thức Cô -si cho hai số x 1; x1 4 4  4  Ta có: x 1  2 x 1.  4  x 1
1  5  y  5  x  1\   x 1 x 1  x 1  4
Dấu “=” xảy ra khi và chỉ khi x 1 
x 1  2  x  3 x 1 PHẦN II: TỰ LUẬN Câu 36. Lời giải
Do a,b 0; 
1 nên 1 a  0;1 b  0; a b  0.
Áp dụng bất đẳng thức CôSi cho ba số không âm, ta có 3        
a  ba b 1 a 1 b a b 1 1 
   a  ba b 8 1 1  .    3  27 1
  a  1 b 1
Đẳng thức xảy ra khi và chỉ khi   a b  1
  b a b 3 Câu 37. Lời giải
Yêu cầu Câu toán   2 m   2
2 x  2(m 1)x 1  0, x      2   0 (m 1)  2 m  2  0 2      m    2 m   1 ( 1)
2  0  2m  1  m  2 a  0  m  2  0 2 1
Vậy m  thỏa mãn. 2 Câu 38. Lời giải
2 a c b
2 a b c
 2 b c a  2 2 2  2 2 2  2 2 2  2 2 2
Ta có m m  5m    5  b c a 4 4  4    2 2 2 2 2 2 2 2 2 2 2 2
 2a  2c b  2a  2b c 10b 10c  5a  9a  9b  9c  0 2 2 2
a b c . a b c
Áp dụng định lí sin trong tam giác ABC ta có    2R . sin A sinB sinC
Khi đó ta có a b c   R A2   R 2  R 2 2 2 2 2 2 2 2 sin 2 sinB
2 sinC  sin A  sin B  sin C . Câu 39. Lời giải
*)Ta thấy điểm A không thuộc hai đường trung tuyến BE : x  2y 1  0,CD : y 1  0 .
BE : x  2y 1;CD : y  1 .
B BE B 2a 1;a;C CD C  ; b  1 .  a  3 
D là trung điểm của AB D a; .    2  a  3 Mà D DC  1 a  1   B 3  ;  1 . 2  b 1 
E là trung điểm của AC E ; 2 .    2  b 1 E BE
 2.2 1  0  b  5  C 5;  1 . 2   *) Ta có: AB   4  ; 4    4  1; 
1 ⇒ vecto chỉ phương của đường thẳng AB là: u AB 1;  1 . 
Vecto pháp tuyến n   AB 1; 1. x  1 t
Phương trình tham số của đường thẳng AB :  . y  3  t
Phương trình tổng quát của đường thẳng AB :1 x  
1 1 y  3  0  x y  2  0 .   
*) Ta có: BC  8;2  24;  1 ⇒ u n   BC 4;  1 ; BC 1; 4 . x  3   4t
Phương trình tham số của đường thẳng BC :  . y  1   t
Phương trình tổng quát của đường thẳng BC :1 x  3  4 y  
1  0  x  4y 1  0 .   
*) Ta có: AC  4; 2    22;  1  u   n AC
2; 1; AC 1;2 . x  1 2t
Phương trình tham số của đường thẳng AC :  . y  3  t
Phương trình tổng quát của đường thẳng AC :1 x  
1  2 y  3  0  x  2y  7  0 .
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 007
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn D
Ta có 5 x  2  9  2x  2y  7  3x  2y  6  0 .
Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào không thỏa bất phương trình trên. Câu 2. Lời giải Chọn C
Vectơ cơ sở của trục Oy là 0;  1 . Câu 3. Lời giải Chọn B
Ta có: y  2x  3  2x y  3  0 . 
Nên đường thẳng đã cho có véc-tơ pháp tuyến là n  2;  1 Câu 4. Lời giải ChọnB
Thử vào dễ thấy rằng D  1  ; 
1 không thỏa mãn bất phương trình nên đáp án là B. Câu 5. Lời giải Chọn B
Đường thẳng đi qua M x ; y
d : ax by c  0 0
o  và song song với đường thẳng có dạng:
a x x b y y  0 (ax by  0) 0   o  . o 0
Nên đường thẳng đi qua điểm O 0 ; 0 và song song với đường thẳng có phương trình 6x  4y  1  0 là
3x  2 y  0 . Câu 6. Lời giải Chọn C • Xét đáp án A:
Thay x  1, y  1
 vào bất phương trình x y  3  0 , ta được: 1   1  3  0  3
  0 ( Vô lý). Vậy cặp số
1; 1 không là nghiệm của bất phương trình x y 3  0. Loại • Xét đáp án B:
Thay x  1, y  1
 vào bất phương trình x y  0 , ta được: 1    
1  0  0  0 ( Vô lý). Vậy cặp số 1;  1
không là nghiệm của bất phương trình x y  0 . Loại • Xét đáp án C:
Thay x  1, y  1
 vào bất phương trình x  3y 1 0 , ta được: 1 3.  1 1  0  1
  0 ( Luôn đúng). Vậy cặp số 1; 
1 là nghiệm của bất phương trình x  3y 1  0 . Chọn C • Xét đáp án D:
Thay x  1, y  1
 vào bất phương trình x  3y 1 0 , ta được: 1   3. 
1 1  0  1  0 ( Vô lý). Vậy cặp số
1; 1 không là nghiệm của bất phương trình x 3y 1 0 . Loại Câu 7. Lời giải Chọn D A a M B C 2 a a 5 2 2 2
BM AB AM a   . 4 2 Câu 8. Lời giải Chọn D Ta có 2
x  3x  4  0  1   x  4 . Câu 9. Lời giải Chọn A 2
Phương trình hệ số góc: y k x x y y   x  3  2  2x  3y 12  0 0  . 0 3 Câu 10. Lời giải Chọn A Câu 11. Lời giải Chọn B 3
Thay các giá trị x  2;1;0; vào bất phương trình thì ta có x  0 là nghiệm. 2 Câu 12. Lời giải Chọn C
2 b c a 2  2 2 2
Theo công thức tính độ dài đường trung tuyến AM . 4 Câu 13. Lời giải Chọn C
Tính chất của bất đẳng thức. Câu 14. Lời giải Chọn A
Ta có 3  x  2  x  3  2 . Câu 15. Lời giải Chọn B
–2 x – y  y  3  2
x  3y  3 .
Thay giá trị từng cặp điểm vào, ta chọn đáp án. D. Câu 16. Lời giải ChọnD 1 
Ta có 2x 1  0  x  . 2 4  Do đó x
không là nghiệm của bất phương trình. 3 Câu 17. Lời giải Chọn C
Điều kiện: 6  3x  0  x  2 . Câu 18. Lời giải Chọn B
Đáp án A sai khi a  1;b  1  .
Đáp án B và D sai khi a b  0. Xét : 2 2 2 2
a b a b a  2ab b a  2 ab b ab ab luôn đúng với mọi số thực a,b . Vậy,chọn B. Câu 19. Lời giải Chọn B
Đáp án A: Do x  1 nên nhân vào hai vế cùng biểu thức 2x 1  0 ta được bất phương trình tương đương. 1
Đáp án B: Hai bất phương trình có cùng tập nghiệm là S  ( ;  ) . 2
Đáp án C: Hai bất phương trình có cùng tập nghiệm là S  ( ;  2  ) .
Đáp án D: Bất phương trình: 2
x (x  2)  0  S  ( 2  ;0)  (0;) , 1
Bất phương trình: x  2  0  S  ( 2  ;) 2
Tập nghiệm hai bất phương trình khác nhau nên chúng không tương đương. Câu 20. Lời giải Chọn A
BA BC AC Áp dụng định lý cosin trong tam giác ta có:  2 2 2 cos ABC  2.B . A BC  2 2 2 2  3  4 3  1   cos ABC    . 2.2.3 12 4 Suy ra góc  ABC  104 2  9 . Câu 21. Lời giải Chọn B
Bất phương trình tương đương với 2
x x 12  0  x  ;  3   4; . Câu 22. Lời giải Chọn B 1 1 h b Ta có: S  . . a h  . . a b h   ABC 2 a 2 b h a b 2 a b b sin B h Mặt khác: a 2       2 . sin A sin B a sin A h 1 b 2 Câu 23. Lời giải Chọn B Ta có: 2 2
1  x y  2xy  2xy  1.
Mặt khác: S   x y2 2 2 2
x  2xy y  2   2  S  2 . Câu 24. Lời giải Chọn D
Ta có: AB  2;6 , trung điểm của AB là I 2;  1 . 
Đường trung trực của đoạn AB qua I 2; 
1 và nhận AB  2;6 làm vectơ pháp tuyến có phương trình:
2 x  2  6 y  
1  0  2x  6y  2  0  x  3y 1  0 . Câu 25. Lời giải Chọn Ax  4  0 x  4      x  4  0  x 4  x  4 
2 x 1   x  4  0  2 x 1  x  4        4   x  2  .  2   x   1   x  4    x  2     x  2    2   x   1  x  4 x  2 Vậy x , 2   2,. Câu 26. Lời giải Chọn D
Giải 2 ta được: x  5. Giải  
1 ta được: x  m .
Hệ có nghiệm  m  5  m  5  . Câu 27. Lời giải Chọn A 
Có AB  4; 2  22;  1 
vtcp của đường thẳng AB là u  2;  1 . Câu 28. Lời giải Chọn D BC 5
Áp dụng định lý sin ta có  2R R   5 . sin  BAC 2.sin 30 Câu 29. Lời giải Chọn C
Phương trình đường thẳng d có dạng: 4x  3y m  0, m  7  . 4  6  mm
Ta có: d M ;d  7 1 
1  m  2  5  . 5  m  3 
Vậy phương trình đường thẳng d là 4x  3y  7  0; 4x  3y  3  0 Câu 30. Lời giải Chọn C 2 m  4  0
Bất phương trình có tập nghiệm là rỗng khi   m  2 . m 1  0 Câu 31. Lời giải Chọn A
Điều kiện: x  1; x  2; x  4 . Bảng xét dấu Vậy x  ;
 2 4; \  1 . Câu 32. Lời giải Chọn A é-2 < x <-1 4 2
x -5x + 4 < 0 Û ( 2 x - )( 2 1 x - )
4 < 0 Û ê1ê< x<2 ë Câu 33. Lời giải. Chọn D
ĐKXĐ: x  3  0  x  3. 3x  6  0 x  2(L)
| 3x  6 | x  3  0 |
 3x  6 | x  3  0    x 3 0    x  3(TM ). Câu 34. Lời giải Chọn Cx  2006  0 x  2006 Điều kiện:     x  2006. 2006  x  0 x  2006
Thay x  2006 vào bất phương trình, ta được: 2006  2006  2006  2006  0  0 (sai).
Vậy bất phương trình vô nghiệm. Câu 35. Lời giải Chọn C 1 y x 1 1 x 1 1 1 1
Cauchy cho 2 số dương x 1, ta có: x 1  x   1 . 1 x 1 x 1 x 1 1 Suy ra x 1 1  2 x 1 Vậy y  1
2 khi và chỉ khi x 1   x  2 min x 1 PHẦN II: TỰ LUẬN Câu 36. Lời giải a b c b Ta có: 1    2 b c a ab c 1    2  c b Tương tự:  c a 1  2  a c
Cộng từng vế các bất đẳng thức trên, ta có đpcm.
Bình luận: Lời giải trên là sự kết nối giữa giả thiết và đpcm. Để ý quan sát ta thấy nếu như cứ nhân 2 số
hạng ở biểu thức điều kiện rồi lấy căn thì ta được một số hạng ở biểu thức cần chứng minh. Chính điều này là
xuất phát điểm của Lời giải như trên. Câu 37. Lời giải Với m  2
 , tam thức bậc hai trở thành 1  0 : luôn đúng với mọi x . Với m  2  , yêu cầu Câu toán 2
 (m  2)x  2(m  2)x m  3  0, x    a  0 m  2  0 m  2  0        m  2   2   0
(m  2)  (m  2)(m  3)  0   m  2  0
Kết hợp hai trường hợp ta được m  2 là giá trị cần tìm. Câu 38. Lời giải 1 1 1 1 1  1 1  1 1 1 1 Ta có          .   2 2  2 2  2 b b c c k b k c k b c k h
k h  hh ha a a a a Câu 39. Lời giải A C' B' G B C
Do B BB ' nên tọa độ của B có dạng 2b 1;b.  b  3 
Vì C ' là trung điểm của AB nên C ' ; b .    2  b  Mặt khác, C ' 3 CC ' nên ta được: 1  0  b  1  hay B  3  ;  1 . 2  c 1 
Tương tự, B ' là trung điểm của AC B ' ; 2    2  c 1
Mặt khác B ' BB ' nên
 2.2 1  0  c  5 hay C 5;  1 . 2
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 008
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn B Câu 2. Lời giải Chọn A
Đáp án A sai khi a  1;b  1  .
Đáp án B và D sai khi a b  0. Xét : 2 2 2 2
a b a b a  2ab b a  2 ab b ab ab luôn đúng với mọi số thực a,b . Vậy,chọn B. Câu 3. Lời giải Chọn A
a b và c d a c b d (Tính chất cộng 2 vế của 2 bất đẳng thức cùng chiều). Câu 4. Lời giải Chọn C Câu 5. Lời giải Chọn A
Lần lượt thay toạ độ điểm ở mỗi phương án vào bất phương trình đã cho, ta thấy  x ; y  2;5 0 0    là nghiệm
của bất phương trình đã cho. Câu 6. Lời giải Chọn C
f x, y  x y . Thay f 2,3  2  3  1   0 . . Câu 7. Lời giải Chọn B 1
2x 1  0  x  . 2 Câu 8. Lời giải Chọn C
Đường thẳng đi qua M x ; y
d : ax by c  0 0
o  và song song với đường thẳng có dạng:
a x x b y y  0 (ax by  0) 0   o  . o 0
Nên đường thẳng đi qua điểm O 0 ; 0 và song song với đường thẳng có phương trình 6x  4y  1  0 là
3x  2 y  0 . Câu 9. Lời giải Chọn B
Áp dụng công thức tình độ dài trung tuyến ta có: 2 2 2 AB AC BC 2 2 2 2  6 5 55 MA      2 4 2 4 2 Câu 10. Lời giải Chọn B
Ta có AB  5 ; BC  7 ; AC  8 . 2 2 2 2 2 2
AC AB BC 8  5  7 1
Từ đó suy ra cos A     A  60. 2A . B AC 2.8.5 2 Câu 11. Lời giải Chọn D
Theo quy tắc xét dấu nhị thức bậc nhất thì đáp án C sai. Câu 12. Lời giải Chọn B Bất phương trình cho 2 2
x  2 5x  5  x  2 5x  5  5
10  4 5x  10  x  . 2 Câu 13. Lời giải Chọn D x y
Ta có phương trình đoạn chắn   1. 4 5  Câu 14. Lời giải Chọn A Câu 15. Lời giải Chọn D
Sai. Vì nếu có một trong ba đường thẳng AB, BC,CA song song hay trùng với y 'Oy thì không có hệ số góc. Câu 16. Lời giải Chọn C
Ta có: Theo định lí về dấu của nhị thức bậc nhất. Câu 17. Lời giải Chọn A
Quan sát đồ thị hàm số ta có, nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng 3x  2y 1  0
(không bao gồm đường thẳng). Câu 18. Lời giải Chọn D
Điều kiện xác định của bất phương trình 1 x  1 x x là 1   x  0   x  1  ;  1 1   x  0 Câu 19. Lời giải Chọn B 2 2 2
a c b 2 2 2 6  5  7 1 Ta có: cos B   . 2ac 2.6.5 5 Câu 20. Lời giải Chọn C Ta thế từng cặp  ;
x y từ đáp án vào, nhận thấy đáp án B không thoả vì 5.1 23  1  1  0 . Câu 21. Lời giải Chọn A BC a a
Theo định lý sin trong tam giác ta có 2R  1 3  R  .  . sin  BAC 2 sin120 3 Câu 22. Lời giải Chọn Dx  2 
x x  2  2  x  2    x  2  ;2 x  2 Câu 23. Lời giải Chọn A Do 2 2 2
6  8  10 nên tam giác ABC vuông và có hai cạnh góc vuông là 6, 8 . 1
Diện tích tam giác ABC là S  .6.8  24 . 2
Gọi r là bán kính đường tròn nội tiếp tam giác. S 24 Ta có: r    2 . p 6  8 10 2 Câu 24. Lời giải Chọn C
Ta có x  2m  2  mx  m  
1 x  2m  2  x  2 ( vì m 1  0 ) Câu 25. Lời giải Chọn B  1 1 
Ta có M là trung điểm AB nên tọa độ điểm M ;  .    2 2 
  7 5    CM   ;   nCM C nCM 5;7 CM
5;7. Đường thẳng đi qua nhận
là véc tơ pháp tuyến có    2 2 
phương trình tổng quát: CM : 5 x  4  7 y  2  0  CM : 5x  7 y  6  0 . Câu 26. Lời giải Chọn C x  1 x  1  
2x  2  x  4 x  2 x  2
2 x 1  x  4    .    x  1 x  1 x  2    
2x  2  x  4 x  2 Câu 27. Lời giải Chọn B 3 Điều kiện: x  . 4 1
Với điều kiện trên thì BPT đã cho tương đương 2
2x  3x 1  0   x  1. 2  1  3
Kết hợp với điều kiện thì tập nghiệm của BPT là S  ;1 \     .  2  4 Câu 28. Lời giải Chọn A
Ta có x x     x  2 2 6 9 0 3  0  x  3 . Câu 29. Lời giải Chọn D
Gọi A là giao điểm của  và Ox , B là giao điểm của  và Oy .
Ta có: A3;0 , B0;5  OA  3 , OB  15 5  S  . OAB 2 Câu 30. Lời giải Chọn A
Ta có  x  3 x   1  0  x  3  ;  1 .
Do x   nên x  3  ; 2  ; 1  ;0;  1 .
Vậy tổng các nghiệm nguyên của bất phương trình  x  3 x   1  0 là 5  . Câu 31. Lời giải Chọn B ĐK: x  3
 ; x  1; x  2; x  4; x  0 . 16  4x 2       2 4 x 16 x  4 x  3   16 4x 4x 4x 48 4  0   0   0   0  2 x x 12 2 x x 12
x  4x 3 x  3  x  4  1 1 1 x x  
1  x x  2   x   1  x  2 2   2  x  0    x 2 0   0   0  
x  2 x 1 x
x x  2 x   1
x x  2 x   1 1
  x  2  x  2
Vậy x  2;01; 22; Câu 32. Lời giải Chọn D 2
x  2mx  5m  6  0 có nghiệm khi và chỉ m  2 2
'  0  m  5m  6  0   m ;  23;   m  3
Vì 1  m  2  m 1;2   ;
 2 3; nên '  0nên phương trình có 2 nghiệm phân biệt. Câu 33. Lời giải Chọn C 
Đường cao BH đi qua B 4;5 và vuông góc với AC   5  ;3 Vậy PTTQ là : 5
 x  4  3 y  5  0  5x  3y  5  0 Câu 34. Lời giải Chọn C
Dễ thấy I) và III) đúng.  1 1 1  1 1 1 1 9
Lại có a b c 3 3    3. abc.3.  9     .Vậy III) cũng đúng.    a b c abc a b c
a b c Câu 35. Lời giải Chọn D 9 2 x 9 4 9 2x 9 13 25 Ta có 2      2  2 .2   x 2  x x 2 2  x 2 2 2
9 2 x 2x 6 Dấu bằng xảy ra khi 2 
x  (thỏa)  a  6; b  5. Vậy a b  11. x 2  x 5 PHẦN II: TỰ LUẬN Câu 36. Lời giải
Áp dụng bất đẳng thức CôSi, ta có  b c   a c   b a 2 2 2 2 2 2  a bc a ,b ac b ,c ba c .        2   2   2  Suy ra 2 2 2 2 2 2
a b b a a c c a b c c b 2 2 2 a bc b ac c ab  .(1) 2
Tiếp tục áp dụng bất đẳng thức CôSi, ta có 3 3 3 3 3 3 3 3 3
a a b
b b a
a a c 2 2 2 a b  ,b a  , a c  , 3 3 3 3 3 3 3 3 3 3 3 3
c c a
b b a
c c b 2 2 2 c a  ,b c  ,c b  3 3 3 Suy ra 2 2 2 2 2 2
a b b a a c c b b c c b   3 3 3
2 a b c . (2) Từ (1) và (2),suy ra 2 2 2 3 3 3 a bc b ac c
ab a b c .
Đẳng thức xảy ra khi và chỉ khi a b c Câu 37. Lời giải Trường hợp 1: 2
4  m  0  m  2  -Với: f x 
f x   
m  2 ta có 1, thoả mãn 0, x -Với: 
f x   
f x   
m  2 ta có
8x 1, không thoả mãn 0, x Trường hợp 2: 2
4  m  0  m  2 
Khi đó: f x   2  m  2 3 4
x  2m  2 x 1  0, x   2 a  0 4  m  0 m   2  ;2        m 1  ;2 '  . 2   0
4m  4m 8  0 m   1  ;2
Từ các trường hợp trên và m   ta được m 1  ;0;1;  2 . Vậy m  1  ;0;1;  2 . Câu 38. Lời giải 1 1  1 Ta có: S S S bc dc sin 45 db sin 45      ABC ABD ACD 2 2 2  1 2bc
bc d(b c)sin 45  d(b c)  d  2 b c Câu 39. Lời giải A C' B' G B M Cy  2  0 x  1 
Do B BB ' BC nên tọa độ điểm B là nghiệm của hệ:    , ta được B  1  ;2.
x  2y  5  0 y  2
Tượng tự, C CC ' BC , ta được C 3;4.
Gọi G là giao điểm của BB ' và CC ', khi đó G 2;2. 
Gọi M là trung điểm của BC , suy ra M 3;  1 và GM   1  ;  1 .
Do G là trọng tâm tam giác ABC nên A ; x y thỏa mãn:   1
  x  3.  1 x  4
AM  3GM    
, ta được A4;0. 3   y  3.1 y  0
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 009
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn B
Thay tọa độ các điểm vào bpt thì  1  ; 
1 thỏa mãn. Các cặp khác không thỏa mãn. Câu 2. Lời giải Chọn C
Ta có 2.2 11  4  0 . Câu 3. Lời giải Chọn B
Thay toạ độ điểm O 0;0 vào từng đáp án. Nhận thấy chỉ có mỗi đáp án D là thoả 2  0 . Câu 4. Lời giải Chọn A Ta có 2 2 2
AC AB BC  2A .
B BC.cos B  76  AC  2 19 . Câu 5. Lời giải Chọn C
Theo lý thuyết về dấu tam thức bậc hai. Câu 6. Lời giải Chọn D Thay x  1
 vào các bất phương trình ta có phương án B đúng. Câu 7. Lời giải Chọn B
Điều kiện: 2  x  0  x  2.
Tập xác định: D   ;  2. Câu 8. Lời giải Chọn B Câu 9. Lời giải Chọn B 13 14 15 Nữa chu vi: p   21. . 2
Diện tích: S p( p 13)( p 14)( p 15)  84.. Câu 10. Lời giải Chọn C
Đường thẳng đi qua A 1
 ;2, nhận n  2; 4
  làm véc tơ pháp tuyến có phương trình:
2(x 1)  4( y  2)  0  2x  4y 10  0  x  2y  5  0 Câu 11. Lời giải Chọn B
Ta có phương án A sai vì f x  g x  0, x
   còn các phương án còn lại đúng theo tính chất về các phép biến đổi bất phương trình. Câu 12. Lời giải Chọn A
Phương trình đường thẳng cần tìm là 2(x 1)  3( y  2)  0  2x  3y  8  0 . Câu 13. Lời giải Chọn D
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy  x ; y  5;3 0 0    là nghiệm của hệ. Câu 14. Lời giải Chọn C Chọn m  1
 thì f x  m  
1 x  2018  2018 không phải là nhị thức bậc nhất. Câu 15. Lời giải Chọn C 2 2 2 b c a 8  4 12 2 AM      3  AM  3 . 2 4 2 4 Câu 16. Lời giải Chọn D
Đáp án A sai khi a  1;b  1  .
Đáp án B và D sai khi a b  0. Xét : 2 2 2 2
a b a b a  2ab b a  2 ab b ab ab luôn đúng với mọi số thực a,b . Vậy,chọn B. Câu 17. Lời giải Chọn A
VTCP của đường thẳng song song với trục Oy là 0;  1 nên VTPT là 1;0 Câu 18. Lời giải Chọn Cx  2006  0
Bất phương trình xác định khi 
x  2006  0  0 vô lý nên bất phương trình vô nghiệm. 2006  x  0 Câu 19. Lời giải Chọn B
a c b d không đúng vì trừ 2 bất đẳng thức cùng chiều thi không được kết quả đúng.
Ví dụ: 7  8; 5  1 nhưng 7  5  2  7  8 1. Câu 20. Lời giải Chọn A
2x 1  x  3  x  4 . Câu 21. Lời giải Chọn D
C  180  40  60  80 . 
Áp đụng định lý sin vào ABC : AB BC AB 5   BC  .sin A  .sin 40  3,26. sin C sin A sin C sin80 Câu 22. Lời giải Chọn D
  m  2 m  4 6 2m d M ;    2 5 2 2 m 1 m 1 m  2  5m 1 3 m2 2 2 2 2 5m 5 m 6m 9 2m 3m 2 0                1 m   2 Câu 23. Lời giải Chọn A  Ta có AB   ;
a b nên vtpt của của đường thẳng AB là  ; b aCâu 24. Lời giải Chọn A 1 3x  5 1 3x  5 5x 12  3    3   0   0 2 x  2 x  2 x  2 x  2 x  4 5x 12
Đặt: f x  . 2 x  4 Bảng xét dấu: x  12  2  2  5 5x 12 - 0 + + + 2 x  4 + + 0 - 0 +
f x - 0 + - + 12 Kết luận: x   hoặc 2   x  2 . 5 Câu 25. Lời giải Chọn B Ta có 2
x 10x 16  0   x  2 x 8  0  2  x  8 . Câu 26. Lời giải Chọn D 1 1 Ta có 2
  1 4.  0  x x   0 4 4 2 1 1
x x   0  x  . 4 2 Câu 27. Lời giải Chọn A Ta có 2
(m  2)(x  3)  m m  6  m  2 x  3  m  2m  3 . Nếu m  2 :  
1  x  3  m  3  x  . m Nếu m  2 :  
1  x  3  m  3  x  . m Nếu m  2 :  
1  0  0 (vô lý). PT vô nghiệm. Câu 28. Lời giải Chọn C B a 2 C a 45° A a 2 D 1 Ta có: 2 S  2S  2. .A . B A .
D sin 45  a . ABCD ABD 2 Câu 29. Lời giải Chọn B  1 2x 1  0 x  1    2  m  2  3  m   . x m  2  2 2 x m  2 Câu 30. Lời giải Chọn A 2x 1   1 2  0 x 1 2x 1 2x 1     Ta có  2  0   2 x 1   x 1     3 . x 1 x 1 2x 1     4x 3  x 1 2     0  4 x 1  x 1  3  Tập x  ,  \     1 .  4  Câu 31. Lời giải Chọn C Ta có
x x    x  2 2 2 1 1  0, x   1  . Do đó bất phương trình x 1 x 1 x 1  0 x  1  0   0     2 x  2x 1 x  2 1 x  1  x  1 
Vậy tập nghiệm của bất phương trình là: S   ;    1   1  ;  1 . Câu 32. Lời giải Chọn C
Từ (1)  1  x  6 Từ (2)  3
  2x 1  3  1   x  2
Khi đó nghiệm của hệ bất phương trình là x  1;2 . Câu 33. Lời giải Chọn A
Đường thẳng d đi qua điểm C có dạng a x 10  by  2  0  ax by 10a  2b  0 . (Với 2 2 a b  0 ) .
a 3 10a  2b 7  a  2b Ta có d  ;
A d    ; 2 2 2 2 a b a b        B d  . a  5 .
b 4 10a 2b 15a 2b d ;  
d A;d   d  ;
B d   7
a  2b  1  5a  2b 2 2 2 2 a b a b 2a b  a 0
Vậy d x  2y 14  0 hoặc y  2  0 . Câu 34. Lời giải Chọn D a b a b a b c a b c Ta có:   2
.  2  I  đúng; 3    3
. .  3  II  đúng; b a b a b c a b c a 1 1 1 1 3     3   1 1 1 9 a b c
abc  a b c 1 1 1    9      III  đúng.     a b c a b c
a b c 3
a b c  3 abc Câu 35. Lời giải Chọn D 2 2 2
Ta có f x  x   x 1 1  2 x   1 . 1  2 2 1. x 1 x 1 x  1  2 x 1    x  2 1  2
Dấu bằng xảy ra khi và chỉ khi  x 1    x  1 2 .     x  1 x 1 PHẦN II: TỰ LUẬN Câu 36. Lời giải
Áp dụng bất đẳng thức CôSi, ta có 1 1 1 1 1 3 2 2 2 3 3
y  3x   3x    3 3x . .  3 . x 2x 2x 2x 2x 4 1 1 1
Dấu “=” xảy ra khi và chỉ khi 2 3
 3x x   x  . 3 2x 6 6 3 1
Vậy giá trị nhỏ nhất của y là 3 3. , khi x  . 4 3 6 Câu 37. Lời giải
Với m  4 , ta có g(x)  -1  0 : đúng với mọi x .
Với m  4 , yêu cầu Câu toán  2
(m  4)x  (2m  8)x m  5  0, x    a  0 m  4  0 m  4        m  4 2   0
(m  4)  (m  4)(m  5)  0   m  4  0
Kết hợp hai trường hợp ta được m  4 . Câu 38. Lời giải 1 1 1 Ta có SSS
bc AM .c.sinAM .b.sin 90   bc AM csinbcosABC MAB MAC 2 2 2 bc Vậy AM  .
b cosc sin Câu 39. Lời giải Định hướng:
- Tọa độ điểm  
B BH BM
- Viết phương trình đường thẳng AC đi qua A và vuông góc với BH .
Suy ra tọa độ M  AC BM C
Gọi BH , BM lần lượt là đường cao và trung tuyến kẻ từ B. 2
x  3y 12  0
Tọa độ điểm B là nghiệm của hệ phương trình   B  3  ;2 2
x  3y  0
Đường thẳng AC đi qua A và vuông góc với BH nên có phương trình 3x  2y 10  0. 2
x  3y  0
Tọa độ điểm M là nghiệm của hệ phương trình   M 6; 4   3
x  2y 10  0
Do M là trung điểm AC suy ra tọa độ điểm C8; 7 Vậy B  3
 ;2,C 8; 7 .
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 010
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn Dx  2  0 x  2
Điều kiện xác định của bất phương trình      x  2 .  x 1  0 x  1 Câu 2. Lời giải Chọn B
Phương trình đường thẳng cần tìm là 2(x 1)  3( y  2)  0  2x  3y  8  0 . Câu 3. Lời giải Chọn A b
Theo bảng xét dấu, ta có:   2  0 . a
Mà a  0  b  0  b a  0 . Câu 4. Lời giải ChọnA 2x  5 x  3  x 1 tương đương với
 0 suy ra x 1. Đáp ánA. 3 2 6 Câu 5. Lời giải Chọn C
Đáp án A sai khi a  1;b  1  .
Đáp án B và D sai khi a b  0. Xét : 2 2 2 2
a b a b a  2ab b a  2 ab b ab ab luôn đúng với mọi số thực a,b . Vậy,chọn B. Câu 6. Lời giải Chọn A
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy  x ; y  0; 2  0 0    là
nghiệm của hệ bất phương trình đã cho. Câu 7. Lời giải Chọn A
Dễ thấy x  1 không là nghiệm của bất pt x 1  x nhưng nó lại là nghiệm của bất pt
2x  1 x 1  2x  1 x . Do đó hai bất pt không tương đương. Câu 8. Lời giải Chọn A Câu 9. Lời giải Chọn B
Thay tọa độ các điểm vào phương trình ta thấy Q 3;2 d . Câu 10. Lời giải Chọn A
Đường thẳng đi qua A 1
 ;2 , nhận n  2; 4 làm vecto pháp tuyến có phương trình là 2 x  
1  4 y  2  0  2x  4y 10  0  x  2y  5  0 . Câu 11. Lời giải Chọn B
a b a c b c (Tính chất cộng 1 số cho 2 vế của bất đẳng thức). Câu 12. Lời giải Chọn B 2 2 2 2 2 2
AB AC BC 3  5  6 1 Ta có cos A     . 2.A . B AC 2.3.5 15 Câu 13. Lời giải Chọn B Câu 14. Lời giải Chọn C Ta có: 4
x 16  0.  16  4x x  4  x 4;. Câu 15. Lời giải Chọn A 3 x  
1  4 y  2  5x  3  2x  4y  8  0  x  2y  4  0 .
Thay lần lượt tọa độ các điểm vào hệ bất phương trình, tọa độ điểm nào thỏa mãn hệ bất phương trình thì
điểm đó thuộc miền nghiệm của bất phương trình đã cho. Câu 16. Lời giải Chọn A
Do  : x  2y  3  0 véc tơ chỉ phương của  là véc tơ khác véc tơ không và cùng phương với u 2;  1  Suy ra: 4; 2
  không là véc tơ chỉ phương của  do không cùng phương với u 2;  1 Câu 17. Lời giải Chọn B
Dễ thấy   9  28  1
 9  0 . Vậy f x  0, x    . Câu 18. Lời giải Chọn D 2 2 2
b a c  2ac cos B 2 2
 8  3  2.8.3cos 60  49  b  7 . Câu 19. Lời giải Chọn D Câu 20. Lời giải Chọn C
Theo công thức độ dài đường trung tuyến. Câu 21. Lời giải Chọn D
Phương trình đường thẳng cần tìm là 2 x  
1  3 y  2  0  2x  3y  8  0 . Câu 22. Lời giải Chọn C
Dựa vào bảng xét dấu ta thấy x  2 là nghiệm của f x nên ta loại các đáp án A, B, Vậy đáp án đúng là Câu 23. Lời giải Chọn C 6  8 10
Nửa chu vi tam giác là: p  12 . 2
S p( p a)( p b)( p c)  12(12  6)(12  8)(12 10)  24 . Câu 24. Lời giải Chọn D
Ta có. x x     x  2 2 4 4 0 2  0 Mà  x  2 2  0 , x    .
Do đó BPT   x  2 2
 0  x  2  0  x  2  . Câu 25. Lời giải Chọn Dx  3  1 x  2 x  3  1  .   x  3  1 x  4 Câu 26. Lời giải Chọn C
Điều kiện: 3  x  0  x  3 .
BPT đã cho tương đương với 1 x x 1  x 1  x 1  x 1  0  x  1.
Vậy tập nghiệm của BPT là  ;   1 . Câu 27. Lời giải Chọn C a b c
Theo định lí hàm số sin ta có:    2R sin A sinB sinC Suy ra: a b . b sin A +   a  . sin A sinB sin B a c . c sin A +   sin C  . sin A sinC a a +
 2R a  2 . R sin A. sin A b b b +
 2R   R sin B   R tan B . sinB 2 2cosB Câu 28. Lời giải Chọn A x y
Phương trình cạnh BC : + = 1 Û BC : 3x + 4y -12 = 0 . 4 3 + -
Độ dài đường cao ứng với cạnh BC là AH = d A BC = = . ( ) 3.1 4.2 12 1 , 5 5 Câu 29. Lời giải Chọn B
Ý nghĩa hình học của bất đẳng thức Cô si. Câu 30. Lời giải Chọn Bx  4 x  4  4  x  0    x  1 2 2
x x  5  4  x   2
 x  2x 1  0   2
x  4  x x  5  4  x  x  1 2 2 x  9  0    3   x  3  x   3  ;1 2  1   2;3 .     Câu 31. Lời giải Chọn C 3
x – 4y 15  0 x  1   
Giao điểm của d và d là nghiệm của hệ  5
x  2y –1  0 y  3 . 1 2
Vậy d cắt d tại A 1  ;3 . 1 2
Để ba đường thẳng d , d , d đồng quy thì d phải đi qua điểm A A thỏa phương trình d 1 2 3 3 3
 m  4.3 15  0  m  3. Câu 32. Lời giải Chọn B Ta có 2 2
x  2x  4  (x 1)  3  0 , x    . Do đó  2
x  2x  4x  3  0  x  3  0  x  3 Câu 33. Lời giải Chọn D x 1 x  2 3  2x 1
Ta có f x      . x  2 x 1
x  2x   1
Lập bảng xét dấu biểu thức f x  
Từ đó suy ra f x   x    1 0 ; 2   ;1 .    2  Câu 34. Lời giải Chọn Am 1  0
Bất phương trình (ẩn x ): (m 1)x  2m  3  0 vô nghiệm    m  1. 2m  3  0 Câu 35. Lời giải Chọn C Ta có 9 4 9 25 4 25 9 25 4 25 25 75 y     x     x 25 2   2 . x  2 . 2 x   . x 2  x x 4 2  x 4 2 x 4 2  x 4 2 2 9 25  xx 4   4 25 6
Dấu “  ” xảy ra   
2 x  x  . 2  x 4  5 0  x  2  75 Vậy min y  6
x   a  6 ; b  5  a b 11. 0;2 2 5 PHẦN II: TỰ LUẬN Câu 36. Lời giải
Áp dụng bất đẳng thức CôSi, ta có 2 2 2 2 2 2
1 a  2 a  2a,1 b  2 b  2 ,
b 1 c  2 c  2c Suy ra 2 a  2  b  2  b  2  c  2  c  2  a    2 2 2 1 1 1
2 a b b c c a.
Tiếp tục áp dụng bất đẳng thức CôSi,ta có 2 2 2 3 2 2 2
a b b c c a  3 a . b b . c c a  3ab . c Suy ra 3 3 3 3 3 3 3 3 3
a a b
b b c
c c a 2 2 2 a b  ,b c  ,c a  3 3 3
Đẳng thức xảy ra khi và chỉ khi a b c  1. Câu 37. Lời giải f x 2
x  2mx  8  m  0, x   R ' 2
   0  m  2m  8  0  4   m  2
Vậy giá trị lớn nhất của tham số m cần tìm là m  2 Câu 38. Lời giải a) Trong M
AB thì MI là trung tuyến nên áp dụng công thức độ dài trung tuyến ta có 2 2 2 MA MB AB 2 AB 2 AB 2 MI    2 2 2
 2MI MA MB  2 2 2
MA MB  2MI  . 2 2 4 2 2
      
     b) 2 M .
A MB  (MI I )
A .(MI IB)  (MI )  MI (IA IB)  I . A IB .
    1   1 
Do I là trung điểm của AB nên thay IA IB  0; IA   A ; B IB
AB vào biểu thức ta được 2 2
  
   1  1  1 2 2 2 M .
A MB  (MI )  MI.0   AB . AB MI AB . Điều phải chứng minh.    2  2 4 Câu 39. Lời giải Định hướng:
- Tọa độ điểm  
B BH BM
- Viết phương trình đường thẳng AC đi qua A và vuông góc với BH .
Suy ra tọa độ M  AC BM C
Gọi BH , BM lần lượt là đường cao và trung tuyến kẻ từ B. 2
x  3y 12  0
Tọa độ điểm B là nghiệm của hệ phương trình   B  3  ;2 2
x  3y  0
Đường thẳng AC đi qua A và vuông góc với BH nên có phương trình 3x  2y 10  0. 2
x  3y  0
Tọa độ điểm M là nghiệm của hệ phương trình   M 6; 4   3
x  2y 10  0
Do M là trung điểm AC suy ra tọa độ điểm C8; 7 Vậy B  3
 ;2,C 8; 7 .
Document Outline

  • 10 DE ON TAP LOP 10 GIUA KY 2 - 2021
  • BTPRO [CD] GIUA KY 2 - LOP 10 - HDG