TOP12 đề ôn tập kiểm tra cuối học kì 1 môn Toán 12 (70% TN + 30% TL)

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra cuối học kỳ 1 môn Giới Toán 12 năm học 2022 – 2023 .Mời bạn đọc đón xem.

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

234 trang 8 tháng trước

Tác giả:

Profile Lan Tường
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 01
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Rút gọn biểu thức
( )
0
aa
Ma
a
=
về dạng
a
thì
thuộc khoảng nào dưới đây?
A.
( )
2;5 .
B.
( )
1;0 .
−
C.
( )
3; 1 .
− −
D.
( )
0;2 .
Câu 2: Cho hàm số
( )
C
và đường thẳng
: 1.d y x= − −
Biết
d
cắt
( )
C
tại ba điểm có
hoành độ lần lượt là
1 2 3
, , .x x x
Tính giá trị
222
1 2 3
.xxx++
A.
3.
B.
6.
C.
0.
D.
9.
Câu 3: Hàm số
3
9 11y x x= − + −
nghịch biến trên khoảng nào sau đây?
A.
( )
; 3 .− −
B.
( )
3; .− +
C.
( )
3; 3 .−
D.
( )
3;3 .−
Câu 4: Cho hình trụ có hai đáy là hai hình tròn
( )
O
và
( )
O
, chiều cao
3R
và bán kính đáy
R
. Một
hình nón có đỉnh là
O
và đáy là hình tròn
( )
;OR
. Tính tỷ số diện tích xung quanh của hình trụ
và hình nón.
A.
3
. B.
2
. C. 2. D. 3.
Câu 5: Cho
0, 1, 0, 0a a b c
. Trong 4 khẳng định sau, có bao nhiêu khẳng định đúng?
I.
( )
log log log
a a a
bc b c=
II.
log log log
a a a
b
cb
c
=−
III.
( )
1
log log 0
aa
bb
=
IV.
1
log log
2
aa
bb=
A. 3. B. 4. C. 1. D. 2.
Câu 6: Cho hàm số
( )
y f x=
xác định trên và có
( )
( )
( )
2021
22
13f x x x x
= − +
. Hỏi
( )
y f x=
có bao
nhiêu điểm cực trị?
A. 3. B. 4. C. 1. D. 2.
Câu 7: Cho
log
=
a
b
thì
( )
23
log=
ab
N a b
thuộc khoảng nào sau đây?
A.
( )
1;1−
. B.
( )
2;4
. C.
( )
1;2
. D.
( )
4;7
.
Câu 8: Trong các mệnh đề sau, mệnh đề nào là sai?
A. Diện tích xung quanh cùa hình trụ tròn xoay bằng tích độ dài đường tròn đáy và độ dài đường
sinh.
B. Thể tích của khối nón tròn xoay bằng tích của diện tích đáy và độ dài đường cao của khối nón
đó.
C. Thể tích của khối trụ tròn xoay là giới hạn của thể tích khối lăng trụ đều nội tiếp khối trụ đó
khi số cạnh tăng lên vô hạn.
D. Diện tích toàn phần của hình nón là tổng của diện tích xung quanh và diện tích đáy của hình
nón đó.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 2
Sưu tầm và biên soạn
Câu 9: Đồ thị nào sau đây là dạng đồ thị của các hàm sổ
log
a
yx=
với
01a
?
A. . B. .
C. . D. .
Câu 10: Cho hàm số
( )
32
1
1
3
y f x x x= = − +
. Tìm giá trị nhỏ nhất của hàm số
( )
y f x=
trên
1;3
.
A.
1−
. B.
1
. C.
1
3
. D.
1
3
−
Câu 11: Cho hàm số
( )
1
2y f x x
x
= = + −
. Gọi
12
,yy
lần lượt là tung độ của điểm cực đại và cực tiểu của
đồ thị hàm số đã cho. Tính giá trị
12
yy−
A.
4
. B.
12−
. C.
4−
. D.
12
Câu 12: Phương trình
( )
3
log 2 1 2x+=
có nghiệm là
A.
3
. B.
4
. C.
13
. D.
1
Câu 13: Hình đa diện nào dưới đây không có tâm đối xứng?
A. Lăng trụ lục giác đều. B. Hình lập phương. C. Bát diện đều. D. Tứ diện đều.
Câu 14: Tính thể tích
V
của khối trụ có bán kính đáy và chiều cao đều bằng
2
.
A.
16
. B.
8
. C.
4
. D.
12
.
Câu 15: Tìm đạo hàm của hàm số
( )
3
12yx
−
=−
.
A.
( )
2
6 1 2yx
−
=−
. B.
( )
2
3 1 2yx
−
= − −
. C.
( )
4
6 1 2yx
−
= − −
. D.
( )
4
6 1 2yx
−
=−
.
Câu 16: Cho hàm số lũy thừa
( )
, .yx
=
Trong các khẳng định sau khẳng định nào sai?
A. Nếu
thì hàm số có tập xác định là
.
B. Nếu
0
−
thì hàm số có tập xác định là
\ 0 .
C. Nếu
thì hàm số có tập xác định là
.
D. Nếu
thì hàm số có tập xác định là
( )
0; .+
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 3
Sưu tầm và biên soạn
Câu 17: Tìm tập xác định của hàm số
( )
2
2
log 1 .yx=−
A.
( )
;1 .= −D
B.
\ 1 .D =
C.
.D =
D.
(
;1 .= −D
Câu 18: Tìm đạo hàm của hàm số
( )
2
3
log 1 .yx=−
A.
( )
2
'.
1 ln3
=
−
y
x
B.
( )
2
1
'.
1 ln3
=
−
y
x
C.
( )
2
2
'.
1 ln3
−
=
−
y
x
D.
( )
2
'.
1 ln3
−
=
−
y
x
Câu 19: Gọi
,l
,h
r
lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của một hình nón. Tính
diện tích xung quanh
xq
S
của hình nón đó.
A.
.
xq
S rh
=
B.
2.
xq
S rl
=
C.
.
xq
S rl
=
D.
2
1
.
3
xq
S r h
=
Câu 20: Cho tứ diện
OABC
có
,OA
,OB
OC
đôi một vuông góc và
,OA a=
,OB b=
.OC c=
Tính thể
tích khối tứ diện
.OABC
A.
.
3
abc
B.
.
6
abc
C.
.
2
abc
D.
.abc
Câu 21: Phương trình
( ) ( )
2
33
1
log 2 log 2 1
2
xx+ + − =
có bao nhiêu nghiệm?
A.
0
B.
1.
C.
2.
D.
3.
Câu 22: Phương trình
1
1
8
2
+
=
x
có nghiệm là:
A.
1.=x
B.
2.=x
C.
3.=−x
D.
4.=−x
Câu 23: Tìm đạo hàm của hàm số
x
ya=
với
A.
ln .
=
x
y a a
B.
.
ln
=
x
a
y
a
C.
1
.
.ln
=y
xa
D.
1
.
.ln
y
aa
=
Câu 24: Cho hàm số
()=y f x
xác định trên
2;2−
có đồ thị trên
2;2−
như hình vẽ:
Biết hàm số
()=y f x
đạt giá trị lớn nhất tại
a
và đath giá
trị nhỏ nhất tại
b
. Tính
4 3 .+ab
A.
12.−
B.
4.
C.
11.−
D.
4
.
3
−
Câu 25: Xét phương trình
( ) ( )
2
1
2022 2021 2022 2021 .
xx−−
− = +
Tổng bình phương các nghiệm
của phương trình đã cho bằng bao nhiêu?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 26: Có bao nhiêu khối đa diện đều?
A.
5.
B.
8.
C.
3.
D.
4.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 4
Sưu tầm và biên soạn
Câu 27: Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có
',BB a=
đáy
ABC
là tam giác vuông cân tại
B
và
.BA BC a==
Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
.Va=
B.
3
.
3
a
V =
C.
3
.
6
a
V =
D.
3
.
2
a
V =
Câu 28: Tập nghiệm của phương trình
1
3
log 1x −
là
A.
3;S
B.
0;3S
C.
.S
D.
;3S
Câu 29: Cho hàm số
( )
y f x=
xác định trên
\1
có bảng biến thiên như hình vẽ. Tìm khẳng định
đúng.
A. Hàm số nghịch biến trên
( )
3; .+
B. Hàm số nghịch biến trên
( ) ( )
; 2 3; .− − +
C. Hàm số đồng biến trên
( )
;1 .−
D. Hàm số đồng biến trên
( )
2;3 .−
Câu 30: Cho hàm số
( )
2
1
x
y f x
x
−
==
−
có đồ thị là hình vẽ nào dưới đây?
A. Hình 4. B. Hình 1. C. Hình 2. D. Hình 4
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 5
Sưu tầm và biên soạn
Câu 31: Cho hàm số
( )
y f x=
xác định trên
\2
. Biết
( )
lim 0
x
fx
→+
=
,
( )
lim 1
x
fx
→−
=
,
( )
2
lim 3
x
fx
−
→
=−
,
( )
2
lim
x
fx
+
→
= −
. Trong các khẳng định sau, khẳng định nào đúng?
A. Đồ thị hàm số có hai đường tiệm cận đứng là
0x =
,
1x =
.
B. Đồ thị hàm số không có tiệm cận đứng.
C. Đồ thị hàm số có hai đường tiệm cận đứng là
2x =
.
D. Đồ thị hàm số có hai đường tiệm cận ngang là
0x =
,
1x =
.
Câu 32: Cho một khối nón có chiều cao bằng
4cm
, độ dài đường sinh bằng
5cm
. Tính thể tích khối nón
này.
A.
( )
3
45 cm
. B.
( )
3
15 cm
. C.
( )
3
12 cm
. D.
( )
3
36 cm
.
Câu 33: Trong mặt phẳng
( )
P
, cho đường thẳng
l
cắt và không vuông góc với
. Khi quay
( )
P
xung
quanh
thì đường thẳng
l
sinh ra
A. Mặt nón tròn xoay. B. Khối nón tròn xoay. C. Mặt trụ tròn xoay. D. Hình nón tròn quay.
Câu 34: Cho hàm số
(x)yf=
xác định trên và có bảng biến thiên như sau:
Tìm số nghiệm của phương trình
2 ( ) 7 0fx−=
?
A.
4.
B.
3.
C.
2.
D.
1.
Câu 35: Đồ thị hàm số
2
2
(x)
9
x
yf
x
−
==
−
có bao nhiêu tiệm cận đứng
A.
4.
B.
1.
C.
2.
D.
3.
II. PHẦN TỰ LUẬN (4 câu – 3 điểm)
Câu 36: Cho
a
và
b
là hai số thực thỏa mãn
2 ab
và
( )
22
log log 7
b
a
a b b+=
. Tính giá trị của biểu
thức
2
log
7
ab
ab
ab
Pa
+
=
.
Câu 37: Cho hình chóp
SABCD
có đáy là nửa lục giác đều
ABCD
nội tiếp trong đường tròn đường kính
4AB a=
. Gọi
H
là trung điểm của
AB
và
( )
SH ABCD⊥
. Khoảng cách từ
B
đến
( )
SAC
bằng
3 10
5
a
. Tính thể tích khối chóp
SABCD
.
Câu 38: Cho hàm số
( ) ( )
32
2 3 4 6 3 3 5y x m x m x m= − + + + − −
có đồ thị
( )
m
C
. Tìm giá trị
0m
để hàm
số có hai cực trị đồng thời khoảng cách từ điểm cực đại của
( )
m
C
đến đường thẳng
( )
: 2 3 5 7 0
m
d m x y m+ − − − =
là lớn nhất.
Câu 39: Tìm tất cả các giá trị của tham số
m
để phương trình
sin cos
33
xx
m
có
20
nghiệm phân biệt
trên
55
;
22
.
-----HẾT-----
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 6
Sưu tầm và biên soạn
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM
Câu 1: Rút gọn biểu thức
( )
0
aa
Ma
a
=
về dạng
a
thì
thuộc khoảng nào dưới đây?
A.
( )
2;5
. B.
( )
1;0
−
. C.
( )
3; 1
− −
. D.
( )
0;2
.
Lời giải
Chọn B
1 3 3
1
2 2 4
4
.a a a a
Ma
a a a
−
= = = =
.
Câu 2: Cho hàm số
( ) ( )
3
21y f x x x C= = − + −
và đường thẳng
:1d y x= − −
. Biết
d
cắt
( )
C
tại 3
điểm phân biệt có hoành độ lần lượt là
12
;xx
và
3
x
. Tính giá trị
232
1 2 3
x x x++
.
A.
3
. B.
6
. C.
0
. D.
9
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm:
33
0
2 1 1 3 0
3
x
x x x x x
x
=
− + − = − − − =
=
.
( ) ( )
22
2 2 2 2
1 2 3
0 3 3 6xxx+ + = + + − =
.
Câu 3: Hàm số
( )
3
9 11y f x x x= = − + −
nghịch biến trên khoảng nào sau đây?
A.
( )
;3− −
B.
( )
3;− +
C.
( )
3; 3−
D.
( )
3;3−
Lời giải
Chọn A
Ta có
2
39yx
= − +
2
3
0 3 9 0
3
x
yx
x
=−
= − + =
=
Hàm số nghịch biến trên
( ) ( )
; 3 ; 3;− − +
Câu 4: Cho hình trụ có hai đáy là hai hình tròn
( )
O
và
( )
O
, chiều cao
3R
và bán kính đáy
R
. Một
hình nón có đỉnh là
O
và đáy là hình tròn
( )
;OR
. Tính tỉ số diện tích xung quanh của hình trụ
và hình nón.
A.
3
. B.
2
. C.
2
. D.
3
.
x
– ∞
-
ξ
3
ξ
3
+ ∞
y'
–
0
+
0
–
y
+ ∞
– ∞
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 7
Sưu tầm và biên soạn
Lời giải
Chọn A
Diện tích xung quanh hình trụ là:
2
1
2 . 3 2 3S R R R

==
Xét tam giác vuông
AOO
tại
O
, ta có
( )
2
2 2 2
32l AO OO AO R R R

= = + = + =
Diện tích xung quanh hình nón đỉnh
O
, đáy là đường tròn
( )
;OR
là
2
2
. .2 2S Rl R R R
= = =
.
Khi đó,
2
1
2
2
23
3
2
SR
SR
==
Câu 5: Cho
0, 1, 0, 0a a b c
. Trong 4 khẳng định sau, có bao nhiêu khẳng định đúng?
I.
( )
log log log
a a a
bc b c=
II.
log log log
a a a
b
cb
c
=−
III.
( )
1
log log 0
aa
bb
=
IV.
1
log log
2
aa
bb=
A. 3. B. 4. C. 1. D. 2.
Lời giải
Chọn C
Chỉ có khẳng định
IV
là đúng.
Câu 6: Cho hàm số
( )
y f x=
xác định trên và có
( )
( )
( )
2021
22
13f x x x x
= − +
. Hỏi
( )
y f x=
có bao
nhiêu điểm cực trị?
A. 3. B. 4. C. 1. D. 2.
Lời giải
Chọn A
Đạo hàm
'( )fx
đổi dấu khi đi qua các nghiệm
1 2 3
3, 1, 1x x x= − = − =
nên hàm số đã cho có 3
cực trị.
Câu 7: Cho
log
a
b
=
thì
( )
23
log
ab
N a b=
thuộc khoảng nào sau đây?
A.
( )
1;1N −
. B.
( )
2;4N
. C.
( )
1;2N
. D.
( )
4;7N
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 8
Sưu tầm và biên soạn
Lời giải
Ta có
( )
( )
( )
( )
23
23
log
2 3log
23
log 2,76 2;4 .
log 1 log 1
a
a
ab
aa
ab
b
N a b
ab b
+
+
= = = =
++
Câu 8: Trong các mệnh đề sau, mệnh đề nào sai?
A. Diện tích xung quanh của hình trụ tròn xoay bằng tích độ dài đường tròn đáy và độ dài đường
sinh.
B. Thể tích của khối nón tròn xoay bằng tích của diện tích đáy và độ dài đường cao của khối nón.
C. Thể tích của khối trụ tròn xoay là giới hạn của thể tích khối lăng trụ đều nội tiếp khối trụ đó
khi số cạnh tăng lên vô hạn.
D. Diện tích toàn phần của hình nón là tổng của diện tích xung quanh và diện tích đáy của hình
nón đó.
Lời giải
Ta có công thức tính thể tích của khối nón tròn xoay
1
.
3
V S h= ⎯⎯→
Đáp án B sai.
Câu 9: Đồ thị nào sau đây là dạng đồ thị của hàm số
log
a
yx=
với
01a
?
A. . B. .
C. . D. .
Lời giải
Chọn B
Hàm số
log
a
yx=
với
01a
nghịch biến trên khoảng
( )
0;+
và có đồ thị nằm bên phải
trục tung. Do đó chọn phương án
B
.
Câu 10: Cho hàm số
( )
32
1
1
3
y f x x x= = − +
. Tìm giá trị nhỏ nhất của hàm số
( )
y f x=
trên
1;3
.
A.
1−
. B.
1
. C.
1
3
. D.
1
3
−
.
Lời giải
Chọn D
Hàm số đã cho xác định và liên tục trên
1;3
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 9
Sưu tầm và biên soạn
Ta có:
( ) ( )
2
0 1;3
2 ; 0
2 1;3
x
f x x x f x
x
=

= − =
=
.
( ) ( ) ( )
11
1 ; 2 ; 3 1
33
f f f= = − =
.
Vậy
( ) ( )
1;3
1
min 2
3
f x f= = −
.
Câu 11: Cho hàm số
( )
1
2.y f x x
x
= = + −
Gọi
12
,yy
lần lượt là tung độ của điểm cực đại và điểm cực
tiểu của đồ thị hàm số đã cho. Tính giá trị
12
.yy−
A.
4.
B.
12.−
C.
4.−
D.
12.
Lời giải
Chọn C
Tập xác định:
\ 0 .D =
Ta có:
2
2
22
11
1 ; 0 1 0 1.
x
y y x x
xx
−

= − = = − = =
Bảng biến thiên:
Hàm số đạt cực đại tại
1, 4
CD
xy= − = −
và đạt cực tiểu tại
1, 0.
CT
xy==
Khi đó ta được
12
4, 0.yy= − =
Vậy
12
4.yy− = −
Câu 12: Phương trình
( )
3
log 2 1 2x+=
có nghiệm là
A.
3.x =
B.
4.x =
C.
13.x =
D.
1.x =
Lời giải
Chọn B
Ta có:
( )
3
1
2 1 0
log 2 1 2 4.
2
2 1 9
4
x
x
xx
x
x
+
−
+ = =

+=
=
Vậy nghiệm của phương trình là
4.x =
Câu 13: Hình đa diện nào dưới đây không có tâm đối xứng?
A. Hình lăng trụ lục giác đều. B. Hình lập phương.
C. Bát diện đều. D. Tứ diện đều.
Lời giải
Chọn D
Ta có hình tứ diện đều không có tâm đối xứng.
Câu 14:
Tính thể tích
V
của khối trụ có bán kính đáy và chiều cao đều bằng
2
.
A.
16V
=
. B.
8V
=
. C.
4V
=
. D.
12V
=
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 10
Sưu tầm và biên soạn
Lời giải
Chọn B
Ta có thể tích khối trụ
22
.2 .2 8V R h
= = =
Câu 15: Tìm đạo hàm của hàm số
( )
3
12yx
−
=−
A.
( )
2
6 1 2yx
−
=−
. B.
( )
2
3 1 2yx
−
= − −
. C.
( )
4
6 1 2yx
−
= − −
. D.
( )
4
6 1 2yx
−
=−
.
Lời giải
Chọn D
Ta có:
( ) ( ) ( ) ( ) ( )
4 4 4
3 1 2 1 2 3 1 2 . 2 6 1 2y x x x x
− − −
= − − − = − − − = −
Câu 16: Cho hàm số lũy thừa
yx
=
,
( )
. Trong các khẳng định sau, khẳng định nào sai?
A. Nếu
*
thì hàm số có tập xác định là .
B. Nếu
0
−
thì hàm số có tập xác định là
\0
.
C. Nếu
thì hàm số có tập xác định là .
D. Nếu
thì hàm số có tập xác định là
( )
0; +
.
Lời giải
Chọn C
Vì nếu
0
=
thì hàm số có tập xác định là
\0
.
Câu 17: Tìm tập xác định của hàm số
( )
2
2
log 1yx=−
.
A.
( )
;1D = −
. B.
\1D =
. C.
D=
. D.
(
;1D = −
.
Lời giải
Chọn B
ĐKXĐ:
( )
2
1 0 1xx−
.
Tìm tập xác định của hàm số là
\1D =
.
Câu 18: Tìm đạo hàm của hàm số
( )
2
3
log 1yx=−
.
A.
( )
2
1 ln3
y
x
=
−
. B.
( )
2
1
1 ln3
y
x
=
−
. C.
( )
2
2
1 ln3
y
x
−
=
−
. D.
( )
2
1 ln3
y
x
−
=
−
.
Lời giải
Chọn D
( )( )
( )
( )
2
2 1 1
2
1 ln3
1 ln3
xx
y
x
x
−−
−
==
−
−
.
Câu 19: Gọi
,,l h r
lần lượt là độ dài dường sinh, chiều cao và bán kính mặt đáy của một hình nón. Tính
diện tích xung quanh
xq
S
của hình nón đó.
A.
xq
S rh
=
. B.
2
xq
S rl
=
. C.
xq
S rl
=
. D.
2
1
3
xq
S r h
=
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 11
Sưu tầm và biên soạn
Chọn C
Câu 20: Cho tứ diện
OABC
có
,,OA OB OC
đôi một vuông góc và
,,OA a OB b OC c= = =
. Tính thể tích
khối tứ diện
OABC
A.
3
abc
. B.
6
abc
. C.
2
abc
. D.
abc
.
Lời giải
Chọn B
Ta có:
1 1 1 1
. . . . . .
3 3 2 6
OBC
V OA S OA OB OC a b c= = =
Câu 21: Phương trình
( ) ( )
2
33
1
log 2 log 2 1
2
xx+ + − =
có bao nhiêu nghiệm?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn D
Điều kiện
( )
2
20
2
2
20
x
x
x
x
+
−

−
.
Ta có
( ) ( ) ( )
2
3 3 3 3
1
log 2 log 2 1 log 2 log 2 1
2
x x x x+ + − = + + − =
.
( ) ( )
3
log 2 . 2 1 2 . 2 3x x x x − + = − + =

2
2
2
2
7
7
43
7
1
2
2
1
43
1
1
x
x
x
x
x
x
x
x
x
x
x
x
x

=
=
−=
=−
=
=−
− + =
=
=−
.
Vậy phương trình đã cho có
3
nghiệm.
Câu 22: Phương trình
1
1
8
2
x+
=
có nghiệm là?
A.
1x =
. B.
2x =
. C.
3x =−
. D.
4x =−
.
Lời giải
Chọn D
Ta có
4
1
1
8 2 1 4 0 4
2
x
x
xx
+
+
= = + = = −
.
Câu 23: Tìm đạo hàm của hàm số
x
ya=
với
0, 1aa
.
A.
' ln
x
y a a=
. B.
'
ln
x
a
y
a
=
. C.
1
'
ln
y
xa
=
. D.
1
'
ln
x
y
aa
=
.
Lời giải
Chọn A
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 12
Sưu tầm và biên soạn
Ta có:
( )
' ' ln
xx
y a a a==
Câu 24: Cho hàm số
( )
y f x=
xác định trên
2;2−
có đồ thị trên
2;2−
như hình vẽ:
Biết hàm số
( )
y f x=
đạt giá trị lớn nhất tại
a
và đạt giá trị nhỏ nhất tại
b
.
Tính giá trị
43ab+
.
A.
12−
. B.
4
. C.
11−
. D.
4
3
−
.
Lời giải
Chọn A
Dựa vào đồ thị, ta thấy: hàm số
( )
y f x=
đạt giá trị lớn nhất trên
2;2−
tại
2x =−
và đạt giá
trị nhỏ nhất tại
4
3
x =−
.
Do đó
( ) ( ) ( )
44
2; 4 3 4. 2 3. 8 4 12
33
a b a b

= − = − + = − + − = − + − = −


Câu 25: Xét phương trình
( ) ( )
2
1
2022 2021 2022 2021 .
xx−−
− = +
Tổng bình phương các nghiệm
của phương trình đã cho bằng bao nhiêu?
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải
Chọn C
Vì
( ) ( )
2022 2021 . 2022 2021 1− + =
nên
( )
1
1
2022 2021 2022 2021 .
2022 2021
−
+ = = −
−
Do đó phương trình
( ) ( ) ( ) ( )
22
11
2022 2021 2022 2021 2022 2021 2022 2021
x x x x− − +
− = + − = −
22
15
2
1 1 0 .
15
2
x
x x x x
x
+
=
= + − − =
−
=
Tổng bình phương các nghiệm của phương trình
đã cho bằng
22
1 5 1 5
3.
22
+−
+=
Câu 26: Có bao nhiêu khối đa diện đều?
A.
5.
B.
8.
C.
3.
D.
4.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 13
Sưu tầm và biên soạn
Lời giải
Chọn A
Theo định lý về sự tồn tại của các khối đa diện đều thì chỉ có năm loại khối đa diện đều.
Câu 27: Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có
',BB a=
đáy
ABC
là tam giác vuông cân tại
B
và
.BA BC a==
Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
.Va=
B.
3
.
3
a
V =
C.
3
.
6
a
V =
D.
3
.
2
a
V =
Lời giải
Chọn D
Vì
. ' ' 'ABC A B C
là lăng trụ đứng nên
'BB
là đường cao của lăng trụ, khi đó
. ' ' '
. ',
ABC A B C ABC
V S BB
=
mà đáy
ABC
là tam giác vuông cân tại
B
và
BA BC a==
nên
2
11
. . . . .
2 2 2
ABC
a
S BA BC a a
= = =
Do đó,
23
. ' ' '
..
22
ABC A B C
aa
Va==
Vậy chọn đáp án D.
Câu 28: Tập nghiệm của phương trình
1
3
log 1x −
là
A.
3;S
B.
0;3S
C.
.S
D.
;3S
Lời giải
Chọn A
Điều kiện
1x
1
13
3
3
log 1 log 1 log 1 3x x x x
−
− − − −
(thỏa mãn). Vậy
1x
Câu 29: Cho hàm số
( )
y f x=
xác định trên
\1
có bảng biến thiên như hình vẽ. Tìm khẳng định
đúng:
A. Hàm số nghịch biến trên
( )
3; +
.
B. Hàm số nghịch biến trên
( ) ( )
;2 3;− +
.
C. Hàm số đồng biến trên
( )
;1−
.
D. Hàm số đồng biến trên
( )
2;3−
.
C'
B'
A'
C
B
A
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 14
Sưu tầm và biên soạn
Lời giải
Chọn A
Hàm số nghịch biến trên các khoảng
( )
3; +
.
Câu 30: Hàm số
( )
2
1
x
y f x
x
−
==
−
có đồ thị là hình vẽ nào dưới đây?
A. Hình 4. B. Hình 1. C. Hình 2. D. Hình 3.
Lời giải
Chọn C
Xét đồ thị hàm số
( )
2
1
x
y f x
x
−
==
−
:
Ta có:
( )
2
1
0, 1
1
yx
x
=
−
nên hàm đã cho luôn đồng biến. Nên ta loại B, D.
Và đồ thị
( )
2
1
x
y f x
x
−
==
−
đi qua điểm
( )
0;2
nên Chọn C
Câu 31: Cho hàm số
( )
y f x=
xác định trên
\2
. Biết
( )
lim 0
x
fx
→+
=
,
( )
lim 1
x
fx
→−
=
,
( )
2
lim 3
x
fx
+
→
=−
và
( )
2
lim
x
fx
−
→
= −
. Trong các khẳng định sau đây khẳng định nào đúng?
A. Đồ thị hàm số có hai đường tiệm cận đứng
0, 1.xx==
B. Đồ thị hàm số không có tiệm cận đứng.
C. Đồ thị hàm số có một đường tiệm cận đứng
2.x =
D. Đồ thị hàm số có hai đường tiệm cận ngang
0, 1.xx==
Lời giải
Chọn C
( )
lim 0
x
fx
→+
=
: Tiệm cận ngang
0.y =
( )
lim 1
x
fx
→−
=
: Tiệm cận ngang
1.y =
( )
2
lim
x
fx
−
→
= −
: Tiệm cận đứng
2.x =
Câu 32: Cho một khối nón có chiều cao bằng
4cm
, độ dài đường sinh bằng
5cm
. Tính thể tích của khối
nón này.
A.
3
45 .cm
B.
3
15 .cm
C.
3
12 .cm
D.
3
36 .cm
Lời giải
Chọn C
Gọi
,,h l r
lần lượt là chiều cao, đường sinh và bán kính của khối nón.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 15
Sưu tầm và biên soạn
22
3r l h cm= − =
.
Thể tích khối nón
23
11
.9.4 12 .
33
V r h cm
= = =
Câu 33: Trong mặt phẳng
( )
,P
cho đường thẳng
l
cắt và không vuông góc với đường thẳng
.
Khi quay
mặt phẳng
( )
P
xung quanh đường thẳng
thì đường thẳng
l
sinh ra
A. Mặt nón tròn xoay. B. Khối nón tròn xoay.
C. Mặt trụ tròn xoay. D. Hình nón tròn xoay.
Lời giải
Câu 34: Cho hàm số
(x)yf=
xác định trên và có bảng biến thiên như sau:
Tìm số nghiệm của phương trình
2 ( ) 7 0fx−=
?
A.
4.
B.
3.
C.
2.
D.
1.
Lời giải
Câu 35: Đồ thị hàm số
−
==
−
2
2
()
9
x
y f x
x
có bao nhiêu tiệm cận đứng
A.
4.
B.
1.
C.
2.
D.
3.
Lời giải
II. PHẦN TỰ LUẬN
Câu 36: Cho
a
và
b
là hai số thực thỏa mãn
2 ab
và
( )
22
log log 7
b
a
a b b+=
. Tính giá trị của biểu
thức
2
log
7
ab
ab
ab
Pa
+
=
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 16
Sưu tầm và biên soạn
Ta có:
( )
22
log log 7
b
a
a b b+=
( )
22
log
2log 7
log
a
a
a
ab
b
b
+ =
2 2log
2log 7
log
a
a
a
b
b
b
+
+ =
( )
2
2 log 5log 2 0
aa
bb − + =
log 2
1
log
2
a
a
b
b
=
=
2
ba
ba
=
=
.
Kiểm tra điều kiện suy ra
2
ba=
.
Khi đó:
2
log
7
ab
ab
ab+
3
2
2
log
8
a
a
a
=
11
log
38
a
=
1
log
2
a
=
.
Do đó,
2
log
7
ab
ab
ab
Pa
+
=
1
log
2
a
a=
1
2
=
.
Câu 37: Cho hình chóp
.S ABCD
có đáy là nửa lục giác đều
ABCD
và nội tiếp đường tròn đường kính
4AB a=
. Gọi
H
là trung điểm của
AB
và
( )
SH ABCD⊥
. Khoảng cách từ
B
đến mặt phẳng
( )
SAC
bằng
3 10
5
a
. Tính thể tích khối chóp
.S ABCD
Lời giải
Ta có
( )
( )
( )
( )
( )
( )
3 10
, 2 , ,
10
a
d B SAC d H SAC d H SAC= =
.
Gọi
O
là giao điểm của
AC
và
DH
. Ta có tứ giác
AHCD
là hình thoi, do đó
OH AC⊥
.
Kẻ
( )
( )
3 10
,
10
a
HI SO d H SAC IH⊥ = =
.
Ta có
AHD
là tam giác đều cạnh bằng
2a OH a=
.
Khi đó
22
2 2 2
1 1 1
93SH a SH a
IH OH SH
= + = =
.
Ta có
( )
2
2
23
3 3. 3 3
4
ABCD ADH
a
S S a
= = =
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 17
Sưu tầm và biên soạn
Vậy thể tích khối chóp
.S ABCD
là
23
1
3 3.3 3 3
3
V a a a==
.
Câu 38: Cho hàm số
( ) ( )
32
2 3 4 6 3 3 5y x m x m x m= − + + + − −
có đồ thị
( )
m
C
. Tìm giá trị
0m
để hàm
số có hai cực trị đồng thời khoảng cách từ điểm cực đại của
( )
m
C
đến đường thẳng
( )
: 2 3 5 7 0
m
d m x y m+ − − − =
là lớn nhất.
Lời giải
Tập xác định
D=
.
Ta có:
( ) ( )
2
6 6 4 6 3y x m x m
= − + + +
.
Cho
( ) ( )
2
0 6 6 4 6 3 0y x m x m
= − + + + =
.
Hàm số có hai cực trị
( ) ( )
2
2
4 4 3 4 4 0m m m m = − + − + = + +


2.m −
Khi đó phương trình
0y
=
có hai nghiệm phân biệt là
1x =
và
3.xm=+
Do hệ số
20a =
và
0m
nên hàm số đạt cực đại tại
1x =
.
Suy ra điểm cực đại của đồ thị
( )
m
C
là:
( )
1;3A
.
( )
( ) ( ) ( )
2 2 2
2 3.3 5 7 4 16
,
2 3 2 9
m
m m m
d M d
mm
+ − − − − −
==
+ + − + +
.
Đường thẳng
m
d
luôn đi qua điểm cố định
(5;1)I
và có 1 VTCP là
( )
3; 2nm=+
.
Gọi
H
là hình chiếu vuông góc của
A
trên
m
d
, ta có
( )
,
m
d A d AH AI=
( )
max
, 2 5
m
d A d AI = =
.
Đẳng thức xảy ra
. 0 12 2( 2) 0 4
m
AI d AI u m m ⊥ = − + = =
.
Vậy
4m =
thỏa yêu cầu bài toán.
Câu 39: Tìm tất cả các giá trị của tham số
m
để phương trình
sin cos
33
xx
m
có
20
nghiệm phân biệt
trên
55
;
22
.
Lời giải
Đặt
sin cos
33
xx
fx
,
55
;
22
x
. Để ý rằng
2
f x f x
nên ta chỉ cần xét
fx
trên đoạn
0;
2
. Khi đó
sin cos
33
xx
fx
. Lại có
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 18
Sưu tầm và biên soạn
, 0; .
22
f x f x x
nên đồ thị hàm số
fx
trên đoạn
0;
2
nhận đường thẳng
4
x
làm trục đối xứng. Xét
fx
trên
0;
4
, ta có
sin cos
cos 3 sin 3 ln 3.
xx
f x x x
Dễ thấy
0x
không là nghiệm của
fx
nên ta xét
0
4
x
, khi đó
sin cos
33
sin cos .
sin cos
xx
f x x x
xx
Đặt
3
t
gt
t
,
21
0
2 ln 3
t
. Do đó
2
3 ln 3 1
0
t
t
gt
t
với
2
0
2
t
. Do đó
gt
là hàm số nghịch biến trên
2
0;
2
. Suy ra, trên
0;
4
ta có
sin cos
33
sin cos sin cos .
sin cos 4
xx
g x g x x x x
xx
Suy ra bảng biến thiên của
fx
trên
0;
2
Bằng cách tịnh tiến liên tiếp đồ thị hàm số
fx
trên
0;
2
, ta thu được đồ thị hàm số
fx
trên
55
;
22
nhận thấy rằng đồ thị này gồm
10
phần đồ thị giống như đồ thị hàm số
fx
trên
0;
2
. Do đó,
fx
có
20
nghiệm trên
55
;
22
khi và chỉ khi
fx
có
2
nghiệm trên
0;
2
. Điều này tương đương
2
2
4 2 3m
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 02
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cắt một hình nón bằng một mặt phẳng qua trục, được thiết diện là một tam giác đều cạnh
2a
.
Tính diện tích xung quanh của hình nón đó.
A.
2
3.a
B.
2
2
3
a
C.
2
2 a
D.
2
4 a
Câu 2: Tìm nghiệm của phương trình
1
31
x
.
A.
2.x =−
B.
1x =
C.
1x = −
D.
2x =
Câu 3: Cho khối lăng trụ
.ABC A B C
có thể tích bằng
36
. Tính thể tích khối tứ diện
A ABC
.
A.
10.
B.
24.
C.
18.
D.
12.
Câu 4: Cho hàm số
( )
2
16
.f x x
x
=+
Tìm giá trị nhỏ nhất của hàm số
( )
fx
trên đoạn
1;4
.
A.
20
B.
4−
C.
17
D.
12
Câu 5: Hàm số nào dưới đây có bảng biến thiên như hình vẽ bên?
A.
3
3y x x=−
B.
1
1
x
y
x
+
=
−
C.
42
2xx−
D.
1
1
x
x
−
+
Câu 6: Đạo hàm của hàm số
lny x x=
trên khoảng
( )
0;+
là
A.
1 ln .yx
=+
B.
1
.y
x
=
C.
ln .yx
=
D.
1 ln .x−
Câu 7: Cho
2
a log 5=
. Khi đó
50
log 100
bằng:
A.
2.
B.
2a 2
.
2a 1
+
+
C.
a2
.
a1
+
+
D.
a2
.
2a 1
+
+
Câu 8: Cho số thực a
(0 a 1)
. Khi đó giá trị của
3
a
P log a=
bằng:
A.
3.
B.
1
.
2
C.
1
.
3
D.
2.
Câu 9: Tìm nghiệm của phương trình
2
log x 1.=−
A.
x.
B.
1
x.
2
=
C.
x 1.=−
D.
x 2.=
Câu 10: Trong các hàm số sau đây, có bao nhiêu hàm số có cực trị?
( ) ( )
4
I f x x=
;
( ) ( )
32
3II f x x x x= − + −
;
( ) ( )
2
III f x x=
;
( ) ( )
IV f x x=
;
A.
1
B.
2
C.
4
D.
3
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 2
Sưu tầm và biên soạn
Câu 11: Cho hàm số
( )
y f x=
xác định trên và có bảng xét dấu của đạo hàm
( )
''y f x=
như sau.
Khẳng định nào sau đây sai?
A. Hàm số có 2 điểm cực đại và 1 điểm cực tiểu.
B. Hàm số có 2 điểm cực tiểu và một điểm cực đại.
C. Hàm số đạt cực đại tại
0x =
.
D. Hàm số có 3 điểm cực trị.
Câu 12: Biết
( )
H
là đa diện đều loại
5;3
với số đỉnh và số cạnh lần lượt là
a
và
b
. Tính
ab−
A.
8ab−=
B.
10ab− = −
C.
8ab− = −
D.
10ab−=
Câu 13: Cho hình vuông
ABCD
cạnh bằng
2a
. Gọi
,MN
lần lượt là trung điểm của hai cạnh
,AB CD
. Quay hình vuông
ABCD
xung quanh trục
MN
. Tính thể tích của khối trụ tạo thành.
A.
3
2
3
a
V
=
. B.
3
2Va
=
. C.
3
Va
=
. D.
3
4Va
=
.
Câu 14: Cho hàm số
( )
y f x=
có đồ thị như hình bên. Phương trình
( )
2 7 0fx−=
có bao nhiêu nghiệm
thực?
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 15: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
;0−
. B.
( )
1; +
. C.
( )
4;5
. D.
( )
0;1
.
Câu 16: Tập xác định
D
của hàm số
2021
2022
x
y

=


là
A.
\0=D
. B.
( )
0;1
. C.
=D
. D.
( )
0;= +D
.
O
x
y
1−
1
2
4
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 3
Sưu tầm và biên soạn
Câu 17: Tính diện tích xung quanh
xq
S
của hình trụ có bán kính bằng
2
và chiều cao bằng
4
.
A.
32
xq
S
=
. B.
16
3
xq
S
=
. C.
8
xq
S
=
. D.
16
xq
S
=
.
Câu 18: Gọi
,,l h R
lần lượt là độ dài đường sinh, đường cao và bán kính đáy của hình nón. Khẳng định
nào sau đây là đúng?
A.
2 2 2
l h R=+
. B.
=lh
. C.
2 2 2
=+h R l
. D.
=Rh
.
Câu 19: Cho
,ab
là hai số thực dương và
,mn
là các số thực tùy ý. Hãy chọn khẳng định đúng.
A.
m n mn
a a a
. B.
2m
mn
a b ab
. C.
mn
mn
a b ab
. D.
m
mm
b
ab
a
.
Câu 20: Một hình trụ có diện tích toàn phần bằng hai lần diện tích xung quanh và thể tích khối trụ là
81
. Tính chiều cao của hình trụ đã cho.
A.
3
. B.
3
33
. C.
33
. D.
3
33
2
.
Câu 21: Khối nón có chiều cao
h
, độ dài đường sinh
l
, bán kính
r
. Thể tích khối nón đó được tính bằng
công thức nào dưới đây?
A.
2
1
3
rl
. B.
2
rl
. C.
rh
. D.
2
1
3
rh
.
Câu 22: Tập nghiệm bất phương trình
1
25 126.5 5 0
xx+
− +
có dạng là
;ab
. Tính
22
ab+
.
A.
16354
.
5625
B.
5.
C.
10.
D.
16354
.
2025
Câu 23: Tìm tập nghiệm của bất phương trình
1 5 3
77
xx+−
.
A.
( )
;1 .−
B.
)
1; .+
C.
( )
1; .+
D.
(
; 1 .− −
Câu 24: Hàm số nào sao đây nghịch biến trên .
A.
0,5
log .yx=
B.
2021
.
2022
x
y

=


C.
2021 .
x
y =
D.
2
log .yx=
Câu 25: Phương trình
( ) ( )
3
9 27 3
2log 2 log 1 2log 2xx− + + =
có bao nhiêu nghiệm?
A.
2.
B.
3.
C.
1.
D.
0.
Câu 26: Tìm
a
để hàm số
( )
2
1
ax
y f x
x
+
==
+
có đồ thị như hình bên.
A.
1.a =
B.
2.a =
C.
2.a =−
D.
1.a =−
Câu 27: Cho hình chóp
.S ABC
có đáy là tam giác đều
ABC
cạnh bằng
2,a
SA
vuông góc với mặt phẳng
( )
ABC
và
.SA a=
Tính
thể tích khối chóp
..S ABC
A.
3
3
.
2
a
B.
3
3
.
4
a
C.
3
3
.
6
a
D.
3
3
.
3
a
Câu 28: Cho hàm số
( )
3
2
2 4 1y x x= − +
. Tính
( )
'0y
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 4
Sưu tầm và biên soạn
A.
12 3
B.
12 3−
C.
43−
D.
43
Câu 29: Tìm tiệm cận ngang của đồ thị hàm số
1
2
y
x
=
−
.
A.
1x =
B.
1y =
C.
2x =
D.
0y =
Câu 30: Cắt khối lăng trụ
. ' ' 'ABC A B C
bởi các mặt phẳng
( )
''AB C
và
( )
'ABC
ta được những khối đa
diện nào?
A. Ba khối tứ diện. B. Hai khối tứ diện và một khối chóp tứ giác.
C. Một khối tứ diện và hai khối chóp tứ giác. D. Hai khối tứ diện và hai khối chóp tứ giác
Câu 31: Cho hàm số
( )
fx
xác định trên và có đồ thị hàm số
( )
y f x
=
là đường cong trong hình dưới đây.
Khẳng định nào sau đây đúng?
A.
( ) ( ) ( )
2 0 1f f f=
.
B.
( ) ( ) ( )
0 1 2f f f
.
C.
( ) ( ) ( )
0 1 2f f f
.
D.
( ) ( ) ( )
2 0 1f f f=
.
Câu 32: Cho hàm số
( )
y f x=
có bảng biến thiên sau:
Tìm giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
1;1−
.
A. 2. B. 3. C. 0. D. 1.
Câu 33: Cho hàm số
( )
3
xa
y
+
=
có đồ thị như hình bên. Giá trị của
a
là
A. 3. B. 2. C. 0. D. 1.
Câu 34: Cho hàm số
( )
log 0 1
a
y x a=
có đồ thị
( )
C
và hàm số
( )
log 0 1
b
y x b=
có đồ thị
( )
C
như hình dưới đây.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 5
Sưu tầm và biên soạn
Khẳng định nào dưới đây đúng?
A.
0 1.ab
B.
0 1.ba
C.
1.ba
D.
1.ab
Câu 35: Cho hàm số
( )
y f x=
có bảng biến thiên sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho?
A.
4.
B.
1.
C.
2.
D.
3.
II. PHẦN TỰ LUẬN (4 câu – 3,0 điểm)
Câu 36: Giải phương trình
( )
2
22
log 4log 3 2 8 0
x
xx− + − =
.
Câu 37: Cho hàm số
32
32y x mx= − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để đồ thị
( )
C
có hai điểm cực trị
,AB
sao cho
25AB =
.
Câu 38: Cho hình lăng trụ đứng
. ' ' 'ABC A B C
, có đáy
ABC
là tam giác vuông tại A,
,AB a=
3AC a=
. Góc tạo bởi mặt phẳng
( )
'B AC
và
( )
ABC
bằng
0
60
.
a) Tính thể tích của khối lăng trụ
. ' ' 'ABC A B C
.
b) Tính khoảng cách giữa hai đường thẳng
'BC
và
AB
Câu 39: Cho
,xy
là các số nguyên dương và nhỏ hơn
2021
và thỏa mãn đẳng thức sau:
( ) ( )
21
5
2 1 5 1 log 25 100
x
x y y
−
− + = + + +
Tính giá trị biểu thức
12T x y=−
…..HẾT…..
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 6
Sưu tầm và biên soạn
BẢNG ĐÁP ÁN
1.C
2.C
3.D
4.D
5.A
6.A
7.B
8.A
9.B
10.D
11.A
12.B
13.B
14.C
15.D
16.C
17.D
18.A
19.D
20.B
21.D
22.B
23.A
24.B
25.C
26.A
27.C
28.C
29.D
30.A
31.B
32.B
33.C
34.C
35.C
HƯỚNG DẪN LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cắt một hình nón bằng một mặt phẳng qua trục, được thiết diện là một tam giác đều cạnh
2a
.
Tính diện tích xung quanh của hình nón đó.
A.
2
3.a
B.
2
2
3
a
C.
2
2 a
D.
2
4 a
Lời giải
Chọn C
Ta có
2
. .2 2
xq
S rl a a a
.
Câu 2: Tìm nghiệm của phương trình
1
31
x
.
A.
2.x =−
B.
1x =
C.
1x = −
D.
2x =
Lời giải
Chọn C
Ta có
1 1 0
3 1 3 3 1 0 1
xx
xx
.
Câu 3: Cho khối lăng trụ
.ABC A B C
có thể tích bằng
36
. Tính thể tích khối tứ diện
A ABC
.
A.
10.
B.
24.
C.
18.
D.
12.
Lời giải
Chọn D
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 7
Sưu tầm và biên soạn
Ta có
..
1 36
3 12
33
ABC A B C A ABC A ABC ABC A B C
V V V V
.
Câu 4: Cho hàm số
( )
2
16
.f x x
x
=+
Tìm giá trị nhỏ nhất của hàm số
( )
fx
trên đoạn
1;4
.
A.
20
B.
4−
C.
17
D.
12
Lời giải
Chọn D
Ta có
( )
2
16
2f x x
x
=−
( )
02f x x
= =
(nhận)
( ) ( ) ( )
1 17; 2 12; 4 20f f f= = =
Vậy
( )
1;4
min 12fx=
.
Câu 5: Hàm số nào dưới đây có bảng biến thiên như hình vẽ bên?
A.
3
3y x x=−
B.
1
1
x
y
x
+
=
−
C.
42
2xx−
D.
1
1
x
x
−
+
Lời giải
Chọn A
Hàm số trong bảng biến thiên trên làm hàm bậc ba có hệ số
0a
Câu 6: Đạo hàm của hàm số
lny x x=
trên khoảng
( )
0;+
là
A.
1 ln .yx
=+
B.
1
.y
x
=
C.
ln .yx
=
D.
1 ln .x−
Lời giải
Chọn A
Ta có
1
ln ln 1y x x x
x
= + = +
.
C'
B'
A
B
C
A'
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 8
Sưu tầm và biên soạn
Câu 7: Cho
2
a log 5=
. Khi đó
50
log 100
bằng:
A.
2.
B.
2a 2
.
2a 1
+
+
C.
a2
.
a1
+
+
D.
a2
.
2a 1
+
+
Lời giải
Chọn B
Có
22
2 2 2
50
2
2 2 2
log 100 log (5 .2 ) 2 2log 5
2 2a
log 100 .
log 50 log (5 .2) 1 2log 5 1 2a
+
+
= = = =
++
Câu 8: Cho số thực a
(0 a 1)
. Khi đó giá trị của
3
a
P log a=
bằng:
A.
3.
B.
1
.
2
C.
1
.
3
D.
2.
Lời giải
Chọn A
Có
3
aa
P log a 3log a 3.= = =
Câu 9: Tìm nghiệm của phương trình
2
log x 1.=−
A.
x.
B.
1
x.
2
=
C.
x 1.=−
D.
x 2.=
Lời giải
Chọn B
ĐK:
x 0.
1
2
1
log x 1 x 2
2
−
= − = =
( Thỏa mãn ĐK).
Câu 10: Trong các hàm số sau đây, có bao nhiêu hàm số có cực trị?
( ) ( )
4
I f x x=
;
( ) ( )
32
3II f x x x x= − + −
;
( ) ( )
2
III f x x=
;
( ) ( )
IV f x x=
;
A.
1
B.
2
C.
4
D.
3
Lời giải
Chọn D
+ Xét hàm số
( ) ( )
4
I f x x=
xác định trên và
( )
3
' 4 0 0f x x x= = =
. Ta thấy
0x =
là
nghiệm bội 3 của
( )
'fx
và
( )
'fx
đổi dấu khi đi qua
0x =
nên hàm số đạt cực trị tại
0.x =
+ Xét hàm số
( ) ( )
32
3II f x x x x= − + −
xác định trên và
( )
2
' 3 2 1 0f x x x= − + =
vô
nghiệm. Ta thấy
( )
'fx
không đổi dấu trên nên hàm số không có cực trị.
+ Xét hàm số
( ) ( )
2
III f x x=
xác định trên và
( )
' 2 0 0f x x x= = =
. Ta thấy
0x =
là
nghiệm đơn của
( )
'fx
và
( )
'fx
đổi dấu khi đi qua
0x =
nên hàm số đạt cực trị tại
0.x =
+ Xét hàm số
( ) ( )
IV f x x=
xác định trên và
( )
'
x
fx
x
=
. Ta thấy
( )
'fx
không xác định
tại
0x =
và
( )
'fx
đổi dấu khi đi qua
0x =
nên hàm số đạt cực trị tại
0.x =
Vậy có 3 hàm số có cực trị.
Câu 11: Cho hàm số
( )
y f x=
xác định trên và có bảng xét dấu của đạo hàm
( )
''y f x=
như sau.
Khẳng định nào sau đây sai?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 9
Sưu tầm và biên soạn
A. Hàm số có 2 điểm cực đại và 1 điểm cực tiểu.
B. Hàm số có 2 điểm cực tiểu và một điểm cực đại.
C. Hàm số đạt cực đại tại
0x =
.
D. Hàm số có 3 điểm cực trị.
Lời giải
Chọn A
Vì đạo hàm đảo dấu từ âm sang dương khi đi qua
6
2
x
=
nên
6
2
x
=
là hai điểm cực tiểu
của hàm số.
Vì đạo hàm đảo dấu từ dương sang âm khi đi qua
0x =
nên
0x =
là điểm cực đại của hàm số.
Do đó khẳng định A là khẳng định sai.
Câu 12: Biết
( )
H
là đa diện đều loại
5;3
với số đỉnh và số cạnh lần lượt là
a
và
b
. Tính
ab−
A.
8ab−=
B.
10ab− = −
C.
8ab− = −
D.
10ab−=
Lời giải
Chọn B
Vì
( )
H
là đa diện đều loại
5;3
nên
( )
H
là khối 12 mặt đều.
Khối 12 mặt đều có 20 đỉnh và 30 cạnh. Suy ra
20a =
;
30b =
.
Khi đó
10ab− = −
Câu 13: Cho hình vuông
ABCD
cạnh bằng
2a
. Gọi
,MN
lần lượt là trung điểm của hai cạnh
,AB CD
. Quay hình vuông
ABCD
xung quanh trục
MN
. Tính thể tích của khối trụ tạo thành.
A.
3
2
3
a
V
=
. B.
3
2Va
=
. C.
3
Va
=
. D.
3
4Va
=
.
Lời giải
Chọn B
Ta có
2
AB
ra==
;
2h AD a==
.
Thể tích khối trụ tạo thành là
2 2 3
. .2 2V r h a a a
= = =
.
M
N
A
D
B
C
r
h
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 10
Sưu tầm và biên soạn
Câu 14: Cho hàm số
( )
y f x=
có đồ thị như hình bên. Phương trình
( )
2 7 0fx−=
có bao nhiêu nghiệm
thực?
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn C
Ta có
( ) ( )
7
2 7 0
2
f x f x− = =
.
Số nghiệm của phương trình
( )
7
2
fx=
chính là số giao điểm của đồ thị hàm số
( )
y f x=
và
đường thẳng
7
2
y =
.
Dựa vào đồ thị, ta thấy phương trình
( )
7
2
fx=
có ba nghiệm thực phân biệt.
Câu 15: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
;0−
. B.
( )
1; +
. C.
( )
4;5
. D.
( )
0;1
.
Lời giải
Chọn D
Dựa vào bảng biến thiên, hàm số
( )
y f x=
đồng biến trên khoảng
( )
0;1
.
O
x
y
1−
1
2
4
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 11
Sưu tầm và biên soạn
Câu 16: Tập xác định
D
của hàm số
2021
2022
x
y

=


là
A.
\0=D
. B.
( )
0;1
. C.
=D
. D.
( )
0;= +D
.
Lời giải
Chọn C
Hàm số đã cho có dạng hàm số mũ nên ta có tập xác định của hàm số
2021
2022
x
y

=


là
=D
.
Câu 17: Tính diện tích xung quanh
xq
S
của hình trụ có bán kính bằng
2
và chiều cao bằng
4
.
A.
32
xq
S
=
. B.
16
3
xq
S
=
. C.
8
xq
S
=
. D.
16
xq
S
=
.
Lời giải
Chọn D
Ta có diện tích xung quanh của hình trụ:
2 . 2 .2.4 16
xq
S r l
= = =
Câu 18: Gọi
,,l h R
lần lượt là độ dài đường sinh, đường cao và bán kính đáy của hình nón. Khẳng định
nào sau đây là đúng?
A.
2 2 2
l h R=+
. B.
=lh
. C.
2 2 2
=+h R l
. D.
=Rh
.
Lời giải
Chọn A
Áp dụng định lý Pitago, trong một hình nón ta có
2 2 2
l h R=+
.
Câu 19: Cho
,ab
là hai số thực dương và
,mn
là các số thực tùy ý. Hãy chọn khẳng định đúng.
A.
m n mn
a a a
. B.
2m
mn
a b ab
. C.
mn
mn
a b ab
. D.
m
mm
b
ab
a
.
Lời giải
Chọn D
Câu 20: Một hình trụ có diện tích toàn phần bằng hai lần diện tích xung quanh và thể tích khối trụ là
81
. Tính chiều cao của hình trụ đã cho.
A.
3
. B.
3
33
. C.
33
. D.
3
33
2
.
Lời giải
Chọn B
Ta có
2
2 2 2 2.2
tp xq
s S rh r rh r h
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 12
Sưu tầm và biên soạn
23
3
81 81 81 3 3V r h r r
.
Câu 21: Khối nón có chiều cao
h
, độ dài đường sinh
l
, bán kính
r
. Thể tích khối nón đó được tính bằng
công thức nào dưới đây?
A.
2
1
3
rl
. B.
2
rl
. C.
rh
. D.
2
1
3
rh
.
Lời giải
Chọn D
Câu 22: Tập nghiệm bất phương trình
1
25 126.5 5 0
xx+
− +
có dạng là
;ab
. Tính
22
ab+
.
A.
16354
.
5625
B.
5.
C.
10.
D.
16354
.
2025
Lời giải
Chọn B
Ta có:
12
1
25 126.5 5 0 25.5 126.5 5 0 5 5 2 1
25
x x x x x
x
+
− + − + −
.
Suy ra:
2; 1ab= − =
. Vậy
22
5ab+=
.
Câu 23: Tìm tập nghiệm của bất phương trình
1 5 3
77
xx+−
.
A.
( )
;1 .−
B.
)
1; .+
C.
( )
1; .+
D.
(
; 1 .− −
Lời giải
Chọn A
Ta có:
1 5 3
7 7 1 5 3 1
xx
x x x
+−
+ −
.
Câu 24: Hàm số nào sao đây nghịch biến trên .
A.
0,5
log .yx=
B.
2021
.
2022
x
y

=


C.
2021 .
x
y =
D.
2
log .yx=
Lời giải
Chọn B
Hàm số
2021
2022
x
y

=


có cơ số
2021
01
2022

, suy ra
2021
2022
x
y

=


nghịch biến trên .
Câu 25: Phương trình
( ) ( )
3
9 27 3
2log 2 log 1 2log 2xx− + + =
có bao nhiêu nghiệm?
A.
2.
B.
3.
C.
1.
D.
0.
Lời giải
Chọn C
Điều kiện:
2.x
Ta có
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 13
Sưu tầm và biên soạn
( ) ( ) ( ) ( )
( )( )
( )( )
3
9 27 3 3 3 3
33
2
2log 2 log 1 2log 2 log 2 log 1 log 4
log 1 2 log 4
1 2 4
60
3
2
x x x x
xx
xx
xx
x
x
− + + = − + + =
+ − =


+ − =
− − =
=
=−
Đối chiếu điều kiện ta có nghiệm của phương trình là
3.x =
Câu 26: Tìm
a
để hàm số
( )
2
1
ax
y f x
x
+
==
+
có đồ thị như hình bên.
A.
1.a =
B.
2.a =
C.
2.a =−
D.
1.a =−
Lời giải
Chọn A
Từ đồ thị hàm số ta có tiệm cận ngang của đồ thị hàm số
( )
y f x=
là
1.y =
Mặt khác
( ) ( )
lim lim
xx
f x f x a y a
→+ →−
= = =
là tiệm cận
ngang của đồ thị hàm số
( )
.y f x=
Vậy
1.a =
Câu 27: Cho hình chóp
.S ABC
có đáy là tam giác đều
ABC
cạnh bằng
2,a
SA
vuông góc với mặt
phẳng
( )
ABC
và
.SA a=
Tính thể tích khối chóp
..S ABC
A.
3
3
.
2
a
B.
3
3
.
4
a
C.
3
3
.
6
a
D.
3
3
.
3
a
Lời giải
Chọn C

Ta có diện tích đáy
ABC
là
là

Vậy thể tích của khối chóp
.S ABC


Câu 28: Cho hàm số
( )
3
2
2 4 1y x x= − +
.
Tính
( )
'0y
.
A.
12 3
B.
12 3−
C.
43−
D.
43
Lời giải
Chọn C
Ta có:
( ) ( )
( )
3 3 1
22
2 4 1 ' 3 2 4 1 . 4 4y x x y x x x
−
= − + = − + −
.
Do đó:
( )
' 0 4 3.y =−
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 14
Sưu tầm và biên soạn
Câu 29: Tìm tiệm cận ngang của đồ thị hàm số
1
2
y
x
=
−
.
A.
1x =
B.
1y =
C.
2x =
D.
0y =
Lời giải
Chọn D
Ta có:
lim 0
x
y
→+
=
và
lim 0
x
y
→−
=
nên ta có tiệm cận ngang của đồ thị hàm số là đường thẳng
0y =
.
Câu 30: Cắt khối lăng trụ
. ' ' 'ABC A B C
bởi các mặt phẳng
( )
''AB C
và
( )
'ABC
ta được những khối đa
diện nào?
A. Ba khối tứ diện. B. Hai khối tứ diện và một khối chóp tứ giác.
C. Một khối tứ diện và hai khối chóp tứ giác. D. Hai khối tứ diện và hai khối chóp tứ giác
Lời giải
Chọn A
Dựa vào hình vẽ trên ta thấy khi cắt khối lăng trụ
. ' ' 'ABC A B C
bới các mặt phẳng
( )
''AB C
và
( )
'ABC
ta được ba khối tứ diện là:
' ' 'AA B C
;
'ABCC
;
''B ABC
.
Câu 31: Cho hàm số
( )
fx
xác định trên và có đồ thị hàm số
( )
y f x
=
là đường cong trong hình dưới
đây.
Khẳng định nào sau đây đúng?
A.
( ) ( ) ( )
2 0 1f f f=
. B.
( ) ( ) ( )
0 1 2f f f
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 15
Sưu tầm và biên soạn
C.
( ) ( ) ( )
0 1 2f f f
. D.
( ) ( ) ( )
2 0 1f f f=
.
Lời giải
Chọn B
Dựa vào đồ thị hàm số
( )
y f x
=
ta suy ra bảng biến thiên của hàm số
( )
fx
Dưa vào bảng biến thiên của hàm số
( )
fx
ta suy ra được
( ) ( ) ( )
0 1 2f f f
.
Câu 32: Cho hàm số
( )
y f x=
có bảng biến thiên sau:
Tìm giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
1;1−
.
A. 2. B. 3. C. 0. D. 1.
Lời giải
Chọn B
Dựa vào bảng biến thiên của hàm số
( )
fx
ta suy ra được
( ) ( )
1;1
max 0 3f x f
−
==
.
Câu 33: Cho hàm số
( )
3
xa
y
+
=
có đồ thị như hình bên. Giá trị của
a
là
A. 3. B. 2. C. 0. D. 1.
Lời giải
Chọn C
Đồ thị hàm số
( )
3
xa
y
+
=
đia qua điểm
( )
0;1
và điểm
( )
2;3
do đó ta có hệ phương trình
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 16
Sưu tầm và biên soạn
( )
( )
0
2
13
0
33
a
a
a
+
+
=
=
=
.
Câu 34: Cho hàm số
( )
log 0 1
a
y x a=
có đồ thị
( )
C
và hàm số
( )
log 0 1
b
y x b=
có đồ thị
( )
C
như hình dưới đây.
Khẳng định nào dưới đây đúng?
A.
0 1.ab
B.
0 1.ba
C.
1.ba
D.
1.ab
Lời giải
Chọn C
Xét sự tương giao của đường thẳng
( )
:1dy=
và các đường
( )
:1x=
,
( )
: log
a
C y x=
,
( )
: log
b
C y x
=
.
Gọi hoành độ giao điểm của
( )
:1dy=
và
( )
:1x=
,
( )
: log
a
C y x=
,
( )
: log
b
C y x
=
lần
lượt là:
12
1; ;x x a x b= = =
Dễ thấy:
21
1 x b x a = =
.
Câu 35: Cho hàm số
( )
y f x=
có bảng biến thiên sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho?
A.
4.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn C
Ta có:
lim ; lim 0
xx
yy
→+ →−
= + =
00
lim ; lim 2
xx
yy
−+
→→
= − =
Nên:
0, 0yx==
lần lượt là tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 17
Sưu tầm và biên soạn
II. PHẦN TỰ LUẬN (4 câu – 3,0 điểm)
Câu 36: Giải phương trình
( )
2
22
log 4log 3 2 8 0
x
xx− + − =
.
Lời giải
Điều kiện xác định:
0
3
28
x
x
x

.
Ta có
( )
2
22
log 4log 3 2 8 0
x
xx− + − =
2
2
22
2
33
2 8 0
log 1 2
log 4log 3 0
8
log 3
x
xx
xx
xx
x
x
==
−=
= =
− + =
=
=
.
Kết hợp điều kiện, phương trình đã cho có 2 nghiệm
12
3, 8xx==
.
Câu 37: Cho hàm số
32
32y x mx= − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để đồ thị
( )
C
có hai điểm cực trị
,AB
sao cho
25AB =
.
Lời giải
Ta có
2
' 3 6y x mx=−
.
( )
0
' 0 3 2 0 .
2
x
y x x m
xm
=
= − =
=
Hàm số có hai điểm cực trị khi và chỉ khi phương trình
'0y =
có hai nghiệm phân biệt, hay
0m
. Khi đó hàm số có hai điểm cực trị
0x =
và
2xm=
.
Tọa độ hai điểm cực trị là
( )
( )
3
0;2 , 2 ; 4 2A B m m−+
.
Theo bài ra
26
2 5 4 16 2 5AB m m= + =
6 2 2
16 4 20 1 1m m m m + = = =
(TM).
Vậy
1m =
.
Câu 38: Cho hình lăng trụ đứng
. ' ' 'ABC A B C
, có đáy
ABC
là tam giác vuông tại A,
,AB a=
3AC a=
. Góc tạo bởi mặt phẳng
( )
'B AC
và
( )
ABC
bằng
0
60
.
c) Tính thể tích của khối lăng trụ
. ' ' 'ABC A B C
.
d) Tính khoảng cách giữa hai đường thẳng
'BC
và
AB
Lời giải
a) Ta có
( ) ( )
'B AC ABC AC=
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 18
Sưu tầm và biên soạn
( )
1
' ( ' ), 'AB B AC AB AC⊥
do
( )
''AC ABB A⊥
( )
2
( ),AB ABC AB AC⊥
do
ABC
là tam giác vuông tại A
( )
3
Từ
( )
1
( )
2
và
( )
3
suy ra góc tạo bởi mặt phẳng
( )
'B AC
và
( )
ABC
là
0
' 60BAB =
Xt tam giác vuông
'BAB
tại B:
00
'
tan60 ' .tan60 3
BB
BB AB a
AB
= = =
3
. ' ' '
1 1 3
=AA'.S AA'. . . 3. . 3
2 2 2
ABC A B C ABC
a
V AB AC a a a
= = =
.
b)Tính khoảng cách giữa hai đường thẳng
'BC
và
AB
k
//CD AB
suy ra
( )
// ' 'AB CDA B
do đó
( ) ( ) ( )
, ' ,( ' ' ) ,( ' ' )d AB B C d AB A B DC d A A B DC==
Từ A hạ
'AH A C⊥
( )
4
mặt khác
( )
''CD ACC A CD AH⊥ ⊥
( )
5
Từ
( )
4
và
( )
5
ta có
( )
''AH A CDB⊥
. Nên
( )
,( ' ')AH d A A CDB=
Xt tam giác vuông cân
'AA C
suy ra
( )
2
2 2 2
1 1 1 6
' AA' 3 3
2 2 2 2
a
AH A C AC a a= = + = + =
.
Vậy khoảng cách giữa hai đường thẳng
'BC
và
AB
bằng
6
2
a
Câu 39: Cho
,xy
là các số nguyên dương và nhỏ hơn
2021
và thỏa mãn đẳng thức sau:
( ) ( )
21
5
2 1 5 1 log 25 100
x
x y y
−
− + = + + +
Tính giá trị biểu thức
12T x y=−
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 19
Sưu tầm và biên soạn
Biến đổi đẳng thức:
( ) ( )
21
5
2 1 5 1 log 25 100
x
x y y
−
− + = + + +
( ) ( )
21
5
2 1 5 2 log 25 4
x
x y y
−
− + = + + +
( ) ( ) ( )
21
5
2 1 5 4 log 4
x
x y y
−
− + = + + +
( )
( ) ( )
21
21
55
5 log 5 4 log 4
x
x
yy
−
−
+ = + + +
( )
*
Xet hàm số
5
( ) logf t t t=+
với
0t
Đạo hàm
1
'( ) 1 0,
.ln5
ft
t
= +
với mọi
0t
nên suy ra hàm
5
( ) logf t t t=+
đồng biến với
0t
. Để phương trình
( )
*
xảy ra khi
21
54
x
y
−
=+
Theo giả thiết
,1 2021 5 4 2025y Z y y
+
+
Suy ra
21
5
5
1 log 2025
5 5 2025 1 2 1 log 2025 1
2
x
xx
−
+
−
Mà
xZ
+
nên có các trường hợp sau
Vậygiá trị biểu thức
12 119.T x y= − =
x
1
2
y
1
121
120T x y=−
119
119
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 03
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Giá trị lớn nhất của hàm số
( )
3
32f x x x= − +
trên đoạn
3;3−
bằng
A.
20
. B.
16−
. C.
4.
D.
0.
Câu 2: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;2−
và có đồ thị như hình
vẽ bên. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
hàm số đã cho trên đoạn
1;2−
. Giá trị
2Mm−
bằng
A.
7
. B.
1−
.
C.
8−
. D.
4
.
Câu 3: Cho hình chóp có đáy là hình vuông cạnh, vuông góc
với mặt phẳng đáy. Tìm tâm mặt cầu ngoại tiếp hình chóp
A. Trung điểm
.SB
B. Trung điểm
.SC
C. Trung điểm
.BC
D. Trung điểm
.AC
Câu 4: Khối hộp chữ nhật có ba cạnh là
3;4;5
có thể tích là
A.
60
B.
8
C.
20
D.
30
Câu 5: Tiệm cận đứng của đồ thị hàm số
3
2
y
x
=
+
là:
A.
0x =
. B.
3x =
. C.
2x =
. D.
2x =−
.
Câu 6: Cho
a
là số thực dương khác
1
. Đẳng thức nào sau đây đúng với mọi số dương
,?xy
A.
log
log
log
a
a
a
x
x
yy
=
. B.
log log log
a a a
x
xy
y
=+
.
C.
log log log
a a a
x
xy
y
=−
. D.
( )
log log
aa
x
xy
y
=−
.
Câu 7: Một hình trụ có bán kính đáy bằng
r
và thiết diện qua trục là một hình vuông. Khi đó diện tích
toàn phần của hình trụ đó bằng.
A.
2
6.r
B.
2
4.r
C.
2
8.r
D.
2
2.r
Câu 8: Tập xác định
D
của hàm số
2021
yx
−
=
là
A.
.D =
B.
)
0; .D = +
C.
( )
0; .D = +
D.
\ 0 .D =
Câu 9: Giả sử
,ab
là các số dương,
,.

Đẳng thức nào sau đây sai?
A.
.
aa
b
b

=


B.
.
a
a
a

−
=
C.
( )
..ab a b

=
D.
.
..a a a
=
Câu 10: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Số nghiệm thực của phương trình
( )
20fx−=
là
A.
0
. B.
2
. C.
4
. D.
3
.
.S ABCD
SA
.S ABCD
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 2
Câu 11: Với
,ab
là các số thực dương tùy ý với
a
khác
1
, đặt
2
36
log log
a
a
P b b=+
. Mệnh đề nào dưới
đây đúng?
A.
6log
a
Pb=
. B.
9log
a
Pb=
. C.
15log
a
Pb=
. D.
27log
a
Pb=
.
Câu 12: Cho hàm số
( )
fx
có bảng xét dấu của đạo hàm như sau:
Hàm số
( )
y f x=
có bao nhiêu điểm cực trị?
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 13: Thể tích
V
của một khối cầu có bán kính
R
bằng
A.
3
4
3
VR
=
. B.
3
4VR
=
. C.
3
1
3
VR
=
. D.
2
4
3
VR
=
.
Câu 14: Gọi
, ,Rlh
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của một hình nón, đẳng thức
nào sau đây đúng?
A.
2 2 2
l h R=+
. B.
2
.l h R=
. C.
2 2 2
R h l=+
. D.
2 2 2
1 1 1
l h R
=+
.
Câu 15: Số nghiệm thực của phương trình
2
4 2 3 0
xx+
− + =
là:
A. 1. B. 0. C. 3. D. 2.
Câu 16: Gọi
, , l h r
lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích
xung quanh
xq
S
của hình nón là
A.
.Sxq rl
=
B.
.Sxq rh
=
C.
2
1
.
3
Sxq r h
=
D.
2.Sxq rl
=
Câu 17: Hình nào sau đây không phải là hình đa diện lồi?
Hình 1
Hình 2
Hình 3
Hình 4
A. Hình 2. B. Hình 4. C. Hình 1. D. Hình 3.
Câu 18: Cho phương trình
21
3 4.3 1 0.
xx+
− + =
Khi đặt
3
x
t =
ta được phương trình nào dưới đây?
A.
2
3 1 0.tt− + =
B.
2
3 4 1 0.tt− + =
C.
2
4 2 0.tt− + =
D.
2
4 1 0.tt− + =
Câu 19: Cho hàm số
( )
fx
có bảng xét dấu của đạo hàm như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
; 1 .− −
B.
( )
1; .+
C.
( )
1;1 .−
D.
( )
3; 1 .−−
Câu 20: Khối trụ tròn xoay có bán kính đáy bằng
a
và chiều cao bằng
2a
có thể tích
V
bằng
A.
3
2.Va
=
B.
3
2
.
3
Va
=
C.
3
4.Va
=
D.
3
4
.
3
Va
=
Câu 21: Hàm số
( )
ln 3 2yx=−
có đạo hàm với mọi
3
2
x
là
A.
1
.
32x−
B.
1
.
32x
−
−
C.
2
.
32x
−
−
D.
3
.
32x−
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 3
Câu 22: Giá trị của
3
1
log
a
a
với
0; 1aa
bằng
A.
.
3
1
B.
.
3
1
−
C.
3.−
D.
3.
Câu 23: Phương trình
( )
22
2log log 3x x+ −=
có bao nhiêu nghiệm?
A.
3.
B.
0.
C.
1.
D.
2.
Câu 24: Nghiệm của phương trình
( )
2
4log 1x+=
là
A.
17.x =
B.
7.x =
C.
15.x =
D.
3.x =
Câu 25: Cho hàm số
( )
y f x=
xác định và liên tục trên
,
có bảng biến thiên như hình sau:
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
( )
; 1 .− −
B. Hàm số đồng biến trên khoảng
( )
1; .− +
C. Hàm số đồng biến trên khoảng
( )
1; .+
D. Hàm số đồng biến trên khoảng
( )
;1 .−
Câu 26: Thể tích khối chóp có diện tích đáy
B
và chiều cao
h
là
A.
1
.
3
Bh
B.
.Bh
C.
1
.
2
Bh
D.
1
.
6
Bh
Câu 27: Hình nào dưới đây là hình đa diện?
A. Hình
3.
B. Hình
2.
C. Hình
1.
D. Hình
4.
Câu 28: Hàm số
2
5
xx
y
−
=
có đạo hàm là
A.
. B.
2
5 .ln5
xx−
. C.
( )
2
2 1 5
xx
x
−
−
. D.
( )
2
21
5
xx
xx
−−
−
.
Câu 29: Tập xác định của hàm số
( )
2021
log 2yx=−
A.
(
;2−
. B.
( )
;2−
. C.
( )
2;+
. D.
)
2;+
.
Câu 30: Nghiệm của phương trình
1
28
x+
=
là:
A.
3x =
. B.
2x =
. C.
4x =
. D.
1x =
.
Câu 31: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại điểm
A.
3.x
B.
1.x
C.
2.x
D.
2.x
Câu 32: Cho
2
log 5 a
và
3
log 5 .b
Hãy tính
6
log 5
theo a và b.
A.
6
1
log 5 .
ab
B.
C.
6
log 5 .ab
D.
6
log 5 .
ab
ab
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 4
Câu 33: Đường cong trong hình bên dưới là đồ thị của hàm số nào trong bốn hàm số được liêt kê ở bốn
phương án dưới đây?
A.
B.
42
1.y x x
C.
32
1.y x x
D.
3
3 1.y x x
Câu 34: Đường tiệm cận ngang của đồ thị hàm số
23
1
x
y
x
−
=
+
là:
A.
0.y =
B.
3.y =−
C.
2.y =
D.
3
.
2
y =
Câu 35: Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
A.
1
1
x
y
x
+
=
−
B.
21
1
x
y
x
+
=
−
C.
3
3 1.y x x= − −
D.
42
1y x x= + +
II. PHẦN TỰ LUẬN (4 câu – 3,0 điểm)
Câu 36: Giải phương trình:
( )
2 2 2
log log 6 log 7.xx+ − =
Câu 37: Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có đáy
ABC
là tam giác vuông cân tại
,A
,AB a=
mặt
phẳng
( )
''AB C
hợp với mặt phẳng đáy một góc
0
30 .
Tính thể tích khối lăng trụ
. ' ' '.ABC A B C
Câu 38: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
12mx
y
xm
+−
=
−
đồng biến trên từng khoảng xác
định của nó.
Câu 39: Giải phương trình:
( ) ( )
3
5 21 7 5 21 2
xx
x+
− + + =
-----HẾT-----
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 5
HƯỚNG DẪN GIẢI
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Giá trị lớn nhất của hàm số
( )
3
32f x x x= − +
trên đoạn
3;3−
bằng
A.
20
. B.
16−
. C.
4.
D.
0.
Lời giải
Chọn A
Hàm số
( )
3
32f x x x= − +
xác định và liên tục trên
3;3−
.
Ta có:
( )
2
33f x x
=−
Do đó:
( )
2
1 3;3
0 3 3 0
1 3;3
x
f x x
x
= −
= − =
= − −
.
Mà:
( )
3 16f − = −
,
( )
14f −=
,
( )
10f −=
,
( )
3 20f =
.
Vậy
( )
3;3
max 3 20yf
−
==
.
Câu 2: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;2−
và có đồ thị như hình vẽ bên. Gọi
M
,
m
lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
1;2−
. Giá trị
2Mm−
bằng
A.
7
. B.
1−
. C.
8−
. D.
4
.
Lời giải
Chọn A
Dựa vào đồ thị ta suy ra được giá trị lớn nhất của hàm số trên đoạn
1;2−
là
3
, giá trị nhỏ nhất
của hàm số trên đoạn
1;2−
là
2−
.
Vậy
3M =
,
2m =−
( )
2 3 2. 2 7Mm − = − − =
.
Câu 3: Cho hình chóp có đáy là hình vuông cạnh, vuông góc với mặt phẳng đáy. Tìm tâm
mặt cầu ngoại tiếp hình chóp
A. Trung điểm
.SB
B. Trung điểm
.SC
C. Trung điểm
.BC
D. Trung điểm
.AC
Lời giải
Chọn B
.S ABCD
SA
.S ABCD
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 6
Ta chứng minh được:
vuông tại .
vuông tại .
vuông tại .
Gọi là trung điểm cạnh . Khi đó: .
Do đó là tâm mặt cầu ngoại tiếp khối chóp .
Câu 4: Khối hộp chữ nhật có ba cạnh là
3;4;5
có thể tích là
A.
60
B.
8
C.
20
D.
30
Lời giải
Chọn A
Thể tích khối hộp chữ nhật là:
3.4.5 60V ==
.
Câu 5: Tiệm cận đứng của đồ thị hàm số
3
2
y
x
=
+
là:
A.
0x =
. B.
3x =
. C.
2x =
. D.
2x =−
.
Lời giải
Chọn D
Ta có:
2
lim
x
y
+
→−
= +
TCĐ:
2x =−
Câu 6: Cho
a
là số thực dương khác
1
. Đẳng thức nào sau đây đúng với mọi số dương
,?xy
A.
log
log
log
a
a
a
x
x
yy
=
. B.
log log log
a a a
x
xy
y
=+
.
C.
log log log
a a a
x
xy
y
=−
. D.
( )
log log
aa
x
xy
y
=−
.
Lời giải
Chọn C
Câu 7: Một hình trụ có bán kính đáy bằng
r
và thiết diện qua trục là một hình vuông. Khi đó diện tích
toàn phần của hình trụ đó bằng.
A.
2
6.r
B.
2
4.r
C.
2
8.r
D.
2
2.r
Lời giải
Chọn A
Thiết diện qua trục là một hình vuông nên chiều cao hình trụ
2hr=
.
Vậy
22
2 2 6 .
tp
S rh r r
= + =
Câu 8: Tập xác định
D
của hàm số
2021
yx
−
=
là
A.
.D =
B.
)
0; .D = +
C.
( )
0; .D = +
D.
\ 0 .D =
Lời giải
Chọn D
Câu 9: Giả sử
,ab
là các số dương,
,.

Đẳng thức nào sau đây sai?
A.
.
aa
b
b

=


B.
.
a
a
a

−
=
C.
( )
..ab a b

=
D.
.
..a a a
=
Lời giải
Chọn D
( )
ΔBC SAB BC SB SBC⊥ ⊥
B
( )
ΔCD SAD CD SD SCD⊥ ⊥
D
( )
ΔSA ABCD SA AC SAC⊥ ⊥
A
O
SC
1
2
OA OC OD OB OS SC= = = = =
O
.S ABCD
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 7
Câu 10: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Số nghiệm thực của phương trình
( )
20fx−=
là
A.
0
. B.
2
. C.
4
. D.
3
.
Lời giải
Chọn C
Phương trình
( ) ( )
2 0 2f x f x− = =
từ BBT
phương trình có 4 nghiệm
Câu 11: Với
,ab
là các số thực dương tùy ý với
a
khác
1
, đặt
2
36
log log
a
a
P b b=+
. Mệnh đề nào dưới
đây đúng?
A.
6log
a
Pb=
. B.
9log
a
Pb=
. C.
15log
a
Pb=
. D.
27log
a
Pb=
.
Lời giải
Chọn A
2
36
log log 3log 3log 6log
a a a a
a
P b b b b b= + = + =
.
Câu 12: Cho hàm số
( )
fx
có bảng xét dấu của đạo hàm như sau:
Hàm số
( )
y f x=
có bao nhiêu điểm cực trị?
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn D
Câu 13: Thể tích
V
của một khối cầu có bán kính
R
bằng
A.
3
4
3
VR
=
. B.
3
4VR
=
. C.
3
1
3
VR
=
. D.
2
4
3
VR
=
.
Lời giải
Chọn A
Câu 14: Gọi
, ,Rlh
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của một hình nón, đẳng thức
nào sau đây đúng?
A.
2 2 2
l h R=+
. B.
2
.l h R=
. C.
2 2 2
R h l=+
. D.
2 2 2
1 1 1
l h R
=+
.
Lời giải
Chọn A
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 8
Câu 15: Số nghiệm thực của phương trình
2
4 2 3 0
xx+
− + =
là:
A. 1. B. 0. C. 3. D. 2.
Lời giải
Chọn D
Ta có:
( )
2
2
2
0
21
4 2 3 0 2 4.2 3 0
log 3
23
x
x x x x
x
x
x
+
=
=
− + = − + =
=
=
.
Vậy phương trình đã cho có 2 nghiệm thực phân biệt.
Câu 16: Gọi
, , l h r
lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích
xung quanh
xq
S
của hình nón là
A.
.Sxq rl
=
B.
.Sxq rh
=
C.
2
1
.
3
Sxq r h
=
D.
2.Sxq rl
=
Lời giải
Chọn A
Câu 17: Hình nào sau đây không phải là hình đa diện lồi?
Hình 1
Hình 2
Hình 3
Hình 4
A. Hình 2. B. Hình 4. C. Hình 1. D. Hình 3.
Lời giải
Chọn A
Dựa vào khái niệm đa diện lồi ta có đáp án A
Câu 18: Cho phương trình
21
3 4.3 1 0.
xx+
− + =
Khi đặt
3
x
t =
ta được phương trình nào dưới đây?
A.
2
3 1 0.tt− + =
B.
2
3 4 1 0.tt− + =
C.
2
4 2 0.tt− + =
D.
2
4 1 0.tt− + =
Lời giải
Chọn B
Ta có
2 1 2
3 4.3 1 0 3.3 4.3 1 0
x x x x+
− + = − + =
Đặt
3
x
t =
ta được phương trình
2
3 4 1 0.tt− + =
Câu 19: Cho hàm số
( )
fx
có bảng xét dấu của đạo hàm như sau:
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 9
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
; 1 .− −
B.
( )
1; .+
C.
( )
1;1 .−
D.
( )
3; 1 .−−
Lời giải
Chọn C
Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên khoảng
( )
1;1 .−
Câu 20: Khối trụ tròn xoay có bán kính đáy bằng
a
và chiều cao bằng
2a
có thể tích
V
bằng
A.
3
2.Va
=
B.
3
2
.
3
Va
=
C.
3
4.Va
=
D.
3
4
.
3
Va
=
Lời giải
Chọn A
Thể tích khối trụ tròn xoay là
23
. .2 2 .V a a a

==
Câu 21: Hàm số
( )
ln 3 2yx=−
có đạo hàm với mọi
3
2
x
là
A.
1
.
32x−
B.
1
.
32x
−
−
C.
2
.
32x
−
−
D.
3
.
32x−
Lời giải
Chọn C
Với
3
2
x
, ta có:
( )
( )
( )
32
2
ln 3 2 .
3 2 3 2
x
yx
xx
−
−
= − = =
−−
Câu 22: Giá trị của
3
1
log
a
a
với
0; 1aa
bằng
A.
.
3
1
B.
.
3
1
−
C.
3.−
D.
3.
Lời giải
Chọn C
Ta có:
3
3
1
3log log
aa
a
a
−
= = −
Câu 23: Phương trình
( )
22
2log log 3x x+ −=
có bao nhiêu nghiệm?
A.
3.
B.
0.
C.
1.
D.
2.
Lời giải
Chọn C
ĐK:
3x
( ) ( )
( )
( )
2 2 2
2
22
1
4 3 4 0
4
log log 3 log 3
3
xx
x
x x x
x
xx
x
+ =
=−
= − − =
=
− = −
−
Kết hợp với điều kiện ta có phương trình có 1 nghiệm là x = 4.
Câu 24: Nghiệm của phương trình
( )
2
4log 1x+=
là
A.
17.x =
B.
7.x =
C.
15.x =
D.
3.x =
Lời giải
Chọn C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 10
ĐK:
1x −
( )
2
4 1 16 15.log 1 xxx + = =+=
Câu 25: Cho hàm số
( )
y f x=
xác định và liên tục trên
,
có bảng biến thiên như hình sau:
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
( )
; 1 .− −
B. Hàm số đồng biến trên khoảng
( )
1; .− +
C. Hàm số đồng biến trên khoảng
( )
1; .+
D. Hàm số đồng biến trên khoảng
( )
;1 .−
Lời giải
Chọn A
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng
( )
; 1 .− −
Câu 26: Thể tích khối chóp có diện tích đáy
B
và chiều cao
h
là
A.
1
.
3
Bh
B.
.Bh
C.
1
.
2
Bh
D.
1
.
6
Bh
Lời giải
Chọn A
Thể tích khối chóp có diện tích đáy
B
và chiều cao
h
là
1
.
3
V Bh=
Câu 27: Hình nào dưới đây là hình đa diện?
A. Hình
3.
B. Hình
2.
C. Hình
1.
D. Hình
4.
Lời giải
Chọn D
Hình 1: có cạnh không phải là cạnh chung của 2 mặt.
Hình 2: có cạnh là cạnh chung của nhiều hơn 2 mặt.
Hình 3: có điểm chung của 2 mặt không phải là đỉnh.
Câu 28: Hàm số
2
5
xx
y
−
=
có đạo hàm là
A.
. B.
2
5 .ln5
xx−
. C.
( )
2
2 1 5
xx
x
−
−
. D.
( )
2
21
5
xx
xx
−−
−
.
Lời giải
Chọn A
Câu 29: Tập xác định của hàm số
( )
2021
log 2yx=−
A.
(
;2−
. B.
( )
;2−
. C.
( )
2;+
. D.
)
2;+
.
Lời giải
Chọn C
Câu 30: Nghiệm của phương trình
1
28
x+
=
là:
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 11
A.
3x =
. B.
2x =
. C.
4x =
. D.
1x =
.
Lời giải
Chọn B
1 1 3
2 8 2 2 1 3 2
xx
xx
++
= = + = =
.
Câu 31: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại điểm
A.
3.x
B.
1.x
C.
2.x
D.
2.x
Lời giải
Chọn A
Căn cứ vào BBT ta có hàm số đã cho đạt cực đại tại điểm
3.x
Câu 32: Cho
2
log 5 a
và
3
log 5 .b
Hãy tính
6
log 5
theo a và b.
A.
6
1
log 5 .
ab
B.
C.
6
log 5 .ab
D.
6
log 5 .
ab
ab
Lời giải
Chọn A
Ta có
6
5 5 5
1 1 1
log 5 .
11
log 6 log 3 log 2
ab
ab
ab
Câu 33: Đường cong trong hình bên dưới là đồ thị của hàm số nào trong bốn hàm số được liêt kê ở bốn
phương án dưới đây?
A.
B.
42
1.y x x
C.
32
1.y x x
D.
3
3 1.y x x
Lời giải
Chọn D
Đồ thị hàm số đã cho là đồ thị hàm số của hàm đa thức bậc ba có hệ số của
3
x
âm.
Câu 34: Đường tiệm cận ngang của đồ thị hàm số
23
1
x
y
x
−
=
+
là:
A.
0.y =
B.
3.y =−
C.
2.y =
D.
3
.
2
y =
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 12
Chọn C
Theo định nghĩa sách giáo khoa.
lim 2
x
y
→
=
nên đồ thị
23
1
x
y
x
−
=
+
có TCN là đường thẳng
2.y =
Câu 35: Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
A.
1
1
x
y
x
+
=
−
B.
21
1
x
y
x
+
=
−
C.
3
3 1.y x x= − −
D.
42
1y x x= + +
Lời giải
Chọn A
Dựa vào dáng điệu đồ thị loại đáp án
,CD
.
Đồ thị
1
1
x
y
x
+
=
−
có TCN là đường thẳng
1,y =
TCN là đường thẳng
1x =
Đồ thị
21
1
x
y
x
+
=
−
có TCN là đường thẳng
2,y =
TCN là đường thẳng
1x =
.
II. PHẦN TỰ LUẬN (4 câu – 3,0 điểm)
Câu 36: Giải phương trình:
( )
2 2 2
log log 6 log 7.xx+ − =
Lời giải
ĐKXĐ:
00
6.
6 0 6
xx
x
xx



−

( )
( )
( )
2 2 2
22
2
22
2
2
log log 6 log 7
log 6 log 7
log 6 log 7
67
6 7 0
1( )
7 ( )
7.
xx
xx
xx
xx
xx
x KTMDK
x TMDK
x
+ − =
− =


− =
− =
− − =
=−
=
=
Vậy nghiệm của phương trình
7.x =
Câu 37: Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có đáy
ABC
là tam giác vuông cân tại
,A
,AB a=
mặt
phẳng
( )
''AB C
hợp với mặt phẳng đáy một góc
0
30 .
Tính thể tích khối lăng trụ
. ' ' '.ABC A B C
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 13
Gọi I là trung điểm của cạnh
' '.BC
Ta có: góc giữa hai mặt phẳng
( )
''AB C
và
( )
ABC
chính là góc giữa hai mặt phẳng
( )
''AB C
và
( )
' ' .AB C
Vì
ABC
là tam giác vuông cân tại
A
nên hai mặt bên
( )
''ABB A
và
( )
''ACC A
là hai hình chữ
nhật bằng nhau. Do đó
' '.AC AB=
Suy ra tam giác
''AB C
là tam giác cân tại
.A
Khi đó:
' '.AI B C⊥
' ' 'A B C
là tam giác vuông cân tại
A
nên
' ' '.A I B C⊥
( ) ( )
( )
( )
( ) ( )
( )
0
' ' ' ' ' ' '
' ', ' ' ' ' , ' ' ' ' 30 .
' ' ', ' ' ' '
AB C A B C B C
AI B C AI AB C AB C A B C AIA
A I B C A I A B C
=
⊥ = =
⊥
0
3
2
. ' ' '
2.
12
'.
22
2 3 6
' ' .tan30 . .
2 3 6
6 1 6
'. . . .
6 2 12
ABC A B C ABC
BC a
a
A I BC
aa
AA A I
aa
V AA S a
=
==
= = =
= = =
Câu 38: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
12mx
y
xm
+−
=
−
đồng biến trên từng khoảng xác
định của nó.
Lời giải
Tập xác định của hàm số:
\Dm=
.
Ta có:
( )
2
2
2
',
mm
y x D
xm
− − +
=
−
.
Hàm số đồng biến trên từng khoảng xác định của nó
' 0,y x D
2
2 0 2 1m m m − − + −
.
Câu 39: Giải phương trình:
( ) ( )
3
5 21 7 5 21 2
xx
x+
− + + =
Lời giải
I
C'
A'
B
A
C
B'
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 14
Ta có
( ) ( )
3
5 21 5 21
5 21 7 5 21 2 7 8
22
xx
xx
x+
−+
− + + = + =
Đặt
5 21 1 5 21
;0
22
xx
tt
t
−+
= =
Phương trình trở thành:
2
1( )
7
8 8 7 0
7( )
tn
t t t
tn
t
=
+ = − + =
=
Với
5 21
1 1 0
2
x
tx

−
= = =



.
Với
( )
5 21
2
5 21
7 7 log 7
2
x
x
tx

−




−
= = =



Vậy phương trình có hai nghiệm
( )
5 21
2
0; log 7
x
xx

−



==
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 04
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
;1− −
. B.
( )
0;1
. C.
( )
1;1−
. D.
( )
1;0−
Câu 2: Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là
A.
3
B.
1
C.
2
D.
0
Câu 3: Giá trị nhỏ nhất của hàm số
( )
42
12 4f x x x= − −
trên đoạn
0;9
bằng
A.
39−
. B.
40−
. C.
36−
. D.
4−
.
Câu 4: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
3=−y x x
. B.
3
3= − +y x x
.
C.
42
2=−y x x
. D.
42
2= − +y x x
.
Câu 5: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
21
1
x
y
x
−
=
−
B.
1
1
x
y
x
+
=
−
C.
42
1y x x= + +
D.
3
31y x x= − −
Câu 6: Tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
−
=
+
là
A.
2y =−
. B.
1y =
. C.
1x =−
. D.
2x =
.
Câu 7: Cho
0, ,a m n
. Khẳng định nào sau đây đúng?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 2
Sưu tầm và biên soạn
A.
.
m n m n
a a a
+
+=
B.
..
m n m n
a a a
−
=
C.
( ) ( )
.
nm
mn
aa=
D.
.
m
nm
n
a
a
a
−
=
Câu 8: Với
a
là số thực dương tùy ý,
( )
5
log 5a
bằng
A.
5
5 log .a+
B.
5
1 log .a+
C.
5
5 log .a−
D.
5
1 log .a−
Câu 9: Tập xác định của hàm số
( )
5
log 2yx=−
là
A.
( )
2; .+
B.
)
2; .+
C.
.
D.
( )
;2 .−
Câu 10: Đạo hàm của hàm số
5
x
y =
là
A.
1
.5 .
x
yx
−
=
B.
5.
x
y
=
C.
5 .ln5.
x
y
=
D.
5
.
ln5
x
y
=
Câu 11: Tìm mệnh đề đúng trong các mệnh đề sau.
A. Hàm số
x
ya=
với
1a
nghịch biến trên khoảng
( )
;− +
.
B. Hàm số
x
ya=
với
01a
đồng biến trên khoảng
( )
;− +
.
C. Hàm số
log
a
yx=
với
1a
đồng biến trên khoảng
( )
0;+
.
D. Hàm số
log
a
yx=
với
01a
nghịch biến trên khoảng
( )
;− +
.
Câu 12: Phương trình
( )
2
log 5 4x−=
có nghiệm là
A.
3.x =
B.
13.x =
C.
21.x =
D.
11.x =
Câu 13: Tập nghiệm của phương trình
9 2.3 3 0
xx
+ − =
là
A.
1; 3 .S =−
B.
0; 3 .S =−
C.
1;3 .S =
D.
0.S =
Câu 14: Tập hợp nghiệm của bất phương trình
( )
2
log 1 3x+
là
A.
( )
; 7 .S = −
B.
( )
1; 7 .S =−
C.
( )
1; 8 .S =−
D.
( )
; 8 .S = −
Câu 15: Trong các hình sau, hình nào không phải đa diện lồi?
A. B. C. D.
Câu 16: Cho khối lăng trụ có diện tích đáy
3B =
và chiều cao
4h =
. Thể tích của khối lăng trụ đã cho
bằng
A.
6
B.
12
C.
36
D.
4
Câu 17: Cho tam giác
SAO
vuông cân tại
O
có diện tích bằng
2
,
quay tam giác
SAO
xung quanh cạnh
SO
. Tính thể tích
V
của khối tròn xoay được tạo thành.
A.
4
3
V
=
B.
8
3
V
=
C.
4
3
V
=
D.
V
=
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 3
Sưu tầm và biên soạn
Câu 18: Cho khối nón có chiều cao
h
, bán kính đáy
r
. Thể tích khối nón đã cho bằng
A.
2
2hr
B.
2
3
hr
C.
2
hr
D.
2
4
3
hr
Câu 19: Cho khối cầu có bán kính
3R =
. Thể tích khối cầu đã cho bằng
A.
4
B.
36
C.
12
D.
108
Câu 20: Diện tích xung quanh của hình nón có chiều cao
4h =
và bán kính đáy
3r =
là
A.
12
B.
15
C.
30
D.
24
Câu 21: Cho hàm số
21
2
x
y
x
−
=
−
. Khẳng định nào dưới đây là SAI?
A. Hàm số nghịch biến trên khoảng
( ;0)−
. B. Hàm số nghịch biến trên
( ;2) (2; )− +
.
C. Hàm số nghịch biến trên khoảng
(0;1)
. D. Hàm số nghịch biến trên khoảng
(2; )+
.
Câu 22: Đồ thị của hàm số
32
35y x x= − + +
có hai điểm cực trị
A
và
B
. Tính diện tích
S
của tam giác
OAB
với
O
là gốc tọa độ.
A.
10
3
S =
. B.
9S =
. C.
10S =
. D.
5S =
.
Câu 23: Giá trị lớn nhất của hàm số
( )
42
21f x x x= − +
trên đoạn
0;2
là
A.
( )
0;2
max 64
x
fx
=
. B.
( )
0;2
max 9
x
fx
=
. C.
( )
0;2
max 0
x
fx
=
. D.
( )
0;2
max 1
x
fx
=
.
Câu 24: Cho hàm số
ax b
y
cx d
+
=
+
( )
0d
có đồ thị như hình bên. Khẳng định nào dưới đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0abc
. C.
0, 0, 0abc
. D.
0, 0, 0abc
.
Câu 25: Hỏi đồ thị hàm số
11
2
x
y
x
−−
=
−
có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
A. 3. B. 2. C. 1. D. 0.
Câu 26: Tập xác định
D
của hàm số
( )
3
2
91yx
−
=−
là
A.
11
;;
33
D
= − − +
. B.
D=
.
C.
11
;
33
D

=−


. D.
11
\;
33
D

=−

.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 4
Sưu tầm và biên soạn
Câu 27: Tìm tập xác định của hàm số
( )
2
log 2 3logy x x= + +
?
A.
( ) ( )
2;0 0;− +
. B.
( )
0;+
. C.
( )
2;− +
. D.
)
2;− +
.
Câu 28: Cho các hàm số
log
a
yx=
và
log
b
yx=
có đồ thị như hình vẽ bên. Đường thẳng
5x =
cắt trục
hoành, đồ thị hàm số
log
a
yx=
và
log
b
yx=
lần lượt tại
,AB
và
C
. Biết rằng
2CB AB=
. Mệnh
đề nào sau đây là đúng?
A.
5ab=
. B.
2
ab=
. C.
3
ab=
. D.
3
ab=
.
Câu 29: Giá trị cực tiểu của hàm số
( )
2
3
x
y e x=−
là:
A.
6
e
. B.
3
6
e
. C.
3e−
. D.
2e−
.
Câu 30: Tổng các nghiệm của phương trình
2
22
log 5log 6 0xx− + =
là
A.
5
. B.
13
. C.
12
. D.
32
.
Câu 31: Gọi
S
là tập nghiệm của phương trình
2 2 2
21
2 2 4 1
x x x x x x− − − − −
+ = +
. Số phần tử của tập
S
là
A.
1
. B.
2
. C.
3
. D.
4
Câu 32: Cho một tấm bìa hình chữ nhật có kích thước
3a
,
6a
. Người ta muốn tạo tấm bìa đó thành bốn
hình không đáy như hình vẽ, trong đó có hai hình trụ lần lượt có chiều cao
3a
,
6a
và hai hình
lăng trụ tam giác đều có chiều cao lần lượt
3a
,
6a
Trong
4
hình H1, H2, H3, H4 lần lượt theo thứ tự có thể tích lớn nhất và nhỏ nhất là
A. H
1
, H
4
. B. H
2
, H
3
. C. H
1
, H
3
. D. H
2
, H
4
.
Câu 33: Cho hình lăng trụ
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
,
3
2
a
AA
=
. Biết rằng hình
chiếu vuông góc của
A
lên
( )
ABC
là trung điểm
BC
. Tính thể tích
V
của khối lăng trụ đó.
A.
3
Va=
. B.
3
2
3
a
V =
. C.
3
3
42
a
V =
. D.
3
3
2
Va=
.
H1
H2
H3
H4
3a
3a
6a
6a
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 5
Sưu tầm và biên soạn
Câu 34: Cho hình trụ có hai đáy là hai hình tròn
( )
O
và
( )
O
, chiều cao
3R
và bán kính đáy
R
. Một hình nón có đỉnh là
O
và đáy là hình tròn
( )
;OR
. Tỷ số diện tích xung quanh của
hình trụ và hình nón bằng
A.
3
. B.
2
. C.
2
. D.
3
.
Câu 35: Một hình nón có đường sinh bằng
2a
và góc giữa đường sinh và mặt phẳng đáy bằng
60
o
.
Tính thể tích của khối nón được tạo nên từ hình nón đó.
A.
3
1
6
6
a
. B.
3
1
6
3
a
. C.
3
1
6
4
a
. D.
3
1
6
12
a
.
II. PHẦN TỰ LUẬN
Câu 36: Giải phương trình
( ) ( )
2
3 9 1
3
log 2 log 5 log 8 0xx+ + − + =
Câu 37: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
A
và
AB a=
,
3AC a=
,
mặt phẳng
( )
A BC
tạo với đáy một góc
30
. Tính thể tích của khối lăng trụ
..ABC A B C
Câu 38: Cho đồ thị hàm số
()y f x
=
như hình vẽ. Tìm các khoảng đồng biến của hàm số:
32
( ) (3 1) 3 1y g x f x x x= = − − + +
.
Câu 39: Xét các số thực
a
và
b
thỏa mãn
1ab
. Tìm giá trị nhỏ nhất của biểu thức
22
log ( ) 3log
ab
b
a
Pa
b

=+


.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 6
Sưu tầm và biên soạn
BẢNG ĐÁP ÁN
1.D
2.A
3.B
4.A
5.B
6.B
7.C
8.B
9.A
10.C
11.C
12.C
13.D
14.B
15.B
16.B
17.B
18.B
19.B
20.B
21.B
22.D
23.B
24.B
25.C
26.D
27.A
28.C
29.D
30.C
31.B
32.D
33.C
34.D
35.D
HƯỚNG DẪN LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM
Câu 1: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
;1− −
. B.
( )
0;1
. C.
( )
1;1−
. D.
( )
1;0−
Lời giải
Chọn D
Hàm số đã cho đồng
biến trên khoảng
( )
1;0−
và
( )
1; +
Câu 2: Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là
A.
3
B.
1
C.
2
D.
0
Lời giải
Chọn A
Hàm số có ba điểm cực trị.
Câu 3: Giá trị nhỏ nhất của hàm số
( )
42
12 4f x x x= − −
trên đoạn
0;9
bằng
A.
39−
. B.
40−
. C.
36−
. D.
4−
.
Lời giải
Chọn B
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 7
Sưu tầm và biên soạn
Ta có:
( )
3
4 24f x x x
=−
;
( )
0 0;9
0 6 0;9
6 0;9
x
f x x
x
=
= =
= −
.
Tính được:
( )
04=−f
;
( )
9 5585=f
và
( )
6 40=−f
.
Suy ra
( )
0;9
min 40=−fx
.
Câu 4: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
3=−y x x
. B.
3
3= − +y x x
. C.
42
2=−y x x
. D.
42
2= − +y x x
.
Lời giải
Chọn A
Đường cong có dạng của đồ thị hàm số bậc
3
với hệ số
0a
nên chỉ có hàm số
3
3y x x=−
thỏa yêu cầu bài toán.
Câu 5: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
21
1
x
y
x
−
=
−
B.
1
1
x
y
x
+
=
−
C.
42
1y x x= + +
D.
3
31y x x= − −
Lời giải
Chọn B
Vì từ đồ thị ta suy ra đồ thị của hàm phân thức có tiệm cận đứng là
1x =
và tiệm cận ngang
1y =
.
Câu 6: Tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
−
=
+
là
A.
2y =−
. B.
1y =
. C.
1x =−
. D.
2x =
.
Lời giải
Chọn B
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 8
Sưu tầm và biên soạn
Ta có
2
lim 1
1
x
x
x
→+
−
=
+
và
2
lim 1
1
x
x
x
→−
−
=
+
.
Suy ra
1y =
là tiệm cận ngang của đồ thị hàm số.
Câu 7: Cho
0, ,a m n
. Khẳng định nào sau đây đúng?
A.
.
m n m n
a a a
+
+=
B.
..
m n m n
a a a
−
=
C.
( ) ( )
.
nm
mn
aa=
D.
.
m
nm
n
a
a
a
−
=
Lời giải
Chọn C
Tính chất lũy thừa
Câu 8: Với
a
là số thực dương tùy ý,
( )
5
log 5a
bằng
A.
5
5 log .a+
B.
5
1 log .a+
C.
5
5 log .a−
D.
5
1 log .a−
Lời giải
Chọn B
Ta có:
( )
5 5 5 5
log 5 log 5 log 1 loga a a= + = +
.
Câu 9: Tập xác định của hàm số
( )
5
log 2yx=−
là
A.
( )
2; .+
B.
)
2; .+
C.
.
D.
( )
;2 .−
Lời giải
Chọn A
Điều kiện xác định:
2 0 2xx−
. Vậy tập xác định của hàm số đã cho là
( )
2;D = +
.
Câu 10: Đạo hàm của hàm số
5
x
y =
là
A.
1
.5 .
x
yx
−
=
B.
5.
x
y
=
C.
5 .ln5.
x
y
=
D.
5
.
ln5
x
y
=
Lời giải
Chọn C
Áp dụng công thức:
( )
.ln
xx
a a a
=
,
( )
01a
ta được:
( )
5 5 .ln5
xx
y
==
.
Câu 11: Tìm mệnh đề đúng trong các mệnh đề sau.
A. Hàm số
x
ya=
với
1a
nghịch biến trên khoảng
( )
;− +
.
B. Hàm số
x
ya=
với
01a
đồng biến trên khoảng
( )
;− +
.
C. Hàm số
log
a
yx=
với
1a
đồng biến trên khoảng
( )
0;+
.
D. Hàm số
log
a
yx=
với
01a
nghịch biến trên khoảng
( )
;− +
.
Lời giải
Chọn C
Câu 12: Phương trình
( )
2
log 5 4x−=
có nghiệm là
A.
3.x =
B.
13.x =
C.
21.x =
D.
11.x =
Lời giải
Chọn C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 9
Sưu tầm và biên soạn
Điều kiện xác định:
5x
.
Phương trình
( )
4
2
log 5 4 5 2 21x x x− = − = =
(thỏa điều kiện).
Vậy phương trình có nghiệm
21x =
.
Câu 13: Tập nghiệm của phương trình
9 2.3 3 0
xx
+ − =
là
A.
1; 3 .S =−
B.
0; 3 .S =−
C.
1;3 .S =
D.
0.S =
Lời giải
Chọn D
( )
2
31
9 2.3 3 0 3 2.3 3 0 0
33 ( )
x
x x x x
x
x
x
=
+ − = + − = =
= −
.
Vậy phương trình có tập nghiệm
0.S =
Câu 14: Tập hợp nghiệm của bất phương trình
( )
2
log 1 3x+
là
A.
( )
; 7 .S = −
B.
( )
1; 7 .S =−
C.
( )
1; 8 .S =−
D.
( )
; 8 .S = −
Lời giải
Chọn B
Ta có:
( )
2
log 1 3x+
3
10
12
x
x
+
+
1
7
x
x
−
17x −
.
Vậy tập nghiệm của bất phương trình đã cho là
( )
1;7S =−
.
Câu 15: Trong các hình sau, hình nào không phải đa diện lồi?
A. B. C. D.
Lời giải
Chọn B
Lấy hai điểm
;AB
như hình vẽ ta thấy đoạn thẳng
AB
có một phần nằm ngoài hình đa diện. nên
hình đa diện này không phải là đa diện lồi.
Câu 16: Cho khối lăng trụ có diện tích đáy
3B =
và chiều cao
4h =
. Thể tích của khối lăng trụ đã cho
bằng
A.
6
B.
12
C.
36
D.
4
Lời giải
Chọn B
Ta có: Thể tích khối lăng trụ là
. 3.4 12V B h= = =
.
A
B
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 10
Sưu tầm và biên soạn
Câu 17: Cho tam giác
SAO
vuông cân tại
O
có diện tích bằng
2
,
quay tam giác
SAO
xung quanh cạnh
SO
. Tính thể tích
V
của khối tròn xoay được tạo thành.
A.
4
3
V
=
B.
8
3
V
=
C.
4
3
V
=
D.
V
=
Lời giải
Chọn B
Tam giác
SAO
vuông cân tại
O
có diện tích là
2
nên độ dài cạnh góc vuông
2SO OA==
.
Khi tam giác
SAO
quay quanh
SO
tạo thành hình nón có đường cao là
2h SO==
và đáy là
hình tròn bán kính
2r AO==
.
Thể tích hình nón là:
2
18
.
33
V h r
==
Câu 18: Cho khối nón có chiều cao
h
, bán kính đáy
r
. Thể tích khối nón đã cho bằng
A.
2
2hr
B.
2
3
hr
C.
2
hr
D.
2
4
3
hr
Lời giải
Chọn B
Khối nón có chiều cao
h
, bán kính đáy
r
có thể tích bằng
2
1
3
V r h
.
Câu 19: Cho khối cầu có bán kính
3R =
. Thể tích khối cầu đã cho bằng
A.
4
B.
36
C.
12
D.
108
Lời giải
Chọn B
Thể tích của khối cầu đã cho là:
33
44
.3 36
33
VR
= = =
.
Câu 20: Diện tích xung quanh của hình nón có chiều cao
4h =
và bán kính đáy
3r =
là
A.
12
B.
15
C.
30
D.
24
Lời giải
Chọn B
Gọi
l
là độ dài đường sinh của hình nón. Khi đó
2 2 2 2
4 3 5.l h r= + = + =
Vậy
. . .3.5 15 .
xq
S r l
= = =
Câu 21: Cho hàm số
21
2
x
y
x
−
=
−
. Khẳng định nào dưới đây là SAI?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 11
Sưu tầm và biên soạn
A. Hàm số nghịch biến trên khoảng
( ;0)−
.
B. Hàm số nghịch biến trên
( ;2) (2; )− +
.
C. Hàm số nghịch biến trên khoảng
(0;1)
.
D. Hàm số nghịch biến trên khoảng
(2; )+
.
Lời giải
Chọn B
+) Tập xác định
\{2}D =
+) Ta có
2
2 1 3
0
2 ( 2)
x
yy
xx
−−
= =
−−
với
xD
.
Vậy hàm số nghịch biến trên khoảng
( ;2)−
và
(2; )+
+) Mặt khác
( ;0) ( ;2)− −
;
(0;1) ( ;2) −
nên đáp án B, C, D đúng.
Câu 22: Đồ thị của hàm số
32
35y x x= − + +
có hai điểm cực trị
A
và
B
. Tính diện tích
S
của tam giác
OAB
với
O
là gốc tọa độ.
A.
10
3
S =
. B.
9S =
. C.
10S =
. D.
5S =
.
Lời giải
Chọn D
Ta có:
2
36y x x
= − +
.
2
0
0 3 6 0
2
x
y x x
x
=
= − + =
=
.
Tọa độ hai điểm cực trị của đồ thị hàm số là
( )
0;5A
và
( )
2;9B
.
( )
2;4 2 5AB AB= =
.
Phương trình đường thẳng
AB
qua
( )
0;5A
có véc tơ pháp tuyến
( )
2;1n =−
:
2 5 0xy− + =
.
( )
( )
2
2
2.0 0 5
,5
21
−+
==
+−
d O AB
.
Vậy diện tích của tam giác
OAB
là:
( )
11
, . . 5.2 5 5
22
S d O AB AB= = =
.
Câu 23: Giá trị lớn nhất của hàm số
( )
42
21f x x x= − +
trên đoạn
0;2
là
A.
( )
0;2
max 64
x
fx
=
. B.
( )
0;2
max 9
x
fx
=
. C.
( )
0;2
max 0
x
fx
=
. D.
( )
0;2
max 1
x
fx
=
.
Lời giải.
Chọn B
Hàm số
( )
42
21f x x x= − +
xác định và liên tục trên
0;2
Ta có:
( )
3
44f x x x
=−
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 12
Sưu tầm và biên soạn
Do đó:
( )
0
0
1
x
fx
x
=
=
=
1 0;2x = −
Ta có:
( )
01f =
,
( )
10f =
,
( )
29f =
Suy ra:
( )
0;2
max 9
x
fx
=
.
Câu 24: Cho hàm số
ax b
y
cx d
+
=
+
( )
0d
có đồ thị như hình bên. Khẳng định nào dưới đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0abc
. C.
0, 0, 0abc
. D.
0, 0, 0abc
.
Lời giải
Chọn B
Dựa vào đồ thị hàm số ta thấy:
+) Đồ thị hàm số có đường tiệm cận đứng
0
d
x
c
= −
, mà
0d
0c
.
+) Đồ thị hàm số có đường tiệm cận ngang
0
a
y
c
=
, mà
0c
0a
.
+) Đồ thị hàm số cắt trục tung tại điểm có tung độ
0
b
y
d
=
, mà
0d
0b
.
Vậy
0, 0, 0abc
.
Câu 25: Hỏi đồ thị hàm số
11
2
x
y
x
−−
=
−
có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
A. 3. B. 2. C. 1. D. 0.
Lời giải
Chọn C
+) Tập xác định
)
1; \ 2D = +
+)
1x
Ta có
xx=
nên
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 13
Sưu tầm và biên soạn
( )
( )
2 2 2 2
1 1 1 1 1 1 1 1
lim lim lim lim
2 2 2
11
2 1 1
x x x x
x x x
xx
x
xx
→ → → →
− − − − − −
= = = =
−−
−+
− − +
.
Suy ra đồ thị hàm số không có tiệm cận đứng.
+) Ta lại có
2
1 1 1
11
lim lim 0
2
2
1
xx
x
x x x
x
x
→+ →+
−−
−−
==
−
−
.
Suy ra đồ thị hàm số có tiệm cận ngang là
0y =
.
Vậy đồ thị hàm số có 1 đường tiệm cận.
Câu 26: Tập xác định
D
của hàm số
( )
3
2
91yx
−
=−
là
A.
11
;;
33
D
= − − +
. B.
D=
.
C.
11
;
33
D

=−


. D.
.
Lời giải
Chọn D
Hàm số đã cho xác định
2
1
9 1 0
3
xx −
.
Suy ra tập xác định của hàm số đã cho là
.
Câu 27: Tìm tập xác định của hàm số
( )
2
log 2 3logy x x= + +
?
A.
( ) ( )
2;0 0;− +
. B.
( )
0;+
. C.
( )
2;− +
. D.
)
2;− +
.
Lời giải
Chọn A
Điều kiện xác định của hàm số là:
2
20
2
0
0
x
x
x
x
+
−

Vậy tập xác định của hàm số là:
( ) ( )
2;0 0;− +
Câu 28: Cho các hàm số
log
a
yx=
và
log
b
yx=
có đồ thị như hình vẽ bên. Đường thẳng
5x =
cắt trục
hoành, đồ thị hàm số
log
a
yx=
và
log
b
yx=
lần lượt tại
,AB
và
C
. Biết rằng
2CB AB=
. Mệnh
đề nào sau đây là đúng?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 14
Sưu tầm và biên soạn
A.
5ab=
. B.
2
ab=
. C.
3
ab=
. D.
3
ab=
.
Lời giải
Chọn C
Dễ thấy
( ) ( ) ( )
5;0 , 5;log 5 , 5;log 5
ab
A B C
và
log 5 log 5 0
ba

.
Do
2CB AB=
nên ta có
( )
log 5 log 5 2 log 5 0
b a a
− = −
.
55
55
3
55
3
log 5 3log 5
13
log log
log 3log
log log
.
ba
ba
ab
ab
ab
=
=
=
=
=
Câu 29: Giá trị cực tiểu của hàm số
( )
2
3
x
y e x=−
là:
A.
6
e
. B.
3
6
e
. C.
3e−
. D.
2e−
.
Lời giải
Chọn D
( ) ( )
22
3 2 2 3
x x x
y e x xe x x e
= − + = + −
.
BBT
Suy ra giá trị cực tiểu của hàm số bằng
2e−
.
Câu 30: Tổng các nghiệm của phương trình
2
22
log 5log 6 0xx− + =
là
A.
5
. B.
13
. C.
12
. D.
32
.
Lời giải
Chọn C
Điều kiện
0x
.
2
22
log 5log 6 0xx− + =
2
2
log 3
8
log 2 4
x
x
xx
=
=
==
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 15
Sưu tầm và biên soạn
Vậy tổng các nghiệm của phương trình là
12.
Câu 31: Gọi
S
là tập nghiệm của phương trình
2 2 2
21
2 2 4 1
x x x x x x− − − − −
+ = +
. Số phần tử của tập
S
là
A.
1
. B.
2
. C.
3
. D.
4
Lời giải
Chọn B
TXĐ:
D=
Xét phương trình:
2
2 2 2 2 2
2 1 1
2
2 2 4 1 2 4 1
4
xx
x x x x x x x x x x
−
− − − − − − − −
+ = + + = +
( )
2
2 2 2 2
2
1
4.2 2 4.4 4 5.2 2 4
xx
x x x x x x x x
−
− − − − −
+ = + = +
( )
2
2
2
2 5.2 4 0
xx
xx
−
−
− + =
. Đặt
2
2 , 0
xx
tt
−
=
Phương trình trở thành:
2
1
5 4 0
4
t
tt
t
=
− + =
=
Với
2
2
0
1 2 1 0
1
xx
x
t x x
x
−
=
= = − =
=
Với
2
22
2
4 2 2 2 0
1
xx
x
t x x
x
−
=
= = − − =
=−
Vậy tập nghiệm của phương trình
1;0;1;2S =−
có
4
phần tử.
Câu 32: Cho một tấm bìa hình chữ nhật có kích thước
3a
,
6a
. Người ta muốn tạo tấm bìa đó thành bốn
hình không đáy như hình vẽ, trong đó có hai hình trụ lần lượt có chiều cao
3a
,
6a
và hai hình
lăng trụ tam giác đều có chiều cao lần lượt
3a
,
6a
Trong
4
hình H1, H2, H3, H4 lần lượt theo thứ tự có thể tích lớn nhất và nhỏ nhất là
A. H
1
, H
4
. B. H
2
, H
3
. C. H
1
, H
3
. D. H
2
, H
4
.
Lời giải
Chọn D
Gọi các hình H
1
, H
2
, H
3
, H
4
lần lượt theo thứ tự có thể tích
1
V
,
2
V
,
3
V
,
4
V
.
Ta có:
2
23
1 1 1
6 27
.3
2
a
V r h a a



= = =


. (Vì
11
6
26
2
a
r a r
= =
).
23
2 2 2
3 27
.6
22
a
V r h a a



= = =


.(Vì
22
3
23
2
a
r a r
= =
).
H1
H2
H3
H4
3a
3a
6a
6a
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 16
Sưu tầm và biên soạn
3
3
13
. 3 . .2 . .2 3 3
22
V h B a a a a

= = =



. (Đáy là tam giác đều cạnh
6 :3 2aa=
).
3
4
1 3 3 3
. 6 . . . .
2 2 2
V h B a a a a

= = =



.(Đáy là tam giác đều cạnh
3 :3aa=
).
Ta có:
1 3 2 4
V V V V
.
Câu 33: Cho hình lăng trụ
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
,
3
2
a
AA
=
. Biết rằng hình
chiếu vuông góc của
A
lên
( )
ABC
là trung điểm
BC
. Tính thể tích
V
của khối lăng trụ đó.
A.
3
Va=
. B.
3
2
3
a
V =
. C.
3
3
42
a
V =
. D.
3
3
2
Va=
.
Lời giải
Chọn C
Gọi
H
là trung điểm
BC
.
Theo giả thiết,
AH
là đường cao hình lăng trụ và
22
6
.
2
a
A H AA AH
= − =
Vậy, thể tích khối lăng trụ là
23
Δ
3 6 3 2
..
4 2 8
ABC
a a a
V S A H= = =
.
Câu 34: Cho hình trụ có hai đáy là hai hình tròn
( )
O
và
( )
O
, chiều cao
3R
và bán kính đáy
R
. Một hình nón có đỉnh là
O
và đáy là hình tròn
( )
;OR
. Tỷ số diện tích xung quanh của
hình trụ và hình nón bằng
A.
3
. B.
2
. C.
2
. D.
3
.
Lời giải
Chọn D
A
B
C
A
B
C
H
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 17
Sưu tầm và biên soạn
Ta có diện tích xung quanh của hình trụ là
2
1
2 2 . 3 2 3.S Rh R R R= = =
Diện tích xung quanh của hình nón là
( )
2
22
2
. 3 2 .S Rl R R R R= = + =
Tỷ số diện tích xung quanh của hình trụ và hình nón bằng
2
1
2
2
23
3.
2
S
R
SR
==
Câu 35: Một hình nón có đường sinh bằng
2a
và góc giữa đường sinh và mặt phẳng đáy bằng
60
o
.
Tính thể tích của khối nón được tạo nên từ hình nón đó.
A.
3
1
6
6
a
. B.
3
1
6
3
a
. C.
3
1
6
4
a
. D.
3
1
6
12
a
.
Lời giải
Chọn D
Xét hình nón đỉnh
S
. Ta có:
60
o
SAI =
và
SA SB l==
suy ra
SAB
đều.
Do đó:
12
2
22
a
AB SA SB a r AI AB= = = = = =
.
( )
2
2
22
26
2
22
aa
h SA AI a

= − = − =



.
2
23
1 1 2 6 1
6
3 3 2 2 12
aa
V r h a

= = =



.
II. PHẦN TỰ LUẬN
Câu 36: Giải phương trình
( ) ( )
2
3 9 1
3
log 2 log 5 log 8 0xx+ + − + =
60
°
a
2
I
A
B
S
O
R
3R
O
O
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 18
Sưu tầm và biên soạn
Lời giải
Điều kiện:
2
5
x
x
−
.
Ta có
( ) ( ) ( )
2
3 9 1 3 3 1
33
log 2 log 5 log 8 0 log 2 log 5 log 8 0x x x x+ + − + = + + − + =
( ) ( ) ( )
33
log 2 5 log 8 2 5 8 *x x x x + − = + − =
TH1:
5x
( ) ( )( )
2
6 (t/m)
* 2 5 8 3 18 0 6
3 ( )
x
x x x x x
xL
=
+ − = − − = =
=−
TH2:
25x−
( ) ( )( )
( )
( )
2
3 17
t/m
2
* 2 5 8 3 2 0
3 17
t/m
2
x
x x x x
x
+
=
+ − + = − + + =
−
=
Vậy tập nghiệm của phương trình là
3 17 3 17
6; ; .
22
S

+−
=


Câu 37: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
A
và
AB a=
,
3AC a=
,
mặt phẳng
( )
A BC
tạo với đáy một góc
30
. Tính thể tích của khối lăng trụ
..ABC A B C
Lời giải
Gọi
AH
là đường cao của tam giác
ABC
, ta có
( )
BC AH
BC AA H BC A H
BC AA
⊥

⊥ ⊥
⊥
nên góc giữa mặt phẳng
( )
A BC
và mặt phẳng
( )
ABC
là góc
30AHA
=
.
Ta có
( )
2
2 2 2 2 2
1 1 1 1 1 4 3
32
3
a
AH
AH AB AC a a
a
= + = + = =
.
31
tan30 .tan30 .
22
3
AA a a
AA AH
AH
= = = =
.
2
1 1 3
. . . . 3
2 2 2
ABC
a
S AB AC a a
= = =
.
Do đó
23
.
33
..
2 2 4
ABC A B C ABC
a a a
V AA S
= = =
.
A'
A
B'
B
C'
C
H
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 19
Sưu tầm và biên soạn
Câu 38: Cho đồ thị hàm số
()y f x
=
như hình vẽ. Tìm các khoảng đồng biến của hàm số:
32
( ) (3 1) 3 1y g x f x x x= = − − + +
.
Lời giải
Ta có:
22
( ) 3 (3 1) 3 6 0 (3 1) 2y g x f x x x f x x x
= = − − + = − = −
Đặt
2
1 4 5
3 1 ( )
9 9 9
x t f t t t
− = = − −
Vẽ đồ thị hàm số
2
1 4 5
9 9 9
y t t= − −
là một parabol đi qua các điểm sau:
(2; 1),−
(5;0),
( 1;0),−
( 4;3)−
Dựa vào đồ thị ta có bảng xét dấu
2
1 4 5
( ) ( )
9 9 9
h t f t t t
= − + +
Suy ra:
4 3 1 4 1
( ) 0 ( ) 0
1 5 1 3 1 5 0 2
t x x
h t g x
t x x
− − − −
− − −
Vậy hàm số đồng biến trên khoảng
(0;2)
và
( ; 1)− −
.
Câu 39: Xét các số thực
a
và
b
thỏa mãn
1ab
. Tìm giá trị nhỏ nhất của biểu thức
22
log ( ) 3log
ab
b
a
Pa
b

=+


.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 20
Sưu tầm và biên soạn
Lời giải
Ta có
2
22
log ( ) 3log 2log 3log
a b a b
bb
aa
P a a
bb

= + = +


2
4 log . 3log
ab
b
aa
b
bb

=+


2
= 4 1 log 3log .
ab
b
a
b
b


++




Đặt
log 0
a
b
tb=
. Vì
1ab
nên
1, 1
a
b
b

. Do đó
0t
Ta có
22
33
4( 1) 4 8 4P t t t
tt
= + + = + + +
Đặt
2
3
( ) 4 8 4.f t t t
t
= + + +
Ta có
3 2 2
2 2 2
3 8 8 3 (2 1)(4 6 3)
( ) 8
t t t t t
f t t t
t t t
+ − − + +
= + − = =
Vậy
1
( ) 0 .
2
f t t
= =
Dễ có
min
1
15
2
Pf

==


ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 05
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
()=y f x
liên tục trên , có đồ thị như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
0;1
. B.
( )
1;0−
. C.
( )
2; 1−−
. D.
( )
1;1−
.
Câu 2: Cho hàm số
( )
=y f x
có đồ thị như hình vẽ. Hàm số đã cho có giá trị cực đại bằng?
A.
2
. B.
1−
. C.
+
. D.
2−
.
Câu 3: Cho hàm số
( )
=y f x
xác định, liên tục trên và có bảng biến thiên sau:
Khẳng định nào sau đây là đúng ?
A. Giá trị lớn nhất của hàm số bằng
2
. B. Giá trị nhỏ nhất của hàm số bằng
1−
.
C. Giá trị nhỏ nhất của hàm số bằng
1
. D. Giá trị nhỏ nhất của hàm số bằng
1−
và
1
.
Câu 4: Đường cong dưới đây là đồ thị của hàm số nào?
A.
32
1.y x x= − + −
B.
42
2 1.y x x= − + −
C.
32
1.y x x= − −
D.
42
2 1.y x x= − −
-2
2
-2
1
-1
2
O
y
x
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 2
Câu 5: Hình vẽ dưới đây là đồ thị của hàm số nào?
A.
1
.
1
x
y
x
−
=
+
B.
21
.
1
x
y
x
+
=
+
C.
23
.
1
x
y
x
−
=
+
D.
25
.
1
x
y
x
+
=
+
Câu 6: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 7: Chọn đáp án đúng, cho
mn
aa
, khi đó
A.
mn
. B.
mn
. C.
mn=
. D.
mn
khi
1a
.
Câu 8: Cho
0, 1,aa
khẳng định nào sau đây sai?
A.
2
log 2.=
a
a
B.
2
1
log .
2
=
a
a
C.
log 2 2.=
a
a
D.
log 2
2
a
a =
.
Câu 9: Giả sử
,xy
là các số thực dương. Trong các khẳng định sau, khẳng định nào sai?
A.
3 3 3
log log log .
x
xy
y
=−
B.
3 3 3
log log log .xy x y=+
C.
( )
3 3 3
1
log log log .
2
xy x y=+
D.
( )
3 3 3
log log log .x y x y+ = +
Câu 10: Hàm số
2
2
xx
y
−
=
có đạo hàm là
A.
( )
2
2 1 .2
xx
x
−
−
. B.
( )
2
21
.2
xx
xx
−−
−
. C.
( )
2
2 . 2 1 .ln2
xx
x
−
−
. D.
2
2 .ln 2
xx−
.
Câu 11: Giá trị thực của
a
để hàm số
21
log
a
yx
−
=
đồng biến trên
( )
0;+
.
A.
1a −
. B.
1a
. C.
01a
. D.
01a
.
Câu 12: Phương trình
2
25
5
5
x
x
−
=
có nghiệm là
A.
2x =
. B.
0=x
. C.
1=−x
. D.
1x =
.
Câu 13: Tập nghiệm
S
của phương trình
23
log 4 2
x−
=
là
A.
15
;
22
S

=


. B.
1
2
S

=


. C.
5
2
S

=


. D.
7
2
S

=


.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 3
Câu 14: Tìm tập nghiệm
S
của bất phương trình
0,5
1
log 2 2
2
x

− −


.
A.
19
;
44
S

=


. B.
19
;
44
S

=

. C.
9
;
4
S

= −


. D.
9
;
4
S

= +


.
Câu 15: Trong một khối đa diện, mệnh đề nào sau đây đúng?
A. Hai cạnh bất kỳ có ít nhất một điểm chung.
B. Ba mặt bất kì có ít nhất một đỉnh chung.
C. Hai mặt bất kì có ít nhất một điểm chung.
D. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
Câu 16: Cho khối lăng trụ có diện tích đáy
3B =
và chiều cao
2h =
. Thể tích của khối lăng trụ đã cho
bằng.
A.
1
. B.
3
. C.
2
. D.
6
.
Câu 17: Cho hình trụ có bán kính đáy
8R =
và độ dài đường sinh
3l =
. Diện tích xung quanh của hình
trụ đã cho bằng:
A.
24 .
B.
192 .
C.
48 .
D.
64 .
Câu 18: Cho hình nón có độ dài đường sinh bằng 25 và bán kính đường tròn đáy bằng 15. Tính thể tích
của khối nón đó.
A.
1500 .
B.
4500 .
C.
375 .
D.
1875 .
Câu 19: Tính thể tích
V
của khối trụ có bán kính
4r =
và chiều cao
42h =
.
A.
32 .V
=
B.
64 2 .V
=
C.
128 .V
=
D.
32 2 .V
=
Câu 20: Thể tích khối cầu bán kính
3cm
bằng
A.
( )
3
36 cm .
B.
( )
3
108 cm .
C.
( )
3
9 cm .
D.
( )
3
54 cm .
Câu 21: Cho hàm số
42
2y x x=−
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
( )
;2− −
. B. Hàm số đồng biến trên khoảng
( )
1;1−
.
C. Hàm số nghịch biến trên khoảng
( )
1;1−
. D. Hàm số đồng biến trên khoảng
( )
;2− −
.
Câu 22: Cho hàm số
( )
fx
có đạo hàm là
( )
( )( )
22
' 1 3 2f x x x x= − − +
x
. Số điểm cực trị của hàm
số
( )
fx
là
A.
4.
B.
3.
C.
2.
D.
1.
Câu 23: Giá trị nhỏ nhất của hàm số
( )
2
2
1
x
fx
x
−
=
−
trên đoạn
2,3
bằng
A.
7
2
B.
5
2
C.
2
. D.
1
.
Câu 24: Cho hàm số
( )
32
f x ax bx cx d= + + +
có đồ thị như hình vẽ. Trong các mệnh đề sau, mệnh đề
nào đúng?
A.
0, 0, 0, 0.a b c d
B.
0, 0, 0, 0.a b c d
C.
0, 0, 0, 0.a b c d
D.
0, 0, 0, 0.a b c d =
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 4
Câu 25: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Số đường tiệm cận ngang của đồ thị hàm số
( )
1
y
fx
=
là
A.
4.
B.
3.
C.
2.
D.
1.
Câu 26: Tập xác định của hàm số
( )
4
2
32y x x
−
= − + −
là
A.
\ 1;2
. B.
( ) ( )
,1 2,− +
. C.
\1
. D.
( )
1,2
.
Lời giải
Chọn A
Hàm số xác định khi
2
3 2 0 1, 2x x x x− + −
.
Vậy tập xác định
\ 1;2D =
.
Câu 27: Tập xác định của hàm số
2
ln
5
x
y
x
−

=

−

là
A.
( )
5,+
. B.
( )
2,5
. C.
( )
,2−
. D.
\ 2;5
.
Câu 28: Cho các hàm số
log
a
yx=
,
log
b
yx=
có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
A.
01ab
. B.
01ba
.
C.
01ab
. D.
01ba
.
Câu 29: Cho các số thực dương
,ab
thỏa mãn
log 2
a
b =
. Giá trị của
( )
2
log
ab
Pa=
bằng
A.
1
6
. B.
1
2
. C.
2
3
. D.
1
.
Câu 30: Nghiệm của phương trình
( ) ( )
33
log 1 1 log 4 1xx+ + = +
là
A.
3x =−
. B.
2x =
. C.
3x =
. D.
4x =
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 5
Câu 31: Cho phương trình
( )
3
4 2 2
log .log 4 2log 0
2
x
xx

+=


. Khi đặt
2
logtx=
, ta được phương trình
nào sau đây?
A.
2
11 0tt+=
. B.
2
11 3 0tt+ − =
. C.
2
14 2 0tt+ − =
. D.
2
14 4 0tt+ − =
.
Câu 32: Hình tứ diện đều có bao nhiêu mặt đối xứng?
A.
3
. B.
4
. C.
6
. D.
9
.
Câu 33: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
cạnh
a
. Cạnh bên
SA
vuông góc
với đáy, góc
60SBD =
. Thể tích khối chóp
.S ABCD
bằng
A.
3
3
a
. B.
3
3
2
a
. C.
3
2
3
a
. D.
3
a
.
Câu 34: Cho hình nón có đường sinh bằng
13,
chiều cao bằng
12.
Diện tích xung quanh của hình nón
bằng
A.
60
. B.
65
. C.
65
. D.
90
.
Câu 35: Thiết diện qua trục của hình trụ là một hình vuông có cạnh bằng
2a
. Thể tích của khối trụ được
tạo bởi hình trụ này là
A.
3
2 a
. B.
3
2
3
a
. C.
3
8 a
. D.
3
8
3
a
.
II. PHẦN TỰ LUẬN
Câu 1: Giải phương trình
( )
( )
2
2
25 5 5
3
1
log log 3 log log 3
2
xx+ − =
?
Câu 2: Cho hình chóp tam giác
.S ABC
có đáy là tam giác đều cạnh
a
, khoảng cách từ
S
đến mặt phẳng
( )
ABC
bằng
6a
. Trên cạnh
SA
lấy điểm
M
, trên cạnh
SB
lấy điểm
N
sao cho
1
2
SM
MA
=
,
2.
SN
NB
=
Mặt phẳng
( )
qua
MN
và song song với
SC
chia khối chóp thành 2 phần. Tính
V
là thể tích của khối đa diện chứa điểm
A
?
Câu 3: Cho hàm số
( )
y f x=
có đạo hàm
( )
2
' 2 3, .f x x x x= + −
Tìm các giá trị thực của tham
số
m
để hàm số
( )
( )
22
3 2 3 2021g x f x x m m m= + + + − +
đồng biến trên khoảng
( )
0;2
?
Câu 4: Tìm
m
để phương trình
( ) ( ) ( )
2
2
33
81
1 log 3 4 5 log 4 1 0
8
3
3
3
m x m m
x

− − − − + − =


−
có nghiệm
trên đoạn
17
1,
9



.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 6
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM
Câu 1: Cho hàm số
()=y f x
liên tục trên , có đồ thị như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
0;1
. B.
( )
1;0−
. C.
( )
2; 1−−
. D.
( )
1;1−
.
Lời giải
Chọn A
Từ đồ thị ta thấy hàm số nghịch biến trên khoảng
( )
0;1
.
Câu 2: Cho hàm số
( )
=y f x
có đồ thị như hình vẽ. Hàm số đã cho có giá trị cực đại bằng?
A.
2
. B.
1−
. C.
+
. D.
2−
.
Lời giải
Chọn A
Giá trị cực đại của hàm số đạt tại
1x =−
là
2
.
Câu 3: Cho hàm số
( )
=y f x
xác định, liên tục trên và có bảng biến thiên sau:
Khẳng định nào sau đây là đúng ?
A. Giá trị lớn nhất của hàm số bằng
2
.
B. Giá trị nhỏ nhất của hàm số bằng
1−
.
C. Giá trị nhỏ nhất của hàm số bằng
1
.
D. Giá trị nhỏ nhất của hàm số bằng
1−
và
1
.
Lời giải
Chọn A
Dựa vào bảng biến thiên nhận thấy:
●
( )
2,f x x
và
( )
02f =
nên GTLN của hàm số bằng 2.
-2
2
-2
1
-1
2
O
y
x
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 7
●
( )
1, − f x x
và vì
lim 1
→−
=−
x
f
nên không tồn tại
0
x
sao cho
( )
0
1=fx
, do đó hàm
số không có GTNN.
Câu 4: Đường cong dưới đây là đồ thị của hàm số nào?
A.
32
1.y x x= − + −
B.
42
2 1.y x x= − + −
C.
32
1.y x x= − −
D.
42
2 1.y x x= − −
Lời giải
Chọn D
Đồ thị hàm số có ba điểm cực trị và phía tay phải của đồ thị hàm số đi lên suy ra hệ số
0a
.
Câu 5: Hình vẽ dưới đây là đồ thị của hàm số nào?
A.
1
.
1
x
y
x
−
=
+
B.
21
.
1
x
y
x
+
=
+
C.
23
.
1
x
y
x
−
=
+
D.
25
.
1
x
y
x
+
=
+
Lời giải
Chọn B
Đồ thị hàm số cắt trục
Oy
tại điểm có tọa độ
( )
0;1
nên ta chọn phương án B.
Câu 6: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 8
Nhìn bảng biến thiên ta thấy
( )
0
lim
x
fx
−
→
= −
nên
0x =
là tiệm cận đứng của đồ thị hàm số.
( )
lim 3 3
x
f x y
→+
= =
là TCN của đồ thị hàm số.
( )
lim 1 1
x
f x y
→−
= =
là TCN của đồ thị hàm số.
Câu 7: Chọn đáp án đúng, cho
mn
aa
, khi đó
A.
mn
. B.
mn
. C.
mn=
. D.
mn
khi
1a
.
Lời giải
Chọn D
Ta có tính chất: Nếu
,1
mn
maa na
.
Câu 8: Cho
0, 1,aa
khẳng định nào sau đây sai?
A.
2
log 2.=
a
a
B.
2
1
log .
2
=
a
a
C.
log 2 2.=
a
a
D.
log 2
2
a
a =
.
Lời giải
Chọn C
Câu 9: Giả sử
,xy
là các số thực dương. Trong các khẳng định sau, khẳng định nào sai?
A.
3 3 3
log log log .
x
xy
y
=−
B.
3 3 3
log log log .xy x y=+
C.
( )
3 3 3
1
log log log .
2
xy x y=+
D.
( )
3 3 3
log log log .x y x y+ = +
Lời giải
Chọn D
Câu 10: Hàm số
2
2
xx
y
−
=
có đạo hàm là
A.
( )
2
2 1 .2
xx
x
−
−
. B.
( )
2
21
.2
xx
xx
−−
−
. C.
( )
2
2 . 2 1 .ln2
xx
x
−
−
. D.
2
2 .ln 2
xx−
.
Lời giải
Chọn C
Ta có:
( )
. .ln
uu
a u a a
=
nên
( )
( )
22
2 2 1 .2 .ln2
x x x x
x
−−
=−
.
Câu 11: Giá trị thực của
a
để hàm số
21
log
a
yx
−
=
đồng biến trên
( )
0;+
.
A.
1a −
. B.
1a
. C.
01a
. D.
01a
.
Lời giải
Chọn B
Ta có hàm số
21
log
a
yx
−
=
đồng biến trên
( )
0;+
2 1 1 1aa −
.
Câu 12: Phương trình
2
25
5
5
x
x
−
=
có nghiệm là
A.
2x =
. B.
0=x
. C.
1=−x
. D.
1x =
.
Lời giải
Chọn A
Ta có
2 2 2
25
5 5 5 2 2 2
5
x x x
x
x x x
− − −
= = − = − =
.
Câu 13: Tập nghiệm
S
của phương trình
23
log 4 2
x−
=
là
A.
15
;
22
S

=


. B.
1
2
S

=


. C.
5
2
S

=


. D.
7
2
S

=


.
Lời giải
Chọn C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 9
Phương trình
( )
2
23
3
2 3 0
3
2
2
5
2
2 3 1
2
2
2 3 2
4 2 3
log 4 2
x
x
x
x
xx
x
x
−
−


− =
−=
=−
=
.
Câu 14: Tìm tập nghiệm
S
của bất phương trình
0,5
1
log 2 2
2
x

− −


.
A.
19
;
44
S

=


. B.
19
;
44
S

=

. C.
9
;
4
S

= −


. D.
9
;
4
S

= +


.
Lời giải
Chọn A
Bất phương trình
( )
2
1
20
2
1
2 0,5
2
x
x
−
−
−
1
4
9
4
x
x
19
44
x
.
Câu 15: Trong một khối đa diện, mệnh đề nào sau đây đúng?
A. Hai cạnh bất kỳ có ít nhất một điểm chung.
B. Ba mặt bất kì có ít nhất một đỉnh chung.
C. Hai mặt bất kì có ít nhất một điểm chung.
D. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
Lời giải
Chọn D
Câu 16: Cho khối lăng trụ có diện tích đáy
3B =
và chiều cao
2h =
. Thể tích của khối lăng trụ đã cho
bằng.
A.
1
. B.
3
. C.
2
. D.
6
.
Lời giải
Chọn D
Thể tích khối lăng trụ là
. 3.2 6V Bh= = =
.
Câu 17: Cho hình trụ có bán kính đáy
8R =
và độ dài đường sinh
3l =
. Diện tích xung quanh của hình
trụ đã cho bằng:
A.
24 .
B.
192 .
C.
48 .
D.
64 .
Lời giải
Chọn C
Diện tích xung quanh của hình trụ
2 48
xq
S rl

==
.
Câu 18: Cho hình nón có độ dài đường sinh bằng 25 và bán kính đường tròn đáy bằng 15. Tính thể tích
của khối nón đó.
A.
1500 .
B.
4500 .
C.
375 .
D.
1875 .
Lời giải
Chọn A
Gọi
h
là chiều cao khối nón
2 2 2 2
25 15 20h l r = − = − =
.
22
11
. .15 .20 1500
33
V r h
= = =
.
Câu 19: Tính thể tích
V
của khối trụ có bán kính
4r =
và chiều cao
42h =
.
A.
32 .V
=
B.
64 2 .V
=
C.
128 .V
=
D.
32 2 .V
=
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 10
Chọn B
2
16.4 2 64 2V r h
= = =
.
Câu 20: Thể tích khối cầu bán kính
3cm
bằng
A.
( )
3
36 cm .
B.
( )
3
108 cm .
C.
( )
3
9 cm .
D.
( )
3
54 cm .
Lời giải
Chọn A
Thể tích khối cầu là:
( )
3 3 3
44
. . . .3 36 cm .
33
VR
= = =
Câu 21: Cho hàm số
42
2y x x=−
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
( )
;2− −
. B. Hàm số đồng biến trên khoảng
( )
1;1−
.
C. Hàm số nghịch biến trên khoảng
( )
1;1−
. D. Hàm số đồng biến trên khoảng
( )
;2− −
.
Lời giải
Chọn A
TXĐ:
.D =
33
0
4 4 ; 0 4 4 0 1
1
x
y x x y x x x
x
=

= − = − = =
=−
Suy ra hàm số đồng biến trên các khoảng
( ) ( )
1;0 , 1;− +
; hàm số nghịch biến trên các khoảng
( ) ( )
; 1 , 0;1− −
. Vậy hàm số nghịch biến trên khoảng
( )
;2− −
.
Câu 22: Cho hàm số
( )
fx
có đạo hàm là
( )
( )( )
22
' 1 3 2f x x x x= − − +
x
. Số điểm cực trị của hàm
số
( )
fx
là
A.
4.
B.
3.
C.
2.
D.
1.
Lời giải
Chọn C
Ta có
( )
( )( )
( )( ) ( )
2
22
' 1 3 2 1 1 2f x x x x x x x= − − + = + − −
.
( )
1
' 0 1
2
x
f x x
x
=−
= =
=
. Do
1, 2xx= − =
là nghiệm đơn,
1x =
là nghiệm bội chẵn nên
( )
'fx
chỉ
đổi dấu khi đi qua
1, 2xx= − =
.
Vậy hàm số
( )
fx
có 2 điểm cực trị
1, 2xx= − =
.
Câu 23: Giá trị nhỏ nhất của hàm số
( )
2
2
1
x
fx
x
−
=
−
trên đoạn
2,3
bằng
A.
7
2
B.
5
2
C.
2
. D.
1
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 11
Chọn C
Ta có
( )
( )
2
2
22
' 0 2,3
1
xx
f x x
x
−+
=
−
.
Mà
( ) ( )
7
2 2, 3
2
ff==
.
Vậy giá trị nhỏ nhất của hàm số
( )
2
2
1
x
fx
x
−
=
−
trên đoạn
2,3
bằng
2
.
Câu 24: Cho hàm số
( )
32
f x ax bx cx d= + + +
có đồ thị như hình vẽ. Trong các mệnh đề sau, mệnh đề
nào đúng?
A.
0, 0, 0, 0.a b c d
B.
0, 0, 0, 0.a b c d
C.
0, 0, 0, 0.a b c d
D.
0, 0, 0, 0.a b c d =
Lời giải
Chọn D
Từ dáng điệu đồ thị ta thấy
( )
lim
x
fx
→+
= +
nên
0a
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên
0d
.
Đồ thị hàm số nhận
1, 1xx= = −
là hai điểm cực trị nên phương trình
( )
2
' 3 2 0f x ax bx c= + + =
có hai nghiệm
1, 1−
.
Theo định lý Vi-et ta có
12
12
22
0
33
1.
33
bb
xx
aa
cc
xx
aa
−−

+ = =




= = −


Do
0a
nên
0, 0bc=
.
Vậy
0, 0, 0, 0.a b c d =
Câu 25: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Số đường tiệm cận ngang của đồ thị hàm số
( )
1
y
fx
=
là
A.
4.
B.
3.
C.
2.
D.
1.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 12
Lời giải
Chọn D
Từ dáng điệu của đồ thị ta thấy
( ) ( )
lim , lim
xx
f x f x
→+ →−
= − = −
.
Do đó
( ) ( )
11
lim 0, lim 0
xx
f x f x
→+ →−
==
.
Đồ thị hàm số
( )
1
y
fx
=
có một đường tiệm cận ngang
0y =
.
Câu 26: Tập xác định của hàm số
( )
4
2
32y x x
−
= − + −
là
A.
\{1,2}
. B.
( ) ( )
,1 2,− +
. C.
\1
. D.
( )
1,2
.
Lời giải
Chọn A
Hàm số xác định khi
2
3 2 0 1, 2x x x x− + −
.
Vậy tập xác định
\ 1;2D =
.
Câu 27: Tập xác định của hàm số
2
ln
5
x
y
x
−

=

−

là
A.
( )
5,+
. B.
( )
2,5
. C.
( )
,2−
. D.
\ 2;5
.
Lời giải
Chọn B
Hàm số xác định khi
2
0 2 5
5
x
x
x
−
−
.
Vậy tập xác định
( )
2,5D =
.
Câu 28: Cho các hàm số
log
a
yx=
,
log
b
yx=
có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
A.
01ab
. B.
01ba
.
C.
01ab
. D.
01ba
.
Lời giải
Chọn B
Ta thấy hàm số
log
b
yx=
nghịch biến nên
01b
.
Mặt khác,
log
a
yx=
đồng biến nên
1a
.
Vậy
01ba
.
Câu 29: Cho các số thực dương
,ab
thỏa mãn
log 2
a
b =
. Giá trị của
( )
2
log
ab
Pa=
bằng
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 13
A.
1
6
. B.
1
2
. C.
2
3
. D.
1
.
Lời giải
Chọn C
Ta có:
2
log 2
a
b b a= =
.
Thay
2
ba=
vào
P
, ta được:
( ) ( )
23
22
.
2
log log
3
a a a
P a a= = =
.
Câu 30: Nghiệm của phương trình
( ) ( )
33
log 1 1 log 4 1xx+ + = +
là
A.
3x =−
. B.
2x =
. C.
3x =
. D.
4x =
.
Lời giải
Chọn B
Điều kiện:
10
1
4 1 0
4
x
x
x
+
−
+
Phương trình đã cho tương đương với phương trình :
( ) ( )
( ) ( )
3 3 3
33
log 1 log 3 log 4 1
log 1 .3 log 4 1
xx
xx
+ + = +
+ = +


( )
1 .3 4 1 2 x x x + = + =
(thỏa mãn đk).
Câu 31: Cho phương trình
( )
3
4 2 2
log .log 4 2log 0
2
x
xx

+=


. Khi đặt
2
logtx=
, ta được phương trình
nào sau đây?
A.
2
11 0tt+=
. B.
2
11 3 0tt+ − =
. C.
2
14 2 0tt+ − =
. D.
2
14 4 0tt+ − =
.
Lời giải
Chọn D
Điều kiện:
0x
.
Ta có:
( ) ( ) ( )
( )
2
4 2 2 2 2 2 2
33
3
2 2 2 2
1 1 1
log .log 4 log log 4 log log . 2 log
2 2 2
log log log 1 3log 1 3 1
22
x x x x x x t t
xx
x x t
= + = + = +
= = − = − = −
Phương trình đã cho có dạng:
22
1
6 2 0 14 4 0
2
t t t t t+ + − = + − =
.
Câu 32: Hình tứ diện đều có bao nhiêu mặt đối xứng?
A.
3
. B.
4
. C.
6
. D.
9
.
Lời giải
Chọn C
Hình tứ diện đều có 6 mặt phẳng đối xứng. Mỗi mặt phẳng đối xứng này được tạo từ một cạnh
của hình tứ diện và trung điểm của cạnh đối diện.
Câu 33: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
cạnh
a
. Cạnh bên
SA
vuông góc
với đáy, góc
60SBD =
. Thể tích khối chóp
.S ABCD
bằng
A.
3
3
a
. B.
3
3
2
a
. C.
3
2
3
a
. D.
3
a
.
Lời giải
Chọn A
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 14
Do
ABCD
là hình vuông
a
nên
2BD a=
và
2
ABCD
Sa=
.
Ta có:
( )
SA AB
SA ABCD
SA AD
⊥
⊥
⊥
Mặt khác ta có:
AB AD=
.
Suy ra hai tam giác vuông
SAB SAD =
(c – g – c)
SB SD=
(hai tam giác bằng nhau có các cặp cạnh tương ứng bằng nhau)
Xét tam giác
SBD
có
SB SD=
và
60SBD =
nên tam giác
SBD
đều
2SB SD BD a = = =
22
SA SB AB a = − =
.
Vậy
3
.
1
..
33
S ABCD ABCD
a
V SA S==
.
Câu 34: Cho hình nón có đường sinh bằng
13,
chiều cao bằng
12.
Diện tích xung quanh của hình nón
bằng
A.
60
. B.
65
. C.
65
. D.
90
.
Lời giải
Chọn C
Ta có
2 2 2 2
13
13 12 5.
12
l
r l h
h
=
= − = − =
=
Khi đó
xq
.5.13 65Sr
= = =
.
Câu 35: Thiết diện qua trục của hình trụ là một hình vuông có cạnh bằng
2a
. Thể tích của khối trụ được
tạo bởi hình trụ này là
A.
3
2 a
. B.
3
2
3
a
. C.
3
8 a
. D.
3
8
3
a
.
Lời giải
Chọn A
Thiết diện qua trục là hình vuông
ABCD
có cạnh bằng
2a
.
Suy ra
22
22
AB a r r a
AD a h h a
= = =


= = =

Vậy thể tích của khối trụ bằng:
2 2 3
. .2 2V r h a a a
= = =
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 15
PHẦN 2 – TỰ LUẬN
Câu 1: Giải phương trình
( )
( )
2
2
25 5 5
3
1
log log 3 log log 3
2
xx+ − =
?
Lời giải
Điều kiện
0
3
x
x
.
Ta có
( )
( )
2
2
25 5 5
3
1
log log 3 log log 3
2
xx+ − =
5 5 5
log log 3 log 2xx + − =
( )
55
log 3 log 2xx − =
( )
( )
32
32
xx
xx
−=
− = −
2
2
3 2 0
3 2 0
xx
xx
− − =
− + =
( )
( )
( )
( )
3 17
2
3 17
2
1
2
x tm
x tm
x tm
x tm
−
=
+
=
=
=
.
Vậy phương trình đã cho có 4 nghiệm là
3 17
2
x
=
,
1x =
,
2x =
.
Câu 2: Cho hình chóp tam giác
.S ABC
có đáy là tam giác đều cạnh
a
, khoảng cách từ
S
đến mặt phẳng
( )
ABC
bằng
6a
. Trên cạnh
SA
lấy điểm
M
, trên cạnh
SB
lấy điểm
N
sao cho
1
2
SM
MA
=
,
2.
SN
NB
=
Mặt phẳng
( )
qua
MN
và song song với
SC
chia khối chóp thành 2 phần. Tính
V
là thể tích của khối đa diện chứa điểm
A
?
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 16
• Ta có
2
0
13
. .sin60
24
ABC
a
S AB AC
==
, nên
23
.
1 1 3 2
. . 6
3 3 4 4
S ABC
aa
V B h a= = =
.
• Trong mặt phẳng
( )
SAC
dựng
MP
song song với
SC
cắt
AC
tại
P
. Trong mặt phẳng
( )
SBC
dựng
NQ
song song với
SC
cắt
BC
tại
.Q
Gọi
D
là giao điểm của
MN
và
PQ
. Dựng
ME
song song với
AB
cắt
SB
tại
E
.
Lại có
1
3
SE SM
SB SA
==
1
3
SE NE NB SB = = =
Suy ra
N
là trung điểm của
BE
và
DM
, đồng thời
1
3
DB ME AB==
11
, .
42
DB DN
DA DM
= =
Do
1
/ / .
2
DQ DN
NQ MP
DP DM
= =
• Ta có
..
.
D AMP D BNQ
V V V=−
.
.
1 1 1 1
. . . .
4 2 2 16
D BNQ
D AMP
V
DB DN DQ
V DA DM DP
= = =
..
1
16
D BNQ D AMP
VV=
..
15 15
. . .
16 16
D AMP M ADP
V V V = =
• Do
1
//
3
QB NB
NQ SC
CB SB
= =
( )
( )
,
1
,3
d Q DB
QB
d C AB CB
= =
( ) ( )
1
, . ,
3
d Q DB d C AB=
( )
1
. , .
2
QDB
S d Q DB DB=
( )
1 1 1 1
. . , .
2 3 3 9
CAB
d C AB AB S==
8
.
9
ADP ABC
SS=
Và
( )
( )
( )
( )
2
,,
3
d M ADP d S ABC=
( )
( )
.
1
. , .
3
M ADP ADP
V d M ADP S=
( )
( )
.
1 2 8 16
. , . .
3 3 9 27
ABC S ABC
d S ABC S V==
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 17
33
..
15 16 5 5 2 5 2
. . . .
16 27 9 9 4 36
S ABC S ABC
aa
V V V = = = =
Câu 3: Cho hàm số
( )
y f x=
có đạo hàm
( )
2
' 2 3, .f x x x x= + −
Tìm các giá trị thực của tham
số m để hàm số
( )
( )
22
3 2 3 2021g x f x x m m m= + + + − +
đồng biến trên khoảng
( )
0;2 ?
Lời giải
Ta có
( ) ( )
2
3
' 2 3 0 * .
1
t
f t t t
t
−
= + −
Ta lại có
( )
( )
( )
( )
2
2
2
2 3 3
' ' 3 2
3
x x x
g x f x x m
xx
++
= + +
+
Vì
( )
( )
( )
2
2
2 3 3
0, 0;2
3
x x x
x
xx
++
+
nên
( )
gx
đồng biến trên
( ) ( ) ( )
0;2 ' 0, 0;2g x x
( )
( )
2
' 3 2 0, 0;2f x x m x + +
( )
( )
( )
( )
22
22
3 2 3, 0;2 3 2 3, 0;2
3 2 1, 0;2 3 2 1, 0;2
x x m x x x m x
x x m x x x m x

+ + − + −



+ + + +

(**)
Có
( )
2
3h x x x=+
luôn đồng biến trên khoảng
( )
0;2
nên
( )
0 10hx
trên khoảng
( )
0;2
Do đó
( )
0 10hx
trên khoảng
( )
0;2
từ (**)
13
2 3 10
2
2 1 0 1
2
m
m
m
m
−
+ −
Vậy giá trị của tham số m cần tìm là
13
2
1
2
m
m
−
.
Câu 4: Tìm
m
để phương trình
( ) ( ) ( )
2
2
33
81
1 log 3 4 5 log 4 1 0
8
3
3
3
m x m m
x

− − − − + − =


−
có nghiệm
trên đoạn
17
1,
9



.
Lời giải
Phương trình
( ) ( ) ( )
2
2
33
81
1 log 3 4 5 log 4 1 0
8
3
3
3
m x m m
x

− − − − + − =


−
( ) ( ) ( )
2
33
88
4 1 log 3 4 5 log 3 4 1 0
33
m x m x m
− − + − − + − =
(1)
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 18
Đặt
3
8
log 3
3
tx

=−


. Do
17
1; 1;1
9
xt

−


Phương trình (1) trở thành
( ) ( )
2
4 1 4( 5) 4 1 0m t m t m− + − + − =
( ) ( )
2
1 5 1 0m t m t m − + − + − =
( )
22
1 5 1m t t t t + + = + +
2
2
51
1
tt
m
tt
++
=
++
* Xét
( )
2
2
51
1
tt
ft
tt
++
=
++
với
1;1t −
( )
( )
2
2
2
44
0
1
t
ft
tt
−
=
++
1;1t −
Hàm số
( )
2
2
51
1
tt
ft
tt
++
=
++
đồng biến trên đoạn
1;1−
( ) ( ) ( )
7
( 1) 1 3
3
f f t f f t − −
* Để phương trình (1) có nghiệm trên đoạn
17
1,
9



thì hai đồ thị của hàm số
( )
2
2
51
;
1
tt
y m f t
tt
++
==
++
cắt nhau
1;1t −
.
7
3
3
m −
.
Vậy
7
3
3
m−
thỏa mãn bài toán.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 06
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
( )
y f x=
xác định, liên tục trên và có bảng biến thiên như hình sau:
Mệnh đề nào sau đây sai?
A. Hàm số nghịch biến trên khoảng
( )
;− +
.
B. Hàm số đồng biến trên khoảng
( )
;− +
.
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên khoảng
( )
1; +
.
Câu 2: Cho hàm số
( )
y f x=
xác định và liên tục trên , có đồ thị như hình vẽ:
Hàm số
( )
y f x=
có giá trị cực đại là:
A.
2.y =
B.
2.y =−
C.
2.x =
D.
0.x =
Câu 3: Cho hàm số
( )
y f x=
có đồ thị trên đoạn
2; 1−
như hình vẽ bên dưới. Giá trị
( )
2; 1
max fx
−
bằng:
A.
1.
B.
3.
C.
0.
D.
3.−
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 2
Sưu tầm và biên soạn
Câu 4: Đường cong trong hình vẽ là đồ thị của hàm số nào trong bốn hàm số sau đây?
A.
32
3 1.y x x= − −
B.
32
3 1.y x x= + −
C.
32
3 1.y x x= − + −
D.
42
3 2.y x x= − + −
Câu 5: Hàm số nào dưới đây có đồ thị dạng như đường cong trong hình bên
A.
42
2 1.y x x= − + +
B.
42
2 2.y x x= + +
C.
42
2 1.y x x= − −
D.
42
2 2.y x x= − + −
Câu 6: Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số
41
23
x
y
x
−
=
−
?
A.
2.x =
B.
3
.
2
y =
C.
3
.
2
x =
D.
2.y =
Câu 7: Tập xác định của hàm số
( )
2yx
=+
là:
A. B.
( )
0; .+
C.
( )
2; .− +
D.
\ 2 .
Câu 8: Tính giá trị biểu thức
19
3
3
1
log 7 2log 49 log
7
A = + −
?
A.
3
log 7.A =
B.
3
2log 7.A =
C.
3
4log 7.A =
D.
3
3log 7.A =
Câu 9: Cho các số dương
a
,
b
,
c
, và
1a
. Khẳng định nào sau đây đúng?
A.
( )
log log log .
a a a
b c bc+=
B.
( )
log log log .
a a a
b c b c+ = +
C.
log log log .
a a a
b c b c+ = −
D.
( )
log log log .
a a a
b c b c+ = −
Câu 10: Đạo hàm của hàm số
( )
3
log 4 1yx=+
là
A.
ln3
.
41
y
x
=
+
B.
( )
4
.
4 1 ln3
y
x
=
+
C.
4ln3
.
41
y
x
=
+
D.
( )
1
.
4 1 ln3
y
x
=
+
Câu 11: Hàm số nào trong bốn hàm số sau đồng biến trên các khoảng xác định của nó?
A.
( )
sin2021 .
x
y =
B.
( )
ln2 .
x
y =
C.
2
.
5
x
y

=


D.
3
.
2 sin2021
x
y

=

+

ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 3
Sưu tầm và biên soạn
Câu 12: Số nghiệm của phương trình
2
21
xx−
=
là:
A.
0.
B.
3.
C.
2.
D.
1.
Câu 13: Phương trình
2
3
log ( 3 5 17) 2xx+− + =
có tập nghiệm
S
là:
A.
8
S= 1; .
3

−


B.
8
S= 1; .
3

−−


C.
8
S= 1; .
3

−


D.
8
S= 2; .
3

−


Câu 14: Cho
( )
3
.e
x
f x x
−
=
. Tập nghiệm của bất phương trình
( )
0fx
là
A.
1
0; .
3



B.
1
;.
3

−


C.
( )
0;1 .
D.
1
;.
3

+


Câu 15: Chọn mệnh đề sai:
A. Khối lập phương là khối đa diện lồi.
B. Khối chóp là khối đa diện lồi.
C. Khối lăng trụ là khối đa diện lồi.
D. Ghép hai khối đa diện lồi ta được một khối đa diện lồi.
Câu 16: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
; hình chiếu của điểm
S
xuống mặt phẳng
()ABCD
trùng với trung điểm của
,3AB SD a=
. Thể tích khối chóp
.S ABCD
là:
A.
3
8
.
3
a
B.
3
83
.
3
a
C.
3
4
.
3
a
D.
3
43
.
3
a
Câu 17: Cho hình nón có chiều cao
23
và chu vi đường tròn đáy bằng
4
. Diện tích xung quanh của
hình nón:
A.
12 .
B.
16 .
C.
8 3 .
D.
8.
Câu 18: Một hình nón có đường sinh
2la=
, góc ở đỉnh bằng
60
. Thể tích khối nón:
A.
3
2
.
3
a
B.
3
2.a
C.
3
3
.
3
a
D.
3
23
.
3
a
Câu 19: Một hình trụ có đường sinh
2a
, đáy là hình tròn ngoại tiếp tam giác đều cạnh bằng
3a
. Thể
tích của khối trụ là:
A.
3
4.a
B.
3
.a
C.
3
2.a
D.
3
.a
Câu 20: Một mặt cầu có diện tích
2
12 ( )S cm
=
. Tìm thể tích V của khối cầu giới hạn bởi mặt cầu đó.
A.
3
4
( ).
3
V cm
=
B.
3
3
( ).
4
V cm
=
C.
3
16 3
( ).
3
cm
D.
3
4 3 ( ).V cm
=
Câu 21: Hỏi hàm số
2
35
1
xx
y
x
−+
=
+
nghịch biến trên các khoảng nào?
A.
( ; 4)− −
và
(2; ).+
B.
( )
4;2 .−
C.
( )
;1− −
và
( )
1; .− +
D.
( )
4; 1−−
và
( )
1;2 .−
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 4
Sưu tầm và biên soạn
Câu 22: Cho hàm số
( )
y f x=
có đạo hàm
' '( )y f x=
và bảng xét dấu
'( )fx
như sau:
Khi đó số điểm cực trị của hàm số
( )
y f x=
là:
A.
1
B.
2
C.
3
D.
4
Câu 23: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2
33
x
y
x
=
+
trên lần lượt là:
A.
0;2
0;2
11
max ,min
33
yy= = −
B.
0;2
0;2
1
max ,min 0
3
yy= =
C.
0;2
0;2
11
max ,min
33
yy= − =
D.
0;2
0;2
1
max 0,min
3
yy= = −
Câu 24: Cho hàm số
( )
0, 0
ax b
y ad bc a
cx d
+
= −
+
có đồ thị như sau:
Khi đó khẳng định nào sau đây đúng?
A.
0, 0, 0.b c d
B.
0, 0, 0.b c d
C.
0, 0, 0.b c d
D.
0, 0, 0.b c d
Câu 25: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Khi đó số tiệm cận của đồ thị hàm số
( )
y f x=
là:
A.
1.
B.
2.
C.
3.
D.
4.
Câu 26: Tập xác định của hàm số
( )
5
1yx
−
=−
là
A.
\ 1 .D =
B.
( )
1; .D = +
C.
( )
;1 .D = −
D.
(
;1 .D = −
Câu 27: Tập xác định của hàm số
là
A.
\ 2 .D =
B.
\ 2 .D =−
C.
( )
; 2 .D = − −
D.
( )
2; .D = − +
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 5
Sưu tầm và biên soạn
Câu 28: Đạo hàm của hàm số
( )
2
53
7
xx
fx
− + −
=
là
A.
( )
2
53
' 7 .
xx
fx
− + −
=
B.
( ) ( )
2
53
' 5 2 7 .
xx
f x x
− + −
=−
C.
( ) ( )
2
53
' ln7. 5 2 7 .
xx
f x x
− + −
=−
D.
( )
2
53
' 7 ln7.
xx
fx
− + −
=
Câu 29: Với
a
là số thực dương tùy ý,
12
9
log a
bằng
A.
3
4 log .a+
B.
3
6log .a
C.
3
24log .a
D.
3
4log .a
Câu 30: Nghiệm của phương trình
( ) ( )
2
2
log 1 log 1 1xx+ − − =
nằm trong khoảng nào
A.
( )
1;0 .−
B.
( )
2;3 .
C.
( )
0;1 .
D.
( )
4;5 .
Câu 31: Hai nghiệm của phương trình
2
log 3log 2 4
x
x +=
là
( )
1 2 1 2
,x x x x
.Tính
21
T x x=−
A.
6.T =
B.
4.T =
C.
2.T =
D.
1.T =
Câu 32: Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ:
Mệnh đề nào sau đây đúng?
A. Khối bát diện đều là loại
4;3
.
B. Khối bát diện đều và khối lập phương đều có cùng số cạnh.
C. Cả năm khối đa diện có số mặt chia hết cho 4.
D. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh.
Câu 33: Cho hình chóp
.S ABCD
đáy là hình vuông cạnh
a
, cạnh
SA
vuông góc với mặt phẳng
( )
,ABCD
góc giữa cạnh
SD
và mặt phẳng
( )
ABCD
bằng
0
60
. Thể tích của khối chóp đã cho bằng:
A.
3
3a
. B.
3
3
3
a
. C.
3
3
6
a
. D.
3
3
9
a
.
Câu 34: Cắt hình trụ
(T)
bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông cạnh
bằng
6
. Diện tích xung quanh của hình trụ
(T)
bằng:
A.
72
. B.
18
. C.
9
. D.
36
.
Câu 35: Cho hình nón tròn xoay đường sinh
4la=
. Thiết diện qua trục của nó là một tam giác cân có
một góc bằng
120
. Thể tích
V
của khối nón đó là:
A.
3
3Va
=
. B.
3
3
a
V
=
. C.
3
3
3
a
V
=
. D.
3
8Va
=
.
II. PHẦN TỰ LUẬN:
Câu 36: Tìm tập tất cả các giá trị nguyên của tham số thực
m
để phương trình sau có bốn nghiệm thực
phân biệt:
( )
22
2 2 2
2 3 1
4 3 2 2 6 1
5 5 25 1.
x m x m m
x x x mx m m
+ − + − +
− + + + − −
+ = +
Câu 37: Cho hình chóp
.S ABC
có đáy là tam giác
ABC
đều cạnh
a
, tam giác
SBA
vuông tại
B
, tam
giác
SAC
vuông tại
C
. Biết góc giữa hai mặt phẳng
( )
SAB
và
( )
ABC
bằng
60
. Tính thể tích
khối chóp
.S ABC
theo
a
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 6
Sưu tầm và biên soạn
Câu 38: Cho hàm số
( )
y f x=
liên tục trên và có bảng biến thiên như sau:
Tìm điểm cực đại của hàm số
( ) ( )
21g x f x=−
.
Câu 39: Cho hàm số
( )
y f x=
có bảng biến thiên như hình dưới đây.
Tìm giá trị lớn nhất của hàm số
( )
( )
2 3 2
11
4 3 8
33
g x f x x x x x= − + − + +
trên đoạn
1;3
.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 7
Sưu tầm và biên soạn
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM:
Câu 1: Cho hàm số
( )
y f x=
xác định, liên tục trên và có bảng biến thiên như hình sau:
Mệnh đề nào sau đây sai?
A. Hàm số nghịch biến trên khoảng
( )
;− +
.
B. Hàm số đồng biến trên khoảng
( )
;− +
.
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên khoảng
( )
1; +
.
Lời giải
Chọn A
Dựa vào bảng biến thiên
' 0,yx
nên hàm số đồng biến trên khoảng
( )
;− +
.
Vậy mệnh đề sai là: “Hàm số nghịch biến trên khoảng
( )
;− +
.”
Câu 2: Cho hàm số
( )
y f x=
xác định và liên tục trên , có đồ thị như hình vẽ:
Hàm số
( )
y f x=
có giá trị cực đại là:
A.
2.y =
B.
2.y =−
C.
2.x =
D.
0.x =
Lời giải
Chọn A
Dựa vào đồ thị hàm số, suy ra giá trị cực đại của hàm số là
2y =
.
Câu 3: Cho hàm số
( )
y f x=
có đồ thị trên đoạn
2; 1−
như hình vẽ bên dưới. Giá trị
( )
2; 1
max fx
−
bằng:
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 8
Sưu tầm và biên soạn
A.
1.
B.
3.
C.
0.
D.
3.−
Lời giải
Chọn A
Giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
2; 1−
là điểm cao nhất của đồ thị hàm số
( )
y f x=
trên đoạn
2; 1−
. Dựa vào đồ thị ta thấy
( )
2; 1
max 1fx
−
=
.
Câu 4: Đường cong trong hình vẽ là đồ thị của hàm số nào trong bốn hàm số sau đây?
A.
32
3 1.y x x= − −
B.
32
3 1.y x x= + −
C.
32
3 1.y x x= − + −
D.
42
3 2.y x x= − + −
Lời giải
Chọn C
Dựa vào đồ thị ta thấy đây là hàm bậc ba. Nhánh cuối đi xuống nên ta có hệ số
0a
.
Câu 5: Hàm số nào dưới đây có đồ thị dạng như đường cong trong hình bên
A.
42
2 1.y x x= − + +
B.
42
2 2.y x x= + +
C.
42
2 1.y x x= − −
D.
42
2 2.y x x= − + −
Lời giải
Chọn C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 9
Sưu tầm và biên soạn
Dựa vào đồ thị ta thấy đây là hàm trùng phương. Nhánh cuối đi lên nên ta có hệ số
0a
; giao
điềm của đồ thị với trục tung nằm phía dưới trục
Ox
nên hệ số
0c
.
Câu 6: Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số
41
23
x
y
x
−
=
−
?
A.
2.x =
B.
3
.
2
y =
C.
3
.
2
x =
D.
2.y =
Lời giải
Chọn D
Hàm số
ax b
y
cx d
+
=
+
có đường tiệm cận đứng là
d
x
c
=−
; đường tiệm cận ngang là
a
y
c
=
.
Theo đề ra ta có đường tiệm cận ngang của đồ thị hàm số
41
23
x
y
x
−
=
−
là đường thẳng
2y =
.
Câu 7: Tập xác định của hàm số
( )
2yx
=+
là:
A. B.
( )
0; .+
C.
( )
2; .− +
D.
\ 2 .
Lời giải
Chọn C
Vì số mũ
là một số thực nên điều kiện xác định của hàm số
( )
2yx
=+
là:
2 0 2xx+ −
Vậy
( )
2;D = − +
.
Câu 8: Tính giá trị biểu thức
19
3
3
1
log 7 2log 49 log
7
A = + −
?
A.
3
log 7.A =
B.
3
2log 7.A =
C.
3
4log 7.A =
D.
3
3log 7.A =
Lời giải
Chọn D
1 2 1
2
21
19
3
33
3
3
1
log 7 2log 49 log log 7 2log 7 log 7
7
A
−
−
= + − = + −
3 3 3 3
log 7 2log 7 2log 7 3log 7A = − + + =
Phân tích
Áp dụng công thức biến đổi logarit, công thức lũy thừa cơ bản
Câu 9: Cho các số dương
a
,
b
,
c
, và
1a
. Khẳng định nào sau đây đúng?
A.
( )
log log log .
a a a
b c bc+=
B.
( )
log log log .
a a a
b c b c+ = +
C.
log log log .
a a a
b c b c+ = −
D.
( )
log log log .
a a a
b c b c+ = −
Lời giải
Chọn A
Theo tính chất logarit ta có:
( )
log log log
a a a
b c bc+=
.
Phân tích
Công thức cơ bản của logarit
Câu 10: Đạo hàm của hàm số
( )
3
log 4 1yx=+
là:
A.
ln3
.
41
y
x
=
+
B.
( )
4
.
4 1 ln3
y
x
=
+
C.
4ln3
.
41
y
x
=
+
D.
( )
1
.
4 1 ln3
y
x
=
+
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 10
Sưu tầm và biên soạn
Chọn B
( )
( ) ( )
41
4
4 1 ln3 4 1 ln3
x
y
xx
+
==
++
.
Phân tích
Công thức đạo hàm của hàm logarit.
Câu 11: Hàm số nào trong bốn hàm số sau đồng biến trên các khoảng xác định của nó?
A.
( )
sin2021 .
x
y =
B.
( )
ln2 .
x
y =
C.
2
.
5
x
y

=


D.
3
2 sin2021
x
y

=

+

Lời giải
Chọn D
Hàm số
x
ya=
đồng biến trên các khoảng xác định của nó
1a
.
Phân tích
Áp dụng tính chất của hàm số mũ
Câu 12: Số nghiệm của phương trình
2
21
xx−
=
là:
A.
0.
B.
3.
C.
2.
D.
1.
Lời giải
Chọn C
Ta có:
2
21
xx−
=
2
0
22
xx−
=
2
0xx − =
0
1
x
x
=
=
. Vậy phương trình có
2
nghiệm.
Phân tích
Phương trình mũ cơ bản
Câu 13: Phương trình
2
3
log ( 3 5 17) 2xx+− + =
có tập nghiệm
S
là:
A.
8
S= 1; .
3

−


B.
8
S= 1; .
3

−−


C.
8
S= 1; .
3

−


D.
8
S= 2; .
3

−


Lời giải
Chọn C
Điều kiện:
2
3 5 17 0xx− + +
5 229 5 229
66
x
−+

.
2
3
log ( 3 5 17) 2xx+− + =
2
3 5 17 9xx− + =+
1
8
3
x
x
=−
=
(thỏa điều kiện).
Phân tích
Phương trình cơ bản của logarit.
Câu 14: Cho
( )
3
.e
x
f x x
−
=
. Tập nghiệm của bất phương trình
( )
0fx
là
A.
1
0; .
3



B.
1
;.
3

−


C.
( )
0;1 .
D.
1
;.
3

+


Lời giải
Chọn B
Ta có:
( )
33
e 3 .e
xx
f x x
−−
=−
( )
3
1 3 e
x
x
−
=−
.
( )
0fx
( )
3
1 3 e 0
x
x
−
−
1
3
x
. Vậy tập nghiệm của bất phương trình:
1
;
3

−


.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 11
Sưu tầm và biên soạn
Phân tích
Công thức đạo hàm hàm mũ và công thức đạo hàm và tính đồng biến và nghịch biến của hàm
số mũ
Câu 15: Chọn mệnh đề sai:
A. Khối lập phương là khối đa diện lồi
B. Khối chóp là khối đa diện lồi
C. Khối lăng trụ là khối đa diện lồi
D. Ghép hai khối đa diện lồi ta được một khối đa diện lồi.
Lời giải
Chọn D
Câu 16: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
; hình chiếu của điểm
S
xuống mặt phẳng
()ABCD
trùng với trung điểm của
,3AB SD a=
. Thể tích khối chóp
.S ABCD
là:
A.
3
8
.
3
a
B.
3
83
.
3
a
C.
3
4
.
3
a
D.
3
43
.
3
a
Lời giải
Chọn A
Gọi H là trung điểm của AB
()SH ABCD⊥
Trong tam giác vuông
AHD
có:
2 2 2 2 2 2
45HD AD AH a a a= + = + =
Trong tam giác vuông
SHD
có:
2 2 2 2 2 2
9 5 4 2SH SD HD a a a SH a= − = − = =
Vậy
3
2
.
1 1 8
. .4 .2
3 3 3
S ABCD ABCD
a
V S SH a a= = =
Câu 17: Cho hình nón có chiều cao
23
và chu vi đường tròn đáy bằng
4
. Diện tích xung quanh của
hình nón:
A.
12 .
B.
16 .
C.
8 3 .
D.
8.
Lời giải
Chọn D
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 12
Sưu tầm và biên soạn
Gọi
r
là bán kính đường tròn đáy, nên chu vi đường tròn đáy là
2.r
Ta có:
2 4 2rr

= =
22
12 4 4.l h r = + = + =
Vậy
8
xq
S rl

==
(đvdt).
Câu 18: Một hình nón có đường sinh
2la=
, góc ở đỉnh bằng
60
. Thể tích khối nón:
A.
3
2
.
3
a
B.
3
2.a
C.
3
3
.
3
a
D.
3
23
.
3
a
Lời giải
Chọn C
Tam giác vuông
SOA
có
.sin30
30 .
.cos30 3
OA SA a
OSA
SO SA a
= =
=
= =
Vậy
3
22
1 1 3
.3
3 3 3
a
V r h a a

= = =
(đvtt).
Câu 19: Một hình trụ có đường sinh
2a
, đáy là hình tròn ngoại tiếp tam giác đều cạnh bằng
3a
. Thể
tích của khối trụ là
A.
3
4.a
B.
3
.a
C.
3
2.a
D.
3
.a
Lời giải
Chọn C
Tam giác đều cạnh
3a
bán kính đường tròn ngoại tiếp:
3
2
sin60
a
R R a= =
.
Vậy
2 2 3
2V R h R l a
= = =
.
Câu 20: Một mặt cầu có diện tích
2
12 ( )S cm
=
. Tìm thể tích V của khối cầu giới hạn bởi mặt cầu đó.
A.
3
4
()
3
V cm
=
B.
3
3
()
4
V cm
=
C.
3
16 3
()
3
cm
D.
3
4 3 ( )V cm
=
Lời giải
Chọn D
Ta có:
2
4 12 3( )S R R cm

= = =
. Vậy
33
4
4 3 ( )
3
V R cm

==
.
Câu 21: Hỏi hàm số
2
35
1
xx
y
x
−+
=
+
nghịch biến trên các khoảng nào?
A.
( ; 4)− −
và
(2; ).+
B.
( )
4;2 .−
C.
( )
;1− −
và
( )
1; .− +
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 13
Sưu tầm và biên soạn
D.
( )
4; 1−−
và
( )
1;2 .−
Lời giải
Chọn D
Ta có :
\1D =−
22
22
(2 3)( 1) ( 3 5) 2 8
'
( 1) ( 1)
x x x x x x
y
xx
− + − − + + −
==
++
Cho
2
2
' 0 2 8 0
4
x
y x x
x
=
= + − =
=−
(nhận)
Bảng xét dấu đạo hàm:
Vậy hàm số nghịch biến trên khoảng
( )
4; 1−−
và
( )
1;2−
Câu 22: Cho hàm số
( )
y f x=
liên tục trên , có đạo hàm
' '( )y f x=
x
và bảng xét dấu
'( )fx
như sau:
Khi đó số điểm cực trị của hàm số
( )
y f x=
là:
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải
Chọn B
Ta có:
0
x
là điểm cực trị của hàm số khi
0
'( ) 0fx=
và
'( )fx
đổi dấu qua
0
x
.
Từ bảng xét dấu
'( )fx
ta thấy
'( )fx
chỉ đổi dấu qua
2
x
và
3
x
.
Do đó: Hàm số có hai điểm cực trị là
2
x
và
3
x
.
Câu 23: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2
33
x
y
x
=
+
trên lần lượt là
A.
0;2
0;2
11
max ,min
33
yy= = −
B.
0;2
0;2
1
max ,min 0
3
yy= =
C.
0;2
0;2
11
max ,min
33
yy= − =
D.
0;2
0;2
1
max 0,min
3
yy= = −
Lời giải
Chọn A
Áp dụng quy tắc tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số ta có:
Tập xác định của hàm số:
D =
.
( )
( ) ( )
2
2
22
22
2 3 3 2 .6
66
'.
3 3 3 3
x x x
x
y
xx
+−
−+
==
++
1
' 0 .
1
x
y
x
=−
=
=
Bảng biến thiên:
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 14
Sưu tầm và biên soạn
Vậy:
11
max ,min
33
yy= = −
Câu 24: Cho hàm số
( )
0, 0
ax b
y ad bc a
cx d
+
= −
+
có đồ thị như sau:
Khi đó khẳng định nào sau đây đúng?
A.
0, 0, 0.b c d
B.
0, 0, 0.b c d
C.
0, 0, 0.b c d
D.
0, 0, 0.b c d
Lời giải
Chọn C
Từ đồ thị của hàm số ta có:
Đường thẳng
a
y
c
=
là tiệm cận ngang nên
0,
a
ac
c

cùng dấu
0c
.
Đường thẳng
1x =
là tiệm cận đứng nên:
1 0 0 0
dd
d
cc
− =
.
Mà giao điểm đồ thị hàm số với trục tung có tọa độ âm nên
0,
b
bd
d

trái dấu
0.b
Vậy:
0, 0, 0b c d
.
Câu 25: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
x
−
1
x
2
x
3
x
+
( )
'fx
+
0
−
−
0
+
( )
fx
( )
1
fx
+
+
−
−
( )
3
fx
Khi đó số tiệm cận của đồ thị hàm số
( )
y f x=
là
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải
Chọn A
Theo định nghĩa đường tiệm cận của đồ thị hàm số:
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 15
Sưu tầm và biên soạn
0
lim
x
yy
→
=
thì đường thẳng
0
yy=
là tiệm cận ngang của đồ thị hàm số.
Nếu ít nhất một trong các điều kiện sau được thỏa mãn:
0 0 0 0
lim , lim , lim , lim
x x x x x x x x
yyyy
+ − − −
→ → → →
= + = − = + = −
hoặc
0
lim
xx
y
→
=
thì đường thẳng
0
xx=
là tiệm cận
đứng của đồ thị hàm số.
Đồng thời, dựa vào bảng biến thiên ta thấy:
lim
x
y
→
= 
nên đồ thị hàm số không có tiệm cận ngang.
2
lim
xx
y
→
= 
nên đường thẳng
2
xx=
là tiệm cận đứng của đồ thị hàm số.
Do đó đồ thị của hàm số chỉ có một đường tiệm cận.
Câu 26: Tập xác định của hàm số
( )
5
1yx
−
=−
là
A.
\1D =
B.
( )
1;D = +
C.
( )
;1D = −
D.
(
;1D = −
Lời giải
Chọn A
Điều kiện của hàm số
yu
=
với
nguyên âm là
0u
.
Do đó điều kiện của hàm số
( )
5
1yx
−
=−
là:
1 0 1xx−
.
Vậy: Tập xác định của hàm số
( )
5
1yx=−
là
\1D =
Câu 27: Tập xác định của hàm số
( )
2
log 3 6yx=+
là
A.
\2D =
B.
\2D = −
C.
( )
;2D = − −
D.
( )
2;D = − +
Lời giải
Chọn D
Điều kiện của hàm số
( )
log
a
y f x=
là
( )
0fx
.
Do đó điều kiện của hàm số
( )
2
log 3 6yx=+
là:
3 6 2xx+ −
.
Vậy: Tập xác định của hàm số
( )
2
log 3 6yx=+
là
( )
2;D = − +
Câu 28: Đạo hàm của hàm số
( )
2
53
7
xx
fx
− + −
=
là
A.
( )
2
53
' 7 .
xx
fx
− + −
=
B.
( ) ( )
2
53
' 5 2 7 .
xx
f x x
− + −
=−
C.
( ) ( )
2
53
' ln7. 5 2 7 .
xx
f x x
− + −
=−
D.
( )
2
53
' 7 ln7.
xx
fx
− + −
=
Lời giải
Chọn B
Đạo hàm của hàm số
( )
u
f x a=
là
( )
' ln . '.
u
f x a au=
Do đó đạo của hàm số
( )
2
53
7
xx
fx
− + −
=
là:
( )
( )
( )
22
5 3 2 5 3
' 7 ln7. 5 3 ' ln7 5 2 7 .
x x x x
f x x x x
− + − − + −
= − + − = −
Câu 29: Với
a
là số thực dương tùy ý,
12
9
log a
bằng
A.
3
4 log a+
. B.
3
6log a
. C.
3
24log a
. D.
3
4log a
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 16
Sưu tầm và biên soạn
Chọn B
Ta có:
( )
2
12
9 3 3
3
1
log 12log 12. log 6log
2
a a a a= = =
.
Câu 30: Nghiệm của phương trình
( ) ( )
2
2
log 1 log 1 1xx+ − − =
nằm trong khoảng nào
A.
( )
1;0−
. B.
( )
2;3
. C.
( )
0;1
D.
( )
4;5
Lời giải
Chọn C
Điều kiện
10
1 1
10
x
x
x
−
−
+
.
Phương trình
( ) ( )
22
2log 1 log 1 1xx + − − =
.
( ) ( )
2 2 2
2log 1 log 1 log 2xx + = − +
.
( ) ( )
2
22
log 1 log 2 1xx + = −


.
2
2 1 2 2x x x + + = −
.
( )
2
25
4 1 0
25
x
xx
xL
= − +
+ − =
= − −
.
Vậy tập nghiệm phương trình là
25S = − +
.
Câu 31: Hai nghiệm của phương trình
2
log 3log 2 4
x
x +=
là
( )
1 2 1 2
,x x x x
.Tính
21
T x x=−
A.
6T =
. B.
4T =
. C.
2T =
. D.
1T =
.
Lời giải
Chọn A
Điều kiện:
01x
.
2
log 3log 2 4
x
x +=
2
2
3
log 4
log
x
x
+ =
2
22
log 4log 3 0xx − + =
2
2
log 1
log 3
x
x
=
=
2
8
x
x
=
=
.
Tập nghiệm của phương trình là
2;8S =
. Vậy
8 2 6T = − =
.
Câu 32: Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ:
Mệnh đề nào sau đây đúng?
A. Khối bát diện đều là loại
4;3
.
B. Khối bát diện đều và khối lập phương đều có cùng số cạnh.
C. Cả năm khối đa diện có số mặt chia hết cho 4.
D. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh.
Lời giải
Chọn B
+ A sai, vì khối bát diện đều là loại
3;4
.
+ B đúng, vì khối lập phương có 12 cạnh; khối bát diện đều có 12 cạnh.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 17
Sưu tầm và biên soạn
+ C sai, vì khối lập phương có
6
mặt và 6 không chia hết cho 4.
+ D sai, vì khối
12
mặt đều có
20
đỉnh, còn khối
20
mặt đều có
12
đỉnh.
Câu 33: Cho hình chóp
.S ABCD
đáy là hình vuông cạnh
a
, cạnh
SA
vuông góc với mặt phẳng
( )
,ABCD
góc giữa cạnh
SD
và mặt phẳng
( )
ABCD
bằng
0
60
. Thể tích của khối chóp đã cho bằng:
A.
3
3a
. B.
3
3
3
a
. C.
3
3
6
a
. D.
3
3
9
a
.
Lời giải
Chọn B
( )
SA ABCD⊥
AD
là hình chiếu của
SD
lên mặt phẳng
( )
ABCD
.
Suy ra
( )
(
)
( )
0
, , 60SD ABCD SD AD SDA= = =
.
.tan 3SA AD SDA a==
.
Ta có:
.D
1
..
3
S ABCD ABC
V S SA=
3
3
3
a
=
(đvtt).
Câu 34: Cắt hình trụ
(T)
bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông cạnh
bằng
6
. Diện tích xung quanh của hình trụ
(T)
bẳng:
A.
72
. B.
18
. C.
9
. D.
36
.
Lời giải
Chọn D
Ta có
3, 6 2 36
xq
r l S rl

= = = =
.
Câu 35: Cho hình nón tròn xoay đường sinh
4la=
. Thiết diện qua trục của nó là một tam giác cân có
một góc bằng
120
. Thể tích
V
của khối nón đó là:
60
°
a
D
C
B
A
S
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 18
Sưu tầm và biên soạn
A.
3
3Va
=
. B.
3
3
a
V
=
. C.
3
3
3
a
V
=
. D.
3
8Va
=
.
Lời giải
Chọn D
Gọi thiết diện qua trục của hình nón là
SAB
như hình vẽ.
Ta có
SAB
cân tại
S
có một góc
120
120ASB =
.
1
60
2
OSA ASB= =
(
SAB
cân tại
S
).
Xét
SAO
vuông tại
O
có:
.cos 4 .cos60 2h SO SA ASO a a= = = =
3
.sin 4 . 2 3
2
r OA SA ASO a a= = = =
.
Thể tích của khối nón là:
( )
2
23
11
. 2 3 .2 8
33
V r h a a a
= = =
.
II. PHẦN TỰ LUẬN:
Câu 36: Tìm tập tất cả các giá trị nguyên của tham số thực
m
để phương trình sau có bốn nghiệm thực
phân biệt:
( )
22
2 2 2
2 3 1
4 3 2 2 6 1
5 5 25 1.
x m x m m
x x x mx m m
+ − + − +
− + + + − −
+ = +
Lời giải
Ta có:
( )
22
2 2 2
2 3 1
4 3 2 2 6 1
5 5 25 1
x m x m m
x x x mx m m
+ − + − +
− + + + − −
+ = +
( )
22
2 2 2
2 2 2 2 6 2
4 3 2 2 6 1
5 5 5 1
x m x m m
x x x mx m m
+ − + − +
− + + + − −
+ = +
(1).
Đặt
2
43a x x= − +
;
22
2 2 6 1b x mx m m= + + − −
( )
22
2 2 2 2 6 2a b x m x m m + = + − + − +
Ta có (1)
5 5 5 1
a b a b+
+ = +
5 5 5 .5 1
a b a b
+ = +
( )( )
1 5 1 5 0
ab
− − =
51
51
a
b
=
=
0
0
a
b
=
=
.
+)
0a =
2
4 3 0xx − + =
1
3
x
x
=
=
.
+)
0b =
22
2 2 6 1 0x mx m m + + − − =
(*).
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 19
Sưu tầm và biên soạn
Yêu câu bài toán
Phương trình (*) có hai nghiệm phân biệt khác
1
và khác
3
2
2
0
2 4 0
2 8 0
mm
m

−
+
2 2 2
2 6 1 0 6 1 0
00
22
m m m m m
mm
mm

= − + + − + +





3 10 3 10
0
2
− +

m
m
m
.
Ta có:
1;3;4;5;6=S
. Vậy có năm giá trị của tham số
m
thỏa mãn yêu cầu bài toán.
Câu 37: Cho hình chóp
.S ABC
có đáy là tam giác
ABC
đều cạnh
a
, tam giác
SBA
vuông tại
B
, tam
giác
SAC
vuông tại
C
. Biết góc giữa hai mặt phẳng
( )
SAB
và
( )
ABC
bằng
60
.
Tính thể tích khối chóp
.S ABC
theo
a
.
Lời giải
Gọi
D
là hình chiếu của
S
lên mặt phẳng
( )
ABC
, suy ra
( )
SD ABC⊥
.
Ta có
SD AB⊥
và
SB AB⊥
(gt) suy ra
( )
AB SBD BA BD⊥ ⊥
.
Tương tự có
AC DC⊥
hay tam giác
ACD
vuông ở
C
.
Dễ thấy
SBA SCA =
(cạnh huyền và cạnh góc vuông), suy ra
SB SC=
. Từ đó ta chứng minh
được
SBD SCD =
nên cũng có
DB DC=
.
Vậy
DA
là đường trung trực của
BC
nên cũng là đường phân giác của góc
BAC
.
Ta có
30DAC =
, suy ra
3
a
DC =
. Ngoài ra góc giữa hai mặt phẳng
( )
SAB
và
( )
ABC
là
60SBD =
, suy ra
tan
SD
SBD
BD
=
.tanSD BD SBD=
.3
3
a
a==
.
Vậy
23
.
1 1 3 3
. . . .
3 3 4 12
S ABC ABC
aa
V S SD a
= = =
.
Câu 38: Cho hàm số
( )
y f x=
liên tục trên và có bảng biến thiên như sau:
Tìm điểm cực đại của hàm số
( ) ( )
21g x f x=−
.
Lời giải
Ta có:
( ) ( ) ( ) ( )
2 1 . 2 1 2 2 1g x x f x f x
= − − = −
.
S
D
B
A
C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 20
Sưu tầm và biên soạn
( )
0gx
=
( )
0
2 1 1
1
2 1 0 2 1 0
2
2 1 1
1
x
x
f x x x
x
x
=
− = −
− = − = =
−=
=
.
Ta có bảng biến thiên của
( )
gx
như sau:
Vậy hàm số
( )
gx
đạt cực đại tại
1
2
x =
.
Câu 39: Cho hàm số
( )
y f x=
có bảng biến thiên như hình dưới đây.
Tìm giá trị lớn nhất của hàm số
( )
( )
2 3 2
11
4 3 8
33
g x f x x x x x= − + − + +
trên đoạn
1;3
.
Lời giải
( ) ( )
( )
22
4 2 4 6 8g x x f x x x x

= − − + − +
( )
( )
2
2 2 4 4x f x x x

= − − + −

.
Với
1;3x
thì
40x−
;
2
3 4 4xx −
nên
( )
2
40f x x
−
.
Suy ra
( )
2
2 4 4 0f x x x
− + −
,
1;3x
.
Bảng biến thiên:
Suy ra
( ) ( )
1;3
max 2g x g=
( )
4 7 12f= + =
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 07
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào sau
đây?
A.
( )
1;1−
. B.
( )
;1−
. C.
( )
0;1
. D.
( )
1;0−
.
Câu 2: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng
A.
2
. B.
0
. C.
1
. D.
5
.
Câu 3: Giá trị lớn nhất của hàm số
42
49y x x= − +
trên đoạn
2;3−
bằng
A.
2
. B.
5
. C.
54
. D.
9
.
Câu 4: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
A.
42
2 4 1y x x= − +
. B.
42
2 4 1y x x= − + +
. C.
3
2 3 1y x x= − +
. D.
3
2 3 1y x x= − + +
.
Câu 5: Đường cong trong hình dưới đây là đồ thị của hàm số nào trong các hàm số sau?
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 2
Sưu tầm và biên soạn
A.
1
1
x
y
x
+
=
−
. B.
24
1
x
y
x
−
=
−
. C.
1
22
x
y
x
+
=
−
. D.
2
33
x
y
x
=
−
.
Câu 6: Tiệm cận ngang của đồ thị hàm số
21
1
x
y
x
+
=
+
là đường thẳng có phương trình
A.
2y =
. B.
2x =
. C.
1y =−
. D.
1x =−
.
Câu 7: Kết luận nào đúng về số thực
a
nếu
37
aa
?
A.
12a
. B.
1a
. C.
01a
. D.
1a
.
Câu 8: Tập xác định
D
của hàm số
( )
3
log 2 1yx=+
là
A.
1
;
2
D

= − −


. B.
1
;
2
D

= +


. C.
( )
0;D = +
. D.
1
;
2
D

= − +


.
Câu 9: Cho
a
,
b
,
c
là ba số thực dương khác
1
. Đồ thị các hàm số
x
ya=
,
x
yb=
,
x
yc=
được cho
trong hình vẽ bên. Mệnh đề nào sau đây đúng?
A.
c a b
. B.
b c a
. C.
a c b
. D.
abc
.
Câu 10: Đạo hàm của hàm số
logyx=
là
A.
1
y
x
=
. B.
ln10
y
x
=
. C.
1
ln10
y
x
=
. D.
1
10ln
y
x
=
.
Câu 11: Đạo hàm của hàm số
2
3
x
y =
là
A.
2
3
x
y
=
. B.
2
3 .ln3
x
y
=
. C.
2
2 .3
x
yx
=
. D.
2
2 .ln3.3
x
yx
=
.
Câu 12: Phương trình
21
2 32
x+
=
có nghiệm là
x
y
2
1
1
1
O
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 3
Sưu tầm và biên soạn
A.
5
2
x =
. B.
2x =
. C.
3
2
x =
. D.
3x =
.
Câu 13: Nghiệm của phương trình
( )
2
log 7 5x+=
là
A.
39x =
. B.
18x =
. C.
25x =
. D.
3x =
.
Câu 14: Tập nghiệm của bất phương trình
( )
3
log 1 1x−
là
A.
(
1;4
. B.
( )
;4−
. C.
(
;4−
. D.
(
0;4
.
Câu 15: Khối lập phương là khối đa diện đều loại nào?
A.
3;3
. B.
5;3
. C.
4;3
. D.
3;4
.
Câu 16: Thể tích khối lập phương có cạnh
2a
bằng
A.
3
8a
. B.
3
2a
. C.
3
a
. D.
3
6a
.
Câu 17: Cho hình nón có bán kính đáy là
3r =
và đường sinh
4l =
. Diện tích xung quanh của hình
nón đã cho là
A.
16 3S
=
. B.
24S
=
. C.
83S
=
. D.
43S
=
.
Câu 18: Cho hình chữ nhật
ABCD
có
AB a=
,
2AD a=
. Thể tích của khối trụ tạo thành khi quay hình
chữ nhật
ABCD
quanh cạnh
AB
bằng
A.
3
4 a
. B.
3
a
. C.
3
2a
. D.
3
a
.
Câu 19: Cho khối nón có độ dài đường cao bằng
2a
và bán kính đáy bằng
a
. Thể tích của khối nón đã
cho bằng
A.
3
2
3
a
. B.
3
4
3
a
. C.
3
3
a
. D.
3
2 a
.
Câu 20: Cắt hình trụ
( )
T
bởi một mặt phẳng đi qua trục của nó, ta được thiết diện là một hình vuông cạnh
là 7. Diện tích xung quanh của
( )
T
bằng
A.
49
2
. B.
49
. C.
98
. D.
49
4
.
Câu 21: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên và có đồ thị của hàm số
( )
y f x
=
như hình
vẽ bên. Mệnh đề nào dưới đây sai?
A. Hàm số
( )
y f x=
đồng biến trên
( )
2;+
.
B. Hàm số
( )
y f x=
nghịch biến trên
( )
1;0−
.
C. Hàm số
( )
y f x=
đồng biến trên
( )
1; +
.
D. Hàm số
( )
y f x=
nghịch biến trên
( )
;2−
.
Câu 22: Cho hàm số
3
35y x x= − +
. Điểm cực tiểu của đồ thị hàm
số đã cho là
A.
( )
7; 1−
. B.
( )
1;7−
. C.
( )
3;1
. D.
( )
1;3
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 4
Sưu tầm và biên soạn
Câu 23: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;3−
và có đồ thị như hình vẽ dưới đây. Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;3−
. Giá trị của
Mm−
bằng
A.
4
. B.
1
. C.
5
. D.
0
.
Câu 24: Cho hàm số
2ax
y
bx c
+
=
+
,
,,abc
có đồ thị như hình vẽ
Khẳng định nào dưới đây đúng?
A.
0b a c
. B.
0b a c
. C.
0a b c
. D.
0b c a
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 5
Sưu tầm và biên soạn
Câu 25: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 26: Rút gọn biểu thức
5
3
3
:Q b b=
với
0b
. Kết quả nào sau đây đúng
A.
5
9
.Qb=
B.
2
.Qb=
C.
4
3
.Qb=
D.
4
3
.Qb
−
=
Câu 27: Cho các số thực dương
a
,
b
,
c
,
d
. Biểu thức
ln ln ln ln
a b c d
S
b c d a
= + + +
bằng
A.
0
. B.
( )
ln . . .abc d
. C.
1
. D.
ln
a b c d
b c d a

+ + +


.
Câu 28: Một người gửi tiết kiệm vào một ngân hàng với lãi suất
7,5%
/năm. Biết rằng nếu không rút tiền
ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp
theo. Hỏi sau bao nhiêu năm người đó thu được (cả số tiền gửi ban đầu và lãi) ít nhất gấp đôi số
tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và người đó không
rút tiền ra?
A.
11
năm. B.
10
năm. C.
12
năm. D.
9
năm.
Câu 29: Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
ln( 2 1)= − + +y x x m
có tập xác định là
.
A.
0m =
. B.
03m
. C.
1m −
hoặc
0m
. D.
0m
.
Câu 30: Gọi
S
là tổng tất cả các nghiệm của phương trình
( )
1
2 64.
x
x
−
=
Giá trị của
S
là
A.
1
S.
2
=
B.
S 6.=−
C.
S 3.=−
D.
S 1.=
Câu 31: Số nghiệm của phương trình
( ) ( )
33
log 6 log 9 5 0xx+ + − =
là
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 32: Mặt phẳng
( ' ')AB C
chia khối lăng trụ
. ' ' 'ABC A B C
thành các khối đa diện nào?
A. Hai khối chóp tứ giác.
B. Một khối chóp tam giác và một khối chóp tứ giác.
C. Hai khối chóp tam giác.
D. Một khối chóp tam giác và một khối chóp ngũ giác.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 6
Sưu tầm và biên soạn
Câu 33: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
,AB a=
3,AD a=
SA
vuông góc
với mặt phẳng đáy và mặt phẳng
( )
SBC
tạo với đáy một góc
60
. Thể tích
V
của khối chóp
.S ABCD
là
A.
3
3
a
V =
. B.
3
3
3
a
V =
. C.
3
Va=
. D.
3
3Va=
.
Câu 34: Cho khối nón có độ dài đường sinh bằng
2a
và bán kính đáy bằng
a
. Thể tích của khối nón đã
cho bằng
A.
3
3
2
a
. B.
3
3
3
a
. C.
3
2
3
a
. D.
3
3
a
.
Câu 35: Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng
2
, thiết diện
thu được là hình vuông có diện tích bằng
16
. Diện tích xung quanh của hình trụ đã cho bằng
A.
86
. B.
24 6
. C.
10 6
. D.
12 6
.
II. PHẦN TỰ LUẬN (4 câu – 3 điểm)
Câu 36: Cho hàm số
( )
fx
có đồ thị
( )
fx
như hình vẽ bên. Tìm giá trị nhỏ nhất của hàm số
( ) ( )
32
1 3 3
2019
3 4 2
g x f x x x x= − − + +
trên đoạn
3;1−
.
Câu 37: Cho lăng trụ đứng
.ABC AB C
có đáy là tam giác vuông cân tại
B
,
2AC a=
; biết góc giữa
mặt phẳng
( )
A BC
và mặt phẳng đáy bằng
60
. Tính thể tích
V
của khối lăng trụ
.ABC AB C
.
Câu 38: Ông A dự định sử dụng hết
2
5 m
kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Câu 39: Cho phương trình
( )
5
5 log+ = −
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
( )
20;20−m
để phương trình đã cho có nghiệm?
---------- HẾT ----------
HƯỚNG DẪN GIẢI CHI TIẾT
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 7
Sưu tầm và biên soạn
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào sau
đây?
A.
( )
1;1−
. B.
( )
;1−
. C.
( )
0;1
. D.
( )
1;0−
.
Lời giải
Chọn D
Dựa vào đồ thị hàm số, ta có bảng biến thiên sau
Câu 2: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng
A.
2
. B.
0
. C.
1
. D.
5
.
Lời giải
Chọn D
Dựa vào bảng biến thiên hàm số có giá trị cực đại bằng
5
.
Câu 3: Giá trị lớn nhất của hàm số
42
49y x x= − +
trên đoạn
2;3−
bằng
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 8
Sưu tầm và biên soạn
A.
2
. B.
5
. C.
54
. D.
9
.
Lời giải
Chọn C
Tập xác định:
2;3D = −
Ta có
( )
( )
3
0 2;3
4 8 ; 0
2 2;3
x
y x x y
x
= −

= − =
= −
.
Ta có
( ) ( ) ( )
( )
0 9; 2 9; 3 54; 2 5y y y y= − = = =
.
Vậy giá trị lớn nhất của hàm số đã cho bằng
54
.
Câu 4: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
A.
42
2 4 1y x x= − +
. B.
42
2 4 1y x x= − + +
. C.
3
2 3 1y x x= − +
. D.
3
2 3 1y x x= − + +
.
Lời giải
Chọn B
Từ hình vẽ ta thấy đây là đồ thị hàm trùng phương
42
y ax bx c= + +
nên loại C,. D.
Lại thấy
lim
x
y
→
= −
nên
0a
, suy ra loại A chọn. B.
Câu 5: Đường cong trong hình dưới đây là đồ thị của hàm số nào trong các hàm số sau?
x
y
2
1
1
1
O
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 9
Sưu tầm và biên soạn
A.
1
1
x
y
x
+
=
−
. B.
24
1
x
y
x
−
=
−
. C.
1
22
x
y
x
+
=
−
. D.
2
33
x
y
x
=
−
.
Lời giải
Chọn C
Dựa vào đò thị hàm số ta thấy :
Đồ thị hàm số có đường tiệm cận ngang là
1
2
y =
và đường tiệm cận đứng là
1x =
.
Câu 6: Tiệm cận ngang của đồ thị hàm số
21
1
x
y
x
+
=
+
là đường thẳng có phương trình
A.
2y =
. B.
2x =
. C.
1y =−
. D.
1x =−
.
Lời giải
Chọn A
Câu 7: Kết luận nào đúng về số thực
a
nếu
37
aa
?
A.
12a
. B.
1a
. C.
01a
. D.
1a
.
Lời giải
Chọn C
Ta có
37
mà
37
aa
nên
0 1.a
Câu 8: Tập xác định
D
của hàm số
( )
3
log 2 1yx=+
là
A.
1
;
2
D

= − −


. B.
1
;
2
D

= +


. C.
( )
0;D = +
. D.
1
;
2
D

= − +


.
Lời giải
Chọn D
Hàm số xác định khi
1
2 1 0
2
xx+ −
.
Vậy tập xác định của hàm số là
1
;
2
D

= − +


.
Câu 9: Cho
a
,
b
,
c
là ba số thực dương khác
1
. Đồ thị các hàm số
x
ya=
,
x
yb=
,
x
yc=
được cho
trong hình vẽ bên. Mệnh đề nào sau đây đúng?
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 10
Sưu tầm và biên soạn
A.
c a b
. B.
b c a
. C.
a c b
. D.
abc
.
Lời giải
Chọn C
Dựng đường thẳng
1x =
, cắt 3 đồ thị hàm số theo thứ tự như hình vẽ
Câu 10: Đạo hàm của hàm số
logyx=
là
A.
1
y
x
=
. B.
ln10
y
x
=
. C.
1
ln10
y
x
=
. D.
1
10ln
y
x
=
.
Lời giải
Chọn C
Đạo hàm của hàm số
logyx=
là
1
ln10
y
x
=
.
Câu 11: Đạo hàm của hàm số
2
3
x
y =
là
A.
2
3
x
y
=
. B.
2
3 .ln3
x
y
=
. C.
2
2 .3
x
yx
=
. D.
2
2 .ln3.3
x
yx
=
.
Lời giải
Chọn D
Ta có
22
3 2 .ln3.3
xx
y y x
= =
.
Câu 12: Phương trình
21
2 32
x+
=
có nghiệm là
A.
5
2
x =
. B.
2x =
. C.
3
2
x =
. D.
3x =
.
Lời giải
Chọn B
Ta có
21
2 32 2 1 5 2
x
xx
+
= + = =
Câu 13: Nghiệm của phương trình
( )
2
log 7 5x+=
là
A.
39x =
. B.
18x =
. C.
25x =
. D.
3x =
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 11
Sưu tầm và biên soạn
Chọn C
Ta có
( )
5
2
log 7 5 7 2 7 32 25x x x x+ = + = + = =
.
Câu 14: Tập nghiệm của bất phương trình
( )
3
log 1 1x−
là
A.
(
1;4
. B.
( )
;4−
. C.
(
;4−
. D.
(
0;4
.
Lời giải
Chọn A
Ta có:
( )
3
1 0 1
log 1 1 1 4
1 3 4
xx
xx
xx
−

−

−

.
Vậy tập nghiệm
(
1;4S =
.
Câu 15: Khối lập phương là khối đa diện đều loại nào?
A.
3;3
. B.
5;3
. C.
4;3
. D.
3;4
.
Lời giải
Chọn C
Khối lập phương là khối đa diện đều loại
4;3
.
Câu 16: Thể tích khối lập phương có cạnh
2a
bằng
A.
3
8a
. B.
3
2a
. C.
3
a
. D.
3
6a
.
Lời giải
Chọn A
Thể tích khối lập phương có cạnh
2a
bằng:
( )
3
3
2 8 .aa=
Câu 17: Cho hình nón có bán kính đáy là
3r =
và đường sinh
4l =
. Diện tích xung quanh của hình
nón đã cho là
A.
16 3S
=
. B.
24S
=
. C.
83S
=
. D.
43S
=
.
Lời giải
Chọn D
Diện tích xung quanh của hình nón
43S rl

==
.
Câu 18: Cho hình chữ nhật
ABCD
có
AB a=
,
2AD a=
. Thể tích của khối trụ tạo thành khi quay hình
chữ nhật
ABCD
quanh cạnh
AB
bằng
A.
3
4 a
. B.
3
a
. C.
3
2a
. D.
3
a
.
Lời giải
Chọn A
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 12
Sưu tầm và biên soạn
Hình trụ tạo thành có
h AB a==
,
2r AD a==
.
Thể tích của khối trụ tạo thành khi quay hình chữ nhật
ABCD
quanh cạnh
AB
bằng
( )
2
23
. . 2 . 4V B h r h a a a
= = = =
.
Câu 19: Cho khối nón có độ dài đường cao bằng
2a
và bán kính đáy bằng
a
. Thể tích của khối nón đã
cho bằng
A.
3
2
3
a
. B.
3
4
3
a
. C.
3
3
a
. D.
3
2 a
.
Lời giải
Chọn A
Thể tích của khối nón đã cho là
3
22
1 1 2
. .2
3 3 3
a
V r h a a

= = =
.
Câu 20: Cắt hình trụ
( )
T
bởi một mặt phẳng đi qua trục của nó, ta được thiết diện là một hình vuông cạnh
là 7. Diện tích xung quanh của
( )
T
bằng
A.
49
2
. B.
49
. C.
98
. D.
49
4
.
Lời giải
Chọn B
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 13
Sưu tầm và biên soạn
Ta có bán kính đáy hình trụ là
7
2
, chiều cao là 7.
Diện tích xung quanh của
( )
T
bằng
7
2 2 . .7 49
2
xq
S rl
= = =
.
THÔNG HIỂU
Câu 21: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên và có đồ thị của hàm số
( )
y f x
=
như hình
vẽ bên. Mệnh đề nào dưới đây sai?
A. Hàm số
( )
y f x=
đồng biến trên
( )
2;+
.
B. Hàm số
( )
y f x=
nghịch biến trên
( )
1;0−
.
C. Hàm số
( )
y f x=
đồng biến trên
( )
1; +
.
D. Hàm số
( )
y f x=
nghịch biến trên
( )
;2−
.
Lời giải
Chọn C
D=
.
Theo đồ thị hàm số
( )
y f x
=
ta có bảng biến thiên
Dựa theo bảng biến thiên ta thấy phương án C sai.
Câu 22: Cho hàm số
3
35y x x= − +
. Điểm cực tiểu của đồ thị hàm số đã cho là
A.
( )
7; 1−
. B.
( )
1;7−
. C.
( )
3;1
. D.
( )
1;3
.
Lời giải
Chọn D
Tập xác định của hàm số là
D=
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 14
Sưu tầm và biên soạn
Ta có
2
1
3 3, 0 .
1
x
y x y
x
=

= − =
=−
Mặt khác,
( ) ( )
6 , 1 6 0, 1 6 0y x y y
= = − = −
.
Do đó, hàm số đạt cực tiểu tại
1, 3.
CT
xy==
Vậy điểm cực tiểu của đồ thị hàm số đã cho là
( )
1;3
.
Câu 23: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;3−
và có đồ thị như hình vẽ dưới đây. Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;3−
. Giá trị của
Mm−
bằng
A.
4
. B.
1
. C.
5
. D.
0
.
Lời giải
Chọn C
Dựa vào đồ thị ta có
[ 1;3]
max 3My
−
==
,
[ 1;3]
min 2my
−
= = −
.
Vậy
( )
3 2 5Mm− = − − =
.
Câu 24: Cho hàm số
2ax
y
bx c
+
=
+
,
,,abc
có đồ thị như hình vẽ
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 15
Sưu tầm và biên soạn
Khẳng định nào dưới đây đúng?
A.
0b a c
. B.
0b a c
. C.
0a b c
. D.
0b c a
.
Lời giải
Chọn C
Ta có đồ thị đi qua điểm
( )
0;1
2
12c
c
= =
.
Đồ thị có đường tiệm cận đứng
1 1 2
c
x b c
b
−
= = = − = −
.
Đồ thị có đường tiệm cận ngang
2 2 2 4
a
y a b
b
= = = = −
.
Vậy
0a b c
.
Câu 25: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn C
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 16
Sưu tầm và biên soạn
Dựa vào bảng biến thiên ta có:
Tập xác định của hàm số là
\1D
.
lim 5, lim
xx
f x f x
nên đồ thị có 1 đường tiệm cận ngang là
5y
.
11
lim , lim 3
xx
f x f x
nên đồ thị có 1 đường tiệm cận đứng là đường thẳng
1x
.
Câu 26: Rút gọn biểu thức
5
3
3
:Q b b=
với
0b
. Kết quả nào sau đây đúng
A.
5
9
.Qb=
B.
2
.Qb=
C.
4
3
.Qb=
D.
4
3
.Qb
−
=
Lời giải
Chọn C
5 5 1 5 1 4
3
3 3 3 3 3 3
: : .Q b b b b b b
−
= = = =
Câu 27: Cho các số thực dương
a
,
b
,
c
,
d
. Biểu thức
ln ln ln ln
a b c d
S
b c d a
= + + +
bằng
A.
0
. B.
( )
ln . . .abc d
. C.
1
. D.
ln
a b c d
b c d a

+ + +


.
Lời giải
Chọn A
Ta có:
( )
ln ln ln ln ln . . . ln 1 0
a b c d a b c d
S
b c d a b c d a

= + + + = = =


.
Câu 28: Một người gửi tiết kiệm vào một ngân hàng với lãi suất
7,5%
/năm. Biết rằng nếu không rút tiền
ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp
theo. Hỏi sau bao nhiêu năm người đó thu được (cả số tiền gửi ban đầu và lãi) ít nhất gấp đôi số
tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và người đó không
rút tiền ra?
A.
11
năm. B.
10
năm. C.
12
năm. D.
9
năm.
Lời giải
Chọn B
Gọi
A
là số tiền người đó gửi ban đầu.
Theo công thức lãi kép, để người đó thu được ít nhất gấp đôi số tiền gửi ban đầu ta cần
( ) ( )
1,075
. 1 2 1 0,075 2 log 2 9,58
nn
A r A n+ +
.
Do
10nn =
.
Vậy người đó cần gửi ít nhất
10
năm.
Câu 29: Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
ln( 2 1)= − + +y x x m
có tập xác định là
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 17
Sưu tầm và biên soạn
.
A.
0m =
. B.
03m
. C.
1m −
hoặc
0m
. D.
0m
.
Lời giải
Chọn D
Hàm số
( )
2
ln 2 1= − + +y x x m
có tập xác định là
khi và chỉ khi:
2
2 1 0, − + + x x m x
0 1 1 0 0
− − mm
.
Câu 30: Gọi
S
là tổng tất cả các nghiệm của phương trình
( )
1
2 64.
x
x
−
=
Giá trị của
S
là
A.
1
S.
2
=
B.
S 6.=−
C.
S 3.=−
D.
S 1.=
Lời giải
Chọn D
( )
( )
( )
1
1
62
3
2 64 2 2 1 6 6 0 .
2
x
xx
x
x
x x x x
x
−
−
=
= = − = − − =
=−
Vậy
( )
3 2 1.S = + − =
Câu 31: Số nghiệm của phương trình
( ) ( )
33
log 6 log 9 5 0xx+ + − =
là
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn C
Ta có:
( ) ( )
( )
( )
33
5
3
0
0
log 6 log 9 5 0
log 9 6 5
9 6 3
x
x
xx
xx
xx
+ + − =

+=

+=

2
0
0
3
9
9 54 243 0
3
x
x
x
x
xx
x
=
=−

+ − =
=
.
Vậy phương trình có nghiệm
3x =
.
Câu 32: Mặt phẳng
( ' ')AB C
chia khối lăng trụ
. ' ' 'ABC A B C
thành các khối đa diện nào?
A. Hai khối chóp tứ giác.
B. Một khối chóp tam giác và một khối chóp tứ giác.
C. Hai khối chóp tam giác.
D. Một khối chóp tam giác và một khối chóp ngũ giác.
Lời giải
Chọn B
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 18
Sưu tầm và biên soạn
Mặt phẳng
( ' ')AB C
chia khối lăng trụ
. ' ' 'ABC A B C
thành các khối chóp tam giác
. ' ' 'A A B C
và khối chóp tứ giác
. ' 'ABCC B
. Vậy chọn đáp án
B.
Câu 33: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
,AB a=
3,AD a=
SA
vuông góc
với mặt phẳng đáy và mặt phẳng
( )
SBC
tạo với đáy một góc
60
. Thể tích
V
của khối chóp
.S ABCD
là
A.
3
3
a
V =
. B.
3
3
3
a
V =
. C.
3
Va=
. D.
3
3Va=
.
Lời giải
Chọn C
Ta có
( ) ( ) ( )
(
)
, 60SA ABCD SBC ABCD SBA⊥ = =
.
ABCD
là hình chữ nhật
2
.3
ABCD
S AB AD a = =
.
SAB
vuông tại
S
.tan .tan60 3SA AB SBA a SA a = = =
.
2
.
11
. 3. 3
33
S ABCD ABCD
V S SA a a = =
3
.S ABCD
Va=
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 19
Sưu tầm và biên soạn
Vậy
3
.S ABCD
Va=
.
Câu 34: Cho khối nón có độ dài đường sinh bằng
2a
và bán kính đáy bằng
a
. Thể tích của khối nón đã
cho bằng
A.
3
3
2
a
. B.
3
3
3
a
. C.
3
2
3
a
. D.
3
3
a
.
Lời giải
Chọn B
Ta có:
22
3h l r a= − =
.
Suy ra: thể tích của khối nón đã cho bằng
3
2
13
..
33
a
rh
=
.
Câu 35: Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng
2
, thiết diện
thu được là hình vuông có diện tích bằng
16
. Diện tích xung quanh của hình trụ đã cho bằng
A.
86
. B.
24 6
. C.
10 6
. D.
12 6
.
Lời giải
Chọn A
Gọi hình trụ đã cho có trục
OO
và thiết diện song song trục là hình vuông
ABCD
. Gọi
H
là
trung điểm của
AD OH AD⊥
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 20
Sưu tầm và biên soạn
Ta có
16 4
ABCD
S AB AD OO
= = = =
và
( )
( )
( )
( )
; ; 2d OO ABCD d O ABCD OH
= = =
.
Xét tam giác
AOH
vuông tại
H
có
22
6OA AH OH= + =
.
Diện tích xung quanh của hình nón đã cho
2 2 . . 8 6
xq
S Rh OAOO
= = =
.
II. PHẦN TỰ LUẬN (4 câu – 3 điểm)
Câu 36: Cho hàm số
( )
fx
có đồ thị
( )
fx
như hình vẽ bên. Tìm giá trị nhỏ nhất của hàm số
( ) ( )
32
1 3 3
2019
3 4 2
g x f x x x x= − − + +
trên đoạn
3;1−
.
Lời giải
Tính được
( ) ( )
2
33
.
22
g x f x x x

= − − +
Khi đó
( ) ( ) ( )
2
33
0 .
22
g x f x x x

= = + −
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 21
Sưu tầm và biên soạn
Hàm số
( )
2
33
22
h x x x= + −
có đồ thị như hình vẽ.
Dựa vào tương giao của hai đồ thị
( )
fx
và
( )
hx
ta thấy trên
3;1−
phương trình
( )
có các
nghiệm
3; 1; 1x x x= − = − =
.
Trên
( )
3; 1−−
, đồ thị hàm số
( )
fx
nằm phía dưới đồ thị hàm số
( )
hx
nên
( )
0gx
.
Trên
( )
1;1−
, đồ thị hàm số
( )
fx
nằm phía trên đồ thị hàm số
( )
hx
nên
( )
0gx
.
Ta có bảng biến thiên
Vậy
( ) ( )
3;1
min 1g x g
−
=−
khi
1x =−
.
Câu 37: Cho lăng trụ đứng
.ABC AB C
có đáy là tam giác vuông cân tại
B
,
2AC a=
; biết góc giữa
mặt phẳng
( )
A BC
và mặt phẳng đáy bằng
60
. Tính thể tích
V
của khối lăng trụ
.ABC AB C
.
Lời giải
Tam giác
ABC
vuông cân tại
, 2 .tan 45 .B AC a BA BC AC a= = = =
Ta có:
( )
.
BC AB
BC A AB BC A B
BC AA
⊥

⊥ ⊥
⊥
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 22
Sưu tầm và biên soạn
Lại có
( ) ( )
( ) ( )
(
)
60 , .
A BC ABC BC
BC AB A BC ABC ABA
BC A B
=

⊥ = =
⊥
Tam giác
A AB
vuông tại
A
nên
tan60 3.AA AB a
= =
Vậy
3
13
. . . .
22
ABC
a
V S AA BA BC AA

= = =
Câu 38: Ông A dự định sử dụng hết
2
5 m
kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Lời giải
Gọi
, , h a b
lần lượt là chiều cao, chiều rộng và chiều dài của bể. Suy ra
2ba=
.
Diện tích đáy:
2
1
2S ab a==
.
Diện tích xunh quanh:
( )
2
26S a b h ah= + =
.
Theo giả thiết ta có
12
5SS+=
2
2 6 5a ah + =
2
52
6
a
h
a
−
=
với
5
0
2
a
.
Thể tích bể cá:
23
2
1
5 2 5 2
. .2
63
a a a
V h S a
a
−−
= = =
Đạo hàm:
2
5
'2
3
Va=−
5
'0
6
Va= =
.
Bể cá có thể tích lớn nhất bằng:
3
5 30
1,01
27
m
khi chiều rộng
5
6
a =
.
Câu 39: Cho phương trình
( )
5
5 log+ = −
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
( )
20;20−m
để phương trình đã cho có nghiệm?
Lời giải
Điều kiện:
xm
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 23
Sưu tầm và biên soạn
Từ phương trình
( )
5
5 log+ = −
x
m x m
( )
5
5 log + = − + −
x
x x m x m
( )
55
5 log 5 log + = − + −
xx
x m x m
(1).
Xét
( )
5
log=+f x x x
với
0x
.
Ta có
( )
1
' 1 0
ln5
= + fx
x
với
0x
. Hàm số
( )
5
log=+f x x x
đồng biến trên
( )
0;+
.
Phương trình (1) tương đương
( )
( )
5 =−
x
f f x m
5 = −
x
xm
5 = −
x
mx
.
Đặt
( )
5=−
x
h x x
ta có
( )
' 1 5 ln5=−
x
hx
cho
( ) ( )
5
' 0 1 5 ln5 0 log ln5= − = = −
x
h x x
.
Bảng biến thiên
Dựa vào đồ thị
( )
5
1
; log ln5
ln5

− − −


m
kết hợp với giá trị nguyên của
( )
20;20−m
.
Vậy
19; 18; 17;...; 1 − − − −m
hay có 19 giá trị
m
nguyên thỏa mãn.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 08
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
32
y ax bx cx d= + + +
có đồ thị như hình vẽ. Số điểm cực trị của hàm số đã cho là
A. 1. B. 3. C. 0. D. 2.
Câu 2: Cho hàm số
( )
y f x=
có bảng biến
thiên như hình vẽ. Giá trị lớn nhất
của hàm số đã cho trên tập hợp
bằng
A. 1. B.
1−
.
C.
1
3
. D. 3.
Câu 3: Hình sau là đồ thị của hàm số nào trong các hàm số sau đây?
A.
3
1yx
B.
3
31y x x
C.
3
31y x x
D.
3
1yx
.
Câu 4: Hình sau là đồ thị của hàm số nào trong các hàm số sau đây?
A.
5
logyx
B.
1
5
logyx
C.
5
x
y
D.
1
5
x
y
Câu 5: Tập xác định của hàm số
1
3
3yx
là
A.
\3
. B.
3;
.
C.
3;
. D. .
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 2
Sưu tầm và biên soạn
Câu 6: Khẳng định nào sau đây là đúng?
A.
( )
y
x xy
ee=
,y .x
B.
x y x y
e e e
−
=−
,y .x
C.
( )
.
y
x x y
e e e=
,y .x
D.
x y x y
e e e
+
=+
,y .x
Câu 7: Khẳng định nào sau đây là đúng?
A.
2
2
2
log
log , , 0, 1
log
x
x
x y y
yy

=


. B.
2
2
log , , 0, 1
log
xx
x y y
yy

=


.
C.
2 2 2
log log log , , 0
x
x y x y
y

= +


. D.
2 2 2
log log log , , 0
x
x y x y
y

= −


.
Câu 8: Hàm số nào trong các hàm số sau đây nghịch biến trên
?
A.
0,9
logyx=
. B.
9
x
y =
. C.
9
logyx=
. D.
( )
0,9
x
y =
.
Câu 9: Tập nghiệm của bất phương trình
( )
0,8 3
x
là
A.
( )
0,8
log 3;+
. B.
( )
0,8
;log 3−
. C.
3
4
log ;
5

+


. D.
3
4
;log
5

−


.
Câu 10: Nếu các số dương
,ab
thỏa mãn
2020
a
b=
thì
A.
1
2020
b
a =
. B.
1
2020
b
a =
. C.
2020
logab=
. D.
1
2020
logab=
.
Câu 11: Cho biểu thức
Khẳng định nào sau đây là đúng?
A.
30
Px=
. B.
5
6
Px=
. C.
6
5
Px=
. D.
5
6
Px=
.
Câu 12: Phương trình đường tiệm cận ngang của đồ thị hàm số
65
6
x
y
x
−
=
+
là
A.
6x =−
. B.
5
6
y =−
. C.
6x =
. D.
6y =
Câu 13: Nếu một hình nón có đường kính đường tròn đáy bằng
a
và độ dài đường sinh bằng
l
thì có diện
tích xung quanh bằng
A.
al
. B.
2 al
. C.
1
2
al
. D.
1
3
al
.
Câu 14: Trên khoảng
( )
0;+
đạo hàm của hàm số
8
15
yx=
bằng
A.
8
7
x
. B.
7
8
x
. C.
8
7
15
8
x
. D.
7
8
15
8
x
.
Câu 15: Cho
ABCD
là hình chữ nhật,
,AB a AD b==
. Quay hình chữ nhật
ABCD
xung quanh cạnh
AB
ta được một khối tròn xoay có thể tích bằng
A.
2
1
.
3
ab
B.
2
1
.
3
ba
C.
2
.ba
D.
2
.ab
Câu 16: Tập hợp các giá trị
m
để phương trình
2020
log xm=
có nghiệm thực là
A.
.
B.
( )
0; .+
C.
( )
;0 .−
D.
\ 1 .
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 3
Sưu tầm và biên soạn
Câu 17: Cho hàm số
( )
y f x=
có đạo hàm trên thỏa mãn
( ) ( )
' 0, 0;1f x x
và
( ) ( )
' 0, 1;2f x x
. Khẳng định nào sau đây là đúng?
A. Hàm số đã cho nghịch biến trên
( )
0;1
và đồng biến trên
( )
1;2 .
B. Hàm số đã cho nghịch biến trên
( )
0;1
và nghịch biến trên
( )
1;2 .
C. Hàm số đã cho đồng biến trên
( )
0;1
và đồng biến trên
( )
1;2 .
D. Hàm số đã cho đồng biến trên
( )
0;1
và nghịch biến trên
( )
1;2 .
Câu 18: Nếu hàm số
( )
y f x=
liên tục trên thỏa mãn
( ) ( ) ( )
0 2;2 \ 0f x f x −
thì
A.
0x =
là một điểm cực tiểu của hàm số đã cho.
B.
0x =
là một điểm cực đại của hàm số đã cho.
C. Hàm số đã cho có giá trị nhỏ nhất trên tập số bằng
( )
0.f
D. Hàm số đã cho có giá trị lớn nhất trên tập số bằng
( )
0.f
Câu 19: Hàm số
1
y
x
=
nghịch biến trên khoảng nào trong các khoảng sau?
A.
( )
;.− +
B.
( )
;1 .−
C.
( )
1; .− +
D.
( )
0; .+
Câu 20: Cho khối chóp
.S ABC
có
( )
, , , ,⊥ = = =SA ABC SA h AB c AC b
BAC .
=
Thể tích khối chóp
.S ABC
bằng
A.
1
.sin .
3
bch
B.
1
.cos .
3
bch
C.
1
.cos .
6
bch
D.
1
.sin .
6
bch
Câu 21: Tập nghiệm của bất phương trình
( )
1
2
log 1 0x −
A.
( )
2;+
. B.
( )
1;2
. C.
( )
;2−
. D.
( )
1; +
.
Câu 22: Cho
73
log 5, log 5ab==
. Biểu thức
21
log 5M =
bằng
A.
ab
M
ab
+
=
. B.
ab
M
ab
=
+
. C.
M ab=
. D.
1
M
ab
=
.
Câu 23: Tập hợp các số thực m để phương trình
( )
( )
2
log 2020 logx mx−=
có nghiệm là
A. . B.
( )
0; .+
C.
( )
;0−
. D.
\0
.
Câu 24: Cho tam giác
ABC
là tam giác vuông tại đỉnh
A
,
AB a=
,
AC b=
. Quay hình tam giác
ABC
quanh cạnh
AC
ta được một khối tròn xoay có diện tích xung quanh bằng
A.
22
.+a a b
B.
22
.+b a b
C.
22
1
.
3
+a a b
D.
22
1
.
3
+b a b
Câu 25: Nếu tăng bán kính của một khối cầu gấp
2
lần thì thể tích thay đổi như thế nào?
A. Thể tích tăng gấp
2
lần. B. Thể tích tăng gấp
4
lần.
C. Thể tích tăng gấp
8
lần. D. Thể tích tăng gấp
4
3
lần.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 4
Sưu tầm và biên soạn
Câu 26: Một cái xúc xích hình trụ có đường kính đáy
2 cm
và chiều cao
6 cm
, giả sử giá bán mỗi
3
cm
xúc xích là
500
đồng. Bạn An cần trả tiền mua một gói 4 cái xúc xích. Số tiền gần đúng nhất cho
4
cái xúc xích là
A.
19000
. B.
76000
. C.
38000
. D.
30000
.
Câu 27: Một người gửi số tiền 100 triệu đồng vào một ngân hàng với lãi suất
6,8% /
năm. Biết rằng nếu
không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu
(người ta gọi là lãi kép). Nếu người đó gửi tiền trong đúng 4 năm và trong khoảng thời gian đó
không rút tiền ra thì người đó có số tiền là.
A.
4
100.1,068
(đồng). B.
5
100.1,068
(triệu đồng).
C.
3
100.1,068
(triệu đồng). D.
4
100.1,068
(triệu đồng).
Câu 28: Cho hàm số
( )
( )
2
0,5
log 6f x x x=−
. Tập nghiệm của bất phương trình
( )
0fx
là.
A.
( )
3; +
. B.
( )
;3−
. C.
( )
3;6
. D.
( )
0;3
.
Câu 29: Một khối bê tông có dạng hình lăng trụ đứng với độ dài các cạnh
đáy là
3 dm, 4dm, 5dm
độ dài cạnh bên là
6 dm
. Thể tích khối bê
tông bằng
A.
( )
3
72 dm
. B.
( )
3
24 dm
.
C.
( )
3
216 dm
. D.
( )
3
36 dm
.
Câu 30: Một dụng cụ đựng chất lỏng có dạng hình nón với chiều cao là
30 cm
và bán kính đáy là
15 cm
. Dụng cụ này đựng được tối
đa bao nhiêu
3
cm
chất lỏng?
A.
( )
3
2250 .cm
B.
( )
3
750 .cm
C.
( )
3
2250 .cm
D.
( )
3
750 .cm
Câu 31: Nếu
.S ABC
là hình chóp đều có chiều cao bằng
h
và cạnh đáy bằng
a
thì có thể tích bằng
A.
2
3
3
ah
. B.
2
3
6
ah
. C.
2
3
12
ah
. D.
2
3
4
ah
.
Câu 32: Tập hợp các giá trị m để hàm số
( )
3
2
10 25 1
3
x
y mx m x= − + − +
có hai điểm cực trị là:
A.
R
. B.
\5R −
. C.
\5R
. D.
( )
5; +
.
Câu 33: Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
10 20xx
y
x
− + −
=
là:
A.
3
. B.
2
. C.
1
. D.
0
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 5
Sưu tầm và biên soạn
Câu 34: Cho hình hộp
có thể tích bằng
V
. Thể tích của khối tứ diện
ACB D

bằng
A.
1
6
V
. B.
1
4
V
. C.
1
3
V
. D.
1
2
V
.
Câu 35: Cho hàm số
( )
y f x=
có đồ thị đạo hàm
( )
y f x
=
như hình bên dưới. Hàm số đã cho nghịch
biến trên khoảng
A.
( )
1;2
. B.
( )
0;1
. C.
1
;0
2

−


. D.
( )
0;2
.
II. PHẦN TỰ LUẬN
Câu 36: Có báo nhiêu giá trị nguyên của tham số
m
để hàm số
2 3 2
( 6) ( 3) 2 1y m m x m x x= − − + − − +
nghịch biến trên ?
Câu 37: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và
2 2 , 3AB AC a BC a= = =
. Tam
giác
SAD
vuông cân tại S, hai mặt phẳng
( )
SAD
và
( )
ABCD
vuông góc nhau. Tính thể tích
khối chóp
.S ABCD
.
Câu 38: Số các giá trị nguyên của tham số
m
để phương trình
2 3 4 1
xx
m+ = +
có đúng một nghiệm là
Câu 39: Có bao nhiêu giá trị nguyên thuộc
2021;2021−
của tham số để phương trình sau có nghiệm
duy nhất
( )
2
2 3 2 3
log 1 log 0.x mx m x
+−
+ + − + =
------------- HẾT -------------
m
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 6
Sưu tầm và biên soạn
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
32
y ax bx cx d= + + +
có đồ thị như hình vẽ. Số điểm cực trị của hàm số đã cho là
A. 1. B. 3. C. 0. D. 2.
Lời giải
Chọn D
Căn cứ vào hình vẽ ta thấy hàm số có 2 điểm cực trị.
Câu 2: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ. Giá trị lớn nhất của hàm số đã cho trên
tập hợp bằng
A. 1. B.
1−
. C.
1
3
. D. 3.
Lời giải
Chọn D
Căn cứ vào hình vẽ ta thấy giá trị lớn nhất của hàm số đã cho trên tập bằng 3.
Câu 3: Hình sau là đồ thị của hàm số nào trong các hàm số sau đây?
A.
3
1yx
B.
3
31y x x
C.
3
31y x x
D.
3
1yx
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 7
Sưu tầm và biên soạn
Lời giải
Chọn B
Ta thấy đồ thị đi qua điểm
1;1M
nên ta loại A, C, D.
Câu 4: Hình sau là đồ thị của hàm số nào trong các hàm số sau đây?
A.
5
logyx
B.
1
5
logyx
C.
5
x
y
D.
1
5
x
y
Lời giải
Chọn C
Đồ thị nằm phía trên trục hoành nên ta loại A, B.
Đồ thị hàm số đi lên nên có hệ số
1a
, do đó loại D.
Câu 5: Tập xác định của hàm số
1
3
3yx
là
A.
\3
. B.
3;
. C.
3;
. D. .
Lời giải
Chọn B
Vì
1
3
nên điều kiện của hàm số đã cho là
3 0 3.xx
Vậy tập xác định
3; .D
Câu 6: Khẳng định nào sau đây là đúng?
A.
( )
y
x xy
ee=
,y .x
B.
x y x y
e e e
−
=−
,y .x
C.
( )
.
y
x x y
e e e=
,y .x
D.
x y x y
e e e
+
=+
,y .x
Lời giải
Chọn A
Ta có:
( )
y
x xy
ee=
,y .x
Câu 7: Khẳng định nào sau đây là đúng?
A.
2
2
2
log
log , , 0, 1
log
x
x
x y y
yy

=


. B.
2
2
log , , 0, 1
log
xx
x y y
yy

=


.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 8
Sưu tầm và biên soạn
C.
2 2 2
log log log , , 0
x
x y x y
y

= +


. D.
2 2 2
log log log , , 0
x
x y x y
y

= −


.
Lời giải
Chọn D
Ta có:
2 2 2
log log log
x
xy
y

=−


,
, 0.xy
(đây là định lí 2, trang 64 sgk).
Câu 8: Hàm số nào trong các hàm số sau đây nghịch biến trên
?
A.
0,9
logyx=
. B.
9
x
y =
. C.
9
logyx=
. D.
( )
0,9
x
y =
.
Lời giải
Chọn D
Hàm số:
0,9
logyx=
nghịch biến trên
( )
0;+
.
Hàm số:
9
x
y =
đồng biến trên .
Hàm số:
9
logyx=
đồng biến trên
( )
0;+
.
Hàm số:
( )
0,9
x
y =
nghịch biến trên .
Vậy đáp án D đúng.
Câu 9: Tập nghiệm của bất phương trình
( )
0,8 3
x
là
A.
( )
0,8
log 3;+
. B.
( )
0,8
;log 3−
. C.
3
4
log ;
5

+


. D.
3
4
;log
5

−


.
Lời giải
Chọn A
( )
0,8
0,8 3 log 3
x
x
.
Vậy tập nghiệm của bất phương trình đã cho là:
( )
0,8
log 3;S= +
.
Câu 10: Nếu các số dương
,ab
thỏa mãn
2020
a
b=
thì
A.
1
2020
b
a =
. B.
1
2020
b
a =
. C.
2020
logab=
. D.
1
2020
logab=
.
Lời giải
Chọn C
2020
2020 log
a
b a b= =
.
Câu 11: Cho biểu thức
Khẳng định nào sau đây là đúng?
A.
30
Px=
. B.
5
6
Px=
. C.
6
5
Px=
. D.
5
6
Px=
.
Lời giải
Chọn C
Với
0x
, ta có:
6
5
6
5
P x x==
.
Câu 12: Phương trình đường tiệm cận ngang của đồ thị hàm số
65
6
x
y
x
−
=
+
là
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 9
Sưu tầm và biên soạn
A.
6x =−
. B.
5
6
y =−
. C.
6x =
. D.
6y =
Lời giải
Chọn D
Ta có
65
lim lim 6
6
xx
x
y
x
→− →−
−
==
+
,
65
lim lim 6
6
xx
x
y
x
→+ →+
−
==
+
, suy ra đồ thị hàm số có đường tiện
cậng ngang
6y =
.
Câu 13: Nếu một hình nón có đường kính đường tròn đáy bằng
a
và độ dài đường sinh bằng
l
thì có diện
tích xung quanh bằng
A.
al
. B.
2 al
. C.
1
2
al
. D.
1
3
al
.
Lời giải
Chọn C
Hình nón có đường kính đường tròn đáy bằng
a
nên bán kính
2
a
r =
.
Câu 14: Trên khoảng
( )
0;+
đạo hàm của hàm số
8
15
yx=
bằng
A.
8
7
x
. B.
7
8
x
. C.
8
7
15
8
x
. D.
7
8
15
8
x
.
Lời giải
Chọn C
Đạo hàm của hàm số
15
8
15
8
y x x==
là
7
8
7
8
15 15
88
y x x
==
.
Câu 15: Cho
ABCD
là hình chữ nhật,
,AB a AD b==
. Quay hình chữ nhật
ABCD
xung quanh cạnh
AB
ta được một khối tròn xoay có thể tích bằng
A.
2
1
.
3
ab
B.
2
1
.
3
ba
C.
2
.ba
D.
2
.ab
Lời giải
Chọn C
Quay hình chữ nhật
ABCD
quanh trục
AB
ta được hình trụ có bán kính đáy
R AD b==
,
chiều cao
h AB a==
Thể tích khối trụ là
2
V b a=
.
Câu 16: Tập hợp các giá trị
m
để phương trình
2020
log xm=
có nghiệm thực là
A.
.
B.
( )
0; .+
C.
( )
;0 .−
D.
\ 1 .
Lời giải
Chọn A
Điều kiện của phương trình:
0x
.
2020
log 2020 0,
m
x m x m= =
.
Với
m
phương trình luôn có nghiệm.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 10
Sưu tầm và biên soạn
Câu 17: Cho hàm số
( )
y f x=
có đạo hàm trên thỏa mãn
( ) ( )
' 0, 0;1f x x
và
( ) ( )
' 0, 1;2f x x
. Khẳng định nào sau đây là đúng?
A. Hàm số đã cho nghịch biến trên
( )
0;1
và đồng biến trên
( )
1;2 .
B. Hàm số đã cho nghịch biến trên
( )
0;1
và nghịch biến trên
( )
1;2 .
C. Hàm số đã cho đồng biến trên
( )
0;1
và đồng biến trên
( )
1;2 .
D. Hàm số đã cho đồng biến trên
( )
0;1
và nghịch biến trên
( )
1;2 .
Lời giải
Chọn D
( ) ( )
' 0, 0;1f x x
nên hàm số đã cho đồng biến trên
( )
0;1
.
( ) ( )
' 0, 1;2f x x
nên hàm số đã cho nghịch biến trên
( )
1;2 .
Câu 18: Nếu hàm số
( )
y f x=
liên tục trên thỏa mãn
( ) ( ) ( )
0 2;2 \ 0f x f x −
thì
A.
0x =
là một điểm cực tiểu của hàm số đã cho.
B.
0x =
là một điểm cực đại của hàm số đã cho.
C. Hàm số đã cho có giá trị nhỏ nhất trên tập số bằng
( )
0.f
D. Hàm số đã cho có giá trị lớn nhất trên tập số bằng
( )
0.f
Lời giải
Chọn B
Theo định nghĩa cực đại, cực tiểu của hàm số trang
13
sgk
12
cơ bản thì
0x =
là một điểm
cực đại của hàm số đã cho.
Câu 19: Hàm số
1
y
x
=
nghịch biến trên khoảng nào trong các khoảng sau?
A.
( )
;.− +
B.
( )
;1 .−
C.
( )
1; .− +
D.
( )
0; .+
Lời giải
Chọn D
Ta có
TXĐ:
\0D =
2
11
' 0,y x D
xx
−

= =


Do đó hàm số nghịch biến trên
( )
;0−
và
( )
0; .+
Câu 20: Cho khối chóp
.S ABC
có
( )
, , , ,⊥ = = =SA ABC SA h AB c AC b
BAC .
=
Thể tích khối chóp
.S ABC
bằng
A.
1
.sin .
3
bch
B.
1
.cos .
3
bch
C.
1
.cos .
6
bch
D.
1
.sin .
6
bch
Lời giải
Chọn D
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 11
Sưu tầm và biên soạn
Diện tích tam giác ABC:
11
. .sin sin
22
S AB AC A bc
==
Thể tích khối chóp S.ABC:
1 1 1 1
. sin sin
3 3 2 6
SABC
V SAS h bc bch

= = =
.
Câu 21: Tập nghiệm của bất phương trình
( )
1
2
log 1 0x −
A.
( )
2;+
. B.
( )
1;2
. C.
( )
;2−
. D.
( )
1; +
.
Lời giải
Chọn B
Ta có
( )
1
2
log 1 0 0 1 1 1 2x x x− −
. Vậy tập nghiệm của bất phương trinh là
( )
1;2
.
Câu 22: Cho
73
log 5, log 5ab==
. Biểu thức
21
log 5M =
bằng
A.
ab
M
ab
+
=
. B.
ab
M
ab
=
+
. C.
M ab=
. D.
1
M
ab
=
.
Lời giải
Chọn B
Ta có
73
log 5, log 5ab==
nên
55
11
log 7 ,log 3
ab
==
.
Từ
21
5 5 5
1 1 1
log 5
11
log 21 log 7 log 3
ab
M
ab
ab
= = = = =
++
+
.
Vậy
ab
M
ab
=
+
.
Câu 23: Tập hợp các số thực m để phương trình
( )
( )
2
log 2020 logx mx−=
có nghiệm là
A. . B.
( )
0; .+
C.
( )
;0−
. D.
\0
.
Lời giải
Chọn D
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 12
Sưu tầm và biên soạn
Phương trình
( )
( )
2
2
2
2020 0
log 2020 log
2020
x
x mx
x mx
−
− =
−=
( ) ( )
( ) ( )
; 2020 2020;
2020
,*
x
m x f x
x
− − +
= − =
.
Phương trình đã cho có nghiệm
phương trình
( )
*
có nghiệm thỏa mãn
( ) ( )
; 2020 2020;x − − +
.
Ta có
( )
( ) ( )
2
2020
1 0, ; 2020 2020;f x x
x
= + − − +
Bảng biến thiên
Phương trình đã cho có nghiệm khi
0m
.
Câu 24: Cho tam giác
ABC
là tam giác vuông tại đỉnh
A
,
AB a=
,
AC b=
. Quay hình tam giác
ABC
quanh cạnh
AC
ta được một khối tròn xoay có diện tích xung quanh bằng
A.
22
.+a a b
B.
22
.+b a b
C.
22
1
.
3
+a a b
D.
22
1
.
3
+b a b
Lời giải
Chọn A
Khi quay hình tam giác
ABC
là tam giác vuông tại đỉnh
A
quanh cạnh
AC
ta được một khối
nón tròn xoay có độ dài bán kính đáy là
ra=
và chiều cao là
hb=
. Do đó độ dài đường sinh
của hình nón là
22
l a b=+
Vậy diện tích xung quanh của hình nón là
22
S rl a a b

= = +
Câu 25: Nếu tăng bán kính của một khối cầu gấp
2
lần thì thể tích thay đổi như thế nào?
A. Thể tích tăng gấp
2
lần. B. Thể tích tăng gấp
4
lần.
C. Thể tích tăng gấp
8
lần. D. Thể tích tăng gấp
4
3
lần.
Lời giải
Chọn C
Gọi
1
R
là bán kính của khối cầu đã cho. Khi đó thể tích của khối cầu đã cho bằng
3
11
4
3
VR
=
.
Nếu tăng bán kính của khối cầu gấp
2
lần thì ta có bán kính mới của khối cầu là
21
2RR=
. Khi
đó thể tích của khối cầu mới là
( ) ( )
33
3
2 2 1 1 1
4 4 4
2 8. 8
3 3 3
V R R R V
= = = =
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 13
Sưu tầm và biên soạn
Vậy thể tích của khối cầu tăng gấp
8
lần.
Câu 26: Một cái xúc xích hình trụ có đường kính đáy
2 cm
và chiều cao
6 cm
, giả sử giá bán mỗi
3
cm
xúc xích là
500
đồng. Bạn An cần trả tiền mua một gói 4 cái xúc xích. Số tiền gần đúng nhất
cho
4
cái xúc xích là
A.
19000
. B.
76000
. C.
38000
. D.
30000
.
Lời giải
Chọn C
Gọi bán kính đáy của hình trụ là
r
.
Ta có:
( )
1 r cm=
.
Thể tích 1 cái xúc xích là:
( )
2 2 3
.1 .6 6 V r h cm
= = =
.
Giá tiền 4 cái xúc xích là:
4.6 .500 37700
đ.
Vậy số tiền gần đúng nhất cho
4
cái xúc xích là
38000
đ.
Câu 27: Một người gửi số tiền 100 triệu đồng vào một ngân hàng với lãi suất
6,8% /
năm. Biết rằng nếu
không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu
(người ta gọi là lãi kép). Nếu người đó gửi tiền trong đúng 4 năm và trong khoảng thời gian đó
không rút tiền ra thì người đó có số tiền là.
A.
4
100.1,068
(đồng). B.
5
100.1,068
(triệu đồng).
C.
3
100.1,068
(triệu đồng). D.
4
100.1,068
(triệu đồng).
Lời giải
Chọn D
Gọi
n
T
là số tiền người đó thu được sau
n
năm.
Số tiền thu được sau một năm là:
( )
1
100. 1 6,8%T =+
(triệu đồng).
Số tiền thu được sau 2 năm là:
( )
21
1 6,8%TT=+
( )
2
100. 1 6,8%=+
(triệu đồng).
Số tiền thu được sau 3 năm là:
( ) ( )
3
32
. 1 6,8% 100. 1 6,8%TT= + = +
(triệu đồng).
Vậy số tiền thu được sau 4 năm là:
( )
4
4
4
100. 1 6,8% 100.1,068T = + =
(triệu đồng).
Câu 28: Cho hàm số
( )
( )
2
0,5
log 6f x x x=−
. Tập nghiệm của bất phương trình
( )
0fx
là.
A.
( )
3; +
. B.
( )
;3−
. C.
( )
3;6
. D.
( )
0;3
.
Lời giải
Chọn C
Tập xác định:
( )
0;6D =
. (1)
Ta có
( )
( )
2
62
6 ln0,5
x
fx
xx
−
=
−
.
( )
0fx
( )
2
62
0
6 ln0,5
x
xx
−

−
2
62
0
6
x
xx
−

−
0
36
x
x

.
Kết hợp (1) suy ra tâp nghiệm của bất phương trình
( )
0fx
là
( )
3;6S =
.
Câu 29: Một khối bê tông có dạng hình lăng trụ đứng với độ dài các cạnh đáy là
3 dm, 4dm, 5dm
độ dài
cạnh bên là
6 dm
. Thể tích khối bê tông bằng
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 14
Sưu tầm và biên soạn
A.
( )
3
72 dm
. B.
( )
3
24 dm
. C.
( )
3
216 dm
. D.
( )
3
36 dm
.
Lời giải
Chọn D
Ta có thể tích khối bê tông là thể tích khối lăng trụ đứng có đáy là tam giác vuông.
Thể tích cầm tìm là
( )
3
1
3.4.6 36 dm
2
V ==
.
Câu 30: Một dụng cụ đựng chất lỏng có dạng hình nón với chiều cao là
30 cm
và bán kính đáy là
15 cm
. Dụng cụ này đựng được tối đa bao nhiêu
3
cm
chất lỏng?
A.
( )
3
2250 .cm
B.
( )
3
750 .cm
C.
( )
3
2250 .cm
D.
( )
3
750 .cm
Lời giải
Chọn A
Khối nón có chiều cao
30h cm
và bán kính đáy
15r cm
có thể tích là
2 2 3
11
.15 .30 2250 .
33
V πr h π π cm
Câu 31: Nếu
.S ABC
là hình chóp đều có chiều cao bằng
h
và cạnh đáy bằng
a
thì có thể tích bằng
A.
2
3
3
ah
. B.
2
3
6
ah
. C.
2
3
12
ah
. D.
2
3
4
ah
.
Lời giải
Chọn C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 15
Sưu tầm và biên soạn
Gọi
O
là tâm đường tròn ngoại tiếp tam giác
ABC
.
Diện tích tam giác
ABC
là
2
3
4
ABC
a
S =
Thể tích khồi chóp là
2
13
.
3 12
ABC
ah
V S SO==
.
Câu 32: Tập hợp các giá trị m để hàm số
( )
3
2
10 25 1
3
x
y mx m x= − + − +
có hai điểm cực trị là:
A.
R
. B.
\5R −
. C.
\5R
. D.
( )
5; +
.
Lời giải
Chọn C
Ta có
( )
3
22
10 25 1 2 x 10 25
3
x
y mx m x y x m m
= − + − + = − + −
.
Để hàm số có hai điểm cực trị
2
2 x 10 25y x m m
= − + −
có hai nghiệm phân biệt
( )
2
2
0 10 25 0 5 0 5m m m m
− + −
.
Câu 33: Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
10 20xx
y
x
− + −
=
là:
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn D
Điều kiện:
10 20x
.
Vì
10 20x
nên không thể tính được
( )
lim
x
fx
→+
và
( )
lim
x
fx
→−
không tồn tại.
Vì
10 20x
nên không thể tính được
( )
0
lim
x
fx
+
→
và
( )
0
lim
x
fx
−
→
không tồn tại.
Vậy đồ thị hàm số không có đường tiệm cận nào.
Câu 34: Cho hình hộp
có thể tích bằng
V
. Thể tích của khối tứ diện
ACB D

bằng
A.
1
6
V
. B.
1
4
V
. C.
1
3
V
. D.
1
2
V
.
Lời giải
Chọn C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 16
Sưu tầm và biên soạn
Ta có
. . . .ACB D A A B D C D B C B ABC D ACD
V V V V V V
= − − − −
.
Mà
. . . . .
1 1 1 1
.
2 2 3 6
A A B D C D B C B ABC D ACD D ABCD
V V V V V V V
= = = = = =
1
4.
63
ACB D
V
V V V

= − =
Câu 35: Cho hàm số
( )
y f x=
có đồ thị đạo hàm
( )
y f x
=
như hình bên dưới. Hàm số đã cho nghịch
biến trên khoảng
A.
( )
1;2
. B.
( )
0;1
. C.
1
;0
2

−


. D.
( )
0;2
.
Lời giải
Chọn C
Dựa vào đồ thị của hàm số
( )
y f x
=
ta có bảng xét dấu như sau:
Vì
( )
1
0, ;0
2
f x x

−


nên chọn phương án C.
II. PHẦN TỰ LUẬN
Câu 36: Có báo nhiêu giá trị nguyên của tham số
m
để hàm số
2 3 2
( 6) ( 3) 2 1y m m x m x x= − − + − − +
nghịch biến trên ?
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 17
Sưu tầm và biên soạn
TH1:
2
3
60
2
m
mm
m
=
− − =
=−
Với
3 2 1m y x= = − +
hàm số nghịch biến trên .
Với
2
2 5 2 1m y x x= − = − − +
không nghịch biến trên .
TH2:
2
60mm− −
,
2 3 2 2 2
( 6) ( 3) 2 1 3( 6) 2( 3) 2y m m x m x x y m m x m x
= − − + − − + = − − + − −
.
Để hàm số nghịch biến trên thì
2
2
23
60
9
3
7 12 27 0
7
m
mm
m
mm
−
− −

−
= − −
Suy ra
1,0,1,2,3m−
Câu 37: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và
2 2 , 3AB AC a BC a= = =
. Tam
giác
SAD
vuông cân tại S, hai mặt phẳng
( )
SAD
và
( )
ABCD
vuông góc nhau. Tính thể tích
khối chóp
.S ABCD
.
Lời giải
Theo giả thiết
2 2 , 3AB AC a BC a= = =
nên tam giác
ABC
có
2 2 2
2 , , 3AB a AC a BC a AB AC BC= = = = +
, do đó
ABC
là tam giác vuông tại
C
.
Suy ra
2
2 . 3
ABCD ABC
S S CACB a= = =
.
Gọi
H
là trung điểm của
AD
, tam giác
SAD
vuông cân tại S nên
SH AD⊥
.
Mặt khác
( ) ( ) ( )
SAD ABCD SH ABCD⊥ ⊥
.
Lại có tam giác
SAD
vuông cân tại
13
22
a
S SH AD = =
.
A
H
C
B
D
S
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 18
Sưu tầm và biên soạn
Vậy thể tích khối chóp
.S ABCD
là
3
2
.
1 1 3
. . . 3
3 3 2 2
S ABCD ABCD
aa
V SH S a= = =
.
Câu 38: Số các giá trị nguyên của tham số
m
để phương trình
2 3 4 1
xx
m+ = +
có đúng một nghiệm là
Lời giải
Đặt
20
x
t =
. Phương trình trở thành:
2
2
3
31
1
t
t m t m
t
+
+ = + =
+
Xét hàm số
( )
2
3
1
t
ft
t
+
=
+
.
Ta có:
( )
( )
( )
3
2
1 3 1
,0
3
1
t
f t f t t
t
−

= = =
+
Bảng biến thiên:
Để phương trình
2 3 4 1
xx
m+ = +
có đúng một nghiệm
10
13
m
m
=

Vậy có 2 giá trị nguyên của m là
2;3m
.
Câu 39: Có bao nhiêu giá trị nguyên thuộc
2021;2021−
của tham số để phương trình sau có nghiệm
duy nhất
( )
2
2 3 2 3
log 1 log 0.x mx m x
+−
+ + − + =
Lời giải
Ta có:
( )
2
2 3 2 3
log 1 log 0x mx m x
+−
+ + − + =
( )
2
2 3 2 3
log 1 log 0x mx m x
++
+ + − − =
2
1
0
x mx m x
x
+ + − =
2
1
1
0
xx
m
x
x
− + +
=
+
m
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 19
Sưu tầm và biên soạn
Xét
2
1
( ) , 0
1
xx
f x x
x
− + +
=
+
.
Khi đó
( )
+
= −
+
2
2
2
'( ) 0, 0.
1
xx
f x x
x
Ta có bảng biến thiên
Để phương trình trên có nghiệm duy nhất thì
1m
.
Vì
;m
2021;2021 2021; 2020; ; 1;0 − − − − mm
có 2022 giá trị
m
thỏa mãn.
------------- HẾT -------------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ I
MÔN: TOÁN 12 – ĐỀ SỐ: 09
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Hàm số
4
2
3
22
x
yx= − + +
có bao nhiêu điểm cực trị?
A.
4
. B.
2
. C.
0
. D.
3
.
Câu 2: Khối lăng trụ có diện tích đáy bằng
2
3a
, chiều cao bằng
a
có thể tích bằng
A.
3
a
. B.
3
3a
. C.
3
3
2
a
. D.
3
1
2
a
.
Câu 3: Phương trình
1
28
x+
=
có nghiệm là
A.
2x=
. B.
1x =
. C.
3x=
. D.
4x=
.
Câu 4: Cho khối tứ diện
OABC
có
OA
,
OB
,
OC
đôi một vuông góc với nhau tại
O
và
2OA =
,
4OB =
,
6OC =
. Thể tích khối tứ diện đã cho bằng
A.
8
. B.
24
. C.
48
. D.
16
.
Câu 5: Cho khối chóp
.S ABC
có thể tích
V
. Các điểm
B
;
C
tương ứng là trung điểm các cạnh
SB
,
SC
. Thể tích khối chóp
.S AB C

bằng
A.
8
V
. B.
2
V
. C.
4
V
. D.
16
V
.
Câu 6: Cho hàm số
2019
2
y
x
=
−
có đồ thị
( )
H
. Số đường tiệm cân của
( )
H
là
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 7: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình
vẽ bên
A.
3
31y x x= − − +
. B.
3
31y x x= − + −
.
C.
3
31y x x= − +
. D.
3
31y x x= + +
.
Câu 8: Cho
a
là một số dương, biểu thức
2
3
aa
viết dưới dạng lũy thừa
với số mũ hữu tỉ là
A.
4
3
.a
B.
5
6
.a
C.
7
6
.a
D.
6
7
.a
Câu 9: Với
a
là số thực dương bất kì, mệnh đề nào sau đây đúng?
A.
5
1
ln ln .
5
aa=
B.
ln3 ln3 ln .aa=+
C.
1
ln ln .
33
a
a=
D.
( )
ln 3 ln3 ln .aa+ = +
Câu 10: Cho hàm số
32
32y x x= − +
có đồ thị
( )
C
. Gọi
m
là số giao điểm của
( )
C
và trục hoành. Tìm
m
.
A.
2m =
. B.
1m =
. C.
3m =
. D.
0m =
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 2
Sưu tầm và biên soạn
Câu 11: Hàm số
( )
2
2
41yx= − +
có giá trị lớn nhất trên đoạn
1;1−
bằng
A.
10
. B.
12
. C.
14
. D.
17
.
Câu 12: Tập xác định của hàm số
( )
5
3yx
−
=−
là
A.
( )
3; +
. B.
( )
1;3
. C. . D.
\3
.
Câu 13: Cho hàm số
( )
fx
có bảng biến thiên sau:
Khẳng định nào sau đây đúng?
A. Giá trị cực tiểu của hàm số bằng
2
.
B. Hàm số đạt cực tiểu tại
1x =
và đạt cực đại tại
5x =
.
C. Hàm số đạt cực đại tại
0x =
và đạt cực tiểu tại
2x =
.
D. Giá trị cực đại của hàm số bằng
0
.
Câu 14: Hàm số
32
3y x x=+
đồng biến trên khoảng nào dưới đây?
A.
( )
;2− −
và
( )
0;+
. B. . C.
( )
2;0−
. D.
( )
1:− +
.
Câu 15: Cho khối chóp có đáy là tam giác đều cạnh bằng
2
và có chiều cao
4.
Thể tích khối chóp bằng
A.
23
. B.
2
. C.
43
3
. D.
4
.
Câu 16: Đồ thị hàm số
2
2
6
34
x
y
xx
−
=
+−
có tất cả bao nhiêu đường tiệm cận?
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 17: Hàm số
3
32y x x= − +
đạt cực đại tại điểm
A.
2x =−
. B.
1x =
. C.
1x =−
. D.
0x =
.
Câu 18: Tổng diện tích các mặt của một khối lập phương là
2
96cm
. Thể tích khối lập phương đó bằng
A.
3
84cm
. B.
3
48cm
. C.
3
64cm
. D.
3
91cm
.
Câu 19: Hình trụ có hai đường tròn đáy ngoại tiếp hai mặt của một hình lập phương cạnh
a
thì có diện
tích xung quanh bằng
A.
2
a
. B.
2
2 a
. C.
2
22a
. D.
2
2 a
.
Câu 20: Trong các hàm số sau hàm số nào đồng biến trên ?
A.
3
logyx=
. B.
2018
x
y =
. C.
3
1
2
xx
y
+

=−


. D.
5
2
1
log
x



.
Câu 21: Cho hàm số
1
1
x
y
x
+
=
−
có đồ thị
( )
C
và đườngthẳng
:2 1 0d x y− − =
. Biết
d
cắt
( )
C
tại hai
điểm phân biệt
( )
11
;M x y
và
( )
22
;N x y
. Tính
12
yy+
.
A.
4−
. B.
5
. C.
2
. D.
2−
.
Câu 22: Tập nghiệm
S
của phương trình
21
2 5.2 2 0
xx+
− + =
là
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 3
Sưu tầm và biên soạn
A.
0;1S =
. B.
1S =
. C.
1;0S =−
. D.
1;1S =−
.
Câu 23: Cho hình nón có bán kính đáy bằng
3cm
, độ dài đường sinh bằng
5cm
. Thể tích của khối nón được
giới hạn bởi hình nón đó bằng
A.
3
75 cm
. B.
3
12 cm
. C.
3
45 cm
. D.
3
16 cm
.
Câu 24: Tập xác định
D
của hàm số
( )
3
1
log 2 1
y
x
=
−
là
A.
1
;
2

−


. B.
1
; \ 1
2

+


. C.
\1
. D.
1
;
2

+


.
Câu 25: Tìm các giá trị thực của tham số
m
để phương trình
2
33
log 3log 2 7 0x x m− + − =
có hai nghiệm
thực
12
;xx
thỏa mãn
( )( )
12
3 3 72xx+ + =
.
A.
9
2
m =
. B.
61
2
m =
. C.
3m =
. D. không tồn tại.
Câu 26: Cho hàm số
( )
fx
có đạo hàm
( ) ( )
( )
22
1 3 2
= − − +f x x x x x
,
x
. Số điểm cực trị của hàm
số là
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 27: Cho hàm số
21
1
−
=
−
x
y
x
có đồ thị
( )
C
. Số các giá trị nguyên của tham số
2020;2020−m
để
đường thẳng
: = − +d y x m
cắt
( )
C
tại hai điểm phân biệt là
A.
4035
. B.
4036
. C.
4037
. D.
2020
.
Câu 28: Cho hình hộp đứng
.ABCD A B C D
có đáy
ABCD
là hình thoi cạnh a, góc nhọn
60BCD =
và
BD AC
=
. Tính thể tích của khối chóp đó bằng
A.
3
3
2
a
. B.
3
3a
. C.
3
a
. D.
3
6
2
a
.
Câu 29: Cho hàm số
x
ya=
,
x
yb=
với a, b là hai số thực dương khác 1, lần lượt có đồ thị là
12
,CC
như
hình vẽ, mệnh đề nào sau đây đúng?
A.
01ab
. B.
01ab
. C.
01ba
. D.
01ba
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 4
Sưu tầm và biên soạn
Câu 30: Nghiệm của phương trình
( ) ( )
33
log 1 1 log 1+ = + −xx
là
=xa
. Tính giá trị biểu thức
2
1= + +T a a
.
A.
2=T
. B.
4=T
. C.
7=T
. D.
5=T
.
Câu 31: Cho hàm số
32
34= + − −y x x mx
. Tập hợp tất cả các giá trị của tham số
m
để hàm số đồng
biến trên khoảng
( )
;− +
là
A.
( )
1;5−
. B.
(
;3− −
. C. . D.
( )
1;− +
.
Câu 32: Cho hàm số
( )
y f x=
xác định, liên tục trên và có bảng biến thiên như sau:
Tìm tất cả các các giá trị thực của tham số
m
để phương trình
( )
1f x m−=
có đúng hai
nghiệm.
A.
0
1
m
m
=−
. B.
2
1
m
m
=−
−
. C.
21m− −
. D.
2
1
m
m
=−
−
.
Câu 33: Một chiếc cốc có dạng hình trụ, chiều cao
16cm
, đường kính đáy bằng
8cm
, bề dày của thành
cốc và đáy cốc bằng
1cm
. Nếu đổ lượng nước vào cốc cách miệng cốc
5cm
thì được thể tích
1
V
, nếu đổ đầy cốc ta được khối trụ (tính cả thành cốc và đáy cốc) có thể tích
2
V
. Tỉ số
1
2
V
V
bằng
A.
2
3
. B.
245
512
. C.
45
128
. D.
11
16
.
Câu 34: Cho hàm số
( )
y f x=
có đồ thị
( )
fx
như hình vẽ bên. Hàm số
( )
53y f x=−
nghịch biến trên
khoảng nào trong các khoảng dưới đây.
A.
( )
2;5
. B.
( )
2;+
. C.
( )
3;1−
. D.
( )
0;3
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 5
Sưu tầm và biên soạn
Câu 35: Cho hàm số
( )
ln ln 2020
2
x
fx
x

=−

+

. Biết
( ) ( ) ( )
2 4 ... 2020
a
f f f
b
+ + =
, với
,*a b N
và
a
b
là phân số tối giản. Tính giá trị biểu thức
2S b a=−
.
A.
2021
2022
S =
. B.
0S =
. C.
1S =
. D.
1S =−
.
II. PHẦN TỰ LUẬN
Câu 36: Tìm tham số
m
để hàm số
5mx
y
xm
+
=
−
đạt giá trị nhỏ nhất trên đoạn
0;1
bằng
7−
.
A.
5m =
. B.
2m =
. C.
0m =
. D.
1m =
.
Câu 37: Cho khối chóp tam giác
.S ABC
có các góc
60ASB BSC CSA= = =
và độ dài các cạnh
1SA =
,
2, 3SB SC==
. Thể tích khối chóp
.S ABC
bằng:
A.
3
2
. B.
2
2
. C.
6
2
. D.
32
2
.
Câu 38: Cho hàm số
( )
y f x=
. Hàm số
( )
y f x
=
có bảng biến thiên như hình vẽ bên. Hỏi hàm số
( ) ( )
2g x f x x=−
có bao nhiêu điểm cực trị?
Câu 39: Giải phương trình sau:
( ) ( ) ( )
2
33
3
11
log 3 log 1 log 4
22
x x x+ + − =
.
---------- HẾT ----------
+
∞
x
1
+
∞
1
1
∞
∞
f'
(
x
)
1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 6
Sưu tầm và biên soạn
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Hàm số
4
2
3
22
x
yx= − + +
có bao nhiêu điểm cực trị?
A.
4
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn D
Ta có
( )
32
2 2 2 1y x x x x
= − + = − −
. Suy ra
( )
2
1
0 2 1 0 0
1
x
y x x x
x
=−
= − − = =
=
Vì
0y
=
có 3 nghiệm phân biệt và đổi dấu khi qua ba nghiệm đó nên hàm số đã cho có 3 cực
trị.
Câu 2: Khối lăng trụ có diện tích đáy bằng
2
3a
, chiều cao bằng
a
có thể tích bằng
A.
3
a
. B.
3
3a
. C.
3
3
2
a
. D.
3
1
2
a
.
Lời giải
Chọn B
Áp dụng công thức tính thể tích khối lăng trụ ta có
23
. 3 . 3V B h a a a= = =
.
Câu 3: Phương trình
1
28
x+
=
có nghiệm là
A.
2x=
. B.
1x =
. C.
3x=
. D.
4x=
.
Lời giải
Chọn A
Ta có
1
28
x+
=
13
22
x+
=
13x + =
2x=
.
Câu 4: Cho khối tứ diện
OABC
có
OA
,
OB
,
OC
đôi một vuông góc với nhau tại
O
và
2OA =
,
4OB =
,
6OC =
. Thể tích khối tứ diện đã cho bằng
A.
8
. B.
24
. C.
48
. D.
16
.
Lời giải
Chọn A
Thể tích khối tứ diện
OABC
là
11
. . .2.4.6 8
66
V OAOB OC= = =
.
Câu 5: Cho khối chóp
.S ABC
có thể tích
V
. Các điểm
B
;
C
tương ứng là trung điểm các cạnh
SB
,
SC
. Thể tích khối chóp
.S AB C

bằng
A.
8
V
. B.
2
V
. C.
4
V
. D.
16
V
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 7
Sưu tầm và biên soạn
Chọn C
Ta có:
.
.
1
4
S AB C
S ABC
V
SA SB SC
V SA SB SC


= =
.
Vậy:
.
4
S AB C
V
V

=
.
Câu 6: Cho hàm số
2019
2
y
x
=
−
có đồ thị
( )
H
. Số đường tiệm cân của
( )
H
là
A.
3
. B.
1
. C.
0
. D.
2
.
Lời giải
Chọn D
Ta có
2019
2019
lim lim 0
2
2
1
xx
x
x
x
→+ →+
==
−
−
,
2019
2019
lim lim 0
2
2
1
xx
x
x
x
→− →−
==
−
−
.
Vậy đường thẳng
0y =
là tiệm cận ngang của đồ thị hàm số.
2
2
2019 2019
lim ;lim
22
x
x
xx
+
→−
→
= − = +
−−
.
Vậy đường thẳng
2x =
là tiệm cận đứng của đồ thị hàm số
Câu 7: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 8
Sưu tầm và biên soạn
A.
3
31y x x= − − +
. B.
3
31y x x= − + −
. C.
3
31y x x= − +
. D.
3
31y x x= + +
.
Lời giải
Chọn C
Giả sử hàm số cần tìm có dạng
32
y ax bx cx d= + + +
với
0a
.
Dựa vào đồ thị hàm số ta thấy
lim
x
y
→+
= +
nên suy ra
0a
. Vậy loại đáp án A, B.
Đồ thị hàm số đạt cực đại tại điểm có tọa độ là
( )
1;3−
và đạt cực tiểu tại điểm có tọa độ là
( )
1; 1−
phương trình
0y
=
phải có hai nghiệm
1; 1xx= − =
. Ta thấy chỉ có hàm số
3
31y x x= − +
có
22
1
3 3; 0 3 3 0
1
x
y x y x
x
=−

= − = − =
=
.
Vậy chọn
3
31y x x= − +
Câu 8: Cho
a
là một số dương, biểu thức
2
3
aa
viết dưới dạng lũy thừa với số mũ hữu tỉ là
A.
4
3
.a
B.
5
6
.a
C.
7
6
.a
D.
6
7
.a
Lời giải
Chọn C
Ta có:
2 2 7
1
3 3 6
2
..a a a a a==
Câu 9: Với
a
là số thực dương bất kì, mệnh đề nào sau đây đúng?
A.
5
1
ln ln .
5
aa=
B.
ln3 ln3 ln .aa=+
C.
1
ln ln .
33
a
a=
D.
( )
ln 3 ln3 ln .aa+ = +
Lời giải
Chọn B
Dựa vào quy tắc tính logarit với ba số dương
,,abc
và
1a
, ta có
( )
log log log .
a a a
bc b c=+
Câu 10: Cho hàm số
32
32y x x= − +
có đồ thị
( )
C
. Gọi
m
là số giao điểm của
( )
C
và trục hoành. Tìm
m
.
A.
2m =
. B.
1m =
. C.
3m =
. D.
0m =
.
Lời giải
Chọn C
Xét phương trình hoành độ giao điểm của
( )
C
và trục hoành:
32
3 2 0xx− + =
. Sử dụng MTBT,
ta có phương trình trên có 3 nghiệm phân biệt:
1; 1 3xx= =
. Mỗi hoành độ tương ứng với
một giao điểm. Vậy có 3 giao điểm của
( )
C
và trục hoành. Ta Chọn C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 9
Sưu tầm và biên soạn
Câu 11: Hàm số
( )
2
2
41yx= − +
có giá trị lớn nhất trên đoạn
1;1−
bằng
A.
10
. B.
12
. C.
14
. D.
17
.
Lời giải
Chọn D
TXĐ:
D=
.
Xét
( )
( )
2
2 1;1
2 4 2 0 0
2 1;1
x
y x x x
x
= − −
= − − = =
= −
.
Ta so sánh các giá trị sau:
( ) ( )
1 10; 0 17ff = =
, ta có:
Giá trị lớn nhất của hàm số trên đoạn
1;1−
bằng
17
khi
0x =
. Ta chọn phương án D.
Câu 12: Tập xác định của hàm số
( )
5
3yx
−
=−
là
A.
( )
3; +
. B.
( )
1;3
. C. . D.
\3
.
Lời giải
Chọn A
Điều kiện xác định:
3 0 3xx−
.
Vậy tập xác định của hàm số là
( )
3;D = +
.
Câu 13: Cho hàm số
( )
fx
có bảng biến thiên sau:
Khẳng định nào sau đây đúng?
A. Giá trị cực tiểu của hàm số bằng
2
.
B. Hàm số đạt cực tiểu tại
1x =
và đạt cực đại tại
5x =
.
C. Hàm số đạt cực đại tại
0x =
và đạt cực tiểu tại
2x =
.
D. Giá trị cực đại của hàm số bằng
0
.
Lời giải
Chọn C
Theo bảng biến thiên thì hàm số đạt cực đại tại
0x =
và đạt cực tiểu tại
2x =
.
Câu 14: Hàm số
32
3y x x=+
đồng biến trên khoảng nào dưới đây?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 10
Sưu tầm và biên soạn
A.
( )
;2− −
và
( )
0;+
. B. . C.
( )
2;0−
. D.
( )
1:− +
.
Lời giải
Chọn A
Tập xác định
.
Ta có
2
0
3 6 ; 0 .
2
x
y x x y
x
=

= + =
=−
Bảng xét dấu của
y
Vậy hàm số đồng biến trên khoảng
( )
;2− −
và
( )
0; .+
Câu 15: Cho khối chóp có đáy là tam giác đều cạnh bằng
2
và có chiều cao
4.
Thể tích khối chóp bằng
A.
23
. B.
2
. C.
43
3
. D.
4
.
Lời giải
Thể tích của khối chóp là
1 1 1 4 3
. . . 2.2.sin60 .4 .
3 3 2 3
V B h= = =
Câu 16: Đồ thị hàm số
2
2
6
34
x
y
xx
−
=
+−
có tất cả bao nhiêu đường tiệm cận?
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn A
Ta có tập xác định của hàm số là
6; 6 \ 1D

=−

.
Ta có
2
2
11
6
lim lim
34
xx
x
y
xx
++
→→
−
= = +
+−
suy ra đồ thị hàm số có tiệm cận đứng là
1x =
.
Đồ thị hàm số không có tiệm cận ngang.
Vậy đồ thị hàm số có 1 đường tiệm cận.
Câu 17: Hàm số
3
32y x x= − +
đạt cực đại tại điểm
A.
2x =−
. B.
1x =
. C.
1x =−
. D.
0x =
.
Lời giải
Chọn C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 11
Sưu tầm và biên soạn
Ta có:
3
32y x x= − +
2
33yx
= −
01yx
= =
hoặc
1x =−
Mà
6yx

=
nên hàm số đạt cực đại tại
1x =−
vì
( )
1 6 0y

− = −
Câu 18: Tổng diện tích các mặt của một khối lập phương là
2
96cm
. Thể tích khối lập phương đó bằng
A.
3
84cm
. B.
3
48cm
. C.
3
64cm
. D.
3
91cm
.
Lời giải
Chọn C
Khối lập phương có 6 mặt bằng nhau nên diện tích 1 mặt
2
0
96
16cm
6
S ==
Độ dài cạnh khối lập phương
4cm
.
Thể thích khối lập phương
33
4 64cm=
Câu 19: Hình trụ có hai đường tròn đáy ngoại tiếp hai mặt của một hình lập phương cạnh
a
thì có diện
tích xung quanh bằng
A.
2
a
. B.
2
2 a
. C.
2
22a
. D.
2
2 a
.
Lời giải
Chọn A
Hình trụ có hai đường tròn đáy ngoại tiếp hai mặt của một hình lập phương có chiều cao là
cạnh của hình lập phương, tức
ha=
. Bán kính đường tròn đáy là
2
a
r =
.
Diện tích xung quanh hình trụ là
2
2 2 . . 2
2
a
rh a a
==
.
Câu 20: Trong các hàm số sau hàm số nào đồng biến trên ?
A.
3
logyx=
. B.
2018
x
y =
. C.
3
1
2
xx
y
+

=−


. D.
5
2
1
log
x



.
Lời giải
Chọn C
Các hàm số
35
2
1
log ; 2018 ; log
x
y x y y
x

= = =


không có tập xác định trên nên loại.
Với
( ) ( )
3 3 2
22
1 1 1 1
3 1 .ln . 3 1 ln2. 0
2 2 2 2
x x x x x x
y y x x x
+ + +
= − = − + = +
Ta Chọn C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 12
Sưu tầm và biên soạn
Câu 21: Cho hàm số
1
1
x
y
x
+
=
−
có đồ thị
( )
C
và đườngthẳng
:2 1 0d x y− − =
. Biết
d
cắt
( )
C
tại hai
điểm phân biệt
( )
11
;M x y
và
( )
22
;N x y
. Tính
12
yy+
.
A.
4−
. B.
5
. C.
2
. D.
2−
.
Lời giải
Chọn C
Ta có phương trình hoành độ giao điểm:
2
01
1
2 1 2 4 0
23
1
xy
x
x x x
xy
x
= = −
+
= − − =
= =
−
.
Do đó đặt
( )
0; 1M −
và
( )
2;3N
.
Vậy
12
2yy+=
Câu 22: Tập nghiệm
S
của phương trình
21
2 5.2 2 0
xx+
− + =
là
A.
0;1S =
. B.
1S =
. C.
1;0S =−
. D.
1;1S =−
.
Lời giải
Chọn D
Đặt
2 , 0
x
tt=
.
2 1 2
2
2 5.2 2 0 2 5 2 0
1
2
xx
t
tt
t
+
=
− + = − + =
=
(thỏa).
Với
2 2 2 1
x
tx= = =
.
Với
11
21
22
x
tx= = = −
.
Vậy tập nghiệm của phương trình đã cho là
1;1S =−
.
Câu 23: Cho hình nón có bán kính đáy bằng
3cm
, độ dài đường sinh bằng
5cm
. Thể tích của khối nón được giới
hạn bởi hình nón đó bằng
A.
3
75 cm
. B.
3
12 cm
. C.
3
45 cm
. D.
3
16 cm
.
Lời giải
Chọn B
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 13
Sưu tầm và biên soạn
Ta có chiều cao của khối nón
22
5 3 4cmh = − =
.
Diện tích đáy
2
9 cmS
=
.
Thể tích khối nón được giới hạn bởi hình nón:
3
1
.9 .4 12 cm
3
V

==
.
Câu 24: Tập xác định
D
của hàm số
( )
3
1
log 2 1
y
x
=
−
là
A.
1
;
2

−


. B.
1
; \ 1
2

+


. C.
\1
. D.
1
;
2

+


.
Lời giải
Chọn B
Hàm số xác định khi và chỉ khi
( )
3
log 2 1x−
xác định và
( )
3
1
2 1 0
log 2 1 0
2
2 1 1
1
x
x
x
x
x
−
−

−
.
1
; \ 1
2
D

= +


.
Câu 25: Tìm các giá trị thực của tham số
m
để phương trình
2
33
log 3log 2 7 0x x m− + − =
có hai nghiệm
thực
12
;xx
thỏa mãn
( )( )
12
3 3 72xx+ + =
.
A.
9
2
m =
. B.
61
2
m =
. C.
3m =
. D. không tồn tại.
Lời giải
Chọn A
Đặt
3
logtx=
. Phương trình trở thành
( )
2
3 2 7 0 1t t m− + − =
.
Phương trình có hai nghiệm
( ) ( )
1 2 1 2
;1x x x x
có hai nghiệm
12
;tt
.
( )
37
9 4 2 7 0
8
mm = − −
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 14
Sưu tầm và biên soạn
Theo viét
12
3tt+=
và
12
. 2 7t t m=−
.
Ta có
12
12
3 ; 3
tt
xx==
.
( )( )
( )
( )
1 2 1 2 1 2
12
3 3 72 3 3 3 3 9 72 3 3 12 2
t t t t t t
xx
+
+ + = + + + = + =
.
Thế
21
3tt=−
vào phương trình
( )
2
ta được
11
3
3 3 12
tt−
+=
11
2
3 12.3 27 0
tt
− + =
Giải phương trình ta được
1
2
1
2
1
33
2
39
t
t
t
t
=
=
=
=
.
12
9
. 2 2 7 2
2
t t m m= − = =
(nhận).
Câu 26: Cho hàm số
( )
fx
có đạo hàm
( ) ( )
( )
22
1 3 2
= − − +f x x x x x
,
x
. Số điểm cực trị của hàm
số là
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn B
Hàm số
( )
fx
đã cho có đạo hàm là hàm đa thức nên hàm số
( )
fx
liên tục trên .
Ta có
( ) ( )
( )
22
1 3 2
= − − +f x x x x x
( ) ( )
2
2
12= − −x x x
.
( )
0
=fx
0
1
2
=
=
=
x
x
x
.
Bảng biến thiên (BBT)
Dựa vào BBT, ta thấy hàm số
( )
fx
có duy nhất một điểm cực trị.
Câu 27: Cho hàm số
21
1
−
=
−
x
y
x
có đồ thị
( )
C
. Số các giá trị nguyên của tham số
2020;2020−m
để
đường thẳng
: = − +d y x m
cắt
( )
C
tại hai điểm phân biệt là
A.
4035
. B.
4036
. C.
4037
. D.
2020
.
Lời giải
Chọn B
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 15
Sưu tầm và biên soạn
Phương trình hoành độ giao điểm của
( )
C
và
d
là
21
1
−
= − +
−
x
xm
x
( )( )
2 1 1 − = − − +x x x m
(Vì
1=x
không phải là nghiệm của phương trình)
( )
2
1 1 0 + − + − =x m x m
( )
*
.
Đường thẳng
d
cắt
( )
C
tại hai điểm phân biệt
( )
*
có hai nghiệm phân biệt
( ) ( )
2
1 4 1 0 − − − mm
2
6 5 0 − + mm
5
1
m
m
.
Theo giả thiết:
2020;2020−m
và
m
2020; 2019;...; 1;0;6;7;8;...;2020 − − −m
có
4036
số nguyên thỏa mãn đề bài.
Câu 28: Cho hình hộp đứng
.ABCD A B C D
có đáy
ABCD
là hình thoi cạnh a, góc nhọn
60BCD =
và
BD AC
=
. Tính thể tích của khối chóp đó bằng
A.
3
3
2
a
. B.
3
3a
. C.
3
a
. D.
3
6
2
a
.
Lời giải
Chọn D
Ta có tam giác
BCD
đều nên
BD a=
và
3AC a=
,
3BD a
=
.
Trong tam giác vuông
BDD
:
22
2DD BD BD a

= − =
.
3
.
16
. 2. . 3
22
ABCD A B C D ABCD
a
V DD S a a a
= = =
.
Câu 29: Cho hàm số
x
ya=
,
x
yb=
với a, b là hai số thực dương khác 1, lần lượt có đồ thị là
12
,CC
như
hình vẽ, mệnh đề nào sau đây đúng?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 16
Sưu tầm và biên soạn
A.
01ab
. B.
01ab
. C.
01ba
. D.
01ba
.
Lời giải
Chọn D
Ta thấy hàm số có đồ thị
1
C
đồng biến nên
1a
, hàm số có đồ thị
2
C
nghịch biến nên
01b
. Vậy
01ba
.
Câu 30: Nghiệm của phương trình
( ) ( )
33
log 1 1 log 1+ = + −xx
là
=xa
. Tính giá trị biểu thức
2
1= + +T a a
.
A.
2=T
. B.
4=T
. C.
7=T
. D.
5=T
.
Lời giải
Chọn C
Phương trình
( ) ( )
33
log 1 1 log 1+ = + −xx
(1),
Điều kiện:
10
1
10
+

−
x
x
x
.
Phương trình (1)
( ) ( )
33
log 1 log 3 3 + = −xx
3 3 1 − = +xx
2=x
(nhận), suy ra
2=a
.
Vây
2
2 2 1 7= + + =T
.
Câu 31: Cho hàm số
32
34= + − −y x x mx
. Tập hợp tất cả các giá trị của tham số
m
để hàm số đồng
biến trên khoảng
( )
;− +
là
A.
( )
1;5−
. B.
(
;3− −
. C. . D.
( )
1;− +
.
Lời giải
Chọn B
Ta có
2
36
= + −y x x m
.
Để hàm số đồng biến trên khoảng
( )
;− +
thì
2
0, 3 6 0,
+ − y x x x m x
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 17
Sưu tầm và biên soạn
Có
30
, nên suy ra
9 3 0 3
= + −mm
hay
(
;3 − −m
.
Câu 32: Cho hàm số
( )
y f x=
xác định, liên tục trên và có bảng biến thiên như sau:
Tìm tất cả các các giá trị thực của tham số
m
để phương trình
( )
1f x m−=
có đúng hai
nghiệm.
A.
0
1
m
m
=−
. B.
2
1
m
m
=−
−
. C.
21m− −
. D.
2
1
m
m
=−
−
.
Lời giải
Chọn D
Ta có
( ) ( )
11f x m f x m− = = +
. Để phương trình đã cho có đúng 2 nghiệm thì
1 1 2
1 0 1
mm
mm
+ = − = −


+ −

Câu 33: Một chiếc cốc có dạng hình trụ, chiều cao
16cm
, đường kính đáy bằng
8cm
, bề dày của thành
cốc và đáy cốc bằng
1cm
. Nếu đổ lượng nước vào cốc cách miệng cốc
5cm
thì được thể tích
1
V
, nếu đổ đầy cốc ta được khối trụ (tính cả thành cốc và đáy cốc) có thể tích
2
V
. Tỉ số
1
2
V
V
bằng
A.
2
3
. B.
245
512
. C.
45
128
. D.
11
16
.
Lời giải
Chọn C
Khi đổ nước vào cách miệng cốc
5cm
thì thể tích nước là
1
V
có dạng hình trụ với chiều cao
bằng
16 1 5 10cm− − =
, đường kính đáy là
8 2 6cm−=
.
Do đó:
3
1
2
3 .10 90 cmV

==
.
Thể tích khi đổ đầy nước (tính cả thành cốc và đáy cốc):
3
2
2
4 .16 256 cmV

==
.
Suy ra:
1
2
90 45
256 128
V
V
==
.
Câu 34: Cho hàm số
( )
y f x=
có đồ thị
( )
fx
như hình vẽ bên. Hàm số
( )
53y f x=−
nghịch biến trên
khoảng nào trong các khoảng dưới đây.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 18
Sưu tầm và biên soạn
A.
( )
2;5
. B.
( )
2;+
. C.
( )
3;1−
. D.
( )
0;3
.
Lời giải
Chọn C
Ta có
( ) ( ) ( )
5 3 5 3 3 5 3y x f x f x
= − − = − −
.
Hàm số nghịch biến
( ) ( )
3 ' 5 3 0 ' 5 3 0f x f x − − −
.
Quan sát đồ thị ta thấy
( )
5 3 0 5 3 2 1f x x x
− −
.
Dựa vào các đáp án ta Chọn C
Câu 35: Cho hàm số
( )
ln ln 2020
2
x
fx
x

=−

+

. Biết
( ) ( ) ( )
2 4 ... 2020
a
f f f
b
+ + =
, với
,*a b N
và
a
b
là phân số tối giản. Tính giá trị biểu thức
2S b a=−
.
A.
2021
2022
S =
. B.
0S =
. C.
1S =
. D.
1S =−
.
Lời giải
Chọn C
( )
ln ln 2020
2
x
fx
x

=−

+

điều kiện:
0
0
2
2
x
x
x
x

−
+
.
Ta có
( )
( )
( )
2
2
2
2 1 1
2
22
22
x
x
x
fx
xx
x x x x
xx


+
+

= = = = −
++
++
.
Khi đó:
( ) ( ) ( )
2 4 ... 2020f f f
++
1 1 1 1 1 1 1 1 1 1 1010 505
...
2 4 4 6 2018 2020 2020 2022 2 2022 2022 1011
= − + − + + − + − = − = =
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 19
Sưu tầm và biên soạn
Ta có
505
1011
là phân số tối giản
505
2 1011 1010 1
1011
a
S b a
b
=
= − = − =
=
.
II. PHẦN TỰ LUẬN
Câu 36: Tìm tham số
m
để hàm số
5mx
y
xm
+
=
−
đạt giá trị nhỏ nhất trên đoạn
0;1
bằng
7−
.
A.
5m =
. B.
2m =
. C.
0m =
. D.
1m =
.
Lời giải
Chọn B
Ta có
( )
2
2
5
0;
m
y x m
xm
−−
=
−
.
Hàm số đạt giá trị nhỏ nhất trên đoạn
0;1
bằng
7−
( )
17
0;1
y
m
= −
5
7
1
0;1
m
m
m
+
=−
−
2
2
0;1
m
m
m
=
=
. Vậy
2m =
.
Câu 37: Cho khối chóp tam giác
.S ABC
có các góc
60ASB BSC CSA= = =
và độ dài các cạnh
1SA =
,
2, 3SB SC==
. Thể tích khối chóp
.S ABC
bằng:
A.
3
2
. B.
2
2
. C.
6
2
. D.
32
2
.
Lời giải
Chọn B
Gọi
H
là hình chiếu của
C
lên mặt
( )
SAB
,
M
và
N
là hình chiếu của
H
lên
SA
và
SB
.
Ta có:
( )
M
C SAB
SA C
A HM
H
S
⊥
⊥
⊥
(Định lý 3 đường vuông góc).
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 20
Sưu tầm và biên soạn
Tương tự:
SB CN⊥
.
Xét hai tam giác vuông
CSM
và
CSN
có:
60
1
CSN CSM
CNS CMS v
= =
==
và cạnh
SH
chung.
Suy ra:
CSM CSN =
(g.c.g)
HM HN H =
thuộc phân giác trong
BSA
.
Xét tam giác vuông
3
cos60
2
33
.sin60
2
.SN SC
C
CS
S
CN
N
=
= =
=
.
Xét tam giác vuông
2
.
3
tan30SHN HN SN= =
.
Xét tam giác vuông
2 2 2
66CHN CH CN HN CH = − = =
.
Diện tích tam giác
SAB
:
s
1
..
2
3
in60
2
SAB
S SA SB
= =
.
Thể tích khối chóp
.S ABC
:
.
12
.
32
ABC SBS A
V CH S
==
.
Cách 2.
Trên các cạnh
,SB SC
lấy các điểm
B
và
C
sao cho
1SB SC SA

= = =
.
Do
60ASB BSC CSA= = =
nên hình chóp
.S AB C

là tứ diện đều cạnh bằng 1.
Suy ra
.
2
12
S AB C
V

=
.
Ta có:
.
..
.
12
.6
62
S AB C
S ABC S AB C
S ABC
V
SB SC
VV
V SB SC



= = = =
.
Câu 38: Cho hàm số
( )
y f x=
. Hàm số
( )
y f x
=
có bảng biến thiên như hình vẽ bên. Hỏi hàm số
( ) ( )
2g x f x x=−
có bao nhiêu điểm cực trị?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 21
Sưu tầm và biên soạn
Lời giải
Ta có
( ) ( )
2 2 1g x f x

=−
.
Cho
( ) ( )
1
02
2
g x f x

= =
(1).
Đặt
2tx=
.
Phương trình (1) là phương trình hoành độ giao điểm của đồ thị
( )
2y f x
=
và
1
2
y =
trở thành
phương trình hoành độ giao điểm của đồ thị
( )
y f t
=
và
1
2
y =
.
Ta có bảng biến thiên
Từ bảng biến thiên suy ra phương trình
( )
1
2
ft
=
có ba nghiệm
t
phân biệt nên
( )
1
2
2
fx
=
có
ba nghiệm
x
phân biệt.
Vậy hàm số
( )
gx
có
3
điểm cực trị.
Câu 39: Giải phương trình sau:
( ) ( ) ( )
2
33
3
11
log 3 log 1 log 4
22
x x x+ + − =
.
Lời giải
( ) ( ) ( )
2
33
3
11
log 3 log 1 log 4
22
x x x+ + − =
.
Điều kiện:
( )
2
30
3
1
1 0 1
0
0
40
x
x
x
xx
x
x
x
+
−
−

Với điều kiện trên phương trình đã cho tương đương
( ) ( )
3 3 3
log 3 log 1 log 4x x x+ + − =
( ) ( )
33
log 3 1 log 4x x x + − =

( )
3 1 4x x x + − =
Trường hợp 1:
1x
( )( )
3 1 4x x x + − =
+
∞
x
1
+
∞
1
1
∞
∞
f'
(
x
)
1
+
∞
t
1
+
∞
1
1
∞
∞
f'
(
t
)
1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 22
Sưu tầm và biên soạn
2
2 3 0
1
3
xx
x
x
− − =
=−
=
Trường hợp 2:
01x
( )( )
3 1 4x x x + − =
2
6 3 0
3 2 3
3 2 3
xx
x
x
+ − =
= − +
= − −
Vậy phương trình đã cho có hai nghiệm
3x =
và
3 2 3x = − +
.
---------- HẾT ----------
(loại)
(loại)
(thỏa mãn)
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 1
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 10
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
()y f x=
có bảng xét dấu đạo hàm như sau:
Hàm số
()y f x=
nghịch biến trong khoảng nào trong các khoảng sau?
B.
( ;3)−
. B.
(1; )+
. C.
(1;3)
. D.
( ;1)−
.
Câu 2: Cho hàm số
( )
y f x=
có đồ thị là hình vẽ sau:
Điểm cực đại của hàm số
( )
y f x=
là
A.
2.x =−
B.
0.x =
C.
2.x =
D.
2.y =
Câu 3: Hàm số
( )
y f x=
liên tục trên
1;3−
và có bảng biến thiên như sau
Giá trị nhỏ nhất của hàm số
( )
y f x=
trên đoạn
1;3−
là
A.
1
. B.
5
. C.
2
. D.
2−
.
Câu 4: Hàm số nào có đồ thị là hnh vẽ sau đây?
B.
42
34y x x= + −
. B.
21
35
x
y
x
+
=
−
. C.
32
34y x x= + +
. D.
32
34y x x= + −
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 2
Câu 5: Hàm số nào có bảng biến thiên là hàm sau đây?
A.
2
1
x
y
x
−−
=
−
. B.
2
1
x
y
x
+
=
−
. C.
2
1
x
y
x
−
=
−
. D.
2
1
x
y
x
−
=
+
.
Câu 6: Đồ thị
( )
C
của hàm số
24
1
x
y
x
−
=
+
có phương trnh đường tiệm cận đứng là
A.
2.y =
B.
1.y =−
C.
1.x =−
D.
2.x =
Câu 7: Với
,ab
là các số thực dương và
,

là các số thực, mệnh đề nào sau đây là sai?
A.
( )
+
=aa
. B.
( )
..=ab a b

. C.
( )
.
=aa
. D.
−
=
a
a
a

.
Câu 8: Với các số
,,abc
là các số dương và
1a
, mệnh đề nào sau đây sai?
A.
( )
log log log=+
a a a
bc b c
. B.
( )
log log .log=
a a a
bc b c
.
C.
log log=
c
aa
b c b
. D.
log log log=−
a a a
b
bc
c
.
Câu 9: Cho
,ab
là các số thực dương thỏa mãn
1a
và
log 3.
a
b =
Tính
( )
2
log
a
ab
.
A.
4
. B.
5
. C.
6
. D.
3
Câu 10: Tập xác định của hàm số
( )
3
log 1yx=−
là
A.
( )
1; +
. B.
( )
;1−
. C.
)
1; +
. D.
( )
;− +
.
Câu 11: Đạo hàm của hàm số
5
logyx=
là
A.
ln5
x
y
=
. B.
1
ln5
y
x
=
. C.
ln5yx
=
. D.
ln5
y
x
=
.
Câu 12: Phương trnh
ln 5 ln 1xx
có nghiệm là
A.
2x
. B.
3x
. C.
2x
. D.
1x
.
Câu 13: Phương trnh
2 3 4 5
33
xx+−
=
có nghiệm là
A.
3x =
. B.
4x =
. C.
2x =
. D.
1x =
.
Câu 14: Cho
( )
2
log 3 1 3x−=
. Giá trị biểu thức
( )
( )
2
log 2 1
3
log 10 3 2
x
Kx
−
= − +
bằng
A. 8. B. 35. C. 32. D. 14.
Câu 15: Mỗi mặt của hình bát diện đều là hình nào trong các hình sau?
A. Tam giác đều. B. Hình vuông. C. Bát giác đều. D. Ngũ giác đều.
Câu 16: Thể tích của khối hộp chữ nhật có ba kích thước
2,3
và
4
là
A.
24
. B.
8
. C.
9
. D.
20
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 3
Câu 17: Cho khối nón có chiều cao
9ha=
và bán kính đáy
2ra=
. Thể tích của khối nón đ cho là
A.
3
12Va
=
. B.
3
6Va
=
. C.
3
24Va
=
. D.
3
36Va
=
.
Câu 18: Cho khối trụ có chiều cao
4ha=
và bán kính đường tròn đáy
2ra=
. Thể tích của khối trụ đ
cho bằng
A.
3
8 a
. B.
3
16 a
. C.
3
6 a
. D.
3
16
3
a
.
Câu 19: Cho hnh nón có bán kính đường tròn đáy
3ra=
và đường sinh
2lr=
. Diện tích xung quanh
của hình nón bằng
A.
2
6 a
. B.
2
9 a
. C.
2
36 a
. D.
2
18 a
.
Câu 20: Thể tích của khối cầu có bán kính
2r =
là
A.
32
3
V
=
. B.
33
2
V
=
. C.
16V
=
. D.
32V
=
.
Câu 21: Cho hàm số
21
1
x
y
x
−
=
+
. Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên .
B.
Hàm số nghịch biến trên khoảng
( )
1;− +
.
C.
Hàm số nghịch biến trên các khoảng
( )
;1− −
và
( )
1;− +
.
D. Hàm số đồng biến trên khoảng
( )
;1− −
.
Câu 22: Hàm số nào sau đây có ba điểm cực trị?
A.
24
1
x
y
x
−
=
+
. B.
42
4 2020y x x= − − +
.
C.
32
35y x x= − +
. D.
42
3 2019y x x= − +
.
Câu 23: Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
34y x x= − +
trên đoạn
0;2
. Giá trị của biểu thức
22
Mm+
bằng
A. 52. B. 20. C. 8. D. 40.
Câu 24: Cho hàm số
( )
42
f x ax bx c= + +
có đồ thị như sau:
Khẳng định nào sau đây đúng?
A.
0, 0, 0.a b c
B.
0, 0, 0.abc
C.
0, 0, 0.abc
D.
0, 0, 0.abc
Câu 25: Số đường tiệm cận ngang của đồ thị hàm số
2
2
41
x
y
x
+
=
+
là
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 4
A.
2
. B.
1
. C.
4
. D.
0
.
Câu 26: Tập xác định của hàm số
( )
2
9 18y x x
= − +
là
A.
( ) ( )
;3 6;− +
. B.
\ 3;6
. C.
( )
3;6
. D.
3;6
.
Câu 27: Đạo hàm của hàm số
( )
4 2019x
f x e
+
=
là
A.
( )
4 2019
'
4
x
e
fx
+
=
. B.
( )
4
'f x e=
. C.
( )
4 2019
'4
x
f x e
+
=
. D.
( )
4 2019
'
x
f x e
+
=
.
Câu 28: Hãy tìm tập xác định
D
của hàm số
( )
2
ln 2 3y x x= − −
.
A.
( )
1;3D =−
. B.
( ) ( )
; 1 3;D = − − +
.
C.
(
)
; 1 3;D = − − +
. D.
1;3D =−
.
Câu 29: Hàm số
log
a
yx=
và
log
b
yx=
có đồ thị như hnh vẽ dưới đây.
Đường thẳng
3y =
cắt đồ thị tại hai điểm có hoành độ là
12
,xx
. Biết rằng
21
2xx =
, giá trị của
a
b
bằng
A.
1
3
. B.
3
. C.
2
. D.
3
2
.
Câu 30: Gọi
1
x
và
2
x
là hai nghiệm của phương trnh
25 7.5 10 0.
xx
Giá trị biểu thức
12
xx
bằng
A.
5
log 7
. B.
5
log 20
. C.
5
log 10
. D.
5
log 70
.
Câu 31: Phương trnh
2
24
2 3 7
xx
m
++
=−
có nghiệm khi
A.
23
;
3
m

+

. B.
7
;
3
m

+


. C.
7
;
3
m

+

. D.
)
5;m +
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 5
Câu 32: Leonhard Euler là nhà toán học rất nỗi tiếng người Thụy Sĩ đ khám phá ra công thức rất thú vị
và có ứng dụng nhiều trong khoa họ C. Đó là trong các khối đa diện bất kì thì
V E F− + =
“hằng số”, hằng số này được gọi là “đặc trưng Euler” (với V là số đỉnh, E là số cạnh và F là
số mặt của đa diện).
Em hy tính “đặc trưng Euler” của khối lập phương.
A. 2. B. 3. C. 1. D. 4.
Câu 33: Cho hình chóp
.S ABCD
có
( )
SA ABCD⊥
,
ABCD
là hình chữ nhật,
22AB BC a==
,
3SC a=
. Thể tích khối chóp
.S ABCD
bằng
A.
3
a
. B.
3
4
3
a
. C.
3
3
a
. D.
3
2
3
a
.
Câu 34: Cho hình chữ nhật
ABCD
có
23AB a=
,
60ADB =
. Gọi M, N lần lượt là trung điểm của AD,
BC. Khối trụ tròn xoay tạo thành khi quay hình chữ nhật
ABCD
(kể cả điểm trong) xung quanh
cạnh MN có thể tích bằng bao nhiêu?
A.
3
83Va
=
. B.
3
23
3
a
V
=
. C.
3
23Va
=
. D.
3
83
3
a
V
=
.
Câu 35: Cho
ABC
vuông tại
A
có
4 , 3AB a AC a==
. Quay
ABC
xung quanh cạnh
AB
, đường gấp
khúc
ACB
tạo nên một hình nón tròn xoay. Diện tích xung quanh của hnh nón đó là
A.
2
24
xq
Sa
=
. B.
2
12
xq
Sa
=
. C.
2
30
xq
Sa
=
. D.
2
15
xq
Sa
=
.
II. PHẦN TỰ LUẬN
Câu 36: Có bao nhiêu giá trị nguyên của tham số
m
để phương trnh
( )
22
2 1 4
2
2 log log 3 log 3x x m x+ − = −
có nghiệm
)
0
64;x +
?
Câu 37: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật, mặt bên
SAD
là tam giác đều cạnh
bằng
4a
và nằm trong mặt phẳng vuông góc với mặt phẳng
( )
ABCD
. Góc giữa mặt phẳng
( )
SBC
và mặt phẳng
( )
ABCD
là
30
. Thể tích của khối chóp
.S ABCD
là
A.
3
24 3a
. B.
3
16 3a
. C.
3
43a
. D.
3
48 3a
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 6
Câu 38: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên và hàm số
( )
y f x
=
có đồ thị như sau:
Đặt
( )
2
1
11
3 2 3
mm
g x f x x m
= − − − − + +
với
m
là tham số. Gọi
S
là tập hợp tất cả các giá
trị nguyên dương của
m
để hàm số
( )
y g x=
đồng biến trên khoảng
( )
7;8
. Tìm tập hợp
S
.
Câu 39: Cho
x
và
y
là các số thực dương thỏa mn điều kiện
( ) ( )
33
2 2 2 2x xy x y y xy x y+ + = + +
.
Tìm tất cả các giá trị của tham số
m
để phương trnh
22
2
33
4
log .log 2 4 0
2
xy
mm
yx
− + − =
có nghiệm
x
thuộc đoạn
1;3
.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 7
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
()y f x=
có bảng xét dấu đạo hàm như sau:
Hàm số
()y f x=
nghịch biến trong khoảng nào trong các khoảng sau?
B.
( ;3)−
. B.
(1; )+
. C.
(1;3)
. D.
( ;1)−
.
Lời giải
Chọn C
Câu 2: Cho hàm số
( )
y f x=
có đồ thị là hình vẽ sau:
Điểm cực đại của hàm số
( )
y f x=
là
A.
2.x =−
B.
0.x =
C.
2.x =
D.
2.y =
Lời giải
Chọn B
Dựa vào đồ thị ta có hàm số đạt cực đại tại
0; 2.
CD
xy==
Vậy điểm cực đại của hàm số là
0.x =
Câu 3: Hàm số
( )
y f x=
liên tục trên
1;3−
và có bảng biến thiên như sau
Giá trị nhỏ nhất của hàm số
( )
y f x=
trên đoạn
1;3−
là
A.
1
. B.
5
. C.
2
. D.
2−
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 8
Chọn D
Dựa vào bảng biến thiên ta thấy
1;3
min 2y
−
=−
.
Câu 4: Hàm số nào có đồ thị là hnh vẽ sau đây?
B.
42
34y x x= + −
. B.
21
35
x
y
x
+
=
−
. C.
32
34y x x= + +
. D.
32
34y x x= + −
.
Lời giải
Chọn D
Dựa vào đồ thị hàm số ta thấy:
Tập xác định của hàm số là . Suy ra loại phương án
B
v tập xác định của hàm số
21
35
x
y
x
+
=
−
là
5
\
3



.
lim ; lim
xx
yy
→+ →−
= + = −
. Suy ra loại phương án
A
v
42
lim( 3 4)
x
xx
→
+ − = +
.
Đồ thị hàm số luôn đi qua điểm
(0; 4)−
. Suy ra loại phương án
C
v đồ thị hàm số
32
34y x x= + +
luôn đi qua điểm
(0;4)
.
Hàm số
32
34y x x= + −
có tập xác định là ;
3 2 3 2
lim( 3 4) ; lim( 3 4)
xx
x x x x
→+ →−
+ − = + + − = −
và đồ thị hàm số luôn đi qua điểm
(0; 4)−
. Vậy
chọn phương án
D
.
Câu 5: Hàm số nào có bảng biến thiên là hàm sau đây?
A.
2
1
x
y
x
−−
=
−
. B.
2
1
x
y
x
+
=
−
. C.
2
1
x
y
x
−
=
−
. D.
2
1
x
y
x
−
=
+
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 9
Lời giải
Chọn A
Từ bảng biến thiên ta thấy, đồ thị hàm số nhận
1y =−
làm tiệm cận ngang.
Mà tiệm cận ngang trong hàm số
ax b
y
cx d
+
=
+
là đường thẳng
a
y
c
=
, nên ta loại ngay 3 đáp án
cuối là B, C, D. Vậy ta chọn đáp án A.
Câu 6: Đồ thị
( )
C
của hàm số
24
1
x
y
x
−
=
+
có phương trnh đường tiệm cận đứng là
A.
2.y =
B.
1.y =−
C.
1.x =−
D.
2.x =
Lời giải
Chọn C
Câu 7: Với
,ab
là các số thực dương và
,

là các số thực, mệnh đề nào sau đây là sai?
A.
( )
+
=aa
. B.
( )
..=ab a b

. C.
( )
.
=aa
. D.
−
=
a
a
a

.
Lời giải
Chọn A
Công thức sai:
( )
+
=aa
. Công thức đúng là
( )
.
=aa
.
Câu 8: Với các số
,,abc
là các số dương và
1a
, mệnh đề nào sau đây sai?
A.
( )
log log log=+
a a a
bc b c
. B.
( )
log log .log=
a a a
bc b c
.
C.
log log=
c
aa
b c b
. D.
log log log=−
a a a
b
bc
c
.
Lời giải
Chọn B
Với các số
,,abc
là các số dương và
1a
, ta có:
( )
log log log=+
a a a
bc b c
A đúng, B sai.
log log=
c
aa
b c b
C đúng
log log log=−
a a a
b
bc
c
D đúng.
Câu 9: Cho
,ab
là các số thực dương thỏa mãn
1a
và
log 3.
a
b =
Tính
( )
2
log
a
ab
.
A.
4
. B.
5
. C.
6
. D.
3
Lời giải
Chọn B
( )
22
log log log 2 3 5.
a a a
a b a b= + = + =
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 10
Câu 10: Tập xác định của hàm số
( )
3
log 1yx=−
là
A.
( )
1; +
. B.
( )
;1−
. C.
)
1; +
. D.
( )
;− +
.
Lời giải
Chọn A
Hàm số có nghĩa khi
.
Vậy tập xác định của hàm số là
( )
1;D = +
.
Câu 11: Đạo hàm của hàm số
5
logyx=
là
A.
ln5
x
y
=
. B.
1
ln5
y
x
=
. C.
ln5yx
=
. D.
ln5
y
x
=
.
Lời giải
Chọn B
Ta có:
5
1
log
ln5
y x y
x
= =
.
Câu 12: Phương trnh
ln 5 ln 1xx
có nghiệm là
A.
2x
. B.
3x
. C.
2x
. D.
1x
.
Lời giải
Chọn C
Điều kiện:
5 0 5
1 5.
1 0 1
xx
x
xx
Phương trnh đ cho tương đương với
5 1 2x x x
(thoả mãn).
Vậy
2.S
Câu 13: Phương trnh
2 3 4 5
33
xx+−
=
có nghiệm là
A.
3x =
. B.
4x =
. C.
2x =
. D.
1x =
.
Lời giải
Chọn B
Ta có:
2 3 4 5
3 3 2 3 4 5 2 8 4
xx
x x x x
+−
= + = − = =
.
Câu 14: Cho
( )
2
log 3 1 3x−=
. Giá trị biểu thức
( )
( )
2
log 2 1
3
log 10 3 2
x
Kx
−
= − +
bằng
A. 8. B. 35. C. 32. D. 14.
Lời giải
Chọn A
Ta có:
( )
2
log 3 1 3x−=
3 1 8 3.xx − = =
Với
3x=
khi đó giá trị biểu thức đ cho trở thành:
2
log 5
3
log 27 2K =+
3 5 8= + =
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 11
Câu 15: Mỗi mặt của hình bát diện đều là hình nào trong các hình sau?
A. Tam giác đều. B. Hình vuông. C. Bát giác đều. D. Ngũ giác đều.
Lời giải
Chọn A
Câu 16: Thể tích của khối hộp chữ nhật có ba kích thước
2,3
và
4
là
A.
24
. B.
8
. C.
9
. D.
20
.
Lời giải
Chọn A
Thể tích khối hộp chữ nhật là
2.3.4 24V ==
.
Câu 17: Cho khối nón có chiều cao
9ha=
và bán kính đáy
2ra=
. Thể tích của khối nón đ cho là
A.
3
12Va
=
. B.
3
6Va
=
. C.
3
24Va
=
. D.
3
36Va
=
.
Lời giải
Chọn A
Thể tích của khối nón đ cho là
2 2 3
11
(2 ) (9 ) 12
33
V r h a a a
= = =
.
Câu 18: Cho khối trụ có chiều cao
4ha=
và bán kính đường tròn đáy
2ra=
. Thể tích của khối trụ đ
cho bằng
A.
3
8 a
. B.
3
16 a
. C.
3
6 a
. D.
3
16
3
a
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 12
Chọn B
Ta có: Diện tích đường tròn đáy:
( )
2
22
. . 2 4S r a a
= = =
.
Vậy thể tích của khối trụ đ cho là:
23
. 4 .4 16V S h a a a

= = =
.
Câu 19: Cho hình nón có bán kính đường tròn đáy
3ra=
và đường sinh
2lr=
. Diện tích xung quanh
của hình nón bằng
A.
2
6 a
. B.
2
9 a
. C.
2
36 a
. D.
2
18 a
.
Lời giải
Chọn D
Ta có
26l r a==
.
Diện tích xung quanh của hình nón
( )
N
là:
S rl
=
.3 .6aa
=
2
18 a
=
.
Câu 20: Thể tích của khối cầu có bán kính
2r =
là
A.
32
3
V
=
. B.
33
2
V
=
. C.
16V
=
. D.
32V
=
.
Lời giải
Chọn A
Ta có
33
4 4 32
.2
3 3 3
Vr

= = =
.
THÔNG HIỂU
Câu 21: Cho hàm số
21
1
x
y
x
−
=
+
. Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên .
B.
Hàm số nghịch biến trên khoảng
( )
1;− +
.
C.
Hàm số nghịch biến trên các khoảng
( )
;1− −
và
( )
1;− +
.
D. Hàm số đồng biến trên khoảng
( )
;1− −
.
Lời giải
Chọn D
Tập xác định
\{ 1}D =−
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 13
2
3
'0
( 1)
y x D
x
=
+
.
Vậy hàm số đồng biến trên khoảng
( ; 1)− −
.
Câu 22: Hàm số nào sau đây có ba điểm cực trị?
A.
24
1
x
y
x
−
=
+
. B.
42
4 2020y x x= − − +
.
C.
32
35y x x= − +
. D.
42
3 2019y x x= − +
.
Lời giải
Chọn D
Hàm số có ba cực trị nên ta loại đáp án A và C.
Xét đáp án B
3
' 4 8y x x= − −
3
' 0 4 8 0 0y x x x= − − = =
Đạo hàm có một nghiệm đơn nên đổi dấu một lần qua nghiệm
0x =
nên hàm số có 1 cực trị.
Loại đáp án B.
Câu 23: Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
34y x x= − +
trên đoạn
0;2
. Giá trị của biểu thức
22
Mm+
bằng
A. 52. B. 20. C. 8. D. 40.
Lời giải
Chọn D
( )
( )
2
1 0;2
3 3; 0
1 0;2
x
y x y
x
=

= − =
= −
.
Ta có
( ) ( ) ( )
0 4; 1 2; 2 6y y y= = =
Do đó
22
6; 2 40M m M m= = + =
.
Câu 24: Cho hàm số
( )
42
f x ax bx c= + +
có đồ thị như sau:
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 14
Khẳng định nào sau đây đúng?
A.
0, 0, 0.a b c
B.
0, 0, 0.abc
C.
0, 0, 0.abc
D.
0, 0, 0.abc
Lời giải
Chọn A
Quan sát đồ thị ta thấy
( )
lim 0
x
f x a
→+
= −
.
Giao điểm của đồ thị với
Oy
là
( )
0;c
nằm phía trên trục hoành
0c
.
( )
( )
( )
( )
32
2
0
4 2 2 2 , 0
2 0 *
x
f x ax bx x ax b f x
ax b
=

= + = + =
+=
.
Hàm số có 3 điểm cực trị nên phương trnh
( )
*
có 2 nghiệm phân biệt khác
0
2 0 0ab b −
.
Vậy
0, 0, 0a b c
.
Câu 25: Số đường tiệm cận ngang của đồ thị hàm số
2
2
41
x
y
x
+
=
+
là
A.
2
. B.
1
. C.
4
. D.
0
.
Lời giải
Chọn A
Ta có:
2
2
lim
41
x
x
x
→+
+
+
2
2
1
lim
1
4
x
x
x
→+
+
=
+
1
2
=
.
Và:
2
2
lim
41
x
x
x
→−
+
+
2
2
lim
1
4
x
x
x
x
→−
+
=
−+
1
2
=−
.
Vậy có hai đường tiệm cận ngang của đồ thị hàm số
2
2
41
x
y
x
+
=
+
.
Câu 26: Tập xác định của hàm số
( )
2
9 18y x x
= − +
là
A.
( ) ( )
;3 6;− +
. B.
\ 3;6
. C.
( )
3;6
. D.
3;6
.
Lời giải
Chọn A
Hàm số xác định
2
9 18 0 3 6x x x x− +
.
Nên tập xác định của hàm số là
( ) ( )
;3 6;D = − +
. Chọn đáp án A.
Câu 27: Đạo hàm của hàm số
( )
4 2019x
f x e
+
=
là
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 15
A.
( )
4 2019
'
4
x
e
fx
+
=
. B.
( )
4
'f x e=
. C.
( )
4 2019
'4
x
f x e
+
=
. D.
( )
4 2019
'
x
f x e
+
=
.
Lời giải
Chọn C
Ta có:
( ) ( )
4 2019 4 2019
' . 4 2019 ' 4.
xx
f x e x e
++
= + =
. Chọn đáp án C.
Câu 28: Hãy tìm tập xác định
D
của hàm số
( )
2
ln 2 3y x x= − −
.
A.
( )
1;3D =−
. B.
( ) ( )
; 1 3;D = − − +
.
C.
(
)
; 1 3;D = − − +
. D.
1;3D =−
.
Lời giải
Chọn B
Điều kiện:
( )( )
2
2 3 0 1 3 0x x x x− − + −
1x −
hoặc
3x
.
Câu 29: Hàm số
log
a
yx=
và
log
b
yx=
có đồ thị như hnh vẽ dưới đây.
Đường thẳng
3y =
cắt đồ thị tại hai điểm có hoành độ là
12
,xx
. Biết rằng
21
2xx =
, giá trị của
a
b
bằng
A.
1
3
. B.
3
. C.
2
. D.
3
2
.
Lời giải
Chọn D
Ta có
3
11
3 log
b
x x b= =
3
22
3 log
a
x x a= =
Mà
33
3
21
2x 2 2
a
x a b
b
= = =
.
Câu 30: Gọi
1
x
và
2
x
là hai nghiệm của phương trnh
25 7.5 10 0.
xx
Giá trị biểu thức
12
xx
bằng
A.
5
log 7
. B.
5
log 20
. C.
5
log 10
. D.
5
log 70
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 16
Lời giải
Chọn C
Đặt
5
x
t
0.t
Phương trnh đ cho trở thành
2
5
1
5 5 5
7 10 0 .
log 2
2
52
x
x
x
t
tt
x
t
Khi đó
1 2 5 5 5 5
1 log 2 log 5 log 2 log 10.xx
Câu 31: Phương trnh
2
24
2 3 7
xx
m
++
=−
có nghiệm khi
A.
23
;
3
m

+

. B.
7
;
3
m

+


. C.
7
;
3
m

+

. D.
)
5;m +
.
Lời giải
Chọn D
Ta có:
2
24xx++
( )
2
1 3 3x= + +
,
x
. Suy ra
2
2 4 3
2 2 8
xx++
=
,
x
.
Phương trnh
2
24
2 3 7
xx
m
++
=−
có nghiệm khi
3 7 8m−
5m
.
Vậy, phương trnh có nghiệm khi
)
5;m +
.
Câu 32: Leonhard Euler là nhà toán học rất nỗi tiếng người Thụy Sĩ đ khám phá ra công thức rất thú vị
và có ứng dụng nhiều trong khoa họ C. Đó là trong các khối đa diện bất kì thì
V E F− + =
“hằng số”, hằng số này được gọi là “đặc trưng Euler” (với V là số đỉnh, E là số cạnh và F là
số mặt của đa diện).
Em hy tính “đặc trưng Euler” của khối lập phương.
A. 2. B. 3. C. 1. D. 4.
Lời giải
Chọn A
Bảng công thức đa diện Euler.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 17
Đặc trưng Euler
được định nghĩa cổ điển cho các khối đa diện lồi,
theo công thức:
2V E F
= − + =
.
Câu 33: Cho hình chóp
.S ABCD
có
( )
SA ABCD⊥
,
ABCD
là hình chữ nhật,
22AB BC a==
,
3SC a=
. Thể tích khối chóp
.S ABCD
bằng
A.
3
a
. B.
3
4
3
a
. C.
3
3
a
. D.
3
2
3
a
.
Lời giải
Chọn B
Ta có:
22
5AC AB BC a= + =
;
22
2SA SC AC a= − =
.
Thể tích khối chóp
.S ABCD
là
.
1
..
3
S ABCD
V SA AB BC=
Vậy:
3
.
14
2 .2 .
33
S ABCD
a
V a a a= =
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 18
Câu 34: Cho hình chữ nhật
ABCD
có
23AB a=
,
60ADB =
. Gọi M, N lần lượt là trung điểm của AD,
BC. Khối trụ tròn xoay tạo thành khi quay hình chữ nhật
ABCD
(kể cả điểm trong) xung quanh
cạnh MN có thể tích bằng bao nhiêu?
A.
3
83Va
=
. B.
3
23
3
a
V
=
. C.
3
23Va
=
. D.
3
83
3
a
V
=
.
Lời giải
Chọn C
Ta có
23
2 2tan60
23
AD AB a
ra= = = =
.
Thể tích khối trụ là:
2 2 3
2 3 2 3V Bh r h a a a
= = = =
.
Câu 35: Cho
ABC
vuông tại
A
có
4 , 3AB a AC a==
. Quay
ABC
xung quanh cạnh
AB
, đường gấp
khúc
ACB
tạo nên một hình nón tròn xoay. Diện tích xung quanh của hnh nón đó là
A.
2
24
xq
Sa
=
. B.
2
12
xq
Sa
=
. C.
2
30
xq
Sa
=
. D.
2
15
xq
Sa
=
.
Lời giải
Chọn D
Trong
ABC
:
22
5BC AB AC a= + =
.
Diện tích xung quanh của hình nón:
2
. . .3 .5 15
xq
S Rl AC BC a a a
= = = =
.
II. PHẦN TỰ LUẬN
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 19
Câu 36: Có bao nhiêu giá trị nguyên của tham số
m
để phương trnh
( )
22
2 1 4
2
2 log log 3 log 3x x m x+ − = −
có nghiệm
)
0
64;x +
?
Lời giải
( )
22
2 1 4
2
2 log log 3 log 3x x m x+ − = −
.
( )
1
Giả sử
x
là nghiệm của phương trnh
( )
1
2
log 6x
.
Đặt
2
log , 6t x t=
.
( ) ( )
( )
2
2 2 2
2
4 4 12
1 2 3 3 4 4 12 6 9
69
tt
t t m t t t m t t m
tt
−−
− − = − − − = − + =
−+
.
( )
2
( )
2
là phương trnh cho hoành độ giao điểm của
2
đồ thị hàm số
2
2
4 4 12
69
ym
tt
y
tt
=
−−
=
−+
Xét
2
2
4 4 12
69
tt
y
tt
−−
=
−+
,
)
6;t +
.
( )
2
2
2
20 48 36
'
69
tt
y
tt
− + +
=
−+
, cho
3
'0
3
5
t
y
t
=
=
=−
.
Bảng biến thiên:
Để phương trnh có nghiệm thì
4 12m
;
5;6;7;8;9;10;11;12mm
.
Vậy có
8
giá trị nguyên thỏa điều kiện bài toán.
Câu 37: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật, mặt bên
SAD
là tam giác đều cạnh
bằng
4a
và nằm trong mặt phẳng vuông góc với mặt phẳng
( )
ABCD
. Góc giữa mặt phẳng
( )
SBC
và mặt phẳng
( )
ABCD
là
30
. Thể tích của khối chóp
.S ABCD
là
A.
3
24 3a
. B.
3
16 3a
. C.
3
43a
. D.
3
48 3a
.
Lời giải
Chọn B
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 20
Gọi
,HK
lần lượt là trung điểm của
AD
và
BC
. Khi đó
( )
⊥AH ABCD
, suy ra
( )
⊥BC SKH
, nên
( )
( )
, 30= = SKH SB ABC
.
Có
.3
23
2
==
AD
SH a
.cot30 6 = =HK SH a
.
Vậy
3
.
1
. . . 16 3
3
==
S ABCD
V SH AD HK a
.
Câu 38: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên và hàm số
( )
y f x
=
có đồ thị như sau:
Đặt
( )
2
1
11
3 2 3
mm
g x f x x m
= − − − − + +
với
m
là tham số. Gọi
S
là tập hợp tất cả các giá
trị nguyên dương của
m
để hàm số
( )
y g x=
đồng biến trên khoảng
( )
7;8
. Tìm tập hợp
S
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 21
( )
1
33
mm
g x f x x

= − − − −
Cho
( )
0 ' 1
33
mm
g x f x x
= − = − −
11
33
11
33
33
33
mm
xx
mm
xx
mm
xx

− = − = −



− = = +



− = = +


Bảng xét dấu:
Để hàm số
( )
y g x=
đồng biến trên khoảng
( )
7;8
thì
37
3
12
17
21 24
3
18
3
m
m
m
m
m
+
−



+
.
Vậy
(
;12 21;24 .S = −
Câu 39: Cho
x
và
y
là các số thực dương thỏa mn điều kiện
( ) ( )
33
2 2 2 2x xy x y y xy x y+ + = + +
.
Tìm tất cả các giá trị của tham số
m
để phương trnh
22
2
33
4
log .log 2 4 0
2
xy
mm
yx
− + − =
có nghiệm
x
thuộc đoạn
1;3
.
Lời giải
Ta có:
( ) ( )
3 3 3 2 3
2 2 2 2 3 2 0x xy x y y xy x y x xy y+ + = + + − − =
( )
( )
( )( )
22
2 0 2 0 2x y x xy y x y x y x y + − − = + − = =
.
Với
2xy=
phương trnh
22
2
33
4
log .log 2 4 0
2
xy
mm
yx
− + − =
. (*) trở thành:
2
33
log log 2 4 0x m x m− + − =
.(1)
Đặt
3
log , 0;1t x t=
, phương trnh (1) trở thành:
2
2 4 0t mt m− + − =
2mt = +
.(2)
Yêu cầu bài toán
phương trnh (2) có nghiệm
0;1 2 3tm
.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Page 22
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 11
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
y f x
xác định và có đạo hàm trên khoảng
K.
Khẳng định nào sau đây là sai?
A. Nếu hàm số
y f x
đồng biến trên khoảng K thì
' 0, K.f x x
B. Nếu
' 0, Kf x x
thì hàm số
fx
đồng biến trên khoảng K.
C. Nếu
' 0, Kf x x
thì hàm số
fx
đồng biến trên khoảng K
D. Nếu
' 0, Kf x x
và
'0fx
chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên
khoảng K.
Câu 2: Cho hàm số
()y f x=
có đồ thị như hình vẽ:
Đồ thị hàm số
()y f x=
có mấy điểm cực trị?
A. 2. B. 1. C. 0. D. 3.
Câu 3: Giả sử hàm số f xác định trên tập hợp
D
. Nếu tồn tại một điểm
0
xD
sao cho
0
( ) ( ),f x f x x D
. Khẳng định nào sau đây là khẳng định đúng?
A. Số
0
()M f x=
được gọi là giá trị lớn nhất của hàm số f trên
D
.
B. Số
0
()m f x=
được gọi là giá trị nhỏ nhất của hàm số f trên
D
.
C. Số
0
()M f x=
được gọi là giá trị nhỏ nhất của hàm số f trên D tại
0
x
.
D. Số
0
()M f x=
được gọi là giá trị lớn nhất của hàm số f trên tập xác định.
Câu 4: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
32
32y x x= − +
. B.
42
32y x x= − +
. C.
42
22y x x= − + +
. D.
32
32y x x= − + +
.
Câu 5: Cho đường cong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào?
A.
23
1
x
y
x
+
=
+
. B.
21
1
x
y
x
−
=
+
. C.
22
1
x
y
x
−
=
−
. D.
21
1
x
y
x
+
=
−
.
x
y
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 2
Câu 6: Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
21
1
x
y
x
−
=
+
.
A.
1
;1
2
xy= = −
. B.
1 ; 2xy= = −
. C.
1; 2xy= − =
. D.
1
1;
2
xy= − =
.
Câu 7: Cho
01a
và
0; 1.bb
Mệnh đề nào sau đây sai?
A.
1
log .
log
a
b
b
a
=
B.
log 0.
a
a =
C.
log
.
a
b
ab=
D.
1
log log .
a
a
a
bb
a
=
Câu 8: Cho
a
là số thực dương khác
1
. Đẳng thức nào sau đây là đúng với mọi số thực dương
,xy
?
A.
log log log
a a a
x
xy
y
=+
. B.
( )
log log
aa
x
xy
y
=−
.
C.
log
log
log
a
a
a
x
x
yy
=
. D.
log log log
a a a
x
xy
y
=−
.
Câu 9: Tập xác định
D
của hàm số
log ( ).yx=−
2016
2017
A.
)
;.D = +0
B.
)
;.D = +2017
C.
( )
;.D = +0
D.
( )
;.D = +2017
Câu 10: Hàm số
2
2
xx
y
−
=
có đạo hàm là
A.
( )
2
21
2
xx
xx
−−
−
B.
( )
2
2 1 .2
xx
x
−
−
. C.
2
2 .ln2
xx−
. D.
( )
2
2 1 .2 .ln2
xx
x
−
−
.
Câu 11: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
( )
2
x
y =
B.
yx=
C.
2
x
y =
D.
( )
2
x
y
−
=
Câu 12: Nghiệm của phương trình
1
39
−
=
x
là
A.
2=−x
B.
3=x
C.
2=x
D.
3=−x
Câu 13: Tập nghiệm của phương trình
1
2
1
125
25
x
x
+

=


là
A.
1
.
8

−


B.
1
.
4

−


C.
4.
D.
3.
Câu 14: Tìm tập nghiệm S của bất phương trình
( )
0,5
log 2 0x −
A.
( )
;3 .S = −
B.
( )
2;3 .S =
C.
( ) ( )
; 1 3; .S = − − +
D.
( )
3; .S = +
x
y
2
1
2
O
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 3
Câu 15: Mỗi hình sau đấy gồm hữu hạn các đa giác.Hình nào là hình đa diện?
A. B. C. D.
Câu 16: Khẳng định nào sau đây là sai?
A. Thể tích của khối chóp có diện tích đáy
B
và chiều cao
h
là
1
3
V Bh=
.
B. Thể tích của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
V Bh=
.
C. Thể tích của một khối hộp chữ nhật bằng tích ba kính thước của nó.
D. Thể tích của khối chóp có diện tích đáy
B
và chiều cao
h
là
3V Bh=
.
Câu 17: Gọi
, ,rlh
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Đẳng thức nào
sau đây luôn đúng.
A.
2 2 2
l h r=+
B.
2 2 2
1 1 1
l h r
=+
C.
2 2 2
r h l=+
D.
2
l hr=
Câu 18: Cho hình nón
( )
N
có chiều cao h, độ dài đường sinh l, bán kính đáy r. Ký hiệu
tp
S
là diện tích
toàn phần của
( )
N
. Công thức nào sau đây là đúng?
A.
tp
S rl
=
. B.
2
tp
S rl r

=+
. C.
2
tp
S rl r

=+
. D.
2
2
tp
S rl r

=+
.
Câu 19: Thể tích
V
của khối trụ có bán kính đáy bằng
2
a
và chiều cao bằng
2a
là:
A.
3
.
2
a
V
=
B.
3
.
3
a
V
=
C.
3
2
.
3
a
V
=
D.
3
.
6
a
V
=
Câu 20: Bán kính
r
của khối cầu có thể tích
( )
3
64 cmV
=
là
A.
3.r cm=
B.
27r cm=
C.
3
48r cm=
D.
3
9.r cm=
Câu 21: Cho hàm số
()y f x=
xác định trên và có bảng biến thiên như hình vẽ dưới đây. Hàm số
()y f x=
đồng biến trên khoảng nào sau đây?
A.
( )
0;4 .
B.
( )
2;1 .−
C.
( )
1;4 .
D.
( )
4; .+
Câu 22: Cho hàm số
( )
y f x=
có đạo hàm là
( ) ( ) ( )
2
2
2 1 1f x x x x
= − +
. Số điểm cực trị của hàm số đã
cho là
A.
0
. B.
1
. C.
2
. D.
3
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 4
Câu 23: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
3y x x=−
trên
1;2
bằng:
A.
0
. B.
2
. C.
14
27
. D.
7−
.
Câu 24: Cho hàm số
( )
42
0y ax bx c a= + +
có đồ thị như hình bên. Xác định dấu của
,,abc
.
A.
0, 0, 0abc
. B.
0, 0, 0a b c
. C.
0, 0, 0abc
. D.
0, 0, 0a b c
.
Câu 25: Số đường tiệm cận của đồ thị hàm số (hình vẽ sau) là:
A.
0.
B.
1.
C.
2.
D.
3.
Câu 26: Tập xác định của hàm số
22
(3 1)yx
−
=−
là:
A.
B.
1
.
3
D

=


C.
11
; ; .
33
D
= − − +
D.
11
;.
33

−


Câu 27: Tập xác định của hàm số
0,5
log ( 1)yx=+
là:
A.
( 1; ).D = − +
B.
\{ 1}.D =−
C.
(0; ).D = +
D.
( ; 1).− −
Câu 28: Cho hàm số
log
a
yx=
và
log
b
yx=
có đồ thị như
sau:
Mệnh đề nào dưới đây là sai?
A.
1.ab
B.
0 1 .ba
C.
0 1 .ab
D.
0.ab
Câu 29: Hàm số nào trong các hàm số cho dưới đây nghịch
biến trên tập xác định của nó?
x
y
-2
2
-1
1
y=
log
b
x
y=
log
a
x
1
O
y
x
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 5
A.
ln .yx=
B.
log .yx
=
C.
.
3
x
y

=


D.
3
.
x
y

=


Câu 30: Trong các phương trình cho dưới đây, phương trình nào có tập ngiệm là
2?S =
A.
( )
2
log log .x x x−=
B.
C.
4 5.2 4 0.
xx
− + =
D.
5.3 4 0.
x
+=
Câu 31: Với phương trình
33
4 5.2 4 0,
xx−−
+ + =
nếu đặt
3
2
x
t
−
=
thì điều kiện của
t
là
A.
0.t
B.
1.t
C.
3.t
D.
.t
Câu 32:
Cho hình chóp tam giác đều
.S ABC
có
O
là trọng tâm tam giác
.ABC
Gọi
I
là trung điểm của
BC
và
E
là điểm thuộc đoạn thẳng
AI
sao cho
3.AI AE=
Đường cao của hình chóp
.S ABC
là
A.
.SO
B.
.SI
C.
.SA
D.
.SE
Câu 33: Cho khối lăng trụ tam giác đều
.ABC AB C
có
,2AB a A C a
==
(hình vẽ bên).
Thể tích
V
của khối lăng trụ
.ABC AB C
là
A.
3
.
4
a
V =
B.
3
3
.
4
a
V =
C.
3
3
.
4
a
V =
D.
3
15
.
4
a
V =
Câu 34: Cho một hình nón có bán kính đáy bằng
a
và góc ở đỉnh bằng
60
. Tính diện tích xung quanh
của hình nón đó.
A.
2
4
xq
Sa
=
. B.
2
23
3
xq
a
S
=
. C.
2
43
3
xq
a
S
=
. D.
2
2
xq
Sa
=
.
Câu 35: Cho hình trụ có chiều cao bằng
53
. Cắt hình trụ đã cho bởi mặt phẳng song song với trục và
cách trục một khoảng bằng
1
, thiết diện thu được có diện tích bằng
30
. Diện tích xung quanh
của hình trụ đã cho bằng
A.
10 3
. B.
5 39
. C.
20 3
. D.
10 39
.
II. PHẦN TỰ LUẬN (4 câu – 3 điểm)
Câu 36: Giải phương trình sau :
( ) ( ) ( )
8
93
3
11
log 3 log 1 log 4
24
x x x+ + − =
Câu 37: Cho hình lăng trụ
.ABC A B C
có đáy là tam giác đều cạnh bằng
a
,hình chiếu vuông góc của
A
lên mặt phẳng
( )
ABC
trùng với trọng tâm
G
của tam giác
ABC
. Biết khoảng cách giữa
BC
và
AA
bằng
3
4
a
. Tính thể tích khối chóp
.B ABC
.
Câu 38: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ sau. Tìm
m
để hàm số
( )
y f x m=+
đồng biến trên khoảng
( )
4;+
.
2a
a
C'
B'
A
B
C
A'
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 6
Câu 39: Có bao nhiêu số nguyên
y
sao cho với mỗi
y
không có quá
50
số nguyên
x
thoả mãn bất phương
trình sau:
( )
32
3
2 log
yx
xy
−
+
?
-----HẾT-----
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 7
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM
Câu 1: Cho hàm số
y f x
xác định và có đạo hàm trên khoảng
K.
Khẳng định nào sau đây là sai?
A. Nếu hàm số
y f x
đồng biến trên khoảng K thì
' 0, K.f x x
B. Nếu
' 0, Kf x x
thì hàm số
fx
đồng biến trên khoảng K.
C. Nếu
' 0, Kf x x
thì hàm số
fx
đồng biến trên khoảng K
D. Nếu
' 0, Kf x x
và
'0fx
chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên
khoảng K.
Lời giải
Chọn C
Nếu
' 0, Kf x x
thì hàm số
fx
đồng biến trên khoảng K (Dấu bằng xảy ra tại hữu hạn
điểm).
Câu 2: Cho hàm số
()y f x=
có đồ thị như hình vẽ:
Đồ thị hàm số
()y f x=
có mấy điểm cực trị?
A. 2. B. 1. C. 0. D. 3.
Lời giải
Chọn A
Câu 3: Giả sử hàm số f xác định trên tập hợp
D
. Nếu tồn tại một điểm
0
xD
sao cho
0
( ) ( ),f x f x x D
. Khẳng định nào sau đây là khẳng định đúng?
A. Số
0
()M f x=
được gọi là giá trị lớn nhất của hàm số f trên
D
.
B. Số
0
()m f x=
được gọi là giá trị nhỏ nhất của hàm số f trên
D
.
C. Số
0
()M f x=
được gọi là giá trị nhỏ nhất của hàm số f trên D tại
0
x
.
D. Số
0
()M f x=
được gọi là giá trị lớn nhất của hàm số f trên tập xác định.
Lời giải
Chọn A
Câu 4: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 8
A.
32
32y x x= − +
. B.
42
32y x x= − +
. C.
42
22y x x= − + +
. D.
32
32y x x= − + +
.
Lời giải
Chọn A
Dựa vào đồ thị ta thấy đây là đồ thị của hàm số bậc ba
( )
32
,0y ax bx cx d a= + + +
với
0a
.
Câu 5: Cho đường cong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào?
A.
23
1
x
y
x
+
=
+
. B.
21
1
x
y
x
−
=
+
. C.
22
1
x
y
x
−
=
−
. D.
21
1
x
y
x
+
=
−
.
Lời giải
Chọn B
Từ đồ thị ta thấy đây là đồ thị hàm số
ax b
y
cx d
+
=
+
có tiện cận đứng là
1x =−
(loại đáp án C và D)
và là hàm số đồng biến (loại đáp án A).
Câu 6: Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
21
1
x
y
x
−
=
+
.
A.
1
;1
2
xy= = −
. B.
1 ; 2xy= = −
. C.
1; 2xy= − =
. D.
1
1;
2
xy= − =
.
Lời giải
Chọn C
Vì
1
2
21
lim lim 2
1
1
1
xx
x
x
x
x
→ →
−
−
==
+
+
nên đường thẳng
2y =
là tiệm cận ngang của đồ thị hàm số.
Vì
1
21
lim
1
x
x
x
+
→−
−
= −
+
,
1
21
lim
1
x
x
x
−
→−
−
= +
+
nên đường thẳng
1x =
là tiệm cận đứng của đồ thị hàm
số.
x
y
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 9
Câu 7: Cho
01a
và
0; 1.bb
Mệnh đề nào sau đây sai?
A.
1
log .
log
a
b
b
a
=
B.
log 0.
a
a =
C.
log
.
a
b
ab=
D.
1
log log .
a
a
a
bb
a
=
Lời giải
Chọn B
log 1.
a
a =
Câu 8: Cho
a
là số thực dương khác
1
. Đẳng thức nào sau đây là đúng với mọi số thực dương
,xy
?
A.
log log log
a a a
x
xy
y
=+
. B.
( )
log log
aa
x
xy
y
=−
.
C.
log
log
log
a
a
a
x
x
yy
=
. D.
log log log
a a a
x
xy
y
=−
.
Lời giải
Chọn D
Theo tính chất lôgarit của một thương, ta có
log log log
a a a
x
xy
y
=−
.
Câu 9: Tập xác định
D
của hàm số
log ( ).yx=−
2016
2017
A.
)
;.D = +0
B.
)
;.D = +2017
C.
( )
;.D = +0
D.
( )
;.D = +2017
Lời giải
Chọn D
Điều kiện là:
xx− 2017 0 2017
Hay TXĐ:
( )
;.D = +2017
Câu 10: Hàm số
2
2
xx
y
−
=
có đạo hàm là
A.
( )
2
21
2
xx
xx
−−
−
B.
( )
2
2 1 .2
xx
x
−
−
. C.
2
2 .ln2
xx−
. D.
( )
2
2 1 .2 .ln2
xx
x
−
−
.
Lời giải
Chọn D
Áp dụng quy tắc đạo hàm hàm số mũ
( )
. .ln
uu
a u a a
=
.
Ta có:
( )
( )
22
2
.2 .ln2 2 1 .2 .ln2
x x x x
y x x x
−−
= − = −
.
Câu 11: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
x
y
2
1
2
O
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 10
A.
( )
2
x
y =
B.
yx=
C.
2
x
y =
D.
( )
2
x
y
−
=
Lời giải
Chọn A
Đồ thị hàm số là đường cong đi qua hai điểm
( ) ( )
0;1 ; 2;2
. Chỉ có hàm số
( )
2
x
y =
thỏa mãn.
Câu 12: Nghiệm của phương trình
1
39
−
=
x
là
A.
2=−x
B.
3=x
C.
2=x
D.
3=−x
Lời giải
Chọn B
1
3 9 1 2 3
−
= − = =
x
xx
Câu 13: Tập nghiệm của phương trình
1
2
1
125
25
x
x
+

=


là
A.
1
.
8

−


B.
1
.
4

−


C.
4.
D.
3.
Lời giải
Chọn B
Phương trình
1
2 2 2 6
11
125 5 5 2 2 6 .
25 4
x
x x x
x x x
+
−−

= = − − = = −


Câu 14: Tìm tập nghiệm S của bất phương trình
( )
0,5
log 2 0x −
A.
( )
;3 .S = −
B.
( )
2;3 .S =
C.
( ) ( )
; 1 3; .S = − − +
D.
( )
3; .S = +
Lời giải
Chọn D
Ta có:
( )
0,5
0
20
2
log 2 0 3
3
2 0,5
x
x
xx
x
x
−
−

−
Câu 15: Mỗi hình sau đấy gồm hữu hạn các đa giác.Hình nào là hình đa diện?
A. B. C. D.
Lời giải
Chọn A
Quan sát bốn hình trên ta thấy chỉ có một hình A là hình đa diện.
Hình B,C, D không phải là hình đa diện, vì vi phạm điều b) Mỗi cạnh của đa giác nào cũng là
cạnh chung của đúng hai đa giác.
Câu 16: Khẳng định nào sau đây là sai?
A. Thể tích của khối chóp có diện tích đáy
B
và chiều cao
h
là
1
3
V Bh=
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 11
B. Thể tích của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
V Bh=
.
C. Thể tích của một khối hộp chữ nhật bằng tích ba kính thước của nó.
D. Thể tích của khối chóp có diện tích đáy
B
và chiều cao
h
là
3V Bh=
.
Lời giải
Chọn D
Theo công thức tính thể tích khối chóp, khối lăng trụ và khối hộp chữ nhật ta thấy các khẳng định
đúng là A, B, C.
Câu 17: Gọi
, ,rlh
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Đẳng thức nào
sau đây luôn đúng.
A.
2 2 2
l h r=+
B.
2 2 2
1 1 1
l h r
=+
C.
2 2 2
r h l=+
D.
2
l hr=
Lời giải
Chọn A
Theo giả thiết, ta có
2 2 2
l r R=+
Câu 18: Cho hình nón
( )
N
có chiều cao h, độ dài đường sinh l, bán kính đáy r. Ký hiệu
tp
S
là diện tích
toàn phần của
( )
N
. Công thức nào sau đây là đúng?
A.
tp
S rl
=
. B.
2
tp
S rl r

=+
. C.
2
tp
S rl r

=+
. D.
2
2
tp
S rl r

=+
.
Lời giải
Chọn C
Câu 19: Thể tích
V
của khối trụ có bán kính đáy bằng
2
a
và chiều cao bằng
2a
là:
A.
3
.
2
a
V
=
B.
3
.
3
a
V
=
C.
3
2
.
3
a
V
=
D.
3
.
6
a
V
=
Lời giải
Chọn B
Ta có
2
3
2
. . . .2
22
aa
V B h r h a

= = = =


Câu 20: Bán kính
r
của khối cầu có thể tích
( )
3
64 cmV
=
là
A.
3.r cm=
B.
27r cm=
C.
3
48r cm=
D.
3
9.r cm=
Lời giải
Chọn C
+
33
3
4
. 64 48 48
3
V r r r cm

= = = =
.
Câu 21: Cho hàm số
()y f x=
xác định trên và có bảng biến thiên như hình vẽ dưới đây. Hàm số
()y f x=
đồng biến trên khoảng nào sau đây?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 12
A.
( )
0;4 .
B.
( )
2;1 .−
C.
( )
1;4 .
D.
( )
4; .+
Lời giải
Chọn C
Dựa vào bảng biến thiên ta chọn đáp án
C
.
Câu 22: Cho hàm số
( )
y f x=
có đạo hàm là
( ) ( ) ( )
2
2
2 1 1f x x x x
= − +
. Số điểm cực trị của hàm số đã
cho là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Ta có bảng biến thiên
Dựa vào bảng biến thiên, hàm số đã cho có 1 cực trị.
Câu 23: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
3y x x=−
trên
1;2
bằng:
A.
0
. B.
2
. C.
14
27
. D.
7−
.
Lời giải
Chọn A
2
1 1;2
' 3 3 0
1 1;2
x
yx
x
=
= − =
= −
( )
( )
12
22
y
y
=−
=
1;2
1;2
max 2
min 2
y
y
=
=−
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
3y x x=−
trên
1;2
bằng 0.
Câu 24: Cho hàm số
( )
42
0y ax bx c a= + +
có đồ thị như hình bên. Xác định dấu của
,,abc
.
A.
0, 0, 0abc
. B.
0, 0, 0a b c
. C.
0, 0, 0abc
. D.
0, 0, 0a b c
.
Lời giải
Chọn B
Khi
x
dần về
+
thì đồ thị đi lên nên
0a
.
Hàm số có 3 điểm cực trị nên
.0ab
. Suy ra
0b
.
x
– ∞
-1
0
+ ∞
y'
–
0
+
0
+
0
+
y
+ ∞
1
+ ∞
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 13
Đồ thị cắt trục tung tại điểm có tung độ âm nên
0c
.
Câu 25: Số đường tiệm cận của đồ thị hàm số (hình vẽ sau) là:
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn C
Từ hình vẽ, ta thấy đồ thị hàm số có một đường tiệm cận đứng và một đường tiệm cận ngang.
Câu 26: Tập xác định của hàm số
22
(3 1)yx
−
=−
là:
A.
B.
1
.
3
D

=


C.
11
; ; .
33
D
= − − +
D.
11
;.
33

−


Lời giải
Chọn A
Vì
2
−
−
nên hàm số
22
(3x 1)y
−
=−
xác định khi
2
1
3x 1 0
3
x−
.
Câu 27: Tập xác định của hàm số
0,5
log ( 1)yx=+
là:
A.
( 1; ).D = − +
B.
\{ 1}.D =−
C.
(0; ).D = +
D.
( ; 1).− −
Lời giải
Chọn A
Hàm số
0,5
log ( 1)x +
xác định khi
1 0 1xx+ −
.
Câu 28: Cho hàm số
log
a
yx=
và
log
b
yx=
có đồ thị như sau:
x
y
-2
2
-1
1
y=
log
b
x
y=
log
a
x
1
O
y
x
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 14
Mệnh đề nào dưới đây là sai?
A.
1.ab
B.
0 1 .ba
C.
0 1 .ab
D.
0.ab
Lời giải
Chọn B
Dựa vào đồ thị ta thấy
01a
và
1.b
Do đó các mệnh đề ở các đáp án A, C, D là đúng và
mệnh đề ở đáp án B là sai.
Câu 29: Hàm số nào trong các hàm số cho dưới đây nghịch biến trên tập xác định của nó?
A.
ln .yx=
B.
log .yx
=
C.
.
3
x
y

=


D.
3
.
x
y

=


Lời giải
Chọn D
Các hàm số
ln ,yx=
log ,yx
=
3
x
y

=


ở các đáp án A, B, C là hàm số lôgarit, hàm số mũ có
cơ số lớn hơn
1
nên đồng biến trên tập xác định của nó và hàm số
3
x
y

=


ở đáp án D là hàm
số mũ có cơ số
3
thỏa mãn
3
01

nên nghịch biến trên tập xác định của nó.
Câu 30: Trong các phương trình cho dưới đây, phương trình nào có tập ngiệm là
2?S =
A.
( )
2
log log .x x x−=
B.
C.
4 5.2 4 0.
xx
− + =
D.
5.3 4 0.
x
+=
Lời giải
Chọn A
( )
2
2
1
log log 2.
20
x
x x x x
xx
− = =
−=
Tập nghiệm phương trình là
2.S =
( )
22
2
1
log 1 2 0 .
2
x
x x x x
x
=−
− = − − =
=
Tập nghiệm phương trình là
1;2 .S =−
2 1 0
4 5.2 4 0 .
2
24
x
xx
x
x
x
==
− + =
=
=
Tập nghiệm phương trình là
0;2 .S =
4
5.3 4 0 3 :
5
xx
+ = = −
phương trình vô nghiệm.
Câu 31: Với phương trình
33
4 5.2 4 0,
xx−−
+ + =
nếu đặt
3
2
x
t
−
=
thì điều kiện của
t
là
A.
0.t
B.
1.t
C.
3.t
D.
.t
Lời giải
Chọn B
Với
3x
thì
3
2
x
t
−
=
luôn lớn hơn hoặc bằng
1.
Câu 32:
Cho hình chóp tam giác đều
.S ABC
có
O
là trọng tâm tam giác
.ABC
Gọi
I
là trung điểm của
BC
và
E
là điểm thuộc đoạn thẳng
AI
sao cho
3.AI AE=
Đường cao của hình chóp
.S ABC
là
A.
.SO
B.
.SI
C.
.SA
D.
.SE
Lời giải
Chọn A
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 15
Vì
.S ABC
là hình chóp tam giác đều có
O
là trọng tâm tam giác
ABC
nên
SO
là đường cao của
hình chóp.
Câu 33: Cho khối lăng trụ tam giác đều
.ABC AB C
có
,2AB a A C a
==
(hình vẽ bên).
Thể tích
V
của khối lăng trụ
.ABC AB C
là
A.
3
.
4
a
V =
B.
3
3
.
4
a
V =
C.
3
3
.
4
a
V =
D.
3
15
.
4
a
V =
Lời giải
Chọn C
Vì
.ABC AB C
là khối lăng trụ tam giác đều nên cạnh bên là đường cao khối chóp và đáy là tam
giác đều.
Tam giác
( )
0
90A AC A
=
nên có:
2 2 2 2
4 3.AA A C AC a a a

= − = − =
Thể tích
V
của khối lăng trụ
.ABC AB C
là
23
33
. . 3 .
44
ABC
aa
V S AA a
= = =
Câu 34: Cho một hình nón có bán kính đáy bằng
a
và góc ở đỉnh bằng
60
. Tính diện tích xung quanh
của hình nón đó.
A.
2
4
xq
Sa
=
. B.
2
23
3
xq
a
S
=
. C.
2
43
3
xq
a
S
=
. D.
2
2
xq
Sa
=
.
Lời giải
Chọn D
Giả sử hình nón có đỉnh là
S
,
O
là tâm của đường tròn đáy và
AB
là một đường kính của đáy.
r OA a==
,
60 30ASB ASO= =
.
Độ dài đường sinh là
2
sin30
OA
l SA a= = =
.
Vậy diện tích xung quanh của hình nón là
2
. .2 2
xq
S rl a a a
= = =
.
2a
a
C'
B'
A
B
C
A'
A
B
S
O
a
60
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 16
Câu 35: Cho hình trụ có chiều cao bằng
53
. Cắt hình trụ đã cho bởi mặt phẳng song song với trục và
cách trục một khoảng bằng
1
, thiết diện thu được có diện tích bằng
30
. Diện tích xung quanh
của hình trụ đã cho bằng
A.
10 3
. B.
5 39
. C.
20 3
. D.
10 39
.
Lời giải
Chọn C
Gọi
,
OO
lần lượt là tâm của hai đáy và
ABCD
là thiết diện song song với trục với
( )
, A B O
;
( )
,
C D O
. Gọi
H
là trung điểm của
AB
( )
( )
,1
= =OH d OO ABCD
.
Vì
30
30 . 30 2 3 3
53
= = = = = =
ABCD
S AB BC AB HA HB
.
Bán kính của đáy là
22
3 1 2= + = + =r OH HA
.
Diện tích xung quanh của hình trụ bằng
2 2 .2.5 3 20 3
= = =
xq
S rh
.
II. PHẦN TỰ LUẬN
Câu 36: Giải phương trình sau :
( ) ( ) ( )
8
93
3
11
log 3 log 1 log 4
24
x x x+ + − =
Lời giải
Điều kiện:
1
0
x
x
.
Ta có:
( ) ( ) ( )
8
93
3
11
log 3 log 1 log 4
24
x x x+ + − =
( ) ( )
3 3 3
log 3 log 1 log 4x x x + + − =
( ) ( )
33
log 3 . 1 log 4x x x + − =

( )
3 . 1 4x x x + − =
( )
1
.
+ Nếu
01x
thì phương trình
( )
1
trở thành
( ) ( )
( )
( )
2
3 2 3
3 . 1 4 6 3 0
3 2 3
x tm
x x x x x
xl
= − +
+ − = − − + =
= − −
.
+ Nếu
1x
thì phương trình
( )
1
trở thành
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 17
( ) ( )
( )
( )
2
3
3 . 1 4 2 3 0
1
x tm
x x x x x
xl
=
+ − = − − =
=−
.
Vậy tập nghiệm của phương trình là:
3 2 3;3S = − +
.
Câu 37: Cho hình lăng trụ
.ABC A B C
có đáy là tam giác đều cạnh bằng
a
,hình chiếu vuông góc của
A
lên mặt phẳng
( )
ABC
trùng với trọng tâm
G
của tam giác
ABC
. Biết khoảng cách giữa
BC
và
AA
bằng
3
4
a
. Tính thể tích khối chóp
.B ABC
.
Lời giải
Gọi
M
là trung điểm của
BC
. Vì tam giác
ABC
đều cạnh
a
nên ta có
2
33
;;
24
ABC
aa
AM BC AM S
⊥ = =
( đvdt).
Mặt khác
( )
AG ABC AG BC⊥ ⊥
.
Như vậy
( )
.
BC AM
BC A G BC AA M
AM A G G
⊥

⊥ ⊥
=
Trong
( )
AA M
, kẻ
MH AA
⊥
ta có
( )
3
,.
4
a
d BC AA HM
==
Xét tam giác vuông
AMH
có
3
1
4
sin 30 .
2
3
2
a
HM
AM
a

= = = =
Xét tam giác vuông
AA G
2 2 3
.tan .tan . .tan30 .
3 3 2 3
aa
A G AG AM

= = = =
Vậy
23
..
1 1 3 3
. . . .
3 3 3 4 36
B ABC A ABC ABC
a a a
V V A G S

= = = =
(đvdt).
Câu 38: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ sau. Tìm
m
để hàm số
( )
y f x m=+
đồng biến trên khoảng
( )
4;+
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 18
Lời giải
+ Bảng biến thiên của hàm số
( )
y f x=
+ Suy ra bảng biến thiên của hàm số
( )
y f x m=+
+ Hàm số
( )
y f x m=+
đồng biến trên khoảng
( )
4;+
44mm − −
.
Câu 39: Có bao nhiêu số nguyên
y
sao cho với mỗi
y
không có quá
50
số nguyên
x
thoả mãn bất phương
trình sau:
( )
32
3
2 log
yx
xy
−
+
?
Lời giải
Điều kiện:
2
0xy+
Xét hàm số:
( )
32
3
( ) 2 log
yx
f x x y
−
= − +
với
( )
2
;xy − +
Ta có:
( )
32
2
1
( ) 3.3 ln3 0, ;
( )ln3
yx
f x x y
xy
−
= − − − +
+
Bảng biến thiên
Từ đó suy ra bất phương trình có nghiệm
(
2
o
;x y x
−
Để tập nghiệm của bất phương trình không chứa quá
50
số nguyên thì
2
( 51) 0fy− +
( )
2
3 51
3
2 log 51
yy− − +

( )
2
23
3 153 log log 51yy + −
7,35 7,02y −
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 19
Vì
y
nên
7; 6;....;6;7y − −
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 12
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
( )
fx
đồng biến trên tập số thực , mệnh đề nào sau đây là đúng?
A. Với mọi
12
,xx
.mà
12
xx
( ) ( )
12
f x f x
.
B. Với mọi
( ) ( )
1 2 1 2
,x x f x f x
.
C. Với mọi
( ) ( )
1 2 1 2
,x x f x f x
.
D. Với mọi
12
,xx
.mà
12
xx
( ) ( )
12
f x f x
.
Câu 2: Cho hàm số
( )
y f x=
xác định và liên tục trên , có đồ thị như hình vẽ.
Hàm số
( )
y f x=
có điểm cực tiểu là
A.
1x =
. B.
2x =
. C.
2x =−
. D.
1x =−
.
Câu 3: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị nhỏ nhất bằng −1. B. Hàm số có giá trị nhỏ nhất bằng 0.
C. Hàm số không xác định tại
1x =−
. D. Hàm số luôn có giá trị lớn nhất.
Câu 4: Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
32
23y x x x= − + − −
. B.
32
2 7 2y x x x= + − −
.
C.
32
22y x x x= − + −
. D.
42
23y x x= − −
.
-1
+
∞
+
∞
+
∞
0
0
-1
-
∞
y'
y
x
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 2
Sưu tầm và biên soạn
Câu 5: Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây:
A.
2
2
x
y
x
−+
=
+
. B.
22
1
x
y
x
−
=
+
. C.
2
1
x
y
x
−
=
+
. D.
22
1
x
y
x
−+
=
+
.
Câu 6: Đồ thị hàm số
2
4
x
y
x
=
−
có bao nhiêu đường tiệm cận
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 7: Tìm tập xác định
D
của hàm số
( )
2
5
1.yx=−
A.
D=
. B.
( )
1;D = +
. C.
( )
;1D = −
. D.
\1D =
.
Câu 8: Cho
0a
;
1a
và
x
;
y
là hai số thực dương. Phát biểu nào sau đây là đúng?
A.
( )
log log log
a a a
x y x y+ = +
. B.
( )
log log log
a a a
xy x y=+
.
C.
( )
log log .log
a a a
xy x y=
. D.
( )
log log .log
a a a
x y x y+=
.
Câu 9: Tập xác định của hàm số
( )
=−
3
log 2yx
là
A.
(
−
;2
. B.
)
+
2;
. C.
( )
−;2
. D.
( )
+2;
.
Câu 10: Ham số
2
x
y
−
=
có đạo hàm là:
A.
1
2
x−−
−
. B.
2 ln2
x−
−
. C.
2 ln2
x−
. D.
2
ln 2
x−
−
.
Câu 11: Trong các hàm số sau, hàm số nào nghịch biến trên khoảng
( )
0;+
?
A.
2021
y
2020
x

=


B.
y
3
x

=


C.
y log x=
D.
2
3
logyx=
Câu 12: Tìm nghiệm của phương trình
58
x
=
.
A.
8
log 5x =
. B.
5
log 8x =
. C.
8
5x =
. D.
5
8x =
.
Câu 13: Nghiệm của phương trình:
24
x
=
là
A.
2x =
. B.
1x =
. C.
3x =
. D.
4x =
.
Câu 14: Nghiệm của bất phương trình:
2
log 1x
là
A.
2x
. B.
2x
. C.
1x
. D.
2x
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 3
Sưu tầm và biên soạn
Câu 15: Khối đa diện đều loại
4;3
có bao nhiêu mặt?
A.
5
. B.
6
. C.
4
. D.
3
.
Câu 16: Thể tích của khối chóp có chiều cao bằng
h
và có diện tích đáy
B
là
A.
1
2
Bh
B.
1
6
Bh
C.
1
3
Bh
D.
Bh
Câu 17: Cho tam giác
ABC
đều có cạnh bằng
a
quay xung quanh cạnh
AC
của nó. Tính thể tích
V
của
khối tròn xoay tạo thành.
A.
3
9
.
18
a
V
=
B.
3
.
4
a
V
=
C.
3
27
.
18
a
V
=
D.
3
27
.
8
a
V
=
Câu 18: Cho tam giác đều
ABC
cạnh
a
quay quanh đường cao
AH
tạo nên hình nón. Diện tích xung
quanh của hình nón đó là
A.
2
3
.
4
a
B.
2
.
2
a
C.
2
.a
D.
2
.a
Câu 19: Diện tích của mặt cầu có bán kính
R
bằng
A.
2
2.R
B.
2
.R
C.
2
4.R
D.
2.R
Câu 20: Thể tích khối trụ có bán kính đáy
,r
đường sinh
l
là
A.
2.V rl
=
B.
2
1
.
3
V rl
=
C.
2
.V rl
=
D.
2
.V r l
=
Câu 21: Cho hàm số
( )
=y f x
xác định trên
\{ 1}−
và có bảng dấu của
( )
fx
như hình bên dưới
Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số
( )
=y f x
đồng biến trên khoảng
( )
1;2 .
B. Hàm số
( )
=y f x
đồng biến trên
.
C. Hàm số
( )
=y f x
đồng biến trên khoảng
( )
3;2 .−
D. Hàm số
( )
=y f x
đồng biến trên khoảng
( )
;2 .−
Câu 22: Điểm cực đại của đồ thị hàm số
32
69y x x x= − +
có tổng hoành độ và tung độ bằng
A.
5
. B.
1
. C.
3
. D.
1−
.
Câu 23: Giá trị lớn nhất của hàm số
42
49y x x= − +
trên đoạn
2;3−
bằng
A.
201
B.
2
C.
9
D.
54
Câu 24: Cho hàm số
32
y ax bx cx d= + + +
có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0a b c d
.
B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
.
D.
0, 0, 0, 0a b c d
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 4
Sưu tầm và biên soạn
Câu 25: Đồ thị hàm số dưới đây có TCĐ và TCN là đường thẳng có phương trình
A.
2; 1xy==
. B.
1; 2xy==
. C.
0; 1xy==
. D.
0; 1xy==
.
Câu 26: Tìm tập xác định của hàm số
( )
31
2
1yx
−
=−
.
A.
D =
. B.
\ 1; 1D =−
. C.
( ) ( )
;1 1;D = − +
.D.
( )
1;1D =−
.
Câu 27: Tìm tập xác định hàm số
( )
2
log 2y x x=−
.
A.
D =
. B.
( ) ( )
;0 2;D = − +
. C.
\ 0;2D =
.
D.
( )
0;2
.
Câu 28: Tìm a để hàm số
log
a
yx=
( )
0 1, 0ax
có đồ thị là hình bên:
A.
1
2
a =
. B.
2a =
. C.
2a =
. D.
1
2
a =
.
Câu 29: Cho hàm số
( )
21
x
y =−
. Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số có đường tiệm cận đứng là trục hoành.
B. Hàm số đồng biến trên khoảng
( )
0;+
.
C. Đồ thi hàm số có đường tiệm cận ngang là trục tung.
D. Hàm số nghịch biến trên khoảng
( )
;− +
.
Câu 30: Tập nghiệm của phương trình
3
log 1 2x −=
là:
A.
{3}
. B.
{-3;4}
. C.
{-3;-2}
. D.
{4;-2}
.
Câu 31: Gọi
12
,xx
là các nghiệm của phương trình
( ) ( )
7 4 3 4 2 3 1.
xx
+ − + = −
Khi đó giá trị của
22
12
xx+
bằng
A.
2.
B.
0.
C.
14.
D.
4.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 5
Sưu tầm và biên soạn
Câu 32: Số mặt phẳng đối xứng của khối chóp tứ diện đều là
A.
7
B.
8.
C.
9.
D.
6.
Câu 33: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
.a
Hình chiếu của
S
lên mặt phẳng
( )
ABCD
trùng với trung điểm của cạnh
,AB
đường thẳng
SD
tạo với mặt phẳng đáy một góc
45 .
o
Tính thể tích khối chóp
.S ABCD
theo
.a
A.
3
5
.
12
a
B.
3
5
.
3
a
C.
3
5
.
2
a
D.
3
5
.
6
a
Câu 34: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh a, góc
120=BAD
. Cạnh bên
SA
vuông góc với đáy
( )
ABCD
và
3=SA a
. Tính bán kính
R
của mặt cầu ngoại tiếp khối chóp
.S BCD
.
A.
3
3
=
a
R
. B.
5
3
=
a
R
. C.
5
3
=
a
R
. D.
4
3
=
a
R
.
Câu 35: Cho hình thang cân
ABCD
có đáy nhỏ
1=AB
, đáy lớn
3=CD
, cạnh bên
2==BC DA
. Cho
hình thang đó quay quanh
AB
thì được vật tròn xoay có thể tích bằng
A.
4
3
. B.
5
3
. C.
2
3
. D.
7
3
.
II. PHẦN TỰ LUẬN
Câu 36: Giải phương trình:
( )
( )
2
2
49 7 7
3
1
log log 1 log log 3
2
xx+ − =
.
Câu 37: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA
vuông góc với mặt đáy. Gọi
M
là trung điểm
BC
. Mặt phẳng
( )
P
đi qua
A
và vuông góc với
SM
cắt
SB
,
SC
lần lượt tại
E
,
F
. Biết thể tích khối chóp
.S ABC
gấp
4
lần thể tích khối chóp
.S AEF
. Tính thể tích của
khối chóp
.S ABC
.
Câu 38: Cho hàm số
( )
=y f x
liên tục trên và có bảng biến thiên bên dưới.
Tìm các khoảng đồng biến của hàm số
( )
( )
2
12y g x f x x= = + −
Câu 39: Cho các số thực
,xy
thỏa mãn
0 , 1xy
và
( )( )
3
log 1 1 2 0
1
xy
xy
xy

+
+ + + − =

−

. Tìm giá trị
nhỏ nhất của
P
với
2P x y=+
.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 6
Sưu tầm và biên soạn
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
( )
fx
đồng biến trên tập số thực , mệnh đề nào sau đây là đúng?
A. Với mọi
12
,xx
.mà
12
xx
( ) ( )
12
f x f x
.
B. Với mọi
( ) ( )
1 2 1 2
,x x f x f x
.
C. Với mọi
( ) ( )
1 2 1 2
,x x f x f x
.
D. Với mọi
12
,xx
.mà
12
xx
( ) ( )
12
f x f x
.
Lời giải
Chọn D
Theo định nghĩa về tính đơn điệu của hàm số: Với mọi
12
,xx
mà
( ) ( )
1 2 1 2
x x f x f x
.
Câu 2: Cho hàm số
( )
y f x=
xác định và liên tục trên , có đồ thị như hình vẽ.
Hàm số
( )
y f x=
có điểm cực tiểu là
A.
1x =
. B.
2x =
. C.
2x =−
. D.
1x =−
.
Lời giải
Chọn A
Câu 3: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị nhỏ nhất bằng −1. B. Hàm số có giá trị nhỏ nhất bằng 0.
C. Hàm số không xác định tại
1x =−
. D. Hàm số luôn có giá trị lớn nhất.
Lời giải
Chọn A
Nhìn BBT ta thấy
1y =−
là giá trị nhỏ nhất của hàm số.
-1
+
∞
+
∞
+
∞
0
0
-1
-
∞
y'
y
x
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 7
Sưu tầm và biên soạn
Câu 4: Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
32
23y x x x= − + − −
. B.
32
2 7 2y x x x= + − −
.
C.
32
22y x x x= − + −
. D.
42
23y x x= − −
.
Lời giải
Chọn C
Từ đồ thị ta thấy hình dạng trên là dạng đồ thị hàm số bậc
3
có hệ số
0a
.
Ngoài ra các điểm cực trị của đồ thị hàm số đều có hoành độ dương nên ta chọn đáp án C
Câu 5: Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây:
A.
2
2
x
y
x
−+
=
+
. B.
22
1
x
y
x
−
=
+
. C.
2
1
x
y
x
−
=
+
. D.
22
1
x
y
x
−+
=
+
.
Lời giải
Chọn D
Đồ thị hàm số đã cho đi qua điểm
( )
1;0
và
( )
0;2
nên ta loại phương án A, B và C.
Đồ thị hàm số
22
1
x
y
x
−+
=
+
đi qua điểm
( )
1;0
,
( )
0;2
, có tiệm cận đứng
1x =−
và tiệm cận ngang
2y =−
nên thỏa mãn yêu cầu bài toán.
Vậy đường cong đã cho là đồ thị hàm số
22
1
x
y
x
−+
=
+
.
Câu 6: Đồ thị hàm số
2
4
x
y
x
=
−
có bao nhiêu đường tiệm cận
A.
2
. B.
1
. C.
4
. D.
3
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 8
Sưu tầm và biên soạn
Lời giải
Chọn D
Điều kiện xác định:
2
40x −
2x
.
Ta có:
22
lim lim 0
44
xx
xx
xx
→+ →−
==
−−
đường thẳng
0y =
là đường tiệm cận ngang của đồ thị
hàm số.
−
→
= −
−
2
2
lim
4
x
x
x
đường thẳng
2x =
là đường tiệm cận đứng của đồ thị hàm số.
( )
−
→−
= −
−
2
2
lim
4
x
x
x
đường thẳng
2x =−
là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có 3 đường tiệm cận.
Câu 7: Tìm tập xác định
D
của hàm số
( )
2
5
1.yx=−
A.
D=
. B.
( )
1;D = +
. C.
( )
;1D = −
. D.
\1D =
.
Lời giải
Chọn B
Do
2
5
nên hàm số xác định khi
( )
1;D = +
.
Câu 8: Cho
0a
;
1a
và
x
;
y
là hai số thực dương. Phát biểu nào sau đây là đúng?
A.
( )
log log log
a a a
x y x y+ = +
. B.
( )
log log log
a a a
xy x y=+
.
C.
( )
log log .log
a a a
xy x y=
. D.
( )
log log .log
a a a
x y x y+=
.
Lời giải
Chọn B
Ta có logarit của một tích bằng tổng hai logarit.
Câu 9: Tập xác định của hàm số
( )
=−
3
log 2yx
là
A.
(
−
;2
. B.
)
+
2;
. C.
( )
−;2
. D.
( )
+2;
.
Lời giải
Chọn D
Hàm số
( )
=−
3
log 2yx
có nghĩa
− 2 0 2xx
.
Vậy tập xác định của hàm số là
( )
+2;
.
Câu 10: Ham số
2
x
y
−
=
có đạo hàm là:
A.
1
2
x−−
−
. B.
2 ln2
x−
−
. C.
2 ln2
x−
. D.
2
ln 2
x−
−
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 9
Sưu tầm và biên soạn
Lời giải
Chọn B
( )
22
xx
yy
−−
= =
( )
.2 .ln 2
x
x
−
=−
2 .ln2
x−
=−
.
Câu 11: Trong các hàm số sau, hàm số nào nghịch biến trên khoảng
( )
0;+
?
A.
2021
y
2020
x

=


B.
y
3
x

=


C.
y log x=
D.
2
3
logyx=
Lời giải
Chọn D
Ta có:
2021
1
2020
nên hàm số
2021
y
2020
x

=


đồng biến trên . Do đó phương án A sai.
1
3
nên hàm số
y
3
x

=


đồng biến trên . Do đó phương án B sai.
10 1
nên hàm số
y log x=
đồng biến trên khoảng
( )
0;+
. Do đó phương án C sai.
2
1
3
nên hàm số
2
3
logyx=
nghịch biến trên khoảng
( )
0;+
. Do đó phương án D đúng.
Câu 12: Tìm nghiệm của phương trình
58
x
=
.
A.
8
log 5x =
. B.
5
log 8x =
. C.
8
5x =
. D.
5
8x =
.
Lời giải
Chọn B
5
5 8 log 8
x
x= =
.
Câu 13: Nghiệm của phương trình:
24
x
=
là
A.
2x =
. B.
1x =
. C.
3x =
. D.
4x =
.
Lời giải
Chọn A
Ta có
2 4 2
x
x= =
.
Câu 14: Nghiệm của bất phương trình:
2
log 1x
là
A.
2x
. B.
2x
. C.
1x
. D.
2x
.
Lời giải
Chọn A
Điều kiện:
0x
Ta có
2
log 1 2xx
.
Câu 15: Khối đa diện đều loại
4;3
có bao nhiêu mặt?
A.
5
. B.
6
. C.
4
. D.
3
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 10
Sưu tầm và biên soạn
Lời giải
Chọn B
Khối đa diện đều loại
4;3
chính là khối lập phương nên có
6
mặt.
Câu 16: Thể tích của khối chóp có chiều cao bằng
h
và có diện tích đáy
B
là
A.
1
2
Bh
B.
1
6
Bh
C.
1
3
Bh
D.
Bh
Lời giải
Chọn C
Câu 17: Cho tam giác
ABC
đều có cạnh bằng
a
quay xung quanh cạnh
AC
của nó. Tính thể tích
V
của
khối tròn xoay tạo thành.
A.
3
9
.
18
a
V
=
B.
3
.
4
a
V
=
C.
3
27
.
18
a
V
=
D.
3
27
.
8
a
V
=
Lời giải
Chọn B
Khi quay tam giác đều
ABC
quanh cạnh
AC
, khối tròn xoay tạo thành là hai khối nón tròn xoay
có trục là
AC
, đường tròn có bán kính bằng chiều cao hạ từ
B
.
2
3
2
3 1 1 3
, , 2. 2. . .
2 2 3 3 2 2 4
a a a a a
BO r OA h V r h


= = = = = = =



Câu 18: Cho tam giác đều
ABC
cạnh
a
quay quanh đường cao
AH
tạo nên hình nón. Diện tích xung
quanh của hình nón đó là
A.
2
3
.
4
a
B.
2
.
2
a
C.
2
.a
D.
2
.a
Lời giải
Chọn B
Với hình nón có chiều cao hạ từ đỉnh là
h
, đường sinh
,l
độ dài bán kính mặt đáy là
r
thì ta có
diện tích xung quanh của hình nón là:
.
xq
S rl
=
Ta có
,
2
a
r l a==
nên
2
.
2
xq
a
S
=
Câu 19: Diện tích của mặt cầu có bán kính
R
bằng
A.
2
2.R
B.
2
.R
C.
2
4.R
D.
2.R
Lời giải
Chọn C
Diện tích của mặt cầu có bán kính
R
bằng
2
4 R
.
Câu 20: Thể tích khối trụ có bán kính đáy
,r
đường sinh
l
là
A.
2.V rl
=
B.
2
1
.
3
V rl
=
C.
2
.V rl
=
D.
2
.V r l
=
Lời giải
Chọn D
Thể tích khối trụ có bán kính đáy
,r
đường sinh
l
là
2
.V r l
=
Câu 21: Cho hàm số
( )
=y f x
xác định trên
\{ 1}−
và có bảng dấu của
( )
fx
như hình bên dưới
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 11
Sưu tầm và biên soạn
Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số
( )
=y f x
đồng biến trên khoảng
( )
1;2 .
B. Hàm số
( )
=y f x
đồng biến trên
.
C. Hàm số
( )
=y f x
đồng biến trên khoảng
( )
3;2 .−
D. Hàm số
( )
=y f x
đồng biến trên khoảng
( )
;2 .−
Lời giải
Chọn A
Ta có
( )
0,fx
( )
1;2x
nên hàm số
( )
=y f x
đồng biến trên khoảng
( )
1;2 .
Câu 22: Điểm cực đại của đồ thị hàm số
32
69y x x x= − +
có tổng hoành độ và tung độ bằng
A.
5
. B.
1
. C.
3
. D.
1−
.
Lời giải
Chọn A
Ta có:
2
1
' 3 12 9 0
3
x
y x x
x
=
= − + =
=
Bảng biến thiên
Khi đó:
1 4 5.
CD CD CD CD
x y x y= = + =
Câu 23: Giá trị lớn nhất của hàm số
42
49y x x= − +
trên đoạn
2;3−
bằng
A.
201
B.
2
C.
9
D.
54
Lời giải
Chọn D
3
48
=−y x x
;
0
0
2
=
=
=
x
y
x
.
Ta có
( )
29y −=
;
( )
3 54y =
;
( )
09y =
;
( )
25y =
.
Vậy
2;3
max 54y
−
=
.
Câu 24: Cho hàm số
32
y ax bx cx d= + + +
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 12
Sưu tầm và biên soạn
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Lời giải
Chọn D
Ta có:
2
32y ax bx c
= + +
,
62y ax b

=+
Từ đồ thị ta thấy:
+
lim
x
y
→+
= −
. Ta suy ra
0a
.
+
( )
0 0 0yd
.
Đồ thị hàm số có hai điểm cực trị với hoành độ
1
x
,
2
x
trái dấu và
12
0xx+
. Ta suy ra phương
trình
'0y =
có hai nghiệm trái dấu và
12
0xx+
.
Ta suy ra
12
0
3
c
xx
a
=
,
0c
.
Hơn nữa,
12
2
0
0
3
0
b
xx
b
a
a
+ = −

.
Vậy
0, 0, 0, 0a b c d
Câu 25: Đồ thị hàm số dưới đây có TCĐ và TCN là đường thẳng có phương trình
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 13
Sưu tầm và biên soạn
A.
2; 1xy==
. B.
1; 2xy==
. C.
0; 1xy==
. D.
0; 1xy==
.
Lời giải
Chọn A
Nhìn vào đồ thị ta thấy TCĐ và TCN lần lượt là
2; 1xy==
.
Câu 26: Tìm tập xác định của hàm số
( )
31
2
1yx
−
=−
.
A.
D =
. B.
\ 1; 1D =−
.
C.
( ) ( )
;1 1;D = − +
. D.
( )
1;1D =−
.
Lời giải
Chọn C
Ta có:
2
1
10
1
x
x
x
−
−
Vậy: TXĐ
( ) ( )
; 1 1;D = − − +
.
Câu 27: Tìm tập xác định hàm số
( )
2
log 2y x x=−
.
A.
D =
. B.
( ) ( )
;0 2;D = − +
.
C.
\ 0;2D =
. D.
( )
0;2
.
Lời giải
Chọn B
Hàm số xác định khi
2
2
20
0
x
xx
x
−
Vậy TXĐ của hàm số là
( ) ( )
;0 2;D = − +
.
Câu 28: Tìm a để hàm số
log
a
yx=
( )
0 1, 0ax
có đồ thị là hình bên:
A.
1
2
a =
. B.
2a =
. C.
2a =
. D.
1
2
a =
.
Lời giải
Chọn C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 14
Sưu tầm và biên soạn
Đồ thị đi qua
(2;2)A
2
2 log 2 2 2
a
aa = = =
.
Câu 29: Cho hàm số
( )
21
x
y =−
. Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số có đường tiệm cận đứng là trục hoành.
B. Hàm số đồng biến trên khoảng
( )
0;+
.
C. Đồ thi hàm số có đường tiệm cận ngang là trục tung.
D. Hàm số nghịch biến trên khoảng
( )
;− +
.
Lời giải
Chọn D
Vì
0 2 1 1 −
nên hàm số
( )
21
x
y =−
nghịch biến trên khoảng
( )
;− +
.
Câu 30: Tập nghiệm của phương trình
3
log 1 2x −=
là:
A.
{3}
. B.
{-3;4}
. C.
{-3;-2}
. D.
{4;-2}
.
Lời giải
Chọn D
Đkxđ:
1x
.
PT
( )
2
1 3 3x − = =
13
13
4
()
2
x
x
x
TM
x
−=
− = −
=
=−
Vậy
{4; 2}x−
.
Câu 31: Gọi
12
,xx
là các nghiệm của phương trình
( ) ( )
7 4 3 4 2 3 1.
xx
+ − + = −
Khi đó giá trị của
22
12
xx+
bằng
A.
2.
B.
0.
C.
14.
D.
4.
Lời giải
Chọn A
Ta có:
( ) ( ) ( ) ( )
( )
2
7 4 3 4 2 3 1 2 3 4 2 3 1 0 1 .
x x x x
+ − + = − + − + + =
Đặt
( )
( )
2 3 , 0
x
tt= +
phương trình
( )
1
trở thành:
2
23
4.
2
1
3
0t
t
t
t +
−
=
=+
−
=
Với
2 3 :t =+
( )
2 3 2 3 1.
x
x+ = + =
Với
2 3 :t =−
( ) ( ) ( )
1
2 3 2 3 2 3 2 3 1
xx
x
−
+ = − + = + = −
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 15
Sưu tầm và biên soạn
Vậy phương trình đã cho có
2
nghiệm
12
1, 1.xx= − =
Khi đó
22
12
2.xx+=
Câu 32: Số mặt phẳng đối xứng của khối chóp tứ diện đều là
A.
7
B.
8.
C.
9.
D.
6.
Lời giải
Chọn D
Các mặt phẳng đối xứng của khối chóp tứ diện đều là các mặt phẳng chứa một cạnh và qua trung
điểm của cạnh đối diện.
Câu 33: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
.a
Hình chiếu của
S
lên mặt phẳng
( )
ABCD
trùng với trung điểm của cạnh
,AB
đường thẳng
SD
tạo với mặt phẳng đáy một góc
45 .
o
Tính thể tích khối chóp
.S ABCD
theo
.a
A.
3
5
.
12
a
B.
3
5
.
3
a
C.
3
5
.
2
a
D.
3
5
.
6
a
Lời giải
Chọn D
Gọi
H
là trung điểm của
( )
AB SH ABCD⊥
nên hình chiếu của hình chiếu của
SD
lên mặt
phẳng
( )
ABCD
là
.HD
Do đó
( )
(
)
( )
, , 45 .SD ABCD SD SH SDH
= = =
2
2 2 2
5
.
22
aa
HD AD AH a

+ = + = + =


+
SHD
vuông cân tại
H
nên
5
.
2
a
SH HD==
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 16
Sưu tầm và biên soạn
Thể tích khối chóp
.:S ABCD
3
2
.
1 1 5 5
. . . .
3 3 2 6
S ABCD ABCD
aa
V SH S a= = =
Câu 34: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh a, góc
120=BAD
. Cạnh bên
SA
vuông góc với đáy
( )
ABCD
và
3=SA a
. Tính bán kính
R
của mặt cầu ngoại tiếp khối chóp
.S BCD
.
A.
3
3
=
a
R
. B.
5
3
=
a
R
. C.
5
3
=
a
R
. D.
4
3
=
a
R
.
Lời giải
Chọn C
Xét hình thoi
ABCD
có
120=BAD
nên
==AD AC AB
, suy ra
A
là tâm đường tròn ngoại
tiếp đa giác đáy
BCD
.
Theo giả thiết
SA
vuông góc với đáy
( )
ABCD
nên đường thẳng
SA
là trục của đáy
BCD
.
Gọi
M
là trung điểm
SD
, trong mặt phẳng
( )
SAD
kẻ đường thẳng
d
vuông góc với
SD
tại
M
,
d
cắt
SA
tại
I
. Ta có
I
là tâm mặt cầu ngoại tiếp khối chóp
.S BCD
.
Lúc đó
=R IS
.
Ta có
10
. 10
.5
2
33
= = = =
a
a
IS SM SM DS a
ISM DSA IS
DS SA SA a
∽
.
Câu 35: Cho hình thang cân
ABCD
có đáy nhỏ
1=AB
, đáy lớn
3=CD
, cạnh bên
2==BC DA
. Cho
hình thang đó quay quanh
AB
thì được vật tròn xoay có thể tích bằng
A.
4
3
. B.
5
3
. C.
2
3
. D.
7
3
.
Lời giải
Chọn D
S
I
D
A
B
C
M
d
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 17
Sưu tầm và biên soạn
Gọi
V
là thể tích vật tròn xoay cần tìm.
1
V
,
2
V
lần lượt là thể tích của khối nón đỉnh
A
, và đỉnh
B
,
T
V
là thể tích khối trụ trục
OO
như hình vẽ.
Gọi
A
,
B
lần lượt là hình chiếu vuông góc của
A
,
B
trên cạnh
CD
.
Suy ra

= AA D BB C
(cạnh huyền – góc nhọn).
Suy ra
2 3 1 2
= − = − =A D CD A B
. Suy ra
1

==A D B C
.
Mặt khác
22
1

= − =O C BC BO
Ta có
1
==AO BO
và
1
==OD O C
nên ta có
12
=VV
.
Thể tích vật tròn xoay cần tìm là
2 2 2
1
12
2 . 2. .
33

= − = − = −


T
V V V R CD R AO R CD AO
.
2
27
.1 . 3
33

= − =


V

.
II. PHẦN TỰ LUẬN
Câu 36: Giải phương trình:
( )
( )
2
2
49 7 7
3
1
log log 1 log log 3
2
xx+ − =
.
Lời giải
Điều kiện
0
1
x
x
.
( )
( )
2
2
49 7 7
3
1
log log 1 log log 3
2
xx+ − =
7 7 7
log log 1 log 2xx + − =
( )
77
log 1 log 2xx − =
( )
( )
12
12
xx
xx
−=
− = −
2
2
20
20
xx
xx
− − =
− + =
2
1
x
x
=
=−
.
Kết hợp điều kiện ta được tập nghiệm của phương trình là
1;2 .S =−
Câu 37: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA
vuông góc với mặt đáy. Gọi
M
là trung điểm
BC
. Mặt phẳng
( )
P
đi qua
A
và vuông góc với
SM
cắt
SB
,
SC
lần lượt tại
E
,
F
. Biết thể tích khối chóp
.S ABC
gấp
4
lần thể tích khối chóp
.S AEF
. Tính thể tích của
khối chóp
.S ABC
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 18
Sưu tầm và biên soạn
Lời giải
Ta có
BC SM⊥
.
Gọi
H
là hình chiếu vuông góc của
A
trên
SM
.
Do
( ) ( )
FE P SBC=
FE SM⊥
FE BC
và
FE
đi qua
H
.
..
1
4
S AEF S ABC
VV=
1
.
4
SE SF
SB SC
=
2
1
4
SH
SM

=


1
2
SH
SM
=
.
Do đó
H
là trung điểm cạnh
SM
.
Suy ra
SAM
vuông cân tại
A
3
2
a
SA=
.
Vậy
2
1 3 3
..
3 2 4
SABC
aa
V =
3
8
a
=
.
Câu 38: Cho hàm số
( )
=y f x
liên tục trên và có bảng biến thiên bên dưới.
Tìm các khoảng đồng biến của hàm số
( )
( )
2
12y g x f x x= = + −
Lời giải
Ta có
( ) ( )
( )
2
2 2 . 1 2g x x f x x

= − + −
.
( )
( )
2
2 2 0
0
1 2 0
x
gx
f x x
−=
=
+ − =
2
2
1
1 2 1
1 2 2
x
xx
xx
=
+ − =
+ − =
( )
=
=
=
0
1 nghiÖm béi ba
2
x
x
x
.
F
E
M
S
B
C
A
H
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 19
Sưu tầm và biên soạn
+ Với
( ) ( )
3 3 4. 2 0x g f

= = − −
(do
( )
20f
−
)
Từ đó ta có bảng biến thiên:
Dựa vào bảng biến thiên hàm số
( )
gx
đồng biến trên khoảng
( )
;0−
và
( )
1;2
.
Câu 39: Cho các số thực
,xy
thỏa mãn
0 , 1xy
và
( )( )
3
log 1 1 2 0
1
xy
xy
xy

+
+ + + − =

−

. Tìm giá trị
nhỏ nhất của
P
với
2P x y=+
.
Lời giải
Điều kiện:
0 , 1
0
1
xy
xy
xy

+
−
0 , 1
0; 1 0
xy
x y xy

+ −
.
Khi đó
( )( )
3
log 1 1 2 0
1
xy
xy
xy

+
+ + + − =

−

( ) ( )
33
log log 1 1 0x y xy x y xy + − − + + + − =
( ) ( ) ( ) ( )
33
log log 1 1 (*)x y x y xy xy + + + = − + −
Xét hàm số
( )
3
logf t t t=+
với
0t
, ta thấy
( )
1
1 0, 0
ln3
f t t
t
= +
nên hàm số
( )
ft
đồng
biến trên khoảng
( )
0;+
.
Do đó
( )
*1x y xy + = −
( )
1
11
1
x
y x x y
x
−
+ = − =
+
. Thay vào
2P x y=+
ta được
1
2
1
x
Px
x
−
=+
+
.
Xét hàm số
( )
1
2
1
x
f x x
x
−
=+
+
trên đoạn
0;1
.
Ta có:
( )
( )
2
2
2
1
fx
x
=−
+
.
+
( )
( )
( )
0 0;1
0
2 0;1
x
fx
x
=
=
= −
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 20
Sưu tầm và biên soạn
+
( ) ( )
0 1; 1 2ff==
Vậy
( ) ( )
0;1
min min 0 1P f x f= = =
khi
0, 1xy==
.
| 1/234
| | Tải xuống

Có thể bạn quan tâm:

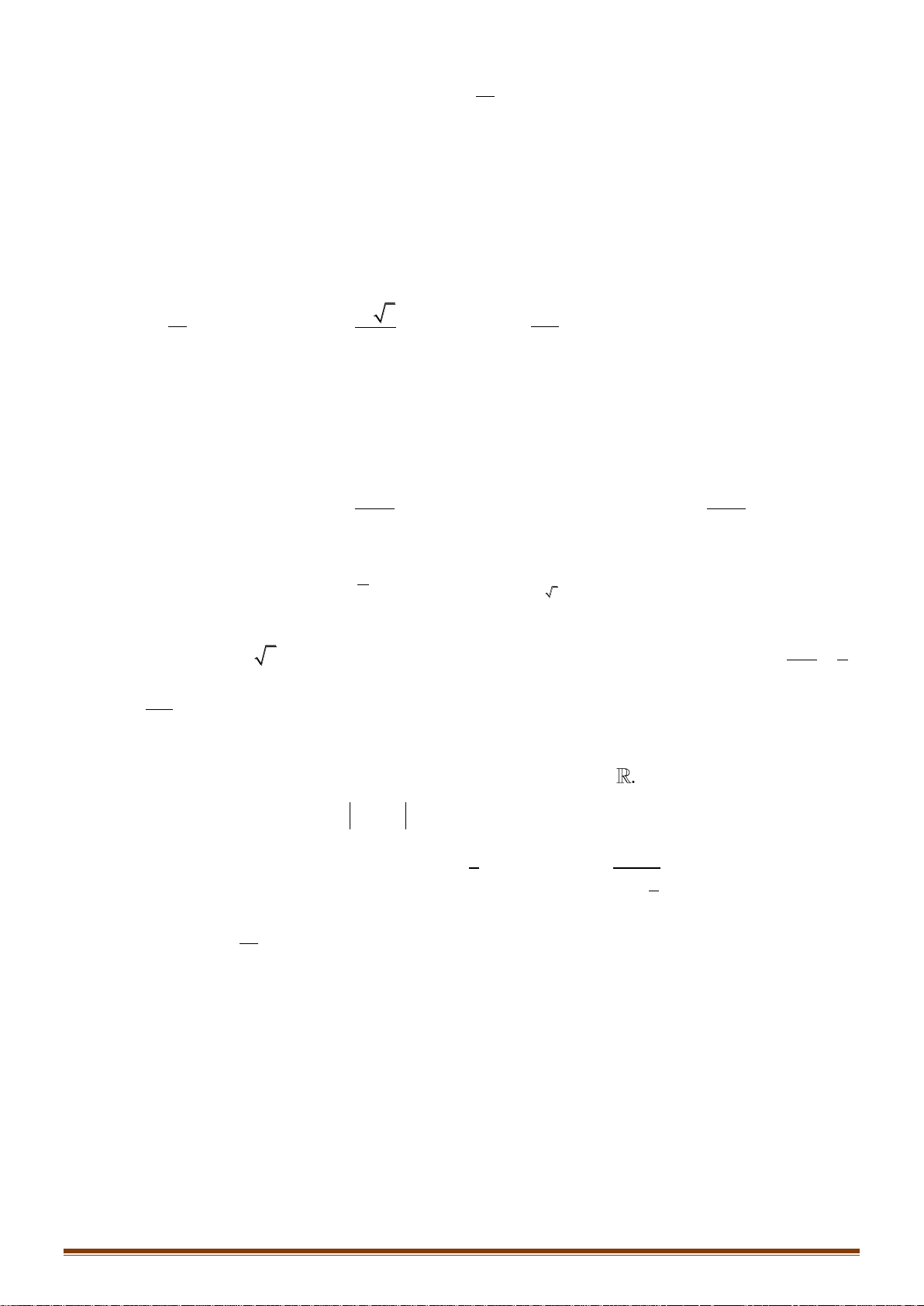
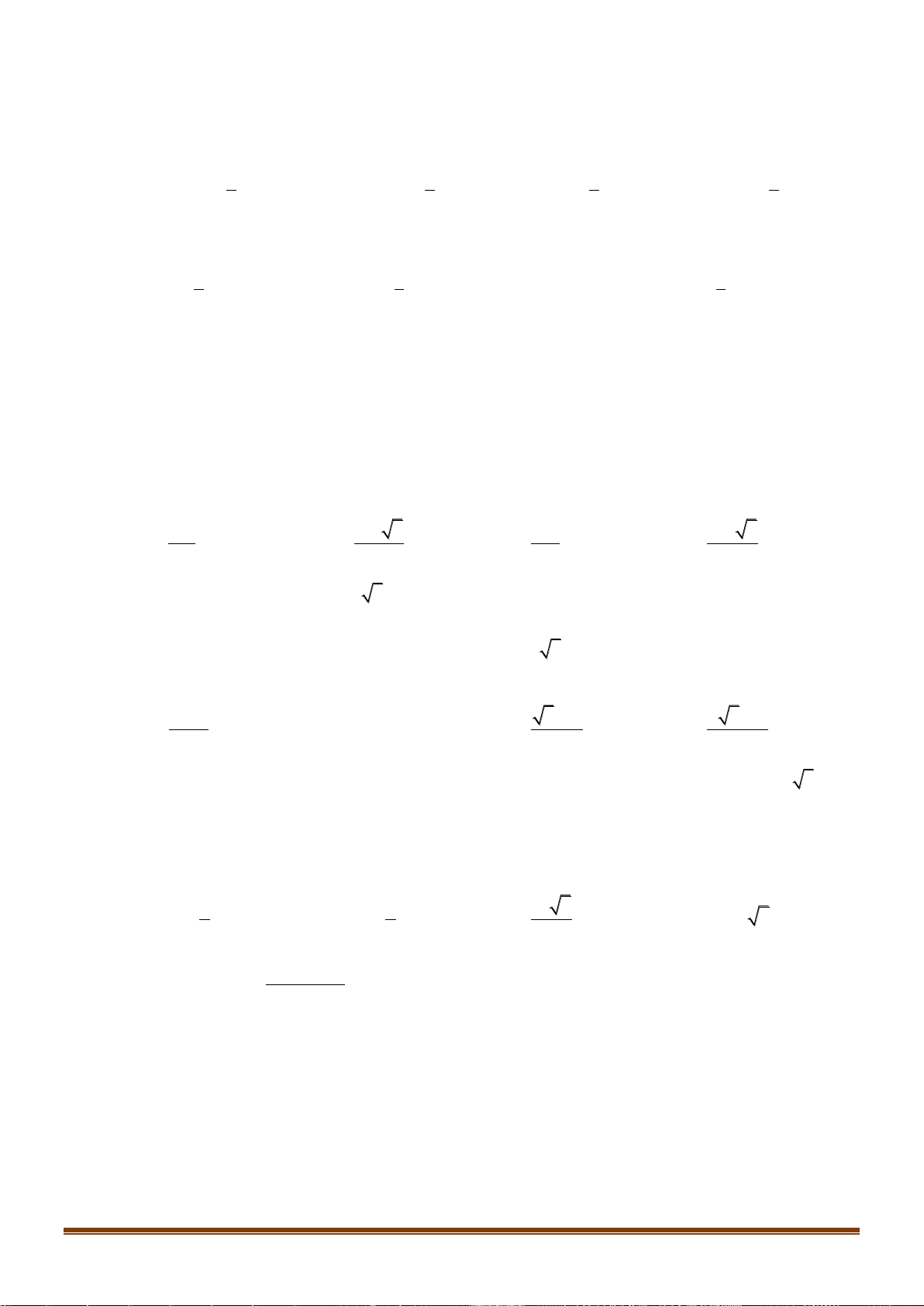
Preview text:

ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 01
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) a aCâu 1:
Rút gọn biểu thức M =
(a  0) về dạng a thì  thuộc khoảng nào dưới đây? a A.  (2;5). B.  ( 1 − ;0). C.  ( 3 − ;− ) 1 . D.  (0;2). Câu 2: Cho hàm số 3
y = −x + 2x −1. (C ) và đường thẳng d : y = −x −1. Biết d cắt (C ) tại ba điểm có
hoành độ lần lượt là + + 1 x , 2 x , 3 x . Tính giá trị 2 2 2 1 x 2 x 3 x . A. 3. B. 6. C. 0. D. 9. Câu 3: Hàm số 3
y = −x + 9x −11 nghịch biến trên khoảng nào sau đây? A. ( ; − − 3). B. (− 3;+). C. (− 3; 3). D. ( 3 − ; ) 3 . Câu 4:
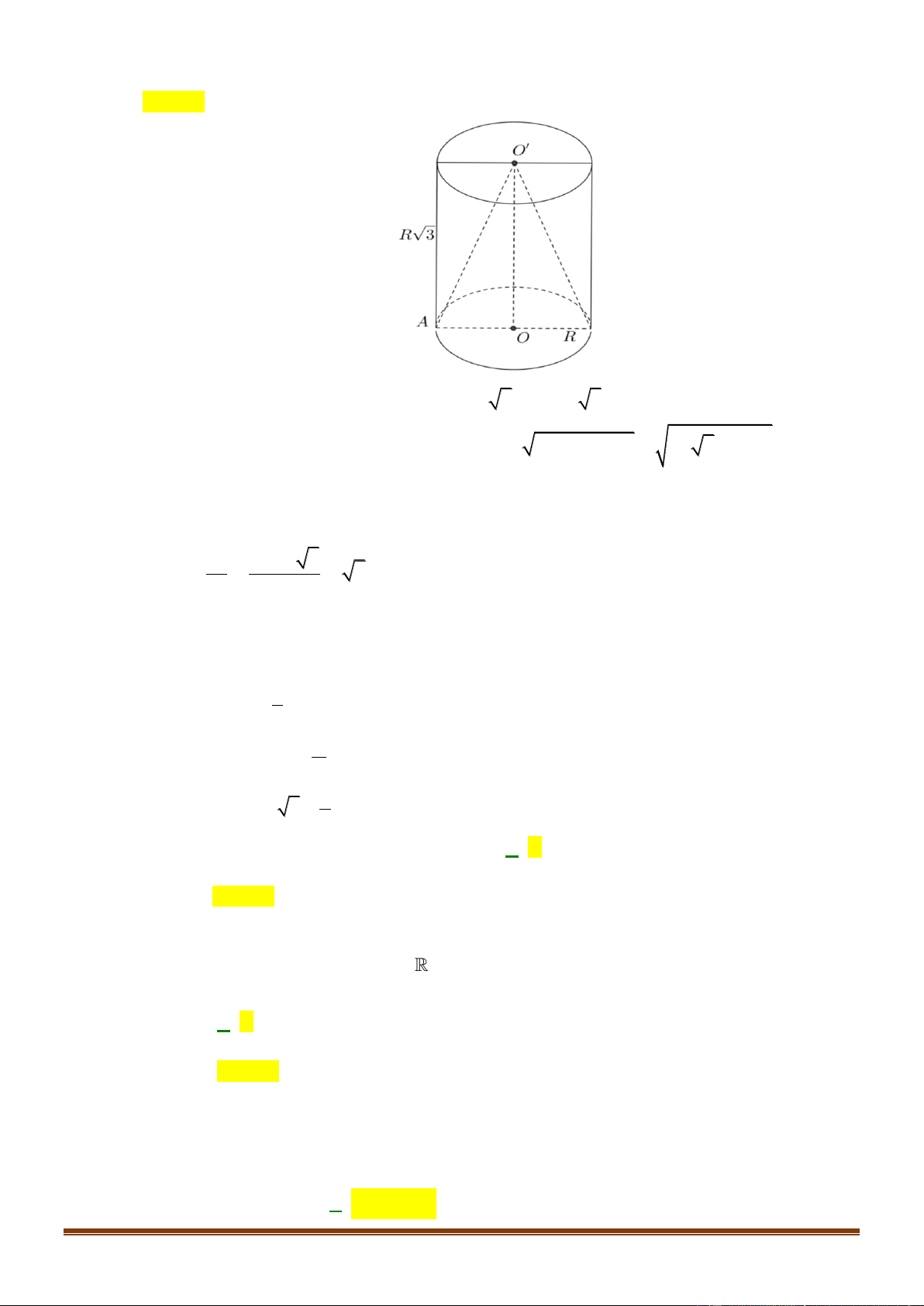
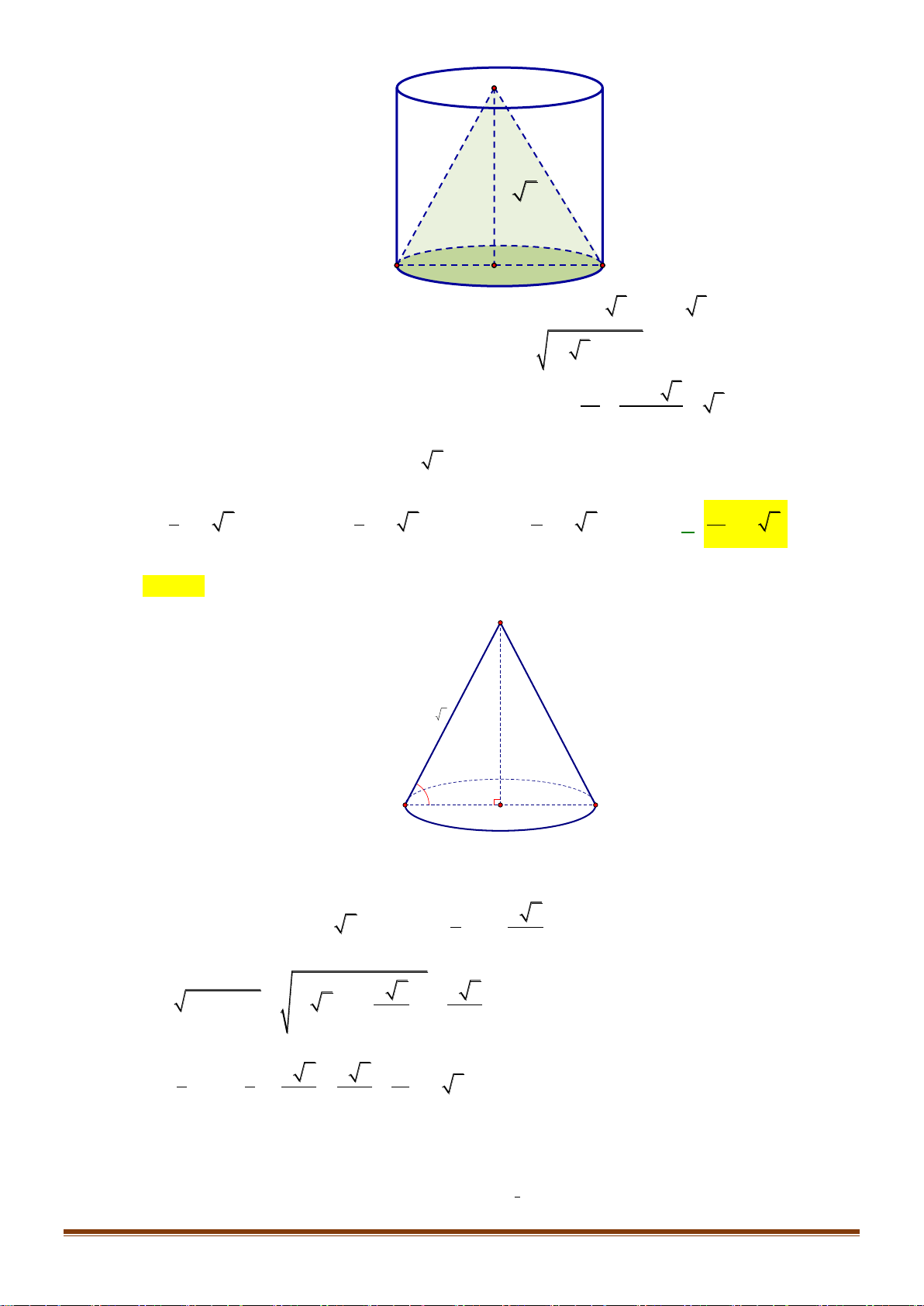
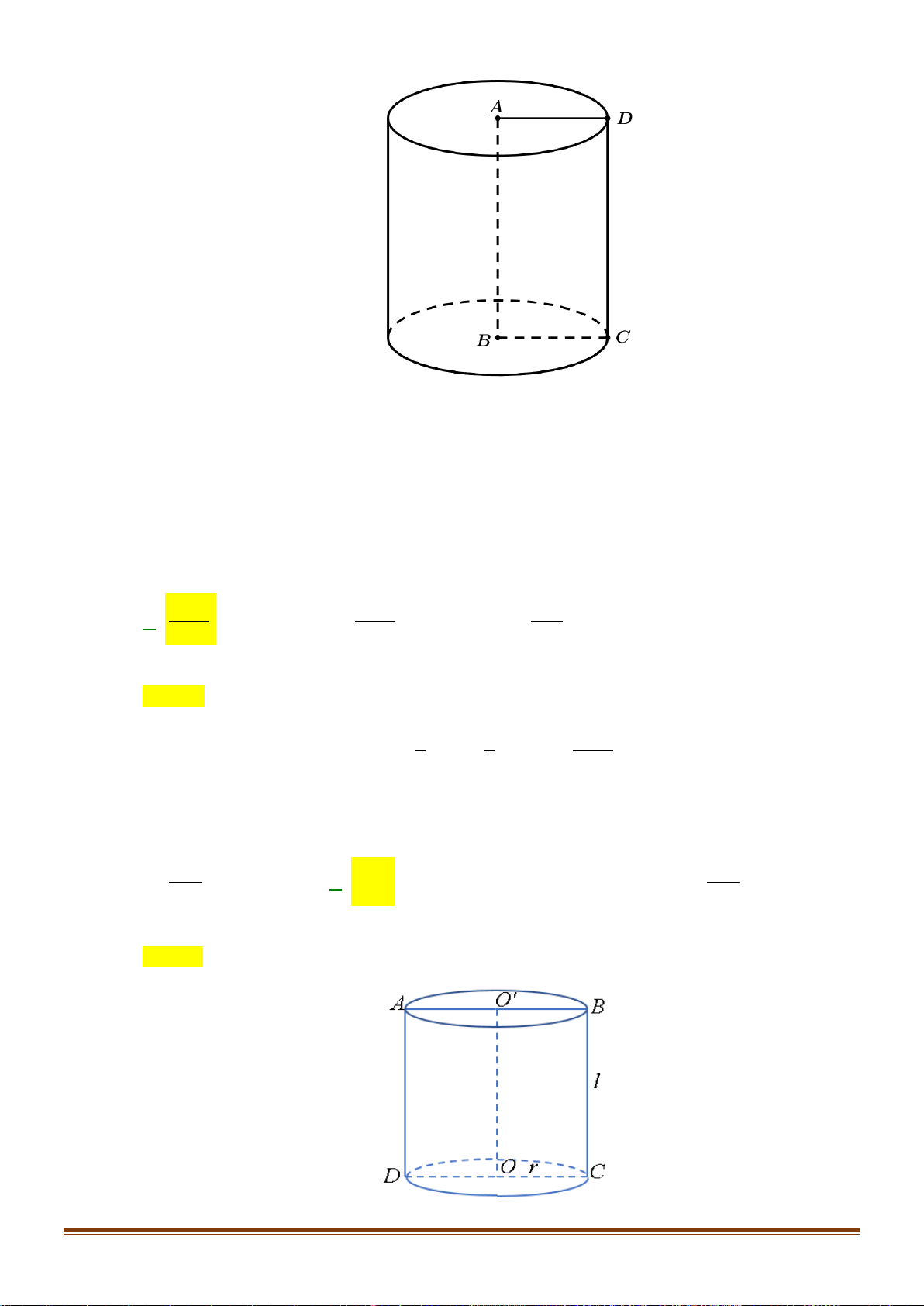
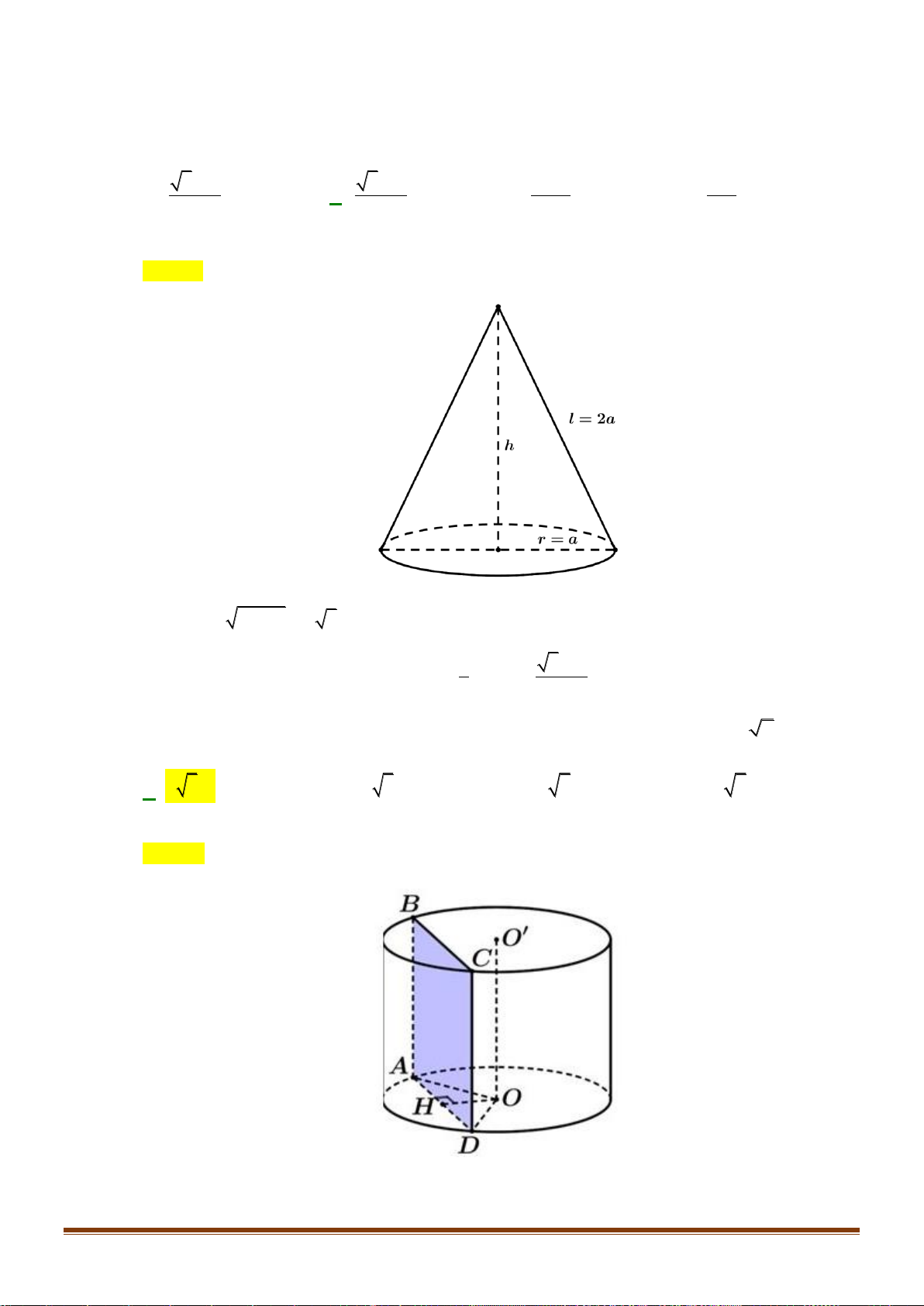
Cho hình trụ có hai đáy là hai hình tròn (O) và (O) , chiều cao R 3 và bán kính đáy R . Một
hình nón có đỉnh là O và đáy là hình tròn ( ;
O R) . Tính tỷ số diện tích xung quanh của hình trụ và hình nón. A. 3 . B. 2 . C. 2. D. 3. Câu 5:
Cho a  0, a  1,b  0, c  0 . Trong 4 khẳng định sau, có bao nhiêu khẳng định đúng? b
I. log (bc) = log blog c II. log
= log c − log b a a a a a a c  1 1 III. log b =
log b (   0 IV. log b = log b a a )  a 2 a A. 3. B. 4. C. 1. D. 2. 2021 Câu 6:
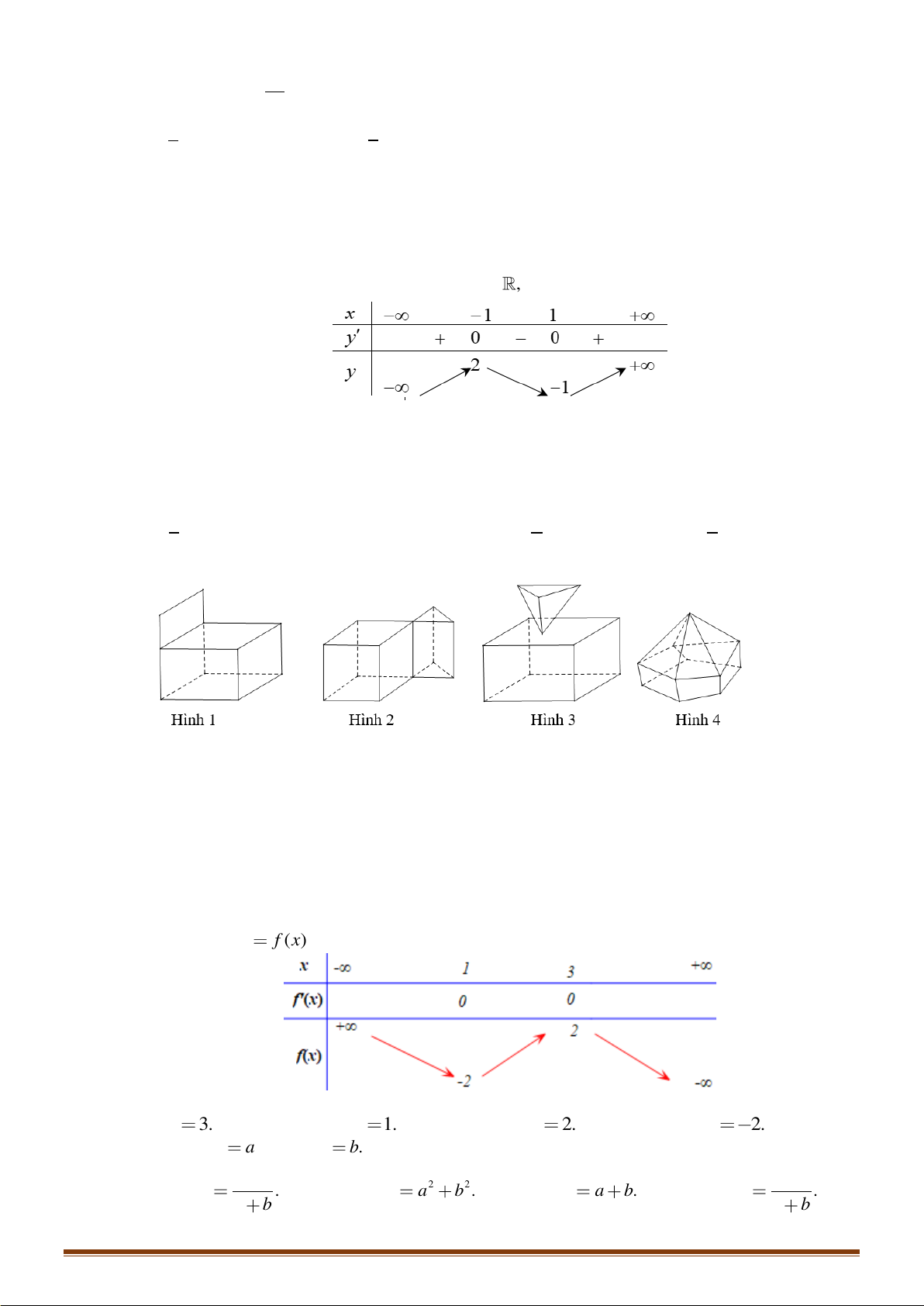
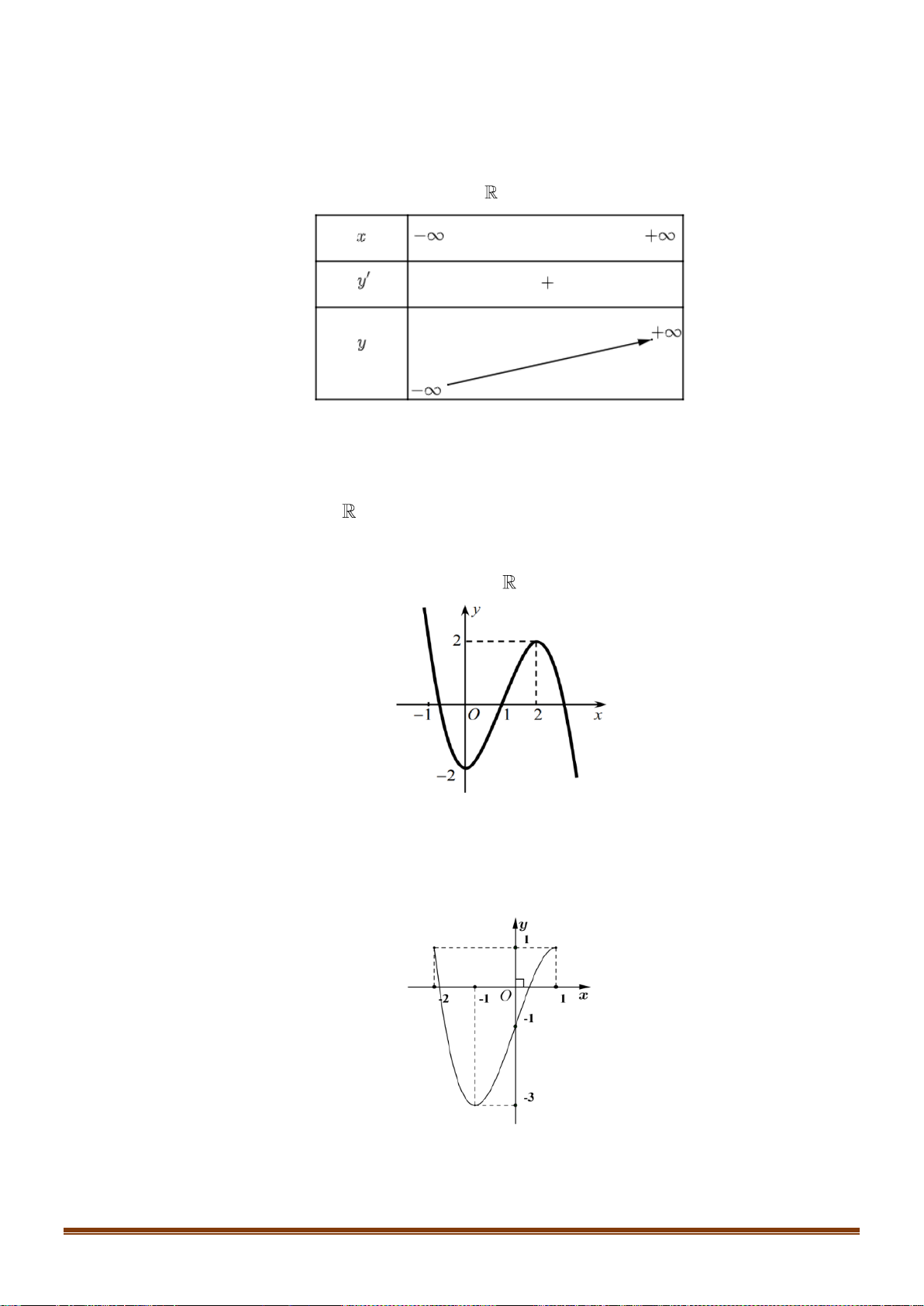
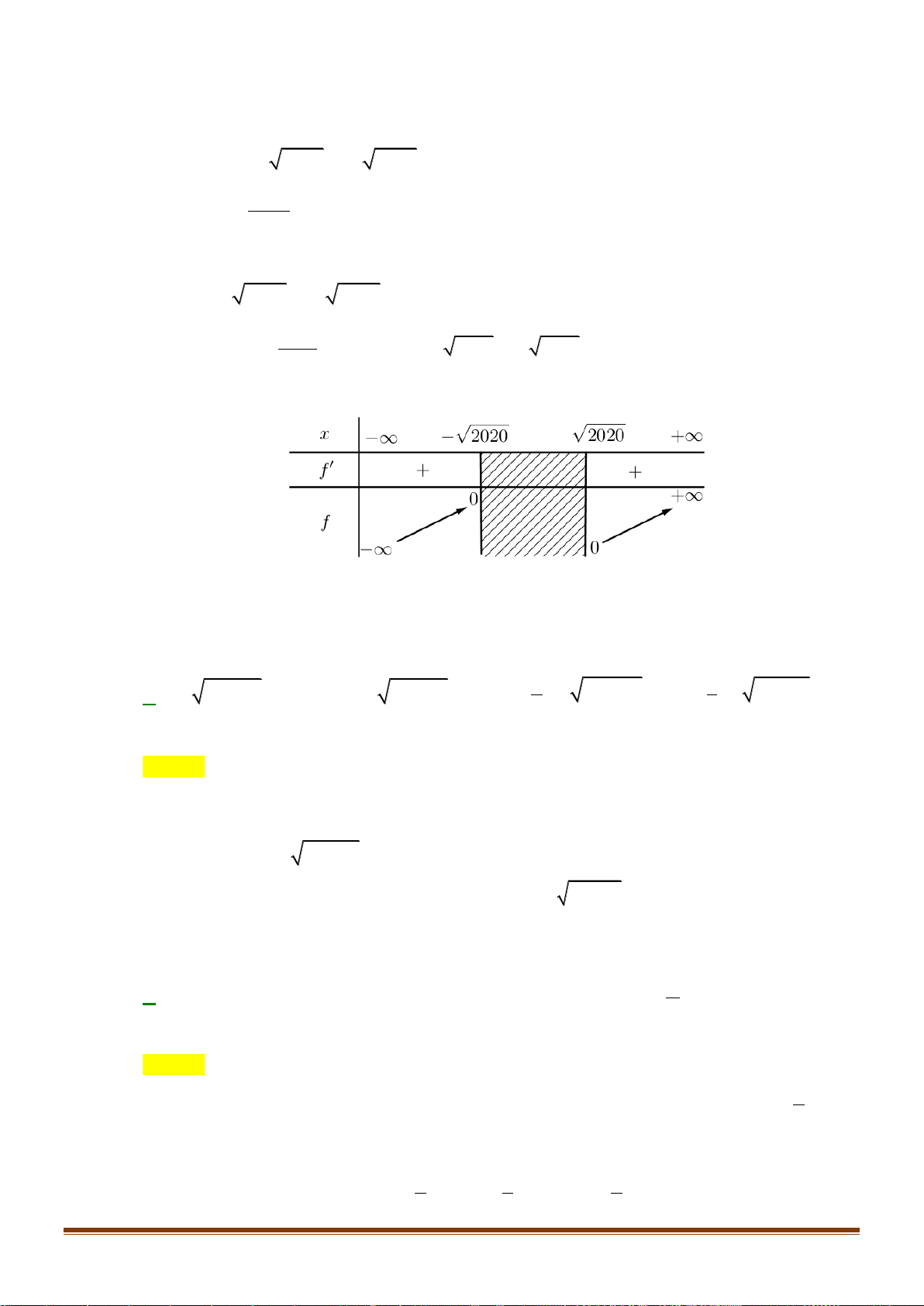
Cho hàm số y = f (x) xác định trên và có f ( x) = ( 2 x − ) 2 1
x ( x + 3) . Hỏi y = f (x) có bao
nhiêu điểm cực trị? A. 3. B. 4. C. 1. D. 2. Câu 7:
Cho log b =  thì N = a b
thuộc khoảng nào sau đây? ab ( 2 3 log ) a A. ( 1 − ; ) 1 . B. (2;4) . C. (1; 2) . D. (4;7) . Câu 8:
Trong các mệnh đề sau, mệnh đề nào là sai?
A. Diện tích xung quanh cùa hình trụ tròn xoay bằng tích độ dài đường tròn đáy và độ dài đường sinh.
B. Thể tích của khối nón tròn xoay bằng tích của diện tích đáy và độ dài đường cao của khối nón đó.
C. Thể tích của khối trụ tròn xoay là giới hạn của thể tích khối lăng trụ đều nội tiếp khối trụ đó
khi số cạnh tăng lên vô hạn.
D. Diện tích toàn phần của hình nón là tổng của diện tích xung quanh và diện tích đáy của hình nón đó. Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Câu 9:
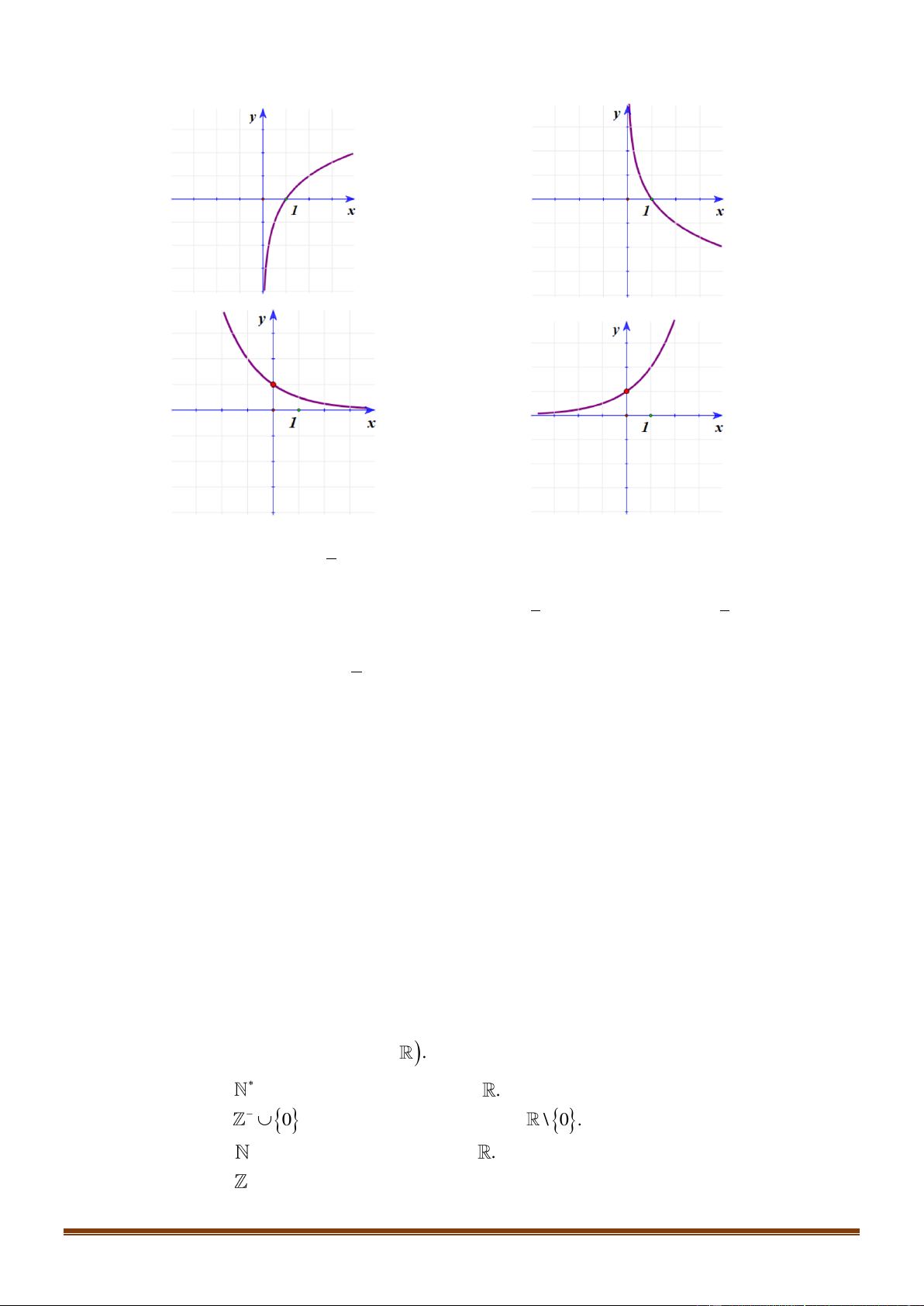
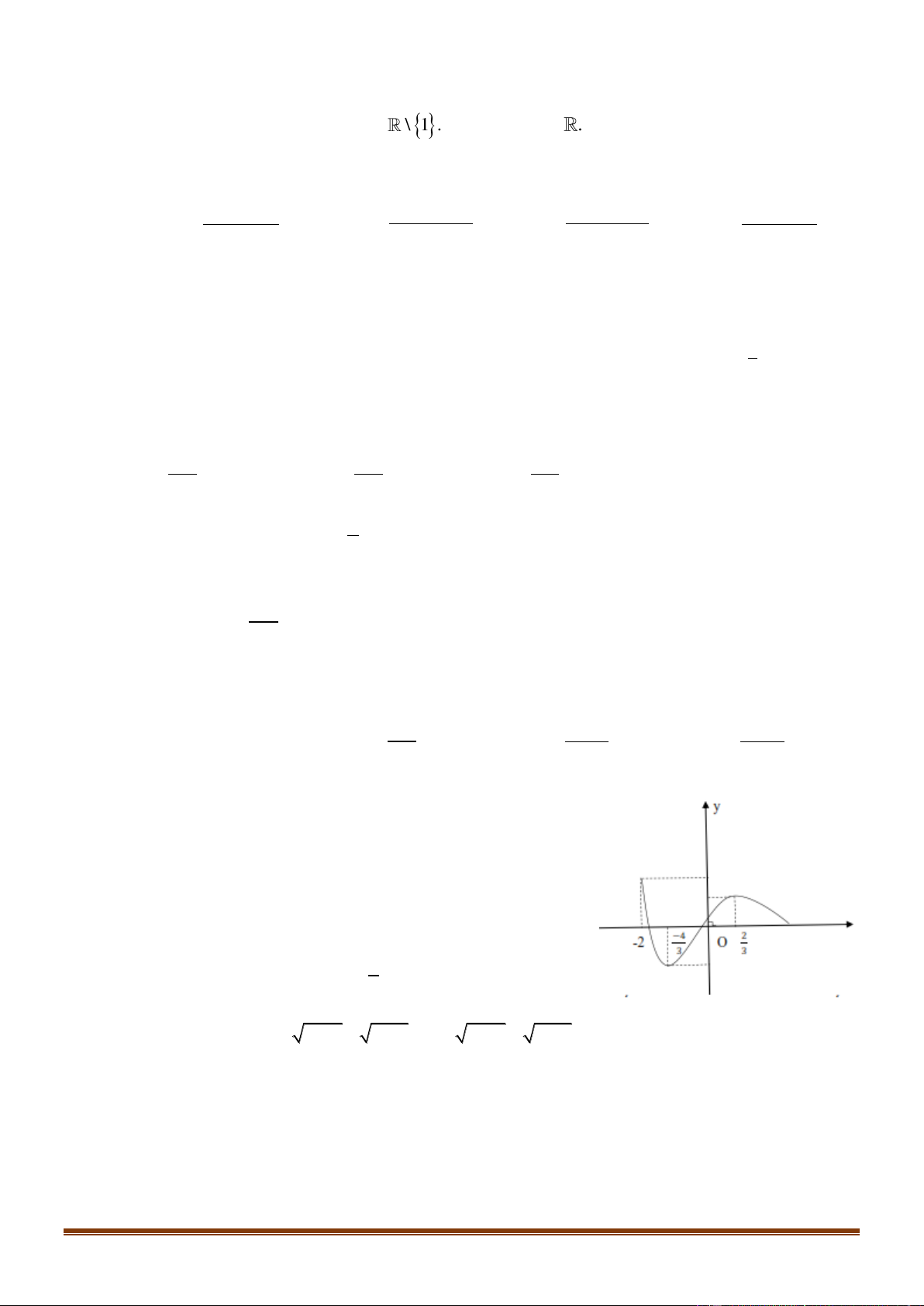
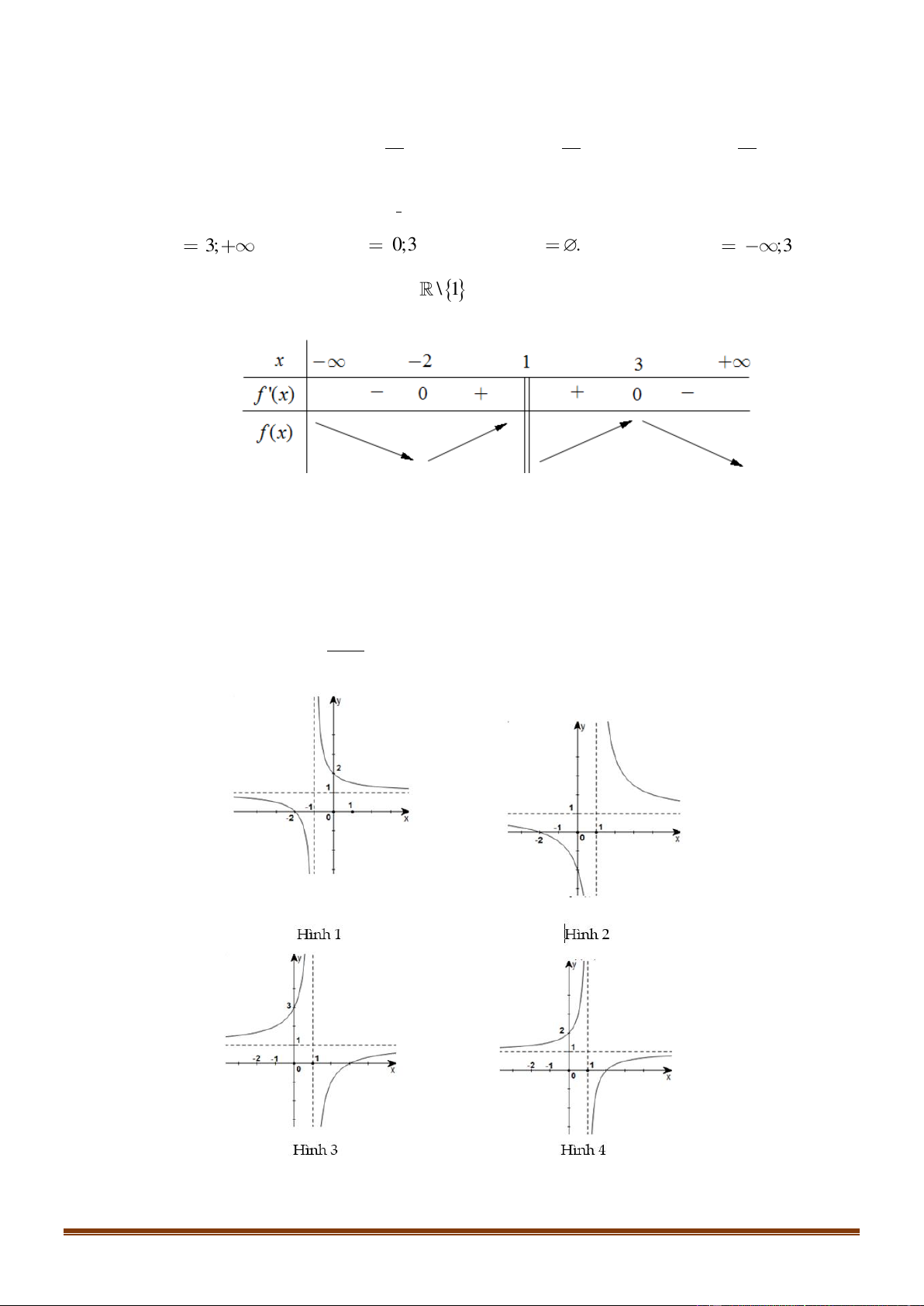
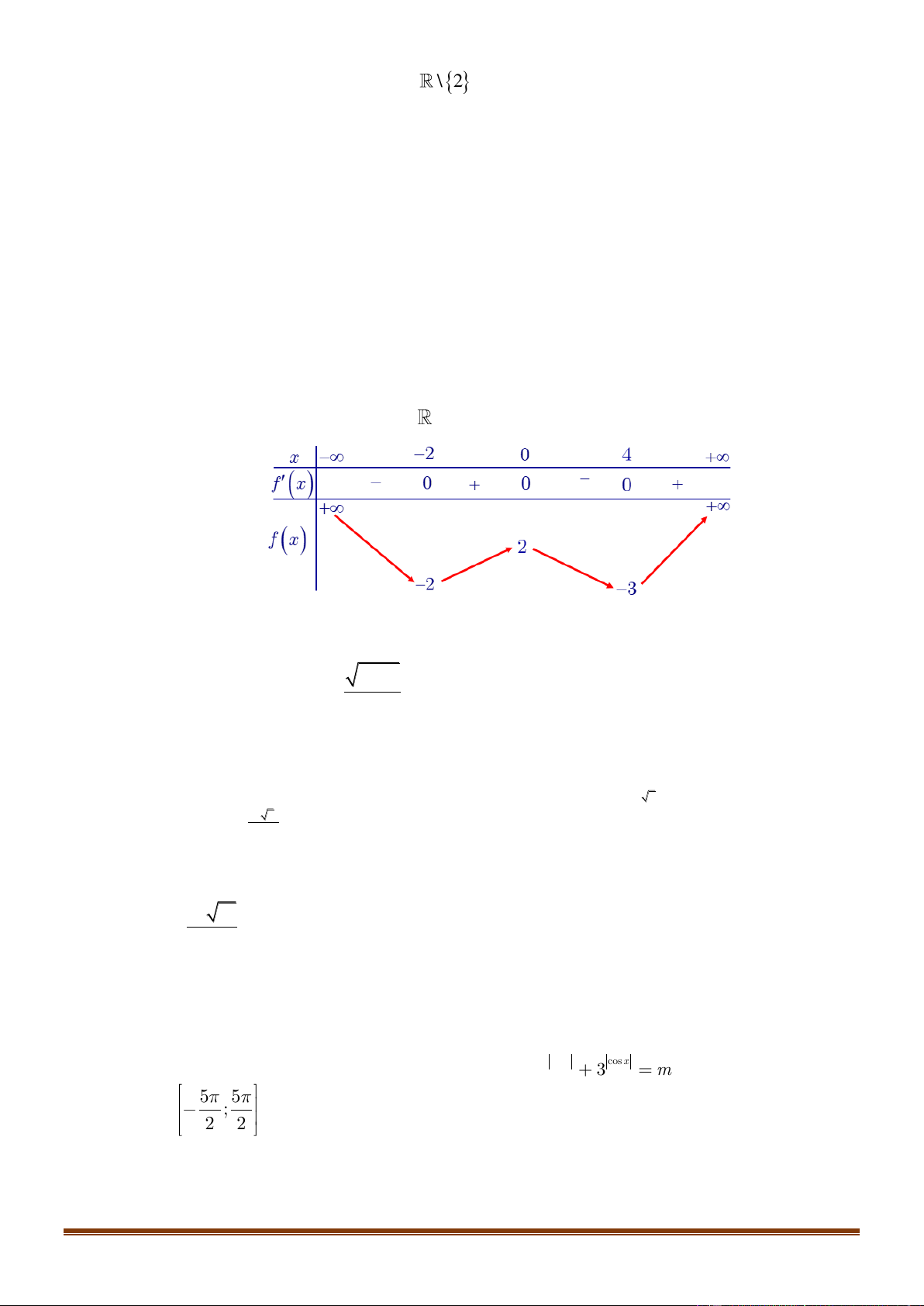
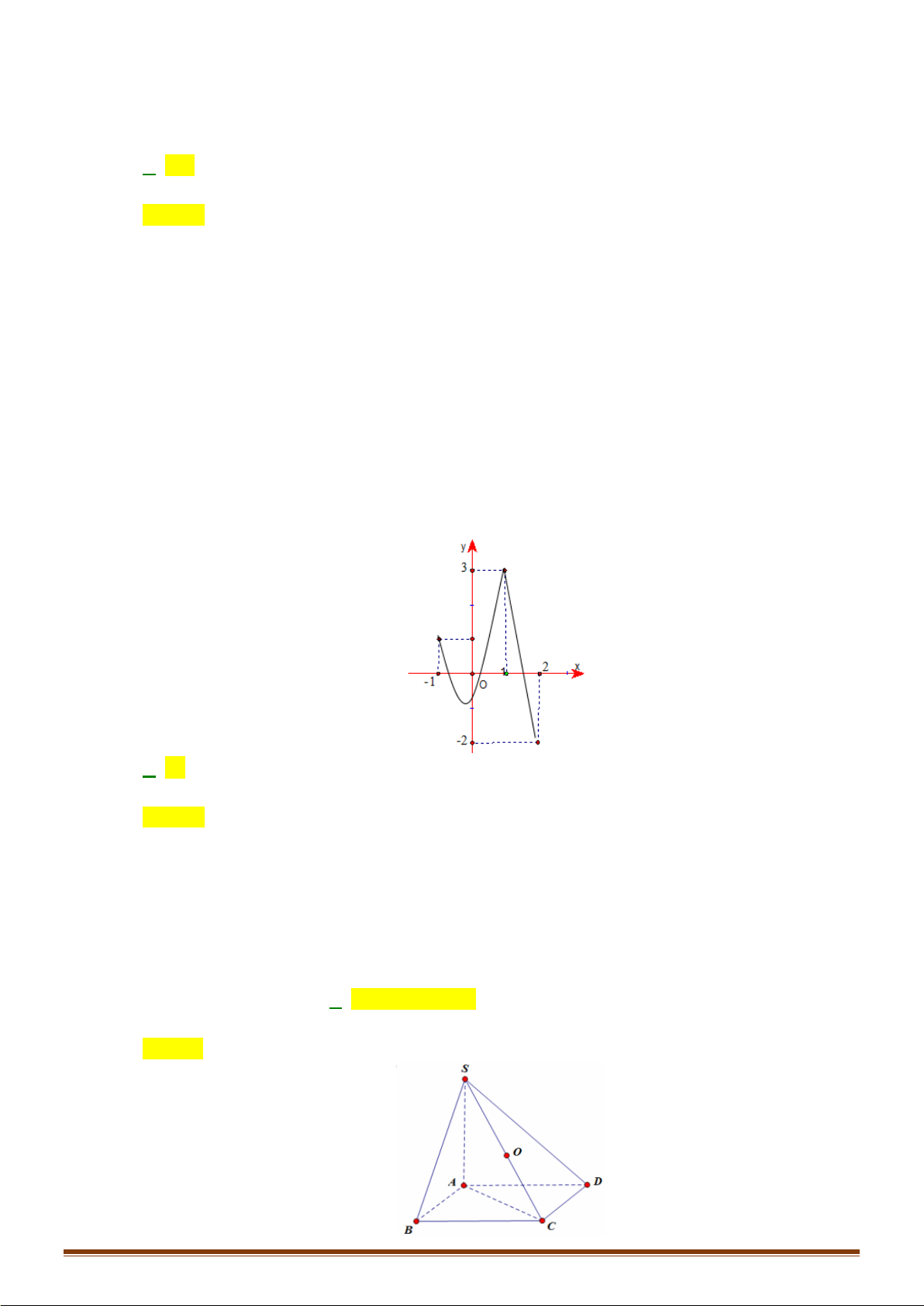
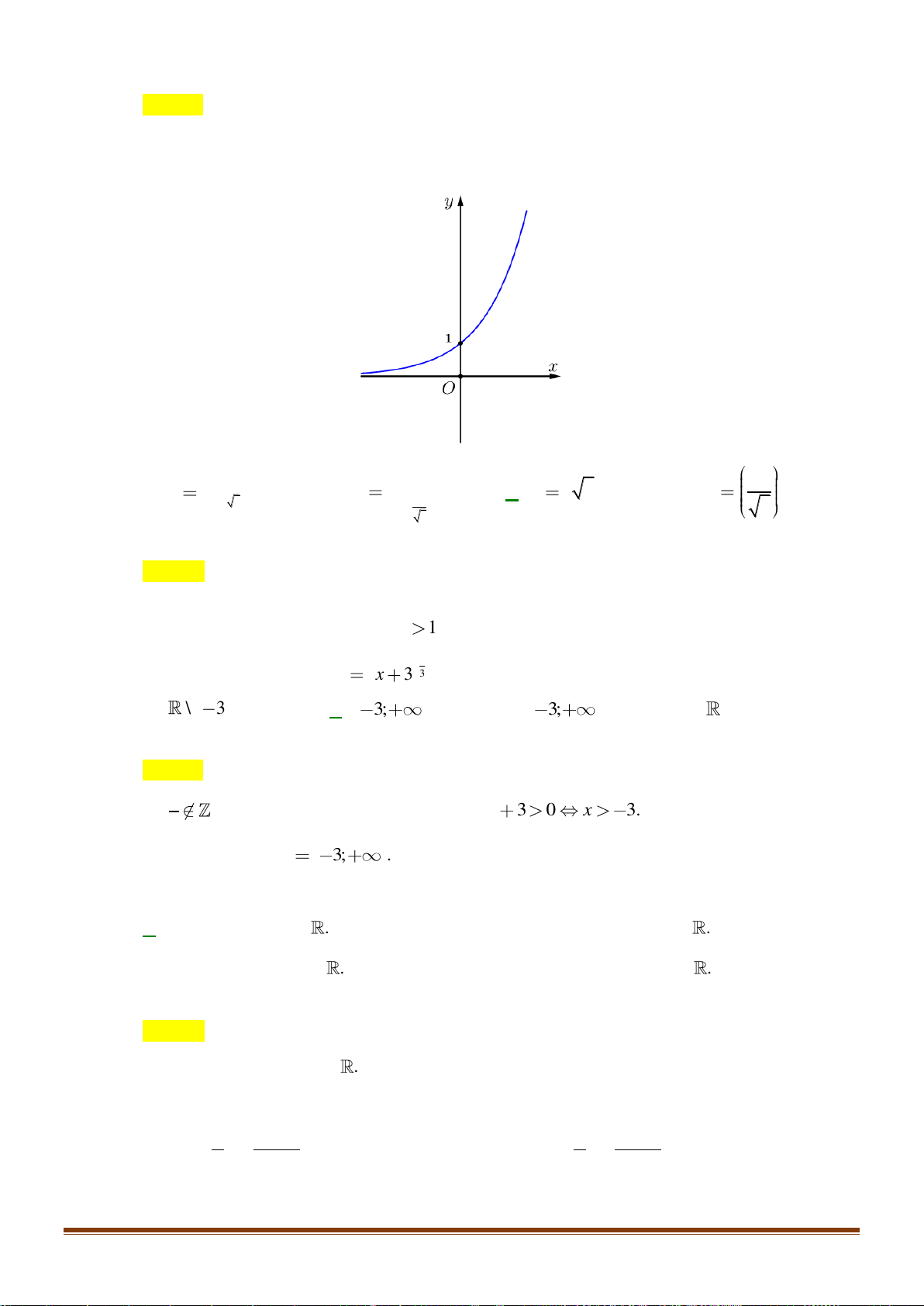
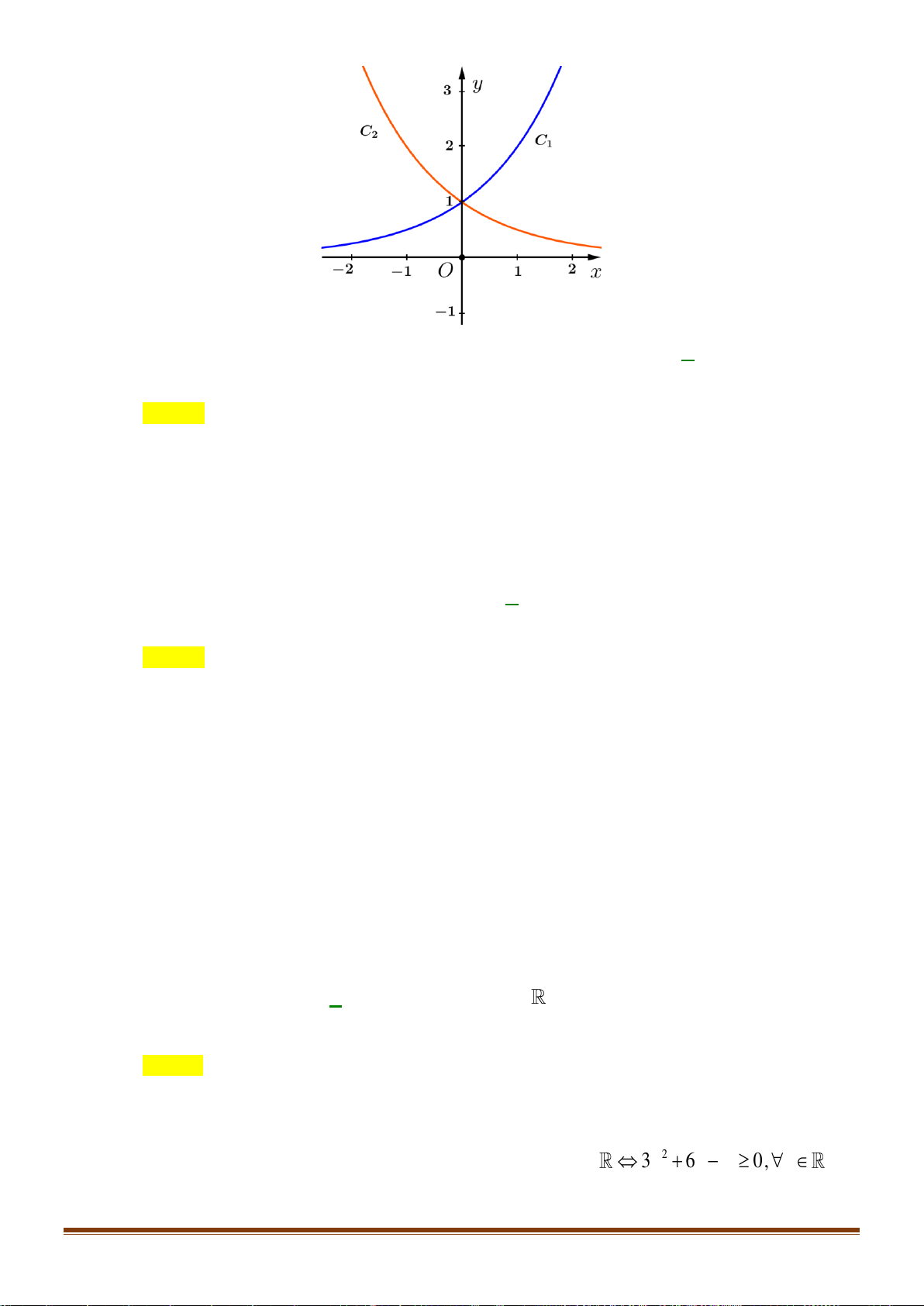
Đồ thị nào sau đây là dạng đồ thị của các hàm sổ y = log x với 0 a 1? a A. . B. . C. . D. . 1
Câu 10: Cho hàm số y = f ( x) 3 2
= x − x +1. Tìm giá trị nhỏ nhất của hàm số y = f (x) trên 1;  3 . 3 1 1 A. 1 − . B. 1. C. . D. − 3 3
Câu 11: Cho hàm số y = f ( x) 1
= x + − 2 . Gọi y , y lần lượt là tung độ của điểm cực đại và cực tiểu của x 1 2
đồ thị hàm số đã cho. Tính giá trị y − y 1 2 A. 4 . B. 12 − . C. 4 − . D. 12
Câu 12: Phương trình log 2x +1 = 2 có nghiệm là 3 ( ) A. 3 . B. 4 . C. 13 . D. 1
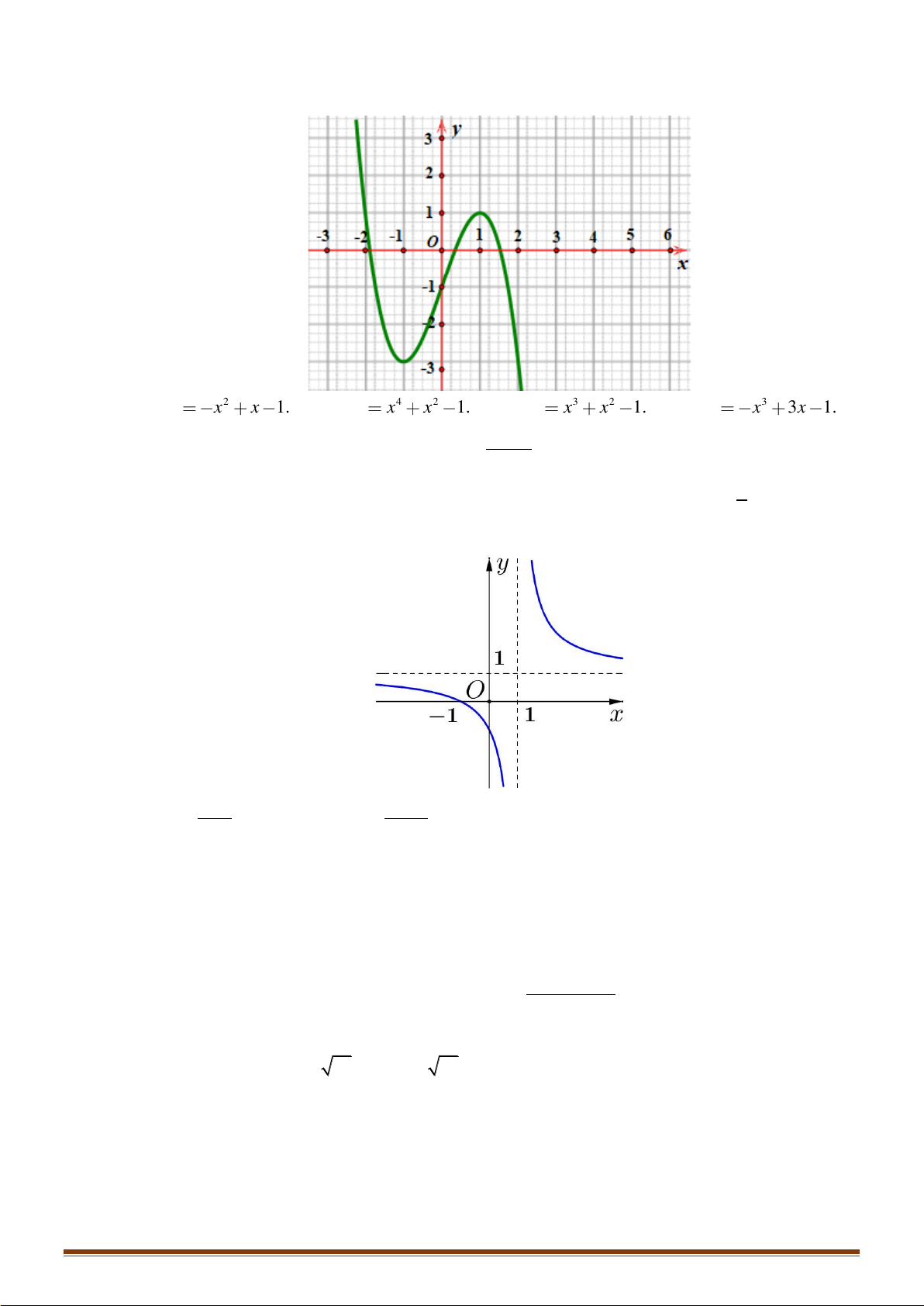
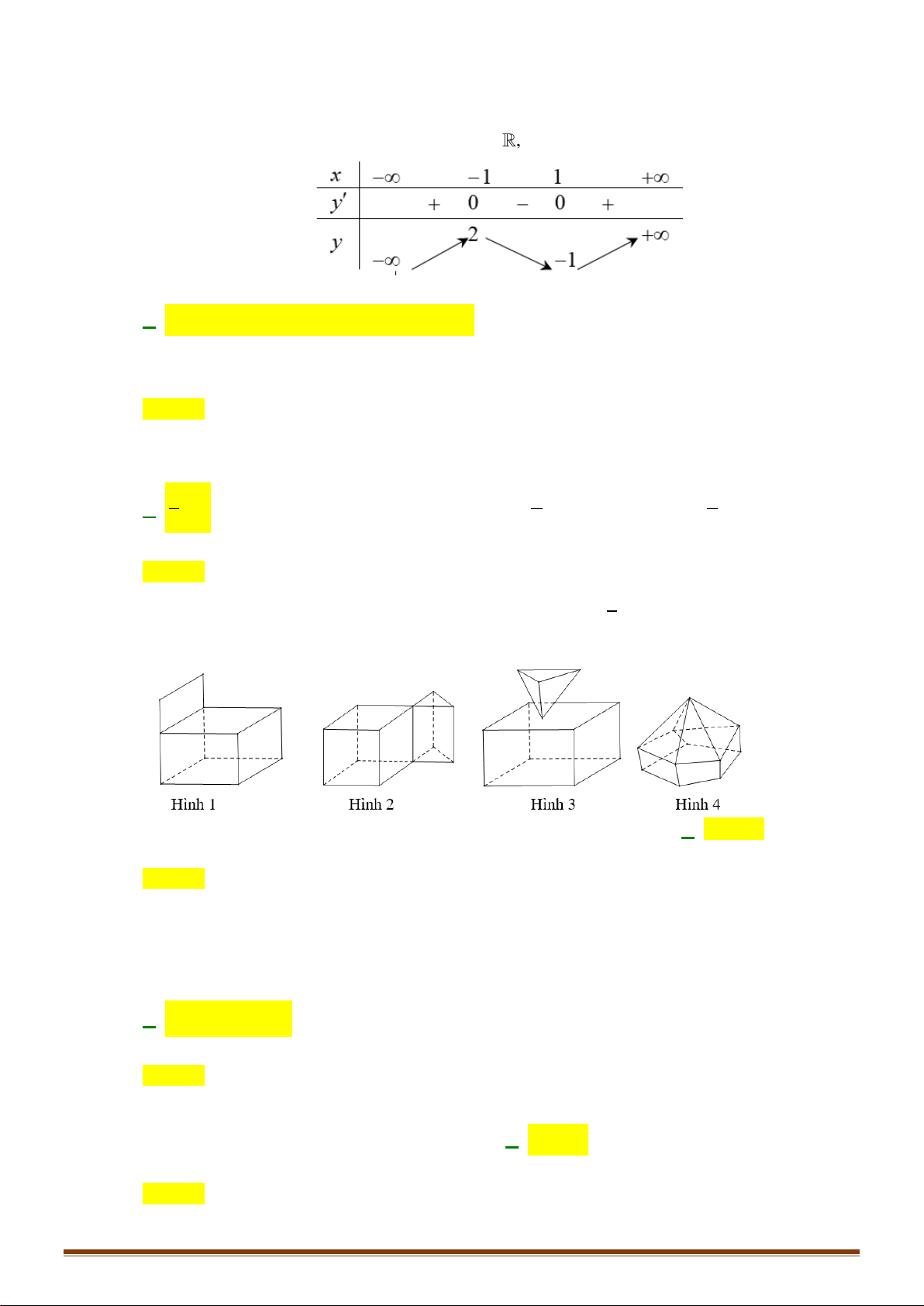
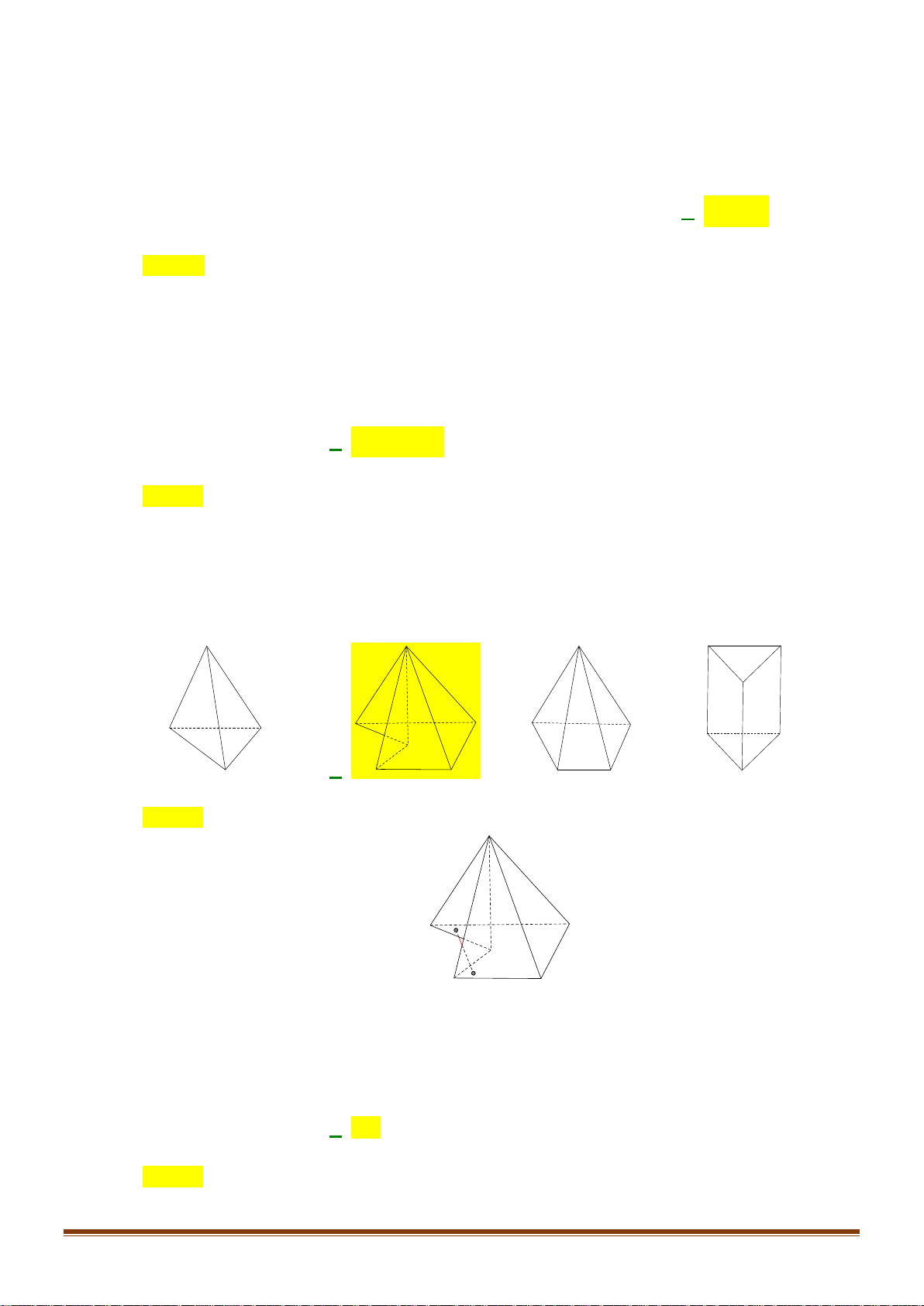
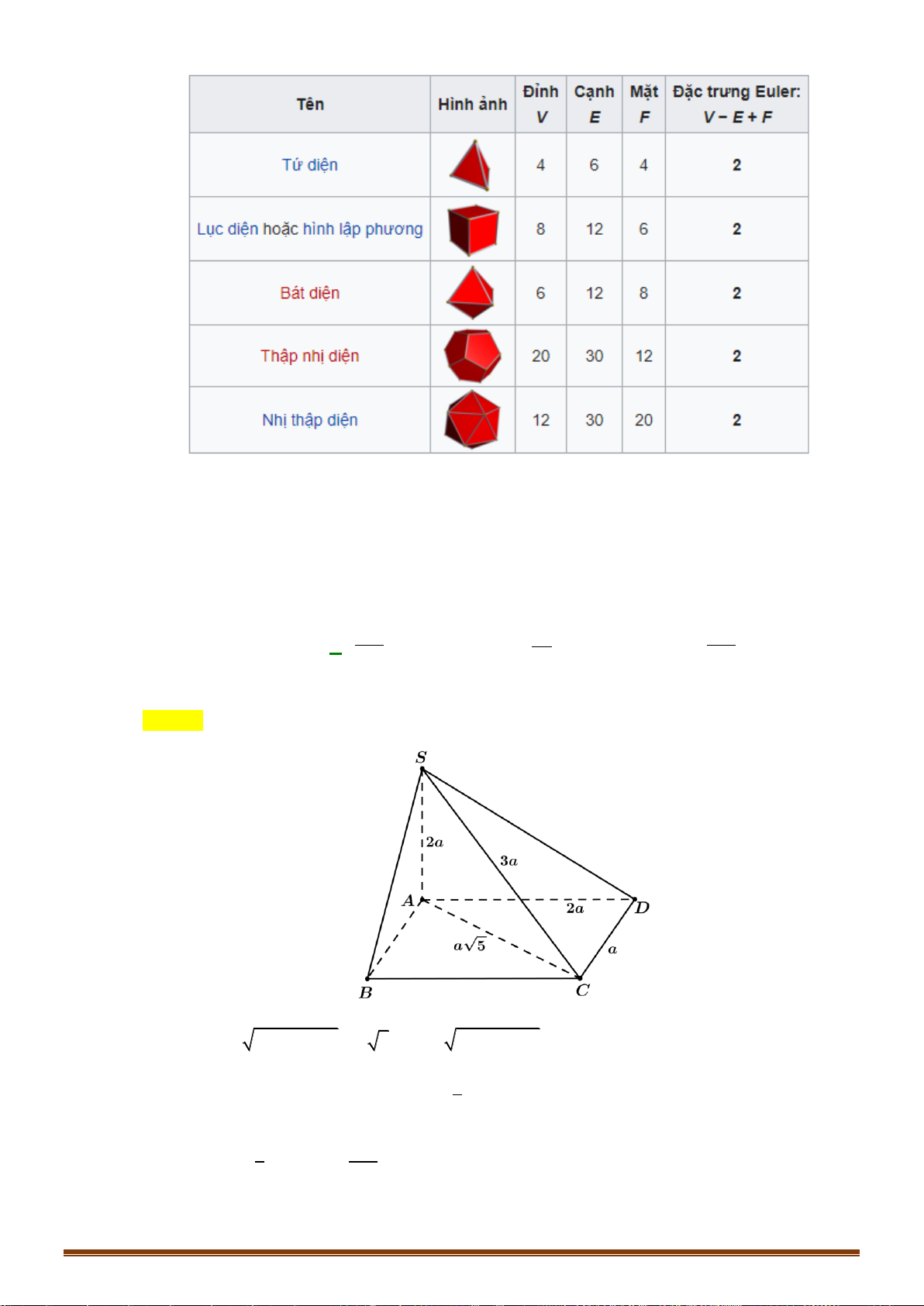
Câu 13: Hình đa diện nào dưới đây không có tâm đối xứng?
A. Lăng trụ lục giác đều. B. Hình lập phương. C. Bát diện đều. D. Tứ diện đều.
Câu 14: Tính thể tích V của khối trụ có bán kính đáy và chiều cao đều bằng 2 . A. 16 . B. 8 . C. 4 . D. 12 . −
Câu 15: Tìm đạo hàm của hàm số y = ( − x) 3 1 2 . − − − −
A. y = ( − x) 2 6 1 2 .
B. y = − ( − x) 2 3 1 2
. C. y = − ( − x) 4 6 1 2
. D. y = ( − x) 4 6 1 2 .
Câu 16: Cho hàm số lũy thừa y = x , (  ). Trong các khẳng định sau khẳng định nào sai? A. Nếu   
thì hàm số có tập xác định là . B. Nếu  −   
0 thì hàm số có tập xác định là \   0 . C. Nếu  
thì hàm số có tập xác định là .
D. Nếu   thì hàm số có tập xác định là (0;+). Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
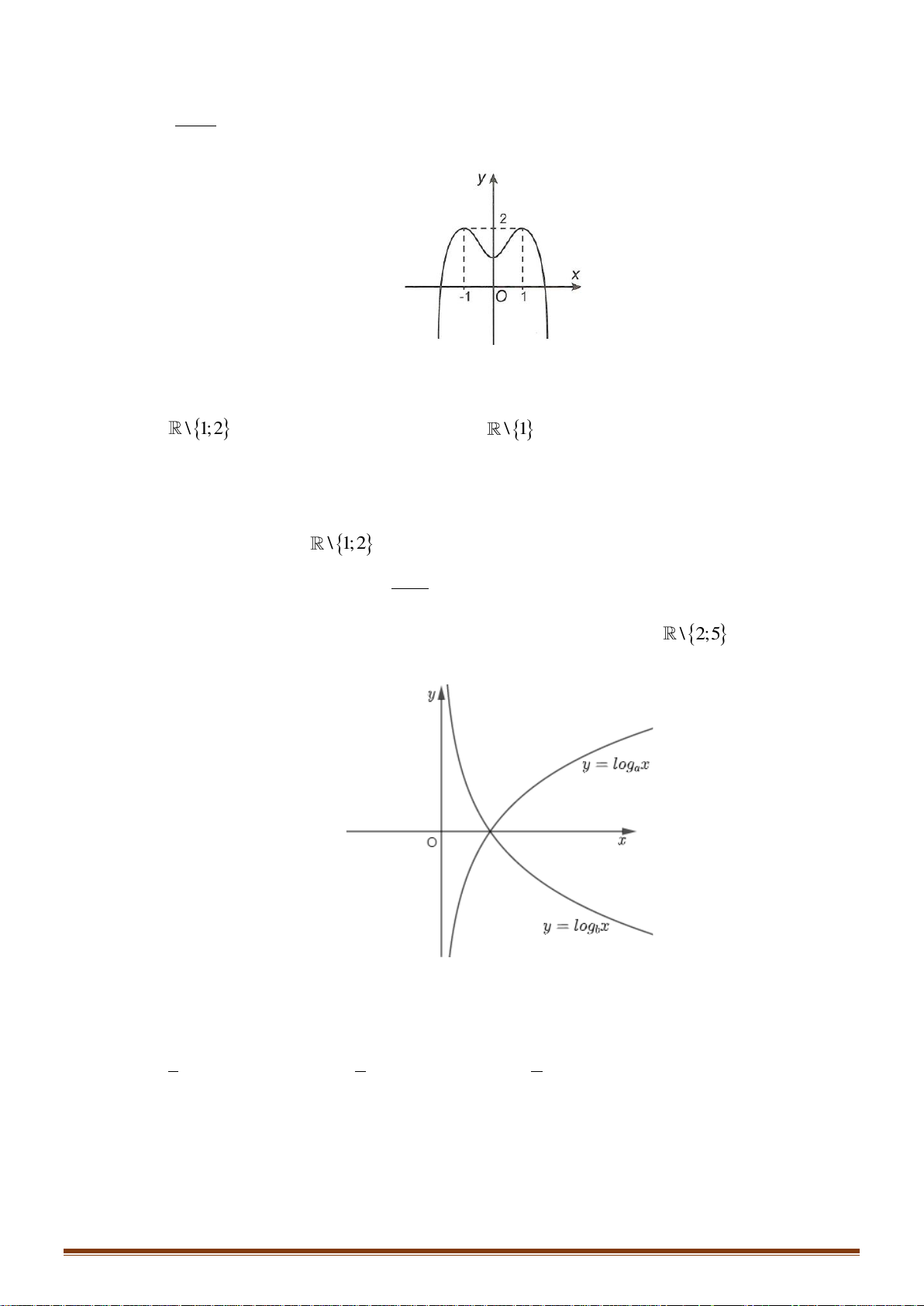
Câu 17: Tìm tập xác định của hàm số y = log (1− x)2 . 2 A. D = (− ;  ) 1 . B. D = \   1 . C. D = . D. D = (− ;   1 .
Câu 18: Tìm đạo hàm của hàm số y = log (1− x)2 . 3 2 1 2 − 2 − A. y ' = ( B. y ' = . C. y ' = . D. y ' = . − x) . 1 ln 3 (1− x)2 ln3 (1− x)2 ln3 (1− x)ln3
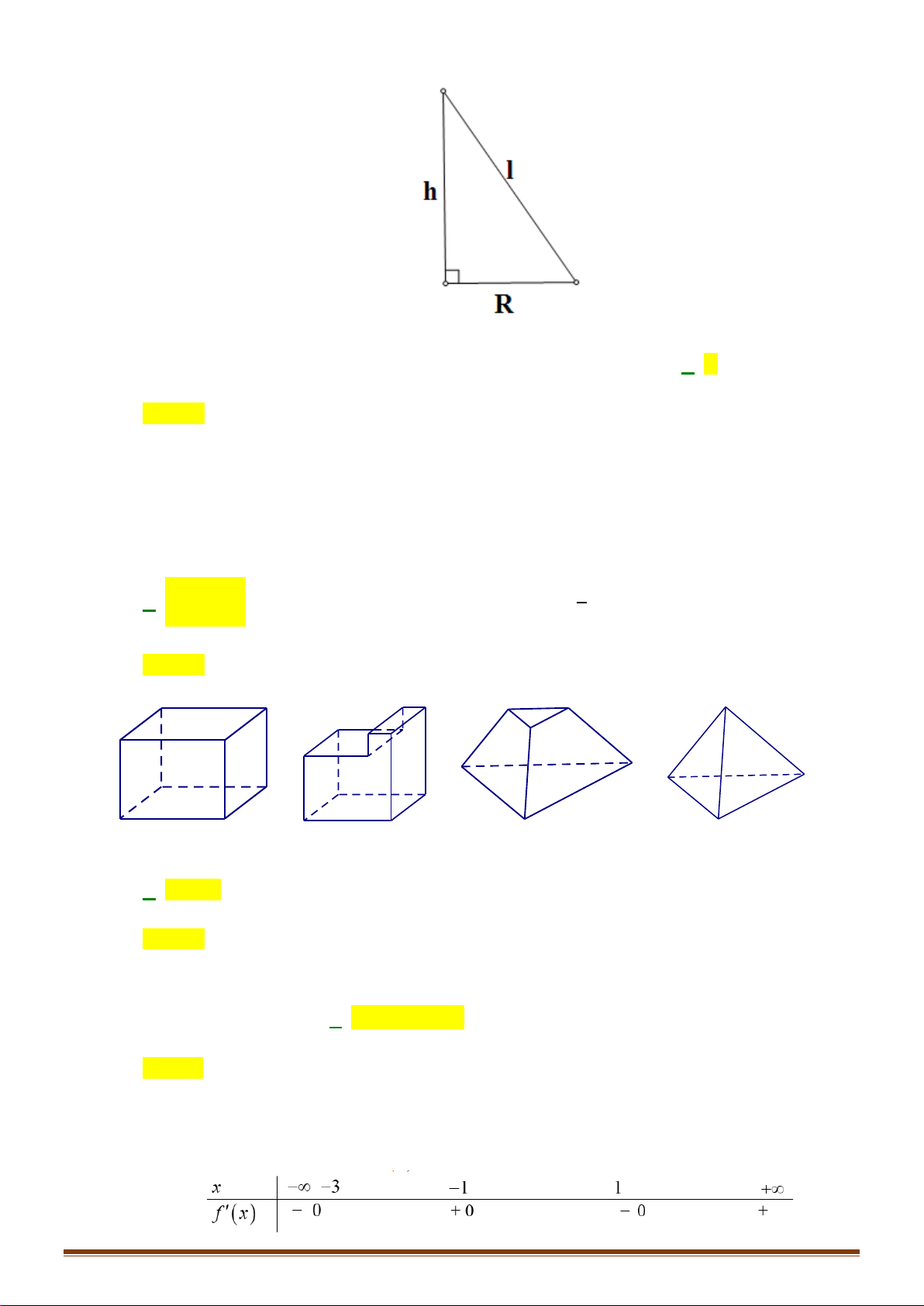
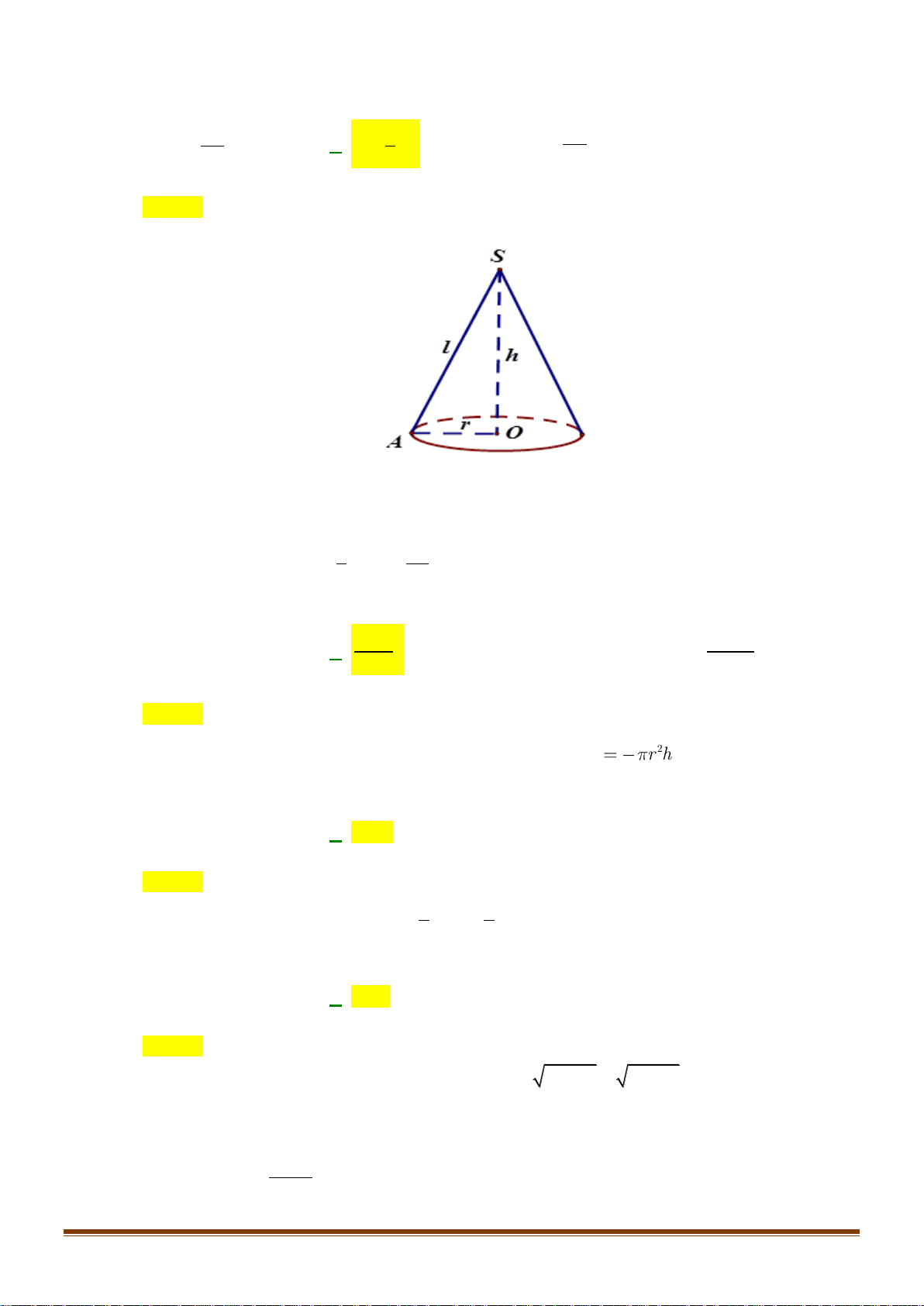
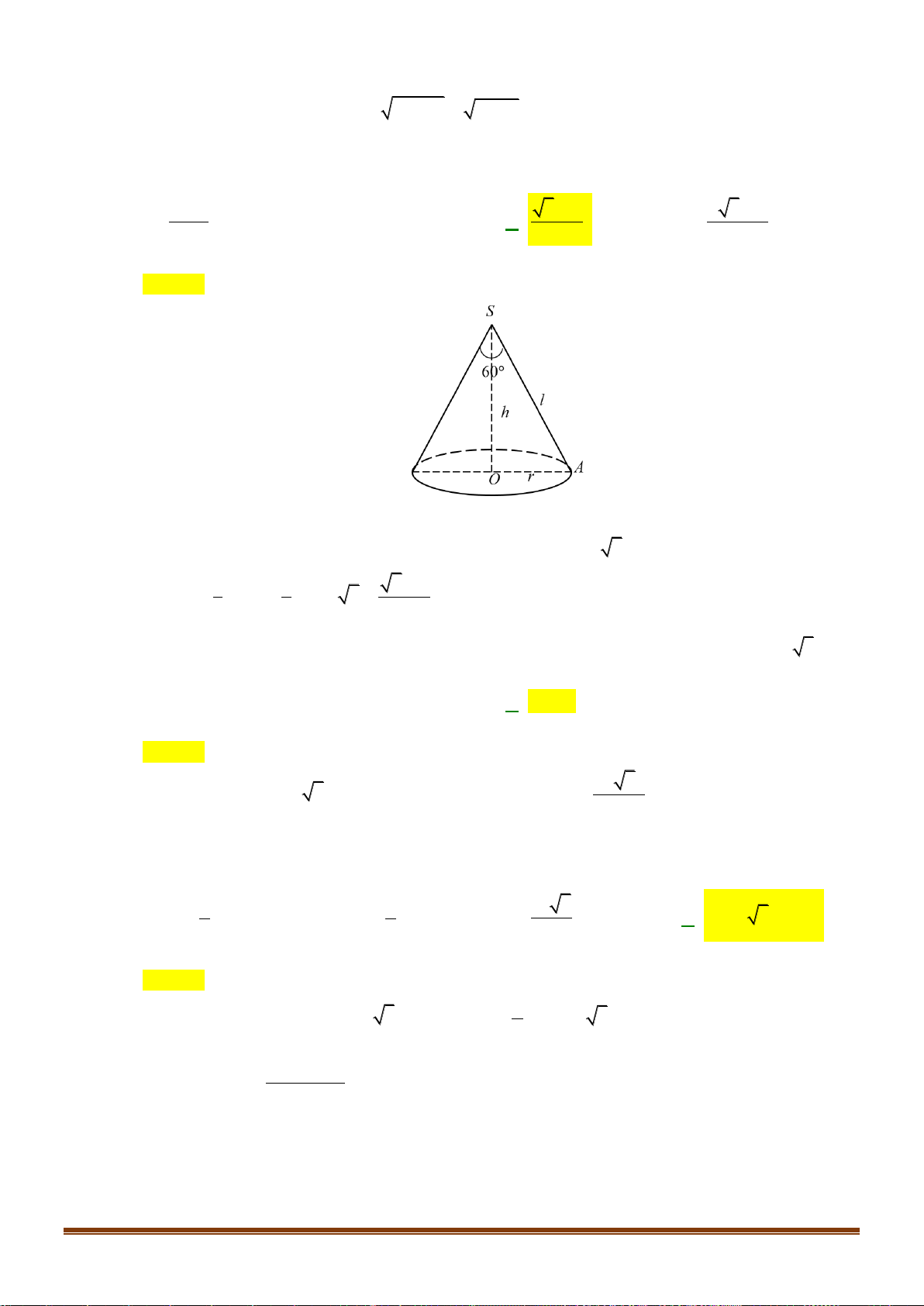
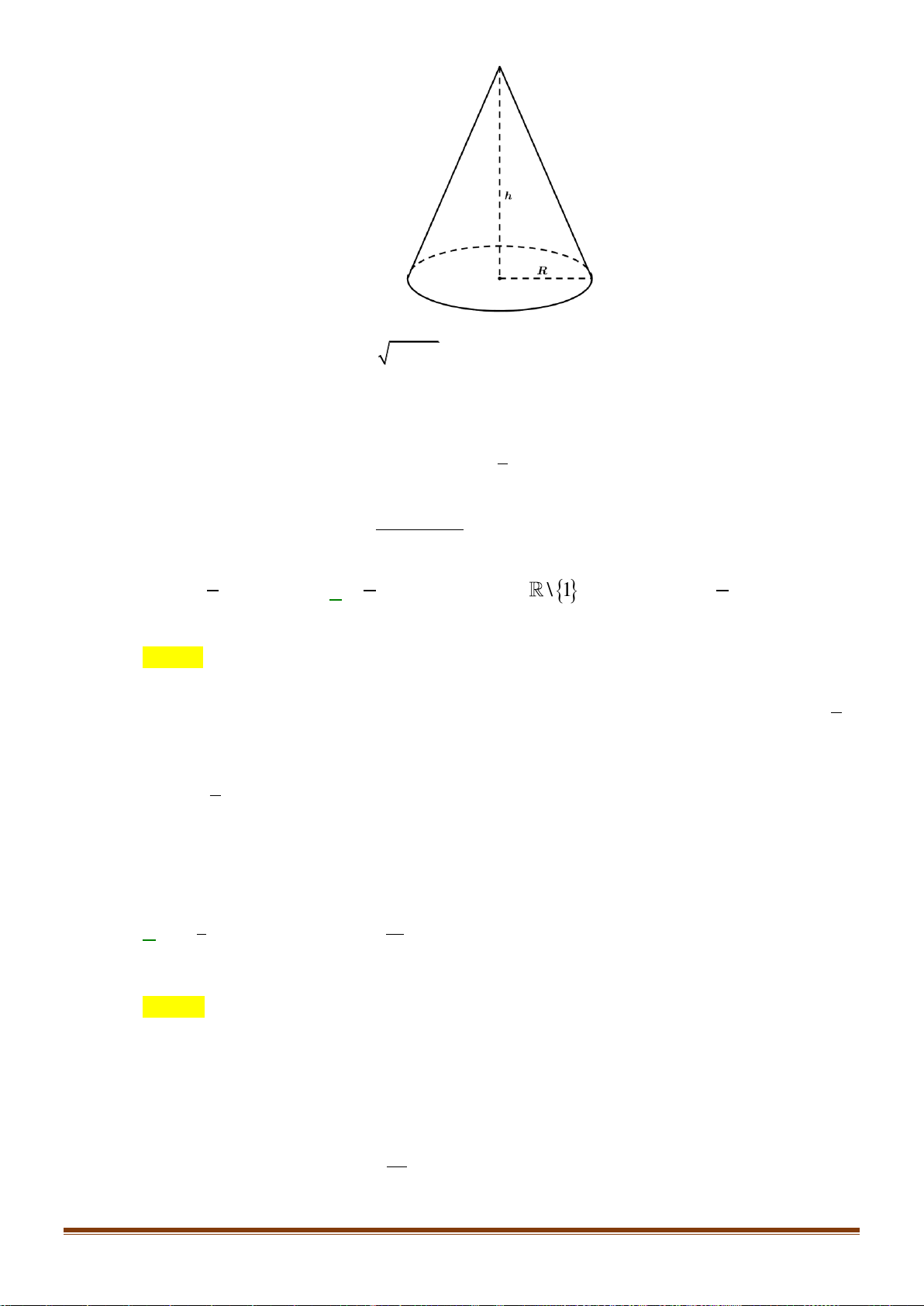
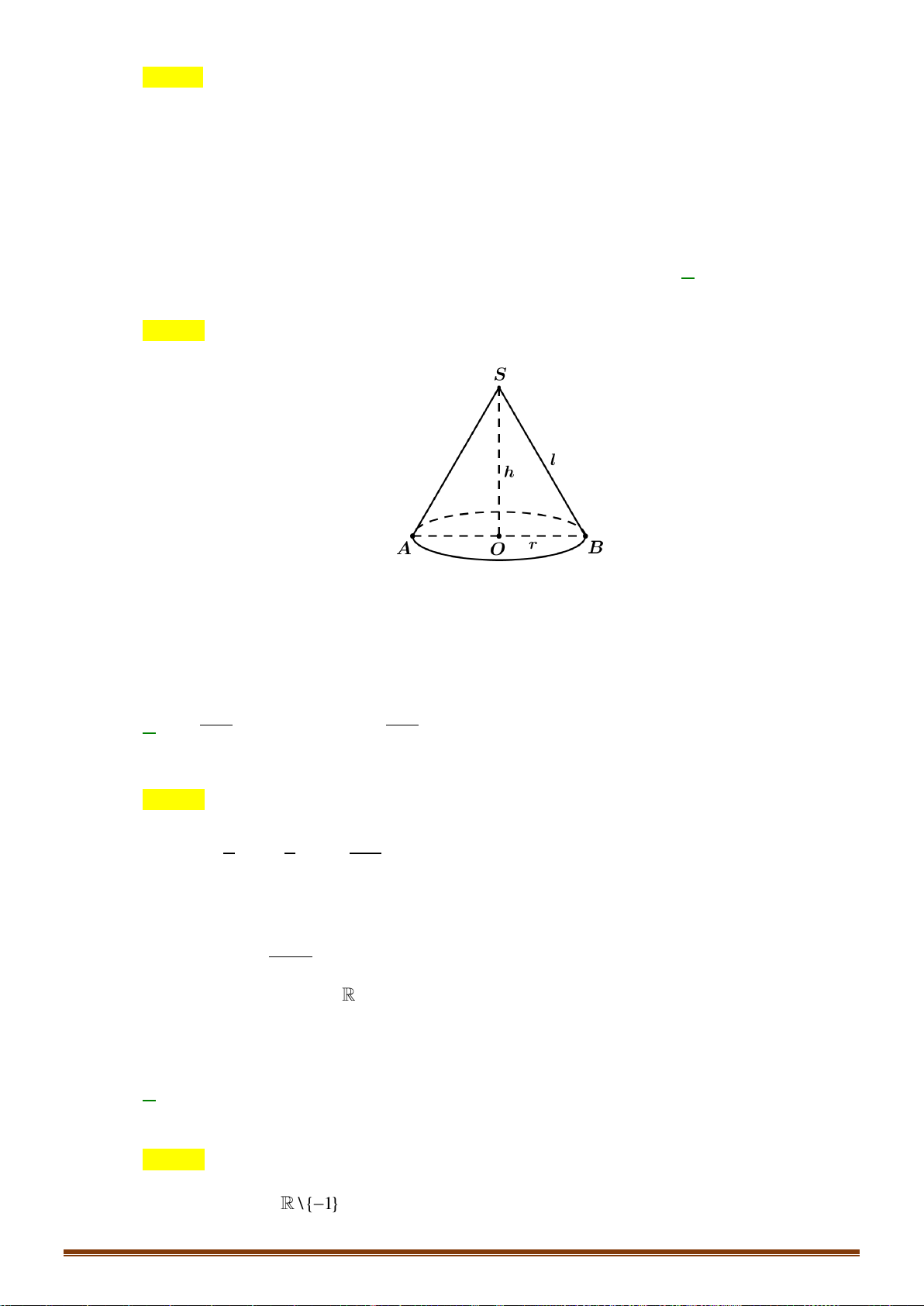
Câu 19: Gọi l, h, r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của một hình nón. Tính
diện tích xung quanh Sxq của hình nón đó. 1 A. S =  r . h B. S = 2 rl. C. S =  rl. D. 2 S =  r . h xq xq xq xq 3
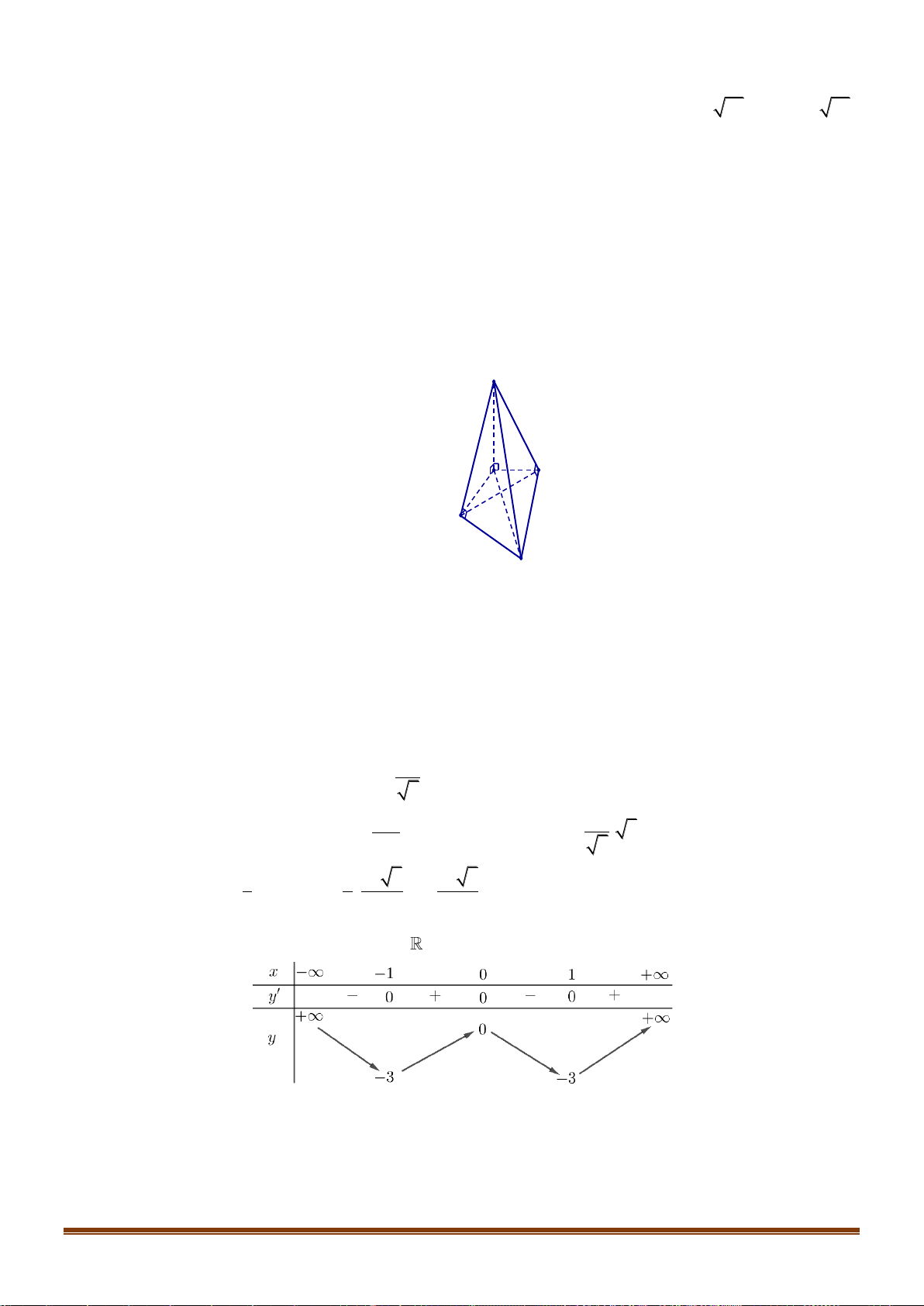
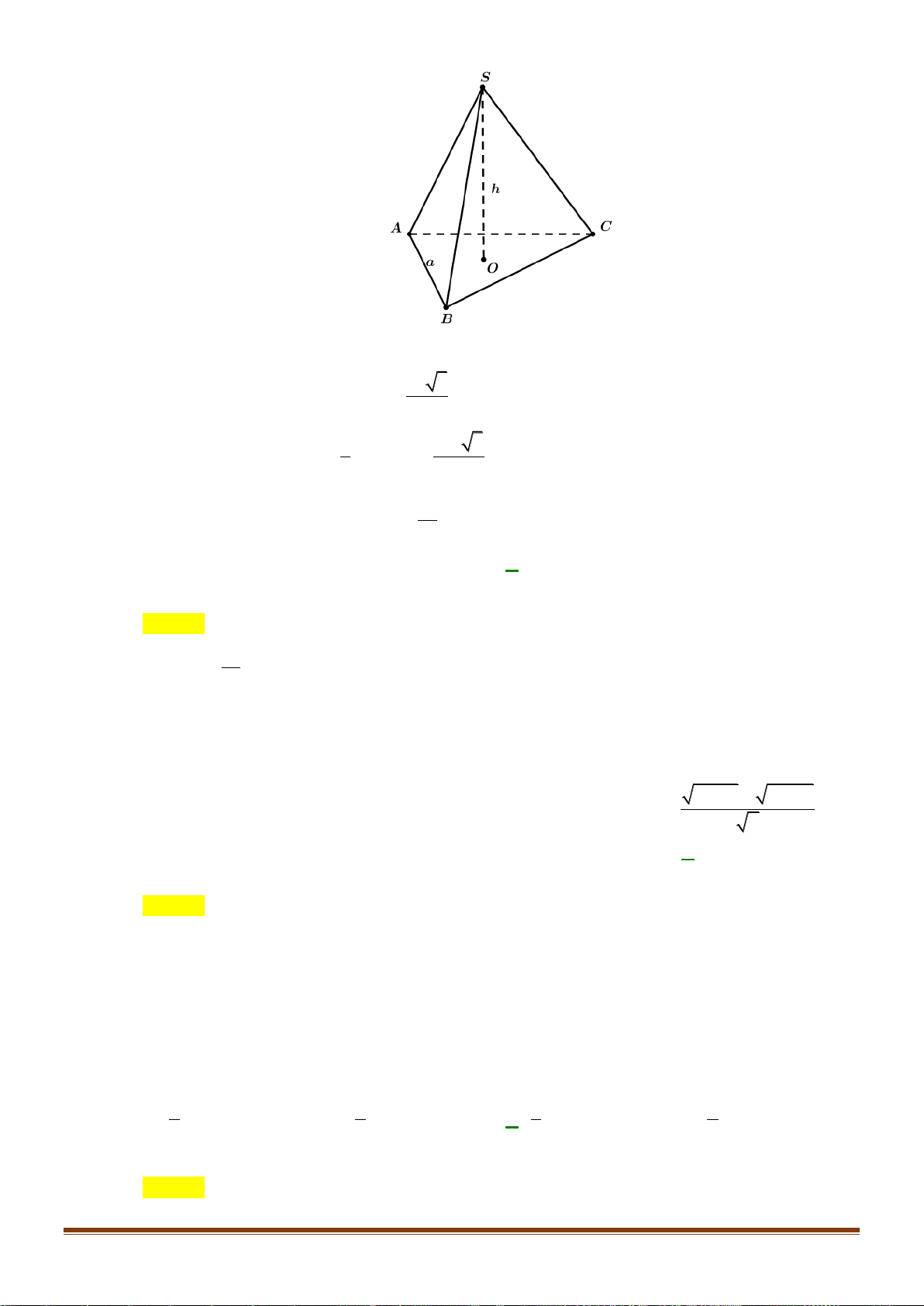
Câu 20: Cho tứ diện OABC có ,
OA OB, OC đôi một vuông góc và OA = a, OB = , b OC = . c Tính thể
tích khối tứ diện OAB . C abc abc abc A. . B. . C. . D. . abc 3 6 2 1
Câu 21: Phương trình log ( x + 2) + log ( x − 2)2 = 1 3 3 có bao nhiêu nghiệm? 2 A. 0 B. 1. C. 2. D. 3. 1
Câu 22: Phương trình = 8 có nghiệm là: x 1 2 + A. x = 1. B. x = 2. C. x = 3. − D. x = 4. −
Câu 23: Tìm đạo hàm của hàm số x y = a với x a 1 1 A.  = x y a ln . a B. y = . C. y = . D. y = . ln a . x ln a . a ln a
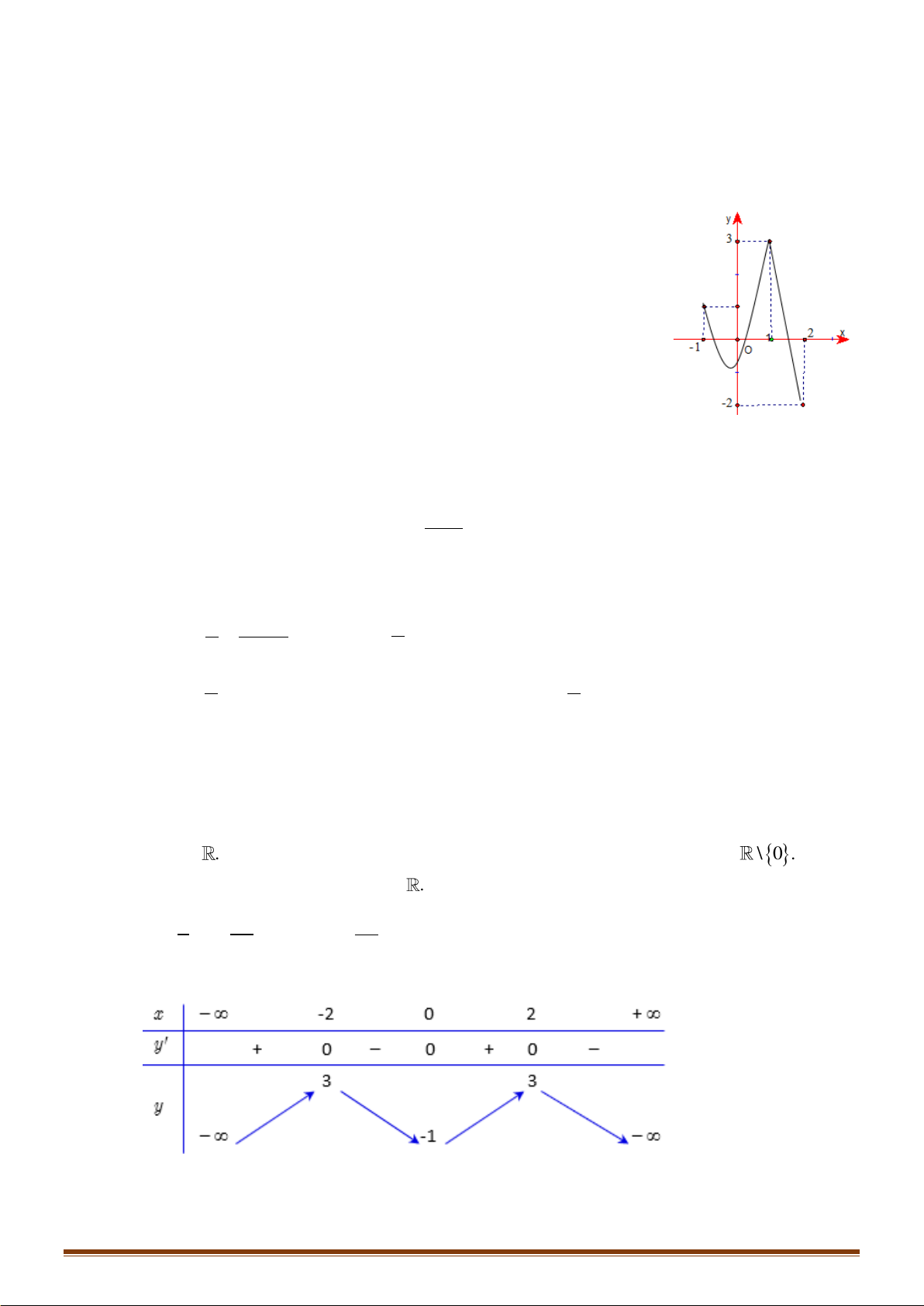
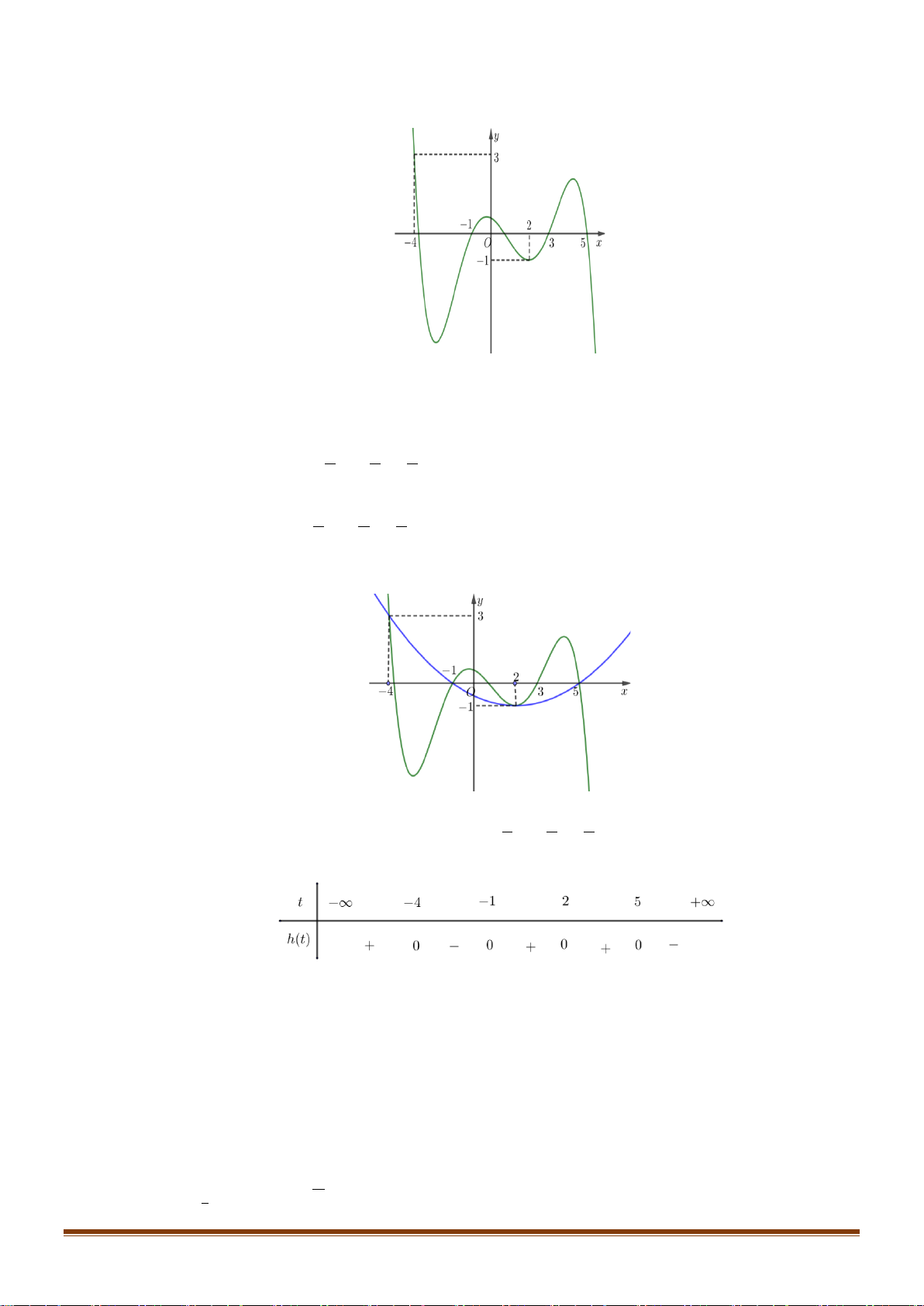
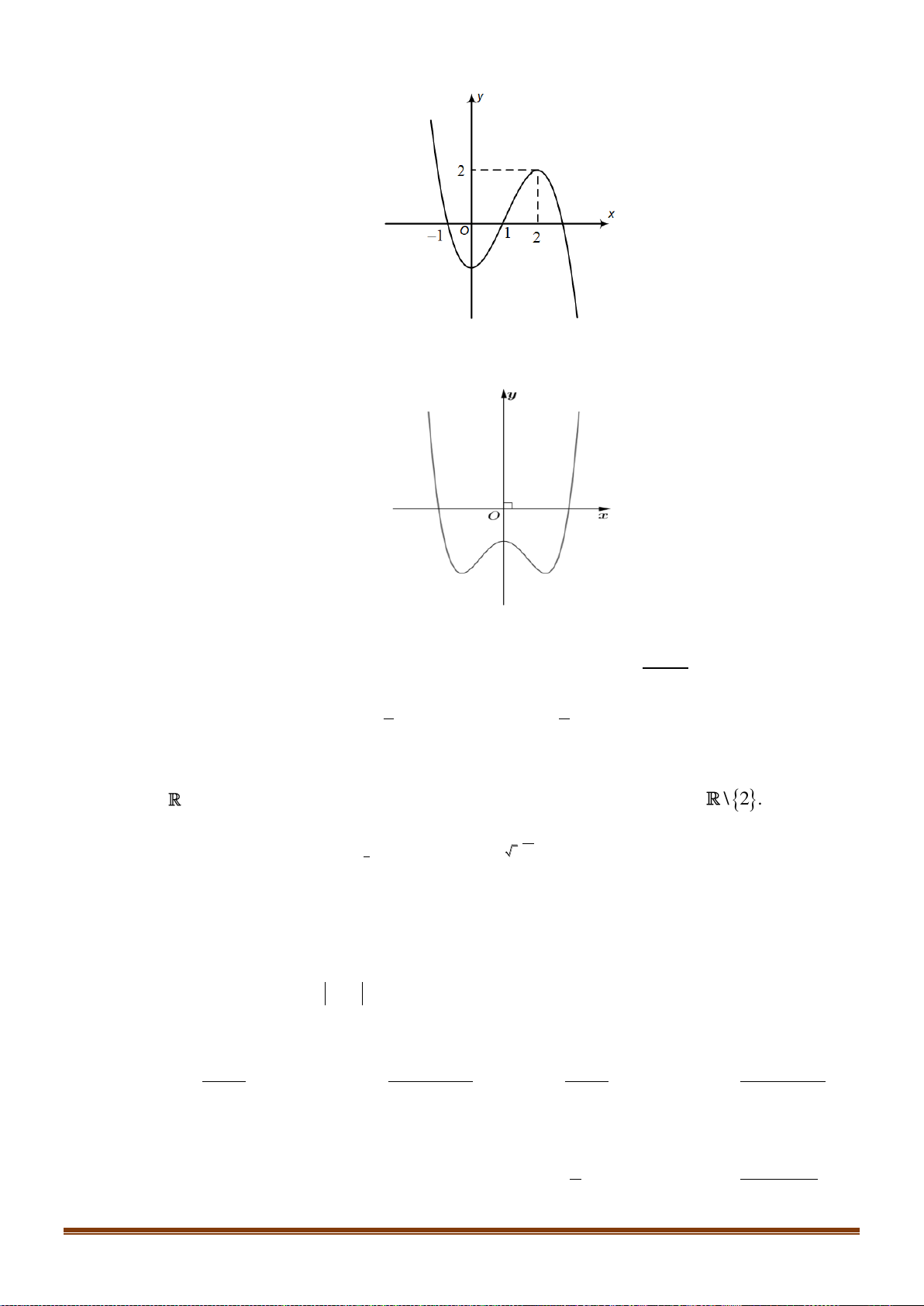
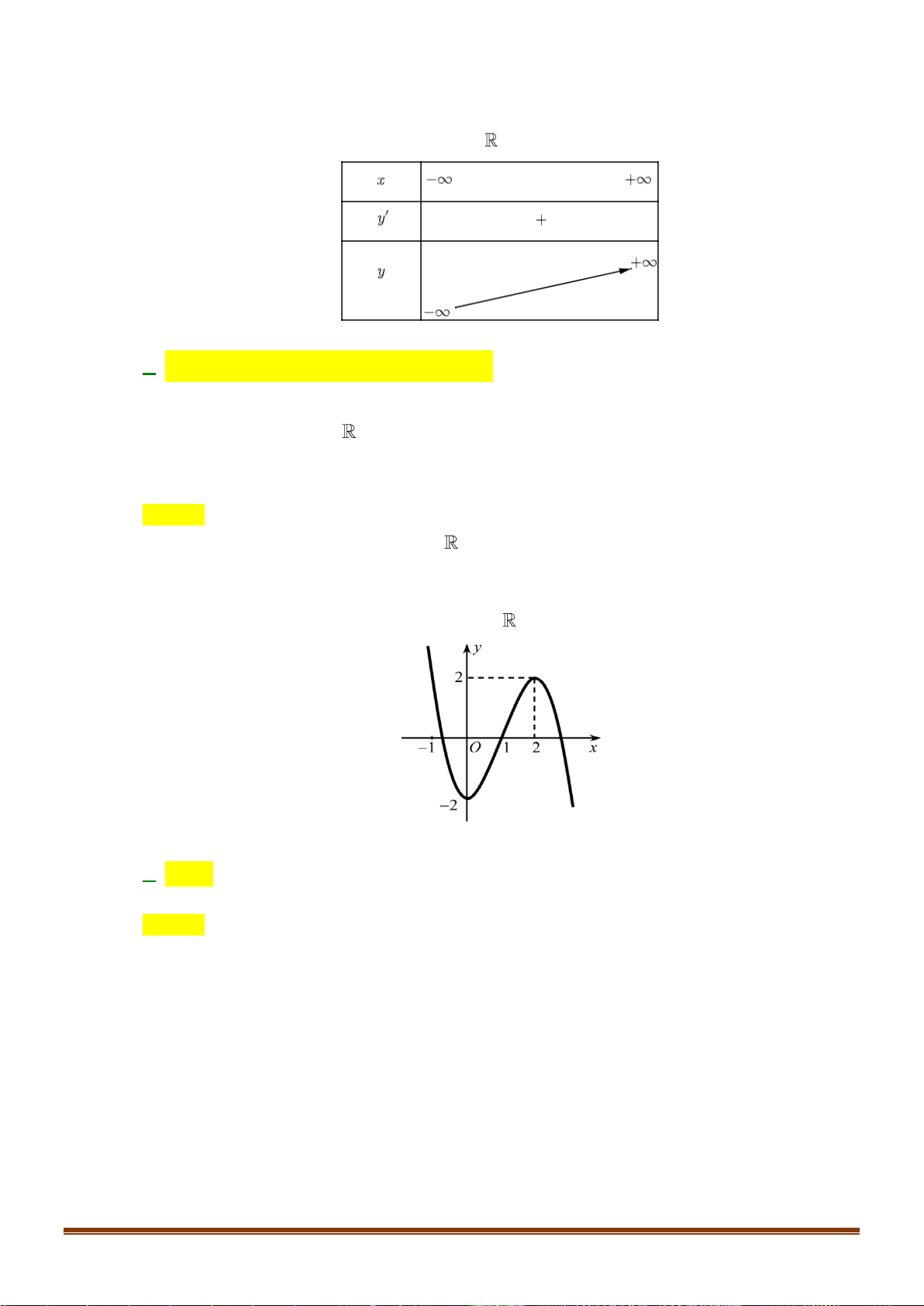
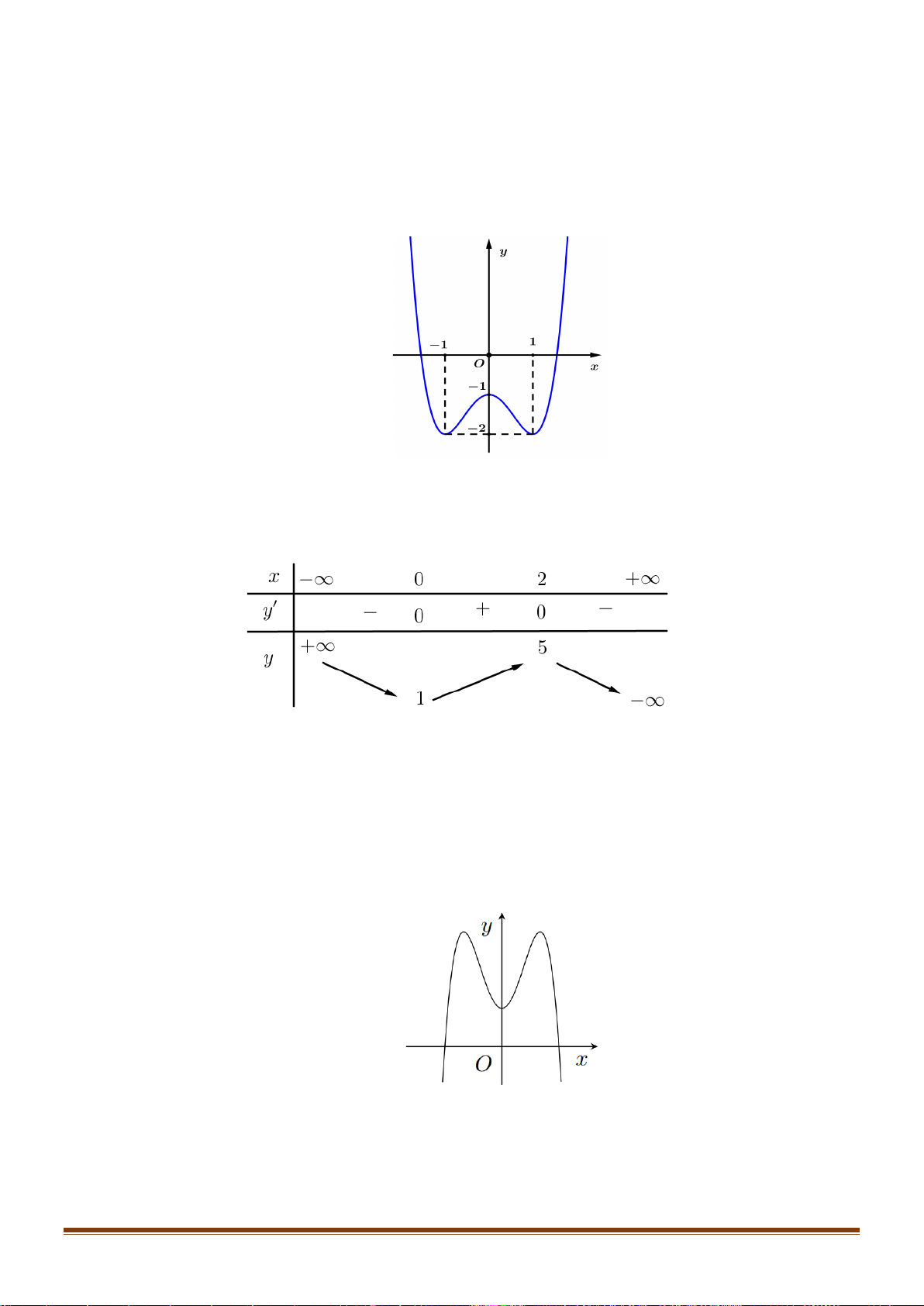
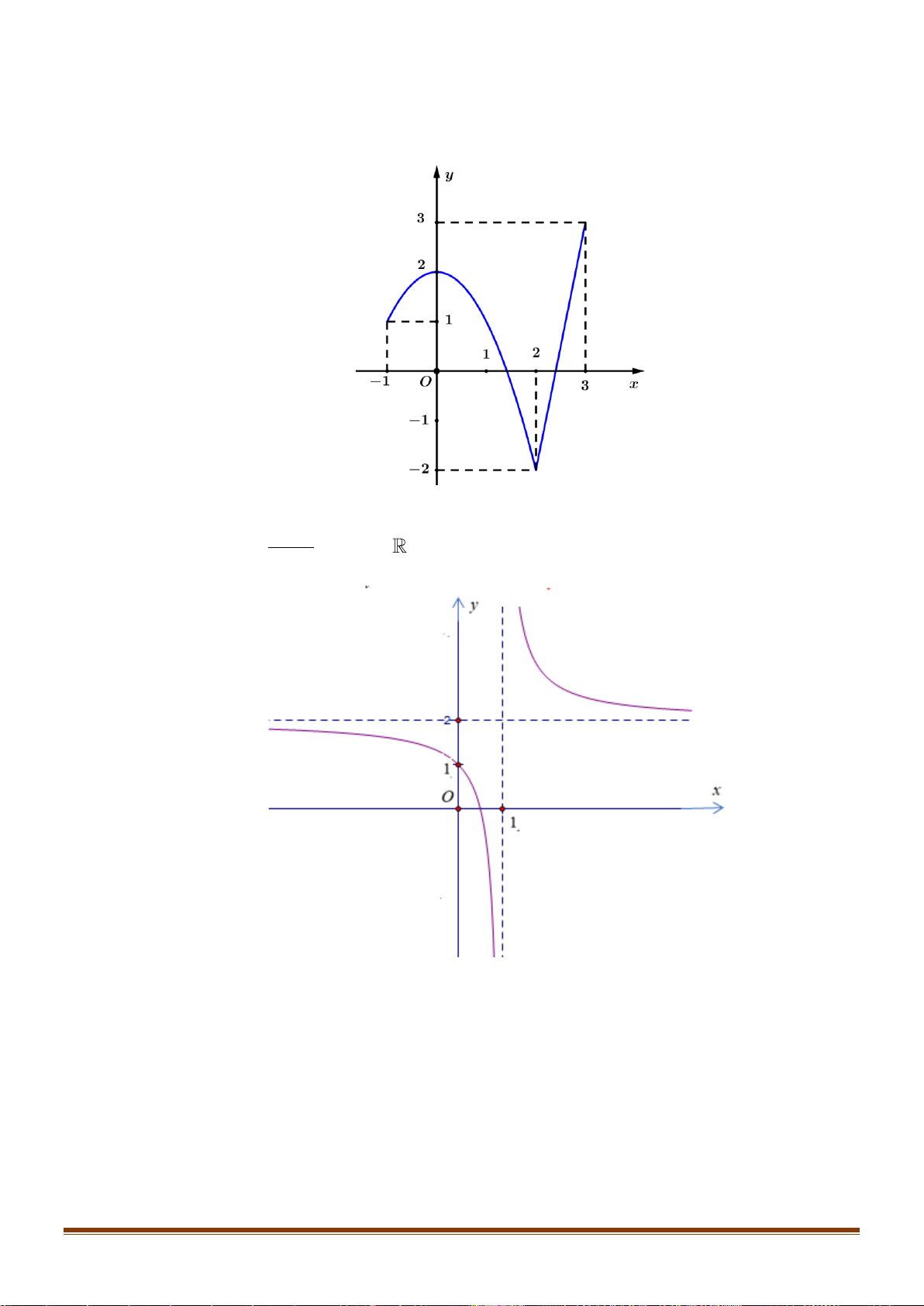
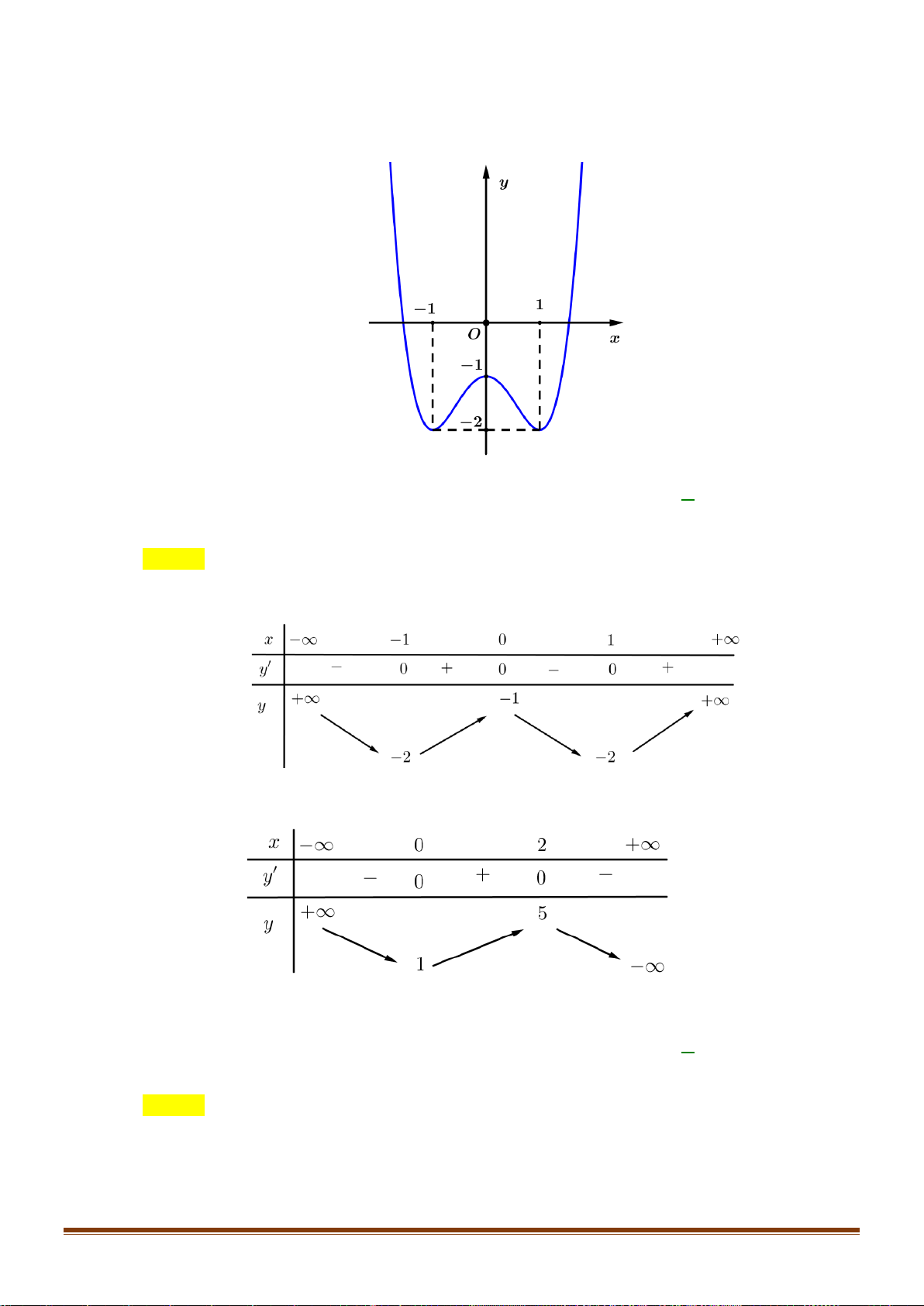
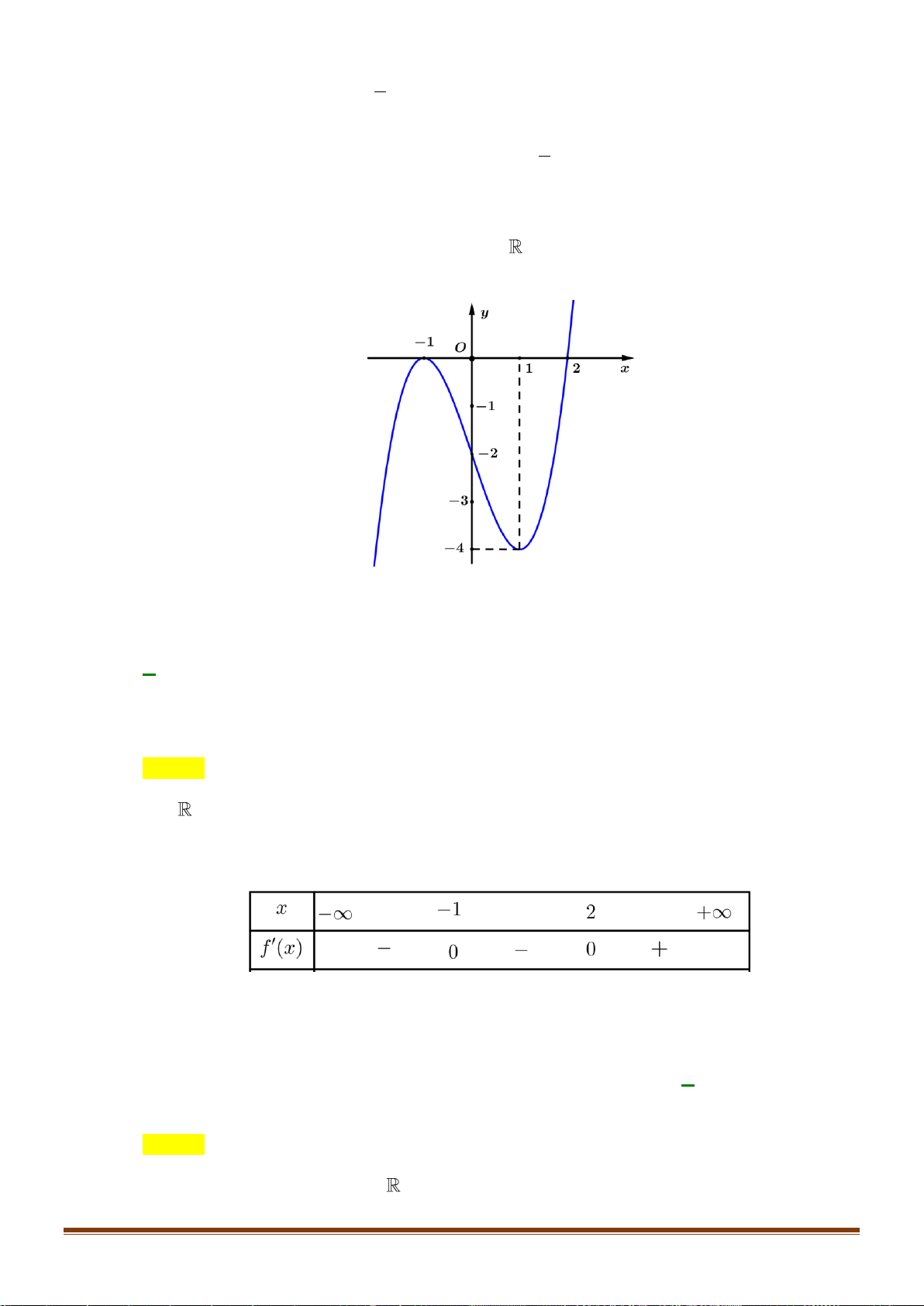
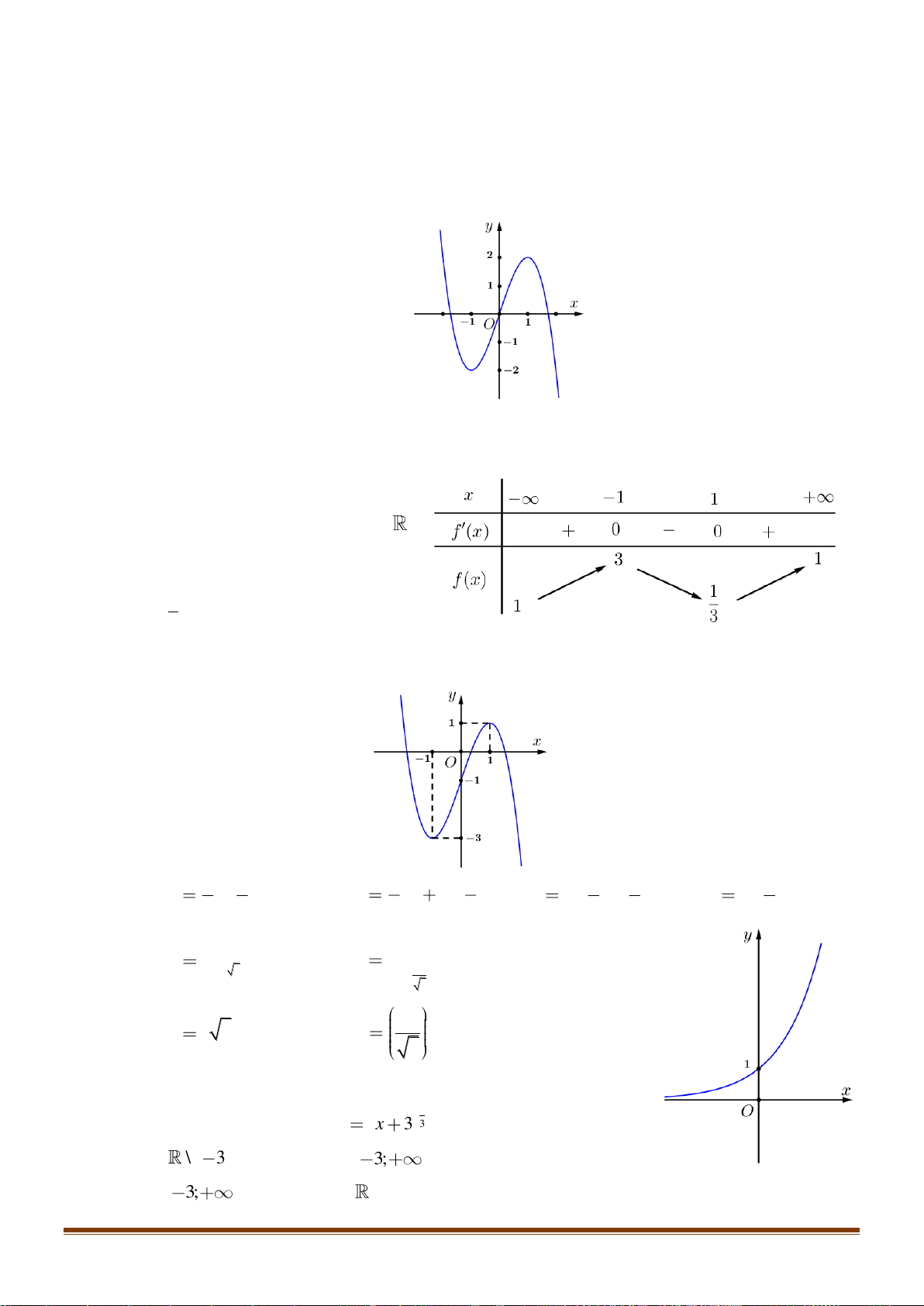
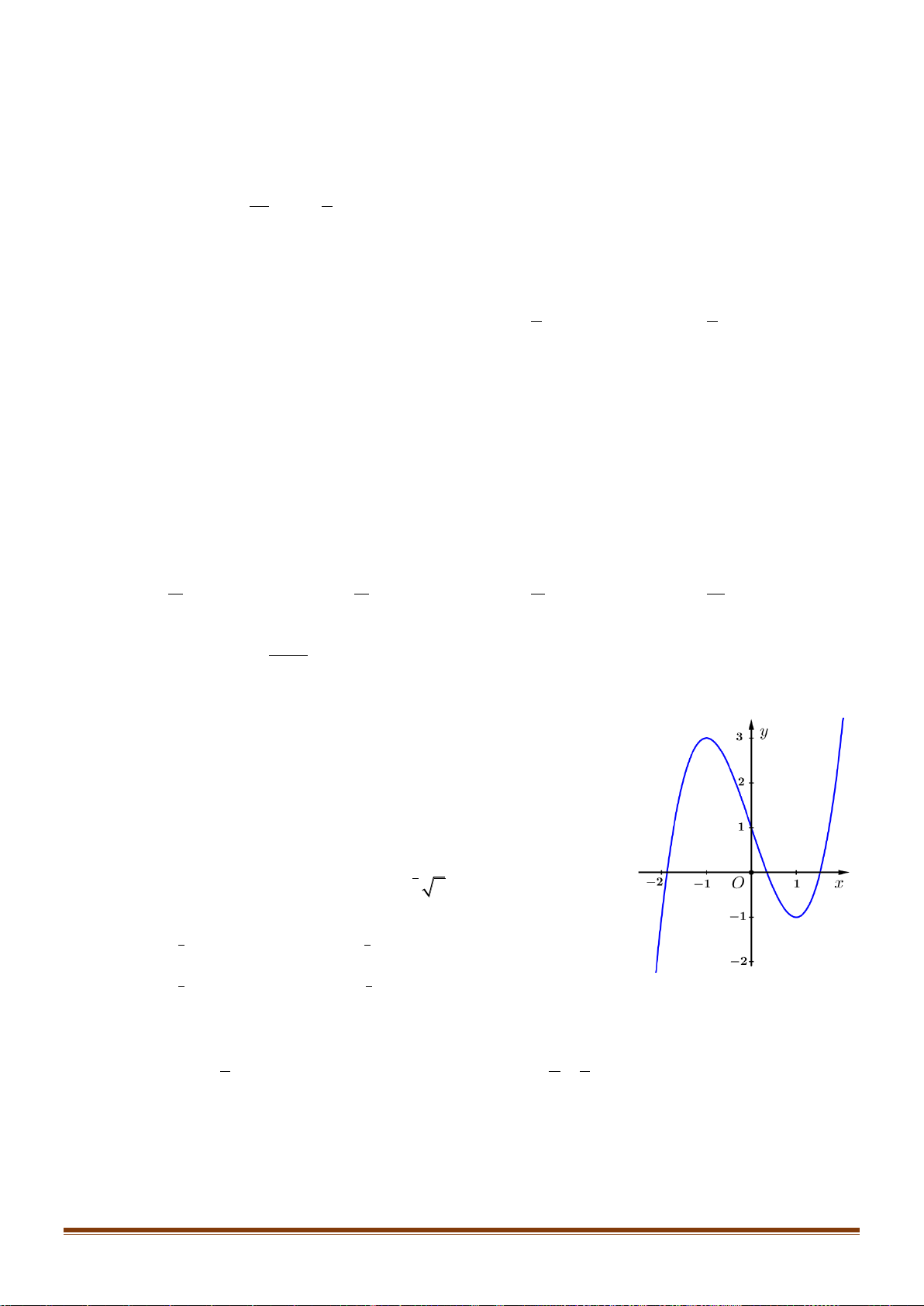
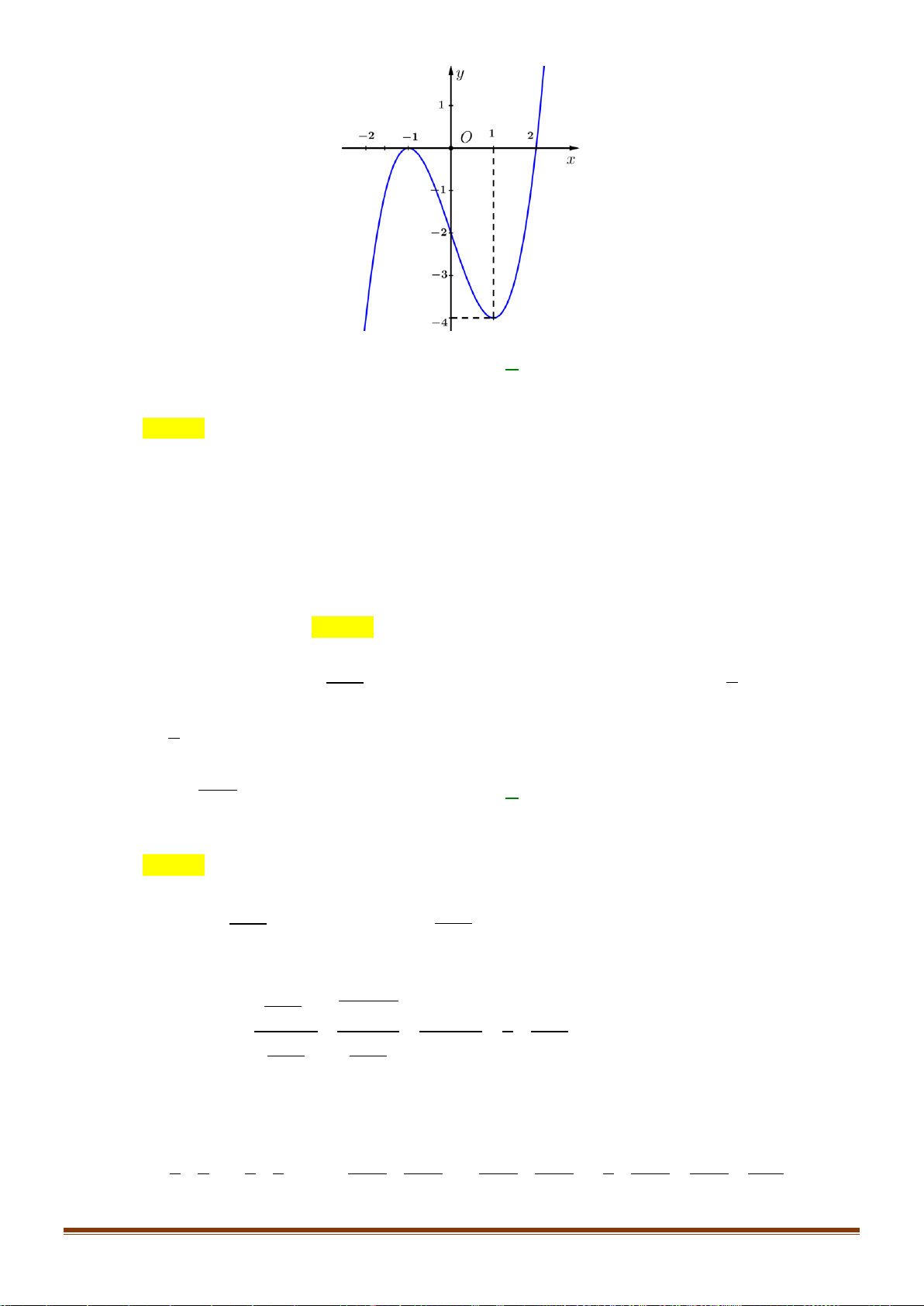
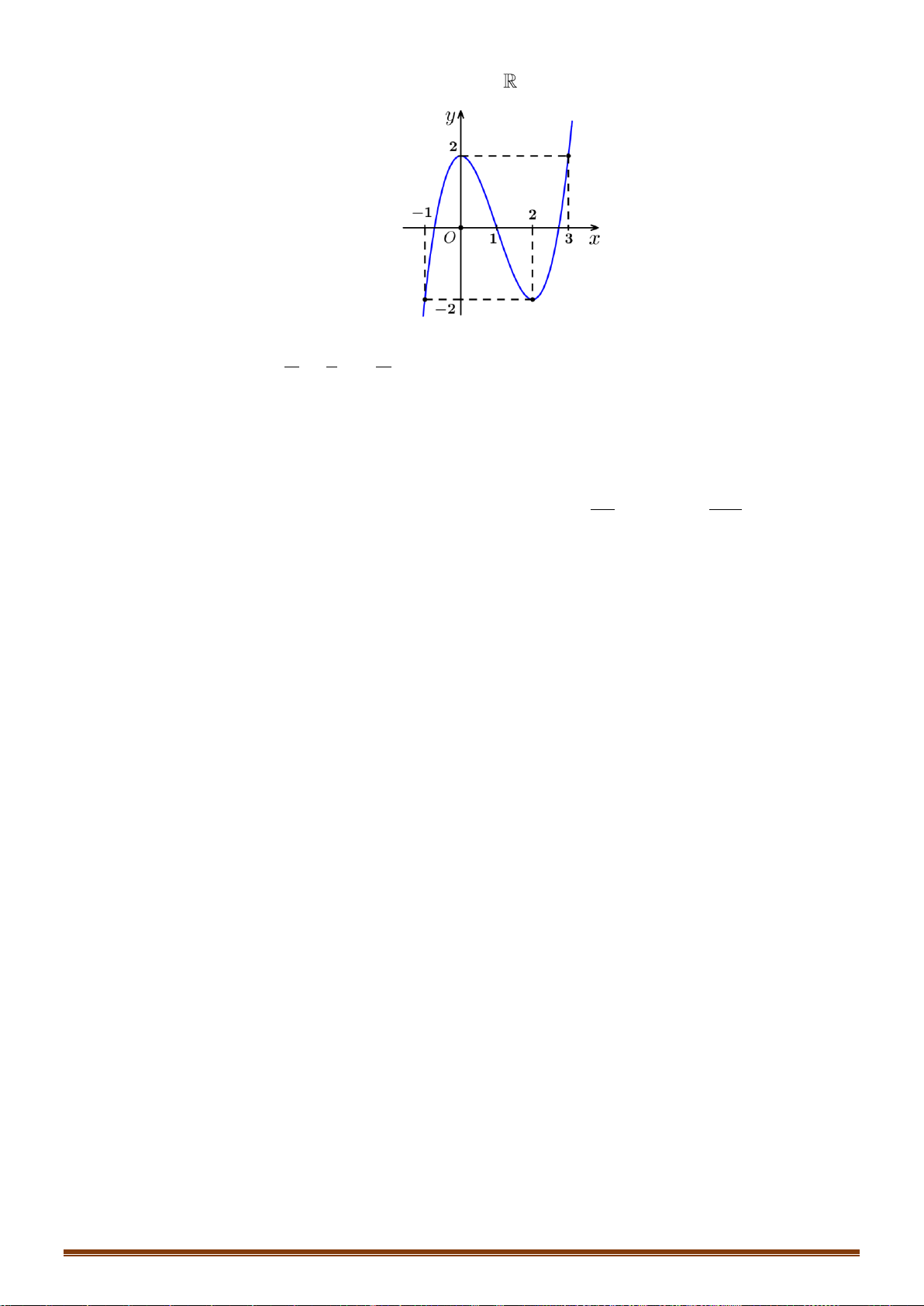
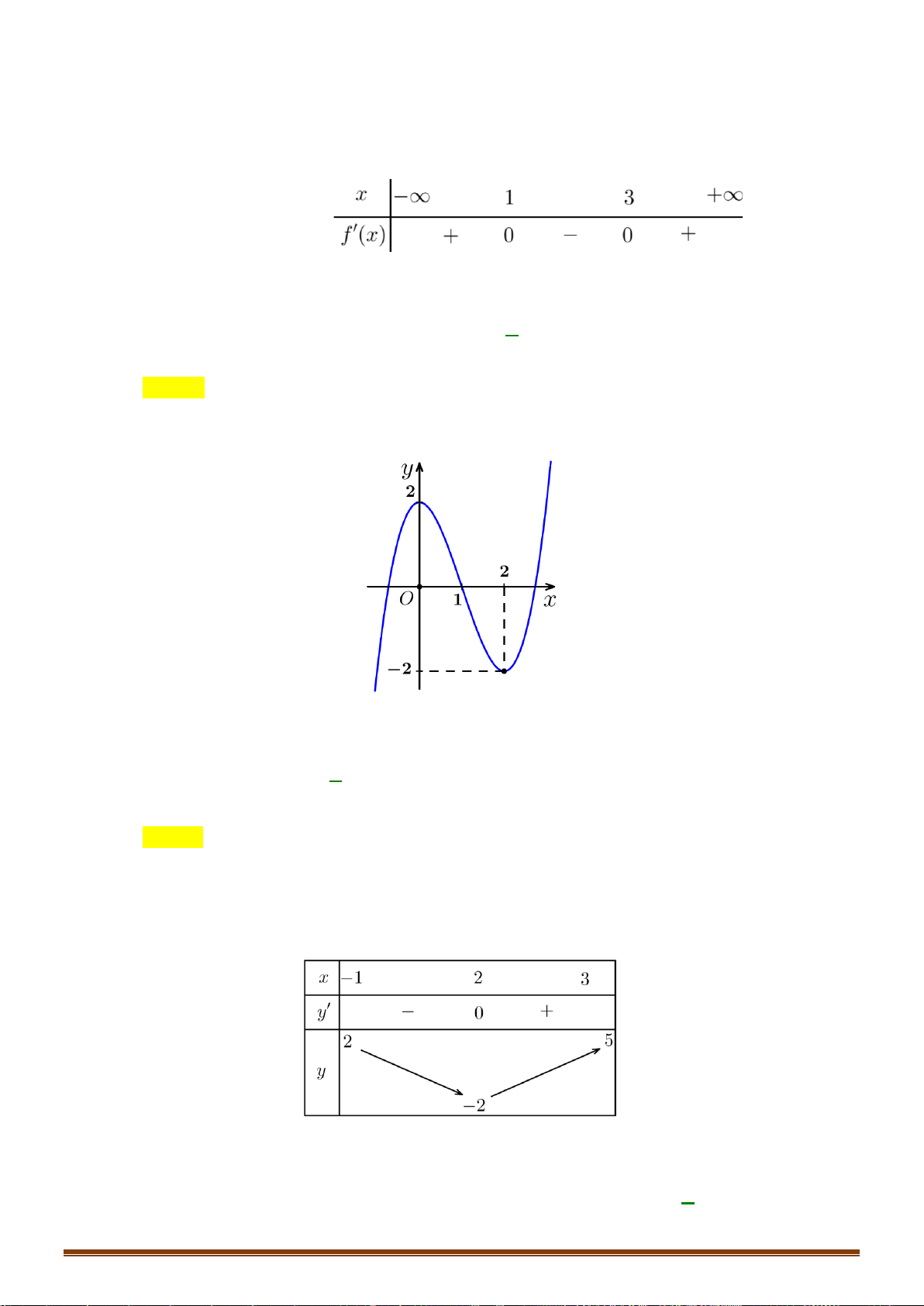
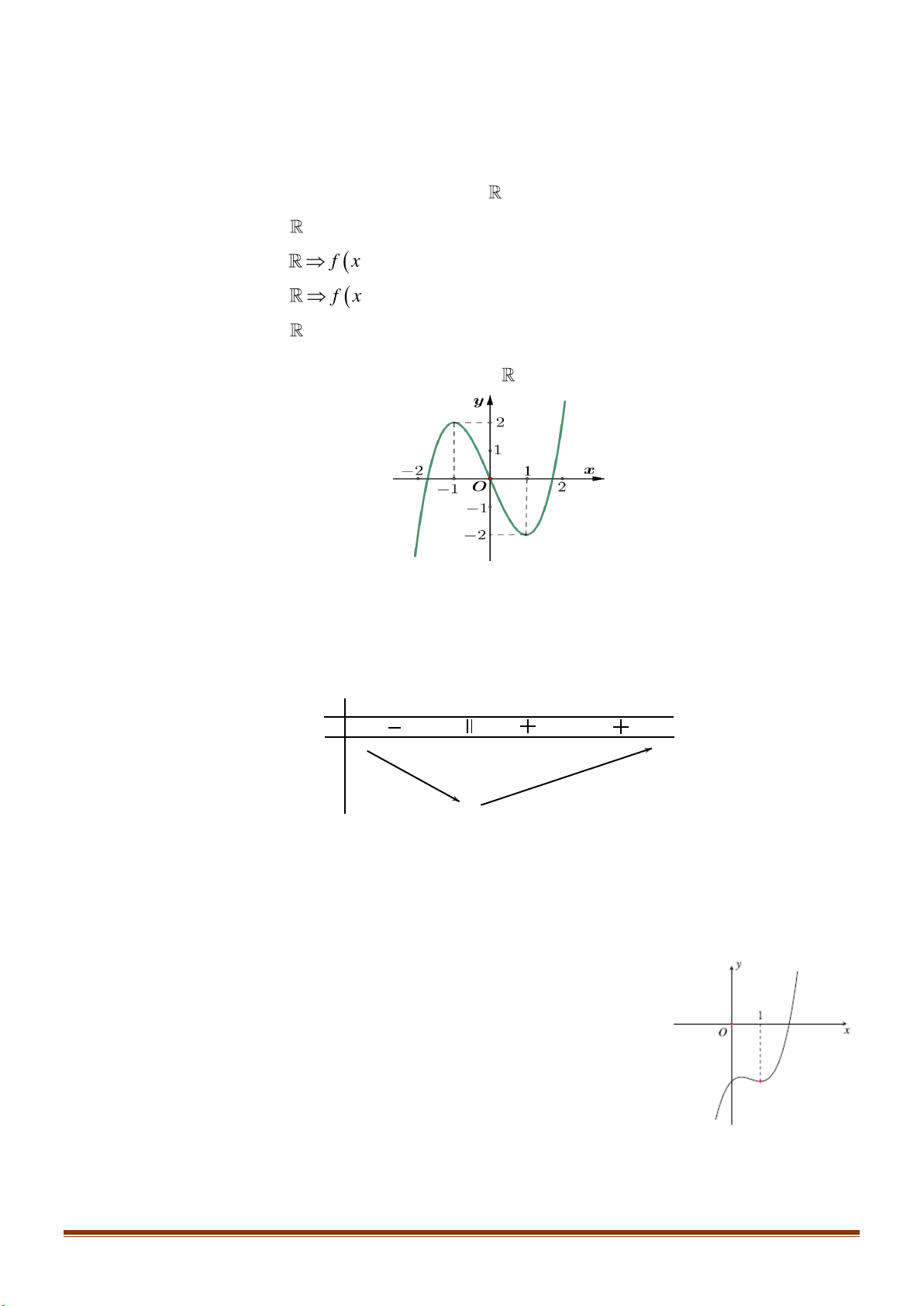
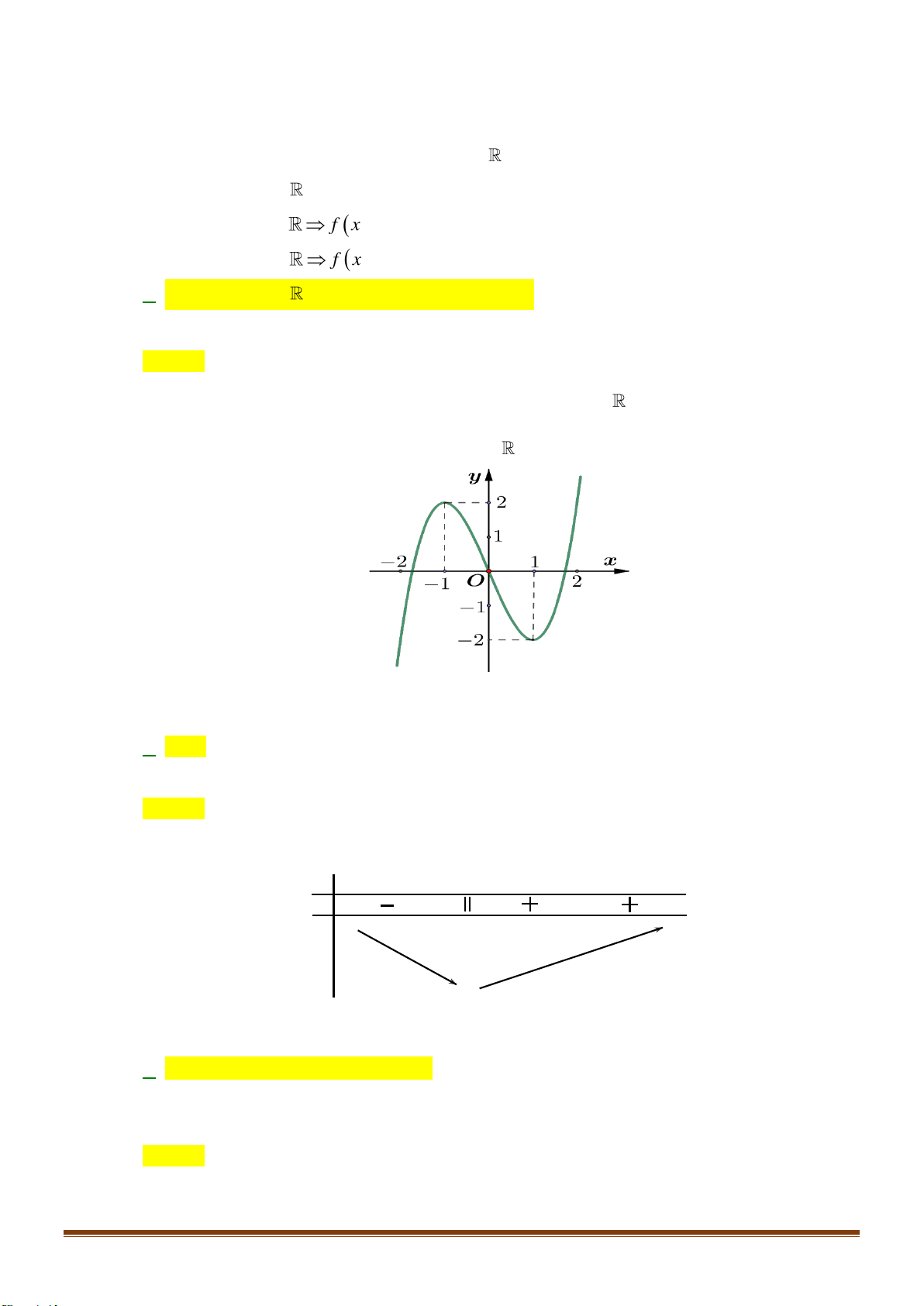
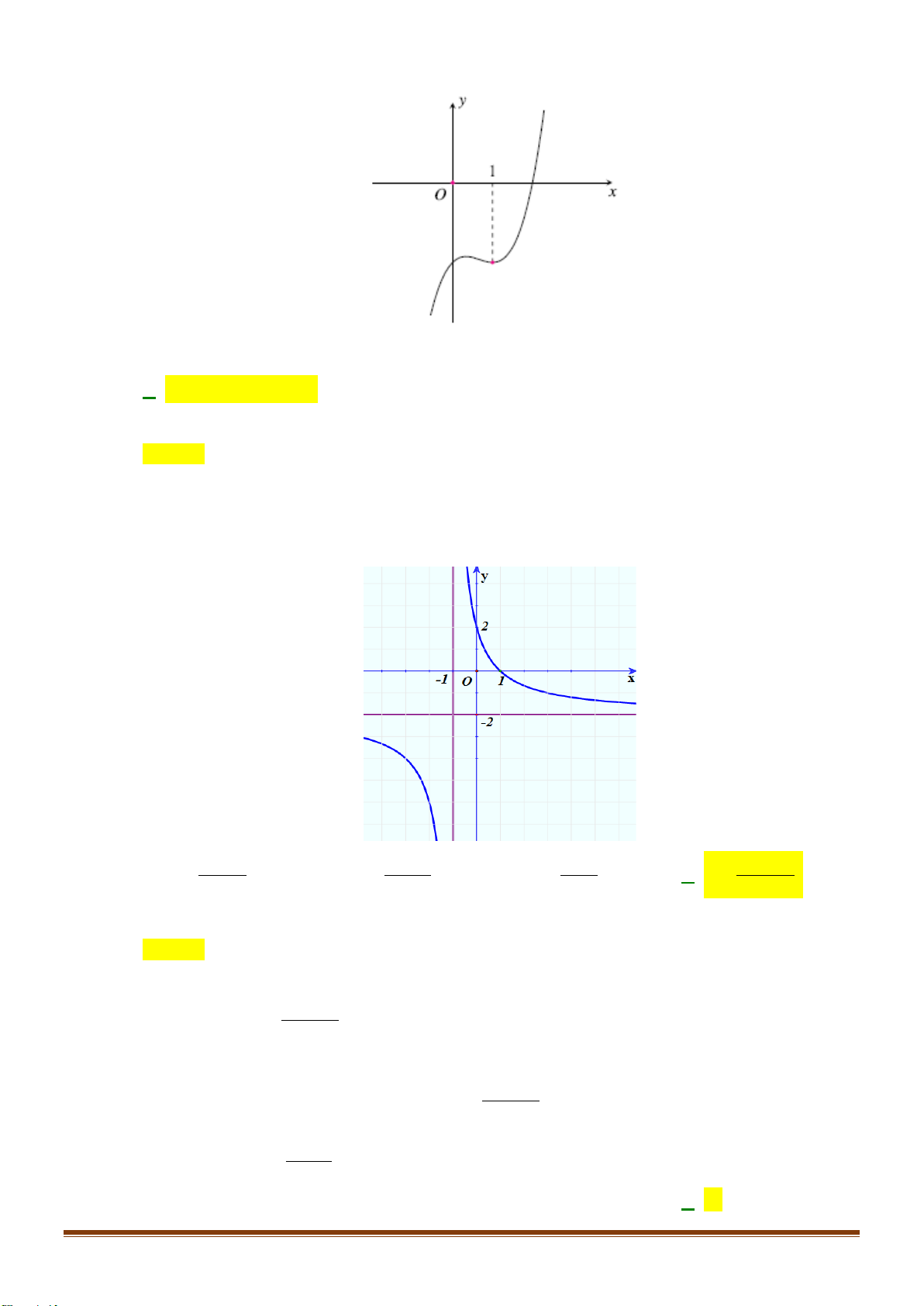
Câu 24: Cho hàm số y = f (x) xác định trên  2 − ;  2 có đồ thị trên  2 − ;  2 như hình vẽ:
Biết hàm số y = f (x) đạt giá trị lớn nhất tại a và đath giá
trị nhỏ nhất tại b . Tính 4a +3 . b A. 12. − B. 4. 4 C. 11. − D. − . 3 2 x −x 1 −
Câu 25: Xét phương trình ( 2022 − 2021) = ( 2022 + 2021)
. Tổng bình phương các nghiệm
của phương trình đã cho bằng bao nhiêu? A. 1. B. 2. C. 3. D. 4.
Câu 26: Có bao nhiêu khối đa diện đều? A. 5. B. 8. C. 3. D. 4. Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
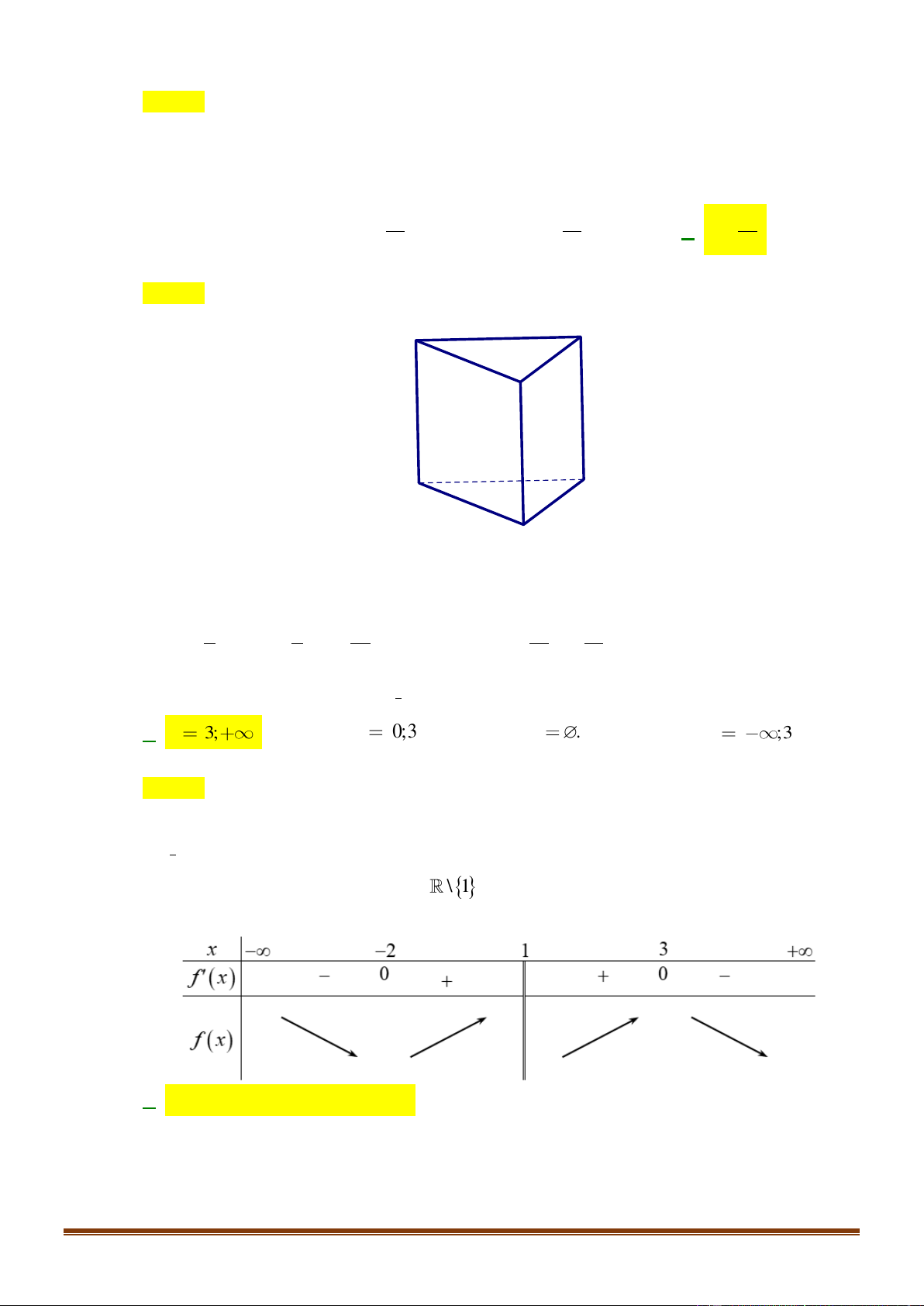
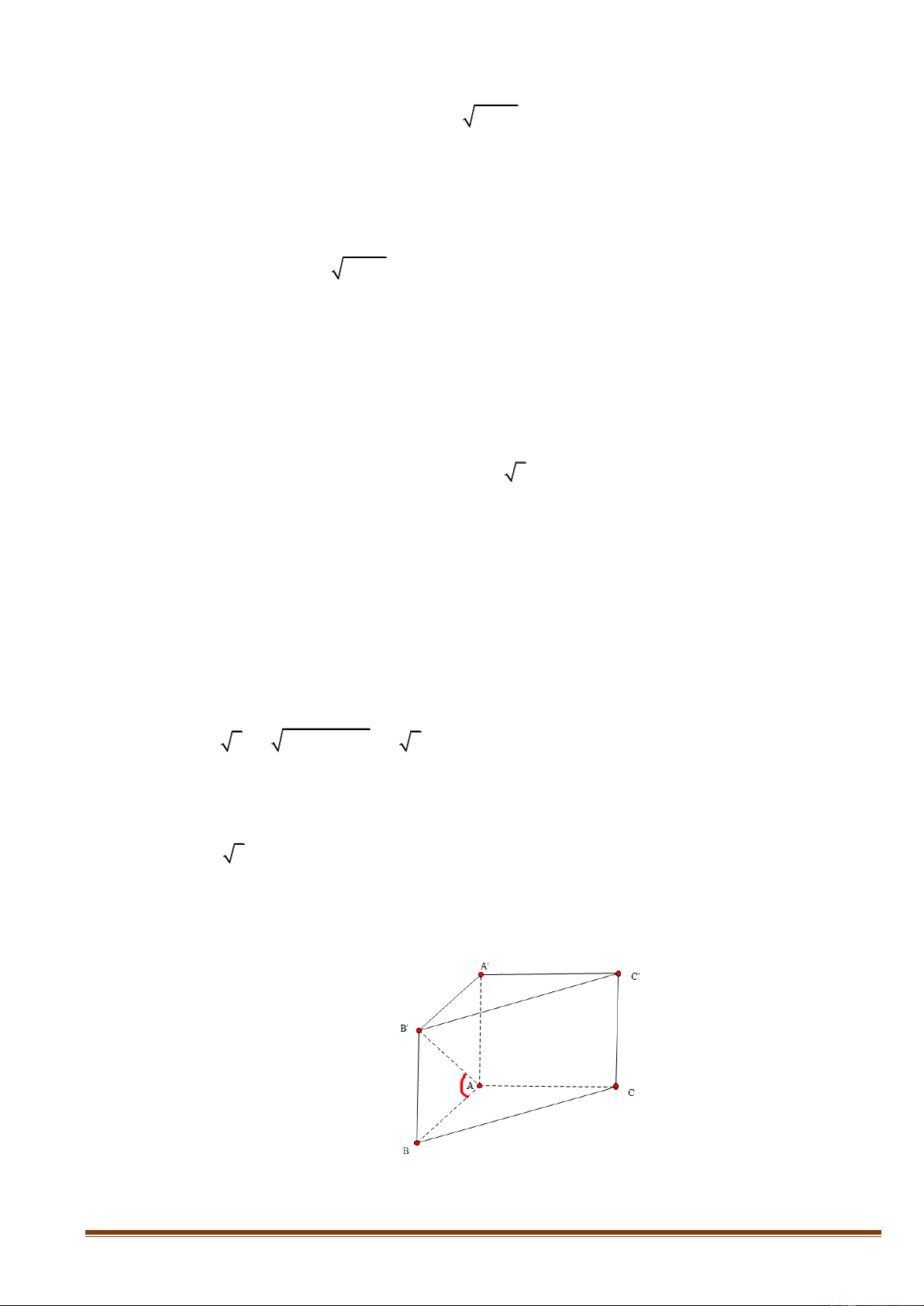
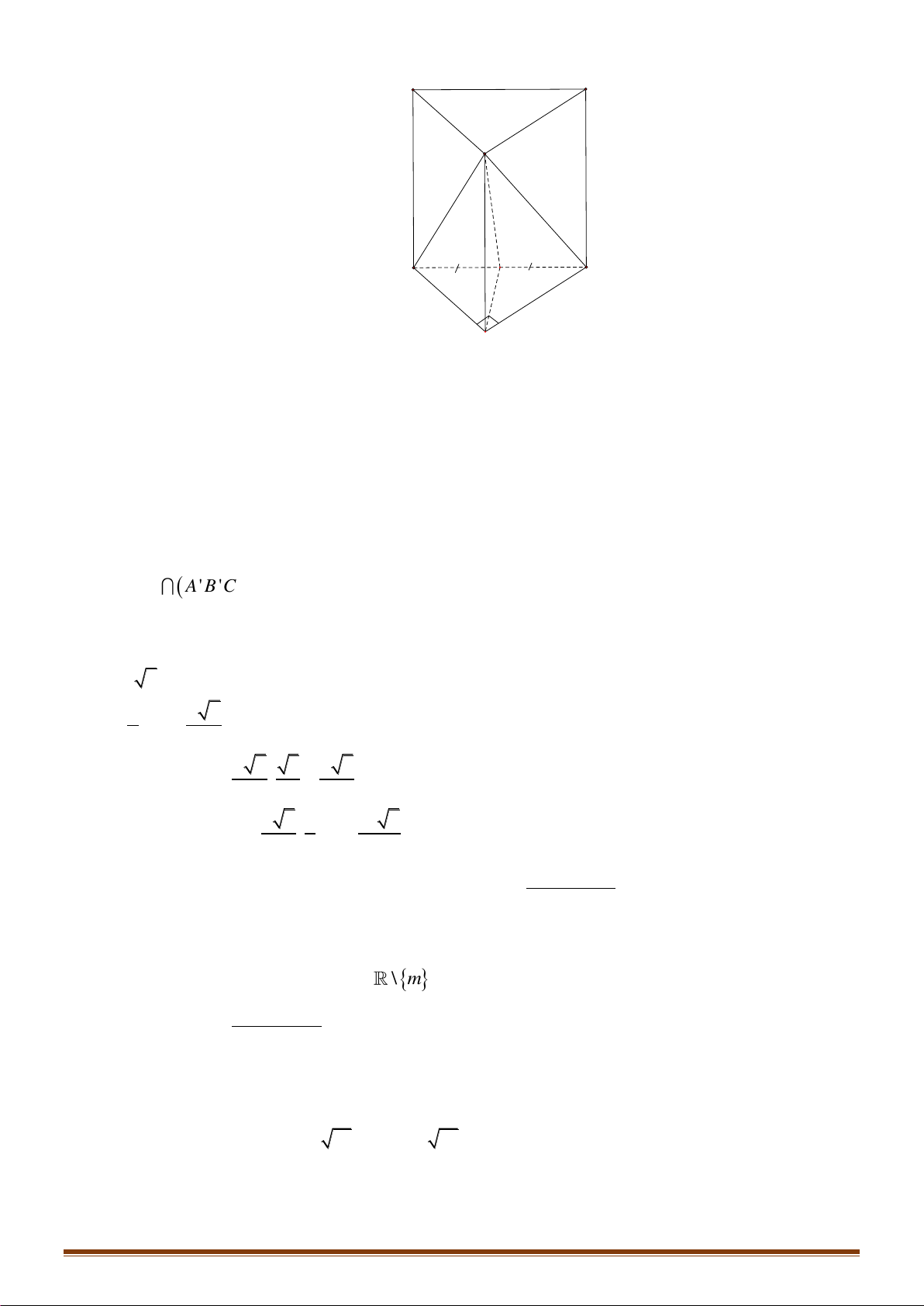
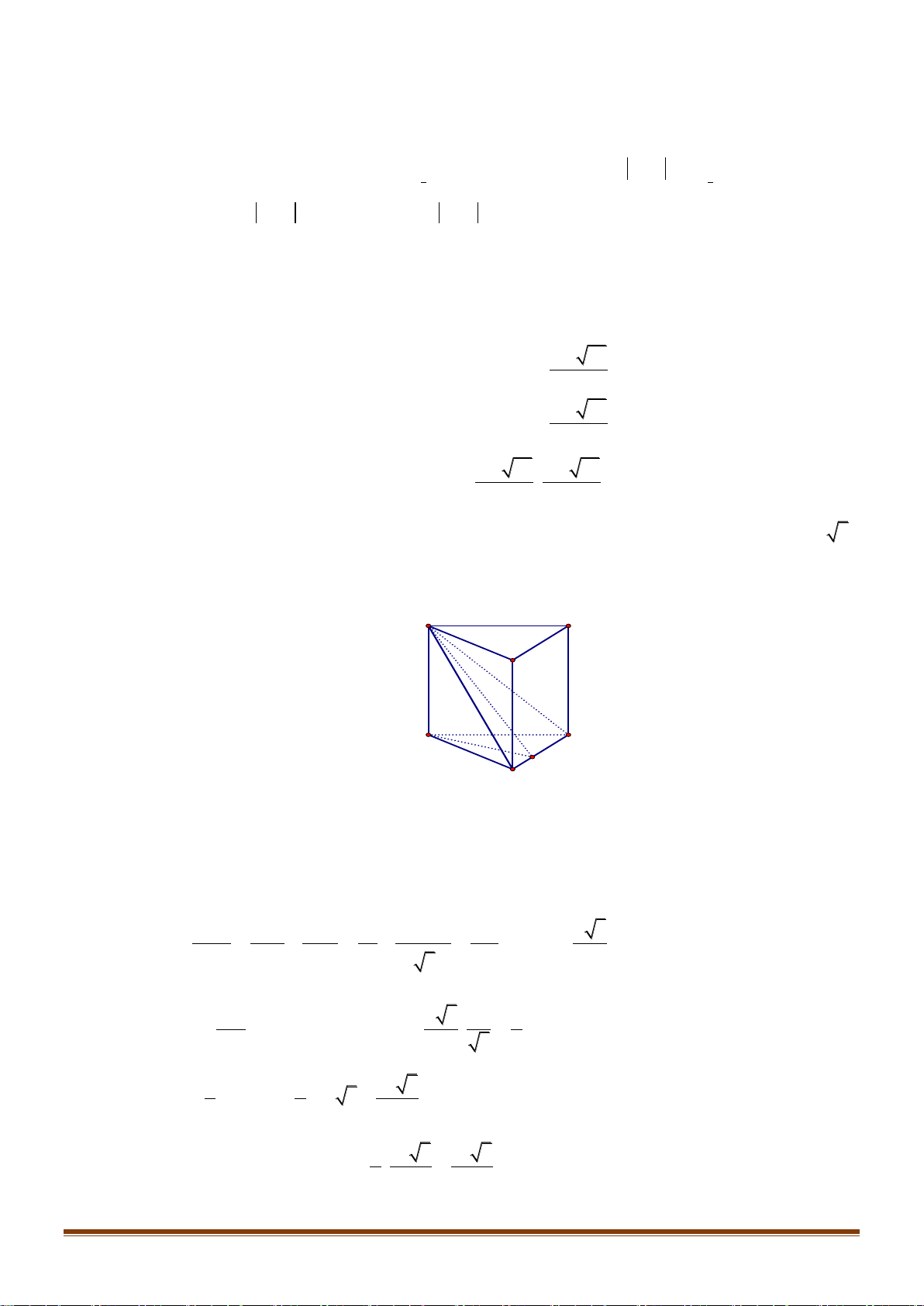
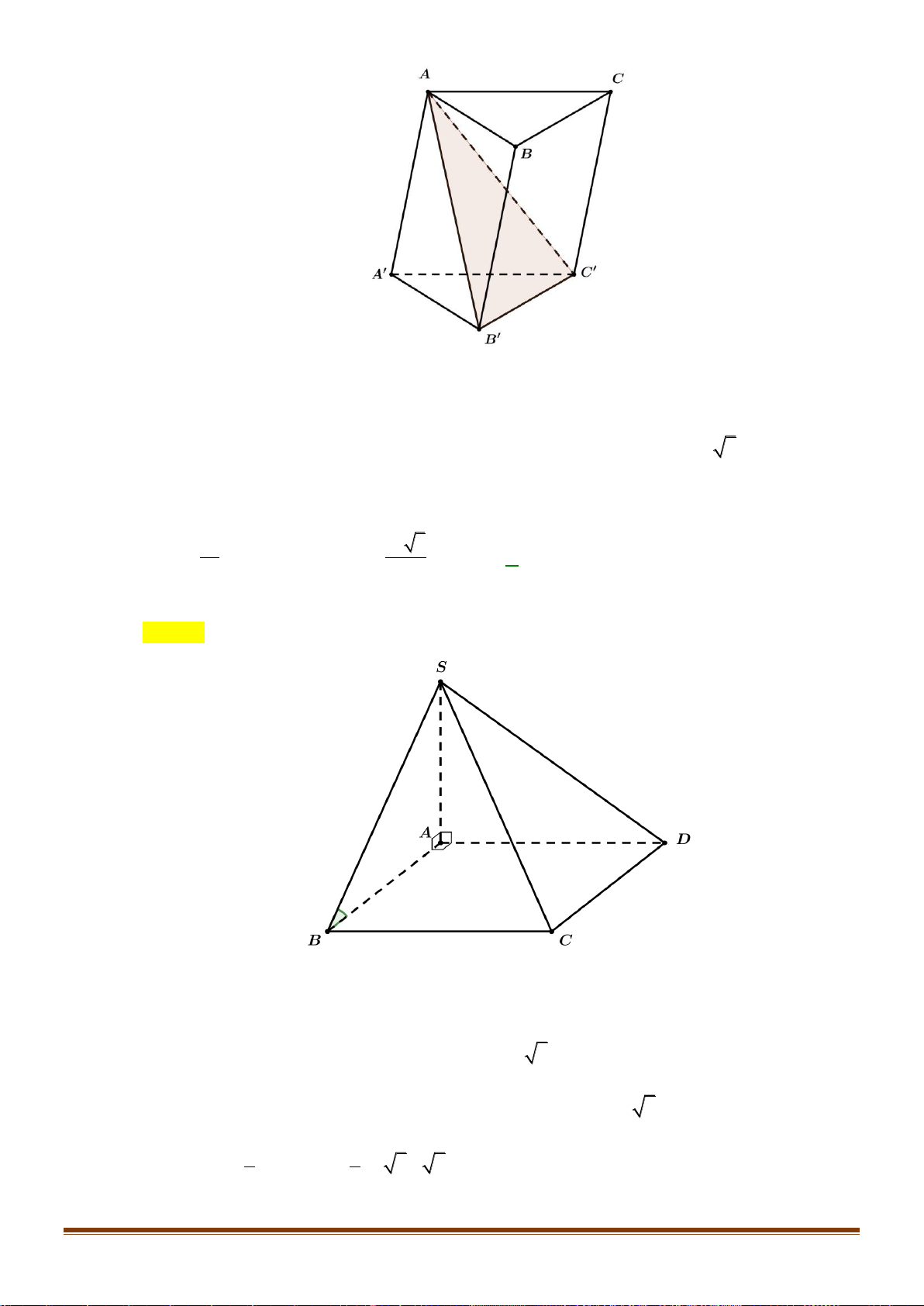
Câu 27: Cho khối lăng trụ đứng AB .
C A' B 'C ' có BB ' = a, đáy ABC là tam giác vuông cân tại B và BA = BC = .
a Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a 3 a A. 3 V = a . B. V = . C. V = . D. V = . 3 6 2
Câu 28: Tập nghiệm của phương trình log x  1 − là 1 3 A. S 3; B. S 0;3 C. S . D. S ;3
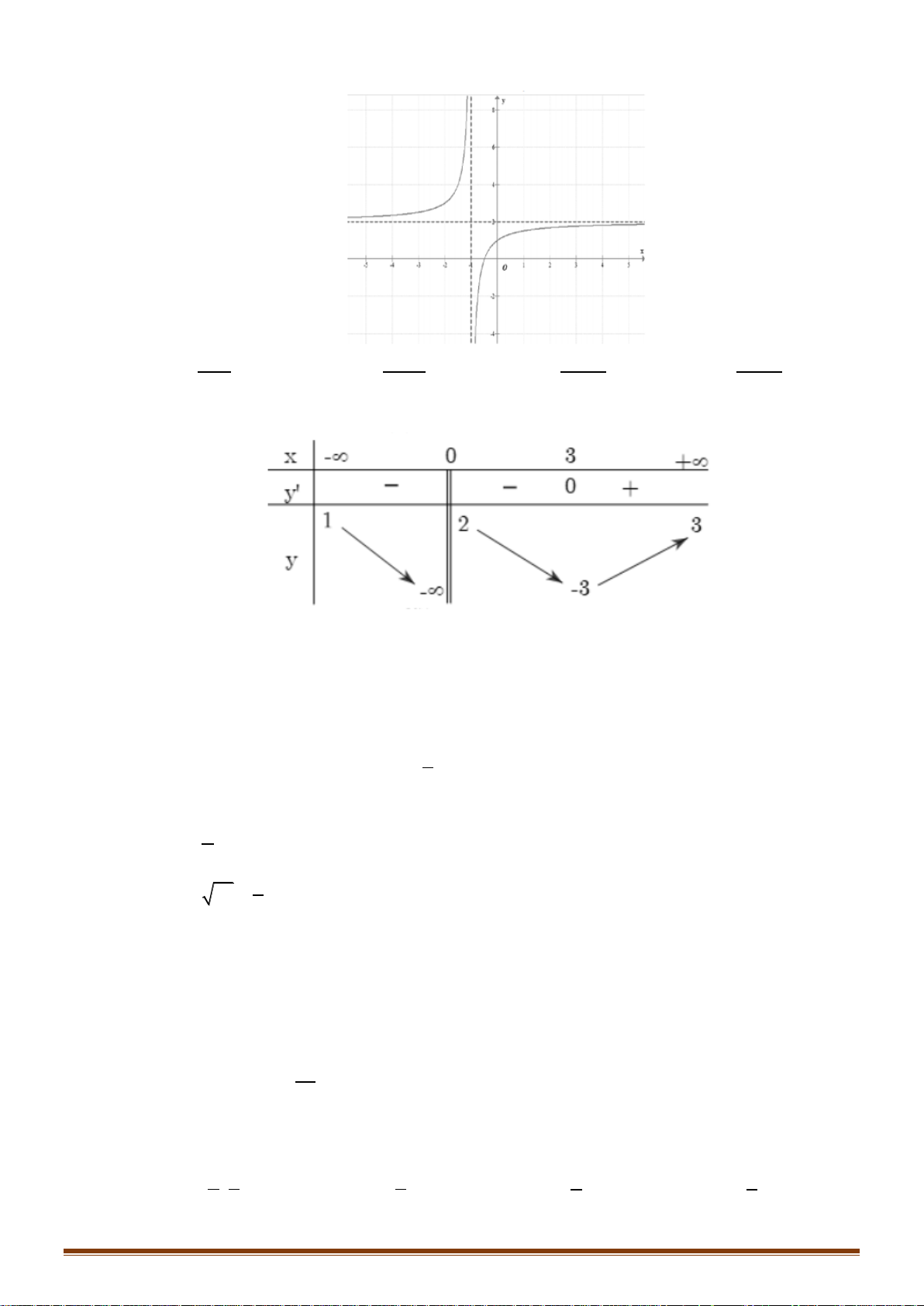
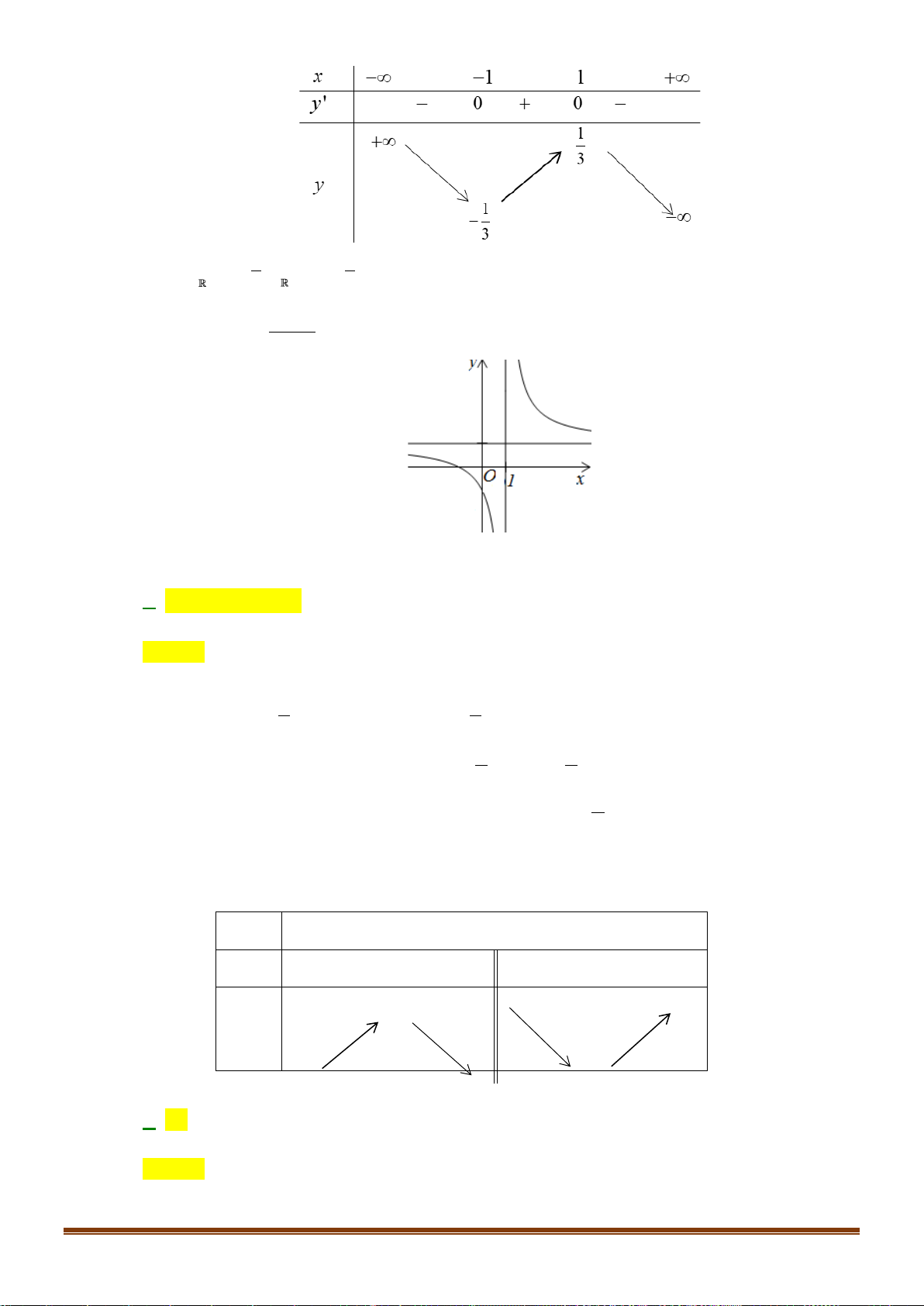
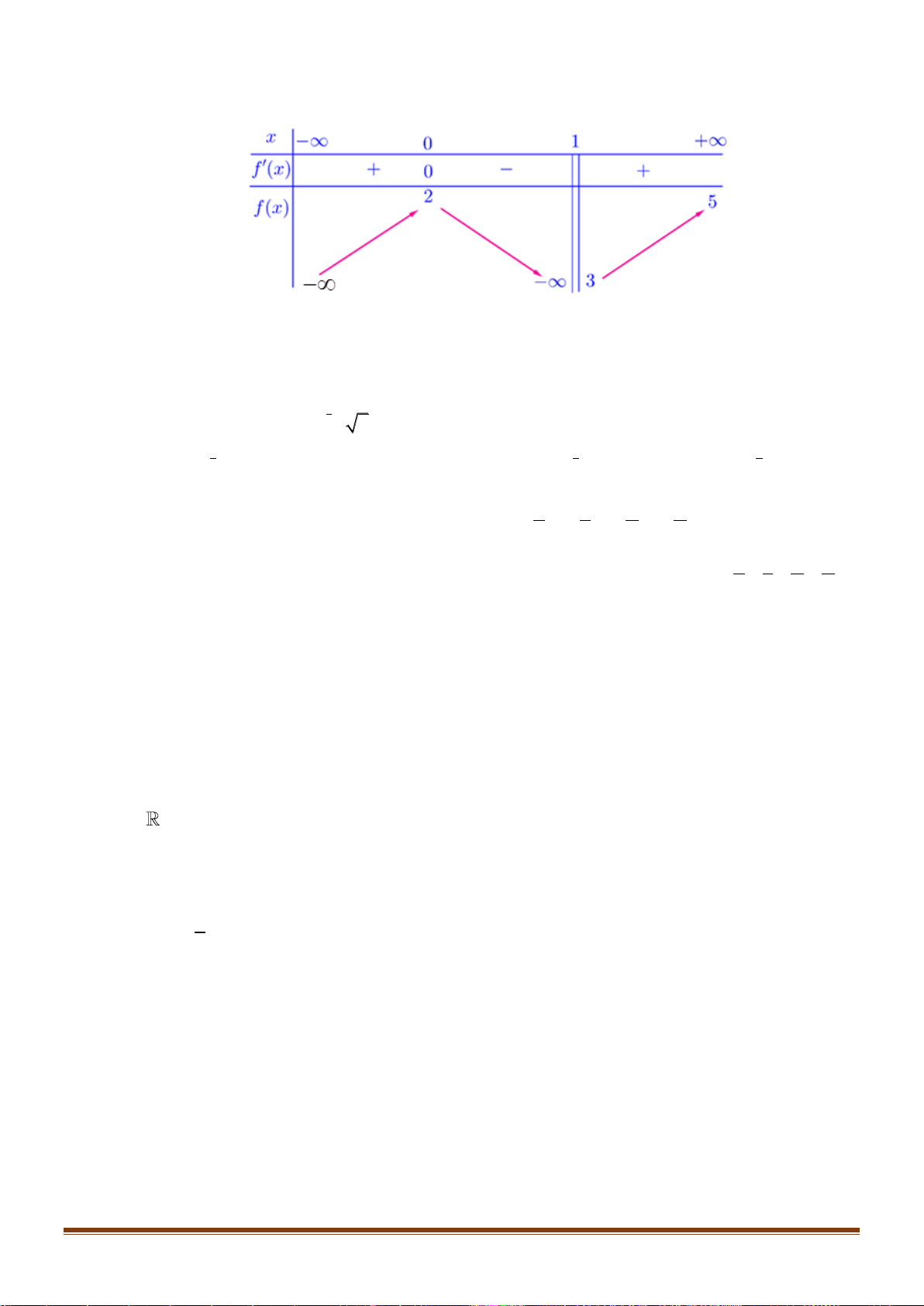
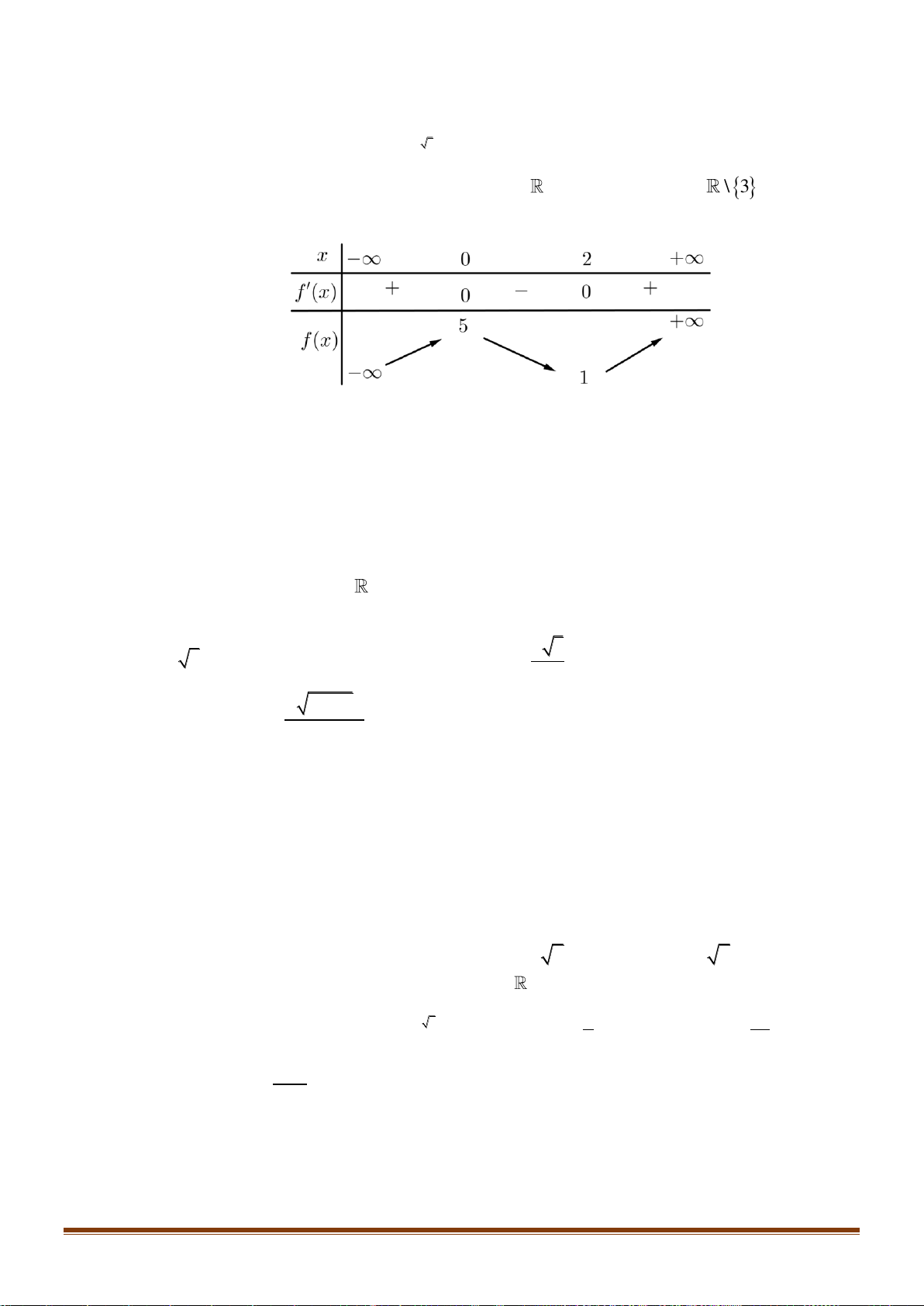
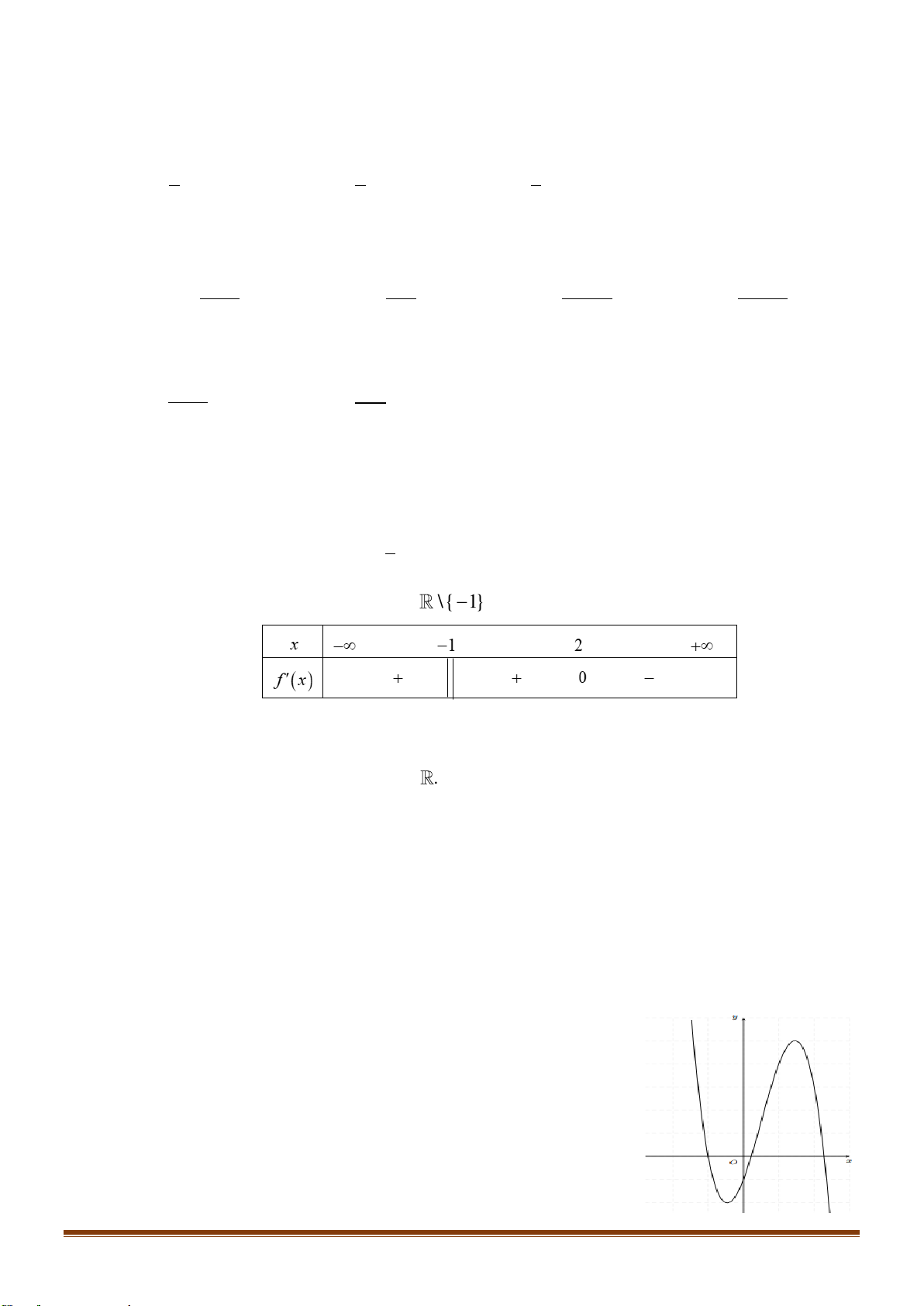
Câu 29: Cho hàm số y = f ( x) xác định trên \ 
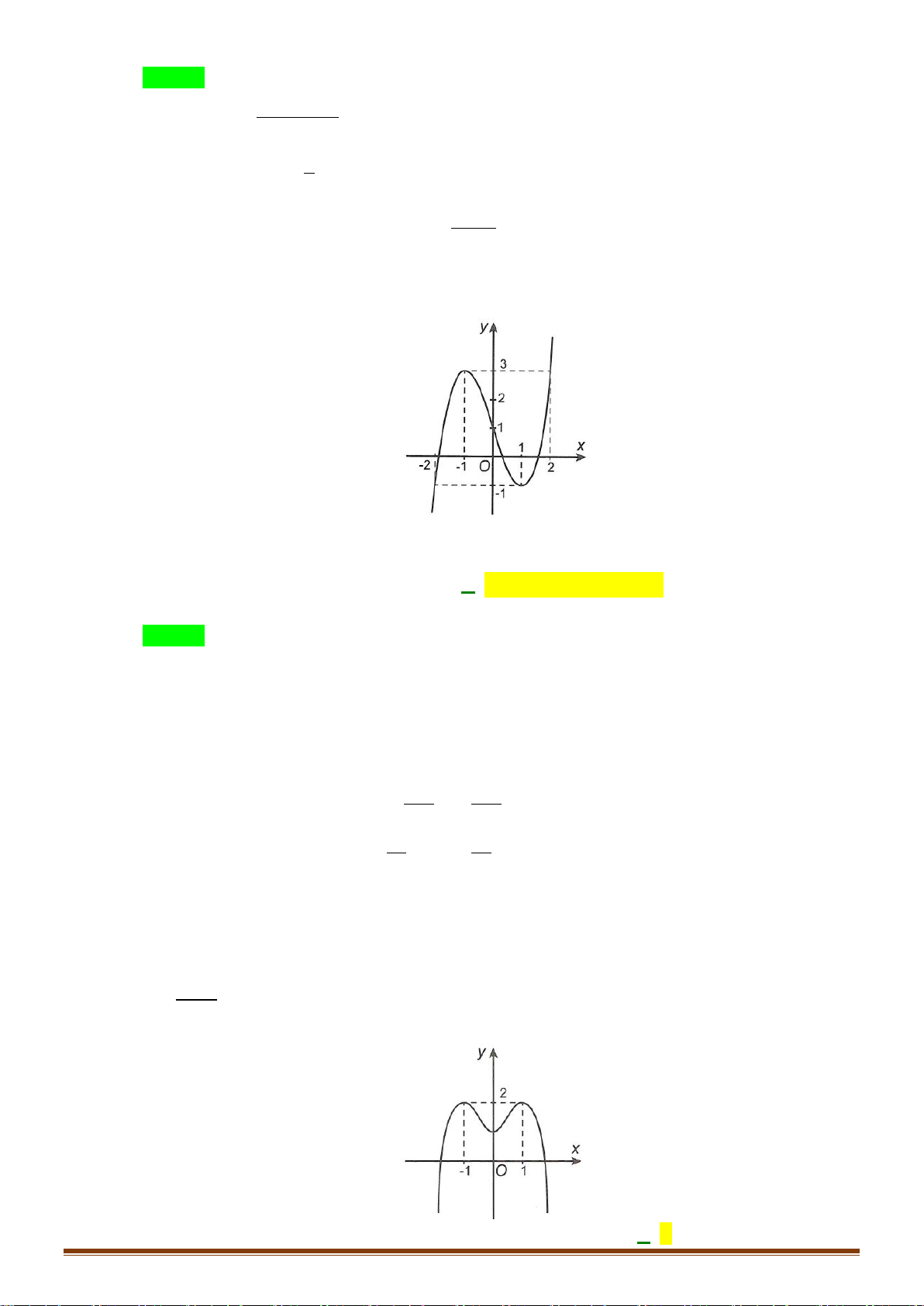
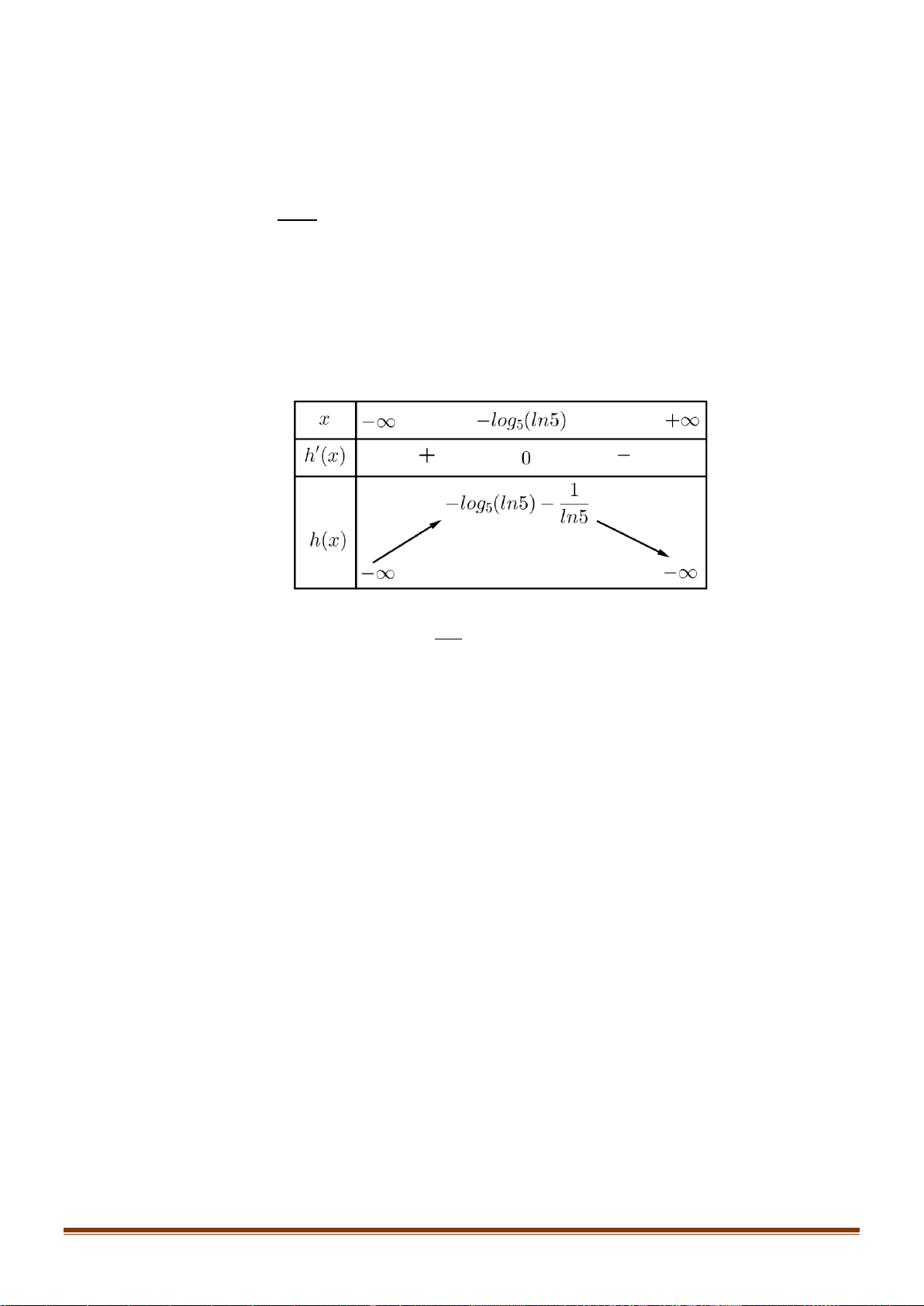
1 có bảng biến thiên như hình vẽ. Tìm khẳng định đúng.
A. Hàm số nghịch biến trên (3;+).
B. Hàm số nghịch biến trên (− ;  2 − )(3;+).
C. Hàm số đồng biến trên ( ; − ) 1 .
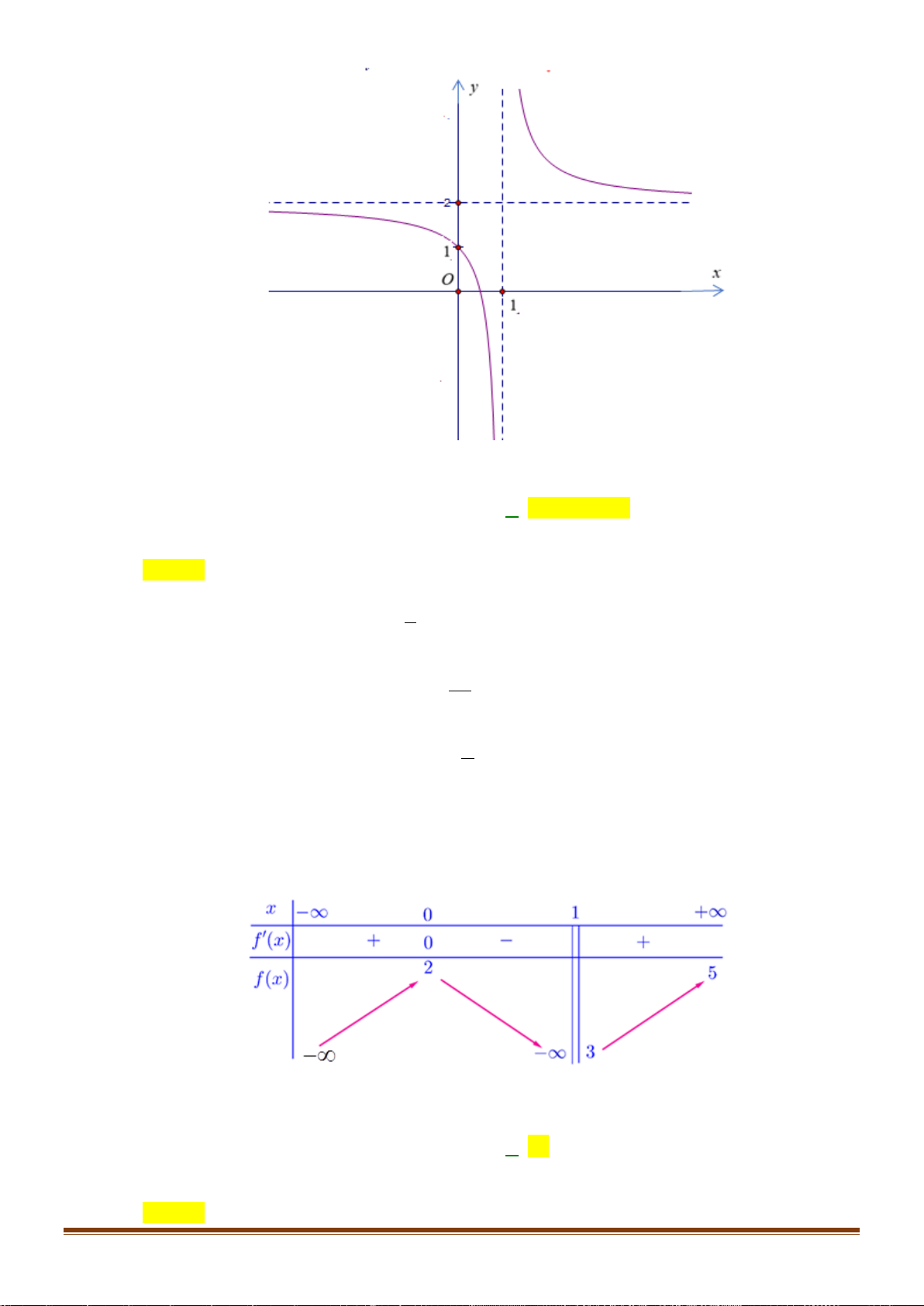
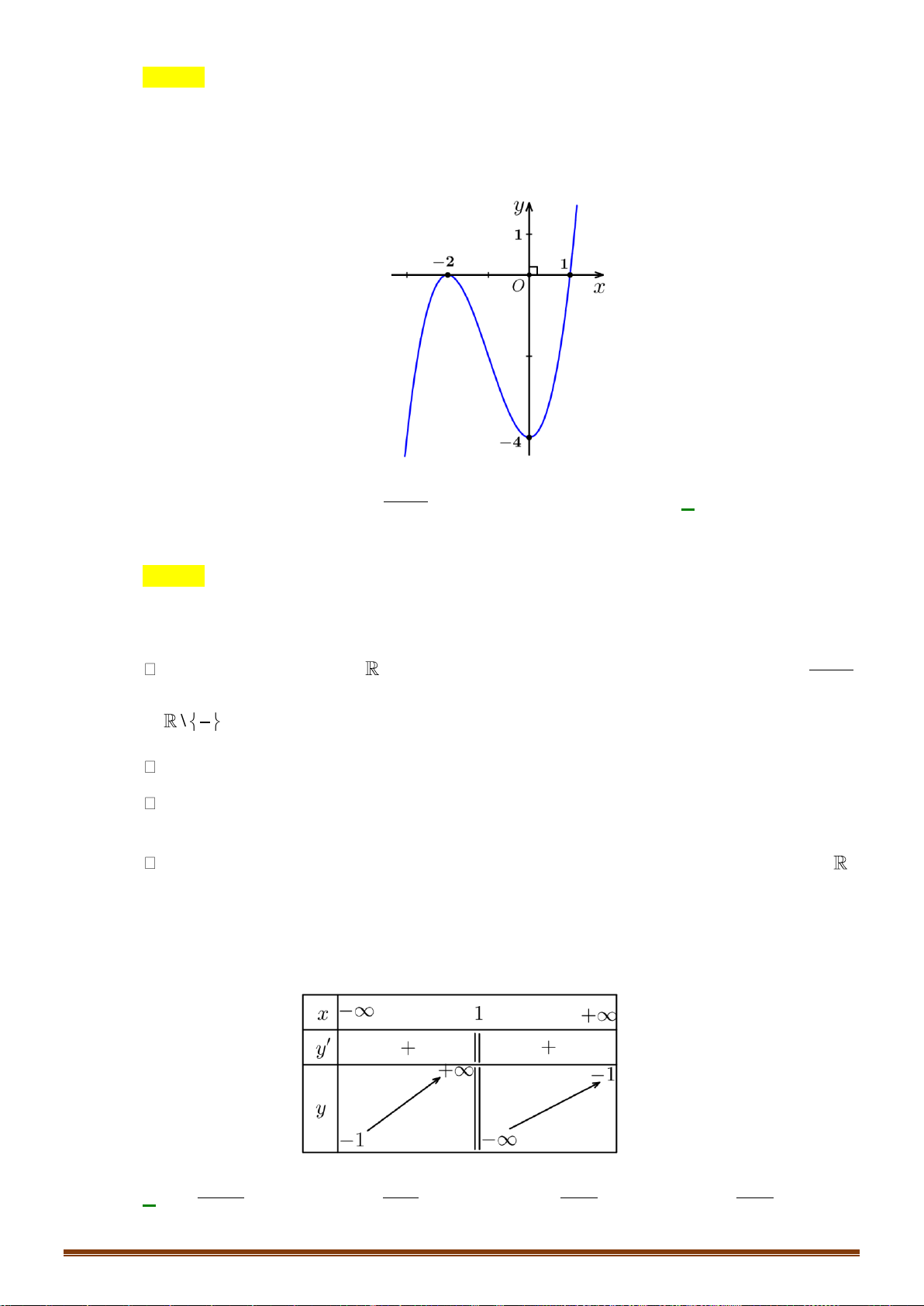
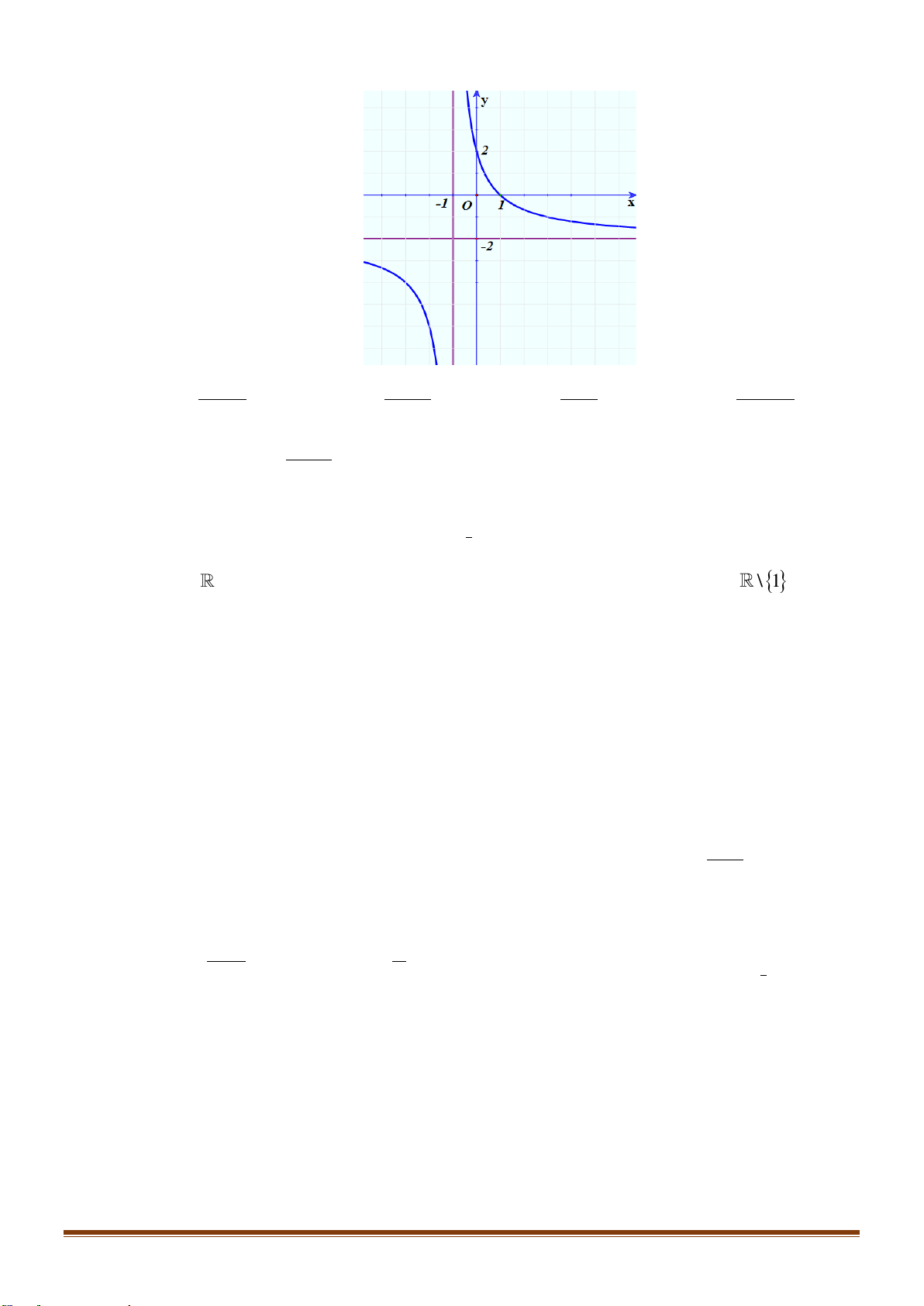
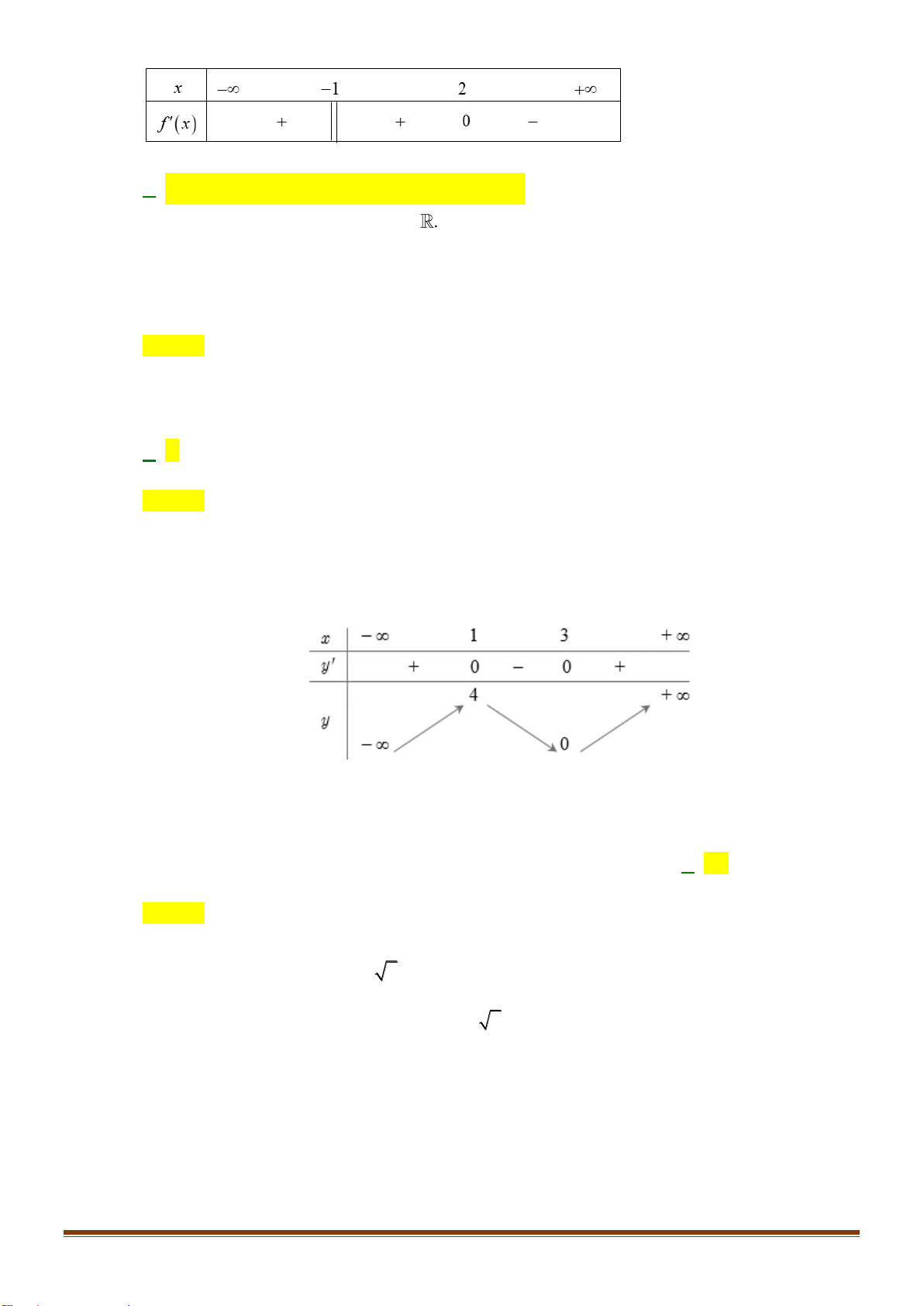
D. Hàm số đồng biến trên ( 2 − ; ) 3 . x −
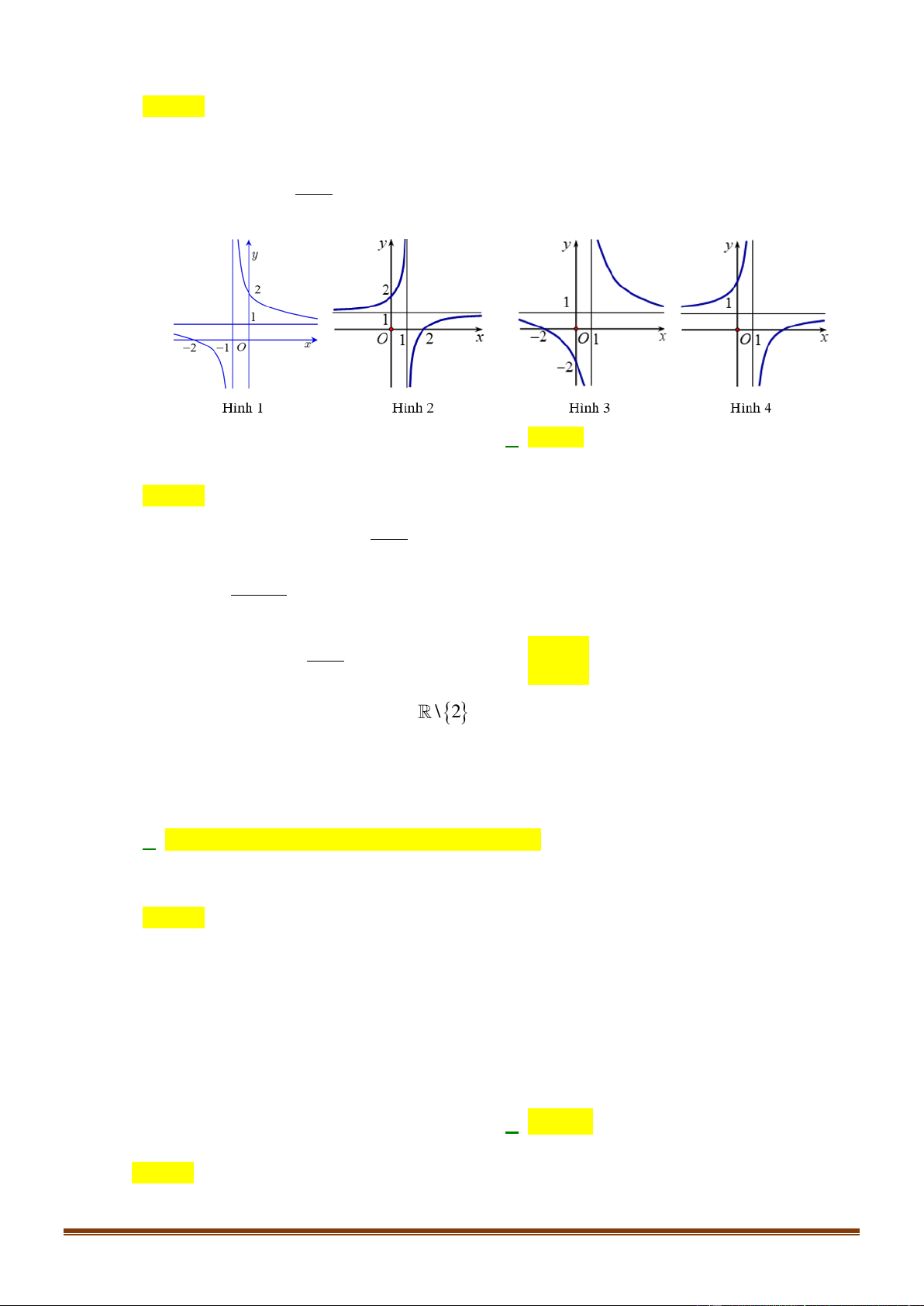
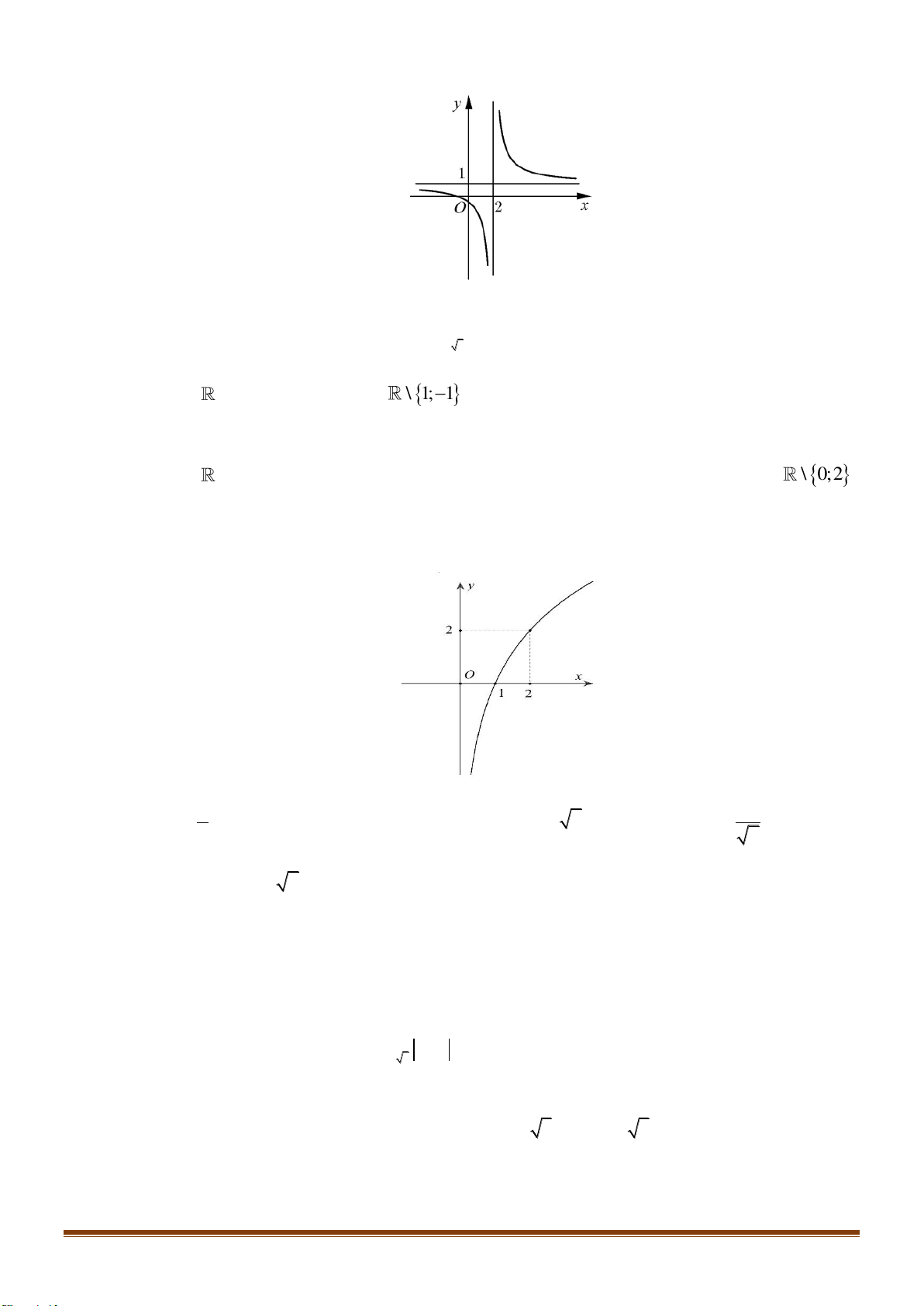
Câu 30: Cho hàm số y = f ( x) 2
= x− có đồ thị là hình vẽ nào dưới đây? 1 A. Hình 4. B. Hình 1. C. Hình 2. D. Hình 4 Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
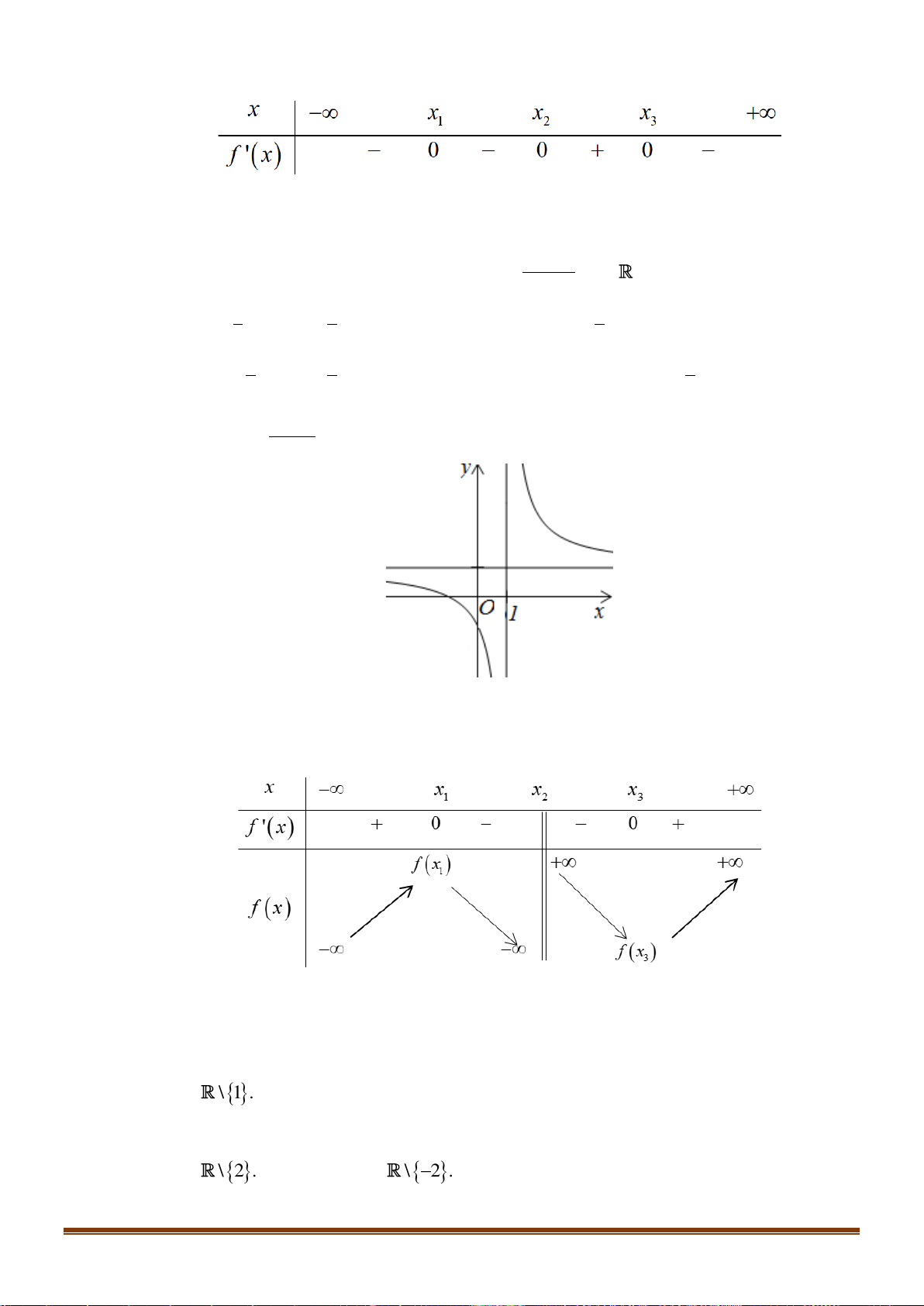
Câu 31: Cho hàm số y = f ( x) xác định trên \  
2 . Biết lim f ( x) = 0 , lim f ( x) = 1, lim f ( x) = 3 − x→+ x→− − x→2
, lim f ( x) = − . Trong các khẳng định sau, khẳng định nào đúng? + x→2
A. Đồ thị hàm số có hai đường tiệm cận đứng là x = 0 , x =1 .
B. Đồ thị hàm số không có tiệm cận đứng.
C. Đồ thị hàm số có hai đường tiệm cận đứng là x = 2 .
D. Đồ thị hàm số có hai đường tiệm cận ngang là x = 0 , x =1 .
Câu 32: Cho một khối nón có chiều cao bằng 4cm , độ dài đường sinh bằng 5cm . Tính thể tích khối nón này. A.  ( 3 45 cm ) . B.  ( 3 15 cm ). C.  ( 3 12 cm ). D.  ( 3 36 cm ).
Câu 33: Trong mặt phẳng ( P) , cho đường thẳng l cắt và không vuông góc với  . Khi quay ( P) xung
quanh  thì đường thẳng l sinh ra
A. Mặt nón tròn xoay.
B. Khối nón tròn xoay. C. Mặt trụ tròn xoay. D. Hình nón tròn quay.
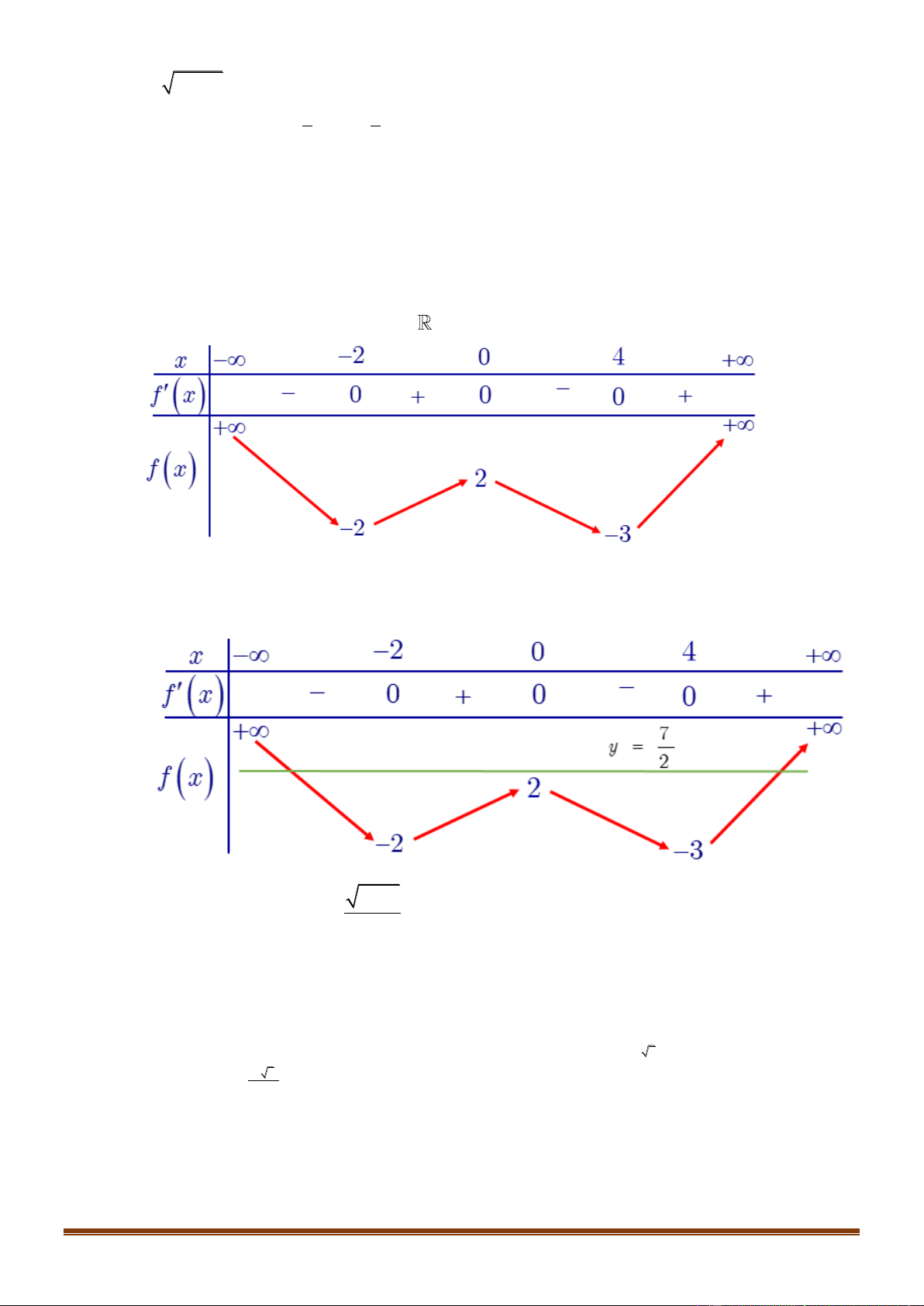
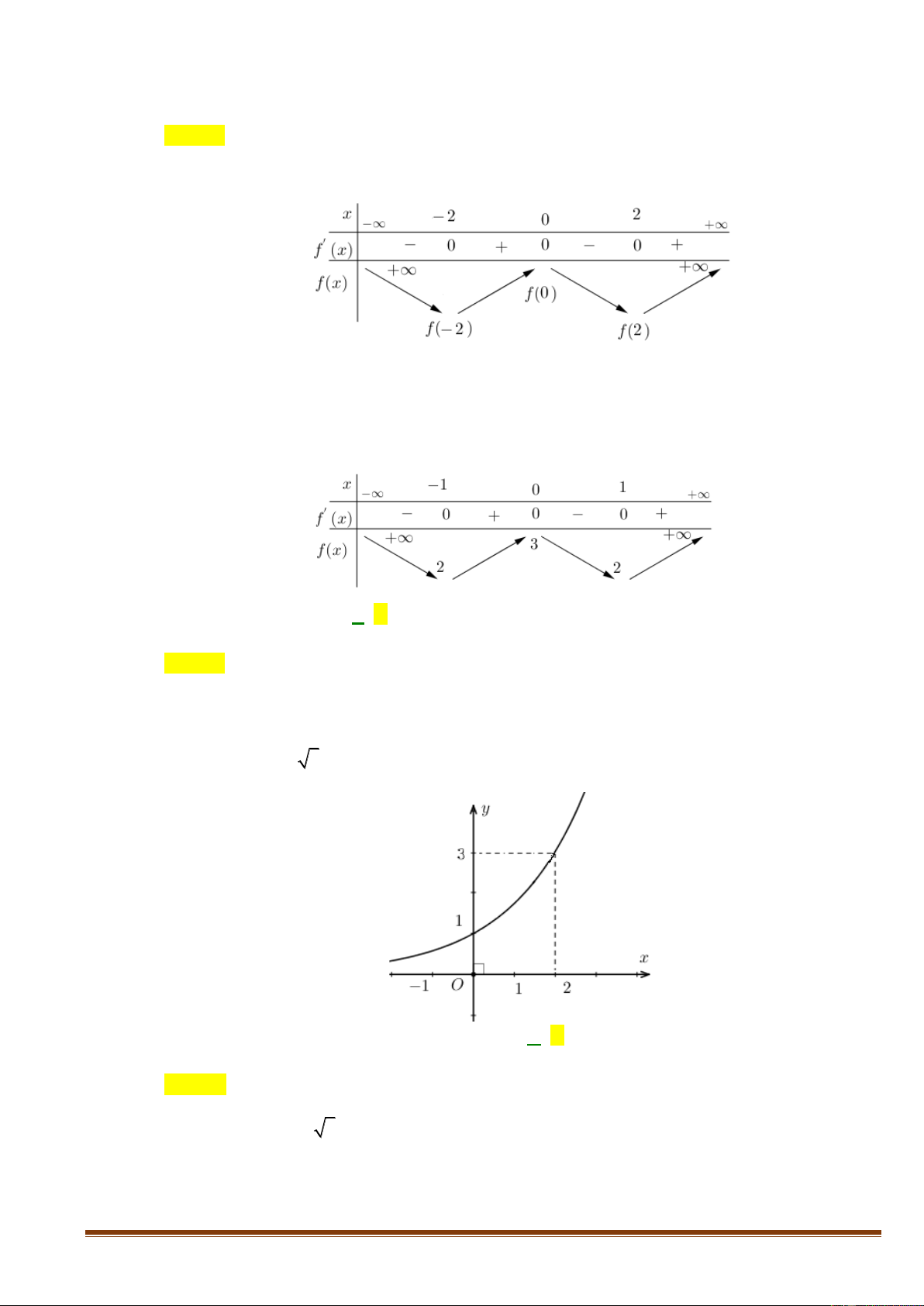
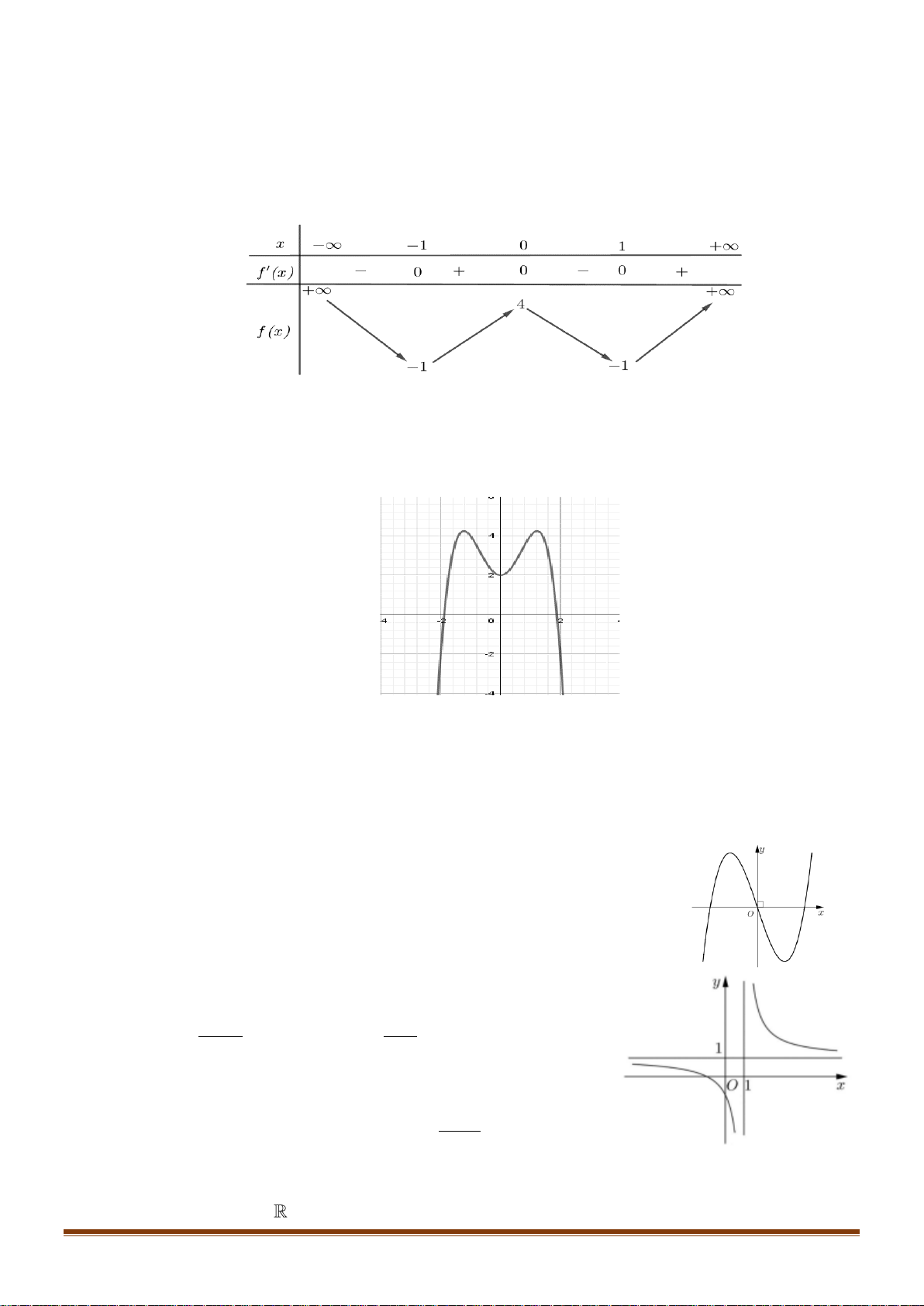
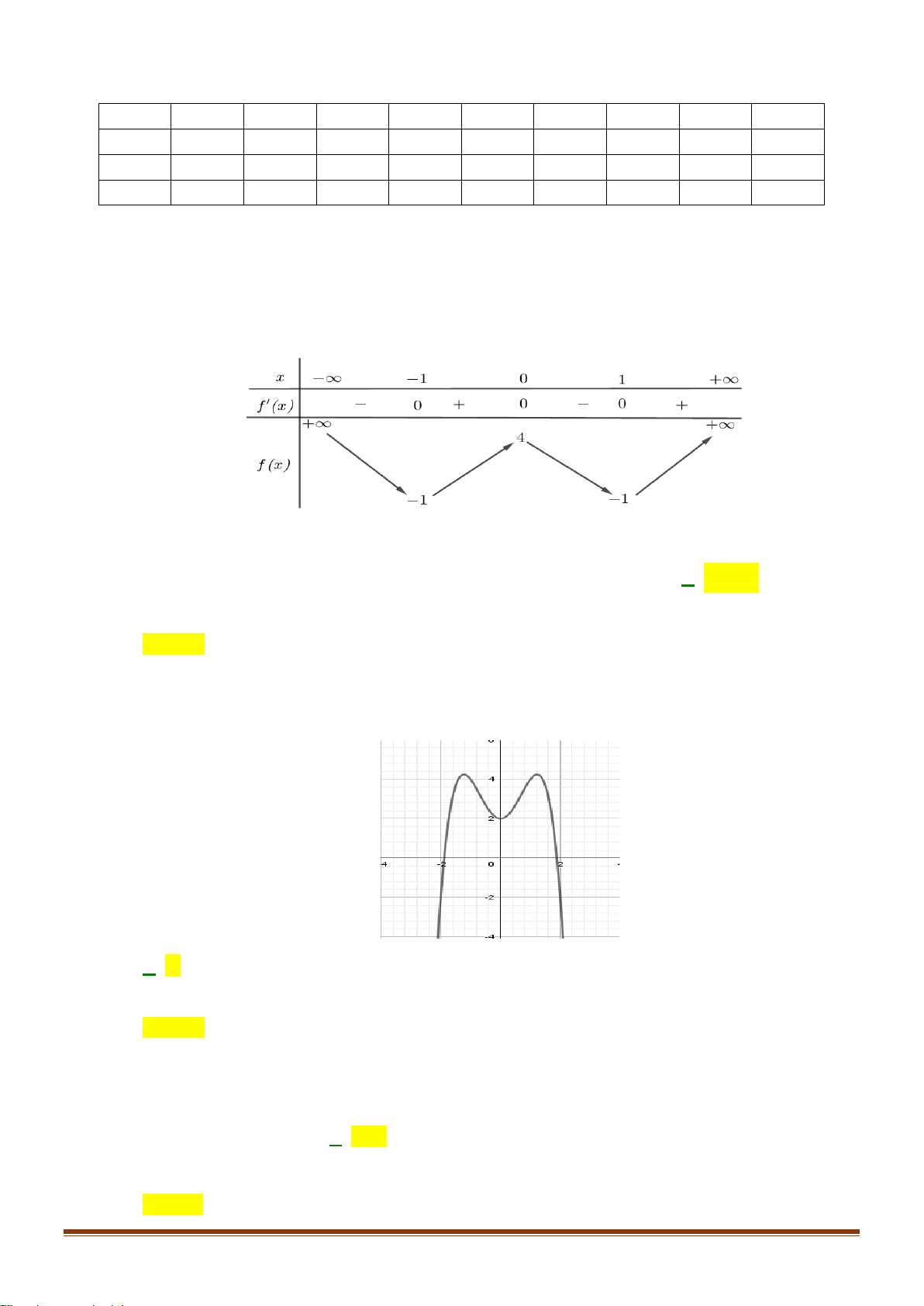
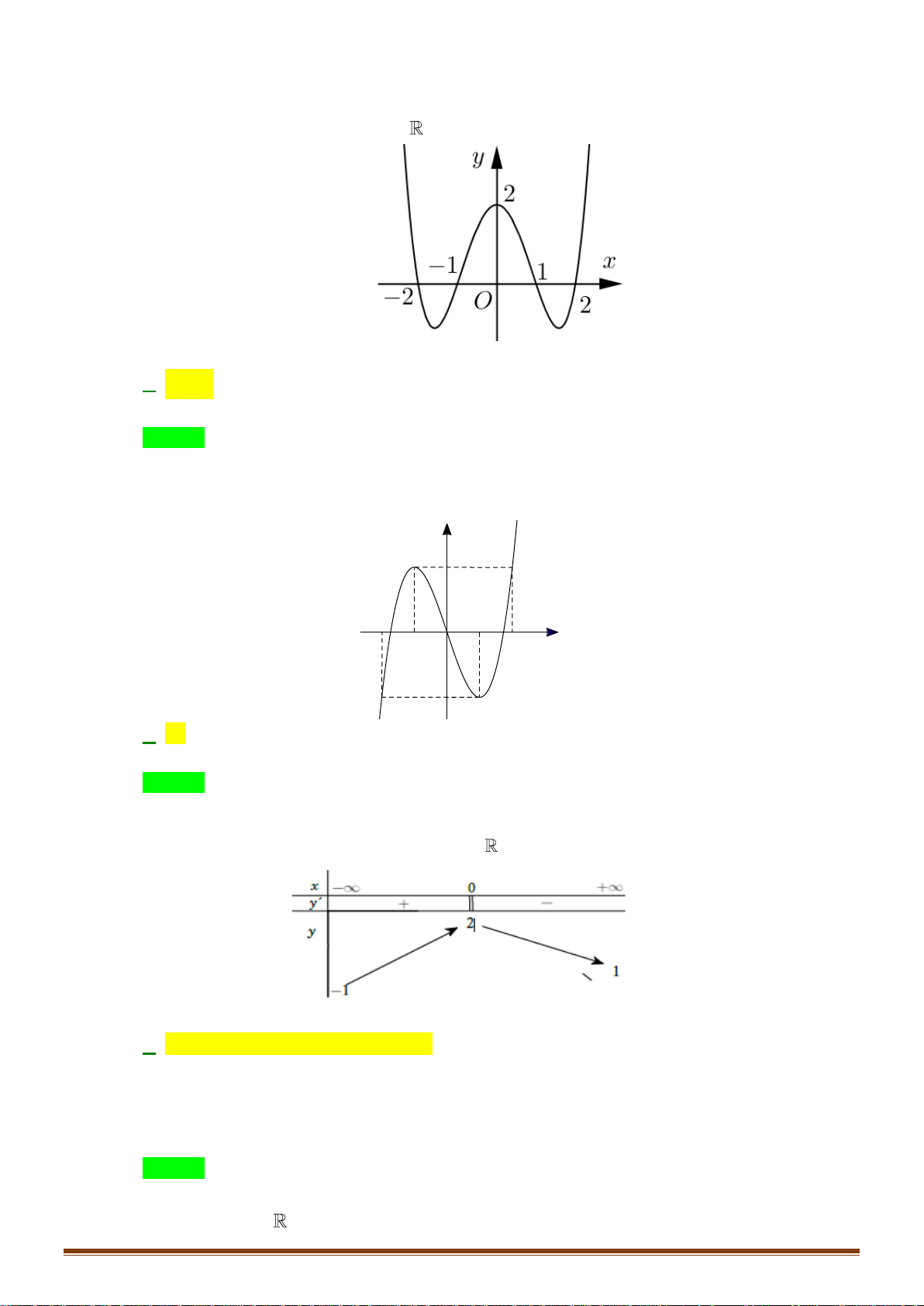
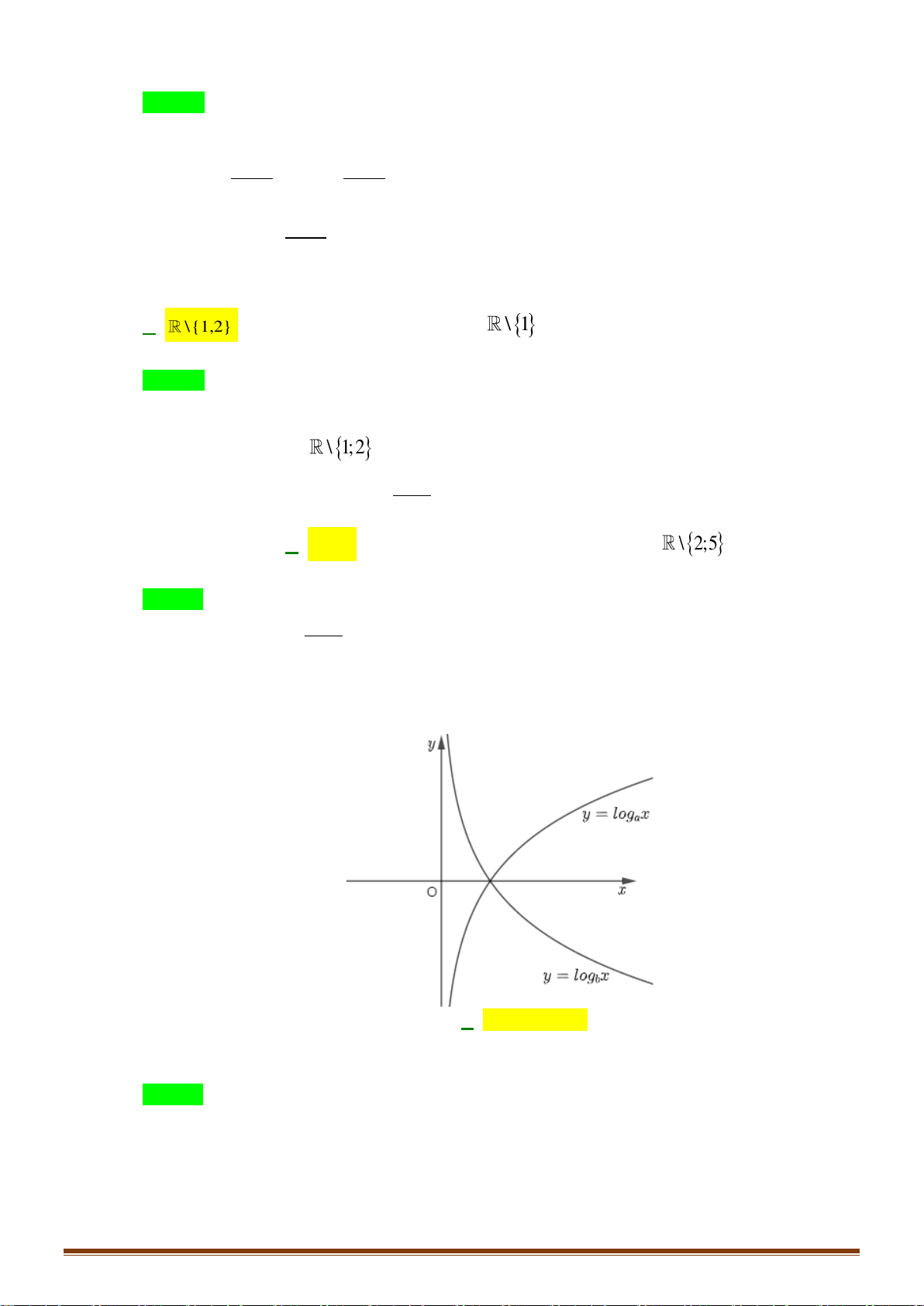
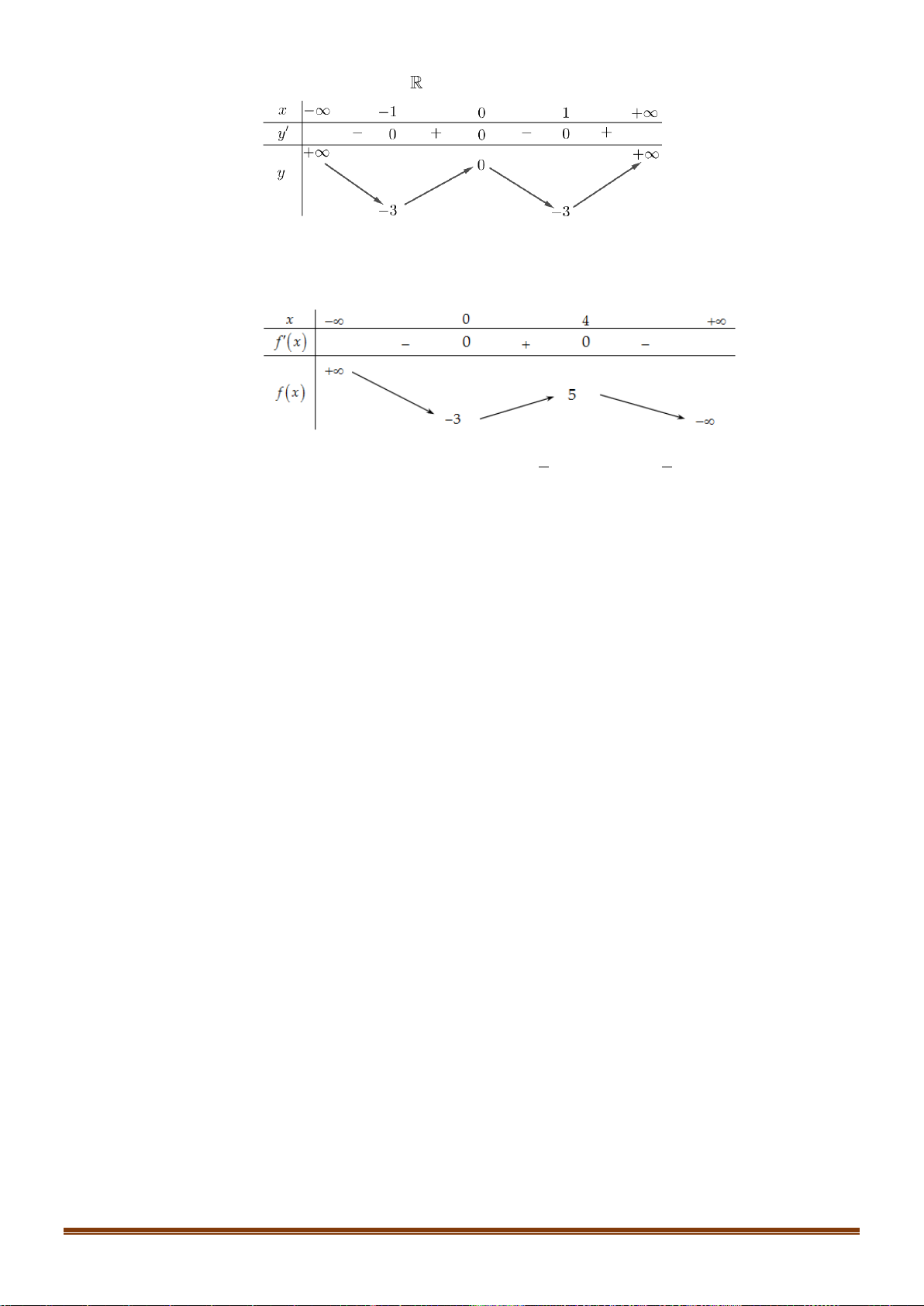
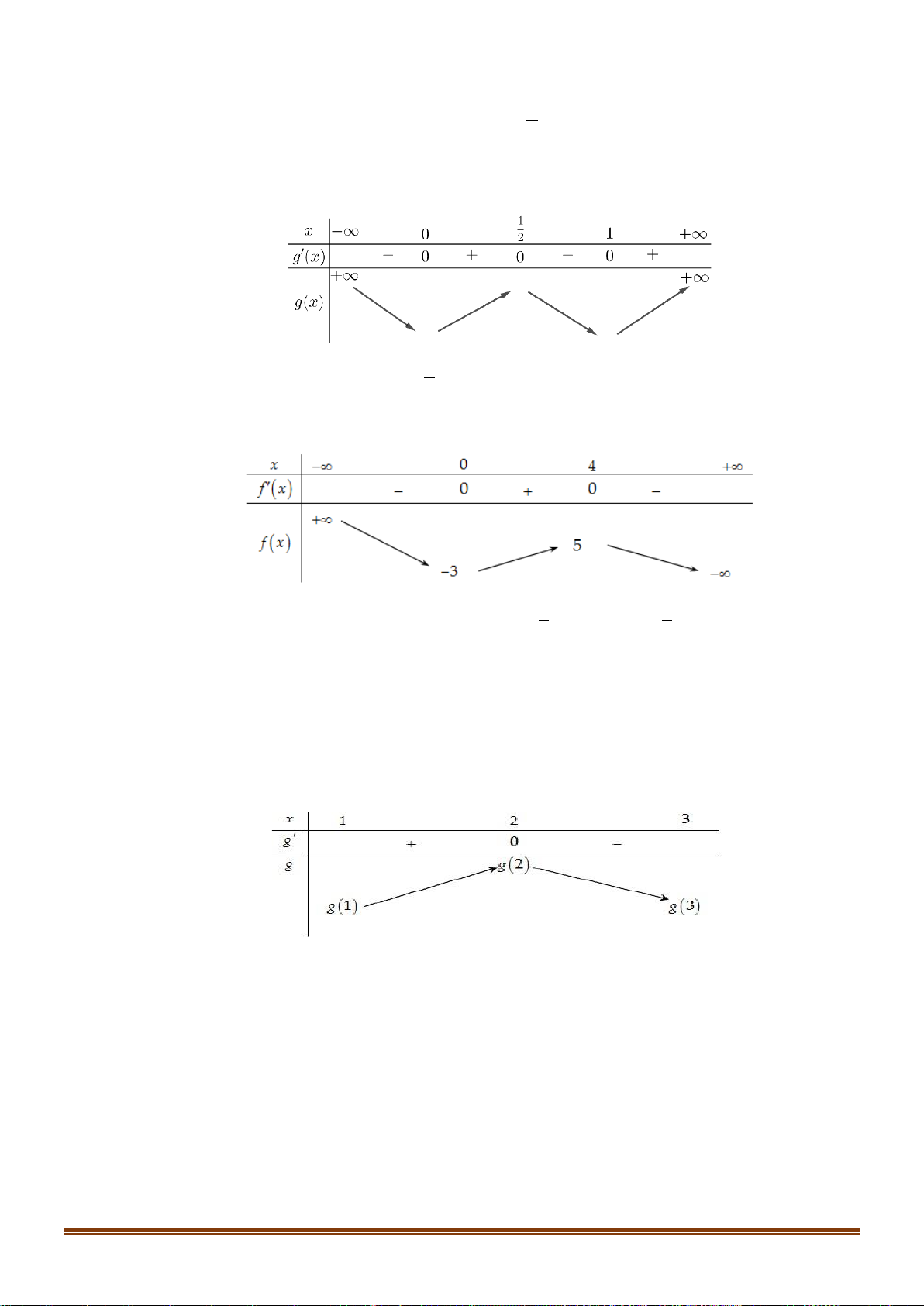
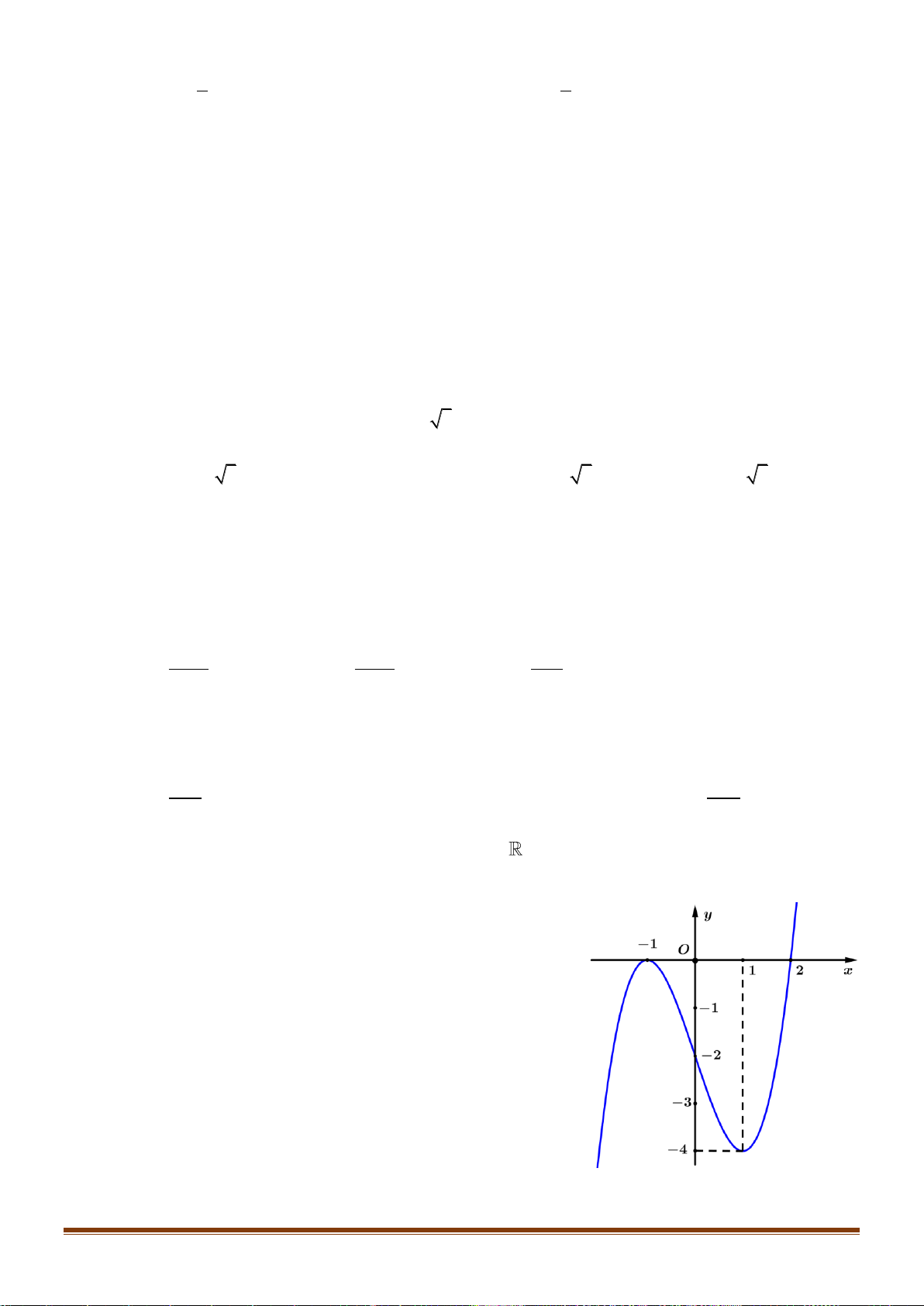
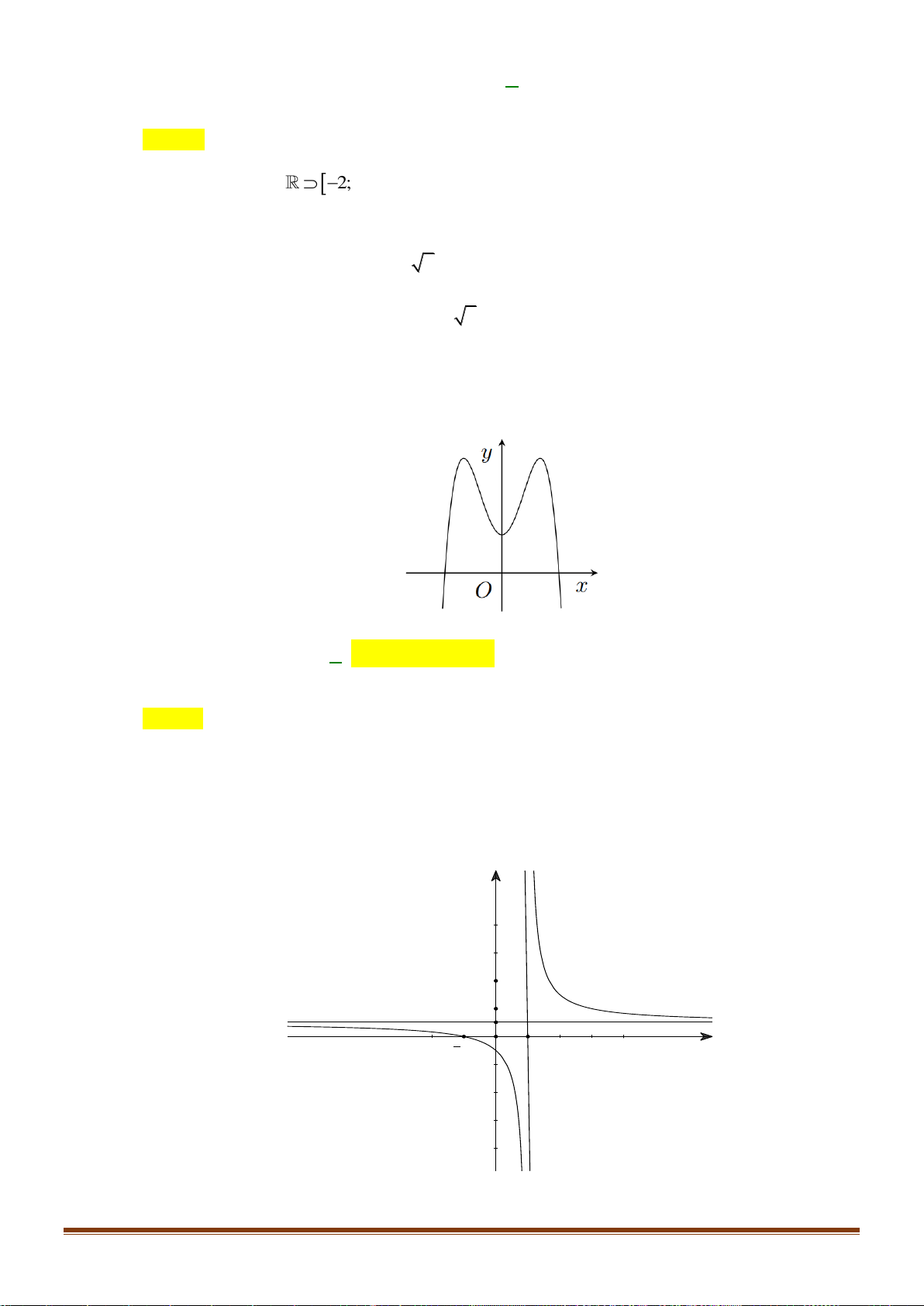
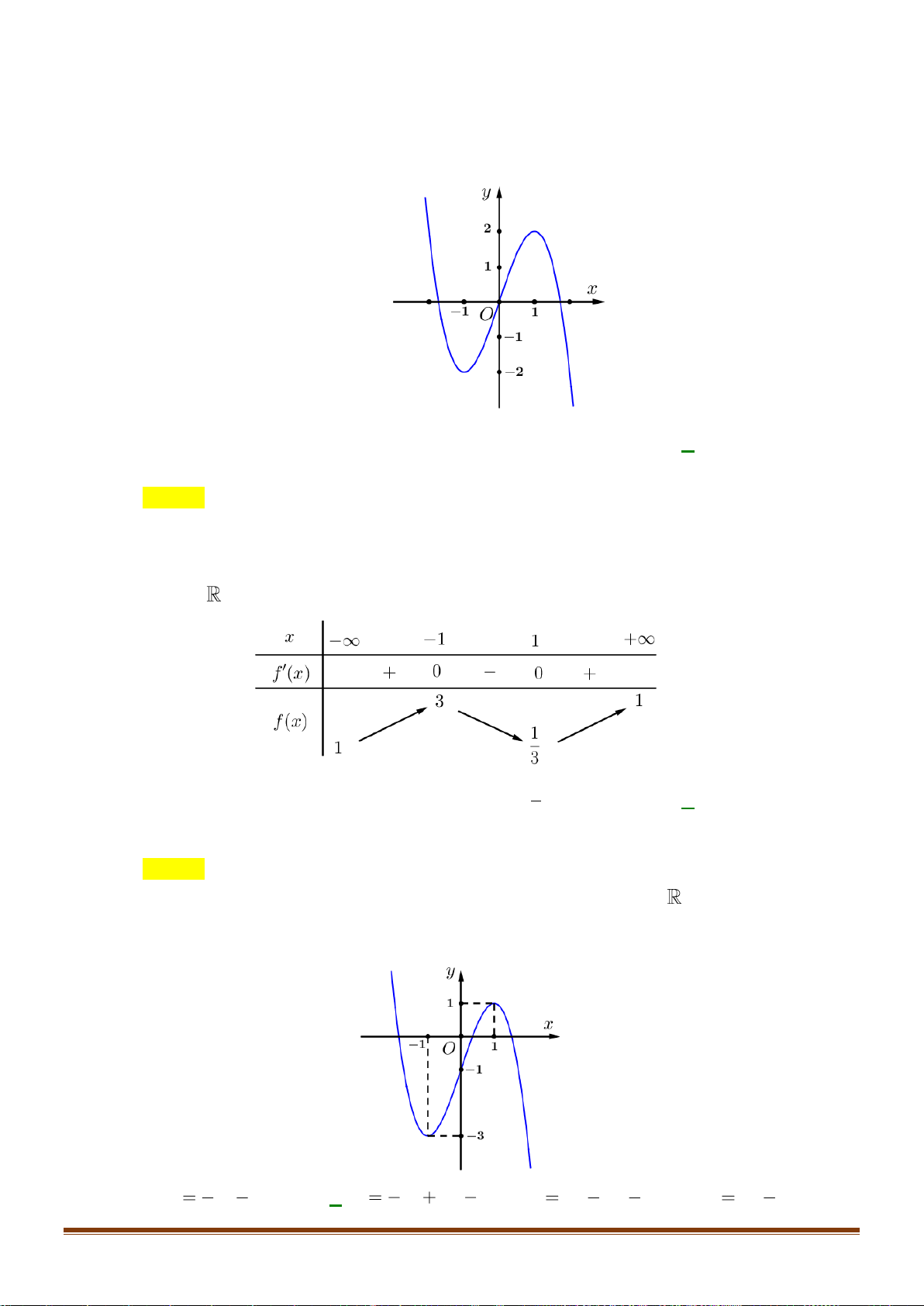
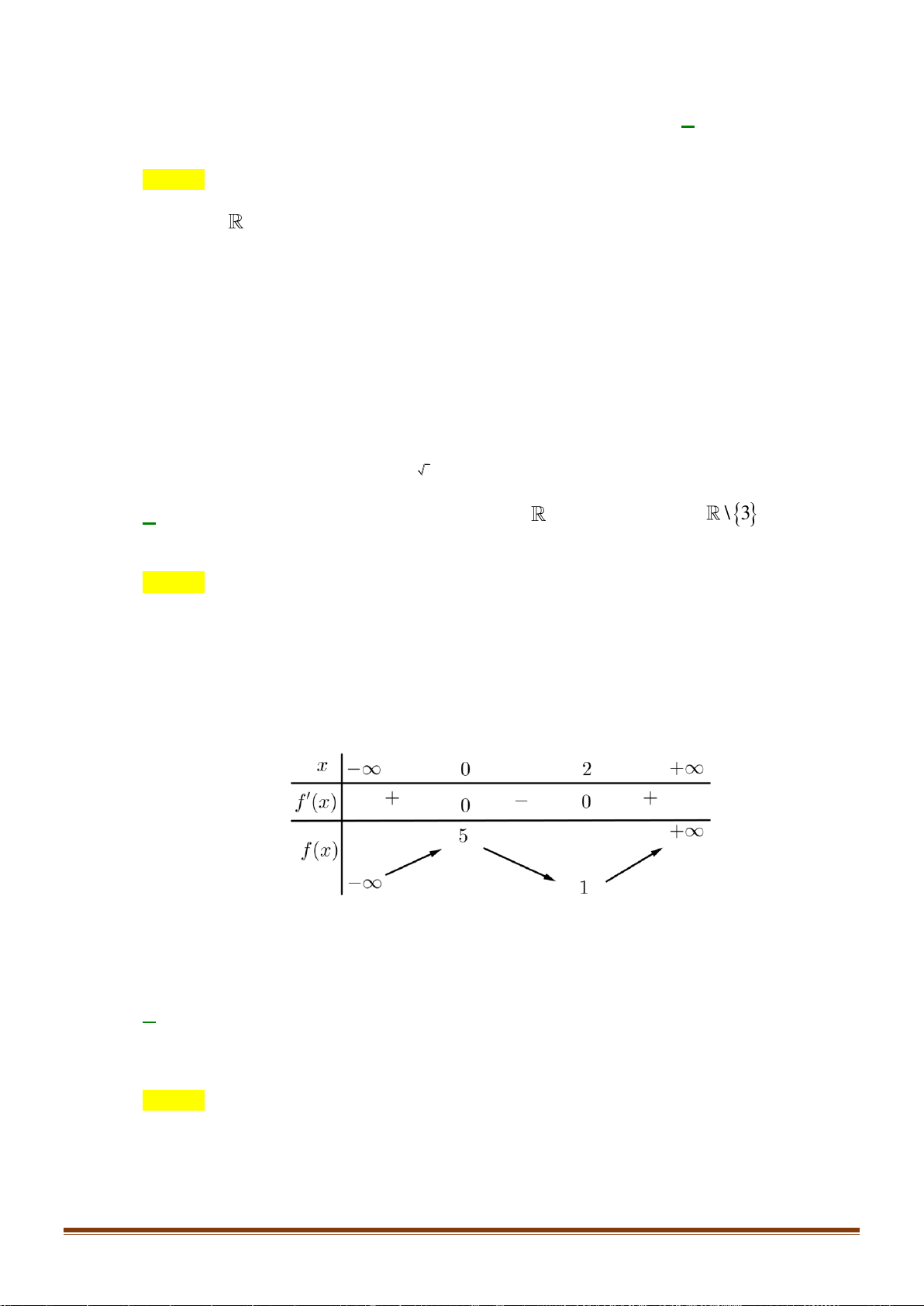
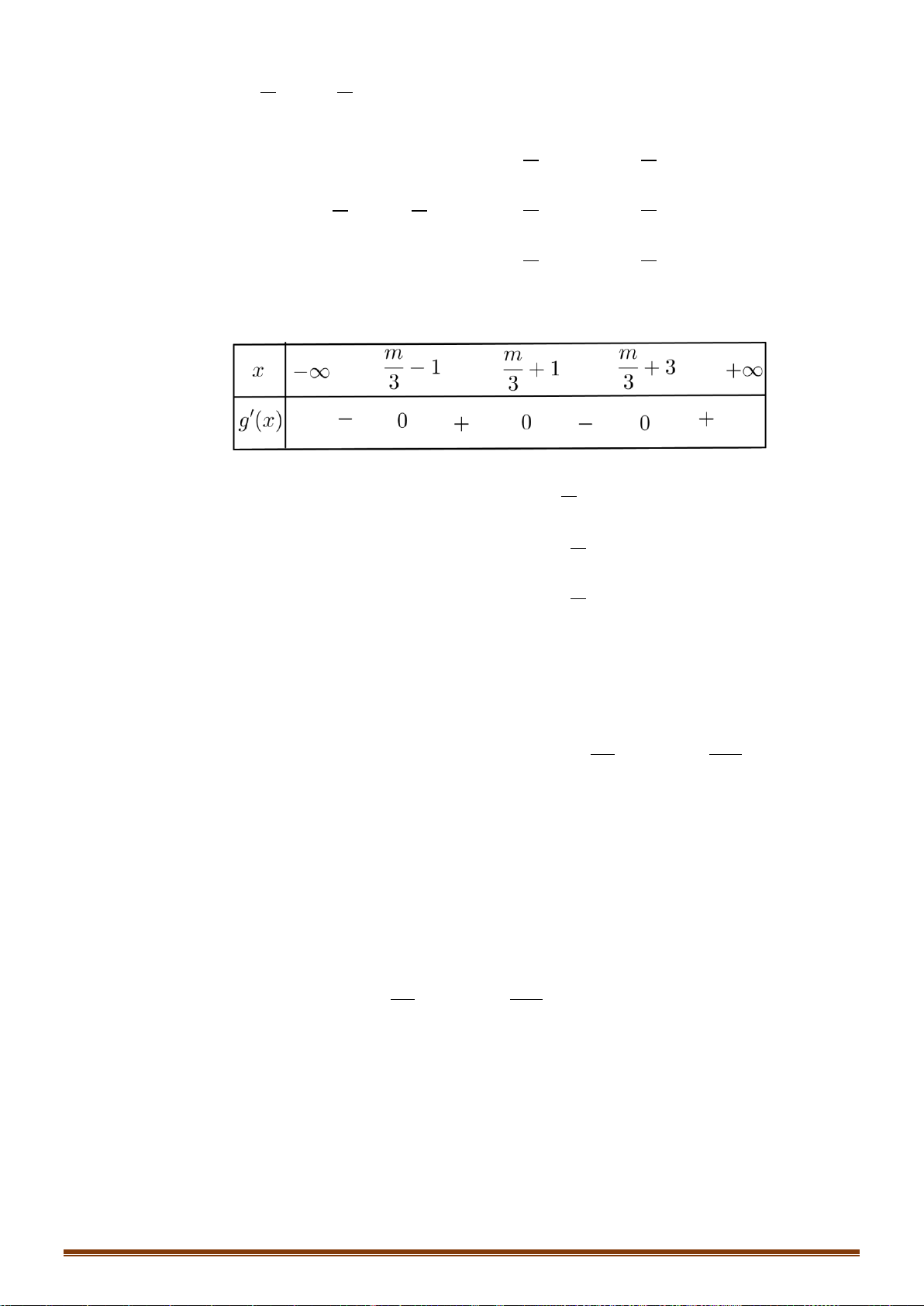
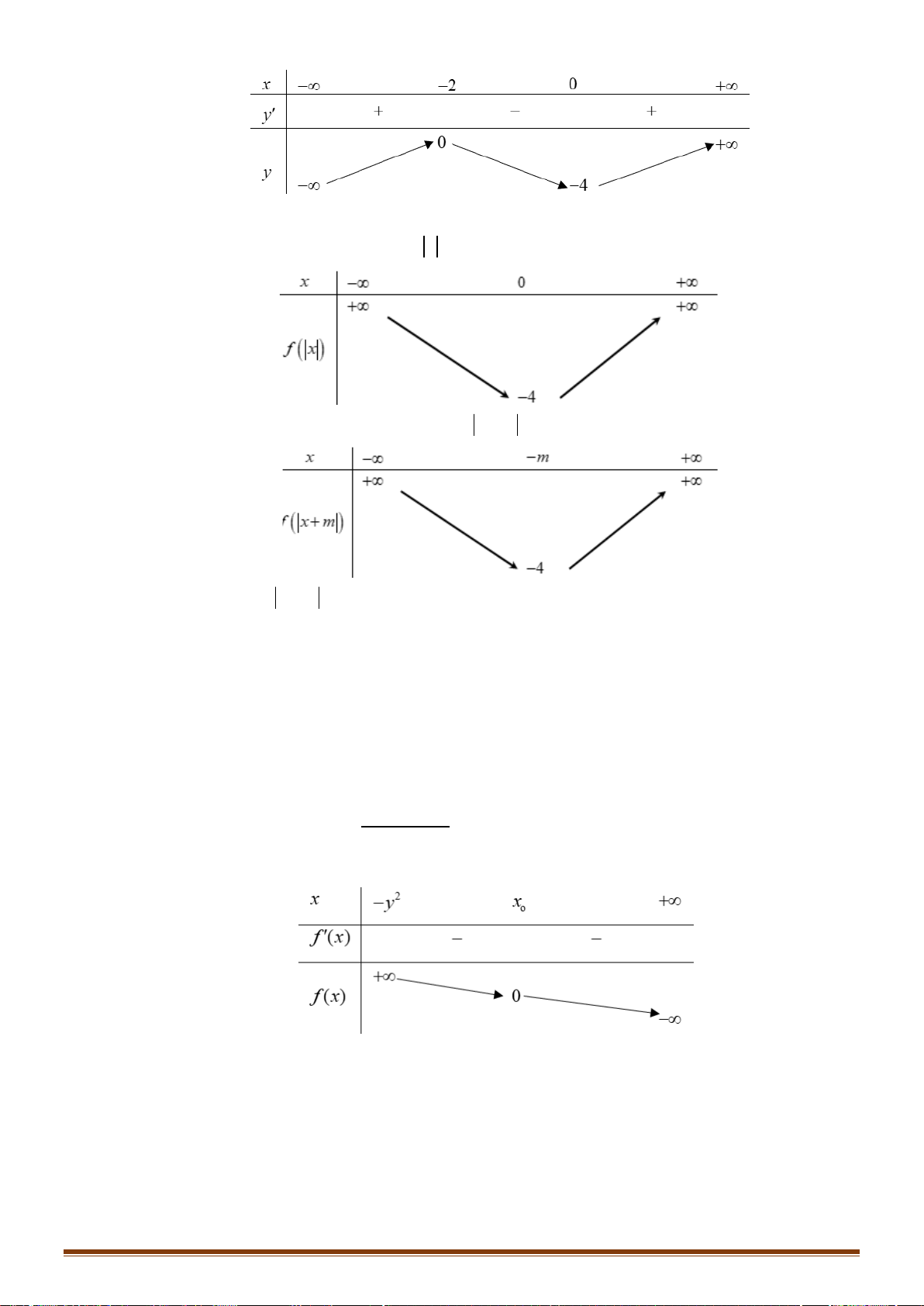
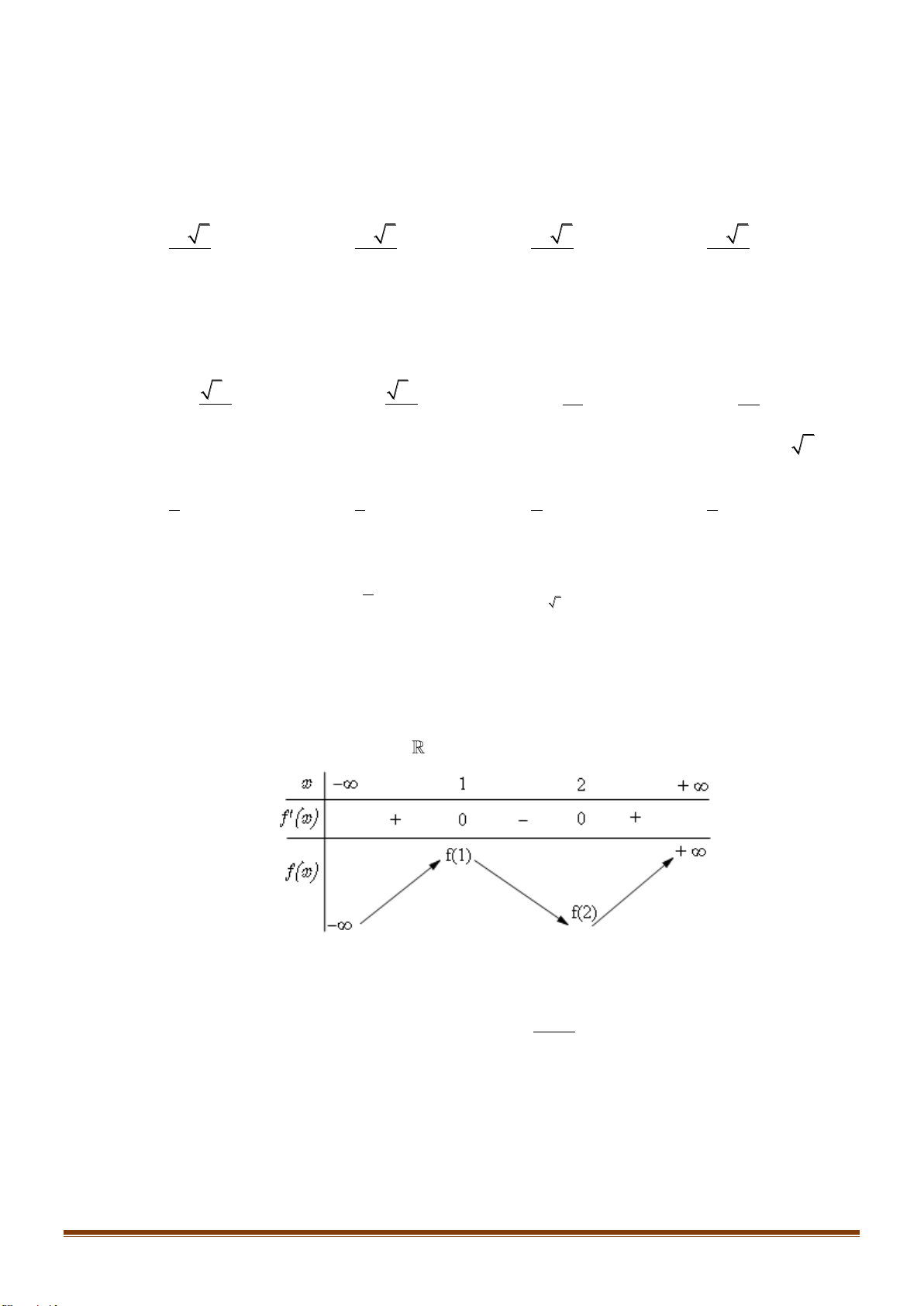
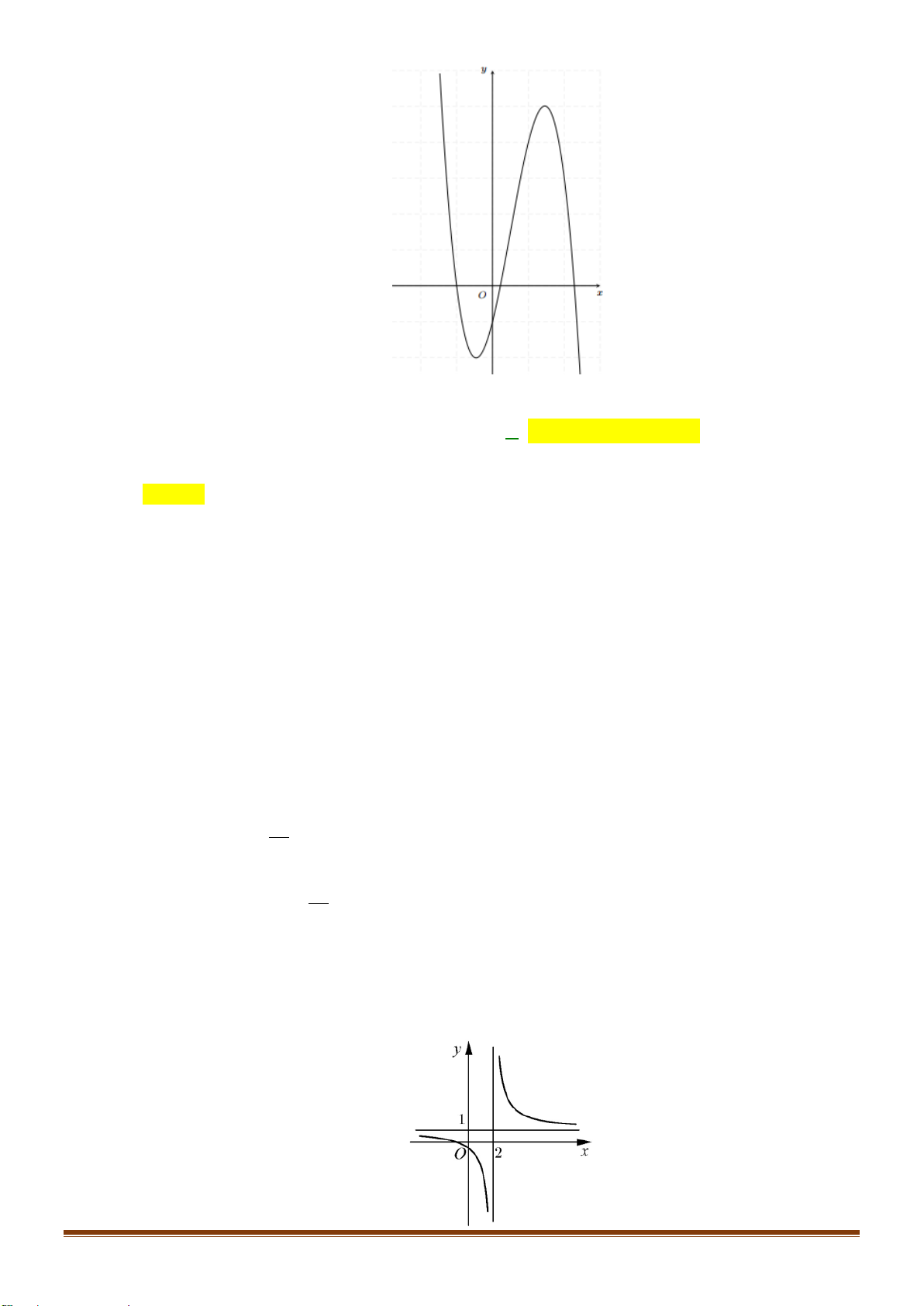
Câu 34: Cho hàm số y = f (x) xác định trên
và có bảng biến thiên như sau:
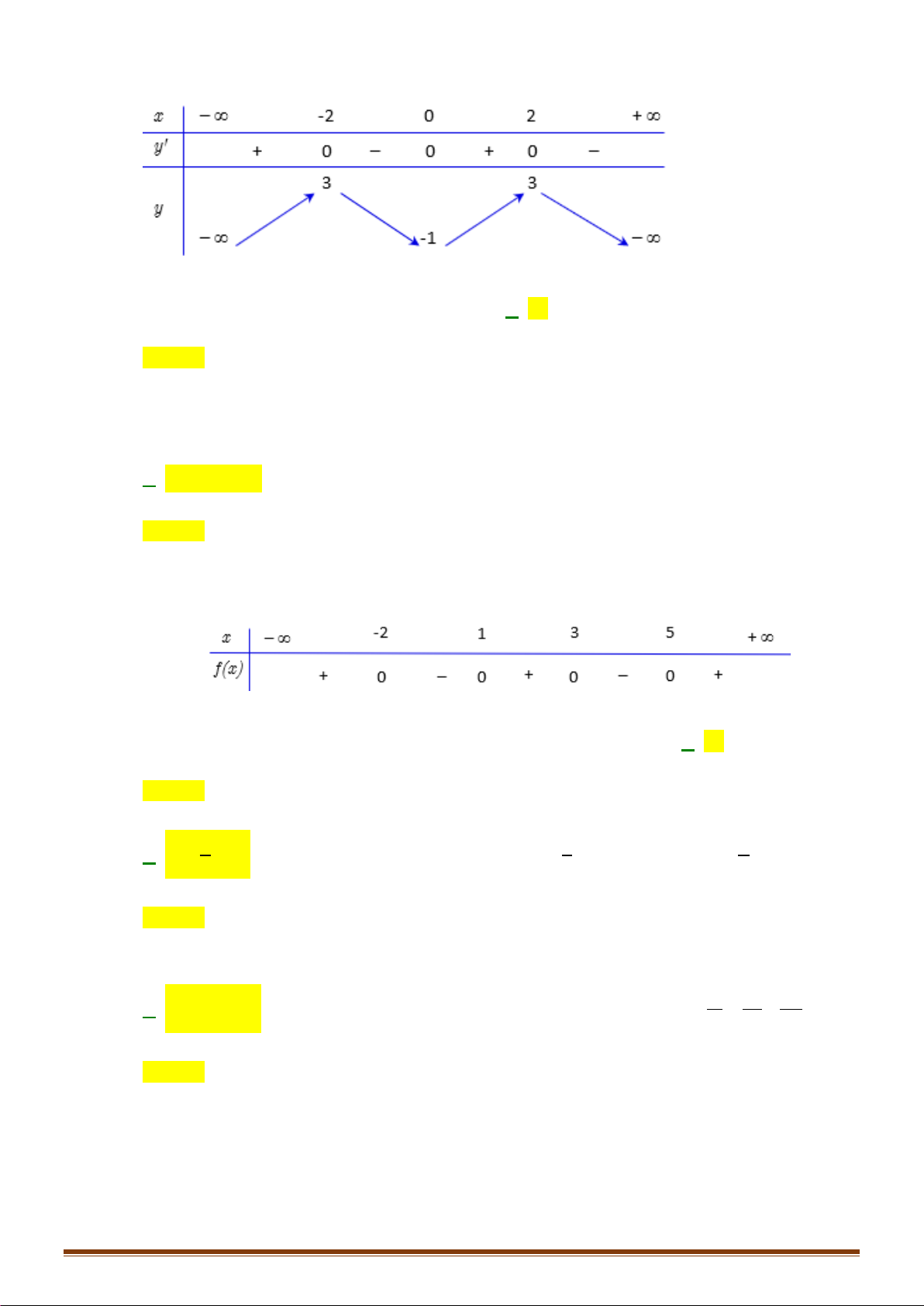
Tìm số nghiệm của phương trình 2 f (x) − 7 = 0 ? A. 4. B. 3. C. 2. D. 1. x − 2
Câu 35: Đồ thị hàm số y = f (x) = 2 x
có bao nhiêu tiệm cận đứng − 9 A. 4. B. 1. C. 2. D. 3.
II. PHẦN TỰ LUẬN (4 câu – 3 điểm)
Câu 36: Cho a và b là hai số thực thỏa mãn 2  a b và ( 2 2 log
a b ) + log b = 7 . Tính giá trị của biểu b a a b logab thức 2 a 7b P a + = .
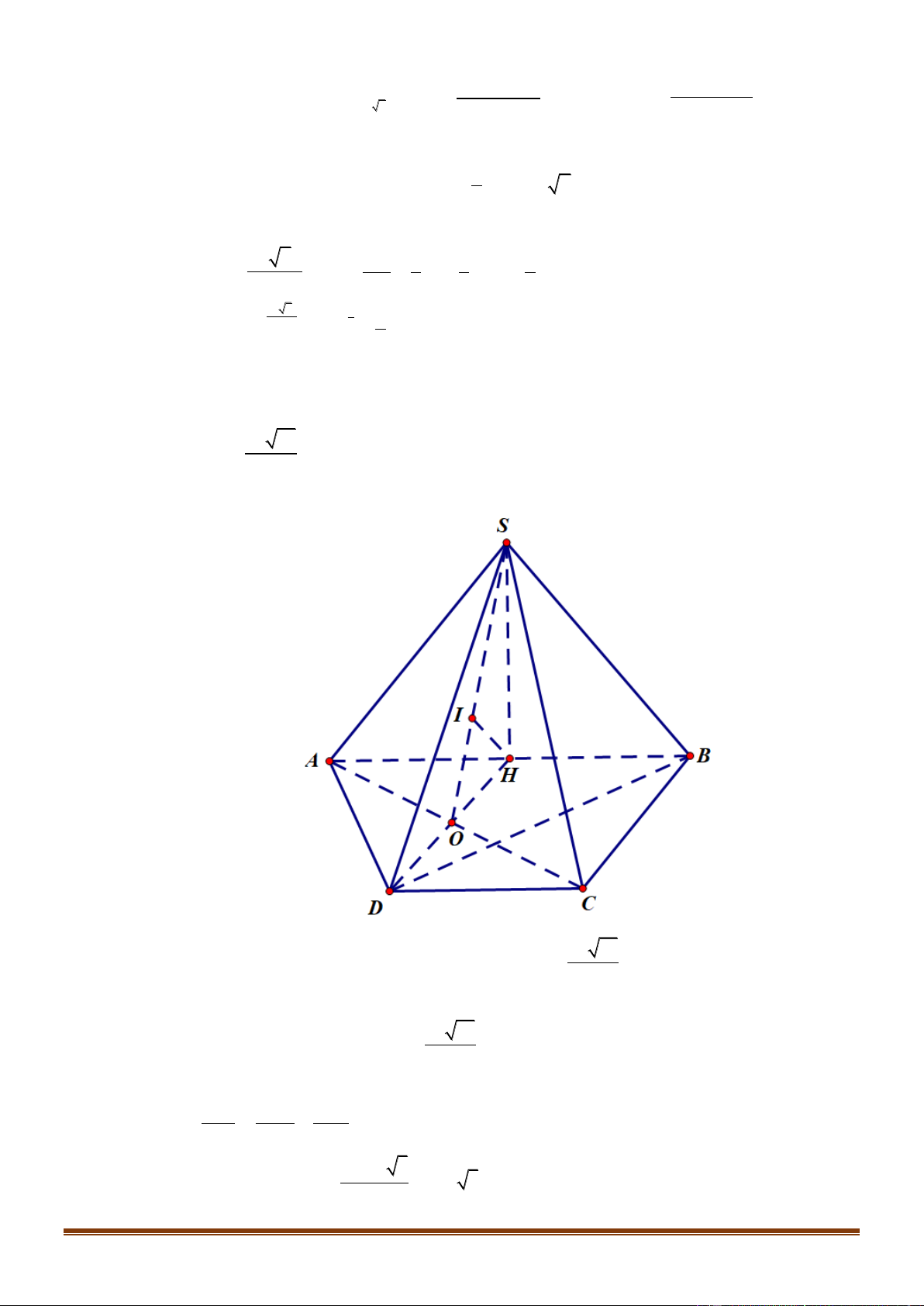
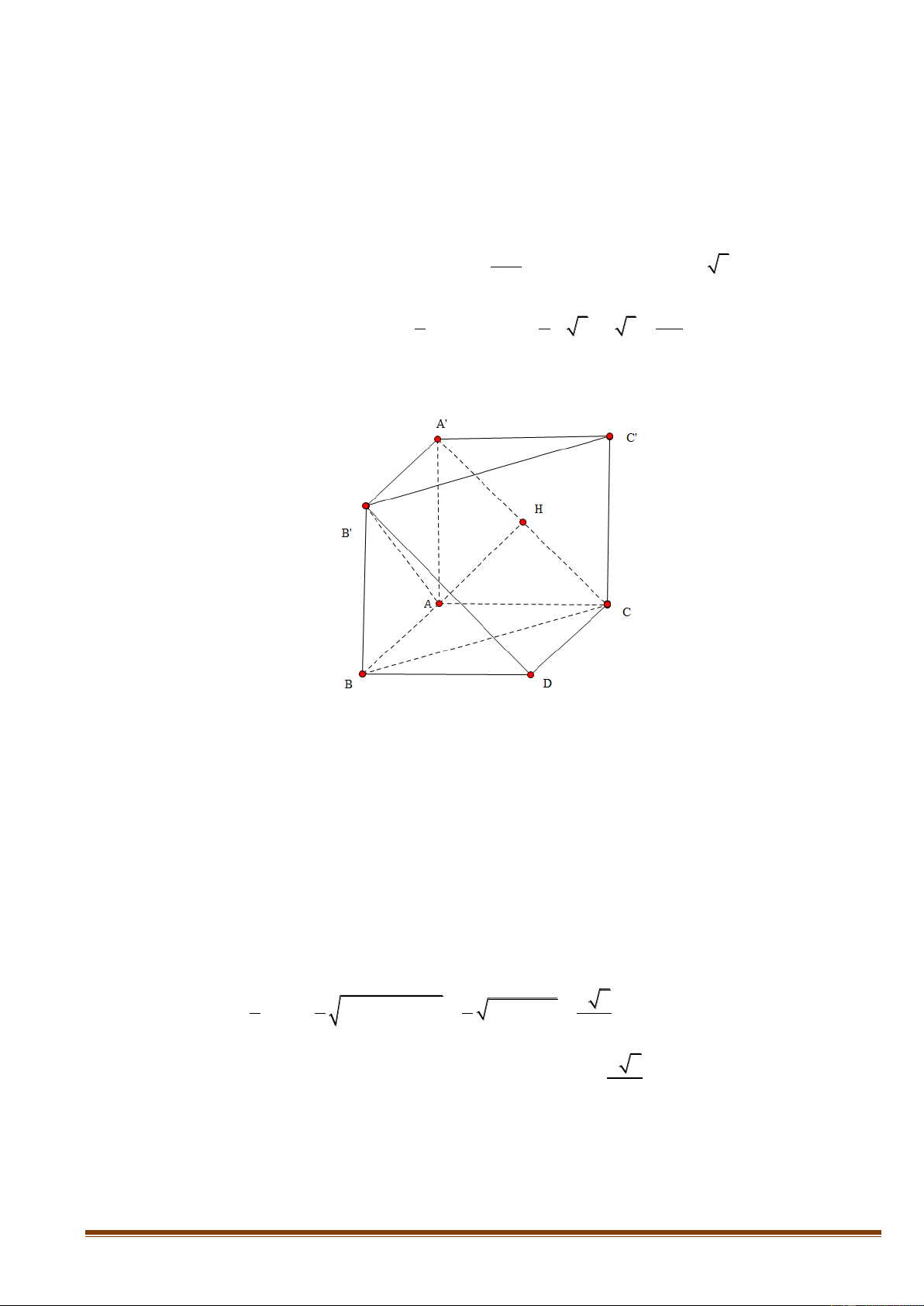
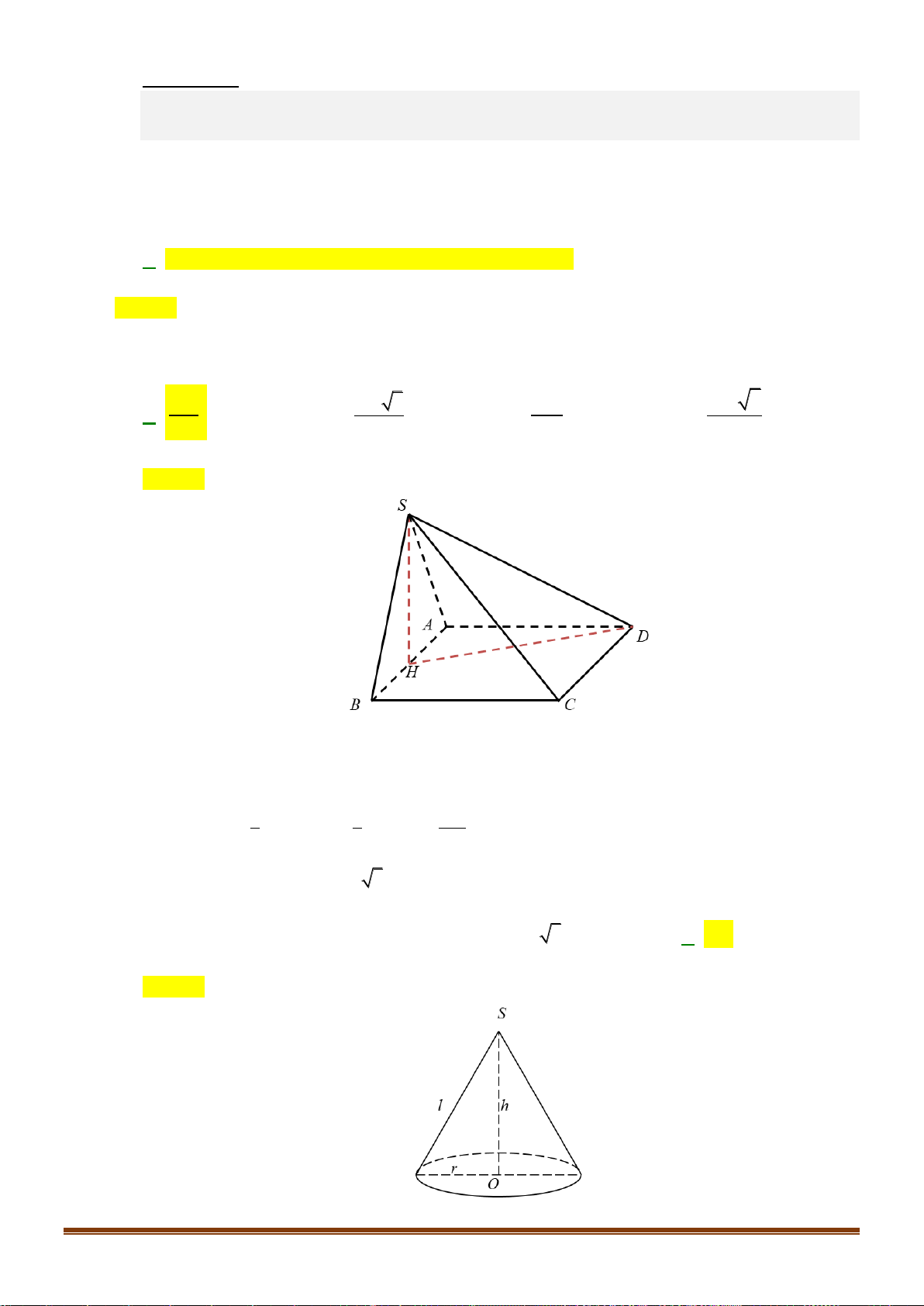
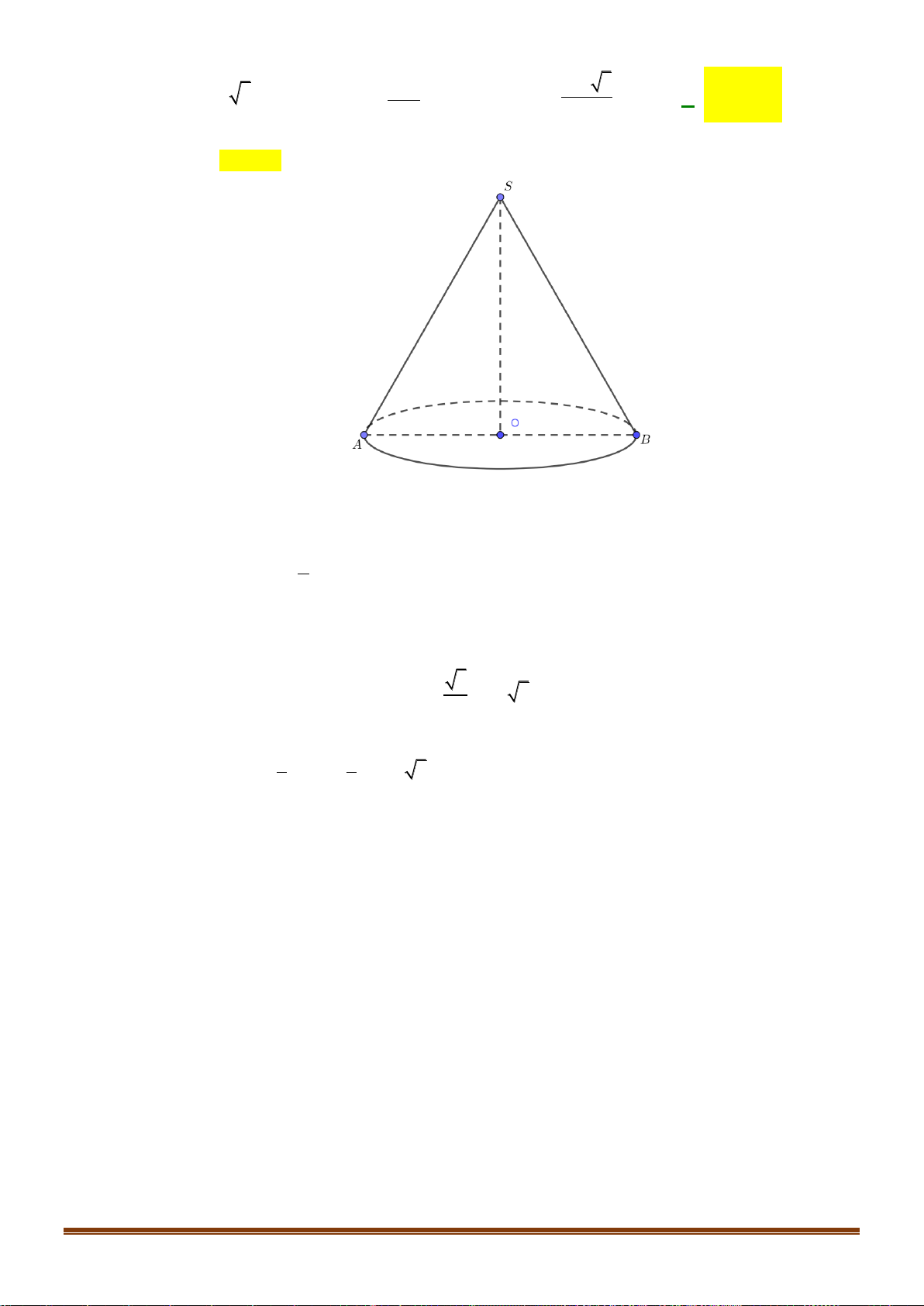
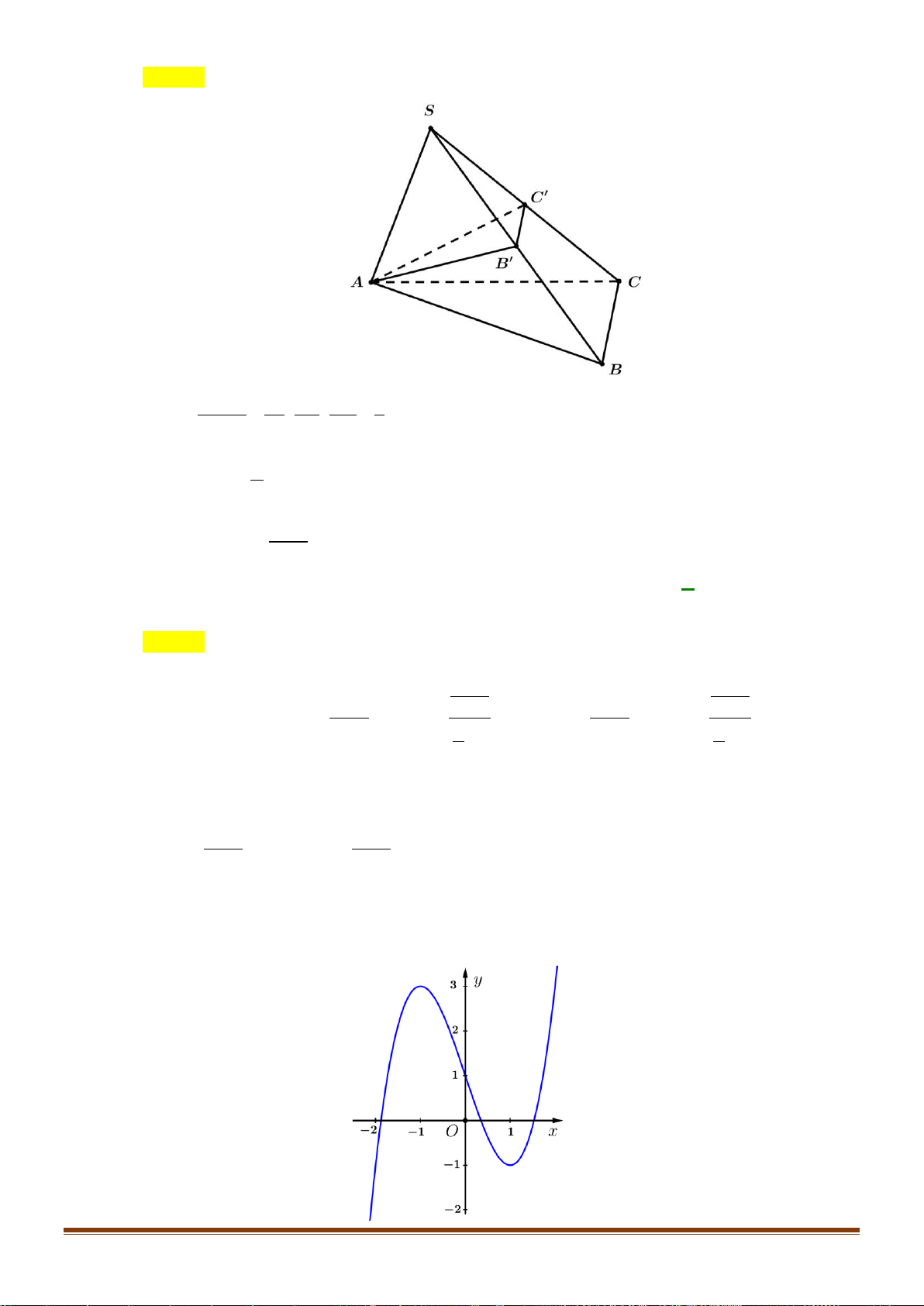
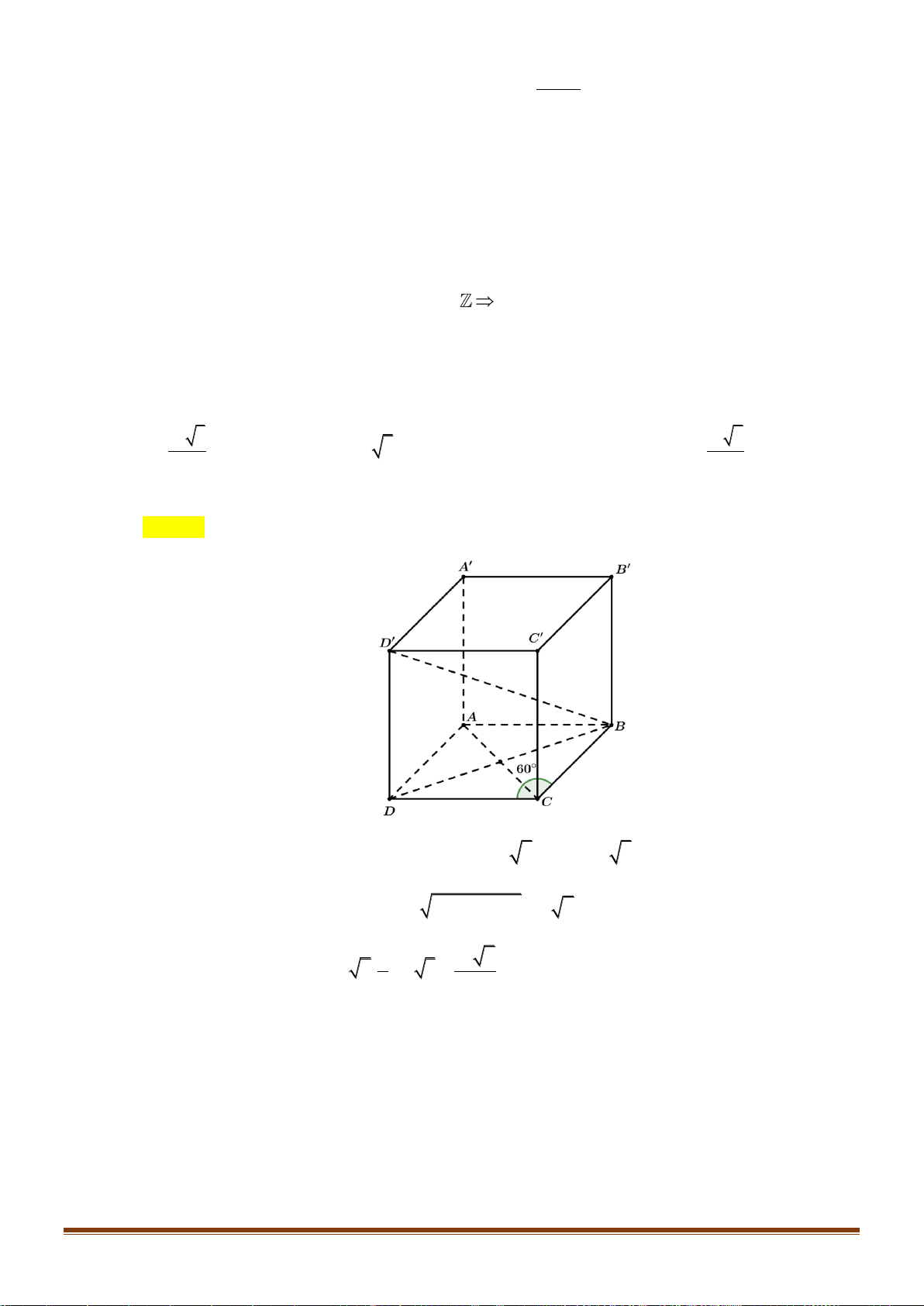
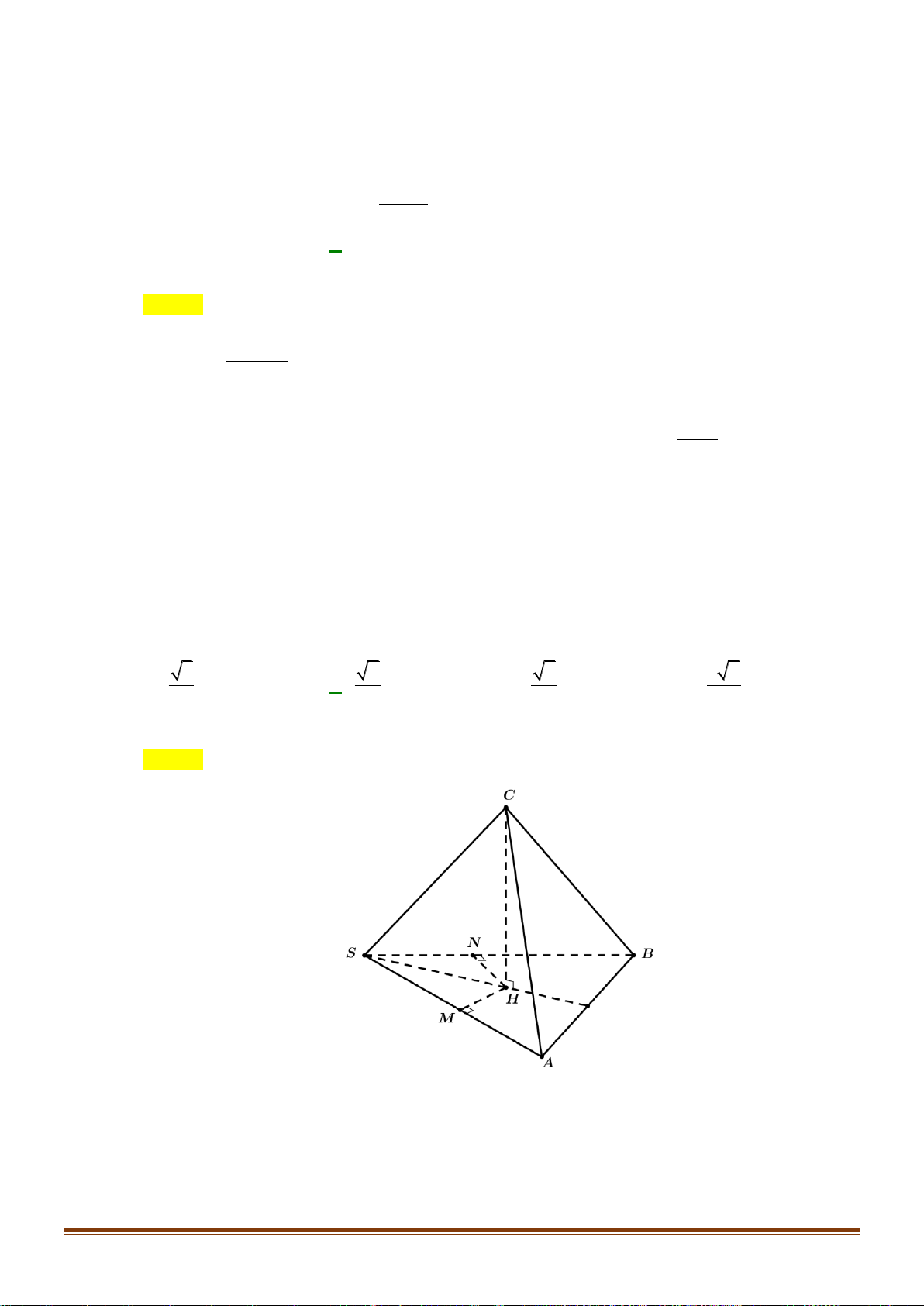
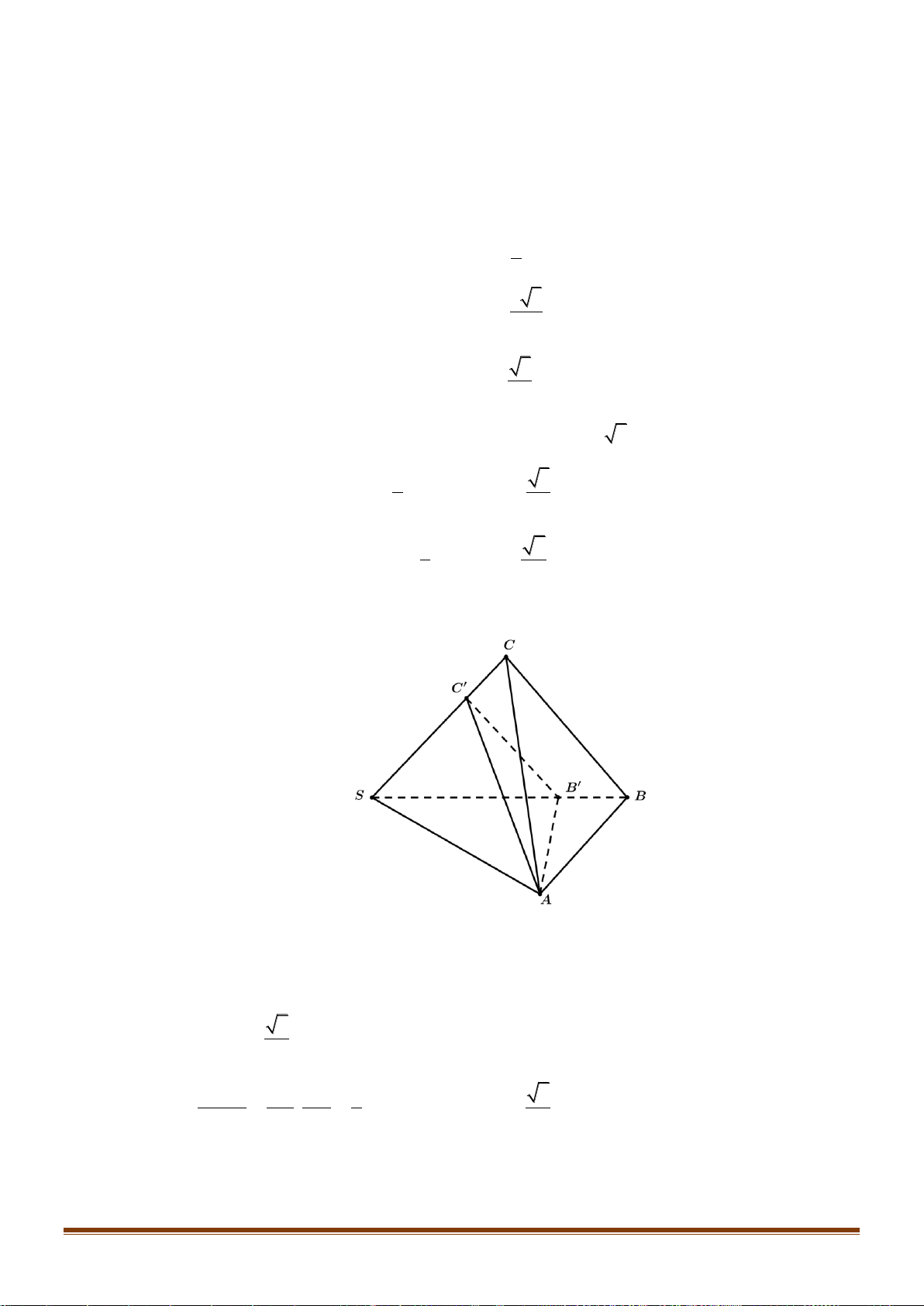
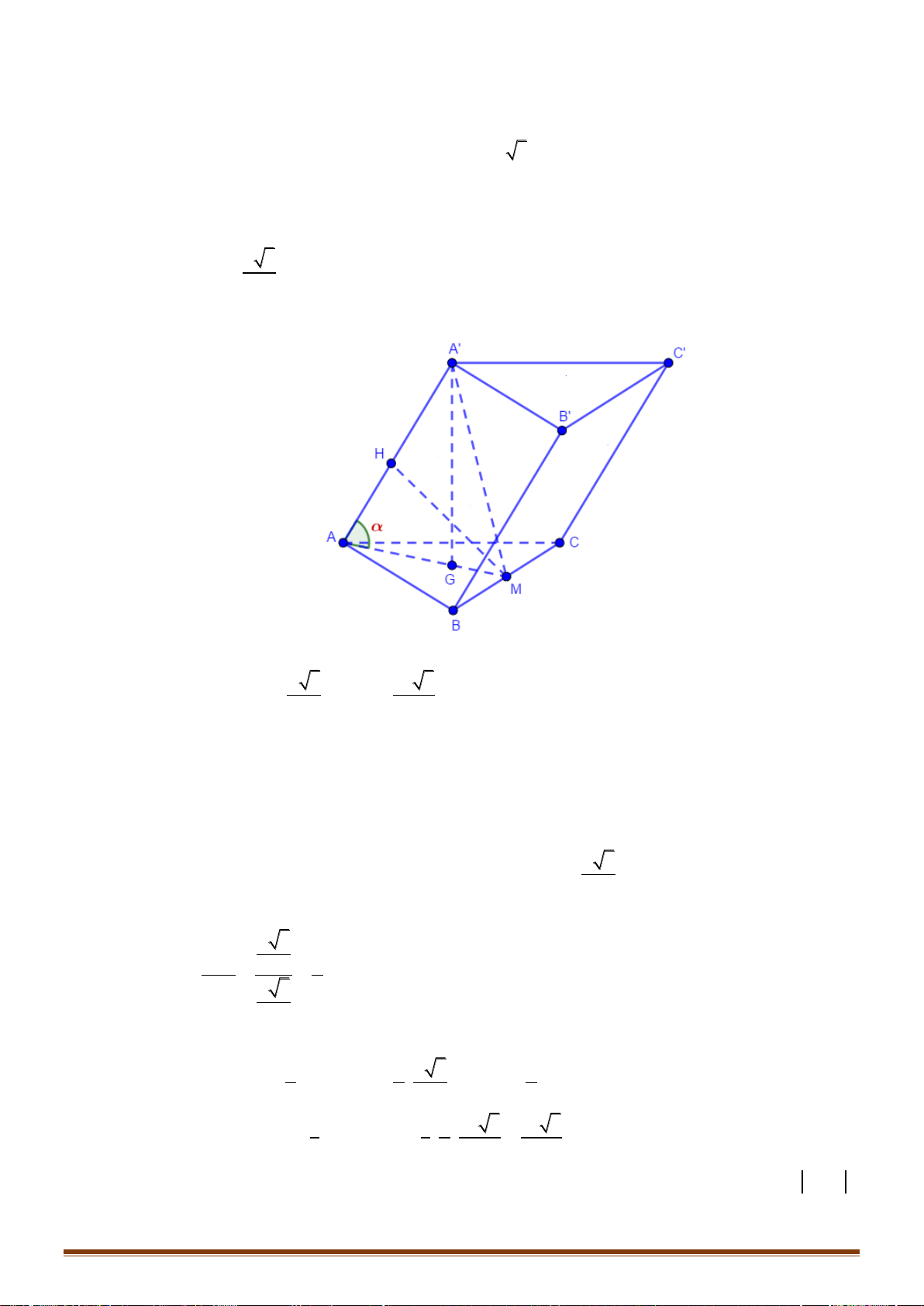
Câu 37: Cho hình chóp SABCD có đáy là nửa lục giác đều ABCD nội tiếp trong đường tròn đường kính
AB = 4a . Gọi H là trung điểm của AB và SH ⊥ ( ABCD). Khoảng cách từ B đến (SAC) 3a 10 bằng
. Tính thể tích khối chóp SABCD . 5 Câu 38: Cho hàm số 3
y = x − (m + ) 2 2 3 4 x + 6(m + )
3 x − 3m − 5 có đồ thị (C
. Tìm giá trị m  0 để hàm m )
số có hai cực trị đồng thời khoảng cách từ điểm cực đại của (C đến đường thẳng m )
d : (m + 2) x −3y −5m − 7 = 0 là lớn nhất. m x x
Câu 39: Tìm tất cả các giá trị của tham số m để phương trình sin cos 3 3
m có 20 nghiệm phân biệt 5 5 trên ; . 2 2 -----HẾT----- Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM a a Câu 1: Rút gọn biểu thức  M =
(a  0) về dạng a thì  thuộc khoảng nào dưới đây? a
A.  (2;5) . B.  ( 1 − ;0) . C.  ( 3 − ;− ) 1 . D.  (0;2) . Lời giải Chọn B 1 3 3 1 2 2 4 . a a a a −4 M = = = = a . a a a Câu 2:
Cho hàm số y = f (x) 3
= −x + 2x −1 (C) và đường thẳng d : y = −x −1. Biết d cắt (C) tại 3
điểm phân biệt có hoành độ lần lượt là x ; x và x . Tính giá trị 2 3 2
x + x + x . 1 2 3 1 2 3 A. 3 . B. 6 . C. 0 . D. 9 . Lời giải Chọn B x = 0
Phương trình hoành độ giao điểm: 3 3
−x + 2x −1 = −x −1  x − 3x = 0   . x =  3
x + x + x = 0 + ( 3)2 + (− 3)2 2 2 2 2 = 6. 1 2 3 Câu 3:
Hàm số y = f ( x) 3
= −x + 9x −11nghịch biến trên khoảng nào sau đây?
A. (−;− 3)
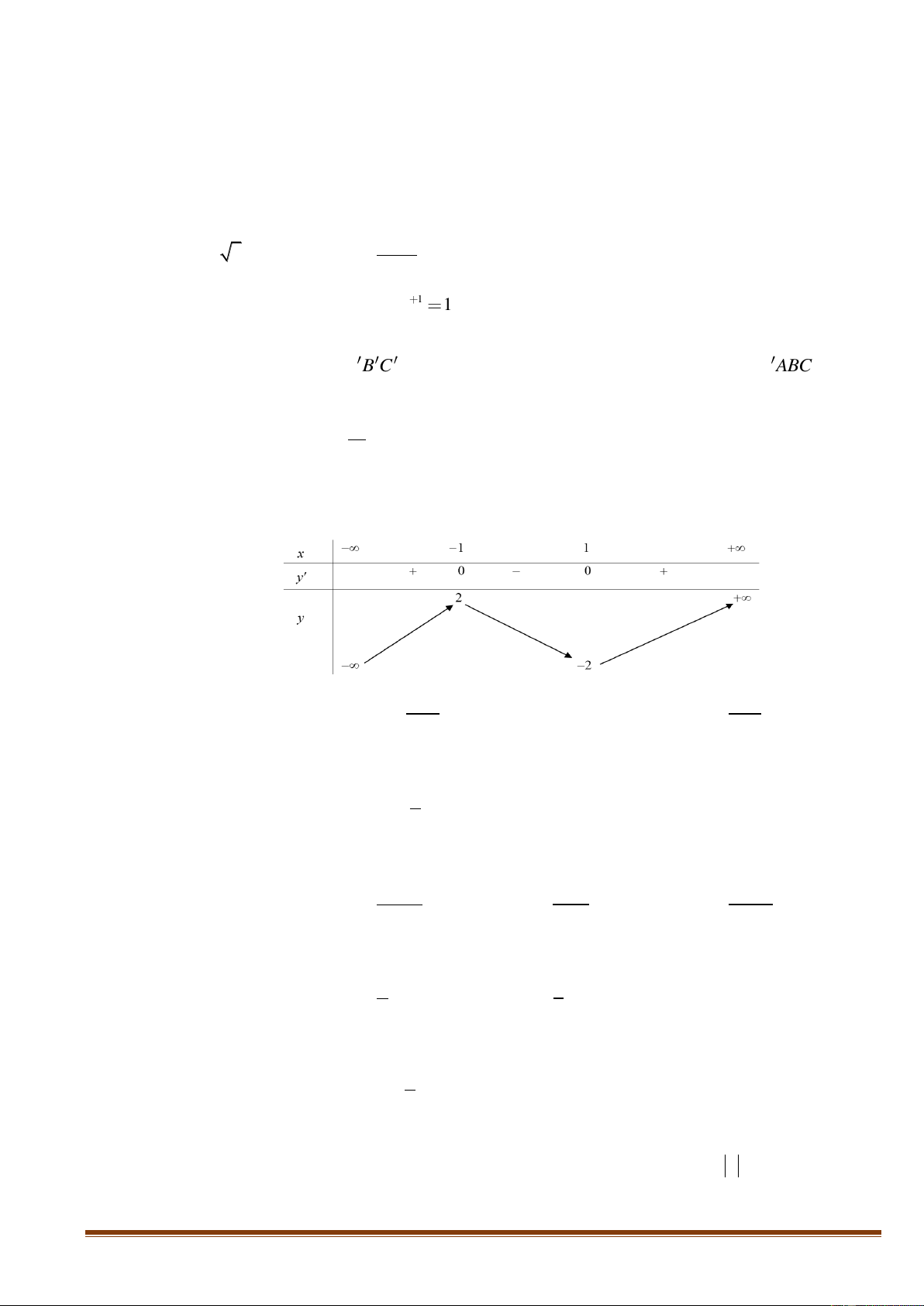
B. (− 3;+) C. (− 3; 3) D. ( 3 − ; ) 3 Lời giải Chọn A Ta có 2 y = 3 − x + 9 x = − 3 2 y = 0  3 − x + 9 = 0   x = 3 x – ∞ -ξ3 ξ3 + ∞ y' – 0 + 0 – + ∞ y – ∞
Hàm số nghịch biến trên (−;− 3);( 3;+) Câu 4:
Cho hình trụ có hai đáy là hai hình tròn (O) và (O) , chiều cao R 3 và bán kính đáy R . Một
hình nón có đỉnh là O và đáy là hình tròn ( ;
O R). Tính tỉ số diện tích xung quanh của hình trụ và hình nón. A. 3 . B. 2 . C. 2 . D. 3 . Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải Chọn A
Diện tích xung quanh hình trụ là: 2 S = 2 . R R 3 = 2 R 3 1
Xét tam giác vuông AOO tại O , ta có l = AO =
OO + AO = (R )2 2 2 2 3 + R = 2R
Diện tích xung quanh hình nón đỉnh O , đáy là đường tròn ( ; O R)là 2 S =  . R l =  .
R 2R = 2 R . 2 2 S 2 R 3 Khi đó, 1 = = 3 2 S 2 R 2 Câu 5:
Cho a  0, a  1,b  0, c  0 . Trong 4 khẳng định sau, có bao nhiêu khẳng định đúng?
I. log (bc) = log blog c a a a b II. log
= log c − log b a a a c  1 III. log b = log b (   0 a a )  1 IV. log b = log b a 2 a A. 3. B. 4. C. 1. D. 2. Lời giải Chọn C
Chỉ có khẳng định IV là đúng. 2021 Câu 6:
Cho hàm số y = f (x) xác định trên và có f ( x) = ( 2 x − ) 2 1
x ( x + 3) . Hỏi y = f (x) có bao
nhiêu điểm cực trị? A. 3. B. 4. C. 1. D. 2. Lời giải Chọn A
Đạo hàm f '(x) đổi dấu khi đi qua các nghiệm x = 3 − , x = 1
− , x =1 nên hàm số đã cho có 3 1 2 3 cực trị. Câu 7:
Cho log b =  thì N = ( 2 3 log a b
thuộc khoảng nào sau đây? ab ) a A. N ( 1 − ; ) 1 .
B. N (2;4) .
C. N (1;2) . D. N (4;7) . Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải 2 3 log a b + +  a 2 3log b 2 3 Ta có N = log ( 2 3 a b ) ( ) a = = =   ab ab + b + a ( ) 2, 76 (2;4). log 1 log 1 a Câu 8:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Diện tích xung quanh của hình trụ tròn xoay bằng tích độ dài đường tròn đáy và độ dài đường sinh.
B. Thể tích của khối nón tròn xoay bằng tích của diện tích đáy và độ dài đường cao của khối nón.
C. Thể tích của khối trụ tròn xoay là giới hạn của thể tích khối lăng trụ đều nội tiếp khối trụ đó
khi số cạnh tăng lên vô hạn.
D. Diện tích toàn phần của hình nón là tổng của diện tích xung quanh và diện tích đáy của hình nón đó. Lời giải 1
Ta có công thức tính thể tích của khối nón tròn xoay V = S.h ⎯⎯ → Đáp án B sai. 3 Câu 9:
Đồ thị nào sau đây là dạng đồ thị của hàm số y = log x với 0  a 1? a A. . B. . C. . D. . Lời giải Chọn B
Hàm số y = log x với 0  a 1 nghịch biến trên khoảng (0;+) và có đồ thị nằm bên phải a
trục tung. Do đó chọn phương án B . 1
Câu 10: Cho hàm số y = f ( x) 3 2
= x − x +1 . Tìm giá trị nhỏ nhất của hàm số y = f (x) trên 1;  3 . 3 1 1 A. 1 − . B. 1. C. . D. − . 3 3 Lời giải Chọn D
Hàm số đã cho xác định và liên tục trên 1;  3 . Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x = 01;  3
Ta có: f ( x) 2 = x − 2 ; x
f ( x) = 0   . x = 2  1; 3 f ( ) 1 = f ( ) 1 1 ; 2 = − ; f (3) = 1. 3 3 Vậy
f ( x) = f ( ) 1 min 2 = − . 1  ;3 3
Câu 11: Cho hàm số y = f ( x) 1
= x + − 2. Gọi y , y lần lượt là tung độ của điểm cực đại và điểm cực 1 2 x
tiểu của đồ thị hàm số đã cho. Tính giá trị y − y . 1 2 A. 4. B. 12. − C. 4. − D. 12. Lời giải Chọn C
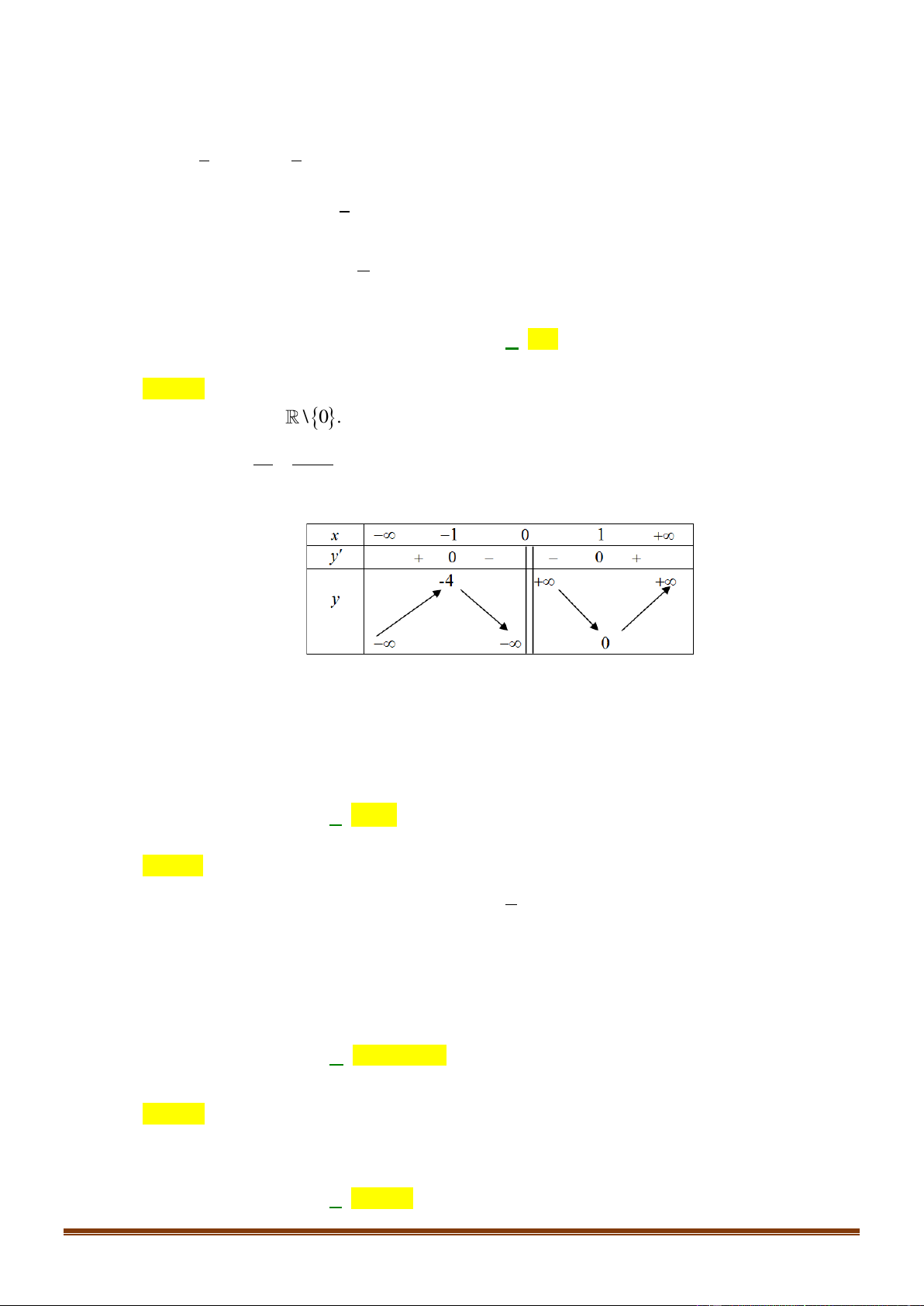
Tập xác định: D = \  0 . 2 1 x −1 Ta có: 2 y = 1− =
; y = 0  x −1 = 0  x = 1. 2 2 x x Bảng biến thiên:
Hàm số đạt cực đại tại x = −1, y
= −4 và đạt cực tiểu tại x =1, y = 0. Khi đó ta được CD CT
y = −4, y = 0. 1 2
Vậy y − y = 4. − 1 2
Câu 12: Phương trình log 2x +1 = 2 có nghiệm là 3 ( )
A. x = 3.
B. x = 4.
C. x = 13. D. x = 1. Lời giải Chọn B  1 2x +1  0 x  − Ta có: log 2x +1 = 2     2  x = 4. 3 ( ) 2x +1 = 9 x = 4
Vậy nghiệm của phương trình là x = 4.
Câu 13: Hình đa diện nào dưới đây không có tâm đối xứng?
A. Hình lăng trụ lục giác đều.
B. Hình lập phương. C. Bát diện đều. D. Tứ diện đều. Lời giải Chọn D
Ta có hình tứ diện đều không có tâm đối xứng.
Câu 14: Tính thể tích V của khối trụ có bán kính đáy và chiều cao đều bằng 2 .
A. V = 16 .
B. V = 8 .
C. V = 4 . D. V = 12 . Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải Chọn B
Ta có thể tích khối trụ 2 2
V =  R h = .2 .2 = 8 −
Câu 15: Tìm đạo hàm của hàm số y = ( − x) 3 1 2 − − − −
A. y = ( − x) 2 6 1 2 .
B. y = − ( − x) 2 3 1 2 .
C. y = − ( − x) 4 6 1 2 .
D. y = ( − x) 4 6 1 2 . Lời giải Chọn D 4 − 4 − 4 −  Ta có: y = 3
− (1− 2x) (1− 2x) = 3 − (1− 2x) .( 2 − ) = 6(1− 2x) 
Câu 16: Cho hàm số lũy thừa y = x , (  ) . Trong các khẳng định sau, khẳng định nào sai? A. Nếu *
  thì hàm số có tập xác định là . B. Nếu  −   
0 thì hàm số có tập xác định là \   0 . C. Nếu  
thì hàm số có tập xác định là .
D. Nếu   thì hàm số có tập xác định là (0; + ) . Lời giải Chọn C
Vì nếu  = 0 thì hàm số có tập xác định là \  0 .
Câu 17: Tìm tập xác định của hàm số y = log (1− x)2 . 2 A. D = (− ) ;1 . B. D = \   1 . C. D = .
D. D = (−  ;1 . Lời giải Chọn B ĐKXĐ: ( − x)2 1  0  x 1.
Tìm tập xác định của hàm số là D = \  1 .
Câu 18: Tìm đạo hàm của hàm số y = log (1− x)2 . 3 2 1 2 − 2 − A. y =   ( . B. y = . C. y = . D. y = . 1− x)ln 3 (1− x)2 ln3 (1− x)2 ln3 (1− x)ln3 Lời giải Chọn D
2(1− x)(1− x) 2 − y = = ( . 1− x)2 ln 3 (1− x)ln3
Câu 19: Gọi l, h, r lần lượt là độ dài dường sinh, chiều cao và bán kính mặt đáy của một hình nón. Tính
diện tích xung quanh S của hình nón đó. xq 1 A. S =  rh . B. S = 2 rl . C. S =  rl . D. 2 S =  r h . xq xq xq xq 3 Lời giải Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Chọn C
Câu 20: Cho tứ diện OABC có O , A O ,
B OC đôi một vuông góc và OA = , a OB = ,
b OC = c . Tính thể tích
khối tứ diện OABC abc abc abc A. . B. . C. . D. abc . 3 6 2 Lời giải Chọn B 1 1 1 1 Ta có: V = O . A S = .O . A O . B OC = . a . b c 3 OBC 3 2 6 1
Câu 21: Phương trình log ( x + 2) + log ( x − 2)2 = 1 3 3 2 có bao nhiêu nghiệm? A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn D x + 2  0  x  −2 Điều kiện   (  .  x − 2  )2  0 x  2 1 2 Ta có log x + 2 + log x − 2
=1  log x + 2 + log x − 2 =1. 3 ( ) 3 ( ) 3 ( ) 3 2
 log  x − 2 . x + 2  =1 x − 2 . x + 2 = 3 3  ( ) ( ) x  2  x  2   x = 7     x = 7 2 x − 4 = 3  x = − 7     x = 1   . x  2 x  2    x = 1 −    2
−x + 4 = 3 x =1  x = 1 −
Vậy phương trình đã cho có 3 nghiệm. 1
Câu 22: Phương trình = 8 1 2x+ có nghiệm là? A. x =1 . B. x = 2 . C. x = 3 − . D. x = 4 − . Lời giải Chọn D 1 + Ta có x 4 = 8  2
=1  x + 4 = 0  x = 4 − . x 1 2 + x =  
Câu 23: Tìm đạo hàm của hàm số y
a với a 0,a 1. x a 1 1 A. ' x
y = a ln a . B. y ' = . C. y ' = . D. y ' = . ln a x ln a x a ln a Lời giải Chọn A Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Ta có: ' = ( x )' x y a
= a ln a
Câu 24: Cho hàm số y = f ( x) xác định trên  2 − ;  2 có đồ thị trên  2 − ;  2 như hình vẽ:
Biết hàm số y = f ( x) đạt giá trị lớn nhất tại a và đạt giá trị nhỏ nhất tại b .
Tính giá trị 4a + 3b . 4 A. 12 − . B. 4 . C. 11 − . D. − . 3 Lời giải Chọn A
Dựa vào đồ thị, ta thấy: hàm số y = f ( x) đạt giá trị lớn nhất trên  2 − ;  2 tại x = 2 − và đạt giá 4
trị nhỏ nhất tại x = − . 3 4  4  Do đó a = 2
− ;b = −  4a + 3b = 4.( 2 − ) + 3. − =   ( 8 − ) + (−4) = −12 3  3  2 x −x 1 −
Câu 25: Xét phương trình ( 2022 − 2021) = ( 2022 + 2021)
. Tổng bình phương các nghiệm
của phương trình đã cho bằng bao nhiêu? A. 1. B. 2. C. 3. D. 4. Lời giải Chọn C
Vì ( 2022 − 2021).( 2022 + 2021) =1 nên + = = ( − ) 1 1 − 2022 2021 2022 2021 . Do đó phương trình 2022 − 2021 ( − ) 2x =( + )−x− ( − ) 2 1 x = ( − )x 1+ 2022 2021 2022 2021 2022 2021 2022 2021  1+ 5 x = 2 2 2
x = x +1  x − x −1 = 0  
. Tổng bình phương các nghiệm của phương trình  1− 5 x =  2 2 2  +   −  đã cho bằ 1 5 1 5 ng   +   = 3.     2 2    
Câu 26: Có bao nhiêu khối đa diện đều? A. 5. B. 8. C. 3. D. 4. Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải Chọn A
Theo định lý về sự tồn tại của các khối đa diện đều thì chỉ có năm loại khối đa diện đều.
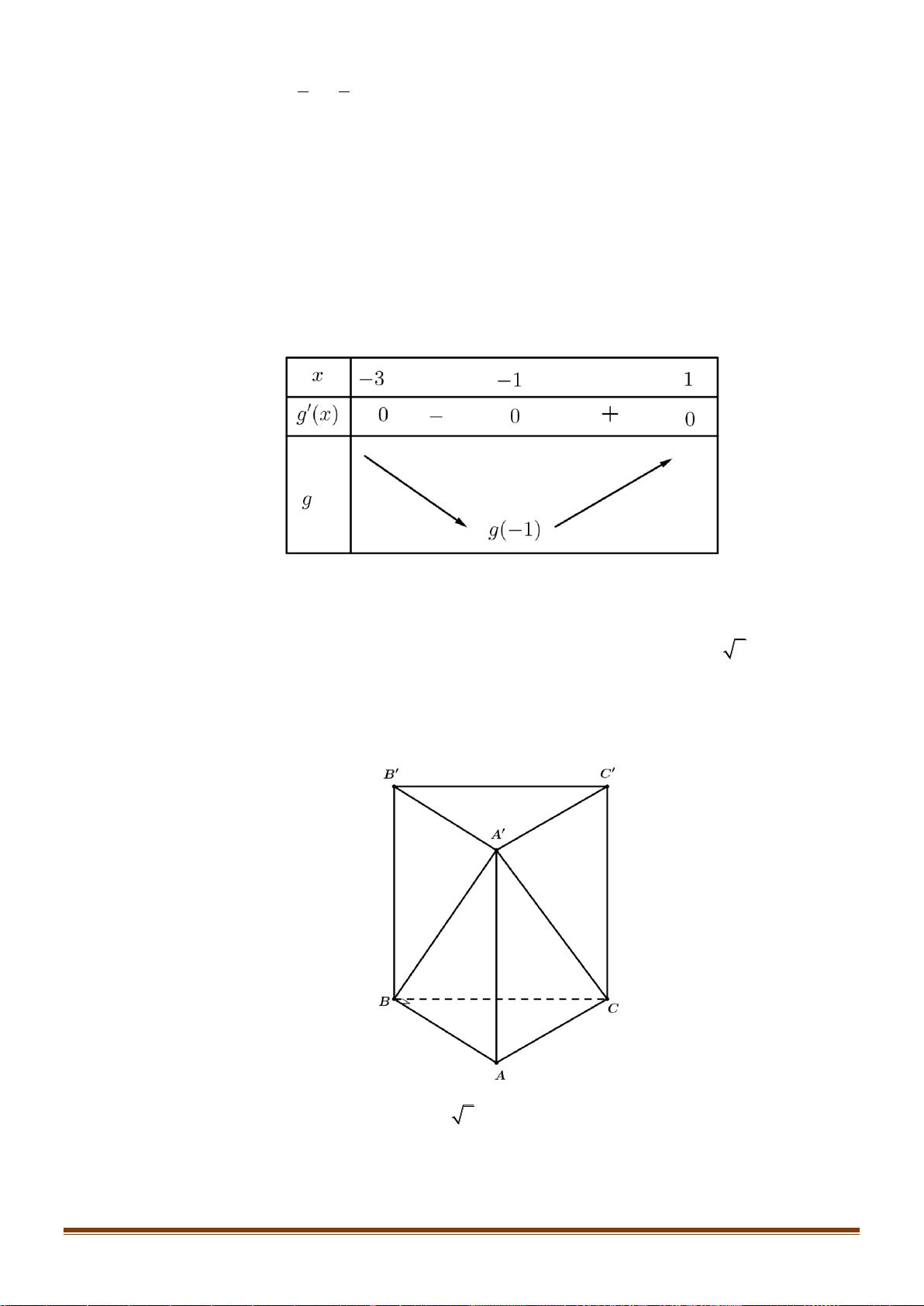
Câu 27: Cho khối lăng trụ đứng AB .
C A' B 'C ' có BB ' = a, đáy ABC là tam giác vuông cân tại B và BA = BC = .
a Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a 3 a A. 3 V = a . B. V = . C. V = . D. V = . 3 6 2 Lời giải Chọn D A' C' B' C A B Vì AB .
C A' B 'C ' là lăng trụ đứng nên BB ' là đường cao của lăng trụ, khi đó V = S
.BB ', mà đáy ABC là tam giác vuông cân tại B và BA = BC = a nên
ABC. A' B 'C ' ABC 2 1 1 a 2 3 a a S = .B . A BC = . . a a = . Do đó, V = .a = . Vậy chọn đáp án D. ABC  2 2 2
ABC. A' B 'C ' 2 2
Câu 28: Tập nghiệm của phương trình log x  1 − là 1 3 A. S 3; B. S 0;3 C. S . D. S ;3 Lời giải Chọn A
Điều kiện x 1 log x  1 −  log  −  −  −   − x 1 log x 1 x
3 (thỏa mãn). Vậy x 1 1 1 3 3 3
Câu 29: Cho hàm số y = f ( x) xác định trên \ 
1 có bảng biến thiên như hình vẽ. Tìm khẳng định đúng:
A. Hàm số nghịch biến trên (3;+) .
B. Hàm số nghịch biến trên (− ;  2)(3;+).
C. Hàm số đồng biến trên ( ) ;1 − .
D. Hàm số đồng biến trên ( 2 − ;3). Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải Chọn A
Hàm số nghịch biến trên các khoảng (3;+) . x −
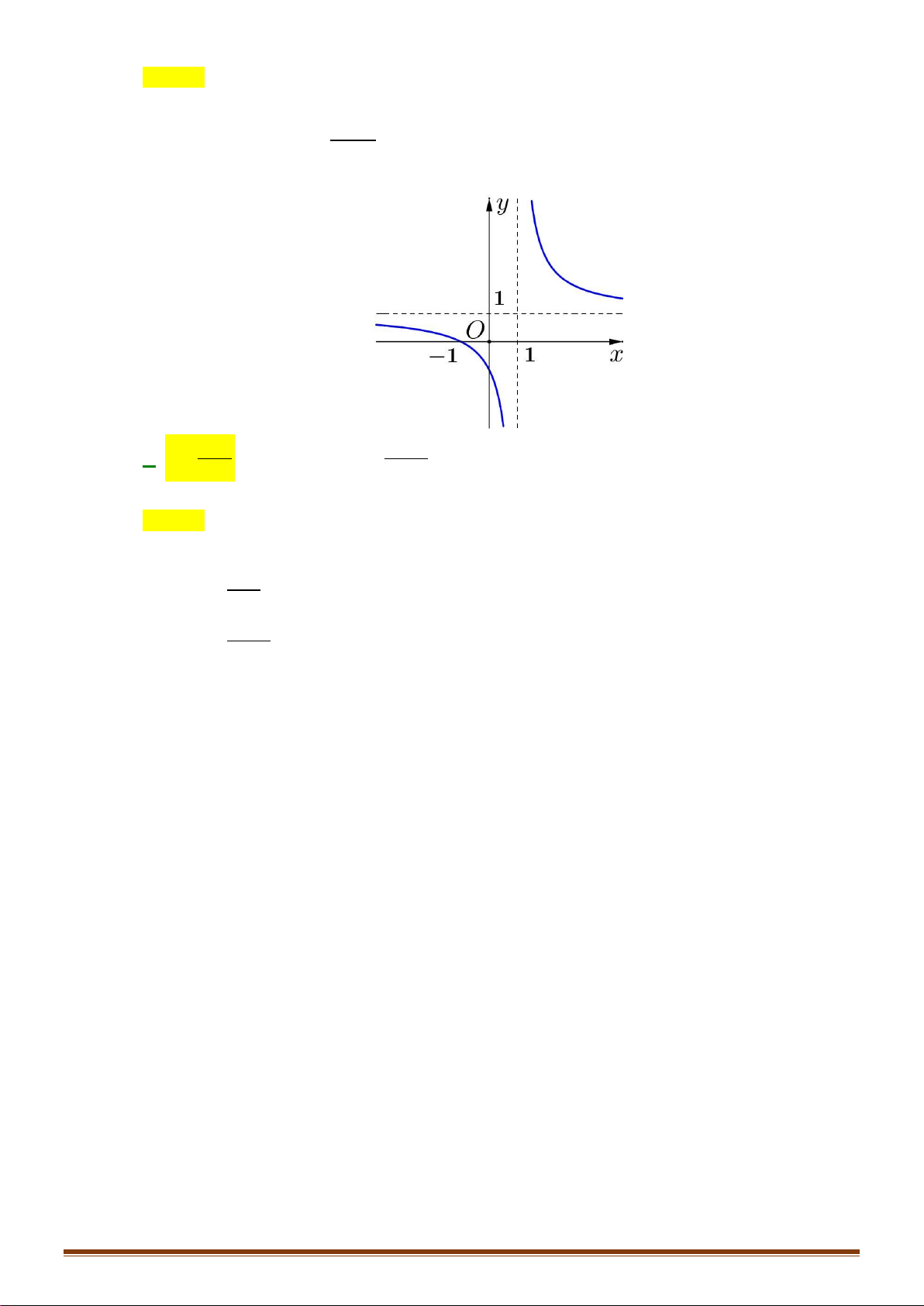
Câu 30: Hàm số y = f ( x) 2
= x− có đồ thị là hình vẽ nào dưới đây? 1 A. Hình 4. B. Hình 1. C. Hình 2. D. Hình 3. Lời giải Chọn C − Xét đồ x
thị hàm số y = f ( x) 2 = x− : 1 1 Ta có: y =    (
nên hàm đã cho luôn đồng biến. Nên ta loại B, D. x − ) 0, x 1 2 1 x −
Và đồ thị y = f ( x) 2 = 0; 2 nên Chọn C x − đi qua điểm ( ) 1
Câu 31: Cho hàm số y = f ( x) xác định trên \  
2 . Biết lim f ( x) = 0 , lim f ( x) = 1, lim f ( x) = 3 − x→+ x→− + x→2
và lim f ( x) = − . Trong các khẳng định sau đây khẳng định nào đúng? − x→2
A. Đồ thị hàm số có hai đường tiệm cận đứng x = 0, x = 1.
B. Đồ thị hàm số không có tiệm cận đứng.
C. Đồ thị hàm số có một đường tiệm cận đứng x = 2.
D. Đồ thị hàm số có hai đường tiệm cận ngang x = 0, x = 1. Lời giải Chọn C
lim f ( x) = 0 : Tiệm cận ngang y = 0. x→+
lim f ( x) = 1: Tiệm cận ngang y = 1. x→−
lim f ( x) = − : Tiệm cận đứng x = 2. − x→2
Câu 32: Cho một khối nón có chiều cao bằng 4cm , độ dài đường sinh bằng 5cm . Tính thể tích của khối nón này. A. 3 45 cm . B. 3 15 cm . C. 3 12 cm . D. 3 36 cm . Lời giải Chọn C
Gọi h,l, r lần lượt là chiều cao, đường sinh và bán kính của khối nón. Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 2 2
r = l − h = 3cm . Thể tích khối nón 1 1 2 3
V =  r h =  .9.4 = 12 cm . 3 3
Câu 33: Trong mặt phẳng ( P), cho đường thẳng l cắt và không vuông góc với đường thẳng .  Khi quay
mặt phẳng ( P) xung quanh đường thẳng  thì đường thẳng l sinh ra
A. Mặt nón tròn xoay.
B. Khối nón tròn xoay.
C. Mặt trụ tròn xoay.
D. Hình nón tròn xoay. Lời giải
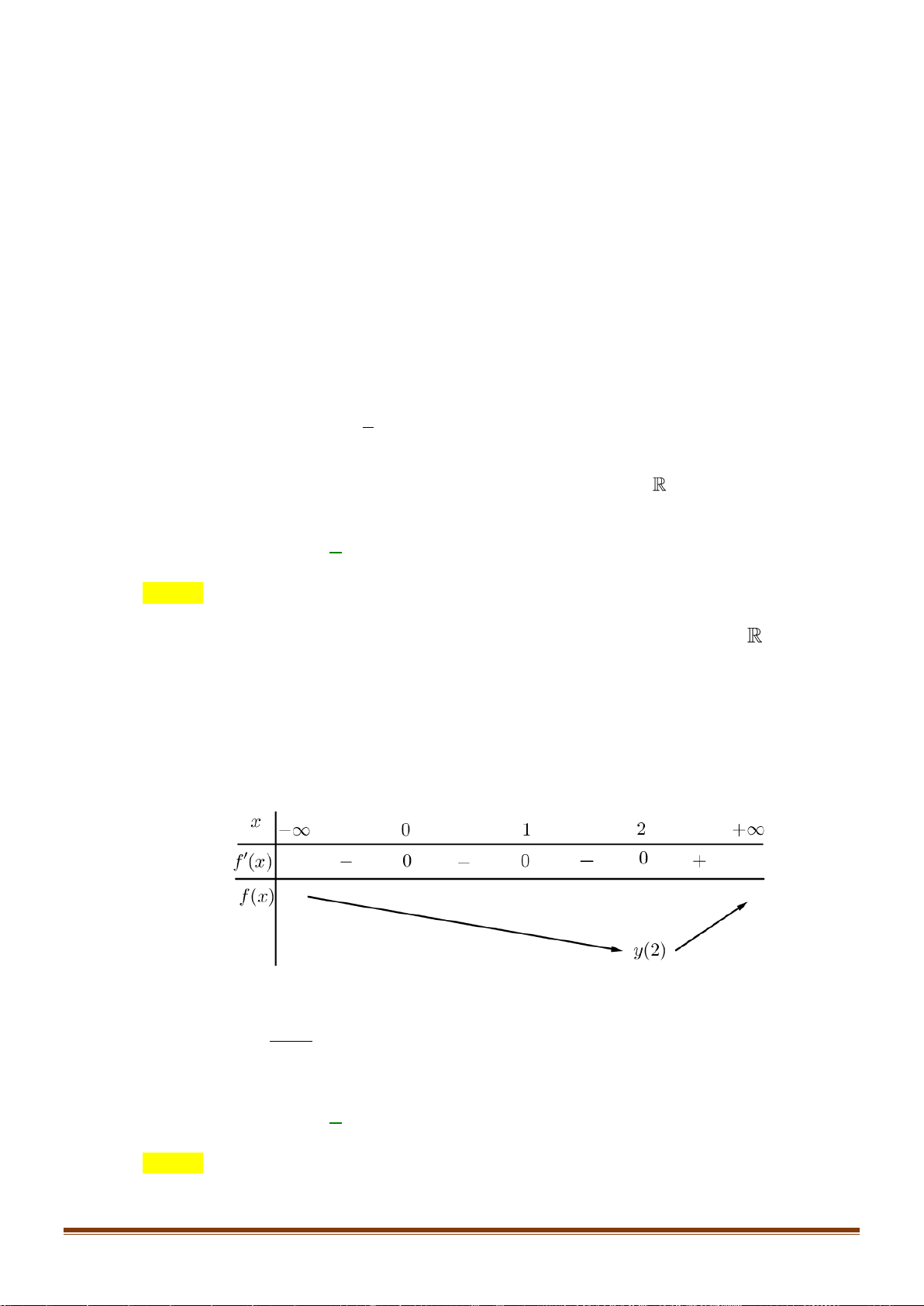
Câu 34: Cho hàm số y = f (x) xác định trên
và có bảng biến thiên như sau:
Tìm số nghiệm của phương trình 2 f (x) − 7 = 0 ? A. 4. B. 3. C. 2. D. 1. Lời giải x − 2
Câu 35: Đồ thị hàm số y = f (x) = 2 x
có bao nhiêu tiệm cận đứng − 9 A. 4. B. 1. C. 2. D. 3. Lời giải II. PHẦN TỰ LUẬN
Câu 36: Cho a và b là hai số thực thỏa mãn 2  a b và ( 2 2 log
a b ) + log b = 7 . Tính giá trị của biểu b a a b logab thức 2 a 7b P a + = . Lời giải Page 15
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 a b + a ( 2 2 log ) b Ta có: ( 2 2 log
a b ) + log b = 7  + 2log b = 2 2 log 7 a  + 2log b = 7 b a a log a b log b a a log b = 2 a 2 b = a  (  b)2 2 log −5log b + 2 = 0    . a a 1 log b = b = a a  2
Kiểm tra điều kiện suy ra 2 b = a . a b 2 Khi đó: a log = 1 1 log = 1 log = log . ab 2 a + 3 7b a 2 8a 3 a 8 a 2 a b 1 log Do đó, ab log 2 a a 7b P a + = 2 = 1 a = . 2
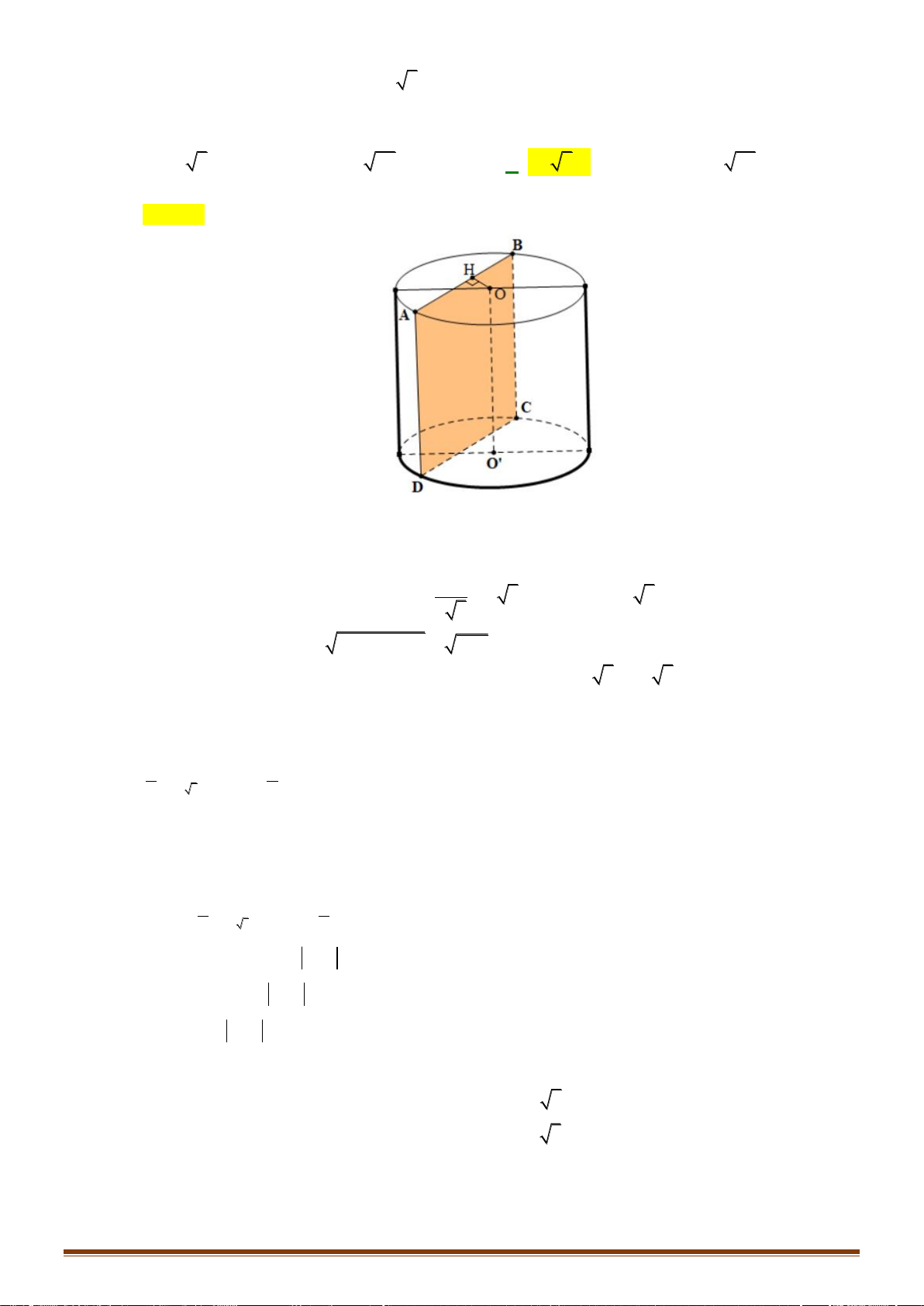
Câu 37: Cho hình chóp S.ABCD có đáy là nửa lục giác đều ABCD và nội tiếp đường tròn đường kính
AB = 4a . Gọi H là trung điểm của AB và SH ⊥ ( ABCD) . Khoảng cách từ B đến mặt phẳng ( 3a 10 SAC ) bằng
. Tính thể tích khối chóp S.ABCD 5 Lời giải a
Ta có d ( B (SAC )) = d ( H (SAC ))  d (H (SAC )) 3 10 , 2 , , = . 10
Gọi O là giao điểm của AC và DH . Ta có tứ giác AHCD là hình thoi, do đó OH ⊥ AC . a
Kẻ HI ⊥ SO d (H (SAC )) 3 10 , = IH = . 10 Ta có A
HD là tam giác đều cạnh bằng 2a OH = a . 1 1 1 Khi đó 2 2 = +
SH = 9a SH = 3a . 2 2 2 IH OH SH (2a)2 3 Ta có 2 S = 3S = 3. = 3a 3 . ABCD ADH 4 Page 16
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Vậy thể tích khối chóp 1 S.ABCD là 2 3 V = 3a 3.3a = 3a 3 . 3 Câu 38: Cho hàm số 3
y = x − (m + ) 2 2 3 4 x + 6(m + )
3 x − 3m − 5 có đồ thị (C
. Tìm giá trị m  0 để hàm m )
số có hai cực trị đồng thời khoảng cách từ điểm cực đại của (C đến đường thẳng m )
d : (m + 2) x −3y −5m − 7 = 0 là lớn nhất. m Lời giải
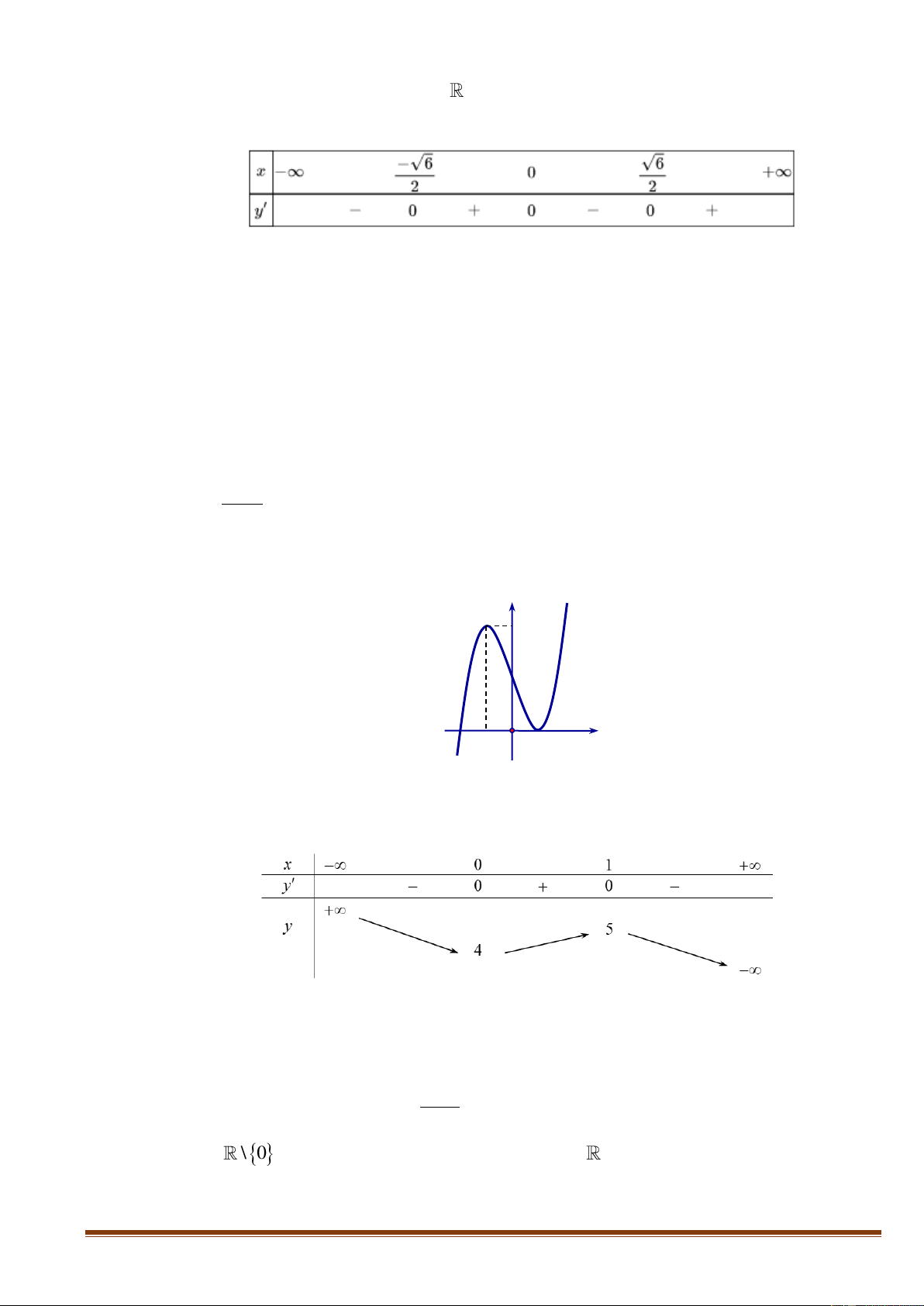
Tập xác định D = . Ta có: 2
y = 6x − 6(m + 4) x + 6(m + ) 3 . Cho 2
y = 0  6x − 6(m + 4) x + 6(m + ) 3 = 0 .
Hàm số có hai cực trị   = −  (m + ) 2  −  (m+ ) 2 4 4
3 = m + 4m + 4  0  m  2. −
Khi đó phương trình y = 0 có hai nghiệm phân biệt là x =1 và x = m+3.
Do hệ số a = 2  0 và m  0 nên hàm số đạt cực đại tại x =1.
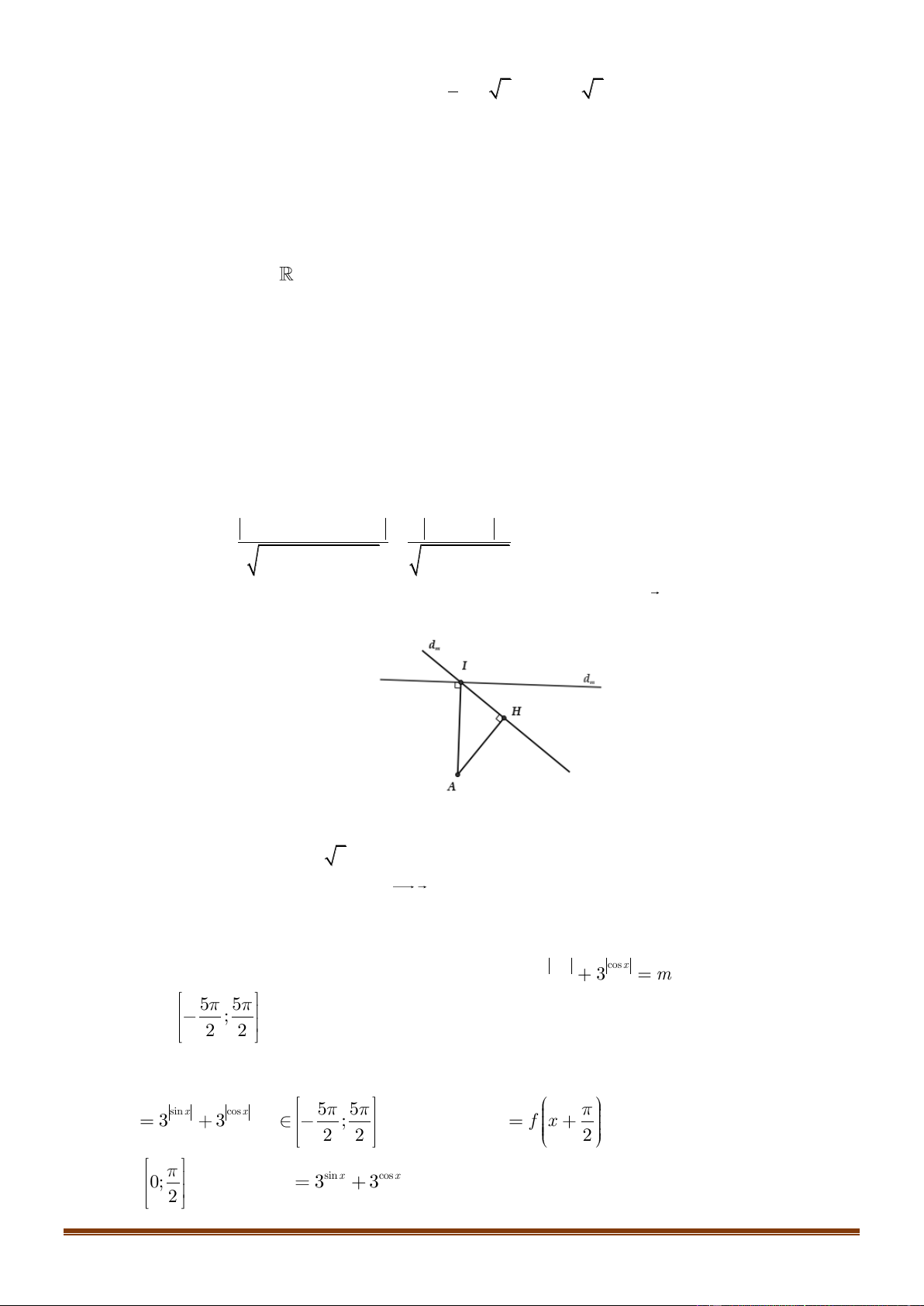
Suy ra điểm cực đại của đồ thị (C là: A(1;3) . m ) ( m + − − m − − m − d M d = = . m ) 2 3.3 5 7 4 16 , (m + 2)2 +(−3)2 (m + 2)2 +9
Đường thẳng d luôn đi qua điểm cố định I (5;1) và có 1 VTCP là n = (3;m + 2). m
Gọi H là hình chiếu vuông góc của A trên d , ta có d ( , A d = AH AI m ) md ( , A d ) = AI = 2 5 . m max
Đẳng thức xảy ra  AI ⊥ d AI.u = 0 12− 2(m + 2) = 0  m = 4 . m
Vậy m = 4 thỏa yêu cầu bài toán. x x
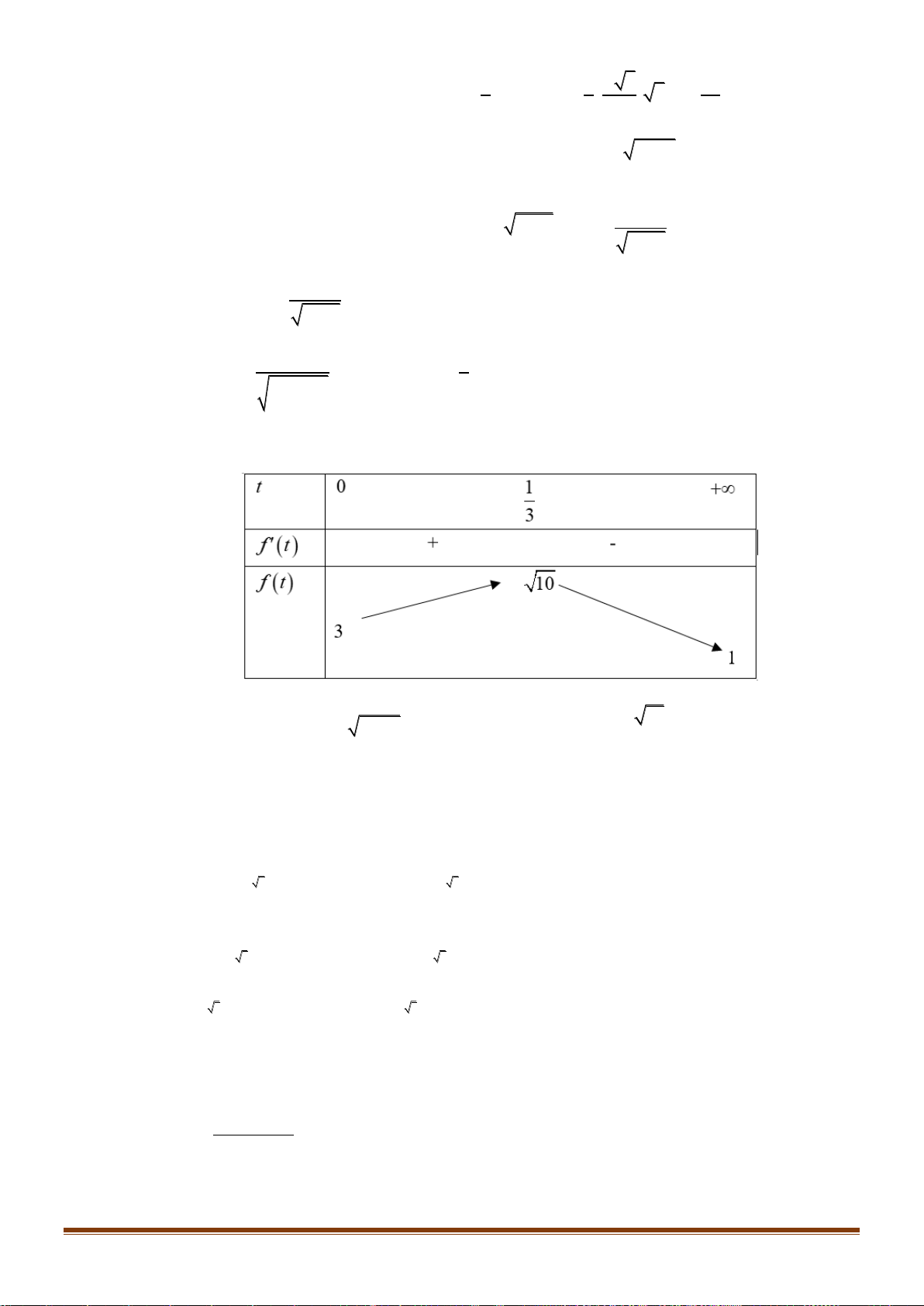
Câu 39: Tìm tất cả các giá trị của tham số m để phương trình sin cos 3 3
m có 20 nghiệm phân biệt 5 5 trên ; . 2 2 Lời giải 5 5 Đặt sin x cos 3 3 x f x , x ; . Để ý rằng f x f x
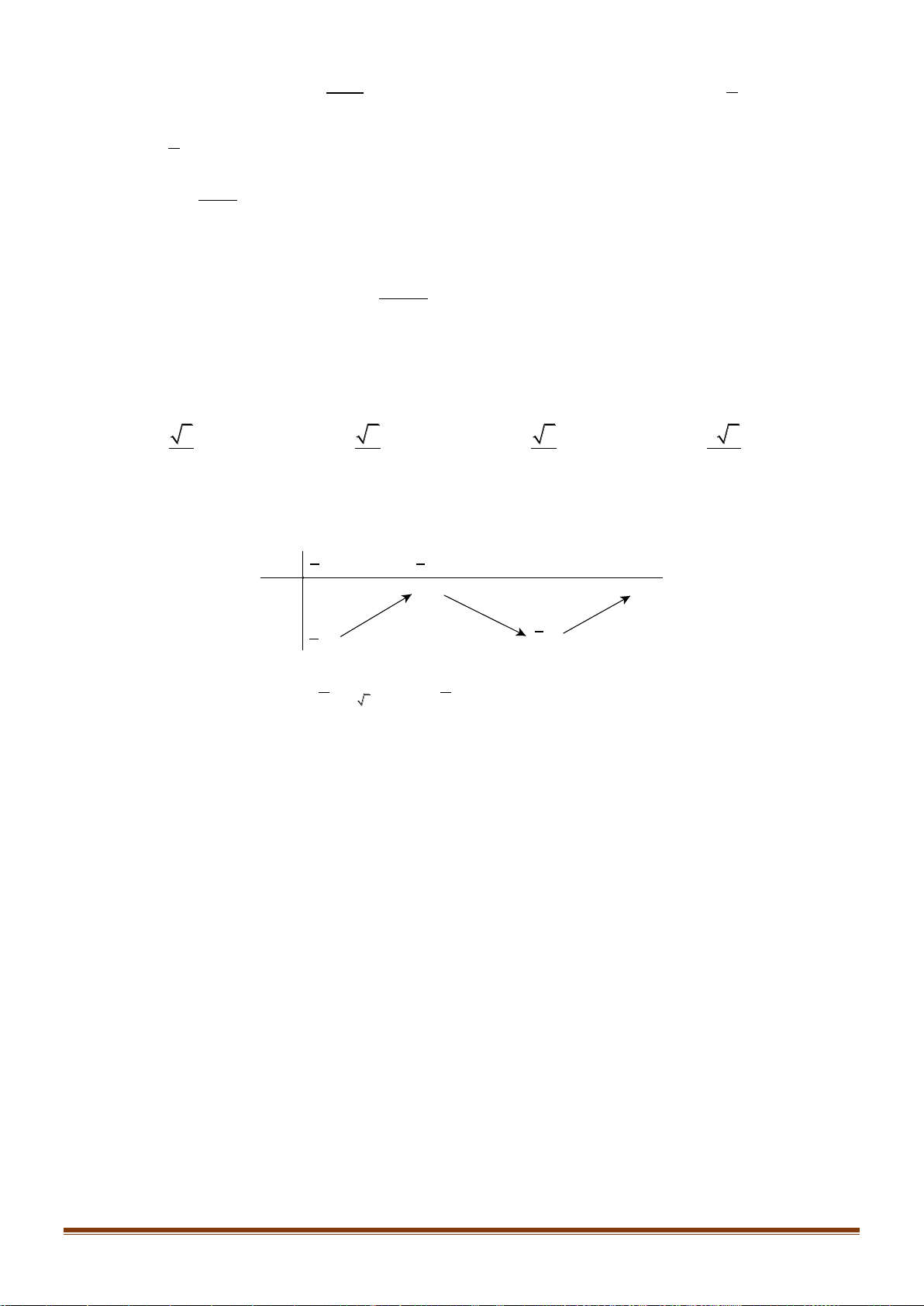
nên ta chỉ cần xét f x trên đoạn 2 2 2 0; . Khi đó sinx cos 3 3 x f x . Lại có 2 Page 17
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 f x f x , x 0; . 2 2
nên đồ thị hàm số f x trên đoạn 0;
nhận đường thẳng x
làm trục đối xứng. Xét f x trên 2 4 0; , ta có 4 sin x cos cos 3 sin 3 x f x x x ln 3. Dễ thấy x
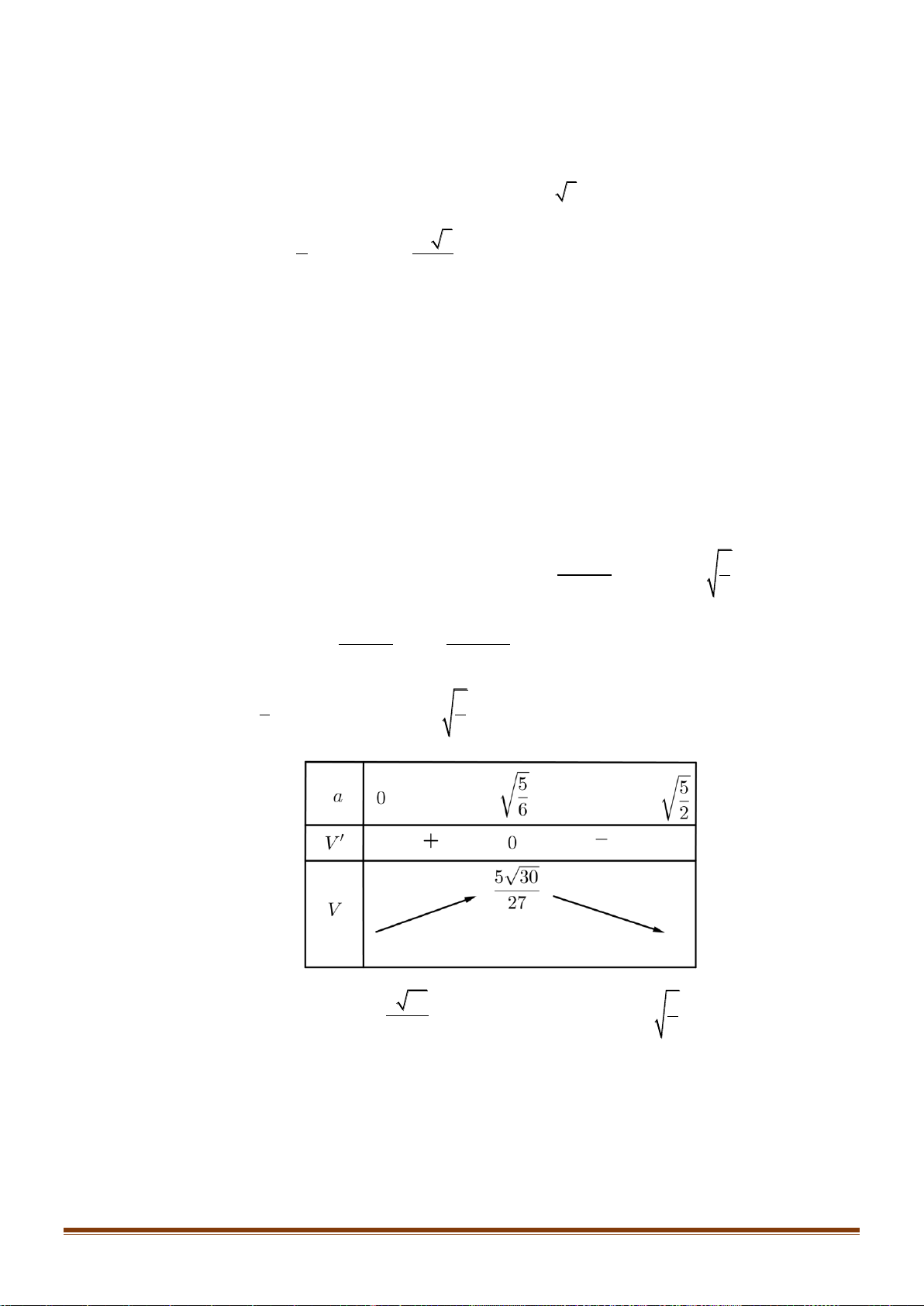
0 không là nghiệm của f x nên ta xét 0 x , khi đó 4 sin x cos 3 3 x f x sin x cos x . sin x cos x 3t 2 1 3t t ln 3 1 2 Đặt g t , 0 t . Do đó g t 0 với 0 t . Do đó t 2 ln 3 2 t 2 2
g t là hàm số nghịch biến trên 0; . Suy ra, trên 0; ta có 2 4 sin x cos 3 3 x g sin x g cos x sin x cos x x . sin x cos x 4
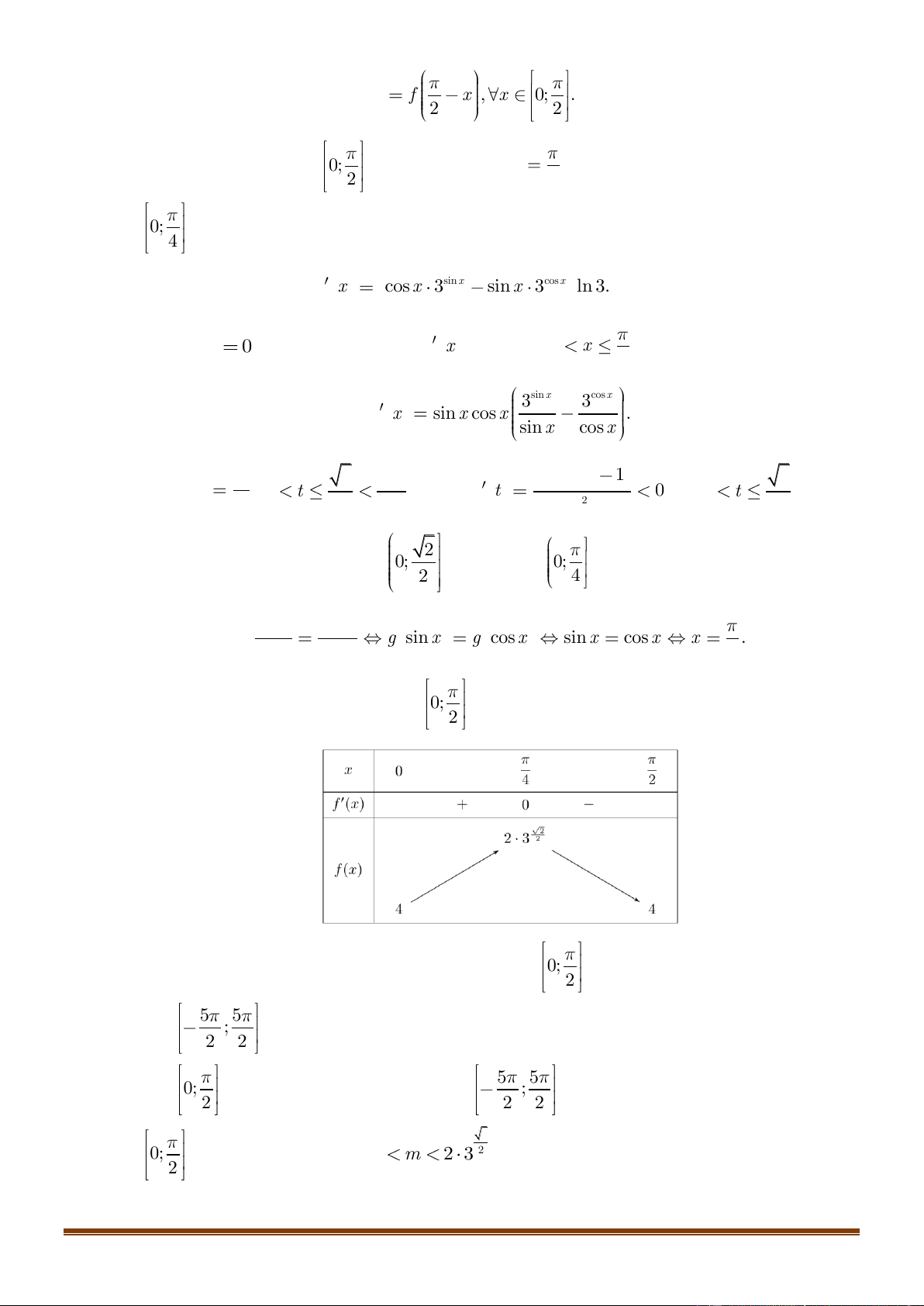
Suy ra bảng biến thiên của f x trên 0; 2
Bằng cách tịnh tiến liên tiếp đồ thị hàm số f x trên 0;
, ta thu được đồ thị hàm số f x 2 5 5 trên ;
nhận thấy rằng đồ thị này gồm 10 phần đồ thị giống như đồ thị hàm số f x 2 2 5 5 trên 0;
. Do đó, f x có 20 nghiệm trên ;
khi và chỉ khi f x có 2 nghiệm trên 2 2 2 2 0;
. Điều này tương đương 2 4 m 2 3 . 2 Page 18
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 02
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Cắt một hình nón bằng một mặt phẳng qua trục, được thiết diện là một tam giác đều cạnh 2a .
Tính diện tích xung quanh của hình nón đó. 2 2 a A. 2  a 3. B. C. 2 2 a D. 2 4 a 3 Câu 2:
Tìm nghiệm của phương trình x 1 3 1 . A. x = 2. −
B. x = 1 C. x = 1 − 
D. x = 2 Câu 3:
Cho khối lăng trụ AB .
C A B C có thể tích bằng 36 . Tính thể tích khối tứ diện A ABC . A. 10. B. 24. C. 18. D. 12. 16 Câu 4:
Cho hàm số f ( x) 2 = x +
. Tìm giá trị nhỏ nhất của hàm số f ( x) trên đoạn 1;  4 . x A. 20 B. 4 − C. 17 D. 12 Câu 5:
Hàm số nào dưới đây có bảng biến thiên như hình vẽ bên? x +1 x −1 A. 3
y = x − 3x B. y = C. 4 2
x − 2x D. x −1 x +1 Câu 6:
Đạo hàm của hàm số y = x ln x trên khoảng (0;+)là 1
A. y = 1+ ln . x B. y = . C. y = ln . x D. 1− ln . x x a = log 5 log 100 Câu 7: Cho 2 . Khi đó 50 bằng: 2a + 2 a + 2 a + 2 A. 2. B. . C. . . 2a +1 a + D. 1 2a + 1 Câu 8:
Cho số thực a (0  a  1) . Khi đó giá trị của 3 P = log a bằng: a 1 1 A. 3. B. . C. . D. 2. 2 3 Câu 9:
Tìm nghiệm của phương trình l og x = 1. − 2 1 A. x .  B. x = . C. x = 1 − . D. x = 2. 2
Câu 10: Trong các hàm số sau đây, có bao nhiêu hàm số có cực trị? ( ) ( ) 4 I
f x = x ; (II ) f ( x) 3 2
= x − x + x −3; ( ) ( ) 2 III
f x = x ; (IV ) f ( x) = x ; A. 1 B. 2 C. 4 D. 3 Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 11: Cho hàm số y = f ( x) xác định trên
và có bảng xét dấu của đạo hàm y ' = f '( x) như sau.
Khẳng định nào sau đây sai?
A. Hàm số có 2 điểm cực đại và 1 điểm cực tiểu.
B. Hàm số có 2 điểm cực tiểu và một điểm cực đại.
C. Hàm số đạt cực đại tại x = 0 .
D. Hàm số có 3 điểm cực trị.
Câu 12: Biết (H ) là đa diện đều loại 5; 
3 với số đỉnh và số cạnh lần lượt là a và b . Tính a − b A. − = −
a − b = 8
B. a − b = 10 − C. a b 8
D. a −b =10
Câu 13: Cho hình vuông ABCD cạnh bằng 2a . Gọi M , N lần lượt là trung điểm của hai cạnh A , B CD
. Quay hình vuông ABCD xung quanh trục MN . Tính thể tích của khối trụ tạo thành. 3 2 a A. V = . B. 3 V = 2 a . C. 3 V =  a . D. 3 V = 4 a . 3
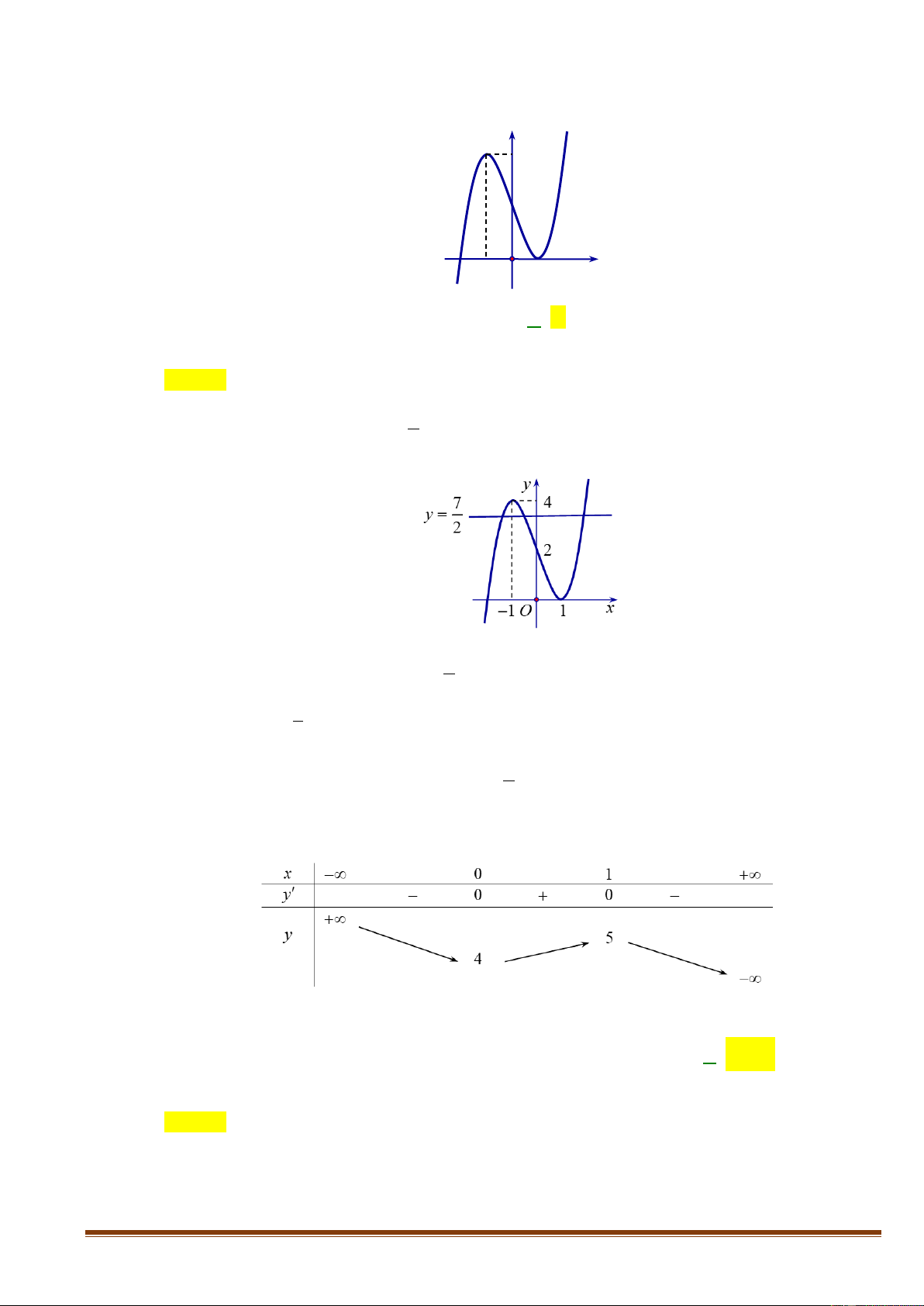
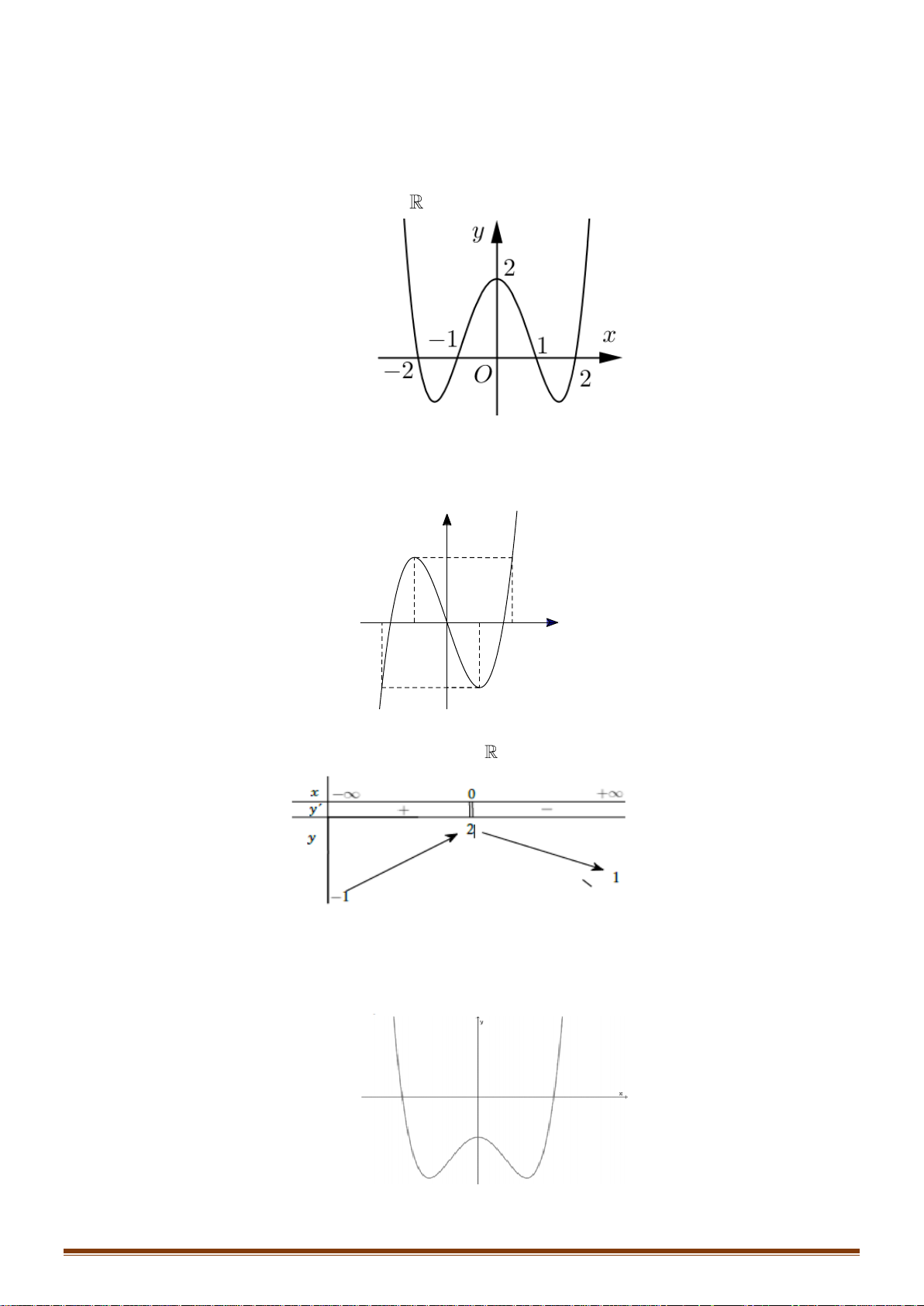
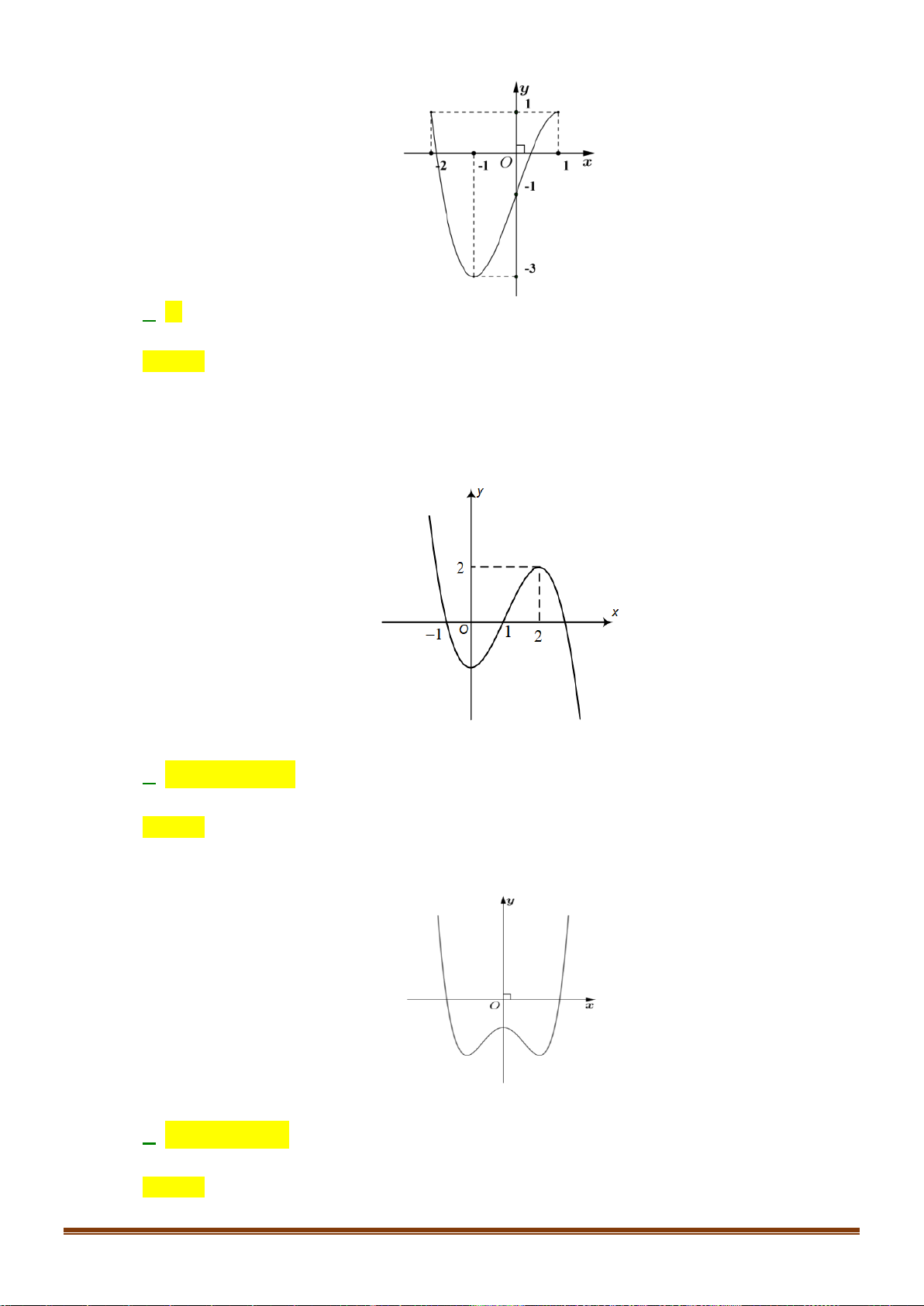
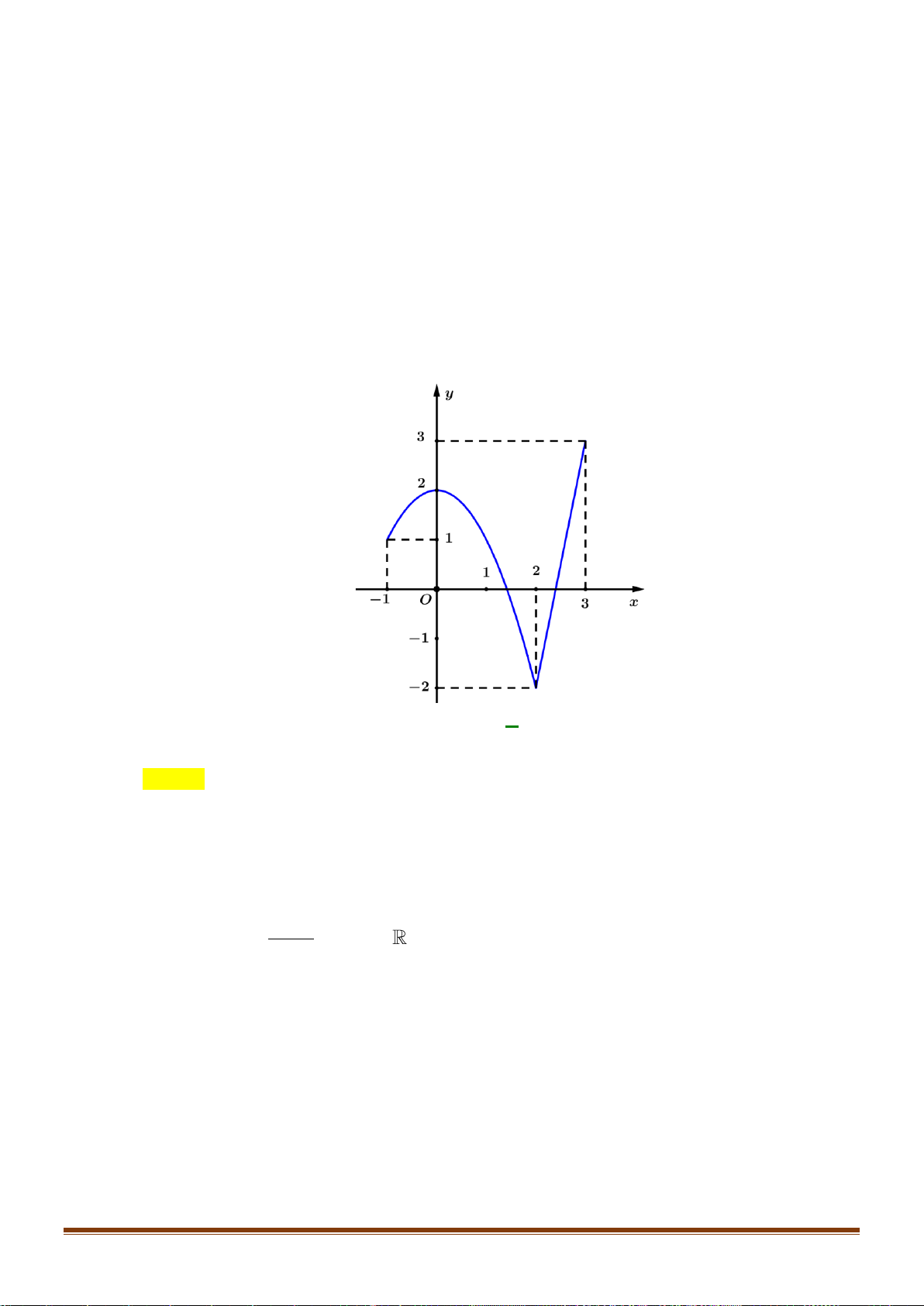
Câu 14: Cho hàm số y = f ( x) có đồ thị như hình bên. Phương trình 2 f ( x) − 7 = 0 có bao nhiêu nghiệm thực? y 4 2 1 − O x 1 A. 4 . B. 1. C. 3 . D. 2 .
Câu 15: Cho hàm số y = f ( x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ( ;0 − ). B. (1;+ ) . C. (4;5) . D. (0 ) ;1 .  2021 x
Câu 16: Tập xác định D của hàm số y =  2022  là   A. D = \   0 . B. (0 ) ;1 . C. D = .
D. D = (0;+) . Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 17: Tính diện tích xung quanh Sxq của hình trụ có bán kính bằng 2 và chiều cao bằng 4 . 16 A. S = 32 S =  S =  S =  xq . B. xq 3 . C. 8 xq . D. 16 xq . Câu 18: Gọi , l ,
h R lần lượt là độ dài đường sinh, đường cao và bán kính đáy của hình nón. Khẳng định nào sau đây là đúng? A. 2 2 2
l = h + R .
B. l = h . C. 2 2 2
h = R + l .
D. R = h .
Câu 19: Cho a, b là hai số thực dương và ,
m n là các số thực tùy ý. Hãy chọn khẳng định đúng. m 2m mn b A. m n mn a a a . B. m n a b ab . C. m n a b ab . D. m m a b . a
Câu 20: Một hình trụ có diện tích toàn phần bằng hai lần diện tích xung quanh và thể tích khối trụ là 81
. Tính chiều cao của hình trụ đã cho. 3 3 3 A. 3 . B. 3 3 3 . C. 3 3 . D. . 2
Câu 21: Khối nón có chiều cao h , độ dài đường sinh l , bán kính r . Thể tích khối nón đó được tính bằng
công thức nào dưới đây? 1 1 A. 2 r l . B. 2 r l . C. rh . D. 2 r h . 3 3 +
Câu 22: Tập nghiệm bất phương trình x 1 25
−126.5x + 5  0 có dạng là  ; a b. Tính 2 2 a + b . 16354 16354 A. . B. 5. C. 10. D. . 5625 2025
Câu 23: Tìm tập nghiệm của bất phương trình x 1 + 5−3 7  7 x . A. ( ; − ) 1 . B. 1;+). C. (1;+). D. (− ;  −  1 .
Câu 24: Hàm số nào sao đây nghịch biến trên . x  2021  A. y = log . x B. y = . C. 2021x y = . D. y = log . x 0,5    2 2022 
Câu 25: Phương trình 2log (x − 2) + log ( x + )3
1 = 2log 2 có bao nhiêu nghiệm? 9 27 3 A. 2. B. 3. C. 1. D. 0. ax +
Câu 26: Tìm a để hàm số y = f ( x) 2 =
có đồ thị như hình bên. x + 1
A. a = 1.
B. a = 2. C. a = 2. − D. a = 1. −
Câu 27: Cho hình chóp S.ABC có đáy là tam giác đều ABC cạnh bằng
a 2 , SA vuông góc với mặt phẳng ( ABC ) và SA = . a Tính
thể tích khối chóp S.AB . C 3 3 a 3 3 a 3 3 a 3 a 3 A. . B. . C. . D. . 2 4 6 3
Câu 28: Cho hàm số y = ( x − x + ) 3 2 2 4 1 . Tính y '(0) . Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 A. 12 3 B. −12 3 C. −4 3 D. 4 3 1
Câu 29: Tìm tiệm cận ngang của đồ thị hàm số y = x − . 2 A. x =1 B. y = 1
C. x = 2
D. y = 0
Câu 30: Cắt khối lăng trụ AB .
C A' B 'C ' bởi các mặt phẳng ( AB 'C ') và ( ABC ') ta được những khối đa diện nào?
A. Ba khối tứ diện.
B. Hai khối tứ diện và một khối chóp tứ giác.
C. Một khối tứ diện và hai khối chóp tứ giác.
D. Hai khối tứ diện và hai khối chóp tứ giác
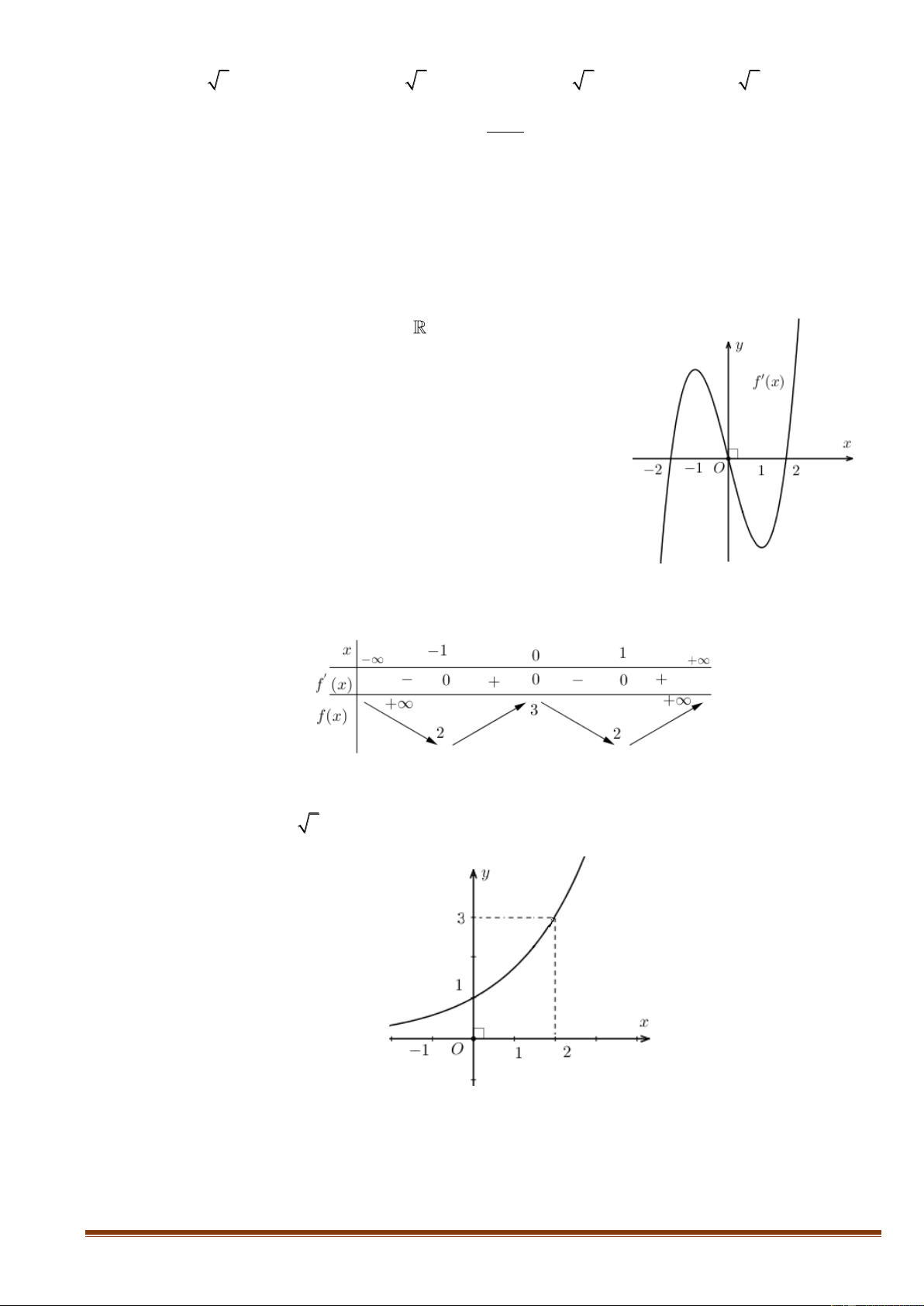
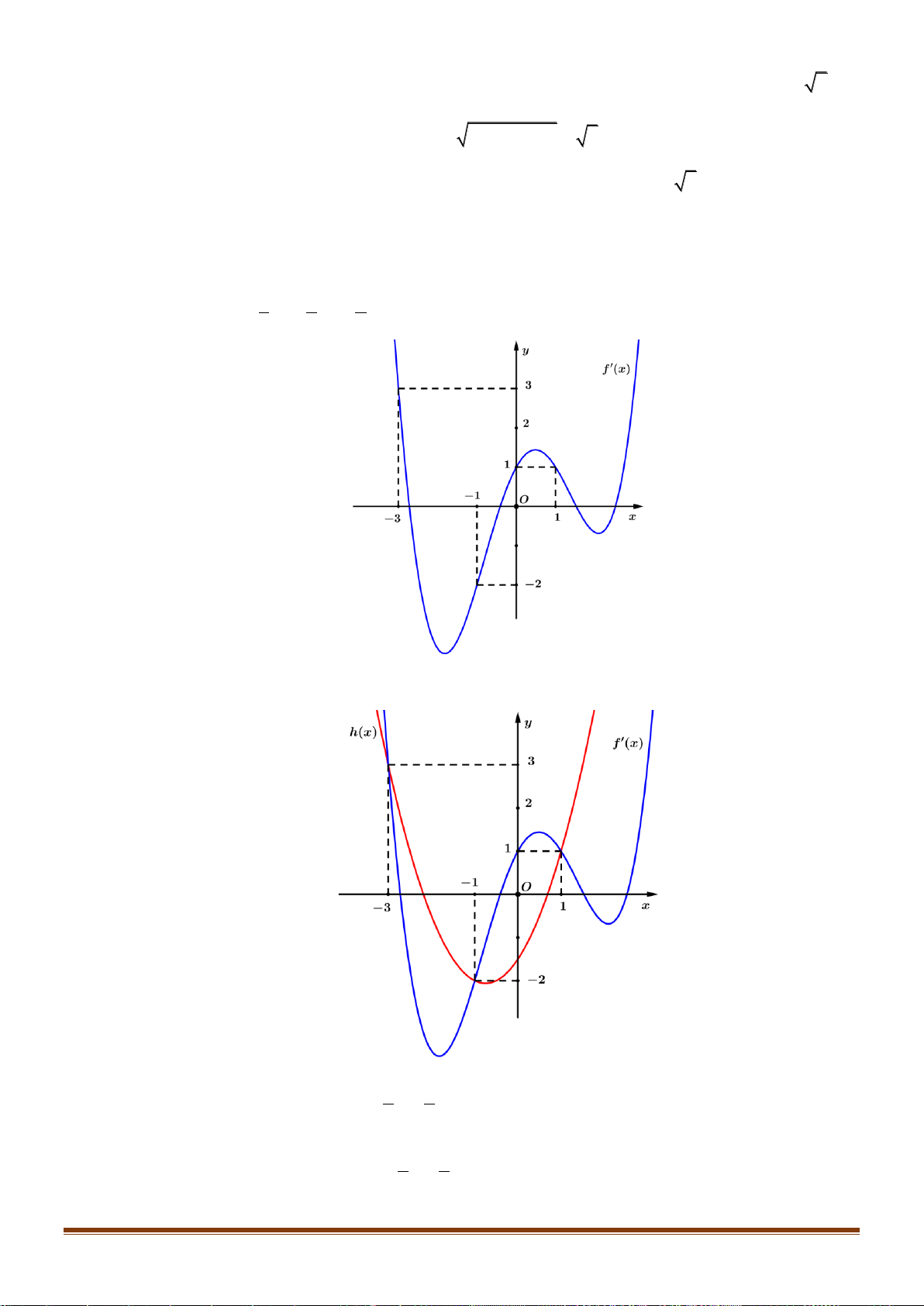
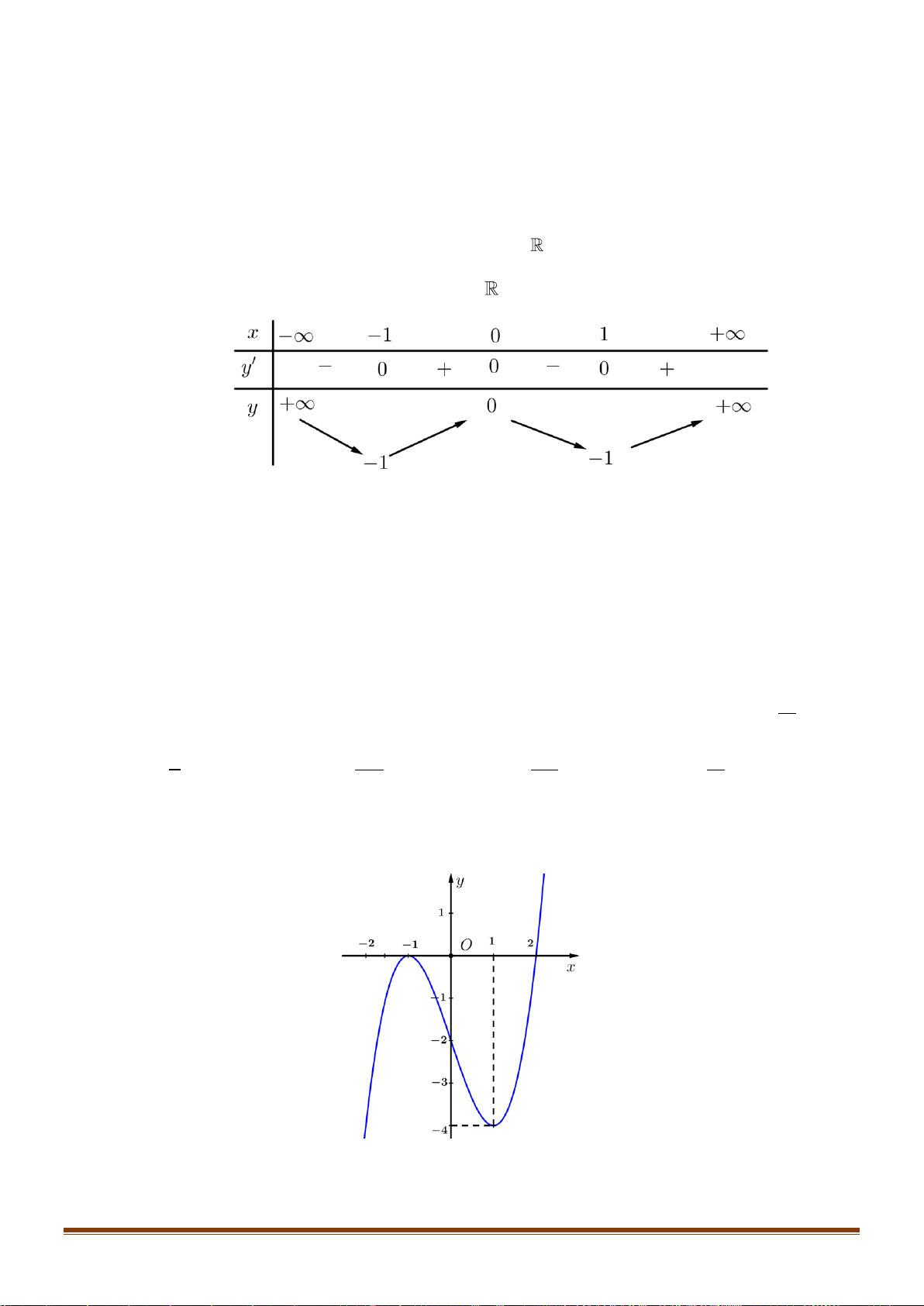
Câu 31: Cho hàm số f ( x) xác định trên và có đồ thị hàm số
y = f ( x) là đường cong trong hình dưới đây.
Khẳng định nào sau đây đúng?
A. f (2) = f (0)  f ( ) 1 .
B. f (0)  f ( ) 1  f (2) .
C. f (0)  f ( ) 1  f (2) .
D. f (2) = f (0)  f ( ) 1 .
Câu 32: Cho hàm số y = f ( x) có bảng biến thiên sau:
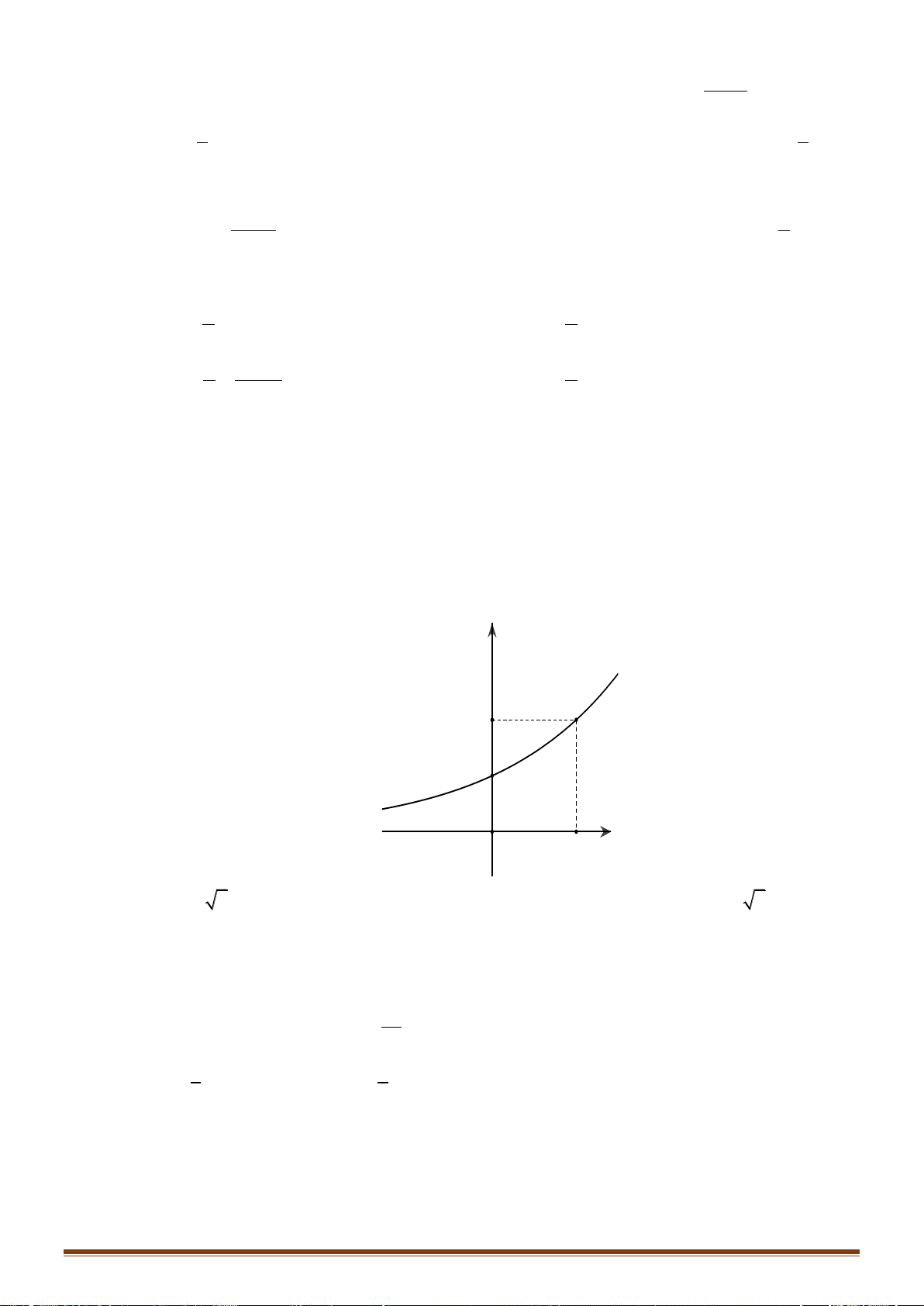
Tìm giá trị lớn nhất của hàm số y = f ( x) trên đoạn  1 − ;  1 . A. 2. B. 3. C. 0. D. 1. x+a
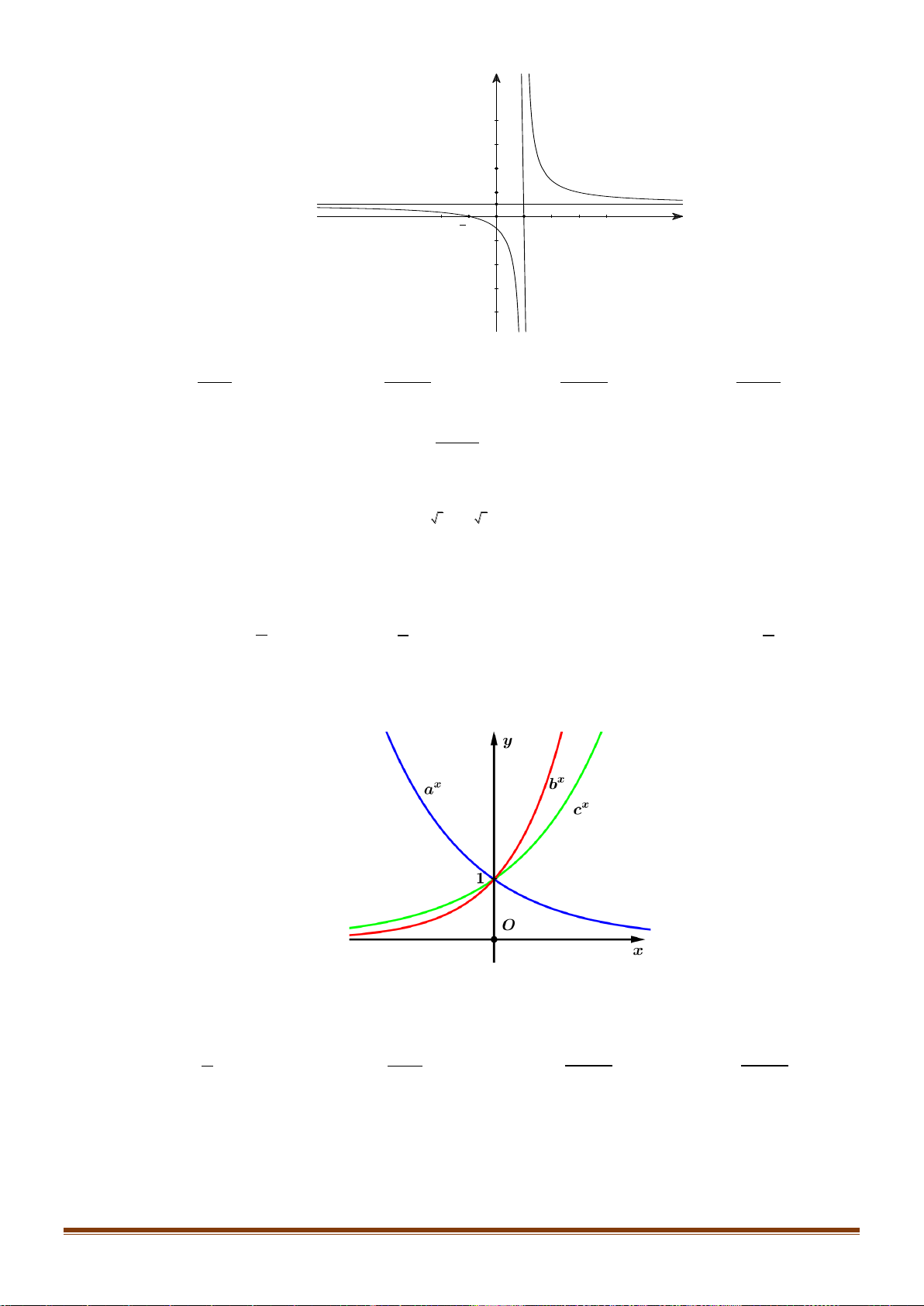
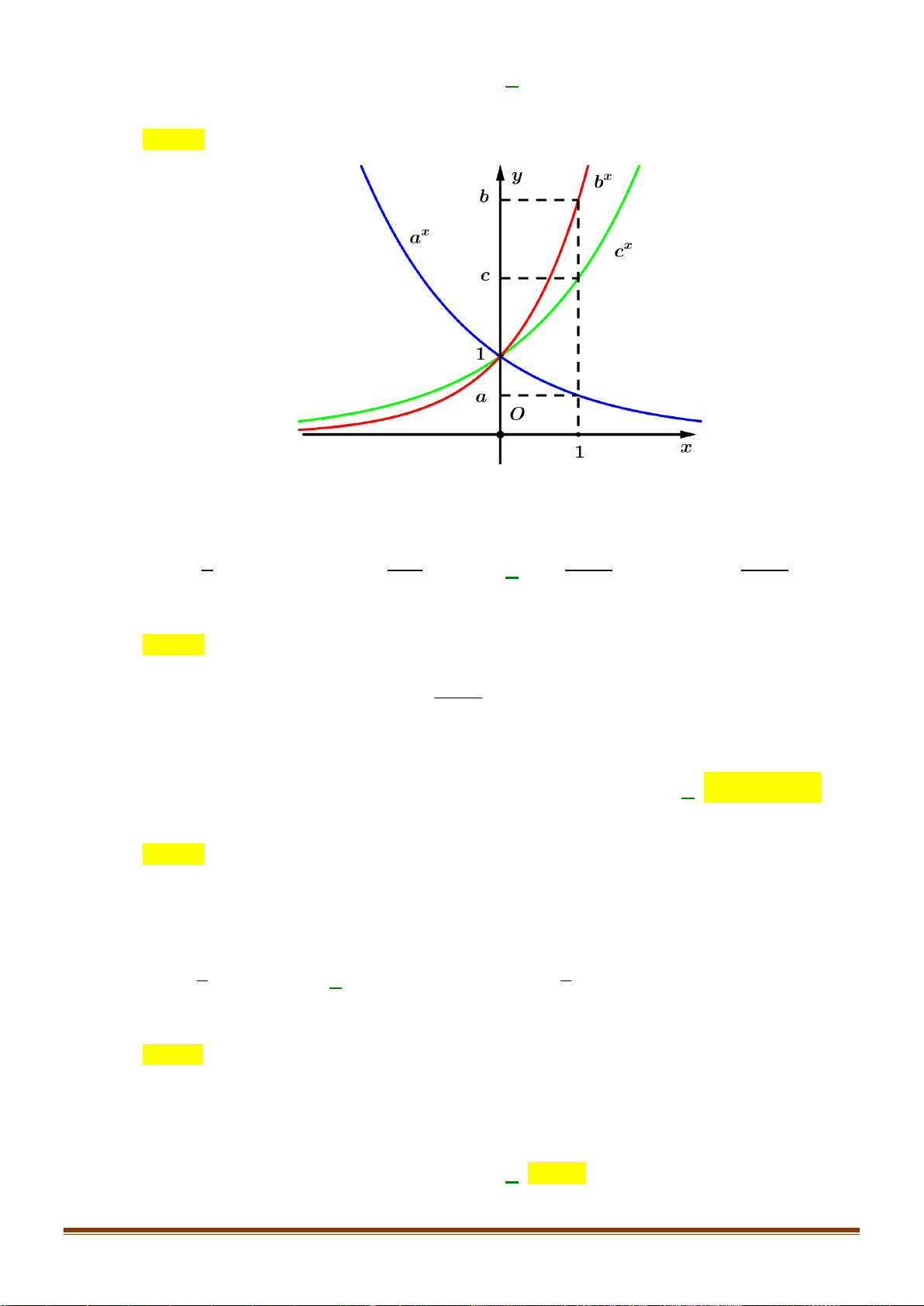
Câu 33: Cho hàm số y = ( 3) có đồ thị như hình bên. Giá trị của a là A. 3. B. 2. C. 0. D. 1.
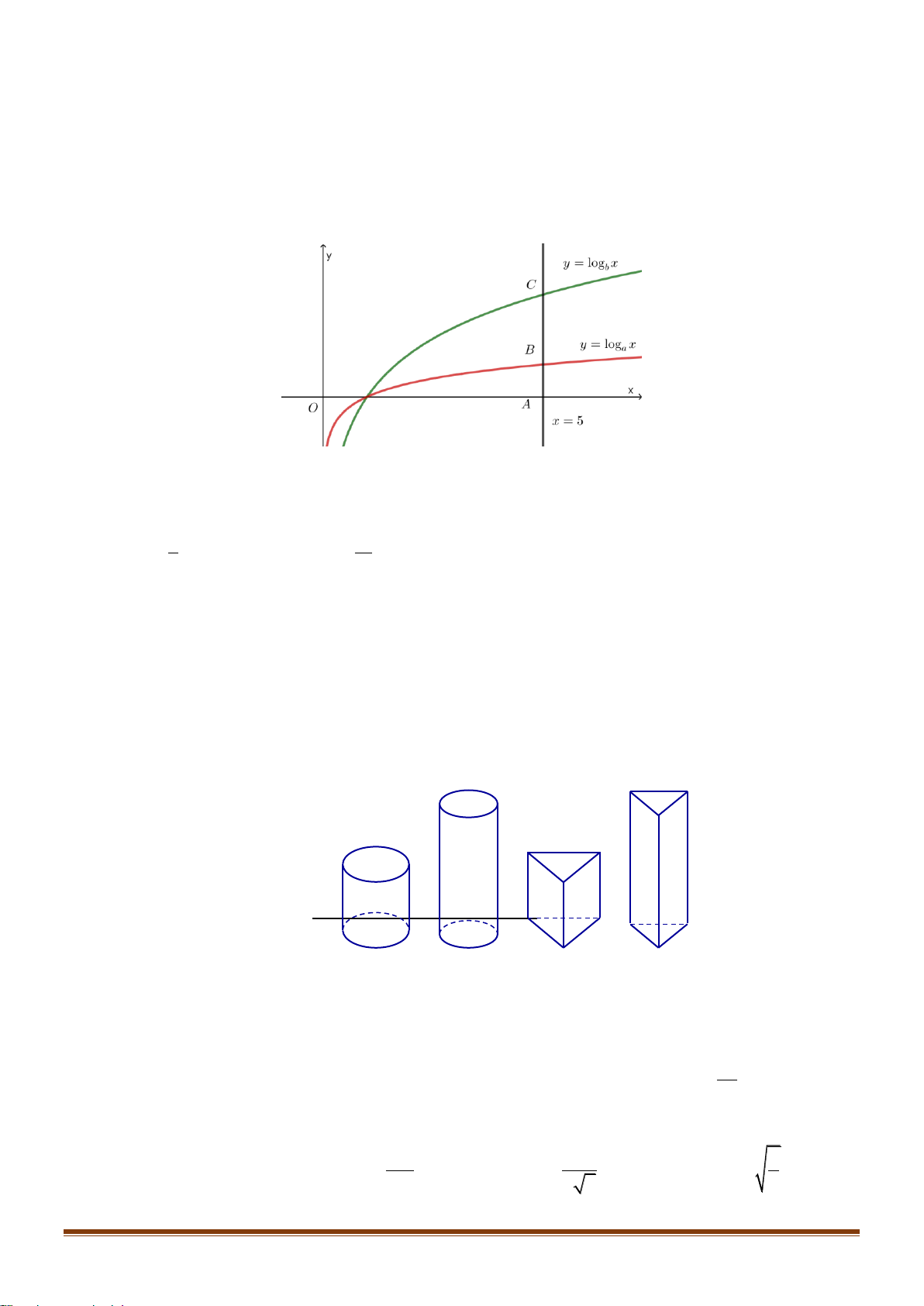
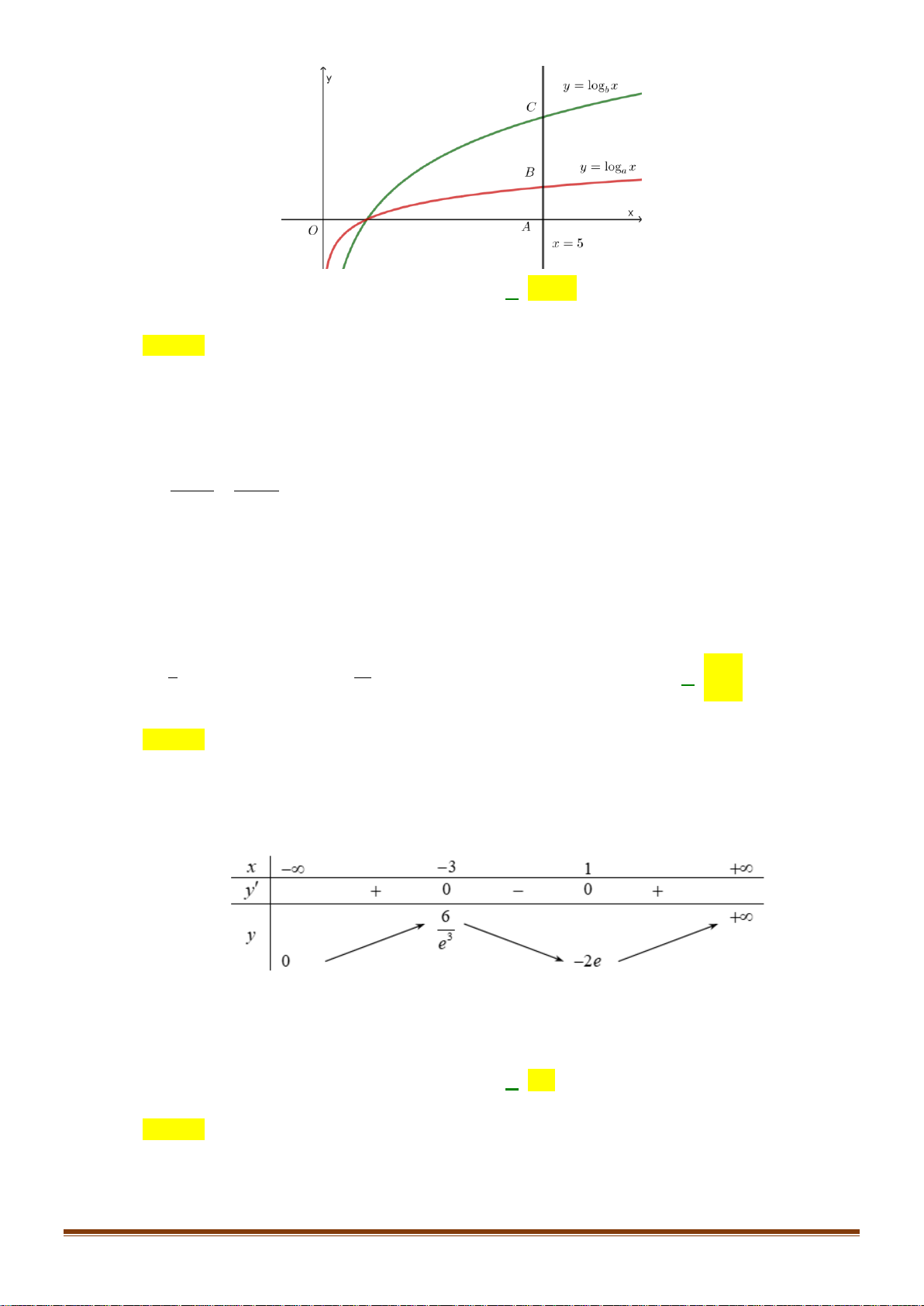
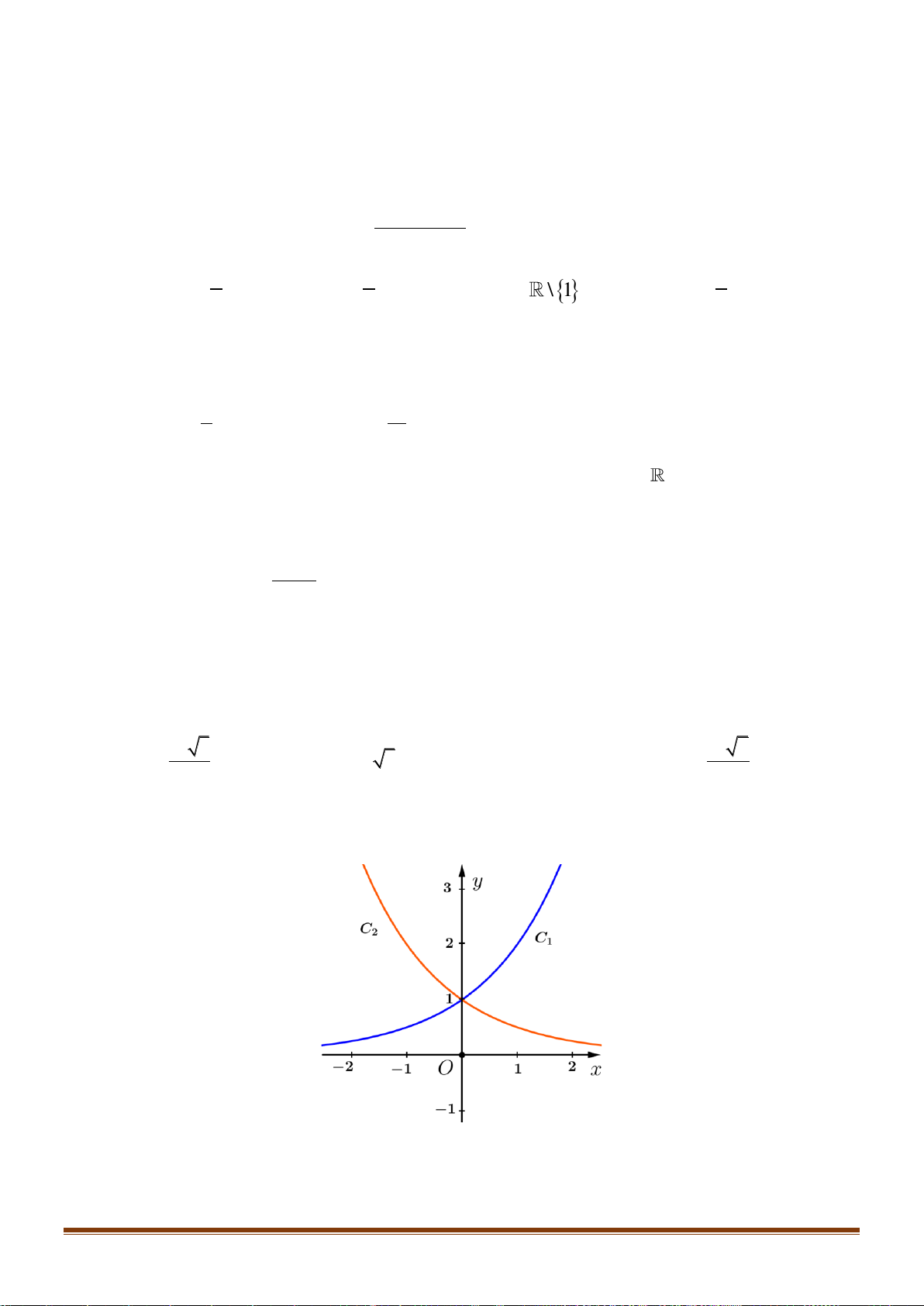
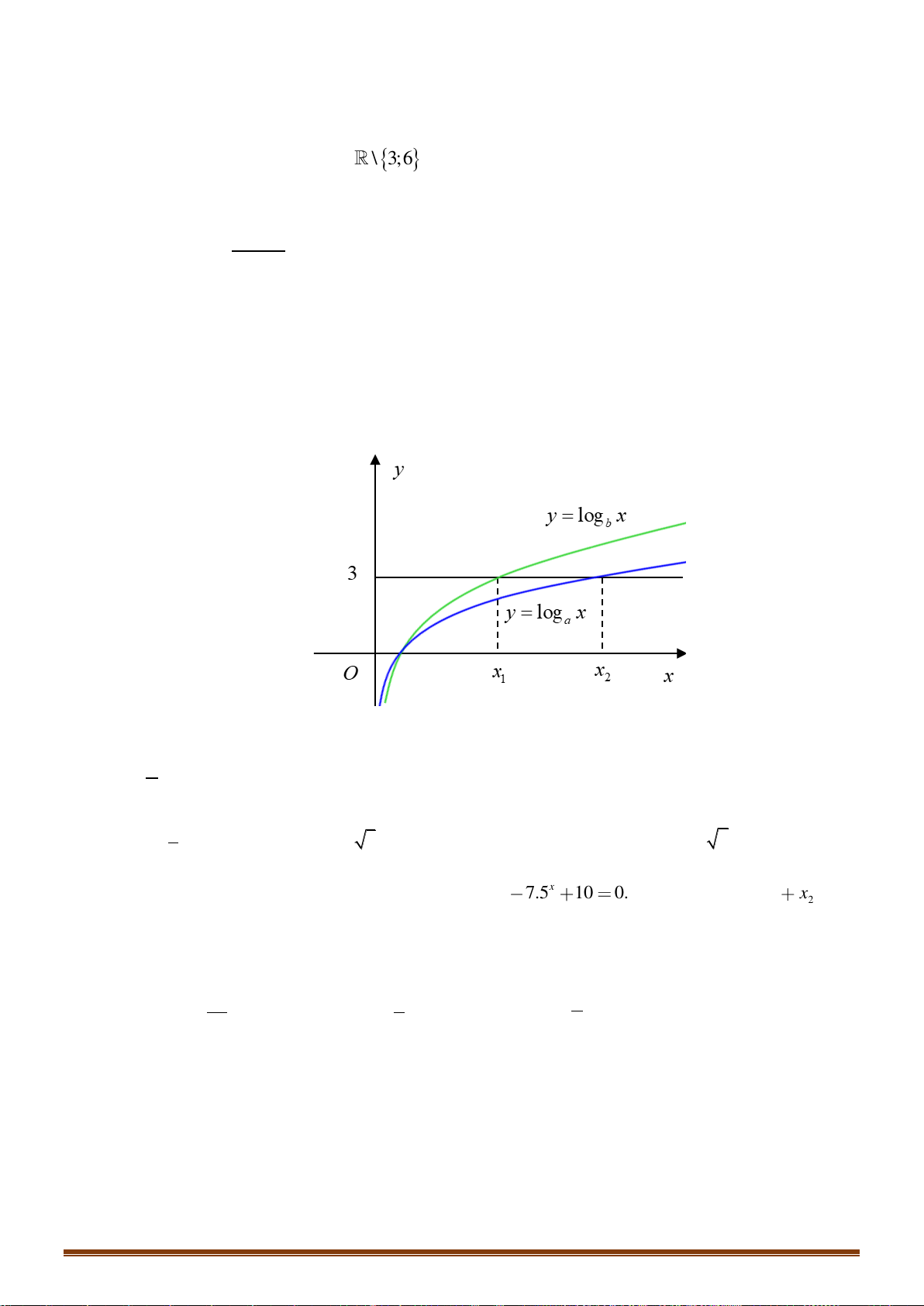
Câu 34: Cho hàm số y = log x (0  a  )
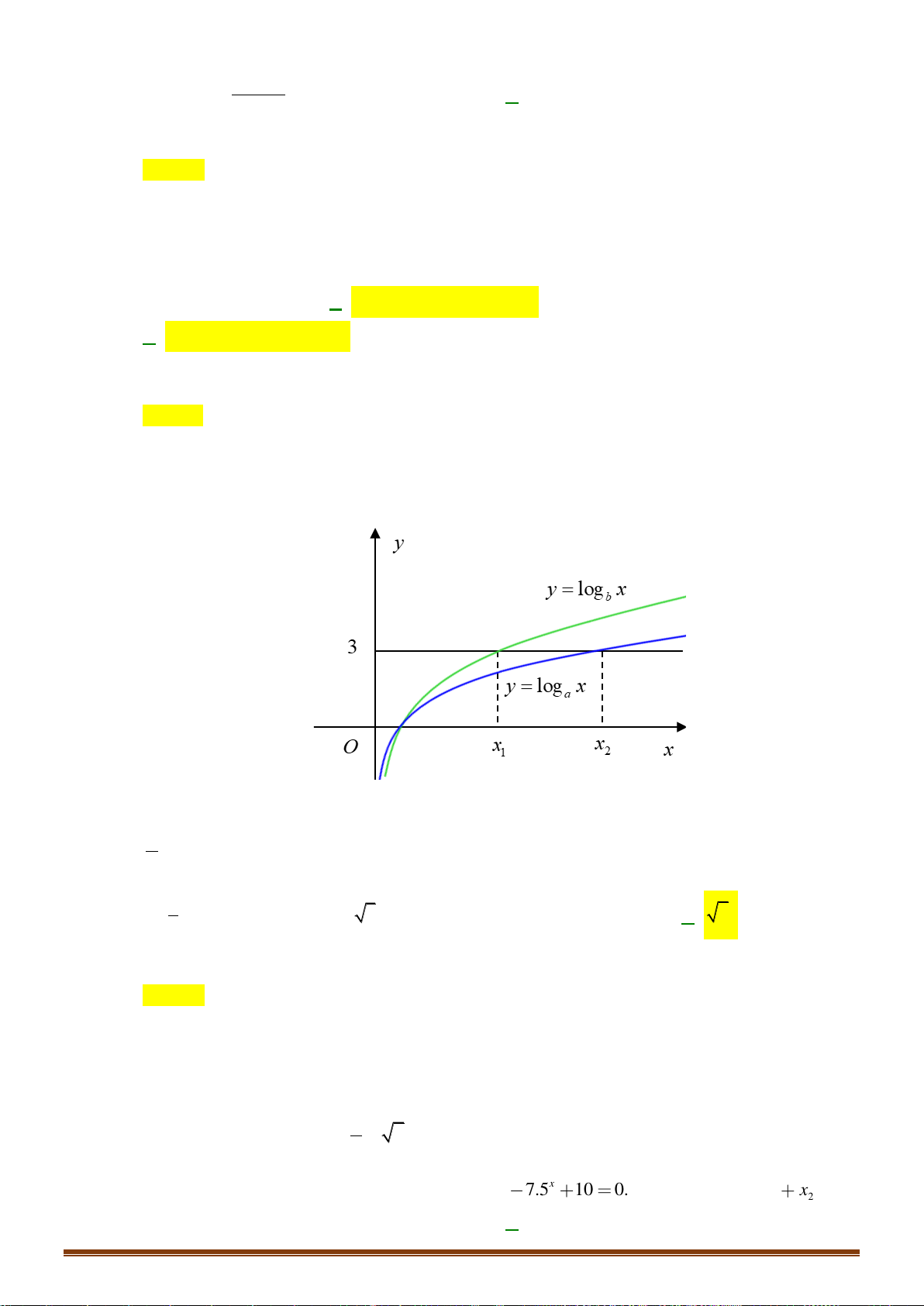
1 có đồ thị (C ) và hàm số y = log x
b  có đồ thị (C) b (0 )1 a như hình dưới đây. Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Khẳng định nào dưới đây đúng?
A. 0  a b 1.
B. 0  b a 1. C. 1  b  . a D. 1  a  . b
Câu 35: Cho hàm số y = f ( x) có bảng biến thiên sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho? A. 4. B. 1. C. 2. D. 3.
II. PHẦN TỰ LUẬN (4 câu – 3,0 điểm)
Câu 36: Giải phương trình ( 2 log − 4log + 3 2x x x −8 = 0. 2 2 ) Câu 37: Cho hàm số 3 2
y = x − 3mx + 2 có đồ thị (C ) . Tìm tất cả các giá trị thực của tham số m để đồ thị
(C) có hai điểm cực trị ,
A B sao cho AB = 2 5 .
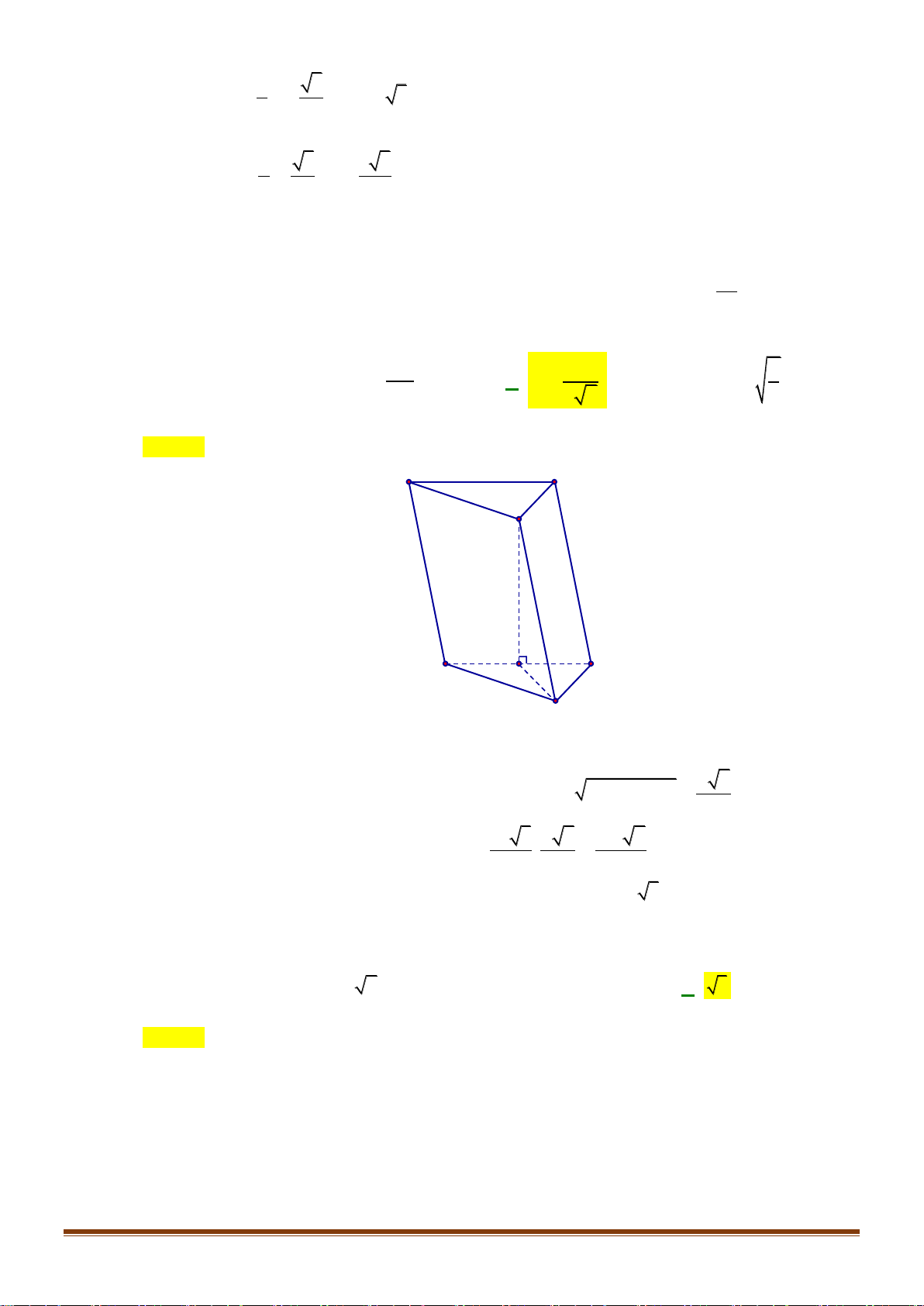
Câu 38: Cho hình lăng trụ đứng AB .
C A' B 'C ' , có đáy ABC là tam giác vuông tại A, AB = , a
AC = a 3 . Góc tạo bởi mặt phẳng (B ' AC) và ( ABC) bằng 0 60 .
a) Tính thể tích của khối lăng trụ AB .
C A' B 'C ' .
b) Tính khoảng cách giữa hai đường thẳng B 'C và AB Câu 39: Cho ,
x y là các số nguyên dương và nhỏ hơn 2021và thỏa mãn đẳng thức sau: 2( x ) 2x 1 1 5 − − +
= y +1+ log 25y +100 5 ( )
Tính giá trị biểu thức T = 12x − y …..HẾT….. Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 BẢNG ĐÁP ÁN 1.C 2.C 3.D 4.D 5.A 6.A 7.B 8.A 9.B 10.D 11.A 12.B 13.B 14.C 15.D 16.C 17.D 18.A 19.D 20.B 21.D 22.B 23.A 24.B 25.C 26.A 27.C 28.C 29.D 30.A 31.B 32.B 33.C 34.C 35.C
HƯỚNG DẪN LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Cắt một hình nón bằng một mặt phẳng qua trục, được thiết diện là một tam giác đều cạnh 2a .
Tính diện tích xung quanh của hình nón đó. 2 2 a A. 2  a 3. B. C. 2 2 a D. 2 4 a 3 Lời giải Chọn C Ta có 2 S rl . . a 2a 2 a . xq Câu 2:
Tìm nghiệm của phương trình x 1 3 1 . A. x = 2. −
B. x = 1 C. x = 1 − 
D. x = 2 Lời giải Chọn C Ta có x 1 x 1 0 3 1 3 3 x 1 0 x 1. Câu 3:
Cho khối lăng trụ AB .
C A B C có thể tích bằng 36 . Tính thể tích khối tứ diện A ABC . A. 10. B. 24. C. 18. D. 12. Lời giải Chọn D Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 A' C' B' A C B 1 36 Ta có V 3V V V 12 . ABC. A B C A ABC A ABC ABC. 3 A B C 3 16 Câu 4:
Cho hàm số f ( x) 2 = x +
. Tìm giá trị nhỏ nhất của hàm số f ( x) trên đoạn 1;  4 . x A. 20 B. 4 − C. 17 D. 12 Lời giải Chọn D 16
Ta có f ( x) = 2x − 2 x
f ( x) = 0  x = 2 (nhận) f ( )
1 =17; f (2) =12; f (4) = 20
Vậy min f ( x) = 12 . 1;4 Câu 5:
Hàm số nào dưới đây có bảng biến thiên như hình vẽ bên? x +1 x −1 A. 3
y = x − 3x B. y = C. 4 2
x − 2x D. x −1 x +1 Lời giải Chọn A
Hàm số trong bảng biến thiên trên làm hàm bậc ba có hệ số a  0 Câu 6:
Đạo hàm của hàm số y = x ln x trên khoảng (0;+)là 1
A. y = 1+ ln . x B. y = . C. y = ln . x D. 1− ln . x x Lời giải Chọn A 1
Ta có y = ln x + x = ln x +1. x Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 a = log 5 log 100 Câu 7: Cho 2 . Khi đó 50 bằng: 2a + 2 a + 2 a + 2 A. 2. B. . C. . . 2a +1 a + D. 1 2a + 1 Lời giải Chọn B 2 2 log 100 log (5 .2 ) 2 + 2 log 5 2 + 2a Có 2 2 2 log 100 = = = = . 50 2 log 50 log (5 .2) 1+ 2 log 5 1+ 2a 2 2 2 Câu 8:
Cho số thực a (0  a  1) . Khi đó giá trị của 3 P = log a bằng: a 1 1 A. 3. B. . C. . D. 2. 2 3 Lời giải Chọn A Có 3 P = log a = 3log a = 3. a a Câu 9:
Tìm nghiệm của phương trình l og x = 1. − 2 1 A. x .  B. x = . C. x = 1 − . D. x = 2. 2 Lời giải Chọn B ĐK: x  0. − 1 1 l og x = 1
−  x = 2 = ( Thỏa mãn ĐK). 2 2
Câu 10: Trong các hàm số sau đây, có bao nhiêu hàm số có cực trị? ( ) ( ) 4 I
f x = x ; (II ) f ( x) 3 2
= x − x + x −3; ( ) ( ) 2 III
f x = x ; (IV ) f ( x) = x ; A. 1 B. 2 C. 4 D. 3 Lời giải Chọn D + Xét hàm số ( ) ( ) 4 I
f x = x xác định trên và f ( x) 3 '
= 4x = 0  x = 0. Ta thấy x = 0 là
nghiệm bội 3 của f '( x) và f '( x) đổi dấu khi đi qua x = 0 nên hàm số đạt cực trị tại x = 0.
+ Xét hàm số (II ) f ( x) 3 2
= x − x + x −3 xác định trên và f (x) 2 '
= 3x − 2x +1= 0 vô
nghiệm. Ta thấy f '( x) không đổi dấu trên
nên hàm số không có cực trị. + Xét hàm số ( ) ( ) 2 III
f x = x xác định trên
và f '( x) = 2x = 0  x = 0 . Ta thấy x = 0 là
nghiệm đơn của f '( x) và f '( x) đổi dấu khi đi qua x = 0 nên hàm số đạt cực trị tại x = 0. x
+ Xét hàm số (IV ) f ( x) = x xác định trên và f '( x) =
. Ta thấy f '( x) không xác định x
tại x = 0 và f '( x) đổi dấu khi đi qua x = 0 nên hàm số đạt cực trị tại x = 0.
Vậy có 3 hàm số có cực trị.
Câu 11: Cho hàm số y = f ( x) xác định trên
và có bảng xét dấu của đạo hàm y ' = f '( x) như sau.
Khẳng định nào sau đây sai? Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
A. Hàm số có 2 điểm cực đại và 1 điểm cực tiểu.
B. Hàm số có 2 điểm cực tiểu và một điểm cực đại.
C. Hàm số đạt cực đại tại x = 0 .
D. Hàm số có 3 điểm cực trị. Lời giải Chọn A   Vì đạo hàm đả 6
o dấu từ âm sang dương khi đi qua 6 x = nên x = là hai điểm cực tiểu 2 2 của hàm số.
Vì đạo hàm đảo dấu từ dương sang âm khi đi qua x = 0 nên x = 0 là điểm cực đại của hàm số.
Do đó khẳng định A là khẳng định sai.
Câu 12: Biết (H ) là đa diện đều loại 5; 
3 với số đỉnh và số cạnh lần lượt là a và b . Tính a − b
A. a − b = 8
B. a − b = 10 −
C. a − b = 8 −
D. a −b =10 Lời giải Chọn B
Vì (H ) là đa diện đều loại 5; 
3 nên (H ) là khối 12 mặt đều.
Khối 12 mặt đều có 20 đỉnh và 30 cạnh. Suy ra a = 20 ; b = 30 .
Khi đó a −b = 10 −
Câu 13: Cho hình vuông ABCD cạnh bằng 2a . Gọi M , N lần lượt là trung điểm của hai cạnh A , B CD
. Quay hình vuông ABCD xung quanh trục MN . Tính thể tích của khối trụ tạo thành. 3 2 a A. V = . B. 3 V = 2 a . C. 3 V =  a . D. 3 V = 4 a . 3 Lời giải Chọn B A M r B h D N C AB Ta có r =
= a ; h = AD = 2a . 2
Thể tích khối trụ tạo thành là 2 2 3
V =  r h =  .a .2a = 2 a . Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 14: Cho hàm số y = f ( x) có đồ thị như hình bên. Phương trình 2 f ( x) − 7 = 0 có bao nhiêu nghiệm thực? y 4 2 1 − O x 1 A. 4 . B. 1. C. 3 . D. 2 . Lời giải Chọn C
Ta có f ( x) − =  f ( x) 7 2 7 0 = . 2
Số nghiệm của phương trình f ( x) 7
= chính là số giao điểm của đồ thị hàm số y = f (x) và 2 đườ 7 ng thẳng y = . 2
Dựa vào đồ thị, ta thấy phương trình f ( x) 7
= có ba nghiệm thực phân biệt. 2
Câu 15: Cho hàm số y = f ( x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ( ;0 − ). B. (1;+). C. (4;5) . D. (0 ) ;1 . Lời giải Chọn D
Dựa vào bảng biến thiên, hàm số y = f ( x) đồng biến trên khoảng (0 ) ;1 . Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12  2021 x
Câu 16: Tập xác định D của hàm số y =  2022  là   A. D = \   0 . B. (0 ) ;1 . C. D = .
D. D = (0;+) . Lời giải Chọn C  2021 x
Hàm số đã cho có dạng hàm số mũ nên ta có tập xác định của hàm số y =  2022  là D = .  
Câu 17: Tính diện tích xung quanh Sxq của hình trụ có bán kính bằng 2 và chiều cao bằng 4 . 16 A. S = 32 S =  S =  S =  xq . B. xq 3 . C. 8 xq . D. 16 xq . Lời giải Chọn D
Ta có diện tích xung quanh của hình trụ:
S = 2r.l = 2.2.4 =16 xq Câu 18: Gọi , l ,
h R lần lượt là độ dài đường sinh, đường cao và bán kính đáy của hình nón. Khẳng định nào sau đây là đúng? A. 2 2 2
l = h + R .
B. l = h . C. 2 2 2
h = R + l .
D. R = h . Lời giải Chọn A
Áp dụng định lý Pitago, trong một hình nón ta có 2 2 2
l = h + R .
Câu 19: Cho a, b là hai số thực dương và ,
m n là các số thực tùy ý. Hãy chọn khẳng định đúng. m 2m mn b A. m n mn a a a . B. m n a b ab . C. m n a b ab . D. m m a b . a Lời giải Chọn D
Câu 20: Một hình trụ có diện tích toàn phần bằng hai lần diện tích xung quanh và thể tích khối trụ là 81
. Tính chiều cao của hình trụ đã cho. 3 3 3 3 A. 3 . B. 3 3 . C. 3 3 . D. . 2 Lời giải Chọn B Ta có 2 s 2S 2 rh 2 r 2.2 rh r h . tp xq Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 2 3 3 V 81 r h 81 r 81 r 3 3 .
Câu 21: Khối nón có chiều cao h , độ dài đường sinh l , bán kính r . Thể tích khối nón đó được tính bằng
công thức nào dưới đây? 1 1 A. 2 r l . B. 2 r l . C. rh . D. 2 r h . 3 3 Lời giải Chọn D
Câu 22: Tập nghiệm bất phương trình x 1
25 + −126.5x + 5  0 có dạng là  ; a b. Tính 2 2 a + b . 16354 16354 A. . B. 5. C. 10. D. . 5625 2025 Lời giải Chọn B x+ x x x 1 Ta có: 1 2 25
−126.5 + 5  0  25.5 −126.5 + 5  0   5x  5  2 −  x  1. 25 Suy ra: a = 2 − ;b =1. Vậy 2 2 a + b = 5 .
Câu 23: Tìm tập nghiệm của bất phương trình x 1 + 5−3 7  7 x . A. ( ; − ) 1 . B. 1;+). C. (1;+). D. (− ;  −  1 . Lời giải Chọn A Ta có: x 1 + 5−3 7
 7 x x +1 5 − 3x x 1.
Câu 24: Hàm số nào sao đây nghịch biến trên . x  2021  x A. y = log . x = y = y = log . x 0,5 B. y .   C. 2021 . D.  2 2022  Lời giải Chọn B xx 2021  2021  2021  Hàm số y =   có cơ số 0   1 , suy ra y =   nghịch biến trên .  2022  2022  2022 
Câu 25: Phương trình 2log (x − 2) + log ( x + )3
1 = 2log 2 có bao nhiêu nghiệm? 9 27 3 A. 2. B. 3. C. 1. D. 0. Lời giải Chọn C
Điều kiện: x  2. Ta có Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
2log ( x − 2) + log ( x + )3 1 = 2log 2  log x − 2 + log x +1 = log 4 9 27 3 3 ( ) 3 ( ) 3
 log  x +1 x − 2  = log 4 3 ( )( ) 3  (x + ) 1 ( x − 2) = 4 2
x − x − 6 = 0 x = 3  x = 2 − 
Đối chiếu điều kiện ta có nghiệm của phương trình là x = 3. ax +
Câu 26: Tìm a để hàm số y = f ( x) 2 =
có đồ thị như hình bên. x + 1
A. a = 1.
B. a = 2. C. a = 2. − D. a = 1. − Lời giải Chọn A
Từ đồ thị hàm số ta có tiệm cận ngang của đồ thị hàm số
y = f ( x) là y =1.
Mặt khác lim f (x) = lim f (x) = a y = a là tiệm cận x→+ x→−
ngang của đồ thị hàm số y = f ( x). Vậy a = 1.
Câu 27: Cho hình chóp S.ABC có đáy là tam giác đều ABC cạnh bằng a 2, SA vuông góc với mặt
phẳng ( ABC) và SA = .
a Tính thể tích khối chóp S.AB . C 3 3 3 3 a 3 A. a 3 a 3 a 3 . B. . C. . D. . 2 4 6 3 Lời giải Chọn C
Ta có diện tích đáy ABC là 𝑆𝛥𝐴𝐵𝐶 = 2 (𝑎√2) √3 𝑎2 = √3. 4 2
Vậy thể tích của khối chóp S.ABC là 𝑉𝑆.𝐴𝐵𝐶 = 1 1 𝑎2 𝑎3 𝑆𝐴. 𝑆 . 𝑎. √3 = √3. 3 𝛥𝐴𝐵𝐶 = 3 2 6
Câu 28: Cho hàm số y = ( x − x + ) 3 2 2 4 1 . Tính y '(0) . A. 12 3 B. −12 3 C. −4 3 D. 4 3 Lời giải Chọn C 3 3 1 − 2 2
Ta có: y = (2x − 4x + ) 1
y ' = 3 (2x − 4x + ) 1 .(4x − 4) . Do đó: y '(0) = 4 − 3. Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 1
Câu 29: Tìm tiệm cận ngang của đồ thị hàm số y = . x − 2 A. x =1 B. y = 1
C. x = 2
D. y = 0 Lời giải Chọn D
Ta có: lim y = 0 và lim y = 0 nên ta có tiệm cận ngang của đồ thị hàm số là đường thẳng x→+ x→− y = 0 .
Câu 30: Cắt khối lăng trụ AB .
C A' B 'C ' bởi các mặt phẳng ( AB'C ') và ( ABC ') ta được những khối đa diện nào?
A. Ba khối tứ diện.
B. Hai khối tứ diện và một khối chóp tứ giác.
C. Một khối tứ diện và hai khối chóp tứ giác.
D. Hai khối tứ diện và hai khối chóp tứ giác Lời giải Chọn A
Dựa vào hình vẽ trên ta thấy khi cắt khối lăng trụ AB .
C A' B 'C ' bới các mặt phẳng ( AB 'C ') và
(ABC') ta được ba khối tứ diện là: AA'B'C'; ABCC'; B' ABC'.
Câu 31: Cho hàm số f ( x) xác định trên và có đồ thị hàm số y = f ( x) là đường cong trong hình dưới đây.
Khẳng định nào sau đây đúng?
A. f (2) = f (0)  f ( ) 1 .
B. f (0)  f ( ) 1  f (2) . Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
C. f (0)  f ( ) 1  f (2) .
D. f (2) = f (0)  f ( ) 1 . Lời giải Chọn B
Dựa vào đồ thị hàm số y = f ( x) ta suy ra bảng biến thiên của hàm số f ( x)
Dưa vào bảng biến thiên của hàm số f (x) ta suy ra được f (0)  f ( ) 1  f (2) .
Câu 32: Cho hàm số y = f ( x) có bảng biến thiên sau:
Tìm giá trị lớn nhất của hàm số y = f ( x) trên đoạn  1 − ;  1 . A. 2. B. 3. C. 0. D. 1. Lời giải Chọn B
Dựa vào bảng biến thiên của hàm số f ( x) ta suy ra được max f ( x) = f (0) = 3 .  1 − ;  1 x+a
Câu 33: Cho hàm số y = ( 3) có đồ thị như hình bên. Giá trị của a là A. 3. B. 2. C. 0. D. 1. Lời giải Chọn C x+a
Đồ thị hàm số y = ( 3) đia qua điểm (0 )
;1 và điểm (2;3) do đó ta có hệ phương trình Page 15
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 +a 1=  ( 3)0   a = . +a 3  =  ( 3) 0 2
Câu 34: Cho hàm số y = log x (0  a  )
1 có đồ thị (C ) và hàm số y = log x
b  có đồ thị (C) b (0 )1 a như hình dưới đây.
Khẳng định nào dưới đây đúng?
A. 0  a b 1.
B. 0  b a 1. C. 1  b  . a D. 1  a  . b Lời giải Chọn C
Xét sự tương giao của đường thẳng (d ) : y =1 và các đường () : x =1, (C) : y = log x , a
(C): y = log x . b
Gọi hoành độ giao điểm của (d ) : y =1 và () : x =1, (C) : y = log x , (C) : y = log x lần a b
lượt là: x = 1; x = a; x = b 1 2
Dễ thấy: 1  x = b x = a . 2 1
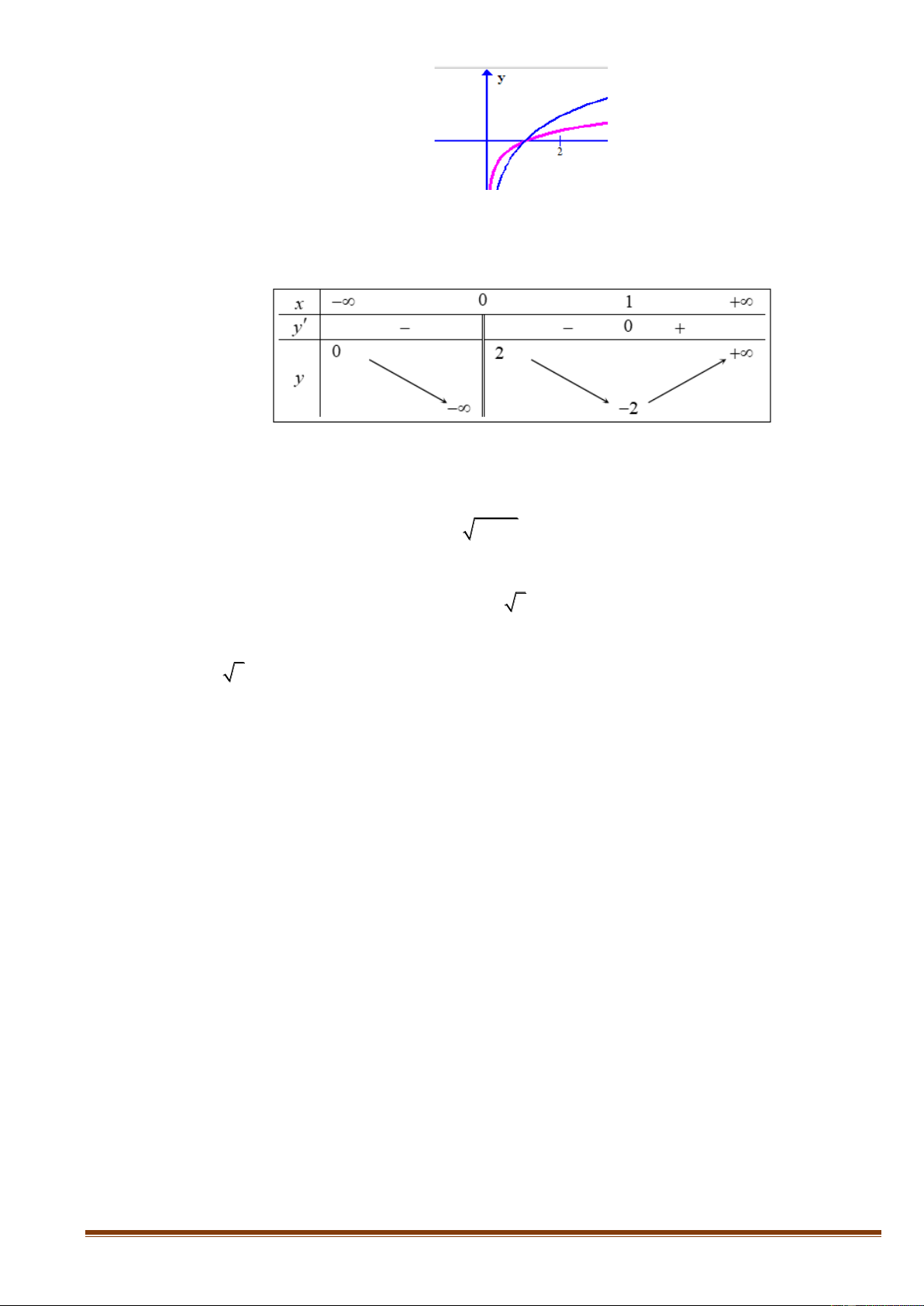
Câu 35: Cho hàm số y = f ( x) có bảng biến thiên sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho? A. 4. B. 1. C. 2. D. 3. Lời giải Chọn C Ta có: lim y = + ;  lim y = 0 x→+ x→− lim y = − ;  lim y = 2 − + x 0 → x 0 →
Nên: y = 0, x = 0 lần lượt là tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho Page 16
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
II. PHẦN TỰ LUẬN (4 câu – 3,0 điểm)
Câu 36: Giải phương trình ( 2 log − 4log + 3 2x x x −8 = 0. 2 2 ) Lời giải x  0
Điều kiện xác định:   x  3 . 2x  8 Ta có ( 2 log − 4log + 3 2x x x −8 = 0 2 2 ) x = 3 x = 3 2x −8 = 0    
 log x = 1  x = 2 . 2 2  
log x − 4log x + 3 = 0  2 2 log x = 3 x = 8   2
Kết hợp điều kiện, phương trình đã cho có 2 nghiệm x = 3, x = 8 . 1 2 Câu 37: Cho hàm số 3 2
y = x − 3mx + 2 có đồ thị (C ) . Tìm tất cả các giá trị thực của tham số m để đồ thị
(C) có hai điểm cực trị ,
A B sao cho AB = 2 5 . Lời giải Ta có 2
y ' = 3x − 6mx .  = y =
x(x − m) x 0 ' 0 3 2 = 0  .  x = 2m
Hàm số có hai điểm cực trị khi và chỉ khi phương trình y ' = 0 có hai nghiệm phân biệt, hay
m  0 . Khi đó hàm số có hai điểm cực trị x = 0 và x = 2m .
Tọa độ hai điểm cực trị là A( ) B( 3 0; 2 , 2 ; m 4 − m + 2). Theo bài ra 2 6
AB = 2 5  4m +16m = 2 5 6 2 2
16m + 4m = 20  m =1 m = 1  (TM). Vậy m = 1  .
Câu 38: Cho hình lăng trụ đứng AB .
C A' B 'C ' , có đáy ABC là tam giác vuông tại A, AB = , a
AC = a 3 . Góc tạo bởi mặt phẳng (B ' AC) và ( ABC) bằng 0 60 .
c) Tính thể tích của khối lăng trụ AB .
C A' B 'C ' .
d) Tính khoảng cách giữa hai đường thẳng B 'C và AB Lời giải
a) Ta có (B' AC) ( ABC) = AC Page 17
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 ( )1
AB '  (B ' AC), AB ' ⊥ AC
do AC ⊥ ( ABB' A') (2)
AB  ( ABC), AB ⊥ AC do ABC là tam giác vuông tại A ( ) 3 Từ ( ) 1 (2) và ( )
3 suy ra góc tạo bởi mặt phẳng (B ' AC) và ( ABC) là 0 BAB ' = 60 BB '
Xét tam giác vuông BAB' tại B: 0 0 tan 60 =  BB ' = A . B tan 60 = a 3 AB 3 1 1 3a V =AA'.S = AA '.A . B AC = .a 3. . a a 3 = .
ABC. A' B 'C ' ABC 2 2 2
b)Tính khoảng cách giữa hai đường thẳng B 'C và AB
kẻ CD // AB suy ra AB // (CDA' B') do đó d ( A ,
B B 'C) = d ( A ,
B (A' B ' DC)) = d ( ,
A (A' B ' DC))
Từ A hạ AH ⊥ A'C (4)
mặt khác CD ⊥ ( ACC ' A')  CD ⊥ AH (5)
Từ (4) và (5) ta có AH ⊥ ( A'CDB') . Nên AH = d ( ,
A (A'CDB '))
Xét tam giác vuông cân AA'C suy ra 1 1 a AH = A 'C = (AA')2 1 6 2 2 2 + AC = 3a + 3a = . 2 2 2 2 a 6
Vậy khoảng cách giữa hai đường thẳng B 'C và AB bằng 2 Câu 39: Cho ,
x y là các số nguyên dương và nhỏ hơn 2021và thỏa mãn đẳng thức sau: − 2( x − ) 2x 1 1 + 5
= y +1+ log 25y +100 5 ( )
Tính giá trị biểu thức T = 12x − y Lời giải Page 18
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 −
Biến đổi đẳng thức: 2( x − ) 2x 1 1 + 5
= y +1+ log 25y +100 5 ( ) −
 (2x − ) 2x 1 1 + 5
= y + 2+ log 25 y + 4 5 ( ) −
 (2x − ) 2x 1 1 + 5
= ( y + 4)+log y +4 5 ( ) 2x 1 − (2x− ) 1  5 + log 5
= y + 4 + log y + 4 ( ) * 5 ( ) 5 ( )
Xet hàm số f (t) = t + log t với t  0 5 1
Đạo hàm f '(t) = 1+
 0, với mọi t  0 nên suy ra hàm f (t) = t + log t đồng biến với t.ln 5 5
t  0 . Để phương trình ( ) * xảy ra khi 2x 1 5 − = y + 4 Theo giả thiết y Z + 
,1  y  2021  5  y + 4  2025 + x− 1 log 2025 Suy ra 2 1 5 5  5
 2025 1 2x −1 log 2025 1 x  5 2 Mà x Z + 
nên có các trường hợp sau x 1 2 y 1 121 119 119
T = 120x − y
Vậygiá trị biểu thức T = 12x − y = 119. Page 19
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 03
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Giá trị lớn nhất của hàm số f ( x) 3
= x −3x + 2 trên đoạn −3;  3 bằng A. 20 . B. 16 − . C. 4. D. 0. Câu 2:
Cho hàm số y = f ( x) liên tục trên đoạn  1 − ; 
2 và có đồ thị như hình
vẽ bên. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
hàm số đã cho trên đoạn  1 − ; 
2 . Giá trị M − 2m bằng A. 7 . B. 1 − . C. 8 − . D. 4 . Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh, SA vuông góc
với mặt phẳng đáy. Tìm tâm mặt cầu ngoại tiếp hình chóp S.ABCD
A. Trung điểm . SB
B. Trung điểm SC.
C. Trung điểm . BC
D. Trung điểm . AC Câu 4:
Khối hộp chữ nhật có ba cạnh là 3; 4;5 có thể tích là A. 60 B. 8 C. 20 D. 30 Câu 5:
Tiệm cận đứng của đồ thị hàm số 3 y = x + là: 2
A. x = 0 .
B. x = 3.
C. x = 2 . D. x = 2 − . Câu 6:
Cho a là số thực dương khác 1. Đẳng thức nào sau đây đúng với mọi số dương x, y ? x log x x A. log a = . B. log
= log x + log y . a a a a y log y y a x x C. log
= log x − log y . D. log
= log x − y . a a ( ) a a a y y Câu 7:
Một hình trụ có bán kính đáy bằng r và thiết diện qua trục là một hình vuông. Khi đó diện tích
toàn phần của hình trụ đó bằng. A. 2 6 r . B. 2 4 r . C. 2 8 r . D. 2 2 r . − Câu 8:
Tập xác định D của hàm số 2021 y = x là A. D = .
B. D = 0;+).
C. D = (0;+). D. D = \   0 . Câu 9:
Giả sử a, b là các số dương, ,   . Đẳng thức nào sau đây sai?     a a a −        A. = .   B. = a .
C. (ab) = a .b . D. . a .a = a .  b    b a
Câu 10: Cho hàm số y = f ( x) có bảng biến thiên như sau:
Số nghiệm thực của phương trình f (x) − 2 = 0 là A. 0 . B. 2 . C. 4 . D. 3 . Page 1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 11: Với a, b là các số thực dương tùy ý với a khác 1, đặt 3 6
P = log b + log b . Mệnh đề nào dưới 2 a a đây đúng?
A. P = 6 log b .
B. P = 9 log b .
C. P = 15log b .
D. P = 27 log b . a a a a
Câu 12: Cho hàm số f ( x) có bảng xét dấu của đạo hàm như sau:
Hàm số y = f (x) có bao nhiêu điểm cực trị? A. 1. B. 3 . C. 2 . D. 4 .
Câu 13: Thể tích V của một khối cầu có bán kính R bằng 4 1 4 A. 3 V =  R . B. 3 V = 4 R . C. 3
V =  R . D. 2 V =  R . 3 3 3
Câu 14: Gọi l, ,
h R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của một hình nón, đẳng thức nào sau đây đúng? 1 1 1 A. 2 2 2
l = h + R . B. 2 l = . h R . C. 2 2 2
R = h + l . D. = + . 2 2 2 l h R
Câu 15: Số nghiệm thực của phương trình x x+2 4 − 2 + 3 = 0 là: A. 1. B. 0. C. 3. D. 2.
Câu 16: Gọi l, ,
h r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích
xung quanh S của hình nón là xq 1
A. Sxq =  rl.
B. Sxq =  r . h C. 2 Sxq =  r . h
D. Sxq = 2 rl. 3
Câu 17: Hình nào sau đây không phải là hình đa diện lồi? Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 2. B. Hình 4. C. Hình 1. D. Hình 3.
Câu 18: Cho phương trình 2x 1
3 + − 4.3x +1 = 0. Khi đặt 3x t =
ta được phương trình nào dưới đây? A. 2
3t − t +1 = 0. B. 2
3t − 4t +1 = 0. C. 2
t − 4t + 2 = 0. D. 2
t − 4t +1 = 0.
Câu 19: Cho hàm số f ( x) có bảng xét dấu của đạo hàm như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. (− ;  − ) 1 . B. (1;+). C. ( 1 − ; ) 1 . D. ( 3 − ;− ) 1 .
Câu 20: Khối trụ tròn xoay có bán kính đáy bằng a và chiều cao bằng 2a có thể tích V bằng 2 4 A. 3
V = 2 a . B. 3 V =  a . C. 3
V = 4 a . D. 3 V =  a . 3 3 3
Câu 21: Hàm số y = ln (3 − 2x) có đạo hàm với mọi x  là 2 1 1 −2 3 A. . − . . . 3 − B. 2x 3 − C. 2x 3 − D. 2x 3 − 2x Page 2
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 1
Câu 22: Giá trị của log
với a  0; a  1 bằng a 3 a 1 1 A. . B. − . C. 3. − D. 3. 3 3
Câu 23: Phương trình log x + log
x − 3 = 2 có bao nhiêu nghiệm? 2 2 ( ) A. 3. B. 0. C. 1. D. 2.
Câu 24: Nghiệm của phương trình log x +1 = 4 là 2 ( )
A. x = 17.
B. x = 7.
C. x = 15. D. x = 3.
Câu 25: Cho hàm số y = f ( x) xác định và liên tục trên , có bảng biến thiên như hình sau:
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng (− ;  − ) 1 .
B. Hàm số đồng biến trên khoảng ( 1 − ;+).
C. Hàm số đồng biến trên khoảng (1;+).
D. Hàm số đồng biến trên khoảng ( ; − ) 1 .
Câu 26: Thể tích khối chóp có diện tích đáy B và chiều cao h là 1 1 1 A. . Bh B. . Bh C. . Bh D. . Bh 3 2 6
Câu 27: Hình nào dưới đây là hình đa diện? A. Hình 3. B. Hình 2. C. Hình 1. D. Hình 4. 2 Câu 28: Hàm số 5x x y − = có đạo hàm là 2 − A. ( ) 2 2 1 5x . x x − − ln 5 .
B. 5x x.ln 5 . C. ( ) 2 2 1 5x x x − − . D. ( ) 2 2 1 5x x x x − − − .
Câu 29: Tập xác định của hàm số y = log x − 2 2021 ( ) A. ( ; −  2 . B. ( ; − 2) . C. (2;+) . D. 2;+) .
Câu 30: Nghiệm của phương trình x 1 2 + = 8 là:
A. x = 3.
B. x = 2 .
C. x = 4 .
D. x =1 .
Câu 31: Cho hàm số y
f (x) có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại điểm A. x 3. B. x 1. C. x 2. D. x 2. log 5 a log 5 . b log 5 Câu 32: Cho 2 và 3 Hãy tính 6 theo a và b. 1 ab A. log 5 . B. 2 2 log 5 a b . C. log 5 a . b D. log 5 . 6 a b 6 6 6 a b Page 3
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 33: Đường cong trong hình bên dưới là đồ thị của hàm số nào trong bốn hàm số được liêt kê ở bốn
phương án dưới đây? A. 2 y x x 1. B. 4 2 y x x 1. C. 3 2 y x x 1. D. 3 y x 3x 1. 2x − 3
Câu 34: Đường tiệm cận ngang của đồ thị hàm số y = là: x +1 3
A. y = 0. B. y = 3. −
C. y = 2. D. y = . 2
Câu 35: Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây? x +1 2x +1 A. y = B. y = C. 3
y = x − 3x −1. D. 4 2
y = x + x +1 x −1 x −1
II. PHẦN TỰ LUẬN (4 câu – 3,0 điểm)
Câu 36: Giải phương trình: log x + log x − 6 = log 7. 2 2 ( ) 2
Câu 37: Cho hình lăng trụ đứng AB .
C A' B 'C ' có đáy ABC là tam giác vuông cân tại , A AB = , a mặt
phẳng ( AB'C ') hợp với mặt phẳng đáy một góc 0
30 . Tính thể tích khối lăng trụ AB .
C A' B 'C '. (m + ) 1 x − 2
Câu 38: Tìm tất cả các giá trị của tham số m để hàm số y = x −
đồng biến trên từng khoảng xác m định của nó. x x
Câu 39: Giải phương trình: ( − ) + ( + ) x+3 5 21 7 5 21 = 2 -----HẾT----- Page 4
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 HƯỚNG DẪN GIẢI
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Giá trị lớn nhất của hàm số f ( x) 3
= x −3x + 2 trên đoạn −3;  3 bằng A. 20 . B. 16 − . C. 4. D. 0. Lời giải Chọn A Hàm số f ( x) 3
= x −3x + 2 xác định và liên tục trên  3 − ;  3 .
Ta có: f ( x) 2 = 3x −3 x = 1−3;  3
Do đó: f ( x) 2
= 0  3x − 3 = 0   . x = −1  −3;  3 Mà: f (− ) 3 = 1 − 6 , f (− ) 1 = 4, f (− ) 1 = 0 , f ( ) 3 = 20 .
Vậy max y = f (3) = 20 .  3 −  ;3 Câu 2:
Cho hàm số y = f ( x) liên tục trên đoạn  1 − ; 
2 và có đồ thị như hình vẽ bên. Gọi M , m lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn  1 − ; 
2 . Giá trị M − 2m bằng A. 7 . B. 1 − . C. 8 − . D. 4 . Lời giải Chọn A
Dựa vào đồ thị ta suy ra được giá trị lớn nhất của hàm số trên đoạn  1 − ; 
2 là 3 , giá trị nhỏ nhất
của hàm số trên đoạn  1 − ;  2 là 2 − .
Vậy M = 3 , m = 2
−  M − 2m = 3− 2.( 2 − ) = 7. Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh, SA vuông góc với mặt phẳng đáy. Tìm tâm
mặt cầu ngoại tiếp hình chóp S.ABCD
A. Trung điểm . SB
B. Trung điểm SC.
C. Trung điểm . BC
D. Trung điểm . AC Lời giải Chọn B Page 5
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Ta chứng minh được:
BC ⊥ (SAB)  BC ⊥ SB  ΔSBC vuông tại B .
CD ⊥ (SAD)  CD ⊥ SD  ΔSCD vuông tại D .
SA ⊥ ( ABCD)  SA ⊥ AC  ΔSAC vuông tại A . 1
Gọi O là trung điểm cạnh SC . Khi đó: OA = OC = OD = OB = OS = SC . 2
Do đó O là tâm mặt cầu ngoại tiếp khối chóp S.ABCD . Câu 4:
Khối hộp chữ nhật có ba cạnh là 3; 4;5 có thể tích là A. 60 B. 8 C. 20 D. 30 Lời giải Chọn A
Thể tích khối hộp chữ nhật là: V = 3.4.5 = 60 . Câu 5:
Tiệm cận đứng của đồ thị hàm số 3 y = x + là: 2
A. x = 0 .
B. x = 3.
C. x = 2 . D. x = 2 − . Lời giải Chọn D
Ta có: lim y = + TCĐ: x = 2 − + x 2 →− Câu 6:
Cho a là số thực dương khác 1. Đẳng thức nào sau đây đúng với mọi số dương x, y ? x log x x A. log a = . B. log
= log x + log y . a a a a y log y y a x x C. log
= log x − log y . D. log
= log x − y . a a ( ) a a a y y Lời giải Chọn C Câu 7:
Một hình trụ có bán kính đáy bằng r và thiết diện qua trục là một hình vuông. Khi đó diện tích
toàn phần của hình trụ đó bằng. A. 2 6 r . B. 2 4 r . C. 2 8 r . D. 2 2 r . Lời giải Chọn A
Thiết diện qua trục là một hình vuông nên chiều cao hình trụ h = 2r . Vậy 2 2 = 2 + 2 = 6 . tp S rh r r − Câu 8:
Tập xác định D của hàm số 2021 y = x là A. D = .
B. D = 0;+).
C. D = (0;+). D. D = \   0 . Lời giải Chọn D Câu 9:
Giả sử a, b là các số dương, ,   . Đẳng thức nào sau đây sai?     a a a −        A. = .   B. = a .
C. (ab) = a .b . D. . a .a = a .  b    b a Lời giải Chọn D Page 6
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 10: Cho hàm số y = f ( x) có bảng biến thiên như sau:
Số nghiệm thực của phương trình f (x) − 2 = 0 là A. 0 . B. 2 . C. 4 . D. 3 . Lời giải Chọn C
Phương trình f (x) −2 = 0  f (x) = 2 từ BBT phương trình có 4 nghiệm
Câu 11: Với a, b là các số thực dương tùy ý với a khác 1, đặt 3 6
P = log b + log b . Mệnh đề nào dưới 2 a a đây đúng?
A. P = 6 log b .
B. P = 9 log b .
C. P = 15log b .
D. P = 27 log b . a a a a Lời giải Chọn A 3 6
P = log b + log b = 3log b + 3log b = 6log b . 2 a a a a a
Câu 12: Cho hàm số f ( x) có bảng xét dấu của đạo hàm như sau:
Hàm số y = f (x) có bao nhiêu điểm cực trị? A. 1. B. 3 . C. 2 . D. 4 . Lời giải Chọn D
Câu 13: Thể tích V của một khối cầu có bán kính R bằng 4 1 4 A. 3 V =  R . B. 3 V = 4 R . C. 3
V =  R . D. 2 V =  R . 3 3 3 Lời giải Chọn A
Câu 14: Gọi l, ,
h R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của một hình nón, đẳng thức nào sau đây đúng? 1 1 1 A. 2 2 2
l = h + R . B. 2 l = . h R . C. 2 2 2
R = h + l . D. = + . 2 2 2 l h R Lời giải Chọn A Page 7
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 15: Số nghiệm thực của phương trình x x+2 4 − 2 + 3 = 0 là: A. 1. B. 0. C. 3. D. 2. Lời giải Chọn D 2x =1 x = 0
Ta có: 4x − 2x+ + 3 = 0  (2x )2 2
− 4.2x + 3 = 0     . 2x = 3 x = log 3  2
Vậy phương trình đã cho có 2 nghiệm thực phân biệt.
Câu 16: Gọi l, ,
h r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích
xung quanh S của hình nón là xq 1
A. Sxq =  rl.
B. Sxq =  r . h C. 2 Sxq =  r . h
D. Sxq = 2 rl. 3 Lời giải Chọn A
Câu 17: Hình nào sau đây không phải là hình đa diện lồi? Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 2. B. Hình 4. C. Hình 1. D. Hình 3. Lời giải Chọn A
Dựa vào khái niệm đa diện lồi ta có đáp án A
Câu 18: Cho phương trình 2x 1
3 + − 4.3x +1 = 0. Khi đặt 3x t =
ta được phương trình nào dưới đây? A. 2
3t − t +1 = 0. B. 2
3t − 4t +1 = 0. C. 2
t − 4t + 2 = 0. D. 2
t − 4t +1 = 0. Lời giải Chọn B Ta có 2x 1 + x 2 3
− 4.3 +1= 0  3.3 x − 4.3x +1= 0 Đặt 3x t = ta được phương trình 2
3t − 4t +1 = 0.
Câu 19: Cho hàm số f ( x) có bảng xét dấu của đạo hàm như sau: Page 8
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. (− ;  − ) 1 . B. (1;+). C. ( 1 − ; ) 1 . D. ( 3 − ;− ) 1 . Lời giải Chọn C
Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên khoảng ( 1 − ; ) 1 .
Câu 20: Khối trụ tròn xoay có bán kính đáy bằng a và chiều cao bằng 2a có thể tích V bằng 2 4 A. 3
V = 2 a . B. 3 V =  a . C. 3
V = 4 a . D. 3 V =  a . 3 3 Lời giải Chọn A
Thể tích khối trụ tròn xoay là 2 3
V =  .a .2a = 2 a . 3
Câu 21: Hàm số y = ln (3 − 2x) có đạo hàm với mọi x  là 2 1 1 −2 3 A. . − . . . 3 − B. 2x 3 − C. 2x 3 − D. 2x 3 − 2x Lời giải Chọn C 3 Với x  , ta có: 2  −  −
y = ( ( − x)) (3 2x) 2 ln 3 2 = = . 3 − 2x 3 − 2x 1
Câu 22: Giá trị của log
với a  0; a  1 bằng a 3 a 1 1 A. . B. − . C. 3. − D. 3. 3 3 Lời giải Chọn C 1 − Ta có: 3 log = log a = 3 − a 3 a a
Câu 23: Phương trình log x + log
x − 3 = 2 có bao nhiêu nghiệm? 2 2 ( ) A. 3. B. 0. C. 1. D. 2. Lời giải Chọn C
ĐK: x  3 log x + log x − 3 = 2  log x x − 3 = 2 2 2 ( ) 2 ( ( ))  ( x = − x x − 3) 1 2
= 4  x − 3x − 4 = 0   x = 4
Kết hợp với điều kiện ta có phương trình có 1 nghiệm là x = 4.
Câu 24: Nghiệm của phương trình log x +1 = 4 là 2 ( )
A. x = 17.
B. x = 7.
C. x = 15. D. x = 3. Lời giải Chọn C Page 9
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 ĐK: x  1 − log
x +1 = 4  x +1 = 16  x = 15. 2 ( )
Câu 25: Cho hàm số y = f ( x) xác định và liên tục trên , có bảng biến thiên như hình sau:
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng (− ;  − ) 1 .
B. Hàm số đồng biến trên khoảng ( 1 − ;+).
C. Hàm số đồng biến trên khoảng (1;+).
D. Hàm số đồng biến trên khoảng ( ; − ) 1 . Lời giải Chọn A
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng (− ;  − ) 1 .
Câu 26: Thể tích khối chóp có diện tích đáy B và chiều cao h là 1 1 1 A. . Bh B. . Bh C. . Bh D. . Bh 3 2 6 Lời giải Chọn A 1
Thể tích khối chóp có diện tích đáy B và chiều cao h là V = B . h 3
Câu 27: Hình nào dưới đây là hình đa diện? A. Hình 3. B. Hình 2. C. Hình 1. D. Hình 4. Lời giải Chọn D
Hình 1: có cạnh không phải là cạnh chung của 2 mặt.
Hình 2: có cạnh là cạnh chung của nhiều hơn 2 mặt.
Hình 3: có điểm chung của 2 mặt không phải là đỉnh. 2 Câu 28: Hàm số 5x x y − = có đạo hàm là 2 − A. ( ) 2 2 1 5x . x x − − ln 5 .
B. 5x x.ln 5 . C. ( ) 2 2 1 5x x x − − . D. ( ) 2 2 1 5x x x x − − − . Lời giải Chọn A
Câu 29: Tập xác định của hàm số y = log x − 2 2021 ( ) A. ( ; −  2 . B. ( ; − 2) . C. (2;+) . D. 2;+) . Lời giải Chọn C
Câu 30: Nghiệm của phương trình x 1 2 + = 8 là: Page 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
A. x = 3.
B. x = 2 .
C. x = 4 .
D. x =1 . Lời giải Chọn B x 1 + x 1 + 3 2 = 8  2
= 2  x +1= 3  x = 2 .
Câu 31: Cho hàm số y
f (x) có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại điểm A. x 3. B. x 1. C. x 2. D. x 2. Lời giải Chọn A
Căn cứ vào BBT ta có hàm số đã cho đạt cực đại tại điểm x 3. log 5 a log 5 . b log 5 Câu 32: Cho 2 và 3 Hãy tính 6
theo a và b. 1 ab A. log 5 . B. 2 2 log 5 a b . C. log 5 a . b D. log 5 . 6 a b 6 6 6 a b Lời giải Chọn A 1 1 1 ab Ta có log 5 . 6 log 6 log 3 log 2 1 1 a b 5 5 5 a b
Câu 33: Đường cong trong hình bên dưới là đồ thị của hàm số nào trong bốn hàm số được liêt kê ở bốn
phương án dưới đây? A. 2 y x x 1. B. 4 2 y x x 1. C. 3 2 y x x 1. D. 3 y x 3x 1. Lời giải Chọn D
Đồ thị hàm số đã cho là đồ thị hàm số của hàm đa thức bậc ba có hệ số của 3 x âm. 2x − 3
Câu 34: Đường tiệm cận ngang của đồ thị hàm số y = là: x +1 3
A. y = 0. B. y = 3. −
C. y = 2. D. y = . 2 Lời giải Page 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Chọn C
Theo định nghĩa sách giáo khoa. 2x − 3
lim y = 2 nên đồ thị y =
có TCN là đường thẳng y = 2. + x→ x 1
Câu 35: Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây? x +1 2x +1 A. y = B. y = C. 3
y = x − 3x −1. D. 4 2
y = x + x +1 x −1 x −1 Lời giải Chọn A
Dựa vào dáng điệu đồ thị loại đáp án C, D . + Đồ x 1 thị y =
có TCN là đường thẳng y = 1, TCN là đường thẳng x =1 x −1 + Đồ 2x 1 thị y =
có TCN là đường thẳng y = 2, TCN là đường thẳng x =1 . x −1
II. PHẦN TỰ LUẬN (4 câu – 3,0 điểm)
Câu 36: Giải phương trình: log x + log x − 6 = log 7. 2 2 ( ) 2 Lời giảix  0 x  0 ĐKXĐ:     x  6. x − 6  0 x  6 log x + log x − 6 = log 7 2 2 ( ) 2
 log x x − 6  = log 7 2  ( ) 2  log ( 2 x − 6x = log 7 2 ) 2 2  x − 6x = 7 2
x − 6x − 7 = 0
x = −1 (KTMDK )
  x = 7 (TMDK)  x = 7.
Vậy nghiệm của phương trình x = 7.
Câu 37: Cho hình lăng trụ đứng AB .
C A' B 'C ' có đáy ABC là tam giác vuông cân tại , A AB = , a mặt
phẳng ( AB'C ') hợp với mặt phẳng đáy một góc 0
30 . Tính thể tích khối lăng trụ AB .
C A' B 'C '. Lời giải Page 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 B C A B' C' I A'
Gọi I là trung điểm của cạnh B 'C '.
Ta có: góc giữa hai mặt phẳng ( AB'C ') và ( ABC) chính là góc giữa hai mặt phẳng ( AB'C ') và (AB'C').
Vì ABC là tam giác vuông cân tại A nên hai mặt bên ( ABB' A') và ( ACC ' A') là hai hình chữ
nhật bằng nhau. Do đó AC ' = AB '.
Suy ra tam giác  AB 'C ' là tam giác cân tại .
A Khi đó: AI ⊥ B 'C '.
A' B 'C ' là tam giác vuông cân tại A nên A'I ⊥ B'C'.
 ( AB'C ') ( A'B'C ') = B'C ' 
AI ⊥ B 'C ', AI  ( AB'C ')  (( AB'C '),( A' B'C ')) 0 = AIA' = 30 .
A'I ⊥ B'C ', A'I   (A'B'C ') BC = a 2. 1 a 2 A ' I = BC = . 2 2 a 2 3 a 6 0
AA ' = A ' I. tan 30 = . = . 2 3 6 3 a 6 1 a 6 2 V = AA'.S = . .a = .
ABC. A' B 'C '  ABC 6 2 12 (m + ) 1 x − 2
Câu 38: Tìm tất cả các giá trị của tham số m để hàm số y = x −
đồng biến trên từng khoảng xác m định của nó. Lời giải
Tập xác định của hàm số: D = \   m . 2 −m − m + 2 Ta có: y ' =   ( . x − m) , x D 2 Hàm số
đồng biến trên từng khoảng xác định của nó  y '  0, x   D 2
 −m − m + 2  0  2 −  m 1. x x
Câu 39: Giải phương trình: ( − ) + ( + ) x+3 5 21 7 5 21 = 2 Lời giải Page 13
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x x x x  −   +  x+ 5 21 5 21 Ta có (5 − 21) + 7(5 + 21) 3 = 2    + 7  = 8     2 2     x x  −   +  Đặt 5 21 1 5 21 t =    =   ;t  0     2 t 2     7 t  =1( ) n Phương trình trở thành: 2 t +
= 8  t −8t + 7 = 0   t t  = 7( ) n x  −  Với 5 21 t = 1    = 1  x = 0   . 2   x  −  Với 5 21 t = 7    = 7  x = log x ( 7 )    5− 21 2        2  
Vậy phương trình có hai nghiệm x = 0; x = log . x ( 7)  5− 21      2   Page 14
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 04
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Cho hàm số f ( x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (− ;  − ) 1 . B. (0 ) ;1 . C. ( 1 − ; ) 1 . D. ( 1 − ;0) Câu 2:
Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là A. 3 B. 1 C. 2 D. 0 Câu 3:
Giá trị nhỏ nhất của hàm số f ( x) 4 2
= x −12x − 4 trên đoạn 0;9 bằng A. 39 − . B. 40 − . C. 36 − . D. 4 − . Câu 4:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y = x − 3x . B. 3
y = −x + 3x . C. 4 2
y = x − 2x . D. 4 2
y = −x + 2x . Câu 5:
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? 2x −1 x +1 A. y = y = x − B. 1 x − 1 C. 4 2
y = x + x +1 D. 3
y = x − 3x −1 x − 2 Câu 6:
Tiệm cận ngang của đồ thị hàm số y = x + là 1 A. y = 2 − .
B. y = 1. C. x = 1 − .
D. x = 2 . Câu 7: Cho a  0, , m n
. Khẳng định nào sau đây đúng? Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 m n m a A. m n m n a a a + + = . B. m. n m n a a a − = .
C. ( m ) = ( n a a ) . D. n−m = a . n a Câu 8:
Với a là số thực dương tùy ý, lo 5 g (5a) bằng A. 5 + log + − − 5 . a B. 1 log5 . a C. 5 log5 . a D. 1 log5 . a Câu 9:
Tập xác định của hàm số y = lo − 5 g ( x 2) là A. (2;+). B. 2;+). C. . D. ( ; − 2).
Câu 10: Đạo hàm của hàm số 5x y = là x − 5 A. x 1 y = . x 5 . B. 5 . x y = C. 5 . x y = ln 5. D. y = . ln 5
Câu 11: Tìm mệnh đề đúng trong các mệnh đề sau. A. Hàm số x
y = a với a 1 nghịch biến trên khoảng (− ;  +) . B. Hàm số x
y = a với 0  a  1 đồng biến trên khoảng (− ;  +) .
C. Hàm số y = loga x với a 1 đồng biến trên khoảng (0;+) .
D. Hàm số y = log   − + a x với 0
a 1 nghịch biến trên khoảng ( ; ).
Câu 12: Phương trình log = 2 ( x − 5) 4 có nghiệm là
A. x = 3.
B. x = 13.
C. x = 21.
D. x = 11.
Câu 13: Tập nghiệm của phương trình 9x 2.3x + − 3 = 0là
A. S = 1;−  3 .
B. S = 0;−  3 . C. S = 1;  3 . D. S =   0 .
Câu 14: Tập hợp nghiệm của bất phương trình log  2 ( x + ) 1 3 là A. S = (− ;  7). B. S = ( 1 − ; 7). C. S = ( 1 − ; 8). D. S = (− ;  8).
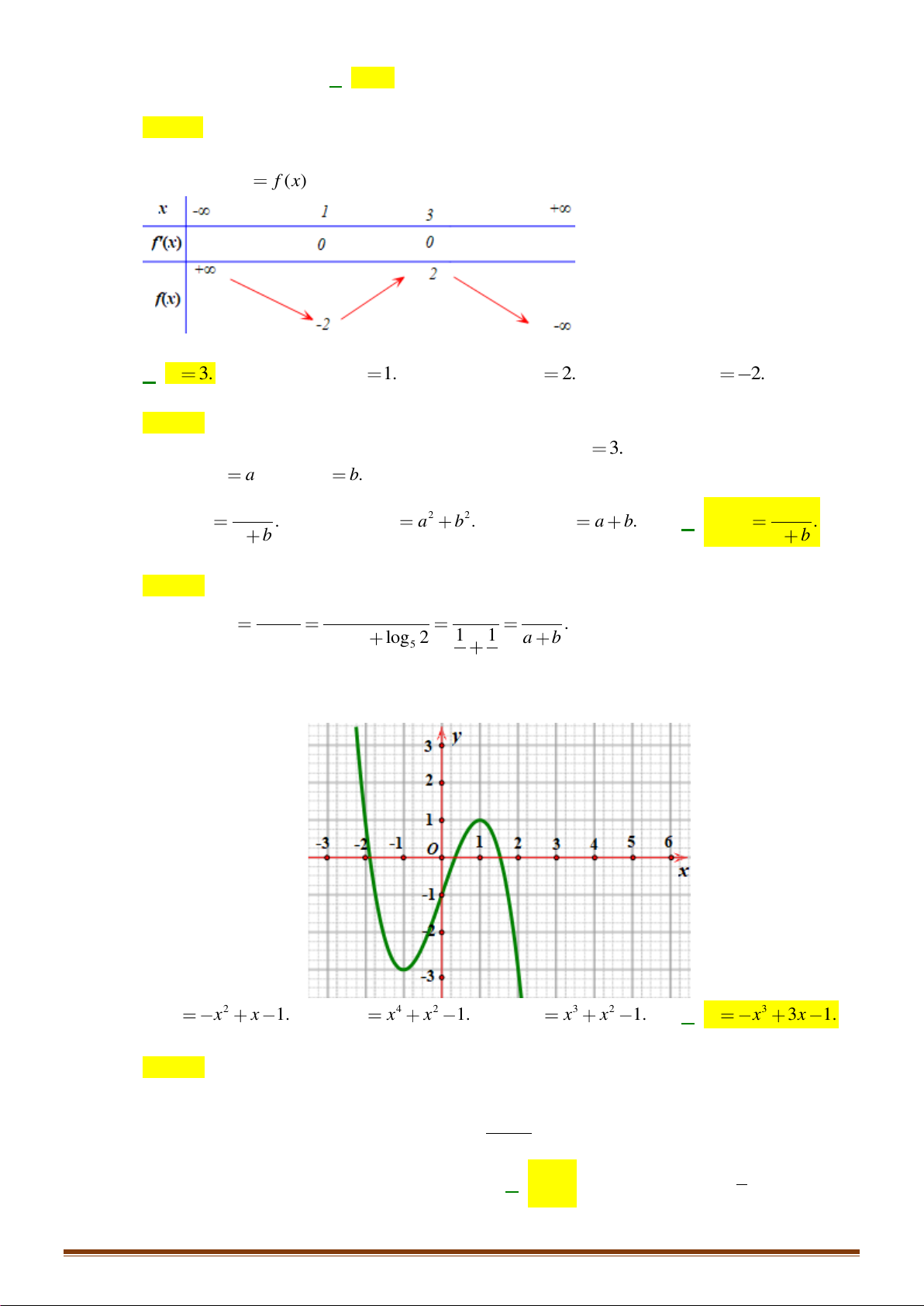
Câu 15: Trong các hình sau, hình nào không phải đa diện lồi? A. B. C. D.
Câu 16: Cho khối lăng trụ có diện tích đáy B = 3 và chiều cao h = 4 . Thể tích của khối lăng trụ đã cho bằng A. 6  B. 12 C. 36 D. 4 
Câu 17: Cho tam giác SAO vuông cân tại O có diện tích bằng 2 , quay tam giác SAO xung quanh cạnh
SO . Tính thể tích V của khối tròn xoay được tạo thành. 4 8 4 A. V = 
B. V =   C. V =  D. V =   3 3 3 Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 18: Cho khối nón có chiều cao h , bán kính đáy r . Thể tích khối nón đã cho bằng 2 hr 2 4hr A. 2
2hr B. C. 2
hr D. 3 3
Câu 19: Cho khối cầu có bán kính R = 3. Thể tích khối cầu đã cho bằng A. 4  B. 36  C. 12  D. 108 
Câu 20: Diện tích xung quanh của hình nón có chiều cao h = 4 và bán kính đáy r = 3 là A. 12  B. 15  C. 30  D. 24  2x −1
Câu 21: Cho hàm số y = x − . Khẳng định nào dưới đây là SAI? 2
A. Hàm số nghịch biến trên khoảng ( ; − 0).
B. Hàm số nghịch biến trên (− ;  2) (2;+ )  .
C. Hàm số nghịch biến trên khoảng (0;1) .
D. Hàm số nghịch biến trên khoảng (2; +) .
Câu 22: Đồ thị của hàm số 3 2
y = −x + 3x + 5 có hai điểm cực trị A và B . Tính diện tích S của tam giác
OAB với O là gốc tọa độ. 10 A. S = .
B. S = 9 .
C. S =10 . D. S = 5. 3
Câu 23: Giá trị lớn nhất của hàm số f ( x) 4 2
= x − 2x +1trên đoạn 0;2là
A. max f ( x) = 64 .
B. max f ( x) = 9 .
C. max f ( x) = 0 .
D. max f ( x) = 1. x   0;2 x   0;2 x   0;2 x   0;2 ax + b
Câu 24: Cho hàm số y =
(d  0) có đồ thị như hình bên. Khẳng định nào dưới đây đúng? cx + d
A. a  0,b  0, c  0 .
B. a  0,b  0, c  0 . C. a  0,b  0, c  0 . D. a  0,b  0, c  0 . x − −
Câu 25: Hỏi đồ thị hàm số 1 1 y =
có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang? x − 2 A. 3. B. 2. C. 1. D. 0. −
Câu 26: Tập xác định D của hàm số y = ( x − ) 3 2 9 1 là  1   1  A. D = − ;  −  ; +     . B. D = .  3   3   1 1   1 1 C. D = − ;   . D. D = \ − ;  .  3 3   3 3 Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 27: Tìm tập xác định của hàm số y = (x+ ) 2 log 2 + 3log x ? A. ( 2 − ;0)(0;+). B. (0;+) . C. ( 2; − +). D.  2; − +).
Câu 28: Cho các hàm số y = log x và y = log x có đồ thị như hình vẽ bên. Đường thẳng x = 5cắt trục a b
hoành, đồ thị hàm số y = log x và y = log x lần lượt tại ,
A B và C . Biết rằng CB = 2AB . Mệnh a b
đề nào sau đây là đúng?
A. a = 5b . B. 2 a = b . C. 3 a = b . D. 3 a = b .
Câu 29: Giá trị cực tiểu của hàm số x y = e ( 2 x − ) 3 là: 6 6 A. . B. . C. 3 − e. D. 2 − e . e 3 e
Câu 30: Tổng các nghiệm của phương trình 2
log x − 5 log x + 6 = 0 là 2 2 A. 5 . B. 13 . C. 12 . D. 32 . − − − − −
Câu 31: Gọi S là tập nghiệm của phương trình 2 2 2 x x x x 2 x x 1 2 + 2 = 4
+1 . Số phần tử của tập S là A. 1. B. 2 . C. 3 . D. 4
Câu 32: Cho một tấm bìa hình chữ nhật có kích thước 3a , 6a . Người ta muốn tạo tấm bìa đó thành bốn
hình không đáy như hình vẽ, trong đó có hai hình trụ lần lượt có chiều cao 3a , 6a và hai hình
lăng trụ tam giác đều có chiều cao lần lượt 3a , 6a 6a 6a 3a 3a H1 H 2 H 3 H 4
Trong 4 hình H1, H2, H3, H4 lần lượt theo thứ tự có thể tích lớn nhất và nhỏ nhất là A. H1, H 4 . B. H 2 , H 3 . C. H1, H 3 . D. H 2 , H 4 . 3a
Câu 33: Cho hình lăng trụ AB . C A BC
  có đáy ABC là tam giác đều cạnh a , AA = . Biết rằng hình 2
chiếu vuông góc của A lên ( ABC) là trung điểm BC . Tính thể tích V của khối lăng trụ đó. 3 2a 3 3a 3 A. 3 V = a . B. V = . C. V = . D. 3 V = a . 3 4 2 2 Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 34: Cho hình trụ có hai đáy là hai hình tròn (O) và (O) , chiều cao R 3 và bán kính đáy
R . Một hình nón có đỉnh là O và đáy là hình tròn ( ;
O R) . Tỷ số diện tích xung quanh của
hình trụ và hình nón bằng A. 3 . B. 2 . C. 2 . D. 3 .
Câu 35: Một hình nón có đường sinh bằng a 2 và góc giữa đường sinh và mặt phẳng đáy bằng 60o .
Tính thể tích của khối nón được tạo nên từ hình nón đó. 1 1 1 1 A. 3 a 6 . B. 3  a 6 . C. 3 a 6 . D. 3  a 6 . 6 3 4 12 II. PHẦN TỰ LUẬN
Câu 36: Giải phương trình log ( x + 2) + log ( x − 5)2 + log 8 = 0 3 9 1 3
Câu 37: Cho lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông tại A và AB = a , AC = a 3 , mặt phẳng ( A B
C) tạo với đáy một góc 30. Tính thể tích của khối lăng trụ AB . C A BC  .
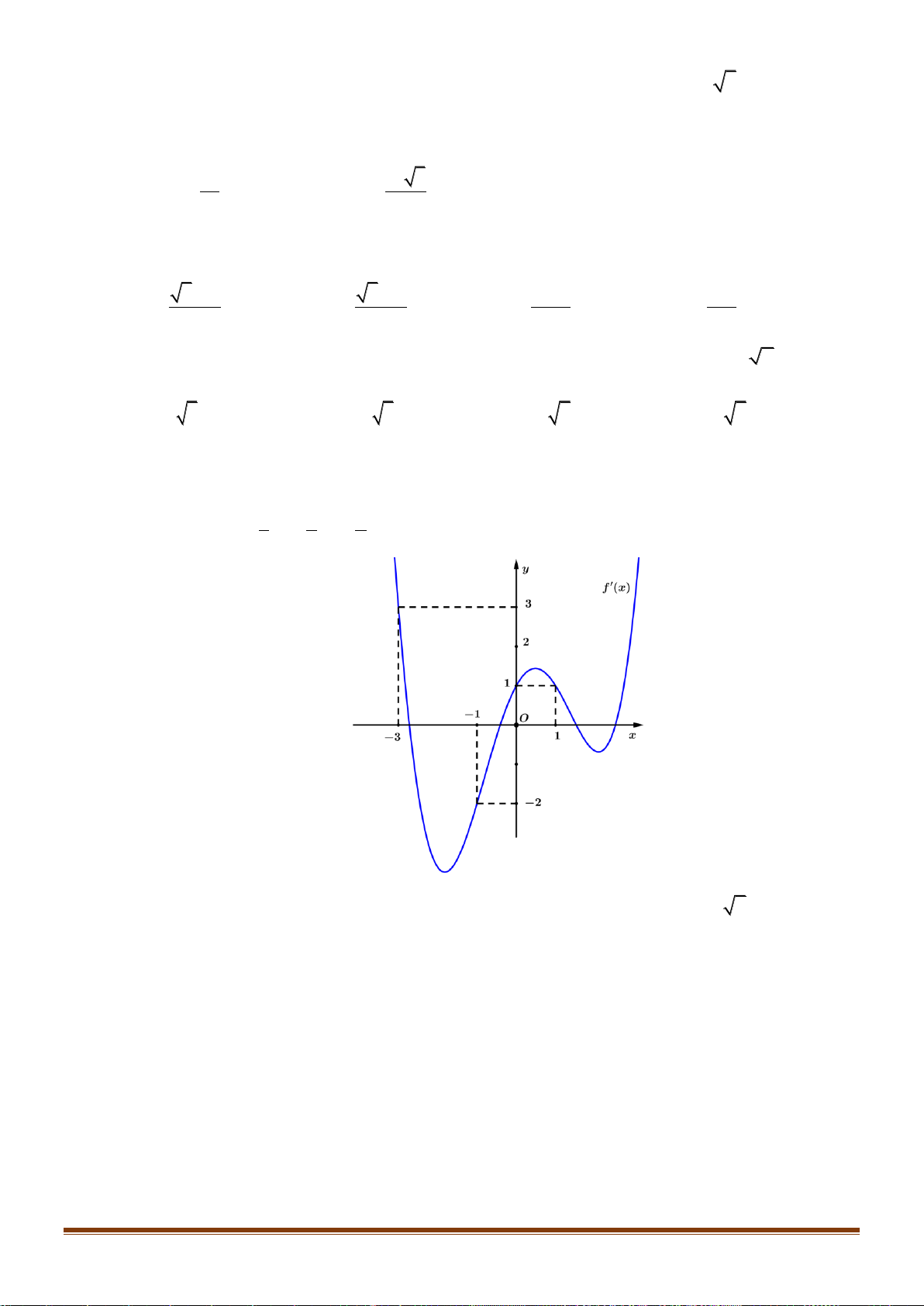
Câu 38: Cho đồ thị hàm số y = f (
x) như hình vẽ. Tìm các khoảng đồng biến của hàm số: 3 2
y = g(x) = f (3x −1) − x + 3x +1.
Câu 39: Xét các số thực a và b thỏa mãn a b  1. Tìm giá trị nhỏ nhất của biểu thức  a  2 2
P = log (a ) + 3log . a b    b b
---------- HẾT ---------- Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 BẢNG ĐÁP ÁN 1.D 2.A 3.B 4.A 5.B 6.B 7.C 8.B 9.A 10.C 11.C 12.C 13.D 14.B 15.B 16.B 17.B 18.B 19.B 20.B 21.B 22.D 23.B 24.B 25.C 26.D 27.A 28.C 29.D 30.C 31.B 32.D 33.C 34.D 35.D
HƯỚNG DẪN LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM Câu 1:
Cho hàm số f ( x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (− ;  − ) 1 . B. (0 ) ;1 . C. ( 1 − ; ) 1 . D. ( 1 − ;0) Lời giải Chọn D
Hàm số đã cho đồng biến trên khoảng ( 1 − ;0) và (1;+) Câu 2:
Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là A. 3 B. 1 C. 2 D. 0 Lời giải Chọn A
Hàm số có ba điểm cực trị. Câu 3:
Giá trị nhỏ nhất của hàm số f ( x) 4 2
= x −12x − 4 trên đoạn 0;9 bằng A. 39 − . B. 40 − . C. 36 − . D. 4 − . Lời giải Chọn B Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x = 00;9 
Ta có: f ( x) 3
= 4x − 24x ; f (x) = 0  x = 6 0;9 .  x = − 6   0;9
Tính được: f (0) = 4
− ; f (9) = 5585 và f ( 6) = 4 − 0 .
Suy ra min f ( x) = 4 − 0. 0;9 Câu 4:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y = x − 3x . B. 3
y = −x + 3x . C. 4 2
y = x − 2x . D. 4 2
y = −x + 2x . Lời giải Chọn A
Đường cong có dạng của đồ thị hàm số bậc 3 với hệ số a  0 nên chỉ có hàm số 3
y = x − 3x
thỏa yêu cầu bài toán. Câu 5:
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? 2x −1 x +1 A. y = y =
y = x + x + D. 3
y = x − 3x −1 x − B. 1 x − C. 4 2 1 1 Lời giải Chọn B
Vì từ đồ thị ta suy ra đồ thị của hàm phân thức có tiệm cận đứng là x =1 và tiệm cận ngang y = 1. x − 2 Câu 6:
Tiệm cận ngang của đồ thị hàm số y = x + là 1 A. y = 2 − .
B. y = 1. C. x = 1 − .
D. x = 2 . Lời giải Chọn B Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x − 2 x − 2 Ta có lim = 1 lim = 1 x→+ x + và 1 x→− x + . 1
Suy ra y = 1 là tiệm cận ngang của đồ thị hàm số. Câu 7: Cho a  0, , m n
. Khẳng định nào sau đây đúng? m n m a A. m n m n a a a + + = . B. m. n m n a a a − = .
C. ( m ) = ( n − a a ) . D. n m = a . n a Lời giải Chọn C Tính chất lũy thừa Câu 8:
Với a là số thực dương tùy ý, lo 5 g (5a) bằng A. 5 + log + − − 5 . a B. 1 log5 . a C. 5 log5 . a D. 1 log5 . a Lời giải Chọn B Ta có: lo = + = + 5 g (5a) lo 5 g 5 lo 5 g a 1 lo 5 g a . Câu 9:
Tập xác định của hàm số y = lo − 5 g ( x 2) là A. (2;+). B. 2;+). C. . D. ( ; − 2). Lời giải Chọn A
Điều kiện xác định: x − 2  0  x  2 . Vậy tập xác định của hàm số đã cho là D = (2;+) .
Câu 10: Đạo hàm của hàm số 5x y = là x − 5 A. x 1 y = . x 5 . B. 5 . x y = C. 5 . x y = ln 5. D. y = . ln 5 Lời giải Chọn C  
Áp dụng công thức: ( x ) x a
= a .ln a , (0  a  )
1 ta được:  = (5x ) = 5 .x y ln 5 .
Câu 11: Tìm mệnh đề đúng trong các mệnh đề sau. A. Hàm số x
y = a với a 1 nghịch biến trên khoảng (− ;  +) . B. Hàm số x
y = a với 0  a  1 đồng biến trên khoảng (− ;  +) .
C. Hàm số y = loga x với a 1 đồng biến trên khoảng (0;+) .
D. Hàm số y = log   − + a x với 0
a 1 nghịch biến trên khoảng ( ; ) . Lời giải Chọn C
Câu 12: Phương trình log = 2 ( x − 5) 4 có nghiệm là
A. x = 3.
B. x = 13.
C. x = 21.
D. x = 11. Lời giải Chọn C Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Điều kiện xác định: x  5.
Phương trình log (x −5) 4 =  − =  = 2 4 x 5 2 x 21 (thỏa điều kiện).
Vậy phương trình có nghiệm x = 21.
Câu 13: Tập nghiệm của phương trình 9x 2.3x + − 3 = 0là
A. S = 1;−  3 .
B. S = 0;−  3 . C. S = 1;  3 . D. S =   0 . Lời giải Chọn D  = x x + − =  ( x ) x 2 3 1 9 2.3 3 0 3
+ 2.3x − 3 = 0    x = 0 .
3x = −3 (x)
Vậy phương trình có tập nghiệm S =   0 .
Câu 14: Tập hợp nghiệm của bất phương trình log  2 ( x + ) 1 3 là A. S = (− ;  7). B. S = ( 1 − ; 7). C. S = ( 1 − ; 8). D. S = (− ;  8). Lời giải Chọn B x +1  0  x  1 − Ta có: log     −   2 ( x + ) 1 3   1 x 7 . 3 x +1 2 x  7
Vậy tập nghiệm của bất phương trình đã cho là S = ( 1 − ;7).
Câu 15: Trong các hình sau, hình nào không phải đa diện lồi? A. B. C. D. Lời giải Chọn B A B Lấy hai điểm ;
A B như hình vẽ ta thấy đoạn thẳng AB có một phần nằm ngoài hình đa diện. nên
hình đa diện này không phải là đa diện lồi.
Câu 16: Cho khối lăng trụ có diện tích đáy B = 3 và chiều cao h = 4 . Thể tích của khối lăng trụ đã cho bằng A. 6  B. 12 C. 36 D. 4  Lời giải Chọn B
Ta có: Thể tích khối lăng trụ là V = . B h = 3.4 =12. Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 17: Cho tam giác SAO vuông cân tại O có diện tích bằng 2 , quay tam giác SAO xung quanh cạnh
SO . Tính thể tích V của khối tròn xoay được tạo thành. 4 8 4 A. V = 
B. V =   C. V = 
D. V =   3 3 3 Lời giải Chọn B
Tam giác SAO vuông cân tại O có diện tích là 2 nên độ dài cạnh góc vuông SO = OA = 2 .
Khi tam giác SAO quay quanh SO tạo thành hình nón có đường cao là h = SO = 2 và đáy là
hình tròn bán kính r = AO = 2 . 1 8 Thể tích hình nón là: 2 V = hr = . 3 3
Câu 18: Cho khối nón có chiều cao h , bán kính đáy r . Thể tích khối nón đã cho bằng 2 hr 2 4hr A. 2
2hr B. C. 2
hr D. 3 3 Lời giải Chọn B 1
Khối nón có chiều cao h , bán kính đáy r có thể tích bằng 2 V r h . 3
Câu 19: Cho khối cầu có bán kính R = 3 . Thể tích khối cầu đã cho bằng A. 4  B. 36  C. 12  D. 108  Lời giải Chọn B 4 4
Thể tích của khối cầu đã cho là: 3 3 V =
R = .3 = 36 . 3 3
Câu 20: Diện tích xung quanh của hình nón có chiều cao h = 4 và bán kính đáy r = 3 là A. 12  B. 15  C. 30  D. 24  Lời giải Chọn B
Gọi l là độ dài đường sinh của hình nón. Khi đó 2 2 2 2
l = h + r = 4 + 3 = 5. Vậy S
= .r.l = .3.5 = 15. xq 2x −1
Câu 21: Cho hàm số y = x − . Khẳng định nào dưới đây là SAI? 2 Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
A. Hàm số nghịch biến trên khoảng ( ; − 0).
B. Hàm số nghịch biến trên (− ;  2) (2;+ )  .
C. Hàm số nghịch biến trên khoảng (0;1) .
D. Hàm số nghịch biến trên khoảng (2; +) . Lời giải Chọn B
+) Tập xác định D = \{2} 2x −1 3 − +) Ta có y =  y =  0 với x   D 2 . x − 2 (x − 2)
Vậy hàm số nghịch biến trên khoảng ( ; − 2) và (2;+) +) Mặt khác (− ;  0)  (− ;  2) ; (0;1)  (− ;
 2) nên đáp án B, C, D đún g.
Câu 22: Đồ thị của hàm số 3 2
y = −x + 3x + 5 có hai điểm cực trị A và B . Tính diện tích S của tam giác
OAB với O là gốc tọa độ. 10 A. S = .
B. S = 9 .
C. S =10 . D. S = 5. 3 Lời giải Chọn D Ta có: 2
y = −3x + 6x . x = 0 2 y = 0  3
− x + 6x = 0   . x = 2
Tọa độ hai điểm cực trị của đồ thị hàm số là A(0;5) và B(2;9) .
AB = (2;4)  AB = 2 5 .
Phương trình đường thẳng AB qua A(0;5) có véc tơ pháp tuyến n = ( 2 − ; )
1 : 2x − y + 5 = 0 . d (O AB) 2.0 − 0 + 5 , = = 5 . 2 + (− )2 2 1 1 1
Vậy diện tích của tam giác OAB là: S = d ( ,
O AB).AB = . 5.2 5 = 5 . 2 2
Câu 23: Giá trị lớn nhất của hàm số f ( x) 4 2
= x − 2x +1trên đoạn 0;2là
A. max f ( x) = 64 .
B. max f ( x) = 9 .
C. max f ( x) = 0 .
D. max f ( x) = 1. x   0;2 x   0;2 x   0;2 x   0;2 Lời giải. Chọn B Hàm số f ( x) 4 2
= x − 2x +1 xác định và liên tục trên 0;2
Ta có: f ( x) 3 = 4x − 4x Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x =
Do đó: f (x) 0 = 0  x = 1 x = 1 − 0;  2
Ta có: f (0) =1, f ( ) 1 = 0, f (2) = 9
Suy ra: max f ( x) = 9 . x   0;2 ax + b
Câu 24: Cho hàm số y =
(d  0) có đồ thị như hình bên. Khẳng định nào dưới đây đúng? cx + d
A. a  0,b  0, c  0 .
B. a  0,b  0, c  0 . C. a  0,b  0, c  0 . D. a  0,b  0, c  0 . Lời giải Chọn B
Dựa vào đồ thị hàm số ta thấy: d
+) Đồ thị hàm số có đường tiệm cận đứng x = −
 0, mà d  0  c  0 . c a
+) Đồ thị hàm số có đường tiệm cận ngang y =
 0 , mà c  0  a  0. c b
+) Đồ thị hàm số cắt trục tung tại điểm có tung độ y =
 0 , mà d  0  b  0 . d
Vậy a  0,b  0,c  0 . x − −
Câu 25: Hỏi đồ thị hàm số 1 1 y =
có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang? x − 2 A. 3. B. 2. C. 1. D. 0. Lời giải Chọn C
+) Tập xác định D = 1;+) \  2 +) x
 1Ta có x = x nên Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x −1 −1 x −1 −1 x −1−1 1 1 lim = lim = lim = lim = . x→2 x→2 x→2 x − 2 x − 2
(x −2)( x−1+ ) x→2 1 x −1 +1 2
Suy ra đồ thị hàm số không có tiệm cận đứng. 1 1 1 − − 2 − − +) Ta lại có x 1 1 x x x lim = lim = 0 . x→+ x − 2 x→+ 2 1− x
Suy ra đồ thị hàm số có tiệm cận ngang là y = 0.
Vậy đồ thị hàm số có 1 đường tiệm cận. −
Câu 26: Tập xác định D của hàm số y = ( x − ) 3 2 9 1 là  1   1  A. D = − ;  −  ; +     . B. D = .  3   3   1 1   1 1 C. D = − ;   . D. D = \ − ;  .  3 3   3 3 Lời giải Chọn D 1
Hàm số đã cho xác định 2
 9x −1  0  x   . 3  
Suy ra tập xác định của hàm số đã cho là 1 1 D = \ − ;  .  3 3
Câu 27: Tìm tập xác định của hàm số y = (x+ ) 2 log 2 + 3log x ? A. ( 2
− ;0)(0;+). B. (0;+). C. ( 2; − +). D.  2; − +). Lời giải Chọn A x + 2  0 x  2 −
Điều kiện xác định của hàm số là:    2 x  0 x  0
Vậy tập xác định của hàm số là: ( 2 − ;0)(0;+)
Câu 28: Cho các hàm số y = log x và y = log x có đồ thị như hình vẽ bên. Đường thẳng x = 5cắt trục a b
hoành, đồ thị hàm số y = log x và y = log x lần lượt tại ,
A B và C . Biết rằng CB = 2AB . Mệnh a b
đề nào sau đây là đúng? Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
A. a = 5b . B. 2 a = b . C. 3 a = b . D. 3 a = b . Lời giải Chọn C
Dễ thấy A(5;0), B(5;log 5), C(5;log 5 và log 5  log 5  0 . a b ) b a
Do CB = 2AB nên ta có log 5 − log 5 = 2(log 5−0 . b a a )  log 5 = 3log 5 b a 1 3  = log b log a 5 5
 log a = 3log b 5 5 3
 log a = log b 5 5 3  a = b .
Câu 29: Giá trị cực tiểu của hàm số x y = e ( 2 x − ) 3 là: 6 6 A. . B. . C. 3 − e. D. 2 − e . e 3 e Lời giải Chọn D x  = ( 2 − ) x + = ( 2 3 2 + 2 −3) x y e x xe x x e . BBT
Suy ra giá trị cực tiểu của hàm số bằng 2 − e .
Câu 30: Tổng các nghiệm của phương trình 2
log x − 5 log x + 6 = 0 là 2 2 A. 5 . B. 13 . C. 12 . D. 32 . Lời giải Chọn C
Điều kiện x  0 . log x = 3 x = 8 2
log x − 5 log x + 6 = 0  2  2 2   log x = 2  x = 4 2 Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Vậy tổng các nghiệm của phương trình là 12.
Câu 31: Gọi S là tập nghiệm của phương trình 2 2 2 x −x x −x−2 x −x 1 2 2 4 − + =
+1 . Số phần tử của tập S là A. 1. B. 2 . C. 3 . D. 4 Lời giải Chọn B TXĐ: D = 2 − x − x x − x− x − x− x − x 2x x Xét phương trình: 2 2 2 2 2 2 1 x − x 1 2 2 4 1 2 4 − + = +  + = +1 4 − − ( 2 2 2 2 2 2 − − − − 1 x x x x x x x x x x )  4.2 + 2 = 4.4 + 4  5.2 = 2 + 4 ( 2 2 x −x) 2  2 − 2
−5.2x −x + 4 = 0. Đặt = 2x x t , t  0 t =1
Phương trình trở thành: 2
t − 5t + 4 = 0   t = 4  = 2 x 0 Với x −x 2 t = 1  2
=1  x − x = 0    x =1  = 2 x 2 Với x −x 2 2 t = 4  2
= 2  x − x − 2 = 0   x = 1 −
Vậy tập nghiệm của phương trình S =  1 − ;0;1;  2 có 4 phần tử.
Câu 32: Cho một tấm bìa hình chữ nhật có kích thước 3a , 6a . Người ta muốn tạo tấm bìa đó thành bốn
hình không đáy như hình vẽ, trong đó có hai hình trụ lần lượt có chiều cao 3a , 6a và hai hình lăng trụ tam giác đều có chiều cao lần lượt 3a , 6a 6a 6a 3a 3a H1 H 2 H 3 H 4
Trong 4 hình H1, H2, H3, H4 lần lượt theo thứ tự có thể tích lớn nhất và nhỏ nhất là A. H1, H 4 . B. H 2 , H 3 . C. H1, H 3 . D. H 2 , H 4 . Lời giải Chọn D
Gọi các hình H1, H 2 , H 3 , H 4 lần lượt theo thứ tự có thể tích V , V ,V ,V . 1 2 3 4 2  6a  27 6a Ta có: 2 3
V =  r h =  .3a =
a . (Vì 2 r = 6a r = ). 1 1 1    2   1 1 2  3a  27 2 3 3a
V =  r h =  .6a =
a .(Vì 2 r = 3a r = ). 2 2 2    2  2 2 2 2 Page 15
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12  1 3  3 V = . h B = 3 . a  .2 . a
.2a  = 3 3a . (Đáy là tam giác đều cạnh 6a : 3 = 2a ). 3   2 2    1 3  3 3 3 V = . h B = 6 . a  . . a .a  =
a .(Đáy là tam giác đều cạnh 3a : 3 = a ). 4   2 2 2  
Ta có: V V V V . 1 3 2 4 3a
Câu 33: Cho hình lăng trụ AB . C A BC
  có đáy ABC là tam giác đều cạnh a , AA = . Biết rằng hình 2
chiếu vuông góc của A lên ( ABC) là trung điểm BC . Tính thể tích V của khối lăng trụ đó. 3 2a 3 3a 3 A. 3 V = a . B. V = . C. V = . D. 3 V = a . 3 4 2 2 Lời giải Chọn C BCAH C B A
Gọi H là trung điểm BC . a 6 Theo giả thiết, A H
 là đường cao hình lăng trụ và 2 2 AH = AA − AH = . 2 2 3 a 3 a 6 3a 2
Vậy, thể tích khối lăng trụ là V = S  = = Δ .A H . . ABC 4 2 8
Câu 34: Cho hình trụ có hai đáy là hai hình tròn (O) và (O) , chiều cao R 3 và bán kính đáy
R . Một hình nón có đỉnh là O và đáy là hình tròn ( ;
O R) . Tỷ số diện tích xung quanh của
hình trụ và hình nón bằng A. 3 . B. 2 . C. 2 . D. 3 . Lời giải Chọn D Page 16
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 OR 3 R O
Ta có diện tích xung quanh của hình trụ là 2 S = 2 Rh = 2 . R R 3 = 2 R  3. 1
Diện tích xung quanh của hình nón là S = Rl =  . R (R 3)2 2 2 + R = 2 R  . 2 2 S 2 R  3
Tỷ số diện tích xung quanh của hình trụ và hình nón bằng 1 = = 3. 2 S 2 R  2
Câu 35: Một hình nón có đường sinh bằng a 2 và góc giữa đường sinh và mặt phẳng đáy bằng 60o .
Tính thể tích của khối nón được tạo nên từ hình nón đó. 1 1 1 1 A. 3  a 6 . B. 3  a 6 . C. 3  a 6 . D. 3  a 6 . 6 3 4 12 Lời giải Chọn D S a 2 60° A I B
Xét hình nón đỉnh S . Ta có: 60o SAI =
và SA = SB = l suy ra SAB đều. 1 a 2
Do đó: AB = SA = SB = a 2  r = AI = AB = . 2 2 = − = (  aa h SA AI a 2 ) 2 2 2 6 2 2 −   =   . 2 2   2 1 1  a 2  a 6 1 2 3
V =  r h =    =  a 6   . 3 3 2 2 12   II. PHẦN TỰ LUẬN
Câu 36: Giải phương trình log ( x + 2) + log ( x − 5)2 + log 8 = 0 3 9 1 3 Page 17
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải x  2 − Điều kiện:  . x  5 2 Ta có log x + 2 + log x − 5
+ log 8 = 0  log x + 2 + log x −5 + log 8 = 0 3 ( ) 9 ( ) 1 3 ( ) 3 1 3 3
 log x + 2 x − 5 = log 8  x + 2 x − 5 = 8 * 3 ( ) 3 ( ) ( ) TH1: x  5 ( x =
*)  ( x + 2)( x − 5) 6 (t/m) 2
= 8  x − 3x −18 = 0   x = 6  x = 3 −  ( ) L TH2: 2 −  x  5  3 + 17 x = (t/m)
( )  (x + )(−x + ) 2 2 * 2
5 = 8  − x + 3x + 2 = 0    3 − 17 x =  (t/m)  2  3+ 17 3− 17 
Vậy tập nghiệm của phương trình là S = 6; ; . 2 2  
Câu 37: Cho lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông tại A và AB = a , AC = a 3 , mặt phẳng ( A B
C) tạo với đáy một góc 30. Tính thể tích của khối lăng trụ AB . C A BC  . Lời giải A' C' B' A C H BBC ⊥ AH
Gọi AH là đường cao của tam giác ABC , ta có 
BC ⊥ ( AA H
 )  BC ⊥ A H  BC ⊥ AA
nên góc giữa mặt phẳng ( A B
C) và mặt phẳng ( ABC) là góc AHA = 30 . 1 1 1 1 1 4 a 3 Ta có = + = + =  AH = . 2 2 2 2 AH AB AC a (a )2 2 3a 2 3 AAa 3 1 a tan 30 =
AA = AH.tan30 = . = . AH 2 3 2 2 1 1 a 3 S = . . AB AC = . . a a 3 = . ABC  2 2 2 2 3 Do đó a a 3 a 3 V =  = =    AA .S . . ABC. A B C ABC  2 2 4 Page 18
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 38: Cho đồ thị hàm số y = f (
x) như hình vẽ. Tìm các khoảng đồng biến của hàm số: 3 2
y = g(x) = f (3x −1) − x + 3x +1. Lời giải Ta có: 2 2 y = g (
x) = 3 f (3x −1) − 3x + 6x = 0  f (3x −1) = x − 2x Đặ 1 4 5 t 2
3x −1 = t f (
t) = t − t − 9 9 9 1 4 5 Vẽ đồ thị hàm số 2 y = t − t −
là một parabol đi qua các điểm sau: (2; 1 − ), (5;0), ( 1 − ;0), 9 9 9 ( 4 − ;3) 1 4 5
Dựa vào đồ thị ta có bảng xét dấu 2
h(t) = f (
t) − t + t + 9 9 9 Suy ra: t  4 − 3x −1  4 − x  1 − h(t)  0 
g (x)  0      1 −  t  5 1 −  3x −1 5 0  x     2
Vậy hàm số đồng biến trên khoảng (0; 2) và (− ;  1 − ) .
Câu 39: Xét các số thực a và b thỏa mãn a b  1. Tìm giá trị nhỏ nhất của biểu thức  a  2 2
P = log (a ) + 3log . a b    b b Page 19
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải 2  a     a  Ta có 2 2
P = log (a ) + 3log =
  2log a + 3log a b a b    b     b b b 2  2  a   a    =  a  4 log .b   + 3log = 4 1  + log b + 3log . a b       b   b a b    b b b Đặ a
t t = log b  0. Vì a b 1 nên
 1,b  1 . Do đó t  0 a b b 3 3 Ta có 2 2 P = 4(t +1) + = 4t + 8t + + 4 t t Đặ 3 t 2
f (t) = 4t + 8t + + 4. t 3 2 2 3 8t + 8t − 3
(2t −1)(4t + 6t + 3) Ta có f (
t) = 8t + t − = = 2 2 2 t t t 1  1  Vậy f (
t) = 0  t = . Dễ có P = f = 15 min   2  2  Page 20
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 05
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Cho hàm số y = f (x) liên tục trên , có đồ thị như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. (0 ) ;1 . B. ( 1 − ;0) . C. ( 2 − ;− ) 1 . D. ( 1 − ; ) 1 . Câu 2:
Cho hàm số y = f ( x) có đồ thị như hình vẽ. Hàm số đã cho có giá trị cực đại bằng? y 2 -2 1 -1 O 2 x -2 A. 2 . B. 1 − . C. + . D. 2 − . Câu 3:
Cho hàm số y = f (x) xác định, liên tục trên và có bảng biến thiên sau:
Khẳng định nào sau đây là đúng ?
A. Giá trị lớn nhất của hàm số bằng 2 .
B. Giá trị nhỏ nhất của hàm số bằng 1 − .
C. Giá trị nhỏ nhất của hàm số bằng 1.
D. Giá trị nhỏ nhất của hàm số bằng 1 − và 1. Câu 4:
Đường cong dưới đây là đồ thị của hàm số nào? A. 3 2
y = −x + x −1. B. 4 2
y = −x + 2x −1. C. 3 2
y = x − x −1. D. 4 2
y = x − 2x −1. Page 1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Câu 5:
Hình vẽ dưới đây là đồ thị của hàm số nào? x −1 2x +1 2x − 3 2x + 5 A. y = . B. y = . C. y = . D. y = . x +1 x +1 x +1 x +1 Câu 6:
Cho hàm số y = f (x) có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: A. 2 . B. 4 . C. 3 . D. 1. Câu 7:
Chọn đáp án đúng, cho m n
a a , khi đó
A. m n .
B. m n .
C. m = n .
D. m n khi a 1. Câu 8:
Cho a  0, a  1, khẳng định nào sau đây sai? 1 A. 2 log a = 2. B. log a = . C. log 2a = 2. D. log 2 a a = 2 . a 2 a a 2 Câu 9: Giả sử ,
x y là các số thực dương. Trong các khẳng định sau, khẳng định nào sai? x A. log = log x − log . y
B. log xy = log x + log y. 3 3 3 y 3 3 3 1 C. log xy = log x + log y . D. log
x + y = log x + log . y 3 ( ) 3 ( 3 3 ) 2 3 3 2 Câu 10: Hàm số 2x x y − = có đạo hàm là 2 2 − A. ( ) 2 2 1 .2x x x − − . B. ( ) 2 2 1 .2x x x x − − − . C. 2x − . x (2x − ) 1 .ln 2 . D. 2x . x ln 2 .
Câu 11: Giá trị thực của a để hàm số y = log
x đồng biến trên (0;+) . 2a 1 − A. a  1 − . B. a 1.
C. 0  a  1.
D. 0  a  1. x− 25
Câu 12: Phương trình 2 5 = có nghiệm là 5x A. x = 2 . B. x = 0 . C. x = 1 − . D. x =1 .
Câu 13: Tập nghiệm S của phương trình log 4 = 2 là 2 x−3 1 5  1  5  7 
A. S =  ;  .
B. S =   .
C. S =   .
D. S =   . 2 2   2   2   2  Page 2
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12  1 
Câu 14: Tìm tập nghiệm S của bất phương trình log  2x −   2 − . 0,5  2   1 9  1 9   9   9  A. S =  ;  S = ; S =  ; −  S =  ; +      . C. 4 4  . B. 4 4   4  . D.  4  .
Câu 15: Trong một khối đa diện, mệnh đề nào sau đây đúng?
A. Hai cạnh bất kỳ có ít nhất một điểm chung.
B. Ba mặt bất kì có ít nhất một đỉnh chung.
C. Hai mặt bất kì có ít nhất một điểm chung.
D. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
Câu 16: Cho khối lăng trụ có diện tích đáy B = 3 và chiều cao h = 2 . Thể tích của khối lăng trụ đã cho bằng. A. 1. B. 3 . C. 2 . D. 6 .
Câu 17: Cho hình trụ có bán kính đáy R = 8 và độ dài đường sinh l = 3 . Diện tích xung quanh của hình trụ đã cho bằng: A. 24. B. 192. C. 48. D. 64.
Câu 18: Cho hình nón có độ dài đường sinh bằng 25 và bán kính đường tròn đáy bằng 15. Tính thể tích của khối nón đó. A. 1500. B. 4500. C. 375. D. 1875.
Câu 19: Tính thể tích V của khối trụ có bán kính r = 4 và chiều cao h = 4 2 .
A. V = 32.
B. V = 64 2 .
C. V = 128.
D. V = 32 2 .
Câu 20: Thể tích khối cầu bán kính 3 cm bằng A.  ( 3 36 cm ). B.  ( 3 108 cm ). C.  ( 3 9 cm ). D.  ( 3 54 cm ). Câu 21: Cho hàm số 4 2
y = x − 2x . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng (− ;
 − 2) . B. Hàm số đồng biến trên khoảng ( 1 − ; ) 1 .
C. Hàm số nghịch biến trên khoảng ( 1 − ; ) 1 .
D. Hàm số đồng biến trên khoảng (− ;  − 2) .
Câu 22: Cho hàm số f ( x) có đạo hàm là f ( x) = ( 2 x − )( 2 '
1 x − 3x + 2) x
  . Số điểm cực trị của hàm số f ( x) là A. 4. B. 3. C. 2. D. 1. x −
Câu 23: Giá trị nhỏ nhất của hàm số f ( x) 2 2 = trên đoạn 2,  3 bằng x −1 7 5 A. B. C. 2 . D. 1. 2 2 Câu 24: Cho hàm số ( ) 3 2
f x = ax + bx + cx + d có đồ thị như hình vẽ. Trong các mệnh đề sau, mệnh đề nào đúng?
A. a  0,b  0, c  0, d  0.
B. a  0,b  0, c  0, d  0.
C. a  0,b  0, c  0, d  0.
D. a  0,b = 0, c  0, d  0. Page 3
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 25: Cho hàm số y = f ( x) có đồ thị như hình vẽ. Số đường tiệm cận ngang của đồ thị hàm số 1 y = là f ( x) A. 4. B. 3. C. 2. D. 1. −
Câu 26: Tập xác định của hàm số y = (−x + x − ) 4 2 3 2 là A. \ 1;  2 . B. (− ) ,1 (2,+) . C. \   1 . D. (1, 2) . Lời giải Chọn A Hàm số xác định khi 2
−x + 3x − 2  0  x  1, x  2 .
Vậy tập xác định D = \ 1;  2 .  2 − x
Câu 27: Tập xác định của hàm số y = ln   là  x − 5  A. (5, +) . B. (2,5) . C. ( , − 2) . D. \ 2;  5 .
Câu 28: Cho các hàm số y = log x , y = log x có đồ thị như hình vẽ. Khẳng định nào sau đây đúng? a b
A. 0  a 1 b .
B. 0  b 1 a .
C. 0  a b 1.
D. 0  b a 1.
Câu 29: Cho các số thực dương a, b thỏa mãn log b = 2 . Giá trị của P = ( 2 log a bằng ab ) a 1 1 2 A. . B. . C. . D. 1. 6 2 3
Câu 30: Nghiệm của phương trình log
x +1 +1 = log 4x +1 là 3 ( ) 3 ( ) A. x = 3 − . B. x = 2 . C. x = 3. D. x = 4 . Page 4
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x
Câu 31: Cho phương trình log . x log (4x) 3
+ 2log   = 0 . Khi đặt t = log x , ta được phương trình 4 2 2  2  2 nào sau đây? A. 2 t +11t = 0 . B. 2
t +11t − 3 = 0 . C. 2
t +14t − 2 = 0 . D. 2
t +14t − 4 = 0 .
Câu 32: Hình tứ diện đều có bao nhiêu mặt đối xứng? A. 3 . B. 4 . C. 6 . D. 9 .
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a . Cạnh bên SA vuông góc
với đáy, góc SBD = 60 . Thể tích khối chóp S.ABCD bằng 3 a 3 a 3 3 2a A. . B. . C. . D. 3 a . 3 2 3
Câu 34: Cho hình nón có đường sinh bằng 13, chiều cao bằng 12. Diện tích xung quanh của hình nón bằng A. 60 . B. 65 . C. 65 . D. 90 .
Câu 35: Thiết diện qua trục của hình trụ là một hình vuông có cạnh bằng 2a . Thể tích của khối trụ được
tạo bởi hình trụ này là 3 2 a 3 8 a A. 3 2 a . B. . C. 3 8 a . D. . 3 3 II. PHẦN TỰ LUẬN 1 Câu 1:
Giải phương trình log x + log ( x − 3)2 2 = log log 3 ? 25 5 5 ( 3 ) 2 Câu 2:
Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh a , khoảng cách từ S đến mặt phẳng ( SM 1
ABC)bằng a 6 . Trên cạnh SA lấy điểm M , trên cạnh SB lấy điểm N sao cho = , MA 2
SN = 2. Mặt phẳng ( ) qua MN và song song với SC chia khối chóp thành 2 phần. Tính V NB
là thể tích của khối đa diện chứa điểm A ? Câu 3:
Cho hàm số y = f ( x) có đạo hàm f ( x) 2 '
= x + 2x −3, x
  .Tìm các giá trị thực của tham
số m để hàm số g ( x) = f ( 2
x + x + m) 2 3 2
+ m − 3m + 2021 đồng biến trên khoảng (0;2)? 2  8  1 Câu 4:
Tìm m để phương trình (m − ) 2 1 log 3x − − 4 m − 5 log
+ 4 m −1 = 0 có nghiệm 3   ( ) 3 ( )  3 8  3x − 3   trên đoạ 17 n 1,   .  9 
---------- HẾT ---------- Page 5
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM Câu 1:
Cho hàm số y = f (x) liên tục trên , có đồ thị như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. (0 ) ;1 . B. ( 1 − ;0) . C. ( 2 − ;− ) 1 . D. ( 1 − ; ) 1 . Lời giải Chọn A
Từ đồ thị ta thấy hàm số nghịch biến trên khoảng (0 ) ;1 . Câu 2:
Cho hàm số y = f ( x) có đồ thị như hình vẽ. Hàm số đã cho có giá trị cực đại bằng? y 2 -2 1 -1 O 2 x -2 A. 2 . B. 1 − . C. + . D. 2 − . Lời giải Chọn A
Giá trị cực đại của hàm số đạt tại x = 1 − là 2 . Câu 3:
Cho hàm số y = f (x) xác định, liên tục trên và có bảng biến thiên sau:
Khẳng định nào sau đây là đúng ?
A. Giá trị lớn nhất của hàm số bằng 2 .
B. Giá trị nhỏ nhất của hàm số bằng 1 − .
C. Giá trị nhỏ nhất của hàm số bằng 1.
D. Giá trị nhỏ nhất của hàm số bằng 1 − và 1. Lời giải Chọn A
Dựa vào bảng biến thiên nhận thấy:
● f (x)  2, x
  và f (0) = 2 nên GTLN của hàm số bằng 2. Page 6
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
● f (x)  1
− ,x và vì lim f = 1
− nên không tồn tại x  sao cho f (x =1, do đó hàm 0 ) 0 x→− số không có GTNN. Câu 4:
Đường cong dưới đây là đồ thị của hàm số nào? A. 3 2
y = −x + x −1. B. 4 2
y = −x + 2x −1. C. 3 2
y = x − x −1. D. 4 2
y = x − 2x −1. Lời giải Chọn D
Đồ thị hàm số có ba điểm cực trị và phía tay phải của đồ thị hàm số đi lên suy ra hệ số a  0 . Câu 5:
Hình vẽ dưới đây là đồ thị của hàm số nào? x −1 2x +1 2x − 3 2x + 5 A. y = . B. y = . C. y = . D. y = . x +1 x +1 x +1 x +1 Lời giải Chọn B
Đồ thị hàm số cắt trục Oy tại điểm có tọa độ (0 )
;1 nên ta chọn phương án B. Câu 6:
Cho hàm số y = f (x) có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: A. 2 . B. 4 . C. 3 . D. 1. Lời giải Chọn C Page 7
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Nhìn bảng biến thiên ta thấy lim f (x) = − nên x = 0 là tiệm cận đứng của đồ thị hàm số. − x→0
lim f ( x) = 3  y = 3 là TCN của đồ thị hàm số. x→+
lim f ( x) =1 y =1 là TCN của đồ thị hàm số. x→− Câu 7:
Chọn đáp án đúng, cho m n
a a , khi đó
A. m n .
B. m n .
C. m = n .
D. m n khi a 1. Lời giải Chọn D
Ta có tính chất: Nếu m n
a a m  , n a  1. Câu 8:
Cho a  0, a  1, khẳng định nào sau đây sai? 1 A. 2 log a = 2. B. log a = . C. log 2a = 2. D. log 2 a a = 2 . a 2 a a 2 Lời giải Chọn C Câu 9: Giả sử ,
x y là các số thực dương. Trong các khẳng định sau, khẳng định nào sai? x A. log = log x − log . y
B. log xy = log x + log y. 3 3 3 y 3 3 3 1 C. log xy = log x + log y . D. log
x + y = log x + log . y 3 ( ) 3 ( 3 3 ) 2 3 3 Lời giải Chọn D 2 Câu 10: Hàm số 2x x y − = có đạo hàm là 2 2 A. ( ) 2 − 2 1 .2x x x − − . B. ( ) 2 2 1 .2x x x x − − − . C. 2x − . x (2x − ) 1 .ln 2 . D. 2x . x ln 2 . Lời giải Chọn C   2 2
Ta có: ( u ) = . u a
ua .ln a nên (2x −x ) = (2 − ) 1 .2x − . x x ln 2 .
Câu 11: Giá trị thực của a để hàm số y = log
x đồng biến trên (0;+) . 2a 1 − A. a  1 − . B. a 1.
C. 0  a  1.
D. 0  a  1. Lời giải Chọn B
Ta có hàm số y = log
x đồng biến trên (0;+)  2a −11 a 1. 2a 1 − x− 25
Câu 12: Phương trình 2 5 = có nghiệm là 5x A. x = 2 . B. x = 0 . C. x = 1 − . D. x =1 . Lời giải Chọn A x− 25 Ta có 2 x−2 2 5 =  5
= 5 −x x − 2 = 2 − x x = 2 . 5x
Câu 13: Tập nghiệm S của phương trình log 4 = 2 là 2 x−3 1 5  1  5  7 
A. S =  ;  .
B. S =   .
C. S =   .
D. S =   . 2 2   2   2   2  Lời giải Chọn C Page 8
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 2x − 3  0 3 3  x  2     x  2 Phương trình 5
 2x − 3  1  2   2  x = .    log 4 = 2 4 = x −    x − = x− (2 3)2 2 2 3 2 2 3  1 
Câu 14: Tìm tập nghiệm S của bất phương trình log  2x −   2 − . 0,5  2   1 9  1 9   9   9  A. S =  ;  S = ; S =  ; −  S =  ; +      . C. 4 4  . B. 4 4   4  . D.  4  . Lời giải Chọn A  1  1 2x −  0    x  4 1 9 Bất phương trình  2      x  . 1 −  9 4 4 2x −  (0,5) 2    x  2  4
Câu 15: Trong một khối đa diện, mệnh đề nào sau đây đúng?
A. Hai cạnh bất kỳ có ít nhất một điểm chung.
B. Ba mặt bất kì có ít nhất một đỉnh chung.
C. Hai mặt bất kì có ít nhất một điểm chung.
D. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt. Lời giải Chọn D
Câu 16: Cho khối lăng trụ có diện tích đáy B = 3 và chiều cao h = 2 . Thể tích của khối lăng trụ đã cho bằng. A. 1. B. 3 . C. 2 . D. 6 . Lời giải Chọn D
Thể tích khối lăng trụ là V = . B h = 3.2 = 6 .
Câu 17: Cho hình trụ có bán kính đáy R = 8 và độ dài đường sinh l = 3 . Diện tích xung quanh của hình trụ đã cho bằng: A. 24. B. 192. C. 48. D. 64. Lời giải Chọn C
Diện tích xung quanh của hình trụ S = 2 rl = 48 . xq
Câu 18: Cho hình nón có độ dài đường sinh bằng 25 và bán kính đường tròn đáy bằng 15. Tính thể tích của khối nón đó. A. 1500. B. 4500. C. 375. D. 1875. Lời giải Chọn A
Gọi h là chiều cao khối nón 2 2 2 2
h = l − r = 25 −15 = 20. 1 1 2 2
V = r h = ..15 .20 =1500 . 3 3
Câu 19: Tính thể tích V của khối trụ có bán kính r = 4 và chiều cao h = 4 2 .
A. V = 32.
B. V = 64 2 .
C. V = 128.
D. V = 32 2 . Lời giải Page 9
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Chọn B 2
V =  r h = 16.4 2 = 64 2 .
Câu 20: Thể tích khối cầu bán kính 3 cm bằng A.  ( 3 36 cm ). B.  ( 3 108 cm ). C.  ( 3 9 cm ). D.  ( 3 54 cm ). Lời giải Chọn A 4 4 Thể tích khối cầu là: 3 3 V =
. .R = ..3 = 36 ( 3 cm ). 3 3 Câu 21: Cho hàm số 4 2
y = x − 2x . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng (− ;
 − 2) . B. Hàm số đồng biến trên khoảng ( 1 − ; ) 1 .
C. Hàm số nghịch biến trên khoảng ( 1 − ; ) 1 .
D. Hàm số đồng biến trên khoảng (− ;  − 2) . Lời giải Chọn A TXĐ: D = . x = 0  3 3
y = 4x − 4 ;
x y = 0  4x − 4x = 0  x = 1  x = 1 − 
Suy ra hàm số đồng biến trên các khoảng ( 1
− ;0),(1;+); hàm số nghịch biến trên các khoảng (− ;  − ) 1 ,(0; )
1 . Vậy hàm số nghịch biến trên khoảng (− ;  − 2) .
Câu 22: Cho hàm số f ( x) có đạo hàm là f ( x) = ( 2 x − )( 2 '
1 x − 3x + 2) x
  . Số điểm cực trị của hàm số f ( x) là A. 4. B. 3. C. 2. D. 1. Lời giải Chọn C
Ta có f ( x) = ( x − )( x − x + ) = ( x + )( x − )2 2 2 ' 1 3 2 1 1 ( x − 2) . x = −1 
f '( x) = 0  x = 1  . Do x = 1
− , x = 2 là nghiệm đơn, x =1 là nghiệm bội chẵn nên f '(x) chỉ x = 2 
đổi dấu khi đi qua x = 1 − , x = 2 .
Vậy hàm số f ( x) có 2 điểm cực trị x = 1 − , x = 2 . x −
Câu 23: Giá trị nhỏ nhất của hàm số f ( x) 2 2 = 2,3 bằng x − trên đoạn   1 7 5 A. B. C. 2 . D. 1. 2 2 Lời giải Page 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Chọn C 2 − + Ta có f ( x) x 2x 2 ' =  0 x   2,3 . 2   (x − ) 1 Mà f ( ) = f ( ) 7 2 2, 3 = . 2 x −
Vậy giá trị nhỏ nhất của hàm số f ( x) 2 2 = 2,3 bằng 2 . x − trên đoạn   1 Câu 24: Cho hàm số ( ) 3 2
f x = ax + bx + cx + d có đồ thị như hình vẽ. Trong các mệnh đề sau, mệnh đề nào đúng?
A. a  0,b  0, c  0, d  0.
B. a  0,b  0, c  0, d  0.
C. a  0,b  0, c  0, d  0.
D. a  0,b = 0, c  0, d  0. Lời giải Chọn D
Từ dáng điệu đồ thị ta thấy lim f ( x) = + nên a  0 . x→+
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên d  0 .
Đồ thị hàm số nhận x =1, x = 1
− là hai điểm cực trị nên phương trình f (x) 2 '
= 3ax + 2bx +c = 0 có hai nghiệm 1, 1 − .  2 − b  2 − b x + x = = 0  1 2  Theo đị   nh lý Vi-et ta có 3a 3a    c cx x  = = 1. − 1 2  3a 3a
Do a  0 nên b = 0, c  0 .
Vậy a  0,b = 0, c  0, d  0.
Câu 25: Cho hàm số y = f ( x) có đồ thị như hình vẽ. Số đường tiệm cận ngang của đồ thị hàm số 1 y = là f ( x) A. 4. B. 3. C. 2. D. 1. Page 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải Chọn D
Từ dáng điệu của đồ thị ta thấy lim f ( x) = − ,
 lim f (x) = − . x→+ x→− 1 1 Do đó lim = = . →+ ( ) 0, lim →− ( ) 0 x x f x f x 1
Đồ thị hàm số y =
có một đường tiệm cận ngang y = 0 . f ( x) −
Câu 26: Tập xác định của hàm số y = (−x + x − ) 4 2 3 2 là A. \ {1,2}. B. (− ) ,1 (2,+) . C. \  1 . D. (1, 2) . Lời giải Chọn A 2
Hàm số xác định khi −x + 3x − 2  0  x  1, x  2 .
Vậy tập xác định D = \1;  2 .  2 − x
Câu 27: Tập xác định của hàm số y = ln   là  x − 5  A. (5, +) . B. (2,5) . C. ( , − 2) . D. \2;  5 . Lời giải Chọn B 2 − x Hàm số xác định khi
 0  2  x  5 . x − 5
Vậy tập xác định D = (2,5) .
Câu 28: Cho các hàm số y = log x y = x a ,
logb có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
A. 0  a 1  b .
B. 0  b 1  a .
C. 0  a b 1.
D. 0  b a 1. Lời giải Chọn B
Ta thấy hàm số y = log x   b nghịch biến nên 0 b 1.
Mặt khác, y = log x a
đồng biến nên a 1.
Vậy 0  b 1  a .
Câu 29: Cho các số thực dương a, b thỏa mãn log b = 2 2 = a . Giá trị của P log a bằng ab ( ) Page 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 1 1 2 A. . B. . C. . D. 1. 6 2 3 Lời giải Chọn C 2
Ta có: log b = 2  b = a a . 2 Thay 2
b = a vào P , ta được: 2 2 P = log a = log a = . 2 a.a ( ) 3 a ( ) 3
Câu 30: Nghiệm của phương trình log
x +1 +1= log 4x +1 là 3 ( ) 3 ( ) A. x = 3 − . B. x = 2 . C. x = 3. D. x = 4 . Lời giải Chọn B x +1 0 Điề 1 u kiện:   x  − 4x +1 0 4
Phương trình đã cho tương đương với phương trình : log x +1 + log 3 = log 4x +1 3 ( ) 3 3 ( ) 
log  x +1 .3 = log 4x +1 3 ( )  3 ( )  (x+ )
1 .3 = 4x +1  x = 2 (thỏa mãn đk).  x
Câu 31: Cho phương trình = log . x log (4x) 3
+ 2log   = 0 . Khi đặt t log x , ta được phương trình 4 2 2 2  2  nào sau đây? A. 2 t +11t = 0 . B. 2
t +11t − 3 = 0 . C. 2
t +14t − 2 = 0 . D. 2
t +14t − 4 = 0 . Lời giải Chọn D
Điều kiện: x  0 . Ta có: log . x log (4x) 1
= log x(log 4 + log x) 1 = log . x (2 + log x) 1 2 = t + t 4 2 2 2 2 2 2 2 2 2 3 3  x   x  log   = log   = ( 3
log x −1 = 3log x −1 = 3t −1 2 2 2 ) 2  2   2 
Phương trình đã cho có dạ 1 ng: 2 2 t +
t + 6t − 2 = 0  t +14t − 4 = 0 . 2
Câu 32: Hình tứ diện đều có bao nhiêu mặt đối xứng? A. 3 . B. 4 . C. 6 . D. 9 . Lời giải Chọn C
Hình tứ diện đều có 6 mặt phẳng đối xứng. Mỗi mặt phẳng đối xứng này được tạo từ một cạnh
của hình tứ diện và trung điểm của cạnh đối diện.
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a . Cạnh bên SA vuông góc
với đáy, góc SBD = 60 . Thể tích khối chóp S.ABCD bằng 3 a 3 a 3 3 2a A. . B. . C. . D. 3 a . 3 2 3 Lời giải Chọn A Page 13
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 2
Do ABCD là hình vuông =
a nên BD = a 2 và S a ABCD .  ⊥ Ta có: ⊥ ( ) SA AB SA ABCD   SA ⊥ AD
Mặt khác ta có: AB = AD .
Suy ra hai tam giác vuông SAB = S
AD (c – g – c)
SB = SD (hai tam giác bằng nhau có các cặp cạnh tương ứng bằng nhau)
Xét tam giác SBD có SB = SD và SBD = 60 nên tam giác SBD đều
SB = SD = BD = 2 2 a 2  SA =
SB − AB = a . 3 1 a Vậy V = .S . A S = S .ABCD . 3 ABCD 3
Câu 34: Cho hình nón có đường sinh bằng 13, chiều cao bằng 12. Diện tích xung quanh của hình nón bằng A. 60 . B. 65 . C. 65 . D. 90 . Lời giải Chọn C l  =13 Ta có 2 2 2 2 
r = l − h = 13 −12 = 5. h =12
Khi đó S =  r = .5.13 = 65 xq .
Câu 35: Thiết diện qua trục của hình trụ là một hình vuông có cạnh bằng 2a . Thể tích của khối trụ được
tạo bởi hình trụ này là 3 2 a 3 8 a A. 3 2 a . B. . C. 3 8 a . D. . 3 3 Lời giải Chọn A
Thiết diện qua trục là hình vuông ABCD có cạnh bằng 2a .
AB = 2a = 2rr = a Suy ra   
AD = 2a = hh = 2a
Vậy thể tích của khối trụ bằng: 2 2 3
V =  r h =  .a .2a = 2 a . Page 14
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 PHẦN 2 – TỰ LUẬN 1 Câu 1:
Giải phương trình log x + log ( x − 3)2 2 = log log 3 ? 25 5 5 ( 3 ) 2 Lời giải x  0 Điều kiện  . x  3 1
Ta có log x + log ( x − 3)2 2 = log log 3 25 5 5 ( 3 ) 2
 log x +log x −3 = log 2 5 5 5
 log x x −3 = log 2 5 ( ) 5
x(x − 3) = 2   x  ( x − 3) = −2  3 − 17 x = (tm) 2  2
x −3x − 2 = 0    3 + 17  x = (tm). 2
x − 3x + 2 = 0 2  x = 1(tm)  x = 2  (tm) 3  17
Vậy phương trình đã cho có 4 nghiệm là x =
, x =1 , x = 2 . 2 Câu 2:
Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh a , khoảng cách từ S đến mặt phẳng (ABC) SM 1
bằng a 6 . Trên cạnh SA lấy điểm M , trên cạnh SB lấy điểm N sao cho = , MA 2
SN = 2. Mặt phẳng ( ) qua MN và song song với SC chia khối chóp thành 2 phần. Tính V NB
là thể tích của khối đa diện chứa điểm A ? Lời giải Page 15
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 2 2 3 • 1 a 3 1 1 a 3 a 2 0 Ta có S = . AB AC.sin 60 = , nên V = . B h = .a 6 = . ABC  2 4 S . ABC 3 3 4 4
• Trong mặt phẳng (SAC) dựng MP song song với SC cắt AC tại P . Trong mặt phẳng
(SBC) dựng NQ song song với SC cắt BC tại Q. Gọi D là giao điểm của MN và PQ
. Dựng ME song song với AB cắt SB tại E . SE SM 1 Lại có = = 1
SE = NE = NB = SB SB SA 3 3 1 DB DN
Suy ra N là trung điểm của BE và DM , đồng thời DB = ME = 1 1 AB  = , = . 3 DA 4 DM 2 DQ DN 1 Do NQ / /MP  = = . DP DM 2 • Ta có V = V −V . D.AMP D.BNQ VD.BNQ DB DN DQ 1 1 1 1 = 1 15 15 . . = . . =  V = VV = .V = .V . V DA DM DP 4 2 2 16 D.BNQ D. 16 AMP D. AMP M . 16 16 ADP D.AMP d ( , Q DB) • QB 1 QB NB 1 1 Do NQ // SC  = =  =
=  d (Q, DB) = .d (C, AB) CB SB 3 d (C, AB) CB 3 3 1  1 1 1 1 S
= .d Q DB DB = . .d (C, AB). AB = 8 SS = .S QDB ( , ). 2 2 3 3 9 CAB ADP 9 ABC 2
Và d (M ,( ADP)) = d (S,( ABC)) 3 1  1 2 8 16 V
= .d M , ADP .S
= . d (S,( ABC)). S = .V M . ADP ( ( )) 3 ADP ABC S . 3 3 9 27 ABC Page 16
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 3 3 15 16 5 5 a 2 5a 2  V = . .V = .V = . = S . ABC S . 16 27 9 ABC 9 4 36 Câu 3:
Cho hàm số y = f ( x) có đạo hàm f ( x) 2 '
= x + 2x −3, x
  .Tìm các giá trị thực của tham
số m để hàm số g ( x) = f ( 2
x + x + m) 2 3 2
+ m − 3m + 2021 đồng biến trên khoảng (0;2)? Lời giải t   3 − Ta có f '(t ) 2
= t + 2t − 3  0   ( ) * . t  1
(2x +3)( 2x +3x)
Ta lại có g '( x) = f '( 2
x + 3x + 2m 2 ) x + 3x
(2x +3)( 2x +3x) Vì  0, x  (0;2)
g x đồng biến trên (0;2)  g '(x)  0, x  (0;2) 2 x + nên ( ) 3xf ( 2
' x + 3x + 2m)  0, x  (0;2) 2
x + 3x + 2m  3 − , x  (0;2) 2
x + 3x  2m −3, x  (0;2)     (**) 2
x + 3x + 2m 1, x  (0;2) 2
x + 3x  2m +1, x  (0;2)   Có h( x) 2
= x +3x luôn đồng biến trên khoảng(0;2) nên 0  h(x) 10trên khoảng(0;2)  13 m   −   Do đó 2m 3 10
0  h( x) 10 trên khoảng (0;2) từ (**)  2    2m +1  0 1 − m   2  13 m  
Vậy giá trị của tham số m cần tìm là 2  . −1 m   2 2  8  1 Câu 4:
Tìm m để phương trình (m − ) 2 1 log 3x − − 4 m − 5 log
+ 4 m −1 = 0 có nghiệm 3   ( ) 3 ( )  3 8  3x − 3  17  trên đoạn 1,   .  9  Lời giải 2  8  1
Phương trình (m − ) 2 1 log 3x − − 4 m − 5 log + 4 m −1 = 0 3   ( ) 3 ( )  3 8  3x − 3      4(m − ) 8 8 2 1 log 3x −
+ 4 m − 5 log 3x − + 4 m −1 = 0 (1) 3   ( ) 3   ( )  3   3  Page 17
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12  8   17 
Đặt t = log 3x − . Do x  1;  t −1;  1 3      3   9 
Phương trình (1) trở thành (m− ) 2 4
1 t + 4(m −5)t + 4(m− ) 1 = 0  (m− ) 2
1 t + (m −5)t + m −1= 0
m( 2t +t + ) 2 1 = t + 5t +1 2 t + 5t +1
m = 2t +t + 1 t + 5t +1 * Xét f (t ) 2 = t  1 − ;1 2 t + t + với   1 ( ) 2 4 − 4t f t = t   1 − ;  (  1 t + t + ) 0 2 2 1  t + 5t +1
Hàm số f (t ) 2 = 1 − ;1 2 t + t +
đồng biến trên đoạn   1
f −  f (t)  f ( )  −  f (t) 7 ( 1) 1 3  3  17 
* Để phương trình (1) có nghiệm trên đoạn 1, 
 thì hai đồ thị của hàm số  9  + +
y = m f (t ) 2 t 5t 1 ; = t   1 − ;1 . 2
t + t + cắt nhau   1 7  3 −  m  . 3 7 Vậy 3
−  m  thỏa mãn bài toán. 3 Page 18
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 06
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Cho hàm số y = f (x) xác định, liên tục trên và có bảng biến thiên như hình sau:
Mệnh đề nào sau đây sai?
A. Hàm số nghịch biến trên khoảng (− ;  +) .
B. Hàm số đồng biến trên khoảng (− ;  +) .
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên khoảng (1;+). Câu 2:
Cho hàm số y = f (x) xác định và liên tục trên , có đồ thị như hình vẽ:
Hàm số y = f (x) có giá trị cực đại là:
A. y = 2. B. y = 2. −
C. x = 2.
D. x = 0. Câu 3:
Cho hàm số y = f (x) có đồ thị trên đoạn  2 − ; 
1 như hình vẽ bên dưới. Giá trị max f ( x) bằng:  2 − ;  1 A. 1. B. 3. C. 0. D. 3. − Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Câu 4:
Đường cong trong hình vẽ là đồ thị của hàm số nào trong bốn hàm số sau đây? A. 3 2
y = x − 3x −1. B. 3 2
y = x + 3x −1. C. 3 2
y = −x + 3x −1. D. 4 2
y = −x + 3x − 2. Câu 5:
Hàm số nào dưới đây có đồ thị dạng như đường cong trong hình bên A. 4 2
y = −x + 2x +1. B. 4 2
y = x + 2x + 2. C. 4 2
y = x − 2x −1. D. 4 2
y = −x + 2x − 2. 4x −1 Câu 6:
Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số y = ? 2x − 3 3 3
A. x = 2. B. y = . C. x = . D. y = 2. 2 2  Câu 7:
Tập xác định của hàm số y = ( x + 2) là: A. B. (0;+). C. ( 2 − ;+). D. \   2 . 1 Câu 8:
Tính giá trị biểu thức A = log 7 + 2 log 49 − log ? 1 9 3 7 3
A. A = log 7.
B. A = 2 log 7.
C. A = 4 log 7.
D. A = 3log 7. 3 3 3 3 Câu 9:
Cho các số dương a , b , c , và a  1 . Khẳng định nào sau đây đúng?
A. log b + log c = log (bc).
B. log b + log c = log b + c a a a ( ). a a a
C. log b + log c = log b − c .
D. log b + log c = log b − c a a a ( ). a a a
Câu 10: Đạo hàm của hàm số y = log 4x +1 là 3 ( ) ln 3 4 4 ln 3 1 A. y = . B. y = . C. y = . D. y = . 4x +1 (4x + ) 1 ln 3 4x +1 (4x + ) 1 ln 3
Câu 11: Hàm số nào trong bốn hàm số sau đồng biến trên các khoảng xác định của nó? x x x x  2   3 
A. y = (sin 202 ) 1 .
B. y = (ln 2) . C. y = .   D. y = .    5   2 + sin 2021 Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 −
Câu 12: Số nghiệm của phương trình 2 2x x = 1 là: A. 0. B. 3. C. 2. D. 1.
Câu 13: Phương trình 2
log (−3x + 5x +17) = 2 có tập nghiệm S là: 3  8   8   8   8  A. S= 1  ; − .
B. S= −1; − .
C. S= −1; .
D. S= 2; − .  3   3   3   3  Câu 14: Cho ( ) 3 .e x f x x − =
. Tập nghiệm của bất phương trình f ( x)  0 là  1   1   1  A. 0; .   B. −; .   C. (0; ) 1 . D. ; +  .    3   3   3 
Câu 15: Chọn mệnh đề sai:
A. Khối lập phương là khối đa diện lồi.
B. Khối chóp là khối đa diện lồi.
C. Khối lăng trụ là khối đa diện lồi.
D. Ghép hai khối đa diện lồi ta được một khối đa diện lồi.
Câu 16: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a ; hình chiếu của điểm S xuống mặt phẳng
( ABCD) trùng với trung điểm của A ,
B SD = 3a . Thể tích khối chóp S.ABCD là: 3 8a 3 8a 3 3 4a 3 4a 3 A. . B. . C. . D. . 3 3 3 3
Câu 17: Cho hình nón có chiều cao 2 3 và chu vi đường tròn đáy bằng 4 . Diện tích xung quanh của hình nón: A. 12. B. 16. C. 8 3 . D. 8.
Câu 18: Một hình nón có đường sinh l = 2a , góc ở đỉnh bằng 60 . Thể tích khối nón: 3 2 a 3 3 a 3 2 3 a A. . B. 3 2 a . C. . D. . 3 3 3
Câu 19: Một hình trụ có đường sinh 2a , đáy là hình tròn ngoại tiếp tam giác đều cạnh bằng a 3 . Thể tích của khối trụ là: A. 3 4 a . B. 3  a . C. 3 2 a . D. 3  a .
Câu 20: Một mặt cầu có diện tích 2
S = 12 (cm ) . Tìm thể tích V của khối cầu giới hạn bởi mặt cầu đó. 4 3 16 3 A. 3 V =  (cm ). B. 3 V =  (cm ). C. 3  (cm ). D. 3
V = 4 3 (cm ). 3 4 3 2 x − 3x + 5
Câu 21: Hỏi hàm số y =
nghịch biến trên các khoảng nào? x +1 A. (− ;  4 − ) và (2; ) + . B. ( 4 − ;2). C. (− ;  − ) 1 và ( 1 − ;+). D. ( 4 − ;− ) 1 và ( 1 − ;2). Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 22: Cho hàm số y = f ( x) có đạo hàm y ' = f '(x) và bảng xét dấu f '(x) như sau:
Khi đó số điểm cực trị của hàm số y = f (x) là: A. 1 B. 2 C. 3  D. 4 2x
Câu 23: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 3x + trên lần lượt là: 3 1 1 1 A. max y =
, min y = − 
B. max y = , min y = 0  0;2 0;2 3 3 0;2 0;2 3 1 1 1
C. max y = − , min y = 
D. max y = 0, min y = −  0;2 0;2 3 3 0;2 0;2 3 ax + b
Câu 24: Cho hàm số y =
(ad − bc  0, a  0) cx + có đồ thị như sau: d
Khi đó khẳng định nào sau đây đúng?
A. b  0, c  0, d  0.
B. b  0, c  0, d  0. C. b  0, c  0, d  0. D. b  0, c  0, d  0.
Câu 25: Cho hàm số y = f ( x) có bảng biến thiên như sau:
Khi đó số tiệm cận của đồ thị hàm số y = f (x) là: A. 1. B. 2. C. 3. D. 4. −
Câu 26: Tập xác định của hàm số y = ( − x) 5 1 là A. D = \   1 .
B. D = (1;+). C. D = (− ;  ) 1 . D. D = (− ;   1 .
Câu 27: Tập xác định của hàm số y = log 3x + 6 là 2 ( ) A. D = \  2 . B. D = \ −  2 . C. D = (− ;  2 − ). D. D = ( 2 − ;+). Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 28: Đạo hàm của hàm số ( ) 2 5 3 7 x x f x − + − = là − + − − + − A. f ( x) 2 x 5x 3 ' = 7 .
B. f ( x) = ( − x) 2 x 5x 3 ' 5 2 7 . − + − − + −
C. f ( x) =
( − x) 2x 5x 3 ' ln 7. 5 2 7 . D. f ( x) 2 x 5x 3 ' = 7 ln 7.
Câu 29: Với a là số thực dương tùy ý, 12 log a bằng 9 A. 4 + log . a B. 6 log . a C. 24 log . a D. 4 log . a 3 3 3 3
Câu 30: Nghiệm của phương trình log
(x+ )1−log 1− x =1 nằm trong khoảng nào 2 ( ) 2 A. ( 1 − ;0). B. (2; ) 3 . C. (0; ) 1 . D. (4;5).
Câu 31: Hai nghiệm của phương trình log x + 3log 2 = 4 là x , x x x .Tính T = x − x 1 2 ( 1 2 ) 2 x 2 1
A. T = 6.
B. T = 4.
C. T = 2. D. T = 1.
Câu 32: Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ:
Mệnh đề nào sau đây đúng?
A. Khối bát diện đều là loại 4;  3 .
B. Khối bát diện đều và khối lập phương đều có cùng số cạnh.
C. Cả năm khối đa diện có số mặt chia hết cho 4.
D. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh.
Câu 33: Cho hình chóp S.ABCD đáy là hình vuông cạnh a , cạnh SA vuông góc với mặt phẳng ( ABCD),
góc giữa cạnh SD và mặt phẳng ( ABCD) bằng 0
60 . Thể tích của khối chóp đã cho bằng: 3 3a 3 3a 3 3a A. 3 3a . B. . C. . D. . 3 6 9
Câu 34: Cắt hình trụ (T) bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông cạnh
bằng 6 . Diện tích xung quanh của hình trụ (T) bằng: A. 72 . B. 18 . C. 9 . D. 36 .
Câu 35: Cho hình nón tròn xoay đường sinh l = 4a . Thiết diện qua trục của nó là một tam giác cân có
một góc bằng 120 . Thể tích V của khối nón đó là: 3 3  3  a a 3
A. V =  a 3 . B. V = . C. V = . D. 3 V = 8 a . 3 3
II. PHẦN TỰ LUẬN:
Câu 36: Tìm tập tất cả các giá trị nguyên của tham số thực m để phương trình sau có bốn nghiệm thực 2 2 2 2 x −4 x+3
x +2mx+2m −6m 1 − x +(m−2) 2
x+m −3m 1 + phân biệt: 5 + 5 = 25 +1.
Câu 37: Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a , tam giác SBA vuông tại B , tam
giác SAC vuông tại C . Biết góc giữa hai mặt phẳng (SAB) và ( ABC) bằng 60 . Tính thể tích
khối chóp S.ABC theo a . Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 38: Cho hàm số y = f (x) liên tục trên và có bảng biến thiên như sau:
Tìm điểm cực đại của hàm số g (x) = f (2x − ) 1 .
Câu 39: Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây. 1 1
Tìm giá trị lớn nhất của hàm số g ( x) = f ( 2 4x − x ) 3 2
+ x − 3x + 8x + trên đoạn 1;  3 . 3 3
---------- HẾT ---------- Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM: Câu 1:
Cho hàm số y = f (x) xác định, liên tục trên và có bảng biến thiên như hình sau:
Mệnh đề nào sau đây sai?
A. Hàm số nghịch biến trên khoảng (− ;  +) .
B. Hàm số đồng biến trên khoảng (− ;  +) .
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên khoảng (1;+). Lời giải Chọn A
Dựa vào bảng biến thiên  y '  0, x
  nên hàm số đồng biến trên khoảng (− ;  +) .
Vậy mệnh đề sai là: “Hàm số nghịch biến trên khoảng (− ;  +) .” Câu 2:
Cho hàm số y = f (x) xác định và liên tục trên , có đồ thị như hình vẽ:
Hàm số y = f (x) có giá trị cực đại là:
A. y = 2. B. y = 2. −
C. x = 2.
D. x = 0. Lời giải Chọn A
Dựa vào đồ thị hàm số, suy ra giá trị cực đại của hàm số là y = 2 . Câu 3:
Cho hàm số y = f (x) có đồ thị trên đoạn  2 − ; 
1 như hình vẽ bên dưới. Giá trị max f ( x) bằng:  2 − ;  1 Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 A. 1. B. 3. C. 0. D. 3. − Lời giải Chọn A
Giá trị lớn nhất của hàm số y = f (x) trên đoạn  2 − ; 
1 là điểm cao nhất của đồ thị hàm số
y = f (x) trên đoạn  2 − ; 
1 . Dựa vào đồ thị ta thấy max f ( x) = 1.  2 − ;  1 Câu 4:
Đường cong trong hình vẽ là đồ thị của hàm số nào trong bốn hàm số sau đây? A. 3 2
y = x − 3x −1. B. 3 2
y = x + 3x −1. C. 3 2
y = −x + 3x −1. D. 4 2
y = −x + 3x − 2. Lời giải Chọn C
Dựa vào đồ thị ta thấy đây là hàm bậc ba. Nhánh cuối đi xuống nên ta có hệ số a  0 . Câu 5:
Hàm số nào dưới đây có đồ thị dạng như đường cong trong hình bên A. 4 2
y = −x + 2x +1. B. 4 2
y = x + 2x + 2. C. 4 2
y = x − 2x −1. D. 4 2
y = −x + 2x − 2. Lời giải Chọn C Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Dựa vào đồ thị ta thấy đây là hàm trùng phương. Nhánh cuối đi lên nên ta có hệ số a  0 ; giao
điềm của đồ thị với trục tung nằm phía dưới trục Ox nên hệ số c  0 . 4x −1 Câu 6:
Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số y = ? 2x − 3 3 3
A. x = 2. B. y = . C. x = . D. y = 2. 2 2 Lời giải Chọn D ax + b d a Hàm số y =
có đường tiệm cận đứng là x = −
; đường tiệm cận ngang là y = . cx + d c c − Theo đề 4x 1
ra ta có đường tiệm cận ngang của đồ thị hàm số y =
là đường thẳng y = 2 . 2x − 3  Câu 7:
Tập xác định của hàm số y = ( x + 2) là: A. B. (0;+). C. ( 2 − ;+). D. \   2 . Lời giải Chọn C Vì số mũ 
 là một số thực nên điều kiện xác định của hàm số y = ( x + 2) là: x + 2  0  x  2 − Vậy D = ( 2; − +) . 1 Câu 8:
Tính giá trị biểu thức A = log 7 + 2 log 49 − log ? 1 9 3 7 3
A. A = log 7.
B. A = 2 log 7.
C. A = 4 log 7.
D. A = 3log 7. 3 3 3 3 Lời giải Chọn D 1 2 1 A log 7 2 log 49 log log − = + − = + − − 7 2 log 7 log 7 1 2 1 1 9 3 3 3 2 7 3 3
A = − log 7 + 2 log 7 + 2 log 7 = 3log 7 3 3 3 3  Phân tích
Áp dụng công thức biến đổi logarit, công thức lũy thừa cơ bản Câu 9:
Cho các số dương a , b , c , và a  1 . Khẳng định nào sau đây đúng?
A. log b + log c = log (bc).
B. log b + log c = log b + c a a a ( ). a a a
C. log b + log c = log b − c .
D. log b + log c = log b − c a a a ( ). a a a Lời giải Chọn A
Theo tính chất logarit ta có: log b + log c = log bc . a a a ( )  Phân tích
Công thức cơ bản của logarit
Câu 10: Đạo hàm của hàm số y = log 4x +1 là: 3 ( ) ln 3 4 4 ln 3 1 A. y = . B. y = . C. y = . D. y = . 4x +1 (4x + ) 1 ln 3 4x +1 (4x + ) 1 ln 3 Lời giải Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Chọn B (  4x + ) 1 4 y = ( = . 4x + ) 1 ln 3 (4x + ) 1 ln 3  Phân tích
Công thức đạo hàm của hàm logarit.
Câu 11: Hàm số nào trong bốn hàm số sau đồng biến trên các khoảng xác định của nó? x x x x  2   3 
A. y = (sin 202 ) 1 .
B. y = (ln 2) . C. y = .   D. y =    5   2 + sin 2021 Lời giải Chọn D Hàm số x
y = a đồng biến trên các khoảng xác định của nó  a 1.  Phân tích
Áp dụng tính chất của hàm số mũ −
Câu 12: Số nghiệm của phương trình 2 2x x = 1 là: A. 0. B. 3. C. 2. D. 1. Lời giải Chọn C  = 2 − − x Ta có: 2x x = 2 1 x x 0  2 = 2 2  x − x = 0 0  
. Vậy phương trình có 2 nghiệm. x =1  Phân tích
Phương trình mũ cơ bản
Câu 13: Phương trình 2
log (−3x + 5x +17) = 2 có tập nghiệm S là: 3  8   8   8   8  A. S= 1  ; − .
B. S= −1; − .
C. S= −1; .
D. S= 2; − .  3   3   3   3  Lời giải Chọn C − + Điều kiện: 2 3
− x + 5x +17  0  5 229 5 229  x  . 6 6 x = 1 − 2 
log (−3x + 5x +17) = 2  2 3
− x + 5x +17 = 9  (thỏa điều kiện). 3 8 x =  3  Phân tích
Phương trình cơ bản của logarit. Câu 14: Cho ( ) 3 .e x f x x − =
. Tập nghiệm của bất phương trình f ( x)  0 là  1   1   1  A. 0; .   B. −; .   C. (0; ) 1 . D. ; +  .    3   3   3  Lời giải Chọn B − − Ta có: ( ) 3x 3 = e −3 .e x f x x ( ) 3 1 3 e x x − = − . 1  1  f ( x)  0 ( ) 3 1 3 e x x −  −
 0  x  . Vậy tập nghiệm của bất phương trình: −;   . 3  3  Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Phân tích
Công thức đạo hàm hàm mũ và công thức đạo hàm và tính đồng biến và nghịch biến của hàm số mũ
Câu 15: Chọn mệnh đề sai:
A. Khối lập phương là khối đa diện lồi
B. Khối chóp là khối đa diện lồi
C. Khối lăng trụ là khối đa diện lồi
D. Ghép hai khối đa diện lồi ta được một khối đa diện lồi. Lời giải Chọn D
Câu 16: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a ; hình chiếu của điểm S xuống mặt phẳng
( ABCD) trùng với trung điểm của A ,
B SD = 3a . Thể tích khối chóp S.ABCD là: 3 8a 3 3 3 8a 3 4a 4a 3 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn A
Gọi H là trung điểm của AB  SH ⊥ ( ABCD)
Trong tam giác vuông AHD có: 2 2 2 2 2 2
HD = AD + AH = 4a + a = 5a
Trong tam giác vuông SHD có: 2 2 2 2 2 2
SH = SD − HD = 9a − 5a = 4a SH = 2a 3 1 1 8a Vậy 2 V = S
.SH = .4a .2a = S . ABCD 3 ABCD 3 3
Câu 17: Cho hình nón có chiều cao 2 3 và chu vi đường tròn đáy bằng 4 . Diện tích xung quanh của hình nón: A. 12. B. 16. C. 8 3 . D. 8. Lời giải Chọn D Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Gọi r là bán kính đường tròn đáy, nên chu vi đường tròn đáy là 2 . r
Ta có: 2 r = 4  r = 2 2 2
l = h + r = 12+ 4 = 4. Vậy S
=  rl = 8 (đvdt). xq
Câu 18: Một hình nón có đường sinh l = 2a , góc ở đỉnh bằng 60 . Thể tích khối nón: 3 2 a 3 3 a 3 2 3 a A. . B. 3 2 a . C. . D. . 3 3 3 Lời giải Chọn C OA = S . A sin 30 = a
Tam giác vuông SOA có OSA = 30   . SO = S .
A cos 30 = a 3 3 1 1 3 a Vậy 2 2 V =
r h =  a .a 3 = (đvtt). 3 3 3
Câu 19: Một hình trụ có đường sinh 2a , đáy là hình tròn ngoại tiếp tam giác đều cạnh bằng a 3 . Thể tích của khối trụ là A. 3 4 a . B. 3  a . C. 3 2 a . D. 3  a . Lời giải Chọn C Tam giác đề a 3
u cạnh a 3  bán kính đường tròn ngoại tiếp:
= 2R R = a . sin 60 Vậy 2 2 3
V =  R h =  R l = 2 a .
Câu 20: Một mặt cầu có diện tích 2
S = 12 (cm ) . Tìm thể tích V của khối cầu giới hạn bởi mặt cầu đó. 4 3 16 3 A. 3 V =  (cm ) B. 3 V =  (cm ) C. 3  (cm ) D. 3
V = 4 3 (cm ) 3 4 3 Lời giải Chọn D 4 Ta có: 2
S = 4 R = 12  R = 3(cm) . Vậy 3 3 V =
R = 4 3 (cm ) . 3 2 x − 3x + 5
Câu 21: Hỏi hàm số y =
nghịch biến trên các khoảng nào? x +1 A. (− ;  4 − ) và (2; ) + . B. ( 4 − ;2). C. (− ;  − ) 1 và ( 1 − ;+). Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 D. ( 4 − ;− ) 1 và ( 1 − ;2). Lời giải Chọn D Ta có : D = \−  1 2 2
(2x − 3)(x +1) − (x − 3x + 5) x + 2x − 8 y ' = = 2 2 (x +1) (x +1) x = 2 Cho 2
y ' = 0  x + 2x − 8 = 0   (nhận) x = 4 −
Bảng xét dấu đạo hàm:
Vậy hàm số nghịch biến trên khoảng ( 4 − ;− ) 1 và ( 1 − ;2)
Câu 22: Cho hàm số y = f ( x) liên tục trên
, có đạo hàm y ' = f '(x) x
  và bảng xét dấu f '(x) như sau:
Khi đó số điểm cực trị của hàm số y = f (x) là: A. 1. B. 2. C. 3. D. 4. Lời giải Chọn B
Ta có: x là điểm cực trị của hàm số khi f '(x ) = 0 và f '(x) đổi dấu qua x . 0 0 0
Từ bảng xét dấu f '(x) ta thấy f '(x) chỉ đổi dấu qua x và x . 2 3
Do đó: Hàm số có hai điểm cực trị là x và x . 2 3 2x
Câu 23: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 3x + trên lần lượt là 3 1 1 1 A. max y =
, min y = −  B. max y =
, min y = 0  0;2 0;2 3 3 0;2 0;2 3 1 1 1
C. max y = − , min y = 
D. max y = 0, min y = −  0;2 0;2 3 3 0;2 0;2 3 Lời giải Chọn A
Áp dụng quy tắc tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số ta có:
Tập xác định của hàm số: D = . 2( 2 3x + 3) 2 − 2 . x 6x 6 − x + 6 y ' = ( = 3x + 3) . 2 (3x +3)2 2 2 x = 1 − y ' = 0  .  x =1 Bảng biến thiên: Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 1 1 Vậy: max y = , min y = −  3 3 ax + b
Câu 24: Cho hàm số y =
(ad − bc  0, a  0) cx + có đồ thị như sau: d
Khi đó khẳng định nào sau đây đúng?
A. b  0, c  0, d  0.
B. b  0, c  0, d  0.
C. b  0, c  0, d  0.
D. b  0, c  0, d  0. Lời giải Chọn C
Từ đồ thị của hàm số ta có: a a
Đường thẳng y = là tiệm cận ngang nên  0  a,c cùng dấu  c  0 . c c Đườ d d
ng thẳng x =1 là tiệm cận đứng nên: − =1  0   0  d  0 . c c b
Mà giao điểm đồ thị hàm số với trục tung có tọa độ âm nên
 0  b, d trái dấu  b  0. d
Vậy: b  0, c  0, d  0 .
Câu 25: Cho hàm số y = f ( x) có bảng biến thiên như sau: x − x x x 1 2 3 +
f '(x) + 0 − − 0 +
f (x + + 1 ) f ( x)
− − f (x 3 )
Khi đó số tiệm cận của đồ thị hàm số y = f (x) là A. 1. B. 2. C. 3. D. 4. Lời giải Chọn A
Theo định nghĩa đường tiệm cận của đồ thị hàm số: Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
lim y = y thì đường thẳng y = y là tiệm cận ngang của đồ thị hàm số. 0 0 x→
Nếu ít nhất một trong các điều kiện sau được thỏa mãn: lim y = + ,  lim y = − ,  lim y = + ,
 lim y = − hoặc lim y =  thì đường thẳng x = x là tiệm cận + − − −  0 x→x x→x x→x x→x x→x 0 0 0 0 0
đứng của đồ thị hàm số.
Đồng thời, dựa vào bảng biến thiên ta thấy:
lim y =  nên đồ thị hàm số không có tiệm cận ngang. x→
lim y =  nên đường thẳng x = x là tiệm cận đứng của đồ thị hàm số.  2 x→x2
Do đó đồ thị của hàm số chỉ có một đường tiệm cận. −
Câu 26: Tập xác định của hàm số y = ( − x) 5 1 là A. D = \  1 
B. D = (1;+) C. D = (− ) ;1 
D. D = (−  ;1  Lời giải Chọn A
Điều kiện của hàm số y = u với  nguyên âm là u  0 . Do đó điề −
u kiện của hàm số y = ( − x) 5 1
là: 1− x  0  x  1.
Vậy: Tập xác định của hàm số y = ( − x)5 1 là D = \  1 
Câu 27: Tập xác định của hàm số y = log 3x + 6 là 2 ( ) A. D = \  2  B. D = \−  2  C. D = (− ;  2 − ) D. D = ( 2; − +) Lời giải Chọn D
Điều kiện của hàm số y = log f x là f (x)  0 . a ( )
Do đó điều kiện của hàm số y = log 3x + 6 là: 3x + 6  x  2 − . 2 ( )
Vậy: Tập xác định của hàm số y = log 3x + 6 là D = ( 2; − +) 2 ( )
Câu 28: Đạo hàm của hàm số ( ) 2 5 3 7 x x f x − + − = là A. f ( x) 2 −x +5x−3 ' = 7 .
B. f ( x) = ( − x) 2 −x +5x−3 ' 5 2 7 .
C. f ( x) = ( − x) 2 −x +5x−3 ' ln 7. 5 2 7 . D. f ( x) 2 −x +5x−3 ' = 7 ln 7. Lời giải Chọn B
Đạo hàm của hàm số ( ) u
f x = a là '( ) u f x = a ln . a u '.
Do đó đạo của hàm số ( ) 2 5 3 7 x x f x − + − = là: f ( x) 2 −x + x− =
(−x + x− ) = ( − x) 2 5 3 2 −x +5x−3 ' 7 ln 7. 5 3 ' ln 7 5 2 7 .
Câu 29: Với a là số thực dương tùy ý, 12 log a 9 bằng A. 4 + log a 6log a 24 log a 4 log a 3 . B. 3 . C. 3 . D. 3 . Lời giải Page 15
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Chọn B 1 Ta có: log ( 12 a
=12log a =12. log a = 6log a . 9 ) 2 3 3 3 2
Câu 30: Nghiệm của phương trình log (x+ )
1 − log 1− x =1 nằm trong khoảng nào 2 ( ) 2 A. ( 1 − ;0) . B. (2;3). C. (0 ) ;1 D. (4;5) Lời giải Chọn C 1  − x  0 Điều kiện   1 −  x 1 . x +1  0
Phương trình  2log x +1 − log 1− x =1 . 2 ( ) 2 ( )
 2log x +1 = log 1− x +log 2 2 ( ) 2 ( ) 2 .  log (x + )2 1 = log 2 1− x  2 2  ( ) . 2
x + 2x +1 = 2 − 2x . x = 2 − + 5 2
x + 4x −1 = 0 x = 2−− 5  (L) .
Vậy tập nghiệm phương trình là S =  2 − + 5.
Câu 31: Hai nghiệm của phương trình log x + 3log 2 = 4
x , x x x
T = x − x 2 x là .Tính 1 2 ( 1 2 ) 2 1
A. T = 6 .
B. T = 4.
C. T = 2 . D. T = 1. Lời giải Chọn A
Điều kiện: 0  x  1. 3 log x =1 x = 2
log x + 3log 2 = 4  log x + = 4 2
 log x − 4log x + 3 = 0 2   . 2 x 2   log x 2 2 log x = 3 x = 8 2  2
Tập nghiệm của phương trình là S = 2 ; 
8 . Vậy T = 8 − 2 = 6 .
Câu 32: Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ:
Mệnh đề nào sau đây đúng?
A. Khối bát diện đều là loại 4;  3 .
B. Khối bát diện đều và khối lập phương đều có cùng số cạnh.
C. Cả năm khối đa diện có số mặt chia hết cho 4.
D. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh. Lời giải Chọn B
+ A sai, vì khối bát diện đều là loại 3;  4 .
+ B đúng, vì khối lập phương có 12 cạnh; khối bát diện đều có 12 cạnh. Page 16
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
+ C sai, vì khối lập phương có 6 mặt và 6 không chia hết cho 4.
+ D sai, vì khối 12 mặt đều có 20 đỉnh, còn khối 20 mặt đều có 12 đỉnh.
Câu 33: Cho hình chóp S.ABCD đáy là hình vuông cạnh a , cạnh SA vuông góc với mặt phẳng ( ABCD),
góc giữa cạnh SD và mặt phẳng ( ABCD) bằng 0
60 . Thể tích của khối chóp đã cho bằng: 3 3a 3 3a 3 3a A. 3 3a . B. . C. . D. . 3 6 9 Lời giải Chọn B S A 60° D B a C
SA ⊥ ( ABCD)  AD là hình chiếu của SD lên mặt phẳng ( ABCD) .
Suy ra (SD ( ABCD)) = (SD AD) 0 , , = SDA = 60 . SA = A . D tan SDA = 3a . 1 3 a 3 Ta có: V = .S .SA = (đvtt). S . ABCD AB D 3 C 3
Câu 34: Cắt hình trụ (T) bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông cạnh
bằng 6 . Diện tích xung quanh của hình trụ (T) bẳng: A. 72 . B. 18 . C. 9 . D. 36 . Lời giải Chọn D
Ta có r = 3, l = 6  S = 2 rl = 36 . xq
Câu 35: Cho hình nón tròn xoay đường sinh l = 4a . Thiết diện qua trục của nó là một tam giác cân có
một góc bằng 120 . Thể tích V của khối nón đó là: Page 17
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 3 3  3  a a 3
A. V =  a 3 . B. V = . C. V = . D. 3 V = 8 a . 3 3 Lời giải Chọn D
Gọi thiết diện qua trục của hình nón là S
AB như hình vẽ. Ta có S
AB cân tại S có một góc 120  ASB =120 . 1 OSA = ASB = 60 ( S
AB cân tại S ). 2
Xét  SAO vuông tại O có:
h = SO = S . A cos ASO = 4 .
a cos60 = 2a 3 r = OA = . SA sin ASO = 4 . a = 2a 3 . 2
Thể tích của khối nón là: 1 1 V =
r h = .(2a 3)2 2 3 .2a = 8a  . 3 3
II. PHẦN TỰ LUẬN:
Câu 36: Tìm tập tất cả các giá trị nguyên của tham số thực m để phương trình sau có bốn nghiệm thực 2 2 2 2 x −4 x+3
x +2mx+2m −6m 1 − x +(m−2) 2 + − + phân biệt: x m 3m 1 5 + 5 = 25 +1. Lời giải 2 2 2 2 x −4 x+3
x +2mx+2m −6m 1 − x +(m−2) 2 + − + Ta có: x m 3m 1 5 + 5 = 25 +1 2 2 2 2 x −4 x+3
x +2mx+2m −6m 1 − 2 x +2(m−2) 2
x+2m −6m+2  5 + 5 = 5 +1 (1). Đặt 2
a = x − 4x + 3; 2 2
b = x + 2mx + 2m − 6m −1 2
a +b = x + (m− ) 2 2 2
2 x + 2m − 6m + 2 a  = a = 0
Ta có (1)  5a + 5b = 5a+b +1 5a 5b 5 . a 5b  + = +1 (1 5a)(1 5b  − − ) = 5 1 0     . 5b = 1 b  = 0 x = +) a = 0 2
x − 4x + 3 = 1 0   . x = 3 +) b = 0 2 2
x + 2mx + 2m − 6m −1= 0 (*). Page 18
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Yêu câu bài toán  Phương trình (*) có hai nghiệm phân biệt khác 1 và khác 3   0 2 2 2
 = m − 2m + 6m +1  0
−m + 6m +1  0 3
 − 10  m  3+ 10     2
 2m − 4m  0 m  0  m  0  m  0     2 2m + 8  0  m  2 m  2   m  2  .
Ta có: S = 1;3;4;5; 
6 . Vậy có năm giá trị của tham số m thỏa mãn yêu cầu bài toán.
Câu 37: Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a , tam giác SBA vuông tại B , tam
giác SAC vuông tại C . Biết góc giữa hai mặt phẳng (SAB) và ( ABC) bằng 60.
Tính thể tích khối chóp S.ABC theo a . Lời giải S D C B A
Gọi D là hình chiếu của S lên mặt phẳng ( ABC) , suy ra SD ⊥ ( ABC) .
Ta có SD ⊥ AB và SB ⊥ AB (gt) suy ra AB ⊥ (SBD)  BA ⊥ BD.
Tương tự có AC ⊥ DC hay tam giác ACD vuông ở C . Dễ thấy SBA = S
CA (cạnh huyền và cạnh góc vuông), suy ra SB = SC . Từ đó ta chứng minh được SBD = S
CD nên cũng có DB = DC .
Vậy DA là đường trung trực của BC nên cũng là đường phân giác của góc BAC . a
Ta có DAC = 30 , suy ra DC =
. Ngoài ra góc giữa hai mặt phẳng (SAB) và ( ABC) là 3 SD a
SBD = 60 , suy ra tan SBD =  SD = . BD tan SBD = . 3 = a . BD 3 2 3 1 1 a 3 a 3 Vậy V = .S .SD = . .a = . S . ABC  3 ABC 3 4 12
Câu 38: Cho hàm số y = f (x) liên tục trên và có bảng biến thiên như sau:
Tìm điểm cực đại của hàm số g (x) = f (2x − ) 1 . Lời giải
Ta có: g( x) = (2x − )
1 . f (2x − )
1 = 2 f (2x − ) 1 . Page 19
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x = 0 2x −1 = 1 −   1
g(x) = 0  f (2x − )
1 = 0  2x −1 = 0  x =  .  2 2x −1 =1  x =1 
Ta có bảng biến thiên của g ( x) như sau: 1
Vậy hàm số g ( x) đạt cực đại tại x = . 2
Câu 39: Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây. 1 1
Tìm giá trị lớn nhất của hàm số g ( x) = f ( 2 4x − x ) 3 2
+ x − 3x + 8x + trên đoạn 1;  3 . 3 3 Lời giải
g( x) = ( − x) f ( 2 x − x ) 2 4 2 4
+ x − 6x +8 = ( − x)  f   ( 2 2 2
4x − x ) + 4 − x . Với x 1;  3 thì 4 − x  0 ; 2
3  4x − x  4 nên f ( 2
4x − x )  0 . Suy ra f ( 2 2
4x − x ) + 4 − x  0, x  1;  3 . Bảng biến thiên:
Suy ra max g ( x) = g (2) = f (4) + 7 =12 . 1;  3 Page 20
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 07
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Cho hàm số y = f ( x) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào sau đây? A. ( 1 − ; ) 1 . B. ( ) ;1 − . C. (0 ) ;1 . D. ( 1 − ;0) . Câu 2:
Cho hàm số y = f ( x) có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng A. 2 . B. 0 . C. 1. D. 5 . Câu 3:
Giá trị lớn nhất của hàm số 4 2
y = x − 4x + 9 trên đoạn  2 − ;  3 bằng A. 2 . B. 5 . C. 54 . D. 9 . Câu 4:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? A. 4 2
y = 2x − 4x +1 . B. 4 2 y = 2
− x + 4x +1. C. 3
y = 2x − 3x +1. D. 3 y = 2 − x + 3x +1. Câu 5:
Đường cong trong hình dưới đây là đồ thị của hàm số nào trong các hàm số sau? Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 y 1 1 O 1 2 x x +1 2x − 4 x +1 2x A. y = y = y = y = x − . B. 1 x − . C. 1 2x − . D. 2 3x − . 3 2x +1 Câu 6:
Tiệm cận ngang của đồ thị hàm số y =
là đường thẳng có phương trình x +1 A. y = 2 . B. x = 2 . C. y = 1 − . D. x = 1 − . Câu 7:
Kết luận nào đúng về số thực a  nếu 3 7 a a ?
A. 1  a  2. B. a 1 .
C. 0  a  1. D. a 1. Câu 8:
Tập xác định D của hàm số y = log 2x +1 là 3 ( )  1   1   1 
A. D = −; −   . B. D = ; +   .
C. D = (0;+) .
D. D = − ; +   .  2   2   2  Câu 9:
Cho a , b , c là ba số thực dương khác 1. Đồ thị các hàm số x y = a , x y = b , x
y = c được cho
trong hình vẽ bên. Mệnh đề nào sau đây đúng?
A. c a b .
B. b c a .
C. a c b .
D. a b c .
Câu 10: Đạo hàm của hàm số y = log x là 1 ln10 1 1 A. y = . B. y = . C. y = . D. y = . x x x ln10 10 ln x 2
Câu 11: Đạo hàm của hàm số 3x y = là 2 2 2 2 A. 3x y = . B. 3x y = .ln 3. C.  = 2 .3x y x .
D.  = 2 .ln 3.3x y x . +
Câu 12: Phương trình 2x 1 2 = 32 có nghiệm là Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 5 3 A. x = . B. x = 2 . C. x = . D. x = 3. 2 2
Câu 13: Nghiệm của phương trình log x + 7 = 5 là 2 ( )
A. x = 39 .
B. x =18.
C. x = 25 .
D. x = 3.
Câu 14: Tập nghiệm của bất phương trình log x −1 1 là 3 ( ) A. (1;  4 . B. ( ; − 4) . C. ( ; −  4 . D. (0; 4.
Câu 15: Khối lập phương là khối đa diện đều loại nào? A. 3;  3 . B. 5;  3 . C. 4;  3 . D. 3;  4 .
Câu 16: Thể tích khối lập phương có cạnh 2a bằng A. 3 8a . B. 3 2a . C. 3 a . D. 3 6a .
Câu 17: Cho hình nón có bán kính đáy là r =
3 và đường sinh l = 4 . Diện tích xung quanh của hình nón đã cho là
A. S = 16 3 . B. S = 24 . C. S = 8 3 . D. S = 4 3 .
Câu 18: Cho hình chữ nhật ABCD có AB = a , AD = 2a . Thể tích của khối trụ tạo thành khi quay hình
chữ nhật ABCD quanh cạnh AB bằng A. 3 4 a . B. 3  a . C. 3 2a . D. 3 a .
Câu 19: Cho khối nón có độ dài đường cao bằng 2a và bán kính đáy bằng a . Thể tích của khối nón đã cho bằng 3 2 a 3 4 a 3  a A. . B. . C. . D. 3 2 a . 3 3 3
Câu 20: Cắt hình trụ (T ) bởi một mặt phẳng đi qua trục của nó, ta được thiết diện là một hình vuông cạnh
là 7. Diện tích xung quanh của (T ) bằng 49 49 A. . B. 49 . C. 98 . D. . 2 4
Câu 21: Cho hàm số y = f ( x) có đạo hàm liên tục trên
và có đồ thị của hàm số y = f (x) như hình
vẽ bên. Mệnh đề nào dưới đây sai?
A. Hàm số y = f ( x) đồng biến trên (2;+) .
B. Hàm số y = f ( x) nghịch biến trên ( 1 − ;0) .
C. Hàm số y = f ( x) đồng biến trên (1;+).
D. Hàm số y = f ( x) nghịch biến trên ( ; − 2) . Câu 22: Cho hàm số 3
y = x − 3x + 5 . Điểm cực tiểu của đồ thị hàm số đã cho là A. (7;− ) 1 . B. ( 1 − ;7). C. (3; ) 1 . D. (1;3) . Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Câu 23: Cho hàm số y = f ( x) liên tục trên đoạn  1 − ; 
3 và có đồ thị như hình vẽ dưới đây. Gọi M và
m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  1 − ; 
3 . Giá trị của M − m bằng A. 4 . B. 1. C. 5 . D. 0 . ax + 2
Câu 24: Cho hàm số y = a b c
có đồ thị như hình vẽ bx + , , , c
Khẳng định nào dưới đây đúng?
A. b a  0  c .
B. b  0  a c .
C. a b  0  c .
D. b  0  c a . Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Câu 25: Cho hàm số y = f (x) có bảng biến thiên như sau:
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 1. B. 3 . C. 2 . D. 4 . 5
Câu 26: Rút gọn biểu thức 3 3
Q = b : b với b  0. Kết quả nào sau đây đúng 5 4 4 − A. 9 Q = b . B. 2 Q = b . C. 3 Q = b . D. 3 Q = b . a b c d
Câu 27: Cho các số thực dương a , b , c , d . Biểu thức S = ln + ln + ln + ln bằng b c d aa b c d A. 0 . B. ln ( . a . b . c d ) . C. 1. D. ln + + +   .  b c d a
Câu 28: Một người gửi tiết kiệm vào một ngân hàng với lãi suất 7, 5% /năm. Biết rằng nếu không rút tiền
ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp
theo. Hỏi sau bao nhiêu năm người đó thu được (cả số tiền gửi ban đầu và lãi) ít nhất gấp đôi số
tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và người đó không rút tiền ra? A. 11 năm. B. 10 năm. C. 12 năm. D. 9 năm.
Câu 29: Tìm tất cả các giá trị thực của tham số m để hàm số 2
y = ln(x − 2x + m +1) có tập xác định là . A. m = 0 .
B. 0  m  3. C. m  1
− hoặc m  0. D. m  0. x−
Câu 30: Gọi S là tổng tất cả các nghiệm của phương trình ( x ) 1 2
= 64. Giá trị của S là 1 A. S = . B. S = 6 − . C. S = 3 − . D. S = 1. 2
Câu 31: Số nghiệm của phương trình log 6 + x + log 9x − 5 = 0 là 3 ( ) 3 ( ) A. 0 . B. 2 . C. 1. D. 3 .
Câu 32: Mặt phẳng ( AB 'C ') chia khối lăng trụ AB .
C A' B 'C ' thành các khối đa diện nào?
A. Hai khối chóp tứ giác.
B. Một khối chóp tam giác và một khối chóp tứ giác.
C. Hai khối chóp tam giác.
D. Một khối chóp tam giác và một khối chóp ngũ giác. Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Câu 33: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = a 3, SA vuông góc
với mặt phẳng đáy và mặt phẳng (SBC) tạo với đáy một góc 60 . Thể tích V của khối chóp S.ABCD là 3 a 3 a 3 A. V = . B. V = . C. 3 V = a . D. 3 V = 3a . 3 3
Câu 34: Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a . Thể tích của khối nón đã cho bằng 3 3 a 3 3 a 3 2 a 3  a A. . B. . C. . D. . 2 3 3 3
Câu 35: Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 2 , thiết diện
thu được là hình vuông có diện tích bằng 16 . Diện tích xung quanh của hình trụ đã cho bằng A. 8 6 . B. 24 6 . C. 10 6 . D. 12 6 .
II. PHẦN TỰ LUẬN (4 câu – 3 điểm)
Câu 36: Cho hàm số f ( x) có đồ thị f ( x) như hình vẽ bên. Tìm giá trị nhỏ nhất của hàm số
g ( x) = f ( x) 1 3 3 3 2
− x − x + x + 2019 trên đoạn  3 − ;  1 . 3 4 2
Câu 37: Cho lăng trụ đứng AB . C A BC
  có đáy là tam giác vuông cân tại B , AC = a 2 ; biết góc giữa mặt phẳng ( A B
C) và mặt phẳng đáy bằng 60. Tính thể tích V của khối lăng trụ AB . C A BC   .
Câu 38: Ông A dự định sử dụng hết 2
5 m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Câu 39: Cho phương trình 5x + m = log
x − m với m là tham số. Có bao nhiêu giá trị nguyên của 5 ( ) m( 2
− 0;20) để phương trình đã cho có nghiệm?
---------- HẾT ----------
HƯỚNG DẪN GIẢI CHI TIẾT Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Cho hàm số y = f ( x) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào sau đây? A. ( 1 − ; ) 1 . B. ( ) ;1 − . C. (0 ) ;1 . D. ( 1 − ;0) . Lời giải Chọn D
Dựa vào đồ thị hàm số, ta có bảng biến thiên sau Câu 2:
Cho hàm số y = f ( x) có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng A. 2 . B. 0 . C. 1. D. 5 . Lời giải Chọn D
Dựa vào bảng biến thiên hàm số có giá trị cực đại bằng 5 . Câu 3:
Giá trị lớn nhất của hàm số 4 2
y = x − 4x + 9 trên đoạn  2 − ;  3 bằng Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 A. 2 . B. 5 . C. 54 . D. 9 . Lời giải Chọn C Tập xác định: D =   2 − ;  3 x = 0(−2;3) Ta có 3
y = 4x − 8 ; x y = 0   . x =  2   (−2;3)
Ta có y (0) = 9; y ( 2
− ) = 9; y(3) = 54; y( 2) = 5.
Vậy giá trị lớn nhất của hàm số đã cho bằng 54 . Câu 4:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? A. 4 2
y = 2x − 4x +1 . B. 4 2 y = 2
− x + 4x +1. C. 3
y = 2x − 3x +1. D. 3 y = 2 − x + 3x +1. Lời giải Chọn B
Từ hình vẽ ta thấy đây là đồ thị hàm trùng phương 4 2
y = ax + bx + c nên loại C,. D.
Lại thấy lim y = − nên a  0 , suy ra loại A chọn. B. x→ Câu 5:
Đường cong trong hình dưới đây là đồ thị của hàm số nào trong các hàm số sau? y 1 1 O 1 2 x Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 x +1 2x − 4 x +1 2x A. y = y = y = y = x − . B. 1 x − . C. 1 2x − . D. 2 3x − . 3 Lời giải Chọn C
Dựa vào đò thị hàm số ta thấy : Đồ 1
thị hàm số có đường tiệm cận ngang là y =
và đường tiệm cận đứng là x =1. 2 2x +1 Câu 6:
Tiệm cận ngang của đồ thị hàm số y =
là đường thẳng có phương trình x +1 A. y = 2 . B. x = 2 . C. y = 1 − . D. x = 1 − . Lời giải Chọn A Câu 7:
Kết luận nào đúng về số thực a  nếu 3 7 a a ?
A. 1  a  2. B. a 1 .
C. 0  a  1. D. a 1. Lời giải Chọn C Ta có 3  7 mà 3 7 a
a nên 0  a 1. Câu 8:
Tập xác định D của hàm số y = log 2x +1 là 3 ( )  1   1   1 
A. D = −; −   . B. D = ; +   .
C. D = (0;+) .
D. D = − ; +   .  2   2   2  Lời giải Chọn D 1
Hàm số xác định khi 2x +1  0  x  − . 2  1 
Vậy tập xác định của hàm số là D = − ; +   .  2  Câu 9:
Cho a , b , c là ba số thực dương khác 1. Đồ thị các hàm số x y = a , x y = b , x
y = c được cho
trong hình vẽ bên. Mệnh đề nào sau đây đúng? Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
A. c a b .
B. b c a .
C. a c b .
D. a b c . Lời giải Chọn C
Dựng đường thẳng x =1 , cắt 3 đồ thị hàm số theo thứ tự như hình vẽ
Câu 10: Đạo hàm của hàm số y = log x là 1 ln10 1 1 A. y = . B. y = . C. y = . D. y = . x x x ln10 10 ln x Lời giải Chọn C Đạ 1
o hàm của hàm số y = log x là y = . x ln10 2
Câu 11: Đạo hàm của hàm số 3x y = là 2 2 2 2 A. 3x y = . B. 3x y = .ln 3. C.  = 2 .3x y x .
D.  = 2 .ln 3.3x y x . Lời giải Chọn D 2 2 Ta có
= 3x   = 2 .ln3.3x y y x . +
Câu 12: Phương trình 2x 1 2 = 32 có nghiệm là 5 3 A. x = . B. x = 2 . C. x = . D. x = 3. 2 2 Lời giải Chọn B + Ta có 2x 1 2
= 32  2x +1= 5  x = 2
Câu 13: Nghiệm của phương trình log x + 7 = 5 là 2 ( )
A. x = 39 .
B. x =18 .
C. x = 25 .
D. x = 3. Lời giải Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 Chọn C Ta có log ( x + 7) 5
= 5  x + 7 = 2  x + 7 = 32  x = 25 . 2
Câu 14: Tập nghiệm của bất phương trình log x −1 1 là 3 ( ) A. (1;  4 . B. ( ; − 4) . C. ( ; −  4 . D. (0; 4. Lời giải Chọn A x −1  0 x 1 Ta có: log x −1  1     1 x  4. 3 ( ) x −1 3 x  4
Vậy tập nghiệm S = (1;  4 .
Câu 15: Khối lập phương là khối đa diện đều loại nào? A. 3;  3 . B. 5;  3 . C. 4;  3 . D. 3;  4 . Lời giải Chọn C
Khối lập phương là khối đa diện đều loại 4;  3 .
Câu 16: Thể tích khối lập phương có cạnh 2a bằng A. 3 8a . B. 3 2a . C. 3 a . D. 3 6a . Lời giải Chọn A
Thể tích khối lập phương có cạnh 2a (2a)3 3 = bằng: 8a .
Câu 17: Cho hình nón có bán kính đáy là r =
3 và đường sinh l = 4 . Diện tích xung quanh của hình nón đã cho là
A. S = 16 3 . B. S = 24 . C. S = 8 3 . D. S = 4 3 . Lời giải Chọn D
Diện tích xung quanh của hình nón S =  rl = 4 3 .
Câu 18: Cho hình chữ nhật ABCD có AB = a , AD = 2a . Thể tích của khối trụ tạo thành khi quay hình
chữ nhật ABCD quanh cạnh AB bằng A. 3 4 a . B. 3  a . C. 3 2a . D. 3 a . Lời giải Chọn A Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Hình trụ tạo thành có h = AB = a , r = AD = 2a .
Thể tích của khối trụ tạo thành khi quay hình chữ nhật ABCD quanh cạnh AB bằng
V = B h =  r h =  ( a)2 2 3 . . 2 .a = 4 a .
Câu 19: Cho khối nón có độ dài đường cao bằng 2a và bán kính đáy bằng a . Thể tích của khối nón đã cho bằng 3 2 a 3 4 a 3  a A. . B. . C. . D. 3 2 a . 3 3 3 Lời giải Chọn A 3 1 1 2 a
Thể tích của khối nón đã cho là 2 2
V =  r h =  .a .2a = . 3 3 3
Câu 20: Cắt hình trụ (T ) bởi một mặt phẳng đi qua trục của nó, ta được thiết diện là một hình vuông cạnh
là 7. Diện tích xung quanh của (T ) bằng 49 49 A. . B. 49 . C. 98 . D. . 2 4 Lời giải Chọn B Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Ta có bán kính đáy hình trụ 7 là , chiều cao là 7. 2 7
Diện tích xung quanh của (T ) bằng S = 2 rl = 2. .7 = 49 . xq 2 THÔNG HIỂU
Câu 21: Cho hàm số y = f ( x) có đạo hàm liên tục trên
và có đồ thị của hàm số y = f (x) như hình
vẽ bên. Mệnh đề nào dưới đây sai?
A. Hàm số y = f ( x) đồng biến trên (2;+) .
B. Hàm số y = f ( x) nghịch biến trên ( 1 − ;0) .
C. Hàm số y = f ( x) đồng biến trên (1;+).
D. Hàm số y = f ( x) nghịch biến trên ( ; − 2) . Lời giải Chọn C D = .
Theo đồ thị hàm số y = f (x) ta có bảng biến thiên
Dựa theo bảng biến thiên ta thấy phương án C sai. Câu 22: Cho hàm số 3
y = x − 3x + 5 . Điểm cực tiểu của đồ thị hàm số đã cho là A. (7;− ) 1 . B. ( 1 − ;7). C. (3; ) 1 . D. (1;3) . Lời giải Chọn D
Tập xác định của hàm số là D = . Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 x =1 Ta có 2
y = 3x − 3, y = 0  .  x = 1 − Mặt khác, y = 6 , x y ( )
1 = 6  0, y (− ) 1 = 6 −  0 .
Do đó, hàm số đạt cực tiểu tại x = 1, y = 3. CT
Vậy điểm cực tiểu của đồ thị hàm số đã cho là (1;3) .
Câu 23: Cho hàm số y = f ( x) liên tục trên đoạn  1 − ; 
3 và có đồ thị như hình vẽ dưới đây. Gọi M và
m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  1 − ; 
3 . Giá trị của M − m bằng A. 4 . B. 1. C. 5 . D. 0 . Lời giải Chọn C
Dựa vào đồ thị ta có M = max y = 3 , m = min y = 2 − . [ 1 − ;3] [ 1 − ;3]
Vậy M − m = 3 − ( 2 − ) = 5. ax + 2
Câu 24: Cho hàm số y = a b c
có đồ thị như hình vẽ bx + , , , c Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Khẳng định nào dưới đây đúng?
A. b a  0  c .
B. b  0  a c .
C. a b  0  c .
D. b  0  c a . Lời giải Chọn C 2
Ta có đồ thị đi qua điểm (0; ) 1  = 1  c = 2 . c −c
Đồ thị có đường tiệm cận đứng x = 1 
= 1 b = −c = −2 . b a
Đồ thị có đường tiệm cận ngang y = 2 
= 2  a = 2b = −4. b
Vậy a b  0  c .
Câu 25: Cho hàm số y = f (x) có bảng biến thiên như sau:
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 1. B. 3 . C. 2 . D. 4 . Lời giải Chọn C Page 15
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Dựa vào bảng biến thiên ta có:
Tập xác định của hàm số là D \ 1 . lim f x 5, lim f x
nên đồ thị có 1 đường tiệm cận ngang là y 5 . x x lim f x , lim f x
3 nên đồ thị có 1 đường tiệm cận đứng là đường thẳng x 1. x 1 x 1 5
Câu 26: Rút gọn biểu thức 3 3
Q = b : b với b  0. Kết quả nào sau đây đúng 5 4 4 − A. 9 Q = b . B. 2 Q = b . C. 3 Q = b . D. 3 Q = b . Lời giải Chọn C 5 5 1 5 1 4 − 3 3 3 3 3 3 3
Q = b : b = b : b = b = b . a b c d
Câu 27: Cho các số thực dương a , b , c , d . Biểu thức S = ln + ln + ln + ln bằng b c d aa b c d A. 0 . B. ln ( . a . b . c d ) . C. 1. D. ln + + +   .  b c d a Lời giải Chọn A a b c da b c d  Ta có: S = ln + ln + ln + ln = ln . . . = ln   ( ) 1 = 0 . b c d ab c d a
Câu 28: Một người gửi tiết kiệm vào một ngân hàng với lãi suất 7, 5% /năm. Biết rằng nếu không rút tiền
ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp
theo. Hỏi sau bao nhiêu năm người đó thu được (cả số tiền gửi ban đầu và lãi) ít nhất gấp đôi số
tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và người đó không rút tiền ra? A. 11 năm. B. 10 năm. C. 12 năm. D. 9 năm. Lời giải Chọn B
Gọi A là số tiền người đó gửi ban đầu.
Theo công thức lãi kép, để người đó thu được ít nhất gấp đôi số tiền gửi ban đầu ta cần n n .
A (1+ r)  2A  (1+ 0,075)  2  n  log 2  9,58 . 1,075 Do n  n =10.
Vậy người đó cần gửi ít nhất 10 năm.
Câu 29: Tìm tất cả các giá trị thực của tham số m để hàm số 2
y = ln(x − 2x + m +1) có tập xác định là Page 16
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 . A. m = 0 .
B. 0  m  3. C. m  1
− hoặc m  0. D. m  0. Lời giải Chọn D Hàm số y = ( 2
ln x − 2x + m + ) 1 có tập xác định là khi và chỉ khi: 2
x − 2x + m +1  0, x   
  0 1− m−1 0  m  0. x−
Câu 30: Gọi S là tổng tất cả các nghiệm của phương trình ( x ) 1 2
= 64. Giá trị của S là 1 A. S = . B. S = 6 − . C. S = 3 − . D. S = 1. 2 Lời giải Chọn D (  = x− x − 2x ) 1 x( x ) 3 1 6 = 64  2
= 2  x(x − ) 2
1 = 6  x − x − 6 = 0  .  x = 2 − Vậy S = 3 + ( 2 − ) =1.
Câu 31: Số nghiệm của phương trình log 6 + x + log 9x − 5 = 0 là 3 ( ) 3 ( ) A. 0 . B. 2 . C. 1. D. 3 . Lời giải Chọn C x  0  x  0
 Ta có: log 6 + x + log 9x − 5 = 0     3 ( ) 3 ( ) log 9x   (6 + x) = 5 9x   (6 + x) 5 = 3 3  x  0 x  0     x = 9 −  x = 3. 2 9
x + 54x − 243 = 0   x = 3
 Vậy phương trình có nghiệm x = 3.
Câu 32: Mặt phẳng ( AB 'C ') chia khối lăng trụ AB .
C A' B 'C ' thành các khối đa diện nào?
A. Hai khối chóp tứ giác.
B. Một khối chóp tam giác và một khối chóp tứ giác.
C. Hai khối chóp tam giác.
D. Một khối chóp tam giác và một khối chóp ngũ giác. Lời giải Chọn B Page 17
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Mặt phẳng ( AB 'C ') chia khối lăng trụ AB .
C A' B 'C ' thành các khối chóp tam giác .
A A' B 'C ' và khối chóp tứ giác .
A BCC ' B ' . Vậy chọn đáp án B.
Câu 33: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = a 3, SA vuông góc
với mặt phẳng đáy và mặt phẳng (SBC) tạo với đáy một góc 60 . Thể tích V của khối chóp S.ABCD là 3 a 3 a 3 A. V = . B. V = . C. 3 V = a . D. 3 V = 3a . 3 3 Lời giải Chọn C
Ta có SA ⊥ ( ABCD)  ((SBC),( ABCD)) = SBA = 60 .
ABCD là hình chữ nhật 2  S = A . B AD = a 3 . ABCD S
AB vuông tại S SA = A . B tan SBA = .
a tan 60  SA = a 3 . 1 1 2  V = S .SA = a 3.a 3 3 V = a . S . ABCD 3 ABCD 3 S.ABCD Page 18
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 Vậy 3 V = a . S.ABCD
Câu 34: Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a . Thể tích của khối nón đã cho bằng 3 3 a 3 3 a 3 2 a 3  a A. . B. . C. . D. . 2 3 3 3 Lời giải Chọn B Ta có: 2 2
h = l − r = a 3 . 3 1 3 a
Suy ra: thể tích của khối nón đã cho bằng 2 .r .h = . 3 3
Câu 35: Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 2 , thiết diện
thu được là hình vuông có diện tích bằng 16 . Diện tích xung quanh của hình trụ đã cho bằng A. 8 6 . B. 24 6 . C. 10 6 . D. 12 6 . Lời giải Chọn A
Gọi hình trụ đã cho có trục OO và thiết diện song song trục là hình vuông ABCD . Gọi H là
trung điểm của AD OH ⊥ AD. Page 19
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 Ta có S
=16  AB = AD = OO = 4
d (OO ; ABCD ) = d ( ; O ( ABCD)) = = ABCD và ( ) OH 2 .
Xét tam giác AOH vuông tại H có 2 2
OA = AH + OH = 6 .
Diện tích xung quanh của hình nón đã cho S = 2 Rh = 2 . O . AOO = 8 6 . xq
II. PHẦN TỰ LUẬN (4 câu – 3 điểm)
Câu 36: Cho hàm số f ( x) có đồ thị f ( x) như hình vẽ bên. Tìm giá trị nhỏ nhất của hàm số
g ( x) = f ( x) 1 3 3 3 2
− x − x + x + 2019 trên đoạn  3 − ;  1 . 3 4 2 Lời giải 3 3
Tính được g( x) = f ( x) 2 − x − x + . 2 2 3 3
Khi đó g( x) = 0  f ( x) 2
= x + x − (). 2 2 Page 20
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 3 3 Hàm số h ( x) 2
= x + x − có đồ thị như hình vẽ. 2 2
Dựa vào tương giao của hai đồ thị f ( x) và h( x) ta thấy trên  3 − ;  1 phương trình ( )  có các nghiệm x = 3 − ; x = 1 − ; x =1. Trên ( 3 − ;− )
1 , đồ thị hàm số f ( x) nằm phía dưới đồ thị hàm số h( x) nên g( x)  0 . Trên ( 1 − ; )
1 , đồ thị hàm số f ( x) nằm phía trên đồ thị hàm số h( x) nên g( x)  0 . Ta có bảng biến thiên
Vậy min g ( x) = g (− ) 1 khi x = 1 − .  3 − ;  1
Câu 37: Cho lăng trụ đứng AB . C A BC
  có đáy là tam giác vuông cân tại B , AC = a 2 ; biết góc giữa mặt phẳng ( A B
C) và mặt phẳng đáy bằng 60. Tính thể tích V của khối lăng trụ AB . C A BC   . Lời giải
Tam giác ABC vuông cân tại B, AC = a 2  BA = BC = AC. tan 45 = . a BC ⊥ AB  Ta có:
  BC ⊥ ( A A
B)  BC ⊥ A . B BC ⊥ AA Page 21
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 (A B
C)( ABC) = BC
Lại có BC ⊥ AB   60 = (( A B
C),( ABC)) = ABA.  BC ⊥ A B   Tam giác A A
B vuông tại A nên AA = AB tan 60 = a 3. 3 1 a 3 Vậy V = S .AA = . BA BC.AA = . ABC 2 2
Câu 38: Ông A dự định sử dụng hết 2
5 m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)? Lời giải Gọi ,
h a, b lần lượt là chiều cao, chiều rộng và chiều dài của bể. Suy ra b = 2a . Diện tích đáy: 2
S = ab = 2a . 1
Diện tích xunh quanh: S = 2 a + b h = 6ah . 2 ( ) 2 5 − 2a 5
Theo giả thiết ta có S + S = 5 2
 2a + 6ah = 5  h = với 0  a  . 1 2 6a 2 2 3 5 − 2a 5a − 2a Thể tích bể cá: 2 V = . h S = .2a = 1 6a 3 Đạ 5 o hàm: 2 V ' = − 2a  5 V ' = 0  a = . 3 6 5 30 5
Bể cá có thể tích lớn nhất bằng: 3
1,01 m khi chiều rộng a = . 27 6
Câu 39: Cho phương trình 5x + m = log
x − m với m là tham số. Có bao nhiêu giá trị nguyên của 5 ( ) m( 2
− 0;20) để phương trình đã cho có nghiệm? Lời giải
Điều kiện: x m . Page 22
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Từ phương trình 5x + m = log
x − m  5x + x = log
x − m + x − m 5 ( ) 5 ( )
 5x + log 5x = x − m+ log x − m (1). 5 5 ( )
Xét f ( x) = x + log x với x  0 . 5 Ta có f ( x) 1 ' =1+
 0 với x  0 . Hàm số f (x) = x +log x đồng biến trên (0;+). x ln 5 5
Phương trình (1) tương đương (5x f
) = f (x−m) 5x = x−m  = −5x m x . Đặt ( ) = −5x h x x ta có '( ) =1−5x h x
ln 5 cho '( ) = 0 1−5x h x
ln 5 = 0  x = −log ln 5 . 5 ( ) Bảng biến thiên  1 
Dựa vào đồ thị m  − ;  −log ln 5 − 
kết hợp với giá trị nguyên của m( 2 − 0;20) . 5 ( )   ln 5  Vậy m 1 − 9; 1 − 8; 1 − 7;...;− 
1 hay có 19 giá trị m nguyên thỏa mãn.
---------- HẾT ---------- Page 23
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 08
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ. Số điểm cực trị của hàm số đã cho là A. 1. B. 3. C. 0. D. 2. Câu 2:
Cho hàm số y = f ( x) có bảng biến
thiên như hình vẽ. Giá trị lớn nhất
của hàm số đã cho trên tập hợp bằng A. 1. B. 1 − . 1 C. . D. 3. 3 Câu 3:
Hình sau là đồ thị của hàm số nào trong các hàm số sau đây? A. 3 y x 1 B. 3 y x 3x 1 C. 3 y x 3x 1 D. 3 y x 1 . Câu 4:
Hình sau là đồ thị của hàm số nào trong các hàm số sau đây? A. y log x B. y log x 5 1 5 x x 1 C. y 5 D. y 5 1 Câu 5:
Tập xác định của hàm số 3 y x 3 là A. \ 3 . B. 3; . C. 3; . D. . Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Câu 6:
Khẳng định nào sau đây là đúng? A. ( )y x xy e = e x  , y . B. x−y x y e
= e − e x  , y . y C. ( x ) x = . y e e e x  , y . D. x+y x y e
= e + e x  , y . Câu 7:
Khẳng định nào sau đây là đúng?  x  log xx x A. 2 log = , ,
x y  0, y  1. B. log = , ,
x y  0, y  1 . 2      y  log y
2  y  log y 2 2  x   x C. log
= log x + log y, , x y  0 . D. log
= log x − log y, , x y  0 . 2   2 2    y  2 2 2  y Câu 8:
Hàm số nào trong các hàm số sau đây nghịch biến trên ? x A. y = log x . B. 9x y = .
C. y = log x . D. y = (0,9) . 0,9 9 x Câu 9:
Tập nghiệm của bất phương trình (0, ) 8  3 là  4   4  A. (log 3;+ . B. ( ; − log 3 . C. log ; + . D. −;log . 0,8 ) 0,8 )  3     5  3  5 
Câu 10: Nếu các số dương ,
a b thỏa mãn 2020a = b thì 1 1 A. 2020b a = . B. a = . C. a = log b . D. a = log b . 2020b 2020 1 2020
Câu 11: Cho biểu thức 5 6 P =
x ( x  0). Khẳng định nào sau đây là đúng? 6 5 5 A. 30 P = x . B. 6 P = x . C. 5 P = x . D. 6 P = x . 6x − 5
Câu 12: Phương trình đường tiệm cận ngang của đồ thị hàm số y = là x + 6 5 A. x = 6 − . B. y = − . C. x = 6 . D. y = 6 6
Câu 13: Nếu một hình nón có đường kính đường tròn đáy bằng a và độ dài đường sinh bằng l thì có diện tích xung quanh bằng 1 1 A. al . B. 2 al . C. al . D. al . 2 3
Câu 14: Trên khoảng (0;+) đạo hàm của hàm số 8 15 y = x bằng 15 15 A. 8 7 x . B. 7 8 x . C. 8 7 x . D. 7 8 x . 8 8
Câu 15: Cho ABCD là hình chữ nhật, AB = a, AD = b . Quay hình chữ nhật ABCD xung quanh cạnh
AB ta được một khối tròn xoay có thể tích bằng 1 1 A. 2  a . b B. 2 b . a C. 2 b . a D. 2  a . b 3 3
Câu 16: Tập hợp các giá trị m để phương trình log
x = m có nghiệm thực là 2020 A. . B. (0;+). C. ( ; − 0). D. \   1 . Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 17: Cho hàm số y = f ( x) có đạo hàm trên thỏa mãn
f '( x)  0, x  (0; ) 1 và
f '( x)  0, x
 (1;2). Khẳng định nào sau đây là đúng?
A. Hàm số đã cho nghịch biến trên (0 )
;1 và đồng biến trên (1;2).
B. Hàm số đã cho nghịch biến trên (0 )
;1 và nghịch biến trên (1;2).
C. Hàm số đã cho đồng biến trên (0 )
;1 và đồng biến trên (1;2).
D. Hàm số đã cho đồng biến trên (0 )
;1 và nghịch biến trên (1;2).
Câu 18: Nếu hàm số y = f ( x) liên tục trên thỏa mãn f ( x)  f (0) x  ( 2 − ;2) \  0 thì
A. x = 0 là một điểm cực tiểu của hàm số đã cho.
B. x = 0 là một điểm cực đại của hàm số đã cho.
C. Hàm số đã cho có giá trị nhỏ nhất trên tập số bằng f (0).
D. Hàm số đã cho có giá trị lớn nhất trên tập số bằng f (0). 1
Câu 19: Hàm số y =
nghịch biến trên khoảng nào trong các khoảng sau? x A. (− ;  +). B. ( ; − ) 1 . C. ( 1 − ;+). D. (0;+).
Câu 20: Cho khối chóp S.ABC có SA ⊥ ( ABC), SA = , h AB = , c AC = ,
b BAC =  .Thể tích khối chóp S.ABC bằng 1 1 1 1 A. bc . h sin. B. bc . h cos. C. b . ch cos. D. bc . h sin. 3 3 6 6
Câu 21: Tập nghiệm của bất phương trình log x −1  0 1 ( ) 2 A. (2;+) . B. (1; 2) . C. ( ;2 − ). D. (1;+) .
a = log 5,b = log 5 M = log 5 Câu 22: Cho 7 3 . Biểu thức 21 bằng a + b ab 1 A. M = . B. M = = . D. M = . ab a + . C. M ab b ab
Câu 23: Tập hợp các số thực m để phương trình ( 2
log x − 2020) = log(mx) có nghiệm là A. . B. (0;+). C. ( ;0 − ) . D. \   0 .
Câu 24: Cho tam giác ABC là tam giác vuông tại đỉnh A , AB = a , AC = b . Quay hình tam giác ABC
quanh cạnh AC ta được một khối tròn xoay có diện tích xung quanh bằng 1 1 2 2 2 2 A. 2 2 a a + b . B. 2 2 b a + b .
C. a a + b .
D. b a + b . 3 3
Câu 25: Nếu tăng bán kính của một khối cầu gấp 2 lần thì thể tích thay đổi như thế nào?
A. Thể tích tăng gấp 2 lần.
B. Thể tích tăng gấp 4 lần. 4
C. Thể tích tăng gấp 8 lần.
D. Thể tích tăng gấp lần. 3 Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 26: Một cái xúc xích hình trụ có đường kính đáy 2 cm và chiều cao 6 cm , giả sử giá bán mỗi 3 cm
xúc xích là 500 đồng. Bạn An cần trả tiền mua một gói 4 cái xúc xích. Số tiền gần đúng nhất cho 4 cái xúc xích là A. 19000 . B. 76000 . C. 38000 . D. 30000 .
Câu 27: Một người gửi số tiền 100 triệu đồng vào một ngân hàng với lãi suất 6,8% / năm. Biết rằng nếu
không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu
(người ta gọi là lãi kép). Nếu người đó gửi tiền trong đúng 4 năm và trong khoảng thời gian đó
không rút tiền ra thì người đó có số tiền là. A. 4 100.1, 068 (đồng). B. 5 100.1, 068 (triệu đồng). C. 3 100.1, 068 (triệu đồng). D. 4 100.1, 068 (triệu đồng).
Câu 28: Cho hàm số f ( x) = log ( 2 6x − x
. Tập nghiệm của bất phương trình f (x)  0 là. 0,5 ) A. (3;+) . B. ( ) ;3 − . C. (3;6). D. (0;3) .
Câu 29: Một khối bê tông có dạng hình lăng trụ đứng với độ dài các cạnh
đáy là 3 dm, 4dm, 5dm độ dài cạnh bên là 6 dm . Thể tích khối bê tông bằng A. ( 3 72 dm ) . B. ( 3 24 dm ) . C. ( 3 216 dm ). D. ( 3 36 dm ) .
Câu 30: Một dụng cụ đựng chất lỏng có dạng hình nón với chiều cao là
30 cm và bán kính đáy là 15 cm . Dụng cụ này đựng được tối đa bao nhiêu 3 cm chất lỏng? A.  ( 3 2250 cm ). B.  ( 3 750 cm ). C. ( 3 2250 cm ). D. ( 3 750 cm ).
Câu 31: Nếu S.ABC là hình chóp đều có chiều cao bằng h và cạnh đáy bằng a thì có thể tích bằng 2 2 2 a h 3 2 a h 3 a h 3 a h 3 A. . B. . C. . D. . 3 6 12 4 3 x
Câu 32: Tập hợp các giá trị m để hàm số 2 y =
− mx + (10m − 25) x +1 có hai điểm cực trị là: 3 A. R .
B. R \ −  5 . C. R \  5 . D. (5;+) .
x −10 + 20 − x
Câu 33: Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = là: x A. 3 . B. 2 . C. 1. D. 0 . Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 34: Cho hình hộp ABC . D A BCD
  có thể tích bằng V . Thể tích của khối tứ diện ACB D   bằng 1 1 1 1 A. V . B. V . C. V . D. V . 6 4 3 2
Câu 35: Cho hàm số y = f (x) có đồ thị đạo hàm y = f ( x) như hình bên dưới. Hàm số đã cho nghịch biến trên khoảng  1  A. (1; 2) . B. (0 ) ;1 . C. − ; 0   . D. (0;2) .  2  II. PHẦN TỰ LUẬN
Câu 36: Có báo nhiêu giá trị nguyên của tham số m để hàm số 2 3 2
y = (m − m − 6)x + (m − 3)x − 2x +1 nghịch biến trên ?
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và AB = 2 AC = 2a, BC = a 3 . Tam
giác SAD vuông cân tại S, hai mặt phẳng (SAD) và ( ABCD) vuông góc nhau. Tính thể tích
khối chóp S.ABCD .
Câu 38: Số các giá trị nguyên của tham số m để phương trình 2x + 3 = 4x m
+1 có đúng một nghiệm là
Câu 39: Có bao nhiêu giá trị nguyên thuộc  2 − 021;202 
1 của tham số m để phương trình sau có nghiệm duy nhất log + + − + = +
( 2x mx m 1 log x 0. 2 3 ) 2− 3
------------- HẾT ------------- Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ. Số điểm cực trị của hàm số đã cho là A. 1. B. 3. C. 0. D. 2. Lời giải Chọn D
Căn cứ vào hình vẽ ta thấy hàm số có 2 điểm cực trị. Câu 2:
Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ. Giá trị lớn nhất của hàm số đã cho trên tập hợp bằng 1 A. 1. B. 1 − . C. . D. 3. 3 Lời giải Chọn D
Căn cứ vào hình vẽ ta thấy giá trị lớn nhất của hàm số đã cho trên tập bằng 3. Câu 3:
Hình sau là đồ thị của hàm số nào trong các hàm số sau đây? A. 3 y x 1 B. 3 y x 3x 1 C. 3 y x 3x 1 D. 3 y x 1 . Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải Chọn B
Ta thấy đồ thị đi qua điểm M 1; 1 nên ta loại A, C, D. Câu 4:
Hình sau là đồ thị của hàm số nào trong các hàm số sau đây? x x 1 A. y log x B. y log x C. y 5 D. y 5 1 5 5 Lời giải Chọn C
Đồ thị nằm phía trên trục hoành nên ta loại A, B.
Đồ thị hàm số đi lên nên có hệ số a 1, do đó loại D. 1 Câu 5:
Tập xác định của hàm số 3 y x 3 là A. \ 3 . B. 3; . C. 3; . D. . Lời giải Chọn B 1 Vì
nên điều kiện của hàm số đã cho là x 3 0 x 3. 3
Vậy tập xác định D 3; . Câu 6:
Khẳng định nào sau đây là đúng? A. ( )y x xy e = e − x  , y . B. x y x y e
= e − e x  , y . y C. ( x ) x = . y e e e + x  , y . D. x y x y e
= e + e x  , y . Lời giải Chọn A Ta có: ( )y x xy e = e x  , y . Câu 7:
Khẳng định nào sau đây là đúng?  x  log xx x A. 2 log = , ,
x y  0, y  1. B. log = , ,
x y  0, y  1 . 2      y  log y
2  y  log y 2 2 Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x   x C. log
= log x + log y, , x y  0 . D. log
= log x − log y, , x y  0 . 2   2 2    y  2 2 2  y Lời giải Chọn D x  Ta có: log
= log x − log y ,  ,
x y  0. (đây là định lí 2, trang 64 sgk). 2   2 2  y Câu 8:
Hàm số nào trong các hàm số sau đây nghịch biến trên ? x A. y = log x . B. 9x y = .
C. y = log x . D. y = (0,9) . 0,9 9 Lời giải Chọn D Hàm số: y = log
x nghịch biến trên (0;+) . 0,9 Hàm số: 9x y = đồng biến trên .
Hàm số: y = log x đồng biến trên (0;+) . 9 x
Hàm số: y = (0,9) nghịch biến trên . Vậy đáp án D đúng. x Câu 9:
Tập nghiệm của bất phương trình (0, ) 8  3 là  4   4  A. (log 3;+ . B. ( ; − log 3 . C. log ; + . D. −;log . 0,8 ) 0,8 )  3     5  3  5  Lời giải Chọn A ( x 0, ) 8  3 x  log 3. 0,8
Vậy tập nghiệm của bất phương trình đã cho là: S= (log 3;+ . 0,8 )
Câu 10: Nếu các số dương ,
a b thỏa mãn 2020a = b thì 1 1 A. 2020b a = . B. a = . C. a = log b . D. a = log b . 2020b 2020 1 2020 Lời giải Chọn C
2020a = b a = log b . 2020
Câu 11: Cho biểu thức 5 6 P =
x ( x  0). Khẳng định nào sau đây là đúng? 6 5 5 A. 30 P = x . B. 6 P = x . C. 5 P = x . D. 6 P = x . Lời giải Chọn C 6
Với x  0 , ta có: 5 6 5 P = x = x . 6x − 5
Câu 12: Phương trình đường tiệm cận ngang của đồ thị hàm số y = là x + 6 Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 5 A. x = 6 − . B. y = − . C. x = 6 . D. y = 6 6 Lời giải Chọn D 6x − 5 6x − 5 Ta có lim y = lim = 6 , lim y = lim
= 6 , suy ra đồ thị hàm số có đường tiện x→− x→− x + 6 x→+ x→+ x + 6 cậng ngang y = 6 .
Câu 13: Nếu một hình nón có đường kính đường tròn đáy bằng a và độ dài đường sinh bằng l thì có diện tích xung quanh bằng 1 1 A. al . B. 2 al . C. al . D. al . 2 3 Lời giải Chọn C
Hình nón có đường kính đường tròn đáy bằ a
ng a nên bán kính r = . 2
Câu 14: Trên khoảng (0;+) đạo hàm của hàm số 8 15 y = x bằng 15 15 A. 8 7 x . B. 7 8 x . C. 8 7 x . D. 7 8 x . 8 8 Lời giải Chọn C 15 7 15 15 Đạ 8 15 8 7 o hàm của hàm số 8 y = x = x là 8 y = x = x . 8 8
Câu 15: Cho ABCD là hình chữ nhật, AB = a, AD = b . Quay hình chữ nhật ABCD xung quanh cạnh
AB ta được một khối tròn xoay có thể tích bằng 1 1 A. 2  a . b B. 2 b . a C. 2 b . a D. 2  a . b 3 3 Lời giải Chọn C
Quay hình chữ nhật ABCD quanh trục AB ta được hình trụ có bán kính đáy R = AD = b ,
chiều cao h = AB = a Thể tích khối trụ là 2 V = ba .
Câu 16: Tập hợp các giá trị m để phương trình log
x = m có nghiệm thực là 2020 A. . B. (0;+). C. ( ; − 0). D. \   1 . Lời giải Chọn A
Điều kiện của phương trình: x  0 . log =  = 2020m x m x  0, m   . 2020 Với m
  phương trình luôn có nghiệm. Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 17: Cho hàm số y = f ( x) có đạo hàm trên thỏa mãn
f '( x)  0, x  (0; ) 1 và
f '( x)  0, x
 (1;2). Khẳng định nào sau đây là đúng?
A. Hàm số đã cho nghịch biến trên (0 )
;1 và đồng biến trên (1;2).
B. Hàm số đã cho nghịch biến trên (0 )
;1 và nghịch biến trên (1;2).
C. Hàm số đã cho đồng biến trên (0 )
;1 và đồng biến trên (1;2).
D. Hàm số đã cho đồng biến trên (0 )
;1 và nghịch biến trên (1;2). Lời giải Chọn D
f '( x)  0, x  (0; )
1 nên hàm số đã cho đồng biến trên (0 ) ;1 .
f '( x)  0, x
 (1;2) nên hàm số đã cho nghịch biến trên (1;2).
Câu 18: Nếu hàm số y = f ( x) liên tục trên
thỏa mãn f ( x)  f (0) x  ( 2 − ;2) \  0 thì
A. x = 0 là một điểm cực tiểu của hàm số đã cho.
B. x = 0 là một điểm cực đại của hàm số đã cho.
C. Hàm số đã cho có giá trị nhỏ nhất trên tập số bằng f (0).
D. Hàm số đã cho có giá trị lớn nhất trên tập số bằng f (0). Lời giải Chọn B
Theo định nghĩa cực đại, cực tiểu của hàm số trang 13 sgk 12 cơ bản thì x = 0 là một điểm
cực đại của hàm số đã cho. 1
Câu 19: Hàm số y =
nghịch biến trên khoảng nào trong các khoảng sau? x A. (− ;  +). B. ( ; − ) 1 . C. ( 1 − ;+). D. (0;+). Lời giải Chọn D Ta có TXĐ: D = \   0   1  1 − y ' = =  0, x   D   2  x x
Do đó hàm số nghịch biến trên ( ;0 − ) và (0;+).
Câu 20: Cho khối chóp S.ABC có SA ⊥ ( ABC), SA = , h AB = , c AC = ,
b BAC =  .Thể tích khối chóp S.ABC bằng 1 1 1 1 A. bc . h sin. B. bc . h cos. C. b . ch cos. D. bc . h sin. 3 3 6 6 Lời giải Chọn D Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 1 1
Diện tích tam giác ABC: S = A . B AC.sin A = bc sin 2 2 1 1 1 1
Thể tích khối chóp S.ABC: V = S . A S
= h bcsin = bchsin . 3 SABC 3 2 6
Câu 21: Tập nghiệm của bất phương trình log x −1  0 1 ( ) 2 A. (2;+) . B. (1; 2) . C. ( ;2 − ). D. (1;+) . Lời giải Chọn B Ta có log
x −1  0  0  x −1  1  1  x  2 . Vậy tập nghiệm của bất phương trinh là 1 ( ) 2 (1;2).
a = log 5,b = log 5 M = log 5 Câu 22: Cho 7 3 . Biểu thức 21 bằng a + b ab 1 A. M = . B. M = = . D. M = . ab a + . C. M ab b ab Lời giải Chọn B 1 1
Ta có a = log 5,b = log 5 nên log 7 = , log 3 = . 7 3 5 5 a b 1 1 1 ab Từ M = log 5 = = = = . 21 log 21 log 7 + log 3 1 1 a + b 5 5 5 + a b ab
Vậy M = a + . b
Câu 23: Tập hợp các số thực m để phương trình ( 2
log x − 2020) = log(mx) có nghiệm là A. . B. (0;+). C. ( ;0 − ) . D. \   0 . Lời giải Chọn D Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 2 x − 2020  0 Phương trình log( 2
x − 2020) = log(mx)   2
x − 2020 = mxx ( ;
− − 2020)  ( 2020;+)    . 2020 m = x − = f (x),( ) *  x
Phương trình đã cho có nghiệm  phương trình ( ) * có nghiệm thỏa mãn x  ( ;
− − 2020)  ( 2020;+) . 2020
Ta có f ( x) = 1+  0, x   − ;  − 2020  2020; + 2 ( ) ( ) x Bảng biến thiên
Phương trình đã cho có nghiệm khi m  0 .
Câu 24: Cho tam giác ABC là tam giác vuông tại đỉnh A , AB = a , AC = b . Quay hình tam giác ABC
quanh cạnh AC ta được một khối tròn xoay có diện tích xung quanh bằng 1 1 2 2 2 2 A. 2 2 a a + b . B. 2 2 b a + b .
C. a a + b .
D. b a + b . 3 3 Lời giải Chọn A
Khi quay hình tam giác ABC là tam giác vuông tại đỉnh A quanh cạnh AC ta được một khối
nón tròn xoay có độ dài bán kính đáy là r = a và chiều cao là h = b . Do đó độ dài đường sinh của hình nón là 2 2
l = a + b
Vậy diện tích xung quanh của hình nón là 2 2
S = rl = a a + b
Câu 25: Nếu tăng bán kính của một khối cầu gấp 2 lần thì thể tích thay đổi như thế nào?
A. Thể tích tăng gấp 2 lần.
B. Thể tích tăng gấp 4 lần. 4
C. Thể tích tăng gấp 8 lần.
D. Thể tích tăng gấp lần. 3 Lời giải Chọn C 4
Gọi R là bán kính của khối cầu đã cho. Khi đó thể tích của khối cầu đã cho bằng 3 V =  R . 1 1 1 3
Nếu tăng bán kính của khối cầu gấp 2 lần thì ta có bán kính mới của khối cầu là R = 2R 2 1 . Khi đó thể 4 4 4
tích của khối cầu mới là V =
 (R )3 =  (2R )3 3
= 8.  R = 8V . 2 2 1 1 1 3 3 3 Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Vậy thể tích của khối cầu tăng gấp 8 lần.
Câu 26: Một cái xúc xích hình trụ có đường kính đáy 2 cm và chiều cao 6 cm , giả sử giá bán mỗi 3 cm
xúc xích là 500 đồng. Bạn An cần trả tiền mua một gói 4 cái xúc xích. Số tiền gần đúng nhất cho 4 cái xúc xích là A. 19000 . B. 76000 . C. 38000 . D. 30000 . Lời giải Chọn C
Gọi bán kính đáy của hình trụ là r .
Ta có: r =1 (cm).
Thể tích 1 cái xúc xích là: 2 2
V =  r h =  =  ( 3 .1 .6 6 cm ) .
Giá tiền 4 cái xúc xích là: 4.6.500  37700 đ.
Vậy số tiền gần đúng nhất cho 4 cái xúc xích là 38000 đ.
Câu 27: Một người gửi số tiền 100 triệu đồng vào một ngân hàng với lãi suất 6,8% / năm. Biết rằng nếu
không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu
(người ta gọi là lãi kép). Nếu người đó gửi tiền trong đúng 4 năm và trong khoảng thời gian đó
không rút tiền ra thì người đó có số tiền là. A. 4 100.1, 068 (đồng). B. 5 100.1, 068 (triệu đồng). C. 3 100.1, 068 (triệu đồng). D. 4 100.1, 068 (triệu đồng). Lời giải Chọn D
Gọi T là số tiền người đó thu được sau n năm. n
Số tiền thu được sau một năm là: T =100. 1+ 6,8% (triệu đồng). 1 ( )
Số tiền thu được sau 2 năm là: T = T 1+ 6,8% = ( + )2
100. 1 6,8% (triệu đồng). 2 1 ( )
Số tiền thu được sau 3 năm là: T = T .(1+ 6,8%) =100.(1+ 6,8%)3 (triệu đồng). 3 2
Vậy số tiền thu được sau 4 năm là: T = 100.(1+ 6,8%)4 4 =100.1,068 (triệu đồng). 4
Câu 28: Cho hàm số f ( x) = log ( 2 6x − x
. Tập nghiệm của bất phương trình f ( x)  0 là. 0,5 ) A. (3;+) . B. ( ) ;3 − . C. (3;6). D. (0;3) . Lời giải Chọn C
Tập xác định: D = (0;6). (1) 6 − 2x Ta có f ( x) = ( . 2 6x − x )ln 0,5 6 − 2x 6 − 2xx  0
f (x)  0  (  0   0   . 2 6x − x )ln 0,5 2 6x − x 3  x  6
Kết hợp (1) suy ra tâp nghiệm của bất phương trình f ( x)  0 là S = (3;6) .
Câu 29: Một khối bê tông có dạng hình lăng trụ đứng với độ dài các cạnh đáy là 3 dm, 4dm, 5dm độ dài
cạnh bên là 6 dm . Thể tích khối bê tông bằng Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 A. ( 3 72 dm ) . B. ( 3 24 dm ) . C. ( 3 216 dm ). D. ( 3 36 dm ) . Lời giải Chọn D
Ta có thể tích khối bê tông là thể tích khối lăng trụ đứng có đáy là tam giác vuông. 1
Thể tích cầm tìm là V = 3.4.6 = 36( 3 dm ) . 2
Câu 30: Một dụng cụ đựng chất lỏng có dạng hình nón với chiều cao là 30 cm và bán kính đáy là
15 cm . Dụng cụ này đựng được tối đa bao nhiêu 3 cm chất lỏng? A.  ( 3 2250 cm ). B.  ( 3 750 cm ). C. ( 3 2250 cm ). D. ( 3 750 cm ). Lời giải Chọn A
Khối nón có chiều cao h
30 cm và bán kính đáy r
15 cm có thể tích là 1 1 2 2 3 V πr h π.15 .30 2250π cm . 3 3
Câu 31: Nếu S.ABC là hình chóp đều có chiều cao bằng h và cạnh đáy bằng a thì có thể tích bằng 2 2 2 a h 3 2 a h 3 a h 3 a h 3 A. . B. . C. . D. . 3 6 12 4 Lời giải Chọn C Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC . 2 a 3
Diện tích tam giác ABC là S = ABC 4 2 1 a h 3
Thể tích khồi chóp là V = S .SO = . 3 ABC 12 3 x
Câu 32: Tập hợp các giá trị m để hàm số 2 y =
− mx + (10m − 25) x +1 có hai điểm cực trị là: 3 A. R .
B. R \ −  5 . C. R \  5 . D. (5;+) . Lời giải Chọn C 3 x Ta có 2 y =
− mx + ( m − ) 2 10
25 x +1  y = x − 2 x m +10m − 25 . 3
Để hàm số có hai điểm cực trị 2
y = x − 2 x
m +10m − 25 có hai nghiệm phân biệt  
   m − m +   (m− )2 2 0 10 25 0 5  0  m  5 .
x −10 + 20 − x
Câu 33: Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = là: x A. 3 . B. 2 . C. 1. D. 0 . Lời giải Chọn D
Điều kiện: 10  x  20 .
Vì 10  x  20 nên không thể tính được lim f ( x) và lim f ( x) không tồn tại. x→+ x→−
Vì 10  x  20 nên không thể tính được lim f ( x) và lim f ( x) không tồn tại. + − x 0 → x 0 →
Vậy đồ thị hàm số không có đường tiệm cận nào.
Câu 34: Cho hình hộp ABC . D A BCD
  có thể tích bằng V . Thể tích của khối tứ diện ACB D   bằng 1 1 1 1 A. V . B. V . C. V . D. V . 6 4 3 2 Lời giải Chọn C Page 15
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Ta có V = − − − −   V
V    V    V V . ACB D . A A B D C.D B C B .ABC D.ACD 1 1 1 1 Mà V = = = = = =    V    V V V  . V V . A A B D C.D B C B .ABC D .ACD D . 2 ABCD 2 3 6 V 1  V = − =   V 4. V ACB D 6 3
Câu 35: Cho hàm số y = f (x) có đồ thị đạo hàm y = f ( x) như hình bên dưới. Hàm số đã cho nghịch biến trên khoảng  1  A. (1; 2) . B. (0 ) ;1 . C. − ; 0   . D. (0;2) .  2  Lời giải Chọn C
Dựa vào đồ thị của hàm số y = f ( x) ta có bảng xét dấu như sau:   Vì f ( x) 1  0,x  − ;0 
 nên chọn phương án C.  2  II. PHẦN TỰ LUẬN
Câu 36: Có báo nhiêu giá trị nguyên của tham số m để hàm số 2 3 2
y = (m − m − 6)x + (m − 3)x − 2x +1 nghịch biến trên ? Lời giải Page 16
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 m = 3 TH1: 2
m − m − 6 = 0   m = 2 −
Với m = 3  y = 2
− x +1 hàm số nghịch biến trên . Với 2 m = 2 −  y = 5
− x − 2x +1 không nghịch biến trên . TH2: 2
m − m − 6  0 , 2 3 2 2 2
y = (m − m − 6)x + (m − 3)x − 2x +1  y = 3(m − m − 6)x + 2(m − 3)x − 2 .
Để hàm số nghịch biến trên thì  2 −  m  3 2 
m − m − 6  0     9 2
 = 7m −12m − 27  0 −  m  3  7 Suy ra m 1 − ,0,1,2,  3
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và AB = 2 AC = 2a, BC = a 3 . Tam
giác SAD vuông cân tại S, hai mặt phẳng (SAD) và ( ABCD) vuông góc nhau. Tính thể tích
khối chóp S.ABCD . Lời giải S A B H D C
Theo giả thiết AB = 2 AC = 2a, BC = a 3 nên tam giác ABC có 2 2 2
AB = 2a, AC = a, BC = a 3  AB = AC + BC , do đó ABC là tam giác vuông tại C . Suy ra 2 S = 2S = C . ACB = 3a . ABCD ABC
Gọi H là trung điểm của AD , tam giác SAD vuông cân tại S nên SH ⊥ AD .
Mặt khác (SAD) ⊥ ( ABCD)  SH ⊥ ( ABCD) . 1 a 3
Lại có tam giác SAD vuông cân tại S SH = AD = . 2 2 Page 17
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 3 1 1 a 3 a
Vậy thể tích khối chóp S.ABCD là 2 V = SH.S = . . 3a = . S . ABCD 3 ABCD 3 2 2
Câu 38: Số các giá trị nguyên của tham số m để phương trình 2x + 3 = 4x m
+1 có đúng một nghiệm là Lời giải t + 3 Đặt 2x t =
 0 . Phương trình trở thành: 2
t + 3 = m t +1  m = 2 t +1 t + 3
Xét hàm số f (t ) = . 2 t +1 1− 3t 1
Ta có: f (t ) =
, f (t ) = 0  t = (t + )3 2 3 1 Bảng biến thiên:  = Để m 10
phương trình 2x + 3 = 4x m
+1 có đúng một nghiệm   1   m  3
Vậy có 2 giá trị nguyên của m là m   2;  3 .
Câu 39: Có bao nhiêu giá trị nguyên thuộc  2 − 021;202 
1 của tham số m để phương trình sau có nghiệm duy nhất log + + − + = +
( 2x mx m 1 log x 0. 2 3 ) 2− 3 Lời giải Ta có: log + + − + = +
( 2x mx m 1 log x 0 2 3 ) 2− 3  log + + − − = +
( 2x mx m 1 log x 0 2 3 ) 2+ 3 2
x + mx + m −1 = x   x  0 2  −x + x +1 m =   x + 1 x  0 Page 18
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 2 −x + x +1 Xét f (x) = , x  0 . x + 1 2 x + 2x
Khi đó f '(x) = −  0, x  0. ( x + )2 1 Ta có bảng biến thiên
Để phương trình trên có nghiệm duy nhất thì m  1.
Vì m  ; m 2 − 021;202  1  m 2 − 021; 2 − 020; ; 1 − ; 
0  có 2022 giá trị m thỏa mãn.
------------- HẾT ------------- Page 19
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ I
MÔN: TOÁN 12 – ĐỀ SỐ: 09
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) 4 x Câu 1: Hàm số 2 3 y = −
+ x + có bao nhiêu điểm cực trị? 2 2 A. 4 . B. 2 . C. 0 . D. 3 . Câu 2:
Khối lăng trụ có diện tích đáy bằng 2
3a , chiều cao bằng a có thể tích bằng 3 1 A. 3 a . B. 3 3a . C. 3 a . D. 3 a . 2 2 Câu 3: Phương trình x+1 2 =8 có nghiệm là A. x = 2 . B. x =1. C. x =3 . D. x = 4 . Câu 4:
Cho khối tứ diện OABC có OA , OB , OC đôi một vuông góc với nhau tại O và OA = 2 , OB = 4
, OC = 6 . Thể tích khối tứ diện đã cho bằng A. 8 . B. 24 . C. 48 . D. 16 . Câu 5:
Cho khối chóp S.ABC có thể tích V . Các điểm B ; C tương ứng là trung điểm các cạnh SB ,
SC . Thể tích khối chóp S.AB C   bằng V V V V A. . B. . C. . D. . 8 2 4 16 2019 Câu 6: Cho hàm số y =
H . Số đường tiệm cân của (H ) là 2 − có đồ thị ( ) x A. 3 . B. 1. C. 0 . D. 2 . Câu 7:
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên A. 3
y = −x − 3x +1 . B. 3
y = −x + 3x −1 . C. 3
y = x − 3x +1 . D. 3
y = x + 3x +1. 2 Câu 8:
Cho a là một số dương, biểu thức 3 a
a viết dưới dạng lũy thừa với số mũ hữu tỉ là 4 5 A. 3 a . B. 6 a . 7 6 C. 6 a . D. 7 a . Câu 9:
Với a là số thực dương bất kì, mệnh đề nào sau đây đúng? 1 a 1 A. 5 ln a = ln . a
B. ln 3a = ln 3+ ln . a C. ln = ln . a
D. ln (3+ a) = ln3+ ln . a 5 3 3 Câu 10: Cho hàm số 3 2
y = x − 3x + 2 có đồ thị (C). Gọi m là số giao điểm của (C) và trục hoành. Tìm m . A. m = 2 . B. m = 1. C. m = 3 . D. m = 0 . Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 11: Hàm số y = ( − x )2 2 4
+1 có giá trị lớn nhất trên đoạn  1 − ;  1 bằng A. 10 . B. 12 . C. 14 . D. 17 . −
Câu 12: Tập xác định của hàm số y = ( x − ) 5 3 là A. (3;+) . B. (1; ) 3 . C. . D. \   3 .
Câu 13: Cho hàm số f ( x) có bảng biến thiên sau:
Khẳng định nào sau đây đúng?
A. Giá trị cực tiểu của hàm số bằng 2 .
B. Hàm số đạt cực tiểu tại x =1 và đạt cực đại tại x = 5.
C. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 2 .
D. Giá trị cực đại của hàm số bằng 0 . Câu 14: Hàm số 3 2
y = x + 3x đồng biến trên khoảng nào dưới đây? A. (− ;  2
− ) và (0;+). B. . C. ( 2 − ;0) . D. ( 1: − +) .
Câu 15: Cho khối chóp có đáy là tam giác đều cạnh bằng 2 và có chiều cao 4. Thể tích khối chóp bằng 4 3 A. 2 3 . B. 2 . C. . D. 4 . 3 2 6 − x
Câu 16: Đồ thị hàm số y =
có tất cả bao nhiêu đường tiệm cận? 2 x + 3x − 4 A. 1. B. 2 . C. 3 . D. 0 . Câu 17: Hàm số 3
y = x − 3x + 2 đạt cực đại tại điểm A. x = 2 − . B. x =1 . C. x = 1 − . D. x = 0 .
Câu 18: Tổng diện tích các mặt của một khối lập phương là 2
96 cm . Thể tích khối lập phương đó bằng A. 3 84 cm . B. 3 48 cm . C. 3 64 cm . D. 3 91cm .
Câu 19: Hình trụ có hai đường tròn đáy ngoại tiếp hai mặt của một hình lập phương cạnh a thì có diện tích xung quanh bằng A. 2  a . B. 2 2 a . C. 2 2 2 a . D. 2 2 a .
Câu 20: Trong các hàm số sau hàm số nào đồng biến trên ? 3 x + x  1   1 
A. y = log x . B. 2018 x y = . C. y = − . D. log . 3      2  5 2  x x +1
Câu 21: Cho hàm số y =
có đồ thị (C ) và đườngthẳng d : 2x − y −1 = 0 . Biết d cắt (C ) tại hai x −1
điểm phân biệt M (x ; y và N (x ; y . Tính y + y . 2 2 ) 1 1 ) 1 2 A. 4 − . B. 5 . C. 2 . D. 2 − .
Câu 22: Tập nghiệm S của phương trình 2x 1
2 + − 5.2x + 2 = 0 là Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 A. S = 0;  1 . B. S =   1 . C. S =  1 − ;  0 . D. S =  1 − ;  1 .
Câu 23: Cho hình nón có bán kính đáy bằng 3cm , độ dài đường sinh bằng 5cm . Thể tích của khối nón được
giới hạn bởi hình nón đó bằng A. 3 75 cm . B. 3 12 cm . C. 3 45 cm . D. 3 16 cm . 1
Câu 24: Tập xác định D của hàm số y = là log 2x −1 3 ( )  1   1   1  A. −;   ; + \ 1   \ 1 ; +    . D. 2  . B.    2  . C.    2  .
Câu 25: Tìm các giá trị thực của tham số m để phương trình 2
log x − 3log x + 2m − 7 = 0 có hai nghiệm 3 3
thực x ; x thỏa mãn ( x + 3 x + 3 = 72 . 1 )( 2 ) 1 2 9 61 A. m = . B. m = . C. m = 3 . D. không tồn tại. 2 2
Câu 26: Cho hàm số f ( x) có đạo hàm f ( x) 2 = x (x − )( 2
1 x − 3x + 2) , x . Số điểm cực trị của hàm số là A. 0 . B. 1. C. 3 . D. 2 . 2x −1
Câu 27: Cho hàm số y =
có đồ thị (C ) . Số các giá trị nguyên của tham số m 2 − 020;202  0 để x −1
đường thẳng d : y = −x + m cắt (C) tại hai điểm phân biệt là A. 4035 . B. 4036 . C. 4037 . D. 2020 .
Câu 28: Cho hình hộp đứng ABC . D A BCD
  có đáy ABCD là hình thoi cạnh a, góc nhọn BCD = 60
và BD = AC . Tính thể tích của khối chóp đó bằng 3 a 3 3 a 6 A. . B. 3 a 3 . C. 3 a . D. . 2 2 Câu 29: Cho hàm số x y = a , x
y = b với a, b là hai số thực dương khác 1, lần lượt có đồ thị là C , C như 1 2
hình vẽ, mệnh đề nào sau đây đúng?
A. 0  a b 1.
B. 0  a 1 b .
C. 0  b a 1.
D. 0  b 1 a . Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 30: Nghiệm của phương trình log x +1 =1+ log
x −1 là x = a . Tính giá trị biểu thức 3 ( ) 3 ( ) 2
T = a + a +1. A. T = 2. B. T = 4. C. T = 7 . D. T = 5 . Câu 31: Cho hàm số 3 2
y = x + 3x − mx − 4 . Tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng (− ;  + ) là A. (−1;5) . B. (− ;  −  3 . C. . D. (−1;+) .
Câu 32: Cho hàm số y = f ( x) xác định, liên tục trên
và có bảng biến thiên như sau:
Tìm tất cả các các giá trị thực của tham số m để phương trình f (x) −1= m có đúng hai nghiệm. m  0 m = 2 − m = 2 − A.  . B.  . C. 2 −  m  1 − . D.  . m = 1 − m  −1 m  1 −
Câu 33: Một chiếc cốc có dạng hình trụ, chiều cao 16cm , đường kính đáy bằng 8cm , bề dày của thành
cốc và đáy cốc bằng 1cm . Nếu đổ lượng nước vào cốc cách miệng cốc 5cm thì được thể tích V1 V
, nếu đổ đầy cốc ta được khối trụ (tính cả thành cốc và đáy cốc) có thể tích V . Tỉ số 1 bằng 2 V2 2 245 45 11 A. . B. . C. . D. . 3 512 128 16
Câu 34: Cho hàm số y = f ( x) có đồ thị f ( x) như hình vẽ bên. Hàm số y = f (5−3x) nghịch biến trên
khoảng nào trong các khoảng dưới đây. A. (2;5) . B. (2;+ ) . C. ( 3 − ; ) 1 . D. (0;3) . Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x a
Câu 35: Cho hàm số f ( x) = ln − ln 2020  
. Biết f (2) + f (4) + ... f (2020) = , với , a b N *  x + 2  b a và
là phân số tối giản. Tính giá trị biểu thức S = b − 2a . b 2021 A. S = . B. S = 0 . C. S = 1. D. S = 1 − . 2022 II. PHẦN TỰ LUẬN mx + 5
Câu 36: Tìm tham số m để hàm số y = 0;1 bằng 7 − . x −
đạt giá trị nhỏ nhất trên đoạn   m A. m = 5 . B. m = 2 . C. m = 0 . D. m = 1.
Câu 37: Cho khối chóp tam giác S.ABC có các góc ASB = BSC = CSA = 60 và độ dài các cạnh SA =1
, SB = 2, SC = 3. Thể tích khối chóp S.ABC bằng: 3 2 6 3 2 A. . B. . C. . D. . 2 2 2 2
Câu 38: Cho hàm số y = f (x) . Hàm số y = f ( x) có bảng biến thiên như hình vẽ bên. Hỏi hàm số
g ( x) = f (2x) − x có bao nhiêu điểm cực trị? x ∞ 1 1 +∞ 1 +∞ f'(x) ∞ 1 1 1 2
Câu 39: Giải phương trình sau: log
(x +3)+ log x −1 = log 4x . 3 ( ) 3 ( ) 3 2 2
---------- HẾT ---------- Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) 4 x Câu 1: Hàm số 2 3 y = −
+ x + có bao nhiêu điểm cực trị? 2 2 A. 4 . B. 2 . C. 0 . D. 3 . Lời giải Chọn D x = 1 −  Ta có 3
y = − x + x = − x ( 2 2 2 2 x − )
1 . Suy ra y = 0  2 − x( 2 x − ) 1 = 0  x = 0  x =1 
Vì y = 0 có 3 nghiệm phân biệt và đổi dấu khi qua ba nghiệm đó nên hàm số đã cho có 3 cực trị. Câu 2:
Khối lăng trụ có diện tích đáy bằng 2
3a , chiều cao bằng a có thể tích bằng 3 1 A. 3 a . B. 3 3a . C. 3 a . D. 3 a . 2 2 Lời giải Chọn B
Áp dụng công thức tính thể tích khối lăng trụ ta có 2 3
V = B .h = 3a .a = 3a . Câu 3: Phương trình x+1 2 =8 có nghiệm là A. x = 2 . B. x =1. C. x =3 . D. x = 4 . Lời giải Chọn A Ta có x+1 2 =8 x +1 3
 2 = 2  x +1=3  x =2 . Câu 4:
Cho khối tứ diện OABC có OA , OB , OC đôi một vuông góc với nhau tại O và OA = 2 , OB = 4
, OC = 6 . Thể tích khối tứ diện đã cho bằng A. 8 . B. 24 . C. 48 . D. 16 . Lời giải Chọn A 1 1
Thể tích khối tứ diện OABC là V = O . A O . B OC = .2.4.6 = 8 . 6 6 Câu 5:
Cho khối chóp S.ABC có thể tích V . Các điểm B ; C tương ứng là trung điểm các cạnh SB ,
SC . Thể tích khối chóp S.AB C   bằng V V V V A. . B. . C. . D. . 8 2 4 16 Lời giải Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Chọn C V     SA SB SC 1 Ta có: S.AB C =   = . V SA SB SC 4 S.ABC V
Vậy: VS.AB C = . 4 2019 Câu 6: Cho hàm số y =
H . Số đường tiệm cân của (H ) là 2 − có đồ thị ( ) x A. 3 . B. 1. C. 0 . D. 2 . Lời giải Chọn D 2019 2019 2019 2019 Ta có lim = lim x = 0 , lim = lim x = 0 . x→+ →+ →− →− 2 x − x 2 x x − 2 − x 2 1 −1 x x
Vậy đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số. 2019 2019 lim = − = + + ;lim → x→2 x 2 − 2 − x 2 − . x
Vậy đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số Câu 7:
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 A. 3
y = −x − 3x +1 . B. 3
y = −x + 3x −1 . C. 3
y = x − 3x +1 . D. 3
y = x + 3x +1. Lời giải Chọn C
Giả sử hàm số cần tìm có dạng 3 2
y = ax + bx + cx + d với a  0 .
Dựa vào đồ thị hàm số ta thấy lim y = + nên suy ra a  0 . Vậy loại đáp án A, B. x→+
Đồ thị hàm số đạt cực đại tại điểm có tọa độ là ( 1
− ;3) và đạt cực tiểu tại điểm có tọa độ là (1;− )
1  phương trình y = 0 phải có hai nghiệm x = 1
− ; x =1. Ta thấy chỉ có hàm số x = 1 − 3
y = x − 3x +1 có 2 2
y = 3x − 3; y = 0  3x − 3 = 0   . x =1 3
Vậy chọn y = x − 3x +1 2 Câu 8:
Cho a là một số dương, biểu thức 3 a
a viết dưới dạng lũy thừa với số mũ hữu tỉ là 4 5 7 6 A. 3 a . B. 6 a . C. 6 a . D. 7 a . Lời giải Chọn C 2 2 1 7 Ta có: 3 3 2 6 a
a = a .a = a . Câu 9:
Với a là số thực dương bất kì, mệnh đề nào sau đây đúng? 1 A. 5 ln a = ln . a
B. ln 3a = ln 3+ ln . a 5 a 1 C. ln = ln . a
D. ln (3+ a) = ln3+ ln . a 3 3 Lời giải Chọn B
Dựa vào quy tắc tính logarit với ba số dương a, ,
b c và a  1, ta có log (bc) = log b + log . c a a a 3 2
Câu 10: Cho hàm số y = x − 3x + 2 có đồ thị (C ) . Gọi m là số giao điểm của (C ) và trục hoành. Tìm m . A. m = 2 . B. m = 1. C. m = 3 . D. m = 0 . Lời giải Chọn C
Xét phương trình hoành độ giao điểm của (C) và trục hoành: 3 2
x − 3x + 2 = 0 . Sử dụng MTBT,
ta có phương trình trên có 3 nghiệm phân biệt: x = 1; x = 1 3 . Mỗi hoành độ tương ứng với
một giao điểm. Vậy có 3 giao điểm của (C ) và trục hoành. Ta Chọn C Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 11: Hàm số y = ( − x )2 2 4
+1 có giá trị lớn nhất trên đoạn  1 − ; 1 bằng A. 10 . B. 12 . C. 14 . D. 17 . Lời giải Chọn D TXĐ: D = . x = 2 −   1 − ;  1  Xét y = 2( 2 4 − x )( 2
− x) = 0  x = 0  . x = 2    1 − ;  1
Ta so sánh các giá trị sau: f ( )
1 =10; f (0) =17 , ta có:
Giá trị lớn nhất của hàm số trên đoạn  1
− ; 1 bằng 17 khi x = 0. Ta chọn phương án D. −
Câu 12: Tập xác định của hàm số y = ( x − ) 5 3 là A. (3;+) . B. (1; ) 3 . C. . D. \   3 . Lời giải Chọn A
Điều kiện xác định: x −3  0  x  3.
Vậy tập xác định của hàm số là D = (3;+) .
Câu 13: Cho hàm số f ( x) có bảng biến thiên sau:
Khẳng định nào sau đây đúng?
A. Giá trị cực tiểu của hàm số bằng 2 .
B. Hàm số đạt cực tiểu tại x =1 và đạt cực đại tại x = 5.
C. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 2 .
D. Giá trị cực đại của hàm số bằng 0 . Lời giải Chọn C
Theo bảng biến thiên thì hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 2 . 3 2
Câu 14: Hàm số y = x + 3x đồng biến trên khoảng nào dưới đây? Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 A. (− ;  2
− ) và (0;+). B. . C. ( 2 − ;0) . D. ( 1: − +) . Lời giải Chọn A Tập xác định . x = 0 Ta có 2 y = 3x + 6 ; x y = 0  .  x = 2 −
Bảng xét dấu của y
Vậy hàm số đồng biến trên khoảng (− ;  2 − ) và (0;+).
Câu 15: Cho khối chóp có đáy là tam giác đều cạnh bằng 2 và có chiều cao 4. Thể tích khối chóp bằng 4 3 A. 2 3 . B. 2 . C. . D. 4 . 3 Lời giải 1 1 1 4 3
Thể tích của khối chóp là V = . . B h = . 2.2.sin 60 .4  = . 3 3 2 3 2 6 − x
Câu 16: Đồ thị hàm số y = 2
x + 3x − có tất cả bao nhiêu đường tiệm cận? 4 A. 1. B. 2 . C. 3 . D. 0 . Lời giải Chọn A
Ta có tập xác định của hàm số là D = − 6; 6  \   1   . 2 6 − x Ta có lim y = lim = + x = . + + 2 x 1 → x 1 → x + 3x −
suy ra đồ thị hàm số có tiệm cận đứng là 1 4
Đồ thị hàm số không có tiệm cận ngang.
Vậy đồ thị hàm số có 1 đường tiệm cận. 3
Câu 17: Hàm số y = x − 3x + 2 đạt cực đại tại điểm A. x = 2 − . B. x =1 . C. x = 1 − . D. x = 0 . Lời giải Chọn C Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 3 2
Ta có: y = x − 3x + 2  y = 3x − 3
y = 0  x = 1 hoặc x = 1 −
Mà y = 6x nên hàm số đạt cực đại tại x = 1 − vì y(− ) 1 = 6 −  0
Câu 18: Tổng diện tích các mặt của một khối lập phương là 2
96 cm . Thể tích khối lập phương đó bằng 3 3 3 3 A. 84 cm . B. 48 cm . C. 64 cm . D. 91cm . Lời giải Chọn C 96
Khối lập phương có 6 mặt bằng nhau nên diện tích 1 mặt 2 S = = 16cm 0 6
 Độ dài cạnh khối lập phương 4cm .
 Thể thích khối lập phương 3 3 4 = 64 cm
Câu 19: Hình trụ có hai đường tròn đáy ngoại tiếp hai mặt của một hình lập phương cạnh a thì có diện tích xung quanh bằng 2 2 A. 2    a . B. 2 2 a . C. 2 2 a . D. 2 a . Lời giải Chọn A
Hình trụ có hai đường tròn đáy ngoại tiếp hai mặt của một hình lập phương có chiều cao là a
cạnh của hình lập phương, tức h = a . Bán kính đường tròn đáy là r = . 2 a 2
Diện tích xung quanh hình trụ là 2 rh = 2 .
.a = 2 a . 2
Câu 20: Trong các hàm số sau hàm số nào đồng biến trên ? 3 x + x  1   1 
A. y = log x = − log 3 . B. 2018 x y = . C. y   . D.   .  5 2 2   x Lời giải Chọn C   x 1
Các hàm số y = log x ; y = 2018 ; y = log
không có tập xác định trên nên loại. 3 5   2  x  3 3 2 x + x x + x x + x  1   1   1   1  Với y = −  y = −( 2 3x + ) 1 .ln . = ( 2 3x + ) 1 ln 2.  0 x           2   2   2   2  Ta Chọn C Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x +1
Câu 21: Cho hàm số y =
có đồ thị (C ) và đườngthẳng d : 2x − y −1 = 0 . Biết d cắt (C ) tại hai x −1
điểm phân biệt M (x ; y và N (x ; y . Tính y + y . 2 2 ) 1 1 ) 1 2 A. 4 − . B. 5 . C. 2 . D. 2 − . Lời giải Chọn C x +1
x = 0  y = 1 −
Ta có phương trình hoành độ giao điểm: 2
= 2x −1  2x − 4x = 0   . x −1
x = 2  y = 3
Do đó đặt M (0;− ) 1 và N (2; ) 3 . Vậy y + y = 2 1 2
Câu 22: Tập nghiệm S của phương trình 2x 1
2 + − 5.2x + 2 = 0 là A. S = 0;  1 . B. S =   1 . C. S =  1 − ;  0 . D. S =  1 − ;  1 . Lời giải Chọn D Đặ x
t t = 2 , t  0 . t = 2 2 x 1 + x 2 2 5.2 2 0 2t 5t 2 0  − + =  − + =  1  (thỏa). t =  2 Với = 2  2x t = 2  x =1. 1 x 1 Với t =  2 =  x = 1 − . 2 2
Vậy tập nghiệm của phương trình đã cho là S =  1 − ;  1 .
Câu 23: Cho hình nón có bán kính đáy bằng 3cm , độ dài đường sinh bằng 5cm . Thể tích của khối nón được giới
hạn bởi hình nón đó bằng 3 3 3 3 A. 75 cm . B. 12 cm . C. 45 cm . D. 16 cm . Lời giải Chọn B Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Ta có chiều cao của khối nón 2 2 h = 5 − 3 = 4cm. Diện tích đáy 2 S = 9 cm . 1
Thể tích khối nón được giới hạn bởi hình nón: 3 V = .9 .4 = 12 cm . 3 1
Câu 24: Tập xác định D của hàm số y = log 2x− là 1 3 ( )  1   1   1  A. −;   . B. ; + \     1 . C. \  1 . D. ; +   .  2   2   2  Lời giải Chọn B  1 2x −1  0 x
Hàm số xác định khi và chỉ khi log 2x −1 xác định và log 2x −1  0     2 . 3 ( ) 3 ( ) 2x −1  1 x 1  1   D = ; + \     1 .  2 
Câu 25: Tìm các giá trị thực của tham số m để phương trình 2
log x − 3log x + 2m − 7 = 0 3 3 có hai nghiệm thực x ; x x + 3 x + 3 = 72 1 2 thỏa mãn ( . 1 )( 2 ) 9 61 A. m = . B. m = . C. m = 3 . D. không tồn tại. 2 2 Lời giải Chọn A Đặt t = log x 2
t − 3t + 2m − 7 = 0 1 3
. Phương trình trở thành ( ).
Phương trình có hai nghiệm x ; x x x  1 có hai nghiệm t ;t . 1 2 ( 1 2 ) ( ) 1 2   = − ( m − ) 37 9 4 2 7  0  m  . 8 Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Theo viét t + t = 3
t .t = 2m − 7 1 2 và 1 2 . t t Ta có 1 2 x = 3 ; x = 3 1 2 . ( + x + ) 3 ( x + ) 1 t t2 3 = 72  3 + 3( 1t t2 3 + 3 ) 1 t t2 + 9 = 72  3 + 3 =12 2 . 1 2 ( )
Thế t = 3 − t 2 t 3−t + = 2 1 vào phương trình ( ) ta được 1 1 3 3 12 2 1 t 1 3 12.3t  − + 27 = 0 t1 3 = 3 t =1 1
Giải phương trình ta được    . t2 3 = 9 t = 2  2 9
t .t = 2  2m − 7 = 2  m = (nhận). 1 2 2
Câu 26: Cho hàm số f ( x) có đạo hàm f ( x) 2 = x (x − )( 2
1 x − 3x + 2) , x . Số điểm cực trị của hàm số là A. 0 . B. 1. C. 3 . D. 2 . Lời giải Chọn B
Hàm số f ( x) đã cho có đạo hàm là hàm đa thức nên hàm số f ( x) liên tục trên . 2 Ta có f ( x) 2 = x (x − )( 2 1 x − 3x + 2) 2 = x (x − ) 1 ( x − 2) . x = 0 
f (x) = 0  x = 1  . x = 2  Bảng biến thiên (BBT)
Dựa vào BBT, ta thấy hàm số f ( x) có duy nhất một điểm cực trị. 2x −1
Câu 27: Cho hàm số y =
có đồ thị (C ) . Số các giá trị nguyên của tham số m 2 − 020;202  0 để x −1
đường thẳng d : y = −x + m cắt (C) tại hai điểm phân biệt là A. 4035 . B. 4036 . C. 4037 . D. 2020 . Lời giải Chọn B Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Phương trình hoành độ 2x −1
giao điểm của (C ) và d là = −x + m x −1
 2x −1= (x− )
1 (−x + m) (Vì x =1 không phải là nghiệm của phương trình) 2
x +(1−m)x+m−1= 0 ( ) * .
Đường thẳng d cắt (C) tại hai điểm phân biệt  ( )
* có hai nghiệm phân biệt m   ( − 5 m)2 1 − 4(m − ) 1  0 2
m − 6m + 5  0   . m 1
Theo giả thiết: m 2 − 020;202 
0 và m  m 2 − 020; 2 − 019;...; 1 − ;0;6;7;8;...;202  0
có 4036 số nguyên thỏa mãn đề bài.
Câu 28: Cho hình hộp đứng ABC . D A BCD
  có đáy ABCD là hình thoi cạnh a, góc nhọn BCD = 60
và BD = AC . Tính thể tích của khối chóp đó bằng 3 a 3 3 3 a 6 A. . B. a 3 . C. 3 a . D. . 2 2 Lời giải Chọn D
Ta có tam giác BCD đều nên BD = a và AC = a 3 , BD = a 3 . 2 2
Trong tam giác vuông BDD : DD =
BD − BD = a 2 . 3 1 a 6 V =  = =     DD .S a 2. . a a 3 . ABCD. A B C D ABCD 2 2 x x
Câu 29: Cho hàm số y = a , y = b với a, b là hai số thực dương khác 1, lần lượt có đồ thị là C ,C 1 2 như
hình vẽ, mệnh đề nào sau đây đúng? Page 15
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
A. 0  a b 1.
B. 0  a 1  b .
C. 0  b a 1.
D. 0  b 1  a . Lời giải Chọn D
Ta thấy hàm số có đồ thị C C
1 đồng biến nên a  1 , hàm số có đồ thị 2 nghịch biến nên
0  b  1. Vậy 0  b 1 a .
Câu 30: Nghiệm của phương trình log x +1 =1+ log
x −1 là x = a . Tính giá trị biểu thức 3 ( ) 3 ( ) 2
T = a + a +1. A. T = 2. B. T = 4. C. T = 7 . D. T = 5 . Lời giải Chọn C
Phương trình log x +1 =1+ log x −1 (1), 3 ( ) 3 ( ) x +1  0 Điều kiện:   x 1. x −1  0
Phương trình (1)  log x +1 = log 3x −3  3x −3 = x +1  x = 2 (nhận), suy ra a = 2 . 3 ( ) 3 ( ) Vây 2 T = 2 + 2 +1 = 7 . 3 2
Câu 31: Cho hàm số y = x + 3x − mx − 4 . Tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng (− ;  + ) là A. (−1;5) . B. (− ;  −  3 . C. . D. (−1;+) . Lời giải Chọn B 2
Ta có y = 3x + 6x − m . Để 2
hàm số đồng biến trên khoảng (− ;
 + ) thì y  0,x  3x + 6x − m  0,x . Page 16
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Có 3  0 , nên suy ra 
 = 9+3m  0  m  −3 hay m(− ;  −  3 .
Câu 32: Cho hàm số y = f ( x) xác định, liên tục trên
và có bảng biến thiên như sau:
Tìm tất cả các các giá trị thực của tham số m để phương trình f ( x) −1= m có đúng hai nghiệm. m  0 m = 2 − m = 2 − A.  . B.  . C. 2 −  m  1 − . D.  . m = 1 − m  −1 m  1 − Lời giải Chọn D
Ta có f ( x) −1 = m f ( x) = m +1. Để phương trình đã cho có đúng 2 nghiệm thì m +1 = 1 − m = 2 −    m +1  0 m  1 −
Câu 33: Một chiếc cốc có dạng hình trụ, chiều cao 16cm , đường kính đáy bằng 8cm , bề dày của thành
cốc và đáy cốc bằng 1cm . Nếu đổ lượng nước vào cốc cách miệng cốc 5cm thì được thể tích V1 V
, nếu đổ đầy cốc ta được khối trụ (tính cả thành cốc và đáy cốc) có thể tích V . Tỉ số 1 bằng 2 V2 2 245 45 11 A. . B. . C. . D. . 3 512 128 16 Lời giải Chọn C
Khi đổ nước vào cách miệng cốc 5cm thì thể tích nước là V có dạng hình trụ với chiều cao 1
bằng 16 −1− 5 =10cm , đường kính đáy là 8 − 2 = 6cm . Do đó: 2 3
V =  3 .10 = 90 cm . 1
Thể tích khi đổ đầy nước (tính cả thành cốc và đáy cốc): 2 3
V =  4 .16 = 256 cm . 2 V 90 45 Suy ra: 1 = = . V 256 128 2
Câu 34: Cho hàm số y = f ( x) có đồ thị f ( x) như hình vẽ bên. Hàm số y = f (5−3x) nghịch biến trên
khoảng nào trong các khoảng dưới đây. Page 17
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 A. (2;5) . B. (2;+ ) . C. ( 3 − ; ) 1 . D. (0;3). Lời giải Chọn C
Ta có y = (5 − 3x) f (5 − 3x) = 3
− f (5 −3x) .
Hàm số nghịch biến  3
− f '(5−3x)  0  f '(5−3x)  0.
Quan sát đồ thị ta thấy f (5−3x)  0  5−3x  2  x 1.
Dựa vào các đáp án ta Chọn C x a
Câu 35: Cho hàm số f ( x) = ln − ln 2020  
. Biết f (2) + f (4) + ... f (2020) = , với , a b N *  x + 2  b a và
là phân số tối giản. Tính giá trị biểu thức S = b − 2a . b 2021 A. S = . B. S = 0 . C. S = 1. D. S = 1 − . 2022 Lời giải Chọn C ( )  x xx  0 f x = ln − ln 2020   điều kiện:  0  .   x + 2  x + 2 x  2 −  2  x  2    x + 2 x + 2  2 1 1 Ta có f ( x) ( ) = = = = − . x x x ( x + 2) x x + 2 x + 2 x + 2
Khi đó: f (2) + f (4) + ... f (2020)  1 1   1 1   1 1   1 1  1 1 1010 505 = − + − +...+ − + − = − = =         .  2 4   4 6 
 2018 2020   2020 2022  2 2022 2022 1011 Page 18
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 505 a = 505 Ta có
là phân số tối giản  
S = b − 2a =1011−1010 =1. 1011 b  =1011 II. PHẦN TỰ LUẬN mx + 5
Câu 36: Tìm tham số m để hàm số y = 0;1 bằng 7 − . x −
đạt giá trị nhỏ nhất trên đoạn   m A. m = 5 . B. m = 2 . C. m = 0 . D. m = 1. Lời giải Chọn B 2 −m − 5 Ta có y =    ( . x − m) 0; x m 2  m + 5 y ( ) 1 = −7 = 7 − 
Hàm số đạt giá trị nhỏ nhất trên đoạn 0;  1 bằng 7 −    1− mm   0; 1  m  0  ;1 m = 2    = . Vậy m = 2 . m     m 2 0;1
Câu 37: Cho khối chóp tam giác S.ABC có các góc ASB = BSC = CSA = 60 và độ dài các cạnh SA =1
, SB = 2, SC = 3. Thể tích khối chóp S.ABC bằng: 3 2 6 3 2 A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn B
Gọi H là hình chiếu của C lên mặt (SAB) , M và N là hình chiếu của H lên SA và SB . C
 H ⊥ (SAB) Ta có: 
SA ⊥ CM (Định lý 3 đường vuông góc).  A S ⊥ HM Page 19
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Tương tự: SB ⊥ CN . C
 SN = CSM = 60
Xét hai tam giác vuông CSM và CSN có:  và cạnh SH chung. C
 NS = CMS =1v Suy ra: CSM = C
SN (g.c.g)  HM = HN H thuộc phân giác trong BSA .  3
SN = SC.cos 60 =  2
Xét tam giác vuông CSN   . 3 3
CN = CS.sin60 =  2 3
Xét tam giác vuông SHN HN = SN. tan 30 = . 2 Xét tam giác vuông 2 2 2
CHN CH = CN − HN = 6  CH = 6 . 1 3
Diện tích tam giác SAB : S = S . A S . B sin 60 =  . SAB 2 2 1 2
Thể tích khối chóp S.ABC : V = CH.S = . S . ABC  3 SAB 2 Cách 2.
Trên các cạnh SB , SC lấy các điểm B và C sao cho SB = SC = SA =1.
Do ASB = BSC = CSA = 60 nên hình chóp S.AB C
  là tứ diện đều cạnh bằng 1. 2 Suy ra V = . S . AB C   12 V     SB SC 1 2 Ta có: S.AB C = . = V = 6V = . S .ABC S .   V SB SC 6 AB C 2 S.ABC
Câu 38: Cho hàm số y = f (x) . Hàm số y = f ( x) có bảng biến thiên như hình vẽ bên. Hỏi hàm số
g ( x) = f (2x) − x có bao nhiêu điểm cực trị? Page 20
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x ∞ 1 1 +∞ 1 +∞ f'(x) ∞ 1 Lời giải
Ta có g( x) = 2 f (2x) −1.
Cho g( x) =  f ( x) 1 0 2 = (1). 2 Đặt t = 2x .
Phương trình (1) là phương trình hoành độ 1
giao điểm của đồ thị y = f (2x) và y = trở thành 2 1
phương trình hoành độ giao điểm của đồ thị y = f (t) và y = . 2 Ta có bảng biến thiên t ∞ 1 1 +∞ 1 +∞ f'(t) ∞ 1
Từ bảng biến thiên suy ra phương trình f (t ) 1
= có ba nghiệm t phân biệt nên f ( x) 1 2 = có 2 2
ba nghiệm x phân biệt.
Vậy hàm số g ( x) có 3 điểm cực trị. 1 1 2
Câu 39: Giải phương trình sau: log
(x +3)+ log x −1 = log 4x . 3 ( ) 3 ( ) 3 2 2 Lời giải 1 (x + ) 1 log 3 + log ( x − )2 1 = log 4x . 3 3 ( ) 3 2 2 x + 3  0 x  3 −   x  1 Điều kiện: (  x − )2 1
 0  x 1     x  0 4x  0 x  0  
Với điều kiện trên phương trình đã cho tương đương
log x + 3 + log x −1 = log 4x 3 ( ) 3 3 ( )
 log  x + 3 x −1 = log 4x 3 ( )  3 ( )  (x + ) 3 x −1 = 4x
Trường hợp 1: x 1  (x + ) 3 (x − ) 1 = 4x Page 21
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 2
x − 2x − 3 = 0 x = −1 (loạ i)
 x =3 (thỏa mãn)
Trường hợp 2: 0  x 1  (x + )
3 (1− x) = 4x 2
x + 6x − 3 = 0 x = −3+ 2 3
 x =−3−2 3 (loại)
Vậy phương trình đã cho có hai nghiệm x = 3 và x = −3 + 2 3 .
---------- HẾT ---------- Page 22
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 10
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau:
Hàm số y = f (x) nghịch biến trong khoảng nào trong các khoảng sau? B. ( ; − 3) . B. (1; +) . C. (1;3) . D. ( ; − 1). Câu 2:
Cho hàm số y = f ( x) có đồ thị là hình vẽ sau:
Điểm cực đại của hàm số y = f (x) là A. x = 2. − B. x = 0. C. x = 2. D. y = 2. Câu 3:
Hàm số y = f (x) liên tục trên  1 − ; 
3 và có bảng biến thiên như sau
Giá trị nhỏ nhất của hàm số y = f (x) trên đoạn  1 − ;  3 là A. 1. B. 5 . C. 2 . D. 2 − . Câu 4:
Hàm số nào có đồ thị là hình vẽ sau đây? 4 2 = + − 2x +1 3 2 = + + 3 2 = + − B. y x 3x 4 . B. y = . C. y x 3x
4 . D. y x 3x 4 . 3x − 5 Page 1
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 Câu 5:
Hàm số nào có bảng biến thiên là hàm sau đây? −x − 2 x + 2 x − 2 x − 2 A. y = . B. y = . C. y = . D. y = . x −1 x −1 x −1 x +1 2x − 4 Câu 6:
Đồ thị (C) của hàm số y =
có phương trình đường tiệm cận đứng là x +1 A. y = 2. B. y = 1. − C. x = 1. − D. x = 2. Câu 7:
Với a, b là các số thực dương và ,  là các số thực, mệnh đề nào sau đây là sai?           a A. (a ) + = a . B. (   .
a b) = a .b . C. (a ) . = a . D.  − =  a  . a Câu 8:
Với các số a , b , c là các số dương và a  1, mệnh đề nào sau đây sai? A. log bc b c . B. log bc b c . a ( ) = log .log a ( ) =log +log a a a a c b
C. log b = c log b . D. = b − . a a log log log c a a a c Câu 9:
Cho a, b là các số thực dương thỏa mãn a  1 và log 3. 2 a b =
Tính loga (a b) . A. 4 . B. 5 . C. 6 . D. 3
Câu 10: Tập xác định của hàm số y = log x −1 là 3 ( ) A. (1;+). B. ( ) ;1 − . C. 1;+) . D. (− ;  +) .
Câu 11: Đạo hàm của hàm số y = log x là 5 x 1 ln 5 A. y = . B. y = .
C. y = x ln 5 . D. y = . ln 5 x ln 5 x
Câu 12: Phương trình ln 5 x ln x 1 có nghiệm là A. x 2 . B. x 3 . C. x 2 . D. x 1. + −
Câu 13: Phương trình 2x 3 4 x 5 3 = 3 có nghiệm là A. x = 3. B. x = 4 . C. x = 2 . D. x =1 . − log 3x 1 − =3 =log 10 −3 + 2 x K x 3 ( ) log 2 1 2 ( ) 2 ( ) Câu 14: Cho . Giá trị biểu thức bằng A. 8. B. 35. C. 32. D. 14.
Câu 15: Mỗi mặt của hình bát diện đều là hình nào trong các hình sau?
A. Tam giác đều.
B. Hình vuông.
C. Bát giác đều. D. Ngũ giác đều.
Câu 16: Thể tích của khối hộp chữ nhật có ba kích thước 2 , 3 và 4 là A. 24 . B. 8 . C. 9 . D. 20 . Page 2
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Câu 17: Cho khối nón có chiều cao h = 9a và bán kính đáy r = 2a . Thể tích của khối nón đã cho là A. 3 V = 12 a . B. 3 V = 6 a . C. 3 V = 24 a . D. 3 V = 36 a .
Câu 18: Cho khối trụ có chiều cao h = 4a và bán kính đường tròn đáy r = 2a . Thể tích của khối trụ đã cho bằng 3 16 a A. 3 8 a . B. 3 16 a . C. 3 6 a . D. . 3
Câu 19: Cho hình nón có bán kính đường tròn đáy r = 3a và đường sinh l = 2r . Diện tích xung quanh của hình nón bằng A. 2 6 a . B. 2 9 a . C. 2 36 a . D. 2 18 a .
Câu 20: Thể tích của khối cầu có bán kính r = 2 là 32 33 A. V = . B. V = . C. V = 16 . D. V = 32 . 3 2 2x −1
Câu 21: Cho hàm số y =
. Mệnh đề nào sau đây đúng? x +1
A. Hàm số đồng biến trên .
B. Hàm số nghịch biến trên khoảng ( 1 − ;+ ).
C. Hàm số nghịch biến trên các khoảng (− ;  − ) 1 và ( 1 − ;+ ).
D. Hàm số đồng biến trên khoảng (− ;  − ) 1 .
Câu 22: Hàm số nào sau đây có ba điểm cực trị? 2x − 4 A. y =
y = −x − x + . x + . B. 4 2 4 2020 1 C. 3 2
y = x − 3x + 5 . D. 4 2
y = 3x − x + 2019 .
Câu 23: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3
y = x − 3x + 4 trên đoạn
0;2. Giá trị của biểu thức 2 2 M + m bằng A. 52. B. 20. C. 8. D. 40. Câu 24: Cho hàm số ( ) 4 2
f x = ax + bx + c có đồ thị như sau:
Khẳng định nào sau đây đúng?
A. a  0, b  0, c  0.
B. a  0, b  0, c  0. C. a  0, b  0, c  0. D. a  0, b  0, c  0. x + 2
Câu 25: Số đường tiệm cận ngang của đồ thị hàm số y = là 2 4x +1 Page 3
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 A. 2 . B. 1. C. 4 . D. 0 . 
Câu 26: Tập xác định của hàm số y = ( 2
x − 9x +18) là A. (− ;  ) 3 (6;+) . B. \ 3;  6 . C. (3;6) . D. 3;6 .
Câu 27: Đạo hàm của hàm số f ( x) 4x 2019 e + = là x e + A. f ( x) 4 2019 ' = . B. f ( x) 4 ' = e . C. ( ) 4 2019 ' 4 x f x e + = . D. ( ) 4 2019 ' x f x e + = . 4
Câu 28: Hãy tìm tập xác định D của hàm số y = ( 2
ln x − 2x − 3) . A. D = ( 1 − ; ) 3 .
B. D = (−;− ) 1 (3;+ ) .
C. D = (−;−  1 3;+ ) . D. D =  1 − ;  3 .
Câu 29: Hàm số y = log x và y = log x có đồ thị như hình vẽ dưới đây. a b
Đường thẳng y = 3 cắt đồ thị tại hai điểm có hoành độ là x , x . Biết rằng x = 2x , giá trị của 1 2 2 1 a bằng b 1 A. . B. 3 . C. 2 . D. 3 2 . 3
Câu 30: Gọi x và x là hai nghiệm của phương trình 25x 7.5x 10
0. Giá trị biểu thức x x bằng 1 2 1 2 A. log 7 . B. log 20 . C. log 10 . D. log 70 . 5 5 5 5 + +
Câu 31: Phương trình 2 x 2 x 4 2
= 3m − 7 có nghiệm khi  23   7  7  A. m  ; +    . B. m  ; +    . C. m  ; +    .
D. m5;+ ) .  3   3   3  Page 4
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Câu 32: Leonhard Euler là nhà toán học rất nỗi tiếng người Thụy Sĩ đã khám phá ra công thức rất thú vị
và có ứng dụng nhiều trong khoa họ
C. Đó là trong các khối đa diện bất kì thì V − E + F =
“hằng số”, hằng số này được gọi là “đặc trưng Euler” (với V là số đỉnh, E là số cạnh và F là
số mặt của đa diện).
Em hãy tính “đặc trưng Euler” của khối lập phương. A. 2. B. 3. C. 1. D. 4.
Câu 33: Cho hình chóp S.ABCD có SA ⊥ ( ABCD), ABCD là hình chữ nhật, AB = 2BC = 2a , SC = 3a
. Thể tích khối chóp S.ABCD bằng 3 4a 3 3 a 2a A. 3 a . B. . C. . D. . 3 3 3
Câu 34: Cho hình chữ nhật ABCD có AB = 2a 3 , ADB = 60 . Gọi M, N lần lượt là trung điểm của AD,
BC. Khối trụ tròn xoay tạo thành khi quay hình chữ nhật ABCD (kể cả điểm trong) xung quanh
cạnh MN có thể tích bằng bao nhiêu? 3 2 a 3 3 8 a 3 A. 3 V = 8 a 3 . B. V = . C. 3 V = 2 a 3 . D. V = . 3 3 Câu 35: Cho ABC
vuông tại A có AB = 4a , AC = 3a . Quay ABC
xung quanh cạnh AB , đường gấp
khúc ACB tạo nên một hình nón tròn xoay. Diện tích xung quanh của hình nón đó là A. 2 S = 24a . B. 2 S =12a . C. 2 S = 30a . D. 2 S =15a . xq xq xq xq II. PHẦN TỰ LUẬN Câu 36: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
2 log x + log x − 3 = m ( 2
log x − 3 có nghiệm x  64; + ? 0  ) 2 1 4 ) 2
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác đều cạnh
bằng 4a và nằm trong mặt phẳng vuông góc với mặt phẳng ( ABCD) . Góc giữa mặt phẳng
(SBC) và mặt phẳng (ABCD) là 30. Thể tích của khối chóp S.ABCD là A. 3 24 3a . B. 3 16 3a . C. 3 4 3a . D. 3 48 3a . Page 5
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Câu 38: Cho hàm số y = f ( x) có đạo hàm liên tục trên
và hàm số y = f ( x) có đồ thị như sau: 2     Đặ m 1 m
t g ( x) = f x − − x − −1 + m +1    
với m là tham số. Gọi S là tập hợp tất cả các giá  3  2  3 
trị nguyên dương của m để hàm số y = g ( x) đồng biến trên khoảng (7;8). Tìm tập hợp S .
Câu 39: Cho x và y là các số thực dương thỏa mãn điều kiện 3
x + xy ( x + y) 3 2
= 2y + 2xy(x + 2y) . 2 2  x   4y
Tìm tất cả các giá trị của tham số m để phương trình 2 log   − . m log   + 2m − 4 = 0 3 3  2y   x
có nghiệm x thuộc đoạn 1;  3 .
---------- HẾT ---------- Page 6
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau:
Hàm số y = f (x) nghịch biến trong khoảng nào trong các khoảng sau? − + − B. ( ;3) . B. (1; ) . C. (1;3) . D. ( ;1) . Lời giải Chọn C Câu 2:
Cho hàm số y = f ( x) có đồ thị là hình vẽ sau:
Điểm cực đại của hàm số y = f (x) là A. x = 2. − B. x = 0. C. x = 2. D. y = 2. Lời giải Chọn B
Dựa vào đồ thị ta có hàm số đạt cực đại tại x = 0; y = 2. CD
Vậy điểm cực đại của hàm số là x = 0. Câu 3:
Hàm số y = f (x) liên tục trên  1 − ; 
3 và có bảng biến thiên như sau
Giá trị nhỏ nhất của hàm số y = f (x) trên đoạn  1 − ;  3 là A. 1. B. 5 . C. 2 . D. 2 − . Lời giải Page 7
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 Chọn D
Dựa vào bảng biến thiên ta thấy min y = 2 − .  1 − ;  3 Câu 4:
Hàm số nào có đồ thị là hình vẽ sau đây? 4 2 = + − 2x +1 3 2 = + + 3 2 = + − B. y x 3x 4 . B. y = . C. y x 3x
4 . D. y x 3x 4 . 3x − 5 Lời giải Chọn D
Dựa vào đồ thị hàm số ta thấy: 2x +1
Tập xác định của hàm số là
. Suy ra loại phương án B vì tập xác định của hàm số y = 3x − 5 5 là \   . 3 lim y = + ;
 lim y = − . Suy ra loại phương án A vì 4 2
lim (x + 3x − 4) = + . x→+ x→− x→
Đồ thị hàm số luôn đi qua điểm (0;− 4) . Suy ra loại phương án C vì đồ thị hàm số 3 2
y = x + 3x + 4 luôn đi qua điểm (0; 4) . Hàm số 3 2
y = x + 3x − 4 có tập xác định là ; 3 2 3 2
lim (x + 3x − 4) = + ;
 lim (x + 3x − 4) = − và đồ thị hàm số luôn đi qua điểm (0;− 4) . Vậy x→+ x→−
chọn phương án D . Câu 5:
Hàm số nào có bảng biến thiên là hàm sau đây? −x − 2 x + 2 x − 2 x − 2 A. y = . B. y = . C. y = . D. y = . x −1 x −1 x −1 x +1 Page 8
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 Lời giải Chọn A
Từ bảng biến thiên ta thấy, đồ thị hàm số nhận y = 1 − làm tiệm cận ngang. ax + b a
Mà tiệm cận ngang trong hàm số y =
là đường thẳng y =
, nên ta loại ngay 3 đáp án cx + d c cuối là B, C,
D. Vậy ta chọn đáp án A. 2x − 4 Câu 6:
Đồ thị (C) của hàm số y =
có phương trình đường tiệm cận đứng là x +1 A. y = 2. B. y = 1. − C. x = 1. − D. x = 2. Lời giải Chọn C Câu 7:
Với a, b là các số thực dương và ,  là các số thực, mệnh đề nào sau đây là sai?           a A. (a ) + = a . B. (   .
a b) = a .b . C. (a ) . = a . D.  − =  a  . a Lời giải Chọn A         Công thức sai: (a ) + = a
. Công thức đúng là (a ) . = a . Câu 8:
Với các số a , b , c là các số dương và a  1, mệnh đề nào sau đây sai? A. log bc b c . B. log bc b c . a ( ) = log .log a ( ) =log +log a a a a c b
C. log b = c log b . D. = b − . a a log log log c a a a c Lời giải Chọn B
Với các số a , b , c là các số dương và a  1, ta có: log bc b
c  A đúng, B sai. a ( ) =log +log a a log c
b = c log b  C đúng a a b log
= log b − log c  D đúng. a a a c Câu 9:
Cho a, b là các số thực dương thỏa mãn a  1 và log 3. 2 a b =
Tính loga (a b) . A. 4 . B. 5 . C. 6 . D. 3 Lời giải Chọn B ( 2ab) 2 log
= log a + log b = 2 + 3 = 5. a a a Page 9
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Câu 10: Tập xác định của hàm số y = log x −1 là 3 ( ) A. (1;+). B. ( ) ;1 − . C. 1;+) . D. (− ;  +) . Lời giải Chọn A
Hàm số có nghĩa khi x −1  0  x 1.
Vậy tập xác định của hàm số là D = (1;+) .
Câu 11: Đạo hàm của hàm số y = log x là 5 x 1 ln 5 A. y = . B. y = .
C. y = x ln 5 . D. y = . ln 5 x ln 5 x Lời giải Chọn B 1
Ta có: y = log x y = . 5 x ln 5
Câu 12: Phương trình ln 5 x ln x 1 có nghiệm là A. x 2 . B. x 3 . C. x 2 . D. x 1. Lời giải Chọn C 5 x 0 x 5 Điều kiện: 1 x 5. x 1 0 x 1
Phương trình đã cho tương đương với 5 x x 1 x 2 (thoả mãn). Vậy S 2 . + −
Câu 13: Phương trình 2x 3 4 x 5 3 = 3 có nghiệm là A. x = 3. B. x = 4 . C. x = 2 . D. x =1 . Lời giải Chọn B + − Ta có: 2x 3 4 x 5 3 = 3
 2x + 3 = 4x − 5  2x = 8  x = 4 . − log 3x 1 − =3 =log 10 −3 + 2 x K x 3 ( ) log 2 1 2 ( ) 2 ( ) Câu 14: Cho . Giá trị biểu thức bằng A. 8. B. 35. C. 32. D. 14. Lời giải Chọn A Ta có: log 3x 1
− =3 3x −1=8 x =3. 2 ( )
Với x =3 khi đó giá trị biểu thức đã cho trở thành: log 5 2 K = log 27 + 2 =3+5=8 . 3 Page 10
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Câu 15: Mỗi mặt của hình bát diện đều là hình nào trong các hình sau?
A. Tam giác đều.
B. Hình vuông.
C. Bát giác đều. D. Ngũ giác đều. Lời giải Chọn A
Câu 16: Thể tích của khối hộp chữ nhật có ba kích thước 2 , 3 và 4 là A. 24 . B. 8 . C. 9 . D. 20 . Lời giải Chọn A
Thể tích khối hộp chữ nhật là V = 2.3.4 = 24 .
Câu 17: Cho khối nón có chiều cao h = 9a và bán kính đáy r = 2a . Thể tích của khối nón đã cho là A. 3 V = 12 a . B. 3 V = 6 a . C. 3 V = 24 a . D. 3 V = 36 a . Lời giải Chọn A 1 1
Thể tích của khối nón đã cho là 2 2 3
V =  r h =  (2a) (9a) = 12 a . 3 3
Câu 18: Cho khối trụ có chiều cao h = 4a và bán kính đường tròn đáy r = 2a . Thể tích của khối trụ đã cho bằng 3 16 a A. 3 8 a . B. 3 16 a . C. 3 6 a . D. . 3 Lời giải Page 11
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 Chọn B
Ta có: Diện tích đường tròn đáy: S = r = ( a)2 2 2 . . 2 =4a .
Vậy thể tích của khối trụ đã cho là: 2 3
V = S.h = 4 a .4a =16 a .
Câu 19: Cho hình nón có bán kính đường tròn đáy r = 3a và đường sinh l = 2r . Diện tích xung quanh của hình nón bằng A. 2 6 a . B. 2 9 a . C. 2 36 a . D. 2 18 a . Lời giải Chọn D
Ta có l = 2r = 6a .
Diện tích xung quanh của hình nón ( N ) là: S = rl = .3 . a 6a 2 = 18 a .
Câu 20: Thể tích của khối cầu có bán kính r = 2 là 32 33 A. V = . B. V = . C. V = 16 . D. V = 32 . 3 2 Lời giải Chọn A 4 4 32 Ta có 3 3 V =  r = .2 = . 3 3 3 THÔNG HIỂU 2x −1
Câu 21: Cho hàm số y =
. Mệnh đề nào sau đây đúng? x +1
A. Hàm số đồng biến trên .
B. Hàm số nghịch biến trên khoảng ( 1 − ;+ ).
C. Hàm số nghịch biến trên các khoảng (− ;  − ) 1 và ( 1 − ;+ ).
D. Hàm số đồng biến trên khoảng (− ;  − ) 1 . Lời giải Chọn D Tập xác định D = \{ 1 − }. Page 12
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 3 y ' =  0 x   D 2 (x + . 1)
Vậy hàm số đồng biến trên khoảng (− ;  1 − ).
Câu 22: Hàm số nào sau đây có ba điểm cực trị? 2x − 4 A. y =
y = −x − x + . x + . B. 4 2 4 2020 1 C. 3 2
y = x − 3x + 5 . D. 4 2
y = 3x − x + 2019 . Lời giải Chọn D
Hàm số có ba cực trị nên ta loại đáp án A và C. Xét đáp án B 3
y ' = −4x − 8x 3 y ' = 0  4
− x − 8x = 0  x = 0
Đạo hàm có một nghiệm đơn nên đổi dấu một lần qua nghiệm x = 0 nên hàm số có 1 cực trị. Loại đáp án B.
Câu 23: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3
y = x − 3x + 4 trên đoạn
0;2. Giá trị của biểu thức 2 2 M + m bằng A. 52. B. 20. C. 8. D. 40. Lời giải Chọn D x = 1(0;2) 2
y = 3x − 3; y = 0   . x = −1  (0;2)
Ta có y (0) = 4; y( ) 1 = 2; y (2) = 6 Do đó 2 2
M = 6; m = 2  M + m = 40 . Câu 24: Cho hàm số ( ) 4 2
f x = ax + bx + c có đồ thị như sau: Page 13
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Khẳng định nào sau đây đúng?
A. a  0, b  0, c  0.
B. a  0, b  0, c  0. C. a  0, b  0, c  0. D. a  0, b  0, c  0. Lời giải Chọn A
Quan sát đồ thị ta thấy lim f (x) = −  a  0 . x→+
Giao điểm của đồ thị với Oy là (0;c) nằm phía trên trục hoành  c  0 .  = f ( x) x 0 3
= 4ax + 2bx = 2x( 2
2ax + b), f ( x) = 0   . 2 2ax + b = 0  (*)
Hàm số có 3 điểm cực trị nên phương trình ( )
* có 2 nghiệm phân biệt khác 0  2
− ab  0  b  0 .
Vậy a  0,b  0, c  0 . x + 2
Câu 25: Số đường tiệm cận ngang của đồ thị hàm số y = là 2 4x +1 A. 2 . B. 1. C. 4 . D. 0 . Lời giải Chọn A 2 1+ x + 2 x + 2 1 Ta có: lim = lim = lim x = . x→+ 2 4x +1 x→+ 1 x→+ 1 2 x 4 + 4 + 2 x 2 x 2 1+ x + 2 x + 2 1 Và: lim = lim = lim x = − . x→− 2 4x +1 x→− 1 x→− − 1 2 x 4 + − 4 + 2 x 2 x x + 2
Vậy có hai đường tiệm cận ngang của đồ thị hàm số y = . 2 4x +1 
Câu 26: Tập xác định của hàm số y = ( 2
x − 9x +18) là A. (− ;  ) 3 (6;+) . B. \ 3;  6 . C. (3;6) . D. 3;6 . Lời giải Chọn A Hàm số xác định  2
x − 9x +18  0  x  3 x  6 .
Nên tập xác định của hàm số là D = (− ;  )
3 (6;+) . Chọn đáp án A.
Câu 27: Đạo hàm của hàm số f ( x) 4x 2019 e + = là Page 14
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 x e + A. f ( x) 4 2019 ' = . B. f ( x) 4 ' = e . C. ( ) 4 2019 ' 4 x f x e + = . D. ( ) 4 2019 ' x f x e + = . 4 Lời giải Chọn C + + Ta có: f ( x) 4x 2019 = e ( x+ ) 4x 2019 ' . 4 2019 ' = 4.e . Chọn đáp án C.
Câu 28: Hãy tìm tập xác định D của hàm số y = ( 2
ln x − 2x − 3) . A. D = ( 1 − ; ) 3 .
B. D = (−;− ) 1 (3;+ ) .
C. D = (−;−  1 3;+ ) . D. D =  1 − ;  3 . Lời giải Chọn B Điều kiện: 2
x − 2x − 3  0  ( x + ) 1 ( x − ) 3  0  x  1 − hoặc x  3.
Câu 29: Hàm số y = log x và y = log x có đồ thị như hình vẽ dưới đây. a b
Đường thẳng y = 3 cắt đồ thị tại hai điểm có hoành độ là x , x . Biết rằng x = 2x , giá trị của 1 2 2 1 a bằng b 1 A. . B. 3 . C. 2 . D. 3 2 . 3 Lời giải Chọn D Ta có 3
3 = log x x = b b 1 1 3
3 = log x x = a a 2 2 a Mà 3 3 3
x = 2x  a = 2b  = 2 . 2 1 b
Câu 30: Gọi x và x là hai nghiệm của phương trình 25x 7.5x 10
0. Giá trị biểu thức x x bằng 1 2 1 2 A. log 7 . B. log 20 . C. log 10 . D. log 70 . 5 5 5 5 Page 15
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 Lời giải Chọn C Đặt 5x t t
0 . Phương trình đã cho trở thành t 5 5x 5 x 1 2 t 7t 10 0 . t 2 5x 2 x log 2 5 Khi đó x x 1 log 2 log 5 log 2 log 10. 1 2 5 5 5 5 + +
Câu 31: Phương trình 2 x 2 x 4 2
= 3m − 7 có nghiệm khi  23   7  7  A. m  ; +    . B. m  ; +    . C. m  ; +    .
D. m5;+ ) .  3   3   3  Lời giải Chọn D 2 + + Ta có: 2
x + 2x + 4 = ( x + )2 1 + 3  3 , x
 . Suy ra x 2x 4 3 2  2 = 8 , x  .
Phương trình 2x+2x+4 2
= 3m − 7 có nghiệm khi 3m−7  8  m  5.
Vậy, phương trình có nghiệm khi m5;+ ) .
Câu 32: Leonhard Euler là nhà toán học rất nỗi tiếng người Thụy Sĩ đã khám phá ra công thức rất thú vị
và có ứng dụng nhiều trong khoa họ
C. Đó là trong các khối đa diện bất kì thì V − E + F =
“hằng số”, hằng số này được gọi là “đặc trưng Euler” (với V là số đỉnh, E là số cạnh và F là
số mặt của đa diện).
Em hãy tính “đặc trưng Euler” của khối lập phương. A. 2. B. 3. C. 1. D. 4. Lời giải Chọn A
 Bảng công thức đa diện Euler. Page 16
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
 Đặc trưng Euler  được định nghĩa cổ điển cho các khối đa diện lồi,
theo công thức:  = V − E + F = 2 .
Câu 33: Cho hình chóp S.ABCD có SA ⊥ ( ABCD), ABCD là hình chữ nhật, AB = 2BC = 2a , SC = 3a
. Thể tích khối chóp S.ABCD bằng 3 4a 3 3 a 2a A. 3 a . B. . C. . D. . 3 3 3 Lời giải Chọn B Ta có: 2 2 AC =
AB + BC = a 5 ; 2 2
SA = SC − AC = 2a . 1
Thể tích khối chóp S.ABCD là V =  S . A A . B BC S . ABCD 3 3 1 4a Vậy: V =  2 .2 a . a a = . S . ABCD 3 3 Page 17
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Câu 34: Cho hình chữ nhật ABCD có AB = 2a 3 , ADB = 60 . Gọi M, N lần lượt là trung điểm của AD,
BC. Khối trụ tròn xoay tạo thành khi quay hình chữ nhật ABCD (kể cả điểm trong) xung quanh
cạnh MN có thể tích bằng bao nhiêu? 3 2 a 3 3 8 a 3 A. 3 V = 8 a 3 . B. V = . C. 3 V = 2 a 3 . D. V = . 3 3 Lời giải Chọn C AD AB 2a 3 Ta có r = = = = a . 2 2 tan 60 2 3 Thể tích khối trụ là: 2 2 3
V = Bh =  r h =  a 2a 3 = 2 a 3 . Câu 35: Cho ABC
vuông tại A có AB = 4a , AC = 3a . Quay ABC
xung quanh cạnh AB , đường gấp
khúc ACB tạo nên một hình nón tròn xoay. Diện tích xung quanh của hình nón đó là A. 2 S = 24a . B. 2 S =12a . C. 2 S = 30a . D. 2 S =15a . xq xq xq xq Lời giải Chọn D Trong ABC  : 2 2 BC =
AB + AC = 5a .
Diện tích xung quanh của hình nón: 2
S =  Rl = .A . C BC = .3 .
a 5a =15 a . xq II. PHẦN TỰ LUẬN Page 18
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 Câu 36: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
2 log x + log x − 3 = m ( 2
log x − 3 có nghiệm x  64; + ? 0  ) 2 1 4 ) 2 Lời giải 2
2 log x + log x − 3 = m ( 2 log x − 3 . ( ) 1 2 1 4 ) 2
Giả sử x là nghiệm của phương trình ( ) 1  log x  6 . 2
Đặt t = log x,t  6. 2 ( ) t − t −
1  2 t − t − 3 = m (t − 3)  4t − 4t −12 = m (t − 6t + 9) 2 4 4 12 2 2 2  m = 2 2 t − 6t + . ( ) 9 y = m ( 
2) là phương trình cho hoành độ giao điểm của 2 đồ thị hàm số 2  4t − 4t −12 y =  2  t − 6t + 9 2 4t − 4t −12 Xét y = t  6; + . 2 t − 6t + ,  ) 9 t = 3 2
−20t + 48t + 36 y ' =  ( , cho y ' = 0  3  . t − 6t + 9)2 2 t = −  5 Bảng biến thiên:
Để phương trình có nghiệm thì 4  m 12 ; m  m   5;6;7;8;9;10;11;1  2 .
Vậy có 8 giá trị nguyên thỏa điều kiện bài toán.
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác đều cạnh
bằng 4a và nằm trong mặt phẳng vuông góc với mặt phẳng ( ABCD) . Góc giữa mặt phẳng
(SBC) và mặt phẳng (ABCD) là 30. Thể tích của khối chóp S.ABCD là A. 3 24 3a . B. 3 16 3a . C. 3 4 3a . D. 3 48 3a . Lời giải Chọn B Page 19
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
Gọi H , K lần lượt là trung điểm của AD và BC . Khi đó AH ⊥ ( ABCD) , suy ra BC ⊥ (SKH )
, nên SKH = (S ,
B ( ABC)) = 30. . AD 3 Có SH =
= 2 3a HK = SH.cot30 = 6a . 2 1 Vậy 3 V = SH AD HK = S. . . . 16 3 ABCD a . 3
Câu 38: Cho hàm số y = f ( x) có đạo hàm liên tục trên
và hàm số y = f ( x) có đồ thị như sau: 2     Đặ m 1 m
t g ( x) = f x − − x − −1 + m +1    
với m là tham số. Gọi S là tập hợp tất cả các giá  3  2  3 
trị nguyên dương của m để hàm số y = g ( x) đồng biến trên khoảng (7;8). Tìm tập hợp S . Lời giải Page 20
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12 ( )  m   m
g x = f x − − x − −1      3   3   mm x − = 1 − x = −1   3 3    m   m m m  
Cho g( x) = 0  f ' x − = x − −1      x − =1  x = +1  3   3   3  3   m mx − = 3 x = + 3  3  3 Bảng xét dấu: m +3 7  3  mm 12
Để hàm số y = g (x) đồng biến trên khoảng (7;8) thì −1  7     . 3 21  m  24 m  +1 8  3 Vậy S = (− ;  1  2 21;2  4 .
Câu 39: Cho x và y là các số thực dương thỏa mãn điều kiện 3
x + xy ( x + y) 3 2
= 2y + 2xy(x + 2y) . 2 2  x   4y
Tìm tất cả các giá trị của tham số m để phương trình 2 log   − . m log   + 2m − 4 = 0 3 3  2y   x
có nghiệm x thuộc đoạn 1;  3 . Lời giải Ta có: 3
x + xy ( x + y) 3
= y + xy(x + y) 3 2 3 2 2 2 2
x −3xy − 2y = 0  (x + y)( 2 2
x − xy − 2 y ) = 0  ( x + y)( x − 2y) = 0  x = 2y . 2 2  x   4y
Với x = 2 y phương trình 2 log   − . m log 
 + 2m − 4 = 0 . (*) trở thành: 3 3  2y   x  2
log x − mlog x + 2m − 4 = 0 .(1) 3 3 Đặt t = log ,
x t  0;1 , phương trình (1) trở thành: 2
t − mt + 2m − 4 = 0 3  
m = t + 2.(2)
Yêu cầu bài toán  phương trình (2) có nghiệm t 0;  1  2  m  3. Page 21
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 12
---------- HẾT ---------- Page 22
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 11
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1: Cho hàm số y
f x xác định và có đạo hàm trên khoảng K. Khẳng định nào sau đây là sai?
A. Nếu hàm số y
f x đồng biến trên khoảng K thì f ' x 0, x K.
B. Nếu f ' x 0, x
K thì hàm số f x đồng biến trên khoảng K.
C. Nếu f ' x 0, x
K thì hàm số f x đồng biến trên khoảng K
D. Nếu f ' x 0, x K và f ' x
0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên khoảng K. Câu 2:
Cho hàm số y = f (x) có đồ thị như hình vẽ:
Đồ thị hàm số y = f (x) có mấy điểm cực trị? A. 2. B. 1. C. 0. D. 3. Câu 3:
Giả sử hàm số f xác định trên tập hợp D . Nếu tồn tại một điểm x D sao cho 0
f (x)  f (x ), x
  D . Khẳng định nào sau đây là khẳng định đúng? 0
A. Số M = f (x ) được gọi là giá trị lớn nhất của hàm số f trên D . 0
B. Số m = f (x ) được gọi là giá trị nhỏ nhất của hàm số f trên D . 0
C. Số M = f (x ) được gọi là giá trị nhỏ nhất của hàm số f trên D tại x . 0 0
D. Số M = f (x ) được gọi là giá trị lớn nhất của hàm số f trên tập xác định. 0 Câu 4:
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? y x A. 3 2
y = x − 3x + 2 . B. 4 2
y = x − 3x + 2 . C. 4 2
y = −x + 2x + 2 . D. 3 2
y = −x + 3x + 2 . Câu 5:
Cho đường cong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? 2x + 3 2x −1 2x − 2 2x +1 A. y = . B. y = . C. y = . D. y = . x +1 x +1 x −1 x −1 Page 1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x − Câu 6:
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số 2 1 y = . x +1 1 1 A. x = ; y = 1 − .
B. x = 1 ; y = 2 − . C. x = 1 − ; y = 2 . D. x = 1 − ; y = . 2 2 Câu 7:
Cho 0  a  1 và b  0;b  1. Mệnh đề nào sau đây sai? 1 1 A. log b = .
B. log a = 0. C. loga b a = . b D. log = a b log . b a log a a a a a b Câu 8:
Cho a là số thực dương khác1. Đẳng thức nào sau đây là đúng với mọi số thực dương x, y ? x x A. log
= log x + log y . B. log
= log x − y . a a ( ) a a a y y x log x x C. log a = . D. log
= log x − log y . a y log y a a a y a Câu 9:
Tập xác định D của hàm số y = log (x − 2017). 2016 A. D =  ; 0 +).
B. D = 2017;+). C. D = ( ; 0 +).
D. D = (2017;+). Câu 10: Hàm số 2 2x x y − = có đạo hàm là 2 − A. ( ) 2 2 1 2x x x x − − − B. ( ) 2 2 1 .2x x x − − . C. 2x . x ln 2 . D. ( ) 2 2 1 .2x . x x − − ln 2 .
Câu 11: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y 2 1 O 2 x x −x
A. y = ( 2)
B. y = x C. 2x y = D. y = ( 2)
Câu 12: Nghiệm của phương trình x 1 3 − = 9 là A. x = 2 − B. x = 3
C. x = 2 D. x = 3 − x 1 +  1 
Câu 13: Tập nghiệm của phương trình 2 =125 x   là  25   1  1  A. − . B. − . C.   4 . D.   3 .  8  4 
Câu 14: Tìm tập nghiệm S của bất phương trình log x − 2  0 0,5 ( ) A. S = (− ;  ) 3 . B. S = (2; ) 3 . C. S = (− ;  − ) 1 (3;+).
D. S = (3;+). Page 2
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 15: Mỗi hình sau đấy gồm hữu hạn các đa giác.Hình nào là hình đa diện? A. B. C. D.
Câu 16: Khẳng định nào sau đây là sai? 1
A. Thể tích của khối chóp có diện tích đáy B và chiều cao h là V = Bh . 3
B. Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là V = Bh .
C. Thể tích của một khối hộp chữ nhật bằng tích ba kính thước của nó.
D. Thể tích của khối chóp có diện tích đáy B và chiều cao h là V = 3Bh .
Câu 17: Gọi l, h, r lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Đẳng thức nào
sau đây luôn đúng. 1 1 1 A. 2 2 2
l = h + r B. = + C. 2 2 2
r = h + l D. 2 l = hr 2 2 2 l h r
Câu 18: Cho hình nón ( N ) có chiều cao h, độ dài đường sinh l, bán kính đáy r. Ký hiệu S là diện tích tp
toàn phần của (N ). Công thức nào sau đây là đúng?
A. S =  rl .
B. S =  rl + 2 r . C. 2
S =  rl +  r . D. 2
S = 2 rl +  r . tp tp tp tp a
Câu 19: Thể tích V của khối trụ có bán kính đáy bằng
và chiều cao bằng 2a là: 2 3 a  3 a  3 2 a  3 aA. V = . B. V = . C. V = . D. V = . 2 3 3 6
Câu 20: Bán kính r của khối cầu có thể tích V =  ( 3 64 cm ) là
A. r = 3c . m B. r = 27cm C. 3 r = 48cm D. 3 r = 9 . cm
Câu 21: Cho hàm số y = f (x) xác định trên
và có bảng biến thiên như hình vẽ dưới đây. Hàm số
y = f (x) đồng biến trên khoảng nào sau đây? A. (0;4). B. ( 2 − ; ) 1 . C. (1;4). D. (4; +). 2
Câu 22: Cho hàm số y = f ( x) có đạo hàm là f ( x) 2 = x (2x − ) 1 ( x + )
1 . Số điểm cực trị của hàm số đã cho là A. 0 . B. 1. C. 2 . D. 3 . Page 3
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 23: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3
y = x − 3x trên 1;  2 bằng: 14 A. 0 . B. 2 . C. . D. 7 − . 27 Câu 24: Cho hàm số 4 2
y = ax + bx + c (a  0) có đồ thị như hình bên. Xác định dấu của a ,b,c .
A. a  0,b  0,c  0 .
B. a  0,b  0,c  0 . C. a  0,b  0,c  0 . D. a  0,b  0,c  0 .
Câu 25: Số đường tiệm cận của đồ thị hàm số (hình vẽ sau) là: y 2 x -2 -1 1 A. 0. B. 1. C. 2. D. 3. −
Câu 26: Tập xác định của hàm số 2 2
y = (3x −1) là:  1   1  A. D = \  . B. D =  .  3   3   1   1   1 1  C. D = − ;  −  ;+ .     D. − ; .    3   3   3 3 
Câu 27: Tập xác định của hàm số y = log (x +1) là: 0,5 A. D = ( 1 − ;+). B. D = \{ −1}. C. D = (0;+ )  . D. (− ;  1 − ).
Câu 28: Cho hàm số y = log x và y = log x có đồ thị như a b y sau: y=logbx
Mệnh đề nào dưới đây là sai? A. a 1  . b
B. 0  b 1 . a
C. 0  a 1 . b D. 0  a  . b O 1 x
Câu 29: Hàm số nào trong các hàm số cho dưới đây nghịch y=logax
biến trên tập xác định của nó? Page 4
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x    x  3  A. y = ln . x B. y = log . x = =  C. y .   D. y .    3    
Câu 30: Trong các phương trình cho dưới đây, phương trình nào có tập ngiệm là S =   2 ? A. ( 2
log x − x) = log . x B. log ( 2
x − x = 1. C. 4x 5.2x −
+ 4 = 0. D. 5.3x + 4 = 0. 2 )
Câu 31: Với phương trình x 3 − x 3 4 5.2 − + + 4 = 0, nếu đặt 3 2 x t − =
thì điều kiện của t là
A. t  0.
B. t 1.
C. t  3.
D. t  .
Câu 32: Cho hình chóp tam giác đều S.ABC có O là trọng tâm tam giác .
ABC Gọi I là trung điểm của
BC và E là điểm thuộc đoạn thẳng AI sao cho AI = 3A .
E Đường cao của hình chóp S.ABC là A. . SO B. SI. C. . SA D. SE.
Câu 33: Cho khối lăng trụ tam giác đều AB . C A BC  có AB = , a A C
 = 2a (hình vẽ bên). A' C' B' 2a A C a B
Thể tích V của khối lăng trụ AB . C A BC   là 3 a 3 a 3 3 3a 3 a 15 A. V = . B. V = . C. V = . D. V = . 4 4 4 4
Câu 34: Cho một hình nón có bán kính đáy bằng a và góc ở đỉnh bằng 60 . Tính diện tích xung quanh của hình nón đó. 2 2 3 a 2 4 3 a A. 2
S = 4 a . B. S = . C. S = . D. 2 S = 2 a . xq xq 3 xq 3 xq
Câu 35: Cho hình trụ có chiều cao bằng 5 3 . Cắt hình trụ đã cho bởi mặt phẳng song song với trục và
cách trục một khoảng bằng 1, thiết diện thu được có diện tích bằng 30 . Diện tích xung quanh
của hình trụ đã cho bằng A. 10 3 . B. 5 39 . C. 20 3 . D. 10 39 .
II. PHẦN TỰ LUẬN (4 câu – 3 điểm)
Câu 36: Giải phương trình sau : 1 (x + ) 1 log 3 + log ( x − )8 1 = log 4x 9 3 ( ) 3 2 4
Câu 37: Cho hình lăng trụ AB . C A BC
  có đáy là tam giác đều cạnh bằng a ,hình chiếu vuông góc của
A lên mặt phẳng ( ABC) trùng với trọng tâm G của tam giác ABC . Biết khoảng cách giữa BC a 3 và AA bằng
. Tính thể tích khối chóp B .  ABC . 4
Câu 38: Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ sau. Tìm m để hàm số y = f ( x + m )
đồng biến trên khoảng (4;+) . Page 5
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 39: Có bao nhiêu số nguyên y sao cho với mỗi y không có quá 50 số nguyên x thoả mãn bất phương trình sau: y−3 2 x  log ( 2 x + y ? 3 ) -----HẾT----- Page 6
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM Câu 1: Cho hàm số y
f x xác định và có đạo hàm trên khoảng K. Khẳng định nào sau đây là sai?
A. Nếu hàm số y
f x đồng biến trên khoảng K thì f ' x 0, x K.
B. Nếu f ' x 0, x
K thì hàm số f x đồng biến trên khoảng K.
C. Nếu f ' x 0, x
K thì hàm số f x đồng biến trên khoảng K
D. Nếu f ' x 0, x K và f ' x
0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên khoảng K. Lời giải Chọn C Nếu f ' x 0, x
K thì hàm số f x đồng biến trên khoảng K (Dấu bằng xảy ra tại hữu hạn điểm). Câu 2:
Cho hàm số y = f (x) có đồ thị như hình vẽ:
Đồ thị hàm số y = f (x) có mấy điểm cực trị? A. 2. B. 1. C. 0. D. 3. Lời giải Chọn A Câu 3:
Giả sử hàm số f xác định trên tập hợp D . Nếu tồn tại một điểm x D sao cho 0
f (x)  f (x ), x
  D . Khẳng định nào sau đây là khẳng định đúng? 0
A. Số M = f (x ) được gọi là giá trị lớn nhất của hàm số f trên D . 0
B. Số m = f (x ) được gọi là giá trị nhỏ nhất của hàm số f trên D . 0
C. Số M = f (x ) được gọi là giá trị nhỏ nhất của hàm số f trên D tại x . 0 0
D. Số M = f (x ) được gọi là giá trị lớn nhất của hàm số f trên tập xác định. 0 Lời giải Chọn A Câu 4:
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? Page 7
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 y x A. 3 2
y = x − 3x + 2 . B. 4 2
y = x − 3x + 2 . C. 4 2
y = −x + 2x + 2 . D. 3 2
y = −x + 3x + 2 . Lời giải Chọn A
Dựa vào đồ thị ta thấy đây là đồ thị của hàm số bậc ba 3 2
y = ax + bx + cx + d,(a  0) với a  0 . Câu 5:
Cho đường cong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? 2x + 3 2x −1 2x − 2 2x +1 A. y = . B. y = . C. y = . D. y = . x +1 x +1 x −1 x −1 Lời giải Chọn B +
Từ đồ thị ta thấy đây là đồ thị hàm số ax b y =
có tiện cận đứng là x = 1
− (loại đáp án C và D) cx + d
và là hàm số đồng biến (loại đáp án A). x − Câu 6:
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số 2 1 y = . x +1 1 1 A. x = ; y = 1 − .
B. x = 1 ; y = 2 − . C. x = 1 − ; y = 2 . D. x = 1 − ; y = . 2 2 Lời giải Chọn C 1 2 − 2x −1 Vì lim = lim
x = 2 nên đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số. x→ x +1 x→ 1 1+ x 2x −1 2x −1 Vì lim = − , lim
= + nên đường thẳng x =1 là tiệm cận đứng của đồ thị hàm + − x 1 →− x +1 x 1 →− x +1 số. Page 8
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Câu 7:
Cho 0  a  1 và b  0;b  1. Mệnh đề nào sau đây sai? 1 1 A. log b = .
B. log a = 0. C. loga b a = . b D. log = a b log . b a log a a a a a b Lời giải Chọn B log a = 1. a Câu 8:
Cho a là số thực dương khác1. Đẳng thức nào sau đây là đúng với mọi số thực dương x, y ? x x A. log
= log x + log y . B. log
= log x − y . a a ( ) a a a y y x log x x C. log a = . D. log
= log x − log y . a y log y a a a y a Lời giải Chọn D x
Theo tính chất lôgarit của một thương, ta có log
= log x − log y . a a a y Câu 9:
Tập xác định D của hàm số y = log (x − 2017). 2016 A. D =  ; 0 +).
B. D = 2017;+). C. D = ( ; 0 +).
D. D = (2017;+). Lời giải Chọn D
Điều kiện là: x − 2017  0  x  2017
Hay TXĐ: D = (2017;+). 2 Câu 10: Hàm số 2x x y − = có đạo hàm là 2 − A. ( ) 2 2 1 2x x x x − − − B. ( ) 2 2 1 .2x x x − − . C. 2x . x ln 2 . D. ( ) 2 2 1 .2x . x x − − ln 2 . Lời giải Chọn D
Áp dụng quy tắc đạo hàm hàm số mũ (  u ) = . u a
ua .ln a . 2 2 
Ta có:  = ( 2 − ) .2x − .xln2 = (2 − ) 1 .2x − . x y x x x ln 2 .
Câu 11: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y 2 1 O 2 x Page 9
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x −x
A. y = ( 2)
B. y = x C. 2x y = D. y = ( 2) Lời giải Chọn A x
Đồ thị hàm số là đường cong đi qua hai điểm (0; )
1 ;(2;2) . Chỉ có hàm số y = ( 2) thỏa mãn.
Câu 12: Nghiệm của phương trình x 1 3 − = 9 là A. x = 2 − B. x = 3
C. x = 2 D. x = 3 − Lời giải Chọn B x 1
3 − = 9  x −1 = 2  x = 3 x 1 +  1 
Câu 13: Tập nghiệm của phương trình 2 =125 x   là  25   1  1  A. − . B. − . C.   4 . D.   3 .  8  4  Lời giải Chọn B x 1 +   Phương trình 1 2x 2 − x−2 6x 1 =125  5 = 5  2
− x − 2 = 6x x = − .    25  4
Câu 14: Tìm tập nghiệm S của bất phương trình log x − 2  0 0,5 ( ) A. S = (− ;  ) 3 . B. S = (2; ) 3 . C. S = (− ;  − ) 1 (3;+).
D. S = (3;+). Lời giải Chọn D x − 2  0 x  2 Ta có: log x − 2  0      x  3 0,5 ( ) 0 x − 2  0,5 x  3
Câu 15: Mỗi hình sau đấy gồm hữu hạn các đa giác.Hình nào là hình đa diện? A. B. C. D. Lời giải Chọn A
Quan sát bốn hình trên ta thấy chỉ có một hình A là hình đa diện.
Hình B,C, D không phải là hình đa diện, vì vi phạm điều b) Mỗi cạnh của đa giác nào cũng là
cạnh chung của đúng hai đa giác.
Câu 16: Khẳng định nào sau đây là sai? 1
A. Thể tích của khối chóp có diện tích đáy B và chiều cao h là V = Bh . 3 Page 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
B. Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là V = Bh .
C. Thể tích của một khối hộp chữ nhật bằng tích ba kính thước của nó.
D. Thể tích của khối chóp có diện tích đáy B và chiều cao h là V = 3Bh . Lời giải Chọn D
Theo công thức tính thể tích khối chóp, khối lăng trụ và khối hộp chữ nhật ta thấy các khẳng định
đúng là A, B,
C.
Câu 17: Gọi l, h, r lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Đẳng thức nào
sau đây luôn đúng. 1 1 1 A. 2 2 2
l = h + r B. = + C. 2 2 2
r = h + l D. 2 l = hr 2 2 2 l h r Lời giải Chọn A Theo giả thiết, ta có 2 2 2
l = r + R
Câu 18: Cho hình nón ( N ) có chiều cao h, độ dài đường sinh l, bán kính đáy r. Ký hiệu S là diện tích tp
toàn phần của ( N ) . Công thức nào sau đây là đúng?
A. S =  rl .
B. S =  rl + 2 r . C. 2
S =  rl +  r . D. 2
S = 2 rl +  r . tp tp tp tp Lời giải Chọn C a
Câu 19: Thể tích V của khối trụ có bán kính đáy bằng
và chiều cao bằng 2a là: 2 3 a  3 a  3 2 a  3 aA. V = . B. V = . C. V = . D. V = . 2 3 3 6 Lời giải Chọn B 2 3  a a  Ta có 2 V = . B h = .  r .h =  .2a =    2  2
Câu 20: Bán kính r của khối cầu có thể tích V =  ( 3 64 cm ) là
A. r = 3c . m B. r = 27cm C. 3 r = 48cm D. 3 r = 9 . cm Lời giải Chọn C 4 + 3 3 3 V =
.r = 64  r = 48  r = 48cm . 3
Câu 21: Cho hàm số y = f (x) xác định trên
và có bảng biến thiên như hình vẽ dưới đây. Hàm số
y = f (x) đồ
ng biến trên khoảng nào sau đây? Page 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 A. (0;4). B. ( 2 − ; ) 1 . C. (1;4). D. (4; +). Lời giải Chọn C
Dựa vào bảng biến thiên ta chọn đáp án C . 2
Câu 22: Cho hàm số y = f ( x) có đạo hàm là f ( x) 2 = x (2x − ) 1 ( x + )
1 . Số điểm cực trị của hàm số đã cho là A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn B
Ta có bảng biến thiên x – ∞ -1 0 + ∞ y' – 0 + 0 + 0 + + ∞ + ∞ y 1
Dựa vào bảng biến thiên, hàm số đã cho có 1 cực trị.
Câu 23: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3
y = x − 3x trên 1;  2 bằng: 14 A. 0 . B. 2 . C. . D. 7 − . 27 Lời giải Chọn A x = 11;2 2
y ' = 3x − 3 = 0   x = −1  1;2 y ( ) 1 = −2 y (2) = 2 max y = 2 1;2 min y = 2 − 1;2
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3
y = x − 3x trên 1;  2 bằng 0. Câu 24: Cho hàm số 4 2
y = ax + bx + c (a  0) có đồ thị như hình bên. Xác định dấu của a ,b,c .
A. a  0,b  0,c  0 .
B. a  0,b  0,c  0 . C. a  0,b  0,c  0 . D. a  0,b  0,c  0 . Lời giải Chọn B
Khi x dần về + thì đồ thị đi lên nên a  0 .
Hàm số có 3 điểm cực trị nên .
a b  0 . Suy ra b  0 . Page 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Đồ thị cắt trục tung tại điểm có tung độ âm nên c  0 .
Câu 25: Số đường tiệm cận của đồ thị hàm số (hình vẽ sau) là: y 2 x -2 -1 1 A. 0. B. 1. C. 2. D. 3. Lời giải Chọn C
Từ hình vẽ, ta thấy đồ thị hàm số có một đường tiệm cận đứng và một đường tiệm cận ngang. −
Câu 26: Tập xác định của hàm số 2 2
y = (3x −1) là:  1   1  A. D = \  . B. D =  .  3   3   1   1   1 1  C. D = − ;  −  ;+ .     D. − ; .    3   3   3 3  Lời giải Chọn A − 1 Vì 2 − −  nên hàm số 2 2
y = (3x −1) xác định khi 2
3x −1  0  x   . 3
Câu 27: Tập xác định của hàm số y = log (x +1) là: 0,5 A. D = ( 1 − ;+). B. D = \{ −1}. C. D = (0;+ )  . D. (− ;  1 − ). Lời giải Chọn A
Hàm số log (x +1) xác định khi x +1 0  x  1 − . 0,5
Câu 28: Cho hàm số y = log x và y = log x có đồ thị như sau: a b y y=logbx O 1 x y=logax Page 13
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Mệnh đề nào dưới đây là sai? A. a 1  . b
B. 0  b 1 . a
C. 0  a 1 . b D. 0  a  . b Lời giải Chọn B
Dựa vào đồ thị ta thấy 0  a  1 và 1  .
b Do đó các mệnh đề ở các đáp án A, C, D là đúng và
mệnh đề ở đáp án B là sai.
Câu 29: Hàm số nào trong các hàm số cho dưới đây nghịch biến trên tập xác định của nó? x    x  3  A. y = ln . x B. y = log . x = =  C. y .   D. y .    3     Lời giải Chọn D x   
Các hàm số y = ln x, y = log x, =  y
  ở các đáp án A, B, C là hàm số lôgarit, hàm số mũ có  3  x   cơ số 3
lớn hơn 1 nên đồng biến trên tập xác định của nó và hàm số y =    ở đáp án D là hàm   3 3 số mũ có cơ số    thỏa mãn 0 1 
nên nghịch biến trên tập xác định của nó.
Câu 30: Trong các phương trình cho dưới đây, phương trình nào có tập ngiệm là S =   2 ? A. ( 2
log x − x) = log . x B. log ( 2
x − x = 1. C. 4x 5.2x −
+ 4 = 0. D. 5.3x + 4 = 0. 2 ) Lời giải Chọn A x  log ( 1 2
x − x) = log x  
x = 2. Tập nghiệm phương trình là S =   2 . 2 x − 2x = 0 x = − log ( 1 2 x − x) 2
=1  x − x − 2 = 0 
. Tập nghiệm phương trình là S =  1 − ;  2 . 2  x = 2 2x =1 x = 0
4x − 5.2x + 4 = 0    . 
Tập nghiệm phương trình là S = 0;  2 . 2x = 4 x = 2 x x 4 5.3 + 4 = 0  3 = −
: phương trình vô nghiệm. 5
Câu 31: Với phương trình x 3 − x 3 4 5.2 − + + 4 = 0, nếu đặt 3 2 x t − =
thì điều kiện của t là
A. t  0.
B. t 1.
C. t  3.
D. t  . Lời giải Chọn B Với x  3 thì 3 2 x t − =
luôn lớn hơn hoặc bằng 1.
Câu 32: Cho hình chóp tam giác đều S.ABC có O là trọng tâm tam giác .
ABC Gọi I là trung điểm của
BC và E là điểm thuộc đoạn thẳng AI sao cho AI = 3A .
E Đường cao của hình chóp S.ABC là A. . SO B. SI. C. . SA D. SE. Lời giải Chọn A Page 14
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Vì S.ABC là hình chóp tam giác đều có O là trọng tâm tam giác ABC nên SO là đường cao của hình chóp. =  =
Câu 33: Cho khối lăng trụ tam giác đều AB . C A BC
 có AB a, A C 2a (hình vẽ bên). A' C' B' 2a A C a B
Thể tích V của khối lăng trụ AB . C A BC   là 3 a 3 a 3 3 3a 3 a 15 A. V = . B. V = . C. V = . D. V = . 4 4 4 4 Lời giải Chọn C Vì AB . C A BC
  là khối lăng trụ tam giác đều nên cạnh bên là đường cao khối chóp và đáy là tam giác đều.
Tam giác AAC ( 0 A = 90 ) nên có: 2 2 2 2 AA = A C
− AC = 4a − a = a 3.
Thể tích V của khối lăng trụ AB . C A BC   là 2 3 a 3 3a V = S .AA = . a 3 = . ABC 4 4
Câu 34: Cho một hình nón có bán kính đáy bằng a và góc ở đỉnh bằng 60 . Tính diện tích xung quanh của hình nón đó. 2 2 3 a 2 4 3 a A. 2
S = 4 a . B. S = . C. S = . D. 2 S = 2 a . xq xq 3 xq 3 xq Lời giải Chọn D S 60 A a O B
Giả sử hình nón có đỉnh là S , O là tâm của đường tròn đáy và AB là một đường kính của đáy.
r = OA = a , ASB = 60  ASO = 30 . Độ dài đường sinh là OA l = SA = = 2a . sin 30
Vậy diện tích xung quanh của hình nón là 2
S =  rl = . .
a 2a = 2 a . xq Page 15
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 35: Cho hình trụ có chiều cao bằng 5 3 . Cắt hình trụ đã cho bởi mặt phẳng song song với trục và
cách trục một khoảng bằng 1, thiết diện thu được có diện tích bằng 30 . Diện tích xung quanh
của hình trụ đã cho bằng A. 10 3 . B. 5 39 . C. 20 3 . D. 10 39 . Lời giải Chọn C Gọi , O
O lần lượt là tâm của hai đáy và ABCD là thiết diện song song với trục với , A B (O) ; C, D ( 
O ) . Gọi H là trung điểm của AB OH = d (OO ,( ABCD)) =1. 30 Vì S = 30  A .
B BC = 30  AB =
= 2 3  HA = HB = 3 . ABCD 5 3 Bán kính của đáy là 2 2
r = OH + HA = 3+1 = 2 .
Diện tích xung quanh của hình trụ bằng S = 2rh = 2.2.5 3 = 20 3 . xq II. PHẦN TỰ LUẬN
Câu 36: Giải phương trình sau : 1 (x + ) 1 log 3 + log ( x − )8 1 = log 4x 9 3 ( ) 3 2 4 Lời giải x 1 Điều kiện:  . x  0 1 1 8 Ta có: log
(x +3)+ log x −1 = log 4x 9 ( ) 3 ( ) 3 2 4
 log x +3 +log x −1 = log 4x 3 ( ) 3 3 ( )
 log  x + 3 . x −1 = log 4x 3 ( )  3 ( )  (x + )
3 . x −1 = 4x ( ) 1 .
+ Nếu 0  x 1 thì phương trình ( ) 1 trở thành x = 3 − + 2 3 (tm) (x +3).(1− x) 2
= 4x  −x − 6x + 3 = 0   . x = 3 − − 2 3  (l)
+ Nếu x 1 thì phương trình ( ) 1 trở thành Page 16
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 x = 3(tm) (x +3).(x − ) 2
1 = 4x x − 2x − 3 = 0   . x = 1 −  (l)
Vậy tập nghiệm của phương trình là: S =  3 − + 2 3;  3 .
Câu 37: Cho hình lăng trụ AB . C A BC
  có đáy là tam giác đều cạnh bằng a ,hình chiếu vuông góc của
A lên mặt phẳng ( ABC) trùng với trọng tâm G của tam giác ABC . Biết khoảng cách giữa BC a 3 và AA bằng
. Tính thể tích khối chóp B .ABC . 4 Lời giải
Gọi M là trung điểm của BC . Vì tam giác ABC đều cạnh a nên ta có 2 a 3 a 3
AM ⊥ BC; AM = ; S = ( đvdt).  2 ABC 4
Mặt khác AG ⊥ ( ABC)  AG ⊥ BC . BC ⊥ AM
Như vậy BC ⊥ AG
BC ⊥ ( AA M  ). AM A G  = Ga Trong ( AA M
 ), kẻ MH ⊥ AA ta có d (BC AA) 3 , = HM = . 4
Xét tam giác vuông AMH có a 3 HM 1 4 sin  = = =   = 30 .  AM a 3 2 2
Xét tam giác vuông AA G  2 2 a 3 a AG = . AG tan  = AM . tan  = . . tan 30 = . 3 3 2 3 2 3 1 1 a a 3 a 3 Vậy V = =  = =  V  .A G. S . . (đvdt). B . ABC A . ABC  3 ABC 3 3 4 36
Câu 38: Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ sau. Tìm m để hàm số y = f ( x + m )
đồng biến trên khoảng (4;+) . Page 17
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải
+ Bảng biến thiên của hàm số y = f ( x )
+ Suy ra bảng biến thiên của hàm số y = f ( x + m )
+ Hàm số y = f ( x + m ) đồng biến trên khoảng (4;+)  m −  4  m  4 − .
Câu 39: Có bao nhiêu số nguyên y sao cho với mỗi y không có quá 50 số nguyên x thoả mãn bất phương trình sau: y−3 2 x  log ( 2 x + y ? 3 ) Lời giải Điều kiện: 2 x + y  0 Xét hàm số: y 3 ( ) = 2 − x f x − log ( 2 x + y với x ( 2 −y ;+) 3 ) y− x 1 Ta có: 3 f (  x) = 3 − .3 ln 3 −  0, x  ( 2 − y ;+ 2 ) (x + y ) ln 3 Bảng biến thiên
Từ đó suy ra bất phương trình có nghiệm x ( 2 −y ; x  o 
Để tập nghiệm của bất phương trình không chứa quá 50 số nguyên thì 2
f (− y + 51)  0 y− ( 2 3 − y +5 ) 1  2  log 51 3 2
 3y + y −153  log log 51 2 ( 3 )  7 − ,35  y  7,02 Page 18
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Vì y  nên y  7 − ; 6 − ;....;6;  7 Page 19
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI
MÔN: TOÁN 12 – ĐỀ SỐ: 12
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Cho hàm số f (x) đồng biến trên tập số thực , mệnh đề nào sau đây là đúng?
A. Với mọi x , x
.mà x x f ( x f x . 1 ) ( 2) 1 2 1 2
B. Với mọi x , x
f x f x . 1 2 ( 1) ( 2)
C. Với mọi x , x
f x f x . 1 2 ( 1) ( 2)
D. Với mọi x , x
.mà x x f ( x f x . 1 ) ( 2) 1 2 1 2 Câu 2:
Cho hàm số y = f ( x) xác định và liên tục trên
, có đồ thị như hình vẽ.
Hàm số y = f ( x) có điểm cực tiểu là
A. x =1 .
B. x = 2 . C. x = 2 − . D. x = 1 − . Câu 3:
Cho hàm số y = f ( x) có bảng biến thiên như sau x -∞ -1 0 +∞ y' 0 +∞ +∞ y -1
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị nhỏ nhất bằng −1.
B. Hàm số có giá trị nhỏ nhất bằng 0.
C. Hàm số không xác định tại x = 1 − .
D. Hàm số luôn có giá trị lớn nhất. Câu 4:
Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào trong các hàm số dưới đây? A. 3 2
y = −x + 2x − x − 3 . B. 3 2
y = x + 2x − 7x − 2 . C. 3 2
y = x − 2x + x − 2 . D. 4 2
y = x − 2x − 3 . Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Câu 5:
Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây: −x + 2 2x − 2 x − 2 2 − x + 2 A. y = . B. y = . C. y = . D. y = . x + 2 x +1 x +1 x +1 x Câu 6:
Đồ thị hàm số y =
có bao nhiêu đường tiệm cận 2 x − 4 A. 2 . B. 1. C. 4 . D. 3 . Câu 7:
Tìm tập xác định D của hàm số y = ( x − )25 1 . A. D = .
B. D = (1;+) . C. D = (− ) ;1 . D. D = \  1 . Câu 8:
Cho a  0 ; a  1 và x ; y là hai số thực dương. Phát biểu nào sau đây là đúng?
A. log ( x + y) = log x + log y . B. log xy = x + y . a ( ) log log a a a a a
C. log ( xy) = log .
x log y . D. log x + y = x y . a ( ) log .log a a a a a Câu 9:
Tập xác định của hàm số y = log (x − 2 là 3 )
A. (−; 2 . B.  + 2; ) .
C. (−; 2) . D. (2; +) . Câu 10: Ham số 2 x y − = có đạo hàm là: −2−x A. − 1 2 x− − . B. 2−x − ln 2 .
C. 2−x ln 2 . D. . ln 2
Câu 11: Trong các hàm số sau, hàm số nào nghịch biến trên khoảng (0;+ ) ? xx 2021     A. y =   B. y =  
C. y = log x
D. y = log x  2020   3  2 3
Câu 12: Tìm nghiệm của phương trình 5x = 8 .
A. x = log 5 .
B. x = log 8 . C. 8 x = 5 . D. 5 x = 8 . 8 5
Câu 13: Nghiệm của phương trình: 2x = 4 là
A. x = 2 .
B. x =1 .
C. x = 3. D. x = 4 .
Câu 14: Nghiệm của bất phương trình: log x  1 là 2
A. x  2 .
B. x  2 .
C. x 1 . D. x  2 . Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 15: Khối đa diện đều loại 4; 
3 có bao nhiêu mặt? A. 5 . B. 6 . C. 4 . D. 3 .
Câu 16: Thể tích của khối chóp có chiều cao bằng h và có diện tích đáy B là 1 1 1 A. Bh B. Bh C. Bh D. Bh 2 6 3
Câu 17: Cho tam giác ABC đều có cạnh bằng a quay xung quanh cạnh AC của nó. Tính thể tích V của
khối tròn xoay tạo thành. 3 9 a 3  a 3 27 a 3 27 a A. V = . B. V = . C. V = . D. V = . 18 4 18 8
Câu 18: Cho tam giác đều ABC cạnh a quay quanh đường cao AH tạo nên hình nón. Diện tích xung
quanh của hình nón đó là 2 3 a 2  a A. . B. . C. 2 a . D. 2 a . 4 2
Câu 19: Diện tích của mặt cầu có bán kính R bằng A. 2 2 R . B. 2  R . C. 2 4 R . D. 2 . R
Câu 20: Thể tích khối trụ có bán kính đáy r, đường sinh l là 1
A. V = 2r . l B. 2
V =  rl . C. 2
V =  rl . D. 2 V =  r l. 3
Câu 21: Cho hàm số y = f ( x) xác định trên
\{ −1} và có bảng dấu của f (x) như hình bên dưới
Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số y = f ( x) đồng biến trên khoảng (1;2).
B. Hàm số y = f ( x) đồng biến trên .
C. Hàm số y = f ( x) đồng biến trên khoảng ( 3 − ;2).
D. Hàm số y = f ( x) đồng biến trên khoảng ( ; − 2).
Câu 22: Điểm cực đại của đồ thị hàm số 3 2
y = x − 6x + 9x có tổng hoành độ và tung độ bằng A. 5 . B. 1. C. 3 . D. 1 − .
Câu 23: Giá trị lớn nhất của hàm số 4 2
y = x − 4x + 9 trên đoạn  2 − ;  3 bằng A. 201 B. 2 C. 9 D. 54 Câu 24: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0 .
C. a  0,b  0, c  0, d  0 .
D. a  0,b  0, c  0, d  0 . Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 25: Đồ thị hàm số dưới đây có TCĐ và TCN là đường thẳng có phương trình
A. x = 2; y = 1.
B. x = 1; y = 2 .
C. x = 0; y = 1 .
D. x = 0; y = 1 . −
Câu 26: Tìm tập xác định của hàm số y = ( x − ) 3 1 2 1 . A. D = . B. D = \ 1;−  1 . C. D = (− ;  )
1  (1;+) .D. D = ( 1 − ; ) 1 .
Câu 27: Tìm tập xác định hàm số y = ( 2
log x − 2x). A. D = . B. D = (− ;  0) (2;+) . C. D = \ 0;  2 . D. (0;2) .
Câu 28: Tìm a để hàm số y = log x (0  a 1, x  0) có đồ thị là hình bên: a 1 1 A. a = .
B. a = 2 . C. a = 2 . D. a = . 2 2 x
Câu 29: Cho hàm số y = ( 2 − )
1 . Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số có đường tiệm cận đứng là trục hoành.
B. Hàm số đồng biến trên khoảng (0;+) .
C. Đồ thi hàm số có đường tiệm cận ngang là trục tung.
D. Hàm số nghịch biến trên khoảng (− ;  +) .
Câu 30: Tập nghiệm của phương trình log x −1 = 2 là: 3 A. {3} . B. {-3;4} . C. {-3;-2} . D. {4;-2} . x x
Câu 31: Gọi x , x là các nghiệm của phương trình (7 + 4 3) − 4(2+ 3) = 1
− . Khi đó giá trị của 1 2 2 2
x + x bằng 1 2 A. 2. B. 0. C. 14. D. 4. Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Câu 32: Số mặt phẳng đối xứng của khối chóp tứ diện đều là A. 7 B. 8. C. 9. D. 6.
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên mặt phẳng
(ABCD) trùng với trung điểm của cạnh AB, đường thẳng SD tạo với mặt phẳng đáy một góc 45 .
o Tính thể tích khối chóp S.ABCD theo a. 3 a 5 3 a 5 3 a 5 3 a 5 A. . B. . C. . D. . 12 3 2 6
Câu 34: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc BAD = 120 . Cạnh bên SA
vuông góc với đáy ( ABCD) và SA = 3a . Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.BCD . 3 5 5 4 A. = a R . B. = a R . C. = a R . D. = a R . 3 3 3 3
Câu 35: Cho hình thang cân ABCD có đáy nhỏ AB =1, đáy lớn CD = 3 , cạnh bên BC = DA = 2 . Cho
hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng 4 5 2 7 A.  . B.  . C.  . D.  . 3 3 3 3 II. PHẦN TỰ LUẬN 1 2
Câu 36: Giải phương trình: 2 log x + log x −1 = log log 3 . 49 7 ( ) 7 ( 3 ) 2
Câu 37: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA vuông góc với mặt đáy. Gọi
M là trung điểm BC . Mặt phẳng ( P) đi qua A và vuông góc với SM cắt SB , SC lần lượt tại
E , F . Biết thể tích khối chóp S.ABC gấp 4 lần thể tích khối chóp S.AEF . Tính thể tích của
khối chóp S.ABC .
Câu 38: Cho hàm số y = f ( x) liên tục trên
và có bảng biến thiên bên dưới.
Tìm các khoảng đồng biến của hàm số y = g ( x) = f ( 2 1+ 2x − x )    x + y
Câu 39: Cho các số thực , x y thỏa mãn 0 , x y 1 và log
+ x +1 y +1 − 2 = 0 . Tìm giá trị 3   ( )( ) 1− xy
nhỏ nhất của P với P = 2x + y .
---------- HẾT ---------- Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Cho hàm số f (x) đồng biến trên tập số thực , mệnh đề nào sau đây là đúng?
A. Với mọi x , x
.mà x x f ( x f x . 1 ) ( 2) 1 2 1 2
B. Với mọi x , x
f x f x . 1 2 ( 1) ( 2)
C. Với mọi x , x
f x f x . 1 2 ( 1) ( 2)
D. Với mọi x , x
.mà x x f ( x f x . 1 ) ( 2) 1 2 1 2 Lời giải Chọn D
Theo định nghĩa về tính đơn điệu của hàm số: Với mọi x , x  mà x x f x f x . 1 2 ( 1) ( 2) 1 2 Câu 2:
Cho hàm số y = f ( x) xác định và liên tục trên
, có đồ thị như hình vẽ.
Hàm số y = f ( x) có điểm cực tiểu là
A. x =1 .
B. x = 2 . C. x = 2 − . D. x = 1 − . Lời giải Chọn A Câu 3:
Cho hàm số y = f ( x) có bảng biến thiên như sau x -∞ -1 0 +∞ y' 0 +∞ +∞ y -1
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị nhỏ nhất bằng −1.
B. Hàm số có giá trị nhỏ nhất bằng 0.
C. Hàm số không xác định tại x = 1 − .
D. Hàm số luôn có giá trị lớn nhất. Lời giải Chọn A
Nhìn BBT ta thấy y = 1
− là giá trị nhỏ nhất của hàm số. Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Câu 4:
Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào trong các hàm số dưới đây? A. 3 2
y = −x + 2x − x − 3 . B. 3 2
y = x + 2x − 7x − 2 . C. 3 2
y = x − 2x + x − 2 . D. 4 2
y = x − 2x − 3 . Lời giải Chọn C
Từ đồ thị ta thấy hình dạng trên là dạng đồ thị hàm số bậc 3 có hệ số a  0 .
Ngoài ra các điểm cực trị của đồ thị hàm số đều có hoành độ dương nên ta chọn đáp án C Câu 5:
Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây: −x + 2 2x − 2 x − 2 2 − x + 2 A. y = . B. y = . C. y = . D. y = . x + 2 x +1 x +1 x +1 Lời giải Chọn D
Đồ thị hàm số đã cho đi qua điểm (1;0) và (0;2) nên ta loại phương án A, B và C. − + Đồ 2x 2 thị hàm số y =
đi qua điểm (1;0) , (0;2) , có tiệm cận đứng x = 1 − và tiệm cận ngang x +1 y = 2
− nên thỏa mãn yêu cầu bài toán. 2 − x + 2
Vậy đường cong đã cho là đồ thị hàm số y = . x +1 x Câu 6:
Đồ thị hàm số y =
có bao nhiêu đường tiệm cận 2 x − 4 A. 2 . B. 1. C. 4 . D. 3 . Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải Chọn D Điề 2
u kiện xác định: x − 4  0  x  2  . x x Ta có: lim = lim
= 0  đường thẳng y = 0 là đường tiệm cận ngang của đồ thị 2 2 x→+ x − 4
x→− x − 4 hàm số. x lim
= − đường thẳng x = 2 là đường tiệm cận đứng của đồ thị hàm số. − x→ 2 2 x − 4 lim
x = −  đường thẳng x = 2
− là đường tiệm cận đứng của đồ thị hàm số. x ( 2)− 2 → − x − 4
Vậy đồ thị hàm số có 3 đường tiệm cận. Câu 7:
Tìm tập xác định D của hàm số y = ( x − )25 1 . A. D = .
B. D = (1;+) . C. D = (− ) ;1 . D. D = \  1 . Lời giải Chọn B 2 Do
 nên hàm số xác định khi x −1 0  x 1  D = (1;+). 5 Câu 8:
Cho a  0 ; a  1 và x ; y là hai số thực dương. Phát biểu nào sau đây là đúng?
A. log ( x + y) = log x + log y . B. log xy = x + y . a ( ) log log a a a a a
C. log ( xy) = log .
x log y . D. log x + y = x y . a ( ) log .log a a a a a Lời giải Chọn B
Ta có logarit của một tích bằng tổng hai logarit. Câu 9:
Tập xác định của hàm số y = log (x − 2 là 3 )
A. (−; 2 . B.  + 2; ) .
C. (−; 2) . D. (2; +) . Lời giải Chọn D
Hàm số y = log (x − 2 có nghĩa  x − 2  0  x  2. 3 )
Vậy tập xác định của hàm số là (2; +) . Câu 10: Ham số 2 x y − = có đạo hàm là: −2−x A. − 1 2 x− − . B. 2−x − ln 2 .
C. 2−x ln 2 . D. . ln 2 Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải Chọn B
= 2−x   = (2−  x y y ) ( ) = − − .2 . x x − ln 2 = 2 − . x ln 2 .
Câu 11: Trong các hàm số sau, hàm số nào nghịch biến trên khoảng (0; + ) ? xx 2021     A. y =   B. y =  
C. y = log x
D. y = log x  2 2020   3  3 Lời giải Chọn D Ta có: x 2021    2021 1 nên hàm số y = 
 đồng biến trên . Do đó phương án A sai. 2020  2020   x    
1 nên hàm số y =   đồng biến trên . Do đó phương án B sai. 3  3 
10  1 nên hàm số y = log x đồng biến trên khoảng (0;+ ) . Do đó phương án C sai.
2 1 nên hàm số y = log x nghịch biến trên khoảng (0;+). Do đó phương án D đúng. 3 2 3
Câu 12: Tìm nghiệm của phương trình 5x = 8 .
A. x = log 5 .
B. x = log 8 . C. 8 x = 5 . D. 5 x = 8 . 8 5 Lời giải Chọn B
5x = 8  x = log 8 . 5
Câu 13: Nghiệm của phương trình: 2x = 4 là
A. x = 2 .
B. x =1 .
C. x = 3. D. x = 4 . Lời giải Chọn A
Ta có 2x = 4  x = 2 .
Câu 14: Nghiệm của bất phương trình: log x  1 là 2
A. x  2 .
B. x  2 .
C. x 1 . D. x  2 . Lời giải Chọn A
Điều kiện: x  0
Ta có log x  1  x  2 . 2
Câu 15: Khối đa diện đều loại 4; 
3 có bao nhiêu mặt? A. 5 . B. 6 . C. 4 . D. 3 . Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải Chọn B
Khối đa diện đều loại 4; 
3 chính là khối lập phương nên có 6 mặt.
Câu 16: Thể tích của khối chóp có chiều cao bằng h và có diện tích đáy B là 1 1 1 A. Bh B. Bh C. Bh D. Bh 2 6 3 Lời giải Chọn C
Câu 17: Cho tam giác ABC đều có cạnh bằng a quay xung quanh cạnh AC của nó. Tính thể tích V của
khối tròn xoay tạo thành. 3 9 a 3  a 3 27 a 3 27 a A. V = . B. V = . C. V = . D. V = . 18 4 18 8 Lời giải Chọn B
Khi quay tam giác đều ABC quanh cạnh AC , khối tròn xoay tạo thành là hai khối nón tròn xoay
có trục là AC , đường tròn có bán kính bằng chiều cao hạ từ B . 2 3 a 3 a 1 1
a 3  a a 2 BO = r = , OA = h =
,V = 2.  r h = 2.    . = .   2 2 3 3 2 2 4  
Câu 18: Cho tam giác đều ABC cạnh a quay quanh đường cao AH tạo nên hình nón. Diện tích xung
quanh của hình nón đó là 2 3 a 2  a A. . B. . C. 2 a . D. 2 a . 4 2 Lời giải Chọn B
Với hình nón có chiều cao hạ từ đỉnh là h , đường sinh l, độ dài bán kính mặt đáy là r thì ta có
diện tích xung quanh của hình nón là: S =  rl. xq a 2  a Ta có r =
, l = a nên S = . 2 xq 2
Câu 19: Diện tích của mặt cầu có bán kính R bằng A. 2 2 R . B. 2  R . C. 2 4 R . D. 2 . R Lời giải Chọn C
Diện tích của mặt cầu có bán kính R bằng 2 4 R .
Câu 20: Thể tích khối trụ có bán kính đáy r, đường sinh l là 1
A. V = 2r . l B. 2
V =  rl . C. 2
V =  rl . D. 2 V =  r l. 3 Lời giải Chọn D
Thể tích khối trụ có bán kính đáy r, đường sinh l là 2
V =  r l.
Câu 21: Cho hàm số y = f ( x) xác định trên
\{ −1} và có bảng dấu của f (x) như hình bên dưới Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số y = f ( x) đồng biến trên khoảng (1;2).
B. Hàm số y = f ( x) đồng biến trên .
C. Hàm số y = f ( x) đồng biến trên khoảng ( 3 − ;2).
D. Hàm số y = f ( x) đồng biến trên khoảng ( ; − 2). Lời giải Chọn A
Ta có f ( x)  0, x
 (1;2) nên hàm số y = f (x) đồng biến trên khoảng (1;2).
Câu 22: Điểm cực đại của đồ thị hàm số 3 2
y = x − 6x + 9x có tổng hoành độ và tung độ bằng A. 5 . B. 1. C. 3 . D. 1 − . Lời giải Chọn A x =1 Ta có: 2
y ' = 3x −12x + 9 = 0  x =3 Bảng biến thiên Khi đó: x
=1 y = 4  x + y = 5. CD CD CD CD
Câu 23: Giá trị lớn nhất của hàm số 4 2
y = x − 4x + 9 trên đoạn  2 − ;  3 bằng A. 201 B. 2 C. 9 D. 54 Lời giải Chọn D x = 0 3
y = 4x − 8x ; y = 0   . x =  2 Ta có y ( 2 − ) = 9 ; y( )
3 = 54; y (0) = 9 ; y ( 2) = 5 . Vậy max y = 54 .  2 −  ;3 Câu 24: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0 .
C. a  0,b  0, c  0, d  0 .
D. a  0,b  0, c  0, d  0 . Lời giải Chọn D Ta có: 2
y = 3ax + 2bx + c , y = 6ax + 2b Từ đồ thị ta thấy:
+ lim y = − . Ta suy ra a  0 . x→+
+ y (0)  0  d  0 .
Đồ thị hàm số có hai điểm cực trị với hoành độ x , x trái dấu và x + x  0 . Ta suy ra phương 1 2 1 2
trình y ' = 0 có hai nghiệm trái dấu và x + x  0 . 1 2 c Ta suy ra x x =
 0 ,  c  0 . 1 2 3a  2bx + x = −  0 Hơn nữa, 1 2  3ab  0 . a  0
Vậy a  0,b  0, c  0, d  0
Câu 25: Đồ thị hàm số dưới đây có TCĐ và TCN là đường thẳng có phương trình Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
A. x = 2; y = 1.
B. x = 1; y = 2 .
C. x = 0; y = 1 .
D. x = 0; y = 1 . Lời giải Chọn A
Nhìn vào đồ thị ta thấy TCĐ và TCN lần lượt là x = 2; y = 1. −
Câu 26: Tìm tập xác định của hàm số y = ( x − ) 3 1 2 1 . A. D = . B. D = \ 1;−  1 . C. D = (− ;  ) 1  (1;+) . D. D = ( 1 − ; ) 1 . Lời giải Chọn C x  1 Ta có: 2 x −1  0   x  1 − Vậy: TXĐ D = (− ;  − ) 1  (1;+).
Câu 27: Tìm tập xác định hàm số y = ( 2
log x − 2x). A. D = . B. D = (− ;  0) (2;+) . C. D = \ 0;  2 . D. (0;2) . Lời giải Chọn B x  2 Hàm số xác định khi 2
x − 2x  0   x  0
Vậy TXĐ của hàm số là D = (− ;  0) (2;+) .
Câu 28: Tìm a để hàm số y = log x (0  a 1, x  0) có đồ thị là hình bên: a 1 1 A. a = .
B. a = 2 . C. a = 2 . D. a = . 2 2 Lời giải Chọn C Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Đồ thị đi qua ( A 2; 2) 2
 2 = log 2  a = 2  a = 2 . a x
Câu 29: Cho hàm số y = ( 2 − )
1 . Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số có đường tiệm cận đứng là trục hoành.
B. Hàm số đồng biến trên khoảng (0;+) .
C. Đồ thi hàm số có đường tiệm cận ngang là trục tung.
D. Hàm số nghịch biến trên khoảng (− ;  +) . Lời giải Chọn D x Vì 0 
2 −1  1 nên hàm số y = ( 2 − )
1 nghịch biến trên khoảng (− ;  +) .
Câu 30: Tập nghiệm của phương trình log x −1 = 2 là: 3 A. {3} . B. {-3;4} . C. {-3;-2} . D. {4;-2} . Lời giải Chọn D Đkxđ: x 1. PT  x − = ( )2 1 3 = 3 x −1 = 3  x−1= 3− x = 4  (TM )  x = 2 − Vậy x {4; 2 − }. x x
Câu 31: Gọi x , x là các nghiệm của phương trình (7 + 4 3) − 4(2+ 3) = 1
− . Khi đó giá trị của 1 2 2 2
x + x bằng 1 2 A. 2. B. 0. C. 14. D. 4. Lời giải Chọn A x x 2x x
Ta có: (7 + 4 3) − 4(2+ 3) = 1
−  (2+ 3) −4(2+ 3) +1= 0 ( ) 1 . x t = 2 + 3
Đặt t = (2+ 3) ,(t  0) phương trình ( ) 1 trở thành: 2
t − 4t +1 = 0   . t = 2 − 3 x
Với t = 2 + 3 : (2+ 3) = 2+ 3  x =1. x x − Với t = 2 − 3 : ( + ) = − ( + ) =( + ) 1 2 3 2 3 2 3 2 3  x = 1 − . Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Vậy phương trình đã cho có 2 nghiệm x = 1 − , x =1. Khi đó 2 2 x + x = 2. 1 2 1 2
Câu 32: Số mặt phẳng đối xứng của khối chóp tứ diện đều là A. 7 B. 8. C. 9. D. 6. Lời giải Chọn D
Các mặt phẳng đối xứng của khối chóp tứ diện đều là các mặt phẳng chứa một cạnh và qua trung
điểm của cạnh đối diện.
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên mặt phẳng
(ABCD) trùng với trung điểm của cạnh AB, đường thẳng SD tạo với mặt phẳng đáy một góc 45 .
o Tính thể tích khối chóp S.ABCD theo a. 3 a 5 3 a 5 3 a 5 3 a 5 A. . B. . C. . D. . 12 3 2 6 Lời giải Chọn D
Gọi H là trung điểm của AB SH ⊥ ( ABCD) nên hình chiếu của hình chiếu của SD lên mặt phẳng ( ABCD) là . HD Do đó (S ,
D ( ABCD)) (S ,
D SH ) SDH 45 . = = = 2  a a 5 2 2 2
+ HD = AD + AH = a + = .    2  2 a 5 + SH
D vuông cân tại H nên SH = HD = . 2 Page 15
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 3 1 1 a 5 a 5
Thể tích khối chóp S.ABCD : 2 V = SH.S = . .a = . S . ABCD 3 ABCD 3 2 6
Câu 34: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc BAD = 120 . Cạnh bên SA
vuông góc với đáy ( ABCD) và SA = 3a . Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.BCD . 3 5 5 4 A. = a R . B. = a R . C. = a R . D. = a R . 3 3 3 3 Lời giải Chọn C S d M I B A C D
Xét hình thoi ABCD có BAD = 120 nên AD = AC = AB , suy ra A là tâm đường tròn ngoại
tiếp đa giác đáy BCD .
Theo giả thiết SA vuông góc với đáy ( ABCD) nên đường thẳng SA là trục của đáy BCD .
Gọi M là trung điểm SD , trong mặt phẳng (SAD) kẻ đường thẳng d vuông góc với SD tại
M , d cắt SA tại I . Ta có I là tâm mặt cầu ngoại tiếp khối chóp S.BCD .
Lúc đó R = IS . a 10 .a 10 IS SM SM .DS 5a Ta có 2
ISM ∽ DSA  =  IS = = = . DS SA SA 3a 3
Câu 35: Cho hình thang cân ABCD có đáy nhỏ AB =1, đáy lớn CD = 3 , cạnh bên BC = DA = 2 . Cho
hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng 4 5 2 7 A.  . B.  . C.  . D.  . 3 3 3 3 Lời giải Chọn D Page 16
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Gọi V là thể tích vật tròn xoay cần tìm. V , V lần lượt là thể tích của khối nón đỉnh A , và đỉnh 1 2
B , V là thể tích khối trụ trục  O O như hình vẽ. T Gọi  A , 
B lần lượt là hình chiếu vuông góc của A , B trên cạnh CD . Suy ra A A D = B
B C (cạnh huyền – góc nhọn). Suy ra 2  A D = CD −  A
B = 3−1 = 2 . Suy ra  A D =  B C =1. Mặt khác 2 2 
O C = BC − B O = 1
Ta có AO = B
O =1 và OD = 
O C =1 nên ta có V = V . 1 2
Thể tích vật tròn xoay cần tìm là 1  2  2 2 2
V = V − 2V =  .R CD − 2.  R .AO =  R CD − AO . T 1   3  3   2  7 2 V =  .1 . 3 − =    .  3  3 II. PHẦN TỰ LUẬN 1 2
Câu 36: Giải phương trình: 2 log x + log x −1 = log log 3 . 49 7 ( ) 7 ( 3 ) 2 Lời giải x  0 Điều kiện  . x 1 1 log x + log ( x − )2 2 1
= log log 3  log x + log x −1 = log 2 49 7 7 ( 3 ) 2 7 7 7 x( x − ) 1 = 2 2  − − =  =  x x 2 0 x 2
log x x −1 = log 2      . 7 ( ) 7  x  ( x − ) 1 = −2 2
x − x + 2 = 0 x = 1 −
Kết hợp điều kiện ta được tập nghiệm của phương trình là S =  1 − ;  2 .
Câu 37: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA vuông góc với mặt đáy. Gọi
M là trung điểm BC . Mặt phẳng ( P) đi qua A và vuông góc với SM cắt SB , SC lần lượt tại
E , F . Biết thể tích khối chóp S.ABC gấp 4 lần thể tích khối chóp S.AEF . Tính thể tích của
khối chóp S.ABC . Page 17
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12 Lời giải S F H E A C M B
Ta có BC ⊥ SM .
Gọi H là hình chiếu vuông góc của A trên SM .
Do FE = (P) (SBC)  FE ⊥ SM FE BC và FE đi qua H . 2 1 SE SFSH  1 SH 1 V = 1 V  . =  =  = . S .AEF S .   4 ABC SB SC 4  SM  4 SM 2
Do đó H là trung điểm cạnh SM . a 3 Suy ra S
AM vuông cân tại A SA = . 2 2 3 a Vậy 1 a 3 a 3 V = . . = . SABC 3 2 4 8
Câu 38: Cho hàm số y = f ( x) liên tục trên
và có bảng biến thiên bên dưới.
Tìm các khoảng đồng biến của hàm số y = g ( x) = f ( 2 1+ 2x − x ) Lời giải
Ta có g( x) = ( − x) f ( 2 2 2 . 1+ 2x − x ) .  = x =  − = x 1 0   g( x) 2 2x 0 = 0   2
 1+ 2x − x =1   x = ( 1 nghiÖm béi b ) a . f     ( 2
1+ 2x − x ) = 0 2
1+ 2x − x = 2  x = 2 Page 18
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
+ Với x = 3  g( ) 3 = 4 − . f ( 2
− )  0 (do f ( 2 − )  0 )
Từ đó ta có bảng biến thiên:
Dựa vào bảng biến thiên hàm số g ( x) đồng biến trên khoảng (−;0) và (1;2) .    x + y
Câu 39: Cho các số thực , x y thỏa mãn 0 , x y 1 và log
+ x +1 y +1 − 2 = 0 . Tìm giá trị 3   ( )( ) 1− xy
nhỏ nhất của P với P = 2x + y . Lời giải
0  x, y 1  0   , x y  1
Điều kiện:  x + y    . 0 
x + y  0; 1− xy  0 1  − xy  +  Khi đó x y log
+ x +1 y +1 − 2 = 0 3   ( )( ) 1− xy
 log x + y −log 1− xy + x + y + xy −1= 0 3 ( ) 3 ( )
 log x + y + x + y = log 1− xy + 1− xy (*) 3 ( ) ( ) 3 ( ) ( )
Xét hàm số f (t) = log t + t với t  0 , ta thấy f (t ) 1 = +1  0, t
  0 nên hàm số f (t) đồng 3 t ln 3
biến trên khoảng (0;+) . − Do đó ( ) x
*  x + y =1− xy y ( x + ) 1
1 = 1− x y =
. Thay vào P = 2x + y ta được x +1 1− x P = 2x + . x +1 − x
Xét hàm số f ( x) 1 = 2x + trên đoạn 0;  1 . x +1 2
Ta có: f ( x) = 2 − ( . x + )2 1 x = 0(0; ) 1
+ f ( x) = 0   . x = 2 −   (0; ) 1 Page 19
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
+ f (0) =1; f ( ) 1 = 2
Vậy min P = min f ( x) = f (0) = 1 khi x = 0, y =1 . 0; 1 Page 20
Sưu tầm và biên soạn
Document Outline

  • CKI_TOAN_12_DE_SO_01(70TN-30TL)_THEO-MA-TRAN-BO_HDG
  • CKI_TOAN_12_DE_SO_02(70TN-30TL)_THEO-MA-TRAN-BO_HDG
  • CKI_TOAN_12_DE_SO_03(70TN-30TL)_THEO-MA-TRAN-BO_HDG
  • CKI_TOAN_12_DE_SO_04(70TN-30TL)_THEO-MA-TRAN-BO_HDG
  • CKI_TOAN_12_DE_SO_05(70TN-30TL)_THEO-MA-TRAN-BO_HDG
  • CKI_TOAN_12_DE_SO_06(70TN-30TL)_THEO-MA-TRAN-BO_HDG
  • CKI_TOAN_12_DE_SO_07(70TN-30TL)_THEO-MA-TRAN-BO_HDG
  • CKI_TOAN_12_DE_SO_08(70TN-30TL)_THEO-MA-TRAN-BO_HDG
  • CKI_TOAN_12_DE_SO_09(70TN-30TL)_THEO-MA-TRAN-BO_HDG
    • Lời giải
  • CKI_TOAN_12_DE_SO_10(70TN-30TL)_THEO-MA-TRAN-BO_HDG
  • CKI_TOAN_12_DE_SO_11(70TN-30TL)_THEO-MA-TRAN-BO_HDG
    • Câu 6: Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số .
    • Câu 6: Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số .
  • CKI_TOAN_12_DE_SO_12(70TN-30TL)_THEO-MA-TRAN-BO_HDG