Top20 đề ôn tập thi học kỳ 1 Toán 12 có đáp án và lời giải chi tiết

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 1

ĐỀ ÔN TẬP SỐ 01

Câu 1. [2D1-1.2-1] Hỏi hàm số

4

2 1

y x

 

đồng biến trên khoảng nào?

A.

 

0;



. B.

1

;

2

 

 

 

 

. C.

 

;0



. D.

1

;

2

 

 

 

 

.

Lời giải

Chọn A

Ta có

3

' 8 , ' 0 0

y x y x

   

. Nên hàm số đã cho đồng biến trên

 

0;



Câu 2. [2D1-2.5-1] Số điểm cực trị của hàm số

3 2

3 1y x x x    

là

A.

2

. B.

3

. C.

1

. D.

0

.

Lời giải

Chọn A

Hàm số bậc ba đã cho có

2

' 3 6 1y x x  

là tam thức bậc 2 có 2 nghiệm phân biệt nên hàm số

đã cho có 2 cực trị.

Câu 3. [2D1-3.3-1] Tìm giá trị lớn nhất của hàm số

3 2

3y x x

   trên đoạn

 

2;1



A.

 

2;1

max 2

y





. B.

 

2;1

max 0

y





. C.

 

2;1

max 20

y





. D.

 

2;1

max 54

y





.

Lời giải

Chọn C

2

' 3 6 0 0

y x x x

     

(thỏa mãn) hoặc

2

x



(loại)

     

2 20; 0 0; 1 2

y y y

    

Vậy:

 

2;1

max 20

y





Câu 4. [2D1-4.3-1] Đồ thị hàm số

2 1

2

x

y

x







có các đường tiệm cận là:

A.

2

y

 

và

2

x

 

. B.

2

y



và

2

x

 

. C.

2

y

 

và

2

x



. D.

2

y



và

2

x



.

Lời giải

Chọn B

Nhắc lại đồ thị hàm số

ax b

y

cx d







có đường tiệm cận ngang là

a

y

c



và đường tiệm cận đứng

là

d

x

c





.

Câu 5. [2D1-5.2-1] Cho đồ thị như hình vẽ bên. Đây là đồ thị của hàm số nào?

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 2

A.

3 2

3y x x

  . B.

3 2

3y x x

   . C.

3 2

3y x x

   . D.

3 2

3 1

y x x

  

Lời giải

Chọn A

Khi

x

tiến tới



thì

y

tiến tới



, do đó hệ số của

3

x

phải dương



Loại B, C

Hàm số đi qua điểm

 

0;0

nên hàm số ở ý D không thỏa mãn

Câu 6. [2D2-1.2-1] Cho biểu thức

4

3

P x x



với

x

là số dương khác

1

. Khẳng định nào sau đây

sai?

A.

2

3

P x x x



. B.

2

3

.P x x

 . C.

13

6

P x

 . D.

6

13

P x



.

Lời giải

Chọn B.

Với

0,

x



1x 

thì

1

1 13 13 13 1

2

4 2 2

6

3 3 3 6 6

. .

P x x x x x x x x x

 

     

 

 

.

Câu 7. [2D2-2.1-1] Tính giá trị của biểu thức

2

1

log

a

A

a



, với

0

a



và

1

a



A.

2A  

. B.

1

2

A

 

. C.

2A 

. D.

1

2

A



.

Lời giải

Chọn A.

Ta có:

2

1

log log 2.log 2

a a a

A a a

a



      

.

Câu 8. [2H1-2.1-1] Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp đôi thì thể tích

khối hộp tương ứng sẽ:

A. tăng 2 lần. B. tăng 4 lần. C. tăng 6 lần. D. tăng 8 lần.

Lời giải

Chọn D.

Giả sử chiều dài, chiều rộng, chiều cao của khối hộp chữ nhật là

, , a b c

.

Thể tích của khối hộp là

V abc

.

Khi tăng tất cả các cạnh của khối hộp lên gấp đôi thì thể tích khối hộp thu được là

’ 2 .2 .2 8 8V a b c abc V  

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 3

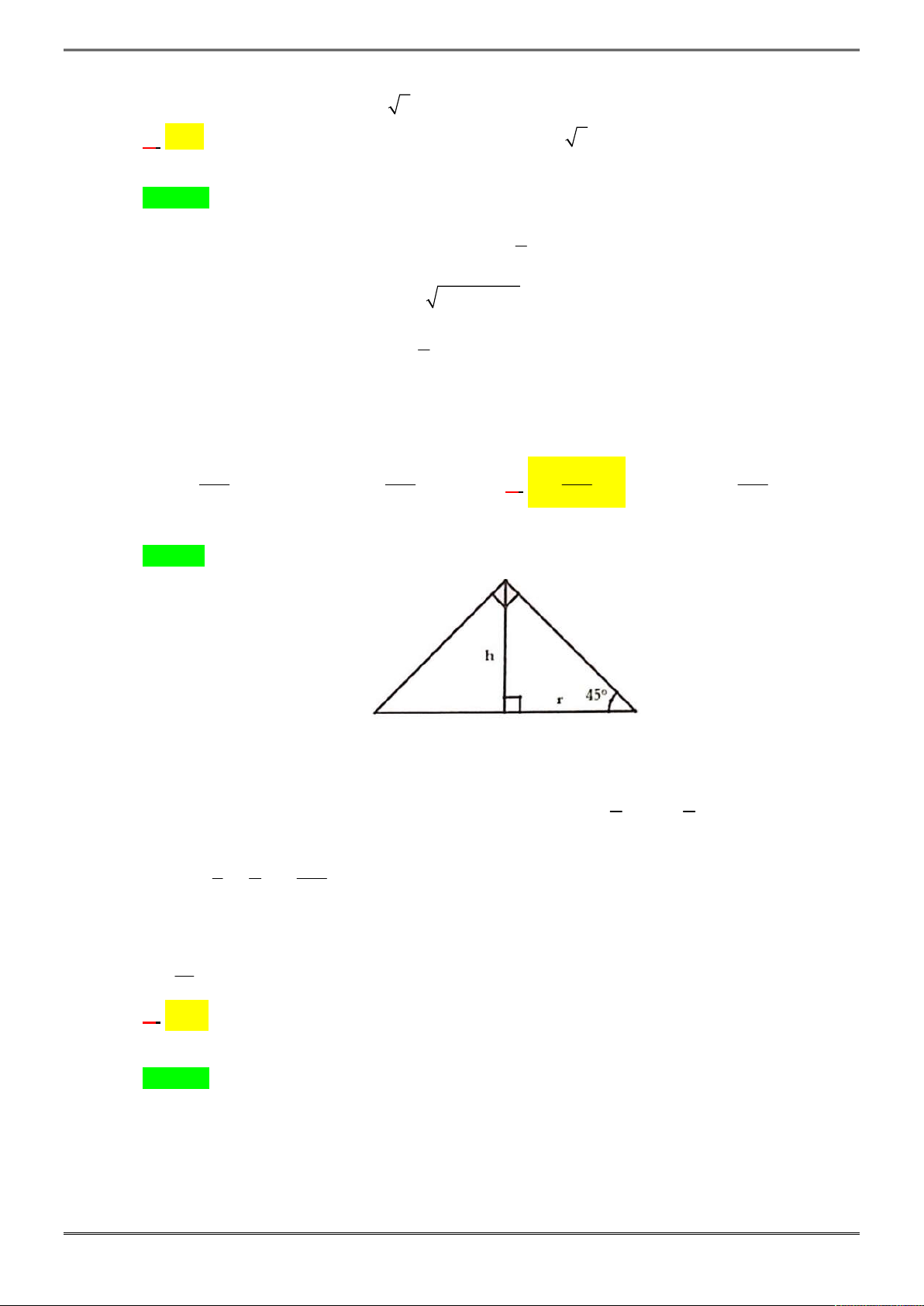
Câu 9. [2H1-2.2-1] Cho hình chóp

.

S ABC

có đáy

ABC

là tam giác vuông tại

A

,

3 , 4AB a AC a 

,

SB

vuông góc

 

ABC

,

5 2SC a



. Tính thể tích khối chóp

.

S ABC

theo

a

.

A.

3

10a

. B.

3

30a

. C.

3

10 2

a

. D.

3

5a

.

Lời giải

Chọn A.

Bước 1: Diện tích tam giác vuông tại

A

:

1

. .

2

ABC

S AB AC





.

Bước 2: Tính độ dài đường cao

2 2

SB SC BC

 

.

Bước 3: Thể tích khối chóp

3

.

1

. . 10

2

S ABC ABC

V S SB a



 

(đvtt).

Câu 10. [2H2-1.4-1] Cho hình nón

 

N

có thiết diện qua trục là một tam giác vuông có cạnh huyền

bằng

 

a cm

. Tính thể tích

V

của khối nón đó.

A.

3

8

a

V cm



 . B.

3

6

a

V cm



 . C.

3

24

a

V cm



 . D.

3

a

V cm



 .

Lời giải

Chọn C

Thiết diện qua trục của hình nón sẽ là một tam giác cân, từ giả thiết suy ra tam giác vuông cân.

Đường cao từ đỉnh có góc vuông của thiết diện chính là đường cao của hình nón và độ dài cạnh

huyền chính là đường kính đáy của hình nón. Do đó ta có:

2

a

r



và

2

a

h



.

Vậy

3

1

3 2 24

a a

V cm



 

 

 

 

.

Câu 11. [2D1-2.7-2] Tìm tất cả các giá trị của tham số thực

m

sao cho hàm số

 

3

2 2

2 1

3

x

y x m m x    

có 2 điểm cực trị.

A.

1

m



. B.

m



. C.

1

m



. D.

 

;1

m

 

.

Lời giải

Chọn A.

TXĐ:

D  

. Ta có:

  

2 2

' 2 2 2 ; ' 0

2

x m

y x x m m x m x m y

x m





         



 



.

Hàm số có 2 điểm cực trị

' 0

y

 

có 2 nghiệm phân biệt

2 1

m m m

    

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 4

Câu 12. [2D1-1.2-2] Hàm số nào nghịch biến trên



A.

1

y

x



B.

4 2

5y x x

  C.

3

2

y x

  

D.

coty x

Lời giải

Chọn C

Để hàm số nghịch biến trên



thì hàm số đó phải xác định trên



.

Các hàm số

1

y

x



và

coty x

không xác định trên toàn tập



Hàm số bậc 4 không thể nghịch biến trên



Hàm số

3

2

y x

  

xác định trên



và có

2

' 3 0

y x

  

nên nghịch biến trên



.

Câu 13. [2D1-2.7-2] Cho hàm số

3 2

2 3 5

y x x

   

. Hàm số có giá trị cực tiểu bằng:

A.

5

B.

6

. C.

0

. D.

1

.

Lời giải

Chọn A

2

' 6 6 0 0

y x x x

     

hoặc

1x 

 

" 12 6; " 0 6 0 0

y x y x

      

là điểm cực tiểu

Giá trị cực tiểu

 

0 5

y



Câu 14. [2D1-2.8-2] Cho hàm số

4 3

4

y x x m  

. Khẳng định nào sau đây là khẳng định sai:

A. Số cực trị của hàm số không phụ thuộc vào tham số

m

.

B. Số cực trị của hàm số phụ thuộc vào tham số

m

.

C. Hàm số có đúng một cực trị.

D. Hàm số có đúng một cực tiểu.

Lời giải

Chọn B

Hàm số có đạo hàm

 

3 2 2

' 4 12 4 3

y x x x x

   

nên số cực trị của hàm số không phụ thuộc

vào tham số m ⇒ Câu B sai

' 0

y



có 2 nghiệm

0

x



và

3

x

 

nhưng y' chỉ đổi dấu khi đi qua giá trị

3

x

 

(từ âm sang

dương) nên hàm số có đúng 1 cực trị và là cực tiểu.

Câu 15. [2D1-3.1-2] Trong tất cả các hình chữ nhật có chu vi

40cm

. Hình chữ nhật có diện tích lớn

nhất có diện tích

S

là

A.

2

100

S cm



B.

2

400

S cm



C.

2

49

S cm



D.

2

40

S cm



Lời giải

Chọn A.

2 2

20

100

2 2

a b

S ab



   

   

   

   

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 5

Câu 16. [2D1-3.15-2] Một chất điểm chuyển động theo quy luật

3 2

3s t t  

. Khi đó vận tốc

 

/v m s

của chuyển động đạt giá trị lớn nhất tại thời điểm

t

(giây) bằng:

A.

2t 

B.

0t 

C.

1t 

D.

1

2

t











Lời giải

Chọn C.

Ta có

 

2

' 3 6 3 1 3 3

v s t t t

        

. Dấu “=” xảy ra

1t 

Vậy vận tốc của chuyển động đạt giá trị lớn nhất tại thời điểm

1t 

Câu 17. [2D1-4.2-2] Cho hàm số

 

y f x



thỏa mãn điều kiện

0

lim ; lim ; lim

x x

y a y y



 



     

.

Chọn mệnh đề sai trong các mệnh đề sau?

A. Đồ thị hàm số

 

y f x



có 2 tiệm cận ngang và 1 tiệm cận đứng.

B. Đồ thị hàm số

 

y f x



có 1 tiệm cận ngang và 1 tiệm cận đứng.

C. Đồ thị hàm số

 

y f x



có tiệm cận ngang

y a

.

D. Đồ thị hàm số

 

y f x



có tiệm cận đứng

0

x x

.

Lời giải

Chọn B.

lim

x

y a y a



   

là 1 đường tiệm cận ngang.

lim

x

y



 

nên ta không thể kết luận được về tiệm cận ngang và đứng.

0

lim

x x

y





 

là tiệm cận đứng.

Câu 18. [2D1-4.5-2] Đồ thị hàm số nào sau đây không có đường tiệm cận:

A.

2

2 1

x

y

x





B.

y x 

C.

2

3 2

x

y

x







D.

1

2

3

y x

x

  



Lời giải

Chọn B

Câu 19. [2D1-6.2-2] Biết rằng đường thẳng

2 2y x  

cắt đồ thị hàm số

3

2

y x x

  

tại điểm duy

nhất; kí hiệu

0 0

;x y

là tọa độ của điểm đó. Tìm

0

y

A.

0

2

y



B.

0

4

y



C.

0

y



D.

0

1

y

 

Lời giải

Chọn A

Phương trình hoành độ giao điểm là

3

2 2 2 0

x x x x

      

. Nên

0 0

2 2

x y

  

Câu 20. [2D1-4.9-2] Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số

2

1

x

y

mx







có hai tiệm cận ngang.

A.

0

m



B.

0

m



C.

0

m



D. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 6

Lời giải

Chọn C

Anh nghĩ câu này khá hay và lạ. Để tìm tiệm cận ngang ta phải tính các giá trị của

lim , lim

x x

y y

 

. Quan sát các đáp án ta dễ dàng thấy được chỉ có giá trị

0

m



thì mới thỏa mãn

yêu cầu đề bài ra.

Nếu

0

m



thì

1y x 

không có tiệm cận,

0

m



thì xét dưới mẫu số ta thấy x có điều kiện

ràng buộc nên không thể xét x tới vô cùng được

Nếu

0

m



thì ta có

2

1

lim

1

x

y

x m

x



 



 

 





sẽ có 2 tiệm cận ngang là

1 1

,y y

m m



 

Câu 21. [2D2-5.2-2] Giải phương trình

 

4

log 1 3

x

 

A.

63

x



B.

65

x



C.

82

x



D.

80

x



Lời giải

Chọn B

 

3

4

log 1 3 1 4 65

x x x

      

Câu 22. [2D2-3.3-2] Cho các số thực dương a, b với

1

a



. Khẳng định nào sau đây là khẳng định

đúng?

A.

 

2

1 1

log log

2 2

a

ab b

 

B.

 

2

log 2 log

a

ab b

 

C.

 

2

1

log log

4

a

ab b



D.

 

2

1

log log

2

a

ab b



Lời giải

Chọn A

Các em áp dụng công thức này nhé:

 

log log ,log log log

x

y

a a a a

a

y

b b xy x y

x

  

ta sẽ được kết quả là đáp án A

Câu 23. [2D2-6.2-2] Tìm nghiệm của bất phương trình

 

1`

2

log 3 1 3

x

 

.

A.

3

8

x



. B.

1 3

3 8

x

 

. C.

3

8

x



. D.

1 5

3 8

x

 

.

Lời giải

Chọn B.

Khi giải bất phương trình logarit chú ý đặt điều kiện và cơ số lớn hơn hay nhỏ hơn 1.

Điều kiện:

 

1

2

1 1 3

3 1 0 ;log 3 1 3 3 1

3 8 8

x x x x x

          

.

Kết hợp điều kiện suy ra nghiệm của bất phương trình là

1 3

3 8

x

 

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 7

Cách khác: Có thể sử dụng MTCT để giải nhanh bài toán này. Nhập MODE + 7 (TABLE)

Nhập

     

1

2

1

:

3

5 1 3

log 3 1 3 : 0, ;

8 3 8

1 5 1

:

15 8 3

Start X

f X X End X f x x

Step X







 

        



 

 



 

 

 



 



.

Câu 24. [2D2-4.2-2] Cho các hàm số sau:

(1)

 

2

y x



 

. (2)

 

2

y x



 

. (3)

 

1

3

2

y x 

.

(4)

1

2

y

x





. (5)

1

2

y

x





. (6)

3

2

y x

 

.

Hỏi có bao nhiêu hàm số có tập xác định là

 

2;D

 

?

A.

1

. B.

2

. C.

3

. D.

4

.

Lời giải

Chọn C.

Các hàm số (1), (3), (5) có tập xác định là

 

2;D

 

; các hàm số (2) (4) có tập xác định là

 

\ 2

; hàm số (6) có tập xác định là



.

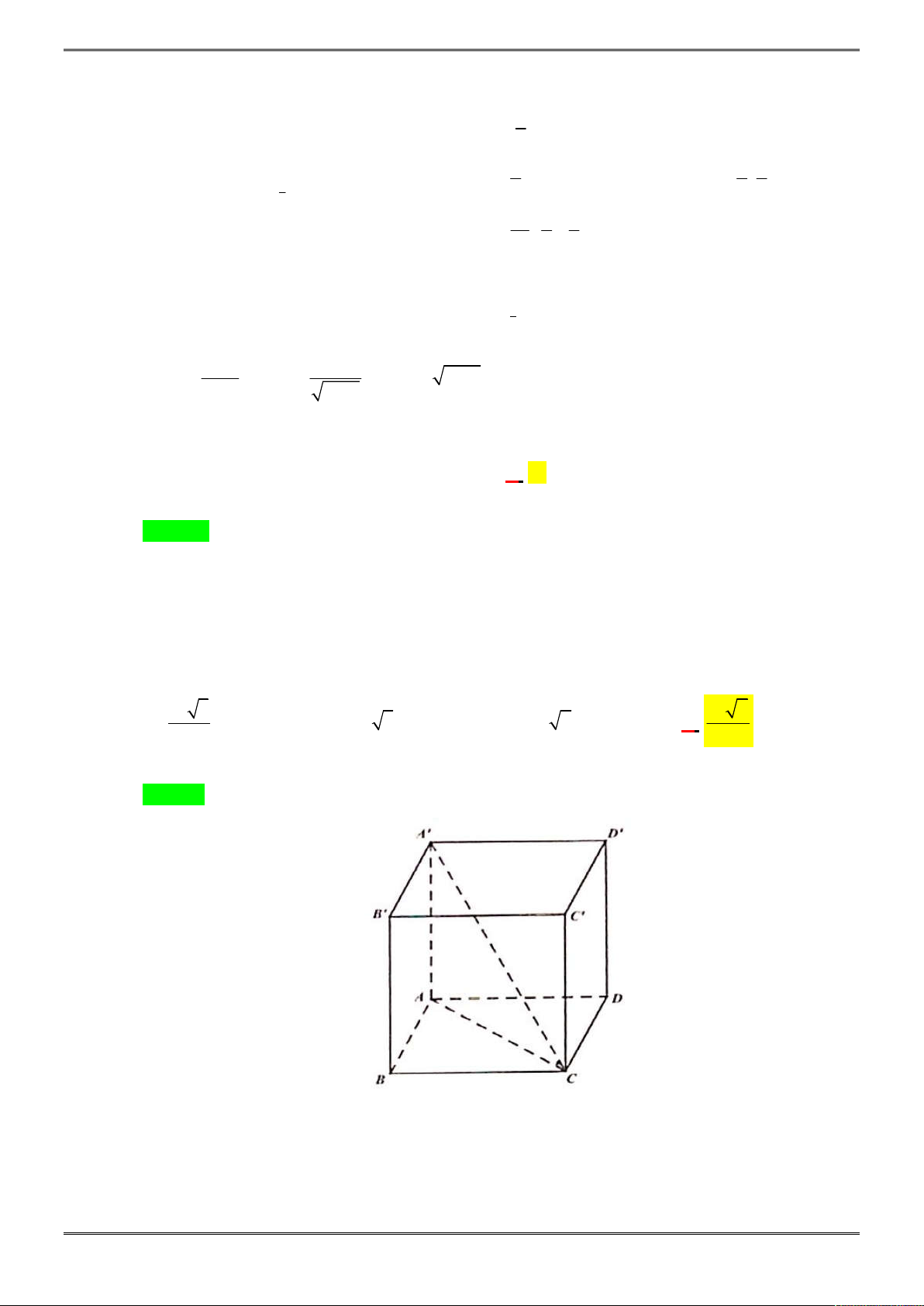
Câu 25. [2H1-3.3-2] Cho hình lăng trụ tứ giác đều

. ' ' ' 'ABCD A B C D

, có cạnh đáy bằng

a

. Góc giữa

'A C

và đáy

 

ABCD

bằng

45

. Tính thể tích của khối lăng trụ

. ' ' 'ABC A B C

theo

a

.

A.

3

2

a

. B.

3

a . C.

2

a

. D.

3

2

a

.

Lời giải

Chọn D

Lăng trụ tứ giác đều

. ' ' ' 'ABCD A B C D

là lăng trụ đứng và có đáy là hình vuông.

Góc giữa

'A C

và đáy

 

ABCD

là



' 45

A CA

 

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 8

Ta có



2

1

, 2, ' .tan ' 2

2

ABC

S a AC a AA AC A CA a

   

Vậy

2 3

. ' ' '

2

'. 2.

2 2

ABC A B C ABC

a a

V AA S a  

.

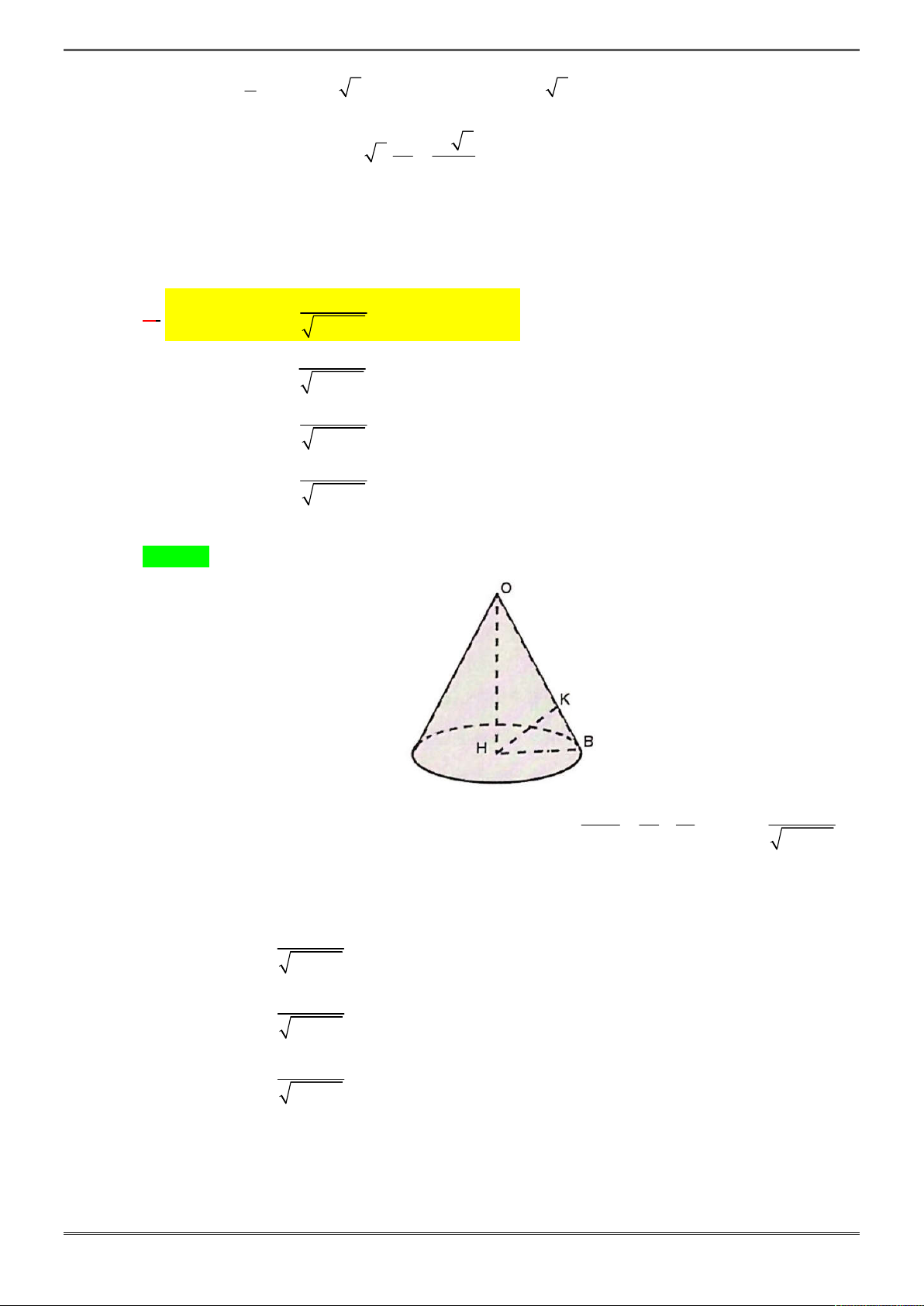
Câu 26. [2H2-1.1-2] Cho hình nón

 

N

có đỉnh

O

và tâm của đáy là

H

.

 



là mặt phẳng qua

O

.

Nên kí hiệu

 

;d H



là khoảng cách từ

H

đến mặt phẳng

 



. Biết chiều cao và bán kính

đáy của hình nón lần lượt là

, h r

. Khẳng định nào sau đây là sai?

A. Nếu

 

2 2

,

rh

d H

r h







thì

   

N



  

.

B. Nếu

 

2 2

,

rh

d H

r h







thì

   

N





là tam giác cân.

C. Nếu

 

2 2

,

rh

d H

r h







thì

   

N





là đoạn thẳng.

D. Nếu

 

2 2

,

rh

d H

r h







thì

   

N





là một điểm.

Lời giải

Chọn A.

Xét tam giác

OBH

vuông tại

H

có đường cao

HK

ta có

2 2 2

2 2

1 1 1 rh

HK

HK h r

r h

   



.

Do đó ta có các vị trí tương đối giữa mặt phẳng qua đỉnh và hình nón là:

Nếu

 

2 2

,

rh

d H

r h







thì

   

N





là tam giác cân.

Nếu

 

2 2

,

rh

d H

r h







thì

   

N





là đoạn thẳng.

Nếu

 

2 2

,

rh

d H

r h







thì

   

N





là một điểm là

O

.

Câu 27. [2H2-1.5-2] Cho khối nón

 

N

đỉnh

O

có bán kính đáy là

r

. Biết thể tích khối nón

 

N

là

0

V

. Tính diện tích

S

của thiết diện qua trục của khối nón.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 9

A.

0

V

S

r





. B.

0

2

3V

S

r





. C.

0

3V

S

r





. D.

0

3 r

S

V





.

Lời giải

Chọn B.

Ta có công thức

2

0

2

3

1

3

V

V r h h

r



  

.

Từ đó diện tích thiết diện qua trục

0 0

2

3 3

1 1

. .2 .

2 2

V V

S AB OH r

r r

 

  

.

Câu 28. [2H1-4.1-2] Cho khối chóp tam giác

.

S ABC

có

 

SBA

và

 

SBC

cùng vuông góc

với

 

ABC

, đáy

ABC

là tam giác đều cạnh

a

,

SC

bằng

7a

. Đường cao của khối chóp

SABC

bằng

A.

a

B.

2 2a

C.

6a

D.

5a

Lời giải

Chọn C

     

   

 

SBA ABC SBC

SB ABC

SBA SBC SB

 



 



 





BC AB AC a  

do tam giác ABC đều

2 2

6SB SC BC a

  

.

Câu 29. [2H1-4.2-2] Cho hình lăng trụ đứng tam giác

. ' ' 'AB A B C

C

có đáy là tam giác vuông cân tại

A

cạnh

AB

bằng

3a

, góc giữa

'A C

và

 

ABC

bằng

0

45

. Khi đó đường cao của lăng trụ

bằng:

A.

a

B.

3a

C.

2a

D.

3a

Lời giải

Chọn B

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 10

A

là hình chiếu của

'A

lên mặt phẳng

 

ABC

 









0

A ' , 45 A 'C ABC CA

  

Lại có

3AC a

 vì tam giác

ABC

cân tại

A

.

Tam giác

'AA C

vuông tại

A

có góc



0

' 45

A CA  nên vuông cân tại

A

' 3AA a

  .

Câu 30. [2H1-2.2-2] Cho hình chóp

.

S ABCD

có

ABCD

là hình chữ nhật,

2 , ,SA a,

AB a BC a

  

SB a 3

 ,

 

SAB

vuông góc với

 

ABCD

. Khi đó thể tích của khối chóp

SABCD

bằng

A.

3

a

B.

3

6

a

C.

3

a D.

3

2 3

a

Lời giải

Chọn A

Dễ thấy

2 2 2 2

4a

SA SB AB  

do đó tam giác

SAB

vuông tại

S

. Dựng

SH AB

, mặt khác

   

DSAB ABC



Do đó

 

SH ABCD



Lại có

. 3

2

SA SB a

SH

AB

 

Do vậy

3

.

1 3

. .

3 3

S ABCD ABCD

a

V SH S 

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 11

Câu 31. [2D1-3.8-3] Tìm giá trị nhỏ nhất của hàm số

3

sin 3siny x x

  trên đoạn

0;

3



 

 

 

A. -2 B. 0 C.

9 3

8



D.

5 2

4



Lời giải

Chọn C

Đặt

sinx

t



với

3

x 0; 0; 1

3 2

t t



 

    

 

 

 

3 2 3

3 9 3

3 ' 3 3 0 sin 3sin

2 8

y t t y t y f x x x f

 

            

 

 

.

Câu 32. [2D1-2.8-3] Cho hàm số

 

4 2 3

9 10

y mx m x

   

. Tìm m để hàm số có 3 điểm cực trị.

A.

1

0 2

m

 





 



B.

3

0 3

m

 





 



C.

3

1 0

m







  



D.

0

1 3

m







 



Lời giải

Chọn B

Xét hàm số

 

4 2 2

x 9 10, xy m m x

     

. Ta có

 

3 2

y' 4mx 2 9m x

  

Phương trình

 

3 2

2 2

0

' 0 4 2 9 0

2 9 *

x

y mx m x

mx m





     



 



Để hàm số đã cho có ba điểm cực trị khi và chỉ khi phương trình (*) có hai nghiệm phân biệt

Hay

2

0

0 3

9

3

0

m





 













 









là giá trị cần tìm.

Câu 33. [2D2-3.3-3] Cho

2 3

log 5 ;log 5

a b 

. Tính

6

log 1080

theo

a

và

b

ta được:

A.

1ab

a b



B.

2 2

a b ab

a b

 



C.

3 3

a b ab

a b

 



D.

2 2

a b ab

a b

 



Lời giải

Chọn C

Ta có

5

2

5 3

log 3

log 5

log 3

log 2 log 5

a

b

  

 

3 3

2

2 2

6

2 2

3

log 2 3 5

3 3log 3 log 5 3 3

log 100

log 6 1 log 5

1

a

b a ab

b

a

a b

b

 

 

 

    

 



.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 12

Câu 34. [2H2-3.2-3] Người thợ cần làm một bể cá hai ngăn, không có

nắp ở phía trên với thể tích 1,296 m

3

. Người thợ này cắt các tấm kính

ghép lại một bể cá dạng hình hộp chữ nhật với 3 kích thước a, b, c như

hình vẽ. Hỏi người thợ phải thiết kế các kích thước a, b, c bằng bao

nhiêu để đỡ tốn kính nhất, giả sử độ dầy của kính không đáng kể.

A.

3,6 ; 0,6 ; 0,6a m b m c m  

B.

2,4 ; 0,9 ; 0,6a m b m c m  

C.

1,8 ; 1,2 ; 0,6a m b m c m  

D.

1, 2 ; 1, 2 ; 0,9a m b m c m  

Lời giải

Chọn C.

Thể tích bể cá là:

1, 296

V abc

 

Diện tích tổng các miếng kính là

2 3S ab ac bc  

(kể cả miếng ở giữa)

Ta có:

3 3

3

1 2 3

3 , ,

1 2 3 1 2 3 3 6 3 6

3 . .

1, 296

Cauchy cho so

c b a

S

abc c b a c b a

abc

     



Dấu “=” xảy ra khi

1,8

1 2 3

1, 2

1,296

0,6

a

b

c b a

abc

c





 

 

 

 

 





.

Câu 35. [2H1-2.1-3] Cho hình chóp

.

S ABCD

có hình chiếu vuông góc của

S

trên mặt đáy

ABCD

là

điểm

I

thuộc

AD

sao cho

7

2 ,

2

a

AI ID SB 

,

ABCD

là hình vuông có cạnh bằng

a

. Khi

đó thể tích của khối chóp

.

S ABCD

bằng:

A.

3

2

6

a

B.

3

11

12

a

C.

3

11

18

a

D.

3

2

18

a

Lời giải

Chọn C.

Ta có

 

.

1

. .

3

S ABCD ABCD

SI ABCD V SI S  

2 2

2 2 13

2

3 3 3

a a

AI ID AI AD BI AI AB       

Xét tam giác vuông SB,

2 2 2

SI IB SB

 

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 13

2 2

7 13 11

2 3 6

a a a

SI SB IB

   

     

   

   

Do đó

3

2

.

1 1 11 11

. . . .

3 3 6 18

S ABCD ABCD

a a

V SI S a  

.

Câu 36. [2D1-6.3-3] Tìm tất cả các giá trị của

m

để đường thẳng

y m

cắt đồ thị hàm số

2 2

y x x

 

tại 6 điểm phân biệt.

A.

0 2.

m

 

B.

0 1.

m

 

C.

1 2.

m

 

D. Không tồn tại

.m

Lời giải

Chọn A.

 Xét hàm số

 

2 2 4 2

2 2 2 4y g x x x x x

    

Ta có

 

3 2

0

8 8 8 1 0

1

x

g x x x x x

x







     



 



.

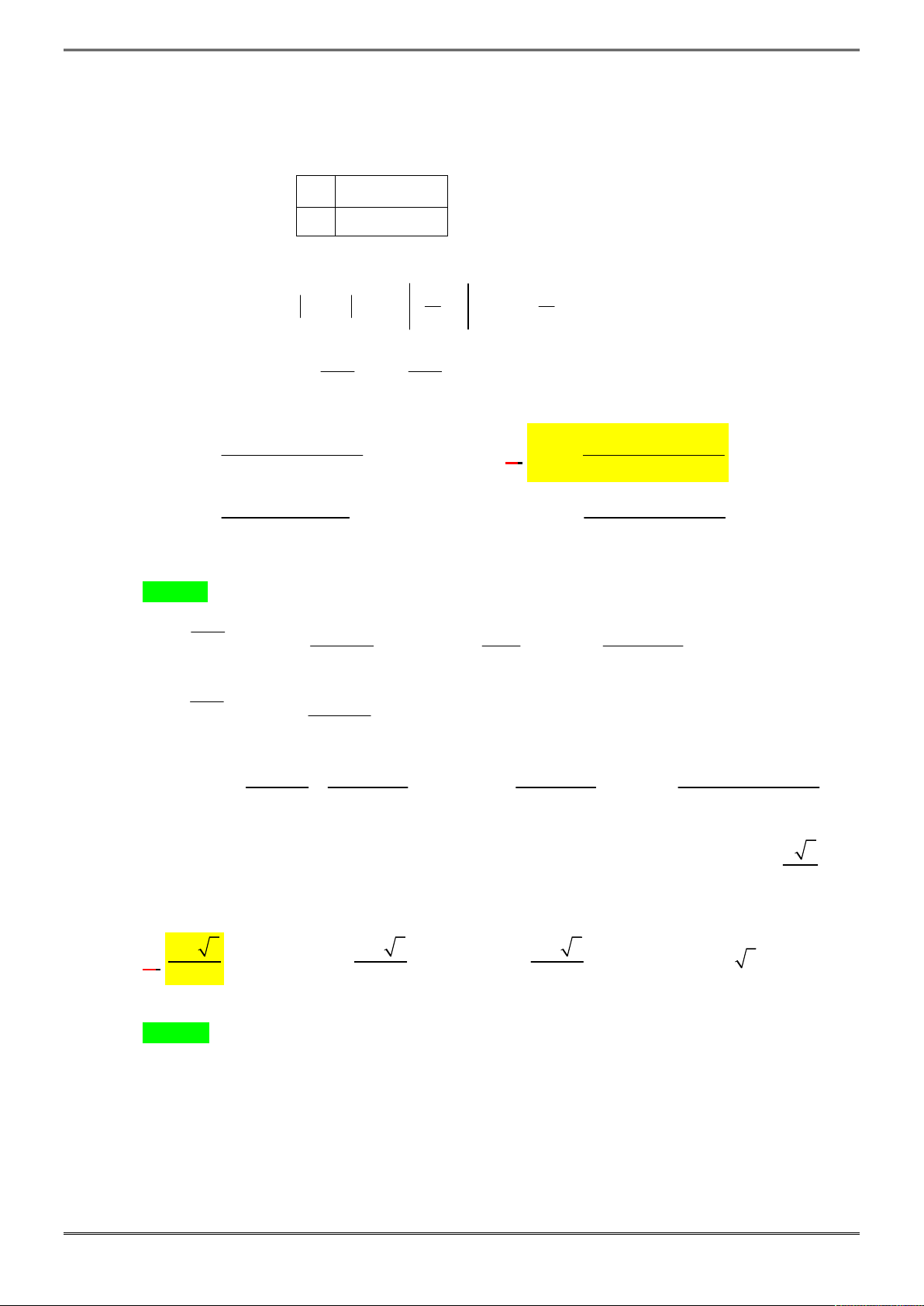
Ta có đồ thị hàm số

 

4 2

2 4g x x x

 

, từ đó suy ra đồ thị hàm số

2 2

y x x

 

Dựa vào đồ thị để phương trình có 6 nghiệm phân biệt khi

0 2.

m

 

Câu 37. [2D1-1.1-4] Có tất cả bao nhiêu giá trị của tham số m sao cho hàm số

 

3 2 2

3 , 0

y mx x m m

   

đồng biến trên khoảng

 

;a b

và nghịch biến trên các khoảng

   

; , ;a b

 

sao cho

2

a b

 

.

A. 0. B. 1. C. 2. D. Vô số m.

Lời giải

Chọn B.

TXĐ:

D  

. Ta có:

1

2 2

2

0

' 3 6 ; ' 0 3 6 0

2

x

y mx x y mx x

x

m







      



 



. Điều kiện

0

m



.

Vẽ bảng xét dấu đạo hàm

'y

ta cần biết dấu của hệ số

3a m

. Ta có nhận xét sau:

Nếu

2 1

3 0

a m x x   

thì ta có bảng xét dấu

x

-∞

2

x

1

x

+∞

'y

+ 0 - 0 +

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 14

Khi đó, hàm số đồng biến trên các khoảng

 

2

; x



và

 

1

;x



. Không thỏa đề nên loại

trường hợp

3 0

a m

 

.

Nếu

1 2

3 0 0

a m m x x     

, ta có bảng xét dấu

x

-∞

1

x

2

x

+∞

'y

- 0 + 0 -

Dựa vào bảng xét dấu ta nhận thấy hàm số chỉ luôn đồng biến trên khoảng

 

1 2

;x x

.

Yêu cầu bài toán

2 1

2 0 2 1 1

x x m

m m

            

.

Câu 38. [2D2-3.1-4] Cho

log log

10 ; 10

m m

n b n c

a b

 

 

với

, , , ,a b c m n

là các số nguyên sao cho các biểu thức

có nghĩa. Tính biểu thức

logc

theo

log a

.

A.

 

2

log

m n a mn

c

n a m

 





. B.

 

2

log

n m a mn

c

n a m

 





.

C.

 

2

log

n m a n

c

n a mn

 





. D.

 

2

log

m n a mn

c

m a n

 





.

Lời giải

Chọn B.

log

10 log log log

log log log

m

n b

m m n a m

a a n b b

n b a a



       



;

log

10 log

log

m

n c

m

b b

n c



  



Ta có

 

2

log

log log

log log log

log log log log

n m a mn

m n a m m a

b n c c

n c a n a m n a m

 



      

  

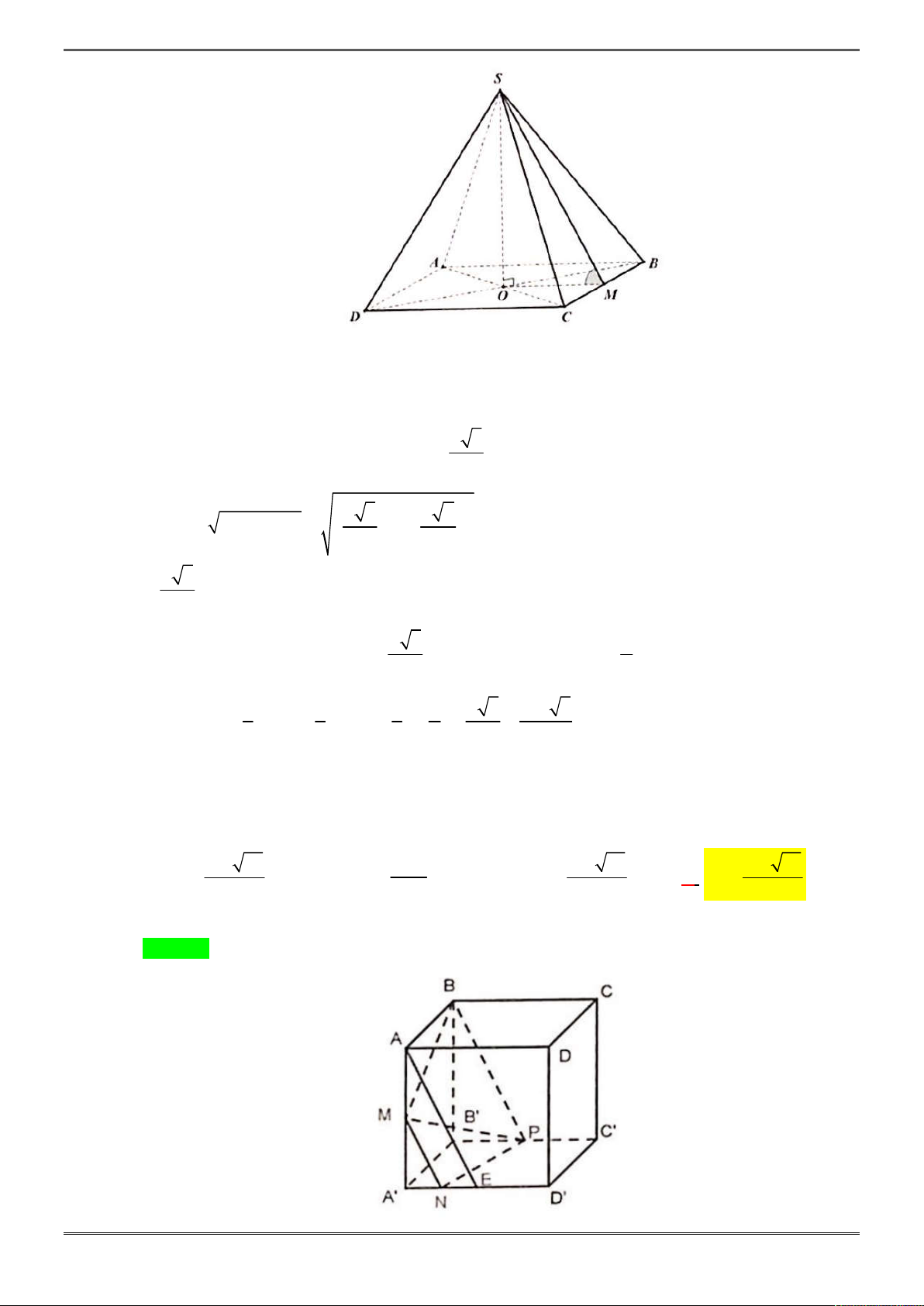
Câu 39. [2H2-1.4-4] Cho hình chóp đều

.

S ABCD

có đáy

ABCD

là hình vuông. Độ dài

5

2

a

SB 

.

Góc giữa mặt bên và mặt đáy bằng

60

. Tính thể tích khối nón có đỉnh

S

và đáy là đường

tròn nội tiếp hình vuông

ABCD

.

A.

3

24

a



. B.

3

8

a



. C.

3

27

a



. D.

3

a



.

Lời giải

Chọn A.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 15

Gọi

M

là trung điểm

BC

. Ta chứng minh được góc giữa mặt bên

 

SBC

và đáy

 

ABCD

bằng góc



60

SMO

 

.

Đặt

AB x

. Độ dài

3

.tan 60

2

x

SO OM  

.

2 2

3 2

2 2

5

2

x x

SB SO OB

x

x a

   

    

   

   

  

Khối nón có chiều cao

3

2

a

h SO 

, bán kính đáy

2

a

R OM

 

.

Thể tích

2

3

2

®ёy

1 1 1 3 3

. . .

3 3 3 2 2 24

a a a

V V h R h



 

 

   

 

 

.

Câu 40. [2H2-2.1-4] Cho hình lập phương

. ' ' ' 'ABCD A B C D

cạnh

a

. Gọi

, M P

lần lượt là trung

điểm của

'AA

và

' 'B C

.

N

là điểm thuộc cạnh

' 'A D

thỏa mãn

3 ' 'A N ND

. Tính diện tích

0

S

của thiết diện của

 

MNP

với hình lập phương.

A.

2

0

3 85

32

a

S 

. B.

2

0

15

32

a

S  . C.

2

0

3 21

8

a

S 

. D.

2

0

3 21

16

a

S 

.

Lời giải

Chọn D.

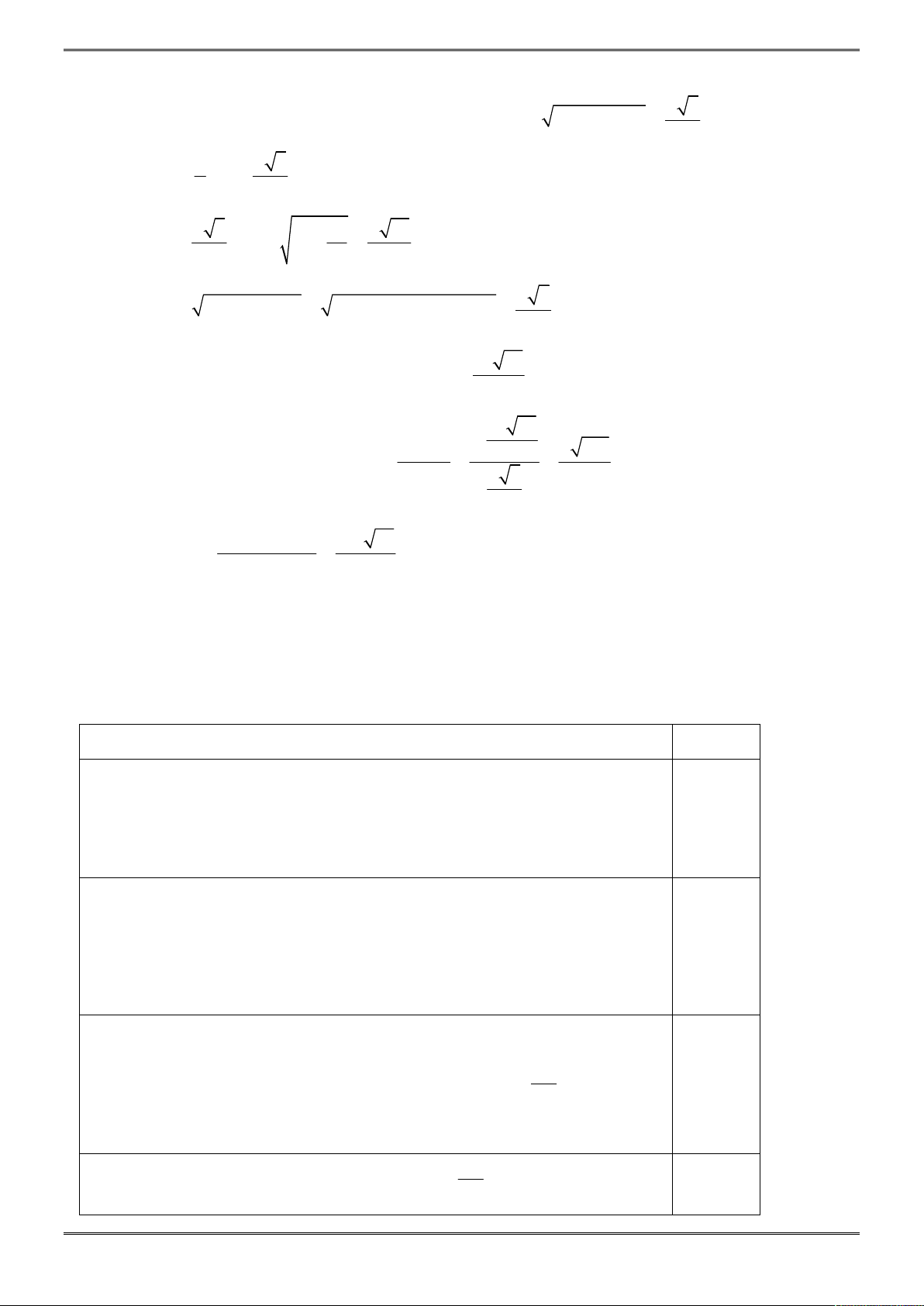
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 16

Gọi

E

là trung điểm của

' 'A D

. Khi đó

/ / / /MN AE BP

. Do đó thiết diện cần tìm là hình

thang

MNPB

. Dựa vào các tam giác vuông thì

2 2

5

' '

2

a

BP BB B P  

và

1 5

2 4

a

MN AE 

.

2

5 17

;

2 16 4

a a a

MB NP a    ;

2 2 2 2 2

6

' ' ' ' ' '

2

a

MP PA A M A B B P A M     

.

Sử dụng công thức Hê-rông để tính

2

21

8

MPB

a

S





.

Ta có chiều cao hình thang là

2

21

2.

2

105

8

10

5

2

MBP

a

S a

h

BP

a



  

.

Vậy

 

2

0

3 21

2 16

h MN BP

a

S



 

.

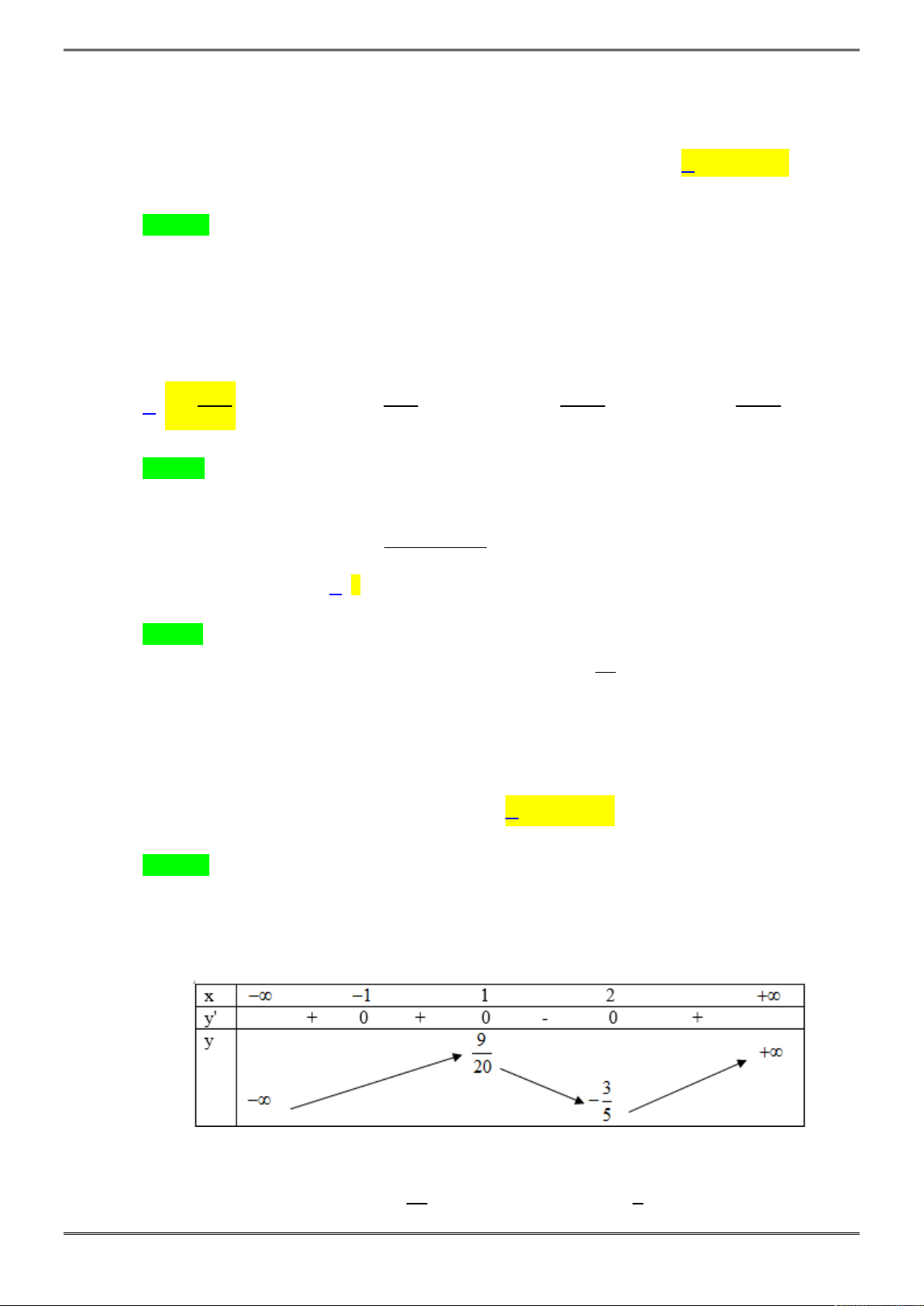
PHẦN II: PHẦN TỰ LUẬN

Bài 1. (1,0 điểm) Tìm tất cả các giá trị của tham số

m

để hàm số

3 2

– 3 –1y x x mx

  có hai điểm cực trị

1 2

,x x

thỏa

2 2

1 2

6

x x

 

.

Đáp án chi tiết Điểm

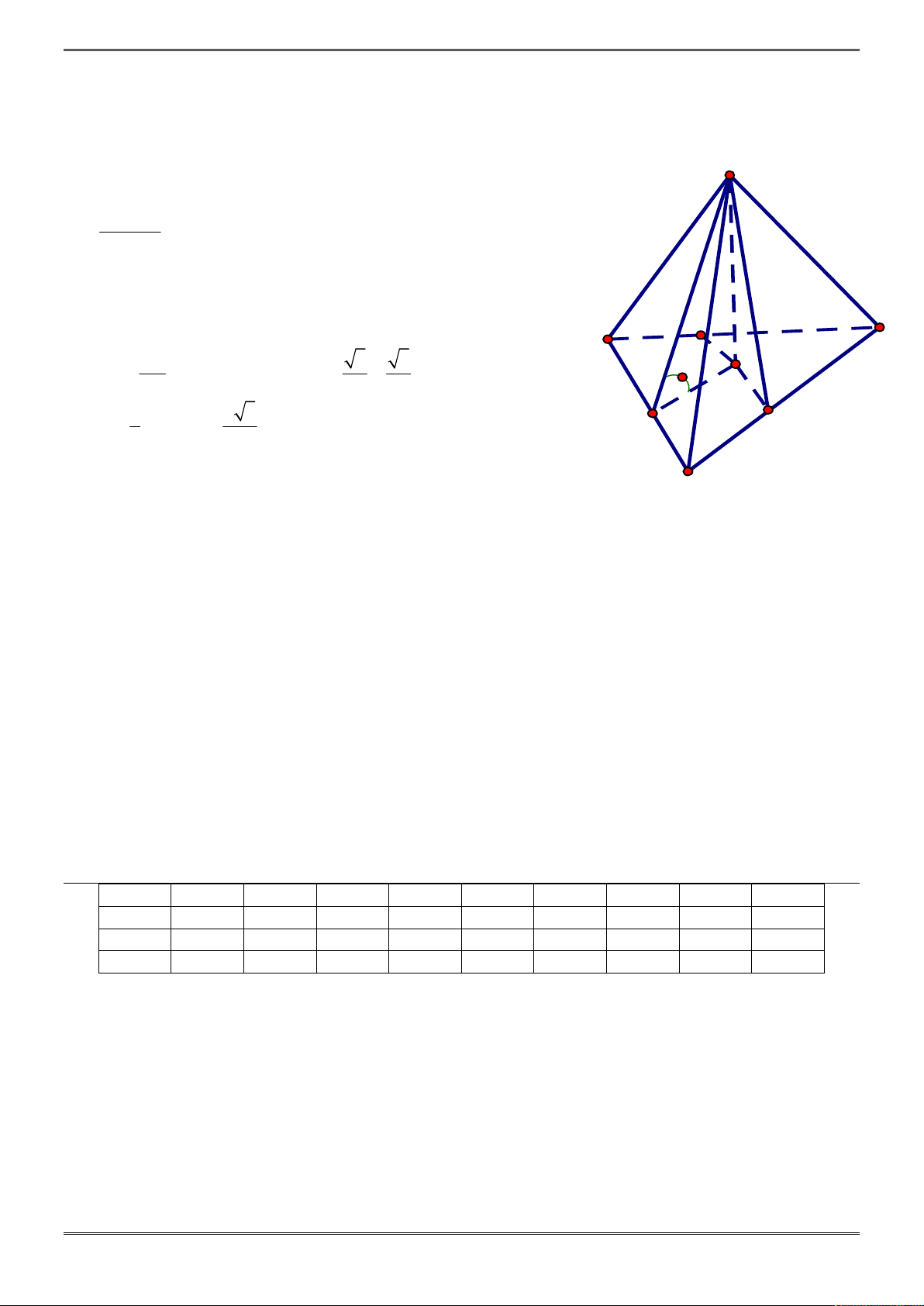
2

3 6

y x x m



  

.

Cho

 

2

0 3 6 0 1

y x x m



    

0,25

Hàm số đã cho có cực trị khi và chỉ khi

 

1

có hai nghiệm phân

biệt

hay

9 3 0 3

m m



     

.

0,25

Khi đó hàm số có cực trị

1 2

,x x

là nghiệm phương trình

 

1

.

Theo Viet, ta có

 

2

2 2

1 2 1 2 1 2

2

2 4

3

m

x x x x x x     

.

0,25

Yêu cầu bài toán tương đương với:

2

4 6 3

3

m

    

 

n

.

0,25

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 17

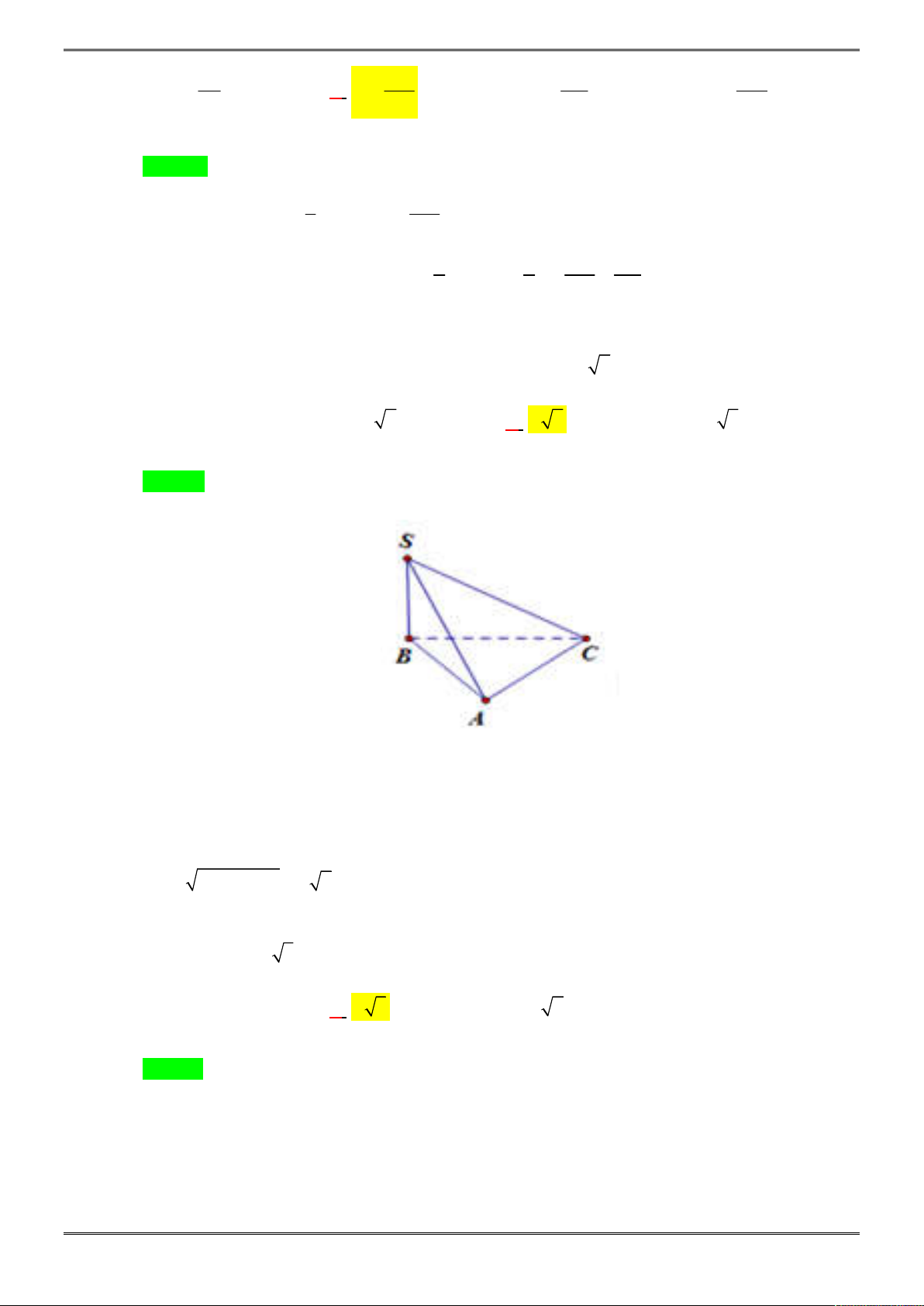
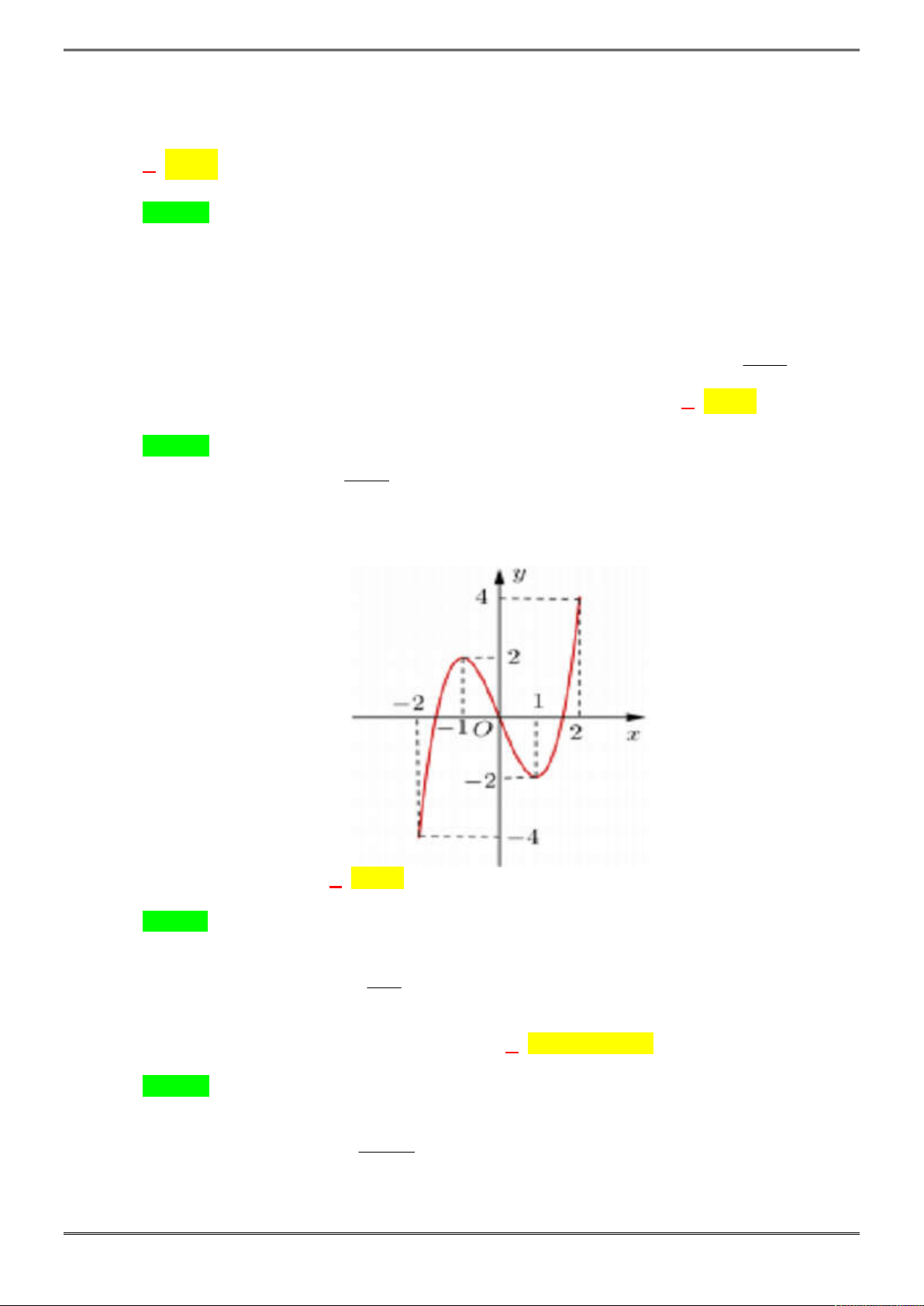
Bài 2. (1,0 điểm)

Cho hình chóp tam giác S.ABC biết

3, 4, 5

AB BC CA

  

.

Tính thể tích hình chóp

.

S ABC

biết các mặt bên của hình chóp đều tạo với đáy một góc 30 độ

Lời giài

Dễ thấy tam giác ABC vuông tại B

6

ABC

S





Gọi p là nữa chu vi

3 4 5

6

2

p

 

 

1S pr r  

Gọi I là tâm đường tròn nội tiếp tam giác ABC, từ giả thiết các

mặt bên tạo với đáy một góc 30 độ ta suy ra I là chân đường cao

của khối chóp

0 0

3 3

tan 30 . an30 1.

3 3

SI

SI MI t

MI

    

.

1 2 3

.

3 3

S ABC ABC

V S SI



 

BẢNG ĐÁP ÁN

1.A

2.A

3.C

4.B

5.A

6.B

7.A

8.D

9.A

10.C

11.A

12.C

13.A

14.B

15.A

16.C

17.B

18.B

19.A

20.C

21.B

22.A

23.B

24.C

25.D

26.A

27.B

28.C

29.B

30.A

31.C

32.B

33.C

34.C

35.C

36.A

37.B

38.B

39.A

40.D

r

A

C

B

I

S

M

30

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 18

ĐỀ ÔN TẬP SỐ 02

PHẦN I: PHẦN TRẮC NGHIỆM

Câu 1. [2D1-1.4-1]: Cho hàm số

3 2

3 9 4y x x x    

. Hàm số đồng biến trên khoảng nào sau đây:

A.

 

1;3



B.

 

3;1



C.

 

; 3 

D.

 

3;



Lời giải

Chọn A.

D  

2

1

' 3x 6x 9; ' 0

3

x

y y

x

 



     







 

' 0, 1;3

y x   

Câu 2. [2D1-4.4-1] Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số

2 1

1

x

y

x







?

A.

1x 

B.

1

y

 

C.

2

y



D.

1

x

 

Lời giải

Chọn D.

Rõ ràng đồ thị hàm số

2x 1

1

y

x







nhận đường thẳng

1

x

 

là tiệm cận đứng.

Câu 3. [2D1-2.5-1] Cho hàm số

 

y f x



xác định, liên tục trên đoạn

 

2;2



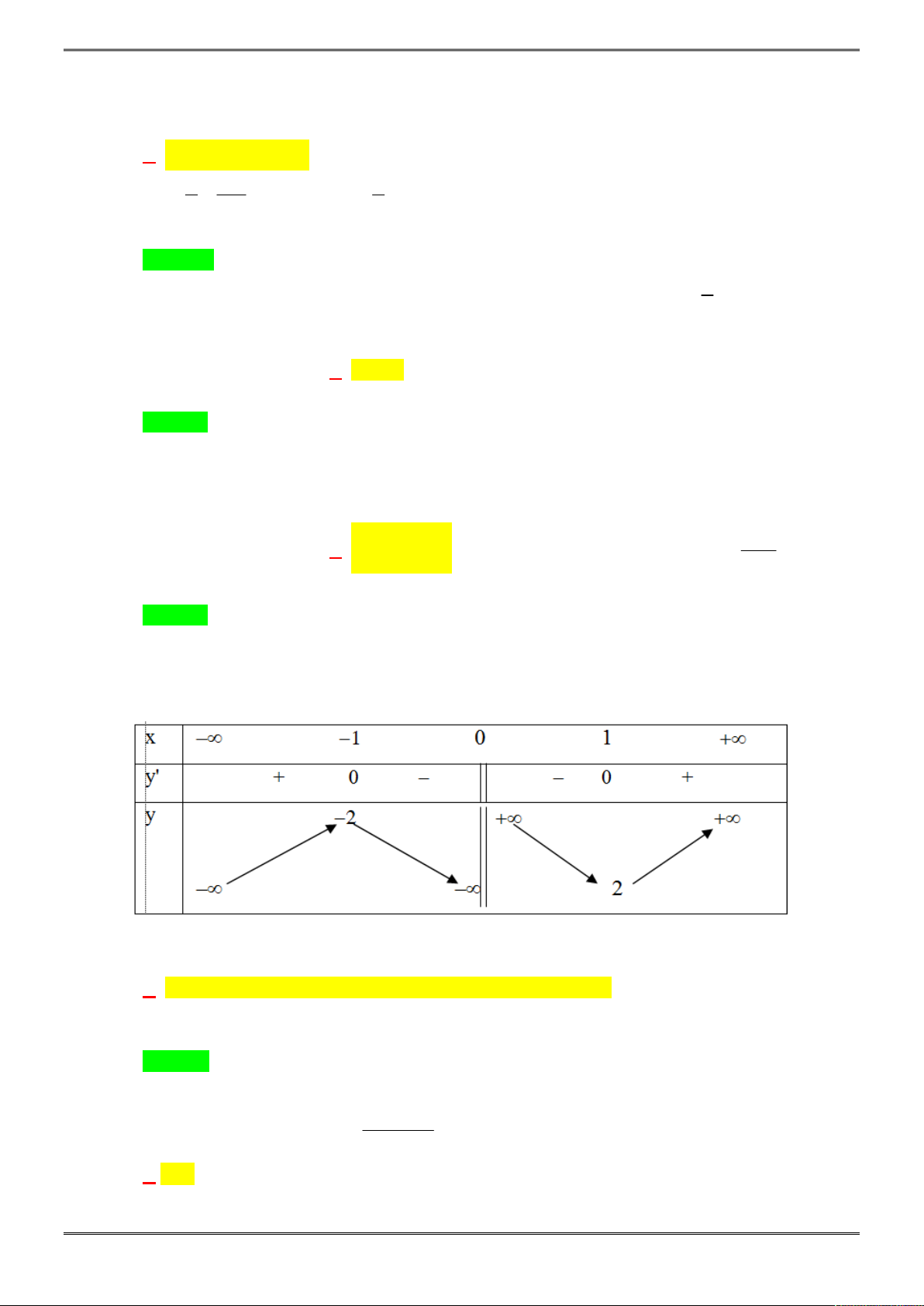
và có đồ thị là đường

cong trong hình vẽ bên. Hàm số f(x) đạt cực đại tại điểm nào dưới đây?

A.

2

x

 

B.

1

x

 

C.

1x 

D.

2

x



Lời giải

Chọn B.

Từ hình vẽ ta có ngay hàm số f(x) đạt cực đại tại điểm

1

x

 

Câu 4. [2D1-2.6-1] Cho hàm số

1

x

y

x







. Hàm số có:

A. Một cực đại. B. Một cực tiểu.

C. Một cực đại và một cực tiểu. D. Không có cực trị.

Lời giải

Chọn D.

Tập xác định

 

\ 1

D 



.

 Đạo hàm:

 

2

' 0

1

y

x

  



với

x D 

⇒ Hàm số không có cực trị.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 19

 Nhận xét rằng hàm phân thức bậc nhất trên bậc nhất không có cực trị nên ta thấy ngay việc

lựa chọn đáp án D là đúng

Câu 5. [2D2-3.2-1] Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng?

A.

 

ln ln lnab a b

 

B.

 

ln ln lnab a b



C.

ln

a a

b b



D.

ln ln ln

a

b a

b

 

Lời giải

Chọn A.

Với các số thực dương a,b bất kì ta có

 

ln . ln lna b a b

 

và

ln ln ln

a

a b

b

 

Câu 6. [2D2-5.1-1] Giải phương trình

 

4

log 1 3

x

 

A.

63

x



B.

65

x



C.

80

x



D.

82

x



Lời giải

Chọn B.

Biến đổi

 

3

4

log 1 3 1 4 65

x x x

      

hoặc sử dụng MTCT thử các kết quả bằng phím

CALC

Câu 7. [2D2-4.2-1] Tính đạo hàm của hàm số

13

x

y  .

A.

1

' .13

x

y x



 B.

' 13 .ln13

x

y  C.

' 13

x

y  D.

13

'

ln13

x

y 

Lời giải

Chọn B.

Áp dụng công thức đạo hàm:

 

' ln ,

x x

a a a x

  

với

0, 1

a a

 

Câu 8. [2D1-2.5-2] Cho hàm số

 

y f x



xác định và liên tục trên

 

0\

R

và có bảng biến thiên:

Khẳng định nào sau đây là khẳng định SAI?

A. Hàm số nghịch biến trên mỗi khoảng

 

1;0



và

 

0;1

B. Hàm số đồng biến trên mỗi khoảng

 

; 1 

và

 

1;



C. Hàm số có giá trị cực đại bằng 2 và giá trị cực tiểu bằng

2

D. Hàm số có hai cực trị.

Lời giải

Chọn C.

Khẳng định C sai vì hàm số có giá trị cực đại bằng -2 và giá trị cực tiểu bằng 2.

Câu 9. [2D1-2.6-2] Cho hàm số

2

4

1

x x

y

x

 





. Tích các giá trị cực đại và cực tiểu của hàm số bằng:

A.

15

. B.

10

. C.

5

. D.

0

.

Lời giải

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 20

Chọn A.

Tập xác định

 

\ 1

D 



.

 Đạo hàm:

 

2

4

' 1

1

y

x

 



,

 

2

1

2

1

4

' 0 1 0 1 4

3

1

x

y x

x

 



       









.

Khi đó, tích các giá trị cực đại và cực tiểu của hàm số bằng:

   

 

2

1 1 4

3 3 4

1 . 3 . 15

1 1 3 1

P y y

  

 

    

  

.

Câu 10. [2D1-4.6-2] Đồ thị hàm số

2

2 3

1

x

y

x







có bao nhiêu đường tiệm cận?

A.

1

B.

2

C.

3

D.

4

Lời giải

Chọn D.

2

2 3

1

x

y

x







TXĐ:

( ;1) (1; )

D

    

.

Ta có:

lim 2

x

y



 

suy ra đường thẳng

2

y

 

là TCN của đồ thị hàm số.

lim 2

x

y



 

suy ra đường thẳng

2

y



là TCN của đồ thị hàm số.

1

lim

x

y





 

suy ra đường thẳng

1x 

là TCN của đồ thị hàm số.

1

lim

x

y





 

suy ra đường thẳng

1

x

 

là TCN của đồ thị hàm số.

Vậy đồ thị của hàm số đã cho có tổng cộng 4 đường tiệm cận.

Câu 11. [2D1-6.1-2] Cho hàm số

 

4 6

:

1

x

C y

x







. Tổng bình phương các hoành độ giao điểm của đồ

thị hàm số (C) với đường thẳng

6 5y x 

bằng:

A.

5

36

. B.

7

36

. C.

11

36

. D.

13

36

.

Lời giải

Chọn D.

Phương trình hoành độ giao điểm:

1

2

1

4 6 1

6 5

1 3

6 5 1 0

x

x x

x

x x







    





  



và

2 2

2 1 2

1 1 1 13

2 3 2 36

x x x

   

     

   

   

.

Câu 12. [2D1-3.4-2] GTNN của hàm số

1

5y x

x

  

trên

1

;5

2

 

 

 

A.

5

2



B.

1

5

C.

3

D.

2

Lời giải

Chọn C.

 

2

2 2

1

1 1

' 1 ' 0

1

x

y y L

x

x x

 





      







   

1 5 1

1 3; ; 5

2 2 5

f f f

 

    

 

 

Vậy GTNN của hàm số là -3.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 21

Câu 13. [2D1-1.4-2] Hàm số nào sau đây luôn đồng biến trên tập xác định (các khoảng xác định)?

A.

3

y x x  

B.

4 2

y x x 

C.

1

2

x

y

x







D.

1

2

x

y

x







Lời giải

Chọn A.

Ta có:

3 2

' 3 1 0

y x x y x

       

với mọi x nên hàm số nghịch biến trên



Hàm trùng phương

4 2

y x x 

luôn có cực trị nên không đồng biến trên R.

 

2

1 1

' 0

2

x

y y

x

 

   



với mọi x thuộc tập xác định nên hàm số nghịch biến.

 

2

1 1

' 0

2

x

y y

x



   



với mọi x thuộc tập xác định nên hàm số đồng biến.

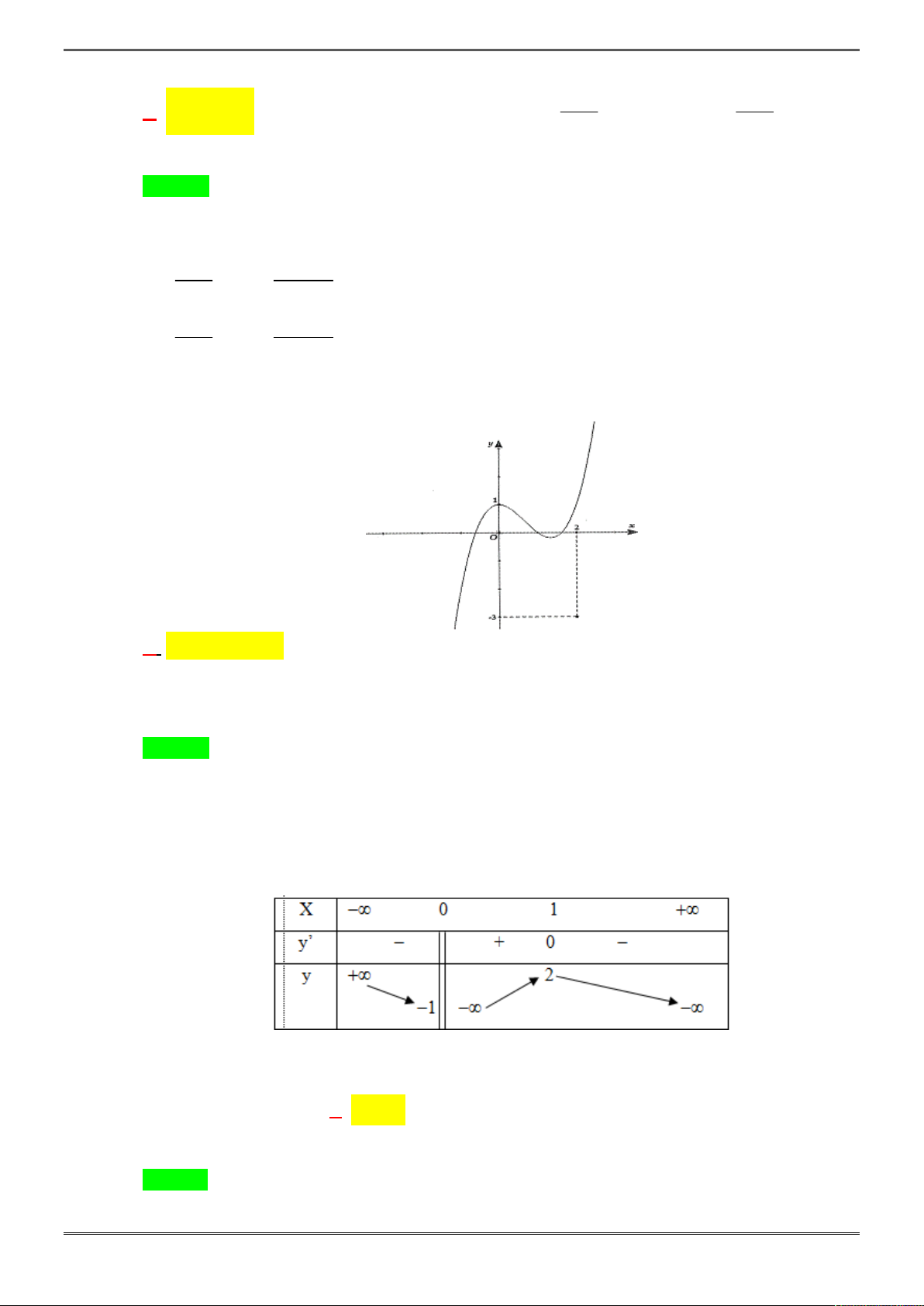
Câu 14. [2D1-5.1-2] Đồ thị hàm số ở hình bên dưới là của đáp án:

A.

3 2

2 1

y x x

  

B.

3 2

1

y x x

  

C.

3 2

2 2

y x x

  

D.

3 2

3 1

y x x

  

Lời giải

Chọn A.

- Đồ thị hàm số đi qua điểm

 

0;1

nên loại C.

- Đồ thị hàm số đi qua điểm

 

1;0

nên loại B, D.

Câu 15. [2D1-6.2-2] Cho hàm số

 

y f x



xác định trên

 

\ 0

, liên tục trên mỗi khoảng xác định và

có bảng biến thiên như sau:

Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình

 

f x m

có ba nghiệm

thực phân biệt.

A.

 

1;2



B.

 

1;2



C.





1;2



D.





;2



Lời giải

Chọn B.

Từ bảng biến thiên trên ta có ngay

 

1 2 1;2

m m     

thỏa mãn bài toán

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 22

Câu 16. [2D1-2.3-2] Cho hàm số

( )y f x

xác định, liên tục trên



và có bảng biến thiên:

Khẳng định nào sau đây là đúng?

A. Hàm số có giá trị cực đại bằng 3.

B. Hàm số có GTLN bằng

1

, GTNN bằng

1

3



C. Hàm số có hai điểm cực trị.

D. Đồ thị hàm số không cắt trục hoành.

Lời giải

Chọn C.

Nhận thấy hàm số đạt cực đại tại

3

CD

x



, giá trị cực đại bằng 1 và đạt cực tiểu tại

1

CT

x



, giá

trị cực tiểu bằng

1

3



.

Câu 17. [2D2-1.2-2] Cho biểu thức

4

3

2 3

. .

P x x x



, với

0

x



. Mệnh đề nào dưới đây đúng ?

A.

1

2

P x

B.

13

24

P x

 C.

1

4

P x

D.

2

3

P x

Lời giải

Chọn B.

Ta có:

6 13

3 7 13

4 4

3 3

4 4

4

3

2 3 2

7 6

2 2 24

x. x x. x . . .

P x x x x x x x x

     

Câu 18. [2D2-3.2-2] Cho các số thực dương a, b với

1

a



. Khẳng định nào sau đây là khẳng định đúng

?

A.

 

3

2

3

log 6 log

2

a

a b b

 

B.

 

3

2

2 1

log log

3 6

a

a b b

 

C.

 

3

2

3

log log

2

a

a b b



D.

 

3

2

1

log log

6

a

a b b



Lời giải

Chọn A.

 

1

3

1 1 1

2 2 2 2

2 2 2

log log 3log 3 log log

a a a

a

a b a b a b a b

     

   

     

     

1 3

3 2 log 6 log

2 2

a a

b b

 

   

 

 

Câu 19. [2D2-6.1-2] Phương trình

   

3 2

3 3

log 6 7 1 log 3 2

x x x x

    

có tập nghiệm là:

A.

1 1

;

2 3

T

 



 

 

. B.

1 1

;

2 3

T

 

 

 

 

. C.

1 1

;

2 3

T

 

 

 

 

. D.

1 1

;

2 3

T

 

 

 

 

.

Lời giải

Chọn D.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 23

 

2

3 2

2

3 2 0

1

6 7 1 3 2

6 4 1 0

2

1 1

1

;

2 3

1 1

1 6 5 1 0

1, ,

2 3

x

x x

x

x x x x

x x x

x

x x

x x x

 





  









 



    







   



 



 

















      



 

 

   

    







Vậy, phương trình có tập nghiệm là

1 1

;

2 3

T

 

  

 

 

.

Câu 20. [2D2-5.3-2] Phương trình

1 1

3 3 10

x x 

 

có tập nghiệm là:

A.

 

1;0

T  

. B.

 

0;1

T 

. C.

 

1;1

T  

. D. Vô nghiệm.

Lời giải

Chọn C.

Biến đổi phương trình về dạng:

3.3 3.3 10

x x

 

.

Đặt

 

3 , 0

x

t t

 

, phương trình có dạng:

2

1

3

1

3

3 10 3 10 3 0

3

1

3

3 3

x

t

t t t

x

t





 







        













.

Vậy, phương trình có tập nghiệm là

 

1

T

 

.

Câu 21. [2D2-1.0-2] Một người đầu tư 100 triệu đồng vào một công ty theo thể thực lãi kép với lãi suất

13% một năm. Hỏi nếu sau 5 năm mới rút lãi thì người đó thu được bao nhiêu tiền lãi ? (Giả sử

rằng lãi suất hàng năm không thay đổi)

A.

 

5

100 1,13 1

 



 

(triệu đồng) B.

 

5

100 1,13 1

 



 

(triệu đồng)

C.

 

5

100 0,13 1

 



 

(triệu đồng) D.

 

5

100 0,13

(triệu đồng)

Lời giải

Chọn A.

Ta có số tiền lãi là

 

5

100 1 13% 1 100 1.13 1

 

   

 

.

Câu 22. [2D1-5.3-3] Cho hàm số

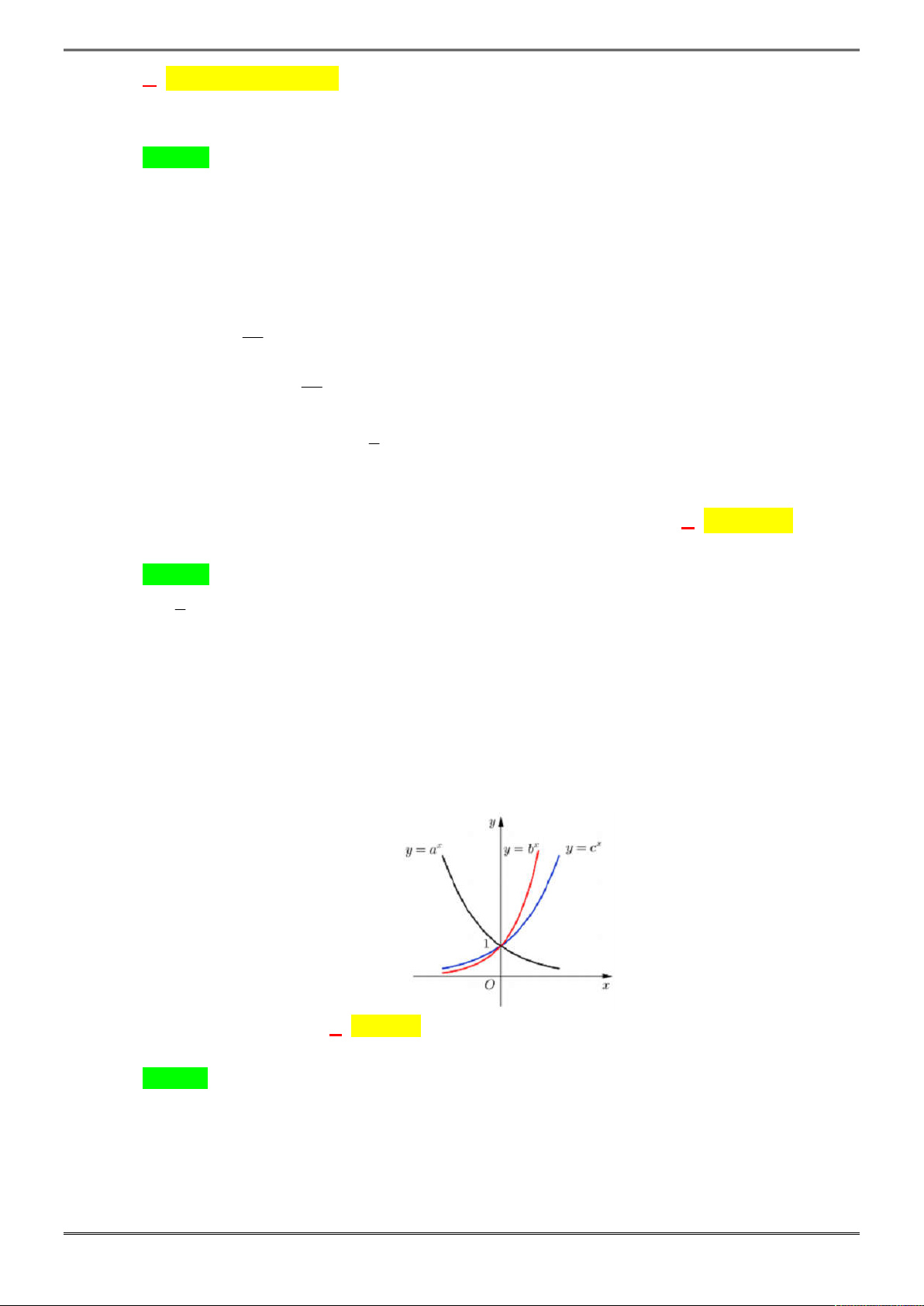
3 2

y ax bx cx d   

có đồ thị như hình vẽ bên. Mệnh đề nào dưới

đây đúng ?

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 24

A.

0, 0, 0, 0

a b c d

   

B.

0, 0, 0, 0

a b c d

   

C.

0, 0, 0, 0

a b c d

   

D.

0, 0, 0, 0

a b c d

   

Lời giải

Chọn A.

Dựa vào đồ thị hàm số

3 2

y ax bx cx d   

, ta có nhận xét sau

* Đồ thị hình chữ N ngược nên hệ số

0

a



* Ta có

 

3 2 2 2

*

' 3 2 0 * ' 3y ax bx cx d y ax bc c b ac

            

Đồ thị hàm số đi qua hai điểm cực trị có hoành độ

1 2

,x x

trái dấu nhau nên

 

*

1 2

' 0

0

. 0

3

c

x x

a

 





 



 





* Dễ thấy

1 2

2

0 0

3

b

x x b

a

     

và đồ thị hàm số cắt Ox tại ba điểm phân biệt nên

0

d



Câu 23. [2D1-1.5-3] Cho hàm số

   

3 2

1

1 2 2016

3

y x m x m m x     

. Tìm tất cả các giá trị m để

hàm số đồng biến trên khoảng

 

3;7

.

A.

1

m



B.

1

m



C.

5

m



D.

5; 1

m m

 

Lời giải

Chọn D.

       

3 2 2

1

1 2 2016 ' 2 1 2

3

y x m x m m x y x m x m m

           

' 0

2

x m

y

x m





 



 



. Lúc này hàm số đồng biến trên các khoảng

   

; , 2;m m

  

Vậy hàm số đồng biến trên khoảng

 

2 3 1

3;7

2 7 5

m m

   







   



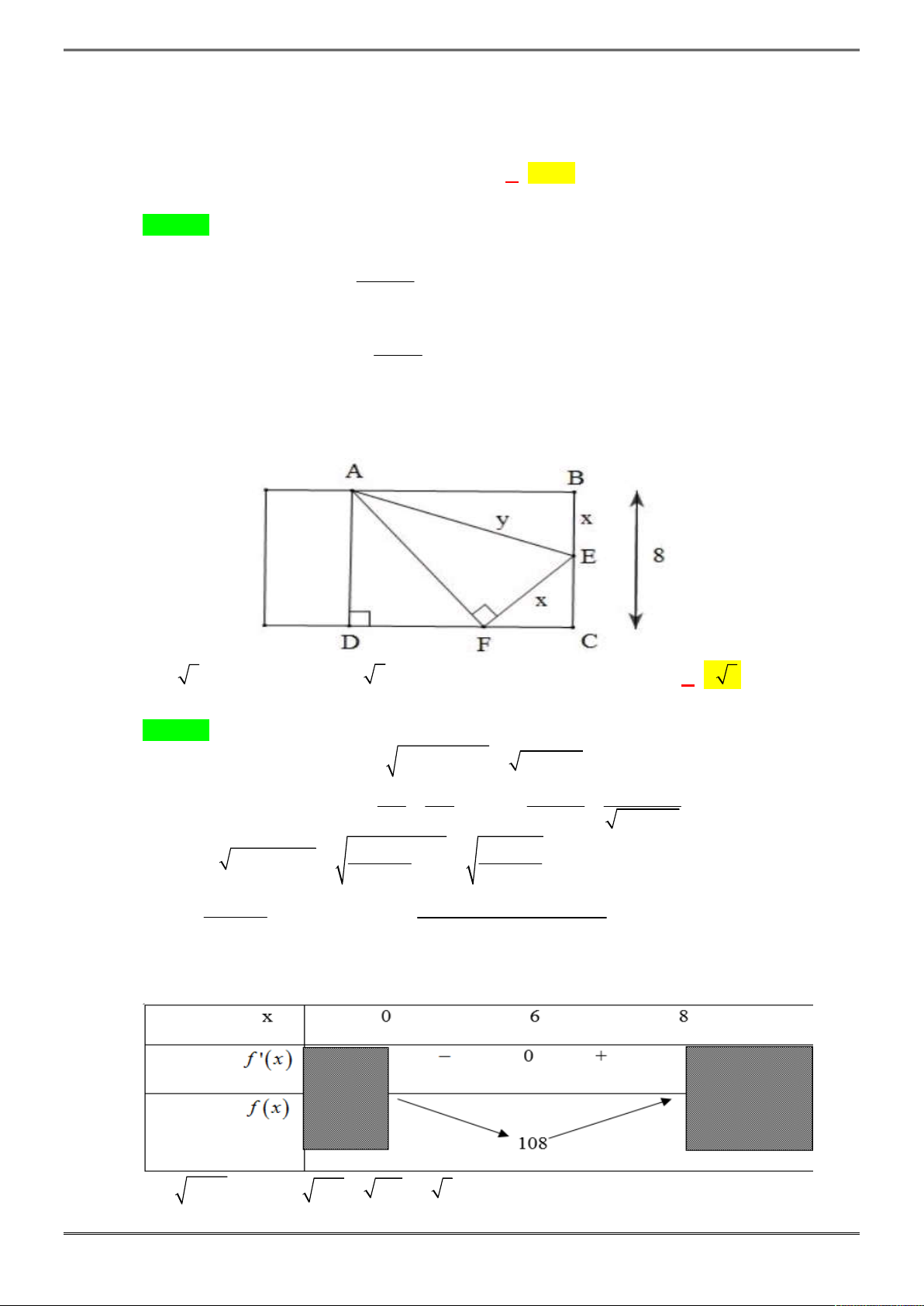
Câu 24. [2D2-4.7-3] Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số , y b ,

x x x

y a y c  

được

cho trong hình vẽ bên. Mệnh đề nào dưới đây đúng ?

A.

a b c 

B.

a c b 

C.

b c a 

D.

c a b 

Lời giải

Chọn B.

Dựa vào đồ thị hàm số, ta có nhận xét sau:

*

1

x

y a

là hàm số nghịch biến trên TXĐ và

2 3

,

x x

y b y c 

là các hàm số đồng biến trên

TXĐ. Do đó

a b

và

a c

.

* Tại điểm

   

0 0

0 2 0 3 0

0

x x

x x y x y x b c b c       

và tương tự tại điểm

0

x x

 

   

0 0

2 0 3 0

x x

y x y x b c b c     

. Do đó

b c a 

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 25

Câu 25. [2D2-7.1-4] Số lượng của loại vi khuẩn A trong một phòng thí nghiệm được tính theo công

thức

   

0 .2

t

s t s

, trong đó

 

0s

là số lượng vi khuẩn

A

lúc ban đầu,

 

s t

là số lượng vi

khuẩn A có sau

t

phút. Biết sau 3 phút thì số lượng vi khuẩn

A

là 625 nghìn con. Hỏi sau bao

lâu, kể từ lúc ban đầu, số lượng vi khuẩn

A

là 10 triệu con ?

A. 48 phút. B. 19 phút. C. 7 phút. D. 12 phút.

Lời giải

Chọn C.

Sau 3 phút số lượng vi khuẩn A là 625 nghìn con, do đó

   

3

625000

625000 0 .2 0 78125

8

s s   

Sau t phút số lượng vi khuẩn A là 10 triệu con, do đó

7

6

2

10

10.10 78125.2 log 7

78125

t

 

   

 

 

Câu 26. [2D1-3.14-4] Cho một tờ giấy hình chữ nhật với chiều dài

12

cm và chiểu rộng 8cm. Gấp góc

bên phải của tờ giấy sao cho sau khi gấp, đỉnh của góc đó chạm đáy dưới như hình vẽ. Để độ

dài nếp gấp là nhỏ nhất thì giá trị nhỏ nhất đó bằng bao nhiêu?

A.

6 5

B.

6 2

C. 6 D.

6 3

Lời giải

Chọn D.

Đặt

 

2

, 8 8 16 64

EF x EC x FC x x x

        

Ta có

 

.

EF CF

ADF FCE g g

AF AD

    



. 8

16 64

EF AD x

AF

FC

x

 



2 3

2 2 2

64 16

16 64 16 64

x x

y AE AF EF x

x x

     

 

   

3

16

0;8

16 64

x

f x x

x

 



;

 

2 3

2

48 16 64 16.16

'

16 64

x x x

f x

x

 





 

3 2 3 3 2

' 0 768 3072 256 0 512 3072 0 6

f x x x x x x x

         

BBT:

 

min min

108 6 3

y f x y f    

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 26

Câu 27. [2D2-3.0-4] Xét các số thực a, b thỏa mãn

1

a b

 

. Tìm giá trị nhỏ nhất

min

P

của biểu thức

 

2 2

log 3log

a b

b

a

P a

b

 

 

 

 

A.

min

19

P



B.

min

13

P



C.

min

14

P



D.

min

15

P



Lời giải

Chọn D.

Ta có:

 

2

2 2

4 3 4 3

2log 3 log 1 3 3

log log

1 log

log

a b

a a

b

a

P a a

b b

ba

b

 

        

 



 

 

 

 

Đặt

log

a

t b

 (Do

1 0 1a b t    

).

Xét

 

2

4 3

3

1

f t

t

  



Khi đó

 

3

2

8 3 1

' 0

3

1

f t t

t



    



. Ta có:

   

0 1

1

lim lim ; 15

3

x x

f t f t f

 

 

 

   

 

 

Do đó

min

15

P



Câu 28. [2D2-5.7-4] Tìm tập hợp tất cả các giá trị của tham số thực

m

để phương trình

 

6 3 2 0

x x

m m

    

có nghiệm thuộc khoảng

 

0;1

.

A.

 

3;4

B.

 

2;4

C.

 

2;4

D.

 

3;4

Lời giải

Chọn C.

Phương trình

 

3.2 6

6 3 .2 0 6 3.2 2 1 0 *

2 1

x x

x x x x x

x

m m m m



          



Đặt

2

log

2

2 log 6 6

t

x x

t x t    

và với

   

0;1 1;2

x t  

.

Khi đó

   

2

log

3 6

1

t

m f t

t



 



Xét hàm số

 

2

log

3 6

1

t

f x

t







trên

   

 

2

log

2

3 6 . ln3 1 ln3

1;2 , ' 0; 1;2

1 .

t

t t

f t t

t t

   

 

   



Nên hàm số

 

f t

là hàm số đồng biến trên

 

1;2

. Do đó để (*) có nghiệm thuộc khoảng

 

0;1

khi và chỉ khi (I) có nghiệm thuộc

     

1;2 1 2 2 4

f m f m

     

.

Vậy

 

2;4

m

là giá trị cần tìm.

Câu 29. [2H1-1.1-1] Số cạnh của một hình bát diện đều là

A.

8

B.

10

C.

12

D.

20

Lời giải

Chọn C.

Câu 30. [2H1-1.4-1] Trong các mệnh đề sau, mệnh đề nào sai?

A. Hình lập phương là hình đa diện lồi

B. Tứ diện là đa diện dồi

C. Hình hộp là là đa diện lồi

D. Hình tạo bởi hai tứ diện đều là ghép với nhau là một hình đa diện lồi

Lời giải

Chọn D.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 27

Câu 31. [2H2-3.5-1] Một hình trụ (T) có bán kính đáy

4r 

và có khoảng cách giữa hai đáy bằng 5.

Tính diện tích xung quanh S của (T)

A.

40

S





B.

80

S





C.

80

3

S





D.

20

S





Lời giải

Chọn A.

Diện tích xung quanh của hình trụ là

2 2 .4.5 40

S rh

  

  

Câu 32. [2H1-3.1-2] Cho lăng trụ đứng

. ’ ’ ’ABC A B C

có đáy

ABC

vuông tại

B

;

AB a

,



0

60

BAC  ;

AA ' 3a

 . Thể tích khối lăng trụ là:

A.

3

2

a

B.

3

2

3

a

C.

3

a

D.

3

9

a

Lời giải

Chọn A.

Ta có:

0

.tan 60 3BC AB a

 

2

. ' ' '

1 3

.AA'= .a.a. 3. 3

2 2

ABC A B C ABC

a

V S a  

Câu 33. [2H1-3.5-2] Một hình nón tròn xoay có thiết diện qua trục là một tam giác vuông cân có cạnh

bằng

a

. Tính diện tích

tp

S

toàn phần của hình nón đó:

A.

2

tp

a

S





. B.

 

2

2 4

2

tp

a

S





 . C.

 

2

2 8

2

tp

a

S





 . D.

 

2

2 1

2

tp

a

S







Lời giải

Chọn A.

l

Theo đề suy ra đường sinh

l a

, và đường tròn đáy có bán kính

2

a

r 

. Khi đó

2

xq

a

S





, diện tích đáy

2

a

S





Vậy

 

2

2 1

2

tp

a

S





 .

Câu 34. [2H1-2.3-2] Cho khối chóp đều

.

S ABCD

có cạnh đáy bằng

3a

, cạnh bên bằng

2a

. Khi đó,

thể tích của khối chóp

.

S ABCD

là:

A.

3

.

10

2

S ABCD

a

V 

B.

3

.

10

4

S ABCD

a

V 

C.

3

.

3

6

S ABCD

a

V 

D.

3

.

3

12

S ABCD

a

V 

Lời giải

Chọn A.

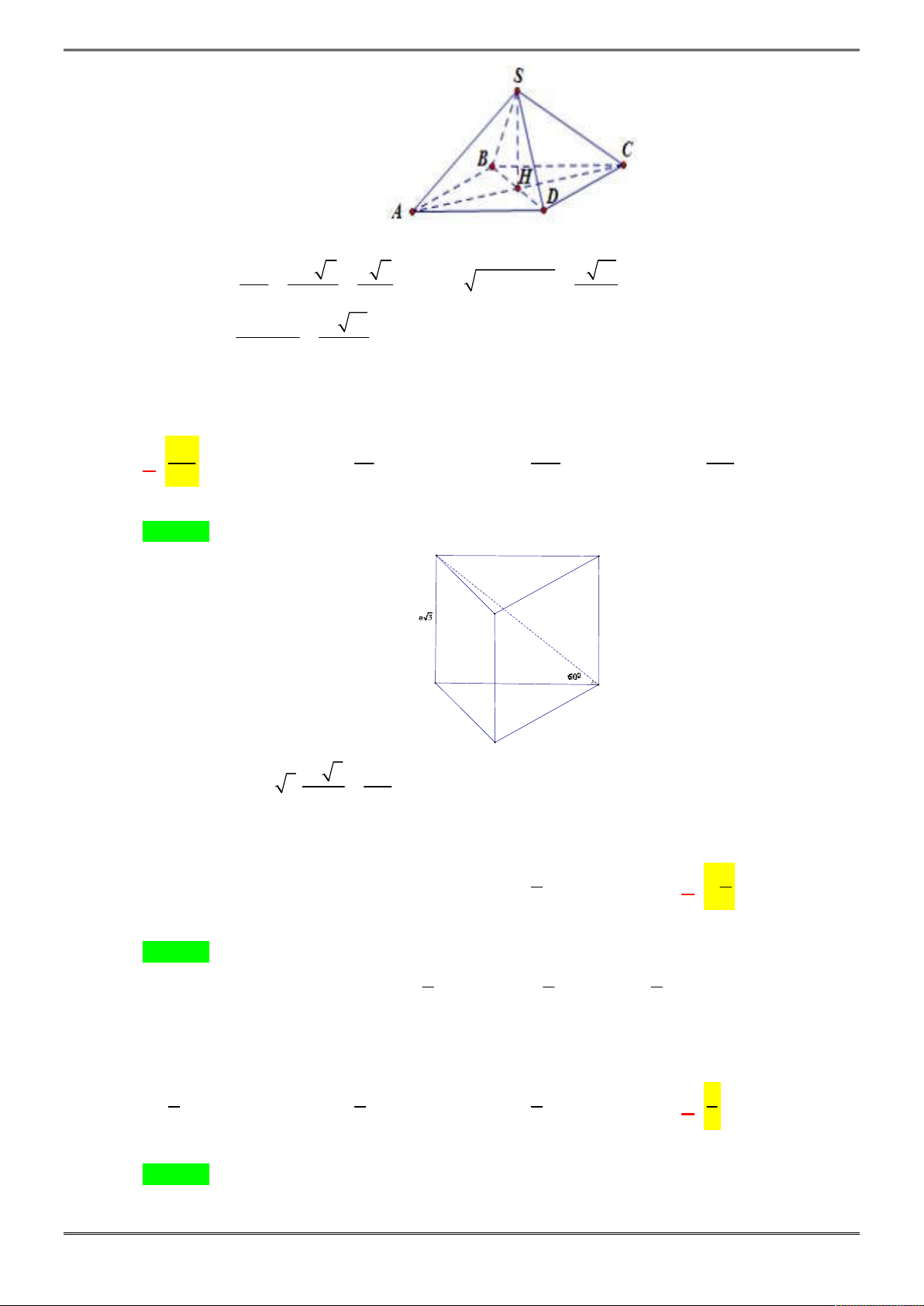
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 28

Gọi H là tâm của hình vuông ABCD

 

SH ABCD

 

Ta có

2 2

2 6 10

2 2 2 2

AC AB a a

AH SH SA HA      

2 3

.

. 10

3 2

S ABCD

SH AB a

V  

Câu 35. [2H1-3.2-2] Cho hình lăng trụ đều

. ’ ’ ’ABC A B C

có cạnh đáy bằng

, ’a A C

hợp với mặt đáy

 

ABC

một góc 60

0

. Thể tích của khối lăng trụ

. ’ ’ ’ABC A B C

bằng:

A.

3

4

a

B.

3

4

a

C.

3

2

3

a

D.

3

8

a

Lời giải

Chọn A.

a

A

C

B

C'

A'

B'

2 3

3 3

' . 3.

4 4

ABC

a a

V A A S a  

Câu 36. [2H1-1.5-2] Cho phép vị tự tâm

O

biến

A

thành

B

, biết rằng

4OA OB

. Khi đó tỉ số vị tự là

bao nhiêu?

A.

4

. B.

4

. C.

1

4

. D.

1

4



.

Lời giải

Chọn D.

Từ giả thiết

4OA OB

, suy ra:

1 1 1

4 4 4

OB OA OB OA k

      

 

Câu 37. [2H1-3.0-2] Cho khối lăng trụ đều

. ’ ’ ’ABC A B C

và

M

là trung điểm của cạnh

AB

. Mặt phẳng

 

’ ’B C M

chia khối lăng trụ thành hai phần. Tính tỷ số thể tích của hai phần đó?

A.

7

5

B.

6

5

C.

1

4

D.

3

8

Lời giải

Chọn D.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 29

Câu 38. [2H1-2.3-3] Cho hình chóp tứ giác đều

.

S ABCD

có cạnh đáy bằng

a

, cạnh bên hợp với đáy

một góc

0

60

. Gọi

M

là điểm đối xứng với

C

qua

;D N

là trung điểm của

SC

, mặt phẳng

 

BMN

chia khối chóp

.

S ABCD

thành hai phần. Tính tỉ số thể tích giữa hai phần đó.

A.

1

5

B.

7

3

C.

1

7

D.

7

5

Lời giải

Chọn D.

Đặt

1

2

?

SABIKN

NBCDIK

V V

V

V V

V





 







*

2 3

.

1 6 6

.

3 2 6

S ABCD

a

V a a

 

*

3

.

1 1 1 6 1 6

. . . . . . .2

3 3 2 3 4 2 12

N BMC BMC BMC

SO a

V NH S S a a a

 

   

* Nhận thấy

K

là trọng tâm của tam giác

SMC

2

3

MK

MN

 

*

.

1 1 2 1

. . . .

2 2 3 6

M DIK

M CBN

V

MD MI MK

V MC MB MN

  

3 3

2 . . .CBN

5 5 6 5 6

.

6 6 12 72

M CBN M DIK M

V V V V a a

     

3

3 3 3

1

1 . 2

3

2

7 6

6 5 6 7 6 7

72

6 72 72 5

5 6

72

S ABCD

a

V

V V V a a a

V

a

        

Câu 39. [2H1-1.5-3] Cho hai đường thẳng song song (

 

’

),

d d

và một điểm

O

không nằm trên chúng.

Có bao nhiêu phép vị tự tâm

O

biến

 

d

thành

 

’d

?

A.

0

. B.

1

. C.

2

. D.

0

hoặc

1

.

Lời giải

Chọn D.

Với giả thiết có hai trường hợp là:

   

 

, 'O d d



hoặc

   

 

, 'O d d



.

Trường hợp 1: Nếu

   

 

, 'O d d



, với

 

M d



ta có:

   

' ' '

k

O

V M M d OM kOM

   

 

.

Gọi

, ’H H

theo thứ tự là hình chiếu vuông góc của

O

lên (d) và (d’), suy ra:

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 30

'

OH kOH



 

⇒ k không đổi.

Vậy, trong trường hợp này có đúng một phép vị tự tâm O biến (d) thành (d’).

Trường hợp 2: Nếu

   

 

, 'O d d



thì không có phép vị tự tâm O nào biến (d) thành (d’), bởi

nếu trái lại với

 

M d



ta có:

   

' ' '

k

O

V M M d OM kOM

   

 

⇒

, , 'O M M

thẳng hàng

   

 

, 'O d d

 

, mâu thuẫn.

Vậy, trong trường hợp này không có phép vị tự tâm O nào biến (d) thành (d’).

Do đó, đáp án D là đúng

Câu 40. [2H1-6.1-4] Một hình nón đỉnh S, đáy là hình tròn tâm O, góc ở đỉnh bằng 120°. Trên đường

tròn đáy lấy một điểm A cố định và điểm M di động. Có bao nhiêu vị trí của M để diện tích tam giác

SAM đạt giá trị lớn nhất?

A. Có 1 vị trí B. Có 2 vị trí C. Có 3 vị trí D. Có vô số vị trí

Lời giải

Chọn B.

Gọi H là hình chiếu vuông góc của M lên SA.

Ta có, diện tích ΔSAM được cho bởi:

1

.

2

S SA MH



.

Do đó, diện tích ΔSAM đạt giá trị lớn nhất khi:

MH đạt giá trị lớn nhất ⇔ MH = MS

MS SA 

.

Tức M là giao điểm của đường tròn đáy hình nón với mặt phẳng (P) qua S và vuông góc với

SA.

Từ giả thiết



120

ASB

 

suy ra tồn tại điểm M trên đường tròn đáy thỏa mãn yêu cầu đề bài.

PHẦN II: PHẦN TỰ LUẬN

Bài 1: [2D1-2.13-3] Cho hàm số

3 2 3

3 4y x mx m

   với giá trị nào của

m

để hàm số có 2 điểm cực trị

A

và

B

sao cho

20

AB 

Lời giải

 

2

0

' 3 6 3 2 0

2

x

y x mx x x m

x m





     







Hàm số đã cho có hai điểm cực trị

, ' 0

A B y

 

có hai nghiệm phân biệt 

0

m



(*)

Giả sử:

 

3 3

3

3 3 3

0 4 0;4

2 ; 4

2 8 12 4 0 2 ;0

A A

B B

x y m A m

AB m m

x m y m m m B m



   



  



      





 

3

2 6 2 2 2

4 16 20 4 5 0 1 1

AB m m m m m m

            

thỏa mãn (*)

Bài 2: [2H1-3.4-4] Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Biết rằng chiều

cao của bình gấp 3 lần bán kính đáy của nó. Người ta thả vào đó một khối trụ và đo được thể tích

nước tràn ra ngoài là

 

3

16

9

dm



. Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón,

các điểm trên đường tròn đáy còn lại đều thuộc các đường sinh của hình nón (như hình dưới) và

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 31

khối trụ có chiều cao bằng đường kính đáy của hình nón. Tính diện tích xung quanh

xq

S

của

bình nước.

Lời giải

Xét mặt cắt và kí hiệu các điểm như hình vẽ, ta có thể tích nước tràn ra chính là thể tích của

khối trụ có bán kính đáy là

0

DH EH r 

và chiều cao

0

HK h

. Còn chiều cao của bình đựng

nước dạng hình nón là

AH h

và bán kính đáy là

BH CH r 

. Để ý rằng

3h r

và

0

2h r

.

Ta có:

0 0 0

0

0 0

3 2

3

r h h h h

MK AK h r r r

r

BH AH r h r r r

 



        

Theo đề, thể tích khối trụ là:

2

2 2 2

0 0 0 0 0

16 16

2 2 2

9 9 3

r

r h r h r r r r



 

      

 

 

 

2 2 3

3 6 2 10 4 10

xq

h r l h r S rl dm

 

         

BẢNG ĐÁP ÁN

1.A

2.D

3.B

4.D

5.A

6.B

7.B

8.C

9.A

10.D

11.D

12.C

13.A

14.A

15.B

16.C

17.B

18.A

19.D

20.C

21.A

22.A

23.D

24.B

25.C

26.D

27.D

28.C

29.C

30.D

31.A

32.A

33.A

34.A

35.A

36.D

37.D

38.D

39.D

40.B

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 32

ĐỀ ÔN TẬP SỐ 03

PHẦN I: PHẦN TRẮC NGHIỆM

Câu 1. [2D1-1.1-1] Hàm số nào sau đây đồng biến trên



?

A.

tan .y x

B.

4 2

2 .y x x

  C.

3

3 1.

y x x

  

D.

3

2.

y x

 

Lời giải

Chọn D.

2

' 3 0, x

y x

  

Nên hàm số

3

2

y x

 

luôn đồng biến trên



.

Câu 2. [2D1-1.1-1] Hàm số nào sau đây đồng biến trên từng khoảng xác định của nó?

A.

1

x

y

x







B.

1

x

y

x







C.

1

x

y

x

 





D.

1

x

y

x

 



 

Lời giải

Chọn A.

' 0

y



trên từng khoảng xác định

Câu 3. [2D1-5.1-1] Đồ thị hàm số

2

1

5 2 3

x x

y

x x

 



  

có bao nhiêu tiệm cận:

A. 1 B. 3 C. 4 D. 2.

Lời giải

Chọn B

Ta có :

2

5 2 3 0

x x

   

có 2 nghiệm phân biệt và

1

lim

5

x

y







nên có 2 tiệm cận đứng

và một

tiệm cận ngang.

Vậy đồ thị HS có 3 tiệm cận

Câu 4. [2D2-5.3-1] Tính đạo hàm của hàm số

2 1x

y xe





A.

 

2 1

2 1 .

x

y e x e





 

B.

 

2

2 1 .

x

y e x e



 

C.

2 1

2 .

x

y e





 D.

2 1x

y e





 .

Lời giải

Chọn C.

 

2 1 2 1 2 1 2 1

' 2 2 1

x x x x

y xe y e xe e x

   

     

.

Câu 5. [2D2-1.3-1] Cho hàm số

 

y f x



xác định, liên tục trên



và có bảng biến thiên:

Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số có ba cực trị.

B. Hàm số có giá trị lớn nhất bằng

9

20

và giá trị nhỏ nhất bằng

3

5



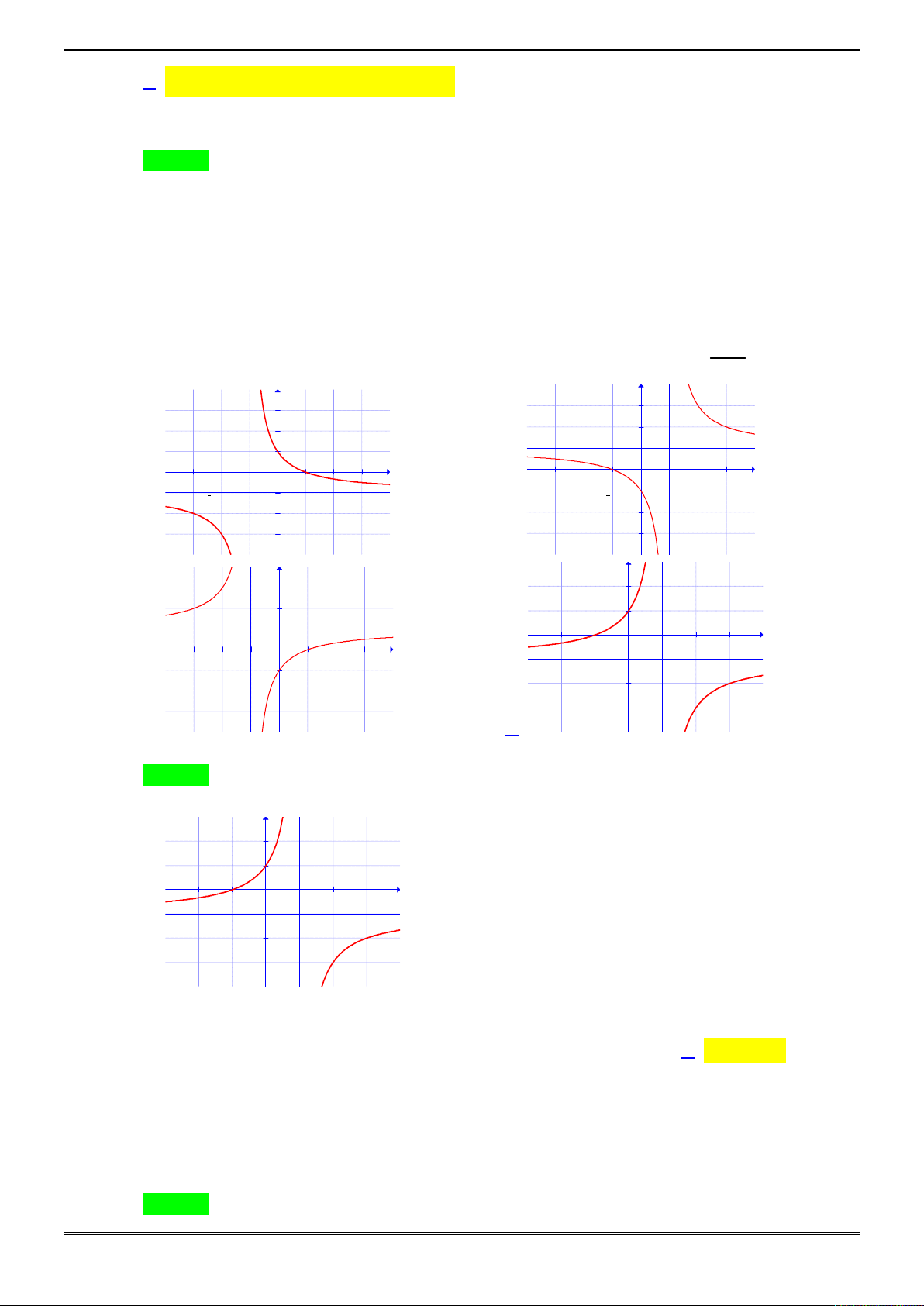
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 33

C. Hàm số đồng biến trên khoảng

 

;1

.

D. Hàm số đạt cực đại tại

2

x



và đạt cực tiểu tại

1x 

.

Lời giải

Chọn C.

Đáp án A sai vì y’ đổi dấu lần 2 khi x qua

0

1

x



và

0

2

x



nên hàm số đã cho có hai cực trị.

Đap án B sai vì tập giá trị của hàm số đã cho là

 

;

 

nên hàm số không có giá trị lớn nhất

và giá trị nhỏ nhất.

Đáp án C đúng vì

 

' 0, x ;1

y

   

và

' 0 1

y x

   

Đáp án D sai vì hàm số đạt cực tiểu tại

2

x



và đạt cực đại tại

1x 

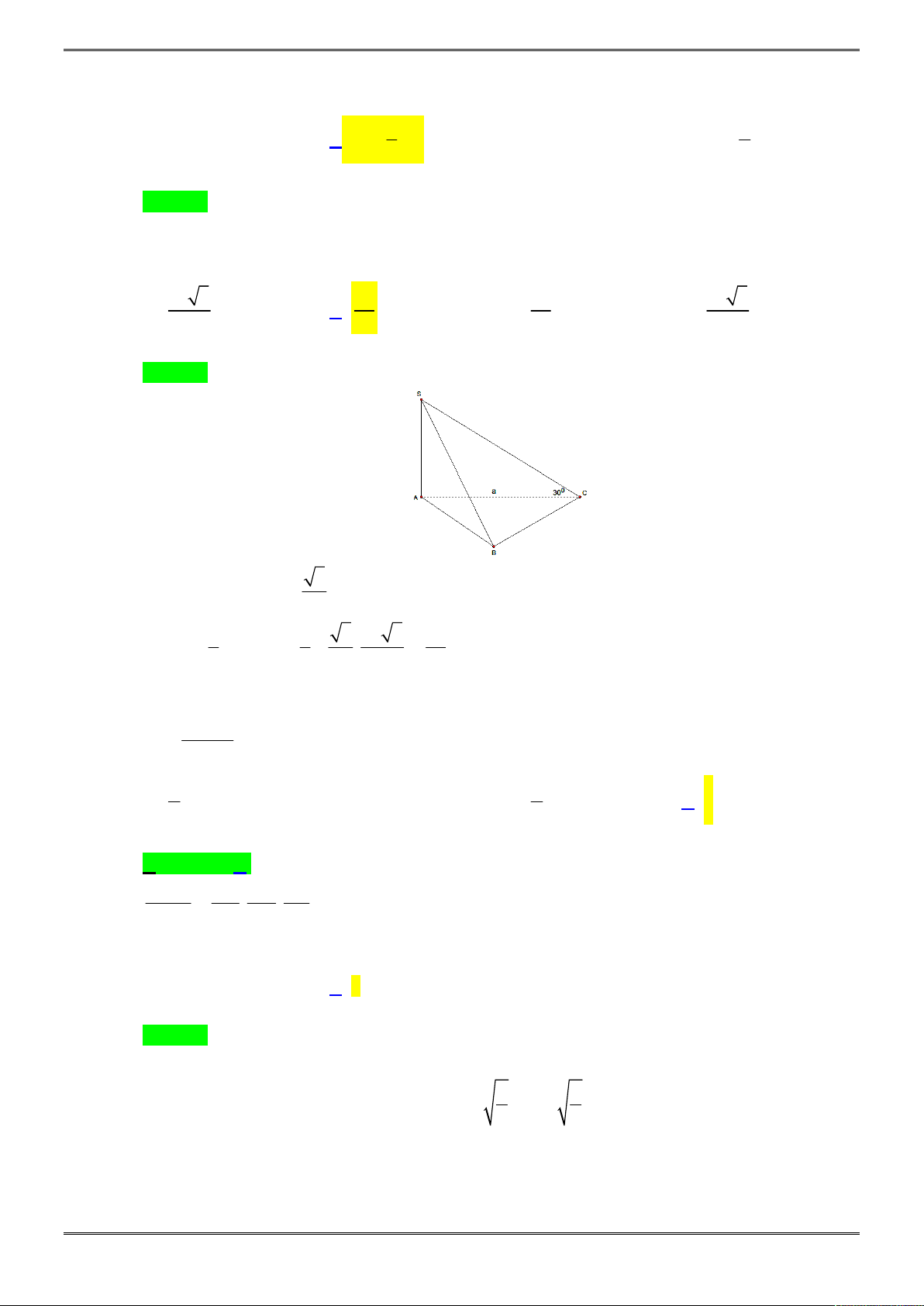
Câu 6. [2D1-7.1-1] Trong các đồ thị dưới đây, đồ thị nào là đồ thị của hàm số

1

x

y

x







?

A.

-3 -2 -1 1 2 3

-3

-2

-1

1

2

3

x

y

B.

-3 -2 -1 1 2 3

-3

-2

-1

1

2

3

x

y

C.

-3 -2 -1 1 2 3

-3

-2

-1

1

2

3

x

y

D.

-2 -1 1 2 3

-3

-2

-1

1

2

x

y

Lời giải

Chọn D.

Tiệm cận đứng

1x 

; tiệm cận ngang

1

y

 

, chọn đáp án D.

D.

-2 -1 1 2 3

-3

-2

-1

1

2

x

y

Câu 7. [2D1-8.2-1] Tiếp tuyến của đồ thị hàm số

3 2

y x x

  

tại điểm

 

1; 2

A

 

là

A.

24 2

y x

 

B.

24 7

y x

 

C.

9 2

y x

 

D.

9 7

y x

 

Ta có:

 

2

' 3 6 ' 1 9

y x x y

    

Phương trình tiếp tuyến của đồ thị hàm số tại điểm

 

1; 2

A

 

là:

    

' 1 1 2 9 1 2 9 7

y y x x x

        

.

Lời giải

Chọn D.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 34

Câu 8. [2H1-4.1-1] Cho khối chóp có diện tích đáy B và chiều cao h.Tính thể tích V của khối chóp

đó.

A.

V Bh

B.

1

3

V Bh



C.

3V Bh

D.

1

2

V Bh



Lời giải

Chọn B.

Câu 9. [2H1-4.1-1] Cho hình chóp

.

S ABC

có đáy là tam giác đều cạnh

,a SA

vuông góc với đáy.

Cạnh bên

SC

hợp với đáy một góc

0

30

. Thể tích của khối chóp

.

S ABC

là:

A.

3

12

a

B.

3

12

a

C.

3

4

a

D.

3

4

a

.

Lời giải

Chọn B.

0

3

.tan 30

3

SA AC a 

2

.

1 1 3 3

. . .

3 3 3 4

S ABC ABC

a

V SA S a 

3

12

a



Câu 10. [2H1-4.1-1] Cho hình chóp

.

S ABC

có

/ /

,A B

lần lượt là trung điểm cáccạnh

,SA SB

. Khi đó,

tỉ số

/ / /

SABC

SA B C

V

bằng

A.

1

2

B.

2

C.

1

4

D. 4.

Lời giải

Chọn D.

. . 2.2.1 4

' '

SABC

SA B C

V

SA SB SC

V SA SB SC

 

  

Câu 11. [2D1-2.3-2] Hàm số

5 3

2 1

y x x

  

có bao nhiêu cực trị?

A. 1 B. 2 C. 3. D. 4.

Lời giải

Chọn B.

Ta có:

5 3 4 2 2

6 6

2x 1 ' 5x 6x 5

5 5

y x y x x x

  

        

  

  

Vì phương trình

' 0

y



có 2 nghiệm đơn phân biệt, tức là đạo hàm đổi dấu hai lần nên hàm số

đã cho có 2 điểm cực trị

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 35

Câu 12. [2D1-2.3-2] Tìm m để hàm số

 

3 2 2

1 2 3y mx m x x    

đạt cực tiểu tại

1x 

?

A.

0

m



. B.

1

m

 

. C.

2

m

 

. D.

3

2

m



.

Lời giải

Chọn D.

Hàm số đã cho đạt cực tiểu tại

1x 

khi

 

0

3

' 1 0

2

" 1 0

m

y m

y







  









Câu 13. [2D1-1.1-2] Cho hàm số

3 2

y x x mx

   

. Tập hợp tất cả các giá trị của m để hàm số đã

cho đồng biến trên khoảng

 

0;



là:

A.

3

m

 

. B.

2

m

 

. C.

1

m

 

. D.

0

m



.

Lời giải

Chọn A.

TXĐ :



2

' 3 6

y x x m  

Hs đồng biến trên khoảng

 



;0

 

2

' 0 0;

3 6 0, 0;

y x

x x m x

    

      

   

2

3 6 , 0; , *

x x m x     

Xét hàm số

   

2

3 6 , 0;g x x x x

    

 

' 6 6

' 0 1

g x x

 

  

Bảng biến thiên :

BPT

3

m

  

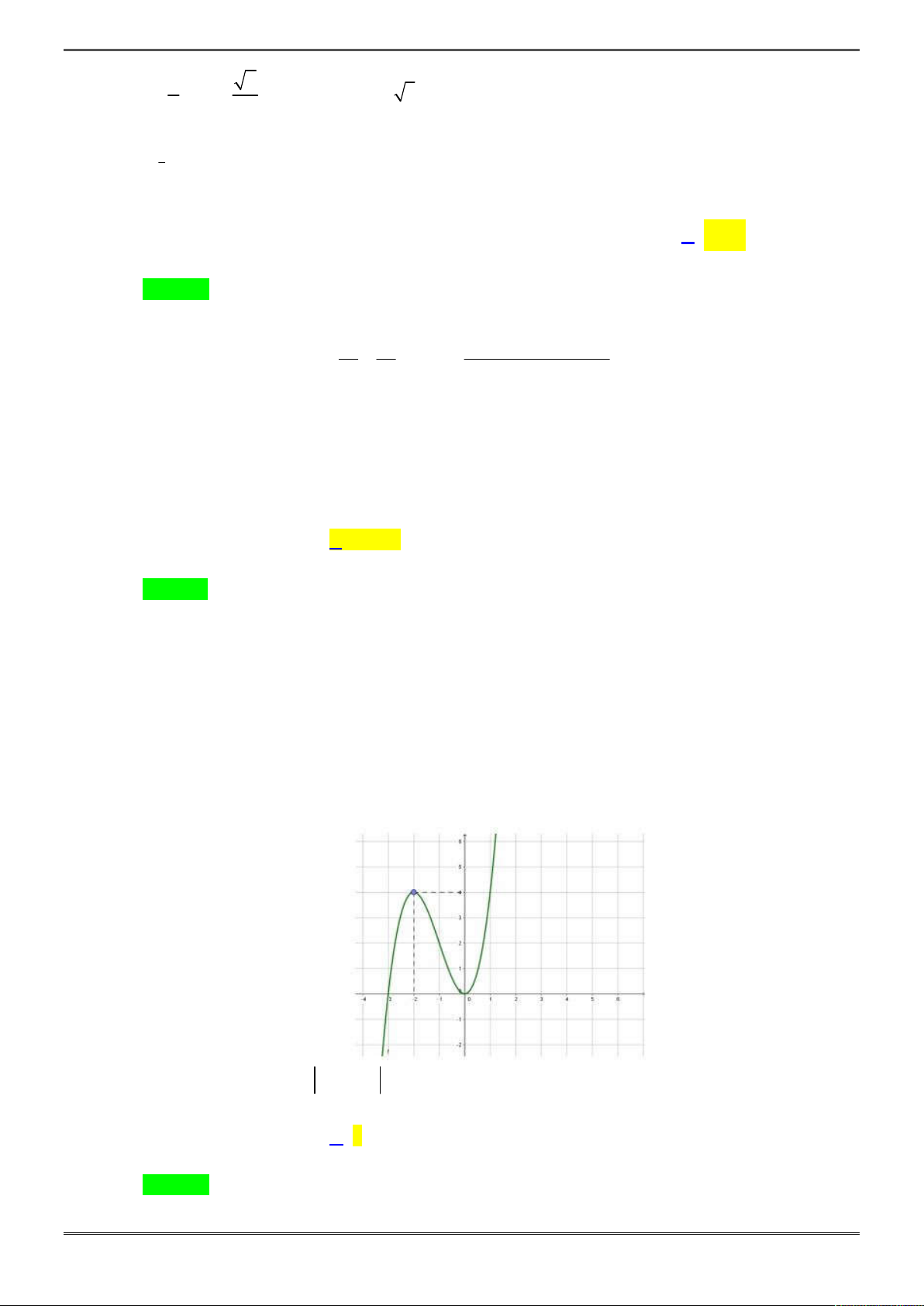
Câu 14. [2D1-3.1-2]Giá trị lớn nhất của hàm số

2

1 4

y x x  

trên đoạn

1

;3

2

 

 

 

là:

A.

1 3

 B.

7

1

2



C. 3 D.

1 2 3



Lời giải

Chọn C.

Tập xác định:

 

0;4

D 

.

2

' 0 2

4

x

y x

x x



   



20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 36

   

1 7

1 , 2 3, 3 3 1

2 2

y y y

 

    

 

 

1

;3

2

maxy 3 2.

x

 

 

 

  

Câu 15. [2D2-7.2-2]Tìm tập nghiệm của phương trình

1 3

5 5 26

x x 

 

A.

 

2;4

B.

 

3;5

C.



D.

 

1;3

Lời giải

Chọn D.

Ta đưa về cùng cơ số 5, rồi đưa về phương trình bậc hai ẩn

5

x

Ta có:

3 2 3

1 3

5 5 5 26.5.5 5.5

5 5 26 26 0

5

5 5.5

x x x

x x

 

 

      

2

1

5 5

5 130.5 625 0

3

5 125

x

x x

x

 





     







Câu 16. [2D2-5.4-2]Cho hàm số

   

2

2 log 2 2 2 1

f x x m mx m x m

 

      

 

(

m

là tham số).

Tìm tất cả các giá trị

m

để hàm số

 

f x

xác định với mọi

x

 

.

A.

0.

m



B.

1.

m



C.

4.

m

 

D.

1 4.

m m

   

Lời giải

Chọn B.

Điều kiện:

   

2

2 2 2 1 0, 1

mx m x m x      



*

0

m



không thỏa

*

 

   

2

0

0: 1

4

3 4 0

' 2 2 1 0

1

m

m m

m m m

m













 

   

 



  

  

     

















Vậy

1

m



.

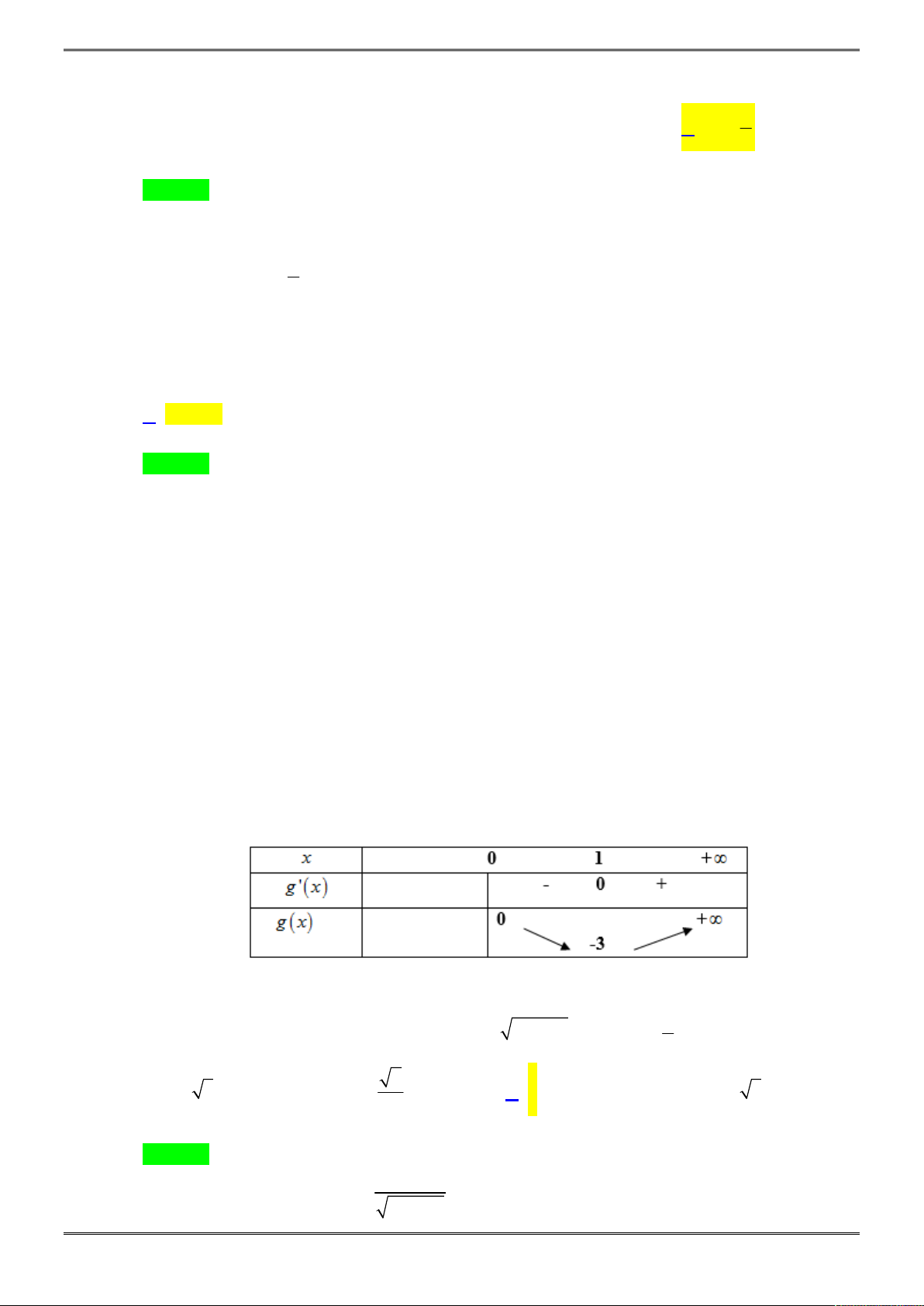
Câu 17. [2D1-6.2-2] Biết rằng đồ thị

3 2

3y x x

  có dạng như sau:

Hỏi đồ thị hàm số

3 2

3y x x

 

có bao nhiêu điểm cực trị?

A. 0 B. 1 C. 2 D. 3

C. 2 D. 3

Lời giải

Chọn D.

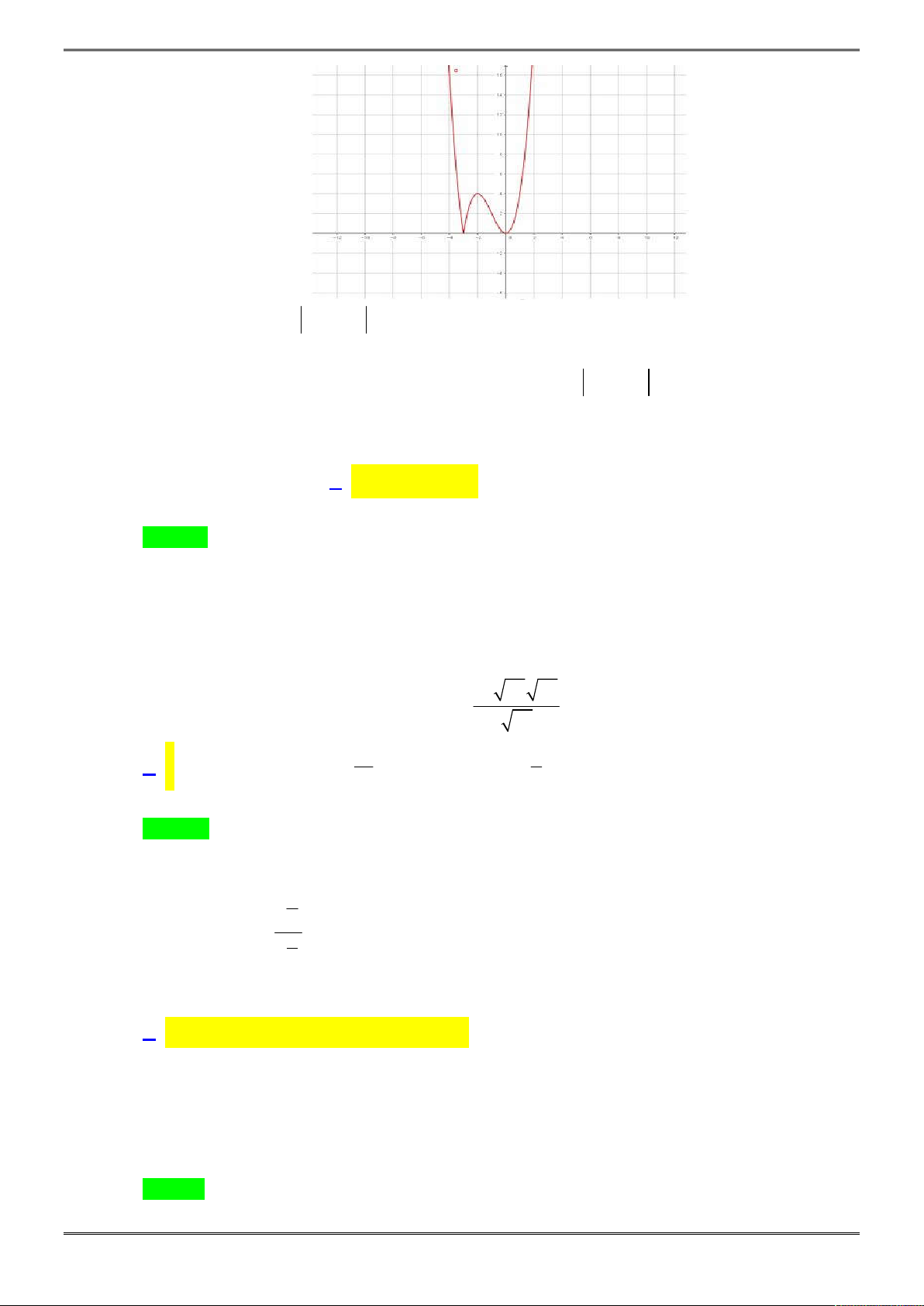
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 37

Đồ thị của hàm

3 2

3y x x

 

có được bằng cách giữ nguyên phần đồ thị phía trên trục hoành

và lấy đối xứng phần đồ thị phía dưới trục hoành qua

Ox

.

Nhìn vào biểu đồ ta thấy có 3 điểm cực trị của hàm số

3 2

3y x x

 

Câu 18. [2D2-4.1-2]Một khu rừng có trữ lượng gỗ

5

4.10

mét khối. Biết tốc độ sinh trưởng của các cây

ở khu rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ?

A.

 

3 3

2016.10

m

B.

 

5 3

4,8666.10

m

C.

 

7 3

125.10

m

D.

 

5 3

35.10

m

Lời giải

Chọn B.

Lượng gỗ ở khu rừng sau năm thứ nhất là:

 

3

1

4% 1

N N N r N m

   

Lượng gỗ ở khu rừng sau năm thứ hai là:

 

2

3

2

4% 1

N N N r N m

   

……….

Như vậy lượng gỗ ở khu rừng sau năm thứ năm là:

 

5

1 4,86661.10

N N r  

Câu 19. [2D2-3.2-2]Giá trị của biểu thức

3 52 2 4

15

7

log

a

a a a

P

a

 



 

 

bằng:

A. 3 B.

12

5

C.

9

5

D. 2

Lời giải

Chọn A.

Thay

100

a



, sử dụng MTCT

Chú ý chỉ cần thay a bằng một giá trị dương nào đó là được.

Cách 2:

52

15

3

7

15

log log 3

a a

a

P a

a

  

.

Câu 20. [2D1-7.1-2] Hàm số

 

f x

có đạo hàm

   

2

' 2

f x x x

 

. Phát biểu nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng

 

2;

 

.

B. Hàm số nghịch biến trên các khoảng

 

; 2 

và

 

0;



.

C. Hàm số đồng biến trên các khoảng

 

; 2 

và

 

0;



.

D. Hàm số nghịc biến trên khoảng

 

2;0



.

Lời giải

Chọn A Đạo hàm chỉ đổi dấu khi x đi qua

2

x

 

Đ

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 38

Câu 21. [2D2-5.3-2]Tìm tập xác định của hàm số

   

2

9

log 1 ln 3 2

y x x

    

A.

 

3;D

 

B.

 

;3

D  

C.

   

; 1 1;3

D     

D.

 

1;3

D  

Lời giải

Chọn C.

Hàm số đã cho xác định khi:

 

   

2

1

1 0

; 1 1;3

3

3 0

x

D

x



 



 



      

 



 







Câu 22. [2D2-5.3-2] Đạo hàm của hàm số

 





2

ln 1

x x

f x e e

  

là:

A.

 

2

1

'

1

x x

f x

e e



 

. B.

 

2

'

1

x

x x

e

f x

e e



 

.

C.

 

2

'

1

x

e

f x

e





. D.

 

2

1

'

1

x

f x

e





.

Lời giải

Chọn C.

 





 

2

2 2

2 2 2 2

1 '

2 1 1

'

1 1 1 1

x

x x

x

x x

x x x x x x x

e

e e

e

e e

f x

e e e e e e e



 

   

      

.

Câu 23. [2D2-9.1-2] Nếu

2

3

4

a a



và

4 6

log log

5 7

b b



thì:

A.

1;0 1

a b

  

. B.

0 1

a b  

. C.

1; 1

a b

 

. D.

0 1; 1

a b

  

.

Lời giải

Chọn B.

+

3 22

3

4 3

34

0 1

a a a



   

+

4 6

5 7

4 6

log log 1

5 7

b b

b



  

0 1

a b   

.

Câu 24. [2D1-2.1-2] Với giá trị nào của m thì hàm số

 

3

2 2017

y m x mx   

không có cực trị?

A.

0 3

m

 

. B.

2

m



. C.

0 2

m

 

. D.

0

m



.

Lời giải

Chọn C.

2

m



HS không có cực trị.

 

3

2 x 2017

y m x m   

không có cực trị

 

2

' 3 2

y m x m   

không có 2 nghiệm phân biệt

 

12 2 0

m m

    

0 2

m

  

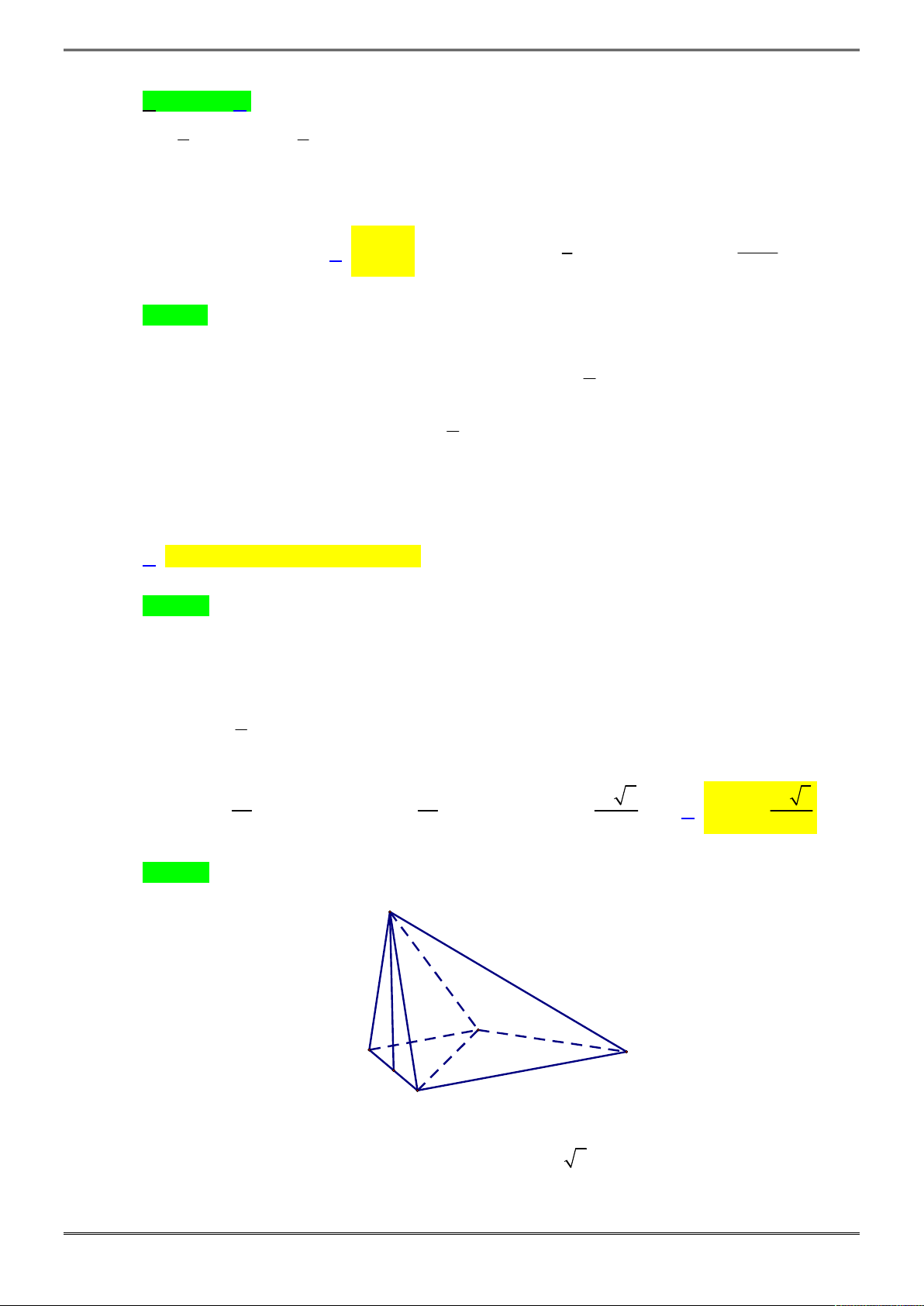
Câu 25. [2H1-4.3-2] Cho tứ diện

.

O ABC

có

, ,OA OB OC

đôi một vuông góc với nhau.

Biết

, 2 , 3OA a OB a OC a  

. Thể tích khối tứ diện là

A.

3

3a

. B.

3

2a

. C.

3

6a

. D.

3

a

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 39

Lời giải

Chọn D.

3

1 1

. .O . .2a.3a=

6 6

V OA OB C a a

 

Câu 26. [2H2-1.4-2]Cho một lập phương có cạnh bằng

a

. Tính diện tích mặt cầu nội tiếp hình lập

phương đó

A.

2

4

S a 

. B.

2

S a 

. C.

2

1

3

S a 

. D.

2

4

3

a

S



 .

Lời giải

Chọn B.

– Tính chất

Mặt cầu nội tiếp hình lập phương cạnh a có bán kính bằng

2

a

Diện tích mặt cầu đó là

2 2

4 R 4

2

a

S a

 

     

 

 

Câu 27. [2H1-1.1-2] Cho khối chóp có đáy là đa giác lồi có

n

cạnh. Trong các mệnh đề sau, mệnh đề

nào đúng?

A. Số mặt của khối chóp bằng

n

. B. Số đỉnh của khối chóp bằng

2n

.

C. Số đỉnh của khối chóp bằng

1n 

. D. Số cạnh của khối chóp bằng số đỉnh.

Lời giải

Chọn C.

Phân tích: Ta chọn luôn được C bởi, mặt đáy của khối chóp có

n

cạnh, và tương ứng với

n

đỉnh của đáy ta có thêm đỉnh

S

. Khi đó có

1n 

đỉnh.

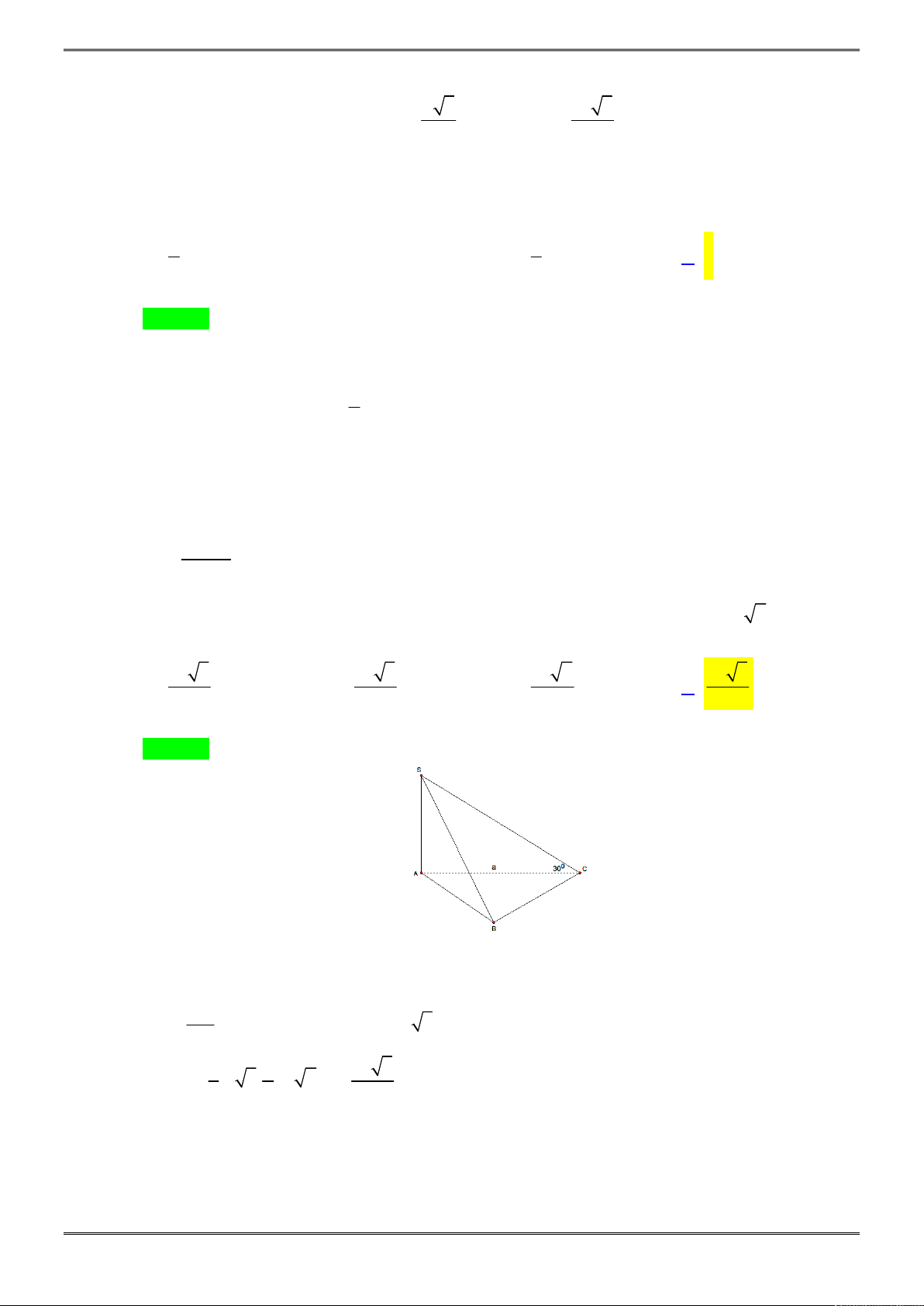
Câu 28. [2H1-4.3-2] Cho hình chóp

.

S ABCD

có đáy ABCDlà hình thang vuông tại

A

và B,

1

2

AB BC AD a  

. Tam giác

SAB

đều và nằm trong mặt phẳng vuông góc với đáy. Tính

thể tích khối chóp

.

S ACD

.

A.

3

.

3

S ACD

a

V  B.

3

.

2

S ACD

a

V  C.

3

.

2

6

S ACD

a

V 

D.

3

.

3

6

S ACD

a

V 

Lời giải

Chọn C.

S

A

D

B

C

H

Ta có: tam giác

ACD

vuông cân tại

C

và

2CA CD a

 

, suy ra

2

ACD

S a





20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 40

Gọi

H

là trung điểm của

AB

vì tam giác

SAB

đều và nằm trong mặt phẳng vuông góc với

đáy, suy ra

 

SH ABCD



và

3

2

a

SH 

. Vậy

3

.

3

6

S ACD

a

V 

.

Câu 29. [2H1-4.4-2]Cho hình lăng trụ

. ' ' 'ABC A B C

vì

M

là trung điểm của

'CC

. Gọi khối đa diện

(H) là phần còn lại của khối lăng trụ

. ' ' 'ABC A B C

sau khi cắt bỏ đi khối chóp

.

M ABC

. Tỷ số

thể tích của (H) và khối chóp

.

M ABC

là:

A.

1

6

B. 6 C.

1

5

D. 5

Lời giải

Chọn D.

Phân tích:

Gọi

M

là trung điểm của

'CC

Theo bài ra ta có:

.ABC '

1

2

M C ABC

V V m 

'

2

C ABC

V m

 

Ta lại có

'

3 6

lt C ABC

V V m

  nên ta có

 

6 5H m m m

  

Vậy

 

.

5

M ABC

H

V



Câu 30. [2H1-4.3-2] Cho hình chóp

SABC

có đáy là tam giác vuông cân tại

A

,

2AB a



,

SA

vuông

góc với đáy. Góc giữa

SBC

và mặt đáy bằng

0

60

. Thể tích của khối chóp

SABC

là:

A.

3

2

a

B.

3

6

a

C.

3

6

3

a

D.

3

a

Lời giải

Chọn D.

Gọi

I

là trung điểm của

BC

, góc giữa

 

SBC

và mặt đáy là



SIA

2

BC

AI a 

;

0

.tan 60 3SA AI a

  .

 

2

.

1 1

. 3. 2

3 2

S ABC

V a a

3

a



Câu 31. [2D1-8.2-3]

Tìm giá trị của

m

để tiếp tuyến của đồ thị hàm số

 

3 2

3 1 1y x mx m x    

tại điểm

có hoành độ

1

x

 

đi qua điểm

 

1;2

A

là:

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 41

A.

3

4

m



B.

4

5

m



C.

2

3

m

 

D.

5

8

m



Lời giải

Chọn D.

TXĐ :



2

' 3 6 1

y x mx m

   

Với

1

x

 

 

1 2 1

f m

   

 

' 1 4 5f m

  

Phương trình tiếp tuyến của (C ) tại điểm

 

1;2 1

m

 

:

  

: 4 5 1 2 1

d y m x m

    

Do

 

1;2

A d

, nên:

 

5

2 4 5 .2 2 1

3

m m m

     

.

Câu 32. [2D2-9.1-3]Tập nghiệm của bất phương trình

4 1

4

3 1 3

log (3 1).log

16 4

x



 

là:

A.



 



1;2 3;

 

B.



 



1;1 4;

  

C.



 



0;4 5;

 

D.



 



0;1 2;

 

Lời giải

Chọn D.

ĐK:

0

x



.

4 1

4

3 1 3

log (3 1).log

16 4

x



 

 

4 4

4log (3 1). 2 log (3 1) 3

x x

    

4

2

4

4log (3 1) 8log (3 1) 3 0

x x

      

4

1

log (3 1)

3 1 2 1

2

3 2

3 1 8

log (3 1)

2

x



 





  



  





 







 





So với ĐK nên có tập nghiệm



 



0;1 2;

 

Câu 33. [2D2-2.3-3]Cho các số thực dương a, b thỏa mãn

 

9 12 16

log log log

a b a b  

. Tính tỉ số

a

T

b



A.

4

3

T



B.

1 3

2

T





C.

1 5

2

T





D.

8

5

T



Lời giải

Chọn C.

– Phương pháp: Đặt cả 3 logarit bằng nhau và bằng

k

– Cách giải

Đặt

 

9 12 16

log log log

k a b a b   

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 42

9

9 3

12 9 12 16 1

16 4

16

k

k k

k k k k

k k

k

a

b

a b







       





 



Đặt

2

1 0

3 1 5

2

4

0

k

t t

t



  

 

   







4 1 5 1

2

3

k

b

T

a t



    

Câu 34. [2H1-4.3-3] Thể tích tứ diện

ABCD

có các mặt

,

ABC BCD

là các tam giác đều cạnh a và

3

2

a

AD 

là:

A.

3

4

a

B.

3

6

a

C.

3

6

a

D.

3

16

a

Lời giải

Chọn D.

Gọi

M

là trung điểm của

BC

;

BC 

 

ADM

3

2

DM AM AD

  

. Suy ra tam giác

ADM

đều.

N

là trung điểmcủa

AM

và

N

à hình chiếu

của

D

lên đáy

 

ABC

.

3 3 3

.

2 2 4

DN a a

 

.

Câu 35. [2H1-4.4-3] Cho hình hộp chữ nhật

. ' ' ' 'ABCD A B C D

có

, 2 , 'AB a BC a AA a  

. Lấy

điểm

M

trên cạnh

AD

sao cho

3

AM MD

. Tính thể tích khối chóp

. 'M AB C

.

A.

3

. '

2

M AB C

a

V  B.

3

. '

4

M AB C

a

V  C.

3

. '

3

4

M AB C

a

V  D.

3

. '

3

2

M AB C

a

V 

Lời giải

Chọn D.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 43

Thể tích khối chóp

. 'M AB C

bằng thể tích khối chóp

'.

B AMC

Ta có:

2

3 3

4 4

AMC ADC

a

S S

 

 

Do đó

3

. ' '.AMC

3

4

M AB C B

a

V V 

Câu 36. [2D1-3.1-4] Một ngọn hải đăng đặt ở vị trí

A

cách bờ biển một khoảng

4kmAB 

. Trên bờ

biển có 1 cái kho ở vị trí

C

cách

B

một khoảng

7km

. Người gác ngọn hải đăng chèo thuyền

từ ngọn hải đăng đến vị trí

M

trên bờ biển rồi đi bộ đến

C

Biết rằng vận tốc chèo thuyền là

3km/h

và vận tốc đi bộ là

5km/h

. Xác định vị trí điểm

M

để người đó đến

C

nhanh nhất.

A.

3km

MN



B.

4km

MN



C.

M

trùng

B

D.

M

trùng

C

Lời giải

Chọn A.

7 -

x

4

x

A

B

M

C

Để người đó đến

C

nhanh nhất thì

M

phải thuộc đoạn

BC

Đặt

 

7 0 7

BM x CM x x

     

2

16

AM x

 

Thời gian để người đó đi từ

A

đến

C

là

 

2

16 7

3 5

x x

t f x

 

  

. Xét hàm số

( )f x

trên

 

0;7

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 44

Với

 

0;7

x 

thì

 

2

1

' 0 5 3 16 3

5

3 16

x

f x x x x

x

       



       

' 0, 0;3 ; ' 0, 3;7

f x x f x x     

   

 

37

3 , 0;7

15

f x f x    

Dấu “



” xảy ra

3

x

 

Câu 37. [2D2-3.4-4] Được sự hỗ trợ từ Ngân hàng Chính sách xã hội địa phương, nhằm giúp đỡ các

sinh viên có hoàn cảnh khó khăn hoàn thành việc đóng học phí học tập, một bạn sinh viên A đã

vay của ngân hàng 20 triệu đồng với lãi suất

12%

/năm, và ngân hàng chỉ bắt đầu tính lãi sau

khi bạn A kết thúc khóa học. Bạn A đã hoàn thành khóa học và đi làm với mức lương là 5,5 t

riệu đồng/tháng. Bạn A dự tính sẽ trả hết nợ gốc lẫn lãi suất cho ngân hàng trong 36 tháng. Hỏi

số tiền

m

mỗi tháng mà bạn A phải trả cho ngân hàng là bao nhiêu?

A.

 

3

1,12 20 0,12

1,12 1 12

m

 



 

triệu B.

 

2

1,12 20 0,12

1,12 1 12

m

 



 

triệu

C.

 

3

1,12 36 0,12

1,12 1 12

m

 



 

triệu D.

 

2

1,12 36 0,12

1,12 1 12

m

 



 

triệu.

Lời giải

Chọn A.

Năm thứ nhất trả gốc và lãi, số tiền còn lại:

 

1 0 0

1 0,12 12. 1,12 12x x m x m

    

,

0

20

x



triệu

Năm thứ hai, số tiền còn lại:

 

2 1 1

1 0,12 12. 1,12 12x x m x m

    

Năm thứ ba, số tiền còn lại:

 

3 2 2

1 12% . 12. 1,12 12 0

x x m x m

     

   

3 3 3

3

2 2

1,12 20 1,12 20 1,12 20 0,12

1,12 1

1 1,12 1,12 12 1,12 1 12

12

1,12 1

m

   

   



    





 

3

1,12 20 0,12

1,12 1 12

m

 



 

triệu

Câu 38. [2D1-3.1-4] Cho một tấm bìa hình vuông cạnh

5dm

. Để làm

một mô hình kim tự tháp Ai Cập, người ta cắt bỏ 4 tam giác cân

bằng nhau có cạnh đáy chính là cạnh của hình vuông rồi gấp lên,

ghép lại thành một hình chóp tứ giác đều. Để mô hình có thể

tích lớn nhất thì cạnh đáy của mô hình là

A.

3 2

dm

2

. B.

5

dm

2

.

C.

5 2

dm

2

. D.

2 2dm

.

Lời giải

Chọn C.

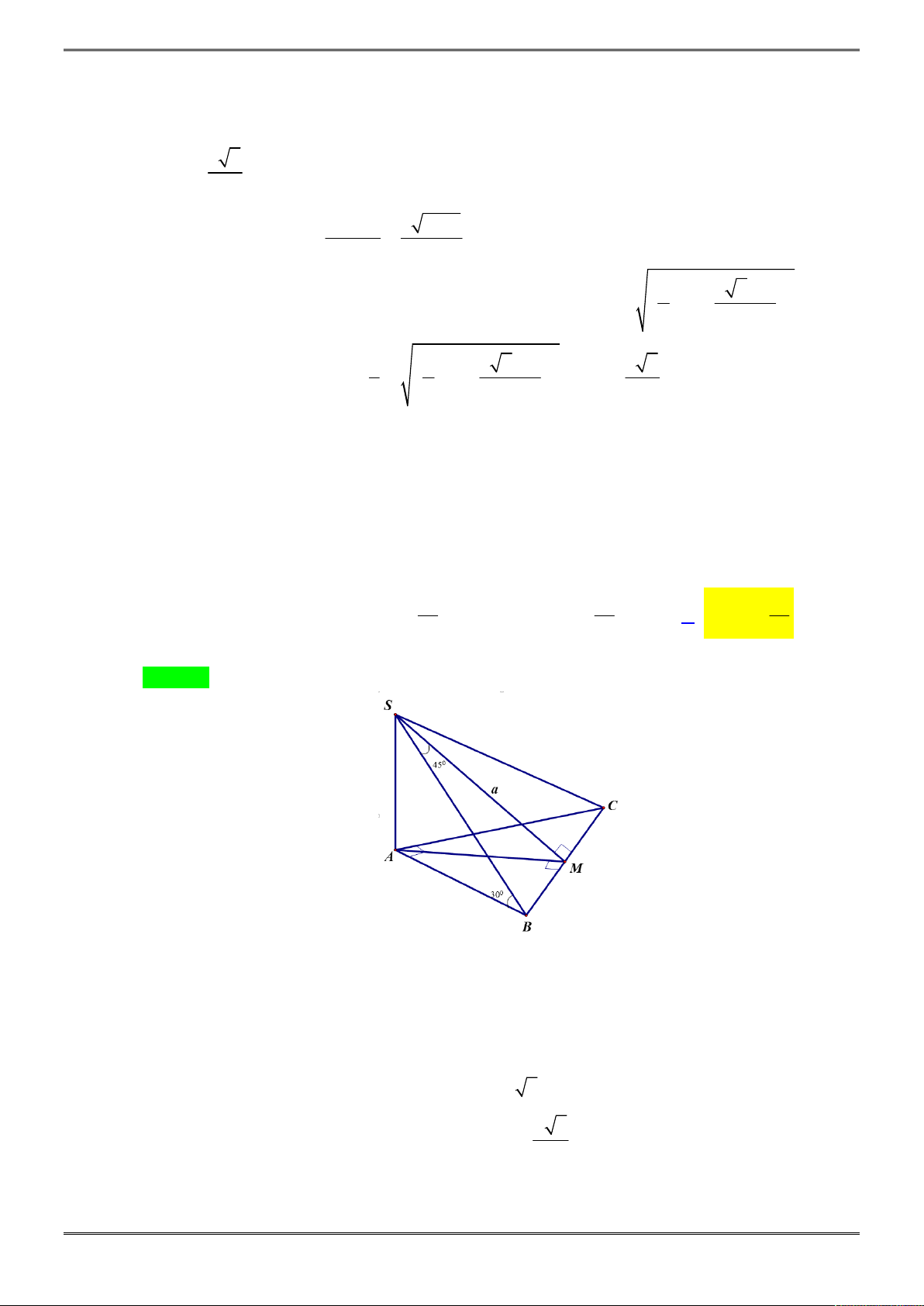
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 45

Phân tích: Đây là bài toán khá hay và khi tính toán cần phải áp dụng bất đẳng thức vào để tìm

giá trị lớn nhất của thể tích.

Đặt tên các đỉnh như hình vẽ. Gọi độ dài cạnh đáy hình của hình chóp tứ giác đều là

x

5 2

0;

2

x

 



 

 

. Theo bài ta ta có chiều cao của hình tam giác (là mặt bên của hình chóp tứ

giác đều) là

5 2

2 2

BD x x

DI BK

 

  

Khi đó chiều cao của hình chóp tứ giác đều được tạo thành là

2

5 2

2 2

x x

h

 



 

 

 

 

Thể tích hình cần tính là:

2

1 5 2 5 2

0;

3 2 2 2

x x

V x x

 

   



 

  

 

   

 

   

 

 

   

 

.

Đến đây có nhiều cách giải nhưng cách giải nhanh nhất có lẽ là ta thay từng đáp án vào và xét

từng giá trị của các đáp án đã cho để tìm kết quả đúng!

Câu 39. [2H1-4.3-4] Cho hình chóp

.

S ABC

có

SA

vuông góc với mặt phẳng

 

ABC

và tam giác

ABC

cân tại

A

. Cạnh bên

SB

lần lượt tạo với mặt phẳng đáy, mặt phẳng trung trực của

BC

các góc bằng

0 0

30 , 45

, khoảng cách từ

S

đến cạnh

BC

bằng a. Tính thể tích khối chóp

.

S ABC

.

A.

3

.S ABC

V a

. B.

3

.ABC

2

S

a

V  . C.

3

.ABC

3

S

a

V  . D.

3

.

6

S ABC

a

V  .

Lời giải

Chọn D.

Ta có

 

SA ABC



nên

AB

là hình chiếu của

SB

trên mặt phẳng

 



0

30

ABC SBA 

. Gọi

G

là trung điểm

BC

, ta có

   

BC AM

BC SAM SAM

BC SA





  







là mặt phẳng trung trực

của

BC

và SM là hình chiếu của SB trên

 



0

45

SAM BSM SBC

   

vuông cân tại

S

. Ta

có

 

,

2, 2

B SC

SM BC d SM a SB SC a BC a

       

Tam giác

SBA

vuông tại

A

, ta có

0

2

.sin30

2

a

SA SB 

Trong tam giác vuông

SAM

, ta có:

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 46

2

2 2 2

2 2

a a

AM SM SA a

 

    

 

 

Vậy

3

.

1

. .

6 6

S ABC

a

V BC AM SA 

Câu 40. [2H2-1.2-4] Cho tứ diện

ABCD

có tam giác

BCD

vuông cân tại

, 2 ,

C BD a AB

vuông góc

với mặt phẳng

 

BCD

. Gọi E là trung điểm cạnh

BD

. Tính bán kính mặt cầu ngoại tiếp tứ

diện

ACDE

A.

7

2

a

. B.

11

2

a

. C.

5

2

a

. D.

14

6

a

.

Lời giải

Chọn B.

Tâm K mặt cầu ngoại tiếp tứ diện

ACDE

là giao điểm trục của tam giác

ADE

và trung trực

của

CE

 

(ADE)

CE 

I là tâm đường tròn ngoại tiếp

EDA

Từ Pythagore và giả thiết đề bài, ta có

2,

BC CD a CE EB ED a    

2, 5AE a AD a

 

   

1 . . 10

2 4 2

AED

AD DE EA

S p p AD p AE p ED ID

S

       

2 2

11

2 2 2

CE a

IK JE R KD IK ID       

.

Phần II: TỰ LUẬN.

Câu 1. [2D2-7.2-3] Tìm tập nghiệm của phương trình

2

log 4 3

2 3 5

x x

 

  

 

.

Lời giải

Phương trình

       

2 2 2 2

2 2

log 2 log 2 3 5 2 3 5 2

x x x x x x x x

           

       

2 2 2 2

2 2

log 2 2 log 2 3 5 2 3 5

x x x x x x x x

           

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 47

Xét hàm

 

2

log , 0

f t t t t

  

. Ta có

 

1

' 1 0, 0

ln 2

f t t

t

     

Hàm f đồng biến trên

 

0;



Do đó:

   

2 2 2 2 2

1

2 2 3 5 2 2 3 5 4 3 0

3

x

f x x f x x x x x x x x

x





               







Vậy tập nghiệm của phương trình đã cho là:

 

1;3

Câu 2. [2H2-1.2-4] Cho khối tứ diện

.

A BCD

có

6 , 7AB cm CD cm 

, khoảng cách giữa hai đường

thẳng

AB

và

CD

là 8cm, góc giữa hai đường thẳng

AB

và

CD

là

0

30

. Thể tích của khối tứ

diện

.

A BCD

là:

Lời giải

Phương pháp: tứ giác có các đỉnh là các đỉnh của hình lăng trụ thì

1

3

tudien langtru

V V

Khoảng cách giữa 2 đường chéo nhau

,a b

bằng khoảng cách giữa đường thẳng

a

tới mặt

phẳng (C) với

 

b C



và

 

//

a C

Cách giải: từ B kẻ

//

BE CD

và

BE CD

Từ C kẻ

//

CF AB

và

CF AB

từ đó ta được hình lăng trụ

.

ABE FCD

Ta có

   

 

, , , 8

d ABE FCD d CD ABE d AB CD

  

 

1 1 21

sin . . sin. . .

2 2 2

ABE

S ABE AB BE ABE AB CD  

   

 

.

. , 84

ABE FCD ABE

V S d ABE FCD

  

.

1

28

3

ABCD ABE FCD

V V

  

.

BẢNG ĐÁP ÁN

1.D 2.A 3.B 4.C 5.C 6.D 7.D 8.B 9.B 10.D

11.B 12.D 13.A 14.C 15.D 16.B 17.D 18.B 19.A 20.A

21.C 22.C 23.B 24.C 25.D 26.B 27.C 28.D 29.D 30.D

31.D 32.D 33.C 34.D 35.C 36.A 37.A 38.C 39.D 40.B

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 48

ĐỀ ÔN TẬP SỐ 04

PHẦN I: PHẦN TRẮC NGHIỆM.

Câu 1. [2D1-4.6-1] Cho hàm số

3

2

y

x





. Số tiệm cận của đồ thị hàm số bằng

A.

0

. B.

2

. C.

3

. D.

1

.

Lời giải

Chọn B.

Đồ thị hàm số có tiệm cận đứng

2

x



Đồ thị hàm số có tiệm cận ngang

0

y



.

Câu 2. [2D1-1.4-2] Hàm số

2

y x x 

nghịch biến trên khoảng:

A.

 

0;1

. B.

 

1;



. C.

 

1;2

. D.

 

0;2

.

Lời giải

Chọn C.

Cách giải: Điều kiện xác định của hàm số là:

2

2 0 0 2

x x x

    

;

2

1

' ' 0 1

2

x

y y x

x x



    



Kết hợp với điều kiện để hàm số nghịch biến ta có

1 2

x

 

.

Câu 3. [2D2-6.1-1] Phương trình

3

log 2

x



có nghiệm x bằng:

A.

1

. B.

9

. C.

2

. D.

3

.

Lời giải

Chọn D.

Cách giải: ta có

 

2

3

log 2 3 3

x x

   

.

Câu 4. [2D2-4.2-2] Cho hàm số

 

.

x

f x x e



. Giá trị của

 

0

f



bằng

A.

1

. B.

2e

. C.

3e

. D.

2

.

Lời giải

Chọn D.

 

2

x x x x

f x e xe f e xe

 

    

 

0 0

0 2 0. 2

f e e



   

.

Câu 5. [2D2-4.1-1] Tìm tập xác định

D

của hàm số

 

3 2

5

log 2y x x x

  

là:

A.

 

0;1

. B.

 

1;



. C.

   

1;0 2;

  

. D.

   

0;2 4;

 

.

Lời giải

Chọn C.

Điều kiện xác định

 

3 2 2

1 0

2 0 2 0

2

x

x x x x x x

x

  



       







Tập xác định

   

1;0 2;D

   

.

Câu 6. [2D2-4.8-4] Một người gửi tiết kiệm với lãi suất

8,4%

năm và lãi hàng năm được nhập vào

vốn, hỏi sau bao nhiêu năm người đó thu được gấp đôi số tiền ban đầu?

A.

6

. B.

7

. C.

8

. D.

9

.

Lời giải

Chọn D.

Từ công thức bài toán lãi kép:

 

1

n

P P r

 

. Theo giả thiết thu được số tiền gấp đôi ban đầu

thì ta có

   

1 1,084

2 1 1 2 log 2 log 2 9

n n

r

P P r r n



        

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 49

Câu 7. [2H1-2.4-1] Cho hình chóp tam giác có đường cao bằng

100cm

và các cạnh đáy bằng

20cm

,

21cm

,

29cm

. Thể tích của hình chóp đó bằng:

A.

3

6000

cm

. B.

3

6213

cm

. C.

3

7000

cm

. D.

3

7000 2

cm

.

Lời giải

Chọn C.

Tam giác đáy của hình chóp của nửa chu vi

 

20 21 29

35

2

p cm

 

 

Và diện tích

   

 

2

13 14 15 210

S p p p p cm

    

Thể tích hình chóp là

 

3

1 1

210.100 7000

3 3

V Sh cm

  

.

Câu 8. [2H1-2.3-2] Cho khối chóp đều

.

S ABC

có cạnh đáy bằng

a

. Tính thể tích khối chóp

.

S ABC

biết cạnh bên bằng

2a

.

A.

3

.

11

12

S ABC

a

V 

. B.

3

.

3

6

S ABC

a

V 

. C.

3

.

12

S ABC

a

V  . D.

3

.

4

S ABC

a

V  .

Lời giải

Chọn A.

Gọi

G

là trọng tâm tam giác

ABC

, do

.

S ABC

là hình chóp đều nên

 

SG ABC



2 2

2 2 3 3

.

3 3 2 3

a a

AG AM SG SA AG

     

2

11

4

3

a a

a  

2 2 3

3 1 1 3 11 11

.

4 3 3 4 12

3

ABC ABC

a a a a

S V S SG

 

     .

Câu 9. [2H2-1.5-3] Cho hình lập phương

.

ABCD A B C D

   

có cạnh bằng

a

. Một hình nón có đỉnh là

tâm của hình vuông

ABCD

và có đường tròn đáy ngoại tiếp hình vuông

A B C D

   

. Diện tích

xung quanh của hình nón đó là

A.

2

3

a



. B.

2

a



. C.

2

3

2

a



. D.

2

6

2

a



Lời giải

Chọn C.

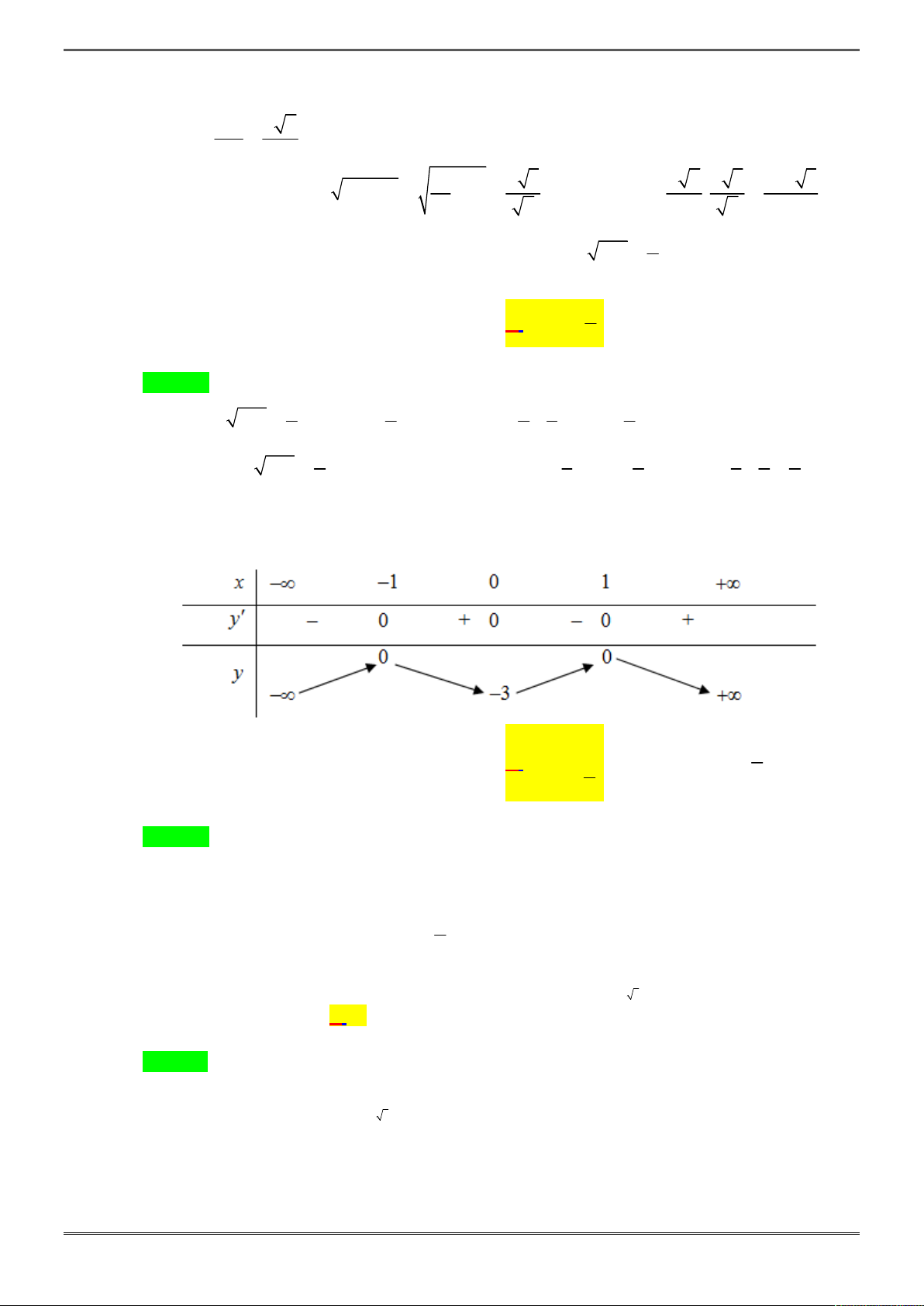
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 50

Hình nón có đỉnh là tâm hình vuông

ABCD

và đường trong đáy ngoại tiếp hình vuông

A B C D

   

thì có chiều cao

h

bằng độ dài cạnh hình lập phương bằng

a

, đường tròn đáy có bán

kính

2

2 2

AC a

R  

Độ dài đường sinh là

2

2 2 2

3

2

a a

l R h a    

2

2 3 3

.

2 2

2

a a a

S Rl



 

    .

Câu 10. [2D2-3.1-3] Cho

a

,

b

là các số hữu tỉ thỏa mãn

6

2 2 2

1

log 360 .log 3 .log 5

2

a b  

. Tính

a b

A.

5

a b

 

. B.

0

a b

 

. C.

1

2

a b

 

. D.

2

a b

 

Lời giải

Chọn C.

Ta có

 

3 2

6

2 2 2 2 2

1 1 1 1 1

log 360 .log 360 .log 2 .3 .5 .log 3 .log 5

6 6 2 3 6

    

Mặt khác

6

2 2 2

1

log 360 .log 3 .log 5

2

a b  

suy ra

1

3

a



và

1

6

b



1 1 1

3 6 2

a b

    

.

Câu 11. [2D1-6.4-3] Cho hàm số

 

y f x



liên tục trên



và có bảng biến thiên như hình vẽ. Tìm tất

cả các giá trị thực của

m

để phương trình

 

2f x m



có đúng hai nghiệm phân biệt.

A.

0

3

m







 



. B.

3

m

 

. C.

0

3

2

m







 



. D.

3

2

m

 

Lời giải

Chọn C.

Dựa vào bảng biến thiên, ta thấy rằng để phương trình

 

2f x m



có đúng hai nghiệm phân

biệt khi và chỉ khi

0

2 0

3

2 3

2

m















 



.

Câu 12. [2D2-6.2-2] Tìm số nghiệm của phương trình:

   

2

3

log 1 log 2 1 2

x x

   

A.

2

. B.

1

. C.

0

. D.

3

.

Lời giải

Chọn B.

Phương trình

   

2

3

3 3

2 1 0; 1

log 1 log 2 1 2

log 1 2log 2 1 2

x x

  





    



   





   

2 2

3

2 1 0; 1

2

log 1 . 2 1 2

1 . 2 1 9

x x

x

x x

  



  



 

   

 

 

  





 



20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 51

Vậy phương trình đã cho có nghiệm duy nhất.

Câu 13. [2H2-1.3-2] Một khối nón có thể tích bằng

30



. Nếu giữ nguyên chiều cao và tăng bán kính

mặt đáy của khối nón lên hai lần thì thể tích khối nón mới bằng

A.

120



. B.

60



. C.

40



. D.

480



Lời giải

Chọn A.

Gọi

h

,

r

lần lượt là chiều cao và bán kính mặt đáy của khối nón.

Thể tích khối nón ban đầu là

2 2

1

30 90

3

non

V r h r h

 

   

Thể tích khối nón sau khi tăng bán kính đáy là

 

2

1 4

2 120

3 3

s

V r h r h

  

  

.

Câu 14. [2D2-4.2-2] Cho hàm số

1

ln

1

y

x





. Hỏi hệ thức nào sau đây đúng?

A. 1

y

xy e



 

. B. 1

y

xy e



 

. C. 1

y

xy e



  

. D. 1

y

xy e



  

Lời giải

Chọn A.

Ta có

 

1 1 1

ln ln 1 . 1 1

1 1 1 1

y

x

y y x x y e

x x x x



 

             

 

 

   

.

Câu 15. [2D1-6.8-2] Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

 

4 2

: 1

m

C y x mx m

   

cắt trục hoành tại bốn điểm phân biệt.

A.

1

m



. B.

1

2

m











. C.

m



. D.

2

m



Lời giải

Chọn C.

Phương trình hoành độ giao điểm của

 

m

C

và

 

d

là

 

4 2 4 2

1 0 1 1

x mx m x m x

       

    

 

2

2 2 2

2

1

1 0

1 1 1

1 *

1

x

x x m x

x m

 



 

     



 



Để

 

m

C

cắt

 

d

tại bốn điểm phân biệt



(*) có hai nghiệm phân biệt khác

1

2

m





 







.

Câu 16. [2D1-1.2-1] Hàm số nào sau đây nghịch biến trên



?

A.

3 2

3 3 2

y x x x

    

. B.

3 2

3 3 2y x x x    

.

C.

3 2

3 3 2

y x x x

   

. D.

3 2

3 3 2y x x x   

Lời giải

Chọn B.

Xét hàm số

3 2

y ax bx cx d   

với

x



, ta có

2

' 3 2

y ax bx c  

Hàm số đã cho nghịch biến trên

2

'

0

' 0;

' 3 0

y

a

y x

b ac







    



   





 

nên hàm số

3 2

3 3 2y x x x    

là hàm số đồng biến trên



.

Câu 17. [2H1-2.1-3] Hình chóp

.

S ABCD

có đáy hình chữ nhật

 

,

AB a SA ABCD

 

,

SC

tạo với

mặt đáy góc

45

. Mặt cầu ngoại tiếp hình chóp

.

S ABCD

có bán kính đáy bằng

2a

. Thể tích

khối chóp

.

S ABCD

bằng

A.

3

2a

. B.

3

2 3

a . C.

3

a

. D.

3

2 3

3

a

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 52

Lời giải

Chọn D.

Gọi O là tâm của hình chữ nhật

ABCD

và I là trung điểm của

SC

.

Khi đó

 

OI ABCD IA IB IC ID

    

mà

SAC

vuông tại

A

IA IS IC  

Do đó I là tâm mặt cầu ngoại tiếp khối chóp

.

S ABCD

suy ra

2 2 2IA a SC a

  

Mặt khác

AC

là hình chiếu của

SC

trên mặt phẳng

   

 



 



0

; ; 45

ABCD SC ABCD SC AC SAC   

Suy ra

SAC

vuông cân

3

.

1 1 2 3

2 . . .2 . . 3

3 3 3

S ABCD ABCD

a

SA AC a V SA S a a a      

.

Câu 18. [2D2-6.1-1] giải bất phương trình

 

1

2

log 2 1 1

x

  

A.

3

;

2

 



 

 

. B.

3

1;

2

 

 

 

. C.

1 3

;

2 2

 

 

 

. D.

3

;

2

 



 

 

Lời giải

Chọn C.

Bất phương trình

 

1

2

2 1 0

1 3

log 2 1 1 ;

2 1 2

2 2

2 1 2

x

x x

x



 



 





 

      

 

 

 

 







.

Câu 19. [2H2-1.6-4] Cho miếng tôn tròn tâm

O

bán kính

R

. Cắt miếng tôn hình quạt

OAB

và gò

phần còn lại thành một hình nón đỉnh

O

không đáy (

AO

trùng với

BO

). Gọi

S

,

S



lần lượt là

diện tích của miếng tôn hình tròn ban đầu và diện tích của miếng tôn còn lại. Tìm tỉ số

S



để

thể tích khối nón lớn nhất.

A.

1

4

. B.

6

3

. C.

2

3

. D.

1

3

.

Lời giải

Chọn B.

Gọi góc



AOB rad





suy ra độ dài dây cung

AB

là

.

AB

L R





Nên độ dài dây cung còn lại là

 

2 2

c

L R R R

   

   

là chu vi của đường tròn đáy của

hình nón.

Bán kính đường tròn đáy hình nón là

 

2

2 2

0 0

2

1 1

1 . . . . 1 .

2 2 3 3 2

R

R R V R h R h

 

 

 

  



   

      

   

   

Mặt khác

 

2

2 2 2

0

2

1

2 2

R

h OA R R R

 

 

 



 

     

 

 

 

 

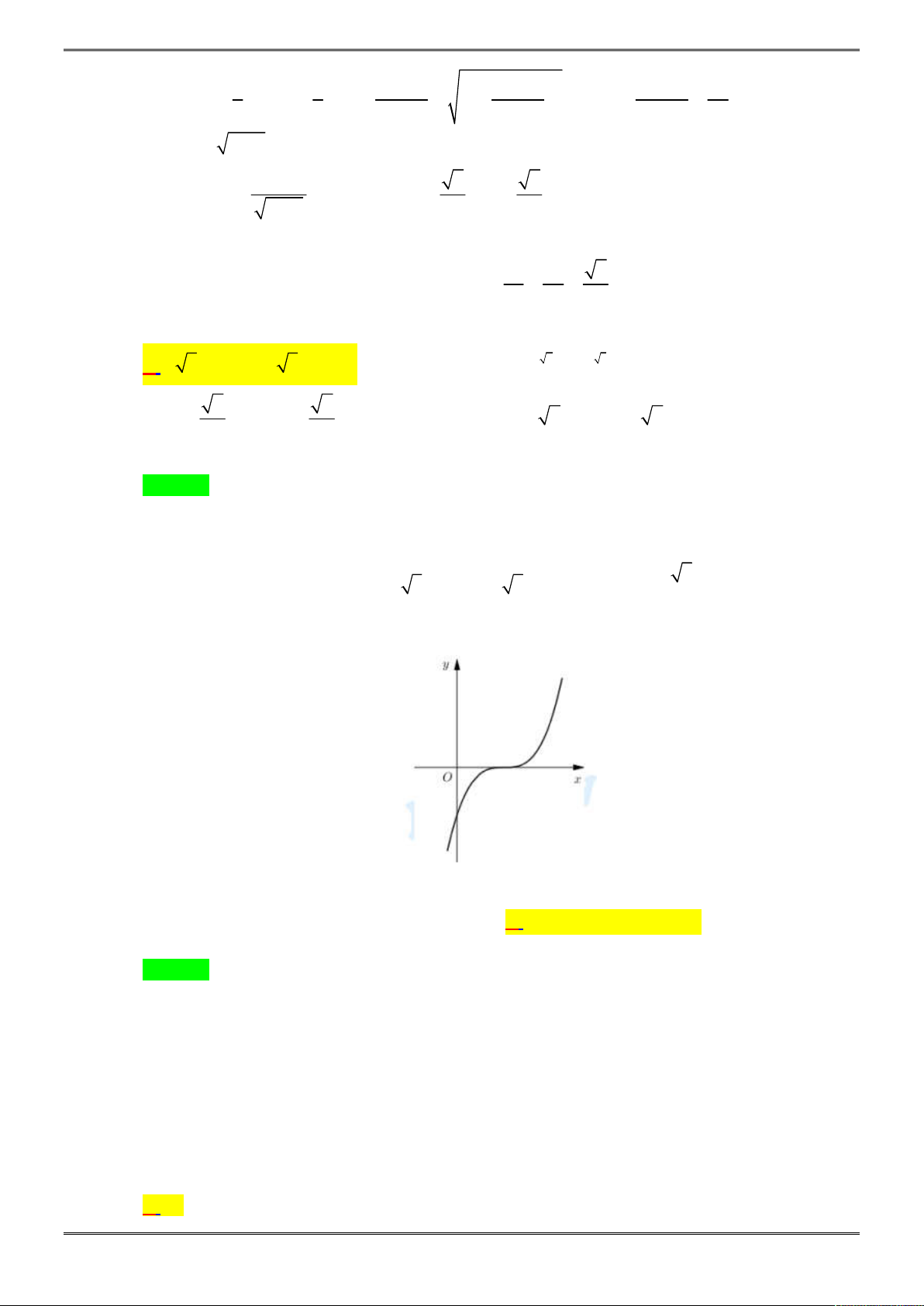
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 53

Khi đó

2 2

2 3

0

1 1 2 2

. . . . 1

3 3 2 2

V R h R

   

 

 

   

  

   

   

. Với

0

2

R

t

R

 





 

, ta xét

 

2 2

. 1

f t t t 

Ta có

   

3

2

2 3 6 6

' ; ' 0

3 3

1

t t

f t f t t f

t

 



    

 



 

đạt giá trị nhỏ nhất

Diện tích xung quanh của hình nón là

2 0 0xq

S S r l rR R

 

  

Diện tích miếng tôn ban đầu là

2

1

S R





suy ra

0

1

2

6

3

R

S

S R

 

.

Câu 20. [2D2-1.3-1] Khẳng định nào sau đây sai?

A.

   

2017 2016

3 1 3 1   . B.

2 1 3

2 2





.

C.

2016 2017

2 2

1 1

2 2

   

  

   

   

. D.

   

2017 2016

2 1 2 1  

Lời giải

Chọn A.

Hàm số

x

y a

là hàm số đồng biến trên



khi

1

a



và là hàm số nghịch biến trên



khi

0 1a 

. Khi đó xét với

1 2

x x

thì

1 2

x x

a a



khi

1

a



và

1 2

x x

a a



khi

0 1a 

Dựa vào các đáp án, ta thấy rằng

   

2017 2016

3 1 3 1   vì

1 2

0 3 1 1

2017 2016

a

x x



   





  





.

Câu 21. [2D1-5.3-2] Cho hàm số

2 2

ax

y bx cx d   

có đồ thị như hình vẽ bên.

Mệnh đề nào dưới đây đúng?

A.

0, 0, 0, 0

a b c d

   

. B.

0, 0, 0, 0

a b c d

   

.

C.

0, 0, 0, 0

a b c d

   

. D.

0, 0, 0, 0

a b c d

   

.

Lời giải

Chọn D.

Dựa vào đồ thị hàm Số, ta có các nhận xét sau

Ta thấy rằng

lim ; lim

x x

y y

 

    

hệ số

0

a



Đồ thị hàm số cắt trục

Ox

tại điểm

( ;0)

A

A x

với

0

A

x



chính là điểm uốn của đồ thị hàm số.

Do đó

2

3 2 6 2 ( ) 0 3 . 0

A A

y ax bx c y ax b y x b a x

  

           

Đồ thị hàm số cắt trục

Oy

tại điểm

(0; )

B

B y

với

0 0

B B

y y d

   

Hàm số đã cho đồng biến trên

2

0; 4 0

y x b ac



       

mà

0 0

a c

  

.

Câu 22. [2D1-3.2-2] Tìm giá trị lớn nhất của hàm số

3 2

2 7 1y x x x    

trên

 

3;2



A.

3

. B.

1

. C.

4

. D.

13

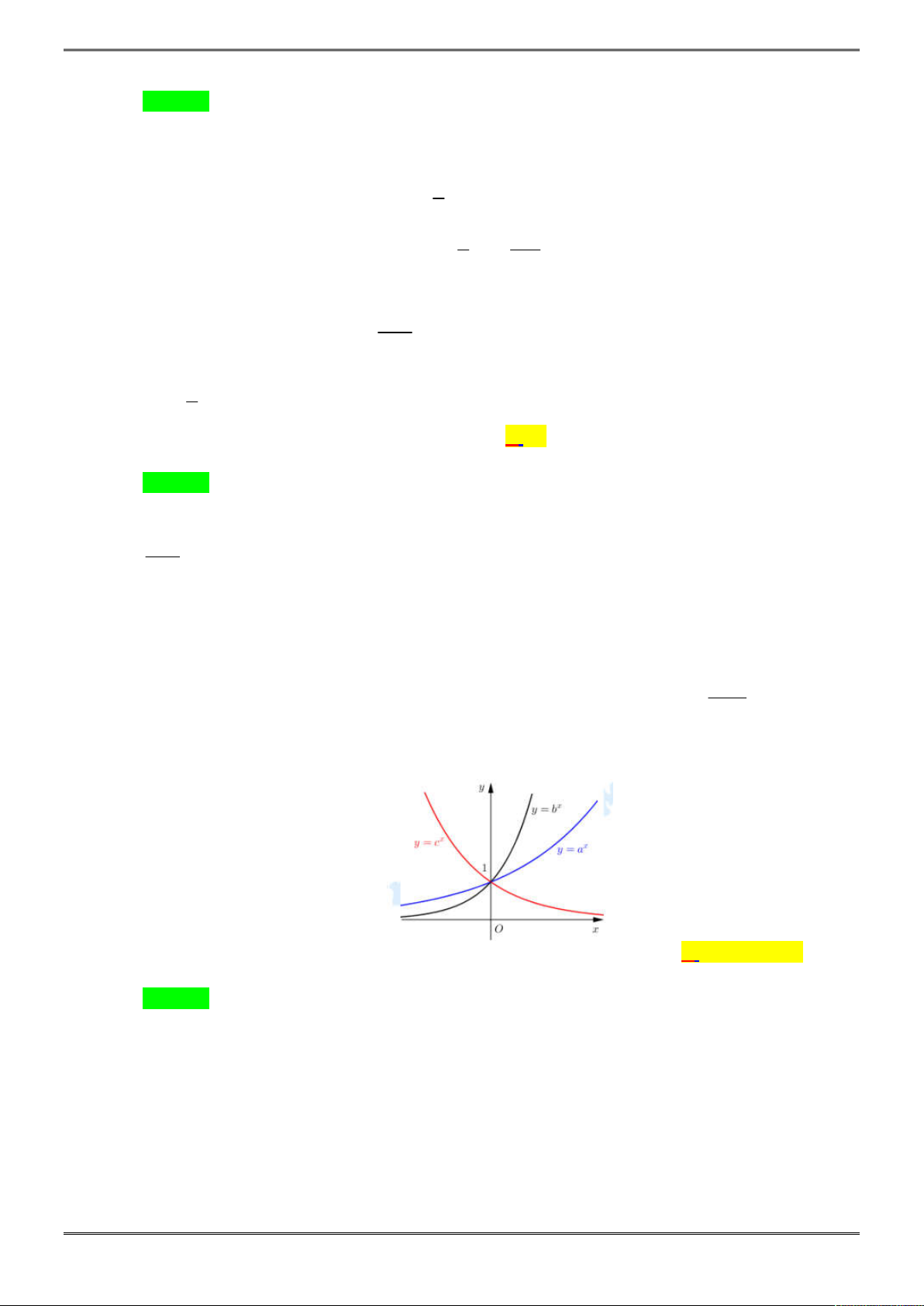
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 54

Lời giải

Chọn A.

Xét hàm số

3 2

2 7 1y x x x    

trên đoạn

[ 3;2]

ta có

2

1

7 4 3 ; 0

7

3

x

y x x y

x







 

    



 



Tính các giá trị

7 419

( 3) 13, (1) 3, , (2) 3

3 27

y y y y

 

        

 

 

Vậy giá trị lớn nhất của hàm số bằng

3

.

Câu 23. [2D1-6.15-3] Cho hàm số

1

x

y

x







và đường thẳng

2 .y x m  

Tìm giá trị của tham số

m

để

đồ thị hàm số đã cho cắt nhau tại 2 điểm phân biệt

A

,

B

và trung điểm của

AB

có hoành độ

bằng

5

2

A.

8

. B.

11

. C.

9

. D.

10

.

Lời giải

Chọn C.

Phương trình hoành độ giao điểm của

 

C

và

 

d

là

2

1

2

1

2 ( 1) 1 0(*)

x

m x

x

x m x m







  





    



Để

 

C

cắt

 

d

tại hai điểm phân biệt

(*)

có hai nghiệm khác 1

2

7

( 1) 8( 1) 0

1

m

m m

m





     



 



Khi đó gọi

,

A B

x x

là hoành độ của hai giao điểm

A

,

B

suy ra

1

5 9

2

A B

m

x x m



    

.

Câu 24. [2D2-4.7-2] Cho ba hàm số , ,

x x x

y a y b y c  

có đồ thị như hình dưới đây. Khẳng định nào

sau đây đúng?

A.

1a b c  

. B.

1

c b a  

. C.

1

c b a  

. D.

1

c a b  

.

Lời giải

Chọn D.

Dựa vào đồ thị hàm số, ta có các nhận xét sau:

Hàm số ,

x x

y a y b 

là các hàm số đồng biến trên



, hàm số

x

y c

là hàm số nghịch biến

trên



Khi đó

 

.ln ; .ln 0

ln ;ln 0

, 1

'

0 1

ln 0

.ln 0

x x

x

a a b b

a b

z b

y

c

c c











 

  

  

 















Ta có

( )

x

f x a

g x b















mà

0 0

( ) ( )f x g x

 (khi

0 0

0

)

x x

x a b a b     

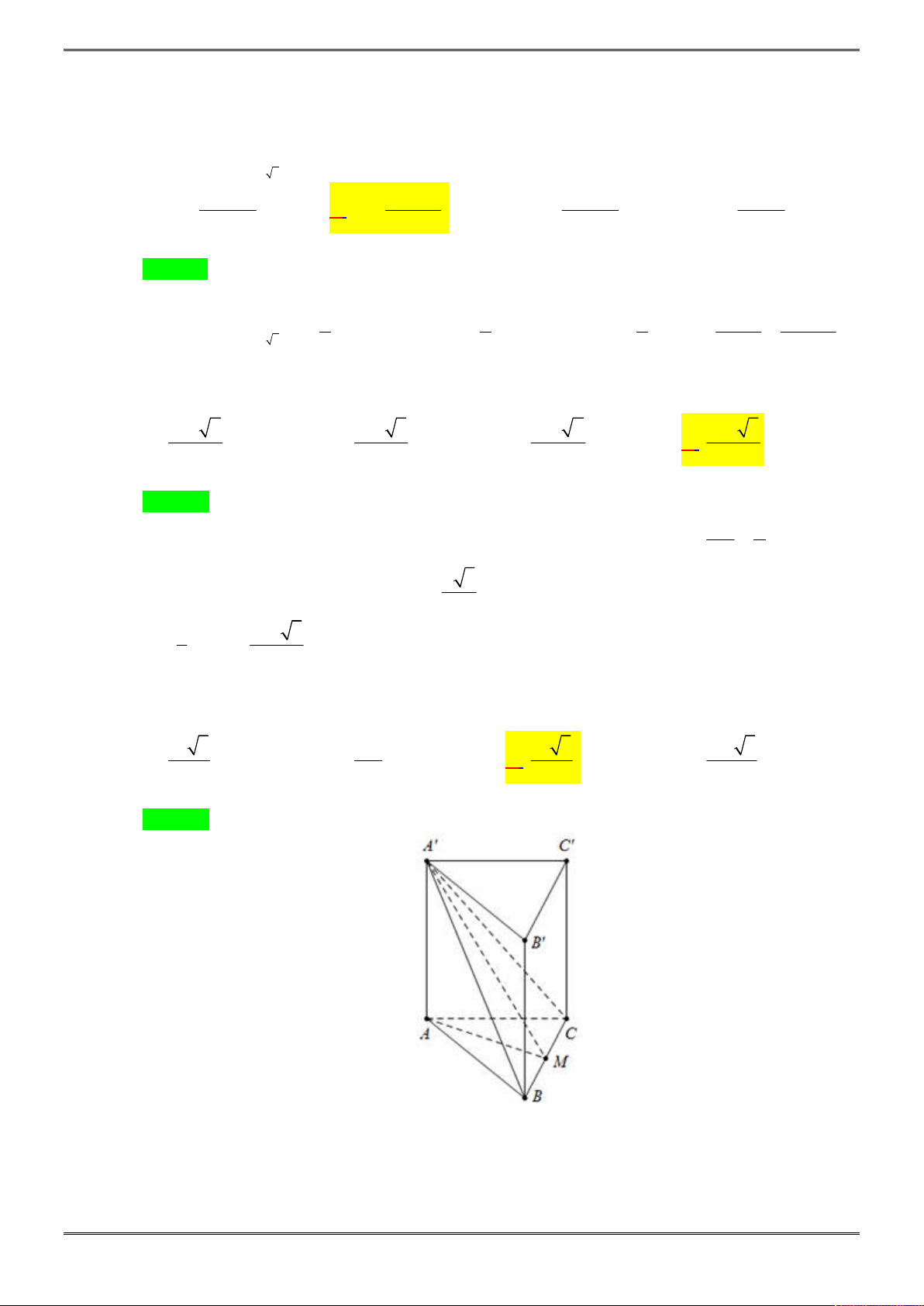
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 55

Hoặc có thể chọn

10

x



thì

10 10

1

a b a b   

Vậy ta được

1 0

b a c

   

.

Câu 25. [2D2-3.1-1] Cho

, 0

a b



và

, 1a b 

. Đặt log

a

b





, tính theo



biểu thức

2

3

log log

b

a

P b a

 

A.

2

2 5

P





 . B.

2

12

2

P





 . C.

2

4 3

2

P





 . D.

2

3

P







Lời giải

Chọn B.

Ta có

2

3 3

1 1 1 6 12

log log .log 2log .log 6.log .log

2 2 2 log 2

a b a b a

b

a

P b a b a b a b

b





         .

Câu 26. [2H2-1.3-1] Cho tam giác

ABC

đều cạnh

a

, đường cao

AH

. Tính thể tích của khối nón sinh

ra khi cho tam giác

ABC

quay xung quanh trục

AH

.

A.

3

6

12

a



. B.

3

12

a



. C.

3

2

24

a



. D.

3

24

a



Lời giải

Chọn D.

Khi quay tam giác

ABC

quanh trục

AH

ta được khối nón có bán kính

2 2

BC a

r

 

Và chiều cao của khối nón là

3

2

a

h AH 

. Vậy thể tích khối nón cần tính là

2

1

.

3

V r h





3

24

a





.

Câu 27. [2H1-3.9-2] Cho lăng trụ tam giác đều

.

ABC A B C

  

có

AB a

; góc giữa hai mặt phẳng

 

A BC



và

 

ABC

là

60

. Tính thể tích khối chóp

ABCC B

 

.

A.

3

8

a

. B.

3

4

a

. C.

3

4

a

. D.

3

3 3

8

a

Lời giải

Chọn C.

Gọi

M

là trung điểm của BC,

ABC

đều nên

AM BC

Tam giác

A BC



đều nền

A M BC





( ' )BC A AM 

Ta có



( ' ) ( ' ) '

( ' );( ) ( ' , ) '

( ' ) ( )

A AM A BC A M

A BC ABC A M AM A MA

A AM ABC AM

 



  



 



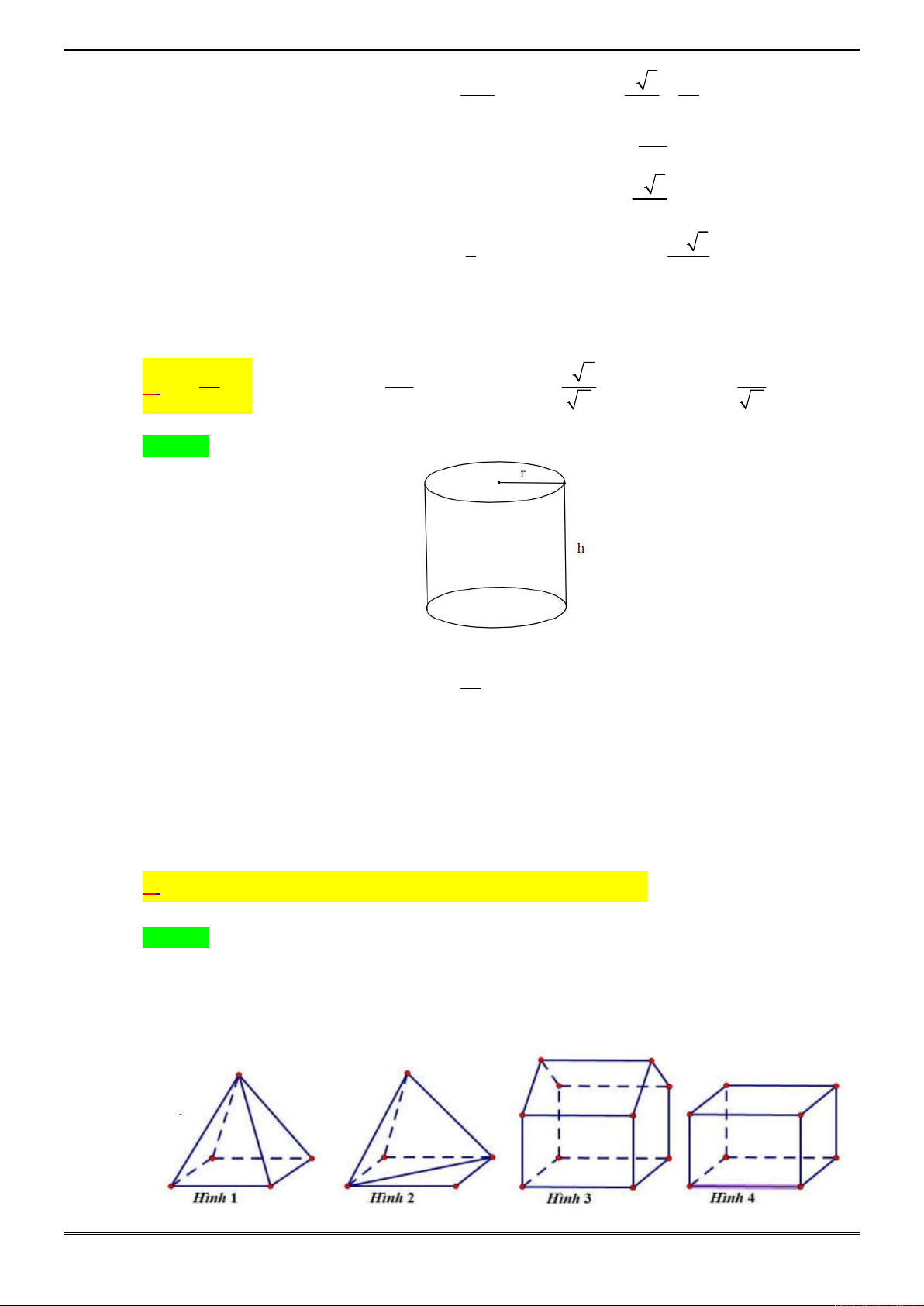
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 56

Xét

AA M





vuông tại

A

, có tan



0

' 3 3

' ' tan 60 .

2 2

AA a a

A MA AA

AM

   

Tứ giác

' 'BCC B

là hình chữ nhật có diện tích

2

'

3

'.

2

BCC C

a

S BB BC 

Mà

3

( ' ') ( ;( ' '))

'

2

AM BC

a

AM BCC B d A BCC B AM

AM BB





    







Thể tích khối chóp

' 'ABCC B

là

3

' ' ' '

1 3

( ;( ' ')).

3 4

ABCC B BCC B

a

V d A BCC B S 

.

Câu 28. [2H2-2.7-3] Một tấm tôn hình chữ nhật có kích thước

50cm x100cm

, người ta gò tấm tôn đó

thành mặt xung quanh của thùng đựng nước hình trụ có chiều cao

50cm

. Tính bán kính

R

của

đáy thùng gò được.

A.

50

R cm





. B.

100

R cm





. C.

5 2

R cm



 . D.

10

R cm





Lời giải

Chọn A.

2 .

xung quanh

S rh





- Cách giải:

50

50.100 2 . .50

xq

S r r



   

.

Câu 29. [2D1-4.1-2] Cho hàm số

 

y f x



có đồ thị (C) và

   

lim 2, lim 2

x x

f x f x

 

  

. Mệnh đề

nào sau đây đúng?

A.

 

C

có đúng một tiệm cận ngang.

B.

 

C

không có tiệm cận ngang.

C.

 

C

có hai tiệm cận ngang là các đường thẳng

2

x



và

2

x

 

.

D.

 

C

có hai tiệm cận ngang là các đường thẳng

2

y



và

2

y

 

.

Lời giải

Chọn D.

lim 2

x

 

đồ thị hàm số có tiệm cận ngang là y = 2

lim 2

x

  

đồ thị hàm số có tiệm cận ngang là

2

y

 

.

Câu 30. [2H1-1.3-1] Hình nào dưới đây không phải hình đa diện?

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 57

A. Hình 3. B. Hình 1. C. Hình 2. D. Hình 4.

Lời giải

Chọn C.

Hình đa diện (gọi tắt là đa diện)

 

H

là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn

hai điều kiện:

Hai đa giác phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có

một cạnh chung.

Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.

Mỗi đa giác như thế được gọi là một mặt của hình đa diện

 

H

. Các đỉnh, cạnh của các đa giác

ấy theo thứ tự gọi là các đỉnh, cạnh của hình đa diện

 

H

.

Từ lí thuyết hình 2 không phải hình đa diện.

Câu 31. [2H1-4.1-2] Cho lăng trụ đứng

.

ABC A B C

  

có đáy

ABC

là tam giác đều cạnh bằng

ă

, cạnh

bên

' 3

AA  . Tính khoảng cách

d

từ điểm

A

đến mặt phẳng

 

A BC



A.

15

5

d 

. B.

2 15

5

d 

. C.

3

2

d 

. D.

3

4

d 

Lời giải

Chọn A.

A'

A

I

C

B

B'

C'

H

Gọi

I

là trung điểm của

BC

Hạ

AH

vuông góc với

A I



Ta có:

 

'

AI BC

BC AA I BC AH

A I BC





   







   

 

'

' ; '

A I AH

AH A BC d A A BC AH

BC AH





   







2 2 2

3 1 1 1 15

2 5

AI AH

AH AA AI

     

.

Câu 32. [2D1-3.2-2] Tìm giá trị lớn nhất của hàm số

3 2

2 7 1y x x x    

trên

 

3;2



A. 3. B.

1

. C. 4. D.

13

Lời giải

Chọn A.

Xét hàm số

3 2

2 7 1y x x x    

trên đoạn

[ 3;2]

ta có

2

1

' 7 4 3 ; ' 0

7

3

x

y x x y

x







    



 



Tính các giá trị

7 419

( 3) 13, (1) 3, , (2) 3

3 27

y y y y

 

        

 

 

Vậy giá trị lớn nhất của hàm số bằng 3.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 58

Câu 33. [2D1-3.14-4] Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm

bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là

 

2 3

45

f t t t 

. Nếu xem

 

f t



là tốc độ truyền bệnh (người / ngày) tạithời điểm

t

. Hỏi tốc độ truyền bệnh sẽ lớn nhất

vào ngày thứ bao nhiêu kể từ ngày xuất hiện bệnh nhân đầu tiên.

A.

30

. B.

12

. C.

15

. D.

20

.

Lời giải

Chọn C.

 

2 3

45

f t t t 

 

2

' 90 3f t t t 

 

" 90 6 0 15

f t t t

    

.

Câu 34. [2H1-2.1-2] Cho hình chóp

.

S ABC

có đáy

ABC

là tam giác đều cạnh

2a

. Cạnh bên

SA

vuông góc với mặt phẳng đáy, thể tích của khối chóp

.

S ABC

bằng

3

4

a

. Tính độ dài

SA

A.

3

4

a

. B.

4

a

. C.

4

3

a

. D.

3

a

.

Lời giải

Chọn A.

Thể tích của khối chớp là

3

2

.

3.

1 3 3

. : 3

3 4 4

S ABC

S ABC ABC

ABC

V

a a

V SA S SA a

S



    

.

Câu 35. [2D1-6.0-2] Đồ thị của hàm số

3 2

( )

f x x ax bx c   

tiếp xúc với trục hoành tại gốc tọa độ

và cắt đường thẳng

1x 

tại điểm có tung độ bằng

3

khi

A.

2; 1; 0

a b c

  

. B.

0, 2

a c b

  

. C.

0, 2

a b c

  

. D.

2, 0

a b c

  

.

Lời giải

Chọn D.

Ta có

Đồ thị hàm số tiếp xúc với hoành độ tại gốc tọa độ, khi đó

 

' 0 0

0 0

0

f

f b

f

c



 



 



 







Đồ thị hàm số cắt đường thẳng

1x 

tại điểm có tung độ bằng

3

, khi đó đồ thị hàm số đi qua

điểm có tọa độ

   

1;3 10 3 1 3 2

f a a

      

.

Suy ra

2, 0.

a b c

  

.

Câu 36. [2D1-3.14-4] Một người nuôi cá thí nghiệm trong hồ. Người đó thấy rằng nếu trên mỗi đơn vị

diện tích của mặt hồ có

n

con cá thì trung bình mỗi con cá sau một vụ cân

nặng

( ) 480 20P n n 

(gam). Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để

sau một vụ thu hoạch được nhiều cá nhất?

A. 12. B. 14. C. 10. D. 18.

Lời giải

Chọn A.

Khối lượng cá mỗi đơn vị diện tích sau khi thu hoạch bằng

   

2

. 480 20 20 144 12 2880

n P n n n n

 

     

 

Suy ra dấu

" "

xảy ra khi

 

2880 12

nP n m

  

Vậy cần thả

12

con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được

nhiều cá nhất.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 59

Câu 37. [2H2-3.5-2] Cho hình chóp tam giác đều

.

S ABC

có đường cao



, 45

SO a SAB

  

. Bán kính

mặt cầu ngoại tiếp hình chóp

.

S ABC

bằng:

A.

3

4

a

. B.

3

2

a

. C.

3

2

a

. D.

3

4

a

.

Lời giải

Chọn C.

Tam giác

SAB

cân tại S có



45

o

SAB SAB

   vuông cân tại S

Suy ra

SA SB

mà

, ,SAB SBC SAC SA SB SC     

đôi một vuông góc với nhau

Khi đó

2 2 2 2

1 1 1 1

SO SA SB SC

  

mà

3SA SB SC x x a

    

Bán kính mặt cầu ngoại tiếp hình chóp

.

S ABC

là

2 2 2

3 3

2 2 2

SA SB SC x a

R

 

  

.

Câu 38. [2D2-4.5-2] Hỏi với giá trị nào của

a

thì hàm số

 

3

x

y a

 

nghịch biến trên 

A.

2 3

a

 

. B.

0 1a 

. C.

2

a



. D.

0

a



Lời giải

Chọn A.

Để hàm số nghịch biến trên



thì

0 3 1 2 3

a a

     

.

Câu 39. [2D2-1.1-4] Cho các số

0, 0, 0

m n p

  

thỏa mãn

4 10 25

m n p

 

. Tính giá trị biểu thức

2 2

n n

T

m p

 

A.

1T 

. B.

5

2

T



. C.

2T 

. D.

1

10

T 

Lời giải

Chọn A.

Từ

log 4 2log 2

4 10 25 log 4 log 25

log 25 2log5

m n p

n

m

m n p

n

p



 



     





 





 

2 log 2 log5 2log10 2 1

n n

T

m p

       

Cách 2: Cho

10 25

1 log 4; log 4

m n p    do đó

1

2 2

n n

T

m p

  

.

Câu 40. [2D1-2.3-2] Tìm điểm cực tiểu của hàm số

3 2

1

2 3 1

3

y x x x   

A.

3

x



. B.

1x 

. C.

1y 

. D.

 

3;1

Lời giải

Chọn A.

2

1

4 3 ; 2 4

3

x

y x x y x

x





 

     







Ta có

 

1 2 0 1y x



    

là điểm cực đại;

 

3 2 0 3

y x



   

là điểm cực tiểu của hàm

số.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 60

PHẦN II: PHẦN TỰ LUẬN.

Câu 1. Tìm giá trị lớn nhất của hàm số

3 2

2 7 1y x x x    

trên

 

3;2



Lời giải

Xét hàm số

3 2

2 7 1y x x x    

trên đoạn

[ 3;2]

ta có

2

1

' 7 4 3 ; ' 0

7

3

x

y x x y

x







    



 



Tính các giá trị

7 419

( 3) 13, (1) 3, , (2) 3

3 27

y y y y

 

        

 

 

Vậy giá trị lớn nhất của hàm số bằng

3

.

Câu 2. Hình chóp

.

S ABCD

có đáy

ABCD

là vuông cạnh

a

, hình chiếu vuông góc của

S

trên mặt

phẳng

 

ABCD

trùng với trung điểm của

AD

;

M

trung điểm

CD

; cạnh bên

SB

hợp với đáy

góc

0

60

. Thể tích của khối chóp

.

S ABM

là:

Lời giải

Gọi

H

là trung điểm của

AD

nên

 

.

1 1

. . . . .

3 6

S ABM ABM

SH ABCD V SH V SH AB BC



   

Ta có

HB

là hình chiếu của

SB

trên mặt phẳng

   

 



 



0

; ; 60

ABCD SB ABCD SB HB SBH   

Xét

SHB

vuông tại

H

, có



0

5 15

tan tan 60 . 3.

2 2

SH a a

SBH SH BH

BH

    

Vậy thể tích của khối chóp

.

S ABM

là

3

2

.

1 15 15

. .

6 2 12

S ABM

a a

V a 

.

BẢNG ĐÁP ÁN

1.B

2.C

3.D

4.D

5.C

6.D

7.C

8.A

9.C

10.C

11.C

12.B

13.A

14.A

15.C

16.B

17.D

18.C

19.B

20.A

21.D

22.A

23.C

24.D

25.B

26.D

27.C

28.A

29.D

30.C

31.A

32.A

33.C

34.A

35.D

36.A

37.C

38.A

39.A

40.A

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 61

ĐÊ ÔN TẬP SỐ 05

PHẦN 1: PHẦN TRẮC NGHIỆM

Câu 1. [2D1-4.2-1] Cho hàm số







2

1

x

y

x

. Xét các mệnh đề sau.

1) Hàm số đã cho đồng biến trên

   

  

;1 1;

.

2) Hàm số đã cho đồng biến trên

 



\ 1

.

3) Hàm số đã cho đồng biến trên từng khoảng xác định.

4) Hàm số đã cho đồng biến trên các khoảng

 

 ; 1

và

 

  

1;

.

Số mệnh đề đúng là

A.

3

. B.

2

. C.

1

. D.

4

.

Lời giải

Chọn B.

Ta có

 



   



2

1

0 x 1

1

y

x

.

Suy ra hàm số đã cho đồng biến các khoảng

 

 ; 1

và

 

  

1;

.

Do đó chỉ có mệnh đề 3 và 4 đúng.

Câu 2. [2H1-3.3-1] Cho lăng trụ tam giác đều

  

.ABC A B C

có tất cả các cạnh đều bằng

2a

. Tính thể

tích của khối lặng trụ.

A.

3

6

2

a

. B.

3

6

a

. C.

3

6

a

. D.

3

8

a

.

Lời giải

Chọn A.

Ta có



 

2 2

3 3

4 2

ABC

AB a

S

,



 

2h AA a

.

Thể tích



 

3

6

.

2

ABC

a

V h S

.

Câu 3. [2D2-6.2-2] Giải phương trình

 

3

log 6 5 2

x

 

.

A.

5

6

x



. B.

0

x



. C.

2

3

x



. D.

9

4

x



.

Lời giải

Chọn C.

 

2

3

2

log 6 5 2 6 5 3

3

x x x

      

.

Câu 4. [2D1-4.2-2]Phương trình đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số

1

2

x

y

x







lần lượt là

A.

2; 1x y 

. B.

2; 1y x 

. C.

2; 1

x y

  

. D.

2; 1x y  

Lời giải

Chọn A.

Tiệm cận đứng:

2

x



, tiệm cận ngang

1y 

.

Câu 5. [2D2-4.2-1] Tính đạo hàm của hàm số

sin 2

x

y e x

 .

A.

 

sin 2 cos2

x

e x x



. B.

 

sin 2 2cos 2

x

e x x



.

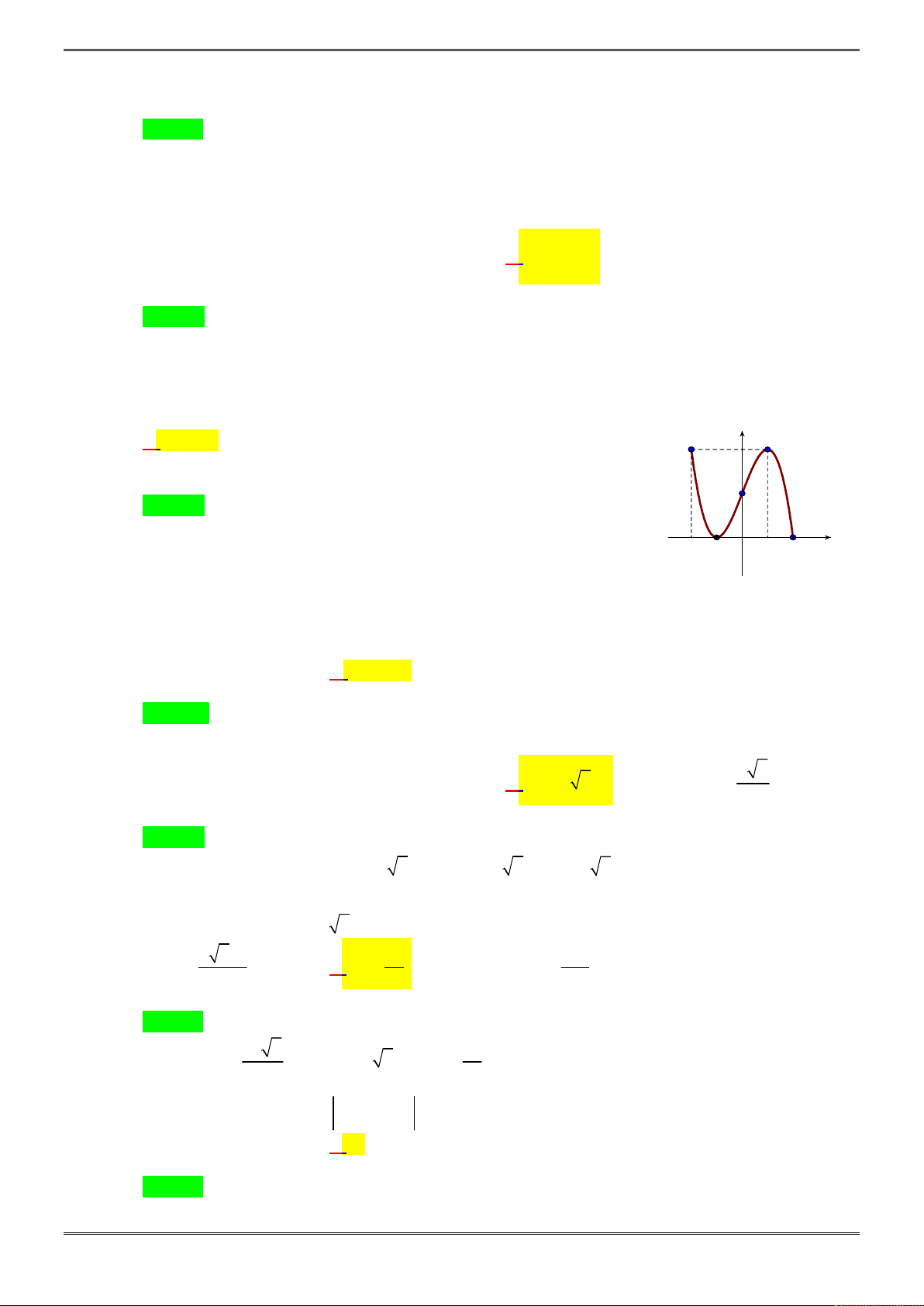
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 62

x

y

4

2

1

-1

-2

2

O

C.

 

sin 2 cos 2

x

e x x



. D.

cos 2

x

e x

.

Lời giải

Chọn B.





   



     

sin 2 . sin 2 sin 2 2 cos 2 sin 2 2cos2

x x x x x

y e x e x e x e x e x x

.

Câu 6. [2D2-6.2-1] Giải bất phương trình

 



2

3

2 4

x x

A.











2

1

x

. B.

 2 4x

. C.

 1 2.x

. D.

 0 x 2.

Lời giải

Chọn C.

 

         

2

3 2 2

2 4 3 2 3 2 0

x x

x x x x

.

Câu 7. [2D1-2.2-2] Cho hàm số

 ( )y f x

xác định và liên tục trên

 



 

2; 2

và có đồ thị là đường cong

trong hình vẽ bên. Hàm số

( )f x

đạt cực tiểu tại điểm nào sau đây?

A.

 1x

. B.

 1x

.

C.

 2x

. D.

 2x

.

Lời giải

Chọn A.

Dựa vào đồ thị ta thấy

( )f x

đạt cực tiểu tại điểm

 1x

và đạt cực

đại tại điểm

 1x

.

Câu 8. [2H1-1.2-1] Chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó

vào chỗ trống mệnh đề sau trở thành mệnh đề đúng:

“ Số cạnh của một hình đa diện luôn ………………. số đỉnh của hình đa diện ấy.”

A. bằng. B. nhỏ hơn hoặc bằng.

C. nhỏ hơn. D. lớn hơn.

Lời giải

Chọn D.

Câu 9. [2H1-3.6-2] Tính thể tích của khối lập phương

. ' ' ' 'ABCD A B C D

biết

' 2AD a

A.



3

V a

. B.



3

8V a

. C.



3

2 2V a

. D.



3

2 2

3

V a

.

Lời giải

Chọn C.

Gọi x là cạnh của hlp =>

   

' 2 2 2AD x a x a





3

2 2V a

.

Câu 10. [2H1-2.2-2] Cho hình chóp tam giác

.S ABC

có đáy

ABC

là tam giác đều cạnh a, cạnh bên

SA

vuông góc đáy và



2 3SA a

. Tính thể tích

V

của khối chóp

.S ABC

A.



3

3 2

2

a

V

. B.



3

2

a

V

. C.



3

2

a

V

. D.



3

V a

.

Lời giải

Chọn B.

Ta có



2

day

3

4

a

S

;

 

2 3h SA a





3

2

a

V

.

Câu 11. [2D1-2.2-2] Hàm số

  

2

5 4

y x x

có bao nhiêu điểm cực trị?

A. 1. B. 3. C. 0. D. 2.

Lời giải

Chọn B.

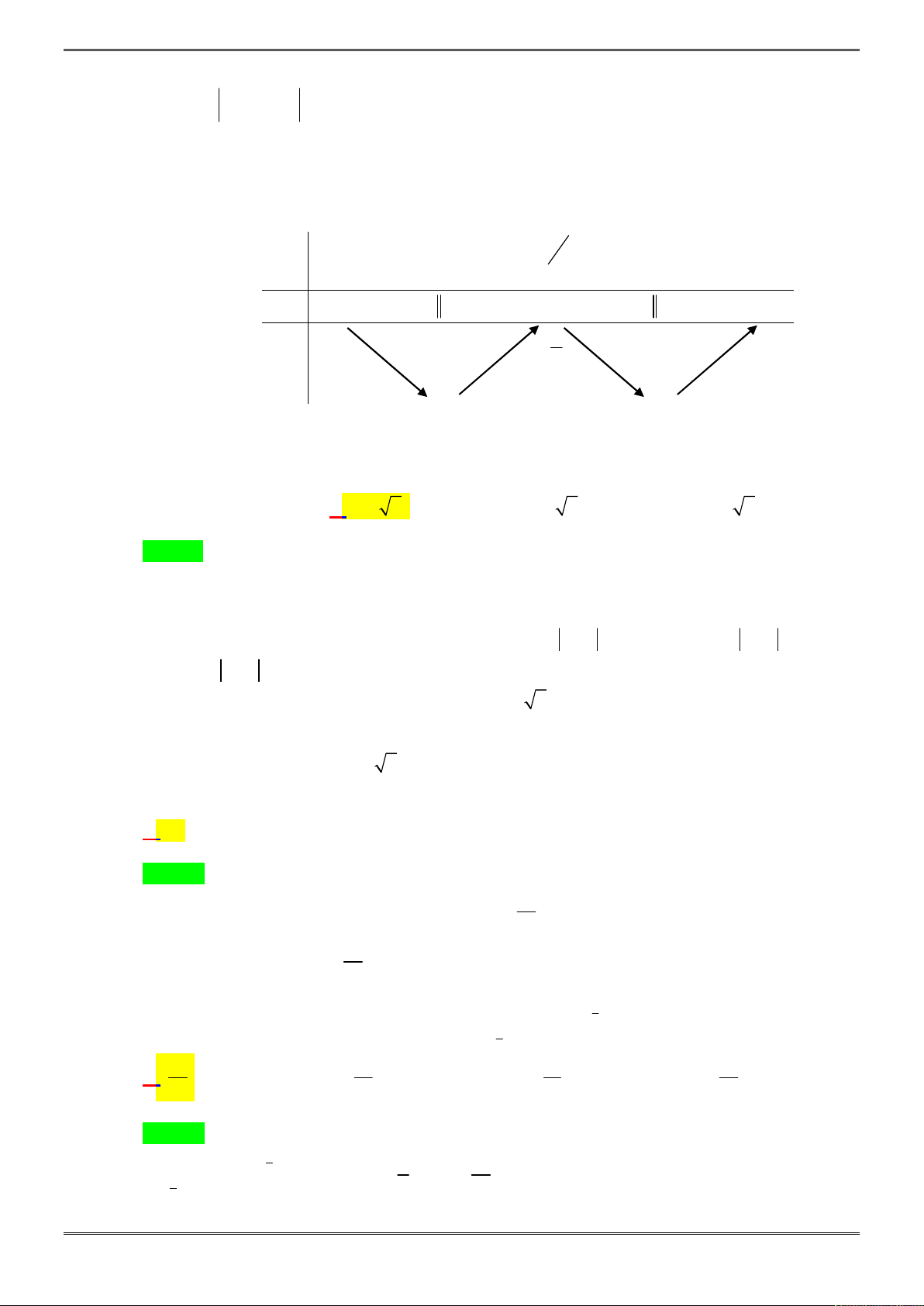
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 63

Ta có



 



   



  





2

5 4

x x

y x x

x x









  

  

2

5 4 0

x x

.



   









    





2

2 5 neu 5 4 0

x x x

y

x x x

.

Ta có bảng biến thiên

Hàm số có 3 cực trị.

Câu 12. [2D2-6.3-2] Tổng tất cả các nghiệm của phương trình

   

2

4 4

2log 3 log 5 0

x x

   

bằng

A. 8. B.

8 2



. C.

8 2



. D.

4 2



.

Lời giải

Chọn B.

Điều kiện:

3

5

x











.

       

2

4 4 4 4 4

2log 3 log 5 0 2log 3 2log 5 0 log 3 5 0

x x x x x x

            

 

3 5 1 (*)

x x   

.

+) Nếu

5

x



thì

  

(*) 3 5 1 4 2

x x x       .

+) Nếu

3 5

x

 

thì

  

(*) 3 5 1 4

x x x

      

.

Vậy tổng các nghiệm bằng

8 2



.

Câu 13. [2D2-4.3-2] Cho

2 2

log 4,log 4

b c

  

. Hãy tính

 

2

log

b c

A.

4

. B.

7

. C.

6

. D.

8

.

Lời giải

Chọn A.

4

2

log 4 2 16

b b

   

,

4

2

1

log 4 2

16

c c



    

.

Vậy

 

2 2

1

log log 16 . 4

16

b c

 

 

 

 

.

Câu 14. [2D2-6.4-2] Tính giá trị của biểu thức sau:

2

1

2 2

2

1

log log ; 1 0.

a

a a a

  

A.

17

4

. B.

13

4

. C.

11

4



. D.

15

4



.

Lời giải

Chọn A.

 

2

1

2

2 2

2

1

1 17

log log 2log + log

4 4

a a

a

a a a a    .

x

–∞

4

5

2



1

+∞

y



–

+ 0 –

+

y

+∞

0

9

4



0

+∞

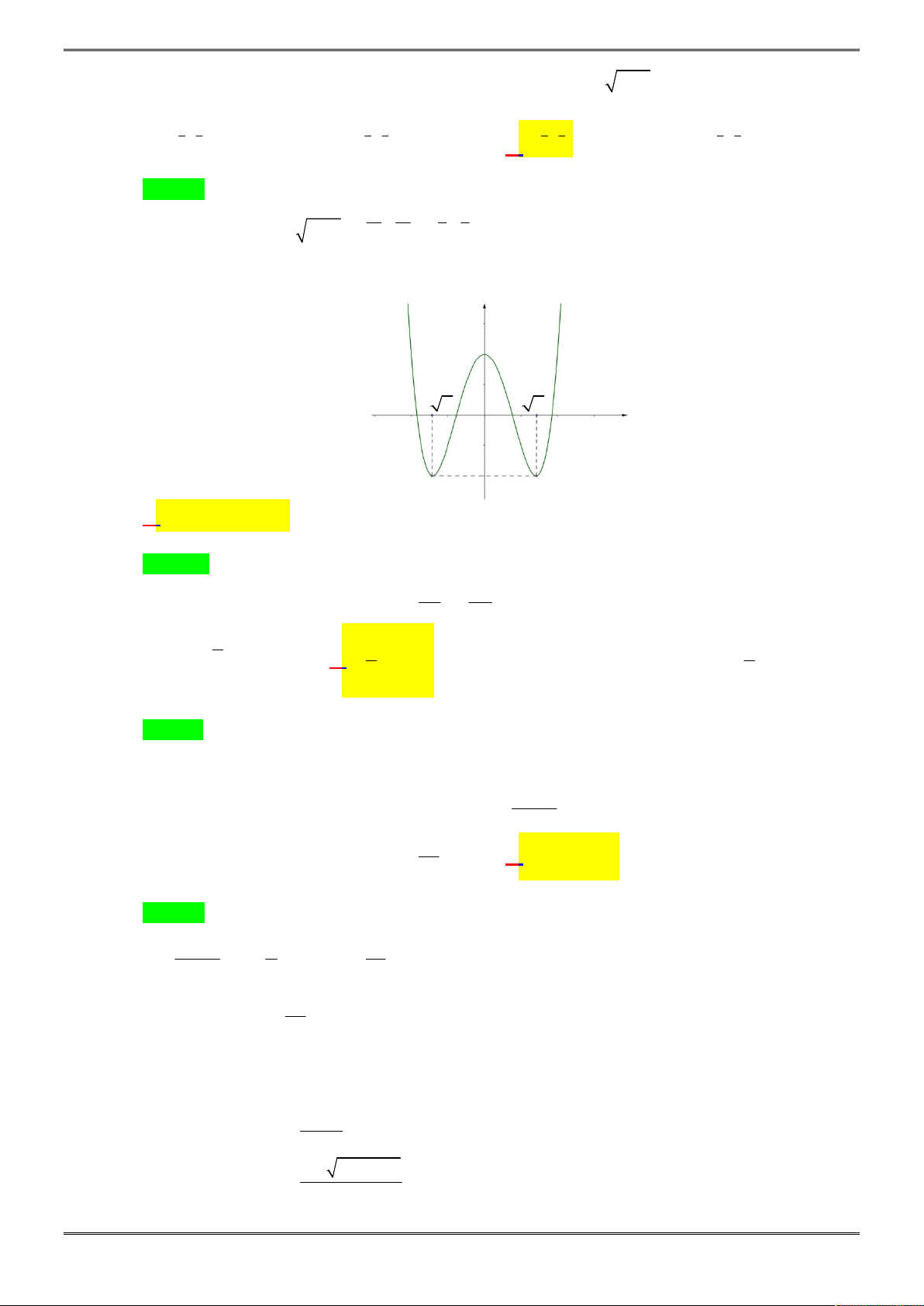
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 64

Câu 15. [2D1-9.1-2] Cho

,a b

là các số thực dương. Viết biểu thức

3 3

12

a b

dưới dạng lũy thừa với số

mũ hữu tỉ.

A.

3 1

4 2

a b

. B.

1

9

4

a b

. C.

1 1

4 4

a b

. D.

1 3

4 4

a b

.

Lời giải

Chọn C.

Do

,a b

dương nên:

 

3 3 1 1

12

3 3

12 12 4 4

. .a b a b a b

.

Câu 16. [2D2-6.4-2]Đường cong trong hình bên là đồ thị một hàm số trong bốn hàm số được liệt kê ở

bốn phương án A, B, C, D dưới đây. Hỏi đó là đồ thị hàm số nào?

A.

  

4 2

y x x

. B.

  

4 2

y x x

. C.

  

4 2

y x x

. D.

   

4 2

y x x

.

Lời giải

Chọn A.

Câu 17. [2D2-5.2-2] Giải bất phương trình

4 1 2 2

2 1 2 1

2 2 1.

x x

 

 

 

A.



 









1

2

1

x

. B.

  

1

2

x

. C.

 1x

. D.

 

1

2

x

.

Lời giải

Chọn B.

Thử với

 0x

ta được:



 

1 2

2 2 1

(đúng).

Câu 18. [2D1-3.3-1] Tìm giá trị lớn nhất của hàm số

2

9

x

y

x



 trên đoạn

 

1;4 .

A.

 

1;4

max 11

y



. B.

 

1;4

25

max

4

y

 

. C.

 

1;4

max 10

y



. D.

 

1;4

max 6

y



.

Lời giải

Chọn C.

2

9 9

x

y x

x x



  

 

2

3 1;4

9

1 0

3 1;4

x

y y

x

  

 

     



  





 

1 10

y



;

 

25

4

y 

;

 

3 6

y



.

Vậy:

 

1;4

max 10

y



.

Câu 19. [2D1-9.1-1] Xét các mệnh đề sau:

1. Đồ thị hàm số

1

2 3

y

x





có một đường tiệm cận đứng và một đường tiệm cận ngang.

2. Đồ thị hàm số

2

1

x x x

y

x

  



có hai đường tiệm cận ngang và một đường tiệm cận đứng.

y

2



2

2

x

O

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 65

3. Đồ thị hàm số

2

2 1

1

x x

y

x

 





có một đường tiệm cận ngang và hai đường tiệm cận đứng.

Số mệnh đề ĐÚNG là

A. 3. B. 2. C. 1. D. 0.

Lời giải

Chọn C.





1

2 3

y

x

có một đường tiệm cận đứng và một đường tiệm cận ngang.



  



2

1

lim 2;

x

x x x

x



  



2

1 1

lim

2

x

x x x

x

  

 

2

1

x x x

y

x

có hai đường tiệm cận

ngang và một đường tiệm cận đứng.

 





2

2 1

1

x x

y

x

có tập xác định

 

 

  





 

1

; \ 1

2

D

nên có tối đa một đường tiệm cận đứng.

Câu 20. [2D2-1.2-1] Cho

,a b

là hai số thực dương. Rút gọn biểu thức

1 1

3 3

2 2

6 6

a b b a

a b



.

A.

1 2

3 3

a b

. B.

2 2

3 3

a b

. C.

3

ab

. D.

2 1

3 3

a b

.

Lời giải

Chọn C.

Ta có

1 1 1 1

3 3 6 6

1 1

1 1 1 1

1 1

3 3

2 2 2 2

3

3 3

1 1 1 1

6 6

6 6 6 6

a b a b

a b b a a b b a

a b ab

a b

a b a b

 



 

 

 

   



 

.

Câu 21. [2D2-6.2-2] Giải bất phương trình:

 

2

1

2

log 3 2 1

x x

   

A.

 

;1

x

 

. B.

[0;2)

x



. C.

[0;1) (2;3]

x

 

. D.

[0;2) (3;7]

x

 

.

Lời giải

Chọn C.

 

2

1

2

log 3 2 1

x x

   

 

2

1

3 2 0

[0;1) (2;3]

2

3 2 2

0 3

x

x x

x

x x

x

 





  

 



    



 



  

 



 



.

Câu 22. [2D2-7.1-2] Giả sử ta có hệ thức

 

2 2

7 , 0

a b ab a b

  

. Hệ thức nào sau đây là đúng?

A.

 

2 2 2

2log log loga b a b

  

. B.

2 2 2

2log log log

3

a b



 

.

C.

 

2 2 2

log 2 log log

3

a b



 

. D. 4

2 2 2

log log log

6

a b



 

.

Lời giải

Chọn B.

Từ

 

2 2

7a b ab

a

2

+ b

2

= 7ab.Ta có

   



       

2 2

2

2 7 9 ( )

3

a b

a b ab ab a b ab ab

Lấy logarit cơ số 2 hai vế ta có:



 

2 2 2

2log log log

3

a b

.

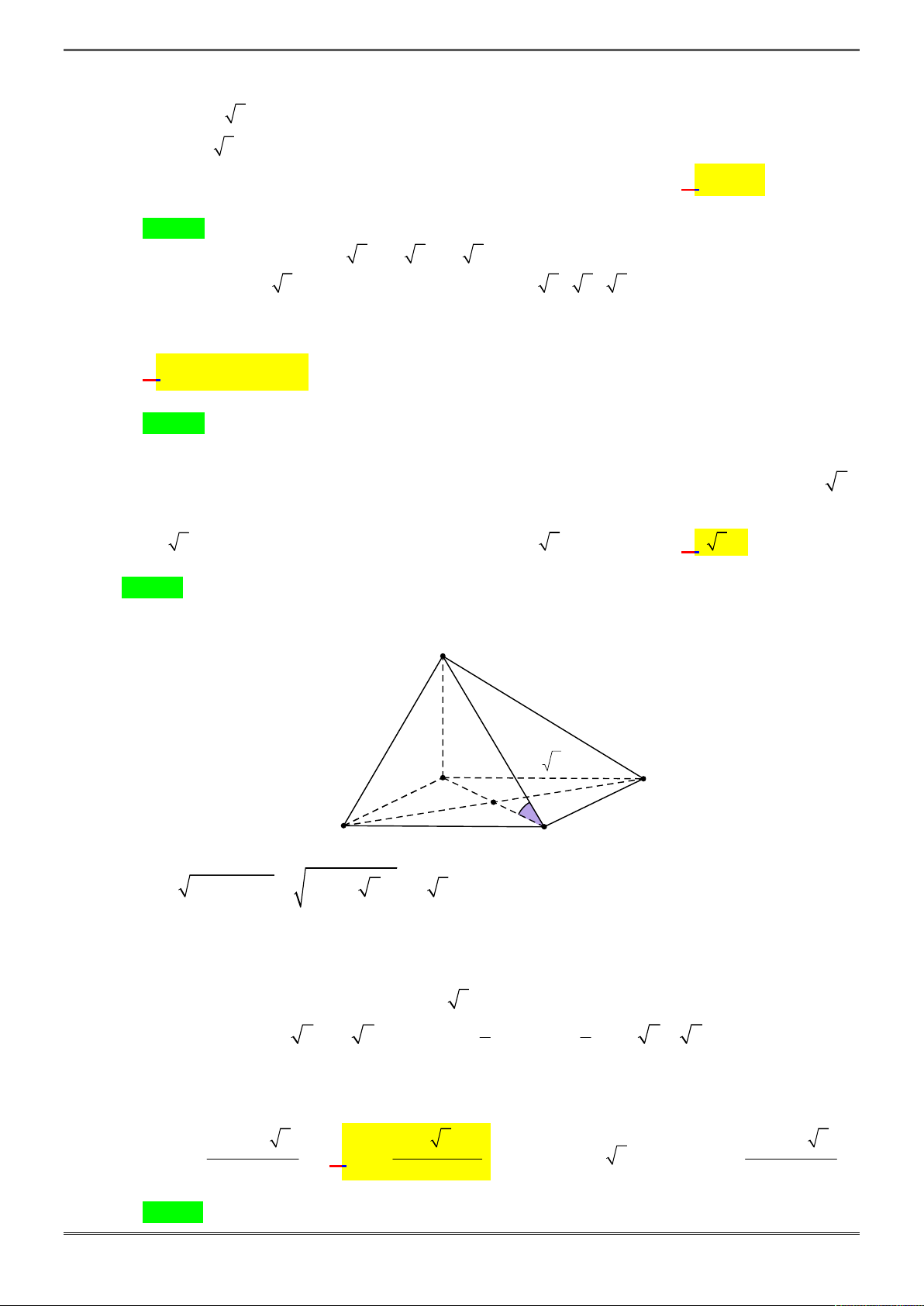
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 66

Câu 23. [2D1-3.1-1] Một hộp giấy hình hộp chữ nhật có thể tích

3

3dm

. Nếu tăng mỗi cạnh của hộp

giấy thêm

3

3 dm

thì thể tích của hộp giấy là

3

24dm

. Hỏi nếu tăng mỗi cạnh của hộp giấy ban

đầu lên

3

2 3 dm

thì thể tích hộp giấy mới là:

A.

3

48dm

. B.

3

192dm

. C.

3

72dm

. D.

3

81dm

.

Lời giải

Chọn D.

Chọn kích thước 3 cạnh là

3

3dm

,

3

3dm

,

3

3dm

thỏa mãn giả thiết bài toán. Khi đó tăng thêm

mỗi kích thước

3

2 3 dm

thì thể tích khối hộp là

 

3

3 3 3

3 3.3 3.3 3 81

V dm

.

Câu 24. [2H2-2.3-2] Diện tích toàn phần của hình trụ có bán kính đáy

R

, chiều cao

h

và độ dài đường

sinh

l

là?

A.

 

 

2

2 2

tp

S R Rl

. B.

 

 

2

tp

S R Rl

. C.

 

 

2

tp

S R Rl

. D.

 

 

2

tp

S R Rl

.

Lời giải

Chọn A.

Áp dụng công thức SGK.

Câu 25. [2H2-4.1-1] Hình chóp tứ giác

.

S ABCD

có đáy là hình chữ nhật cạnh

AB a

,

2AD a



;

( )SA ABCD

, góc giữa

SC

và đáy bằng

60

. Thể tích khối chóp

.

S ABCD

bằng.

A.

3

6 .a

. B.

3

3 .a

. C.

3

3 2 .a

. D.

3

2 .a

Lời giải

Chọn D.

a

a 2

B

D

C

A

S



 

2

2 2 2

2 3.

AC AB BC a a a    



AC

là hình chiếu vuông góc của

SC

trên

 

ABCD

 









 



o

, , 60

SC ABCD SC AC SCA   



SAC

vuôngtại

A



o

tan 3 tan 60 3 .SA AC SCA a a

   



2

. . 2 2.

ABCD

S AB AD a a a  

2 3

.

1 1

. . .3 . 2 2 .

3 3

S ABCD ABCD

V SA S a a a

   

.

Câu 26. [2H2-1.3-2] Thiết diện qua trục của hình nón

 

N

là tam giác vuông cân có cạnh góc vuông

bằng

a

. Tính diện tích toàn phần của hình nón này?

A.

 







2

2 2

2

tp

a

S

. B.

 







2

2 1

2

tp

a

S

. C.

 



 

2

2 1

tp

S a

. D.

 







2

3 2

2

tp

a

S

.

Lời giải

Chọn B.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 67

Thiết diện qua trục của hình nón là tam giác vuông cân tại đỉnh của hình nón.

Do đó đường sinh

l a

và đường kính đáy là

 2d a

bán kính



2

a

R

Diện tích toàn phần của hình nón là:

 



   



    

2

2 1

2

. . . . .

2 2 2

tp

a

a a

S R l R a

.

Câu 27. [2D1-6.3-2]Cho hàm số

  

3

3 2

y x x

có đồ thị

 

C

. Gọi

d

là đường thẳng đi qua

 

3;20

A

và có hệ số góc

m

. Giá trị của

m

để đường thẳng

d

cắt

 

C

tại

3

điểm phân biệt là

A.



15

4

m

. B.

 

15

, 24

4

m m

. C.

 

15

, 24

4

m m

. D.



15

4

m

.

Lời giải

Chọn B.

Đường thẳng

 

  : 3 20

d y m x

Xét phương trình hoành độ giao điểm

   





 

 

           



    





3 2

2

3

3 2 3 20 3 3 6 0

3 6 0

x

x x m x x x x m

g x x x m

Để

d

cắt

 

C

tại 3 điểm phân biệt thì phương trình

 

 0

g x

phải có 2 nghiệm phân biệt

 3x

 



   



 

 

 

  









15

4 15 0

4

3 24 0

24

m

g m

m

.

Câu 28. [2D2-5.3-2] Giải phương trình:

2

3 8.3 15 0

x

  

A.

3

log 5

log 25

x











. B.

3

2

log 5

x











. C.

3

2

log 25

x











. D.

2

3

x











.

Lời giải

Chọn C.

Đặt

 

2

3 0

x

t t

 

. Phương trình đã cho được viết lại

2

3 3

2

2log 5 log 25

5 3 5

8 15 0

3

2 2

3 3

x

x x

t

t t

t

x x



 

 





      

 





 



 







.

Câu 29. [2H1-2.3-2] Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình chữ nhật có

; 5AB a AC a 

. Hai

mặt bên

 

SAB

và

 

SAD

cùng vuông góc với đáy, cạnh bên

SB

tạo với đáy một góc bằng

60

. Tính theo

a

thể tích của khối chóp

.

S ABCD

.

A.

3

2 2a

. B.

3

4 2a

. C.

3

6 2a

. D.

3

2a

.

Lời giải

Chọn A.

S

A

B

C

D

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 68

Hai mặt bên

 

SAB

và

 

SAD

cùng vuông góc với đáy suy ra

 

SA ABCD



.

 



, , 60

SB ABCD SB AB SBA

   

Do đó: Đường cao

tan 60 3SA AB a

  

Diện tích đáy

2 2 2 2 2

. . . 25 2 6

ABCD

S AB BC AB AC AB a a a a     

Thể tích

2 3

1 1

. 3.2 6 2 2

3 3

ABCD

V SA S a a a  

.

Câu 30. [2H1-2.2-2] Hình chóp

.

S ABC

có đáy

ABC

là tam giác vuông tại

A

, cạnh

AB a

,

2BC a

, chiều cao

6SA a

 . Thể tích khối chóp là

A.

3

2

a

V 

. B.

3

6

3

a

V 

. C.

2

a

V 

. D.

3

2 6

V a .

Lời giải

Chọn A.

Xét tam giác vuông

ABC

có

2 2

3AC BC AB a

  

Nên:

3

.

1 1 1 1 1 2

. . . . . . . 6. . 3

3 3 2 6 6 2

S ABC ABC

a

V SA S SA AB AC SA AB AC a a a    

.

Câu 31. [2D2-5.8-3] Tìm tất cả các giá trị của tham số

m

để phương trình

  9 2 .3 2 0

x x

m m

có hai

nghiệm phân biệt

1 2

;x x

sao cho

  

1 2

x x

là

A.

 

3

2

m

. B.



27

2

m

. C.



3 3

m

. D.



9

2

m

.

Lời giải

Chọn B.

 Đặt

 3 , 0

x

t t

. PT trở thành

 





  





2

0

2 2 0 (2)

t

t mt m

 PT đã cho có hai nghiệm phân biệt

1 2

;x x

sao cho

  

1 2

x x

 PT(2) có hai nghiệm dương

phân biệt

1 2

,t t

thoả



1 2

. 27

t t

(vì



  

1 2

3

1 2

3 3 . 27

x x

t t

) 





 













0

27

S

P





27

2

m

.

Câu 32. [2D2-6.5-3] Giải bất phương trình

 



 



 



 

2

0,7 6

log log 0

4

x x

x

A.

   ( 4; 3) (8; )

. B.

 ( 4; 3)

. C.

 ( 4; )

. D.

(8; )

.

Lời giải

Chọn A.

Tập xác định

 

   

( 4;1) 0;D

.

A

B

C

S

6a

2 a

a

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 69

Ta có:

 

    

 

      

 

   

 

2 2 2 2

0,7 6 6

5 24

log log 0 log 1 6 0

4 4 4 4

x x x x x x x x

x x x x

.

      4 3 8x x

.

Câu 33. [2D1-6.17-3] Cho hàm số

 







2 1

1

x

y C

x

. Tìm giá trị

m

để đường thẳng

 :d y x m

cắt

 

C

tại hai điểm phân biệt sao cho tam giác

OAB

vuông tại

A

hoặc

B

.

A.

 

1 5

m

. B.

 

1 3

m

. C.

 

1 2m

. D.

 

1 6

m

.

Lời giải

Chọn A.

Phương trình hoành độ giao điểm :

   



       



2

2 1

3 1 0 *

1

x

x m x m x m

x

.

Ta có

d

cắt

 

C

tại hai điểm phân biệt khi chỉ khi

   



    





    





2

2 5 0

1 3 .1 1 0

m m

(luôn đúng với

mọi

m

).

Gọi

1 2

,x x

là hai nghiệm phương trình

 

*

, ta có



  





 





1 2

3

1

x x m

và

 

C

cắt

d

tại

   

 

1 1 2 2

; , ;

A x x m B x x m

.

Vectơ

 

  



2 1 2 1

;

AB x x x x

cùng phương với vectơ

 





1;1

u

.

Tam giác

OAB

vuông tại

A

khi chỉ khi

   





1

. 0 2 0

OA u x m

.

Ta có hệ phương trình

 



     





 



     



 



 

 



 

   



1 2 1

1 2 2

1

3 2

1 5

1 2 6

1 5

2

6 4 4

x x m x m

m

x x m x m

m

x m

m m m

.

Câu 34. [2H1-4.2-3] Cho tứ diện

ABCD

có

 AB CD a

. Gọi

,M N

lần lượt là trung điểm của

,AD BC

. Biết



3

12

ABCD

a

V

và

 



,

d AB CD a

. Khi đó độ dài

MN

là.

A.



2MN a

hoặc



6MN a

. B.



2MN a

hoặc



3MN a

.

C.



2

a

MN

hoặc



3

2

a

MN

. D.

MN a

hoặc



2MN a

.

Lời giải

Chọn C.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 70

Gọi

P

,

Q

,

E

lần lượt là trung điểm của

AC

,

BD

,

CD

. Ta có tứ giác

MQNP

là hình thoi

cạnh

2

a

. Ta chứng minh được

3

1 3

2 24

CDMQNP ABCD

a

V V 

(dựa vào

 

AB CD MQNP€ €

và

AB

,

CD

chéo nhau).

Mặt khác:

3 3 3 3

. . .

1 3 3 3 3

2.

8 96 24 96 48

C PNE D QME ABCD E MQNP

a a a a

V V V V      

.

Vì

AB

,

CD

chéo nhau và

 

,

d AB CD a

nên

 

,

2

a

d CD MQNP



(thật vậy, gọi



là

đường vuông góc chung của

AB

,

CD

thì

 

MQNP

 

vì

,

NP NQ   

).

Suy ra

 

3

.

3 1 1

, . . .

48 3 3 2

E MQNP MQNP MQNP

a a

V d CD MQNP S S  

.

2

3

8

MQNP

a

S 

 



0

2

0

60

3 3

2

. .sin sin

8 2

3

120

2

a

NQP MN

a

MQ NQ NQP NQP

a

NQP MN



  



    



  





.

Câu 35. [2H1-2.6-3] Cho hình chóp

.

S ABCD

có thể tích bằng 18, đáy là hình bình hành. Điểm

M

thuộc cạnh

SD

sao cho

2

SM MD

. Mặt phẳng

 

ABM

cắt

SC

tại

N

. Tính thể tích khối

chóp

.S ABNM

.

A.

9

. B.

10

. C.

12

. D.

6

Lời giải

Đáp án B.

Có:

   

/ /

M ABM SCD

AB CD

 









   

/ /ABM SCD MN CD

  

.

1 5

.

2 2 2 9

S ABNM SANM SANB

SABCD SACD SACB

V V V

SM SN SN

V V V SD SC SC

 

    

 

 

Vậy:

.

5

. 10

9

S ABNM SABCD

V V

 

.

Câu 36. [2H1-2.2-4] Cho hình chóp

.

S ABCD

có đáy là hình thang

ABCD

vuông tại

A

và

D

có

2 2

AB AD CD 

,

SA

vuông góc với đáy

 

ABCD

. Góc giữa

SC

và đáy bằng

0

60

. Biết

khoảng cách từ

B

đến

 

SCD

là

42

7

a

, khi đó tỉ số

.

3

S ABCD

V

a

bằng.

A.

3

2

. B.

6

3

. C.

6

2

. D.

3

.

Lời giải

Chọn C.

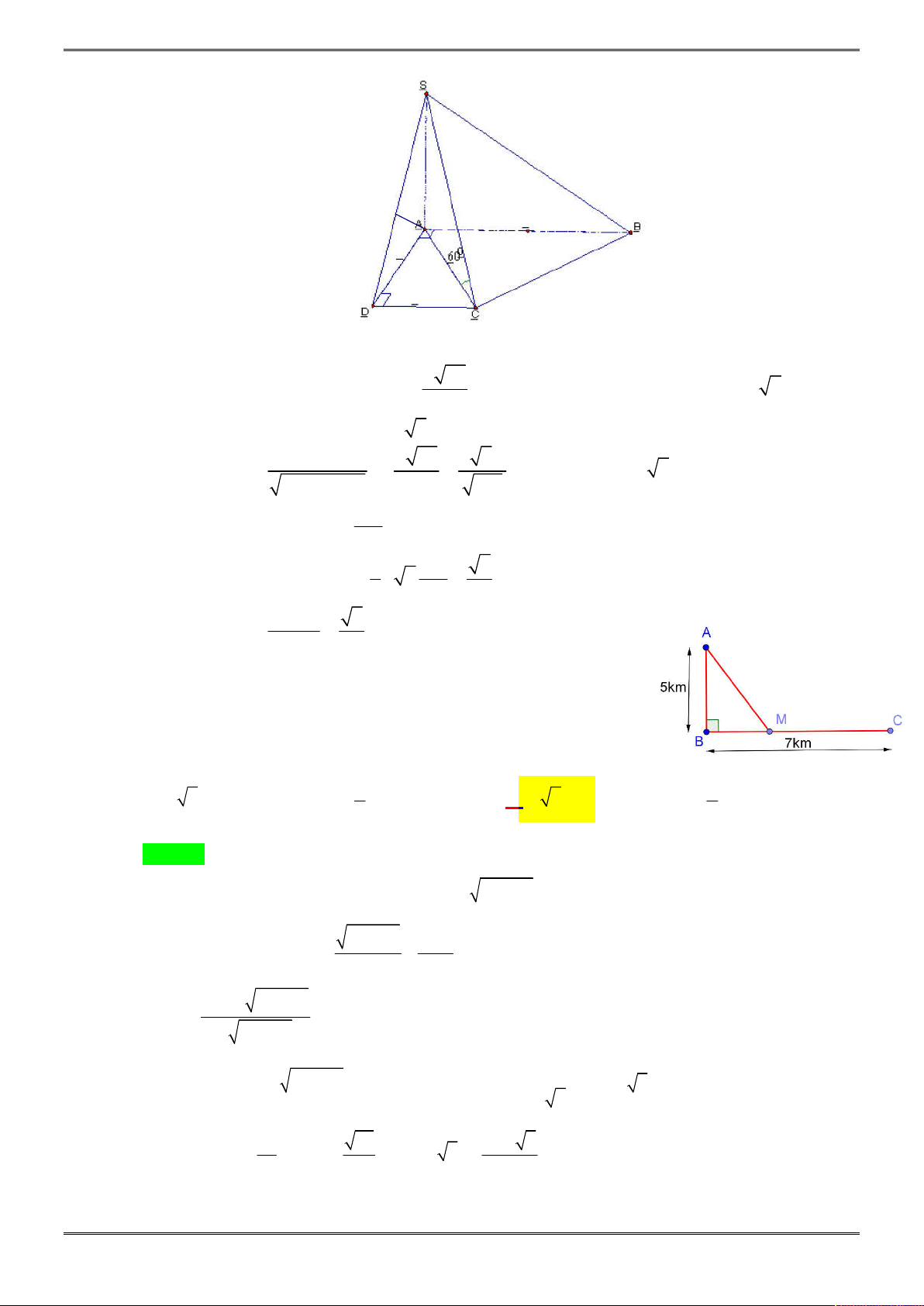
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 71

H

* Ta có :

   

42

,( ) ,( )

7

a

d B SCD d A SCD AH  

Đặt

2 2 2 2AB AD CD x AC x

    



0 0

60 .tan 60 6SCA AS AC x

   

Mặt khác:

2 2 2

. 42 6.

6

7

AS AD a x x

AH x a SA a

AS AD x

      



* Diện tích ABCD:

2

3

2

ABCD

a

S 

* Thể tích

.

S ABCD

:

2

3

.

1 3 6

6

3 2 2

S ABCD

a

V a a

 

Vậy :

.

3

6

2

S ABCD

V

a



Câu 37. [2D1-3.15-4] Một ngọn hải đăng đặt ở vị trí

A

cách bờ

5km

, trên

bờ biển có một kho hàng ở vị trí

C

cách

B

một khoảng

7km

.

Người canh hải đăng có thể chèo thuyền từ

A

đến

M

trên bờ biển

với vận tốc

4 /km h

rồi đi bộ từ

M

đến

C

với vận tốc

6 /km h

. Xác

định độ dài đoạn

BM

để người đó đi từ

A

đến C nhanh nhất.

A.

3 2 .km

. B.

7

.

3

km

. C.

2 5 km.

. D.

7

.

2

km

Lời giải

Chọn C.

Gọi

BM x

 

km

,

 0 7x

. Khi đó:

 

2

25

AM x

và

 7MC x

Theo đề bài ta có:

 

 

 

2

25 7

4 6

x x

f x

 

 







2

3 2 25

4 25

x x

f x

x

Cho

 

 

 



       

 

 







2

0

0 2 25 3 2 5

2 5

20

x

f x x x x

x

Khi đó:

 



29

0

12

f

,

 



74

7

4

f

và

 





14 5

2 5

12

f

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 72

Vậy

 

 

 



 

0;7

14 5

min 2 5

12

x

f x f

.

Câu 38. [2D1-2.10-4] Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

 

4 2

1

y x m x m   

cắt trục hoành tại bốn điểm phân biệt có tổng bình phương các hoành độ

bằng

10

.

A.

1 5

m    . B.

3

m



. C.

2

m



. D.

4

m



.

Lời giải

Chọn D.

PT hđgđ

 

4 2

1 0

x m x m

   

(1).Đặt

2

0

t x

 

, PT (1) trở thành

 

2

0

1 0 (2)

t

t m t m







   



PT (1) có 4 nghiệm phân biệt

1 2 3 4

, , ,x x x x

với tổng bình phương các nghiệm bằng

10

2 2 2 2

1 2 3 4

10

x x x x

   

(PT(2) có 2 nghiệm dương phân biệt

1 2

,t t

thoả

       

2 2 2 2

2 1 1 2

10

t t t t

     



1 2

5

t t

 

() Nếu

1 2

5

t t

 



4

m



4 2

5 4 0

x x

  

() Với

4

m



: PT(1)

4 2

5 4 0

x x

  



2

1

x

 





 



(thoả đk

2 2 2 2

1 2 3 4

10

x x x x

   

).

Câu 39. [2D2-5.3-4] Tập tất cả các giá trị của

m

để phương trình

 

2

1

2

2 2

2 . 2 3 4 . 2 2

x mx

log x x log x m



    

có đúng ba nghiệm phân biệt là:

A.

1 3

; 1;

2 2

 



 

 

. B.

1 3

;1;

2 2

 



 

 

. C.

1 3

;1;

2 2

 



 

 

. D.

1 3

;1; .

2 2

 

 

 

Lời giải

Chọn D.

Ta có

 

2

1

2

2 2

2 . 2 3 4 . 2 2

x mx

log x x log x m



    

 

1

 

2

21

2 2

2 . 1 2 2 . 2 2

x mx

log x log x m



 

     

 

 

2

Xét hàm số

   

2

2 . 2 , 0.

t

f t log t t

  

Vì

 

0, 0

f t t



   

hàm số đồng biến trên

 

0;



Khi đó

   

 

2 2

2 1 2 1 2

f x f x m x x m

 

       

 

 

2

4 1 2 0 3

2 1 4

x x m

x m



   





 





Phương trình

 

1

có đúng ba nghiệm phân biệt nếu xảy ra các trường hợp sau:

+) PT

 

3

có nghiệm kép khác hai nghiệm phân biệt của PT

 

4

.

 

3

2

m

, thay vào PT

 

4

thỏa mãn.

+) PT

 

4

có nghiệm kép khác hai nghiệm phân biệt của PT

 

3

 

1

2

m

, thay vào PT

 

3

thỏa mãn.

+) PT

 

4

có hai nghiệm phân biệt và PT

 

3

có hai nghiệm phân biệt, trong đó có một nghiệm

của hai PT trùng nhau.

 

   4 2 1

x m

,với

 

1 3

.

2 2

m

Thay vào PT

 

3

tìm được

 1.m

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 73

KL:

 



 

 

1 3

;1; .

2 2

m

Câu 40. [2D1-3.2-4] Tìm các giá trị thực của tham số

m

để phương

trình

     

2

2 1

x x m x x

có hai nghiệm phân biệt.

A.

23

5; .

4

m

 



 

 

B.

 

5;6 .

m 

C.

 

23

5; 6 .

4

m

 

 

 

 

D.

 

23

5; 6 .

4

m

 

 





 

Lời giải

Chọn B.

+)

2

2 1

x x m x x     

(

1

)

Điều kiện:

1 2

x

  

+)

 

2 2

1 3 2 2

x x x x m        

Đặt:

2

;x x t  

   

2

; 2 1f x x x f x x



     

   

1 1 1

1 2, 2 2, 2;

2 4 4

f f f t

   

       

 

 

   

 

1 3 2 2 2 2 3

t t m t t m

         

2 2 3m t t    

Đặt

 

2 2 3f t t t   

 

1 1 2

1

2 2

t

f t

t t

 



  

 

.

 

0 1 2 0 1

f t t t



       

.

Bảng biến thiên

23

4

5

6

+



1

4

-1-2

-



f(t)

f'(t)

t

+)

2 2

0x x t x x t       

Để phương trình có hai nghiệm phân biệt

1

1 4 0

4

t t

      

Do đó để phương trình có hai nghiệm phân biệt thì phương trình

 



có nghiệm

1

2;

4

t

 

 

 

 

Từ bảng biến thiên

 

5;6

m 

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 74

PHẦN II: PHẦN TỰ LUẬN

Câu 1. [2H1-4.2-4] Cho hình chóp tứ giác đều

.

S ABCD

có thể tích

2

6

V 

. Gọi

M

là trung điểm

của cạnh

SD

. Nếu

SB SD

thì khoảng cách từ

B

đến mặt phẳng

 

MAC

bằng:

Lời giải

Giả sử hình chóp có đáy

ABCD

là hình vuông cạnh

a

. Khi đó,

2BD a



.

Tam giác

SBD

vuông cân tại

S

nên

SD SB a 

và

2

2 2

BD a

SO  

.

Suy ra các tam giác

,

SCD SAD

là các tam giác đều cạnh

a

và

 

SD MAC



tại

M

.

Thể tích khối chóp là

3

1 2

. .

3 6

ABCD

a

V SO S 

Mà

3

2 2

1

6 6

a

  

Vì

O

là trung điểm

BD

nên

 

1

, ,

2

d B MAC d D MAC DM

  

.

Câu 2. [2D1-1.6-3] Tất cả các giá trị thực của tham số

m

để hàm số

   

3 2

2 3 1 6 2 2017

y x m x m x     

nghịch biến trên khoảng

 

;a b

sao cho

3

b a

 

là

Lời giải

Ta có

   

2

6 6 1 6 2

y x m x m



    

Hàm số nghịch biến trên

       

2

; 1 2 0 ;a b x m x m x a b

       

2

6 9

m m

   

TH1:

   

2

0 1 2 0x m x m x

          

Vô lí

TH2:

0 3

m y



    

có hai nghiệm

 

1 2 2 1

,

x x x x





Hàm số luôn nghịch biến trên

 

1 2

;x x

.

Yêu cầu đề bài:

 

2

2 1 2 1

3 9 4 9

x x x x S P

        

   

2

6

1 4 2 9 6 0

0

m

m m m m

m





        







BẢNG ĐÁP ÁN

1.B

2.A

3.C

4.A

5.B

6.C

7.A

8.D

9.C

10.B

11.B

12.B

13.A

14.A

15.C

16.A

17.B

18.C

19.C

20.C

21.C

22.B

23.D

24.A

25.D

26.B

27.B

28.C

29.A

30.A

31.B

32.A

33.A

34.C

35.B

36.C

37.C

38.D

39.D

40.B

S

M

D

A

O

B

C

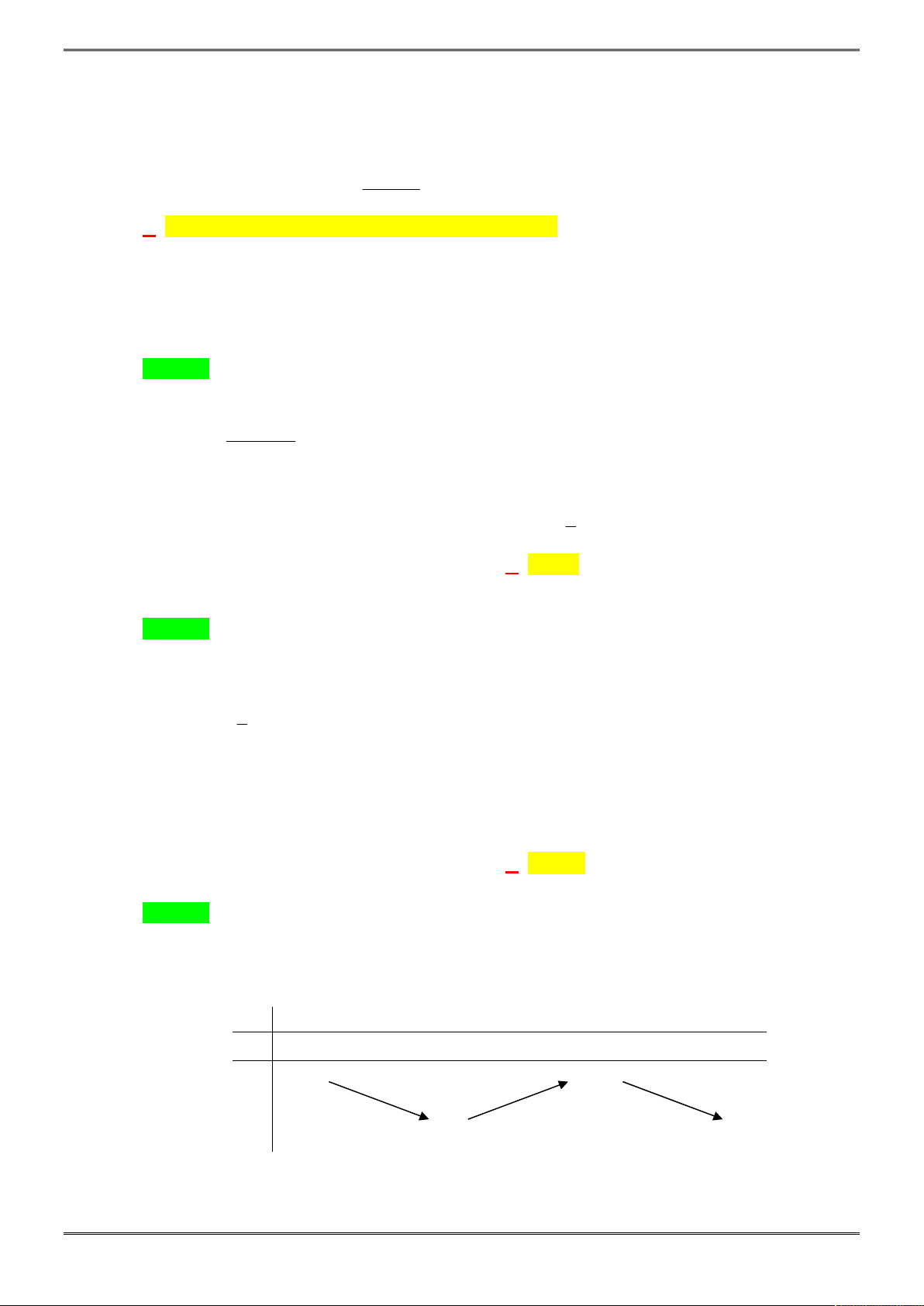
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 1

ĐỀ ÔN TẬP SỐ 06

PHẦN I: PHẦN TRẮC NGHIỆM

Câu 1. [2D1-1.4-1] Cho hàm số

3 1

4 2

x

y

x





 

. Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số luôn nghịch biến trên từng khoảng xác định.

B. Hàm số luôn nghịch biến trên



.

C. Hàm số đồng biến trên các khoảng

 

;2



và

 

2;



.

D. Hàm số nghịch biến trên các khoảng

 

; 2 

và

 

2;

 

.

Lời giải

Chọn A.

Tập xác định của hàm số là

 

\ 2

D 



Ta có

 

2

10

' 0,

2 4

y x D

x



   



Vậy hàm số luôn nghịch biến trên từng khoảng xác định

Câu 2. [2D1-1.5-2] Tìm tất cả giá trị tham số

m

để hàm số

3 2

1

3

y x x mx m   

đồng biến trên



.

A.

3

m



. B.

1

m



. C.

9

m



. D.

3

m

 

.

Lời giải

Chọn C.

Ta có

2

6

y x x m



  

Hàm số

3 2

1

3

y x x mx m   

đồng biến trên



0

y



 

,

x

  

2

6 0

x x m

   

,

x

  

9 0 9

m m



      

.

Câu 3. [2D1-2.6-1] Gọi

,

CD CT

y y

là giá trị cực đại và giá trị cực tiểu của hàm số

3 2

3 1

y x x

   

. Khi

đó giá trị của biểu thức

20 12

CD CT

T y y

  bằng bao nhiêu?

A.

4T 

. B.

40

T

 

. C.

88

T



. D.

6

T

 

.

Lời giải

Chọn C.

Ta có TXĐ:

D  

.

2

3 6 0 0, 2

y x x x x



      

.

Bảng biến thiên

Vậy

5, 1 20.5 12.1 88

CD CT

y y T

     

.

x



0

2



y





0



0



y



1

5



20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 2

Câu 4. [2D1-2.8-2] Đồ thị hàm số

2

2 2

ax b

y

x x





 

có điểm cực trị là

 

3; 1

A

 

.Tính giá trị của biểu

thức

a b

.

A.

1a b 

. B.

9

a b

 

. C.

3

a b

  

. D.

1

a b

  

.

Lời giải

Chọn C.

 

  

   

2

2 2

2

2 2

2 2 2 2

2 2 2

2 2

2 2 2 2

a x x x ax b

ax b ax bx a b

y y

x x

x x x x

    

    



   

 

   

Điểm

 

3; 1

A

 

là điểm cực trị

   

 

   

2

3 2 3 2 2 0

7 4 0 4

4 7 3.

3

3 5 7

1

3 2 3 2

a b a b

a b a

a b

a b b



      



   

 

        

 

  

    

 

 



   



Câu 5. [2D1-2.13-4] Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm

số

3 2

3 3 3

y mx mx m

   

có hai điểm cực trị

,A B

sao cho

2 2 2

2 ( ) 20

AB OA OB

  

( trong

đó

O

là gốc tọa độ).

A.

1.

m

 

B.

1

m



.

C.

1

m

 

hoặc

17

11

m

 

. D.

1

m



hoặc

17

11

m

 

.

Lời giải

Chọn D.

Ta có:

2

(3 6 )y m x x



 

Với mọi

0

m



, ta có

0 3 3

0

2 3

x y m

y

x y m

   





 



    



. Vậy hàm số luôn có hai điểm cực trị.

Giả sử

(0;3 3); (2; 3)

A m B m

  

.

Ta có :

2 2 2 2

1

2 ( ) 20 11 6 17 0

17

11

m

AB OA OB m m

m







       



 



( thỏa mãn)

Vậy giá trị

m

cần tìm là:

1

17

11

m







 



.

Câu 6. [2D1-3.2-1] Tính tổng giá trị nhỏ nhất và giá trị nhỏ nhất của hàm số

 

3 2

3 9 1   f x x x x

trên đoạn

 

4;0



.

A.

24

. B.

21

. C.

22

. D.

29

.

Lời giải

Chọn D.

 

2

3 6 9



  f x x x

 

 

2

1 4;0

0 3 6 9 0

3 4;0

x

f x x x

x

   



     



   





 

4 21 

f

,

 

0 1

f

,

 

3 28 

f

.

 

   

4;0

max 3 28



  

f x f

;

 

   

4;0

min 0 1



 

f x f

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 3

Vậy tổng giá trị nhỏ nhất và giá trị nhỏ nhất của hàm số bằng

29

.

Câu 7. [2D1-3.11-3] Với giá trị nào của

m

thì giá trị nhỏ nhất của hàm số

2

1





x

y

x m

trên đoạn

 

2;5

bằng

1

6

?

A.

1 

m

. B.

2 

m

. C.

3 

m

. D.

4

m

.

Lời giải

Chọn B.

Đạo hàm:

 

 

2

1

' 0, 2;5



   



m

y x

x m

. Hàm số đồng biến trên

 

2;5

.

Do hàm số liên tục trên đoạn

 

2;5

nên

 

 

2

2;5

1 1

min 2 4 2.

2 6

       



y y m m

m

Câu 8. [2D1-3.14-4] Một đường dây điện được nối từ một nhà máy điện ở

A

đến một hòn đảo

C

và

khoảng cách ngắn nhất từ

B

đến

C

là

1km

, khoảng cách từ

B

đến

A

là

4km

được minh họa

bằng hình vẽ sau:

Biết rằng mỗi rằng km dây điện đặt dưới nước mất

5000

USD, còn đặt dưới đất mất

3000

USD. Hỏi điểm

S

trên bờ cách

A

bao nhiêu để khi mắc dây điện từ

A

qua

S

rồi đến

C

là ít

tốn kém nhất ?

A.

15

km

4

. B.

13

km

4

. C.

10

km

4

. D.

19

km

4

.

Lời giải

Chọn A.

Gọi

 

x km

là khoảng cách từ

S

đến tới điểm

 

0 4 km

B SB x x   

. Khi đó khoảng cách

từ

 

2 2 2

4 km 1

SA x SC BC BS x      

(km)

Chi phí mắc dây điện từ

A

qua

S

rồi đến

C

là:

   

2

3000 4 5000 1 ,C x x x

   

với

0 4

x

 

Bài toán trở thành tìm giá trị nhỏ nhất của hàm số

 

C x

với

0 4

x

 

 

2

2 2

5000 5 3 1

' 3000 1000

1 1

x x x

C x

x x

 

 

    

 

 

 

 

2 2 2 2

' 0 5 3 1 3 1 5 9 1 25 0 4

C x x x x x x x do x

           

 

2

3

9

4

0 4

3

16

4

x tm

x do x

x ktm







    



 





. Lại có:

 





 

3

2

5000

'' 0, 0;4

1

C x x

x

   



.

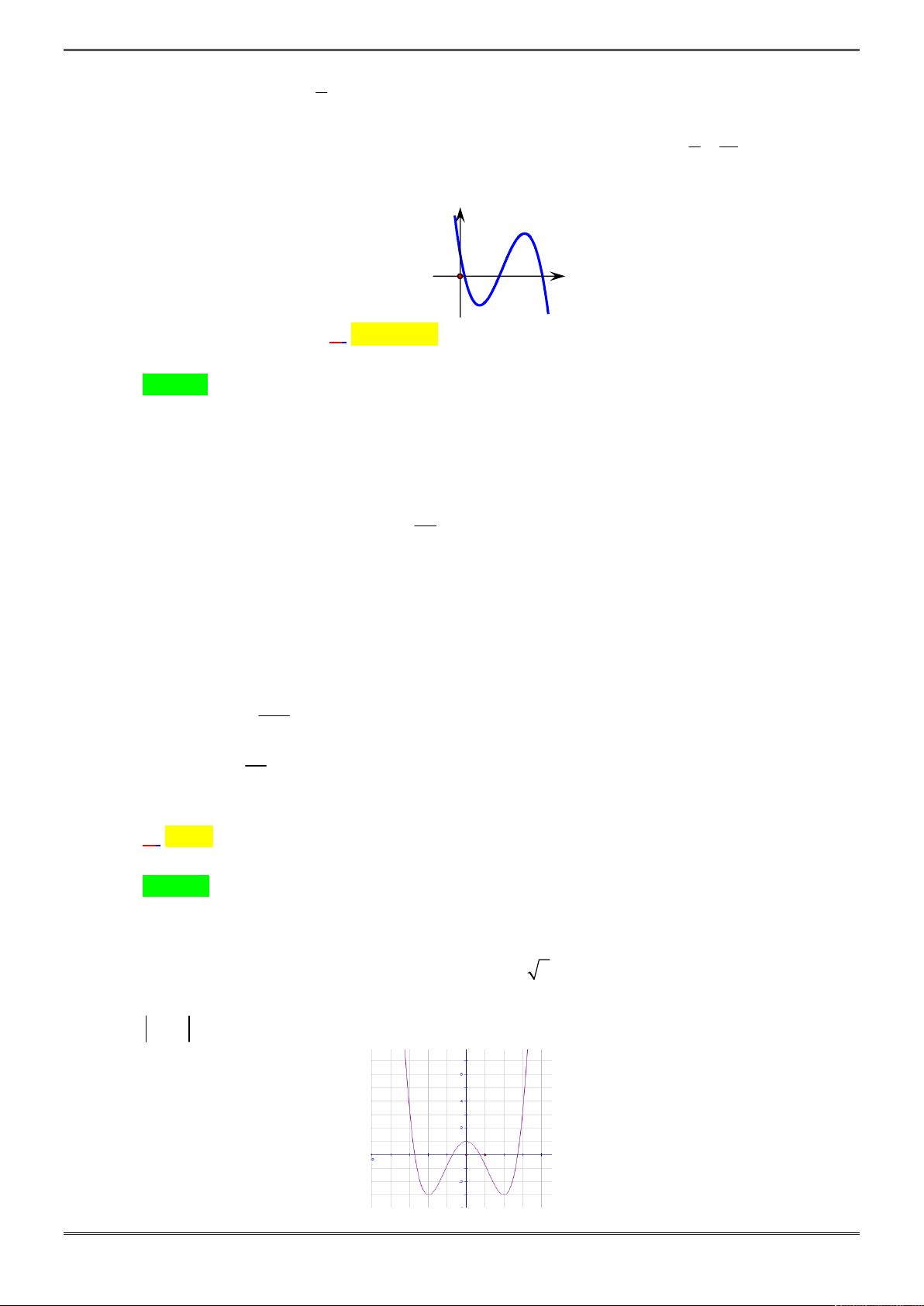
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 4

Do đó

 

0;4

3

min 16000

4

x

C x C



 

 

 

 

(USD).

Vậy, để chi phí ít tốn kém nhất thì điểm

S

phải cách

A

là

3 13

4 km

4 4

AB BS   

.

Câu 9. [2D1-5.3-2] Hàm số

3 2

1y x bx cx    

có đồ thị như hình vẽ. Mệnh đề nào đúng?

A.

0; 0

b c

 

. B.

0; 0

b c

 

. C.

0; 0

b c

 

. D.

0; 0

b c

 

.

Lời giải

Chọn B.

Cách 1:

Nhìn đồ thị ta thấy:

Nhánh cuối đi xuống

0

a



.

Hai điểm cực trị nằm cùng phía với

Oy

:

;a c

cùng dấu

0

c

 

.

Điểm uốn nằm bên phải

Oy

0

3

u

b

x

a



  

;ab 

cùng dấu

0 0

b b

    

.

Cách 2:

Ta có :

2

' 3 2

y x bx c   

Gọi

1 2

;x x

là nghiệm của phương trình

' 0

y



Nhìn đồ thị ta thấy:

Nhánh cuối đi xuống

1 0

a

  

.

1 2

2

0 0 0

3

. 0 0 0

3

b

x x b

c

x x c





     









    







Câu 10. [2D1-6.1-1] Số giao điểm

n

của hai đồ thị

4 2

3

y x x

  

và

2

3 1

y x

 

là:

A.

2

n



. B.

4

n



. C.

3

n



. D.

0

n



.

Lời giải

Chọn A.

Phương trình hoành độ giao điểm

4 2 2

3 3 1   

x x x

4 2

4 4 0   

x x

2

2 2    

x x

.

Câu 11. [2D1-6.6-2] Hình vẽ bên là đồ thị hàm trùng phương. Tìm giá trị của

m

để phương trình

 

f x m

có 4 nghiệm phân biệt

O

x

y

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 5

A.

0

m



. B.

3 1

m

  

. C.

0, 3

m m

 

. D.

1 3

m

 

.

Lời giải

Chọn C.

Đồ thị hàm

 

y f x



có được bằng cách giữ phần đồ thị

 

f x

nằm trên

Ox

và lấy đối xứng

phần đồ thị của

 

f x

nằm phía dưới

Ox

lên trên như hình vẽ.



Phương trình

 

f x m

có 4 nghiệm phân biệt khi

0, 3

m m

 

.

Câu 12. [2D1-6.15-4] Cho hàm số

   

4 2 2

2 2 1 4 1

y x m x m   

. Các giá trị của tham số

m

để đồ thị

hàm số

 

1

cắt trục hoành tại

4

điểm phân biệt có hoành độ

1 2 3 4

, , ,x x x x

thoả mãn

2 2 2 2

1 2 3 4

6

  



x x x x

là:

A.

1

4



m

. B.

1

2

 

m

. C.

1

4

 

m

. D.

1

4

 

m

.

Lời giải

Chọn A.

Phương trình hoành độ giao điểm của đồ thị hàm số

 

1

và trục hoành là:

   

4 2 2

2 2 1 4 0 2

x m x m   

Đặt

 

2

0





t x t

. Phương trình

 

2

trở thành

   

2 2

2 2 1 4 0 3

   t m t m

Đồ thị hàm số

 

1

cắt trục hoành tại

4

điểm phân biệt

 

3



pt

có

2

nghiệm dương phân biệt

1 2

0

 t t

.

 

2

1 2

4 1 0

' 0

1

0 4 0 0

4

0

2 2 1 0

 



 





       

 

 

 



m

t t m m

t t

m

 

*

.

Khi đó các nghiệm của phương trình

 

2

là

2 1 1 2

, , ,

 

t t t t

. Theo giải thiết ta có

       

2 2 2 2

2 1 21 1 2

6 3

    

   

tt t tt t .

Theo định lí Viet

   

1 2

1

2 2 1 2 2 1 3

4

     



t t m m m

.

Câu 13. [2D1-7.1-2] Cho hàm số

 

2 1

1

x

y C

x







. Hệ số góc của tiếp tuyến với đồ thị

 

C

sao cho tiếp

tuyến đó cắt các trục

,Ox Oy

lần lượt tại các điểm

,A B

thỏa mãn

4OA OB

là

A.

1

4



. B.

1

4

. C.

1

4



hoặc

1

4

. D.

1

.

Lời giải

Chọn A.

3

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 6

Ta có

 

2

1

0, 1

1

y x

x





   



.

Gọi



là góc tạo bởi tiếp tuyến

d

với trục

Ox

. Ta có hệ số góc của tiếp tuyến

d

là

tan

k



 

1

4

OB

OA

   

.

Ta lại có hệ số góc của tiếp tuyến với

 

C

tại điểm

 

0 0

;M x y

là

 

0

2

0

1

0

1

y x

x





 



nên

nhận giá trị

1

4

k

 

và loại giá trị

1

4

k



.

Câu 14. [2D1-8.2-3] Cho hàm số

2

3

x

y

x







có đồ thị

 

C

. Có bao nhiêu điểm

M

thuộc

 

C

sao cho

khoảng cách từ điểm

M

đến tiệm cận ngang bằng

5

lần khoảng cách từ

M

đến tiệm cận đứng.

A.

1

. B.

2

. C.

3

. D.

4

.

Lời giải

Chọn B.

TXĐ:

 

\ 3

.

Ta có:

3 3

2

lim lim

3

x x

x

y

x

 

 



  



nên hàm số có tiệm cận đứng là

3

x



.

2

lim lim 1

3

x x

x

y

x

 



 



nên hàm số có tiệm cận ngang là

1y 

.

Gọi

 

0

2

;

3

x

M x C

x

 





 



 

0

3

x



. Khi đó

0

2

1

3

x





là khoảng cách từ điểm

M

đến tiệm cận

ngang.

Và

0

3

x



là khoảng cách từ

M

đến tiệm cận đứng.

Để khoảng cách từ điểm

M

đến tiệm cận ngang bằng

5

lần khoảng cách từ

M

đến tiệm cận

đứng thì

0

2

1 5 3

3

x



  



0 0

0 0 0

2 3

5

5 3 5 3

3 3 3

x x

x x x

 

      

  

 

2

0 0

0 0 0

0 0

3 1 4

1 1

3 3 3 1

3 1 2

3 3

x x

x x x

x x

   



          



   

 



.

Vậy có

2

điểm

M

thỏa mãn đề bài.

Câu 15. [2D1-4.6-2] Đồ thị hàm số

2

9

x

y

x







có bao nhiêu đường tiệm cận?

A.

1

. B.

2

. C.

3

. D.

4

.

Lời giải

Chọn C.

Tập xác định:

 

\ 3 

D

.

Ta có:

2 2

3 3 3 3

2 2

lim lim ; lim lim

9 9

   

   

 

      

 

x x x x

x x

y y

x x

Tiệm cận đứng:

3

x

.

2 2

3 3 3 3

2 2

lim lim ; lim lim

9 9

   

   

 

      

 

x x x x

x x

y y

x x

Tiệm cận đứng:

3 

x

.

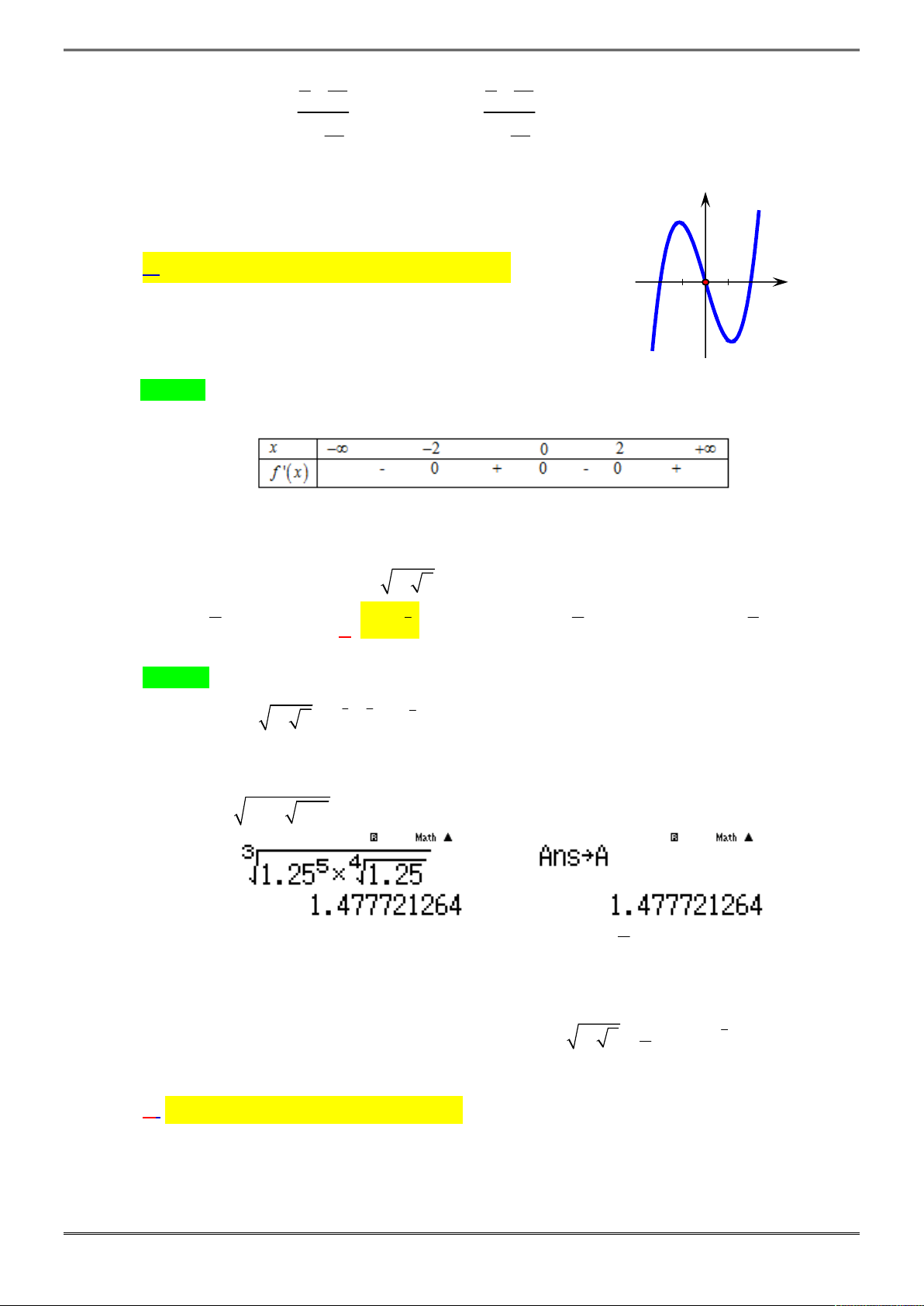
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 7

Lại có:

2 2

1 2 1 2

lim lim 0; lim lim 0

9 9

1 1

   

 

    

 

x x x x

y y

x x

Tiệm cận ngang:

0

y

.

Câu 16. [2D1-5.5-2] Cho hàm số

 

f x

xác định trên



và có đồ thị

 

'y f x



là đường cong trong

hình. Mệnh đề nào dưới đây là đúng?

A. Hàm số

 

f x

nghịch biến trên khoảng

 

1;1



.

B. Hàm số

 

f x

nghịch biến trên khoảng

 

0;2

.

C. Hàm số

 

f x

đồng biến trên khoảng

 

1;2

.

D. Hàm số

 

f x

đồng biến trên khoảng

 

2;1



.

Lời giải

Chọn B.

Dựa vào đồ thị ta có bảng xét dấu:

Dựa vào bảng xét dấu, ta có: + Hàm số đồng biến trên các khoảng

 

2;0



và

 

2;



.

+ Hàm số nghịch biến trên các khoảng

 

; 2 

và

 

0;2

.

Câu 17. [2D2-1.2-1] Cho biểu thức

5

3

4

P x x



với

0.

x



Mệnh đề nào dưới đây đúng?

A.

20

21

.P x

 B.

7

4

.P x

 C.

20

5

.P x

 D.

12

5

.P x



Lời giải

Chọn A.

Tự luận:

1 1

7

5

53

3 4

4

P x x x x

 



 

 

  

Trắc nghiệm:

* Cách1: Chọn

0

x



ví dụ như

1, 25

x



chẳng hạn.

Tính giá trị

5

3

4

1,25 1,25

rồi lưu vào

A

Tiếp theo ta tính hiệu, ví dụ như đáp án A ta cần tính

 

20

21

1,25

A 

. Nếu màn hình máy tính xuất

hiện kết quả bằng 0 thì chứng tỏ đáp án A đúng.

Đáp số chính là B.

* Cách 2: Dùng MTCT thay

2

x



và bấm

7

3 5

4

2

7

log log 2 2 .

4

x

P P x

   

Câu 18. [2D2-4.1-1] Cho

0, 1

a a

 

. Tìm mệnh đề đúng trong các mệnh đề sau

A. Tập giá trị của hàm số

log

a

y x

 là



.

B. Tập xác định của hàm số

x

y a

là

 

0;



.

C. Tập xác định của hàm số

log

a

y x

 là



.

D. Tập giá trị của hàm số

x

y a

là



.

O

x

1

2

1

y

2

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 8

Lời giải

Chọn A.

B. Sai, vì tập xác định của hàm số

x

y a

là



.

C. Sai, vì tập xác định của hàm số

log

a

y x

 là

 

0;



.

D. Sai, vì tập giá trị của hàm số

x

y a

là

 

0;



.

Câu 19. [2D2-3.1-2] Nếu

2

8 4

log log

5

a b



và

2

4 8

log l

7

oga b



thì giá trị của

 

2

log

ab

bằng bao

nhiêu?

A.

9

. B.

18

. C.

1

. D.

3

.

Lời giải

Chọn A.

Từ giải thiết ta có

0, 0

a b

 

và

   

2 2

2 2 2

2 2

1

log log

4

3

log log log

1

3

log log

3

5

12 9

7

a b

a b ab

a b







  













.

Câu 20. [2D2-3.3-2] Cho

2

log 3

a  ,

3

log 5

b  ,

7

log 2

c  . Tính

140

log 63

theo

, ,a b c

.

A.

1 2

ac

c abc



 

. B.

1 2

ac

c abc



 

. C.

1 2

ac

c abc



 

. D.

1 2

ac

c abc



 

.

Lời giải

Chọn A.

Tự luận:

Ta có :

7 7 7 2

140

7 7 7 7 7 2 3

log 63 1 2log 3 1 2log 2.log 3

log 63

log 140 1 2log 2 log 5 1 2log 2 log 2.log 3.log 5

 

  

   

1 2

ac

c abc





 

.

Trắc nghiệm:

Nhập

2

log 3

shift STO A

Nhập

3

log 5

shift STO B

Nhập

7

log 2

shift STO C

Nhập

140

1 2

log 63 0

1 2

AC

C ABC



 

 

.

Câu 21. [2D2-4.2-1] Tính đạo hàm của hàm số

6

x

y :

A.

1

' .6





x

y x . B.

6

'

ln 6



x

y . C.

' 6 .ln 6



x

y . D.

' 6

x

y .

Lời giải

Chọn A.

Ta có:

 

6 6 ln 6





x x

.

Câu 22. [2D2-4.3-2] Gọi

m

và

M

lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số

 

2 3



x

f x e

trên đoạn

 

0;2

. Mối liên hệ giữa

m

và

M

là:

A.

1 

m M

. B.

. M m e

C.

2

1

.



M m

e

. D.

2



M

e

m

.

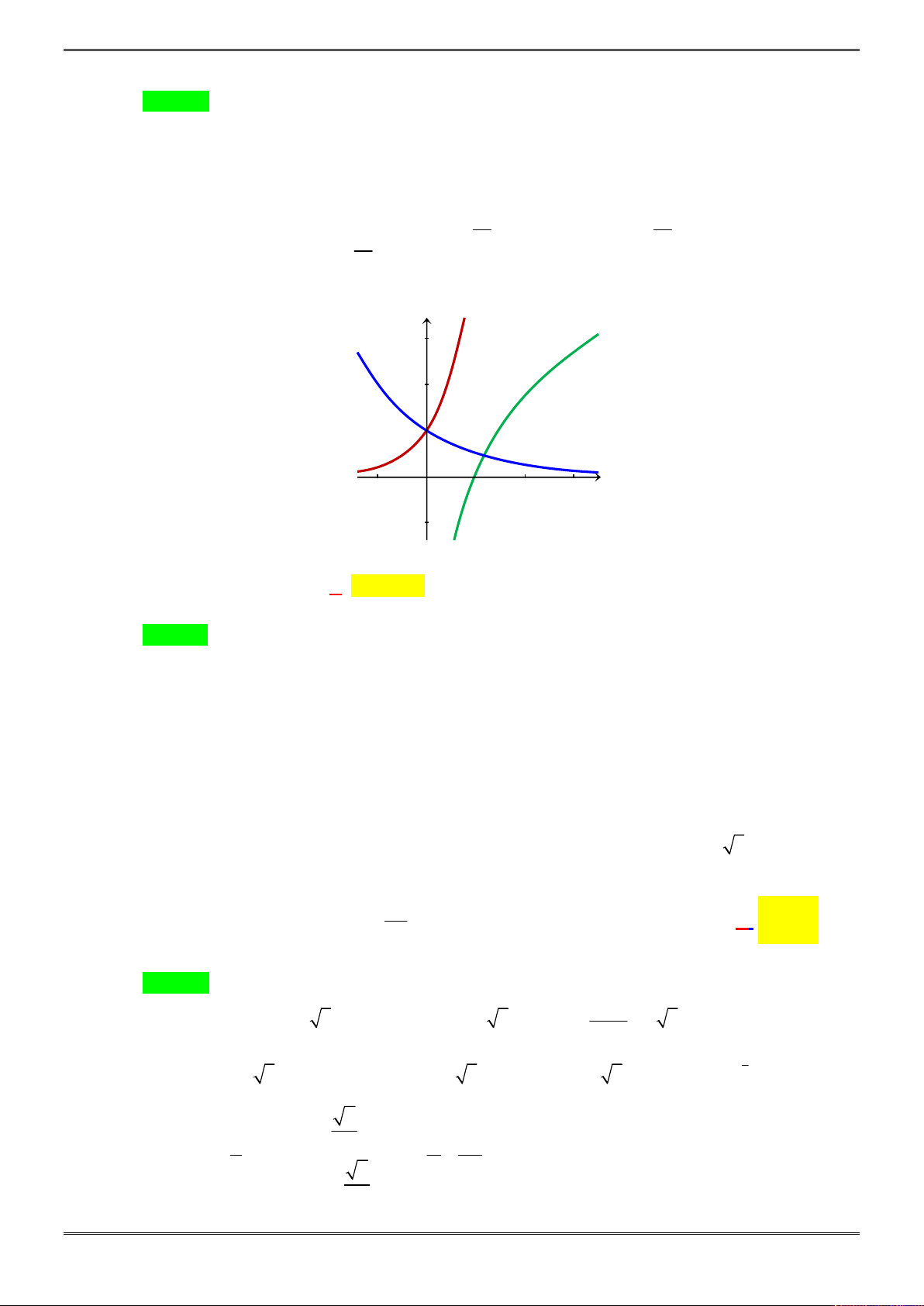
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 9

Lời giải

Chọn A.

Hàm số

 

f x

xác định và liên tục trên đoạn

 

0;2

.

Đạo hàm

 

2 3

' 3 0,



    

x

f x e x

. Do đó hàm số

 

f x

nghịch biến trên

 

0;2

.

Suy ra

 

   

 

   

2

0;2

4

0;2

max 0

1

min 2



 







 



f x f e

f x f

e

. Suy ra

2

4

1

,

 m M e

e

nên

2

1

.



M m

e

.

Câu 23. [2D2-4.7-3] Trong hình vẽ dưới đây có đồ thị của các hàm số

x

y a

,

x

y b

,

log

c

y x



.

Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?

A.

.c a b 

B.

.a c b 

C.

.b c a 

D.

.a b c 

Lời giải

Chọn B.

Từ đồ thị

Ta thấy hàm số

x

y a

nghịch biến

0 1

a

  

.

Hàm số

, log

x

c

y b y x

 

đồng biến

1, 1b c  

,

a b a c  

nên loại A, C

Nếu

b c

thì đồ thị hàm số

x

y b

và

log

c

y x

 phải đối xứng nhau qua đường phân giác góc

phần tư thứ nhất

y x

. Nhưng ta thấy đồ thị hàm số

log

c

y x

 cắt đường

y x

nên loại D.

Câu 24. [2D2-5.3-2] Tính tổng

T

tất cả các nghiệm của phương trình

2 2

sin cos

5 5 2 5

x x

 

trên đoạn

 

0;2 .



A.

.

T





B.

3

.

4

T





C.

2 .

T





D.

4 .

T





Lời giải

Chọn D.

Ta có

2 2 2 2 2

2

sin cos sin 1 sin sin

sin

5

5 5 2 5 5 5 2 5 5 2 5

5

x x x x x

x



       

   

2 2 2 2 2

1

2 2

sin sin sin sin sin

2

5 2 5.5 5 0 5 5 0 5 5 0 5 5

x x x x x

           

2

sin

1

2

sin ,

2 4 2

2

sin

2

x

k

x x k

x

 







      



 







.

O

1

1

2

3

1

2

3

x

y

x

y a

x

y b

log

c

y x

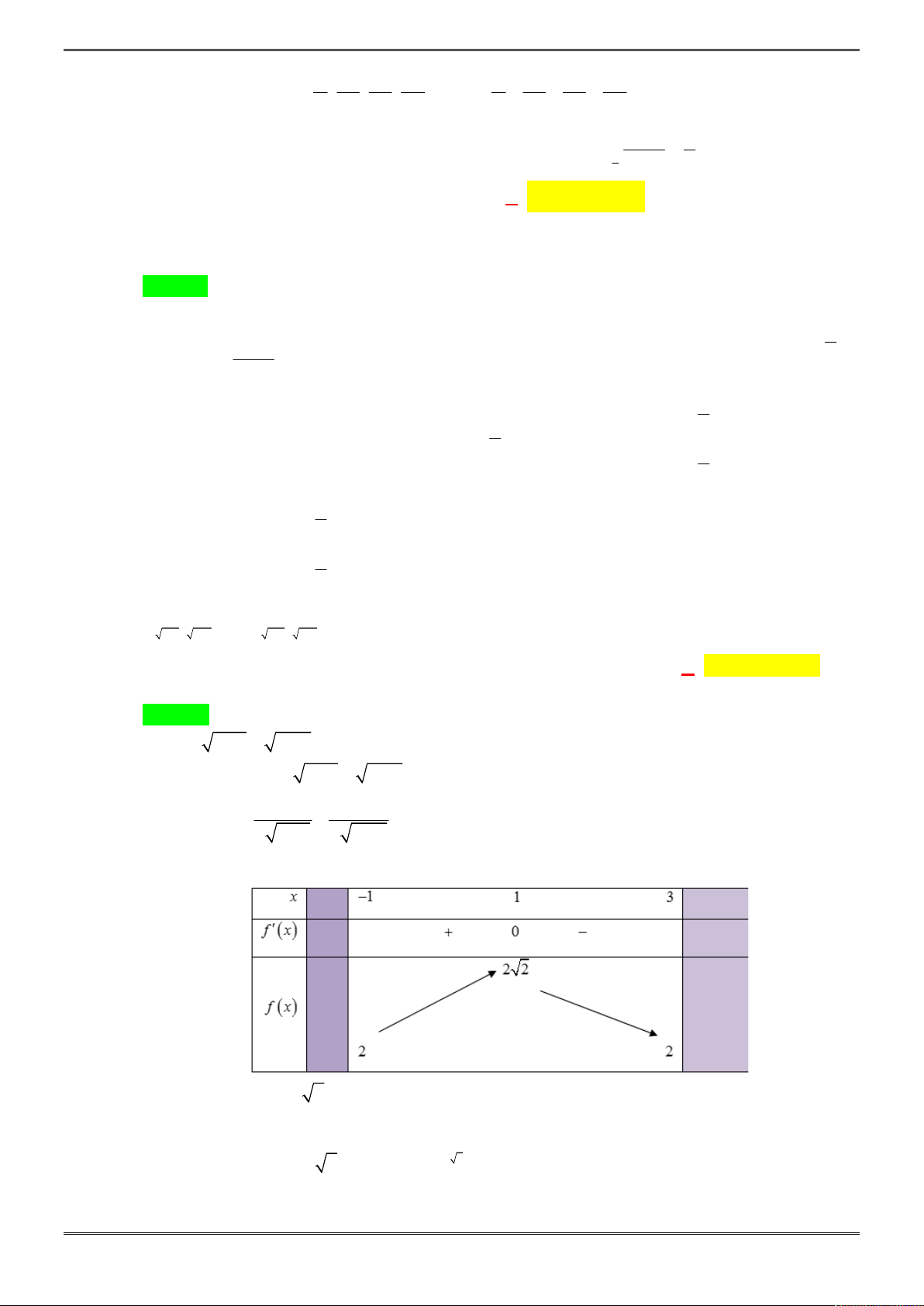
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 10

Do

 

3 5 7 3 5 7

0;2 ; ; ; 4 .

4 4 4 4 4 4 4 4

x x T

       

 

 

        

 

 

Câu 25. [2D2-6.3-2] Tập nghiệm của bất phương trình

 

x

4 1

4

3 1 3

log 3 1 .log

16 4



 

là

A.



 



1;2 3;

 

B.



 



0;1 2;

 

.

C.



 



1;1 4;

  

. D.



 



0;4 5;

 

.

Lời giải

Chọn B.

Điều kiện

x

3 1 0

3 1 x 0

3 1

0

16



 



   











. Khi đó BPT

   

x x

4 4

3

log 3 1 . log 3 1 2

4

 

     

 

.

Đặt

 

x

4

t log 3 1 

. Khi đó, ta có

 

2

3

t

3

2

t t 2 4t 8t 3 0

1

4

t

2







       









Khi đó

 

x

4

x

4

3

log 3 1

x 2

2

1 0 x 1

log 3 1

2



 











 





 





Vậy tập nghiệm của bất phương trình là:



 



0;1 2;

 

Câu 26. [2D2-5.7-4] Tìm tất cả các giá trị thực của tham số

m

để phương trình

1 3 1 3

4 14.2 8

x x x x

m

     

  

có nghiệm.

A.

32

m

 

. B.

41 32

m

  

. C.

41

m

 

. D.

41 32

m

   

.

Lời giải

Chọn D.

Đặt 1 3

t x x   

.

Xét hàm số

 

1 3

f x x x   

trên

 

1;3



.

Ta có

   

1 1

; 0 1

2 1 2 3

f x f x x

x x

 

    

 

.

Bảng biến thiên của hàm số

 

f x

trên

 

1;3



:

Từ đó suy ra

2;2 2

t

 



 

.

Khi đó ta có phương trình:

4 14.2 8

t t

m  

.

Đặt

2

t

a



, do

2;2 2

t

 



 

nên

2

4;4

a

 



 

. Ta có phương trình

2

14 8

a a m  

.

Xét hàm số

     

2

14 8; 2 14; 0 7

g a a a g a a g a a

 

       

.

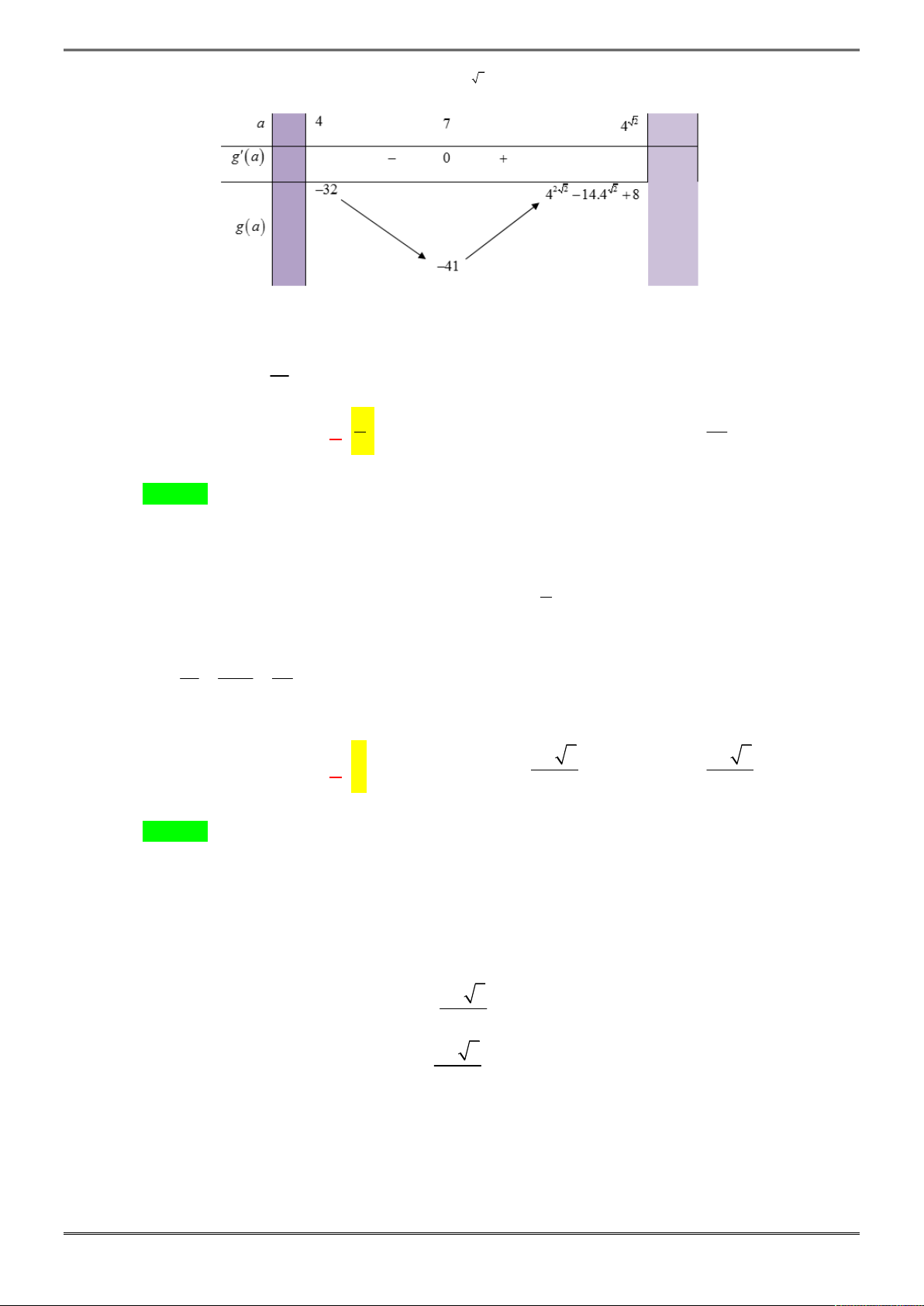
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 11

Bảng biến thiên của hàm số

 

g a

trên

2

4;4

 

 

.

Từ bảng biến thiên ta thấy để phương trình có nghiệm thì

41 32

m

   

.

Câu 27. [2D2-6.2-2] Biết phương trình

 

2log 2 log 4 log 4log3

   x x

có hai nghiệm là

1 2

,x x

 

1 2

x x



. Tỉ số

1

2

x

khi rút gọn là:

A. 4. B.

1

4

. C. 64. D.

1

64

.

Lời giải

Chọn B.

Điều kiện:

0

x

.

Phương trình tương đương với:

   

2 2

4

log 2 log 4 log log3 4 2 81

      

x x x x

  

2 1

2

1

4 65 16 0 4 1 16 0

4

16







        







x

x x x x

x

(thỏa mãn điều kiện).

Vậy

1

2

1 1

4.16 64

 

x

.

Câu 28. [2D2-5.5-2] Tổng của nghiệm nhỏ nhất và lớn nhất phương trình

2 2

1 1 2

2 2 2 2

  

  

x x x x x

bằng:

A.

0

. B.

1

. C.

1 5

2



. D.

1 5

2



.

Lời giải

Chọn B.

Phương trình tương đương với

   

2

1

2 2 1 2 2 1



  

x x x x

 

2

2 2

1

1 1

2 2

2 1 0 2 1

2 1 2 2 0

2 2 0 2 2

0

0 0

.

1 5

1 1 0

2



 

 

  

     

 

  

 

 





 

 



  

 





    



 





x x

x x x

x x x x

x

x x

x x x x

x

Phương trình có ba nghiệm

0

x

,

1 5

2



x

.

Tổng của nghiệm nhỏ nhất và lớn nhất phương trình bằng

1

.

Câu 29. [2H1-1.1-1] Khối đa diện sau có bao nhiêu mặt?

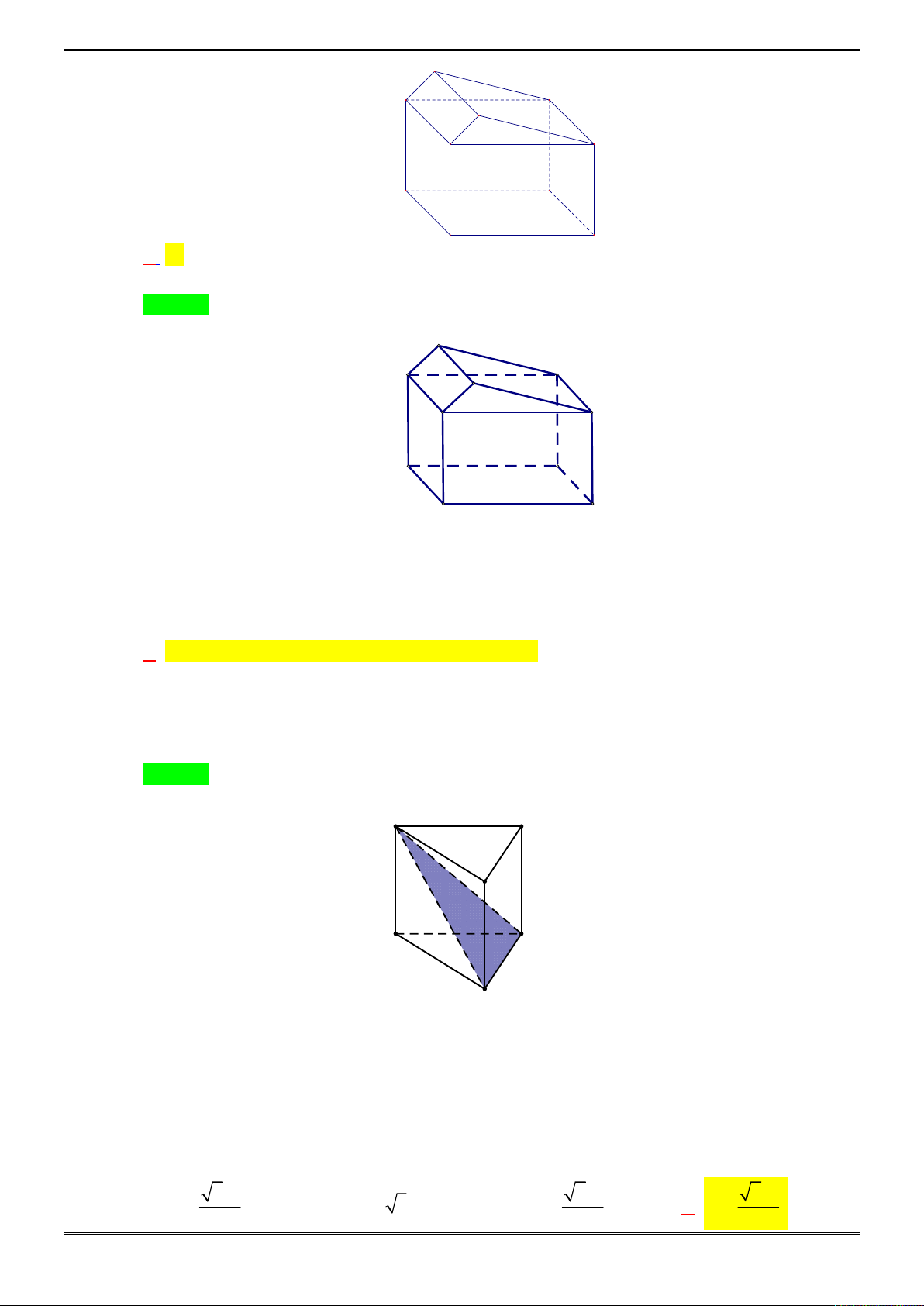
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 12

A.

9

. B.

10

. C.

8

. D.

7

.

Lời giải

Chọn A.

A

D

A'

D'

C'

B'

C

B

F

E

Có 9 mặt:

         

' ' , ' ' , ' ' , ' ' , ' ' ' ' ,ABB A BB C C CC D D DD A A A B C D

 

,ABEF

     

, ,

CDFE BEC ADE

Câu 30. [2H1-1.4-1] Mặt phẳng

 

 

AB C

chia khối lăng trụ

  

.ABC A B C

thành các khối đa diện nào ?

A. Một khối chóp tam giác và một khối chóp tứ giác.

B. Hai khối chóp tam giác.

C. Một khối chóp tam giác và một khối chóp ngũ giác.

D. Hai khối chóp tứ giác.

Lời giải

Chọn A.

C

C'

B'

A'

B

A

Dựa vào hình vẽ, ta thấy mặt phẳng

 

AB C

 

chia khối lăng trụ

.

ABC A B C

  

thành khối chóp

tam giác

.

A A B C

  

và khối chóp tứ giác

. .A BCC B

 

Câu 31. [2H1-2.1-2] Cho hình chóp

.

S ABCD

có đáy là hình thoi cạnh

,a



0

60

ABC  ,

SA

vuông góc

với đáy,

SD

tạo với mặt phẳng

 

SAC

một góc bằng

0

45 .

Tính thể tích

V

của khối chóp

. .S ABCD

A.

3

6

.

18

a

V 

B.

3

3 .V a

 C.

3

6

.

3

a

V 

D.

3

6

.

12

a

V 

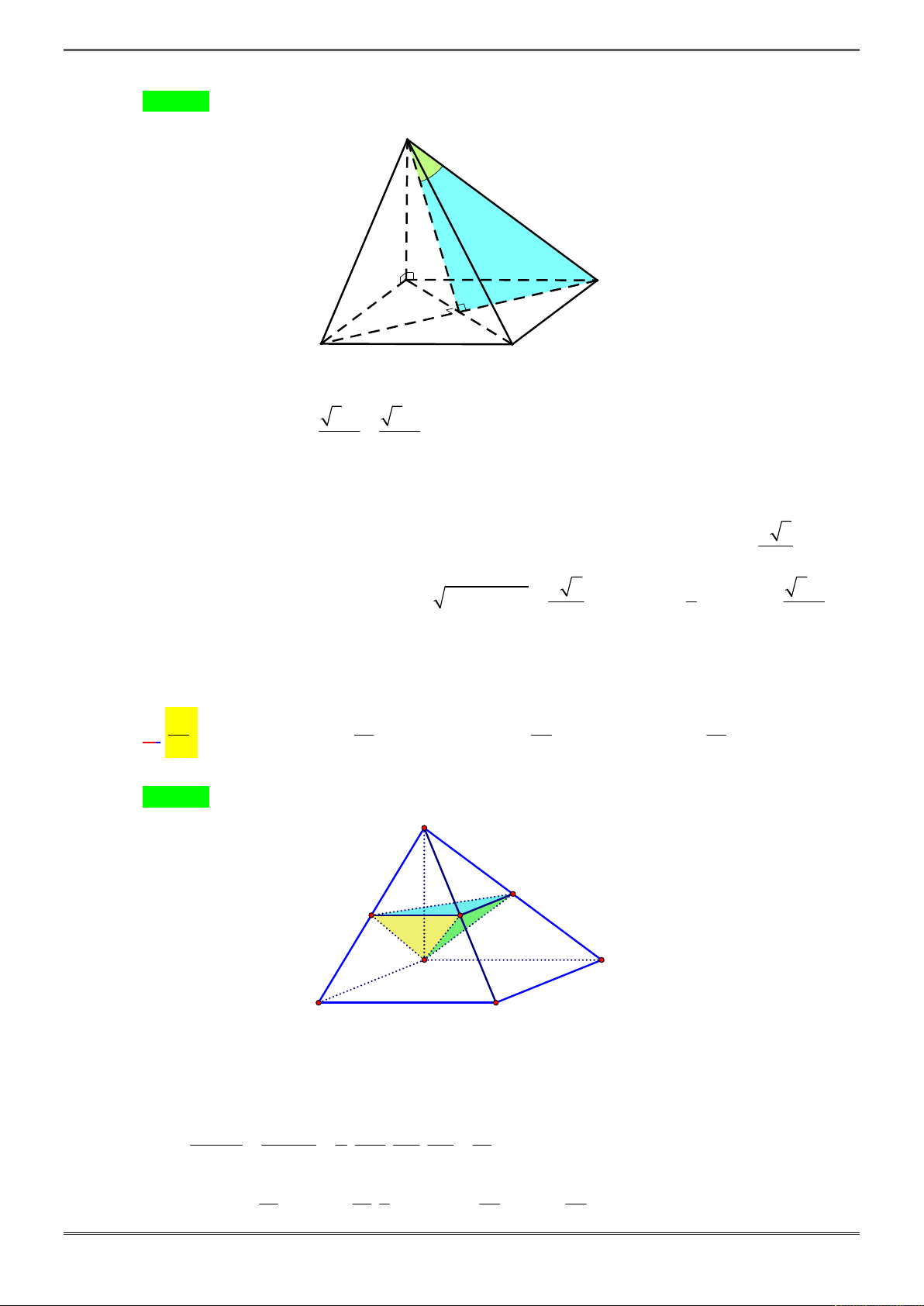
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 13

Lời giải

Chọn D.

O

A

B

C

D

S

45

0

a

Do

ABCD

là hình thoi cạnh

a

và



0

60

ABC  nên tam giác

ABC

đều.

Vậy

2 2

3 3

2 2. .

4 2

ABCD ABC

a a

S S  

Ta có:

 

BD AC

BD SAC

BD SA





 







 



0

, 45 .

SD SAC DSO   Vậy tam giác

SOD

vuông cân tại

3

.

2

a

O SO DO  

Xét tam giác

SAO

vuông tại

:A

2 2

2

a

SA SO AO  

3

.

1 6

. .

3 12

S ABCD ABCD

a

V SA S  

Câu 32. [2H1-2.5-3] Cho hình chóp

.

S ABCD

, đáy

ABCD

là hình vuông cạnh

a

.

SA

vuông góc với

đáy và

2SA a

. Gọi

, , M N P

lần lượt là trung điểm của

, , SB SC SD

. Tính thể tích khối đa

diện

AMNP

.

A.

3

.

24

a

B.

3

.

16

a

C.

3

.

48

a

D.

3

.

8

a

Lời giải

Chọn A.

P

N

M

C

A

D

B

S

Từ giả thiết suy ra (MNP)//(BCD). Suy ra

( ,( )) ( ,( )).h d A MNP d C MNP 

Vì

N

là trung điểm của

SC

nên

( ,( )) ( ,( )).h d C MNP d S MNP 

Do đó

. .

A MNP S MNP

V V .

Ta có:

. .

1 1

. . .

2 2 16

A MNP S MNP

S ABCD S BCD

V V

SM SN SP

V V SB SC SD

  

.

Suy ra:

3

2

. .

1 1 1 1

. . . . .2 .

16 16 3 48 24

A MNP S ABCD ABCD

a

V V SA S a a    .

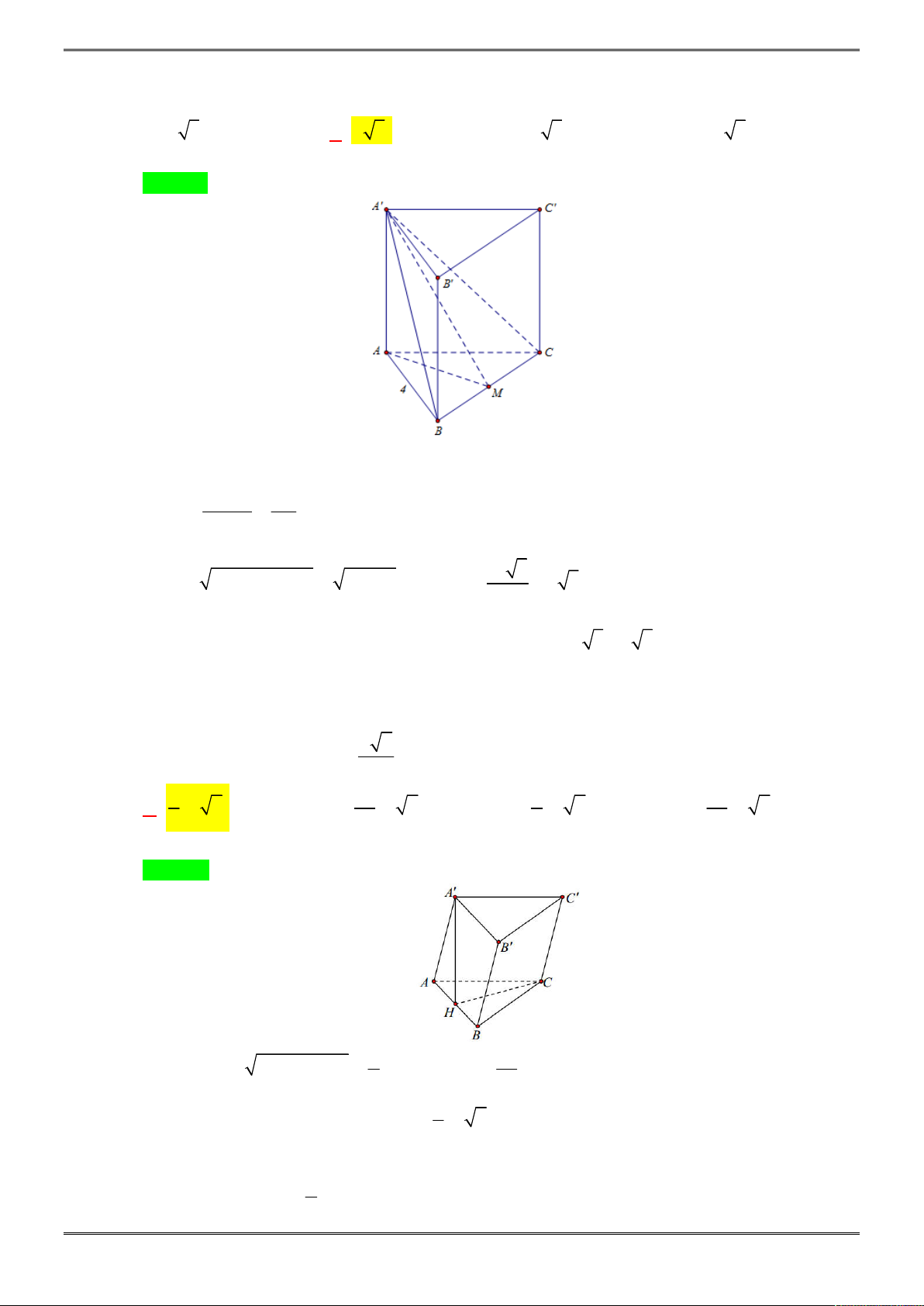
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 14

Câu 33. [2H1-3.2-2] Cho hình lăng trụ đều

.

ABC A B C

  

có cạnh đáy

4

a



, biết diện tích tam giác

A BC



bằng 8. Tính thể tích khối lăng trụ

.

ABC A B C

  

.

A.

4 3

. B.

8 3

. C.

2 3

. D.

10 3

.

Lời giải

Chọn B.

Gọi M là trung điểm của

BC A'M BC 

.

2 2 2

A'BC

2S

2.8

A 'M 4, AM AB BM 16 4 12

BC 4

       

.

2

2 2 2

ABC

a 3

A 'A A 'M AM 4 12 2; S 4 3

4

      

.

Thể tích khối lăng trụ

.

ABC A B C

  

là:

ABC

V A'A.S 2.4 3 8 3

  

.

Câu 34. [2H1-3.4-2] Cho lăng trụ tam giác

.

ABC A B C

  

có đáy là tam giác vuông cân tại C. Hình chiếu

vuông góc A lên mặt phẳng ABC trùng với trung điểm cạnh AB. Biết cạnh bên lăng trụ bằng

2a, đường cao lăng trụ bằng

7

.

2

a

Tính theo a thể tích khối lăng trụ

.

ABC A B C

  

.

A.

3

9

7.

8

a

B.

3

9

7.

24

a

C.

3

9

7.

4

a

D.

3

9

7.

48

a

Lời giải

Chọn A.

Ta có:

'2 ' 2

3 3

; .

2 2

    

a

AH AA A H a CH AH

Thể tích lăng trụ:

' 3

9

.HC.A 7.

8

 V AH H a

Câu 35. [2H1-2.3-2] Hình chóp tứ giác đều

.

S ABCD

có góc tạo bởi mặt bên và mặt đáy bằng

45

. Thể

tích của hình chóp là

3

4

3

a

. Hỏi cạnh hình vuông mặt đáy bằng bao nhiêu?

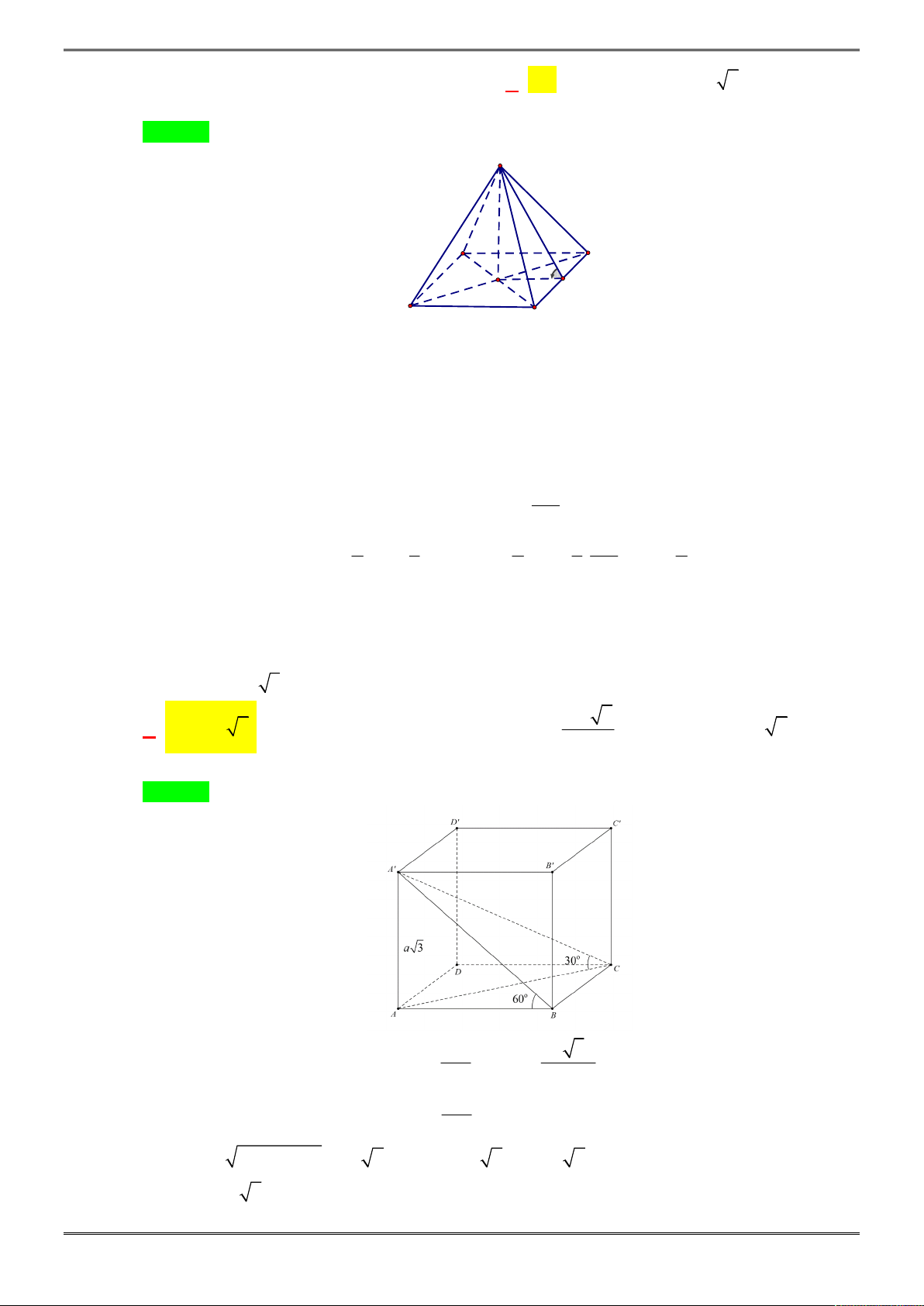
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 15

A.

a

. B.

4a

. C.

2a

.

D.

2a

.

Lời giải

Chọn A.

45

O

A

B

C

D

S

I

Gọi

O

là tâm hình vuông

ABCD

,

I

là trung điểm

CD

.

Vì

.

S ABCD

là hình chóp đều nên

SO

là đường cao của hình chóp.

Ta có :

   

 



 



0

( );( ) 45

SCD ABCD CD

SI CD SCD SCD ABCD SIO

OI CD OCD

cвn

 



   





 



.

Do đó tam giác

SOI

vuông cân tại

2

BC

O SO OI  

Theo đề bài ta có:

3 3 2 3

.

4 1 4 1 4

. . . .

3 3 3 3 2 3

S ABCD ABCD

BC

V a SO S a BC a

    

3 3

8 2BC a BC a   

Câu 36. [2H1-3.6-2] Tính theo

a

thể tích

V

của khối hộp chữ nhật

.

ABCD A B C D

   

biết rằng mặt

phẳng

 

A BC



hợp với mặt đáy

 

ABCD

một góc

o

60

,

A C



hợp với đáy

 

ABCD

một góc

o

30

và

3AA a



 .

A.

3

2 6

V a . B.

3

V a

. C.

3

2 6

3

a

V 

. D.

3

2 2

V a

.

Lời giải

Chọn A.

Xét tam giác vuông

A AB



có

3

tan 60

o

AA a

AB a

AB



   

.

Xét tam giác vuông

A AC



có

tan30 3

o

AA

AC a

AC



  

.

Vậy

2 2

2 2BC AC AB a

  

;

2

2 2. 2 2

ABCD

S a a a 

.

Vậy

3

2 6

V a .

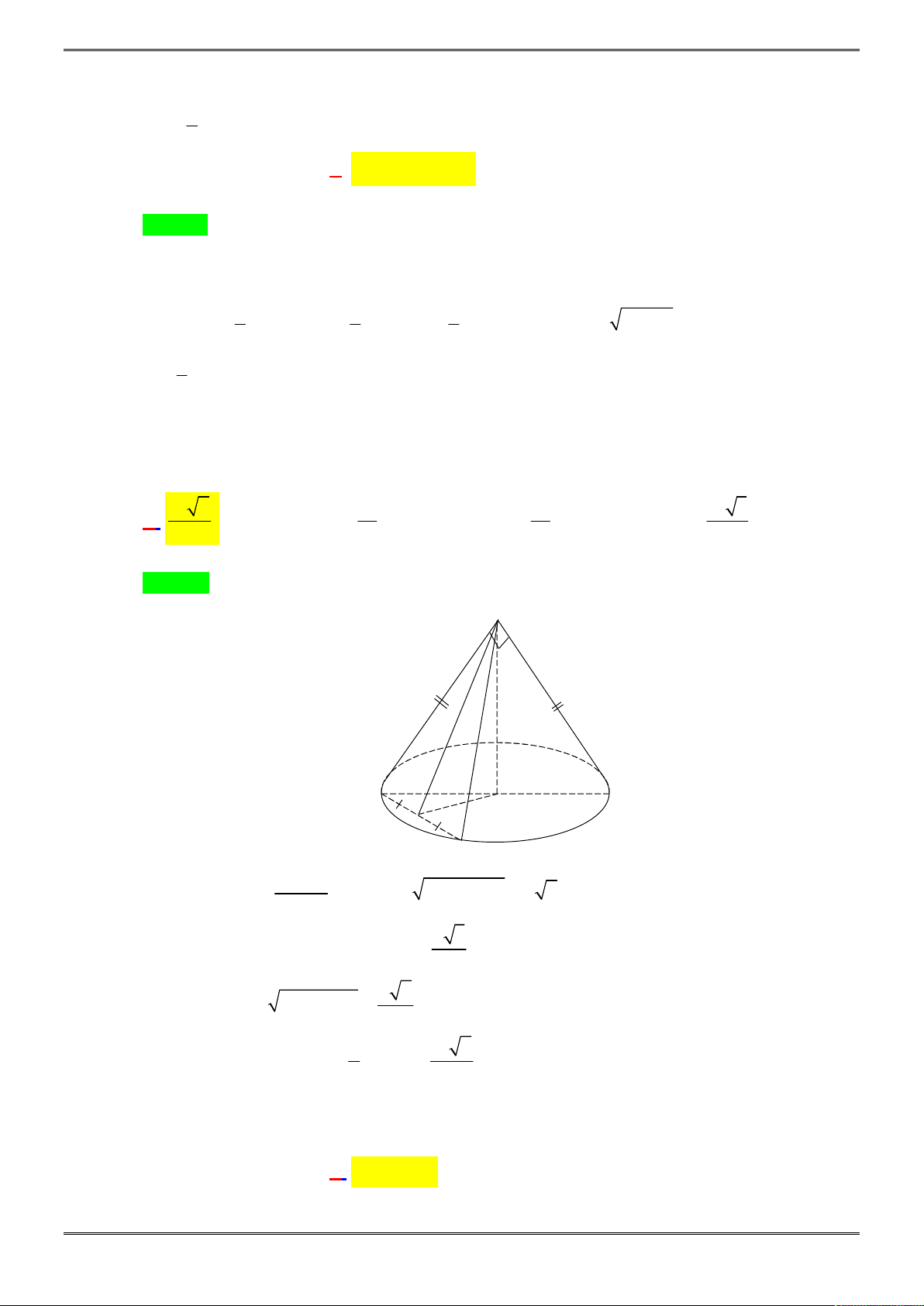
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 16

Câu 37. [2H2-1.3-2] Một hình nón có bán kính đường tròn đáy là

 

6

cm

và diện tích hình tròn đáy

bằng

3

5

diện tích xung quanh của hình nón. Tính thể tích khối nón.

A.

288

V

 

 

3

cm

. B.

 

3

96

V cm

 

. C.

 

3

48

V cm

 

. D.

 

3

64

V cm

 

.

Lời giải

Chọn B.

Gọi

R

,

l

,

h

lần lượt là bán kính, đường cao, đường sinh của hình nón.

Ta có:

 

6

R cm



.

Ta có:

3

5

d xq

S S



2

3

5

R Rl   

5

3

l R

 

10

l

 

 

2 2

8

h l R cm

   

.

2

1

96

3

V R h

   

.

Câu 38. [2H2-1.4-3] Một hình nón đỉnh

S

tâm

O

có bán kính đáy bằng

a

góc ở đỉnh bằng

0

90

. Một

mặt phẳng

 

P

qua đỉnh cắt đường tròn đáy tại

, A B

sao cho



0

AOB = 60

. Diện tích thiết

diện bằng:

A.

2

a 7

4

. B.

2

a

2

. C.

2

a

4

. D.

2

a 3

4

.

Lời giải

Chọn A.

Xét

:SO

tan 45

AO

SOA a  



;

2 2

2SA SO OA a

  

.

OAB

là tam giác đều cạnh

a

3

2

a

OI 

Xét

:SOI

2 2

7

2

a

SI SO OI  

Diện tích thiết diện:

2

1 a 7

. .

2 4

SAB

S AB SI 

.

Câu 39. [2H2-2.2-1] Cho hình trụ

 

T

có chiều cao

h

, độ dài đường sinh

l

, bán kính đáy

r

. Ký hiệu

xq

S

là diện tích xung quanh của

 

T

. Công thức nào sau đây là đúng?

A.

xq

S rh





. B.

2

xq

S rl





. C.

2

xq

S r h





. D.

xq

S rl





.

Lời giải

S

A

O

B

I

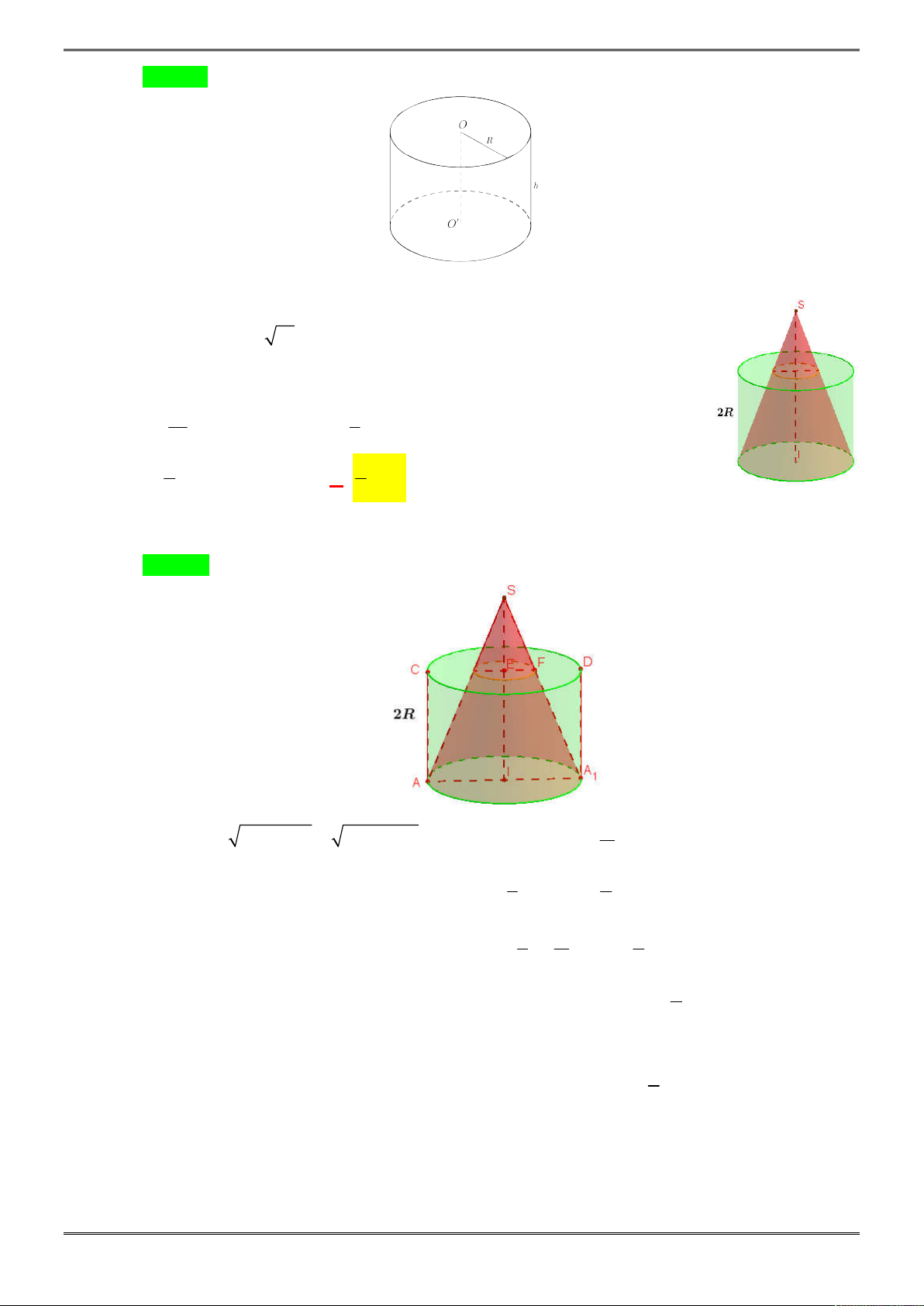
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 17

Chọn B.

Với hình trụ ta có

2 2

xq

h l S rh rl

 

   

.

Câu 40. [2H2-4.1-4] Cho hình nón có độ dài đường kính đáy là

2R

, độ dài

đường sinh là

17

R và hình trụ có chiều cao và đường kính đáy đều

bằng

2R

, lồng vào nhau như hình vẽ. Tính thể tích phần khối trụ không

giao với khối nón.

A.

3

5

12

R



. B.

3

1

3

R



.

C.

3

4

3

R



. D.

3

5

6

R



.

Lời giải

Chọn D.

Ta có

2 2 2 2

17 4 2 ,

2

R

SI SA IA R R R SE R EF

       

.

Thể tích khối nón lớn (có đường cao

SI

) là

2 3

1

1 4

.4R

3 3

V R R

 

 

.

Thể tích khối nón nhỏ (có đường cao

SE

) là

2

3

2

1 1

.2

3 2 6

R

V R R

 

 

 

 

 

Thể tích phần khối giao nhau giữ khối nón và khối trụ là

3

3 1 2

7

6

V V V R



  

.

Thể tích khối trụ là là

2 3

4

.2 2

V R R R

 

 

.

Vậy thể tích phần khối trụ không giao với khối nón là

3

4 3

5

6

V V V R



  

.

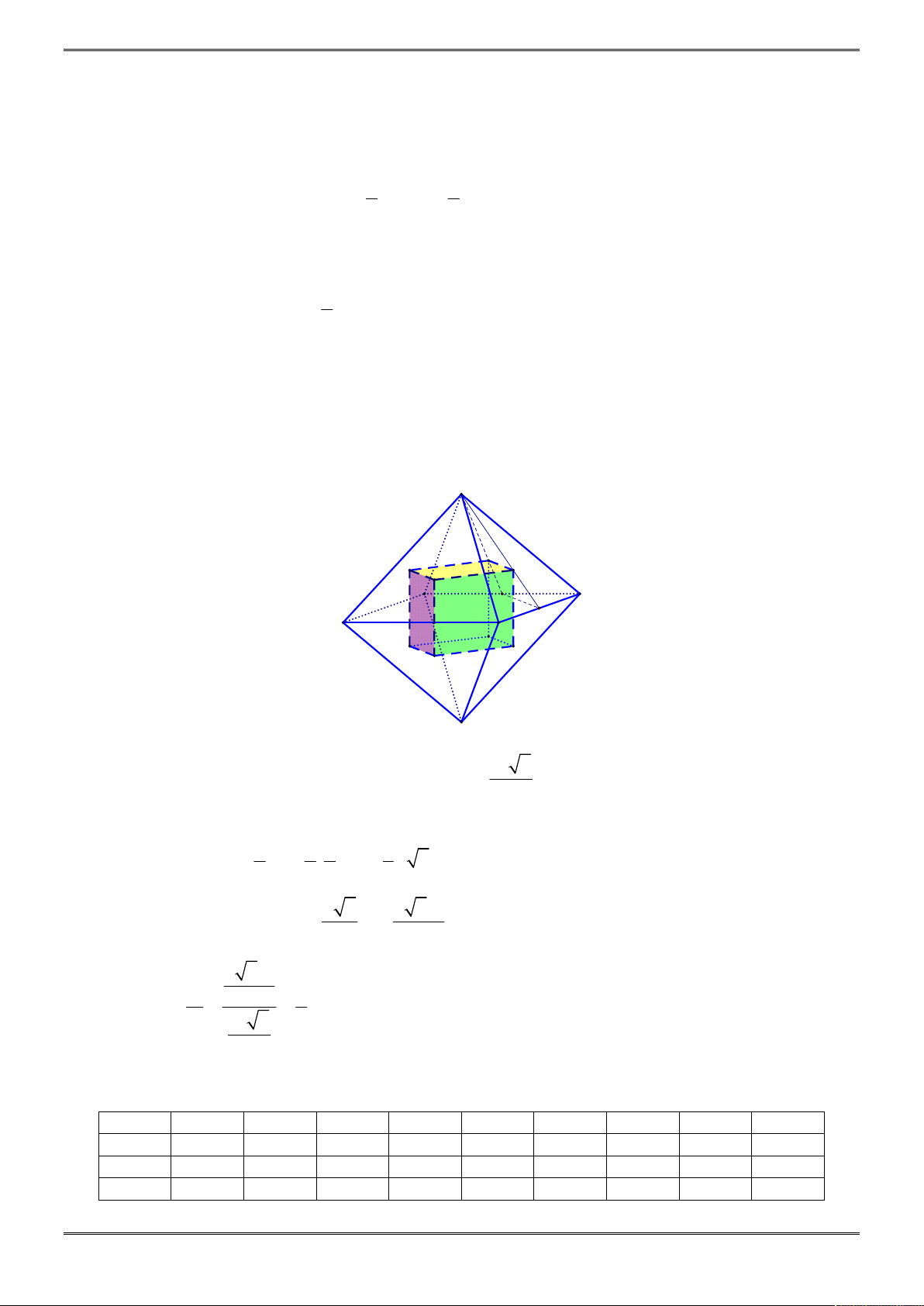
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 18

PHẦN II: PHẦN TỰ LUẬN

Câu 1. [2D2-5.3-3] Giải phương trình sau:

2 2

2 1 2 2

2 9.2 2 0

x x x x  

  

.

Lời giải

Chia cả hai vế của phương trình cho

2 2

2 0

x



ta được:

2 2 2 2 2 2

2 2 1 2 2 2 2 2

1 9

2 9.2 1 0 .2 .2 1 0 2.2 9.2 4 0

2 4

x x x x x x x x x x x x       

          

.

Đặt

2

x x

t



 điều kiện

0t 

. Khi đó phương trình đã cho tương đương với

2

2 2

2

1

4

2 2 2 2

2 9 4 0

1

2 2

2

x x

t

x x x

t t

x

t

x x



 





   





      



 



  

 





Vậy phương trình có hai nghiệm

2

1

x







 



.

Câu 2. [2H1-3.5-4] Cho khối bát diện đều cạnh

a

. Tính tỷ số thể tích của khối lập phương được tạo

nên bằng cách nối các tâm của các mặt bên của khối bát diện với thể tích của khối bát diện.

Lời giải

G

7

G

8

G

6

G

5

S'

G

4

G

1

G

3

G

2

I

J

D

B

C

A

S

Thể tích của khối bát diện đều cạnh

a

là:

3

2

.

6

a

V 

Gọi thể tích khối lập phương

1 2 3 4 5 6 7 8

.

G G G G G G G G

là

1

V

.

Ta có:

2 3

2 2 1 1

. 2.

3 3 2 3

G G IJ BD a  

Khi đó

 

3

1 2 3

2 2 2

.

3 27

a a

V G G

 

  

 

 

Vậy:

3

1

3

2 2

4

27

.

9

2

6

a

V

a

 

BẢNG ĐÁP ÁN

1.A

2.C

3.C

4.C

5.D

6.D

7.B

8.B

9.B

10.A

11.C

12.A

13.A

14.B

15.C

16.B

17.B

18.A

19.A

20.A

21.C

22.A

23.B

24.D

25.B

26.D

27.B

28.B

29.A

30.A

31.D

32.A

33.B

34.A

35.C

36.A

37.B

38.A

39.B

40.D

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 19

ĐỀ ÔN TẬP SỐ 07

PHẦN I: PHẦN TRẮC NGHIỆM

Câu 1. [2D1-4.2-1] Cho hàm số

( )f x

xác định trên

 

\ 1

, liên tục trên mỗi khoảng xác định và có

bảng biến thiên như hình vẽ. Hỏi mệnh đề nào dưới đây sai?

A. Đồ thị hàm số có tiệm cận ngang là

1.

y

 

B. Hàm số đạt cực trị tại điểm

2.

x



C. Hàm số không có đạo hàm tại điểm

1.

x

 

D. Đồ thị hàm số có tiệm cận đứng là

1.

x

 

Lời giải

Chọn A

Vì

lim , lim

x x

y y

 

   

nên đồ thị hàm số không có tiệm cận ngang, chọn. A.

Câu 2. [2D1-2.4-1] Hàm số

4 3 2

1 1 1

4 3 2

y x x x x   

có bao nhiêu điểm cực trị?

A.

2

điểm. B.

4

điểm. C.

3

điểm. D.

1

điểm.

Lời giải

Chọn D

Ta có:

4 3 2 3 2

1 1 1

1

4 3 2

y x x x x y x x x



        

.

Suy ra:

3 2

0 1 0 1

y x x x x



        

.

Bảng xét dấu của

y



:

x



1

1



y





0



0



Vậy hàm số đã cho có 1 điểm cực trị tại

1

x

 

.

Câu 3. [2D2-3.2-1] Cho số thực

x

thỏa mãn

3

log

2 5

x



. Mệnh đề nào sau đây đúng?

A.

5

log

2 3 .

x



B.

2

log 3

5 .

x

C.

3

log 5

2 .

x

D.

2

log 5

3 .

x

Lời giải:

Chọn C

Ta có:

 

3

3 5 3

log 5

log log log 5

2 5 2 5

x x

x   

.

Câu 4. [2D1-1.1-1] Cho hàm số

 

y f x



đơn điệu trên

 

;a b

. Mệnh đề nào dưới đây đúng?

A.

   

0, ; .f x x a b



  

B.

   

0, ; .f x x a b



  

.

C.

 

f x



không đổi dấu trên khoảng

 

;a b

. D.

   

0, ; .f x x a b



  

Lời giải

Chọn C.

x



1

2



y





0



y







1



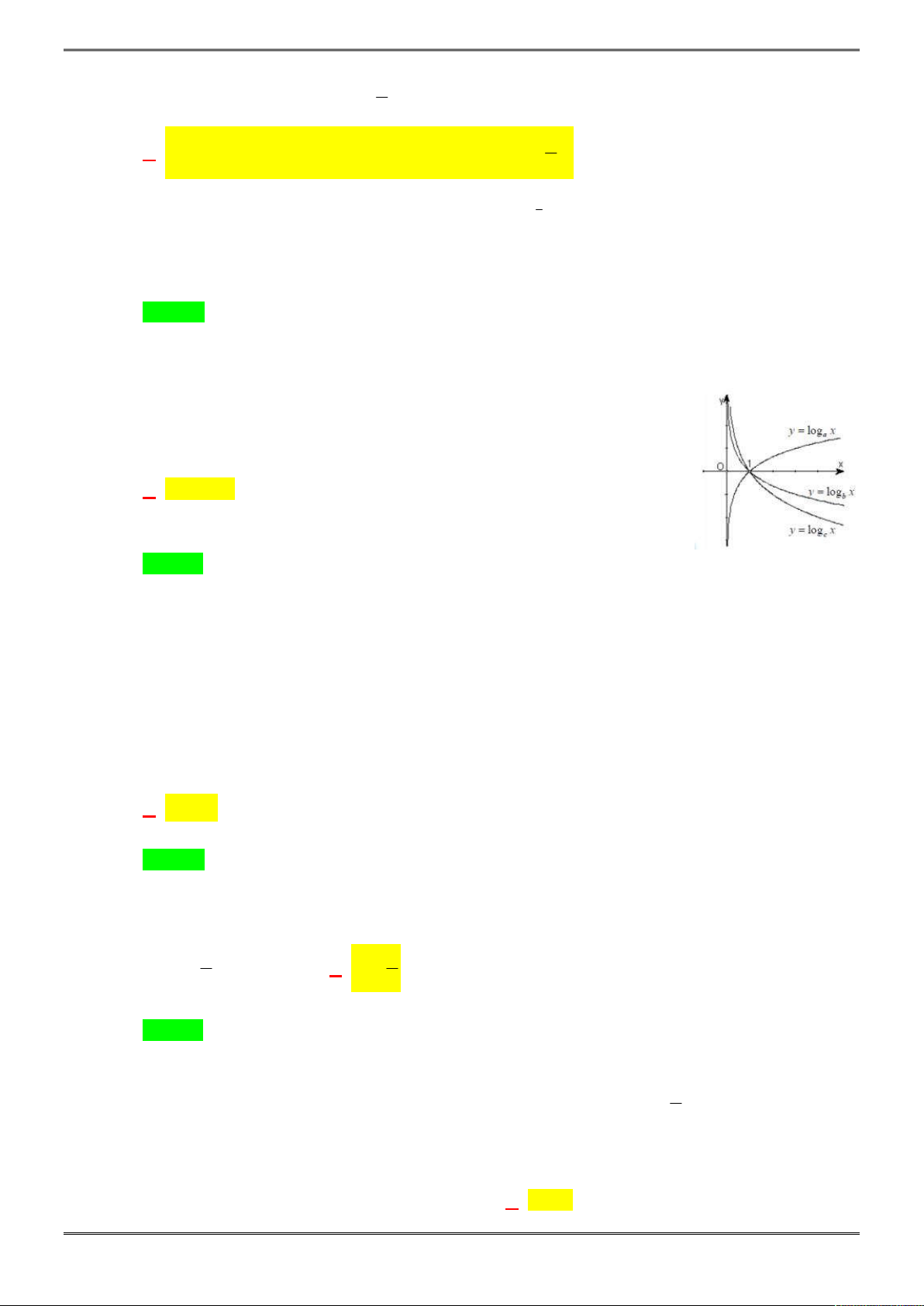
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 20

Câu 5. [2D2-4.7-1] Cho hàm số

1

2

x

y

 



 

 

. Mệnh đề nào sau đây sai?

A. Đồ thị hàm số luôn đi qua hai điểm

 

1; 0

A

,

1

1; .

2

B

 

 

 

.

B. Đồ thị hàm số đối xứng với đồ thị hàm số

1

2

logy x

 qua đường thẳng

y x

.

C. Đồ thị hàm số có một đường tiệm cận.

D. Đồ thị hàm số nằm phía trên trục hoành.

Lời giải

Chọn A

Ta có

 

2

4 4

ln ln 4 4

1

4 4 0

x

x x

x





 



   

 



 



.

Câu 6. [2D2-4.7-2] Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số

log , log , log

a b c

y x y x y x

   được cho trong hình vẽ sau

Mệnh đề nào dưới đây đúng

A.

c a b 

. B.

b c a 

.

C.

a c b 

. D.

a b c 

Lời giải

Chọn B

Dựa vào đồ thị ta thấy

 Hàm số

log

a

y x

 đồng biến, suy ra

1

a



 Hai hàm số

log

b

y x

 và

log

c

y x

 nghịch biến, suy ra

0 , 1b c 

 Với

0 1 log log

1 log log

b c

x x x

   





  



Suy ra

b c a 

.

Câu 7. [2D2-3.1-1] Nếu log

a

b p

, thì

2 4

log

a

a b

bằng

A.

4 2

p



. B.

2 4

a p

. C.

4 2p a

. D.

4

2p a

Lời giải

Chọn A

Ta có

2 4 2 4

log log log 2 4log 2 4

a a a a

a b a b b p

     

.

Câu 8. [2D2-5.7-2] Tìm các giá trị m để phương trình

1 2 3

2 .2 2

x x x

m

  

 

luôn đúng với

x

 

A.

3

2

m



. B.

5

2

m



. C.

3

m



. D.

2

m



Lời giải

Chọn B

Phương trình

   

1 2 3

2 .2 2 2.2 4 .2 8.2 2 5 2 0 *

x x x x x x x

m m m

  

       

Để phương trình (*) nghiệm đúng với mọi

5

5 2 0

2

x m m

     



.

Câu 9. [2H2-2.3-1] Cho khối trụ có độ dài đường sinh bằng 10, biết diện tích mặt đáy của khối trụ

bẳng 90



. Tính thể tích của khối trụ

A.

30



. B.

300



. C.

900



. D.

450



20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 21

Lời giải

Chọn C

. 10.90 900

V B h

 

  

.

Câu 10. [2H1-2.0-1] Cho khối chóp có đường cao h, diện tích mặt đáy S. Gọi V là thể tích của khối

chóp.

Tìm mệnh đề đúng

A.

.V S h

. B.

1

.

2

V S h



. C.

1

.

3

V S h



. D.

1

.

6

V S h



Lời giải

Chọn C

Áp dụng công thức tính thể tích khối chóp

1 1

. .

3 3

V B h S h

 

.

Câu 11. [2H1-2.1-1] Cho hình chóp tam giác S. ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA

vuông góc với mặt phẳng đáy và

2 3SA a

 . Tính thể tích V của khối chóp S.ABC.

A.

3

3 2

2

a

V 

. B.

3

2

a

V  . C.

3

2

a

V  . D.

3

V a

.

Lời giải

Chọn B

Ta có

0 2

1 3

. .sin 60

2 4

ABC

S AB AC a

 

Áp dụng công thức

3

2

1 1 3

. . .2 3

3 3 4 2

ABC

a

V SA S a a  

.

Câu 12. [2D2-4.2-1] Tính đạo hàm của hàm số

2

ln(2 )y x x

  với

0 2

x

 

là:

A.

2

2 2

2

x

y

x x









. B.

2

(2 2 )(2 )y x x x



   .

C.

2

1

2

y

x x







.

D.

2

y x x



 

.

Lời giải

Chọn A

2

2 2

(2x )' 2 2x

ln(2x ) '

2x 2x

x

y x y

x x

 

    

 

Câu 13. [2D2-4.1-2] Tìm tập xác định của hàm số

 

2

3

log 5. 6

y x x

  

là:

A.

( ;2) (3; )

D

   

. B.

(2;3)

D



.

C.

 

2;3

D 

. D.

( ;2] [3; )

D

   

.

Lời giải

Chọn A

Điều kiện

2

5x 6 0 2; 3

x x x

     

Câu 14. [2D2-3.3-2] Cho

2

loga m

 với

0

m



và

1

m



và

log (8 )

m

A m

 . Khi đó mỗi quan hệ giữa

A

và

a

là:

A.

3

a

A

a





. B.

(3 )A a a 

. C.

3

a

A

a





. D.

(3 ).A a a 

.

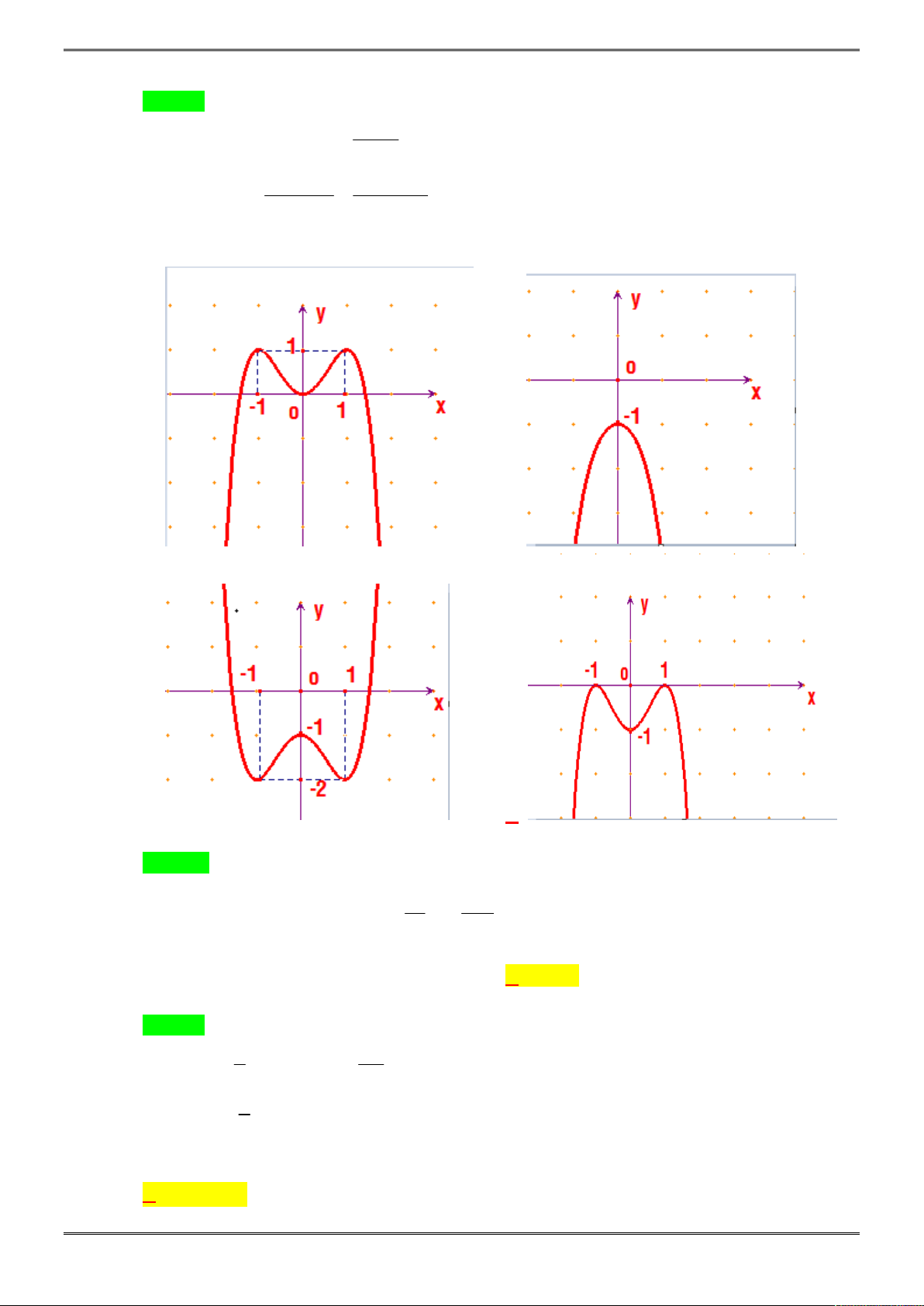
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 22

Lời giải

Chọn A

Sử dụng công thức

log

c

a

c

b

a



, ta được:

2 2

log (8 ) 3 log

log (8 )

log log

m

m m

A m

m m



  

Câu 15. [2D1-5.2-2] Hàm số

4 2

2 1

y x x

   

có đồ thị nào trong các đồ thị sau:

A. . B. .

C. . D.

Lời giải

Chọn D.

Câu 16. [2D1-2.8-2] Biết rằng hàm số

2

3

1

4

3 3

mx

y x



  

đạt cực đại tại

2

x



. Khi đó giá trị của

m

sẽ là:

A.

1

m



. B.

2

m



. C.

3

m



. D.

4

m



.

Lời giải

Chọn C

.

 

2

2 4

' x ' 2 4 0 3

3 3

2

'' 2x '' 2 4 2 2 0 2

3

m

y x m y m

y m y x

        

           

Câu 17. [2D2-5.2-2] Giải bất phương trình:

2

3x

3 81

x 



có nghiệm là:

A.

4 1x  

. B.

1; 4

x x

  

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 23

C.

1 4

x

 

.

D.

4; 1x x 

.

Lời giải

Chọn A

2 2

3x 3x 4 2

3 81 3 3 3x 4

x x

x

 

     

Câu 18.

[2D1-7.1-2] Phương trình tiếp tuyến của đồ thị hàm số

2 1

2

x

y

x





 

tại điểm có hoành độ

1x 

là:

A.

5 8y x  

. B.

5 2

y x

 

. C.

5 2

y x

  

. D.

5 8y x 

.

Lời giải

Chọn B

 

2

5

' ' 1 5

2

y y

x

  

 

loại đáp án A, C

0 0

1; 3 : 5x 2

x y PT y

    

Câu 19. [2D1-3.2-2] Giá trị nhỏ nhất của hàm số

4 2

2 1

y x x

  

trên đoạn

 

1;1



là:

A.

1

.

B.

1

. C.

0

. D.

2

.

Lời giải

Chọn B

 

2

5

' ' 1 5

2

y y

x

  

 

loại đáp án A, C

0 0

1; 3 : 5x 2

x y PT y

    

Chọn đáp án B

( Học sinh có thể sd máy tính để tính kq ).

Câu 20. [2D1-2.4-2] Cho hàm số

3

3y x x  

. Hãy chọn khẳng định đúng

A. Hàm số không có cực trị. B. Hàm số có một cực trị.

C. Hàm số đạt cực tiểu tại

1x 

. D. Giá trị cực đại của hàm số là 2.

Lời giải

Chọn D

2

' 3x 3 0 1

y x

      

hàm số có 2 cực trị loại đáp án A, B

Vẽ bảng biến thiên ta thấy hàm số đạt cực đại tại x = 1, loại đáp án C

Câu 21. [2D2-4.0-2] Mệnh đề nào sau đây đúng.

A.

2017

1 0

2016

x

 

  

 

 

. B.

2016

log 2017 1

.

C.

2017

log 2016 1

. D.

2016

1 0

2017

x

 

  

 

 

.

Lời giải

Chọn D

Ta thấy

x

2016 2016

1 1 x 0

2017 2017

 

    

 

 

.

Câu 22. [2D2-5.2-3] Cho hàm số

 

2

1

3

.

7

x

f x





Khẳng định nào dưới đây là sai?

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 24

A.

 

2

3 7

1

1 log 7 1 log 3

x x

f x



  

 

. B.

 

2

1 2

2

1 .log 3 1 log 7

f x x x   

.

C.

 

2

3

1 1 log 7

f x x x   

. D.

 

2

1 ln3 1 ln 7

f x x x   

.

Lời giải

Chọn B

 

2

x

x x 2 2

1 1 1 1 1

x 1

2 2 2 2 2

3

f x 1 7.3 7 log 7 x log 3 x log 7 x log 3 x 1 log 7

7



         

.

Câu 23. [2D1-3.11-2] Cho hàm số

 

1mx

f x

x m







. Giá trị lớn nhất của hàm số trên

 

1;2

bằng

3

. Khi

đó giá trị

m

bằng:

A.

1

2

m

 

. B.

1

2

m



. C.

1

m



. D.

2

m



.

Lời giải

Chọn B

Tập xác định

 

\

D R m



Trước hết, để hàm số đạt GTLN trên

 

1;2

thì

2

1

m











Ta có:

2

1 1

( ) '( ) 0,

( )

mx m

f x f x x D

x m x m

 

      

 

[1;2]

1 1

( ) (1) 3 3

1 2

max

m

f x f m

m



     



.

Câu 24. [2D1-7.1-3] Có bao nhiêu tiếp tuyến với đồ thị hàm số

2

1

x

y

x







. Biết tiếp tuyến song song

với đường thẳng

3 2

y x

 

A. 0. B. 1. C. 2. D. Không có

Lời giải

Chọn B

Xét phương trình

2

1 1 0

3

1 1 2

( 1)

x x

x

  

 

  

 

    



 

Với

0

x



ta có phương trình tiếp tuyến

3 2

y x

 

( loại)

Với

2

x

 

ta có phương trình tiếp tuyến

3 7

y x

 

( Nhận).

Câu 25. [2D2-4.5-2] Cho

0 1, , .a x y R  

Mệnh đề nào dưới đây đúng?

A. Nếu

x y

a a

thì

  

1 0

a x y

  

. B. Nếu

x y

a a

thì

  

1 0

a x y

  

.

C. Nếu

x y

a a

thì

x y

. D. Nếu

x y

a a

thì

x y

Lời giải

Chọn B

Ta có

 TH1:

1 0

0 1 ( 1)( ) 0

0

x y

a

a a x y

a a x y x y

 



      



     



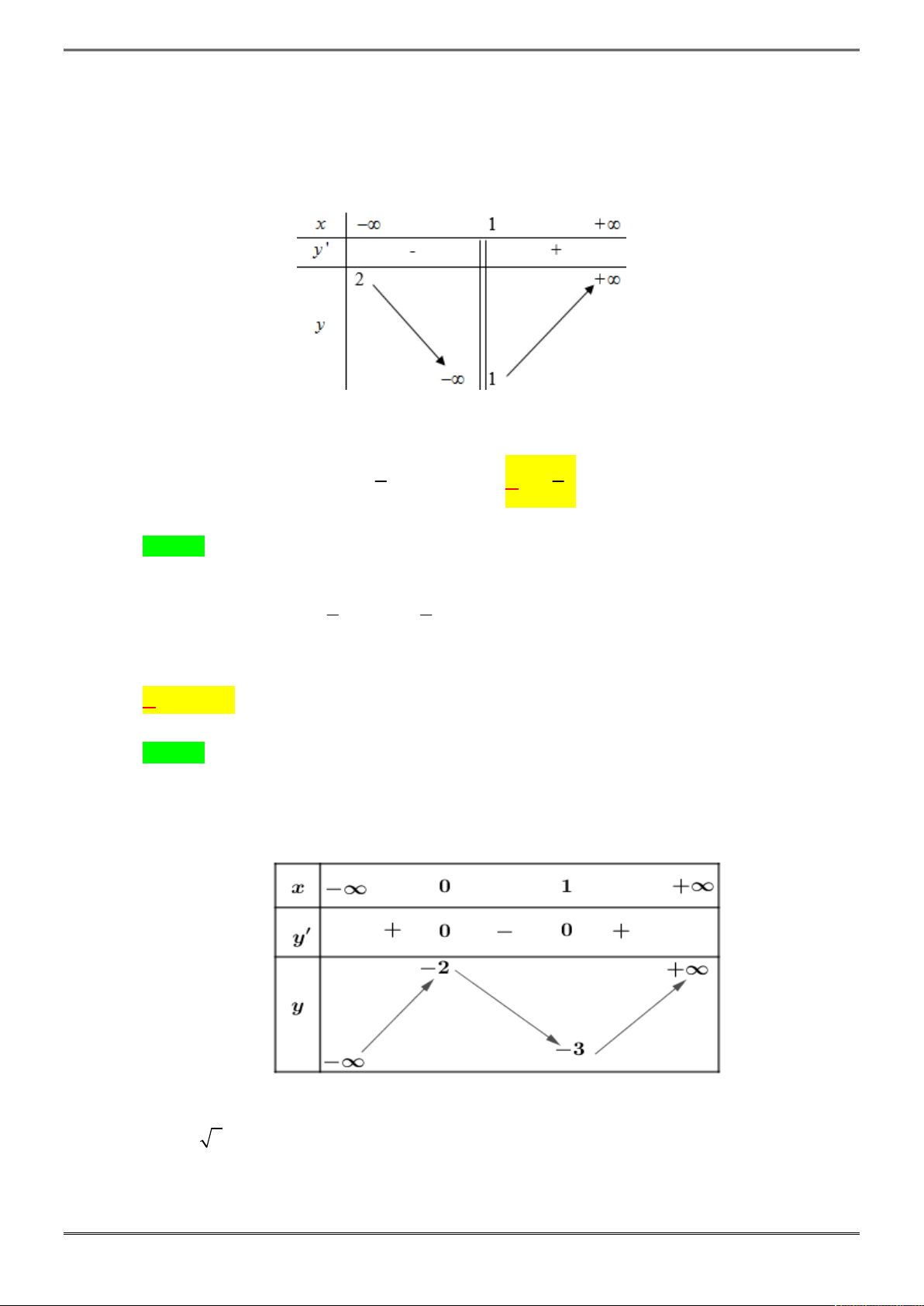
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 25

 TH2:

1 0

1 ( 1)( ) 0

0

x y

a

a a x y

a a x y x y

 



     



     



.

Câu 26. [2D1-6.8-3] Cho hàm số

 

y f x



 

\ 1

R

và liên tục trên từng khoảng xác định có bảng biến

thiên:

Tìm tập hợp tất hợp tất cả các giá trị thực của tham số m để đồ thị hàm số

 

y f x



cắt đường

thẳng

2 1

y m

 

tại hai điểm phân biệt.

A.

 

1;2

. B.

3

1;

2

 

 

 

. C.

3

1;

2

 

 

 

. D.

 

1;2

Lời giải

Chọn C

Đồ thị hàm số

( )y f x

cắt đường thẳng

2 1

y m

 

tại hai điểm phân biệt khi và chỉ khi

3 3

1 2 1 2 1 1;

2 2

m m m

 

       

 

 

.

Câu 27. [2D1-2.6-2] Tìm giá trị cực tiểu

CT

y

của hàm số

3 2

2 3 2

y x x

  

?

A.

3

CT

y

 

. B.

2

CT

y

 

. C.

0

CT

y



. D.

1

CT

y



Lời giải

Chọn A

Tính

2

' 6 6y x x 

, cho

0

' 0

1

x

y

x





 







Bảng biến thiên

.

Câu 28. [2H1-3.1-2] Cho lăng trụ đứng

.

ABC A B C

  

có đáy

ABC

là tam giác vuông tại

B

,

AB a

,

2BC a



, mặt bên

 

A BC



hợp với mặt đáy

 

ABC

một góc

30

. Tính thể tích khối lăng

trụ.

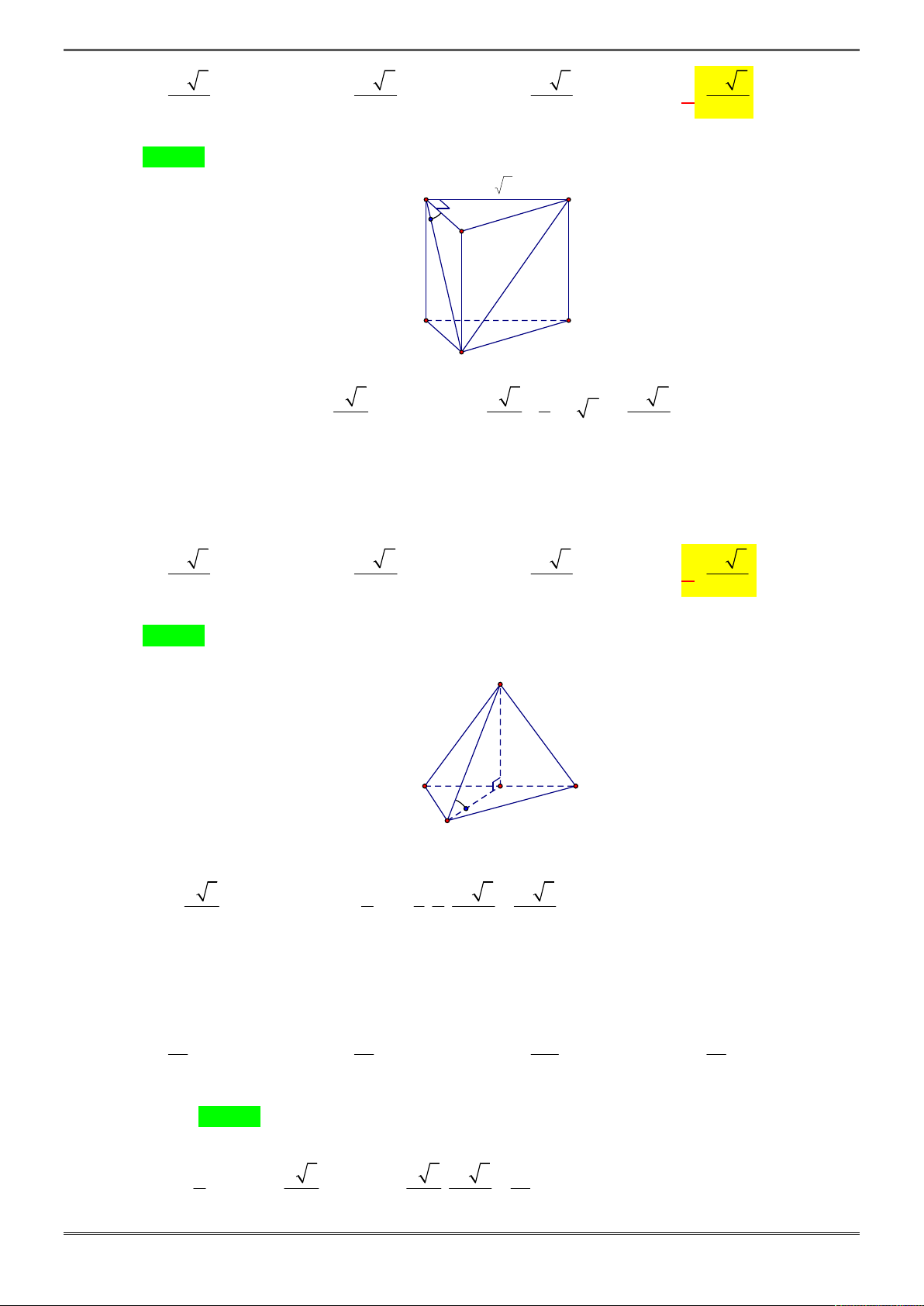
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 26

A.

3

6

a

. B.

3

6

3

a

. C.

3

a

. D.

3

6

a

.

Lời giải

Chọn D

30

0

a

a 2

C'

B'

A'

C

A

B

Ta có:

0

3

AA ' .tan30

3

a

a 

mặt khác:

3

3 1 6

. . 2

3 2 6

a a

V a a

 

 

 

 

Câu 29. [2H1-2.4-2] Cho hình chóp

.

S ABC

có tam giác

ABC

là tam giác đều cạnh

a

. Hình chiếu của

S

trên mặt phẳng

 

ABC

là trung điểm của cạnh

AB

, góc tạo bởi cạnh

SC

và mặt phẳng đáy

 

ABC

bằng

30

. Thể tích của khối chóp

.

S ABC

là:

A.

3

8

a

. B.

3

2

8

a

. C.

3

24

a

. D.

3

2

a

.

Lời giải

Chọn D

30

0

a

S

I

C

B

A

2 3

0

3 1 3 3

, .tan 30 , . .

2 2 3 2 4 24

a a a a a

CI SI CI V    

.

Câu 30. [2H1-3.4-3] Cho hình lăng trụ

.

ABC A B C

  

có đáy

ABC

là tam giác đều cạnh a, hình chiếu

của

C



trên

 

ABC

là trung điểm

I

của

BC

. Góc giữa

AA

và

BC

là

30

. Thể tích của khối

lăng trụ

.

ABC A B C

  

là:

A.

3

4

a

. B.

3

2

a

. C.

3

8

a

. D.

3

8

a

.

Lời giải

Chọn D

Do

AA'

song song với

'CC

nên góc giữa

AA'

và

BC

cũng là góc giữa

'CC

và

BC

. Nên

0

3

' .tan 30

2 6

a a

C I  

. Vậy:

2 3

3 3

.

6 4 8

a a a

V  

Nên chọn đáp án. D.

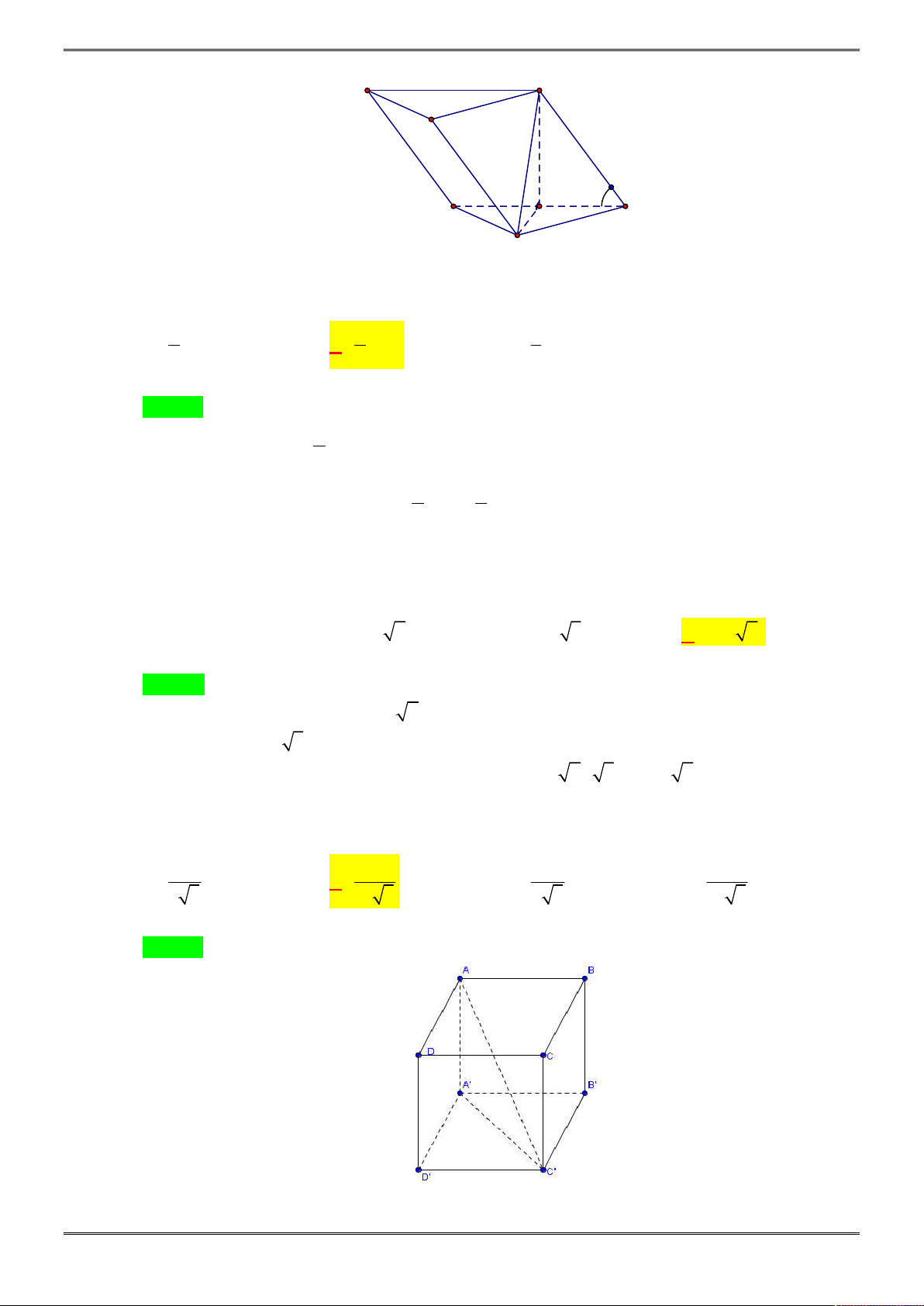
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 27

a

A'

B'

30

0

A

C

C'

I

B

.

Câu 31. [2H2-2.3-2] Một hình trụ có 2 đáy là 2 hình tròn nội tiếp hai mặt của một hình lập phương

cạnh

a

. Thể tích của khối trụ đó là

A.

3

1

2

a



.

B.

3

1

4

a



. C.

3

1

3

a



. D.

3

a



.

Lời giải

Chọn B

+ Bán kính của đáy là

2

a

+ Thể tích khối trụ:

2

2 3

1

. . .

2 4

a

V r h a a

  

 

  

 

 

.

Câu 32. [2H2-1.2-2] Gọi

S

là diện tích xung quanh của hình nón tròn xoay được sinh ra bởi đoạn

thẳng

AC



của hình lập phương

.

ABCD A B C D

   

có cạnh

b

khi quay xung quanh trục

AA



.

Diện tích

S

là

A.

2

b



. B.

2

b



. C.

2

3

b



. D.

2

6

b



.

Lời giải

Chọn D

+ Bán kính hình nón

' ' 2r A C b

 

+Đường sinh

3l b



+ Diện tích xung quanh của hình nón là:

. . . 2 . 3

xq

S r l b b

 

  

2

6

b



.

Câu 33. [2H1-2.4-2] Hình lập phương

. ' ' ' 'ABCD A B C D

có độ dài đường chéo bằng

a

. Khi đó thể

tích khối tứ diện

' ' 'AA B C

là.

A.

2

3 3

a

. B.

3

18 3

a

. C.

3

6 3

a

. D.

2

18 3

a

Lời giải

Chọn B

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 28

Hình lập phương

. ' ' ' 'ABCD A B C D

có độ dài đường chéo bằng

a

. Khi đó thể tích khối tứ diện

' ' 'AA B C

là.

Gọi

x

là cạnh hình lập phương

Ta có

2 2 2

' ' ' 'AA A C AC

 

2 2 2

( 2)

3

a

x x a x   

V=

3

' ' '

1 1

'

3 6

18 3

A B C

a

S AA x 

.

Câu 34. [2H2-1.3-3] Hình nón có thiết diện qua trục là tam giác đều cạnh a, thể tích của hình nón là:

A.

3

24

a

. B.

3

2

24

a

. C.

3

12

a

. D.

3

2

12

a

Lời giải

Chọn A

Hình nón có thiết diện qua trục là tam giác đều cạnh a, thể tích của hình nón là:

3

; ;

2 2

a a

l a R h  

=>

3

2

1 3

3 24

a

V R h



 

.

Câu 35. [2D1-2.13-4] Cho hàm số

3 2

y x x mx

   

(m là tham số) có đồ thị là (C

m

). Các điểm cực

đại và cực tiểu của đồ thị hàm số cách đều đường thẳng

1y x 

khi

A.

0

m



. B.

1

m

 

. C.

2

m

 

. D.

3

m



Lời giải

Chọn A

Ta có:

2

' 3 6

y x x m  

.

Hàm số có CĐ, CT

2

' 3 6 0

y x x m

    

có 2 nghiệm phân biệt

1 2

;x x

' 9 3 0 3

m m

       

(*)

Gọi hai điểm cực trị là

   

1 2

; ; ;

A B x

y y

x

Thực hiện phép chia y cho y ta được:

1 1 2

' 2 2

3 3 3 3

m m

y x y x

     

     

     

     



1 1 2 221

2 2

2 2 ;( 2 2

3

) ( )

3 3 3

y y x y y x

m m m m

x x

   

     

   

 



 

  



Phương trình đường thẳng đi qua 2 điểm cực trị là :

2

2 2

3 3

m m

y x

 

   

 

 

Các điểm cực trị cách đều đường thẳng

1y x 



xảy ra 1 trong 2 trường hợp:

TH1: Đường thẳng đi qua 2 điểm cực trị song song hoặc trùng với đường thẳng

1y x 

2 9

2 1

3 2

m

   



(không thỏa (*))

TH2: Trung điểm I của AB nằm trên đường thẳng

1y x 

   

2

1

2

2 2

1

2

2 2 2 2

3 3

2

2 .2 2 2 0 0

3

1 1

2

3

2

I I

x m m

x x x x

m m

y x

m

y

   

      

   

   

   

      

   

  

 



      

Vậy các giá trị cần tìm của m là:

0

m



.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 29

Câu 36. [2D2-5.7-4] Tìm m để phương trình

3

4 2 3

x x

m



  

có đúng 2 nghiệm

 

1;3

x 

A.

13 9

m

   

. B.

3 9

m

 

. C.

9 3

m

  

. D.

13 3

m

  

Lời giải

Chọn A

đặt

 

2 0

x

t t

 

phương trình đã cho có dạng

2

8 3

t t m  

Yêu cầu bài toán trở thành tìm m để phương trình

2

8 3 0

t t m

   

có đúng hai nghiệm

 

2;8

t 

Ta có

 

64 4 3 0 13

m m

       

Khi đó giả sử phương trình có hai nghiệm

 

1 2 1 2

,

t t t t

. Khi đó ta có

  

 

1 2 1 2 1 2

1 2

1 2 1 2 1 2

2 2 0 2 4 0

2 8

8 8 0 8 64 0

t t t t t t

t t

t t t t t t



      



 

    

 

      





3 2.8 4 0

9

3 8.8 64 0

m

   



   



   



Kết hợp lại ta có

13 9

m

   

.

Câu 37. [2D1-6.8-4] Tìm tập hợp tất cả các giá trị của tham số m để đường thẳng

1y x 

cắt đồ thị

hàm số

2

1

x m

y

x







tại hai điểm phân biệt có hoành độ dương

A.

2 1

m

   

. B.

1

m

 

. C.

1

m



. D.

2 1

m

  

Lời giải

Chọn A

Xét phương trình hoành độ giao điểm của 2 đồ thị:

 

2

1

2

1

2 1 0 *

1 2

1

x

x m

x

x x m

x







   

 

   

  





2 đồ thị cắt nhau tại 2 điểm có hoành độ dương



phương trình (*) có 2 nghiệm dương phân

biệt khác

 

2

1 2

1 2.1 1 0

2

' 1 1 0

1 2 2 1

2 0

1

1 0

m

m m

x x

m

x x m



   

 





    

 

        

 

  

 

 





   



.

Câu 38. [2H1-2.4-4] Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O,



0

, 60

AB a BAD 

 

SO ABCD



và mặt phẳng (SCD) tạo với mặt đáy một góc 60

0

. Tính thể tích khối chóp

S.ABCD

A.

3

.

3

12

S ABCD

a

V 

. B.

3

.

3

24

S ABCD

a

V 

. C.

3

.

3

8

S ABCD

a

V 

. D.

3

.

3

48

S ABCD

a

V 

Lời giải

Chọn C

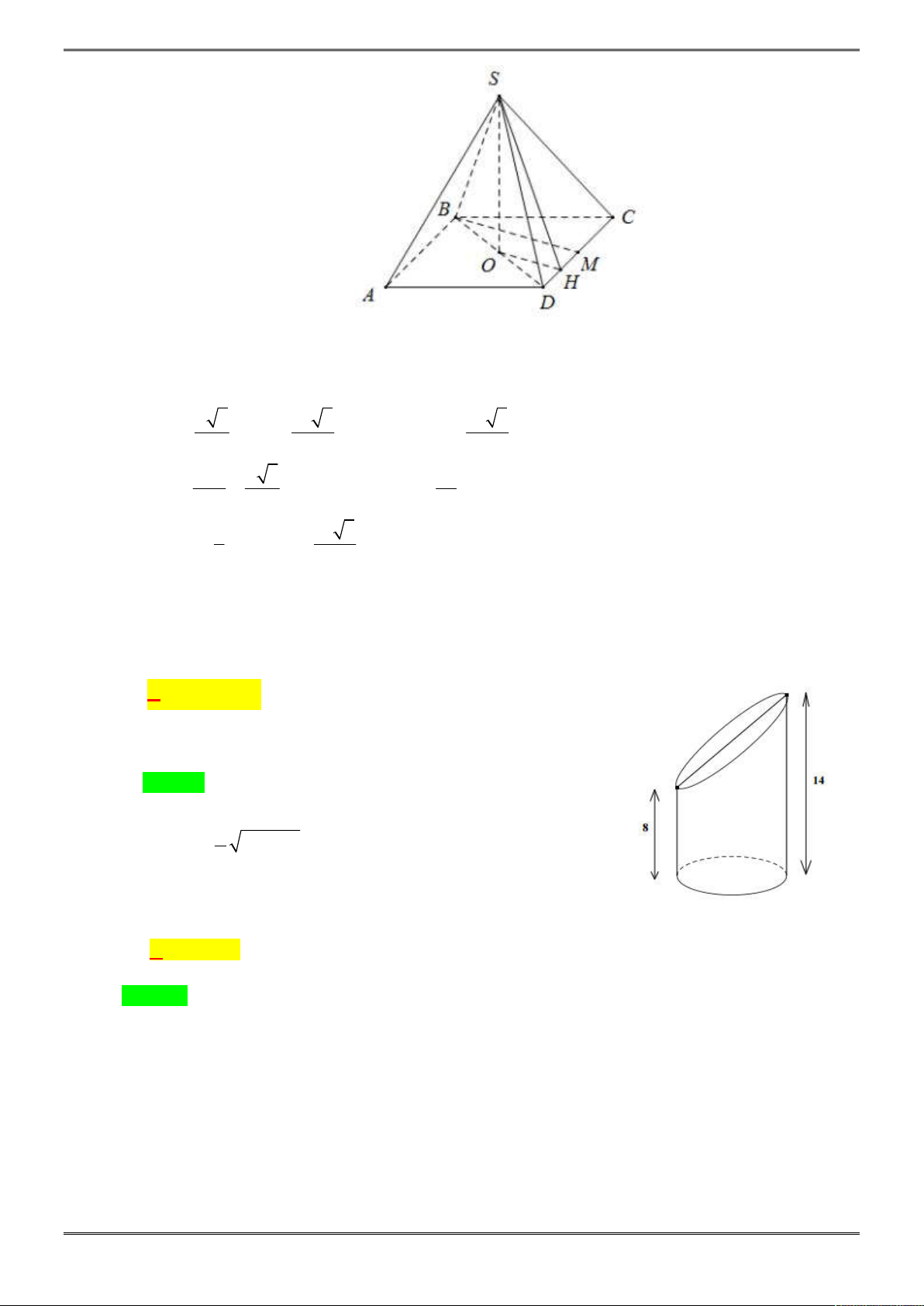
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 30

Gọi M là trung điểm CD,

OH CD

tại H

Có

BCD

đều cạnh a nên

BM CD

Góc giữa (SCD) và (ABCD) là góc

0

60

SHO 

2 2

3 3 3

; ; 2

2 4 2

BCD ABCD BCD

a a a

BM S S S   

0

3 3

; .tan 60

2 4 4

BM a a

OH SO OH   

3

.

1 3

.

3 8

S ABCD ABCD

a

V SO S 

.

Câu 39. Cắt một khối trụ bởi một mặt phẳng ta được một khối (H) như hình vẽ bên. Biết rằng thiết diện

là một hình elip có độ dài trục lớn bằng 10, khoảng cách từ một điểm thuộc thiết diện gần mặt

đáy nhất và điểm thuộc thiết diện xa mặt đáy nhất tới mặt đáy lần lượt là 8 và 14. (xem hình

vẽ). Tính thể tích của hình (H)

.A.

 

176

H

V





. B.

 

275

H

V





.

C.

 

192

H

V





. D.

 

740

H

V





Lời giải

Chọn A

Khối (H) có thể tích bằng thể tích hình trụ chiều cao 11 và bán

kính đáy

2 2

1

10 6 4

2

 

nên

 

2

.4 .11 176

H

V

 

 

Câu 40. [2H2-1.2-2] Cho tam giác

OAB

vuông tại

O

có

3

OA



,

4

OB



. Tính diện tích toàn phần của hình nón tạo thành khi

quay tam giác

OAB

quanh

OA

.

A.

36 .

S





B.

20 .

S





C.

26 .

S





D.

52 .

S





Lời giải

Chọn A

Vì tam giác

OAB

vuông tại

O

có

3, 4

OA OB

 

nên

5.

AB



Ta có

. . .4.5 20 .

xq

S Rl OB AB

   

   

Và diện tích đáy là

2 2 2

. .4 16 .

S R OB

   

   

Vậy

36 .

tp xq

S S S



  

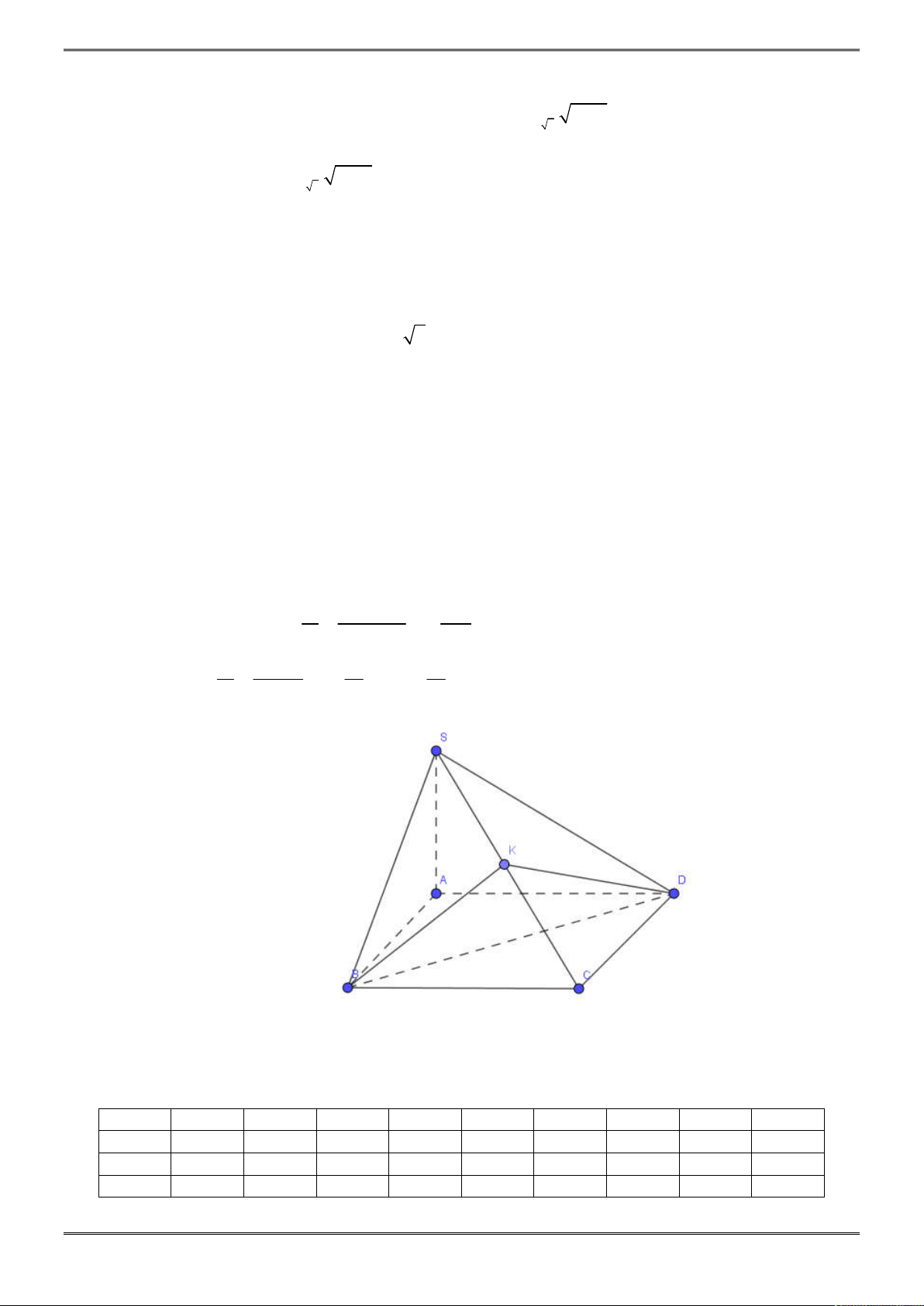
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 31

PHẦN II: PHẦN TỰ LUẬN

Câu 1 . [2D2-7.1-3] Giải phương trình:

2 3

4 8

2

log ( 1) 2 log 4 log (4 )x x x

     

(1)

Lời giải

2

log ( 1) 2

x

 

=

3

8

2

log 4 log (4 ) ;(1)

x x  

.

TXĐ

 

( 4;4) \ 1 

2

2 2 2 2 2

2 2

(1) log | x 1| 2 log (4 ) log (4 ) log 4| 1| log (16 )

4 | x 1| 16 x 4 | 1| 16 0;(2)

x x x x

x x

          

        

*)Xét

4 1

x

   

2

(2) 4 20 0 2 2 6

x x x      

*)Xét

1 4

x

  

2

(2) 4 12 0 2

x x x

     

Câu 2. [2H1-2.4-4] Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình thoi với



0

120

A  ,

BD a

. Cạnh

bên

SA

vuông góc với đáy. Góc giữa mặt phẳng

 

SBC

và đáy bằng

60

o

. Một mặt phẳng (α)

đi qua

BD

và vuông góc với cạnh

SC

. Tính tỉ số thể tích giữa hai phần của hình chóp do mặt

phẳng (α) tạo ra khi cắt hình chóp.

Lời giải

Gọi

1 2

; ;V V V

là thể tích của hình chóp

.

S ABCD

,

.

K BCD

và phần còn lại của hình chop

.

S ABCD

.

S ABCD

:

1

.

2. 13

.

ABCD

BCD

S SA

V SA

V S HK HK

  

Ta được:

1 2 2 2

1 1 1 1

1 13 12

V V V V

V

V V V V



     

BẢNG ĐÁP ÁN

1.A

2.D

3.C

4.C

5.A

6.A

7.A

8.B

9.C

10.C

11.B

12.A

13.A

14.A

15.D

16.C

17.A

18.B

19.B

20.D

21.D

22.B

23.B

24.B

25.B

26.C

27.A

28.D

29.D

30

31.B

32.D

33.B

34.A

35.A

36.A

37.A

38.C

39.A

40.A

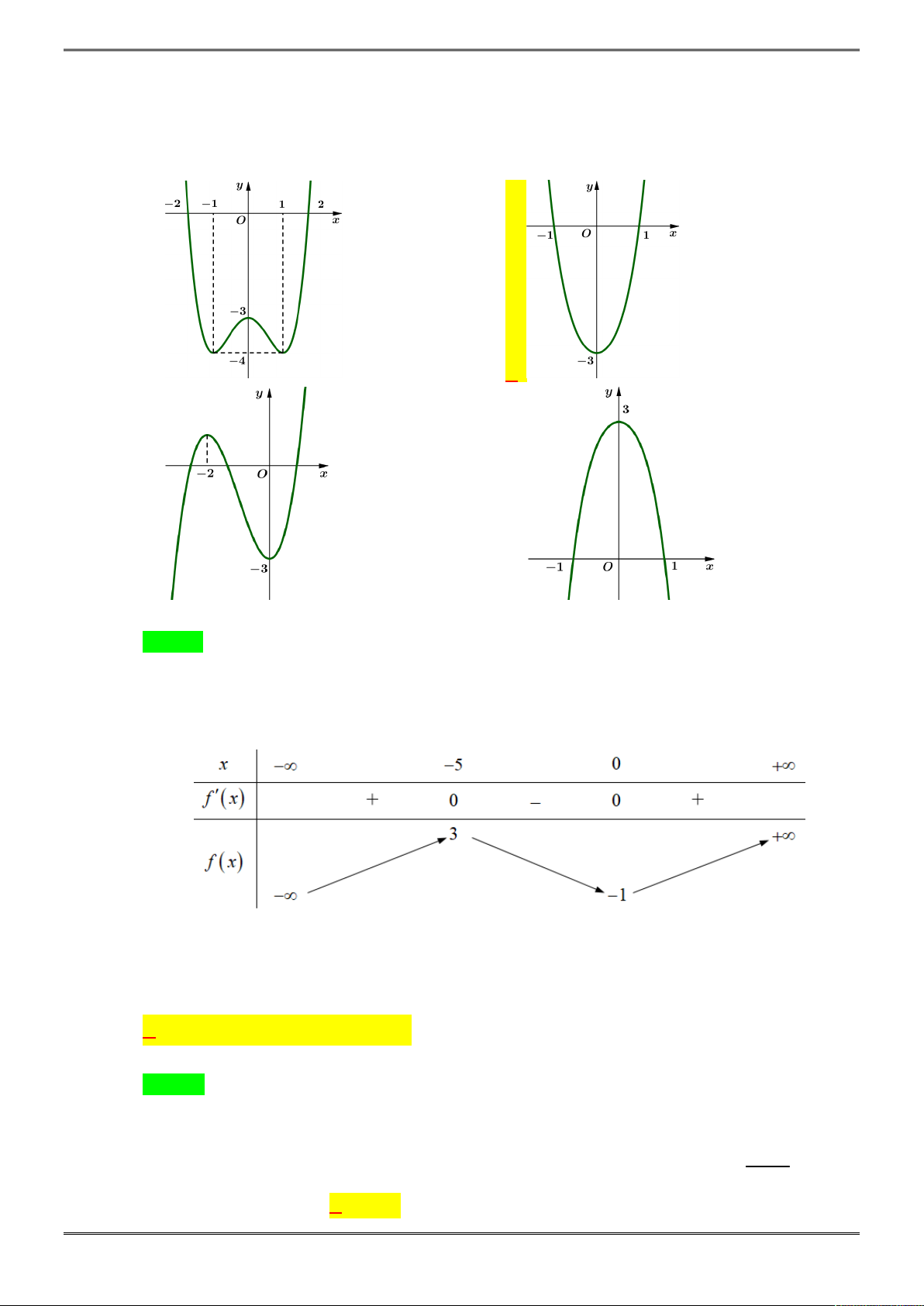
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 32

ĐỀ ÔN TẬP SỐ 08

PHẦN I: PHẦN TRẮC NGHIỆM

Câu 1. [2D1-5.2-1] Hàm số

4 2

2 3

y x x

  

có đồ thị là hình nào sau đây?

A. . B. .

C. . D. .

Lời giải

Chọn B

Hàm số đã cho là hàm trùng phương, có hệ số

0

a



nên loại câu C và D.

Hàm số có hệ số

1

a



và

2

b



cùng dấu nên hàm số chỉ có một cực trị. Loại A.

Câu 2. [2D1-1.3-1] Bảng biến thiên dưới là của hàm số

 

y f x



. Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên

 

;3



và

 

1;

  

.

B. Hàm số nghịch biến trên

 

; 5 

.

C. Hàm số đồng biến trên

 

1;1



.

D. Hàm số nghịch biến trên

 

5;0



.

Lời giải

Chọn D

Ta thấy

 

0 5;0

y x



   

nên hàm số nghịch biến trên

 

5;0



.

Câu 3. [2D1-4.4-1] Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số

2 1

2

x

y

x







?

A.

2

y

 

. B.

2

y



. C.

2

x

 

. D.

2

x



.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 33

Lời giải

Chọn B

Ta có

2 1

lim lim 2 2

2

x x

x

y y

x

 



   



là tiệm cận ngang của đồ thị hàm số.

Câu 4. [2D2-2.1-1] Tìm tập xác định

D

của hàm số

 

2

3

1

y x

 

.

A.

   

; \ 1

D   

. B.

 

;D

  

. C.

 

;1

D

 

. D.





;1

D

 

.

Lời giải

Chọn C

Điều kiện:

1 0 1x x   

.

Tập xác định

 

;1

D

 

.

Câu 5. [2D1-2.4-1] Hàm số

4 2

2017 2018

y x x    có bao nhiêu điểm cực trị?

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Chọn B

Ta có

3

4 4034y x x



   ;

0 0

y x



  

và

y



đổi dấu khi qua điểm

0

x



nên hàm số có

1

điểm cực trị.

Chú ý: Hàm số dạng trùng phương có các hệ số

1

a

 

,

2017

b

 

cùng dấu nên hàm số có

1

điểm cực trị.

Câu 6. [2D2-3.2-1] Cho

0

a



,

0

b



. Khẳng định nào sau đây đúng?

A.

ln lnb a

a b



. B.

 

2 2 2

ln ln lnab a b

 

.

C.

ln

a a

b b

 



 

 

. D.

 

1

ln ln ln

2

ab a b

 

.

Lời giải

Chọn A

Đáp án A đúng vì ta có

log log

b b

c a

a c

nên

ln lnb a

a b



.

Đáp án B sai vì

   

2

2 2 2

ln ln ln ln lnab a b a b

   

.

Đáp án C sai vì

ln

ln ln ln

ln

a a

a b

b b

 

  

 

 

.

Đáp án D sai vì

 

1 1

ln ln ln ln ln

2 2

ab a b a b

   

.

Câu 7. [2D2-4.7-1] Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số

x

y a

và

1

x

y

a

 



 

 

đối xứng nhau qua trục hoành.

B. Đồ thị hàm số

log

a

y x

 và

1

log

a

y x

 đối xứng nhau qua trục tung.

C. Đồ thị hàm số

log

a

y x

 và

x

y a

đối xứng nhau qua đường thẳng

y x

.

D. Đồ thị hàm số

x

y a

và

log

a

y x

 đối xứng nhau qua đường thẳng

y x 

.

Lời giải

Chọn C

Lý thuyết: Đồ thị các hàm số

log

a

y x

 và

x

y a

đối xứng nhau qua đường thẳng

y x

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 34

Đáp án A sai vì đồ thị các hàm số

x

y a

và

1

x

y

a

 



 

 

đối xứng nhau qua trục tung.

Đáp án B sai vì đồ thị hàm số

log

a

y x

 và

1

log

a

y x

 đối xứng nhau qua trục hoành.

Câu 8. [2H1-1.1-1] Cho các khẳng định sau:

(I). Hình chóp đều là hình chóp có đáy là đa giác đều và đường cao hạ từ đỉnh qua tâm của đáy.

(II). Hình hộp là lăng trụ có đáy là hình chữ nhật.

(III). Lăng trụ đều là lăng trụ đứng có đáy là đa giác đều.

(IV). Hình lập phương có

9

mặt phẳng đối xứng.

Số khẳng định đúng là?

A.

1

. B.

2

. C.

3

. D.

4

.

Lời giải

Chọn C

Các khẳng định đúng là (I), (III), (IV).

Câu 9. [2H1-1.1-1] Cho các khẳng định sau:

(I). Tứ diện đều có

6

mặt phẳng đối xứng.

(II). Hình hộp chữ nhật

3

kích thước khác nhau có

3

mặt phẳng đối xứng.

(III). Lăng trụ tam giác đều có

4

mặt phẳng đối xứng.

(IV). Bát diện đều có

9

mặt phẳng đối xứng.

Số khẳng định Sai là?

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Chọn A

Câu 10. [2H2-1.3-1] Thể tích khối nón tròn xoay có đường cao

h

, đường sinh

l

, bán kính đáy

R

có thể

tích là.

A.

2

V Rl





. B.

V Rl





. C.

2

V R h





. D.

2

1

3

V h R





.

Lời giải

Chọn D

Câu 11. [2D1-6.1-2] Đồ thị của hàm số

4 2

4 3 3

y x x

  

và đường thẳng

3y x 

có tất cả bao nhiêu

điểm chung?

A.

4

. B.

2

. C.

1

. D.

3

.

Lời giải

Chọn D

Phương trình hoành độ giao điểm của hai đồ thị là

4 2

4 3 3 3x x x   

4 2

4 3 0

x x x

   

 

3

4 3 1 0

x x x

   

0

1

2

x









 









.

Suy ra hai đồ thị có ba điểm chung.

Câu 12. [2D2-4.2-2] Tính đạo hàm của hàm số

 

2

log 2 1

x

y

 

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 35

A.

 

1

2 1 ln 2

x

y







. B.

1

1 2

x

y









. C.

2 ln 2

2 1

x

y







. D.

ln 2

2 1

x

y







.

Lời giải

Chọn B

Ta có

 

2

log 2 1

x

y



 



 

 

 

2 1

2 1 ln 2

x









 

2 ln 2 1

1 2

2 1 ln 2

x



 



.

Câu 13. [2D1-3.4-2] Tìm giá trị nhỏ nhất của hàm số

3

y x

x

 

trên đoạn

 

2;3

.

A.

 

2;3

15

min

2

y



. B.

 

2;3

19

min

2

y



. C.

 

2;3

min 4

y



. D.

 

2;3

min 28

y



.

Lời giải

Chọn B

2

3

3y x

x



 

.

4

2

1

0 0

x

y

x





  

 

4

1 0 1 2;3

x x      

.

Ta có:

 

19

2

y



,

 

3 28

y



. Vậy

 

2;3

19

min

2

y



.

Câu 14. [2D2-3.3-2] Biết

log 2

a



,

log3

b



thì

log0,018

tính theo

a

và

b

bằng

A.

2

b a

. B.

2 3

b a

 

. C.

2 2

b a

 

. D.

2 2

a b

 

.

Lời giải

Chọn B

Ta có

18

log0,018 log

1000



3

log18 log10

 

log 2 2log3 3  

2 3a b  

.

Câu 15. [2D1-1.5-2] Tìm tất cả các giá trị thực của tham số

m

để hàm số

3 2

1

4 2

3

y x mx x

   

luôn

đồng biến trên tập xác định của nó?

A.

2

m



. B.

2

m

 

. C.

2

m

 









. D.

2 2

m

  

.

Lời giải

Chọn D

Tập xác định:

D  

.

2

2 4y x mx



  

.

Hàm số luôn đồng biến trên



1 0

0

a

 









 



2

4 0

m

  

2 2

m

   

.

Câu 16. [2D1-4.7-2] Cho hàm số

2

1

, 0

2 9

x

y m

x mx



 

 

. Có tất cả bao nhiêu giá trị thực của tham số

m

để đồ thị của hàm số đã cho có đúng một đường tiệm cận đứng?

A.

3

. B.

2

. C.

1

. D.

0

.

Lời giải

Chọn A

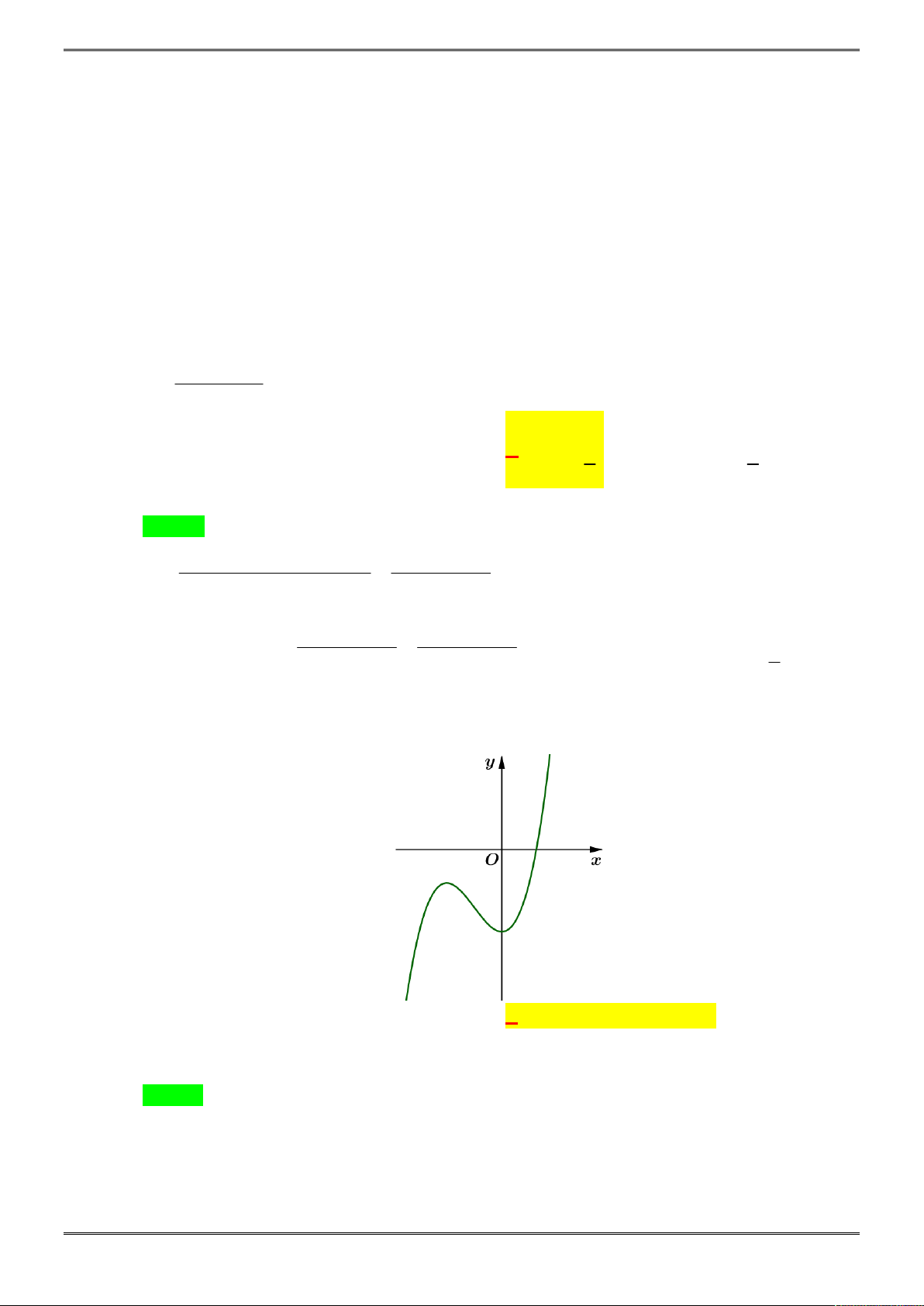
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 36

Để đồ thị hàm số có đúng một tiệm cận đứng thì phương trình

 

2

2 9 0 *

x mx  

có duy nhất

nghiệm khác

1

hoặc có hai nghiệm phân biệt trong đó có một nghiêm bằng

1

.

TH1:

2

9 0

m



   

3

m

  

Khi

3

m



, phương trình có một nghiệm

3

x



(thỏa mãn).

Khi

3

m

 

phương trình có một nghiệm

3

x

 

(thỏa mãn).

TH2: Phương trình

 

*

có một nghiệm bằng 1

1 2 9 0 5

m m

     

.

Thử lại, với

5

m



ta có phương trình

2

1

10 9 0

9

x

x x

x





   







(thỏa mãn)

Vậy với

3

m



,

3

m

 

,

5

m



thì đồ thị hàm số có duy nhất một tiệm cận đứng.

Câu 17. [2D1-3.4-2] Tìm tất cả các giá trị thực của tham số

m

để giá trị lớn nhất của hàm số

2

m x m

y

x

 





trên đoạn

 

2;0



bằng

2

?

A.

6

m



. B.

2

m



. C.

2

5

2

m







 



. D.

2

5

2

m

 









.

Lời giải

Chọn C

 

2 2

2

2 2

2

m x m x m

y

x

   







 

2

2 2

0,

2

m m

m

x

  

   



hàm số nghịch biến trên

 

2;0



 

 

2

2;0

2 2

max 2

2 2

m m

y y



  

   

 

2

2 2

2 2 2 8

5

4

2

m

m m

m





  



      





 



.

Câu 18. [2D1-5.3-2] Cho hàm số

3 2

y ax bx cx d   

có đồ thị là đường cong như hình vẽ bên. Mệnh

đề nào dưới đây đúng?

A.

0, 0, 0, 0

a b c d

   

. B.

0, 0, 0, 0

a b c d

   

.

C.

0, 0, 0, 0

a b c d

   

. D.

0, 0, 0, 0

a b c d

   

.

Lời giải

Chọn B

Dựa vào đồ thị, ta có các nhận xét sau:

+ Ta thấy rằng

lim ; lim 0

x x

y y a

 

     

.

+ Hàm số đạt cực đại tại

1 2

0, 0

x x

 

. Ta có

1 2

,x x

là nghiệm phương trình

2

3 2 0

y ax bx c



   

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 37

Theo hệ thức Viét, ta có

1 2

2

0

3

0

3

b

x x

a

c

x x

a



   







 





0

c

b













+ Đồ thị hàm số đi qua điểm có tọa độ

 

0; 0

d d

 

.

Vậy các hệ số

0, 0, 0, 0

a b c d

   

.

Câu 19. [2D2-6.1-2] Tìm tập nghiệm

S

của bất phương trình

3 1

3

log log 0

x

 



 

 

.

A.

 

0;1

S 

. B.

1

;

3

S

 

 

 

 

. C.

S

 

. D.

1

0;

3

S

 



 

 

.

Lời giải

Chọn D

Điều kiện:

1

3

0

log 0

x

















0

0 1

1

x





   







.

Bất phương trình

1

3

log 1x 

1

3

x

 

.

So với điều kiện, ta có

1

0;

3

S

 



 

 

.

Câu 20. [2D2-5.3-2] Phương trình

2 1

3 4.3 1 0

x x

  

có 2 nghiệm

1 2

,x x

trong đó

1 2

x x

. Chọn phát

biểu đúng?

A.

1 2

. 1

x x

 

. B.

1 2

2 0

x x

 

. C.

1 2

2 1

x x

  

. D.

1 2

2

x x

  

.

Lời giải

Chọn C

Ta có

2 1

3 4.3 1 0

x x

  

2

3.3 4.3 1 0

x x

   

3 1

1

3

x

















0

1

x









 



1

2

1

0

x

 











.

Vậy

1 2

2 1

x x

  

.

Câu 21. [2D2-4.1-2] Tìm tất cả các giá trị thực của tham số

m

sao cho hàm số

 

2

log 2 4

y x mx

  

có tập xác định

D  

.

A.

4

m



. B.

4 4

m

  

. C.

2

m

 

hoặc

2

m



. D.

2 2

m

  

.

Lời giải

Chọn D

Hàm số có tập xác định là



2

2 4 0,x mx x

      

2

4 0

m



    

2 2

m

   

.

Câu 22. [2D1-6.3-2] Tìm

m

để phương trình

4 2

4 1 0

x x m

   

có

2

nghiệm.

A.

1

m



. B.

3 1

m

  

. C.

1

m



hoặc

3

m

 

. D.

1

m

 

hoặc

3

m



.

Lời giải

Chọn C

Ta có

4 2

4 1 0

x x m

   

4 2

4 1

x x m   

.

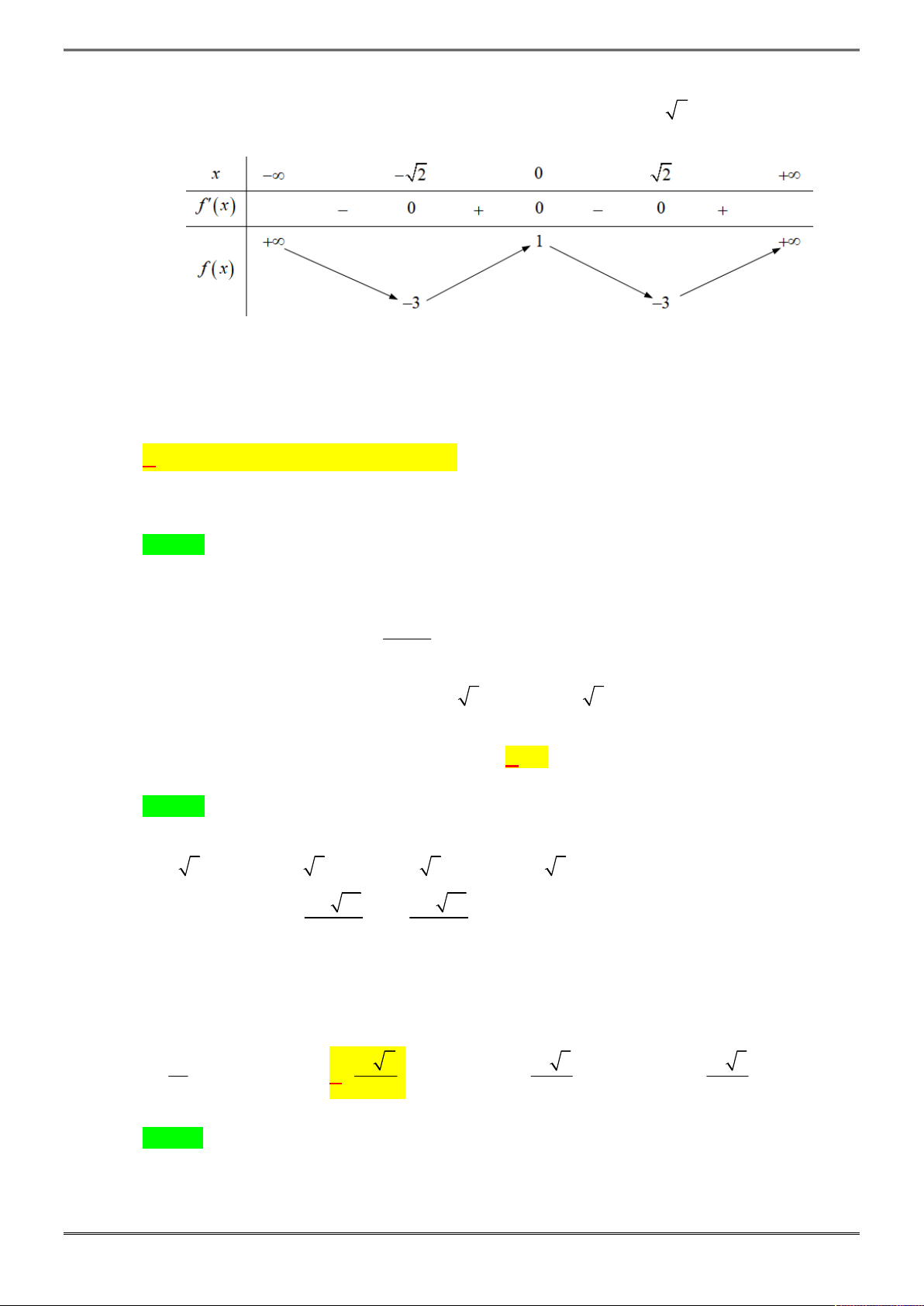
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 38

Đặt

 

4 2

4 1

f x x x

  

. Ta có

 

3

4 8f x x x



 

;

 

0

2

x

f x

x







 



 



.

Bảng biến thiên:

Dựa vào bảng biến thiên ta thấy phương trình có

2

nghiệm



1

m



hoặc

3

m

 

.

Câu 23. [2D2-4.5-2] Trong các khẳng định sau, khẳng định nào đúng?

A.

 

log log loga b a b

  

,

0, 0

a b

  

.

B.

x y x y

a a a



 

,

0

a

 

,

,x y



.

C. Hàm số

10 2017

x

y e



 đồng biến trên



.

D. Hàm số

12

log

y x

 nghịch biến trên khoảng

 

0;



.

Lời giải

Chọn C

+ Các khẳng định A, B sai theo lý thuyết.

+ Xét khẳng định C: Ta có

10 2017

10 0

x

y e





 

x

  

hàm số đồng biến trên



C đúng.

+ Xét khẳng định D: Ta có

1

0 0

ln12

y x

x



    

hàm số đồng biến trên

 

0;





D sai.

Câu 24. [2D2-5.2-2] Giải bất phương trình

   

2

2 2 8

2 3 2 3

x x x   

  

ta được bao nhiêu nghiệm

nguyên?

A.

4

. B.

5

. C.

6

. D. Vô số.

Lời giải

Chọn C

Ta có

   

2

2 2 8

2 3 2 3

x x x   

  

   

2

2 2 8

2 3 2 3

x x x  

   

2

2 2 8x x x    

2

3 6 0

x x

   

3 33 3 33

2 2

x

 

  

.

Vì

x



nên

 

1,0,1,2,3, 4

x  

. Vậy có tất cả

6

nghiệm nguyên.

Câu 25. [2H1-2.3-2] Cho

 

H

là khối chóp tứ giác đều có tất cả các cạnh bằng

a

. Thể tích của

 

H

bằng.

A.

3

a

. B.

3

2

6

a

. C.

3

4

a

. D.

3

2

a

.

Lời giải

Chọn B

Giả sử tứ diện đều

.

S ABCD

.

Tính diện tích

ABCD

:

2

ABCD

S a

.

Xác định chiều cao:

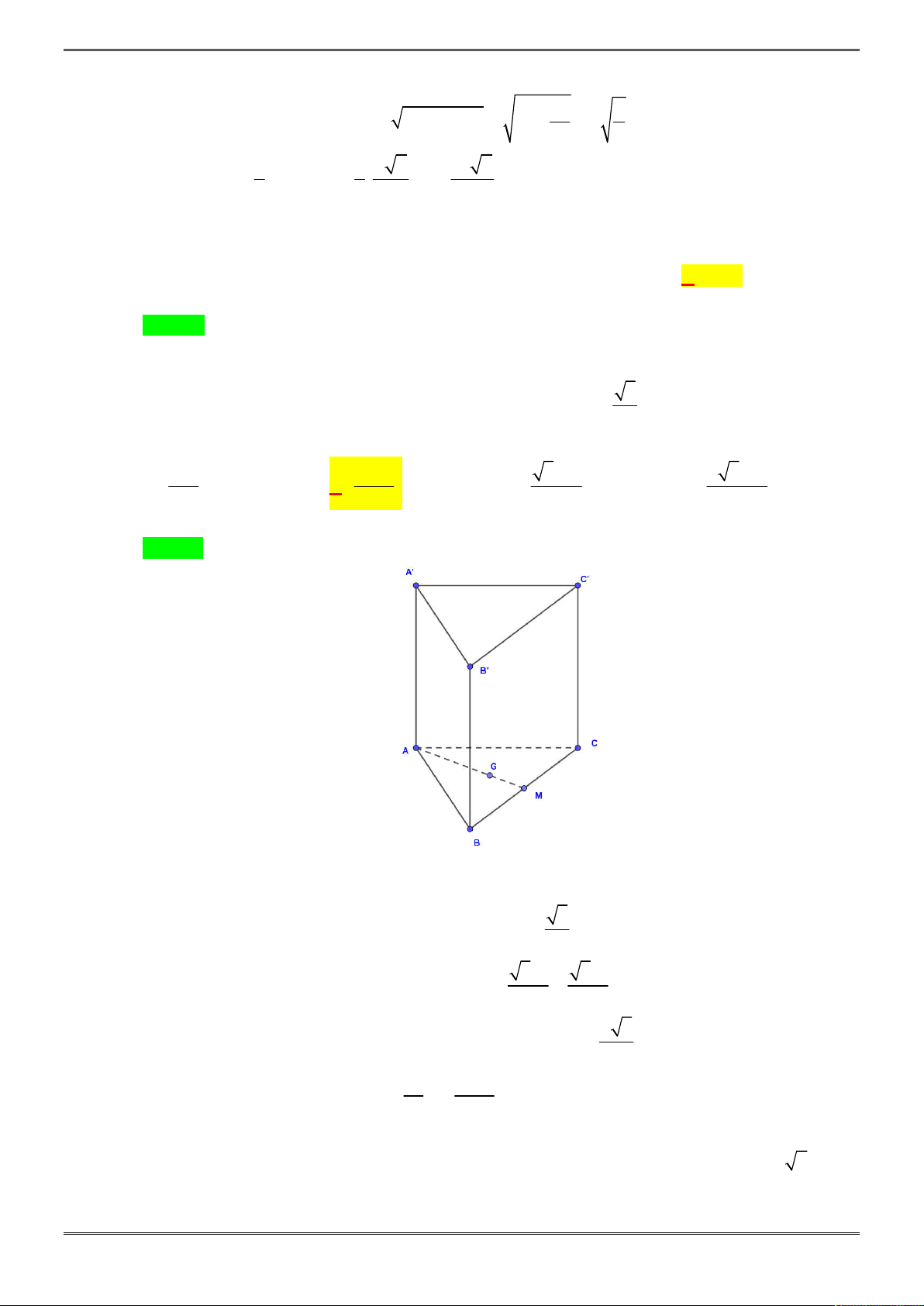
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 39

Gọi

D

O AC B SO  

là chiều cao của khối chóp.

SOA

vuông tại

O

cho ta

2

2 2 2

1

2 2

a

SO SA AO a a     .

Vậy,

3

2

.

1 1 2 2

. . .

3 3 2 6

S ABCD ABCD

a a

V S SO a  

.

Câu 26. [2H2-2.3-2] Một hình trụ có bán kính đáy bằng

2

và có chiều cao bằng

4

. Thể tích của hình

trụ bằng:

A.

8



. B.

24



. C.

32



. D.

16



.

Lời giải

Chọn D

2

.4.4 16

V R h

  

  

.

Câu 27. [2H2-2.5-2] Cho một khối lăng trụ tam giác đều có thể tích là

3

2

a

. Tính thể tích của khối trụ

ngoại tiếp lăng trụ đã cho.

A.

3

a



. B.

3

2

3

a



. C.

3

a



. D.

3

2 3

3

a



.

Lời giải

Chọn B

Giả sử khối lăng trụ tam giác đều là

.

ABC A B C

  

; gọi

G

là trọng tâm tam giác

ABC

.

Gọi

h

là chiều cao của khối lăng trụ và

x

là độ dài cạnh tam giác đáy.

Do đáy là tam giác đều cạnh

x

nên có diện tích :

2

3

4

S x



.

Thể tích của khối lăng trụ tam giác đều là:

2 3

3 3

2

4 2

x a

V h x h a

   

.

Bán kính đường tròn đáy của khối trụ ngoại tiếp là

3

x

r AG 

.

Thể tích khối trụ là :

2 3

2

3 3

T

x a

V r h h



 

   .

Câu 28. [2H2-1.2-2] Cho hình nón có thiết diện qua trục là tam giác vuông có cạnh huyền

2a

. Diện

tích xung quanh của hình nón là.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 40

A.

2

a



. B.

2

3

a



. C.

2

6

a



. D.

2

3

a



.

Lời giải

Chọn A

Gọi

l

,

h

,

R

lần lượt là độ dài đường sinh, đường cao và bán kính đáy của hình nón.

Thiết diện qua trục của hình nón là tam giác

SAB

vuông cân tại

S

có cạnh huyền

2AB a



.

Nên

2 2 2 2 2

2 2

SA SB AB SA a SA a l      

.

Ta có:

1 2

2 2

a

R AO AB  

.

Vậy diện tích xung quanh của hình nón:

2

2 2

.

2 2

a a

S Rl a



 

  

.

Câu 29. [2H1-3.5-2] Tính thể tích

V

của khối lập phương

.

ABCD A B C D

   

, biết tổng diện tích các mặt

của hình lập phương bằng

150

.

A.

25

V



. B.

75

V



. C.

125

V



. D.

100

V



.

Lời giải

Chọn C

Đặt cạnh lập phương là

a

.

Tổng diện tích các mặt lập phương là:

2

6S a



.

Theo bài ta có:

2

6 150 5

S a a

   

.

Vậy thể tích khối lập phương là :

3

125

V a 

.

Câu 30. [2H1-2.1-2] Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình chữ nhật,

2CD a

;

AD a

;

 

SA ABCD



và

3SA a

. Thể tích của khối chóp

.

S ABCD

bằng.

A.

3

a

. B.

3

2a

. C.

3

6a

. D.

3

4a

.

Lời giải

Chọn B

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 41

Diện tích hình chữ nhật

ABCD

là:

2

. 2

ABCD

S AD CD a

 

.

 

SA ABCD SA

 

là đường cao của chóp

.

S ABCD

.

Thể tích khối chóp

.

S ABCD

là:

2 3

.

1 1

. . .3 .2 2

3 3

S ABCD ABCD

V SA S a a a

  

.

Câu 31. [2D1-2.13-3] Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

 

3 2

2 3 1 6y x m x mx

   

có hai điểm cực trị

A

và

B

, sao cho đường thẳng

AB

vuông góc với đường thẳng

2

y x

 

.

A.

0

m



và

2

m



. B.

0

m



,

1

m

 

và

2

m

 

.

C.

0

m



và

1

m

 

. D.

0

m



,

1

m



và

2

m



.

Lời giải

Chọn A

Ta có

 

2

6 6 1 6y x m x m



   

.

 

2

0 6 6 1 6 0

y x m x m



     

1

x

x m













.

Hàm số có hai điểm cực trị

1

m

 

.

Khi đó hai điểm cực trị là

 

1;3 1

A m



,

 

3 2

; 3

B m m m

 

 

3 2

1; 3 3 1

AB m m m m

      



.

Vectơ chỉ phương của đường thẳng

2

y x

 

là

 

1;1

d

u 



.

Đường thẳng

AB

vuông góc với đường thẳng

2

y x

 

. 0

d

AB u

 

 

3 2

1 3 3 1 0

m m m m

      

3 2

3 2 0

m m m

   

  

1 2 0

m m m

   

 

0

2

1

m tm

m l





 







.

Vậy

0

m



hoặc

2

m



.

Câu 32. [2D2-6.2-3] Phương trình

   

2 3

4 8

2

log 1 2 log 4 log 4

x x x

     

có hai nghiệm

1 2

,x x

,

khi đó

1 2

x x

bằng bao nhiêu?

A.

8 2 6

 . B.

8

. C.

2 6

. D.

4 6

.

Lời giải

Chọn C

Điều kiện:

   

1 0

4 0 4;4 \ 1

4 0

x

x x

x

 





     





 



.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 42

Khi đó,

     

2 1 2

2

1

2 3

2

2 2

2

log 1 2 log 4 log 4

PT x x x

      

   

2 2 2 2

log 1 log 4 log 4 log 4

x x x

      

 

2

2 2

log 4 1 log 16

x x

   

 

2

4 1 16 *

x x   

* TH1:

1 0 1 4

x x

     

: Ta có

 

2

* 4 4 16

x x   

2

4 12 0

x x

   

 

2

6

x tm

x l







 





1

2

x

 

.

* TH2:

1 0 4 1

x x

      

:

 

2

* 4 4 16

x x    

2

4 20 0

x x

   

 

2 2 6

x l

x tm



 







 



2

2 2 6

x  

.

Vậy

1 2

2 6

x x  .

Câu 33. [2D1-1.8-3] Tìm các giá trị của tham số

m

để hàm số

tan

tan 1

x m

y

m x







nghịch biến trên khoảng

0;

4



 

 

 

.

A.

 

1;



. B.

   

; 1 1;

   

. C.





 

;0 1;

  

. D.





0;



.

Lời giải

Chọn A

Ta có

 

2

tan 1

cos tan 1

x m m

y

m x

x m x



 

 



 

 



 



.

Hàm số nghịch biến trên khoảng

0;

4



 

 

 

khi

0

y





,

0;

4

x



 

 

 

 

2

1

1 0

1

m

 



   







.

Đồng thời

tan 1 0, 0;

4

m x x



 

   

 

 

1

, 0;

tan 4

m x

x



 

    

 

 

.

Ta có

 

0; tan 0;1

4

x x



 

  

 

 

 

1

; 1

tan x

    

 

; 1

m

   

Vậy

 

1;m

 

.

Câu 34. [2H1-3.4-3] Cho lăng trụ

.

ABC A B C

  

có thể tích

V

và một điểm

M

di động trong tam giác

A B C

  

. Khi đó thể tích khối chóp

.

M ABC

tính theo

V

bằng.

A.

V

. B.

3

V

. C.

6

V

. D.

2

V

.

Lời giải

Chọn B

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 43

Gọi

h

là chiều cao của lăng trụ,

ABC

S S

 . Khi đó chóp

.

M ABC

có chiều cao là

h

.

Thể tích lăng trụ

.V h S

.

Thể tích tứ diện

.

M ABC

là

.

1

.

3 3

M ABC

V

V h S

 

.

Câu 35. [2H1-2.1-3] Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình vuông cạnh

a

, hai mặt bên

 

SAB

và

 

SAD

cùng vuông góc với mặt phẳng đáy. Biết góc giữa

 

SCD

và

 

ABCD

bằng

o

45

. Gọi

H

và

K

lần lượt là trung điểm của

SC

và

SD

. Thể tích của khối chóp

.

S AHK

là.

A.

3

24

a

. B.

3

12

a

. C.

3

6

a

. D.

3

a

.

Lời giải

Chọn A

Ta có:

 

SAB

và

 

SAD

cùng vuông góc với mặt phẳng đáy

 

ABCD

 

SA ABCD

 

   

 



0

, 45

SCD ABCD SDA SA AD a     

.

2 3

.

1 1

.S .

3 3 2 6

S ACD SCD

a a

V SA a



   .

3

.

. .

.

1 1

.

4 4 24

S AHK

S AHK S ACD

S ACD

V

SH SK a

V V

V SC SD

     .

Câu 36. [2D2-7.1-4] Cho hàm số

 

4

4 2

x

f x 



. Tính tổng

1 2 3 2013 2014

...

2015 2015 2015 2015 2015

S f f f f f

         

     

         

         

A.

2014

S



. B.

2015

S



. C.

1008

S



. D.

1007

S



.

Lời giải

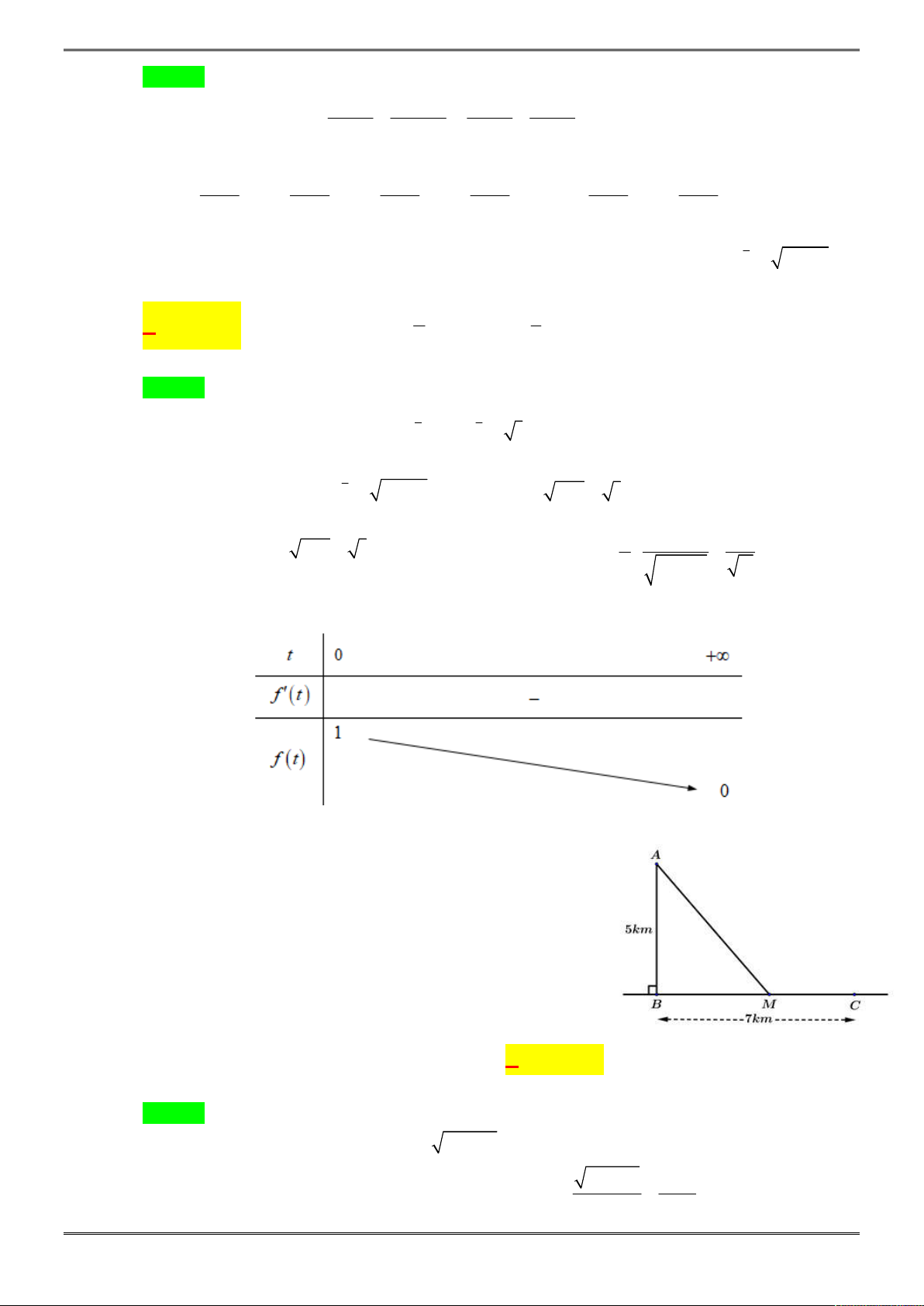
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 44

Chọn D

Ta có

   

1

4 4

1

4 2 4 2

x x

f x f x



   

 

4 2

1

4 2 4 2

x

x x

  

 

.

Suy ra

1 2014 2 2013 1007 1008

... 1007

2015 2015 2015 2015 2015 2015

S f f f f f f

           

       

           

           

.

Câu 37. [2D2-5.7-4] Tìm tất cả các giá trị thực của tham số

m

để phương trình

2

4

2

1

x

m e e

  

có

nghiệm thực.

A.

0 1

m

 

. B.

2

0 m

e

 

. C.

1

m

e

 

. D.

1 0

m

  

.

Lời giải

Chọn A

Đặt

2x

t e



,

0t 

. Ta có

4

2

x

t e e

 

 

 

 

4

2

x

e t 

.

Khi đó phương trình

2

4

2

1

x

m e e

  

trở thành

 

4 4

1 *

m t t  

Xét hàm số

 

4 4

1

f t t t  

trên khoảng

 

0;



, có

 

3 3

4

1 1 1

0; 0

4

1

f t t

t

 

 



    

 



 

.

Suy ra

 

f t

là hàm số nghịch biến trên

 

0;



, kết hợp với

 

lim 0

t

f t





,

 

0

lim 1

t

f t







.

Vậy phương trình (*) có nghiệm khi và chỉ khi

0 1

m

 

.

Câu 38. [2D1-3.14-4] Một ngọn hải đăng đặt ở vị trí

A

cách bờ biển

một khoảng

 

5 km

AB 

. Trên bờ biển có một cái kho ở vị

trí

C

cách

B

một khoảng là

 

7 km

. Người canh hải đăng

có thể chèo đò từ

A

đến vị trí

M

trên bờ biển với vận tốc

 

4 km/h

rồi đi bộ đến

C

với vận tốc

 

6 km/h

Vị trí của

điểm

M

cách

B

một khoảng gần nhất với giá trị nào sau

đây để người đó đến kho nhanh nhất?

A.

 

3,0 km

. B.

 

3,0 km

. C.

 

4,5 km

. D.

 

2,1 km

.

Lời giải

Chọn C

Đặt

, 0 7

x BM x

  

. Khi đó

2

25

AM x

 

,

7

MC x 

.

Thời gian người canh hải đăng đi từ

A

đến

C

là

 

2

25 7

4 6

x x

F x

 

 

(giờ)

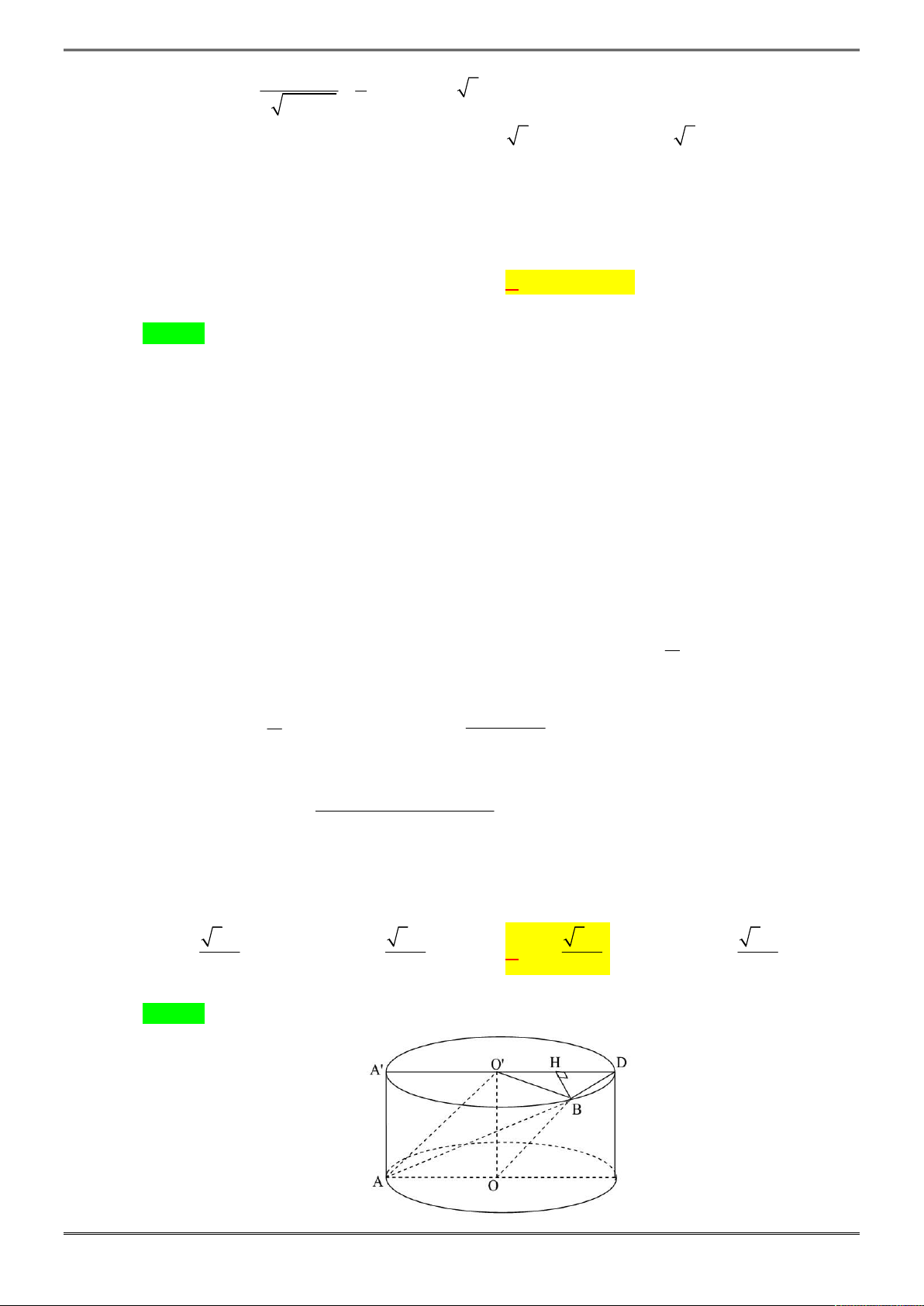
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 45

Ta có:

 

2

1

0 5

6

4 25

x

F x

x

 



  



(km)

Hàm số

 

F x

đạt giá trị nhỏ nhất tại điểm

2 5

x  do đó

2 5 4,5

BM x  

(km).

Câu 39. [2D2-4.8-4] Một anh sinh viên được gia định gởi vào số tiết kiệm ngân hàng số tiền là

8000000

đồng với lãi suất

0,9% /

tháng. Nếu mỗi tháng anh sinh viên đó rút ra một số tiền

như nhau vào ngày ngân hàng trã lãi thì hàng tháng anh ta rút ra bao nhiêu tiền (làm tròn đến

1000

đồng) để sau đúng

5

năm sẻ vừa hết số tiền cả vốn lẫn lãi?

A.

180000

đồng. B.

171000

đồng. C.

173000

đồng. D.

175000

đồng.

Lời giải

Chọn C

Gọi

N

là số tiền gốc gửi vào sổ tiết kiệm, lãi suất là

r

,

A

là số tiền hàng tháng mà anh ta rút

ra. Ta có:

Sau tháng thứ

1

số tiền trong sổ còn lại là:

 

1

N Nr A N r A    

.

Sau tháng thứ

2

số tiền trong sổ còn lại là:

   

1 1

N r A N r A r A     

   

   

   

2

1 1 1

N r A r

     

 

.

Sau tháng thứ

3

số tiền trong sổ còn lại là:

       

 

2 2

1 1 1 1 1 1

N r A r N r A r r A         

   

   

     

3 2

1 1 1 1

N r A r r

 

      

 

.

…………………………………………………………………

Sau tháng thứ

n

số tiền trong sổ còn lại là:

       

1 2

1 1 1 ... 1 1

n n n

n

T N r A r r r

 

 

         

 

   

1 1 1

n n

A

N r r

r

 

    

 

.

Nếu sau tháng thứ

n

số tiền trong sổ anh ta vừa hết thì

   

1 1 1 0

n n

n

A

T N r r

r

 

     

 

 

1

1 1

n

Nr r

A

r



 

 

.

Vậy sau đúng

5

năm hay

60

tháng, anh ta rút hết số tiền trong sổ tiết kiệm thì số tiền hàng

tháng anh ta rút là

60

8000000.0,009.1,009

173000

1,009 1

A  



(đồng).

Câu 40. [2H2-2.3-4] Cho hình trụ có các đáy là

2

hình tròn tâm

O

và

O



, bán kính đáy bằng chiều cao

và bằng

a

. Trên đường tròn đáy tâm

O

lấy điểm

A

, trên đường tròn đáy tâm

O



lấy điểm

B

sao cho

2AB a

. Thể tích khối tứ diện

OO AB



theo

a

là

A.

3

8

a

V 

. B.

3

6

a

V 

. C.

3

12

a

V 

. D.

3

4

a

V 

.

Lời giải

Chọn C

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 46

Kẻ đường sinh

AA



. Gọi

D

là điểm đối xứng với

A



qua

O



và

H

là hình chiếu của

B

trên

đường thẳng

A D



.

Do

BH A D





,

 

BH AA BH AOO A

  

  

.

2 2 2 2

3

A B AB A A a BD A D A B a

   

      

.

O BD





đều nên

3

2

a

BH 

.

2

AOO

a

S





 . Suy ra thể tích khối tứ diện

OO AB



là:

3

12

a

V 

.

PHẦN II : PHẦN TỰ LUẬN

Câu 1. [2D1-2.9-3] Tìm

m

để hàm số

   

3 2

1

2 4 2 6

3

y x m x m x m

      

có cực đại và cực tiểu

với hoành độ

1 2

,x x

thỏa mãn

2 2

1 2

30

x x

 

.

Lời giải

Ta có

 

2

2 2 4

y x m x m



    

.

Hàm số có hai điểm cực trị

1 2

,x x



phương trình

 

2

2 2 4 0

x m x m

    

có hai nghiệm

phân biệt

2

5 0

m m



    

0

5

m













.

Ta có

 

1 2

2 2

x x m

  

,

1 2

. 4

x x m

 

.

2 2

1 2

30

x x

 

 

2

1 2 1 2

2 . 30

x x x x

   

   

2

4 2 2 4 30

m m

    

2

2 9 11 0

m m

   

 

1 tm

11

tm

2

m

 













.

Vậy

1

m

 

hoặc

11

2

m



thỏa yêu cầu đề bài.

Câu 2. [2H2-4.2-4] Một nóc nhà cao tầng có dạng một hình nón. Người

ta muốn xây một bể có dạng hình trụ nội tiếp trong hình nón để

chứa nước (như hình vẽ minh họa). Cho biết

SO h

;

OB R

và

OH x

,

 

0

x h 

. Tìm

x

để hình trụ tạo ra có thể tích lớn

nhất.

Lời giải

x

H

S

O

B

C

A

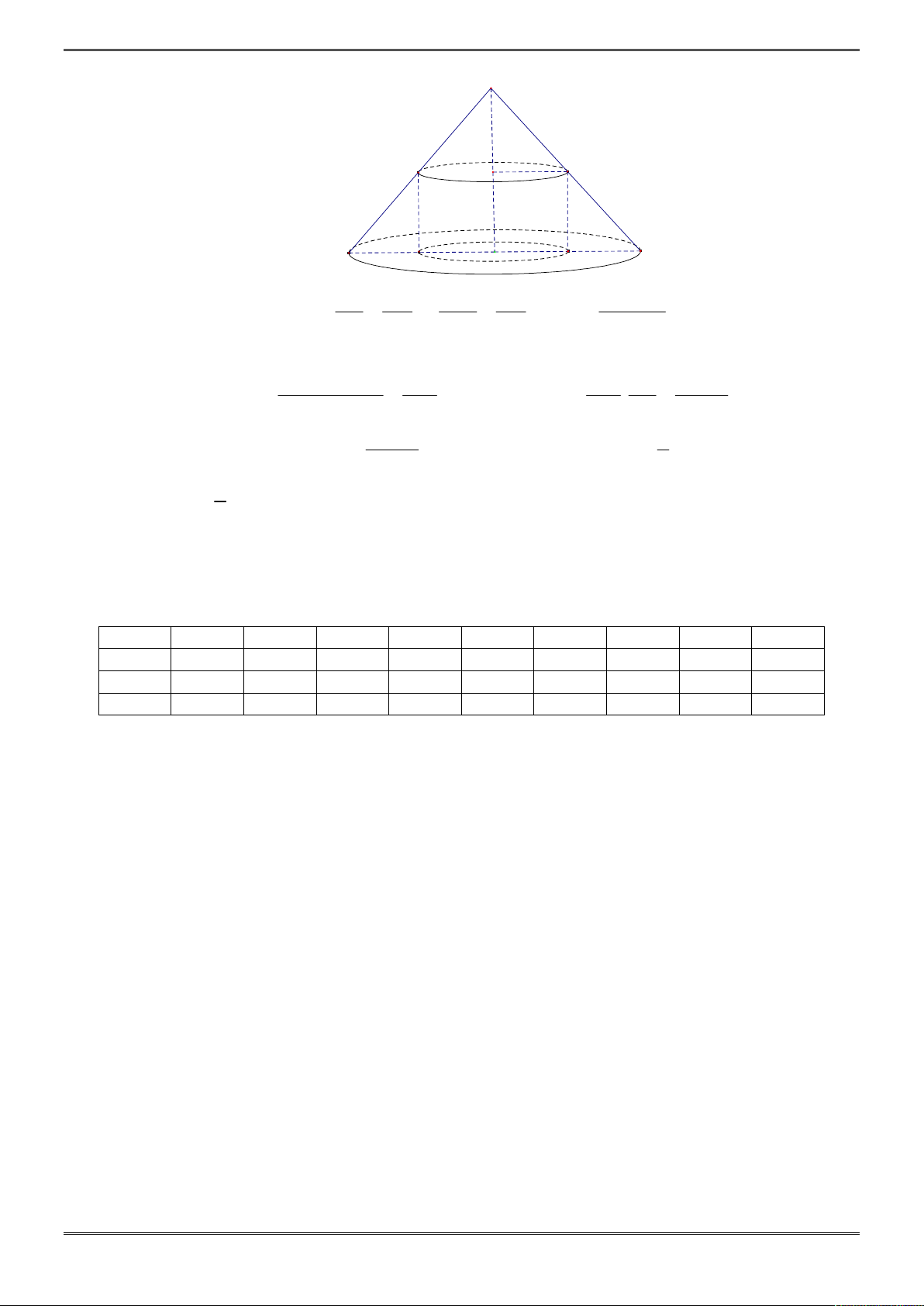
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 47

x

H

S

O

B

C

A

Ta có

SHC SOB ∽

nên

 

R h x

SH HC h x HC

HC

SO OB h R h



     .

Suy ra thể tích khối trụ là:

 

  

2

2 2 3 2

2

2 2 2

8 4

. . . 2 .

2 2 27 27

h x R x

R R h hR

V HC OH h x h x x

h h h



  





       .

Do đó khối trụ lớn nhất bằng

2

4

27

hR



đạt được khi

2

3

h

h x x x

   

.

Vậy,

3

h

x



thì khối trụ có thể tích lớn nhất.

BẢNG ĐÁP ÁN

1.B

2.D

3.B

4.C

5.B

6.A

7.C

8.C

9.A

10.D

11.D

12.B

13.B

14.B

15.D

16.A

17.C

18.B

19.D

20.C

21.D

22.C

23.C

24.C

25.B

26.D

27.B

28.A

29.C

30.B

31.A

32.C

33.A

34.B

35.A

36.D

37.A

38.C

39.C

40.C

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 48

ĐỀ ÔN TẬP SỐ 09

PHẦN I: PHẦN TRẮC NGHIỆM

Câu 1. [2D1-1.5-1] Hàm số nào trong các hàm số sau đồng biến trên



?

A.

3 2

2 10y x x x

   . B.

4 2

7 3y x x

  . C.

4 1

2

x

y

x







. D.

tany x

.

Lời giải

Chọn A.

Vì

2

' 3 4 10 0,y x x x

     

. Nên hàm số luôn đồng biến trên



.

Câu 2. [2H1-3.5-1] Cho khối lập phương có độ dài đường chéo bằng

2 3m.

Tìm thể tích

V

của khối

lập phương đó.

A.

3

24 3m

. B.

3

12m

. C.

3

8m

. D.

3

27m

.

Lời giải

Chọn C.

Gọi độ dài cạnh của khối lập phương là

a

. Khi đó độ dài đường chéo khối lập phương là

3a

.Yêu cầu bài toán

3 3

3 2 3 2 8( )a a V a m

     

.

Câu 3. [2D2-4.0-1] Tìm mệnh đề đúng trong các mệnh đề sau:

A. Hàm số

log

a

y x

 với

1

a



là hàm số nghịch biến trên khoảng

 

0;



.

B. Hàm số

 

log 0 1

a

y x a

  

có tập xác định là



.

C. Hàm số

log

a

y x

 với

0 1a 

là hàm số đồng biến trên khoảng

 

0;



.

D. Đồ thị các hàm số

log

a

y x

 và

 

1

log 0 1

a

y x a

  

đối xứng nhau qua trục hoành.

Lời giải

Chọn D.

A sai vì với

1

a



hàm số đồng biến trên

 

0;



.

B sai vì tập xác định của hàm số là

 

0;



.

C sai vì với

0 1a 

hàm số nghịch biến trên

 

0;



.

D đúng nên ta chọn. D.

Câu 4. [2D1-1.2-1] Cho hàm số

 

y f x



có bảng biến thiên như sau. Chọn phát biểu sai?

A. Hàm số đạt cực đại tại

0

x



. B. Hàm số đạt cực đại tại

3

x

 

.

C. Hàm số đạt cực tiểu tại

4

x

 

. D. Hàm số đạt cực đại tại

4

x

 

.

Lời giải

Chọn A.

x

–∞

1

0

1

+∞

y



– 0 + 0 – 0 +

y

+∞

4

3

4

+∞

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 49

Câu 5. [2D1-4.4-1] Cho hàm số

2 3

3 6

x

y

x







có đồ thị

( ).C

Khẳng định nào là sai?

A.

( )C

có tiệm cận đứng

2.

x

 

. B.

( )C

đi qua điểm

1

1; .

9

A

 

 

 

.

C.

( )C

có tâm đối xứng

2

2; .

3

I

 



 

 

. D.

( )C

có tiệm cận ngang

2

.

3

y



Lời giải

Chọn B.

Ta có

x x

x 2 x 2

2 2

lim y , lim

3 3

lim y , lim y

 

 

 



 









   



phương trình đường tiệm cận đứng và tiệm cận ngang đồ

thị

 

C

lần lượt là

2 2

x 2,y I 2;

3 3

 

    

 

 

là tâm đối xứng của

 

C



A, C, D đúng.

Câu 6. [2D2-4.1-1] Hàm số

 

2

y ln 5 6

x x

   

có tập xác định là

A.

 

2;3 .

D 

. B.

 

0; .

D

 

. C.

 

;0 .

D  

. D.

   

;2 3; .

D

   

Lời giải

Chọn A.

Hàm số logarit xác định khi

2

5 6 0

x x

    

2 3

x

 

.

Câu 7. [2D2-3.2-1] Cho

, ,a b c

là các số thực dương tùy ý và

1.

a



Trong các mệnh đề sau, mệnh đề

nào sai?

A.

 

log . log .log

a a a

b c b c



. B.

log log log

a a a

b

b c

c

 

 

 

 

.

C.

log log

a a

b b





. D.

log

b

a

b

a



.

Lời giải

Chọn A.

Câu 8. [2H1-2.1-1] Cho hình chóp

.

S ABCD

, có đáy là hình chữ nhật có

, 2AB a AD a 

. Cạnh bên

SA

vuông góc với đáy và

SA a

. Thể tích khối chóp là

A.

3

2

3

a

. B.

3

a

. C.

3

2 3

3

a

. D.

3

a

.

Lời giải

Chọn A.

2a

a

C

A

D

B

S

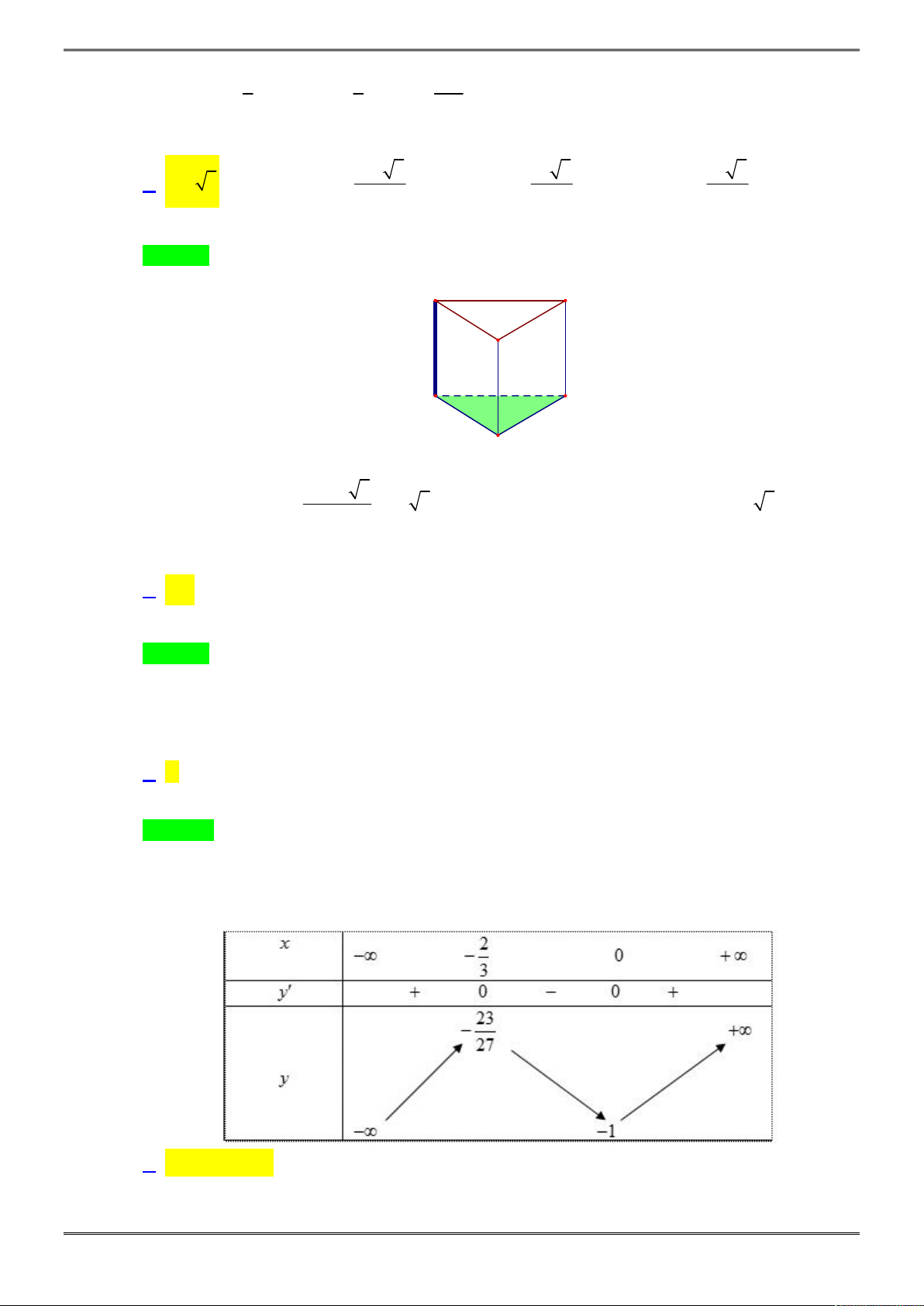
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 50

Thể tích

3

1 1 2

. . . .2 .

3 3 3

a

V AB AD SA a a a   .

Câu 9. [2H1-3.2-1] Thể tích khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng

2a

là

A.

3

2 3

a . B.

3

2 3

3

a

. C.

3

4

a

. D.

3

a

.

Lời giải

Chọn A.

2a

B

C

A'

C'

A

B'

Diện tích đáy

 

2

2 3

3

4

ABC

a

S a 

. Thể tích khối lăng trụ

3

. 2 3

ABC

V S AA a



 

.

Câu 10. [2D2-6.1-1] Tập nghiệm của phương trình

 

2

log 1 3

x

 

là

A.

 

7

. B.

 

2

. C.

 

9

. D.

 

8

.

Lời giải

Chọn A.

PT 

3

1 2

x

 



7

x



.

Câu 11. [2D1-6.1-2] Đồ thị hàm số

3 2

3 4

y x x

  

và đồ thị hàm số

2 1y x 

có tất cả bao nhiêu

điểm chung?

A.

3

. B.

1

. C.

2

. D.

0

.

Lời giải

Chọn A.

Phương trình hoành độ giao điểm

3 2

3 4 2 1x x x   

có 3 nghiệm phân biệt, nên hai đồ thị có

3 điểm chung.

Câu 12. [2D1-1.2-2] Bảng biến thiên sau là của hàm số nào trong bốn hàm số được liệt kê dưới đây?

A.

3 2

1

y x x

  

. B.

3 2

1

y x x

   

. C.

3 2

1

y x x

  

. D.

3 2

1

y x x

  

.

Lời giải

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 51

Chọn A.

Các đáp án đều là hàm số bậc 3 có dạng chung

3 2

y ax bx cx d   

Từ chiều biến thiên ta có

0

a



,

y



có 2 nghiệm phân biệt, thay

2

3

x

 

suy ra

2

0

3

y

 



 

 

 

và

2 23

3 27

y

 

  

 

 

; thay

0

x



suy ra

 

0 0

y





và

 

0 1

y

 

.

Câu 13. [2D2-6.3-2] Tìm tập nghiệm

S

của bất phương trình

 

2 2

2

log 2 2log 4 8 0

x x

  

.

A.

1

;2

4

S

 



 

 

. B.





;2

S  

. C.

 

2;2

S  

. D.





0;2

S 

.

Lời giải

Chọn A.

BPT 

   

2

2 2

4log 2 4log 2 8 0

x x

   

 

2

1 log 2 2

x

   

1 2

2 2 2x



  

1

2

4

x

 

.

Câu 14. [2D2-1.2-2] Cho biểu thức

3

2 4

5

P x x x x



với

0.

x



Biểu thức được đưa về lũy thừa với

số mũ hữu tỷ là

A.

59

60

P x

 . B.

57

60

P x

 . C.

61

60

P x

 . D.

60

59

P x

 .

Lời giải

Chọn A.

1 2 1

1

3 15 60

2

P x x x x

 =

59

60

x

.

Câu 15. [2D1-2.4-2] Cho hàm số

4 2

3 1

y x x

   

. Số điểm cực trị của hàm số là

A.

3

. B.

2

. C.

1

. D.

4

.

Lời giải

Chọn A.

D  

,

3

4 6y x x



 

,

6

2

0 0

6

2

x

y x

x



 





  









,

BBT:

6 0 6

0 0 0

x

y

CT

C

y

Đ

CT

  



   

 

   

Vậy hàm số có 3 điểm cực trị.

Câu 16. [2D2-3.3-2] Nếu

15

log 3

a thì

A.

25

3

log 15

5(1 )



 a

. B.

25

5

log 15

3(1 )



 a

. C.

25

1

log 15

2(1 )



 a

. D.

25

1

log 15

5(1 )



 a

.

Lời giải

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 52

Chọn C.

Ta có

 

15 3 3 3

1 1 1

log 3 log 15 log 5.3 log 5



      

a

a a a

Mặt khác ta có

 

3 3

25

3 3

log 15 1 log 5 1

log 15

log 25 2 log 5 2 1



  

 a

.

Câu 17. [2D2-4.2-2] Đạo hàm của hàm số







x x

e e

y

e e

bằng

A.

 

2

4





x x

e e

. B.





x x

e e

. C.

 

2 2

2





x x

e e

. D.

 

2

5





x x

e e

.

Lời giải

Chọn A.

   

2 2

4

x x x x

x x

x x x x

e e e e

e e

y y

e e

e e e e

 



 

  





   



 

.

Câu 18. [2D2-6.1-2] Bất phương trình

 

2

log 3 1 3 

x

có nghiệm là

A.

10

3

x

. B.

1

3

 

x

. C.

3

x

. D.

3

x

.

Lời giải

Chọn D.

Điều kiện:

x



1

3

 

2

log 3 1 3 3 1 8 3      

x x x

.

Câu 19. [2D2-5.3-2] Nghiệm của bất phương trình

32.4 18.2 1 0  

x x

là

A.

4 1   

x

. B.

1 1

16 2

 

x

. C.

2 4 

x

. D.

1 4 

x

.

Lời giải

Chọn A.

Ta có

1 1

32.4 18.2 1 0 2 4 1

16 2

          

x x x

x

.

Câu 20. [2D2-5.3-2] Số nghiệm của phương trình

2 2

2 2 15

x x 

 

là:

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Chọn C.

2 2 2

2 4

2 2 15 4.2 15.2 4 0 2

1

2

4

x

x x x x

x

 







        



 





.

Câu 21. [2D2-6.3-2] Số nghiệm của phương trình

 

2

log 4 3log 7 0

x x

  

là:

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 53

Chọn C.

TXĐ:

 

0;D

 

   

2 2

2

2 2 2 2 2

2

log 4 3log 7 0 log 2 6log 7 0 log 2log 3 0

x x x x x x

           

2

8

log 3

1

log 1

2

x











 



 





.

Câu 22. [2D2-4.3-2] Giá trị nhỏ nhất, giá trị lớn nhất của hàm số

lny x x 

trên

1

;

2

e

 

 

 

theo thứ tự

là:

A.

1

và

1

ln 2

2



. B.

1

2

và

e

. C.

1

ln 2

2



và

1e 

. D.

1

và

1e 

.

Lời giải

Chọn D.

1

1 0 1y x

x



    

.

   

1 1

ln 2 ; 1 1; 1

2 2

y y y e e

 

    

 

 

.

Câu 23. [2D1-2.2-2] Đồ thị hàm số nào sau đây không có cực trị?

A.

3 2

y x x 

. B.

3 2

y x x  

. C.

3

y x x  

. D.

3 2

1

y x x

  

.

Lời giải

Chọn C.

3 2

y x x 

có

2

3 2y x x



 

,

2

0

3

0

x

y

x









 







y





đổi dấu



Hàm số có cực trị.

3 2

y x x  

có

2

3 2y x x



  

,

0

2

3

x

y

x









 







y





đổi dấu



Hàm số có cực trị.

3

y x x  

có

2

3 1

y x



  

,

0

y





vô nghiệm. Vậy hàm số không có cực trị.

3 2

1

y x x

  

có

2

3 2y x x



 

,

0

2

3

x

y

x









 



 



y





đổi dấu



Hàm số có cực trị.

Câu 24. [2D1-7.1-2] Cho hàm số

3 2

3 1

y x x

   

, có đồ thị là

 

C

. Phương trình tiếp tuyến của đồ thị

hàm số

 

C

tại điểm

 

3;1

A

.

A.

20 9y x 

. B.

9 28 0

x y

  

. C.

9 20

y x

 

. D.

9 28 0

x y

  

.

Lời giải

Chọn B.

Ta có

2

3 6y x x



  

 

3 9

k y



   

. Phương trình tiếp tuyến

 

9 3 1 9 28 0

y x x y

       

.

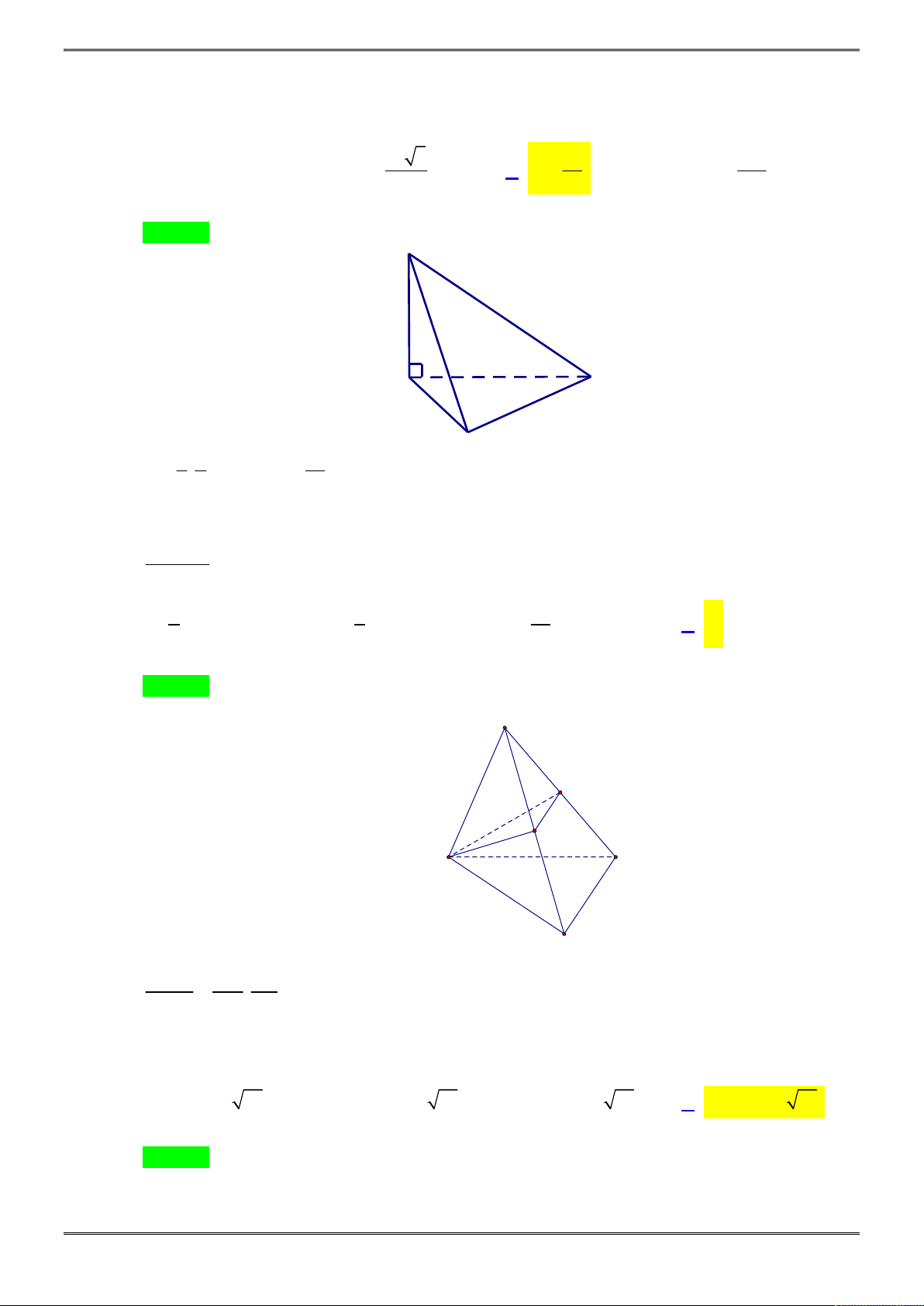
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 54

Câu 25. [2H1-2.1-2] Cho hình chóp

.

S ABC

có đáy

ABC

là tam giác vuông tại

B

và

BA BC a 

.

Cạnh bên

2SA a

và vuông góc với mặt phẳng đáy. Tính theo

a

thể tích

V

khối chóp

.

S ABC

.

A.

3

V a

. B.

3

2

a

V 

. C.

3

a

V  . D.

3

2

3

a

V  .

Lời giải

Chọn C.

3

1 1

. . .

3 2 3

a

V AB BC SA  .

Câu 26. [2H1-2.5-2] Cho hình chóp

SABC

. Gọi

;M N

lần lượt là trung điểm

; SB SC

. Khi đó

V

SABC

V

SAMN

là bao nhiêu?

A.

1

4

. B.

1

8

. C.

1

16

. D.

4

.

Lời giải

Chọn D.

M

N

S

A

C

B

.

. 4

S ABC

S AMN

V

SB SC

V SM SN

 

.

Câu 27. [2H2-1.2-2] Một hình nón có đường cao

20cm

h



, bán kính đáy

25cm

r



. Tính diện tích

xung quanh của hình nón đó.

A.

5 41

xq

S





. B.

25 41

xq

S





. C.

50 41

xq

S





. D.

125 41

xq

S





.

Lời giải

Chọn D.

S

A

B

C

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 55

2 2

5 41 125 41

xq

l h r S rl

 

     

.

Câu 28. [2H2-2.1-2] Một hình trụ có diện tích đáy bằng

 

2

4

m



. Khoảng cách giữa trục và đường

sinh của mặt xung quanh hình trụ đó bằng

A.

2m

. B.

3m

. C.

4m

. D.

1m

.

Lời giải

Chọn A.

l

r

=

2 m

O

O'

Khoảng cách giữa trục và đường sinh bằng bán kính đường tròn đáy

GT: diện tích đáy bằng

 

2

4

m





2

4

r

 





 

2

r m

 .

Câu 29. [2H2-1.3-2] Thể tích

V

của khối nón có đường sinh bằng

10

và bán kính đáy bằng

6

là

A.

96

V





. B.

360

V





. C.

288

V





. D.

60

V





.

Lời giải

Chọn A.

r=6

l=10

h

I

B

A

O

Chiều cao

2 2

h l r  

2 2

10 6 8 

Thể tích khối nón

1

.

3

đ

V S h 

2

1

. 96

3

r h

 



.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 56

Câu 30. [2H1-2.3-2] Cho hình chóp tam giác đều

.

S ABC

có cạnh đáy bằng

a

và cạnh bên bằng

21

6

a

. Tính theo

a

thể tích

V

của khối chóp

.

S ABC

.

A.

3

8

a

V 

. B.

3

12

a

V 

. C.

3

24

a

V 

. D.

3

6

a

V 

.

Lời giải

Chọn C.

Gọi

G

là trọng tâm

ABC



2 2

3

3 2

a a

AG SG SA AG

    

2 3

1 3 3

. .

3 4 2 24

a a a

V  

.

Câu 31. [2D1-1.5-3] Tìm tất cả các giá trị m để hàm số

3 2

3 4 4

y x mx mx

   

luôn tăng trên



.

A.

4

0

3

m

 

. B.

4

0

3

m

  

. C.

3

0

4

m

 

. D.

3

0

4

m

  

.

Lời giải

Chọn B.

Yêu cầu bài toán

   

2

1 0

0

4

0

3

3 3. 4 0

y

a

m

m m













     

 



 

  





.

Câu 32. [2D1-3.4-3] Giá trị nhỏ nhất của hàm số

 

2

1

x m m

f x

x

 





trên đoạn

 

0;1

bằng

2

khi

m

là:

A.

2

m

 

và

1

m



. B.

1

m



. C.

2

m

 

và

1

m

 

. D.

2

m

 

Lời giải

Chọn A.

 

 

   

2

2 2

2

0;1

1

0 Min 0 2 2 0

1

m m

y m f x f m m m m

x

 



              





2; 1

m m

   

.

Câu 33. [2D2-4.2-3] Cho hàm số

 

ln 2 1

y x

 

. Tìm

m

để

 

2 1

y e m



 

.

A.

1 2

4 2

e

m

e







. B.

1 2

4 2

e

m

e







. C.

1 2

4 2

e

m

e







. D.

1 2

4 2

e

m

e







.

Lời giải

Chọn C.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 57

2

2 1

y

x







 

2 2 2 1 1 2

2 1 2 1 2 1

2 1 2 1 2 1 4 2

e e

y e m m m m

e e e e

  



          

   

.

Câu 34. [2H1-2.2-3] Cho hình chóp

.

S ABC

có tam giác

SAB

đều cạnh

,a

tam giác

ABC

cân tại

C

.

Hình chiếu của

S

lên

 

ABC

là trung điểm của cạnh

AB

; góc hợp bởi cạnh

SC

và mặt đáy là

30

o

. Thể tích

V

của khối chóp

.

S ABC

tính theo

a

là

A.

3

4



a

V

. B.

3

2

8



a

V

. C.

3

2



a

V

. D.

3

8



a

V

.

Lời giải

Chọn D.

a

30



H

A

B

C

S

2

3

4



SAB

a

S

.

Gọi

H

là trung điểm

AB

.

( )

( vi ( ) )

`





 



  



CH AB

CH SAB

CH SH SH ABC CH

.

2 3

3

2

tan 30

tan 30 2

3

1 1 3 3 3

. . . .

3 3 4 2 8

o

SABC SAB

a

SH SH a

HC

a a a

V S HC

    

  

.

Câu 35. [2H1-2.3-3] Cho hình chóp tứ giác đều .

S ABCD

có cạnh đáy bằng

1

, cạnh bên hợp với mặt

đáy một góc

0

60

. Tính khoảng cách từ

O

đến mặt phẳng

 

SBC

.

A.

1

2

. B.

2

. C.

7

2

. D.

42

14

.

Lời giải

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 58

Chọn D.

 



0

; 60

SC ABCD SCO 

,

0

2 6

tan 60

2 2

OC SO OC   

Gọi

I

là trung điểm

,BC

kẻ

OH SI

tại

H

   

 

;

OH SBC d O SBC OH

   

2 2 2

1 1 1 42

14

OH

OH OI SO

   

.

Câu 36. [2H1-3.2-4] Cho lăng trụ tam giác đều

.

ABC A B C

  

có cạnh đáy bằng

2a

, khoảng cách từ

A

đến mặt phẳng

 

A BC



bằng

6

2

a

. Khi đó thể tích

V

của lăng trụ bằng

A.

3

V a

. B.

3



V a

. C.

3

4

3



V a

. D.

3

4 3

3



V a

.

Lời giải

Chọn B.

Gọi

I

là trung điểm

BC

.

H

là hình chiếu của

A

lên



A I

.

2a

I

C'

B'

A

B

C

A'

H

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 59

 

€

( ) ( ) theo giao tuye n

; ( )

( )

6

( ;( ))

2





    

   









 

 



 



  

AI BC

BC AA I A BC AA I A I

AA BC

AH A I AH AA I

AH A BC

a

d A A BC AH



A AI

vuông tại

A

:

 

2 2

2 2 2 2

2

3

1 1 1 1 1 1

3. 3

36

2

2 3

. . 3 3 .

4



      

 

 

 

 



  

ABC

AA a

AH AI AA AA

aa

a

V S AA a a

.

Câu 37. [2D2-6.9-4] Tìm

m

để bất phương trình

 

.9 2 1 6 .4 0

x x x

m m m

   

có nghiệm với mọi

 

0;1

x 

.

A.

6

m

 

. B.

6 4

m

   

. C.

4

m

 

. D.

6

m



.

Lời giải

Chọn D.

Ta có

       

 

0 1; 1 6 .9 2 1 .6 .4

x x x

f f m f x m m m       

Để bất phương trình có nghiệm trong đoạn

 

 

0;1

0;1 0 6 0 6

Max f x m m

      

Ta chọn đáp án D.

Câu 38. [2D1-6.4-4] Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

 

4 2

1

y x m x m   

cắt trục hoành tại 4 điểm phân biệt có tổng bình phương các hoành độ bằng 8.

A.

1 2 2

m   

. B.

1

m



. C.

3

m



. D.

3

m

 

.

Lời giải

Chọn C.

Phương trình hoành độ giao điểm:

 

4 2

1 0

x m x m

   

.

Số giao điểm của đồ thị hàm số và

Ox

là số nghiệm của phương trình trên.

Để đồ thị hàm số cắt

Ox

tại 4 điểm phân biệt có tổng bình phương các hoành độ bằng

8

 

2 2

1 0

t m t m t x

     

có 2 nghiệm dương phân biệt có tổng là

4

   

2 2

1 2

0

1 4 0 1 0

1

0

1 0 1

0 3

0

0 0

3

4

4 1 4

m m m

m

S

m m

P

m m

m

t t

S m

 

 



    





 





   

   

      

   



 

   





  

 

  



 

.

Câu 39. [2D1-6.9-4] Cho hàm số

 

3 2

3 1 3 1y x m x x    

có đồ thị

 

C

và đường thẳng

: 1d y x 

. Tìm các giá trị của tham số

m

để đường thẳng

d

cắt

 

C

tại ba điểm phân biệt

 

, 0;1

A B

và

C

sao cho

5 2

AC 

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 60

A.

0 2

m

 

. B.

0

m



hoặc

2

m

 

.

C.

2 0

m

  

. D.

2

m



hoặc

2

m

 

.

Lời giải

Chọn B.

Phương trình hoành độ giao điểm:

 

   

3 2

2

0

3 1 4 0

3 1 4 0 1

x

x m x x

x m x





    



   



Số giao điểm của 2 đồ thị hàm số là số nghiệm của phương trình trên.

Để

d

cắt

 

C

tại 3 điểm phân biệt



phương trình hoành độ giao điểm có 3 nghiệm phân biệt

 

1



có 2 nghiệm phân biệt khác

0

     

 

2

0

9 1 16 0

0 0 3 1 4

4 0

m

g g x x m x

 



  

 

   

 

    

 







.

Theo Viet, ta có:

 

3 1 ; 4

S m P

   

Giả sử

1 2

,x x

là hai nghiệm của (1). Ta có

     

   

2 2 2

2 2

1 2 1 2 1 2

2 2 4 2 9 18 25

AC x x y y x x S P m m           .

 

2 2

0

5 2 2 9 18 25 5 2 9 18 25 25 .

2

m

AC m m m m

m





         



 



.

Câu 40. [2D1-6.0-4] Đường thẳng

d

đi qua

 

1;3

I

và có hệ số góc

k

cắt trục hoành tại điểm

A

và

trục tung tại điểm

B

(hoành độ của điểm

A

và tung độ của điểm

B

là những số dương). Diện

tích tam giác

OAB

nhỏ nhất khi

k

bằng:

A.

1

. B.

2

. C.

3

. D.

4

.

Lời giải

Chọn C

 

: 1 3 3

d y k x y kx k

      

.

Vì

3 0

3

, 0 0

3

0

A B

k

x y k

k

 









    



 











.

 

2

1 1 1 3 6 9 9

. . 3 . 3

2 2 2 2 2 2

OAB A B

k k k k

S OA OB x y k

k k k

   

         .

 

2

1 9

0 9 3 3 0

2 2

OAB

S k k k do k

k



            

0

6 3

OAB

k

Min S k



   

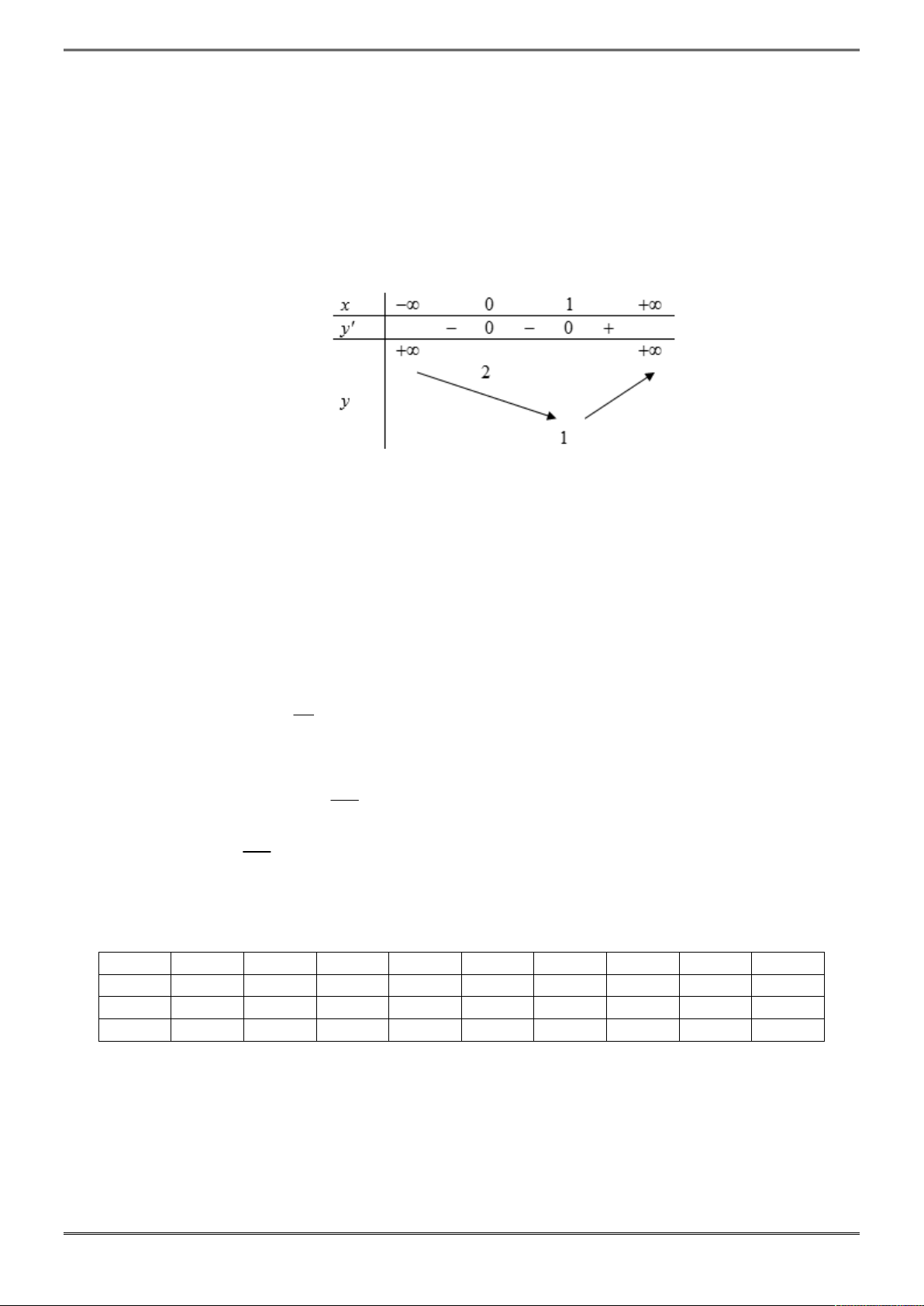
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 61

PHẦN II: PHẦN TỰ LUẬN

Câu 1. [2D2-5.7-3] Xác định m để phương trình

9 2.3 2

x x

m  

có hai nghiệm phân biệt ?

Lời giải

Đặt

3

x

t



, đk

0t 

. Nếu có một giá trị

0t 

tương ứng sẽ có một giá trị

x

PT đã cho trở thành

 

2

2 2 2 , 0

t t m t

   

Đặt

 

2

2 2f t t t  

,

 

2 2f t t



 

,

 

0 1f t t



  

BBT

PT (2) có 2 nghiệm phân biệt khi

1 2

m

 

.

Câu 2. [2H1-3.6-4] Nhân ngày phụ nữ Việt Nam 20/10 năm 2017, ông A quyết định mua tặng vợ một

món quà và đặt nó vào trong một chiếc hộp có thể tích là

 

32 đ

vtt

có đáy hình vuông và

không có nắp. Để món quà trở nên thật đặc biệt và xứng đáng với giá trị của nó ông quyết định

mạ vàng cho chiếc hộp, biết rằng độ dày lớp mạ tại mọi điểm trên hộp là như nhau. Gọi chiều

cao và cạnh đáy của chiếc hộp lần lượt là

;h x

. Giá trị của

;h x

bằng bao nhiêu để lượng vàng

trên hộp là nhỏ nhất

Lời giải

 

2

32

32 0

V hx h x

x

    

(Hình vẽ thầy)

Để lượng vàng trên hộp nhỏ nhất



 

xq day

f x S S

 

nhỏ nhất

 

2

4

f x xh x  

nhỏ nhất

Ta có

 

2 2

128

4

f x xh x x

x

   

   

2

128

2 0 4 48 4; 2

f x x x Min f x x h

x



         

.

BẢNG ĐÁP ÁN

1.A

2.C

3.D

4.A

5.B

6.A

7.A

8.A

9.A

10.A

11.A

12.A

13.A

14.A

15.A

16.C

17.A

18.D

19.A

20.C

21.C

22.D

23.C

24.B

25.C

26.D

27.D

28.A

29.A

30.C

31.B

32.A

33.C

34.D

35.D

36.B

37.D

38.C

39.B

40.C

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 62

ĐÊ ÔN TẬP SỐ 10

PHẦN I: PHẦN TRẮC NGHIỆM

Câu 1. [2D1-1.4-2] Khoảng đồng biến của hàm số

3 2

3 9 4y x x x    

là:

A.

 

; 3 

. B.

 

3;1



. C.

 

3;



. D.

 

1;3



.

Lời giải

Chọn D

2

x 1

y 3x 6x 9;y 0

x 3

 



 

     







. Suy ra

 

y 0, x 1;3



   

.

Câu 2. [2D1-1.5-3] Tìm tất cả các giá trị

m

để hàm số

 

3 2

1 2 1y m x mx x    

luôn nghịch biến

trên



?

A.

3 3 1

m

  

. B.

1 3 3

m   .

C.

m

 

. D.

3 3 3 3

m    .

Lời giải

Chọn A

Hàm số nghịch biến trên

R

thì

 

f ' x 0,x

 

Ta có

 

2

y' 3 m 1 x 2mx 2   

   

 

2

m 1 0

m 1

f ' x 0,x 3 m 1 x 2mx 2 0

' m 6 m 1 0

3 3 m 3 3

 





 

        

 

    

   







3 3 m 1   

.

Câu 3. [2D1-2.6-1] Cho hàm số

4 2

3 1

y x x

   

. Mệnh đề nào dưới đây là đúng?

A. Một cực đại và

2

cực tiểu. B. Một cực tiểu và

2

cực đại.

C. Một cực đại duy nhất. D. Một cực tiểu duy nhất.

Lời giải

Chọn C

4 2

3 1

y x x

   

 

3 2

' 4 6 4 6

y x x x x

      

' 0 0

y x

  

và đổi dấu từ + sang – ( dựa vào bảng biến thiên).=> Hàm số có 1 cực đại duy

nhất.

Câu 4. [2D1-2.7-2] Với tất cả giá trị nào của m thì hàm số

 

4 2

1 1 2y mx m x m

    

chỉ có một

cực trị?

A.

1

m



. B.

0

m



. C.

0 1

m

 

. D.

0 1

m m

  

.

Lời giải

Chọn D

   

 

4 2 3 2

1 1 2 ' 4 2 1 2 2 1

y mx m x m y mx m x x mx m

           

 

2

0

' 0

2 1 0 2

x

y

mx m





 



  



Hàm số chỉ có một cực trị

 

2



vô nghiệm hoặc có nghiệm kép

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 63

 

0 2 1 0 0 1

m m m m

          

.

Câu 5. [2D1-2.14-4] Cho hàm số

4 2

2 1

y x mx m   

. Tìm tất cả các giá trị thực của m để đồ thị

hàm số có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ

O

làm trực tâm.

A.

1

m



. B.

2

m



. C.

0

m



. D.

1

m

 

.

Lời giải

Chọn A

Ta có:

3

2

x 0

y' 4x 4mx 0

x m





   







. Hàm số có 3 điểm cực trị khi

m 0

Khi đó gọi

 

   

A 0;1; m ;B m;1 2m ;C m;1 2m

    là các điểm cực trị của đồ thị hàm số

Ta có:

   

 

OB.AC m;1 2m . m; m 0 m 1 2m m 0 m 1          

 

.

Câu 6. [2D1-3.2-1] Tìm giá trị nhỏ nhất của hàm số

3 2

3 9 6

y x x x

   

trên

 

4;4



.

A.

 

 

4;4

21

Min f x





. B.

 

 

4;4

14

Min f x



 

. C.

 

 

4;4

11

Min f x





. D.

 

 

4;4

70

Min f x



 

.

Lời giải

Chọn D

Đây là một câu hỏi dễ lấy điểm. Để tìm được GTNN của hàm số trên đoạn

 

4;4



ta giải

phương trình

1

' 0

3

x

y

x

 



 







. Ta lần lượt so sánh

   

4 , 4 ,

f f

   

1 , 3f f



thì thấy

 

4 70

f

  

là nhỏ nhất. Vậy đáp án đúng là D.

Câu 7. [2D1-3.4-2] Tìm GTNN

m

của hàm số

1

5y x

x

  

trên

1

;5

2

 

 

 

.

A.

5

2

m

 

. B.

1

5

m



. C.

3

m

 

. D.

2

m

 

.

Lời giải

Chọn C

 

2

2 2

1

1 1 1

5 ' 1 ' 0 1 0

1

x L

x

y x y y x

x x x

x

 



            







Ta có:

   

1 5 1

1 3; ; 5

2 2 5

f f f

 

    

 

 

Vậy GTNN của hàm số bằng

3

m

 

.

Câu 8. [2D1-3.14-4] Một xe buýt của hãng xe A có sức chứa tối đa là 50 hành khách. Nếu một chuyến

xe buýt chở

x

hành khách thì giá tiền cho mỗi hành khách là:

2

20 3

40

x

 



 

 

(nghìn đồng).

Khẳng định nào dưới đây là đúng?

A. Một chuyến xe buýt thu được số tiền nhiều nhất bằng 3.200.000 đồng.

B. Một chuyến xe buýt thu được số tiền nhiều nhất khi có 45 hành khách.

C. Một chuyến xe buýt thu được số tiền nhiều nhất bằng 2.700.000 đồng.

D. Một chuyến xe buýt thu được số tiền nhiều nhất khi có 50 hành khách.

Lời giải

Chọn A

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 64

Số tiền của chuyến xe buýt chở

x

hành khách là:

   

2

2 3

x 3x x

f x 20x. 3 20 9x 0 x 50

40 20 1600

 

      

 

 

     





 

2

0;50

x 40

3x 3x

f x 20 9 f x 0 maxf x f 40 3200000

x 120

10 1600



 





        

 







 

Vậy: một chuyến xe buýt thu được lợi nhuận cao nhất bằng: 3.200.000(đồng).

Câu 9. [2D1-4.4-1] Cho hàm số

3x 1

.

2x 1

y







Khẳng định nào dưới đây đúng?

A. Đồ thị hàm số có tiệm cận đứng là

1

2

x

 

.

B. Đồ thị hàm số có tiệm cận ngang là

1

2

y



.

C. Đồ thị hàm số có tiệm cận đứng là

1

2

y



.

D. Đồ thị hàm số không có tiệm cận.

Lời giải

Chọn B

Đồ thị hàm số có tiệm cận đứng là

1

x

2



và tiệm cận ngang là

1

y

2



.

Câu 10. [2D1-4.6-2] Tìm số tiệm cận của đồ thị hàm số

2

1

x

y

x







.

A.

2

. B.

3

. C.

4

. D.

0

.

Lời giải

Chọn C

Nhận xét: Khi

1

x



hoặc

1

x

 

thì

y  

nên ta có thể thấy ngay

1; 1

x x

  

là hai tiệm

cận đứng của đồ thị hàm số.

Ngoài ra ta có:

2

1 1

lim lim lim

1

x x

x

x x

y

x

 



 

 



2 2

1

lim lim 1

1 1

x x

x

x x

 



   

 

2

1 1

lim lim lim

1

x x

x

x x

y

x

 



 

 



2 2

1

lim lim 1

1 1

x x

x

x x

 



    

   

Như vậy

1

y



và

1

y

 

là hai tiệm cận ngang của đồ thị hàm số.

Vậy đáp án là có 4 tiệm cận.

Câu 11. [2D1-5.2-1] Đường cong trong hình bên là đồ thị của hàm số nào?

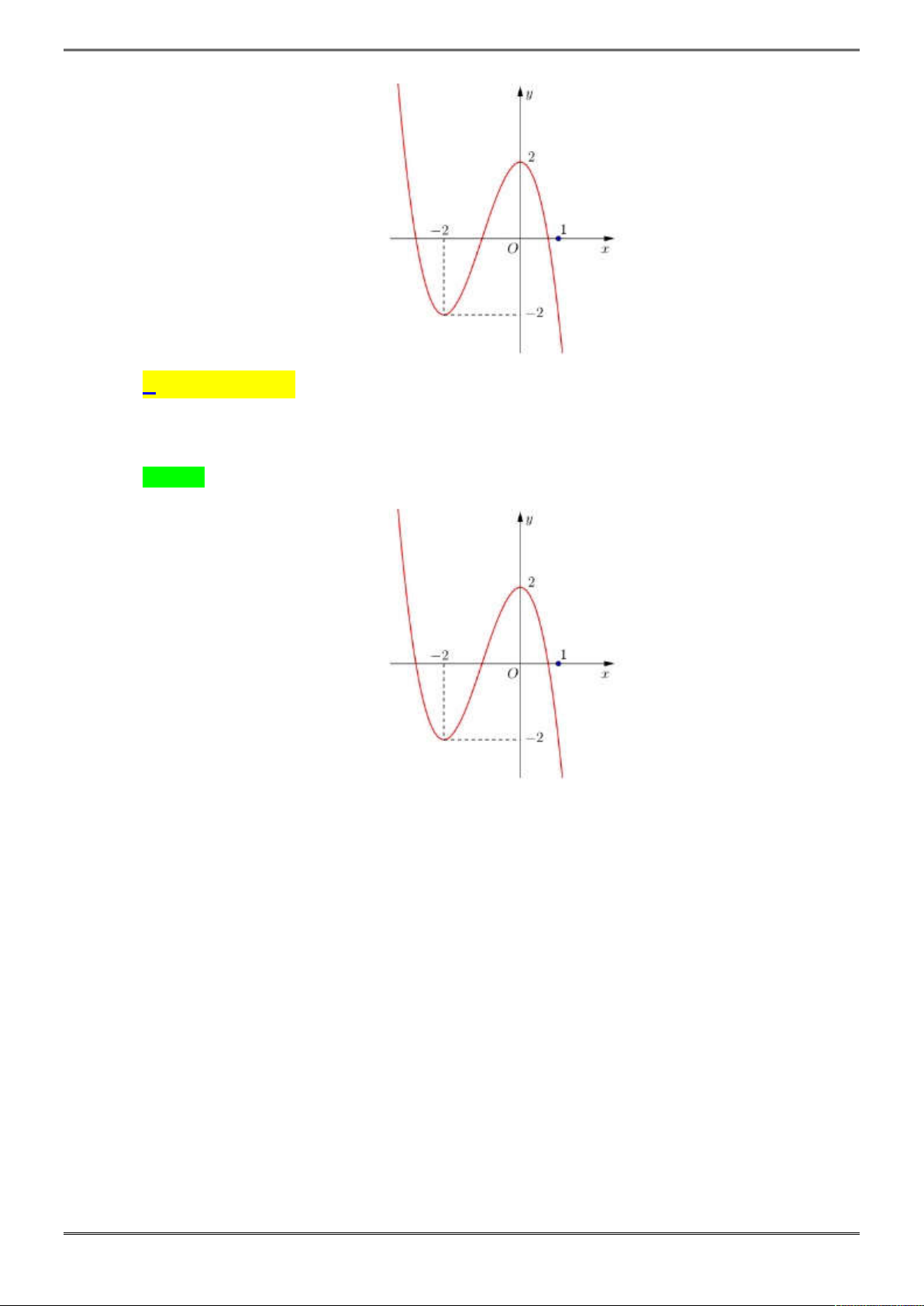
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 65

A.

3 2

y x x

   

. B.

3 2

y x x

   

.

C.

3 2

y x x

  

. D.

3

3 2y x x   

.

Lời giải

Chọn A

Dựa vào đồ thị và đáp án ta thấy

x

lim y





 







 





.

Hàm số đạt cực trị tại các điểm

x 2, x 0  

.

Đồ thị hàm số đi qua các điểm có tọa độ

   

2; 2 , 0;2

 

.

Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.

Câu 12. [2D1-5.2-2] Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt

kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

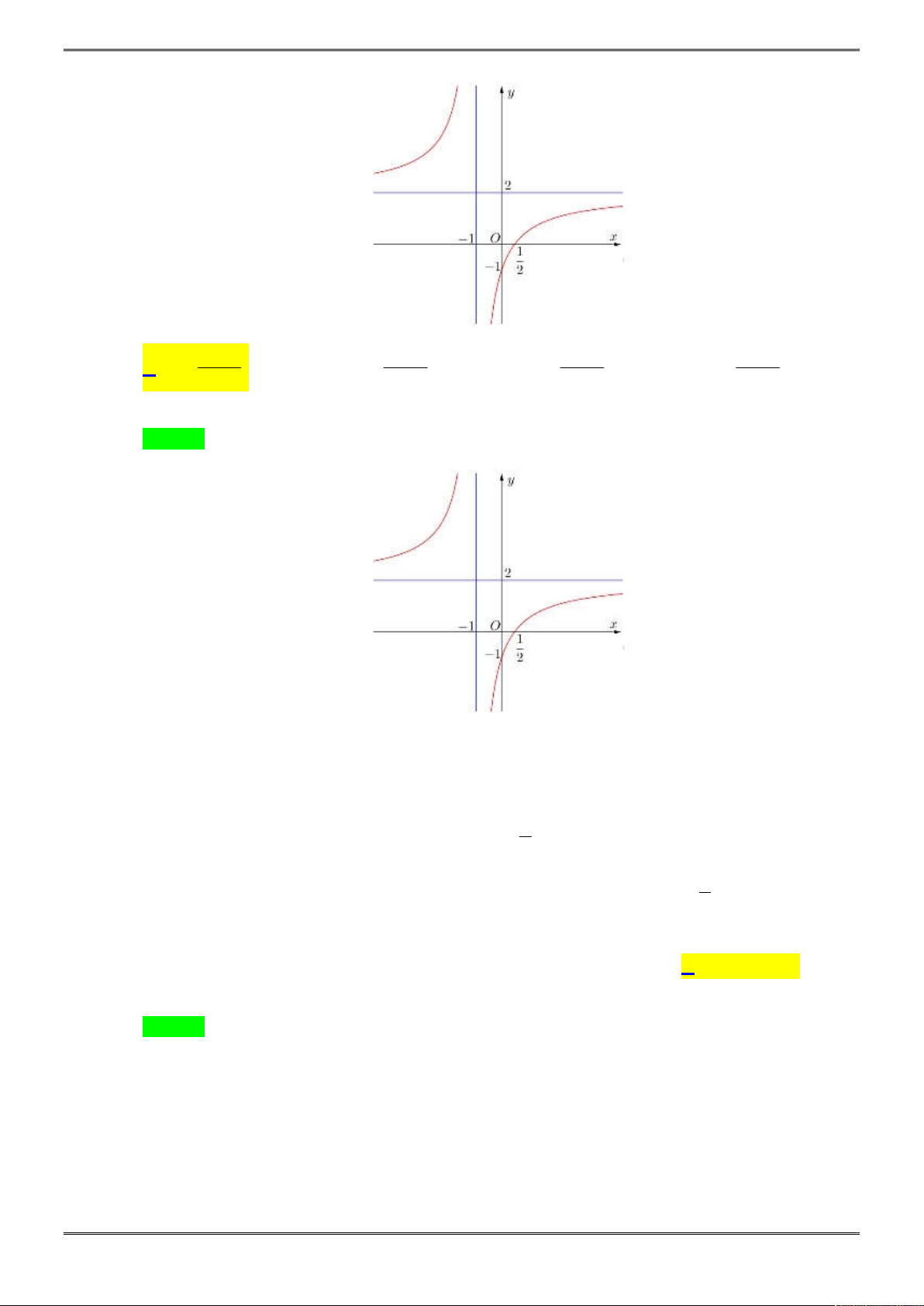
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 66

A.

2 1

1

x

y

x







. B.

2 1

1

x

y

x







. C.

2 1

1

x

y

x







. D.

1 2

1

x

y

x







.

Lời giải

Chọn A

Dựa vào đồ thị hàm số ta thấy

Đồ thị hàm số có tiệm cận đứng và tiệm cận ngang lần lượt là

x 1, y 2  

.

Hàm số đồng biến trên mỗi khoảng xác định.

Đồ thị hàm số đi qua các điểm có tọa độ

 

1

0; 1 , ;0

2

 



 

 

.

Câu 13. [2D1-7.1-2] Viết phương trình tiếp tuyến của đồ thị hàm số

 

3 2

2

1

3

y f x x x

   

tại điểm

có hoành độ

0

x

là nghiệm của phương trình

 

0

'' 10

f x



.

A.

12 23

y x

 

. B.

12 24

y x

 

. C.

12 25

y x

 

. D.

12 26

y x

 

.

Lời giải

Chọn D

   

2

' 2 2 ; '' 4 2f x x x f x x   

Theo đề bài, ta có:

 

0 0 0

'' 10 4 2 10 3

f x x x

     

Với

   

0

3 3 10; ' 3 12

x f f

   

Phương trình tiếp tuyến tại điểm

 

3;10

là

12 26

y x

 

.

Câu 14. [2D1-6.1-2] Đồ thị của hàm số

3 2

3x 2x 1

y x

    

và đồ thị của hàm số

2

2 1y x x  

có

tất cả bao nhiêu điểm chung?

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 67

A.

2

. B.

0

. C.

1

. D.

3

.

Lời giải

Chọn D

Phương trình hoành độ giao điểm của hai đồ thị là

3 2 2

x 3x 2x 1 x 2x 1      

 

3 2 2

x 0

x 2x 4x 0 x x 2x 4 0 x 1 5

x 1 5







            



 



hai đồ thị có 3 điểm chung.

Câu 15. [2D1-6.8-4] Cho hàm số

 

2 1

1

x

y C

x







. Tìm các giá trị

m

để đường thẳng

: 1

d y x m

  

cắt đồ thị tại 2 điểm phân biệt

,A B

sao cho

2 3

AB  .

A.

4 10

m   . B.

2 10

m   . C.

4 3

m   . D.

2 3

m   .

Lời giải

Chọn A

Phương trình hoành độ giao điểm của

( )C

và

d

là:

   

2

2 1

1 2 2 0 *

1

x

x m x m x m

x



        



Vì

,A B

là giao điểm của

( )C

và

d

nên

,A B

thuộc đường thẳng

d

và hoành độ

1 2

;x x

là

nghiệm của phương trình (*)

             

2 2 2

1 1 2 2 1 2 2 1 1 2 1 2 1 2

; 1 ; ; 1 2 2 4 .

A x x m B x x m AB x x x x x x x x x x

 

             

 

Theo viet:

   

1 2 1 2

2 ; 2

x x m x x m

    

2

12 4 10

AB m    .

Câu 16. [2D2-1.2-1] Rút gọn biểu thức

3 6

P x x x



với

0

x



.

A.

2

3

P x

. B.

P x

 . C.

3

P x

 . D.

5

6

P x

.

Lời giải

Chọn D

Ta có

3 6

P x x x



1

1 1

2

3 6

. .x x x

 



 

 

2 1 5

3 6 6

x x



 

.

Câu 17. [2D2-1.2-2] Rút gọn

 

7 1 2 7

2 2

.a a

P

a

 







, với

0

a



.

A.

4

P a

. B.

3

P a

. C.

5

P a

. D.

P a

.

Lời giải

Chọn C

 

7 1 2 7

2 2

.a a

P

a

 







 

  

7 1 2 7

2 2 2 2

a

  

 



3

2

a





5

a

.

Câu 18. [2D2-3.2-1] Cho hai số thực

,a b

thỏa mãn

e a b 

. Khẳng định nào dưới đây là sai?

A.

ln 2

ab



. B.

ln 0

a

b



. C.

ln lnb a

. D.

log log 2

a b

e e

 

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 68

Lời giải

Chọn B

Vì

1

a

b



nên

ln ln1 0

a

b

 

.

Câu 19. [2D2-3.3-2] Cho

3

log 2

a  và

3

log 5

a  . Tính

10

log 60

theo

,a b

.

A.

2 1a b

a b

 



. B.

2 1a b

a b

 



. C.

2 1a b

a b

 



. D.

1a b

a b

 



.

Lời giải

Chọn A

Ta có

10 10 10 10

2 3 3 5

2 1 1

log 60 2log 2 log 3 log 5

1 log 5 log 2 log 5 1 log 2

     

  

3 3

2 1 1 2 1 1 2a b 1

log 5 log 2 b a

log 2 log 5 a b a b

1 1

a blog 2 log 5

 

      

  

 

.

Câu 20. [2D2-3.2-1] Với các số thực dương

,a b

bất kỳ. Mệnh đề nào dưới đây đúng?

A.

log( ) log logab a b 

. B.

log( ) log .logab a b

.

C.

log( ) log logab b a a b 

. D.

log( ) log

b

ab a

 .

Lời giải

Chọn A

Theo qui tắc tính logarit:

log( ) log logab a b 

.

Câu 21. [2D2-3.0-4] Cho

x, y 0

thỏa mãn

 

2 2 2

log log log

x y x y  

. Tìm giá trị nhỏ nhất của biểu

thức

2 2

P x y 

.

A.

min 4P 

. B.

min 4 2

P 

. C.

min 8

P



. D.

min 16

P



.

Lời giải

Chọn C

Ta có:

     

2 2 2 2 2

log x log y log x y log xy log x y     

 

2

x y

x y xy x y 4

4



      

.

Khi đó

 

2

2 2

min

x y

4

P x y 8 P 8

2 2



      

, dấu “=” xảy ra khi và chỉ khi

x y 2 

.

Câu 22. [2D2-4.1-1] Tìm tập xác định

D

của hàm số

 

2

3

( ) log 2y f x x x

  

.

A.

 

;0 (2; )

D

   

.B.

 

/ 0;2

D 



. C.

 

0;2

D 

. D.



.

Lời giải

Chọn A

TXĐ

2

0

2 0

2

x

x x

x





  







.

Câu 23. [2D2-4.2-2] Cho hàm số

2 2016

x

y e



 . Ta có

 

' ln3

y

bằng:

A.

2016

e e

. B.

2016

18.

e

. C.

2016

9.

e

. D.

2016

2. 9

e



.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 69

Lời giải

Chọn B

 

2x 2016 2016

y' 2.e y' ln 3 18.e



   .

Câu 24. [2D2-4.2-2] Tính đạo hàm của hàm số

3

log x

y

x



?

A.

3

2

1 log

'

x

y

x





. B.

2

1 ln

'

ln 3

x

y

x





. C.

3

2

1 log

'

x

y

x





. D.

2

1 ln

'

ln 3

x

y

x





.

Lời giải

Chọn D

3

3 3

2 2 2

1

.x log x

log x 1 ln 3.log x

1 ln x

x ln 3

'

x

x x ln 3 x ln 3



 

  

 

 

.

Câu 25. [2D2-4.9-4] Một tên lửa bay vào không trung với quãng đường đi được quãng đường

 

s t

(km) là hàm phụ thuộc theo biến

t

(giây) theo quy tắc sau:

   

2

3 3 1

2 .

t t

s t e t e km

 

 

. Hỏi vận

tốc của tên lửa sau 1 giây là bao nhiêu (biết hàm biểu thị vận tốc là đạo hàm của hàm biểu thị

quãng đường theo thời gian).

A.

4

5e

(km/s). B.

4

3e

(km/s). C.

4

9e

(km/s). D.

4

10e

(km/s).

Lời giải

Chọn D

Ta có công thức vận tốc:

   

 

2

3 1

' 2 .

t t

v t s t e t e



  

 

2

3 3 1

2 . 6 2

t t

t e t e

 

  

Với

1t 

ta có:

 

4

10 /e km s

.

Câu 26. [2D2-6.2-2] Tìm tập nghiệm

S

của bất phương trình

 

2

1

2

log 3 2 1

x x

   

.

A.

 

1;S

 

. B.





0;2

S 

. C.



 



0;2 3;7

S  

. D.



 



0;1 2;3

S  

.

Lời giải

Chọn C

Điều kiện

 

2

3 2 0

1

x

x x

x





   







Chú ý hệ số a logari

0 1a 

   

2 2

1

2

log 3 2 1 3 2 2 0 3

x x x x x

          

Kết hợp điều kiện chọn C.

Câu 27. [2D2-5.3-2] Phương trình

2.4 7.2 3 0

x x

  

có tất cả các nghiệm thực là:

A.

2

1, log 3

x x   . B.

2

log 3

x  . C.

1

x

 

. D.

2

1, log 3

x x  .

Lời giải

Chọn A

 

x

2

x x

x

2

1

2

x 1

2. 2 7.2 3 0

2

x log 3

2 3



  





    













.

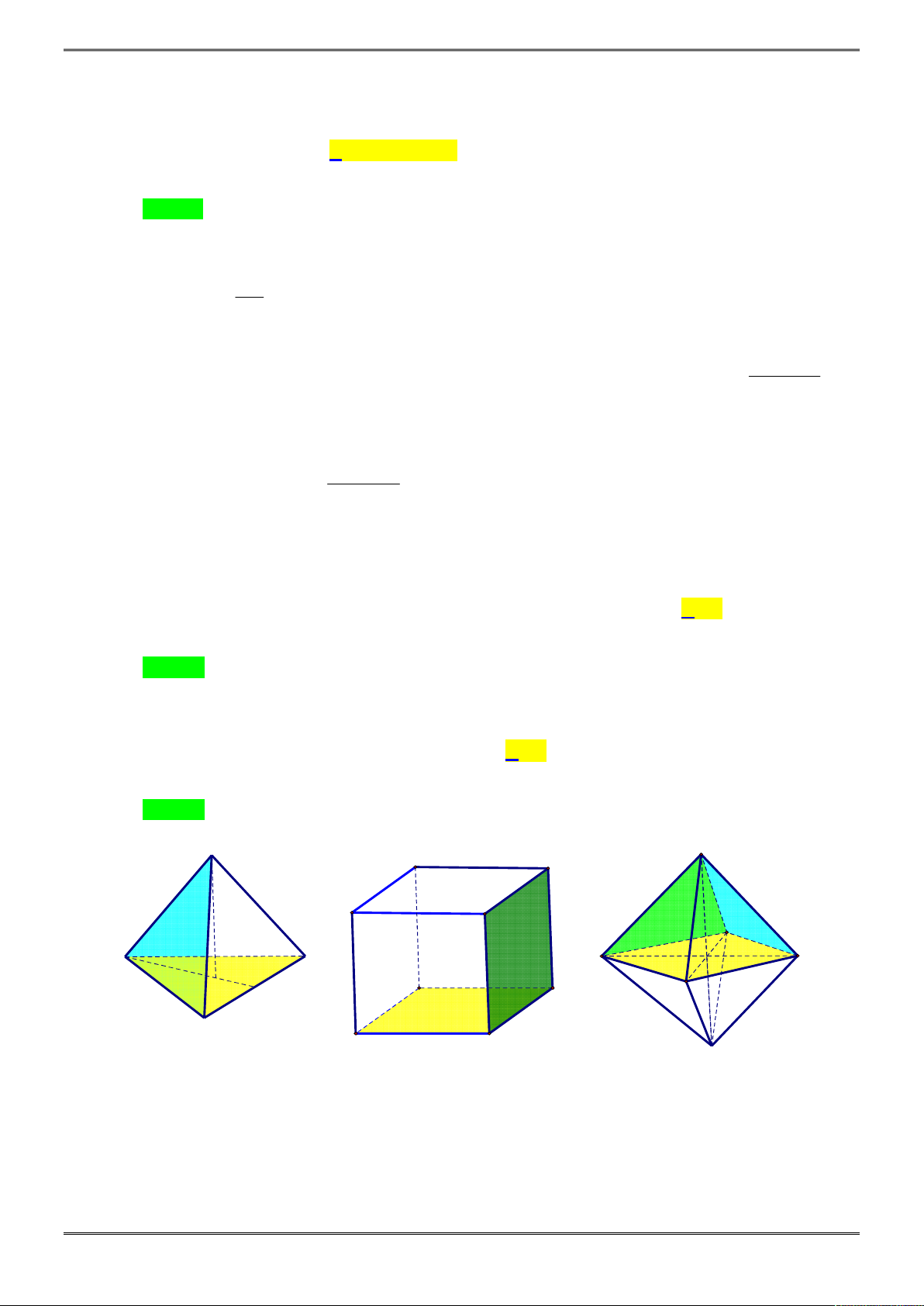
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 70

Câu 28. [2D2-7.1-4] Anh Sơn vay tiền ngân hàng mua nhà trị giá 1 tỉ đồng theo phương thức trả góp.

Nếu cuối mỗi tháng bắt đầu từ tháng thứ nhất anh trả 12 triệu và chịu lãi số tiền chưa trả là

0,5% tháng thì sau bao lâu anh trả hết nợ?

A. 3 năm. B. 3 năm 1 tháng. C. 3 năm 2 tháng. D. 3 năm 3 tháng.

Lời giải

Chọn B

Gọi n là số tháng anh cần trả với

n

tự nhiên

Sau tháng thứ nhất anh còn nợ

9 6 9 6

1

0,5

10 .(1 ) 30.10 10 .1,005 30.10

100

S     

đồng

Sau tháng thứ hai anh còn nợ

 

6 9 6 6

2 1

.1,005 12.10 10 .1,005 30.10 .1,005 30.10

S S    

2

9 2 6

1,005 1

10 .1,005 30.10 .

0,005



 

đồn

g

Tiếp tục quá trình trên thì số tiền anh Sơn còn nợ sau

n

tháng sẽ là

9 6

1,005 1

10 .1,005 30.10 . 0

0,005

n

S



  

1,005

1,005 1,2 log 1,2 36,555

n

n    

Do đó sau 37 tháng sẽ trả hết nợ tức 3 năm 1 tháng.

Câu 29. [2H1-1.0-1] Mỗi đỉnh của khối đa diện lồi là đỉnh chung của ít nhất bao nhiêu mặt?

A.

2

. B.

5

. C.

4

. D.

3

.

Lời giải

Chọn D

Theo lý thuyết.

Câu 30. [2H1-1.1-2] Có tất cả bao nhiêu khối đa diện đều lồi?

A.

3

. B.

4

. C.

5

. D.

6

.

Lời giải

Chọn C

Căn cứ vào định nghĩa về khối đa diện lồi và định lý về khối đa diện đều.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 71

.

Câu 31. [2H1-1.2-2] Hình lập phương có bao nhiêu mặt phẳng đối xứng?

A.

8

. B.

9

. C.

10

. D.

7

.

Lời giải

Chọn B

Hình lập phương có 9 mặt phẳng đối xứng như hình

vẽ.

.

Câu 32. [2H1-2.1-1] Cho hình chóp

.

S ABCD

có đáy là hình chữ nhật,

, 2AB a AD a 

và

2SA a

vuông góc với đáy. Tính thể tích

V

của hình chóp

.

S ABCD

?

A.

3

4

3

V a



(đvtt). B.

3

4V a



(đvtt). C.

3

2

3

V a



(đvtt). D.

3

2V a



(đvtt).

Lời giải

Chọn A

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 72

.

1 1

. . . .

3 3

S ABCD ABCD ABCD

V S h S SA

 

3

1 1 4

. . . . .2 .2

3 3 3

AB AD SA a a a a

  

.

Câu 33. [2H1-3.1-2] Cho một lăng trụ đứng

. ' ' 'ABC A B C

có đáy là một tam giác vuông cân tại

A

.

Cho

2AB a

, góc giữa

'AC

và

( )ABC

bằng

30



. Tính thể tích

V

khối lăng trụ

. ' ' 'ABC A B C

.

A.

3

4 3

2

a

V 

. B.

3

2 3

3

a

V 

. C.

2

4 3

2

a

V 

. D.

3

4 3

3

a

V 

.

Lời giải

Chọn D

B'

A'

C'

A

B

C

Ta có

2

1

. 2

2

ABC

S AB AC a

 

; góc giữa

'AC

và

( )ABC

là góc



'C AC

. Xét tam giác

'ACC

có



0

' 2 3

tan ' ' tan 30 '

3

CC

C AC CC AC CC a

AC

    

. Vậy

3

. ' ' '

4 3

'.

3

ABC A B C ABC

a

V CC S 

.

Câu 34. [2H1-2.2-3] Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình thoi cạnh

a

với

3

,

2 2

a a

SA SB 

,



60

BAD



 và mặt phẳng

( )SAB

vuông góc với mặt phẳng đáy. Gọi

,H K

lần lượt là trung điểm của

,AB BC

. Tính thể tích

V

tứ diện

.

K SCD

.

A.

3

4

a

V  . B.

3

16

a

V  . C.

3

8

a

V  . D.

3

32

a

V  .

Lời giải

Chọn D

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 73

S

K

A

B

C

D

H

M

Từ giả thiết ta có

3

, ,

2 2

a a

AB a SA SB  

Nên

ASB

vuông tại

2

AB

S SH SAH

   

đều

Gọi

M

là trung điểm của

AH

thì

SM AB

Do

     

SAB ABCD SM ABCD

  

Vậy

.

1 1 1

. . . .

3 3 2

KSDC S KCD KCD BAD

V V SM S SM S

 

  

3

1 3 1 . 3

. . .

3 4 2 2.2 32

a a a a

 

(đvtt).

Câu 35. [2H2-1.2-1] Cho hình nón có bán kính đáy bằng

3

và chiều cao bằng

4

. Tính diện tích xung

quanh

xq

S

của hình nón đó.

A.

60

xq

S





. B.

15

xq

S





. C.

20

xq

S





. D.

25

xq

S





.

Lời giải

Chọn B

O

I

M

Ta có

2 2

xq

S rl r r h 15      

.

Câu 36. [2H2-1.0-2] Một hình nón có bán kính đáy

2 3

R  , góc ở đỉnh bằng

120



. Khi đó diện tích

xung quanh

xq

S

và thể tích

V

của khối nón đó lần lượt là:

A.

8 3;8

 

. B.

6 3;8

 

. C.

8 3;6

 

. D.

8 3;4

 

.

Lời giải

Chọn A

Giả sử hình nón có đỉnh

S

, đáy là hình tròn tâm

O

, đường sinh là

l SA

, đường cao

h SO

.

60



20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 74

Khi đó

SOA

vuông tại

O

và



60

OSA





ta có:

2 3

2

tan60

3

OA

SO



  

và

2 3

4

sin 60

3

2

OA

SA



  

.

Vậy

.2 3.4 8 3

xq

S Rl

  

  

và

2

1 1

.12.2 8

3 3

V R h

  

  

.

Câu 37. [2H2-1.5-3] Cho hình chóp tứ giác đều

.

S ABCD

có cạnh đáy bằng

a

và cạnh bên cũng bằng

a

. Tính thể tích

 

N

V

của khối nón

( )N

ngoại tiếp khối chóp

.

S ABCD

.

A.

3

( )

2

12

N

a

V





. B.

3

( )

12

N

a

V



 . C.

3

( )

6

N

a

V



 . D.

3

( )

2

4

N

a

V





.

Lời giải

Chọn A

Phân tích: Hình chóp

.

S ABCD

là hình chóp tứ giác đều có

AB SA a 

nên khối nón ngoại

tiếp hình chóp có bán kính đáy

a 2

r

2



và chiều cao

2

a 2 a 2

SO a

2 2

 

  

 

 

Khi đó:

 

2

3 3

N

a 2 1 a 2 a 2 a 2

V . .

12 3 2 2 12

 

 

   

 

 

.

Câu 38. [2H2-2.3-2] Một hình trụ

( )T

có hai đáy là hai hình tròn nội tiếp hình vuông cạnh

a

. Tính thể

tích

( )T

V

của khối trụ đó, biết chiều cao của khối trụ bằng

h a

?

A.

3

( )

1

2

T

V a





. B.

3

( )

1

4

T

V a





. C.

3

( )

1

3

T

V a





. D.

3

( )T

V a





Lời giải

Chọn B

Phân tích:

Ta có hình vẽ sau

Ta thấy hình tròn nội tiếp hình vuông cạnh

a

có đường kính có độ dài

a

.

Khi đó thể tích của khối trụ là

2

2 3

1

. . . . .

2 4

a

V B h a R a a

  

 

   

 

 

.

Câu 39. [2H2-2.7-4] Khi sản xuất vỏ lon sữa Ông Thọ hình trụ, các nhà sản xuất luôn đặt chỉ tiêu sao

cho chi phí sản xuất vỏ lon là nhỏ nhất, tức là nguyên liệu ( sắt tây) được dùng là ít nhất. Hỏi

B

A

C

D

S

O

I

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 75

khi đó diện tích toàn phần

tp

S

của lon sữa là bao nhiêu, khi nhà sản xuất muốn thể tích của hộp

là

3

V cm

.

A.

2

3

4

tp

V

S



 . B.

2

3

6

4

tp

V

S



 . C.

2

3

4

tp

V

S



 . D.

2

6

4

tp

V

S



 .

Lời giải

Chọn B

SỮA ÔNG THỌ

Đây là bài toán vừa kết hợp yếu tố hình học và yếu tố đại số. Yếu tố hình học ở đây là các công

thức tính diện tích toàn phần, diện tích xung quanh, thể tích của hình trụ. Còn yếu tố đại số ở

đây là tìm GTNN của

tp

S

Ta có yếu tố đề bài cho

2

. .

V

V B h R h h

R



   

(*)

2

2 2. R 2 .

tp xq day

S S S R h

 

   

2 2

2

2 . 2

V V

R R R

R

  



   

   

   

   

Đến đây ta có hai hướng giải quyết, đó là tìm đạo hàm rồi xét

' 0

y



rồi vẽ BBT tìm GTNN.

Tuy nhiên ở đây tôi giới thiệu đến quý độc giả cách làm nhanh bằng BĐT Cauchy.

Ta nhận thấy ở đây chỉ có một biến

R

và bậc của

R

ở hạng tử thứ nhất là bậc 2, nhưng bậc của

R

ở hạng tử thứ 2 chỉ là 1. Vậy làm thế nào để khi áp dụng BĐT Cauchy triệt tiêu được biến

R

. Ta sẽ tìm cách tách

V

R

thành 2 hạng tử bằng nhau để khi nhân vào triệt tiêu được

2

R

ban

đầu. Khi đó ta có như sau:

2

3

2. 2.3

2 2 4

tp

V V V

S R

R R



 

   

 

 

.

Câu 40. [2H2-2.2-2] Cho khối trụ

( )T

có thiết diện qua trục là một hình vuông có diện tích bằng

4

.

Tính diện tích xung quanh S

xq

của khối trụ

( )T

.

A.

4

xq

S





. B.

2

xq

S





. C.

8

xq

S





. D.

4 2

xq

S  .

Lời giải

Chọn A

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 76

Gọi chiều cao của khối trụ là

h

. Ta có:

2

h 4 h 2 l   

.

Bán kính đáy của khối trụ là:

h 2

r 1

2 2

  

Diện tích xung quanh của khối trụ là:

xq

S 2 rl 2 .2.1 4     

.

PHẦN II: PHẦN TỰ LUẬN

Câu 1. [2D2-6.3-3] Giải bất phương trình

2

2 2

log 5log 4 0

x x

  

Lời giải

ĐK:

0x 

2

2 2

2

log 1

2

log 5log 4 0

log 4 16

x

x x





    



 



Kết hợp với đk

0x 

, ta được:

0 2

16

x

 









Vậy tập nghiệm của bpt là:



 



0;2 16;S

  

.

Câu 2. [2H1-2.6-4] Cho tứ diện đều

ABCD

có cạnh bằng

a

. Gọi

,M N

lần lượt là trung điểm của

các cạnh

,AB BC

và

E

là điểm đối xứng với

B

qua

D

. Mặt phẳng

( )MNE

chia khối tứ diện

ABCD

thành hai khối đa diện, trong đó khối đa diện chứa đỉnh

A

có thể tích

V

. Tính

V

.

Lời giải

 

MNE

chia khối tứ diện

ABCD

thành 2 khối đa diện

 

1

: .

AC MNPQ



và

 

2

: .

BD MNPQ



 

MNE

cắt

AD

tại

Q

, cắt

CD

tại

P

.

. . .

AC MNPQ E AMNC E ACPQ

V V V 

 

.

1 1

, . , .

3 3

1 1 1 3 3

, . .2. D, .

3 4 3 4 2

E AMNC AMNC ABC BMN

ABC ABC ABC ABCD

V d E AMNC S d E ABC S S

d E ABC S S d ABC S V

 

  

  

 

   

 

 

 

.

1 1 1 8 8

, . B, . B, .

3 3 3 9 9

E ACPQ ACPQ ACD DPQ ACD ABCD

V d E ACPQ S d ACD S S d ACD S V

  

    

3 3

.

3 8 11 11 2 11 2

.

2 9 18 18 12 216

AC MNPQ ABCD ABCD ABCD

V V V V a a

    

Dựa vào bảng biến thiên ta có

max ( ) 4

g x





. Do đó:

1 4 3.

m m

   

A

B

C

D

Q

P

E

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 1

ĐỀ ÔN TẬP SỐ 11

PHẦN I: PHẦN TRẮC NGHIỆM

Câu 1. [2D1-1.4-2] Cho hàm số

3 2

4 5 2y x x x   

. Mệnh đề nào dưới đây là đúng?

A. Hàm số nghịch biến trên khoảng

 

;1

. B. Hàm số nghịch biến trên khoảng

5

1;

3

 

 

 

.

C. Hàm số nghịch biến trên khoảng

5

;

3

 



 

 

. D. Hàm số đồng biến trên khoảng

5

1;

3

 

 

 

.

Lời giải

Chọn B.

Xét hàm số

3 2

4 5 2y x x x   

trên



, ta có

2

' 3 8 5;y x x x

     

.

Bất phương trình

 

2

5

' 0 3 8 5 0 ;1 ;

3

1

x

y x x x

x





 



          

 



 





.

Tương tự,

2

5

' 0 3 8 5 0 1;

3

y x x x

 

      

 

 

.

Suy ra hàm số nghịch biến trên khoảng

5

1;

3

 

 

 

.

Câu 2. [2D1-1.5-3] Tìm tập hợp tất cả các giá trị của tham số m để hàm số

3 2

3 4y x x mx   

đồng

biến trên khoảng

 

;1

A.





; 3 

. B.

 

; 3 

. C.

 

3;9



. D.

 

3;9



.

Lời giải

Chọn A.

Ta có:

 

3 2 2

3 4 3 6

y x x mx x x m



      

.

Hàm số đồng biến trên khoảng

   

 

2

3 6

3 6 0

;1 ' 0, ;1

;1

m x x f x

x x m

y x

x



  



  

 

       

 

  





Ta có

   

6 6 0 6 6 0 1

f x x f x x x

 

         

.

Xét bảng biến thiên của hàm số trên đoạn

 

;1

ta thấy

 

  



;1

1 3 3 ; 3

f x f m m



          

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 2

Câu 3. [2D1-2.6-1] Cho hàm số

4 3 2

3 8 6 24 1y x x x x    

. Mệnh đề nào dưới đây đúng?

A. Hàm số đạt cực tiểu tại

1x 

. B. Hàm số đạt cực đại tại

2

x



.

C. Hàm số đạt cực trị tại

1

y

 

. D. Hàm số đạt cực đại tại

1x 

.

Lời giải

Chọn D.

Ta có

3 2 3 2

2

' 12 24 12 24 ' 0 12 24 12 24 0

1

x

y x x x y x x x

x





           



 



.

Lại có

 

2

'' 2 36 0

'' 36 48 12 '' 1 24 0

'' 1 72 0

y

y x x y

y

 



       





  



Hàm số đạt cực đại tại

1x 

, đạt cực tiểu

tại

2

x



và

1

x

 

.

Câu 4. [2D1-2.8-2] Tìm tất cả các giá trị của tham số

m

để hàm số

3 2 2

2 x 2y x m m x   

đạt cực

tiểu tại

1.

x



A.

1.

m



B.

3.

m



C.

1 3.

m m

  

D.

1.

m

 

Lời giải

Chọn A.

Tập xác định

.

D

 

2 2

3 4 ; 6 4 .y x mx m y x m

 

    

Do hàm số đã cho là hàm bậc 3 nên hàm số đạt cực tiểu tại

1x 

 

2

1 3

1 0

4 3 0

1.

3

6 4 0

1 0

2

m m

y

m m

m

y

  









  

 

    

  





 











Câu 5. [2D1-2.9-4] Tìm

m

để hàm số

 

4 2

2 1 2

y mx m x

   

có hai cực tiểu và một cực đại.

A.

0.

m



B.

0 1.

m

 

C.

2.

m



D.

1 2.

m

 

Lời giải

Chọn B.

Tập xác định

.

D

 

 

3

4 4 1 .y mx m x



  

;

 

2

0

1

x

y

mx m







 



  



Hàm số có 2 cực tiểu và 1 cực đại khi phương trình

0

y





có 3 nghiệm phân biệt và

0

m



.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 3

Khi đó phương trình

 

2

1

mx m

  

có 2 nghiệm phân biệt khác

0

và

0

m



.

0

0 1.

1

0

m







   





 





Câu 6. [2D1-3.2-1] Tổng của giá trị lớn nhất và giá trị nhỏ nhất của hàm số

3 2

3 9 35

y x x x

   

trên

đoạn

 

5;2



là

A.

1

. B.

102

. C.

92

. D.

82

.

Lời giải

Chọn C.

Ta có

2

3 6 9y x x



  

.

Phương trình

 

2

3 5;2

0 3 6 9 0

1 5;2

x

y x x

x



   





     



  





.

Tính các giá trị

       

5 3 1 2

30; 62; 30; 37

y y y y

 

   

.

So sánh các giá trị ta suy ra GTLN là

62

và GTNN là

30

.

Tổng cần tìm là

92

.

Câu 7. [1D1-1.5-3] Giá trị lớn nhất của hàm số

 

4 6

sin .cosf x x x



là

A.

5

8

. B.

108

3125

. C.

0

. D.

1

.

Lời giải

Chọn B.

Chuyển hàm đã cho về biến là

2

cos x

.

 

   

2 3

4 6 2 2

sin .cos 1 cos . cos .f x x x x x

   .

Đặt

 

     

2

2 3

cos 0;1 1 .x t f x g t t t

     

. Suy ra

     

2

3 2

' .2. 1 3 1

g t t t t t    

.

Phương trình

     

2

0 1 2 3 1 0

g t t t t t



      

 

 

  

2

1 3 5 0

t t t

   

 

0 0;1

1 0;1

3

0;1

5

t





 



  



 





.

Tính giá trị

 

g t

tại

3

0; 1;

5

t 

, ta được GTLN của hàm số là

108

3125

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 4

Câu 8. [2D1-3.4-2] Tìm giá trị nhỏ nhất của hàm số

2

3

1

x

y

x







trên đoạn

 

2;4

.

A.

 

2;4

min 6

y



. B.

 

2;4

min 2

y

 

. C.

 

2;4

min 3

y

 

. D.

 

2;4

19

min

3

y



.

Lời giải

Chọn A.

Ta có

 

2

1 2;4

2 3

' 0

3 2;4

1

x

x x

y

x



  

 

  



 





.

Do hàm số đã cho liên tục trên đoạn

 

2;4

và có

     

19

2 7; 3 6; 4

3

y y y

  

.

Suy ra

 

2;4

min 6

y



.

Câu 9. [2D1-4.4-2] Cho hàm số

 

2

3

2

x

y f x

x



 



có đồ thị (C). Khẳng định nào sau đây là đúng?

A. Đồ thị (C) có một tiệm cận đứng là đường thẳng

2

x 

và không có tiệm cận ngang.

B. Đồ thị (C) có đúng một tiệm cận đứng là đường thẳng

2

x 

và một tiệm cận ngang là

đường thẳng

0

y



.

C. Đồ thị (C) có hai tiệm cận đứng là đường thẳng

2; 2

x x

  

và một tiệm cận ngang là

đường thẳng

0

y



.

D. Đồ thị (C) có hai tiệm cận đứng là hai đường thẳng

2; 2

x x

  

và không có tiệm cận

ngang.

Lời giải

Chọn C.

Nhìn tổng quan thì rõ ràng các phương án đều nói về các tiệm cận của đồ thị hàm số, do đó ta

sẽ đi tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số.

Ta có

2

2 0

2

x





  



 





.

2

3

lim

2

x







 



;

2

3

lim

2

x







 



2

x 

là một tiệm cận đứng của đồ thị hàm số.

2

3

lim

2

x







 



;

2

3

lim

2

x







 



2

x

  

là một tiệm cận đứng của đồ thị hàm số.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 5

2

3 1

3 0

lim lim 0

2

2 1

1

x x

x

x x

x

 



  



.

2

3 1

3 0

lim lim 0

2

2 1

1

x x

x

x x

x

 



  



0

y

 

là một tiệm cận ngang của đồ thì hàm số.

Câu 10. [2D1-4.8-2] Tìm m để đồ thị hàm số

2

1

2 3 4

x

y

x mx m





  

có đúng một đường tiệm cận đứng.

A.

 

1;4

m 

. B.

 

1;4

m 

.

C.

   

; 1 4;m

    

. D.

 

5; 1;4

m  

.

Lời giải

Chọn D.

Phân tích: Đây là dạng bài tìm tiệm cận, ta cùng nhớ lại kiến thức sách giáo khoa như sau:

Đường thẳng

0

x x

được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số

 

y f x



nếu ít nhất một trong các điều kiện sau được thỏa mãn:

 

0 0

lim ; lim

x x x x

f x

 

 

   

 

0 0

lim ; lim

x x x x

f x

 

 

   

Vậy để đồ thị hàm số

2

1

2 3 4

x

y

x mx m





  

chỉ có đúng một tiệm cận đứng thì phải thỏa mãn

một trong các điều kiện trên. Nhận thấy đây là hàm phân thức có bậc tử nhỏ hơn bậc mẫu, khi

đó tiệm cận đứng

0 0

,x x x

 là giá trị làm cho đa thức dưới mẫu không xác định, do đó để đồ thị

hàm số có duy nhất một tiệm cận đứng thì phương trình

2

2 3 4 0

x mx m

   

có duy nhất một

nghiệm, hoặc phương trình

2

2 3 4 0

x mx m

   

có một nghiệm

1

x

 

và một nghiệm khác

1

.

Trường hợp 1: phương trình có duy nhất một nghiệm khi và chỉ khi phương trình có nghiệm

kép

2

4

' 0 3 4 0

1

m

m m

m





       



 



.

Trường hợp 2: phương trình có một nghiệm bằng -1 một nghiệm khác -1, khi đó ta có

   

2

1 2. 1 . 3 4 0

m m

     

5 0 5

m m

     

.

Thử lại thấy với

5

m

 

phương trình có hai nghiệm phân biệt (thỏa mãn).

Vậy đáp án của chúng ta là D.

Câu 11. [2D2-4.7-2] Độ thị bên dưới là đồ thị của hàm số nào?

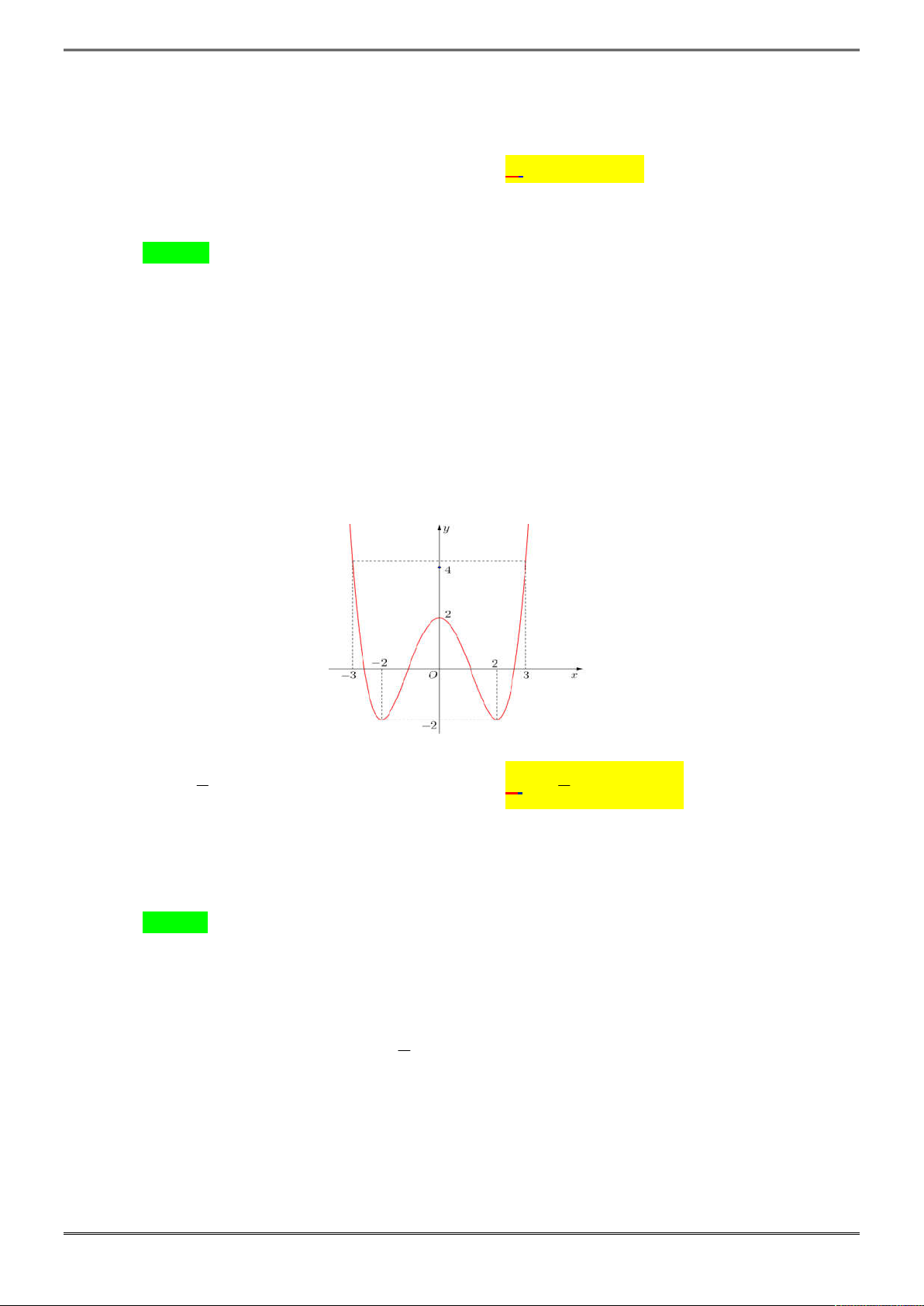
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 6

A.

3

logy x

 . B.

2

log 1y x 

. C.

2

log ( 1)

y x

 

. D.

3

log ( 1)

y x

 

.

Lời giải

Chọn C.

Dựa vào đồ thị hàm số ta thấy

 Hàm số đồng biến trên khoảng xác định.

 Đồ thị hàm số có tiệm cận đứng

x 1. 

 Đồ thị hàm số đi qua các điểm có tọa độ

   

1;1 , 3;2 .

Câu 12. [2D1-5.1-2] Xác định các hệ số

, ,a b c

để hàm số

4 2

y ax bx c  

có đồ thị như hình bên

dưới?

A.

1

, 2, 0

4

a b c

   

. B.

1

, 2, 2

4

a b c

   

.

C.

4, 2, 2

a b c

  

. D.

4, 2, 2

a b c

   

.

Lời giải

Chọn B.

Dựa vào đồ thị hàm số ta thấy



lim y 0.

x

a



   

 Hàm số có 3 cực trị, suy ra

0 0.

b

a

   

 Đồ thị hàm số đi qua điểm có tọa độ

 

0;2 2.

c

 

 Đồ thị hàm số đi qua các điểm có tọa độ

   

2; 2 , 2; 2 .  

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 7

 Hàm số đạt cực trị tại

1

2, 0 ,b 2.

4

x x a

      

Câu 13. [2D1-7.1-2] Cho hàm số:

 

3 2

: 2 6 3

C y x x

  

. Phương trình tiếp tuyến với đồ thị (C) có hệ

số góc nhỏ nhất là

A.

6 3y x 

. B.

6 7y x  

. C.

6 5y x  

. D.

6 5y x 

.

Lời giải

Chọn C.

Phương trình tiếp tuyến tại điểm

 

0 0

;M x y

của đồ thị hàm số (C) cho trước là

 

   

0

0 0

*

x

y y x x y



  

Suy ra hệ số góc của phương trình tiếp tuyến là

 

0

2

0 0 0

' 6 12 6 1 6 6

x

y x x x

      

Hệ số góc tiếp tuyến của đồ thị

 

3 2

: 2 6 3

C y x x

  

đạt nhỏ nhất là

6

khi

0

1

x



.

Thay vào (*), ta được phương trình tiếp tuyến cần tìm.

Câu 14. [2D1-6.1-1] Đường thẳng

2 2y x  

cắt đồ thị hàm số

3 2

5 7 3y x x x   

tại điểm có tung

độ là

A.

0

y



. B.

0

1

y



. C.

0

2

y



. D.

0

2

y

 

.

Lời giải

Chọn A.

Phương trình hoành độ giao điểm của hai đồ thị là

3 2

2 2 5 7 3 1 0

x x x x x y

         

.

Câu 15. [2D2-1.3-1] Cho

   

2 1

3 3

1 1

a a

 

  

. Khi đó ta có thể kết luận về

a

là

A.

1

2

a











. B.

1

2

a











. C.

1 2

a

 

. D.

2

a



.

Lời giải

Chọn D.

Điều kiện

1

a



.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 8

Ta có thể viết lại

   

2 1

3 3

1 1

a a

 

  

 

2

3

2

3

1 1

1

0

1

a a

a



  



  













 

  

2

1 2 0

1 1

2

1

a a

a



   

  



   

 







.

Kết hợp điều kiện suy ra

2

a



.

Sai lầm thường gặp: Không để ý đến điều kiện

3

1

0

1a





khi biến đổi tương đương.

Câu 16. [2D2-1.2-2] Cho biểu thức

3

4

2 3

P x x x



với x > 0. Mệnh đề nào dưới đây là đúng?

A.

5

6

.P x

 B.

2

3

.P x

 C.

5

8

.P x

 D.

3

4

.P x



Lời giải

Chọn C.

Ta có:

11

15 5

3 7

34

3

4

3

4

2 3 2

8 8

2 2

3

. .

P x x x x x x x x x x

 

    

 

 

.

Câu 17. [2D2-3.2-1] Với các số thực dương

,a b

bất kỳ. Mệnh đề nào sau đây là đúng?

A.

4

log 1 4.log log .

10

a

a b

b

 

   

 

 

B.

4

log 1 4.log log .

10

a

a b

b

 

  

 

 

C.

4

log 1 4.log log .

10

a

a b

b

 

  

 

 

D.

4

log 1 4.log log .

10

a

a b

b

 

   

 

 

Lời giải

Chọn A.

Ta có

 

4

log log log 10 4.log 1 log 1 4.log log

10

a

a b b a b

b

 

        

 

 

.

Câu 18. [2D2-3.1-1] Cho a là số thực dương,

1

a



và

3

log .

a

P a

 Mệnh đề nào dưới đây đúng?

A.

3.

P



B.

1.

P



C.

9.

P



D.

1

.

3

P



Lời giải

Chọn C.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 9

Với a là số thực dương khác 1, ta có:

1

3

log 3log 3.3.log 9

a

P a a a

   

.

Câu 19. [2D2-3.3-3] Đặt

3

log 5 .a

Mệnh đề nào sau đây đúng?

A.

15

1

log 75 .

2a 1

a







B.

15

2 1

log 75 .

a 1

a







C.

15

2 1

log 75 .

a 1

a







D.

15

2 1

log 75 .

1

a







Lời giải

Chọn B.

 

2

3

3 3

15

3 3 3

log 3.5

log 75 1 2log 5

1 2a

log 75 .

log 15 log 3.5 1 log 5 1

a



   

 

Thu gọn ta có:

15

1 2a

log 75 .

1 a







Câu 20. [2D2-4.4-4] Cho các số thực a, b thỏa mãn

1, 1

a b

 

. Tìm giá trị nhỏ nhất của biểu thức

 

2

27

2.log log 4log

2

ab ab a

P a b ab

  

.

A.

min

36.

P  B.

min

24.

P  C.

min

32.

P  D.

min

48.

P 

Lời giải

Chọn A.

Ta có

 

2

27 27 2 1

2.log log 4log 4.log 4

2 2 log log

ab ab a a

a b

P a b ab b

ab ab

 

      

 

 

.

Đặt

 

1

log 0 log

a b

t b t a

t

   

, khi đó

2 2

27 2 27 2

. 4 4 . 4 4

2 1 1 2 1

t t

P t t

t t t



   

      

   

  

   

.

Xét hàm số

 

2

27 2

. 4

2 1

t

f t t

t



 

 

 



 

với

 

0;t

 

, ta có

 

  

 

2

3

2 2 5

' ; ' 0 2

1

t t

f t f t t

t

 

   



. Dựa vào bảng biến thiên, ta thấy rằng f(t) đạt giá trị

nhỏ nhất bằng

 

min

2 32 36

f P

  

.

Câu 21. [2D2-4.1-2] Tìm tập xác định của hàm số sau:

 

2

3 2

log

1

x x

f x

x

 





A.

3 17 3 17

; 1 ;1

2 2

D

   

   

  

 

 

 

   

. B.

   

; 3 1;1

D     

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 10

C.

3 17 3 17

; 1;

2 2

D

   

   

   

 

 

 

   

. D.



 



; 3 1;D

    

.

Lời giải

Chọn C.

Ta có để hàm số xác định thì cần hai điều kiện: Điều kiện thứ nhất là điều kiện để

logarit xác định, điều kiện thứ hai là điều kiện để căn thức xác định.

Nên ta có:

2

3 2

0

1

3 2

log 0

1

x x

x

x x

x



 









 











 





   

2

2 2

; 3 1;1

3 2

log log 1

1

x

x x

x

     







 









   

2

; 3 1;1

3 2

1

x

x x

x

     







 









   

; 3 1;1

3 17 3 17

; 1;

2 2

x

    





   



   

   

 

 



 

   



3 17 3 17

; 1;

2 2

x

   

   

    

 

 

 

   

.

Câu 22. [2D2-4.2-1] Tính đạo hàm của hàm số sau:

 

x x

e e

f x

e e









.

A.

 

2

4

x x

f x

e e









. B.

 

x x

f x e e





 

.

C.

 

2

x

x x

e

f x

e e









. D.

 

2

5

x x

f x

e e









.

Lời giải

Chọn A.

Ta có

     

 

2

x x x x x x x x

x x

e e e e e e e e

e e

   





    

 





 



 



   

2 2

2 . 2 . 4

x x x x

e e e e

 

  

 

 

.

Câu 23. [2D2-4.2-2] Đạo hàm của hàm số

   

2

sin 2x.ln 1

f x x 

là

A.

   

 

2

2sin 2 .ln 1

' 2cos 2 .ln 1

1

x x

f x x x

x



  



.

B.

   

 

2

2sin 2 .ln 1

' 2cos 2 .ln 1

1

x x

f x x x

x



  



.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 11

C.

     

2

' 2cos 2 .ln 1 2sin 2 .ln 1

f x x x x x   

.

D.

     

2

' 2cos 2 .ln 1 2sin 2 .ln 1

f x x x x x   

.

Lời giải

Chọn A.

Ta có

   

 

2

' sin 2 .ln 1 'f x x x

 

     

 

2 2

sin 2 '.ln 1 sin 2 . ln 1

x x x x

   

(áp dụng công thức

 

. ' ' 'uu v u v v

 

)

   

 

2

2.cos2 x.ln 1 sin 2 .2 ln 1 '.ln 1

x x x x    

   

2

1

2cos 2 .ln 1 2sin 2 . .ln 1

1

x x x x

x



   



(chú ý rằng

 

2

' 2 '.u u u



)

 

2

2.sin 2 .ln 1

2cos 2 .ln 1

1

x x

x



  



.

Câu 24. [2D2-4.1-3] Tập xác định của hàm số

   

3 2

2 5 7

ln

12

x x

y

x

 





chứa bao nhiêu số nguyên ?

A.

8

. B.

9

. C.

10

. D.

11

.

Lời giải

Chọn A.

Hàm số đã cho xác định khi

   

3 2

2 5 7

0

12

x x

x



 















 

5

7; ; 12

2

7

5

12

5

12

2

5

12;

2

x x x

x

x x l



  







 



 

 

 



 

 









 









Trong khoảng đó có tám số nguyên. Đáp án A.

Câu 25. [2D2-5.2-2] Giải bất phương trình:

 

2

3 1

2

log log 1 1

x

 

.

A.

 

3 3

2; 2 \ ;

2 2 2 2

 

 

 

 

. B.

3 3

2; ; 2

2 2 2 2

   

  

   

   

.

C.

3

2;

2 2

x x  . D.

 

3

; 2 ;

2 2

 

   

 

 

.

Lời giải

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 12

Chọn B.

   

2 2

3 1 3 1 3

2 2

log log 1 1 log log 1 log 3

x x    

   

2 2

1 1 1

2 2 2

1

0 log 1 3 log 1 log

8

x x      

2 2

1 9 3

1 1 2 2

8 8

2 2

x x x         

Với biểu thức cuối thì ta suy ra đáp án đúng là B.

Câu 26. [2D2-6.3-2] Nghiệm của phương trình

3 3

3 log log 3 1 0

x x

  

là

A.

3, 9

x x

 

. B.

9, 27

x x

 

. C.

27, 81

x x

 

. D.

81, 3

x x

 

.

Lời giải

Chọn D.

Điều kiện

3

3 0

0 1

log 0

x

x x

x







  









.

Ta có

 

3 3 3 3 3 3

3 log log 3 1 0 3 log 1 log 1 0 log 3 log 2 0 1

x x x x x x            .

Đặt

 

3

log 0

t x t

 

, khi đó

 

1

tương đương với

3

2

3

log 1

1 3

3 2 0

2 log 4 81

x

t x

t t

t x x



 



 

     



 

  

 



.

Vậy phương trình có hai nghiệm là

81, 3

x x

 

.

Câu 27. [2D2-6.1-1] Tìm tập nghiệm của phương trình

 

3

2 4

x x



.

A.

 

4;1 .



B.

 

3 .

C.

 

1;4 .

D.

 

4;2 .



Lời giải

Chọn A.

 

   

3 4

2

1

2 2 3 4 3 4 0 4;1

4

x x

x

PT x x x x S

x







            



 



.

Câu 28. [2H1-1.1-1] Khối đa diện đều loại

 

4;3

có bao nhiêu mặt?

A.

6

. B.

12

. C.

5

. D.

8

.

Lời giải

Chọn A.

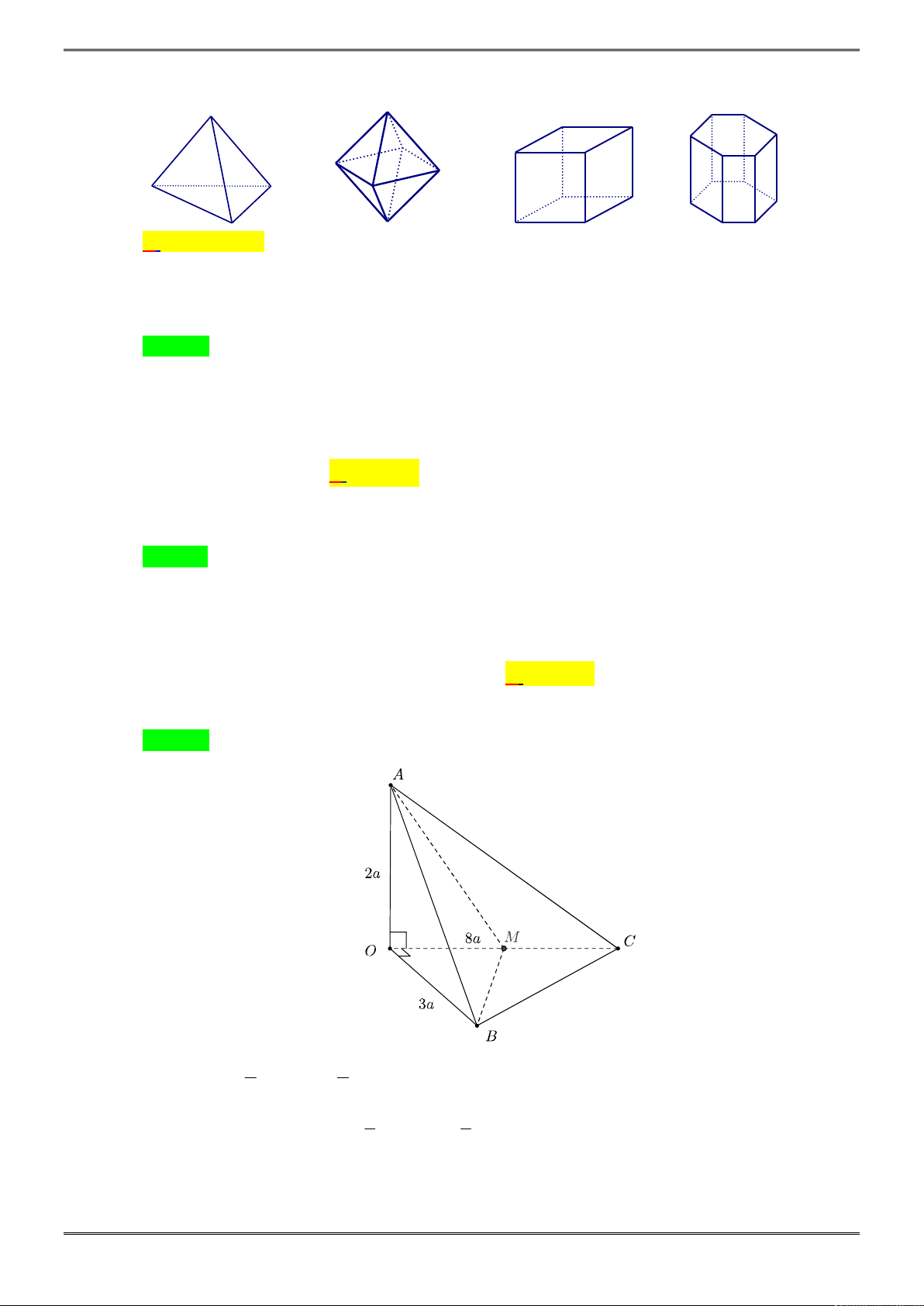
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 13

Câu 29. [2H1-1.2-2] Hình đa diện nào dưới đây không có tâm đối xứng?

A. Tứ diện đều.. B. Bát diện đều.. C. Hình lập phương. D. Lăng trụ lục giác

đều.

Lời giải

Chọn A.

Câu 30. [2H1-1.6-2] Cho hình đa diện đều loại

 

4;3

cạnh

.a

Gọi

S

là tổng diện tích tất cả các mặt

của hình đa diện đó. Mệnh đề nào dưới đây đúng?

A.

2

4 .S a

 B.

2

6 .S a

 C.

2

8 .S a

 D.

2

10 .S a



Lời giải

Chọn B.

Câu 31. [2H1-2.1-2] Cho tứ diện

.

O ABC

có

OA

,

OB

,

OC

đôi một vuông góc với nhau và

2OA a

,

3OB a

,

8OC a

.

M

là trung điểm của

.OC

Tính thể tích

V

của khối tứ diện

.

O ABM

.

A.

3

8V a



. B.

3

6V a



. C.

3

4V a



. D.

3

3V a



.

Lời giải

Chọn C.

Ta có

2

1 1

. 4 .3 6

2 2

OBM

S OM OB a a a

  

.

Vậy thể tích

2 3

. .

1 1

. .6 .2 4 .

3 3

O ABM A OBM OBM

V V S OA a a a

   

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 14

Câu 32. [2H1-2.1-2] Cho khối chóp

.

S ABCD

có đáy

ABCD

là hình chữ nhật với

,AB a

2BD a

;

Cạnh bên

SA

vuông góc với mặt phẳng đáy, góc giữa

 

mp SBD

và

 

mp ABCD

bằng

60

.

Thể tích

V

của khối chóp

.

S ABCD

là

A.

3

6

a

V 

;. B.

3

V a

. C.

3

4

a

V 

;. D.

3

2

a

V 

;.

Lời giải

Chọn B.

Ta có

   









; 60

SBD ABCD SOA

  

.

Vì

ABCD

là hình chữ nhật

,AB a

2BD a

.

nên

1

2

AC a OA AC a   

.

Ta có

.tan 60 3SA OA a

   .

 

2

2 2 2 2

. . . 2 3

ABCD

S AB BC AB AC AB a a a a     

.

Vậy

 

2 3

.

1 1

. . 3. 3

3 3

S ABCD ABCD

V SA S a a a dvtt

  

.

Câu 33. [2H1-2.4-3] Tính thể tích

V

của khối chóp

.

S ABC

có độ dài các cạnh

5 ,SA BC a 

6SB AC a 

và

7 .SC AB a 

A.

3

2 95V a

 . B.

3

35 2

2

V a



. C.

3

35

2

V a



. D.

3

2 105V a

 .

Lời giải

Chọn A.

Gọi

M

,

N

lần lượt là trung điểm của

SA

,

BC

. Khi đó ta có:

SA AN

,

CM BM

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 15

Suy ra:

MN SA

MN BC











. Mà

SA

và

BC

chéo nhau nên

 

,

MN d SA BC



.

Áp dụng công thức:

   



.

1

. . . , .sin ,

6

S ABC

V SA BC d SA BC SA BC



.

Ta có:

2 2 2 2 2 2 2

2

36 49 25 145

2 4 2 4 4

AC SC SA a a a a

MC

 

     .

 

2 2

145 25

, 30

4 4

a a

d SA BC MN MC NC a      .





. . . . . . .cos . .cos

SA BC SA BA SA AC AS AB AS AC AS AB SAB AS AC SAC

     

         

.

Mà



2 2 2 2 2 2

25 49 36 19

cos

2. . 2.5 .7 35

SA AB SB a a a

SAB

SA AB a a

   

   .



2 2 2 2 2 2

25 36 49 1

cos

2. . 2.5 .6 5

SA AC SC a a a

SAC

SA AC a a

   

  

.

Suy ra:

2

19 1

. 5 .7 . 5 .6 . 13

35 5

SA BC a a a a a

  

 

.

Lại có:

     

2

13

. . .cos , 5 .5 .cos , 13 cos ,

25

SA BC SA BC SA BC a a SA BC a SA BC    

       

.

Khi đó:

 



2 114

sin ,

25

SA BC 

.

Vậy thế tích khối chóp là:

2 3

1 2 114

.25 . 30. 2 95

6 25

V a a a 

.

Câu 34. [2H2-1.1-1] Một hình nón có bán kính đáy là

5a

, độ dài đường sinh là

13a

thì đường cao

h

của hình nón là?

A.

7 6a

. B.

12a

. C.

17a

. D.

8a

.

Lời giải

Chọn B.

Áp dụng công thức với đường sinh l, bán kính r và đường cao h thì:

2 2

1

r h 

Áp dụng công thức ta có:

2 2

1 12h r a

  

.

Câu 35. [2H1-1.3-2] Cho khối nón có thiết diện qua trục là một tam giác vuông cân và đường sinh có

độ dài bằng

a

. Thể tích khối nón là

A.

3

12

a



. B.

3

2

12

a



. C.

3

a



. D.

3

2

6

a



.

Lời giải

Chọn B.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 16

Ta có:

; 2AC AB a BD a

  

;

2

2 2

BC

DC r  

.

Thể tích của khối nón là:

2

2 3

1 1 2 2 2

.

3 3 2 2 12

r h a

  

 

 

 

 

.

Câu 36. [2H2-1.3-3] Cho hình nón đỉnh

.S

Xét hình chóp

.

S ABC

có đáy

ABC

là tam giác ngoại tiếp

đường tròn đáy của hình nón và có

10 ,AB BC a 

12AC a

góc tạo bởi hai mặt phẳng

 

SAB

và

 

ABC

bằng

0

45

. Tính thể tích khối nón đã cho.

A.

3

9

a



. B.

3

12

a



. C.

3

27

a



. D.

3

a



.

Lời giải

Chọn A.

Gọi I là tâm đường tròn nội tiếp tam giác ABC cũng là tâm đường tròn đáy của hình nón.

Gọi E là trung điểm của AC khi đó

2 2

8BE AB AE a  

.

16 3

2

ABC

S

AB BC CA

P a r

p

 

    

Dựng

 



0

45

IM AB AB SMI SMI    

Mặt khác

0

3 tan 45 3IM r a SI IM a    

Vậy

 

2 3

1

. 9

3

N

V SI r a

 

 

.

Câu 37. [2H2-2.3-2] Cho hình vuông

ABCD

quay quanh cạnh

AB

tạo ra hình trụ có độ dài của đường

tròn đáy bằng

4 .a



Tính theo

a

thể tích

V

của hình trụ này.

A.

3

4

V a





. B.

3

8

V a





. C.

3

8

3

a

V



 . D.

3

2

V a





.

Lời giải

Chọn B.

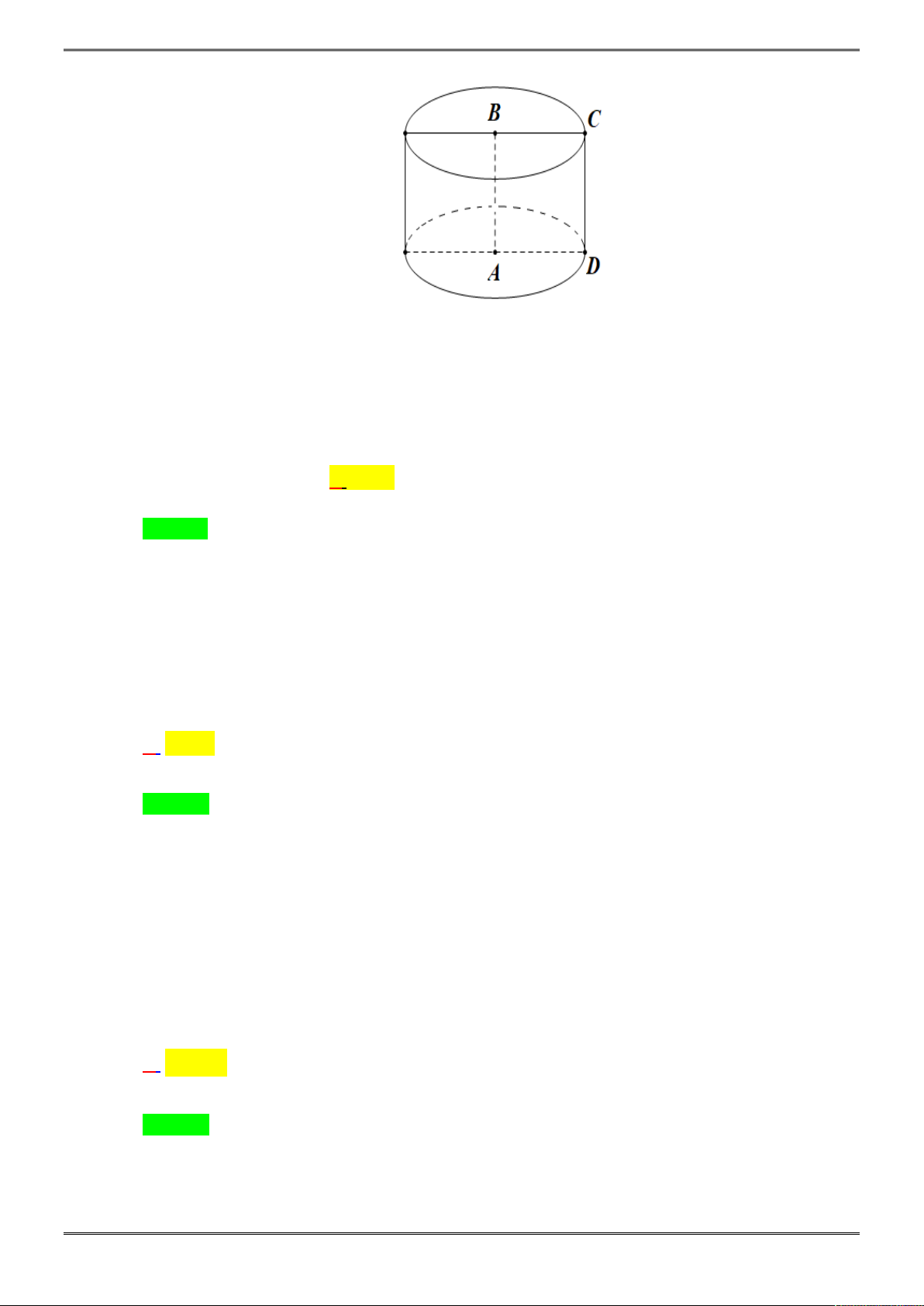
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 17

Theo đề bài, ta có

4 2 2 . 2a C R AD AD a

  

    

Vì

ABCD

là hình vuông nên

2CD AD a 

.

Thể tích khối trụ

 

2

2 3

. 2 .2 8

V R h a a a

  

  

.

Câu 38. [2H2-2.3-2] Hình trụ có bán kính đáy bằng a, chu vi của thiết Diện qua trục bằng 10a. Thể tích

của khối trụ đã cho bằng

A.

3

4 a

. B.

3

3 a

. C.

3

a

. D.

3

5 a

.

Lời giải

Chọn B.

Gọi

l h

là độ Dài đường sinh của khối trụ

Khi đó chu vi thiết Diện qua trục là

   

C 2 2r l 2 2r h 10a h 3a      

Suy ra

 

2 3

T

V R h 3 a   

.

Câu 39. [2H2-2.3-2] Cho khối trụ

 

T

có bán kính đáy bằng

R

và diện tích toàn phần bằng

2

8

R



.

Tính thể tích

V

của khối trụ

 

T

.

A.

3

6 .R



B.

3

3 .R



C.

3

4 .R



D.

3

8 .R



Lời giải

Chọn A.

Gọi

h

là đường cao của hình trụ

 

T

.

Ta có:

2 2 2 2 2 2

2 8 2 8 S 6 . 6 6

tp xq xqđ xq

S S R S R R R h RS R h

     

           

Vậy thể tích khối trụ:

2

. 6 .

đ

V h S R



 

Câu 40. [2H2-2.6-3] Cho hình trụ có tính chất: Thiết diện của hình trụ và mặt phẳng chứa trục của hình

trụ là hình chữ nhật có chu vi là 12cm. Giá trị lớn nhất của thể tích khối trụ là

A.

3

8 cm .



B.

3

16 cm .



C.

3

32 cm .



D.

3

64 cm .



Lời giải

Chọn A.

Sử dụng công thức tính thể tích

2

V r h.

 

Biến đổi đưa thể tích về hàm

số của một biến rồi tìm giá trị lớn nhất.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 18

Gọi chiều rộng, chiều dài của hình chữ nhật lần lượt là a và b. khi đó:

0 a 3; 3 b 6.   

Ta có chu vi của hình chữ nhật bằng 12 nên

 

2 a b 12 

a b 6 b 6 a.     

Để thể tích khối trụ đạt giá trị lơn hơn ta cần chọn

b

h a; r .

2

 

Khi đó:

 

2

2 3 2

b

V r h .a . 6 a .a a 12a 36a .

2 4 4

 

 

        

 

 

Đặt

   

3 2

f a a 12a 36a, a 0;3

   

   

2

a 2

f ' a 3a 24a 36; f ' a 0 a 2.

a 6





       







Bảng biến thiên:

max max

V f a 2 b 4.    

Vậy

max

V 8 . 

PHẦN II: PHẦN TỰ LUẬN

Câu 1. [2D1-3.8-2] Tìm giá trị lớn nhất của hàm số

 

2

5

x

y e x x

  

trên đoạn

 

1;3

.

Lời giải

Ta có:

 

2

5 2 1

x x

y e x x e x



    

 

2

6

x

e x x

  

.

 

2

0 6 0

x

y e x x



    

 

2 1;3

3 1;3

x

  





  





.

Vậy

 

1 5y e 

;

 

2

2 3y e 

;

 

3

y e

.

Vậy giá trị lớn nhất của hàm số trên đoạn

 

1;3

bằng

3

e

.

Câu 2. [2H1-2.8-3] Cho tứ diện

.

S ABC

có thể tích

V

. Gọi

, , ,H M N P

lần lượt là trung điểm của các

cạnh

,SA

, ,AB BC CA

. Tính thể tích khối chóp

.

H MNP

.

Lời giải

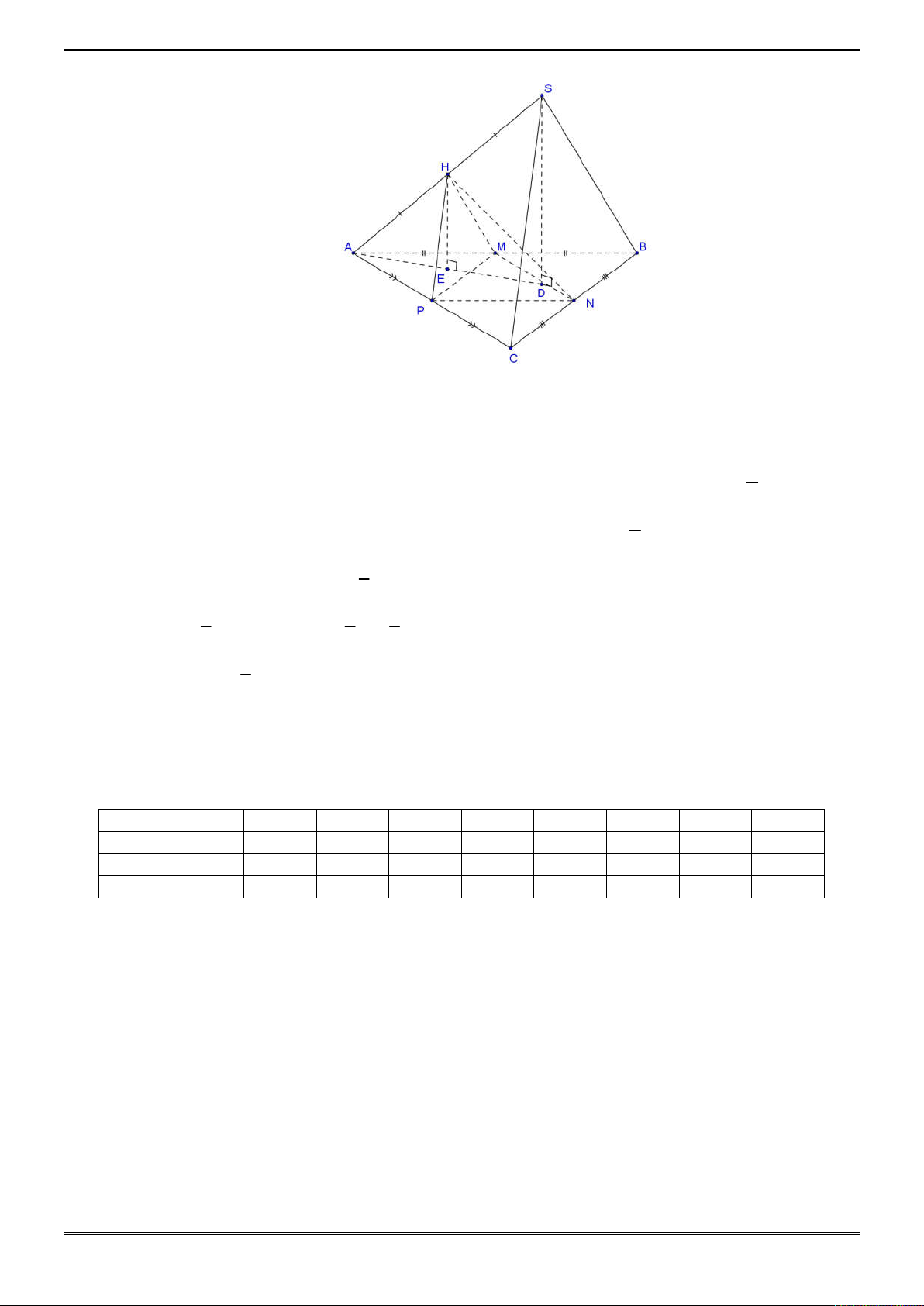
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 19

Kẻ đường thẳng

d

qua

S

và vuông góc với

 

ABC

. Gọi

 

D d ABC

 

.

Khi đó

SD

chính là đường cao của tứ diện

.

S ABC

.

Trong tam giác

ASD

, kẻ

 

HE SD E AD





 

HE ABC

 

hay

 

HE MNP



.

Do

H

là trung điểm của

AS

, nên

HE

là đường trung bình của

ASD

1

2

HE SD

 

.

Do

, ,M N P

lần lượt là trung điểm của

, ,AB BC CA

   

1

4

MNP ABC

S S

 

 

.

Theo giả thiết:

   

.

1

. .

3

S ABC ABC

V V SD S



 

 

1

.2 .4

3

MNP

V HE S



 

 

1 1

. .

8 3

MNP

V HE S



 

Hay

1

8

MNP

V V





.

BẢNG ĐÁP ÁN

1.B

2.A

3.D

4.A

5.B

6.C

7.B

8.A

9.C

10.D

11.C

12.B

13.C

14.A

15.D

16.C

17.A

18.C

19.B

20.A

21.C

22.A

23.A

24.A

25.B

26.D

27.A

28.A

29.A

30.B

31.C

32.B

33.A

34.B

35.B

36.A

37.B

38.B

39.A

40.A

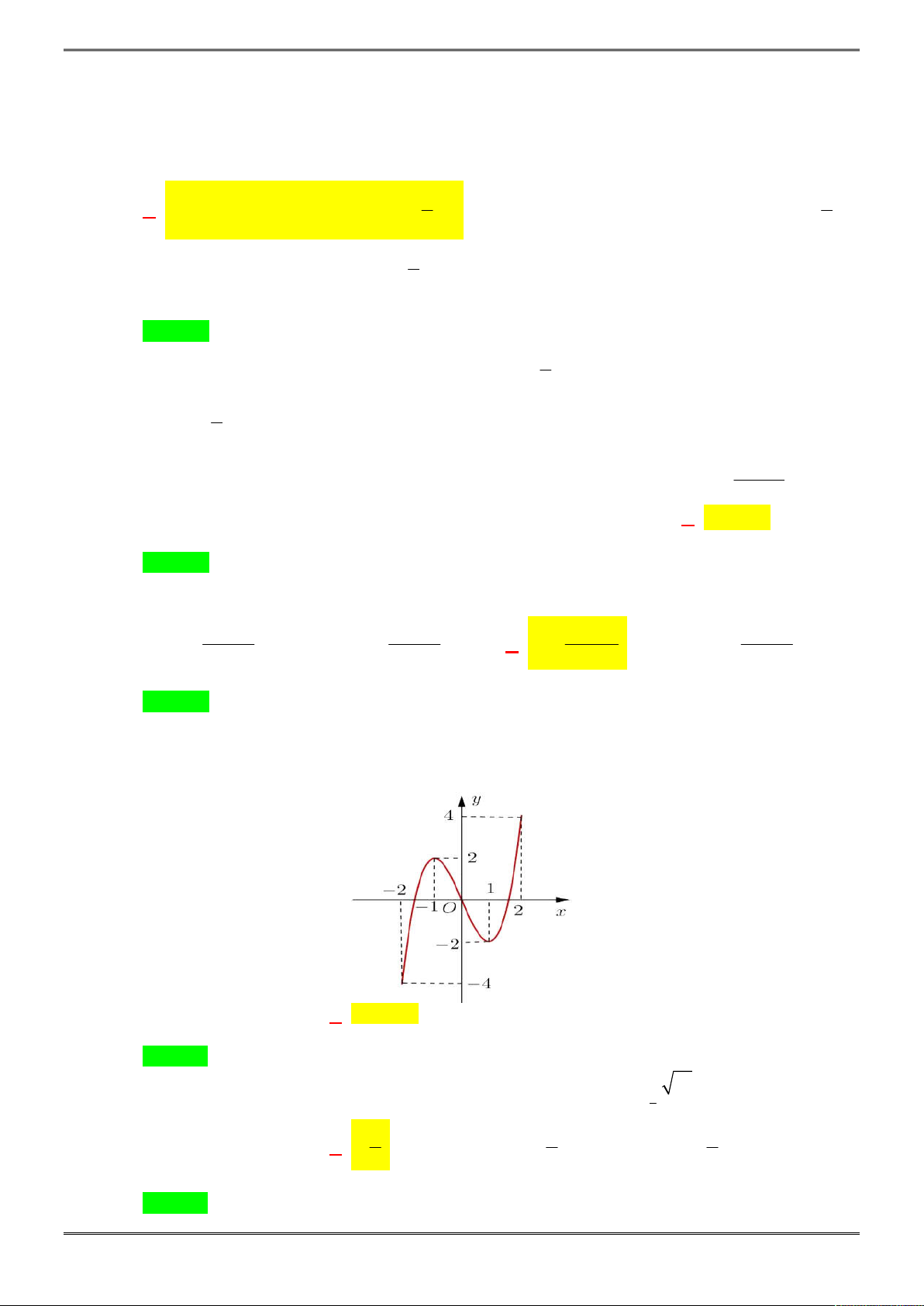
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 20

ĐỀ ÔN TẬP SỐ 12

PHẦN I: PHẦN TRẮC NGHIỆM

Câu 1. [2D1-1.4-1] Cho hàm số

3 2

2 1y x x x   

. Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng

1

;1

3

 

















 

. B. Hàm số nghịch biến trên khoảng

1

;

3

 



















 

.

C. Hàm số đồng biến trên khoảng

1

;1

3

 

















 

. D. Hàm số nghịch biến trên khoảng

 

1;



.

Lời giải

Chọn A.

  

2

' 3 4 1 1 3 1 ' 0

y x x x x y

       

khi

1

3

x

 

nên hàm số nghịch biến trên

khoảng

1

;1

3

 

















 

.

Câu 2. [2D1-4.4-1] Đường thẳng nào sau đây là tiệm cận đứng của đồ thị hàm số

2 1

1

x

y

x







?

A.

1x 

. B.

1y  

. C.

2y 

. D.

1x  

.

Lời giải

Chọn D.

1 0 1x x    

.

Câu 3. [2D1-6.1-1] Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?

A.

2 3

3 1

x

y

x







. B.

3 2

1

x

y

x







. C.

3 4

1

x

y

x







. D.

4 1

2

x

y

x







.

Lời giải

Chọn C.

Câu 4. [2D1-2.5-1] Cho hàm số

( )y f x

xác định và liên tục trên đoạn

2;2

 



 

 

và có đồ thị là đường

cong trong hình vẽ bên. Hàm số

( )f x

đạt cực đại tại điểm nào sau đây?

A.

2x  

. B.

1x  

. C.

1x 

. D.

2x 

.

Lời giải

Chọn B.

Câu 5. [2D2-3.1-1] Cho số thực

a

dương khác

1

. Giá trị của biểu thức

3

7

1

log

a

bằng

A.

4

. B.

7

3



. C.

3

7



. D.

4

3

.

Lời giải

Chọn B.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 21

1

7

3

7

3

1

7

log log

3

a

a a



  

.

Câu 6. [2D2-5.1-1] Tìm các nghiệm của phương trình

1

3 27

x



.

A.

9

. B.

3

. C.

4

. D.

10

.

Lời giải

Chọn C.

1 1 3

3 27 3 3 4

x x

x

 

    

.

Câu 7. [2D2-3.2-1] Với các số thực dương

a

,

b

bất kỳ. Mệnh đề nào dưới đây đúng?

A.

 

ln ln .lna b a b 

. B.

 

ln . ln .lna b a b

.

C.

 

ln . ln lna b a b 

. D.

 

ln ln lna b a b  

.

Lời giải

Chọn C.

Câu 8. [2H1-1.2-1] Hình đa diện nào dưới đây không có tâm đối xứng?

A. Tứ diện đều. B. Bát diện đều. C. Hình lập phương. D. Lăng trụ lục giác

đều.

Lời giải

Chọn C.

Hình tứ diện đều không có tâm đối xứng.

Câu 9. [2H1-3.2-1] Tính thể tích

V

của khối lăng trụ tam giác đều

.ABC A B C

  

có tất cả các cạnh

bằng

2a

.

A.

3

2

a

V



. B.

3

6

a

V



. C.

3

2 3

3

a

V



. D.

3

2 3V a

.

Lời giải

Chọn C.

 

2

0 2

1

2 sin 60 3

2

ABC

S a a 

Thể tích khối lăng trụ là:

2 2

2 . 3 2 3V a a a 

.

Câu 10. [2H2-1.3-1] Cho khối nón

( )N

có bán kính đáy bằng

3

và diện tích xung quanh bằng

15

.

Tính thể tích

V

của khối nón

( )N

.

A.

12V 

. B.

20V 

. C.

36V 

. D.

60V 

.

Lời giải

Chọn C.

Áp dụng công thức diện tích xung quanh hình nón:

15 15 5

xq

S Rl Rl l      

.

2 2

4h l R   

2

1 1

.9.4 12

3 3

V R h

  

   

Câu 11. [2D1-8.2-2] Với giá trị nào của

m

thì đồ thị của hàm số

4 2

y x mx 

đi qua điểm

 

2;8

?

A.

2m 

. B.

2m  

. C.

2m  

. D.

4m  

.

Lời giải

Chọn A.

Thay

2x 

,

8y 

vào

4 2

y x mx 

ta có

4 2

8 2 .2 2m m   

.

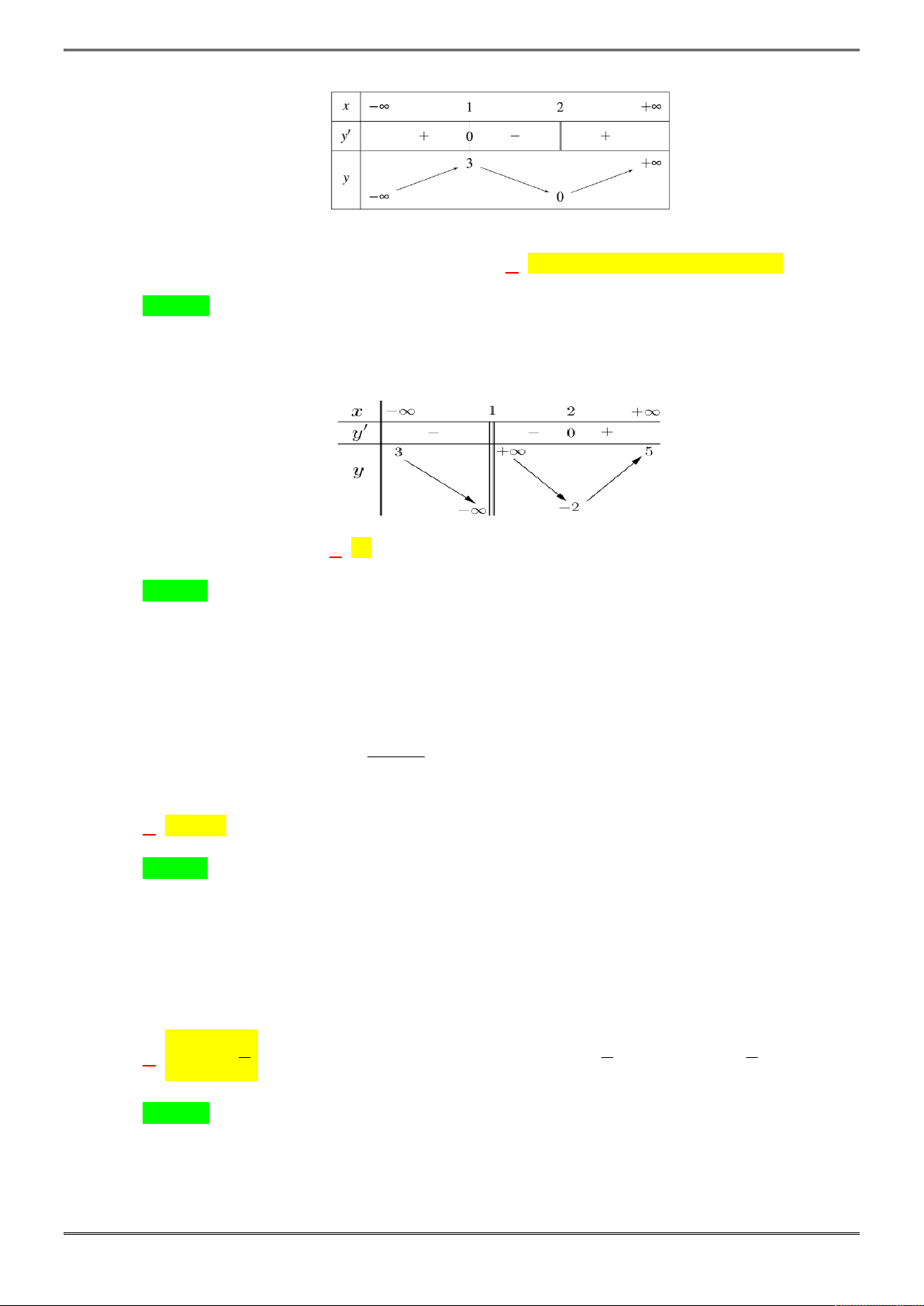
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 22

Câu 12. [2D1-2.3-2] Hàm số

( )y f x

liên tục trên



và có bảng biến thiên như hình vẽ bên dưới.

Mệnh đề nào sau đây dúng?

A. Hàm số đã cho có đúng một điểm cực trị. B. Hàm số đã cho không có giá trị cực tiểu.

C. Hàm số đã cho không có giá trị cực đại. D. Hàm số đã cho có hai điểm cực trị

Lời giải

Chọn C.

Thay

2, 8

x y

 

vào

4 2

y x mx

 

ta có

4 2

8 2 2 2

m m

   

Câu 13. [2D1-4.5-2] Cho hàm số

 

y f x

xác định trên

 

\ 1



, liên tục trên mỗi khoảng xác định và

có bảng biến thiên như sau:

Đồ thị hàm số đã cho có mấy đường tiệm cận?

A.

2

. B.

3

. C.

4

. D.

5

.

Lời giải

Chọn B.

Từ bảng biến thiên thấy được:

1

lim

x

y





 

và

1

lim

x

y





 

nên

1x 

làtiệm cận đứng của đồ thị hàm số.

lim 3

x

y





và

lim 5

x

y





nên

3, 5y y 

là các tiệm cận ngang của đồ thị hàm số.

Vậy số các đường tiệm cận là 3

Câu 14. [2D1-4.9-2] Cho hàm số

1

3

mx

y

x







có đồ thị

 

C

. Tìm

m

để giao điểm hai đường tiệm cận

đồ thị

 

C

cách gốc tọa độ một đoạn bằng

3

?

A.

0m 

. B.

1m 

. C.

3m  

. D.

3m 

.

Lời giải

Chọn B.

TXĐ:

 

\ 3

D





. Ta có tiệm cận đứng và tiệm cận ngang của

 

C

lần lượt là

3;x y m 

nên giao điểm I của hai tiệm cận có tọa độ

 

3;I m

. Từ giả thiết ta có:

2 2 2

3 9 3 9 0.IO IO m m       

Câu 15. [2D1-2.9-2] Tìm tất cả giá trị của tham số m để hàm số

 

3 2

2 1 6

y x x m x

    

có đúng

hai điểm cực trị và hai điểm đó nằm bên phải của trục tung

A.

7

1

3

m

 

. B.

1m 

. C.

7

1

3

m

 

. D.

7

3

m



.

Lời giải

Chọn A.

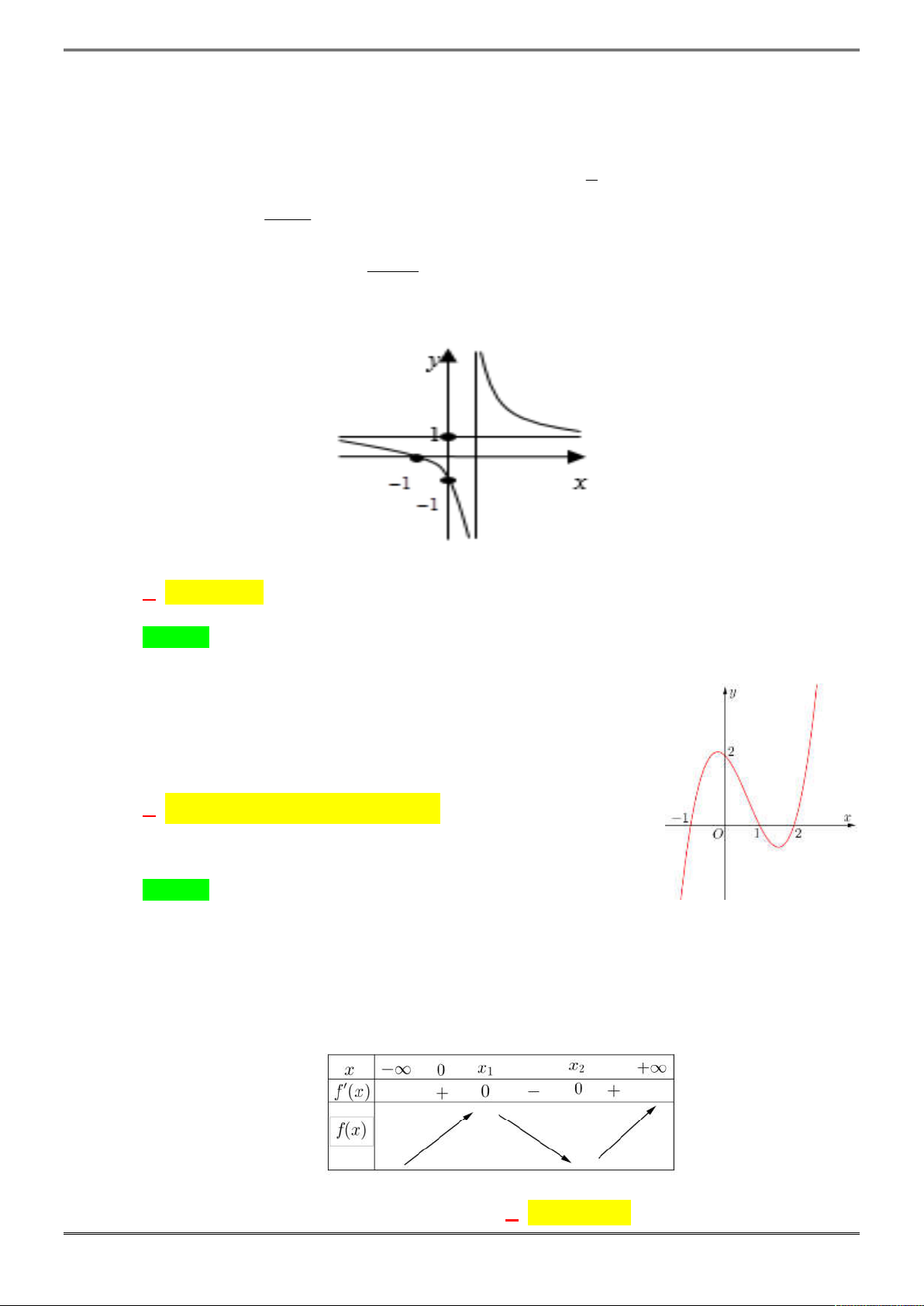
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 23

Hàm số có

2

' 3 4 1y x x m   

, hàm số có hai điểm cực trị và chúng nằm bên phải Oy khi

và chỉ khi y’ có hai nghiệm phân biệt

dương

 

' 4 3 1 7 4 0

7

4 / 3 0 1

4

1

0

3

m m

S m

m

P





      



     









 





Câu 16. [2D1-5.1-2] Cho hàm số

 

,

1

ax b

y a b

x



 





có đồ thị biểu diễn là đường cong

 

C

như

hình vẽ. Tìm a, b.

A.

1, 1a b 

. B.

1, 1a b   

. C.

1, 1a b  

. D.

1, 1a b  

.

Lời giải

Chọn A.

Tiệm cận ngang

1y 

nên

1

a



, giao với trục

Ox

tại

1

x

 

nên

1b 

.

Câu 17. [2D1-2.3-2] Cho hàm số

 

y f x



xác định và có đạo hàm

 

'f x

.

Đồ thị hàm số f'(x) như hình bên. Khẳng định nào sau đây là đúng?

A. Hàm số

 

y f x



đồng biến trên khoảng

 

;2

.

B. Hàm số

 

y f x



đồng biến trên khoảng

 

; 1 

.

C. Hàm số

 

y f x



có ba điểm cực trị.

D. Hàm số

 

y f x



nghịch biến trên khoảng

 

0;1

.

Lời giải

Chọn C.

Dựa vào đồ thị f'(x) và đáp án ta thấy

 Hàm số y = f(x) đồng biến trên các khoảng

 

1;1

và

 

2;



.

 Hàm số y = f(x) nghịch biến trên các khoảng

 

; 1 

và

 

1;2

.

 Hàm số y = f(x) có ba điểm cực trị.

Câu 18. [2D1-5.3-2] Cho hàm số

 

3 2

0

y ax bx cx d a

    

có bảng biến thiên như hình vẽ sau:

Mệnh đề nào sau đây là đúng?

A.

0; 0b c 

. B.

0; 0b c 

. C.

0; 0b c 

. D.

0; 0b c 

.

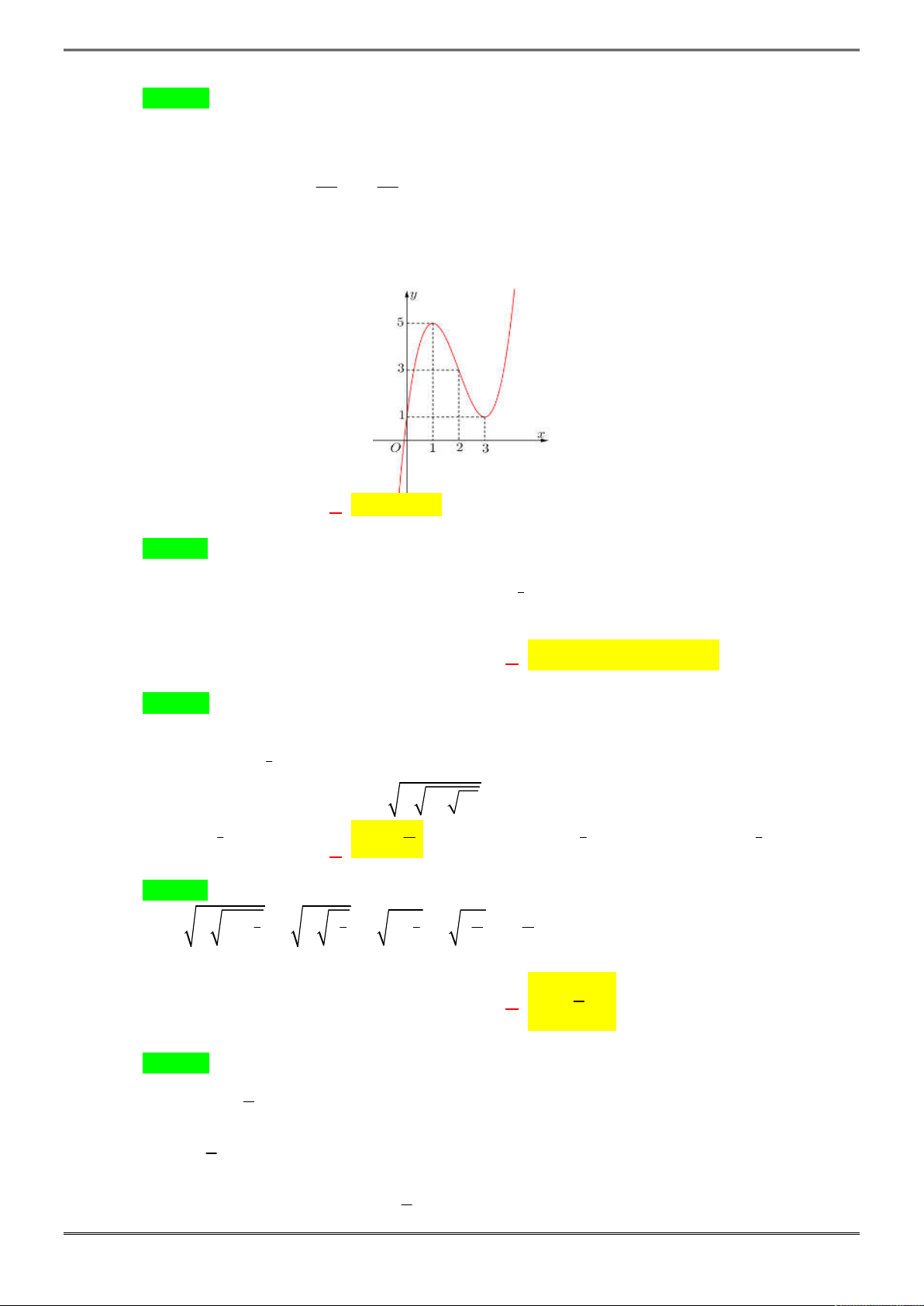
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 24

Lời giải

Chọn C.

Ta có:

2

3 2y ax bx c



  

. Từ bảng biến thiên suy ra

0a 

và hàm số có hai cực trị có

hoành độ dương.

Do đó, ta có:

2

0; 0; 0 0; 0

3 3

b c

a a

       

.

Câu 19. [2D1-6.5-2] Cho hàm số

 

y f x



có đồ thị (C) như hình bên. Tìm tất cả các giá trị thực của

tham số m để đồ thị (C) và đường thẳng

:

d y m

có 2 điểm chung đều có hoành độ lớn hơn

2

.

A.

1 3m 

. B.

1 3m 

. C.

1 3m 

. D.

1 3m 

.

Lời giải

Chọn B.

Câu 20. [2D2-4.1-2] Tìm tập xác định của hàm số

 

2

1

2

log 6 8

y x x

  

là

A.

2;4D

 



 

. B.

 

4; ;2D

 

   

 

.

C.

 

2;4D 

. D.

   

4; ;2D    

.

Lời giải

Chọn D.

Hàm số

 

2

1

2

log 6 8

y x x

  

xác định

2

4

6 8 0

2

x

x x

x







    









.

Câu 21. [2D2-1.2-2] Cho biểu thức

4

3

2 3

. .P x x x

với x>0. Mệnh đề nào dưới đây đúng ?

A.

1

2

P x

. B.

13

24

P x

. C.

1

4

P x

. D.

2

3

P x

.

Lời giải

Chọn B.

7

3 7 13 13

4 4

43 3 4

2

7

2 2 6 24

. . . .P x x x x x x x x x    

.

Câu 22. [2D2-6.2-2] Tìm tập nghiệm S của bất phương trình

A.

 

2;S

 

. B.

 

;2

S

 

. C.

1

;2

2

S

 



















 

. D.

 

1;2

S

 

.

Lời giải

Chọn C.

ĐKXĐ:

1

2

x



.

Do

1

0 1

2

 

nên BPT

1 2 1x x   

hay

2x 

Kết hợp điều kiện xác định suy ra

1

2

x

 

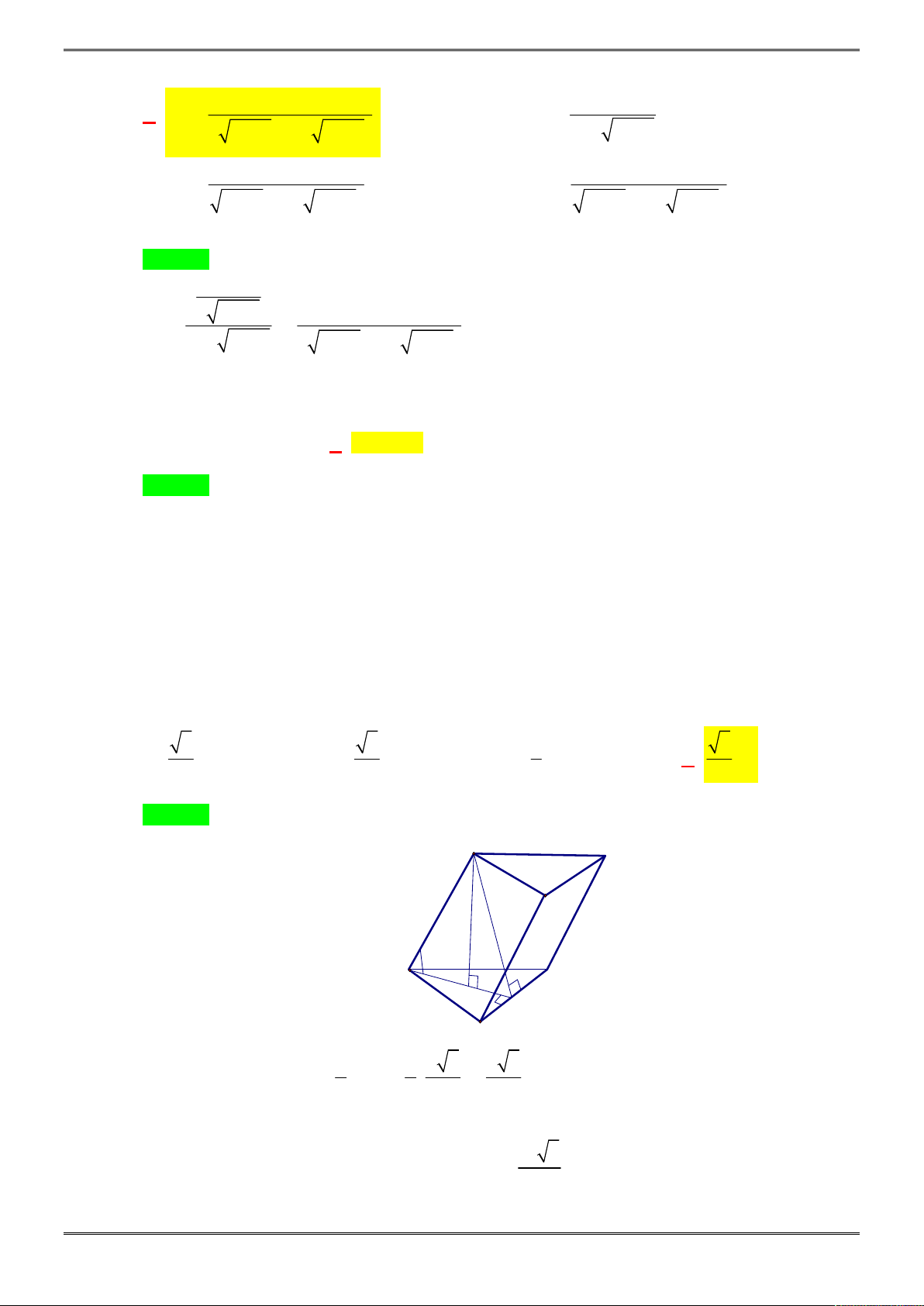
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 25

Câu 23. [2D2-4.2-2] Tính đạo hàm của hàm số .

A.

 

1

'

2 1 1 1

y

x x



  

. B.

1

'

1 1

y

x



 

.

C.

 

1

'

1 1 1

y

x x



  

. D.

 

2

'

1 1 1

y

x x



  

.

Lời giải

Chọn A.

 

1

2 1

'

1 1

2 1 1 1

x

y

x

x x



 

 

  

Câu 24. [2D2-6.3-2] Gọi x

1

, x

2

là nghiệm của phương trình

2

3

log log .log27 4 0

x x

  

. Tính giá trị

của biểu thức

1 2

log logA x x 

A.

3A 

. B.

3A  

. C.

2A  

. D.

4A 

.

Lời giải

Chọn C.

 

2

3

0

log 1

log 3 log .log 3 4 0

log 3 log 4 0

log 4

x

PT

x x

x





















 





  

  



  

  

  







 















1

2

log 1

3

log 3

x

A

x









   





 





.

Câu 25. [2H1-3.2-2] Cho khối lăng trụ có đáy là tam giác đều cạnh

a

, cạnh bên tạo với mặt đáy một

góc

0

60

và hình chiếu của một đỉnh xuống mặt đáy trùng với trọng tâm của mặt đáy đó. Tính

thể tích khối lăng trụ?

A.

3

12

a

. B.

3

8

a

. C.

3

1

2

a

. D.

3

4

a

.

Lời giải

Chọn D.

H

O

o

60

C'

A

a

B'

A'

C

B

ABC

đều nên

2 2 3 3

.

3 3 2 3

a a

AO AH  

.



0

( ' ,( )) ( ' , ) ' 60A A ABC A A AO A AO    

.

0

' .tan 60A O AO a  

.

3

. '

4

ABC

a

V S A O  

.

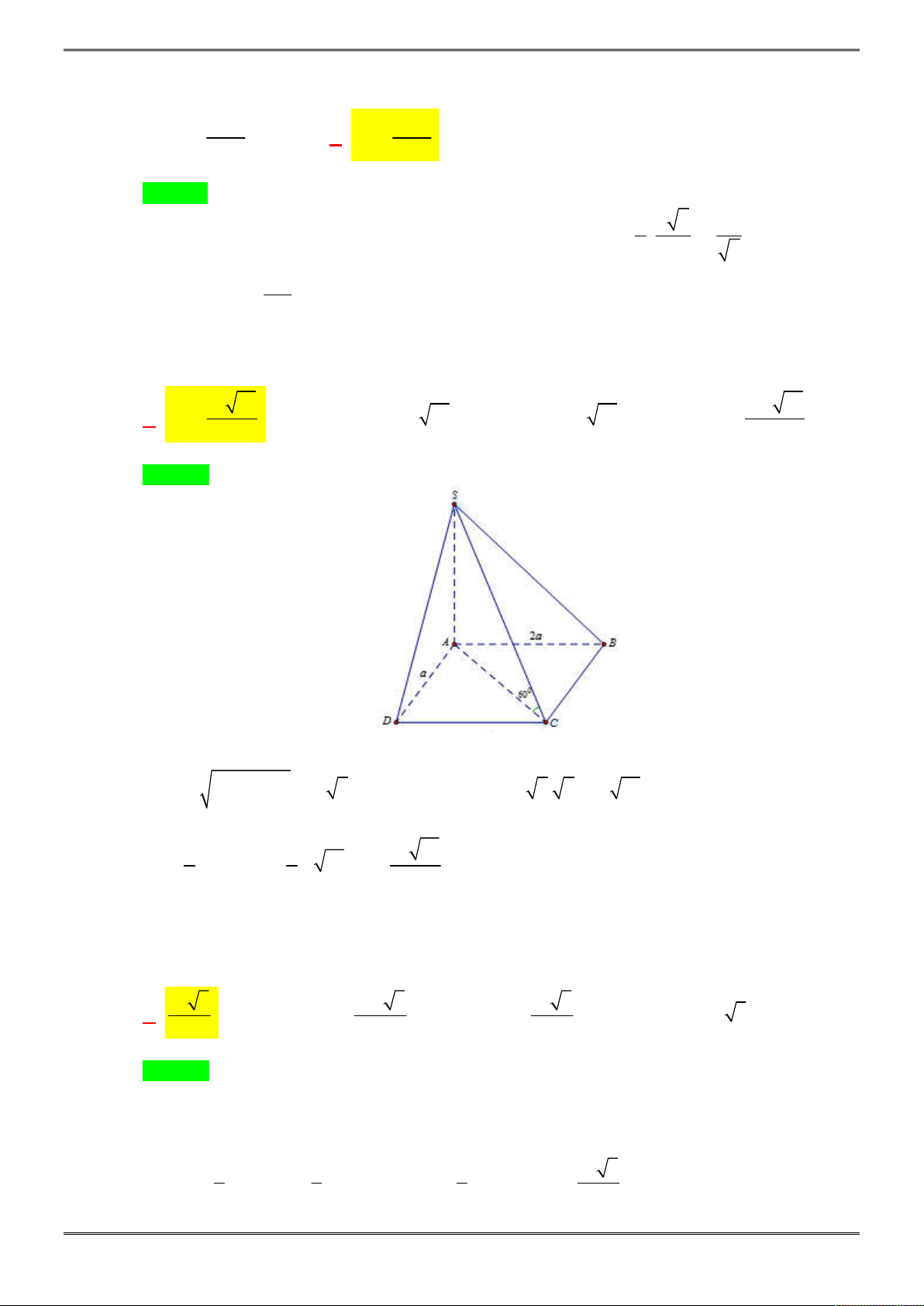
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 26

Câu 26. [2H2-2.5-2] Cho hình lăng trụ tam giác đều

. ' ' 'ABC A B C

có độ dài cạnh đáy bằng a và chiều

cao bằng h. Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho.

A.

2

9

a h

V





. B.

2

3

a h

V





. C.

2

3V a h

. D.

2

V a h

.

Lời giải

Chọn B.

Áp dụng ta sẽ tính bán kính đường tròn ngoại tiếp đáy là chính là

2 3

.

3 2

3

a a



, do đó:

2

3

a h

V R h

  

.

Câu 27. [2H1-2.1-2] Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), đáy ABCD là

hình chữ nhật có

2 ,AB a AD a 

. Cạnh bên SC tạo với mặt phẳng đáy một góc 60

0

. Tính

thể tích V của khối chóp S.ABD theo a.

A.

3

15

3

a

V



. B.

3

2 15V a

. C.

3

15V a

. D.

3

2 15

3

a

V



.

Lời giải

Chọn A.

Ta có:

2

.2 2

ABCD

S a a a 

 

2

2 0

2 5; tan 60 5. 3 15

AC a a a SA AC a a     

Thể tích của khối chóp S.ABD là:

3

2

1 1 15

. . 15.

3 3 3

ABD

a

V SAS a a

  

.

Câu 28. [2H1-2.1-2] Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình vuông có cạnh a và SA vuông

góc đáy

ABCD

và mặt bên

 

SCD

hợp với đáy một góc

60

. Tính thể tích hình chóp

.

S ABCD

A.

3

a

. B.

3

2 3

3

a

. C.

3

6

a

. D.

3

a

.

Lời giải

Chọn A.

Đáy

ABCD

là hình vuông cạnh

a

nên

2

ABCD

S a

Ta có:

   



 



; ; 60

SCD ABCD SD AD SDA

 

   

 



3

2 2

.

1 1 1 3

. .tan . .tan 60 .

3 3 3 3

S ABCD ABCD

a

V S SA a SDA AD a a    

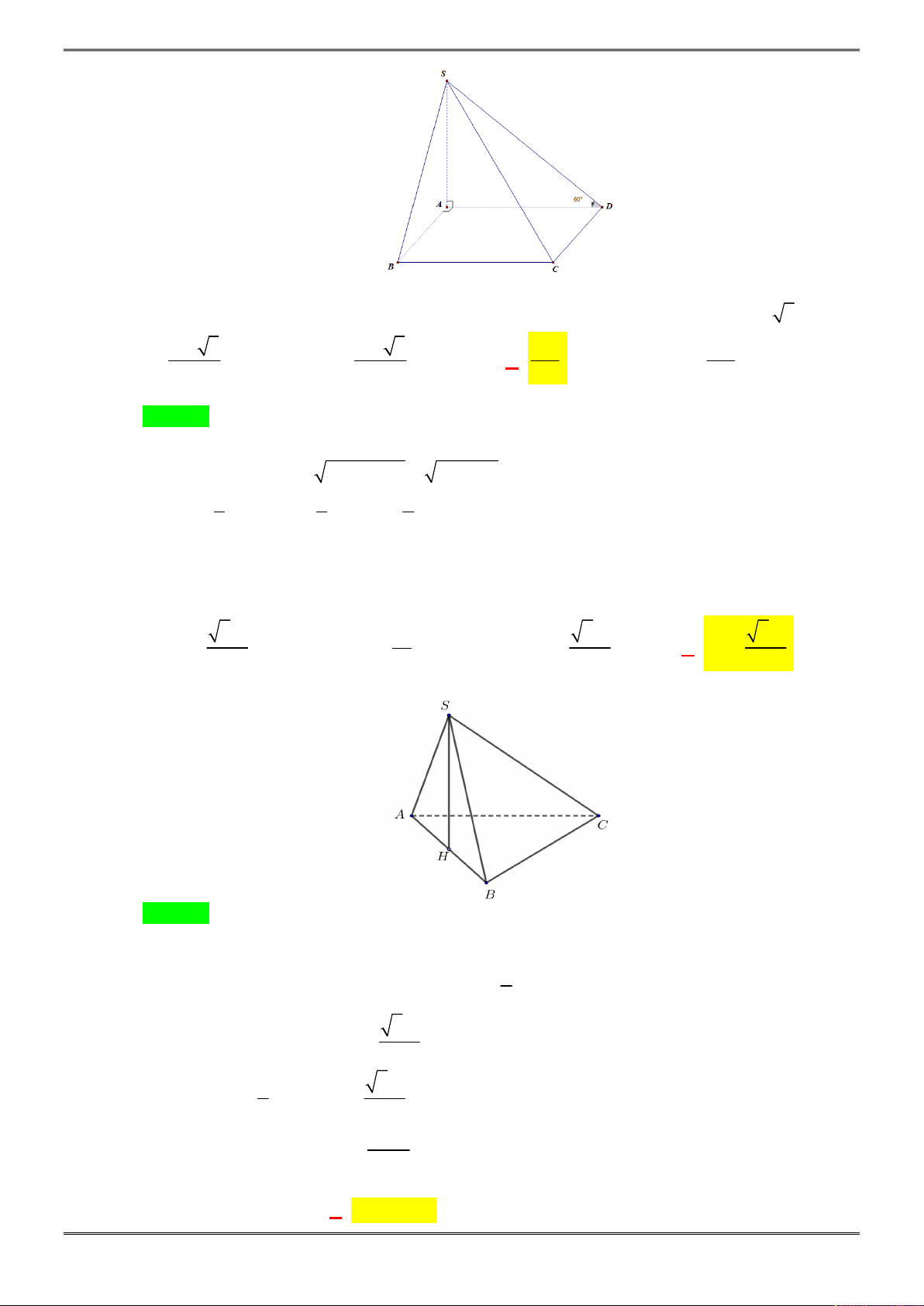
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 27

Câu 29. [2H1-2.4-2] Cho khối chóp

.

S ABCD

có đáy

ABCD

là hình chữ nhật

2 ,

AD a AB a 

. Gọi

H

là trung điểm của

AD

, biết

 

SH ABCD



. Tính thể tích khối chóp biết

5SA a



.

A.

3

2 3

3

a

. B.

3

4 3

3

a

. C.

3

4

3

a

. D.

3

2

3

a

.

Lời giải

Chọn C.

Đáy là hình chữ nhật ABCD nên

2

. 2 . 2

ABCD

S AD AB a a a

  

Xét

2 2 2 2

: 5 2SHA H SH SA HA a a a      

2 3

.

1 1 4

. .2 .2

3 3 3

S ABCD ABCD

V SH S a a a

  

Câu 30. [2H1-2.2-2] Cho hình chóp

.S ABC

có

ABC

là tam giác đều cạnh

,a

tam giác

SAB

vuông

cân tại S và nằm trong mặt phẳng vuông góc với

 

.ABC

Tính thể tích

V

của khối chóp

.ABCD

A.

3

6

a

V



. B.

3

12

a

V



. C.

3

8

a

V



. D.

3

24

a

V



.

Lời giải

Chọn D.

Dựng

,SH BC

do

     

.SAB ABC SH ABC  

Ta có

SAB

vuông cân tại S, AB=a

2

a

SH

 

ABC

đều cạnh a



2

3

.

4

ABC

a

S 

Vậy

3

.

1 3

. .

3 24

S ABC ABC

a

V SH S

 

Câu 31. [2D1-7.1-3] Cho hàm số

1

x

y

x





có đồ thị

( )C

. Tiếp tuyến của đồ thị

( )C

cắt hai trục tọa

độ lần lượt tại hai điểm phân biệt

A

,

B

sao cho tam giác

OAB

cân, có phương trình là:

A.

1y x 

. B.

4y x 

. C.

4y x 

. D.

y x

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 28

Lời giải

Chọn B.

Ta có:

2

1

0

( 1)

y

x



 



,

1x  

.

Vì tiếp tuyến của đồ thị

( )C

cắt hai trục tọa độ lần lượt tại hai điểm phân biệt

A

,

B

sao cho

tam giác

OAB

cân nên tiếp tuyến của

( )C

song song với đường thẳng

y x

.

Suy ra tiếp tuyến của

( )C

có hệ số góc

1k  

.

Gọi

 

0 0

;M x y

là tiếp điểm của

( )C

và tiếp tuyến cần tìm

0

( ) 1y x



 

(vì

0, 1y x



  

).

Ta có:

 

0 0

0

2

0 0

0

0 0 0;0

1

( ) 1 1

2 2 2;2

( 1)

x y M

y x

x y M

x



   





   



     







 Trường hợp 1:

 

0;0M

(loại vì

M O

)

 Trường hợp 2:

 

2;2M  

phương trình tiếp tuyến là:

4y x 

.

Câu 32. [2D2-4.8-3] Một người gửi vào ngân hàng 500 triệu đồng với lãi suất ban đầu 6%/năm và lãi

hằng năm được nhập vào vốn. Cứ sau một năm lãi suất lại tăng 0,5%. Hỏi sau 3 năm tổng số

tiền người đó nhận được gần nhất với giá trị nào sau đây?

A.

602

triệu. B.

604

triệu. C.

603

triệu. D.

605

triệu.

Lời giải

Chọn B.

Năm đầu người đó có

1

(1 )M A r 

Năm 2:

2

(1 )(1 0.5%)M A r r   

Năm 3:

3

(1 )(1 0, 5%)(1 1%) 500.(1 6%)(1 6,5%)(1 7%) 603,9615M A r r r          

Câu 33. [2D2-6.7-3] Gọi

S

là tập hợp các giá trị nguyên của tham số

m

để phương trình

 

2 2 2

2 1 4

2

log log 1 log 3

x x m x

   

có nghiệm thuộc



16;









. Số phần tử của tập

S

là:

A.

2

. B.

7

. C.

10

. D.

3

.

Lời giải

Chọn D.

Điều kiện

0x 

.

Đặt

2

logt x

. Do

 

16; 4;x t

 

    

 

 

. Khi đó phương trình trở thành:

 

2

2 1 3

t t m t

   

.

+ Ta thấy

3t 

không là nghiệm của phương trình.

+ Với

3t 

ta có:

  

2

2 1

, 4;

3

t t

m f t t

t

 



   







,

 



2

4 2

0, 4;

3 . 2 1

t

f x t

t t t

 





    





  

.

Bảng biến thiên:

Từ bảng biến thiên ta thấy phương trình có nghiệm khi

1 23m 

.

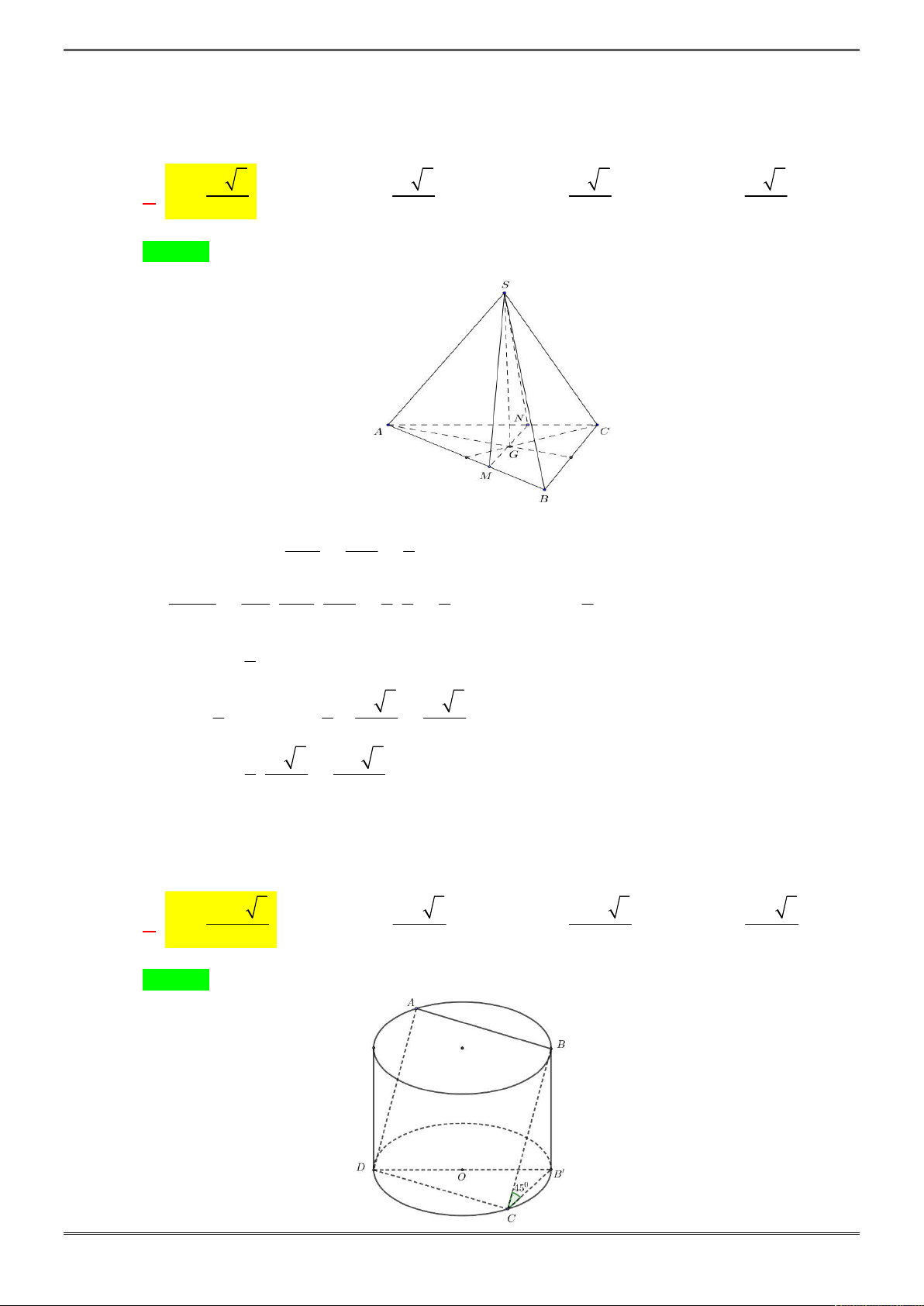
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 29

Vậy

S

có số phần tử là

3

.

Câu 34. [2H1-2.3-3] Cho hình chóp đều

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

, góc giữa cạnh

bên và mặt đáy là

0

60

. Đường thẳng qua trọng tâm

G

của tam giác

ABC

và song song cạnh

BC

cắt hai cạnh

,AB AC

tại

, .M N

Tính thể tích

V

khối chóp

SMNCB

A.

3

27

a

V



. B.

3

18

a

V



. C.

3

48

a

V



. D.

3

24

a

V



.

Lời giải

Chọn A.

Vì

2

/ /

3

AM AN

MN BC

AB AC

  

2 2 4 4

. . .

3 3 9 9

ASMN

ASMN ASBC

ASBC

V

AS AM AN

V V

V AS AB AC

     

5

.

9

SMNCB SABC

V V 

2 3

1 1 3 3

. . . .

3 3 4 12

SABC ABC

a a

V SG S a

  

(đvtt)

3 3

5 3 5 3

.

9 12 108

SMNCB

a a

V  

(đvtt).

Câu 35. [2H2-2.3-3] Bên trong khối trụ (T) có một hình vuông ABCD cạnh bằng a mà hai đỉnh A, B

nằm trên đường tròn đáy thứ nhất, hai đỉnh C, D nằm trên đường tròn đáy thứ hai của hình trụ.

Mặt phẳng chứa hình vuông tạo với mặt đáy hình trụ một góc

0

45

. Tính thể tích V của khối trụ

(T).

A.

3

3 2

16

a

V





. B.

3

2

16

a

V





. C.

3

3 2

8

a

V





. D.

3

2

8

a

V





.

Lời giải

Chọn A.

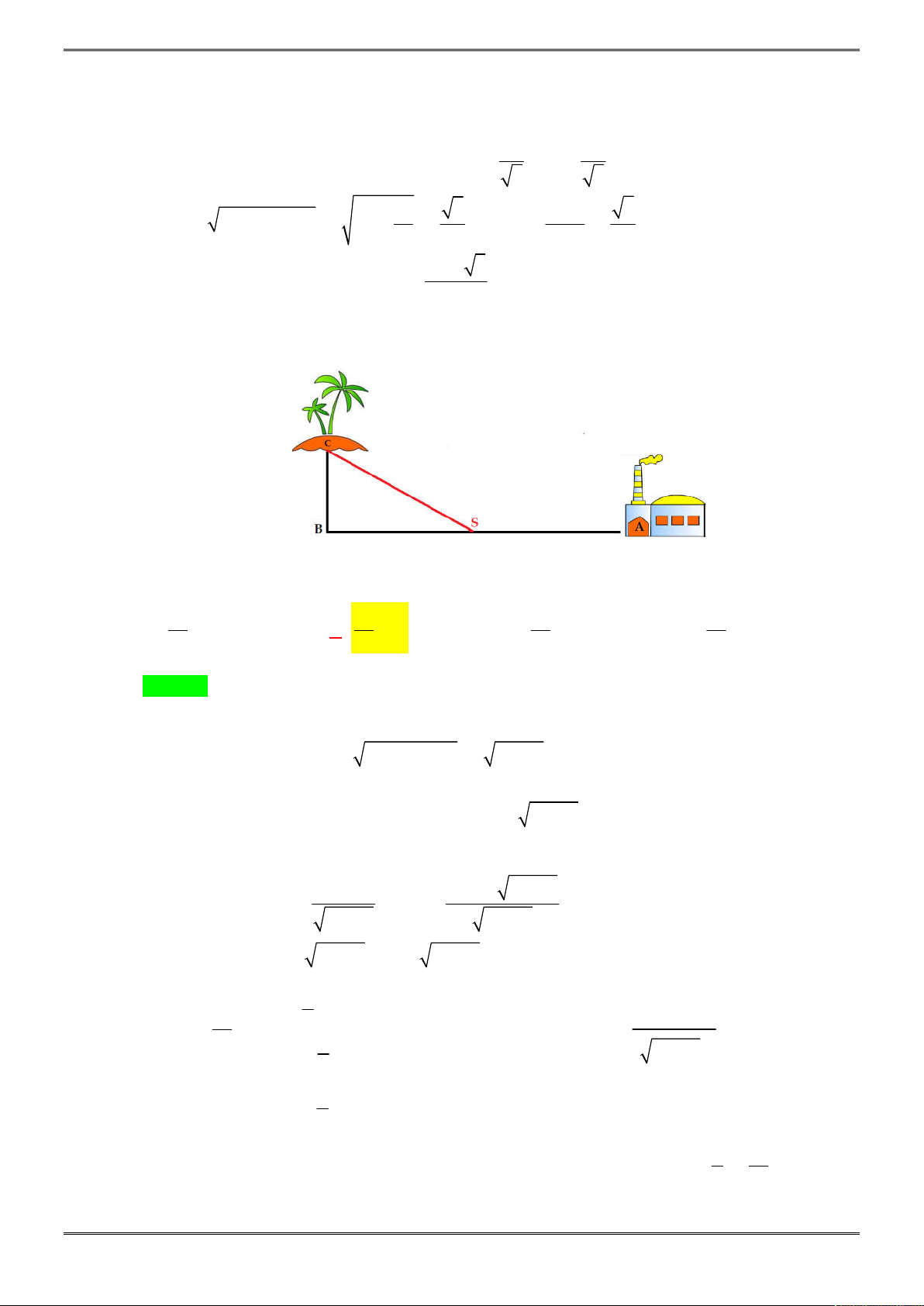
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 30

Kẻ đường sinh BB’. Ta có

', 'DC BB DC CB DC CB   



DB’ là đường kính của

đường tròn đáy.

Góc giữa mp(ABCD) và (B’CD) bằng góc

 

0

' ' 45BCB BCB 

1

' '

2 2

a

h BB B C BC    

2

2 2 2

6

' '

2 2

a

B D CD CB a a

    

' 6

2 4

B D

R a

  

Thể tích khối trụ (T) là

3

2

3 2

16

a

V R h



 

.

Câu 36. [2D1-3.14-4] Một đường dây điện được nối từ một nhà máy điện ở

A

đến một hòn đảo

C

và

khoảng cách ngắn nhất từ

B

đến

C

là 1 km, khoảng cách từ

B

đến

A

là

4

km được minh

họa bằng hình vẽ sau:

Biết rằng mỗi km dây điện đặt dưới nước chi phí mất 5000 USD, còn đặt dưới đất chi phí mất

3000 USD. Hỏi điểm S trên bờ cách A bao nhiêu để khi mắc dây điện từ A qua S rồi đến C là

chi phí là ítnhất ?

A.

15

4

km

. B.

13

4

km

. C.

10

.

4

km

. D.

19

4

km

.

Lời giải

Chọn B.

Gọi

 

x km

là khoảng cách từ

S

đến tới điểm

 

0 4

B SB x x km

   

. Khi đó

 

2 2 2

4 1

SA x km SC BC BS x

      

(km)

Chi phí mắc dây điện từ

A

qua

S

rồi đến

C

là:

   

2

3000 4 5000 1 ,C x x x

   

với

0 4x 

Bài toán trở thành tìm giá trị nhỏ nhất của hàm số

 

C x

với

0 4x 

 

2

2 2

5000 5 3 1

' 3000 1000

1 1

x x x

C x

x x

 



 







    













 

 

 

2 2 2 2

' 0 5 3 1 3 1 5 9 1 25 0 4

C x x x x x x x do x           

 

2

3

9

4

0 4

3

16

4

x tm

x do x

x ktm









    



 





.Lại có:

 

3

2

5000

'' 0, 0;4

1

C x x

x

   



.

Do đó

 

0;4

3

min 16000

4

C x C

 







 











 

(USD).

Vậy, để chi phí ít tốn kém nhất thì điểm

S

phải cách

A

là

3 13

4

4 4

AB BS km

   

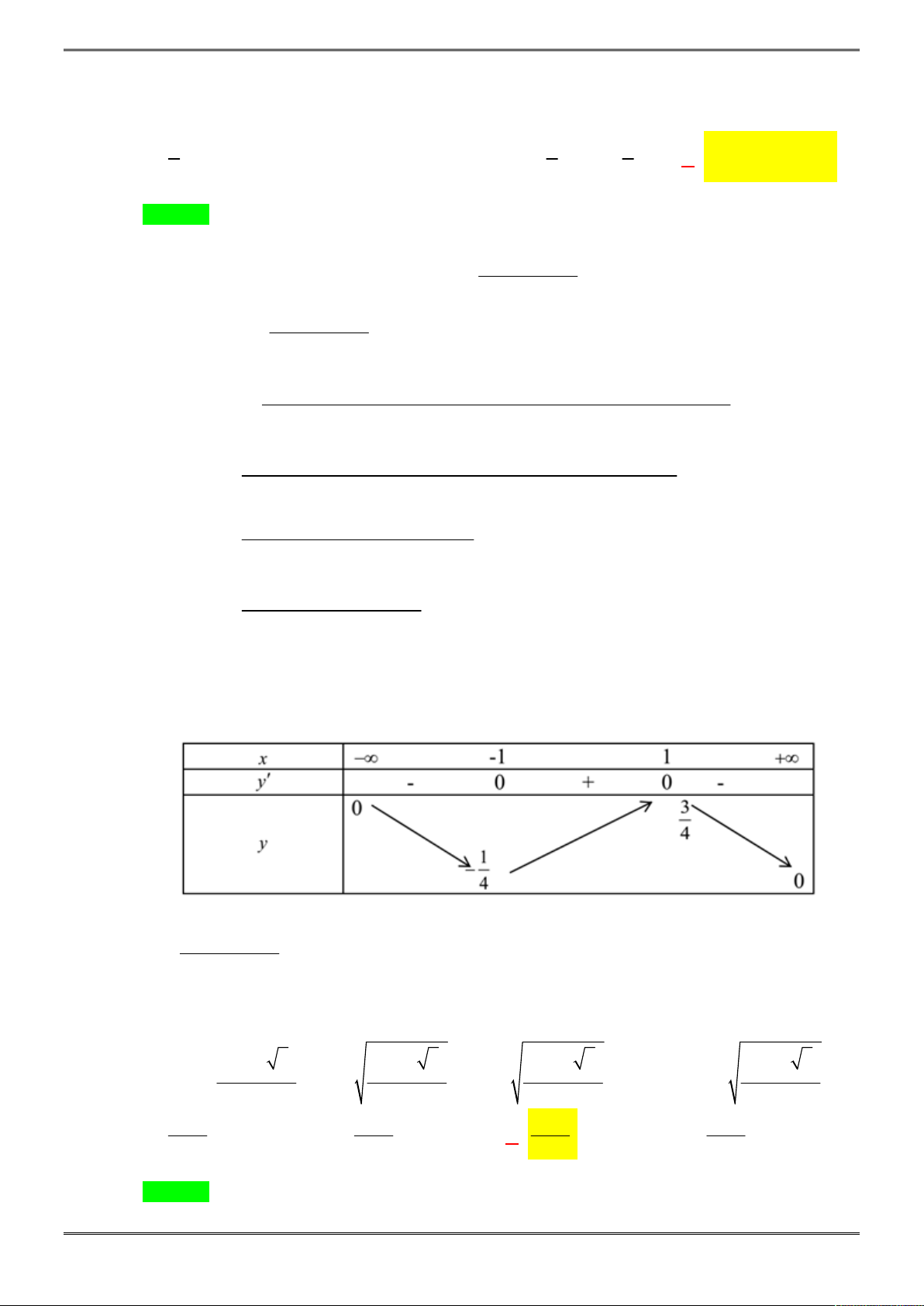
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 31

Câu 37. [2D1-6.3-4] Phương trình

 

2

3 2

1 1

x x x m x   

có bốn nghiệm thực phân biệt khi và

chỉ khi:

A.

1

2

4

m

 

. B.

1 3m  

. C.

1 3

4 4

m

  

. D. Không tồn tại

m

.

Lời giải

Chọn D.

TXĐ:

D  

Ta có

 

3 2

2

3 2

4 2

1 1

2 1

x x x

x x x m x m

x x

 

     

 

(1)

Xét hàm số

3 2

4 2

2 1

x x x

y

x x

 



 

xác định trên



.

      

 

     

 

  

 

3 2 4 2 3 2 4 2

2

4 2

2 4 2 3 2 3

2

4 2

6 5 4 2

2

4 2

2

4 2

2 1 2 1

2 1

3 2 1 2 1 4 4

2 1

2 2 1

2 1

1 2 1

2 1

x x x x x x x x x x

y

x x

x x x x x x x x x

x x

x x x x x

x x

x x x

x x

 

        





 

       



 

     



 

   



 

  

4 2

1

0 1 2 1 0

1

x

y x x x

x









       



 





Bảng biến thiên

Phương trình (1) có bốn nghiệm thực phân biệt khi đường thẳng

y m

cắt đồ thị hàm số

3 2

4 2

2 1

x x x

y

x x

 



 

tại bốn điểm phân biệt. Từ BBT ta thấy không có

m

thỏa mãn yêu cầu.

Câu 38. [2D2-3.1-4] Cho

0; 0a b 

thỏa điều kiện:

 

9 12 16

log log log

a b a b  

. Giá trị của biểu

thức

       

2018

2017

3

4 8 16

2

1 5 1 5 1 5 1 5

log log log ... log

a a a a

S

b b b b

   

    

là:

A.

1

2017

. B.

2018

2017

. C.

2017

2018

. D.

1

2018

.

Lời giải

Chọn C.

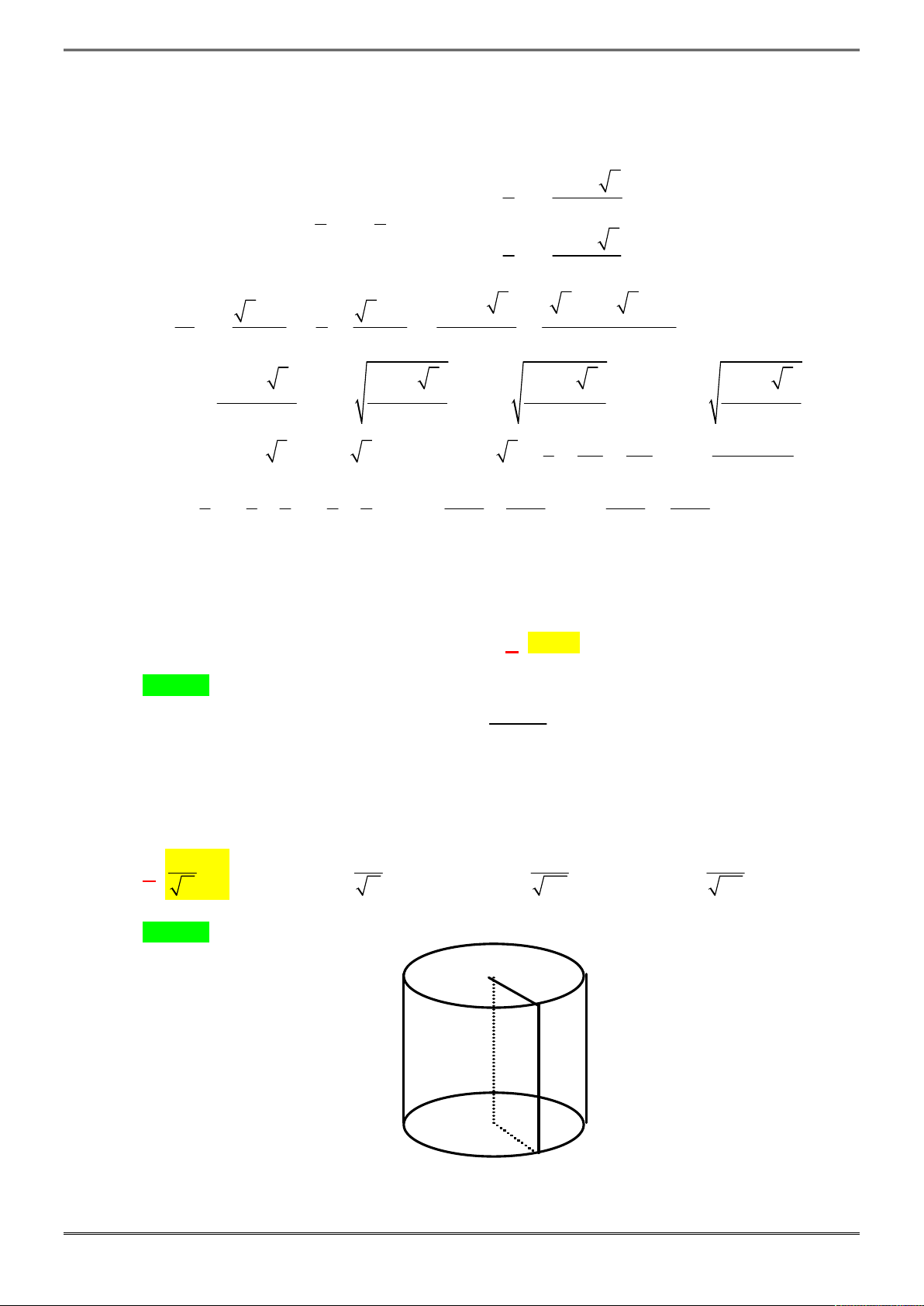
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 32

Đặt

 

9 12 16

9

log log log 12

16

t

a

a b a b t b

a b









     





 





 

2

3 1 5

3 3

4 2

9 12 16 1 0

4 4

3 1 5

4 2

t

t t

t t t

t

vn



 

 



















   





 



 

 

 

       

 



 

 

 

 

 

   



 























 



    

1 5 5 1 5 1

9 5 1 5 1

2

12 2 2 2

t

a

b b

  

 

 







      











 

       

2018

2017

3

4 8 16

2

1 5 1 5 3 5 1 5

log log log ... log

a a a a

S

b b b b

   

   

2018

2017

3

4 8 16

2

log 2 log 2 log 2 ... log 2

    

1 1 1 1

...

2 2.3 3.4 2017.2018

    

1 1 1 1 1 1 1

1 ...

2 2 3 3 4 2017 2018

       

   

   

   

        

   

   

   

   

   

       

1 2017

1

2018 2018

  

Câu 39. [2D2-4.9-4] Số lượng của loại vi khuẩn A trong một phòng thí nghiệm được tính theo công

thức

( ) (0).2 ,

t

s t s

trong đó

(0)s

là số lượng vi khuẩn A lúc ban đầu,

( )s t

là số lượng vi

khuẩn A có sau t (phút). Biết sau 3 phút thì số lượng vi khuẩn A là 625 nghìn con. Hỏi sau

bao lâu, kể từ lúc bắt đầu, số lượng vi khuẩn A là 10 triệu con ?

A. 48 phút. B. 19 phút. C. 7 phút. D. 12 phút.

Lời giải

Chọn C.

Theo giả thiết

   

3

625000

62500 0 .2 0

8

s s   

khi số vi khuẩn là 10 triệu con thì

 

7

10 0 .2 2 128 7

t t

s t

    

(phút)

Câu 40. [2H2-2.7-4] Một nhà sản suất cần thiết kế một thùng đựng dầu nhớt hình trụ có nắp đậy với

dung tích là

3

2000

dm

. Để tiết kiệm nguyên liệu nhất thì bán kính của nắp đậy phải bằng bao

nhiêu.

A.

3

10

dm



. B.

2

20

dm



. C.

3

10

2

dm



. D.

3

20

2

dm



.

Lời giải

Chọn A.

A’

O’

’

O

R

h

A

h

Để tiết kiệm nguyên liệu nhất thì diện tích toàn phần của hình trụ phải nhỏ nhất

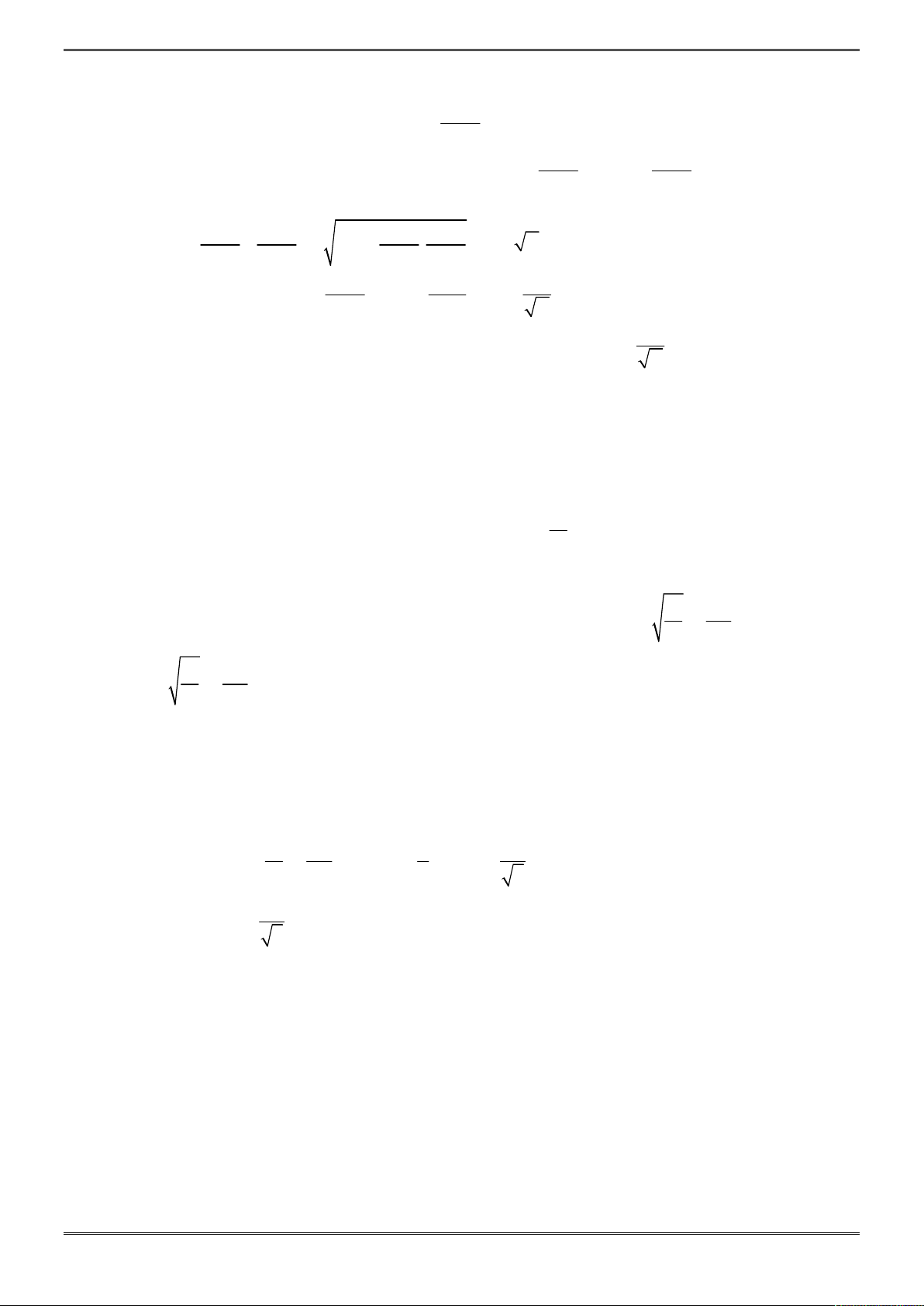
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 33

Gọi bán kính nắp đậy và chiều cao của hình trụ lần lượt là

 

x dm

và

 

h dm

Thể tích hình trụ là

2

2000

2000 x h h

x



  

Diện tích toàn phần

2 2 2

2

2000 4000

2 2 2 2 . 2

tp

S x xh x x x

x x

    



     

Áp dụng bất đẳng thức Côsi cho 3 số dương:

2 2

3

2000 2000 2000 2000

2 3 2 . . 600x x

x x x x

  

   

Stp nhỏ nhất

2 3

3

2000 1000 10

2 x x x

x



     

Vậy để tiết kiệm nguyên liệu nhất thì bán kính nắp đậy phải bằng

3

10



PHẦN II: PHẦN TỰ LUẬN

Câu 1. [2D1-2.14-3] Cho hàm số

4 2

1y x mx m   

( )

m

C

,

m

là tham số thực. Tìm

m

để

( )

m

C

có ba điểm cực trị lập thành một tam giác có một góc bằng

120



.

Lời giải

Ta có:

3 2

2

0

4 2 2 (2 ) 0

2

x

y x mx x x m

m

x







 

     









Hàm số có ba điểm cực trị

0y



 

có ba nghiệm phân biệt

0m 

.

Với

0m 

thì đồ thị

( )

m

C

có ba điểm cực trị là:

(0; 1)A m 

,

2

; 1

2 4

m m

B m

 









   









 

và

2

; 1

2 4

m m

C m

 









  









 

.

Suy ra hai điểm

B

và

C

đối xứng với nhau qua trục tung. Do đó, tam giác

ABC

cân tại

A

.

Suy ra



120BAC 



.

Áp dụng định lí côsin trong tam giác

ABC

, ta có:



2 2 2 2 2

2 . .cos 3BC AB AC AB AC BAC BC AB    

4

3

8 2

2 3

2 16 3

3

m m

m m m

 







      







 

(thỏa mãn điều kiện).

Kết luận:

3

2

3

m 

là giá trị cần tìm.

Câu 2. [2H1-2.3-4] Cho hình chóp tam giác đều

.S ABC

có cạnh đáy bằng

a

, cạnh bên hợp với đáy

một góc

60



. Gọi

M

,

N

lần lượt là trung điểm của

AB

,

BC

. Tính theo

a

thể tích khối chóp

.S ABC

và khoảng cách từ điểm

C

đến mặt phẳng

( )SMN

.

Lời giải

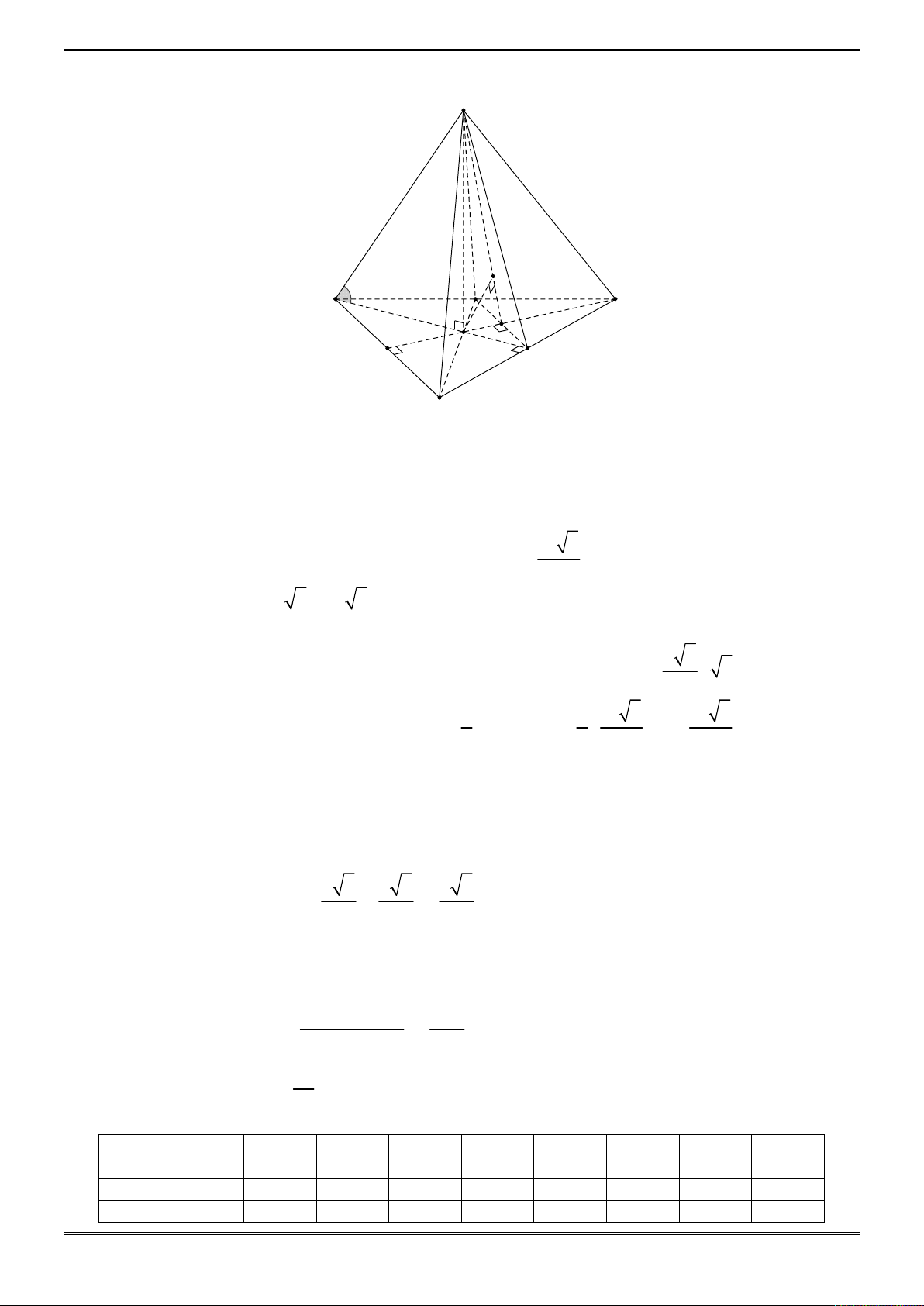
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 34

H

K

I

N

M

C

B

A

S

Gọi

H

là tâm của tam giác đều

ABC

, ta có:

( )SH ABC

.

Suy ra

AH

là hình chiếu vuông góc của đường thẳng

SA

trên mặt phẳng

( )ABC

. Do đó, ta có



SAH

là góc giữa đường thẳng

SA

và mặt phẳng

( )ABC

. Suy ra



60SAH 



.

Tam giác

ABC

đều cạnh

a

nên có diện tích

2

3

4

ABC

a

S





và

2 2 3 3

3 3 2 3

a a

AH AN   

Tam giác

SAH

vuông tại

H

có



60SAH 



3

.tan 60 3

3

a

SH AH a    



.

Vậy thể tích khối chóp

.S ABC

là:

2 3

.

1 1 3 3

.

3 3 4 12

S ABC ABC

a a

V S SH a



    

(đvtt).

Gọi

I AH MN 

, ta có:

( ) ( ) ( )

//

AH BC

AH MN MN SAH SMN SAH

MN BC









     







theo giao tuyến

SI

.

Trong mặt phẳng

( )SAH

, kẻ

HK SI

tại

K

, ta có:

 

( ) ;( )HK SMN HK d H SMN  

.

Ta có:

3 3 3

3 4 12

a a a

HI BH IB    

.

Tam giác

SHI

vuông tại

H

có

HK

là đường cao

2 2 2 2

1 1 1 49

7

a

HK

HK SH HI a

     

.

Ta có:

 

   

;( )

( ) 3 ;( ) 3 ;( ) 3

;( )

d C SMN

CM

CH SMN M d C SMN d H SMN HK

HM

d H SMN

       

.

Vậy

 

3

: ( )

7

a

d C SMN 

.

BẢNG ĐÁP ÁN

1.A

2.D

3.C

4.B

5.B

6.C

7.C

8.A

9.C

10.A

11.A

12.D

13.B

14.A

15.A

16.A

17.C

18.C

19.B

20.D

21.B

22.C

23.A

24.B

25.D

26.B

27.A

28.A

29.C

30.D

31.B

32.B

33.D

34.A

35.A

36.B

37.D

38.C

39.C

40.A

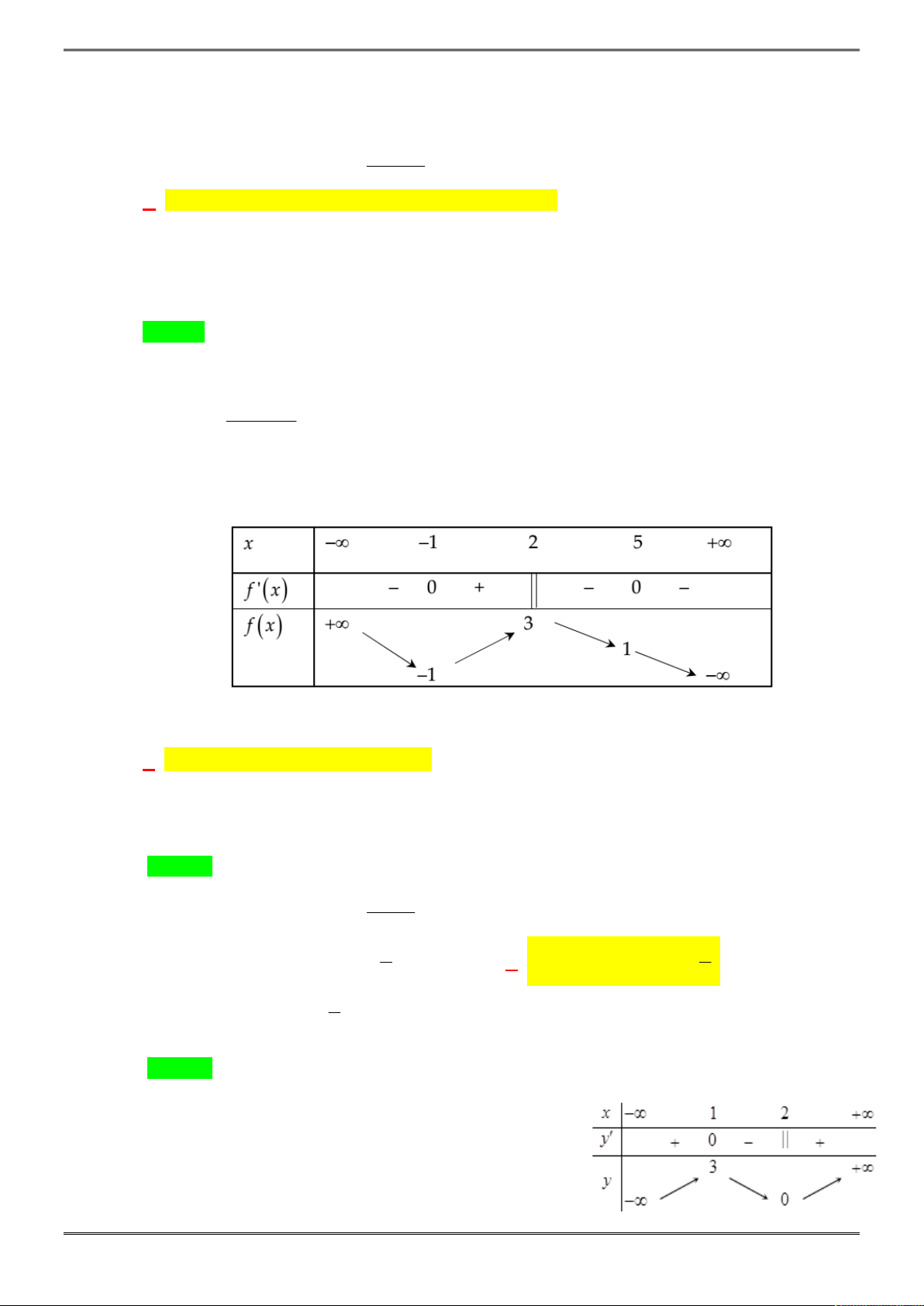
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 35

ĐỀ ÔN TẬP SỐ 13

PHẦN I: CÂU HỎI TRẮC NGHIỆM.

Câu 1. [2D1-1.1-1] Cho hàm số

3 1

4 2

x

y

x





 

. Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số luôn nghịch biến trên từng khoảng xác định.

B. Hàm số luôn nghịch biến trên



.

C. Hàm số đồng biến trên các khoảng

 

; 2



và

 

2;



.

D. Hàm số nghịch biến trên các khoảng

 

; 2 

và

 

2;

 

.

Lời giải

Chọn A

Tập xác định của hàm số là

 

\ 2

D  

Ta có

 

2

10

' 0,

2 4

y x D

x



   



Vậy hàm số luôn nghịch biến trên từng khoảng xác định.

Câu 2. [2D1-2.3-1] Cho hàm số

 

y f x



xác định và liên tục trên

.

Ta có bảng biến thiên sau:

Khẳng định nào sau đây đúng?

A. Hàm số

 

y f x



có 1 cực đại và 2 cực tiểu.

B. Hàm số có 1 cực đại và 1 cực tiểu.

C. Hàm số

 

y f x



có đúng 1 cực trị.

D. Hàm số

 

y f x



có 2 cực đại và 1 cực tiểu.

Lời giải

Chọn B.

Câu 3. [2D1-4.3-1] Cho hàm số

4 5

3 2

x

y

x







có đồ thị là (C ). Khẳng định nào sau đây là đúng?

A. (C) có tiệm cận ngang

5

.

2

y

 

. B. (C) có tiệm ngang

4

.

3

y



.

C. (C) có tiệm đứng

3

.

2

x



. D. (C) không có tiệm cận.

Lời giải

Chọn B.

Câu 4. [2D1-1.3-1] Cho hàm số

 

y f x



có bảng biến thiên

như hình vẽ bên. Mệnh đề nào sau đây là sai?

A. Hàm số đã cho đồng biến trên khoảng

 

2;

 

.

B. Hàm số đã cho đồng biến trên khoảng

 

3;

 

.

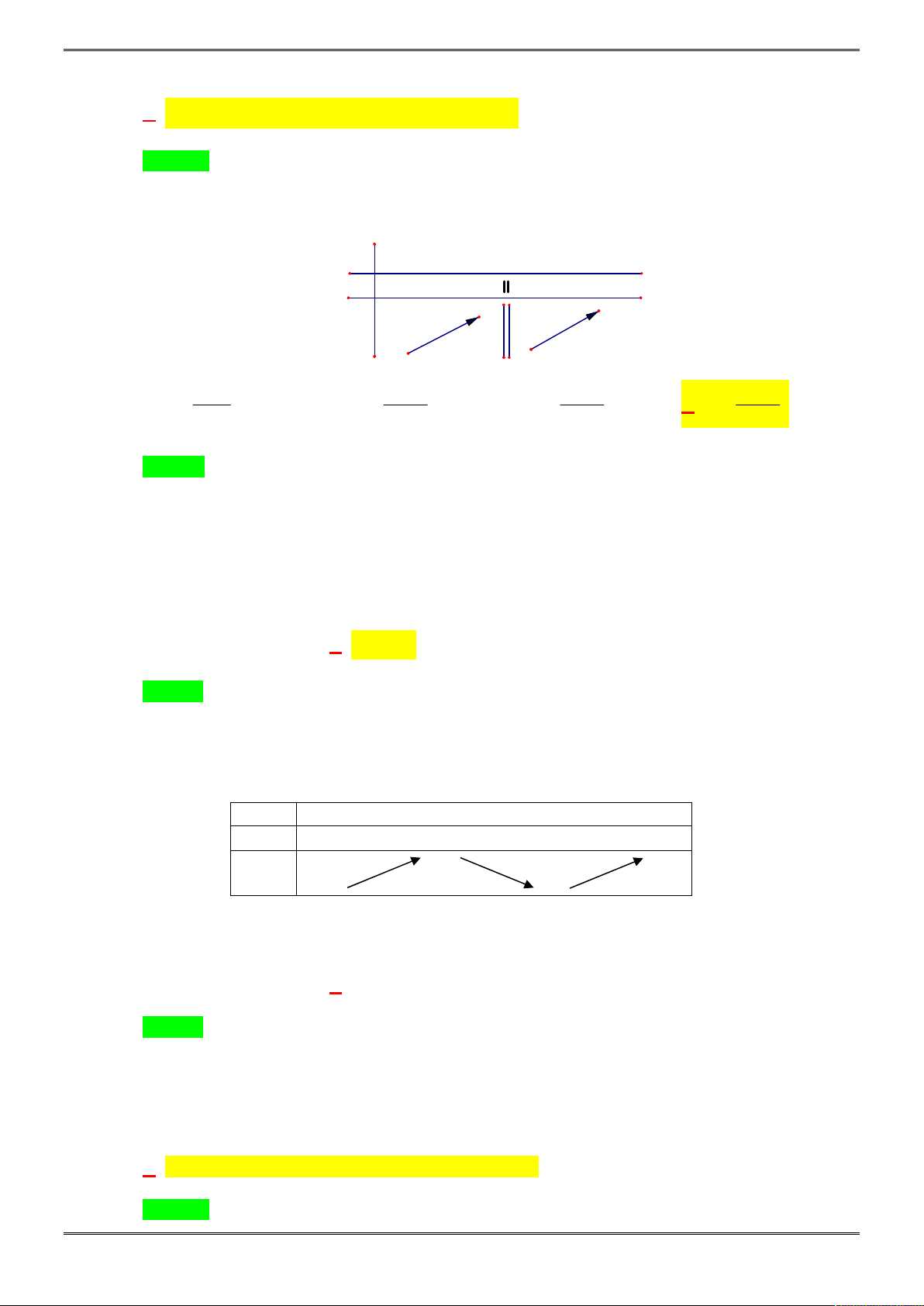
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 36

C. Hàm số đã cho đồng biến trên khoảng

 

; 1



.

D. Hàm số đã cho nghịch biến trên khoảng

 

0; 3

.

Lời giải

Chọn D.

Dựa vào bảng biến thiên.

Câu 5. [2D1-1.2-1] Bảng biến thiên sau đây là của hàm số nào?

2

++

-1

-∞

+∞

-∞

y

y'

x

A.

2

1

x

y

x



 



B.

1

2 1

x

y

x



 



C.

2 1

1

x

y

x



 



D.

2 1

1

x

y

x



 



Lời giải

Chọn D

Dựa vào bảng biến thiên, ta có

Hàm số nhận

2

y



làm tiệm cận ngang.

Hàm số nhận

1

x

 

làm tiệm cận đứng.

Hàm số đồng biến, tức có

0

y





.

Câu 6. [2D1-2.6-1] Giá trị cực tiểu

CT

y

của hàm số

 

3 2

- 3 4

y x x

là.

A.

 1

CT

y

. B.

 0

CT

y

. C.

 4

CT

y

. D.

 2

CT

y

.

Lời giải

Chọn B

 

2

' 3 6 .y x x

 



  

 



  





0 0 4

' 0

2 2 0

x y

y

x y

x



0

2



( )f x





0



0



( )f x

4





0

 

  2 0

CT

y y

.

Câu 7. [2D-6.1-1] Giải phương trình

 

4

log 1 3

x

 

.

A.

63

x



. B.

65

x



. C.

80

x



. D.

82

x



.

Lời giải

Chọn B

Phương trình tương đương

3

1 4 64 65

x x     

.

Câu 8. [2H1-2.8-1] Chọn khái niệm đúng

A. Hai khối đa diện có thể tích bằng nhau thì bằng nhau.

B. Hai khối lăng trụ có chiều cao bằng nhau thì thể tích bằng nhau.

C. Hai khối chóp có hai đáy là hai tam giác đều bằng nhau thì thể tích bằng nhau.

D. Hai khối đa diện bằng nhau có thể tích bằng nhau.

Lời giải

Chọn D.

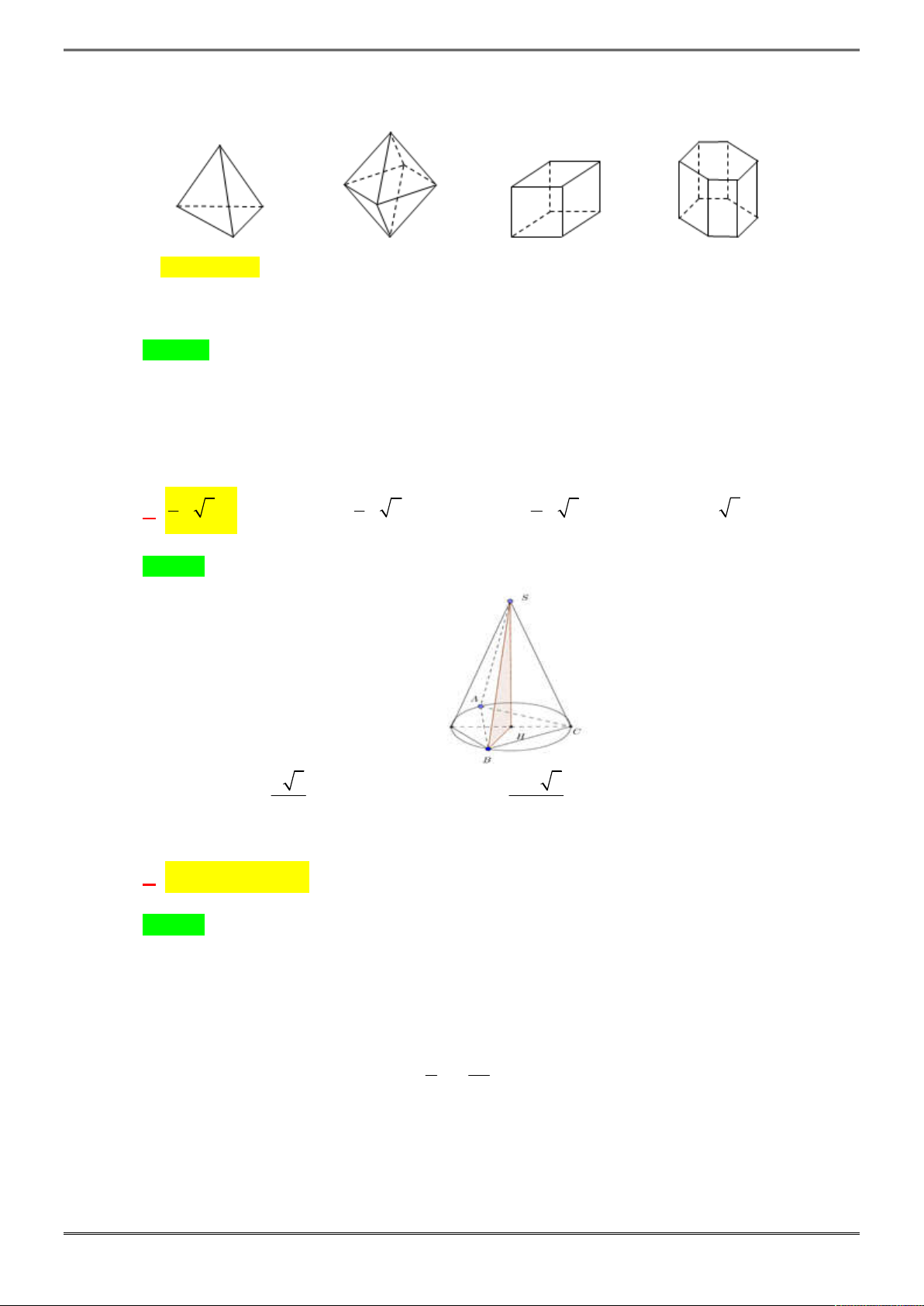
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 37

Câu 9. [2H1-1.2-1] Hình đa diện nào dưới đây không có tâm đối xứng?

A. Tứ diện đều. B. Bát diện đều.

C. Hình lập phương. D. Lăng trụ lục giác đều.

Lời giải

Chọn A.

Dễ dàng thấy bát diện đều, hình lập phương và lăng trục lục giác đều có tâm đối xứng. Còn tứ

diện đều không có tâm đối xứng.

Câu 10. [2H2-1.2-1] Một hình tứ diện đều có cạnh bằng

a

, có một đỉnh trùng với đỉnh của hình nón,

ba đỉnh còn lại nằm trên đường tròn đáy của hình nón. Khi đó diện tích xung quanh của hình

nón là

A.

2

1

3

a



. B.

3

1

2

3

a



. C.

2

1

3

2

a



. D.

2

3a



.

Lời giải

Chọn A

Ta có:

3

a

r BH 

,

l SA a 

2

3

xq

a

S rl



  

.

Câu 11. [2D2-6.10-2] Điều kiện xác định của phươg trình

2

log (2 7 12) 2

x

x x

  

là:

A.

   

0;1 1;x

  

. B.

 

;0

x 

. C.

 

0;1

x

. D.

 

0;x

 

.

Lời giải

Chọn A

Biểu thức

2

log (2 7 12)

x

x x 

xác

định

2

0 0

1 1 (0;1) (1; )

7 47

2 7 12 0

2 ( ) 0

4 16

x x

x x x

x x

x







 



 

       

 

 

  

 





  

 



 



.

Câu 12. [2D2-4.7-2] Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt

kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 38

x

y

1

2

1

O

A.

2

logy x

 . B.

1

2

logy x

 . C.

2

log

y x



. D.

 

2

log 2y x



Lời giải

Chọn A

Nhận thấy đây là đồ thị hàm số

log

a

y x

 . Điểm

1

; 1

2

 



 

 

thuộc đồ thị hàm số nên

1

1 1 1 1

1 log 2

2 2 2

a

a a

a



       

. Hàm số là

2

logy x

 .

Câu 13. [2D1-1.5-2] Tất cả các giá trị của tham số

m

để hàm số

  

3 2

- 3 4

y x mx x

đồng biến trên



là.

A.

2 2m  

. B.

3 3m  

. C.

3m 

. D.

3m  

.

Lời giải

Chọn B

Ta có:

  

2

' 3 2 3

y x mx

Hàm số đồng biến trên R

 

    

' 0,y x x

          

2

' 0, 9 0x m x

 

  

 

3; 3

m

.

Câu 14. [2D1-2.1-2] Cho hàm số

 



y f x

có đạo hàm cấp hai trên

 

a; b

và

 



0

;x a b

khẳng định

nào sau đây là khẳng định đúng?

A. Nếu

 

0

' 0

f x



và

 

0

" 0

f x



thì

0

x

là điểm cực tiểu của hàm số.

B. Nếu hàm số đạt cực tiểu tại

0

x

thì

 

0

' 0

f x



và

 

0

" 0

f x



.

C. Nếu

 

0

' 0

f x



và

 

0

" 0

f x



thì

0

x

là điểm cực tiểu của hàm số.

D. Nếu

0

x

là điểm cực trị của hàm số thì

 

0

' 0

f x



và

 

0

" 0

f x



.

Lời giải

Chọn A.

Câu 15. [2D2-1.3-2] Với điều kiện nào của

a

thì

   

2 1

3 3

1 1

a a

 

  

?

A.

2

a



. B.

1

a



. C.

1 2

a

 

. D.

0 1

a

 

.

Lời giải

Chọn A

Ta có

2 1

3 3

  

, kết hợp với

   

2 1

3 3

1 1

a a

 

  

. Suy ra hàm số đặc trưng

 

1

x

y a 

đồng

biến.Do đó suy ra cơ số

1 1 2

a a

   

.

Câu 16. [2D2-5.3-2] Gọi

1 2

,x x

là 2 nghiệm của phương trình

2 2

1 2

1

4 log 2 log

x x

 

 

. Khi đó

1 2

.x x

bằng:

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 39

A.

1

2

. B.

1

8

. C.

1

4

. D.

3

4

.

Lời giải

Chọn B

[Phương pháp tự luận]

Điều kiện:

0

4

1

16

x



















.

Đặt

2

logt x

 ,điều kiện

4

2

t

 









. Khi đó phương trình trở thành:

2

1

1 2

2

1 3 2 0

2 1

4 2

4

x

t

t t

t

t t

x







 



       



 

 











Vậy

1 2

1

.

8

x x



[Phương pháp trắc nghiệm]

Dùng chức năng SOLVE trên máy tính bỏ túi tìm được 2 nghiệm là

1

2

và

1

4

.

Câu 17. [2D2-4.10-2] Cho ba số thực dương

, ,a b c

khác

1.

Đồ thị các hàm số

log , log , log

a b c

y x y x y x

   được cho trong hình vẽ sau:

Mệnh đề nào dưới đây đúng?

A.

.b c a 

. B.

.a b c 

. C.

.c a b 

. D.

.a c b 

Lời giải

Chọn A.

Do đồ thị hàm số

log

a

y x

 đi lên từ trái sang phải trên khoảng

 

0;



nên hàm số đồng biến,

suy ra

1.

a



Mặc khác đồ thị hàm số

log ; log

b c

y x y x

  đi xuống từ trái sang phải trên khoảng

 

0;



nên hàm số nghịch biến, suy ra

1; 1.

b c

 

Mà từ đồ thị ta xét tại

2 2

1 1

2 log 2 log 2

log log

b c

x

b c

    

nhân hai vế

2 2

log .log 0

b c



Ta được

2 2

log log

c b c b  

.

Vậy:

.a c b 

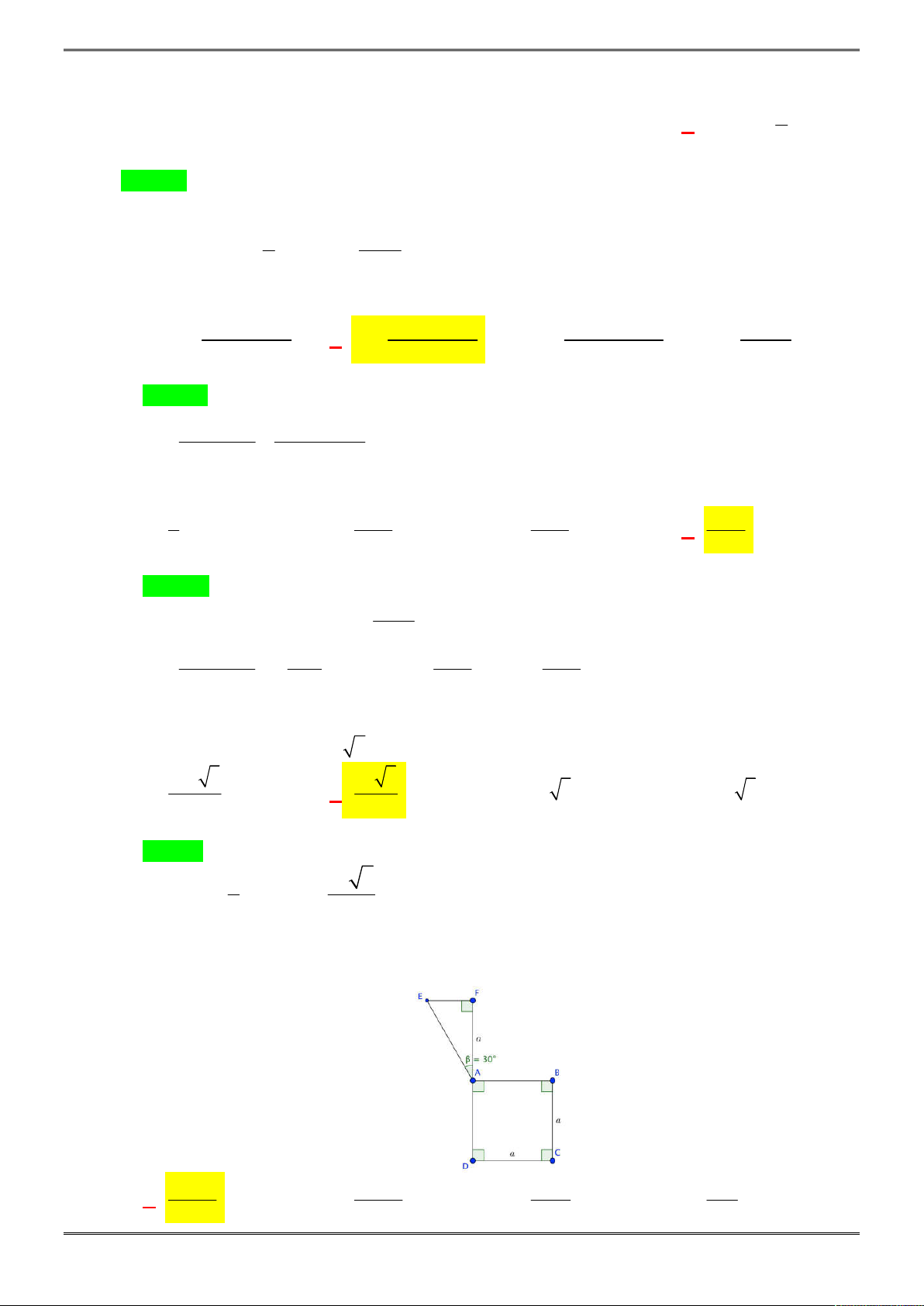
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 40

Câu 18. [2D2-4.5-2] Trong các hàm số sau, hàm số nào nghịch biến trong khoảng

 

0;



?

A.

2

logy x

. B.

2

logy x x 

. C.

2

logy x x 

. D.

2

1

log

y

x



Lời giải

Chọn D.

Ta thấy hàm số

2

logy x

đồng biến trên khoảng

 

0;



nên A, B, C loại.

Kiểm tra

2

1

log

y

x

 có

 

1

' 0, 0;

ln 2

y x

x

     

.

Câu 19. [2D-4.2-2] Tính đạo hàm của hàm số

 

log ln2y x



.

A.

2

ln 2 .ln10

y

x x





. B.

1

ln 2 .ln10

y

x x





. C.

1

2 ln 2 .ln10

y

x x





. D.

1

ln 2

y

x x





Lời giải

Chọn B.

 

ln2

1

ln2 .ln10 .ln 2 .ln10

x

y

x x x



 

.

Câu 20. [2D-4.2-2] Đạo hàm của hàm số

   

3

log 1 2ln 1 2y x x x    

tại điểm

2

x



bằng

A.

1

3

. B.

1

2

3ln3



. C.

1

3ln 3



. D.

1

3ln3

.

Lời giải.

Chọn D.

Sử dụng công thức

 

log

ln

a

u

u a





, ta được

 

1 1 1 1

2. 2 2 2 2

1 ln3 1 3ln3 3ln3

y y

x x

 

       

 

.

Câu 21. [2H1-2.1-2] Cho hình chóp S.ABCD có đáy là hình chữ nhật với

, 2AB a AD a 

, SA vuông

góc với mặt đáy và

3SA a



. Thể tính khối chóp S.ABC bằng

A.

3

2 3

.

3

a

B.

3

.

3

a

C.

3

3.

a

D.

3

2 3.

a

Lời giải

Chọn B

Ta có

3

1 3

.

3 3

ABC

a

V SA S 

.

Câu 22. [2H2-2.8-2] Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục

DF

A.

3

10

9

a



. B.

3

10

7

a



. C.

3

5

2

a



. D.

3

a



.

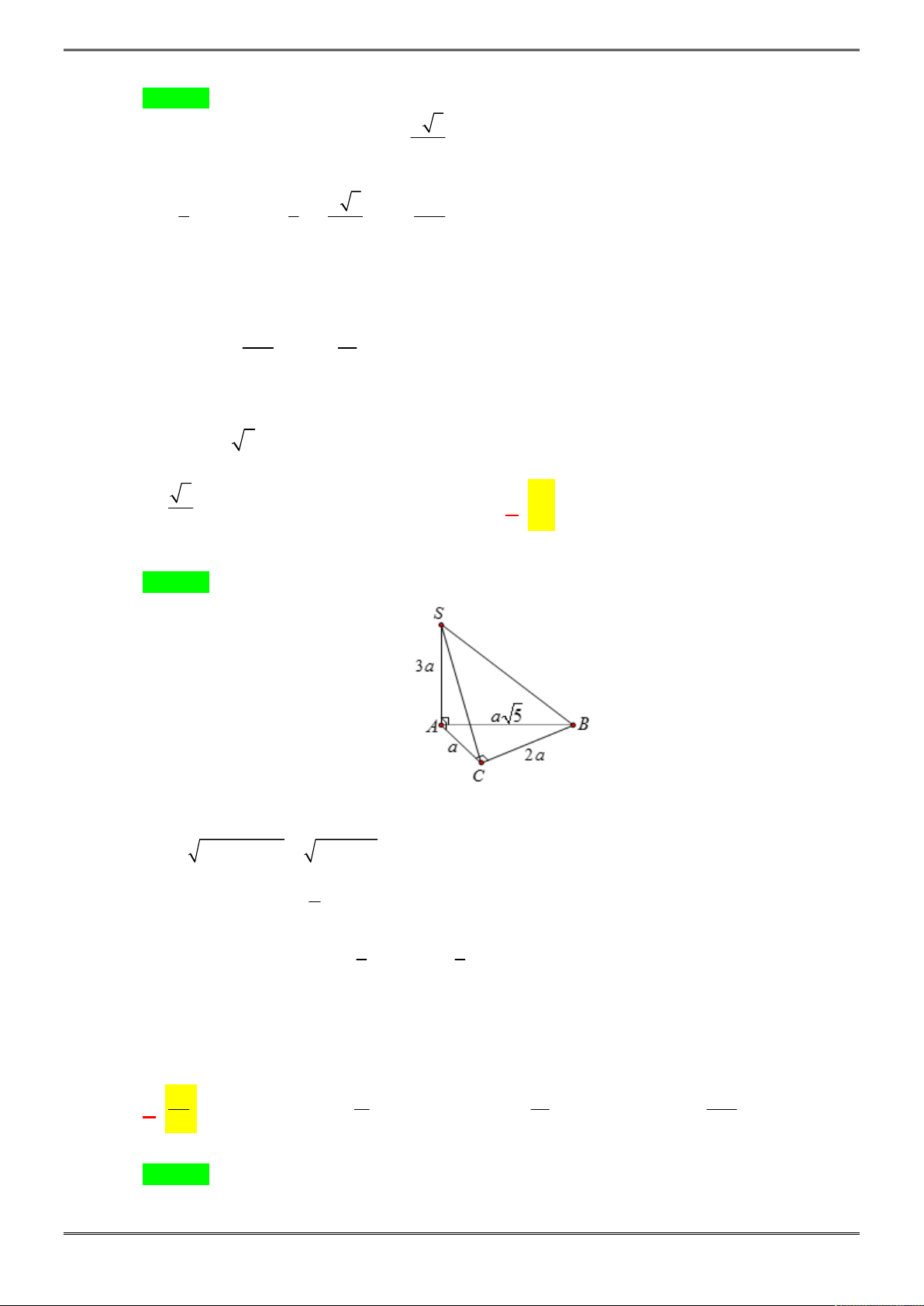
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 41

Lời giải

Chọn A.

Ta có

3

.tan .tan 30

3

a

EF AF a



   

Khi quay quanh trục

DF

, tam giác

AEF

tạo ra một hình nón có thể tích

2

3

2

1

1 1 3

. . . .

3 3 3 9

a a

V EF AF a



 

 

  

 

 

Khi quay quanh trục

DF

, hình vuông

ABCD

tạo ra một hình trụ có thể tích

2 2 3

2

. . . .

V DC BC a a a

  

  

Thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục

DF

là

3

3 3

1 2

10

9 9

a

V V V a a



 

    

.

Câu 23. [2H1-2.1-2] Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

,C

5,

AB a



.AC a

Cạnh bên

3SA a

và vuông góc với mặt phẳng đáy. Thể tích của

khối chóp

.S ABC

. bằng

A.

3

5

.

2

a

. B.

3

3 .a

. C.

3

.a

. D.

3

2 .a

Lời giải

Chọn C.

Vì

ABC

vuông nên áp dụng pitago.

2 2 2 2

5 2 .CB AB AC a a a

    

.

Diện tích đáy

2

1

. .2

2

ABC

S a a a



 

.

Thể tích khối chóp:

2 3

.

1 1

. . . .3 .

3 3

S ABC ABC

V S SA a a a



  

.

Câu 24. [2H1-2.5-2] Cho hình chóp tứ giác

.S ABCD

. Gọi

V

là thể tích khối chóp

.S ABCD

. Lấy

điểm

A



trên cạnh

SA

sao cho

4 'SA SA

. Mặt phẳng qua

A



và song song với đáy của hình

chóp cắt các cạnh

, ,SB SC SD

lần lượt tại các điểm

', ', 'B C D

.Thể tích khối chóp

. ' ' ' 'S A B C D

bằng:

A.

64

V

. B.

4

V

. C.

16

V

. D.

256

V

.

Lời giải

Chọn A.

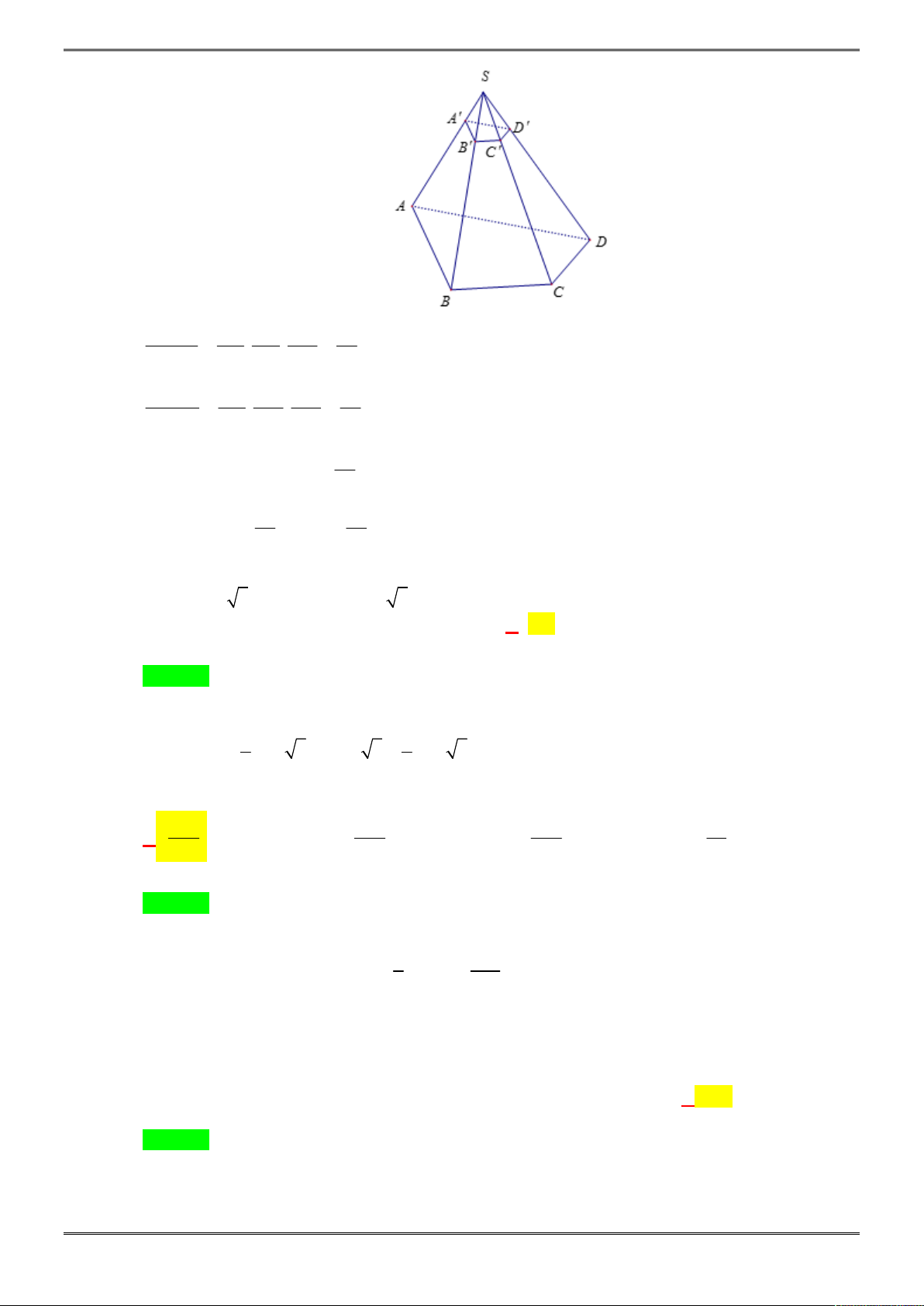
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 42

.

1

. .

64

S A B C

S ABC

V

SA SB SC

V SA SB SC

  

 

.

1

. .

64

S A D C

S ADC

V

SA SD SC

V SA SD SC

  

 

.

Suy ra

 

. . . .

1

64

S A B C S A D C S ABC S ADC

V V V V

     

  

.

hay

. .

1

64 64

S A B C D S ABCD

V

V V

   

 

.

Câu 25. [2H1-2.3-2] Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình vuông. Nếu khối chóp có chiều

cao bằng

3a

và thể tích là

3

3 3

a

thì cạnh đáy có độ dài là:

A.

.a

B.

2 .a

C.

3 .a

D.

4 .a

Lời giải

Chọn C.

Gọi độ dài cạnh đáy là

x

.

Có

2 3 2

.

1 1

. 3 3 3 . 3

3 3

S ABCD

V x a a x a

  

2 2

9 3 .x a x a

   

.

Câu 26. [2H2-1.3-2] Tính thể tích của một khối nón có góc ở đỉnh là

90 ,

bán kính hình tròn đáy là

?a

A.

3

.

3

a



B.

3

.

2

a



C.

3

.

4

a



D.

3

.

3

a

Lời giải

Chọn A.

Hình nón có góc ở đỉnh

90 ,

bán kính hình tròn đáy là

a

nên

, .r a h a 

Khi đó thể tích của hình nón

3

2

1

. . .

3 3

πa

V π a h 

Câu 27. [2D1-2.16-3] Giá trị của tham số

m

để hàm số

 

3 2

- 3 -1y x x mx

có hai đểm cực trị

1 2

,x x

thỏa mãn

 

2 2

1 2

6

x x

là

A.

1

. B.

3

. C.

1

. D.

3

.

Lời giải

Chọn D.

Ta có:

  

2

' 3 6

y x x m

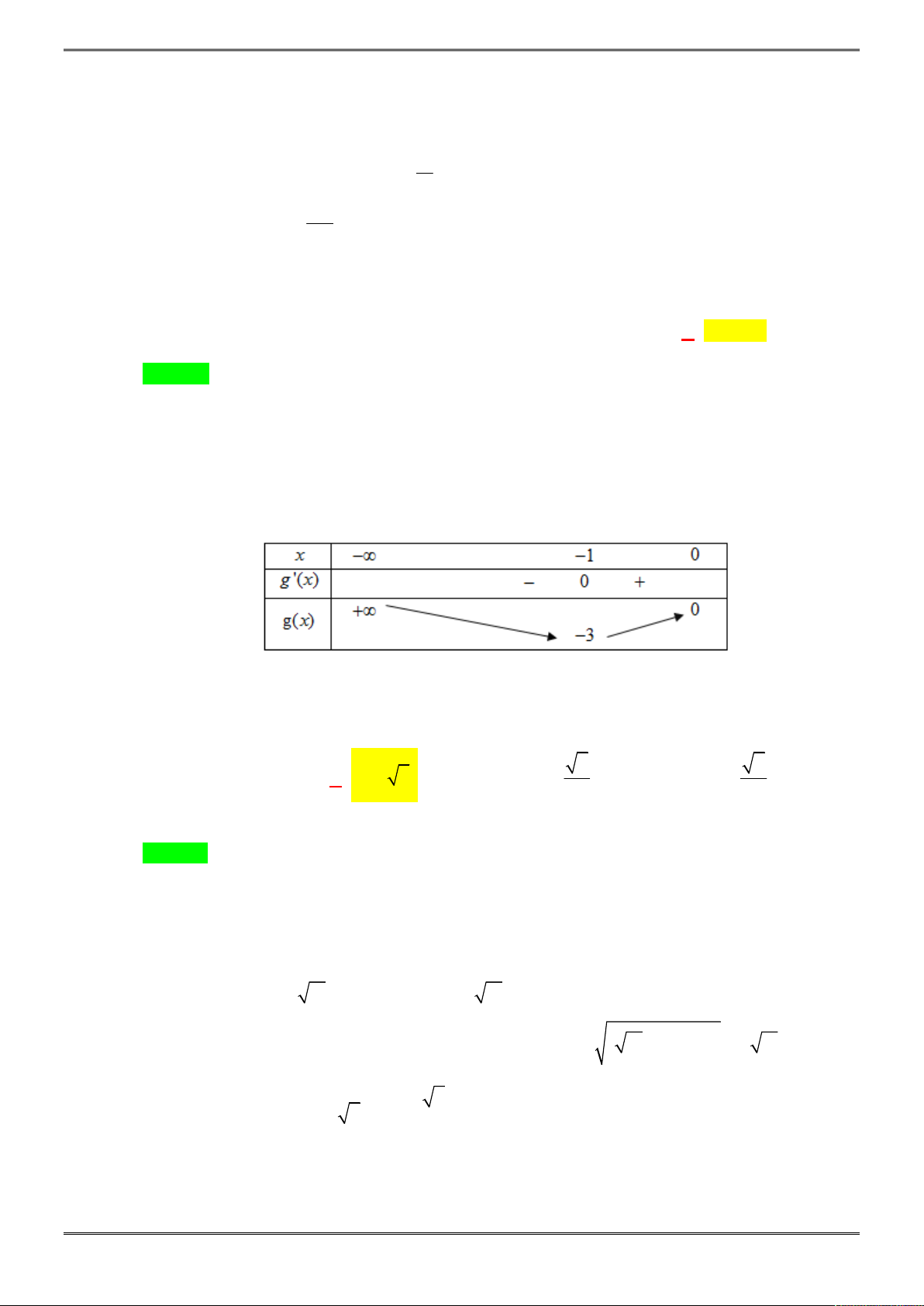
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 43

Hàm số có hai điểm cực trị

' 0

y

 

có hai nghiệm phân

biệt

' 0 9 3m 0 m 3       

.

Áp dụng định lý vi-et ta có:



 











1 2

2

3

x x

m

x x

Có

       

2 2

1 2

2

6 4 6 3

3

m

x x m

(nhận).

Câu 28. [2D1-1.5-3] Tìm tất cả các giá trị của tham số

m

để hàm số

  

3 2

3 - 1y x x mx

đồng biến

trên khoảng

 

;0 .



A.

 0m

. B.

 3m

. C.

 3m

. D.

 3m

.

Lời giải

Chọn D.

  

2

' 3 6

y x x m

Hàm số đồng biến trên khoảng

 

;0



 

    

' 0, ,0

y x

 

      

2

3 6 0, ,0

x x m x

 

     

2

3 6 , ,0

m x x x

Xét hàm số

 

 

2

3 6g x x x

trên

 

;0



có

 

 ' 6 6

g x x

Hàm số đã cho đồng biến trên

     

        ;0 , ;0 3

m g x x m

.

Câu 29. [2D1-2.10-3] Tìm tất cả các giá trị của tham số

m

sao cho đồ thị hàm số

  

4 2 4

- 2 2

y x mx m m

có ba điểm cực trị tạo thành một tam giác đều.

A.

 1m

. B.



3

m

. C.



3

6

2

m

. D.



3

2

m

.

Lời giải

Chọn B.



3

' 4 - 4y x mx

    

2

' 0 0

y x x m

Hàm số có 3 điểm cực trị

  0m

Gọi tọa độ của 3 điểm cực trị là:

 

   

     

4 4 2 4 2

0; 2 ; ; 2 ; ; 2A m m B m m m m C m m m m

Ta thấy

ABC

cân tại

A

nên

ABC

đều

 AB BC

 

  

2

m m m

.

  

4

4m m m

 

 

   









3

0

3 0

3

m

m do m

m

.

Câu 30. [2H1-2.3-3] Cho hình chóp tứ giác đều

.

S ABCD

có cạnh đáy bằng a và mặt bên tạo với đáy

một góc 45

0

. Thể tích

V

khối chóp

.

S ABCD

là

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 44

A.

3

.

2

a

V  B.

3

9

a

V  . C.

3

6

a

V  . D.

3

1

24

V a



.

Lời giải

Chọn C

Gọi H là hình chiếu vuông góc của S trên (ABCD), M là trung điểm của BC



3

0

.

45

2 6

S ABCD

a a

SMH SH HM V      .

Câu 31. [2H1-3.10-3] Một khối lăng trụ tam giác đều có thể tích là

3

V 16a



. Để diện tích toàn phần

của hình lăng trụ đó nhỏ nhất thì cạnh đáy của lăng trụ có độ dài là

A.

2a

. B.

3a

. C.

a 3

. D.

4a

.

Lời giải

Chọn D

- Phương pháp: +Tính diện tích toàn phần của lăng trụ

+Sử dụng phương pháp hàm số để tìm giá trị nhỏ nhất của diện tích toàn phần hình lăng trụ.

- Cách giải:

Gọi độ dài cạnh đáy của hình lăng trụ là

 

0

x x



; chiều cao là h.

Diện tích đáy của lăng trụ là

2 2

3 3

2.

4 2

x x



; diện tích xung quanh của lăng trụ là 3xh.

Ta có:

2 3

3

2

3 64

. 16 .

4

3

d

x a

V S h a h h

x

    

Diện tích toàn phần của lăng trụ

2 2 3 2 3

2

3 3 64 3 64 3

3 3 .

2 2 2

3

x x a x a

S xh x

x

     

3

3 3

2

64 3

' 3 ; ' 0 64 4

a

S x S x a x a

x

      

Suy ra diện tích toàn phần nhỏ nhất khi

4x a

.

Câu 32. [2D1-1.8-4] Có bao nhiêu giá trị nguyên của tham số

 

5;5

m 

để hàm số

-cos

cos

x m

y

x m







đồng biến trên khoảng

2



 

 

 

0;

?

A.

4

. B.

5

. C.

8

. D.

9

.

Lời giải

Chọn A.

Ta có

 

2

2 . sin

'

cos

m x

y

x m

 





. Vậy hàm số đồng biến trên khoảng

0;

2



 

 

 

khi và chỉ khi

 

   

2 2

2 sin

2

' 0, 0; 0, 0; 0, 0;

2 2 2

cos cos

m x

m

y x x x

x m x m

  

 



     

          

     

     

 

 

2 0

0

0;1

m

 





  



 





( Vì

sin 0, 0;

2

x x



 

   

 

 

)

Mặt khác

 

5,5

m 

nên

1, 2,3,4

m



.

Câu 33. [2H1-2.8-4] Khối chóp

.

S ABCD

có đáy là hình thoi cạnh a,

SA SB SC a  

. Thể tích lớn

nhất của khối chóp

.

S ABCD

là

A.

3

.

8

a

B.

3

.

2

a

C.

3

.

8

a

D.

3

.

4

a

Lời giải

Chọn D

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 45

Kẻ

 

SH ABCD



tại H => H là tâm đường tròn ngoại tiếp

ABC

.Mà

ABC

cân tại B và

AC BD H BD  

.Gọi O là giao điểm AC và BD.

Ta có:

1

( . . ) D D

2

SAC BAC c c c SO OB B SB

       

vuông tại S.

D

1 1 1 1 1

. D . D V= . . . D= . D. . . D

3 3 2 6 6

ABC

SH B SB S SH S SH AC B SB S AC a AC S

    

Lại có

2 2 2 2

SD BD SB BD a   

.Mà

2

2 2 2 2 2

2 2 2 4

4

BD

AC OA AB OB a a BD

      

   

2 2 2 2

3

2 2 2 2

4

1

. 4 . . .

6 6 2 4

a BD BD a

a a

V a a BD BD a

  

      .

Câu 34. [2D2-4.8-4] Anh Nam mong muốn rằng sau

6

năm sẽ có

2

tỷ để mua nhà. Hỏi anh Nam phải

gửi vào ngân hàng một khoản tiền tiền tiết kiệm như nhau hàng năm gần nhất với giá trị nào

sau đây, biết rằng lãi suất của ngân hàng là

8%

/năm và lãi hàng năm được nhập vào vốn.

A.

253,5

triệu. B.

251

triệu. C.

253

triệu. D.

252,5

triệu.

Lời giải

Chọn D

Giả sử anh Nam bắt đầu gửi

A

đồng vào ngân hàng từ đầu kì

1

với lãi suất là

r

.

● Cuối kì

1

có số tiền là:

 

1

C A r



 

.

● Đầu kì

2

có số tiền là:

 

2

1

C A r A

  

 

   

2 2

1 1 . 1 1 1 1

1 1

A A

A r r r

r r

   

 

        

   

 

   

 

.

Cuối kì

2

có số tiền là:

   

2

1 1 1

A

C r r

r



 

   

 

 

.

● Đầu kì

3

có số tiền là:

   

2

3

1 1 1

A

C r r A

r

 

    

 

 

     

3 3

1 1 1 1 .

A A

r r r r

r r

   

       

   

   

Cuối kì

3

có số tiền là:

       

3 4

3

1 1 1 1 1

A A

C r r r r

r r



   

       

   

   

.

………….

Tổng quát, ta có cuối kì

N

có số tiền là:

   

1

1 1

N

A

C r r

r



 

   

 

 

.

Suy ra

   

1

.

1 1

N

C r

A

r r





  

.

Áp dụng công thức với

2000000000

6

8% 0,08

N

C

n

r

















  





, ta được

252435900

A



.

Câu 35. [2D2-3.4-4] Cho

2

log log log

log 0;

y

a b c b

x x

p q r ac

    

. Tính

y

theo

, ,p q r

.

A.

2

y q pr 

. B.

2

p r

y

q



 . C.

2

y q p r  

. D.

2

y q pr 

.

Lời giải

Chọn C.

Ta có

2 2

log log

y y

b b

x x

ac ac

  

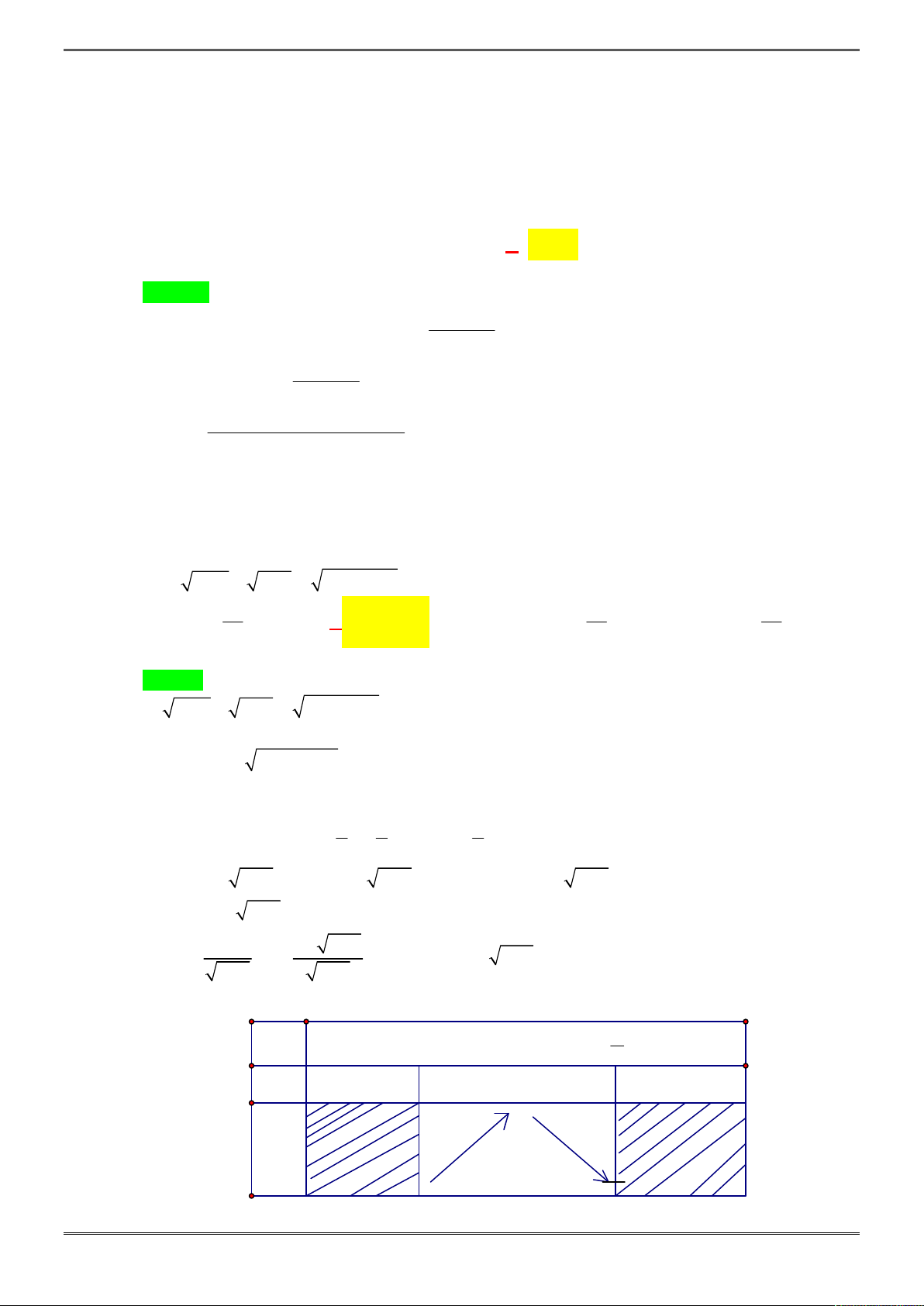
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 46

log 2 log log log 2 log log logy x b a c q x p x r x      

 

.log 2 .logy x q p r x

   

2

y q p r   

(do

log 0

x



).

Câu 36. [2D2-5.7-4] Tìm tập hợp các giá trị của tham số thực

m

để phương trình

 

6 3 2 0

x x

m m

   

có nghiệm thuộc khoảng

 

0;1

.

A.

 

3;4

. B.

 

2;4

. C.

 

2;4

. D.

 

3;4

.

Lời giải

Chọn C.

Ta có:

 

6 3 2 0

x x

m m

   

 

1



6 3.2

2 1

x x

x

m







Xét hàm số

 

6 3.2

2 1

x x

x

f x







xác định trên



, có

 

2

12 .ln 3 6 .ln 6 3.2 .ln 2

0,

2 1

x x x

x

f x x

 



   





nên hàm số

 

f x

đồng biến trên



Suy ra

       

0 1 0 1 2 4

x f f x f f x

       

vì

   

0 2, 1 4

f f

 

Vậy phương trình

 

1

có nghiệm thuộc khoảng

 

0;1

khi

 

2;4

m

.

Câu 37. [2D2-6.4-4] Tìm các giá trị thực của tham số

m

để phương

trình

2

2 1

x x m x x     

có hai nghiệm phân biệt.

A.

23

5; .

4

m

 



 

 

B.

 

5;6 .

m

C.

 

23

5; 6 .

4

m

 

 

 

 

D.

 

23

5; 6 .

4

m

 

 





 

Lời giải

Chọn B

+)

2

2 1

x x m x x     

(

1

)

Điều kiện:

1 2

x

  

+)

 

2 2

1 3 2 2

x x x x m        

Đặt:

2

;x x t  

   

2

; 2 1f x x x f x x



     

   

1 1 1

1 2, 2 2, 2;

2 4 4

f f f t

   

       

 

 

   

 

1 3 2 2 2 2 3

t t m t t m

         

2 2 3m t t    

Đặt

 

2 2 3f t t t   

 

1 1 2

1

2 2

t

f t

t t

 



  

 

.

 

0 1 2 0 1

f t t t



       

Bảng biến thiên

23

4

5

6

+



1

4

-1-2

-



f(t)

f'(t)

t

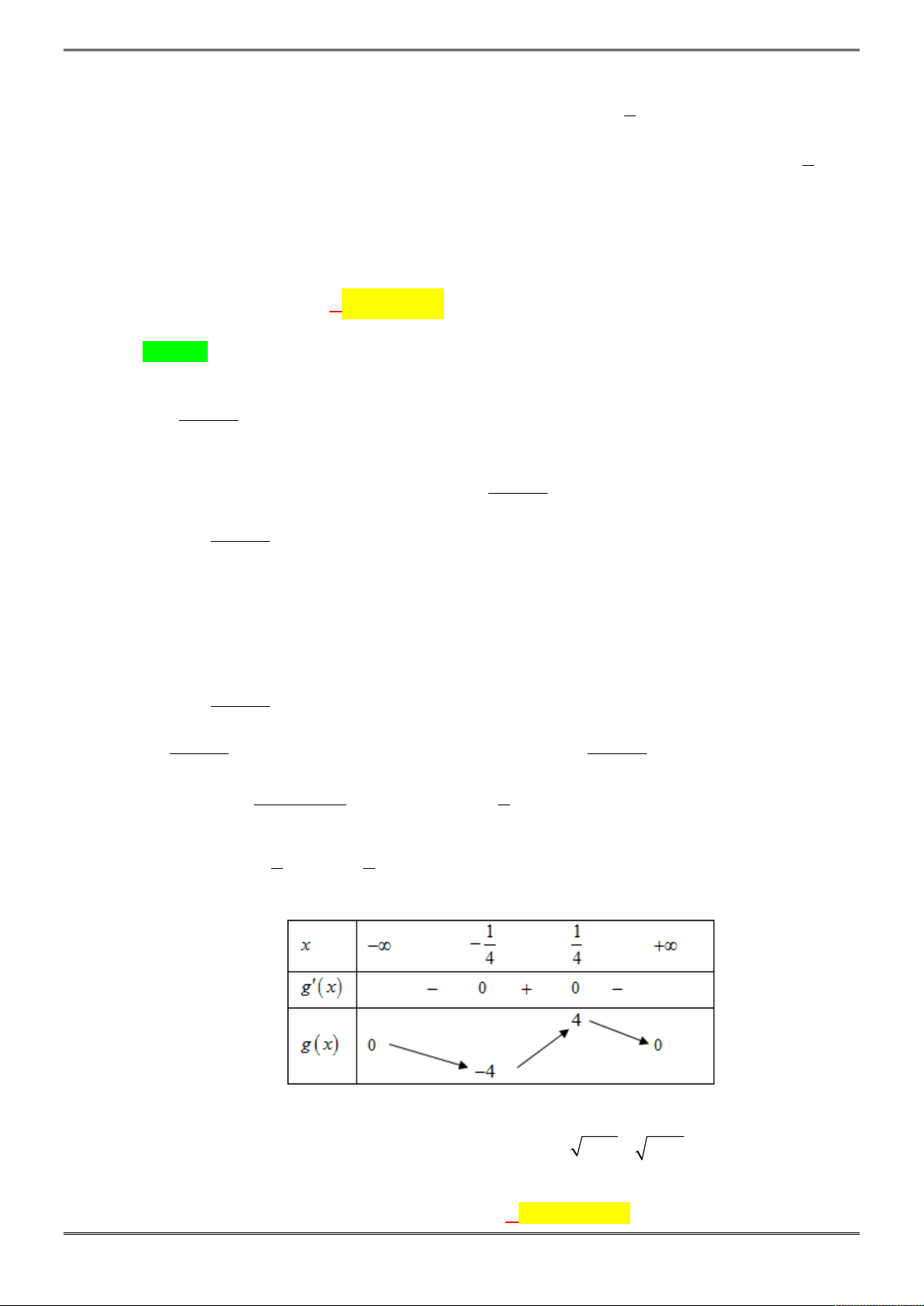
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 47

+)

2 2

0x x t x x t       

Để phương trình có hai nghiệm phân biệt

1

1 4 0

4

t t

      

Do đó để phương trình có hai nghiệm phân biệt thì phương trình

 



có nghiệm

1

2;

4

t

 

 

 

 

. Từ

bảng biến thiên

 

5;6

m 

.

Câu 38. [2D2-4.10-4] Tìm tất cả các giá trị của tham số

m

để hàm số

 

2

ln 16 1 1 2

y x m x m

     

nghịch biến trên khoảng

 

; . 

A.





; 3 .

m

  

B.





3; .

m

 

C.

 

; 3 .

m

  

D.

 

3;3 .

m 

Lời giải

Chọn B.

Ta có:

 

2

ln 16 1 1 2

y x m x m

     

 

2

32

1

16 1

x

y m

x



  



Hàm số nghịch biến trên



khi và chỉ khi

0,y x



  

 

2

32

1 0,

16 1

x

m x

x

     





Cách 1:

 

2

32

1 0,

16 1

x

m x

x

    





 

2

32 1 16 1 0,x m x x

      

   

2

16 1 32 1 0,m x x m x

        

 

2

16 1 0

1

16 32 240 0

16 16 1 0

m

m m

m



  

 





 

 

   



    







1

3.

5

3

m

 





  

 















Cách 2:

 

2

32

1 0

16 1

x

m x

x

    





2

32

1,

16 1

x

m x

x

    





1 max ( ),m g x

  



với

2

32

( )

16 1

x

g x

x





Ta có:

 

2

512 32

( )

16 1

x

g x

x

 







;

1

( ) 0

4

g x x



   

1 1

lim ( ) 0; 4; 4

4 4

x

g x g g



   

    

   

   

Bảng biến thiên:

Dựa vào bảng biến thiên ta có

max ( ) 4

g x





. Do đó:

1 4 3.

m m

   

Câu 39. [2D2-3.12-4] Cho các số thực

,x y

thỏa mãn

 

2 3 3

x y x y

    

. Giá trị nhỏ nhất của

biểu thức

 

2 2

4 15P x y xy

  

là

A.

min 80

P

 

. B.

min 91

P

 

. C.

min 83

P

 

. D.

min 63

P

 

.

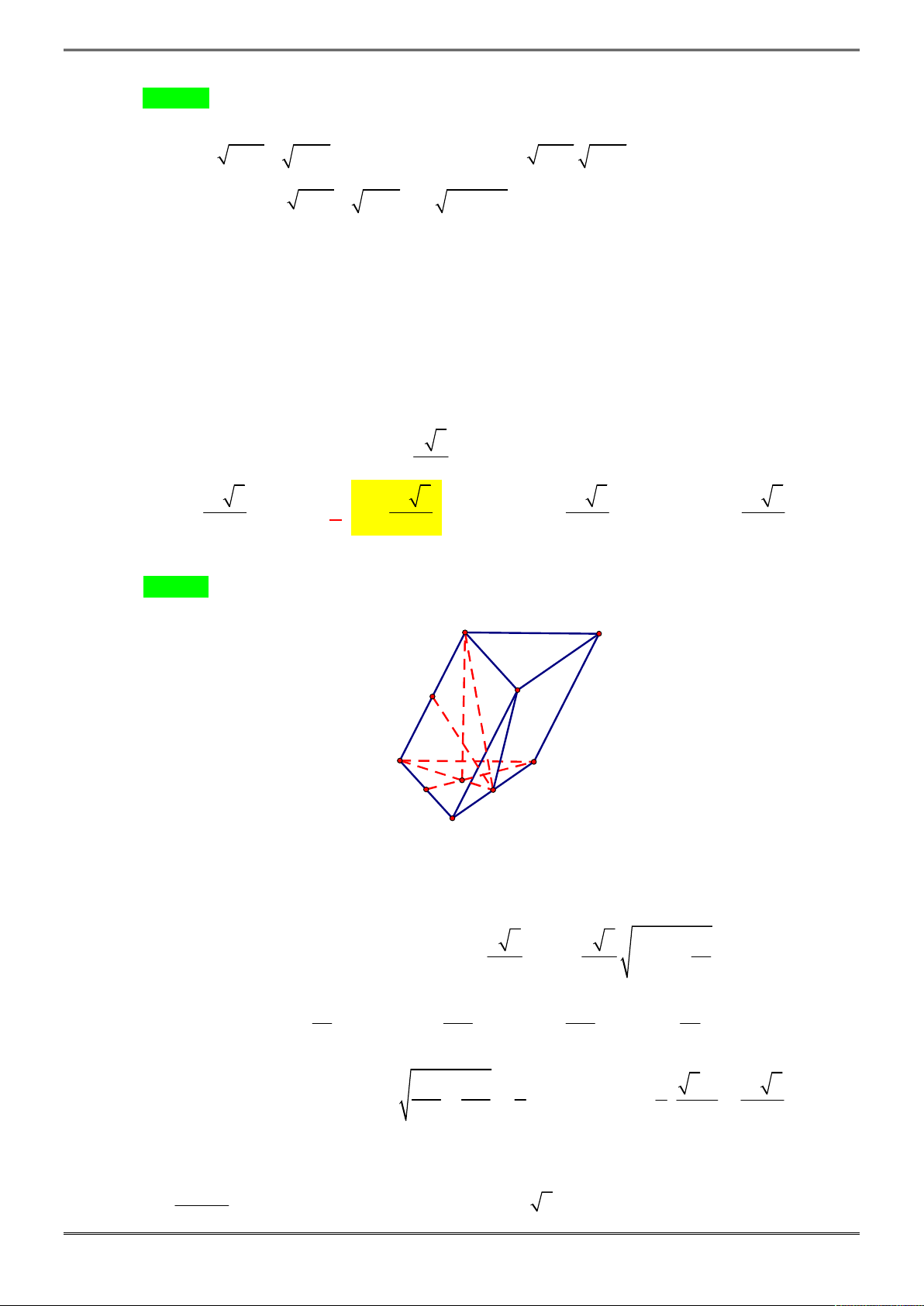
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 48

Lời giải

Chọn C.

Ta có:

2

4

2( 3 3) ( ) 4( ) 8 3. 3 4( )

0

x y

x y x y x y x y x y x y

x y

 



              



 



Mặt khác

 

2( 3 3) 2 2( ) 8 4;8

x y x y x y x y x y            

Xét biểu thức

2 2 2

4( ) 15 4( ) 7 16( ) 7 7 ( 3) 16 5P x y xy x y xy x y xy x y y x            

.

Mà

3 0

16(4 ) 5 64 21

4

y

P x x x

y x

 



     



 



, kết hợp với

 

4 3;7 64 21 83

x y x x

       

Vậy giá trị nhỏ nhất của biểu thức

P

là

83

.

Câu 40. [2D2-3.10-4] Cho hình lăng trụ

ABCA B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông

góc của

A



lên mặt phẳng

 

ABC

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa

hai đường thẳng

AA



và

BC

bằng

3

4

a

. Tính thể tích

V

của khối lăng trụ

.ABCA B C

  

A.

3

.

24

a

V

 B.

3

.

12

a

V

 C.

3

.

3

a

V

 D.

3

.

6

a

V



Lời giải

Chọn B.

H

G

M

B

C

A

C'

B'

A'

M

là trung điểm của

BC

thì

 

BC AA M



 .Gọi

MH

là đường cao của tam giác

A AM



thì

MH A A





và

HM BC

nên

HM

là khoảng cách

AA



và

BC

.Ta có

. .A A HM A G AM

 

 

2

3 3

.

4 2 3

a a a

A A A A

 

 

2 2 2

2 2 2 2

4 4 2

4 3 .

3 3 9 3

a a a a

A A A A A A A A A A

 

    

        

 

 

Đường cao của lăng trụ là

2 2

4 3

9 9 3

a a a

A G



  

.Thể tích

2 3

3 3

.

3 4 12

LT

a a a

V

 

PHẦN 2. TỰ LUẬN.

Câu 1. Tìm tất cả các giá trị thực của tham số

m

để đường thẳng

:

d y x m  

cắt đồ thị hàm số

2 1

1

x

y

x

 





 

C

tại hai điểm

, A B

sao cho

2 2

AB 

.

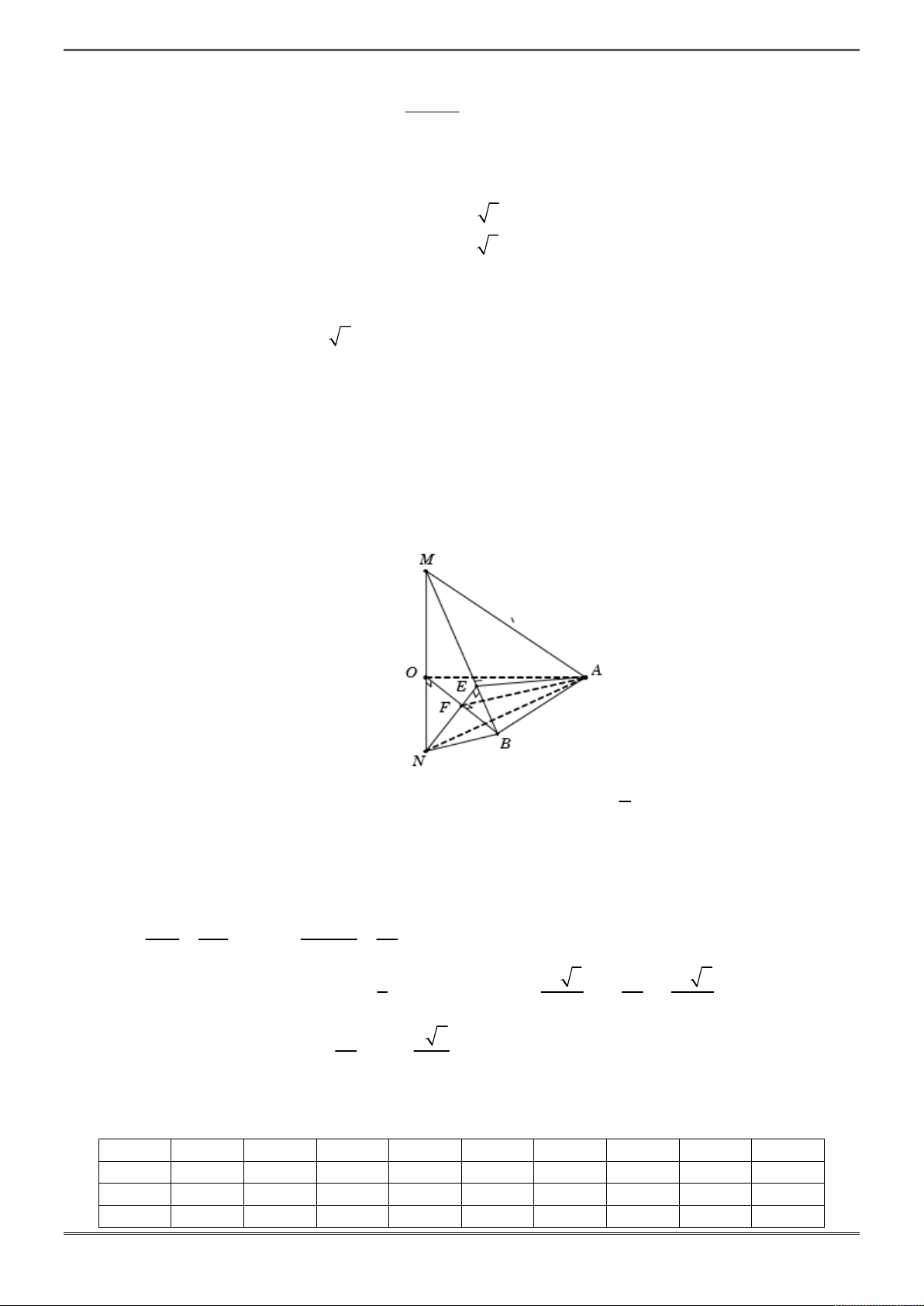
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 49

Lời giải

Phương trình hoành độ giao điểm:

 

2 1

1

x

x m x

x

 

    



    

2

2 1 1 1 1 0.

x x m x x m x m

            

 

*

Để

d

cắt

 

C

tại hai điểm phân biệt



phương trình

 

*

có hai nghiệm phân biệt

   

2

3 2 3

1 4 1 0 .

3 2 3

m

m m

m



  

       



  





Theo đinh lí Viet, ta có

1 2

1

.

1

x x m

  





 



Giả sử

 

1 1

;

A x x m

 

và

 

2 2

;

B x x m 

.

Yêu cầu bài toán

   

2 2

2

2 1 1 2 1 2

2 2 8 2 8 4 4

AB AB x x x x x x

         

   

2

1

1 4 1 4 6 7 0

7

m

m m m m

m





         



 



(thỏa mãn).

Câu 2. Cho tam giác

OAB

đều cạnh

a

. Trên đường thẳng

d

qua

O

và vuông góc với mặt phẳng

 

OAB

lấy điểm

M

sao cho

OM x

. Gọi

, E F

lần lượt là hình chiếu vuông góc của

A

trên

MB

và

OB

. Gọi

N

là giao điểm của

EF

và

d

. Tìm

x

để thể tích tứ diện

ABMN

có giá trị

nhỏ nhất.

Lời giải

Do tam giác

OAB

đều cạnh

a F

là trung điểm

.

2

a

OB OF

 

Ta có

 

.

AF OB

AF MOB AF MB

AF MO





   







Mặt khác,

MB AE

.

Suy ra

 

.MB AEF MB EF

  

Suy ra

OBM ONF 

∽

nên

2

.

2

OB ON OB OF a

ON

OM OF OM x

    .

Ta có

ABMN ABOM ABON

V V V 

 

2 2 3

1 3 6

3 12 2 12

OAB

a a a

S OM ON x

x



 

    

 

 

.

Đẳng thức xảy ra khi

2

2 2

a a

x x

x

  

.

BẢNG ĐÁP ÁN

1.A

2.B

3.B

4.D

5.D

6.B

7.B

8.D

9

10.A

11.A

12.A

13.B

14.A

15.A

16.B

17.A

18.D

19.B

20.D

21.B

22.A

23.C

24.A

25.C

26.A

27.D

28.D

29.B

30.C

31.D

32.A

33.D

34.D

35.C

36.C

37.B

38.B

39.C

40.B

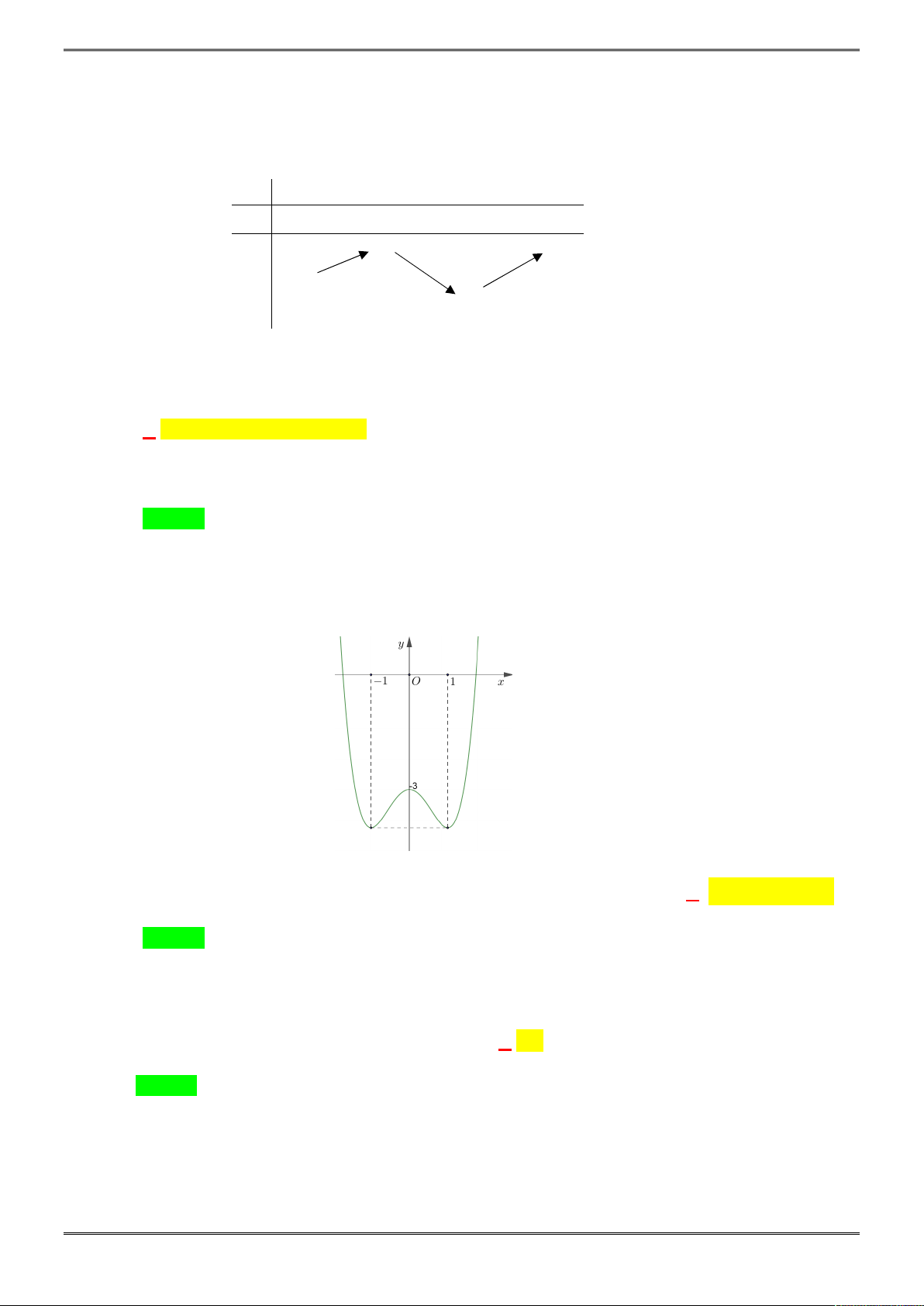
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 50

ĐỀ ÔN TẬP SỐ 14

PHẦN I: PHẦN TRẮC NGHIỆM

Câu 1. [2D1-2.3-1] Cho hàm số

( )y f x

xác định, liên tục trên



và có bảng biến thiên như hình vẽ:

x



0

1



y





||



0



y



2

3



Mệnh đề nào dưới đây đúng?

A. Hàm số chỉ có giá trị nhỏ nhất không có giá trị lớn nhất.

B. Hàm số có một điểm cực trị.

C.Hàm số có hai điểm cực trị.

D. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng – 3.

Lời giải

Chọn C

Tại

0

x



ta thấy

'y

không xác định và đổi dấu từ dương sang âm

0

x

 

là một cực trị.

Tại

1x 

ta thấy

' 0

y



và đổi dấu từ âm sang dương

1x 

là một cực trị.

Câu 2. [2D1-5.1-1] Đường cong sau đây là đồ thị của hàm số nào ?

A.

4 2

2 3   

y x x . B.

4 2

2 3  

y x x . C.

4 2

3  

y x x . D.

4 2

2 3  

y x x .

Lời giải

Chọn D

Nhìn vào đồ thị ta thấy hệ số của

4

x

phải lớn hơn

0

, nên loại A; mặt khác hàm số có hai điểm

cực trị là

1 

x

chỉ có hàm số

4 2

2 3  

y x x thỏa mãn.

Câu 3. [2D1-3.2-1]Giá trị lớn nhất của hàm số

3 2

2 3 12 2y x x x   

trên đoạn

[ 1;2]

là

A.

6

. B.

10

. C.

15

. D.

11

.

Lời giải

Chọn C

 



  

 

    

   





2

1 1;2

6x 6x 12 0

2 1;2

x

y

x

.

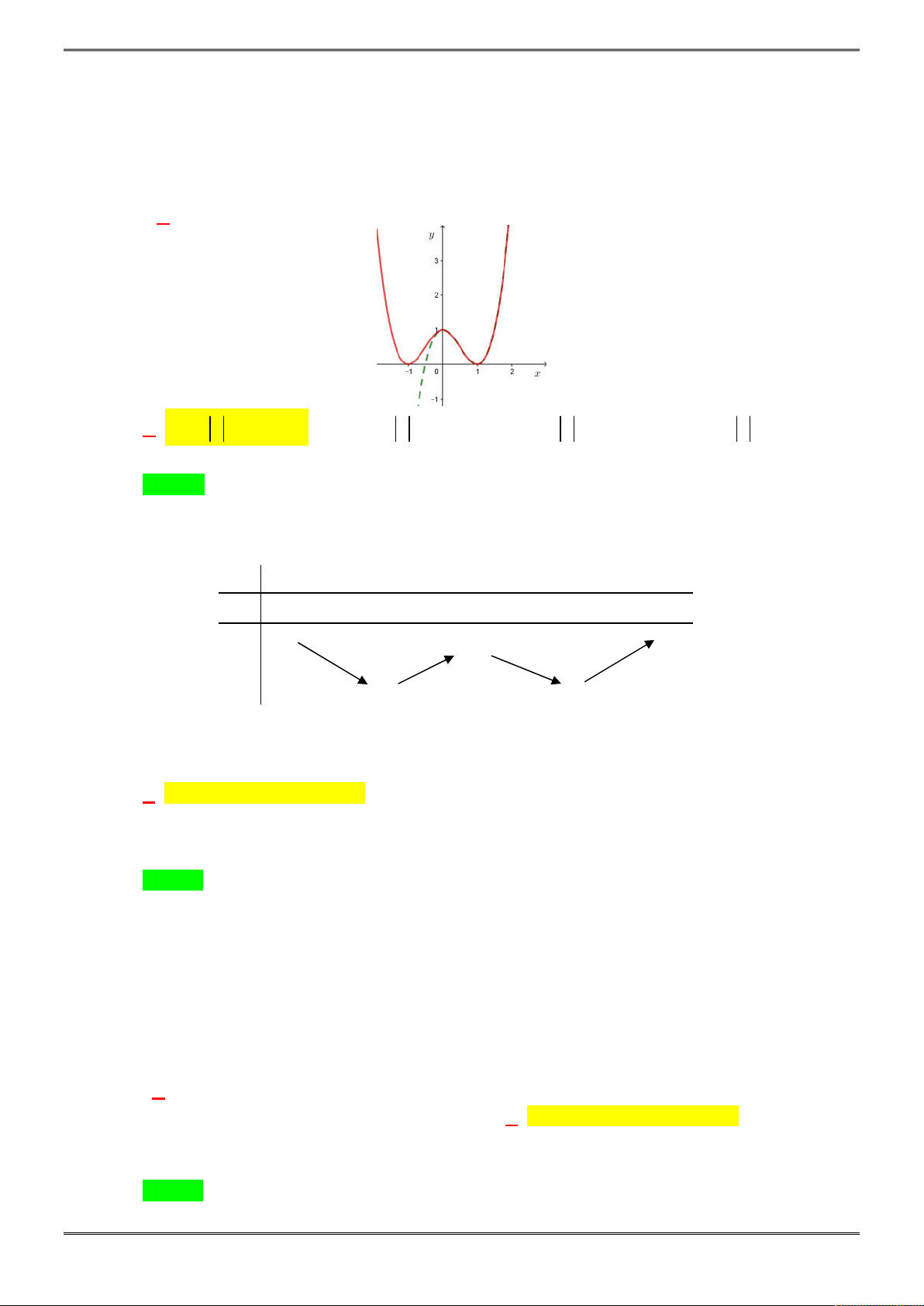
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 51

Ta có



 









 



( 1) 15

(2) 6

(1) 5

y

 



 

 

1;2

15

Max y

.

Câu 4. [2D1-5.1-1] Đồ thị sau đây ( đường nối liền) là của hàm số nào sau đây?

A.

  

3

2

2 3 1

y x x . B.

  

3

2

2 3 2

y x x . C.

  

3

2

3 1

y x x . D.

  

3

2

3 2

y x x .

Lời giải

Chọn A

Đồ thị đi qua điểm

(0;1)

, nên loại B,D. Mặt khác đồ thị đi qua điểm

(1; 0)

nên loại C.

Câu 5. [2D2-3.15-2] Cho hàm số

 

y f x



có bảng biến thiên như sau:

Mệnh đề nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng

 

0;



và nghịch biến trên khoảng

 

;0



.

B. Hàm số có ba điểm cực trị.

C. Hàm số có giá trị lớn nhất bằng

3

và giá trị nhỏ nhất bằng

4.

D. Hàm số có ba giá trị cực trị.

Lời giải

Chọn B

Dựa vào bảng biến thiên, ta có nhận xét:

 Hàm số đồng biến trên các khoảng

 

1;0



,

 

1;



; nghịch biến trên các khoảng

 

; 1 

,

 

0;1

. Do đó A sai.

 Hàm số có ba điểm cực trị là

1, 0, 1.

x x x

   

Do đó B đúng.

 Hàm số có GTNN bằng

4

và không có GTLN. Do đó C sai.

 Hàm số có đúng hai giá trị cực trị là

CD

3

y

 

và

CT

4

y

 

. Do đó D sai.

Câu 6. [2D1-1.1-1] Cho hàm số

    

3 2

3 3 1y x x x

. Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên



. B. Hàm số nghịch biến trên



.

C. Hàm số đạt cực đại tại

 1x

. D. Hàm số đạt cực tiểu tại

 1x

.

Lời giải

Chọn B

y

x

'y





1

4



3





0



1



0

4

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 52

Ta có

          

2 2

' 3 6 3 ' 3( 1) 0,y x x y x x

Nên hàm số nghịch biến trên



.

Câu 7. [2D1-4.5-1] Đồ thị hàm số







3

2

x

y

x

có tiệm cận ngang là đường thẳng:

A.

 1y

. B.

 1y

. C.

 2x

. D.

 2y

Lời giải

Chọn B

Ta có

 



  



3

lim lim 1

2

x x

x

y

x

nên đường thẳng

 1y

là tiệm cận ngang của đồ thị hàm số.

Câu 8. [2D2-1.1-1]Cho hàm số

 

y f x

xác định và có đạo hàm trên

K.

Khẳng định nào sau đây là

sai?

A. Nếu hàm số

 

y f x

đồng biến trên khoảng

K

thì

 

' 0, K.

f x x

  

B. Nếu

 

' 0, K

f x x

  

thì hàm số

 

f x

đồng biến trên

K

.

C. Nếu

 

' 0, K

f x x

  

thì hàm số

 

f x

đồng biến trên

K

.

D. Nếu

 

' 0, K

f x x

  

và

 

' 0

f x



chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên

K

.

Lời giải

Chọn C

Câu 9. [2D1-4.6-1] Số đường tiệm cận của đồ thị hàm số

2

1

20

x

y

x x





 

là:

A.

1

. B.

3

. C.

2

. D.

4

.

Lời giải

Chọn C.

TXĐ:



  

1; \ 5

D  

.

2

1

lim lim 0

20

x

y

x x



 



 

 

 

 

nên đồ thị hàm số nhận đường thẳng

0

y



làm đường tiệm cận

ngang.

5 5

lim , lim

x x

y y

 

 

   

nên đồ thị hàm số nhận đường thẳng

5

x



làm đường tiệm

cận đứng.

Vậy: Đồ thị hàm số đã cho có hai đường tiện cận.

Câu 10. [2D1-1.3-1]Hàm số

2

y x x  

nghịch biến trên khoảng nào?

A.

 

 

 

1

;2

2

. B.

 



 

 

1

1;

2

. C.

 



1;2

. D.

 



2;

.

Lời giải

Chọn A

ĐKXĐ:

1 2

x

  

2

1 2

' ( 1;2)

2 2

x

y x

x x



   

 

,

1

' 0 ( ;2)

2

y x  

.

Câu 11. [2D1-2.1-1]Tập xác định của hàm số:



 

2

3

( 4)

y x

là

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 53

A.

   ( ; 2) (2; )D

. B.

  \{ 2}D

.

C.

 ( 2;2)D

. D.

 D

.

Lời giải

Chọn A

ĐKXĐ:

2

4 0

2

x





  



 



.

Câu 12. [2D1-4.2-1]Đạo hàm của hàm số:





1

100

x

y

là

A.





1

' 100 ln10

x

y

. B.



' 200.100 ln10

x

y

.

C.

 





1

'

1 ln100

y

x

. D.

 

 

' 1 ln100

y x

Lời giải

Chọn B

1

' 100 ln100 200.100 ln10

x x

y



  .

Câu 13. [2D1-6.1-1]Phương trình:

 

4

log (2 8) 2

x

có tập nghiệm là

A.

S

B.

{4}S

C.

{12}S

D.

{4;12}S

Lời giải

Chọn C

2

2 8 4 12

PT x x

    

.

Câu 14. [2D1-4.1-1]Hàm số

  

2

5

log ( 6 9)

y x x

xác định khi

A.

 3x

. B.

 3x

. C.

 3x

. D.

 3x

.

Lời giải

Chọn B

Hàm số xác định

2

6 9 0 3

x x x

     

.

Câu 15. [2D1-5.1-1]Giá trị

x

thỏa mãn phương trình:



  

1

49 7 8 0

x x

là

A.

 0x

. B.



7

log 8

x

. C.

7

0

8

log

x













. D.

8

0

7

log

x













.

Lời giải

Chọn B

Thấy

0

x



không là nghiệm.Vậy chỉ có đáp số của B có thể đúng.

Câu 16. [2D1-6.1-1]Chọn đáp án đúng khi nói về bất phương trình:

    

2 2

1 1

2 2

log (2 1) log ( 4 5)

x x x x

A. Bất phương trình có nghĩa khi:

 5x

.

B. Tập nghiệm

 (1;4]S

.

C. Bất phương trình có nghĩa khi:

1x

.

D. Tập nghiệm

 

  



;1 (4; )

S

.

Lời giải

Chọn B

Điều kiện:





















    

 





 



 





  









 













2

1

2

2 1 0 5

1

4 5 0

5

1

x

x x x

x

x x

x

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 54

                 

2 2 2 2 2

1 1

2 2

log (2 1) log ( 4 5) 2 1 4 5 5 4 0 1 4

x x x x x x x x x x x

Kết hợp với điều kiện ta được:

 1 4x

.

Câu 17. [2D2-3.3-2] Nếu

 

12 12

log 6 ; log 7

a b

thì :

A.





2

log 7

1

a

. B.





2

log 7

1

a

b

. C.





2

log 7

1

a

b

. D.





2

log 7

1

b

a

.

Lời giải

Chọn D

Ta có :

  

 

12 12

2

12 12 12

log 7 log 7

log 7

log 2 log 12 log 6 1

b

a

.

Câu 18. [2D2-1.2-2] Rút gọn biểu thức



3 6

P x x x

với

 0x

.

A.



2

3

P x

. B.



P x

. C.



3

P x

. D.



5

6

P x

.

Lời giải

Chọn D

Ta có



3 6

P x x x

 



 

 

1

1 1

2

3 6

. .x x x



 

2 1 5

3 6 6

x x

.

Câu 19. [2D1-1.3-1]Cho

 0 1a

và

 

 1

. Khẳng định nào sau đây là khẳng định đúng?

A.

 

 1.

a a

B.

 

 

1 .a a

C.

 

 

1 .a a

D.

 

 1.

a a

Lời giải

Chọn A

Dựa vào tính chất:

 



 

 







0 1a

a a

Tương tự:

   

 



 

     



  



0

0 1

1 1

0 1

a

a a a hay a a

.

Câu 20. [2D1-3.2-1]Cho

, , 0a b c

và

1

a

bc











. Khẳng định nào sau đây là khẳng định sai?

A.

2log log

a a

bc bc

. B.

 

 

1

log log log

2

a a a

bc b c

.

C.



1

log

a

bc

a

. D.

 log log log

a a a

bc b c

.

Lời giải

Chọn D

Vì

 

log log log .

a a a

bc b c

Câu 21. [2H1-1.2-1] Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng ?

A.

4

mặt phẳng. B.

1

mặt phẳng.

C.

2

mặt phẳng. D.

3

mặt phẳng.

Lời giải

Chọn A

Hình lăng trụ tam giác đều có

4

mặt phẳng đối xứng (hình vẽ bên dưới).

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 55

Câu 22. [2H1-1.1-1]Cho hình đa diện đều loại

 

4;3

cạnh

.a

Gọi

S

là tổng diện tích tất cả các mặt của

hình đa diện đó. Mệnh đề nào dưới đây đúng?

A.

2

4S a

. B.

2

6S a

. C.

2

8S a

. D.

2

10S a

.

Lời giải

Chọn B

Đa diện đều loại

 

4;3

là khối lập phương nên có 6 mặt là các hình vuông cạnh

a

. Vậy hình

lập phương có tổng diện tích tất cả các mặt là

2

6 .S a

Câu 23. [2H1-2.8-1]Cho một khối chóp có thể tích bằng

V

. Khi giảm diện tích đa giác đáy xuống

1

3

lần thì thể tích khối chóp lúc đó bằng

A.

9

V

. B.

3

V

. C.

6

V

. D.

27

V

.

Lời giải

Chọn B

Câu 24. [2H1-2.1-1]Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh

a

. Biết

 



SA ABCD

và



3SA a

. Thể tích của khối chóp S.ABCD là

A.

3

a

. B.

3

4

a

. C.

3

a

. D.

3

.

12

a

Lời giải

Chọn A

  

3

2

. D D

1 1 3

. 3

3 3 3

S ABC ABC

a

V S SA a a

.

Câu 25. [2H1-1.0-1] Chọn khẳng định sai. Trong một khối đa diện

A. Mỗi đỉnh là đỉnh chung của ít nhất 3 mặt.

B. Mỗi mặt có ít nhất 3 cạnh.

C. Mỗi cạnh của một khối đa diện là cạnh chung của đúng hai mặt phẳng.

D. Hai mặt bất kì luôn có ít nhất một điểm chung.

Lời giải

Chọn D

Dựa vào định nghĩa hình đa diện suy ra: A, B, C đúng.

Hình đa diện (gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai

tính chất:

a) Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung,

hoặc chỉ có một cạnh chung.

b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.

Mỗi đa giác gọi là một mặt của hình đa diện. Các đỉnh, cạnh của các đa giác ấy theo thứ tự

được gọi là các đỉnh, cạnh của hình đa diện.

Đáp án D sai.

Ví dụ: hình lăng trụ

. ' ' 'ABC A B C

có đáy

 

ABC

và

 

' ' 'A B C

song song với nhau nên không có điểm chung.

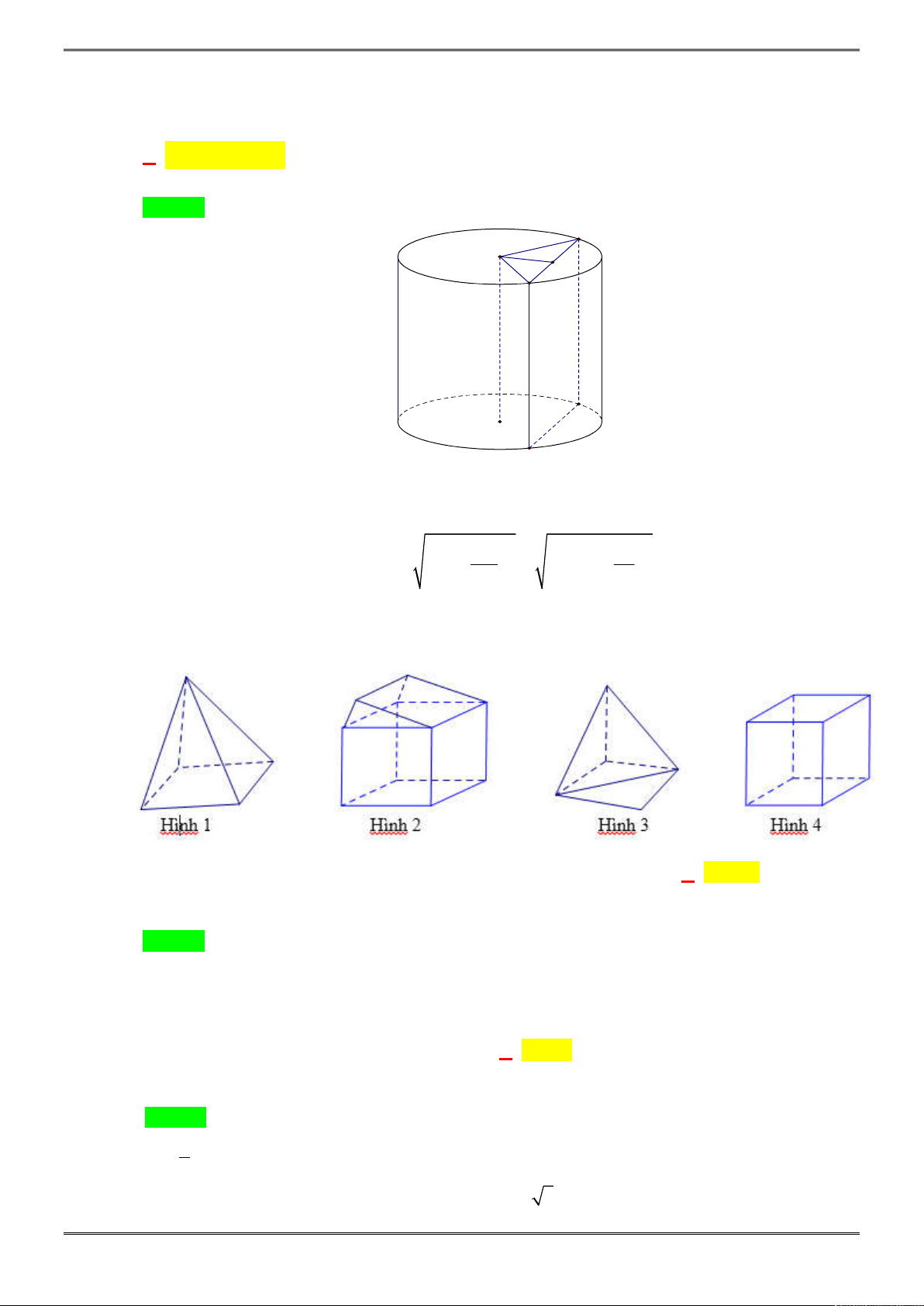
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 56

Câu 26. [2H2-1.2-2] Cho hình trụ có đường cao bằng

8a

. Một mặt phẳng song song với trục và cách

trục hình trụ

3a

, cắt hình trụ theo thiết diện là hình vuông. Diện tích xung quanh và thể tích

khối trụ bằng:

A.

2 3

80 ,200

 

a a

. B.

2 3

60 ,200

 

a a

. C.

2 3

80 ,180

 

a a

. D.

2 3

60 ,180 .a a

 

Lời giải

Chọn A

H

D

C

B

A

O'

O

Thiết diện

ABCD

là hình vuông có cạnh là

8a

 

8



h a

.

Khoảng cách từ trục đến mặt phẳng

 

ABCD

là

3 .d a

Suy ra bán kính đường tròn đáy

 

2 2

2

8

3 5 .

2 2

AB a

r d a a

   

    

   

   

Vậy

2

2 80

 

 

xq

S rh a

,

2 3

200 .

tr

V r h a

 

 

Câu 27. [2H1-1.1-1] Hình nào dưới đây không phải là hình đa diện?

A. Hình 4. B. Hình 1. C. Hình 2. D. Hình 3.

Lời giải

Chọn D

Hình 3 có một tam giác nằm hoàn toàn bên ngoài làm cho hình tạo nên không liền một khối nên

nó không phải là hình đa diện.

Câu 28. [2H1-1.3-1]Cho khối nón có chiều cao bằng

6

và bán kính đường tròn đáy bằng

8

. Thể tích

của khối nón là:

A.



160

. B.



144

. C.



128

. D.

169



.

Lời giải

Chọn C

 

 

1

.64.6 128

3

V

.

Câu 29. [2H2-1.3-2] Một hình nón có đường kính đáy là

2 3a

, góc ở đỉnh là

0

120

. Tính thể tích của

khối nón đó theo

a

.

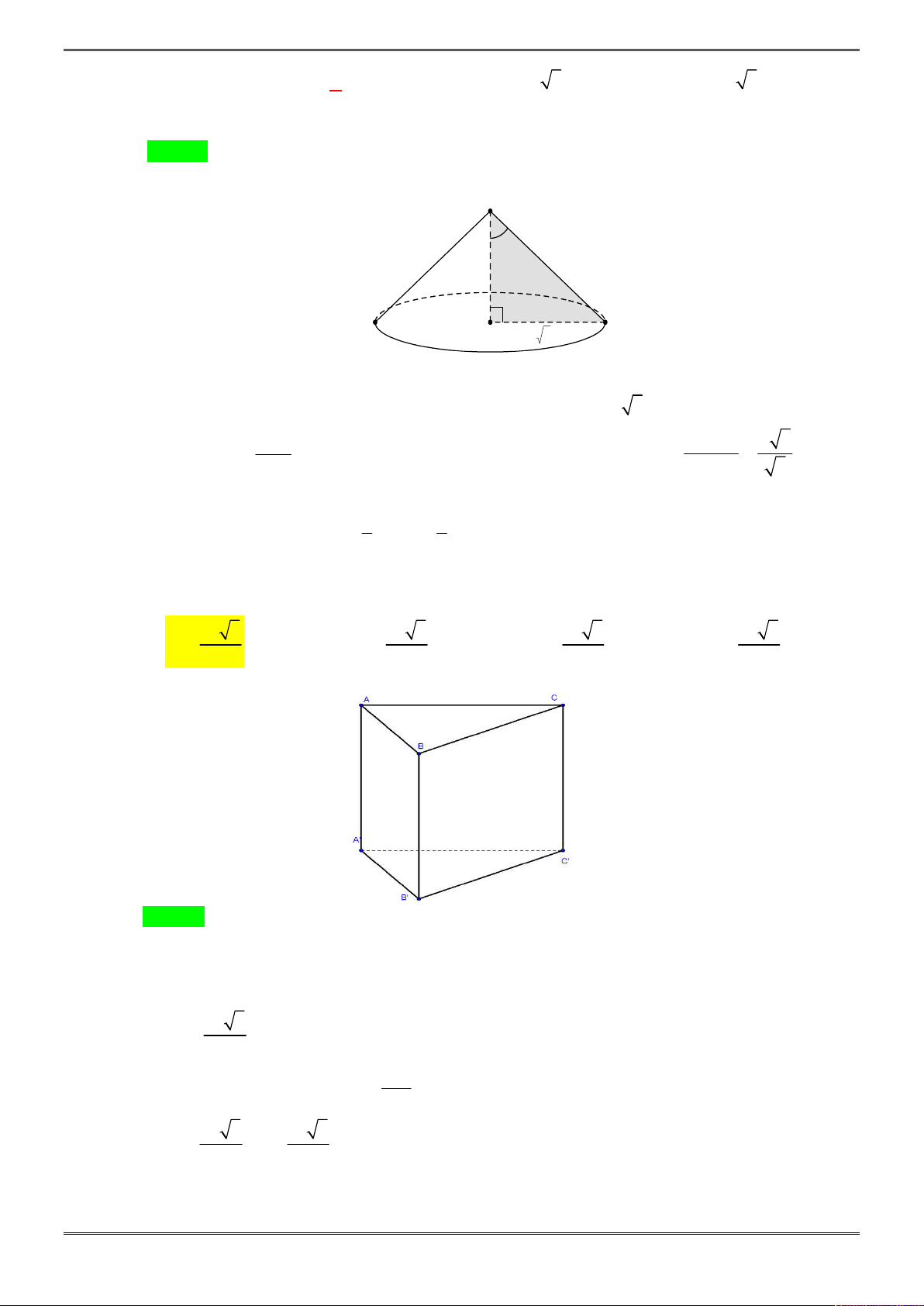
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 57

A.

3

a



. B.

3

a



. C.

3

2 3

a



. D.

3

a



.

Lời giải

Chọn B

a 3

60

0

A

C

B

Gọi

B

là đỉnh hình nón,

A

là tâm đáy,

C

là một điểm thuộc đường tròn đáy.

Theo giả thiết dễ suy ra đường tròn đáy có bán kính

3 (cm)

 R AC a

và góc



0

120

60

2

 ABC

. Xét tam giác

ABC

vuông tại

A

, ta có

0

3

tan 60

3

  

AC a

AB a

.

Do đó chiều cao hình nón là

h a

.

Vậy thể tích khối nón là

2 2 3

1 1

.3 .

3 3

V R h a a a

  

  

.

Câu 30. [2H1-3.2-2]Cho lăng trụ đều

.

ABC A B C

  

có cạnh đáy bằng

a

, diện tích mặt bên

ABB A

 

bằng

2

2a

. Tính thể tích

V

của khối lăng trụ

.

ABC A B C

  

.

A.

3

2

a

V 

. B.

3

6

a

V 

. C.

3

4

a

V 

. D.

3

12

a

V 

.

Lời giải

Chọn A

- Thể tích của khối lăng trụ đều bằng diện tích đáy nhân với chiều cao

- Do

.

ABC A B C

  

là lăng trụ đều nên đáy là tam giác đều cạnh

a

, mặt bên

ABB A

 

là hình chữ

nhật với độ dài cạnh

AA



là chiều cao

2

3

4

ABC

a

S 

.

2

2 . 2

ABB A

a

S a AB AA AA a

a

 

    

2 3

3 3

.2

4 2

a a

V a  

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 58

Câu 31. [2D1-1.9-3]Tìm tất cả các giá trị thực của tham số

m

để hàm số

2cos 3

2cos

x

y

x m







nghịch biến

trên khoảng

0; .

3



 













 

A.

 

3;m

  

. B.

   

; 3 2;m

    

.

C.

 

; 3

m

  

. D.

   

3;1 2;m

   

.

.Lời giải

Chọn C

Đặt

cost x

, với

1

0; ;1

3 2

x t



   

 

 

  

 

 

 

 

   

.

Hàm số trở thành

   

 

2

2 3 2 6

'

2

t m

y t y t

t m

  

  



.

Ta có

' sin 0, 0;

3

t x x



 





    









 

, do đó

cost x

nghịch biến trên

0; .

3



 













 

Do đó YCBT

 

y t

đồng biến trên khoảng

1

;1

2

 













 

 

1

' 0, ;1

2

y t t

 





   









 

 

3

2 6 0 3

1 1

, ;1 , ;1 3.

1;2

2 0 2

2 2

m

m m

t t m

m

t m m t



  



   

   

 

  

 

 

        

 

  

 

 

 

  

   



  

 

 





Nhận xét. Do

 

1

;1 2 1;2

2

t t

 





  









 

. Và

 

1

1;2

2

m







 







.

Câu 32. [2D2-6.10-4]Cho

p

,

q

là các số thực dương thỏa mãn

 

9 12 16

log log log

p q p q  

. Tính

giá trị của biểu thức

.

p

A

q



A.

1 5

2

A





. B.

1 5

2

A

 



. C.

1 5

2

A

 



. D.

1 5

2

A





.

Lời giải

Chọn C

Đặt

 

9 12 16

9

log log log 12

16

t

p

t p q p q q

p q









     





 





9 12 16 .

t t t

p q

    

 

*

Chia hai vế của

 

*

cho

16

t

, ta được

2

9 12 3 3

1 1

16 16 4 4

t t t t

       

   

   

    

   

   

   

   

       

2

3 3 3 1 5

1 0

4 4 4 2

t t t

     

 

  

  

     

  

  

  

  

     

(loại) hoặc

3 1 5

.

4 2

t

 

 















 

Giá trị cần tính

3 1 5

4 2

t

p

A

q

 

 





  









 

.

Câu 33. [2D1-5.10-4]Tính tổng

T

tất cả các nghiệm của phương trình

2 2

sin cos

2017 2017 cos2

x x

x 

trên

đoạn

 

0; .

A.

x 

. B.

4

x





. C.

2

x





. D.

3

4

x





.

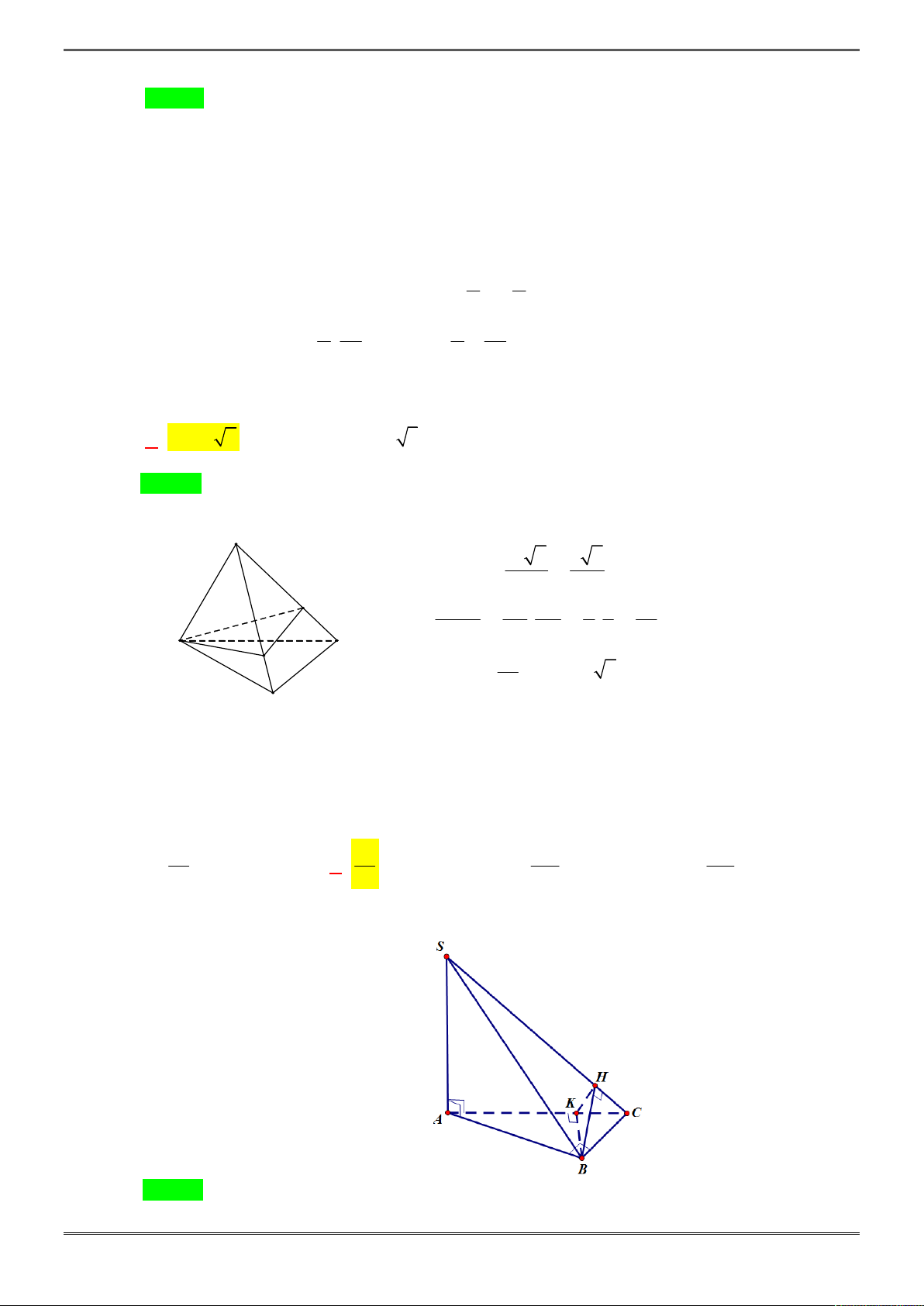
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 59

Lời giả

Chọn A

Phương trình

2 2

sin cos 2 2

2017 2017 cos sin

x x

x x   

2 2

sin 2 cos 2

2017 sin 2017 cos .

x x

x x   

 

*

Xét hàm số

 

2017

t

f t t 

trên

,

ta có

 

' 2017 ln2017 1 0, .

t

f t t

     

Suy ra hàm số

 

f t

đồng biến trên

.

Nhận thấy

 

*

có dạng

   

2 2 2 2

sin cos sin cosf x f x x x  

2 2

cos sin 0 cos 2 0 , .

4 2

x x x x k k

 

         

Vì

 

3 3

0; ;

4 4 4 4

x x T

   

 

 

 

      

 

 

 

.

Câu 34. [2H1-2.5-3]Cho hình chóp

.

S ABC

có

3, 4, 5

SA SB SC

  

và



0

60 .

ASB BSC CSA

  

Tính thể tích

V

của khối chóp đã cho.

A.

5 2

V



. B.

5 3

V



. C.

10

V



. D.

15

V



.

Lời giải

Chọn D

Trên các đoạn

, SB SC

lần lượt lấy các điểm

, E F

sao cho

3.

SE SF

 

Khi đó

.

S AEF

là khối tứ diện đều có cạnh

3.

a



Suy ra

3

.

2 9 2

.

12 4

S AEF

a

V  

Ta có

.

3 3 9

. .

4 5 20

S AEF

S ABC

V

SE SF

V SB SC

  

. .

20

5 2

9

S ABC S AEF

V V  

.

Câu 35. [2H1-2.1-3] Cho hình chóp

. ,

S ABC ABC

là tam giác vuông cân có

BA BC a 

, cạnh bên

SA

vuông góc với đáy, góc giữa hai mặt phẳng

 

SAC

và (SBC) là

0

60

. Tính thể tích hình chóp

.

S ABC

A.

3

7

a

. B.

3

6

a

. C.

3

2

3

a

. D.

3

7

a

Lời giải

Chọn B

F

E

S

A

B

C

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 60

C

B

S

A

H

Gọi H, K lần lượt là hình chiếu vuông góc của B lên SC và AC

( )

SC BHK SC HK  



0

60

BHK 

0

.tan 60

2

2 6

AC a a

BK BK HK    

mà

SAC KCH 

nên ta có

HK CK

SA SC



2 2

2 3SA a SA

  

SA a 

3

.

6

S ABC

a

V

 

.

Câu 36. [2H1-2.8-4]Cho hình chóp

.

S ABC

có

SA a

,

2SB a

,

3SC a

. Tính thể tích lớn nhất

max

V

của khối chóp đã cho.

A.

3

max

6

V a



. B.

3

max

6

2

a

V 

. C.

3

max

6

3

a

V 

. D.

3

max

6

a

V 

.

Lời giải

Chọn D.

Gọi

H

là hình chiếu của

A

trên mặt phẳng

   

.SBC AH SBC 

Ta có



AH AS

.

Dấu

'' ''

xảy ra khi

 

AS SBC

.



1 1

. .sin .

2 2

SBC

S SB SC BSC SB SC



 

.

Dấu

'' ''

xảy ra khi

SB SC

.

Khi đó

1 1 1 1

. . . .

3 3 2 6

SBC

V S AH SB SC AS SA SB SC



 





   









 

Dấu

'' ''

xảy ra khi

, , SA SB SC

đôi một vuông góc với nhau.

Vậy thể tích lớn nhất của khối chóp là

3

max

1 6

. .

6 6

a

V SA SB SC 

.

Câu 37. [2D2-5.8-3]Tìm tất cả các giá trị thực của tham số

m

để bất phương trình

2

2 1 2 3

2

x mx x m

e

  

   

 

 



 

 

 

 

   

nghiệm đúng với mọi

x

.

A.

 

5;0

m

 

. B.

 

5;0

m

 

.

C.

   

; 5 0;m

    

. D.

   

; 5 0;m

    

.

Lời giải

Chọn B

Bất phương trình

2

2 1 2 3

2

2 1 2 3

2 2

x mx x m

e e

x mx x m

   

   

 

 

       

 

 

 

 

   

 

2

2 1 3 1 0.

x m x m

     

Ycbt

 

2

1 0

0

2 1 3 1 0,

' 0

1 3 1 0

a

x m x m x

m m













         

 

 

 

   











2

5 0 5 0

m m m

      

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 61

Câu 38. [2D1-2.16-3] Gọi

 

P

là đường parabol qua ba điểm cực trị của đồ thị hàm

số

4 2 2

1

4

  y x mx m

(m

là tham số thực).Gọi

0

m

là giá trị để

 

P

đi qua điểm

 

2;24

A

.Hỏi

0

m

thuộc khoảng nào sau đây?

A.

 

10;15

. B.

 

6;1



. C.

 

2;10



. D.

 

8;2



.

Lời giải

Chọn C

Hàm số đã cho liên tục trên



.Ta có

4 2 2

1

( )

4

   y f x x mx m

,

3

' '( ) 2 .

  

y f x x mx

+)ĐK để đồ thị của hàm số có ba điểm cực trị là

'( )f x

đổi dấu ba lần

'( ) 0 

f x

có ba

nghiệm phân biệt

0 

m

.

+)Thực hiện phép chia đa thức

( )f x

cho

'( )f x

ta được

2 2

( ) '( ). ( )

2

  

m

f x f x q x x m

.Từ đó

suy ra parabol đi qua ba điểm cực trị của đồ thị hàm số là

2 2

2

  

m

y x m

 

P

+)

 

2

24 2 6

A P m m m

      

(Chú ý

0

m

).

Câu 39. [2D2-5.4-3]Tìm tập nghiệm

S

của phương trình

2 2

1

3 .5 15

x m

x

x m

 





,

m

là tham số khác 2.

A.

 

3

2; log 5

S m



B.

 

3

2; 5

log

S m 

.

C.

 

2

S



. D.

 

3

2; log 5

S m

 

.

Lời giải

Chọn D

Điều kiện:

.x m

Phương trình

 

2 2 2 2 2

1

1 1

1 2

3 .5 3.5 5 3 5 3

x m x m x

x

x x

x m x m x m

    



 

  

     

.

 

*

Lấy logarit cơ số 5 hai vế của

 

*

, ta được

:

   

5 5

2 1

2 log 3 2 log 3 0.

x

x x

x m x m

 







     









 

 

 Với

 

2 0 2 .

x x

thoûa maõn   

 Với

 

5 3

5

1 1

log 3 0 log 5 .

log 3

x m x m

x m

thoûa maõn

        



Vậy phương trình có tập nghiệm

 

3

2; log 5

S m

 

Câu 40. [2D1-2.14-3]Cho hàm số

   

4 2 4

2 2

y x mx m m

. Với những giá trị nào của m thì đồ thị (

m

C

)

có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành một tam giác có diện tích

4

S



?

A.

16m

B.

 

3

16

m

C.



3

16

m

D.



5

16

m

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 62

Lời giải

Chọn D







   







3

2

0

4x 4 x 0

x

y m

x m

Để hàm số có 3 cực trị thì

 0m

, khi đó ba điểm cực trị là:

 



4

0;2

A m m

;

 

 

4 2

, 2B m m m m

;

 

  

4 2

, 2C m m m m

. Gọi I là trung điểm của BC

 

  

4 2

0; 2I m m m

.Ta có

 

4 2

AI m m

và

 4 2

BC m m

.

Theo đề

2

5

4 4 4 16

2

ABC

BCAI

S m m m      

.

PHẦN II: PHẦN TỰ LUẬN

Bài 1. Cho hai số thực dương

,a b

.Biết hàm số

 

2( 1) cos ( )y ab x a b x

   

đồng biến trên



.Tìm giá

trị nhỏ nhất của biểu thức

2F a b 

Lời giải

Vì hàm số đã cho đồng biến trên



nên

' 2( 1) ( )sin[(a b) x] 0 xy ab a b

       

(1)

Đặt

sin[( ) ]t a b x 

,

[ 1;1]

t

 

.Xét

( ) 2( 1) ( )f t ab a b t   

(1) 0 2( 1) ( ) 0

(1)

( 1) 0 2( 1) ( ) 0

f ab a b

    

 

  

 

     

 

(2 1) 2

b a a

  

(2)

Vì

,a b

là các số dương nên từ

(2)

suy ra

1

2

a



và

2

2 1

a

b

a









10

4 2

2 1

b

a

 



.Do đó

10

2 2 4 (2 1) 3 3 2 10

2 1

F a b a

a

       



3 10

2

F



 

(3)

BĐT

(3)

trở thành đẳng thức khi và chỉ khi

2 1 0

1 10

10

2

2 1

2 10

2

4

2 1

a

b

a

b

a





 









 

  

 





 





 











.Vậy

3 2 10

min

2

F





.

Bài 2. Hình lập phương

.

ABCD A B C D

   

có cạnh bằng

a

, một hình nón tròn xoay có đỉnh là tâm của

hình vuông

DABC

và có đáy là đường tròn ngoại tiếp hình vuông

.A B C D

   

a) Tính diện tích xung quanh của hình nón đó

b) Tính thể tích khối nón tương ứng.

Lời giải

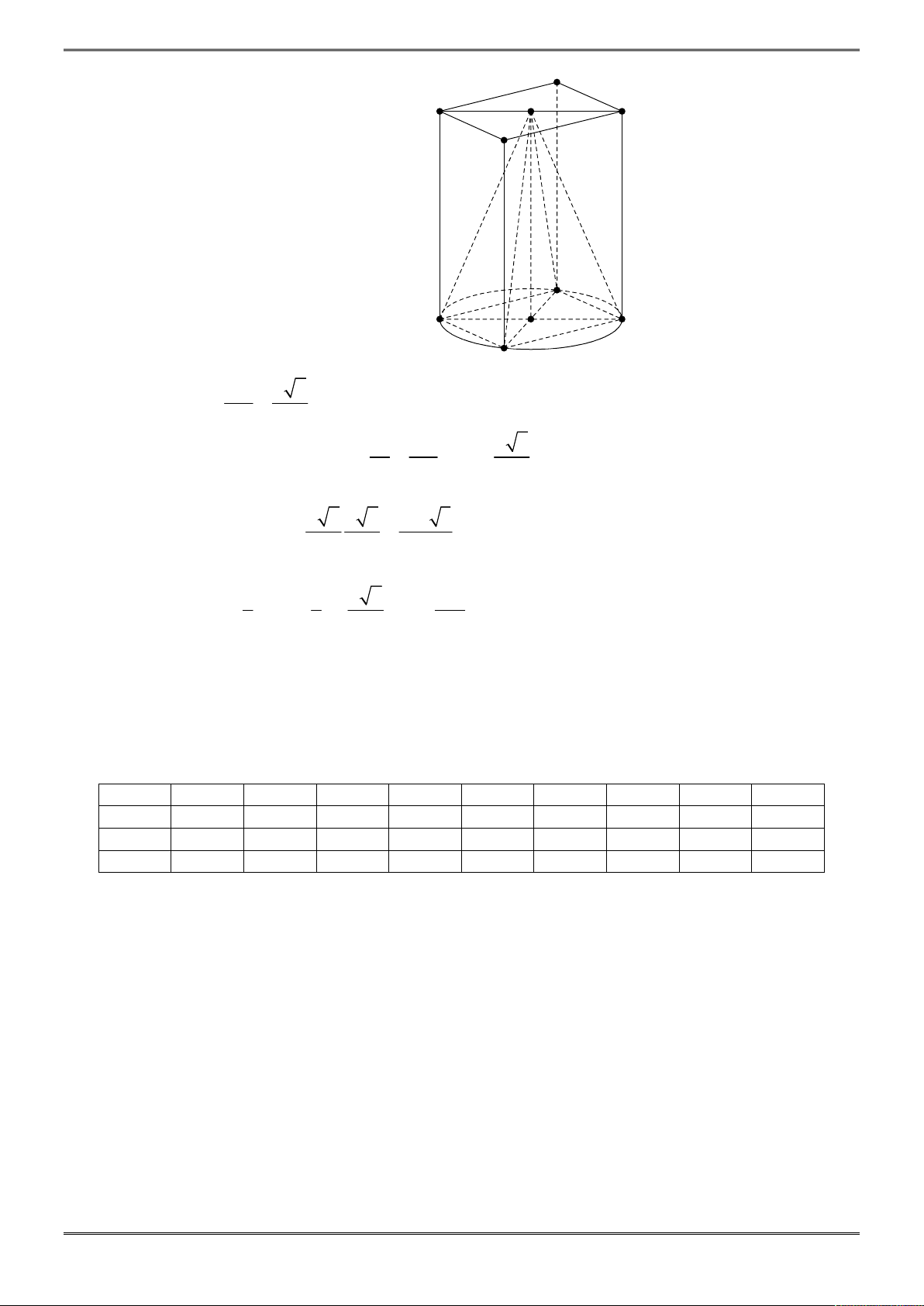
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 63

l

r

h

D'

A'

B'

C'

O

C

A

O'

B

D

Ta có:

2

2 2

AC a

r  

và

h a

2 2

2 2 2 2

3 6

.

2 2 2

a a a

l a r a l       

a) Diện tích xung quanh:

2

2 6 3

.

2 2 2

xq

a a a

S rl



 

  

b) Thể tích hình nón đó là

2

3

2

1 1 2

. .

3 3 2 6

a a

V r h a



 

 

  

 

 

BẢNG ĐÁP ÁN

1.C

2.D

3.C

4.D.A

5.B

6.D.B

7.D.B

8.C

9.C

10.A

11.A

12.B

13.C

14.B

15.B

16.B

17.D

18.D.D

19.A

20.D

21.A

22.B

23.B

24.A

25.D

26.A

27.D

28.C

29.B

30

31.C

32.C

33.A

34.A

35.B

36.D

37.B

38.C

39.D

40.D

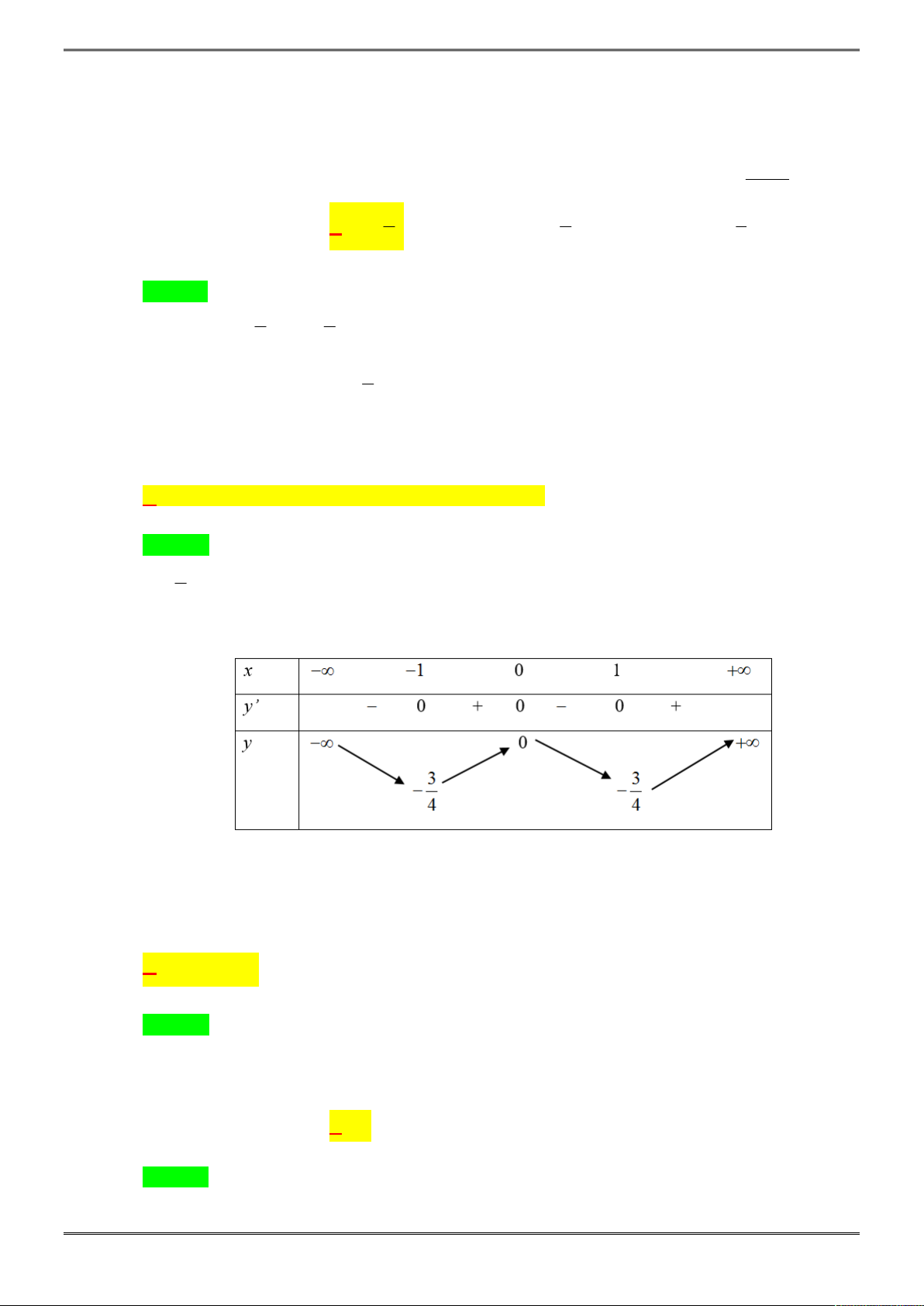
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 64

ĐỀ ÔN TẬP SỐ 15

PHẦN I: PHẦN TRẮC NGHIỆM

Câu 1. [2D1-4.3-1] Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số

3 1

?

2 1

x

y

x







A.

1.

y



B.

3

.

2

y



C.

1

.

2

y



D.

1

.

3

y



Lời giải

Chọn B.

Ta có

3

lim

2

x

y





3

2

y

 

là tiệm cận ngang của đồ thị hàm số.

Câu 2. [2D1-2.1-1] Cho hàm số

4 2

1

.

2

y x x 

Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số đạt cực đại tại các điểm

1; 1

x x

  

.

B. Hàm số có giá trị lớn nhất bằng với giá trị cực đại.

C. Hàm số đạt cực tiểu tại điểm

0

x



.

D. Hàm số có giá trị nhỏ nhất bằng với giá trị cực tiểu.

Lời giải

Chọn D.

4 2

1

2

y x x 

3

' 2 2 , ' 0

y x x y

   

0

.

1

x









 



Bảng biến thiên

Dựa vào bảng biến thiên suy ra đáp án D là đáp án đúng.

Câu 3. [2D2-4.0-1] Cho hàm số

 

0, 1

x

y a a a

  

. Khẳng định nào sau đây là sai ?

A. Tập xác định

D  

B. Hàm số có tiệm cận ngang

0

y



C.

lim

x

y



 

D. Đồ thị hàm số luôn ở phía trên trục hoành

Lời giải

Chọn C.

Vì nếu

0 1a 

thì

lim 0

x

y





Câu 4. [2D2-4.2-1] Tìm khoảng đồng biến của hàm số

sin .y x x  

A.



B.



C.

 

1;2

D.

 

;2



Lời giải

Chọn B.

Ta có

siny x x  

tập xác định

D  

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 65

' 1 cos 0,y x x    

.

Vậy hàm số luôn nghịch biến trên



.

Câu 5. [2D2-4.2-1] Tính đạo hàm của hàm số

2017 .

x

y 

A.

1

' .2017

x

y x



 . B.

' 2017

x

y  . C.

2017

'

ln 2017

x

y  . D.

' 2017 .ln 2017

x

y  .

Lời giải

Chọn D.

' 2017 .ln 2017.

x

y 

Câu 6. [2D2-4.1-1] Cho hàm số

   

2

log 3 4

f x x

 

. Tập hợp nào sau đây là tập xác định của

 

?f x

A.

 

1;D

  

. B.

4

;

3

D

 

  

 

 

. C.





1;D

  

. D.





1;D

 

.

Lời giải

Chọn C.

Hàm số xác định

 

2

3 4 0

log 3 4 0

x

 









 





3 4 0

3 4 1

x

 







 



1.

x

  

Câu 7. [2D2-5.2-1] Giải phương trình

 

2 1

16 8

x





A.

3

x

 

B.

2

x



C.

3

x



D.

2

x

 

Lời giải

Chọn C.

Phương trình

   

 

2 1

4 3

2 2

x x 

 

4 6 6

2 2

x x 

 

4 6 6x x   

3.

x

 

Câu 8. [2H1-1.0-1] Trong các mệnh đề sau, mệnh đề nào SAI?

A. Khối tứ diện là khối đa diện lồi.

B. Lắp ghép hai khối hộp luôn được một khối đa diện lồi.

C. Khối hộp là khối đa diện lồi.

D. Khối lăng trụ tam giác là khối đa diện lồi.

Lời giải

Chọn B.

Đa diện lồi là đa diện mà đoạn thẳng nối hai điểm bất kì của đa

diện đó luôn thuộc chính nó.

Các khối tứ diện, khối hộp, khối lăng trụ tam giác là các khối đa

diện lồi.

Ghép hai khối hộp chưa chắc đã được một khối đa diện lồi, ví dụ

như hình bên, đoạn

''AA

nằm ngoài khối đa diện thu được khi

ghép 2 khối hộp

. ' ' ' 'ABCD A B C D

và

' ' ' '. '' '' '' ''A B C D A B C D

nên khối đa diện thu được không phải khối đa diện lồi.

Câu 9. [2H1-2.1-1] Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình

vuông cạnh bằng 1. Cạnh bên

SA

vuông góc với mặt phẳng

 

ABCD

và

5

SC  . Tính thể

tích khối chóp

. .S ABCD

A.

3

V

3



. B.

3

V

6



. C.

V 3

 . D.

15

V

3



.

Lời giải

Chọn A.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 66

O

B

A

D

C

S

Đường chéo hình vuông

2

AC 

.

Xét

SAC

, ta có

2 2

3

SA SC AC  

.

Chiều cao khối chóp là

3

SA  .

Diện tích hình vuông

ABCD

là

2

1 1

ABCD

S

 

.

Thể tích khối chóp

.

S ABCD

là:

.

1 3

. .

3 3

S ABCD ABCD

V S SA 

(đvtt).

Câu 10. [2H2-1.2-1] Diện tích xung quanh của hình nón tròn xoay ngoại tiếp tứ diện đều cạnh

a

là:

A.

2

3

xq

a

S



 . B.

2

3

xq

a

S



 . C.

2

3

xq

a

S





. D.

2

2 3

3

xq

a

S





.

Lời giải

Chọn C.

Ta có :

3

;

3

a

R 

l a

2

3

.

3

xq

a

S Rl



  

Câu 11. [2D1-6.1-2] Số giao điểm của đường cong

3 2

3 1y x x x   

và đường thẳng

1 2y x 

bằng:

A.

1.

B.

0.

C.

2.

D.

3.

Lời giải

Chọn A.

Xét phương trình hoành độ

3 2

3 1 1 2x x x x    

3 2

3 3 2 0

x x x

    

2

x

 

Vậy số giao điểm là

1

.

Câu 12. [2D1-5.1-2] Đồ thị sau đây là đồ thị của hàm số nào?

A.

4 2

2 1

y x x

  

. B.

4 2

2y x x

 

.

C.

4 2

2y x x

  

. D.

4 2

2 1

y x x

   

.

Lời giải

Chọn B.

Dựa vào đồ thị ta thấy:

Hàm số cần tìm có dạng

4 2

y ax bx c  

Do

lim

x

y



 

0

a

 

mà hàm số đi qua

( 1; 1) 

và

(1; 1)



Hàm số cần tìm là

4 2

2y x x

 

Câu 13. [2D1-7.1-2] Cho hàm số

3 2

1

2 3 1

3

y x x x   

có đồ thị (C). Tiếp tuyến của (C) song song với

đường thẳng

: 3 1y x  

có phương trình là:

A.

3 1y x 

B.

26

3

y x 

C.

3 2

y x

 

D.

29

3

y x 

y

x

-1

2

1

O

1

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 67

Lời giải

Chọn D.

Gọi

3 2

1

; 2 3 1

3

M a a a a

 

  

 

 

là điểm thuộc (C).

Đạo hàm:

2

' 4 3y x x  

.

Suy ra hệ số góc của tiếp tuyến của (C) tại M là

 

2

' 4 3

k y a a a

   

.

Theo giả thiết, ta có:

3

k



2

4 3 3

a a

   

0

.

4

a













Với

     

 

0 0;1 : 3 0 1 3 1

7 7 29

4 4; : y 3 4 3

3 3 3

a M tt y x x L

a M tt x x

       



 



       

 



 



.

Câu 14. [2D1-3.8-2] Cho hàm số

 

2

3 1

1

x

y f x

x



 



, giá trị lớn nhất của hàm số

 

f x

trên tập xác

định của nó là:

A.

2.

B.

4.

C.

2 2.

D.

10.

Lời giải

Chọn D.

Hàm số liên tục trên



.

 

2

3 1 3 1

1

' 0

1

x

x x

x

y

x

  



 



 

2

3 1 3 1

x x x

   

3.

x

 

' 0, 3;

y x

  

' 0, 3

y x

  

.

 

3 10

y 

max 10

y 

.

Câu 15. [2D1-1.5-2] Tìm các giá trị của tham số

m

để hàm số :

   

3 2

1

6 2 1

3

y x mx m x m

     

luôn đồng biến trên



:

A.

2

m

 

. B.

3

m



. C.

2 3

m

  

. D.

2

m

 

hoặc

3

m



.

Lời giải

Chọn C.

2

' 2 6, y' 0

y x mx m

    

2

2 6 0.

x mx m

    

 

2 2

' 6 6

m m m m

      

.

Hàm số đồng biến trên



' 0 xy

    

1 0

' 0

a

 







 



2

6 0

m m

   

2 3.

m

   

Câu 16. [2D1-2.5-2] Gọi giá trị cực đại và giá trị cực tiểu của hàm số

3

3 2y x x  

lần lượt là

,

C

CĐ

T

y y

. Tính

3 2

CT

CĐ

y y

 ?

A.

3 2 12

CĐ CT

y y

  

. B.

3 2 3

CTCĐ

y y

  

.

C.

3 2 3

TĐ CC

y y

 

. D.

3 2 12

CĐ CT

y y

 

.

Lời giải

Chọn D.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 68

Ta có:

2

' 3 3,

y x

 

' 0

y



1

x

  

4

0

CD

CT

y













. Vậy

3 2 12

CD CT

y y

 

.

Câu 17. [2D1-4.4-2] Đồ thị hàm số

2

2017

5

x

y

x







có số đường tiệm cận là:

A.

1.

B.

2.

C.

3.

D.

4.

Lời giải

Chọn D.

Ta có:

2

2017

lim lim 1

5

x x

x

y

x

 



  



1

y









 



là 2 tiệm cận ngang.

Lại có:

5

lim

x

y







 







 





5

x









 





là tiệm cận đứng.

Câu 18. [2D2-6.4-2] Bất phương trình

3

3log ( 1) log (2 1) 3

x x

   

có tập nghiệm là :

A.





1;2

. B.

 

1;2

. C.

1

;2

2



 

 

 

. D.

1

;2

2



 





 

.

Lời giải

Chọn A.

Điều kiện

1x 

.

3 3

3log ( 1) 3log (2 1) 3

x x

   

.

 

3

log ( 1)(2 1) 1

x x

   

.

( 1)(2 1) 3.

x x

   

2

2 3 2 0.

x x

   

1

2.

2

x



  

Kết hợp với điều kiện tập nghiệm là





1;2

S 

.

Câu 19. [2D2-5.2-2] Tổng bình phương các nghiệm của phương trình

2

3 2

1

5

x



 



 

 

bằng:

A.

0

. B.

5

. C.

2

. D.

3

.

Lời giải

Chọn B.

Ta có

2

3 2

1

5

x



 



 

 

2

3 2

5 5

x x



 

2

3 2

x x  

1

.

2

x













Vậy tổng bình phương hai nghiệm bằng

5

.

Câu 20. [2D2-6.4-2] Nghiệm của bất phương trình

2

1

2

3 2

log 0

x x

x

 



là:

A.

0

2 2 2 2

x







   



. B.

2 2 1

2 2 2

x



  



  





C.

2 2 1

2 2 2

x



  



  





. D.

0

2 2

x







 



.

Lời giải

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 69

Chọn B.

ĐK:

0 1

2

x

 









.

2

1

2

3 2

log 0

x x

x

 



.

2

1 1

2 2

3 2

log log 1.

x x

x

 

 

2

3 2

1

x x

x

 

 

.

2

4 2

0.

x x

x

 

 

0

.

2 2 2 2

x









   



Kết hợp đk nghiệm của bất phương trình

2 2 1

2 2 2

x



  



  





.

Câu 21. [2D2-5.3-2] Tập nghiệm của bất phương trình

4 2 2 0

x x

  

là:

A.

 

1;



. B.

 

;1

. C.

 

2;



. D.

 

;2



.

Lời giải

Chọn B.

Đặt

2 , 0

x

t t

 

. Bất phương trình trở thành:

2

2 0

t t

  

1 2t   

2 2

x

 

1.

x

 

Câu 22. [2D2-4.1-2] Cho hàm số

   

log 100 3

f x x 

 

 

. Khẳng định nào sau đây sai ?

A. Tập xác định của hàm số

 

f x

là





3;D

 

.

B.

   

2log 3

f x x

 

với

3

x



.

C. Đồ thị hàm số

 

4;2

đi qua điểm

 

4;2

.

D. Hàm số

 

f x

đồng biến trên

 

3;



.

Lời giải

Chọn A.

Hàm số xác định khi

 

100 3 0

x

 

3

x

 

. Do đó A sai.

Câu 23. [2D2-3.2-2] Với các số thực dương

,x y

bất kì. Mệnh đề nào dưới đây đúng?

A.

2

log

log .

log

x

y y

 



 

 

B.

 

2 2 2

log log log .x y x y

  

C.

2

2 2 2

log 2log log .

x

x y

y

 

 

 

 

D.

 

2 2 2

log log .log .xy x y



Lời giải

Chọn C.

Vì

2

2 2 2 2 2

log log log 2log log

x

x y x y

y

 

   

 

 

.

Câu 24. [2D2-4.1-2] Tìm tất cả các giá trị của

m

để hàm số

 

2

3

log 5

y x x m  

xác định trên



.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 70

A.

25

4

m 

. B.

0

m



. C.

0

m



. D.

25

4

m 

.

Lời giải

Chọn A.

Hàm số đã cho xác định trên



2

5 0; .

x x m x

     

 

2

5 4 0.

m

     

25

.

4

m 

Câu 25. [2H1-4.2-2] Cho hình chóp

.

S ABC

có đáy là tam giác đều cạnh

,a

cạnh bên

SA

vuông góc

với đáy và thể tích của khối chóp đó bằng

3

.

4

a

Tính cạnh bên

.SA

A.

3

.

2

a

B.

2 3.

a C.

3.

a D.

3

.

3

a

Lời giải

Chọn C.

Đáy là tam giác đều cạnh

a

nên diện tích

2

3

4

ABC

a

S 

.

SA

là đường cao nên

.

1

.

3

S ABC ABC

V SA S



3

.

2

3

4

3

4

S ABC

ABC

a

V

SA a

S

a

   

.

Câu 26. [2H1-4.2-2] Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình thoi cạnh

,a

 

.SA ABCD



Gọi

M

là trung điểm

.BC

Biết



120 , 45 .

o o

DAB SMA 

Khoảng cách từ

D

đến mặt phẳng

 

SBC

bằng:

A.

6

a

. B.

6

3

a

. C.

6

5

a

. D.

6

4

a

.

Lời giải

Chọn D.

Xét

3

:

2

a

ABC AM 

3

2

a

SA 

,

6

( ;( )) ( ;( ))

4

a

d D SBC d A SBC AK  

với

AK

vuông

góc với

SM

Cách giải khác :

.

3

(D,(SBC))

S BCD

SBC

V

d

S





.

Câu 27. [2H2-1.2-2] Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông

bằng

a

. Diện tích xung quanh của hình nón bằng:

A.

2

a



. B.

2

a



. C.

2

3

2

a



. D.

2

a



.

Lời giải

Chọn B.

Giả sử

SAB

là thiết diện qua trục của hình nón (như hình vẽ)

SAB

cân tại

S

nên

SA SB a 

.

Do đó,

2 2

2AB SA SB a

  

và

1 2

2 2

a

SO OA AB  

.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 71

Vậy, diện tích xung quanh của hình nón:

2

2 2

. .

2 2

xq

a a

S rl a



 

  

.

Câu 28. [2H2-4.1-2] Một cái phễu rỗng phần trên có kích thước như hình vẽ.

Diện tích xung quanh của phễu là:

A.

2

360 cm

xq

S





. B.

2

424 cm

xq

S





.

C.

2

296 cm

xq

S





. D.

2

960 cm

xq

S





.

Lời giải

Chọn C.

2

2. .8.10 .8.17 296 cm

xq

S

  

  

.

Câu 29. [2H1-3.4-2] Cho hình hộp

. ' ' ' 'ABCD A B C D

có đáy

ABCD

là hình

thoi cạnh

,a



0

BCD 120

 và

7

'

2

a

AA 

. Hình chiếu vuông góc

của

'A

lên mặt phẳng

 

ABCD

trùng với giao điểm của

AC

và

.BD

Tính theo a thể tích khối

hộp

. ' ' ' '.ABCD A B C D

A.

3

12V a



. B.

3

3V a



. C.

3

9V a



. D.

3

6V a



.

Lời giải

Chọn B.

Gọi

O AC BD 

. Từ giả thiết suy ra

 

'

A O ABCD



.

Cũng từ giả thiết, suy ra

ABC

là tam giác đều nên:

2

3

2

ABCD ABC

a

S S



 

.

Đường cao khối hộp:

2

2 2 2

' ' ' 2 3

2

AC

A O AA AO AA a

 

    

 

 

.

Vậy

3

. ' ' '

. ' 3

ABCD A B C D ABCD

V S A O a

 

(đvtt).

Câu 30. [2H1-4.2-2] Khối lăng trụ

. ' ' 'ABC A B C

có thể tích bằng

3

a

, đáy là tam giác đều cạnh bằng

2a

. Tính khoảng

cách giữa

AB

và

' '.B C

A.

4

3

a

. B.

3

a

. C.

a

. D.

3a

.

Lời giải

Chọn B.

Ta có:

/ / ' 'AB A B

 

/ / ' ' 'AB A B C



   

 

; ' ' ' ' ' ' ; ' ' ' .d AB A B d AB A B C d A A B C h   

Mà

 

2

0 2 3

1

. . . 2 sin 60 3

2

ABC

V h S h a ha a   

.

3

a

h 

Câu 31. [2D2-4.5-3] Tìm tập hợp tất cả các giá trị của tham số thực

m

để hàm số

 

2

ln 4 3y x mx   

đồng biến trên khoảng

 

;

 

?

A.

1

;

2

 

 





 

. B.

1

;

2

 

 

 

 

. C.

1 1

;

2 2

 



 

 

. D.

1

;

2

 







 

.

Lời giải

10cm

8cm

17cm

D'

O

B

A

D

C

B'

A'

C'

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 72

Chọn A.

Ta có:

2

'

4

x

y m

x

 



. Để hàm số đồng biến trên

 

;

 

thì

2

' 0

4

x

y m

x

  



.

Xét hàm số

2

4

x

y

x





ta có

 

2

8 2

' ; ' 0

2

4

x

y y

x







  



 





. Ta có

   

1 1

2 ; 2

2 2

y y

   

.

Để

2

4

x

m

x





thì

 

1 1

min ;

2 2

m f x m m

 

       





 

.

Câu 32. [2D2-3.1-3] Cho các số thực

1 0

a b

  

. Tìm giá trị nhỏ nhất của biểu thức

 

4

2

3log log

b

a

P ab

b

  

A.

min

3

P



. B.

min

4

P



. C.

min

5

2

P



. D.

min

3

2

P



.

Lời giải

Chọn A.

Ta có:

 

   

2

3 3

log log 1 log log 1

4 4

a b a b

a

P ab b a

b



      

.

Đặt

 

log 0 1

b

t a t

  

ta có:

   

2

3 1 1 3

1 1 2

4 4 4

P t t t f t

t t



 

        

 

 

.

Khi đó

 

2

3 1

' 2 2 0

4 2

f t t t

t

      

. Lại có:

   

1

0

1

lim ;lim 4; 3

2

x

f t f t f





 

   

 

 

.

Do đó

min

3

P



khi

1

2

t



.

Câu 33. [2H2-2.2-3] Một cái tục lăn sơn nước có dạng một hình trụ. Đường kính của đường tròn đáy

là

5cm

, chiều dài lăn là

23cm

(hình dưới). Sau khi lăn trọn

15

vòng thì trục lăn tạo trên sân

phẳng một diện diện tích là

A.

3

1725 cm .



B.

2

3450 cm .



C.

2

1725 cm .



D.

2

862,5 cm .



Lời giải

Chọn C.

Diện tích xung quanh của mặt trụ là

2

5

2 2 . .23 115 cm

2

xq

S Rl

  

  

.

Sau khi lăn 15 vòng thì diện tích phần sơn được là:

2

115 .15 1725

S cm

 

 

.

Câu 34. [2H1-2.3-3] Người ta cắt miếng bìa hình tam giác cạnh bằng

10cm

như hình bên và gấp theo

các đường kẻ, sau đó dán các mép lại để được hình tứ diện đều. Tính thể tích của khối tứ diện

tạo thành.

23 cm

5 cm

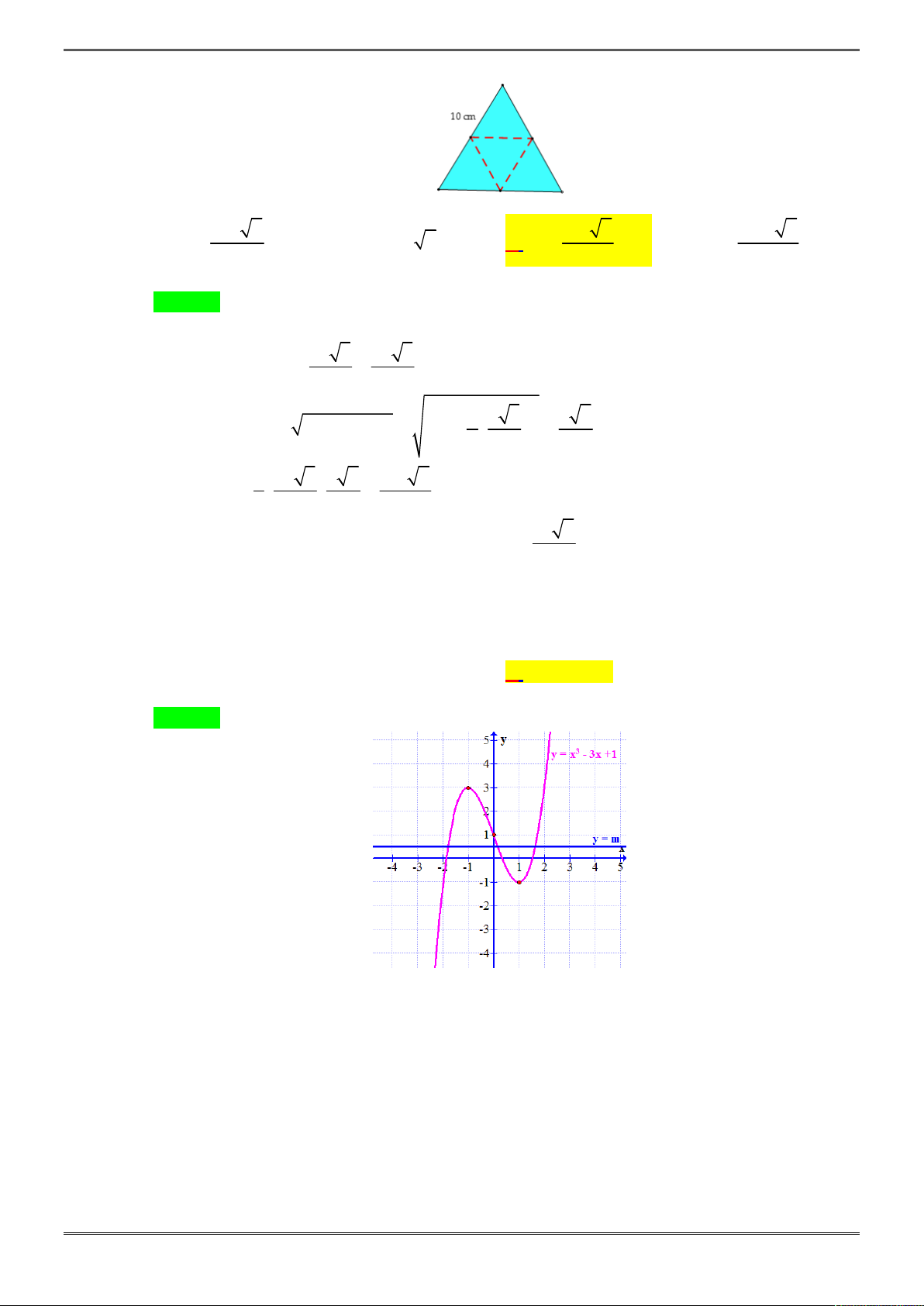
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 73

A.

3

250 2

cm .

12

V 

B.

3

250 2cm .

V 

C.

3

125 2

cm .

12

V 

D.

3

1000 2

cm .

3

V 

Lời giải

Chọn C.

Tứ diện đều tạo thành là tứ diện đều

ABCD

có tất cả các cạnh bằng

5cm

.

Diện tích đáy là

2

3 25 3

cm

4 4

a

S  

.

Đường cao

2

2 2 2

2 5 3 5 6

5

3 2 3

AH AD DH

 

     

 

 

, với

H

là tâm đáy.

Thể tích

3

1 25 3 5 6 125 2

cm

3 4 3 12

V    

.

Ghi nhớ: Thể tích khối tứ diện đều cạnh

a

là

3

2

12

a

V 

Câu 35. [2D1-6.4-3] Tìm tất cả các giá trị thực của tham số

m

sao cho đường thẳng

y m

cắt đồ thị

hàm số

3

3 1y x x  

tại ba điểm phân biệt, trong đó có đúng hai điểm phân biệt có hoành độ

dương ?

A.

1 3.

m

  

B.

1 3.

m

 

C.

1 1.

m

  

D.

1.

m



Lời giải

Chọn C.

Dựa vào đồ thị ta thấy:

1 1

m

  

thì thỏa bài.

Câu 36. [2D1-3.14-4] Nhà Văn hóa Thanh niên của thành phố X muốn trang trí đèn dây led gần cổng.

Ban giám đốc Nhà Văn hóa Thanh niên chỉ cho nhà thiết kế biết chỗ chuẩn bị trang trí đã có

hai trụ đèn cao áp mạ kẽm đặt cố định ở vị trí

A

và

B

có độ cao lần lượt là

10m

và

30m,

khoảng cách giữa hai trụ đèn

24m

và cũng yêu cầu nhà thiết kế chọn một cái chốt ở vị trí

M

trên mặt đất nằm giữa hai chân trụ đèn để giăng đèn dây Led nối đến hai đỉnh

C

và

D

của trụ

đèn (như hình vẽ). Hỏi nhà thiết kế phải đặt chốt ở vị trí cách trụ đèn

B

trên mặt đất là bao

nhiêu để tổng độ dài của hai sợi dây đèn led ngắn nhất ?

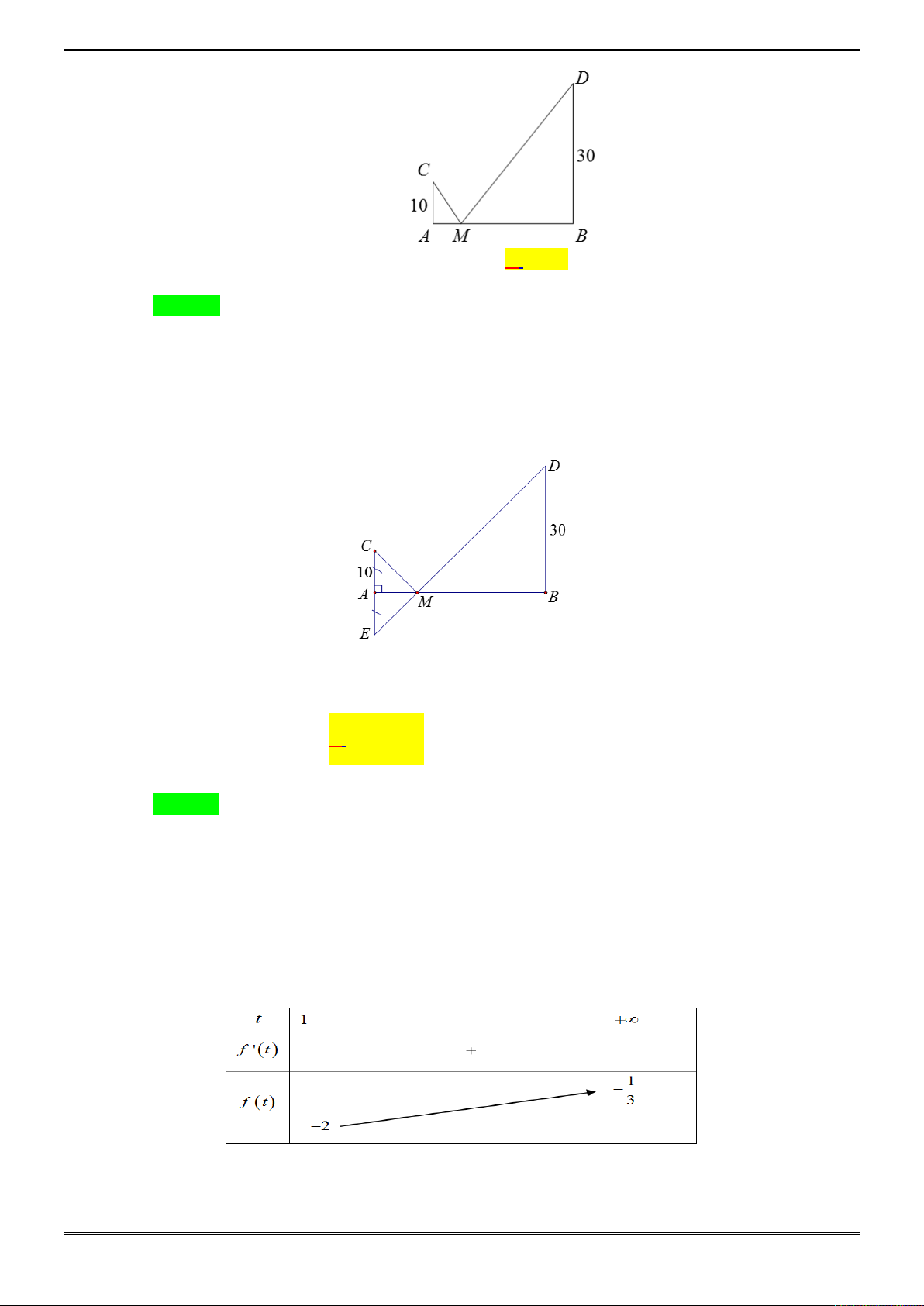
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 74

A.

20m.

B.

6m.

C.

18m.

D.

12m.

Lời giải

Chọn C.

Gọi

E

là điểm đối xứng của

C

qua

AB

.

Gọi

M DE AB 

, khi đó nhà thiết kế đặt chốt ở vị trí

M

thì tổng độ dài hai sợi dây đèn led

ngắn nhất.

Ta có

1

3

AE MA

MB MA

BD MB

   

, mà

24MB MA AB  

, suy ra

6

MA



và

18

MB



.

Câu 37. [2D2-5.7-4] Tất cả các giá trị của

m

để bất phương trình

(3 1)12 (2 )6 3 0

x x x

m m

    

có

nghiệm đúng

0

x

 

là:

A.

 

2;

 

. B.

( ; 2] 

. C.

1

;

3

 

 

 

 

. D.

1

2;

3

 

 

 

 

.

Lời giải

Chọn B.

Đặt

2

x

t

. Do

0 1x t  

.

Khi đó ta có :

2

(3m 1) t (2 m) t 1 0, t 1      

.

2

2 2

2

2 1

(3t t) m t 2 1 t 1 t 1

3

t t

t m

t t

  

           



.

Xét hàm số

 

2

2 1

( ) к 1;

3

t t

f t tr n

t t

  

 



2

2 2

7 6 1

'(t) 0 (1; )

(3t t)

t t

f t

 

     



.

BBT:

Do đó

 

1;

min (t) 2

m f



  

thỏa mãn yêu cầu bài toán.

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 75

Câu 38. [2D2-6.7-4] Cho phương trình

2

log(100 ) log(10 ) 1 log

4.5 25.4 29.10

x x x



  . Gọi

a

và

b

lần lượt là

2

nghiệm của phương trình. Khi đó giá trị biểu thức

2017

ab



bằng:

A.

2017

. B.

10

. C.

2018

. D.

1

10

.

Lời giải

Chọn C.

Điều kiện

0

x



.

2

log(100x ) log(10x) 1 log

4.5 25.4 29.10

x



 

log10 log10 log10

4.25 29.10 25.4 0

x x x

   

.

log10

2log10 log10

log10

5

1

2

5 5

4. 29. 25 0 2017 2018

10

2 2

5 25

10

2 4

x

x x

x

ab

x



 







 



 

   



        

   



   

 









 



 



.

Câu 39. [2D1-2.9-4] Cho hàm số

 

3

2

1

1 4 1

3

m x

y m x x



    

. Hàm số đã cho đạt cực tiểu tại

1

x

, đạt cực đại tại

2

x

đồng thời

1 2

x x

khi và chỉ khi:

A.

5

m



. B.

1

m



hoặc

5

m



.

C.

1

m



hoặc

5

m



. D.

1

m



.

Lời giải

Chọn D.

Hàm số có 2 cực trị



   

2

' 1 2 1 4 0

y m x m x

     

có 2 nghiệm phân biệt.

1

m

 

và

   

2

' 1 4 1 0 5

m m m

       

hoặc

1

m



.

Hàm số có điểm cực tiểu nhỏ hơn điểm cực đại



hệ số của

3

x

âm



1 0 1

m m

   

.

Câu 40. [2D1-3.4-4] Hàm số

2

1

x m

y

x







có giá trị nhỏ nhất trên đoạn

 

0;1

bằng -1 khi:

A.

1

m







 



. B.

3

m







 





. C.

2

m

 

. D.

3

m



.

Lời giải

Chọn A.

 

2

1

' 0,

1

m

y

x



 



 

0;1

x 

.

Do đó:

 

 

2

0;1

min 0

y y m  

.

Theo đề bài:

 

0;1

min 1

y

 

2

1

m

   

1

m

  

.

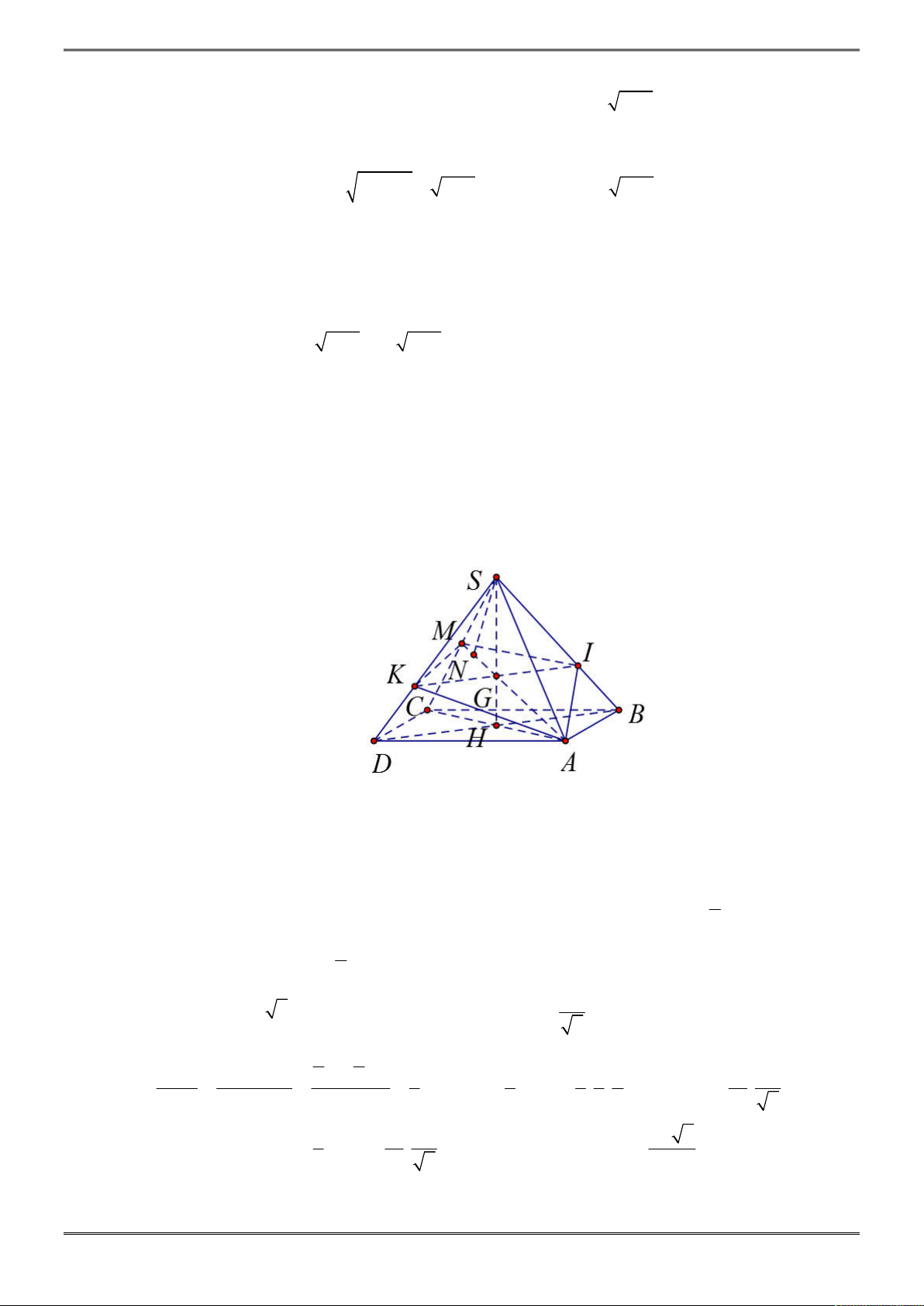
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 76

PHẦN II: PHẦN TỰ LUẬN

Câu 1. [2D1-9.1-3] Giải phương trình:

 

3 2

3 9 10 4 3 4 1 0

x x x x x

      

.

Lời giải

ĐK:

1

x

 

.

PT

   

3 3

3 1 1 3 1 1x x x x       

 

1 1

f x f x

   

.

Xét hàm số:

 

3

3 , 2

f t t t t

   

.

 





2

9 1 0 2;f t t t



      

.



Hàm số

f

liên tục và đồng biến trên





2;

 

.

Do đó:

 

1 1 1 1f x f x x x      

 

2

1

1 1

x

x x











  





1

3

0

3

x







  

















.

So với điều kiên, suy ra: phương trình đã cho có 1 nghiệm:

3

x



.

Câu 2. [2H1-2.6-4] Cho hình chóp đều

.

S ABCD

có cạnh bên và cạnh đáy cùng bằng

m

, gọi

M

là

trung điểm của

SC

. Một mặt phẳng

 

P

chứa

AM

và song song với

BD

, lần lượt cắt

,SB SD

tại

,I K

.

a) Tính thể tích khối đa diện

SMIAK

.

b) Tính khoảng cách từ

S

đến mặt phẳng

 

P

.

Lời giải

a) Gọi

H

là tâm hình vuông

ABCD

 

SH SAC

 

.

Gọi

G SH AM 

, suy ra

, ,K G I

cùng thuộc giao tuyến của hai mp

 

SAC

và

 

P

.

Mà

 

/ / / /P BD KI BD



(1).

,M H

lần lượt là trung điểm

,SC AC

nên

G

là trọng tâm

SAC

2

3

SG SH

 

.

Kết hợp với (1)

2

3

SI SB

 

.

Lại có

2

AC m SAC

  

vuông cân tại

S

2

m

SH 

.

1 2

.

. . 1

2 3

. . . 3

SAMI

SABC

SA SB

V

SA SM SI

V SA SC SB SC SB

  

3

1 1 1 1 1

. . . . . .

3 3 3 2 18

2

SAMI SABC

m

V V BA BC SH   

.

Tương tự

3

1 1

.

3 18

2

SAMK SADC

m

V V  

3

2

18

SAIMK SAMI SAMK

m

V V V   

(đvtt).

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12

NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 77

b) Cách 1:

2

2 2 2

5

4 2

m a

MA SM SA m    

.

2 2 2 2

3 3 3

IK SG a

IK BD

BD SH

    

.

   

BD SAC IK SAC IK AM

    

2

1 10

.

2 6

AIMK

m

S AM IK  

.

Khoảng cách từ

S

đến mp

 

AIMK

là

3 2

3

2 10

:

6 6

5

SAIMK

AIMK

V

m m m

SN

S

  

.

Cách 2: Từ

S

hạ

SN AM

tại

N

, mà

   

BD SAC SN BD SN IK SN AIMK

      

.

SAM

vuông tại

S

2 2 2 2 2

1 1 1 1 4

SN SA SM m m

    

5

m

SN 

.

BẢNG ĐÁP ÁN

1.B

2.D

3.C

4.B

5.D

6.C

7.C

8.B

9.A

10.C

11.A

12.B

13.D

14.D

15.C

16.D

17.D

18.A

19.B

20.B

21.B

22.A

23.C

24.A

25.C

26.D

27.B

28.C

29.B

30.B

31.A

32.A

33.C

34.C

35.C

36.C

37.B

38.C

39.D

40.A

Top20 đề ôn tập thi học kỳ 1 Toán 12 có đáp án và lời giải chi tiết

Đề HK1 Toán 12 458 tài liệu

Toán 12 3.8 K tài liệu

Bình luận

Top20 đề ôn tập thi học kỳ 1 Toán 12 có đáp án và lời giải chi tiết