
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/25
TRƯỜNG THPT
CHUYÊN NGOẠI NGỮ
NHÓM TOÁN 12
ĐỀ THI HỌC KÌ I NĂM HỌC 2016-2017
MÔN: TOÁN – KHỐI 12
Thời gian làm bài: 90 phút
Câu 1. [2D2-2] Tập xác định của hàm số
2
2
3
2
log 2
x x
y
x
là
A.
1; 2
. B.
1;
. C.
1; 2
. D.
2; 2 \ 1
.
Câu 2. [2D1-2] Phát biểu nào sau đây SAI?
A. Hàm số
4 2
0
y ax bx c a
luôn có điểm cực trị.
B. Hàm số
ax b
y
cx d
(với
0
ad bc
) không có cực trị.
C. Hàm số
3 2
0
y ax bx cx d a
luôn có điểm cực trị.
D. Hàm số
2
0
y ax bx c a
luôn có một điểm cực trị duy nhất.
Câu 3. [2D1-2] Cho hàm số
y f x
có bảng biến thiên như sau:
(I): Tập xác định của
f x
là
\ 1
D
. (II): Hàm số
f x
có đúng một điểm cực trị.
(III):
min 2
f x
. (IV):
1;3
A là điểm cực đại của đồ thị hàm số.
Trong các phát biểu trên, có bao nhiêu phát biểu ĐÚNG?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 4. [2H1-2] Cho khối chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt
đáy bằng
45
. Thể tích khối chóp
.
S ABC
bằng bao nhiêu?
A.
3
3 2
4
a
. B.
3
12
a
. C.
3
4
a
. D.
3
3
4
a
.
Câu 5. [2D1-2] Cho hàm số
3 2
1
2 3 1
3
y x x x
có đồ thị
C
. Có bao nhiêu tiếp tuyến của
C
song song với đường thẳng
3 1
y x
?
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 6. [2H2-2] Cho
ABC
vuông tại
A
,
6 cm
AB
,
8 cm
AC
. Gọi
1
V
là thể tích khối nón tạo
thành khi quay
ABC
quanh
AB
và
2
V
là thể tích khối nón tạo thành khi quay
ABC
quanh
AC
. Tỉ số
1
2
V
V
bằng
A.
4
3
. B.
3
4
. C.
16
9
. D.
64
27
.
Câu 7. [2D2-2] Giá tị nhỏ nhất của hàm số
1
4
2 .8
3
x x
y
trên
1;0
bằng bao nhiêu?
A.
5
6
. B.
2
3
. C.
2 2
3
. D.
50
81
.
x
1
1
y
0
||
y
3
2
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/25
Câu 8. [2D1-2] GTNN của hàm số
2sin 2 5 1
f x x x
trên đoạn
0;
2
bằng bao nhiêu?
A.
0
. B.
5
3
4
. C.
5
1
2
. D.
1
.
Câu 9. [2D2-2] Cho
ABC
vuông tại
A
có
log 8
3
a
AB ,
25
log 36
5AC . Biết độ dài
10
BC
thì giá trị
a
bằng bao nhiêu?
A.
9
. B.
1
3
. C.
3
. D.
3
.
Câu 10. [2D2-2] Phương trình
2 2 2
2 5 2 3 7 2 5 12 4
2 2 1 2
x x x x x x
có bao nhiêu nghiệm?
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 11. [2D2-2] Một tên lửa bay vào không trung với quãng đường đi được
km
s t là hàm phụ
thuộc theo biến
t
(giây), với phương trình
2
3 3 1
e 2 .e
t t
s t t
. Khi đó vận tốc của tên lửa sau
1
giây là
A.
4
5e km/h
. B.
4
3e km/h
.
C.
4
9e km/h
. D.
4
10e km/h
.
Câu 12. [2D2-2] Giới hạn
2
0
e 1
lim
4 2
x
x
x
bằng
A.
8
. B.
4
. C.
2
. D.
1
.
Câu 13. [2D1-2] Trong các hàm số sau, hàm số nào đồng biến trên
0;
?
A.
sin 2
y x
. B.
2
1
x
y
x
. C.
2
x
y
x
D.
2
2
1
y x
Câu 14. [2H2-2] Cho hình lăng trụ đứng
.
ABC A B C
có tam giác
ABC
vuông cân tại
B
,
2
AB a
và cạch bên
6
AA a
. Khi đó diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ đứng
đã cho là
A.
2
4 6
a
. B.
2
6
a
. C.
2
4
a
. D.
2
2 6
a
Câu 15. [2D1-2] Biết phương trình
3
3 0
x x m
có ba nghiệm phân biệt. Khẳng định nào sau đây đúng?
A.
2
4
m
. B.
2
4
m
.
C.
2
4
m
. D.
2
4
m
.
Câu 16. [2D1-1] Cho hàm số
f x
xác định, liên tục trên
, có đồ thị như
hình vẽ. Khẳng định nào dưới đây ĐÚNG?
A. Hàm số đạt cực đại tại
0
x
và đạt cực tiểu tại
2
x
.
B. Hàm số có giá trị lớn nhất bằng
3
.
C. Hàm số đồng biến trê khoảng
0;
.
C. Đồ thị hàm số có một đường tiệm cận.
Câu 17. [2D2-1] Cho
0 1, 0 1, 0, 0
a b x y
. Tìm công thức ĐÚNG trong các công thức sau.
A.
log log log
a a a
x y x y
B.
log .log
b
a
a
x b x
.
C.
log log .log
b b a
x a x
. D.
log
log
log
a
a
a
x
x
y y
.
O
x
y
3
2
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/25
Câu 18. [2D1-2] Bảng biến thiên sau đây có thể là bảng biến thiên của hàm số nào?
A.
2
2 3
y x x
. B.
4 2
1
3
4
y x x
. C.
4 2
1
3
2
y x x
. D.
4 2
1
2 3
2
y x x
Câu 19. [2D1-2] Gọi
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 1 7
y x x
.
Khi đó có bao nhiêu số nguyên nằm giữa
m
,
M
?
A.
2
. B.
1
. C. Vô số. D.
0
.
Câu 20. [2D2-2] Cho hàm số
2 sin 2
e
x
f x
. Biết
0
0;
2
x
là giá trị thỏa mãn
0
0.
f x
Khi đó:
A.
0
2
x
. B.
0
3
x
. C.
0
0
x
D.
0
4
x
.
Câu 21. [2H1-1] Cho khối lăng trụ tam giác đều có cạnh đáy bằng
a
. Biết diện tích mỗi mặt bên của
lăng trụ là
2
3
a , khi đó thể tích khối lăng trụ bằng
A.
3
3 3
4
a
. B.
3
3
4
a
. C.
3
4
a
. D.
3
3
4
a
.
Câu 22. [2D2-2] Cho hàm số
ln 1 e
x
y x . Khẳng định nào dưới đây là ĐÚNG?
A. Hàm số đạt cực tiểu tại
1
x
. B. Hàm số đạt cực đại tại
0
x
.
C. Hàm số đồng biến trên
. D. Tập xác định của hàm số là
0;D
.
Câu 23. [2H1-2] Cho khối chóp tứ giác đều
.
S ABCD
có độ dài tất cả các cạnh đều bằng
a
. Thể tích
khối chóp
.
S ABCD
bằng
A.
3
2
a
. B.
3
4
a
. C.
3
2 3
a
. D.
3
3 2
a
.
Câu 24. [2D1-3] Cho hàm số
4 2
2 1
y x mx
. Tìm giá trị của
m
để đồ thị hàm số có ba điểm cực trị
A
,
B
,
C
sao cho
ABC
có diện tích bằng
4 2
.
A.
1
m
. B.
2
m
. C.
2
m
. D.
4
m
.
Câu 25. [2D2-2] Giá trị cực đại của hàm số
2
ln
x
y
x
bằng
A.
e
2
. B.
1
2e
. C.
1
e
. D.
2
1
2e
.
Câu 26. [2D1-3] Biết phương trình
2 2
2 1 2 1 2 3 0
x x x x x x
có nghiệm duy nhất là
a
.
Khi đó
A.
0 1
a
. B.
3 4
a
. C.
1 2
a
. D.
2 3
a
.
Câu 27. [2D1-2] Cho hàm số
3 1
2
x
y
x
có đồ thị
C
. Có bao nhiêu điểm trên
C
mà tổng khoảng
cách từ đó đến hai đường tiệm cận của
C
bằng
6
.
A.
0
. B.
1
. C.
4
. D.
2
.
x
0
y
0
y
3
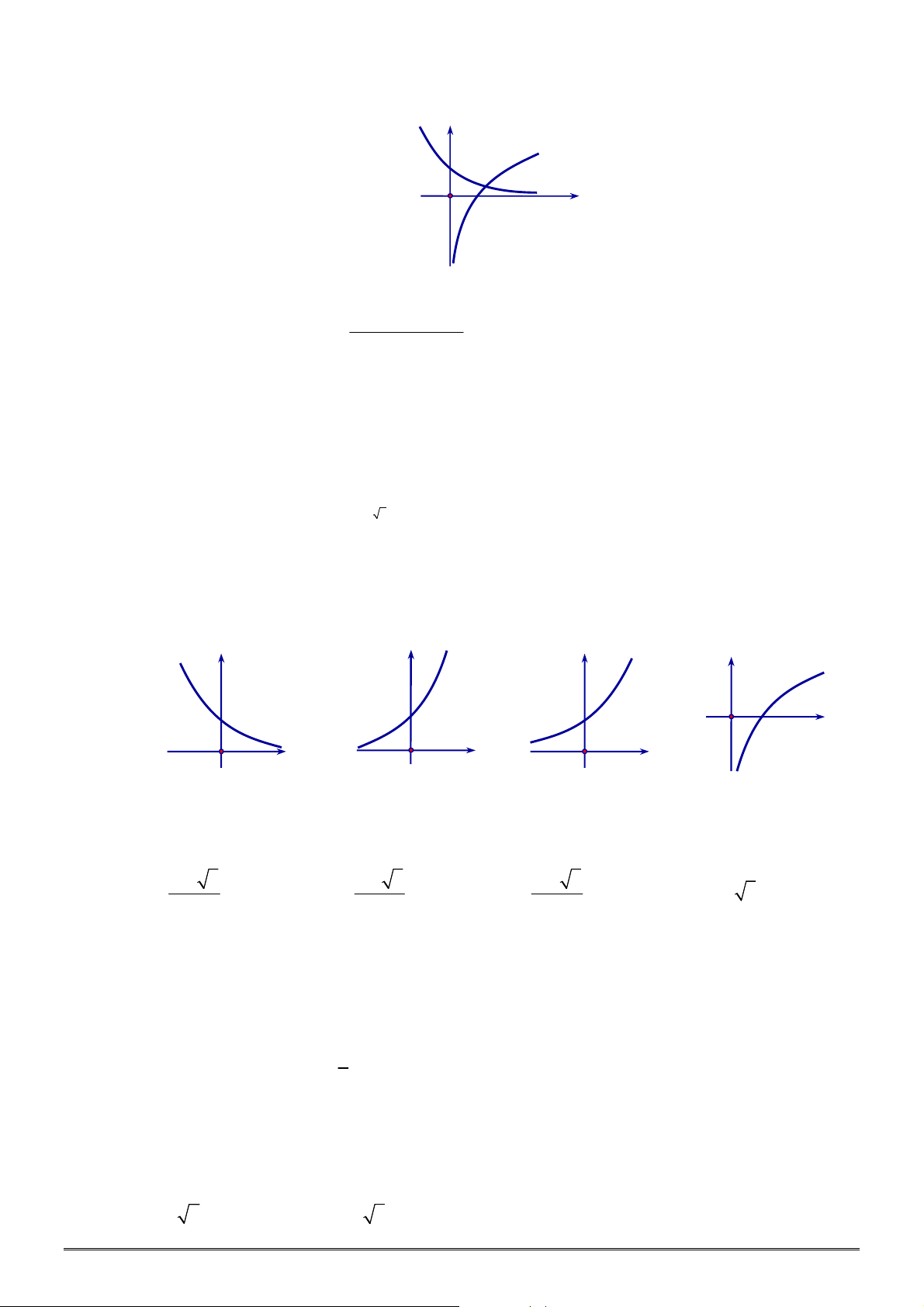
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/25
Câu 28. [2D2-1] Cho đồ thị hàm số
x
y a
và
log
b
y x
như hình vẽ bên. Khẳng định nào dưới đây là
ĐÚNG?
A.
0 1
a b
. B.
1; 1
a b
. C.
0 1,0 1
a b
. D.
0 1
b a
.
Câu 29. [2D1-1] Đồ thị hàm số
2 2
3 1
5 6
x
y
x x x
có bao nhiêu đường tiệm cận đứng?
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 30. [2D1-1] Gọi
x a
và
x b
là các điểm cực trị của hàm số
3 2
2 3 18 1
y x x x
. Khi đó
2
A a b ab
bằng
A.
5
. B.
7
. C.
5
. D.
7
.
Câu 31. [2D2-3] Cho phương trình
2 2
2
2
log 2 2log 4 8 0
x x
1
. Khi đó phương trình
1
tương
đương với phương trình nào dưới đây:
A.
2
3 2 0
x x
. B.
3 5 6 2
x x
x
.
C.
2
4 9 2 0
x x
. D.
2 2
2 2 1
4 2 3 0
x x x x
.
Câu 32. [2D2-1] Đồ thị nào dưới đây là đồ thị của hàm số
3
x
y
?
A. B. C. D.
Câu 33. [2H1-3] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
2
a
,
SAD
cân tại
S
và
nằm trong mặt phẳng vuông góc với đáy. Góc giữa
SBC
và mặt đáy bằng
60
. Tính thể tích
.
S ABCD
bằng
A.
3
2 3
3
a
. B.
3
8 3
3
a
. C.
3
4 3
3
a
. D.
3
2 3
a .
Câu 34. [2H2-1] Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mọi hình hộp đứng đều có mặt cầu ngoại tiếp.
B. Mọi hình hộp chữ nhật đều có mặt cầu ngoại tiếp.
C. Mọi hình hộp có một mặt bên vuông góc với đáy đều có mặt cầu ngoại tiếp.
D. Mọi hình hộp đều có mặt cầu ngoại tiếp.
Câu 35. [2D1-2] Cho hàm số
3 2
1
2 1 5
3
y x x m x
. Tìm điều kiện của
m
để hàm số đồng biến
trên
.
A.
3
m
.
B.
3
m
. C.
3
m
. D.
3
m
.
Câu 36. [2H1-3] Cho khối chóp
.
S ABC
có
3
SA
,
4
SB
,
SC 5
,
60
ASB BSC CSA
Tính thể
tích khối chóp
.
S ABC
bằng
A.
5 2
. B.
5 3
. C.
10
. D.
15.
O
x
y
1
O
x
y
1
O
x
y
1
O
x
y
1
x
y
O
1
1
x
y a
log
b
y x

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/25
Câu 37. [2D2-2] Cho phương trình
2
1 2
2016 1 .2017 1 1
x x
x
. Khẳng định nào dưới đây đúng?
A. Phương trình
1
có nghiệm duy nhất.
B. Phương trình
1
vô nghiệm.
C. Phương trình
1
có tổng các nghiệm bằng
0
.
D. Phương trình
1
có nhiều hơn hai nghiệm.
Câu 38. [2H2-2] Một khối lập phương có thể tích
2 2
. Khi đó thể tích khối cầu ngoại tiếp hình lập
phương đó bằng
A.
2
. B.
6
. C.
2
. D.
6
.
Câu 39. [2H1-3] Cho khối chóp
.
S ABCD
có đáy là hình bình hành,
P
là mặt phẳng chứa
AB
cắt
SC
,
SD
tại
M
,
N
sao cho
1
3
SM SC
. Gọi
1
V
,
2
V
lần lượt là thể tích khối chóp
.
S ABMN
và khối đa diện
ABCDNM
. Khi đó tỉ số
1
2
V
V
bằng
A.
1
2
.
B.
1
8
. C.
2
9
. D.
2
7
.
Câu 40. [2H2-3] Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh bằng
6
, cạnh bên
SA ABC
và
4 6.
SA
Diện tích của mặt cầu ngoại tiếp hình chóp
.
S ABC
bằng
A.
108
. B.
48
. C.
36
. D.
144
.
Câu 41. [2H2-2] Cho hai khối cầu
1
S
có bán kính
1
R
, thể tích
1
V
và
2
S
có bán kính
2
R
, thể tích
2
V
.
Biết
2 1
8
V V
, khẳng định nào dưới đây là ĐÚNG?
A.
2 1
2
R R
. B.
1 2
2
R R
. C.
2 1
4
R R
. D.
2 1
2 2
R R
.
Câu 42. [2D1-2] Gọi
A
,
B
là các giao điểm của đường thẳng
y x m
và đồ thị hàm số
1
x
y
x
.
Khi đó, tìm
m
để
1
A B
x x
.
A.
2
m
. B.
3
m
. C.
0
m
. D.
1
m
.
Câu 43. [2D1-1] Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá tị nhỏ nhất của hàm số
2
3 e
x
f x x
trên đoạn
0; 2
. Giá trị của biểu thức
2016
2
4A m M bằng
A.
2016
e
. B.
1
. C.
2016
2
. D.
0
.
Câu 44. [2D1-2] Phương trình
3 3
3 log log 3 1
x x
có hai nghiệm
1
x
,
2
x
. Khi đó, tích
1 2
x x
bằng
A.
1
. B.
6
3
. C.
243
. D.
81
.
Câu 45. [1H3-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
2
a
. Biết
SAB
là tam
giác đều và nằm trong mặt phẳng vuông góc với
ABCD
. Khoảng cách giữa
AB
và
SD
bằng
A.
42
7
a
. B.
42
14
a
. C.
3
2
a
. D.
2
2
a
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/25
Câu 46. [1H3-3] Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
3
a
. Tính khoảng cách từ
điểm
A
đến
SBC
biết thể tích khối chóp
.
S ABC
bằng
3
6
4
a
.
A.
2 3
3
a
. B.
2
a
. C.
a
. D.
2
2
a
.
Câu 47. [1H3-3] Cho lăng trụ đứng
.
ABC A B C
có đáy là tam giác vuông tại
B
,
AB a
,
2
BC a
.
Biết thể tích của khối lăng trụ
.
ABC A B C
bằng
3
2 2
a
. Gọi
là góc giữa
A BC
với
ABC
. Tính
cos
.
A.
1
3
. B.
3
3
. C.
6
3
. D.
2
3
.
Câu 48. [2H2-3] Công ty
A
cần xây bể chưa hình hộp chữ nhật (không có nắp), đáy là hình vuông cạnh
bằng
m
a , chiều cao bằng
m
h . Biết thể tích bể chứa cần xây là
3
62,5 m
, hỏi kích thước
cạnh đáy và chiều cao phải bằng bao nhiêu để tổng diện tích các mặt xung quanh và mặt đáy là
nhỏ nhất?
A.
5 2
m, 5m
2
a h . B.
5 10
m, 4m
4
a h .
C.
5m, 2,5m
a h
. D.
5 30
3m, m
6
a h .
Câu 49. [2D1-1] Biết đồ thị
1
:
1
ax
C y
bx
,
0, 0
b a b
có tiệm cận ngang là
2
y
. Khi đó, tỷ
số
a
b
là
A.
3
. B.
2
. C.
1
. D.
1
.
Câu 50. [2D2-3] Biết phương trình
2
3 3
2log 2 log 4 0
x x
có hai nghiệm
1 2
,
x x
. Khi đó
2
1 2
x x
bằng
A.
2
. B.
4
. C.
8
. D.
9
.
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/19 - Mã đề thi 485
SỞ GIÁO DỤC VÀ ĐÀO TẠO
--------------
ĐỀ CHÍNH THỨC
(Đề thi gồm có 50 câu)
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2017 - 2018
Môn: Toán, lớp 12
Thời gian làm bài: 90phút;
(không kể thời gian phát đề)
Họ, tên thí sinh……………………………Lớp……………………….
Mã đề thi 485
Câu 1. [2D1-2] Giá trị nhỏ nhất của hàm số
3 2
2 3
y x x m
trên đoạn
0;5
bằng
5
khi
m
là:
A.
6
. B.
10
. C.
7
. D.
5
.
Câu 2. [2D2-2] Phương trình
2
2 2
log log 8 3 0
x x
tương đương với phương trình nào sau đây?
A.
2
2 2
log log 0
x x
. B.
2
2 2
log log 6 0
x x
.
C.
2
2 2
log log 0
x x
. D.
2
2 2
log log 6 0
x x
Câu 3. [2D1-1] Các điểm cực tiểu của hàm số
4 2
3 2
y x x
là
A.
0
x
. B.
1
x
. C.
1
x
và
2
x
. D.
5
x
.
Câu 4. [2D1-1] Cho hàm số
2
3
x
y
x
. Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
;
.
B. Hàm số nghịch biến trên từng khoảng xác định.
C. Hàm số đồng biến trên từng khoảng xác định.
D. Hàm số đồng biến trên khoảng
;
.
Câu 5. [2D1-2] Đường cong bên là đồ thị hàm số nào sau đây?
A.
3
3
y x x
. B.
3
3 1
y x x
. C.
3
3
y x x
. D.
3
3 1
y x x
.
Câu 6. [2D2-2] Hàm số
2
1
8 6 3 ln 2
x x
y x
là đạo hàm của hàm số nào sau đây
A.
2
1
8
x x
y
. B.
2
1
2
x x
y
. C.
2
3 3 1
2
x x
y
. D.
2
3 3 1
8
x x
y
.
Câu 7. [2D2-2] Đạo hàm hàm số
2
ln 1
y x x
là:
A.
1
1.
y
x
B.
ln 1.
y x
C.
1.
y
D.
2ln 1 .
y x x
Câu 8. [2H1-2] Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
2
a
. Tam giác
SAB
là tam giác
cân tại
S
và nằm trong mặt phẳng vuông góc với đáy,
3
SA a
. Tính thể tích
V
của khối chóp
.
S ABCD
.
A.
3
10 3
.
3
V a
B.
3
8 2
.
3
V a
C.
3
15
.
6
V a
D.
3
17
.
6
V a
Câu 9. [2D1-2] Đồ thị hàm số
3 1
1
x
y
x
có tâm đối xứng là
A.
1; 3
I . B.
1;1
I . C.
3;1
I . D.
1; 3
I .
Câu 10. [2D1-2] Cho hàm số
f x
có đạo hàm là
2 4
1 2f x x x x x
. Số điểm cực tiểu
của hàm số
y f x
là
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 11. [2D2-1] Tập xác định của hàm số
2
1
y x là:
A.
;1
D
. B.
D
. C.
1;D
. D.
\ 1
D
.
Câu 12. [2H2-2] Hình nón có bán kính đáy
8 cm
r
, đường sinh
10 cm
l
. Thể tích khối nón là:
A.
3
192
cm
3
V
. B.
3
128 cm
V
. C.
3
128
cm
3
V
. D.
3
192 cm
V
.
O
x
y
2
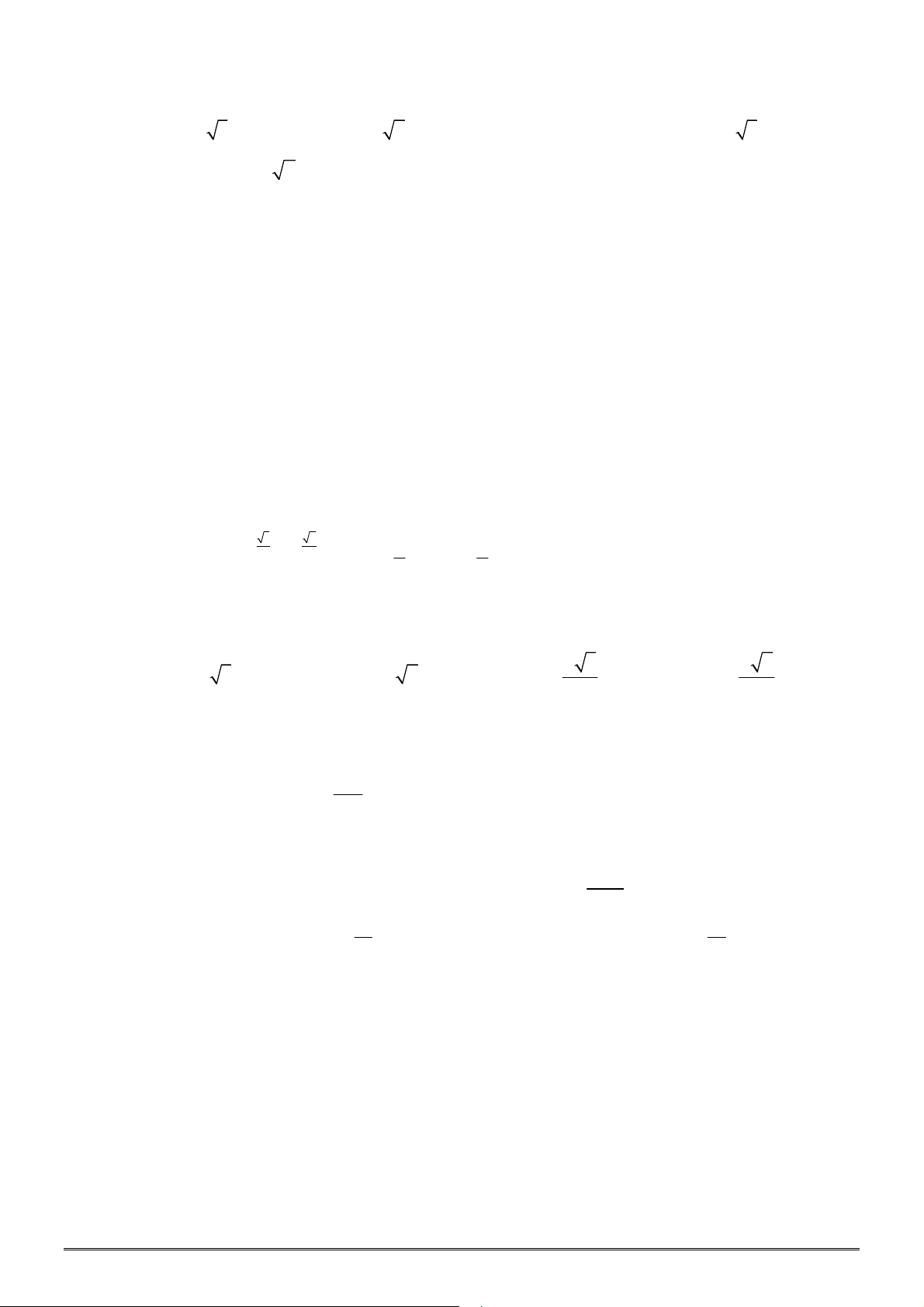
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/19 - Mã đề thi 485
Câu 13. [2H1-4] Xét khối tứ diện
ABCD
có cạnh
AB x
và các cạnh còn lại đều bằng
2
. Tìm
x
để
thể tích khối tứ diện
ABCD
đạt giá trị lớn nhất.
A.
2 3
x . B.
6
x . C.
2
x
. D.
3
x .
Câu 14. [2D2-1] Nếu
log 2
a
thì
log
a
bằng
A.
100
. B.
4
. C.
10
. D.
8
.
Câu 15. [2D1-2] Hàm số
4 2
5
y x mx m
(
m
là tham số) có
3
điểm cực trị khi các giá trị của
m
là:
A.
4 5.
m
B.
0.
m
C.
8
m
. D.
1.
m
Câu 16. [2D2-4] Phương trình
2
log log 1
x mx x m
có nghiệm duy nhất khi giá trị của
m
là:
A.
0.
m
B.
1.
m
C.
5.
m
D.
4 0.
m
Câu 17. [2D2-2] Số nghiệm của phương trình
3 3 3
log 2 log 2 log 5
x x là:
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 18. [2D2-2] Hàm số
2
ln 2 4
y x mx
có tập xác định
D
khi các giá trị của tham số
m
là:
A.
2
m
. B.
2
m
hoặc
2
m
. C.
2
m
. D.
2 2
m
.
Câu 19. [2D2-1] Nếu
3
2
3
2
a a
và
3 4
log log
4 5
b b
thì
A.
0 1
a
,
1
b
. B.
0 1
b
,
1
a
. C.
1
a
,
1
b
. D.
0 1
a
,
0 1
b
.
Câu 20. [2H2-2] Tính bán kính
R
của mặt cầu ngoại tiếp hình lập phương có cạnh bằng
a
.
A.
3
R a
. B.
2
R a
. C.
3
2
a
R . D.
6
2
a
R .
Câu 21. [2D2-1] Cho phương trình
1
25 26.5 1 0
x x
. Đặt
5
x
t
,
0
t
thì phương trình trở thành
A.
2
26 1 0
t t
. B.
2
25 26 0
t t
. C.
2
25 26 1 0
t t
. D.
2
26 0
t t
.
Câu 22. [2D2-2] Cho hàm số
ln
x
y
x
. Mệnh đề nào sau đây đúng?
A. Hàm số có một cực đại. B. Hàm số có một cực tiểu.
C. Hàm số có hai cực trị. D. Hàm số không có cực trị.
Câu 23. [2D2-3] Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
ln
x
y
x
trên đoạn
3
1;e
lần lượt là
A.
3
e
và
1
. B.
3
9
e
và
0
. C.
2
e
và
0
. D.
2
4
e
và
0
.
Câu 24. [2D1-3] Cho hàm số
4 2
2 1
y x x
có đồ thị
C
và đường thẳng
: 1
d y m
(
m
là tham
số). Đường thẳng
d
cắt
C
tại
4
điểm phân biệt khi các giá trị của
m
là:
A.
3 5
m
. B.
1 2
m
. C.
1 0
m
. D.
5 3
m
.
Câu 25. [2D1-1] Cho hàm số
y f x
có đạo hàm
2
1
f x x
. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên
;1
. B. Hàm số nghịch biến trên
;
.
C. Hàm số nghịch biến trên
1;1
. D. Hàm số đồng biến trên
;
.
Câu 26. [2D2-2] Giá trị lớn nhất và nhỏ nhất của hàm số
3 2
2 3 1
y x x
trên đoạn
2;1
lần lượt là
A.
0
và
1
. B.
1
và
2
. C.
7
và
10
. D.
4
và
5
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/19 - Mã đề thi 485
Câu 27. [2D2-2] Nghiệm của phương trình
2 4
log log 1
x
là:
A.
8
x
. B.
16
x
. C.
4
x
. D.
2
x
.
Câu 28. [2H1-2] Cho khối lăng trụ đứng
.
ABC A B C
có
2
CC a
, đáy
ABC
là tam giác vuông cân
tại
B
và
2
AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
V a
. B.
3
2
a
V . C.
3
2
V a
. D.
3
3
a
V .
Câu 29. [2H2-2] Cho hình chóp tứ giác đều
.
S ABCD
có các cạnh đều bằng
2
a
. Tính thể tích
V
của
khối nón có đỉnh
S
và đường tròn đáy là đường tròn nội tiếp tứ giác
ABCD
.
A.
3
3
6
a
V
. B.
3
2
3
a
V
. C.
3
2
6
a
V
. D.
3
3
3
a
V
.
Câu 30. [2D2-2] Nếu
6 5 6 5
x
thì:
A.
1
x
. B.
1
x
. C.
1
x
. D.
1
x
.
Câu 31. [2H2-2] Cho hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng
20
. Khi
đó thể tích của khối trụ là:
A.
10 5
V
. B.
10 2
V
. C.
10
V
. D.
20
V
.
Câu 32. [2D1-1] Đồ thị của hàm số
3 2
3 2
y x x
có tâm đối xứng là:
A.
0;2
I . B.
1;0
I . C.
2; 2
I
. D.
1; 2
I
.
Câu 33. [2D1-1] Hàm số
2 5
1
x
y
x
có bao nhiêu điểm cực trị?
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 34. [2D1-3] Hàm số
2
1 1
2
x m x
y
x
(
m
là tham số) nghịch biến trên mỗi khoảng xác định
của nó khi các giá trị của
m
là:
A.
1
m
. B.
1
m
. C.
5
2
m
. D.
1 1
m
.
Câu 35. [2D1-2] Số đường tiệm cận đứng của đồ thị hàm số
2
2
3 2
4
x x
y
x
là:
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 36. [2H1-1] Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối
xứng?
A.
6
mặt phẳng. B.
4
mặt phẳng. C.
3
mặt phẳng. D.
9
mặt phẳng.
Câu 37. [2D1-1] Cho hàm số
y f x
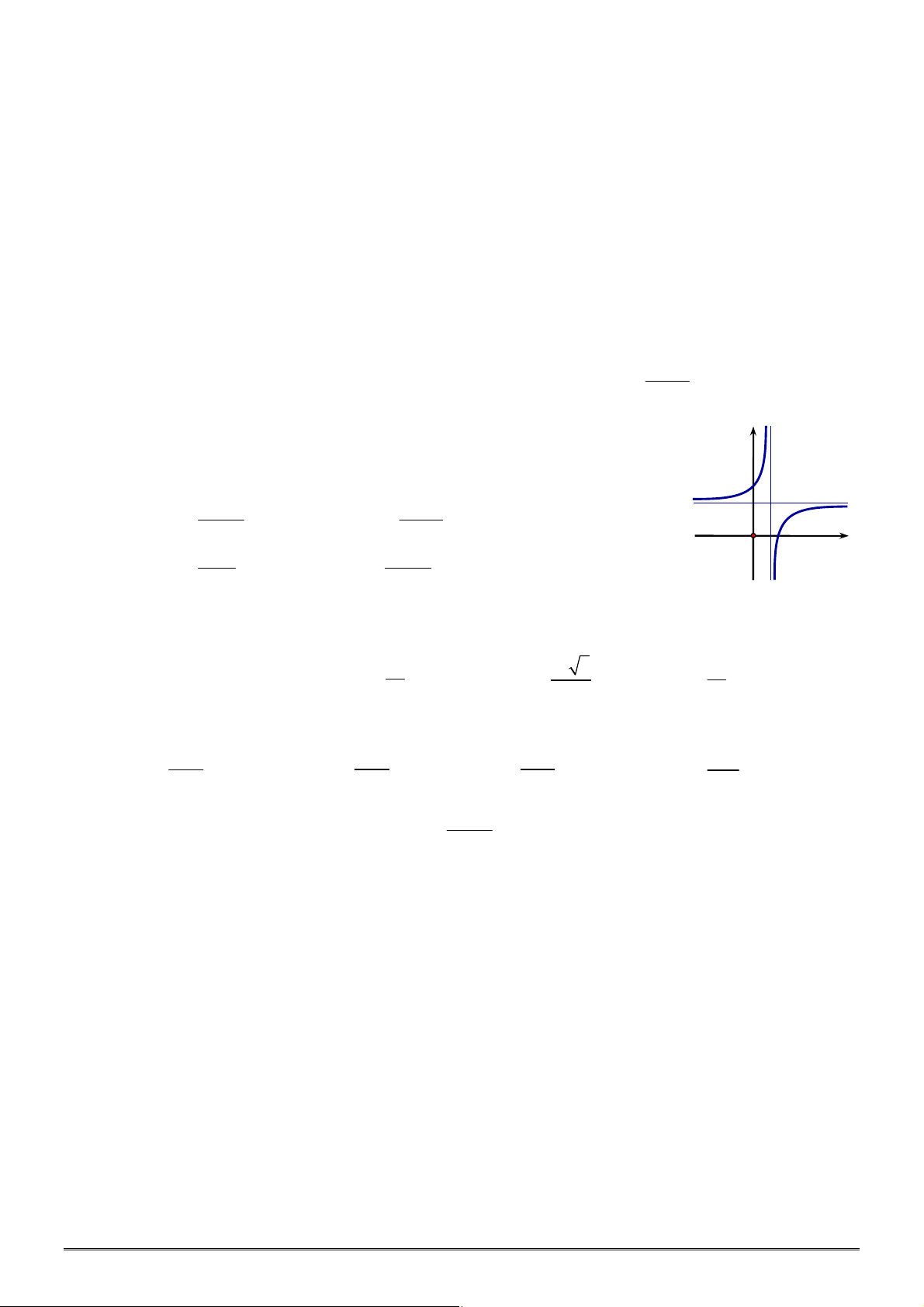
có bảng biến thiên như hình bên. Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại
5
x
. B. Hàm số đạt cực tiểu tại
1
x
.
C. Hàm số không có cực trị. D. Hàm số đạt cực đại tại
0
x
.
Câu 38. [2D2-2] Phương trình
2 2
2 3.2 32 0
x x
có tổng các nghiệm là
A.
2
. B.
12
. C.
6
. D.
5
.
Câu 39. [2D1-2] Đồ thị hàm số
3 2
3 2 1
y x x x
cắt đồ thị hàm số
2
3 1
y x x
tại hai điểm phân
biệt
A
và
B
. Khi đó độ dài đoạn
AB
là:
A.
3
AB
. B.
2
AB
. C.
2 2
AB
. D.
1
AB
.
x
0
2
y
0
0
y
5
1
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/19 - Mã đề thi 485
Câu 40. [2D2-2] Phương trình
2
2 2
1
9 10.3 1 0
x x
x x
có tập nghiệm là:
A.
2; 1;1;2
. B.
2;0;1;2
. C.
2; 1;0;1
. D.
1;0;2
.
Câu 41. [2D2-2] Tập xác định của hàm số
2
log 2
y x x
là:
A.
D 2;0
. B.
D \ 0
.
C.
D ; 2 0;
. D.
D
.
Câu 42. [2D1-2] Cho hàm số
4 2
2 1
y x x
có đồ thị
C
. Phương trình tiếp tuyến của đồ thị
C
tại
1;4
M là:
A.
8 4
y x
. B.
8 4
y x
. C.
8 12
y x
. D.
3
y x
.
Câu 43. [2D1-1] Các đường tiệm cận đứng và ngang của đồ thị hàm số
2 1
1
x
y
x
là:
A.
2
x
;
1
y
. B.
1
x
;
2
y
.
C.
1
x
;
2
y
. D.
1
x
;
2
y
.
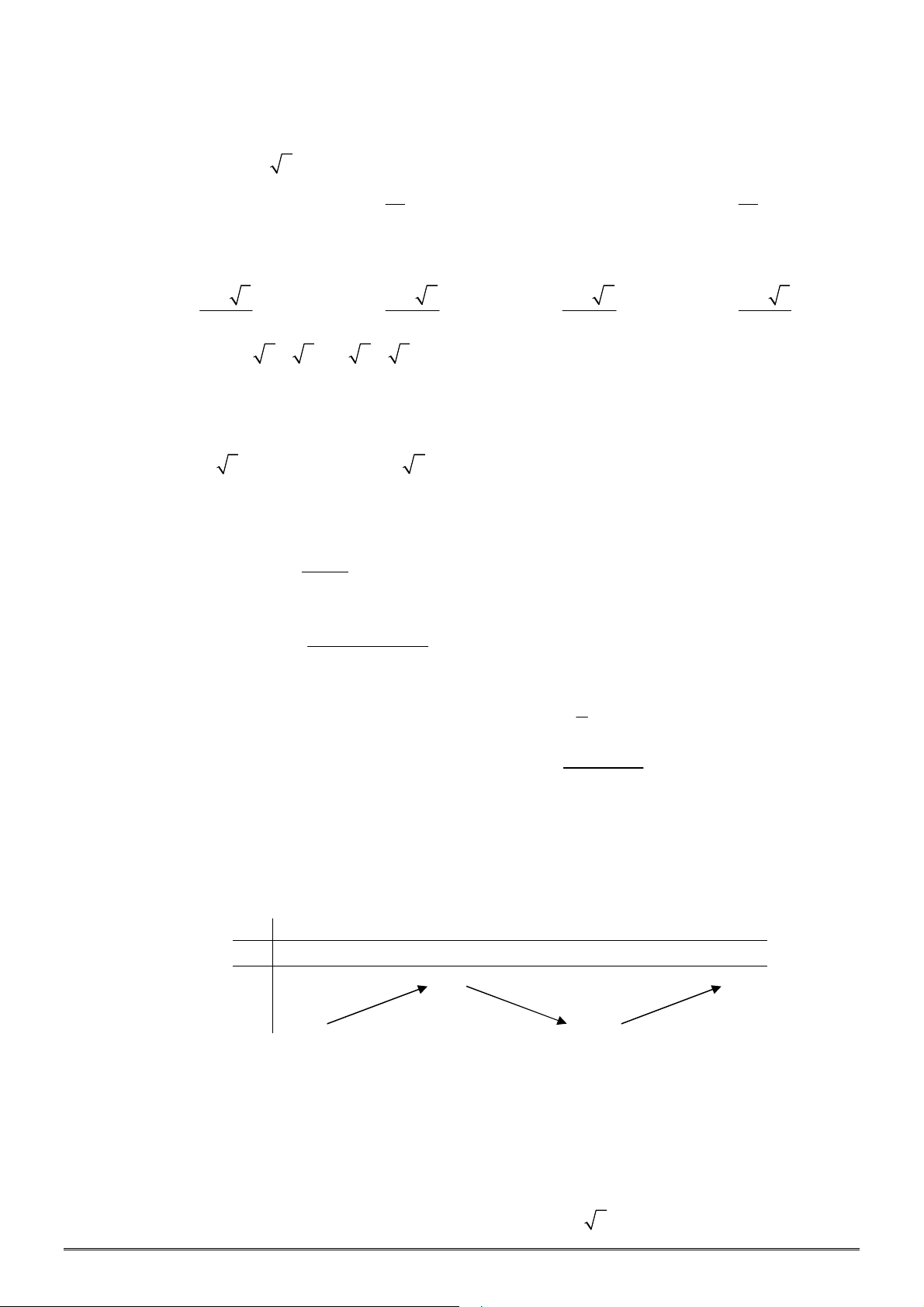
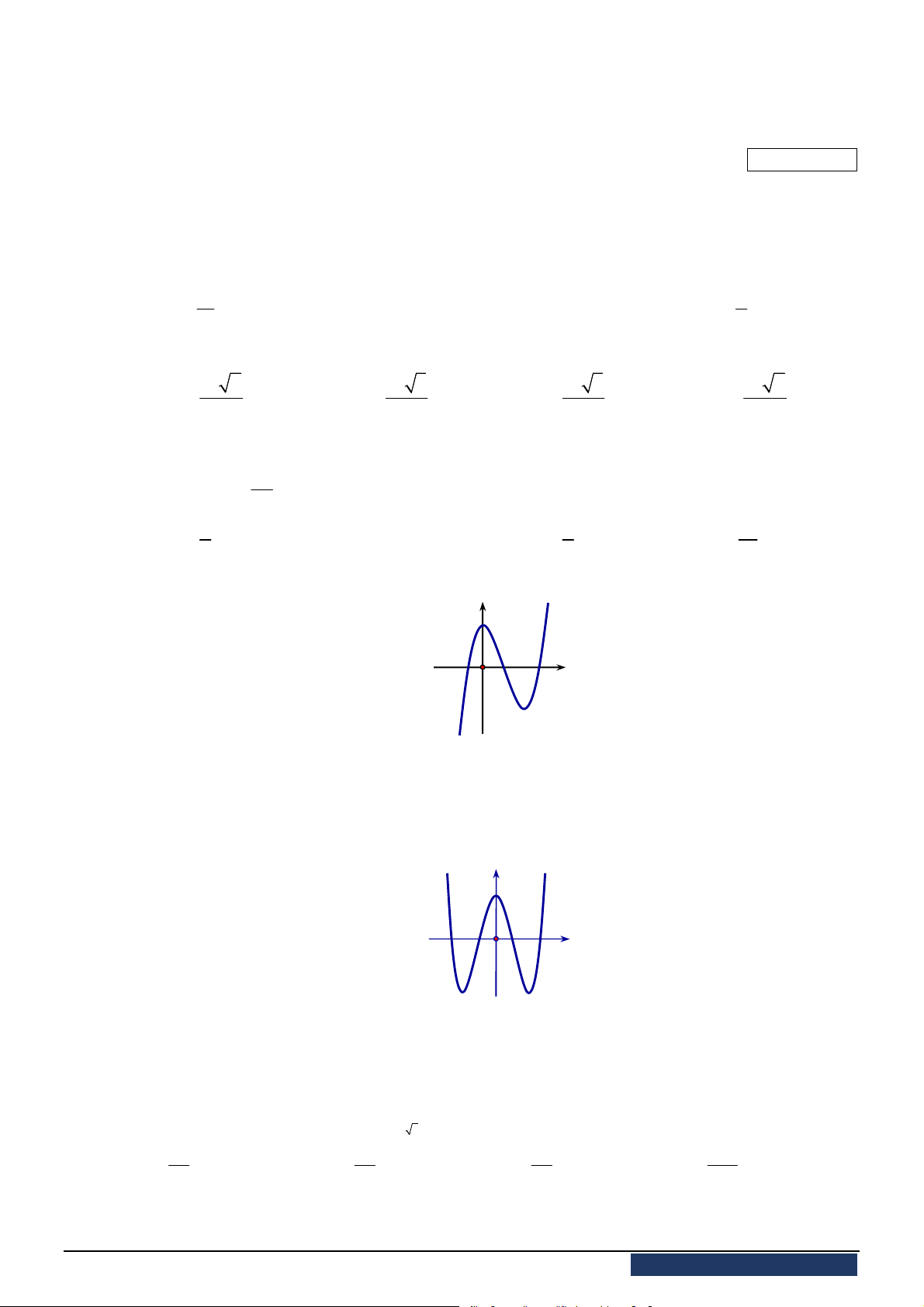
Câu 44. [2D1-2] Đường cong bên là đồ thị của hàm số nào dưới đây?
A.
2 3
1
x
y
x
. B.
2 1
1
x
y
x
.
C.
3
2
x
y
x
. D.
2 3
1
x
y
x
.
Câu 45. [2H1-2] Cho hình chóp .
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
2
AB BC
,
3
AD
. Cạnh bên
2
SA
và vuông góc với đáy. Tính thể tích khối chóp .
S ABCD
.
A.
4
V
. B.
10
3
V
. C.
10 3
3
V
. D.
17
6
.
Câu 46. [2D2-2] Nếu
12
log 6
a
và
12
log 7
b
thì
2
log 7
bằng kết quả nào sau đây:
A.
1
a
a
. B.
1
b
a
. C.
1
a
b
. D.
1
a
b
.
Câu 47. [2D1-1] Giá trị lớn nhất của hàm số
2
4
2
y
x
là
A.
10
. B.
3
. C.
5
. D.
2
.
Câu 48. [2D1-1] Cho hàm số
y f x
có
1
lim
x
f x
và
1
lim 2
x
f x
. Mệnh đề nào sau đây
đúng?
A. Đồ thị hàm số không có tiệm cận. B. Đồ thị hàm số có tiệm cận đứng
1
x
.
C. Đồ thị hàm số có hai tiệm cận. D. Đồ thị hàm số có tiệm cận ngang
2
y
.
Câu 49. [2D1-3] Một ông nông dân có
2400
m hàng rào và muốn rào lại cánh đồng hình chữ nhật tiếp
giáp với một con sông. Ông không cần rào cho phía giáp bờ sông. Hỏi ông có thể rào được
cánh đồng với diện tích lớn nhất là bao nhiêu?
A.
630000
m
2
. B.
720000
m
2
. C.
360000
m
2
. D.
702000
m
2
.
Câu 50. [2H1-1] Khối đa diện đều loại
4;3
là:
A. Khối lập phương. B. Khối bát diện đều. C. Khối hộp chữ nhật. D. Khối tứ diện đều.
----------HẾT----------
O
x
y
1
2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/24 – HKI1819-001-SGD BẠC LIÊU
SỞ GD-ĐT BẠC LIÊU KIỂM TRA HỌC KỲ I NĂM HỌC 2018 – 2019
ĐẾ CHÍNH THỨC Môn kiểm tra: TOÁN 12
(Gồm có 06 trang) Thời gian: 90 phút, không kể thời gian phát đề
Họ, tên học sinh: …………………………………..; Số báo danh: ………………… Mã đề thi 213
Câu 1. Giá trị nhỏ nhất của hàm số
3
3 1
y x x
trên đoạn
1;4
là
A.
1
. B.
3
. C.
4
. D.
1
.
Câu 2. Nghiệm của phương trình
3
log 2 3 2
x
là
A.
11
2
x
. B.
6
x
. C.
5
x
. D.
9
2
x
.
Câu 3. Thể tích
V
của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
là
A.
3
2
3
a
V . B.
3
3
4
a
V . C.
3
3
2
a
V . D.
3
2
4
a
V .
Câu 4. Gọi
1
x
,
2
x
, (với
1 2
x x
) là hai nghiệm của phương trình
2 1
2 5.2 2 0
x x
. Tính giá trị của
biểu thức
2
1
1
3
3
x
x
P
.
A.
5
4
P
. B.
6
P
. C.
2
3
P
. D.
10
9
P
.
Câu 5. Đường cong ở hình vẽ bên dưới là của hàm số nào?
A.
3
3 – 4
y x x . B.
3 2
3 2
y x x
. C.
3
4
y x
. D.
4 2
3 2
y x x
.
Câu 6. Trong các hàm số sau, hàm số nào có 3 điểm cực trị?
A.
4 2
2 – 3 2
y x x
. B.
2
–3 2
y x x
. C.
4 2
2 – 3 2
y x x
. D.
3 2
3 2
y x x
.
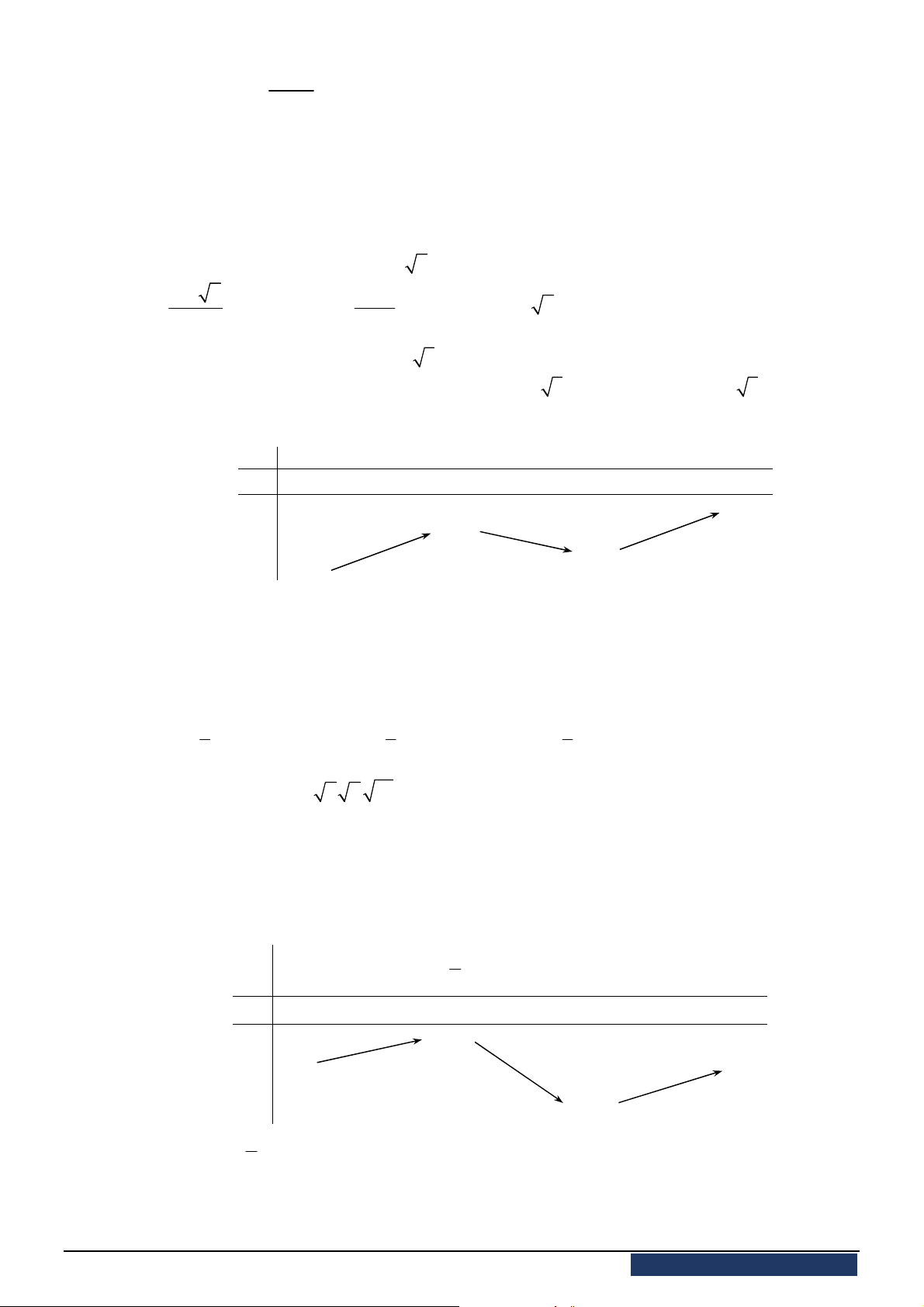
Câu 7. Đường cong ở hình vẽ bên dưới là đồ thị của hàm số nào sau đây?
A.
4 2
4 2
y x x
. B.
3 2
– 3 1
y x x
. C.
4 2
4 2
y x x
. D.
4 2
4 2
y x x
.
Câu 8. Khối bát diện đều là khối đa diện đều loại
A.
4;3
. B.
3;5
. C.
5;3
. D.
3: 4
.
Câu 9. Biết
3 3 9
3
log 3log 2 log 25 log 3
x . Khi đó, giá trị của
x
là
A.
25
9
. B.
40
9
. C.
20
3
. D.
200
3
.
O
x
y
O
x
y
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/24 – HKI1819-001-SGD BẠC LIÊU
Câu 10. Cho hàm số
1
1
x
y
x
. Khẳng định nào sao đây là khẳng định đúng?
A. Hàm số nghịch biến trên khoảng
;1 1;
.
B. Hàm số đồng biến trên khoảng
;1 1;
.
C. Hàm số nghịch biến trên các khoảng
;1
và
1;
.
D. Hàm số đồng biến trên các khoảng
;1
và
1;
.
Câu 11. Một hình trụ có bán kính đáy
2
r a
, chiều cao
h a
. Thể tích của khối trụ bằng
A.
3
2
3
a
. B.
3
2
3
a
. C.
3
2
a
. D.
3
2
a
.
Câu 12. Một khối cầu có đường kính bằng
2 3
có thể tích bằng
A.
4
. B.
12
. C.
4 3
. D.
12 3
.
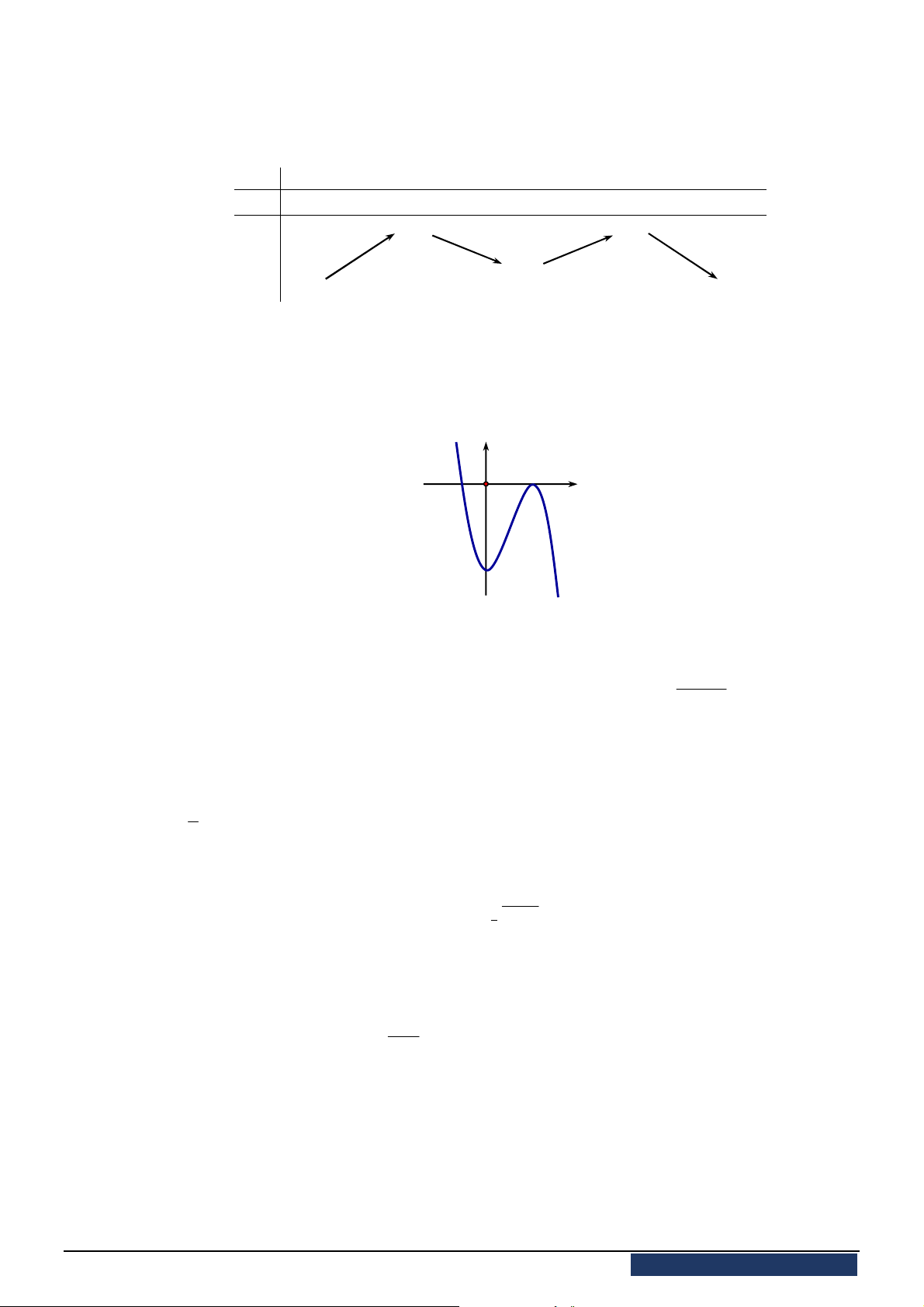
Câu 13. Cho hàm số
y f x
có bảng biến thiên như hình vẽ bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực tiểu tại
2
x
. B. Hàm số đạt cực đại tại
4
x
.
C. Hàm số đạt cực đại tại
3
x
. D. Hàm số đạt cực đại tại
2
x
.
Câu 14. Hình nón có chiều cao
h
, độ dài đường sinh
l
, bán kính đáy
r
. Thể tích
V
của khối nón được
tính theo công thức nào sau đây?
A.
2
1
3
V r l
. B.
1
3
V rh
. C.
2
1
3
V r h
. D.
2
V r l
.
Câu 15. Cho biểu thức
5
12
3 4
f x x x x
. Khi đó, giá trị của
2,7
f bằng
A.
0,027
. B.
27
. C.
2,7
. D.
0,27
.
Câu 16. Một khối nón có bán kính đáy là
r a
và thể tích bằng
3
a
. Chiều cao
h
của khối nón là
A.
2
h a
. B.
h a
. C.
4
h a
. D.
3
h a
.
Câu 17. Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như hình vẽ.
A.
1
max
2
y
. B.
max 1
y
. C.
max 1
y
. D.
max 3
y
.
Câu 18. Tính thể tích
V
của khối hộp chữ nhật
.
ABCD A B C D
, biết
AB a
,
2
AD a
và
3
AA a
.
A.
6
V a
. B.
3
6
V a
. C.
2
6
V a
. D.
3
2
V a
.
x
1
2
2
y
0
0
y
3
1
1
1
x
2
4
y
0
0
y
3
2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/24 – HKI1819-001-SGD BẠC LIÊU
Câu 19. Tiếp tuyến của đồ thị hàm số
3
3 2
y x x
tại điểm có hoành độ
0
2
x
có phương trình là
A.
9 22
y x
. B.
9 22
y x
. C.
9 14
y x
. D.
9 14
y x
.
Câu 20. Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như hình vẽ bên dưới.
Hàm số
y f x
đồng biến trên khoảng nào dưới đây?
A.
;0
. B.
0;1
. C.
1;0
. D.
0;
.
Câu 21. Tìm tất cả các giá trị của tham số
m
để phương trình
3 2
– 3 4 0
x x m
có nghiệm duy nhất
lớn hơn
2
. Biết rằng đồ thị của hàm số
3 2
3 – 4
y x x có hình vẽ như bên dưới.
A.
4
m
hoặc
20
m
. B.
4
m
.
C.
4
m
D.
0
m
.
Câu 22. Tìm tất cả các giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
1
x m
y
x
trên
2;4
bằng
2
A.
m
0. B.
2
m
. C.
2
m
. D.
4
m
.
Câu 23. Gọi
S
tập hợp tất cả các giá trị nguyên của tham số
m
để hàm số
3 2
1
– 2 3 2
3
y x mx m x m
nghịch biến trên
. Số phần tử của là
A.
5
. B.
4
. C.
7
. D.
8
.
Câu 24. Với giá trị nào của
x
thì biểu thức
1
2
1
log
3
x
f x
x
có nghĩa?
A.
\ –3;1
x
. B.
3;1
x . C.
\ 3;1
x
. D.
3;1
x .
Câu 25. Đạo hàm của hàm số
x
y
là
A.
1
ln
x
y x
. B.
ln
x
y
. C.
.ln
x
y
. D.
1
.
x
y x
.
Câu 26. Cho hình nón có đường sinh
5 cm
l
và bán kính đáy
4 cm
r
. Diện diện tích xung quan của
hình nón bằng
A.
2
20 cm
. B.
2
40 cm
. C.
2
40 cm
. D.
2
20 cm
.
Câu 27. Tổng các nghiệm của phương trình
2
log 5 – 2 2
x
x
bằng
A.
3
. B.
1
. C.
2
. D.
0
.
O
x
y
1
2
4
x
1
0
1
y
0
0
0
y
1
1
2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/24 – HKI1819-001-SGD BẠC LIÊU
Câu 28. Biết
log 3
a
b
với
a
,
b
là các số thực dương và
a
khác
1
. Tính giá trị của biểu thức
2
3 2 6
log log
a a
P b b
.
A.
63
P
. B.
45
P
. C.
21
P
. D.
99
P
.
Câu 29. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
và có
AB a
,
3
BC a
. Mặt
bên
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng
ABC
. Tính
theo
a
thể tích của khối chóp
.
S ABC
.
A.
3
6
6
a
V . B.
3
6
12
a
V . C.
3
2 6
3
a
V . D.
3
6
4
a
V .
Câu 30. Đồ thị hàm số
2 1
1
x
y
x
có đường tiệm cận đứng là
A.
2
y
. B.
1
x
. C.
2
y
. D.
1
x
.
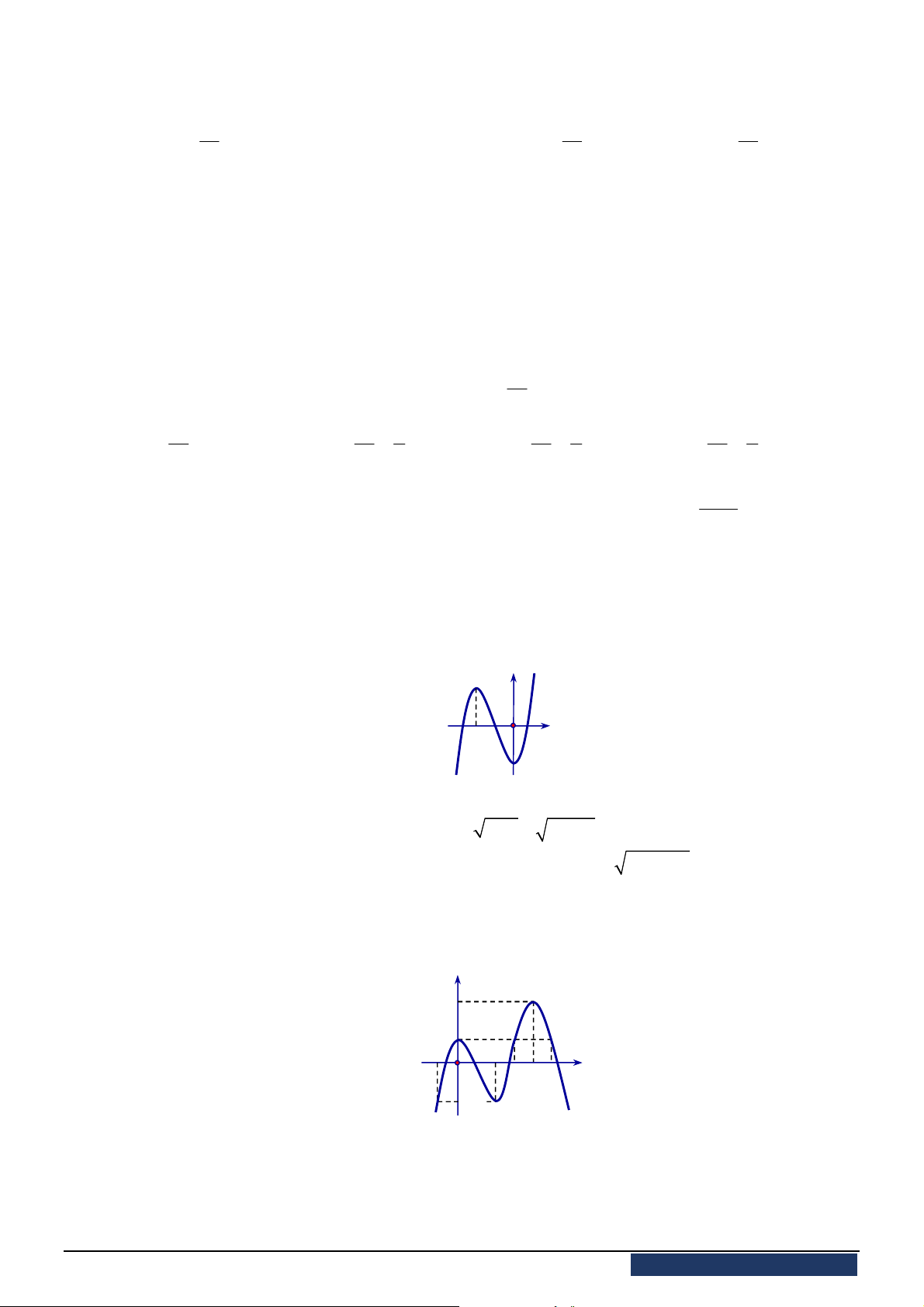
Câu 31. Bảng biến thiên ở hình vẽ bên dưới là của hàm số nào?
A.
3
1
x
y
x
. B.
2
1
x
y
x
. C.
3
1
x
y
x
. D.
3
1
x
y
x
.
Câu 32. Một người gửi
100
triệu đồng vào một ngân hàng với lãi suất
0,65%
/tháng. Biết rằng nếu
không rút tiền khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu để
tính lãi cho tháng tiếp theo. Hỏi sau đúng
12
tháng, người đó được lĩnh số tiền (cả vốn ban đầu
và lãi) là bao nhiêu? Biết rằng trong khoảng thời gian này người đó không rút tiền ra và lãi suất
không thay đổi.
A.
108.085.000
đồng. B.
108.000.000
đồng. C.
108.084.980
đồng. D.
108.084.981
đồng.
Câu 33. Biết hàm số
3 2
3 6
y x x x
đạt cực trị tại hai điểm
1
x
,
2
x
. Khi đó, giá trị của biểu thức
2 2
1 2
x x
bằng
A.
8
. B.
10
. C.
8
. D.
10
.
Câu 34. Cho khối chóp đều
.
S ABC
có cạnh đáy bằng
a
, cạnh bên bằng
2
a
. Gọi
M
là trung điểm
SB
,
N
là điểm trên đoạn
SC
sao cho
2
NS NC
. Thể tích của khối chóp
.
A BCNM
bằng
A.
3
11
18
a
. B.
3
11
24
a
. C.
3
11
36
a
. D.
3
11
16
a
.
Câu 35. Số đường tiệm cận của đồ thị hàm số
2
1 3 1
3 2
x x
y
x x
là
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 36. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên
bằng
2
a
.
A.
2 14
7
a
R . B.
2 7
2
a
R .
C.
2 7
3 2
a
R . D.
2 2
7
a
R .
x
1
y
–
–
y
1
1
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/24 – HKI1819-001-SGD BẠC LIÊU
Câu 37. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
,
SA
vuông góc với mặt đáy và
SA AB a
,
2
AC a
. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
4
a
V . B.
3
V a
. C.
3
2
a
V . D.
3
3
a
V .
Câu 38. Số giao điểm của đồ thị hàm số
3
4
y x x
với đường thẳng
4
y
là
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 39. Tổng lập phương các nghiệm thực của phương trình
2
4 5
3 9
x x
bằng
A.
27
. B.
28
. C.
26
. D.
25
.
Câu 40. Cho tam giác
ABC
vuông tại
A
có
2
BC a
và
30
B
. Quay tam giác vuông này quanh
trục
AB
, ta được một hình nón đỉnh
B
. Gọi
1
S
là diện tích toàn phần của hình nón đó và
2
S
là
diện tích mặt cầu có đường kính
AB
. Tính tỉ số
2
1
S
S
.
A.
2
1
1
S
S
. B.
2
1
2
3
S
S
. C.
2
1
3
2
S
S
. D.
2
1
1
2
S
S
.
Câu 41. Tổng tất cả các giá trị nguyên âm của tham số
m
để hàm số
3
2
3
28
y x mx
x
, đồng biến trên
khoảng
0;
bằng
A.
15
. B.
6
. C.
3
. D.
10
.
Câu 42. Cho hàm số
y f x
xác định và liên tục trên
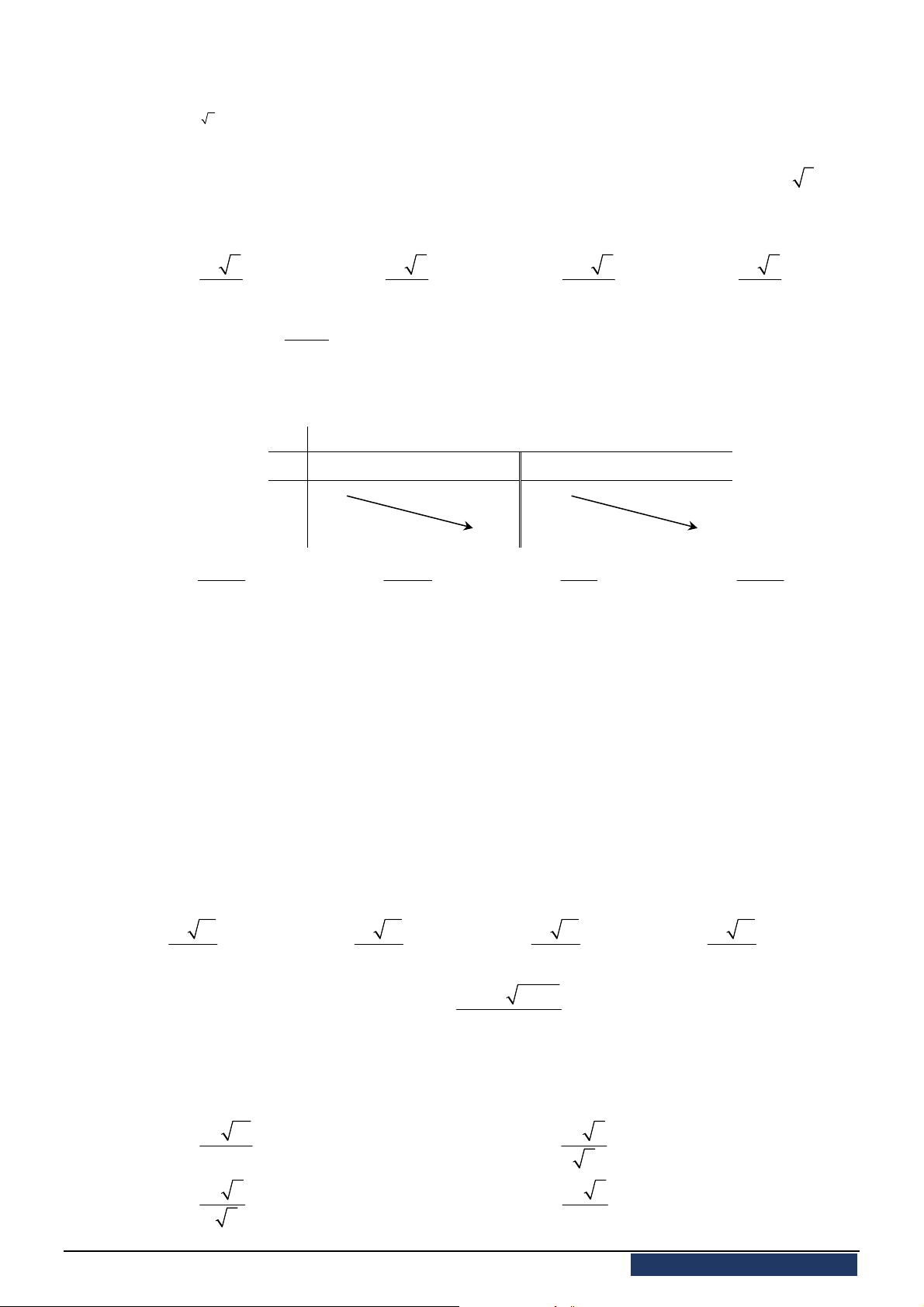
có đồ thị như hình vẽ. Hàm số
2
2 4
g x f x x
có bao nhiêu điểm cực tiểu?
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 43. Cho
x
,
y
là các số thực thỏa mãn
1 2 2
x y x y
. Gọi
M
,
m
lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của
2 2
2 1 1 8 4
P x y x y x y
. Khi đó, giá trị của
M m
bằng
A.
42
. B.
44
. C.
41
. D.
43
.
Câu 44. Cho hàm số
y f x
có đồ thị hàm số
y f x
được cho như hình vẽ.
Hàm số
2
2 2
g x f x x
nghịch biến trên khoảng nào?
A.
0;2
. B.
3;1
. C.
2;3
. D.
1;0
.
x
y
1
1
2
O
3
4
5
3
2
2
x
y
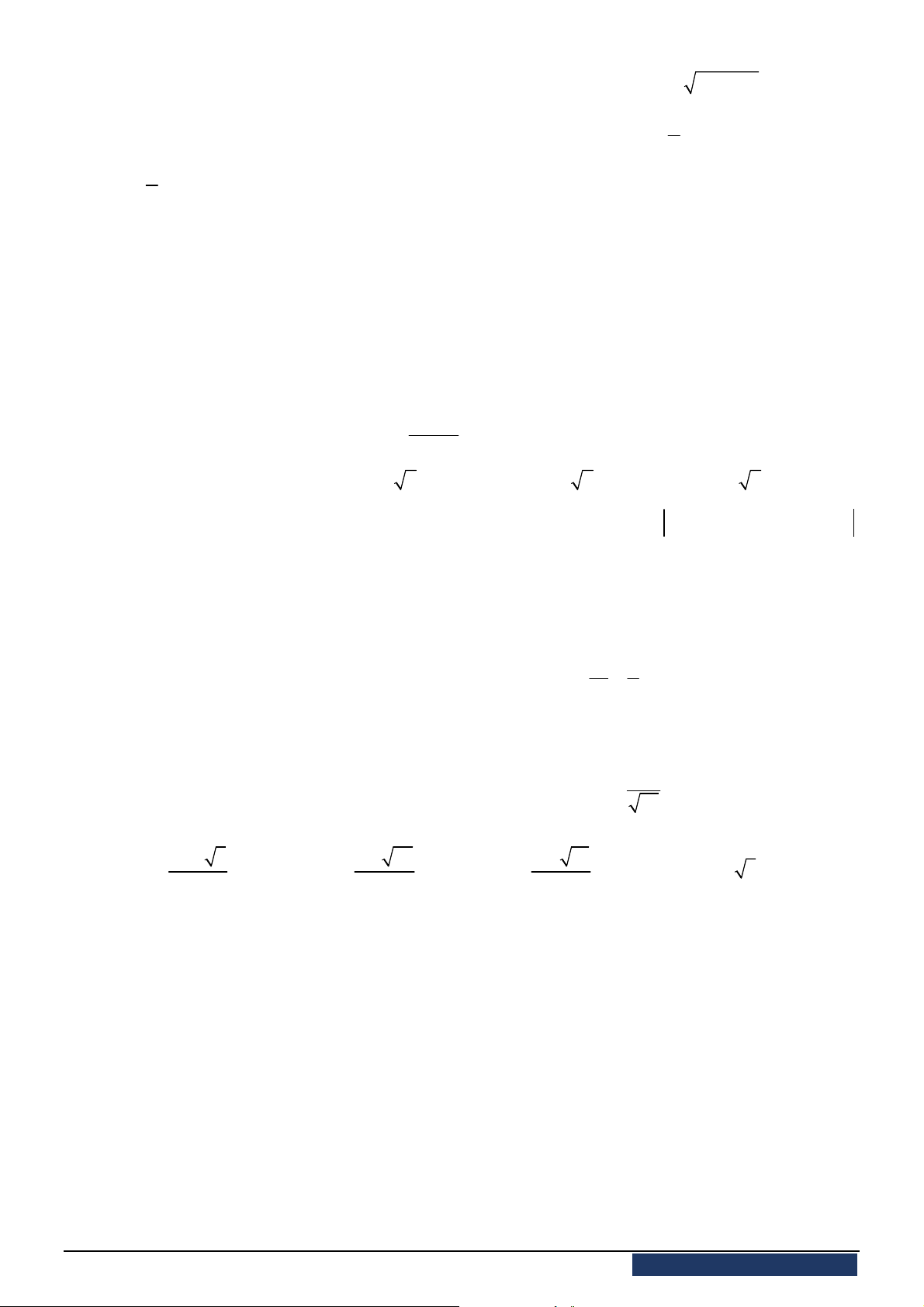
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/24 – HKI1819-001-SGD BẠC LIÊU
Câu 45. Cho hàm số
4 7
3 1 .2 – 6 3
x x
f x x x
, khi phương trình
2
7 4 6 9 3 1 0
f x x m
có số nghiệm nhiều nhất thì giá trị nhỏ nhất của tham số
m
có dạng
a
b
(trong đó
a
,
b
và
a
b
là phân số tối giản). Tính
T a b
.
A.
7
T
. B.
11
T
. C.
8
T
. D.
13
T
.
Câu 46. Cho hàm số
3 2
3 1
y x x
có đồ thị
C
và điểm
1;
A m
. Gọi
S
là tập hợp tất cả các giá trị
nguyên của tham số
m
để qua
A
có thể kể được đúng ba tiếp tuyến tới đồ thị
C
. Số phần tử
của
S
là
A.
9
. B.
7
. C.
3
. D.
5
Câu 47. Cho hai số thực
1
a
,
1
b
. Biết phương trình
2
1
1
x x
a b
có hai nghiệm phân biệt
1
x
,
2
x
. Tìm
giá trị nhỏ nhất của biểu thức
2
1 2
1 2
1 2
4
x x
P x x
x x
.
A.
4
P
. B.
3
3 2
P
. C.
3
3 4
P
. D.
3
4
P
.
Câu 48. Tổng tất cả các giá trị nguyên của tham số
m
để đồ thị hàm số
4 3 2
3 8 6 – 24
y x x x x m
có
7
điểm cực trị là
A.
63
. B.
55
. C.
30
. D.
42
.
Câu 49. Cho hình thang
ABCD
vuông tại
A
và
B
có
AB a
,
3
AD a
và
BC x
với
0 3
x a
.
Gọi
1
V
,
2
V
, lần lượt là thể tích các khối tròn xoay tạo thành khi quay hình thang
ABCD
(kể cả
các điểm trong) quanh đường thẳng
BC
và
AD
. Tìm
x
để
1
2
7
5
V
V
.
A.
x a
. B.
2
x a
. C.
3
x a
. D.
4
x a
.
Câu 50. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
2
a
. Gọi
M
là trung điểm cạnh
SA
,
90
SAB SCB
, biết khoảng cách từ
A
đến
MBC
bằng
6
21
a
. Thể tích của khối chóp
.
S ABC
bằng
A.
3
10 3
9
a
. B.
3
8 39
3
a
. C.
3
4 13
3
a
. D.
3
2 3
a .
----------- HẾT ---------
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/24 - Mã đề thi 640
0SỞ GIÁO DỤC VÀ ĐÀO TẠO BẠC
LIÊU
ĐỀ CHÍNH THỨC
(Đề thi gồm 06 trang)
KIỂM TRA HỌC KỲ I NĂM HỌC: 2017-2018
Môn kiểm tra: TOÁN 12
Thời gian làm bài 90 phút, không kể thời gian phát đề
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 640
Câu 1. [2H1-1] Số mặt phẳng đối xứng của hình chóp đều
.
S ABC
là
A.
4
. B.
2
. C.
6
. D.
3
.
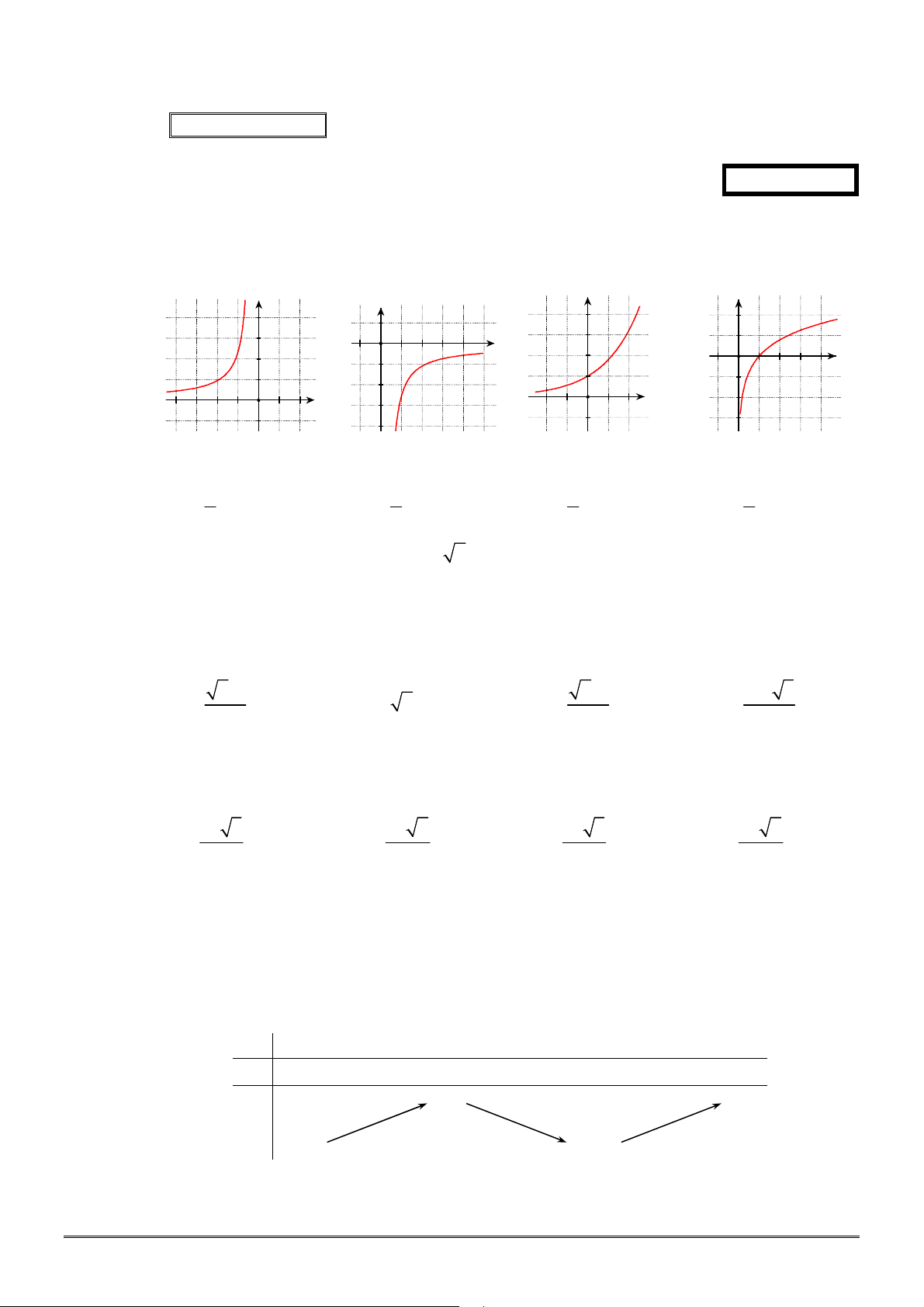
Câu 2. [2D2-1] Cho
a
là số thực dương khác
1
. Hình nào sau đây là đồ thị của hàm số mũ
x
y a
?
A.
x
y
1
1
O
B.
x
y
1
1
O
C.
x
y
1
1
O
D.
x
y
1
1
O
Câu 3. [2H2-1] Khối cầu
S
có bán kính bằng
r
và thể tích bằng
V
. Mệnh đề nào dưới đây đúng?
A.
3
4
3
V r
. B.
2 2
4
3
V r
. C.
2 3
4
3
V r
. D.
4
3
V r
.
Câu 4. [2D2-2] Cho
3
log 6
x
. Tính
3
3
log
K x
.
A.
4
K
. B.
8
K
. C.
2
K
. D.
3
K
.
Câu 5. [2H1-2] Cho khối chóp
.
S ABCD
có đáy là hình chữ nhật
AB a
,
2
BC a
,
SA
vuông góc
với đáy và
SC
tạo với mặt phẳng
SAB
một góc bằng
60
. Tính thể tích
V
của khối chóp đã
cho.
A.
3
6
3
a
V . B.
3
2
V a
. C.
3
2
3
a
V . D.
3
2 3
9
a
V .
Câu 6. [2H2-2] Cho tứ diện
ABCD
có tam giác
BCD
vuông tại
B
,
AC
vuông góc với mặt phẳng
BCD
,
5
AC a
,
3
BC a
và
4
BD a
. Tính bán kính
R
của mặt cầu ngoại tiếp tứ
diện
ABCD
.
A.
5 3
2
a
R . B.
5 2
3
a
R . C.
5 3
3
a
R . D.
5 2
2
a
R .
Câu 7. [2D1-2] Đồ thị hàm số
3 2
3 9 1
y x x x
có hai cực trị
A
và
B
. Điểm nào dưới đây thuộc
đường thẳng
AB
?
A.
0;2
N . B.
1;1
P . C.
1; 8
Q
. D.
0; 1
M
.
Câu 8. [2D1-1] Cho hàm số
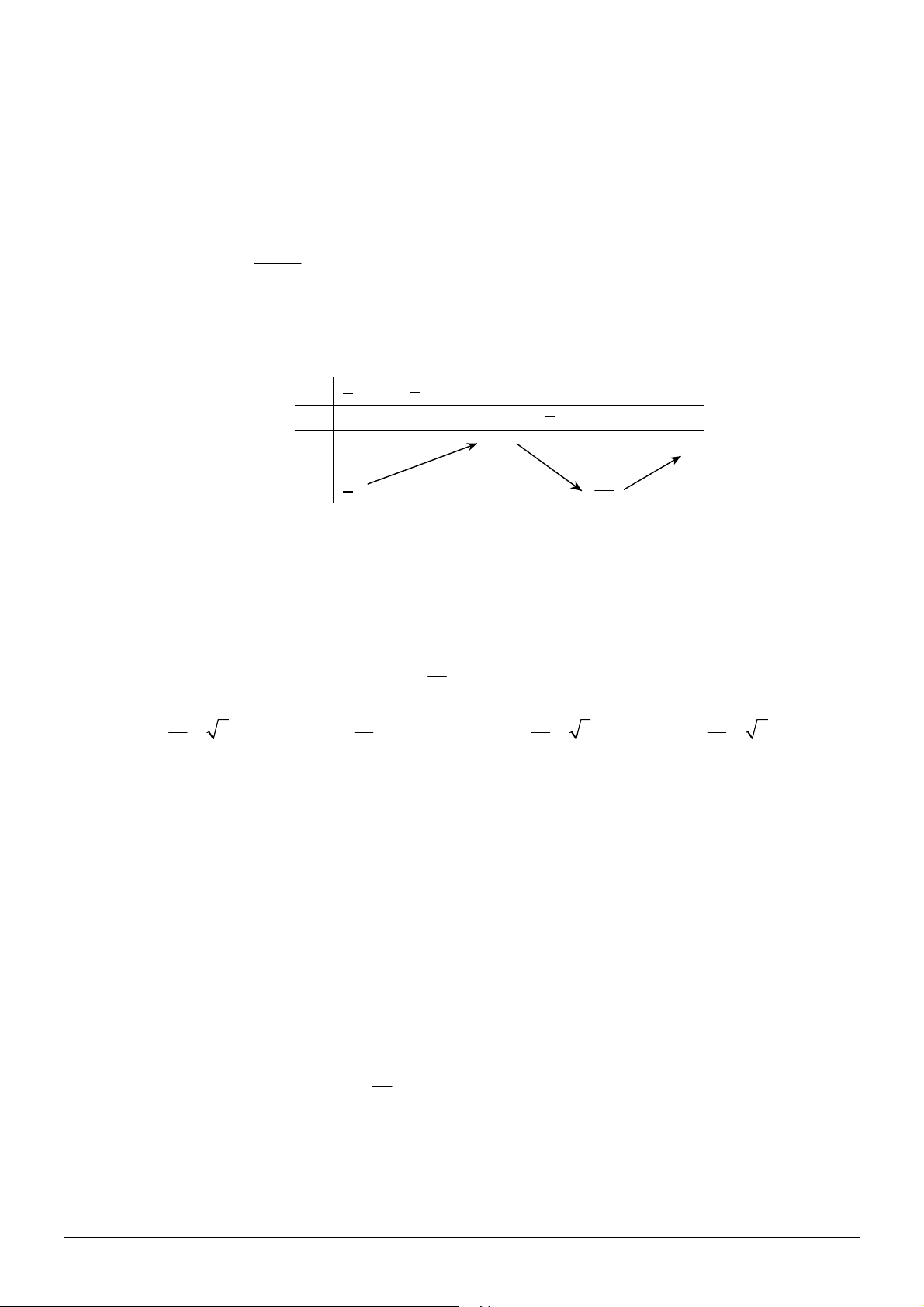
y f x
có bảng biến thiên như hình bên dưới. Tìm giá trị cực đại và
giá trị cực tiểu của hàm số đã cho.
A.
3
CĐ
y
và
0
CT
y
. B.
2
CĐ
y
và
2
CT
y
.
C.
2
CĐ
y
và
2
CT
y
. D.
0
CĐ
y
và
3
CT
y
.
x
0
3
y
0
0
y
2
2
4
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/24 - Mã đề thi 640
Câu 9. [2H1-2] Cho hình chóp
.
S ABC
có
6
AB
,
8
BC
,
10
AC
. Cạnh bên
SA
vuông góc với
đáy và
4
SA
. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
40
V
. B.
32
V
. C.
192
V
. D.
24
V
.
Câu 10. [2D2-1] Cho
a
là số thực dương khác
1
. Mệnh đề nào dưới đây đúng với mọi số thực dương
x
,
y
?
A.
log log .log
a a a
xy x y
. B.
log log log
a a a
xy x y
.
C.
log
log
log
a
a
a
x
xy
y
. D.
log log log
a a a
xy x y
.
Câu 11. [2D1-1] Cho hàm số
y f x
liên tục trên
, bảng biến thiên như sau.Kết luận nào sau đây
đúng.
A. Hàm số có ba điểm cực trị. B. Hàm số có hai điểm cực trị.
C. hàm số đạt cực tiểu tại
1
x
. D. Hàm số đạt cực đại tại
2
x
.
Câu 12. [2H2-4] Cho
S
là một mặt cầu cố định có bán kính
R
. Một hình trụ
H
thay đổi nhưng
luôn có hai đường tròn đáy nằm trên
S
. Gọi
1
V
là thể tích của khối cầu
S
và
2
V
là thể tích
lớn nhất của khối trụ
H
. Tính tỉ số
1
2
V
V
.
A.
1
2
6
V
V
. B.
1
2
2
V
V
. C.
1
2
3
V
V
. D.
1
2
2
V
V
Câu 13. [2H2-2] Cho hình nón tròn xoay có đường sinh bằng
13
(cm), bán kính đường tròn đáy bằng
5
(cm). Thể tích của khối nón tròn xoay là
A.
200
(
3
cm
). B.
150
(
3
cm
). C.
100
(
3
cm
). D.
300
(
3
cm
).
Câu 14. [2D1-2] Cho hàm số
2
1 2
y x x
có đồ thị
C
. Mệnh đề nào dưới đây đúng?
A.
C
không cắt trục hoành. B.
C
cắt trục hoành tại một điểm.
C.
C
cắt trục hoành tại ba điểm. D.
C
cắt trục hoành tại hai điểm.
Câu 15. [2H1-1] Thể tích
V
của một khối lăng trụ có diện tích đáy bằng
B
và chiều cao bằng
h
là
A.
2
1
3
V B h
. B.
V Bh
. C.
1
3
V Bh
. D.
1
2
V Bh
.
Câu 16. [2D2-2] Phương trình
3 4
1
2
32
x
có nghiệm là
A.
3
x
. B.
2
x
. C.
2
x
. D.
3
x
.
Câu 17. [2D2-1] Tập xác định của hàm số
2
log 10 2
y x
là
A.
;2
. B.
5;
. C.
;10
. D.
;5
.
y
y'
x
+++
+
2
2
1
00
1 +
0
19
12

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/24 - Mã đề thi 640
Câu 18. [2D1-3] Gọi
S
là tổng tất cả các giá trị nguyên dương của tham số
m
sao cho hàm số
2
2
4
x m
y
x m
đồng biến trên khoảng
2021;
. Khi đó, giá trị của
S
bằng
A.
2035144
. B.
2035145
. C.
2035146
. D.
2035143
.
Câu 19. [2D1-2] Cho hàm số
4 2
2
y x x
. Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
1;1
. B. Hàm số nghịch biến trên khoảng
; 2
.
C. Hàm số đồng biến trên khoảng
1;1
. D. Hàm số đồng biến trên khoảng
; 2
.
Câu 20. [2H2-1] Cho mặt cầu
S
có tâm
O
, bán kính
r
. Mặt phẳng
cắt mặt cầu
S
theo giao
tuyến là đường tròn
C
có bán kính
R
. Kết luận nào sau đây sai?
A.
2 2
,R r d O
.
B.
,
d O r
.
C. Diện tích của mặt cầu là
2
4
S r
.
D. Đường tròn lớn của mặt cầu có bán kính bằng bán kính mặt cầu.
Câu 21. [2D2-2] Với
a
,
b
,
x
là các số thực dương thỏa mãn
5 5 5
log 4log 3log
x a b
, mệnh đề nào
dưới đây là đúng?
A.
3 4
x a b
. B.
4 3
x a b
. C.
4 3
x a b
. D.
4 3
x a b
.
Câu 22. [2H2-1] Một hình trụ có khoảng cách giữa hai đáy, độ dài đường sinh và bán kính đường tròn
đáy lần lượt bằng
h
,
l
,
r
. Khi đó công thức tính diện tích toàn phần của hình trụ là
A.
2
tp
S r l r
. B.
2 2
tp
S r l r
. C.
tp
S r l r
. D.
2
tp
S r l r
.
Câu 23. [2H2-1] Cho hình nón tròn xoay. Một mặt phẳng
P
đi qua đỉnh
O
của hình nón và cắt
đường tròn đáy của hình nón tại hai điểm. Thiết diện được tạo thành là
A. Một tứ giác. B. Một hình thang cân. C. Một ngũ giác. D. Một tam giác cân.
Câu 24. [2D2-1] Cho
với ,
. Mệnh đề nào dưới đây đúng?
A.
. B.
. C.
. D.
.
Câu 25. [2H1-1] Khối đa diện nào sau đây có công thức thể tích là
1
3
V Bh
? Biết hình đa diện đó có
diện tích đáy bằng
B
và chiều cao bằng
h
?
A. Khối chóp. B. Khối hộp chữ nhật. C. Khối hộp. D. Khối lăng trụ.
Câu 26. [2D1-2] Đồ thị
2
2
4
x
y
x
có bao nhiêu tiệm cận?
A. 2. B. 4. C. 3. D. 1.
Câu 27. [2D2-1] Cho
4
số thực
a
,
b
,
x
,
y
với
a
,
b
là các số dương và khác
1
. Mệnh đề nào dưới
đây đúng? A.
x
x y
y
a
a
a
. B.
y
x x y
a a
. C.
.
.
x y x y
a a a
D.
. .
x
x
a b a b
.
Câu 28. [2D1-3] Hai thành phố A và B ngăn cách nhau bởi một còn sông. Người ta cần xây cây cầu
bắc qua sông và vuông góc với bờ sông. Biết rằng thành phố A cách bờ sông 2 (km), thành phố
B cách bờ sông 5 (km ), khoảng cách giữa đường thẳng đi qua A và đường thẳng đi qua B cùng
vuông góc với bờ sông là 12 (km). Giả sử hai bờ sông là hai đường thẳng song song với nhau.
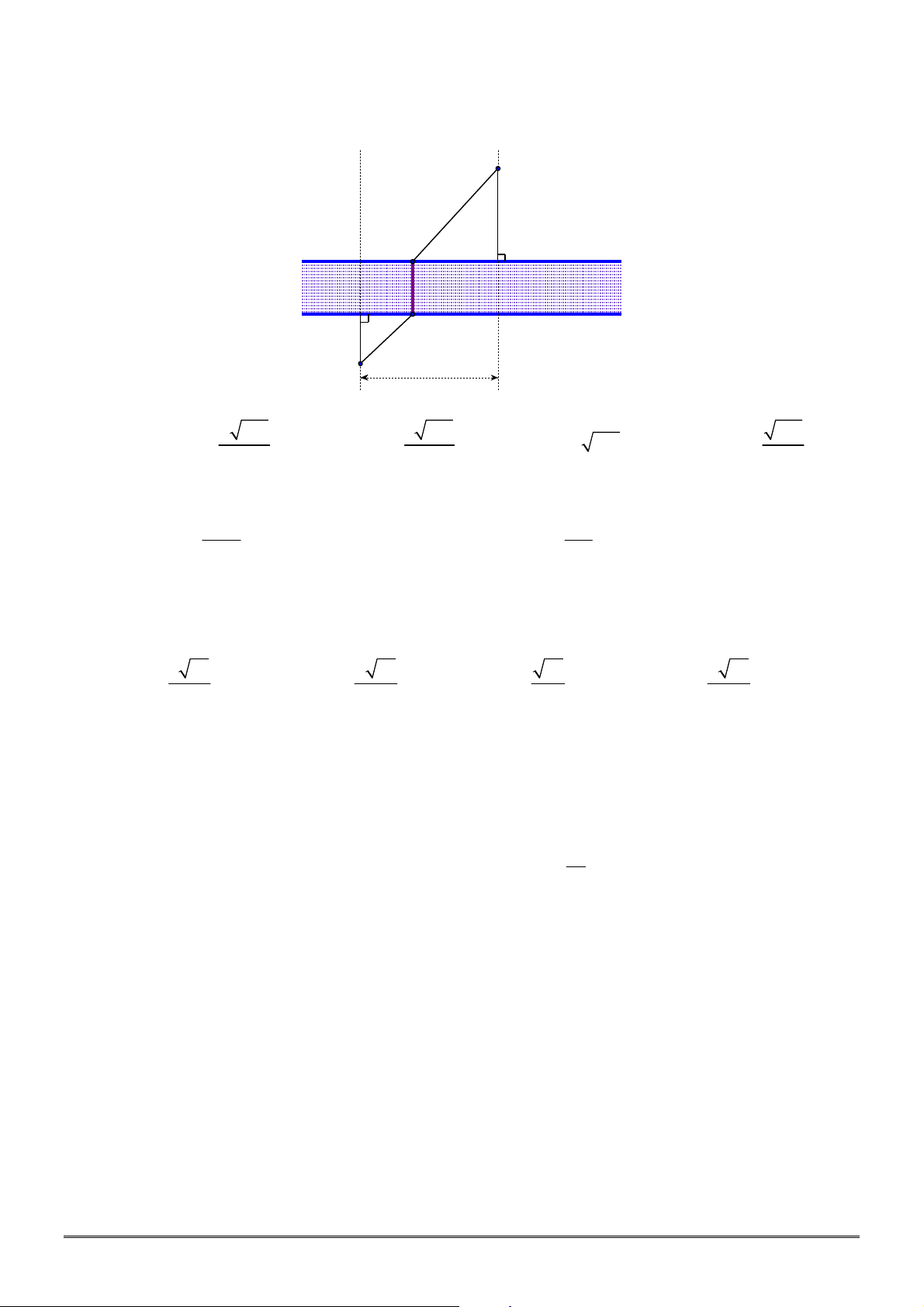
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/24 - Mã đề thi 640
Nhằm tiết kiệm chi phí đi từ thành phố A đến thành phố B, người ta xây cây cầu ở vị trí MN để
quãng đường đi từ thành phố A đến thành phố B là ngắn nhất (hình vẽ). Khi đó, độ dài
đoạn
AM
là
sông
2 km
5 km
12 km
A
M
B
N
A.
2 193
km.
7
AM B.
3 193
km.
7
AM C.
193 km.
AM D.
193
km.
7
AM
Câu 29. [2D1-1] Đạo hàm của hàm số
5 2017
x
y là
A.
5
5ln5
x
y
. B.
5 .ln5
x
y
. C.
5
ln5
x
y
D.
5
x
y
.
Câu 30. [1H3-3] Cho khối chóp
.
S ABCD
có đáy là hình vuông,
SAB
đều và nằm trong mặt phẳng
vuông góc với mặt đáy. Mặt cầu ngoại tiếp khối chóp
.
S ABCD
có diện tích
2
84 cm
. Khoảng
cách giữa hai đường thẳng
SA
và
BD
là
A.
3 21
cm
7
. B.
2 21
cm
7
. C.
21
cm
7
. D.
6 21
cm
7
.
Câu 31. [2D2-2] Tìm tập xác định
D
của hàm số
3
2
2
y x x
.
A.
0;D
. B.
; 2 1;D
.
C.
\ 2;1
D
. D.
D
.
Câu 32. [2D1-2] Tìm các giá trị của tham số
m
để hàm số
3
2 2
3 2 3
3
x
y x m x m
đồng biến trên
.
A.
3
3
m
m
. B.
3 3
m
. C.
3 3
m
. D.
3
3
m
m
.
Câu 33. [2D2-1] Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. Với
0 1
a
, hàm số
log
a
y x
là một hàm nghịch biến trên khoảng
0;
.
B. Với
1
a
, hàm số
log
a
y x
là một hàm đồng biến trên khoảng
;
.
C. Với
1
a
, hàm số
x
y a
là một hàm đồng biến trên khoảng
;
.
D. Với
0 1
a
, hàm số
x
y a
là một hàm nghịch biến trên khoảng
;
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/24 - Mã đề thi 640
Câu 34. [2D2-4] Xét các số thực dương
x
,
y
thỏa mãn
3
1
log 3 3 4
3
y
xy x y
x xy
. Tìm giá trị nhỏ
nhất
min
P
của
P x y
.
A.
min
4 3 4
3
P
. B.
min
4 3 4
3
P
. C.
min
4 3 4
9
P
. D.
min
4 3 4
9
P
.
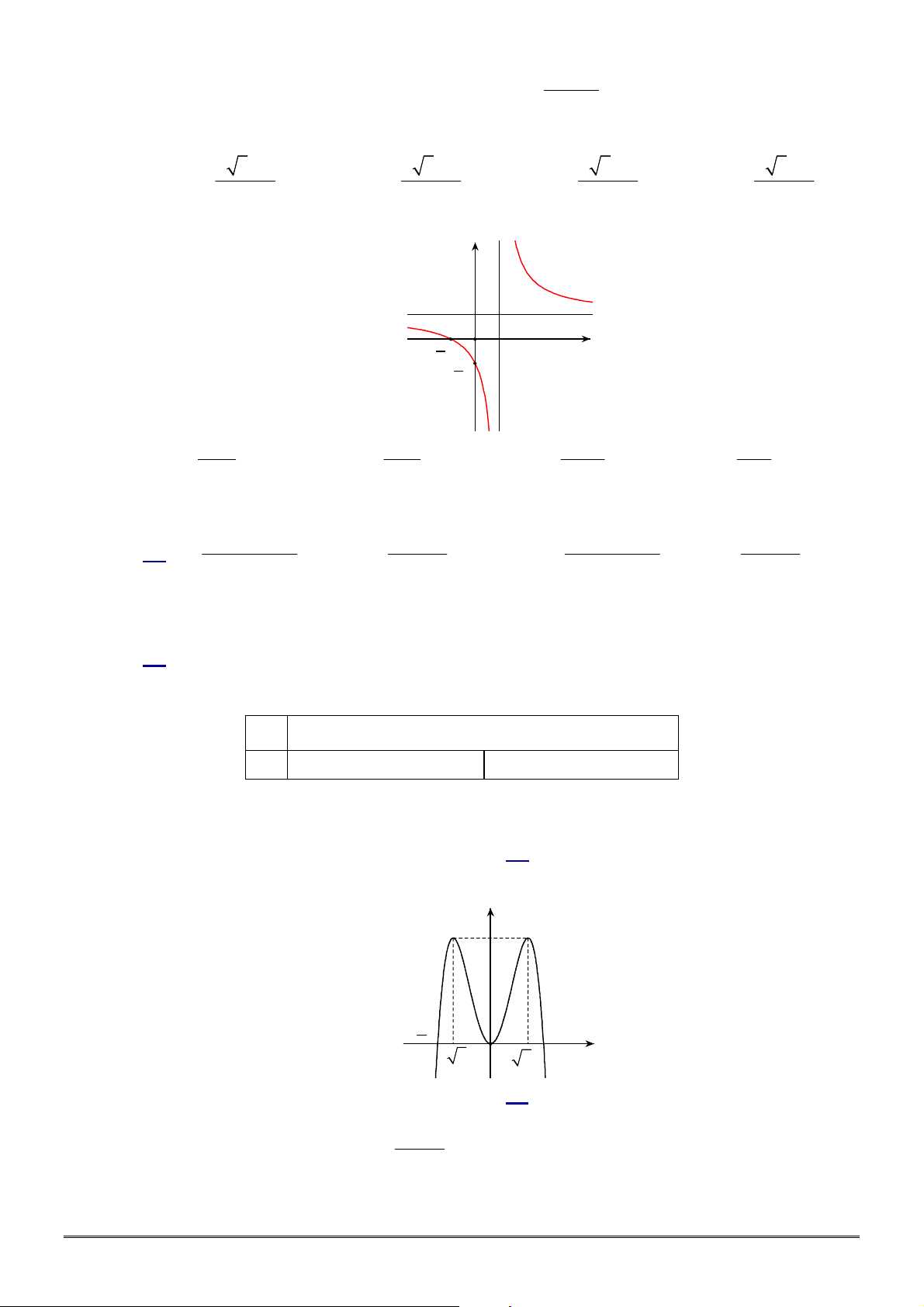
Câu 35. [2D1-1] Hình vẽ sau đây là đồ thị của hàm số nào?
x
y
1
1
1
1
O
A.
2
1
x
y
x
. B.
3
1
x
y
x
. C.
2 1
2 1
x
y
x
. D.
1
1
x
y
x
.
Câu 36. [2D2-2] Tính đạo hàm của hàm số
log 2 1
y x
.
A.
2
2x 1 ln10
y
. B.
2
2x 1
y
. C.
1
2x 1 ln10
y
. D.
1
2x 1
y
.
Câu 37. [2H1-1] Mỗi cạnh của một hình đa diện là cạnh chung của đúng
n
mặt của hình đa diện đó.
Mệnh đề nào dưới đây đúng?
A.
2
n
. B.
5
n
. C.
3
n
. D.
4
n
.
Câu 38. [2D1-1] Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau
x
2
0
2
y
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
;2
. B. Hàm số nghịch biến trên khoảng
; 2
.
C. Hàm số nghịch biến trên khoảng
;0
. D. Hàm số nghịch biến trên khoảng
2;0
.
Câu 39. [2D1-1] Hình vẽ sau đây là đồ thị của hàm số nào?
A.
4 2
2
y x x
. B.
4 2
3 1
y x x
. C.
4 2
4
y x x
. D.
4 2
3
y x x
.
Câu 40. [2D1-2] Cho hàm số
2
,
8
x m
f x
x
với
m
là tham số. Giá trị lớn nhất của
m
để
0;3
min 2
f x
là:
x
y
4
22
O
2
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/24 - Mã đề thi 640
A.
5
m
. B.
6
m
. C.
4
m
. D.
3
m
.
Câu 41. [2D2-2] Tìm giá trị thực của tham số
m
để phương trình
1
9 2.3 0
x x
m
có hai nghiệm
thực
1
x
,
2
x
thỏa mãn
1 2
0
x x
.
A.
6
m
. B.
0
m
. C.
3
m
. D.
1
m
.
Câu 42. [2D1-2] Giá trị lớn nhất của hàm số
4
2
x
y
x
trên đoạn
3;4
.
A.
4
. B.
10
. C.
7
. D.
8
.
Câu 43. [2D1-2] Tìm giá trị thực của tham số
m
để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực tiểu
tại
3
x
.
A.
1
m
. B.
1
m
. C.
5
m
. D.
7
m
.
Câu 44. [2H1-3] Cho khối lăng trụ đứng .
ABC A B C
có đáy là tam giác cân
ABC
với
AB AC a
,
120
BAC
, mặt phẳng
AB C
tạo với đáy một góc
30
. Tính thể tích
V
của khối lăng trụ
đã cho.
A.
3
6
a
V . B.
3
8
a
V . C.
3
3
8
a
V . D.
3
9
8
a
V .
Câu 45. [2H1-2] Cho khối lăng trụ đứng .
ABC A B C
có
AA a
, đáy
ABC
là tam giác vuông cân tại
A
và
2
BC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
V a
. B.
3
2
a
V . C.
3
6
a
V . D.
3
3
a
V .
Câu 46. [2H2-1] Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật
ABCD
có
AB
và
CD
thuộc hai đáy của hình trụ,
4
AB a
,
5
AC a
. Thể tích của khối trụ:
A.
3
8
a
. B.
3
12
a
. C.
3
4
a
. D.
3
16
a
.
Câu 47. [2H2-1] Cho hình nón tròn xoay có bán kính đường tròn đáy
r
, chiều cao
h
và đường sinh
l
.
Kết luận nào sau đây sai?
A.
2
1
3
V r h
. B.
2
tp
S rl r
. C.
2 2 2
h r l
. D.
xq
S rl
.
Câu 48. [2D1-1] Hàm số
y f x
có giới hạn
lim
x a
f x
và đồ thị
C
của hàm số
y f x
chỉ nhận đường thẳng
d
làm tiệm cận đứng. Khẳng định nào sau đây đúng?
A. :
d y a
. B.
:
d x a
. C.
:
d x a
. D. :
d y a
.
Câu 49. [2D2-1] Rút gọn biểu thức
1 3 1
5 10 5
2 1 2
3 3 3
a a a
M
a a a
với
0, 1
a a
, ta được kết quả là:
A.
1
1
a
. B.
1
1
a
. C.
1
1
a
. D.
1
1
a
.
Câu 50. [2D2-3] Đầu mỗi tháng anh A gửi vào ngân hàng
3
triệu đồng với lãi suất kép là
0,6%
mỗi
tháng. Hỏi sau ít nhất bao nhiêu tháng (khi ngân hàng đã tính lãi) thì anh A có được số tiền cả
lãi và gốc nhiều hơn
100
triệu biết lãi suất không đổi trong quá trình gửi.
A.
31
tháng. B.
40
tháng. C.
35
tháng. D.
30
tháng.
---HẾT---

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/29
SỞ GD VÀ ĐT HÀ NỘI
TRƯỜNG THPT KIM LIÊN
(Đề thi gồm 06 trang)
ĐỀ KIỂM TRA HỌC KÌ I MÔN TOÁN KHỐI 12
Năm học: 2017-2018
Thời gian làm bài 90 phút, không kể thời gian phát đề
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 590
Câu 1. [2H1-1] Cho khối chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
2
a
,
SA
vuông góc với mặt
phẳng
ABC
,
3.
SA a Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
6
a
V . B.
3
V a
. C.
3
4
a
V . D.
3
12
a
V .
Câu 2. [2D1-2] Cho hàm số
sin cos 2
y x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại các điểm
3
2 ,
4
x k k
.
B. Hàm số đạt cực đại tại các điểm 2 ,
4
x k k
.
C. Hàm số đạt cực tiểu tại các điểm 2 ,
4
x k k
.
D. Hàm số đạt cực tiểu tại các điểm 2 ,
4
x k k
.
Câu 3. [2D1-1] Tìm số điểm cực trị của hàm số
4 3 2
3 8 6 1
y x x x
.
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 4. [2D1-2] Tìm tất cả các giá trị củar tham số
m
để đồ thị hàm số
8
2
mx
y
x
có tiệm cận đứng.
A.
4
m
. B.
4
m
. C.
4
m
. D.
4
m
.
Câu 5. [1D1-2] Tìm giá trị lớn nhất
M
của hàm số
2
2sin sin2 11
y x x
.
A.
12 2
M
. B.
10 2
M
. C.
12 2
M
. D.
10 2
M
.
Câu 6. [2D1-1] Hàm số
3
3 5
y x x
đồng biến trên khoảng nào dưới đây?
A.
; 1
. B.
1;1
. C.
;1
. D.
1;
.
Câu 7. [2D1-2] Biết đồ thị hai hàm số
1
y x
và
2 1
1
x
y
x
cắt nhau tại hai điểm phân biện
A
,
B
.
Tính độ dài đoạn thẳng
AB
.
A.
2 2
AB
. B.
2
AB
. C.
2
AB
. D.
4
AB
.
Câu 8. [2D2-2] Tìm tập xác định
D
của hàm số
2018
2
2017
log 9 2 3y x x
.
A.
3 3
3; ;3
2 2
D
. B.
3;3
D . C.
3 3
3; ;3
2 2
D
. D.
3
;3
2
D
.
Câu 9. [2D1-2]Cho hàm số
3
3
y x x
với
2;x
. Mệnh đề nào dưới đây đúng?
A. Hàm số có giá trị nhỏ nhất và không có giá trị lớn nhất.
B. Hàm số có cả giá trị nhỏ nhất và giá trị lớn nhất.
C. Hàm số không có cả giá trị nhỏ nhất và giá trị lớn nhất.
D. Hàm số không có giá trị nhỏ nhất và có giá trị lớn nhất.
Câu 10. [2D2-2] Cho
p
,
q
là các số thực thỏa mãn:
2
1
e
p q
m
,
2
p q
n e
, biết
m n
. So sánh
p
và
q
.
A.
p q
. B.
p q
. C.
p q
. D.
p q
.
5
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/29
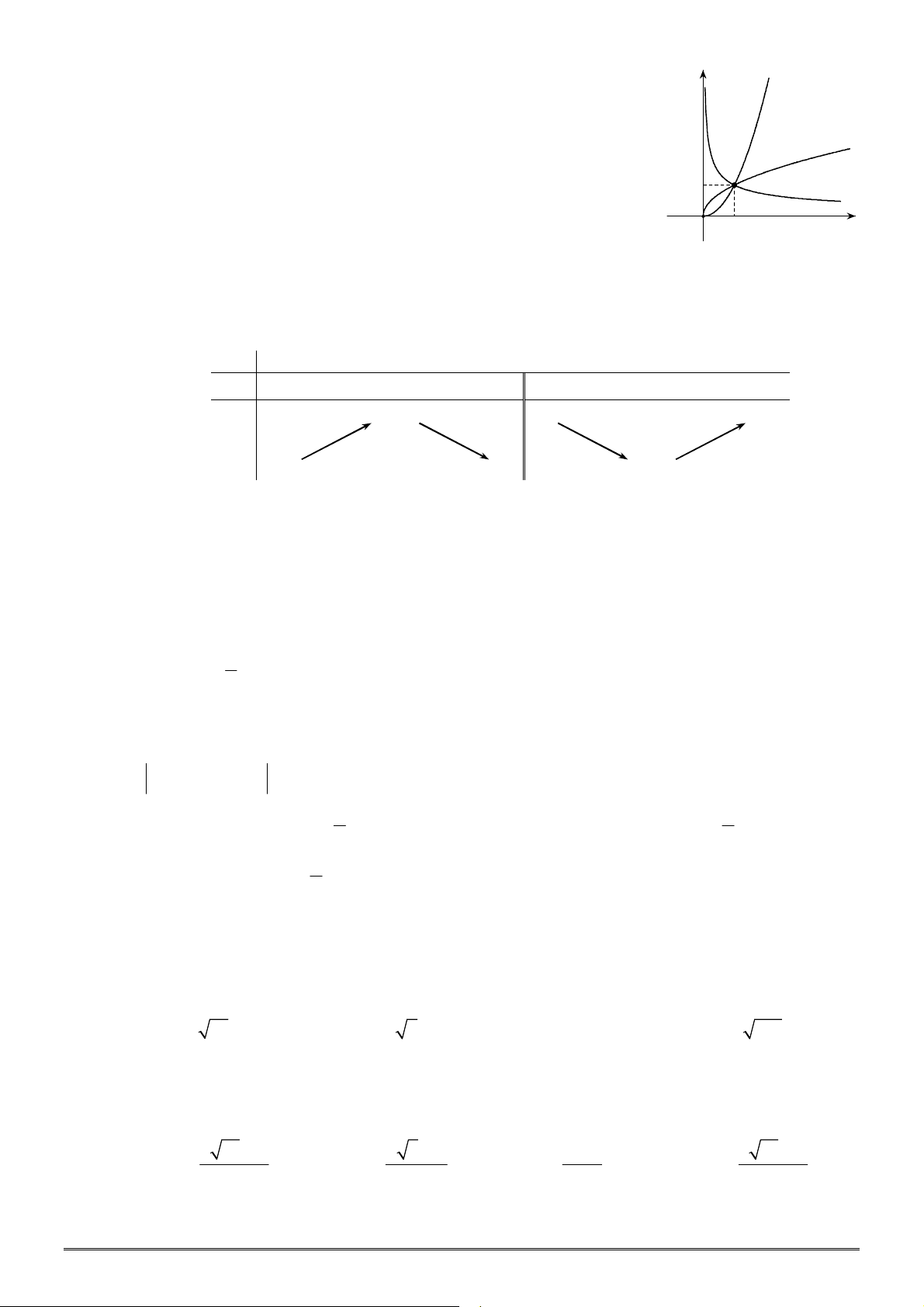
Câu 11. [2D2-2] Hình vẽ sau là đồ thị của ba hàm số
y x
,
y x
,
y x
(với
0
x
và
,
,
là các số thực cho trước). Mệnh
đề nào dưới đây đúng?
A.
. B.
.
C.
. D.
.
Câu 12. [2D1-3] Cho hàm số
3 2
3 2 1
y x x x
. Tiếp tuyến song song với
đường thẳng
2 3 0
x y
của đồ thị hàm số trên có phương trình là
A.
2 1 0.
x y
B.
2 2 0
x y
. C.
2 1 0
x y
. D.
2 1
y x
.
Câu 13. [2D1-2] Cho hàm số
y f x
có bảng biến thiên như hình vẽ. Mệnh đề nào dưới đây sai?
A. Hàm số đồng biến trên khoảng
3; 1
.
B. Đồ thị hàm số không có đường tiệm cận ngang.
C. Đồ thị hàm số có một đường tiệm cận đứng.
D. Hàm số nghịch biến trên
0; 1 1; 2
.
Câu 14. [2D2-2] Tính tổng
1 2
S x x
biết
1
x
,
2
x
là các giá trị thực thỏa mãn đẳng thức
2
3
6 1
1
2
4
x
x x
.
A.
5
S
. B.
8
S
. C.
4
S
. D.
2
S
.
Câu 15. [2H2-3] Cho tam giác
ABC
. Tập hợp các điểm
M
trong không gian thỏa mãn hệ thức
MA MB MC a
(với
a
là số thức dương không đổi) là:
A. Mặt cầu bán kính
3
a
R
. B. Đường tròn bán kính
3
a
R
.
C. Đoạn thẳng độ dài
3
a
. D. Đường thẳng.
Câu 16. [2H2-3] Mặt cầu tâm
I
bán kính
11
R
cm
cắt mặt phẳng
P
theo giao tuyến là đường
tròn đi qua ba điểm
A
,
B
,
C
. Biết
8
AB
cm
,
6
AC
cm
,
10
BC
cm
. Tính khoảng
cách
d
từ
I
đến mặt phẳng
P
.
A.
21
d
cm
. B.
4 6
d
cm
. C.
4
d
cm
. D.
146
d
cm
.
Câu 17. [2H2-3] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Mặt bên
SAB
là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích của khối cầu ngoại tiếp hình
chóp
.
S ABC
.
A.
3
5 15
54
a
V
. B.
3
4 3
27
a
V
. C.
3
5
3
a
V
. D.
3
5 15
18
a
V
.
x
0
1
2
y
0
0
y
1
4
x
y
1
1
O
y x
y x
y x

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/29
Câu 18. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để phương trình
4 2
3 1 0
x x m
có hai
nghiệm phân biệt.
A.
1
m
hoặc
13
4
m
. B.
1
m
.
C.
1
m
. D.
1
m
hoặc
13
4
m
.
Câu 19. [2D1-4] Cho Parabol
2
: 2 1,
P y x x
qua điểm
M
thuộc
P
kẻ tiếp tuyến với
P
cắt
hai trục
Ox
,
Oy
lần lượt tại hai điểm
A
,
B
. Có bao nhiêu điểm
M
để tam giác
ABO
có diện
tích bằng
1
.
4
A.
3
. B.
6.
C.
2
. D.
8
.
Câu 20. [2H2-3] Cho tứ diện đều
ABCD
có cạnh
2 .
a
Tính bán kính
r
của mặt cầu tiếp xúc với tất cả
các mặt của tứ diện.
A.
6
6
a
r . B.
6
.
12
a
r C.
6
8
a
r . D.
6
3
a
r .
Câu 21. [ 2D2-2] Cho hàm số
sin
x
y e
. Mệnh đề nào sau đây sai?
A.
.cos .sin 1
y x y x y
. B.
sin
2 sin sin 2 .
x
y x x e
.
C.
sin
cos .
x
y x e
. D.
.cos .sin 0
y x y x y
.
Câu 22. [2D2-1] Biết
6
log 2
a
0 1
a
. Tính
log 6
a
I .
A.
1
2
I
. B.
64
I
. C.
36
I
. D.
1
4
I
.
Câu 23. [2D2-2] Biết
6 6
log 2 , log 5 .
a b
Tính
3
log 5
I theo
, .
a b
A.
.
b
I
a
B.
.
1
b
I
a
C.
.
1
b
I
a
D.
.
1
b
I
a
Câu 24. [2H1-2] Cho khối lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
với
,
AB a A B
tạo với mặt phẳng
ABC
một góc
.
Biết thể tích lăng trụ
.
ABC A B C
là
3
3
.
2
a
Tính
.
A.
45 .
B.
70 .
C.
60 .
D.
30 .
Câu 25. [2D1-3] Một kim tự tháp Ai Cập có hình dạng là một khối chóp tứ giác đều có độ dài cạnh bên
là một số thực dương không đổi. Gọi
là góc giữa cạnh bên của kim tự tháp với mặt đáy. Khi
thể tích của kim tự tháp lớn nhất, tính
sin
.
A.
3
sin
2
. B.
3
sin
3
. C.
6
sin
3
. D.
5
sin
3
.
Câu 26. [2D2-2] Tìm
n
biết
2 3
2 2
2 2 2
1 1 1 1 465
...
log log log log log
n
x x x x x
luôn đúng với mọi
0,
x
1
x
.
A.
n
. B.
30
n
. C.
31
n
. D.
31
n
.
Câu 27. [2D2-2] Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
2
a
, các mặt bên tạo với đáy
một góc
60
. Tính diện tích
S
của mặt cầu ngoại tiếp hình chóp.
A.
2
25
3
a
S
. B.
2
12
a
S . C.
2
32
3
a
S
. D.
2
8
3
a
S
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/29
Câu 28. [2D1-4] Cho khối chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, cạnh bên hợp với đáy một
góc
60
. Gọi
M
là điểm đối xứng với
C
qua
D
,
N
là trung điểm
SC
. Mặt phẳng
BMN
chia khối chóp
.
S ABCD
thành hai khối đa diện. Tính thể tích
V
của khối đa diện chứa đỉnh
C
.
A.
3
7 6
36
a
V . B.
3
7 6
72
a
V . C.
3
5 6
72
a
V . D.
3
5 6
36
a
V .
Câu 29. [2D1-3] Cho các số thực dương
x
,
y
thỏa mãn
5
2
4
x y
. Tìm giá trị nhỏ nhất
min
P
của biểu
thức
2 1
4
P
x y
.
A.
min
34
5
P . B.
min
65
4
P . C.
min
P
không tồn tại. D.
min
5
P
.
Câu 30. [2D2-1] Số hình đa diện lồi trong các hình dưới đây là:
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 31. [2D1-1] Trong các hàm số sau, hàm số nào không có giá trị nhỏ nhất?
A.
2
1
x
y
x
. B.
4
2
y x x
. C.
2
2 3
y x x
. D.
2 1
y x
.
Câu 32. [2D1-1] Tìm số giao điểm của hai đồ thị hàm số
3
y x
và
1
y x
.
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 33. [2D1-4] Tìm tất cả các giá trị thực của tham số
m
để hàm số sin
y x mx
nghịch biến trên
.
A.
1
m
B.
1
m
. C.
1
m
. D.
1
m
.
Câu 34. [2H1-1]Người ta nối trung điểm các cạnh của một hình hộp chữ nhật
rồi cắt bỏ các hình chóp tam giác ở các góc của hình hộp như hình vẽ
sau. Hình còn lại là một đa diện có số đỉnh và số cạnh là:
A.
12
đỉnh,
24
cạnh. B.
10
đỉnh,
24
cạnh.
C.
12
đỉnh,
20
cạnh. D.
10
đỉnh,
48
cạnh.
Câu 35. [ 2D2-2] Tìm số nguyên
n
lớn nhất thỏa mãn
360 480
3
n .
A.
3
n
. B.
4
n
. C.
2
n
. D.
5
n
.
Câu 36. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
để hàm số
4 2 2
2 2 1 5
y x x m x
đồng biến trên khoảng
1;
.
A.
2 2
2 2
m . B.
2 2
2 2
m .
C.
2
2
m hoặc
2
2
m . D.
2
2
m hoặc
2
2
m .
Câu 37. [2D1-2] Tìm số tiệm cận đứng và ngang của đồ thị hàm số
3
1
3 2
x
y
x x
.
A.
0
. B.
3
. C.
2
. D.
1
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/29
Câu 38. [2D1-3] Cáp tròn truyền nhiệt dưới nước bao gồm một lõi
đồng và bao quanh lõi đồng là một lõi cách nhiệt như hình
vẽ. Nếu
r
x
h
là tỉ lệ bán kính độ dày thì bằng đo đạc thực
nghiệm người ta thấy rằng vận tốc truyền tải tín hiệu được
cho bởi phương trình
2
1
ln
v x
x
với
0 1
x
. Nếu bán kính
lõi cách nhiệt là
2
cm thì vật liệu cách nhiệt có bề dày
h
(cm) bằng bao nhiêu để tốc độ truyền tải tín hiệu lớn nhất?
A.
2
h e
(cm). B.
2
h e
(cm). C.
2
h
e
(cm). D.
2
h
e
(cm).
Câu 39. [2H1-2] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình vuông. Gọi
M
,
N
,
P
,
Q
lần lượt là
trung điểm các cạnh
SB
,
BC
,
CD
,
DA
. Biết thể tích khối chóp
.
S ABCD
là
0
V
. Tính thể tích
khối chóp .
M QPCN
theo
0
V
.
A.
0
3
4
V V
. B.
0
1
16
V V
. C.
0
3
8
V V
. D.
0
3
16
V V
.
Câu 40. [2H1-2] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình thang cân với đáy
AD
và
BC
. Biết
2
AD a
,
AB BC CD a
. Hình chiếu vuông góc của
S
trên mặt phẳng
ABCD
là điểm
H
thuộc đoạn
AD
thỏa mãn
3
HD HA
,
SD
tạo với đáy một góc
45
. Tính thể tích
V
của
khối chóp
.
S ABCD
.
A.
3
3
8
a
V . B.
3
3 3
8
a
V . C.
3
3 3
4
a
V . D.
3
9 3
8
a
V .
Câu 41. [2D1-3] Cho hàm số
3 2
y f x ax bx cx d
với
0
a
. Biết đồ thị hàm số có hai điểm
cực trị là
1; 1 , 1;3
A B . Tính
4
f .
A.
4 53
f
. B.
4 17
f
. C.
4 17
f
. D.
4 53
f
.
Câu 42. [2H1-1] Số mặt phẳng đối xứng của hình lăng trụ đứng có đáy là hình vuông là:
A.
4
. B.
5
. C.
1
. D.
3
.
Câu 43. [2D1-3] Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3
2 2
2 2 4 2 0
m x x x x
có nghiệm thỏa mãn
3
x
.
A.
4
. B.
6
.
C. Không có giá trị nào của
m
. D. Vô số giá trị của
m
.
Câu 44. [2H1-1] Cho tứ diện
OMNP
có
OM
,
ON
,
OP
đôi một vuông góc. Tính thể tích
V
của khối
tứ diện
OMNP
.
A.
1
. .
6
V OM ON OP
. B.
1
. .
2
V OM ON OP
.
C.
1
. .
3
V OM ON OP
. D.
. .
V OM ON OP
.
Câu 45. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để hàm số
4 2 2
1 1 1
y m x m x
có
đúng một cực trị.
A.
1
m
;
1
m
. B.
1
m
. C.
1
m
. D.
1
m
;
1
m
.
Cách nhiệt
Lõi đồng
r
h
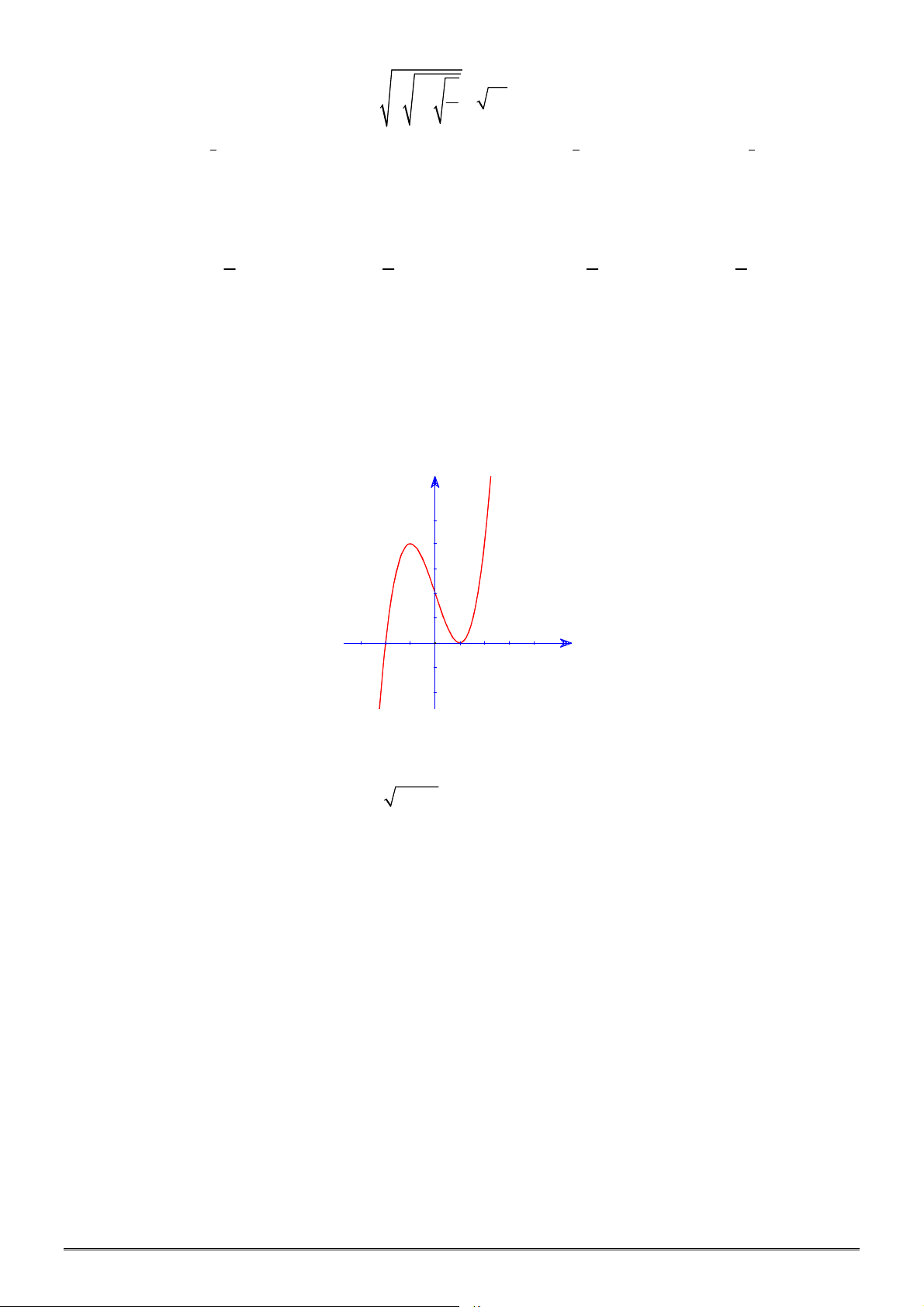
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/29
Câu 46. [2D2-2] Rút gọn biểu thức
2 7
24
3
4
1
:
P a a a
a
, với
0
a
.
A.
2
3
P a
. B.
P a
. C.
1
2
P a
. D.
1
3
P a
.
Câu 47. [2D2-2] Tìm tất các giá trị thực của
x
để đồ thị hàm số
0,5
log
y x
nằm trên đường thẳng
2.
y
A.
1
0
4
x
. B.
1
4
x
. C.
1
0
4
x
. D.
1
4
x
.
Câu 48. [2D2-3] Theo số liệu từ Tổng cục thống kê, dân số Việt Nam năm
2015
là
91,7
triệu người.
Giả sử tỉ lệ tăng dân số hàng năm của Việt Nam trong giai đoạn
2015 2050
ở mức không đổi
là
1,1%
. Hỏi đến năm nào dân số Việt Nam sẽ đạt mức
120,5
triệu người?
A.
2039
. B.
2040
. C.
2042
. D.
2041
.
Câu 49. [2D1-2] Đường cong ở hình vẽ là đồ thị của một trong các hàm số dưới đây:
Hàm số đó là hàm số nào?
x
y
1
O
-2
A.
2
1 2
y x x
. B.
2
1 2
y x x
. C.
2
1 2
y x x . D.
2
1 2
y x x .
Câu 50. [2D1-2] Đồ thị của hàm số nào trong các hàm số dưới đây có tâm đối xứng?
A.
2
2 6
y x x
. B.
2 1
y x
. C.
3 2
2 3
y x x x
. D.
4 2
2 5
y x x
.
----------HẾT----------
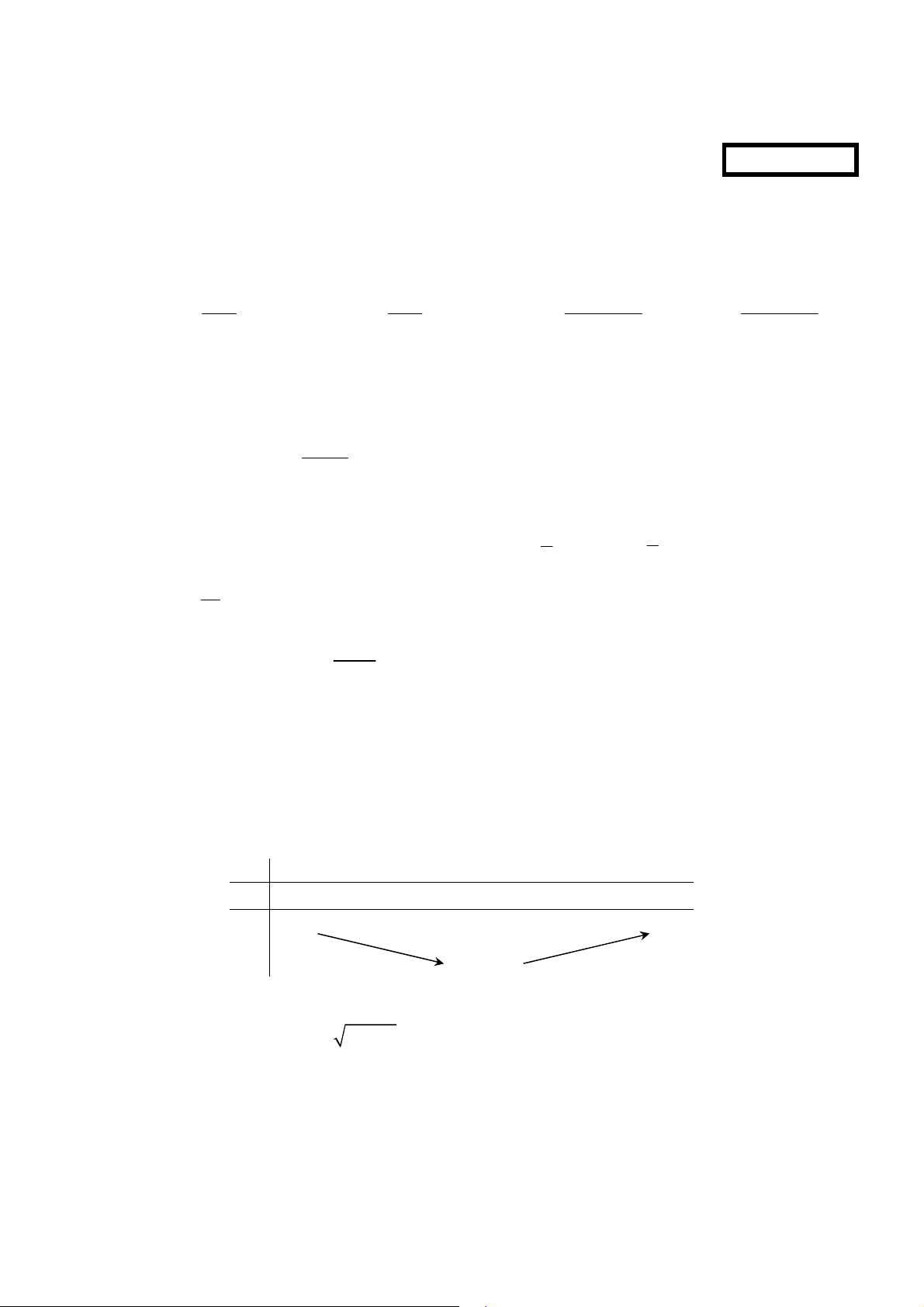
Trang 1/23 - Mã đề thi 132
S
Ở
GD&ĐT HÀ N
Ộ
I
TRƯỜNG THPT LÝ THÁNH TÔNG
(Đề gồm 06 trang)
K
Ỳ
THI H
Ọ
C K
Ỳ
1 NĂM 2017
-
2018
Bài thi: TOÁN 12
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 001
Câu 1: [2D1-1] Cho hàm số
4 2
4 3
y x x
có đồ thị
.
C
Tìm số giao điểm của
C
và trục hoành.
A.
3.
B.
2.
C.
1.
D.
0.
Câu 2: [2D2-1] Tìm đạo hàm của hàm số
2
log 1
y x
.
A.
1
1
y
x
. B.
ln2
1
y
x
. C.
1
1 ln 2
y
x
. D.
1
2ln 1
y
x
.
Câu 3: [2D2-2] Tìm tập nghiệm
S
của bất phương trình
log 2 2 log 1
x x
.
A.
3;
. B.
1;3
. C.
3;
. D.
.
Câu 4: [2D1-1] Hàm số
2 3
1
x
y
x
có bao nhiêu điểm cực trị?
A.
3.
B.
0.
C.
2.
D.
1.
Câu 5: [2D1-2] Tìm giá trị nhỏ nhất
m
của hàm số
2
2
y x
x
trên đoạn
1
;2
2
.
A.
17
.
4
m B.
10.
m
C.
5.
m
D.
3.
m
Câu 6: [2D1-1] Cho hàm số
3 1
1
x
y
x
. Mệnh đề nào dưới đây là đúng?
A. Hàm số đồng biến trên các khoảng
; 1
và
1;
.
B. Hàm số luôn đồng biến trên
\ 1
.
C. Hàm số nghịch biến trên các khoảng
; 1
và
1;
.
D. Hàm số luôn nghịch biến trên
\ 1
.
Câu 7: [2D1-2] Bảng biến thiên dưới đây là của hàm số nào?
A.
4 2
3 1
y x x
. B.
4 2
3 1
y x x
. C.
4 2
3 1
y x x
. D.
4 2
3 1
y x x
.
Câu 8: [2D1-2] Cho hàm số
2
2 1
y x
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
1;1
. B. Hàm số đồng biến trên khoảng
0;
.
C. Hàm số đồng biến trên khoảng
;0
. D. Hàm số nghịch biến trên khoảng
0;
.
Câu 9: [2D2-2] Tìm tất cả các giá trị thực của tham số
m
để phương trình
4 2
2
x x m
có bốn
nghiệm thực phân biệt.
A.
0
m
. B.
0 1
m
. C.
0 1
m
. D.
1
m
.
x
0
y
–
0
y
1
6

Trang 2/23 - Mã đề thi 132
Câu 10: [2D1-3] Một vật chuyển động theo quy luật
3 2
1
6
3
s t t
với
t
(giây) là khoảng thời gian
tính từ khi vật bắt đầu chuyển động và
s
(mét) là quãng đường vật di chuyển được trong
khoảng thời gian đó. Hỏi trong khoảng thời gian
9
giây, kể từ khi bắt đầu chuyển động, vận tốc
lớn nhất của vật đạt được là bao nhiêu?
A.
144 (m/s)
. B.
36 (m/s)
. C.
243 (m/s)
. D.
27 (m/s)
.
Câu 11: [2D1-3] Đồ thị của hàm số
2
2
3 2
x
y
x x
có bao nhiêu tiệm cận?
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 12: [2D2-1] Tính giá trị của biểu thức
3 1 3 4
0
3 2
2 .2 5 .5
10 :10 0,25
K
là
A.
10
. B.
10
. C.
12
. D.
15
.
Câu 13: [2D2-2] Cho
3
7
1
log
a
P a
0, 1
( )
a a
. Mệnh đề nào dưới đây đúng?
A.
7
3
P
. B.
5
3
P
. C.
2
3
P
. D.
7
3
P
.
Câu 14: [2D1-2] Hàm số nào dưới đây nghịch biến trên khoảng
;
.
A.
3 2
3
y x x
. B.
4 2
4 2017
y x x .
C.
3 2
3 3 1
y x x x
. D.
5
1
x
y
x
.
Câu 15: [2D2-2] Cho
0 1
a
. Mệnh đề nào trong các mệnh đề sau là sai?
A.
log 0
a
x
khi
0 1
x
.
B.
log 0
a
x
khi
1
x
.
C. Nếu
1 2
x x
thì
1 2
log log
a a
x x
.
D. Đồ thị hàm số
log
a
y x
có tiệm cận đứng là trục tung.
Câu 16: [2H1-2] Cho
H
là khối chóp tứ giác đều có tất cả các cạnh bằng
a
. Thể tích của
H
bằng
A.
3
3
a
. B.
3
2
6
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Câu 17: [2D1-2] Cho hàm số
4
mx m
y
x m
với
m
là tham số. Gọi
S
là tập hợp tất cả các giá trị nguyên
của
m
để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của
S
.
A.
5
. B.
4
. C. Vô số. D.
3
.
Câu 18: [2D1-3] Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
3 2 3
3 4
y x mx m
có hai
điểm cực trị
A
và
B
sao cho tam giác
OAB
có diện tích bằng
4
với
O
là gốc tọa độ.
A.
4 4
1 1
;
2 2
m m
.B.
1, 1
m m
. C.
1
m
. D.
0
m
.
Câu 19: [2D1-2] Tìm giá trị lớn nhất của hàm số
3
3 1
y x x
trên khoảng
0;
?
A.
1
. B.
3
. C.
5
. D.
4
.
Câu 20: [2H1-1] Trong các mệnh đề sau mệnh đề nào sai?
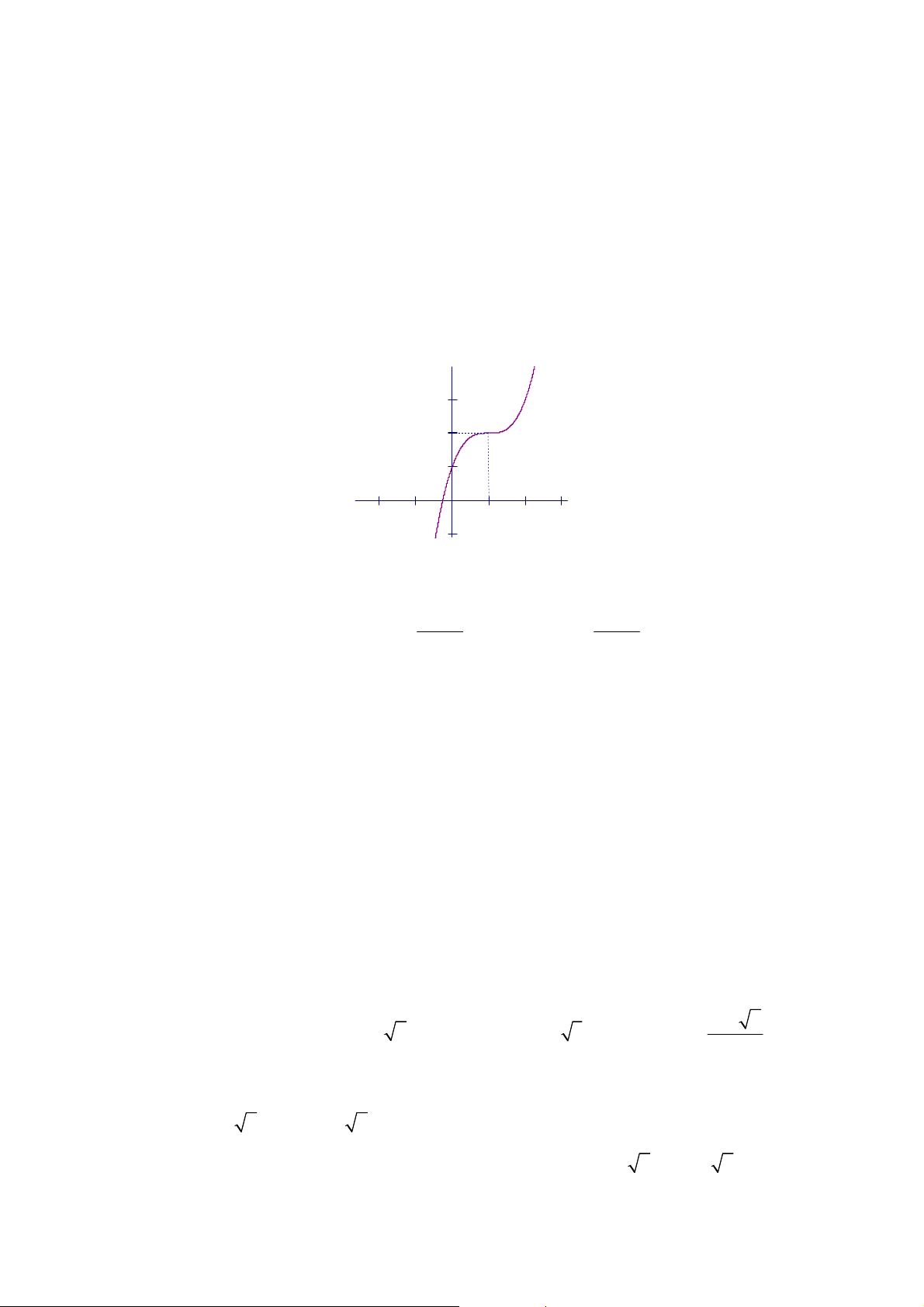
Trang 3/23 - Mã đề thi 132
A. Lắp ghép hai khối hộp sẽ được một khối đa diện lồi.
B. Khối hộp là khối đa diện lồi.
C. Khối tứ diện là khối đa diện lồi.
D. Khối lăng trụ tam giác là khối đa diện lồi.
Câu 21: [2D2-2] Tìm nghiệm của phương trình
2
log 5 4
x
.
A.
21
x
. B.
3
x
. C.
11
x
. D.
13
x
.
Câu 22: [2D2-3] Tìm tập nghiệm của phương trình sau
2
log 3log 2 4
x
x
.
A.
2;8
S . B.
4;3
S . C.
4;16
S . D.
S
.
Câu 23: [2D1-1] Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây.
2
O
1
1
A.
3 2
3 3 1
y x x x
. B.
3 2
3 1
y x x
. C.
3
2 1
y x x
. D.
3 2
3 1
y x x
.
Câu 24: [2D2-1] Cho
a
là số thực dương tùy ý khác
1
. Mệnh đề nào dưới đây đúng?
A.
2
log log 2
a
a . B.
2
2
1
log
log
a
a
. C.
2
1
log
log 2
a
a . D.
2
log log 2
a
a .
Câu 25: [2D2-2] Tìm tập xác định
D
của hàm số
3
2
2
y x x
.
A.
D
. B.
(0; )
D
. C.
( ; 1) (2; )
D
. D.
\{ 1;2}
D
.
Câu 26: [2H2-1] Cho hình nón có thể tích bằng
3
36
V a
và bán kính đáy bằng
3
a
. Tính độ dài
đường cao
h
của hình nón đã cho.
A.
4
a
. B.
2
a
. C.
5
a
. D.
12
a
.
Câu 27: [2D2-1] Tìm tất cả các giá trị thực của tham số
m
để phương trình 3
x
m
có nghiệm thực.
A.
1
m
. B.
0
m
. C.
0
m
. D.
0
m
.
Câu 28: [2H2-2] Cho hình lập phương
.
ABCD A B C D
có cạnh bằng
a
. Gọi
S
là diện tích xung
quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông
ABCD
và
A B C D
. Diện
tích
S
là:
A.
2
a
. B.
2
2
a
. C.
2
3
a
. D.
2
2
2
a
.
Câu 29: [2D2-1] Tìm tập xác định
D
của hàm số
2
3
log 4 3
y x x
A.
2 2;1 3;2 2
D
. B.
1;3
D .
C.
;1 3;D
. D.
;2 2 2 2;D
.
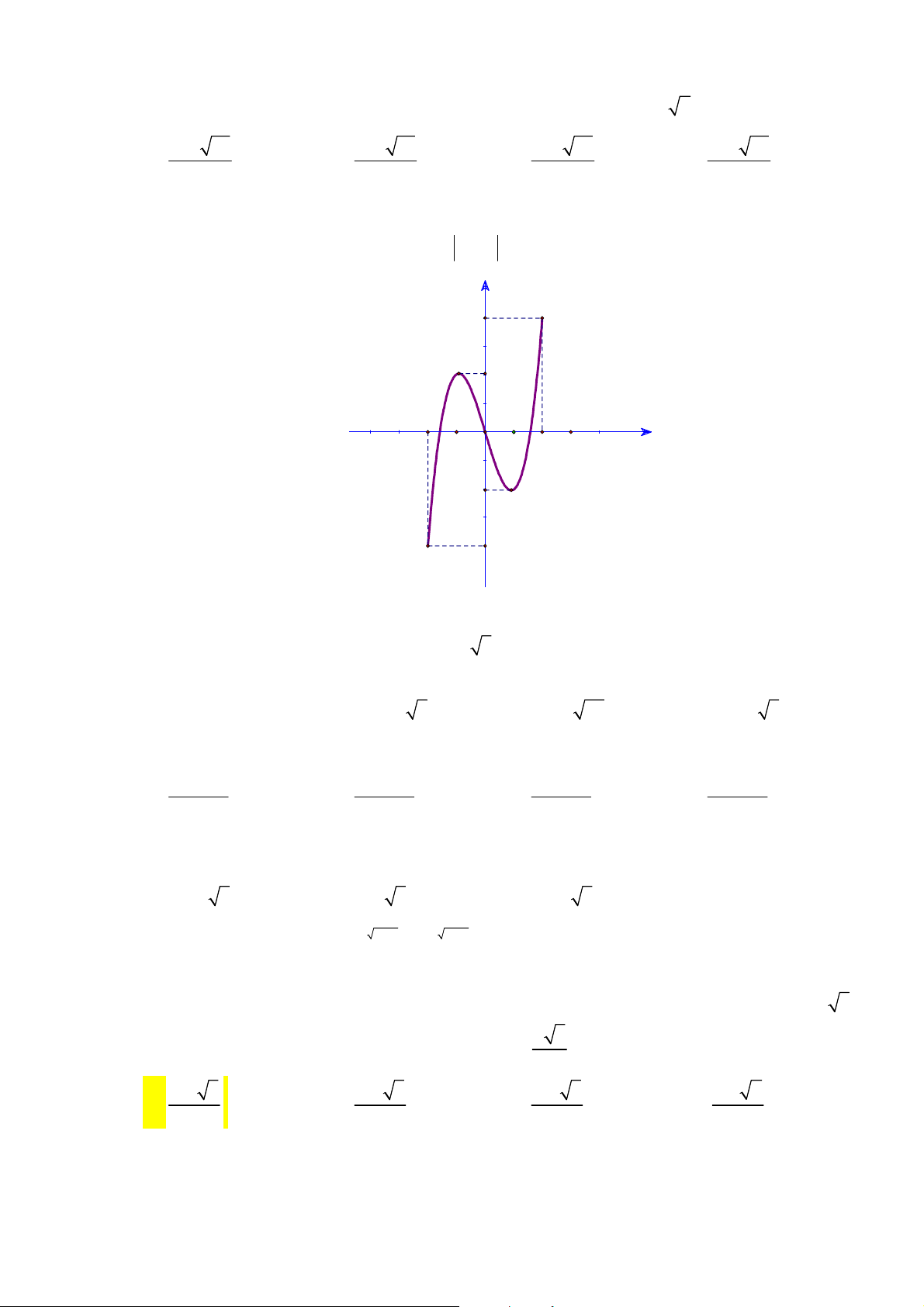
Trang 4/23 - Mã đề thi 132
Câu 30: [2H2-2] Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
và chiều cao bằng
2
a
, diện
tích xung quanh của hình nón đỉnh
S
và đáy là hình tròn nội tiếp
2;2
t
bằng
A.
2
17
4
a
. B.
2
15
4
a
. C.
2
17
6
a
. D.
2
17
8
a
.
Câu 31: [2D1-2] Cho hàm số
y f x
liên tục trên đoạn
2;2
và có đồ thị là đường cong như hình
vẽ bên. Tìm số nghiệm của phương trình
1
f x
trên đoạn
2;2
.
x
y
-2
2
-4
4
2-1-2
O
1
A.
4
. B.
6
. C.
3
. D.
5
.
Câu 32: [2H2-1] Cho hình nón có bán kính đáy
3
r và độ dài đường sinh
4
l
. Tính diện tích xung
quanh
xq
S
của hình nón đã cho.
A.
12
xq
S
. B.
4 3
xq
S
. C.
39
xq
S
. D.
8 3
xq
S
.
Câu 33: [2D2-2] Cho log3
a
, log5
b
. Tính
6
log 1125
.
A.
3 2
1
a b
a b
. B.
2 3
1
a b
a b
. C.
3 2
1
a b
a b
. D.
3 2
1
a b
a b
.
Câu 34: [2H1-1] Cho hình bát diện đều cạnh
a
. Gọi
S
là tổng diện tích tất cả các mặt của hình bát diện
đều đó. Mệnh đề nào dưới đây đúng?
A.
2
4 3
S a
. B.
2
3
S a
. C.
2
2 3
S a
. D.
2
8
S a
.
Câu 35: [2D2-3] Hỏi phương trình
2 5 1 2 5 6
2 2 2 32 0
x x x x
có bao nhiêu nghiệm phân biệt?
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 36: [2H1-2] Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật,
AB a
,
2
AD a
,
3
SA a
,
SA ABCD
.
M
là điểm trên
SA
sao cho
3
3
a
AM . Tính thể tích của khối chóp
.
S BMC
.
A.
3
2 3
9
a
. B.
3
2 3
3
a
. C.
3
4 3
3
a
. D.
3
3 2
9
a
.
Câu 37: [2D2-2] Với mọi
a
,
b
,
x
là các số thực dương thỏa mãn
2 2 2
log 5log 3log
x a b
. Mệnh đề
nào dưới đây đúng?
A.
3 5
x a b
B.
5 3
x a b
C.
5 3
x a b
D.
5 3
x a b

Trang 5/23 - Mã đề thi 132
Câu 38: [2H2-2] Cho khối chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
2
a
. Tính
thể tích
V
của khối chóp
.
S ABC
.
A.
3
13
12
a
V . B.
3
11
12
a
V . C.
3
11
6
a
V . D.
3
11
4
a
V .
Câu 39: [2H2-1] Gọi
l
,
h
,
R
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón.
Đẳng thức nào sau đây luôn đúng?
A.
2 2 2
l h R
. B.
2 2 2
1 1 1
l h R
. C.
2 2 2
R h l
. D.
2
l hR
.
Câu 40: [2D2-3] Hàm số
ln
f x x
có đạo hàm cấp
n
là
A.
n
n
n
f x
x
. B.
1
1 !
1
n
n
n
n
f x
x
.
C.
1
n
n
f x
x
. D.
!
n
n
n
f x
x
.
Câu 41: [2H2-1] Gọi
l
,
h
,
R
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối nón
N
. Thể tích
V
của khối nón
N
bằng
A.
2
1
3
V R h
. B.
2
V R h
. C.
2
V R l
. D.
2
1
3
V R l
.
Câu 42: [2D2-2] Tìm giá trị thực của tham số
m
để phương trình
1
9 2.3 0
x x
m
có hai nghiệm thực
1
x
,
2
x
thỏa mãn
1 2
1
x x
.
A.
6
m
. B.
3
m
. C.
3
m
. D.
1
m
.
Câu 43: [2H1-2] Cho khối chóp
.
S ABCD
có đáy là nửa lục giác đều nội tiếp trong nửa đường tròn
đường kính
2
AB R
. Biết
I
là trung điểm
AB
,
SI
vuông góc với đáy và
SBC
và hợp với
đáy
ABCD
một góc
45
. Tính thể tích khối chóp
.
S ABCD
A.
3
3
4
R
. B.
3
3
8
R
. C.
3
3
6
R
. D.
3
3
2
R
.
Câu 44: [2D1-2] Tìm giá trị thực của tham số
m
để đường thẳng
: 2 1 3
d y m x m
vuông góc
với đường thẳng đi qua hai điểm cực trị của hàm số
3 2
3 1
y x x
.
A.
3
2
m
. B.
3
4
m
. C.
1
2
m
. D.
1
4
m
.
Câu 45: [2D2-3] Hỏi có bao nhiêu giá trị
m
nguyên trong đoạn
2017;2017
để phương trình
3 3 3
log log 2log 1
m x x
luôn có hai nghiệm phân biệt?
A.
4015
. B.
2010
. C.
2018
. D.
2013
.
Câu 46: [2D1-3] Biết hàm số
2 2
4 2 3 2
y x x x x
đạt giá trị lớn nhất tại hai điểm
1
x
,
2
x
. Giá trị
1 2
.
x x
bằng
A.
2
. B.
1
. C.
0
. D.
1
.
Câu 47: [2D2-2] Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
2
ln 2 1
y x x m
xác
định với
x
là
A.
0
. B.
0;3
. C.
; 1 0;
. D.
0;
.

Trang 6/23 - Mã đề thi 132
Câu 48: [2D2-3] Anh Nam gửi 100 triệu đồng vào ngân hàng Vietcombank. Lãi suất hàng năm không
thay đổi là
7,5% /
năm. Nếu anh Nam hàng năm không rút lãi thì sau 5 năm số tiền anh Nam
nhận được cả vốn lẫn tiền lãi (kết quả làm tròn đến hàng ngàn) là
A.
143.563.000
đồng. B.
2.373.047.000
đồng.
C.
137.500.000
đồng. D.
133.547.000
đồng.
Câu 49: [2H1-4] Cho một tấm bìa hình vuông cạnh
5
dm. Để làm một mô hình kim tự tháp Ai Cập,
người ta cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy chính là cạnh của hình vuông rồi gấp
lên, ghép lại thành một hình chóp tứ giác đều. Để mô hình có thể tích lớn nhất thì cạnh đáy của
mô hình là
A.
3 2
2
dm. B.
5
2
dm. C.
5 2
2
dm. D.
2 2
dm.
Câu 50: [2H2-3] Cho tam giác
ABC
vuông cân tại
A
, có
12
AB AC
. Lấy một điểm
M
thuộc cạnh
huyền
BC
và gọi
H
là hình chiếu của
M
lên cạnh góc vuông
AB
. Quay tam giác
AMH
quanh trục là đường thẳng
AB
tạo thành mặt nón tròn xoay
N
, hỏi thể tích
V
của khối nón
tròn xoay
H
lớn nhất bằng bao nhiêu?
A.
256
3
V
. B.
128
3
V
. C.
256
V
. D.
72
V
.
----------HẾT----------
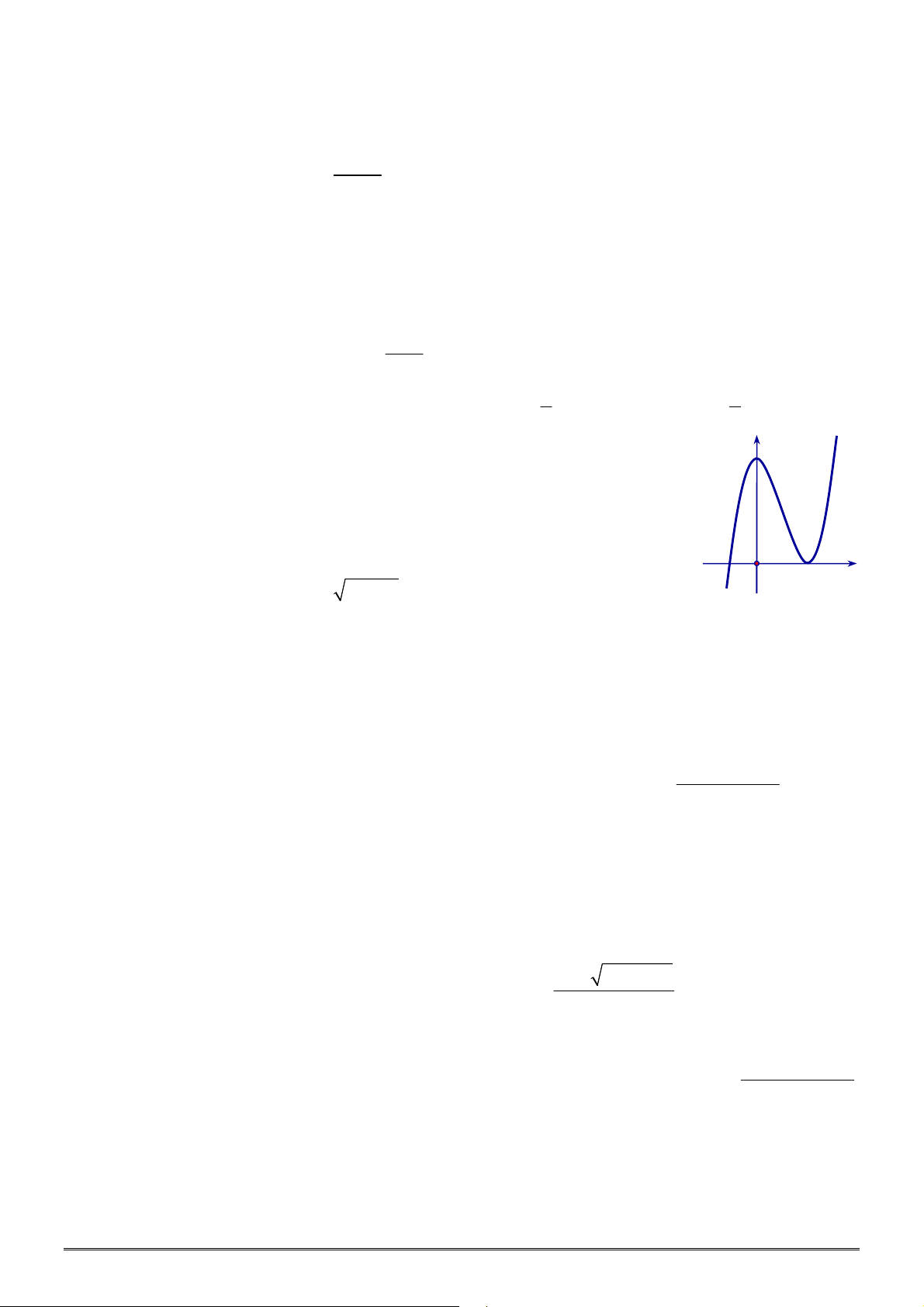
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/26
SỞ GIÁO DỤC ĐÀO TẠO NAM ĐỊNH
ĐỀ CHÍNH THỨC
(Mã đề 102)
ĐỀ THI HỌC KÌ I, NĂM HỌC 2017 – 2018
Môn Toán – Khối 12
Thời gian 90 phút (không kể thời gian phát đề)
Câu 1. [2D1-2] Cho hàm số
3 1
2
x
y
x
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số luôn nghịch biến trên
.
B. Hàm số luôn nghịch biến trên từng khoảng xác định.
C. Hàm số đồng biến trên các khoảng
;2
và
2;
.
D. Hàm số nghịch biến trên các khoảng
; 2
và
2;
.
Câu 2. [2D1-2] Hàm số
3
ln 2
2
y x
x
đồng biến trên khoảng nào?
A.
;1 .
B.
1; .
C.
1
;1 .
2
D.
1
; .
2
Câu 3. [2D1-1] Cho hàm số
y f x
có đồ thị như hình vẽ. Trên
khoảng
1;3
đồ thị hàm số
y f x
có mấy điểm cực trị?
A.
2.
B.
1.
C.
0.
D.
3.
Câu 4. [2D1-2] Cho hàm số
2
3
y x x
. Khẳng định nào sau đây là đúng?
A. Hàm số có hai điểm cực trị. B. Hàm số đạt cực tiểu tại
0.
x
C. Hàm số đạt cực đại tại
3.
x
D. Hàm số không có cực trị.
Câu 5. [2D1-3] Tìm tất cả giá trị của tham số
m
để đồ thị hàm số
4 2
2 2 3
y x mx m
có ba điểm
cực trị là ba đỉnh của tam giác vuông.
A.
1.
m
B.
0.
m
C.
2.
m
D.
1.
m
Câu 6. [2D1-1] Tìm phương trình đường tiệm cận đứng của đồ thị hàm số
2017 2018
1
x
y
x
.
A.
2017
x
. B.
1
x
. C.
2017
y
. D.
1
y
.
Câu 7. [2D1-2] Cho hàm số
y f x
có
lim 1
x
f x
và
lim 1
x
f x
. Tìm phương trình đường
tiệm cận ngang của đồ thị hàm số
2 2017
y f x
.
A.
2017
y
B.
1
y
C.
2017
y
. D.
2019
y
.
Câu 8. [2D1-2] Tìm số đường tiệm cận của đồ thị hàm số
2
2
2 6
1
x x x
y
x
.
A.
1
. B.
2
. C.
0
. D.
4
.
Câu 9. [2D1-3] Hỏi có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
2
2
3 2
5
x x
y
x mx m
không có đường tiệm cận đứng?
A.
9
. B.
10
. C.
11
. D.
8
.
Câu 10. [2D1-2] Phương trình tiếp tuyến của đồ thị hàm số
3 2
3 1
y x x
tại điểm
3;1
A là
A.
9 26
y x
. B.
9 26
y x
. C.
9 3
y x
. D.
9 2
y x
.
O
x
y
1
2
4
7

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/26
Câu 11. [1D5-2] Với
0;
2
x
, hàm số
2 sin 2 cos
y x x
có đạo hàm là
A.
1 1
sin cos
y
x x
. B.
1 1
sin cos
y
x x
.
C.
cos sin
sin cos
x x
y
x x
. D.
cos sin
sin cos
x x
y
x x
.
Câu 12. [2D2-2] Cho hàm số
2
2017 3
x x
y e e
. Mệnh đề nào dưới đây đúng?
A.
3 2 2017
y y y
B.
3 2 3
y y y
.
C.
3 2 0
y y y
. D.
3 2 2
y y y
.
Câu 13. [2D1-2] Đồ thị hình bên là đồ thị của một trong
4
hàm số dưới đây. Hỏi đó là hàm số nào?
A.
3 2
3 3 1
y x x x
.
B.
3
1
3 1
3
y x x
.
C.
3 2
3 3 1
y x x x
.
D.
3
3 1
y x x
.
Câu 14. [2D1-4] Cho hàm số
1
1
x
y
x
có đồ thị
C
. Gọi
A
,
B
0
A B
x x
là hai điểm trên
C
có
tiếp tuyến tại
A
,
B
song song nhau và
2 5
AB . Tính
A B
x x
.
A.
2
A B
x x
. B.
4
A B
x x
. C.
2 2
A B
x x D.
2
A B
x x
Câu 15. [2D2-2] Giá trị nhỏ nhất của hàm số
ln
x
y
x
trên đoạn
1;
e
là
A.
0.
B.
1.
C.
1
.
e
D.
.
e
Câu 16. [2D1-3] Trong các hình chữ nhật có chu vi bằng
16
, hình chữ nhật có diện tích lớn nhất bằng
A.
64
. B.
4
. C.
16
. D.
8
.
Câu 17. [2D1-4] Cho hàm số
1
1
x
y
x
có đồ thị
C
. Gọi
;
M M
M x y
là một điểm trên
C
sao cho
tổng khoảng cách từ điểm
M
đến hai trục tọa độ là nhỏ nhất. Tổng
M M
x y
bằng
A.
2 2 1
. B.
1
. C.
2 2
. D.
2 2 2
.
Câu 18. [2D1-1] Tìm số giao điểm của đồ thị
3 2
: 3 2 2017
C y x x x và đường thẳng
2017
y
.
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 19. [2D1-3] Cho hàm số
3 2
2 8
y mx x x m
có đồ thị
m
C
. Tìm tất cả giá trị của tham số
m
để đồ thị
m
C
cắt trục hoành tại ba điểm phân biệt.
A.
1 1
;
6 2
m
. B.
1 1
;
6 2
m
. C.
1 1
; \ 0
6 2
m
. D.
1
; \ 0
2
m
.
Câu 20. [2D1-4] Tìm tất cả giá trị của tham số
m
để đồ thị hàm số
4 2
1 2 2 3 6 5
y m x m x m
cắt trục hoành tại bốn điểm phân biệt có hoành độ
1
x
,
2
x
,
3
x
,
4
x
thỏa
1 2 3 4
1
x x x x
.
A.
5
1;
6
m
. B.
3; 1
m
. C.
3;1
m . D.
4; 1
m
.
O
x
y
1
1
3
2
1
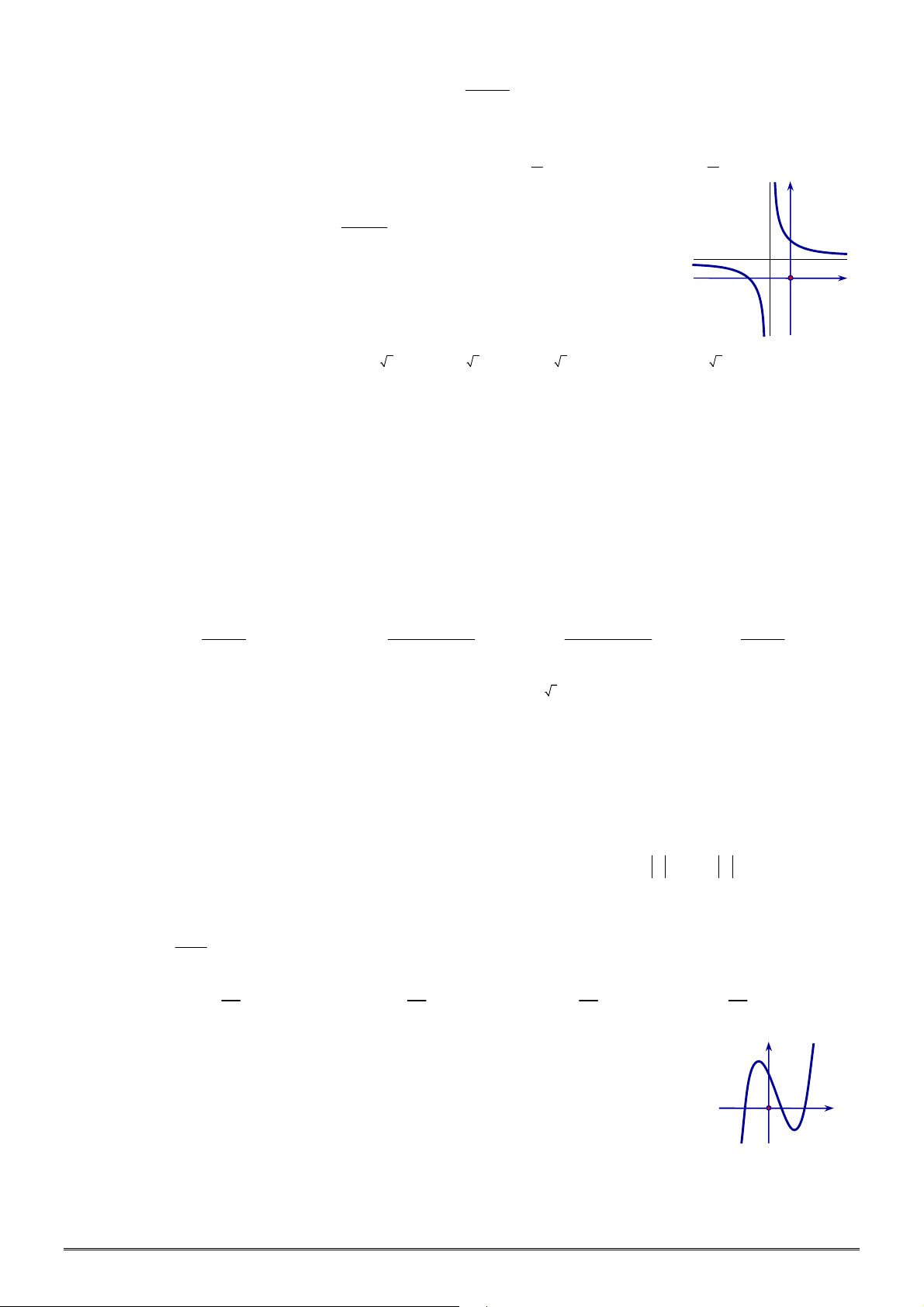
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/26
Câu 21. [1D4-2] Tiếp tuyến với đồ thị hàm số
2 1
1
x
y
x
tại điểm có hoành độ bằng
0
cắt hai trục tọa
độ lần lượt tại
A
và
.
B
Diện tích tam giác
OAB
bằng
A.
2
. B.
3
. C.
1
2
. D.
1
4
.
Câu 22. [2D1-2] Cho hàm số
1
ax b
y
x
có đồ thị như hình vẽ bên.
Tìm khẳng định đúng trong các khẳng định sau?
A.
0
a b
. B.
0
b a
.
C.
0
b a
. D.
0
a b
.
Câu 23. [2D2-3] Tìm tổng
3 20174
2 2 2 2
2 2 2 2
1 2 log 2 3 log 2 4 log 2 ... 2017 log 2
S .
A.
2 2
1008 .2017
S . B.
2 2
1007 .2017
S . C.
2 2
1009 .2017
S . D.
2 2
1010 .2017
S .
Câu 24. [2D2-2] Cho hàm số
ln
y x
. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng
0;
.
B. Hàm số có tập giá trị là
;
.
C. Đồ thị hàm số nhận trục
Oy
làm tiệm cận đứng.
D. Hàm số có tập giá trị là
0;
.
Câu 25. [2D2-1] Tính đạo hàm của hàm số
2
log 2 1
y x
.
A.
2
2 1
y
x
. B.
2
2 1 ln2
y
x
. C.
1
2 1 ln2
y
x
. D.
1
2 1
y
x
.
Câu 26. [2D2-1] Tìm tập xác định
D
của hàm số
1 3
2y x
.
A.
;D
. B.
;2
D . C.
;2
D . D.
2;D
.
Câu 27. [2D2-2] Cho
0, 1
a a
và
,
x y
là hai số thực khác
0
. Khẳng định nào sau đây là khẳng định
đúng?
A.
2
log 2log
a a
x x
. B.
log log log
a a a
xy x y
.
C.
log log log
a a a
x y x y
. D.
log log log
a a a
xy x y
.
Câu 28. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
3
2
7 14 2
3
mx
y mx x m
nghịch biến trên nửa khoảng
1;
.
A.
14
;
15
. B.
14
;
15
. C.
14
2;
15
. D.
14
;
15
.
Câu 29. [2D1-2] Cho đồ thị hàm số
3 2
y ax bx cx d
có đồ thị như
hình bên. Khẳng định nào sau đây là khẳng định đúng?
A.
, , 0; 0
a b c d
. B.
, , 0; 0
a b d c
.
C.
, , 0; 0
a c d b
. D.
, 0; , 0
a d b c
.
Câu 30. [2H1-2] Số mặt phẳng đối xứng của khối lăng trụ tam giác đều là
A.
3
. B.
4
. C.
6
. D.
9
.
O
x
y
O
x
y
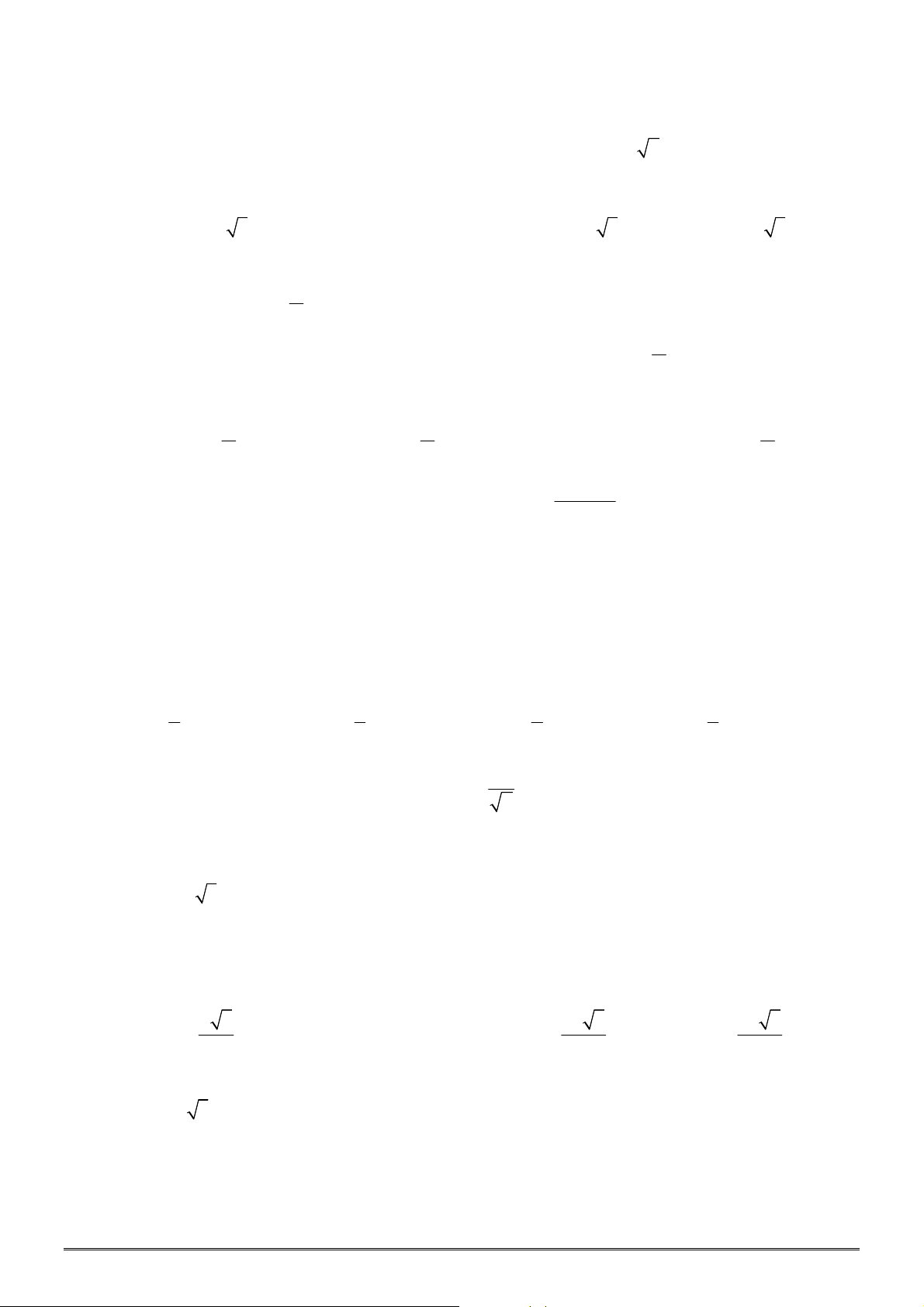
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/26
Câu 31. [2H1-1] Hỏi khối đa diện đều loại
4;3
có bao nhiêu mặt?
A.
4
. B.
20
. C.
6
. D.
12
.
Câu 32. [2H1-3] Cho hình lập phương
.
ABCD A B C D
có cạnh bằng
2 2
a
. Gọi
S
là tổng diện tích
tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương
.
ABCD A B C D
. Tính
.
S
A.
2
4 3
S a . B.
2
8
S a
. C.
2
16 3
S a . D.
2
8 3
S a .
Câu 33. [1D1-1] Khẳng định nào sau đây là khẳng định sai?
A.
cos 0 2
2
x x k
. B.
cos 1 2
x x k
.
C.
cos 1 2
x x k
. D. cos 0
2
x x k
.
Câu 34. [1D1-2] Giải phương trình
cos2 5sin 4 0
x x
.
A.
2
x k
. B.
2
x k
. C.
2
x k
. D.
2
2
x k
.
Câu 35. [1D1-3] Gọi
S
là tổng các nghiệm của phương trình
sin
0
cos 1
x
x
trên đoạn
0;2017
. Tính
S
.
A.
2035153
S
. B.
1001000
S
. C.
1017072
S
. D.
200200
S
.
Câu 36. [1D2-2] Có bao nhiêu số tự nhiên có
3
chữ số đôi một khác nhau?
A.
648
. B.
1000
. C.
729
. D.
720
.
Câu 37. [1D2-2] Một hộp có
5
bi đen,
4
bi trắng. Chọn ngẫu nhiên
2
bi. Xác suất
2
bi được chọn có
cùng màu là
A.
1
4
. B.
1
9
. C.
4
9
. D.
5
9
.
Câu 38. [1D2-2] Trong khai triển đa thức
6
2
P x x
x
(
0
x
), hệ số của
3
x
là
A.
60
. B.
80
. C.
160
. D.
240
.
Câu 39. [1H3-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
;
SA ABC
và
3
SA a
. Tính góc giữa đường thẳng
SB
với mặt phẳng
ABC
.
A.
75
. B.
60
. C.
45
. D.
30
.
Câu 40. [1H3-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
;
SA ABCD
và
2
SA a
. Tính khoảng cách
d
từ điểm
B
đến mặt phẳng
SCD
.
A.
5
5
a
d . B.
d a
. C.
4 5
5
a
d . D.
2 5
5
a
d .
Câu 41. [2H1-2] Cho hình hộp
.
ABCD A B C D
có đáy là hình thoi cạnh
a
,
60
ABC
và thể tích
bằng
3
3
a
. Tính chiều cao
h
của hình hộp đã cho.
A.
2
h a
. B.
h a
. C.
3
h a
. D.
4
h a
.
Câu 42. [2H1-2] Diện tích ba mặt của hình hộp chữ nhật lần lượt bằng
3
20 cm
,
3
28 cm
,
3
35 cm
. Thể
tích của hình hộp đó bằng
A.
3
165 cm
. B.
3
190 cm
. C.
3
140 cm
. D.
3
160 cm
.
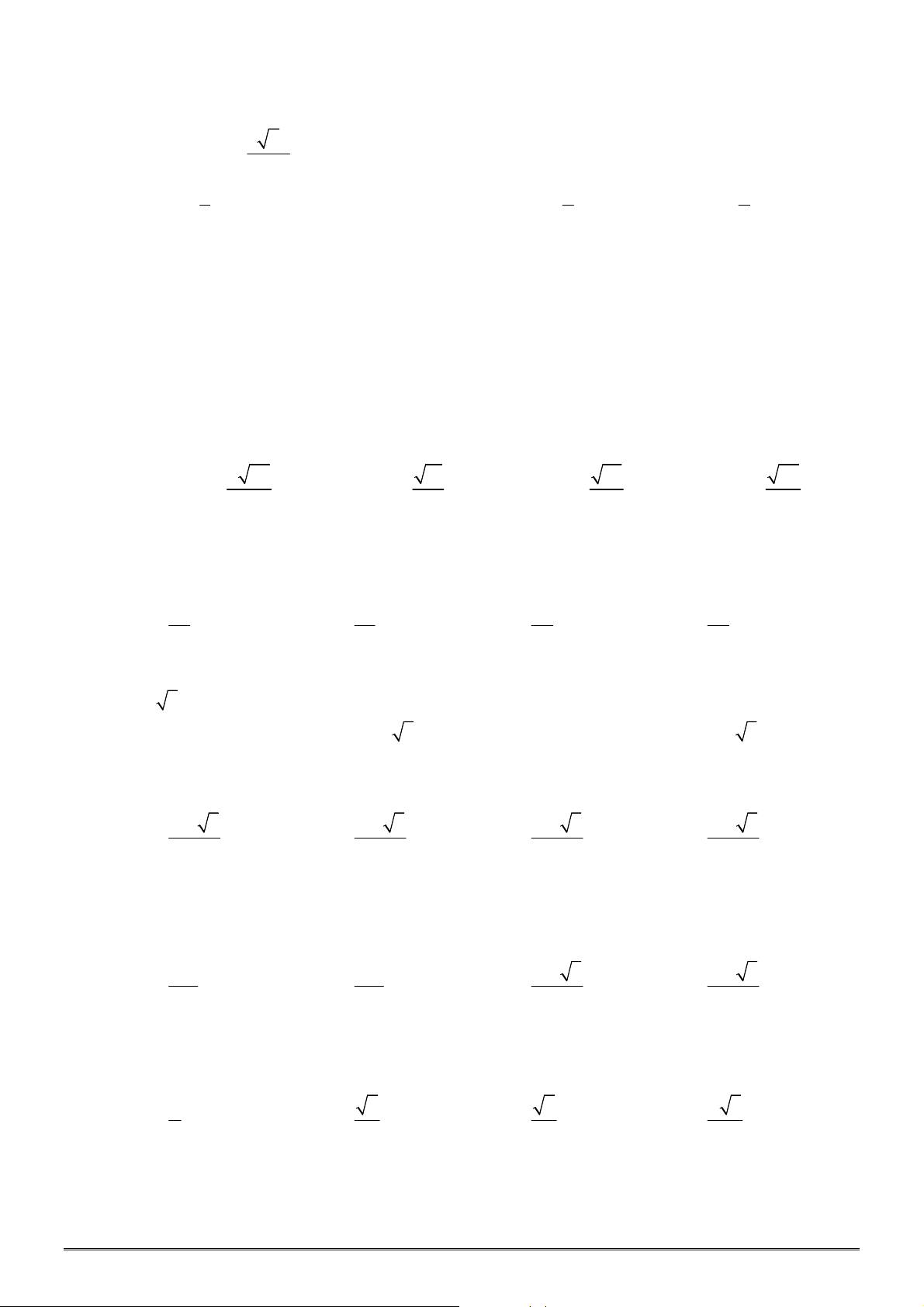
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/26
Câu 43. [2H1-3] Cho hình chóp tứ giác
.
S ABCD
có đáy là hình vuông, mặt bên
SAB
là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm B đến mặt phẳng
SCD
bằng
3 7
7
a
. Tính thể tích V của khối chóp
.
S ABCD
.
A.
3
1
3
V a
. B.
3
V a
. C.
3
2
3
V a
. D.
3
3
2
V a
.
Câu 44. [1H3-4] Cho hình chóp
.
S ABC
có
SA
vuông góc với đáy,
2
SA BC
và
120
BAC
. Hình
chiếu của
A
trên các đoạn
SB
,
SC
lần lượt là
M
,
N
. Tính góc giữa hai mặt phẳng
ABC
và
AMN
.
A.
45
. B.
. C.
15
. D.
.
Câu 45. [1H3-4] Cho hình lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
, tam giác
A BC
đều và nằm trong mặt phẳng vuông góc với mặt phẳng
ABC
,
M
là trung điểm cạnh
CC
.
Tính
cosin
góc
giữa hai đường thẳng
AA
và
BM
.
A.
2 22
cos
11
. B.
11
cos
11
. C.
33
cos
11
. D.
22
cos
11
.
Câu 46. [2H1-4] Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
. Biết
2
AB a
,
AC a
,
4
AA a
. Gọi
M
là điểm thuộc cạnh
AA
sao cho
3
MA MA
. Tính
khoảng cách giữa hai đường thẳng chéo nhau
BC
và
C M
.
A.
6
7
a
. B.
8
7
a
. C.
4
3
a
. D.
4
7
a
.
Câu 47. [2H2-2] Tính diện tích xung quanh của hình trụ biết hình trụ có bán kính đáy
a
và đường cao
3
a
.
A.
2
2
a
. B.
2
2 3
a . C.
2
a
. D.
2
3
a .
Câu 48. [2H2-2] Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài
2
a
. Thể tích
của khối nón là:
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3
2
a
. D.
3
3
12
a
.
Câu 49. [2H2-4] Cho tam giác
ABC
có
120
A
,
AB AC a
. Quay tam giác
ABC
(bao gồm cả
điểm trong tam giác) quanh đường thẳng
AB
ta được một khối tròn xoay. Thể tích khối tròn
xoay đó bằng:
A.
3
3
a
. B.
3
4
a
. C.
3
3
2
a
. D.
3
3
4
a
.
Câu 50. [2H2-4] Trong các khối trụ có cùng diện tích toàn phần bằng
, gọi
là khối trụ có thể tích
lớn nhất, chiều cao của
bằng:
A.
3
. B.
6
3
. C.
6
6
. D.
3
4
.
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/25
SỞ GD VÀ ĐT THÁI NGUYÊN
TRƯỜNG THPT CHUYÊN
(Đề thi gồm 06 trang)
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KỲ I
NĂM HỌC 2017-2018
MÔN: TOÁN 12
Thời gian làm bài 90 phút, không kể thời gian phát đề
Họ và tên thí sinh:...............................SBD:...........
Mã đề thi 295
Câu 1. [2D2-1] Cho
0 1
a
và
0
x
,
0
y
. Chọn mệnh đề đúng trong các mệnh đề sau:
A.
log log .log
a a a
x y x y
. B.
log log log
a a a
xy x y
.
C.
log log .log
a a a
xy x y
. D.
log log log
a a a
x y x y
.
Câu 2. [2D1-3] Có tất cả bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2017;2017
để
hàm số
3 2
6 1
y x x mx
đồng biến trên khoảng
0;
?
A.
2030
. B.
2005
. C.
2018
. D.
2006
.
Câu 3. [2H1-3] Cho lăng trụ đứng
.
ABC A B C
có
AB AC BB a
,
120
BAC
. Gọi
I
là trung
điểm của
CC
. Ta có cosin của góc giữa hai mặt phẳng
ABC
và
AB I
bằng
A.
3
2
. B.
30
10
. C.
3 5
12
. D.
2
2
.
Câu 4. [2H1-2] Gọi
1
V
là thể tích của khối lập phương
.
ABCD A B C D
,
2
V
là thể tích khối tứ diện
A ABD
. Hệ thức nào sau đây là đúng?
A.
1 2
4
V V
. B.
1 2
6
V V
. C.
1 2
2
V V
. D.
1 2
8
V V
.
Câu 5. [2D2-3] Cho
2 6 6
log 3 log 2 log 3 5
a b c
với
, ,
a b c
là các số tự nhiên. Khẳng định nào
đúng trong các khẳng định sau đây?
A.
a b
. B.
a b c
. C.
b c
. D.
b c
.
Gốc:
2 6 6
log 3 log 2 log 5 5
a b c
Câu 6. [2H1-2] Cho khối chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng
đáy và khoảng cách từ
A
đến mặt phẳng
SBC
bằng
2
2
a
. Gọi
M
là điểm thuộc cạnh
SD
sao cho
3
SM MD
. Mặt phẳng
ABM
cắt cạnh
SC
tại điểm
N
. Thể tích khối đa diện
MNABCD
bằng
A.
3
7
32
a
. B.
3
15
32
a
. C.
3
17
32
a
. D.
3
11
96
a
.
Câu 7. [2D1-3] Gọi
S
là tập hợp các giá trị thực của tham số
m
để hàm số
3 2 3
3 4
y x mx m
có hai
điểm cực trị
A
và
B
sao cho tam giác
OAB
có diện tích bằng
4
(
O
là gốc tọa độ). Ta có tổng
giá trị tất cả các phần tử của tập
S
bằng
A.
1
. B.
2
. C.
1
. D.
0
.
Câu 8. [2D2-1] Cho
2
log 5
a
. Tính
2
log 200
theo
a
.
A.
2 2
a
. B.
4 2
a
. C.
1 2
a
. D.
3 2
a
.
Câu 9. [2D1-2] Cho hàm số
4 2
1
2 2017
4
y x x . Khẳng định nào sau đây là đúng?
A. Hàm số có một điểm cực tiểu và không có điểm cực đại.
B. Hàm số có một điểm cực đại và không có điểm cực tiểu.
C. Hàm số có một điểm cực đại và hai điểm cực tiểu.
D. Hàm số có một điểm cực tiểu và hai điểm cực đại.
8

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/25
Câu 10. [2D2-2] Rút gọn biểu thức
2
4log 3
a
A a
với
0 1
a
ta được kết quả là
A.
9
. B.
4
3
. C.
8
3
. D.
6
.
Câu 11. [2H1-1] Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai khối chóp có hai đáy là hai đa giác bằng nhau thì thể tích bằng nhau.
B. Hai khối đa diện có thể tích bằng nhau thì bằng nhau.
C. Hai khối lăng trụ có chiều cao bằng nhau thì thể tích bằng nhau.
D. Hai khối đa diện bằng nhau có thể tích bằng nhau.
Câu 12. [2D1-2] Số điểm chung của đồ thị hàm số
3 2
2 12
y x x x
với trục
Ox
là
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 13. [2D1- 2] Cho hàm số
y f x
có đạo hàm liên tục trên
.
Đồ thị hàm số
y f x
như hình vẽ bên. Số điểm cực trị
của hàm số
2
y f x x
là
A.
2
. B.
1
.
C.
3
. D.
4
.
Câu 14. [2D1-2] Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 2
3 9 1
y x x x
trên đoạn
0;4
. Ta có
2
m M
bằng
A.
14
. B.
24
. C.
37
. D.
57
.
Câu 15. [2D1-1] Hàm số
3 2
1
2 3 1
3
y x x x
nghịch biến trên khoảng nào trong các khoảng sau đây?
A.
1;3
. B.
1;4
. C.
3; 1
. D.
1;3
.
Câu 16. [2H1-2] Cắt khối lăng trụ
.
MNP M N P
bởi các mặt phẳng
MN P
và
MNP
ta được những
khối đa diện nào?
A. Ba khối tứ diện. B. Hai khối tứ diện và hai khối chóp tứ giác.
C. Hai khối tứ diện và một khối chóp tứ giác. D. Một khối tứ diện và một khối chóp tứ giác.
Câu 17. [2H2-1] Thể tích của khối cầu bán kính
R
bằng
A.
3
1
3
R
. B.
3
2
3
R
. C.
3
R
. D.
3
4
3
R
.
Câu 18. [2D1-2] Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 2
1 2 3 1
y m x m x
có đúng một điểm cực tiểu và không có điểm cực đại?
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 19. [2D1-1] Trong số đồ thị của các hàm số
1
;
y
x
2
1;
y x
2
3 7
;
1
x x
y
x
2
1
x
y
x
có tất
cả bao nhiêu đồ thị có tiệm cận ngang?
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 20. [2H1-1] Cho khối chóp tứ giác đều có chiều cao bằng
6
và thể tích bằng
8
. Độ dài cạnh đáy bằng
A.
2
3
. B.
3
. C.
4.
D.
2
.
Câu 21. [2H1-2] Hình lăng trụ tam giác đều có tất cả bao nhiêu mặt phẳng đối xứng
A. 4 mặt phẳng. B. 1 mặt phẳng. C. 3 mặt phẳng. D. 2 mặt phẳng.
O
x
y
1
1
2
4
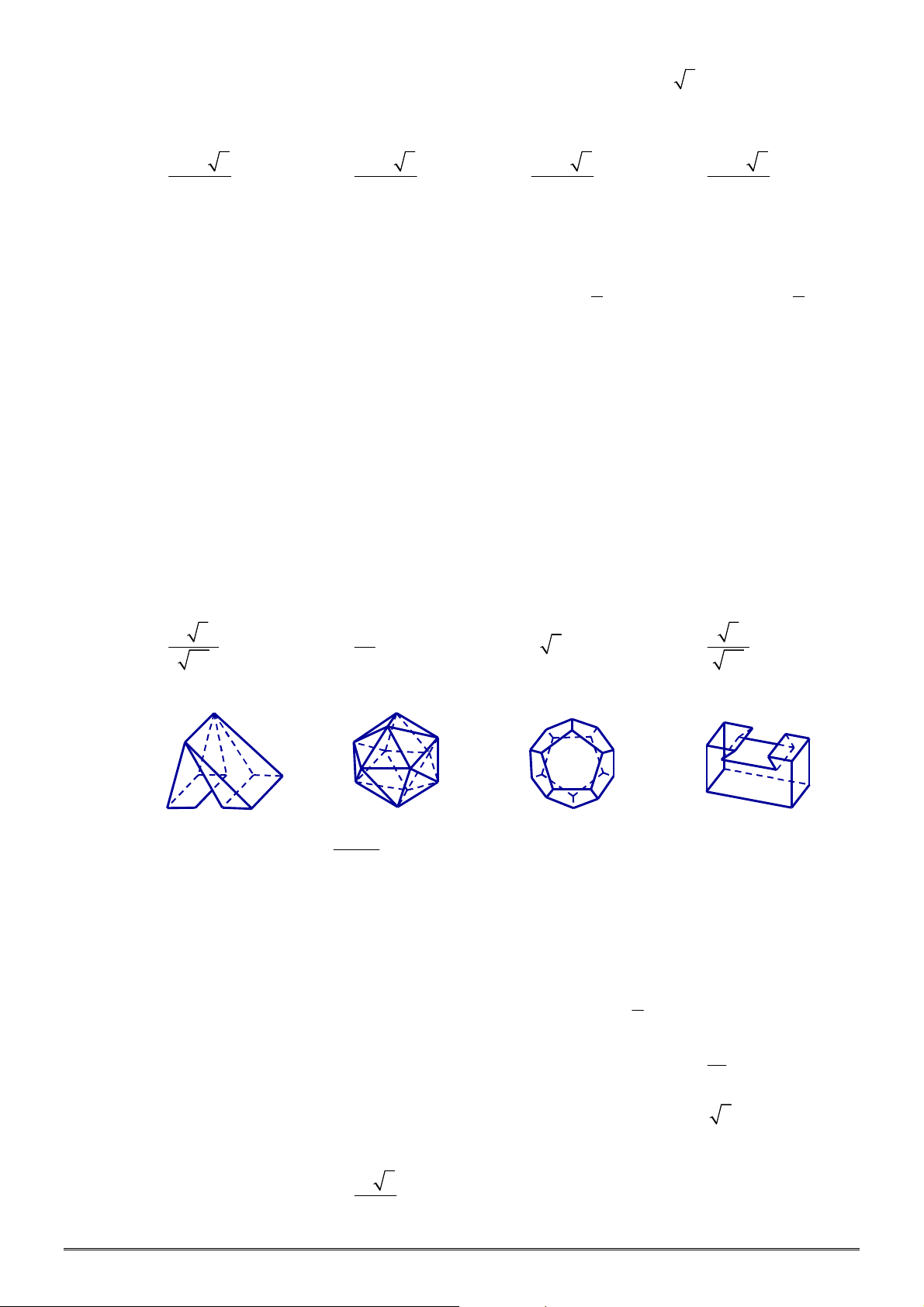
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/25
Câu 22. [2H2-3] Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật,
3
AB a
và
AD a
. Đường
thẳng
SA
vuông góc với mặt phẳng đáy và
SA a
. Thể tích khối cầu ngoại tiếp hình chóp
.
S BCD
bằng
A.
3
5 5
.
6
a
B.
3
5 5
.
24
a
C.
3
3 5
.
25
a
D.
3
3 5
.
8
a
Câu 23. [2D1-3] Gọi
0
m
là giá trị thực của tham số
m
để đồ thị hàm số
4 2
2 4
y x mx
có 3 điểm
cực trị nằm trên các trục tọa độ. Khẳng định nào sau đây là đúng?
A.
0
1;3
m B.
0
5; 3
m
. C.
0
3
;0
2
m
D.
0
3
3;
2
m
Câu 24. [2H2-1] Chọn mệnh đề đúng trong các mệnh đề sau?
A. Hình có đáy là hình bình hành thì có mặt cầu ngoại tiếp.
B. Hình chóp có đáy là hình thang vuông thì có mặt cầu ngoại tiếp.
C. Hình chóp có đáy là hình thang cân thì có mặt cầu ngoại tiếp.
D. Hình có đáy là hình tứ giác thì có mặt cầu ngoại tiếp.
Câu 25. [2D1-2] Hàm số
4 3
8 6
y x x
có tất cả bao nhiêu điểm cực trị?
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 26. [2D1-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
3
AB a
,
4
BC a
và
SA ABC
. Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
60
. Gọi
M
là trung
điểm của cạnh
AC
. Khoảng cách giữa hai đường thẳng
AB
và
SM
bằng
A.
10 3
79
a
. B.
5
2
a
. C.
5 3
a
. D.
5 3
79
a
.
Câu 27. [2H1-1] Vật thể nào trong các vật thể sau đây không phải là khối đa diện?
A. . B. . C. . D.
Câu 28. [2D1-1] Cho hàm số
2 3
4
x
y
x
. Hãy chọn khẳng định đúng trong các khẳng định sau đây:
A. Hàm số nghịch biến trên
.
B. Hàm số đồng biến trên mỗi khoảng xác định.
C. Hàm số đồng biến trên
.
D. Hàm số nghịch biến trên mỗi khoảng xác định.
Câu 29. [2D1-1] Giá trị lớn nhất của hàm số
3
3 5
y x x
trên đoạn
3
0;
2
.
A.
3
. B.
5
. C.
7
. D.
31
8
.
Câu 30. [2H1-2] Cho hình chóp
.
S ABC
có đáy là tam giác vuông tại
C
,
5
AB a
,
AC a
. Cạnh
bên
3
SA a
và vuông góc vói mặt phẳng
ABC
. Thể tích khối chóp
.
S ABC
bằng
A.
3
a
. B.
3
5
3
a
. C.
3
2
a
. D.
3
3
a
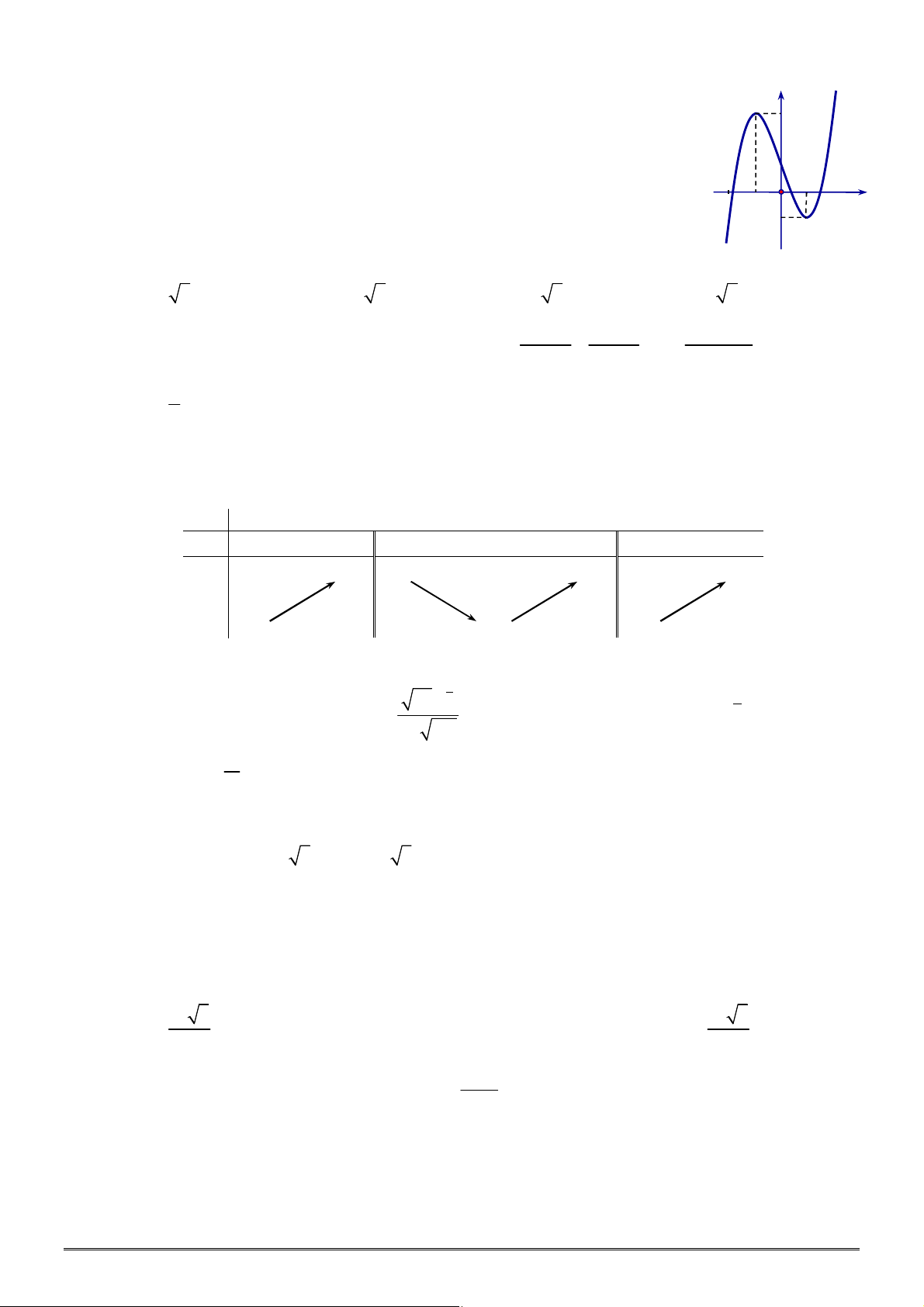
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/25
Câu 31. [2D1-2] Cho biết đồ thị sau là đồ thị của một trong bốn hàm số ở các phương án A, B, C, D. Đó
là đồ thị của hàm số nào?
A.
3 2
2 3 1
y x x
.
B.
3
3 1
y x x
.
C.
3
3 1
y x x
.
D.
3
2 6 1
y x x
.
Câu 32. [2D1-2] Khoảng cách giữa hai điểm cực trị của đồ thị hàm số
3 2
3 4
y x x
là
A.
5
. B.
4 5
. C.
2 5
. D.
3 5
.
Câu 33. [2D2-2] Cho
2017!
x
. Giá trị của biểu thức
2 2 2
2 3 2017
1 1 1
...
log log log
A
x x x
bằng
A.
1
2
. B.
2
. C.
4
. D.
1
.
Câu 34. [2D1-1] Cho hàm số
y f x
xác định và có đạo hàm trên
\ 1
. Hàm số có bảng biến
thiên như hình vẽ dưới đây. Hỏi đồ thị hàm số
y f x
có tất cả bao nhiêu đường tiệm cận?
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 35. [2D2-2] Rút gọn biểu thức
7
3 5
3
7
4 2
.
.
a a
A
a a
với
0
a
ta được kết quả
m
n
A a
, trong đó
m
,
*
n
và
m
n
là phân số tối giản. Khẳng định nào sau đây đúng?
A.
2 2
43
m n
. B.
2
2 15
m n
. C.
2 2
25
m n
. D.
2
3 2 2
m n
.
Câu 36. [2D2-2] Nếu
1
7 4 3 7 4 3
a
thì
A.
1
a
. B.
1
a
. C.
0
a
. D.
0
a
.
Câu 37. [2H1-2] Cho tứ diện
OABC
có
OA
,
OB
,
OC
đôi một vuông góc với nhau. Biết
OA a
,
2
OB a
và đường thẳng
AC
tạo với mặt phẳng
OBC
một góc
60
. Thể tích khối tứ diện
OABC
bằng
A.
3
3
9
a
. B.
3
3
a
. C.
3
a
. D.
3
3
3
a
.
Câu 38. [2D1-2] Tiếp tuyến của đồ thị hàm số
1
2
x
y
x
tại điểm
1; 2
M
có phương trình là
A.
3 5
y x
. B.
3 1
y x
. C.
3 1
y x
. D.
3 2
y x
.
Câu 39. [2H1-1] Tổng số đỉnh, số cạnh và số mặt của một hình bát diện đều là
A.
24
. B.
26
. C.
52
. D.
20
.
x
1
0
1
y
0
y
1
2
3
O
x
y
1
1
2
1
3
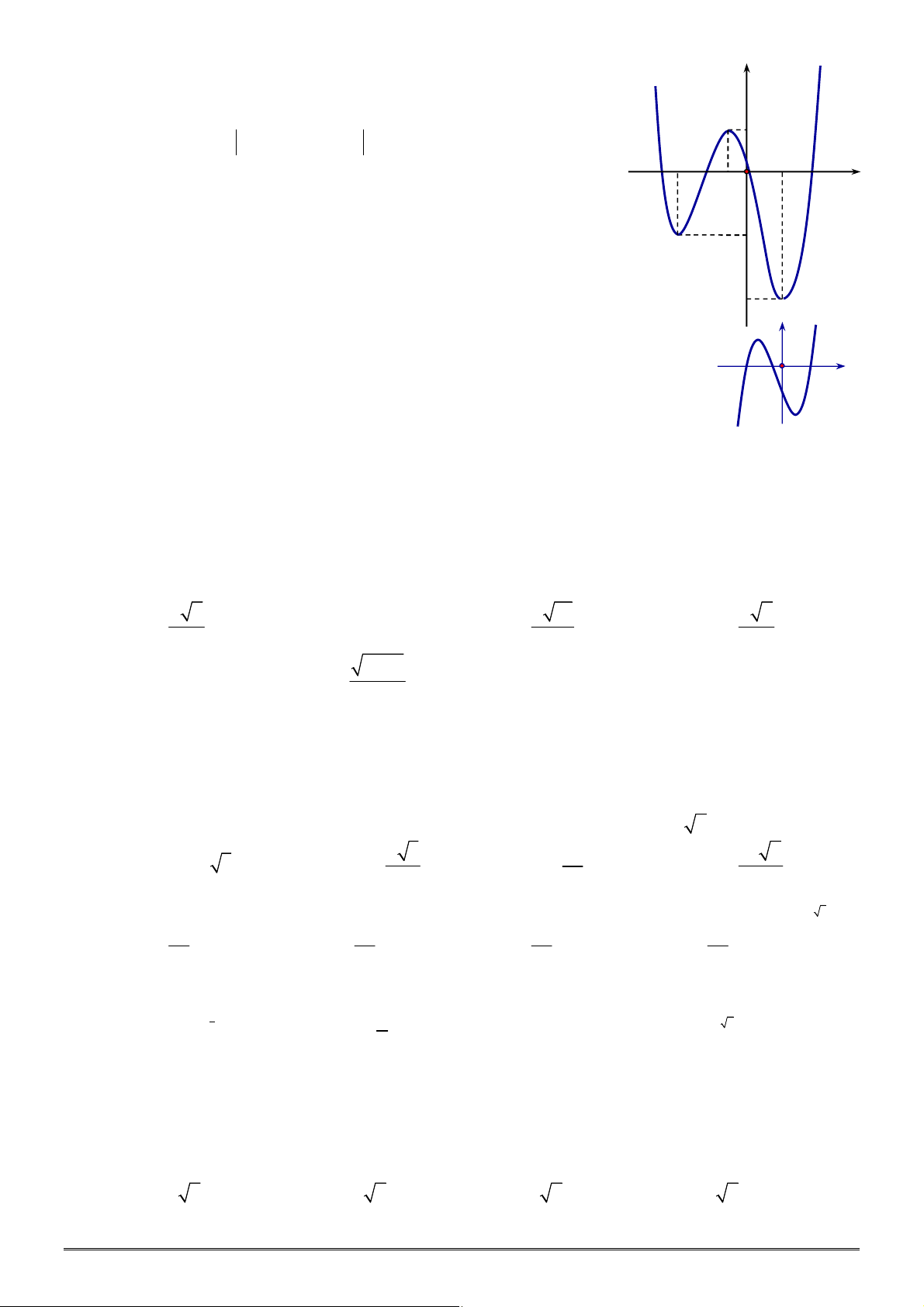
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/25
Câu 40. [2D1-4] Cho đồ thị của hàm số
y f x
như hình bên. Gọi
S
là tập hợp các giá trị nguyên dương của tham số
m
để
hàm số
2017
y f x m
có
5
điểm cực trị. Tổng tất cả
các giá trị của các phần tử của tập
S
bằng
A.
12
. B.
15
.
C.
18
. D.
9
.
Câu 41. [1D1-2] Cho hàm số
y f x
có đạo hàm là hàm số liên tục trên
với đồ thị hàm số
y f x
như hình vẽ. Biết
0
f a
, hỏi đồ
thị hàm số
y f x
cắt trục hoành tại nhiều nhất bao nhiêu điểm?
A.
3
. B.
2
.
C.
4
. D.
0
.
Câu 42. [1D1-3] Có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số:
3 2
1 1 2 2
y m x m x x
nghịch biến trên
?
A.
5
. B.
6
. C.
8
. D.
7
.
Câu 43.
[1H3-5] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA ABC
, góc giữa
đường thẳng
SB
và mặt phẳng
ABC
bằng
60
. Khoảng cách giữa hai đường thẳng
AC
và
SB
bằng
A.
2
2
a
. B.
2
a
. C.
15
5
a
. D.
7
7
a
R .
Câu 44. [2D1-4] Đồ thị hàm số
2
2
1
2
x
y
x x
có tất cả bao nhiêu tiệm cận đứng?
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 45. [2D2-2] Cho
0 1
a
,
0
b
thỏa mãn điều kiện
log 0
a
b
. Khẳng định nào sau đây là đúng?
A.
1
0 1
b a
b a
. B.
1
0 1
a b
a b
. C.
0 1
0 1
a b
b a
. D.
0 1
b a
.
Câu 46. [2H2-3] Tính bán kính
R
mặt cầu ngoại tiếp tứ diện đều
ABCD
cạnh
2
a
.
A.
3
R a
. B.
3
2
a
R . C.
3
2
a
R . D.
3 2
2
a
R .
Câu 47. [2D2-2] Tìm tất cả các giá trị thực của
x
thỏa mãn đẳng thức
3 3 9
3
log 3log 2 log 25 log 3
x .
A.
40
9
. B.
25
9
. C.
28
3
. D.
20
3
.
Câu 48. [2D2-1] Trong các biểu thức sau, biểu thức nào không có nghĩa?
A.
1
3
4
. B.
0
3
4
. C.
4
3
. D.
2
1
.
Câu 49. [2D2-1] Cho
0 1
a
và
.
b
Chọn mệnh đề sai trong các mệnh đề sau:
A.
2
log 2log
a a
b b
. B. log
b
a
a b
. C.
log 1 0
a
. D.
log 1
a
a
.
Câu 50. [2H2-2] Cho mặt cầu tâm
,
O
bán kính
3.
R
Mặt phẳng
P
nằm cách tâm
O
một khoảng
bằng
1
và cắt mặt cầu theo một đường tròn có chu vi bằng
A.
4 2
. B.
6 2
. C.
3 2
. D.
8 2
.
----------HẾT----------
O
x
y
2
3
6
a
x
y
O
b
c

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/21
TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI
TRƯỜNG THPT CHUYÊN
ĐỀ KIỂM TRA HỌC KÌ 1 LỚP 12
NĂM HỌC 2017-2018 - MÔN: TOÁN
Thời gian làm bài 90 phút
Họ và tên thí sinh:...............................SBD:...........
Mã đề thi 485
Câu 1. [2H2-2] Cho hình nón đỉnh
S
có đường cao bằng
6 cm
, bán kính đáy bằng
10 cm
. Trên
đường tròn đáy lấy hai điểm
A
,
B
sao cho
12 cm
AB . Diện tích tam giác
SAB
bằng:
A.
2
100 cm
. B.
2
48 cm
. C.
2
40 cm
. D.
2
60 cm
.
Câu 2. [2H2-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành và có thể tích bằng
1
. Trên
SC
lấy điểm
E
sao cho
2
SE EC
. Tính thể tích
V
của khối tứ diện
SEBD
.
A.
1
3
V
. B.
2
3
V
. C.
1
6
V
. D.
1
12
V
.
Câu 3. [2D2-1] Cho
2
log 3
a
. Hãy tính
4
log 54
theo
a
.
A.
4
1
log 54 1 3
2
a
. B.
4
1
log 54 1 6
2
a
.
C.
4
1
log 54 1 12
2
a
. D.
4
log 54 2 1 6
a
.
Câu 4. [2D2-2] Giải bất phương trình
10 3 10 3
x
có kết quả là
A.
1
x
. B.
1
x
.
C.
1
x
. D.
1
x
.
Câu 5. [2D1-2] Đồ thị dưới đây là của hàm số nào?
A.
2 1
1
x
y
x
. B.
2 5
1
x
y
x
.
C.
2
1
x
y
x
. D.
2 1
1
x
y
x
.
Câu 6. [2D2-2] Phương trình
2 1
3 4.3 1 0
x x
có hai nghiệm
1
x
,
2
x
trong đó
1 2
x x
, chọn phát biểu đúng.
A.
1 2
1
x x
. B.
1 2
2 0
x x
. C.
1 2
2 1
x x
. D.
1 2
2
x x
.
Câu 7. [2D1-1] Tính đạo hàm của hàm số
ln
y x x
.
A.
ln 1
y x
. B.
ln
y x
. C. .
ln 1
y x
. D.
1
x
.
Câu 8. [2D1-2] Các điểm cực đại của hàm số
sin2
y x x
là
A. ,
6
x k k
. B. ,
6
x k k
.
C. ,
6
x k k
. D. 2 ,
3
x k k
.
Câu 9. [2H1-2] Cho hình chóp
.
S ABC
có
SA ABC
, tam giác
ABC
vuông tại .
A
., biết
3
BC a
,
AB a
. Góc giữa mặt phẳng
SBC
và
ABC
bằng
45
. Tính thể tích khối chóp
.
S ABC
theo
a
.
A.
3
.
4
9
S ABC
a
V . B.
3
.
2
6
S ABC
a
V . C.
3
.
2
2
S ABC
a
V . D.
3
.
2
9
S ABC
a
V .
O
x
y
1
1
2
9
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/21
Câu 10. [2H2-1] Khối nón có chiều cao
3 cm
h
và bán kính đáy
2 cm
r
thì thể tích bằng:
A.
2
16 cm
. B.
2
4 cm
. C.
3
4
cm
3
. D. .
3
4 cm
.
Câu 11. [2D1-2] Giá trị nhỏ nhất của số thực
m
để hàm số
3 2
1
3
y x mx mx m
đồng biến trên
là
A.
2
m
. B.
1
m
. C.
1
m
. D.
0
m
.
Câu 12. [2D2-1] Giải phương trình
2
6
log 2
x
được kết quả là.
A.
36
x . B.
6
x
. C.
6
x
. D.
6
x
.
Câu 13. [2H1-1] Cho lăng trụ tứ giác đều
.
ABCD A B C D
có đáy là hình vuông cạnh
a
,
3
AA a
.
Thể tích khối lăng trụ đã cho là
A.
3
12
a
. B.
3
a
. C.
3
6
a
. D.
3
3
a
.
Câu 14. [2H1-1] Khối chóp ngũ giác có số cạnh là
A.
20
. B.
15
. C.
5
. D.
10
.
Câu 15. [2D1-3] Tìm các giá trị thực của tham số
m
sao cho phương trình
3
3 4 1 0
x x m
có ít
nhất
1
nghiệm thực trong đoạn
3;4
?
A.
51 19
4 4
m . B.
51 19
4 4
m . C.
51 19
m
. D.
51 19
m
.
Câu 16. [2D1-3] Giá trị lớn nhất của hàm số
1
2
mx
f x
x m
trên đoạn
3;5
bằng
2
khi và chỉ khi:
A.
7
m
. B.
7;13
m . C.
m
. D.
13
m
.
Câu 17. [2H1-3] Cho hình chóp
.
S ABC
có
SA a
,
SB b
,
SC c
, và
60
ASB BSC CSA
. Tính
thể tích khối chóp
.
S ABC
theo
a
,
b
,
c
.
A.
2
12
abc
. B.
2
12
abc
. C. .
2
4
abc
. D.
2
4
abc
.
Câu 18. [2D1-2] Giá trị nhỏ nhất của hàm số:
2
. 1
y x x
là
A.
2
. B.
1
. C.
1
. D.
1
2
.
Câu 19. [2D1-2] Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2sin cos 1
y x x
. Tích
.
M m
bằng
A.
25
.
4
B.
25
.
8
C.
2.
D.
0.
Câu 20. [2H1-1] Khối đa diện đều loại
4;3
có số đỉnh, số cạnh và số mặt lần lượt là
A.
6
,
12
,
8
. B.
8
,
12
,
6
. C.
12
,
30
,
20
. D.
4
,
6
,
4
.
Câu 21. [2D2-1] Cho bất phương trình
1 1
5 5
log log
f x g x
. Khi đó bất phương trình tương đương
A.
f x g x
. B.
0
g x f x
.
C.
0
g x f x
. D.
f x g x
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/21
Câu 22. [2H1-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA ABCD
và
3
SA a
. Thể tích của khối chóp
.
S ABCD
là
A.
3
3
3
a
. B.
3
3
6
a
. C.
3
2
3
a
. D.
3
2
6
a
.
Câu 23. [2D2-1] Cho các số thực
x
,
y
và
a
thỏa mãn
x y
;
1
a
. Khi đó:
A.
x y
a a
. B.
x y
a a
. C.
x y
a a
. D.
x y
a a
.
Câu 24. [2D2-2] Ông An gửi số tiền
100
triệu đồng vào ngân hàng với lãi suất
7%
trên .
1
. năm, biết
rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn
ban đầu. Sau thời gian
10
năm nếu không rút lãi lần nào thì số tiền mà ông An nhận được tính
cả gốc lẫn lãi là (đơn vị là đồng):
A.
10
8
10 . 1 0,0007
. B. .
10
8
10 . 1 0,07
. C.
8 10
10 .0,07
. D.
10
8
10 . 1 0,7
.
Câu 25. [2D2-1] Giải phương trình
3
log 1 2
x
.
A.
8
. B.
10
. C.
7
. D.
9
.
Câu 26. [2D2-3] Số chữ số của só tự nhiên
2017
3
N là
A.
962
. B.
964
. C.
961
. D.
963
.
Câu 27. [2H1-2] Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, góc tạo bởi mặt bên và mặt
đáy là
. Thể tích khối chóp
.
S ABCD
là:
A.
3
.tan
2
a
. B.
3
.tan
3
a
. C.
3
.tan
6
a
. D.
3
2 .tan
3
a
.
Câu 28. [2D1-2] Giả sử
A
và
B
là các giao điểm của đường cong
3
3 2
y x x
và trục hoành. Tính
độ dài đoạn thẳng
AB
.
A.
6 5
AB . B.
4 2
AB
. C.
3
AB
. D.
5 3
AB .
Câu 29. [2D1-3] Cho hàm số
3 2
2 1
y x mx
có đồ thị
.
m
C Tìm
m
sao cho
m
C
cắt đường thẳng
: 1
d y x
tại ba điểm phân biệt có hoành độ
1 2 3
, ,
x x x
thỏa mãn
1 2 3
101.
x x x
A.
101
.
2
m B.
50.
m
C.
51.
m
D.
49.
m
Câu 30. [2D1-2] Số tiệm cận của đồ thị hàm số
2
2
6 3
3 2
x x
y
x x
là?
A.
6.
B.
2.
C.
1.
D.
3.
Câu 31. [2D1-2] Đồ thị bên là đồ thị của hàm số nào?
A.
4 2
4 3
y x x
. B.
4 2
3 3
y x x
.
C.
4 2
2 3
y x x
. D.
4 2
1
3 3
4
y x x
.
Câu 32. [2D1-3] Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình bên.
Hỏi phương trình
3 2
2 0
ax bx cx d
có bao nhiêu nghiệm?
A. Phương trình có đúng một nghiệm.
B. Phương trình có đúng hai nghiệm.
C. Phương trình khôngg có nghiệm.
D. Phương trình có đúng ba nghiệm.
O
x
y
3
1
1
x
y
1
1
2
3
O
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/21
Câu 33. [2D2-2]Phương trình
2
log log 2 0
x x
có bao nhiêu nghiệm?
A.
1.
B.
2.
C.
3.
D.
0.
Câu 34. [2H2-2]Cho lăng trụ tam giác đều có tất cả các cạnh bằng
a
.Một hình trụ tròn xoay có hai đáy
là hai hình tròn ngoại tiếp hai đáy của lăng trụ.Thể tích của khối trụ tròn xoay bằng:
A.
3
.
9
a
B.
3
.
a
C.
3
3 .
a
D.
3
.
3
a
Câu 35. [2H2-1] Cho hình trụ
T
có độ dài đường sinh
l
, bán kính đáy
r
. Ký hiệu
xq
S
là diện tích
xung quanh của
T
. Công thức nào sau đây là đúng?
A.
3
xq
S rl
. B. 2
xq
S rl
. C.
xq
S rl
. D.
2
2
xq
S r l
.
Câu 36. [2D1-2] Điều kiện cần và đủ của tham số
m
để hàm số
3 2
5
y x x mx
có cực trị là
A.
1
3
m
. B.
1
3
m
. C.
1
3
m
. D.
1
3
m
.
Câu 37. [2D2-1] Tập xác định của hàm số
2
3
log
2
x
y
x
là:
A.
3; 2
. B.
; 3 2;
.
C.
\ 2
. D.
3; 2
.
Câu 38. [2H2-2] Cho hình chóp
.
S ABC
có tam giác
ABC
đều cạnh
3cm
a
,
SA ABC
và
2
SA a
. Tính thể tích khối cầu ngoại tiếp hình chóp
.
S ABC
.
A.
3
3
8
cm
3 3
a
. B.
3
3
4
cm
3
a
. C.
3
32 3cm
. D.
3
16 3cm
.
Câu 39. [2H1-3] Cho hình lăng trụ đứng
.
ABCD A B C D
có thể tích bằng
V
. Các điểm
M
,
N
,
P
lần
lượt thuộc các cạnh
AA
,
BB
,
CC
sao cho
1
2
AM
AA
,
3
4
BN CP
BB CC
. Thể tích khối đa diện
.
ABC MNP
bằng
A.
2
3
V
. B.
1
8
V
. C.
1
3
V
. D.
1
2
V
.
Câu 40. [2H2-2] Tìm nghiệm của phương trình:
log 4 3 2
x
x
.
A.
1
x
. B.
4
x
. C.
x
. D.
1; 4
x
.
Câu 41. [2D1-2] Với giá trị nào của số thực
m
thì hàm số
1
x m
y
x
đồng biến trên từng khoảng xác
định?
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Câu 42. [2H2-1] Khối cầu có bán kính
3 cm
thì có thể tích là
A.
3
9 cm
. B.
3
12 cm
.
C.
3
36 cm
. D.
3
27 cm
.
Câu 43. [2D2-1] Nghiệm của phương trình
2
5 125
x
là
A.
1
x
. B.
5
x
. C.
3
x
. D.
1
x
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/21
Câu 44. [2H1-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
,
30
ABC
. Tam giác
SBC
là tam giác đều cạnh
a
và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp
.
S ABC
là:
A.
3
16
a
. B.
3
3 3
16
a
. C.
3
3
16
a
. D.
3
3
16
a
.
Câu 45. [2D1-2] Gọi
1
y
,
2
y
lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số
4 2
10 9
y x x
.
Khi đó
1 2
y y
bằng:
A.
7
. B.
2 5
. C.
25
. D.
9
.
Câu 46. [2D2-2] Giá trị nhỏ nhất của hàm số
2
e 3e 1
x x
y
trên đoạn
ln2;ln5
là:
A.
2
e
. B.
9
. C.
9
e
. D.
39
.
Câu 47. [2D2-2]
3
7
1
log
a
a
0; 1
a a
bằng
A.
3
7
. B.
7
3
. C.
3
7
. D.
7
3
.
Câu 48. [2D1-1] Tiệm cận đứng của đồ thị hàm số
2 3
7
x
y
x
có phương trình là
A.
7
y
. B.
2
y
. C.
7
x
. D.
2
x
.
Câu 49. [2D2-1] Cho hàm số
3 1
1
x
y
x
. Chọn khẳng định đúng.
A. Hàm số đồng biến trên khoảng
;1 1;
.
B. Hàm số nghịch biến trên từng khoảng xác định của nó.
C. Hàm số đồng biến trên
.
D. Hàm số nghịch biến trên
.
Câu 50. [2D2-1] Tập xác định của hàm số hàm số
1
2
2 1
y x
là
A.
1
;
2
. B.
1
\
2
. C.
1
;
2
. D.
.
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/22
SỞ GD VÀ ĐT HÀ NỘI
TRƯỜNG THPT LƯƠNG THẾ VINH
ĐỀ THI HỌC KÌ 1 – TOÁN 12
NĂM HỌC 2017-2018
Thời gian làm bài 90 phút
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 103
Câu 1. [2D1-1] Hai đường tiệm cận của đồ thị hàm số
2 1
2
x
y
x
là.
A.
2
x
;
2
y
. B.
2
x
;
1
2
y
. C.
2
x
;
2
y
. D.
2
x
;
2
y
.
Câu 2. [2D1-2] Biết đường thẳng
1
y x
cắt đồ thị hàm số
2 1
1
x
y
x
tại hai điểm phân biệt
A
,
B
có hoành độ lần lượt là
A
x
;
B
x
. Tính giá trị của
A B
x x
.
A.
2
A B
x x
. B.
2
A B
x x
. C.
0
A B
x x
. D.
1
A B
x x
.
Câu 3. [2D2-2] Tìm tập xác định
D
của hàm số
2
3
log 3
y x x
.
A.
D
. B.
\ 0;3
D
. C.
;0 3;D
. D.
0;3
.
Câu 4. [2D1-2] Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
A.
4
y x
. B.
2
2 2
y x x
. C.
1
3
x
y
x
. D.
3
y x x
.
Câu 5. [2D1-3]Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
2
4
x
y
x m x
có ba tiệm
cận đứng.
A.
2 2
m
. B.
0
2 2
m
m
. C. Mọi giá trị
m
. D.
2 2
m
.
Câu 6. [2H3-2]Trong không gian
Oxyz
, cho bốn điểm
1;0;0
A ,
0;2;0
B ,
0;0;3
C ,
1;2;3
D .
Phương trình mặt cầu đi qua bốn điểm
A
,
B
,
C
,
D
là:
A.
2 2 2
2 3 0
x y z x y z
. B.
2 2 2
2 3 14 0
x y z x y z
.
C.
2 2 2
2 3 6 0
x y z x y z
. D.
2 2 2
2 4 6 0
x y z x y z
Câu 7. [2D1-1] Cho hàm số
2 1
2
x
y
x
. Khẳng định nào dưới đây đúng?
A. Đồ thị hàm số có tiệm cận đứng là
2
x
. B. Hàm số có tiệm cận đứng là
2
x
.
C. Đồ thị hàm số không có tiệm cận. D. Đồ thị hàm số có tiệm cận ngang là
1
2
y
.
Câu 8. [2D2-2] Tìm tập nghiệm
S
của phương trình
4 6.2 8 0
x x
.
A.
1;2
S . B.
2
S . C.
1
S . D.
1;2
S .
Câu 9. [2H2-4] Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
,
B
,
AB BC a
,
2
SA AD a
,
SA ABCD
, gọi
E
là trung điểm của
AD
. Tính bán kính
R
của mặt cầu
ngoại tiếp khối chóp
.
S CDE
theo
a
.
A.
3 2
2
a
R . B.
10
2
a
R . C.
11
2
a
R . D.
2
2
a
R .
10

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/22
Câu 10. [2D2-2] Cho hàm số
2
1
2
x
y x e
. Giá trị của biểu thức 2
y y y
tại
0
x
là
A.
1
. B.
e
. C.
0
. D.
1
e
.
Câu 11. [2H2-3] Trong các hình hộp chữ nhật nằm trong mặt cầu bán kính
R
, thể tích lớn nhất có thể
của khối hộp chữ nhật là
A.
3
4 3
3
R
. B.
3
8 3
9
R
. C.
3
16 3
3
R
. D.
3
8 3
3
R
.
Câu 12. [2D1-2] Viết phương trình tiếp tuyến của đồ thị hàm số
3
3 2
y x x
tại giao điểm của đồ thị
hàm số với trục tung.
A.
2
y
. B.
3 2
y x
. C.
3 2
y x
. D.
3 2
y x
.
Câu 13. [2D2-3] Tìm tất cả các giá trị thực của tham số
m
để phương trình
3
4 2 3
x x
m
có đúng
2
nghiệm thực phân biệt trong khoảng
1;3
.
A.
13 9
m
. B.
9 3
m
. C.
13 3
m
. D.
3 9
m
.
Câu 14. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 2
3 0
x x m
có
2
nghiệm phân biệt
A. Không có
m
. B.
4;0
m . C.
4;0
m . D.
0
m
.
Câu 15. [2D1-2] Đồ thị hàm số
2
2
9
6 8
x
y
x x
có bao nhiêu đường tiệm cận?
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 16. [2D1-3] Giá trị thực của tham số
m
để đồ thị hàm số
4 2
2
y x mx m
có ba điểm cực trị tạo
thành một tam giác nhận gốc tọa độ làm trọng tâm là
A.
1
m
. B. không có
m
. C.
3
2
m
. D.
1
2
m
.
Câu 17. [2D1-2] Hàm số
4 2
2017 2018
y x x có giá trị cực đại là
A.
CÑ
2017
y . B.
CÑ
0
y
. C.
CÑ
2018
y . D.
CÑ
2018
y .
Câu 18. [2D1-2] Cho hàm số
y f x
liên tục trên
và có đạo hàm được xác định bởi hàm số
3
2
1 3
f x x x x
. Hỏi đồ thị hàm số
y f x
có bao nhiêu điểm cực trị?
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 19. [2H1-2] Cho hình trụ có diện tích toàn phần lớn hơn diện tích xung quanh là
4 .
Bán kính của
hình trụ là?
A.
2
.
2
B.
2.
C.
2.
D.
1.
Câu 20. [2D2-1] Tìm tập xác định
D
của hàm số
3
2
1 .
y x
A.
; 1 1; .
D
B.
.
D
C.
.
D
D.
\ 1 .
D

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/22
Câu 21. [0H3-2] Trong không gian
Oxyz
, cho hai điểm
1;2;0
A ,
2; 1;1
B . Tìm điểm
C
có hoành
độ dương trên trục
Ox
sao cho tam giác
ABC
vuông tại
C
.
A.
3;0;0
C . B.
2;0;0
C . C.
1;0;0
C . D.
5;0;0
C .
Câu 22. [0H3-2] Trong không gian
Oxyz
, cho hai điểm
1;2; 2
A
,
2; 1;2
B . Tìm tọa độ điểm
M
trên mặt phẳng
Oxyz
cho
MA MB
đạt giá trị nhỏ nhất.
A.
1;1;0
M . B.
3 1
; ;0
2 2
M
. C.
2;1;0
M . D.
1 3
; ;0
2 2
M
.
Câu 23. [2D2-2] Tập nghiệm của bất phương trình
2
1
2
4
x
x
là
A.
1;S
. B.
;1
S
. C.
;2
S . D.
2;S
.
Câu 24. [2D1-1] Số điểm cực trị của hàm số
4 2
3 5
y x x
là
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 25. [2D2-1] Giải phương trình
3
log 1 2
x
.
A.
8
. B.
10
. C.
7
. D.
9
.
Câu 26. [2D2-3] Số chữ số của só tự nhiên
2017
3
N là
A.
962
. B.
964
. C.
961
. D.
963
.
Câu 27. [2D2-2] Cho hàm số
1
1
x x
y f x e
. Tính giá trị biểu thức
2018
1 . 2 ... 2017 .
T f f f e
.
A.
1
T
. B.
T e
. C.
1
T
e
. D.
1
2018
T e
.
Câu 28. [2H1-2] Cho khối hộp
.
ABCD A B C D
có thể tích là
36
. Tính thể tích
V
của khối chóp
.
ACB D
.
A.
18
V
. B.
6
V
. C.
9
V
. D.
12
V
.
Câu 29. [2H1-1] Cho hình chóp
.
S ABCD
có cạnh bên
SA
tạo với đáy một góc
60
và
3
SA a
, đáy
là tứ giác có hai đường chéo vuông góc,
2
AC BD a
. Tính thể tích
V
của khối chóp theo
a
.
A.
3
2 3
3
a
V . B.
3
3
V a
. C.
3
V a
. D.
3
3
2
a
V .
Câu 30. [2D2-2] Hàm số
3
3
y x x
đồng biến trên khoảng nào?
A.
1;1
. B.
; 1
. C.
;
. D.
0;
.
Câu 31. [2D2-3] Cho bất phương trình
2
3 2
2 2 2 3
x x x
x x
có tập nghiệm là
;
a b
. Giá trị của
2
T a b
là
A.
1
T
. B.
5
T
. C.
3
T
. D.
2
T
.
Câu 32. [2D1-3] Cho hàm số
1
mx
y
x n
,
trong đó
m
,
n
là tham số. Biết giao điểm của hai đường tiệm
cận của đồ thị hàm số nằm trên đường thẳng
2 3 0
x y
và đồ thị hàm số đi qua điểm
0;1
A . Giá trị của
m n
là
A.
3
m n
. B.
3
m n
.
C.
1
m n
. D.
1
m n
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/22
Câu 33. [2D1-2] Biết rằng hàm số
3 2
y f x x ax bx c
đạt cực tiểu tại điểm
1
x
, giá trị cực
tiểu bằng
3
và đồ thị hàm số cắt trục tung tại điểm có tung độ
2
. Tìm giá trị của hàm số tại
2
x
.
A.
2 8.
f
B.
2 0.
f
C.
2 0.
f
D.
2 4.
f
Câu 34. [2D2-3] Cho phương trình
2017 2017
4
4034
tan 12 tan
1 1
12 12
2017.
2 3
1 tan 1 tan 1 tan
12 12 12
x x
x
.
Tính tổng tất cả các nghiệm thực của phương trình đã cho.
A.
0
B.
1
C.
1
D.
2017
Câu 35. [2H2-2] Tính thể tích
V
khối lập phương biết rằng khối cầu ngoại tiếp khối lập phương có thể
tích là
32
3
.
A.
64 3
9
V . B.
8
V
. C.
8 3
9
V . D.
8 3
3
V .
Câu 36. [2D2-1] Hàm số nào trong bốn hàm số liệt kê ở dưới đồng biến trên các khoảng xác định của
hàm số?
A.
2 1
x
y
e
. B.
3
x
y
. C.
sin 2017
x
y . D.
2
x
y
e
.
Câu 37. [1D5-4] Cho hàm số
3 2
3 2
y x x
. Gọi
A
,
B
là các điểm thuộc đồ thị hàm số đã cho có
hoành độ lần lượt là
A
x
;
B
x
, tiếp tuyến của đồ thị hàm số tại
A
,
B
song song với nhau và
đường thẳng
AB
tạo với
2
trục toạ độ một tam giác cân, đường thẳng
AB
có hệ số góc
dương. Tính giá trị
A B
x x
.
A.
1
A B
x x
. B.
3
A B
x x
. C.
2
A B
x x
. D.
2
A B
x x
.
Câu 38. [1D5-2] Tiếp tuyến với đồ thị
2 1
2
x
y
x
tại điểm có tung độ bằng
5
có hệ số góc
k
là
A.
1
3
k
. B.
1
k
. C.
3
k
. D.
1
3
k
.
Câu 39. [2H2-2] Cho hình nón tròn xoay có đường cao
4
h
và diện tích đáy là
9
. Tính diện tích
xung quanh của hình nón.
A.
10
xq
S
. B.
15
xq
S
. C.
25
xq
S
. D.
30
xq
S
.
Câu 40. [2D1-2] Tìm giá trị nhỏ nhất của hàm số
4
1y x
x
trên
1;3
.
A.
1;3
Min 4
x
y
. B.
1;3
Min 5
x
y
. C.
1;3
16
Min
3
x
y
. D.
1;3
Min 6
x
y
.
Câu 41. [2D1-1] Đường cong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây.
A.
3
3 2
y x x
.
B.
4 2
2 2
y x x
.
C.
4 2
2 2
y x x
.
D.
4 2
2 2
y x x
.
O
x
y
2
1
1
3

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/22
Câu 42. [2D2-2] Tập nghiệm của bất phương trình
1 1
2 2
log 3 log 9 2
x x
.
A.
3;4
S . B.
;4
S . C.
9
3;
4
S
. D.
3;4
S .
Câu 43. [2H1-2] Diện tích toàn phần của một hình hộp chữ nhật là
2
8
tp
S a
. Đáy của hình hộp là hình
vuông cạnh
a
. Tính thể tích của khối hộp theo
a
.
A.
3
3 .
V a
B.
3
V a
. C.
3
3
.
2
a
V D.
3
7
.
4
V a
Câu 44. [2H3-1] Trong không gian
Oxyz
, phương trình mặt cầu tâm
1;2;0
I và đi qua điểm
2; 2;0
A là
A.
2 2
2
1 2 100.
x y z B.
2 2
2
1 2 5.
x y z
C.
2 2
2
1 2 10.
x y z D.
2 2
2
1 2 25.
x y z
Câu 45. [2D1-2] Tìm tập hợp tất cả các giá trị của tham số thực
m
để hàm số
1
mx
y
x m
đồng biến trên
từng khoảng xác định.
A.
; 1
. B.
1;1
. C.
1;
. D.
;1
.
Câu 46. [2H2-2] Hình nón có chiều cao bằng đường kính đáy. Tỉ số giữa diện tích xung quanh và diện
tích toàn phần của hình nón là:
A.
1
2
. B.
1 5
4
. C.
1
4
. D.
5 5
4
.
Câu 47. [2H1-1] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA a
và vuông góc với
đáy. Thể tích
V
của khối chóp
.
S ABC
theo
a
là
A.
3
.
3
12
S ABC
a
V . B.
3
.
2
12
S ABC
a
V . C.
3
.
3
3
S ABC
a
V . D.
3
.
3
4
S ABC
a
V .
Câu 48. [2D2-2] Đạo hàm của hàm số
2
2
log 2
y x x
là
A.
2
1
2 ln2
y
x x
. B.
2
1
2
x
y
x x
.
C.
2
1
2 ln2
x
y
x x
. D.
2
1
2 ln 2
x
y
x x
.
Câu 49. [2H3-2] Trong không gian
Oxyz
, cho ba vecto
1;2;1
a
,
0;2; 1
b
,
;1;0
c m
. Tìm giá
trị thực của tham số
m
để ba véctơ
a
,
b
,
c
đồng phẳng.
A.
1
m
. B.
0
m
. C.
1
4
m
. D.
1
4
m
.
Câu 50. [2H2-1] Khối cầu có thể tích là
36
. Diện tích xung quanh của mặt cầu là
A.
9
xq
S
. B.
27
xq
S
. C.
18
xq
S
. D.
36
xq
S
.
----------HẾT----------
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/32 – Mã đề 101
TRƯỜNG TRUNG HỌC PHỔ THÔNG
CHUYÊN HẠ LONG
(Đề thi gồm 08 trang)
KIỂM TRA HỌC KÌ I
Năm học 2017 - 2018
Môn: Toán 12 (Chương trình chuẩn)
(Chương trình nâng cao)
(Thời gian làm bài: 90 phút)
Họ và tên thí sinh: .......................................................... SBD: ................................
Mã đề 101
A. PHẦN CHUNG (80%, gồm 40 câu)
Câu 1. [2H1-2] Hình đa diện đều nào dưới đây không có tâm đối xứng?
A. Hình bát diện đều. B. Hình tứ diện đều.
C. Hình lăng trụ lục giác đều. D. Hình lập phương.
Câu 2. [2D1-1] Tìm giá trị cựa đại
C
Đ
y
của hàm số
4 2
2 2
y x x
.
A.
2
CĐ
y
. B.
2
CĐ
y
. C.
1
CĐ
y
. D.
1
CĐ
y
.
Câu 3. [2D1-2] Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D
dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3 2
3 2.
y x x
B.
3 2
3 2.
y x x
C.
4 2
2 2.
y x x
D.
3 2
3 2.
y x x
Câu 4. [2D2-2] Tính đạo hàm của hàm số
2 1
7
x
y
.
A.
2
2.7
x
y
. B.
2 1
7
x
y
. C.
2 1
2.7 .ln7
x
y
. D.
2 1
2.7
ln7
x
y
.
Câu 5. [2D1-2] Tìm khoảng nghịch biến của hàm số
3 2
3 2
y x x
.
A.
0; 2
. B.
0; 3
. C.
0; +
. D.
2; 0
.
Câu 6. [2D1-2] Tiệm cận đứng và tiện cận ngang của đồ thị hàm số
2 1
1
x
y
x
.
A.
1
y
;
2
x
. B.
1
x
;
2
y
. C.
1
x
;
2
y
. D.
1
x
;
2
y
.
Câu 7. [2D1-2] Tìm giá trị lớn nhất
M
của hàm số
3 2
3 2
y x x
trên đoạn
2;3 .
A.
22.
M
B.
6.
M
C.
22.
M
D.
6.
M
Câu 8. [2D1-2] Biết đường thẳng
1
y x
cắt đồ thị hàm số
3 1
1
x
y
x
tại hai điểm phân biệt
A
,
B
có hoành độ lần lượt
A
x
,
B
x
. Hãy tính tổng
.
A B
x x
A.
1.
A B
x x
B.
3.
A B
x x
C.
3.
A B
x x
D.
1.
A B
x x
Câu 9. [2H1-2] Cho tam giác đều
ABC
có đường cao
.
AH
Khi tam giác
ABC
quay quanh trục là
đường thẳng
AH
một góc
360
thì các cạnh của tam giác
ABC
sinh ra hình gì?
A. Một hình trụ. B. Một mặt nón.
C. Hai hình nón. D. Một hình nón.
O
x
y
11
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/32 – Mã đề 101
Câu 10. [2H1-1] Hình đa diện bên có bao nhiêu mặt?
A.
6
. B.
11
.
C.
12
. D.
10
.
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
3
1
y x
.
A.
;D
. B.
\ 1
D
. C.
; 1
D . D.
; 1
D .
Câu 12. [2D2-2] Phương trình
2
2 7 5
2 1
x x
có bao nhiêu nghiệm?
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 13. [2H2-1] Cho tấm tôn hình chữ nhật quay quanh trục là đường thẳng chứa một cạnh của tấm tôn
đó một góc
360
ta được một vật tròn xoay nào dưới đây?
A. Mặt trụ. B. Khối lăng trụ. C. Hình trụ. D. Khối trụ.
Câu 14. [2D2-1] Giải phương trình
3
log 2 2.
x
A.
6.
x
B.
7.
x
C.
11.
x
D.
4.
x
Câu 15. [2H2-1] Cho đường tròn quay quanh một đường thẳng đi qua tâm đường tròn đó một góc
360
thì sinh ra hình gì?
A. Hai mặt cầu. B. Một khối cầu. C. Hai khối cầu. D. Một mặt cầu.
Câu 16. [2H1-1] Cho khối lăng trụ đứng
.
ABC A B C
có thể tích bằng
3
.
a
Biết
ABC
vuông tại
,
A
AB a
,
2
AC a
. Tính độ dài đường cao của khối lăng trụ.
A.
3
a
. B.
a
. C.
3
a
. D.
2
a
.
Câu 17. [2D1-1] Tìm số đường tiệm cận của đồ thị hàm số
2
15 11
2017
x
y
x
.
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 18. [2H1-2] Tính thể tích khối chóp
.
S ABC
biết
SA a
,
ABC
đều,
SAB
vuông cân tại
S
và
nằm trong mặt phẳng vuông góc với mặt phẳng đáy.
A.
3
6
24
a
. B.
3
6
12
a
. C.
3
3
12
a
. D.
3
6
6
a
.
Câu 19. [2D1-3] Cho khối lăng trụ
.
ABC A B C
. Gọi
M
là trung điểm
CC
. Mặt phẳng
ABM
chia
khối lăng trụ
.
ABC A B C
thành hai khối. Tính tỉ số thể tích (số bé chia số lớn) của hai khối đó.
A.
1
3
. B.
2
5
. C.
1
6
. D.
1
5
.
Câu 20. [2D2-2] Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, góc
60
SAB
. Tính thể
tích của khối nón đỉnh
S
có đáy là đường tròn ngoại tiếp tứ giác
ABCD
.
A.
3
2
12
a
. B.
3
3
12
a
. C.
3
3
6
a
. D.
3
2
6
a
.
Câu 21. [2D2-2] Cho
a
và
b
là các số thực dương khác
1
,
x
và
y
là hai số thực dương. Khẳng định
nào dưới đây đúng?
A.
log
log
log
a
a
a
x
x
y y
. B.
1 1
log
log
a
a
x x
.
C.
log log log
a a a
x y x y
. D.
log log .log
b b a
x a x
.
Câu 22. [2D1-2] Tìm giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
2
sin cos 2.
y x x
A.
3
; 3.
4
M m
B.
3
3;
4
M m
C.
3; 1.
M m
D.
3
3;
4
M m
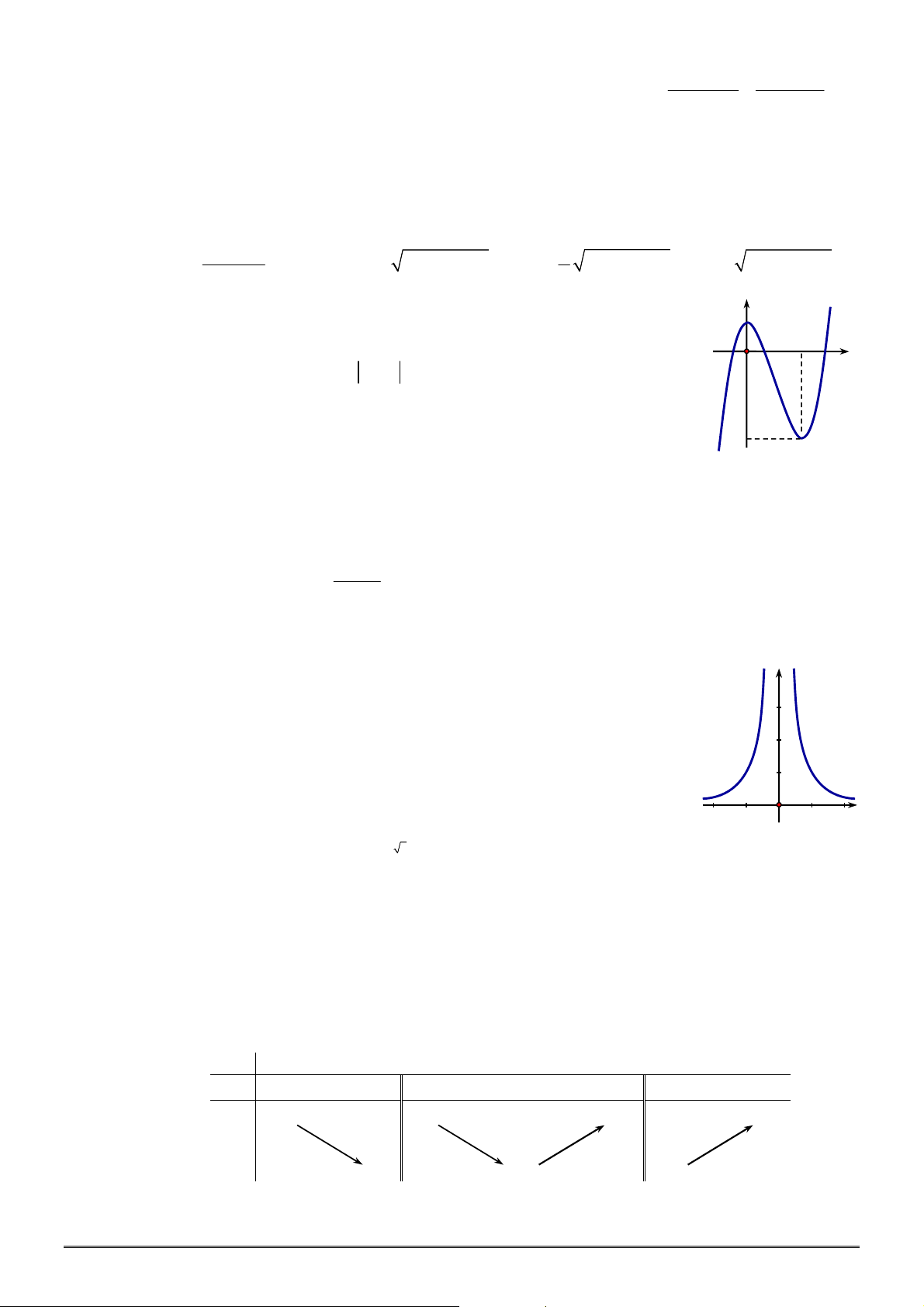
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/32 – Mã đề 101
Câu 23. [2D2-2] Số tuổi của An và Bình là các nghiệm của phương trình
2 2
1 2
1
5 log 1 logx x
.
Tính tổng số tuổi của An và Bình.
A.
21.
B.
16.
C.
12.
D.
13.
Câu 24. [2H2-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
,
A
biết
SA ABC
và
SA a
,
AB b
,
AC c
. Tính bán kính
r
của mặt cầu ngoại tiếp hình chóp
. .
S ABC
A.
2
a b c
r
B.
2 2 2
2 .
r a b c
C.
2 2 2
1
.
2
r a b c
D.
2 2 2
.
r a b c
Câu 25. [2D1-3]Cho hàm số
y f x
liên tục trên
và có đồ thị hàm số
là đường cong trong hình vẽ bên. Tìm tất cả các giá trị thực của
tham số
m
để phương trình
f x m
có
3
nghiệm phân biệt.
A.
0;3
m .
B.
1 3
m
.
C.
3 1
m
.
D. Không có giá trị nào của
m
.
Câu 26. [2D1-2] Cho hàm số
y f x
có đạo hàm
3
2
1 .
f x x x
Hỏi hàm số có bao nhiêu điểm
cực trị?
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 27. [2D1-1] Cho hàm số
2 4
.
1
x
y
x
Khẳng định nào sau đây sai?
A. Đồ thị hàm số có tiệm cận đứng là đường thẳng
1
x
và tiệm cận ngang là đường
thẳng
4
y
.
B. Đồ thị hàm số cắt trục hoành tại điểm
2;0
và cắt trục tung tại điểm
0;4
.
C. Hàm số không có cực trị.
D. Hàm số đồng biến trên các khoảng
;1
và
1;
.
Câu 28. [2D2-2] Đường cong hình bên là đồ thị của một trong bốn hàm
số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó
là hàm số nào?
A.
4
y x
. B.
2
y x
. C.
2
x
y
. D.
2
y x
.
Câu 29. [2H2-2] Tính diện tích xung quanh
xq
S
của hình trụ có đường cao
h a
và thể tích
3
V a
.
A.
2
4
xq
S a
. B.
2
6
xq
S a
. C.
2
2
xq
S a
. D.
2
8
xq
S a
.
Câu 30. [2D1-2] Cho hàm số
y f x
xác định trên
\ 1
, liên tục trên mỗi khoảng xác định và có
bảng biến thiên như hình bên dưới. Tìm tập hợp tất cả các giá trị thực của tham số
m
sao cho
phương trình
f x m
vô nghiệm.
A.
; 2
. B.
1;
. C.
2;1
. D.
2;
.
x
1
0
1
y
0
y
2
1
2
O
x
y
1
2
1
2
1
2
O
x
y
3
2
1
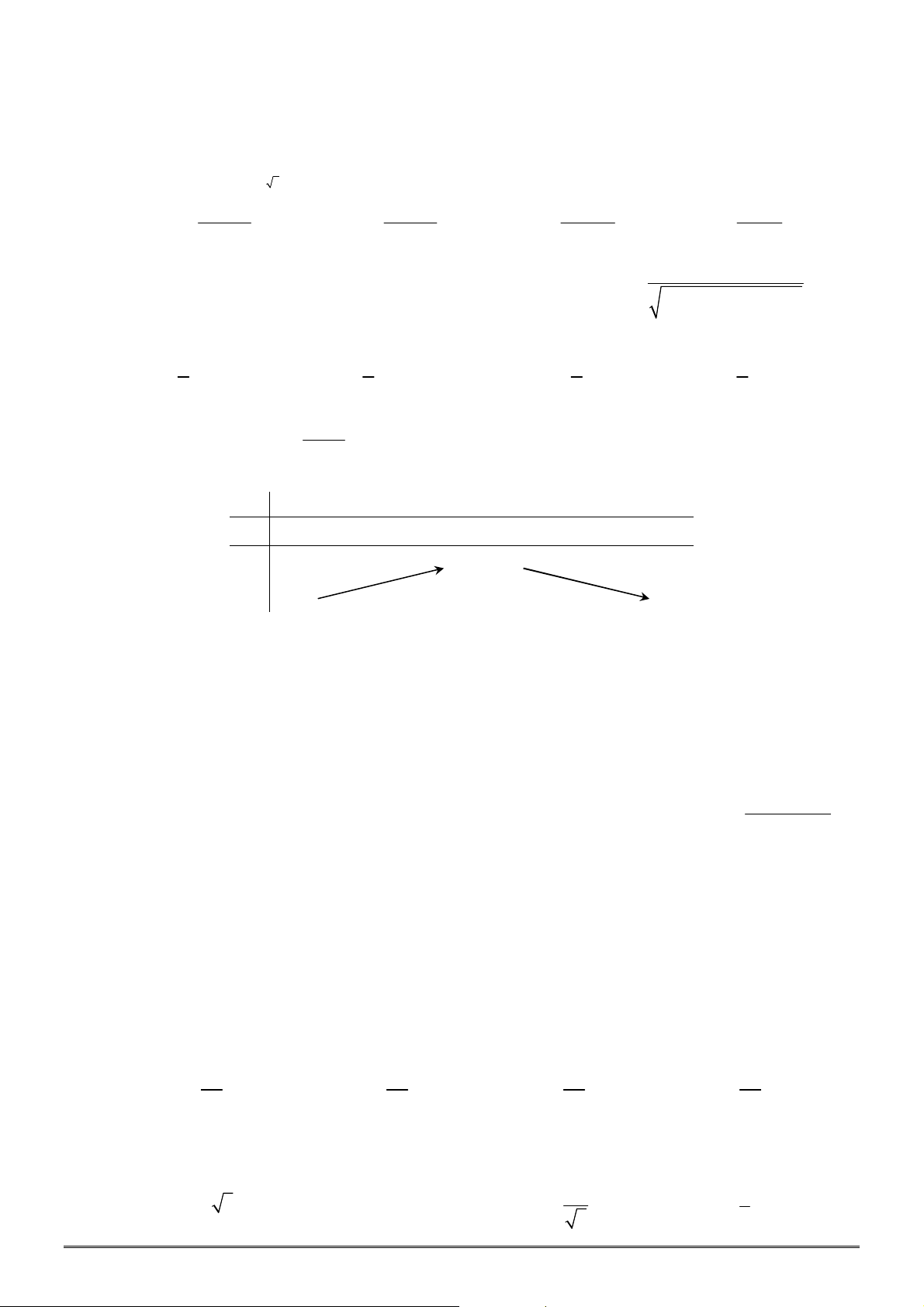
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/32 – Mã đề 101
Câu 31. [0D2-1] Phương trình
2 3 4
9 27
x x
tương đương với phương trình nào sau đây?
A.
6 0
x
. B.
7 6 0
x
. C.
7 6 0
x
. D.
6 0
x
.
Câu 32. [0D2-2] Cho
a
,
b
là hai số dương khác
1.
Đặt
log .
a
b m
Tính theo
m
giá trị của biểu thức
2
3
log log
ba
P b a
.
A.
2
12
2
m
P
m
. B.
2
12
m
P
m
. C.
2
4 3
2
m
P
m
. D.
2
3
m
P
m
.
Câu 33. [0D2-2] Tìm tất cả các giá trị của tham số
m
sao cho hàm số
2
3
1
log 2 3
y
x x m
có tập
xác định là
.
A.
2
;
3
. B.
2
;
3
. C.
2
;
3
. D.
2
;
3
.
Câu 34. [2D1-1] Hàm số
2
4
1
y
x
có bảng biến thiên như bên dưới. Xét trên tập xác định của hàm số,
khẳng định nào sau đây đúng?
A. Hàm số có giá trị lớn nhất bằng
4
và không có giá trị nhỏ nhất.
B. Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
C. Hàm số có giá trị lớn nhất bằng
4
và giá trị nhỏ nhất bằng
0
.
D. Hàm số có giá trị nhỏ nhất bằng
0
và không có giá trị lớn nhất.
Câu 35. [2D2-2] Tính tổng tất cả các nghiệm của phương trình
9 4.3 3 0
x x
.
A.
3
. B.
1
. C.
1
. D.
2
.
Câu 36. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị hàm số
2
1
2
x
y
x x m
có
đúng hai đường tiệm cận đứng.
A.
1
m
. B.
3
m
. C.
1
m
. D.
1
3
m
m
.
Câu 37. [2D2-2] Biết tập nghiệm của bất phương trình
2 2 2
log 1 log 5 1 log 2
x x x
là
khoảng
;
a b
. Tính
.
P a b
A.
6
P
. B.
5
P
. C.
7
P
. D.
8
P
.
Câu 38. [2D2-2] Tìm tất cả các giá trị của tham số
m
để phương trình
2 3
2 2 5
x
m
có nghiệm.
A.
5
2
m
. B.
5
2
m
. C.
5
2
m
. D.
5
2
m
.
Câu 39. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị hàm số
4 2
2 1
y x mx
có
ba điểm cực trị tạo thành ba đỉnh của một tam giác đều.
A.
3
3
m
. B.
3
m
. C.
3
1
3
m
. D.
1
3
m
.
x
0
y
0
y
1
4
2
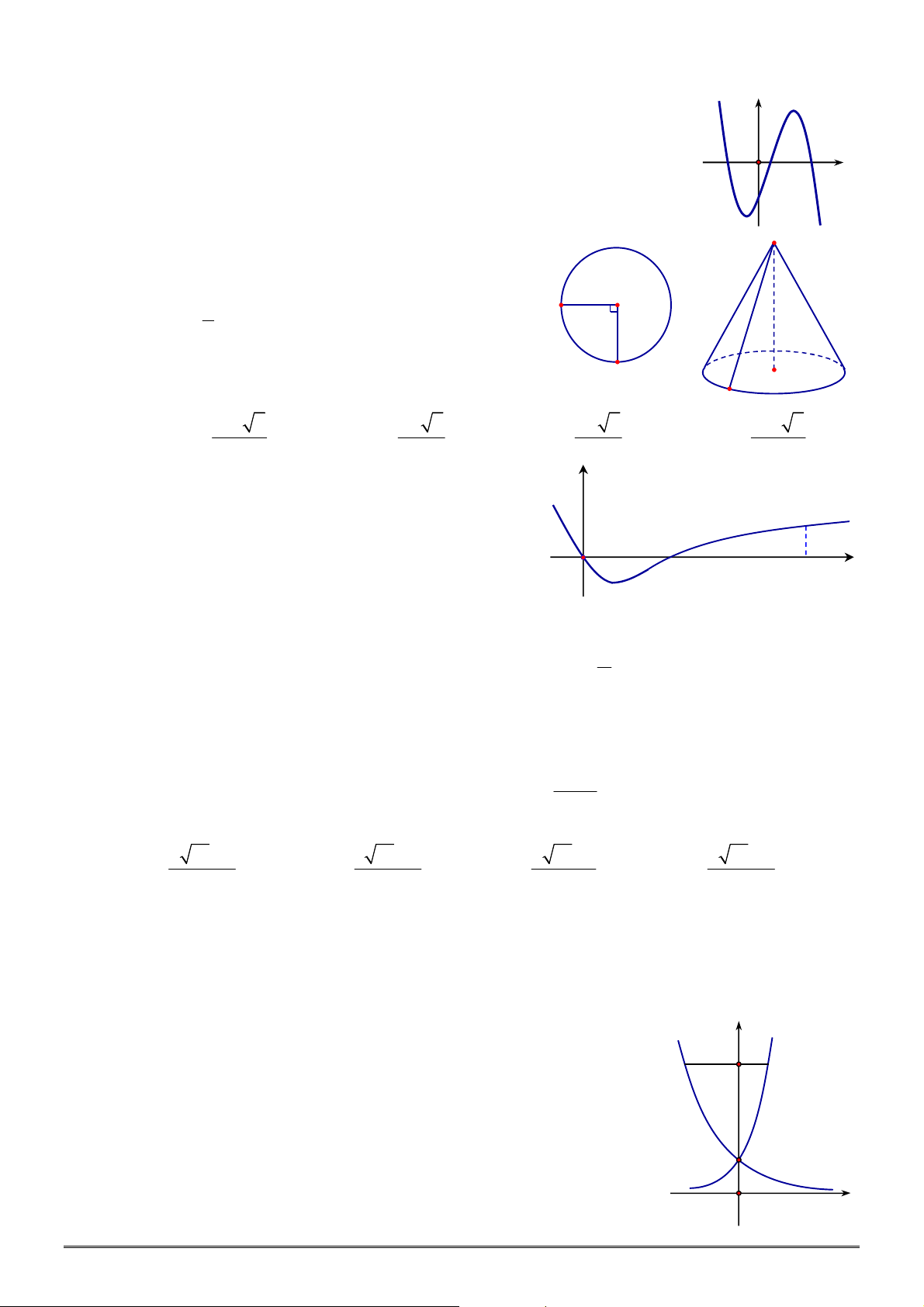
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/32 – Mã đề 101
Câu 40. [2D1-3] Cho hàm số
3 2
y ax bx cx d
có đồ thị hình bên. Hỏi khẳng định nào sau đây
đúng?
A.
0
a
,
0
b
,
0
c
,
0
d
.
B.
0
a
,
0
b
,
0
c
,
0
d
.
C.
0
a
,
0
b
,
0
c
,
0
d
.
D.
0
a
,
0
b
,
0
c
,
0
d
.
B. PHẦN RIÊNG ( 20%, gồm 10 câu )
1. Phần dành cho học sinh không chuyên
Câu 41. [2H2-3] Cho tấm tôn hình tròn có bán kính
6.
r
Cắt bỏ
1
4
hình tròn giữa 2 bán kính
OA
,
OB
, rồi
đem tấm tôn còn lại ghép hai bán kính đó lại để
được một hình nón (như hình vẽ). Tính thể tích
khối nón giới hạn bởi hình nón đó.
A.
81 7
4
. B.
9 7
8
. C.
9 7
2
. D.
81 7
8
.
Câu 42. [2D1-3] Cho hàm số
f x
có đạo hàm
f x
.
Biết đồ thị hàm số
y f x
là hình bên và
0 3 2 5
f f f f . Tìm giá trị lớn nhất
của hàm số
f x
trên đoạn
0;5
.
A.
5
f
. B.
3
f
. C.
0
f . D.
2
f .
Câu 43. [2D2-2] Tìm tất cả các giá trị của tham số
m
để hàm số
3 2
3 3 11
1
x mx mx
y
đồng biến trên
.
A.
; 0 1;m
. B.
0;1
m .
C.
0;1
m . D.
; 0 1;m
.
Câu 44. [2D2-4] Xét các số thực
a
,
b
dương thỏa mãn
2
1
log 2 3
ab
ab a b
a b
. Tìm giá trị nhỏ
nhất của biểu thức
2
P a b
.
A.
2 10 3
2
. B.
3 10 7
2
. C.
2 10 1
2
. D.
2 10 5
2
.
Câu 45. [2D2-2] Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức
0
. 1 4
t
Q t Q
, với
t
là khoảng thời gian tính bằng giờ và
0
Q
là dung lượng nạp tối đa (pin
đầy). Nếu điện thoại nạp pin từ lúc cạn pin ( dung lượng
0%
) thì sau bao lâu nạp được
90%
?
A.
1,5
giờ. B.
1,66
giờ. C.
2,66
giờ. D.
1,26
giờ.
Câu 46. [2D2-3] Cho hai số thực dương
a
,
b
khác
1.
Biết rằng bất kì
đường thẳng nào song song với trục hoành mà cắt các đường
x
y a
,
x
y b
và trục tung lần lượt tại
M
,
N
,
A
thì
3
AN AM
( hình vẽ bên). Hỏi khẳng định nào sau đây đúng?
A.
2
1
ab
.
B.
3
b a
.
C.
3
1
a b
.
D.
3
1
ab
.
O
x
y
A
B
6
O
B
A
O
y
x
O
2
5
O
x
y
N
M
A
x
y b
x
y a
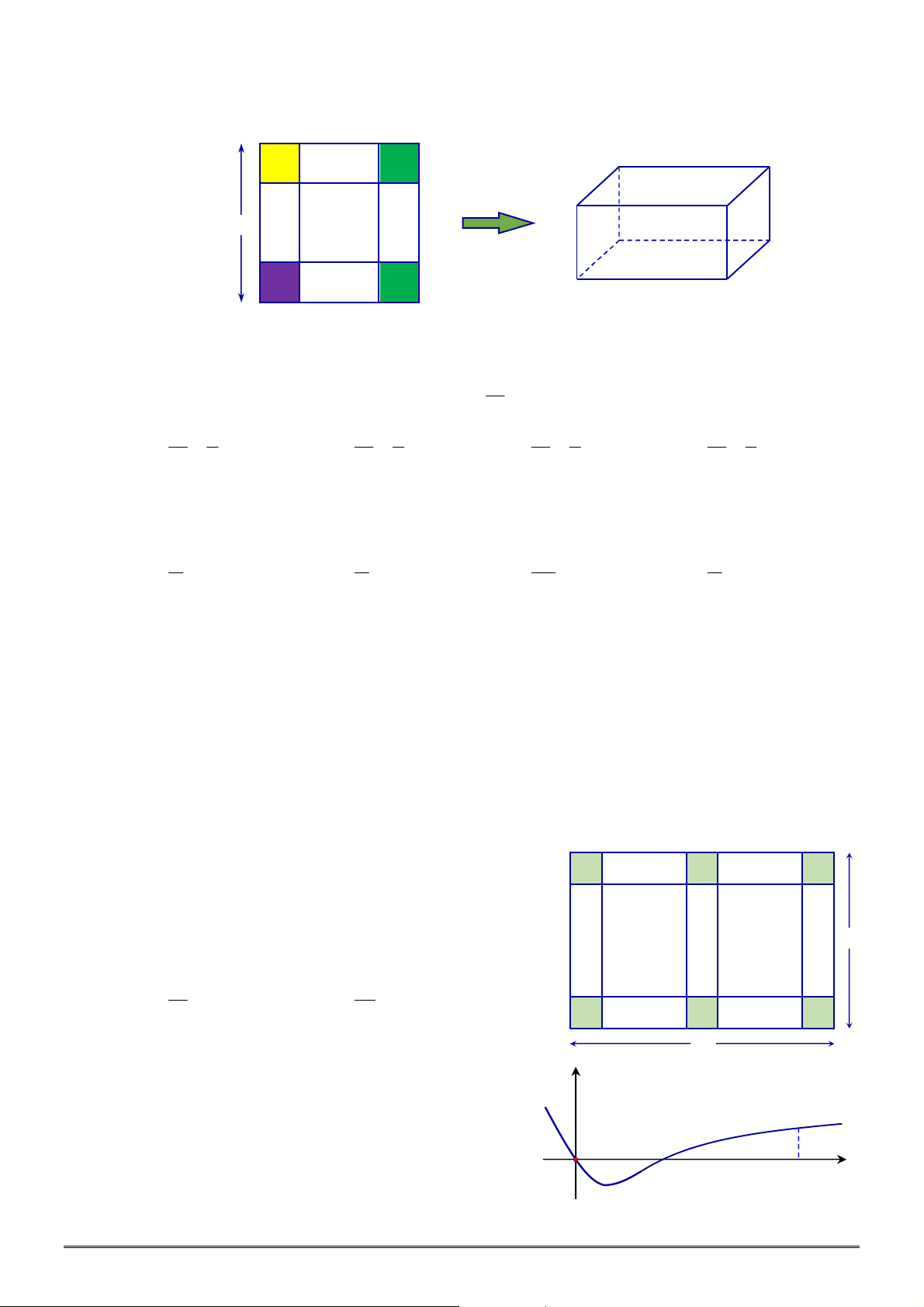
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/32 – Mã đề 101
Câu 47. [2D1-3] Từ một tấm tôn hình vuông cạnh
12
(mét) người ta cắt đi bốn góc bốn hình vuông
cạnh
x
(mét) rồi gấp tấm tôn còn lại để được một cái hộp không có nắp như hình vẽ dưới đây.
Tìm
x
để hộp nhận được có thể tích lớn nhất.
A.
4m.
B.
2m.
C.
2,5m.
D.
3m.
Câu 48. [2H1-3] Cho khối tứ diện có thể tích
.
V
Gọi
V
là thể tích khối đa diện có các đỉnh là trung
điểm các cạnh của khối tứ diện đó. Tính tỉ số
V
V
A.
1
2
V
V
B.
2
3
V
V
C.
1
4
V
V
D.
5
8
V
V
Câu 49. [2H1-2] Cho khối lăng trụ
.
ABC A B C
có thể tích
.
V
Gọi
M
là điểm bất kì trên đường thẳng
.
CC
Tính thể tích khối chóp
.
M ABB A
theo
.
V
A.
2
V
. B.
3
V
. C.
2
3
V
. D.
4
V
.
Câu 50. [2H2-1] Một hình trụ có bán kính đáy bằng
r
và có thiết diện qua trục là một hình vuông. Tính
diện tích xung quanh của hình trụ đó
A.
2
2 .
r
B.
2
.
r
C.
2
4 .
r
D.
2
8 .
r
2. Phần dành cho học sinh chuyên
Câu 51. [2D1-3] Đồ thị hàm số
3 2
3 9 1
y x x x
có hai điểm cực trị
A
,
B
. Điểm nào dưới đây
thuộc đường thẳng
.
AB
A.
1; 10 .
N B.
1;0 .
P C.
Q 0; 1 .
D.
1;10 .
M
Câu 52. [2D1-3] Từ một tấm tôn hình chữ nhật có chiều dài và
rộng là
60 cm
,
40 cm
. Người ta cắt đi
6
hình vuông
cạnh
(cm)
x rồi gấp tấm tôn còn lại để được một cái
hộp có nắp như hình vẽ dưới đây. Tìm
x
để hộp nhận
được có thể tích lớn nhất.
A.
10
cm .
3
B.
20
cm .
3
C.
4 cm .
D.
5 cm .
Câu 53. [2D1-3] Cho hàm số
f x
có đạo hàm
f x
.
Biết đồ thị hàm số
y f x
là hình bên và
0 3 2 5
f f f f . Tìm giá trị lớn nhất
của hàm số
f x
trên đoạn
0;5
.
A.
3
f
. B.
2
f . C.
5
f
. D.
0
f .
x
12
x
x
60
40
y
x
O
2
5
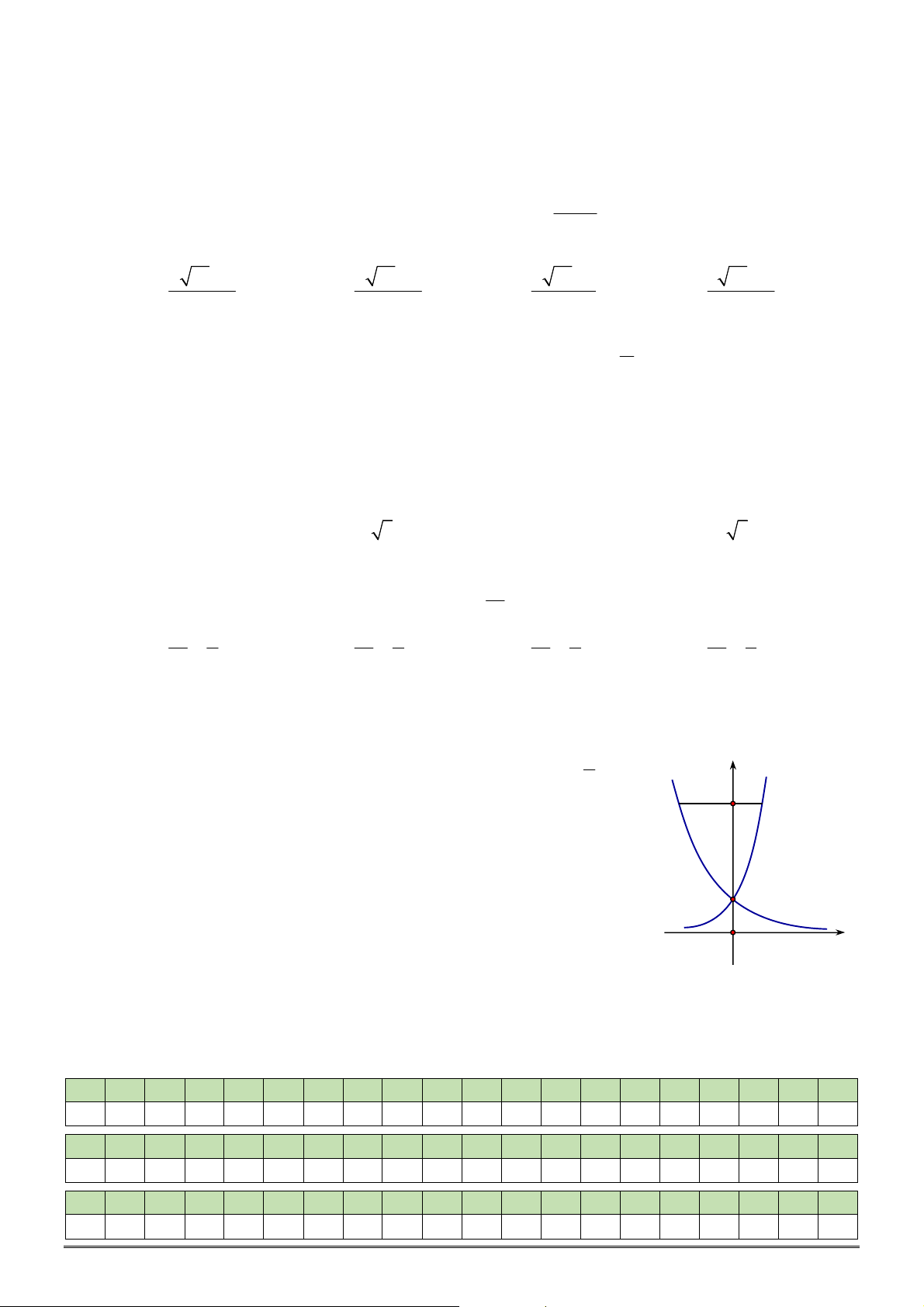
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/32 – Mã đề 101
Câu 54. [2D2-3] Ông A vay ngân hàng
300
triệu đồng để mua nhà theo phương thức trả góp với lãi
suất
0,5%
mỗi tháng. Nếu cuối mỗi tháng, bắt đầu từ tháng thứ nhất ông hoàn nợ cho ngân
hàng
5.500.000
đồng và chịu lãi số tiền chưa trả. Hỏi sau bao nhiêu tháng ông A sẽ trả hết số
tiền đã vay?
A. 64 tháng. B. 65 tháng. C. 63 tháng. D. 62 tháng.
Câu 55. [2D2-4] Xét các số thực
a
,
b
dương thỏa mãn
2
1
log 2 3
ab
ab a b
a b
. Tìm giá trị nhỏ
nhất của biểu thức
2
P a b
.
A.
2 10 3
2
B.
2 10 5
2
C.
2 10 1
2
D.
3 10 7
2
Câu 56. [2D2-3] Tìm tất cả các giá trị của tham số
m
để hàm số
3 2
3 3 11
1
x mx mx
y
đồng biến trên
khoảng
0; .
A.
0;1 .
m B.
0;1 .
m C.
0; .
D.
0; .
Câu 57. [2H2-3] Cho tứ diện đều
ABCD
có cạnh
6 .
a
Hình nón
N
có đỉnh
A
và đường tròn đáy là
đường tròn ngoại tiếp tam giác
.
BCD
Tính diện tích xung quanh của hình nón
N
.
A.
2
24 .
a
B.
2
12 3 .
a
C.
2
48 .
a
D.
2
24 3 .
a
Câu 58. [2H1-3] Cho khối tứ diện có thể tích
.
V
Gọi
V
là thể tích khối đa diện có các đỉnh là trung
điểm các cạnh của khối tứ diện đó. Tính tỉ số
V
V
A.
2
3
V
V
B.
1
2
V
V
C.
1
4
V
V
D.
5
8
V
V
Câu 59. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
1
y mx m
cắt đồ thị
hàm số
3 2
3 2
y x x x
tại ba điểm
A
,
B
,
C
phân biệt sao cho
.
AB BC
A.
( ;0] [4; ).
m
B.
5
; .
4
m
C.
2; .
m
D.
.
m
Câu 60. [2D2-3] Cho hai số thực dương
a
,
b
khác
1.
Biết rằng bất kì
đường thẳng nào song song với trục hoành mà cắt các đường
x
y a
,
x
y b
và trục tung lần lượt tại
M
,
N
,
A
thì
3
AN AM
(hình vẽ bên). Hỏi khẳng định nào sau đây đúng?
A.
3
b a
. B.
3
1
a b
. C.
2
1
ab
. D.
3
1
ab
.
----------HẾT----------
BẢNG ĐÁP ÁN THAM KHẢO
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
B B B C A D A C D B C D D B D B C B D A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
D B C C A D A D C C B A A A B D B A A C
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
D A C A B D B A C C A B C A A D B B C D
O
x
y
N
M
A
x
y b
x
y a
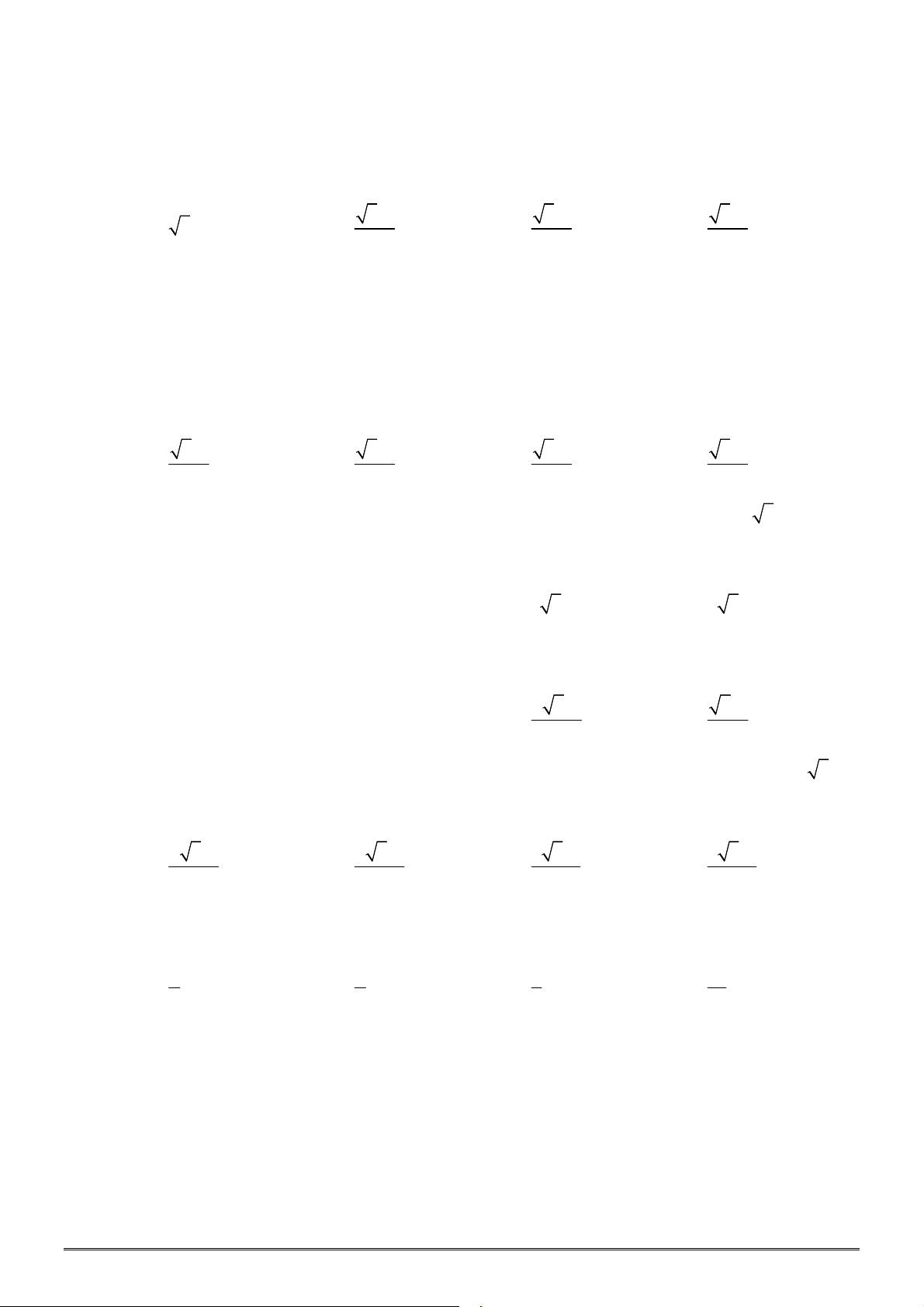
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/24
TRƯỜNG THPT
CHUYÊN NGOẠI NGỮ
NHÓM TOÁN 12
ĐỀ MINH HỌA THI THI HỌC KÌ I NĂM HỌC 2017-2018
MÔN: TOÁN – KHỐI 12
Thời gian làm bài: 90 phút
Câu 1. [2H1-2] Cho hình lăng trụ đứng
.
ABC A B C
có đáy là tam giác vuông cân,
AB AC a
,
2
A C a
. Thể tích của khối lăng trụ đó bằng
A.
3
3
a
. B.
3
3
6
a
. C.
3
3
3
a
. D.
3
3
2
a
.
Câu 2. [2H1-2] Hình hộp chữ nhật
.
ABCD A B C D
có diện tích các mặt
ABCD
,
ADD A
,
CDD C
lần lượt là
15
cm
2
,
20
cm
2
,
12
cm
2
. Thể tích khối hộp chữ nhật đó là
A.
30
cm
3
. B.
60
cm
3
. C.
45
cm
3
. D.
90
cm
3
.
Câu 3. [2H1-2] Cho lăng trụ
.
ABC A B C
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của
C
trên
A B C
là trung điểm của
B C
, góc giữa
CC
với
A B C
bằng
45
. Thể tích khối
lăng trụ
.
ABC A B C
là
A.
3
3
4
a
. B.
3
3
12
a
. C.
3
3
8
a
. D.
3
3
24
a
.
Câu 4. [2H1-2] Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật có
2
AB a
,
3
BC a
. Biết rằng
SAB
là tam giác cân tại
S
và
SAB
vuông góc với
ABCD
; góc giữa
SC
và
ABCD
bằng
60
. Thể tích khối chóp
.
S ABCD
là
A.
3
4
a
. B.
3
3
a
. C.
3
3 3
a
. D.
3
2 3
a
.
Câu 5. [2H1-2] Cho hình chóp
.
S ABC
có
SA
vuông góc với
ABC
và đáy là tam giác vuông tại
B
.
Biết
SA a
,
2
AB a
,
3
AC a
. Thể tích khối chóp
.
S ABC
là
A.
3
2
a
. B.
3
a
. C.
3
2 5
3
a
. D.
3
5
3
a
.
Câu 6. [2H1-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a
,
3
AD a
và
2
SA a
vuông góc với mặt đáy. Gọi
M
,
N
,
E
,
F
lần lượt là trung điểm của
SA
,
SB
,
SC
,
SD
. Thể tích của khối chóp cụt
.
ABCD MNEF
bằng
A.
3
7 3
12
a
. B.
3
7 3
6
a
. C.
3
5 3
8
a
. D.
3
5 3
4
a
.
Câu 7. [2H1-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
,
N
,
P
,
Q
lần
lượt là trung điểm của
SA
,
SB
,
SC
,
SD
. Tỉ lệ
. .
:
S MNPQ S ABCD
V V bằng
A.
1
2
. B.
1
4
. C.
1
8
. D.
1
16
.
Câu 8. [2D1-2] Trong tất cả các hình chữ nhật có cùng chu vi bằng
16
cm thì hình chữ nhật có diện
tích lớn nhất bằng
A.
36
cm
2
. B.
20
cm
2
. C.
16
cm
2
. D.
30
cm
2
.
Câu 9. [2D2-3] Ông
A
gửi
15
triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn
1
quý, với lãi
suất
1,65%
/quý. Hỏi sau bao nhiêu quý thì ông
A
có ít nhất
20
triệu đồng (bao gồm cả vốn
lẫn lãi) từ số vốn ban đầu? (Giả sử lãi suất không thay đổi).
A.
16
quý. B.
18
quý.
C.
17
quý. D.
19
quý.
12

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/24
Câu 10. [2H2-2] Cho hình chóp đều
.
S ABCD
có cạnh đáy bằng
2
a
, góc giữa mặt bên và mặt đáy bằng
45
. Khi đó bán kính mặt cầu ngoại tiếp hình chóp
.
S ABCD
bằng
A.
3
2
a
. B.
2
a
. C.
2
2
a
. D.
3
3
a
.
Câu 11. [2H2-2] Cho
1
S
,
2
S
là hai mặt cầu có bán kính lần lượt là
1
R
,
2
R
. Tính tỉ số diện tích của
mặt cầu
1
S
, và mặt cầu
2
S
biết
1 2
2
R R
.
A.
6
. B.
8
. C.
4
. D.
2
.
Câu 12. [2H2-2] Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
2
a
, đường cao bằng
a
. Thể
tích của khối nón đỉnh
S
, đường tròn đáy là đường tròn ngoại tiếp tam giác
ABC
bằng
A.
3
2
9
a
. B.
3
2
3
a
. C.
3
4
3
a
. D.
3
4
9
a
.
Câu 13. [2H2-2] Cho hình vuông
ABCD
cạnh
4 cm
. Gọi
M
,
N
lần lượt là trung điểm của
AD
,
BC
.
Cho hình vuông đó quay xung quanh trục
MN
ta được khối trụ có thể có thể tích bằng bao
nhiêu?
A.
3
8
cm
3
. B.
3
16
cm
3
. C.
3
8 cm
. D.
3
16 cm
.
Câu 14. [2H2-2] Một khối lập phương có thể tích
3
8 cm
. Khi đó thể tích khối cầu ngoại tiếp hình lập
phương đó bằng?
A.
3
4 3 cm
. B.
3
2 3 cm
. C.
3
8 3 cm
. D.
3
6 3 cm
.
Câu 15. [1H3-2] Cho tứ diện
ABCD
có
AB
,
AC
,
AD
đôi một vuông góc. Tính khoảng cách từ
A
đến
BCD
biết
2 cm
AB AC
,
3 cm
AD
.
A.
3 11
cm
2
. B.
3 2
cm
11
. C.
3 22
cm
11
. D.
3 11
cm
11
.
Câu 16. [1H3-2] Cho hình hộp chữ nhật
.
ABCD A B C D
có
4 cm
AB
,
3 cm
AD
và đường chéo
A C
tạo với mặt phẳng
ABCD
góc
60
. Gọi
M
là trung điểm của
BC
. Khoảng cách giữa
AM
và
A D
là
A.
5 cm
. B.
5 3 cm
. C.
4 cm
. D.
4 3 cm
.
Câu 17. [1H3-2] Cho hình chóp đều
.
S ABCD
có đường cao bằng
a
và thể tích bằng
3
4
3
a
. Tính góc
giữa mặt bên và mặt đáy.
A.
75
. B.
60
. C.
45
. D.
30
.
Câu 18. [2D2-2] Chọn khẳng định sai?
A.
log 0 0 1
x x
. B.
ln 0 1
x x
.
C.
2 2
3 3
log log 0
a b a b
. D.
2 2
log log 0
a b a b
.
Câu 19. [2D2-2] Số nghiệm của phương trình
2
2 9 5
2 1
x x
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 20. [1D4-2] Hàm số
2
ln 1
y x x
có đạo hàm bằng
A.
2
1
1
x x
. B.
2
1
1
x
. C.
2
1
x
x x
. D.
2
1
x
x
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/24
Câu 21. [2D2-3] Đặt
2 3
log 5 , log 2
a b
. Biểu diễn
12
log 100
theo
,
a b
.
A.
2 1
2 1
b a
b
. B.
2 1
2 1
a
b
. C.
2 1
2
a
b
. D.
2 1
2
b a
b
.
Câu 22. [2D2-2] Rút gọn
3
2
log
log
9 4
a
b
được
A.
3 2
a b
. B.
9 4
a b
. C.
2 2
a b
. D.
a b
.
Câu 23. [2D2-3] Tập xác định của hàm số
1
3
log 3 1
y x
là
A.
3;
. B.
10
3;
3
. C.
10
3;
3
. D.
10
;
3
.
Câu 24. [2D2-2] Tổng tất cả các nghiệm của phương trình
2
2
log 1 3
x
là
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 25. [2D2-2] Phương trình
4 3.6 2.9 0
x x x
có hai nghiệm
0
x
và
2
1
x
y
x
, với
0
a b
.
Khi đó
b
a
là
A.
2
. B.
3
. C.
4
. D.
3
2
.
Câu 26. [2D2-2] Phương trình
2017
log 2016 2017
x x
có bao nhiêu nghiệm?
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 27. [2D2-2] Cho
,
a b
là các số dương và
1
a
. Chọn khẳng định đúng.
A.
2
3 2
3
log 1 log
2
a
a
a b b
. B.
2
3 2
1
log 3 log
2
a
a
a b b
.
C.
2
3 2
3
log log
2
a
a
a b b
. D.
2
3 2
3
log log
2
a
a
a b b
.
Câu 28. [2D2-2] Cho hàm số
e
x
y x
. Chọn khẳng định sai.
A. Hàm số đồng biến trên khoảng
0;
. B. Hàm số nghịch biến trên khoảng
; 1
.
C.
min 0
y
. D. Hàm số đạt cực tiểu tại
1
x
.
Câu 29. [2D2-2] Cho hàm số
1
.
2
x
x
y
Khi đó
1
y
bằng
A.
1
2
. B.
1
4
. C.
0
. D.
4
.
Câu 30. [2D2-3] Số nghiệm của phương trình
3 3 3
log log log
2 7 5
x x x
là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 31. [2D1-1] Hàm số nào sau đây đồng biến trên
?
A.
1
x
y
x
. B.
2
3 1
y x x
. C.
3 2
3 3 1
y x x x
. D.
4 2
2 1
y x x
.
Câu 32. [2D1-1] Chọn khẳng định sai?
A. Đồ thị hàm số bậc ba có tâm đối xứng.
B. Đồ thị hàm số
ax b
y
mx n
,
0,
m an bm
có tiệm cận ngang.
C. Đồ thị hàm số bậc ba có tiệm cận đứng.
D. Đồ thị hàm số bậc bốn luôn có điểm cực trị.
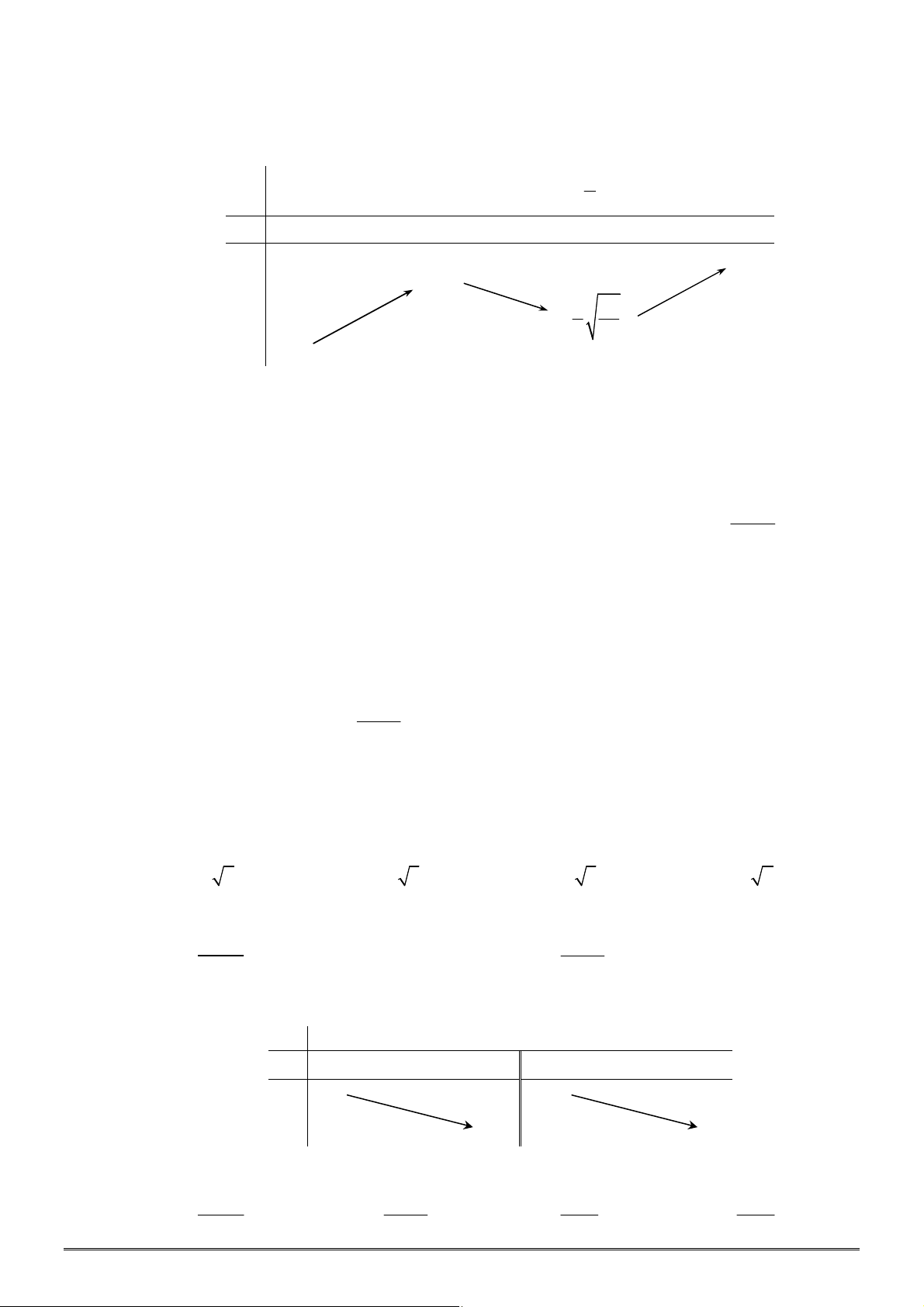
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/24
Câu 33. [2D1-2] Giá trị cực đại của hàm số
4 2
3 3
y x x
bằng
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 34. [2D1-2] Cho hàm số
y f x
xác định, liên tục trên
và có bảng biến thiên như sau:
Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số cắt trục hoành tại ba điểm phân biệt.
B. Hàm số có đúng một cực trị.
C. Hàm số có giá trị lớn nhất bằng
0
.
D. Hàm số đồng biến trên khoảng
1; 2017
.
Câu 35. [2D1-2] Gọi
M
,
m
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3
1
x
y
x
trên đoạn
2; 4
. Khi đó tổng
M m
bằng
A.
7
. B.
13
. C.
14
. D.
6
.
Câu 36. [2D1-2] Tiếp tuyến của đồ thị hàm số
3
2
y x x
tại điểm
0; 2
M có phương trình dạng
y ax b
. Khi đó giá trị của hệ số
b
là
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 37. [2D1-2] Đồ thị hàm số
2 1
2
x
y
x
cắt đường thẳng
3 2
y x
tại điểm duy nhất
A
. Khi đó
tung độ của
A
là
A.
2
. B.
1
. C.
1
. D.
2
.
Câu 38. [2D1-3] Tìm tất cả các giá trị của
m
để đồ thị hàm số
4 2 2
2 1
y x m x
có ba điểm cực trị tạo
thành một tam giác đều.
A.
3
6
m . B.
6
3
m
. C.
3
3
m
. D.
3
2
m
.
Câu 39. [2D1-2] Đồ thị hàm số nào dưới đây có tiệm cận ngang?
A.
2
2
1
x
y
x
. B.
3
2
y x x
. C.
2 1
2
x
y
x
. D.
2
2 2
y x x
.
Câu 40. [2D1-1] Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số
y f x
là hàm số nào sau đây?
A.
2 3
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2
1
x
y
x
. D.
2
1
x
y
x
.
x
0
2
5
y
||
0
y
0
3
3 4
5 25
x
1
y
–
–
y
2
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/24
Câu 41. [2D1-2] Đồ thị hàm số
3 2
3 2
y x x
có tâm đối xứng là điểm
I
. Khi đó hoành độ của
I
là
A.
2
. B.
0
. C.
2
. D.
1
.
Câu 42. [2D1-3] Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
3 1
x x
với
0;3
x . Mệnh đề
nào sau đây sai?
A.
0;3
min 1
y
. B.
0;3
max 19
y
.
C.
0;3
min 0
y
. D. Hàm số đạt giá trị lớn nhất tại
3
x
.
Câu 43. [2D1-2] Có bao nhiêu giá trị nguyên của
m
để phương trình
3
3 1
x x m
có ba nghiệm phân
biệt.
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 44. [2D1-3] Tìm
m
để bất phương trình
2
3 1
x m x
có nghiệm?
A.
1
m
. B.
10
m . C.
1
m
. D.
1 10
m .
Câu 45. [2D1-2] Cho hàm số
2
1
x
y
x
có đồ thị
C
và
1;1
I . Khi đó có bao nhiêu điểm thuộc đồ thị
C
sao cho khoảng cách tới
I
bằng
10
.
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 46. [2D1-3] Phương trình
4 2
2 3
x x k
có
6
nghiệm phân biệt khi và chỉ khi
A.
3 4
k
. B.
0 3
k
. C.
3
k
. D.
4
k
.
Câu 47. [2D1-3] Tìm
m
để hàm số
3 2 2
2 2
2 3 1
3 3
y x mx m x
có hai điểm cực trị
1
x
,
2
x
thỏa
mãn
1 2 1 2
2 0
x x x x
.
A.
1
m
;
1
3
m
. B.
1
m
. C.
2
m
,
1
m
. D.
2
m
.
Câu 48. [2D1-1] Hàm số
3
3 2
y x x
.
A. Đồng biến trên khoảng
0;
. B. Nghịch biến trên khoảng
1;1
.
C. Đồng biến trên khoảng
;1
. D. Nghịch biến trên khoảng
0;2
.
Câu 49. [2D2-1] Cho hàm số
y f x
có đồ thị
C
như hình vẽ sau:
Khẳng định nào sau đây sai?
A. Hàm số nghịch biến trên
.
B. Đồ thị hàm số có một đường tiệm cận.
C. Phương trình của đồ thị
C
có dạng
x
y a
với
1
a
.
D. Đồ thị hàm số cắt trục tung.
Câu 50. [2D2-2] Phương trình
2
3 5
3
2
5
4 2 log
2 6
x x x
x
x x
có hai nghiệm là
1
x
,
2
x
. Khi đó tổng
1 2
x x
bằng
A.
5
. B.
5
2
. C.
5
. D.
5
2
.
----------HẾT----------
O
x
y
1
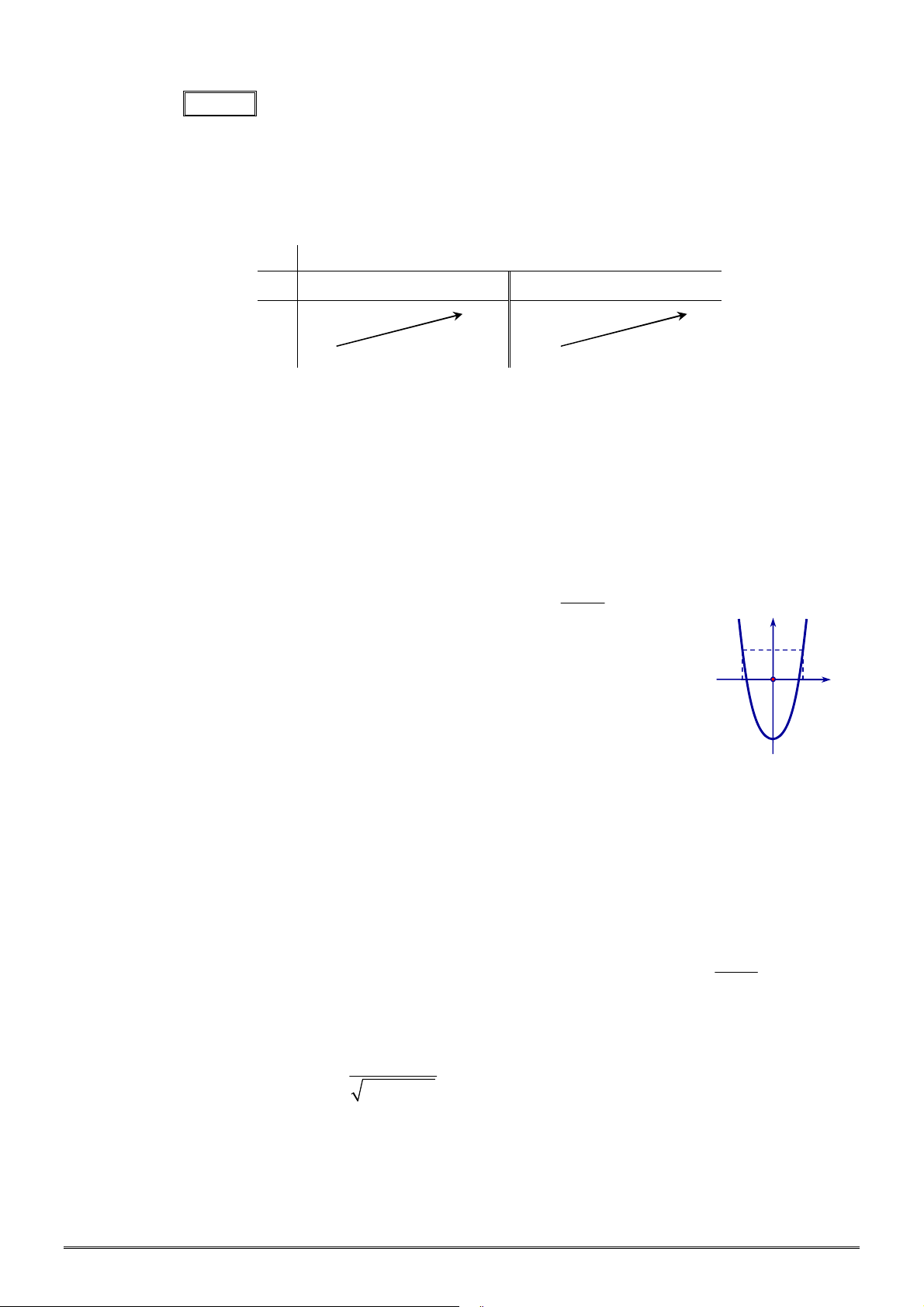
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/27
TRƯỜNG THPT KIM LIÊN – HÀ NỘI ĐỀ ÔN TẬP HỌC KỲ I NĂM HỌC 2017 – 2018
ĐỀ SỐ 1 MÔN TOÁN - LỚP 12
------- ------------------
Câu 1. [2D1-2] Đồ thị hàm số
4 2
20 2016 11
y x x
cắt trục hoành tại mấy điểm?
A.
4
. B.
3
. C.
2
. D.
0
.
Câu 2. [2D1-2] Cho hàm số
y f x
xác định, liên tục trên tập
\ 1
và có bảng biến thiên:
Khẳng định nào dưới đây là sai?
A. Hàm số không có cực trị.
B. Đồ thị hàm số và đường thẳng
25
y
có
1
điểm chung.
C. Đồ thị hàm số có tiệm cận ngang là đường thẳng
2
y
.
D. Hàm số đồng biến trên tập
\ 1
.
Câu 3. [2D1-2] Hàm số nào sau đây nghịch biến trên
?
A.
3 2
3 2
y x x
. B.
3 2
2 2
y x x x
.
C.
4 2
2 2
y x x
. D.
3
2 1
x
y
x
.
Câu 4. [2D1-3] Đường cong trong hình dưới đây là đồ thị của hàm
số nào được liệt kê sau đây?
A.
4 2
2 2
y f x x x
. B.
2
2
y f x x
.
C.
4 2
2 2
y f x x x
. D.
2
2
y f x x
.
Câu 5. [2D1-2] Số điểm cực trị của hàm số
4 3
2 3
y x x
là
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 6. [1D1-2] Giá trị nhỏ nhất của hàm số
3sin5 4cos5
y x x
là
A.
3
. B.
4
. C.
5
. D.
3
.
Câu 7. [2D1-2] Điểm cực đại của đồ thị hàm số
3
12 12
y x x
là
A.
2; 4
. B.
2;28
. C.
4;28
. D.
2;2
.
Câu 8. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
3 1
x
y
x m
có tiệm cận
đứng nằm bên trái trục
Oy
.
A.
0
m
. B.
0
m
. C.
0
m
. D. Đáp án khác.
Câu 9. [2D1-2] Đồ thị hàm số
2
11
2016
x
y
x
có bao nhiêu đường tiệm cận ngang?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 10. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
4 2 2
2016
y x m m x
có
3
điểm cực trị?
A.
1
m
hoặc
0
m
. B.
0 1
m
. C.
1 0
m
. D.
0
m
hoặc
1
m
.
x
1
y
+ +
y
2
2
O
x
y
1
1
2
1
13

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/27
Câu 11. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
1
mx
y
x m
đồng biến trên
khoảng
1;
.
A.
1 1
m
. B.
1
m
. C.
\ 1;1
m
. D.
1
m
.
Câu 12. [2D1-2] Cho hàm số
2
2
3 2
2 3
x x
y
x x
khẳng định nào sau đây sai?
A. Đồ thị hàm số có hai tiệm cận đứng.
B. Đồ thị hàm số có ba đường tiệm cận.
C. Đồ thị hàm số có tiệm cận ngang là đường thẳng
2
y
.
D. Đồ thị hàm số có tiệm cận ngang là đường thẳng
1
2
y
.
Câu 13. [2D1-2] Cho hàm số
4 2
2 2017
f x x x , khẳng định nào sau đây sai?
A.
f x
nghịch biến trên
0;1
. B.
f x
đồng biến trên
0;
.
C.
f x
đồng biến trên
1;0
. D.
f x
nghịch biến trên
; 1
.
Câu 14. [2D1-2] Giá trị nhỏ nhất của hàm số
1
y x
x
bằng bao nhiêu?
A.
2
. B.
0
. C.
2
. D.
1
.
Câu 15. [2D1-2] Cho hàm số
3
3sin 4sin
y x x
. Giá trị lớn nhất của hàm số trên khoảng
;
2 2
bằng
A.
1
. B.
1
. C.
7
. D.
3
.
Câu 16. [2D1-2] Tìm
m
để hàm số
2
2017
y x m x đồng biến trên khoảng
1;2
.
A.
1
m
. B.
3
m
. C.
1
m
. D.
2
m
.
Câu 17. [1D5-3] Một chất điểm chuyển động có phương trình
2 3
6 9 1
s s t t t t
. Thời điểm
t
(giây) tại đó vận tốc
m/s
v của chuyển động đạt giá trị lớn nhất là
A.
3
t
. B.
1
t
. C.
2
t
. D.
4
t
.
Câu 18. [2D1-2] Hàm số
3 2 2
1
1 1
3
y x mx m m x
đạt cực trị tại điểm
1
x
khi
A.
1
m
hoặc
2
m
. B.
1
m
. C.
2
m
. D.
m
.
Câu 19. [2D1-2] Phương trình tiếp tuyến với đồ thị hàm số
4 2
2 1
y x x
tại điểm cực tiểu của đồ thị
hàm số là
A.
1 0
y
. B.
0
y
. C.
1 0
x y
. D.
y x
.
Câu 20. [1D5-3] Cho hàm số
3
3 2
y x x
. Có bao nhiêu tiếp tuyến của đồ thị hàm số song song với
trục hoành?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 21. [2D1-2] Cho hàm số
y f x
có đồ thị như hình vẽ bên.
Khẳng định nào dưới đây là đúng?
A.
max 4
f x
.
B. Hàm số đồng biến trên khoảng
;1
.
C. Giá trị cực tiểu của hàm số bằng
1
.
D.
2;1
min 0
f x
O
x
y
2
2
1
4
1
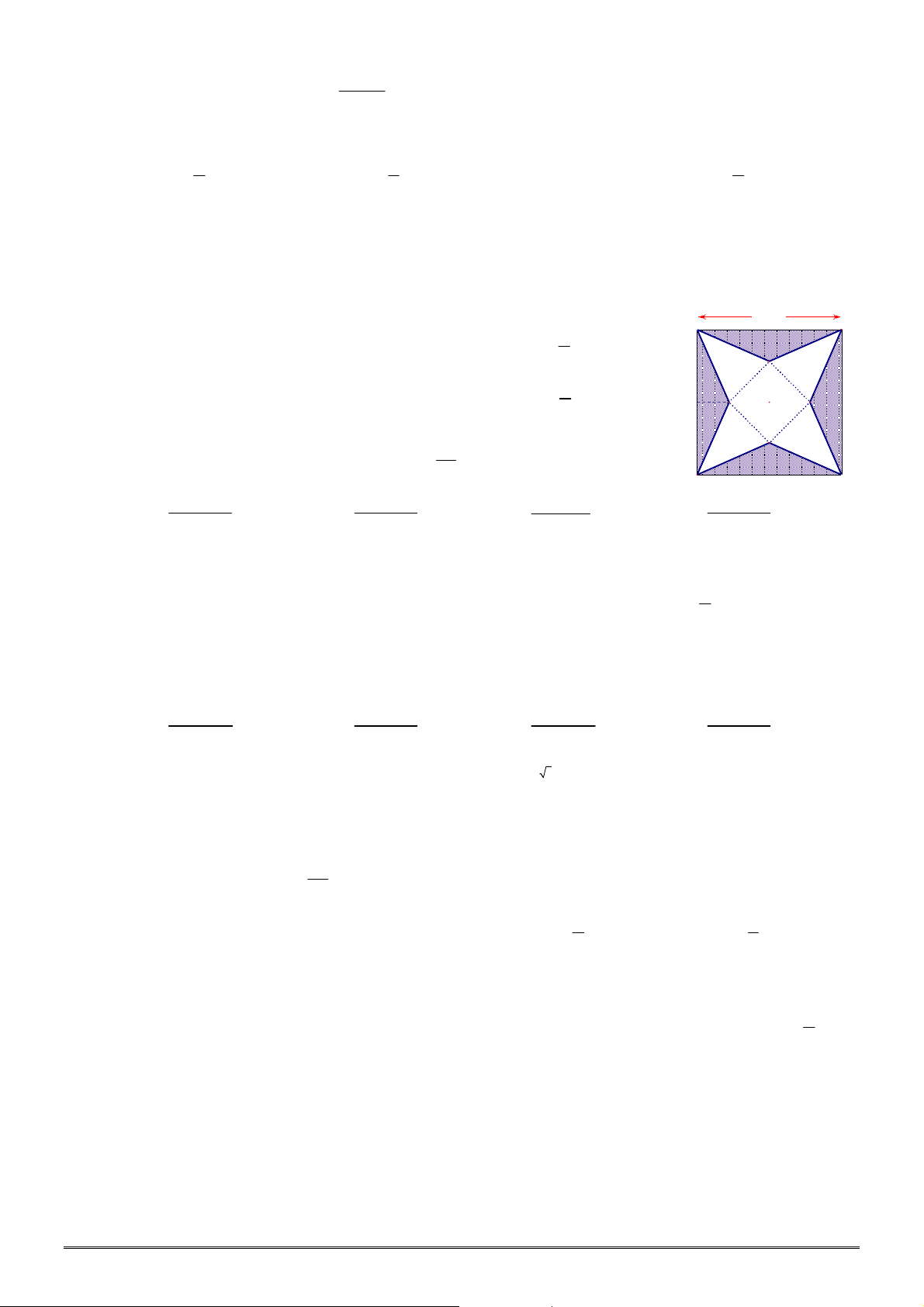
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/27
Câu 22. [2D1-4] Cho hàm số
2 3
2
x
y
x
có đồ thị
C
. Tìm trên
C
những điểm sao cho tiếp tuyến
với
C
tại
M
cắt hai tiệm cận của
C
tại
A
,
B
sao cho
AB
ngắn nhất.
A.
3
0; , 1; 1
2
. B.
5
1; , 3;3
3
. C.
3;3 , 1;1
. D.
5
4; ; 3;3
2
.
Câu 23. [2H1-3] Cho một tấm nhôm hình vuông cạnh
10cm
, tại bốn cạnh tấm nhôm người ta cắt ra
bốn tam giác cân bằng nhau, độ dài đường cao xuất phát từ đỉnh của mỗi tam giác cân bằng
cm
x . Sau đó gập tấm nhôm theo đường chấm chấm (xem hình vẽ bên) để được một khối
chóp tứ giác đều. Tìm
x
để khối chóp nhận được có thể tích lớn nhất.
A.
2
x
. B.
5
2
x
.
C.
1
x
. D.
1
2
x
.
Câu 24. [2D2-2] Tính đạo hàm của hàm số
2
x
x
y
.
A.
1 ln2
4
x
x
. B.
1 ln2
4
x
x
. C.
1 ln 2
2
x
x
. D.
1 ln2
2
x
x
.
Câu 25. [2D2-3] Cho các số thực dương
x
,
y
thỏa mãn
2 2
4 12
x y xy
. Khẳng định nào sau đây đúng?
A.
log 2 8 log log
x y x y
. B.
1
log 2 2log2 log log
2
x y x y
.
C.
log 2log log12 log
x y xy
. D.
2 2
log log4 log12
x y xy
.
Câu 26. [2D2-3] Cho
27
log 5
a
,
8
log 7
b
,
2
log 3
c
. Hãy biểu diễn
12
log 35
theo
a
,
b
và
c
.
A.
3 2
2
b ac
c
. B.
3 3
2
b ac
c
. C.
3 2
3
b ac
c
. D.
3 3
1
b ac
c
.
Câu 27. [2D2-2] Tìm tập xác định
D
của hàm số
3
2 3
1
y x x
.
A.
1;1
D . B.
0;1
D . C.
\ 1;1
D
. D.
1;1 \ 0
D .
Câu 28. [2D2-2] Tìm
x
biết
1
2
1
125
25
x
x
.
A.
1
x
. B.
4
x
. C.
1
4
x
. D.
1
8
x
.
Câu 29. [2D2-3] Hàm số
2
2 1
log
a a
y x
nghịch biến trên khoảng
0;
khi
A.
1
a
và
0 2
a
. B.
1
a
. C.
0
a
. D.
1
a
và
1
2
a
.
Câu 30. [2D2-2] Hàm số
2
e
x
y x
nghịch biến trên khoảng nào trong các phương án sau.
A.
; 2
. B.
2;0
. C.
1;
. D.
;1
.
Câu 31. [2D2-3] Tìm giá trị nhỏ nhất của hàm số
1 3
2 2
x x
f x
.
A.
4
. B.
6
. C.
2
. D.
1
.
x
10 cm

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/27
Câu 32. [2D2-2] Giá trị lớn nhất của hàm số
2
ln ln 1
y x x
trên đoạn
1
;2
2
đạt tại
A.
1
x
. B.
1
2
x
. C.
3
2
x
. D.
3
4
.
Câu 33. [2D2-3] Tính
1 2
.
x x
biết
1
x
,
2
x
thỏa mãn
16
log 2 log 0
x
x
.
A.
1
. B.
1
. C.
0
. D.
4
.
Câu 34. [2D2-2] Tìm
x
biết
2
5 4
1
4
2
x x
.
A.
5 17
2
x
hoặc
5 17
2
x
. B.
5 17 5 17
2 2
x
.
C.
3
x
hoặc
2
x
. D.
2 3
x
.
Câu 35. [2D2-3] Dân số thế được tính theo công thức
.e
ni
S A
trong đó
A
là dân số của năm lấy làm
mốc tính,
S
là dân số sau
n
năm,
i
là tỉ lệ tăn dân số hàng năm. Cho biết năm
2003
Việt Nam
có khoảng
80.902.400
người và tỉ lệ tăng dân số là
1,47%
một năm. Như vậy, nếu tỉ lệ tăng dân
số hàng năm không đổi thì đến năm
2017
số dân của Việt Nam sẽ gần với số nào nhất sau đây?
A.
99.389.200
. B.
99.386.600
. C.
100.861.100
. D.
99.251.200
.
Câu 36. [2H1-1] Có tất cả bao nhiêu loại khối đa diện đều.
A.
3
. B.
5
. C.
6
. D.
7
.
Câu 37. [2D1-4] Cho hàm số
3 2
f x x ax bx c
và giả sử
A
,
B
là hai điểm cực trị của đồ thị
hàm số. Giả sử đường thẳng
AB
đi qua gốc tọa độ. Tìm giá trị nhỏ nhất của
P abc ab c
.
A.
16
25
. B.
1
. C.
9
. D.
25
9
.
Câu 38. [2H1-2] Cho khối hộp
.
ABCD A B C D
có thể tích
V
. Khi đó thể tích khối tứ diện
AB CD
bằng
A.
2
3
V
. B.
3
4
V
. C.
3
V
. D.
6
V
.
Câu 39. [2H2-3] Mặt cầu tâm
O
bán kính
17dm
R
. Mặt phẳng
P
cắt mặt cầu sao cho giao tuyến đi qua
ba điểm
A
,
B
,
C
mà
18dm
AB
,
24dm
BC
,
30dm
CA
. Tính khoảng cách từ
O
đến
P
.
A.
14dm
. B.
7dm
. C.
8dm
. D.
16dm
.
Câu 40. [2H1-3] Để chế tác đồ vật trang trí trong nhà từ khối đá có hình dạng một tứ diện đều cạnh
8dm
.
Ở bốn đỉnh tứ diện, người ta cần cắt đi các tứ diện đều bằng nhau có cạnh bằng
x
, sao cho phần
còn lại của khối đá sau khi cắt có thể tích bằng
3
4
thể tích khối đá ban đầu. Giá trị của
x
là
A.
3 2 dm
. B.
3
3 4 dm
. C.
2 2 dm
. D.
3
2 4 dm
.
Câu 41. [2H1-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt
phẳng
ABCD
, góc tạo bởi đường thẳng
SD
và mặt phẳng
ABCD
bằng
45
. Thể tích khối
chóp
.
S ABCD
bằng.
A.
3
a
. B.
3
2
3
a
. C.
3
3
a
. D.
3
2
a
.
Câu 42. [2H2-2] Cho hình hộp chữ nhật có kích thước
3
,
4
,
5
. Bán kính mặt cầu ngoại tiếp hình hộp là
A.
5 2
. B.
5 2
2
. C.
2 5
. D.
5
.
Câu 43. [2H2-3] Cho hình chóp tứ giác đều
.
S ABCD
có
2
AC a
, góc giữa cạnh bên và mặt đáy bằng
60
. Diện tích mặt cầu ngoại tiếp hình chóp bằng.
A.
2
16
3
a
. B.
2
8
3
a
. C.
2
4
3
a
. D.
2
2
3
a
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/27
Câu 44. [2H1-2] Cho lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
2,
AB a
3
BC a
. Góc giữa đường thẳng
A B
và mặt đáy là
60
. Tính theo
a
thể tích khối lăng trụ
.
ABC A B C
.
A.
3
2 3
a . B.
3
3 3
a . C.
3
3
3
a
. D.
3
3
a .
Câu 45. [2H2-1] Cho mặt cầu
S
có tâm
I
, bán kính
5
và mặt phẳng
P
cắt
S
theo một đường
tròn
C
có bán kính
3
r
. Kết luận nào sau đây sai?
A. Tâm của
C
là hình chiếu vuông góc của
I
trên
P
.
B. Khoảng cách từ
I
đến
P
bằng
4
.
C.
C
là giao tuyến của
S
và
P
.
D.
C
là đường tròn lớn của mặt cầu.
Câu 46. [2H1-3] Cho hình chóp .
S ABC
có đáy
ABC
là tam giác vuông tại
A
, với
2
a
AC ,
BC a
.
Hai mặt phẳng
SAB
và
SAC
cùng tạo với mặt đáy
ABC
góc
60
. Tính khoảng cách từ
điểm
B
tới mặt phẳng
SAC
, biết rằng mặt phẳng
SBC
vuông góc với đáy
ABC
.
A.
3
4
a
.
B.
3
4
a
. C.
4
5
a
. D.
3
a
.
Câu 47. [2H2-3] Một khối cầu thủy tinh có bán kính bằng
4dm
. Người
ta muốn cắt bỏ một chỏm cầu có diện tích mặt cắt là
2
15 dm
để lấy phần còn lại làm bể nuôi cá. Hỏi thể tích
nước tối đa mà bể này chứa là bao nhiêu?
A.
3
175
dm
3
. B.
3
175
dm
4
. C.
3
125
dm
3
. D.
3
175
dm
4
.
Câu 48. [2H2-2] Cho hình chóp .
S ABC
có đáy là tam giác vuông cân tại
B
,
AB a
. Cạnh bên
SA
vuông góc mặt phẳng
ABC
và
SC
hợp với đáy một góc bằng
60
. Thể tích khối cầu ngoại
tiếp hình chóp .
S ABC
.
A.
3
4 2
3
a
. B.
3
8 2
3
a
. C.
3
5 2
3
a
. D.
3
2 2
3
a
.
Câu 49. [2H2-3] Cho hình chóp .
S ABCD
có đáy là hình thang cân
ABCD
với
2
AB a
,
BC CD DA a
và
SA ABCD
. Một mặt phẳng qua
A
vuông góc với
SB
và cắt
,
SB
SC
,
SD
lần lượt tại
M
,
N
,
P
. Tính đường kính khối cầu ngoại tiếp khối đa diện
ABCDMNP
.
A.
3
a
. B.
2
a
. C.
a
. D.
3
2
a
.
Câu 50. [2H2-2] Cho tứ diện
ABCD
có
O
là trung điểm của đoạn thẳng nối trung điểm của hai cạnh
đối diện. Tập hợp các điểm
M
trong không gian thỏa mãn hệ thức
MA MB MC MD a
(với
0
a không đổi) là
A. Mặt cầu tâm
O
bán kính
3
a
r
. B. Mặt cầu tâm
O
bán kính
2
a
r
.
C. Mặt cầu tâm
O
bán kính
r a
. D. Mặt cầu tâm
O
bán kính
4
a
r
.
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/24
TRƯỜNG THPT KIM LIÊN – HÀ NỘI ĐỀ ÔN TẬP HỌC KỲ I NĂM HỌC 2017 – 2018
ĐỀ SỐ 2 MÔN TOÁN - LỚP 12
------- ------------------
Câu 1. [2D1-1] Cho hàm số
4 2
5 2
y x x
. Hàm số nghịch biến trên khoảng nào?
A.
0;
. B.
1;1
. C.
0;1
. D.
;0
.
Câu 2. [2D1-1] Cho hàm số
2 1
1
x
y
x
có đạo hàm
2
3
0, 1
1
y x
x
. Có hai học sinh phát biểu
như sau:
Học sinh
X
: “ Hàm số luôn nghịch biến trên tập xác định”
Học sinh
Y
: “ Hàm số luôn nghịch biến trên từng khoảng xác định”.
Phát biểu nào đúng, phát biểu nào sai?
A.
X
đúng và
Y
sai. B.
X
sai và
Y
đúng. C.
X
và
Y
đều đúng. D.
X
và
Y
đều sai.
Câu 3. [2D1-2] Với các giá trị nào của
m
thì hàm số
3 2
1
2 1
3 2
m
y x x x
luôn đồng biến trên
?
A.
2 2
m
. B.
2 2
m . C. Không có
m
. D.
2
m
.
Câu 4. [2D1-2] Tìm các giá trị của
m
để hàm số
1 2 2
m x m
y
x m
nghịch biến trên khoảng
1;
?
A.
1
m
. B.
2
m
. C.
1
m
hoặc
2
m
. D.
1 2
m
.
Câu 5. [2D1-1] Trong các khẳng định sau về hàm số
4 2
1 1
x 3
4 2
y x
. Khẳng định nào đúng:
A. Hàm số có điểm cực tiểu là
0
x
. B. Hàm số có hai điểm cực đại là
1
x
.
C. Cả
A
và
B
đều đúng. D. Có
A
đúng,
B
sai.
Câu 6. [2D1-2] Cho hàm số
3
2
y x x
. Hệ thức liên hệ giữa giá trị cực đại
Đ
C
y
và giá trị cực tiểu
CT
y
là
A. 2
CT C
Đ
y y
. B.
2
C C
Đ
T
y y
. C.
CT C
Đ
y y
. D.
Đ
CT C
y y
.
Câu 7. [2D1-2] Giá trị của
m
để hàm số
3 2 2
1
1 1
3
y x mx m m x
đạt cực tiểu tại điểm
1
x
là
A.
1
. B.
2
. C.
3
. D. Không có
m
.
Câu 8. [2D1-2] Giá trị của
m
để hàm số
4 2
1 1 2
y mx m x m
chỉ có đúng một cực trị là
A.
1
m
. B.
0
m
. C.
0 1
m
. D.
0
m
hoặc
1
m
.
Câu 9. [2D1-1] Cho hàm số
3 2
3x 3
y x
xác định trên
1;3
. Gọi
M,m
lần lượt là giá trị lớn nhất
và nhỏ nhất của hàm số thì
M + m
bằng
A.
2
. B.
4
. C.
6
. D.
8
.
Câu 10. [2D1-2] Giá trị nhỏ nhất của hàm số
2
4
y x x
trên
1;2
là
A.
1;2
min 0
y
. B.
1;2
min 3 1
y
. C.
1;2
min 2 2
y
. D.
1;2
min 2
y
.
Câu 11. [2D1-3] Các giá trị của
m
để giá trị lớn nhất của hàm số
2
1
x m m
y
x
trên đoạn
0;1
bằng
5
m
là
A.
11 4 5
2
. B.
11 5 5
2
. C.
11 6 5
2
. D. Không có giá trị nào.
14
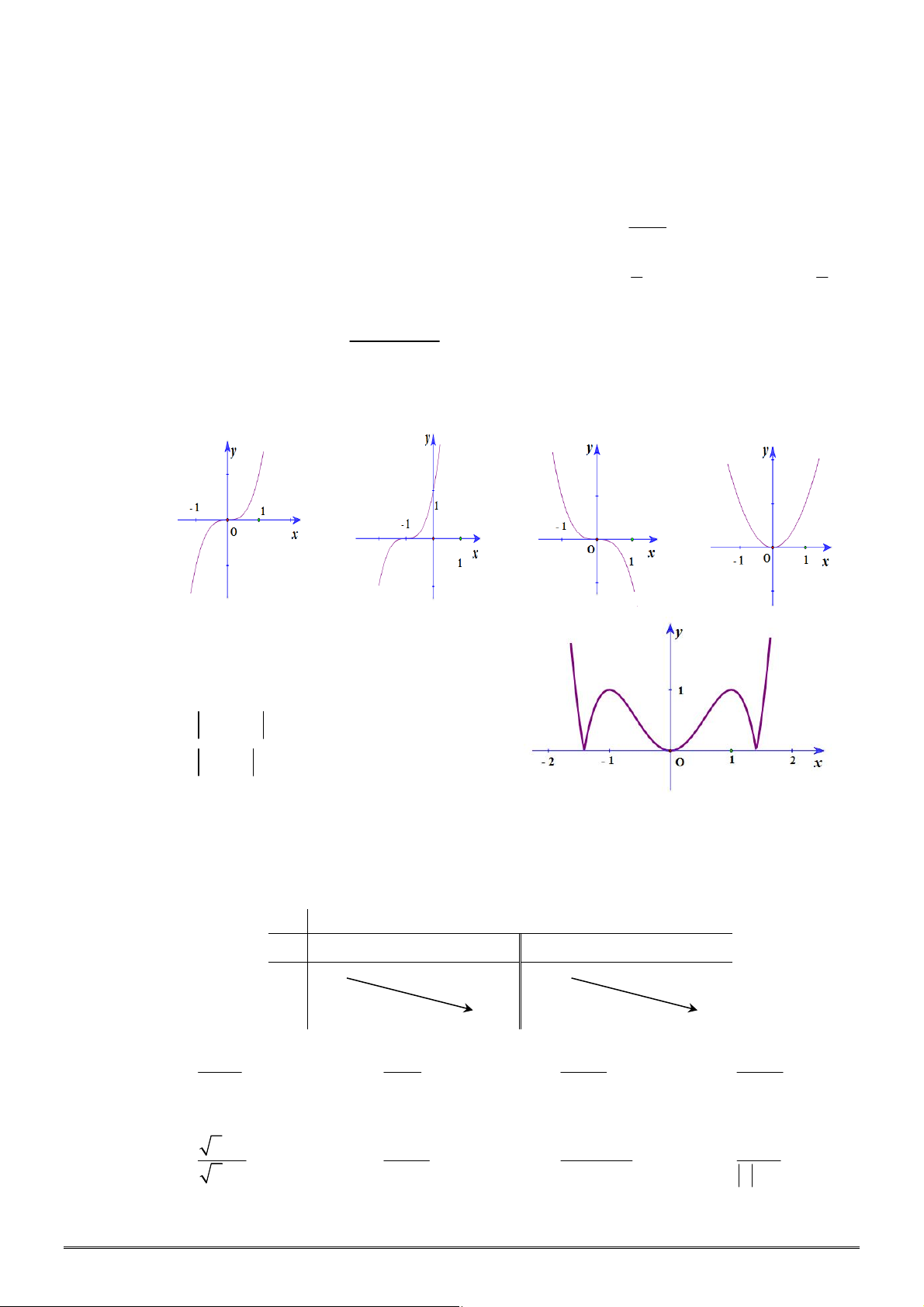
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/24
Câu 12. [2D1-3] Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: nếu mỗi đơn vị diện
tích của mặt hồ có
n
con cá thì trung bình mỗi con cá sau một vụ cân nặng
480 20 gam
P n n . Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ
để sau một vụ thu hoạch được nhiều cá nhất.
A.
10
. B.
16
. C.
26
. D.
12
.
Câu 13. [2D1-1] Phương trình các đường tiệm cận của đồ thị hàm số
3
2
x
y
x
là
A.
1
x
và
2
y
. B.
2
x
và
1
y
. C.
2
x
và
1
2
y
. D.
1
x
và
1
2
y
.
Câu 14. [2D1-2] Đồ thị hàm số
2
2
3 7 6
2 7 3
x x
y
x x
có bao nhiêu đường tiệm cận?
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 15. [2D1-2] Hàm số
3 2
3 3 1
y x x x
có đồ thị là hình nào sau đây?
A. . B. . C. . D. .
Câu 16. [2D1-3] Hình bên là đồ thị của hàm số nào sau đây?
A.
4 2
2
y x x
.
B.
4 2
2
y x x
.
C.
4 2
2
y x x
.
D.
3
3
y x x
.
Câu 17. [2D1-2] Tìm tất cả các giá trị của tham số
m
sao cho phương trình
3 2
3 0
x x m
có ba
nghiệm phân biệt?
A.
0 4
m
. B.
0
m
. C.
4
m
. D.
0 4
m
.
Câu 18. [2D1-2] Hàm số nào sau đây không có bảng biến thiên như hình dưới đây?
A.
2 1
2
x
y
x
. B.
3
2
x
y
x
. C.
2 3
2
x
y
x
. D.
2 3
2
x
y
x
.
Câu 19. [2D1-2] Đồ thị hàm số nào dưới đây có đúng hai đường tiệm cận?
A.
1
1
x
y
x
. B.
2
1
y
x x
. C.
2
5
7
x
y
x x
. D.
1
2
y
x
.
x
2
y
–
–
y
2
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/24
Câu 20. [2D1-2] Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số
3 2
1
2 3 5
3
y x x x
A. Song song với đường thẳng
1
x
. B. Song song với trục hoành.
C. Có hệ số góc dương. D. Có hệ số góc bằng
1
.
Câu 21. [2D1-2] Phương trình tiếp tuyến của đồ thị hàm số
4 2
2 1
y x x
mà vuông góc với đường
thẳng
8 0
x y
là
A.
8 6
y x
. B.
8 10
y x
. C.
8 6
y x
. D.
8
y x
.
Câu 22. [2D1-3] Cho hàm số
1
1
x
y
x
có đồ thị
H
và đường thẳng
: 2
d y x m
. Tìm các giá trị
của
m
để đường thẳng
d
cắt
H
tại hai điểm phân biệt
A
và
B
sao cho độ dài đoạn
AB
ngắn nhất?
A.
1 2
m
. B.
1
m
. C.
0
m
. D.
2
m
.
Câu 23. [2D2-1] Trong các biểu thức sau, biểu thức nào có nghĩa?
A.
5
2
. B.
1
3
8
. C.
3
4
5
. D.
3
0
.
Câu 24. [2D2-2] Các giá trị của
x
thỏa mãn đẳng thức
1
4
4
x x
là
A.
0
x
. B.
0
x
.
C.
0
x
. D. Không có giá trị nào.
Câu 25. [2D2-2] Biến đổi thành dạng lũy thừa với số mũ hữu tỉ của biểu thức
2002
2003
2017
...
a
(với
0
a
) là
A.
1
2017
a
. B.
2001!
2017 !
a
. C.
2002
2017
a
. D.
2002
2017 !
a
.
Câu 26. [2D2-3] Giá trị của biểu thức
log tan1 log tan 2 log tan3 ... log tan89
là
A.
1
. B.
0
. C. Không xác định. D.
44
.
Câu 27. [2D2-3] So sánh giá trị của biểu thức
2 3 2017
log 3.log 4...log 2018
P và
2
1 log 1009
Q ta có:
A.
P Q
. B.
P Q
.
C.
P Q
. D. Không so sánh được.
Câu 28. [2D2-2] Các giá trị của
x
thỏa mãn
2
1
2
log 5 7 0
x x
là
A.
2 3
x
. B.
2
x
hoặc
3
x
. C.
3
x
. D.
2
x
.
Câu 29. [2D2-2] Biểu thức
2
2 2
ln log e ln log e
a a
A a a được đơn giản thành
A.
2
. B.
2
2ln 2
a
. C.
2
ln 2
a
. D.
2
5ln 2
a
.
Câu 30. [2D2-3] Cho hai số dương
a
và
b
. Đặt
2
e e
e ;
2
a b
a b
X Y
. Khi đó:
A.
X Y
. B.
X Y
. C.
X Y
. D.
X Y
.
Câu 31. [2D2-2] Tập xác định của hàm số:
2016
2
1y x
là
A.
. B.
; 1 1;
.
C.
1;1
. D.
\ 1;1
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/24
Câu 32. [2D2-2] Tập xác định của hàm số:
1
2
2017
2y x x là
A.
; 1 2;
. B.
; 1 2;
. C.
1;2
. D.
\ 1;2
.
Câu 33. [2D2-2] Hàm số
2
e
x
y x
đồng biến trong khoảng
A.
;0
. B.
2;
. C.
0;2
. D.
;
.
Câu 34. [2D2-1] Cho
0 1
a
. Khẳng định nào dưới đây là đúng:
A.
1 0
x
a x
. B.
1 0
x
a x
. C.
1 0
x
a x
. D.
1 0 1
x
a x
.
Câu 35. [2D2-1] Cho
1
x
. Khẳng định nào dưới đây là đúng:
A.
log 0 0;1
a
x a . B.
log 0 0
a
x a
.
C.
log 0 0 1
a
x a
. D.
log 0 1
a
x a
.
Câu 36. [2D2-2] Đạo hàm của hàm số
ln 1
y x x
là
A.
ln 1
x
. B.
ln
x
. C.
1
1
x
. D.
1
.
Câu 37. [2D2-4] Một xe máy điện trị giá
10
triệu được bán trả góp
11
lần, mỗi lần trả góp với số tiền là
1
triệu (lần đầu trả sau khi nhận xe được một tháng). Tính lãi suất tiền hàng tháng?
A. 1,62%/
tháng
. B. t2,1% /
háng
. C. t1,1%/
háng
. D. 1,922%/
tháng
.
Câu 38. [2H1-2] Cho
H
là khối chóp tứ giác đều có tất cả các cạnh bằng
a
. Thể tích của
H
bằng
A.
3
3
a
. B.
3
2
6
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Câu 39. [2H1-2] Cho hình hộp chữ nhật
.
ABCD A B C D
. Gọi
E
,
F
lần lượt thuộc cạnh
BB
,
DD
sao cho
1
2
BE EB
,
1
2
DF FD
. Mặt phẳng
AEF
cắt cạnh
CC
tại
K
và chia khối hộp
thành hai khối đa diện là
A. Khối đa diện
A B C D AEKF
và khối đa diện
BCDEKF
.
B. Khối đa diện
A B C D AEKF
và khối đa diện
ABCDEKF
.
C. Khối đa diện
A B C D EKF
và khối đa diện
ABCDEKF
.
D. Khối đa diện
A B C D AEKF
và khối đa diện
ACDEKF
.
Câu 40. [2H1-2] Đáy của một hình hộp đứng là một hình thoi có đường chéo nhỏ bằng
d
và góc nhọn
bằng
. Diện tích của mặt bên bằng
S
. Thể tích của hình hộp đã cho là
A.
cos
2
dS
. B.
sin
2
dS
. C.
1
sin
2
dS
. D.
sin
dS
.
Câu 41. [2H1-3] Cho hình chóp đều
.
S ABCD
. Người ta tăng cạnh đáy của hình chóp lên
k
lần nhưng
muốn giữ nguyên thể tích. Khi đó tỉ số tan của góc giữa cạnh bên và mặt phẳng đáy của hình
chóp đều
.
S ABCD
và hình chóp sau khi tăng cạnh đáy là
A.
3
k
. B.
2
k
. C.
1
. D.
2
.
Câu 42. [2H2-2] Cho hình lập phương
.
ABCD A B C D
cạnh
a
. Tâm và bán kính của mặt cầu đi qua
8
đỉnh của hình lập phương là
A.
2
a
. B.
3
2
a
. C.
2
2
a
. D.
5
2
a
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/24
Câu 43. [2H2-2] Cho ba điểm
A
,
B
,
C
nằm trên mặt cầu, biết rằng góc
ACB
bằng
90
. Trong các
khẳng định sau, khẳng định nào đúng?
A. Có
AB
là một đường kính của mặt cầu.
B. Tam giác
ABC
vuông cân tại
C
.
C. Mặt phẳng
ABC
cắt mặt cầu theo giao tuyến là một đường tròn lớn.
D. Luôn có một đường tròn nằm trên mặt cầu ngoại tiếp tam giác
ABC
.
Câu 44. [2H2-4] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
1
, mặt bên
SAB
là tam giác
đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích
V
của khối cầu ngoại tiếp
hình chóp là
A.
5 15
18
. B.
5 15
54
. C.
4 3
27
. D.
5
3
.
Câu 45. [2H2-1] Cho mặt cầu
;
S I R
và mặt phẳng
.
P
Giả sử
d
là khoảng cách từ tâm
I
của mặt
cầu đến mặt phẳng
.
P
Biết mặt phẳng
P
tiếp xúc mặt cầu. Khẳng định nào sau đây đúng?
A.
2
d R
. B.
R d
. C.
2
d R
. D.
3 3
0
d R
.
Câu 46. [2H2-3] Một mặt cầu
S
ngoại tiếp một hình lập phương cạnh là
3 cm
. Một mặt phẳng
P
cách tâm
I
của hình lập phương một khoảng
1cm
cắt mặt cầu
S
theo một đường tròn. Diện
tích của hình tròn bằng
A.
2
3
. B.
3
5
. C.
5
. D.
5
4
.
Câu 47. [2H2-3] Một khối cầu bán kính bằng
5
dm người ta cắt bỏ hai đầu bằng mặt phẳng vuông góc
với đường kính của khối cầu và cách tâm một khoảng bằng
4
dm để làm một chiếc lu đựng
nước. Tính thể tích của cái lu.
A.
3
500
dm
3
. B.
3
dm
1
22
5
96
. C.
3
952
dm
27
. D.
3
472
dm
3
.
Câu 48. [2H2-3] Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
B
biết
AB BC a
,
2
AD a
,
SA ABCD
và
SA
2
a
. Gọi
E
là trung điểm của
AD
. Kẻ
EK
SD
tại
K
.
Bán kính mặt cầu đi qua sáu điểm
S
,
A
,
B
,
C
,
E
,
K
bằng
A.
a
. B.
3
2
a
. C.
1
2
a
. D.
6
2
a
.
Câu 49. [2H2-4] Một hình chóp tứ giác đều có cạnh đáy bằng
a
và cạnh bên bằng
2
x
. Điều kiện cần
và đủ của
x
để tâm mặt cầu ngoại tiếp hình chóp ở ngoài hình chóp là
A.
2
2 2
a a
x
. B.
2
2 2
a a
x
. C.
2
a
x
. D.
2
a
x
.
Câu 50. [2H2-3] Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp
. .
S ABCD
A.
21
6
a
. B.
21
3
a
. C.
2 21
6
a
. D.
21
6
a
.
----------HẾT----------
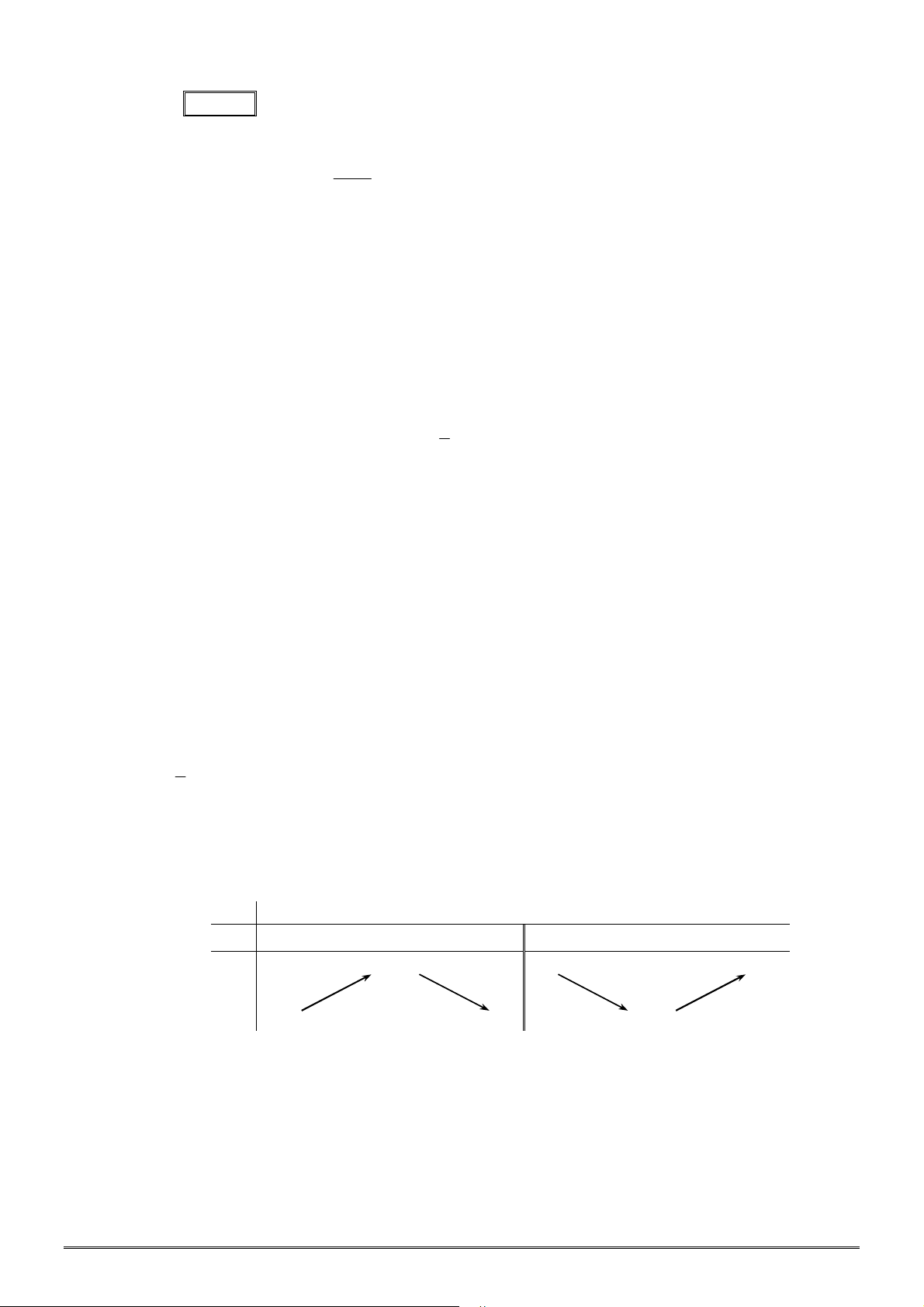
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/25
TRƯỜNG THPT KIM LIÊN – HÀ NỘI ĐỀ ÔN TẬP HỌC KỲ I NĂM HỌC 2017 – 2018
ĐỀ SỐ 3 MÔN TOÁN - LỚP 12
------- ------------------
Câu 1. [2D1-2] Cho hàm số
1
2
x
y
x
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đơn điệu trên
.
B. Hàm số đồng biến trên
\ 2
.
C. Hàm số nghịch biến trên
\ 2
.
D. Hàm số đồng biến trên các khoảng
; 2
và
2;
.
Câu 2. [2D1-2] Hỏi hàm số
3 2
3 4
y x x
nghịch biến trên khoảng nào?
A.
2;0
. B.
; 2
. C.
0;
. D.
.
Câu 3. [2D1-3] Tìm
m
bé nhất để hàm số
3 2
1
4 2016
3
y x mx x đồng biến trên tập xác định?
A.
4
m
. B.
2
m
. C.
2
m
. D.
0
m
.
Câu 4. [2D1-4] Một chất điểm chuyển động theo quy luật
3 2
6
s t t t
. Tính thời điểm
t
(giây) tại
đó vận tốc
v
(m/s) của chuyển động đạt giá trị lớn nhất.
A.
0
t
. B.
6
t
. C.
4
t
. D.
2
t
.
Câu 5. [2D1-2] Số điểm cực trị của hàm số
4 2
1
y x x
là
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 6. [2D1-2] Tìm giá trị cực tiểu
CT
y
của hàm số
3 2
6 9 5
y x x x
.
A.
5
CT
y
. B.
1
CT
y
. C.
3
CT
y
. D.
9
CT
y
.
Câu 7. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
3 2 2
1
1 1
3
y x mx m m x
đạt cực đại tại điểm
1
x
.
A.
1
m
. B.
2
m
. C.
0
m
. D.
4
m
.
Câu 8. [2D1-1] Cho hàm số
y f x
xác định, liên tục trên các khoảng
;1
,
1;
và có bảng
biến thiên như hình dưới. Khẳng định nào sau đây đúng?
A. Hàm số có giá trị cực tiểu bằng
1
.
B. Hàm số có giá trị lớn nhất bằng
1
và giá trị nhỏ nhất bằng
5
.
C. Hàm số đạt cực đại tại
0
x
và đạt cực tiểu tại
2
x
.
D. Hàm số nhiều hơn hai cực trị.
Câu 9. [2D1-2] Hàm số nào sau đây có giá trị nhỏ nhất trên
?
A.
3 2
2
y x x
. B.
3 2
2 5
y x x
.
C.
4 2
2 5
y x x
. D.
4 2
3
y x x
.
x
0
1
2
y
0
0
y
1
5
15
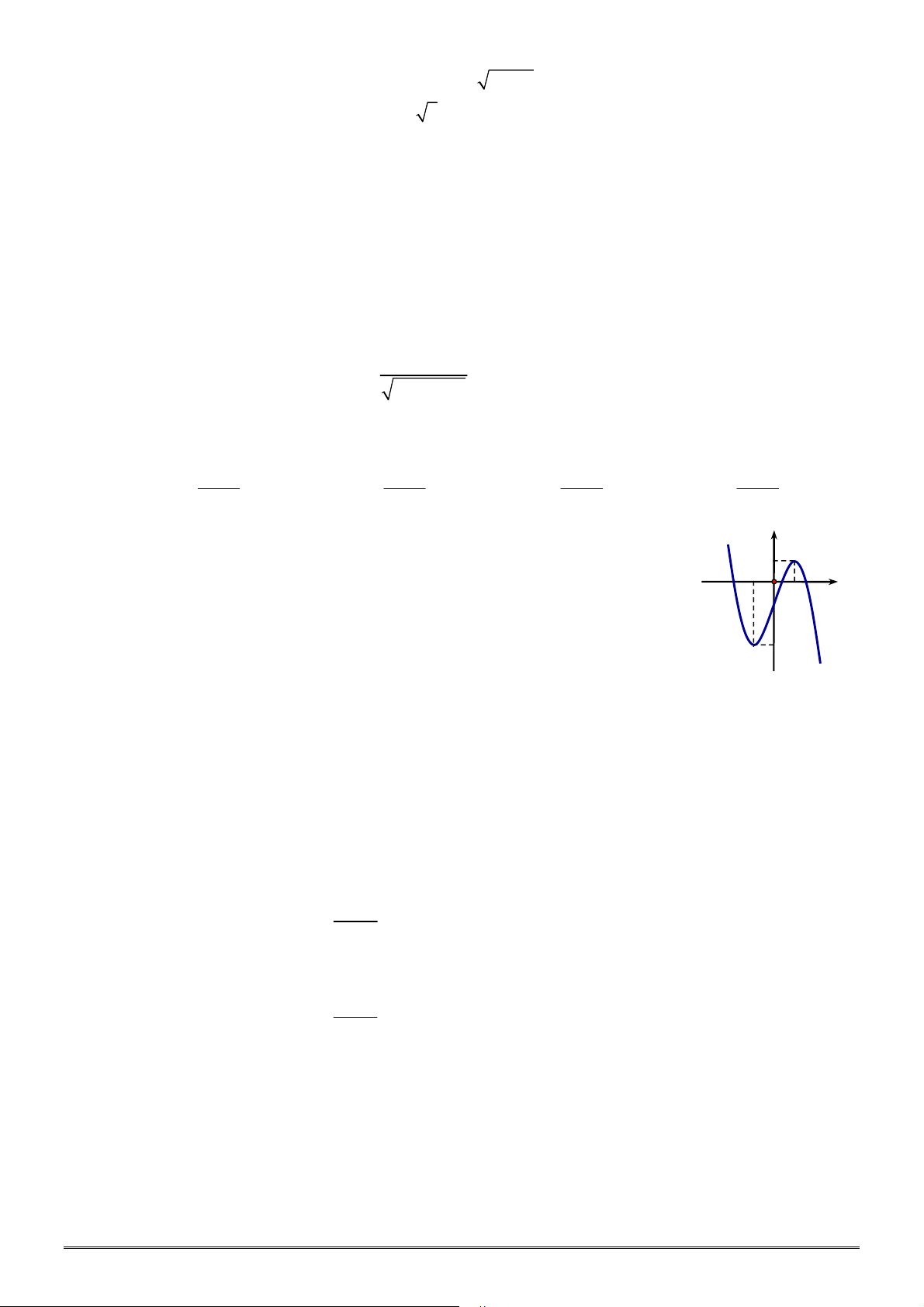
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/25
Câu 10. [2D1-2] Tìm giá trị nhỏ nhất của hàm số
6 3
y x
trên đoạn
1;1
.
A.
1;1
min 3
y
. B.
1;1
min 3
y
. C.
1;1
min 0
y
. D.
1;1
min 1
y
.
Câu 11. [2D1-2] Tìm giá trị
m
để hàm số
3 2
3
y x x m
có giá trị nhỏ nhất trên đoạn
1;1
bằng
0
?
A.
6
m
. B.
0
m
. C.
2
m
. D.
4
m
.
Câu 12. [2H2-3] Một người thợ thủ công pha một khối thạch cao vào nước tạo thành một hỗn hợp có
thể tích
3
330cm
V , sau đó đổ vào khuôn để đúc thành những viên phấn hình trụ có bán kính
đáy
0,5cm
R
và chiều cao
6cm
h
. Biết rằng trong quá trình đúc sự tiêu hao nguyên liệu là
không đáng kể. Hỏi người thợ thủ công đó đúc được bao nhiêu viên phấn?
A.
50
viên. B.
70
viên. C.
24
viên. D.
23
viên.
Câu 13. [2D1-2] Đồ thị của hàm số
2
2 3
2016
x
y
x
có bao nhiêu đường tiệm cận ngang?
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 14. [2D1-2] Đồ thị hàm số nào sau đây có tiệm cận đứng là đường thẳng
1
x
?
A.
2
1
1
x
y
x
. B.
2
3
1
x
y
x
. C.
2
1
1
x
y
x
. D.
2
3
1
x
y
x
.
Câu 15. [2D1-1] Đường cong trong hình bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi
hàm số đó là hàm số nào?
A.
2
1
y x x
. B.
4 2
1
y x x
.
C.
3
3 1
y x x
. D.
3 2
1
y x x
.
Câu 16. [2D1-1] Cho hàm số
4 2
2 3
y x x
. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số có tập xác định là
.
B. lim
x
y
và lim
x
y
.
C. Đồ thị hàm số có ba điểm cực trị.
D. Đồ thị hàm số nhận trục hoành
Ox
làm trục đối xứng.
Câu 17. [2D1-2] Cho hàm số
4 2
2
y x x
. Có bao nhiêu tiếp tuyến của đồ thị hàm số song song với
trục hoành?
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 18. [2D1-1] Cho hàm số
2 1
1
x
y
x
. Khẳng định nào sau đây là khẳng định đúng?
A.
1
lim
x
y
. B.
1
lim
x
y
. C.
1
lim
x
y
. D.
1
lim
x
y
.
Câu 19. [2D1-1] Cho hàm số
2 1
1
x
y
x
. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số không có cực trị.
B.
lim 2
x
y
và
lim 2
x
y
.
C. Đồ thị hàm số không cắt trục tung.
D. Đồ thị hàm số có tâm đối xứng là điểm
1;2
I .
Câu 20. [2D1-1] Cho hàm số
3 2
4 4
y x x x
. Tìm phương trình tiếp tuyến của đồ thị hàm số tại gốc
toạ độ?
A.
y x
. B.
4
y x
. C.
4
y x
. D.
y x
.
O
x
y
1
1
2
3
1
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/25
Câu 21. [2D1-1] Tìm số giao điểm của đồ thị hàm số
2
1 3
y x x x
với trục hoành.
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 22. [2D1-2] Tìm điều kiện của
m
để đường thẳng
y m
cắt đồ thị hàm số
4 2
y x x
tại bốn
điểm phân biệt.
A.
1
0
4
m
. B.
1
0
4
m
. C.
1
4
m
. D.
1
4
m
.
Câu 23. [2D2-1] Cho
,
a b
là hai số thực dương,
m
là một số nguyên còn
n
là một số nguyên dương.
Khẳng định nào dưới đây là khẳng định sai?
A. .
m n m n
a a a
. B.
m
m n
n
a
a
a
. C.
n
m m n
a a
. D.
m
n
m
n
a a
.
Câu 24. [2D2-1] Cho
2 3 2 3
m n
với ,m n
. Khẳng định nào sau đây là khẳng định đúng?
A.
m n
. B.
m n
. C.
m n
. D.
m n
.
Câu 25. [2D2-1] Cho
a
là số thực dương. Rút gọn biểu thức
3 1
3 1
5 3 4 5
.
a
P
a a
A.
2
P a
. B.
1
P a
. C.
1
P
. D.
P a
.
Câu 26. [2D2-3] Một người đầu tư
200
triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
14%
một năm. Hỏi sau ba năm mới rút lãi thì người đó thu được bao nhiêu triệu đồng tiền lãi?
(Giả sử rằng lãi suất hàng năm không thay đổi).
A.
59,92
triệu đồng. B.
96,31
triệu đồng. C.
84
triệu đồng. D.
137,79
triệu đồng.
Câu 27. [2D2-1] Cho
,
a b
là hai số thực dương. Tìm
x
biết
2 2 2
log 2log 4log
x a b
.
A.
2 4
.
x a b
. B.
2 2
.
x a b
. C.
2
.
x a b
. D.
4
.
x a b
.
Câu 28. [2D2-2] Cho các số thực dương
,
x y
thỏa mãn
2 2
7
x y xy
. Khẳng định nào sau đây đúng?
A.
1
log log log
3 2
x y
x y
. B.
2 2
log
log log
7
x y
x y
.
C.
2 2
log log log
3
x y
x y
. D.
2 2
log 2 log log
7
x y
x y
.
Câu 29. [2H1-2] Cho khối hộp
.
ABCD A B C D
có thể tích là
V
. Tính theo
V
thể tích khối tứ diện
AB CD
.
A.
2
3
V
. B.
3
4
V
. C.
3
V
. D.
6
V
.
Câu 30. [2D2-1] Đặt
ln 2
a
,
ln3
b
. Hãy biểu diễn
7
ln21 2ln14 3ln
2
Q theo
a
và
b
.
A. 5
Q a b
. B. 5
Q b a
. C. 6
Q a b
. D.
11 5
Q a b
.
Câu 31. [2D2-1] Trong các khẳng định sau, khẳng định nào sai?
A. Hàm số
log
y x
là hàm số lôgarit.
B. Hàm số
1
3
x
y
là hàm số mũ.
C. Hàm số
x
y
nghịch biến trên
.
D. Hàm số
ln
y x
đồng biến trên khoảng
0;
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/25
Câu 32. [2D2-2] Cho hàm số
2
ln 4
f x x x
. Tìm tập nghiệm của phương trình
0
f x
.
A.
;0 4;
. B.
4
. C.
2
. D.
.
Câu 33. [2D2-2] Cho hàm số
1
.ln
8
2016.e
x
y . Khẳng định nào sau đây là khẳng định đúng?
A.
2 ln 2 0
y y
. B.
3 ln 2 0
y y
. C.
8 ln 2 0
y y
. D.
8 ln 2 0
y y
.
Câu 34. [2D2-2] Tìm tập xác định
D
của hàm số
2
2 2
1
y x x
.
A.
1;1
D . B.
0;1
D . C.
\ 1;1
D
. D.
1;1 \ 0
D .
Câu 35. [2H1-2] Tìm số mặt phẳng đối xứng của hình chóp tứ giác đều.
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 36. [2D2-2] Tìm giá trị của
x
để đồ thị hàm số
2
log
y x
nằm ở phía trên đường thẳng
2
y
.
A.
4
x
. B.
4
x
. C.
4
x
. D.
0 4
x
.
Câu 37. [2D2-2] Số giá trị của
a
để
2
3 2
2 0,25
a a
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 38. [2H2-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
SA ABC
. Tìm tâm
mặt cầu ngoại tiếp hình chóp.
A. Trung điểm
SB
. B. Trung điểm
SC
.
C. Trung điểm
BC
. D. Một đáp án khác.
Câu 39. [2H1-2] Cho lăng trụ đứng .
ABC A B C
có đáy
ABC
là tam giác vuông tại
B
.
2
AB a
,
5
AC a
,
2 3
AA a
. Tính thể tích
V
của khối lăng trụ .
ABC A B C
.
A.
3
2 3
3
a
V . B.
3
3
3
a
V . C.
3
4 3
V a . D.
3
2 3
V a .
Câu 40. [2H1-3] Người ta cắt miếng bìa hình tam giác đều cạnh bằng 2 như hình
dưới và gấp theo các đường kẻ, sau đó dán các mép lại để được hình tứ
diện đều. Tính thể tích
V
của khối tứ diện tạo thành.
A.
2
96
V . B.
2
12
V .
C.
3
96
V . D.
3
16
V .
Câu 41. [2H1-2] Cho hình chóp
.
S ABC
có
M
,
N
và
P
lần lượt là trung điểm các cạnh
AB
,
BC
và
CA
. Gọi
1 .
S ABC
V V ,
2 .
S MNP
V V . Khẳng định nào sau đây là khẳng định đúng?
A.
1 2
2
V V
. B.
1 2
4
V V
.
C.
1 2
8
V V
. D.
1 2
3 8
V V
.
Câu 42. [2H1-3] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
; biết
2
AB AD a
,
CD a
. Góc giữa hai mặt phẳng
SBC
và
ABCD
bằng
60
. Gọi
I
là
trung điểm
AD
, biết hai mặt phẳng
SBI
và
SCI
cùng vuông góc với mặt phẳng
ABCD
.
Tính thể tích
V
của khối chóp
.
S ABCD
.
A.
3
3 5
5
a
V B.
3
3 5
8
a
V C.
3
3 15
8
a
V . D.
3
3 15
5
a
V .

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/25
Câu 43. [2H2-1] Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình chóp nào cũng có mặt cầu ngoại tiếp.
B. Hình hộp đứng nào cũng có mặt cầu ngoại tiếp.
C. Hình lăng trụ tam giác có cạnh bên không vuông góc với đáy có thể nội tiếp một mặt cầu.
D. Hình tứ diện nào cũng có mặt cầu ngoại tiếp.
Câu 44. [2H2-2] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
SA
vuông
góc với mặt phẳng đáy và
SA a
. Tính diện tích
S
của mặt cầu ngoại tiếp hình chóp đã cho.
A.
2
4
S a
. B.
2
3
S a
. C.
2
3
S a
. D.
2
6
S a
.
Câu 45. [2H2-2] Cho mặt cầu tâm
O
bán kính
R
và mặt phẳng
P
cách tâm
O
một khoảng
2
R
.Tìm
bán kính
r
của đường tròn giao tuyến giữa mặt phẳng
P
và mặt cầu đã cho?
A.
3
2
R
r . B.
3
4
R
r . C.
2
2
R
r . D.
2
4
R
r .
Câu 46. [2H1-2] Trong các mệnh đề sau, mệnh đề nào sai?
A. Chỉ có năm loại khối đa diện đều.
B. Hình chóp tam giác đều là hình chóp có bốn mặt là những tam giác đều.
C. Mỗi cạnh của hình đa diện đều là cạnh chung của đúng hai mặt.
D. Mỗi khối đa diện đều là một khối đa diện lồi.
Câu 47. [2H1-3] Trong không gian cho ba điểm cố định
A
,
B
,
C
phân biệt và không thẳng hàng. Tìm
tập hợp các điểm
M
trong không gian sao cho thể tích khối chóp
.
M ABC
là một số dương
không đổi?
A. Hai đường thẳng song song. B. Một mặt cầu.
C. Một mặt phẳng. D. Hai mặt phẳng song song.
Câu 48. [2H2-3] Cho hình chóp
.
S ABCD
có
SA ABCD
,
SA a
. Đáy
ABCD
là hình thang vuông
tại
A
và
B
,
AB BC a
và
2
AD a
. Tính theo
a
thể tích khối cầu ngoại tiếp hình chóp
.
S ACD
.
A.
3
5 5
9
a
V
. B.
3
5 5
6
a
V
. C.
3
5 5
3
a
V
. D.
3
5 5
12
a
V
.
Câu 49. [1H2-2] Cho hình lăng trụ
.
ABCD A B C D
có đáy
ABCD
là hình vuông. Hình chiếu vuông
góc của
A
lên
mp ABCD
là trung điểm
AB
, góc giữa
mp A CD
và
mp ABCD
là
60
.
Thể tích của khối chóp
.
B ABCD
là
3
8 3
3
a
. Tính theo
a
độ dài đoạn thẳng
AC
?
A.
3
2 2
a
. B.
2
a
. C.
2
a
. D.
2 2
a
.
Câu 50. [2H1-4] Cho khối chóp
.
S ABCD
có đáy là hình bình hành và có thể tích là
V
. Gọi
M
là trung
điểm của
SB
,
P
là điểm thuộc cạnh
SD
sao cho
2
SP DP
. Mặt phẳng
AMP
cắt cạnh
SC
tại
N
. Tính thể tích của khối đa diện
ABCDMNP
theo
V
.
A.
23
30
V
. B.
19
30
V
. C.
2
5
V
. D.
7
30
V
.
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/22
TRƯỜNG THPT KIM LIÊN – HÀ NỘI ĐỀ ÔN TẬP HỌC KỲ I NĂM HỌC 2017 – 2018
ĐỀ SỐ 4 MÔN TOÁN - LỚP 12
------- ------------------
Câu 1. [2D1-1] Hàm số
3 2
6 9 7
y x x x
đồng biến trên
A. Khoảng
1;3
. B. Đoạn
1;3
.
C. Tập
;1 3;
. D. Các khoảng
;1
,
3;
.
Câu 2. [2D1-1] Cho hàm số
2 1
1
x
y
x
. Kết luận nào sau đây đúng:
A. Hàm số đồng biến trên
\ 1
.
B. Hàm số đồng biến trên các khoảng
;1
,
3;
.
C. Hàm số đồng biến trên tập
;1 1;
.
D. Hàm số nghịch biến trên các khoảng
;1
,
3;
.
Câu 3. [2D1-3] Giá trị của tham số
m
để hàm số
3 2
1
2 2 2 2 5
3
m
y x m x m x
nghịch
biến trên
là
A.
2 3
m
. B.
2
m
. C.
1
m
. D.
2 3
m
.
Câu 4. [2D1-2] Điểm cực đại của hàm số
3 2
3 1
y x x
là
A.
0
x
. B.
2
x
. C.
0;2
. D.
2;6
.
Câu 5. [2D1-2] Giá trị của tham số
m
để hàm số
3
2 1
y x mx
đạt cực tiểu tại
1
x
A.
3
2
m
. B.
3
2
m
. C.
2
3
m
. D.
2
3
m
.
Câu 6. [2D1-2] Hàm số
4 2
3 2 1
y mx m x m
chỉ có cực đại mà không có cực tiểu với:
A.
3
m
. B.
3
m
. C.
3
0
m
m
. D.
3 0
m
.
Câu 7. [2D1-2] Giá trị lớn nhất của hàm số
2
4
y x x
là
A.
2
. B.
0
. C.
4
. D.
1
.
Câu 8. [2D1-2] Giá trị lớn nhất của hàm số
3 1
3
x
y
x
trên đoạn
0;2
là
A.
1
3
. B.
5
. C.
4
. D.
1
3
.
Câu 9. [2D1-1] Số giao điểm của đồ thị hai hàm số
3 2
6 9 1
y x x x
và
1
y x
là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 10. [2D1-3] Tìm
m
để đường thẳng
1
y x m
cắt đồ thị
2 1
1
x
y
x
tại hai điểm phân biệt
A
,
B
và
2 3
AB .
A.
4 3
m . B.
2 10
m . C.
4 10
m . D.
2 3
m .
Câu 11. [2D1-2] Đồ thị hàm số nào sau đây có tiệm cận đứng là đường thẳng
1
x
và tiệm cận ngang
là
2
y
.
A.
2
1
x
y
x
. B.
1
1
x
y
x
. C.
2
1
x
y
x
. D.
2
1
x
y
x
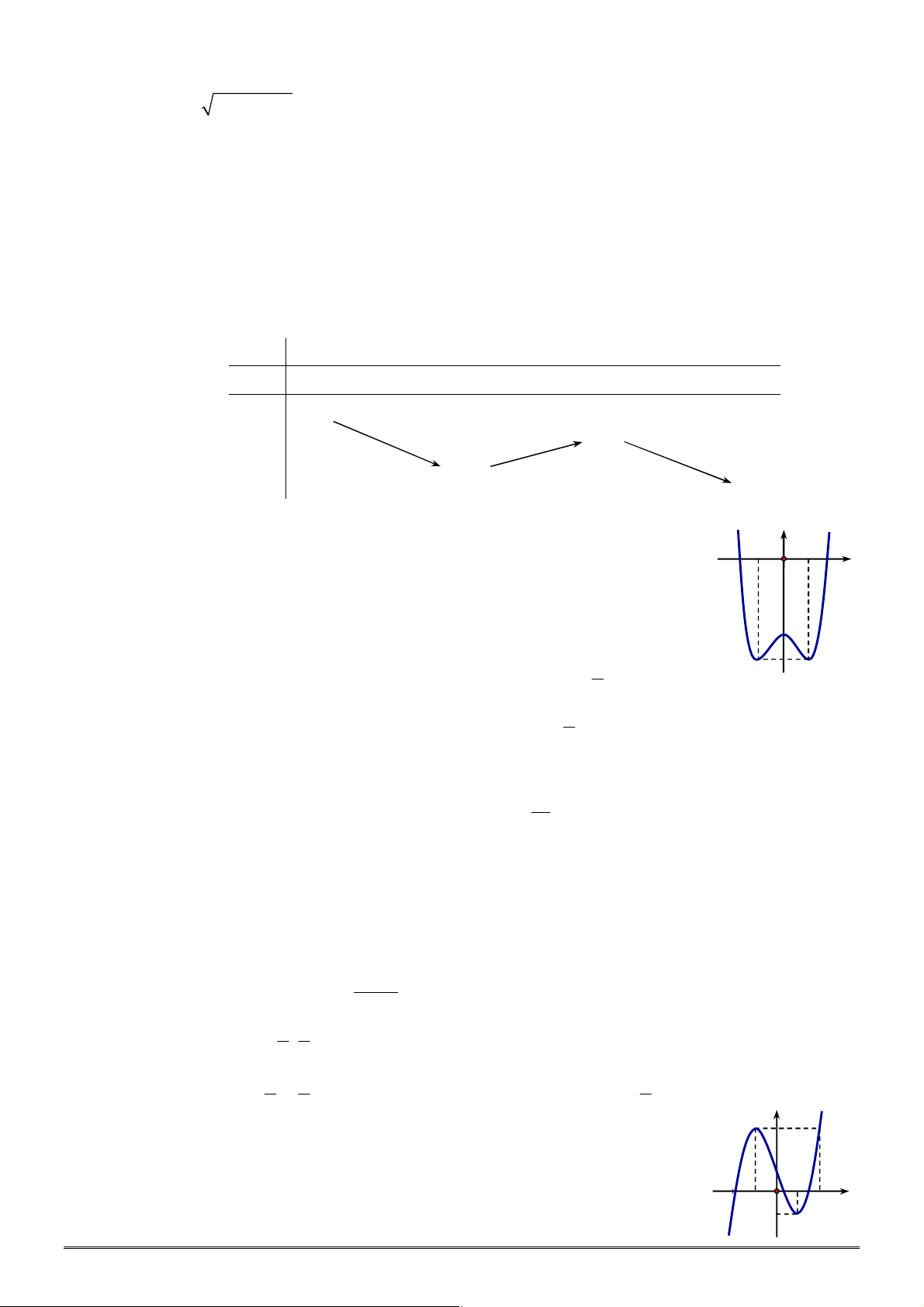
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/22
Câu 12. [2D1-3] Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
2
2 3
y x x x
là
A.
3
. B.
2
. C.
1
. D.
0
Câu 13. [2D1-2] Cho hàm số
3 2
3 1
y x x
. Phương trình tiếp tuyến tại điểm
3;1
A là
A.
9 20
y x
. B.
9 28
y x
. C.
9 20
y x
. D.
9 28
y x
.
Câu 14. [2D1-3] Trong các tiếp tuyến của đồ thị hàm số
3 2
3 2
y x x
, hệ số góc nhỏ nhất của các
tiếp tuyến đó là
A.
3
. B.
3
. C.
4
. D.
0
Câu 15. [2D1-2] Bảng biến thiên trong hình dưới đây là bảng biến thiên của hàm số nào?
A.
3 2
3 1
y x x
. B.
3 2
3 1
y x x
.
C.
3 2
3 1
y x x
. D.
3 2
3 1
y x x
Câu 16. [2D1-2] Đồ thị trong hình dưới đây là đồ thị của hàm số nào?
A.
4 2
3
y x x
. B.
4 2
3
y x x
.
C.
4 2
2 3
y x x
. D.
4 2
3
y x x
.
Câu 17. [2D1-3] Giá trị của tham số
m
để đồ thị của hai hàm số
3
5
2
4
y x x
và
2
y x x m
tiếp xúc là
A.
2
m
. B.
2
m
. C.
2
3
m
. D.
3
m
.
Câu 18. [2D1-2] Giá trị nhỏ nhất của hàm số
2
3sin 4cos 2
y x x
là
A.
2
. B.
6
. C.
19
3
. D. Không tồn tại.
Câu 19. [2D1-3] Xét phương trình
3 2
3 2 0
x x m
. Phát biểu nào sau đây là đúng:
A. Với
7
m
, phương trình trên có ba nghiệm phân biệt.
B. Với
1
m
, phương trình trên có hai nghiệm phân biệt.
C. Với
2 6
m
, phương trình trên có ba nghiệm phân biệt.
D. Phương trình trên có ba nghiệm phân biệt khi
2
m
hoặc
6
m
.
Câu 20. [2D1-2] Đồ thị hàm số
2
2 1
x
y
x
A. Nhận điểm
1 1
;
2 2
làm tâm đối xứng. B. Không có tâm đối xứng.
C. Nhận điểm
1 1
;
2 2
làm tâm đối xứng. D. Nhận điểm
1
;2
2
làm tâm đối xứng.
Câu 21. [2D1-1] Đồ thị hình bên là đồ thị của hàm số nào?
A.
3
3 1
y x x
. B.
3 2
1
y x x
.
C.
3
3 1
y x x
. D.
3
3 1
y x x
.
x
0
2
y
0
0
y
3
1
O
x
y
4
3
1
1
O
x
y
1
1
1
3
2
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/22
Câu 22. [2D1-1] Biết hàm số
2
4 1
1
x x
y
x
có hai cực trị
1
x
,
2
x
. Tích
1 2
.
x x
bằng
A.
2
. B.
5
. C.
1
. D.
4
.
Câu 23. [2D2-1] Biểu thức
a a a a
;
0
a
bằng
A.
13
16
a
. B.
11
64
a
. C.
15
16
a
. D.
15
8
a
.
Câu 24. [2D2-1] Xét mệnh đề: “Với mọi số thực
a
,
x
,
y
, nếu
x y
thì
x y
a a
”. Với điều kiện sau
đây của
a
thì mệnh đề trên đúng.
A.
a
bất kì. B.
0
a
. C.
1
a
. D.
0 1
a
.
Câu 25. [2D2-2] Tỉ lệ tăng dân số hàng năm của một nước là
1,5%
. Năm
2000
, dân số nước này là
212942000
. Dân số nước đó vào năm
2008
xấp xỉ:
A.
239877584
người. B.
240090000
người.
C.
230081000
người. D.
24078100
người.
Câu 26. [2D2-2] Đẳng thức
7 7 7
1
log log log
3 2
a b
a b
, với
, 0
a b
tương đương với:
A.
2 2
7
a b ab
. B.
2 2
14
a b ab
. C.
2 2
5
a b ab
. D.
3 3
7
a b ab
.
Câu 27. [2D2-2] Cho
12
log 27
a
. Khi đó
36
log 24
bằng
A.
9
6 2
a
a
. B.
9
6 2
a
a
. C.
9
6 2
a
a
. D.
9
6 2
a
a
.
Câu 28. [2D2-1] Giá trị của biểu thức
2
8log 7
a
a
,
0, 1
a a
bằng
A.
2
7
. B.
4
7
. C.
8
7
. D.
16
7
.
Câu 29. [2D2-1] Biết
ln 2
a
,
ln3
b
. Biểu diễn
1
ln
12
theo
a
,
b
được kết quả:
A.
2
a b
. B.
2
a b
. C.
2
a b
. D.
2
a b
.
Câu 30. [2D2-1] Biết
log 0
a
, khi đó
a
thỏa mãn:
A.
a
bất kì. B.
0
a
. C.
1
a
. D.
0 1
a
.
Câu 31. [2D2-2] Tập xác định của hàm số
2
1
2
log 1
y x
là
A.
; 1 1;D
. B.
D
.
C.
1;1
D
. D.
; 1 1;D
.
Câu 32. [2D2-3] Đạo hàm của hàm số
2x
1 e
y x là hàm số
A.
2
2 1 e
x
y x . B.
2 1 e
x
x . C.
2
2 1 e
2
x
x
. D.
2
2 e
x
x
.
Câu 33. [2D2-1] Đồ thị của hàm số
2
x
y
A. Nhận trục tung làm tiệm cận đứng.
B. Có trục đối xứng.
C. Đối xứng với đồ thị hàm số
1
2
x
y
qua trục hoành.
D. Nhận trục hoành là tiệm cận ngang.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/22
Câu 34. [2D2-3] Đạo hàm của hàm số
3
2
ln 2
y x
tại điểm
1
x
là
A.
1
3
2
ln 2
3
. B.
1
3
2
ln 2
3
. C.
1
3
1
ln 2
3
. D.
1
3
1
ln 2
3
.
Câu 35. [2D2-1] Cho hàm số
4
y x
. Trong các khẳng định sau, khẳng định nào sai?
A. Tập xác định của hàm số là
0;D
. B. Hàm số nghịch biến trên tập xác định.
C. Đồ thị hàm số qua điểm
1;1
. D. Đồ thị hàm số không có đường tiệm cận.
Câu 36. [2D2-3] Cho hàm số
2
ln 1
y x
. Số nghiệm của phương trình
0
y
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 37. [2D2-3] Số điểm cực trị của hàm số
e
1
x
y
x
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 38. [2D2-3] Giá trị của
x
thỏa mãn đẳng thức
3 5
5 3
x x
là
A.
5 3
3
log log 5
x . B.
5 5
3
log log 3
x .
C.
3 5
5
log log 3
x . D.
3 3
5
log log 5
x .
Câu 39. [2H1-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
3
a
. Biết tam giác
SAB
là tam giác cân tại
S
và nằm trong mặt phẳng vuông góc với đáy, tam giác
SAB
vuông. Thể
tích khối chóp
.
S ABCD
là
A.
3
9 3
a . B.
3
9 3
2
a
. C.
3
9
a
. D.
3
9
2
a
.
Câu 40. [2D1-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật
2
AD a
,
AC a
. Gọi
H
là trọng tâm tam giác
ABD
,
SH
vuông góc với đáy, góc giữa
SD
và mặt phẳng
ABCD
bằng
30
. Thể tích khối chóp
.
S ABCD
là
A.
3
a
. B.
3
2
a
. C.
3
2 35
9
a
. D.
3
5
3
a
.
Câu 41. [2H1-3] Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
2
BC a
. Biết
A C
tạo với mặt đáy một góc
60
. Thể tích khối lăng trụ
.
ABC A B C
là
A.
3
3 3
a . B.
3
6 3
a . C.
3
3 3
2
a
. D.
3
3
2
a
.
Câu 42. [2H1-3] Cho hình lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác đều,
3
AB a
. Biết hình
chiếu của
A
lên mặt phẳng
ABC
trùng với trung điểm của
BC
và cạnh bên bằng
2
a
. Thể
tích khối lăng trụ
.
ABC A B C
là
A.
3
21
8
a
. B.
3
3 21
8
a
. C.
3
14
12
a
. D.
3
14
8
a
.
Câu 43. [2H1-3] Cho khối tứ diện có thể tích là
V
. Gọi
V
là thể tích của khối đa diện có đỉnh là trung
điểm các cạnh của khối tứ diện đã cho. Ta có
V
bằng
A.
3
.
4
V
B.
4
.
5
V
C.
.
2
V
D.
2
.
3
V

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/22
Câu 44. [2H1-2] Cho nửa hình tròn đường kính
3
AB a
quay quanh trục
AB
, ta được khối tròn
xoay có thể tích là
A.
3
2 3
a . B.
3
3
2
a
. C.
3
3
2
a
. D.
3
2 3
3
a
.
Câu 45. [2H1-2] Cho hình lăng trụ đứng có đáy là hình vuông cạnh
a
, chiều cao bằng
2
a
. Diện tích
mặt cầu ngoại tiếp hình lăng trụ đó là
A.
2
6
a
. B.
2
6
4
a
. C.
2
6
4
a
. D.
2
6
a
.
Câu 46. [2H1-1] Tên gọi của khối đa diện đều loại
3;4
là khối:
A. Bát diện đều. B. Lập phương.
C. Hai mươi mặt đều. D. Mười hai mặt đều.
Câu 47. [2H1-3] Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
6
3
a
. Gọi
O
là tâm đáy. Trong các khẳng định sau, khẳng định nào đúng khi nói về mặt cầu ngoại tiếp tứ
diện
.
S ABC
?
A. Mặt cầu có tâm trùng với
O
và bán kính
3
3
a
R .
B. Mặt cầu có tâm trùng với
O
và bán kính
6
6
a
R .
C. Mặt cầu có tâm là trung điểm
SO
và bán kính
3
6
a
R .
D. Mặt cầu có tâm là trung điểm
SO
và bán kính
3
2
a
R .
Câu 48. [2H1-2] Cho hình chóp có đáy là đa giác
n
cạnh. Trong các khẳng định sau, khẳng định nào đúng?
A. Số cạnh của hình chóp bằng
1
n
. B. Số mặt của hình chóp bằng
2
n
.
C. Số đỉnh của hình chóp bằng
2 1
n
. D. Số mặt của hình chóp bằng số đỉnh.
Câu 49. [2H1-3] Cho hình chóp
.
S ABCD
có
SA ABCD
. Đáy
ABCD
là hình thoi,
2
AC a
,
3
BD a
,
I
là trung điểm của
SC
. Bán kính mặt cầu tâm
I
và tiếp xúc với mặt phẳng
SAB
là
A.
3
2
a
. B.
3
4
a
. C.
21
7
a
. D.
2
4
a
.
Câu 50. [2H1-3] Cho hình chóp
.
S ABC
có
SA ABC
,
2
SA a
. Đáy
ABC
là tam giác đều cạnh
a
.
Bán kính mặt cầu tâm
S
và tiếp xúc với đường thẳng
BC
là
A.
3
2
a
. B.
3 5
2
a
. C.
15
2
a
. D.
19
2
a
.
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/13 - Mã đề thi 132
SỞ GD VÀ ĐT LONG AN
TRƯỜNG THPT CHUYÊN
LONG AN
ĐỀ THI HỌC KỲ 1
MÔN: TOÁN 12 – Hệ không chuyên
(Thời gian làm bài 90 phút)
Họ và tên thí sinh:..............................................................SBD:.....................
Câu 1. Đồ thị hàm số nào sau đây có ba điểm cực trị?
A.
4 2
2 1
y x x
. B.
4 2
2 1
y x x
. C.
4 2
2 1
y x x
. D.
4 2
2 4 1
y x x
.
Câu 2. Tính đạo hàm của hàm số
2
x
f x
?
A.
1
.2 ln 2
x
f x x
. B.
1
.2
x
f x x
. C.
1
2 ln 2
x
f x
. D.
2 ln 2
x
f x
.
Câu 3. Số nghiệm của phương trình
2
log 1 2
x
là:
A. Kết quả khác. B.
1
. C.
0
. D.
2
.
Câu 4. Tập nghiệm của bất phương trình
2
1 1
3 3
log 2 1 log 1
x x x
là:
A.
1;2
. B.
3;
. C.
2;
. D.
1;
.
Câu 5. Tìm giá trị nhỏ nhất của hàm số
2 1
1
x
y
x
trên đoạn
2;3
?
A.
0
. B.
1
. C.
5
. D.
2
.
Câu 6. Cho lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
2 , 2
BC a AA a
.
Tính thể tích
V
của lăng trụ
.
ABC A B C
.
A.
3
8
3
a
V . B.
3
2
3
a
V . C.
3
2
V a
. D.
3
4
V a
.
Câu 7. Cho hàm số
2 3
1
x
y
x
có đồ thị
C
. Tiếp tuyến của
C
tại điểm có hoành độ bằng
2
cắt
các trục
Ox
và
Oy
tại các điểm
;0
A a
,
0;
B b
. Khi đó, giá trị của
5
P a b
bằng:
A.
17
5
P . B.
0
P
. C.
17
P
. D.
34
P
.
Câu 8. Gọi
1
x
,
2
x
là các nghiệm của phương trình
2
1 3
3
log 3 1 log 3 0
x x
. Khi đó, tích
1 2
x x
:
A.
3
. B.
3
3
. C.
3 1
3
. D.
3
3
.
Câu 9. Hàm số
3 2
1 1 1
3 2 2
y x mx
đạt cực tiểu tại
2
x
khi
m
nhận giá trị nào sau đây?
A.
2
m
. B.
4
m
. C.
1
m
. D.
3
m
.
Câu 10. Số điểm cực đại của hàm số
4
100
y x là:
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 11. Cho khối chóp
.
S ABC
có
SA ABC
,
SA a
, đáy
ABC
là tam giác đều cạnh bằng
a
. Tính
thể tích
V
của khối tứ diện
.
S ABC
.
A.
3
3
4
a
V . B.
3
3
12
a
V . C.
3
3
7
a
V . D.
3
3
3
a
V .
17
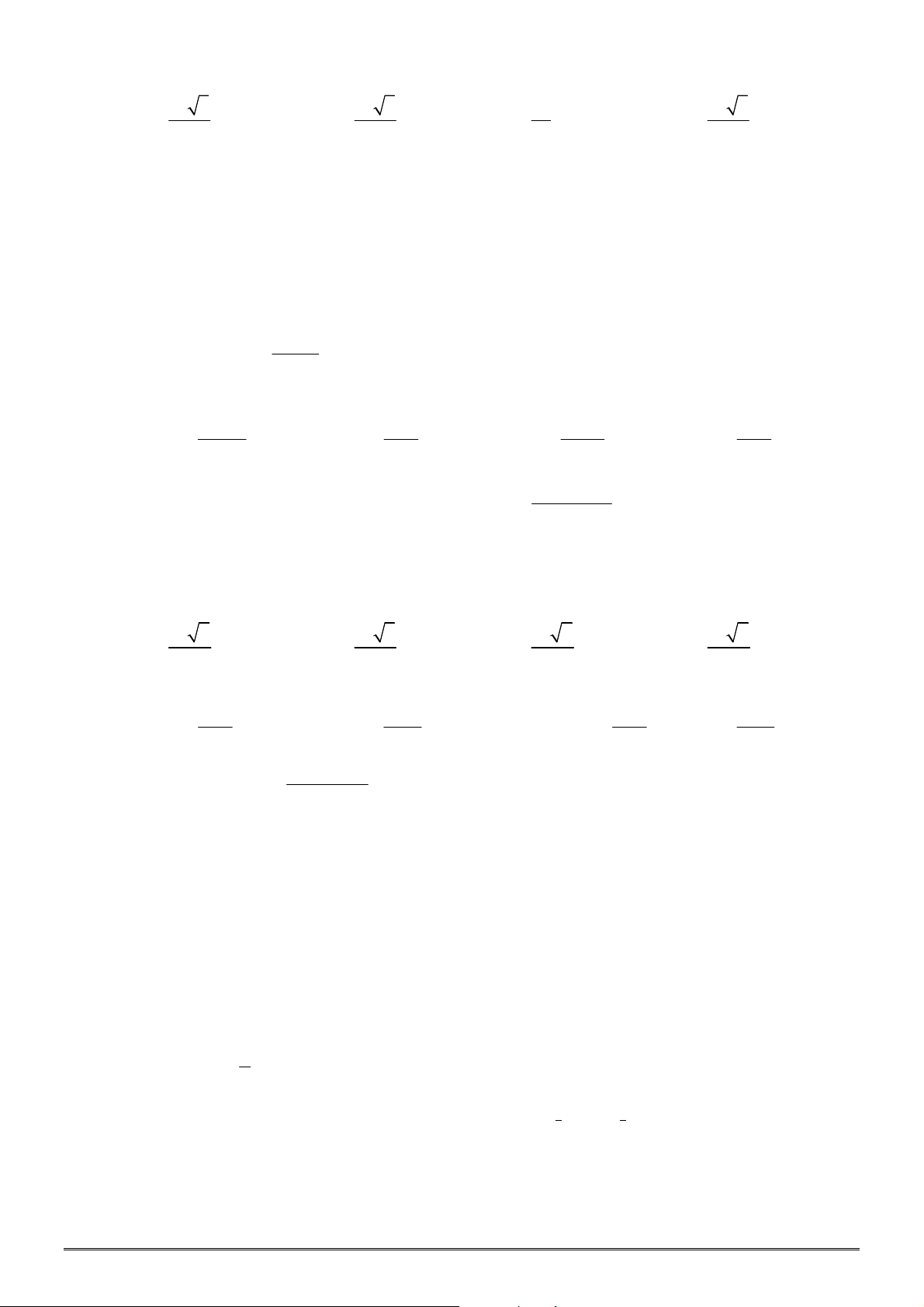
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/13 - Mã đề thi 132
Câu 12. Cho lăng trụ đứng
.
ABC A B C
có tất cả các cạnh bằng
a
. Tính thể tích khối tứ diện
A B AC
?
A.
3
3
4
a
. B.
3
3
12
a
. C.
3
6
a
. D.
3
3
6
a
.
Câu 13. Một người gửi tiền vào ngân hàng
100
triệu đồng thể thức lãi kép, kỳ hạn là
1
tháng với lãi
suất
0,5%
một tháng. Hỏi sau ít nhất bao nhiêu tháng, người đó có nhiều hơn
125
triệu đồng?
A.
44
tháng. B.
45
tháng. C.
47
tháng. D.
46
tháng.
Câu 14. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật với
3
AB a
,
4
BC a
,
12
SA a
và
SA
vuông góc mặt đáy. Tính diện tích mặt cầu ngoại tiếp khối chóp
.
S ABCD
.
A.
25
S
. B.
289
S
. C.
169
S
. D.
144
S
.
Câu 15. Tìm hàm số
ax b
y
cx d
biết rằng đồ thị hàm số cắt trục tung tại điểm
0;1
M vào giao điểm
hai đường tiệm cận của hàm số là
1; 1
I
.
A.
2
2
x
y
x
. B.
1
1
x
y
x
. C.
2 1
1
x
y
x
. D.
1
1
x
y
x
.
Câu 16. Tìm tất cả các tiệm cận đứng của đồ thị hàm số
2
2
3 2
4
x x
y
x
.
A.
2
x
. B.
2, 2
x x
. C.
4
x
. D.
2
x
.
Câu 17. Cho hình chóp đều
.
S ABCD
có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt đáy bằng
60
.
Tính thể tích khối chóp
.
S ABCD
?
A.
3
6
3
a
. B.
3
3
6
a
. C.
3
6
2
a
. D.
3
6
6
a
.
Câu 18. Hàm số nào sau đây có đồ thị nhận đường thẳng
2
x
làm tiệm cận đứng?
A.
1
1
y
x
. B.
2
2
y
x
. C.
1
2
1
y x
x
. D.
5
2
x
y
x
.
Câu 19. Đồ thị hàm số
2
2 3
4 4
x
y
x x
có tiệm cận đứng
x a
và tiệm cận ngang
y b
. Khi đó giá trị
của
2
a b
bằng:
A.
2
. B.
2
. C.
4
. D.
4
.
Câu 20. Cho khối chóp tam giác
.
S ABC
. Gọi
A
,
B
,
C
lần lượt là trung điểm của cạnh
SA
,
SB
,
SC
. Khi đó thể tích khối chóp
.
S ABC
gấp bao nhiêu lần thể tích khối chóp
.
S A B C
?
A.
6
. B.
4
. C.
8
. D.
2
.
Câu 21. Giá trị nhỏ nhất của hàm số
2
2 4
y x x
trên đoạn
2;4
là:
A.
1
. B.
4
. C.
4
. D.
2
.
Câu 22. Cho các số thực dương
,
a b
. Mệnh đề nào sau đây đúng?
A.
2
2 2
1
log log
2
a a
. B.
2 2
1 1
log log
a a
a b a b
.
C.
2 2
2 2
log 2log
a b a b
. D.
3 3
4 4
log log
a b a b
.
Câu 23. Cho hàm số
4 2
2 1
y x x
biết
;
a b
là khoảng nghịch biến dài nhất của hàm số với
,a b
. Tính giá trị của
5
a b
là:
A.
1
. B.
6
. C.
5
. D.
2
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/13 - Mã đề thi 132
Câu 24. Thể tích khối hộp chữ nhật có ba cạnh xuất phát từ một đỉnh lần lượt có độ dài
, ,
a b c
là:
A.
1
6
V abc
. B.
1
3
V abc
. C.
V abc
. D.
4
3
V abc
.
Câu 25. Số nghiệm nguyên của bất phương trình
2
log 2 11 25 1
x x
là:
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 26. Tập xác định của hàm số
1
2
1
y x
là:
A.
D ;1
. B.
D 1;
. C.
D 0;1
. D.
D 1;
.
Câu 27. Chọn phát biểu đúng trong các phát biểu sau?
A. Đồ thị hàm số logarit không nằm bên dưới trục hoành.
B. Đồ thị hàm số mũ với cơ số dương nhỏ hơn 1 thì nằm dưới trên trục hoành.
C. Đồ thị hàm số logarit luôn nằm bên phải trục tung.
D. Đồ thị hàm số mũ với số mũ âm luôn có hai tiệm cận.
Câu 28. Cho hình chóp đều
.
S ABC
có cạnh đáy bằng
a
, góc giữa mặt bên và đáy bằng
60
. Tính diện
tích xung quanh
xq
S
của hình nón có đỉnh
S
và có đường tròn đáy là đường tròn ngoại tiếp tam
giác đáy
ABC
.
A.
2
10
8
xq
a
S
. B.
2
7
6
xq
a
S
. C.
2
3
3
xq
a
S
. D.
2
7
4
xq
a
S
.
Câu 29. Hàm số
1
2
x
y
x
có đồ thị
H
. Tiếp tuyến của
H
tại giao điểm của
H
với trục hoành là:
A.
1 1
3 3
y x
. B.
3
y x
. C.
3
y x
. D.
3 3
y x
.
Câu 30. Cho khối hộp chữ nhật
.
ABCD A B C D
có
8
AD
,
6
CD
,
12
AC
. Tính diện tích toàn
phần của khối trụ có hai đường tròn đáy ngoại tiếp hai hình chữ nhật
ABCD
và
A B C D
.
A.
5 4 11 5
tp
S
. B.
26
tp
S
.
C.
576
tp
S
. D.
10 2 11 5
tp
S
.
Câu 31. Đồ thị hàm số
3 2
3 9 2
y x x x
có tâm đối xứng là:
A.
2; 20
I . B.
1;7
I . C.
2;0
I . D.
1; 9
I
.
Câu 32. Cho hình lăng trụ đứng
.
ABCD A B C D
có đáy
ABCD
là hình thang cân với cạnh
,
AB BC a
2
AD a
. Chiều cao của hình lăng trụ bằng
2
a
. Tính tổng thể tích
V
khối trụ
ngoại tiếp lăng trụ đã cho.
A.
2
3
V a
. B.
2
4
V a
. C.
3
V a
. D.
3
2
V a
.
Câu 33. Cho hàm số
y f x
xác định trên
\ 1
và có bảng biến thiên như hình vẽ dưới đây.
Kết luận nào sau đây là đúng?
A. Hàm số đạt giá trị nhỏ nhất là
4
.
B. Hàm số đạt cực đại tại
1
x
.
C. Đồ thị hàm số có điểm cực tiểu
0
x
.
D. Đồ thị hàm số chỉ có hai tiệm cận.
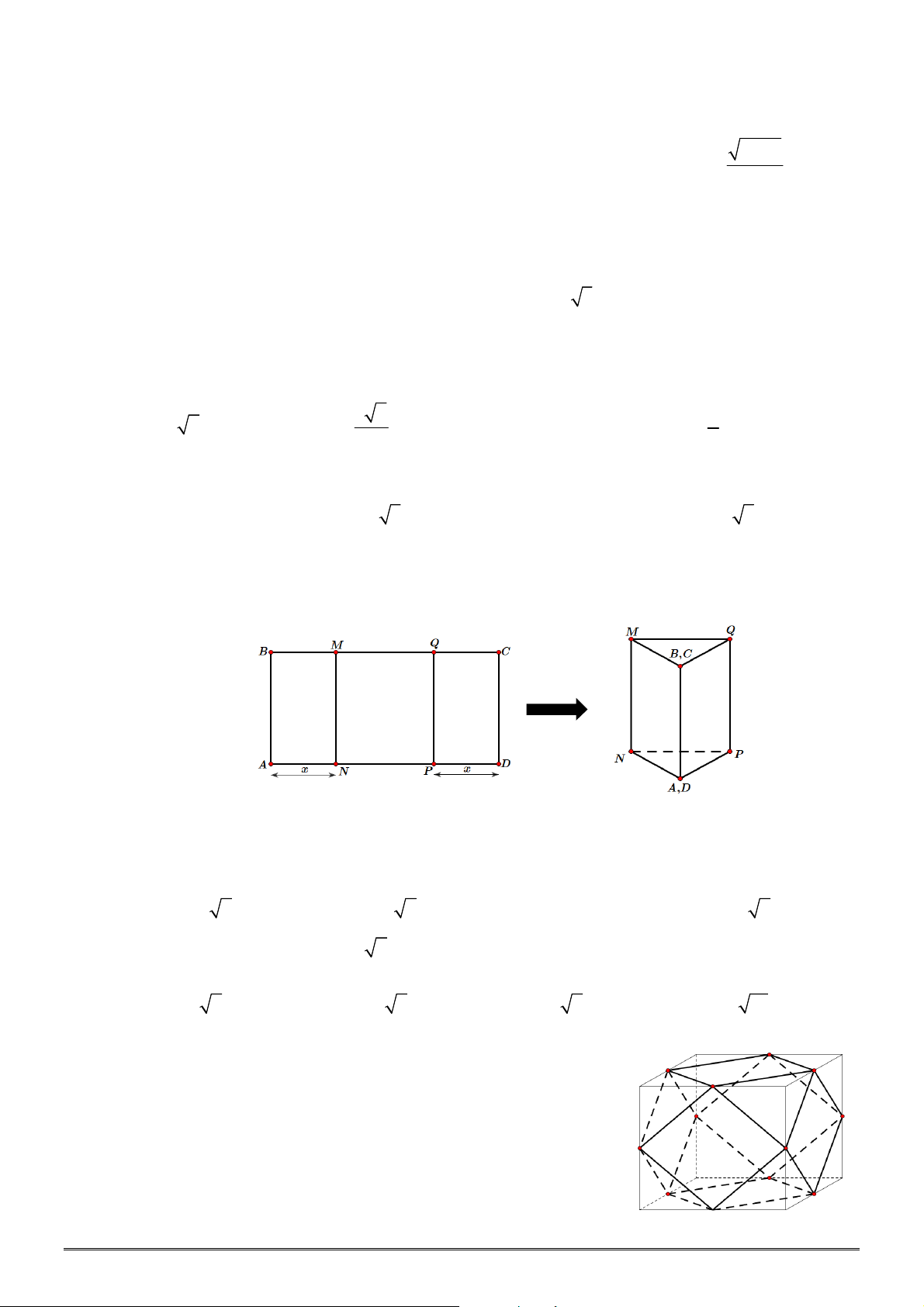
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/13 - Mã đề thi 132
Câu 34. Tìm số các giá trị nguyên của tham số
m
để hàm số
4 2
1 3 10 2
y m x m x
có ba cực trị?
A.
3
. B.
5
. C.
4
. D.
0
.
Câu 35. Gọi
n
,
d
lần lượt số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
2
1
x
y
x
. Tính giá
trị của
2 3
T n d
?
A.
7
T
. B.
4
T
. C.
5
T
. D.
8
T
.
Câu 36. Cho đồ thị hàm số
3 2
3 4
y x x
có hai điểm cực trị là
A
,
B
. Tính diện tích tam giác
OAB
?
A.
4
S
. B.
8
S
. C.
2 5
S . D.
2
S
.
Câu 37. Cho hình vuông
ABCD
có cạnh bằng
4
. Tính tỉ số thể tích của hai khối tròn xoay sinh ra khi
lần lượt quay hình vuông đã cho quanh các đường thẳng chứa cạnh
AB
và đường chéo
AC
của hình vuông?
A.
3 2
. B.
3 2
2
. C.
3
. D.
3
2
.
Câu 38. Cho hàm số
2
2
x
y x x e
. Xác định tổng các nghiệm của phương trình
0
y y
?
A.
3
. B.
3 5
. C.
3
. D.
3 5
.
Câu 39. Cho một tấm nhôm hình chữ nhật
ABCD
có
24 cm
AD
. Ta gấp tấm nhôm theo hai cạnh
MN
,
QP
vào phía trong đến khi
,
AB CD
trùng nhau như hình vẽ dưới đây để được một hình
lăng trụ khuyết hai đáy. Tìm
x
để thể tích khối lăng trụ lớn nhất?
A.
8
x
. B.
10
x
. C.
9
x
. D.
6
x
.
Câu 40. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
2 2
sin cos
2 2
x x
y lần lượt là
m
,
M
. Tính giá trị
.
P M m
?
A.
4 2
P
. B.
3 2
P
. C.
6
P
. D.
6 2
P
.
Câu 41. Cho hình trụ có trục
2 7
OO
,
ABCD
là hình vuông có cạnh bằng 8 sao cho các đỉnh nằm
trên đường tròn đáy và tâm hình vuông trùng với trung điểm
OO
. Thể tích khối trụ là:
A.
25 7
. B.
50 7
. C.
16 7
. D.
25 14
.
Câu 42. Người ta nối trung điểm các cạnh của hình hộp chữ nhật rồi
cắt bỏ các hình chóp tam giác ở các góc của hình hộp như hình
vẽ bên. Hình còn lại là một đa diện có số đỉnh và số cạnh là:
A.
12
đỉnh,
24
cạnh.
B.
10
đỉnh,
24
cạnh.
C.
10
đỉnh,
48
cạnh.
D.
12
đỉnh,
20
cạnh.
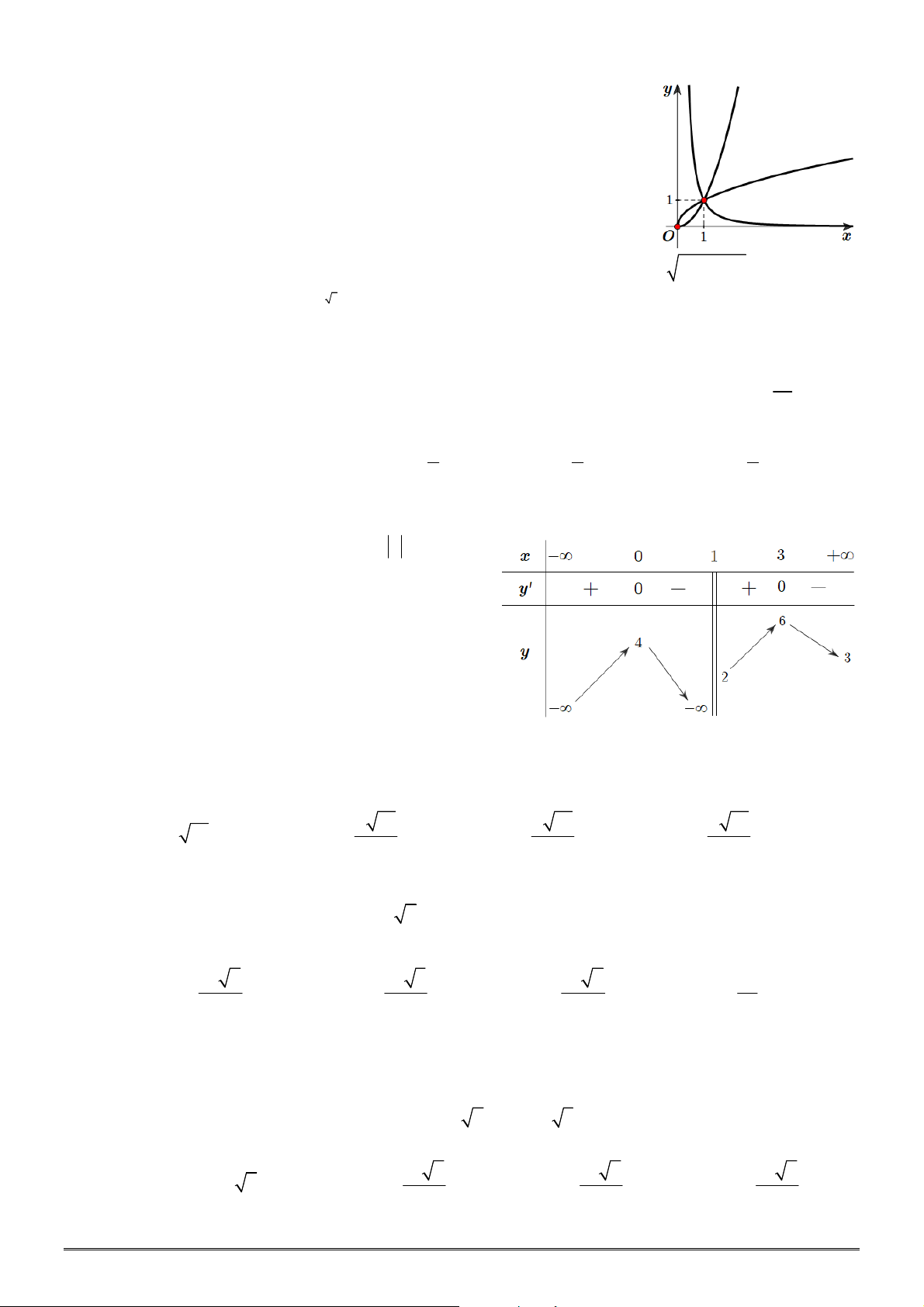
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/13 - Mã đề thi 132
Câu 43. Hình vẽ sau là đồ thị của ba hàm số
y x
,
y x
,
y x
với
điều kiện
0
x
và
,
,
là các số thực cho trước. Mệnh đề
nào dưới đây đúng?
A.
.
B.
.
C.
.
D.
.
Câu 44. Tìm tập hợp các giá trị của tham số
m
để phương trình
2 2
5 5
log 2 log 1 2 0
x x m
có
nghiệm thuộc đoạn
3
1;5
?
A.
2;3
. B.
2;6
. C.
0;5
. D.
1;6
.
Câu 45. Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
3
3
1
3 2x mx
x
nghiệm
đúng với mọi
1
x
?
A.
;1
m . B.
2
;
3
m
. C.
2
;1
3
m
. D.
2
;
3
m
.
Câu 46. Cho hàm số
y f x
xác định trên
\ 1
và có bảng biến thiên như hình vẽ dưới đây.
Hỏi khi đó đồ thị hàm số
y f x
có bao
nhiêu tiệm cận?
A.
4
.
B.
3
.
C.
1
.
D.
2
.
Câu 47. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật có
AB a
,
3
BC a
và
SA ABCD
.
Gọi
G
là trọng tâm tam giác
SAB
. Tính khoảng cách từ
G
đến mặt phẳng
SAC
bằng:
A.
10
a . B.
10
3
a
. C.
10
2
a
. D.
10
10
a
.
Câu 48. Cắt hình nón
N
có đỉnh
S
bởi một mặt phẳng chứa trục hình nón ta được một tam giác
vuông cân có cạnh huyền bằng
2
a
;
BC
là một dây cung của hình tròn đáy của
N
sao cho
mặt phẳng
SBC
tạo với đáy góc
60
. Tính diện tích
S
của tam giác
SBC
.
A.
2
2
2
a
S . B.
2
3
3
a
S . C.
2
2
3
a
S . D.
2
3
a
S .
Câu 49. Cho khối chóp
.
S ABCD
có thể tích bằng 81. Gọi
M
,
N
,
P
,
Q
lần lượt là trọng tâm các mặt
bên
SAB
,
SBC
,
SCD
,
SDA
. Tính thể tích
V
của khối chóp .
S MNPQ
?
A.
18
V
. B.
24
V
. C.
12
V
. D.
54
V
.
Câu 50. Cho hình chóp
.
S ABC
có
SA a
,
2
SB a
,
3
SC a
. Tính thể tích lớn nhất
max
V
của khối
chóp đã cho.
A.
3
max
6.
V a B.
3
max
6
.
2
a
V C.
3
max
6
.
3
a
V D.
3
max
6
.
6
a
V
----------HẾT----------
y x
y x
y x
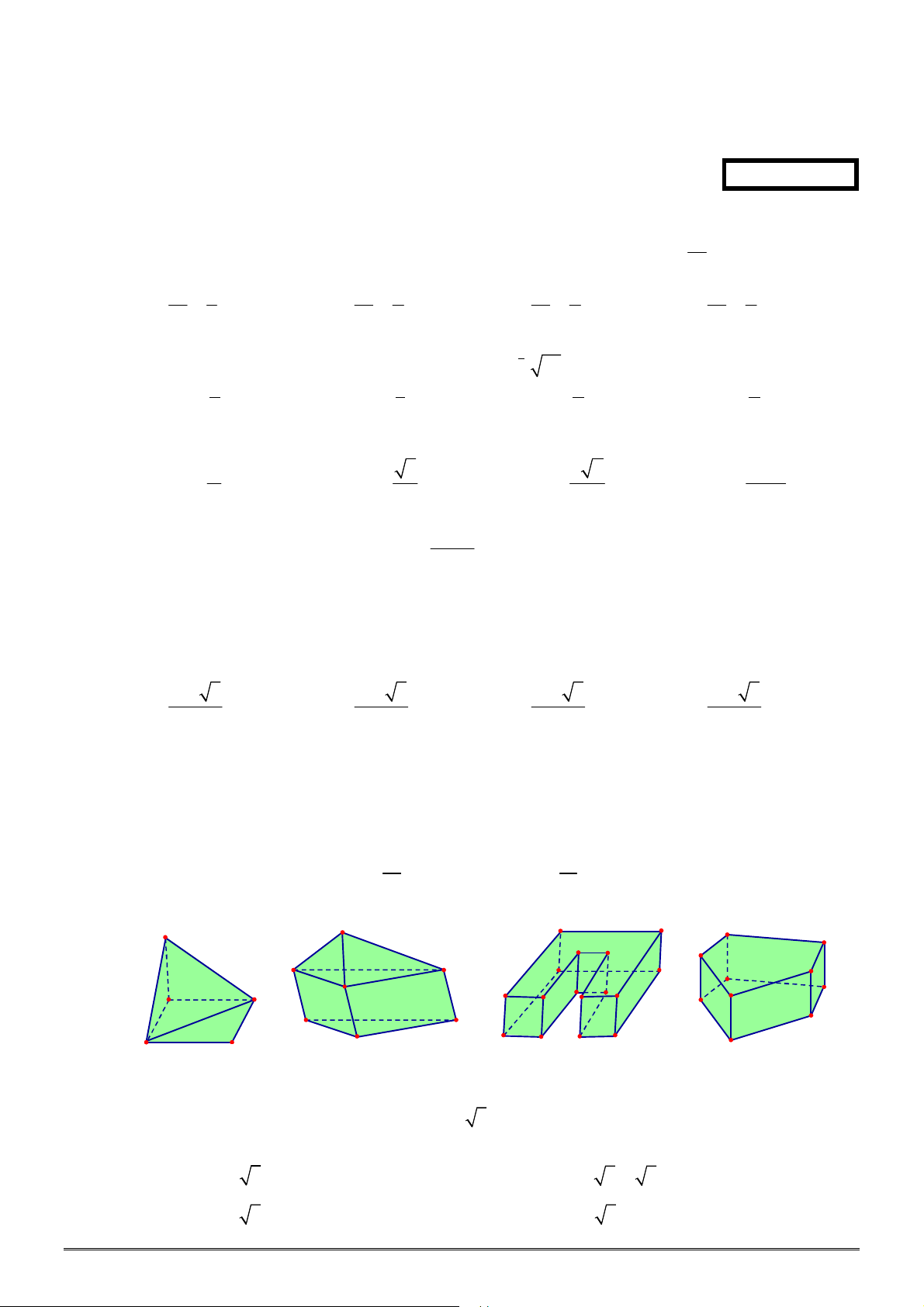
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/26 - Mã đề thi 357
SỞ GIÁO DỤC VÀ ĐÀO TẠO
LÂM ĐỒNG
KIỂM TRA CHẤT LƯỢNG HỌC KỲ 1
Năm học 2017-2018
MÔN: TOÁN 12
Thời gian làm bài 90 phút
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 357
Câu 1. [2H1-2] Cho lăng trụ
.
ABC A B C
. Gọi
O
là tâm của mặt bên
ACC A
. Gọi
1
V
,
2
V
lần lượt là
thể tích của khối chóp
.
O ABC
và khối lăng trụ
.
ABC A B C
. Tính tỷ số
1
2
V
V
.
A.
1
2
1
3
V
V
. B.
1
2
1
4
V
V
. C.
1
2
1
2
V
V
. D.
1
2
1
6
V
V
.
Câu 2. [2D2-1] Cho
x
là số thực dương. Biểu diễn
1
5
4
4
.
P x x
thành dạng lũy thừa với số mũ hữu tỷ.
A.
3
10
P x
. B.
11
4
P x
. C.
7
20
P x
. D.
21
20
P x
.
Câu 3. [2D2-2] Hàm số nào sau đây nghịch biến trên
?
A.
3
x
y
. B.
5
2
x
y
. C.
2 2
3
x
y
. D.
2018
2017
x
y
.
Câu 4. [2D1-2] Biết rằng đồ thị hàm số
2 1
1
x
y
x
và đường thẳng
7
y x
cắt nhau tại hai điểm
1 1
;
A x y
,
2 2
;
B x y
. Tính giá trị của tổng
1 2
S x x
.
A.
6
S
. B.
10
S
. C.
6
S
. D.
8
S
.
Câu 5. [2H2-2] Thiết diện qua trục của hình nón là một tam giác đều cạnh bằng
a
. Tính thể tích
V
của khối nón đã cho.
A.
3
3
24
a
. B.
3
3
12
a
. C.
3
3
8
a
. D.
3
3
48
a
.
Câu 6. [2D1-2] Tìm giá trị nhỏ nhất của hàm số
3 2
5 1
y x x x
trên đoạn
2;0
:
A.
2;0
min 5
y
. B.
2;0
min 1
y
. C.
2;0
min 1
y
. D.
2;0
min 4
y
.
Câu 7. [2D2-2] Tìm nghiệm của phương trình
3
log 2 5 2
x
.
A.
2
x
. B.
13
2
x
. C.
11
2
x
. D.
7
x
.
Câu 8. [2H1-1] Hình nào trong các hình dưới đây không phải hình đa diện?
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 9. [2H2-1] Cho khối trụ có bán kính đáy là
2 3
và chiều cao bằng
3
. Tính diện tích xung quanh
xq
S
của hình trụ.
A.
12 3
xq
S
. B.
4 3 2 3 3
xq
S
.
C.
18 3
xq
S
. D.
6 3
xq
S
.
Hình 1.
Hình 3.
Hình 4.
Hình 2.
18
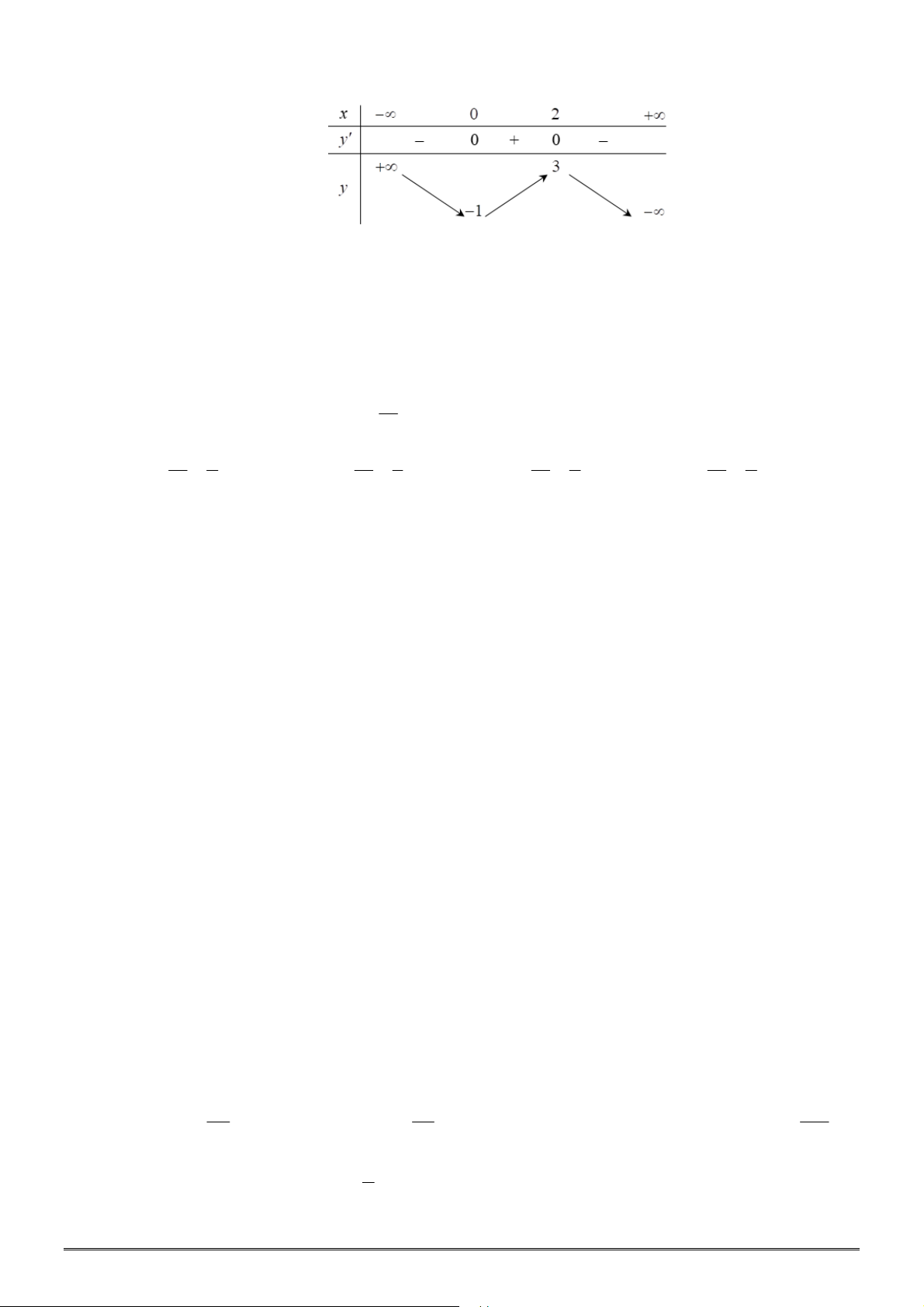
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/26 - Mã đề thi 357
Câu 10. [2D1-1] Cho hàm số
y f x
có bảng biến thiên như hình vẽ.
Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
1; 3
. B. Hàm số nghịch biến trên khoảng
0; 2
.
C. Hàm số đồng biến trên khoảng
0; 2
. D. Hàm số nghịch biến trên khoảng
; 2
.
Câu 11. [2H1-2] Cho hình chóp
.
S ABC
, gọi
M
là trung điểm của
SB
và
D
là điểm đối xứng của
B
qua
C
. Cạnh
SC
cắt mặt phẳng
AMD
tại
N
. Gọi
1
V
,
2
V
lần lượt là thể tích của khối chóp
.
S AMN
và
.
S ABC
. Tính tỉ số
1
2
V
V
.
A.
1
2
2
3
V
V
. B.
1
2
1
3
V
V
. C.
1
2
1
6
V
V
. D.
1
2
1
4
V
V
.
Câu 12. [2H2-1] Cho hình chữ nhật
ABCD
có
3
AB
,
4
AD
. Gọi
M
,
N
lần lượt là trung điểm của
các cạnh
AD
,
BC
. Quay hình chữ nhật
ABCD
quanh trục
MN
, tính thể tích
V
của khối trụ
nhận được.
A.
4
V
. B.
12
V
. C.
48
V
. D.
36
V
.
Câu 13. [2D2-2] Tìm đạo hàm của hàm số
3 2
x
y x .
A.
2 1 3 ln3
x
y x
. B.
2 4
x
y x
.
C.
2 1 3 log2
x
y x
. D.
2 1 3 ln2
x
y x
.
Câu 14. [2D1-2] Cho hàm số
3 2
4 6 5
y x x
. Tính giá trị cực tiểu
CT
y
của hàm số.
A.
0
CT
y
. B.
5
CT
y
. C.
3
CT
y
. D.
1
CT
y
.
Câu 15. [2D1-1] Hàm số
4 2
8 3
y x x
có bao nhiêu điểm cực trị?
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 16. [2H1-1] Khối tứ diện đều có bao nhiêu mặt phẳng đối xứng?
A.
6
. B.
3
. C. Vô số. D.
4
.
Câu 17. [2H2-2] Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lăng trụ đứng có đáy là tam giác nội tiếp được trong một mặt cầu.
B. Hình hộp chữ nhật có ba kích thước phân biệt nội tiếp được trong một mặt cầu.
C. Hình chóp
.
S ABCD
có đáy là hình bình hành nội tiếp được trong một mặt cầu.
D. Hình chóp
.
S ABCD
có đáy là hình chữ nhật nội tiếp được trong một mặt cầu.
Câu 18. [2D2-1] Cho số thực
a
dương, khác 1 và số thực
tùy ý. Mệnh đề nào dưới đây đúng?
A.
1
a
a
. B.
1
a
a
. C.
a a
. D.
1
a
a
.
Câu 19. [2D1-1] Đồ thị hàm số
3
y
x
có bao nhiêu đường tiệm cận?
A.
1
. B.
0
. C.
3
. D.
2
.
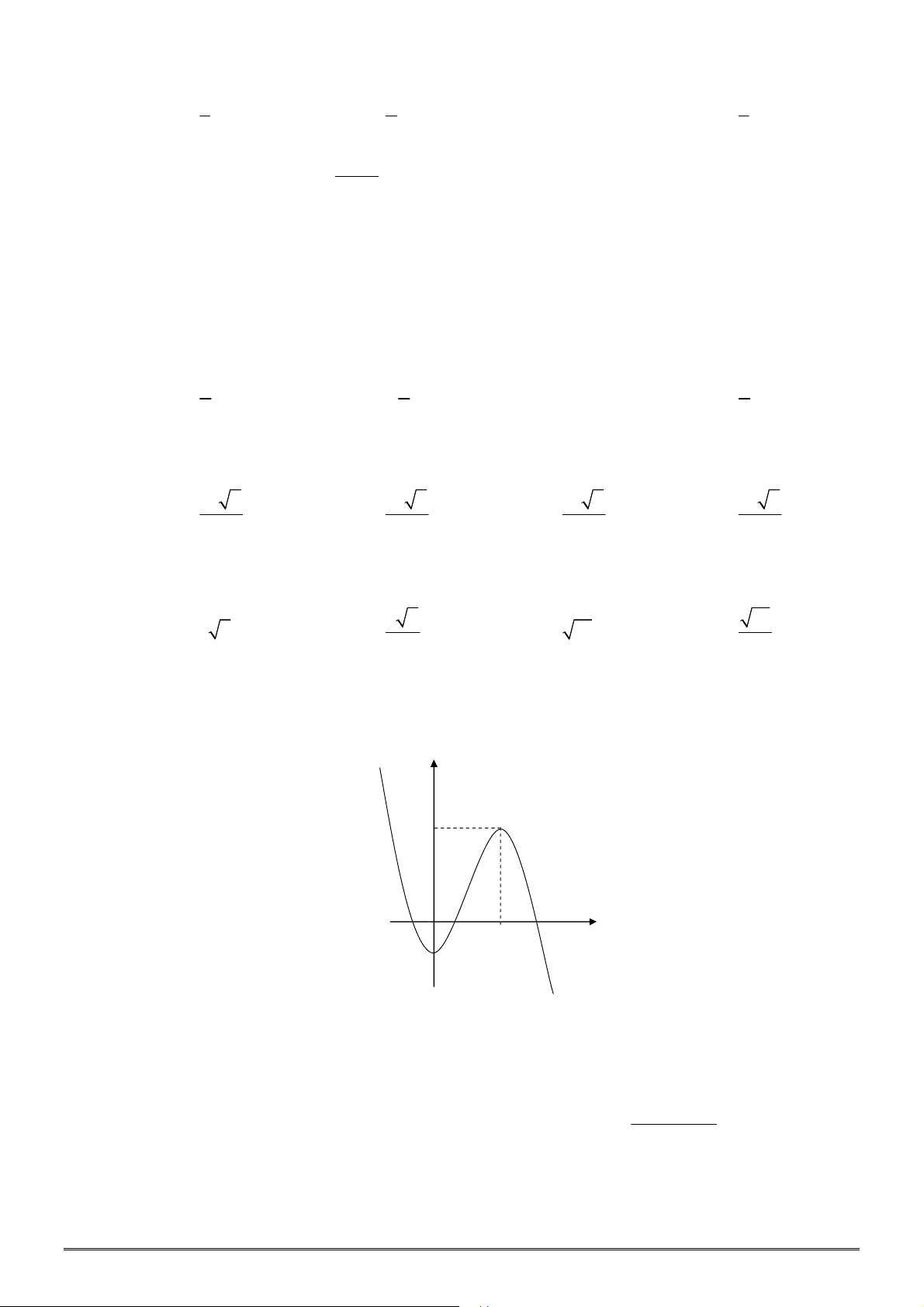
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/26 - Mã đề thi 357
Câu 20. [2H1-1] Viết công thức tính thể tích
V
của khối chóp có diện tích là
S
và chiều cao
h
.
A.
1
3
V S h
. B.
1
.
2
V S h
. C.
.
V S h
. D.
1
.
3
V S h
.
Câu 21. [2D1-2] Cho hàm số
2 1
2
x
y
x
. Gọi
M
là giá trị lớn nhất của hàm số trên đoạn
1;2
. Mệnh
đề nào sau đây đúng?
A.
1;2
M . B.
1;0
M . C.
0;1
M . D.
4;2
M .
Câu 22. [2D1-1] Đồ thị hàm số
3 2
2 1
y x x x
và đường thẳng
1
y x
có bao nhiêu giao điểm?
A.
2
. B.
0
. C.
3
. D.
1
.
Câu 23. [2D2-2] Cho số thực
a
dương và khác
1
. Tính
2
3
log .
a
P a
A.
2
.
3
P
B.
2
.
3
P
C.
6.
P
D.
3
.
2
P
Câu 24. [2H2-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông và cạnh bên
SA
vuông góc với
đáy. Cho biết
SAC
là tam giác vuông cân và
SC a
. Tính thể tích
V
của hình chóp
.
S ABCD
.
A.
3
2
.
8
a
V B.
3
2
.
24
a
V C.
3
2
.
12
a
V D.
3
2
.
3
a
V
Câu 25. [2H2-2] Tính bán kính
R
của mặt cầu ngoại tiếp hình hộp chữ nhật có kích thước lần lượt là
3,4,5
.
A.
5 2
R
. B.
5 2
2
R . C.
15
R . D.
12
2
R .
Câu 26. [2D1-2] Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hãy tìm hàm số
đó.
A.
3 2
3 1
y x x
. B.
3 2
3 1
y x x
. C.
3 2
3 1
y x x
. D.
3 2
2 1
y x x
.
x
y
O
3
2
-1
Câu 27. [2H1-1] Khối nào trong các khối sau là khối đa diện đều loại
3;4
?
A. Khối tứ diện đều. B. Khối bát diện đều .
C. Khối nhị thập diện đều . D. Khối lập phương .
Câu 28. [2D1-3] Tìm tất cả giá trị của tham số
m
để đồ thị hàm số
2
3
4
x
y
x x m
có ba đường tiệm
cận .
A.
4
m
. B.
4
3
m
m
. C.
4
m
. D.
4
3
m
m
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/26 - Mã đề thi 357
Câu 29. [2H1-2] Cho hình hộp đứng
.
ABCD A B C D
có đáy là hình vuông, tam giác
B AC
đều có
cạnh bằng
a
. Tính thể tích
V
của khối hộp đã cho.
A.
3
2
8
a
V . B.
3
3
9
a
V . C.
3
2
4
a
V . D.
3
2
12
a
V .
Câu 30. [2H2-1] Viết công thức tính diện tích xung quanh của hình nón có bán kính đáy là
r
và chiều
cao
h
.
A.
2 2
2
xq
S r r h
. B.
xq
S rh
. C.
2 2
xq
S r r h
. D.
xq
S r r h
.
Câu 31. [2D2-2] Cho phương trình
2
2
2
2
log log 6 0
8
x
x
với điều kiện
0
x
, nếu đặt
2
log
t x
ta
được phương trình nào sau đây?
A.
2
4 2 9 0
t t
. B.
2
2 2 3 0
t t
. C.
2
3 3 0
t
. D.
2
4 2 3 0
t t
.
Câu 32. [2D1-2] Cho hàm số
3 2
3 1 1
y x x . Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số
1
đồng biến trên các khoảng
;0 , 2;
và nghịch biến trên khoảng
0;2
.
B. Hàm số
1
đồng biến trên các khoảng
; 2 , 0;
và nghịch biến trên khoảng
2;0
.
C. Hàm số
1
nghịch biến trên các khoảng
;0 , 2;
và đồng biến trên khoảng
0;2
.
D. Hàm số
1
nghịch biến trên các khoảng
; 2 , 0;
và đồng biến trên khoảng
2;0
.
Câu 33. [2H1-2] Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh
a
và cạnh bên
SA
vuông góc với
đáy,
2
SA a
. Tính thể tích
V
của khối chóp
.
S ABC
?
A.
3
2
6
a
. B.
3
3
6
a
. C.
3
3
12
a
. D.
3
2 3
9
a
.
Câu 34. [2D2-2] Tìm tập xác định
D
của hàm số
3
2
4
4
y x
.
A.
\ 2; 2
D
. B.
D
.
C.
; 2 2;D
. D.
; 2 2;D
.
Câu 35. [2H1-2] Cho hình lăng trụ
.
ABC A B C
có diện tích đáy bằng
2
a
, cạnh bên
AA a
và hợp với
đáy
ABC
một góc
60
. Tính thể tích
V
của khối lăng trụ
.
ABC A B C
.
A.
3
3
2
a
V . B.
3
3
6
a
V . C.
3
2
a
V . D.
3
3
3
a
V .
Câu 36. [2D1-2] Cho hàm số
1
mx m
y
x m
, (
m
là tham số). Tìm giá trị của
m
để
0;2
max 2
y
.
A.
1
m
. B.
3
m
. C.
5
m
. D.
1
3
m
.
Câu 37. [2D1-3] Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ bên. Khẳng định nào sau đây
đúng ?
A.
0, 0, 0, 0.
a b c d
B.
0, 0, 0, 0.
a b c d
C.
0, 0, 0, 0.
a b c d
D.
0, 0, 0, 0.
a b c d
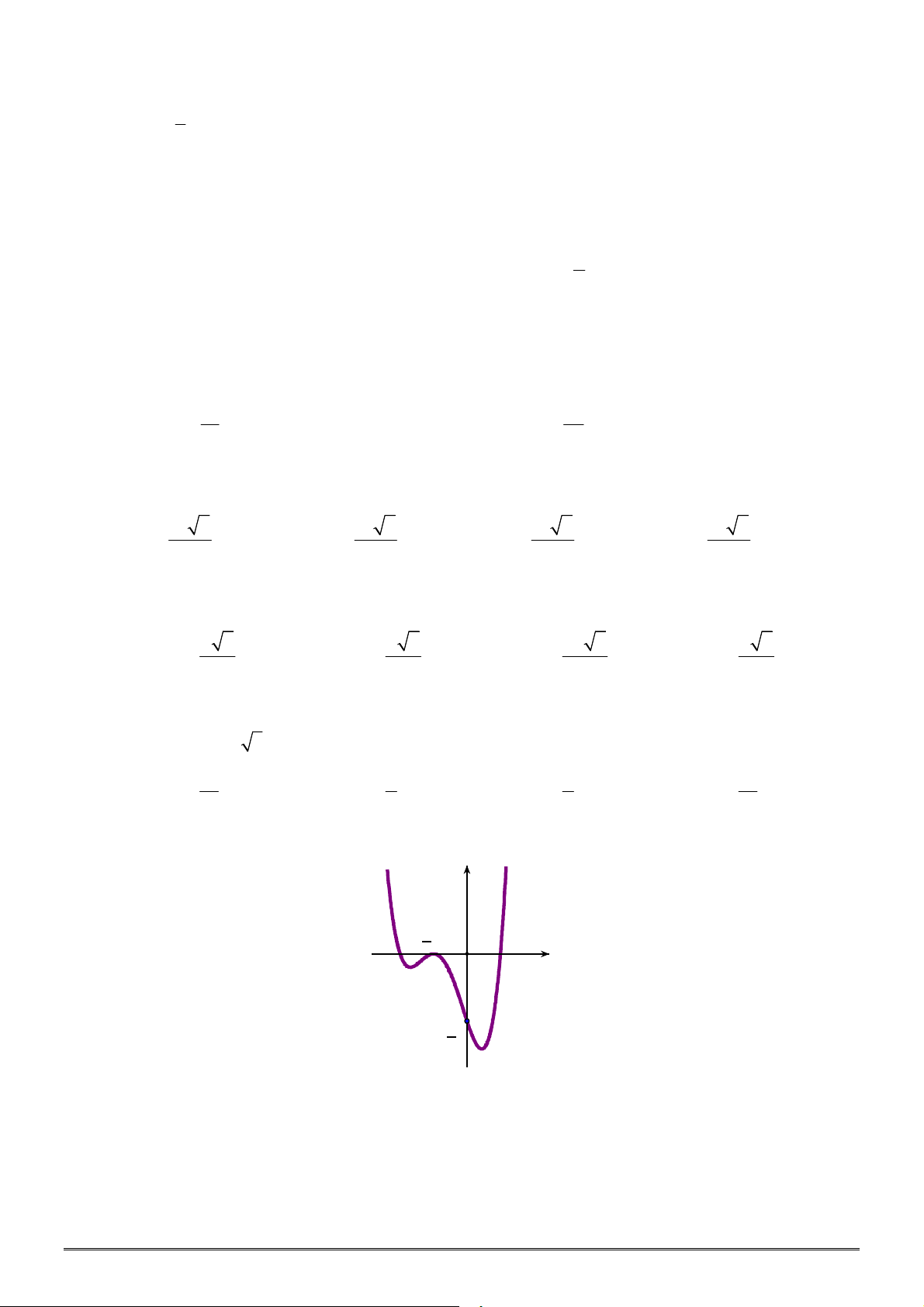
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/26 - Mã đề thi 357
Câu 38. [2D1-3] Gọi
S
là tập hợp các giá trị nguyên của
m
trên đoạn
10;10
để hàm số
3 2
1
2 1 2 2
3
y x m x m x
có cực đại và cực tiểu. Tìm số phần tử của
S
.
A.
20
. B.
19
. C.
18
. D.
21
.
Câu 39. [2D2-2] Tìm tất cả các giá trị của tham số
m
để phương trình
9 2 1 3 2 1 0
x x
m m
có
hai nghiệm thực phân biệt.
A.
0
m
. B.
1
0
m
m
. C.
1
2
0
m
m
. D.
0
m
.
Câu 40. [2D2-2] Tìm giá trị của tham số
m
để phương trình
2 2
3 3
log 2 log 1 4 0
x m x m
có hai
nghiệm thực phân biệt
1 2
;
x x
thỏa điều kiện
1 2
9
x x
.
A.
13
2
m
. B.
3
m
. C.
1
4
m
. D.
2
m
.
Câu 41. [2H1-2]Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy là
a
và tất cả các mặt bên của hình
chóp là các tam giác vuông cân. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
2
8
a
. B.
3
6
18
a
. C.
3
2
12
a
. D.
3
2
24
a
.
Câu 42. [2H2-2]Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy là
a
và cạnh bên hợp với đáy góc
60
. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp.
A.
6
3
a
R . B.
6
2
a
R . C.
2 6
3
a
R . D.
6
6
a
R .
Câu 43. [2D2-2] Cho biết
log 2
a
b
và
log 3
b
c
,
0 1,0 1, 0
a b c
. Tính giá trị của biểu thức
2
log
ab
P b c
.
A.
10
3
P
. B.
7
4
P
. C.
7
3
P
. D.
16
3
P
.
Câu 44. [2D1-3] Cho hàm số
y f x
liên tục trên
và hàm số
y f x
có đồ thị như hình vẽ.
x
y
1
1
2
O
Đặt
2
g x f x x
. Khẳng định nào dưới đây đúng?
A. Hàm số
g x
có một điểm cực đại và một điểm cực tiểu.
B. Hàm số
g x
chỉ có một điểm cực đại.
C. Hàm số
g x
có một điểm cực đại và hai điểm cực tiểu.
D. Hàm số
g x
chỉ có một điểm cực tiểu.
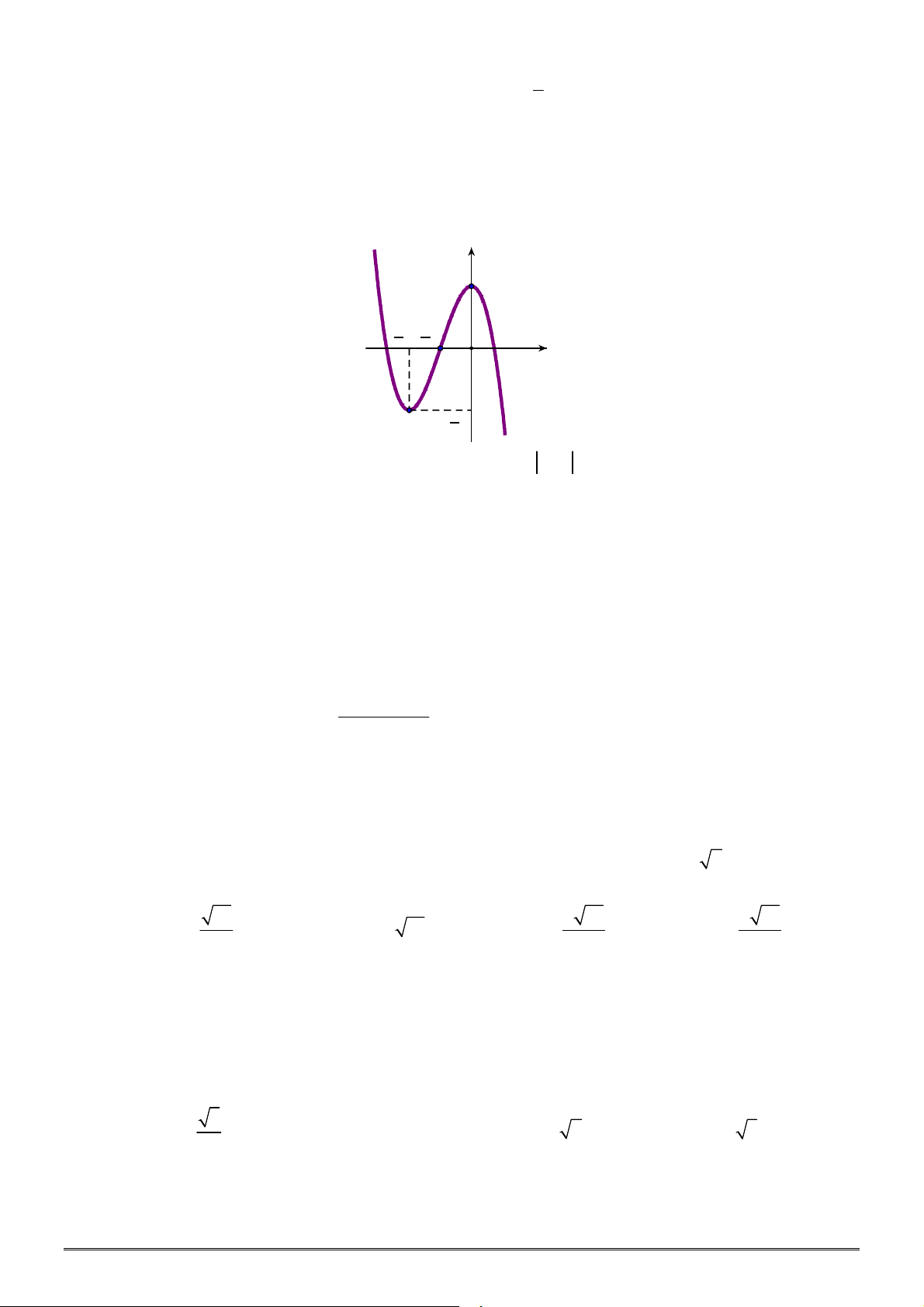
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/26 - Mã đề thi 357
Câu 45. [2D1-2] Tìm giá trị của tham số m để hàm số
3 2 2
1
1 2 1
3
y x mx m x m
đạt cực tiểu
tại điểm
0
2
x
.
A.
3
m
hoặc
1
m
. B.
3
m
hoặc
1
m
.
C.
1
m
D.
3
m
.
Câu 46. [2D1-3] Cho hàm số
2
1 2 2
y x x x
có đồ thị như hình vẽ bên
x
y
2
2
12
O
Tìm tất cả giá trị của tham số m để phương trình
2
1 2 2
x x x m
có 4 nghiệm thực
phân biệt.
A.
0 2
m
. B. Không tồn tại m. C.
2
m
. D.
0 2
m
.
Câu 47. [2D2-3] Sự tăng trưởng của một loài vi khuẩn trong phòng thí nghiệm được tính theo công thức
.3
rt
f t F
trong đó
F
là lượng vi khuẩn ban đầu,
r
là tỉ lệ tăng trưởng
0
r
và
t
là thời
gian(đơn vị: giờ). Biết rằng số lượng vi khuẩn ban đầu là
6
10
con và sau
3
giờ là
6
5.10
con.
Hỏi sau thời gian mấy giờ, số lượng vi khuẩn là
125
triệu con?
A.
75
giờ. B.
9
giờ. C.
6
giờ. D.
60
giờ.
Câu 48. [2D2-3] Cho hàm số
3 2
3
x
x
m m
y
m
, (
m
tham số). Tìm tất cả các giá trị của tham số
m
để
hàm số đồng biến trên
0;1
.
A.
3
2
m
m
. B.
3 1
2
m
m
. C.
1
2
m
m
. D.
3
1
m
m
.
Câu 49. [2H1-3] Cho tứ diện
ABCD
có
2
AB
, tất cả các cạnh còn lại bằng
2 2
. Thể tích
V
của
khối tứ diện
ABCD
A.
10
3
V . B.
2 10
V . C.
4 10
3
V . D.
2 10
3
V .
Câu 50. [2H2-4] Cho mặt cầu
S
có tâm
O
, bán kính bằng
2
. Hai mặt phẳng
P
và
Q
song song
với nhau và cách đều tâm
O
một khoảng cách là
x
0 2
x
lần lượt cắt mặt cầu
S
theo
giao tuyến là hai đường tròn
C
và
C
. Xác định
x
để hình trụ có hai đường tròn đáy là
C
và
C
có diện tích xung quanh lớn nhất.
A.
3
2
x . B.
1
x
. C.
2
x
. D.
3
x .
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/25 - Mã đề thi 753
ĐẠI HỌC QUỐC GIA HÀ NỘI
TRƯỜNG ĐẠI HỌC NGOẠI NGỮ
TRƯỜNG THPT CHUYÊN NGOẠI NGỮ
ĐỀ KIỂM TRA HỌC KỲ 1 – LỚP 12
Năm học 2017 - 2018
Môn: Toán – Thời gian làm bài 90 phút
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 753
Câu 1. [2D2-2] Đặt
2
log 3
a
,
3
log 5
b
. Biểu diễn
15
log 18
theo
a
,
b
là:
A.
2 1
1
b
a b
. B.
2 1
1
b
b a
. C.
2 1
1
a
b a
. D.
2 1
1
a
a b
.
Câu 2. [2H1-2] Cho hình chóp
.
S ABCD
có
SA
vuông góc với
ABCD
và đáy
ABCD
là hình thoi.
Biết
3
SA a
và
SC
tạo với
ABCD
góc
60
. Tính độ dài
BD
biết thể tích của khối chóp
.
S ABCD
bằng
3
3
a
.
A.
2
BD a
. B.
3
BD a
. C.
2 2
BD a
. D.
2 3
BD a
.
Câu 3. [2D1-1] Hàm số nào trong số bốn hàm số sau đồng biến trên khoảng
0:
?
A.
ln
y x x
. B.
x
y
. C.
1
x
y e
x
. D.
2
1
y x
.
Câu 4. [2H1-2] Cho hình lập phương có diện tích toàn phần bằng
24
2
cm
. Khi đó thể tích của khối lập
phương là?
A.
12
3
cm
. B.
27
3
cm
. C.
8
3
cm
. D.
24
3
cm
.
Câu 5. [2D1-3] Tiếp tuyến với đồ thị hàm số
2 1
1
x
y
x
tại điểm
M
có
0
M
x
cắt hai trục tọa độ lần
lượt tại
A
và
B
. Tính diện tích
S
của tam giác
OAB
.
A.
1
2
. B.
2
. C.
3
. D.
1
4
V
.
Câu 6. [2H2-3] Cho hình chóp
.
S ABC
có
SA
,
SB
,
SC
đôi một vuông góc và
2
SA SB a
,
SC a
.
Tính thể tích
V
của khối cầu ngoại tiếp hình chóp
.
S ABC
.
A.
3
9
2
a
V
. B.
3
36
V a
. C.
3
27
V a
. D.
3
27
2
a
V
.
Câu 7. [1H3-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
,
B
và
SA
vuông
góc với
ABCD
. Biết
2
SA AD a
,
AB BC a
. Tính khoảng cách
h
từ
C
đến
SBD
.
A.
6
6
a
h . B.
3
3
a
h . C.
6
2
a
h . D.
2
2
a
h .
Câu 8. [2D1-2] Hàm số
3
3
1
y x
x
đạt giá trị nhỏ nhất trên
0;
tại
0
x
. Khẳng định nào
ĐÚNG?
A.
0
1
;1
2
x
. B.
0
1
0;
2
x
. C.
0
3
1;
2
x
. D.
0
3
;2
2
x
.
Câu 9. [2D2-3] Tìm giá trị của tham số
m
để phương trình
2
2 2
log log 2 6 0
x m x m
có hai
nghiệm
1
x
,
2
x
thỏa mãn
1 2
16
x x
.
A.
4
m
. B.
11
m
. C.
4
m
. D.
5
m
.
19

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/25 - Mã đề thi 753
Câu 10. [1D5-2] Có bao nhiêu tiếp tuyến của đồ thị hàm số
4 2
2 1
y x x
song song với trục hoành?
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 11. [2H2-2] Khẳng định nào dưới đây là SAI?
A. Hình chóp đều bất kì luôn nội tiếp trong một hình cầu.
B. Hình chóp tam giác bất kì luôn nội tiếp trong một hình nón.
C. Hình lăng trụ tam giác bất kì luôn nội tiếp trong một hình trụ.
D. Hình lăng trụ đều bất kì luôn nội tiếp trong một hình trụ.
Câu 12. [2H2-2] Một hình trụ có thiết diện qua trục là hình vuông chu vi
16cm
. Tính thể tích
V
khối
trụ đã cho.
A.
3
8 cm
V
. B.
3
16
cm
3
V
. C.
3
16 cm
V
. D.
3
32 cm
V
.
Câu 13. [2D2-2] Phương trình
3 3
log 2 1 log 1 0
x x
có bao nhiêu nghiệm?
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 14. [2D2-1] Cho hàm số
log
y x
. Khẳng định nào sau đây khẳng định SAI?
A. Hàm số có tập giá trị là
0;
. B. Hàm số đồng biến trên khoảng
0;
.
C. Hàm số có tập xác định là
0;
. D. Hàm số có tập giá trị là
;
.
Câu 15. [2D2-2] Hàm số
3
ln 1
1
y x
x
đồng biến trên khoảng nào?
A.
1;2
. B.
1
;1
2
. C.
1
;
2
. D.
2;
.
Câu 16. [2D1-3] Tìm tập hợp tất cả các giá trị của tham số
m
để hàm số
3 2
1 1
y x m x mx
đồng biến trên khoảng
0;1
.
A.
;0
. B.
0;
. C.
;0
. D.
0;
.
Câu 17. [2H2-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật và
SA
vuông góc với mặt
đáy. Biết
2
SA a
,
4
BD a
. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp
.
S ABCD
.
A.
5
R a
. B.
2 5
R a
. C.
2 3
R a
. D.
3
R a
.
Câu 18. [2D1-2] Cho hàm số
f x
có tính chất:
0
f x
0; 3
x và
0
f x
1; 2
x .
Khẳng định nào dưới đây là SAI?
A. Hàm số
f x
là hàm hằng trên khoảng
1; 2
.
B. Hàm số
f x
đồng biến trên khoảng
0; 1
.
C. Hàm số
f x
đồng biến trên khoảng
0; 3
.
D. Hàm số
f x
đồng biến trên khoảng
2; 3
.
Câu 19. [2H1-2] Hình lăng trụ có đáy là thập giác lồi có bao nhiêu cạnh?
A.
20
. B.
12
. C.
30
. D.
22
.
Câu 20. [2D1-2] Cho hàm số
y f x
xác định trên
\ 0
, liên tục trên mỗi khoảng xác định và có
bảng biến thiên như hình bên.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/25 - Mã đề thi 753
Tìm tập hợp tất cả các giá trị của tham số thực
m
sao cho phương trình
2 0
m f x
có ba
nghiệm thực phân biệt.
A.
4;2
. B.
; 4
. C.
4;2
. D.
4;2
.
Câu 21. [2D2-1] Cho
a
là số thực dương tùy ý. Mệnh đề nào dưới đây SAI?
A.
3
3
4
2
2 2 2
5
log log
18
a a a
. B.
2
1
log
log 2
a
a .
C.
2
2 2
log 2log
a a
. D.
2 3 2
log log .log 3
a a .
Câu 22. [2D2-2] Tập xác định của hàm số
ln log
y x
là
A.
0;1
. B.
1;
. C.
0;
. D.
0;
.
Câu 23. [2D1-2] Cho hàm số
f x
có đạo hàm liên tục trên
;
a b
và đồ thị hàm số
y f x
được
cho như hình bên. Gọi
n
là số điểm cực trị của hàm số
y f x
trên khoảng
;
a b
thì
n
bằng bao nhiêu?
x
y
21 b
a
O
A.
0.
n
B.
1.
n
C.
3
n
D.
2.
n
Câu 24. [2D1-2] Đồ thị hàm số
3 2
2 3 1
y x x x
và đường thẳng
2
y x
cắt nhau tại điểm
; .
A A
A x y
Tìm
.
A
y
A.
0.
A
y
B.
3.
A
y
C.
2.
A
y
D.
1.
A
y
Câu 25. [2D2-2] Phương trình
1
5 5. 0,2 26
x
x
có hai nghiệm
1
x
,
2
x
. Tính tổng
1 2
S x x
.
A.
13
. B.
26
. C.
1
. D.
0
.
Câu 26. [2D1-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
O
là giao điểm của
AC
và
BD
. Gọi
M
,
N
lần lượt là trung điểm của
SB
,
SC
. Tính tỉ số
.
OBCNM
S ABCD
V
k
V
.
A.
3
16
k . B.
1
8
k
. C.
3
8
k
. D.
1
16
k .
Câu 27. [2D1-2] Cho hàm số
y f x
có
lim 1
x
f x
và
lim 1
x
f x
. Tìm phương trình đường
tiệm cận ngang của đồ thị hàm số
1 2018.
y f x
.
A.
1
y
. B.
2019
y
. C.
1
y
. D.
2017
y
.
x
0
1
y
0
y
1
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/25 - Mã đề thi 753
Câu 28. [2D1-2] Đồ thị hình bên là đồ thị của hàm số nào?
A.
3 2
3 3 1
y x x x
. B.
3
1
3 1
3
y x x
.
C.
3 2
3 3 1
y x x x
. D.
3
3 1
y x x
.
Câu 29. [2D1-1] Cho hàm số
y f x
xác định, liên tục trên
và có bảng biến thiên như hình dưới
đây. Khẳng định nào sau đây là sai:
A. Hàm số có ba điểm cực trị.
B.
0
1
x
được gọi là điểm cực tiểu của hàm số.
C.
0
1
y
được gọi là giá trị cực tiểu của hàm số.
D.
0;2
M được gọi là điểm cực đại của hàm số.
Câu 30. [2D2-1] Tính đạo hàm của hàm số
2
log 5 1
y x
.
A.
5
5 1 ln2
y
x
. B.
1
5 1
y
x
. C.
5
5 1
y
x
. D.
1
5 1 ln2
y
x
.
Câu 31. [2D1-3] Tìm các giá trị của
m
để đồ thị hàm số
3 2 2
1
1 2 1 3
3
y x m x m x
có hai
điểm cực trị cách đều trục tung.
A.
1
m
. B.
1
m
. C.
2
m
. D.
1
m
.
Câu 32. [2D2-2] Cho
3
log 2
a
và
2
1
log
2
b
. Tính
2
3 3 1
4
2log log 3 log
I a b
.
A.
4
I
. B.
5
4
I
. C.
3
2
I
. D.
0
I
.
Câu 33. [2H1-1] Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
,
AC a
và
5
BC a
. Biết góc giữa
AB C
và
ABC
bằng
45
, tính thể tích
V
của khối lăng trụ
đã cho.
A.
3
6
V a
. B.
3
2
V a
. C.
3
5
V a
. D.
3
4
V a
.
Câu 34. [2D2-2] Đặt
3
5
0
1
lim
1
x
x
x
e
a
e
. Tính giá trị của
5 4
P a
.
A.
4
P
. B.
1
P
. C.
3
P
. D.
7
P
.
x
1
0
1
y
0
0
0
y
1
2
1
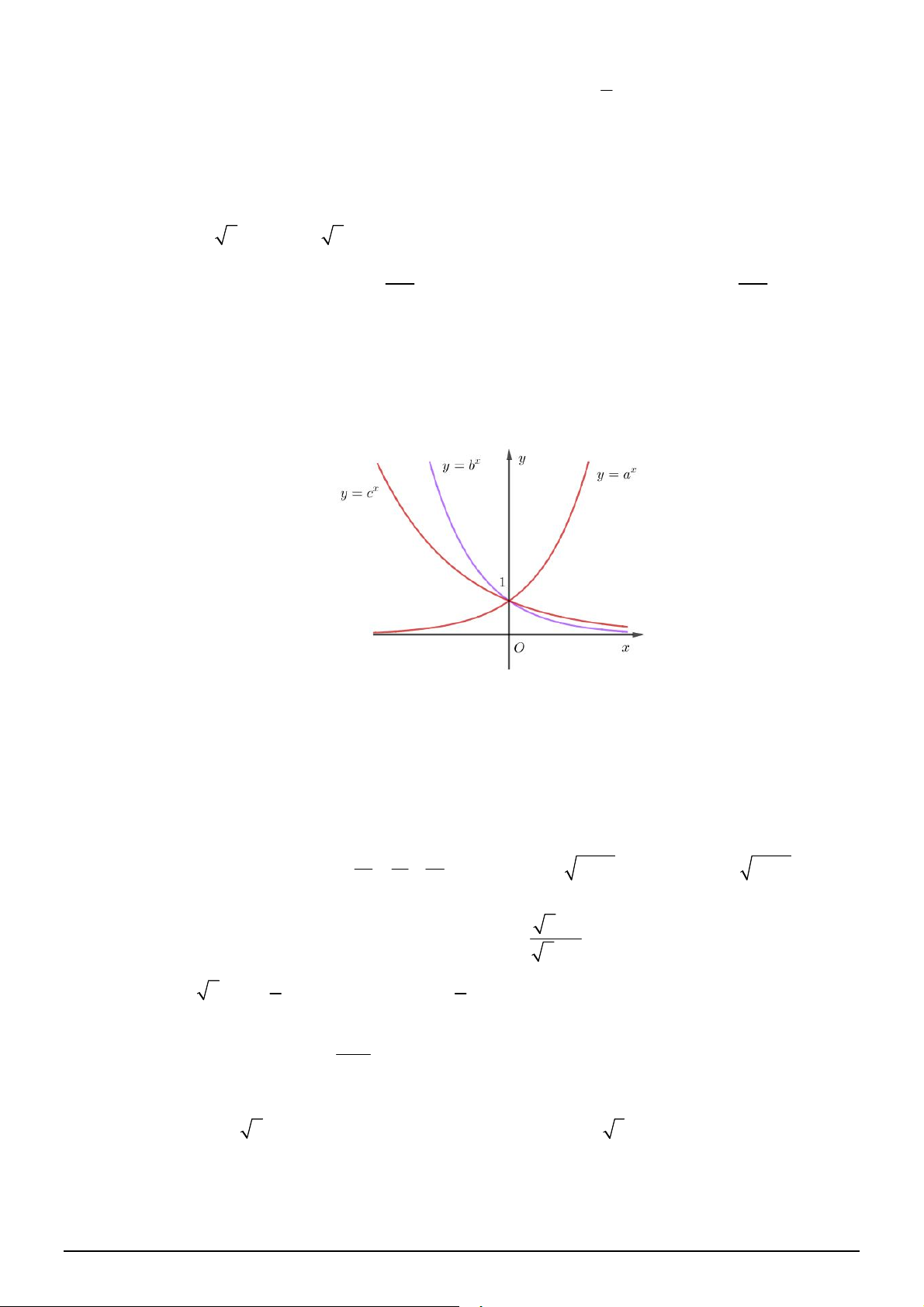
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/25 - Mã đề thi 753
Câu 35. [2D1-2] Cho chuyển thẳng xác định bởi phương trình
4 2
1
3
2
S t t
, trong đó
t
tính bằng
giây
s
,
S
được tính bằng mét
m
. Tính vận tốc của chuyển động tại thời điểm
4
t s
.
A.
232 m/s
v
. B.
140 m/s
v
. C.
116 m/s
v
. D.
280 m/s
v
.
Câu 36. [2H1-2] Cho hình chóp
.
S ABC
có
SA
,
SB
,
SC
đôi một vuông góc. Biết
2
SAB
S a
,
2
2
SBC
S a ,
2
2
SCA
S a . Tính thể tích
V
của khối chóp
.
S ABC
theo
a
?
A.
3
2
V a
. B.
3
4
3
a
V . C.
3
4
V a
. D.
3
2
3
a
V .
Câu 37. [2D2-3] Huyện
A
có
300
nghìn người. Với mức tăng dân số bình quân
1,2%
/năm thì sau
n
năm dân số sẽ vượt lên
330
nghìn người. Hỏi
n
nhỏ nhất bằng bao nhiêu?
A.
9
năm. B.
7
năm. C.
10
năm. D.
8
năm.
Câu 38. [2D2-3] Cho đồ thị các hàm số , ,
x x x
y a y b y c
có hình vẽ bên. Tìm khẳng định ĐÚNG.
A.
a c b
. B.
b c a
. C.
c b a
. D.
a b c
.
Câu 39. [2H2-2] Cho hình trụ
T
có trục
2
OO a
, bán kính đường tròn đáy bằng
a
. Gọi
S
là mặt
cầu tiếp xúc với hai mặt đáy của hình trụ và tiếp xúc với các đường sinh của hình trụ. Gọi
N
là hình nón đỉnh
O
và đáy là hình tròn
O
của hình trụ. Gọi
1
V
,
2
V
,
3
V
là thể tích của khối
trụ
T
, khối cầu
S
và khối nón
N
. Khẳng định nào ĐÚNG?
A.
1 2 3
V V V
. B.
3 1 2
1 1 1
V V V
. C.
2 3 1
.
V V V
. D.
3 1 2
.
V V V
.
Câu 40. [2D1-2] Các đường tiệm cận của đồ thị hàm số
1
2
x
y
x
là:
A.
2
x
;
1
2
y
. B.
4
x
;
1
2
y
. C.
2
x
;
1
y
. D.
4
x
;
1
y
.
Câu 41. [2D1-3] Cho hàm số
1
1
x
y
x
có đồ thị
C
và
A
là một điểm thuộc
C
. Gọi
S
là tổng các
khoảng cách từ
A
đến các đường tiệm cận của
C
. Tìm
min
S
.
A.
min 2 2
S
. B.
min 2
S
. C.
min 2 3
S . D.
min 3
S
.
Câu 42. [2D2-3] Cho phương trình
.2017 2 .2018 2 1 0
x x
x x x
. Tìm khẳng định ĐÚNG?
A. Phương trình có đúng một nghiệm nguyên. B. Phương trình không có nghiệm nguyên.
C. Phương trình có nghiệm nguyên lớn hơn
5
. D. Phương trình có nghiệm nguyên âm.
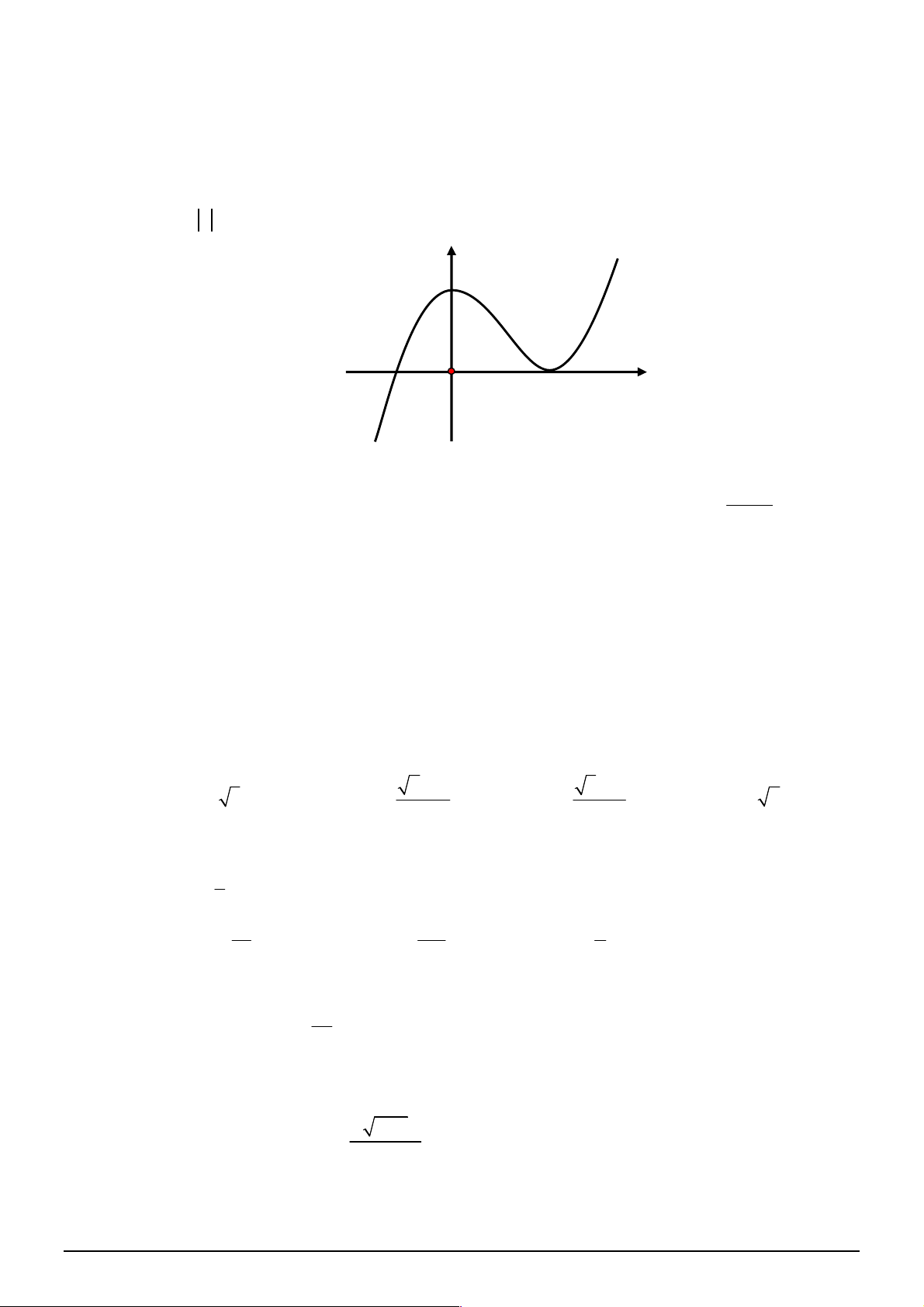
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/25 - Mã đề thi 753
Câu 43. [2H1-3] Cho hình hộp
.
ABCD A B C D
có thể tích
48
đvtt
. Tính thể tích khối tứ diện
BCD B
.
A.
12
đvtt
. B.
6
đvtt
. C.
8
đvtt
. D.
16
đvtt
.
Câu 44. [2D1-3] Cho hàm số
y f x
có đồ thị như hình bên. Trên đoạn
1;3
, đồ thị hàm số
y f x
có mấy điểm cực trị?
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 45. [2D1-2] Tìm tập hợp tất cả các giá trị của tham số
m
để đồ thị hàm sô
2 3
2
x
y
x
cắt đường
thẳng
2
y x m
tại hai điểm phân biệt.
A.
3;
. B.
;1 3;
. C.
1;3
. D.
;1
.
Câu 46. [2D2-1] Tìm tập xác định
D
của hàm số
5
2
2
y x x
.
A.
D
. B.
; 1 2;
. C.
0;D
. D.
\ 1;2
D
.
Câu 47. [2H2-2] Cho hình chóp đều
.
S ABC
cạnh đáy
3
AB a
, góc giữa cạnh bên và mặt đáy bằng
45 .
Tính diện tích xung quanh
xq
S
của hình nón đỉnh
S
và đường tròn đáy là đường tròn
ngoại tiếp tam giác
ABC
.
A.
2
3 3
xq
S a
. B.
2
2
3
xq
a
S
. C.
2
3
3
xq
a
S
. D.
2
3 2
xq
S a
.
Câu 48. [2D1-3] Cho
x
,
y
là hai số thực không âm thỏa mãn
2
x y
. Tìm giá trị nhỏ nhất của biểu
thức
3 2 2
1
1
3
P x x y x
.
A.
17
min
3
P
. B.
115
min
3
P . C.
7
min
3
P
. D.
min 5
P
.
Câu 49. [2H1-3] Cho hình lăng trụ tam giác đều
.
ABC A B C
có
2
AB a
. Biết khoảng cách từ điểm
B
đến
AB C
bằng
3
2
a
. Kí hiệu
là góc giữa hai mặt phẳng
AB C
và
ABC
. Số đo
bằng
A.
30
. B.
60
. C.
90
. D.
45
.
Câu 50. [2D1-3] Đồ thị hàm số
2
1
2
x
y
x x
có bao nhiêu đường tiệm cận?
A.
3
. B.
1
. C.
2
. D.
0
.
----------HẾT----------
O
x
y
4
2
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/22 - Mã đề thi 132
UBND TỈNH BẮC NINH
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA ĐỊNH KỲ LẦN 1 NĂM HỌC 2017 – 2018
MÔN TOÁN 12
Thời gian làm bài 90 phút;
Họ, tên thí sinh……………………………Lớp……………………….
Mã đề thi 132
Câu 1. [2D2-2] Đặt
3
log 45
a . Mệnh đề nào dưới đây đúng?
A.
45
2
log 5
a
a
. B.
45
1
log 5
a
a
. C.
45
2
log 5
a
a
. D.
45
2
log 5
a
a
.
Câu 2. [2D1-2] Cho hàm số
3 2
3 9 1
y x x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
3;1
. B. Hàm số nghịch biến trên khoảng
3;1
.
C. Hàm số nghịch biến trên khoảng
; 3
. D. Hàm số nghịch biến trên khoảng
1;
.
Câu 3. [2D1-3] Đồ thị của hàm số
2
2
4 1
x
y
x
có bao nhiêu đường tiệm cận?
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 4. [2H1-1] Cho một hình đa diện. Mệnh đề nào dưới đây sai?
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh. B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C. Mỗi cạnh là cạnh chung của ít nhất ba mặt. D. Mỗi mặt có ít nhất ba cạnh.
Câu 5. [2D1-1] Đồ thị hàm số
2
2
1 2
6 9
x
y
x x
có tiệm cân đứng
x a
và tiệm cận ngang
y b
. Tính
giá trị
2
T a b
.
A.
4
T
. B.
1
T
. C.
8
T
. D.
6
T
.
Câu 6. [2H1-1] Cho lăng trụ đứng
1 1 1
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
C
,
2
AC a
.
Biết tam giác
1
ABC
có chu vi bằng
5
a
. Tính thể tích
V
của khối lăng trụ
1 1 1
.
ABC A B C
.
A.
3
3
2
a
V . B.
3
2
a
V . C.
3
1
3
V a
. D.
3
V a
.
Câu 7. [2D1-2] Tìm giá trị lớn nhất của hàm số
2
4
x
y
x
trên đoạn
1;5
.
A.
1;5
1
max
5
y
. B.
1;5
1
max
4
y
. C.
1;5
5
max
29
y . D.
1;5
2
max
6
y .
Câu 8. [2D1-2] Cho hàm số
f x
có đạo hàm
2
1 3
f x x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại
3
x
. B. Hàm số đạt cực tiểu tại
3
x
.
C. Hàm số đạt cực tiểu tại
1
x
. D. Hàm số đạt cực đại tại
1
x
.
Câu 9. [2D2-1] Cho
0
a
. Hãy viết biểu thức
4 5
4
3
a a
a a
dưới dạng lũy thừa với số mũ hữu tỉ.
A.
23
4
a
B.
3
4
a
. C.
19
4
a
. D.
9
2
a
.
Câu 10. [2D2-2] Tính tổng lập phương các nghiệm của phương trình
2 3 2 3
log .log 1 log log
x x x x
.
A.
5
. B.
35
. C.
13
. D.
125
.
Câu 11. [2D2-1] Cho
a
là số thực dương khác
1
. Mệnh đề nào dưới đây đúng với mọi số dương
x
,
y
.
A.
log log
a a
xy x y
. B.
log log log
a a a
xy x y
.
C.
log log
a a
xy x y
. D.
log log .log
a a a
xy x y
.
20
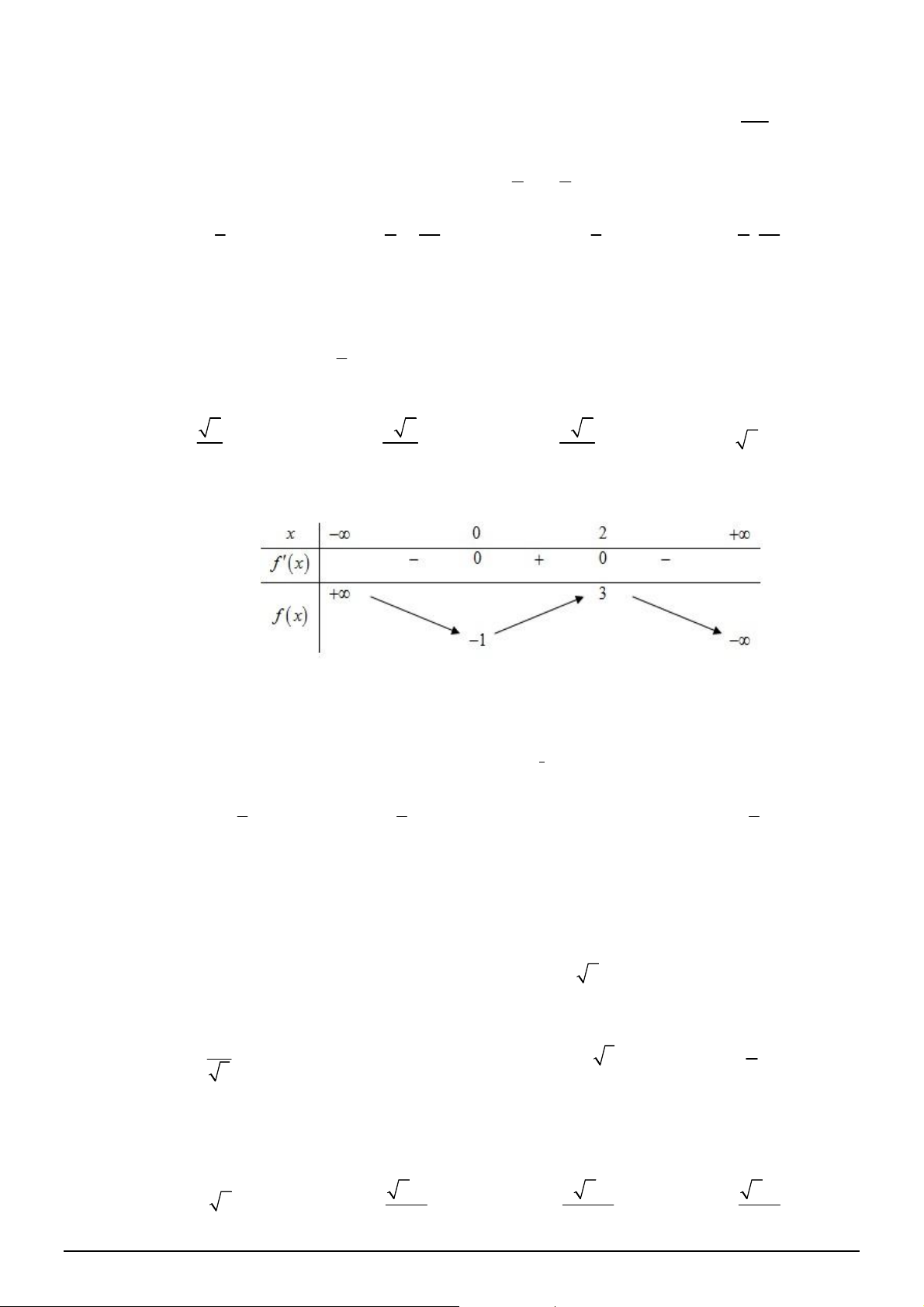
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/22 - Mã đề thi 132
Câu 12. [2D2-1] Tính đạo hàm của hàm số
3
x
y
.
A.
3 .ln3
x
y
. B.
1
.3
x
y x
. C.
3
x
y
. D.
1
.3
ln3
x
y
.
Câu 13. [2D1-1] Tìm điểm cực đại của đồ thị hàm số
3 2
2 5
2 1
3 2
y x x x
.
A.
1
2;
3
M
. B.
1 35
;
2 24
M
. C.
1
2;
3
M
. D.
1 35
;
2 24
M
.
Câu 14. [2H2-2] Tính thể tích của khối hộp chữ nhật
.
ABCD A B C D
có
3
AB
,
4
AD
,
5
AA
.
A.
60
V
. B.
10
V
. C.
20
V
. D.
12
V
.
Câu 15. [2D1-3] Cho hàm số
3 2
1
2 2 1
3
y x x x C
. Biết đồ thị
C
có hai tiếp tuyến cùng vuông
góc với đường thẳng :
d y x
. Gọi
h
là khoảng cách giữa hai tiếp tuyến đó. Tính
h
.
A.
2
3
h . B.
4 2
3
h . C.
2 2
3
h . D.
2
h
.
Câu 16. [2D1-2] Cho hàm số
y f x
có bảng biến thiên như sau:
Tìm tất cả các giá trị của tham số
m
để phương trình
f x m
có ba nghiệm thực phân biệt.
A.
1;3
m . B.
1;m
. C.
1;3
m . D.
;3
m .
Câu 17. [2D2-1] Tìm tập xác định
D
của hàm số
1
3
3 1
y x
.
A.
1
\
3
D
. B.
1
;
3
D
. C.
D
. D.
1
;
3
D
.
Câu 18. [2D1-2] Tìm số giao điểm của đồ thị hàm số
2
1 2
y x x x
với trục hoành.
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 19. [2D1-2] Tìm giá trị cực tiểu
CT
y
của hàm số
4 2
4 3
y x x
.
A.
3
CT
y
. B.
0
CT
y
. C.
2
CT
y . D.
1
CT
y
.
Câu 20. [2D2-1] Trong các hàm số sau, hàm số nào đồng biến trên
?
A.
2
3
x
y
. B.
0,99
x
y . C.
2 3
x
y . D.
2
3
x
y
.
Câu 21. [2H1-2] Cho khối chóp
.
S ABCD
có đáy là hình chữ nhật cạnh
2
AB a
,
AD a
. Hình chiếu
của đỉnh
S
lên mặt đáy là trung điểm cạnh
AB
, cạnh bên
SC
tạo với mặt phẳng đáy một góc
45
. Tính thể tích
V
của khối chóp đã cho.
A.
3
2 2
V a
. B.
3
2
3
a
V . C.
3
2 2
3
a
V . D.
3
2
6
a
V .
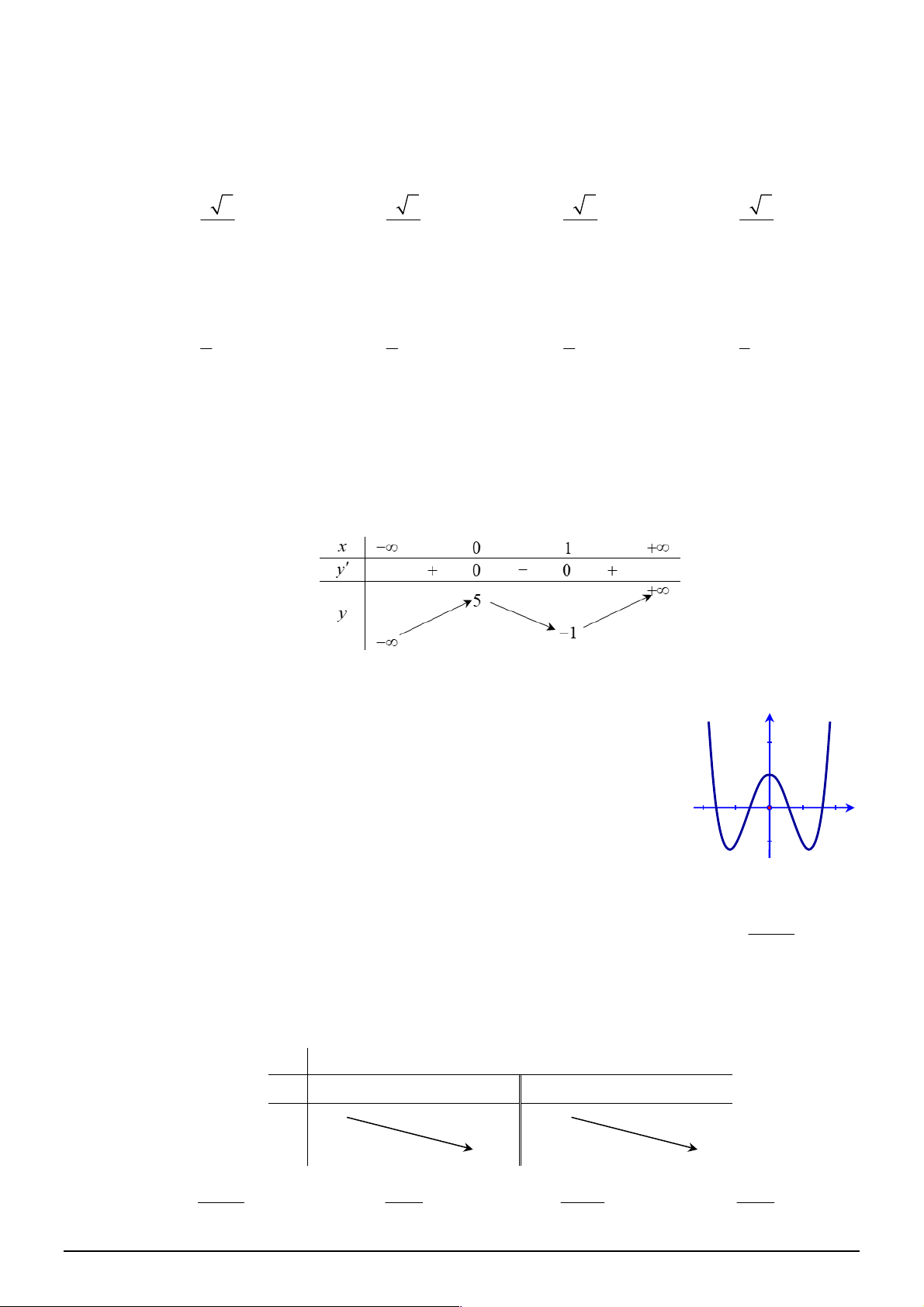
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/22 - Mã đề thi 132
Câu 22. [2D2-2] Cho hàm số
2
ln
f x x x
. Tính
e
f
?
A.
e
. B.
3e
. C.
2e
. D.
2 e
.
Câu 23. [2D1-3] Cho hàm số
3
1
y x mx
(với
m
là tham số). Tìm tất cả các giá trị của
m
để đồ thị
hàm số cắt trục hoành tại ba điểm phân biệt.
A.
3
3 2
2
m . B.
3
3 2
.
2
m C.
3
3 2
2
m . D.
3
3 2
.
2
m
Câu 24. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để hàm số
3 2
2 1 2
y x x m x
nghịch biến trên khoảng
;
.
A.
7
3
m
. B.
7
3
m
. C.
7
3
m
. D.
1
3
m
.
Câu 25. [2D2-1] Tìm tập xác định
D
của hàm số
2
ln 3
y x x
.
A.
; 0 3; D
. B.
; 0 3; D
.
C.
0; 3
D . D.
0; 3
D .
Câu 26. [2D1-1] Cho hàm số
y f x
có bảng biến thiên như hình bên. Mệnh đề nào dưới đây đúng?
A. Hàm số có điểm cực tiểu bằng
0
. B. Hàm số có điểm cực đại bằng
5
.
C. Hàm số có điểm cực tiểu bằng
1
. D. Hàm số có điểm cực tiểu bằng
1
.
Câu 27. [2D1-1] Đường cong ở hình vẽ là đồ thị của một trong bốn hàm
số dưới đây. Hàm số đó là hàm số nào?
A.
4 2
3 1
y x x
. B.
3 2
2 1
y x x
.
C.
3
3 1
y x x
. D.
4 2
3 1
y x x
.
Câu 28. [2D2-2] Gọi
S
là tập nghiệm của phương trình
2 1 1
2 5.2 3 0
x x
. Tìm
S
.
A.
3
1;log 2
S . B.
2
0;log 3
S . C.
2
1;log 3
S . D.
1
S .
Câu 29. [2D1-1] Đường thẳng nào cho dưới đây là tiệm cận ngang của đồ thị hàm số
2 3
1
x
y
x
.
A.
2
x
. B.
2
y
. C.
1
y
. D.
2
y
.
Câu 30. [2D1-2] Bảng sau là bảng biến thiên của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
A.
2 3
2
x
y
x
. B.
1
2
x
y
x
. C.
2 1
2
x
y
x
. D.
4
2
x
y
x
.
x
2
y
–
–
y
2
2
O
y
x
2
1
1
2
2
1
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/22 - Mã đề thi 132
Câu 31. [2D2-3] Ông A gửi vào ngân hàng
100
triệu đồng theo hình thức lãi suất kép. Lãi suất ngân
hàng là
8%
trên năm và không thay đổi qua các năm ông gửi tiền. Sau
5
năm ông cần tiền để
sửa nhà, ông đã rút toàn bộ số tiền và sử dụng một nửa số tiền đó vào công việc, số còn lại ông
tiếp tục gửi ngân hàng với hình thức như trên. Hỏi sau
10
năm ông A đã thu được số tiền lãi là
bao nhiêu? (đơn vị tính là triệu đồng).
A.
81,412.
B.
80,412.
C.
79,412.
D.
100,412.
Câu 32. [2D1-1] Cho đồ thị hàm số
3
: 3
C y f x x x
. Mệnh đề nào dưới đây sai?
A. Đồ thị
C
cắt trục tung tại một điểm.
B. Đồ thị
C
nhận gốc tọa độ
O
là tâm đối xứng.
C. Đồ thị
C
cắt trục hoành tại ba điểm phân biệt.
D. Đồ thị
C
nhận trục
Oy
làm trục đối xứng.
Câu 33. [2D1-2] Cho hàm số
2 1
1
x
y
x
. Phương trình tiếp tuyến tại điểm
2;5
M của đồ thị hàm số
trên là:
A.
3 11
y x
. B.
3 11
y x
. C.
3 11
y x
. D.
3 11
y x
.
Câu 34. [2H1-2] Cho khối chóp
.
S ABC
có
SA
,
SB
,
SC
đôi một vuông góc với nhau và
SA a
,
SB b
,
SC c
. Tính thể tích khối chóp
.
S ABC
.
A.
1
3
V abc
. B.
V abc
. C.
1
2
V abc
. D.
1
6
V abc
.
Câu 35. [2D1-2] Hàm số nào sau đây đồng biến trên khoảng
;
?
A.
3
1
y x
. B.
4
3
y x x
. C.
x
y e
. D.
1
2
x
y
x
.
Câu 36. [2H1-2] Cho khối tứ diện
ABCD
,
M
là trung điểm
AB
. Mặt phẳng
MCD
chia khối tứ diện
ABCD
thành hai khối đa diện nào?
A. Hai khối lăng trụ tam giác. B. Một lăng trụ tam giác và một khối tứ diện.
C. Hai khối tứ diện. D. Hai khối chóp tứ giác.
Câu 37. [2H2-1] Viết công thức thể tích
V
của khối cầu có bán kính
r
.
A.
3
1
3
V r
. B.
3
4
3
V r
. C.
3
V r
. D.
2
4
V r
.
Câu 38. [2H1-2] Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng
6
gần bằng số nào sau đây
nhất?
A.
46
. B.
48
. C.
52
. D.
51
.
Câu 39. [2H1-2] Cho hình chóp tứ giác đều có cạnh đáy bằng
a
và biết diện tích xung quanh gấp đôi
diện tích đáy. Tính thể tích của khối chóp.
A.
3
3
12
a
V . B.
3
3
3
a
V . C.
3
3
2
a
V . D.
3
3
6
a
V .
Câu 40. [2H1-2] Cho hình chóp tam giác đều có cạnh bên là
b
và chiều cao là
h
,
b h
. Tính thể tích
khối chóp đó.
A.
2 2
3
4
V b h h
. B.
2 2
3
12
V b h h
. .C.
2 2
3
4
V b h b
. D.
2 2
3
8
V b h h
.
Câu 41. [2D1-2] Tìm giá trị nhỏ nhất của hàm số
3 2
3 9 2
y x x x
trên đoạn
0;4
.
A.
0;4
min 2
y
. B.
0;4
min 34
y
. C.
0;4
min 25
y
. D.
0;4
min 18
y
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/22 - Mã đề thi 132
Câu 42. [2H1-1] Nếu tăng chiều cao một khối chóp lên
2
lần và giảm diện tích đáy đi
6
lần thì thể tích
khối chóp đó tăng hay giảm bao nhiêu lần?
A. Tăng
3
lần. B. Giảm
3
lần.
C. Giảm
12
lần. D. Không tăng, không giảm.
Câu 43. [2D2-1] Tìm nghiệm của phương trình:
2
log 2 1 3
x
.
A.
9
2
x
. B.
8
x
. C.
7
2
x
. D.
5
x
.
Câu 44. [2H2-2] Cho tứ diện
ABCD
có
DA
vuông góc với mặt phẳng
ABC
và
AD a
,
2
AC a
;
cạnh
BC
vuông góc với cạnh
AB
. Tính bán kính
r
mặt cầu ngoại tiếp tứ diện
ABCD
.
A.
3
2
a
r . B.
r a
. C.
5
2
a
r . D.
5
r a
.
Câu 45. [2H1-2] Cho hình hộp chữ nhật
.
ABCD A B C D
có tâm
I
. Gọi
V
,
1
V
lần lượt là thể tích của
khối hộp
.
ABCD A B C D
và khối chóp
.
I ABCD
. Tính tỉ số
1
V
k
V
.
A.
1
6
k
. B.
1
12
k . C.
1
8
k
. D.
1
3
k
.
Câu 46. [2H2-1] Viết công thức diện tích xung quanh
xq
S
của hình nón tròn xoay có độ dài đường sinh
l
và bán kính đường tròn đáy
r
.
A.
xq
S rl
. B. 2
xq
S rl
. C.
xq
S rl
. D.
1
2
xq
S rl
.
Câu 47. [2H2-1] Một hình trụ có bán kính đáy
5
r
(cm), chiều cao
7
h
(cm). Tính diện tích xung quanh
của hình trụ.
A.
35
xq
S
(cm
2
). B.
70
xq
S
(cm
2
). C.
70
3
xq
S
(cm
2
). D.
35
3
xq
S
(cm
2
).
Câu 48. [2D1-1] Đồ thị hàm số nào dưới đây đi qua điểm
2; 1
M
?
A.
4 2
4 1
y x x
. B.
3
1
x
y
x
. C.
3
3 1
y x x
. D.
2 3
3
x
y
x
.
Câu 49. [2D2-2] Cho hàm số
1
1
x
y
x
. Gọi
M
là giá trị lớn nhất và
m
là giá trị nhỏ nhất của hàm số
trên đoạn
5; 1
. Tính
M m
.
A.
6.
B.
3
.
2
C.
6
.
5
D.
2
.
3
Câu 50. [2D2-2] Tìm
2017
0
e 1
lim .
x
x
x
A.
0.
B.
1.
C.
2017.
D.
.
----------HẾT----------

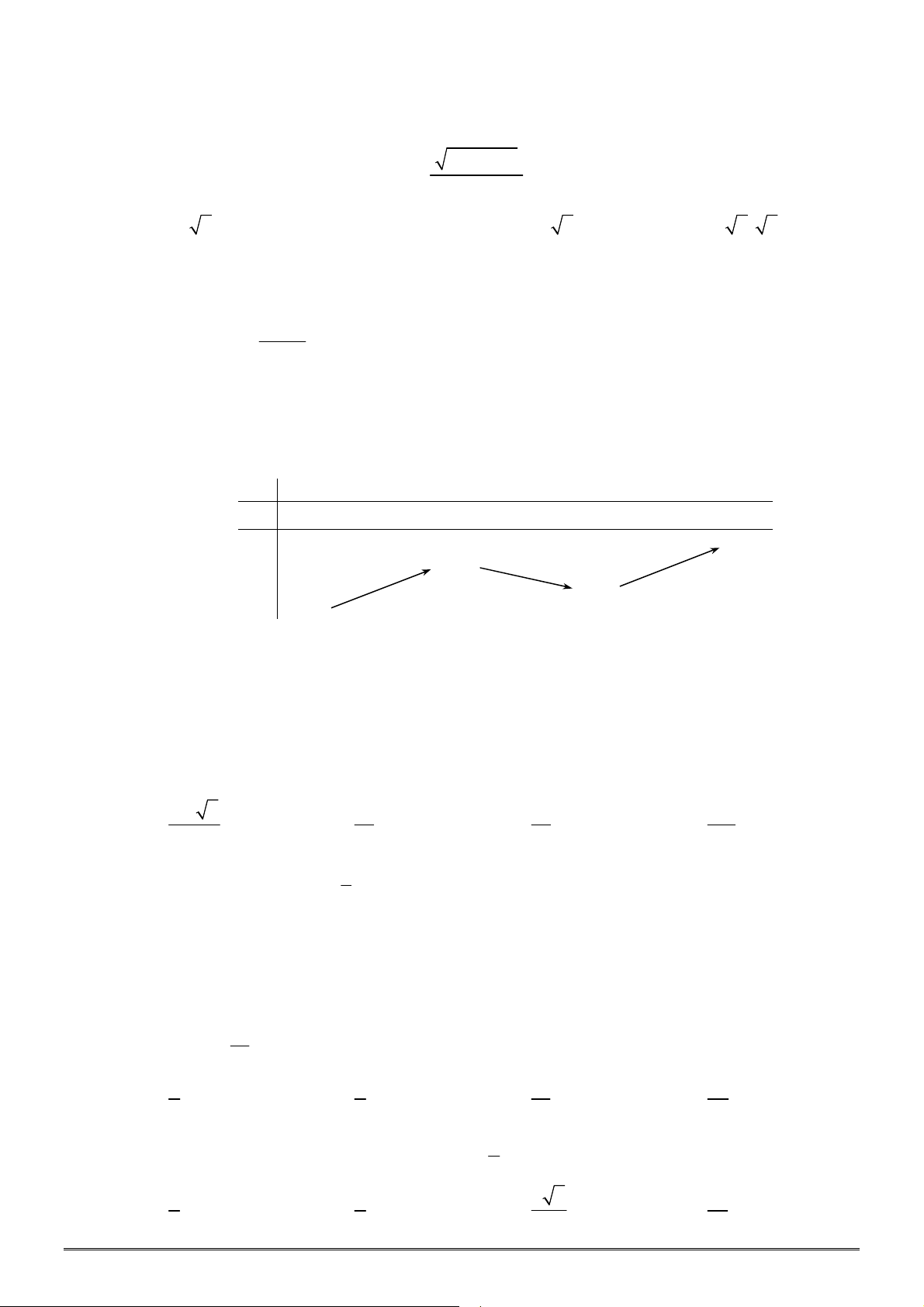
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/25
TRƯỜNG THPT
CHUYÊN NGOẠI NGỮ
NHÓM TOÁN 12
ĐỀ THI HỌC KÌ I NĂM HỌC 2016-2017
MÔN: TOÁN – KHỐI 12
Thời gian làm bài: 90 phút
Câu 1. [2D2-2] Tập xác định của hàm số
2
2
3
2
log 2
x x
y
x
là
A.
1; 2
. B.
1;
. C.
1; 2
. D.
2; 2 \ 1
.
Câu 2. [2D1-2] Phát biểu nào sau đây SAI?
A. Hàm số
4 2
0
y ax bx c a
luôn có điểm cực trị.
B. Hàm số
ax b
y
cx d
(với
0
ad bc
) không có cực trị.
C. Hàm số
3 2
0
y ax bx cx d a
luôn có điểm cực trị.
D. Hàm số
2
0
y ax bx c a
luôn có một điểm cực trị duy nhất.
Câu 3. [2D1-2] Cho hàm số
y f x
có bảng biến thiên như sau:
(I): Tập xác định của
f x
là
\ 1
D
. (II): Hàm số
f x
có đúng một điểm cực trị.
(III):
min 2
f x
. (IV):
1;3
A là điểm cực đại của đồ thị hàm số.
Trong các phát biểu trên, có bao nhiêu phát biểu ĐÚNG?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 4. [2H1-2] Cho khối chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt
đáy bằng
45
. Thể tích khối chóp
.
S ABC
bằng bao nhiêu?
A.
3
3 2
4
a
. B.
3
12
a
. C.
3
4
a
. D.
3
3
4
a
.
Câu 5. [2D1-2] Cho hàm số
3 2
1
2 3 1
3
y x x x
có đồ thị
C
. Có bao nhiêu tiếp tuyến của
C
song song với đường thẳng
3 1
y x
?
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 6. [2H2-2] Cho
ABC
vuông tại
A
,
6 cm
AB
,
8 cm
AC
. Gọi
1
V
là thể tích khối nón tạo
thành khi quay
ABC
quanh
AB
và
2
V
là thể tích khối nón tạo thành khi quay
ABC
quanh
AC
. Tỉ số
1
2
V
V
bằng
A.
4
3
. B.
3
4
. C.
16
9
. D.
64
27
.
Câu 7. [2D2-2] Giá tị nhỏ nhất của hàm số
1
4
2 .8
3
x x
y
trên
1;0
bằng bao nhiêu?
A.
5
6
. B.
2
3
. C.
2 2
3
. D.
50
81
.
x
1
1
y
0
||
y
3
2
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/25
Câu 8. [2D1-2] GTNN của hàm số
2sin 2 5 1
f x x x
trên đoạn
0;
2
bằng bao nhiêu?
A.
0
. B.
5
3
4
. C.
5
1
2
. D.
1
.
Câu 9. [2D2-2] Cho
ABC
vuông tại
A
có
log 8
3
a
AB ,
25
log 36
5AC . Biết độ dài
10
BC
thì giá trị
a
bằng bao nhiêu?
A.
9
. B.
1
3
. C.
3
. D.
3
.
Câu 10. [2D2-2] Phương trình
2 2 2
2 5 2 3 7 2 5 12 4
2 2 1 2
x x x x x x
có bao nhiêu nghiệm?
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 11. [2D2-2] Một tên lửa bay vào không trung với quãng đường đi được
km
s t là hàm phụ
thuộc theo biến
t
(giây), với phương trình
2
3 3 1
e 2 .e
t t
s t t
. Khi đó vận tốc của tên lửa sau
1
giây là
A.
4
5e km/h
. B.
4
3e km/h
.
C.
4
9e km/h
. D.
4
10e km/h
.
Câu 12. [2D2-2] Giới hạn
2
0
e 1
lim
4 2
x
x
x
bằng
A.
8
. B.
4
. C.
2
. D.
1
.
Câu 13. [2D1-2] Trong các hàm số sau, hàm số nào đồng biến trên
0;
?
A.
sin 2
y x
. B.
2
1
x
y
x
. C.
2
x
y
x
D.
2
2
1
y x
Câu 14. [2H2-2] Cho hình lăng trụ đứng
.
ABC A B C
có tam giác
ABC
vuông cân tại
B
,
2
AB a
và cạch bên
6
AA a
. Khi đó diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ đứng
đã cho là
A.
2
4 6
a
. B.
2
6
a
. C.
2
4
a
. D.
2
2 6
a
Câu 15. [2D1-2] Biết phương trình
3
3 0
x x m
có ba nghiệm phân biệt. Khẳng định nào sau đây đúng?
A.
2
4
m
. B.
2
4
m
.
C.
2
4
m
. D.
2
4
m
.
Câu 16. [2D1-1] Cho hàm số
f x
xác định, liên tục trên
, có đồ thị như
hình vẽ. Khẳng định nào dưới đây ĐÚNG?
A. Hàm số đạt cực đại tại
0
x
và đạt cực tiểu tại
2
x
.
B. Hàm số có giá trị lớn nhất bằng
3
.
C. Hàm số đồng biến trê khoảng
0;
.
C. Đồ thị hàm số có một đường tiệm cận.
Câu 17. [2D2-1] Cho
0 1, 0 1, 0, 0
a b x y
. Tìm công thức ĐÚNG trong các công thức sau.
A.
log log log
a a a
x y x y
B.
log .log
b
a
a
x b x
.
C.
log log .log
b b a
x a x
. D.
log
log
log
a
a
a
x
x
y y
.
O
x
y
3
2
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/25
Câu 18. [2D1-2] Bảng biến thiên sau đây có thể là bảng biến thiên của hàm số nào?
A.
2
2 3
y x x
. B.
4 2
1
3
4
y x x
. C.
4 2
1
3
2
y x x
. D.
4 2
1
2 3
2
y x x
Câu 19. [2D1-2] Gọi
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 1 7
y x x
.
Khi đó có bao nhiêu số nguyên nằm giữa
m
,
M
?
A.
2
. B.
1
. C. Vô số. D.
0
.
Câu 20. [2D2-2] Cho hàm số
2 sin 2
e
x
f x
. Biết
0
0;
2
x
là giá trị thỏa mãn
0
0.
f x
Khi đó:
A.
0
2
x
. B.
0
3
x
. C.
0
0
x
D.
0
4
x
.
Câu 21. [2H1-1] Cho khối lăng trụ tam giác đều có cạnh đáy bằng
a
. Biết diện tích mỗi mặt bên của
lăng trụ là
2
3
a , khi đó thể tích khối lăng trụ bằng
A.
3
3 3
4
a
. B.
3
3
4
a
. C.
3
4
a
. D.
3
3
4
a
.
Câu 22. [2D2-2] Cho hàm số
ln 1 e
x
y x . Khẳng định nào dưới đây là ĐÚNG?
A. Hàm số đạt cực tiểu tại
1
x
. B. Hàm số đạt cực đại tại
0
x
.
C. Hàm số đồng biến trên
. D. Tập xác định của hàm số là
0;D
.
Câu 23. [2H1-2] Cho khối chóp tứ giác đều
.
S ABCD
có độ dài tất cả các cạnh đều bằng
a
. Thể tích
khối chóp
.
S ABCD
bằng
A.
3
2
a
. B.
3
4
a
. C.
3
2 3
a
. D.
3
3 2
a
.
Câu 24. [2D1-3] Cho hàm số
4 2
2 1
y x mx
. Tìm giá trị của
m
để đồ thị hàm số có ba điểm cực trị
A
,
B
,
C
sao cho
ABC
có diện tích bằng
4 2
.
A.
1
m
. B.
2
m
. C.
2
m
. D.
4
m
.
Câu 25. [2D2-2] Giá trị cực đại của hàm số
2
ln
x
y
x
bằng
A.
e
2
. B.
1
2e
. C.
1
e
. D.
2
1
2e
.
Câu 26. [2D1-3] Biết phương trình
2 2
2 1 2 1 2 3 0
x x x x x x
có nghiệm duy nhất là
a
.
Khi đó
A.
0 1
a
. B.
3 4
a
. C.
1 2
a
. D.
2 3
a
.
Câu 27. [2D1-2] Cho hàm số
3 1
2
x
y
x
có đồ thị
C
. Có bao nhiêu điểm trên
C
mà tổng khoảng
cách từ đó đến hai đường tiệm cận của
C
bằng
6
.
A.
0
. B.
1
. C.
4
. D.
2
.
x
0
y
0
y
3
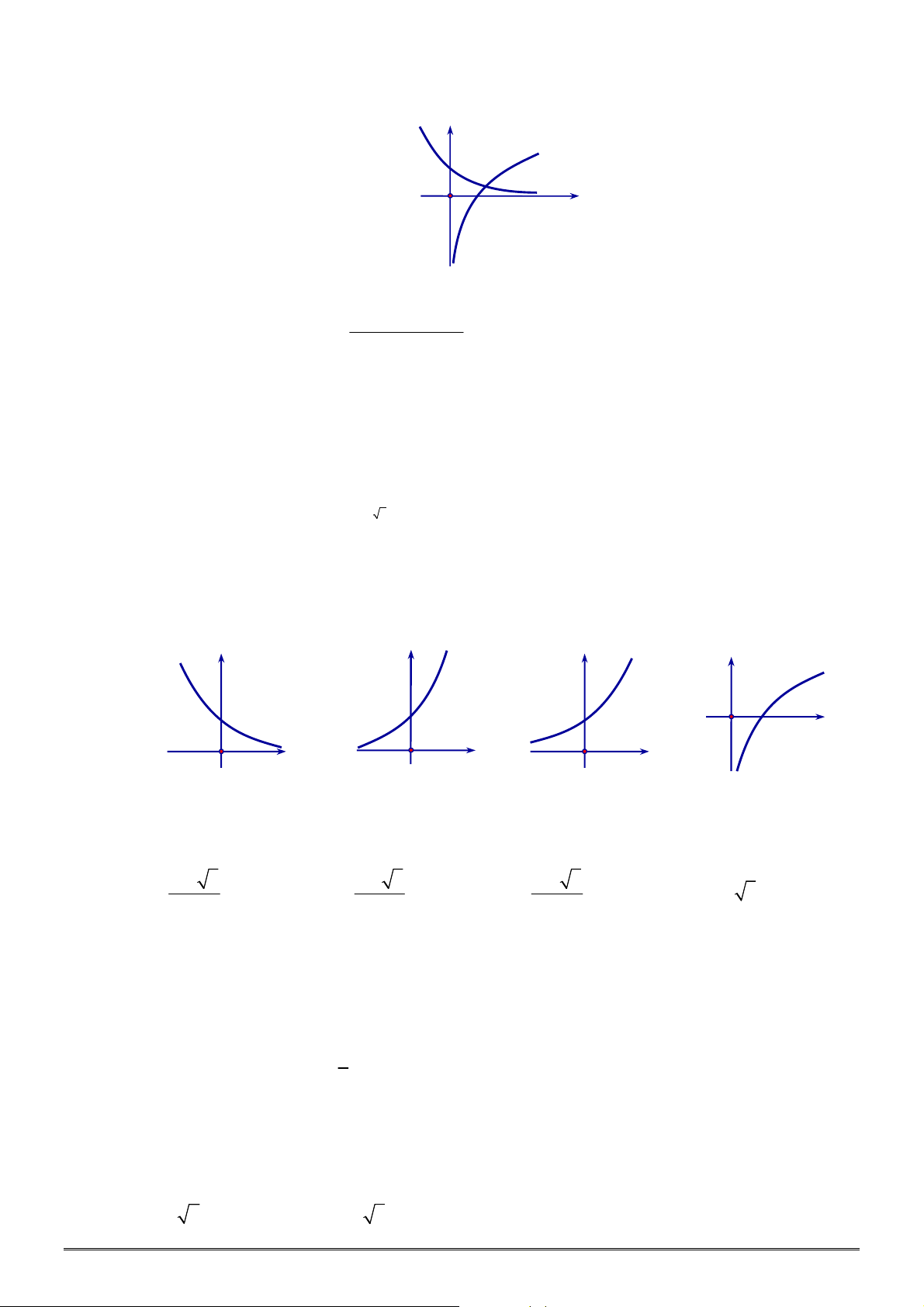
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/25
Câu 28. [2D2-1] Cho đồ thị hàm số
x
y a
và
log
b
y x
như hình vẽ bên. Khẳng định nào dưới đây là
ĐÚNG?
A.
0 1
a b
. B.
1; 1
a b
. C.
0 1,0 1
a b
. D.
0 1
b a
.
Câu 29. [2D1-1] Đồ thị hàm số
2 2
3 1
5 6
x
y
x x x
có bao nhiêu đường tiệm cận đứng?
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 30. [2D1-1] Gọi
x a
và
x b
là các điểm cực trị của hàm số
3 2
2 3 18 1
y x x x
. Khi đó
2
A a b ab
bằng
A.
5
. B.
7
. C.
5
. D.
7
.
Câu 31. [2D2-3] Cho phương trình
2 2
2
2
log 2 2log 4 8 0
x x
1
. Khi đó phương trình
1
tương
đương với phương trình nào dưới đây:
A.
2
3 2 0
x x
. B.
3 5 6 2
x x
x
.
C.
2
4 9 2 0
x x
. D.
2 2
2 2 1
4 2 3 0
x x x x
.
Câu 32. [2D2-1] Đồ thị nào dưới đây là đồ thị của hàm số
3
x
y
?
A. B. C. D.
Câu 33. [2H1-3] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
2
a
,
SAD
cân tại
S
và
nằm trong mặt phẳng vuông góc với đáy. Góc giữa
SBC
và mặt đáy bằng
60
. Tính thể tích
.
S ABCD
bằng
A.
3
2 3
3
a
. B.
3
8 3
3
a
. C.
3
4 3
3
a
. D.
3
2 3
a .
Câu 34. [2H2-1] Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mọi hình hộp đứng đều có mặt cầu ngoại tiếp.
B. Mọi hình hộp chữ nhật đều có mặt cầu ngoại tiếp.
C. Mọi hình hộp có một mặt bên vuông góc với đáy đều có mặt cầu ngoại tiếp.
D. Mọi hình hộp đều có mặt cầu ngoại tiếp.
Câu 35. [2D1-2] Cho hàm số
3 2
1
2 1 5
3
y x x m x
. Tìm điều kiện của
m
để hàm số đồng biến
trên
.
A.
3
m
.
B.
3
m
. C.
3
m
. D.
3
m
.
Câu 36. [2H1-3] Cho khối chóp
.
S ABC
có
3
SA
,
4
SB
,
SC 5
,
60
ASB BSC CSA
Tính thể
tích khối chóp
.
S ABC
bằng
A.
5 2
. B.
5 3
. C.
10
. D.
15.
O
x
y
1
O
x
y
1
O
x
y
1
O
x
y
1
x
y
O
1
1
x
y a
log
b
y x

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/25
Câu 37. [2D2-2] Cho phương trình
2
1 2
2016 1 .2017 1 1
x x
x
. Khẳng định nào dưới đây đúng?
A. Phương trình
1
có nghiệm duy nhất.
B. Phương trình
1
vô nghiệm.
C. Phương trình
1
có tổng các nghiệm bằng
0
.
D. Phương trình
1
có nhiều hơn hai nghiệm.
Câu 38. [2H2-2] Một khối lập phương có thể tích
2 2
. Khi đó thể tích khối cầu ngoại tiếp hình lập
phương đó bằng
A.
2
. B.
6
. C.
2
. D.
6
.
Câu 39. [2H1-3] Cho khối chóp
.
S ABCD
có đáy là hình bình hành,
P
là mặt phẳng chứa
AB
cắt
SC
,
SD
tại
M
,
N
sao cho
1
3
SM SC
. Gọi
1
V
,
2
V
lần lượt là thể tích khối chóp
.
S ABMN
và khối đa diện
ABCDNM
. Khi đó tỉ số
1
2
V
V
bằng
A.
1
2
.
B.
1
8
. C.
2
9
. D.
2
7
.
Câu 40. [2H2-3] Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh bằng
6
, cạnh bên
SA ABC
và
4 6.
SA
Diện tích của mặt cầu ngoại tiếp hình chóp
.
S ABC
bằng
A.
108
. B.
48
. C.
36
. D.
144
.
Câu 41. [2H2-2] Cho hai khối cầu
1
S
có bán kính
1
R
, thể tích
1
V
và
2
S
có bán kính
2
R
, thể tích
2
V
.
Biết
2 1
8
V V
, khẳng định nào dưới đây là ĐÚNG?
A.
2 1
2
R R
. B.
1 2
2
R R
. C.
2 1
4
R R
. D.
2 1
2 2
R R
.
Câu 42. [2D1-2] Gọi
A
,
B
là các giao điểm của đường thẳng
y x m
và đồ thị hàm số
1
x
y
x
.
Khi đó, tìm
m
để
1
A B
x x
.
A.
2
m
. B.
3
m
. C.
0
m
. D.
1
m
.
Câu 43. [2D1-1] Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá tị nhỏ nhất của hàm số
2
3 e
x
f x x
trên đoạn
0; 2
. Giá trị của biểu thức
2016
2
4A m M bằng
A.
2016
e
. B.
1
. C.
2016
2
. D.
0
.
Câu 44. [2D1-2] Phương trình
3 3
3 log log 3 1
x x
có hai nghiệm
1
x
,
2
x
. Khi đó, tích
1 2
x x
bằng
A.
1
. B.
6
3
. C.
243
. D.
81
.
Câu 45. [1H3-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
2
a
. Biết
SAB
là tam
giác đều và nằm trong mặt phẳng vuông góc với
ABCD
. Khoảng cách giữa
AB
và
SD
bằng
A.
42
7
a
. B.
42
14
a
. C.
3
2
a
. D.
2
2
a
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/25
Câu 46. [1H3-3] Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
3
a
. Tính khoảng cách từ
điểm
A
đến
SBC
biết thể tích khối chóp
.
S ABC
bằng
3
6
4
a
.
A.
2 3
3
a
. B.
2
a
. C.
a
. D.
2
2
a
.
Câu 47. [1H3-3] Cho lăng trụ đứng
.
ABC A B C
có đáy là tam giác vuông tại
B
,
AB a
,
2
BC a
.
Biết thể tích của khối lăng trụ
.
ABC A B C
bằng
3
2 2
a
. Gọi
là góc giữa
A BC
với
ABC
. Tính
cos
.
A.
1
3
. B.
3
3
. C.
6
3
. D.
2
3
.
Câu 48. [2H2-3] Công ty
A
cần xây bể chưa hình hộp chữ nhật (không có nắp), đáy là hình vuông cạnh
bằng
m
a , chiều cao bằng
m
h . Biết thể tích bể chứa cần xây là
3
62,5 m
, hỏi kích thước
cạnh đáy và chiều cao phải bằng bao nhiêu để tổng diện tích các mặt xung quanh và mặt đáy là
nhỏ nhất?
A.
5 2
m, 5m
2
a h . B.
5 10
m, 4m
4
a h .
C.
5m, 2,5m
a h
. D.
5 30
3m, m
6
a h .
Câu 49. [2D1-1] Biết đồ thị
1
:
1
ax
C y
bx
,
0, 0
b a b
có tiệm cận ngang là
2
y
. Khi đó, tỷ
số
a
b
là
A.
3
. B.
2
. C.
1
. D.
1
.
Câu 50. [2D2-3] Biết phương trình
2
3 3
2log 2 log 4 0
x x
có hai nghiệm
1 2
,
x x
. Khi đó
2
1 2
x x
bằng
A.
2
. B.
4
. C.
8
. D.
9
.
----------HẾT----------
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/25
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
C
C
B B A
B C
C
B
D
A
B D
B A
C
B B D
C
C
D
C
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
C
A
D
D
C
C
B B
B
A
C
B D
D
A
A
D
C
A
B A
C
B A
HƯỚNG DẪN GIẢI
Câu 1. [2D2-2] Tập xác định của hàm số
2
2
3
2
log 2
x x
y
x
là
A.
1; 2
. B.
1;
. C.
1; 2
. D.
2; 2 \ 1
.
Lời giải
Chọn C.
Đkxđ của hàm số:
2
2
2 0
2 0
x x
x
2
1
2 2
x
x
x
1 2
x
.
Câu 2. [2D1-2] Phát biểu nào sau đây SAI?
A. Hàm số
4 2
0
y ax bx c a
luôn có điểm cực trị.
B. Hàm số
ax b
y
cx d
(với
0
ad bc
) không có cực trị.
C. Hàm số
3 2
0
y ax bx cx d a
luôn có điểm cực trị.
D. Hàm số
2
0
y ax bx c a
luôn có một điểm cực trị duy nhất.
Lời giải
Chọn C.
Hàm số
3 2
0
y ax bx cx d a
là hàm bậc ba có
2
3 2
y ax bx c
nếu
2
3 0
b ac
thì
y
không đổi dấu nên không có điểm cực trị.
Câu 3. [2D1-2] Cho hàm số
y f x
có bảng biến thiên như sau:
(I): Tập xác định của
f x
là
\ 1
D
. (II): Hàm số
f x
có đúng một điểm cực trị.
(III):
min 2
f x
. (IV):
1;3
A là điểm cực đại của đồ thị hàm số.
Trong các phát biểu trên, có bao nhiêu phát biểu ĐÚNG?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C.
Từ bảng biến thiên của hàm số ta có: (I), (II), (III) đều là các phát biểu sai. Chỉ có (IV) là phát
biểu đúng.Do đó số phát biểu đúng là
1
.
x
1
1
y
0
||
y
3
2
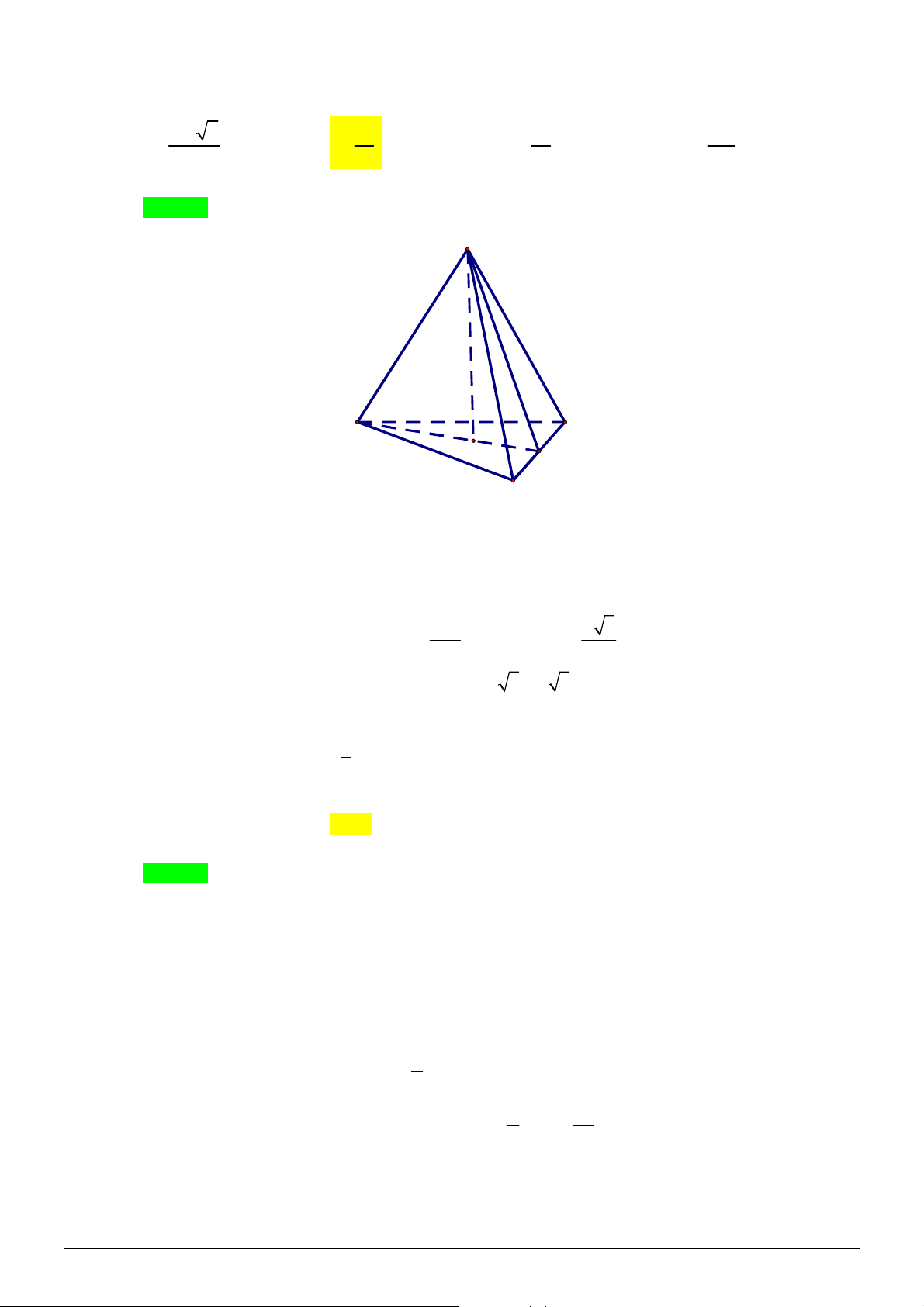
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/25
Câu 4. [2H1-2] Cho khối chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt
đáy bằng
45
. Thể tích khối chóp
.
S ABC
bằng bao nhiêu?
A.
3
3 2
4
a
. B.
3
12
a
. C.
3
4
a
. D.
3
3
4
a
.
Lời giải
Chọn B.
M
A
C
B
S
H
Gọi
H
là trọng tâm tam giác
ABC
. Khi đó:
SH ABC
và góc giữa cạnh bên
SA
và
ABC
là
SAH
.
Do đó:
45
SAH
. Khi đó: tan 45
SH
AH
3
3
a
SH AH .
Thể tích khối chóp là
.
1
. .
3
S ABC ABC
V SH S
2 3
1 3 3
. .
3 3 4 12
a a a
.
Câu 5. [2D1-2] Cho hàm số
3 2
1
2 3 1
3
y x x x
có đồ thị
C
. Có bao nhiêu tiếp tuyến của
C
song song với đường thẳng
3 1
y x
?
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn B.
Ta có:
2
4 3
y x x
.
Xét phương trình:
3
y
2
4 3 3
x x
0
4
x
x
.
Với
0
x
, ta có tiếp điểm là
0;1
M và phương trình tiếp tuyến của
C
là
3 0 1
y x
3 1
x l
.
Với
4
x
, ta có tiếp điểm là
7
4;
3
M
và phương trình tiếp tuyến của
C
là
7 29
3 4 3
3 3
y x x .

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/25
Câu 6. [2H2-2] Cho
ABC
vuông tại
A
,
6 cm
AB
,
8 cm
AC
. Gọi
1
V
là thể tích khối nón tạo
thành khi quay
ABC
quanh
AB
và
2
V
là thể tích khối nón tạo thành khi quay
ABC
quanh
AC
. Tỉ số
1
2
V
V
bằng
A.
4
3
. B.
3
4
. C.
16
9
. D.
64
27
.
Lời giải
Chọn A.
Khi quay
ABC
quanh
AB
, ta được khối nón có chiều cao
1
6 cm
h AB , bán kính đáy
1
8 cm
r AC nên thể tích khối nón tạo thành là
2 3
1
1
.6.8 cm
3
V
.
Khi quay
ABC
quanh
AC
, ta được khối nón có chiều cao
2
8 cm
h AC , bán kính đáy
2
6 cm
r AB nên thể tích khối nón tạo thành là
2 3
2
1
.8.6 cm
3
V
.
Ta có tỉ số:
1
2
4
3
V
V
.
Câu 7. [2D2-2] Giá tị nhỏ nhất của hàm số
1
4
2 .8
3
x x
y
trên
1;0
bằng bao nhiêu?
A.
5
6
. B.
2
3
. C.
2 2
3
. D.
50
81
.
Lời giải
Chọn B.
Ta có:
3
4
2.2 . 2
3
x x
y . Đặt
2
x
t
, với
1;0
x
1
1
2
t
.
Khi đó xét:
3
4
2
3
y t t
trên
1
;1
2
.
Ta có:
2
4 2
y t
,
1
2
0
1
2
t
y
t l
.
Xét
1 5
2 6
y
,
2
1
3
y
,
1 2 2
3
2
y
. Suy ra: GTNN của hàm số đã cho là
2
3
.
Câu 8. [2D1-2] GTNN của hàm số
2sin 2 5 1
f x x x
trên đoạn
0;
2
bằng bao nhiêu?
A.
0
. B.
5
3
4
. C.
5
1
2
. D.
1
.
Lời giải
Chọn C.
Ta có: 4cos2 5 0
y x x R
. Do đó hàm số đã cho nghịch biến trên đoạn
0;
2
. Suy ra:
GTNN của hàm số đã cho là
5
1
2 2
f
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/25
Câu 9. [2D2-2] Cho
ABC
vuông tại
A
có
log 8
3
a
AB ,
25
log 36
5AC . Biết độ dài
10
BC
thì giá trị
a
bằng bao nhiêu?
A.
9
. B.
1
3
. C.
3
. D.
3
.
Lời giải
Chọn C.
Ta có:
2 2 2
AC AB BC
2
36 100
AC
8
AC
log 8
3 8
a
. Do đó:
log 3
8 8
a
log 3 1
a
3
a
.
Câu 10. [2D2-2] Phương trình
2 2 2
2 5 2 3 7 2 5 12 4
2 2 1 2
x x x x x x
có bao nhiêu nghiệm?
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
Chọn B.
Phương trình
2 2
2 5 2 3 7 2
2 1 2 1 0
x x x x
2
2
2 5 2 0 1
3 7 2 0 2
x x
x x
Xét
2
1
1
2
x
x
và
2
2
1
3
x
x
.
Vậy phương trình bài ra có
3
nghiệm.
Câu 11. [2D2-2] Một tên lửa bay vào không trung với quãng đường đi được
km
s t là hàm phụ
thuộc theo biến
t
(giây), với phương trình
2
3 3 1
e 2 .e
t t
s t t
. Khi đó vận tốc của tên lửa sau
1
giây là
A.
4
5e km/h
. B.
4
3e km/h
. C.
4
9e km/h
. D.
4
10e km/h
.
Lời giải
Chọn D.
Ta có
2
3 3 1 3 1
2 .e 2e 6 .e
t t t
v t s t t t
.
Do đó
4
1 10.e km/h
v .
Câu 12. [2D2-2] Giới hạn
2
0
e 1
lim
4 2
x
x
x
bằng
A.
8
. B.
4
. C.
2
. D.
1
.
Lời giải
Chọn A.
Ta có:
2
2
0 0
2 e 1 4 2
e 1
lim lim 8
2
4 2
x
x
x x
x
x
x
.
Câu 13. [2D1-2] Trong các hàm số sau, hàm số nào đồng biến trên
0;
?
A.
sin 2
y x
. B.
2
1
x
y
x
. C.
2
x
y
x
D.
2
2
1
y x
Lời giải
Chọn B.
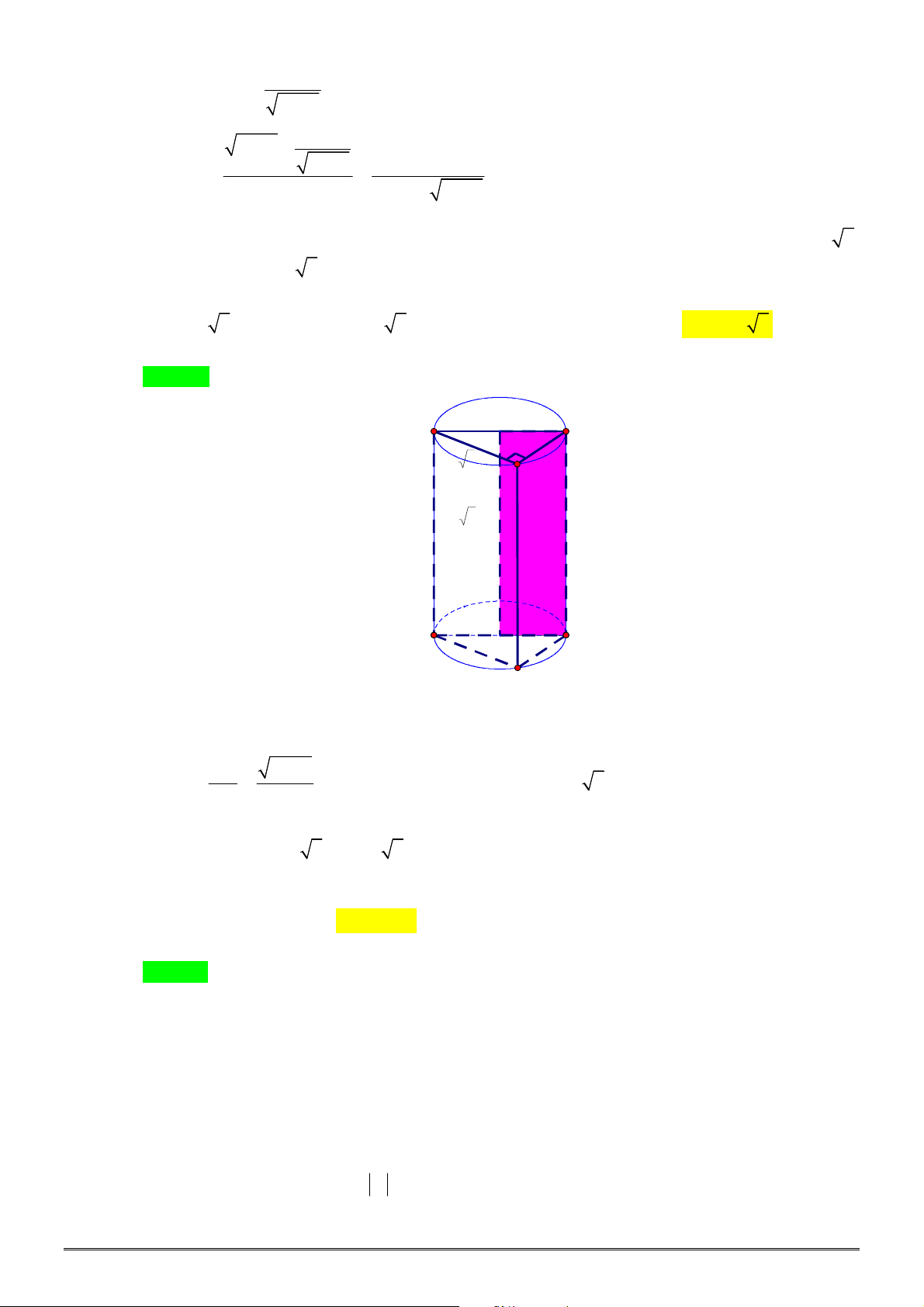
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/25
Xét hàm số
2
1
x
y
x
Ta có
2
2
2
2
2 2
1
1
1
0;
1
1 1
x
x
x
y x
x
x x
nên hàm số đồng biến trên
.
Câu 14. [2H2-2] Cho hình lăng trụ đứng
.
ABC A B C
có tam giác
ABC
vuông cân tại
B
,
2
AB a
và cạch bên
6
AA a
. Khi đó diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ đứng
đã cho là
A.
2
4 6
a
. B.
2
6
a
. C.
2
4
a
. D.
2
2 6
a
Lời giải
Chọn D.
a 2
a 6
r
h
O
O'
A
B
B'
A'
C'
C
Ta có: tam giác
ABC
vuông cân tại
B
nên tâm đường tròn ngoại tiếp đáy lăng trụ là trung điểm
của
AC
Nên
2
2
2 2
AC BA
r a
, chiều cao hình trụ
6
h AA a
Suy ra diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ đứng đã cho là
2
2 . . 2 . . 6 2 6
xq
S r h a a a
.
Câu 15. [2D1-2] Biết phương trình
3
3 0
x x m
có ba nghiệm phân biệt. Khẳng định nào sau đây đúng?
A.
2
4
m
. B.
2
4
m
. C.
2
4
m
. D.
2
4
m
.
Lời giải
Chọn B.
Số nghiệm của phương trình
3
3 0
x x m
bằng số giao điểm của đồ thị hàm số
3
3
y x x
và đường thẳng
y m
Để phương trình đã cho có ba nghiệm phân biệt điều
kiện là hàm số có cực đại, cực tiểu và
CT C
Đ
y m y
.
Ta có:
2
1 2
3 3 0
1 2
CT
CĐ
x y
y x y
x y
Để đường thẳng
y m
cắt đồ thị hàm số
3
3
y x x
tại ba điểm phân biệt điều kiện là
2
2 2 2 2 2 4
m m m m
.
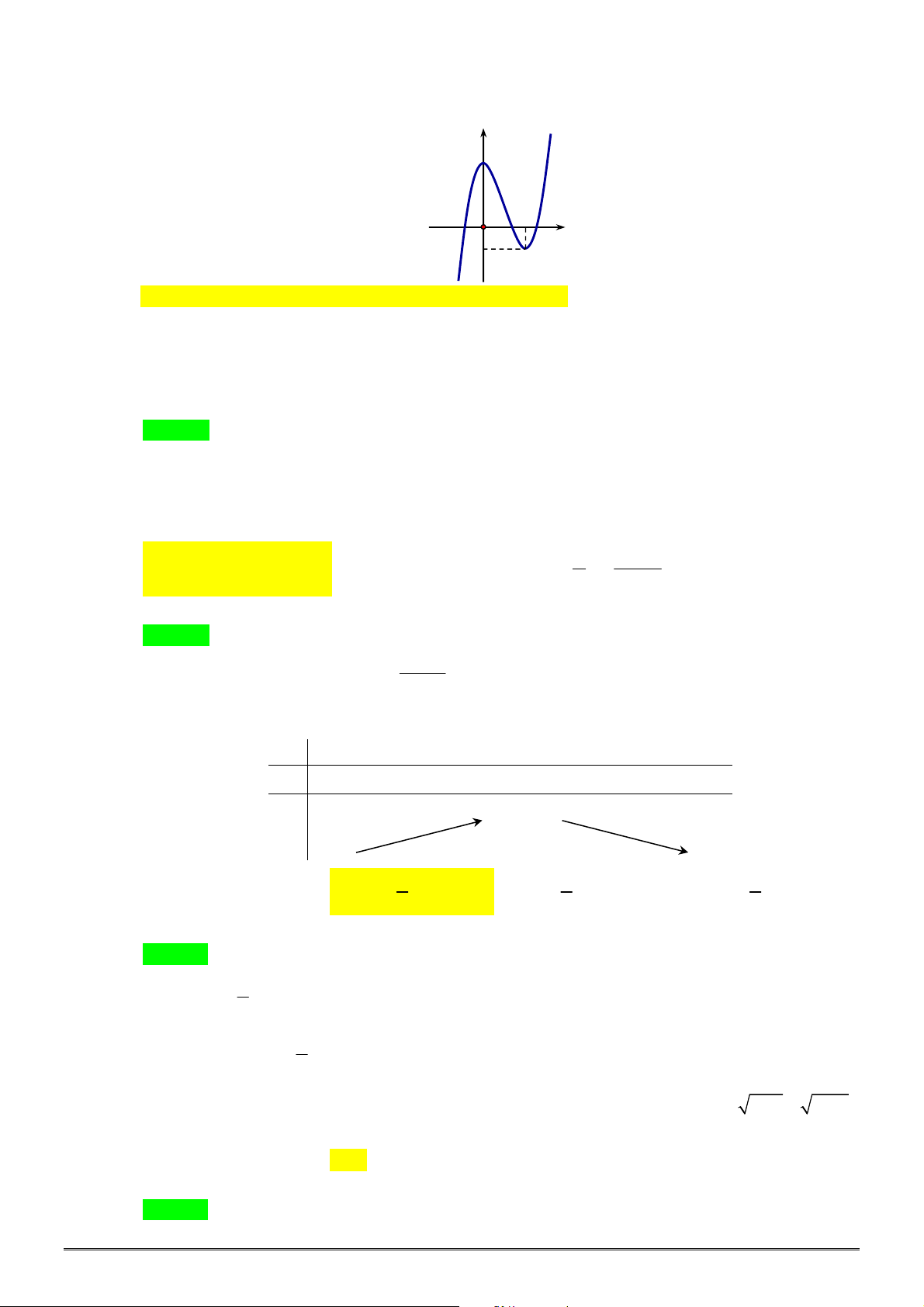
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/25
Câu 16. [2D1-1] Cho hàm số
f x
xác định, liên tục trên
, có đồ thị như hình vẽ. Khẳng định nào
dưới đây ĐÚNG?
A. Hàm số đạt cực đại tại
0
x
và đạt cực tiểu tại
2
x
.
B. Hàm số có giá trị lớn nhất bằng
3
.
C. Hàm số đồng biến trê khoảng
0;
.
C. Đồ thị hàm số có một đường tiệm cận.
Lời giải
Chọn A.
Từ đồ thị hàm số ta suy ra hàm số đạt cực đại tại
0
x
và đạt cực tiểu tại
2
x
.
Câu 17. [2D2-1] Cho
0 1, 0 1, 0, 0
a b x y
. Tìm công thức ĐÚNG trong các công thức sau.
A.
log log log
a a a
x y x y
B.
log .log
b
a
a
x b x
.
C.
log log .log
b b a
x a x
. D.
log
log
log
a
a
a
x
x
y y
.
Lời giải
Chọn C.
Theo công thức đổi cơ số
log
log log log .log
log
b
a b b a
b
x
x x a x
a
.
Câu 18. [2D1-2] Bảng biến thiên sau đây có thể là bảng biến thiên của hàm số nào?
A.
2
2 3
y x x
. B.
4 2
1
3
4
y x x
. C.
4 2
1
3
2
y x x
. D.
4 2
1
2 3
2
y x x
Lời giải
Chọn B.
Ta có:
4 2 3
2
0
1
3 2 0
4
2 0
x
y x x y x x x
x
Suy ra hàm số
4 2
1
3
4
y x x
là hàm số có bảng biến thiên đã cho.
Câu 19. [2D1-2] Gọi
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 1 7
y x x
.
Khi đó có bao nhiêu số nguyên nằm giữa
m
,
M
?
A.
2
. B.
1
. C. Vô số. D.
0
.
Lời giải
Chọn B.
x
0
y
0
y
3
O
x
y
3
2
1
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/25
Tập xác định:
1;7
D .
Theo bất đẳng thức Côsi ta có:
0 2 1 7 1 7 6
x x x x
.
2 2
6 2 1 7 6 12 6 2 3
y x x y y
Suy ra
6; 2 3
m M nên chỉ có 1 số nguyên nằm giữa
m
,
M
là số 3.
Câu 20. [2D2-2] Cho hàm số
2 sin 2
e
x
f x
. Biết
0
0;
2
x
là giá trị thỏa mãn
0
0.
f x
Khi đó:
A.
0
2
x
. B.
0
3
x
. C.
0
0
x
D.
0
4
x
.
Lời giải
Chọn D.
Ta có:
2 sin 2
e .2cos2
x
f x x
0 0 0 0
0 cos2 0 do 0;
4 2
f x x x x
.
Câu 21. [2H1-1] Cho khối lăng trụ tam giác đều có cạnh đáy bằng
a
. Biết diện tích mỗi mặt bên của
lăng trụ là
2
3
a , khi đó thể tích khối lăng trụ bằng
A.
3
3 3
4
a
. B.
3
3
4
a
. C.
3
4
a
. D.
3
3
4
a
.
Lời giải
Chọn C.
Gọi
h
là chiều cao của khối lăng trụ, ta có:
2
. 3 3
a h a h a
.
Mặt đáy là tam giác đều cạnh
a
nên diện tích mặt đáy là
2
3
4
a
S .
Vậy, thể tích khối lăng trụ đã cho là
2 3
3 3
. . 3
4 4
a a
V S h a .
Câu 22. [2D2-2] Cho hàm số
ln 1 e
x
y x . Khẳng định nào dưới đây là ĐÚNG?
A. Hàm số đạt cực tiểu tại
1
x
. B. Hàm số đạt cực đại tại
0
x
.
C. Hàm số đồng biến trên
. D. Tập xác định của hàm số là
0;D
.
Lời giải
Chọn C.
Ta có
e 1
1 0,
1 e 1 e
x
x x
y x
. Do đó hàm số đã cho đồng biến trên
.
a
h
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/25
Câu 23. [2H1-2] Cho khối chóp tứ giác đều
.
S ABCD
có độ dài tất cả các cạnh đều bằng
a
. Thể tích
khối chóp
.
S ABCD
bằng
A.
3
2
a
. B.
3
4
a
. C.
3
2 3
a
. D.
3
3 2
a
.
Lời giải
Chọn D.
Gọi
H
là tâm của hình vuông
ABCD
, khi đó
SH ABCD
,
2
2 2
AC a
HA , nên:
2
2
2 2 2 2
2 2
2 2 2
a a a
SH SA HA a SH
.
Thể tích khối chóp
.
S ABCD
là
3
2
1 1 2
. .
3 3 2
3 2
ABCD
a a
V S SH a .
Câu 24. [2D1-3] Cho hàm số
4 2
2 1
y x mx
. Tìm giá trị của
m
để đồ thị hàm số có ba điểm cực trị
A
,
B
,
C
sao cho
ABC
có diện tích bằng
4 2
.
A.
1
m
. B.
2
m
. C.
2
m
. D.
4
m
.
Lời giải
Chọn C.
Ta có:
3 2
4 4 4
y x mx x x m
;
2
0
0
x
y
x m
.
Đồ thị hàm số đã cho có ba điểm cực trị khi và chỉ khi
0
y
có ba nghiệm phân biệt
0
m
.
Khi đó
0
y
có ba nghiệm là
0
x
,
x m
và
x m
.
Tọa độ các điểm cực trị của đồ thị hàm số là
0;1
A ,
2
;1
B m m
,
2
;1
C m m
. Ba
điểm cực trị
A
,
B
,
C
tạo thành
ABC
cân đỉnh
A
.
Gọi
H
là trung điểm
BC
thì
2
0;1
H m
. Từ đó 2
BC m
,
2
AH m
.
Diện tích
ABC
là
2 2
1 1
. .2 .
2 2
S BC AH m m m m
.
Bởi vậy
2
4 2 4 2 2
S m m m
.
C
B
A
H
S
D

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/25
Câu 25. [2D2-2] Giá trị cực đại của hàm số
2
ln
x
y
x
bằng
A.
e
2
. B.
1
2e
. C.
1
e
. D.
2
1
2e
.
Lời giải
Chọn B.
Tập xác định của hàm số:
0;D
.
Ta có:
3
1 2ln
0 1 2ln 0 e
x
y x x
x
.
Ta có bảng biến thiên
Từ bảng biến thiên, ta thấy giá trị cực đại của hàm số
2
ln
x
y
x
bằng
1
2e
.
Câu 26. [2D1-3] Biết phương trình
2 2
2 1 2 1 2 3 0
x x x x x x
có nghiệm duy nhất là
a
.
Khi đó
A.
0 1
a
. B.
3 4
a
. C.
1 2
a
. D.
2 3
a
.
Lời giải
Chọn A.
Ta có:
2 2
2 1 2 1 2 3 0
x x x x x x
2
2
2 1 1 1 2 0 *
x x x x x x
Xét hàm số:
2
2
f t t t t
với
t
.
Ta có
2
2
2
1 2 0,
2
t
f t t t
t
.
Do đó, hàm số
f t
đồng biến trên
. Bởi vậy:
1
* 1 1
2
f x f x x x x
.
Như vậy, phương trình có nghiệm duy nhất
1
0;1
2
a .
Câu 27. [2D1-2] Cho hàm số
3 1
2
x
y
x
có đồ thị
C
. Có bao nhiêu điểm trên
C
mà tổng khoảng
cách từ đó đến hai đường tiệm cận của
C
bằng
6
.
A.
0
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn C.
Đồ thị
C
hàm số có tiệm cận đứng là đường thẳng
2
x
và tiệm cận ngang là đường thẳng
3
y
.
x
0
e
y
0
y
1
2e
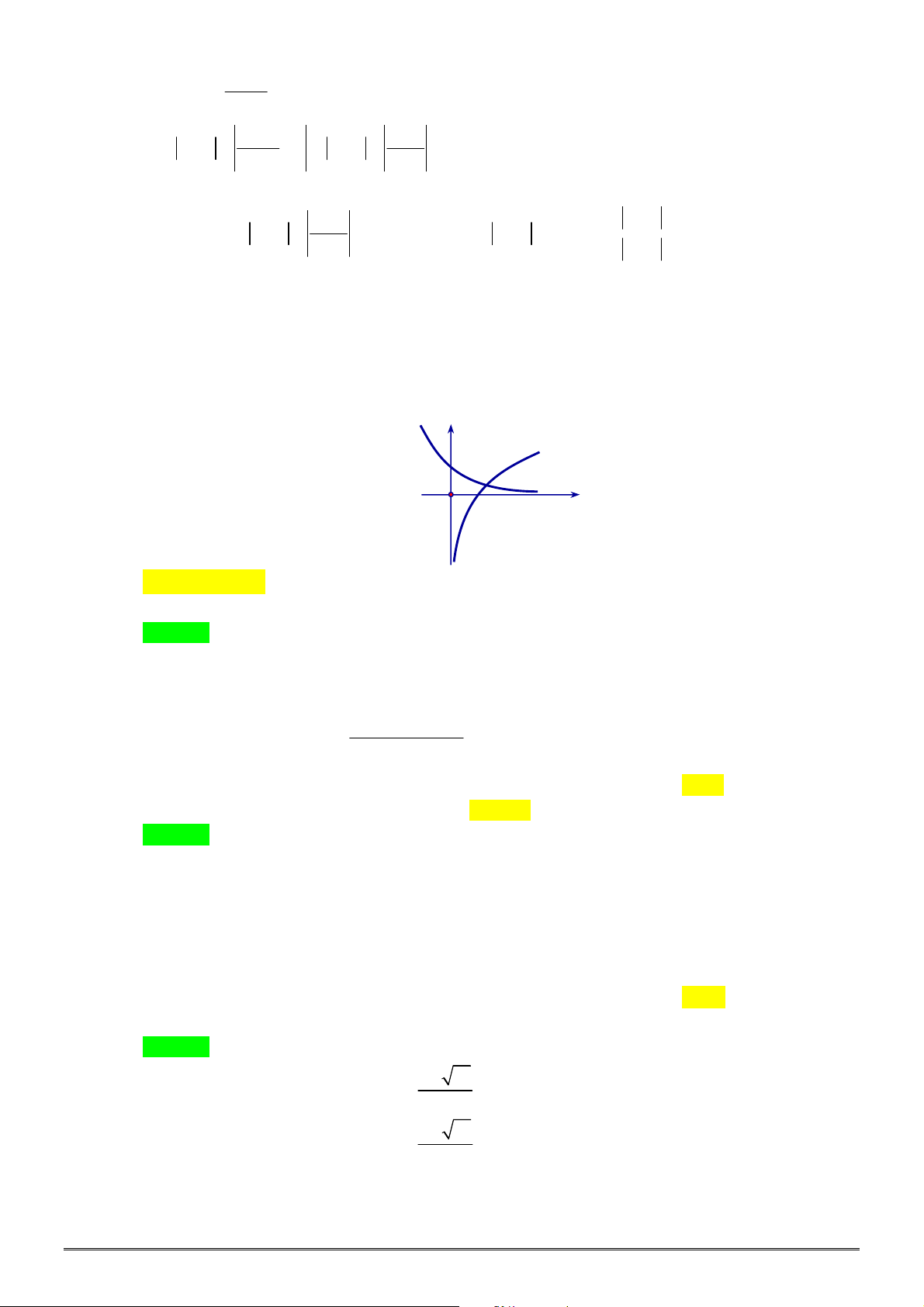
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/25
Gọi
3 1
;
2
x
M x C
x
, tổng khoảng cách từ
M
đến hai đường tiệm cận là
3 1 5
2 3 2
2 2
x
T x x
x x
Nên
2
1
2 1
3
5
6 2 6 2 6 2 5 0
3
2
2 5
7
x
x
x
T x x x
x
x
x
x
.
Như vậy, có
4
điểm trên
C
mà tổng khoảng cách từ đó đến hai đường tiệm cận của
C
bằng
6
.
Câu 28. [2D2-1] Cho đồ thị hàm số
x
y a
và
log
b
y x
như hình vẽ bên. Khẳng định nào dưới đây là
ĐÚNG?
A.
0 1
a b
. B.
1; 1
a b
. C.
0 1,0 1
a b
. D.
0 1
b a
.
Lời giải
Chọn A.
Từ đồ thị hàm số
x
y a
và
log
b
y x
suy ra hàm số
x
y a
nghịch biến và
log
b
y x
đồng
biến nên
0 1
a b
.
Câu 29. [2D1-1] Đồ thị hàm số
2 2
3 1
5 6
x
y
x x x
có bao nhiêu đường tiệm cận đứng?
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn D.
Hàm số đã cho có tập xác định
\ 0;2;3
D
.
Ta có
0
lim
x
y
;
2
lim
x
y
và
3
lim
x
y
nên đồ thị hàm số có
3
đường tiệm cận đứng.
Câu 30. [2D1-1] Gọi
x a
và
x b
là các điểm cực trị của hàm số
3 2
2 3 18 1
y x x x
. Khi đó
2
A a b ab
bằng
A.
5
. B.
7
. C.
5
. D.
7
.
Lời giải
Chọn D.
Ta có:
2
1 13
2
6 6 18 0
1 13
2
x
y x x
x
.
x
y
O
1
1
x
y a
log
b
y x
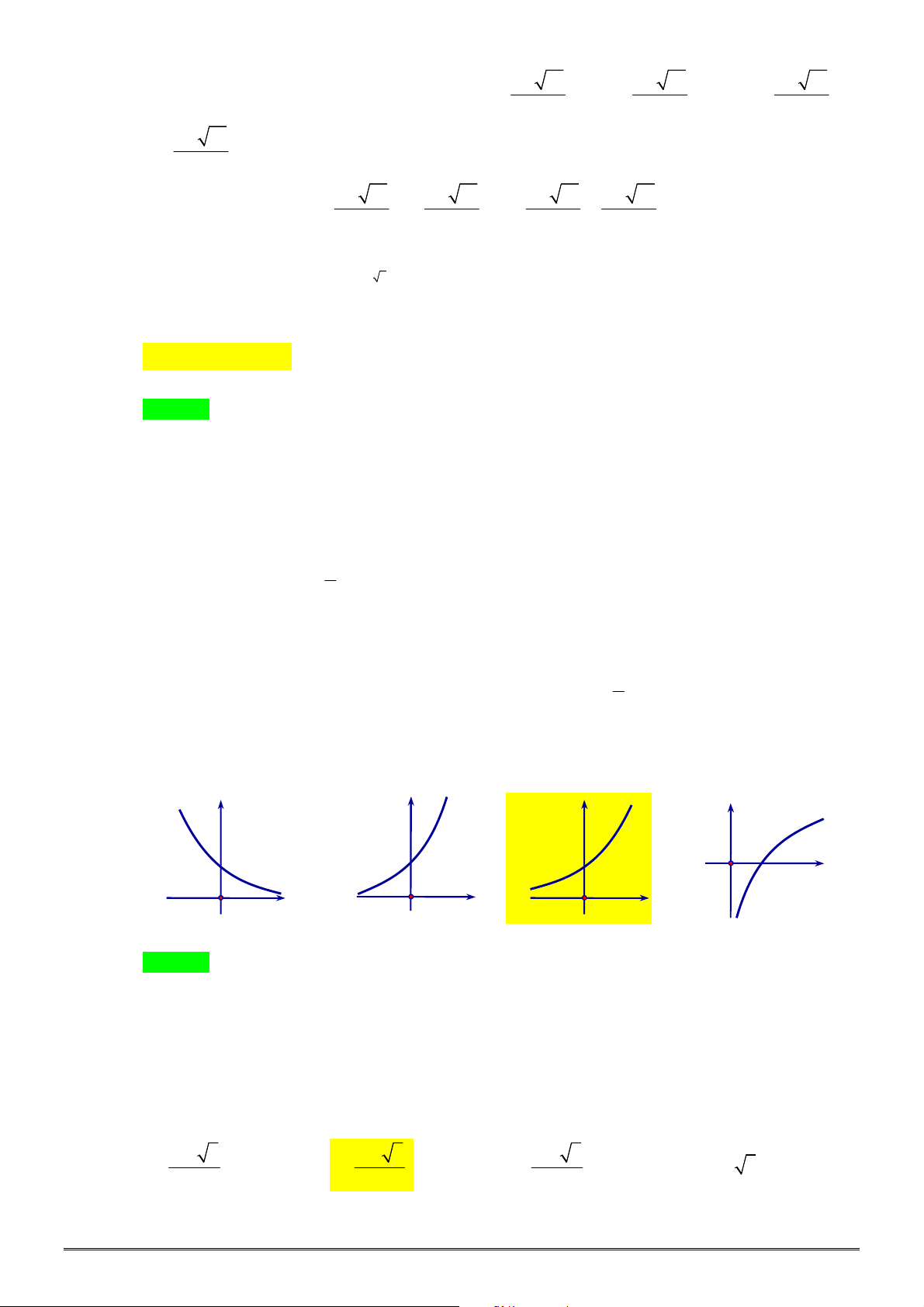
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/25
Như vậy, hàm số đạt cực trị tại các điểm
1 13
2
x
và
1 13
2
x
. Hay
1 13
2
a
và
1 13
2
b
.
Từ đó
1 13 1 13 1 13 1 13
2 2 7
2 2 2 2
A a b ab
.
Câu 31. [2D2-3] Cho phương trình
2 2
2
2
log 2 2log 4 8 0
x x
1
. Khi đó phương trình
1
tương
đương với phương trình nào dưới đây:
A.
2
3 2 0
x x
. B.
3 5 6 2
x x
x
.
C.
2
4 9 2 0
x x
. D.
2 2
2 2 1
4 2 3 0
x x x x
.
Lời giải
Chọn C.
1
2
2
2 2 2 2
4 log 2 log 2 log 4 log 8 0
x x
2
2
2 2
4 log 2log 1 4 4log 8 0
x x x
2
2
2
4log 4log 8 0
x x
2
2
2
log log 2 0
x x
2
2
2
log 1
1
log 2
4
x
x
x
x
. Do đó
1
có tập nghiệm là
2
2; 2
S
.
Phương trình
2
3 2 0
x x
và phương trình
3 5 6 2
x x
x
đều có
1
x
là một nghiệm nên
loại A và B. Phương trình
2 2
2 2 1
4 2 3 0
x x x x
có
0
x
là một nghiệm.
Phương trình
2
4 9 2 0
x x
có hai nghiệm là
2
x
và
1
4
x
nên tương đương với phương
trình
1
.
Câu 32. [2D2-1] Đồ thị nào dưới đây là đồ thị của hàm số
3
x
y
?
A. B. C. D.
Lời giải
Chọn C.
Hàm số
2
x
y
là hàm đồng biến. Đồ thị hàm số
2
x
y
đi qua điểm
1;2
, cắt trục tung tại
0;1
.
Câu 33. [2H1-3] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
2
a
,
SAD
cân tại
S
và
nằm trong mặt phẳng vuông góc với đáy. Góc giữa
SBC
và mặt đáy bằng
60
. Tính thể tích
.
S ABCD
bằng
A.
3
2 3
3
a
. B.
3
8 3
3
a
. C.
3
4 3
3
a
. D.
3
2 3
a .
Lời giải
O
x
y
1
O
x
y
1
O
x
y
1
O
x
y
1
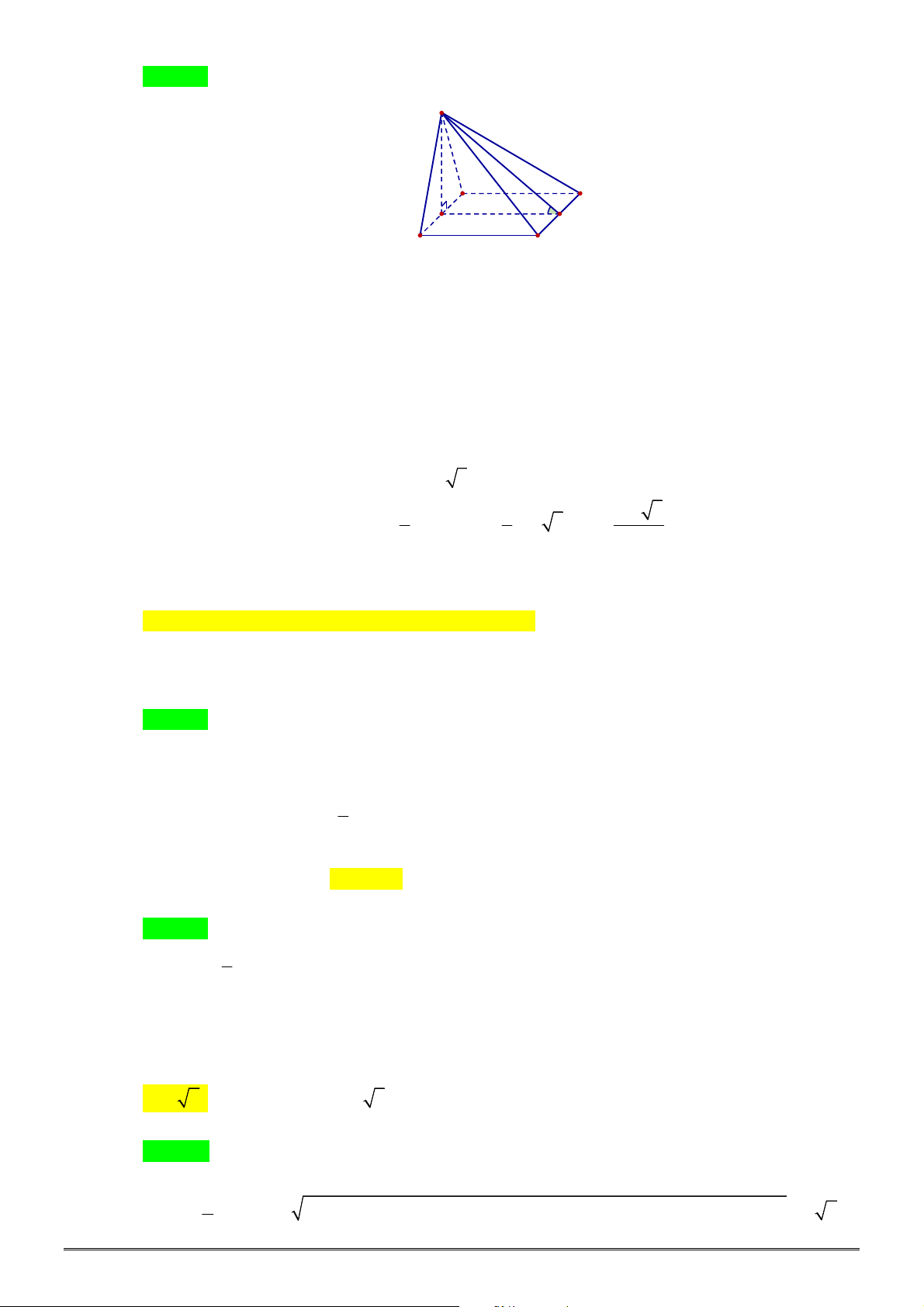
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/25
Chọn B.
Gọi
H
là trung điểm
AD
. Ta có:
SAD ABCD
SAD ABCD AD
SH AD
SH ABCD
.
ABCD
là hình vuông cạnh
2
a
nên
2 2
4
ABCD
S AB a
.
Tam giác
SBC
cân tại
S
nên
SM BC
, mà
HM BC
góc giữa mặt phẳng
SBC
và
mặt phẳng
ABCD
là góc giữa hai đường thẳng
HM
,
SM
chính là góc
SMH
. Theo bài ra
có
60
SMH
2 .tan 60 2 3
SH a a
.
Vậy thể tích
.
S ABCD
là
3
2
1 1 8 3
. .2a 3.4 .
3 3 3
SABCD ABCD
a
V SH S a
Câu 34. [2H2-1] Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mọi hình hộp đứng đều có mặt cầu ngoại tiếp.
B. Mọi hình hộp chữ nhật đều có mặt cầu ngoại tiếp.
C. Mọi hình hộp có một mặt bên vuông góc với đáy đều có mặt cầu ngoại tiếp.
D. Mọi hình hộp đều có mặt cầu ngoại tiếp.
Lời giải
Chọn B.
A., C., D. sai vì nếu đa giác ở đáy không phải là tứ giác nội tiếp một đường tròn thì không có
mặt cầu ngoại tiếp.
Câu 35. [2D1-2] Cho hàm số
3 2
1
2 1 5
3
y x x m x
. Tìm điều kiện của
m
để hàm số đồng biến
trên
.
A.
3
m
.
B.
3
m
. C.
3
m
. D.
3
m
.
Lời giải
Chọn B.
Ta có
3 2
1
2 1 5
3
y x x m x
2
4 1
y x x m
,
3
m
. Để hàm số đồng biến
trên
thì
3 0
m
3
m
.
Câu 36. [2H1-3] Cho khối chóp
.
S ABC
có
3
SA
,
4
SB
,
SC 5
,
60
ASB BSC CSA
Tính thể
tích khối chóp
.
S ABC
bằng
A.
5 2
. B.
5 3
. C.
10
. D.
15.
Lời giải
Chọn A.
Áp dụng công thức nhanh cho tứ diện biết ba cạnh và ba góc cùng suất phát một đỉnh ta có.
2 2 2
1
. . . 1 cos cos cos 2cos .cos .cos 5 2
6
SABC
V SA SB SC ASB BSC CSA ASB BSC CSA
A
D
C
B
H
S
60
M

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/25
Câu 37. [2D2-2] Cho phương trình
2
1 2
2016 1 .2017 1 1
x x
x
. Khẳng định nào dưới đây đúng?
A. Phương trình
1
có nghiệm duy nhất.
B. Phương trình
1
vô nghiệm.
C. Phương trình
1
có tổng các nghiệm bằng
0
.
D. Phương trình
1
có nhiều hơn hai nghiệm.
Lời giải
Chọn C.
2 2
2 1 1 2
1 0 2016 1 2016 1 .2017 1
x x x
x x
.
2 2
2 1 1 2
1 0 2016 1 2016 1 .2017 1
x x x
x x
.
Vậy
2
1 0 1.
x x
Câu 38. [2H2-2] Một khối lập phương có thể tích
2 2
. Khi đó thể tích khối cầu ngoại tiếp hình lập
phương đó bằng
A.
2
. B.
6
. C.
2
. D.
6
.
Lời giải
Chọn B.
Giả sử khối lập phương có cạnh
3
2 2 2
a a a
.
Độ dài đường chéo của hình lập phương là
6
.
Bán kính mặt cầu ngoại tiếp hình lập phương là
6
2
r .
Thể tích khối cầu ngoại tiếp hình lập phương là
3
3
4 4 6
6 .
3 3 2
V r
Câu 39. [2H1-3] Cho khối chóp
.
S ABCD
có đáy là hình bình hành,
P
là mặt phẳng chứa
AB
cắt
SC
,
SD
tại
M
,
N
sao cho
1
3
SM SC
. Gọi
1
V
,
2
V
lần lượt là thể tích khối chóp
.
S ABMN
và khối đa diện
ABCDNM
. Khi đó tỉ số
1
2
V
V
bằng
A.
1
2
.
B.
1
8
. C.
2
9
. D.
2
7
.
Lời giải
Chọn D.
Ta có
1
// //
3
SN
MN AB MN CD
SD
S
A
B
C
D
N
M
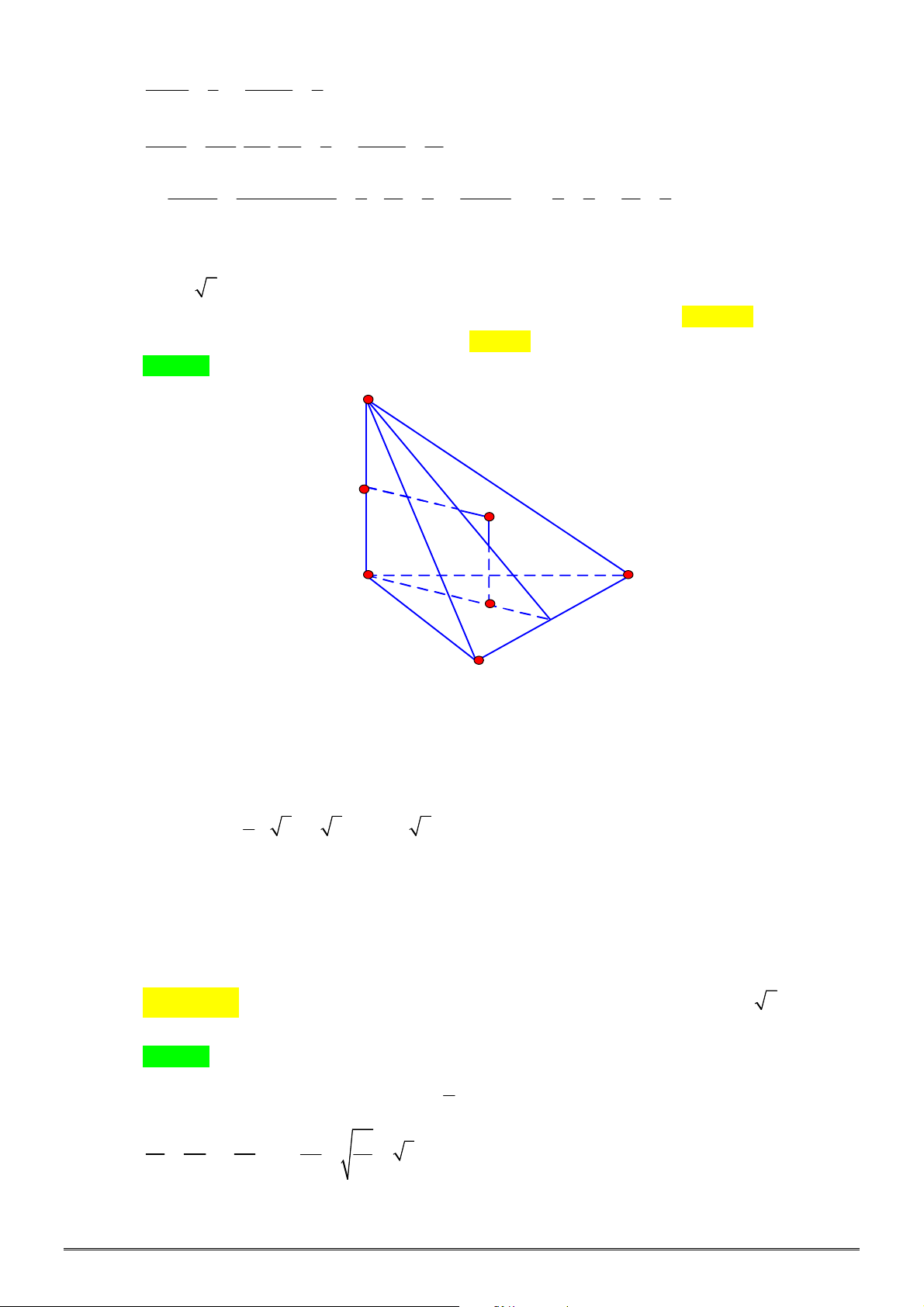
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/25
1 1
3 6
SABM SABM
SABC SABCD
V V
V V
.
1 1
. . .
9 18
SABN SABN
SABC SABCD
V V
SM SN SA
V SC SD SA V
1
. 2
1 1 2 2 7 2
1 .
6 18 9 9 9 7
SABMN SABM SAMN ABCDN
SABCD S ABCD SABCD
V V V V
V
V S V V
Câu 40. [2H2-3] Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh bằng
6
, cạnh bên
SA ABC
và
4 6.
SA
Diện tích của mặt cầu ngoại tiếp hình chóp
.
S ABC
bằng
A.
108
. B.
48
. C.
36
. D.
144
.
Lời giải
Chọn D.
S
A
B
C
I
G
M
Gọi
O
là trọng tâm tam giác
ABC
.
Dựng đường thẳng
d
đi qua
O
và vuông góc với
.
ABC
Trong
SAO
dựng đường trung trực của
SA
cắt
SA
tại
M
và cắt
d
tại
I
.
Suy ra
I
là tâm của mặt cầu ngoại tiếp hình chóp
.
S ABC
và
R IA
.
Ta có:
2
.3 3 2 3, 2 6
3
AO AM
2 2 2
36 6
IA IM MA R IA
Diện tích mặt cầu:
2
4 4 .36 144 .
S R
Câu 41. [2H2-2] Cho hai khối cầu
1
S
có bán kính
1
R
, thể tích
1
V
và
2
S
có bán kính
2
R
, thể tích
2
V
.
Biết
2 1
8
V V
, khẳng định nào dưới đây là ĐÚNG?
A.
2 1
2
R R
. B.
1 2
2
R R
. C.
2 1
4
R R
. D.
2 1
2 2
R R
.
Lời giải
Chọn A.
Từ công thức tính thể tích khối cầu
3
4
3
V R
, ta có được biểu thức tỷ lệ
3
3
2 2 2
3
1 1 1
V R R
V R R
3
2 2
3
1 1
8 2
R V
R V
2 1
2
R R

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/25
Câu 42. [2D1-2] Gọi
A
,
B
là các giao điểm của đường thẳng
y x m
và đồ thị hàm số
1
x
y
x
.
Khi đó, tìm
m
để
1
A B
x x
.
A.
2
m
. B.
3
m
. C.
0
m
. D.
1
m
.
Lời giải
Chọn A.
Xét phương trình hoành độ giao điểm giữa đường thẳng
y x m
và đồ thị hàm số
1
x
y
x
:
1
x
x m
x
2
0
1 1 0 1
x
f x x m x
.
Với
A
,
B
là các giao điểm thì
,
A B
x x
là các nghiệm (khác 0) của phương trình (1), ta cần điều
kiện:
1
0
0 0
f
2
1 4 0
1 0
m
(luôn đúng với mọi
m
).
Khi đó, theo Viet, ta có
1
A B
x x m
1 1
m
2
m
.
Câu 43. [2D1-1] Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá tị nhỏ nhất của hàm số
2
3 e
x
f x x
trên đoạn
0; 2
. Giá trị của biểu thức
2016
2
4A m M bằng
A.
2016
e
. B.
1
. C.
2016
2
. D.
0
.
Lời giải
Chọn D.
Ta có
2
2 3 e
x
f x x x
.
Nên
0
f x
2
2 3 e 0
x
x x
2
2 3 0
x x
1 0;2
3 0;2
x
x
Khi đó, ta có
0
0 3.e 2;
f
2 2
2 4 3 .e e ;
f
1
1 1 3 .e 2e
f
.
Nên ta có
2e
m
,
2
e
M
. Vậy
2016
2
4A m M
2016
2 2
4e 4e 0
.
Câu 44. [2D1-2] Phương trình
3 3
3 log log 3 1
x x
có hai nghiệm
1
x
,
2
x
. Khi đó, tích
1 2
x x
bằng
A.
1
. B.
6
3
. C.
243
. D.
81
.
Lời giải
Chọn C.
Với điều kiện
1
x
, phương trình tương đương với
3 3
3 log log 1 1
x x
3 3
log 3 log 2 0
x x
3
3
log 1
log 2
x
x
3
3
log 1
log 4
x
x
4
3
3
x
x
.
Khi đó, ta có
4 5
1 2
3.3 3 243
x x .
Câu 45. [1H3-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
2
a
. Biết
SAB
là tam
giác đều và nằm trong mặt phẳng vuông góc với
ABCD
. Khoảng cách giữa
AB
và
SD
bằng
A.
42
7
a
. B.
42
14
a
. C.
3
2
a
. D.
2
2
a
.
Lời giải
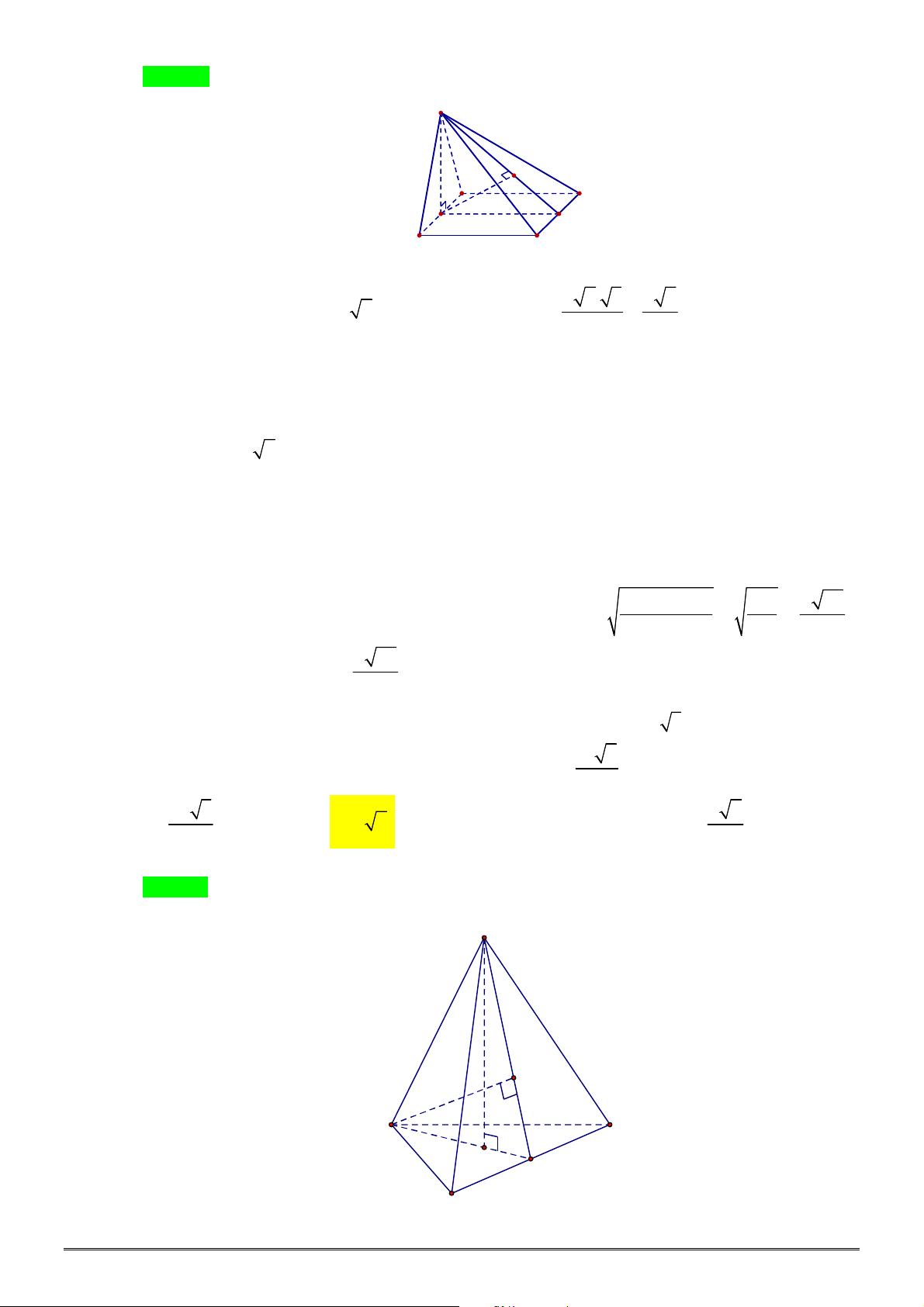
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/25
Chọn A.
Gọi
H
,
M
lần lượt là trung điểm của các cạnh
AB
,
CD
.
Tam giác
SAB
đều, cạnh
2
a
nên
SH AB
và
2. 3 6
2 2
a a
SH .
Ta chứng minh được
SH ABCD
. Do //
AB CD
nên
//
AB SCD
. Vậy
,
d AB SD
,
d AB SCD
,
d H SCD
.
Có
HM
là đường trung bình của hình vuông
ABCD
nên // //
HM AD CB HM CD
và
2
HM AD a
.
Ta có:
CD SH
CD HM
CD SHM
SHM SCD
.
Gọi
K
là hình chiếu vuông góc của
H
trên
SM
nên
HK SM
. Ta chứng minh được
HK SCD
nên
,
d H SCD HK
.
HK
là đường cao của tam giác vuông
SHM
nên ta có
2 2
2 2
.HS HM
HK
HS HM
2
6
7
a
42
7
a
.
Vậy
,
d H SCD HK
42
7
a
.
Câu 46. [1H3-3] Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
3
a
. Tính khoảng cách từ
điểm
A
đến
SBC
biết thể tích khối chóp
.
S ABC
bằng
3
6
4
a
.
A.
2 3
3
a
. B.
2
a
. C.
a
. D.
2
2
a
.
Lời giải
Chọn B.
I
D
A
C
B
S
H
A
B
C
D
K
H
S
M

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 23/25
Xét tam giác đều
ABC
với
D
là trung điểm của
BC
và
I
là trọng tâm của tam giác
ABC
nên
ta có
,
A
I
,
D
thẳng hàng và
3. 3 3
2 2
a a
AD ,
2
3
AI AD a
,
1
3 2
a
ID AD
. Đồng thời
2
3 3
4
ABC
a
S
.
Hình chóp
.
S ABC
là chóp tam giác đều nên ta có
SI ABC
. Khi đó, ta có:
.
1
.
3
S ABC ABC
V SI S
3
.
2
6
3.
3
4
2
3 3
4
S ABC
ABC
a
V
SI a
S
a
.
Ta chứng minh được
BC SAD
và
SBC SAD
. Gọi
H
là hình chiếu vuông góc của
A
trên
SD
. Khi đó
AH SBC
nên
,
d A SBC AH
.
Xét tam giác vuông
SID
có
2
2 2 2
3
2
4 2
a a
SD SI ID a .
Xét tam giác
SAD
có
. .
AH SD SI AD
3
2.
.
2
2
3
2
a
a
SI AD
AH a
a
SD
.
Vậy
, 2
d A SBC a
Câu 47. [1H3-3] Cho lăng trụ đứng
.
ABC A B C
có đáy là tam giác vuông tại
B
,
AB a
,
2
BC a
.
Biết thể tích của khối lăng trụ
.
ABC A B C
bằng
3
2 2
a
. Gọi
là góc giữa
A BC
với
ABC
. Tính
cos
.
A.
1
3
. B.
3
3
. C.
6
3
. D.
2
3
.
Lời giải
Chọn A.
Ta có
,
BC AB
,
BC BB
AB BB B
nên
BC ABB A
. Khi đó, ta có:
;
;
A BC ABC BC
AB ABC AB BC
A B A BC A B BC
,
ABC A BC ABA
.
Từ giả thiết, ta có:
3
.
.
2 2
. 2 2
1
. .2
2
ABC A B C
ABC A B C ABC
ABC
V a
V S AA AA a
S
a a
.
Xét tam giác vuông
A AB
có:
2 2 2 2
8 3
A B AA AB a a a
.
A
C
B
A
C
B

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 24/25
Nên ta có
1
cos
3 3
AB a
ABA
A B a
. Vậy
1
cos
3
.
Câu 48. [2H2-3] Công ty
A
cần xây bể chưa hình hộp chữ nhật (không có nắp), đáy là hình vuông cạnh
bằng
m
a , chiều cao bằng
m
h . Biết thể tích bể chứa cần xây là
3
62,5 m
, hỏi kích thước
cạnh đáy và chiều cao phải bằng bao nhiêu để tổng diện tích các mặt xung quanh và mặt đáy là
nhỏ nhất?
A.
5 2
m, 5m
2
a h . B.
5 10
m, 4m
4
a h .
C.
5m, 2,5m
a h
. D.
5 30
3m, m
6
a h .
Lời giải
Chọn C.
Từ giả thiết, ta có:
Thể tích bể chứa cần xây là
2
. 62,5 1
V h a .
Tổng diện tích tích các mặt xung quanh và mặt đáy là
2
4 2
đxq
S S S ah a .
Từ (1), ta có
2
62,5
h
a
, thế vào (2) ta được
2 2
2
62,5 250
4 .
S a a a f a
a a
.
Ta có:
3
2 2
250 2 250
2
a
f a a
a a
.
3
3
2
2 250
0 0 2 250 0 5
a
f a a a
a
.
Ta có bảng xét dấu của
f a
như sau:
a
0
5
f
–
0
Trên khoảng
0;
, hàm số
f a
có duy nhất một điểm cực tiểu là
5
a
.
Tại đó
2
62,5
5m, 2,5m
5
a h , tổng diện tích đạt giá trị nhỏ nhất.
Câu 49. [2D1-1] Biết đồ thị
1
:
1
ax
C y
bx
,
0, 0
b a b
có tiệm cận ngang là
2
y
. Khi đó, tỷ
số
a
b
là
A.
3
. B.
2
. C.
1
. D.
1
.
Lời giải
Chọn B.
Đồ thị hàm số
1
1
ax
y
bx
có đường tiệm cận ngang là
a
y
b
, nên ta có được
2
a
b
.
Câu 50. [2D2-3] Biết phương trình
2
3 3
2log 2 log 4 0
x x
có hai nghiệm
1 2
,
x x
. Khi đó
2
1 2
x x
bằng
A.
2
. B.
4
. C.
8
. D.
9
.
Lời giải
Chọn A.
Phương trình đã cho tương đương với:

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 25/25
3 3
2log 2 2log 4 0
x x
3 3
log 2 log 4
x x
1
2
4
x
x
1
2 khi 4
4
1
2 khi 2 4
4
x x
x
x x
x
.
Khi
4
x
, ta có
1
2
4
x
x
2
6 7 0
x x
3 2
3 2
x TM
x L
.
Khi
2 4
x
, ta có
1
2
4
x
x
2
6 9 0
x x
3
x TM
.
Vậy, hai nghiệm của phương trình ban đầu là
1 2
3, 3 2
x x .
Khi đó:
2
2
1 2
2 2
x x
.
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/19 - Mã đề thi 485
SỞ GIÁO DỤC VÀ ĐÀO TẠO
--------------
ĐỀ CHÍNH THỨC
(Đề thi gồm có 50 câu)
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2017 - 2018
Môn: Toán, lớp 12
Thời gian làm bài: 90phút;
(không kể thời gian phát đề)
Họ, tên thí sinh……………………………Lớp……………………….
Mã đề thi 485
Câu 1. [2D1-2] Giá trị nhỏ nhất của hàm số
3 2
2 3
y x x m
trên đoạn
0;5
bằng
5
khi
m
là:
A.
6
. B.
10
. C.
7
. D.
5
.
Câu 2. [2D2-2] Phương trình
2
2 2
log log 8 3 0
x x
tương đương với phương trình nào sau đây?
A.
2
2 2
log log 0
x x
. B.
2
2 2
log log 6 0
x x
.
C.
2
2 2
log log 0
x x
. D.
2
2 2
log log 6 0
x x
Câu 3. [2D1-1] Các điểm cực tiểu của hàm số
4 2
3 2
y x x
là
A.
0
x
. B.
1
x
. C.
1
x
và
2
x
. D.
5
x
.
Câu 4. [2D1-1] Cho hàm số
2
3
x
y
x
. Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
;
.
B. Hàm số nghịch biến trên từng khoảng xác định.
C. Hàm số đồng biến trên từng khoảng xác định.
D. Hàm số đồng biến trên khoảng
;
.
Câu 5. [2D1-2] Đường cong bên là đồ thị hàm số nào sau đây?
A.
3
3
y x x
. B.
3
3 1
y x x
. C.
3
3
y x x
. D.
3
3 1
y x x
.
Câu 6. [2D2-2] Hàm số
2
1
8 6 3 ln 2
x x
y x
là đạo hàm của hàm số nào sau đây
A.
2
1
8
x x
y
. B.
2
1
2
x x
y
. C.
2
3 3 1
2
x x
y
. D.
2
3 3 1
8
x x
y
.
Câu 7. [2D2-2] Đạo hàm hàm số
2
ln 1
y x x
là:
A.
1
1.
y
x
B.
ln 1.
y x
C.
1.
y
D.
2ln 1 .
y x x
Câu 8. [2H1-2] Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
2
a
. Tam giác
SAB
là tam giác
cân tại
S
và nằm trong mặt phẳng vuông góc với đáy,
3
SA a
. Tính thể tích
V
của khối chóp
.
S ABCD
.
A.
3
10 3
.
3
V a
B.
3
8 2
.
3
V a
C.
3
15
.
6
V a
D.
3
17
.
6
V a
Câu 9. [2D1-2] Đồ thị hàm số
3 1
1
x
y
x
có tâm đối xứng là
A.
1; 3
I . B.
1;1
I . C.
3;1
I . D.
1; 3
I .
Câu 10. [2D1-2] Cho hàm số
f x
có đạo hàm là
2 4
1 2f x x x x x
. Số điểm cực tiểu
của hàm số
y f x
là
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 11. [2D2-1] Tập xác định của hàm số
2
1
y x là:
A.
;1
D
. B.
D
. C.
1;D
. D.
\ 1
D
.
Câu 12. [2H2-2] Hình nón có bán kính đáy
8 cm
r
, đường sinh
10 cm
l
. Thể tích khối nón là:
A.
3
192
cm
3
V
. B.
3
128 cm
V
. C.
3
128
cm
3
V
. D.
3
192 cm
V
.
O
x
y
2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/19 - Mã đề thi 485
Câu 13. [2H1-4] Xét khối tứ diện
ABCD
có cạnh
AB x
và các cạnh còn lại đều bằng
2
. Tìm
x
để
thể tích khối tứ diện
ABCD
đạt giá trị lớn nhất.
A.
2 3
x . B.
6
x . C.
2
x
. D.
3
x .
Câu 14. [2D2-1] Nếu
log 2
a
thì
log
a
bằng
A.
100
. B.
4
. C.
10
. D.
8
.
Câu 15. [2D1-2] Hàm số
4 2
5
y x mx m
(
m
là tham số) có
3
điểm cực trị khi các giá trị của
m
là:
A.
4 5.
m
B.
0.
m
C.
8
m
. D.
1.
m
Câu 16. [2D2-4] Phương trình
2
log log 1
x mx x m
có nghiệm duy nhất khi giá trị của
m
là:
A.
0.
m
B.
1.
m
C.
5.
m
D.
4 0.
m
Câu 17. [2D2-2] Số nghiệm của phương trình
3 3 3
log 2 log 2 log 5
x x là:
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 18. [2D2-2] Hàm số
2
ln 2 4
y x mx
có tập xác định
D
khi các giá trị của tham số
m
là:
A.
2
m
. B.
2
m
hoặc
2
m
. C.
2
m
. D.
2 2
m
.
Câu 19. [2D2-1] Nếu
3
2
3
2
a a
và
3 4
log log
4 5
b b
thì
A.
0 1
a
,
1
b
. B.
0 1
b
,
1
a
. C.
1
a
,
1
b
. D.
0 1
a
,
0 1
b
.
Câu 20. [2H2-2] Tính bán kính
R
của mặt cầu ngoại tiếp hình lập phương có cạnh bằng
a
.
A.
3
R a
. B.
2
R a
. C.
3
2
a
R . D.
6
2
a
R .
Câu 21. [2D2-1] Cho phương trình
1
25 26.5 1 0
x x
. Đặt
5
x
t
,
0
t
thì phương trình trở thành
A.
2
26 1 0
t t
. B.
2
25 26 0
t t
. C.
2
25 26 1 0
t t
. D.
2
26 0
t t
.
Câu 22. [2D2-2] Cho hàm số
ln
x
y
x
. Mệnh đề nào sau đây đúng?
A. Hàm số có một cực đại. B. Hàm số có một cực tiểu.
C. Hàm số có hai cực trị. D. Hàm số không có cực trị.
Câu 23. [2D2-3] Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
ln
x
y
x
trên đoạn
3
1;e
lần lượt là
A.
3
e
và
1
. B.
3
9
e
và
0
. C.
2
e
và
0
. D.
2
4
e
và
0
.
Câu 24. [2D1-3] Cho hàm số
4 2
2 1
y x x
có đồ thị
C
và đường thẳng
: 1
d y m
(
m
là tham
số). Đường thẳng
d
cắt
C
tại
4
điểm phân biệt khi các giá trị của
m
là:
A.
3 5
m
. B.
1 2
m
. C.
1 0
m
. D.
5 3
m
.
Câu 25. [2D1-1] Cho hàm số
y f x
có đạo hàm
2
1
f x x
. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên
;1
. B. Hàm số nghịch biến trên
;
.
C. Hàm số nghịch biến trên
1;1
. D. Hàm số đồng biến trên
;
.
Câu 26. [2D2-2] Giá trị lớn nhất và nhỏ nhất của hàm số
3 2
2 3 1
y x x
trên đoạn
2;1
lần lượt là
A.
0
và
1
. B.
1
và
2
. C.
7
và
10
. D.
4
và
5
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/19 - Mã đề thi 485
Câu 27. [2D2-2] Nghiệm của phương trình
2 4
log log 1
x
là:
A.
8
x
. B.
16
x
. C.
4
x
. D.
2
x
.
Câu 28. [2H1-2] Cho khối lăng trụ đứng
.
ABC A B C
có
2
CC a
, đáy
ABC
là tam giác vuông cân
tại
B
và
2
AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
V a
. B.
3
2
a
V . C.
3
2
V a
. D.
3
3
a
V .
Câu 29. [2H2-2] Cho hình chóp tứ giác đều
.
S ABCD
có các cạnh đều bằng
2
a
. Tính thể tích
V
của
khối nón có đỉnh
S
và đường tròn đáy là đường tròn nội tiếp tứ giác
ABCD
.
A.
3
3
6
a
V
. B.
3
2
3
a
V
. C.
3
2
6
a
V
. D.
3
3
3
a
V
.
Câu 30. [2D2-2] Nếu
6 5 6 5
x
thì:
A.
1
x
. B.
1
x
. C.
1
x
. D.
1
x
.
Câu 31. [2H2-2] Cho hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng
20
. Khi
đó thể tích của khối trụ là:
A.
10 5
V
. B.
10 2
V
. C.
10
V
. D.
20
V
.
Câu 32. [2D1-1] Đồ thị của hàm số
3 2
3 2
y x x
có tâm đối xứng là:
A.
0;2
I . B.
1;0
I . C.
2; 2
I
. D.
1; 2
I
.
Câu 33. [2D1-1] Hàm số
2 5
1
x
y
x
có bao nhiêu điểm cực trị?
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 34. [2D1-3] Hàm số
2
1 1
2
x m x
y
x
(
m
là tham số) nghịch biến trên mỗi khoảng xác định
của nó khi các giá trị của
m
là:
A.
1
m
. B.
1
m
. C.
5
2
m
. D.
1 1
m
.
Câu 35. [2D1-2] Số đường tiệm cận đứng của đồ thị hàm số
2
2
3 2
4
x x
y
x
là:
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 36. [2H1-1] Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối
xứng?
A.
6
mặt phẳng. B.
4
mặt phẳng. C.
3
mặt phẳng. D.
9
mặt phẳng.
Câu 37. [2D1-1] Cho hàm số
y f x
có bảng biến thiên như hình bên. Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại
5
x
. B. Hàm số đạt cực tiểu tại
1
x
.
C. Hàm số không có cực trị. D. Hàm số đạt cực đại tại
0
x
.
Câu 38. [2D2-2] Phương trình
2 2
2 3.2 32 0
x x
có tổng các nghiệm là
A.
2
. B.
12
. C.
6
. D.
5
.
Câu 39. [2D1-2] Đồ thị hàm số
3 2
3 2 1
y x x x
cắt đồ thị hàm số
2
3 1
y x x
tại hai điểm phân
biệt
A
và
B
. Khi đó độ dài đoạn
AB
là:
A.
3
AB
. B.
2
AB
. C.
2 2
AB
. D.
1
AB
.
x
0
2
y
0
0
y
5
1
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/19 - Mã đề thi 485
Câu 40. [2D2-2] Phương trình
2
2 2
1
9 10.3 1 0
x x
x x
có tập nghiệm là:
A.
2; 1;1;2
. B.
2;0;1;2
. C.
2; 1;0;1
. D.
1;0;2
.
Câu 41. [2D2-2] Tập xác định của hàm số
2
log 2
y x x
là:
A.
D 2;0
. B.
D \ 0
.
C.
D ; 2 0;
. D.
D
.
Câu 42. [2D1-2] Cho hàm số
4 2
2 1
y x x
có đồ thị
C
. Phương trình tiếp tuyến của đồ thị
C
tại
1;4
M là:
A.
8 4
y x
. B.
8 4
y x
. C.
8 12
y x
. D.
3
y x
.
Câu 43. [2D1-1] Các đường tiệm cận đứng và ngang của đồ thị hàm số
2 1
1
x
y
x
là:
A.
2
x
;
1
y
. B.
1
x
;
2
y
.
C.
1
x
;
2
y
. D.
1
x
;
2
y
.
Câu 44. [2D1-2] Đường cong bên là đồ thị của hàm số nào dưới đây?
A.
2 3
1
x
y
x
. B.
2 1
1
x
y
x
.
C.
3
2
x
y
x
. D.
2 3
1
x
y
x
.
Câu 45. [2H1-2] Cho hình chóp .
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
2
AB BC
,
3
AD
. Cạnh bên
2
SA
và vuông góc với đáy. Tính thể tích khối chóp .
S ABCD
.
A.
4
V
. B.
10
3
V
. C.
10 3
3
V
. D.
17
6
.
Câu 46. [2D2-2] Nếu
12
log 6
a
và
12
log 7
b
thì
2
log 7
bằng kết quả nào sau đây:
A.
1
a
a
. B.
1
b
a
. C.
1
a
b
. D.
1
a
b
.
Câu 47. [2D1-1] Giá trị lớn nhất của hàm số
2
4
2
y
x
là
A.
10
. B.
3
. C.
5
. D.
2
.
Câu 48. [2D1-1] Cho hàm số
y f x
có
1
lim
x
f x
và
1
lim 2
x
f x
. Mệnh đề nào sau đây
đúng?
A. Đồ thị hàm số không có tiệm cận. B. Đồ thị hàm số có tiệm cận đứng
1
x
.
C. Đồ thị hàm số có hai tiệm cận. D. Đồ thị hàm số có tiệm cận ngang
2
y
.
Câu 49. [2D1-3] Một ông nông dân có
2400
m hàng rào và muốn rào lại cánh đồng hình chữ nhật tiếp
giáp với một con sông. Ông không cần rào cho phía giáp bờ sông. Hỏi ông có thể rào được
cánh đồng với diện tích lớn nhất là bao nhiêu?
A.
630000
m
2
. B.
720000
m
2
. C.
360000
m
2
. D.
702000
m
2
.
Câu 50. [2H1-1] Khối đa diện đều loại
4;3
là:
A. Khối lập phương. B. Khối bát diện đều. C. Khối hộp chữ nhật. D. Khối tứ diện đều.
----------HẾT----------
O
x
y
1
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/19 - Mã đề thi 485
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
C
A
C
C
A
D
B D
D
C
B
B
B
B B C
D
A
C
C
A
D
C
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
B A
B A
A
B A
C
A
C
D
D
D
C
C
A
D
A
B B D
B B A
Câu 1. [2D1-2] Giá trị nhỏ nhất của hàm số
3 2
2 3
y x x m
trên đoạn
0;5
bằng
5
khi
m
là:
A.
6
. B.
10
. C.
7
. D.
5
.
Lời giải
Chọn A.
Hàm số xác định và liên tục trên:
0;5
D
.
2
6 6
y x x
;
2
0
0 6 6 0
1
x D
y x x
x D
.
0
f m
;
1 1
f m
;
5 175
f m
Dễ thấy
5 0 1 ,f f f m
nên
0;5
min 1 1
f x f m
.
Theo đề bài,
0;5
min 5 1 5 6
f x m m
.
Câu 2. [2D2-2] Phương trình
2
2 2
log log 8 3 0
x x
tương đương với phương trình nào sau đây?
A.
2
2 2
log log 0
x x
. B.
2
2 2
log log 6 0
x x
.
C.
2
2 2
log log 0
x x
. D.
2
2 2
log log 6 0
x x
Lời giải
Chọn C.
Với điều kiện
0
x
:
2
2 2
log log 8 3 0
x x
2 2
2 2 2 2 2
log log 8 log 3 0 log log 0
x x x x
.
Câu 3. [2D1-1] Các điểm cực tiểu của hàm số
4 2
3 2
y x x
là
A.
0
x
. B.
1
x
. C.
1
x
và
2
x
. D.
5
x
.
Lời giải
Chọn A.
Tập xác định:
D
.
3 2
4 6 4 6
y x x x x
.
2
0 4 6 0 0
y x x x
.
Vậy hàm số có điểm cực tiểu là
0
x
.
Câu 4. [2D1-1] Cho hàm số
2
3
x
y
x
. Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
;
.
B. Hàm số nghịch biến trên từng khoảng xác định.
x
0
y
0
y
2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/19 - Mã đề thi 485
C. Hàm số đồng biến trên từng khoảng xác định.
D. Hàm số đồng biến trên khoảng
;
.
Lời giải
Chọn C.
Tập xác định:
\ 3
D
.
2
5
0,
3
y x D
x
.
Vậy hàm số đồng biến trên các khoảng
; 3
và
3;
.
Câu 5. [2D1-2] Đường cong bên là đồ thị hàm số nào sau đây?
A.
3
3
y x x
. B.
3
3 1
y x x
. C.
3
3
y x x
. D.
3
3 1
y x x
.
Lời giải
Chọn C.
Dựa vào đồ thị ta thấy đồ thị hàm số đã cho đi qua gốc toạ độ nên loại B, D.
Đồng thời đồ thị cắt trục hoành tại 3 điểm trong đó có 2 điểm có hoành độ trái dấu nên loại A.
Câu 6. [2D2-2] Hàm số
2
1
8 6 3 ln 2
x x
y x
là đạo hàm của hàm số nào sau đây
A.
2
1
8
x x
y
. B.
2
1
2
x x
y
. C.
2
3 3 1
2
x x
y
. D.
2
3 3 1
8
x x
y
.
Lời giải
Chọn A.
Để ý thấy:
2
1
8 6 3 ln 2
x x
y x
có chứa
2
1
8
x x
nên loại B, C.
Xét đáp án A:
3
1
8
x x
f x
.
2 2 2
2 1 1 3 1
1 .8 .ln8 2 1 .8 .ln2 8 6 3 ln 2
x x x x x x
f x x x x x
.
Câu 7. [2D2-2] Đạo hàm hàm số
2
ln 1
y x x
là:
A.
1
1.
y
x
B.
ln 1.
y x
C.
1.
y
D.
2ln 1 .
y x x
Lời giải
Chọn D.
Ta có
2 2
1
ln 1 2 ln 1 . 2ln 1
y x x y x x x x x
x
.
Câu 8. [2H1-2] Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
2
a
. Tam giác
SAB
là tam giác
cân tại
S
và nằm trong mặt phẳng vuông góc với đáy,
3
SA a
. Tính thể tích
V
của khối chóp
.
S ABCD
.
A.
3
10 3
.
3
V a
B.
3
8 2
.
3
V a
C.
3
15
.
6
V a
D.
3
17
.
6
V a
Lời giải
O
x
y

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/19 - Mã đề thi 485
Chọn B.
Gọi
H
là trung điểm của
AB
.
SH ABCD
2 2 2 3
1 8 2
4 ; 9 2 2 . . .
3 3
ABCD ABCD
S a SH a a a V SH S a
Câu 9. [2D1-2] Đồ thị hàm số
3 1
1
x
y
x
có tâm đối xứng là
A.
1; 3
I . B.
1;1
I . C.
3;1
I . D.
1; 3
I .
Lời giải
Chọn D.
Ta có
1 1
3 1
lim lim
1
x x
x
y
x
và
1 1
3 1
lim lim
1
x x
x
y
x
nên đường thẳng
1
x
là tiệm cận
đứng của đồ thị hàm số.
Lại có
3 1
lim lim 3
1
x x
x
y
x
nên đường thẳng
3
y là tiệm cận ngang của đồ thị hàm số.
Giao điểm của hai đường tiệm cận là tâm đối xứng của đồ thị. Do đó
1; 3
I .
Câu 10. [2D1-2] Cho hàm số
f x
có đạo hàm là
2 4
1 2f x x x x x
. Số điểm cực tiểu
của hàm số
y f x
là?
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn D.
Ta có
2 4
0 1 2 0
f x x x x . Do
0
x
là nghiệm đơn, còn các nghiệm
1
x
và
2
x
là các nghiệm bội chẵn nên chỉ có
0
x
là nghiệm mà
f x
đổi dấu từ “âm” sang
“dương” theo chiều từ trái sang phải. Do đó
0
x
là điểm cực tiểu duy nhất của hàm số đã cho.
Câu 11. [2D2-1] Tập xác định của hàm số
2
1
y x là:
A.
;1
D
. B.
D
. C.
1;D
. D.
\ 1
D
.
Lời giải
Chọn C.
Hàm số
2
1
y x có số mũ không nguyên nên để hàm số có nghĩa thì
1 0 1
x x
.
Câu 12. [2H2-2] Hình nón có bán kính đáy
8 cm
r
, đường sinh
10 cm
l
. Thể tích khối nón là:
A.
3
192
cm
3
V
. B.
3
128 cm
V
. C.
3
128
cm
3
V
. D.
3
192 cm
V
.
Lời giải
Chọn B.
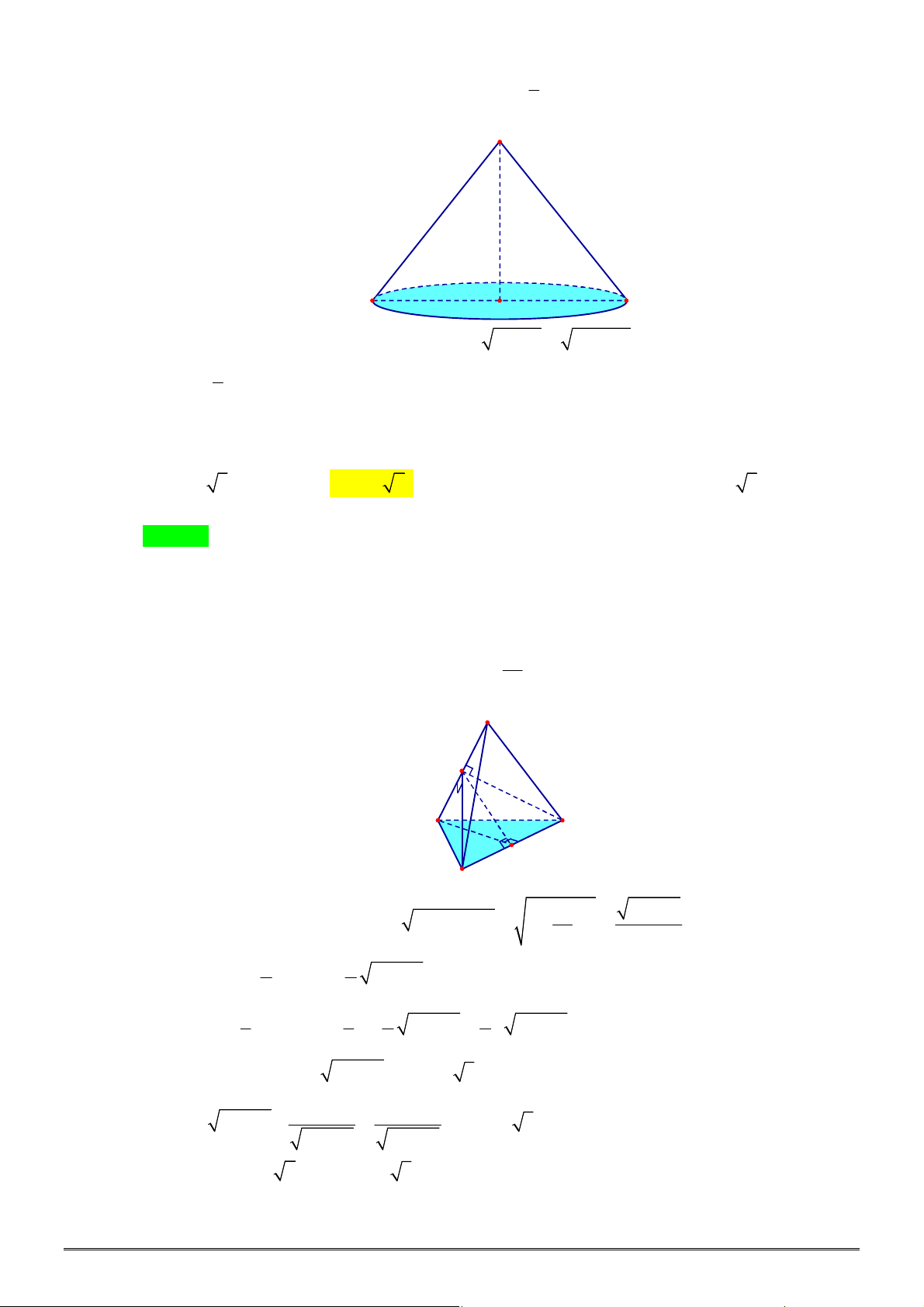
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/19 - Mã đề thi 485
Áp dụng công thức tính thể tích khối nón ta có
1
.h
3
V B
với
2
64
B r
,
Gọi
I
là tâm đường tròn đáy ta có:
2 2 2 2
10 8 6
h OI l r
.
Vậy
3
1
.64 .6 128 cm
3
V
.
Câu 13. [2H1-4] Xét khối tứ diện
ABCD
có cạnh
AB x
và các cạnh còn lại đều bằng
2
. Tìm
x
để
thể tích khối tứ diện
ABCD
đạt giá trị lớn nhất.
A.
2 3
x . B.
6
x . C.
2
x
. D.
3
x .
Lời giải
Chọn B.
Cách 1. Gọi
H
là trung điểm
AB
CH AB
DH AB
(do
ABC
,
ABD
cân đáy
AB
)
AB CDH
.
Mặt khác
CDH
cân tại
H
,
2
2 2
4
4
x
HC HD
.
Gọi
I
là trung điểm
CD
2 2
2 2
12
4 1
4 2
x x
HI HC CI
.
Suy ra
2
1 1
. 12
2 2
CDH
S HI CD x
Vậy
2 2
1 1 1 1
. 12 12
3 3 2 6
ABCD CDH
V AB S x x x x
.
Cách 1a: Xét
2
12 , 0;2 3
f x x x x
2 2
2
2 2
12 2
12 , 0;2 3
12 12
x x
f x x x
x x
0 6
f x x
do
0;2 3
x
.
Bảng biến thiên:
A
B
C
D
H
x
I
A
B
l
O
I
r
h
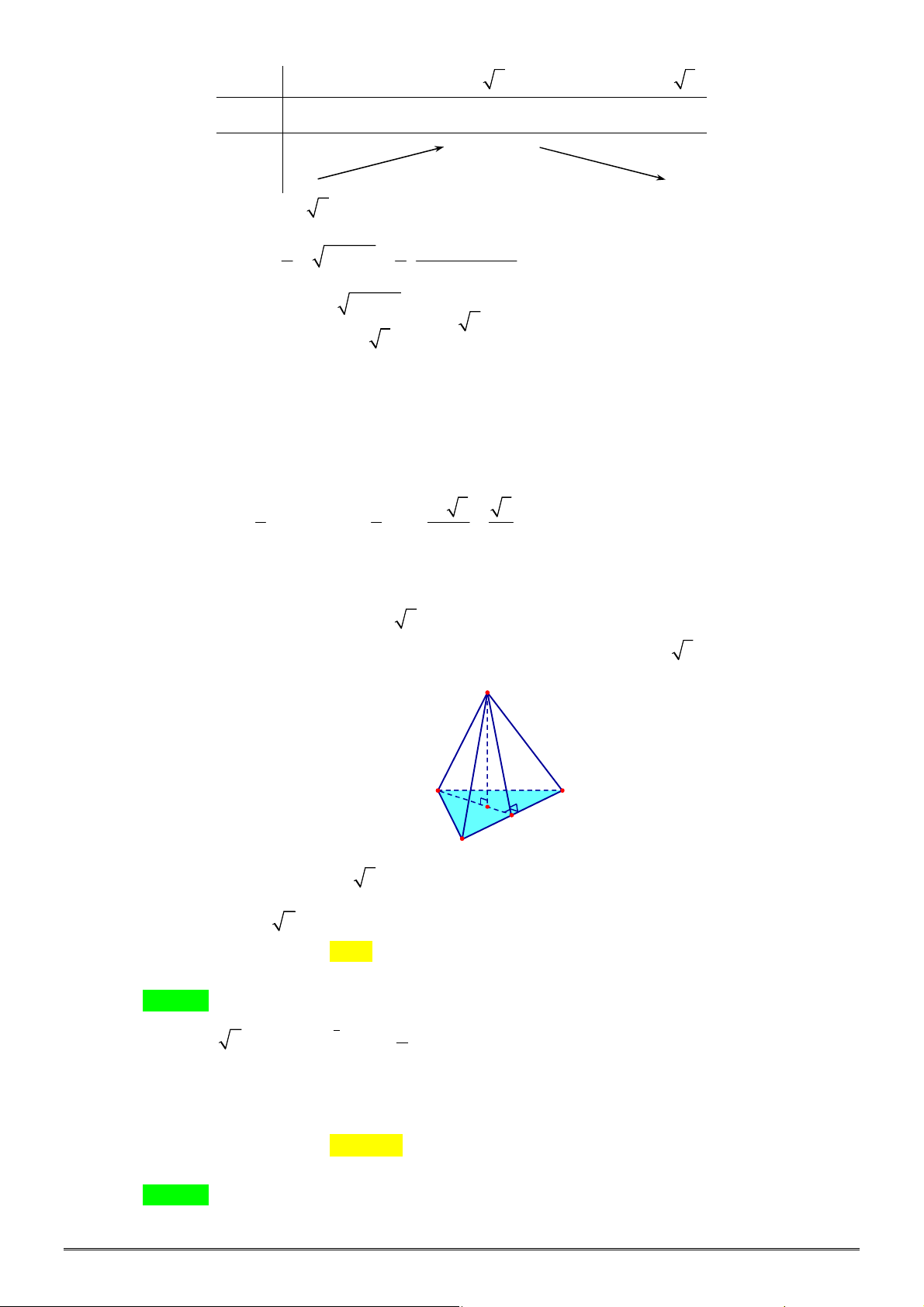
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/19 - Mã đề thi 485
Vậy
max
2
V
khi
6
x .
Cách 1b:
2 2
2
12
1 1
12 1
6 6 2
ABCD
x x
V x x
Dấu
“ ”
xảy ra khi
2
12
6
0;2 3
x x
x
x
.
Cách 2: Gọi
H
là trung điểm
CD
, dễ thấy
AH CD
BH CD
(do
ACD
,
BCD
cân đáy
CD
) Suy
ra
CD ABH ABH BCD
theo giao tuyến
BH
.
Vì vậy trong
ABH
kẻ
AK BH
tại
K BH
thì
AK BCD
Do đó
2
1 1 2 3 3
3 3 4 3
ABCD BCD
V AK S AK AK
.
Vậy
ABCD
V lớn nhất
max
AK
.
Trong
AHK
có
AK AH
nên
AK
lớn nhất khi
K H AH BH
.
2 2 2
6 6
AB AH BH x .
(Vì
ACD
,
BCD
là các tam giác đều cạnh bằng
2
nên
3
AH BH )
Vậy
ABCD
V lớn nhất khi
6
x .
Câu 14. [2D2-1] Nếu
log 2
a
thì
log
a
bằng
A.
100
. B.
4
. C.
10
. D.
8
.
Lời giải
Chọn B.
Ta có
1
2
1
log 2 log 2 log 2 log 4
2
a a a a
.
Câu 15. [2D1-2] Hàm số
4 2
5
y x mx m
(
m
là tham số) có
3
điểm cực trị khi các giá trị của
m
là:
A.
4 5.
m
B.
0.
m
C.
8
m
. D.
1.
m
Lời giải
Chọn B.
Hàm số có 3 điểm cực trị
. 0 0
a b m
.
A
B
C
D
x
H
K
x
0
6
2 3
f x
–
0
f x
0
1
0

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/19 - Mã đề thi 485
Câu 16. [2D2-4] Phương trình
2
log log 1
x mx x m
có nghiệm duy nhất khi giá trị của
m
là:
A.
0.
m
B.
1.
m
C.
5.
m
D.
4 0.
m
Lời giải
Chọn B.
Phương trình
2 2
1 1 1 0 1
1 0 1
g x x mx x m g x x m x m
x m x m
.
PT đã cho có nghiệm duy nhất khi và chỉ khi xảy ra
1
trong
2
TH sau:
TH1: PT
1
có nghiệm kép
1
x m
2
1
0
1 4 1 0
3
1
1
1 0
2
1
m
m m
m
m
m
m
m
m
TH2: PT
1
có hai nghiệm phân biệt thỏa mãn
1 2
1
x m x
Đk:
2
2
0 2 3 0
1
1 1
2 2
1 0
1 1 1 1 0
m m
S m
m m
g m
m m m m
:Không có
m
thỏa mãn.
TH3:Phương trình có hai nghiệm phân biệt thỏa mãn
1 2
1
x m x
ĐK:
1 2
0
1 1 0
x m x m
*
trong đó
1 2
1 2
1
1
x x m
x x m
Khi đó
*
thành
2
2
2
1 2 1 2
2 3 0
2 3 0
1
1 0
1 1 0
m m
m m
m
m
x x m x x m
.
KL:
1.
m
Câu 17. [2D2-2] Số nghiệm của phương trình
3 3 3
log 2 log 2 log 5
x x là:
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Chọn C.
3 3 3
log 2 log 2 log 5 1
x x
Điều kiện:
2
x
.
Với điều kiện trên,
2
3 3
3
1 log 2 2 log 5 4 5
3
x
x x x
x
.
Đối chiếu với điều kiện, ta được nghiệm phương trình:
3
x
.
Câu 18. [2D2-2] Hàm số
2
ln 2 4
y x mx
có tập xác định
D
khi các giá trị của tham số
m
là:
A.
2
m
. B.
2
m
hoặc
2
m
.
C.
2
m
. D.
2 2
m
.
Lời giải
Chọn D.
Hàm số
2
ln 2 4
y x mx
có tập xác định
khi
2
2 4 0, 1
x mx x
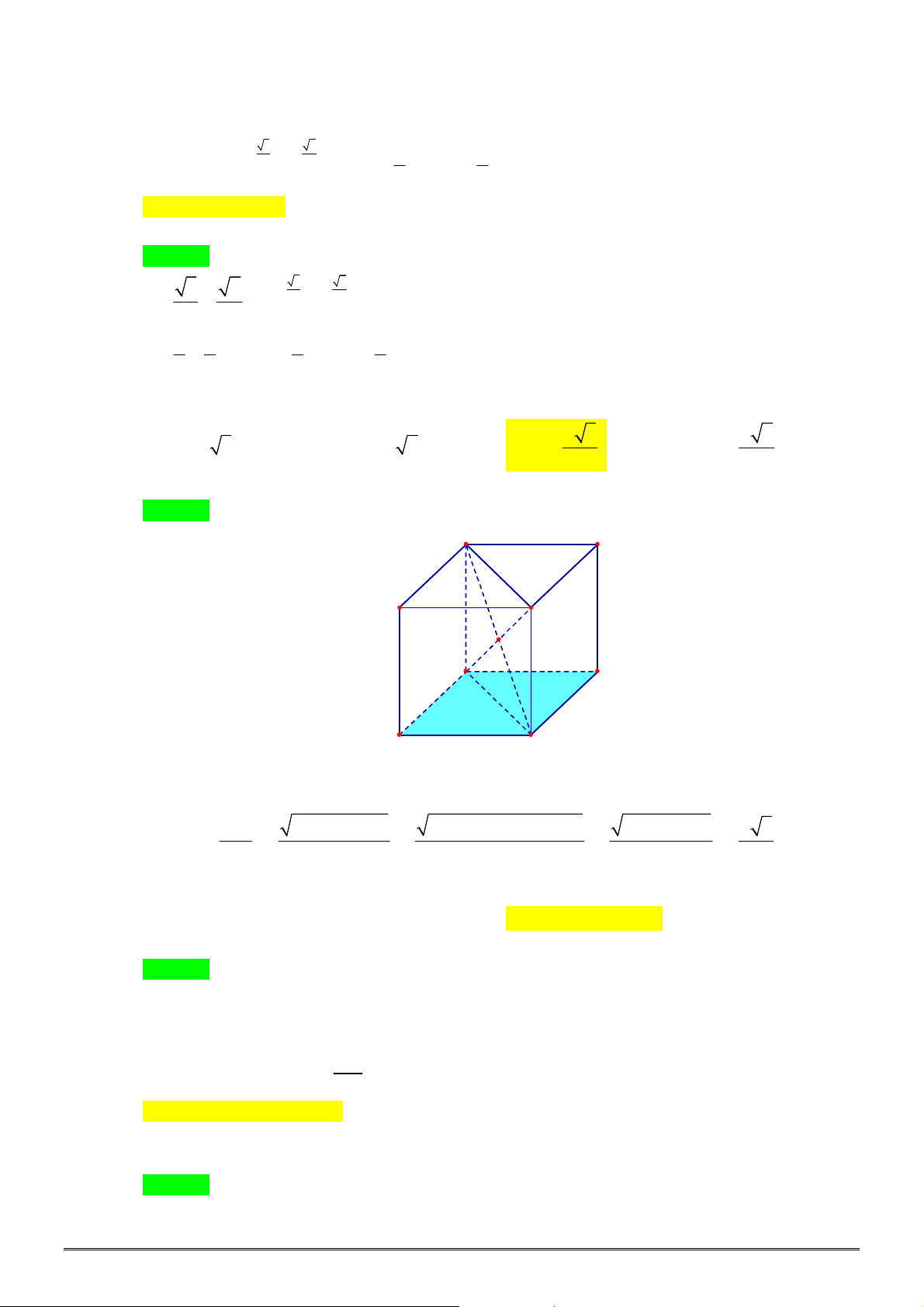
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/19 - Mã đề thi 485
2
1 0
1 4 0 2 2
0
a
m m
.
Câu 19. [2D2-1] Nếu
3
2
3
2
a a
và
3 4
log log
4 5
b b
thì
A.
0 1
a
,
1
b
. B.
0 1
b
,
1
a
. C.
1
a
,
1
b
. D.
0 1
a
,
0 1
b
.
Lời giải
Chọn A.
Do
3 2
3 2
và
3
2
3
2
a a
nên suy ra
0 1
a
.
Do
3 4
4 5
và
3 4
log log
4 5
b b
nên suy ra
1
b
.
Câu 20. [2H2-2] Tính bán kính
R
của mặt cầu ngoại tiếp hình lập phương có cạnh bằng
a
.
A.
3
R a
. B.
2
R a
. C.
3
2
a
R . D.
6
2
a
R .
Lời giải
Chọn C.
Gọi
I
là giao điểm của
AC
và
A C
. Khi đó,
I
chính là tâm của mặt cầu ngoại tiếp hình lập
phương. Bán kính
R
được tính bởi
R IA
2
AC
2 2
2
AA A C
2 2 2
2
AA A B A D
2 2 2
2
a a a
3
2
a
.
Câu 21. [2D2-1] Cho phương trình
1
25 26.5 1 0
x x
. Đặt
5
x
t
,
0
t
thì phương trình trở thành
A.
2
26 1 0
t t
. B.
2
25 26 0
t t
. C.
2
25 26 1 0
t t
. D.
2
26 0
t t
.
Lời giải
Chọn C.
Ta có
1
25 26.5 1 0
x x
2
25.5 26.5 1 0
x x
.
Vậy nếu đặt
5
x
t
,
0
t
thì phương trình trên trở thành
2
25 26 1 0
t t
.
Câu 22. [2D2-2] Cho hàm số
ln
x
y
x
. Mệnh đề nào sau đây đúng?
A. Hàm số có một cực đại. B. Hàm số có một cực tiểu.
C. Hàm số có hai cực trị. D. Hàm số không có cực trị.
Lời giải
Chọn A.
Điều kiện
0
x
.
A
B
C
D
D
C
B
A
I
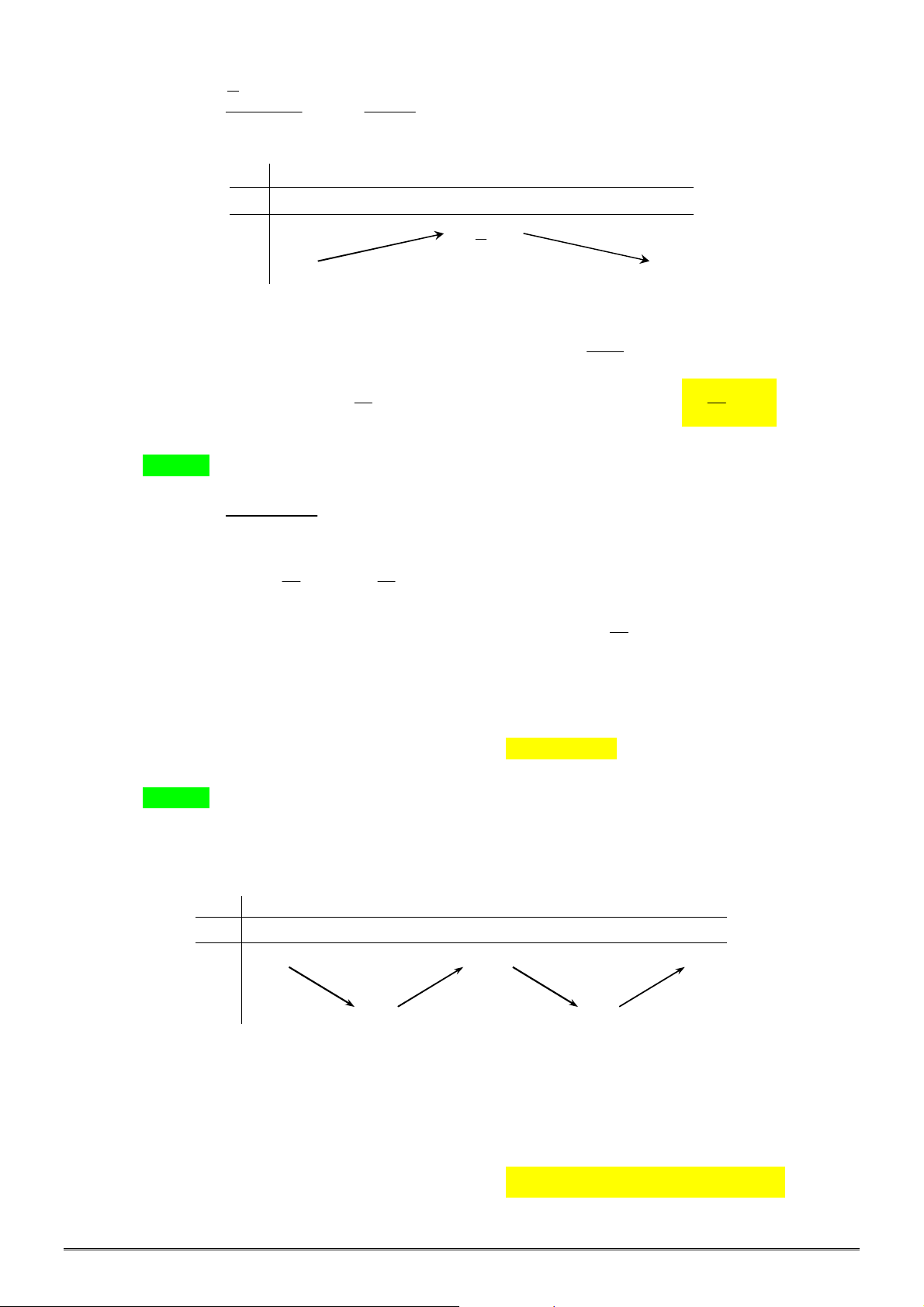
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/19 - Mã đề thi 485
Ta có
2
1
ln
x x
x
y
x
2
1 ln
x
y
x
0
y
ln 1 0
x
x e
.
Bảng biến thiên
Vậy hàm số có một cực đại.
Câu 23. [2D2-3] Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
ln
x
y
x
trên đoạn
3
1;e
lần lượt là
A.
3
e
và
1
. B.
3
9
e
và
0
. C.
2
e
và
0
. D.
2
4
e
và
0
.
Lời giải
Chọn D.
Ta có
2
2
2ln ln
x x
y
x
. Khi đó
2
0 2ln ln 0
y x x
3
2 3
1 1;e
ln 0
ln 2
1;e
x
x
x
x e
.
1 0,
y
2
2
4
e ,
e
y
3
3
9
e
e
y
.
Vậy giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là:
2
4
e
và
0
.
Câu 24. [2D1-3] Cho hàm số
4 2
2 1
y x x
có đồ thị
C
và đường thẳng
: 1
d y m
(
m
là tham
số). Đường thẳng
d
cắt
C
tại
4
điểm phân biệt khi các giá trị của
m
là:
A.
3 5
m
. B.
1 2
m
. C.
1 0
m
. D.
5 3
m
.
Lời giải
Chọn C.
Xét hàm số
4 2
2 1
y x x
có
3
0
4 4 , 0
1
x
y x x y
x
.
Ta có bảng biến thiên
Dựa vào bảng biến thiên ta có đường thẳng
d
cắt
C
tại
4
điểm phân biệt khi
0 1 1 1 0
m m
.
Câu 25. [2D1-1] Cho hàm số
y f x
có đạo hàm
2
1
f x x
. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên
;1
. B. Hàm số nghịch biến trên
;
.
C. Hàm số nghịch biến trên
1;1
. D. Hàm số đồng biến trên
;
.
Lời giải
x
1
0
1
y
0
0
0
y
0
1
0
x
0
e
y
0
y
1
e
0
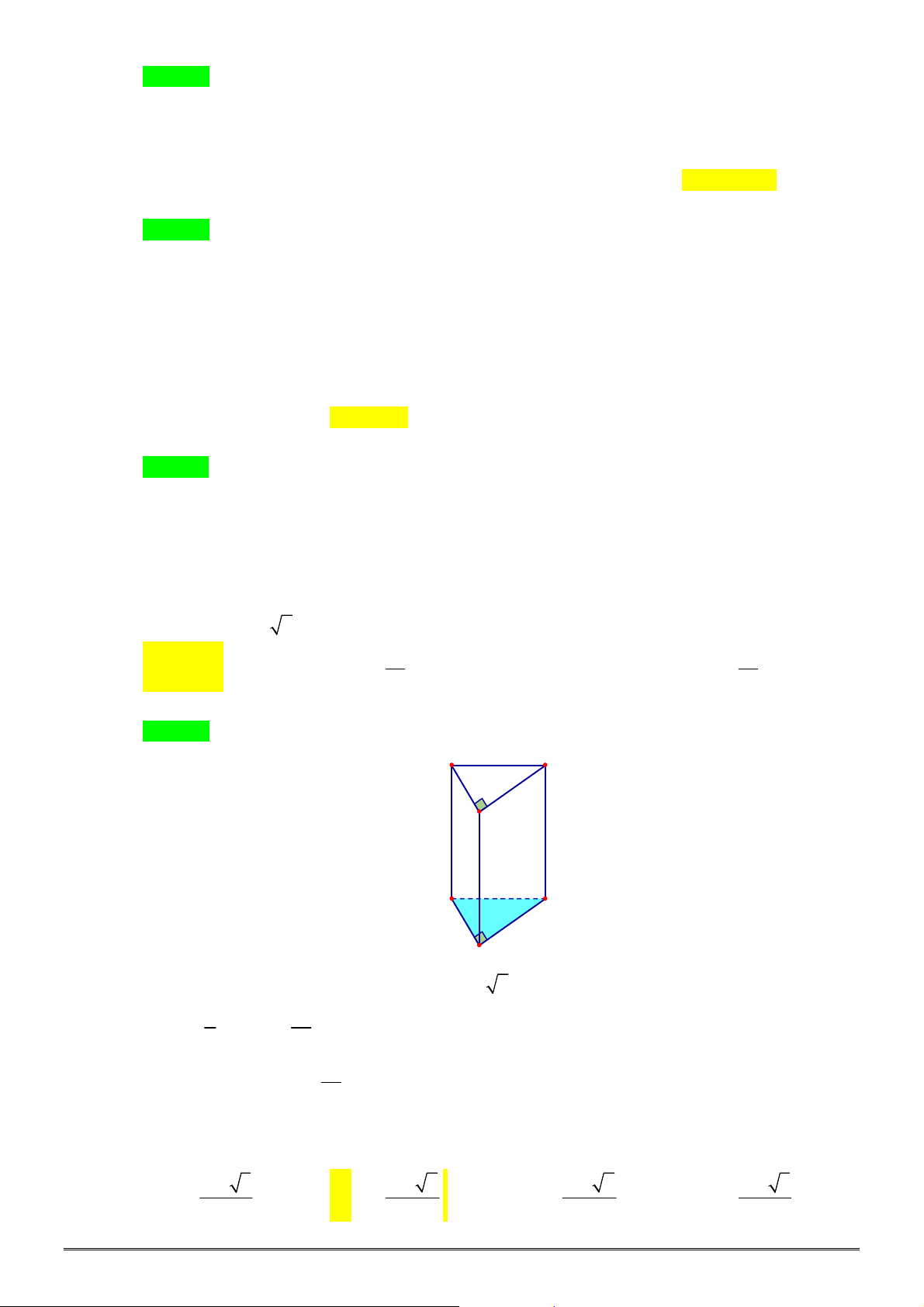
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/19 - Mã đề thi 485
Chọn D.
Do
2
1 0
f x x
với mọi
x
nên hàm số luôn đồng biến trên
.
Câu 26. [2D2-2] Giá trị lớn nhất và nhỏ nhất của hàm số
3 2
2 3 1
y x x
trên đoạn
2;1
lần lượt là
A.
0
và
1
. B.
1
và
2
. C.
7
và
10
. D.
4
và
5
.
Lời giải
Chọn D.
Ta có
2
6 6
y x x
2
0 6 6 0
y x x
0
1
x
x
.
0 1
y
,
1 0
y
,
1 4
y
,
2 5
y
.
Vậy giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là
4
và
5
.
Câu 27. [2D2-2] Nghiệm của phương trình
2 4
log log 1
x
là:
A.
8
x
. B.
16
x
. C.
4
x
. D.
2
x
.
Lời giải
Chọn B.
Điều kiện:
4
0
log 0
x
x
*
2 4 4
log log 1 log 2 16
x x x
: T/m
*
.
Câu 28. [2H1-2] Cho khối lăng trụ đứng
.
ABC A B C
có
2
CC a
, đáy
ABC
là tam giác vuông cân
tại
B
và
2
AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
V a
. B.
3
2
a
V . C.
3
2
V a
. D.
3
3
a
V .
Lời giải
Chọn A.
ABC
là tam giác vuông cân tại
B
và
2
AC a
suy ra
AB AC a
.
2
1
.
2 2
ABC
a
S AB BC
.
2
3
.
. .2
2
ABC A B C ABC
a
V S CC a a
Câu 29. [2H2-2] Cho hình chóp tứ giác đều
.
S ABCD
có các cạnh đều bằng
2
a
. Tính thể tích
V
của
khối nón có đỉnh
S
và đường tròn đáy là đường tròn nội tiếp tứ giác
ABCD
.
A.
3
3
6
a
V
. B.
3
2
3
a
V
. C.
3
2
6
a
V
. D.
3
3
3
a
V
.
A
B
C
A
C
B
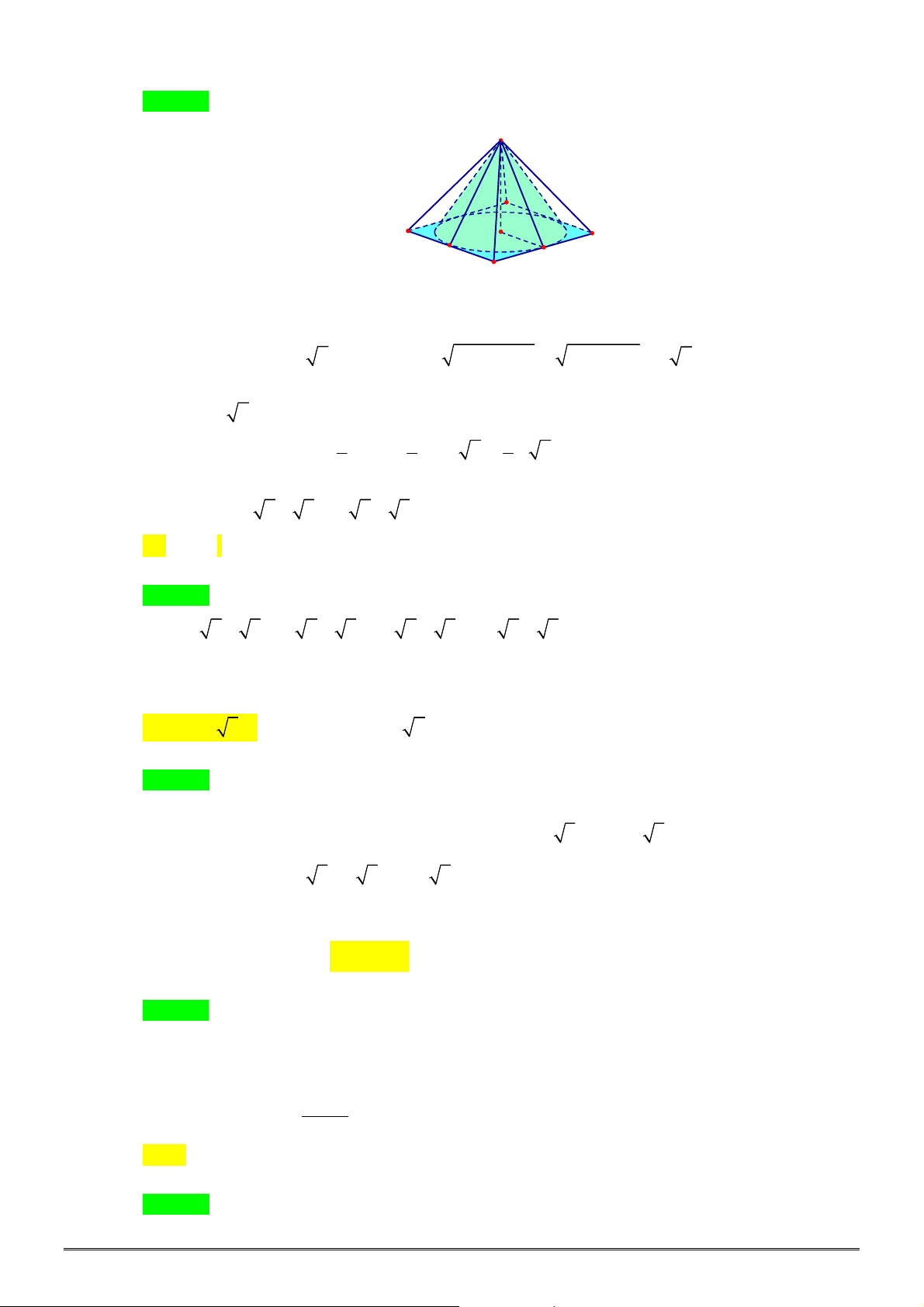
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/19 - Mã đề thi 485
Lời giải
Chọn B.
Gọi
M
là trung điểm của
,
BC
ta có
OM a
.
Vì hình chóp
.
S ABCD
là hình chóp tứ giác đều có các cạnh đều bằng
2
a
.
Do đó
2 2
AC BD a
. Khi đó
2 2
SO SA AO
2 2
4 2 2
a a a .
Khối nón có đỉnh
S
và đường tròn đáy là đường tròn nội tiếp tứ giác
ABCD
nên có chiều cao
2
h SO a
và
r OM a
.
Thể tích khối nón là:
2
1
3
V r h
2
1
2
3
a a
3
1
2
3
a
.
Câu 30. [2D2-2] Nếu
6 5 6 5
x
thì:
A.
1
x
. B.
1
x
. C.
1
x
. D.
1
x
.
Lời giải
Chọn A.
Ta có
6 5 6 5
x
6 5 6 5
x
1
x
1
x
.
Câu 31. [2H2-2] Cho hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng
20
. Khi
đó thể tích của khối trụ là:
A.
10 5
V
. B.
10 2
V
. C.
10
V
. D.
20
V
.
Lời giải
Chọn A.
Do thiết diện qua trục là hình vuông nên
2
h R
.
Ta có: 2
xq
S Rh
2 .2 20
R R
2
5
R
5
R
2 5
h .
Khi đó
2
2
. 2 5. . 5 10 5
V h R
.
Câu 32. [2D1-1] Đồ thị của hàm số
3 2
3 2
y x x
có tâm đối xứng là:
A.
0;2
I . B.
1;0
I . C.
2; 2
I
. D.
1; 2
I
.
Lời giải
Chọn B.
Đồ thị hàm số bậc ba nhận điểm uốn làm tâm đối xứng.
Ta có:
6 6
y x
;
0 1 0
y x y
1;0
I là tâm đối xứng.
Câu 33. [2D1-1] Hàm số
2 5
1
x
y
x
có bao nhiêu điểm cực trị?
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn A.
A
B
C
D
S
M
O
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/19 - Mã đề thi 485
Tập xác định
\ 1
D
. Đạo hàm:
2
7
0,
1
y x D
x
.
Hàm số đồng biến trên từng khoảng xác định nên đồ thị không có điểm cực trị nào.
Câu 34. [2D1-3] Hàm số
2
1 1
2
x m x
y
x
(
m
là tham số) nghịch biến trên mỗi khoảng xác định
của nó khi các giá trị của
m
là:
A.
1
m
. B.
1
m
. C.
5
2
m
. D.
1 1
m
.
Lời giải
Chọn C.
Tập xác định
\ 2
D
. Đạo hàm:
2
2 2
4 2 1
2 2
g x
x x m
y
x x
.
Hàm số nghịch biến trên mỗi khoảng xác định của nó khi và chỉ khi 0,
y x D
( Dấu
' '
chỉ xảy ra tại hữu hạn điểm trên
D
)
2
4 2 1 0,g x x x m x
Điều kiện:
0
(vì
1 0
a
)
4 1 . 2 1 0
m
2 5 0
m
5
2
m
.
Câu 35. [2D1-2] Số đường tiệm cận đứng của đồ thị hàm số
2
2
3 2
4
x x
y
x
là:
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải
Chọn A.
Hàm số
2
2
3 2
4
x x
y
x
có TXĐ
\ 2;2
D
.
Ta có
2 2
2
2
2
1 2
1 1
lim lim lim
2
2
4
4 2 2
3
x x x
x x
x x
x
x
x x x
và
2
2
2
3
lim
2 1
4 4
x
x x
x
.
2 2
2
2
2
1 2
1
lim lim lim
2 2 2
3 2
4
x x x
x
x
x
x
x
x
x x x
và
2
2
2
3 2
4
lim
x
x x
x
.
Vậy đồ thị hàm số chỉ có một đường tiệm cận đứng là
2
x
.
Câu 36. [2H1-1] Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối
xứng?
A.
6
mặt phẳng. B.
4
mặt phẳng. C.
3
mặt phẳng. D.
9
mặt phẳng.
Lời giải
Chọn C.
Câu 37. [2D1-1] Cho hàm số
y f x
có bảng biến thiên như hình bên. Mệnh đề nào dưới đây đúng?

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/19 - Mã đề thi 485
A. Hàm số đạt cực đại tại
5
x
. B. Hàm số đạt cực tiểu tại
1
x
.
C. Hàm số không có cực trị. D. Hàm số đạt cực đại tại
0
x
.
Lời giải
Chọn D.
Qua bảng biến thiên ta thấy hàm số có
y
đổi dấu từ dương sang âm qua
0
x
nên hàm số đạt
cực đại tại
0
x
.
Câu 38. [2D2-2] Phương trình
2 2
2 3.2 32 0
x x
có tổng các nghiệm là
A.
2
. B.
12
. C.
6
. D.
5
.
Lời giải
Chọn D.
Phương trình đã cho
2
2 12.2 32 0
x x
. Đặt
2
x
t
,
0
t
Khi đó phương trình trở thành:
2
12 32 0
t t
1
2
4 2 4 2
8 2 8 3
x
x
t x
t x
1 2
5
x x
.
Câu 39. [2D1-2] Đồ thị hàm số
3 2
3 2 1
y x x x
cắt đồ thị hàm số
2
3 1
y x x
tại hai điểm phân
biệt
A
và
B
. Khi đó độ dài đoạn
AB
là
A.
3
AB
. B.
2
AB
. C.
2 2
AB
. D.
1
AB
.
Lời giải
Chọn D.
3 2
3 2 1 1
y x x x ;
2
3 1 2
y x x
Phương trình hoành độ giao điểm của
1
và
2
là:
3 2 2
3 2 1 3 1
x x x x x
3 2
4 5 2 0
x x x
1
2
x
x
Suy ra
1; 1
A
và
2; 1
B
. Khi đó
1;0
AB
1
AB
.
Câu 40. [2D2-2] Phương trình
2
2 2
1
9 10.3 1 0
x x
x x
có tập nghiệm là:
A.
2; 1;1;2
. B.
2;0;1;2
. C.
2; 1;0;1
. D.
1;0;2
.
Lời giải
Chọn C.
Ta có
2
2 2
1
9 10.3 1 0
x x
x x
2
2 1
1
10
9 .3 1 0
3
x x
x x
2
1
2
1
3 3
1
3
3
x x
x x
2
2
1 1
1 1
x x
x x
2
2
2 0
0
x x
x x
1
2
1
0
x
x
x
x
Tập nghiệm của phương trình là:
2; 1;0;1
S .
Câu 41. [2D2-2] Tập xác định của hàm số
2
log 2
y x x
là:
x
0
2
y
0
0
y
5
1
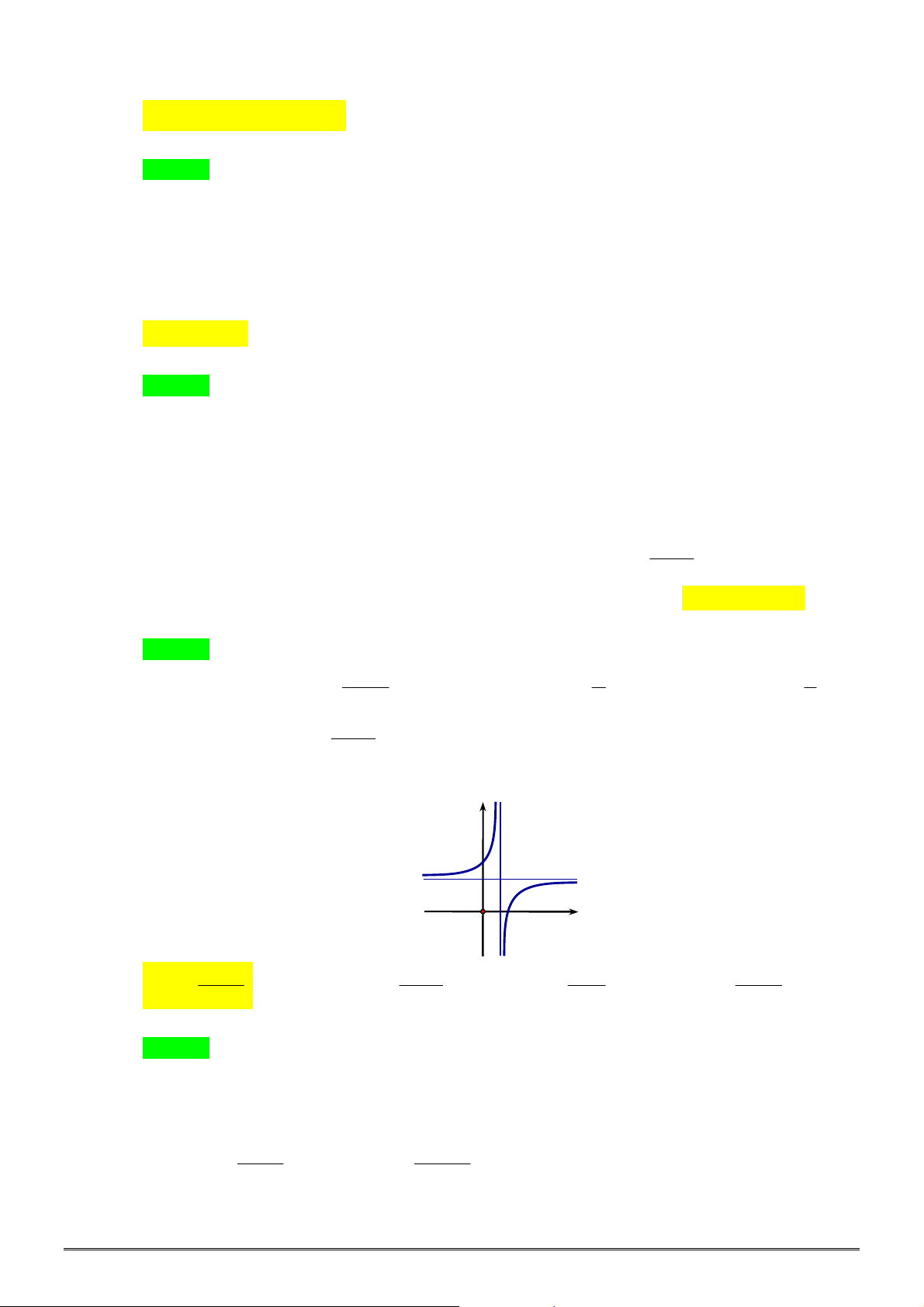
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/19 - Mã đề thi 485
A.
D 2;0
. B.
D \ 0
.
C.
D ; 2 0;
. D.
D
.
Lời giải
Chọn C.
Hàm số
2
log 2
y x x
xác định khi
2
2
2 0
0
x
x x
x
.
Câu 42. [2D1-2] Cho hàm số
4 2
2 1
y x x
có đồ thị
C
. Phương trình tiếp tuyến của đồ thị
C
tại
1;4
M là:
A.
8 4
y x
. B.
8 4
y x
. C.
8 12
y x
. D.
3
y x
.
Lời giải
Chọn A.
Tập xác định
D
.
Ta có:
3
4 4
y x x
,
x
.
Do
0 0
1 1 8
x y x y
. Nên phương trình tiếp tuyến của đồ thị
C
tại
1;4
M là:
8 1 4 8 4
y x x
.
Câu 43. [2D1-1] Các đường tiệm cận đứng và ngang của đồ thị hàm số
2 1
1
x
y
x
là:
A.
2
x
;
1
y
. B.
1
x
;
2
y
. C.
1
x
;
2
y
. D.
1
x
;
2
y
.
Lời giải
Chọn D.
Đồ thị hàm phân thức
ax b
y
cx d
có tiệm cận đứng là
d
x
c
và tiệm cận ngang là
a
y
c
.
Do đó đồ thị hàm số
2 1
1
x
y
x
có tiệm cận đứng và tiệm cận ngang lần lượt là
1
x
;
2
y
.
Câu 44. [2D1-2] Đường cong bên là đồ thị của hàm số nào dưới đây?
A.
2 3
1
x
y
x
. B.
2 1
1
x
y
x
. C.
3
2
x
y
x
. D.
2 3
1
x
y
x
.
Lời giải
Chọn A.
Đồ thị hàm số có tiệm cận đứng
1
x
và tiệm cận ngang
2
y
.
Từ đó ta loại đáp án C.
Từ hình vẽ ta được hàm số đồng biến trên các khoảng xác định.
Hàm số
2 3
1
x
y
x
có đạo hàm
2
1
0
1
y
x
,
1
x
.
O
x
y
1
2
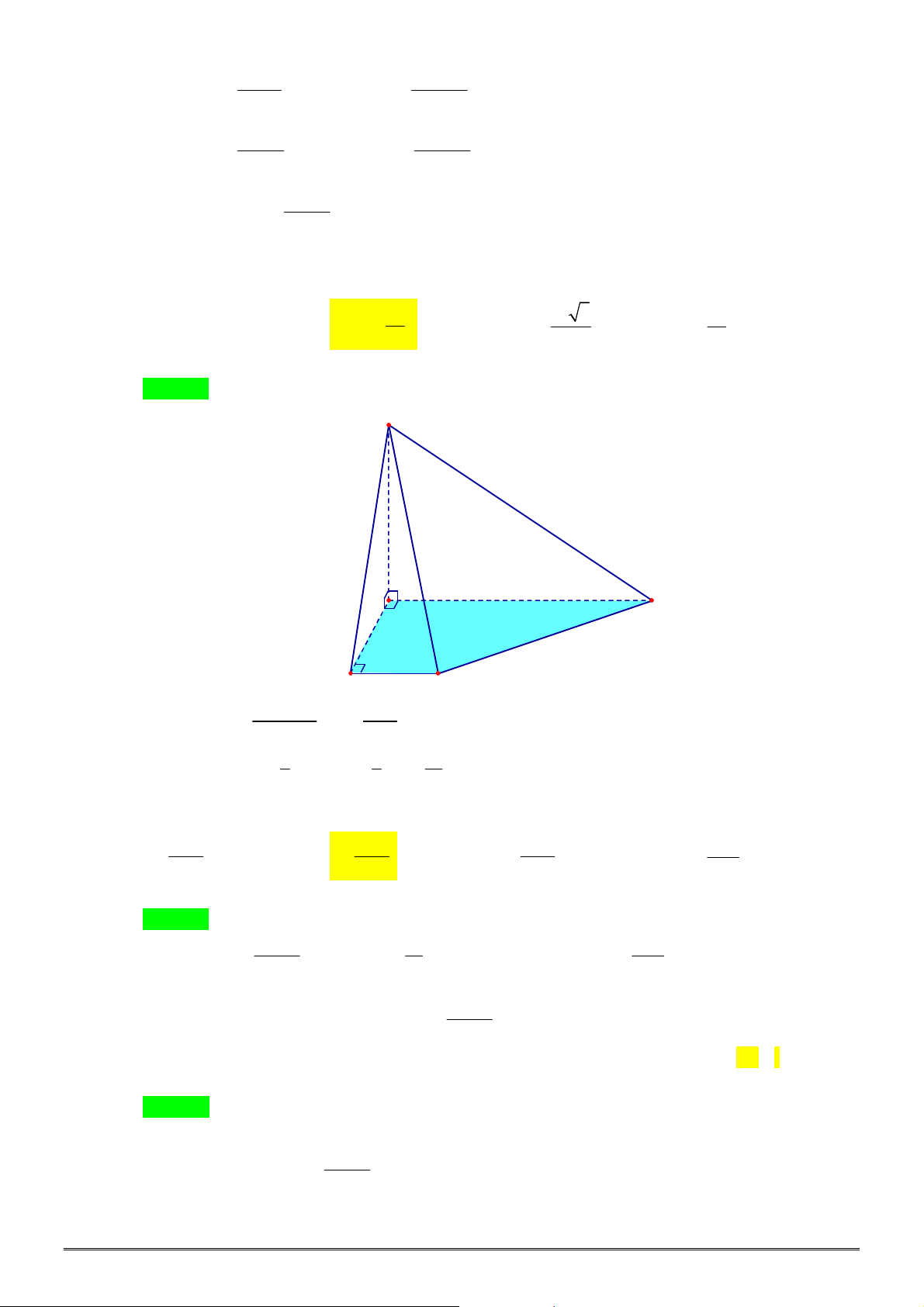
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/19 - Mã đề thi 485
Hàm số
2 1
1
x
y
x
có đạo hàm
2
1
0
1
y
x
,
1
x
.
Hàm số
2 3
1
x
y
x
có đạo hàm
2
5
0
1
y
x
,
1
x
.
Do đó hàm số
2 3
1
x
y
x
thỏa mãn bài toán.
Câu 45. [2H1-2] Cho hình chóp .
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
2
AB BC
,
3
AD
. Cạnh bên
2
SA
và vuông góc với đáy. Tính thể tích khối chóp .
S ABCD
.
A.
4
V
. B.
10
3
V
. C.
10 3
3
V
. D.
17
6
.
Lời giải
Chọn B.
Ta có:
2 3
. .2 5
2 2
ABCD
AB CD
S AD
Thể tích:
.
1 1 10
. . .2.5
3 3 3
S ABCD ABCD
V SA S
.
Câu 46. [2D2-2] Nếu
12
log 6
a
và
12
log 7
b
thì
2
log 7
bằng kết quả nào sau đây:
A.
1
a
a
. B.
1
b
a
. C.
1
a
b
. D.
1
a
b
.
Lời giải
Chọn B.
Ta có:
12
2 12 12 12 12 12
12
log 7
12
log 7 log 7:log log 7: log 12 log 6
log 2 6 1
b
a
.
Câu 47. [2D1-1] Giá trị lớn nhất của hàm số
2
4
2
y
x
là
A.
10
. B.
3
. C.
5
. D.
2
.
Lời giải
Chọn D.
TXĐ:
D
.
Ta có
2
2 2
x
suy ra
2
4
2 2
2
y
x
nên
max 2
y
.
Cách khác: dùng đạo hàm.
A
D
C
B
S

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/19 - Mã đề thi 485
Câu 48. [2D1-1] Cho hàm số
y f x
có
1
lim
x
f x
và
1
lim 2
x
f x
. Mệnh đề nào sau đây
đúng?
A. Đồ thị hàm số không có tiệm cận. B. Đồ thị hàm số có tiệm cận đứng
1
x
.
C. Đồ thị hàm số có hai tiệm cận. D. Đồ thị hàm số có tiệm cận ngang
2
y
.
Lời giải
Chọn B.
Vì
1
lim
x
f x
nên đồ thi hàm số có tiệm cận đứng
1
x
.
Câu 49. [2D1-3] Một ông nông dân có
2400
m hàng rào và muốn rào lại cánh đồng hình chữ nhật tiếp
giáp với một con sông. Ông không cần rào cho phía giáp bờ sông. Hỏi ông có thể rào được
cánh đồng với diện tích lớn nhất là bao nhiêu?
A.
630000
m
2
. B.
720000
m
2
. C.
360000
m
2
. D.
702000
m
2
.
Lời giải
Chọn B.
Gọi hai kích thước của hình chữ nhật là
x
và
y
, với
2 2400
x y
0 , 2400
x y .
Diện tích của mảnh vườn hình chữ nhật là:
2
2
2
1 2400
2 . 720000
2 8 8
AM GM
x y
S xy x y
.
Vậy ông nông dân có thể rào được cánh đồng với diện tích lớn nhất là
720000
m
2
.
Câu 50. [2H1-1] Khối đa diện đều loại
4;3
là:
A. Khối lập phương. B. Khối bát diện đều. C. Khối hộp chữ nhật. D. Khối tứ diện đều.
Lời giải
Chọn A.
Theo định nghĩa khối đa diện đều loại
4;3
là khối có: Mỗi mặt là 1 đa giác đều có
4
cạnh
(hình vuông), mỗi đỉnh là đỉnh chung của đúng
3
mặt. Vậy nó là khối lập phương.
Theo bảng tóm tắt về năm loại khối đa diện đều
Loại Tên gọi Số đỉnh Số cạnh Số mặt
3;3
Tứ diện đều
4
6
4
4;3
Lập phương
8
12
6
3;4
Bát diện đều
6
12
8
5;3
Mười hai mặt đều
20
30
12
3;5
Hai mươi mặt đều
12
30
20
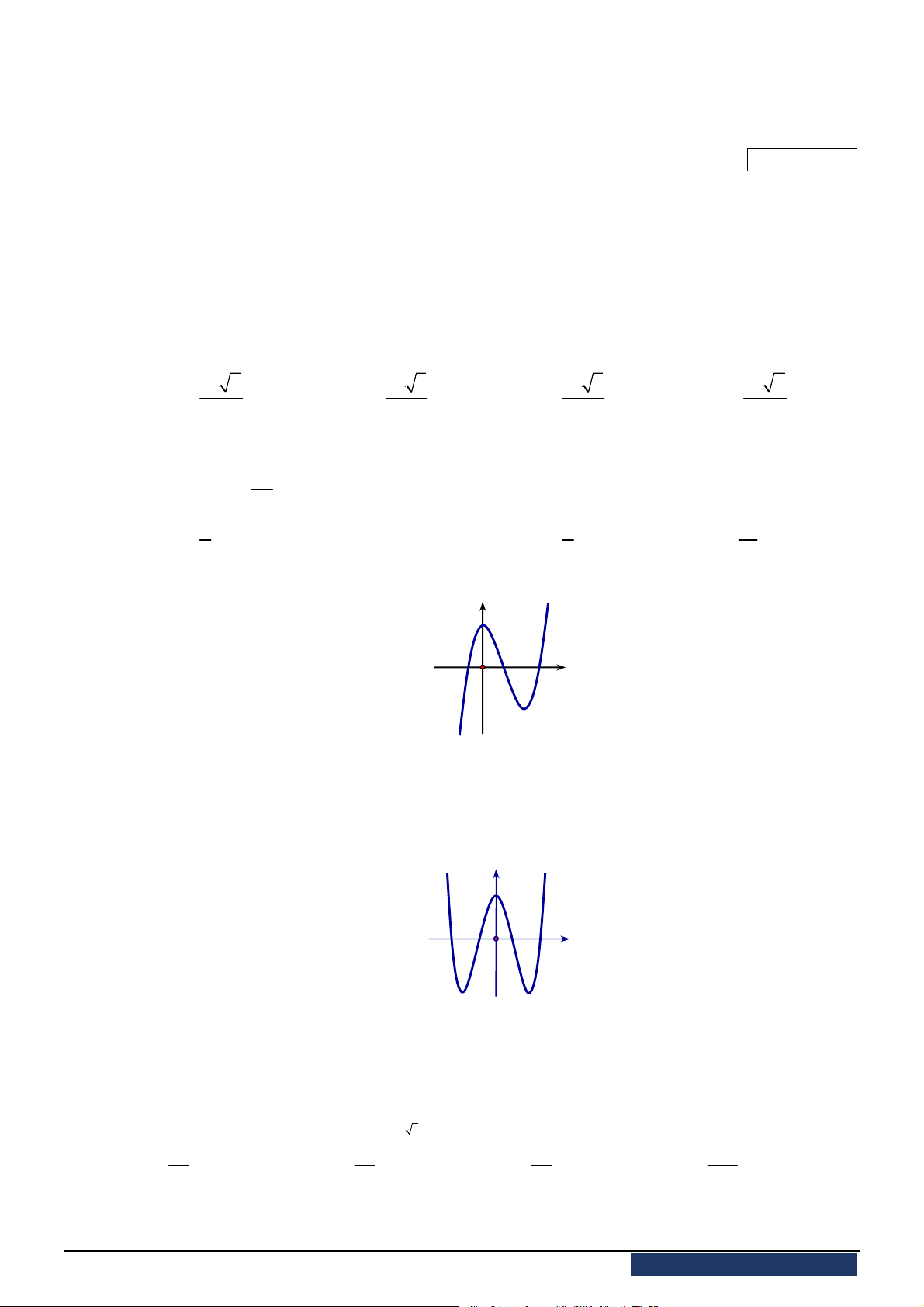
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/24 – HKI1819-001-SGD BẠC LIÊU
SỞ GD-ĐT BẠC LIÊU KIỂM TRA HỌC KỲ I NĂM HỌC 2018 – 2019
ĐẾ CHÍNH THỨC Môn kiểm tra: TOÁN 12
(Gồm có 06 trang) Thời gian: 90 phút, không kể thời gian phát đề
Họ, tên học sinh: …………………………………..; Số báo danh: ………………… Mã đề thi 213
Câu 1. Giá trị nhỏ nhất của hàm số
3
3 1
y x x
trên đoạn
1;4
là
A.
1
. B.
3
. C.
4
. D.
1
.
Câu 2. Nghiệm của phương trình
3
log 2 3 2
x
là
A.
11
2
x
. B.
6
x
. C.
5
x
. D.
9
2
x
.
Câu 3. Thể tích
V
của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
là
A.
3
2
3
a
V . B.
3
3
4
a
V . C.
3
3
2
a
V . D.
3
2
4
a
V .
Câu 4. Gọi
1
x
,
2
x
, (với
1 2
x x
) là hai nghiệm của phương trình
2 1
2 5.2 2 0
x x
. Tính giá trị của
biểu thức
2
1
1
3
3
x
x
P
.
A.
5
4
P
. B.
6
P
. C.
2
3
P
. D.
10
9
P
.
Câu 5. Đường cong ở hình vẽ bên dưới là của hàm số nào?
A.
3
3 – 4
y x x . B.
3 2
3 2
y x x
. C.
3
4
y x
. D.
4 2
3 2
y x x
.
Câu 6. Trong các hàm số sau, hàm số nào có 3 điểm cực trị?
A.
4 2
2 – 3 2
y x x
. B.
2
–3 2
y x x
. C.
4 2
2 – 3 2
y x x
. D.
3 2
3 2
y x x
.
Câu 7. Đường cong ở hình vẽ bên dưới là đồ thị của hàm số nào sau đây?
A.
4 2
4 2
y x x
. B.
3 2
– 3 1
y x x
. C.
4 2
4 2
y x x
. D.
4 2
4 2
y x x
.
Câu 8. Khối bát diện đều là khối đa diện đều loại
A.
4;3
. B.
3;5
. C.
5;3
. D.
3: 4
.
Câu 9. Biết
3 3 9
3
log 3log 2 log 25 log 3
x . Khi đó, giá trị của
x
là
A.
25
9
. B.
40
9
. C.
20
3
. D.
200
3
.
O
x
y
O
x
y
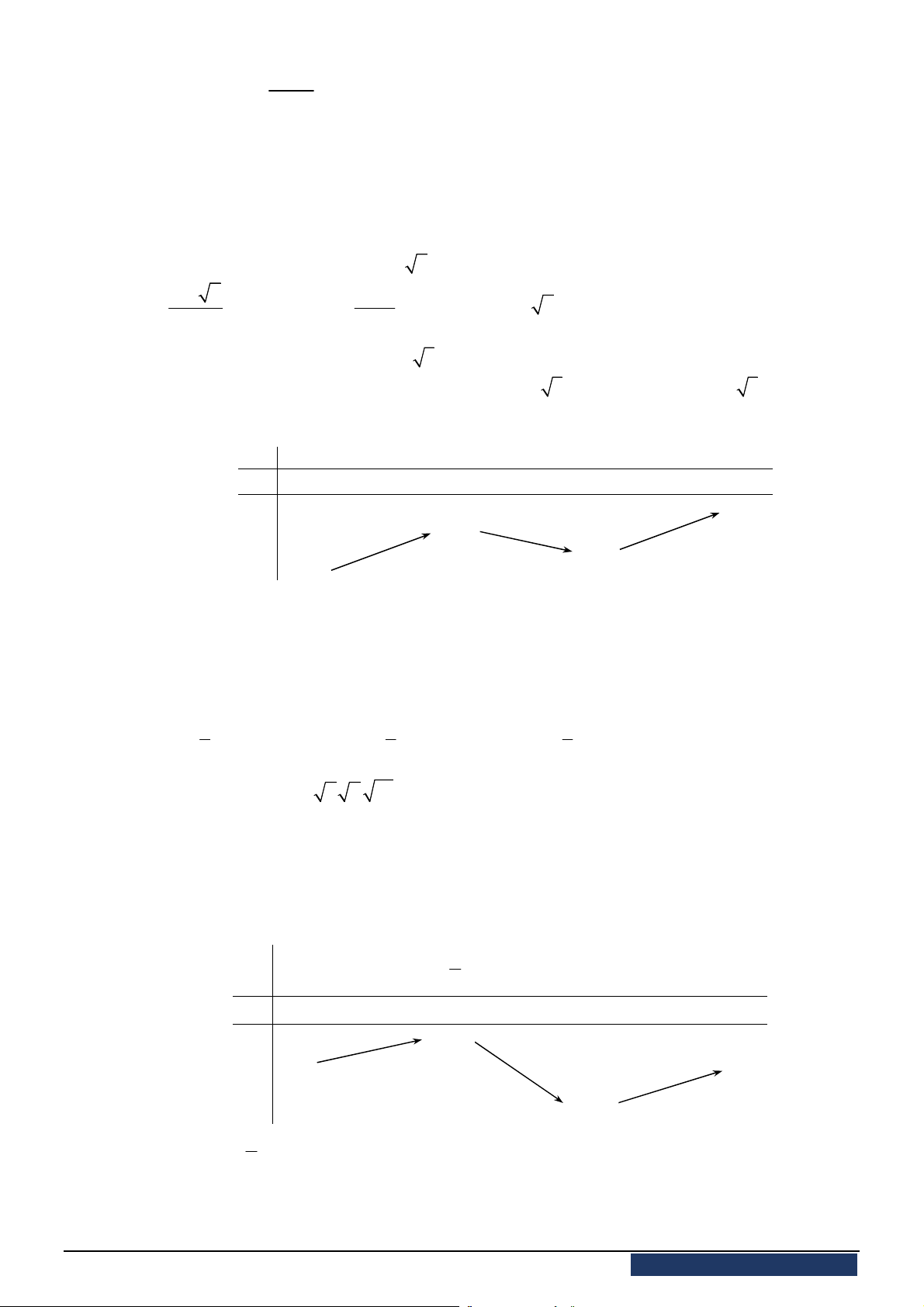
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/24 – HKI1819-001-SGD BẠC LIÊU
Câu 10. Cho hàm số
1
1
x
y
x
. Khẳng định nào sao đây là khẳng định đúng?
A. Hàm số nghịch biến trên khoảng
;1 1;
.
B. Hàm số đồng biến trên khoảng
;1 1;
.
C. Hàm số nghịch biến trên các khoảng
;1
và
1;
.
D. Hàm số đồng biến trên các khoảng
;1
và
1;
.
Câu 11. Một hình trụ có bán kính đáy
2
r a
, chiều cao
h a
. Thể tích của khối trụ bằng
A.
3
2
3
a
. B.
3
2
3
a
. C.
3
2
a
. D.
3
2
a
.
Câu 12. Một khối cầu có đường kính bằng
2 3
có thể tích bằng
A.
4
. B.
12
. C.
4 3
. D.
12 3
.
Câu 13. Cho hàm số
y f x
có bảng biến thiên như hình vẽ bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực tiểu tại
2
x
. B. Hàm số đạt cực đại tại
4
x
.
C. Hàm số đạt cực đại tại
3
x
. D. Hàm số đạt cực đại tại
2
x
.
Câu 14. Hình nón có chiều cao
h
, độ dài đường sinh
l
, bán kính đáy
r
. Thể tích
V
của khối nón được
tính theo công thức nào sau đây?
A.
2
1
3
V r l
. B.
1
3
V rh
. C.
2
1
3
V r h
. D.
2
V r l
.
Câu 15. Cho biểu thức
5
12
3 4
f x x x x
. Khi đó, giá trị của
2,7
f bằng
A.
0,027
. B.
27
. C.
2,7
. D.
0,27
.
Câu 16. Một khối nón có bán kính đáy là
r a
và thể tích bằng
3
a
. Chiều cao
h
của khối nón là
A.
2
h a
. B.
h a
. C.
4
h a
. D.
3
h a
.
Câu 17. Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như hình vẽ.
A.
1
max
2
y
. B.
max 1
y
. C.
max 1
y
. D.
max 3
y
.
Câu 18. Tính thể tích
V
của khối hộp chữ nhật
.
ABCD A B C D
, biết
AB a
,
2
AD a
và
3
AA a
.
A.
6
V a
. B.
3
6
V a
. C.
2
6
V a
. D.
3
2
V a
.
x
1
2
2
y
0
0
y
3
1
1
1
x
2
4
y
0
0
y
3
2
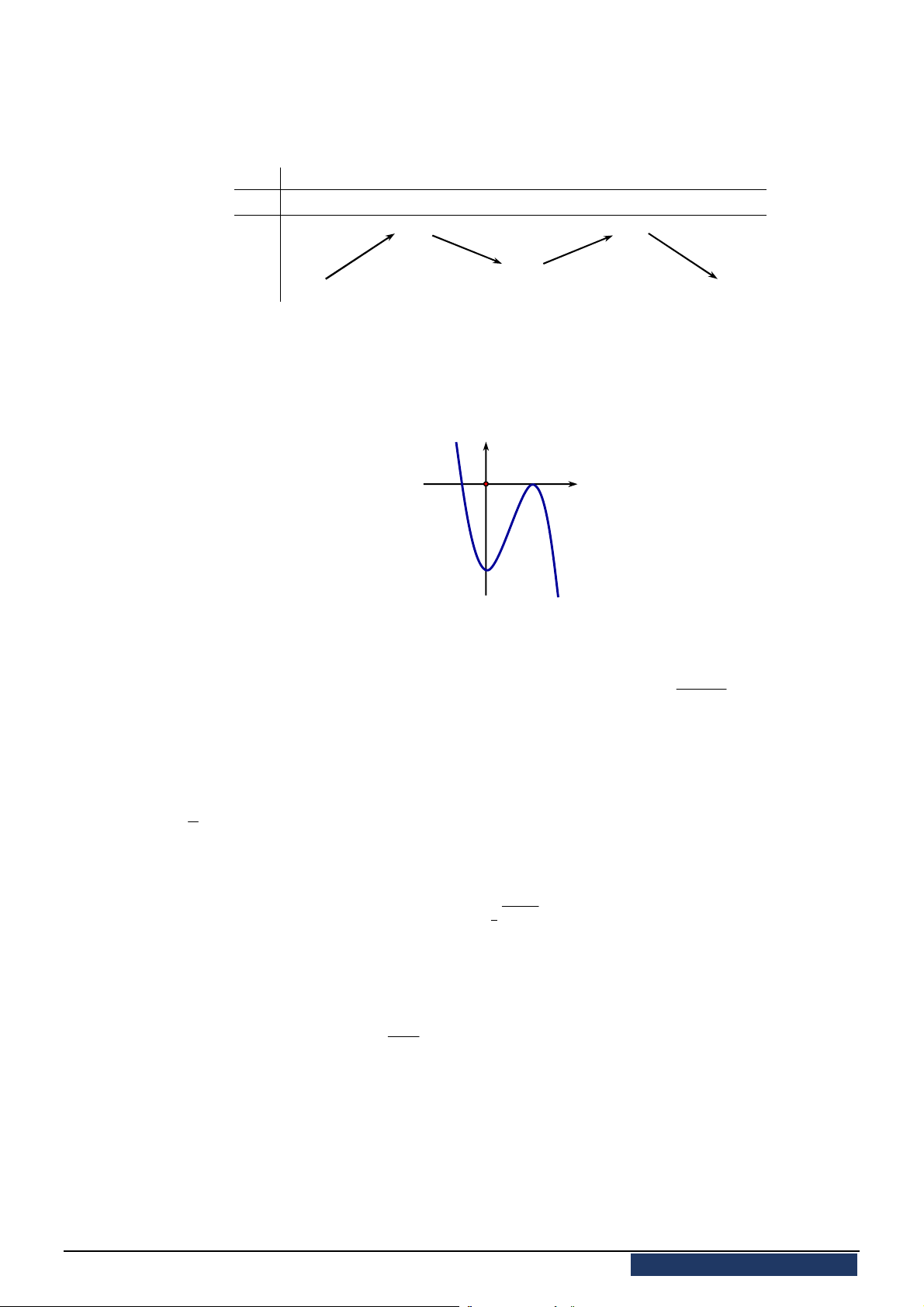
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/24 – HKI1819-001-SGD BẠC LIÊU
Câu 19. Tiếp tuyến của đồ thị hàm số
3
3 2
y x x
tại điểm có hoành độ
0
2
x
có phương trình là
A.
9 22
y x
. B.
9 22
y x
. C.
9 14
y x
. D.
9 14
y x
.
Câu 20. Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như hình vẽ bên dưới.
Hàm số
y f x
đồng biến trên khoảng nào dưới đây?
A.
;0
. B.
0;1
. C.
1;0
. D.
0;
.
Câu 21. Tìm tất cả các giá trị của tham số
m
để phương trình
3 2
– 3 4 0
x x m
có nghiệm duy nhất
lớn hơn
2
. Biết rằng đồ thị của hàm số
3 2
3 – 4
y x x có hình vẽ như bên dưới.
A.
4
m
hoặc
20
m
. B.
4
m
.
C.
4
m
D.
0
m
.
Câu 22. Tìm tất cả các giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
1
x m
y
x
trên
2;4
bằng
2
A.
m
0. B.
2
m
. C.
2
m
. D.
4
m
.
Câu 23. Gọi
S
tập hợp tất cả các giá trị nguyên của tham số
m
để hàm số
3 2
1
– 2 3 2
3
y x mx m x m
nghịch biến trên
. Số phần tử của là
A.
5
. B.
4
. C.
7
. D.
8
.
Câu 24. Với giá trị nào của
x
thì biểu thức
1
2
1
log
3
x
f x
x
có nghĩa?
A.
\ –3;1
x
. B.
3;1
x . C.
\ 3;1
x
. D.
3;1
x .
Câu 25. Đạo hàm của hàm số
x
y
là
A.
1
ln
x
y x
. B.
ln
x
y
. C.
.ln
x
y
. D.
1
.
x
y x
.
Câu 26. Cho hình nón có đường sinh
5 cm
l
và bán kính đáy
4 cm
r
. Diện diện tích xung quan của
hình nón bằng
A.
2
20 cm
. B.
2
40 cm
. C.
2
40 cm
. D.
2
20 cm
.
Câu 27. Tổng các nghiệm của phương trình
2
log 5 – 2 2
x
x
bằng
A.
3
. B.
1
. C.
2
. D.
0
.
O
x
y
1
2
4
x
1
0
1
y
0
0
0
y
1
1
2
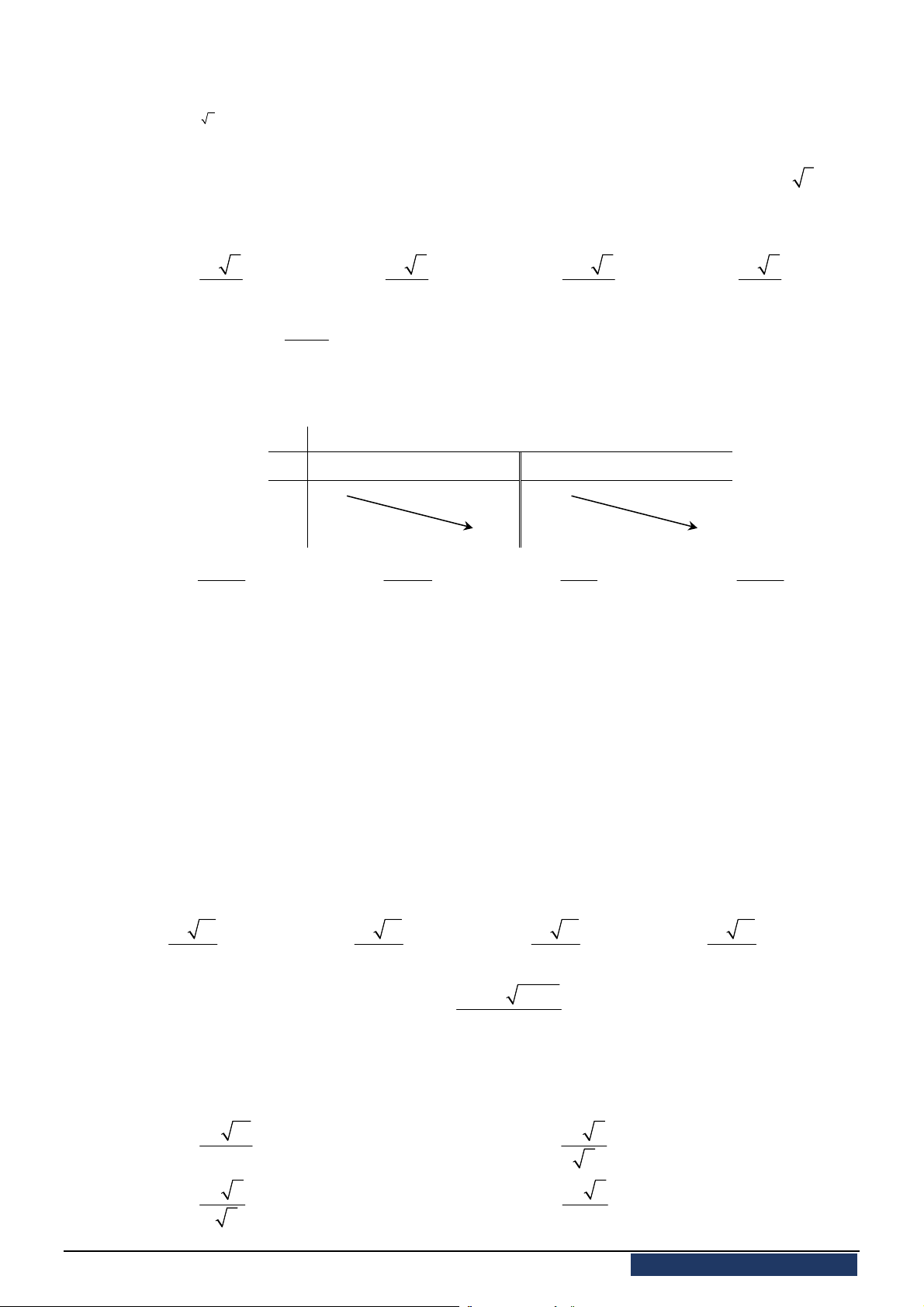
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/24 – HKI1819-001-SGD BẠC LIÊU
Câu 28. Biết
log 3
a
b
với
a
,
b
là các số thực dương và
a
khác
1
. Tính giá trị của biểu thức
2
3 2 6
log log
a a
P b b
.
A.
63
P
. B.
45
P
. C.
21
P
. D.
99
P
.
Câu 29. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
và có
AB a
,
3
BC a
. Mặt
bên
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng
ABC
. Tính
theo
a
thể tích của khối chóp
.
S ABC
.
A.
3
6
6
a
V . B.
3
6
12
a
V . C.
3
2 6
3
a
V . D.
3
6
4
a
V .
Câu 30. Đồ thị hàm số
2 1
1
x
y
x
có đường tiệm cận đứng là
A.
2
y
. B.
1
x
. C.
2
y
. D.
1
x
.
Câu 31. Bảng biến thiên ở hình vẽ bên dưới là của hàm số nào?
A.
3
1
x
y
x
. B.
2
1
x
y
x
. C.
3
1
x
y
x
. D.
3
1
x
y
x
.
Câu 32. Một người gửi
100
triệu đồng vào một ngân hàng với lãi suất
0,65%
/tháng. Biết rằng nếu
không rút tiền khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu để
tính lãi cho tháng tiếp theo. Hỏi sau đúng
12
tháng, người đó được lĩnh số tiền (cả vốn ban đầu
và lãi) là bao nhiêu? Biết rằng trong khoảng thời gian này người đó không rút tiền ra và lãi suất
không thay đổi.
A.
108.085.000
đồng. B.
108.000.000
đồng. C.
108.084.980
đồng. D.
108.084.981
đồng.
Câu 33. Biết hàm số
3 2
3 6
y x x x
đạt cực trị tại hai điểm
1
x
,
2
x
. Khi đó, giá trị của biểu thức
2 2
1 2
x x
bằng
A.
8
. B.
10
. C.
8
. D.
10
.
Câu 34. Cho khối chóp đều
.
S ABC
có cạnh đáy bằng
a
, cạnh bên bằng
2
a
. Gọi
M
là trung điểm
SB
,
N
là điểm trên đoạn
SC
sao cho
2
NS NC
. Thể tích của khối chóp
.
A BCNM
bằng
A.
3
11
18
a
. B.
3
11
24
a
. C.
3
11
36
a
. D.
3
11
16
a
.
Câu 35. Số đường tiệm cận của đồ thị hàm số
2
1 3 1
3 2
x x
y
x x
là
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 36. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên
bằng
2
a
.
A.
2 14
7
a
R . B.
2 7
2
a
R .
C.
2 7
3 2
a
R . D.
2 2
7
a
R .
x
1
y
–
–
y
1
1
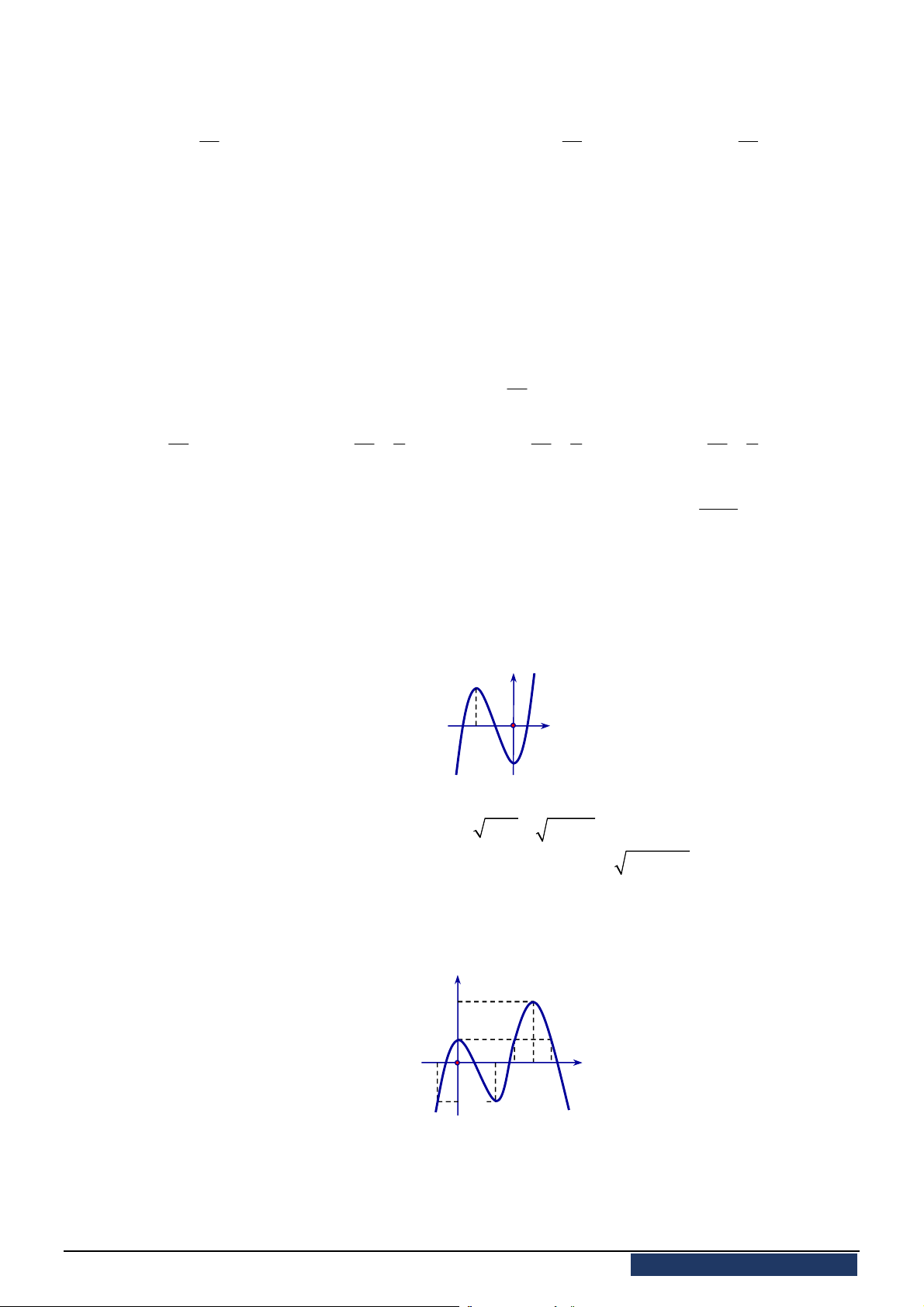
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/24 – HKI1819-001-SGD BẠC LIÊU
Câu 37. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
,
SA
vuông góc với mặt đáy và
SA AB a
,
2
AC a
. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
4
a
V . B.
3
V a
. C.
3
2
a
V . D.
3
3
a
V .
Câu 38. Số giao điểm của đồ thị hàm số
3
4
y x x
với đường thẳng
4
y
là
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 39. Tổng lập phương các nghiệm thực của phương trình
2
4 5
3 9
x x
bằng
A.
27
. B.
28
. C.
26
. D.
25
.
Câu 40. Cho tam giác
ABC
vuông tại
A
có
2
BC a
và
30
B
. Quay tam giác vuông này quanh
trục
AB
, ta được một hình nón đỉnh
B
. Gọi
1
S
là diện tích toàn phần của hình nón đó và
2
S
là
diện tích mặt cầu có đường kính
AB
. Tính tỉ số
2
1
S
S
.
A.
2
1
1
S
S
. B.
2
1
2
3
S
S
. C.
2
1
3
2
S
S
. D.
2
1
1
2
S
S
.
Câu 41. Tổng tất cả các giá trị nguyên âm của tham số
m
để hàm số
3
2
3
28
y x mx
x
, đồng biến trên
khoảng
0;
bằng
A.
15
. B.
6
. C.
3
. D.
10
.
Câu 42. Cho hàm số
y f x
xác định và liên tục trên
có đồ thị như hình vẽ. Hàm số
2
2 4
g x f x x
có bao nhiêu điểm cực tiểu?
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 43. Cho
x
,
y
là các số thực thỏa mãn
1 2 2
x y x y
. Gọi
M
,
m
lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của
2 2
2 1 1 8 4
P x y x y x y
. Khi đó, giá trị của
M m
bằng
A.
42
. B.
44
. C.
41
. D.
43
.
Câu 44. Cho hàm số
y f x
có đồ thị hàm số
y f x
được cho như hình vẽ.
Hàm số
2
2 2
g x f x x
nghịch biến trên khoảng nào?
A.
0;2
. B.
3;1
. C.
2;3
. D.
1;0
.
x
y
1
1
2
O
3
4
5
3
2
2
x
y
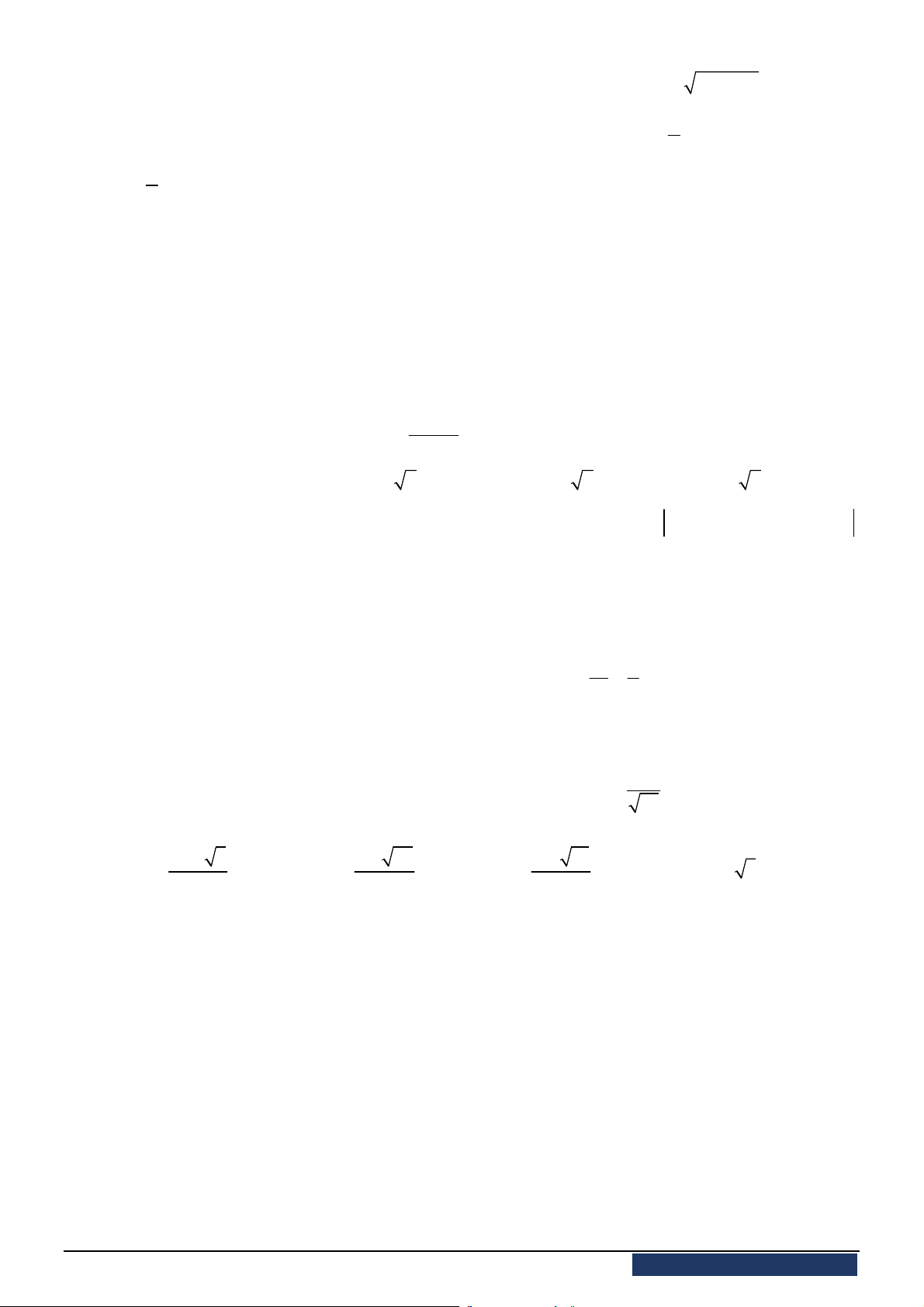
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/24 – HKI1819-001-SGD BẠC LIÊU
Câu 45. Cho hàm số
4 7
3 1 .2 – 6 3
x x
f x x x
, khi phương trình
2
7 4 6 9 3 1 0
f x x m
có số nghiệm nhiều nhất thì giá trị nhỏ nhất của tham số
m
có dạng
a
b
(trong đó
a
,
b
và
a
b
là phân số tối giản). Tính
T a b
.
A.
7
T
. B.
11
T
. C.
8
T
. D.
13
T
.
Câu 46. Cho hàm số
3 2
3 1
y x x
có đồ thị
C
và điểm
1;
A m
. Gọi
S
là tập hợp tất cả các giá trị
nguyên của tham số
m
để qua
A
có thể kể được đúng ba tiếp tuyến tới đồ thị
C
. Số phần tử
của
S
là
A.
9
. B.
7
. C.
3
. D.
5
Câu 47. Cho hai số thực
1
a
,
1
b
. Biết phương trình
2
1
1
x x
a b
có hai nghiệm phân biệt
1
x
,
2
x
. Tìm
giá trị nhỏ nhất của biểu thức
2
1 2
1 2
1 2
4
x x
P x x
x x
.
A.
4
P
. B.
3
3 2
P
. C.
3
3 4
P
. D.
3
4
P
.
Câu 48. Tổng tất cả các giá trị nguyên của tham số
m
để đồ thị hàm số
4 3 2
3 8 6 – 24
y x x x x m
có
7
điểm cực trị là
A.
63
. B.
55
. C.
30
. D.
42
.
Câu 49. Cho hình thang
ABCD
vuông tại
A
và
B
có
AB a
,
3
AD a
và
BC x
với
0 3
x a
.
Gọi
1
V
,
2
V
, lần lượt là thể tích các khối tròn xoay tạo thành khi quay hình thang
ABCD
(kể cả
các điểm trong) quanh đường thẳng
BC
và
AD
. Tìm
x
để
1
2
7
5
V
V
.
A.
x a
. B.
2
x a
. C.
3
x a
. D.
4
x a
.
Câu 50. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
2
a
. Gọi
M
là trung điểm cạnh
SA
,
90
SAB SCB
, biết khoảng cách từ
A
đến
MBC
bằng
6
21
a
. Thể tích của khối chóp
.
S ABC
bằng
A.
3
10 3
9
a
. B.
3
8 39
3
a
. C.
3
4 13
3
a
. D.
3
2 3
a .
----------- HẾT ---------
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/24 – HKI1819-001-SGD BẠC LIÊU
ĐÁP ÁN THAM KHẢO ĐỀ HKI1819-001-SGD BẠC LIÊU
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
B B B B A
C
D
B
D
D
C
D
C
C
D
D
B D
B C
A
A
A
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
C
D
B B A
D
C
A
A
A
D
A
B A
C
B D
D
C
B C
D
A
A
HƯỚNG DẪN GIẢI
Câu 1. Giá trị nhỏ nhất của hàm số
3
3 1
y x x
trên đoạn
1;4
là
A.
1
. B.
3
. C.
4
. D.
1
.
Lời giải
Chọn A.
Xét hàm số
3
3 1
y x x
liên tục trên đoạn
1;4
có:
2
3 3 0 1 1;4
1 1; 1 3; 4 53
y x y x
y y y
Vậy
1;4
min 1
y
.
Câu 2. Nghiệm của phương trình
3
log 2 3 2
x
là
A.
11
2
x
. B.
6
x
. C.
5
x
. D.
9
2
x
.
Lời giải
Chọn B.
Điều kiện:
3
2 3 0
2
x x
.
3
log 2 3 2 2 3 9 6
x x x
Vậy
6
x
.
Câu 3. Thể tích
V
của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
là
A.
3
2
3
a
V . B.
3
3
4
a
V . C.
3
3
2
a
V . D.
3
2
4
a
V .
Lời giải
Chọn B.
Ta có
2
3
4
ABC
a
S
Vậy
2 3
3 3
.
4 4
a a
V a .
A
C
B
A
C
B
a
a
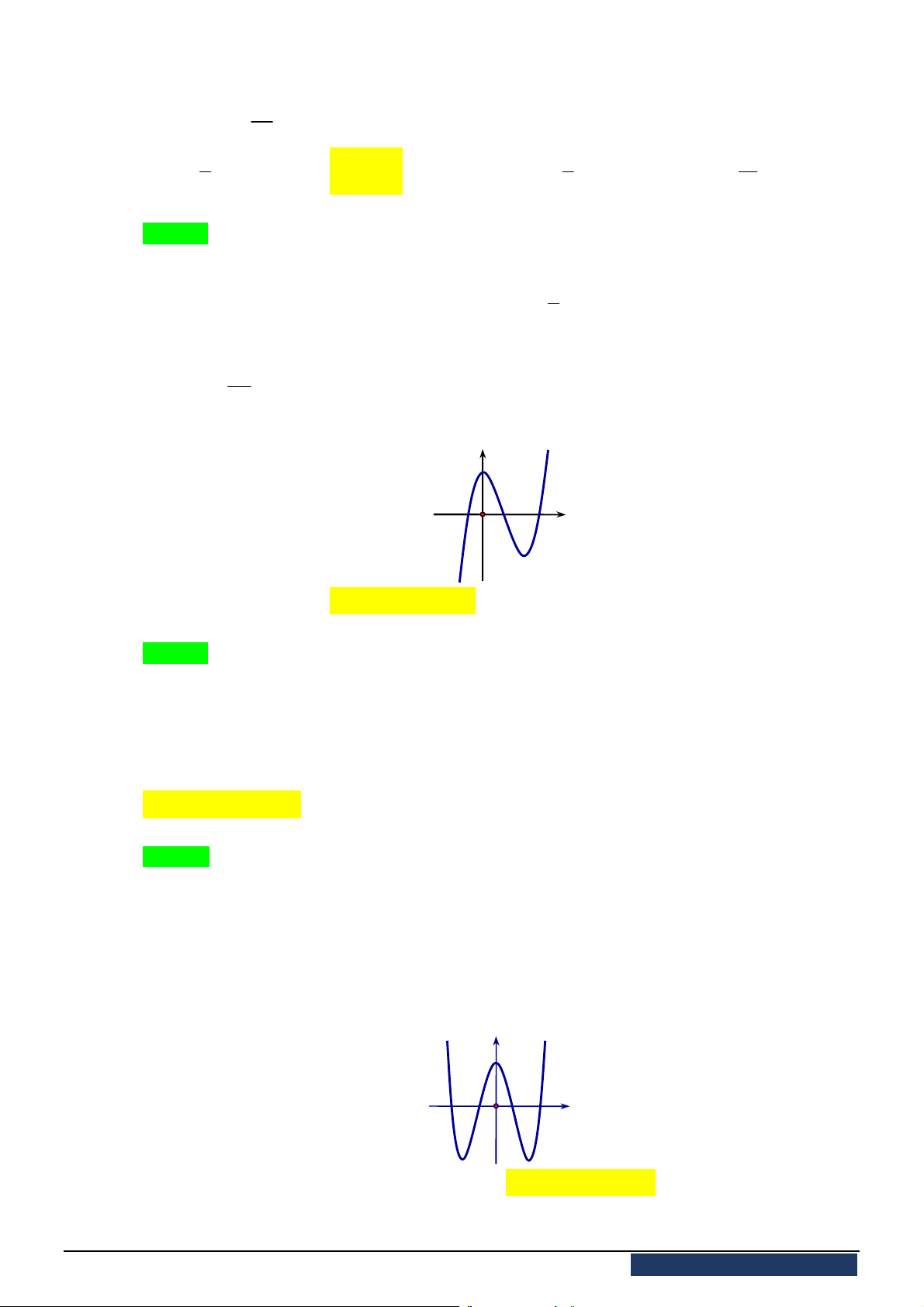
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/24 – HKI1819-001-SGD BẠC LIÊU
Câu 4. Gọi
1
x
,
2
x
, (với
1 2
x x
) là hai nghiệm của phương trình
2 1
2 5.2 2 0
x x
. Tính giá trị của
biểu thức
2
1
1
3
3
x
x
P
.
A.
5
4
P
. B.
6
P
. C.
2
3
P
. D.
10
9
P
.
Lời giải
Chọn B.
2 1
2 5.2 2 0
x x
2
2. 2 5.2 2 0
x x
2 2
1
1
1
2
2
x
x
x
x
Vậy
1 2
1; 1
x x
Do đó
1
1
1
3 6
3
P
.
Câu 5. Đường cong ở hình vẽ bên dưới là của hàm số nào?
A.
3
3 – 4
y x x . B.
3 2
3 2
y x x
. C.
3
4
y x
. D.
4 2
3 2
y x x
.
Lời giải
Chọn B.
Đồ thị hàm số là đồ thị hàm số bậc
3
, hệ số
0
a
Loại đáp án C, D.
Xét hàm số
3
3 4
y x x
có
2
3 3 0,y x x
nên loại đáp án A.
Xét hàm số
3 2
3 2
y x x
có
2
3 6 3 2
y x x x x
có hai nghiệm phân biệt nên thỏa mãn.
Câu 6. Trong các hàm số sau, hàm số nào có 3 điểm cực trị?
A.
4 2
2 – 3 2
y x x
. B.
2
–3 2
y x x
. C.
4 2
2 – 3 2
y x x
. D.
3 2
3 2
y x x
.
Lời giải
Chọn A.
Hàm số có
3
điểm cực trị
Loại đáp án B, D.
Xét hàm số
4 2
2 3 2
y x x
3 2
8 6 2 4 3
y x x x x
Giải
0 0
y x
. Vậy hàm số
4 2
2 3 2
y x x
có
1
điểm cực trị
Loại đáp án C.
Xét hàm số
4 2
2 3 2
y x x
có
3 2
8 6 2 4 3
y x x x x
có ba nghiệm phân biệt nên thỏa mãn.
Câu 7. Đường cong ở hình vẽ bên dưới là đồ thị của hàm số nào sau đây?
A.
4 2
4 2
y x x
. B.
3 2
– 3 1
y x x
. C.
4 2
4 2
y x x
. D.
4 2
4 2
y x x
.
Lời giải
O
x
y
O
x
y
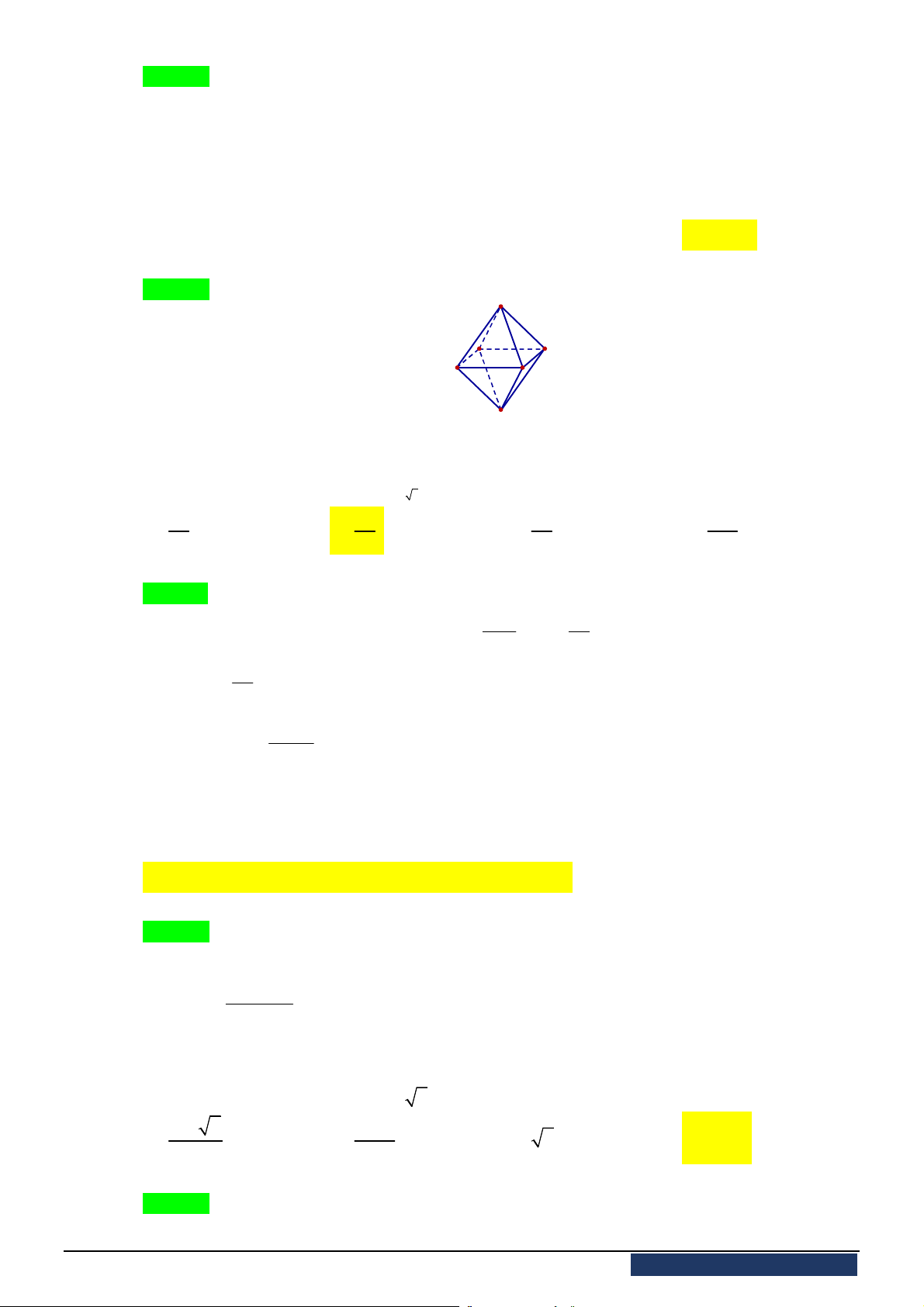
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/24 – HKI1819-001-SGD BẠC LIÊU
Chọn C.
Hàm số có dạng
4 2
y ax bx c
0
a
.
lim
x
y
nên
0
a
.
Hàm số có
3
điểm cực trị nên
. 0
a b
0
b
.
Câu 8. Khối bát diện đều là khối đa diện đều loại
A.
4;3
. B.
3;5
. C.
5;3
. D.
3: 4
.
Lời giải
Chọn D.
Số cạnh trên một mặt là
3
.
Mỗi đỉnh là đỉnh chung của đúng của đúng
4
mặt.
Câu 9. Biết
3 3 9
3
log 3log 2 log 25 log 3
x . Khi đó, giá trị của
x
là
A.
25
9
. B.
40
9
. C.
20
3
. D.
200
3
.
Lời giải
Chọn B.
Ta có:
3 2
3 3 3 3 3 3
8 5 40
log log 2 log 5 log 3 =log log .
9 9
x
Suy ra:
40
9
x .
Câu 10. Cho hàm số
1
1
x
y
x
. Khẳng định nào sao đây là khẳng định đúng?
A. Hàm số nghịch biến trên khoảng
;1 1;
.
B. Hàm số đồng biến trên khoảng
;1 1;
.
C. Hàm số nghịch biến trên các khoảng
;1
và
1;
.
D. Hàm số đồng biến trên các khoảng
;1
và
1;
.
Lời giải
Chọn D.
TXĐ
\ 1
D
Ta có
2
2
0, 1
1
y x
x
.
Suy ra hàm số đồng biến trên khoảng
;1
và
1;
.
Câu 11. Một hình trụ có bán kính đáy
2
r a
, chiều cao
h a
. Thể tích của khối trụ bằng
A.
3
2
3
a
. B.
3
2
3
a
. C.
3
2
a
. D.
3
2
a
.
Lời giải
Chọn D.
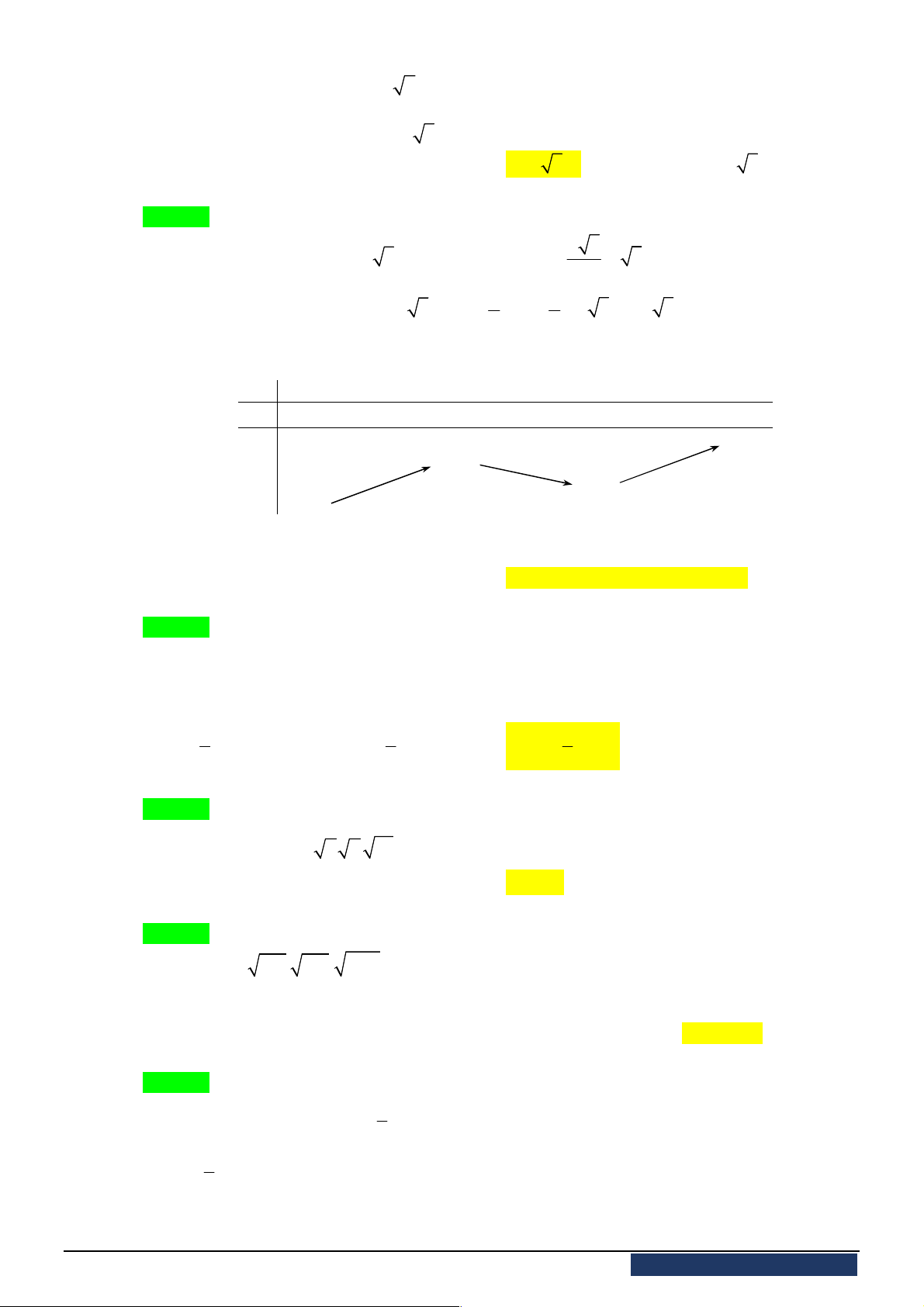
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/24 – HKI1819-001-SGD BẠC LIÊU
Thể tích khối trụ
2
2 3
2 2
V r h a a a
.
Câu 12. Một khối cầu có đường kính bằng
2 3
có thể tích bằng
A.
4
. B.
12
. C.
4 3
. D.
12 3
.
Lời giải
Chọn C.
Khối cầu có đường kính bằng
2 3
nên có bánkính là
2 3
3
2
r .
Thể tích của khối cầu bán kính
3
r là
3
3
4 4
. 3 4 3
3 3
V r
.
Câu 13. Cho hàm số
y f x
có bảng biến thiên như hình vẽ bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực tiểu tại
2
x
. B. Hàm số đạt cực đại tại
4
x
.
C. Hàm số đạt cực đại tại
3
x
. D. Hàm số đạt cực đại tại
2
x
.
Lời giải
Chọn D.
Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại
2
x
.
Câu 14. Hình nón có chiều cao
h
, độ dài đường sinh
l
, bán kính đáy
r
. Thể tích
V
của khối nón được
tính theo công thức nào sau đây?
A.
2
1
3
V r l
. B.
1
3
V rh
. C.
2
1
3
V r h
. D.
2
V r l
.
Lời giải
Chọn C.
Câu 15. Cho biểu thức
5
12
3 4
f x x x x
. Khi đó, giá trị của
2,7
f bằng
A.
0,027
. B.
27
. C.
2,7
. D.
0,27
.
Lời giải
Chọn C.
5
12
3
4
2,7 2,7. 2,7. 2,7 2,7
f x .
Câu 16. Một khối nón có bán kính đáy là
r a
và thể tích bằng
3
a
. Chiều cao
h
của khối nón là
A.
2
h a
. B.
h a
. C.
4
h a
. D.
3
h a
.
Lời giải
Chọn D.
Ta có thể tích khối nón là:
2
1
3
V r h
Suy ra:
2 3
1
3
3
a h a h a
.
Câu 17. Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như hình vẽ.
x
2
4
y
0
0
y
3
2
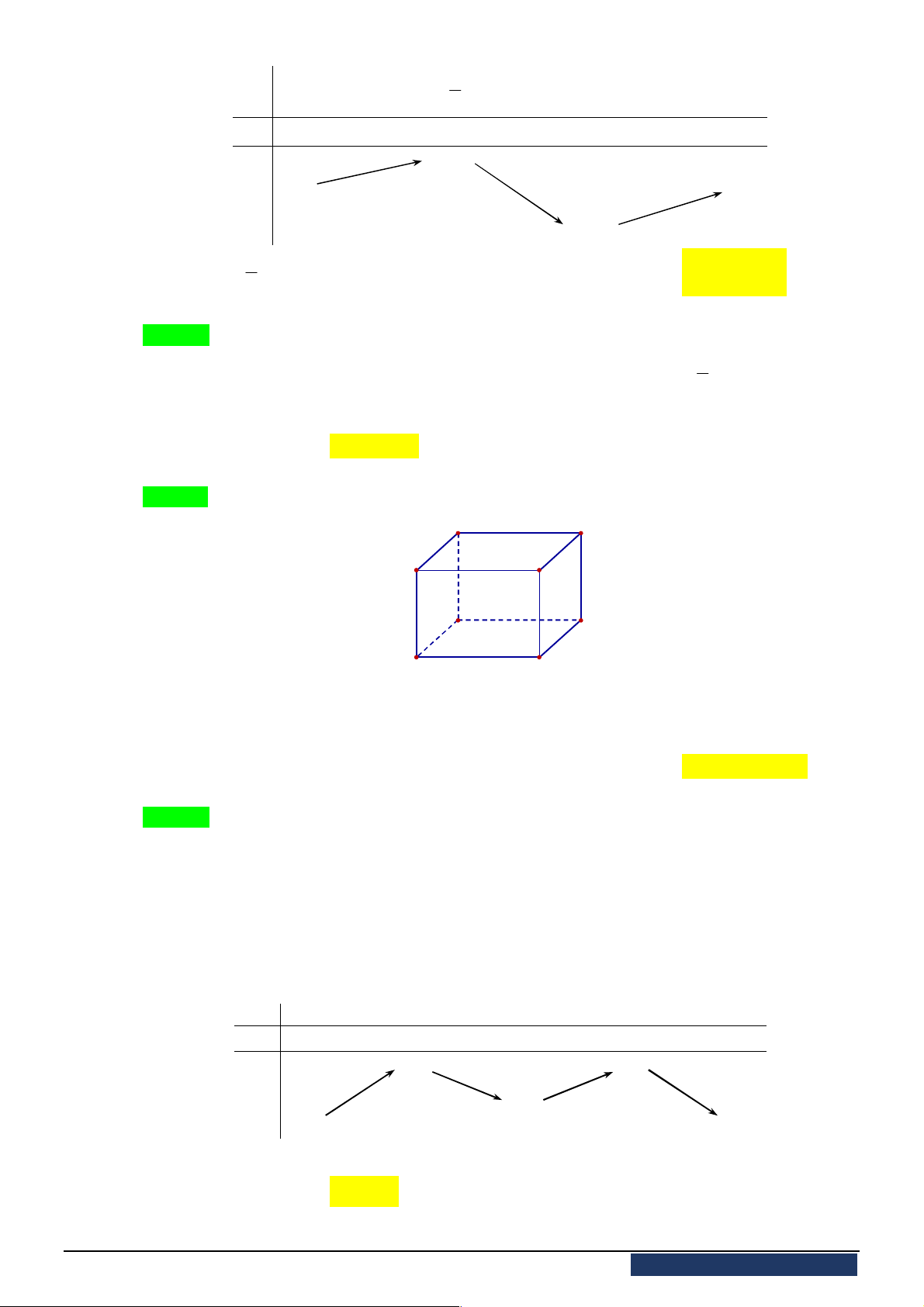
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/24 – HKI1819-001-SGD BẠC LIÊU
A.
1
max
2
y
. B.
max 1
y
. C.
max 1
y
. D.
max 3
y
.
Lời giải
Chọn D.
Dựa vào bảng biến thiên ta có hàm số đạt giá trị lớn nhất bằng
3
tại
1
2
x
.
Câu 18. Tính thể tích
V
của khối hộp chữ nhật
.
ABCD A B C D
, biết
AB a
,
2
AD a
và
3
AA a
.
A.
6
V a
. B.
3
6
V a
. C.
2
6
V a
. D.
3
2
V a
.
Lời giải
Chọn B.
Ta có
3
.
. . . 3 . .2 6
ABCD A B C D ABCD
V A A S A A AB AD a a a a
.
Câu 19. Tiếp tuyến của đồ thị hàm số
3
3 2
y x x
tại điểm có hoành độ
0
2
x
có phương trình là
A.
9 22
y x
. B.
9 22
y x
. C.
9 14
y x
. D.
9 14
y x
.
Lời giải
Chọn D.
Ta có:
2
3 3
y x
.
Với
0 0
2 4
x y
.
Hệ số góc của tiếp tuyến tai điểm có hoành độ
0
2
x
là:
2 9
k y
.
Phương trình tiếp tuyến tại điểm có hoành độ
0
2
x
là:
9 2 4 9 14
y x x
.
Câu 20. Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như hình vẽ bên dưới.
Hàm số
y f x
đồng biến trên khoảng nào dưới đây?
A.
;0
. B.
0;1
. C.
1;0
. D.
0;
.
Lời giải
A
B
C
D
B
A
C
D
x
1
2
2
y
0
0
y
3
1
1
1
x
1
0
1
y
0
0
0
y
1
1
2
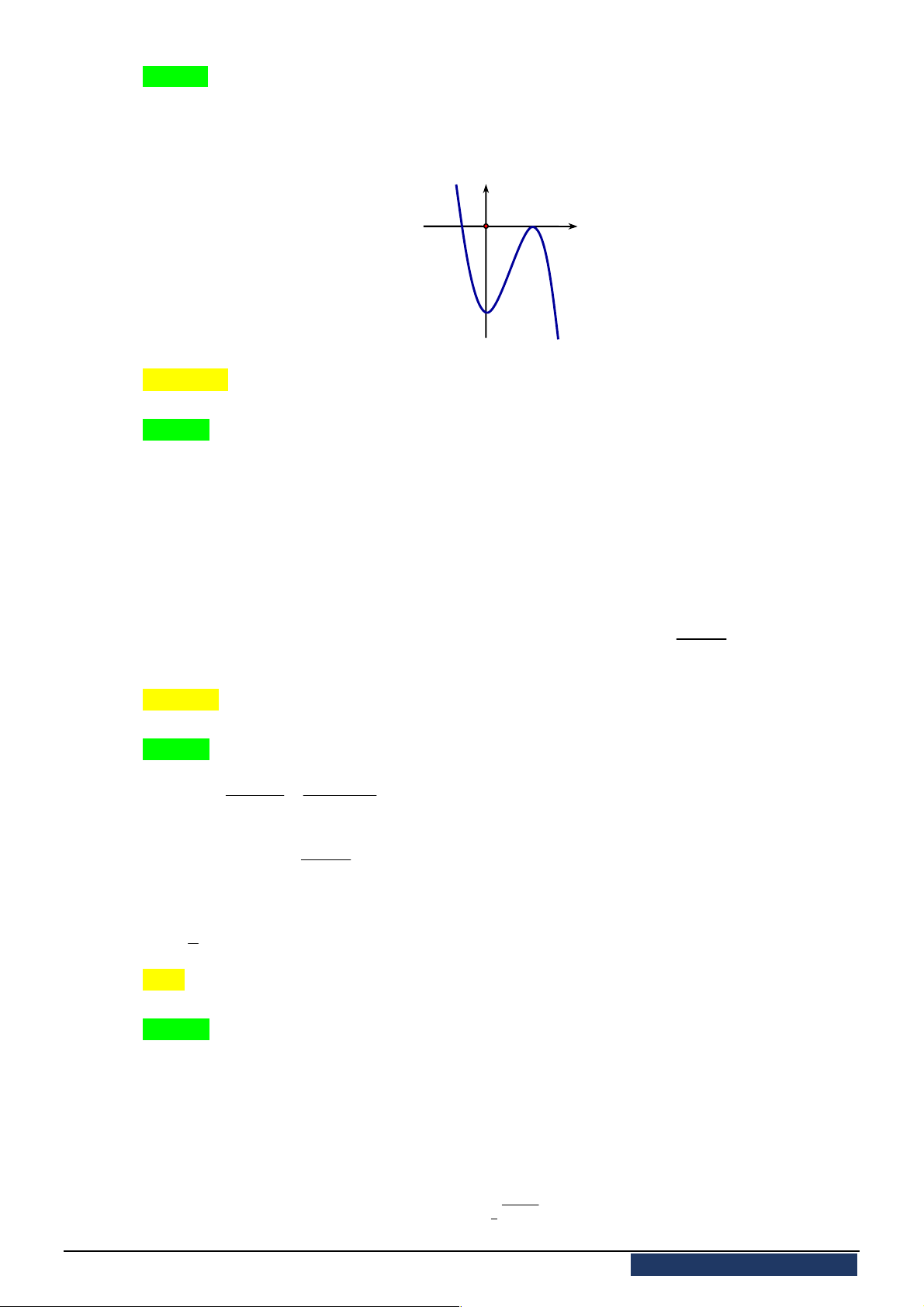
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/24 – HKI1819-001-SGD BẠC LIÊU
Chọn B.
Dựa vào bảng biến thiên hàm số
y f x
đồng biến
; 1
và
0;1
. Chỉ có đáp án B thỏa.
Câu 21. Tìm tất cả các giá trị của tham số
m
để phương trình
3 2
– 3 4 0
x x m
có nghiệm duy nhất
lớn hơn
2
. Biết rằng đồ thị của hàm số
3 2
3 – 4
y x x có hình vẽ như bên dưới.
A.
4
m
hoặc
20
m
. B.
4
m
.
C.
4
m
. D.
0
m
.
Lời giải
Chọn C.
Ta có
3 2 3 2
3 4 0 3 4 .
x x m x x m
Do đó, số nghiệm của phương trình
3 2
3 4 0
x x m
là số giao điểm giữa đồ thị
C
của
hàm số
3 2
3 4
y x x
và đường thẳng
y m
.
Chính vì vậy, để phương trình
3 2
3 4 0
x x m
có nghiệm duy nhất lớn hơn
2
thì
y m
phải cắt
C
tại một điểm duy nhất có hoành độ lớn hơn
2,
dựa vào đồ thị ta có
4.
m
Câu 22. Tìm tất cả các giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
1
x m
y
x
trên
2;4
bằng
2
.
A.
m
0. B.
2
m
. C.
2
m
. D.
4
m
.
Lời giải
Chọn A.
Ta có
2
2
2 2
1
1
0, 1
1 1
m
m
y x
x x
. Do đó trên
2;4
hàm số đã cho nghịch biến.
Vậy
2
2;4
2
max 2 2 0
2 1
m
y y m
.
Câu 23. Gọi
S
tập hợp tất cả các giá trị nguyên của tham số
m
để hàm số
3 2
1
– 2 3 2
3
y x mx m x m
nghịch biến trên
. Số phần tử của
S
là
A.
5
. B.
4
. C.
7
. D.
8
.
Lời giải
Chọn A.
2
2 2 3
y x mx m
Hàm số đã cho nghịch biến trên
2
2 3 0
0, 3 1
1 0
m m
y x m
/
Suy ra
3; 2; 1;0;1
S .
Câu 24. Với giá trị nào của
x
thì biểu thức
1
2
1
log
3
x
f x
x
có nghĩa?
O
x
y
1
2
4

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/24 – HKI1819-001-SGD BẠC LIÊU
A.
\ –3;1
x
. B.
3;1
x . C.
\ 3;1
x
. D.
3;1
x .
Lời giải
Chọn A.
Biểu thức
1
2
1
log
3
x
f x
x
có nghĩa khi
3
1
0
1
3
x
x
x
x
.
Câu 25. Đạo hàm của hàm số
x
y
là
A.
1
ln
x
y x
. B.
ln
x
y
. C.
.ln
x
y
. D.
1
.
x
y x
.
Lời giải
Chọn C.
Ta có:
.ln
x
y
.
Câu 26. Cho hình nón có đường sinh
5 cm
l
và bán kính đáy
4 cm
r
. Diện diện tích xung quan của
hình nón bằng
A.
2
20 cm
. B.
2
40 cm
. C.
2
40 cm
. D.
2
20 cm
.
Lời giải
Chọn D.
Có
2
20 cm
xp
S rl
.
Câu 27. Tổng các nghiệm của phương trình
2
log 5 – 2 2
x
x
bằng
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn C.
Điều kiện:
5 2 0.
x
2 2
2
4
log 5 2 2 5 2 2 5 2 2 5.2 4 0.
2
2 1 0
.
2
2 4
x x x x x x
x
x
x
x
x
tmdk
x
Vậy tổng các nghiệm của phương trình đã cho là bằng
2
.
Câu 28. Biết
log 3
a
b
với
a
,
b
là các số thực dương và
a
khác
1
. Tính giá trị của biểu thức
2
3 2 6
log log
a a
P b b
.
A.
63
P
. B.
45
P
. C.
21
P
. D.
99
P
.
Lời giải
Chọn D.
Ta có
2
2 2
3 2 6
log log 2.3log 3log 2.3.3 3.3 99
a
a a
a
P b b b b
.
Câu 29. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
và có
AB a
,
3
BC a
. Mặt
bên
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng
ABC
. Tính
theo
a
thể tích của khối chóp
.
S ABC
.
A.
3
6
6
a
V . B.
3
6
12
a
V . C.
3
2 6
3
a
V . D.
3
6
4
a
V .
Lời giải
Chọn B.
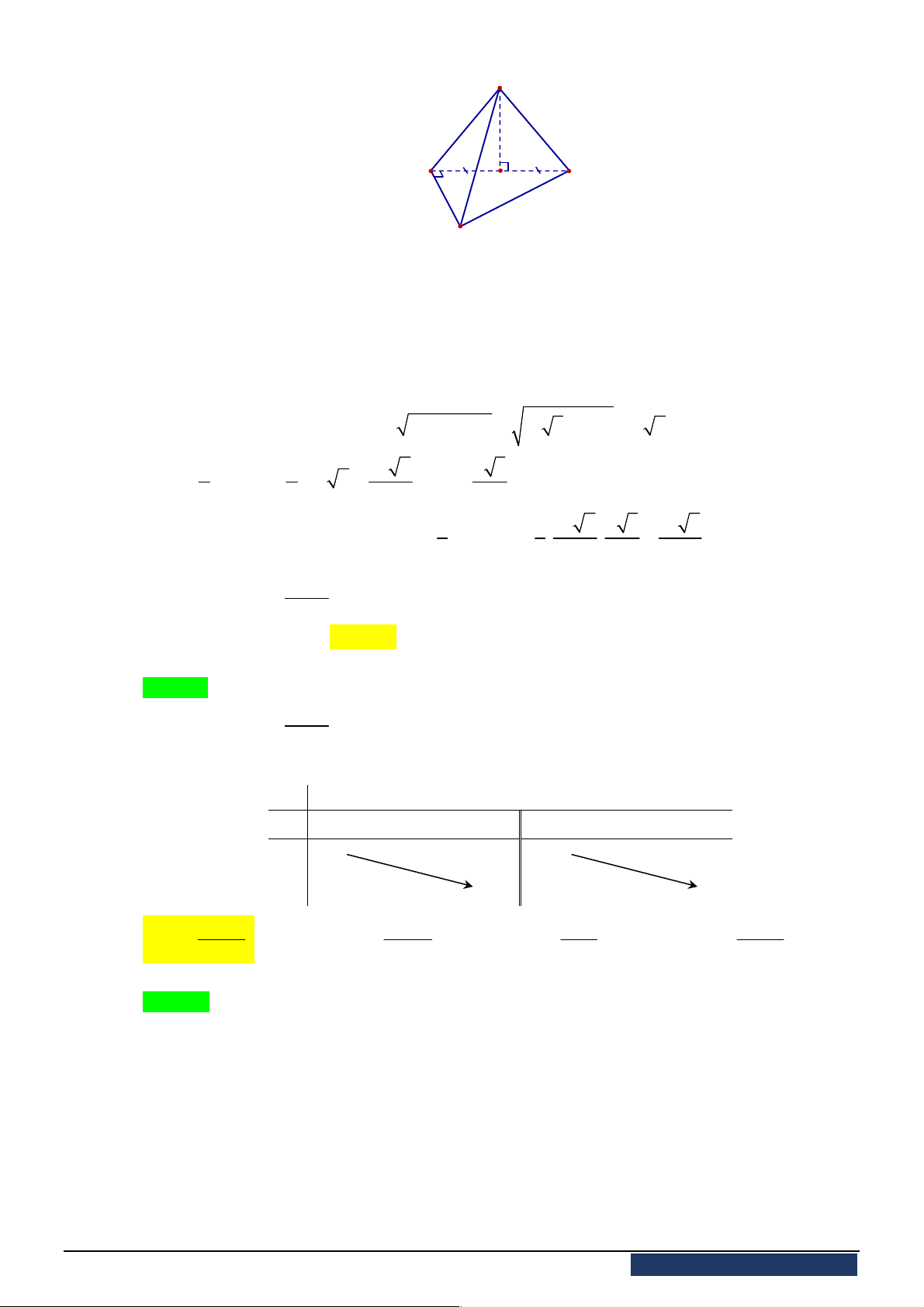
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/24 – HKI1819-001-SGD BẠC LIÊU
Gọi
H
là trung điểm của cạnh
AB
. Do
SAB
đều nên
SH AB
,
SAB ABC
SAB ABC AB SH ABC
SH SAB SH AB
Vậy
SH
là chiều cao của khối chóp
.
S ABC
.
ABC
vuông tại
A
, ta có:
2
2 2 2
3 2
AC BC AB a a a
2
1 1 2
. . . 2
2 2 2
ABC
a
S AB AC a a ,
3
2
a
SH
Thể tích khối chóp
.
S ABC
là:
2 3
.
1 1 2 3 6
. . . .
3 3 2 2 12
S ABC ABC
a a a
V S SH .
Câu 30. Đồ thị hàm số
2 1
1
x
y
x
có đường tiệm cận đứng là
A.
2
y
. B.
1
x
. C.
2
y
. D.
1
x
.
Lời giải
Chọn B.
Đồ thị hàm số
2 1
1
x
y
x
có đường tiệm cận đứng là
1
x
.
Câu 31. Bảng biến thiên ở hình vẽ bên dưới là của hàm số nào?
A.
3
1
x
y
x
. B.
2
1
x
y
x
. C.
3
1
x
y
x
. D.
3
1
x
y
x
.
Lời giải
Chọn A.
Từ bảng biến thiên ta thấy: Hàm số cần tìm phải nghịch biến trên mỗi khoảng xác định nên loại
đáp án B và D (do hai hàm số này đồng biến). Đồ thị hàm số cần tìm có tiệm cận ngang là
đường thẳng
1
y
nên loại đáp án C.
Câu 32. Một người gửi
100
triệu đồng vào một ngân hàng với lãi suất
0,65%
/tháng. Biết rằng nếu
không rút tiền khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu để
tính lãi cho tháng tiếp theo. Hỏi sau đúng
12
tháng, người đó được lĩnh số tiền (cả vốn ban đầu
và lãi) là bao nhiêu? Biết rằng trong khoảng thời gian này người đó không rút tiền ra và lãi suất
không thay đổi.
x
1
y
–
–
y
1
1
S
A
C
B
H
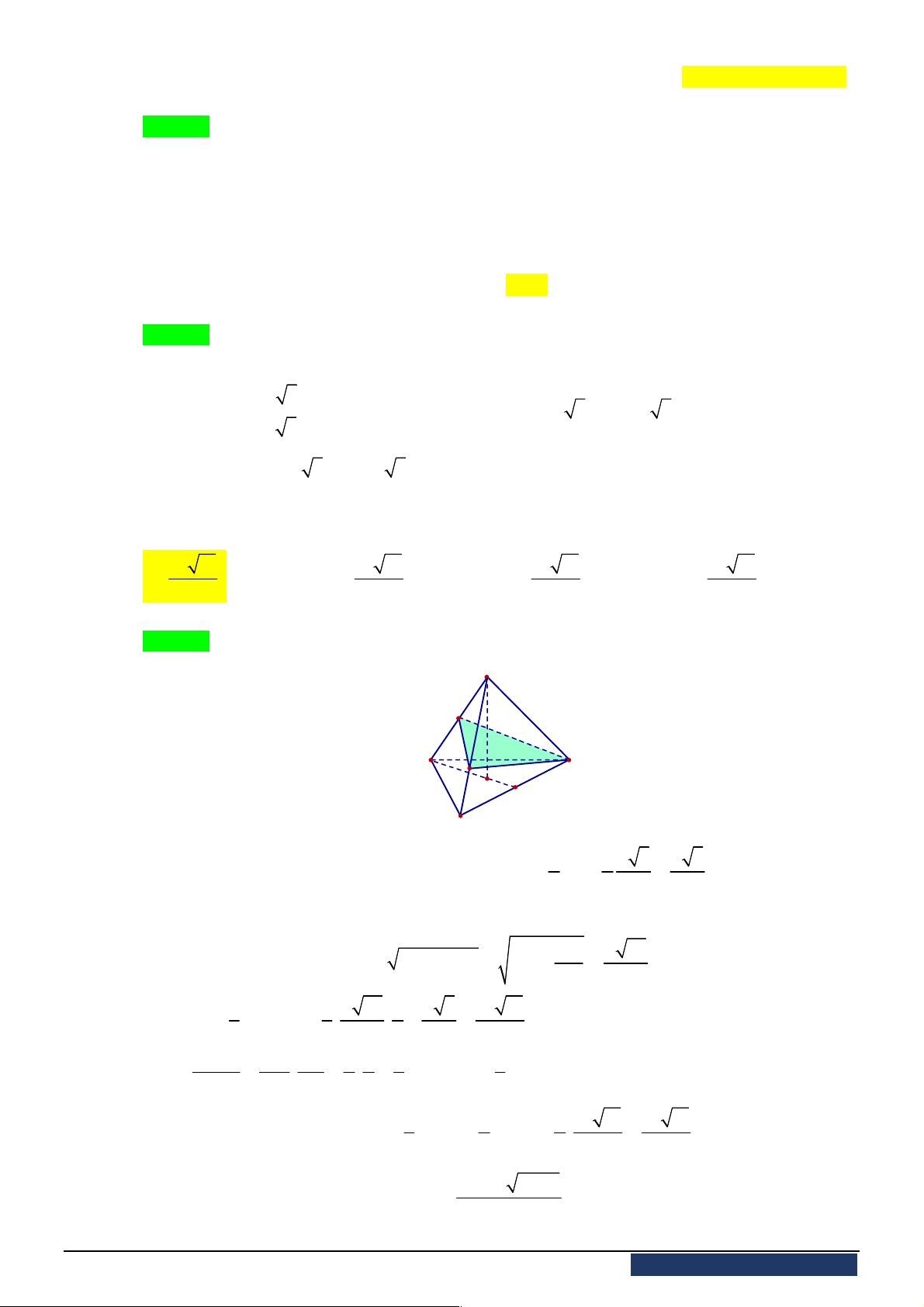
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/24 – HKI1819-001-SGD BẠC LIÊU
A.
108.085.000
đồng. B.
108.000.000
đồng. C.
108.084.980
đồng. D.
108.084.981
đồng.
Lời giải
Chọn D.
Sau
12
tháng, người đó lĩnh được số tiền (cả vốn lẫn lãi) là:
12
1 100 1 0,65% 108084981
n
T A r (đồng)
Câu 33. Biết hàm số
3 2
3 6
y x x x
đạt cực trị tại hai điểm
1
x
,
2
x
. Khi đó, giá trị của biểu thức
2 2
1 2
x x
bằng
A.
8
. B.
10
. C.
8
. D.
10
.
Lời giải
Chọn C.
3 2 2
3 6 3 6 6
y x x x y x x
1
2
1 3
0
1 3
x x
y
x x
, hàm số đạt cực trị tại
1 2
1 3; 1 3
x x
Khi đó
2 2
2 2
1 2
1 3 1 3 8
x x
.
Câu 34. Cho khối chóp đều
.
S ABC
có cạnh đáy bằng
a
, cạnh bên bằng
2
a
. Gọi
M
là trung điểm
SB
,
N
là điểm trên đoạn
SC
sao cho
2
NS NC
. Thể tích của khối chóp
.
A BCNM
bằng
A.
3
11
18
a
. B.
3
11
24
a
. C.
3
11
36
a
. D.
3
11
16
a
.
Lời giải
Chọn A.
Gọi
O
là trọng tâm của tam giác
ABC
. Khi đó
2 2 3 3
3 3 2 3
a a
BO BI .
Khối chóp
.
S ABC
đều và
O
là trọng tâm tam giác
ABC
lên
SO ABC SO OB
SOB
vuông tại
O
2
2 2 2
3 33
4
9 3
a a
SO SB OB a .
3
.
1 1 33 1 3 11
. . . .
3 3 3 2 2 12
S ABC ABC
a a a
V SO S a .
Ta có
.
. .
.
1 2 1 1
. .
2 3 3 3
S AMN
S AMN S ABC
S ABC
V
SM SN
V V
V SB SC
.
3 3
. . . . . .
1 2 2 11 11
.
3 3 3 12 18
A BCNM S ABC S AMN S ABC S ABC S ABC
a a
V V V V V V .
Câu 35. Số đường tiệm cận của đồ thị hàm số
2
1 3 1
3 2
x x
y
x x
là
S
B
C
A
M
N
G
I
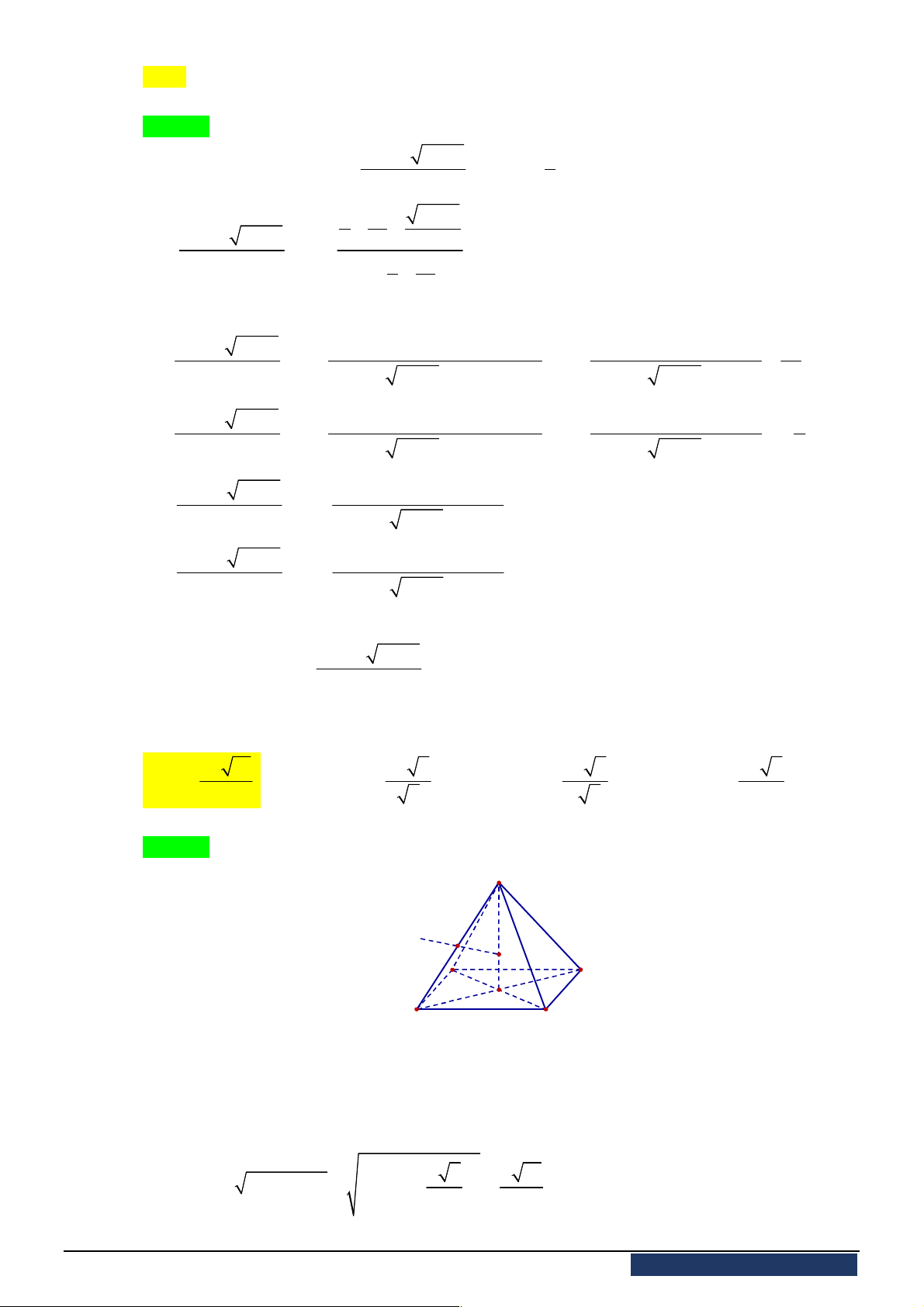
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/24 – HKI1819-001-SGD BẠC LIÊU
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Chọn A.
Tập xác định của hàm số
2
1 3 1
3 2
x x
y
x x
là
1
;1 1;2 2; .
3
D
2 2
2
2
1 1 3 1
1 3 1
lim lim 0
3 2
3 2
1
x x
x
x x
x x x
x x
x x
đường thẳng
0
y
là tiệm cận ngang của đồ thị hàm số.
2
2
2
1 1 1
1 3 1
1 3 1 1
lim lim lim
3 2 4
1 3 1 3 2 1 3 1 2
x x x
x x
x x x
x x
x x x x x x x
2
2
2
1 1 1
1 3 1
1 3 1 1
lim lim lim
3 2 4
1 3 1 3 2 1 3 1 2
x x x
x x
x x x
x x
x x x x x x x
.
2
2 2
2
2 2
1 3 1
lim lim
3 2
1 3 1 2
1 3 1
lim lim
3 2
1 3 1 2
x x
x x
x x x
x x
x x x
x x x
x x
x x x
đường thẳng
2
x
là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số
2
1 3 1
3 2
x x
y
x x
có
2
đường tiệm cận.
Câu 36. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên
bằng
2
a
.
A.
2 14
7
a
R . B.
2 7
2
a
R . C.
2 7
3 2
a
R . D.
2 2
7
a
R .
Lời giải
Chọn A.
Gọi
.
S ABCD
là hình chóp tứ giác đều thỏa mãn đầu bài. Gọi
O
là tâm của đáy,
M
là trung
điểm của
SA
. Khi đó
SO
là trục của đường tròn ngoại tiếp hình vuông
ABCD
.
Trong mặt phẳng
SAC
, gọi
là đường trung trực của cạnh
SA
và
I SO
thì
I
là tâm mặt cầu ngoại tiếp hình chóp
.
S ABCD
.
Ta có
2
2
2 2
2 14
2
2 2
a a
SO SA AO a
.
S
A
B
C
D
O
M
I
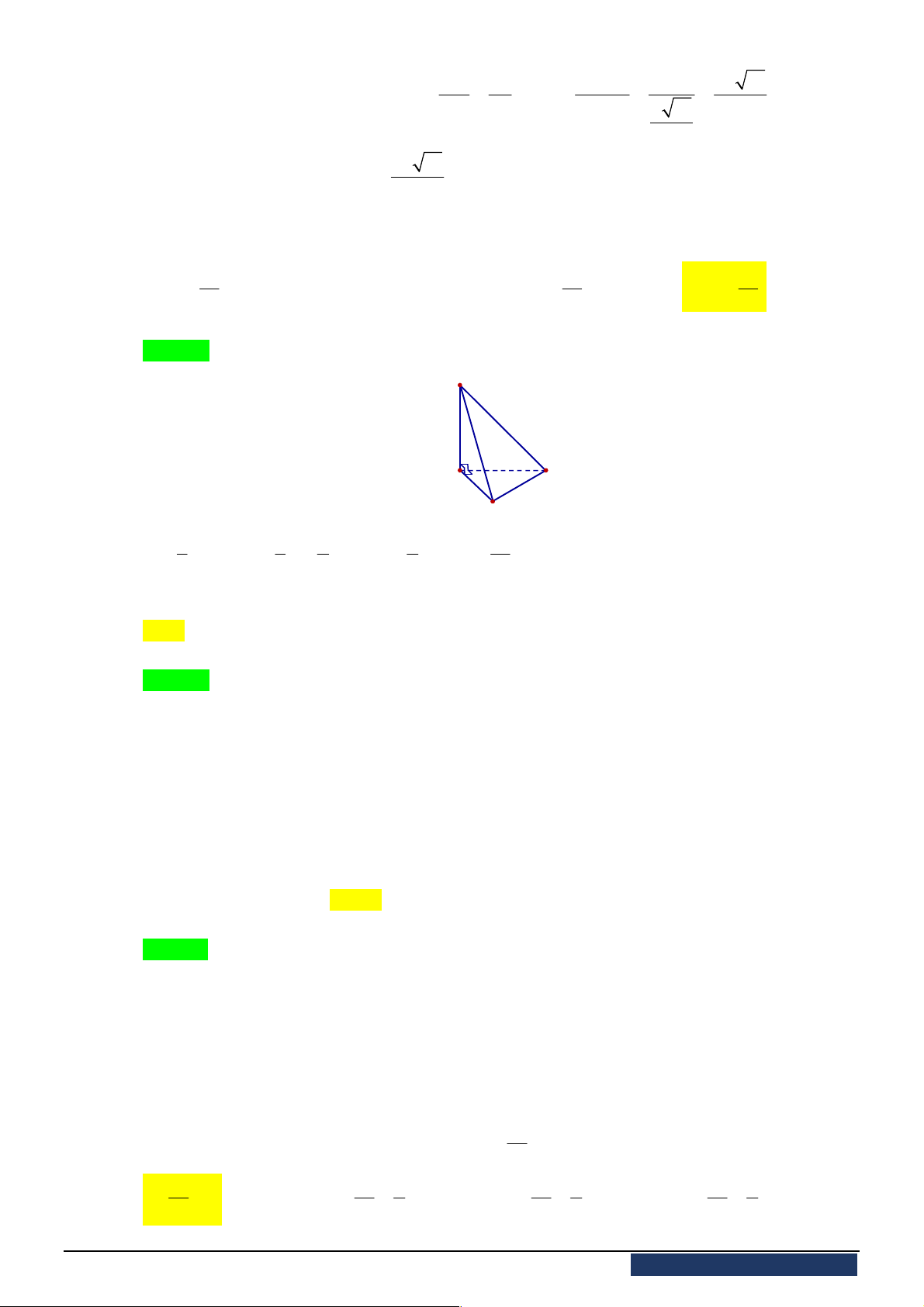
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/24 – HKI1819-001-SGD BẠC LIÊU
Ta có
SMI
và
SOA
đồng dạng nên
. .2 2 14
7
14
2
SM SI SM SA a a a
SI
SO SA SO
a
.
Bán kính mặt cầu ngoại tiếp
2 14
7
a
R .
Câu 37. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
,
SA
vuông góc với mặt đáy và
SA AB a
,
2
AC a
. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
4
a
V . B.
3
V a
. C.
3
2
a
V . D.
3
3
a
V .
Lời giải
Chọn D.
1
. .
3
ABC
V SA S
1 1
. . .
3 2
SA AB AC
1
. . .2
6
a a a
3
3
a
.
Câu 38. Số giao điểm của đồ thị hàm số
3
4
y x x
với đường thẳng
4
y
là
A.
3
. B.
1
. C.
0
. D.
2
.
Lời giải
Chọn A.
Phương trình hoành độ giao điểm:
3
4 4
x x
1
3 2
1
1 0 1 0 0
1
x
x x x x x
x
Vậy đồ thị hàm số
3
4
y x x
và đường thẳng
4
y
cắt nhau tại
3
điểm
Câu 39. Tổng lập phương các nghiệm thực của phương trình
2
4 5
3 9
x x
bằng
A.
27
. B.
28
. C.
26
. D.
25
.
Lời giải
Chọn B.
Ta có:
2 2
4 5 4 5 2 2 2
1
3 9 3 3 4 5 2 4 3 0
3
x x x x
x
x x x x
x
Suy ra tổng lập phương các nghiệm thực của phương trình là:
3 3
1 3 28
S
,
Câu 40. Cho tam giác
ABC
vuông tại
A
có
2
BC a
và
30
B
. Quay tam giác vuông này quanh
trục
AB
, ta được một hình nón đỉnh
B
. Gọi
1
S
là diện tích toàn phần của hình nón đó và
2
S
là
diện tích mặt cầu có đường kính
AB
. Tính tỉ số
2
1
S
S
.
A.
2
1
1
S
S
. B.
2
1
2
3
S
S
. C.
2
1
3
2
S
S
. D.
2
1
1
2
S
S
.
S
A
C
B
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/24 – HKI1819-001-SGD BẠC LIÊU
Lời giải
Chọn A.
Ta có:
3 1
2 , .cos30 2 . 3 , .sin30 2 .
2 2
BC a l BA BC a a h AC BC a a r
Diện tích toàn phần của hình nón là:
2 2 2
1
. . . . .2 3
S r l r a a a a
,
Diện tích mặt cầu là:
2
2
2
2
3
4 . 4 . 3
2 2
AB
S a a
. Suy ra:
1
2
1.
S
S
Câu 41. Tổng tất cả các giá trị nguyên âm của tham số
m
để hàm số
3
2
3
28
y x mx
x
, đồng biến trên
khoảng
0;
bằng
A.
15
. B.
6
. C.
3
. D.
10
.
Lời giải
Chọn C.
Xét hàm số
3
2
3
28
y x mx
x
trên khoảng
0;
, ta có:
3
2
3
3
14
y x m
x
.
Hàm số đã cho đồng biến trên khoảng
0;
2
3
3
3 0,
14
y x m
x
0;x
(dấu
“=” xảy ra tại hữu hạn điểm trên
0;
).
2
3
3
3
14
m x
x
,
0;x
; dấu “=” xảy ra tại hữu hạn điểm trên
0;
.
*
Xét hàm số
3
2
3
3 , 0;
14
f x x x
x
, có:
4 4
5
9 9 84
6
14 14
x
f x x
x x
,
5
3
0
28
f x x
.
Ta có:
0
lim , lim
x
x
f x f x
.
Bảng biến thiên:
x
0
5
3
28
f x
0
f x
5
15 21952
28 27
B
C
D
A
O
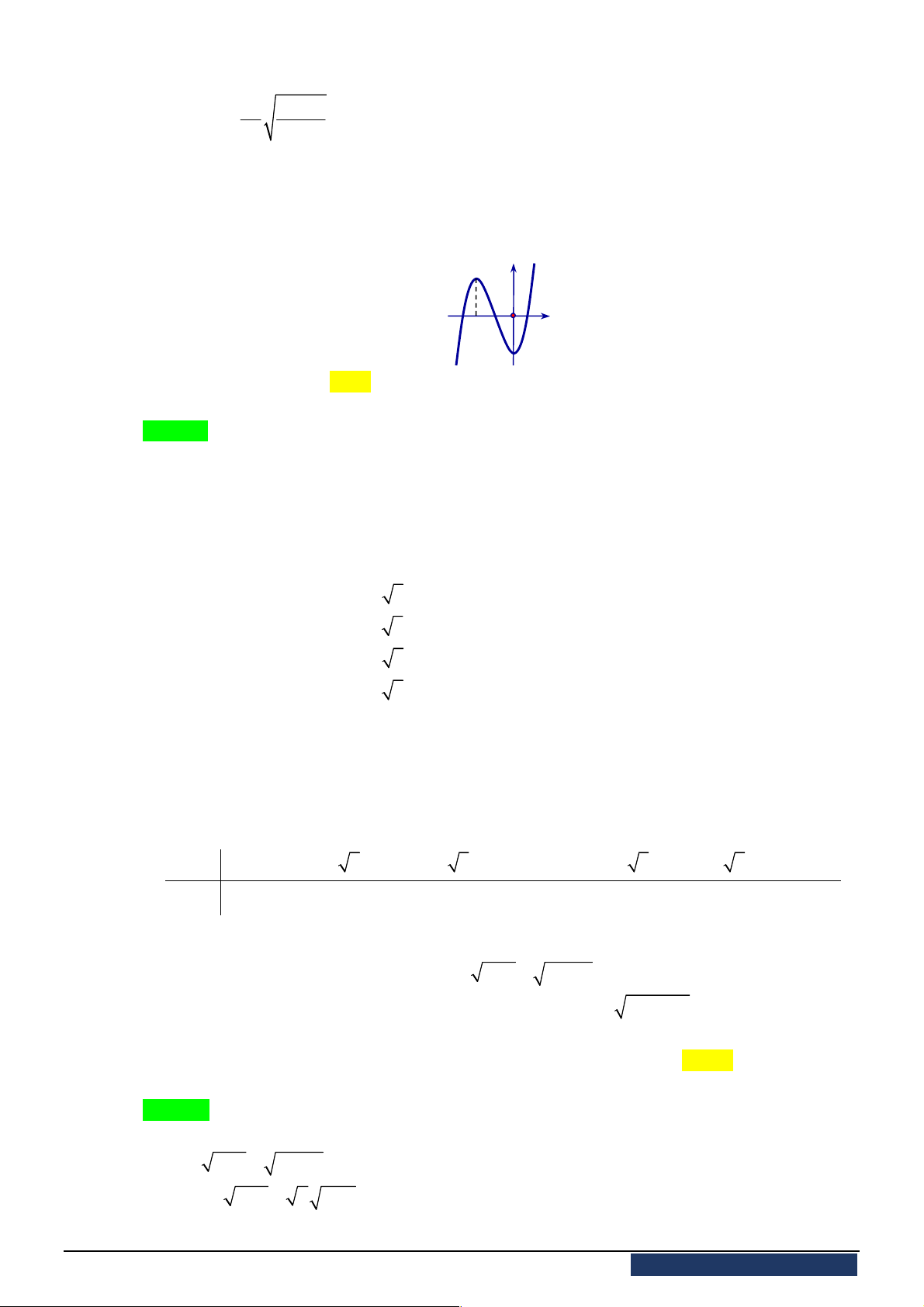
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/24 – HKI1819-001-SGD BẠC LIÊU
Dựa vào bảng biến thiên ta có:
5
15 21952
*
28 27
m . Mà
m
là số nguyên âm
2; 1
m
.
Tổng tất cả các giá trị nguyên âm của tham số
m
thỏa mãn yêu cầu đề bài là:
2 1 3
.
Câu 42. Cho hàm số
y f x
xác định và liên tục trên
có đồ thị như hình vẽ. Hàm số
2
2 4
g x f x x
có bao nhiêu điểm cực tiểu?
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn B.
Ta có:
2
2 1 2 4
g x x f x x
.
2
2
1
0 1 2 4 0
2 4 0
x
g x x f x x
f x x
2
2
1
1 3
1
2 4 2 1 3
2 4 0
1 5
1 5
x
x
x
x x x
x x
x
x
(Tất cả đều là nghiệm bội lẻ).
Ta chọn
2
x
để xét dấu của
g x
:
2 2. 3 . 4
g f
.
Vì hàm số
y f x
đồng biến trên khoảng
0;
do đó:
4 0
f
.
Suy ra:
2 0
g
.
Theo tính chất qua nghiệm bội lẻ
g x
đổi dấu, ta có bảng xét dấy
g x
như sau:
x
1 5
1 3
1
1 3
1 5
g x
0
0
0
0
0
Từ bảng xét dấu, suy ra hàm số
y g x
có 3 điểm cực tiểu.
Câu 43. Cho
x
,
y
là các số thực thỏa mãn
1 2 2
x y x y
. Gọi
M
,
m
lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của
2 2
2 1 1 8 4
P x y x y x y
. Khi đó, giá trị của
M m
bằng
A.
42
. B.
44
. C.
41
. D.
43
.
Lời giải
Chọn D.
Ta có
1 2 2
x y x y
1 2 1
x y x y
2
x
y
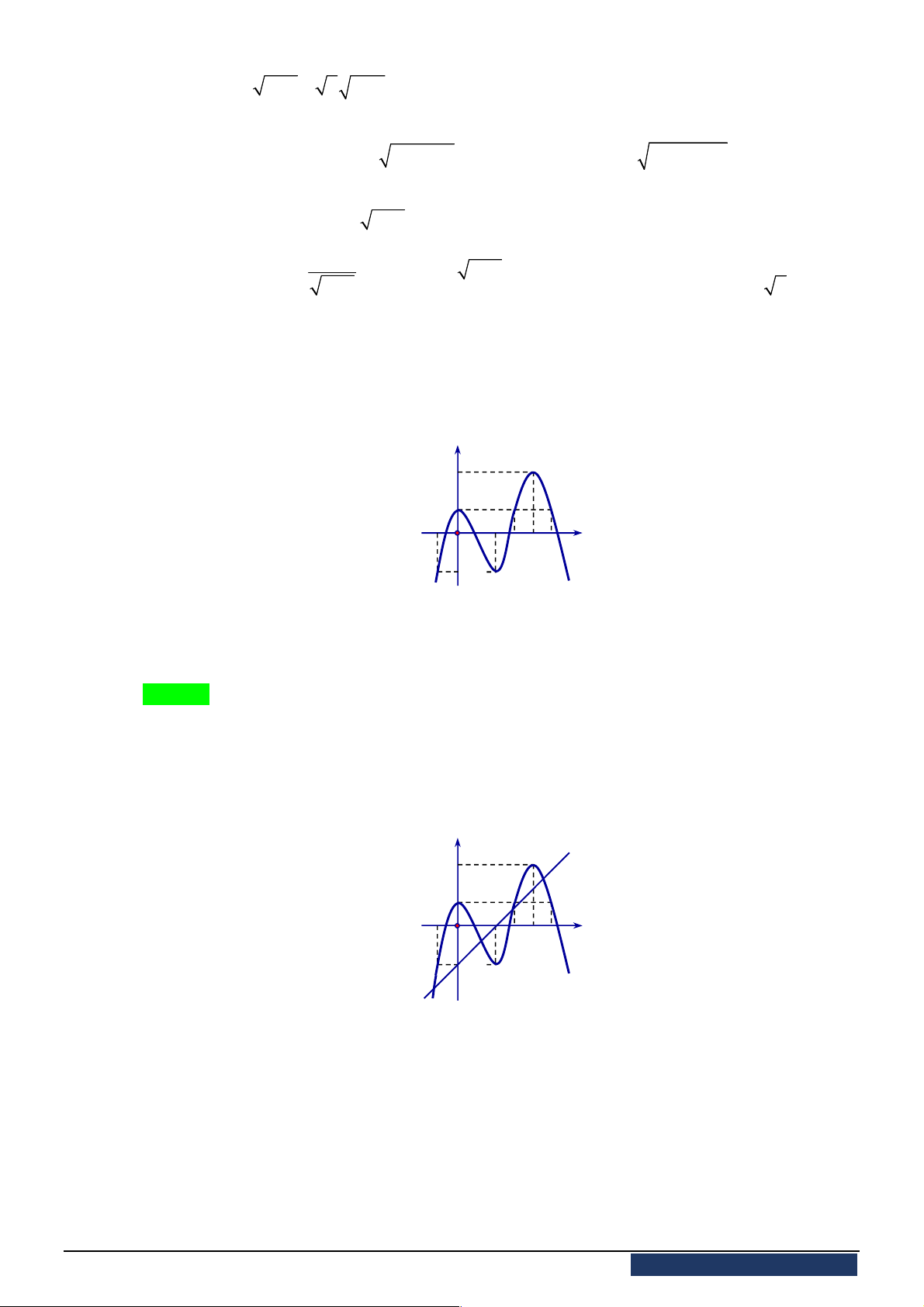
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/24 – HKI1819-001-SGD BẠC LIÊU
2
2
1 2 1 1 2 ( )
x y x y x y B TCauchy ShwĐ
art
0 3
x y
2
2 2
2 1 1 8 4 2 8 4 2
P x y x y x y x y x y x y
Đặt
t x y
,
0 3
t
.
Xét hàm số
2
2 8 4 2
f t t t t
,
0;3
t .
Ta có
3 2
0
4
2 2 0 1 4 2 2 7 0
4
1 2 2 ( )
t
f t t t t t t t
t
t L
Ta tính
0 18, 3 25
f f
.
Suy ra
min 0 18
P f m
và
max 3 25
P f M
.
Vậy
18 25 43
M m
.
Câu 44. Cho hàm số
y f x
có đồ thị hàm số
y f x
được cho như hình vẽ.
Hàm số
2
2 2
g x f x x
nghịch biến trên khoảng nào?
A.
0;2
. B.
3;1
. C.
2;3
. D.
1;0
.
Lời giải
Chọn D.
Ta có
Ta có
2
2 2
g x f x x
, suy ra
2 2 2
g x f x x
0 2 0 2 2 2
g x f x x f x x
Đặt
2
u x
ta có
2
f u u
.
Xét sự tương giao của hai hàm
y f u
và
2
y u
Ta có để hàm
g x
nghịch biến thì
0
g x
hay
2
f x x
Tức đồ thị hàm số
y f u
nằm dưới đồ thị hàm số
: 2
d y u
Nhận thấy
1;0
x thỏa mãn.
x
y
1
1
2
O
3
4
5
3
2
x
y
1
1
2
O
3
4
5
3
2
d
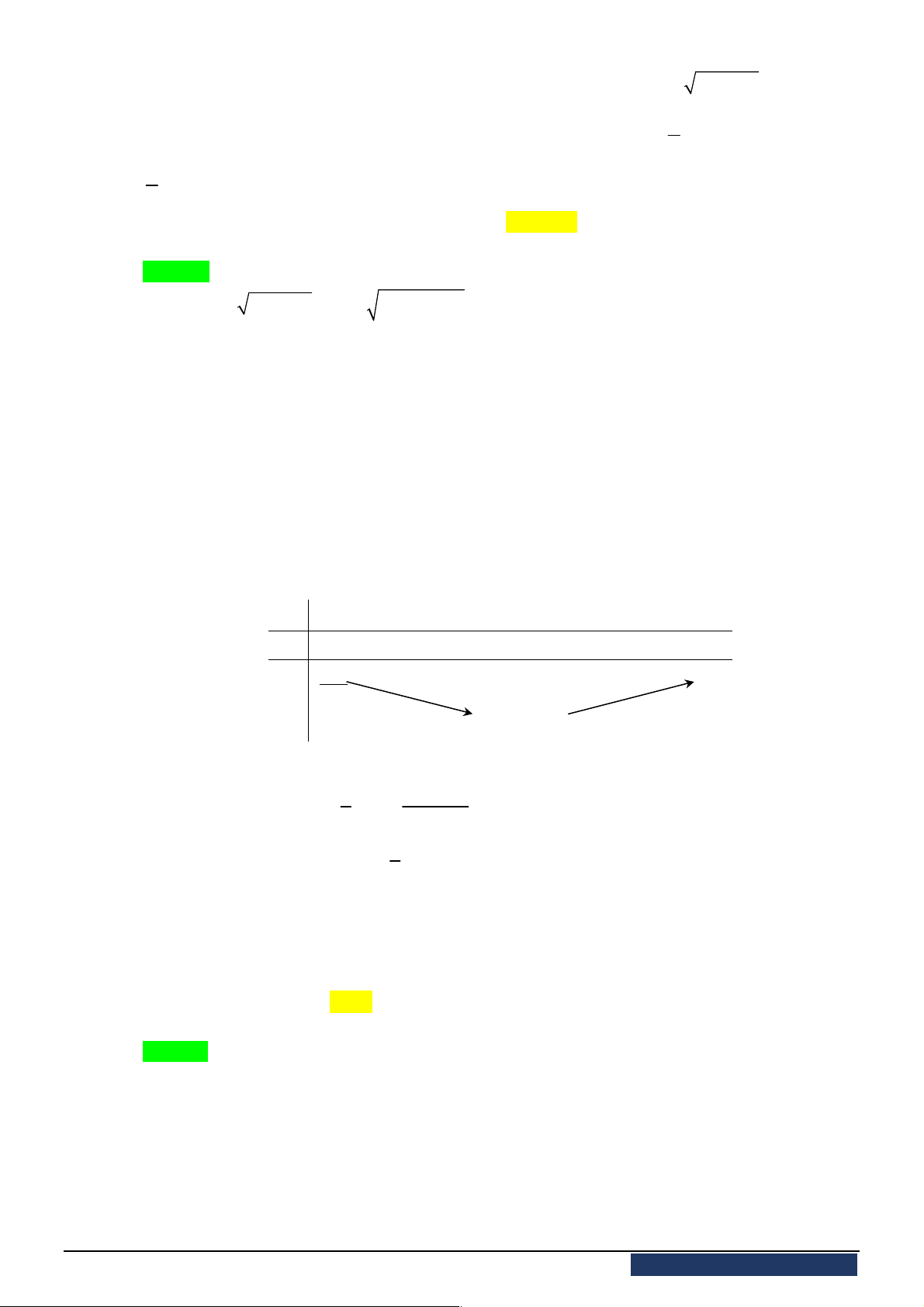
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/24 – HKI1819-001-SGD BẠC LIÊU
Câu 45. Cho hàm số
4 7
3 1 .2 – 6 3
x x
f x x x
, khi phương trình
2
7 4 6 9 3 1 0
f x x m
có số nghiệm nhiều nhất thì giá trị nhỏ nhất của tham số
m
có dạng
a
b
(trong đó
a
,
b
và
a
b
là phân số tối giản). Tính
T a b
.
A.
7
T
. B.
11
T
. C.
8
T
. D.
13
T
.
Lời giải
Chọn C.
Đặt
2
2
7 4 6 9 7 4 1 3 1 3;7 .
t x x x Khi đó
1 3 .
f t m
Xét hàm số
4 7
3 1 2 6 3
t t
f t t t
trên đoạn
3;7 .
Ta có
4 7 7
3 ln3 2 1 2 ln2 6;
t t t
f t t
2 2
4 7 7 7
3 ln3 2 ln 2 2 ln 2 1 2 ln 2
t t t t
f t t
2
4 7
0, 3;7
3 ln3 2 1 ln2 2 ln 2 0.
t t
t
t
Suy ra hàm số
f t
đồng biến trên
3;7 .
Lại có
3 0
0
7 0
f
f x
f
có nghiệm duy nhất
0
t
thuộc
3;7 .
Dựa vào BBT, ta thấy phương trình
1 3
f t m
có số nghiệm nhiều nhất
0
0
1
5
1 3 4 .
3 3
f t
f t m m
Suy ra giá trị nhỏ nhất của
m
là
5
5
3
3
a
b
nên
8
a b
.
Câu 46. Cho hàm số
3 2
3 1
y x x
có đồ thị
C
và điểm
1;
A m
. Gọi
S
là tập hợp tất cả các giá trị
nguyên của tham số
m
để qua
A
có thể kể được đúng ba tiếp tuyến tới đồ thị
C
. Số phần tử
của
S
là
A.
9
. B.
7
. C.
3
. D.
5
Lời giải
Chọn B.
Gọi
k
là hệ số góc của đường thẳng
d
qua
A
.
Ta có phương trình của
d
có dạng:
y kx m k
.
d
tiếp xúc
C
hệ sau có nghiệm:
3
3 2
2
2
2 6 1 *
3 1
3 6
3 6
m x x
kx m k x x
k x x
k x x
t
3
0
t
7
f
0
f
148
3
0
f t
4
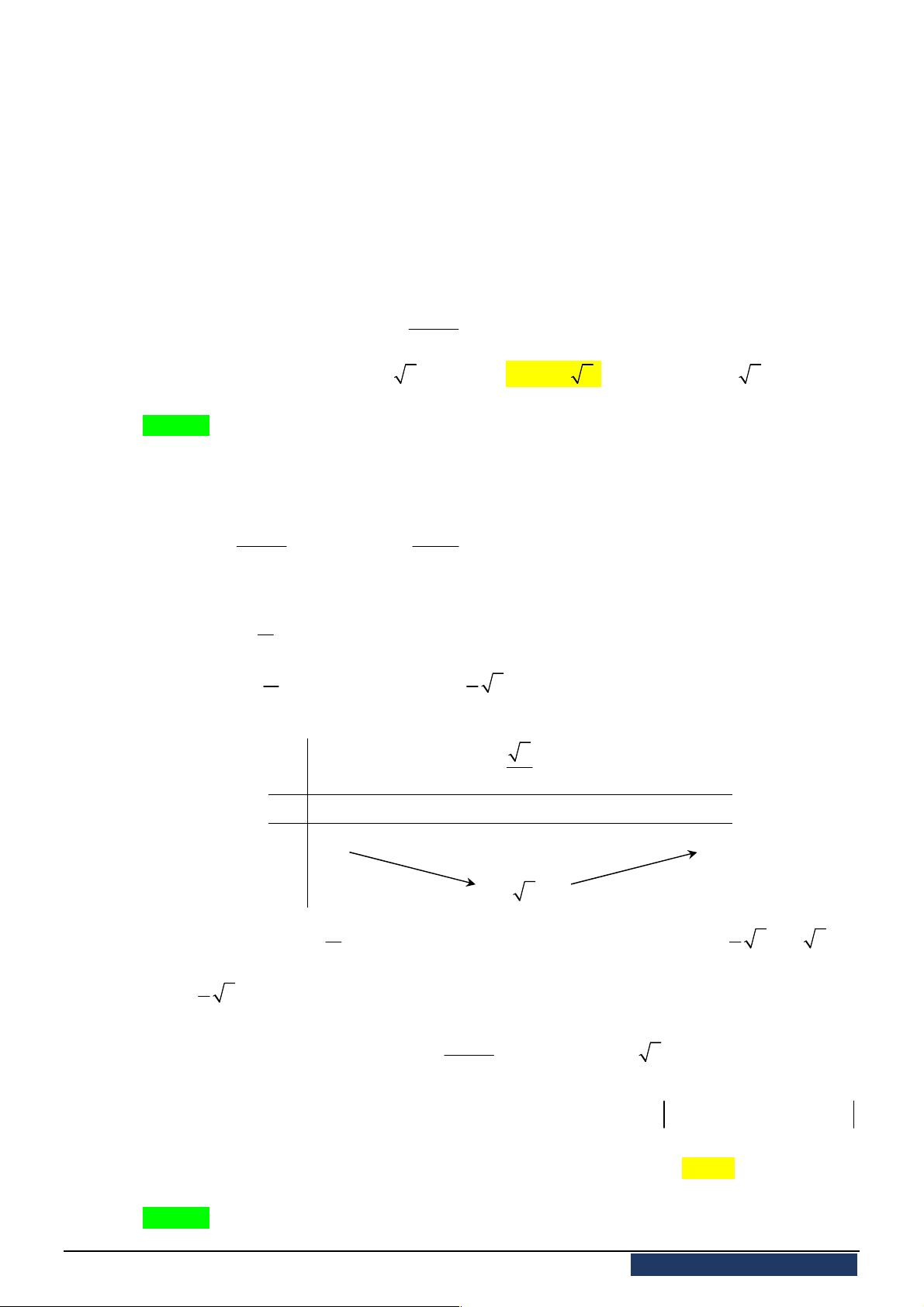
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/24 – HKI1819-001-SGD BẠC LIÊU
Để qua
A
có thể được đúng 3 tiếp tuyến tới
C
thì phương trình (*) phải có 3 nghiệm phân
biệt
C
CT
Đ
y m y
với
3
2 6 1
f x x x
.
Ta có
2
6 6; 0 1
f x x f x x
.
1 5 ; 1 3
C
CĐ
T
f f f f
.
Suy ra
3 5
m
.
Vậy số phần tử của
S
là
7
.
Câu 47. Cho hai số thực
1
a
,
1
b
. Biết phương trình
2
1
1
x x
a b
có hai nghiệm phân biệt
1
x
,
2
x
. Tìm
giá trị nhỏ nhất của biểu thức
2
1 2
1 2
1 2
4
x x
P x x
x x
.
A.
4
P
. B.
3
3 2
P
. C.
3
3 4
P
. D.
3
4
P
.
Lời giải
Chọn C.
Ta có
2
1
. 1
x x
a b
2
1
log . log 1
x x
b b
a b
2
log . 1 0
b
x a x
.
Khi đó, phương trình có hai nghiệm phân biệt
1
x
,
2
x
thì
1 2
log
b
x x a
và
1 2
1
x x
.
Do đó
2
1 2
1 2
2
1 2
1
4 4log
log
b
b
x x
P x x a
x x a
.
Đặt
log
b
t a
với
0
t
.
2
1
4
P f t t
t
với
0
t
.
Ta có
3
2
4
f t
t
nên
3
1
0 4
2
f t t
.
Lập bảng biến thiên
ta suy ra hàm số
2
1
4
f t t
t
đạt giá trị nhỏ nhất trên khoảng
0;
là
3 3
1
4 3 4
2
f
khi
tại
3
1
4
2
t
Vậy giá trị nhỏ nhất của biểu thức
2
1 2
1 2
1 2
4
x x
P x x
x x
là
3
3 4
.
Câu 48. Tổng tất cả các giá trị nguyên của tham số
m
để đồ thị hàm số
4 3 2
3 8 6 – 24
y x x x x m
có
7
điểm cực trị là
A.
63
. B.
55
. C.
30
. D.
42
.
Lời giải
Chọn D.
t
0
3
4
2
f
0
f
0
3
3 4
0
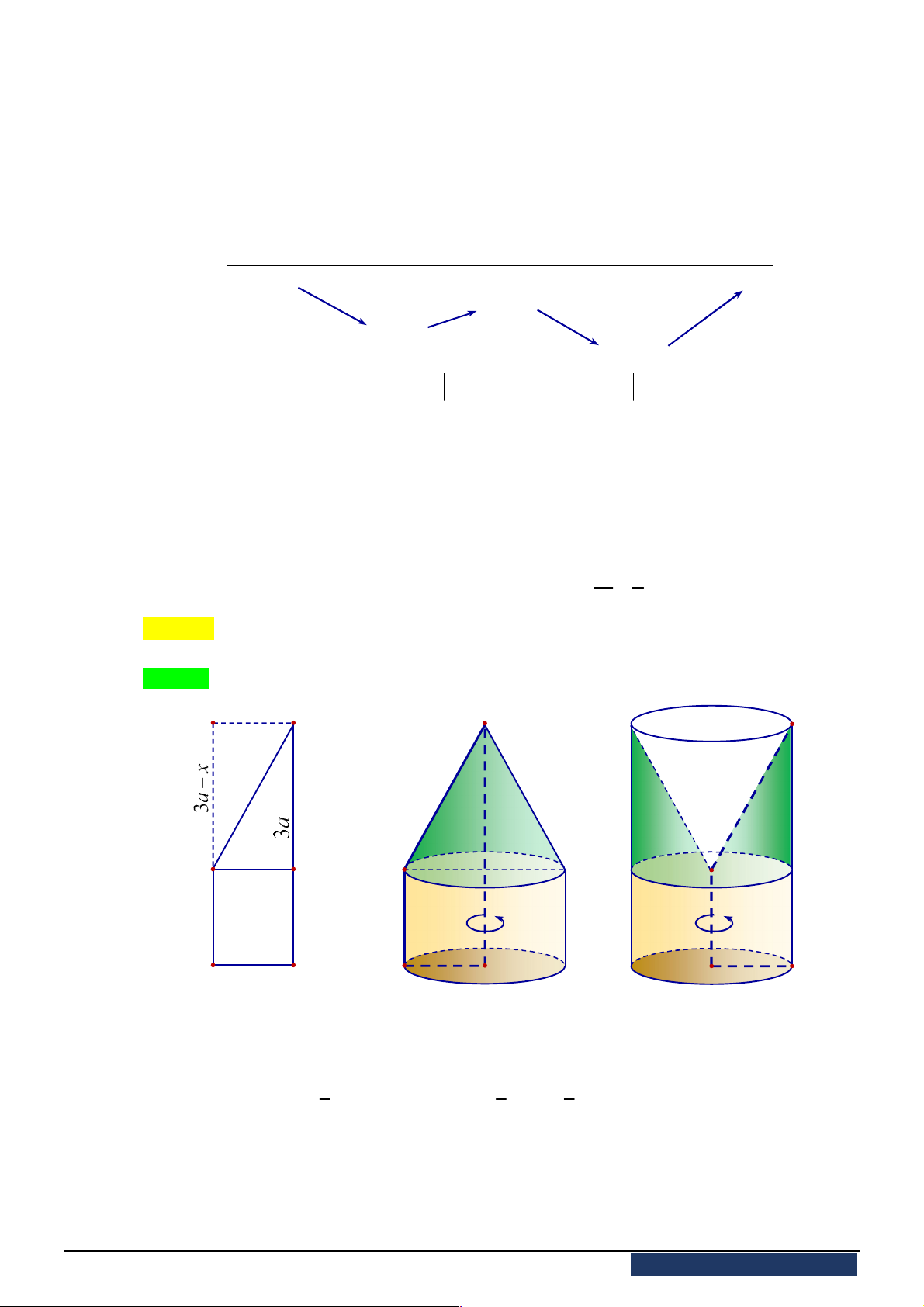
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 23/24 – HKI1819-001-SGD BẠC LIÊU
Xét hàm số
4 3 2
3 8 6 24
y x x x x m
.
3 2
12 24 12 24
y x x x
;
1
0 1
2
x
y x
x
.
Bảng biến thiên:
Từ bảng biến thiến, ta thấy hàm số
4 3 2
3 8 6 24
y x x x x m
có
7
điểm cực trị khi và chỉ
khi:
8 0
8 13
13 0
m
m
m
.
Do
9;10;11;12
m m
9 10 11 12 42
.
Câu 49. Cho hình thang
ABCD
vuông tại
A
và
B
có
AB a
,
3
AD a
và
BC x
với
0 3
x a
.
Gọi
1
V
,
2
V
, lần lượt là thể tích các khối tròn xoay tạo thành khi quay hình thang
ABCD
(kể cả
các điểm trong) quanh đường thẳng
BC
và
AD
. Tìm
x
để
1
2
7
5
V
V
.
A.
x a
. B.
2
x a
. C.
3
x a
. D.
4
x a
.
Lời giải
Chọn A.
Dựng các điểm
E
,
F
để có các hình chữ nhật
ABED
và
ABCF
như hình vẽ.
Khi quay hình thang
ABCD
(kể các điểm trong) quanh đường thẳng
BC
ta được khối tròn
xoay có thể tích là
3 2
1 3 4
1
3π π 3
3
V V V a a x a
3 2
1
2
π π
3
a xa
2
1
π 6
3
a a x
.
Trong đó,
3
V
là thể tích khối trụ tròn xoay có bán kính đáy bằng
a
, chiều cao bằng
3
a
;
4
V
là thể tích khối nón tròn xoay có bán kính đáy bằng
a
, chiều cao bằng
3
a x
.
Khi quay hình thang
ABCD
(kể các điểm trong) quanh đường thẳng
AD
ta được khối tròn
xoay có thể tích là
x
2
1
1
y
0
0
0
y
13
m
8
m
19
m
B
A
C
D
B
A
C
D
B
B
A
C
D
F
E
a
a
a
x
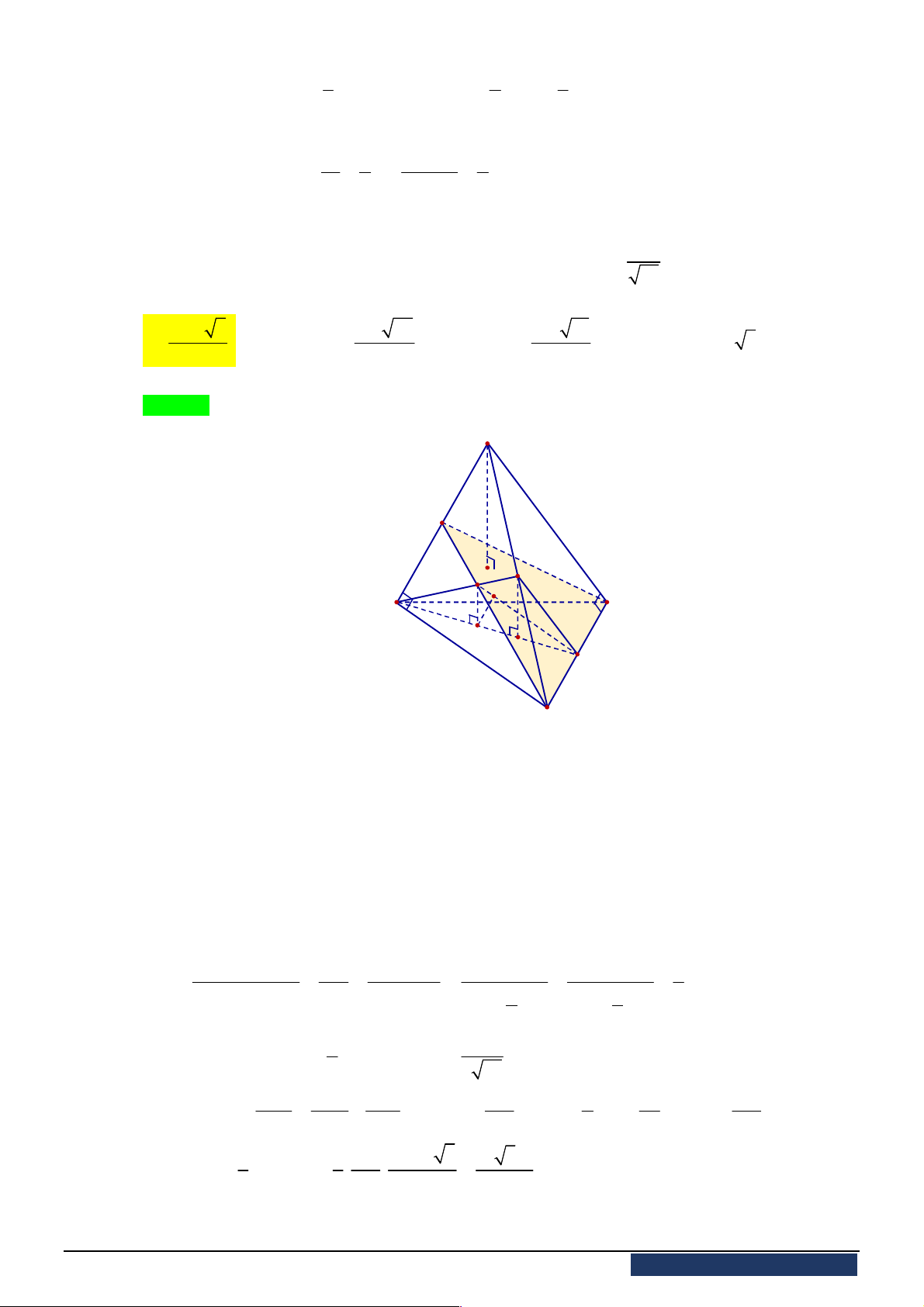
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 24/24 – HKI1819-001-SGD BẠC LIÊU
2 2
2 5 4
1
π π 3
3
V V V a x a x a
3 2
2
π π
3
a xa
2
1
π 3 2
3
a a x
.
Trong đó,
5
V
là thể tích khối trụ tròn xoay có bán kính đáy bằng
a
, chiều cao bằng
x
.
Theo giả thiết ta có:
1
2
7
5
V
V
6 7
3 2 5
a x
a x
x a
.
Câu 50. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
2
a
. Gọi
M
là trung điểm cạnh
SA
,
90
SAB SCB
, biết khoảng cách từ
A
đến
MBC
bằng
6
21
a
. Thể tích của khối chóp
.
S ABC
bằng
A.
3
10 3
9
a
. B.
3
8 39
3
a
. C.
3
4 13
3
a
. D.
3
2 3
a .
Lời giải
Chọn A.
Vì
90
SAB SCB
, , ,
S A B C
cùng thuộc mặt cầu đường kính
SB
.
Gọi
D
là trung điểm
BC
,
I
là trung điểm
SB
và
O
là tâm đường tròn ngoại tiếp
ABC
, ta có
OI ABC
.
Gọi
H
là điểm đối xứng với
B
qua
O
SH ABC
(vì
OI
là đường trung bình
SHB
).
Gọi
BM AI J
, ta có
J
trọng tâm
SAB
.
Trong
AID
, kẻ
//
JN IO
. Khi đó, vì
BC JND
nên
JND MBC
.
Kẻ
NE JD
, ta có
NE MBC
. Do đó
;
d N MBC NE
.
Ta có
,
,
d A MBC
AD AD
ND AD AN
d N MBC
9
2 4
5
3 9
AD AD
AD AO AD AD
.
Suy ra,
5 10
, ,
9
3 21
a
d N MBC d A MBC
.
Xét
JND
có
2 2 2
1 1 1
NE ND NJ
nên
10
9
a
NJ
3 5
2 3
a
OI NJ
10
3
a
SH .
Vậy
2
3
2 3
1 1 10 10 3
. . .
3 3 3 4 9
SABC ABC
a
a a
V SH S .
----------HẾT----------
S
M
A
B
C
O
N
J
H
I
E
D
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/24 - Mã đề thi 640
0SỞ GIÁO DỤC VÀ ĐÀO TẠO BẠC
LIÊU
ĐỀ CHÍNH THỨC
(Đề thi gồm 06 trang)
KIỂM TRA HỌC KỲ I NĂM HỌC: 2017-2018
Môn kiểm tra: TOÁN 12
Thời gian làm bài 90 phút, không kể thời gian phát đề
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 640
Câu 1. [2H1-1] Số mặt phẳng đối xứng của hình chóp đều
.
S ABC
là
A.
4
. B.
2
. C.
6
. D.
3
.
Câu 2. [2D2-1] Cho
a
là số thực dương khác
1
. Hình nào sau đây là đồ thị của hàm số mũ
x
y a
?
A.
x
y
1
1
O
B.
x
y
1
1
O
C.
x
y
1
1
O
D.
x
y
1
1
O
Câu 3. [2H2-1] Khối cầu
S
có bán kính bằng
r
và thể tích bằng
V
. Mệnh đề nào dưới đây đúng?
A.
3
4
3
V r
. B.
2 2
4
3
V r
. C.
2 3
4
3
V r
. D.
4
3
V r
.
Câu 4. [2D2-2] Cho
3
log 6
x
. Tính
3
3
log
K x
.
A.
4
K
. B.
8
K
. C.
2
K
. D.
3
K
.
Câu 5. [2H1-2] Cho khối chóp
.
S ABCD
có đáy là hình chữ nhật
AB a
,
2
BC a
,
SA
vuông góc
với đáy và
SC
tạo với mặt phẳng
SAB
một góc bằng
60
. Tính thể tích
V
của khối chóp đã
cho.
A.
3
6
3
a
V . B.
3
2
V a
. C.
3
2
3
a
V . D.
3
2 3
9
a
V .
Câu 6. [2H2-2] Cho tứ diện
ABCD
có tam giác
BCD
vuông tại
B
,
AC
vuông góc với mặt phẳng
BCD
,
5
AC a
,
3
BC a
và
4
BD a
. Tính bán kính
R
của mặt cầu ngoại tiếp tứ
diện
ABCD
.
A.
5 3
2
a
R . B.
5 2
3
a
R . C.
5 3
3
a
R . D.
5 2
2
a
R .
Câu 7. [2D1-2] Đồ thị hàm số
3 2
3 9 1
y x x x
có hai cực trị
A
và
B
. Điểm nào dưới đây thuộc
đường thẳng
AB
?
A.
0;2
N . B.
1;1
P . C.
1; 8
Q
. D.
0; 1
M
.
Câu 8. [2D1-1] Cho hàm số
y f x
có bảng biến thiên như hình bên dưới. Tìm giá trị cực đại và
giá trị cực tiểu của hàm số đã cho.
A.
3
CĐ
y
và
0
CT
y
. B.
2
CĐ
y
và
2
CT
y
.
C.
2
CĐ
y
và
2
CT
y
. D.
0
CĐ
y
và
3
CT
y
.
x
0
3
y
0
0
y
2
2
4
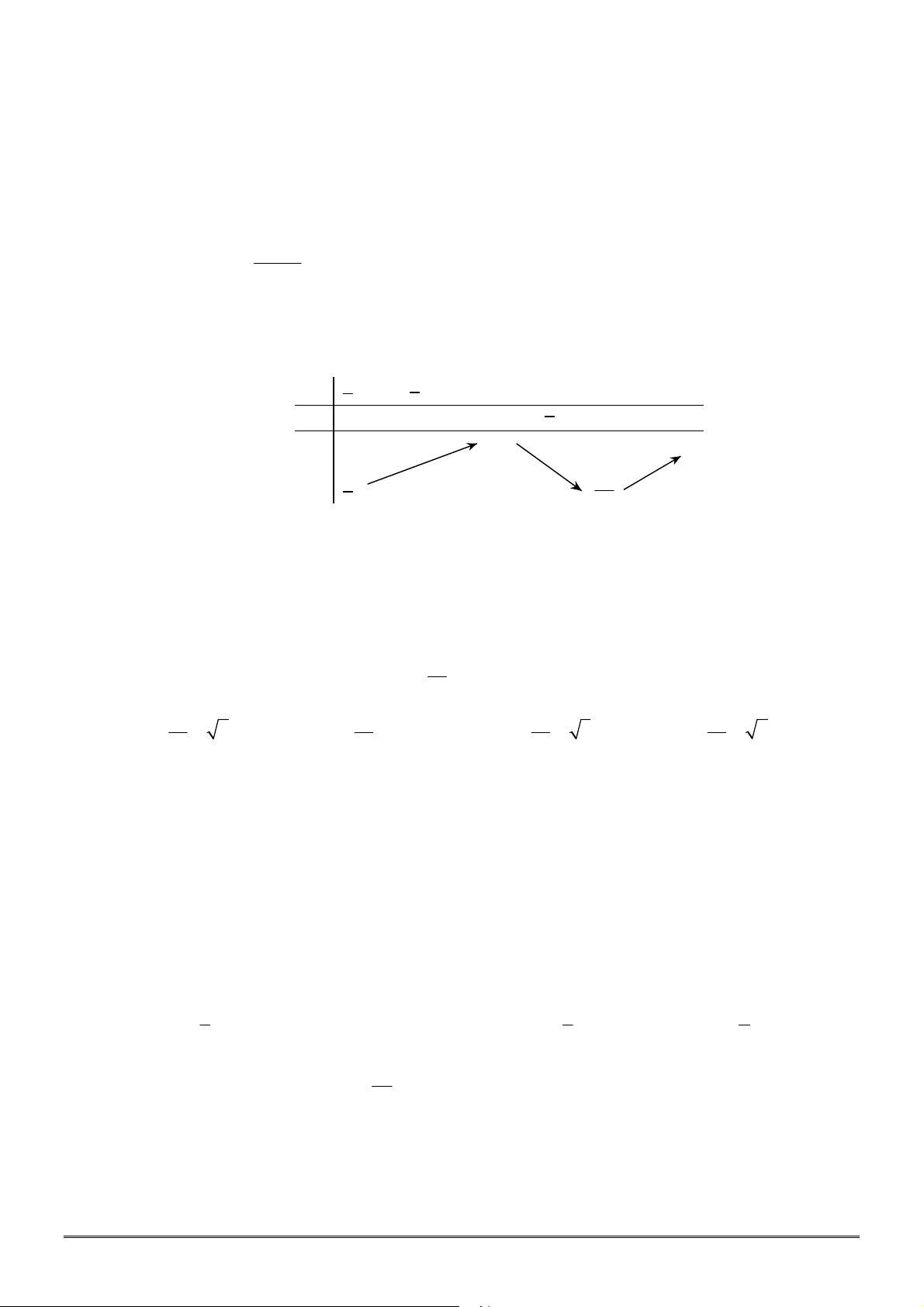
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/24 - Mã đề thi 640
Câu 9. [2H1-2] Cho hình chóp
.
S ABC
có
6
AB
,
8
BC
,
10
AC
. Cạnh bên
SA
vuông góc với
đáy và
4
SA
. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
40
V
. B.
32
V
. C.
192
V
. D.
24
V
.
Câu 10. [2D2-1] Cho
a
là số thực dương khác
1
. Mệnh đề nào dưới đây đúng với mọi số thực dương
x
,
y
?
A.
log log .log
a a a
xy x y
. B.
log log log
a a a
xy x y
.
C.
log
log
log
a
a
a
x
xy
y
. D.
log log log
a a a
xy x y
.
Câu 11. [2D1-1] Cho hàm số
y f x
liên tục trên
, bảng biến thiên như sau.Kết luận nào sau đây
đúng.
A. Hàm số có ba điểm cực trị. B. Hàm số có hai điểm cực trị.
C. hàm số đạt cực tiểu tại
1
x
. D. Hàm số đạt cực đại tại
2
x
.
Câu 12. [2H2-4] Cho
S
là một mặt cầu cố định có bán kính
R
. Một hình trụ
H
thay đổi nhưng
luôn có hai đường tròn đáy nằm trên
S
. Gọi
1
V
là thể tích của khối cầu
S
và
2
V
là thể tích
lớn nhất của khối trụ
H
. Tính tỉ số
1
2
V
V
.
A.
1
2
6
V
V
. B.
1
2
2
V
V
. C.
1
2
3
V
V
. D.
1
2
2
V
V
Câu 13. [2H2-2] Cho hình nón tròn xoay có đường sinh bằng
13
(cm), bán kính đường tròn đáy bằng
5
(cm). Thể tích của khối nón tròn xoay là
A.
200
(
3
cm
). B.
150
(
3
cm
). C.
100
(
3
cm
). D.
300
(
3
cm
).
Câu 14. [2D1-2] Cho hàm số
2
1 2
y x x
có đồ thị
C
. Mệnh đề nào dưới đây đúng?
A.
C
không cắt trục hoành. B.
C
cắt trục hoành tại một điểm.
C.
C
cắt trục hoành tại ba điểm. D.
C
cắt trục hoành tại hai điểm.
Câu 15. [2H1-1] Thể tích
V
của một khối lăng trụ có diện tích đáy bằng
B
và chiều cao bằng
h
là
A.
2
1
3
V B h
. B.
V Bh
. C.
1
3
V Bh
. D.
1
2
V Bh
.
Câu 16. [2D2-2] Phương trình
3 4
1
2
32
x
có nghiệm là
A.
3
x
. B.
2
x
. C.
2
x
. D.
3
x
.
Câu 17. [2D2-1] Tập xác định của hàm số
2
log 10 2
y x
là
A.
;2
. B.
5;
. C.
;10
. D.
;5
.
y
y'
x
+++
+
2
2
1
00
1 +
0
19
12

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/24 - Mã đề thi 640
Câu 18. [2D1-3] Gọi
S
là tổng tất cả các giá trị nguyên dương của tham số
m
sao cho hàm số
2
2
4
x m
y
x m
đồng biến trên khoảng
2021;
. Khi đó, giá trị của
S
bằng
A.
2035144
. B.
2035145
. C.
2035146
. D.
2035143
.
Câu 19. [2D1-2] Cho hàm số
4 2
2
y x x
. Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
1;1
. B. Hàm số nghịch biến trên khoảng
; 2
.
C. Hàm số đồng biến trên khoảng
1;1
. D. Hàm số đồng biến trên khoảng
; 2
.
Câu 20. [2H2-1] Cho mặt cầu
S
có tâm
O
, bán kính
r
. Mặt phẳng
cắt mặt cầu
S
theo giao
tuyến là đường tròn
C
có bán kính
R
. Kết luận nào sau đây sai?
A.
2 2
,R r d O
.
B.
,
d O r
.
C. Diện tích của mặt cầu là
2
4
S r
.
D. Đường tròn lớn của mặt cầu có bán kính bằng bán kính mặt cầu.
Câu 21. [2D2-2] Với
a
,
b
,
x
là các số thực dương thỏa mãn
5 5 5
log 4log 3log
x a b
, mệnh đề nào
dưới đây là đúng?
A.
3 4
x a b
. B.
4 3
x a b
. C.
4 3
x a b
. D.
4 3
x a b
.
Câu 22. [2H2-1] Một hình trụ có khoảng cách giữa hai đáy, độ dài đường sinh và bán kính đường tròn
đáy lần lượt bằng
h
,
l
,
r
. Khi đó công thức tính diện tích toàn phần của hình trụ là
A.
2
tp
S r l r
. B.
2 2
tp
S r l r
. C.
tp
S r l r
. D.
2
tp
S r l r
.
Câu 23. [2H2-1] Cho hình nón tròn xoay. Một mặt phẳng
P
đi qua đỉnh
O
của hình nón và cắt
đường tròn đáy của hình nón tại hai điểm. Thiết diện được tạo thành là
A. Một tứ giác. B. Một hình thang cân. C. Một ngũ giác. D. Một tam giác cân.
Câu 24. [2D2-1] Cho
với ,
. Mệnh đề nào dưới đây đúng?
A.
. B.
. C.
. D.
.
Câu 25. [2H1-1] Khối đa diện nào sau đây có công thức thể tích là
1
3
V Bh
? Biết hình đa diện đó có
diện tích đáy bằng
B
và chiều cao bằng
h
?
A. Khối chóp. B. Khối hộp chữ nhật. C. Khối hộp. D. Khối lăng trụ.
Câu 26. [2D1-2] Đồ thị
2
2
4
x
y
x
có bao nhiêu tiệm cận?
A. 2. B. 4. C. 3. D. 1.
Câu 27. [2D2-1] Cho
4
số thực
a
,
b
,
x
,
y
với
a
,
b
là các số dương và khác
1
. Mệnh đề nào dưới
đây đúng? A.
x
x y
y
a
a
a
. B.
y
x x y
a a
. C.
.
.
x y x y
a a a
D.
. .
x
x
a b a b
.
Câu 28. [2D1-3] Hai thành phố A và B ngăn cách nhau bởi một còn sông. Người ta cần xây cây cầu
bắc qua sông và vuông góc với bờ sông. Biết rằng thành phố A cách bờ sông 2 (km), thành phố
B cách bờ sông 5 (km ), khoảng cách giữa đường thẳng đi qua A và đường thẳng đi qua B cùng
vuông góc với bờ sông là 12 (km). Giả sử hai bờ sông là hai đường thẳng song song với nhau.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/24 - Mã đề thi 640
Nhằm tiết kiệm chi phí đi từ thành phố A đến thành phố B, người ta xây cây cầu ở vị trí MN để
quãng đường đi từ thành phố A đến thành phố B là ngắn nhất (hình vẽ). Khi đó, độ dài
đoạn
AM
là
sông
2 km
5 km
12 km
A
M
B
N
A.
2 193
km.
7
AM B.
3 193
km.
7
AM C.
193 km.
AM D.
193
km.
7
AM
Câu 29. [2D1-1] Đạo hàm của hàm số
5 2017
x
y là
A.
5
5ln5
x
y
. B.
5 .ln5
x
y
. C.
5
ln5
x
y
D.
5
x
y
.
Câu 30. [1H3-3] Cho khối chóp
.
S ABCD
có đáy là hình vuông,
SAB
đều và nằm trong mặt phẳng
vuông góc với mặt đáy. Mặt cầu ngoại tiếp khối chóp
.
S ABCD
có diện tích
2
84 cm
. Khoảng
cách giữa hai đường thẳng
SA
và
BD
là
A.
3 21
cm
7
. B.
2 21
cm
7
. C.
21
cm
7
. D.
6 21
cm
7
.
Câu 31. [2D2-2] Tìm tập xác định
D
của hàm số
3
2
2
y x x
.
A.
0;D
. B.
; 2 1;D
.
C.
\ 2;1
D
. D.
D
.
Câu 32. [2D1-2] Tìm các giá trị của tham số
m
để hàm số
3
2 2
3 2 3
3
x
y x m x m
đồng biến trên
.
A.
3
3
m
m
. B.
3 3
m
. C.
3 3
m
. D.
3
3
m
m
.
Câu 33. [2D2-1] Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. Với
0 1
a
, hàm số
log
a
y x
là một hàm nghịch biến trên khoảng
0;
.
B. Với
1
a
, hàm số
log
a
y x
là một hàm đồng biến trên khoảng
;
.
C. Với
1
a
, hàm số
x
y a
là một hàm đồng biến trên khoảng
;
.
D. Với
0 1
a
, hàm số
x
y a
là một hàm nghịch biến trên khoảng
;
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/24 - Mã đề thi 640
Câu 34. [2D2-4] Xét các số thực dương
x
,
y
thỏa mãn
3
1
log 3 3 4
3
y
xy x y
x xy
. Tìm giá trị nhỏ
nhất
min
P
của
P x y
.
A.
min
4 3 4
3
P
. B.
min
4 3 4
3
P
. C.
min
4 3 4
9
P
. D.
min
4 3 4
9
P
.
Câu 35. [2D1-1] Hình vẽ sau đây là đồ thị của hàm số nào?
x
y
1
1
1
1
O
A.
2
1
x
y
x
. B.
3
1
x
y
x
. C.
2 1
2 1
x
y
x
. D.
1
1
x
y
x
.
Câu 36. [2D2-2] Tính đạo hàm của hàm số
log 2 1
y x
.
A.
2
2x 1 ln10
y
. B.
2
2x 1
y
. C.
1
2x 1 ln10
y
. D.
1
2x 1
y
.
Câu 37. [2H1-1] Mỗi cạnh của một hình đa diện là cạnh chung của đúng
n
mặt của hình đa diện đó.
Mệnh đề nào dưới đây đúng?
A.
2
n
. B.
5
n
. C.
3
n
. D.
4
n
.
Câu 38. [2D1-1] Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau
x
2
0
2
y
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
;2
. B. Hàm số nghịch biến trên khoảng
; 2
.
C. Hàm số nghịch biến trên khoảng
;0
. D. Hàm số nghịch biến trên khoảng
2;0
.
Câu 39. [2D1-1] Hình vẽ sau đây là đồ thị của hàm số nào?
A.
4 2
2
y x x
. B.
4 2
3 1
y x x
. C.
4 2
4
y x x
. D.
4 2
3
y x x
.
Câu 40. [2D1-2] Cho hàm số
2
,
8
x m
f x
x
với
m
là tham số. Giá trị lớn nhất của
m
để
0;3
min 2
f x
là:
x
y
4
22
O
2
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/24 - Mã đề thi 640
A.
5
m
. B.
6
m
. C.
4
m
. D.
3
m
.
Câu 41. [2D2-2] Tìm giá trị thực của tham số
m
để phương trình
1
9 2.3 0
x x
m
có hai nghiệm
thực
1
x
,
2
x
thỏa mãn
1 2
0
x x
.
A.
6
m
. B.
0
m
. C.
3
m
. D.
1
m
.
Câu 42. [2D1-2] Giá trị lớn nhất của hàm số
4
2
x
y
x
trên đoạn
3;4
.
A.
4
. B.
10
. C.
7
. D.
8
.
Câu 43. [2D1-2] Tìm giá trị thực của tham số
m
để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực tiểu
tại
3
x
.
A.
1
m
. B.
1
m
. C.
5
m
. D.
7
m
.
Câu 44. [2H1-3] Cho khối lăng trụ đứng .
ABC A B C
có đáy là tam giác cân
ABC
với
AB AC a
,
120
BAC
, mặt phẳng
AB C
tạo với đáy một góc
30
. Tính thể tích
V
của khối lăng trụ
đã cho.
A.
3
6
a
V . B.
3
8
a
V . C.
3
3
8
a
V . D.
3
9
8
a
V .
Câu 45. [2H1-2] Cho khối lăng trụ đứng .
ABC A B C
có
AA a
, đáy
ABC
là tam giác vuông cân tại
A
và
2
BC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
V a
. B.
3
2
a
V . C.
3
6
a
V . D.
3
3
a
V .
Câu 46. [2H2-1] Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật
ABCD
có
AB
và
CD
thuộc hai đáy của hình trụ,
4
AB a
,
5
AC a
. Thể tích của khối trụ:
A.
3
8
a
. B.
3
12
a
. C.
3
4
a
. D.
3
16
a
.
Câu 47. [2H2-1] Cho hình nón tròn xoay có bán kính đường tròn đáy
r
, chiều cao
h
và đường sinh
l
.
Kết luận nào sau đây sai?
A.
2
1
3
V r h
. B.
2
tp
S rl r
. C.
2 2 2
h r l
. D.
xq
S rl
.
Câu 48. [2D1-1] Hàm số
y f x
có giới hạn
lim
x a
f x
và đồ thị
C
của hàm số
y f x
chỉ nhận đường thẳng
d
làm tiệm cận đứng. Khẳng định nào sau đây đúng?
A. :
d y a
. B.
:
d x a
. C.
:
d x a
. D. :
d y a
.
Câu 49. [2D2-1] Rút gọn biểu thức
1 3 1
5 10 5
2 1 2
3 3 3
a a a
M
a a a
với
0, 1
a a
, ta được kết quả là:
A.
1
1
a
. B.
1
1
a
. C.
1
1
a
. D.
1
1
a
.
Câu 50. [2D2-3] Đầu mỗi tháng anh A gửi vào ngân hàng
3
triệu đồng với lãi suất kép là
0,6%
mỗi
tháng. Hỏi sau ít nhất bao nhiêu tháng (khi ngân hàng đã tính lãi) thì anh A có được số tiền cả
lãi và gốc nhiều hơn
100
triệu biết lãi suất không đổi trong quá trình gửi.
A.
31
tháng. B.
40
tháng. C.
35
tháng. D.
30
tháng.
---HẾT---
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/24 - Mã đề thi 640
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
C
A
C
D
D
A
B B D
B C
C
C
B C
D
D
B A
C
A
D
A
A
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
C
A
A
B D
C
D
B B D
A
A
D
C
C
D
C
A
B B B C
B A
A
HƯỚNG DẪN GIẢI
Câu 1. [2H1-1] Số mặt phẳng đối xứng của hình chóp đều
.
S ABC
là
A.
4
. B.
2
. C.
6
. D.
3
.
Lời giải
Chọn D.
N
C
B
A
S
O
O
O
S
A
B
C
P
M
C
B
A
S
Hình chóp đều
.
S ABC
có
3
mặt phẳng đối xứng lần lượt là
SAM
,
SCP
và
SBN
.
Câu 2. [2D2-1] Cho
a
là số thực dương khác
1
. Hình nào sau đây là đồ thị của hàm số mũ
x
y a
?
A.
x
y
1
1
O
B.
x
y
1
1
O
C.
x
y
1
1
O
D.
x
y
1
1
O
Lời giải
Chọn C.
Đồ thị của hàm
x
y a
đi qua hai điểm
0;1
A và
1;
B a
.
Câu 3. [2H2-1] Khối cầu
S
có bán kính bằng
r
và thể tích bằng
V
. Mệnh đề nào dưới đây đúng?
A.
3
4
3
V r
. B.
2 2
4
3
V r
. C.
2 3
4
3
V r
. D.
4
3
V r
.
Lời giải
Chọn A.
Theo công thức trong SGK.
Câu 4. [2D2-2] Cho
3
log 6
x
. Tính
3
3
log
K x
.
A.
4
K
. B.
8
K
. C.
2
K
. D.
3
K
.
Lời giải
Chọn C.
3
log 6
x
6
3
x
. Do đó:
3
3
log
K x
3
6
3
log 3
2
3
log 3
2
.
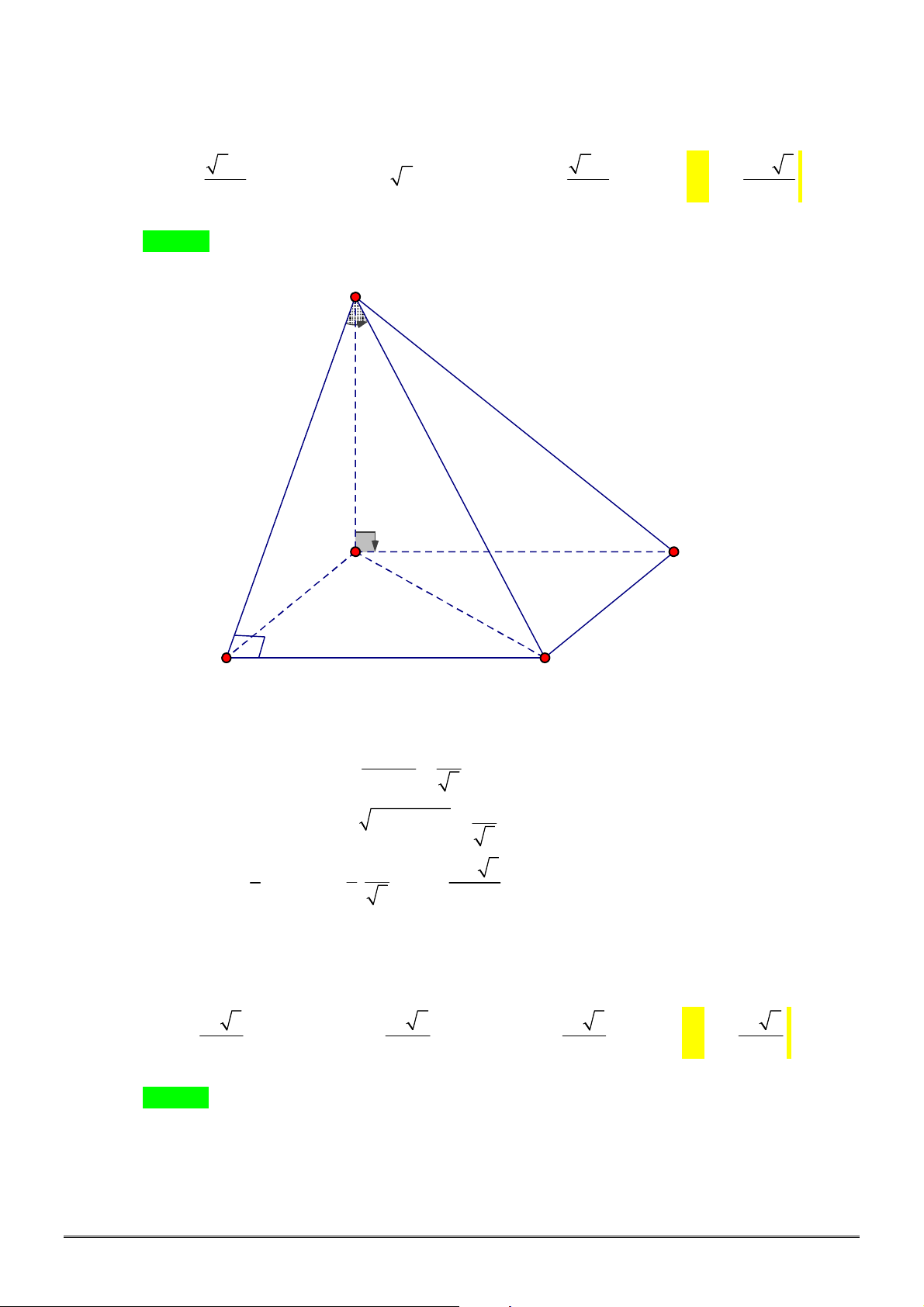
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/24 - Mã đề thi 640
Câu 5. [2H1-2] Cho khối chóp
.
S ABCD
có đáy là hình chữ nhật
AB a
,
2
BC a
,
SA
vuông góc
với đáy và
SC
tạo với mặt phẳng
SAB
một góc bằng
60
. Tính thể tích
V
của khối chóp đã
cho.
A.
3
6
3
a
V . B.
3
2
V a
. C.
3
2
3
a
V . D.
3
2 3
9
a
V .
Lời giải
Chọn D.
2a
a
60
o
S
D
C
B
A
Theo đề bài:
; ;
SC SAB SC SB
BSC
60
.
SBC
vuông tại
B
tan60
BC
SB
2
3
a
.
SAB
vuông tại
A
2 2
SA SB AB
3
a
.
Vậy
.
1
.
3
S ABCD ABCD
V SA S
1
. . .2
3
3
a
a a
3
2 3
9
a
.
Câu 6. [2H2-2] Cho tứ diện
ABCD
có tam giác
BCD
vuông tại
B
,
AC
vuông góc với mặt phẳng
BCD
,
5
AC a
,
3
BC a
và
4
BD a
. Tính bán kính
R
của mặt cầu ngoại tiếp tứ
diện
ABCD
.
A.
5 3
2
a
R . B.
5 2
3
a
R . C.
5 3
3
a
R . D.
5 2
2
a
R .
Lời giải
Chọn B.
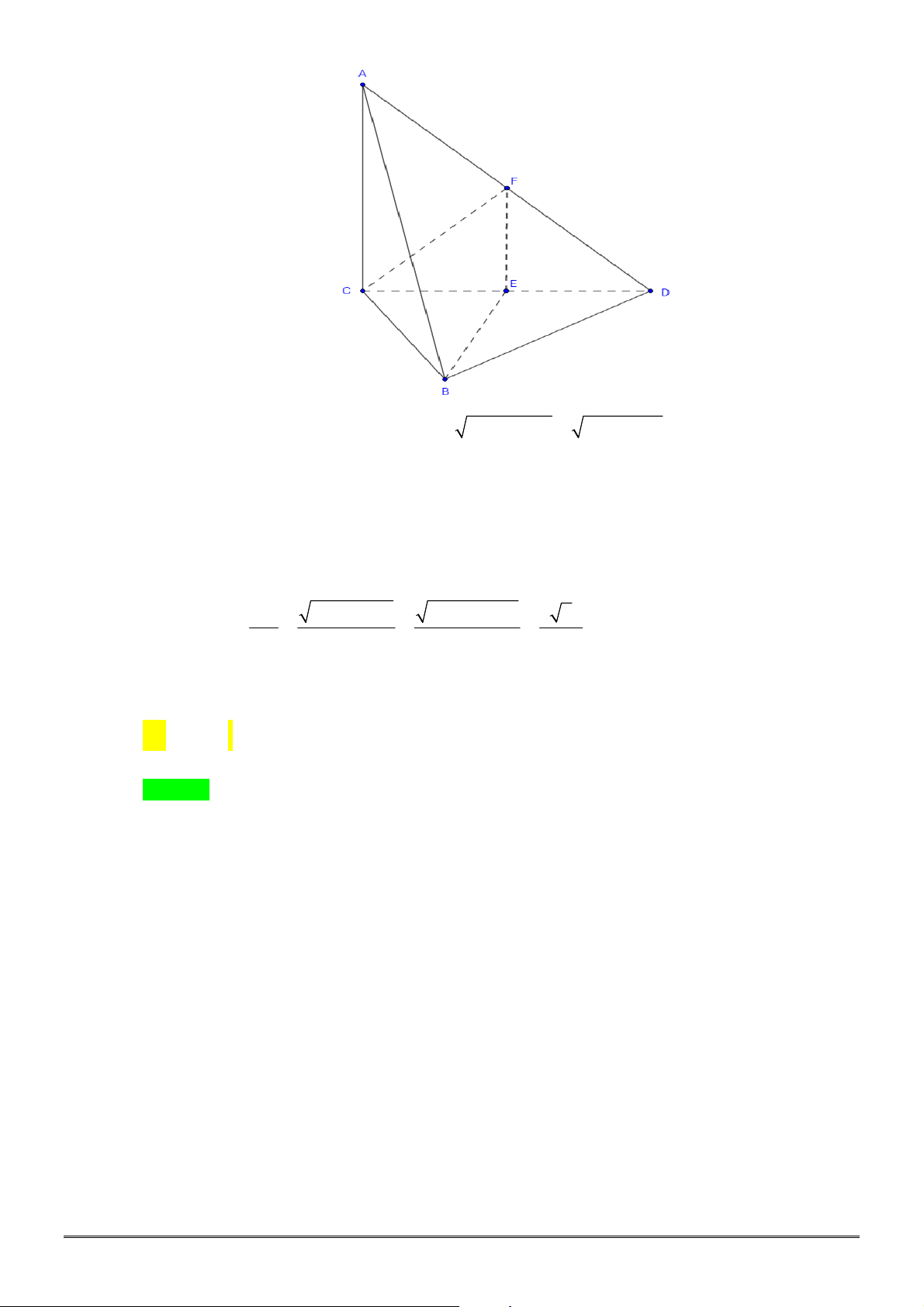
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/24 - Mã đề thi 640
Trong tam giác vuông
CBD
, ta có
2 2 2 2
9 16 5
DC BC BD a a a
.
Tam giác
ACD
có
5
AC CD a
nên
ACD
là tam giác vuông cân.
Gọi
E
là trung điểm
CD
. Do tam giác
CBD
vuông tại
B
nên
E
là tâm đường tròn ngoại tiếp
tam giác
CBD
.
Trong tam giác
ACD
, qua
E
kẻ đường thẳng vuông góc với
CD
và cắt
AD
tại điểm
F
.
Do
//
EF AC
và
E
là trung điểm
CD
nên
F
là trung điểm
AD
. Và ta có
F
chính là tâm của
mặt cầu ngoại tiếp tứ diện
ABCD
vì
FA FC FD FB
.
Bán kính
2 2 2 2
25 25 5 2
2 2 2 2
AD CA CD a a a
R
.
Câu 7. [2D1-2] Đồ thị hàm số
3 2
3 9 1
y x x x
có hai cực trị
A
và
B
. Điểm nào dưới đây thuộc
đường thẳng
AB
?
A.
0;2
N . B.
1;1
P . C.
1; 8
Q
. D.
0; 1
M
.
Lời giải
Chọn A.
Ta có
2 2
1
3 6 9 0 3 6 9 0
3
x
y x x y x x
x
.
Với
1
x
, ta có
6
y
. Vậy điểm
1; 6
A
.
Với
3
x
, ta có
26
y
. Vậy điểm
3;26
B .
4;32
AB
, suy ra đường thẳng
AB
nhận
8;1
u
làm véctơ pháp tuyến.
Vậy phương trình đường thẳng
AB
là
8. 1 1. 6 0 8 2 0
x y x y
1
.
Điểm
0;2
N thỏa mãn
1
nên
N
thuộc đường thẳng
AB
.
Câu 8. [2D1-1] Cho hàm số
y f x
có bảng biến thiên như hình bên dưới. Tìm giá trị cực đại và
giá trị cực tiểu của hàm số đã cho.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/24 - Mã đề thi 640
A.
3
CĐ
y
và
0
CT
y
. B.
2
CĐ
y
và
2
CT
y
.
C.
2
CĐ
y
và
2
CT
y
. D.
0
CĐ
y
và
3
CT
y
.
Lời giải
Chọn B.
Dựa vào bảng biến thiên, ta thấy
2
CĐ
y
và
2
CT
y
.
Câu 9. [2H1-2] Cho hình chóp
.
S ABC
có
6
AB
,
8
BC
,
10
AC
. Cạnh bên
SA
vuông góc với
đáy và
4
SA
. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
40
V
. B.
32
V
. C.
192
V
. D.
24
V
.
Lời giải
Chọn B.
Ta có
2 2 2 2 2
6 8 100
AB BC AC
nên suy ra tam giác
ABC
vuông tại
B
và
1 1
6 8 24
2 2
ABC
S AB BC
.
Vậy
.
1 1
4 24 32
3 3
S ABC ABC
V SA S
.
Câu 10. [2D2-1] Cho
a
là số thực dương khác
1
. Mệnh đề nào dưới đây đúng với mọi số thực dương
x
,
y
?
A.
log log .log
a a a
xy x y
. B.
log log log
a a a
xy x y
.
C.
log
log
log
a
a
a
x
xy
y
. D.
log log log
a a a
xy x y
.
Lời giải
Chọn D.
Ta có
log log log
a a a
xy x y
nên D đúng.
Câu 11. [2D1-1] Cho hàm số
y f x
liên tục trên
, bảng biến thiên như sau.Kết luận nào sau đây
đúng.
x
0
3
y
0
0
y
2
2
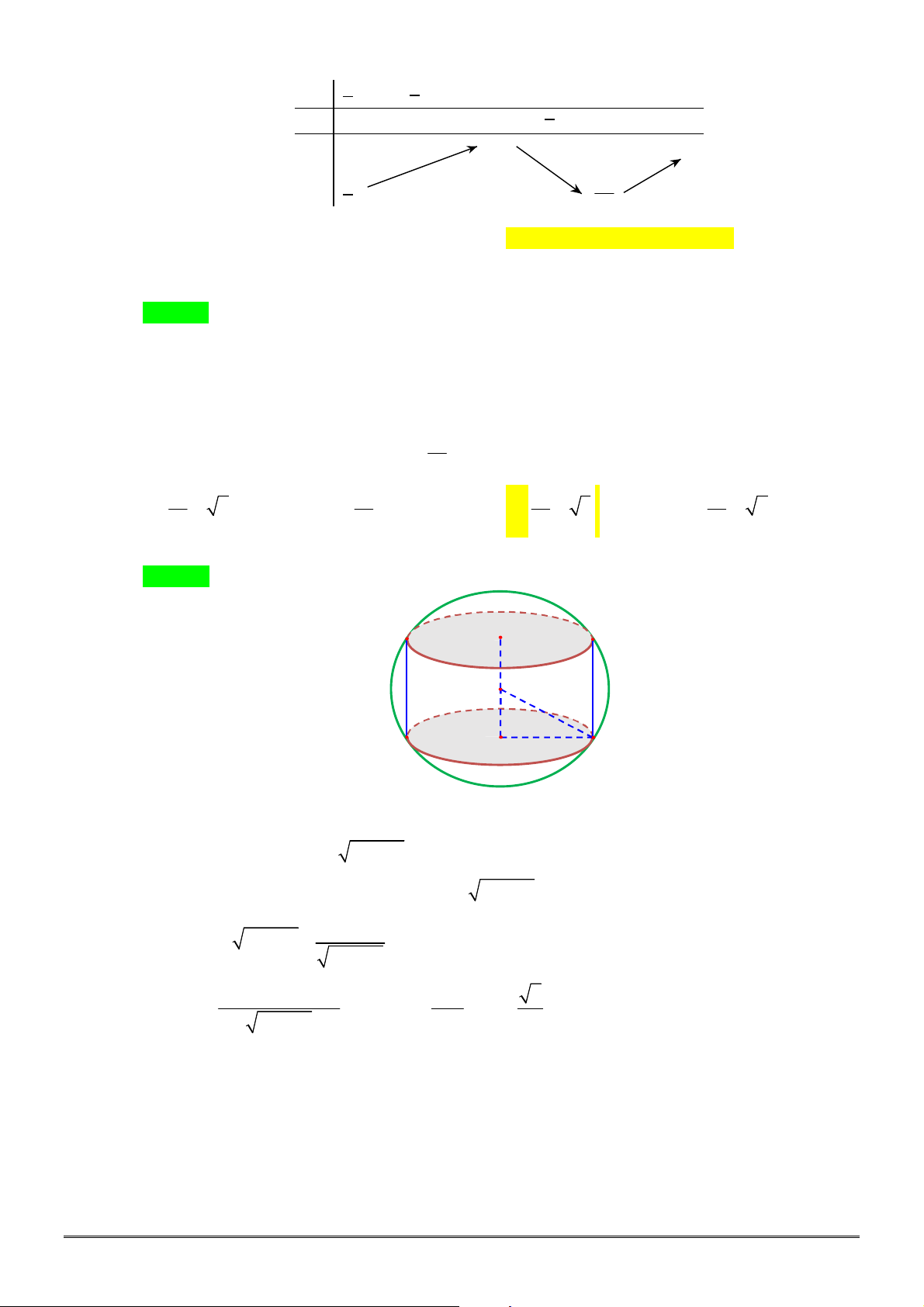
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/24 - Mã đề thi 640
A. Hàm số có ba điểm cực trị. B. Hàm số có hai điểm cực trị.
C. hàm số đạt cực tiểu tại
1
x
. D. Hàm số đạt cực đại tại
2
x
.
Lời giải
Chọn B.
Dựa vào bảng biến thiên, ta dễ dàng nhận thấy hàm số có hai điểm cực trị.
Câu 12. [2H2-4] Cho
S
là một mặt cầu cố định có bán kính
R
. Một hình trụ
H
thay đổi nhưng
luôn có hai đường tròn đáy nằm trên
S
. Gọi
1
V
là thể tích của khối cầu
S
và
2
V
là thể tích
lớn nhất của khối trụ
H
. Tính tỉ số
1
2
V
V
.
A.
1
2
6
V
V
. B.
1
2
2
V
V
. C.
1
2
3
V
V
. D.
1
2
2
V
V
Lời giải
Chọn C.
Gọi
I
là tâm mặt cầu
S
,
,
r h
là bán kính đáy và chiều cao hình trụ
H
.
Ta có:
2 2
2 , 2.
h d I C R r
với
C
là giao tuyến của
S
và
H
.
Thể tích khối trụ
H
là:
2 2 2 2
2
2
V r h r R r
.
3
2 2
2
2 2
2 2
r
V r R r
R r
.
2 2 3
2
2
2
2 2
2
2 6
0 0
3 3
r R r r
R
V r r R
R r
.
I
R
r
y
y'
x
+++
+
2
2
1
00
1 +
0
19
12

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/24 - Mã đề thi 640
Bảng biến thiên:
Dựa vào bảng biến thiên,
3
2
4 3
max
9
V R
.
Lại có thể tích khối cầu
S
là:
3
1
4
3
V R
.
Vậy
3
1
3
2
4
3
3
4 3
9
R
V
V
R
.
Câu 13. [2H2-2] Cho hình nón tròn xoay có đường sinh bằng
13
(cm), bán kính đường tròn đáy bằng
5
(cm). Thể tích của khối nón tròn xoay là
A.
200
(
3
cm
). B.
150
(
3
cm
). C.
100
(
3
cm
). D.
300
(
3
cm
).
Lời giải
Chọn C.
Chiều cao hình nón:
2 2
12 cm
h l R .
Thể tích khối nón:
2 3
1
100 cm
3
V R h
.
Câu 14. [2D1-2] Cho hàm số
2
1 2
y x x
có đồ thị
C
. Mệnh đề nào dưới đây đúng?
A.
C
không cắt trục hoành. B.
C
cắt trục hoành tại một điểm.
C.
C
cắt trục hoành tại ba điểm. D.
C
cắt trục hoành tại hai điểm.
Lời giải
Chọn C.
Phương trình hoành độ giao điểm giữa
C
và
Ox
:
2
1 2 0
x x
2
1
1 0
2 0
2
x
x
x
x
.
Số nghiệm của phương trình hoành độ giao điểm chính là số giao điểm của
C
và
Ox
.
Vậy
C
cắt trục hoành tại ba điểm.
Câu 15. [2H1-1] Thể tích
V
của một khối lăng trụ có diện tích đáy bằng
B
và chiều cao bằng
h
là
A.
2
1
3
V B h
. B.
V Bh
. C.
1
3
V Bh
. D.
1
2
V Bh
.
Lời giải
Chọn B.
r
0
6
3
R
2
R
2
V
0
2
V
0
3
4 3
9
R
0

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/24 - Mã đề thi 640
Câu 16. [2D2-2] Phương trình
3 4
1
2
32
x
có nghiệm là
A.
3
x
. B.
2
x
. C.
2
x
. D.
3
x
.
Lời giải
Chọn C.
Ta có
3 4 3 4 5
1
2 2 2
32
x x
3 4 5 2
x x
.
Câu 17. [2D2-1] Tập xác định của hàm số
2
log 10 2
y x
là
A.
;2
. B.
5;
. C.
;10
. D.
;5
.
Lời giải
Chọn D.
Điều kiện:
10 2 0 5
x x
.
Vậy tập xác định của hàm số là
; 5
D .
Câu 18. [2D1-3] Gọi
S
là tổng tất cả các giá trị nguyên dương của tham số
m
sao cho hàm số
2
2
4
x m
y
x m
đồng biến trên khoảng
2021;
. Khi đó, giá trị của
S
bằng
A.
2035144
. B.
2035145
. C.
2035146
. D.
2035143
.
Lời giải
Chọn D.
Tập xác định:
\ 4
D m
.
Đạo hàm:
2
2
2 8
4
m m
y
x m
.
Hàm số đồng biến trên khoảng
0, 2021;
2021;
4 2021;
y x
m
Hay
2
2 8 0
4 2021
m m
m
2 4
2017
m m
m
4 2017
m
.
Tổng các số nguyên dương từ
1
đến
2017
là
2017. 2017 1
2035153
2
T
.
Khi đó
1 2 3 4 20135143
S T .
Câu 19. [2D1-2] Cho hàm số
4 2
2
y x x
. Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
1;1
. B. Hàm số nghịch biến trên khoảng
; 2
.
C. Hàm số đồng biến trên khoảng
1;1
. D. Hàm số đồng biến trên khoảng
; 2
.
Lời giải
Chọn B.
Tập xác định:
D
.
Đạo hàm:
3
4 4
y x x
;
1
0 0
1
x
y x
x
.
Bảng biến thiên:

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/24 - Mã đề thi 640
Từ bảng biến thiên ta thấy hàm số nghịch biến trên khoảng
; 2
.
Câu 20. [2H2-1] Cho mặt cầu
S
có tâm
O
, bán kính
r
. Mặt phẳng
cắt mặt cầu
S
theo giao
tuyến là đường tròn
C
có bán kính
R
. Kết luận nào sau đây sai?
A.
2 2
,R r d O
.
B.
,
d O r
.
C. Diện tích của mặt cầu là
2
4
S r
.
D. Đường tròn lớn của mặt cầu có bán kính bằng bán kính mặt cầu.
Lời giải
Chọn A.
Công thức tính bán kính đường tròn giao tuyến là
2 2
,R r d O
.
Câu 21. [2D2-2] Với
a
,
b
,
x
là các số thực dương thỏa mãn
5 5 5
log 4log 3log
x a b
, mệnh đề nào
dưới đây là đúng?
A.
3 4
x a b
. B.
4 3
x a b
. C.
4 3
x a b
. D.
4 3
x a b
.
Lời giải
Chọn C.
Ta có:
4 3 4 3
5 5 5 5 5
log 4log 3log log log .
x a b x a b x a b
Câu 22. [2H2-1] Một hình trụ có khoảng cách giữa hai đáy, độ dài đường sinh và bán kính đường tròn
đáy lần lượt bằng
h
,
l
,
r
. Khi đó công thức tính diện tích toàn phần của hình trụ là
A.
2
tp
S r l r
. B.
2 2
tp
S r l r
. C.
tp
S r l r
. D.
2
tp
S r l r
.
Lời giải
Chọn A.
Công thức tính diện tích toàn phần của hình trụ là
2
2 2 2 .
tp
S r rl r l r
Câu 23. [2H2-1] Cho hình nón tròn xoay. Một mặt phẳng
P
đi qua đỉnh
O
của hình nón và cắt
đường tròn đáy của hình nón tại hai điểm. Thiết diện được tạo thành là
A. Một tứ giác. B. Một hình thang cân. C. Một ngũ giác. D. Một tam giác cân.
Lời giải
Chọn D.
Thiết diện là một tam giác cân đỉnh
.
O
Câu 24. [2D2-1] Cho
với ,
. Mệnh đề nào dưới đây đúng?
A.
. B.
. C.
. D.
.
Lời giải
Chọn A.
Do
1
nên
.
x
1
0
1
y
0
0
0
y
1
0
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/24 - Mã đề thi 640
Câu 25. [2H1-1] Khối đa diện nào sau đây có công thức thể tích là
1
3
V Bh
? Biết hình đa diện đó có
diện tích đáy bằng
B
và chiều cao bằng
h
?
A. Khối chóp. B. Khối hộp chữ nhật. C. Khối hộp. D. Khối lăng trụ.
Lời giải
Chọn A.
Công thức tính thể tích của khối chóp là
1
3
V Bh
.
Câu 26. [2D1-2] Đồ thị
2
2
4
x
y
x
có bao nhiêu tiệm cận?
A. 2. B. 4. C. 3. D. 1.
Lời giải
Chọn C.
Tập xác định của hàm số là.
2
2 2
2
1
2 2
lim lim lim lim 1
4 4
4
1 1
x x x x
x x
x
y
x
x
x x
1
y
là tiệm cận ngang của đồ thị.
2
2 2
2
1
2 2
lim lim lim lim 1
4 4
4
1 1
x x x x
x x
x
y
x
x
x x
1
y
là tiệm cận ngang của
đồ thị.
2
2
2 2 2 2
2
2 2
lim lim lim lim 0
2 2 2
4
x x x x
x
x x
y
x x x
x
.
2
2
2 2 2 2
2
2 2
lim lim lim lim
2 2 2
4
x x x x
x
x x
y
x x x
x
. Suy ra
2
x
là
tiệm cận đứng của đồ thị.
Câu 27. [2D2-1] Cho
4
số thực
a
,
b
,
x
,
y
với
a
,
b
là các số dương và khác
1
. Mệnh đề nào dưới
đây đúng? A.
x
x y
y
a
a
a
. B.
y
x x y
a a
. C.
.
.
x y x y
a a a
D.
. .
x
x
a b a b
.
Lời giải
Chọn A.
Câu hỏi lý thuyết.
Câu 28. [2D1-3] Hai thành phố A và B ngăn cách nhau bởi một còn sông. Người ta cần xây cây cầu
bắc qua sông và vuông góc với bờ sông. Biết rằng thành phố A cách bờ sông 2 (km), thành phố
B cách bờ sông 5 (km ), khoảng cách giữa đường thẳng đi qua A và đường thẳng đi qua B cùng
vuông góc với bờ sông là 12 (km). Giả sử hai bờ sông là hai đường thẳng song song với nhau.
Nhằm tiết kiệm chi phí đi từ thành phố A đến thành phố B, người ta xây cây cầu ở vị trí MN để
quãng đường đi từ thành phố A đến thành phố B là ngắn nhất (hình vẽ). Khi đó, độ dài
đoạn
AM
là
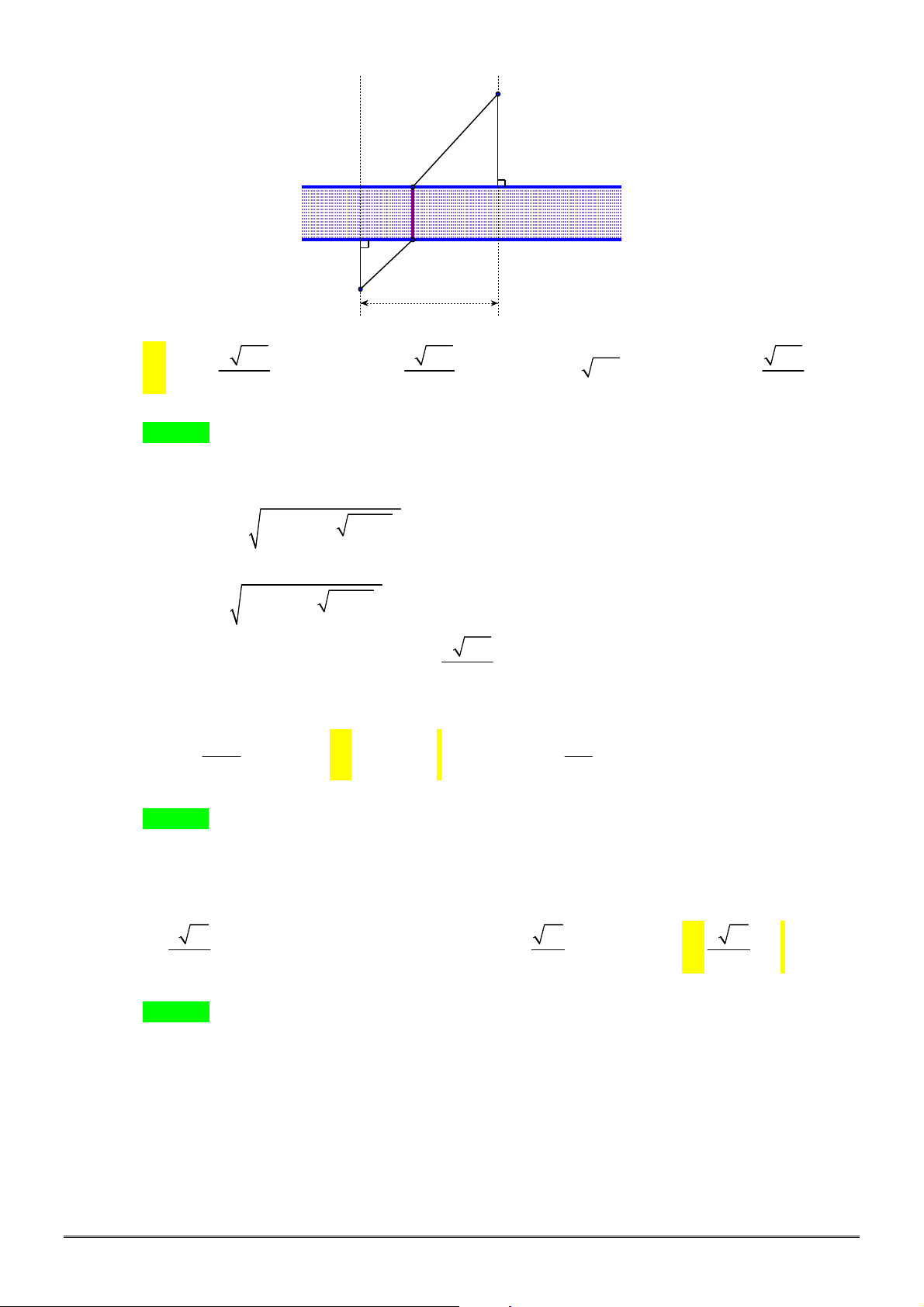
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/24 - Mã đề thi 640
sông
2 km
5 km
12 km
A
M
B
N
A.
2 193
km.
7
AM B.
3 193
km.
7
AM C.
193 km.
AM D.
193
km.
7
AM
Lời giải
Chọn A.
Đặt
AM x
0 12
x .
Khi đó tổng quãng đường từ thành phố
A
đến thành phố
B
là
2
25 12 4
S MN x x
.
Do khoảng cách giữa hai bờ không đổi nên quãng đường ngắn nhất khi
2
25 12 4
f x x x
nhỏ nhất.
Thử trực tiếp các đáp án ta được
2 193
km
7
AM .
Câu 29. [2D1-1] Đạo hàm của hàm số
5 2017
x
y là
A.
5
5ln5
x
y
. B.
5 .ln5
x
y
. C.
5
ln5
x
y
D.
5
x
y
.
Lời giải
Chọn B.
Câu 30. [1H3-3] Cho khối chóp
.
S ABCD
có đáy là hình vuông,
SAB
đều và nằm trong mặt phẳng
vuông góc với mặt đáy. Mặt cầu ngoại tiếp khối chóp
.
S ABCD
có diện tích
2
84 cm
. Khoảng
cách giữa hai đường thẳng
SA
và
BD
là
A.
3 21
cm
7
. B. . C.
21
cm
7
. D.
6 21
cm
7
.
Lời giải
Chọn D.
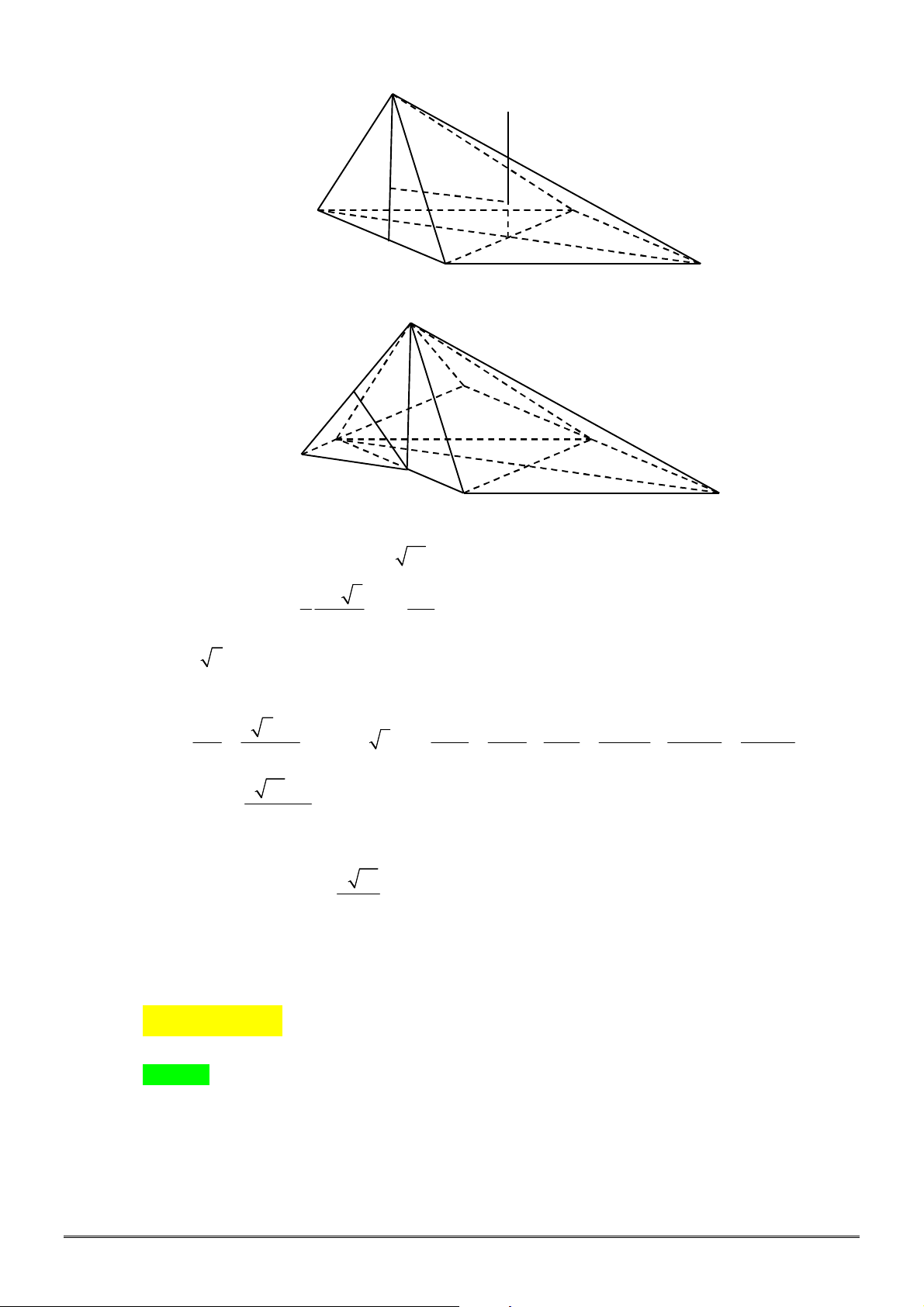
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/24 - Mã đề thi 640
Ta có
2 2
4 84 cm
S r
21cm
r .
2 2 2
SG GI r
2
2
2
2 3
21cm
3 2 2
AB AB
6cm
AB
.
6 2cm
AC . Dựng hình bình hành
ABDE
. Kẻ
HK AE K AE
,
HF SK F SK
.
Suy ra
HF SAE
.
3 2 cm
4 2
AC
HK ,
3 3 cm
SH ,
2 2 2 2 2 2
1 1 1 4 1 7
18cm 27cm 27cm
HF HK SH
.
Suy ra
3 21cm
7
HF .
Do
//
BD SAE
, , , 2 ,
d SA BD d BD SAE d B SAE d H SAE
.
Vậy
6 21
, 2 cm
7
d SA BD HF .
Câu 31. [2D2-2] Tìm tập xác định
D
của hàm số
3
2
2
y x x
.
A.
0;D
. B.
; 2 1;D
.
C.
\ 2;1
D
. D.
D
.
Lời giải
Chọn C.
Do số mũ nguyên âm nên hàm số xác định khi và chỉ khi
2
1
2 0
2
x
x x
x
.
Vậy tập xác định
\ 2;1
D
.
H
A
B
C
D
E
K
F
O
S
S
d
A
H
B
C
D
I
G
O

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/24 - Mã đề thi 640
Câu 32. [2D1-2] Tìm các giá trị của tham số
m
để hàm số
3
2 2
3 2 3
3
x
y x m x m
đồng biến trên
.
A.
3
3
m
m
. B.
3 3
m
. C.
3 3
m
. D.
3
3
m
m
.
Lời giải
Chọn D.
TXĐ:
D
.
2 2
6
y x x m
.
Hàm số
y
đồng biến trên
2 2
0, 6 0,y x x x m x
2
1 0
0 3
0 3
9 0
a m
m
m
.
Câu 33. [2D2-1] Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. Với
0 1
a
, hàm số
log
a
y x
là một hàm nghịch biến trên khoảng
0;
.
B. Với
1
a
, hàm số
log
a
y x
là một hàm đồng biến trên khoảng
;
.
C. Với
1
a
, hàm số
x
y a
là một hàm đồng biến trên khoảng
;
.
D. Với
0 1
a
, hàm số
x
y a
là một hàm nghịch biến trên khoảng
;
.
Lời giải
Chọn B.
Hàm số
log
a
y x
có tập xác định là
0;D
nên với
1
a
, hàm số
log
a
y x
là một
hàm đồng biến trên khoảng
0;
.
Câu 34. [2D2-4] Xét các số thực dương
x
,
y
thỏa mãn
3
1
log 3 3 4
3
y
xy x y
x xy
. Tìm giá trị nhỏ
nhất
min
P
của
P x y
.
A.
min
4 3 4
3
P
. B.
min
4 3 4
3
P
. C.
min
4 3 4
9
P
. D.
min
4 3 4
9
P
.
Lời giải
Chọn B.
Điều kiện:
0 1, 0
y x
.
Ta có:
3 3 3
1
log 3 3 4 log 1 log 3 3 3 4
3
y
xy x y y x xy xy x y
x xy
3 4
log 3 1 3 1 log 3 3
y y xy x xy x
.
Xét hàm số
3
log
f t t t
trên khoảng
0;
.
Ta có:
1
1 0
.ln3
f t
t
,
0;t
nên hàm số
f t
đồng biến trên khoảng
0;
.
Do đó:
3
3 1 3 3 1 3
3 1
x
y xy x y x x y
x
.
3
3 1
x
P x y x
x
.
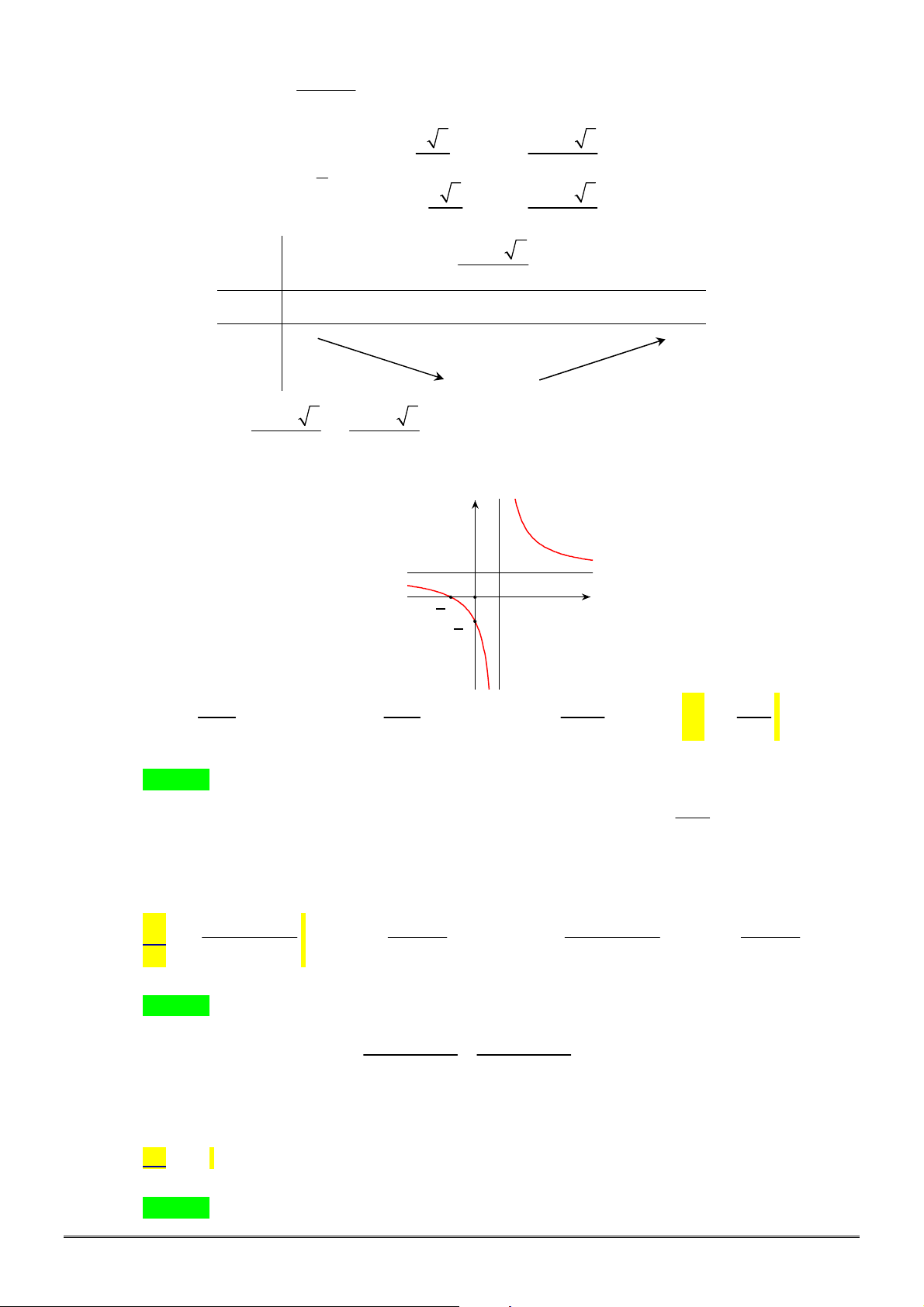
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/24 - Mã đề thi 640
Xét hàm
3
3 1
x
g x x
x
với
0
x
.
2
2 3 3 2 3
1
4
3 3
0 1
3
2 3 3 2 3
1
3 3
x x
g x x
x x l
Vậy
min
3 2 3 4 4 3
3 3
P g
.
Câu 35. [2D1-1] Hình vẽ sau đây là đồ thị của hàm số nào?
x
y
1
1
1
1
O
A.
2
1
x
y
x
. B.
3
1
x
y
x
. C.
2 1
2 1
x
y
x
. D.
1
1
x
y
x
.
Lời giải
Chọn D.
Đồ thị hàm số đi qua điểm có tọa độ
1;0
. Chỉ có đồ thị hàm số
1
1
x
y
x
trong
4
hàm số đề
cho thỏa ý này.
Câu 36. [2D2-2] Tính đạo hàm của hàm số
log 2 1
y x
.
A.
2
2x 1 ln10
y
. B.
2
2x 1
y
. C.
1
2x 1 ln10
y
. D.
1
2x 1
y
.
Lời giải
Chọn A.
Ta có
2 1
2
log 2 1
2 1 ln10 2 1 ln10
x
y x y
x x
.
Câu 37. [2H1-1] Mỗi cạnh của một hình đa diện là cạnh chung của đúng
n
mặt của hình đa diện đó.
Mệnh đề nào dưới đây đúng?
A.
2
n
. B.
5
n
. C.
3
n
. D.
4
n
.
Lời giải
Chọn A.
x
0
3 2 2
3
g x
–
0
g x
GTNN
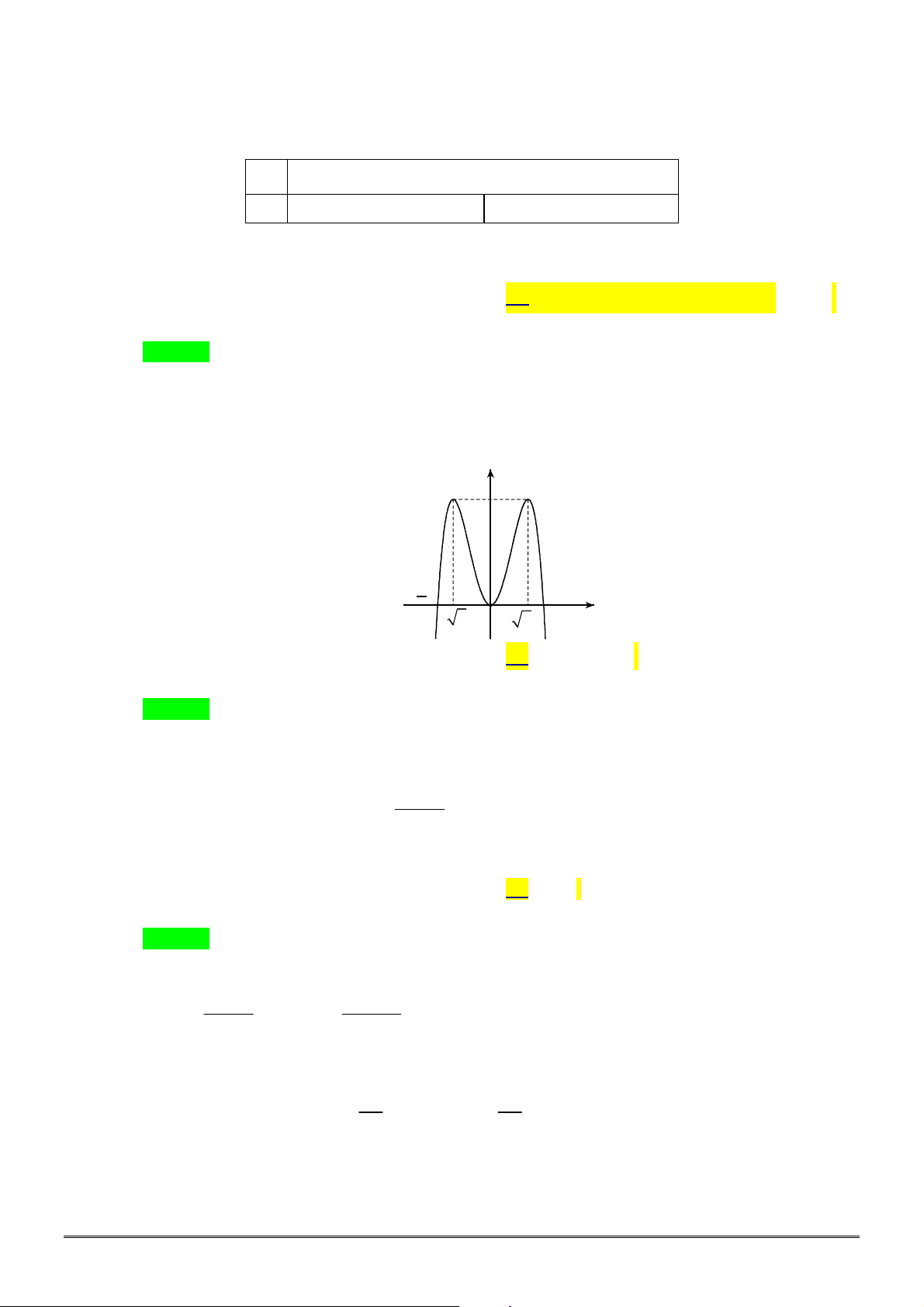
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/24 - Mã đề thi 640
Theo định nghĩa hình đa diện (SGK hình học 12), mỗi cạnh thuộc một mặt là cạnh chung của
đúng hai mặt.
Câu 38. [2D1-1] Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau
x
2
0
2
y
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
;2
. B. Hàm số nghịch biến trên khoảng
; 2
.
C. Hàm số nghịch biến trên khoảng
;0
. D. Hàm số nghịch biến trên khoảng
2;0
.
Lời giải
Chọn D.
Dựa vào bảng xét dấu đạo hàm, ta có trong khoảng
2;0
, đạo hàm mang dấu âm nên hàm số
nghịch biến trên khoảng
2;0
.
Câu 39. [2D1-1] Hình vẽ sau đây là đồ thị của hàm số nào?
A.
4 2
2
y x x
. B.
4 2
3 1
y x x
. C.
4 2
4
y x x
. D.
4 2
3
y x x
.
Lời giải
Chọn C.
Dựa vào hình vẽ trên và bốn đáp án, ta có đồ thị là của hàm số bậc bốn trùng phương có hệ số
0
a
, có ba điểm cực trị và đi qua gốc tọa độ. Chỉ có hàm số ở đáp án C thỏa.
Câu 40. [2D1-2] Cho hàm số
2
,
8
x m
f x
x
với
m
là tham số. Giá trị lớn nhất của
m
để
0;3
min 2
f x
là:
A.
5
m
. B.
6
m
. C.
4
m
. D.
3
m
.
Lời giải
Chọn C.
Tập xác định
\ 8
D
nên hàm số xác định và liên tục trên
0; 3
. Ta có
22
2
8
0
8
8
x m
f x f
m
x
x
x
8
x
suy ra hàm số đồng biến trên từng khoảng xác
định của nó nên cũng đồng biến trên
0; 3
.
Suy ra
2
0;3
min 0
8
m
f x f , theo đề bài
2
2
2 16 4
8
m
m m
.
Vậy chọn
4
m
.
Câu 41. [2D2-2] Tìm giá trị thực của tham số
m
để phương trình
1
9 2.3 0
x x
m
có hai nghiệm
thực
1
x
,
2
x
thỏa mãn
1 2
0
x x
.
x
y
4
22
O
2
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/24 - Mã đề thi 640
A.
6
m
. B.
0
m
. C.
3
m
. D.
1
m
.
Lời giải
Chọn D.
Ta có:
1 2 1 2
0
1 2
0 3 3 3 .3 1
x x x x
x x
.
Và:
1
9 2.3 0 9 6.3 0
x x x x
m m
.
Đặt
3
x
t
với
0
t
, phương trình đã cho trở thành:
2
6 0
t t m
*
.
Ta tìm
m
để phương trình
*
có hai nghiệm
1
t
,
2
t
thỏa mãn
1 2
1
t t
9 0 9
1
1 1
m m
m
m m
.
Câu 42. [2D1-2] Giá trị lớn nhất của hàm số
4
2
x
y
x
trên đoạn
3;4
.
A.
4
. B.
10
. C.
7
. D.
8
.
Lời giải
Chọn C.
Tập xác định:
\ 2
D
.
Đạo hàm:
2
6
0
2
y
x
x D
.
Ta thấy
2 3;4
,
3 7
y
và
4 4
y
. Vậy
3;4
max 3 7
y y
.
Câu 43. [2D1-2] Tìm giá trị thực của tham số
m
để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực tiểu
tại
3
x
.
A.
1
m
. B.
1
m
. C.
5
m
. D.
7
m
.
Lời giải
Chọn A.
Tập xác định:
D
.
Đạo hàm cấp 1:
2 2
2 4
y x mx m
.
Đạo hàm cấp 2:
2 2
y x m
.
Hàm số đã cho đạt cực tiểu tại
2
1
3 3 0 6 5 0
5
m
x y m m
m
.
Với
1 3 2.3 2.1 6 2 4 0
m y
. Suy ra hàm số đạt cực tiểu tại
3
x
.
Với
5 3 2.3 2.5 6 10 4 0
m y
. Suy ra hàm số đạt cực đại tại
3
x
.
Vậy
1
m
là giá trị cần tìm.
Câu 44. [2H1-3] Cho khối lăng trụ đứng .
ABC A B C
có đáy là tam giác cân
ABC
với
AB AC a
,
120
BAC
, mặt phẳng
AB C
tạo với đáy một góc
30
. Tính thể tích
V
của khối lăng trụ
đã cho.
A.
3
6
a
V . B.
3
8
a
V . C.
3
3
8
a
V . D.
3
9
8
a
V .
Lời giải
Chọn B.
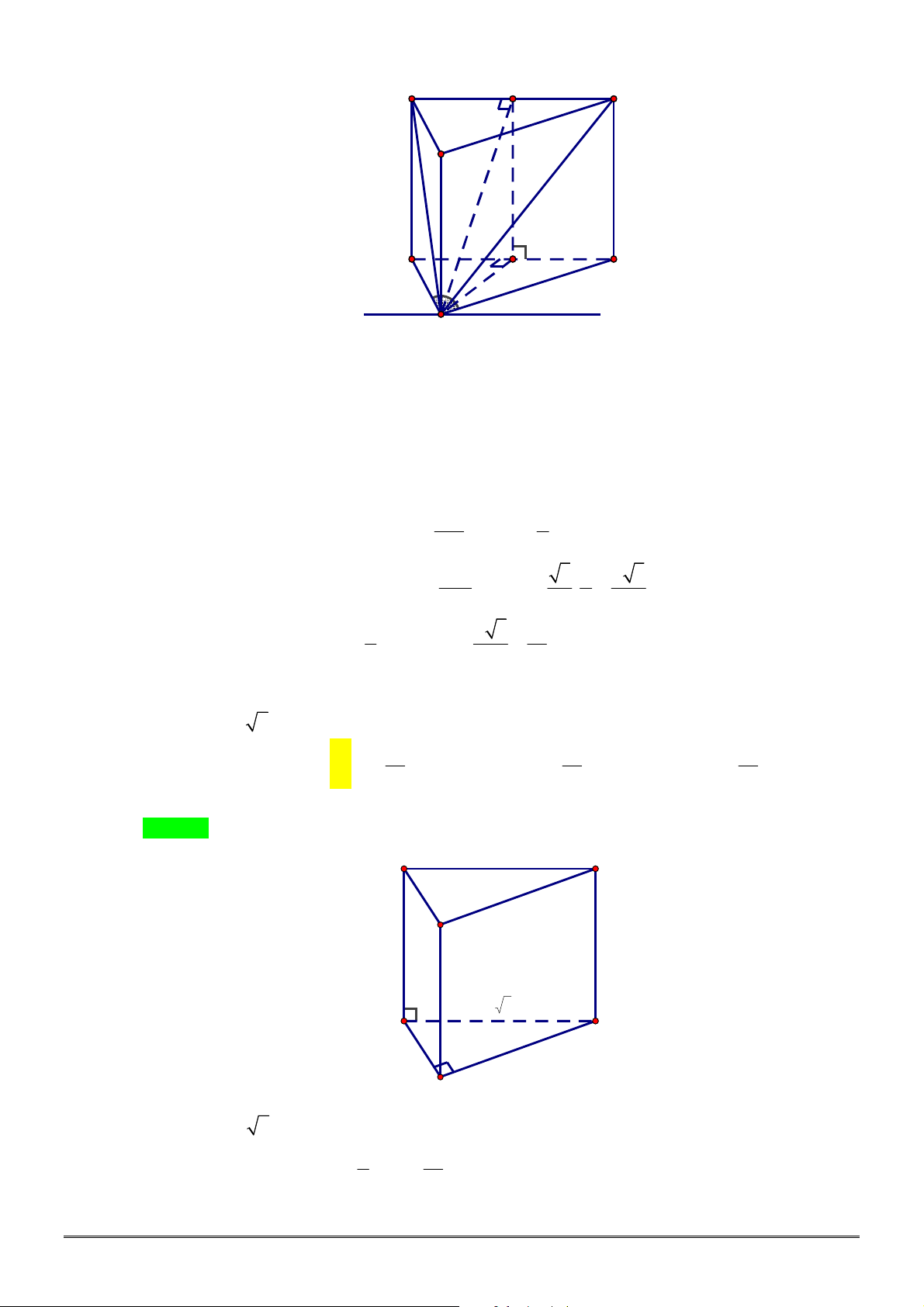
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/24 - Mã đề thi 640
a a
x
120°
N
M
C'
A'
B
A
C
B'
Gọi
M
,
N
lần lượt là trung điểm của
B C
và
BC
. Suy ra:
MN BC
và
MN B C
.
Ta có:
// //
AB C ABC Ax BC B C
.
Do
ABC
cân tại
A
nên
AN BC AN Ax
.
Do
AB C
cân tại
A
nên
AM B C AM Ax
.
Suy ra:
, 30
ABC AB C NAM
(do
90
MNA
).
Xét
ANB
vuông tại
N
có: cos60
2
AN a
AN
AB
.
Xét
ANM
vuông tại
N
có:
3 3
tan30 .
3 2 6
MN a a
MN
AN
.
Vậy:
3
.
1 3
. . .sin120 .
2 6 8
ABC A B C ABC
a a
V S MN a a
.
Câu 45. [2H1-2] Cho khối lăng trụ đứng .
ABC A B C
có
AA a
, đáy
ABC
là tam giác vuông cân tại
A
và
2
BC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
V a
. B.
3
2
a
V . C.
3
6
a
V . D.
3
3
a
V .
Lời giải
Chọn B.
a
a
2
C'
A'
C
A
B
B'
Ta có
2
BC a AB AC a
.
Vậy
3
2
.
1
. .
2 2
ABC A B C ABC
a
V S AA a a
.
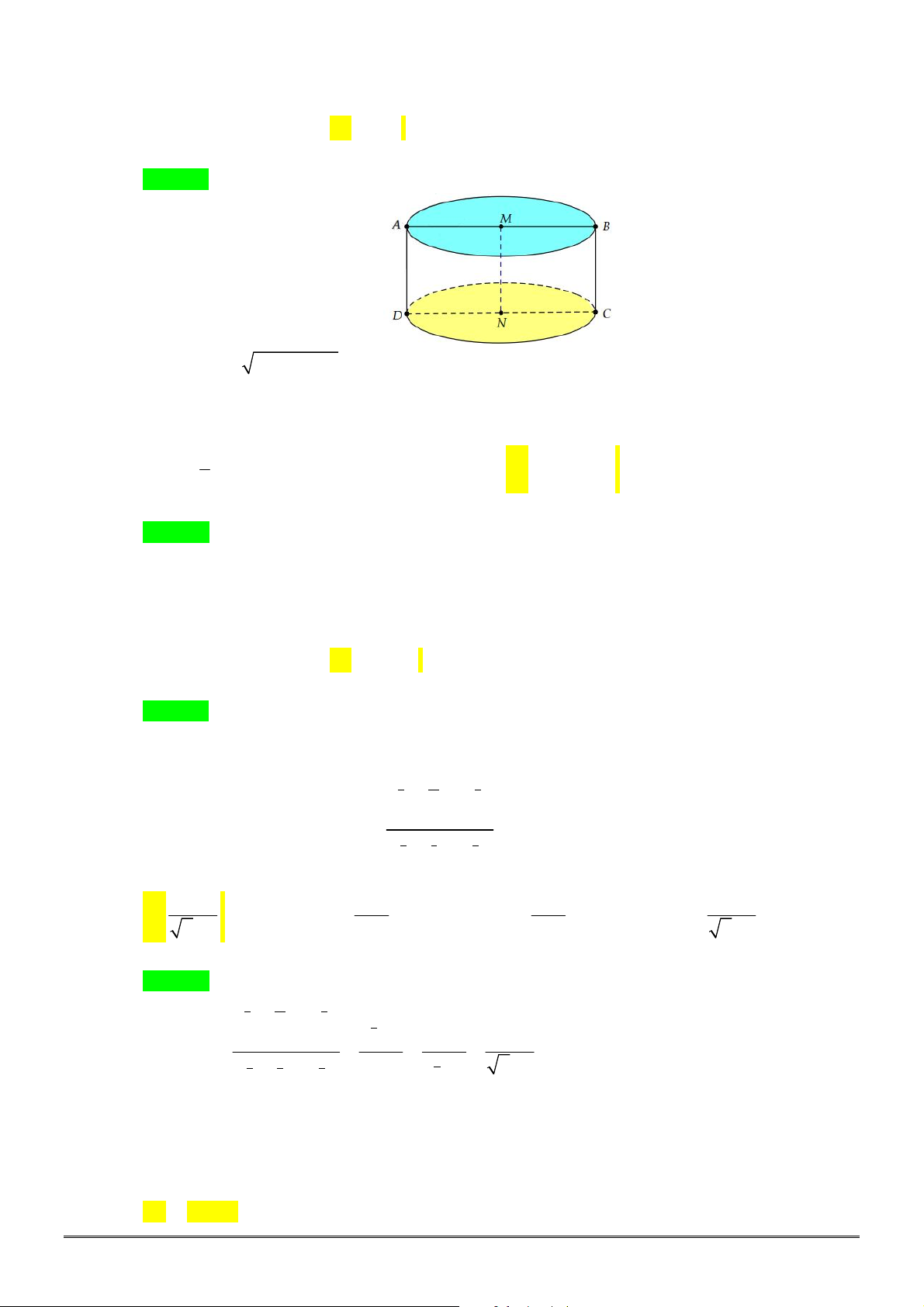
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 23/24 - Mã đề thi 640
Câu 46. [2H2-1] Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật
ABCD
có
AB
và
CD
thuộc hai đáy của hình trụ,
4
AB a
,
5
AC a
. Thể tích của khối trụ:
A.
3
8
a
. B.
3
12
a
. C.
3
4
a
. D.
3
16
a
.
Lời giải
Chọn B.
Ta có:
2 2
3
BC AC AB a
. Thể tích
2
2 3
. 2 .3 12
V R h a a a
.
Câu 47. [2H2-1] Cho hình nón tròn xoay có bán kính đường tròn đáy
r
, chiều cao
h
và đường sinh
l
.
Kết luận nào sau đây sai?
A.
2
1
3
V r h
. B.
2
tp
S rl r
. C.
2 2 2
h r l
. D.
xq
S rl
.
Lời giải
Chọn C.
2 2 2
h l r
.
Câu 48. [2D1-1] Hàm số
y f x
có giới hạn
lim
x a
f x
và đồ thị
C
của hàm số
y f x
chỉ nhận đường thẳng
d
làm tiệm cận đứng. Khẳng định nào sau đây đúng?
A. :
d y a
. B.
:
d x a
. C.
:
d x a
. D. :
d y a
.
Lời giải
Chọn B.
Ta có lim
x a
, suy ra đồ thị
C
nhận đường thẳng
x a
làm tiệm cận đứng.
Câu 49. [2D2-1] Rút gọn biểu thức
1 3 1
5 10 5
2 1 2
3 3 3
a a a
M
a a a
với
0, 1
a a
, ta được kết quả là:
A.
1
1
a
. B.
1
1
a
. C.
1
1
a
. D.
1
1
a
.
Lời giải
Chọn A.
Ta có:
1 3 1
5 10 5
1
2
1
2 1 2
2
3 3 3
1 1 1
1
1
1
a a a
a
M
a
a
a
a a a
.
Câu 50. [2D2-3] Đầu mỗi tháng anh A gửi vào ngân hàng
3
triệu đồng với lãi suất kép là
0,6%
mỗi
tháng. Hỏi sau ít nhất bao nhiêu tháng (khi ngân hàng đã tính lãi) thì anh A có được số tiền cả
lãi và gốc nhiều hơn
100
triệu biết lãi suất không đổi trong quá trình gửi.
A.
31
tháng. B.
40
tháng. C.
35
tháng. D.
30
tháng.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 24/24 - Mã đề thi 640
Lời giải
Chọn A.
Ta có:
Số tiền cả gốc và lãi thu được sau tháng
1
là:
1 0 0 0
(1 ) (1 ) 1
S S r S S r
Số tiền cả gốc và lãi thu được sau tháng
1
là:
2
2 1 0 0 0 0 0
(1 ) (1 ) (1 ) (1 ) (1 ) 1
S S r S S r S r S S r r
..........................................................................................................................................................
Số tiền cả gốc và lãi thu được sau tháng n là:
1
0
1 2
1 0 0
(1 ) 1
(1 ) (1 ) (1 ) ... (1 ) (1 ) 1
n
n n
n n
S r
S S r S S r r r r
r
1
3 (1,006) 1
0,006
n
n
S
Để sau
n
tháng thu được ít nhất
100
triệu (tháng cuối cùng không đóng thêm
3
triệu) điều kiện
là:
1
1
0
3 1,006 1
100 3 100 1,006 1,206
0,006
n
n
n
S S
1,006
log 1,206 1 31
n n
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/29
SỞ GD VÀ ĐT HÀ NỘI
TRƯỜNG THPT KIM LIÊN
(Đề thi gồm 06 trang)
ĐỀ KIỂM TRA HỌC KÌ I MÔN TOÁN KHỐI 12
Năm học: 2017-2018
Thời gian làm bài 90 phút, không kể thời gian phát đề
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 590
Câu 1. [2H1-1] Cho khối chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
2
a
,
SA
vuông góc với mặt
phẳng
ABC
,
3.
SA a Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
6
a
V . B.
3
V a
. C.
3
4
a
V . D.
3
12
a
V .
Câu 2. [2D1-2] Cho hàm số
sin cos 2
y x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại các điểm
3
2 ,
4
x k k
.
B. Hàm số đạt cực đại tại các điểm 2 ,
4
x k k
.
C. Hàm số đạt cực tiểu tại các điểm 2 ,
4
x k k
.
D. Hàm số đạt cực tiểu tại các điểm 2 ,
4
x k k
.
Câu 3. [2D1-1] Tìm số điểm cực trị của hàm số
4 3 2
3 8 6 1
y x x x
.
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 4. [2D1-2] Tìm tất cả các giá trị củar tham số
m
để đồ thị hàm số
8
2
mx
y
x
có tiệm cận đứng.
A.
4
m
. B.
4
m
. C.
4
m
. D.
4
m
.
Câu 5. [1D1-2] Tìm giá trị lớn nhất
M
của hàm số
2
2sin sin2 11
y x x
.
A.
12 2
M
. B.
10 2
M
. C.
12 2
M
. D.
10 2
M
.
Câu 6. [2D1-1] Hàm số
3
3 5
y x x
đồng biến trên khoảng nào dưới đây?
A.
; 1
. B.
1;1
. C.
;1
. D.
1;
.
Câu 7. [2D1-2] Biết đồ thị hai hàm số
1
y x
và
2 1
1
x
y
x
cắt nhau tại hai điểm phân biện
A
,
B
.
Tính độ dài đoạn thẳng
AB
.
A.
2 2
AB
. B.
2
AB
. C.
2
AB
. D.
4
AB
.
Câu 8. [2D2-2] Tìm tập xác định
D
của hàm số
2018
2
2017
log 9 2 3y x x
.
A.
3 3
3; ;3
2 2
D
. B.
3;3
D . C.
3 3
3; ;3
2 2
D
. D.
3
;3
2
D
.
Câu 9. [2D1-2]Cho hàm số
3
3
y x x
với
2;x
. Mệnh đề nào dưới đây đúng?
A. Hàm số có giá trị nhỏ nhất và không có giá trị lớn nhất.
B. Hàm số có cả giá trị nhỏ nhất và giá trị lớn nhất.
C. Hàm số không có cả giá trị nhỏ nhất và giá trị lớn nhất.
D. Hàm số không có giá trị nhỏ nhất và có giá trị lớn nhất.
Câu 10. [2D2-2] Cho
p
,
q
là các số thực thỏa mãn:
2
1
e
p q
m
,
2
p q
n e
, biết
m n
. So sánh
p
và
q
.
A.
p q
. B.
p q
. C.
p q
. D.
p q
.
5
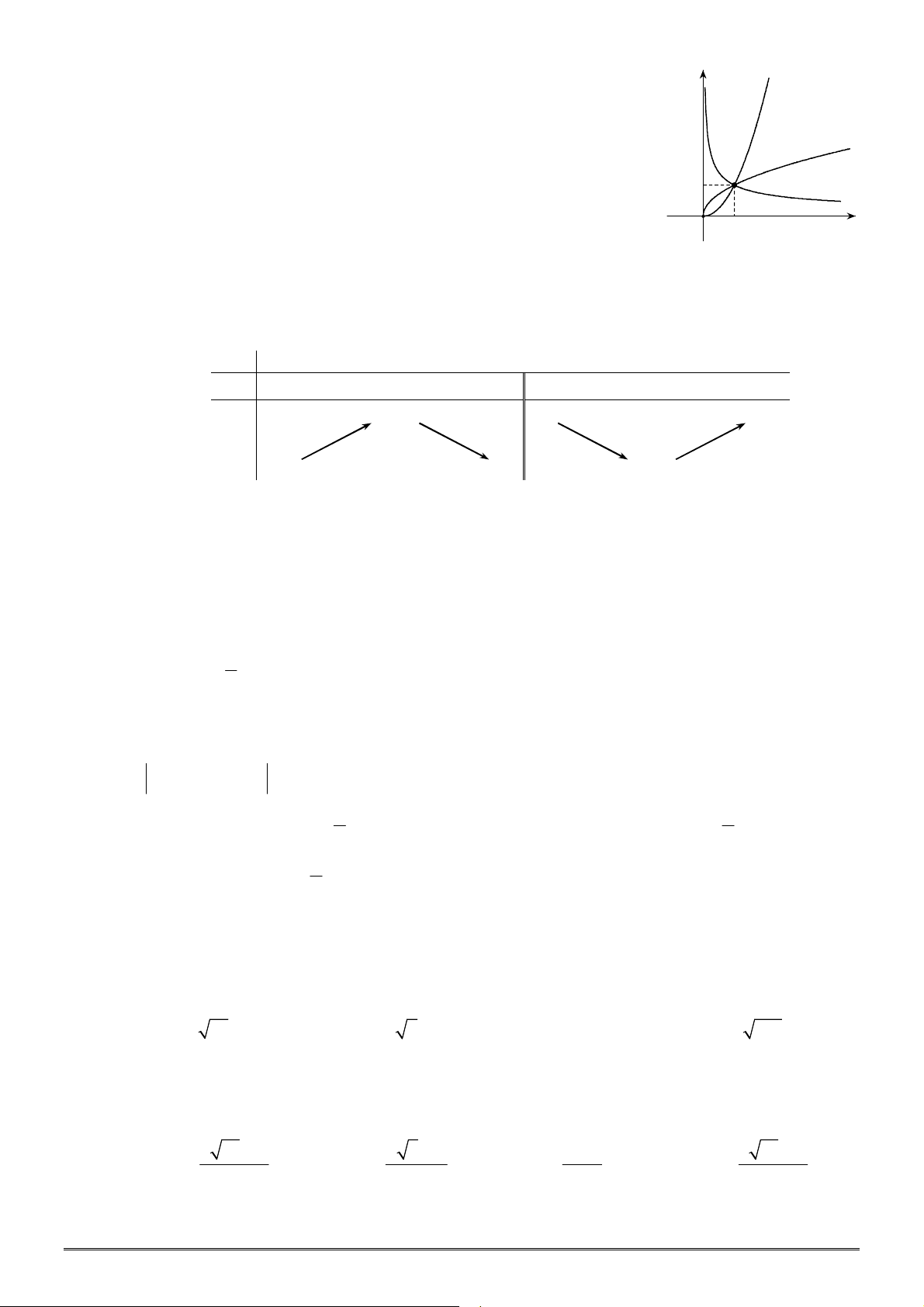
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/29
Câu 11. [2D2-2] Hình vẽ sau là đồ thị của ba hàm số
y x
,
y x
,
y x
(với
0
x
và
,
,
là các số thực cho trước). Mệnh
đề nào dưới đây đúng?
A.
. B.
.
C.
. D.
.
Câu 12. [2D1-3] Cho hàm số
3 2
3 2 1
y x x x
. Tiếp tuyến song song với
đường thẳng
2 3 0
x y
của đồ thị hàm số trên có phương trình là
A.
2 1 0.
x y
B.
2 2 0
x y
. C.
2 1 0
x y
. D.
2 1
y x
.
Câu 13. [2D1-2] Cho hàm số
y f x
có bảng biến thiên như hình vẽ. Mệnh đề nào dưới đây sai?
A. Hàm số đồng biến trên khoảng
3; 1
.
B. Đồ thị hàm số không có đường tiệm cận ngang.
C. Đồ thị hàm số có một đường tiệm cận đứng.
D. Hàm số nghịch biến trên
0; 1 1; 2
.
Câu 14. [2D2-2] Tính tổng
1 2
S x x
biết
1
x
,
2
x
là các giá trị thực thỏa mãn đẳng thức
2
3
6 1
1
2
4
x
x x
.
A.
5
S
. B.
8
S
. C.
4
S
. D.
2
S
.
Câu 15. [2H2-3] Cho tam giác
ABC
. Tập hợp các điểm
M
trong không gian thỏa mãn hệ thức
MA MB MC a
(với
a
là số thức dương không đổi) là:
A. Mặt cầu bán kính
3
a
R
. B. Đường tròn bán kính
3
a
R
.
C. Đoạn thẳng độ dài
3
a
. D. Đường thẳng.
Câu 16. [2H2-3] Mặt cầu tâm
I
bán kính
11
R
cm
cắt mặt phẳng
P
theo giao tuyến là đường
tròn đi qua ba điểm
A
,
B
,
C
. Biết
8
AB
cm
,
6
AC
cm
,
10
BC
cm
. Tính khoảng
cách
d
từ
I
đến mặt phẳng
P
.
A.
21
d
cm
. B.
4 6
d
cm
. C.
4
d
cm
. D.
146
d
cm
.
Câu 17. [2H2-3] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Mặt bên
SAB
là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích của khối cầu ngoại tiếp hình
chóp
.
S ABC
.
A.
3
5 15
54
a
V
. B.
3
4 3
27
a
V
. C.
3
5
3
a
V
. D.
3
5 15
18
a
V
.
x
0
1
2
y
0
0
y
1
4
x
y
1
1
O
y x
y x
y x

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/29
Câu 18. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để phương trình
4 2
3 1 0
x x m
có hai
nghiệm phân biệt.
A.
1
m
hoặc
13
4
m
. B.
1
m
.
C.
1
m
. D.
1
m
hoặc
13
4
m
.
Câu 19. [2D1-4] Cho Parabol
2
: 2 1,
P y x x
qua điểm
M
thuộc
P
kẻ tiếp tuyến với
P
cắt
hai trục
Ox
,
Oy
lần lượt tại hai điểm
A
,
B
. Có bao nhiêu điểm
M
để tam giác
ABO
có diện
tích bằng
1
.
4
A.
3
. B.
6.
C.
2
. D.
8
.
Câu 20. [2H2-3] Cho tứ diện đều
ABCD
có cạnh
2 .
a
Tính bán kính
r
của mặt cầu tiếp xúc với tất cả
các mặt của tứ diện.
A.
6
6
a
r . B.
6
.
12
a
r C.
6
8
a
r . D.
6
3
a
r .
Câu 21. [ 2D2-2] Cho hàm số
sin
x
y e
. Mệnh đề nào sau đây sai?
A.
.cos .sin 1
y x y x y
. B.
sin
2 sin sin 2 .
x
y x x e
.
C.
sin
cos .
x
y x e
. D.
.cos .sin 0
y x y x y
.
Câu 22. [2D2-1] Biết
6
log 2
a
0 1
a
. Tính
log 6
a
I .
A.
1
2
I
. B.
64
I
. C.
36
I
. D.
1
4
I
.
Câu 23. [2D2-2] Biết
6 6
log 2 , log 5 .
a b
Tính
3
log 5
I theo
, .
a b
A.
.
b
I
a
B.
.
1
b
I
a
C.
.
1
b
I
a
D.
.
1
b
I
a
Câu 24. [2H1-2] Cho khối lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
với
,
AB a A B
tạo với mặt phẳng
ABC
một góc
.
Biết thể tích lăng trụ
.
ABC A B C
là
3
3
.
2
a
Tính
.
A.
45 .
B.
70 .
C.
60 .
D.
30 .
Câu 25. [2D1-3] Một kim tự tháp Ai Cập có hình dạng là một khối chóp tứ giác đều có độ dài cạnh bên
là một số thực dương không đổi. Gọi
là góc giữa cạnh bên của kim tự tháp với mặt đáy. Khi
thể tích của kim tự tháp lớn nhất, tính
sin
.
A.
3
sin
2
. B.
3
sin
3
. C.
6
sin
3
. D.
5
sin
3
.
Câu 26. [2D2-2] Tìm
n
biết
2 3
2 2
2 2 2
1 1 1 1 465
...
log log log log log
n
x x x x x
luôn đúng với mọi
0,
x
1
x
.
A.
n
. B.
30
n
. C.
31
n
. D.
31
n
.
Câu 27. [2D2-2] Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
2
a
, các mặt bên tạo với đáy
một góc
60
. Tính diện tích
S
của mặt cầu ngoại tiếp hình chóp.
A.
2
25
3
a
S
. B.
2
12
a
S . C.
2
32
3
a
S
. D.
2
8
3
a
S
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/29
Câu 28. [2D1-4] Cho khối chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, cạnh bên hợp với đáy một
góc
60
. Gọi
M
là điểm đối xứng với
C
qua
D
,
N
là trung điểm
SC
. Mặt phẳng
BMN
chia khối chóp
.
S ABCD
thành hai khối đa diện. Tính thể tích
V
của khối đa diện chứa đỉnh
C
.
A.
3
7 6
36
a
V . B.
3
7 6
72
a
V . C.
3
5 6
72
a
V . D.
3
5 6
36
a
V .
Câu 29. [2D1-3] Cho các số thực dương
x
,
y
thỏa mãn
5
2
4
x y
. Tìm giá trị nhỏ nhất
min
P
của biểu
thức
2 1
4
P
x y
.
A.
min
34
5
P . B.
min
65
4
P . C.
min
P
không tồn tại. D.
min
5
P
.
Câu 30. [2D2-1] Số hình đa diện lồi trong các hình dưới đây là:
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 31. [2D1-1] Trong các hàm số sau, hàm số nào không có giá trị nhỏ nhất?
A.
2
1
x
y
x
. B.
4
2
y x x
. C.
2
2 3
y x x
. D.
2 1
y x
.
Câu 32. [2D1-1] Tìm số giao điểm của hai đồ thị hàm số
3
y x
và
1
y x
.
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 33. [2D1-4] Tìm tất cả các giá trị thực của tham số
m
để hàm số sin
y x mx
nghịch biến trên
.
A.
1
m
B.
1
m
. C.
1
m
. D.
1
m
.
Câu 34. [2H1-1]Người ta nối trung điểm các cạnh của một hình hộp chữ nhật
rồi cắt bỏ các hình chóp tam giác ở các góc của hình hộp như hình vẽ
sau. Hình còn lại là một đa diện có số đỉnh và số cạnh là:
A.
12
đỉnh,
24
cạnh. B.
10
đỉnh,
24
cạnh.
C.
12
đỉnh,
20
cạnh. D.
10
đỉnh,
48
cạnh.
Câu 35. [ 2D2-2] Tìm số nguyên
n
lớn nhất thỏa mãn
360 480
3
n .
A.
3
n
. B.
4
n
. C.
2
n
. D.
5
n
.
Câu 36. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
để hàm số
4 2 2
2 2 1 5
y x x m x
đồng biến trên khoảng
1;
.
A.
2 2
2 2
m . B.
2 2
2 2
m .
C.
2
2
m hoặc
2
2
m . D.
2
2
m hoặc
2
2
m .
Câu 37. [2D1-2] Tìm số tiệm cận đứng và ngang của đồ thị hàm số
3
1
3 2
x
y
x x
.
A.
0
. B.
3
. C.
2
. D.
1
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/29
Câu 38. [2D1-3] Cáp tròn truyền nhiệt dưới nước bao gồm một lõi
đồng và bao quanh lõi đồng là một lõi cách nhiệt như hình
vẽ. Nếu
r
x
h
là tỉ lệ bán kính độ dày thì bằng đo đạc thực
nghiệm người ta thấy rằng vận tốc truyền tải tín hiệu được
cho bởi phương trình
2
1
ln
v x
x
với
0 1
x
. Nếu bán kính
lõi cách nhiệt là
2
cm thì vật liệu cách nhiệt có bề dày
h
(cm) bằng bao nhiêu để tốc độ truyền tải tín hiệu lớn nhất?
A.
2
h e
(cm). B.
2
h e
(cm). C.
2
h
e
(cm). D.
2
h
e
(cm).
Câu 39. [2H1-2] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình vuông. Gọi
M
,
N
,
P
,
Q
lần lượt là
trung điểm các cạnh
SB
,
BC
,
CD
,
DA
. Biết thể tích khối chóp
.
S ABCD
là
0
V
. Tính thể tích
khối chóp .
M QPCN
theo
0
V
.
A.
0
3
4
V V
. B.
0
1
16
V V
. C.
0
3
8
V V
. D.
0
3
16
V V
.
Câu 40. [2H1-2] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình thang cân với đáy
AD
và
BC
. Biết
2
AD a
,
AB BC CD a
. Hình chiếu vuông góc của
S
trên mặt phẳng
ABCD
là điểm
H
thuộc đoạn
AD
thỏa mãn
3
HD HA
,
SD
tạo với đáy một góc
45
. Tính thể tích
V
của
khối chóp
.
S ABCD
.
A.
3
3
8
a
V . B.
3
3 3
8
a
V . C.
3
3 3
4
a
V . D.
3
9 3
8
a
V .
Câu 41. [2D1-3] Cho hàm số
3 2
y f x ax bx cx d
với
0
a
. Biết đồ thị hàm số có hai điểm
cực trị là
1; 1 , 1;3
A B . Tính
4
f .
A.
4 53
f
. B.
4 17
f
. C.
4 17
f
. D.
4 53
f
.
Câu 42. [2H1-1] Số mặt phẳng đối xứng của hình lăng trụ đứng có đáy là hình vuông là:
A.
4
. B.
5
. C.
1
. D.
3
.
Câu 43. [2D1-3] Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3
2 2
2 2 4 2 0
m x x x x
có nghiệm thỏa mãn
3
x
.
A.
4
. B.
6
.
C. Không có giá trị nào của
m
. D. Vô số giá trị của
m
.
Câu 44. [2H1-1] Cho tứ diện
OMNP
có
OM
,
ON
,
OP
đôi một vuông góc. Tính thể tích
V
của khối
tứ diện
OMNP
.
A.
1
. .
6
V OM ON OP
. B.
1
. .
2
V OM ON OP
.
C.
1
. .
3
V OM ON OP
. D.
. .
V OM ON OP
.
Câu 45. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để hàm số
4 2 2
1 1 1
y m x m x
có
đúng một cực trị.
A.
1
m
;
1
m
. B.
1
m
. C.
1
m
. D.
1
m
;
1
m
.
Cách nhiệt
Lõi đồng
r
h
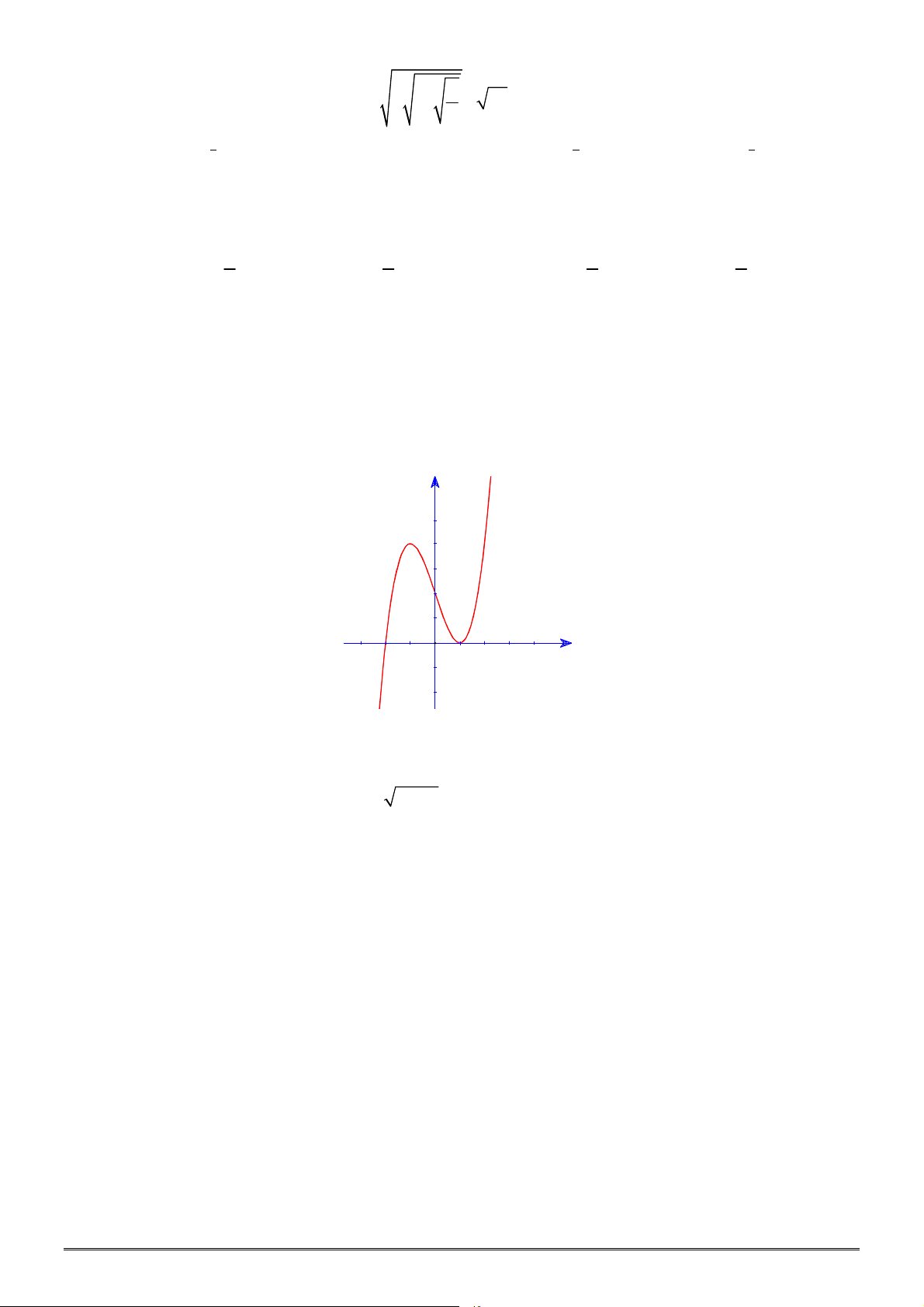
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/29
Câu 46. [2D2-2] Rút gọn biểu thức
2 7
24
3
4
1
:
P a a a
a
, với
0
a
.
A.
2
3
P a
. B.
P a
. C.
1
2
P a
. D.
1
3
P a
.
Câu 47. [2D2-2] Tìm tất các giá trị thực của
x
để đồ thị hàm số
0,5
log
y x
nằm trên đường thẳng
2.
y
A.
1
0
4
x
. B.
1
4
x
. C.
1
0
4
x
. D.
1
4
x
.
Câu 48. [2D2-3] Theo số liệu từ Tổng cục thống kê, dân số Việt Nam năm
2015
là
91,7
triệu người.
Giả sử tỉ lệ tăng dân số hàng năm của Việt Nam trong giai đoạn
2015 2050
ở mức không đổi
là
1,1%
. Hỏi đến năm nào dân số Việt Nam sẽ đạt mức
120,5
triệu người?
A.
2039
. B.
2040
. C.
2042
. D.
2041
.
Câu 49. [2D1-2] Đường cong ở hình vẽ là đồ thị của một trong các hàm số dưới đây:
Hàm số đó là hàm số nào?
x
y
1
O
-2
A.
2
1 2
y x x
. B.
2
1 2
y x x
. C.
2
1 2
y x x . D.
2
1 2
y x x .
Câu 50. [2D1-2] Đồ thị của hàm số nào trong các hàm số dưới đây có tâm đối xứng?
A.
2
2 6
y x x
. B.
2 1
y x
. C.
3 2
2 3
y x x x
. D.
4 2
2 5
y x x
.
----------HẾT----------
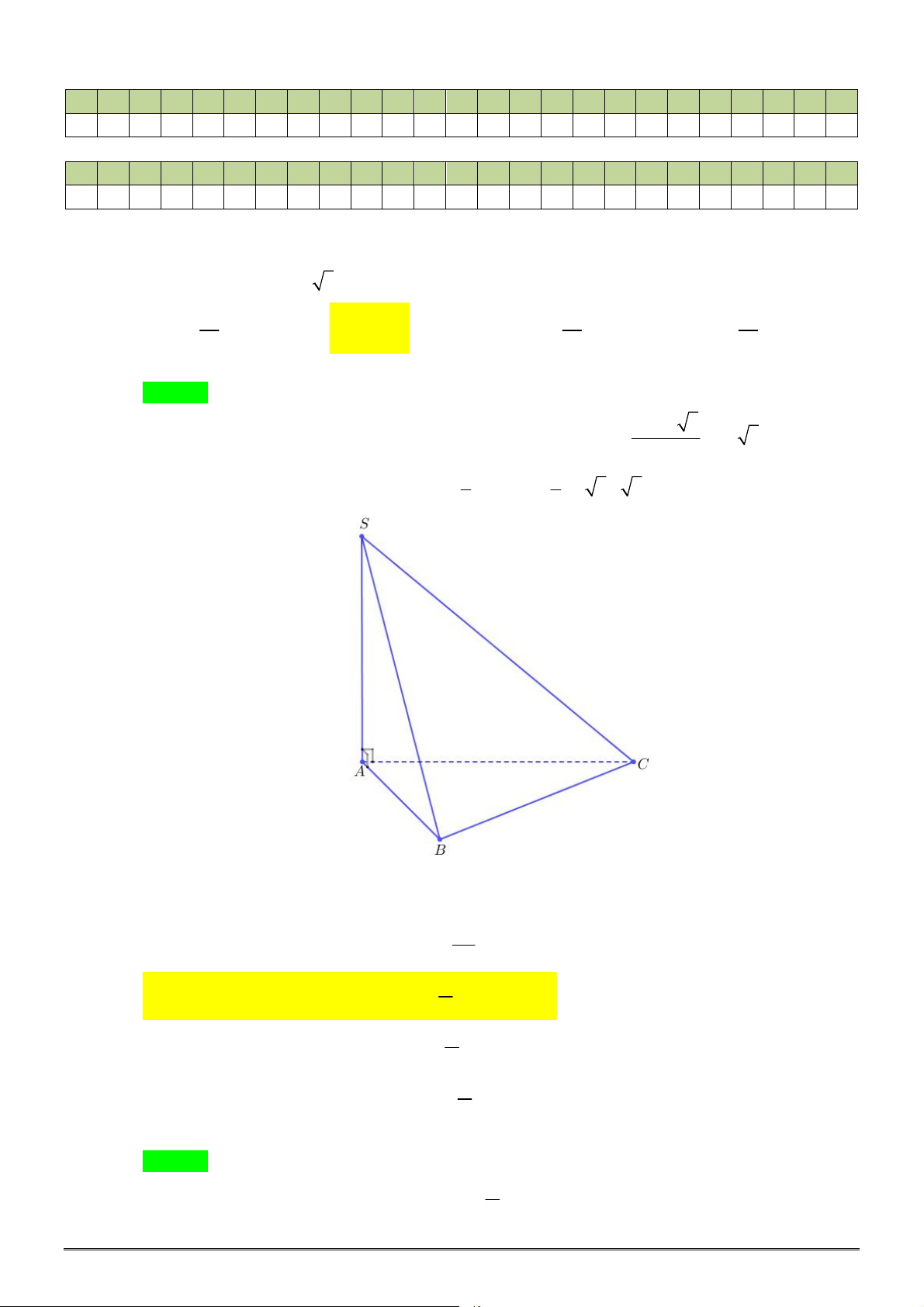
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/29
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B B C
C
C
B A
C
A
A
D
A
D
C
A
B A
D
C
A
A
A
D
C
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B A
C
D
D
A
D
B A
B C
B
A
D
B D
B C
A
D
C
A
B B C
HƯỚNG DẪN GIẢI
Câu 1. [2H1-1] Cho khối chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
2
a
,
SA
vuông góc với mặt
phẳng
ABC
,
3.
SA a Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
6
a
V . B.
3
V a
. C.
3
4
a
V . D.
3
12
a
V .
Lời giải
Chọn B.
Tam giác
ABC
là tam giác đều cạnh
2
a
nên có diện tích
2
2
2 3
3
4
ABC
a
S a .
Thể tích
V
của khối chóp
.
S ABC
là:
2 3
1 1
. . 3. 3
3 3
ABC
V S SA a a a
.
Câu 2. [2D1-2] Cho hàm số
sin cos 2
y x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại các điểm
3
2 ,
4
x k k
.
B. Hàm số đạt cực đại tại các điểm 2 ,
4
x k k
.
C. Hàm số đạt cực tiểu tại các điểm 2 ,
4
x k k
.
D. Hàm số đạt cực tiểu tại các điểm 2 ,
4
x k k
.
Lời giải
Chọn B.
Ta có cos sin 0 tan 1 ,
4
y x x x x k k
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/29
Hay
0 2
4
y x k
hoặc
3
2 ,
4
x k k
.
Mặt khác:
sin cos
y x x
;
Nên:
2 sin 2 cos 2 sin cos 2 0
4 4 4 4 4
y k k k
3 3 3 3 3
2 sin 2 cos 2 sin cos 2 0
4 4 4 4 4
y k k k
.
Do đó, hàm số đạt cực đại tại các điểm 2 ,
4
x k k
.
Câu 3. [2D1-1] Tìm số điểm cực trị của hàm số
4 3 2
3 8 6 1
y x x x
.
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Chọn C.
Ta có:
3 2 2
12 24 12 12 1
y x x x x x x
Xét
0 0
y x
.Ta thấy
y
đổi dấu từ âm sang dương khi đi qua giá trị
0
x
Hàm số có 1
điểm cực trị (cực tiểu).
Câu 4. [2D1-2] Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
8
2
mx
y
x
có tiệm cận đứng.
A.
4
m
. B.
4
m
. C.
4
m
. D.
4
m
.
Lời giải
Chọn C.
*TXĐ:
\ 2
D
.
*Ta có:
2 2
8
lim lim
2
x x
mx
y
x
Để đồ thị hàm số
8
2
mx
y
x
có tiệm cận đứng điều kiện là:
2
lim 2 8 0 4
x
y m m
.
Câu 5. [1D1-2] Tìm giá trị lớn nhất
M
của hàm số
2
2sin sin2 11
y x x
.
A.
12 2
M
. B.
10 2
M
. C.
12 2
M
. D.
10 2
M
.
Lời giải
Chọn C.
Tập xác định
D
.
Ta có
2
2sin sin2 11
y x x
1 cos2 sin2 11
x x
12 2cos 2
4
x
.
Suy ra
max 12 2
M y
. Dấu
" "
xảy ra khi
cos 2 1
4
x
.
Câu 6. [2D1-1] Hàm số
3
3 5
y x x
đồng biến trên khoảng nào dưới đây?
A.
; 1
. B.
1;1
. C.
;1
. D.
1;
.
Lời giải
Chọn B.
Tập xác định
D
. Đạo hàm
2
3 3
y x
.
Ta có
0
y
2
3 3 0
x
1 1
x
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/29
Vậy hàm số đã cho đồng biến trên khoảng
1;1
.
Câu 7. [2D1-2] Biết đồ thị hai hàm số
1
y x
và
2 1
1
x
y
x
cắt nhau tại hai điểm phân biện
A
,
B
.
Tính độ dài đoạn thẳng
AB
.
A.
2 2
AB
. B.
2
AB
. C.
2
AB
. D.
4
AB
.
Lời giải
Chọn A.
Xét phương trình hoành độ giao điểm của hai hàm số đã cho:
2 1
1,
1
x
x
x
1
x
.
0 1
2 1
x y
x y
Toạ độ giao điểm lần lượt là.
0; 1
. và
2;1
.
Vậy độ dài đoạn thẳng
2 2
AB
.
Câu 8. [2D2-2] Tìm tập xác định
D
của hàm số
2018
2
2017
log 9 2 3y x x
.
A.
3 3
3; ;3
2 2
D
. B.
3;3
D .
C.
3 3
3; ;3
2 2
D
. D.
3
;3
2
D
.
Lời giải
Chọn C.
Hàm số xác định
2
9 0
2 3 0
x
x
3 3
3
2
x
x
. Vậy tập xác định là:
3 3
3; ;3
2 2
D
.
Câu 9. [2D1-2]Cho hàm số
3
3
y x x
với
2;x
. Mệnh đề nào dưới đây đúng?
A. Hàm số có giá trị nhỏ nhất và không có giá trị lớn nhất.
B. Hàm số có cả giá trị nhỏ nhất và giá trị lớn nhất.
C. Hàm số không có cả giá trị nhỏ nhất và giá trị lớn nhất.
D. Hàm số không có giá trị nhỏ nhất và có giá trị lớn nhất.
Lời giải
Chọn A.
Tập xác định:
3;0 3;D
. Hàm số xác định và liên tục với
2;x
.
Ta có
2
3
3 3
2 3
x
y
x x
;
0 1
y x
;
y
xác định với mọi
2;x
.
Thấy ngay
0
y
,
2;x
do đó hàm số có giá trị nhỏ nhất tại
2
x
và không có giá trị
lớn nhất.
Câu 10. [2D2-2] Cho
p
,
q
là các số thực thỏa mãn:
2
1
p q
m
e
,
2
p q
n e
, biết
m n
. So sánh
p
và
q
.
A.
p q
. B.
p q
. C.
p q
. D.
p q
.
Lời giải
Chọn A.
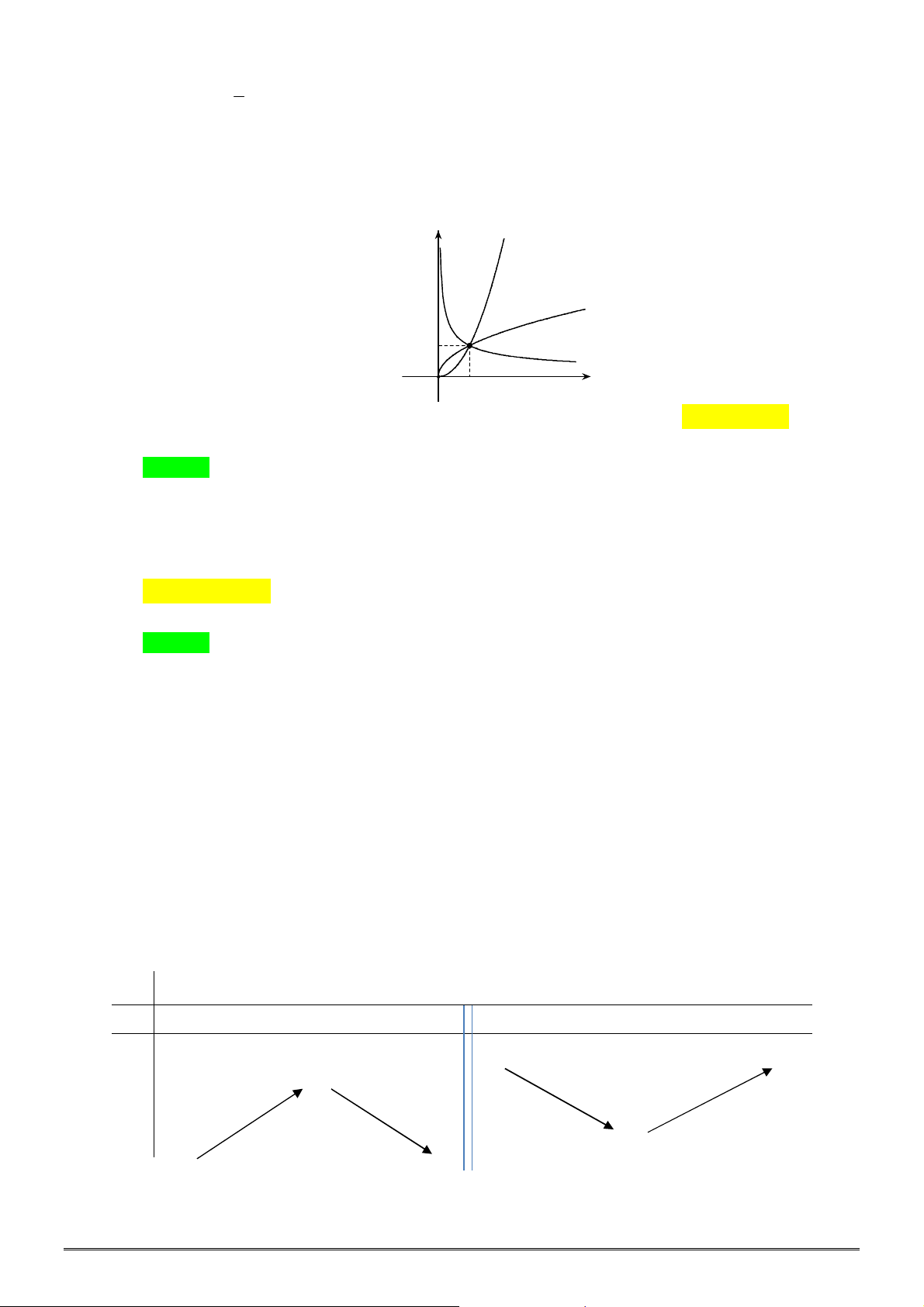
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/29
Ta có
2
2
1
p q
q p
m e
e
.
Theo giả thiết:
2 2
2 2
q p p q
m n e e q p p q
(do cơ số
1
e
)
p q
.
Câu 11. [2D2-2] Hình vẽ sau là đồ thị của ba hàm số
y x
,
y x
,
y x
(với
0
x
và
,
,
là
các số thực cho trước). Mệnh đề nào dưới đây đúng?
A.
. B.
. C.
. D.
.
Lời giải
Chọn D.
Theo hình vẽ các đồ thị tương ứng thì
1
,
0 1
và
0
nên suy ra
.
Câu 12. [2D1-3] Cho hàm số
3 2
3 2 1
y x x x
. Tiếp tuyến song song với đường thẳng
2 3 0
x y
của đồ thị hàm số trên có phương trình là
A.
2 1 0.
x y
B.
2 2 0
x y
. C.
2 1 0
x y
. D.
2 1
y x
.
Lời giải
Chọn A.
Đường thẳng
: 2 3 0
x y
được viết lại dưới dạng
2 3
y x
. Suy ra, hệ số góc của
bằng
2.
Gọi
0 0
;
x y
là tọa độ tiếp điểm. Tiếp tuyến song song với
, suy ra:
0
2
y x
0 0
2 2
0 0 0 0
0 0
0 1
3 6 2 2 3 6
2 y 7
x y
x x x x
x
Tại điểm
0; 1
, ta được phương trình tiếp tuyến
2 0 1 2 1 2 1 0
y x x x y
.
Tại điểm
2;7
, ta được phương trình tiếp tuyến
2 2 7 2 3
y x x
(loại, do trùng
với đường thẳng
).
Vậy, tiếp tuyến cần tìm có phương trình là
2 1 0
x y
.
Câu 13. [2D1-2] Cho hàm số
y f x
có bảng biến thiên như hình vẽ. Mệnh đề nào dưới đây sai?
x
0
1
2
y
0
0
y
1
4
A. Hàm số đồng biến trên khoảng
3; 1
.
B. Đồ thị hàm số không có đường tiệm cận ngang.
x
y
1
1
O
y x
y x
y x

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/29
C. Đồ thị hàm số có một đường tiệm cận đứng.
D. Hàm số nghịch biến trên
0; 1 1; 2
.
Lời giải
Chọn D.
Từ bảng biến thiên suy ra:
Hàm số đồng biến trên khoảng
; 0
nên cũng đồng biến trên khoảng
3; 1
nên A đúng.
lim
x
y
và lim
x
y
nên đồ thị hàm số không có tiệm cận ngang do đó B đúng.
1 1
lim ; lim
x x
y y
nên đồ thị hàm số có một đường tiệm cận đứng do đó C đúng.
Xét phương án D “Hàm số nghịch biến trên
0; 1 1; 2
” là mệnh đề sai vì ta chỉ xét tính đơn
điệu của hàm số trên khoảng
K
, với
K
là khoảng, đoạn hoặc nửa khoảng.
Câu 14. [2D2-2] Tính tổng
1 2
S x x
biết
1
x
,
2
x
là các giá trị thực thỏa mãn đẳng thức
2
3
6 1
1
2
4
x
x x
.
A.
5
S
. B.
8
S
. C.
4
S
. D.
2
S
.
Lời giải
Chọn C.
Ta có
2 2
3
2 3
6 1 6 1 2
1
2 2 2 6 1 2 6
4
x
x
x x x x
x x x
1
2
1 2
2
1
4 5 0 4
5
x
x x S x x
x
.
Câu 15. [2H2-3] Cho tam giác
ABC
. Tập hợp các điểm
M
trong không gian thỏa mãn hệ thức
MA MB MC a
(với
a
là số thức dương không đổi) là:
A. Mặt cầu bán kính
3
a
R
. B. Đường tròn bán kính
3
a
R
.
C. Đoạn thẳng độ dài
3
a
. D. Đường thẳng.
Lời giải
Chọn A.
Gọi
G
là trọng tâm tam giác
ABC
. Theo bài ra ta có,
MA MB MC MG GA MG GB MG GC
3
MG GA GB GC
3
MG
.
Thay vào
MA MB MC a
ta được
3 *
3
a
MG a MG
. Vì
G
cố định nên tập hợp
các điểm
M
thỏa mãn
*
là mặt cầu tâm
G
bán kính
3
a
.
Câu 16. [2H2-3] Mặt cầu tâm
I
bán kính
11
R
cm
cắt mặt phẳng
P
theo giao tuyến là đường
tròn đi qua ba điểm
A
,
B
,
C
. Biết
8
AB
cm
,
6
AC
cm
,
10
BC
cm
. Tính khoảng
cách
d
từ
I
đến mặt phẳng
P
.
A.
21
d
cm
. B.
4 6
d
cm
. C.
4
d
cm
. D.
146
d
cm
.
Lời giải
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/29
Chọn B.
Gọi
J
là hình chiếu của
I
lên
P
. Theo bài ra
IA IB IC R
nên
J
là tâm đường tròn
ngoại tiếp tam giác
ABC
.
Ta có
12 cm
2
AB AC BC
p
,
ABC
S p p a p b p c
2
12.4.6.2 24 cm
Đặt
1
R
là bán kính đường tròn ngoại tiếp tam giác
ABC
. Ta có
1
. .
4
ABC
AB AC BC
S
R
1
. .
4
AB AC BC
R
S
8.6.10
5 cm
4.24
.
Từ đó suy ra
2 2
d IJ IA AJ
2 2
1
R R
121 25
4 6 cm
.
Chú ý: Tam giác
ABC
vuông tại
A
nên
J
là trung điểm
BC
nên
1
5
2
BC
R
.
Câu 17. [2H2-3] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Mặt bên
SAB
là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích của khối cầu ngoại tiếp hình
chóp
.
S ABC
.
A.
3
5 15
54
a
V
. B.
3
4 3
27
a
V
. C.
3
5
3
a
V
. D.
3
5 15
18
a
V
.
Lời giải
Chọn A.
a
a
a
a
O
H
C
A
B
S
G
I
Gọi
H
là trung điểm của
AB
. Dễ thấy
SH ABC
.
I
J
A
B
C
P

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/29
Gọi
G
và
I
lần lượt là trọng tâm của tam giác
ABC
và
SAB
. Do tam giác
ABC
và
SAB
là
tam giác đều nên
G
và
I
lần lượt là tâm đường tròn ngoại tiếp của tam giác
ABC
và
SAB
.
Dựng trục của hai đường tròn ngoại tiếp tam giác
ABC
và
SAB
cắt nhau tại
O
.
Ta có
OA
OB
OC
OS
.
Vậy
O
là tâm mặt cầu ngoại tiếp hình chóp
.
S ABC
.
Dễ thấy,
OIHG
là hình vuông.
Vậy
OI
GH
IH
1
3
CH
3
6
a
.
Xét tam giác vuông
OCG
có
2 2
OC OG CG
2 2
3 3
36 9
a a
15
6
a
.
Vậy thể tích khối cầu ngoại tiếp hình chóp
.
S ABC
là:
3
4 15 15
.
3 216
a
V
3
5 15
54
a
.
Câu 18. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để phương trình
4 2
3 1 0
x x m
có hai
nghiệm phân biệt.
A.
1
m
hoặc
13
4
m
. B.
1
m
.
C.
1
m
. D.
1
m
hoặc
13
4
m
.
Lời giải
Chọn D.
4 2
3 1 0
x x m
4 2
3 1 *
x x m .
Số nghiệm của phương trình
*
bằng số giao điểm của đồ thị hàm số
4 2
3 1
y x x
và
đường thẳng
y m
.
Xét hàm số
4 2
3 1
y x x
.
D
.
3
4 6
y x x
2
2 2 3
x x
.
0
y
2
2 2 3 0
x x
0
6
2
6
2
x
x
x
.
Lập bảng biến thiên
Vậy phương trình
*
có hai nghiệm phân biệt khi và chỉ khi
1
m
hoặc
13
4
m
.
x
6
2
0
6
2
y
0
0
0
y
13
4
1
13
4

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/29
Câu 19. [2D1-4] Cho Parabol
2
: 2 1,
P y x x
qua điểm
M
thuộc
P
kẻ tiếp tuyến với
P
cắt
hai trục
Ox
,
Oy
lần lượt tại hai điểm
A
,
B
. Có bao nhiêu điểm
M
để tam giác
ABO
có diện
tích bằng
1
.
4
A.
3
. B.
6.
C.
2
. D.
8
.
Lời giải
Chọn C.
2 2.
y x
Điểm
2
0 0 0
; 2 1 .
M P M x x x
Tiếp tuyến của đồ thị
P
tại
M
có phương trình là
2
0 0 0 0
: 2 2 2 1.
d y x x x x x
Với
0
1,
x
d Ox
tại
2
0
0
1
;0 ,
2 1
x
A d Oy
x
tại
2
0
0; 1 .
B x
Ta có
2
2
2 2
0
0 0 0
0
11 1 1
. . 1 1 1 3 .
2 2 2 1 4
OAB
x
S OAOB x x x
x
TH1:
0
4 2 3
0 0 0 0 0 0
3
0 0
0
1: 3 2 1 1 2 1 0
2 1 0 *
o
x TM
x PT x x x x x x
x x
Xét hàm số
3 2
2 1, 3 2 0, 0; .
f x x x f x x x
Ta có hàm số
f x
liên tục trên
0;
f x
đồng biến trên khoảng
0; .
Ta có
0 . 1 2 0 *
f f PT có
1
nghiệm duy nhất thuộc
0;1
.
TH2:
4 2 4 2
0 0 0 0 0 0 0
1: 3 2 1 1 2 2 0 ** .
x PT x x x x x x
Xét hàm số
4 2 3
2 2; 4 4 1 0, 1.
g x x x x g x x x x
Hàm số
g x
liên tục trên
; 1
g x
nghịch biến trên
; 1
.
Ta có
1 1 4 **
x g x g PT vô nghiệm.
Vậy có
2
giá trị
0
x
thỏa mãn
có
2
điểm
M
thỏa mãn yêu cầu.
Câu 20. [2H2-3] Cho tứ diện đều
ABCD
có cạnh
2 .
a
Tính bán kính
r
của mặt cầu tiếp xúc với tất cả
các mặt của tứ diện.
A.
6
6
a
r . B.
6
.
12
a
r C.
6
8
a
r . D.
6
3
a
r .
Lời giải
Chọn A.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/29
Gọi
O
là tâm đường tròn ngoại tiếp
.
BCD AO BCD
Giả sử mặt cầu tiếp xúc với tất cả các mặt của tứ diện có tâm
,
I
bán kính
r
.
Ta có
. . . . .
1
4 4. . . .
3
ABCD I BCD I ABC I ABD I ACD I BCD BCD
V V V V V V r S
Ta có
3 2
2 2 2 3
; .
12 4
ABCD BCD
a a
V S
Suy ra
3
2
8 2
3.
3
6
12
.
4. 6
4 3
4.
4
ABCD
BCD
a
V a
r
S
a
Cách khác
Bốn đường cao trong tứ diện đều
ABCD
cùng bằng
2 6
3
a
và đồng quy tại điểm
I
chia các
đường cao theo cùng một tỉ lệ
3:1
.
Vì vậy
I
là điểm cách đều các mặt, hay
I
là tâm mặt cầu tiếp xúc với các mặt của tứ diện.
Khi đó bán kính mặt cầu tâm
I
tiếp xúc với các mặt chính là
1 2 6 6
4 3 6
a a
r .

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/29
Câu 21. [ 2D2-2] Cho hàm số
sin
x
y e
. Mệnh đề nào sau đây sai?
A.
.cos .sin 1
y x y x y
. B.
sin
2 sin sin 2 .
x
y x x e
.
C.
sin
cos .
x
y x e
. D.
.cos .sin 0
y x y x y
.
Lời giải
Chọn A.
Ta có:
sin
cos .
x
y x e
nên loại C.
sin
2 sin 2cos . .sin
x
y x x e x
sin
sin2 .
x
x e
nên loại B.
sin 2 sin
sin . cos .
x x
y x e x e
.cos .sin
y x y x y
2 sin sin sin 2 sin
cos . sin .e sin . cos .
x x x x
x e x x e x e
0
nên loại D.
Vậy chọn đáp án A.
Câu 22. [2D2-1] Biết
6
log 2
a
0 1
a
. Tính
log 6
a
I .
A.
1
2
I
. B.
64
I
. C.
36
I
. D.
1
4
I
.
Lời giải
Chọn A.
Ta có
6
1 1
log 6 .
log 2
a
I
a
Câu 23. [2D2-2] Biết
6 6
log 2 , log 5 .
a b
Tính
3
log 5
I theo
, .
a b
A.
.
b
I
a
B.
.
1
b
I
a
C.
.
1
b
I
a
D.
.
1
b
I
a
Lời giải
Chọn D.
Ta có
3
5 5 5
5
1 1 1
log 5 .
1
log 3 log 6 log 2
log 2
I
b
Lại có
5 6 5
1 1
. log 6.log 2 log 2 .
1
1
b
a I
a
b a
b b
Cách khác:
6 6
3
6 6 6
log 5 log 5
log 5 .
log 3 log 6 log 2 1
b
I
a
Câu 24. [2H1-2] Cho khối lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
với
,
AB a A B
tạo với mặt phẳng
ABC
một góc
.
Biết thể tích lăng trụ
.
ABC A B C
là
3
3
.
2
a
Tính
.
A.
45 .
B.
70 .
C.
60 .
D.
30 .
Lời giải
Chọn C.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/29
C
B
A
C'
B'
A'
Lăng trụ đứng
. ;
ABC A B C A A ABC A B ABC A BA
tan
A A A A
A BA
AB a
(1)
Ta có
3
.
3 1 1
. . . . . 3.
2 2 2
ABC A B C ABC
a
V A A S A A AB AC A A a a A A a
Thế vào (1) ta được
tan 3 60 .
Câu 25. [2D1-3] Một kim tự tháp Ai Cập có hình dạng là một khối chóp tứ giác đều có độ dài cạnh bên
là một số thực dương không đổi. Gọi
là góc giữa cạnh bên của kim tự tháp với mặt đáy. Khi
thể tích của kim tự tháp lớn nhất, tính
sin
.
A.
3
sin
2
. B.
3
sin
3
. C.
6
sin
3
. D.
5
sin
3
.
Lời giải
Chọn B.
S
A
B
C
D
O
Vì hình dạng của kim tự tháp là một hình chóp tứ giác đều nên hình vẽ có dạng như trên. Giả
sử gọi cạnh bên của kim tự tháp là
x
với 0, x x
.
SO
là chiều cao của hình chóp.
SA SB SC SD x
, góc giữa cạnh bên của hình chóp với mặt đáy là
SBO
.
Ta có
.sin
SO x
;
.cos
OB x
suy ra
2 .cos
BD x
.
Vậy thể tích:
2
3 2
.
1 1 1 2
. .sin . 2 .cos sin .cos
3 3 2 3
S ABCD ABCD
V SO S x x x
.
.S ABCD
V V
3 2
2
sin .cos
3
x
Suy ra
3 2
2
sin . 1 sin
3
V x
.
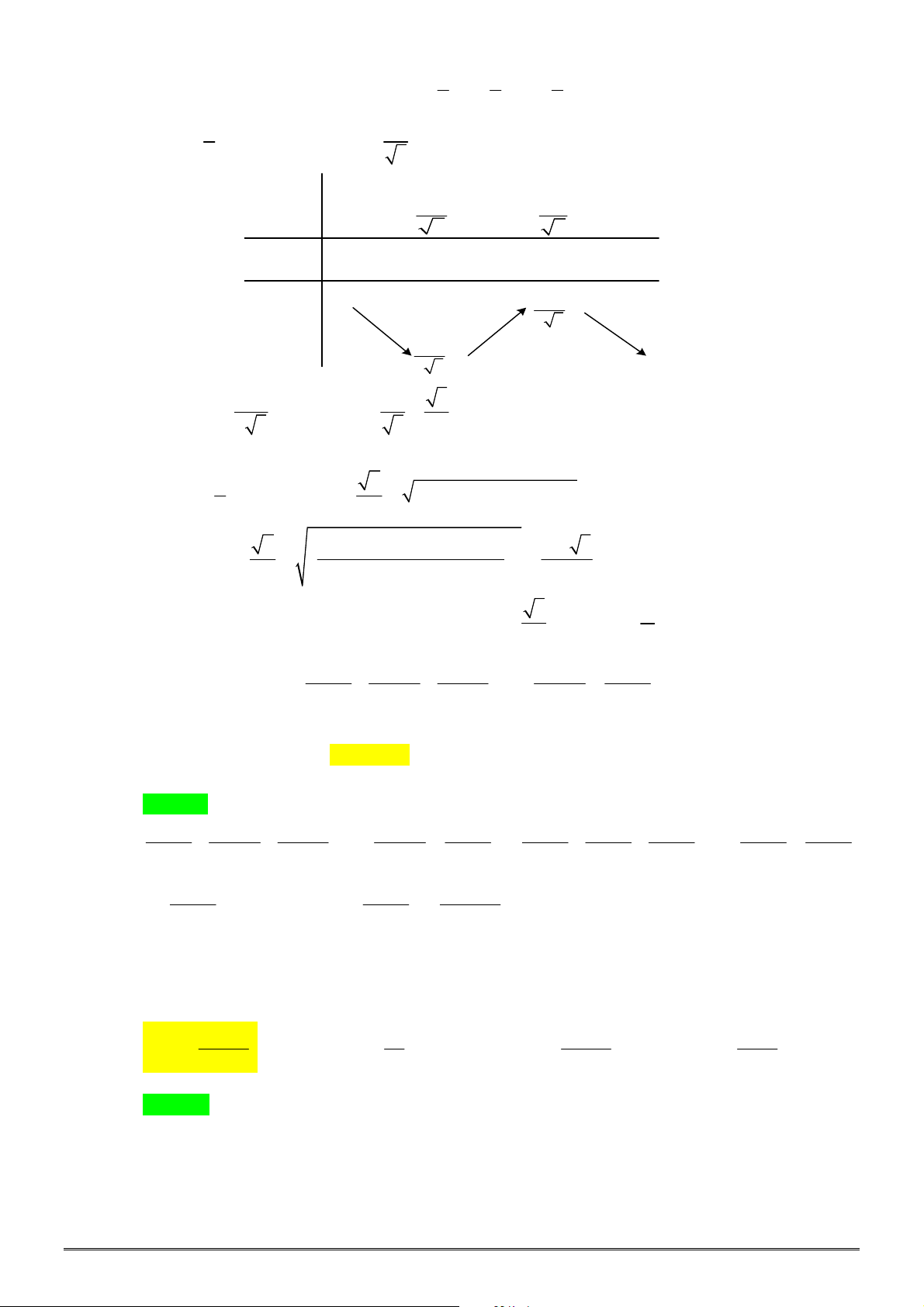
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/29
Ta khảo sát hàm
3 3 3 3 3
2 2 2
3 3 3
V t x t x t x t t
với
sin 1;1
t
.
3 3 2
2 1
2 0
3
3
V t x x t t
. Ta có bảng biến thiên:
t
V t
V t
1
1
1
3
1
3
0
0
0
0
3
4
9 3
x
3
4
9 3
x
3
1;1
4
max
9 3
V t x
khi
1 3
sin
3
3
.
Cách khác:
3 2 3 2 2 2
.
2 2
sin .cos 2sin .cos .cos
3 3
S ABCD
V x x
Vậy
3
2 2 2 3
3
.
2 2sin cos cos 4 3
3 3 27
S ABCD
x
V x
.
Dấu
" "
xảy ra khi
2 2
2sin cos
hay
3
sin
3
(do
0 sin 0
2
).
Câu 26. [2D2-2] Tìm
n
biết
2 3
2 2
2 2 2
1 1 1 1 465
...
log log log log log
n
x x x x x
luôn đúng với mọi
0,
x
1
x
.
A.
n
. B.
30
n
. C.
31
n
. D.
31
n
.
Lời giải
Chọn B.
2 3
2 2
2 2 2
1 1 1 1 465
...
log log log log log
n
x x x x x
2 2 2 2 2
1 2 3 465
...
log log log log log
n
x x x x x
2 2
1 465
1 2 3 ...
log log
n
x x
1
465
2
n n
2
930 0
n n
30
31
n
n
.
Do
n
là số nguyên dương nên
30
n
.
Câu 27. [2D2-2] Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
2
a
, các mặt bên tạo với đáy
một góc
60
. Tính diện tích
S
của mặt cầu ngoại tiếp hình chóp.
A.
2
25
3
a
S
. B.
2
12
a
S . C.
2
32
3
a
S
. D.
2
8
3
a
S
.
Lời giải
Chọn A.
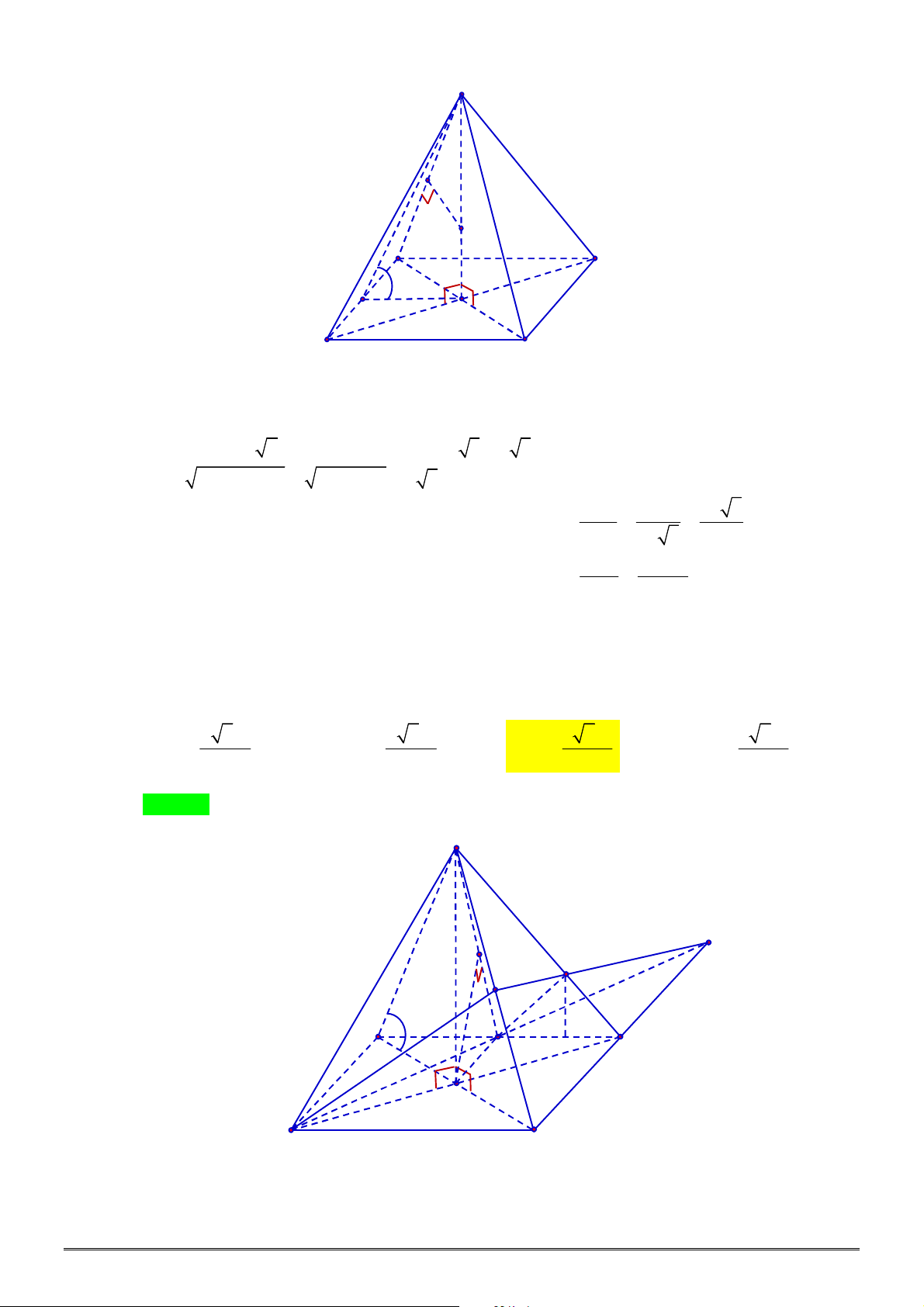
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/29
Gọi
H
là tâm đáy,
K
và
M
lần lượt là trung điểm của
SA
và
AB
, 60
SAB ABCD SMH
.
Kẻ
KI SA
,
I SH
suy ra
I
là tâm mặt cầu ngoại tiếp hình chóp
.
S ABCD
.
Ta có:
2
AH a
,
.tan60 . 3 3
SH MH a a
,
2 2 2 2
3a 2a 5
SA SH AH a
.
Suy ra bán kính mặt cầu ngoại tiếp hình chóp là:
2 2
5 5 3
2 6
2 3
SA a a
R SI
SH
a
.
Diện tích mặt cầu ngoại tiếp hình chóp là:
2 2
2
25 25
4 4 .
12 3
a a
S R
.
Câu 28. [2D1-4] Cho khối chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, cạnh bên hợp với đáy một
góc
60
. Gọi
M
là điểm đối xứng với
C
qua
D
,
N
là trung điểm
SC
. Mặt phẳng
BMN
chia khối chóp
.
S ABCD
thành hai khối đa diện. Tính thể tích
V
của khối đa diện chứa đỉnh
C
.
A.
3
7 6
36
a
V . B.
3
7 6
72
a
V . C.
3
5 6
72
a
V . D.
3
5 6
36
a
V .
Lời giải
Chọn C.
Gọi
P MN SD
,
Q BM AD
. Suy ra
BNPQ
là thiết diện của
BMN
với hình chóp
.
S ABCD
.
S
H
C
D
A
B
I
R
K
60
2
a
M
S
H
C
D
A
B
60
a
N
M
P
Q
I
K

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/29
Gọi
H
là tâm của đáy, ta có:
2 6
.tan60 . 3
2 2
a a
SH ABCD SH AH .
Ta có:
. .
CDPQBN N BCDQ N DPQ
V V V .
Do
N
là trung điểm của
SC
, suy ra
1
,
2
d N BCDQ SH
.
Ta lại có:
M
là điểm đối xứng với
C
qua
D
, suy ra
Q
là trung điểm của
AD
.
nên
2
.
.
3
2
2 2 4
BCDQ
a
a a
BC DQ CD
a
S
,
2 3
.
1 1 6 3 3 6
. . . .
6 6 2 4 48
N BCDQ BCDQ
a a a
V SH S .
Ta có:
,
1
2
,
d N DPQ
NS
CS
d C DPQ
,
,
2
,
d C SAD
CA
HA
d H SAD
,
, ,
d N DPQ d H SAD
.
Mà
HQ AD
, kẻ
HI SQ I
,
d H SAD HI
.
2 2 2 2 2 2
1 1 1 2 4 14
3 3
HI SH HQ a a a
3
.
14
HI a
.
Xét
SCM
, có
N
và
D
là trung điểm của
SC
và
CM
suy ra
P
là trọng tâm
SCM
.
1
3
DP SD
. Kẻ
PK DQ K
,
2 2
2 2
3
7
2 4
3 3 3 6
a a
SH HQ
SQ a
PK
.
Suy ra:
2
1 1 7 7
. . .
2 2 2 6 24
DPQ
a a a
S DQ PK ,
2 3
.
1 3 7 6
. . .
3 14 24 144
N DPQ
a a
V a .
Vậy
3 3 3
3 6 6 5 6
48 144 72
CDPQBN
a a a
V .
Cách khác
Gọi
P MN SD
,
Q BM AD
. Suy ra
BNPQ
là thiết diện của
BMN
với hình chóp
.
S ABCD
.
Gọi
H
là tâm của đáy, ta có:
2 6
.tan60 . 3
2 2
a a
SH ABCD SH AH .
Gọi
3
2
.
1 1 6 6
.
3 3 2 6
S ABCD ABCD
a a
V V SH S a .
Do
N
là trung điểm của
SC
,
D
là trung điểm
CM
nên
P
là trọng tâm tam giác
SCM
,
3
2
,
d N BCM
NM
PM
d P BCM
.
Dễ thấy
1
4
ABQ QDM BCM
S S S nên
3
. .
1 6
2 12
N BCM S ABCD
a
V V
và
. . .
2 1 1
.
3 4 6
P DQM N BCM N BCM
V V V .
Vậy
3 3
. . . .
1 5 6 5 6
6 6 12 72
NPBCDQ N BCM P DQM N BCM N BCM
a a
V V V V V .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/29
Câu 29. [2D1-3] Cho các số thực dương
x
,
y
thỏa mãn
5
2
4
x y
. Tìm giá trị nhỏ nhất
min
P
của biểu
thức
2 1
4
P
x y
.
A.
min
34
5
P . B.
min
65
4
P . C.
min
P
không tồn tại. D.
min
5
P
.
Lời giải
Chọn D.
Từ giả thiết ta có
5
2
4
y x
. Vì
0
y
nên
5 5
2 0
4 8
x x
. Do đó
5
0
8
x
.
Ta có
2
2 1 2 1 10 15
5
5 8 8 5
4 2
4
x
P
x x x x x
x
với
5
0
8
x
.
2
2
2
120 160 50
8 5
x x
P
x x
. Có
2
5 5
0;
6 8
0 120 160 50 0
1 5
0;
2 8
x
P x x
x
.
Bảng biến thiên
Dựa vào bảng biến thiên ta có
min
5
P
.
Câu 30. [2D2-1] Số hình đa diện lồi trong các hình dưới đây là:
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn D.
Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn
thuộc(H). Khi đó đa diện giới hạn (H) được gọi là đa diện lồi.
Do đó chỉ có hình cuối là hình đa diện lồi.
Câu 31. [2D1-1] Trong các hàm số sau, hàm số nào không có giá trị nhỏ nhất?
A.
2
1
x
y
x
. B.
4
2
y x x
. C.
2
2 3
y x x
. D.
2 1
y x
.
Lời giải
Chọn A.
Ta có
1
2
lim
1
x
x
x
nên
2
1
x
y
x
không có giá trị nhỏ nhất.
Câu 32. [2D1-1] Tìm số giao điểm của hai đồ thị hàm số
3
y x
và
1
y x
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/29
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn D.
Phương trình hoành độ giao điểm
3 1
x x
2
1 0
3 1
x
x x
2
1
2 0
x
x x
1
1
2
x
x n
x l
1
x
có một nghiệm nên có 1 giao điểm.
Câu 33. [2D1-4] Tìm tất cả các giá trị thực của tham số
m
để hàm số sin
y x mx
nghịch biến trên
.
A.
1
m
B.
1
m
. C.
1
m
. D.
1
m
.
Lời giải
Chọn B.
Ta có: cos
y x m
Hàm số luôn nghịch biến trên
khi:
0, cos 0, cos ,y x x m x x m x
Mà
cos [ 1;1]
x
Vậy
1
m
Câu 34. [2H1-1]Người ta nối trung điểm các cạnh của một hình hộp chữ nhật rồi cắt bỏ các hình chóp
tam giác ở các góc của hình hộp như hình vẽ sau.
Hình còn lại là một đa diện có số đỉnh và số cạnh là:
A.
12
đỉnh,
24
cạnh. B.
10
đỉnh,
24
cạnh. C.
12
đỉnh,
20
cạnh. D.
10
đỉnh,
48
cạnh.
Lời giải
Chọn A.
Đa diện có
4
đỉnh thuộc mặt đáy trên,
4
đỉnh thuộc mặt đáy dưới và
4
đỉnh thuộc
4
cạnh
bên.
Vậy có
12
đỉnh.
Mỗi mặt của hình hộp có 4 cạnh của đa diện. vậy có 24 cạnh.
Câu 35. [ 2D2-2] Tìm số nguyên
n
lớn nhất thỏa mãn
360 480
3
n .
A.
3
n
. B.
4
n
. C.
2
n
. D.
5
n
.
Lời giải
Chọn B.
120 120
360 480 3 4 3
3 3
3 3 81 81 3 3 3 3
n n n n
Mà
n
là số nguyên lớn nhất
4
n
.
Câu 36. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
để hàm số
4 2 2
2 2 1 5
y x x m x
đồng biến trên khoảng
1;
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 23/29
A.
2 2
2 2
m . B.
2 2
2 2
m .
C.
2
2
m hoặc
2
2
m . D.
2
2
m hoặc
2
2
m .
Lời giải
Chọn C.
3 2
4 4 2 1
y x x m
Hàm số đồng biến trên khoảng
1;
3 2
4 4 2 1 0, 1;x x m x
3 2
4 4 1 2 , 1;x x m x
1
Xét hàm số
3
4 4
g x x x
trên
1;
2
12 4
g x x
3
0
3
g x x
1
2
1 2 0
m
2
2
2
2
m
m
.
Câu 37. [2D1-2] Tìm số tiệm cận đứng và ngang của đồ thị hàm số
3
1
3 2
x
y
x x
.
A.
0
. B..
3
. C.
2
. D.
1
.
Lời giải
Chọn B.
Tập xác định:
\ 1;2
D
.
lim 0
x
y
đường thẳng
0
y
là đường tiệm cận ngang của đồ thị hàm số.
2
1 1 1
1 1
lim lim lim
1 2
1 2
x x x
x
y
x x
x x
đường thẳng
1
x
là đường
tiệm cận đứng của đồ thị hàm số.
2 2
1
lim lim
1 2
x x
y
x x
đường thẳng
2
x
là đường tiệm cận đứng của đồ thị hàm
số.
Vậy số tiệm cận đứng và ngang của đồ thị hàm số là
3
.
Câu 38. [2D1-3] Cáp tròn truyền nhiệt dưới nước bao gồm một lõi đồng và bao quanh lõi đồng là một
lõi cách nhiệt như hình vẽ. Nếu
r
x
h
là tỉ lệ bán kính độ dày thì bằng đo đạc thực nghiệm
người ta thấy rằng vận tốc truyền tải tín hiệu được cho bởi phương trình
2
1
ln
v x
x
với
x
g x
g x
1
0
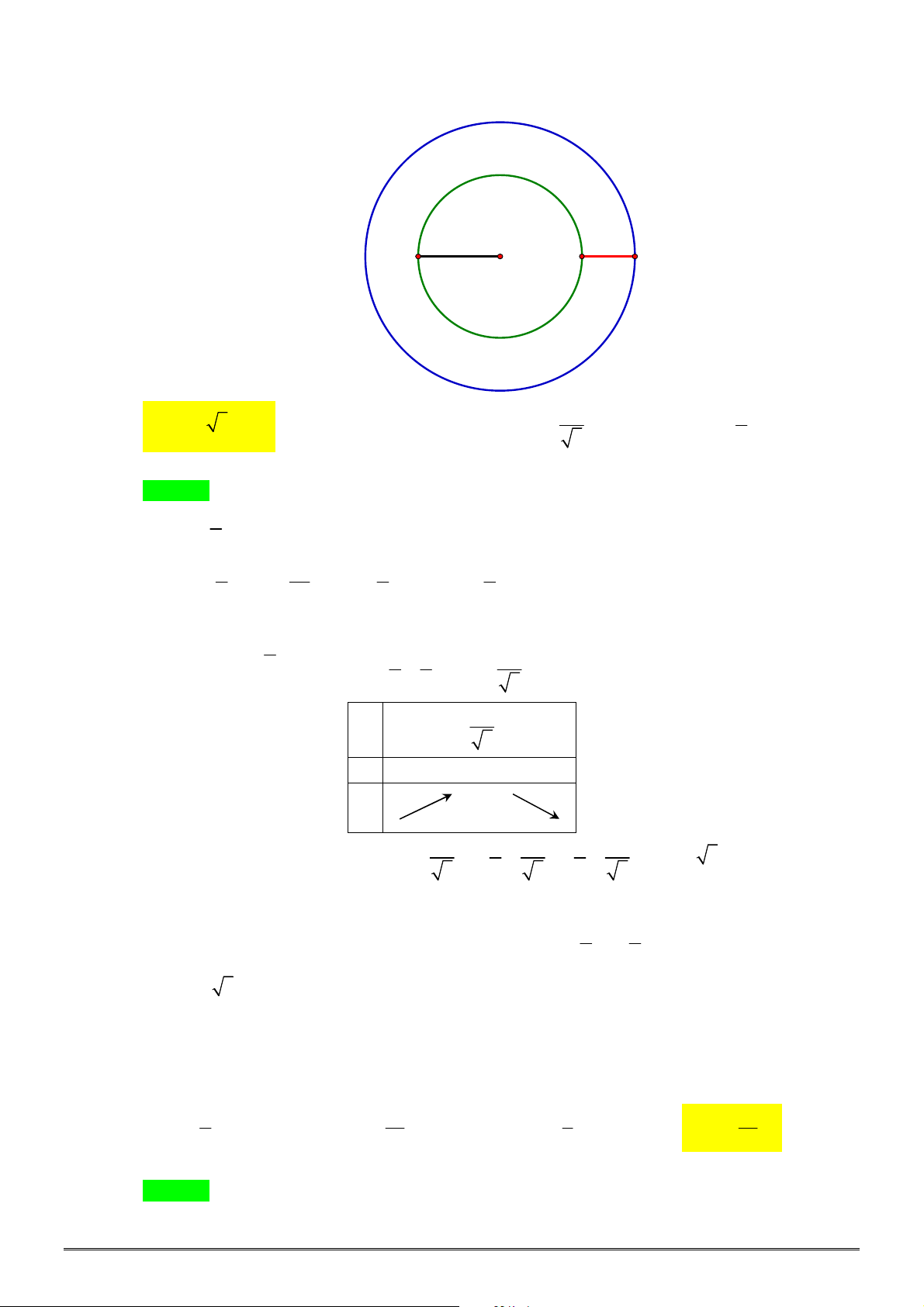
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 24/29
0 1
x
. Nếu bán kính lõi cách nhiệt là
2
cm thì vật liệu cách nhiệt có bề dày
h
(cm) bằng
bao nhiêu để tốc độ truyền tải tín hiệu lớn nhất?
Cách nhiệt
Lõi đồng
r
h
A.
2
h e
(cm). B.
2
h e
(cm). C.
2
h
e
(cm). D.
2
h
e
(cm).
Lời giải
Chọn A.
2
1
ln
v x
x
là hàm số xác định là liên tục trên
0 1
x
.
2
2
1 1 1 1
2 ln . . 2 ln 2ln 1
v x x x x x x
x x x x
.
0
0
1
0 2ln 1 0
1 1
1
ln
2
x l
x
v x
x
x n
x
e
.
x
0
1
e
1
v
0
v
GTLN
Vậy tốc độ truyền tải lớn nhất khi
1
x
e
1 2 1
2
r
h e
h h
e e
(cm).
Cách làm trắc nghiệm
Thay các giá trị
h
cho trong các đáp án vào hàm số
2
2
ln
2
h
v
h
, ta được kết quả
v
lớn nhất
khi
2
h e
.
Câu 39. [2H1-2] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình vuông. Gọi
M
,
N
,
P
,
Q
lần lượt là
trung điểm các cạnh
SB
,
BC
,
CD
,
DA
. Biết thể tích khối chóp
.
S ABCD
là
0
V
. Tính thể tích
khối chóp .
M QPCN
theo
0
V
.
A.
0
3
4
V V
. B.
0
1
16
V V
. C.
0
3
8
V V
. D.
0
3
16
V V
.
Lời giải
Chọn D.
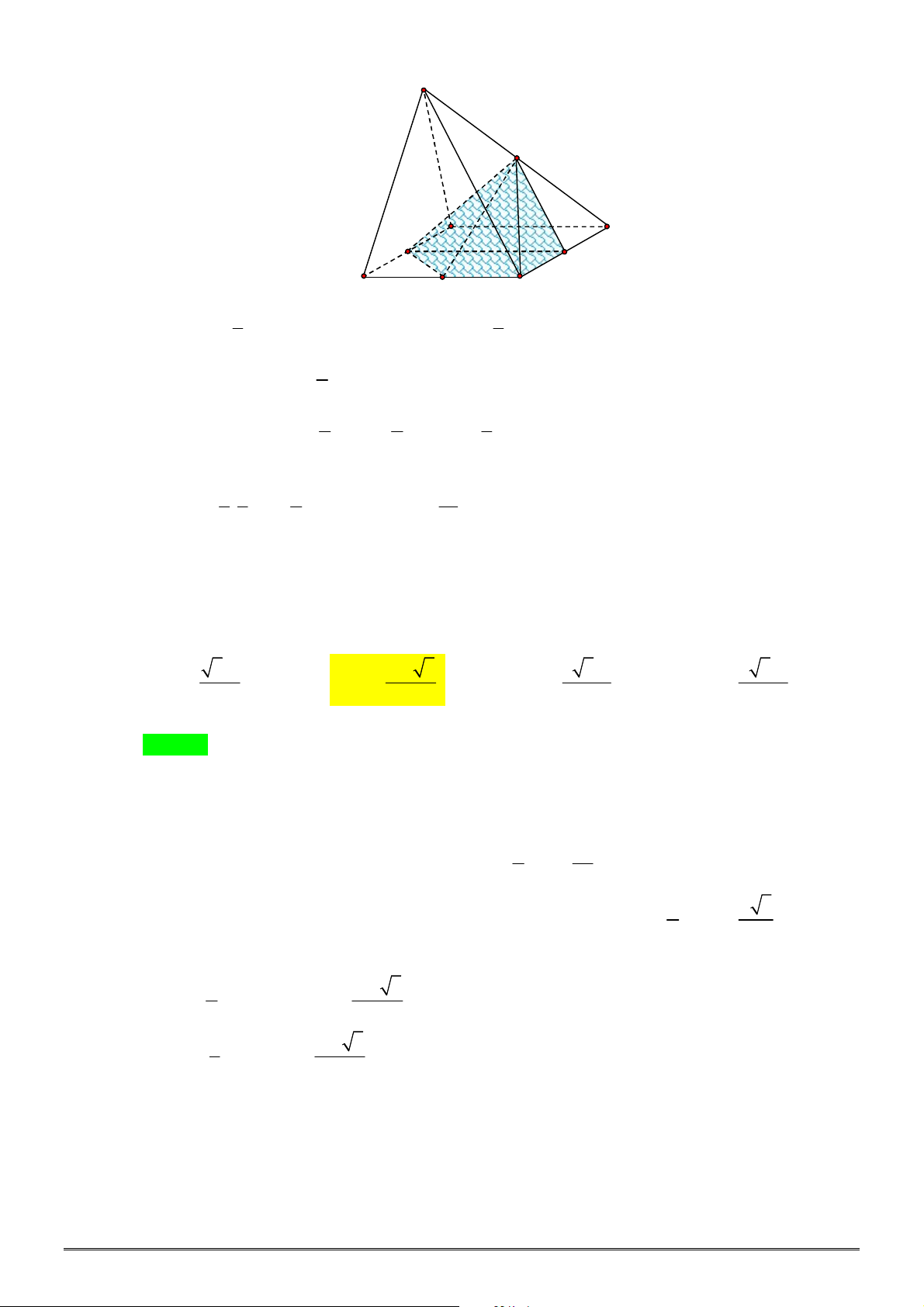
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 25/29
Ta có:
0
1
. ,
3
ABCD
V S d S ABCD
;
.
1
. ,
3
M QPCN QPCN
V S d M QPCN
Mà
1
, ,
2
d M QPCN d S ABCD
;
1 1 3
.
2 2 8
QPCN CDQN DPQ ABCD ABCD
S S S S DP DQ S .
Khi đó:
. 0
1 3 1 3
. . ,
3 8 2 16
M QPCN abcd
V S d A ABCD V
.
Câu 40. [2H1-2] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình thang cân với đáy
AD
và
BC
. Biết
2
AD a
,
AB BC CD a
. Hình chiếu vuông góc của
S
trên mặt phẳng
ABCD
là điểm
H
thuộc đoạn
AD
thỏa mãn
3
HD HA
,
SD
tạo với đáy một góc
45
. Tính thể tích
V
của
khối chóp
.
S ABCD
.
A.
3
3
8
a
V . B.
3
3 3
8
a
V . C.
3
3 3
4
a
V . D.
3
9 3
8
a
V .
Lời giải
Chọn B.
Ta có
HD
là hình chiếu vuông góc của
SD
lên mặt phẳng
ABCD
, 45
SD ABCD SDH
Tam giác
SHD
vuông cân tại
H
có
3 3
4 2
a
SH HD AD
Trong mặt phẳng
ABCD
, kẻ
BE AD
,
CF AD
thì
2
a
AE DF
;
3
2
a
BE .
Khi đó:
2
1 3 3
.
2 4
ABCD
a
S AD BC BE
3
1 3 3
. .
3 8
SABCD ABCD
a
V S SH .
S
B
A
C
D
M
P
N
Q
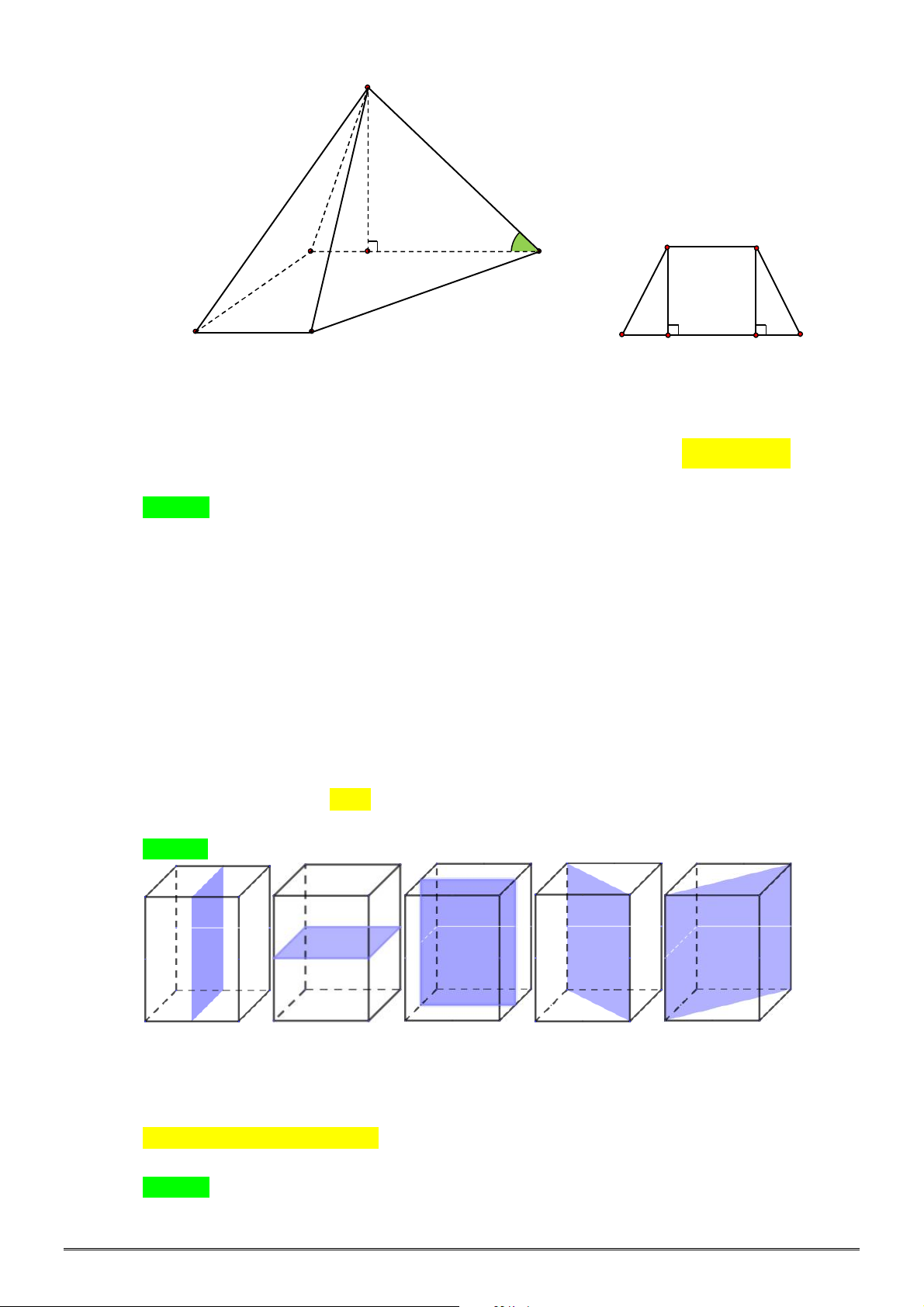
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 26/29
Câu 41. [2D1-3] Cho hàm số
3 2
y f x ax bx cx d
với
0
a
. Biết đồ thị hàm số có hai điểm
cực trị là
1; 1 , 1;3
A B . Tính
4
f .
A.
4 53
f
. B.
4 17
f
. C.
4 17
f
. D.
4 53
f
.
Lời giải
Chọn D.
Ta có
2
3 2
f x ax bx c
.
Đồ thị hàm số có hai điểm cực trị là
1; 1 , 1;3
A B khi và chỉ khi
1 0
1 0
1 1
1 3
f
f
f
f
3 2 0
3 2 0
1
3
a b c
a b c
a b c d
a b c d
1
0
3
1
a
b
c
d
.
Khi đó
3
3 1
f x x x
. Vậy
4 53
f
.
Câu 42. [2H1-1] Số mặt phẳng đối xứng của hình lăng trụ đứng có đáy là hình vuông là:
A.
4
. B.
5
. C.
1
. D.
3
.
Lời giải
Chọn B.
Câu 43. [2D1-3] Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3
2 2
2 2 4 2 0
m x x x x
có nghiệm thỏa mãn
3
x
.
A.
4
. B.
6
.
C. Không có giá trị nào của
m
. D. Vô số giá trị của
m
.
Lời giải
Chọn C.
Đặt
2
2
t x x
.
45
A
B
C
D
E
F
S
A
D
C
B
H
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 27/29
Xét
2
2
g x x x
,
3
x
ta được miền giá trị của
t
là
3; )
.
Phương trình đã cho viết lại:
3
2 2 0
mt t
2
.
Do đó: phương trình đã cho có nghiệm
3
x
khi và chỉ khi phương trình
2
có nghiệm
3;t
.
Ta có:
2
3
3
2 2
2 2
t
mt t m
t
.
Xét
3
2 2
t
f t
t
ta có:
4
4 6
0, t 3
t
f t
t
.
nên hàm số
f t
nghịch biến trên
3;
mà:
lim 0
t
f t
;
4
3
27
f .
Bảng biến thiên:
t
3
f t
f t
4
27
0
Vậy: Phương trình đã cho có nghiệm thỏa mãn
3
x
khi và chỉ
4
0
27
m mà
m
nguyên
nên không có giá trị nào của
m
.
Câu 44. [2H1-1] Cho tứ diện
OMNP
có
OM
,
ON
,
OP
đôi một vuông góc. Tính thể tích
V
của khối
tứ diện
OMNP
.
A.
1
. .
6
V OM ON OP
. B.
1
. .
2
V OM ON OP
.
C.
1
. .
3
V OM ON OP
. D.
. .
V OM ON OP
.
Lời giải
Chọn A.
Tứ diện
OMNP
có
OM
,
ON
,
OP
đôi một vuông góc nên thể tích
V
của khối tứ diện
OMNP
là:
1 1
. . .
3 6
ONP
V OM S OM ON OP
.
Câu 45. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để hàm số
4 2 2
1 1 1
y m x m x
có
đúng một cực trị.
A.
1
m
;
1
m
. B.
1
m
. C.
1
m
. D.
1
m
;
1
m
.
Lời giải
Chọn D.
Tập xác định:
D
.
3 2
4 1 2 1
y m x m x
;
2 2
0
0
2 1 1 1
x
y
m x m
.
Hàm số có đúng một cực trị
0
y
có một nghiệm.
Nếu
1
m
thì
1
y
hàm số không có cực trị.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 28/29
Nếu
1
m
thì
2
1
1
2
m
x
. Do đó hàm số có đúng một cực trị
1
0 1
2
m
m
.
Vậy khi
1
m
;
1
m
thì hàm số có đúng một cực trị.
Cách trình bày khác:
1
m
hàm số trở thành
1
y
không có cực trị. Vậy loại
1
m
.
1
m
hàm số là hàm trùng phương, vì vậy điều kiện cần và đủ để hàm số có một cực trị
là
2
2
1 1 0
; 1 1;1
; 1 1;1
1 0
1
1 0
m m
m
m
m
m
m
.
Câu 46. [2D2-2] Rút gọn biểu thức
2 7
24
3
4
1
:
P a a a
a
, với
0
a
.
A.
2
3
P a
. B.
P a
. C.
1
2
P a
. D.
1
3
P a
.
Lời giải
Chọn C.
Ta có:
1
1 1 1 7
1 7 1
1
24
2
2 3 24 24
2 24 2
6
1
:
P a a a a a
a
.
Câu 47. [2D2-2] Tìm tất các giá trị thực của
x
để đồ thị hàm số
0,5
log
y x
nằm trên đường thẳng
2.
y
A.
1
0
4
x
. B.
1
4
x
. C.
1
0
4
x
. D.
1
4
x
.
Lời giải
Chọn A.
Điều kiện:
0
x
.
Đồ thị hàm số
0,5
log
y x
nằm trên đường thẳng
2
y
khi và chỉ khi
0,5
log 2
x
2
1
0,5
4
x x
. Vậy
1
0
4
x
.
Câu 48. [2D2-3] Theo số liệu từ Tổng cục thống kê, dân số Việt Nam năm
2015
là
91,7
triệu người.
Giả sử tỉ lệ tăng dân số hàng năm của Việt Nam trong giai đoạn
2015 2050
ở mức không đổi
là
1,1%
. Hỏi đến năm nào dân số Việt Nam sẽ đạt mức
120,5
triệu người?
A.
2039
. B.
2040
. C.
2042
. D.
2041
.
Lời giải
Chọn B.
Áp dụng công thức lãi kép, dân số Việt Nam sau
n
năm kể từ năm
2015
là:
0,011
91,7.
n
P e (triệu người).
Ta có:
0,011 0,011
1205
ln
1205
917
91,7. 120,5 24,8
917 0,011
n n
e e n
năm.
Vậy khoảng đến năm
2015 25 2040
dân số Việt Nam sẽ đạt mức
120,5
triệu người.
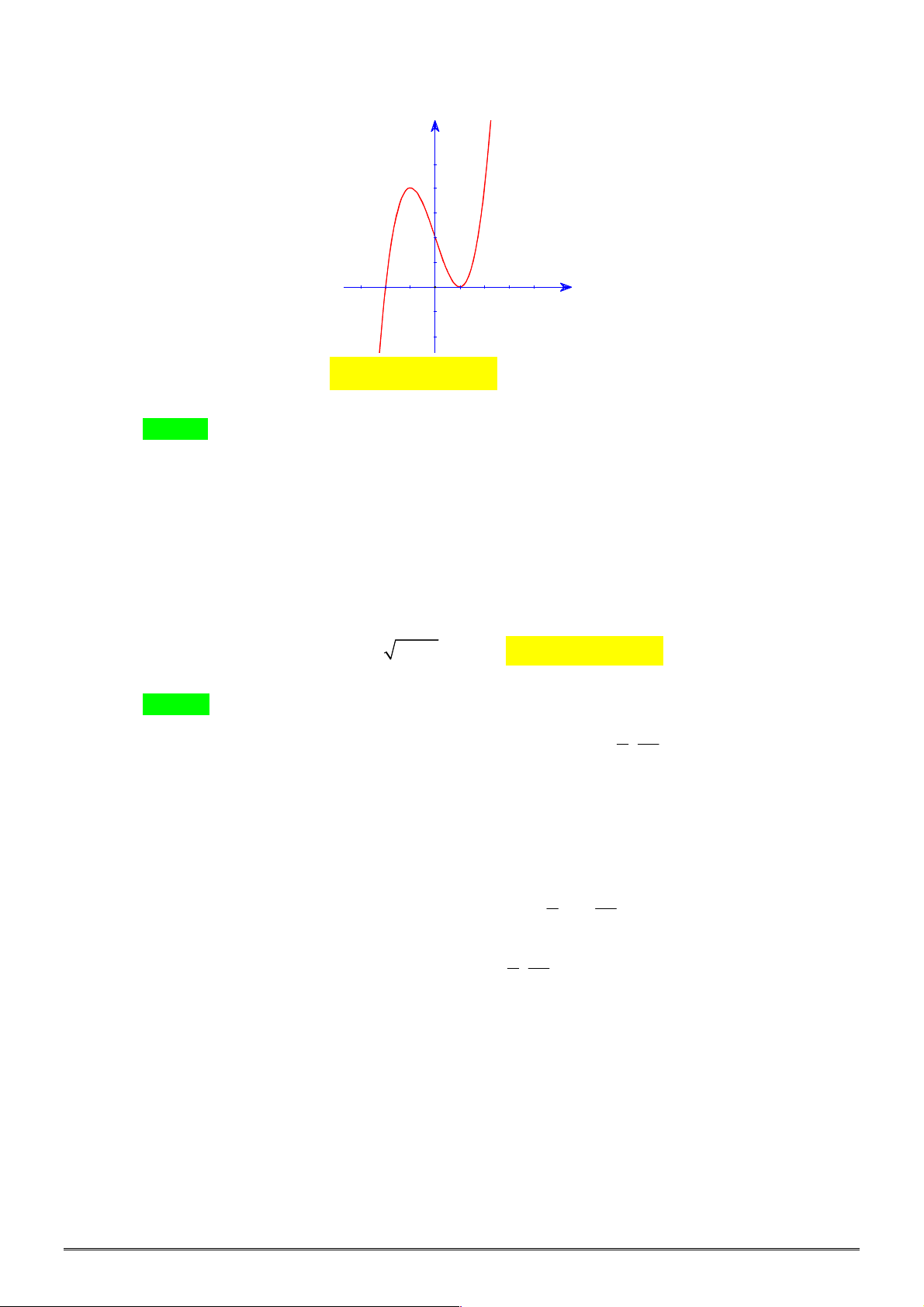
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 29/29
Câu 49. [2D1-2] Đường cong ở hình vẽ là đồ thị của một trong các hàm số dưới đây:
Hàm số đó là hàm số nào?
x
y
1
O
-2
A.
2
1 2
y x x
. B.
2
1 2
y x x
. C.
2
1 2
y x x . D.
2
1 2
y x x .
Lời giải
Chọn B.
Từ hình vẽ ta nhận thấy đồ thị cắt trục hoành tại điểm có hoành độ
2
x
nên hàm số có dạng
2 .
y x g x
Đồ thị hàm số tiếp xúc với trục hoành tại điểm có hoành độ
1
x
nên hàm số có dạng
2
1 .
y x h x
Đối chiếu kết quả trong 4 đáp án ta được hàm số cần tìm là:
2
1 2
y x x
.
Câu 50. [2D1-2] Đồ thị của hàm số nào trong các hàm số dưới đây có tâm đối xứng?
A.
2
2 6
y x x
. B.
2 1
y x
. C.
3 2
2 3
y x x x
. D.
4 2
2 5
y x x
.
Lời giải
Chọn C.
Đồ thị hàm số bậc 3 có tâm đối xứng là điểm uốn của đồ thị
2 38
;
3 27
I
.
Chứng minh: Gọi
;
I a b
là tâm đối xứng khi đó tồn tại số thỏa mãn
2
f a x f a x b
Ta có
3 2
2 3
f a x a x a x a x
,
3 2
2 3
f a x a x a x a x
3 2 2 2 2 3
2 6 4 4 6 2 3 2 2 4 6
f a x f a x a ax a x a a x a a
3
3 2 0
2 38
2 ,
3 27
2 4 6 2
a
f a x f a x b a b
a a b
.
Hàm số
3 2
2 3
y x x x
có tâm đối xứng là
2 38
;
3 27
I
.
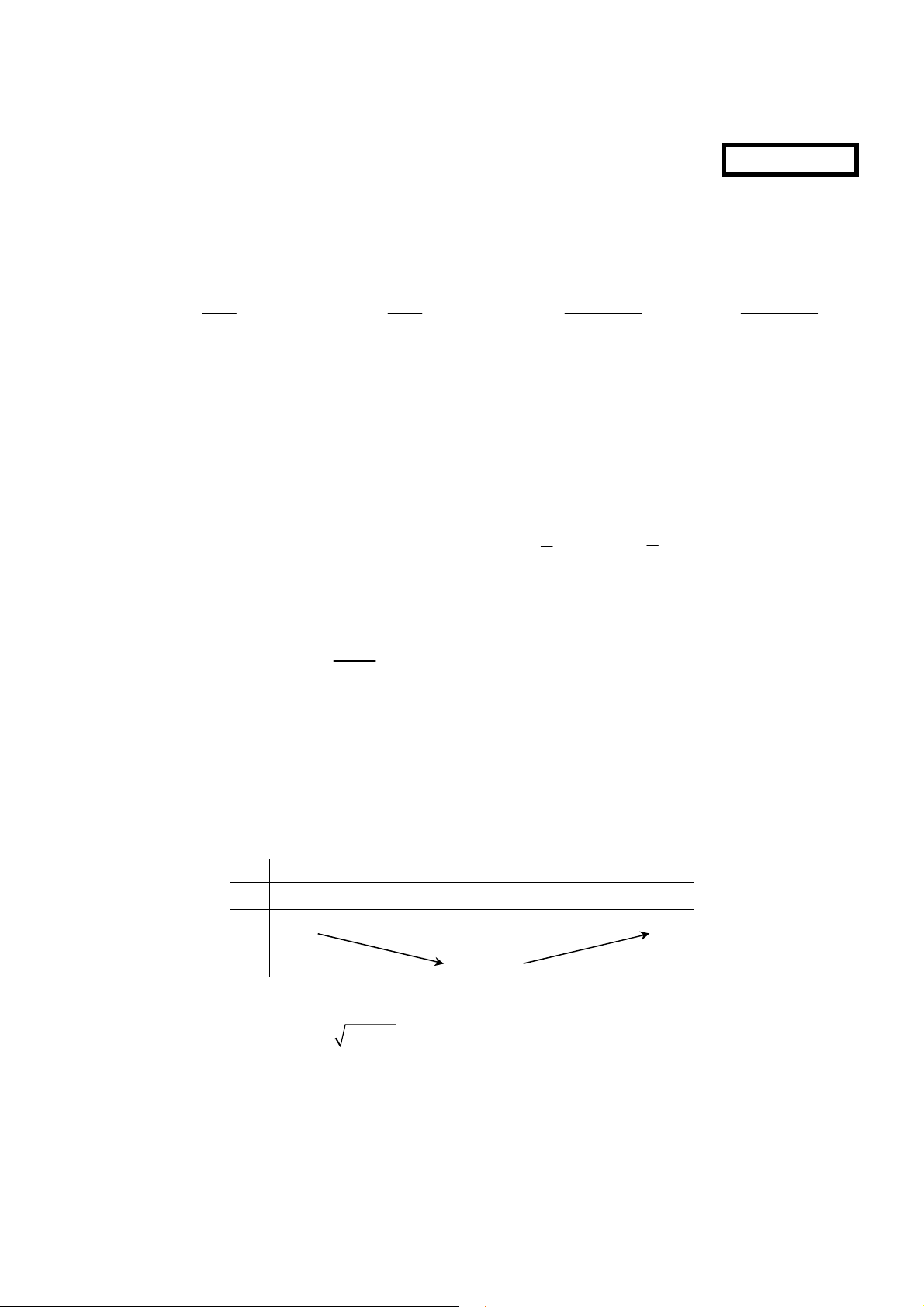
Trang 1/23 - Mã đề thi 132
S
Ở
GD&ĐT HÀ N
Ộ
I
TRƯỜNG THPT LÝ THÁNH TÔNG
(Đề gồm 06 trang)
K
Ỳ
THI H
Ọ
C K
Ỳ
1 NĂM 2017
-
2018
Bài thi: TOÁN 12
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 001
Câu 1: [2D1-1] Cho hàm số
4 2
4 3
y x x
có đồ thị
.
C
Tìm số giao điểm của
C
và trục hoành.
A.
3.
B.
2.
C.
1.
D.
0.
Câu 2: [2D2-1] Tìm đạo hàm của hàm số
2
log 1
y x
.
A.
1
1
y
x
. B.
ln2
1
y
x
. C.
1
1 ln 2
y
x
. D.
1
2ln 1
y
x
.
Câu 3: [2D2-2] Tìm tập nghiệm
S
của bất phương trình
log 2 2 log 1
x x
.
A.
3;
. B.
1;3
. C.
3;
. D.
.
Câu 4: [2D1-1] Hàm số
2 3
1
x
y
x
có bao nhiêu điểm cực trị?
A.
3.
B.
0.
C.
2.
D.
1.
Câu 5: [2D1-2] Tìm giá trị nhỏ nhất
m
của hàm số
2
2
y x
x
trên đoạn
1
;2
2
.
A.
17
.
4
m B.
10.
m
C.
5.
m
D.
3.
m
Câu 6: [2D1-1] Cho hàm số
3 1
1
x
y
x
. Mệnh đề nào dưới đây là đúng?
A. Hàm số đồng biến trên các khoảng
; 1
và
1;
.
B. Hàm số luôn đồng biến trên
\ 1
.
C. Hàm số nghịch biến trên các khoảng
; 1
và
1;
.
D. Hàm số luôn nghịch biến trên
\ 1
.
Câu 7: [2D1-2] Bảng biến thiên dưới đây là của hàm số nào?
A.
4 2
3 1
y x x
. B.
4 2
3 1
y x x
. C.
4 2
3 1
y x x
. D.
4 2
3 1
y x x
.
Câu 8: [2D1-2] Cho hàm số
2
2 1
y x
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
1;1
. B. Hàm số đồng biến trên khoảng
0;
.
C. Hàm số đồng biến trên khoảng
;0
. D. Hàm số nghịch biến trên khoảng
0;
.
Câu 9: [2D2-2] Tìm tất cả các giá trị thực của tham số
m
để phương trình
4 2
2
x x m
có bốn
nghiệm thực phân biệt.
A.
0
m
. B.
0 1
m
. C.
0 1
m
. D.
1
m
.
x
0
y
–
0
y
1
6

Trang 2/23 - Mã đề thi 132
Câu 10: [2D1-3] Một vật chuyển động theo quy luật
3 2
1
6
3
s t t
với
t
(giây) là khoảng thời gian
tính từ khi vật bắt đầu chuyển động và
s
(mét) là quãng đường vật di chuyển được trong
khoảng thời gian đó. Hỏi trong khoảng thời gian
9
giây, kể từ khi bắt đầu chuyển động, vận tốc
lớn nhất của vật đạt được là bao nhiêu?
A.
144 (m/s)
. B.
36 (m/s)
. C.
243 (m/s)
. D.
27 (m/s)
.
Câu 11: [2D1-3] Đồ thị của hàm số
2
2
3 2
x
y
x x
có bao nhiêu tiệm cận?
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 12: [2D2-1] Tính giá trị của biểu thức
3 1 3 4
0
3 2
2 .2 5 .5
10 :10 0,25
K
là
A.
10
. B.
10
. C.
12
. D.
15
.
Câu 13: [2D2-2] Cho
3
7
1
log
a
P a
0, 1
( )
a a
. Mệnh đề nào dưới đây đúng?
A.
7
3
P
. B.
5
3
P
. C.
2
3
P
. D.
7
3
P
.
Câu 14: [2D1-2] Hàm số nào dưới đây nghịch biến trên khoảng
;
.
A.
3 2
3
y x x
. B.
4 2
4 2017
y x x .
C.
3 2
3 3 1
y x x x
. D.
5
1
x
y
x
.
Câu 15: [2D2-2] Cho
0 1
a
. Mệnh đề nào trong các mệnh đề sau là sai?
A.
log 0
a
x
khi
0 1
x
.
B.
log 0
a
x
khi
1
x
.
C. Nếu
1 2
x x
thì
1 2
log log
a a
x x
.
D. Đồ thị hàm số
log
a
y x
có tiệm cận đứng là trục tung.
Câu 16: [2H1-2] Cho
H
là khối chóp tứ giác đều có tất cả các cạnh bằng
a
. Thể tích của
H
bằng
A.
3
3
a
. B.
3
2
6
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Câu 17: [2D1-2] Cho hàm số
4
mx m
y
x m
với
m
là tham số. Gọi
S
là tập hợp tất cả các giá trị nguyên
của
m
để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của
S
.
A.
5
. B.
4
. C. Vô số. D.
3
.
Câu 18: [2D1-3] Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
3 2 3
3 4
y x mx m
có hai
điểm cực trị
A
và
B
sao cho tam giác
OAB
có diện tích bằng
4
với
O
là gốc tọa độ.
A.
4 4
1 1
;
2 2
m m
.B.
1, 1
m m
. C.
1
m
. D.
0
m
.
Câu 19: [2D1-2] Tìm giá trị lớn nhất của hàm số
3
3 1
y x x
trên khoảng
0;
?
A.
1
. B.
3
. C.
5
. D.
4
.
Câu 20: [2H1-1] Trong các mệnh đề sau mệnh đề nào sai?
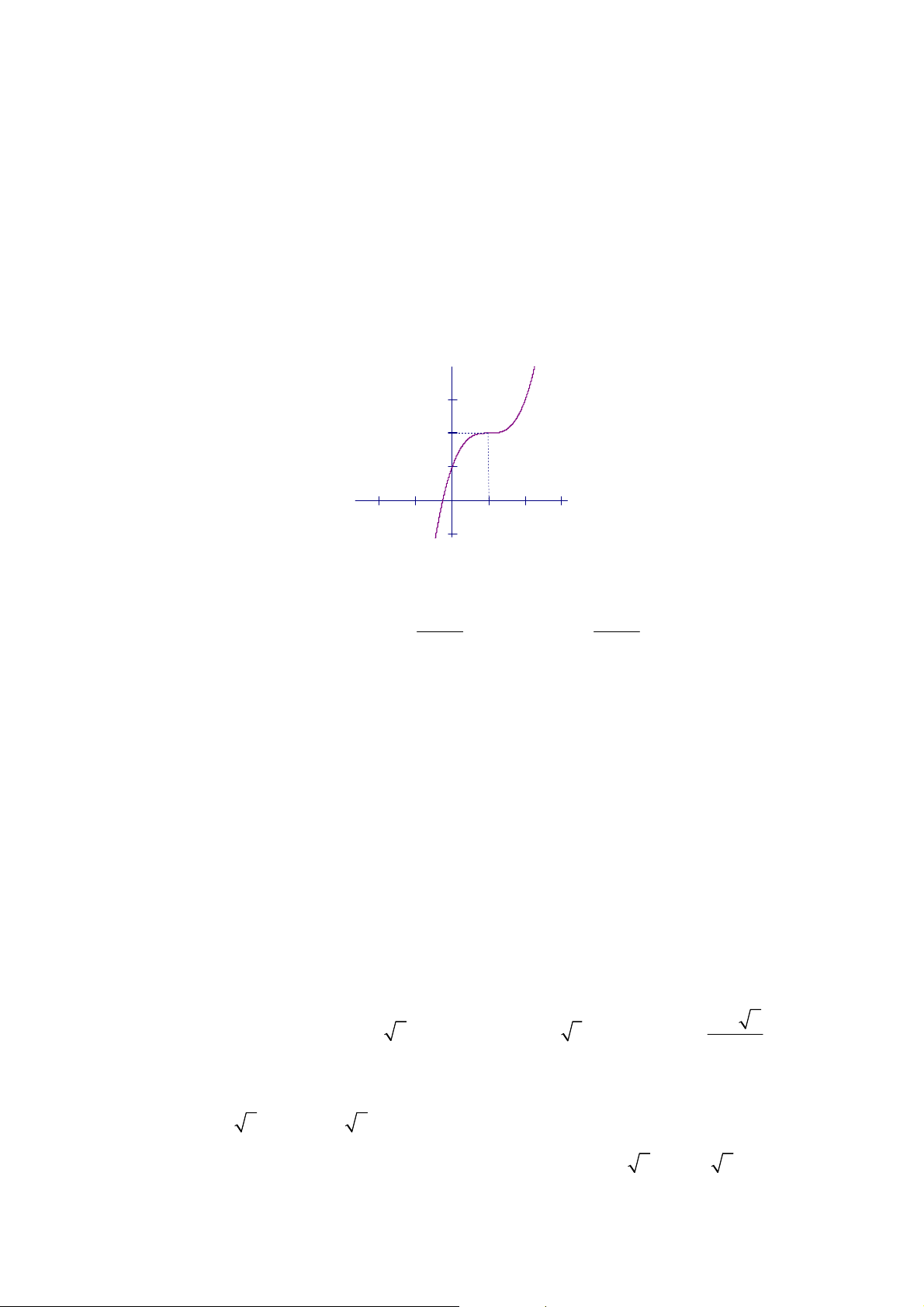
Trang 3/23 - Mã đề thi 132
A. Lắp ghép hai khối hộp sẽ được một khối đa diện lồi.
B. Khối hộp là khối đa diện lồi.
C. Khối tứ diện là khối đa diện lồi.
D. Khối lăng trụ tam giác là khối đa diện lồi.
Câu 21: [2D2-2] Tìm nghiệm của phương trình
2
log 5 4
x
.
A.
21
x
. B.
3
x
. C.
11
x
. D.
13
x
.
Câu 22: [2D2-3] Tìm tập nghiệm của phương trình sau
2
log 3log 2 4
x
x
.
A.
2;8
S . B.
4;3
S . C.
4;16
S . D.
S
.
Câu 23: [2D1-1] Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây.
2
O
1
1
A.
3 2
3 3 1
y x x x
. B.
3 2
3 1
y x x
. C.
3
2 1
y x x
. D.
3 2
3 1
y x x
.
Câu 24: [2D2-1] Cho
a
là số thực dương tùy ý khác
1
. Mệnh đề nào dưới đây đúng?
A.
2
log log 2
a
a . B.
2
2
1
log
log
a
a
. C.
2
1
log
log 2
a
a . D.
2
log log 2
a
a .
Câu 25: [2D2-2] Tìm tập xác định
D
của hàm số
3
2
2
y x x
.
A.
D
. B.
(0; )
D
. C.
( ; 1) (2; )
D
. D.
\{ 1;2}
D
.
Câu 26: [2H2-1] Cho hình nón có thể tích bằng
3
36
V a
và bán kính đáy bằng
3
a
. Tính độ dài
đường cao
h
của hình nón đã cho.
A.
4
a
. B.
2
a
. C.
5
a
. D.
12
a
.
Câu 27: [2D2-1] Tìm tất cả các giá trị thực của tham số
m
để phương trình 3
x
m
có nghiệm thực.
A.
1
m
. B.
0
m
. C.
0
m
. D.
0
m
.
Câu 28: [2H2-2] Cho hình lập phương
.
ABCD A B C D
có cạnh bằng
a
. Gọi
S
là diện tích xung
quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông
ABCD
và
A B C D
. Diện
tích
S
là:
A.
2
a
. B.
2
2
a
. C.
2
3
a
. D.
2
2
2
a
.
Câu 29: [2D2-1] Tìm tập xác định
D
của hàm số
2
3
log 4 3
y x x
A.
2 2;1 3;2 2
D
. B.
1;3
D .
C.
;1 3;D
. D.
;2 2 2 2;D
.
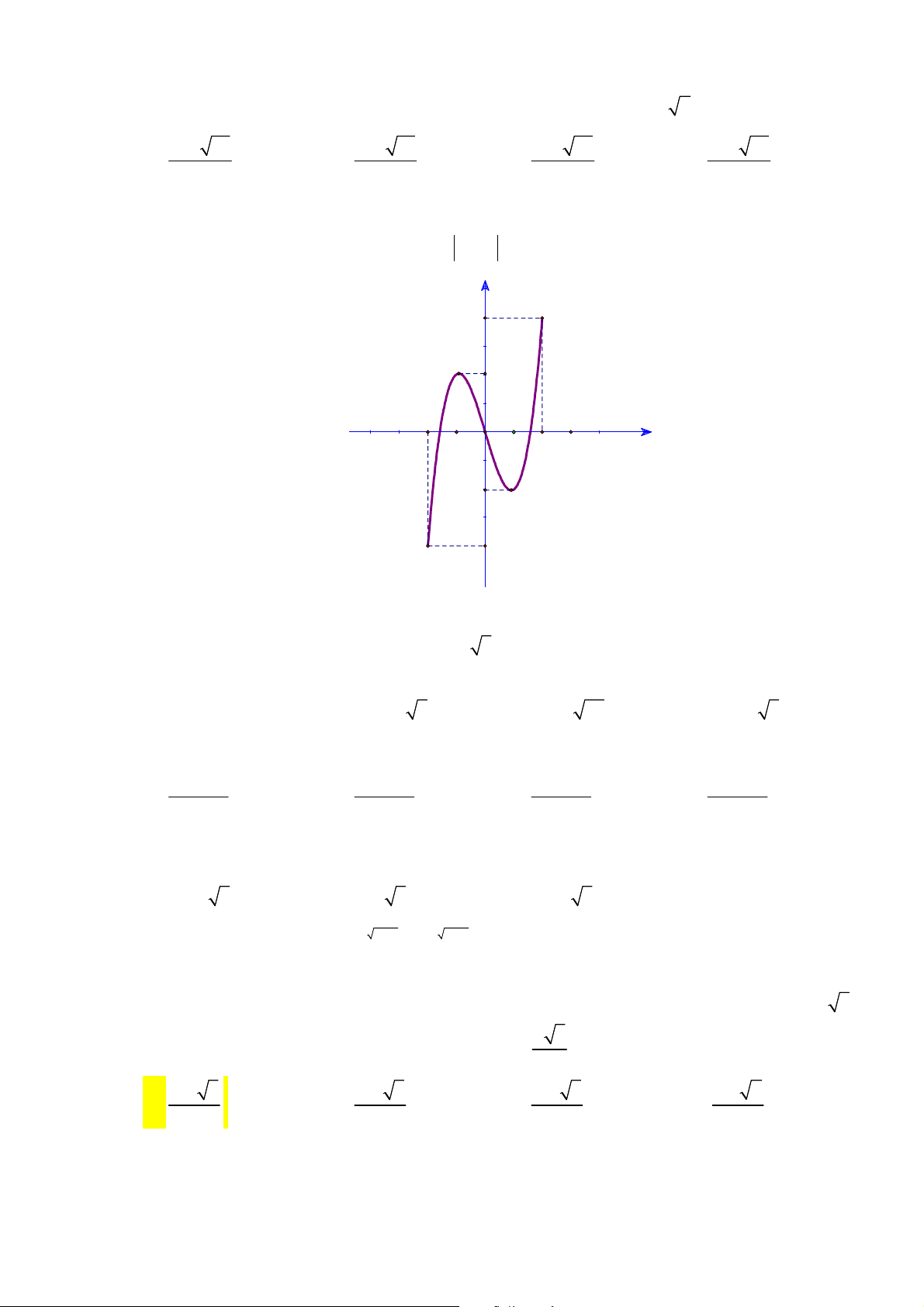
Trang 4/23 - Mã đề thi 132
Câu 30: [2H2-2] Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
và chiều cao bằng
2
a
, diện
tích xung quanh của hình nón đỉnh
S
và đáy là hình tròn nội tiếp
2;2
t
bằng
A.
2
17
4
a
. B.
2
15
4
a
. C.
2
17
6
a
. D.
2
17
8
a
.
Câu 31: [2D1-2] Cho hàm số
y f x
liên tục trên đoạn
2;2
và có đồ thị là đường cong như hình
vẽ bên. Tìm số nghiệm của phương trình
1
f x
trên đoạn
2;2
.
x
y
-2
2
-4
4
2-1-2
O
1
A.
4
. B.
6
. C.
3
. D.
5
.
Câu 32: [2H2-1] Cho hình nón có bán kính đáy
3
r và độ dài đường sinh
4
l
. Tính diện tích xung
quanh
xq
S
của hình nón đã cho.
A.
12
xq
S
. B.
4 3
xq
S
. C.
39
xq
S
. D.
8 3
xq
S
.
Câu 33: [2D2-2] Cho log3
a
, log5
b
. Tính
6
log 1125
.
A.
3 2
1
a b
a b
. B.
2 3
1
a b
a b
. C.
3 2
1
a b
a b
. D.
3 2
1
a b
a b
.
Câu 34: [2H1-1] Cho hình bát diện đều cạnh
a
. Gọi
S
là tổng diện tích tất cả các mặt của hình bát diện
đều đó. Mệnh đề nào dưới đây đúng?
A.
2
4 3
S a
. B.
2
3
S a
. C.
2
2 3
S a
. D.
2
8
S a
.
Câu 35: [2D2-3] Hỏi phương trình
2 5 1 2 5 6
2 2 2 32 0
x x x x
có bao nhiêu nghiệm phân biệt?
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 36: [2H1-2] Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật,
AB a
,
2
AD a
,
3
SA a
,
SA ABCD
.
M
là điểm trên
SA
sao cho
3
3
a
AM . Tính thể tích của khối chóp
.
S BMC
.
A.
3
2 3
9
a
. B.
3
2 3
3
a
. C.
3
4 3
3
a
. D.
3
3 2
9
a
.
Câu 37: [2D2-2] Với mọi
a
,
b
,
x
là các số thực dương thỏa mãn
2 2 2
log 5log 3log
x a b
. Mệnh đề
nào dưới đây đúng?
A.
3 5
x a b
B.
5 3
x a b
C.
5 3
x a b
D.
5 3
x a b

Trang 5/23 - Mã đề thi 132
Câu 38: [2H2-2] Cho khối chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
2
a
. Tính
thể tích
V
của khối chóp
.
S ABC
.
A.
3
13
12
a
V . B.
3
11
12
a
V . C.
3
11
6
a
V . D.
3
11
4
a
V .
Câu 39: [2H2-1] Gọi
l
,
h
,
R
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón.
Đẳng thức nào sau đây luôn đúng?
A.
2 2 2
l h R
. B.
2 2 2
1 1 1
l h R
. C.
2 2 2
R h l
. D.
2
l hR
.
Câu 40: [2D2-3] Hàm số
ln
f x x
có đạo hàm cấp
n
là
A.
n
n
n
f x
x
. B.
1
1 !
1
n
n
n
n
f x
x
.
C.
1
n
n
f x
x
. D.
!
n
n
n
f x
x
.
Câu 41: [2H2-1] Gọi
l
,
h
,
R
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối nón
N
. Thể tích
V
của khối nón
N
bằng
A.
2
1
3
V R h
. B.
2
V R h
. C.
2
V R l
. D.
2
1
3
V R l
.
Câu 42: [2D2-2] Tìm giá trị thực của tham số
m
để phương trình
1
9 2.3 0
x x
m
có hai nghiệm thực
1
x
,
2
x
thỏa mãn
1 2
1
x x
.
A.
6
m
. B.
3
m
. C.
3
m
. D.
1
m
.
Câu 43: [2H1-2] Cho khối chóp
.
S ABCD
có đáy là nửa lục giác đều nội tiếp trong nửa đường tròn
đường kính
2
AB R
. Biết
I
là trung điểm
AB
,
SI
vuông góc với đáy và
SBC
và hợp với
đáy
ABCD
một góc
45
. Tính thể tích khối chóp
.
S ABCD
A.
3
3
4
R
. B.
3
3
8
R
. C.
3
3
6
R
. D.
3
3
2
R
.
Câu 44: [2D1-2] Tìm giá trị thực của tham số
m
để đường thẳng
: 2 1 3
d y m x m
vuông góc
với đường thẳng đi qua hai điểm cực trị của hàm số
3 2
3 1
y x x
.
A.
3
2
m
. B.
3
4
m
. C.
1
2
m
. D.
1
4
m
.
Câu 45: [2D2-3] Hỏi có bao nhiêu giá trị
m
nguyên trong đoạn
2017;2017
để phương trình
3 3 3
log log 2log 1
m x x
luôn có hai nghiệm phân biệt?
A.
4015
. B.
2010
. C.
2018
. D.
2013
.
Câu 46: [2D1-3] Biết hàm số
2 2
4 2 3 2
y x x x x
đạt giá trị lớn nhất tại hai điểm
1
x
,
2
x
. Giá trị
1 2
.
x x
bằng
A.
2
. B.
1
. C.
0
. D.
1
.
Câu 47: [2D2-2] Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
2
ln 2 1
y x x m
xác
định với
x
là
A.
0
. B.
0;3
. C.
; 1 0;
. D.
0;
.

Trang 6/23 - Mã đề thi 132
Câu 48: [2D2-3] Anh Nam gửi 100 triệu đồng vào ngân hàng Vietcombank. Lãi suất hàng năm không
thay đổi là
7,5% /
năm. Nếu anh Nam hàng năm không rút lãi thì sau 5 năm số tiền anh Nam
nhận được cả vốn lẫn tiền lãi (kết quả làm tròn đến hàng ngàn) là
A.
143.563.000
đồng. B.
2.373.047.000
đồng.
C.
137.500.000
đồng. D.
133.547.000
đồng.
Câu 49: [2H1-4] Cho một tấm bìa hình vuông cạnh
5
dm. Để làm một mô hình kim tự tháp Ai Cập,
người ta cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy chính là cạnh của hình vuông rồi gấp
lên, ghép lại thành một hình chóp tứ giác đều. Để mô hình có thể tích lớn nhất thì cạnh đáy của
mô hình là
A.
3 2
2
dm. B.
5
2
dm. C.
5 2
2
dm. D.
2 2
dm.
Câu 50: [2H2-3] Cho tam giác
ABC
vuông cân tại
A
, có
12
AB AC
. Lấy một điểm
M
thuộc cạnh
huyền
BC
và gọi
H
là hình chiếu của
M
lên cạnh góc vuông
AB
. Quay tam giác
AMH
quanh trục là đường thẳng
AB
tạo thành mặt nón tròn xoay
N
, hỏi thể tích
V
của khối nón
tròn xoay
H
lớn nhất bằng bao nhiêu?
A.
256
3
V
. B.
128
3
V
. C.
256
V
. D.
72
V
.
----------HẾT----------

Trang 7/23 - Mã đề thi 132
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
C C B D
A
C B C B D
A
D
C
C B D
B B A
A
A
A
C D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
C B C A
B B B C A
A
D
B
A
B A
C B B D
D
D
A
D
A
HƯỚNG DẪN GIẢI
Câu 1: [2D1-1] Cho hàm số
4 2
4 3
y x x
có đồ thị
.
C
Tìm số giao điểm của
C
và trục hoành.
A.
3.
B.
2.
C.
1.
D.
0.
Lời giải
Chọn D.
Phương trình hoành độ giao điểm
4 2
4 3 0,
x x
phương trình này vô nghiệm.
Số giao điểm của
C
và trục hoành chính là số nghiệm của phương trình
4 2
4 3 0.
x x
Câu 2: [2D2-1] Tìm đạo hàm của hàm số
2
log 1
y x
.
A.
1
1
y
x
. B.
ln2
1
y
x
. C.
1
1 ln 2
y
x
. D.
1
2ln 1
y
x
.
Lời giải
Chọn C.
Ta có
1
.
1 ln2
y
x
Câu 3: [2D2-2] Tìm tập nghiệm
S
của bất phương trình
log 2 2 log 1
x x
.
A.
3;
. B.
1;3
. C.
3;
. D.
.
Lời giải
Chọn C.
Điều kiện
2 2 0
1
1 0
x
x
x
(*)
BPT
2 2 1 3,
x x x
kết hợp với (*) ta được
3
x
thỏa mãn.
Câu 4: [2D1-1] Hàm số
2 3
1
x
y
x
có bao nhiêu điểm cực trị?
A.
3.
B.
0.
C.
2.
D.
1.
Lời giải
Chọn B.
Ta có
2
1
0, 1
1
y x
x
hàm số
2 3
1
x
y
x
có
0
điểm cực trị.
Câu 5: [2D1-2] Tìm giá trị nhỏ nhất
m
của hàm số
2
2
y x
x
trên đoạn
1
;2
2
.
A.
17
.
4
m B.
10.
m
C.
5.
m
D.
3.
m
Lời giải
Chọn D.
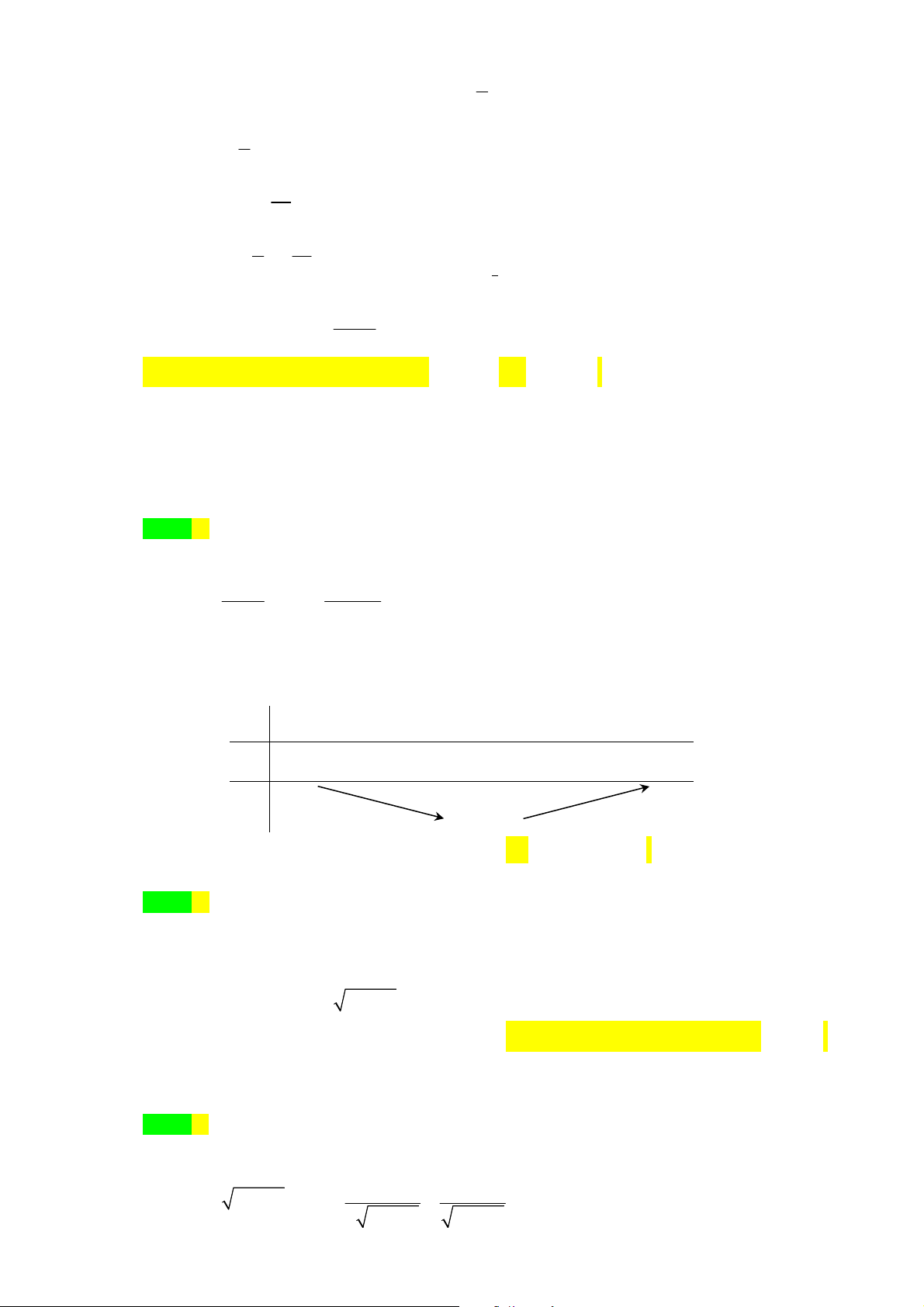
Trang 8/23 - Mã đề thi 132
Hàm số đã cho đã xác định và liên tục trên
1
;2
2
.
Ta có
2
1
;2
2
1.
2
2 0
x
x
y x
x
Tính được
1
;2
2
1 17
, 2 5, 1 3 min 1 3 3.
2 4
f f f y f m
Câu 6: [2D1-1] Cho hàm số
3 1
1
x
y
x
. Mệnh đề nào dưới đây là đúng?
A. Hàm số đồng biến trên các khoảng
; 1
và
1;
.
B. Hàm số luôn đồng biến trên
\ 1
.
C. Hàm số nghịch biến trên các khoảng
; 1
và
1;
.
D. Hàm số luôn nghịch biến trên
\ 1
.
Lời giải
Chọn A.
Tập xác định
\ 1
D
.
Ta có
2
3 1 4
0
1
1
x
y y
x
x
với mọi
x D
.
Vậy hàm số đồng biến trên các khoảng
; 1
và
1;
.
Câu 7: [2D1-2] Bảng biến thiên dưới đây là của hàm số nào?
A.
4 2
3 1
y x x
. B.
4 2
3 1
y x x
. C.
4 2
3 1
y x x
. D.
4 2
3 1
y x x
.
Lời giải
Chọn C.
Đồ thị hàm số có nhánh đầu tiên “đi xuống” nên hệ số
0
a
nên loại phương án B, D.
Hàm số có một điểm cực trị
. 0
a b
nên loại phương án A.
Câu 8: [2D1-2] Cho hàm số
2
2 1
y x
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
1;1
. B. Hàm số đồng biến trên khoảng
0;
.
C. Hàm số đồng biến trên khoảng
;0
. D. Hàm số nghịch biến trên khoảng
0;
.
Lời giải
Chọn B.
Tập xác định
D
.
Ta có
2
2
2 2
2 1
2
2 1 0 0
2 2 1 2 1
x
x
y x y y x
x x
.
x
0
y
–
0
y
1
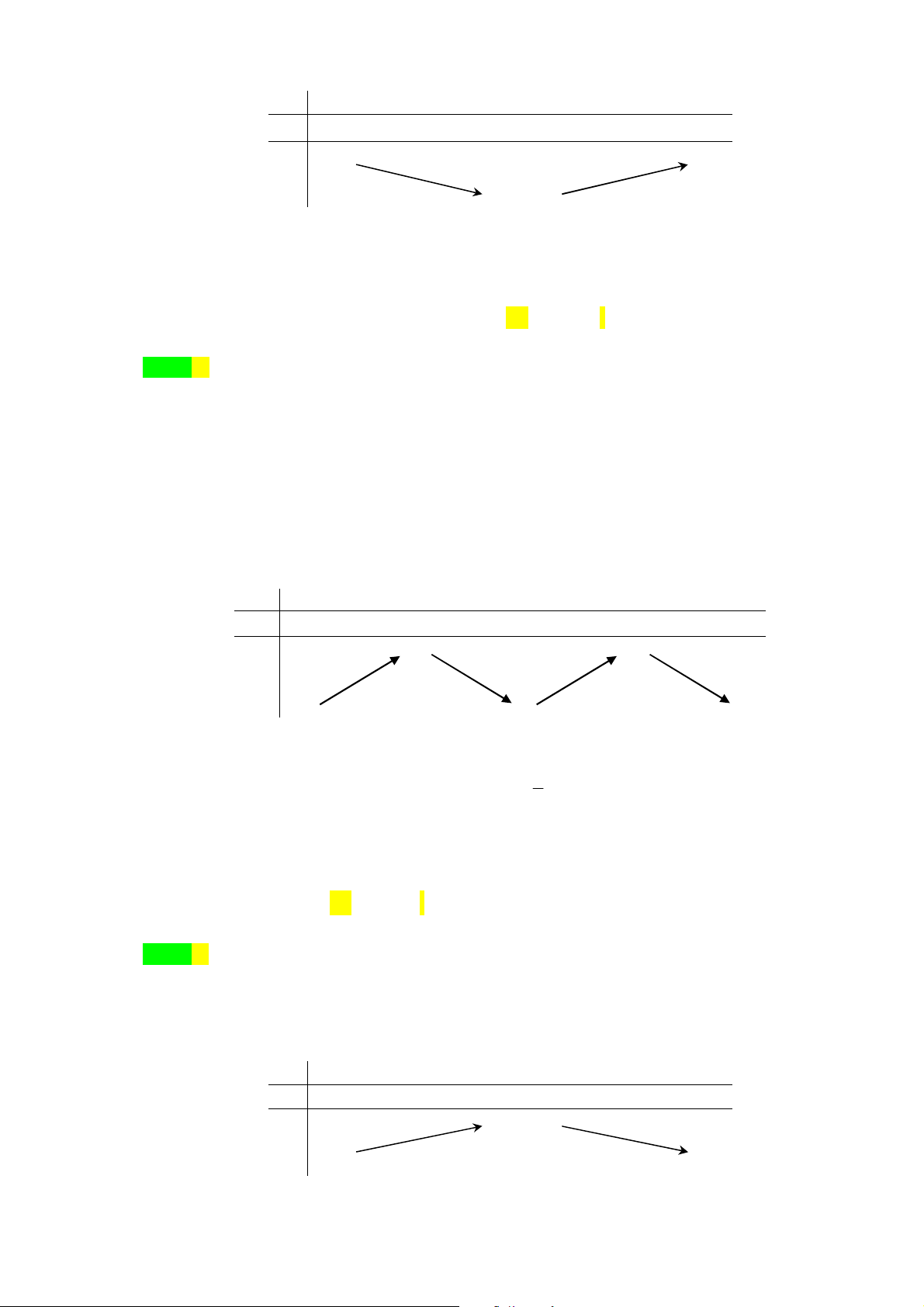
Trang 9/23 - Mã đề thi 132
Bảng biến thiên
Vậy hàm số đồng biến trên khoảng
0;
.
Câu 9: [2D2-2] Tìm tất cả các giá trị thực của tham số
m
để phương trình
4 2
2
x x m
có bốn
nghiệm thực phân biệt.
A.
0
m
. B.
0 1
m
. C.
0 1
m
. D.
1
m
.
Lời giải
Chọn C.
Tập xác định
D
.
Số nghiệm của phương trình
4 2
2
x x m
là số hoành độ giao điểm của đồ thị hàm số
4 2
2
y x x
và đường thẳng
y m
.
Xét hàm số
4 2
2
y x x
, ta có
3 3
0 0
4 4 0 4 4 0 1 1
1 1
x y
y x x y x x x y
x y
.
Bảng biến thiên
Dựa vào bảng biến thiên, ta thấy phương trình ban đầu có bốn nghiệm phân biệt khi
0 1
m
.
Câu 10: [2D1-3] Một vật chuyển động theo quy luật
3 2
1
6
3
s t t
với
t
(giây) là khoảng thời gian
tính từ khi vật bắt đầu chuyển động và
s
(mét) là quãng đường vật di chuyển được trong
khoảng thời gian đó. Hỏi trong khoảng thời gian
9
giây, kể từ khi bắt đầu chuyển động, vận tốc
lớn nhất của vật đạt được là bao nhiêu?
A.
144 (m/s)
. B.
36 (m/s)
. C.
243 (m/s)
. D.
27 (m/s)
.
Lời giải
Chọn B.
Vận tốc chuyển động của vật được tính bởi công thức
2
12 m/s
v t s t t t
.
Ta có
2 12 0 2 12 0 6
v t t v t t t
.
Bảng biến thiên
Vậy vận tốc lớn nhất mà vật đạt được là
36 (m/s)
.
x
0
y
–
0
y
1
x
1
0
1
y
0
0
0
y
1
0
1
t
0
6
9
v
0
v
0
36
27

Trang 10/23 - Mã đề thi 132
Câu 11: [2D1-3] Đồ thị của hàm số
2
2
3 2
x
y
x x
có bao nhiêu tiệm cận?
A.
0
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn D.
Ta có: TXĐ
\ 1;2
D
.
2
2 1
3 2 1
x
y
x x x
.
Do đó:
1
lim
x
y
Đồ thị hàm số có một tiệm cận đứng
1
x
.
lim 0
x
y
Đồ thị hàm số có một tiệm cận ngang
0
y
.
Câu 12: [2D2-1] Tính giá trị của biểu thức
3 1 3 4
0
3 2
2 .2 5 .5
10 :10 0,25
K
là
A.
10
. B.
10
. C.
12
. D.
15
.
Lời giải
Chọn A.
Ta có:
3 1 3 4 2
0
1
3 2
2 .2 5 .5 2 5 9.10
10
10 1 9
10 :10 0,25
K
.
Câu 13: [2D2-2] Cho
3
7
1
log
a
P a
0, 1
( )
a a
. Mệnh đề nào dưới đây đúng?
A.
7
3
P
. B.
5
3
P
. C.
2
3
P
. D.
7
3
P
.
Lời giải
Chọn D.
Ta có:
7
3 7
3
1
7 7
log log log
3 3
a a
a
P a a a
.
Câu 14: [2D1-2] Hàm số nào dưới đây nghịch biến trên khoảng
;
.
A.
3 2
3
y x x
. B.
4 2
4 2017
y x x .
C.
3 2
3 3 1
y x x x
. D.
5
1
x
y
x
.
Lời giải
Chọn C.
Xét hàm số
3 2
3 3 1
y x x x
:
Ta có
2
2
3 6 3 3 1 0,y x x x x
. Do đó hàm số nghịch biến trên
;
.
Câu 15: [2D2-2] Cho
0 1
a
. Mệnh đề nào trong các mệnh đề sau là sai?
A.
log 0
a
x
khi
0 1
x
.
B.
log 0
a
x
khi
1
x
.
C. Nếu
1 2
x x
thì
1 2
log log
a a
x x
.
D. Đồ thị hàm số
log
a
y x
có tiệm cận đứng là trục tung.
Lời giải
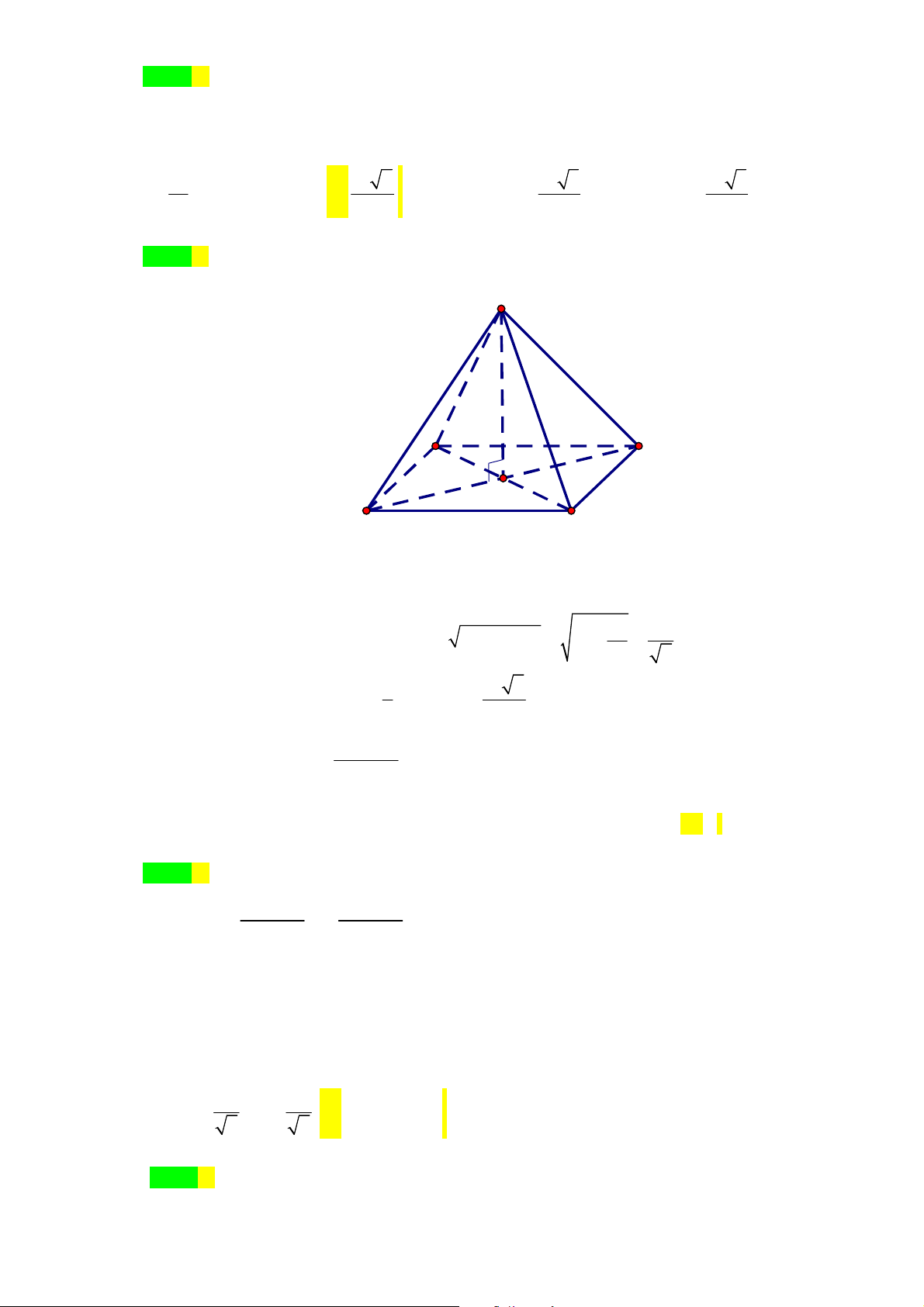
Trang 11/23 - Mã đề thi 132
Chọn C.
Với
0 1
a
, ta có
1 2
x x
thì
1 2
log log
a a
x x
.
Câu 16: [2H1-2] Cho
H
là khối chóp tứ giác đều có tất cả các cạnh bằng
a
. Thể tích của
H
bằng
A.
3
3
a
. B.
3
2
6
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Lời giải
Chọn B.
O
B
A
C
D
S
Xét hình chóp đều
.
S ABCD
có các cạnh đều bằng
a
ta có:
Diện tích đáy là:
2
ABCD
S a
Chiều cao là:
2
2 2 2
;
2
2
a a
h d S ABCD SO SA AO a
Thể tích hình chóp là:
3
.
1 2
.
3 6
S ABCD ABCD
a
V S SO .
Câu 17: [2D1-2] Cho hàm số
4
mx m
y
x m
với
m
là tham số. Gọi
S
là tập hợp tất cả các giá trị nguyên
của
m
để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của
S
.
A.
5
. B.
4
. C. Vô số. D.
3
.
Lời giải
Chọn D.
Ta có:
2
2
4 4
mx m m m
y
x m
x m
Để hàm số nghịch biến trên các khoảng xác định điều kiện là
2
0; 4 0
y x m m m
0 4 1; 2; 3
m S .
Câu 18: [2D1-3] Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
3 2 3
3 4
y x mx m
có hai
điểm cực trị
A
và
B
sao cho tam giác
OAB
có diện tích bằng
4
với
O
là gốc tọa độ.
A.
4 4
1 1
;
2 2
m m
.B.
1, 1
m m
. C.
1
m
. D.
0
m
.
Lời giải
Chọn B.
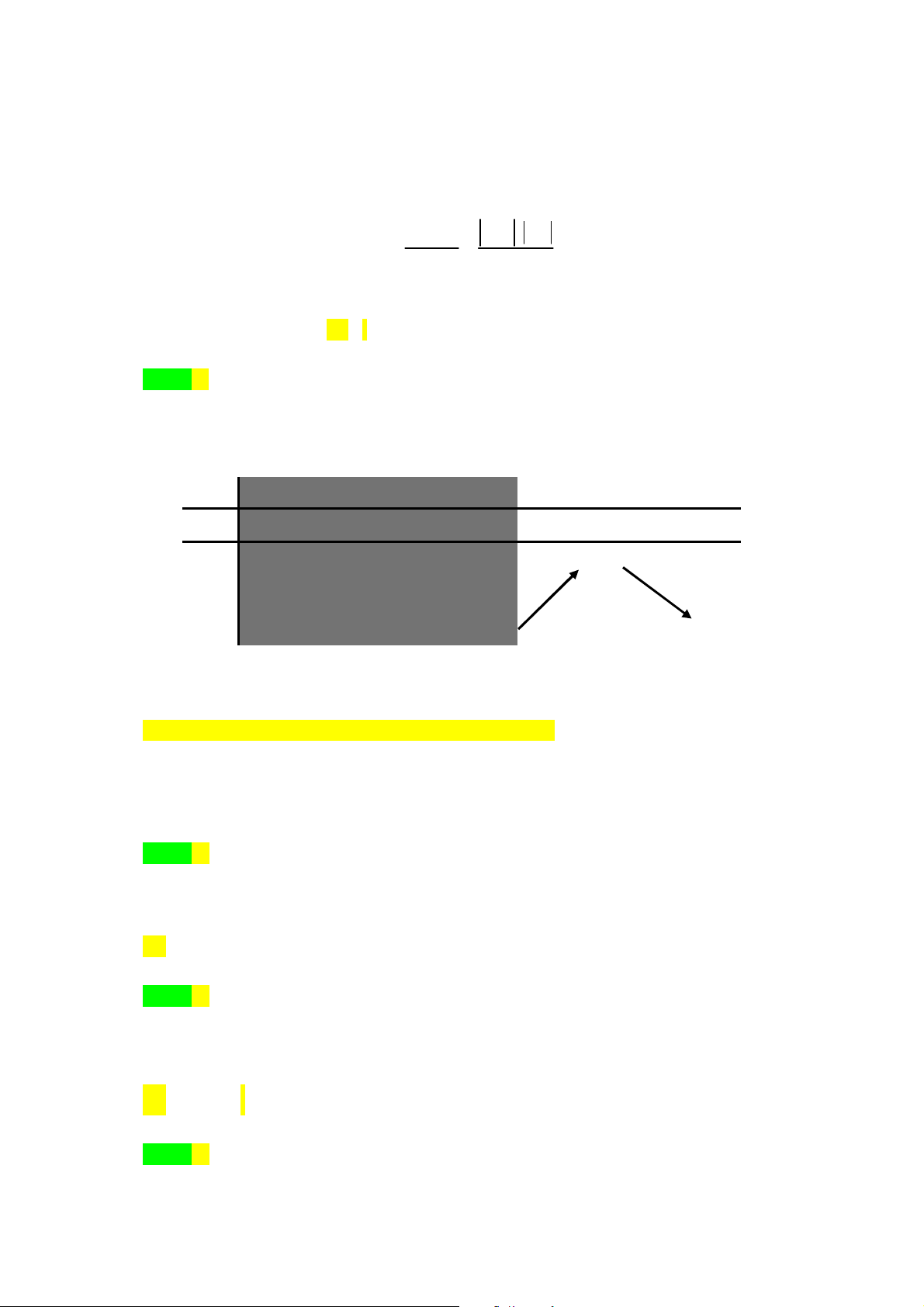
Trang 12/23 - Mã đề thi 132
Ta có:
2 2
0
3 6 0 2 0
2
x
y x mx y x mx
x m
* Để hàm số có hai điểm cực trị điều kiện là phương trình
0
y
có hai nghiệm phân biệt
0
m
.
* Với
0
m
ta có
3
0;4
A m
và
2 ;0
B m
3
0;4 , 2 ;0
OA m OB m
. 0
OAOB
ABC
vuông tại
O
3
4 4
4 . 2
.
4 4 1 1
2 2
ABC
m m
OAOB
S m m m
Câu 19: [2D1-2] Tìm giá trị lớn nhất của hàm số
3
3 1
y x x
trên khoảng
0;
?
A.
1
. B.
3
. C.
5
. D.
4
.
Lời giải
Chọn B.
Ta có:
2
1
3 3 0
1
x
y x y
x
Bảng biến thiên:
x
1
0
1
y
0
0
0
y
1
3
Từ BBT suy ra
0;
max 3
y
.
Câu 20: [2H1-1] Trong các mệnh đề sau mệnh đề nào sai?
A. Lắp ghép hai khối hộp sẽ được một khối đa diện lồi.
B. Khối hộp là khối đa diện lồi.
C. Khối tứ diện là khối đa diện lồi.
D. Khối lăng trụ tam giác là khối đa diện lồi.
Lời giải
Chọn A.
Ta dùng phương pháp loại trừ do B, C, D là các mệnh đề đúng nên A là mệnh đề sai.
Câu 21: [2D2-2] Tìm nghiệm của phương trình
2
log 5 4
x
.
A.
21
x
. B.
3
x
. C.
11
x
. D.
13
x
.
Lời giải
Chọn D.
Ta có
2
log 5 4 5 16 21
x x x
.
Câu 22: [2D2-3] Tìm tập nghiệm của phương trình sau
2
log 3log 2 4
x
x
.
A.
2;8
S . B.
4;3
S . C.
4;16
S . D.
S
.
Lời giải
Chọn A.
ĐK:
0 1
x
.
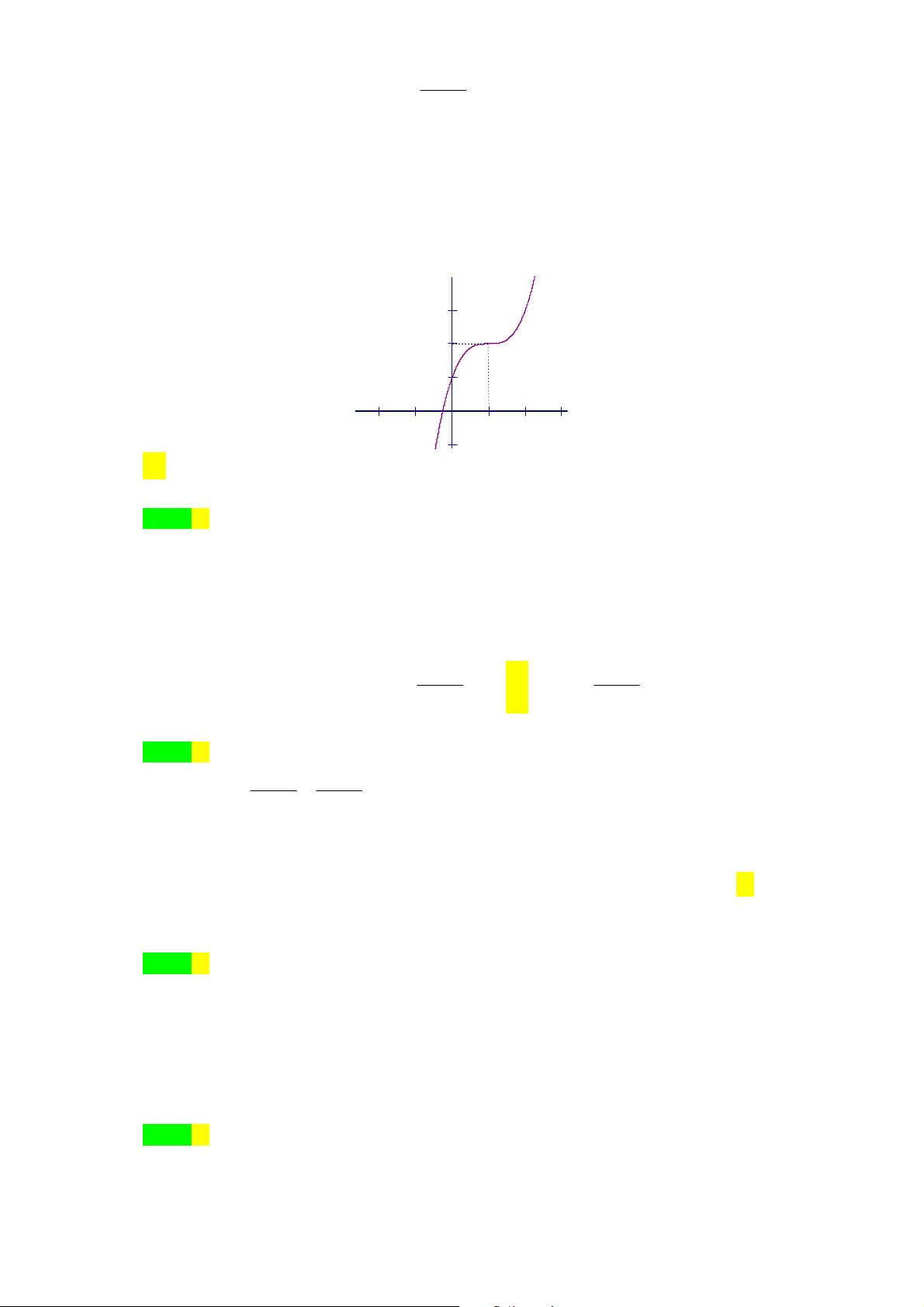
Trang 13/23 - Mã đề thi 132
Phương trình tương đương
2
2 2 2
2
1
log 3 4 log 4log 3 0
log
x x x
x
2
2
log 1
2
log 3 8
x
x
x x
.
Vậy tập nghiệm của pt là
2;8
S .
Câu 23: [2D1-1] Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây.
2
O
1
1
A.
3 2
3 3 1
y x x x
. B.
3 2
3 1
y x x
. C.
3
2 1
y x x
. D.
3 2
3 1
y x x
.
Lời giải
Chọn A.
Ta có đồ thị hàm số luôn đi qua điểm
0;1
I ;
1;2
A ;
1 0
y
và đồ thị có
x
thì
y
nên hệ số
0
a
, đồ thị hàm số là hàm số đồng biến trên
suy ra
0
y
với
x
suy ra hàm số cần tìm là
3 2
3 3 1
y x x x
.
Câu 24: [2D2-1] Cho
a
là số thực dương tùy ý khác
1
. Mệnh đề nào dưới đây đúng?
A.
2
log log 2
a
a . B.
2
2
1
log
log
a
a
. C.
2
1
log
log 2
a
a . D.
2
log log 2
a
a .
Lời giải
Chọn C.
Ta có
2
log
1
log
log 2 log 2
a
a a
a
a .
Câu 25: [2D2-2] Tìm tập xác định
D
của hàm số
3
2
2
y x x
.
A.
D
. B.
(0; )
D
. C.
( ; 1) (2; )
D
. D.
\{ 1;2}
D
.
Lời giải
Chọn D.
Điều kiện để hàm số xác định là
2
2 0 1;2
x x x suy ra
\{ 1;2}
D
.
Câu 26: [2H2-1] Cho hình nón có thể tích bằng
3
36
V a
và bán kính đáy bằng
3
a
. Tính độ dài
đường cao
h
của hình nón đã cho.
A.
4
a
. B.
2
a
. C.
5
a
. D.
12
a
.
Lời giải
Chọn D.
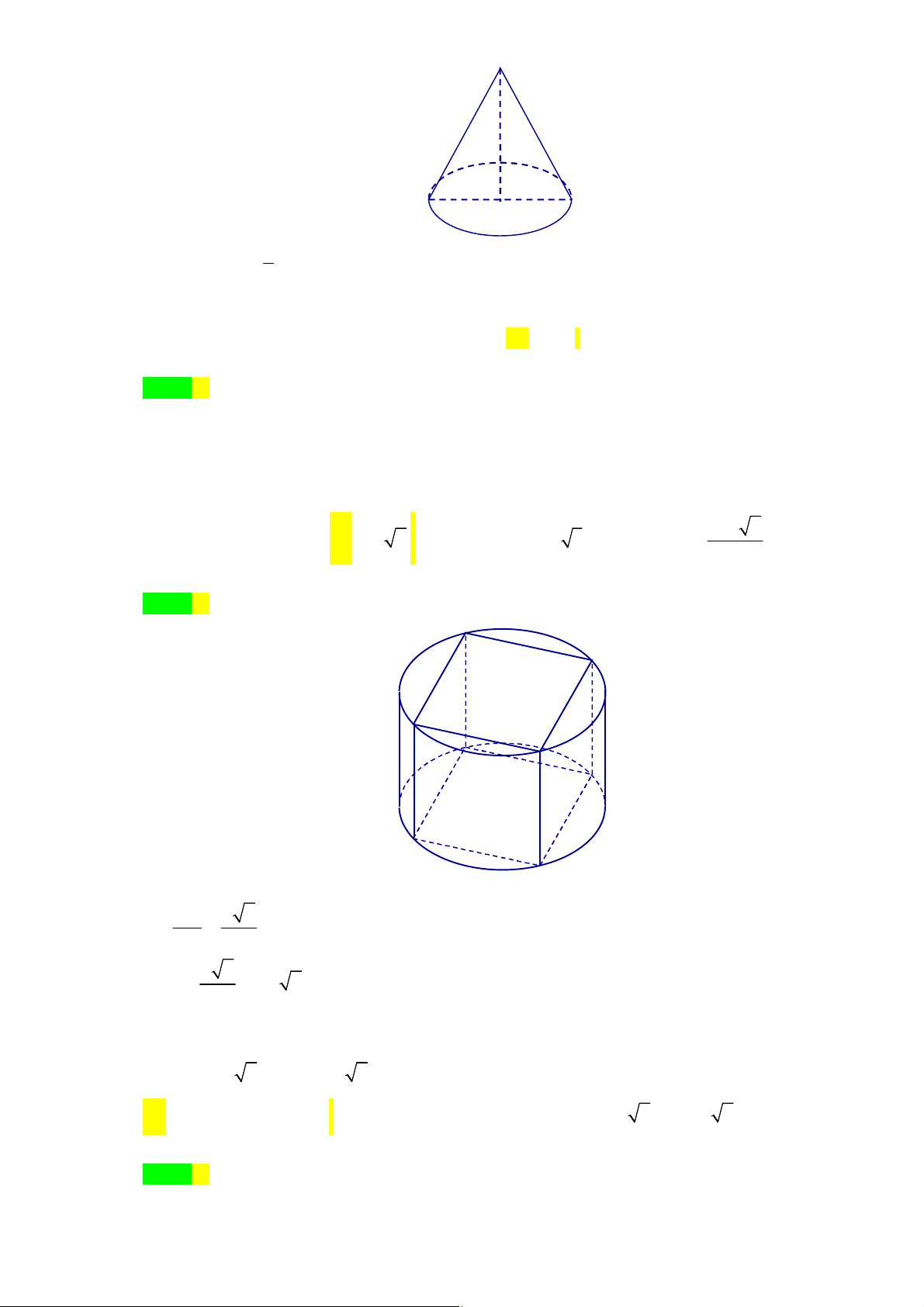
Trang 14/23 - Mã đề thi 132
Ta có:
2
3
1
36 3
3
a a h
12
h a
.
Câu 27: [2D2-1] Tìm tất cả các giá trị thực của tham số
m
để phương trình 3
x
m
có nghiệm thực.
A.
1
m
. B.
0
m
. C.
0
m
. D.
0
m
.
Lời giải
Chọn C.
Phương trình có nghiệm khi
0
m
.
Câu 28: [2H2-2] Cho hình lập phương
.
ABCD A B C D
có cạnh bằng
a
. Gọi
S
là diện tích xung
quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông
ABCD
và
A B C D
. Diện
tích
S
là:
A.
2
a
. B.
2
2
a
. C.
2
3
a
. D.
2
2
2
a
.
Lời giải
Chọn B.
2
2 2
AC a
r
2
2
2 2
2
a
S a a
.
Câu 29: [2D2-1] Tìm tập xác định
D
của hàm số
2
3
log 4 3
y x x
A.
2 2;1 3;2 2
D
. B.
1;3
D .
C.
;1 3;D
. D.
;2 2 2 2;D
.
Lời giải
Chọn C.
A
B
B
C
A
C
D
D
h
r
O
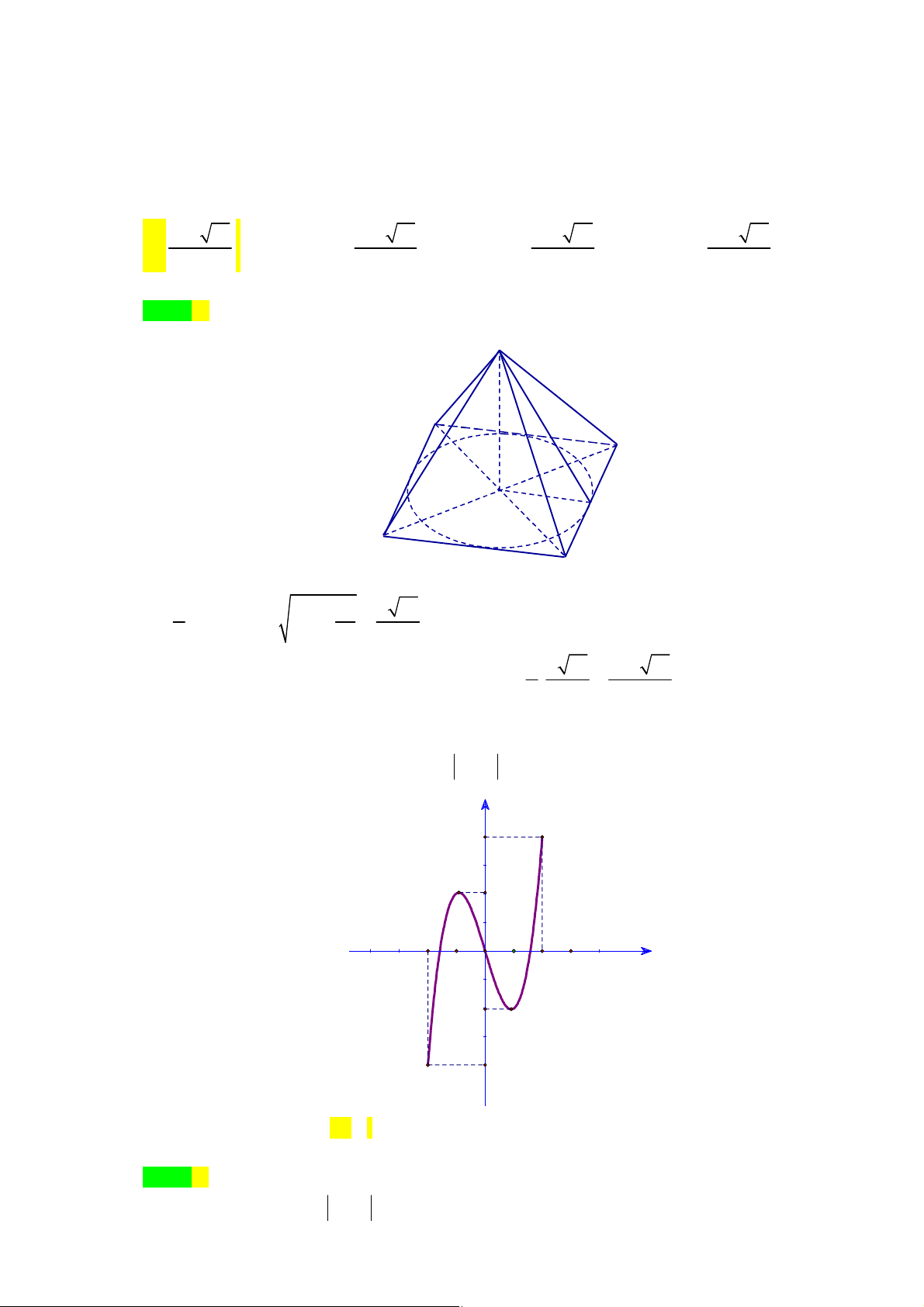
Trang 15/23 - Mã đề thi 132
Hàm số xác định khi:
2
4 3 0
x x
1
3
x
x
.
Vậy tập xác định của hàm số là:
;1 3;D
.
Câu 30: [2H2-2] Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
và chiều cao bằng
2
a
, diện
tích xung quanh của hình nón đỉnh
S
và đáy là hình tròn nội tiếp
ABCD
bằng
A.
2
17
4
a
. B.
2
15
4
a
. C.
2
17
6
a
. D.
2
17
8
a
.
Lời giải
Chọn A.
2
a
r
;
2
h a
;
2
2
17
4
4 2
a a
l a
Vậy diện tích xung quanh của hình nón là:
2
17 17
. .
2 2 4
xq
a a a
S
.
Câu 31: [2D1-2] Cho hàm số
y f x
liên tục trên đoạn
2;2
và có đồ thị là đường cong như hình
vẽ bên. Tìm số nghiệm của phương trình
1
f x
trên đoạn
2;2
.
x
y
-2
2
-4
4
2-1-2
O
1
A.
4
. B.
6
. C.
3
. D.
5
.
Lời giải
Chọn B.
Ta có đồ thị hàm số
y f x
trên đoạn
2;2
:
S
D
A
B
C
O

Trang 16/23 - Mã đề thi 132
x
y
2
4
2-1-2
O
1
Số nghiệm phương trình
1
f x
là số giao điểm của đồ thị hàm số
y f x
với đường
thẳng
1
y
.
Vậy phương trình
1
f x
có
6
nghiệm.
Câu 32: [2H2-1] Cho hình nón có bán kính đáy
3
r và độ dài đường sinh
4
l
. Tính diện tích xung
quanh
xq
S
của hình nón đã cho.
A.
12
xq
S
. B.
4 3
xq
S
. C.
39
xq
S
. D.
8 3
xq
S
.
Lời giải
Chọn B.
Áp dụng công thức tính diện tích xung quanh hình nón, ta được
4 3
xq
S rl
.
Câu 33: [2D2-2] Cho log3
a
, log5
b
. Tính
6
log 1125
.
A.
3 2
1
a b
a b
. B.
2 3
1
a b
a b
. C.
3 2
1
a b
a b
. D.
3 2
1
a b
a b
.
Lời giải
Chọn B.
Ta có:
10
log5 log 1 log2 log2 1
2
b
.
2 3
6
log1125 log3 log5 2 3
log 1125
log6 log2 log3 1
a b
a b
.
[phương pháp trắc nghiệm]
Lưu các giá trị
a
,
b
vào các biến nhớ rồi lần lượt so sánh các đáp án với
6
log 1125
.
Câu 34: [2H1-1] Cho hình bát diện đều cạnh
a
. Gọi
S
là tổng diện tích tất cả các mặt của hình bát diện
đều đó. Mệnh đề nào dưới đây đúng?
A.
2
4 3
S a
. B.
2
3
S a
. C.
2
2 3
S a
. D.
2
8
S a
.
Lời giải
Chọn C.
Hình bát diện đều có tám mặt là các tam giác đều cạnh
a
.
Tổng diện tích tất cả các mặt này bằng:
2
2
3
8 2 3
4
a
S a .
Câu 35: [2D2-3] Hỏi phương trình
2 5 1 2 5 6
2 2 2 32 0
x x x x
có bao nhiêu nghiệm phân biệt?
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn A.
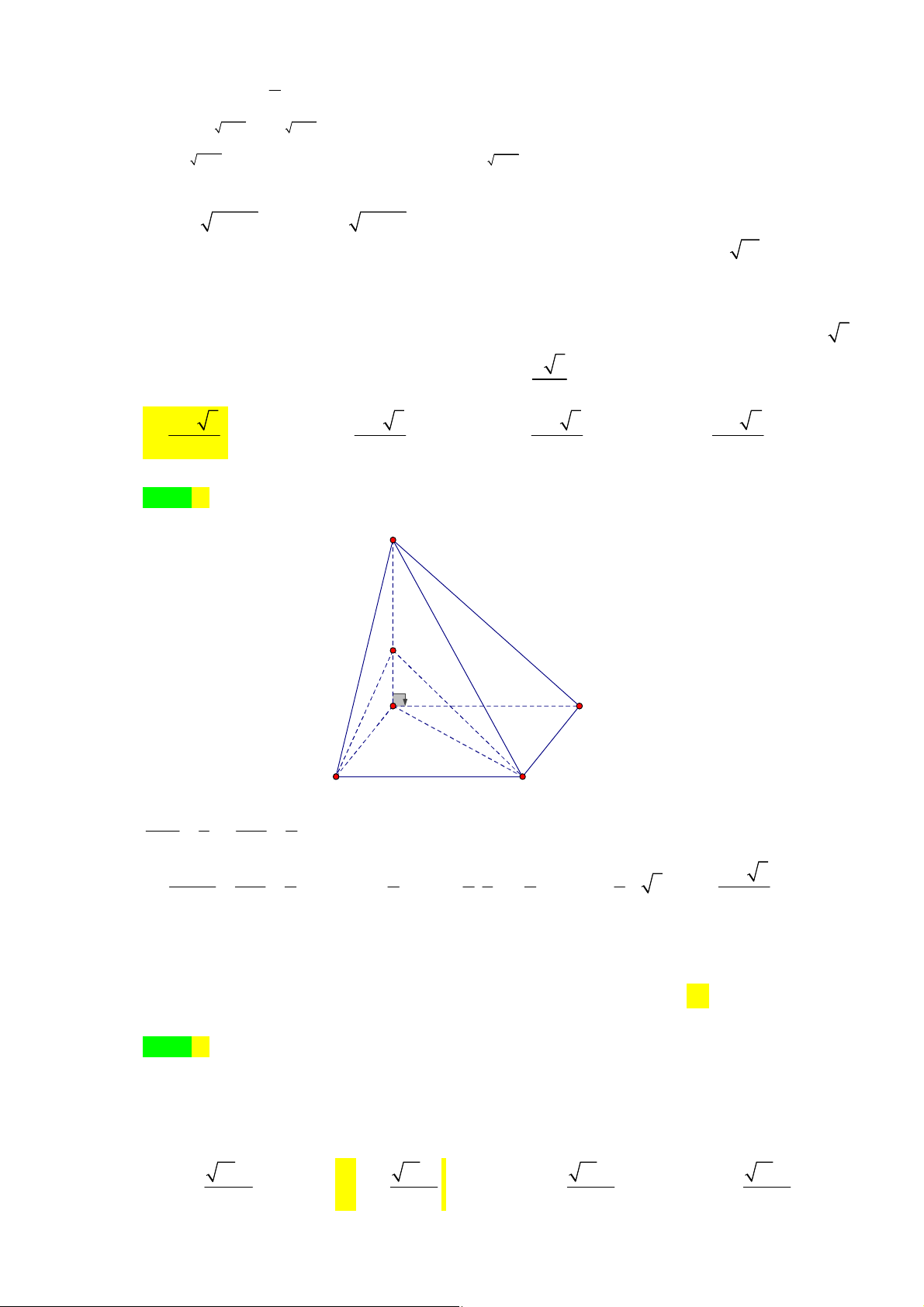
Trang 17/23 - Mã đề thi 132
Điều kiện:
5
2
x
.
Ta có
2 5 1 2 5 6
2 2 2 32 0
x x x x
1 2 5 1 6 1
2 2 1 2 1 2 0
x x x x
1 2 5 6 1
2 2 2 1 0
x x x
1 2 5 6 2 5 5
1 0 1
x x x x
x x
2
5 0
1
12 20 0
6 2 14
1
x
x
x x
x
x
.
Vậy phương trình có hai nghiệm phân biệt.
Câu 36: [2H1-2] Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật,
AB a
,
2
AD a
,
3
SA a
,
SA ABCD
.
M
là điểm trên
SA
sao cho
3
3
a
AM . Tính thể tích của khối chóp
.
S BMC
.
A.
3
2 3
9
a
. B.
3
2 3
3
a
. C.
3
4 3
3
a
. D.
3
3 2
9
a
.
Lời giải
Chọn A.
M
D
C
B
A
S
1 2
3 3
AM SM
SA SA
.
.
.
2
3
S BMC
S BAC
V
SM
V SA
3
. .
2 2 1 1 1 2 3
. . . . . . 3. .2
3 3 3 2 9 9
S BMC S BAC
a
V V SA AB BC a a a .
Câu 37: [2D2-2] Với mọi
a
,
b
,
x
là các số thực dương thỏa mãn
2 2 2
log 5log 3log
x a b
. Mệnh đề
nào dưới đây đúng?
A.
3 5
x a b
B.
5 3
x a b
C.
5 3
x a b
D.
5 3
x a b
Lời giải
Chọn D.
2 2 2
log 5log 3log
x a b
5 3
2 2 2
log log log
x a b
5 3
2 2
log log
x a b
5 3
x a b
.
Câu 38: [2H2-2] Cho khối chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
2
a
. Tính
thể tích
V
của khối chóp
.
S ABC
.
A.
3
13
12
a
V . B.
3
11
12
a
V . C.
3
11
6
a
V . D.
3
11
4
a
V .
Lời giải
Trang 18/23 - Mã đề thi 132
Chọn B.
O
M
C
B
A
S
Gọi
O
là tâm mặt đáy,
M
là trung điểm
BC
.
2 3
3 3
a
AM AM .
Tam giác
SAO
vuông tại
O
:
2 2
11
3
a
SO SA AO .
Vậy thể tích khối chóp
.
S ABC
là:
2 3
1 1 11 3 11
. .
3 3 4 12
3
ABC
a a a
V SO S .
Câu 39: [2H2-1] Gọi
l
,
h
,
R
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón.
Đẳng thức nào sau đây luôn đúng?
A.
2 2 2
l h R
. B.
2 2 2
1 1 1
l h R
. C.
2 2 2
R h l
. D.
2
l hR
.
Lời giải
Chọn A.
R
l
h
O
B
A
S
Theo định lí Pytago trong tam giác
SOB
vuông tại
O
:
2 2 2
l h R
.
Câu 40: [2D2-3] Hàm số
ln
f x x
có đạo hàm cấp
n
là
A.
n
n
n
f x
x
. B.
1
1 !
1
n
n
n
n
f x
x
.
C.
1
n
n
f x
x
. D.
!
n
n
n
f x
x
.
Lời giải
Chọn B.

Trang 19/23 - Mã đề thi 132
1
f x
x
.
2
2
1
f x
x
.
3
3 3
1.2 2!
f x
x x
.
4
4 4
1.2.3 3!
f x
x x
.
…
1
1 !
1 .
n
n
n
n
f
x
.
Sau đó dễ dàng chứng minh bằng quy nạp.
Câu 41: [2H2-1] Gọi
l
,
h
,
R
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối nón
N
. Thể tích
V
của khối nón
N
bằng
A.
2
1
3
V R h
. B.
2
V R h
. C.
2
V R l
. D.
2
1
3
V R l
.
Lời giải
Chọn A.
Câu 42: [2D2-2] Tìm giá trị thực của tham số
m
để phương trình
1
9 2.3 0
x x
m
có hai nghiệm thực
1
x
,
2
x
thỏa mãn
1 2
1
x x
.
A.
6
m
. B.
3
m
. C.
3
m
. D.
1
m
.
Lời giải
Chọn C.
Phương trình tương đương với
2
3 6.3 0 1
x x
m .
Đặt
3
x
t
, điều kiện
0
t
. Phương trình trở thành
2
6 0 2
t t m .
Để tồn tại
1
x
,
2
x
thì phương trình
2
có hai nghiệm dương
1
t
,
2
t
. Giả sử có
1
t
,
2
t
dương khi
đó ta có
1 2
1 2
. 3 3
x x
t t
3
m
.
Thử lại ta thấy với
3
m
thì phương trình
2
có hai nghiệm dương phân biệt. Vậy
3
m
.
Câu 43: [2H1-2] Cho khối chóp
.
S ABCD
có đáy là nửa lục giác đều nội tiếp trong nửa đường tròn
đường kính
2
AB R
. Biết
I
là trung điểm
AB
,
SI
vuông góc với đáy và
SBC
và hợp với
đáy
ABCD
một góc
45
. Tính thể tích khối chóp
.
S ABCD
A.
3
3
4
R
. B.
3
3
8
R
. C.
3
3
6
R
. D.
3
3
2
R
.
Lời giải
Chọn B.
Trang 20/23 - Mã đề thi 132
Tam giác
IBC
đều nên nếu gọi
J
là trung điểm của
BC
thì
SIJ BC
,
3
2
R
IJ và
45
SJI
. Suy ra
3
2
R
SI .
Vậy thể tích
2 3
.
1 1 3 3 3
. .3
3 3 2 4 8
S ABCD ABCD IBC
R R R
V SI S SI S .
Câu 44: [2D1-2] Tìm giá trị thực của tham số
m
để đường thẳng
: 2 1 3
d y m x m
vuông góc
với đường thẳng đi qua hai điểm cực trị của hàm số
3 2
3 1
y x x
.
A.
3
2
m
. B.
3
4
m
. C.
1
2
m
. D.
1
4
m
.
Lời giải
Chọn B.
Hàm số có hai cực trị có tọa độ là
0;1
A và
2; 3
B
.
Phương trình đường thẳng qua cực đại cực tiểu là
: 2 1
y x
.
Để đường thẳng
d
vuông góc với đường thẳng
thì
1 3
2 1
2 4
m m
.
Câu 45: [2D2-3] Hỏi có bao nhiêu giá trị
m
nguyên trong đoạn
2017;2017
để phương trình
3 3 3
log log 2log 1
m x x
luôn có hai nghiệm phân biệt?
A.
4015
. B.
2010
. C.
2018
. D.
2013
.
Lời giải
Chọn D.
Điều kiện
0
0
m
x
.
Phương trình tương đương với
2
3 3
log log 1
mx x
2
2 1
mx x x
2
2 1 0 *
x m x

Trang 21/23 - Mã đề thi 132
Để phương trình đầu có hai nghiệm phân biệt thì phương trình
*
có hai nghiệm dương phân
biệt
0
0
0
S
P
2
4 0
2 0
m m
m
m
4
m
Vì
m
và
4;2017
m nên có
2013
số thỏa mãn.
Câu 46: [2D1-3] Biết hàm số
2 2
4 2 3 2
y x x x x
đạt giá trị lớn nhất tại hai điểm
1
x
,
2
x
. Giá trị
1 2
.
x x
bằng
A.
2
. B.
1
. C.
0
. D.
1
.
Lời giải
Chọn D.
Đặt
2
2
2 3 1 2 2
t x x x .
Ta có hàm số
2
4 3
f t t t
,
2;t
.
2 4 0 2
f t t t
.
Suy ra
0
f t
khi
2;2
t
và
0
f t
khi
2;t
Do đó
2;
max 2
f t f
khi
2 2
2 2 3 2 2 1 0
t x x x x
.
Vậy
1 2
. 1
x x
.
Câu 47: [2D2-2] Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
2
ln 2 1
y x x m
xác
định với
x
là
A.
0
. B.
0;3
. C.
; 1 0;
. D.
0;
.
Lời giải
Chọn D.
Hàm số có tập xác định là
2
2 1 0
x x m
với
x
1 1 0 0
m m
.
Câu 48: [2D2-3] Anh Nam gửi 100 triệu đồng vào ngân hàng Vietcombank. Lãi suất hàng năm không
thay đổi là
7,5% /
năm. Nếu anh Nam hàng năm không rút lãi thì sau 5 năm số tiền anh Nam
nhận được cả vốn lẫn tiền lãi (kết quả làm tròn đến hàng ngàn) là
A.
143.563.000
đồng. B.
2.373.047.000
đồng.
C.
137.500.000
đồng. D.
133.547.000
đồng.
Lời giải
Chọn A.
Đặt
6
100.10
A đồng. Theo công thức lãi kép thì tổng số tiền cả vốn và lãi sau 5 năm của anh
Nam là
5
6
100.10 1 7,5% 143.563.000
đồng.
Câu 49: [2H1-4] Cho một tấm bìa hình vuông cạnh
5
dm. Để làm một mô hình kim tự tháp Ai Cập,
người ta cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy chính là cạnh của hình vuông rồi gấp
lên, ghép lại thành một hình chóp tứ giác đều. Để mô hình có thể tích lớn nhất thì cạnh đáy của
mô hình là
A.
3 2
2
dm. B.
5
2
dm. C.
5 2
2
dm. D.
2 2
dm.
Trang 22/23 - Mã đề thi 132
Lời giải
Chọn D.
Đặt
MN x
,
5dm
a
. Ta có
2
x
OI
,
2 2
2 2 2
a a x
OA AI
.
Vậy đường cao
2
2
2 2
2
2
2 2 2 2
a x x a
h AI OI a x
Vậy thể tích của hình chóp là
2 4
1 1 2
2 2 2 4
3 2 3 8
a a
V x a x a x x
Áp dụng bất đẳng thức Côsi cho 5 số thực dương
2 2 4
a x
và 4 số
x
, ta có
5
5
4
2 2 4 4
2 2 4 2 2 128 2
5
a x x
a x x
.
Vậy
3
max
160
dm
3
V khi
2 2
2 2 4 2 2
5
a
a x x x dm.
Câu 50: [2H2-3] Cho tam giác
ABC
vuông cân tại
A
, có
12
AB AC
. Lấy một điểm
M
thuộc cạnh
huyền
BC
và gọi
H
là hình chiếu của
M
lên cạnh góc vuông
AB
. Quay tam giác
AMH
quanh trục là đường thẳng
AB
tạo thành mặt nón tròn xoay
N
, hỏi thể tích
V
của khối nón
tròn xoay
H
lớn nhất bằng bao nhiêu?
A.
256
3
V
. B.
128
3
V
. C.
256
V
. D.
72
V
.
Lời giải
Chọn A.
Đặt
AH x
, khi đó ta có 12
MH BH
MH BH x
AC BA
.
A
C
M
B
H
N
x
A
B
C
D
M
N
P
Q
O
I

Trang 23/23 - Mã đề thi 132
Khi đó
2
1
12
3
N
V x x
.
Áp dụng BĐT Côsi cho ba số dương
12
x
,
12
x
,
x
ta có
3
2
24 2 2 256
12 .2
6 6 3 6
x x
V x x
Vậy
max
256
V
x
khi
12 2 4
x x x
.
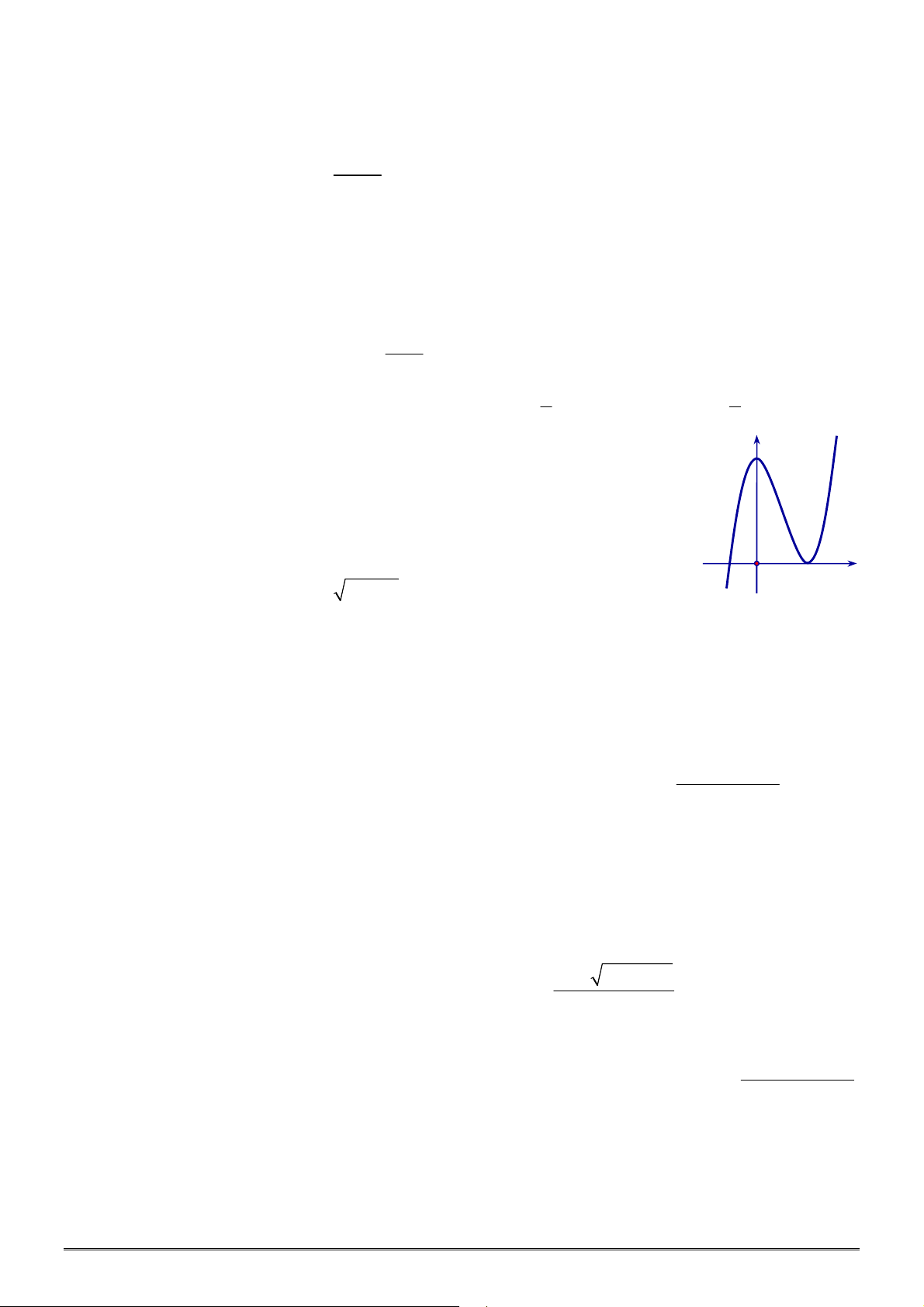
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/26
SỞ GIÁO DỤC ĐÀO TẠO NAM ĐỊNH
ĐỀ CHÍNH THỨC
(Mã đề 102)
ĐỀ THI HỌC KÌ I, NĂM HỌC 2017 – 2018
Môn Toán – Khối 12
Thời gian 90 phút (không kể thời gian phát đề)
Câu 1. [2D1-2] Cho hàm số
3 1
2
x
y
x
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số luôn nghịch biến trên
.
B. Hàm số luôn nghịch biến trên từng khoảng xác định.
C. Hàm số đồng biến trên các khoảng
;2
và
2;
.
D. Hàm số nghịch biến trên các khoảng
; 2
và
2;
.
Câu 2. [2D1-2] Hàm số
3
ln 2
2
y x
x
đồng biến trên khoảng nào?
A.
;1 .
B.
1; .
C.
1
;1 .
2
D.
1
; .
2
Câu 3. [2D1-1] Cho hàm số
y f x
có đồ thị như hình vẽ. Trên
khoảng
1;3
đồ thị hàm số
y f x
có mấy điểm cực trị?
A.
2.
B.
1.
C.
0.
D.
3.
Câu 4. [2D1-2] Cho hàm số
2
3
y x x
. Khẳng định nào sau đây là đúng?
A. Hàm số có hai điểm cực trị. B. Hàm số đạt cực tiểu tại
0.
x
C. Hàm số đạt cực đại tại
3.
x
D. Hàm số không có cực trị.
Câu 5. [2D1-3] Tìm tất cả giá trị của tham số
m
để đồ thị hàm số
4 2
2 2 3
y x mx m
có ba điểm
cực trị là ba đỉnh của tam giác vuông.
A.
1.
m
B.
0.
m
C.
2.
m
D.
1.
m
Câu 6. [2D1-1] Tìm phương trình đường tiệm cận đứng của đồ thị hàm số
2017 2018
1
x
y
x
.
A.
2017
x
. B.
1
x
. C.
2017
y
. D.
1
y
.
Câu 7. [2D1-2] Cho hàm số
y f x
có
lim 1
x
f x
và
lim 1
x
f x
. Tìm phương trình đường
tiệm cận ngang của đồ thị hàm số
2 2017
y f x
.
A.
2017
y
B.
1
y
C.
2017
y
. D.
2019
y
.
Câu 8. [2D1-2] Tìm số đường tiệm cận của đồ thị hàm số
2
2
2 6
1
x x x
y
x
.
A.
1
. B.
2
. C.
0
. D.
4
.
Câu 9. [2D1-3] Hỏi có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
2
2
3 2
5
x x
y
x mx m
không có đường tiệm cận đứng?
A.
9
. B.
10
. C.
11
. D.
8
.
Câu 10. [2D1-2] Phương trình tiếp tuyến của đồ thị hàm số
3 2
3 1
y x x
tại điểm
3;1
A là
A.
9 26
y x
. B.
9 26
y x
. C.
9 3
y x
. D.
9 2
y x
.
O
x
y
1
2
4
7

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/26
Câu 11. [1D5-2] Với
0;
2
x
, hàm số
2 sin 2 cos
y x x
có đạo hàm là
A.
1 1
sin cos
y
x x
. B.
1 1
sin cos
y
x x
.
C.
cos sin
sin cos
x x
y
x x
. D.
cos sin
sin cos
x x
y
x x
.
Câu 12. [2D2-2] Cho hàm số
2
2017 3
x x
y e e
. Mệnh đề nào dưới đây đúng?
A.
3 2 2017
y y y
B.
3 2 3
y y y
.
C.
3 2 0
y y y
. D.
3 2 2
y y y
.
Câu 13. [2D1-2] Đồ thị hình bên là đồ thị của một trong
4
hàm số dưới đây. Hỏi đó là hàm số nào?
A.
3 2
3 3 1
y x x x
.
B.
3
1
3 1
3
y x x
.
C.
3 2
3 3 1
y x x x
.
D.
3
3 1
y x x
.
Câu 14. [2D1-4] Cho hàm số
1
1
x
y
x
có đồ thị
C
. Gọi
A
,
B
0
A B
x x
là hai điểm trên
C
có
tiếp tuyến tại
A
,
B
song song nhau và
2 5
AB . Tính
A B
x x
.
A.
2
A B
x x
. B.
4
A B
x x
. C.
2 2
A B
x x D.
2
A B
x x
Câu 15. [2D2-2] Giá trị nhỏ nhất của hàm số
ln
x
y
x
trên đoạn
1;
e
là
A.
0.
B.
1.
C.
1
.
e
D.
.
e
Câu 16. [2D1-3] Trong các hình chữ nhật có chu vi bằng
16
, hình chữ nhật có diện tích lớn nhất bằng
A.
64
. B.
4
. C.
16
. D.
8
.
Câu 17. [2D1-4] Cho hàm số
1
1
x
y
x
có đồ thị
C
. Gọi
;
M M
M x y
là một điểm trên
C
sao cho
tổng khoảng cách từ điểm
M
đến hai trục tọa độ là nhỏ nhất. Tổng
M M
x y
bằng
A.
2 2 1
. B.
1
. C.
2 2
. D.
2 2 2
.
Câu 18. [2D1-1] Tìm số giao điểm của đồ thị
3 2
: 3 2 2017
C y x x x và đường thẳng
2017
y
.
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 19. [2D1-3] Cho hàm số
3 2
2 8
y mx x x m
có đồ thị
m
C
. Tìm tất cả giá trị của tham số
m
để đồ thị
m
C
cắt trục hoành tại ba điểm phân biệt.
A.
1 1
;
6 2
m
. B.
1 1
;
6 2
m
. C.
1 1
; \ 0
6 2
m
. D.
1
; \ 0
2
m
.
Câu 20. [2D1-4] Tìm tất cả giá trị của tham số
m
để đồ thị hàm số
4 2
1 2 2 3 6 5
y m x m x m
cắt trục hoành tại bốn điểm phân biệt có hoành độ
1
x
,
2
x
,
3
x
,
4
x
thỏa
1 2 3 4
1
x x x x
.
A.
5
1;
6
m
. B.
3; 1
m
. C.
3;1
m . D.
4; 1
m
.
O
x
y
1
1
3
2
1
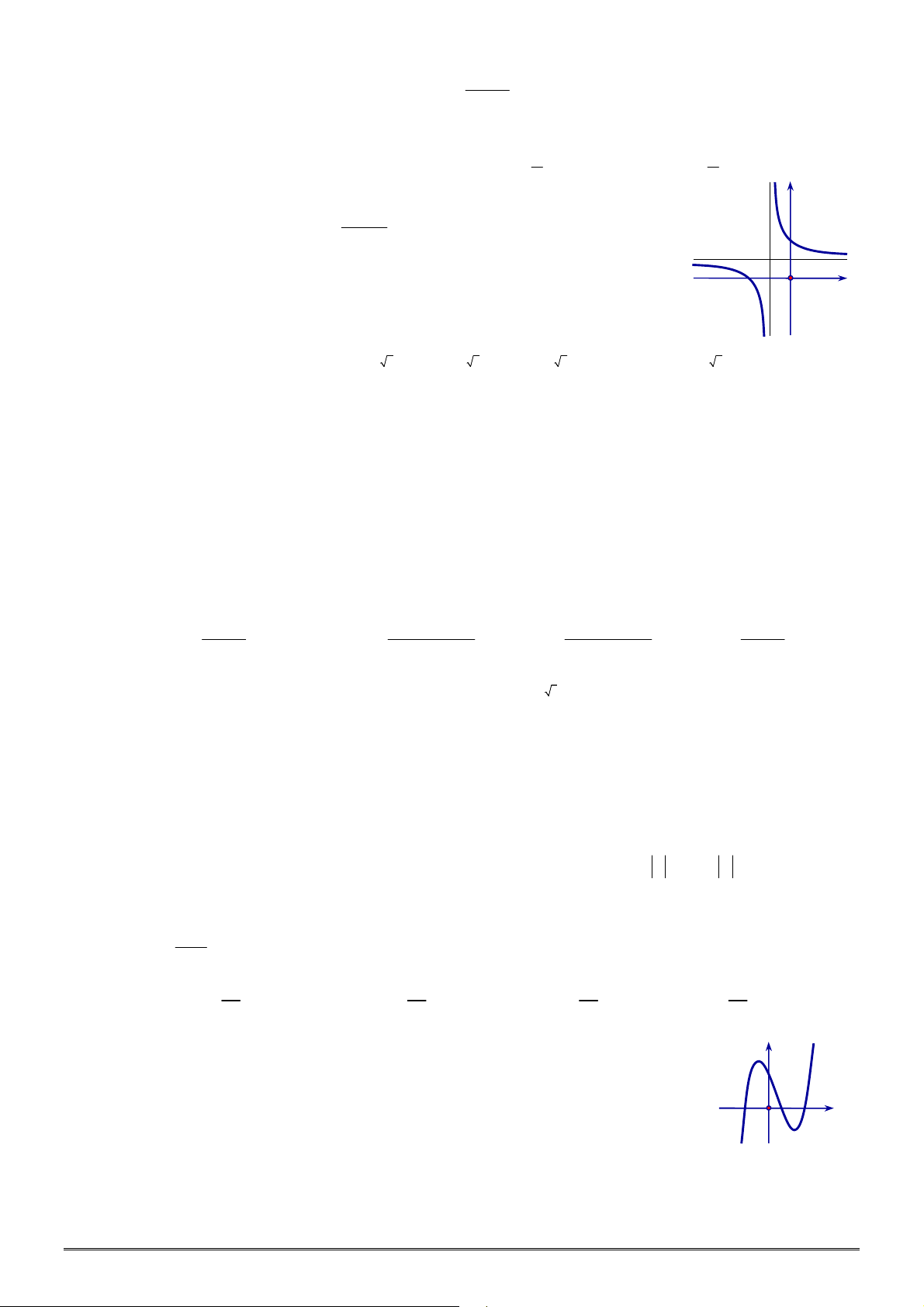
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/26
Câu 21. [1D4-2] Tiếp tuyến với đồ thị hàm số
2 1
1
x
y
x
tại điểm có hoành độ bằng
0
cắt hai trục tọa
độ lần lượt tại
A
và
.
B
Diện tích tam giác
OAB
bằng
A.
2
. B.
3
. C.
1
2
. D.
1
4
.
Câu 22. [2D1-2] Cho hàm số
1
ax b
y
x
có đồ thị như hình vẽ bên.
Tìm khẳng định đúng trong các khẳng định sau?
A.
0
a b
. B.
0
b a
.
C.
0
b a
. D.
0
a b
.
Câu 23. [2D2-3] Tìm tổng
3 20174
2 2 2 2
2 2 2 2
1 2 log 2 3 log 2 4 log 2 ... 2017 log 2
S .
A.
2 2
1008 .2017
S . B.
2 2
1007 .2017
S . C.
2 2
1009 .2017
S . D.
2 2
1010 .2017
S .
Câu 24. [2D2-2] Cho hàm số
ln
y x
. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng
0;
.
B. Hàm số có tập giá trị là
;
.
C. Đồ thị hàm số nhận trục
Oy
làm tiệm cận đứng.
D. Hàm số có tập giá trị là
0;
.
Câu 25. [2D2-1] Tính đạo hàm của hàm số
2
log 2 1
y x
.
A.
2
2 1
y
x
. B.
2
2 1 ln2
y
x
. C.
1
2 1 ln2
y
x
. D.
1
2 1
y
x
.
Câu 26. [2D2-1] Tìm tập xác định
D
của hàm số
1 3
2y x
.
A.
;D
. B.
;2
D . C.
;2
D . D.
2;D
.
Câu 27. [2D2-2] Cho
0, 1
a a
và
,
x y
là hai số thực khác
0
. Khẳng định nào sau đây là khẳng định
đúng?
A.
2
log 2log
a a
x x
. B.
log log log
a a a
xy x y
.
C.
log log log
a a a
x y x y
. D.
log log log
a a a
xy x y
.
Câu 28. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
3
2
7 14 2
3
mx
y mx x m
nghịch biến trên nửa khoảng
1;
.
A.
14
;
15
. B.
14
;
15
. C.
14
2;
15
. D.
14
;
15
.
Câu 29. [2D1-2] Cho đồ thị hàm số
3 2
y ax bx cx d
có đồ thị như
hình bên. Khẳng định nào sau đây là khẳng định đúng?
A.
, , 0; 0
a b c d
. B.
, , 0; 0
a b d c
.
C.
, , 0; 0
a c d b
. D.
, 0; , 0
a d b c
.
Câu 30. [2H1-2] Số mặt phẳng đối xứng của khối lăng trụ tam giác đều là
A.
3
. B.
4
. C.
6
. D.
9
.
O
x
y
O
x
y
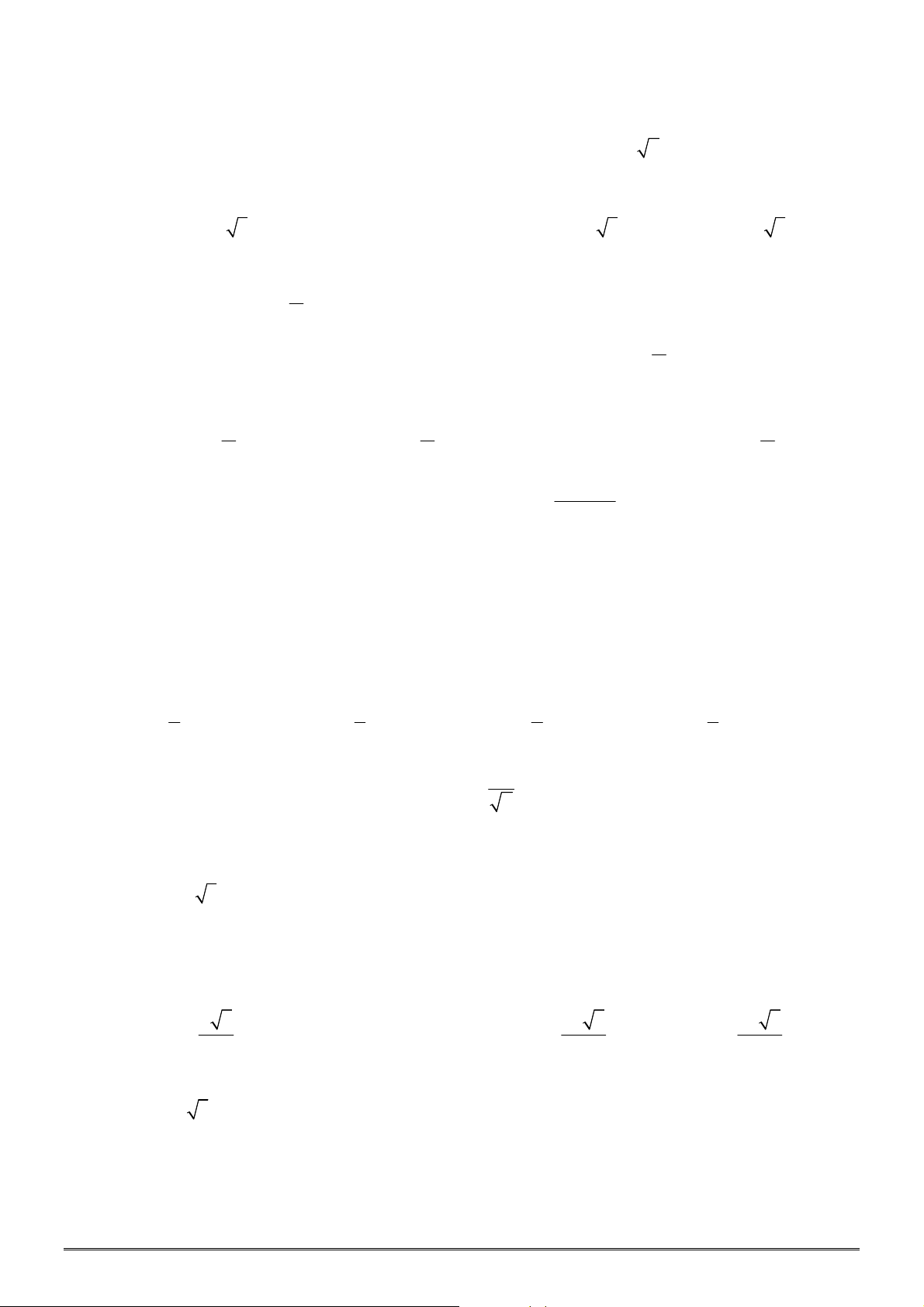
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/26
Câu 31. [2H1-1] Hỏi khối đa diện đều loại
4;3
có bao nhiêu mặt?
A.
4
. B.
20
. C.
6
. D.
12
.
Câu 32. [2H1-3] Cho hình lập phương
.
ABCD A B C D
có cạnh bằng
2 2
a
. Gọi
S
là tổng diện tích
tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương
.
ABCD A B C D
. Tính
.
S
A.
2
4 3
S a . B.
2
8
S a
. C.
2
16 3
S a . D.
2
8 3
S a .
Câu 33. [1D1-1] Khẳng định nào sau đây là khẳng định sai?
A.
cos 0 2
2
x x k
. B.
cos 1 2
x x k
.
C.
cos 1 2
x x k
. D. cos 0
2
x x k
.
Câu 34. [1D1-2] Giải phương trình
cos2 5sin 4 0
x x
.
A.
2
x k
. B.
2
x k
. C.
2
x k
. D.
2
2
x k
.
Câu 35. [1D1-3] Gọi
S
là tổng các nghiệm của phương trình
sin
0
cos 1
x
x
trên đoạn
0;2017
. Tính
S
.
A.
2035153
S
. B.
1001000
S
. C.
1017072
S
. D.
200200
S
.
Câu 36. [1D2-2] Có bao nhiêu số tự nhiên có
3
chữ số đôi một khác nhau?
A.
648
. B.
1000
. C.
729
. D.
720
.
Câu 37. [1D2-2] Một hộp có
5
bi đen,
4
bi trắng. Chọn ngẫu nhiên
2
bi. Xác suất
2
bi được chọn có
cùng màu là
A.
1
4
. B.
1
9
. C.
4
9
. D.
5
9
.
Câu 38. [1D2-2] Trong khai triển đa thức
6
2
P x x
x
(
0
x
), hệ số của
3
x
là
A.
60
. B.
80
. C.
160
. D.
240
.
Câu 39. [1H3-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
;
SA ABC
và
3
SA a
. Tính góc giữa đường thẳng
SB
với mặt phẳng
ABC
.
A.
75
. B.
60
. C.
45
. D.
30
.
Câu 40. [1H3-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
;
SA ABCD
và
2
SA a
. Tính khoảng cách
d
từ điểm
B
đến mặt phẳng
SCD
.
A.
5
5
a
d . B.
d a
. C.
4 5
5
a
d . D.
2 5
5
a
d .
Câu 41. [2H1-2] Cho hình hộp
.
ABCD A B C D
có đáy là hình thoi cạnh
a
,
60
ABC
và thể tích
bằng
3
3
a
. Tính chiều cao
h
của hình hộp đã cho.
A.
2
h a
. B.
h a
. C.
3
h a
. D.
4
h a
.
Câu 42. [2H1-2] Diện tích ba mặt của hình hộp chữ nhật lần lượt bằng
3
20 cm
,
3
28 cm
,
3
35 cm
. Thể
tích của hình hộp đó bằng
A.
3
165 cm
. B.
3
190 cm
. C.
3
140 cm
. D.
3
160 cm
.
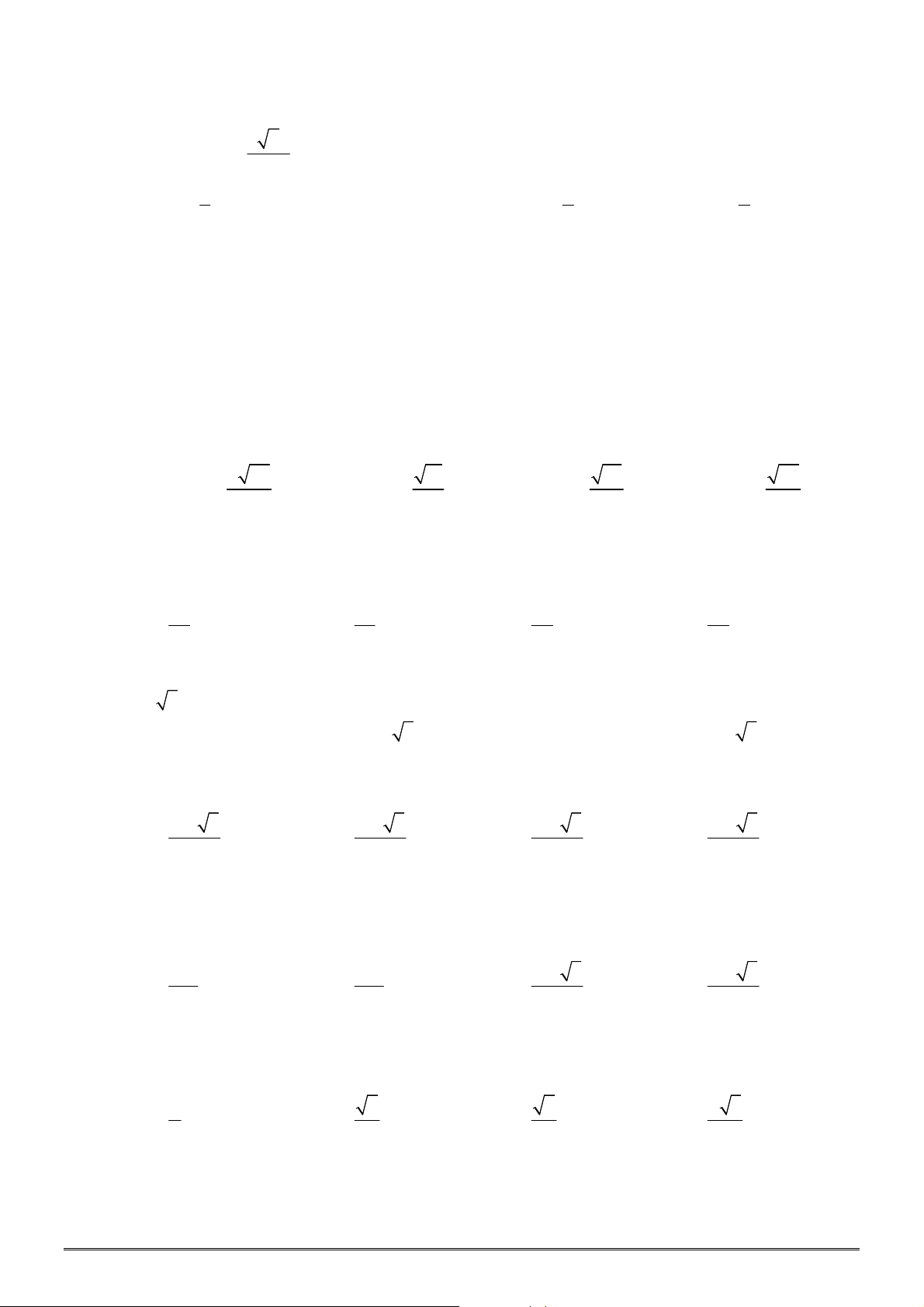
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/26
Câu 43. [2H1-3] Cho hình chóp tứ giác
.
S ABCD
có đáy là hình vuông, mặt bên
SAB
là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm B đến mặt phẳng
SCD
bằng
3 7
7
a
. Tính thể tích V của khối chóp
.
S ABCD
.
A.
3
1
3
V a
. B.
3
V a
. C.
3
2
3
V a
. D.
3
3
2
V a
.
Câu 44. [1H3-4] Cho hình chóp
.
S ABC
có
SA
vuông góc với đáy,
2
SA BC
và
120
BAC
. Hình
chiếu của
A
trên các đoạn
SB
,
SC
lần lượt là
M
,
N
. Tính góc giữa hai mặt phẳng
ABC
và
AMN
.
A.
45
. B.
. C.
15
. D.
.
Câu 45. [1H3-4] Cho hình lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
, tam giác
A BC
đều và nằm trong mặt phẳng vuông góc với mặt phẳng
ABC
,
M
là trung điểm cạnh
CC
.
Tính
cosin
góc
giữa hai đường thẳng
AA
và
BM
.
A.
2 22
cos
11
. B.
11
cos
11
. C.
33
cos
11
. D.
22
cos
11
.
Câu 46. [2H1-4] Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
. Biết
2
AB a
,
AC a
,
4
AA a
. Gọi
M
là điểm thuộc cạnh
AA
sao cho
3
MA MA
. Tính
khoảng cách giữa hai đường thẳng chéo nhau
BC
và
C M
.
A.
6
7
a
. B.
8
7
a
. C.
4
3
a
. D.
4
7
a
.
Câu 47. [2H2-2] Tính diện tích xung quanh của hình trụ biết hình trụ có bán kính đáy
a
và đường cao
3
a
.
A.
2
2
a
. B.
2
2 3
a . C.
2
a
. D.
2
3
a .
Câu 48. [2H2-2] Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài
2
a
. Thể tích
của khối nón là:
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3
2
a
. D.
3
3
12
a
.
Câu 49. [2H2-4] Cho tam giác
ABC
có
120
A
,
AB AC a
. Quay tam giác
ABC
(bao gồm cả
điểm trong tam giác) quanh đường thẳng
AB
ta được một khối tròn xoay. Thể tích khối tròn
xoay đó bằng:
A.
3
3
a
. B.
3
4
a
. C.
3
3
2
a
. D.
3
3
4
a
.
Câu 50. [2H2-4] Trong các khối trụ có cùng diện tích toàn phần bằng
, gọi
là khối trụ có thể tích
lớn nhất, chiều cao của
bằng:
A.
3
. B.
6
3
. C.
6
6
. D.
3
4
.
----------HẾT----------
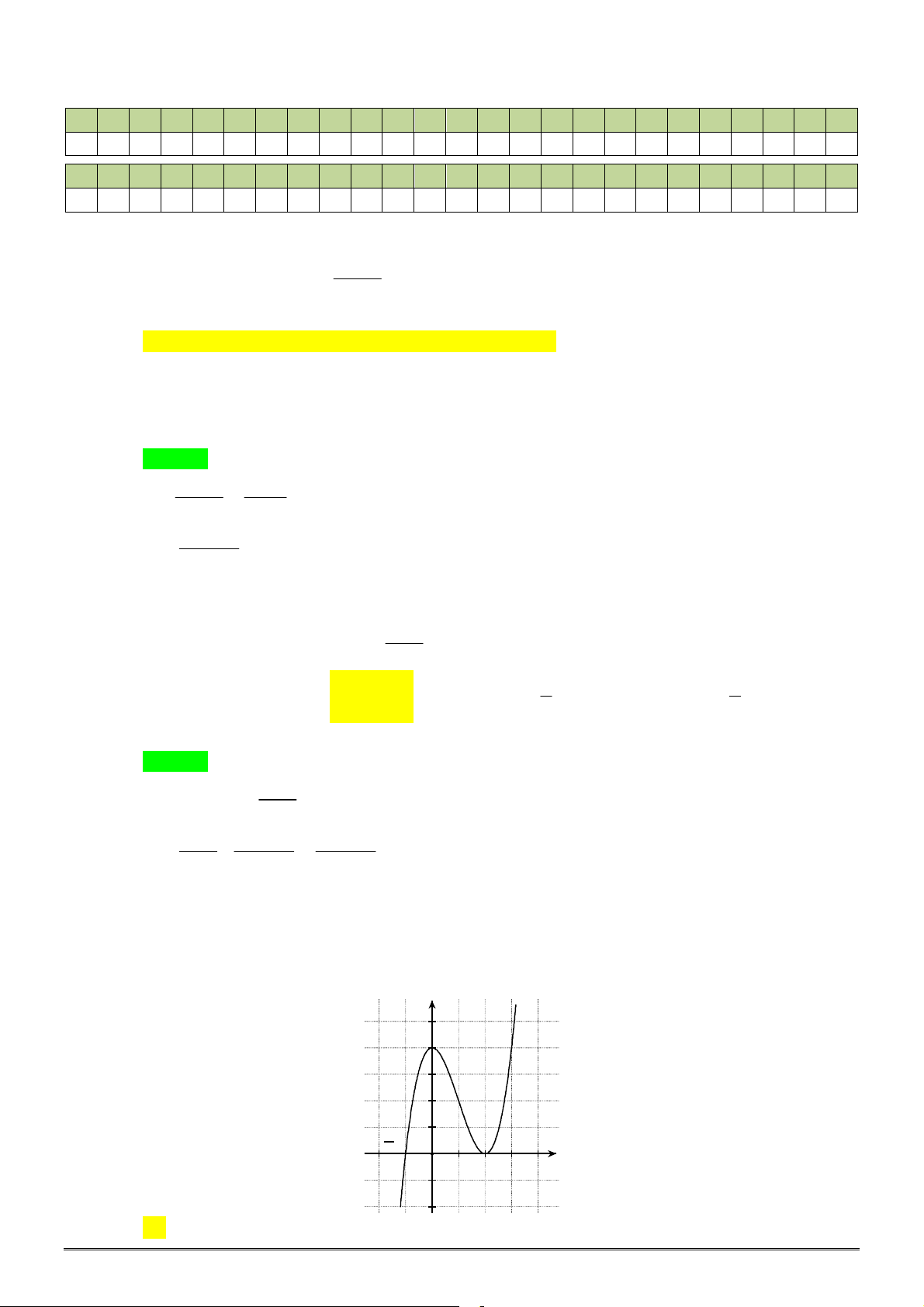
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/26
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B B A
D
D
B D
A
B B D
C
D
A
A
C
D
A
C
D
C
D
C
D
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
C
D
B D
B C
D
A
D
C
A
C
A
B
D
A
C
D
D
C
B B B B B
BẢNG ĐÁP ÁN
Câu 1. [2D1-2] Cho hàm số
3 1
2
x
y
x
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số luôn nghịch biến trên
.
B. Hàm số luôn nghịch biến trên từng khoảng xác định.
C. Hàm số đồng biến trên các khoảng
;2
và
2;
.
D. Hàm số nghịch biến trên các khoảng
; 2
và
2;
.
Lời giải
Chọn B.
3 1
2
x
y
x
3 1
2
x
x
. TXĐ:
\ 2
D
.
2
5
2
y
x
0
,
x D
.
Suy ra hàm số luôn nghịch biến trên từng khoảng xác định.
Câu 2. [2D1-2] Hàm số
3
ln 2
2
y x
x
đồng biến trên khoảng nào?
A.
;1 .
B.
1; .
C.
1
;1 .
2
D.
1
; .
2
Lời giải
Chọn B.
3
ln 2
2
y x
x
. TXĐ:
2;D
.
2
1 3
2
2
y
x
x
2
1
2
x
x
.
0
y
1
x
Hàm số luôn đồng biến trên
1;
.
Câu 3. [2D1-1] Cho hàm số
y f x
có đồ thị như hình vẽ. Trên khoảng
1;3
đồ thị hàm số
y f x
có mấy điểm cực trị?
x
y
2
4
1
O
A.
2.
B.
1.
C.
0.
D.
3.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/26
Lời giải
Chọn A.
Dựa vào đồ thị, trên khoảng
1;3
đồ thị hàm số có 2 điểm cực trị lần lượt là
0;4
và
2;0
.
Câu 4. [2D1-2] Cho hàm số
2
3
y x x
. Khẳng định nào sau đây là đúng?
A. Hàm số có hai điểm cực trị.
B. Hàm số đạt cực tiểu tại
0.
x
C. Hàm số đạt cực đại tại
3.
x
D. Hàm số không có cực trị.
Lời giải
Chọn D.
2
3
y x x
. TXĐ:
;0 3;D
.
2
2 3
2 3
x
y
x x
.
0
y
3;x
Hàm số luôn đồng biến trên
3;
.
0
y
;0
x
Hàm số luôn nghịch biến trên
;0
.
Vậy hàm số không có cực trị.
Câu 5. [2D1-3] Tìm tất cả giá trị của tham số
m
để đồ thị hàm số
4 2
2 2 3
y x mx m
có ba điểm
cực trị là ba đỉnh của tam giác vuông.
A.
1.
m
B.
0.
m
C.
2.
m
D.
1.
m
Lời giải
Chọn D.
4 2
2 2 3
y x mx m
. TXĐ:
D
.
3
4 4
y x mx
.
2
0
0
x
y
x m
. Hàm số có ba điểm cực trị
0
m
*
.
Giả sử ba điểm cực trị lần lượt là:
0;2 3
A m
,
2
; 2 3
B m m m
,
2
; 2 3
C m m m
.
2
;
AB m m
,
2
;
AC m m
.
Dễ thấy: tam giác
ABC
cân tại
A
.
Yêu cầu bài toán
AB AC
. 0
AB AC
4
0
m m
0
1
m
m
.
So với ĐK
*
suy ra:
1
m
thoả mãn yêu cầu bài toán.
Câu 6. [2D1-1] Tìm phương trình đường tiệm cận đứng của đồ thị hàm số
2017 2018
1
x
y
x
.
A.
2017
x
. B.
1
x
. C.
2017
y
. D.
1
y
.
Lời giải
Chọn B.
Ta có
1
lim
x
y
và
1
lim
x
y
nên
1
x
là đường tiệm cận đứng của đồ thị hàm số.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/26
Câu 7. [2D1-2] Cho hàm số
y f x
có
lim 1
x
f x
và
lim 1
x
f x
. Tìm phương trình đường
tiệm cận ngang của đồ thị hàm số
2 2017
y f x
.
A.
2017
y
B.
1
y
C.
2017
y
. D.
2019
y
.
Lời giải
Chọn D.
Ta có
lim lim 2 2017. 2 2017. 1 2019
lim lim 2 2017. 2 2017. 1 2019
x x
x x
y f x
y f x
nên
2019
y
là đường tiệm cận
ngang của đồ thị hàm số
2 2017
y f x
.
Câu 8. [2D1-2] Tìm số đường tiệm cận của đồ thị hàm số
2
2
2 6
1
x x x
y
x
.
A.
1
. B.
2
. C.
0
. D.
4
.
Lời giải
Chọn A.
Tập xác định của hàm số là
; 2 3;D
.
Do
lim 0
x
y
nên đường thẳng
0
y
là đường tiệm cận ngang của đồ thị hàm số.
Do các giới hạn
1
lim
x
y
,
1
lim
x
y
,
1
lim
x
y
,
1
lim
x
y
không tồn tại nên đồ thị hàm số không có
đường tiệm cận đứng.
Câu 9. [2D1-3] Hỏi có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
2
2
3 2
5
x x
y
x mx m
không có đường tiệm cận đứng?
A.
9
. B.
10
. C.
11
. D.
8
.
Lời giải
Chọn B.
Xét các trường hợp sau:
TH1: Phương trình
2
5 0
x mx m
vô nghiệm
2
4 20 0
m m
.
Giải ra ta được
2 2 6 2 2 6
m . Do
m
nguyên nên
6; 5;...; 2
m .
TH2: Phương trình
2
5 0
x mx m
có
1
nghiệm trùng với nghiệm của tử số (không xảy ra).
TH3: Phương trình
2
5 0
x mx m
có
2
nghiệm trùng với hai nghiệm
1
và
2
của tử số.
Điều này tương đương với
2
4 20 0
1 5 0
4 2 5 0
m m
m m
m m
2 2 6 2 2 6
3
m m
m
3
m
.
Vậy có
10
giá trị nguyên của
m
thỏa yêu cầu bài toán.
Câu 10. [2D1-2] Phương trình tiếp tuyến của đồ thị hàm số
3 2
3 1
y x x
tại điểm
3;1
A là
A.
9 26
y x
. B.
9 26
y x
. C.
9 3
y x
. D.
9 2
y x
.
Lời giải
Chọn B.
Ta có
2
3 6 3 9
y x x y
.
Phương trình tiếp tuyến cần tìm
9 3 1 9 26
y x y x
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/26
Câu 11. [1D5-2] Với
0;
2
x
, hàm số
2 sin 2 cos
y x x
có đạo hàm là
A.
1 1
sin cos
y
x x
. B.
1 1
sin cos
y
x x
.
C.
cos sin
sin cos
x x
y
x x
. D.
cos sin
sin cos
x x
y
x x
.
Lời giải
Chọn D.
2 sin 2 cos
cos sin
2 sin 2 cos sin cos
x x
x x
y
x x x x
.
Câu 12. [2D2-2] Cho hàm số
2
2017 3
x x
y e e
. Mệnh đề nào dưới đây đúng?
A.
3 2 2017
y y y
B.
3 2 3
y y y
.
C.
3 2 0
y y y
. D.
3 2 2
y y y
.
Lời giải
Chọn C.
2
2017 6
x x
y e e
2
2017 12
x x
y e e
Ta có:
3 2
y y y
2 2 2
2017 12 3 2017 6 2 2017 3
x x x x x x
e e e e e e
0
.
Câu 13. [2D1-2] Đồ thị hình bên là đồ thị của một trong
4
hàm số dưới đây. Hỏi đó là hàm số nào?
x
y
1
2
1
3
1
1
O
A.
3 2
3 3 1
y x x x
. B.
3
1
3 1
3
y x x
.
C.
3 2
3 3 1
y x x x
. D.
3
3 1
y x x
.
Lời giải
Chọn D.
+Đồ thị cắt trục
Oy
tại điểm
0; 1
nên loại đáp án C
+ Xét hàm
3
1
3 1
3
y x x
có
2
3 0
y x
. Hàm số luôn đồng biến nên loại B.
+ Xét hàm
3
3 1
y x x
có
2
3 3
y x x
,
1
0
1
x
y
x
(thỏa mãn)
Câu 14. [2D1-4] Cho hàm số
1
1
x
y
x
có đồ thị
C
. Gọi
A
,
B
0
A B
x x
là hai điểm trên
C
có
tiếp tuyến tại
A
,
B
song song nhau và
2 5
AB . Tính
A B
x x
.
A.
2
A B
x x
. B.
4
A B
x x
. C.
2 2
A B
x x D.
2
A B
x x

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/26
Lời giải
Chọn A.
+ Gọi
;
A A
A x y
,
;
B B
B x y
Theo giả thiết
A B
y x y x
2 2
2 2
2 2
1 1
1 1
A B
A B
x x
x x
Suy ra
1 1 2
A B A B
x x x x
1
+
2
2
2 2
1 1
1 1
B A
B A
AB x x
x x
2
2
2
1 1
A B
B A
B A
x x
x x
x x
2
2
2
4
20 1 20
. 1
B A
A B A B
AB x x
x x x x
2
4
1 20
. 1
A B
A B
x x
x x
có 2
B A
x x
2
2
4
4 . . 1 20
. 1
A B A B
A B
x x x x
x x
+ Đặt:
2
.
A B
A B
x x
x x a
Phương trình
tương đương với
2
4
4 4 1 20
1
a
a
16
4 1 20
1
a
a
.
Đặt
1
a m
2
16
4 20 4 20 16 0
m m m
m
4
1
m
m
+
. 3
4 1 4 3
2
A B
A B
x x
m a a
x x
A
x
,
B
x
là nghiệm của phương trình
2
2 3 0
X X
Suy ra
, 3; 1
A B
x x
(không thỏa mãn ĐK) hoặc
, 1;3
A B
x x (không thỏa mãn ĐK)
+
. 0
1 1 1 0
2
A B
A B
x x
m a a
x x
A
x
,
B
x
là nghiệm của phương trình
2
2 0
X X
Suy ra
, 0;2
A B
x x
2 0
A B
x x ktm
, 2;0
A B
x x
2 0
A B
x x tm
.
Câu 15. [2D2-2] Giá trị nhỏ nhất của hàm số
ln
x
y
x
trên đoạn
1;
e
là
A.
0.
B.
1.
C.
1
.
e
D.
.
e
Lời giải
Chọn A.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/26
2 2
1
. ln
1 ln
x x
x
x
y
x x
,
0 1 ln 0 1;
y x x e e
1 0
y
,
1
y e
e
1;
min 0
e
y
Câu 16. [2D1-3] Trong các hình chữ nhật có chu vi bằng
16
, hình chữ nhật có diện tích lớn nhất bằng
A.
64
. B.
4
. C.
16
. D.
8
.
Lời giải
Chọn C.
Gọi
x
0 8
x
là một cạnh của hình chữ nhật, suy ra cạnh còn lại:
8
x
.
Diện tích của hình chữ nhật:
2
8
8 16
2
x x
S x x S
.
Do đó
max
16 8
S x x
4
x
.
Câu 17. [2D1-4] Cho hàm số
1
1
x
y
x
có đồ thị
C
. Gọi
;
M M
M x y
là một điểm trên
C
sao cho
tổng khoảng cách từ điểm
M
đến hai trục tọa độ là nhỏ nhất. Tổng
M M
x y
bằng
A.
2 2 1
. B.
1
. C.
2 2
. D.
2 2 2
.
Lời giải
Chọn D.
Tập xác định:
\ 1
D
.
Đặt:
1
; ;
1
x
d M d M Ox d M Oy x
x
.
Nhận xét: với
0;1
M thì ta có:
1
d M
. Do đó để tìm giá trị nhỏ nhất của
d M
ta chỉ cần
xét khi
1
x
1 1
x
.
Nếu
0 1
x
thì
1
1
x
d M g x x
x
.
Ta có:
2
2
1 0; 0;1
1
g x x
x
g x
nghịch biến trên
0;1
do đó
0;1
min 0 1
g x g
.
Nếu
1 0
x
thì
1
1
x
d M g x x
x
.
Ta có:
2
2
1
1
g x
x
1 2 1; 0
0
1 2 1; 0
x
g x
x
.
Ta có:
0 1
g
;
1 1
g
;
1 2 2 2 2
g
0;1
min 1 2 2 2 2
g x g
.
Do đó
;
M M
M x y
thỏa đề bài là:
1 2;1 2
M
suy ra:
2 2 2
M M
x y .

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/26
Câu 18. [2D1-1] Tìm số giao điểm của đồ thị
3 2
: 3 2 2017
C y x x x và đường thẳng
2017
y
.
A.
3
. B.
0
. C.
1
. D.
2
.
Lời giải
Chọn A.
Phương trình hoành độ giao điểm:
3 2
3 2 2017 2017
x x x
3 2
3 2 0
x x x
0
1
2
x
x
x
.
Do đó giữa đường thẳng và
C
có
3
điểm chung.
Câu 19. [2D1-3] Cho hàm số
3 2
2 8
y mx x x m
có đồ thị
m
C
. Tìm tất cả giá trị của tham số
m
để đồ thị
m
C
cắt trục hoành tại ba điểm phân biệt.
A.
1 1
;
6 2
m
. B.
1 1
;
6 2
m
. C.
1 1
; \ 0
6 2
m
. D.
1
; \ 0
2
m
.
Lời giải
Chọn C.
Phương trình hoành độ giao điểm:
3 2
2 8 0
mx x x m
2
2
2 1 4 0
x
g x mx m x m
Do đó
m
C
cắt trục hoành tại ba điểm phân biệt
0
g x
có hai nghiệm phân biệt khác
2
2
2
0
2 1 16 0
2 12 2 0
m
m m
g m
2
0
12 4 1 0
1
6
m
m m
m
0
1 1
6 2
1
6
m
m
m
0
1 1
6 2
m
m
.
Câu 20. [2D1-4] Tìm tất cả giá trị của tham số
m
để đồ thị hàm số
4 2
1 2 2 3 6 5
y m x m x m
cắt trục hoành tại bốn điểm phân biệt có hoành độ
1
x
,
2
x
,
3
x
,
4
x
thỏa
1 2 3 4
1
x x x x
.
A.
5
1;
6
m
. B.
3; 1
m
. C.
3;1
m . D.
4; 1
m
.
Lời giải
Chọn D.
Phương trình hoành độ giao điểm:
4 2
1 2 2 3 6 5 0 1
m x m x m .
Đặt
2
t x
;
0
t
phương trình trở thành:
2
1 2 2 3 6 5 0 2
m t m t m .
Phương trình
1
có bốn nghiệm thỏa
1 2 3 4
1
x x x x
khi và chỉ khi phương trình
2
có
hai nghiệm
1
t
,
2
t
thỏa
1 2
0 1
t t
1 2
1 2
0
1 1 0
t t
t t
1 2
1 2 1 2
0
1 0
t t
t t t t
.
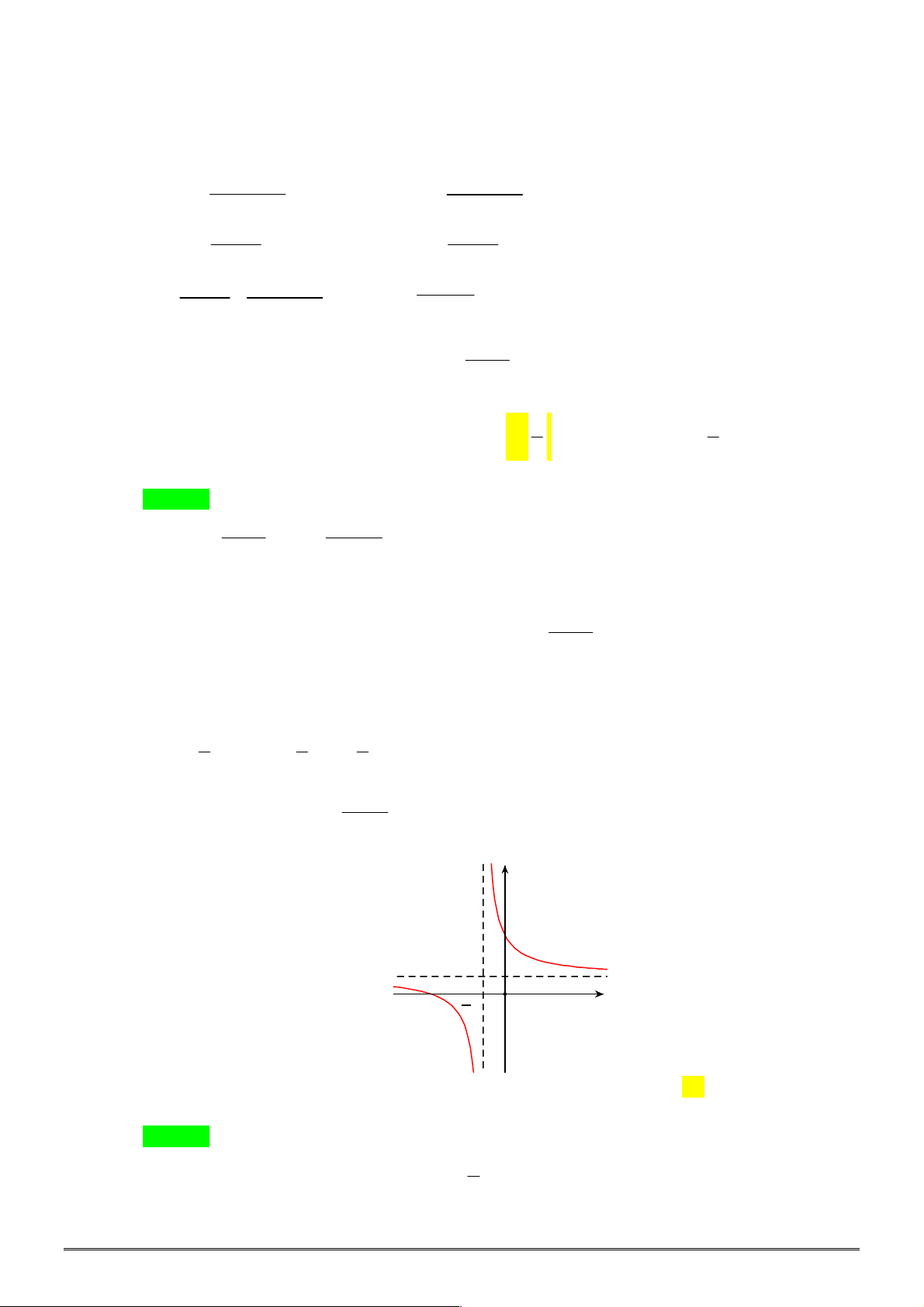
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/26
2
1 0
2 23 4 0
2 2 3
0
1
6 5
0
1
2 2 3
6 5
1 0
1 1
m
m m
m
S
m
m
P
m
m
m
m m
2
1 0
2 23 4 0
2 2 3
0
1
6 5
0
1
3 12
0
1
m
m m
m
S
m
m
P
m
m
m
4 1
m
.
Câu 21. [1D4-2] Tiếp tuyến với đồ thị hàm số
2 1
1
x
y
x
tại điểm có hoành độ bằng
0
cắt hai trục tọa
độ lần lượt tại
A
và
.
B
Diện tích tam giác
OAB
bằng
A.
2
. B.
3
. C.
1
2
. D.
1
4
.
Lời giải
Chọn C.
Ta có
2
2 1 1
1
1
x
y y
x
x
.
Với
0
0
x
, ta có
0 1
y
và
0 1
y
.
Vậy phương trình tiếp tuyến
d
của đồ thị hàm số
2 1
1
x
y
x
tại điểm
0;1
là
1. 0 1 1
y x y x
.
d
cắt
Ox
tại điểm
1;0
A ,
d
cắt
Oy
tại điểm
0;1
B .
1 1 1
1 1
2 2 2
AOB
S OA OB
.
Câu 22. [2D1-2] Cho hàm số
1
ax b
y
x
có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các
khẳng định sau?
x
y
1
O
A.
0
a b
. B.
0
b a
. C.
0
b a
. D.
0
a b
.
Lời giải
Chọn D.
Đồ thị hàm số cắt trục hoành tại điểm
;0
b
A
a
.
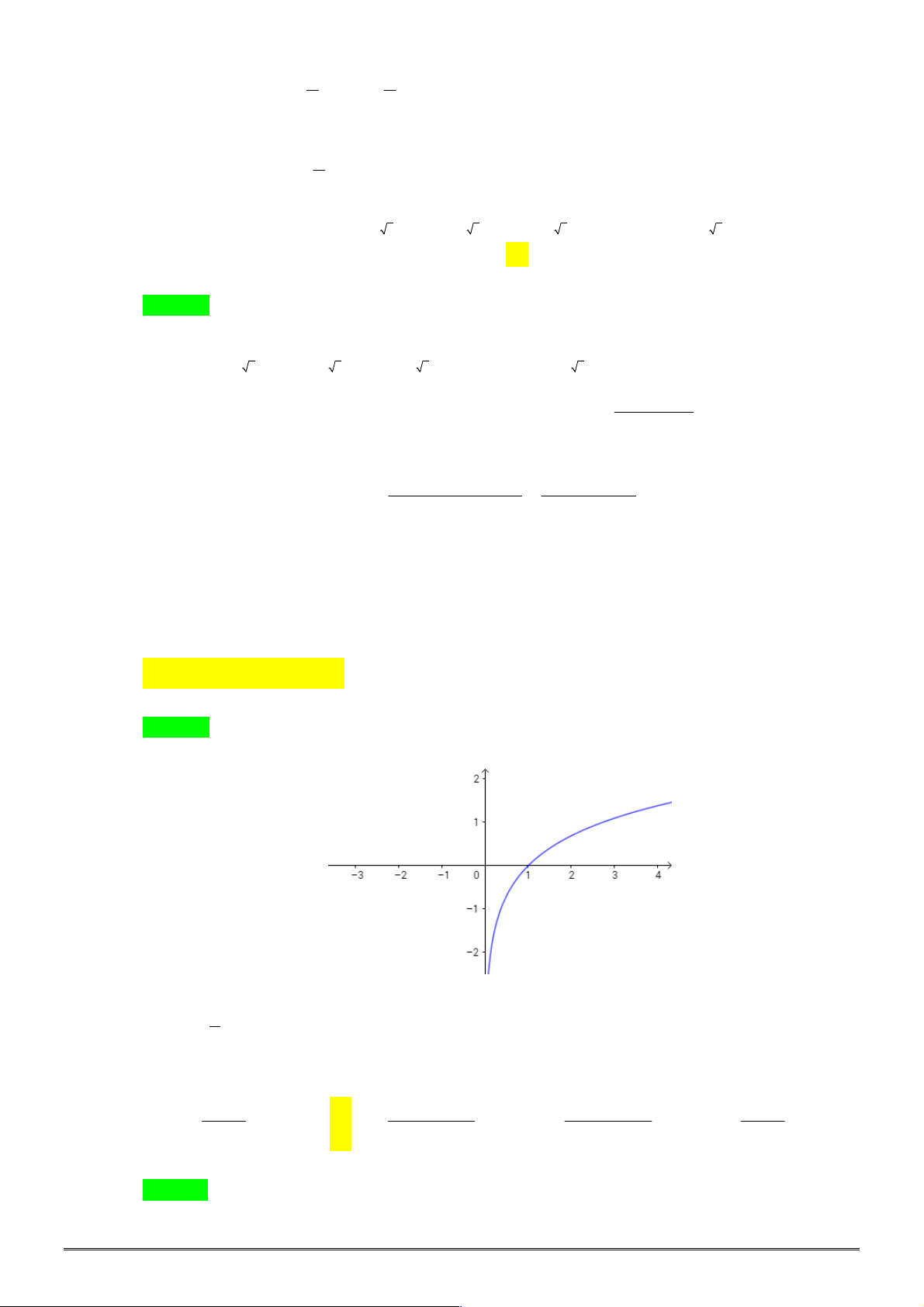
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/26
Theo hình vẽ, ta có
1 1 . 0
b b
a b
a a
. Vậy loại phương án B.
Đồ thị hàm số có đường tiệm cận ngang
y a
. Theo hình vẽ, ta có
0
a
.
Kết hợp với điều kiện
1
b
a
, ta suy ra
0
b a
.
Câu 23. [2D2-3] Tìm tổng
3 20174
2 2 2 2
2 2 2 2
1 2 log 2 3 log 2 4 log 2 ... 2017 log 2
S .
A.
2 2
1008 .2017
S . B.
2 2
1007 .2017
S . C.
2 2
1009 .2017
S . D.
2 2
1010 .2017
S .
Lời giải
Chọn C.
Ta có
3 20174
2 2 2 2 3 3 3 3
2 2 2 2
1 2 log 2 3 log 2 4 log 2 ... 2017 log 2 1 2 3 4 ... 2017
S .
Bằng quy nạp, ta chứng minh được rằng:
2
2
3 3 3 3
. 1
1 2 3 ...
4
n n
n
với mọi
*
n
.
Áp dụng với
2017
n
, ta có
2
2
2 2
3 3 3 3 2 2
2017 . 2017 1
2017 .2018
1 2 3 4 ... 2017 1009 .2017
4 4
S
.
Câu 24. [2D2-2] Cho hàm số
ln
y x
. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng
0;
.
B. Hàm số có tập giá trị là
;
.
C. Đồ thị hàm số nhận trục
Oy
làm tiệm cận đứng.
D. Hàm số có tập giá trị là
0;
.
Lời giải
Chọn D.
Đồ thị hàm số
ln
y x
có dạng
Qua đồ thị ta thấy, các khẳng định A, B, C đúng.
Ta có
1
1
ln ln 1 0
e
e
nên khẳng định D sai.
Câu 25. [2D2-1] Tính đạo hàm của hàm số
2
log 2 1
y x
.
A.
2
2 1
y
x
. B.
2
2 1 ln2
y
x
. C.
1
2 1 ln2
y
x
. D.
1
2 1
y
x
.
Lời giải
Chọn B.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/26
Ta có
2
2 1
2
log 2 1
2 1 .ln 2 2 1 .ln2
x
y x y
x x
.
Câu 26. [2D2-1] Tìm tập xác định
D
của hàm số
1 3
2y x
.
A.
;D
. B.
;2
D . C.
;2
D . D.
2;D
.
Lời giải
Chọn C.
Hàm số
1 3
2y x
là hàm số luỹ thừa, có số mũ
1 3
nên có tập xác định là
;2
D .
Câu 27. [2D2-2] Cho
0, 1
a a
và
,
x y
là hai số thực khác
0
. Khẳng định nào sau đây là khẳng định
đúng?
A.
2
log 2log
a a
x x
. B.
log log log
a a a
xy x y
.
C.
log log log
a a a
x y x y
. D.
log log log
a a a
xy x y
.
Lời giải
Chọn D.
Câu hỏi lý thuyết.
Câu 28. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
3
2
7 14 2
3
mx
y mx x m
nghịch biến trên nửa khoảng
1;
.
A.
14
;
15
. B.
14
;
15
. C.
14
2;
15
. D.
14
;
15
.
Lời giải
Chọn B.
Tập xác định
D
.
2
14 14
y mx mx
.
Hàm số nghịch biến trên nửa khoảng
1;
0
y
với
1;x
.
2
14 14 0
mx mx
với
1;x
2
14 14
m x x
với
1;x
2
14
14
m
x x
với
1;x
.
Xét hàm số
2
14
14
f x
x x
với
1;x
Ta có
2
2
28 7
0
14
x
f x
x x
với
1;x
.
Hàm số đồng biến trên với
1;x
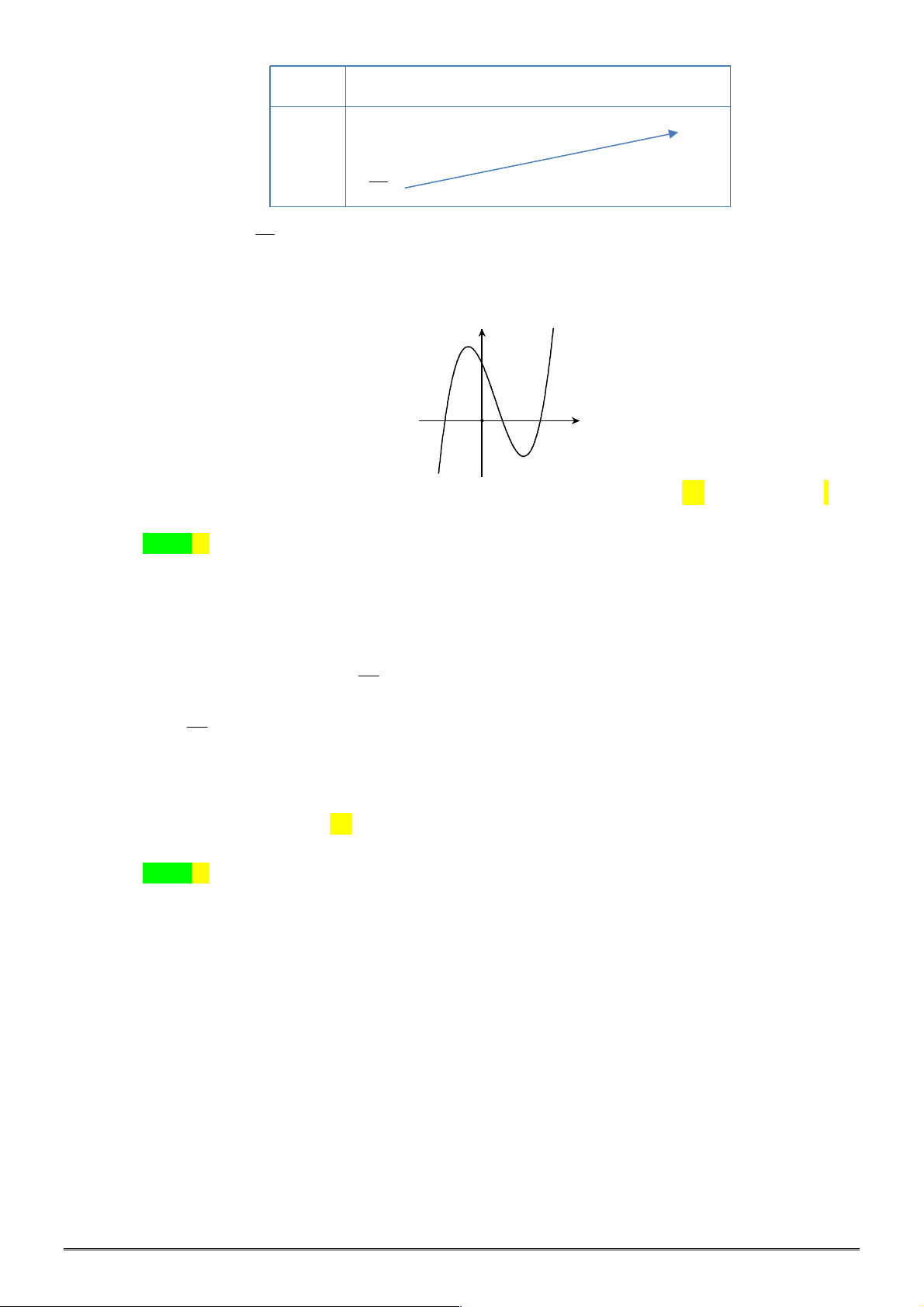
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/26
Vậy với
14
15
m
thì hàm số nghịch biến trên nửa khoảng
1;
.
Câu 29. [2D1-2] Cho đồ thị hàm số
3 2
y ax bx cx d
có đồ thị như hình bên. Khẳng định nào sau
đây là khẳng định đúng?
x
y
O
A.
, , 0; 0
a b c d
. B.
, , 0; 0
a b d c
. C.
, , 0; 0
a c d b
. D.
, 0; , 0
a d b c
.
Lời giải
Chọn D.
Ta thấy lim
x
y
0
a
loại đáp án A.
2
3 2
y ax bx c
Theo đồ thị thì hàm số có hai điểm cực trị trái dấu
0
ac
0
c
.
6 2 0
y ax b
3
b
x
a
. Đồ thị có điểm uốn có hoành độ dương suy ra
0
3
b
x
a
0
b
.
Do đó đáp án đúng là D.
Câu 30. [2H1-2] Số mặt phẳng đối xứng của khối lăng trụ tam giác đều là
A.
3
. B.
4
. C.
6
. D.
9
.
Lời giải
Chọn B.
xx
f x
1
14
15
0
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/26
Ta có các mặt phẳng đối xứng của khối lăng trụ tam giác đều là các mặt phẳng trung trực của
các đoạn thẳng
AB
,
BC
,
CA
,
AA
.
Câu 31. [2H1-1] Hỏi khối đa diện đều loại
4;3
có bao nhiêu mặt?
A.
4
. B.
20
. C.
6
. D.
12
.
Lời giải
Chọn C.
Khối đa diện đều loại
4;3
chính là khối lập phương nên có
6
mặt.
Câu 32. [2H1-3] Cho hình lập phương
.
ABCD A B C D
có cạnh bằng
2 2
a
. Gọi
S
là tổng diện tích
tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương
.
ABCD A B C D
. Tính
.
S
A.
2
4 3
S a . B.
2
8
S a
. C.
2
16 3
S a . D.
2
8 3
S a .
Lời giải
Chọn D.
N
I
M
F
E
J
B'
C'
D'
B
D
C
A
A'
Gọi
, , , , ,
E F I J M N
lần lượt là tâm của sáu mặt của hình lập phương (như hình vẽ), khi đó
, , , , ,
E F I J M N
là các đỉnh của một bát diện đều.
A
B
C
A
B
C

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/26
N
I
M
F
E
J
B'
D'
C
A
Thật vậy, xét tứ diện đều
ACB D
khi đó
, , , , ,
E F I J M N
là trung điểm của các cạnh của tứ
diện nên mỗi mặt của bát diện là những tam giác đều bằng nhau có cạnh bằng
2
AC
Mà
AC
là đường chéo hình vuông cạnh bằng
2 2
a
suy ra
4
AC a
.
Suy ra diện tích một mặt
2
2
2 3
3
4
IEF
a
S a
.
Vậy tổng
2
8 3
S a .
Câu 33. [1D1-1] Khẳng định nào sau đây là khẳng định sai?
A.
cos 0 2
2
x x k
. B.
cos 1 2
x x k
.
C.
cos 1 2
x x k
. D. cos 0
2
x x k
.
Lời giải
Chọn A.
Ta có cos 0
2
x x k
.
Câu 34. [1D1-2] Giải phương trình
cos2 5sin 4 0
x x
.
A.
2
x k
. B.
2
x k
. C.
2
x k
. D.
2
2
x k
.
Lời giải
Chọn D.
Ta có
2
cos2 5sin 4 0 1 2sin 5sin 4 0
x x x x
.
2
sin 1
2sin 5sin 3 0
3
sin
2
x n
x x
x l
sin 1
3
sin
2
x
x VN
sin 1 2 ,
2
x x k k
.
Câu 35. [1D1-3] Gọi
S
là tổng các nghiệm của phương trình
sin
0
cos 1
x
x
trên đoạn
0;2017
. Tính
S
.
A.
2035153
S
. B.
1001000
S
. C.
1017072
S
. D.
200200
S
.
Lời giải
Chọn C.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/26
Ta có
2
sin 0
cos 1
sin
0
cos 1cos 1
cos 1
x
x
x
xx
x
cos 1 2
x x k
,
k
.
Vì
0;2017 0 2017
x x
suy ra
2017
0 2 2017 0 1008,5
2
k k
.
Vậy
0; 1; 2; ...; 1008
k , do đó ta được
1009
nghiệm là:
0 1 2 1007 1008
0, 1.2 , 2.2 , ..., 1007.2 , 1008.2
x x x x x
.
Tổng của các nghiệm là;
0 1.2 2.2 ... 1007.2 1008.2
S
1008.1009
2 1 2 ... 1008 2 1017072
2
.
Câu 36. [1D2-2] Có bao nhiêu số tự nhiên có
3
chữ số đôi một khác nhau?
A.
648
. B.
1000
. C.
729
. D.
720
.
Lời giải
Chọn A.
Số tự nhiên gồm ba chữ số đôi một khác nhau là:
3 2
10 9
648
A A số.
Câu 37. [1D2-2] Một hộp có
5
bi đen,
4
bi trắng. Chọn ngẫu nhiên
2
bi. Xác suất
2
bi được chọn có
cùng màu là
A.
1
4
. B.
1
9
. C.
4
9
. D.
5
9
.
Lời giải
Chọn C.
Chọn
2
bi bất kỳ từ
9
bi ta có:
2
9
36
n C
Gọi
A
là biến cố hai bi được chọn cùng màu ta có:
2 2
4 5
16
n A C C
.
Vậy xác suất của biến cố
A
là:
4
9
n A
P A
n
.
Câu 38. [1D2-2] Trong khai triển đa thức
6
2
P x x
x
(
0
x
), hệ số của
3
x
là
A.
60
. B.
80
. C.
160
. D.
240
.
Lời giải
Chọn A.
Số hạng tổng quát trong khai triển trên là:
6
6
2
.
k
k k
T C x
x
--
3
6
2
6
2
k
k k
C x
Để có số hạng chứa
3
x
khi
3
6 3
2
k
2
k
.
Vậy hệ số của
3
x
trong khai triển trên là:
2 2
6
2 . 60
C
.
Câu 39. [1H3-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
;
SA ABC
và
3
SA a
. Tính góc giữa đường thẳng
SB
với mặt phẳng
ABC
.
A.
75
. B.
60
. C.
45
. D.
30
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/26
Lời giải
Chọn B.
Vì
SA ABC
nên hình chiếu của đường thẳng
SB
trên mặt phẳng
ABC
là
AB
. Khi đó
góc giữa đường thẳng
SB
với mặt phẳng
ABC
là
SBA
.
Trong tam giác vuông
SBA
có
3
tan 3
SA a
SBA
AB a
60
SBA
.
Vậy góc giữa đường thẳng
SB
với mặt phẳng
ABC
là
60
.
Câu 40. [1H3-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
;
SA ABCD
và
2
SA a
. Tính khoảng cách
d
từ điểm
B
đến mặt phẳng
SCD
.
A.
5
5
a
d . B.
d a
. C.
4 5
5
a
d . D.
2 5
5
a
d .
Lời giải
Chọn D.
Gọi
H
là hình chiếu của
A
trên
SD
ta có:
CD AD
CD SAD
CD SA
mà
AH SAD AH CD
.
AH CD
AH SCD
AH SD
,
AH d A SCD
Vì //
AB CD
, ,
d B SCD d A SCD
2 2
. 2 2 5
5
5
SA AD a a
AH
SA AD
.
S
C
A
B
S
A
C
B
D
H
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/26
Câu 41. [2H1-2] Cho hình hộp
.
ABCD A B C D
có đáy là hình thoi cạnh
a
,
60
ABC
và thể tích
bằng
3
3
a
. Tính chiều cao
h
của hình hộp đã cho.
A.
2
h a
. B.
h a
. C.
3
h a
. D.
4
h a
.
Lời giải
Chọn A.
Do đáy là hình thoi cạnh
a
,
60
ABC
nên diện tích đáy là:
2 2
3 3
2
4 2
a a
B .
Thể tích của hình hộp là
3
2
3
. 2
3
2
V a
V B h h a
B
a
.
Câu 42. [2H1-2] Diện tích ba mặt của hình hộp chữ nhật lần lượt bằng
3
20 cm
,
3
28 cm
,
3
35 cm
. Thể
tích của hình hộp đó bằng
A.
3
165 cm
. B.
3
190 cm
. C.
3
140 cm
. D.
3
160 cm
.
Lời giải
Chọn C.
Gọi
a
,
b
,
c
là ba kích thước của hình hộp chữ nhật, theo giả thiết ta có
20
ab
,
28
bc
,
35
ca
.
Mà
3
. . 20.28.35 140cm
V abc ab bc ca .
Câu 43. [2H1-3] Cho hình chóp tứ giác
.
S ABCD
có đáy là hình vuông, mặt bên
SAB
là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm B đến mặt phẳng
SCD
bằng
3 7
7
a
. Tính thể tích V của khối chóp
.
S ABCD
.
A.
3
1
3
V a
. B.
3
V a
. C.
3
2
3
V a
. D.
3
3
2
V a
.
Lời giải
Chọn D.
Vì
SAB
đều, gọi
H
là trung điểm
AB
, từ giả thiết
SH ABCD
.
Vì
3 7
; ;
7
a
d B SCD d H SCD .
Gọi
M
là trung điểm của
CD
, theo hình vẽ ta có
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/26
3 7
,
7
a
d H SCD HK .
Gọi
x
là độ dài cạnh đáy. Khi đó, do
SAB
đều cạnh
x
nên
3
2
x
SH ,
HM x
2 2 2 2 2 2
1 1 1 7 4 1
3
9 3
x a
HK SH HM a x x
.
Vậy
2
3
ABCD
S a
;
3
.
3 1 3
.
2 3 2
S ABCD ABCD
a a
SH V SH S .
Câu 44. [1H3-4] Cho hình chóp
.
S ABC
có
SA
vuông góc với đáy,
2
SA BC
và
120
BAC
. Hình
chiếu của
A
trên các đoạn
SB
,
SC
lần lượt là
M
,
N
. Tính góc giữa hai mặt phẳng
ABC
và
AMN
.
A.
45
. B.
. C.
15
. D.
.
Lời giải
Chọn D.
Gọi
O
là tâm đường tròn ngoại tiếp
,
ABC D
là điểm đối xứng của
A
qua
.
O
Ta có
AB BD
BD SAB BD AM
SA BD
, mà
AM SB
nên
AM SBD
AM SD
.
Tương tự
AN SD
.
Vậy
,
SD AMN
mà
SA ABC
nên
; ;
AMN ABC SA SD ASD
vì
SAD
vuông tại
.
A
Ta có
tan ,
AD
ASD
SA
mà
AD
là đường kính của đường tròn ngoại tiếp
ABC
nên
2
sin120
3 3
BC BC SA
AD
.
Vậy
1
tan 30
3
ASD ASD
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 23/26
Câu 45. [1H3-4] Cho hình lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
, tam giác
A BC
đều và nằm trong mặt phẳng vuông góc với mặt phẳng
ABC
,
M
là trung điểm cạnh
CC
.
Tính
cosin
góc
giữa hai đường thẳng
AA
và
BM
.
A.
2 22
cos
11
. B.
11
cos
11
. C.
33
cos
11
. D.
22
cos
11
.
Lời giải
Chọn C.
Gọi
H
là trung điểm
BC A H ABC
.
Ta có
3
2
a
A H AH
nên
6
2
a
AA
.
Do
/ /
AA CC
nên
; ;
AA BM CC BM
.
Ta tính góc
BMC
.
Vì
M
là trung điểm
CC
nên
1 1 6
2 2 4
a
CM CC AA
.
Gọi
N
là giao điểm của
A M
với
AC
. Do
/ /
CM AA
,
1
2
CM AA
nên
CM
là đường trung
bình của
AA N C
là trung điểm
AN
.
Ta có
A C AC CN
nên
AA N
vuông tại
A
,
2
AN a
,
6
2
a
AA
10
2
a
A N
.
Tương tự,
ABN
vuông tại
B
,
AB a
,
2
AN a
3
BN a
.
Xét
A BN
có
A B a
,
3
BN a
,
10
2
a
A N
,
BM
là đường trung tuyến nên
2 2 2 2 2 2 2
2
3 5 11 22
2 4 2 8 8 4
BN A B A N a a a a a
BM BM
.
Xét
BMC
có
2 2
2
2 2 2
11 3
33
8 8
cos
2 . 11
22 6
2. .
4 4
a a
a
BM CM BC
BMC
BM CM
a a
.
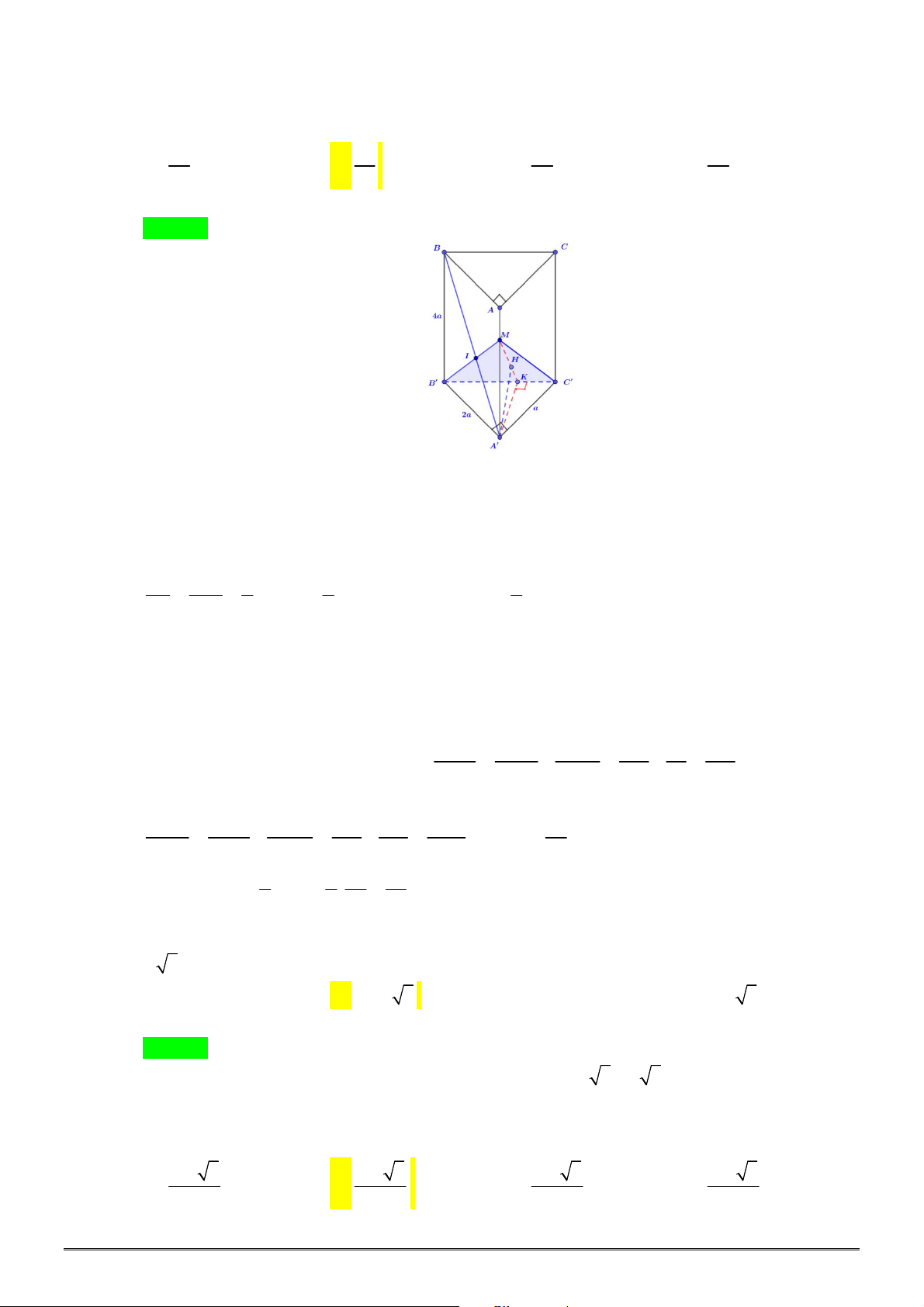
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 24/26
Câu 46. [2H1-4] Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
. Biết
2
AB a
,
AC a
,
4
AA a
. Gọi
M
là điểm thuộc cạnh
AA
sao cho
3
MA MA
. Tính
khoảng cách giữa hai đường thẳng chéo nhau
BC
và
C M
.
A.
6
7
a
. B.
8
7
a
. C.
4
3
a
. D.
4
7
a
.
Lời giải
Chọn B.
Gọi
I B M BA
, ta có:
//
//
BC B C MB C
BC MB C
BC MB C
, , ,
d BC C M d BC MB C d B MB C
.
Mà hai tam giác
IMA
và
IB B
đồng dạng, có:
3 3 4
, ,
4 4 3
IA MA
IA IB d B MB C d A MB C
IB BB
.
Dựng
A K B C
tại
K
,
A H MK
tại
H
, ta có:
,
B C A K
B C MA K A H B C
A H MB C d A MB C A H
B C MA
A H MK
.
Xét tam giác
A B C
vuông tại
A
có:
2 2 2 2 2 2
1 1 1 1 1 5
4 4
A K A B A C a a a
.
Xét tam giác
MA K
vuông tại
A
có:
2 2 2 2 2 2
1 1 1 5 1 49
4 9 36
A H A K A M a a a
6
7
a
A H
. Vậy,
4 4 6 8
, .
3 3 7 7
a a
d BC C M A H
.
Câu 47. [2H2-2] Tính diện tích xung quanh của hình trụ biết hình trụ có bán kính đáy
a
và đường cao
3
a
.
A.
2
2
a
. B.
2
2 3
a . C.
2
a
. D.
2
3
a .
Lời giải
Chọn B.
Diện tích xung quanh hình trụ:
2
2 2 2 . . 3 2 3
xq
S Rl Rh a a a
.
Câu 48. [2H2-2] Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài
2
a
. Thể tích
của khối nón là:
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3
2
a
. D.
3
3
12
a
.
Lời giải
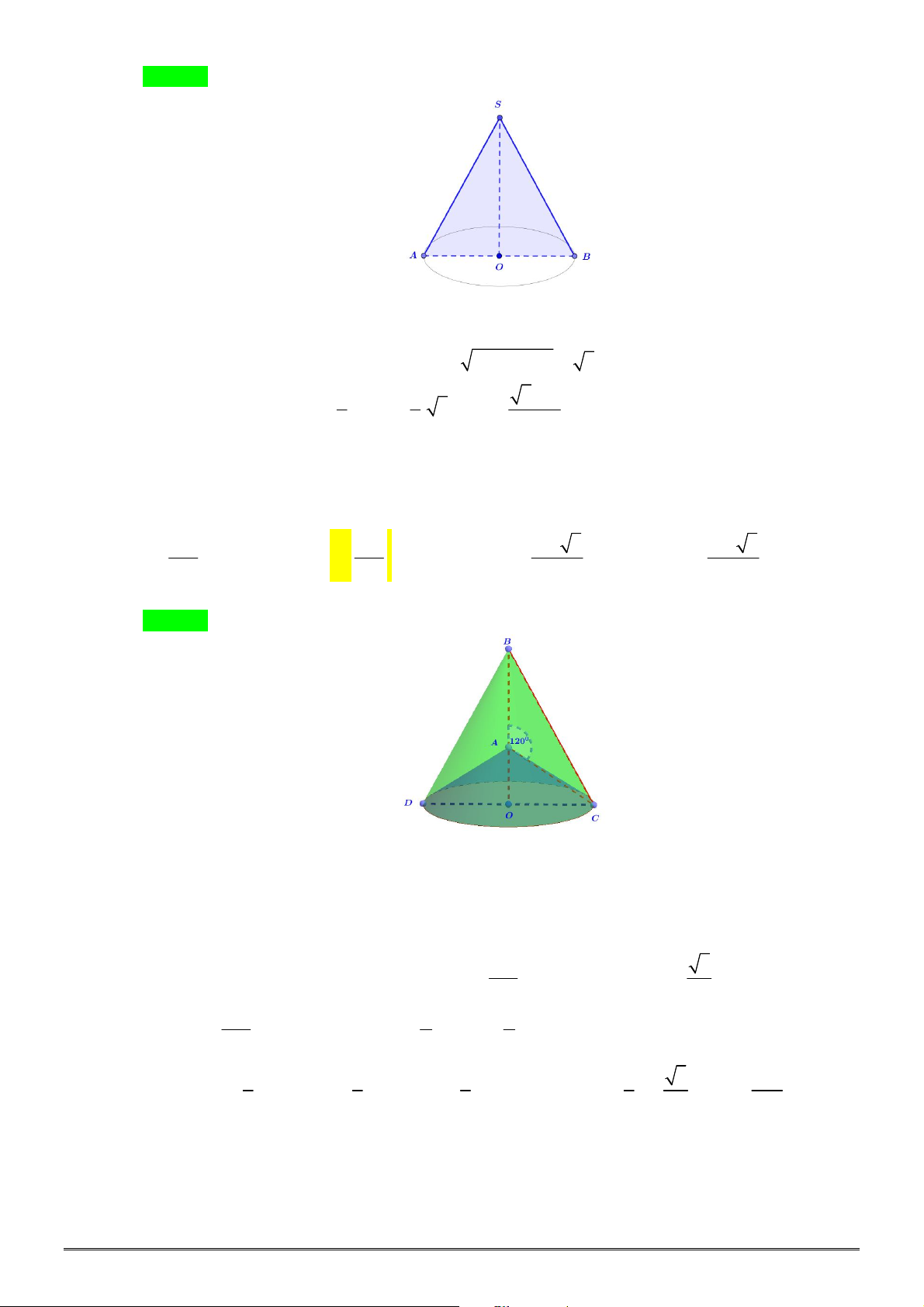
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 25/26
Chọn B.
Giả sử hình nón có đỉnh là
S
, tâm đáy là
O
, thiết diện qua trục là
SAB
.
Ta có:
SAB
đều cạnh
2
a R a
.
Tam giác
SOA
vuông tại
O
có:
2 2
3
h SO SA AO a
.
Thể tích khối nón là:
3
2 2
1 1 3
. 3 .
3 3 3
a
V h R a a
.
Câu 49. [2H2-4] Cho tam giác
ABC
có
120
A
,
AB AC a
. Quay tam giác
ABC
(bao gồm cả
điểm trong tam giác) quanh đường thẳng
AB
ta được một khối tròn xoay. Thể tích khối tròn
xoay đó bằng:
A.
3
3
a
. B.
3
4
a
. C.
3
3
2
a
. D.
3
3
4
a
.
Lời giải
Chọn B.
Quay tam giác
ABC
quanh đường thẳng
AB
ta được khối tròn xoay có thể tích bằng
1
V
thể
tích khối nón lớn có đỉnh
B
và thiết diện qua trục là
BDC
(hình vẽ) trừ đi
2
V
thể tích khối nón
nhỏ có đỉnh
A
và thiết diện qua trục là
ADC
.
Gọi
O
là tâm đường tròn ngoại tiếp đáy của hai khối nón.
Xét tam giác
AOC
vuông tại
O
có:
3
sin60 sin60
2
OC
OC AC a
AC
.
3
cos60 cos60
2 2
AO a
OA AC BO a
AC
.
2
3
2 2 2
1 2
1 1 1 1 3
.. . . .
3 3 3 3 2 4
a
V V V BO OC AO OC OC BO AO a a
.
Câu 50. [2H2-4] Trong các khối trụ có cùng diện tích toàn phần bằng
, gọi
là khối trụ có thể tích
lớn nhất, chiều cao của
bằng:
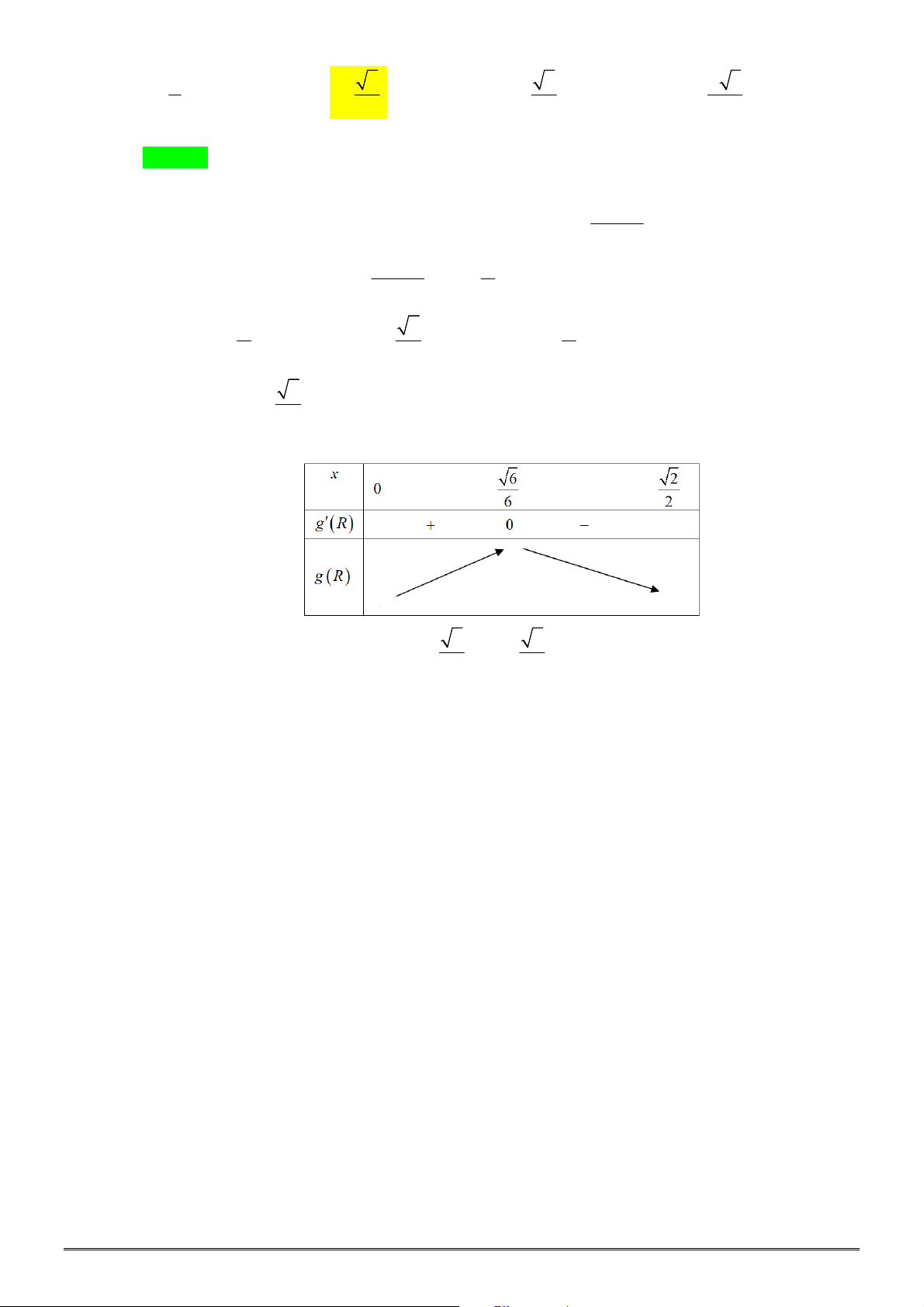
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 26/26
A.
3
. B.
6
3
. C.
6
6
. D.
3
4
.
Lời giải
Chọn B.
Gọi
R
,
h
lần lượt là bán kính đáy và chiều cao khối trụ.
Diện tích toàn phần hình trụ:
2
2
1 2
2 2
2
tp
R
S Rh R h
R
.
Thể tích khối trụ:
2
2 2 3
1 2
. 2
2 2
R
V h R R R R
R
.
Xét
3
2
2
g R R R
trên
2
0;
2
. Ta có:
2
1 6
2
g R R
.
6
0
6
g R R
.
Bản biến thiên:
Vậy, thể tích khối trụ lớn nhất khi
6 6
6 3
R h .

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/25
SỞ GD VÀ ĐT THÁI NGUYÊN
TRƯỜNG THPT CHUYÊN
(Đề thi gồm 06 trang)
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KỲ I
NĂM HỌC 2017-2018
MÔN: TOÁN 12
Thời gian làm bài 90 phút, không kể thời gian phát đề
Họ và tên thí sinh:...............................SBD:...........
Mã đề thi 295
Câu 1. [2D2-1] Cho
0 1
a
và
0
x
,
0
y
. Chọn mệnh đề đúng trong các mệnh đề sau:
A.
log log .log
a a a
x y x y
. B.
log log log
a a a
xy x y
.
C.
log log .log
a a a
xy x y
. D.
log log log
a a a
x y x y
.
Câu 2. [2D1-3] Có tất cả bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2017;2017
để
hàm số
3 2
6 1
y x x mx
đồng biến trên khoảng
0;
?
A.
2030
. B.
2005
. C.
2018
. D.
2006
.
Câu 3. [2H1-3] Cho lăng trụ đứng
.
ABC A B C
có
AB AC BB a
,
120
BAC
. Gọi
I
là trung
điểm của
CC
. Ta có cosin của góc giữa hai mặt phẳng
ABC
và
AB I
bằng
A.
3
2
. B.
30
10
. C.
3 5
12
. D.
2
2
.
Câu 4. [2H1-2] Gọi
1
V
là thể tích của khối lập phương
.
ABCD A B C D
,
2
V
là thể tích khối tứ diện
A ABD
. Hệ thức nào sau đây là đúng?
A.
1 2
4
V V
. B.
1 2
6
V V
. C.
1 2
2
V V
. D.
1 2
8
V V
.
Câu 5. [2D2-3] Cho
2 6 6
log 3 log 2 log 3 5
a b c
với
, ,
a b c
là các số tự nhiên. Khẳng định nào
đúng trong các khẳng định sau đây?
A.
a b
. B.
a b c
. C.
b c
. D.
b c
.
Gốc:
2 6 6
log 3 log 2 log 5 5
a b c
Câu 6. [2H1-2] Cho khối chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng
đáy và khoảng cách từ
A
đến mặt phẳng
SBC
bằng
2
2
a
. Gọi
M
là điểm thuộc cạnh
SD
sao cho
3
SM MD
. Mặt phẳng
ABM
cắt cạnh
SC
tại điểm
N
. Thể tích khối đa diện
MNABCD
bằng
A.
3
7
32
a
. B.
3
15
32
a
. C.
3
17
32
a
. D.
3
11
96
a
.
Câu 7. [2D1-3] Gọi
S
là tập hợp các giá trị thực của tham số
m
để hàm số
3 2 3
3 4
y x mx m
có hai
điểm cực trị
A
và
B
sao cho tam giác
OAB
có diện tích bằng
4
(
O
là gốc tọa độ). Ta có tổng
giá trị tất cả các phần tử của tập
S
bằng
A.
1
. B.
2
. C.
1
. D.
0
.
Câu 8. [2D2-1] Cho
2
log 5
a
. Tính
2
log 200
theo
a
.
A.
2 2
a
. B.
4 2
a
. C.
1 2
a
. D.
3 2
a
.
Câu 9. [2D1-2] Cho hàm số
4 2
1
2 2017
4
y x x . Khẳng định nào sau đây là đúng?
A. Hàm số có một điểm cực tiểu và không có điểm cực đại.
B. Hàm số có một điểm cực đại và không có điểm cực tiểu.
C. Hàm số có một điểm cực đại và hai điểm cực tiểu.
D. Hàm số có một điểm cực tiểu và hai điểm cực đại.
8

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/25
Câu 10. [2D2-2] Rút gọn biểu thức
2
4log 3
a
A a
với
0 1
a
ta được kết quả là
A.
9
. B.
4
3
. C.
8
3
. D.
6
.
Câu 11. [2H1-1] Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai khối chóp có hai đáy là hai đa giác bằng nhau thì thể tích bằng nhau.
B. Hai khối đa diện có thể tích bằng nhau thì bằng nhau.
C. Hai khối lăng trụ có chiều cao bằng nhau thì thể tích bằng nhau.
D. Hai khối đa diện bằng nhau có thể tích bằng nhau.
Câu 12. [2D1-2] Số điểm chung của đồ thị hàm số
3 2
2 12
y x x x
với trục
Ox
là
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 13. [2D1- 2] Cho hàm số
y f x
có đạo hàm liên tục trên
.
Đồ thị hàm số
y f x
như hình vẽ bên. Số điểm cực trị
của hàm số
2
y f x x
là
A.
2
. B.
1
.
C.
3
. D.
4
.
Câu 14. [2D1-2] Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 2
3 9 1
y x x x
trên đoạn
0;4
. Ta có
2
m M
bằng
A.
14
. B.
24
. C.
37
. D.
57
.
Câu 15. [2D1-1] Hàm số
3 2
1
2 3 1
3
y x x x
nghịch biến trên khoảng nào trong các khoảng sau đây?
A.
1;3
. B.
1;4
. C.
3; 1
. D.
1;3
.
Câu 16. [2H1-2] Cắt khối lăng trụ
.
MNP M N P
bởi các mặt phẳng
MN P
và
MNP
ta được những
khối đa diện nào?
A. Ba khối tứ diện. B. Hai khối tứ diện và hai khối chóp tứ giác.
C. Hai khối tứ diện và một khối chóp tứ giác. D. Một khối tứ diện và một khối chóp tứ giác.
Câu 17. [2H2-1] Thể tích của khối cầu bán kính
R
bằng
A.
3
1
3
R
. B.
3
2
3
R
. C.
3
R
. D.
3
4
3
R
.
Câu 18. [2D1-2] Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 2
1 2 3 1
y m x m x
có đúng một điểm cực tiểu và không có điểm cực đại?
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 19. [2D1-1] Trong số đồ thị của các hàm số
1
;
y
x
2
1;
y x
2
3 7
;
1
x x
y
x
2
1
x
y
x
có tất
cả bao nhiêu đồ thị có tiệm cận ngang?
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 20. [2H1-1] Cho khối chóp tứ giác đều có chiều cao bằng
6
và thể tích bằng
8
. Độ dài cạnh đáy bằng
A.
2
3
. B.
3
. C.
4.
D.
2
.
Câu 21. [2H1-2] Hình lăng trụ tam giác đều có tất cả bao nhiêu mặt phẳng đối xứng
A. 4 mặt phẳng. B. 1 mặt phẳng. C. 3 mặt phẳng. D. 2 mặt phẳng.
O
x
y
1
1
2
4
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/25
Câu 22. [2H2-3] Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật,
3
AB a
và
AD a
. Đường
thẳng
SA
vuông góc với mặt phẳng đáy và
SA a
. Thể tích khối cầu ngoại tiếp hình chóp
.
S BCD
bằng
A.
3
5 5
.
6
a
B.
3
5 5
.
24
a
C.
3
3 5
.
25
a
D.
3
3 5
.
8
a
Câu 23. [2D1-3] Gọi
0
m
là giá trị thực của tham số
m
để đồ thị hàm số
4 2
2 4
y x mx
có 3 điểm
cực trị nằm trên các trục tọa độ. Khẳng định nào sau đây là đúng?
A.
0
1;3
m B.
0
5; 3
m
. C.
0
3
;0
2
m
D.
0
3
3;
2
m
Câu 24. [2H2-1] Chọn mệnh đề đúng trong các mệnh đề sau?
A. Hình có đáy là hình bình hành thì có mặt cầu ngoại tiếp.
B. Hình chóp có đáy là hình thang vuông thì có mặt cầu ngoại tiếp.
C. Hình chóp có đáy là hình thang cân thì có mặt cầu ngoại tiếp.
D. Hình có đáy là hình tứ giác thì có mặt cầu ngoại tiếp.
Câu 25. [2D1-2] Hàm số
4 3
8 6
y x x
có tất cả bao nhiêu điểm cực trị?
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 26. [2D1-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
3
AB a
,
4
BC a
và
SA ABC
. Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
60
. Gọi
M
là trung
điểm của cạnh
AC
. Khoảng cách giữa hai đường thẳng
AB
và
SM
bằng
A.
10 3
79
a
. B.
5
2
a
. C.
5 3
a
. D.
5 3
79
a
.
Câu 27. [2H1-1] Vật thể nào trong các vật thể sau đây không phải là khối đa diện?
A. . B. . C. . D.
Câu 28. [2D1-1] Cho hàm số
2 3
4
x
y
x
. Hãy chọn khẳng định đúng trong các khẳng định sau đây:
A. Hàm số nghịch biến trên
.
B. Hàm số đồng biến trên mỗi khoảng xác định.
C. Hàm số đồng biến trên
.
D. Hàm số nghịch biến trên mỗi khoảng xác định.
Câu 29. [2D1-1] Giá trị lớn nhất của hàm số
3
3 5
y x x
trên đoạn
3
0;
2
.
A.
3
. B.
5
. C.
7
. D.
31
8
.
Câu 30. [2H1-2] Cho hình chóp
.
S ABC
có đáy là tam giác vuông tại
C
,
5
AB a
,
AC a
. Cạnh
bên
3
SA a
và vuông góc vói mặt phẳng
ABC
. Thể tích khối chóp
.
S ABC
bằng
A.
3
a
. B.
3
5
3
a
. C.
3
2
a
. D.
3
3
a
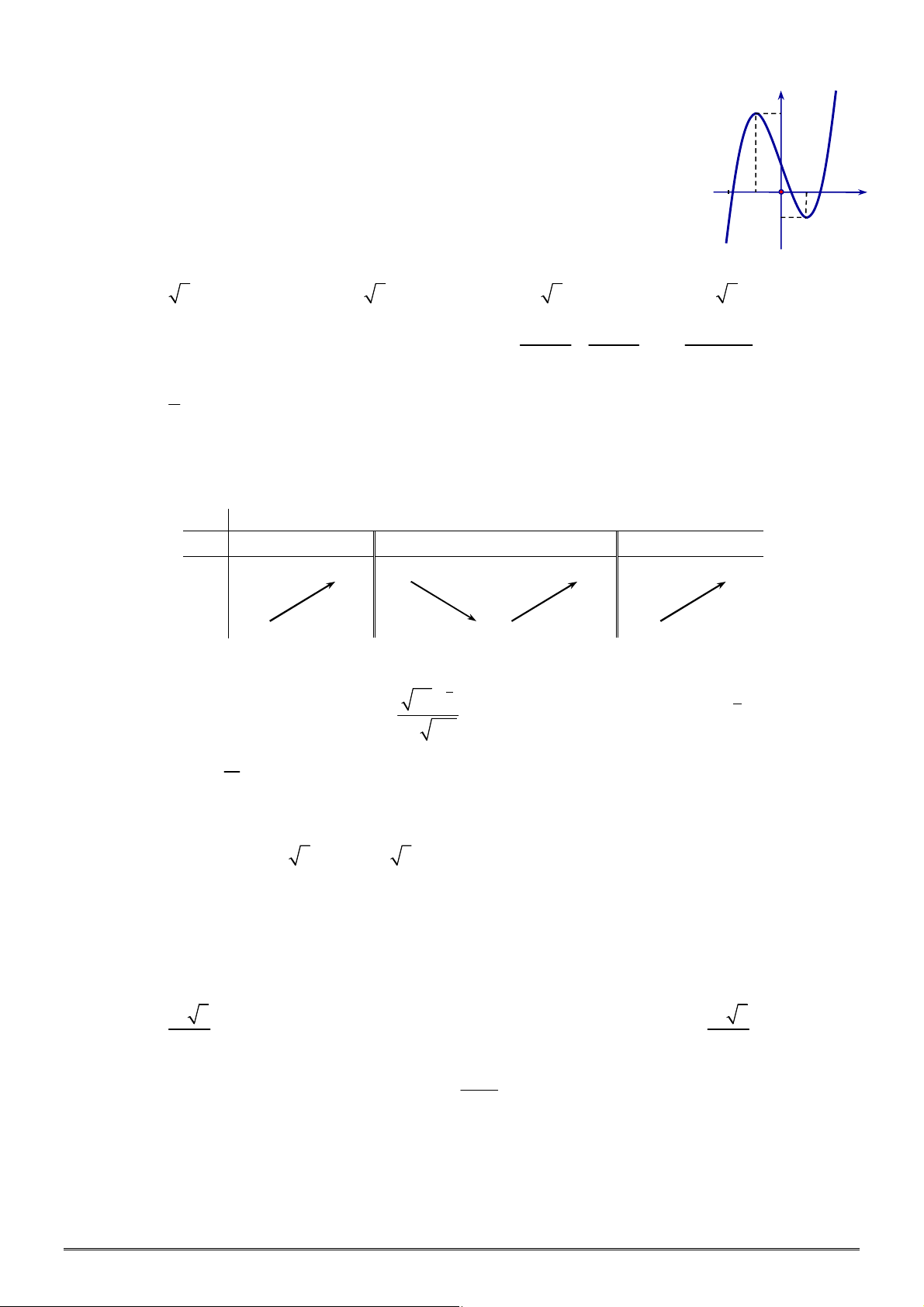
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/25
Câu 31. [2D1-2] Cho biết đồ thị sau là đồ thị của một trong bốn hàm số ở các phương án A, B, C, D. Đó
là đồ thị của hàm số nào?
A.
3 2
2 3 1
y x x
.
B.
3
3 1
y x x
.
C.
3
3 1
y x x
.
D.
3
2 6 1
y x x
.
Câu 32. [2D1-2] Khoảng cách giữa hai điểm cực trị của đồ thị hàm số
3 2
3 4
y x x
là
A.
5
. B.
4 5
. C.
2 5
. D.
3 5
.
Câu 33. [2D2-2] Cho
2017!
x
. Giá trị của biểu thức
2 2 2
2 3 2017
1 1 1
...
log log log
A
x x x
bằng
A.
1
2
. B.
2
. C.
4
. D.
1
.
Câu 34. [2D1-1] Cho hàm số
y f x
xác định và có đạo hàm trên
\ 1
. Hàm số có bảng biến
thiên như hình vẽ dưới đây. Hỏi đồ thị hàm số
y f x
có tất cả bao nhiêu đường tiệm cận?
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 35. [2D2-2] Rút gọn biểu thức
7
3 5
3
7
4 2
.
.
a a
A
a a
với
0
a
ta được kết quả
m
n
A a
, trong đó
m
,
*
n
và
m
n
là phân số tối giản. Khẳng định nào sau đây đúng?
A.
2 2
43
m n
. B.
2
2 15
m n
. C.
2 2
25
m n
. D.
2
3 2 2
m n
.
Câu 36. [2D2-2] Nếu
1
7 4 3 7 4 3
a
thì
A.
1
a
. B.
1
a
. C.
0
a
. D.
0
a
.
Câu 37. [2H1-2] Cho tứ diện
OABC
có
OA
,
OB
,
OC
đôi một vuông góc với nhau. Biết
OA a
,
2
OB a
và đường thẳng
AC
tạo với mặt phẳng
OBC
một góc
60
. Thể tích khối tứ diện
OABC
bằng
A.
3
3
9
a
. B.
3
3
a
. C.
3
a
. D.
3
3
3
a
.
Câu 38. [2D1-2] Tiếp tuyến của đồ thị hàm số
1
2
x
y
x
tại điểm
1; 2
M
có phương trình là
A.
3 5
y x
. B.
3 1
y x
. C.
3 1
y x
. D.
3 2
y x
.
Câu 39. [2H1-1] Tổng số đỉnh, số cạnh và số mặt của một hình bát diện đều là
A.
24
. B.
26
. C.
52
. D.
20
.
x
1
0
1
y
0
y
1
2
3
O
x
y
1
1
2
1
3
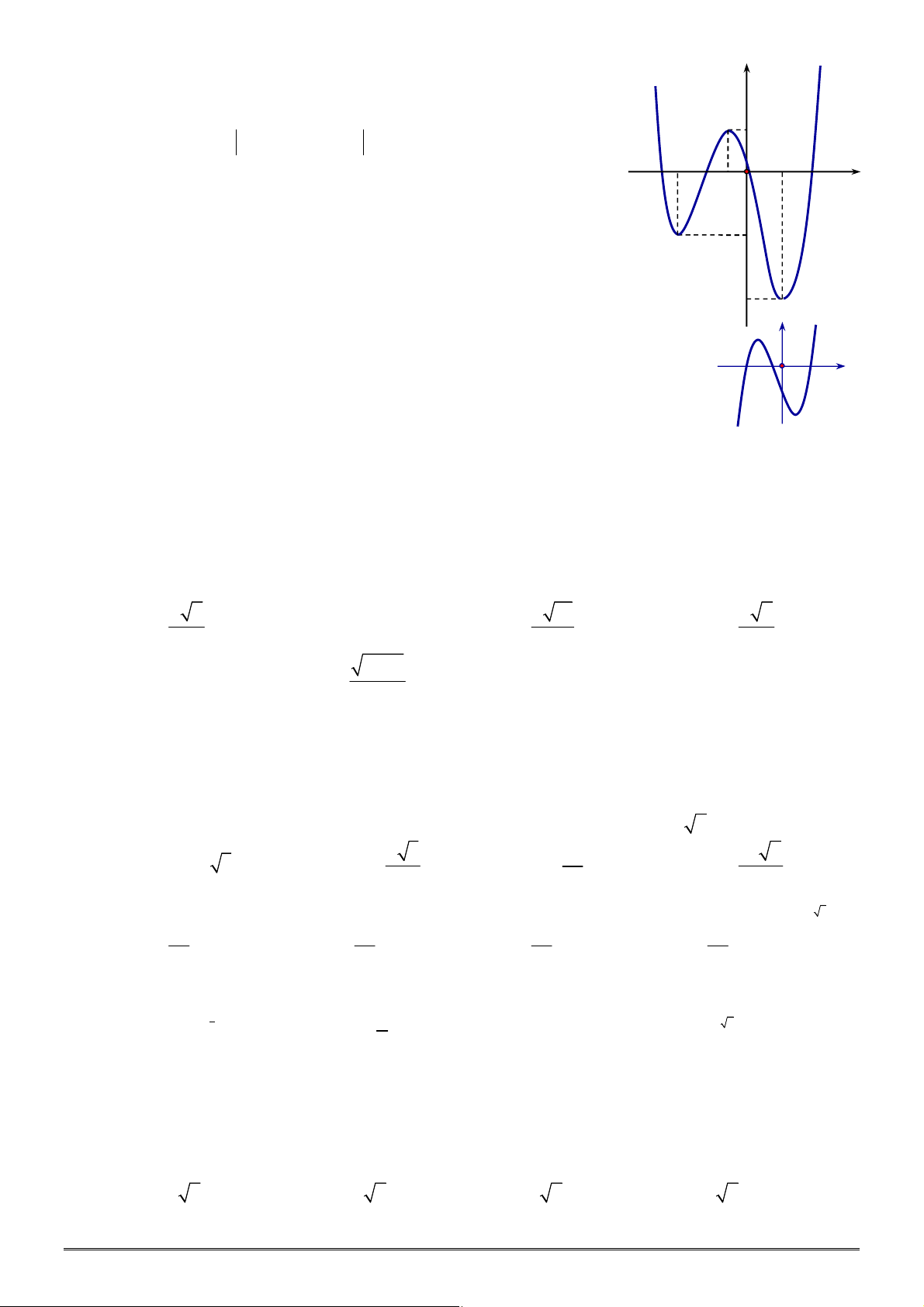
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/25
Câu 40. [2D1-4] Cho đồ thị của hàm số
y f x
như hình bên. Gọi
S
là tập hợp các giá trị nguyên dương của tham số
m
để
hàm số
2017
y f x m
có
5
điểm cực trị. Tổng tất cả
các giá trị của các phần tử của tập
S
bằng
A.
12
. B.
15
.
C.
18
. D.
9
.
Câu 41. [1D1-2] Cho hàm số
y f x
có đạo hàm là hàm số liên tục trên
với đồ thị hàm số
y f x
như hình vẽ. Biết
0
f a
, hỏi đồ
thị hàm số
y f x
cắt trục hoành tại nhiều nhất bao nhiêu điểm?
A.
3
. B.
2
.
C.
4
. D.
0
.
Câu 42. [1D1-3] Có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số:
3 2
1 1 2 2
y m x m x x
nghịch biến trên
?
A.
5
. B.
6
. C.
8
. D.
7
.
Câu 43.
[1H3-5] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA ABC
, góc giữa
đường thẳng
SB
và mặt phẳng
ABC
bằng
60
. Khoảng cách giữa hai đường thẳng
AC
và
SB
bằng
A.
2
2
a
. B.
2
a
. C.
15
5
a
. D.
7
7
a
R .
Câu 44. [2D1-4] Đồ thị hàm số
2
2
1
2
x
y
x x
có tất cả bao nhiêu tiệm cận đứng?
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 45. [2D2-2] Cho
0 1
a
,
0
b
thỏa mãn điều kiện
log 0
a
b
. Khẳng định nào sau đây là đúng?
A.
1
0 1
b a
b a
. B.
1
0 1
a b
a b
. C.
0 1
0 1
a b
b a
. D.
0 1
b a
.
Câu 46. [2H2-3] Tính bán kính
R
mặt cầu ngoại tiếp tứ diện đều
ABCD
cạnh
2
a
.
A.
3
R a
. B.
3
2
a
R . C.
3
2
a
R . D.
3 2
2
a
R .
Câu 47. [2D2-2] Tìm tất cả các giá trị thực của
x
thỏa mãn đẳng thức
3 3 9
3
log 3log 2 log 25 log 3
x .
A.
40
9
. B.
25
9
. C.
28
3
. D.
20
3
.
Câu 48. [2D2-1] Trong các biểu thức sau, biểu thức nào không có nghĩa?
A.
1
3
4
. B.
0
3
4
. C.
4
3
. D.
2
1
.
Câu 49. [2D2-1] Cho
0 1
a
và
.
b
Chọn mệnh đề sai trong các mệnh đề sau:
A.
2
log 2log
a a
b b
. B. log
b
a
a b
. C.
log 1 0
a
. D.
log 1
a
a
.
Câu 50. [2H2-2] Cho mặt cầu tâm
,
O
bán kính
3.
R
Mặt phẳng
P
nằm cách tâm
O
một khoảng
bằng
1
và cắt mặt cầu theo một đường tròn có chu vi bằng
A.
4 2
. B.
6 2
. C.
3 2
. D.
8 2
.
----------HẾT----------
O
x
y
2
3
6
a
x
y
O
b
c

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/25
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B D
B B D
D
D
D
C
A
D
B
C
B
D
A
D
A
C
D
A
A
D
C
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
A
B B A
C
C
B C
B D
A
B
B
A
B D
C
C
C
B A
A
A
A
HƯỚNG DẪN GIẢI
Câu 1. [2D2-1] Cho
0 1
a
và
0
x
,
0
y
. Chọn mệnh đề đúng trong các mệnh đề sau:
A.
log log .log
a a a
x y x y
. B.
log log log
a a a
xy x y
.
C.
log log .log
a a a
xy x y
. D.
log log log
a a a
x y x y
.
Lời giải
Chọn B.
Câu 2. [2D1-3] Có tất cả bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2017;2017
để
hàm số
3 2
6 1
y x x mx
đồng biến trên khoảng
0;
?
A.
2030
. B.
2005
. C.
2018
. D.
2006
.
Lời giải
Chọn D.
Do hàm số
3 2
6 1
y x x mx
đồng biến trên khoảng
0;
tương đương với hàm số đồng
biến trên
0;
.
Ta có
2
3 12 0
y x x m
,
0;x
2
3 12
m x x
,
0;x
2
0;
max 3 12
m x x
.
Xét hàm số
2
3 12
y x x
có hoành độ đỉnh là
0
2
2
b
x
a
.
Và
2 12
y
,
0 0
y
. Suy ra
2
0;
max 3 12 2 12
x x y
.
Vậy giá trị
m
cần tìm là
12;13;14;...;2017
m . Suy ra có
2017 12 1 2006
giá trị nguyên
của tham số
m
cần tìm.
Câu 3. [2H1-3] Cho lăng trụ đứng
.
ABC A B C
có
AB AC BB a
,
120
BAC
. Gọi
I
là trung
điểm của
CC
. Ta có cosin của góc giữa hai mặt phẳng
ABC
và
AB I
bằng
A.
3
2
. B.
30
10
. C.
3 5
12
. D.
2
2
.
Lời giải
Chọn B.
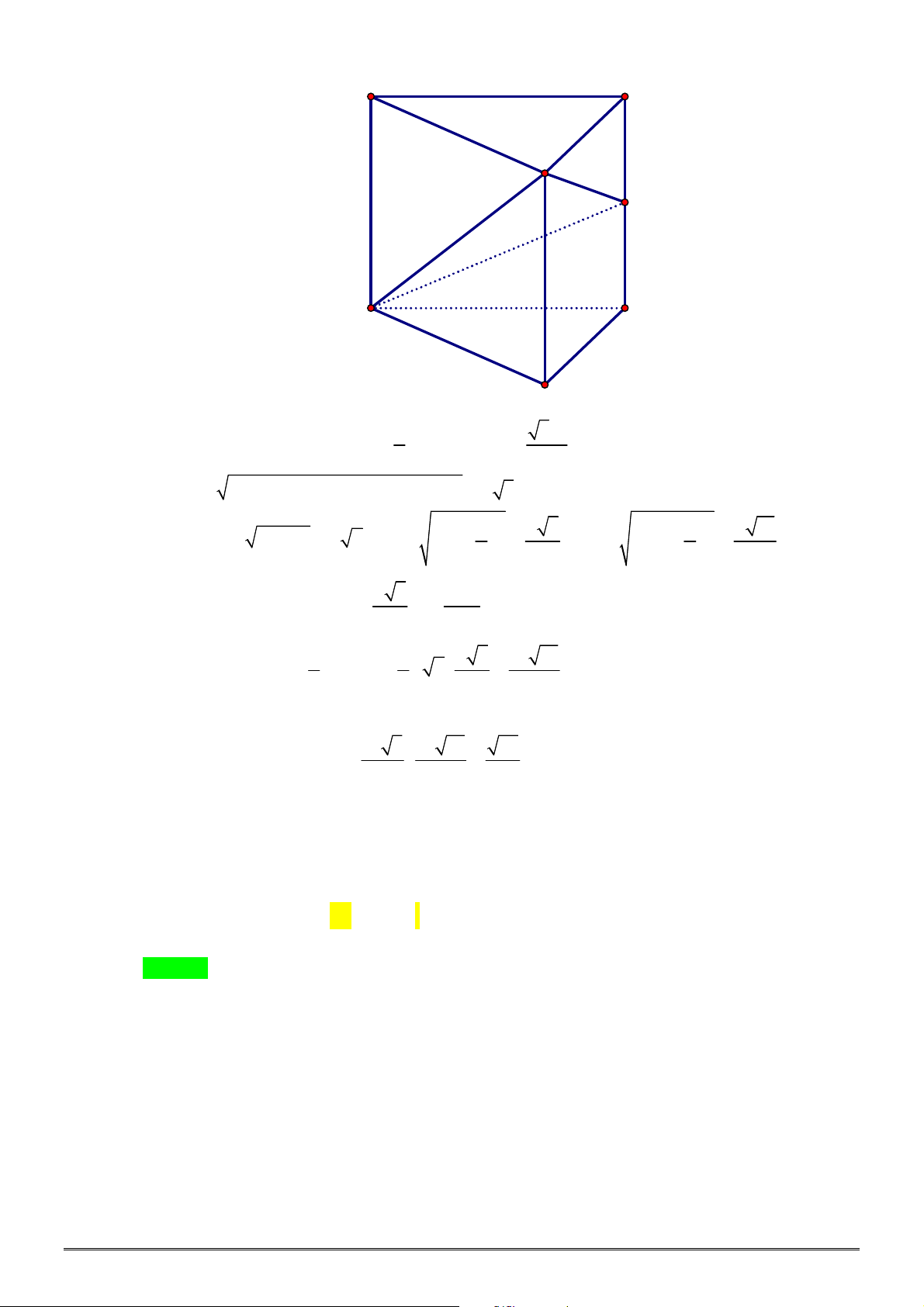
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/25
I
C'
B'
A
C
B
A'
Diện tích tam giác
ABC
:
2
1 3
. . .sin
2 4
ABC
a
S AB AC A .
Có
2 2
2 . .cos 3
BC AB AC AB AC BAC a
.
Ta có:
2 2
2
AB a a a
,
2
2
5
2 2
a a
AI a
,
2
2
13
3
2 2
a a
B I a
.
Ta được
2
2
2 2 2 2
5 13
2
2 4
a a
AB AI a B I
. Suy ra tam giác
AB I
vuông tại
A
, có
diện tích bằng
2
1 1 5 10
. . 2
2 2 2 4
AB I
a a
S AB AI a
.
Tam giác
ABC
là hình chiếu vuông góc của tam giác
AB I
trên
ABC
nên ta có:
2 2
3 10 30
cos . cos :
4 4 10
ABC AB I
a a
S S
.
Chú ý: Nếu không được “may mắn có
AB I
vuông”, ta có thể sử dụng công thức He-rong để
tính diện tích tam giác
AB I
.
Câu 4. [2H1-2] Gọi
1
V
là thể tích của khối lập phương
.
ABCD A B C D
,
2
V
là thể tích khối tứ diện
A ABD
. Hệ thức nào sau đây là đúng?
A.
1 2
4
V V
. B.
1 2
6
V V
. C.
1 2
2
V V
. D.
1 2
8
V V
.
Lời giải
Chọn B.
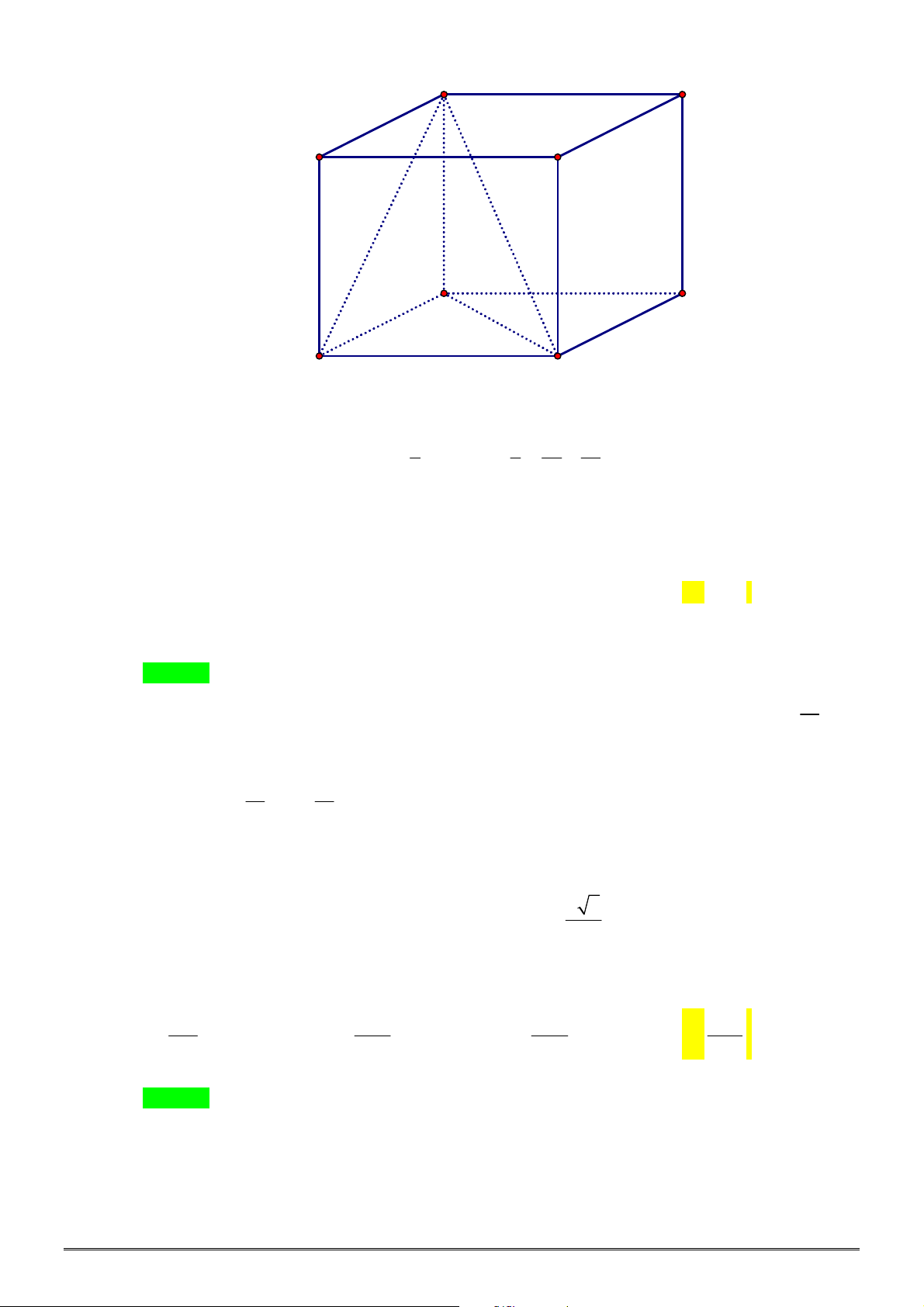
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/25
D'
D
C'
B'
A
C
B
A'
.
Gọi
a
là độ dài cạnh hình lập phương. Thể tích khối lập phương:
3
1
V a
.
Thể tích khối tứ diện
ABDA
:
2 3
2
1 1
. . . .
3 3 2 6
ABD
a a
V AA S a
.
Vậy
1 2
6
V V
.
Câu 5. [2D2-3] Cho
2 6 6
log 3 log 2 log 3 5
a b c
với
, ,
a b c
là các số tự nhiên. Khẳng định nào
đúng trong các khẳng định sau đây?
A.
a b
. B.
a b c
. C.
b c
. D.
b c
.
Gốc:
2 6 6
log 3 log 2 log 5 5
a b c
Lời giải
Chọn D.
5
2 6 6 6 6 2 2
log 3 log 2 log 3 5 log 2 log 3 log 2 log 3
b c a
a b c
5
6 2
2
log 2 3 log
3
b c
a
.
Đặt
6
5
5
5
2
0
log 2 3
2 3 6
2 3 6
5
22
2 3 2
2
log
5
3
3
b c
b c t
b c t
a t
t
aa
a
t
t
t
b c
(vì
, ,
a b c
là các số tự nhiên).
Vậy
b c
.
Câu 6. [2H1-2] Cho khối chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng
đáy và khoảng cách từ
A
đến mặt phẳng
SBC
bằng
2
2
a
. Gọi
M
là điểm thuộc cạnh
SD
sao cho
3
SM MD
. Mặt phẳng
ABM
cắt cạnh
SC
tại điểm
N
. Thể tích khối đa diện
MNABCD
bằng
A.
3
7
32
a
. B.
3
15
32
a
. C.
3
17
32
a
. D.
3
11
96
a
.
Lời giải
Chọn D.
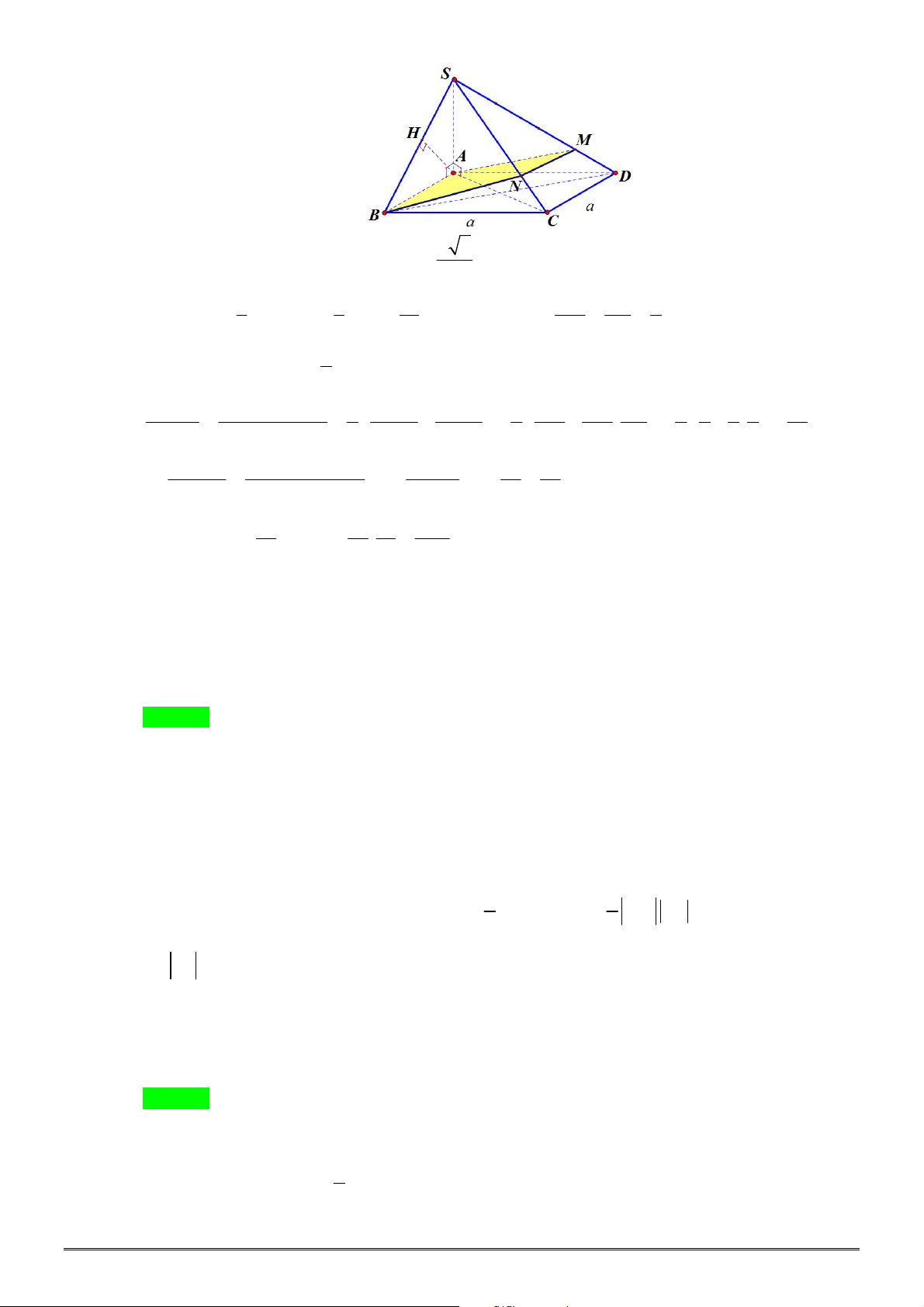
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/25
Kẻ
AH SB
2
,
2
a
d A SBC AH
SAB
vuông cân tại
A
SA a
.
3
2
.
1 1
. . .
3 3 3
S ABCD ABCD
a
V SA S a a . Kẻ
3
//
4
SM SN
MN CD
SD SC
.
Ta có:
. . .
1
2
S ABD S BCD S ABCD
V V V
. . . . .
. . . .
1 1 1 3 3 3 21
. .
2 2 2 2 4 4 4 32
S AMNB S ABM S BMN S ABM S BMN
S ABCD S ABD S ABD S BCD
V V V V V SM SM SN
V V V V SD SD SC
.
. . .
. . .
21 11
1 1
32 32
MNABCD S ABCD S AMNB S AMNB
S ABCD S ABCD S ABCD
V V V V
V V V
.
Vậy
3 3
.
11 11 11
.
32 32 3 96
MNABCD S ABCD
a a
V V .
Câu 7. [2D1-3] Gọi
S
là tập hợp các giá trị thực của tham số
m
để hàm số
3 2 3
3 4
y x mx m
có hai
điểm cực trị
A
và
B
sao cho tam giác
OAB
có diện tích bằng
4
(
O
là gốc tọa độ). Ta có tổng
giá trị tất cả các phần tử của tập
S
bằng
A.
1
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn D.
3 2 3 2
3 4 3 6
y x mx m y x mx
. Ta có
0
0
2
x
y
x m
.
Để hàm số đã cho có hai điểm cực trị thì
0
m
. Khi đó:
3 3
0 0 4 0; 4
0
2 2 0 2 ; 0
x y m A m Oy
y
x m y m B m Ox
Vậy tam giác
OAB
vuông tại
O
nên
3
1 1
. 4 4 2
2 2
OAB
S OAOB m m
4
1
1 1; 1
1
m
m S
m
.
Câu 8. [2D2-1] Cho
2
log 5
a
. Tính
2
log 200
theo
a
.
A.
2 2
a
. B.
4 2
a
. C.
1 2
a
. D.
3 2
a
.
Lời giải
Chọn D.
2 3
2 2 2 2
log 200 log 5 .2 2log 5 3log 2 2 3
a
.
Câu 9. [2D1-2] Cho hàm số
4 2
1
2 2017
4
y x x . Khẳng định nào sau đây là đúng?
A. Hàm số có một điểm cực tiểu và không có điểm cực đại.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/25
B. Hàm số có một điểm cực đại và không có điểm cực tiểu.
C. Hàm số có một điểm cực đại và hai điểm cực tiểu.
D. Hàm số có một điểm cực tiểu và hai điểm cực đại.
Lời giải
Chọn C.
3
0
4 0
2
x
y x x
x
.
Ta thấy, phương trình
0
y
có 3 nghiệm phân biệt và
1
0
4
a
nên hàm số có ba cực trị
trong đó có một điểm cực đại và hai điểm cực tiểu.
Câu 10. [2D2-2] Rút gọn biểu thức
2
4log 3
a
A a
với
0 1
a
ta được kết quả là
A.
9
. B.
4
3
. C.
8
3
. D.
6
.
Lời giải
Chọn A.
2
4log 3
2log 3 log 9
9
a a a
A a a a
.
Câu 11. [2H1-1] Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai khối chóp có hai đáy là hai đa giác bằng nhau thì thể tích bằng nhau.
B. Hai khối đa diện có thể tích bằng nhau thì bằng nhau.
C. Hai khối lăng trụ có chiều cao bằng nhau thì thể tích bằng nhau.
D. Hai khối đa diện bằng nhau có thể tích bằng nhau.
Lời giải
Chọn D.
Câu hỏi lý thuyết “Khái niệm về thể tích khối đa diện” (SGK hình học 12 trang 21, mục I phần b).
Câu 12. [2D1-2] Số điểm chung của đồ thị hàm số
3 2
2 12
y x x x
với trục
Ox
là
A.
2
. B.
1
. C.
3
. D.
0
.
Lời giải
Chọn B.
Phương trình hoành độ giao điểm của đồ thị hàm số với trục
Ox
3 2
2 12 0
x x x
2
3 4 0
x x x
.
2
2
3
3 4 0 3
4 0 VN
x
x x x x
x x
.
Câu 13. [2D1- 2] Cho hàm số
y f x
có đạo hàm liên tục trên
.
Đồ thị hàm số
y f x
như hình
vẽ sau:
x
y
4
-1
0
1
2
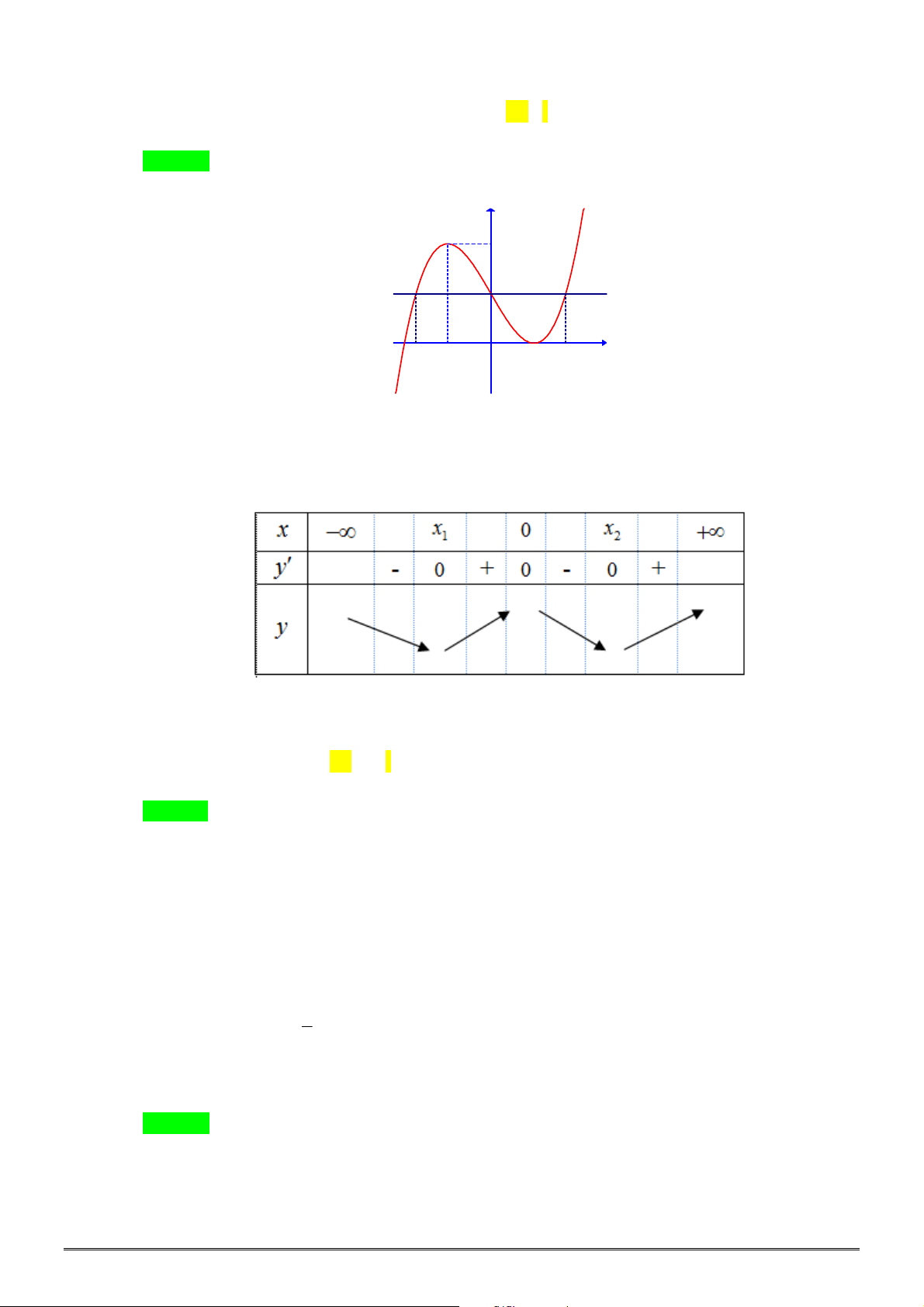
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/25
Số điểm cực trị của hàm số
2
y f x x
là
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn C.
2 2
y f x x y f x
.
x
y
4
-1
0
1
2
1
x
2
x
Ta có
1
2
0 2 0 2 0
x x
y f x f x x
x x
.
Bảng biến thiên:
Câu 14. [2D1-2] Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 2
3 9 1
y x x x
trên đoạn
0;4
. Ta có
2
m M
bằng
A.
14
. B.
24
. C.
37
. D.
57
.
Lời giải
Chọn B.
Xét hàm số
3 2
3 9 1
y x x x
trên đoạn
0;4
.
2
3 6 9
y x x
.
2
1 0;4
0 3 6 9 0
3 0;4
x
y x x
x
.
Tính
0 1; 3 26; 4 19
y y y
. Suy ra
1, 26 2 24
M m m M
.
Câu 15. [2D1-1] Hàm số
3 2
1
2 3 1
3
y x x x
nghịch biến trên khoảng nào trong các khoảng sau đây?
A.
1;3
. B.
1;4
. C.
3; 1
. D.
1;3
.
Lời giải
Chọn D.
Tập xác định
D
.
2
4 3
y x x
;
1
0
3
x
y
x
.
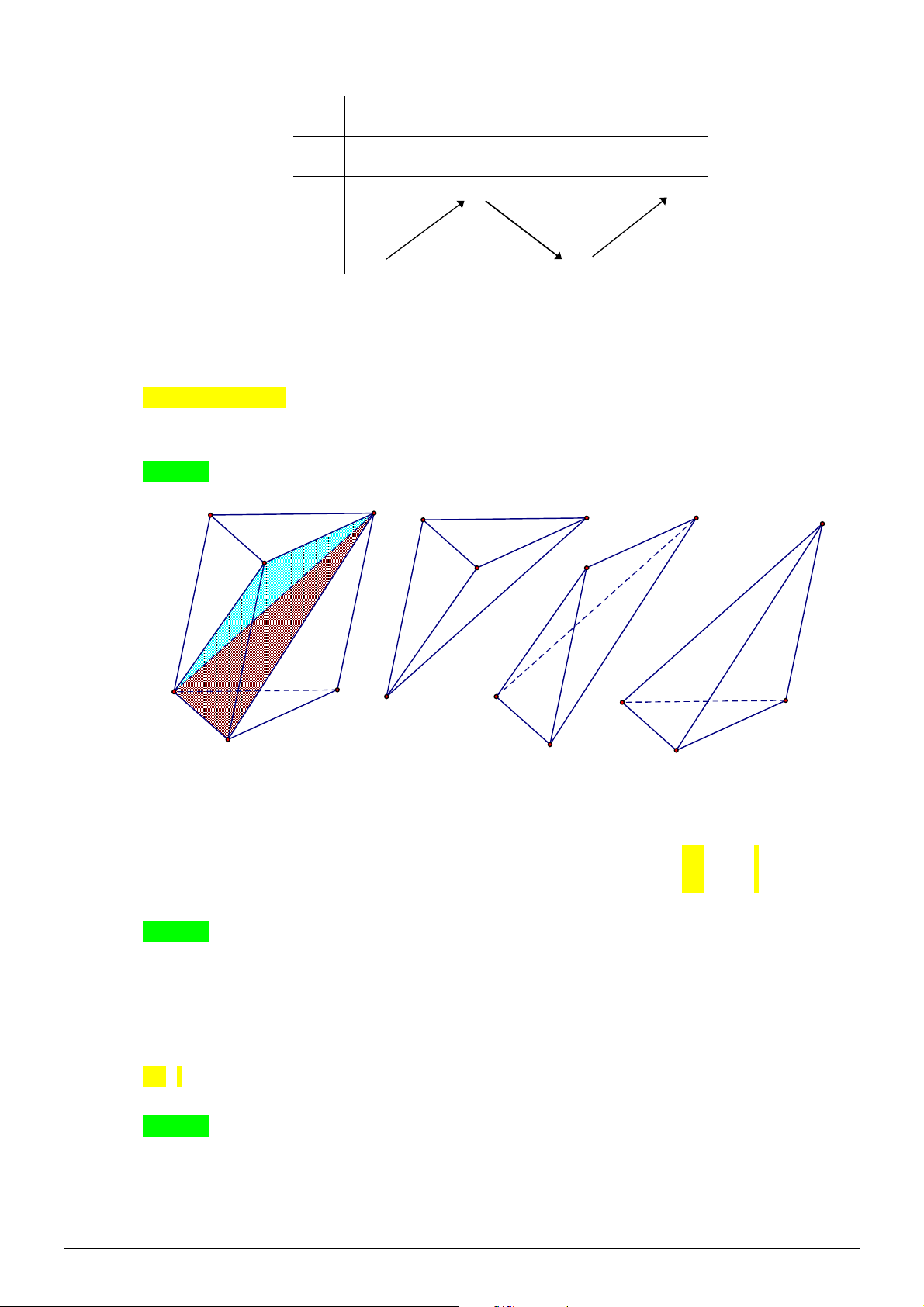
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/25
Bảng biến thiên:
Từ bảng biến thiên, ta thấy hàm số nghịch biến trên
1;3
.
Câu 16. [2H1-2] Cắt khối lăng trụ
.
MNP M N P
bởi các mặt phẳng
MN P
và
MNP
ta được những
khối đa diện nào?
A. Ba khối tứ diện. B. Hai khối tứ diện và hai khối chóp tứ giác.
C. Hai khối tứ diện và một khối chóp tứ giác. D. Một khối tứ diện và một khối chóp tứ giác.
Lời giải
Chọn A.
P'
P'
N'
P'
N'
P'
N'
M
N
P
M'
M
M'
M
N
M
N
P
Dựa vào hình vẽ ta chọn đáp án
A
.
Câu 17. [2H2-1] Thể tích của khối cầu bán kính
R
bằng
A.
3
1
3
R
. B.
3
2
3
R
. C.
3
R
. D.
3
4
3
R
.
Lời giải
Chọn D.
Công thức tính thể tích của khối cầu bán kính
R
là
3
4
3
V R
.
Câu 18. [2D1-2] Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 2
1 2 3 1
y m x m x
có đúng một điểm cực tiểu và không có điểm cực đại?
A.
1
. B.
3
. C.
2
. D.
0
.
Lời giải
Chọn A.
Tập xác định
.
Trường hợp
1
:
1 0
m
1
m
, ta có
2
8 1
y x
có đồ thị là parabol, bề lõm quay lên trên
nên hàm số chỉ có
1
cực tiểu và không có cực đại.
x
1
3
y
0
0
y
1
3
1
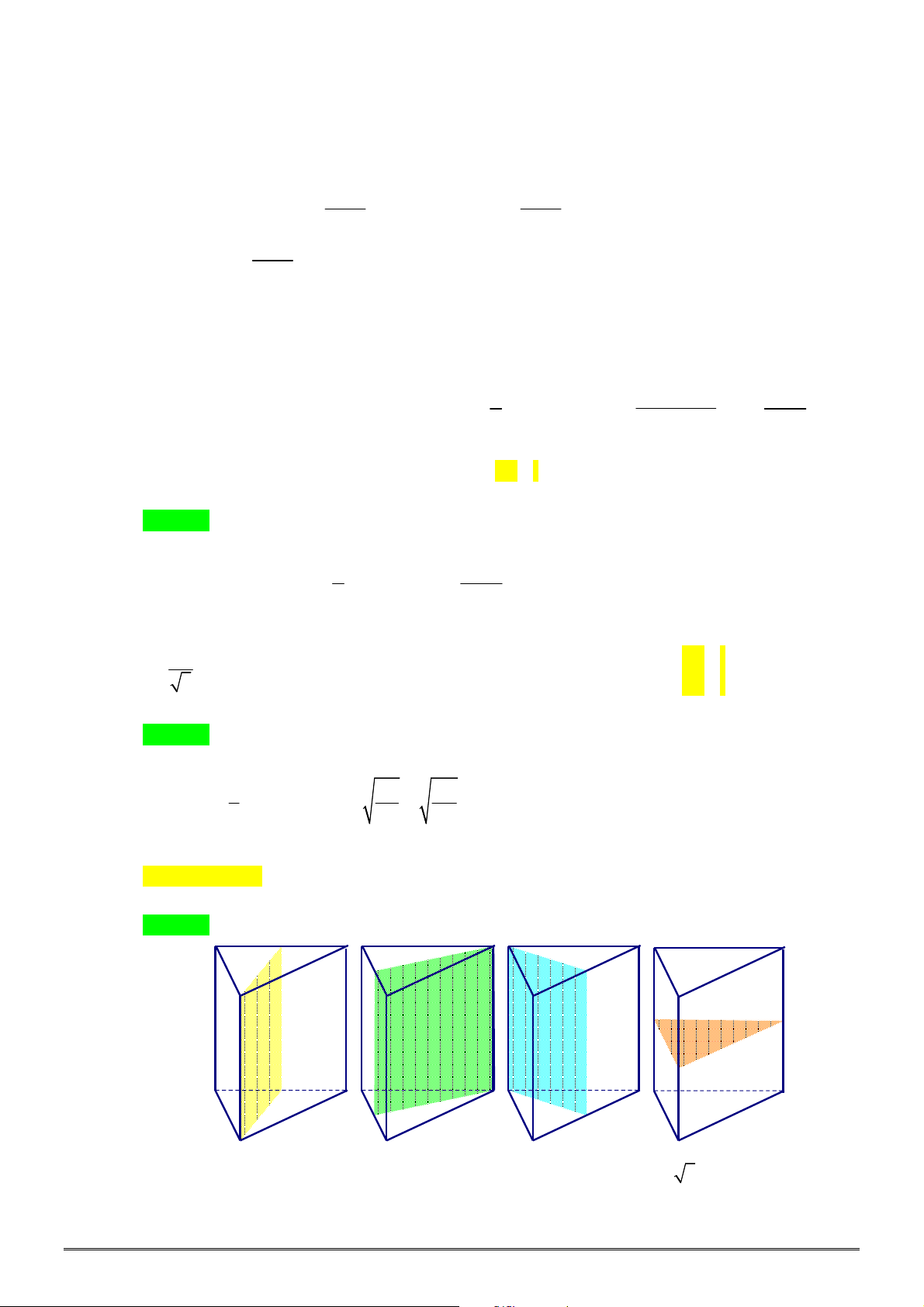
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/25
Trường hợp
2
:
1 0 1.
m m
Vì hàm số trùng phương nên để hàm số chỉ có cực tiểu mà
không có cực đại thì
1
m
và phương trình
0
y
có đúng một nghiệm.
Vậy ta có
3
4 1 4 3 0
m x m x
3
1 3 0
m x m x
2
0
1 3 0
x
m x m
.
Do
1
m
nên ta có
2
3
1
m
x
m
. Phương trình
2
3
1
m
x
m
có một nghiệm
0
x
hoặc vô nghiệm
khi và chỉ khi
3
0
1
m
m
3 1.
m
(thỏa điều kiện
1
m
).
Do đó không có
m
nguyên dương thỏa mãn trong trường hợp này.
Kết luận: Vậy
1
m
thì hàm số
4 2
1 2 3 1
y m x m x
có đúng một điểm cực tiểu và
không có điểm cực đại.
Câu 19. [2D1-1] Trong số đồ thị của các hàm số
1
;
y
x
2
1;
y x
2
3 7
;
1
x x
y
x
2
1
x
y
x
có tất
cả bao nhiêu đồ thị có tiệm cận ngang?
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn C.
Để hàm số có tiệm cận ngang thì hàm số là hàm phân thức có bậc tử nhỏ hơn hoặc bằng bậc
mẫu. Vậy có hàm số
1
y
x
và hàm số
2
1
x
y
x
có tiệm cận ngang.
Câu 20. [2H1-1] Cho khối chóp tứ giác đều có chiều cao bằng
6
và thể tích bằng
8
. Độ dài cạnh đáy bằng
A.
2
3
. B.
3
. C.
4.
D.
2
.
Lời giải
Chọn D.
Gọi độ dài cạnh đáy của hình chóp tứ giác đều là
a
và chiều cao hình chóp tứ giác đều là
h
.
Ta có:
2
1
.
3
V a h
Suy ra
3 3.8
2
6
V
a
h
.
Câu 21. [2H1-2] Hình lăng trụ tam giác đều có tất cả bao nhiêu mặt phẳng đối xứng
A. 4 mặt phẳng. B. 1 mặt phẳng. C. 3 mặt phẳng. D. 2 mặt phẳng.
Lời giải
Chọn A.
Câu 22. [2H2-3] Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật,
3
AB a
và
AD a
. Đường
thẳng
SA
vuông góc với mặt phẳng đáy và
SA a
. Thể tích khối cầu ngoại tiếp hình chóp
.
S BCD
bằng
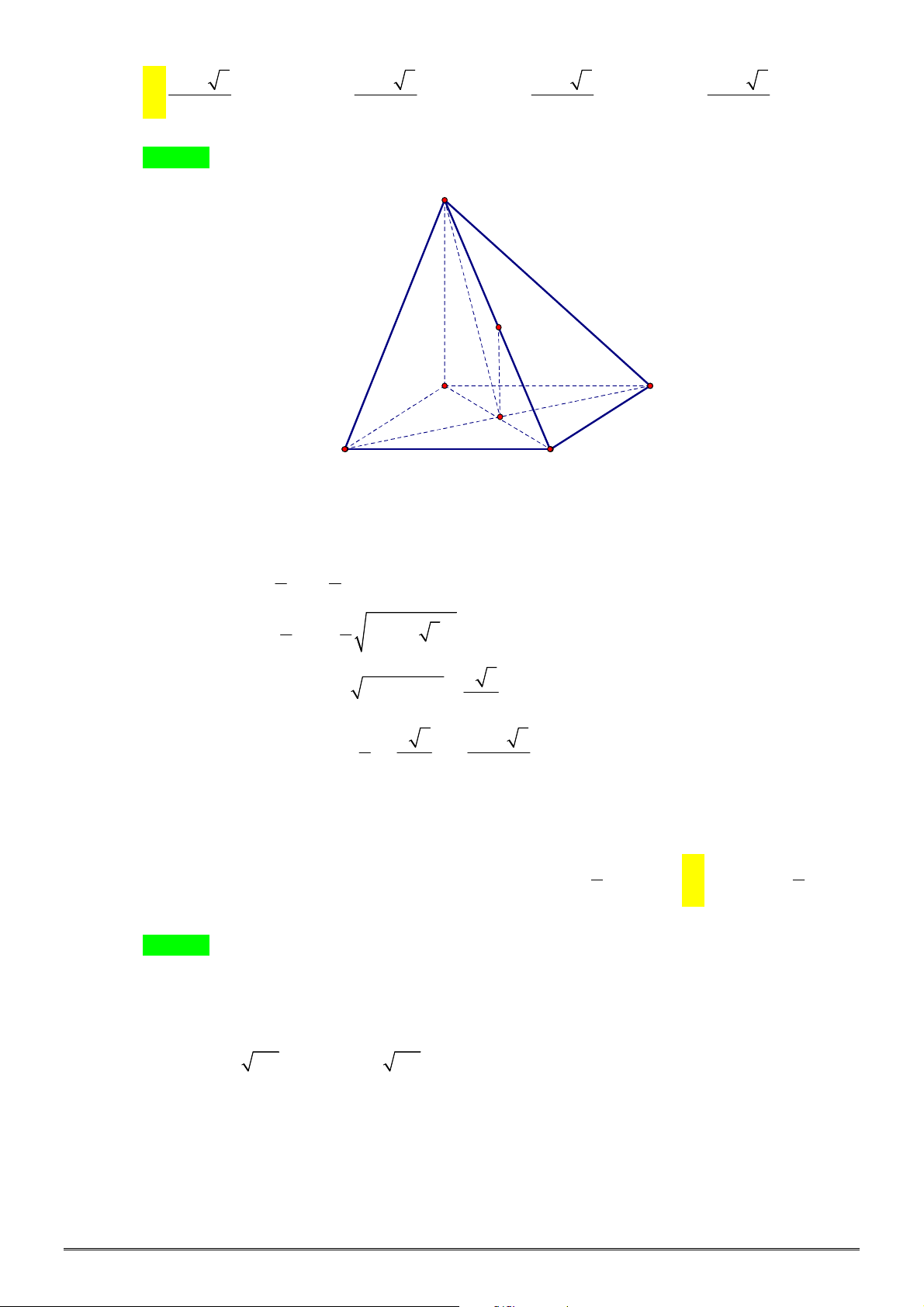
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/25
A.
3
5 5
.
6
a
B.
3
5 5
.
24
a
C.
3
3 5
.
25
a
D.
3
3 5
.
8
a
Lời giải
Chọn A.
A
D
B
C
S
O
I
Gọi
O
là giao điểm của hai đường chéo
AC
và
BD
, từ
O
dựng đường thẳng song song với
SA
và cắt
SC
tại trung điểm
I
của
SC
, suy ra
I
là tâm mặt cầu ngoại tiếp hình chóp
.
S BCD
.
Mặt khác:
2
2
1
2 2
1 1
3
2 2
a
OI SA
OC AC a a a
Theo bài ra ta có:
2 2
5
.
2
a
R IC OC OI
Vậy thể tích khối cầu là
3
3
4 5 5 5
.
3 2 6
a a
V
Câu 23. [2D1-3] Gọi
0
m
là giá trị thực của tham số
m
để đồ thị hàm số
4 2
2 4
y x mx
có 3 điểm
cực trị nằm trên các trục tọa độ. Khẳng định nào sau đây là đúng?
A.
0
1;3
m B.
0
5; 3
m
. C.
0
3
;0
2
m
D.
0
3
3;
2
m
Lời giải
Chọn D.
3
' 4 4
y x mx
.
2
0
' 0
x
y
x m
Hàm số có 3 điểm cực trị
0
m
. Khi đó đồ thị hàm số có 3 điểm cực trị là
2 2
0;4 , ; 4 , ; 4
A B m m C m m
Ta có
A Oy
nên 3 điểm cực trị nằm trên các trục tọa độ
2
2
4 0
2
m KTM
m
m TM
Câu 24. [2H2-1] Chọn mệnh đề đúng trong các mệnh đề sau?
A. Hình có đáy là hình bình hành thì có mặt cầu ngoại tiếp.
B. Hình chóp có đáy là hình thang vuông thì có mặt cầu ngoại tiếp.
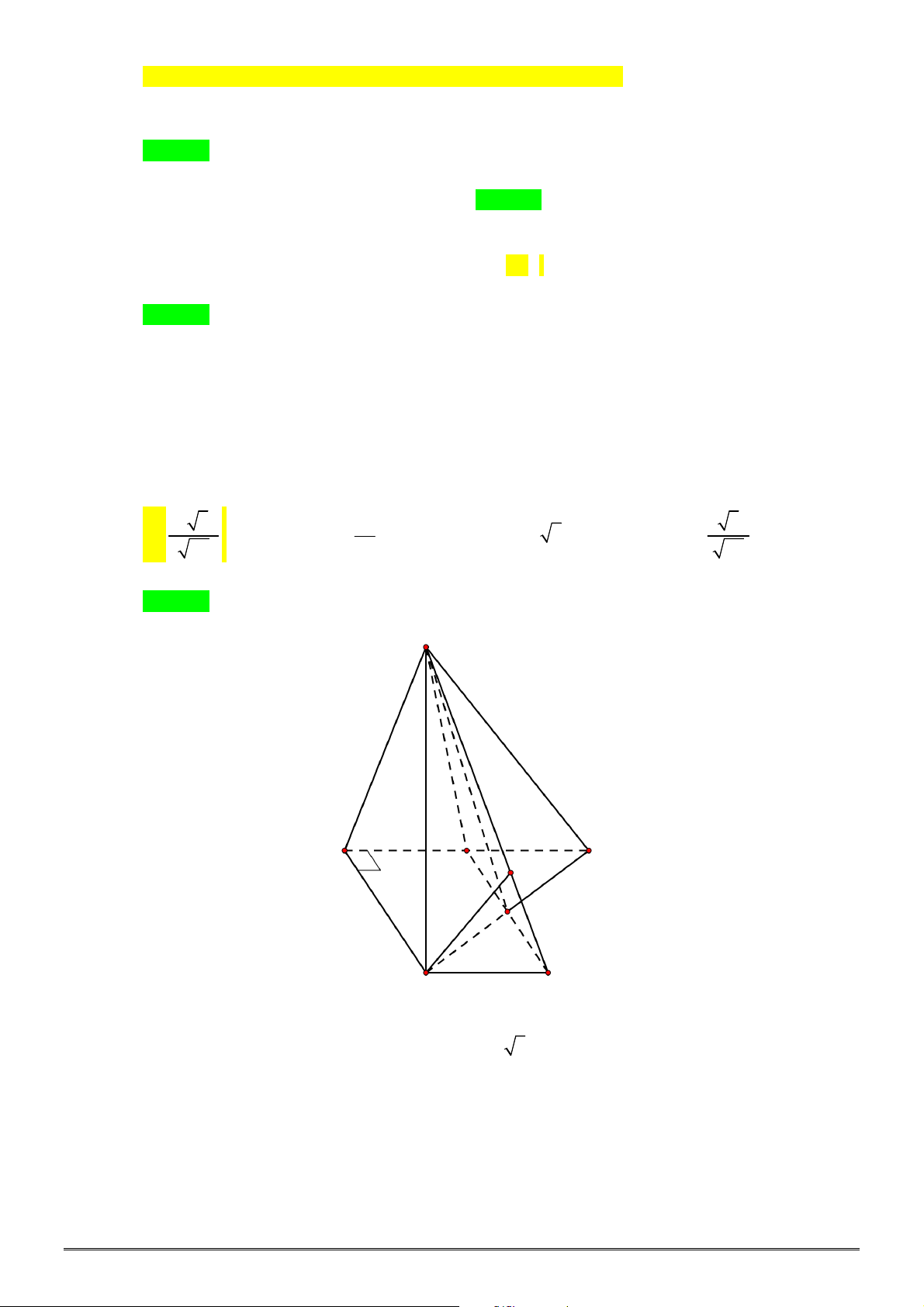
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/25
C. Hình chóp có đáy là hình thang cân thì có mặt cầu ngoại tiếp.
D. Hình có đáy là hình tứ giác thì có mặt cầu ngoại tiếp.
Lời giải
Chọn C.
Trong các hình: hình bình hành, hình thang vuông, hình thang cân, hình tứ giác chỉ có hình
thang cân là có đường tròn ngoại tiếp nên ta Chọn C.
Câu 25. [2D1-2] Hàm số
4 3
8 6
y x x
có tất cả bao nhiêu điểm cực trị?
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn C.
Ta có
3 2 2
0
4 24 4 6 0
6
x
y x x x x
x
. Do
0
x
là nghiệm kép nên hàm số chỉ có
1 cực trị
6
x
.
Câu 26. [2D1-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
3
AB a
,
4
BC a
và
SA ABC
. Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
60
. Gọi
M
là trung
điểm của cạnh
AC
. Khoảng cách giữa hai đường thẳng
AB
và
SM
bằng
A.
10 3
79
a
. B.
5
2
a
. C.
5 3
a
. D.
5 3
79
a
.
Lời giải
Chọn A.
Do
SA ABC
nên góc giữa
SC
và
ABC
là góc
60
SCA
.
Vì
ABC
vuông tại
B
nên
5 5 3
AC a SA a
.
Gọi
N
là trung điểm
BC
nên
// //
MN AB AB SMN
; ; ;
d AB SM d AB SMN d A SMN
. Từ
A
kẻ đường thẳng song song với
BC
cắt
MN
tại
D
. Do
BC AB BC MN AD MN
. Từ
A
kẻ
AH
vuông góc với
SD
.
Ta có
MD AD
MD SAD MD AH
MD SA
S
B
A
M
C
N
D
H
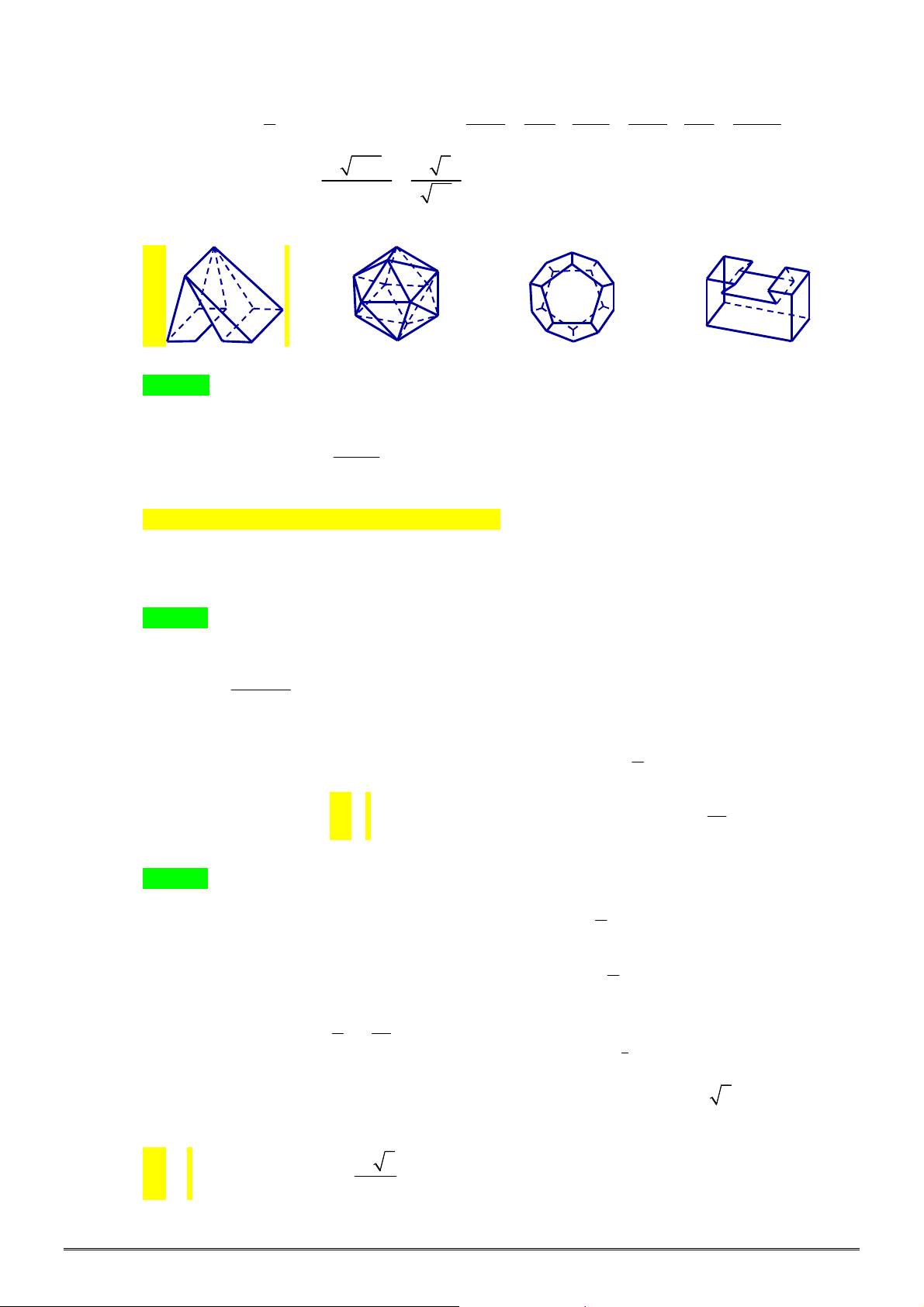
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/25
Mà
AH SD AH SMD
hay
;
AH SMN d A SMN AH
Do
1
2
2
AD BN BC a
. Xét
SAD
có
2 2 2 2 2 2
1 1 1 1 1 79
75 4 300
AH SA AD a a a
10 237 10 3
;
79
79
a a
d AB SM AH .
Câu 27. [2H1-1] Vật thể nào trong các vật thể sau đây không phải là khối đa diện?
A. . B. . C. . D.
Lời giải
Chọn A.
Vì có một cạnh là cạnh chung của bốn đa giác, điều này trái với định nghĩa về khối đa diện.
Câu 28. [2D1-1] Cho hàm số
2 3
4
x
y
x
. Hãy chọn khẳng định đúng trong các khẳng định sau đây:
A. Hàm số nghịch biến trên
.
B. Hàm số đồng biến trên mỗi khoảng xác định.
C. Hàm số đồng biến trên
.
D. Hàm số nghịch biến trên mỗi khoảng xác định.
Lời giải
Chọn B.
Hàm số có tập xác định:
\ 4
.
Ta có:
2
3
0, 4
4
y x
x
, nên hàm số đồng biến trên mỗi khoảng xác định của nó.
Câu 29. [2D1-1] Giá trị lớn nhất của hàm số
3
3 5
y x x
trên đoạn
3
0;
2
.
A.
3
. B.
5
. C.
7
. D.
31
8
.
Lời giải
Chọn B.
Ta có
2
3 3
y x
, cho
2
3
1 0;
2
0 3 3 0
3
1 0;
2
x
y x
x
3 31
0 5, 1 3,
2 8
f f f
. So sánh ba giá trị, ta được
3
0;
2
max 0 5
f x f
.
Câu 30. [2H1-2] Cho hình chóp
.
S ABC
có đáy là tam giác vuông tại
C
,
5
AB a
,
AC a
. Cạnh
bên
3
SA a
và vuông góc vói mặt phẳng
ABC
. Thể tích khối chóp
.
S ABC
bằng
A.
3
a
. B.
3
5
3
a
. C.
3
2
a
. D.
3
3
a
Lời giải

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/25
Chọn A.
Ta có
2 2
2
BC AB AC a
.
2
1
.
2
ABC
S BC AC a
, suy ra:
3
1
. .
3
ABC
V S SA a
.
Câu 31. [2D1-2] Cho biết đồ thị sau là đồ thị của một trong bốn hàm số ở các phương án A, B, C, D. Đó
là đồ thị của hàm số nào?
x
y
1
3
1
1
O
A.
3 2
2 3 1
y x x
. B.
3
3 1
y x x
. C.
3
3 1
y x x
. D.
3
2 6 1
y x x
.
Lời giải
Chọn C.
Từ hình dáng đồ thị, suy ra
0
a
loại đáp án B.
Đồ thị qua hai điểm
1;3
và
1; 1
. Thay trực tiếp vào 3 đáp án còn lại, ta thấy đáp án C
thỏa.
Câu 32. [2D1-2] Khoảng cách giữa hai điểm cực trị của đồ thị hàm số
3 2
3 4
y x x
là
A.
5
. B.
4 5
. C.
2 5
. D.
3 5
.
Lời giải
Chọn C.
D
;
2
3 6
y x x
;
0 0
y x
hoặc
2
x
.
Tọa độ hai điểm cực trị là
0; 4
A
,
2;0
B ;
Khoảng cách giữa hai điểm cực trị là
2 2
20 2 5
B A B A
AB x x y y .
Câu 33. [2D2-2] Cho
2017!
x
. Giá trị của biểu thức
2 2 2
2 3 2017
1 1 1
...
log log log
A
x x x
bằng
A.
1
2
. B.
2
. C.
4
. D.
1
.
Lời giải
Chọn B.
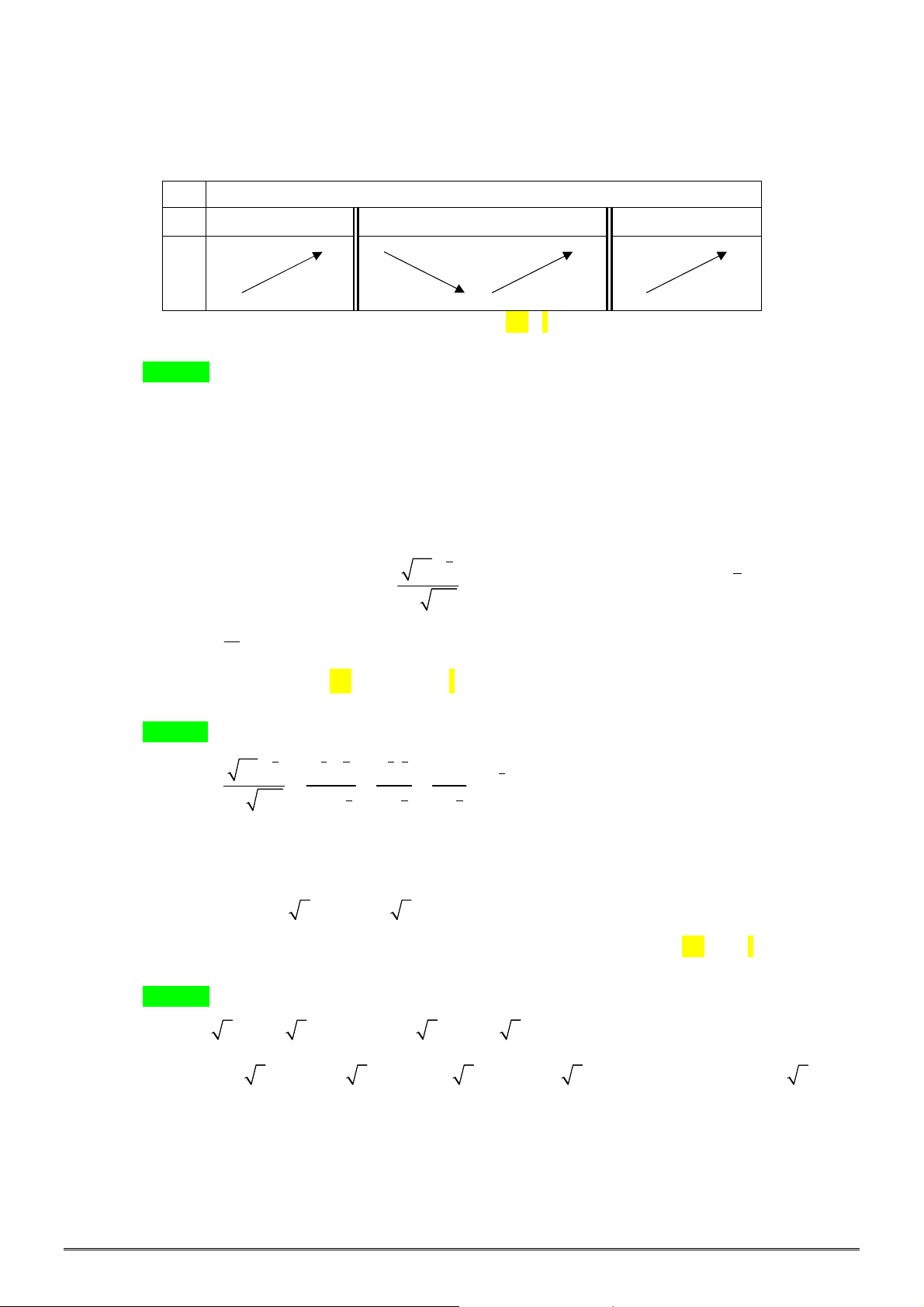
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/25
Ta có:
2 2 2
log 2 log 3 ... log 2017
x x x
A
2
log 2.3...2017
x
2log 2017!
x
2
.
Câu 34. [2D1-1] Cho hàm số
y f x
xác định và có đạo hàm trên
\ 1
. Hàm số có bảng biến
thiên như hình vẽ dưới đây. Hỏi đồ thị hàm số
y f x
có tất cả bao nhiêu đường tiệm cận?
x
1
0
1
y
0
y
1
3
2
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn C.
Ta có:
1
lim
x
y
1
x
là tiệm cận đứng;
1
lim
x
y
1
x
là tiệm cận đứng;
lim 3
x
y
3
y
là tiệm cận ngang.
Vậy đồ thị hàm số
y f x
có tất cả ba đường tiệm cận.
Câu 35. [2D2-2] Rút gọn biểu thức
7
3 5
3
7
4 2
.
.
a a
A
a a
với
0
a
ta được kết quả
m
n
A a
, trong đó
m
,
*
n
và
m
n
là phân số tối giản. Khẳng định nào sau đây đúng?
A.
2 2
43
m n
. B.
2
2 15
m n
. C.
2 2
25
m n
. D.
2
3 2 2
m n
.
Lời giải
Chọn B.
Ta có
7
3 5
3
7
4 2
.
.
a a
A
a a
5 7
3 3
2
4
7
.
.
a a
a a
5 7
3 3
2
4
7
a
a
4
2
4
7
a
a
2
7
a
.
Suy ra
2
m
,
7
n
. Do đó
2
2 15
m n
.
Ghi chú: Với
2
m
,
7
n
thì
2 2
53
m n
;
2 2
45
m n
;
2
3 2 2
m n
.
Câu 36. [2D2-2] Nếu
1
7 4 3 7 4 3
a
thì
A.
1
a
. B.
1
a
. C.
0
a
. D.
0
a
.
Lời giải
Chọn D.
Vì
7 4 3 7 4 3 1
nên
1
7 4 3 7 4 3
.
Do đó:
1
7 4 3 7 4 3
a
1 1
7 4 3 7 4 3
a
1 1
a
(do
7 4 3 1
)
0
a
.
Câu 37. [2H1-2] Cho tứ diện
OABC
có
OA
,
OB
,
OC
đôi một vuông góc với nhau. Biết
OA a
,
2
OB a
và đường thẳng
AC
tạo với mặt phẳng
OBC
một góc
60
. Thể tích khối tứ diện
OABC
bằng
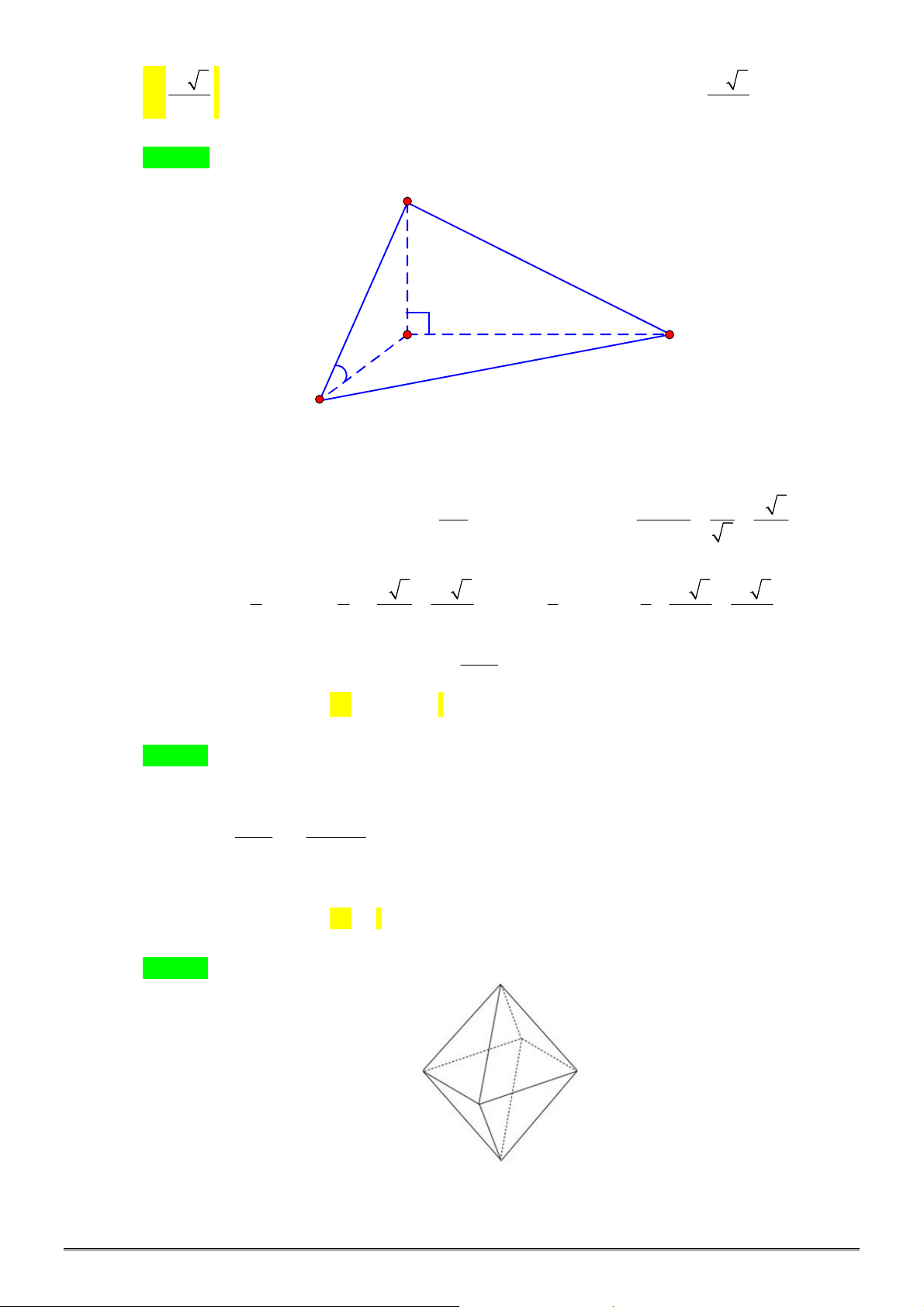
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/25
A.
3
3
9
a
. B.
3
3
a
. C.
3
a
. D.
3
3
3
a
.
Lời giải
Chọn A.
O
A
60
B
C
Theo giả thiết
OA
,
OB
,
OC
đôi một vuông góc với nhau nên
OA OBC
,
OC
là hình
chiếu của
AC
lên mặt phẳng
OBC
. Do đó
60
ACO
,
OA
là chiều cao của tứ diện
OABC
.
Xét tam giác vuông
AOC
có tan60
OA
OC
với
OA a
3
tan60 3
3
OA a a
OC
;
2
OB a
.
Ta có:
2
1 1 3 3
. 2 .
2 2 3 3
OBC
a a
S OB OC a ;
2 3
1 1 3 3
. .
3 3 3 9
OABC OBC
a a
V OA S a .
Câu 38. [2D1-2] Tiếp tuyến của đồ thị hàm số
1
2
x
y
x
tại điểm
1; 2
M
có phương trình là
A.
3 5
y x
. B.
3 1
y x
. C.
3 1
y x
. D.
3 2
y x
.
Lời giải
Chọn B.
Phương trình tiếp tuyến tại điểm
1; 2
M
có dạng:
1 1 2
y y x
Ta có
2
1 3
2
2
x
y
x
x
;
1 3
y
suy ra
3 1 2 3 1
y x x
.
Câu 39. [2H1-1] Tổng số đỉnh, số cạnh và số mặt của một hình bát diện đều là
A.
24
. B.
26
. C.
52
. D.
20
.
Lời giải
Chọn B.
Số cạnh: 12, số đỉnh: 6, số mặt: 8.
Câu 40. [2D1-4] Cho đồ thị của hàm số
y f x
như hình vẽ dưới đây:
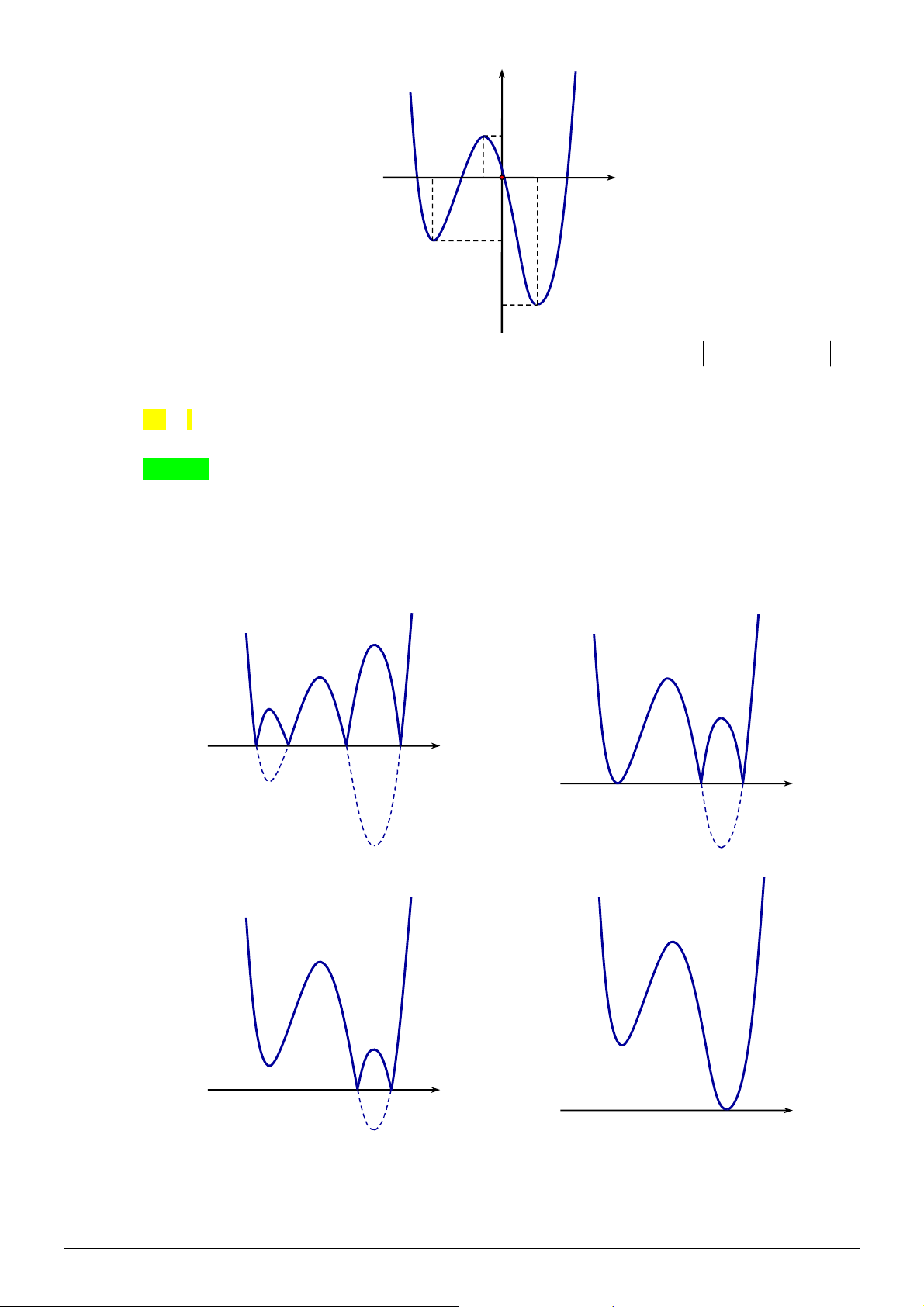
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/25
Gọi
S
là tập hợp các giá trị nguyên dương của tham số
m
để hàm số
2017
y f x m
có
5
điểm cực trị. Tổng tất cả các giá trị của các phần tử của tập
S
bằng
A.
12
. B.
15
. C.
18
. D.
9
.
Lời giải
Chọn A.
Nhận xét: Số giao điểm của
:
C y f x
với
Ox
bằng số giao điểm của
: 2017
C y f x
với
Ox
.
Vì
0
m
nên
: 2017
C y f x m
có được bằng cách tịnh tiến
: 2017
C y f x
lên trên
m
đơn vị.
TH1:
0 3
m
. Đồ thị hàm số có
7
điểm cực trị. Loại.
TH2:
3
m
. Đồ thị hàm số có
5
điểm cực trị. Nhận.
TH3:
3 6
m
. Đồ thị hàm số có
5
điểm cực trị. Nhận.
x
x
TH3:3 6
m
TH4: 6
m
O
x
y
2
3
6
x
x
TH1:0 3
m
TH2: 3
m
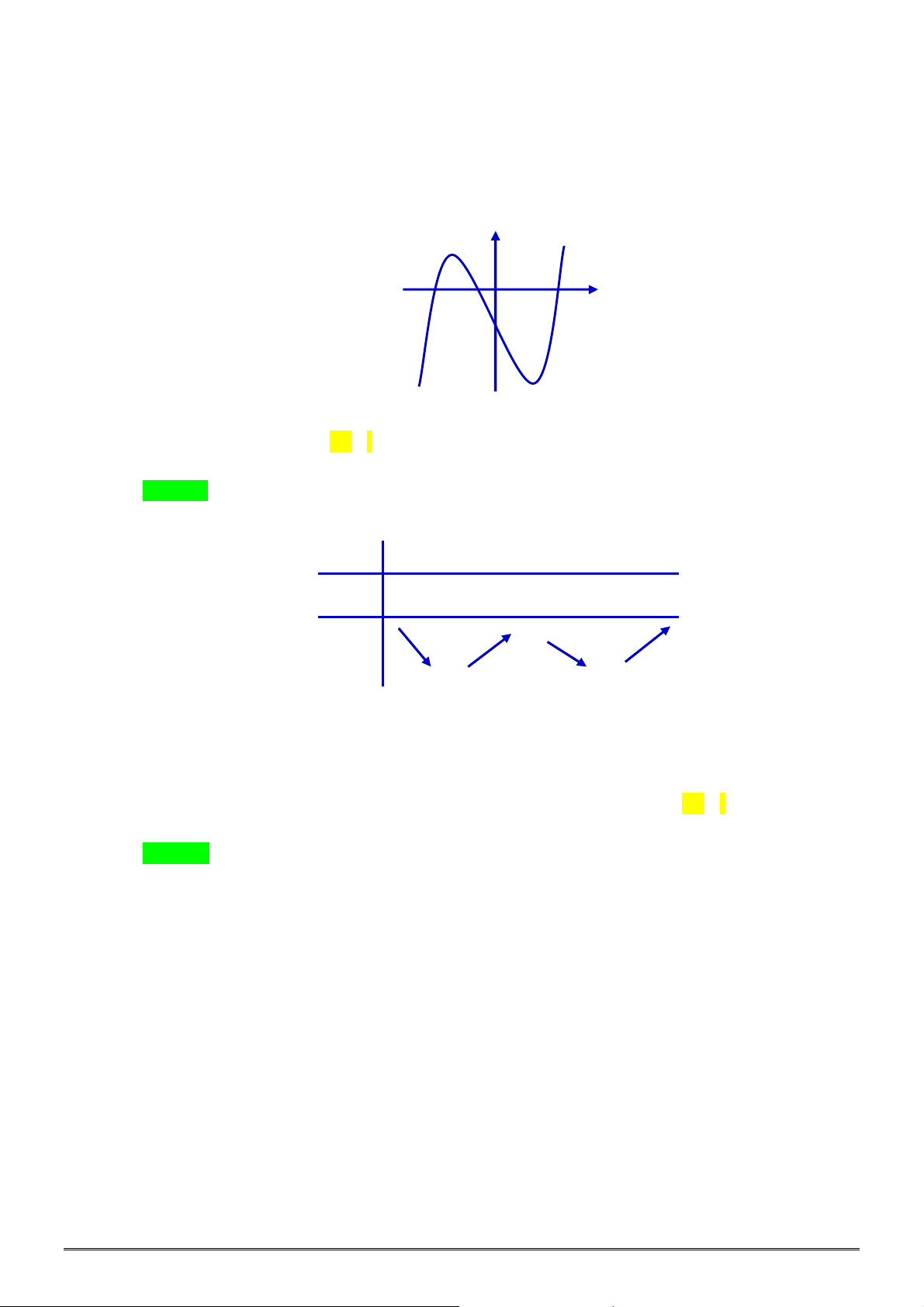
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/25
TH4:
6
m
. Đồ thị hàm số có
3
điểm cực trị. Loại.
Vậy
3 6
m
. Do
*
m
nên
3;4;5
m .
Vậy tổng giá trị tất cả các phần tử của
S
bằng
12
.
Câu 41. [1D1-2] Cho hàm số
y f x
có đạo hàm là hàm số liên tục trên
với đồ thị hàm số
y f x
như hình vẽ.
Biết
0
f a
, hỏi đồ thị hàm số
y f x
cắt trục hoành tại nhiều nhất bao nhiêu điểm?
A.
3
. B.
2
. C.
4
. D.
0
.
Lời giải
Chọn B.
Từ đồ thị hàm số
y f x
, ta có bảng biến thiên:
Do
0
f a
, suy ra
y f x
có thể cắt trục hoành nhiều nhất tại
2
điểm.
Câu 42. [1D1-3] Có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số:
3 2
1 1 2 2
y m x m x x
nghịch biến trên
?
A.
5
. B.
6
. C.
8
. D.
7
.
Lời giải
Chọn D.
Ta có:
2
3 1 2 1 2
y m x m x
.
Để hàm số
3 2
1 1 2 2
y m x m x x
nghịch biến trên
thì
0
y
với
x
x
f x
f x
a
b
c
0
0
0
f a
f b
f c
y
x
O
b
a
c
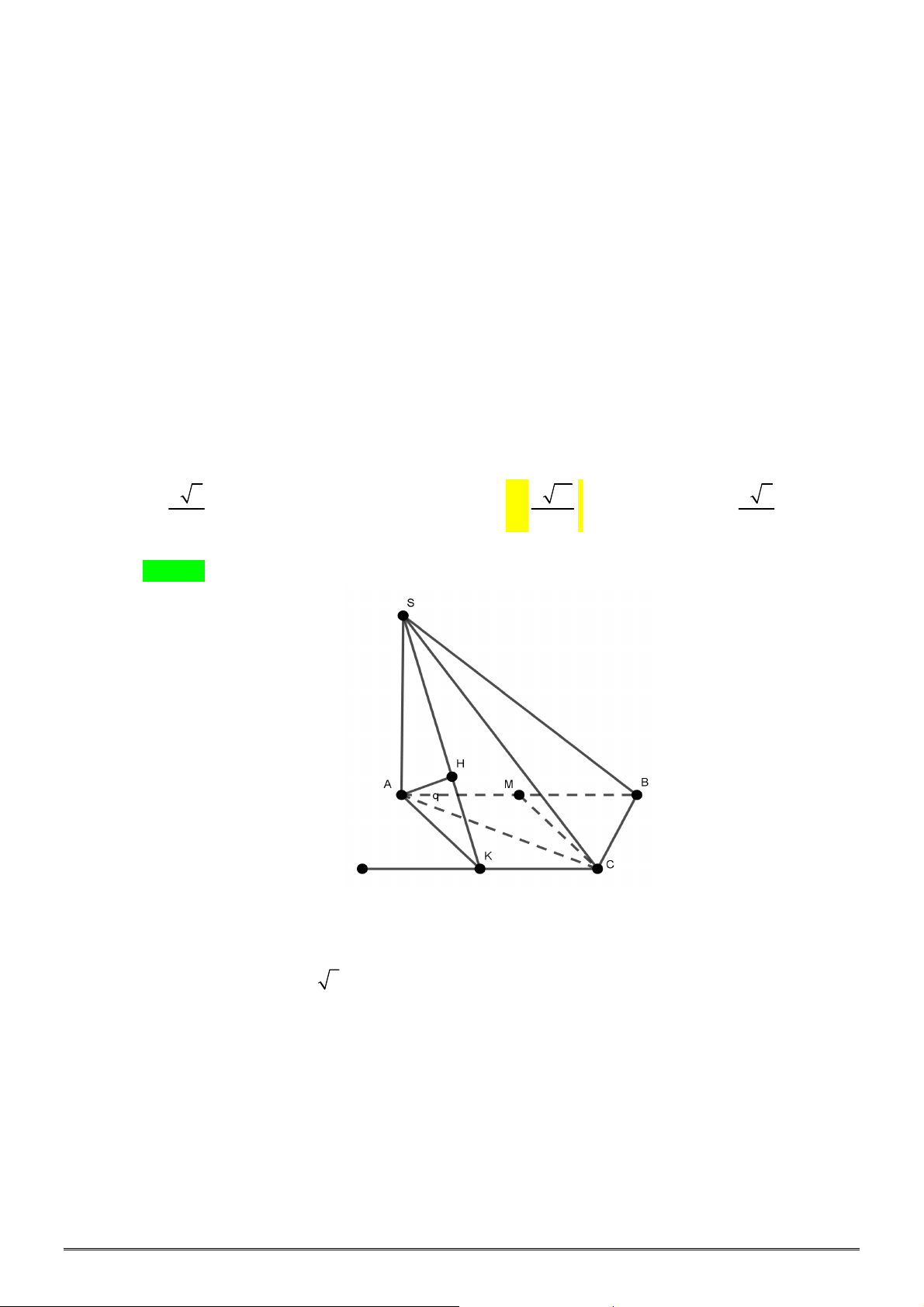
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/25
suy ra:
2
3 1 2 1 2 0
m x m x
với
x
,
0
0
0
0
0
a
bx c
a
a
2
1
2 0
1
8 7 0
/l
m
đ
m
m m
1
7; 1
m
m
. Theo đầu bài:
m
,
7; 6; 5; 4; 3; 2; 1
m
.
Câu 43.
[1H3-5] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA ABC
, góc giữa
đường thẳng
SB
và mặt phẳng
ABC
bằng
60
. Khoảng cách giữa hai đường thẳng
AC
và
SB
bằng
A.
2
2
a
. B.
2
a
. C.
15
5
a
. D.
7
7
a
R .
Lời giải
Chọn C.
SA ABC
AB
là hình chiếu vuông góc của
SB
lên
ABC
, , 60
SB ABC SB AB SBA
.tan60 3
SA AB a
Dựng
d
qua
B
và
//
d AC
Dựng
AK d
tại
K
Dựng
AH SK
tại
H
Ta có:
BK AK
BK SAK
BK SA
BK AH
BK AH
AH SBK
SK AH
,
d A SBK AH

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 23/25
//
//
BK AC
BK SBK AC SBK
AC SBK
, ,
d AC SB d A SBK AH
Gọi
M
là trung điểm
AC
1
BM AC
2
//
BK AK
AK AC
BK AC
1 , 2 //
AK BM
AKBM
là hình bình hành
3
2
a
AK BM
Xét tam giác
SAK
vuông tại
A
ta có:
2 2 2 2
1 1 1 5
3
AH AK SA a
15
5
a
AH
Vậy
15
,
5
a
d AC SB
Câu 44. [2D1-4] Đồ thị hàm số
2
2
1
2
x
y
x x
có tất cả bao nhiêu tiệm cận đứng?
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn C.
Hàm số xác định
2
2
1 0
2 0
x
x x
1;1 \ 0
x
0
lim
x
y
đường thẳng
0
x
là tiệm cận đứng.
1
lim 0
x
y
;
1
lim 0
x
y
Vậy hàm số đã cho có 1 tiệm cận đứng.
Câu 45 – 46_ THPT Chuyên Thái Nguyên_Thọ Bùi
Câu 45. [2D2-2] Cho
0 1
a
,
0
b
thỏa mãn điều kiện
log 0
a
b
. Khẳng định nào sau đây là đúng?
A.
1
0 1
b a
b a
. B.
1
0 1
a b
a b
. C.
0 1
0 1
a b
b a
. D.
0 1
b a
.
Lời giải
Chọn C.
Ta có
log 0 log log 1
a a a
b b . Xét
2
trường hợp:
TH1:
1
a
suy ra
log log 1 1
a a
b b
. Kết hợp điều kiện ta được
0 1
b a
.
TH2:
0 1
a
suy ra
log log 1 1
a a
b b
. Kết hợp điều kiện ta được
0 1
a b
.
Vậy khẳng định đúng là
0 1
0 1
a b
b a
.
Câu 46. [2H2-3] Tính bán kính
R
mặt cầu ngoại tiếp tứ diện đều
ABCD
cạnh
2
a
.
A.
3
R a
. B.
3
2
a
R . C.
3
2
a
R . D.
3 2
2
a
R .
Lời giải
Chọn B.
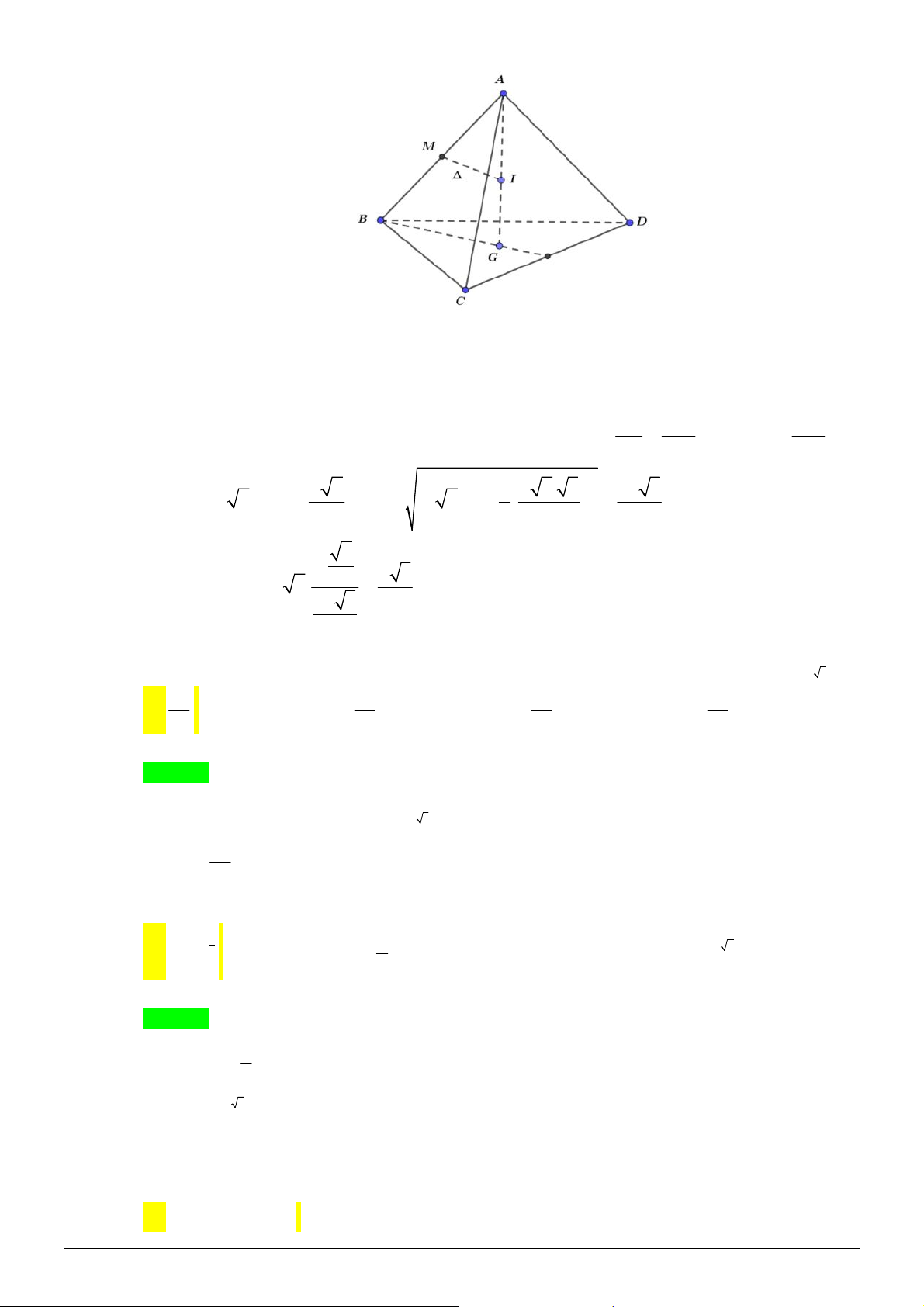
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 24/25
Gọi
G
là trọng tâm
BCD
, ta có
AG BCD
nên
AG
là trục của
BCD
.
Gọi
M
là trung điểm của
AB
. Qua
M
dựng đường thẳng
AB
, gọi
I AG
.
Do đó mặt cầu ngoại tiếp tứ diện
ABCD
có tâm là
I
và bán kính
R IA
.
Ta có
AMI
và
AGB
là hai tam giác vuông đồng dạng nên: .
AI AM AM
AI AB
AB AG AG
.
Do
2
2,
2
a
AB a AM ,
2
2
2 2. 3 2 3
2 .
3 2 3
a a
AG a
.
Khi đó
2
3
2
2.
2
2 3
3
a
a
R AI a
a
.
Câu 47. [2D2-2] Tìm tất cả các giá trị thực của
x
thỏa mãn đẳng thức
3 3 9
3
log 3log 2 log 25 log 3
x .
A.
40
9
. B.
25
9
. C.
28
3
. D.
20
3
.
Lời giải
Chọn A.
Ta có
3 3 9 3 3 3 3
3
40
log 3log 2 log 25 log 3 log 8 log 5 log 9 log
9
x .
Vậy
40
9
x .
Câu 48. [2D2-1] Trong các biểu thức sau, biểu thức nào không có nghĩa?
A.
1
3
4
. B.
0
3
4
. C.
4
3
. D.
2
1
.
Lời giải
Chọn A.
Lũy thừa
0
3
4
và
4
3
có số mũ nguyên âm hoặc bằng
0
thì cơ số phải khác
0
(thỏa mãn).
Lũy thừa
2
1
có số mũ không nguyên thì cơ số phải dương (thỏa mãn).
Lũy thừa
1
3
4
có số mũ không nguyên thì cơ số phải dương (không thỏa mãn).
Câu 49. [2D2-1] Cho
0 1
a
và
.
b
Chọn mệnh đề sai trong các mệnh đề sau:
A.
2
log 2log
a a
b b
. B. log
b
a
a b
. C.
log 1 0
a
. D.
log 1
a
a
.
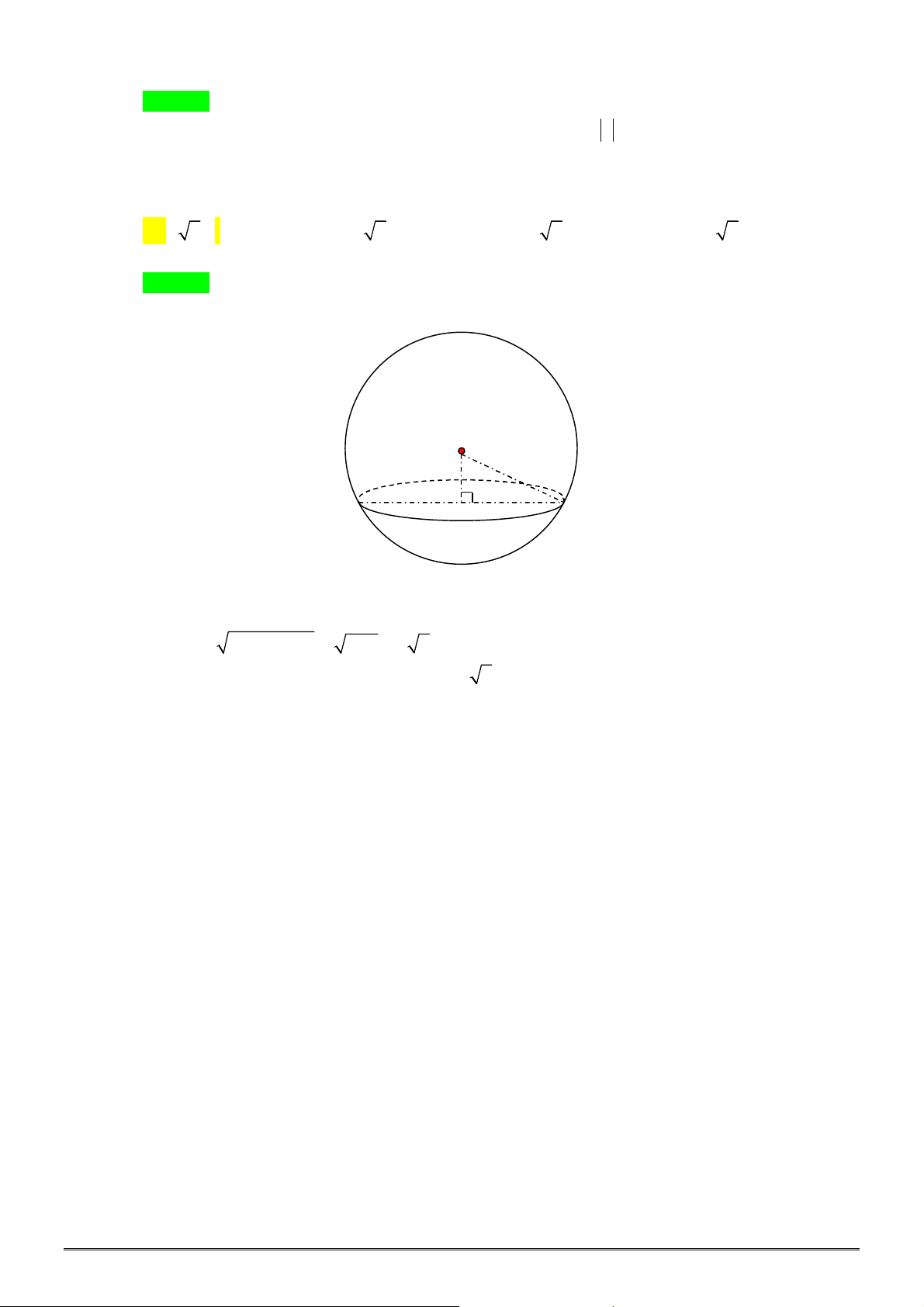
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 25/25
Lời giải
Chọn A.
Do
b
nên
b
chưa biết rõ về dấu, vì vậy:
2
log 2log .
a a
b b
Câu 50. [2H2-2] Cho mặt cầu tâm
,
O
bán kính
3.
R
Mặt phẳng
P
nằm cách tâm
O
một khoảng
bằng
1
và cắt mặt cầu theo một đường tròn có chu vi bằng
A.
4 2
. B.
6 2
. C.
3 2
. D.
8 2
.
Lời giải
Chọn A.
Mặt phẳng
P
cắt mặt cầu tâm
O
theo một đường tròn tâm
H
và bán kính
.
r HA
Ta có
, 1
OH d O P
;
3.
OA R
Áp dụng định lý Pytago cho tam giác vuông
HOA
ta có
2 2
9 1 2 2.
r HA OA OH
Vậy chu vi đường tròn thiết diện là
2 4 2 .
r
A
3
R
O
H
r

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/21
TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI
TRƯỜNG THPT CHUYÊN
ĐỀ KIỂM TRA HỌC KÌ 1 LỚP 12
NĂM HỌC 2017-2018 - MÔN: TOÁN
Thời gian làm bài 90 phút
Họ và tên thí sinh:...............................SBD:...........
Mã đề thi 485
Câu 1. [2H2-2] Cho hình nón đỉnh
S
có đường cao bằng
6 cm
, bán kính đáy bằng
10 cm
. Trên
đường tròn đáy lấy hai điểm
A
,
B
sao cho
12 cm
AB . Diện tích tam giác
SAB
bằng:
A.
2
100 cm
. B.
2
48 cm
. C.
2
40 cm
. D.
2
60 cm
.
Câu 2. [2H2-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành và có thể tích bằng
1
. Trên
SC
lấy điểm
E
sao cho
2
SE EC
. Tính thể tích
V
của khối tứ diện
SEBD
.
A.
1
3
V
. B.
2
3
V
. C.
1
6
V
. D.
1
12
V
.
Câu 3. [2D2-1] Cho
2
log 3
a
. Hãy tính
4
log 54
theo
a
.
A.
4
1
log 54 1 3
2
a
. B.
4
1
log 54 1 6
2
a
.
C.
4
1
log 54 1 12
2
a
. D.
4
log 54 2 1 6
a
.
Câu 4. [2D2-2] Giải bất phương trình
10 3 10 3
x
có kết quả là
A.
1
x
. B.
1
x
.
C.
1
x
. D.
1
x
.
Câu 5. [2D1-2] Đồ thị dưới đây là của hàm số nào?
A.
2 1
1
x
y
x
. B.
2 5
1
x
y
x
.
C.
2
1
x
y
x
. D.
2 1
1
x
y
x
.
Câu 6. [2D2-2] Phương trình
2 1
3 4.3 1 0
x x
có hai nghiệm
1
x
,
2
x
trong đó
1 2
x x
, chọn phát biểu đúng.
A.
1 2
1
x x
. B.
1 2
2 0
x x
. C.
1 2
2 1
x x
. D.
1 2
2
x x
.
Câu 7. [2D1-1] Tính đạo hàm của hàm số
ln
y x x
.
A.
ln 1
y x
. B.
ln
y x
. C. .
ln 1
y x
. D.
1
x
.
Câu 8. [2D1-2] Các điểm cực đại của hàm số
sin2
y x x
là
A. ,
6
x k k
. B. ,
6
x k k
.
C. ,
6
x k k
. D. 2 ,
3
x k k
.
Câu 9. [2H1-2] Cho hình chóp
.
S ABC
có
SA ABC
, tam giác
ABC
vuông tại .
A
., biết
3
BC a
,
AB a
. Góc giữa mặt phẳng
SBC
và
ABC
bằng
45
. Tính thể tích khối chóp
.
S ABC
theo
a
.
A.
3
.
4
9
S ABC
a
V . B.
3
.
2
6
S ABC
a
V . C.
3
.
2
2
S ABC
a
V . D.
3
.
2
9
S ABC
a
V .
O
x
y
1
1
2
9
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/21
Câu 10. [2H2-1] Khối nón có chiều cao
3 cm
h
và bán kính đáy
2 cm
r
thì thể tích bằng:
A.
2
16 cm
. B.
2
4 cm
. C.
3
4
cm
3
. D. .
3
4 cm
.
Câu 11. [2D1-2] Giá trị nhỏ nhất của số thực
m
để hàm số
3 2
1
3
y x mx mx m
đồng biến trên
là
A.
2
m
. B.
1
m
. C.
1
m
. D.
0
m
.
Câu 12. [2D2-1] Giải phương trình
2
6
log 2
x
được kết quả là.
A.
36
x . B.
6
x
. C.
6
x
. D.
6
x
.
Câu 13. [2H1-1] Cho lăng trụ tứ giác đều
.
ABCD A B C D
có đáy là hình vuông cạnh
a
,
3
AA a
.
Thể tích khối lăng trụ đã cho là
A.
3
12
a
. B.
3
a
. C.
3
6
a
. D.
3
3
a
.
Câu 14. [2H1-1] Khối chóp ngũ giác có số cạnh là
A.
20
. B.
15
. C.
5
. D.
10
.
Câu 15. [2D1-3] Tìm các giá trị thực của tham số
m
sao cho phương trình
3
3 4 1 0
x x m
có ít
nhất
1
nghiệm thực trong đoạn
3;4
?
A.
51 19
4 4
m . B.
51 19
4 4
m . C.
51 19
m
. D.
51 19
m
.
Câu 16. [2D1-3] Giá trị lớn nhất của hàm số
1
2
mx
f x
x m
trên đoạn
3;5
bằng
2
khi và chỉ khi:
A.
7
m
. B.
7;13
m . C.
m
. D.
13
m
.
Câu 17. [2H1-3] Cho hình chóp
.
S ABC
có
SA a
,
SB b
,
SC c
, và
60
ASB BSC CSA
. Tính
thể tích khối chóp
.
S ABC
theo
a
,
b
,
c
.
A.
2
12
abc
. B.
2
12
abc
. C. .
2
4
abc
. D.
2
4
abc
.
Câu 18. [2D1-2] Giá trị nhỏ nhất của hàm số:
2
. 1
y x x
là
A.
2
. B.
1
. C.
1
. D.
1
2
.
Câu 19. [2D1-2] Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2sin cos 1
y x x
. Tích
.
M m
bằng
A.
25
.
4
B.
25
.
8
C.
2.
D.
0.
Câu 20. [2H1-1] Khối đa diện đều loại
4;3
có số đỉnh, số cạnh và số mặt lần lượt là
A.
6
,
12
,
8
. B.
8
,
12
,
6
. C.
12
,
30
,
20
. D.
4
,
6
,
4
.
Câu 21. [2D2-1] Cho bất phương trình
1 1
5 5
log log
f x g x
. Khi đó bất phương trình tương đương
A.
f x g x
. B.
0
g x f x
.
C.
0
g x f x
. D.
f x g x
.
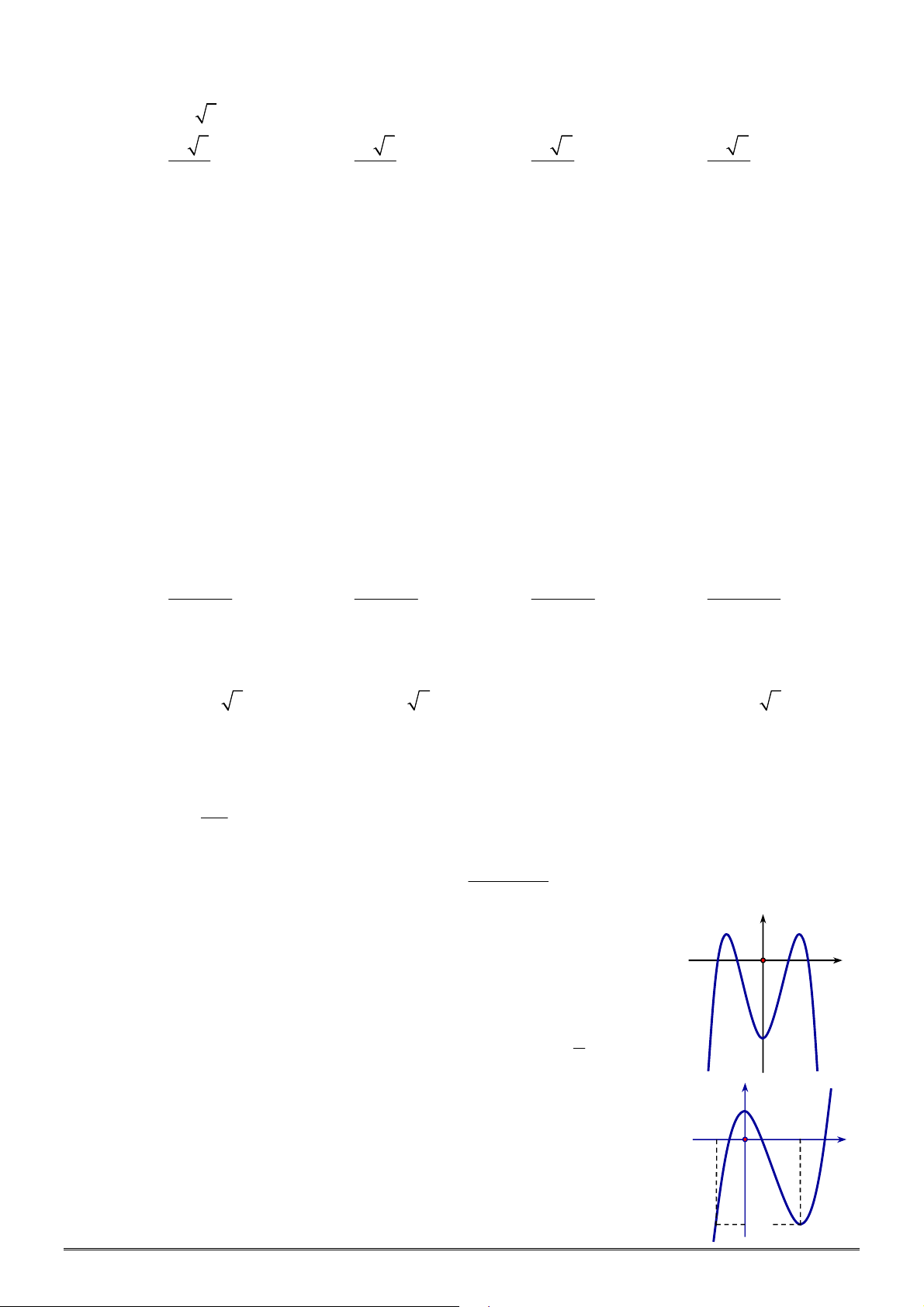
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/21
Câu 22. [2H1-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA ABCD
và
3
SA a
. Thể tích của khối chóp
.
S ABCD
là
A.
3
3
3
a
. B.
3
3
6
a
. C.
3
2
3
a
. D.
3
2
6
a
.
Câu 23. [2D2-1] Cho các số thực
x
,
y
và
a
thỏa mãn
x y
;
1
a
. Khi đó:
A.
x y
a a
. B.
x y
a a
. C.
x y
a a
. D.
x y
a a
.
Câu 24. [2D2-2] Ông An gửi số tiền
100
triệu đồng vào ngân hàng với lãi suất
7%
trên .
1
. năm, biết
rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn
ban đầu. Sau thời gian
10
năm nếu không rút lãi lần nào thì số tiền mà ông An nhận được tính
cả gốc lẫn lãi là (đơn vị là đồng):
A.
10
8
10 . 1 0,0007
. B. .
10
8
10 . 1 0,07
. C.
8 10
10 .0,07
. D.
10
8
10 . 1 0,7
.
Câu 25. [2D2-1] Giải phương trình
3
log 1 2
x
.
A.
8
. B.
10
. C.
7
. D.
9
.
Câu 26. [2D2-3] Số chữ số của só tự nhiên
2017
3
N là
A.
962
. B.
964
. C.
961
. D.
963
.
Câu 27. [2H1-2] Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, góc tạo bởi mặt bên và mặt
đáy là
. Thể tích khối chóp
.
S ABCD
là:
A.
3
.tan
2
a
. B.
3
.tan
3
a
. C.
3
.tan
6
a
. D.
3
2 .tan
3
a
.
Câu 28. [2D1-2] Giả sử
A
và
B
là các giao điểm của đường cong
3
3 2
y x x
và trục hoành. Tính
độ dài đoạn thẳng
AB
.
A.
6 5
AB . B.
4 2
AB
. C.
3
AB
. D.
5 3
AB .
Câu 29. [2D1-3] Cho hàm số
3 2
2 1
y x mx
có đồ thị
.
m
C Tìm
m
sao cho
m
C
cắt đường thẳng
: 1
d y x
tại ba điểm phân biệt có hoành độ
1 2 3
, ,
x x x
thỏa mãn
1 2 3
101.
x x x
A.
101
.
2
m B.
50.
m
C.
51.
m
D.
49.
m
Câu 30. [2D1-2] Số tiệm cận của đồ thị hàm số
2
2
6 3
3 2
x x
y
x x
là?
A.
6.
B.
2.
C.
1.
D.
3.
Câu 31. [2D1-2] Đồ thị bên là đồ thị của hàm số nào?
A.
4 2
4 3
y x x
. B.
4 2
3 3
y x x
.
C.
4 2
2 3
y x x
. D.
4 2
1
3 3
4
y x x
.
Câu 32. [2D1-3] Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình bên.
Hỏi phương trình
3 2
2 0
ax bx cx d
có bao nhiêu nghiệm?
A. Phương trình có đúng một nghiệm.
B. Phương trình có đúng hai nghiệm.
C. Phương trình khôngg có nghiệm.
D. Phương trình có đúng ba nghiệm.
O
x
y
3
1
1
x
y
1
1
2
3
O
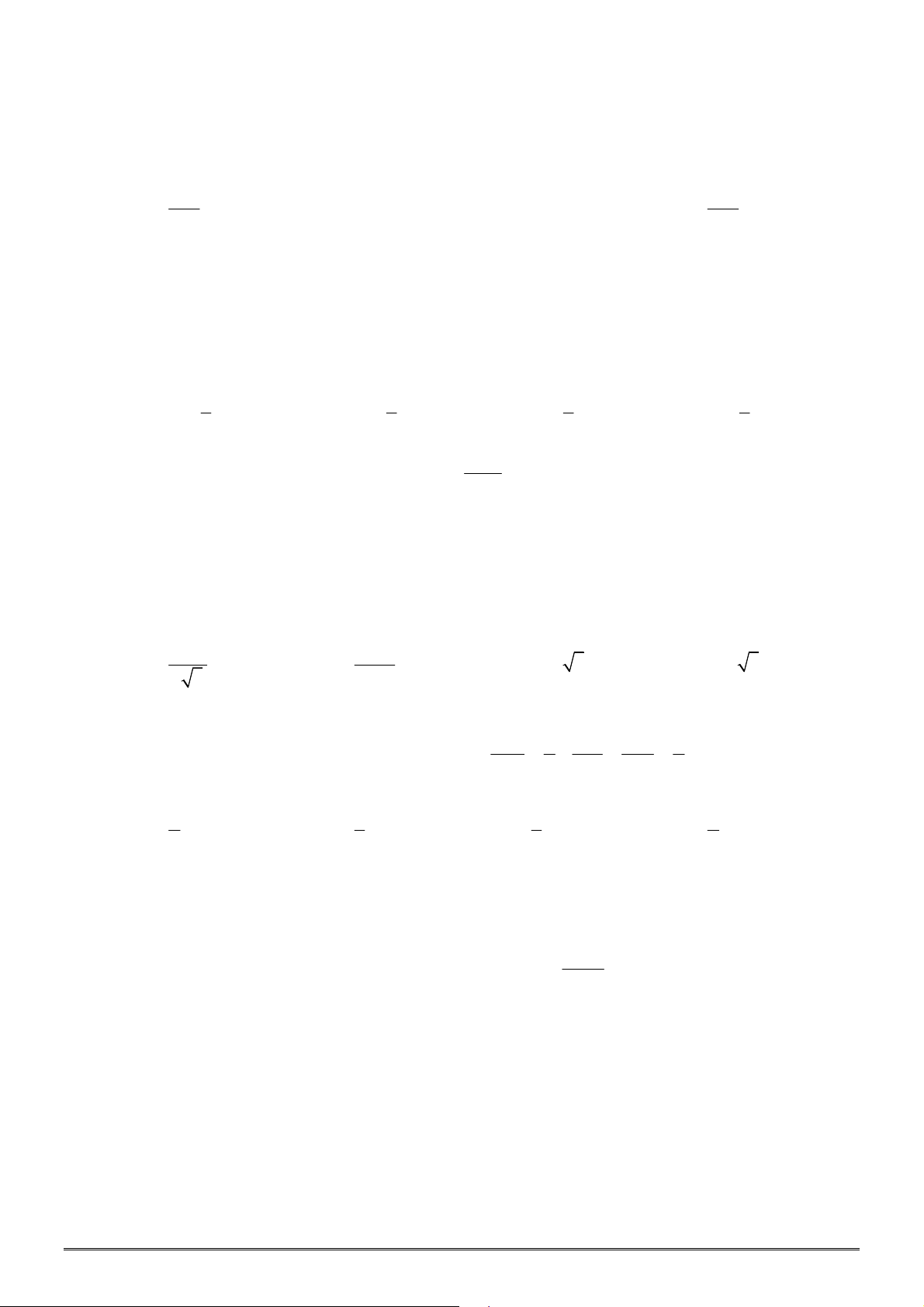
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/21
Câu 33. [2D2-2]Phương trình
2
log log 2 0
x x
có bao nhiêu nghiệm?
A.
1.
B.
2.
C.
3.
D.
0.
Câu 34. [2H2-2]Cho lăng trụ tam giác đều có tất cả các cạnh bằng
a
.Một hình trụ tròn xoay có hai đáy
là hai hình tròn ngoại tiếp hai đáy của lăng trụ.Thể tích của khối trụ tròn xoay bằng:
A.
3
.
9
a
B.
3
.
a
C.
3
3 .
a
D.
3
.
3
a
Câu 35. [2H2-1] Cho hình trụ
T
có độ dài đường sinh
l
, bán kính đáy
r
. Ký hiệu
xq
S
là diện tích
xung quanh của
T
. Công thức nào sau đây là đúng?
A.
3
xq
S rl
. B. 2
xq
S rl
. C.
xq
S rl
. D.
2
2
xq
S r l
.
Câu 36. [2D1-2] Điều kiện cần và đủ của tham số
m
để hàm số
3 2
5
y x x mx
có cực trị là
A.
1
3
m
. B.
1
3
m
. C.
1
3
m
. D.
1
3
m
.
Câu 37. [2D2-1] Tập xác định của hàm số
2
3
log
2
x
y
x
là:
A.
3; 2
. B.
; 3 2;
.
C.
\ 2
. D.
3; 2
.
Câu 38. [2H2-2] Cho hình chóp
.
S ABC
có tam giác
ABC
đều cạnh
3cm
a
,
SA ABC
và
2
SA a
. Tính thể tích khối cầu ngoại tiếp hình chóp
.
S ABC
.
A.
3
3
8
cm
3 3
a
. B.
3
3
4
cm
3
a
. C.
3
32 3cm
. D.
3
16 3cm
.
Câu 39. [2H1-3] Cho hình lăng trụ đứng
.
ABCD A B C D
có thể tích bằng
V
. Các điểm
M
,
N
,
P
lần
lượt thuộc các cạnh
AA
,
BB
,
CC
sao cho
1
2
AM
AA
,
3
4
BN CP
BB CC
. Thể tích khối đa diện
.
ABC MNP
bằng
A.
2
3
V
. B.
1
8
V
. C.
1
3
V
. D.
1
2
V
.
Câu 40. [2H2-2] Tìm nghiệm của phương trình:
log 4 3 2
x
x
.
A.
1
x
. B.
4
x
. C.
x
. D.
1; 4
x
.
Câu 41. [2D1-2] Với giá trị nào của số thực
m
thì hàm số
1
x m
y
x
đồng biến trên từng khoảng xác
định?
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Câu 42. [2H2-1] Khối cầu có bán kính
3 cm
thì có thể tích là
A.
3
9 cm
. B.
3
12 cm
.
C.
3
36 cm
. D.
3
27 cm
.
Câu 43. [2D2-1] Nghiệm của phương trình
2
5 125
x
là
A.
1
x
. B.
5
x
. C.
3
x
. D.
1
x
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/21
Câu 44. [2H1-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
,
30
ABC
. Tam giác
SBC
là tam giác đều cạnh
a
và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp
.
S ABC
là:
A.
3
16
a
. B.
3
3 3
16
a
. C.
3
3
16
a
. D.
3
3
16
a
.
Câu 45. [2D1-2] Gọi
1
y
,
2
y
lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số
4 2
10 9
y x x
.
Khi đó
1 2
y y
bằng:
A.
7
. B.
2 5
. C.
25
. D.
9
.
Câu 46. [2D2-2] Giá trị nhỏ nhất của hàm số
2
e 3e 1
x x
y
trên đoạn
ln2;ln5
là:
A.
2
e
. B.
9
. C.
9
e
. D.
39
.
Câu 47. [2D2-2]
3
7
1
log
a
a
0; 1
a a
bằng
A.
3
7
. B.
7
3
. C.
3
7
. D.
7
3
.
Câu 48. [2D1-1] Tiệm cận đứng của đồ thị hàm số
2 3
7
x
y
x
có phương trình là
A.
7
y
. B.
2
y
. C.
7
x
. D.
2
x
.
Câu 49. [2D2-1] Cho hàm số
3 1
1
x
y
x
. Chọn khẳng định đúng.
A. Hàm số đồng biến trên khoảng
;1 1;
.
B. Hàm số nghịch biến trên từng khoảng xác định của nó.
C. Hàm số đồng biến trên
.
D. Hàm số nghịch biến trên
.
Câu 50. [2D2-1] Tập xác định của hàm số hàm số
1
2
2 1
y x
là
A.
1
;
2
. B.
1
\
2
. C.
1
;
2
. D.
.
----------HẾT----------
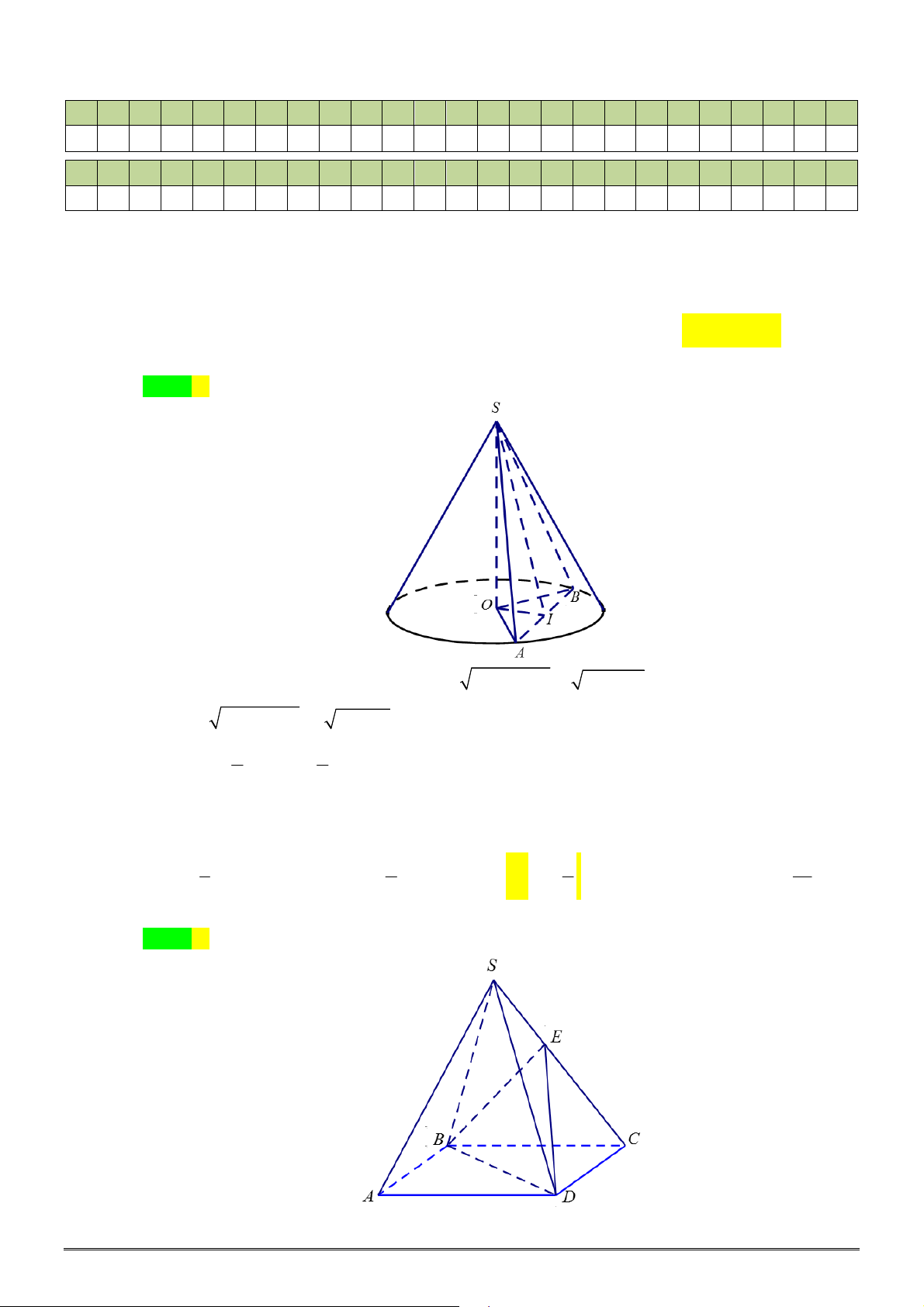
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/21
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
C A
C D
C A
B A
D
C B
D
D
A
A
B D
D
B C A
C B B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
C C A
D
A
D
B D
B B D
C
A
C A
C A
A
C B D
C B C
HƯỚNG DẪN GIẢI
Câu 1. [2H2-2] Cho hình nón đỉnh
S
có đường cao bằng
6 cm
, bán kính đáy bằng
10 cm
. Trên
đường tròn đáy lấy hai điểm
A
,
B
sao cho
12 cm
AB . Diện tích tam giác
SAB
bằng:
A.
2
100 cm
. B.
2
48 cm
. C.
2
40 cm
. D.
2
60 cm
.
Lời giải
Chọn D.
Gọi
I
là trung điểm của
AB
. Ta có
2 2
OI OA AI
100 36
8
cm
.
2 2
SI SO OI
.
36 64
10
cm
.
Vậy
1
.
2
SAB
S SI AB
.
1
10.12
2
.
2
60 cm
.
Câu 2. [2H2-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành và có thể tích bằng
1
. Trên
SC
lấy điểm
E
sao cho
2
SE EC
. Tính thể tích
V
của khối tứ diện
SEBD
.
A.
1
3
V
. B.
2
3
V
. C.
1
6
V
. D.
1
12
V
.
Lời giải
Chọn C.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/21
Vì .
ABCD
. là hình bình hành nên ta có
. .
1 1
2 2
S ABD S ABCD
V V
, mà
.
.
1
3
S EBD
S CBD
V
SE
V SC
.
Từ đó suy ra
. .
1 1
3 6
S EBD S CBD
V V
.
Câu 3. [2D2-1] Cho
2
log 3
a
. Hãy tính
4
log 54
theo
a
.
A.
4
1
log 54 1 3
2
a
. B.
4
1
log 54 1 6
2
a
.
C.
4
1
log 54 1 12
2
a
. D.
4
log 54 2 1 6
a
.
Lời giải
Chọn A.
Ta có:
4 2 2 2 2
1 1 1
log 54 log 2.27 log 2 log 27 1 3log 3
2 2 2
.
Vậy
4
1
log 54 1 3
2
a
.
Câu 4. [2D2-2] Giải bất phương trình
10 3 10 3
x
có kết quả là
A.
1
x
. B.
1
x
. C.
1
x
. D.
1
x
.
Lời giải
Chọn C.
Ta có:
1
10 3 10 3 10 3 10 3 1
x x
x
.
Câu 5. [2D1-2] Đồ thị dưới đây là của hàm số nào?
A.
2 1
1
x
y
x
. B.
2 5
1
x
y
x
. C.
2
1
x
y
x
. D.
2 1
1
x
y
x
.
Lời giải
Chọn D.
Ta thấy đồ thị hàm số trên hình vẽ có tiệm cận đứng
1
x
và tiệm cận ngang là nên hàm số
thoả mãn là ở đáp án B hoặc D.
Mặt khác đồ thị trên hình vẽ cắt trục hoành tại điểm có tung độ nhỏ hơn
2
nên đáp án đúng là
D.
Câu 6. [2D2-2] Phương trình
2 1
3 4.3 1 0
x x
có hai nghiệm
1
x
,
2
x
trong đó
1 2
x x
, chọn phát biểu
đúng.
A.
1 2
1
x x
. B.
1 2
2 0
x x
. C.
1 2
2 1
x x
. D.
1 2
2
x x
.
Lời giải
Chọn C.
O
x
y
1
1
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/21
Ta có
2 1
3 4.3 1 0
x x
2
3. 3 4.3 1 0
x x
3 1
1
3
3
x
x
0
1
x
x
.
Vậy
1
1
x
,
2
0
x
1 2
2 1
x x
.
Câu 7. [2D1-1] Tính đạo hàm của hàm số
ln
y x x
.
A.
ln 1
y x
. B.
ln
y x
. C. .
ln 1
y x
. D.
1
x
.
Lời giải
Chọn A.
1
ln . ln 1
y x x x
x
.
Câu 8. [2D1-2] Các điểm cực đại của hàm số
sin2
y x x
là
A. ,
6
x k k
. B. ,
6
x k k
.
C. ,
6
x k k
. D. 2 ,
3
x k k
.
Lời giải
Chọn B.
sin2 1 2cos2 ; 4sin 2
y x x y x y x
.
1
6
0 1 2cos2 0 cos 2 ,
2
6
x k
y x x k
x k
3
4sin 2 4sin 4 2 3 0
6 3 3 2
y k k
6
x k
là điểm cực tiểu của hàm số đã cho.
3
4sin 2 4sin 4 2 3 0
6 3 3 2
y k k
6
x k
là điểm cực đại của hàm số đã cho.
Câu 9. [2H1-2] Cho hình chóp
.
S ABC
có
SA ABC
, tam giác
ABC
vuông tại .
A
., biết
3
BC a
,
AB a
. Góc giữa mặt phẳng
SBC
và
ABC
bằng
45
. Tính thể tích khối chóp
.
S ABC
theo
a
.
A.
3
.
4
9
S ABC
a
V . B.
3
.
2
6
S ABC
a
V . C.
3
.
2
2
S ABC
a
V . D.
3
.
2
9
S ABC
a
V .
Lời giải
Chọn A.
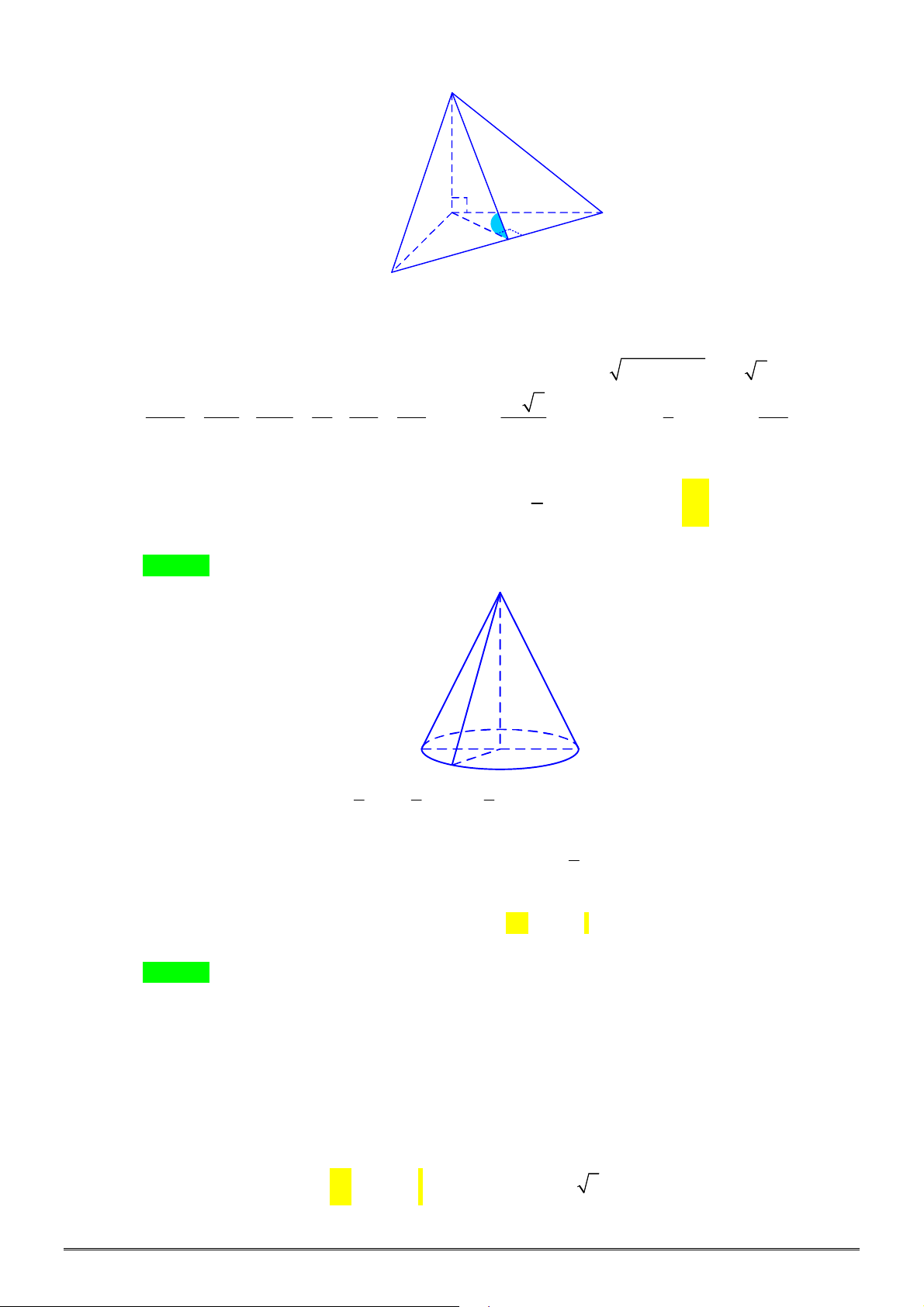
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/21
S
A
B
C
45
H
Kẻ
AH BC
. Vì
SA ABC
nên
SA AH
,
SH BC
. Do đó góc giữa mặt phẳng
SBC
và
ABC
là
45
SHA
và tam giác
SAH
vuông cân tại
A
suy ra
SA AH
.
Xét tam giác
ABC
vuông tại
A
, có
3
BC a
,
AB a
:
2 2
2 2
AC BC AB a
,
2 2 2 2 2 2
1 1 1 1 1 9
8 8
AH AB AC a a a
2 2
3
a
AH SA
.
3
.
1 4
.
3 9
S ABC ABC
a
V SA S
.
Câu 10. [2H2-1] Khối nón có chiều cao
3 cm
h
và bán kính đáy
2 cm
r
thì thể tích bằng:
A.
2
16 cm
. B.
2
4 cm
. C.
3
4
cm
3
. D. .
3
4 cm
.
Lời giải
Chọn D.
S
O
h
r
Ta có thể tích hình nón
2 2 3
1 1 1
. . .2 .3 4 cm
3 3 3
V B h r h
.
Câu 11. [2D1-2] Giá trị nhỏ nhất của số thực
m
để hàm số
3 2
1
3
y x mx mx m
đồng biến trên
là
A.
2
m
. B.
1
m
. C.
1
m
. D.
0
m
.
Lời giải
Chọn C.
.
2
2
y x mx m
.
Hàm số đồng biến trên
.
0,y x
2
2 0,x mx m x
2
0
0 1 0
0
a
m m m
.
Vậy giá trị nhỏ nhất của
m
cần tìm là:
1
m
Câu 12. [2D2-1] Giải phương trình
2
6
log 2
x
được kết quả là.
A.
36
x . B.
6
x
. C.
6
x
. D.
6
x
.
Lời giải
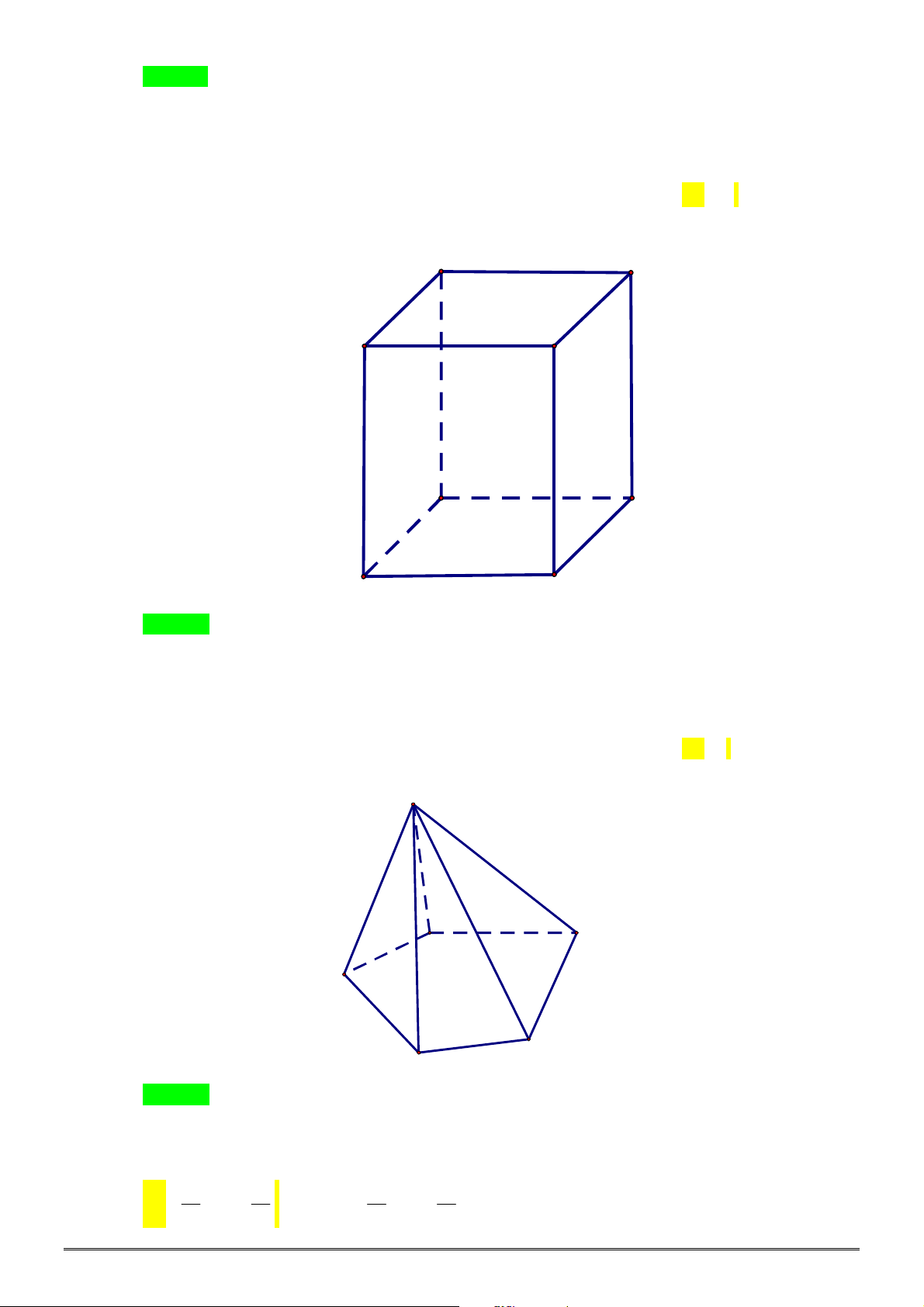
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/21
Chọn B.
2
6
log 2
x
2 2
6 6
x x
.
Câu 13. [2H1-1] Cho lăng trụ tứ giác đều
.
ABCD A B C D
có đáy là hình vuông cạnh
a
,
3
AA a
.
Thể tích khối lăng trụ đã cho là
A.
3
12
a
. B.
3
a
. C.
3
6
a
. D.
3
3
a
.
Lời giải
B
C
A
D
A'
D'
C'
B'
Chọn D.
Lăng trụ trên có chiều cao
3
AA a
, Diện tích đáy là
2
ABCD
S S a
Thể tích của khối lăng trụ
.
ABCD A B C D
là
2 3
. 3 . 3
ABCD
V AA S a a a
.
Câu 14. [2H1-1] Khối chóp ngũ giác có số cạnh là
A.
20
. B.
15
. C.
5
. D.
10
.
Lời giải
E
D
A
B
C
S
Chọn D.
Câu 15. [2D1-3] Tìm các giá trị thực của tham số
m
sao cho phương trình
3
3 4 1 0
x x m
có ít
nhất
1
nghiệm thực trong đoạn
3;4
?
A.
51 19
4 4
m . B.
51 19
4 4
m . C.
51 19
m
. D.
51 19
m
.
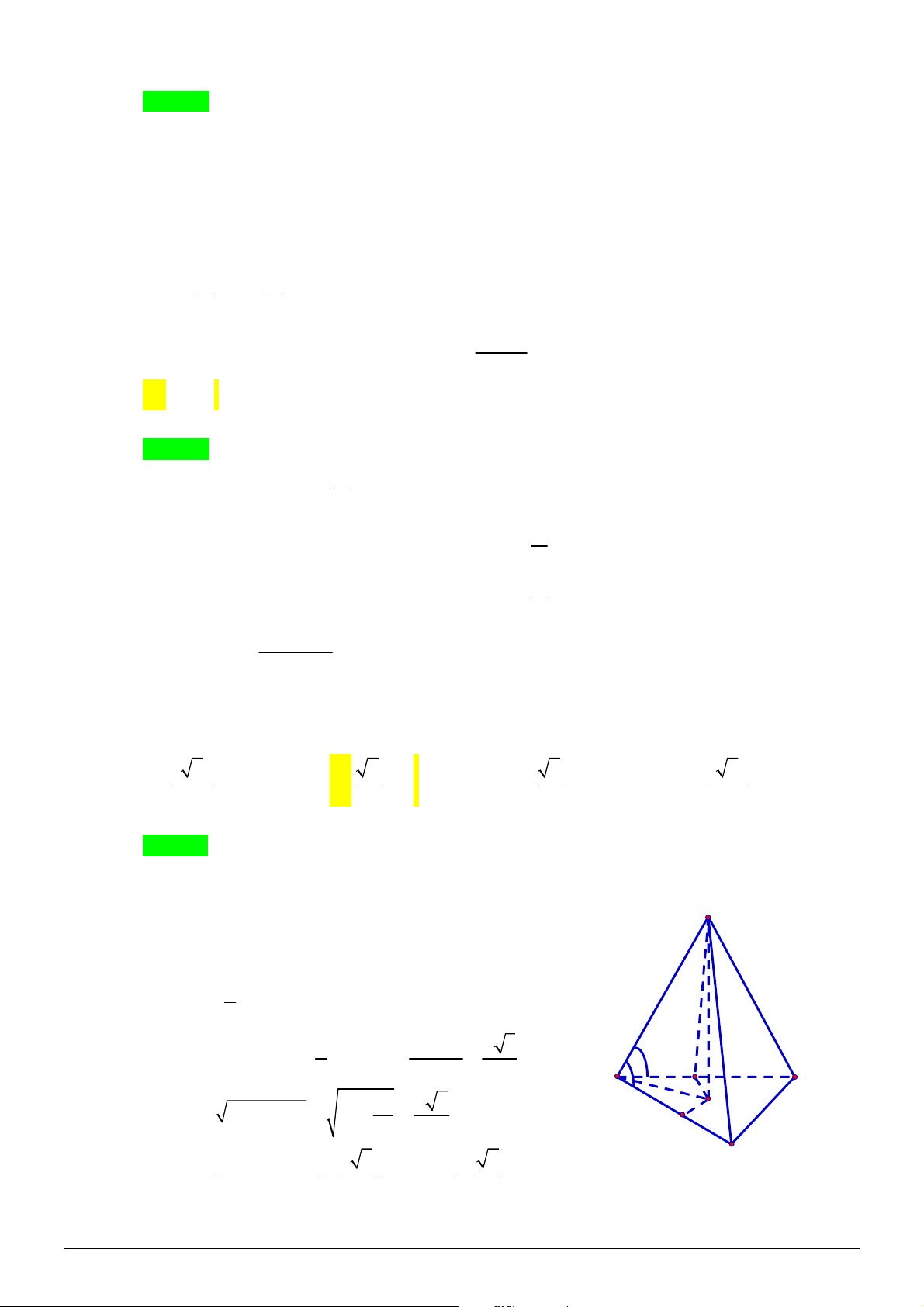
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/21
Lời giải
Chọn A.
Ta có phương trình
3 3
3 4 1 0 4 3 1
x x m m x x
.
1
Đặt
3
3 1
f x x x
.
Phương trình
1
có ít nhất
1
nghiệm thực trong đoạn
3;4
thì
3;4
3;4
min 4 max
f x m f x
.
Do
2
3 3 0
f x x
có hai nghiệm
1 3;4
x nên
3;4
min 51
f x
,
3;4
max 19
f x
.
Vậy
51 19
4 4
m .
Câu 16. [2D1-3] Giá trị lớn nhất của hàm số
1
2
mx
f x
x m
trên đoạn
3;5
bằng
2
khi và chỉ khi:
A.
7
m
. B.
7;13
m . C.
m
. D.
13
m
.
Lời giải
Chọn A.
Tập xác định: \
2
m
D
.
Để hàm số có giá trị lớn nhất trên đoạn
3;5
thì
5
10
2
6
3
2
m
m
m m
.
Ta có .
2
2
2
0
2
m
f x
x m
.,
3;5
x nên
3;5
max 2 5 2 7
f x f m
(thỏa đk).
Câu 17. [2H1-3] Cho hình chóp
.
S ABC
có
SA a
,
SB b
,
SC c
, và
60
ASB BSC CSA
. Tính
thể tích khối chóp
.
S ABC
theo
a
,
b
,
c
.
A.
2
12
abc
. B.
2
12
abc
. C. .
2
4
abc
. D.
2
4
abc
.
Lời giải
Chọn B.
Gọi
H
là chân đường cao hạ từ
A
xuống mặt phẳng
SBC
,
kẻ
HK SB
,
HI SC
.
AK SB
,
AI SC
.
Ta có:
SAK SAI
vì
90
K I
,
60
ASK ASI
,
SA
chung.
SK SI
,
SHK SHI
1
30
2
HSK BSC
.
Mà .cos60
2
a
SK SA
,
3
cos30 3
SK a
SH
.
2
2 2 2
6
3 3
a a
AH SA SH a .
Vậy
1 1 6 sin 60 2
. .
3 3 3 2 12
SBC
a bc
V AH S abc
.
c
S
B
C
A
H
I
K
a
b
60

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/21
Câu 18. [2D1-2] Giá trị nhỏ nhất của hàm số:
2
. 1
y x x
là
A.
2
. B.
1
. C.
1
. D.
1
2
.
Lời giải
Chọn D.
TXĐ:
1; 1
D .
Ta có: .
2 2
2
2 2
1 2
1
1 1
x x
y x
x x
.
Xét
2
2
1 2 2
0 0
2
1
x
y x
x
.
Ta có:
1 0
f
,
2 1
2 2
f
,
2 1
2 2
f
. Vậy
1; 1
1
min
2
y
.
Câu 19. [2D1-2] Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2sin cos 1
y x x
. Tích
.
M m
bằng
A.
25
.
4
B.
25
.
8
C.
2.
D.
0.
Lời giải
Chọn D.
Cách 1: Ta có:
2
2sin cos 1
y x x
2
2cos cos 3
x x
Đặt
cos
t x
,
1;1
t , ta có hàm số
2
2 3
g t t t
Xét hàm số
g t
trên , ta có:
4 1
g t t
1
0 .
4
g t t
Khi đó:
1 2
g
,
1 25
4 8
g
,
1 0
g
.
Vậy
25
8
M và
0
m
, suy ra
. 0
M m
.
Cách 2: Sử dụng chức năng Table của casio.
Câu 20. [2H1-1] Khối đa diện đều loại
4;3
có số đỉnh, số cạnh và số mặt lần lượt là
A.
6
,
12
,
8
. B.
8
,
12
,
6
. C.
12
,
30
,
20
. D.
4
,
6
,
4
.
Lời giải
Chọn B.
Khối đa diện đều
4;3
thực ra là khối lập phương.
Câu 21. [2D2-1] Cho bất phương trình
1 1
5 5
log log
f x g x
. Khi đó bất phương trình tương đương
A.
f x g x
. B.
0
g x f x
. C.
0
g x f x
. D.
f x g x
.
Lời giải
Chọn C.
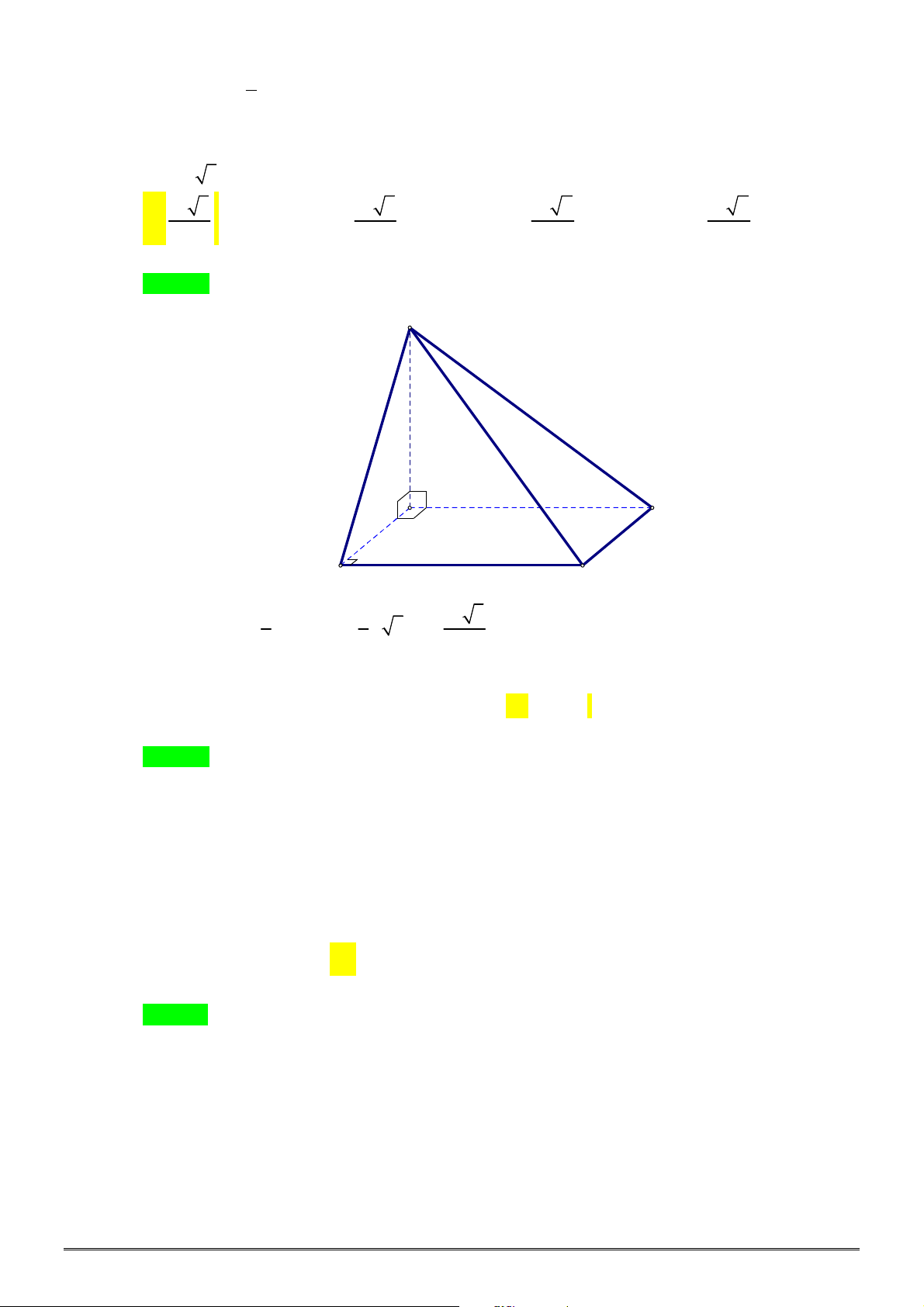
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/21
Do cơ số
1
1
5
a
, đổi chiều bất phương trình và biểu thức trong logarit phải dương.
Câu 22. [2H1-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA ABCD
và
3
SA a
. Thể tích của khối chóp
.
S ABCD
là
A.
3
3
3
a
. B.
3
3
6
a
. C.
3
2
3
a
. D.
3
2
6
a
.
Lời giải
Chọn A.
B
A
D
C
S
Ta có
3
2
.
1 1 3
. 3.
3 3 3
S ABCD ABCD
a
V SA S a a .
Câu 23. [2D2-1] Cho các số thực
x
,
y
và
a
thỏa mãn
x y
;
1
a
. Khi đó:
A.
x y
a a
. B.
x y
a a
. C.
x y
a a
. D.
x y
a a
.
Lời giải
Chọn C.
x
y a
là hàm số mũ có tập xác định
D
và có cơ số
1
a
nên hàm số đồng biến trên
.
Khi đó:
x y
x y a a
.
Câu 24. [2D2-2] Ông An gửi số tiền
100
triệu đồng vào ngân hàng với lãi suất
7%
trên .
1
. năm, biết
rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn
ban đầu. Sau thời gian
10
năm nếu không rút lãi lần nào thì số tiền mà ông An nhận được tính
cả gốc lẫn lãi là (đơn vị là đồng):
A.
10
8
10 . 1 0,0007
. B. .
10
8
10 . 1 0,07
. C.
8 10
10 .0,07
. D.
10
8
10 . 1 0,7
.
Lời giải
Chọn B.
Gọi
100
A
triệu đồng,
7% 0,07
r
.
Sau
1
năm ông An nhận được số tiền là:
1
1
A A Ar A r
.
Sau
2
năm ông An nhận được số tiền là:
2
2 1 1 1
1 1
A A Ar A r A r
.
…
Sau
10
năm ông An nhận được số tiền là:
10 10
10
1 100. 1 0,07
A A r (triệu đồng) hay
10 10
8
10
1 10 . 1 0,07
A A r đồng.
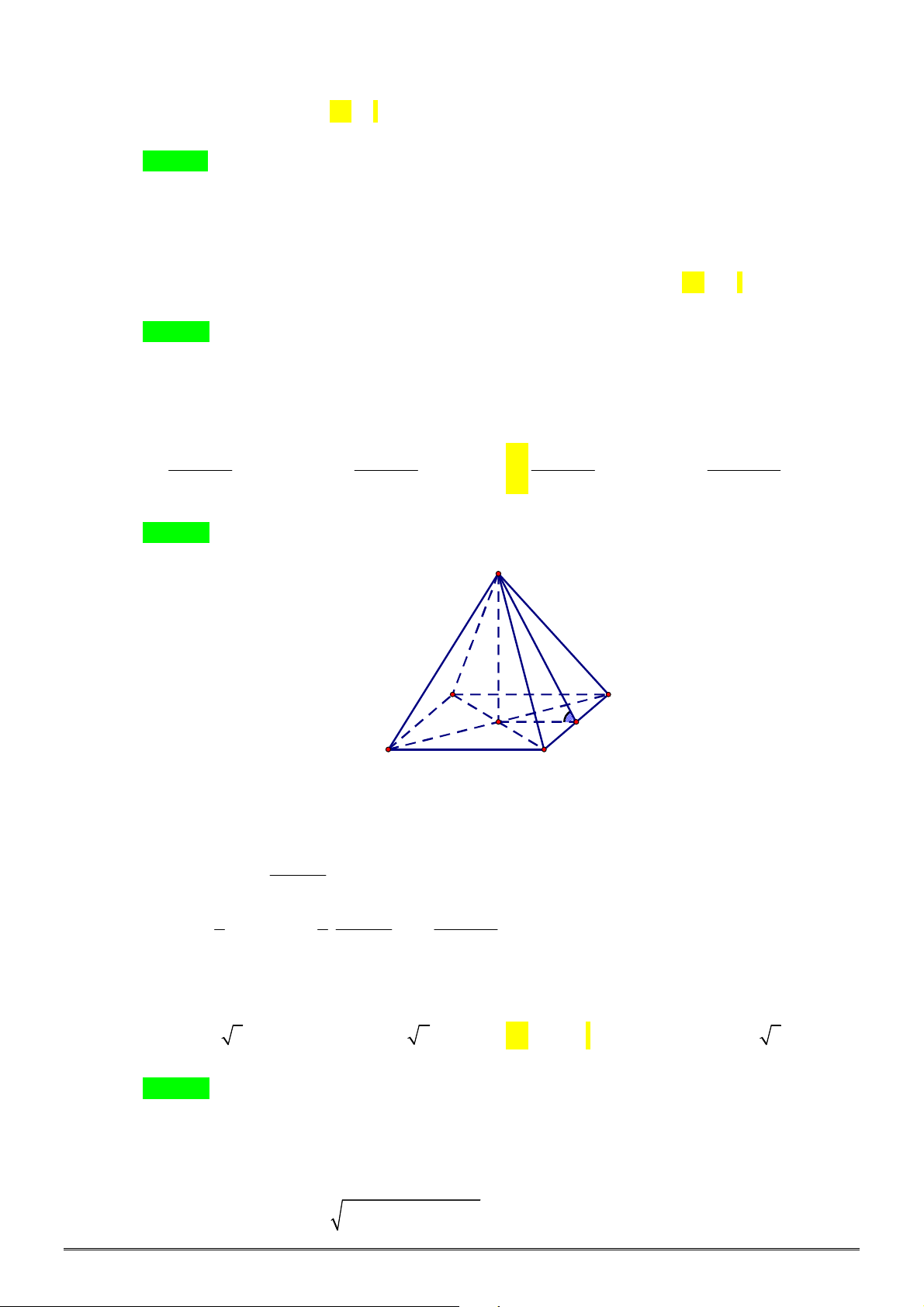
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/21
Câu 25. [2D2-1] Giải phương trình
3
log 1 2
x
.
A.
8
. B.
10
. C.
7
. D.
9
.
Lời giải
Chọn B.
Ta có
3
log 1 2
x
1 0
10
1 9
x
x
x
.
Câu 26. [2D2-3] Số chữ số của só tự nhiên
2017
3
N là
A.
962
. B.
964
. C.
961
. D.
963
.
Lời giải
Chọn D.
Ta có số chữ số của só tự nhiên
2017
3
N là
2017
log3 1 963
.
Câu 27. [2H1-2] Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, góc tạo bởi mặt bên và mặt
đáy là
. Thể tích khối chóp
.
S ABCD
là:
A.
3
.tan
2
a
. B.
3
.tan
3
a
. C.
3
.tan
6
a
. D.
3
2 .tan
3
a
.
Lời giải
Chọn C.
α
I
O
B
D
A
C
S
Gọi
O
là tâm của hình vuông
ABCD
. Do đó
.
SO ABCD
Gọi
I
là trung điểm của
BC
. Khi đó
, .
SBC ABCD SIO
.tan
tan . .
2
a
SO OI
3
2
.
1 1 .tan .tan
. . . . .
3 3 2 6
S ABCD ABCD
a a
V SO S a
Câu 28. [2D1-2] Giả sử
A
và
B
là các giao điểm của đường cong
3
3 2
y x x
và trục hoành. Tính
độ dài đoạn thẳng
AB
.
A.
6 5
AB . B.
4 2
AB
. C.
3
AB
. D.
5 3
AB .
Lời giải
Chọn C.
Ta có: Phương trình hoành độ giao điểm
3
1
3 2 0
2
x
x x
x
.
Do đó tọa độ hai điểm
1; 0 ,
A
2; 0
B .
Độ dài đoạn thẳng
2 2
2 1 0 0 3
AB
.
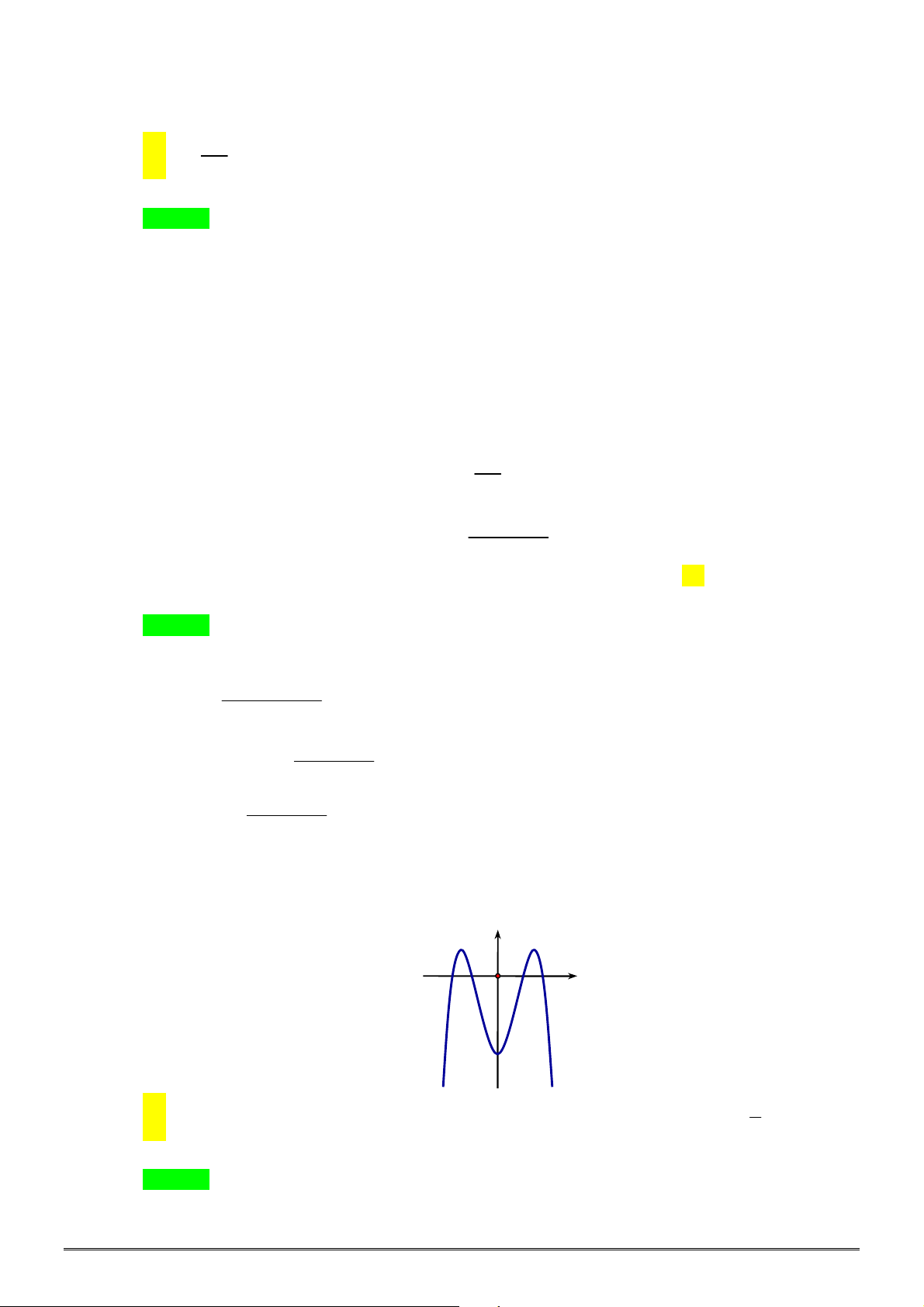
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/21
Câu 29. [2D1-3] Cho hàm số
3 2
2 1
y x mx
có đồ thị
.
m
C Tìm
m
sao cho
m
C
cắt đường thẳng
: 1
d y x
tại ba điểm phân biệt có hoành độ
1 2 3
, ,
x x x
thỏa mãn
1 2 3
101.
x x x
A.
101
.
2
m B.
50.
m
C.
51.
m
D.
49.
m
Lời giải
Chọn A.
Phương trình hoành độ giao điểm
3 2 2
2
0
2 1 1 2 1 0
2 1 0 (1)
x
x mx x x x mx
x mx
Ta có
d
cắt
m
C
tại 3 điểm phân biệt
(1) có 2 nghiệm phân biệt khác 0
2
2
1 0
0 2 .0 1 0
m
m
m
(*)
Giả sử
3
0
x
khi đó
1 2
,
x x
là 2 nghiệm của (1), theo Viet có
1 2
2 .
x x m
Do đó
1 2 3
101
101 2 101 .
2
x x x m m
Câu 30. [2D1-2] Số tiệm cận của đồ thị hàm số
2
2
6 3
3 2
x x
y
x x
là?
A.
6.
B.
2.
C.
1.
D.
3.
Lời giải
Chọn D.
TXĐ:
\ 1;2 .
D
Ta có
2
6 3
1 2
x x
y
x x
tiệm cận đứng
1, 2.
x x
Lại có
2
2
6 3
lim lim 1
3 2
x x
x x
y
x x
tiệm cận ngang
1.
y
2
2
6 3
lim lim 1
3 2
x x
x x
y
x x
tiệm cận ngang
1.
y
Tóm lại đồ thị hàm số đã cho có
3
tiệm cận.
31-32
Câu 31. [2D1-2] Đồ thị bên là đồ thị của hàm số nào?
A.
4 2
4 3
y x x
. B.
4 2
3 3
y x x
. C.
4 2
2 3
y x x
. D.
4 2
1
3 3
4
y x x
.
Lời giải
Chọn A.
* Đồ thị hàm số quay xuống nên loại phương án B và C.
* Đồ thị hàm số cắt trục
Ox
tại
1
nên chọn đáp án A.
O
x
y
3
1
1
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/21
Câu 32. [2D1-3] Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình bên. Hỏi phương trình
3 2
2 0
ax bx cx d
có bao nhiêu nghiệm?
A. Phương trình có đúng một nghiệm. B. Phương trình có đúng hai nghiệm.
C. Phương trình khôngg có nghiệm. D. Phương trình có đúng ba nghiệm.
Lời giải
Chọn A.
* Phương trình
3 2
2
ax bx cx d
.
* Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số
3 2
y ax bx cx d
và
đường thẳng
2
y
mà đường thẳng
2
y
cắt đồ thị hàm số
3 2
y ax bx cx d
tại 3
điểm phân biệt nên phương trình đã cho có tất cả 3 nghiệm.
Câu 33. [2D2-2]Phương trình
2
log log 2 0
x x
có bao nhiêu nghiệm?
A.
1.
B.
2.
C.
3.
D.
0.
Lời giải
Chọn B.
Ta có
2
log log 2 0
x x
log 1
log 2
x
x
1
2
10
10
x
x
1
10
100
x
x
.
Câu 34. [2H2-2]Cho lăng trụ tam giác đều có tất cả các cạnh bằng
a
.Một hình trụ tròn xoay có hai đáy
là hai hình tròn ngoại tiếp hai đáy của lăng trụ.Thể tích của khối trụ tròn xoay bằng:
A.
3
.
9
a
B.
3
.
a
C.
3
3 .
a
D.
3
.
3
a
Lời giải
Chọn D.
G
I
C'
B'
A'
C
B
A
Gọi
G
là trọng tâm tam giác
ABC
thì
G
cũng là tâm đường tròn đáy của hình trụ.
O
x
y
1
2
3
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/21
bán kính đáy của hình trụ là
2 3
3 3
a
r AG AI và đường sinh của hình trụ là
'
l AA a
.
Vậy thể tích của khối trụ tròn xoay là
2
3
2
3
' .
3 3
a a
V r AA a
Câu 35. [2H2-1] Cho hình trụ
T
có độ dài đường sinh
l
, bán kính đáy
r
. Ký hiệu
xq
S
là diện tích
xung quanh của
T
. Công thức nào sau đây là đúng?
A.
3
xq
S rl
. B. 2
xq
S rl
. C.
xq
S rl
. D.
2
2
xq
S r l
.
Lời giải
Chọn B.
Công thức tính diện tích xung quanh của hình trụ
T
có độ dài đường sinh
l
, bán kính đáy
r
là 2
xq
S rl
.
Câu 36. [2D1-2] Điều kiện cần và đủ của tham số
m
để hàm số
3 2
5
y x x mx
có cực trị là
A.
1
3
m
. B.
1
3
m
. C.
1
3
m
. D.
1
3
m
.
Lời giải
Chọn B.
Tập xác định của hàm số là
D
.
Đạo hàm
2
3 2
y x x m
.
Hàm số đã cho có cực trị khi và chỉ khi
0
y
có hai nghiệm phân biệt và
y
đổi dấu khi qua
các nghiệm này.
Ta có
2
0 3 2 0
y x x m
có hai nghiệm phân biệt .
1
1 3 0
3
m m
.
Câu 37. [2D2-1] Tập xác định của hàm số
2
3
log
2
x
y
x
là:
A.
3; 2
. B.
; 3 2;
.
C.
\ 2
. D.
3; 2
.
Lời giải
Chọn D.
Hàm số
2
3
log
2
x
y
x
xác định
3
0 3 2
2
x
x
x
.
Vây tập xác định của hàm số là
3; 2
.
Câu 38. [2H2-2] Cho hình chóp
.
S ABC
có tam giác
ABC
đều cạnh
3cm
a
,
SA ABC
và
2
SA a
. Tính thể tích khối cầu ngoại tiếp hình chóp
.
S ABC
.
A.
3
3
8
cm
3 3
a
. B.
3
3
4
cm
3
a
. C.
3
32 3cm
. D.
3
16 3cm
.
Lời giải
Chọn C.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/21
Gọi
1
R
là bán kính đường tròn ngoại tiếp tam giác
ABC
. Do tam giác
ABC
đều, cạnh bằng
a
nên
1
2 3 3
3 2 3
a a
R .
Bán kính khối cầu ngoại tiếp hình chóp
.
S ABC
là:
2 2
2 2
1
2 3
4 3 3
SA a a
R R a .
Thể tích khối cầu ngoại tiếp hình chóp
.
S ABC
là:
3
3
3
4 4 2 3 32 3
32 3
3 3 3 27
a a
V R
3
cm
.
Câu 39. [2H1-3] Cho hình lăng trụ đứng
.
ABCD A B C D
có thể tích bằng
V
. Các điểm
M
,
N
,
P
lần
lượt thuộc các cạnh
AA
,
BB
,
CC
sao cho
1
2
AM
AA
,
3
4
BN CP
BB CC
. Thể tích khối đa diện
.
ABC MNP
bằng
A.
2
3
V
. B.
1
8
V
. C.
1
3
V
. D.
1
2
V
.
Lời giải
Chọn A.
P
N
M
A
C
B
A'
B'
C'
M'
Gọi
M
là trung điểm
A M
. Ta có
.
3 3
. .
4 4
M NP ABC M NP ABC
V AM S AA S V
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/21
Ta có
.
1 1 1 1
. . .
3 3 4 12
M M NP M NP ABC
V MM S AA S V
.
Do đó
. . .
3 1 2
4 12 3
ABC MNP M NP ABC M M NP
V V V V V V
.
Câu 40. [2H2-2] Tìm nghiệm của phương trình:
log 4 3 2
x
x
.
A.
1
x
. B.
4
x
. C.
x
. D.
1; 4
x
.
Lời giải
Chọn C.
Điều kiện:
4 3 0
4
0 0 , 1
3
1
x
x x x
x
.
Ta có
log 4 3 2
x
x
2 2
1
4 3 3 4 0
4
x
x x x x
x
.
Kết hợp với điều kiện ta được:
x
.
Câu 41. [2D1-2] Với giá trị nào của số thực
m
thì hàm số
1
x m
y
x
đồng biến trên từng khoảng xác
định?
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Lời giải
Chọn A.
Tập xác định
\ 1
D
.
Đạo hàm
2
1
1
m
y
x
.
Hàm số đồng biến trên từng khoảng xác định khi
1 0 1
m m
.
Câu 42. [2H2-1] Khối cầu có bán kính
3 cm
thì có thể tích là
A.
3
9 cm
. B.
3
12 cm
. C.
3
36 cm
. D.
3
27 cm
.
Lời giải
Chọn C.
Thể tích khối cầu là
3 3 3
4 4
.3 36 cm
3 3
V R
.
Câu 43. [2D2-1] Nghiệm của phương trình
2
5 125
x
là
A.
1
x
. B.
5
x
. C.
3
x
. D.
1
x
.
Lời giải
Chọn A.
2 2 3
5 125 5 5
x x
2 3 1
x x
.
Câu 44. [2H1-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
,
30
ABC
. Tam giác
SBC
là tam giác đều cạnh
a
và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp
.
S ABC
là:
A.
3
16
a
. B.
3
3 3
16
a
. C.
3
3
16
a
. D.
3
3
16
a
.
Lời giải
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/21
Chọn A.
H
B
C
A
S
Gọi
H
là trung điểm đoạn
BC
.
Tam giác
SBC
đều cạnh
a
nên
SH BC
.
Lại có
SBC ABC
,
SBC ABC BC
suy ra
SH ABC
,
3
2
a
SH .
Do tam giác
ABC
vuông tại
A
,
30
ABC
,
BC a
suy ra
3
,
2
a
AB
2
a
AC
.
Thể tích khối chóp
.
S ABC
bằng:
3
1 1
. . .
3 2 16
a
V SH AB AC
Câu 45. [2D1-2] Gọi
1
y
,
2
y
lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số
4 2
10 9
y x x
.
Khi đó
1 2
y y
bằng:
A.
7
. B.
2 5
. C.
25
. D.
9
.
Lời giải
Chọn C.
Tập xác định:
D
. Đạo hàm:
3
4 20
y x x
.
Xét
3
0 9
0 4 20 0
5 16
x y
y x x
x y
.
Bảng biến thiên:
x
5
0
5
y
+
0
0
+
0
y
16
16
9
Suy ra:
1
16
y
và
2
9
y
. Vậy
1 2
25
y y
.
Câu 46. [2D2-2] Giá trị nhỏ nhất của hàm số
2
e 3e 1
x x
y
trên đoạn
ln2;ln5
là:
A.
2
e
. B.
9
. C.
9
e
. D.
39
.
Lời giải
Chọn B.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/21
Tập xác định:
D
. Đạo hàm:
2
2e 3e 0
x x
y
x
.
Suy ra hàm số
2
e 3e 1
x x
y
đồng biến trên
nên cũng đồng biến trên đoạn
ln2;ln5
.
Vậy
2ln2 ln2
ln2;ln5
min ln 2 e 3e 1 4 3.2 1 9
y y
.
Câu 47. [2D2-2]
3
7
1
log
a
a
0; 1
a a
bằng
A.
3
7
. B.
7
3
. C.
3
7
. D.
7
3
.
Lời giải
Chọn D.
Ta có:
7
3 7
3
1
7
log log
3
a
a
a a
.
Câu 48. [2D1-1] Tiệm cận đứng của đồ thị hàm số
2 3
7
x
y
x
có phương trình là
A.
7
y
. B.
2
y
. C.
7
x
. D.
2
x
.
Lời giải
Chọn C.
Tập xác định:
\ 7
D
.
Ta có:
7
lim
x
y
7
x
là tiệm cận đứng.
Câu 49. [2D2-1] Cho hàm số
3 1
1
x
y
x
. Chọn khẳng định đúng.
A. Hàm số đồng biến trên khoảng
;1 1;
.
B. Hàm số nghịch biến trên từng khoảng xác định của nó.
C. Hàm số đồng biến trên
.
D. Hàm số nghịch biến trên
.
Lời giải
Chọn B.
Ta có
2
4
0
1
y
x
với
\ 1
x
suy ra hàm số nghịch biến trên từng khoảng xác định
của nó.
Câu 50. [2D2-1] Tập xác định của hàm số hàm số
1
2
2 1
y x
là
A.
1
;
2
. B.
1
\
2
. C.
1
;
2
. D.
.
Lời giải
Chọn C.
ĐK:
1
2 1 0
2
x x
suy ra tập xác định của hàm số là
1
;
2
D
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/22
SỞ GD VÀ ĐT HÀ NỘI
TRƯỜNG THPT LƯƠNG THẾ VINH
ĐỀ THI HỌC KÌ 1 – TOÁN 12
NĂM HỌC 2017-2018
Thời gian làm bài 90 phút
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 103
Câu 1. [2D1-1] Hai đường tiệm cận của đồ thị hàm số
2 1
2
x
y
x
là.
A.
2
x
;
2
y
. B.
2
x
;
1
2
y
. C.
2
x
;
2
y
. D.
2
x
;
2
y
.
Câu 2. [2D1-2] Biết đường thẳng
1
y x
cắt đồ thị hàm số
2 1
1
x
y
x
tại hai điểm phân biệt
A
,
B
có hoành độ lần lượt là
A
x
;
B
x
. Tính giá trị của
A B
x x
.
A.
2
A B
x x
. B.
2
A B
x x
. C.
0
A B
x x
. D.
1
A B
x x
.
Câu 3. [2D2-2] Tìm tập xác định
D
của hàm số
2
3
log 3
y x x
.
A.
D
. B.
\ 0;3
D
. C.
;0 3;D
. D.
0;3
.
Câu 4. [2D1-2] Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
A.
4
y x
. B.
2
2 2
y x x
. C.
1
3
x
y
x
. D.
3
y x x
.
Câu 5. [2D1-3]Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
2
4
x
y
x m x
có ba tiệm
cận đứng.
A.
2 2
m
. B.
0
2 2
m
m
. C. Mọi giá trị
m
. D.
2 2
m
.
Câu 6. [2H3-2]Trong không gian
Oxyz
, cho bốn điểm
1;0;0
A ,
0;2;0
B ,
0;0;3
C ,
1;2;3
D .
Phương trình mặt cầu đi qua bốn điểm
A
,
B
,
C
,
D
là:
A.
2 2 2
2 3 0
x y z x y z
. B.
2 2 2
2 3 14 0
x y z x y z
.
C.
2 2 2
2 3 6 0
x y z x y z
. D.
2 2 2
2 4 6 0
x y z x y z
Câu 7. [2D1-1] Cho hàm số
2 1
2
x
y
x
. Khẳng định nào dưới đây đúng?
A. Đồ thị hàm số có tiệm cận đứng là
2
x
. B. Hàm số có tiệm cận đứng là
2
x
.
C. Đồ thị hàm số không có tiệm cận. D. Đồ thị hàm số có tiệm cận ngang là
1
2
y
.
Câu 8. [2D2-2] Tìm tập nghiệm
S
của phương trình
4 6.2 8 0
x x
.
A.
1;2
S . B.
2
S . C.
1
S . D.
1;2
S .
Câu 9. [2H2-4] Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
,
B
,
AB BC a
,
2
SA AD a
,
SA ABCD
, gọi
E
là trung điểm của
AD
. Tính bán kính
R
của mặt cầu
ngoại tiếp khối chóp
.
S CDE
theo
a
.
A.
3 2
2
a
R . B.
10
2
a
R . C.
11
2
a
R . D.
2
2
a
R .
10

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/22
Câu 10. [2D2-2] Cho hàm số
2
1
2
x
y x e
. Giá trị của biểu thức 2
y y y
tại
0
x
là
A.
1
. B.
e
. C.
0
. D.
1
e
.
Câu 11. [2H2-3] Trong các hình hộp chữ nhật nằm trong mặt cầu bán kính
R
, thể tích lớn nhất có thể
của khối hộp chữ nhật là
A.
3
4 3
3
R
. B.
3
8 3
9
R
. C.
3
16 3
3
R
. D.
3
8 3
3
R
.
Câu 12. [2D1-2] Viết phương trình tiếp tuyến của đồ thị hàm số
3
3 2
y x x
tại giao điểm của đồ thị
hàm số với trục tung.
A.
2
y
. B.
3 2
y x
. C.
3 2
y x
. D.
3 2
y x
.
Câu 13. [2D2-3] Tìm tất cả các giá trị thực của tham số
m
để phương trình
3
4 2 3
x x
m
có đúng
2
nghiệm thực phân biệt trong khoảng
1;3
.
A.
13 9
m
. B.
9 3
m
. C.
13 3
m
. D.
3 9
m
.
Câu 14. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 2
3 0
x x m
có
2
nghiệm phân biệt
A. Không có
m
. B.
4;0
m . C.
4;0
m . D.
0
m
.
Câu 15. [2D1-2] Đồ thị hàm số
2
2
9
6 8
x
y
x x
có bao nhiêu đường tiệm cận?
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 16. [2D1-3] Giá trị thực của tham số
m
để đồ thị hàm số
4 2
2
y x mx m
có ba điểm cực trị tạo
thành một tam giác nhận gốc tọa độ làm trọng tâm là
A.
1
m
. B. không có
m
. C.
3
2
m
. D.
1
2
m
.
Câu 17. [2D1-2] Hàm số
4 2
2017 2018
y x x có giá trị cực đại là
A.
CÑ
2017
y . B.
CÑ
0
y
. C.
CÑ
2018
y . D.
CÑ
2018
y .
Câu 18. [2D1-2] Cho hàm số
y f x
liên tục trên
và có đạo hàm được xác định bởi hàm số
3
2
1 3
f x x x x
. Hỏi đồ thị hàm số
y f x
có bao nhiêu điểm cực trị?
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 19. [2H1-2] Cho hình trụ có diện tích toàn phần lớn hơn diện tích xung quanh là
4 .
Bán kính của
hình trụ là?
A.
2
.
2
B.
2.
C.
2.
D.
1.
Câu 20. [2D2-1] Tìm tập xác định
D
của hàm số
3
2
1 .
y x
A.
; 1 1; .
D
B.
.
D
C.
.
D
D.
\ 1 .
D

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/22
Câu 21. [0H3-2] Trong không gian
Oxyz
, cho hai điểm
1;2;0
A ,
2; 1;1
B . Tìm điểm
C
có hoành
độ dương trên trục
Ox
sao cho tam giác
ABC
vuông tại
C
.
A.
3;0;0
C . B.
2;0;0
C . C.
1;0;0
C . D.
5;0;0
C .
Câu 22. [0H3-2] Trong không gian
Oxyz
, cho hai điểm
1;2; 2
A
,
2; 1;2
B . Tìm tọa độ điểm
M
trên mặt phẳng
Oxyz
cho
MA MB
đạt giá trị nhỏ nhất.
A.
1;1;0
M . B.
3 1
; ;0
2 2
M
. C.
2;1;0
M . D.
1 3
; ;0
2 2
M
.
Câu 23. [2D2-2] Tập nghiệm của bất phương trình
2
1
2
4
x
x
là
A.
1;S
. B.
;1
S
. C.
;2
S . D.
2;S
.
Câu 24. [2D1-1] Số điểm cực trị của hàm số
4 2
3 5
y x x
là
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 25. [2D2-1] Giải phương trình
3
log 1 2
x
.
A.
8
. B.
10
. C.
7
. D.
9
.
Câu 26. [2D2-3] Số chữ số của só tự nhiên
2017
3
N là
A.
962
. B.
964
. C.
961
. D.
963
.
Câu 27. [2D2-2] Cho hàm số
1
1
x x
y f x e
. Tính giá trị biểu thức
2018
1 . 2 ... 2017 .
T f f f e
.
A.
1
T
. B.
T e
. C.
1
T
e
. D.
1
2018
T e
.
Câu 28. [2H1-2] Cho khối hộp
.
ABCD A B C D
có thể tích là
36
. Tính thể tích
V
của khối chóp
.
ACB D
.
A.
18
V
. B.
6
V
. C.
9
V
. D.
12
V
.
Câu 29. [2H1-1] Cho hình chóp
.
S ABCD
có cạnh bên
SA
tạo với đáy một góc
60
và
3
SA a
, đáy
là tứ giác có hai đường chéo vuông góc,
2
AC BD a
. Tính thể tích
V
của khối chóp theo
a
.
A.
3
2 3
3
a
V . B.
3
3
V a
. C.
3
V a
. D.
3
3
2
a
V .
Câu 30. [2D2-2] Hàm số
3
3
y x x
đồng biến trên khoảng nào?
A.
1;1
. B.
; 1
. C.
;
. D.
0;
.
Câu 31. [2D2-3] Cho bất phương trình
2
3 2
2 2 2 3
x x x
x x
có tập nghiệm là
;
a b
. Giá trị của
2
T a b
là
A.
1
T
. B.
5
T
. C.
3
T
. D.
2
T
.
Câu 32. [2D1-3] Cho hàm số
1
mx
y
x n
,
trong đó
m
,
n
là tham số. Biết giao điểm của hai đường tiệm
cận của đồ thị hàm số nằm trên đường thẳng
2 3 0
x y
và đồ thị hàm số đi qua điểm
0;1
A . Giá trị của
m n
là
A.
3
m n
. B.
3
m n
.
C.
1
m n
. D.
1
m n
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/22
Câu 33. [2D1-2] Biết rằng hàm số
3 2
y f x x ax bx c
đạt cực tiểu tại điểm
1
x
, giá trị cực
tiểu bằng
3
và đồ thị hàm số cắt trục tung tại điểm có tung độ
2
. Tìm giá trị của hàm số tại
2
x
.
A.
2 8.
f
B.
2 0.
f
C.
2 0.
f
D.
2 4.
f
Câu 34. [2D2-3] Cho phương trình
2017 2017
4
4034
tan 12 tan
1 1
12 12
2017.
2 3
1 tan 1 tan 1 tan
12 12 12
x x
x
.
Tính tổng tất cả các nghiệm thực của phương trình đã cho.
A.
0
B.
1
C.
1
D.
2017
Câu 35. [2H2-2] Tính thể tích
V
khối lập phương biết rằng khối cầu ngoại tiếp khối lập phương có thể
tích là
32
3
.
A.
64 3
9
V . B.
8
V
. C.
8 3
9
V . D.
8 3
3
V .
Câu 36. [2D2-1] Hàm số nào trong bốn hàm số liệt kê ở dưới đồng biến trên các khoảng xác định của
hàm số?
A.
2 1
x
y
e
. B.
3
x
y
. C.
sin 2017
x
y . D.
2
x
y
e
.
Câu 37. [1D5-4] Cho hàm số
3 2
3 2
y x x
. Gọi
A
,
B
là các điểm thuộc đồ thị hàm số đã cho có
hoành độ lần lượt là
A
x
;
B
x
, tiếp tuyến của đồ thị hàm số tại
A
,
B
song song với nhau và
đường thẳng
AB
tạo với
2
trục toạ độ một tam giác cân, đường thẳng
AB
có hệ số góc
dương. Tính giá trị
A B
x x
.
A.
1
A B
x x
. B.
3
A B
x x
. C.
2
A B
x x
. D.
2
A B
x x
.
Câu 38. [1D5-2] Tiếp tuyến với đồ thị
2 1
2
x
y
x
tại điểm có tung độ bằng
5
có hệ số góc
k
là
A.
1
3
k
. B.
1
k
. C.
3
k
. D.
1
3
k
.
Câu 39. [2H2-2] Cho hình nón tròn xoay có đường cao
4
h
và diện tích đáy là
9
. Tính diện tích
xung quanh của hình nón.
A.
10
xq
S
. B.
15
xq
S
. C.
25
xq
S
. D.
30
xq
S
.
Câu 40. [2D1-2] Tìm giá trị nhỏ nhất của hàm số
4
1y x
x
trên
1;3
.
A.
1;3
Min 4
x
y
. B.
1;3
Min 5
x
y
. C.
1;3
16
Min
3
x
y
. D.
1;3
Min 6
x
y
.
Câu 41. [2D1-1] Đường cong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây.
A.
3
3 2
y x x
.
B.
4 2
2 2
y x x
.
C.
4 2
2 2
y x x
.
D.
4 2
2 2
y x x
.
O
x
y
2
1
1
3

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/22
Câu 42. [2D2-2] Tập nghiệm của bất phương trình
1 1
2 2
log 3 log 9 2
x x
.
A.
3;4
S . B.
;4
S . C.
9
3;
4
S
. D.
3;4
S .
Câu 43. [2H1-2] Diện tích toàn phần của một hình hộp chữ nhật là
2
8
tp
S a
. Đáy của hình hộp là hình
vuông cạnh
a
. Tính thể tích của khối hộp theo
a
.
A.
3
3 .
V a
B.
3
V a
. C.
3
3
.
2
a
V D.
3
7
.
4
V a
Câu 44. [2H3-1] Trong không gian
Oxyz
, phương trình mặt cầu tâm
1;2;0
I và đi qua điểm
2; 2;0
A là
A.
2 2
2
1 2 100.
x y z B.
2 2
2
1 2 5.
x y z
C.
2 2
2
1 2 10.
x y z D.
2 2
2
1 2 25.
x y z
Câu 45. [2D1-2] Tìm tập hợp tất cả các giá trị của tham số thực
m
để hàm số
1
mx
y
x m
đồng biến trên
từng khoảng xác định.
A.
; 1
. B.
1;1
. C.
1;
. D.
;1
.
Câu 46. [2H2-2] Hình nón có chiều cao bằng đường kính đáy. Tỉ số giữa diện tích xung quanh và diện
tích toàn phần của hình nón là:
A.
1
2
. B.
1 5
4
. C.
1
4
. D.
5 5
4
.
Câu 47. [2H1-1] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA a
và vuông góc với
đáy. Thể tích
V
của khối chóp
.
S ABC
theo
a
là
A.
3
.
3
12
S ABC
a
V . B.
3
.
2
12
S ABC
a
V . C.
3
.
3
3
S ABC
a
V . D.
3
.
3
4
S ABC
a
V .
Câu 48. [2D2-2] Đạo hàm của hàm số
2
2
log 2
y x x
là
A.
2
1
2 ln2
y
x x
. B.
2
1
2
x
y
x x
.
C.
2
1
2 ln2
x
y
x x
. D.
2
1
2 ln 2
x
y
x x
.
Câu 49. [2H3-2] Trong không gian
Oxyz
, cho ba vecto
1;2;1
a
,
0;2; 1
b
,
;1;0
c m
. Tìm giá
trị thực của tham số
m
để ba véctơ
a
,
b
,
c
đồng phẳng.
A.
1
m
. B.
0
m
. C.
1
4
m
. D.
1
4
m
.
Câu 50. [2H2-1] Khối cầu có thể tích là
36
. Diện tích xung quanh của mặt cầu là
A.
9
xq
S
. B.
27
xq
S
. C.
18
xq
S
. D.
36
xq
S
.
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/22
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C A
D
C B A
A
D
C A
B B
A
C
D
C D
B C D
A
B D
A
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
B D
C B B B D
D
A
A
B
C
B
B B D
C D
B D
A
D
D
D
HƯỚNG DẪN GIẢI
Câu 1. [2D1-1] Hai đường tiệm cận của đồ thị hàm số
2 1
2
x
y
x
là.
A.
2
x
;
2
y
. B.
2
x
;
1
2
y
. C.
2
x
;
2
y
. D.
2
x
;
2
y
.
Lời giải
Chọn C.
TXĐ:
\ 2
D
.
2
2
lim
lim
x
x
y
y
2
x
là đường tiệm cận đứng.
lim 2
x
y
2
y
là đường tiệm cận ngang.
Câu 2. [2D1-2] Biết đường thẳng
1
y x
cắt đồ thị hàm số
2 1
1
x
y
x
tại hai điểm phân biệt
A
,
B
có hoành độ lần lượt là
A
x
;
B
x
. Tính giá trị của
A B
x x
.
A.
2
A B
x x
. B.
2
A B
x x
. C.
0
A B
x x
. D.
1
A B
x x
.
Lời giải
Chọn A.
: 1
d y x
;
2 1
:
1
x
H y
x
.
Phương trình hoành độ giao điểm của
d
và
H
:
2 1
1
1
x
x
x
1
:
1
ĐK x
.
2 2
1 2 1 2 2 0 1 3
x x x x x .
Vì
d
cắt
H
tại hai điểm phân biệt
A
,
B
nên hoành độ hai điểm
A
,
B
là nghiệm của
phương trình
1
.
Vậy
2
A B
x x
.
Câu 3. [2D2-2] Tìm tập xác định
D
của hàm số
2
3
log 3
y x x
.
A.
D
. B.
\ 0;3
D
. C.
;0 3;D
. D.
0;3
.
Lời giải
Chọn D.
Điều kiện:
2
3 0 0 3
x x x
. Vậy
0;3
D .
Câu 4. [2D1-2] Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
A.
4
y x
. B.
2
2 2
y x x
. C.
1
3
x
y
x
. D.
3
y x x
.
Lời giải
Chọn C.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/22
Hàm số
1
3
x
y
x
có đạo hàm
2
4
0
3
y
x
3
x
nên hàm số này không có cực trị.
Câu 5. [2D1-3]Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
2
4
x
y
x m x
có ba tiệm
cận đứng.
A.
2 2
m
. B.
0
2 2
m
m
. C. Mọi giá trị
m
. D.
2 2
m
.
Lời giải
Chọn B.
Tập xác định
2;2 \
D m
.
Xét
2
2
lim
4
x
x
x m x
do
2
lim 2
x
x
,
2
2
lim 4 0
x
x m x
nên
2
lim
x
y
.
Suy ra
2
x
là tiệm cận đứng của đồ thị.
Tương tự, xét
2
2
lim
4
x
x
x m x
, ta được
2
x
là tiệm cận đứng của đồ thị.
Để đồ thị hàm số có ba tiệm cận đứng thì:
2
lim
4
x m
x
x m x
2
lim 0
0
lim 4 0
x m
x m
x
m
x m x
.
Vậy để đồ thị hàm số có ba đường tiệm cận thì
0
2 2
m
m
.
Câu 6. [2H3-2]Trong không gian
Oxyz
, cho bốn điểm
1;0;0
A ,
0;2;0
B ,
0;0;3
C ,
1;2;3
D .
Phương trình mặt cầu đi qua bốn điểm
A
,
B
,
C
,
D
là:
A.
2 2 2
2 3 0
x y z x y z
. B.
2 2 2
2 3 14 0
x y z x y z
.
C.
2 2 2
2 3 6 0
x y z x y z
. D.
2 2 2
2 4 6 0
x y z x y z
Lời giải
Chọn A
Phương trình mặt cầu có dạng
S
:
2 2 2
2 2 2 0
x y z ax by cz d
Ta có
A S
B S
C S
D S
1 2 0
4 4 0
9 6 0
14 2 4 6 0
a d
b d
c d
a b d d
1
2
1
3
2
0
a
b
c
d
.
Vậy phương trình mặt cầu đi qua bốn điểm
A
,
B
,
C
, là:
2 2 2
: 2 3 0
S x y z x y z
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/22
Câu 7. [2D1-1] Cho hàm số
2 1
2
x
y
x
. Khẳng định nào dưới đây đúng?
A. Đồ thị hàm số có tiệm cận đứng là
2
x
. B. Hàm số có tiệm cận đứng là
2
x
.
C. Đồ thị hàm số không có tiệm cận. D. Đồ thị hàm số có tiệm cận ngang là
1
2
y
.
Lời giải
Chọn A.
Câu 8. [2D2-2] Tìm tập nghiệm
S
của phương trình
4 6.2 8 0
x x
.
A.
1;2
S . B.
2
S . C.
1
S . D.
1;2
S .
Lời giải
Chọn D.
Ta có
2 2 1
4 6.2 8 0
2
2 4
x
x x
x
x
x
Câu 9. [2H2-4] Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
,
B
,
AB BC a
,
2
SA AD a
,
SA ABCD
, gọi
E
là trung điểm của
AD
. Tính bán kính
R
của mặt cầu
ngoại tiếp khối chóp
.
S CDE
theo
a
.
A.
3 2
2
a
R . B.
10
2
a
R . C.
11
2
a
R . D.
2
2
a
R .
Lời giải
Chọn C.
Vì
E
là trung điểm
AD
nên
2
AD
AE a
, khi đó
ABCE
là hình vuông cạnh
a
. Từ đó ta có
CE AD
1
.
Từ giả thiết
SA ABCD
suy ra
SA CE
2
.
Từ
1
và
2
ta có
CE SAD
.
Ta coi hình chóp
.
S CDE
là hình chóp
.
C SED
, ta xác định tâm và bán kính mặt cầu ngoại tiếp
hình chóp
.
C SED
.
Gọi
I
là tâm đường tròn ngoại tiếp tam giác
SED
, gọi
là đường thẳng đi qua
I
và vuông
góc với mặt phẳng
SED
. Khi đó
//
EC
. Mặt phẳng trung trực của đoạn thẳng
CE
cắt
tại
O
, ta có
OIEM
là hình chữ nhật (với
M
là trung điểm
CE
).
Do
O
nằm trên
nên
OE OS OD
, do
O
nằm trên mặt phẳng trung trực của đoạn thẳng
CE
nên
OE OC
.
Như vậy
OC OE OS OD
nên
O
là tâm mặt cầu ngoại tiếp hình chóp
.
C SED
.
Tam giác
SAD
vuông cân đỉnh
A
nên
2 2 2
SD SA a
và
45
SDE
.
Tam giác
SAE
vuông tại
A
và
2
SA a
,
AE a
nên
2
2 2 2
2 5
SE SA AE a a a
.
Gọi
r
là bán kính đường tròn ngoại tiếp tam giác
SED
, áp dụng định lí sin trong tam giác
SED
ta có:
5 10
2
2sin 45 2
sin 2sin
SE SE a a
r r
SDE SDE
, hay
10
2
a
IE r .
Mặt khác
2 2
EC a
EM
, nên bán kính mặt cầu ngoại tiếp hình chóp
.
S CDE
là:
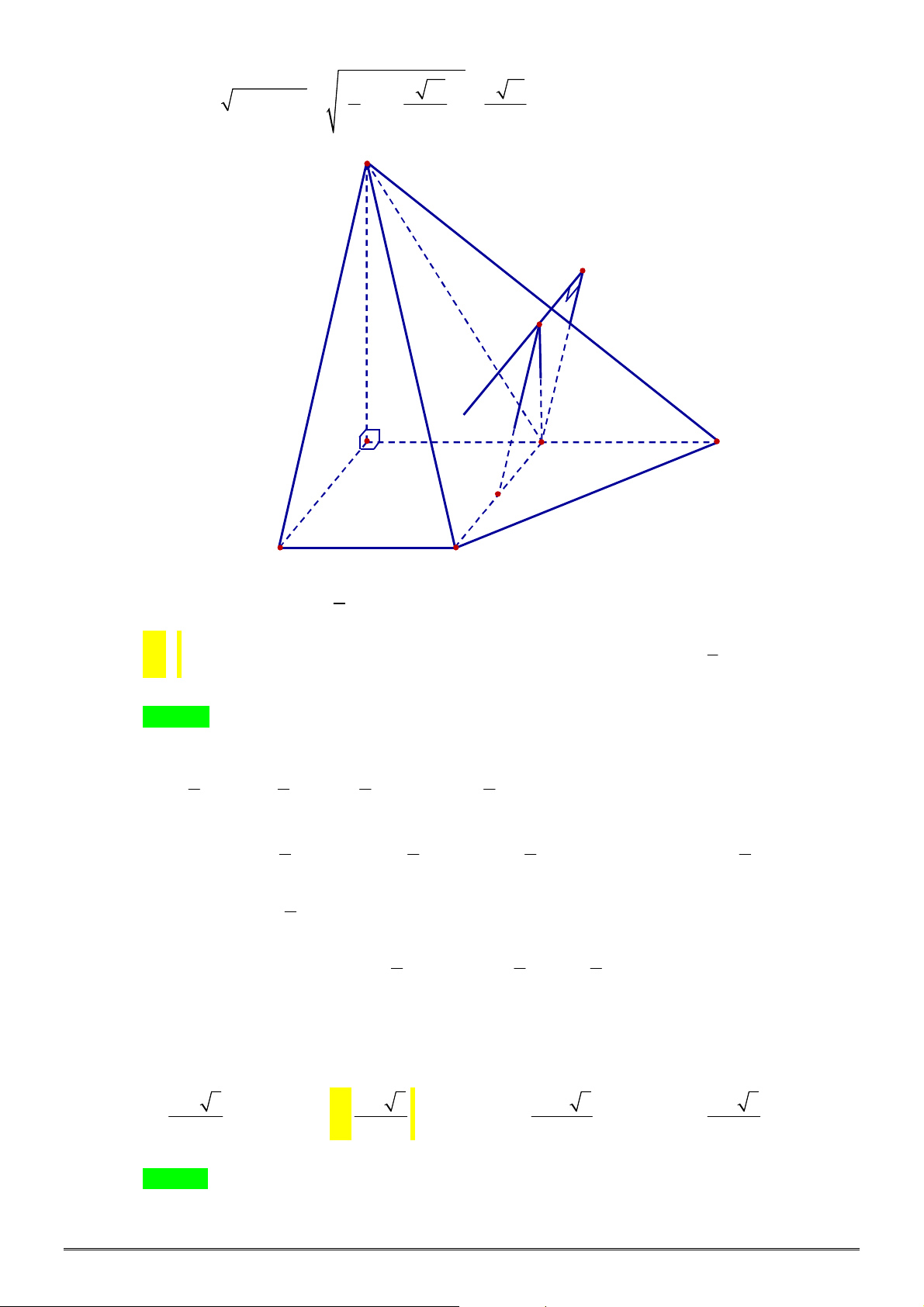
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/22
2
2
2 2
10 11
2 2 2
a a a
R OE OI IE
.
Câu 10. [2D2-2] Cho hàm số
2
1
2
x
y x e
. Giá trị của biểu thức 2
y y y
tại
0
x
là
A.
1
. B.
e
. C.
0
. D.
1
e
.
Lời giải
Chọn A.
Ta có:
2 2 2 2
1 1 1 1
2 2 2 2
x x x x
y x e x e x e x x e
;
2 2 2 2
1 1 1 1
1
2 2 2 2
x x x x x
y y x x e x x e x x e x e x x e
Hay
2
1
1 2
2
x
y x x e
.
Như vậy:
2 2 2
1 1 1
2 1 2 2
2 2 2
x x x x
y y y x x e x x e x e e
.
Do đó, giá trị của biểu thức 2
y y y
tại
0
x
là
0
1
e
.
Câu 11. [2H2-3] Trong các hình hộp chữ nhật nằm trong mặt cầu bán kính
R
, thể tích lớn nhất có thể
của khối hộp chữ nhật là
A.
3
4 3
3
R
. B.
3
8 3
9
R
. C.
3
16 3
3
R
. D.
3
8 3
3
R
.
Lời giải
Chọn B.
A
C
O
I
S
D
E
B
M
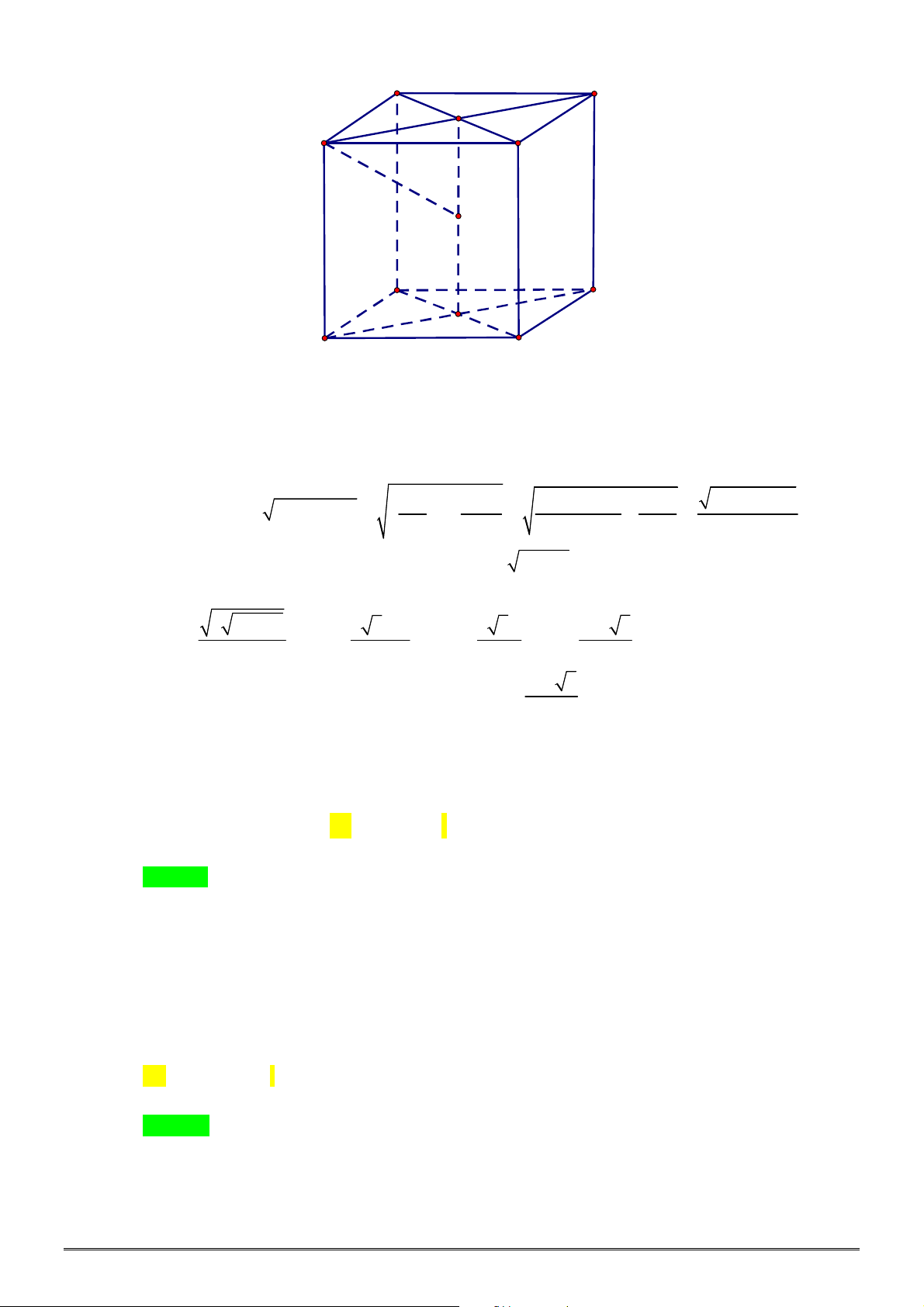
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/22
I
O'
O
A
D
C
B
D'
C'
B'
A'
Gọi
AB CD O
,
A B C D O
.
Ta có
OO
là trục đường tròn ngoại tiếp hai đáy hình hộp chữ nhật. Gọi là
I
trung điểm
OO
.
Vậy
I
là tâm mặt cầu ngoại tiếp khối hộp chữ nhật
.
ABCD A B C D
Gọi
AB a
,
AD b
,
AA c
. Thể tích khối hộp
.ABCD A B C D
V abc
Ta có
2
2 2 2 2 2 2 2
2 2
2 2 4 4 2
BD OO AB AD AA a b c
R ID DO OI
.
Áp dụng bất đẳng thức AM-GM:
3
2 2 2 2 2 2
3
a b c a b c
.
Dấu bằng xảy ra khi và chỉ khi
a b c
.
3 2 2 2
3
3 3 3
2 8
a b c abc
R R
3
3
3 3 8 3
8 9
V R
R V .
Thể tích lớn nhất có thể của khối hộp chữ nhật là
3
8 3
9
R
, khi đó
.
ABCD A B C D
là hình lập
phương.
Câu 12. [2D1-2] Viết phương trình tiếp tuyến của đồ thị hàm số
3
3 2
y x x
tại giao điểm của đồ thị
hàm số với trục tung.
A.
2
y
. B.
3 2
y x
. C.
3 2
y x
. D.
3 2
y x
.
Lời giải
Chọn B.
Đồ thị hàm số giao với trục tung tại điểm
0;2
.
Ta có
2
3 3
y x
,
0 3
y
. Phương trình tiếp tuyến tại điểm
0;2
có dạng:
0 . 0 2
y y x
3 2
y x
.
Câu 13. [2D2-3] Tìm tất cả các giá trị thực của tham số
m
để phương trình
3
4 2 3
x x
m
có đúng
2
nghiệm thực phân biệt trong khoảng
1;3
.
A.
13 9
m
. B.
9 3
m
. C.
13 3
m
. D.
3 9
m
.
Lời giải
Chọn A.
Ta có
3 2
4 2 3 2 8.2 3
x x x x
m m
. Đặt
2 0
x
t t
, phương trình đã cho trở thành
2
8 3
t t m
1
. Để phương trình đã cho có đúng
2
nghiệm thực phân biệt trong khoảng
1;3
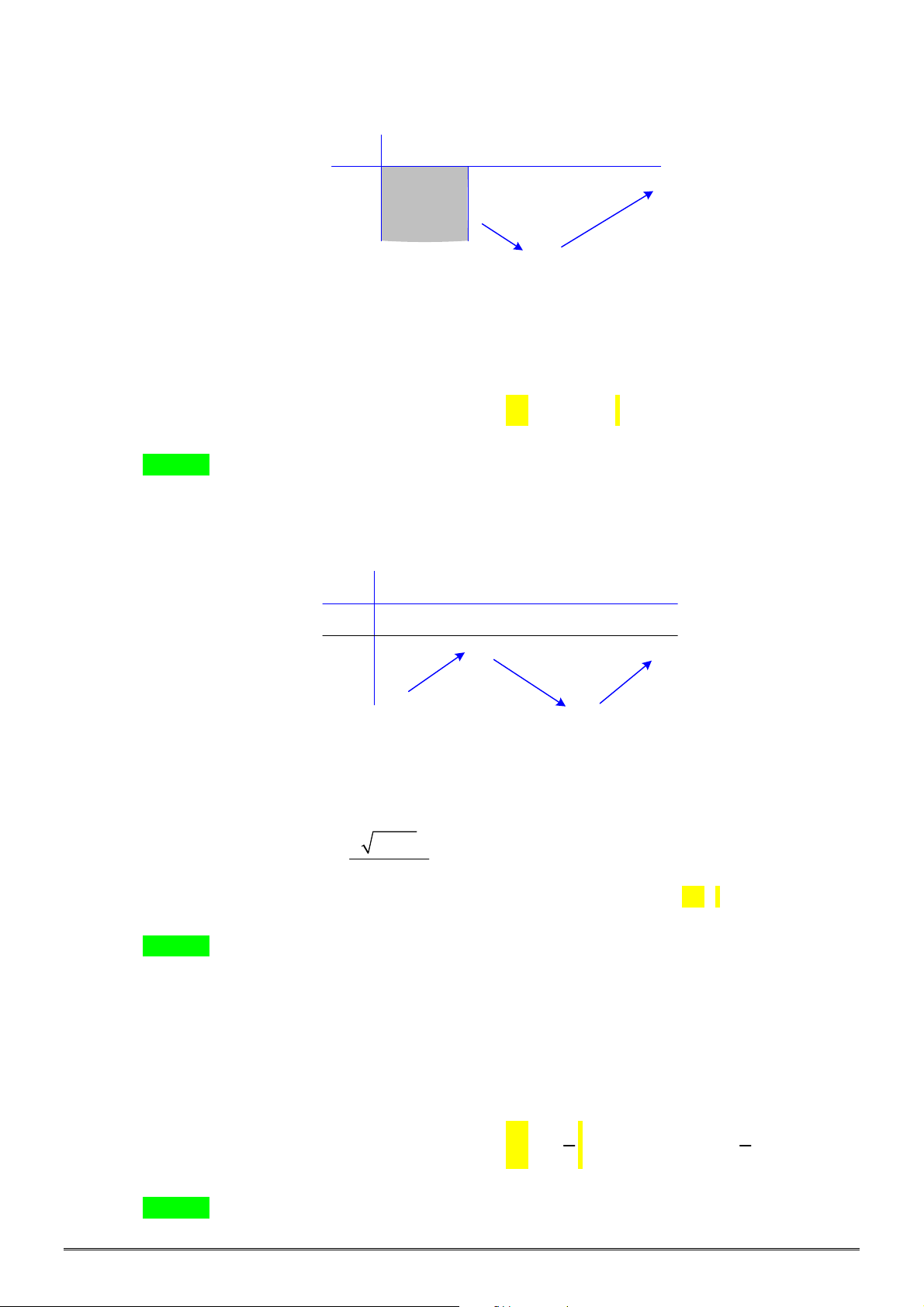
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/22
Thì phương trình
1
có hai nghiệm phân biệt
2;8
t .
Hàm số
2
8 3
f t t t
có bảng biến thiên:
t
f t
0
2
8
4
13
9
3
Để phương trình
1
có hai nghiệm phân biệt
2;8
t thì đường thẳng
y m
cắt đồ thị hàm
số
2
8 3
f t t t
tại hai điểm phân biệt. Khi đó
13 9
m
.
Câu 14. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 2
3 0
x x m
có
2
nghiệm phân biệt
A. Không có
m
. B.
4;0
m . C.
4;0
m . D.
0
m
.
Lời giải
Chọn C.
Ta có
3 2 3 2
3 0 3
x x m x x m
.
Xét hàm số
3 2
3
y x x
:
TXĐ:
D
,
2
3 6 0 0
y x x x
hoặc
2
x
. Bảng biến thiên:
x
y
0
2
y
0
0
4
0
Dựa vào bảng biến thiên suy ra hình dạng đồ thị của hàm số
3 2
3
y x x
, để phương trình
3 2
3 0
x x m
có
2
nghiệm phân biệt thì đường thẳng
y m
cắt đồ thị hàm số
3 2
3
y x x
tại hai điểm phân biệt suy ra
0
m
hoặc
4
m
. Vậy
4;0
m .
Câu 15. [2D1-2] Đồ thị hàm số
2
2
9
6 8
x
y
x x
có bao nhiêu đường tiệm cận?
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn D.
Tập xác định:
3;3 \ 2
D . Do hàm số không xác định trên khoảng vô hạn nên đồ thị hàm
số không có tiệm cận ngang.
Ta có:
2
lim
x
y
2
x
là tiệm cận đứng.
Câu 16. [2D1-3] Giá trị thực của tham số
m
để đồ thị hàm số
4 2
2
y x mx m
có ba điểm cực trị tạo
thành một tam giác nhận gốc tọa độ làm trọng tâm là
A.
1
m
. B. không có
m
. C.
3
2
m
. D.
1
2
m
.
Lời giải
Chọn C.
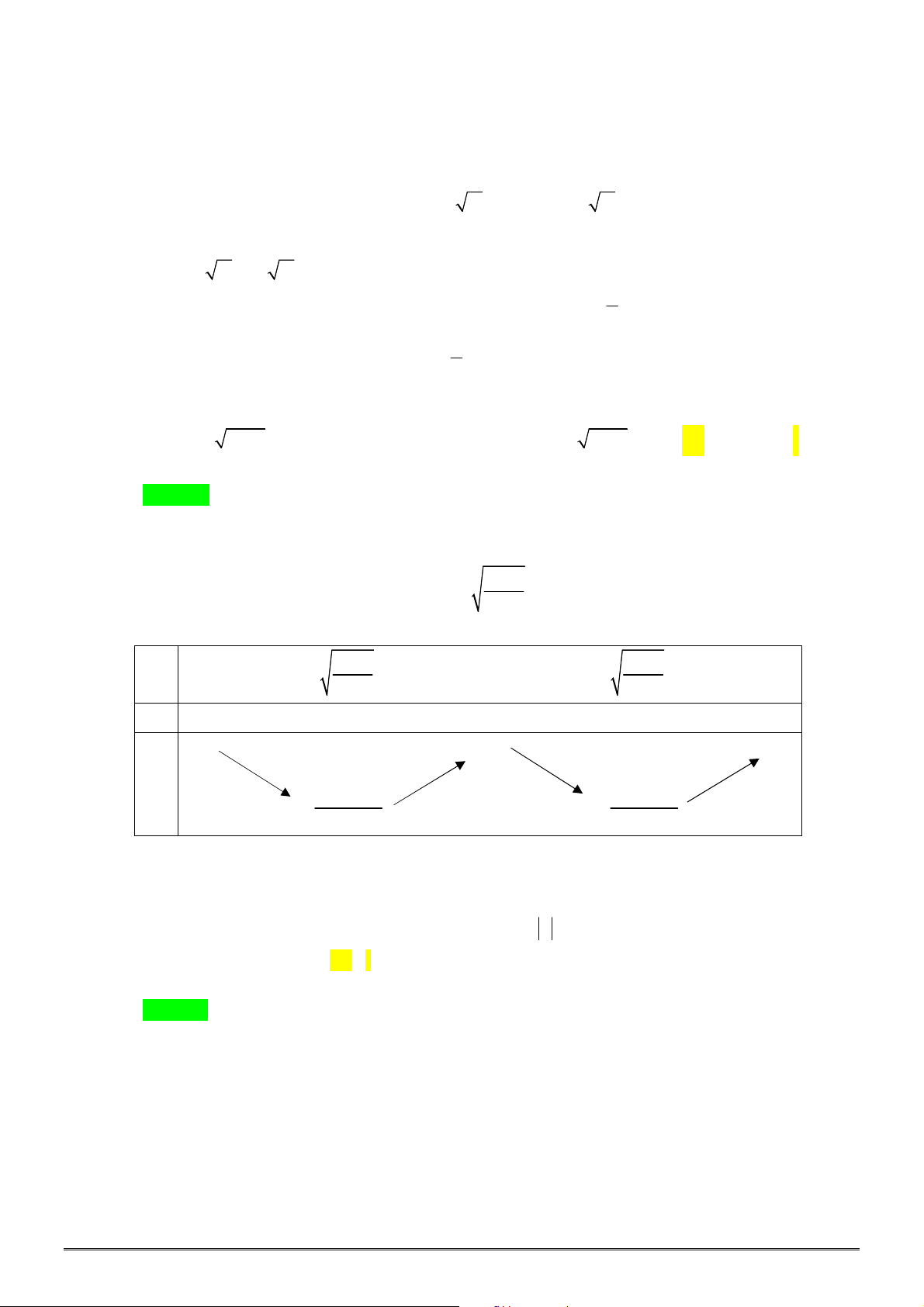
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/22
Tập xác định:
D
.
Ta có:
3
4 4
y x mx
;
2
0
0
x
y
x m
.
Đồ thị hàm số
4 2
2
y x mx m
có ba điểm cực trị
0 *
m .
Tọa độ các điểm cực trị là:
0;
A m
,
2
;
B m m m
;
2
;
C m m m
.
Theo đề bài ta có gốc tọa độ là trọng tâm
ABC
2 2
0 3.0
3.0
m m
m m m m m
2
3 2 0
m m
0
3
2
m
m
.
Đối chiếu với điều kiện
*
ta được
3
2
m
thỏa mãn.
Câu 17. [2D1-2] Hàm số
4 2
2017 2018
y x x có giá trị cực đại là
A.
CÑ
2017
y . B.
CÑ
0
y
. C.
CÑ
2018
y . D.
CÑ
2018
y .
Lời giải
Chọn D.
Tập xác định:
D
.
Ta có:
3
4 4034
y x x
0
0
2017
2
x
y
x
.
Bảng biến thiên:
x
2017
2
0
2017
2
y
0
0
0
y
2018
4060217
4
4060217
4
Từ bảng biến thiên suy ra
CÑ
2018
y .
Câu 18. [2D1-2] Cho hàm số
y f x
liên tục trên
và có đạo hàm được xác định bởi hàm số
3
2
1 3
f x x x x
. Hỏi đồ thị hàm số
y f x
có bao nhiêu điểm cực trị?
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn B.
Ta có:
0
0 1
3
x
f x x
x
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/22
Bảng biến thiên:
x
3
0
1
f x
0
0
0
f x
Ta có:
neáu 0
neáu 0
f x x
y f x
f x x
.
Do đó ta có bảng biến thiên của hàm số
y f x
như sau:
x
1
0
1
f x
0
0
0
f x
Từ bảng biến thiên suy ra đồ thị hàm số
y f x
có ba điểm cực trị.
Câu 19. [2H1-2] Cho hình trụ có diện tích toàn phần lớn hơn diện tích xung quanh là
4 .
Bán kính của
hình trụ là?
A.
2
.
2
B.
2.
C.
2.
D.
1.
Lời giải
Chọn C.
Ta có
2
2
2 4 2.
2
tp
tp xq
xq
S r h r
S S r r
S rh
Câu 20. [2D2-1] Tìm tập xác định
D
của hàm số
3
2
1 .
y x
A.
; 1 1; .
D
B.
.
D
C.
.
D
D.
\ 1 .
D
Lời giải
Chọn D.
Hàm số đã cho xác định
2
1 0 1.
x x
Câu 21. [0H3-2] Trong không gian
Oxyz
, cho hai điểm
1;2;0
A ,
2; 1;1
B . Tìm điểm
C
có hoành
độ dương trên trục
Ox
sao cho tam giác
ABC
vuông tại
C
.
A.
3;0;0
C . B.
2;0;0
C . C.
1;0;0
C . D.
5;0;0
C .
Lời giải
Chọn A.
Do
C
có hoành độ dương trên trục
Ox
nên
;0;0 , 0
C x x
.
Ta có:
1; 2;0
AC x
,
2;1; 1
BC x
.
Vì tam giác
ABC
vuông tại
C
nên
. 0 1 2 2 0
AC BC x x
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/22
2
0
3 0
3
x l
x x
x
. Vậy
3;0;0
C .
Câu 22. [0H3-2] Trong không gian
Oxyz
, cho hai điểm
1;2; 2
A
,
2; 1;2
B . Tìm tọa độ điểm
M
trên mặt phẳng
Oxyz
cho
MA MB
đạt giá trị nhỏ nhất.
A.
1;1;0
M . B.
3 1
; ;0
2 2
M
. C.
2;1;0
M . D.
1 3
; ;0
2 2
M
.
Lời giải
Chọn B.
Ta có:
1; 3;4
AB
,
1; 2; 2
AM x y z
.
Ta có:
MA MB AB
, dấu bằng xảy ra khi
M
nằm giữa
A
và
B
AM k AB
.
3
2
1 1
1 1
2 3 3 2 0
2 2
2 4 4 2
0
x
x k x k
y k y k z k y
z k z k
z
.
Vậy
3 1
; ;0
2 2
M
.
Câu 23. [2D2-2] Tập nghiệm của bất phương trình
2
1
2
4
x
x
là
A.
1;S
. B.
;1
S
. C.
;2
S . D.
2;S
.
Lời giải
Chọn D.
Ta có
2 2 2
1
2 2 2
4
x
x x x
2 2 2
x x x
.
Vậy tập nghiệm của bất phương trình là
2;S
.
Câu 24. [2D1-1] Số điểm cực trị của hàm số
4 2
3 5
y x x
là
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn A.
Hàm số đã cho là hàm trùng phương có hệ số
,
a b
trái dấu nên hàm số có
3
điểm cực trị.
Câu 25. [2D2-1] Giải phương trình
3
log 1 2
x
.
A.
8
. B.
10
. C.
7
. D.
9
.
Lời giải
Chọn B.
Ta có
3
log 1 2
x
1 0
10
1 9
x
x
x
.
Câu 26. [2D2-3] Số chữ số của só tự nhiên
2017
3
N là
A.
962
. B.
964
. C.
961
. D.
963
.
Lời giải

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/22
Chọn D.
Ta có số chữ số của só tự nhiên
2017
3
N là
2017
log3 1 963
.
Câu 27. [2D2-2] Cho hàm số
1
1
x x
y f x e
. Tính giá trị biểu thức
2018
1 . 2 ... 2017 .
T f f f e
.
A.
1
T
. B.
T e
. C.
1
T
e
. D.
1
2018
T e
.
Lời giải
Chọn B.
Ta có
1
1
x x
f x e
1
1
1
x
x
x
e
f
e
.
1
1
1
20172
2018
2018
1 1 1
2 3 2018
1 . 2 ... 2017 . . ... .
e e e
T f f f e e
e
e e
T e
.
Câu 28. [2H1-2] Cho khối hộp
.
ABCD A B C D
có thể tích là
36
. Tính thể tích
V
của khối chóp
.
ACB D
.
A.
18
V
. B.
6
V
. C.
9
V
. D.
12
V
.
Lời giải
Chọn D.
Ta có
. . .
4.
ABCD A B C D A CB D C C B D
V V V
.
Mà
1
2
B C D A B C D
S S
,
. .
6.
ABCD A B C D C C B D
V V
.
. . .
4
.
6
ABCD A B C D A CB D ABCD A B C D
V V V
. .
1
.
3
ABCD A B C D A CB D
V V
.
1
.36 12
3
A CB D
V
.
Câu 29. [2H1-1] Cho hình chóp
.
S ABCD
có cạnh bên
SA
tạo với đáy một góc
60
và
3
SA a
, đáy
là tứ giác có hai đường chéo vuông góc,
2
AC BD a
. Tính thể tích
V
của khối chóp theo
a
.
A.
3
2 3
3
a
V . B.
3
3
V a
. C.
3
V a
. D.
3
3
2
a
V .
Lời giải
Chọn C.
A
B
C
D
D
C
B
A
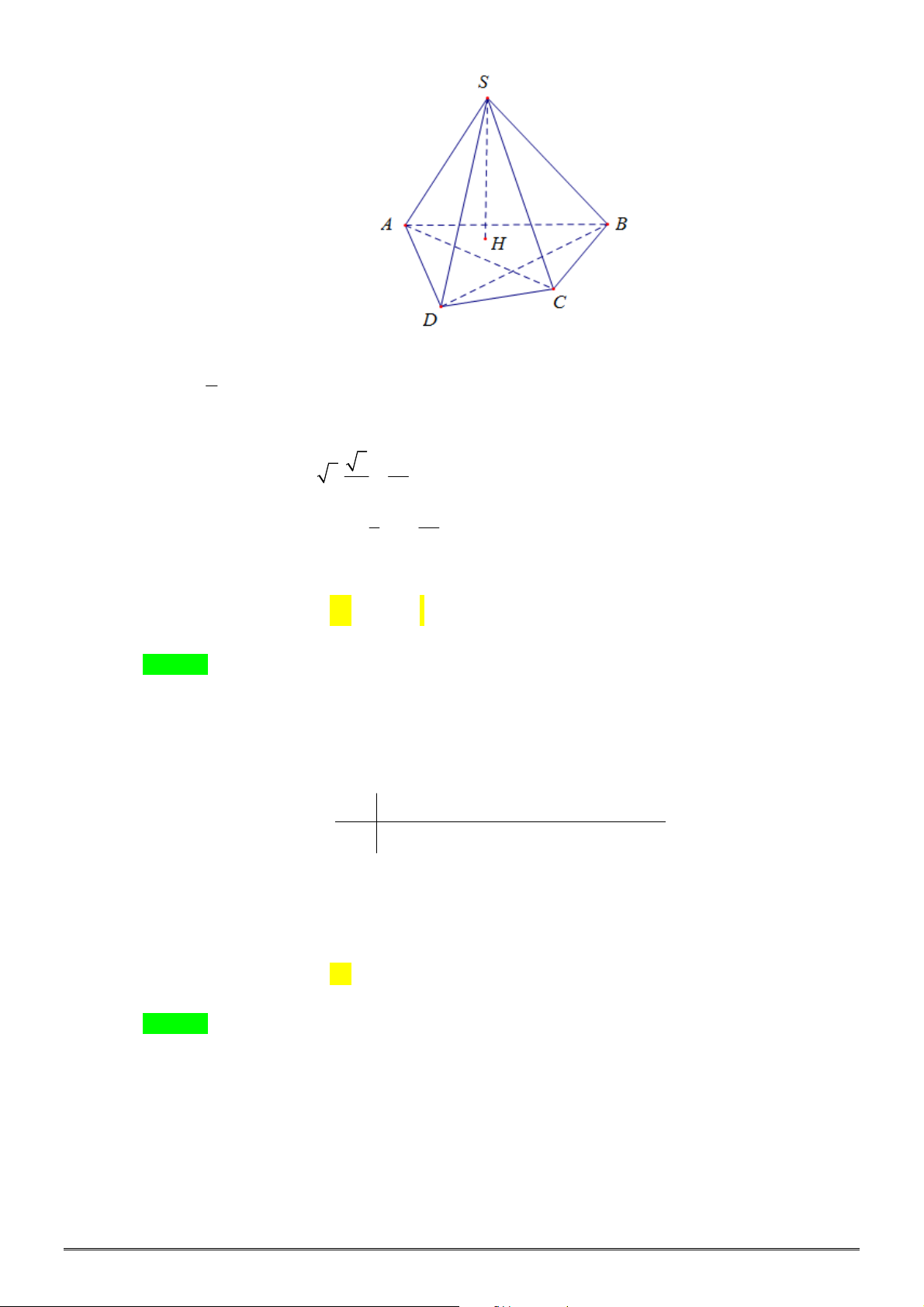
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/22
2
1
. 2
2
ABCD
S AC BD a
Hạ
( )
SH ABCD
góc giữa
SA
và đáy là
60
SAH
3 3
.sin60 3.
2 2
a
SH SA a .
Vậy thể tích khối chóp là
2 3
1 3
.2 .
3 2
a
V a a
.
Câu 30. [2D2-2] Hàm số
3
3
y x x
đồng biến trên khoảng nào?
A.
1;1
. B.
; 1
. C.
;
. D.
0;
.
Lời giải
Chọn B.
TXĐ:
D
2
3 3
y x
.
1
0
1
x
y
x
hàm số đồng biến trên
; 1
.
Câu 31. [2D2-3] Cho bất phương trình
2
3 2
2 2 2 3
x x x
x x
có tập nghiệm là
;
a b
. Giá trị của
2
T a b
là
A.
1
T
. B.
5
T
. C.
3
T
. D.
2
T
.
Lời giải
Chọn B.
Ta có
2 2
3 2 2 3
2 2 2 3 2 2 3 1
x x x x x x
x x x x x
.
Xét hàm số
2
t
f t t
, có
2 .ln 2 1 0
t
f t t
Vậy hàm số
f t
đồng biến trên
.
2 2
1 3 3 3 1
f x x f x x x x x
3;1
x .
3, 1 2 5
a b T a b
.
x
y
1
1
0
0

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/22
Câu 32. [2D1-3] Cho hàm số
1
mx
y
x n
,
trong đó
m
,
n
là tham số. Biết giao điểm của hai đường tiệm
cận của đồ thị hàm số nằm trên đường thẳng
2 3 0
x y
và đồ thị hàm số đi qua điểm
0,1
A . Giá trị của
m n
là
A.
3
m n
. B.
3
m n
.
C.
1
m n
. D.
1
m n
.
Lời giải
Chọn B.
Đồ thị hàm số
1
mx
y
x n
có đường tiệm cận ngang là
y m
, đường tiệm cận đứng là
x n
.
Gọi
I
là giao điểm của hai đường tiệm cận
;
I n m
. Đặt
: 2 3 0
d x y
Ta có
: 2 3 0
I d x y
2 3 0
n m
.
Đồ thị hàm số đi qua điểm
0;1
A
.0 1
1
0
m
n
Ta có hệ phương trình:
2 3 0
1
3
.0 1
2
1
0
n m
n
m n
m
m
n
.
Câu 33. [2D1-2] Biết rằng hàm số
3 2
y f x x ax bx c
đạt cực tiểu tại điểm
1
x
, giá trị cực
tiểu bằng
3
và đồ thị hàm số cắt trục tung tại điểm có tung độ
2
. Tìm giá trị của hàm số tại
2
x
.
A.
2 8.
f
B.
2 0.
f
C.
2 0.
f
D.
2 4.
f
Lời giải
Chọn C.
Theo đề bài ta có:
3 2
1 2 3 0
1
1 1 3 5 5 2 2 4
2
0 2
f a b
a
f a b c b f x x x x f
c
f c
.
Câu 34. [2D2-3] Cho phương trình
2017 2017
4
4034
tan 12 tan
1 1
12 12
2017.
2 3
1 tan 1 tan 1 tan
12 12 12
x x
x
.
Tính tổng tất cả các nghiệm thực của phương trình đã cho.
A.
0
B.
1
C.
1
D.
2017
Lời giải
Chọn D.
Ta có:
tan
3 1
12
2
1 tan
12
;
1 3 1
2 3
1 tan
12
, đặt
4034
x
t phương trình trở thành:
2 2
4
12 3 1
3 1 3 1 1
2017
2 2
2 3 2 3
t t
t

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/22
2
4
12 3 1
3 3
2017 0
2
2 3 2 3
t t
Đặt
3
2 3
t
X
ta có:
4
2
12 3 1
2017. 0
2
X X
suy ra phương trình có các nghiệm
1 2
,
X X
thỏa mãn
1 2 1 2
4
1 2 1 2
12 3 1
3 3 3 1
. .
2 2
2 3 2 3 2 3
t t t t
X X t t
1 2
1 2
1
2017
4034 4034 2
x x
x x
Câu 35. [2H2-2] Tính thể tích
V
khối lập phương biết rằng khối cầu ngoại tiếp khối lập phương có thể
tích là
32
3
.
A.
64 3
9
V . B.
8
V
. C.
8 3
9
V . D.
8 3
3
V .
Lời giải
Chọn A.
Gọi độ dài cạnh hình lập phương là
x
.
Khi đó bán kính mặt cầu ngoại tiếp khối lập phương là:
3
2 2
AC x
R
. Thể tích khối cầu này là
3
4
3
R
.
Theo bài ra, ta có:
3
4 32
3 3
R
3
4 3 32
3 2 3
x
3
64 3
9
x .
Vậy thể tích
V
khối lập phương là:
3
64 3
9
V x .
Câu 36. [2D2-1] Hàm số nào trong bốn hàm số liệt kê ở dưới đồng biến trên các khoảng xác định của
hàm số?
A.
2 1
x
y
e
. B.
3
x
y
. C.
sin 2017
x
y . D.
2
x
y
e
.
Lời giải
Chọn A.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/22
Với hàm số
2 1
x
y
e
ta có
2 1
2. .ln 0,
x
y x
e e
.
Suy ra hàm số
2 1
x
y
e
đồng biến trên
.
Câu 37. [1D5-4] Cho hàm số
3 2
3 2
y x x
. Gọi
A
,
B
là các điểm thuộc đồ thị hàm số đã cho có
hoành độ lần lượt là
A
x
;
B
x
, tiếp tuyến của đồ thị hàm số tại
A
,
B
song song với nhau và
đường thẳng
AB
tạo với
2
trục toạ độ một tam giác cân, đường thẳng
AB
có hệ số góc
dương. Tính giá trị
A B
x x
.
A.
1
A B
x x
. B.
3
A B
x x
. C.
2
A B
x x
. D.
2
A B
x x
.
Lời giải
Chọn B.
Hàm số
3 2
3 2
y x x
có tập xác định
D
. Đạo hàm
2
3 6
y x x
.
Gọi
;
A A
A x y
,
;
B B
B x y
. Từ giả thiết ta suy ra
A B
x x
.
* Hệ số góc của tiếp tuyến của đồ thị hàm số tại
A
,
B
lần lượt là:
2
3 6
A A A A
k y x x x
;
2
3 6
B B B B
k y x x x
.
Vì tiếp tuyến của đồ thị hàm số tại
A
,
B
song song với nhau nên
A B
k k
2 2
3 6 3 6
A A B B
x x x x
2 2
2
A B A B
x x x x
2
A B
x x
(do
A B
x x
).
* Đường thẳng
AB
tạo với
2
trục toạ độ một tam giác cân, đường thẳng
AB
có hệ số góc
dương nên
1
AB
k
1
B A
B A
y y
x x
3 2 3 2
3 2 3 2
A A B B B A
x x x x x x
3 3 2 2
3
A B A B B A
x x x x x x
2 2
3 1
A A B B A B
x x x x x x
2
3 1
A B A B A B
x x x x x x
2
2 3.2 1
A B
x x
3
A B
x x
.
Câu 38. [1D5-2] Tiếp tuyến với đồ thị
2 1
2
x
y
x
tại điểm có tung độ bằng
5
có hệ số góc
k
là
A.
1
3
k
. B.
1
k
. C.
3
k
. D.
1
3
k
.
Lời giải
Chọn C.
Hàm số
2 1
2
x
y
x
có tập xác định
\ 2
D
. Đạo hàm
2
3
2
y
x
.
Gọi
0 0
;
x y
là tiếp điểm,
0
2
x
. Theo giả thiết ta có
0
5
y
0
0
2 1
5
2
x
x
0 0
2 1 5 2
x x
0
3 9
x
0
3
x
.
Vậy hệ số góc của tiếp tuyến cần tìm là
2
3
3 3
3 2
k y
.
Câu 39. [2H2-2] Cho hình nón tròn xoay có đường cao
4
h
và diện tích đáy là
9
. Tính diện tích
xung quanh của hình nón.
A.
10
xq
S
. B.
15
xq
S
. C.
25
xq
S
. D.
30
xq
S
.
Lời giải
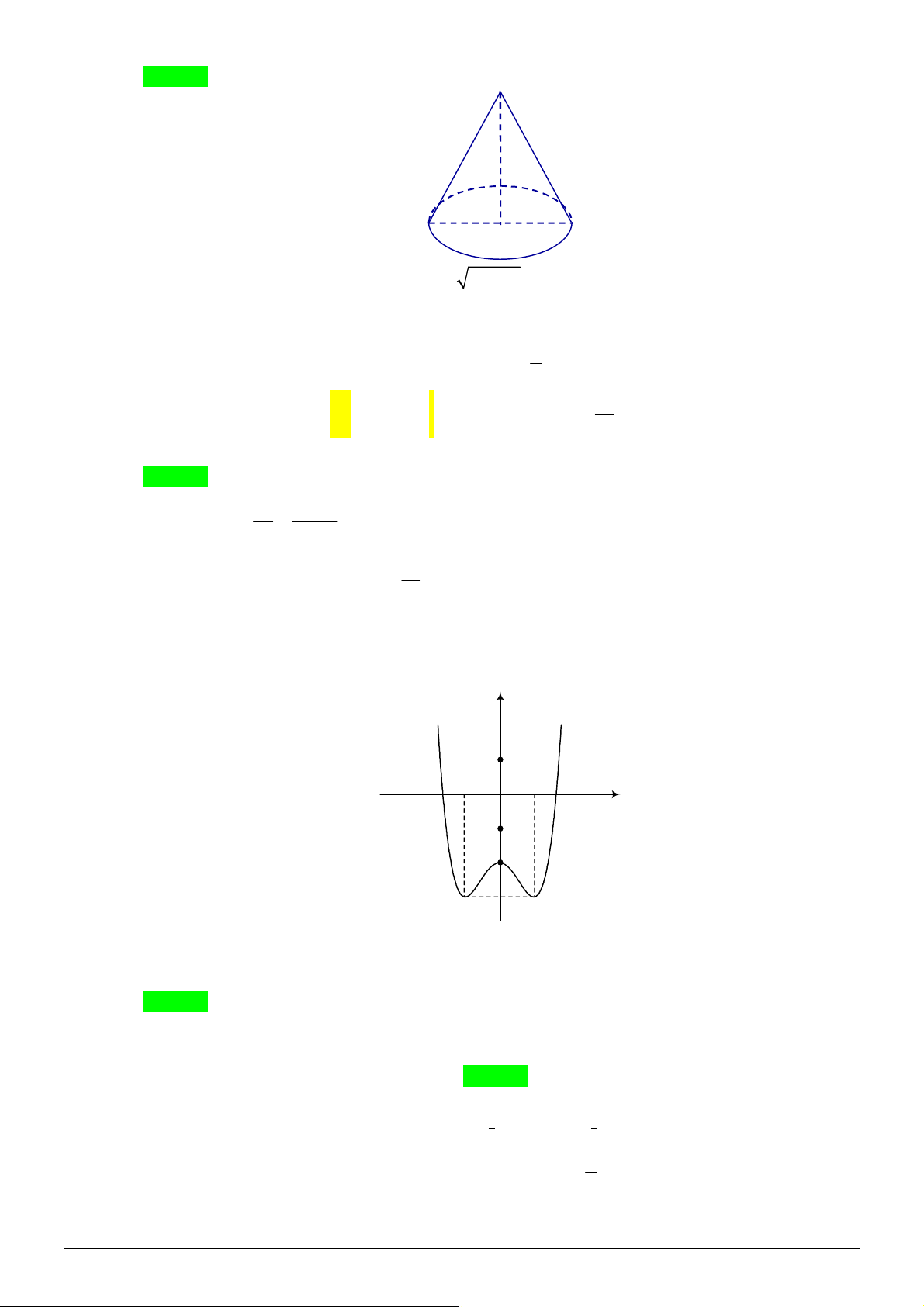
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/22
Chọn B.
Ta có:
2
B r
2
9
r
3
r
;
2 2
5
l r h
.
Diện tích xung quanh:
.3.5 15
xq
S
Câu 40. [2D1-2] Tìm giá trị nhỏ nhất của hàm số
4
1y x
x
trên
1;3
.
A.
1;3
Min 4
x
y
. B.
1;3
Min 5
x
y
. C.
1;3
16
Min
3
x
y
. D.
1;3
Min 6
x
y
.
Lời giải
Chọn B.
Ta có:
2
2 2
4 4
1
x
y
x x
;
0
y
2 1;3
2
x
x
Tính:
1 6
y
;
2 5
y
;
16
3
3
y
.
Vậy
1;3
min 5
x
y
.
Câu 41. [2D1-1] Đường cong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây.
x
y
1
2
3
1
1
1
A.
3
3 2
y x x
. B.
4 2
2 2
y x x
. C.
4 2
2 2
y x x
. D.
4 2
2 2
y x x
.
Lời giải
Chọn B.
Loại A vì đồ thị là của hàm số bậc 4 trùng phương.
Nhìn vào đồ thị xác định được hệ số
0
a
nên loại C.
Do hàm số có 3 cực trị nên
0
ab
. Vậy Chọn B.
Câu 42. [2D2-2] Tập nghiệm của bất phương trình
1 1
2 2
log 3 log 9 2
x x
.
A.
3;4
S . B.
;4
S . C.
9
3;
4
S
. D.
3;4
S .
Lời giải
h
r
O

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/22
Chọn D.
Điều kiện xác định:
9
3
2
x
.
Bất phương trình cho
3 9 2 4
x x x
So điều kiện, ta được:
3 4
x
.
Câu 43. [2H1-2] Diện tích toàn phần của một hình hộp chữ nhật là
2
8
tp
S a
. Đáy của hình hộp là hình
vuông cạnh
a
. Tính thể tích của khối hộp theo
a
.
A.
3
3 .
V a
B.
3
V a
. C.
3
3
.
2
a
V D.
3
7
.
4
V a
Lời giải
Chọn C.
Gọi
h
là chiều cao hình hộp chữ nhật, theo bài ra ta có
2
2 8
tp
S ah ah aa a
3
2
a
h .
Vậy thể tích khối hộp:
3
3
.
2
a
V Bh
Câu 44. [2H3-1] Trong không gian
Oxyz
, phương trình mặt cầu tâm
1;2;0
I và đi qua điểm
2; 2;0
A là
A.
2 2
2
1 2 100.
x y z B.
2 2
2
1 2 5.
x y z
C.
2 2
2
1 2 10.
x y z D.
2 2
2
1 2 25.
x y z
Lời giải
Chọn D.
Ta có:
2 2
3 4 5
R IA
.
Vậy phương trình mặt cầu có dạng:
2 2
2
1 2 25.
x y z
Câu 45. [2D1-2] Tìm tập hợp tất cả các giá trị của tham số thực
m
để hàm số
1
mx
y
x m
đồng biến trên
từng khoảng xác định.
A.
; 1
. B.
1;1
. C.
1;
. D.
;1
.
Lời giải
Chọn B.
Tập xác định:
\
D m
.
Ta có
2
2
1
m
y
x m
, để hàm số đồng biến trên từng khoảng xác định thì
2
2
1
0
m
y
x m
2
1 0 1 1
m m
.
Câu 46. [2H2-2] Hình nón có chiều cao bằng đường kính đáy. Tỉ số giữa diện tích xung quanh và diện
tích toàn phần của hình nón là:
A.
1
2
. B.
1 5
4
. C.
1
4
. D.
5 5
4
.
Lời giải
Chọn D.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/22
Gọi bán kính đáy là
r
thì
2 5
h r l r
.
Diện tích xung quanh
2
5
xq
S rl r
và diện tích toàn phần
2 2
1 5
tp
S rl r r
.
Vậy tỉ số giữa diện tích xung quanh và diện tích toàn phần của hình nón là:
5 5
4
.
Câu 47. [2H1-1] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA a
và vuông góc với
đáy. Thể tích
V
của khối chóp
.
S ABC
theo
a
là
A.
3
.
3
12
S ABC
a
V . B.
3
.
2
12
S ABC
a
V . C.
3
.
3
3
S ABC
a
V . D.
3
.
3
4
S ABC
a
V .
Lời giải
Chọn A.
Ta có
2
3
4
ABC
S a
và
h SA a
.
Khi đó
2 3
.
1 1 3 3
.
3 3 4 12
S ABC ABC
V S h a a a
.
Câu 48. [2D2-2] Đạo hàm của hàm số
2
2
log 2
y x x
là
A.
2
1
2 ln2
y
x x
. B.
2
1
2
x
y
x x
.
C.
2
1
2 ln2
x
y
x x
. D.
2
1
2 ln 2
x
y
x x
.
Lời giải
Chọn D.
Áp dụng công thức
log
ln
a
u
u
u a
ta được:
2
2
2
2 2
2
2
2 2 1
log 2
2 ln 2 2 ln2
2 ln 2
x x
x x
x x
x x x x
x x
.
Câu 49. [2H3-2] Trong không gian
Oxyz
, cho ba vecto
1;2;1
a
,
0;2; 1
b
,
;1;0
c m
. Tìm giá
trị thực của tham số
m
để ba véctơ
a
,
b
,
c
đồng phẳng.
A.
1
m
. B.
0
m
. C.
1
4
m
. D.
1
4
m
.
Lời giải
Chọn D.
Ba véctơ
a
,
b
,
c
đồng phẳng
, . 0
a b c
Ta có
, 4;1;2
a b
,
, . 4 1 0
a b c m
1
.
4
m
Câu 50. [2H2-1] Khối cầu có thể tích là
36
. Diện tích xung quanh của mặt cầu là
A.
9
xq
S
. B.
27
xq
S
. C.
18
xq
S
. D.
36
xq
S
.
Lời giải
Chọn D.
3
4
36
3
V R
2
3 4 36 .
xq
R S R
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/32 – Mã đề 101
TRƯỜNG TRUNG HỌC PHỔ THÔNG
CHUYÊN HẠ LONG
(Đề thi gồm 08 trang)
KIỂM TRA HỌC KÌ I
Năm học 2017 - 2018
Môn: Toán 12 (Chương trình chuẩn)
(Chương trình nâng cao)
(Thời gian làm bài: 90 phút)
Họ và tên thí sinh: .......................................................... SBD: ................................
Mã đề 101
A. PHẦN CHUNG (80%, gồm 40 câu)
Câu 1. [2H1-2] Hình đa diện đều nào dưới đây không có tâm đối xứng?
A. Hình bát diện đều. B. Hình tứ diện đều.
C. Hình lăng trụ lục giác đều. D. Hình lập phương.
Câu 2. [2D1-1] Tìm giá trị cựa đại
C
Đ
y
của hàm số
4 2
2 2
y x x
.
A.
2
CĐ
y
. B.
2
CĐ
y
. C.
1
CĐ
y
. D.
1
CĐ
y
.
Câu 3. [2D1-2] Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D
dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3 2
3 2.
y x x
B.
3 2
3 2.
y x x
C.
4 2
2 2.
y x x
D.
3 2
3 2.
y x x
Câu 4. [2D2-2] Tính đạo hàm của hàm số
2 1
7
x
y
.
A.
2
2.7
x
y
. B.
2 1
7
x
y
. C.
2 1
2.7 .ln7
x
y
. D.
2 1
2.7
ln7
x
y
.
Câu 5. [2D1-2] Tìm khoảng nghịch biến của hàm số
3 2
3 2
y x x
.
A.
0; 2
. B.
0; 3
. C.
0; +
. D.
2; 0
.
Câu 6. [2D1-2] Tiệm cận đứng và tiện cận ngang của đồ thị hàm số
2 1
1
x
y
x
.
A.
1
y
;
2
x
. B.
1
x
;
2
y
. C.
1
x
;
2
y
. D.
1
x
;
2
y
.
Câu 7. [2D1-2] Tìm giá trị lớn nhất
M
của hàm số
3 2
3 2
y x x
trên đoạn
2;3 .
A.
22.
M
B.
6.
M
C.
22.
M
D.
6.
M
Câu 8. [2D1-2] Biết đường thẳng
1
y x
cắt đồ thị hàm số
3 1
1
x
y
x
tại hai điểm phân biệt
A
,
B
có hoành độ lần lượt
A
x
,
B
x
. Hãy tính tổng
.
A B
x x
A.
1.
A B
x x
B.
3.
A B
x x
C.
3.
A B
x x
D.
1.
A B
x x
Câu 9. [2H1-2] Cho tam giác đều
ABC
có đường cao
.
AH
Khi tam giác
ABC
quay quanh trục là
đường thẳng
AH
một góc
360
thì các cạnh của tam giác
ABC
sinh ra hình gì?
A. Một hình trụ. B. Một mặt nón.
C. Hai hình nón. D. Một hình nón.
O
x
y
11
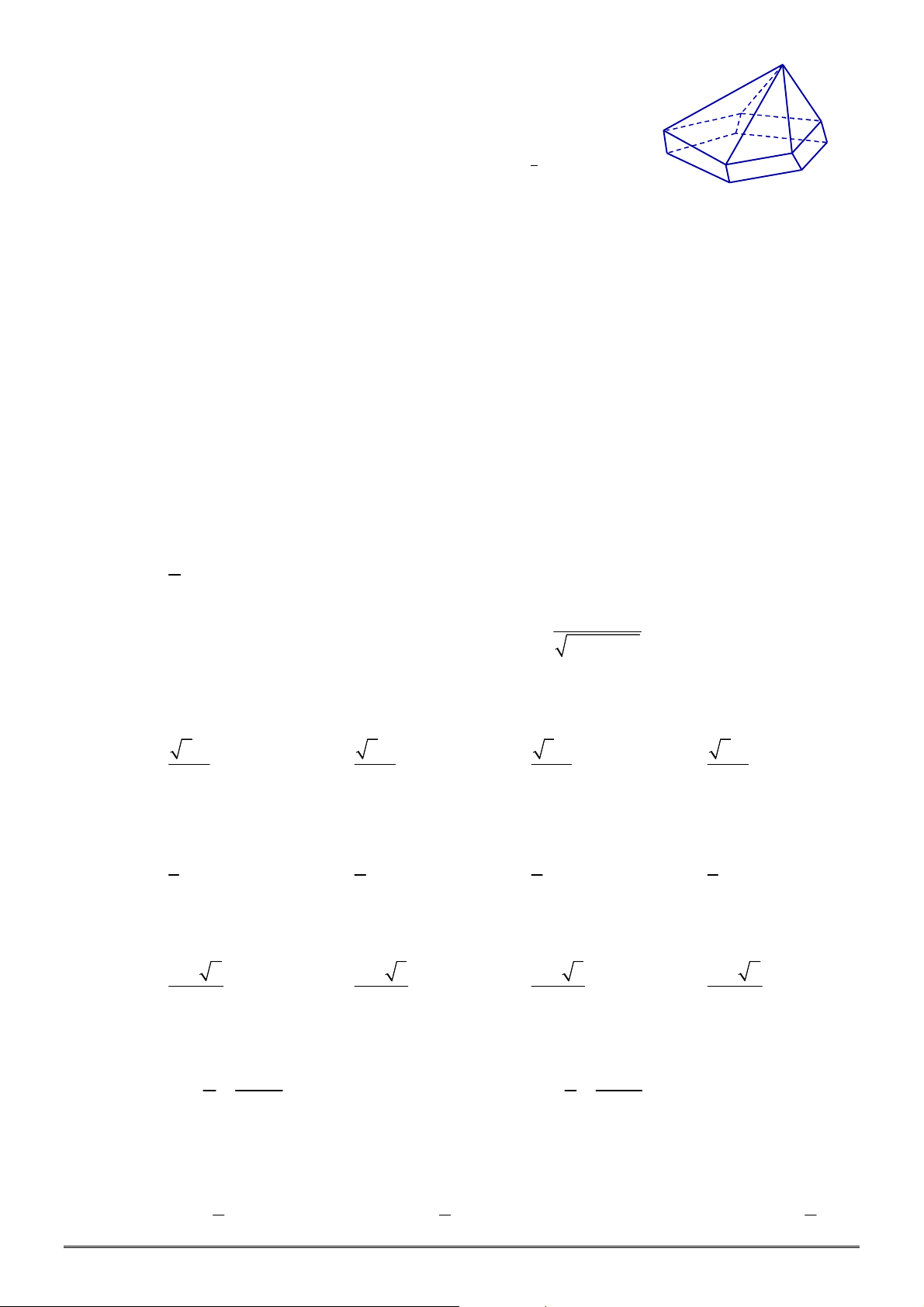
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/32 – Mã đề 101
Câu 10. [2H1-1] Hình đa diện bên có bao nhiêu mặt?
A.
6
. B.
11
.
C.
12
. D.
10
.
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
3
1
y x
.
A.
;D
. B.
\ 1
D
. C.
; 1
D . D.
; 1
D .
Câu 12. [2D2-2] Phương trình
2
2 7 5
2 1
x x
có bao nhiêu nghiệm?
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 13. [2H2-1] Cho tấm tôn hình chữ nhật quay quanh trục là đường thẳng chứa một cạnh của tấm tôn
đó một góc
360
ta được một vật tròn xoay nào dưới đây?
A. Mặt trụ. B. Khối lăng trụ. C. Hình trụ. D. Khối trụ.
Câu 14. [2D2-1] Giải phương trình
3
log 2 2.
x
A.
6.
x
B.
7.
x
C.
11.
x
D.
4.
x
Câu 15. [2H2-1] Cho đường tròn quay quanh một đường thẳng đi qua tâm đường tròn đó một góc
360
thì sinh ra hình gì?
A. Hai mặt cầu. B. Một khối cầu. C. Hai khối cầu. D. Một mặt cầu.
Câu 16. [2H1-1] Cho khối lăng trụ đứng
.
ABC A B C
có thể tích bằng
3
.
a
Biết
ABC
vuông tại
,
A
AB a
,
2
AC a
. Tính độ dài đường cao của khối lăng trụ.
A.
3
a
. B.
a
. C.
3
a
. D.
2
a
.
Câu 17. [2D1-1] Tìm số đường tiệm cận của đồ thị hàm số
2
15 11
2017
x
y
x
.
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 18. [2H1-2] Tính thể tích khối chóp
.
S ABC
biết
SA a
,
ABC
đều,
SAB
vuông cân tại
S
và
nằm trong mặt phẳng vuông góc với mặt phẳng đáy.
A.
3
6
24
a
. B.
3
6
12
a
. C.
3
3
12
a
. D.
3
6
6
a
.
Câu 19. [2D1-3] Cho khối lăng trụ
.
ABC A B C
. Gọi
M
là trung điểm
CC
. Mặt phẳng
ABM
chia
khối lăng trụ
.
ABC A B C
thành hai khối. Tính tỉ số thể tích (số bé chia số lớn) của hai khối đó.
A.
1
3
. B.
2
5
. C.
1
6
. D.
1
5
.
Câu 20. [2D2-2] Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, góc
60
SAB
. Tính thể
tích của khối nón đỉnh
S
có đáy là đường tròn ngoại tiếp tứ giác
ABCD
.
A.
3
2
12
a
. B.
3
3
12
a
. C.
3
3
6
a
. D.
3
2
6
a
.
Câu 21. [2D2-2] Cho
a
và
b
là các số thực dương khác
1
,
x
và
y
là hai số thực dương. Khẳng định
nào dưới đây đúng?
A.
log
log
log
a
a
a
x
x
y y
. B.
1 1
log
log
a
a
x x
.
C.
log log log
a a a
x y x y
. D.
log log .log
b b a
x a x
.
Câu 22. [2D1-2] Tìm giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
2
sin cos 2.
y x x
A.
3
; 3.
4
M m
B.
3
3;
4
M m
C.
3; 1.
M m
D.
3
3;
4
M m
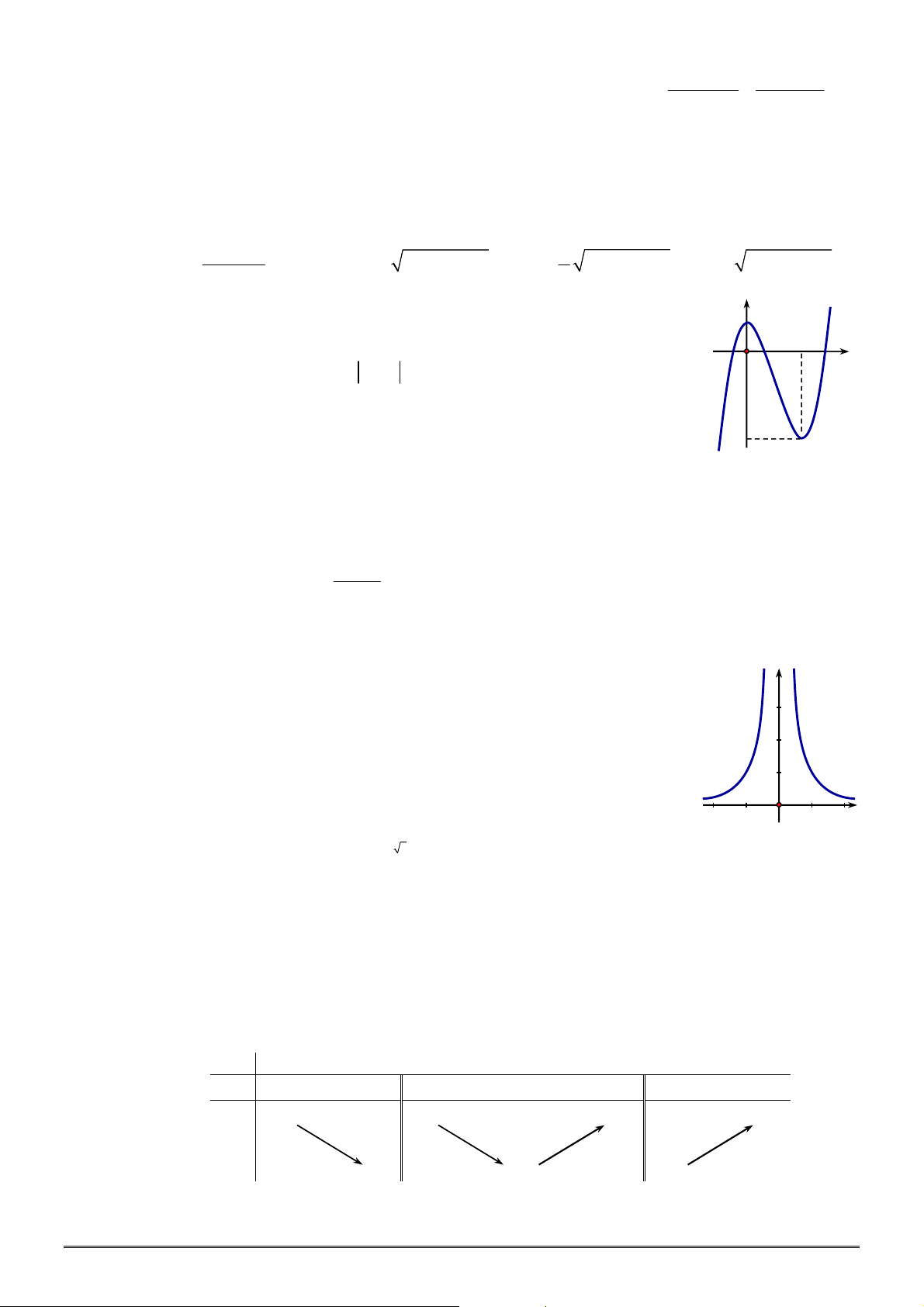
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/32 – Mã đề 101
Câu 23. [2D2-2] Số tuổi của An và Bình là các nghiệm của phương trình
2 2
1 2
1
5 log 1 logx x
.
Tính tổng số tuổi của An và Bình.
A.
21.
B.
16.
C.
12.
D.
13.
Câu 24. [2H2-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
,
A
biết
SA ABC
và
SA a
,
AB b
,
AC c
. Tính bán kính
r
của mặt cầu ngoại tiếp hình chóp
. .
S ABC
A.
2
a b c
r
B.
2 2 2
2 .
r a b c
C.
2 2 2
1
.
2
r a b c
D.
2 2 2
.
r a b c
Câu 25. [2D1-3]Cho hàm số
y f x
liên tục trên
và có đồ thị hàm số
là đường cong trong hình vẽ bên. Tìm tất cả các giá trị thực của
tham số
m
để phương trình
f x m
có
3
nghiệm phân biệt.
A.
0;3
m .
B.
1 3
m
.
C.
3 1
m
.
D. Không có giá trị nào của
m
.
Câu 26. [2D1-2] Cho hàm số
y f x
có đạo hàm
3
2
1 .
f x x x
Hỏi hàm số có bao nhiêu điểm
cực trị?
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 27. [2D1-1] Cho hàm số
2 4
.
1
x
y
x
Khẳng định nào sau đây sai?
A. Đồ thị hàm số có tiệm cận đứng là đường thẳng
1
x
và tiệm cận ngang là đường
thẳng
4
y
.
B. Đồ thị hàm số cắt trục hoành tại điểm
2;0
và cắt trục tung tại điểm
0;4
.
C. Hàm số không có cực trị.
D. Hàm số đồng biến trên các khoảng
;1
và
1;
.
Câu 28. [2D2-2] Đường cong hình bên là đồ thị của một trong bốn hàm
số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó
là hàm số nào?
A.
4
y x
. B.
2
y x
. C.
2
x
y
. D.
2
y x
.
Câu 29. [2H2-2] Tính diện tích xung quanh
xq
S
của hình trụ có đường cao
h a
và thể tích
3
V a
.
A.
2
4
xq
S a
. B.
2
6
xq
S a
. C.
2
2
xq
S a
. D.
2
8
xq
S a
.
Câu 30. [2D1-2] Cho hàm số
y f x
xác định trên
\ 1
, liên tục trên mỗi khoảng xác định và có
bảng biến thiên như hình bên dưới. Tìm tập hợp tất cả các giá trị thực của tham số
m
sao cho
phương trình
f x m
vô nghiệm.
A.
; 2
. B.
1;
. C.
2;1
. D.
2;
.
x
1
0
1
y
0
y
2
1
2
O
x
y
1
2
1
2
1
2
O
x
y
3
2
1
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/32 – Mã đề 101
Câu 31. [0D2-1] Phương trình
2 3 4
9 27
x x
tương đương với phương trình nào sau đây?
A.
6 0
x
. B.
7 6 0
x
. C.
7 6 0
x
. D.
6 0
x
.
Câu 32. [0D2-2] Cho
a
,
b
là hai số dương khác
1.
Đặt
log .
a
b m
Tính theo
m
giá trị của biểu thức
2
3
log log
ba
P b a
.
A.
2
12
2
m
P
m
. B.
2
12
m
P
m
. C.
2
4 3
2
m
P
m
. D.
2
3
m
P
m
.
Câu 33. [0D2-2] Tìm tất cả các giá trị của tham số
m
sao cho hàm số
2
3
1
log 2 3
y
x x m
có tập
xác định là
.
A.
2
;
3
. B.
2
;
3
. C.
2
;
3
. D.
2
;
3
.
Câu 34. [2D1-1] Hàm số
2
4
1
y
x
có bảng biến thiên như bên dưới. Xét trên tập xác định của hàm số,
khẳng định nào sau đây đúng?
A. Hàm số có giá trị lớn nhất bằng
4
và không có giá trị nhỏ nhất.
B. Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
C. Hàm số có giá trị lớn nhất bằng
4
và giá trị nhỏ nhất bằng
0
.
D. Hàm số có giá trị nhỏ nhất bằng
0
và không có giá trị lớn nhất.
Câu 35. [2D2-2] Tính tổng tất cả các nghiệm của phương trình
9 4.3 3 0
x x
.
A.
3
. B.
1
. C.
1
. D.
2
.
Câu 36. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị hàm số
2
1
2
x
y
x x m
có
đúng hai đường tiệm cận đứng.
A.
1
m
. B.
3
m
. C.
1
m
. D.
1
3
m
m
.
Câu 37. [2D2-2] Biết tập nghiệm của bất phương trình
2 2 2
log 1 log 5 1 log 2
x x x
là
khoảng
;
a b
. Tính
.
P a b
A.
6
P
. B.
5
P
. C.
7
P
. D.
8
P
.
Câu 38. [2D2-2] Tìm tất cả các giá trị của tham số
m
để phương trình
2 3
2 2 5
x
m
có nghiệm.
A.
5
2
m
. B.
5
2
m
. C.
5
2
m
. D.
5
2
m
.
Câu 39. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị hàm số
4 2
2 1
y x mx
có
ba điểm cực trị tạo thành ba đỉnh của một tam giác đều.
A.
3
3
m
. B.
3
m
. C.
3
1
3
m
. D.
1
3
m
.
x
0
y
0
y
1
4
2
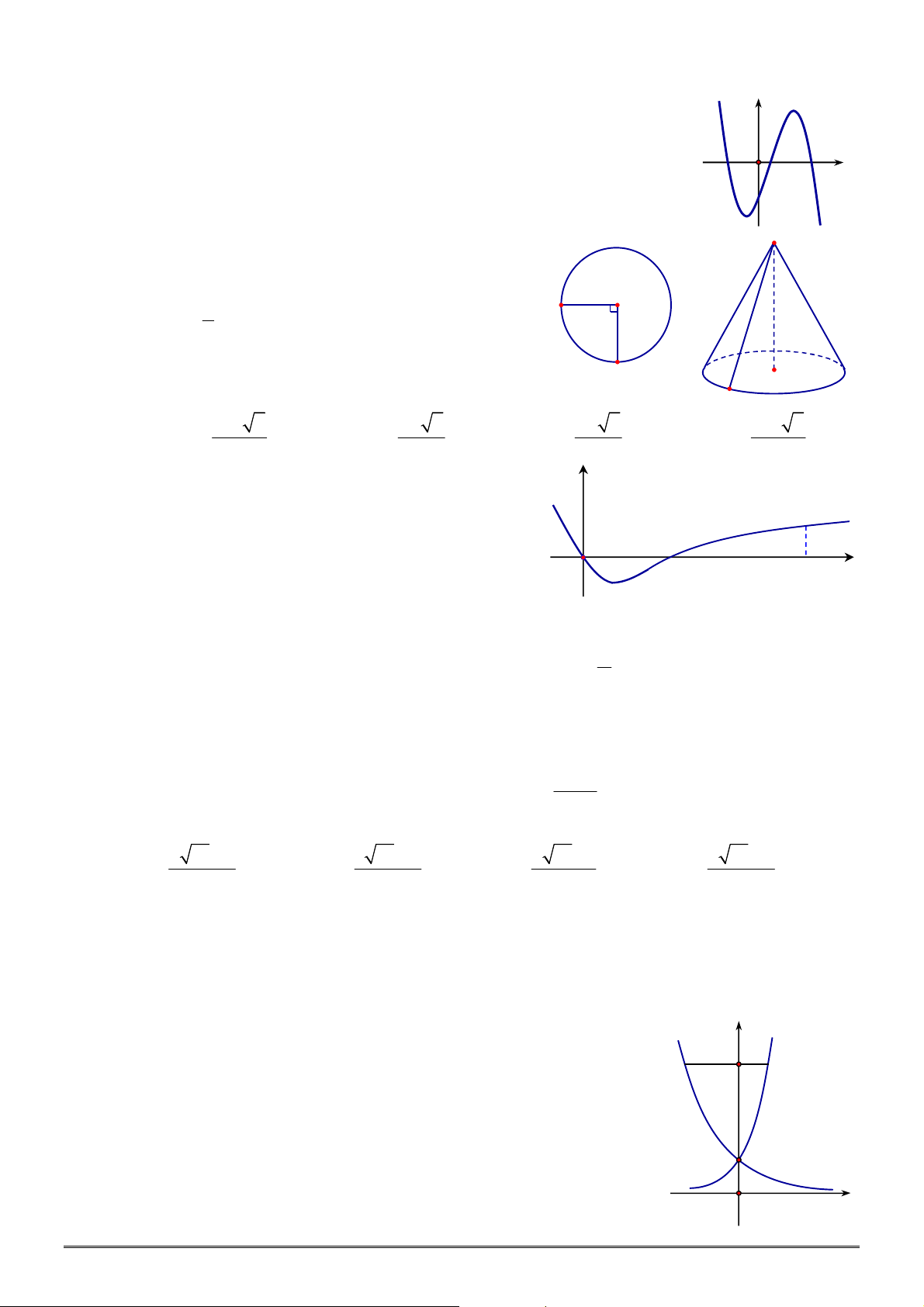
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/32 – Mã đề 101
Câu 40. [2D1-3] Cho hàm số
3 2
y ax bx cx d
có đồ thị hình bên. Hỏi khẳng định nào sau đây
đúng?
A.
0
a
,
0
b
,
0
c
,
0
d
.
B.
0
a
,
0
b
,
0
c
,
0
d
.
C.
0
a
,
0
b
,
0
c
,
0
d
.
D.
0
a
,
0
b
,
0
c
,
0
d
.
B. PHẦN RIÊNG ( 20%, gồm 10 câu )
1. Phần dành cho học sinh không chuyên
Câu 41. [2H2-3] Cho tấm tôn hình tròn có bán kính
6.
r
Cắt bỏ
1
4
hình tròn giữa 2 bán kính
OA
,
OB
, rồi
đem tấm tôn còn lại ghép hai bán kính đó lại để
được một hình nón (như hình vẽ). Tính thể tích
khối nón giới hạn bởi hình nón đó.
A.
81 7
4
. B.
9 7
8
. C.
9 7
2
. D.
81 7
8
.
Câu 42. [2D1-3] Cho hàm số
f x
có đạo hàm
f x
.
Biết đồ thị hàm số
y f x
là hình bên và
0 3 2 5
f f f f . Tìm giá trị lớn nhất
của hàm số
f x
trên đoạn
0;5
.
A.
5
f
. B.
3
f
. C.
0
f . D.
2
f .
Câu 43. [2D2-2] Tìm tất cả các giá trị của tham số
m
để hàm số
3 2
3 3 11
1
x mx mx
y
đồng biến trên
.
A.
; 0 1;m
. B.
0;1
m .
C.
0;1
m . D.
; 0 1;m
.
Câu 44. [2D2-4] Xét các số thực
a
,
b
dương thỏa mãn
2
1
log 2 3
ab
ab a b
a b
. Tìm giá trị nhỏ
nhất của biểu thức
2
P a b
.
A.
2 10 3
2
. B.
3 10 7
2
. C.
2 10 1
2
. D.
2 10 5
2
.
Câu 45. [2D2-2] Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức
0
. 1 4
t
Q t Q
, với
t
là khoảng thời gian tính bằng giờ và
0
Q
là dung lượng nạp tối đa (pin
đầy). Nếu điện thoại nạp pin từ lúc cạn pin ( dung lượng
0%
) thì sau bao lâu nạp được
90%
?
A.
1,5
giờ. B.
1,66
giờ. C.
2,66
giờ. D.
1,26
giờ.
Câu 46. [2D2-3] Cho hai số thực dương
a
,
b
khác
1.
Biết rằng bất kì
đường thẳng nào song song với trục hoành mà cắt các đường
x
y a
,
x
y b
và trục tung lần lượt tại
M
,
N
,
A
thì
3
AN AM
( hình vẽ bên). Hỏi khẳng định nào sau đây đúng?
A.
2
1
ab
.
B.
3
b a
.
C.
3
1
a b
.
D.
3
1
ab
.
O
x
y
A
B
6
O
B
A
O
y
x
O
2
5
O
x
y
N
M
A
x
y b
x
y a
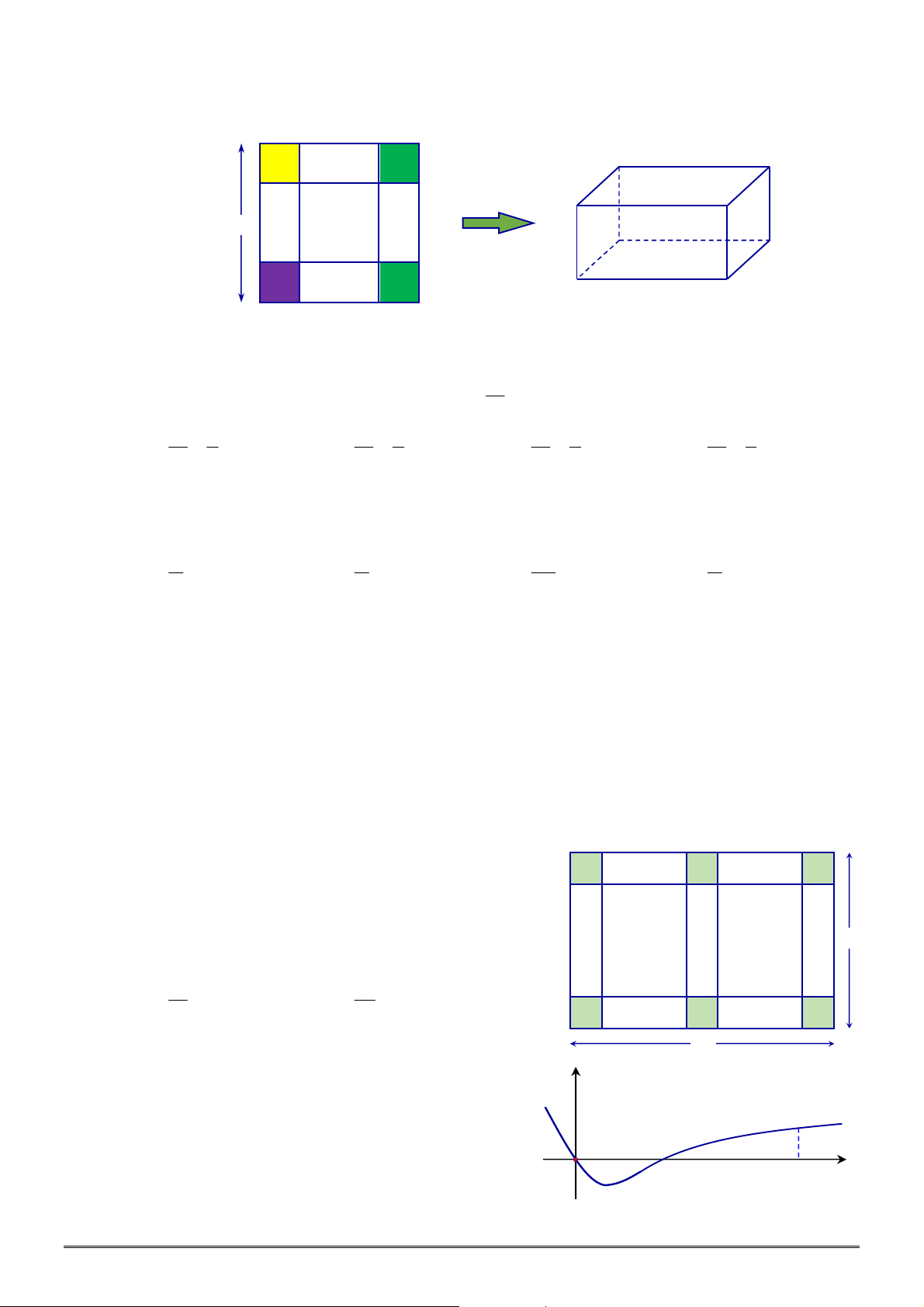
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/32 – Mã đề 101
Câu 47. [2D1-3] Từ một tấm tôn hình vuông cạnh
12
(mét) người ta cắt đi bốn góc bốn hình vuông
cạnh
x
(mét) rồi gấp tấm tôn còn lại để được một cái hộp không có nắp như hình vẽ dưới đây.
Tìm
x
để hộp nhận được có thể tích lớn nhất.
A.
4m.
B.
2m.
C.
2,5m.
D.
3m.
Câu 48. [2H1-3] Cho khối tứ diện có thể tích
.
V
Gọi
V
là thể tích khối đa diện có các đỉnh là trung
điểm các cạnh của khối tứ diện đó. Tính tỉ số
V
V
A.
1
2
V
V
B.
2
3
V
V
C.
1
4
V
V
D.
5
8
V
V
Câu 49. [2H1-2] Cho khối lăng trụ
.
ABC A B C
có thể tích
.
V
Gọi
M
là điểm bất kì trên đường thẳng
.
CC
Tính thể tích khối chóp
.
M ABB A
theo
.
V
A.
2
V
. B.
3
V
. C.
2
3
V
. D.
4
V
.
Câu 50. [2H2-1] Một hình trụ có bán kính đáy bằng
r
và có thiết diện qua trục là một hình vuông. Tính
diện tích xung quanh của hình trụ đó
A.
2
2 .
r
B.
2
.
r
C.
2
4 .
r
D.
2
8 .
r
2. Phần dành cho học sinh chuyên
Câu 51. [2D1-3] Đồ thị hàm số
3 2
3 9 1
y x x x
có hai điểm cực trị
A
,
B
. Điểm nào dưới đây
thuộc đường thẳng
.
AB
A.
1; 10 .
N B.
1;0 .
P C.
Q 0; 1 .
D.
1;10 .
M
Câu 52. [2D1-3] Từ một tấm tôn hình chữ nhật có chiều dài và
rộng là
60 cm
,
40 cm
. Người ta cắt đi
6
hình vuông
cạnh
(cm)
x rồi gấp tấm tôn còn lại để được một cái
hộp có nắp như hình vẽ dưới đây. Tìm
x
để hộp nhận
được có thể tích lớn nhất.
A.
10
cm .
3
B.
20
cm .
3
C.
4 cm .
D.
5 cm .
Câu 53. [2D1-3] Cho hàm số
f x
có đạo hàm
f x
.
Biết đồ thị hàm số
y f x
là hình bên và
0 3 2 5
f f f f . Tìm giá trị lớn nhất
của hàm số
f x
trên đoạn
0;5
.
A.
3
f
. B.
2
f . C.
5
f
. D.
0
f .
x
12
x
x
60
40
y
x
O
2
5
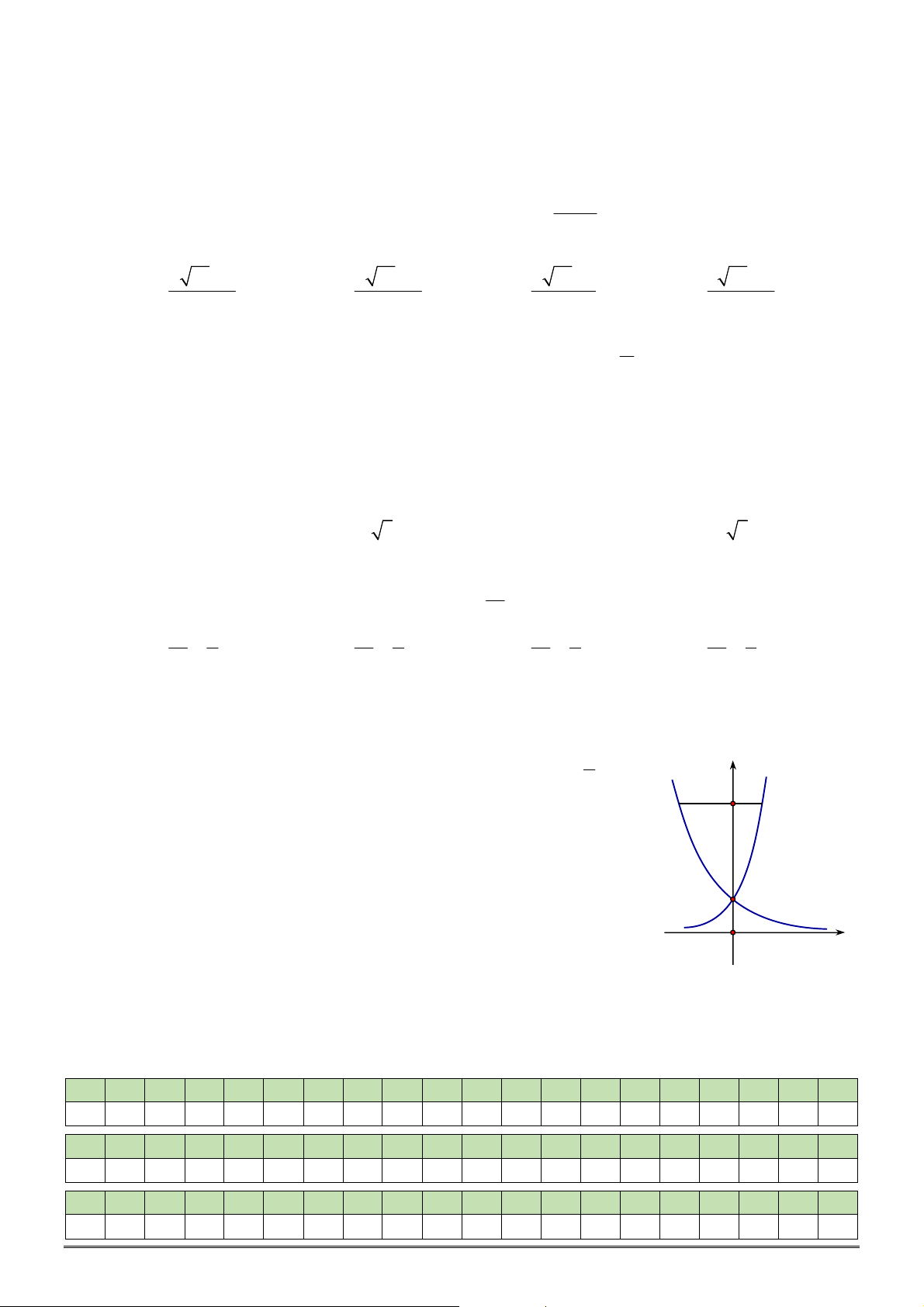
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/32 – Mã đề 101
Câu 54. [2D2-3] Ông A vay ngân hàng
300
triệu đồng để mua nhà theo phương thức trả góp với lãi
suất
0,5%
mỗi tháng. Nếu cuối mỗi tháng, bắt đầu từ tháng thứ nhất ông hoàn nợ cho ngân
hàng
5.500.000
đồng và chịu lãi số tiền chưa trả. Hỏi sau bao nhiêu tháng ông A sẽ trả hết số
tiền đã vay?
A. 64 tháng. B. 65 tháng. C. 63 tháng. D. 62 tháng.
Câu 55. [2D2-4] Xét các số thực
a
,
b
dương thỏa mãn
2
1
log 2 3
ab
ab a b
a b
. Tìm giá trị nhỏ
nhất của biểu thức
2
P a b
.
A.
2 10 3
2
B.
2 10 5
2
C.
2 10 1
2
D.
3 10 7
2
Câu 56. [2D2-3] Tìm tất cả các giá trị của tham số
m
để hàm số
3 2
3 3 11
1
x mx mx
y
đồng biến trên
khoảng
0; .
A.
0;1 .
m B.
0;1 .
m C.
0; .
D.
0; .
Câu 57. [2H2-3] Cho tứ diện đều
ABCD
có cạnh
6 .
a
Hình nón
N
có đỉnh
A
và đường tròn đáy là
đường tròn ngoại tiếp tam giác
.
BCD
Tính diện tích xung quanh của hình nón
N
.
A.
2
24 .
a
B.
2
12 3 .
a
C.
2
48 .
a
D.
2
24 3 .
a
Câu 58. [2H1-3] Cho khối tứ diện có thể tích
.
V
Gọi
V
là thể tích khối đa diện có các đỉnh là trung
điểm các cạnh của khối tứ diện đó. Tính tỉ số
V
V
A.
2
3
V
V
B.
1
2
V
V
C.
1
4
V
V
D.
5
8
V
V
Câu 59. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
1
y mx m
cắt đồ thị
hàm số
3 2
3 2
y x x x
tại ba điểm
A
,
B
,
C
phân biệt sao cho
.
AB BC
A.
( ;0] [4; ).
m
B.
5
; .
4
m
C.
2; .
m
D.
.
m
Câu 60. [2D2-3] Cho hai số thực dương
a
,
b
khác
1.
Biết rằng bất kì
đường thẳng nào song song với trục hoành mà cắt các đường
x
y a
,
x
y b
và trục tung lần lượt tại
M
,
N
,
A
thì
3
AN AM
(hình vẽ bên). Hỏi khẳng định nào sau đây đúng?
A.
3
b a
. B.
3
1
a b
. C.
2
1
ab
. D.
3
1
ab
.
----------HẾT----------
BẢNG ĐÁP ÁN THAM KHẢO
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
B B B C A D A C D B C D D B D B C B D A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
D B C C A D A D C C B A A A B D B A A C
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
D A C A B D B A C C A B C A A D B B C D
O
x
y
N
M
A
x
y b
x
y a
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/32 – Mã đề 101
HƯỚNG DẪN GIẢI
A. PHẦN CHUNG (80%, gồm 40 câu)
Câu 1. [2H1-2] Hình đa diện đều nào dưới đây không có tâm đối xứng?
A. Hình bát diện đều. B. Hình tứ diện đều.
C. Hình lăng trụ lục giác đều. D. Hình lập phương.
Lời giải
A'
G
A
B
C
D
Chọn B.
Nếu lấy đối xứng 1 đỉnh của tứ diện qua trọng tâm của nó ta được một đỉnh không thuộc tứ
diện.
Câu 2. [2D1-1] Tìm giá trị cựa đại
C
Đ
y
của hàm số
4 2
2 2
y x x
.
A.
2
CĐ
y
. B.
2
CĐ
y
. C.
1
CĐ
y
. D.
1
CĐ
y
.
Lời giải
Chọn B.
3
4 4
y x x
.
0
0
1
x
y
x
.
Do hệ số của
4
x
dương nên giá trị cực đại của hàm số bằng
0 2
y
.
Câu 3. [2D1-2] Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A, B, C, D dưới đây.
O
x
y

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/32 – Mã đề 101
Hỏi hàm số đó là hàm số nào?
A.
3 2
3 2.
y x x
B.
3 2
3 2.
y x x
C.
4 2
2 2.
y x x
D.
3 2
3 2.
y x x
Lời giải
Chọn B.
Dạng đồ thị hình chữ
N
nên không phải đồ thị của hàm bậc bốn và hàm bậc ba có hệ số của
3
x
âm. Suy ra loại A, C
Từ đồ thị suy ra
0
y
có một nghiệm dương (một nghiệm bằng
0
).
Xét D,
3 2 2
0
3 2 3 6 ; 0
2
x
y x x y x x y
x
. Vậy loại D
Xét B thấy thỏa mãn.
Câu 4. [2D2-2] Tính đạo hàm của hàm số
2 1
7
x
y
.
A.
2
2.7
x
y
. B.
2 1
7
x
y
. C.
2 1
2.7 .ln7
x
y
. D.
2 1
2.7
ln7
x
y
.
Lời giải
Chọn C.
Ta có
2 1
7
x
y
2 1
2.7 .ln7
x
y
.
Câu 5. [2D1-2] Tìm khoảng nghịch biến của hàm số
3 2
3 2
y x x
.
A.
0; 2
. B.
0; 3
. C.
0; +
. D.
2; 0
.
Lời giải
Chọn A.
Ta có
3 2
3 2
y x x
2
3 6
y x x
.
Xét
0
y
2
3 6 0
x x
0
2
x
x
.
Do đó
0 0 2.
y x
Vậy hàm số nghịch biến trên khoảng
0; 2
.
Câu 6. [2D1-2] Tiệm cận đứng và tiện cận ngang của đồ thị hàm số
2 1
1
x
y
x
.
A.
1
y
;
2
x
. B.
1
x
;
2
y
. C.
1
x
;
2
y
. D.
1
x
;
2
y
.
Lời giải
Chọn D.
TXĐ:
\ 1
D
.
Ta có
1
2 1
lim
1
x
x
x
,
1
2 1
lim
1
x
x
x
.
Suy ra đường thẳng
1
x
là tiệm cận đứng của đồ thị hàm số.
1
2
2 1
lim lim 2
1
1
1
x x
x
x
x
x
,
1
2
2 1
lim lim 2
1
1
1
x x
x
x
x
x
.
Suy ra đường thẳng
2
y
là tiệm cận ngang của đồ thị hàm số.
Câu 7. [2D1-2] Tìm giá trị lớn nhất
M
của hàm số
3 2
3 2
y x x
trên đoạn
2;3 .
A.
22.
M
B.
6.
M
C.
22.
M
D.
6.
M
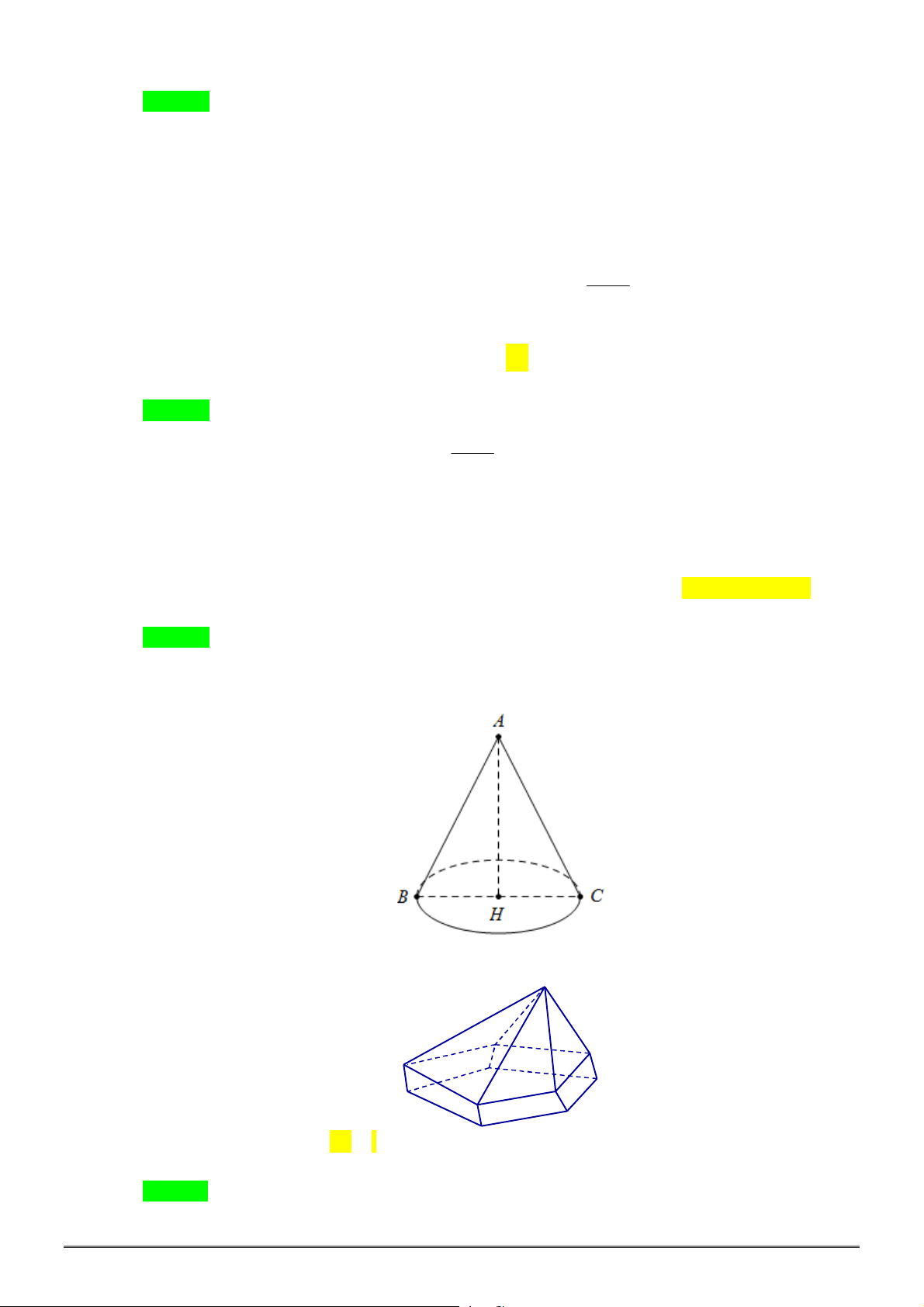
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/32 – Mã đề 101
Lời giải
Chọn A.
Hàm số đã cho đã xác định và liên tục trên
2;3 .
Ta có
2
0 2;3
3 6 3 2 0
2 2;3
x
y x x x x
x
Tính được
2 22;
y
3 2;
y
0 2;
y
2 6 22.
y M
Câu 8. [2D1-2] Biết đường thẳng
1
y x
cắt đồ thị hàm số
3 1
1
x
y
x
tại hai điểm phân biệt
A
,
B
có hoành độ lần lượt
A
x
,
B
x
. Hãy tính tổng
.
A B
x x
A.
1.
A B
x x
B.
3.
A B
x x
C.
3.
A B
x x
D.
1.
A B
x x
Lời giải
Chọn C.
Phương trình hoành độ giao điểm
2
1
3 1
1
1
3 2 0 (1)
x
x
x
x
x x
Bài ra có
A
x
,
B
x
là hai nghiệm của
(1)
nên theo hệ thức Viet ta được
3.
A B
x x
Câu 9. [2H1-2] Cho tam giác đều
ABC
có đường cao
.
AH
Khi tam giác
ABC
quay quanh trục là
đường thẳng
AH
một góc
360
thì các cạnh của tam giác
ABC
sinh ra hình gì?
A. Một hình trụ. B. Một mặt nón. C. Hai hình nón. D. Một hình nón.
Lời giải
Chọn D.
Khi tam giác
ABC
quay quanh trục là đường thẳng
AH
một góc
360
thì các cạnh của tam
giác
ABC
sinh ra một hình nón có chiều cao
AH
và đường sinh
AB
,
AC
.
Câu 10. [2H1-1] Hình đa diện bên có bao nhiêu mặt?
A.
6
. B.
11
. C.
12
. D.
10
.
Lời giải
Chọn B.
Đếm số mặt ta được
11
mặt.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/32 – Mã đề 101
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
3
1
y x
.
A.
;D
. B.
\ 1
D
. C.
; 1
D . D.
; 1
D .
Lời giải
Chọn C.
Hàm dạng lũy thừa có số mũ không nguyên nên cơ số phải dương
Nghĩa là
1 0 1
x x
.
Vậy
; 1
D .
Câu 12. [2D2-2] Phương trình
2
2 7 5
2 1
x x
có bao nhiêu nghiệm?
A.
3
. B.
1
. C.
0
. D.
2
.
Lời giải
Chọn D.
Ta có
2
2 7 5 2
2 1 2 7 5 0
x x
x x
1
x
hoặc
5
2
x
.
Câu 13. [2H2-1] Cho tấm tôn hình chữ nhật quay quanh trục là đường thẳng chứa một cạnh của tấm tôn
đó một góc
360
ta được một vật tròn xoay nào dưới đây?
A. Mặt trụ. B. Khối lăng trụ. C. Hình trụ. D. Khối trụ.
Lời giải
Chọn D.
Câu 14. [2D2-1] Giải phương trình
3
log 2 2.
x
A.
6.
x
B.
7.
x
C.
11.
x
D.
4.
x
Lời giải
Chọn B.
Điều kiện:
2 0 2
x x
*
Khi đó phương trình đã cho
2
3
log 2 2 2 3 9 7
x x x
.
Câu 15. [2H2-1] Cho đường tròn quay quanh một đường thẳng đi qua tâm đường tròn đó một góc
360
thì sinh ra hình gì?
A. Hai mặt cầu. B. Một khối cầu. C. Hai khối cầu. D. Một mặt cầu.
Lời giải
Chọn D.
Câu 16. [2H1-1] Cho khối lăng trụ đứng
.
ABC A B C
có thể tích bằng
3
.
a
Biết
ABC
vuông tại
,
A
AB a
,
2
AC a
. Tính độ dài đường cao của khối lăng trụ.
A.
3
a
. B.
a
. C.
3
a
. D.
2
a
.
Lời giải
Chọn B.
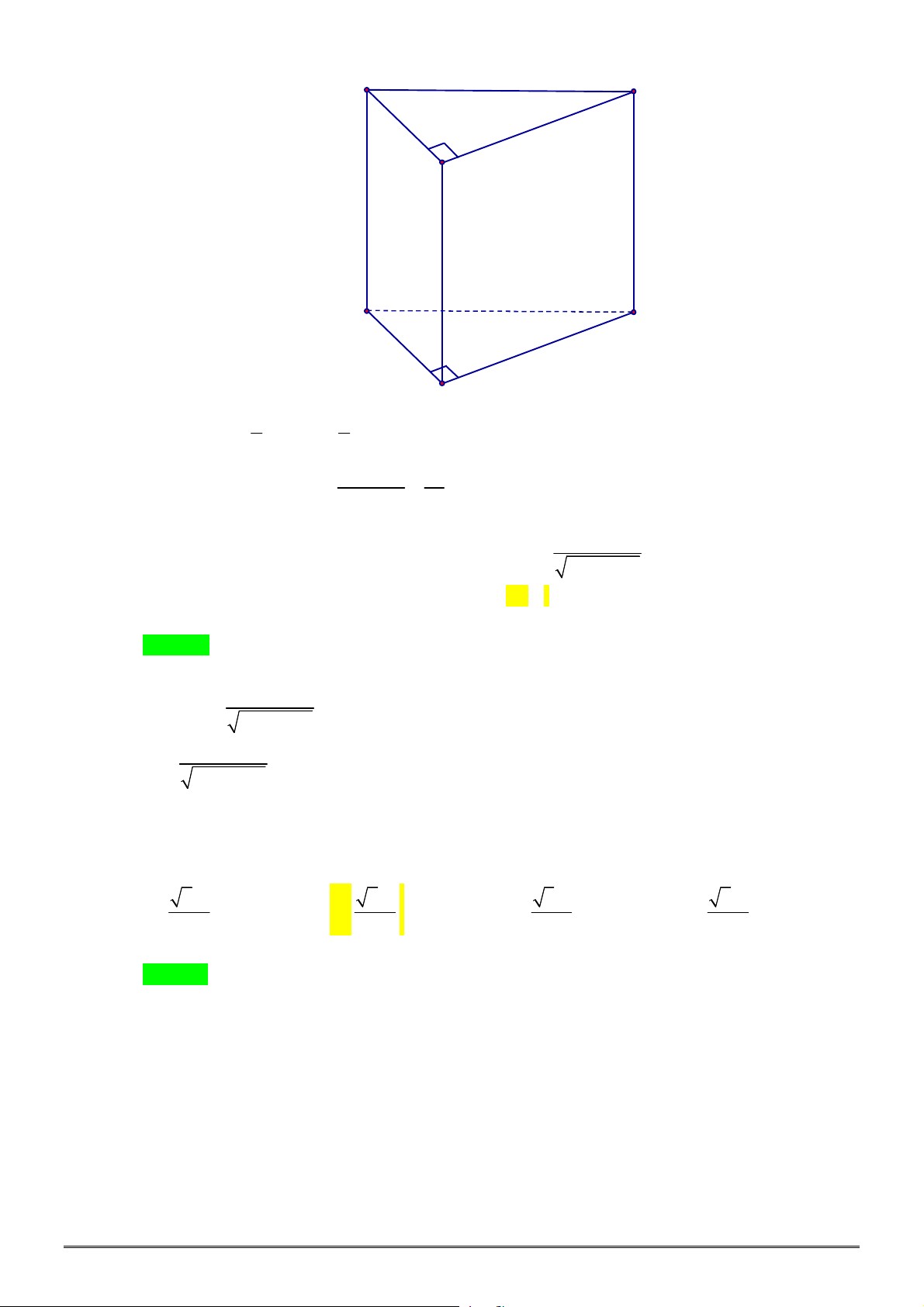
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/32 – Mã đề 101
Ta có
2
1 1
. 2 .
2 2
ABC
S AB AC a a a
.
.
.
ABC A B C ABC
V h S
3
.
2
ABC A B C
ABC
V
a
h a
S a
.
Câu 17. [2D1-1] Tìm số đường tiệm cận của đồ thị hàm số
2
15 11
2017
x
y
x
.
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C.
Tập xác định:
D
.
Ta có
2
15 11
lim 15
2017
x
x
x
.
2
15 11
lim 15
2017
x
x
x
.
Vậy hàm số có 2 tiệm cận ngang
15
y
và
15
y
và không có tiệm cận đứng.
Câu 18. [2H1-2] Tính thể tích khối chóp
.
S ABC
biết
SA a
,
ABC
đều,
SAB
vuông cân tại
S
và
nằm trong mặt phẳng vuông góc với mặt phẳng đáy.
A.
3
6
24
a
. B.
3
6
12
a
. C.
3
3
12
a
. D.
3
6
6
a
.
Lời giải
Chọn B.
B
A
C
A
C
B
a
2
a
h
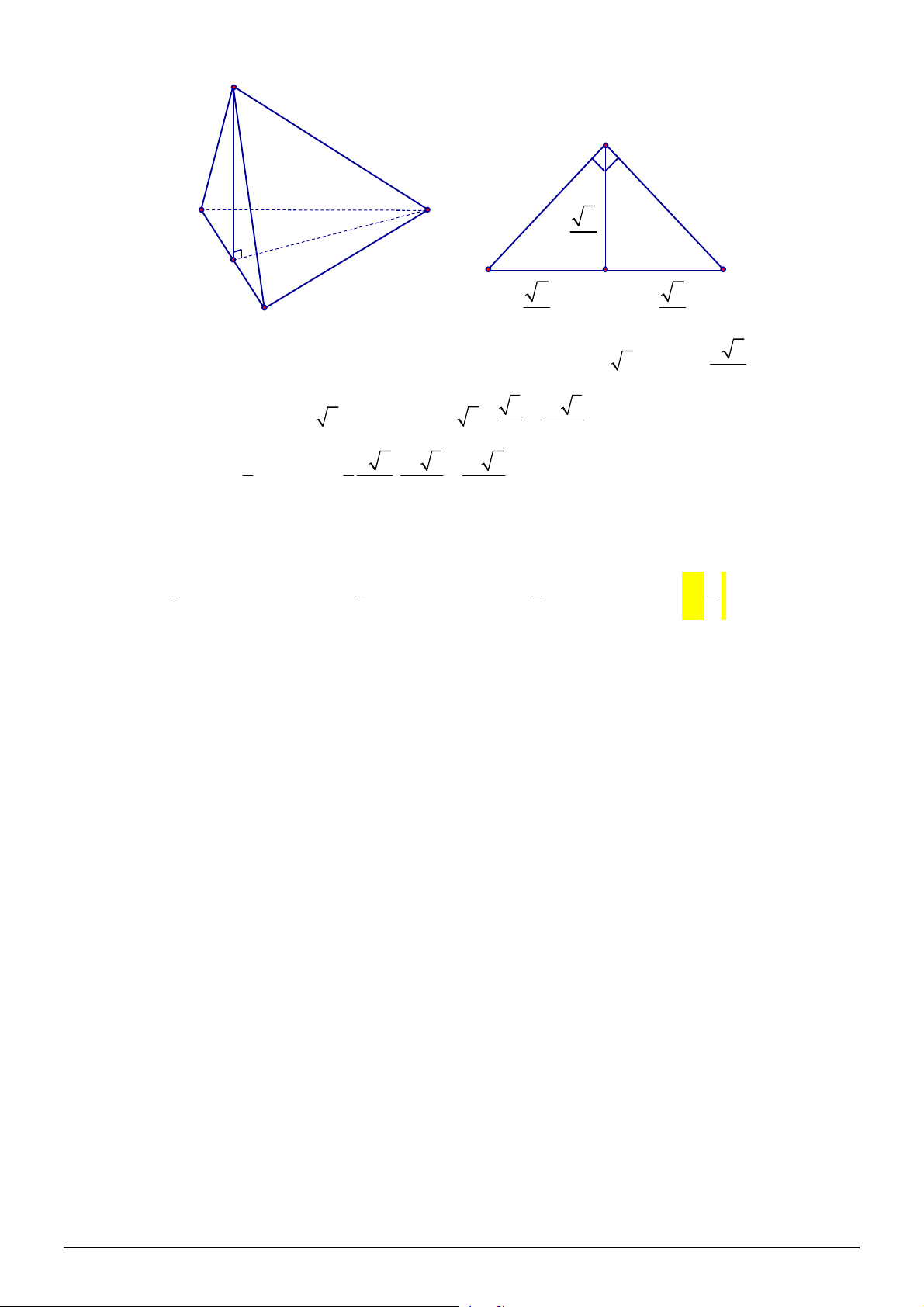
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/32 – Mã đề 101
Ta có
SAB
vuông cân tại
S
mà
SA a
nên
SB a
;
2
AB a
và
2
2
a
SH .
ABC
đều mà
2
AB a
nên
2
2
3 3
2
4 2
ABC
a
S a
.
Vậy
2 3
.
1 1 2 3 6
. .
3 3 2 2 12
S ABC ABC
a a a
V SH S
.
Câu 19. [2D1-3] Cho khối lăng trụ
.
ABC A B C
. Gọi
M
là trung điểm
CC
. Mặt phẳng
ABM
chia
khối lăng trụ
.
ABC A B C
thành hai khối. Tính tỉ số thể tích (số bé chia số lớn) của hai khối đó.
A.
1
3
. B.
2
5
. C.
1
6
. D.
1
5
.
A
S
B
H
a
2
2
a
a
2
2
a
2
2
a
S
A
B
C
H
a
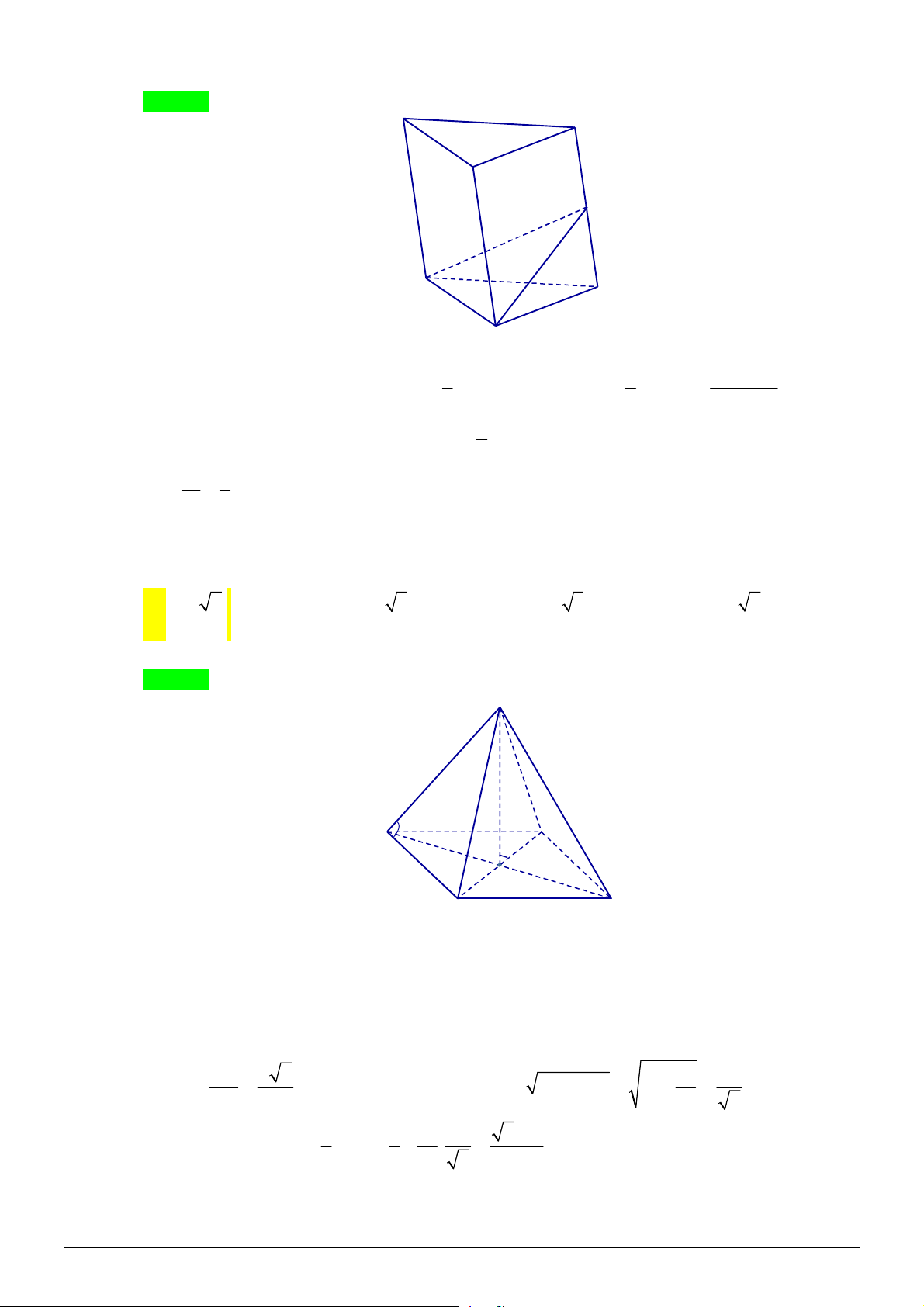
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/32 – Mã đề 101
Lời giải
Chọn D.
Gọi
h
là chiều cao của lăng trụ
.
ABC A B C
.
Thể tích của khối chóp
.
M ABC
là
.
1
1 1
; . .
3 6 6
ABC A B C
ABC ABC
V
V d M ABC S h S
.
Thể tích của phần còn lại là
2 . .
5
6
A B C MAB ABC A B C
V V V
.
Vậy
1
2
1
5
V
V
.
Câu 20. [2D2-2] Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, góc
60
SAB
. Tính thể
tích của khối nón đỉnh
S
có đáy là đường tròn ngoại tiếp tứ giác
ABCD
.
A.
3
2
12
a
. B.
3
3
12
a
. C.
3
3
6
a
. D.
3
2
6
a
.
Lời giải
Chọn A.
Gọi
I AC BD
. Suy ra
IA IB IC ID
vì
ABCD
là hình vuông.
SI ABCD
vì
.
S ABCD
là hình chóp tứ giác đều.
Tam giác
SAB
là tam giác cân có
60
SAB
nên tam giác
SAB
là tam giác đều.
Suy ra
SA AB a
.
Khối nón đỉnh
S
có đáy là đường tròn ngoại tiếp tứ giác
ABCD
có bán kính đáy là
2
2 2
AC a
r IA , độ dài đường cao là
2
2 2 2
2
2
a a
h SI SA IA a .
Thể tích cần tìm là
2 3
2
1 1 2
.
3 3 2 12
2
a a a
V r h
.
Câu 21. [2D2-2] Cho
a
và
b
là các số thực dương khác
1
,
x
và
y
là hai số thực dương. Khẳng định
nào dưới đây đúng?
C
A
B
C
A
B
M
S
B
C
A
D
I
60

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/32 – Mã đề 101
A.
log
log
log
a
a
a
x
x
y y
. B.
1 1
log
log
a
a
x x
.
C.
log log log
a a a
x y x y
. D.
log log .log
b b a
x a x
.
Lời giải
Chọn D.
Phương án A sai vì
log log log
a a a
x
x y
y
.
Phương án B sai vì
1
1
log log log
a a a
x x
x
.
Phương án C sai vì
log log log
a a a
xy x y
.
Vậy phương án đúng là D.
Cách 2: Theo công thức đổi cơ số ta có
log
log log log .log
log
b
a b b a
b
x
x x a x
a
, vậy D đúng.
Câu 22. [2D1-2] Tìm giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
2
sin cos 2.
y x x
A.
3
; 3.
4
M m
B.
3
3;
4
M m
C.
3; 1.
M m
D.
3
3;
4
M m
Lời giải
Chọn B.
Ta có:
2
sin sin 1.
y f x x x
Đặt
sin ; 1;1
t x t hàm số trở thành:
2
1.
y g t t t
2 1
g t t
Xét
1
0 1;1
2
g t t
Ta có:
1;1
1;1
1 1
1 3 3
min min ; max max 3
2 4 4
1 3
g
g f x g t f x g t
g
.
Câu 23. [2D2-2] Số tuổi của An và Bình là các nghiệm của phương trình
2 2
1 2
1
5 log 1 logx x
.
Tính tổng số tuổi của An và Bình.
A.
21.
B.
16.
C.
12.
D.
13.
Lời giải
Chọn C.
Điều kiện:
2
2
0 0
5 log 0 32
1
1 log 0
2
x x
x x
x
x
.
Đặt
2
log
t x
phương trình đã cho trở thành:
2
2
3
2 2 4
1 2
1 5 6 0; 1;5
3
5 1
2 8
t x
t t t
t
t t
x
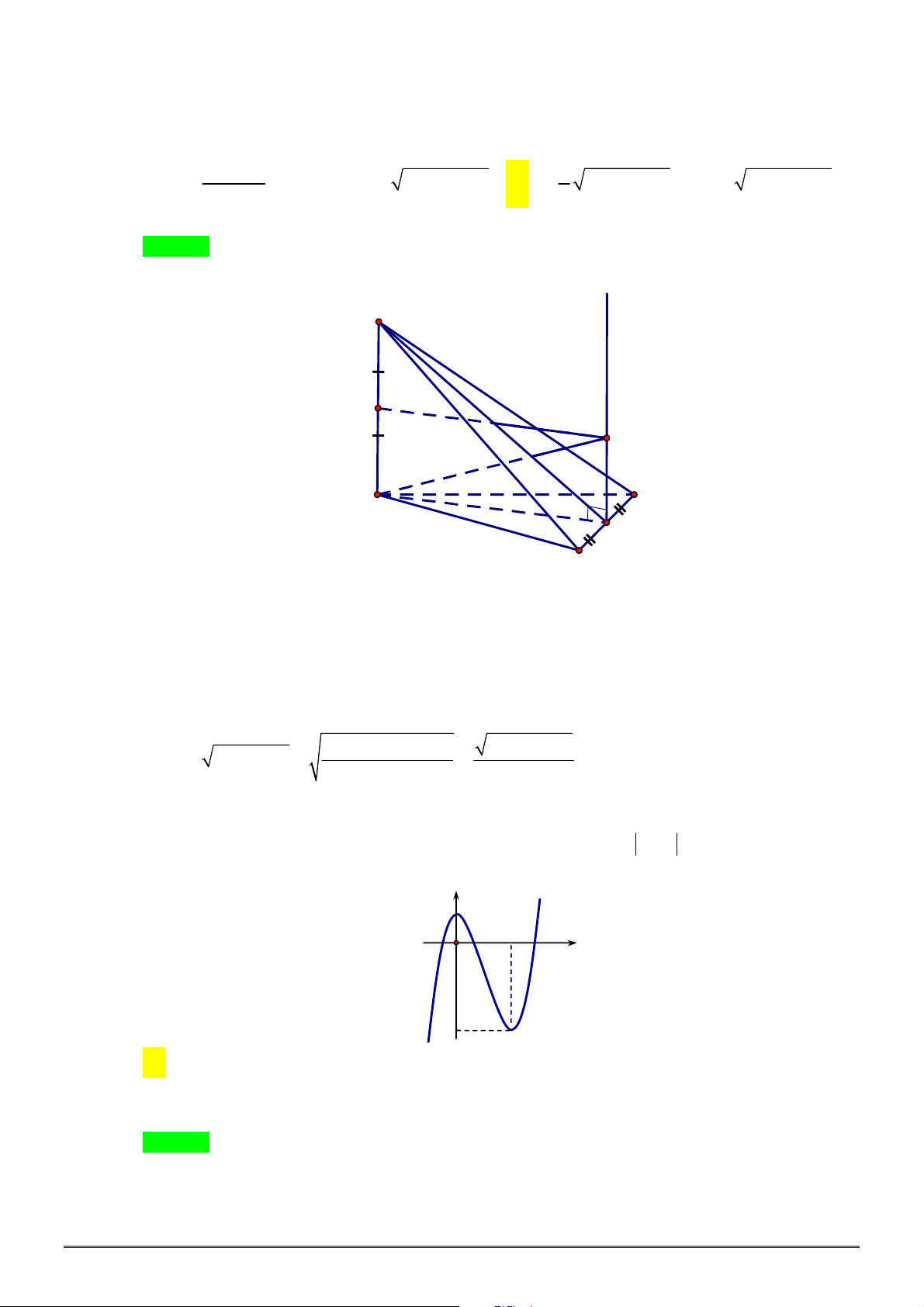
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/32 – Mã đề 101
Vậy tổng số tuổi An và Bình là
12
.
Câu 24. [2H2-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
,
A
biết
SA ABC
và
SA a
,
AB b
,
AC c
. Tính bán kính
r
của mặt cầu ngoại tiếp hình chóp
. .
S ABC
A.
2
a b c
r
B.
2 2 2
2 .
r a b c
C.
2 2 2
1
.
2
r a b c
D.
2 2 2
.
r a b c
Lời giải
Chọn C.
Gọi
I
là tâm đường tròn ngoại tiếp tam giác
ABC I
là trung điểm của đoạn
BC
.
d
M
I
A
B
C
S
O
Gọi
O
là tâm mặt cầu ngoại tiếp hình chóp, do
O
cách đều các điểm
A
,
B
,
C
nên
O
thuộc
đường thẳng
d
đi qua tâm
I
và vuông góc với
ABC
. Do
O
cách đều các điểm
,
A S
nên
O
thuộc đường thẳng
là đường trung trực của đoạn
SI
nằm trong
SAI
từ đó ta có:
O d
.
Bán kính mặt cầu ngoại tiếp hình chóp là:
r OA OB OC OS
.
2 2 2 2 2 2
2 2
4 2
AB AC SA a b c
r AI OI
.
Câu 25. [2D1-3]Cho hàm số
y f x
liên tục trên
và có đồ thị hàm số là đường cong trong hình vẽ
bên. Tìm tất cả các giá trị thực của tham số
m
để phương trình
f x m
có
3
nghiệm phân
biệt.
A.
0;3
m .
B.
1 3
m
.
C.
3 1
m
.
D. Không có giá trị nào của
m
.
Lời giải
Chọn A.
O
x
y
3
2
1
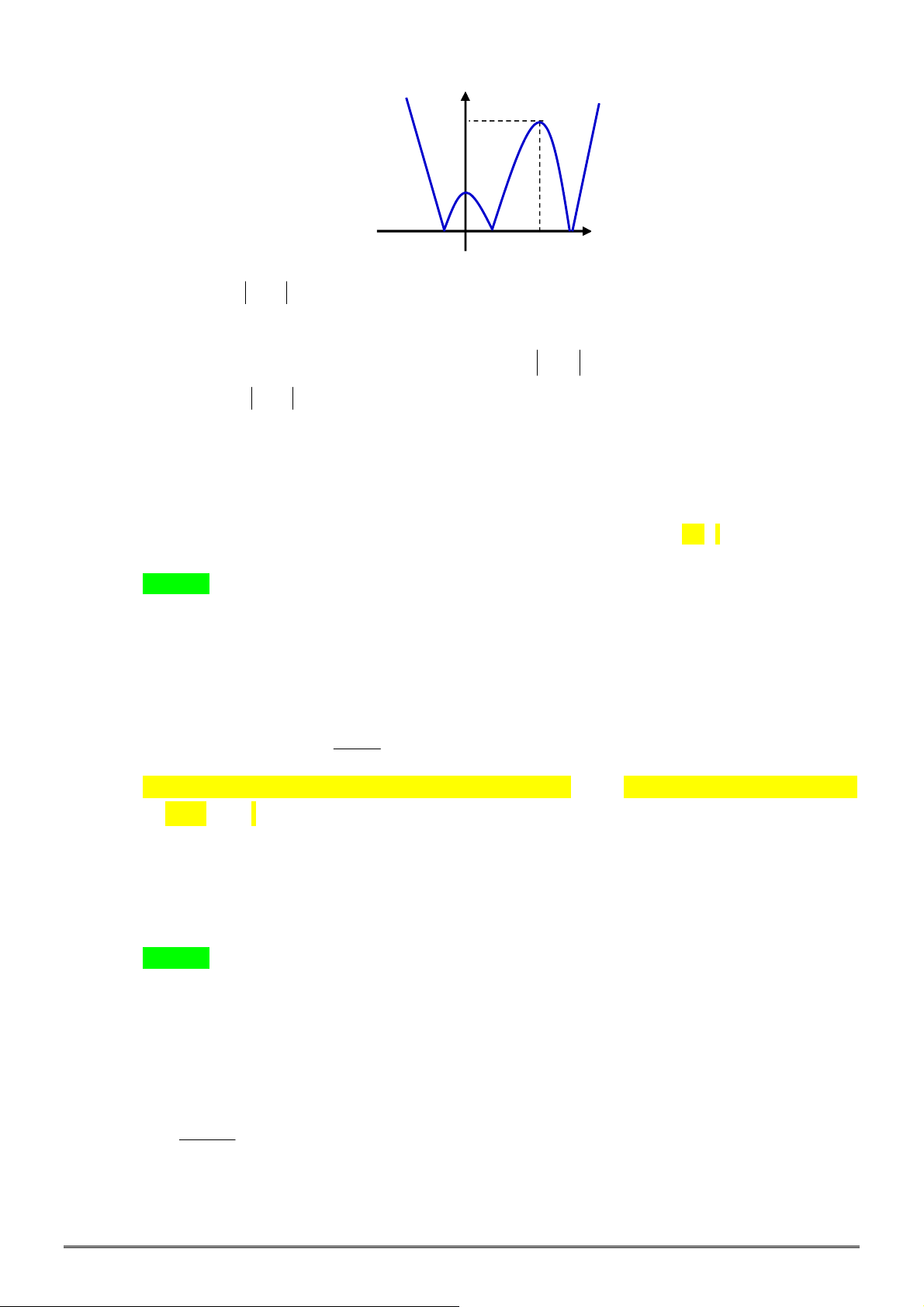
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/32 – Mã đề 101
Phương trình
f x m
là phương trình hoành độ giao điểm của đường thẳng :
d y m
và đồ
thị hàm số
y f x
Từ đồ thị hàm số
y f x
, ta có đồ thị hàm số
y f x
như hình vẽ.
Phương trình
f x m
có ba nghiệm phân biệt khi đường thẳng :
d y m
cắt đồ thị hàm số
y f x
tại 3 điểm phân biệt. Khi đó:
0;3 .
m
Câu 26. [2D1-2] Cho hàm số
y f x
có đạo hàm
3
2
1 .
f x x x
Hỏi hàm số có bao nhiêu điểm
cực trị?
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
Chọn D.
3
2
0
0 1 0
1
x
f x x x
x
trong đó nghiệm
0
có số nghiệm chẵn nên qua nghiệm
0
,
f x
không đổi dấu, nghiệm
1
có số nghiệm lẻ nên qua nghiệm
1
,
f x
đổi dấu.
Vậy hàm số có một điểm cực trị.
Câu 27. [2D1-1] Cho hàm số
2 4
.
1
x
y
x
Khẳng định nào sau đây sai?
A. Đồ thị hàm số có tiệm cận đứng là đường thẳng
1
x
và tiệm cận ngang là đường
thẳng
4
y
.
B. Đồ thị hàm số cắt trục hoành tại điểm
2;0
và cắt trục tung tại điểm
0;4
.
C. Hàm số không có cực trị.
D. Hàm số đồng biến trên các khoảng
;1
và
1;
.
Lời giải
Chọn A.
1
lim
x
y
đường thẳng
1
x
là tiệm cận đứng của đồ thị hàm số.
lim 2
x
y
đường thẳng
2
y
là tiệm cận ngang của đồ thị hàm số.
0 4
x y
;
0 2
y x
. Vậy đồ thị hàm số cắt trục hoành tại điểm
2;0
và cắt trục tung
tại điểm
0;4
.
2
2
0 1
1
y x
x
nên hàm số không có cực trị và luôn đồng biến trên các khoảng
;1
và
1;
.
㕸
㖖
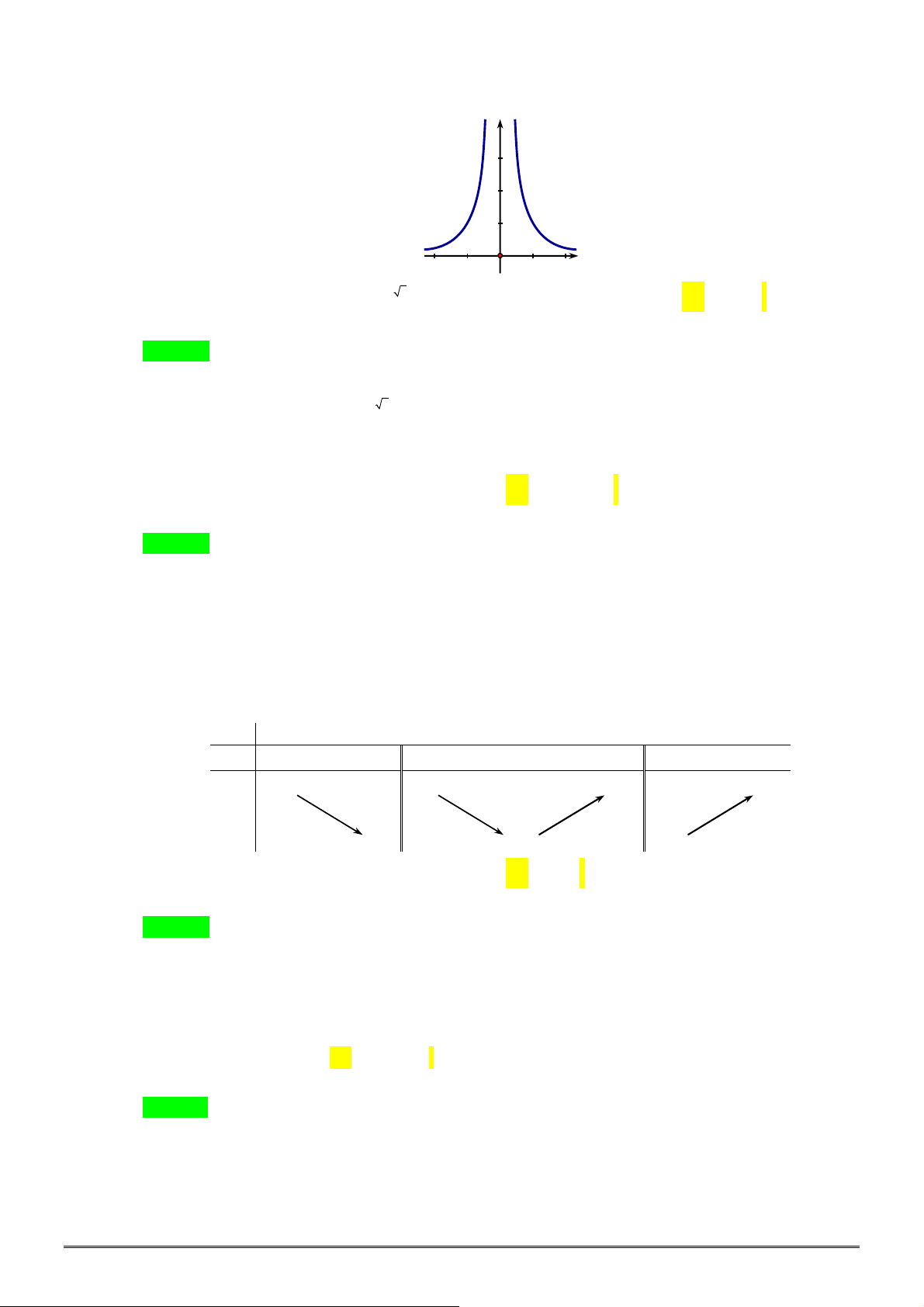
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/32 – Mã đề 101
Câu 28. [2D2-2] Đường cong hình bên là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi đó là hàm số nào?
A.
4
y x
. B.
2
y x
. C.
2
x
y
. D.
2
y x
.
Lời giải
Chọn D.
Đồ thị hàm số trên không cắt trục
Oy
nên loại đáp án A, C. .
Tập xác định của hàm số
2
y x
là
0;D
nên loại B.
Câu 29. [2H2-2] Tính diện tích xung quanh
xq
S
của hình trụ có đường cao
h a
và thể tích
3
V a
.
A.
2
4
xq
S a
. B.
2
6
xq
S a
. C.
2
2
xq
S a
. D.
2
8
xq
S a
.
Lời giải
Chọn C.
Ta có
2 2 3
V r h r a a r a
.
Vậy
2
2 2 . 2
xq
S rl a a a
.
Câu 30. [2D1-2] Cho hàm số
y f x
xác định trên
\ 1
, liên tục trên mỗi khoảng xác định và có
bảng biến thiên như hình bên dưới. Tìm tập hợp tất cả các giá trị thực của tham số
m
sao cho
phương trình
f x m
vô nghiệm.
A.
; 2
. B.
1;
. C.
2;1
. D.
2;
.
Lời giải
Chọn C.
Phương trình
f x m
vô nghiệm khi và chỉ khi đường thẳng
y m
không cắt đồ thị hàm số
y f x
2 1
m
.
Câu 31. [0D2-1] Phương trình
2 3 4
9 27
x x
tương đương với phương trình nào sau đây?
A.
6 0
x
. B.
7 6 0
x
. C.
7 6 0
x
. D.
6 0
x
.
Lời giải
Chọn B.
Ta có:
2 2 3 3 4
2 3 4
9 27 3 3
x x
x x
.
2 2 3 3 4 7 6 0
x x x
.
O
x
y
1
2
1
2
1
2
x
1
0
1
y
0
y
2
1
2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/32 – Mã đề 101
Câu 32. [0D2-2] Cho
a
,
b
là hai số dương khác
1.
Đặt
log .
a
b m
Tính theo
m
giá trị của biểu thức
2
3
log log
ba
P b a
.
A.
2
12
2
m
P
m
. B.
2
12
m
P
m
. C.
2
4 3
2
m
P
m
. D.
2
3
m
P
m
.
Lời giải
Chọn A.
Ta có:
2
2
3
1 1 1 12
log log log 6log 6
2 2 2
a b
b
a
m
P b a b a m
m m
.
Câu 33. [0D2-2] Tìm tất cả các giá trị của tham số
m
sao cho hàm số
2
3
1
log 2 3
y
x x m
có tập
xác định là
.
A.
2
;
3
. B.
2
;
3
. C.
2
;
3
. D.
2
;
3
.
Lời giải
Chọn A.
Để hàm số có tập xác định là
2
3
2
log 2 3 0,
2 3 0
x x m x
x x m
.
2 2
2 3 1, 2 3 1 0
x x m x x x m
.
2
1 3 1 0
3
m m
.
Câu 34. [2D1-1] Hàm số
2
4
1
y
x
có bảng biến thiên như bên dưới. Xét trên tập xác định của hàm số,
khẳng định nào sau đây đúng?
A. Hàm số có giá trị lớn nhất bằng
4
và không có giá trị nhỏ nhất.
B. Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
C. Hàm số có giá trị lớn nhất bằng
4
và giá trị nhỏ nhất bằng
0
.
D. Hàm số có giá trị nhỏ nhất bằng
0
và không có giá trị lớn nhất.
Lời giải
Chọn A.
Dựa vào bảng biến thiên, ta thấy hàm số có giá trị lớn nhất bằng
4
khi
0
x
và không có giá
trị nhỏ nhất.
Câu 35. [2D2-2] Tính tổng tất cả các nghiệm của phương trình
9 4.3 3 0
x x
.
A.
3
. B.
1
. C.
1
. D.
2
.
Lời giải
Chọn B.
Ta có
9 4.3 3 0
x x
2
3 4.3 3 0
x x
3 1 0
1
3 3
x
x
x
x
.
x
0
y
0
y
1
4
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/32 – Mã đề 101
Vậy tổng các nghiệm của phương trình bằng
1
.
Câu 36. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị hàm số
2
1
2
x
y
x x m
có
đúng hai đường tiệm cận đứng.
A. .
1
m
. B.
3
m
. C.
1
m
. D.
1
3
m
m
.
Lời giải
Chọn D.
Để đồ thị hàm số có hai đường tiệm cận đứng thì phương trình
2
2 0
x x m
phải có hai
nghiệm phân biệt khác
1
. Điều này xảy ra khi
1 0 1
1 2 0 3
m m
m m
.
Câu 37. [2D2-2] Biết tập nghiệm của bất phương trình
2 2 2
log 1 log 5 1 log 2
x x x
là
khoảng
;
a b
. Tính
.
P a b
A.
6
P
. B.
5
P
. C.
7
P
. D.
8
P
.
Lời giải
Chọn B.
Điều kiện:
2 5
x
.
Ta có
2 2 2 2 2 2 2
log 1 log 5 1 log 2 log 1 log 2 log 2 log 5
x x x x x x
Hay
2 2
log 1 2 log 2 5
x x x
1 2 2 5
x x x
2
12 0
x x
4 3
x
.
So điều kiện ta được
2 3
x
. Do đó
2;3
S .
Vậy
2 3 5
P
.
Câu 38. [2D2-2] Tìm tất cả các giá trị của tham số
m
để phương trình
2 3
2 2 5
x
m
có nghiệm.
A.
5
2
m
. B.
5
2
m
. C.
5
2
m
. D.
5
2
m
.
Lời giải
Chọn A.
Ta có
2 3 2 3
2 2 5 2 2 5
x x
m m
có nghiệm khi và chỉ khi
5
2 5 0
2
m m
.
Câu 39. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị hàm số
4 2
2 1
y x mx
có
ba điểm cực trị tạo thành ba đỉnh của một tam giác đều.
A.
3
3
m
. B.
3
m
. C.
3
1
3
m
. D.
1
3
m
.
Lời giải
Chọn A.
Đạo hàm:
3
4 4
y x mx
.
Đồ thị hàm số có ba điểm cực trị
0
y
có ba nghiệm phân biệt
0
m
.
Tọa độ ba điểm cực trị:
0;1
A ,
2
;1
B m m
,
2
;1
C m m
.
Do tam giác
ABC
cân tại
A
nên để tam giác
ABC
đều thì
AC BC
.
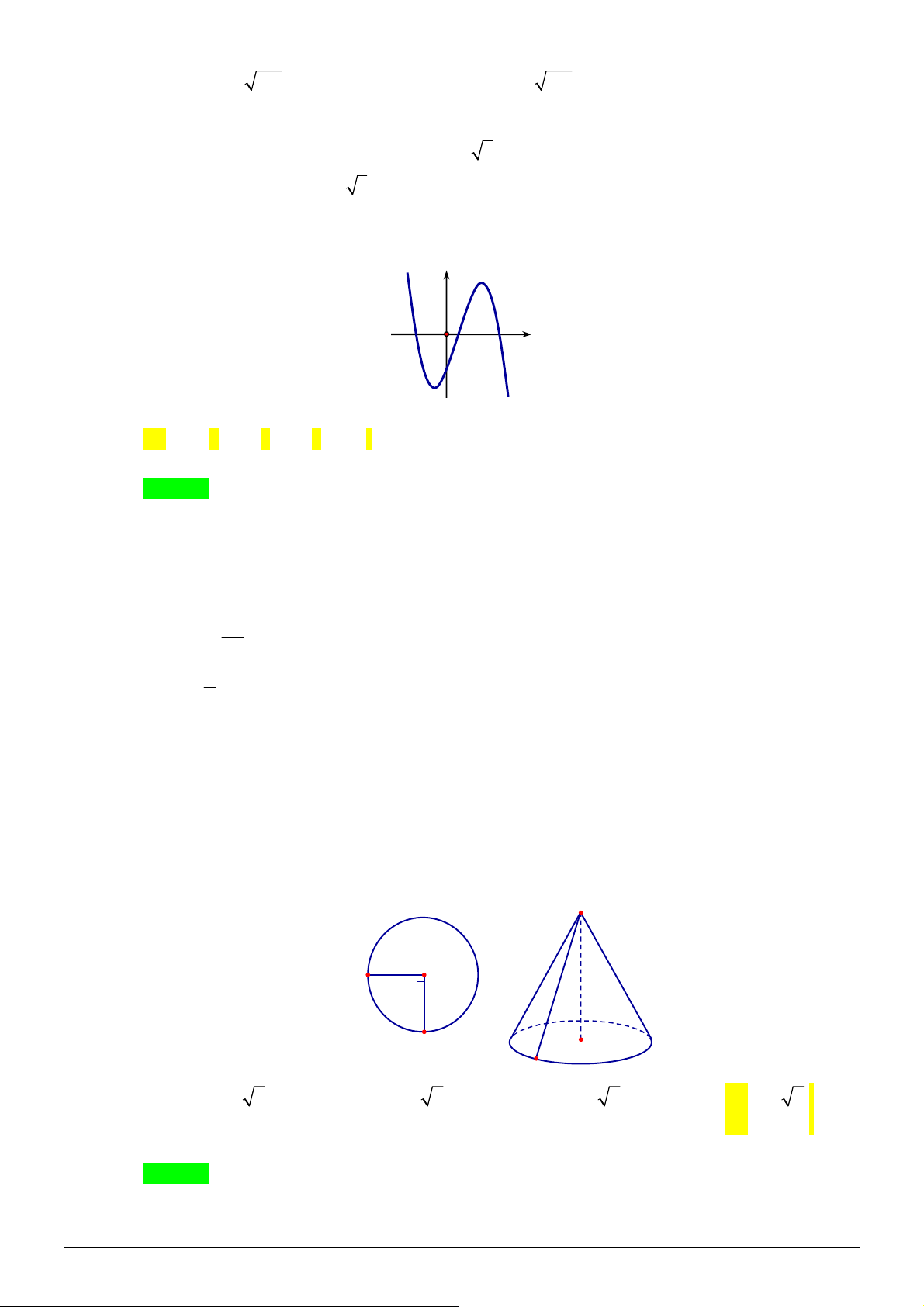
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/32 – Mã đề 101
Ta có
2
;
AC m m
4
AC m m
;
2 ; 0
BC m
4
BC m
.
Khi đó
AC BC
4
3 0
m m
3
0
3
m
m
.
So điều kiện ta nhận
3
3
m
.
Câu 40. [2D1-3] Cho hàm số
3 2
y ax bx cx d
có đồ thị hình bên. Hỏi khẳng định nào sau đây
đúng?
A.
0
a
,
0
b
,
0
c
,
0
d
. B.
0
a
,
0
b
,
0
c
,
0
d
.
C.
0
a
,
0
b
,
0
c
,
0
d
. D.
0
a
,
0
b
,
0
c
,
0
d
.
Lời giải
Chọn C.
Quan sát đồ thị ta có
0
a
. Khi
0
x
thì
0
y d
. Vì đồ thị có hai điểm cực trị có hoành độ
trái dấu nên phương trình
2
3 2 0
y ax bx c
có hai nghiệm
1
x
,
2
x
phân biệt thỏa mãn
1 2
1 2
0
0
0
0
0
a
b
b
x x
c
a
c
x x
a
.
B. PHẦN RIÊNG ( 20%, gồm 10 câu )
1. Phần dành cho học sinh không chuyên
Câu 41. [2H2-3] Cho tấm tôn hình tròn có bán kính
6.
r
Cắt bỏ
1
4
hình tròn giữa 2 bán kính
OA
,
OB
, rồi đem tấm tôn còn lại ghép hai bán kính đó lại để được một hình nón (như hình vẽ).
Tính thể tích khối nón giới hạn bởi hình nón đó.
A.
81 7
4
. B.
9 7
8
. C.
9 7
2
. D.
81 7
8
.
Lời giải
Chọn D.
A
B
6
O
B
A
O
O
x
y
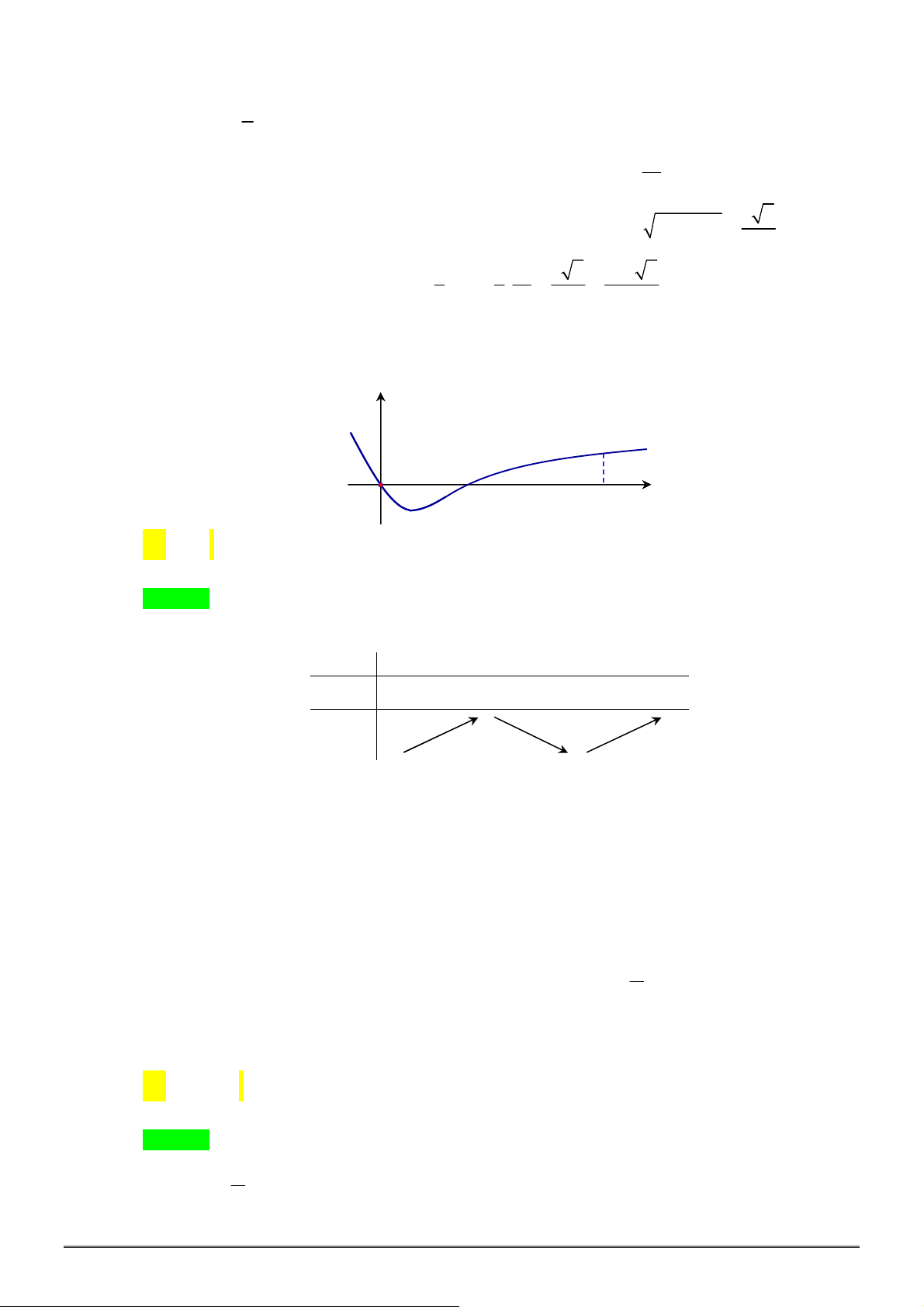
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/32 – Mã đề 101
Ta có chu vi đường tròn lúc chưa cắt là
0
2 12
C R
, sau khi cắt thì chu vi của đáy hình
nón là
1 0
3
9
4
C C
. Khi đó nếu gọi bán kính đường tròn đáy của hình nón là
r
thì
2 9 4,5
r r
lúc đó ta có diện tích đáy hình nón
2
81
4
B r
.
Hình nón được tạo thành có đường sinh
6
OA
nên chiều cao
2 2
3 7
6 4,5
2
h .
Vậy thể tích khối nón tạo thành là
1 1 81 3 7 81 7
.h . .
3 3 4 2 8
V B
.
Câu 42. [2D1-3] Cho hàm số
f x
có đạo hàm
f x
. Biết đồ thị hàm số
y f x
là hình bên và
0 3 2 5
f f f f . Tìm giá trị lớn nhất của hàm số
f x
trên đoạn
0;5
.
A.
5
f
. B.
3
f
. C.
0
f . D.
2
f .
Lời giải
Chọn A.
Dựa vào đồ thị của hàm số
y f x
ta có bảng biến thiên của hàm số
y f x
:
0 2 0
f f nên
0
x
và
2
x
là hai điểm cực trị của
y f x
. Đồng thời
2 3 5
f f f
và
0 2
f f .
Mặt khác
0 3 2 5
f f f f
3 2 5 0 0 5 0
f f f f f f
Trên đoạn
0;5
hàm số
y f x
có:
2 0 5
f f f .
Vậy giá trị lớn nhất của hàm số
f x
trên đoạn
0;5
là
5
f
.
Câu 43. [2D2-2] Tìm tất cả các giá trị của tham số
m
để hàm số
3 2
3 3 11
1
x mx mx
y
đồng biến trên
.
A.
; 0 1;m
. B.
0;1
m .
C.
0;1
m . D.
; 0 1;m
.
Lời giải
Chọn C.
Ta có
3 2
3 2
3 3 11
3 3 11
1
x mx mx
x mx mx
y
.
x
0
2
f x
0
0
f x
y
x
O
2
5

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 23/32 – Mã đề 101
Đạo hàm
3 2
3 3 11
2
3. 2 ln
x mx mx
y x mx m
.
Hàm số đồng biến trên
nên
3 2
3 3 11
2
0 3. 2 ln 0
x mx mx
y x mx m
2
2 0
x mx m
2
0 0
m m
,
0;1
m .
Câu 44. [2D2-4] Xét các số thực
a
,
b
dương thỏa mãn
2
1
log 2 3
ab
ab a b
a b
. Tìm giá trị nhỏ
nhất của biểu thức
2
P a b
.
A.
2 10 3
2
. B.
3 10 7
2
. C.
2 10 1
2
. D.
2 10 5
2
.
Lời giải
Chọn A.
Điều kiện
1
0
ab
a b
. Ta có:
2
1
log 2 3
ab
ab a b
a b
2 2
log 1 log 2 3
ab a b ab a b
2 2
log 2 1 2 1 log
ab ab a b a b
.
Xét hàm số
2
log
f t t t
, có đạo hàm
1
1 0
ln2
f t
t
,
0
t
.
Do đó
2 1
f ab f a b
2
0
1 2
a
b
a
0 2
a
.
Ta có
2
P a b
2
2 2 4
2.
1 2 1 2
a a a
a
a a
.
Từ đó ta có
2
2 4
1 2
a a
P f a
a
với
0 2
a
.
Đạo hàm
2
2
4 4 9
1 2
a a
f a
a
. Xét
2
10 1
0;2
2
0 4 4 9 0
10 1
0
2
a
f a a a
a
.
Lập bảng biến thiên của hàm số
f a
trên
0;2
ta được
min
10 1 2 10 3
2 2
P P
.
Câu 45. [2D2-2] Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức
0
( ) . 1 4 ,
t
Q t Q
với
t
là khoảng thời gian tính bằng giờ và
0
Q
là dung lượng nạp tối đa (
pin đầy). Nếu điện thoại nạp pin từ lúc cạn pin ( dung lượng
0%
) thì sau bao lâu nạp được
90%
?
A.
1,5
giờ. B.
1,66
giờ. C.
2,66
giờ. D.
1,26
giờ.
Lời giải
Chọn B.
Gọi
0
t
là thời điểm nạp được
90%
.
Từ giả thiết ta có
0
0 0
0,9 . 1 4
t
Q Q
0
0,9 1 4
t
0
4 0,1
t
0 4
log 0,1
t
0
1,66
t .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 24/32 – Mã đề 101
Câu 46. [2D2-3] Cho hai số thực dương
a
,
b
khác
1.
Biết rằng bất kì đường thẳng nào song song với
trục hoành mà cắt các đường
x
y a
,
x
y b
và trục tung lần lượt tại
M
,
N
,
A
thì
3
AN AM
( hình vẽ bên). Hỏi khẳng định nào sau đây đúng?
A.
2
1
ab
. B.
3
b a
. C.
3
1
a b
. D.
3
1
ab
.
Lời giải
Chọn D.
Giả sử
N
,
M
có hoành độ lần lượt là
n
,
m
khác
0
. Theo đề, ta có:
3
n m
,
n m
b a
Vậy
3
m m
b a
3
m
m
b a
3
b a
3
1
a
b
3
1
ab
.
Câu 47. [2D1-3] Từ một tấm tôn hình vuông cạnh
12
(mét) người ta cắt đi bốn góc bốn hình vuông
cạnh
x
(mét) rồi gấp tấm tôn còn lại để được một cái hộp không có nắp như hình vẽ dưới đây.
Tìm
x
để hộp nhận được có thể tích lớn nhất.
A.
4m.
B.
2m.
C.
2,5m.
D.
3m.
Lời giải
Chọn B.
Thể tích của hình hộp là:
2
3 2
12 2 . 4 48 144 0 6
V x x x x x x x
.
2
2 0;6
12 96 144; 0
6 0;6
x
V x x x V x
x
Ta có bảng biến thiên của hàm số
V x
:
Căn cứ vào bảng biến thiên ta có
0;6
max 128 2.
x
V x x
Câu 48. [2H1-3] Cho khối tứ diện có thể tích
.
V
Gọi
V
là thể tích khối đa diện có các đỉnh là trung
điểm các cạnh của khối tứ diện đó. Tính tỉ số
V
V
x
12
x
0
2
6
V x
0
V x
0
128
b
O
x
y
N
M
A
x
y b
x
y a
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 25/32 – Mã đề 101
A.
1
2
V
V
B.
2
3
V
V
C.
1
4
V
V
D.
5
8
V
V
Lời giải
Chọn A.
. . . . . .
. .
1
A QEP B QMF C MNE D NPF A QEP B QMF
C MNE D NPF
V V V V V V V
V VV
V V V V V V
1 1 1 1 1 1 1 1 1 1 1 1 1
1 . . . . . . . .
2 2 2 2 2 2 2 2 2 2 2 2 2
.
Câu 49. [2H1-2] Cho khối lăng trụ
.
ABC A B C
có thể tích
.
V
Gọi
M
là điểm bất kì trên đường thẳng
.
CC
Tính thể tích khối chóp
.
M ABB A
theo
.
V
A.
2
V
. B.
3
V
. C.
2
3
V
. D.
4
V
.
Q
P
N
M
D
C
B
A
E
F
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 26/32 – Mã đề 101
Lời giải
Chọn C.
M
C'
C
B
B'
A'
A
. . .
1 1
. .
3 3
M ABB A M ABC M A B C ABC A B C
V V V V V MC S MC S
1 1 2
.
3 3 3 3
ABC ABC
V V
V S MC MC V S CC V
.
Câu 50. [2H2-1] Một hình trụ có bán kính đáy bằng
r
và có thiết diện qua trục là một hình vuông. Tính
diện tích xung quanh của hình trụ đó
A.
2
2 .
r
B.
2
.
r
C.
2
4 .
r
D.
2
8 .
r
Lời giải
Chọn C.
D
C
r
B
A
Giả sử thiết diện qua trục là hình vuông
ABCD
2
l AD r
.
Vậy diện tích xung quanh cần tìm là:
2
2 2 . .2 4
xq
S rl r r r
2. Phần dành cho học sinh chuyên
Câu 51. [2D1-3] Đồ thị hàm số
3 2
3 9 1
y x x x
có hai điểm cực trị
A
,
B
. Điểm nào dưới đây
thuộc đường thẳng
.
AB
A.
1; 10 .
N B.
1;0 .
P C.
Q 0; 1 .
D.
1;10 .
M
Lời giải
Chọn A.
Tập xác định:
D
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 27/32 – Mã đề 101
Ta có
2
3 6 9
y x x
;
2
1 6
0 3 6 9 0
3 26
x y
y x x
x y
.
Đồ thị hàm số có hai điểm cực trị
1;6
A và
3; 26
B .
Cách 1:
4; 32 4 1; 8
AB
;
2;16 2 1; 8
AN
Suy ra
2
AB AN
, suy ra hai vec tơ
AB
,
AN
cùng phương nên giá của chúng song song hoặc
trùng nhau. Vì hai véctơ
AB
,
AN
có chung gốc
A
, vậy chúng có giá trùng nhau hay ba điểm
A
,
B
,
N
thẳng hàng hay
N
thuộc đường thẳng
AB
.
Cách 2: viết phương trình đường thẳng
AB
sau đó lần lượt kiểm tra từng điểm.
Câu 52. [2D1-3] Từ một tấm tôn hình chữ nhật có chiều dài và rộng là
60 cm
,
40 cm
. Người ta cắt đi
6
hình vuông cạnh
(cm)
x rồi gấp tấm tôn còn lại để được một cái hộp có nắp như hình vẽ
dưới đây. Tìm
x
để hộp nhận được có thể tích lớn nhất.
A.
10
cm .
3
B.
20
cm .
3
C.
4 cm .
D.
5 cm .
Lời giải
Chọn B.
Sau khi gập ta được hình hộp có các kích thước là
60 3
20
2
x
x
,
40 2
x
,
x
.ĐK:
0 20
x
Thể tích khối hộp tương ứng là :
40 20
V x x x
.
Xét
3 2
3 120 1200
f x x x x
,
0 20
x
2
9 240 1200
f x x x
20
0 0;20
3
f x x
Lập bảng biến thiên của hàm số
f x
ta thấy hàm số đạt giá trị lớn nhất khi
20
3
x .Vậy thể
tích khối hộp lớn nhất khi
20
3
x .
Chú ý: Học sinh có thể sử dụng phương pháp khác đó là: Tìm giá trị lớn nhất của hàm số
2
3 20 ; 0;20
f x x x x .
Câu 53. [2D1-3] Cho hàm số
f x
có đạo hàm
f x
. Biết đồ thị hàm số
y f x
là hình bên và
0 3 2 5
f f f f . Tìm giá trị lớn nhất của hàm số
f x
trên đoạn
0;5
.
x
x
60
40
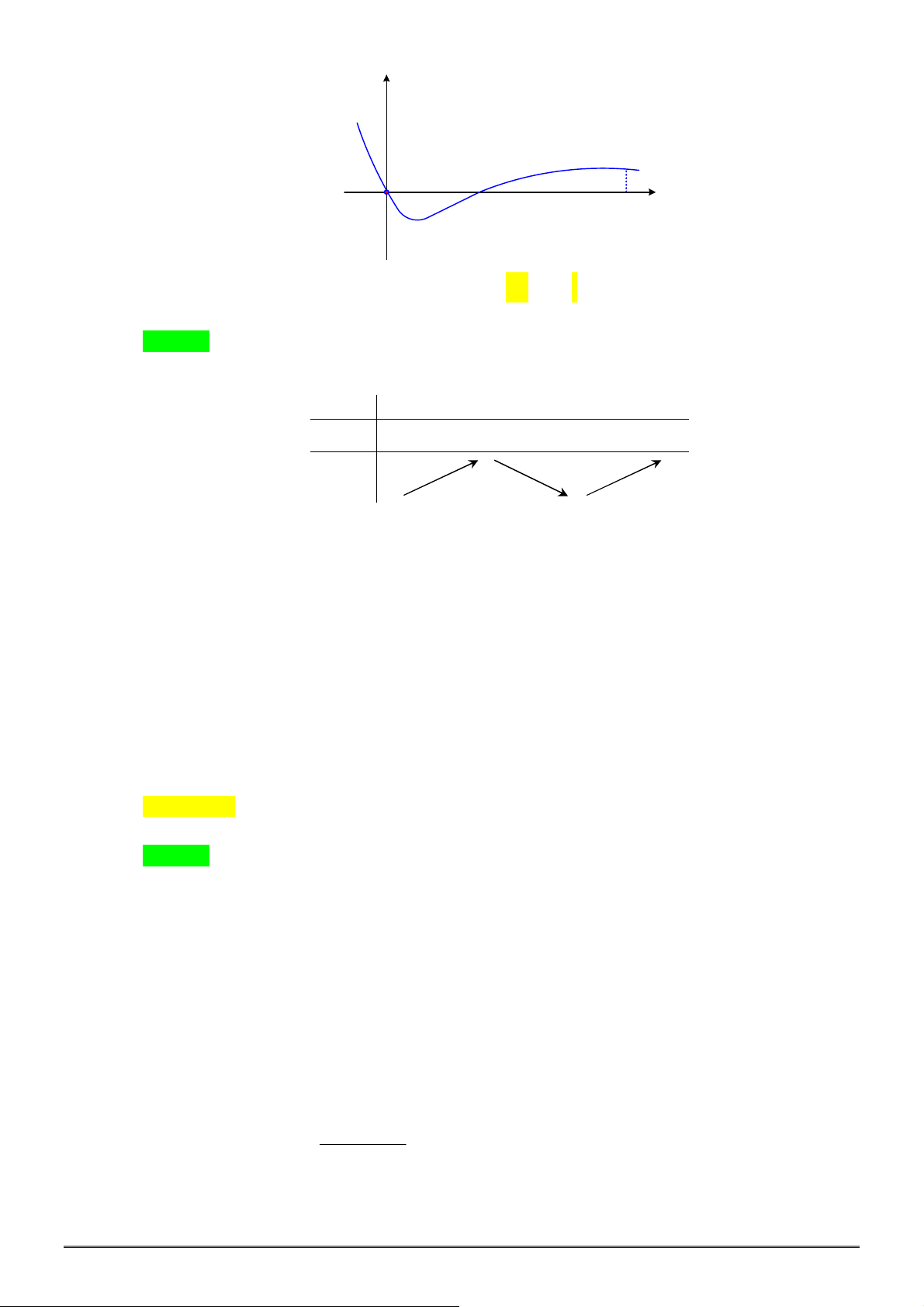
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 28/32 – Mã đề 101
y
x
5
O
2
A.
3
f
. B.
2
f . C.
5
f
. D.
0
f .
Lời giải
Chọn C.
Dựa vào đồ thị của hàm số
y f x
ta có bảng biến thiên của hàm số
y f x
:
0 2 0
f f nên
0
x
và
2
x
là hai điểm cực trị của
y f x
. Đồng thời
2 3 5
f f f
và
0 2
f f .
Mặt khác
0 3 2 5
f f f f
3 2 5 0 0 5 0
f f f f f f
Trên đoạn
0;5
hàm số
y f x
có:
2 0 5
f f f .
Vậy giá trị lớn nhất của hàm số
f x
trên đoạn
0;5
là
5
f
.
Câu 54. [2D2-3] Ông A vay ngân hàng
300
triệu đồng để mua nhà theo phương thức trả góp với lãi
suất
0,5%
mỗi tháng. Nếu cuối mỗi tháng, bắt đầu từ tháng thứ nhất ông hoàn nợ cho ngân
hàng
5.500.000
đồng và chịu lãi số tiền chưa trả. Hỏi sau bao nhiêu tháng ông A sẽ trả hết số
tiền đã vay?
A. 64 tháng. B. 65 tháng. C. 63 tháng. D. 62 tháng.
Lời giải
Chọn A.
Đặt
300000000
B
,
5500000
b
.
Cuối tháng thứ nhất ông A còn nợ số tiền là:
1
.1,005
T B b
Cuối tháng thứ hai ông A còn nợ số tiền là:
2
2 1
.1,005 1,005 .1,005
T T b B b b
Cuối tháng thứ ba ông A còn nợ số tiền là:
3 2
3 2
.1,005 1,005 . 1,005 .1,005
T T b B b b b
………………………..
Cuối tháng thứ
n
ông A còn nợ số tiền là:
1 1
1
.1,005 1,005 . 1,005 . 1,005 .......
n n n
n n
T T b B b b b
1
1.005 1
. 1.005 1.
0.005
n
n
n
T B b
s
Để tháng thứ
n
trả hết tiền thì
0
n
T
. Vậy
64
n
.
x
0
2
f x
0
0
f x

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 29/32 – Mã đề 101
Câu 55. [2D2-4] Xét các số thực
a
,
b
dương thỏa mãn
2
1
log 2 3
ab
ab a b
a b
. Tìm giá trị nhỏ
nhất của biểu thức
2
P a b
.
A.
2 10 3
2
B.
2 10 5
2
C.
2 10 1
2
D.
3 10 7
2
Lời giải
Chọn A.
Điều kiện
1
0
ab
a b
. Ta có:
2
1
log 2 3
ab
ab a b
a b
2 2
log 1 log 2 3
ab a b ab a b
2 2
log 2 1 2 1 log
ab ab a b a b
.
Xét hàm số
2
log
f t t t
, có đạo hàm
1
1 0
ln2
f t
t
,
0
t
.
Do đó
2 1
f ab f a b
2
1 2
a
b
a
,
0 2
a
.
Ta có
2
P a b
2
2 2 4
2.
1 2 1 2
a a a
a
a a
.
Từ đó ta có
2
2 4
1 2
a a
P f a
a
,
0 2
a
.
Đạo hàm
2
2
4 4 9
1 2
a a
f a
a
, ta có
2
10 1
0;2
2
0 4 4 9 0
10 1
0
2
a
f a a a
a
.
Lập bảng biến thiên của hàm số
f a
trên
0 2
a
ta được
min
10 1 2 10 3
2 2
P P
.
Câu 56. [2D2-3] Tìm tất cả các giá trị của tham số
m
để hàm số
3 2
3 3 11
1
x mx mx
y
đồng biến trên
khoảng
0; .
A.
0;1 .
m B.
0;1 .
m C.
0; .
D.
0; .
Lời giải
Chọn D.
Ta có
3 2
3 2
3 3 11
3 3 11
1
x mx mx
x mx mx
y
.
Đạo hàm
3 2
3 3 11
2
3. 2 ln
x mx mx
y x mx m
.
Hàm số đồng biến trên
0;
nên
3 2
3 3 11
2
0 3. 2 ln 0
x mx mx
y x mx m
trên
0;
. Khi đó
2
2 0
x mx m
trên
0;
.
Cách 1:
Trường hợp
1
:
2
0 0 0;1
m m m
.
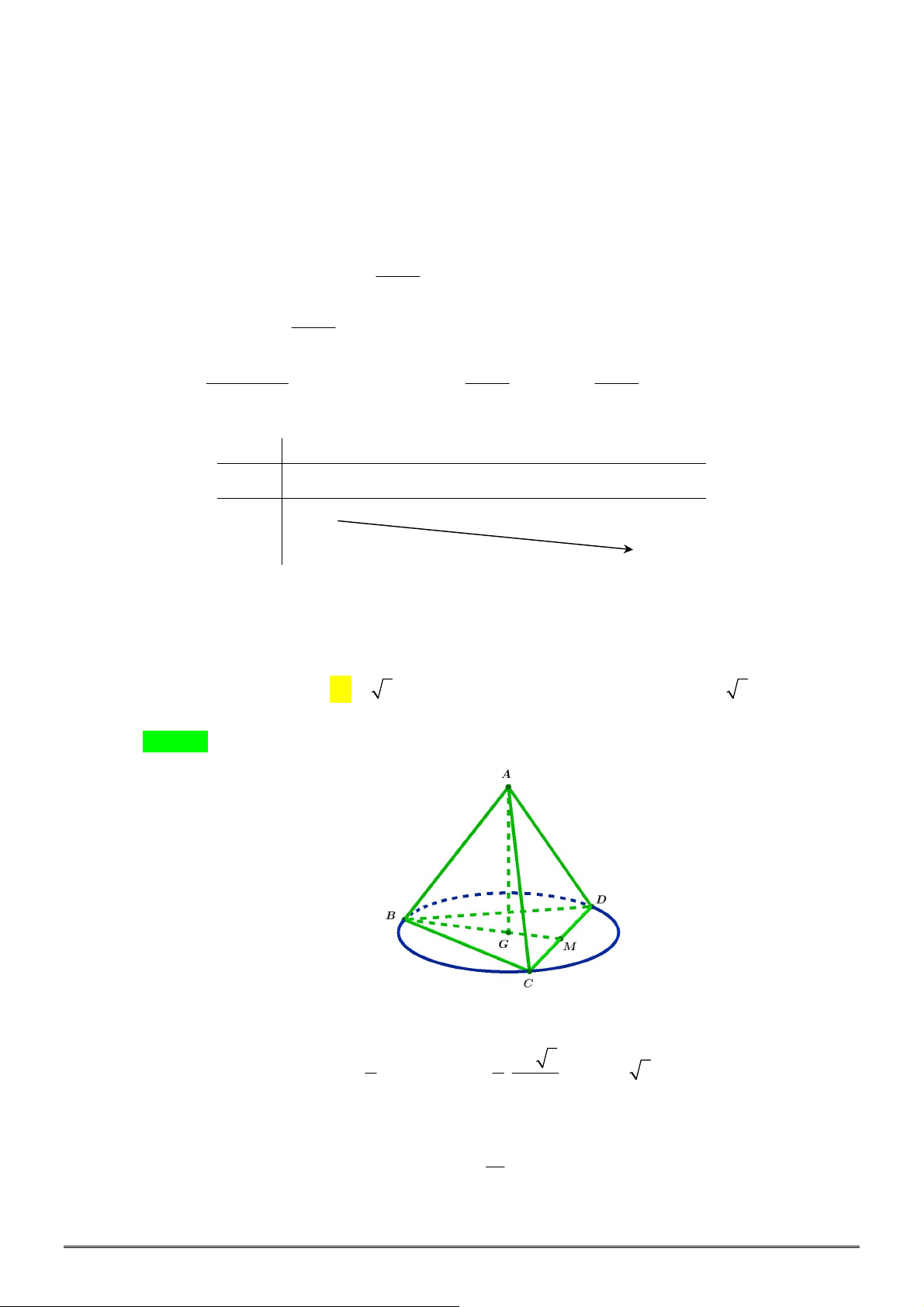
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 30/32 – Mã đề 101
Trường hợp
2
: Tam thức
2
2
g x x mx m
có hai nghiệm
1
x
,
2
x
thỏa mãn
1 2
0
x x
.
Khi đó
1 2
1 2
0
0
0
x x
x x
2
0
2 0
0
m m
m
m
; 0 1;
0
0
m
m
m
1;m
.
Kết hợp hai trường hợp ta có
0;m
.
Cách 2:
Ta có
2
2
2 0
2 1
x
x mx m m
x
, vì
0; 2 1 0
x x
Xét hàm số
2
, 0;
2 1
x
g x x
x
2
2
2
0, 0;
2 1
x x
g x x
x
;
2
lim
2 1
x
x
x
;
2
0
lim 0
2 1
x
x
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên, yêu cầu bài toán
0
m
hay
0;m
.
Câu 57. [2H2-3] Cho tứ diện đều
ABCD
có cạnh
6 .
a
Hình nón
N
có đỉnh
A
và đường tròn đáy là
đường tròn ngoại tiếp tam giác
.
BCD
Tính diện tích xung quanh của hình nón
N
.
A.
2
24 .
a
B.
2
12 3 .
a
C.
2
48 .
a
D.
2
24 3 .
a
Lời giải
Chọn B.
Diện tích xung quanh của hình nón
N
là:
2
2 2 6 . 3
. . . . . . .6 . . .6 12 3 .
3 3 2
xq
a
S R l BG AB BM a a a
Câu 58. [2H1-3] Cho khối tứ diện có thể tích
.
V
Gọi
V
là thể tích khối đa diện có các đỉnh là trung
điểm các cạnh của khối tứ diện đó. Tính tỉ số
V
V
x
0
g x
g x
0
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 31/32 – Mã đề 101
A.
2
3
V
V
B.
1
2
V
V
C.
1
4
V
V
D.
5
8
V
V
Lời giải
Chọn B.
. . . . . .
. .
1
A QEP B QMF C MNE D NPF A QEP B QMF
C MNE D NPF
V V V V V V V
V VV
V V V V V V
1 1 1 1 1 1 1 1 1 1 1 1 1
1 . . . . . . . .
2 2 2 2 2 2 2 2 2 2 2 2 2
.
Câu 59. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
1
y mx m
cắt đồ thị
hàm số
3 2
3 2
y x x x
tại ba điểm
A
,
B
,
C
phân biệt sao cho
.
AB BC
A.
( ;0] [4; ).
m
B.
5
; .
4
m
C.
2; .
m
D.
.
m
Lời giải
Chọn C.
Đặt
: 1
d y mx m
và
3 2
: 3 2
C y x x x
.
Phương trình hoành độ giao điểm của
d
và
C
là:
3 2 3 2
3 2 1 3 1 1 0 1
x x x mx m x x m x m
2
2
1
1 2 1 0
2 1 0 2
x
x x x m
x x m
Để
d
cắt
C
tại ba điểm
A
,
B
,
C
phân biệt thì
1
có ba nghiệm phân biệt
2
có hai nghiệm phân biệt khác
1
2
0
2 0
2 *
2
1 2.1 1 0
m
m
m
m
.
Nhận xét: với điều kiện
*
thì
1
có 3 nghiệm phân biệt
1
1
x
,
2
x
và
3
x
và ta có
2 3 1
2 2
x x x m
nên ba giao điểm
A
,
B
,
C
luôn thỏa mãn
.
AB BC
Câu 60. [2D2-3] Cho hai số thực dương
a
,
b
khác
1.
Biết rằng bất kì đường thẳng nào song song với
trục hoành mà cắt các đường
x
y a
,
x
y b
và trục tung lần lượt tại
M
,
N
,
A
thì
3
AN AM
(hình vẽ bên). Hỏi khẳng định nào sau đây đúng?
Q
P
N
M
D
C
B
A
E
F
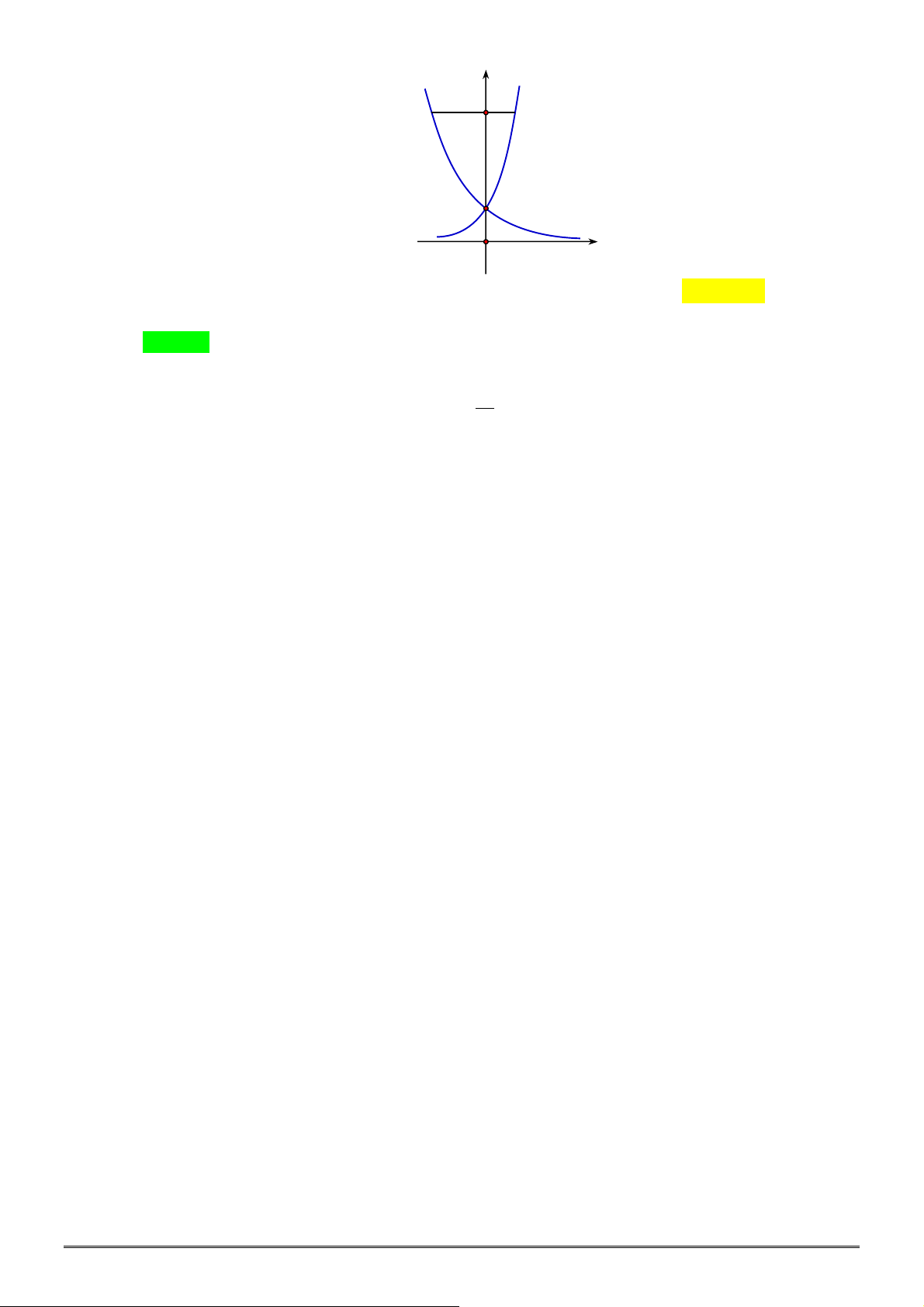
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 32/32 – Mã đề 101
A.
3
b a
. B.
3
1
a b
. C.
2
1
ab
. D.
3
1
ab
.
Lời giải
Chọn D.
Giả sử
N
,
M
có hoành độ lần lượt là
n
,
m
khác
0
. Theo đề, ta có:
3
n m
,
n m
b a
Vậy
3
m m
b a
3
m
m
b a
3
b a
3
1
a
b
3
1
ab
.
O
x
y
N
M
A
x
y b
x
y a
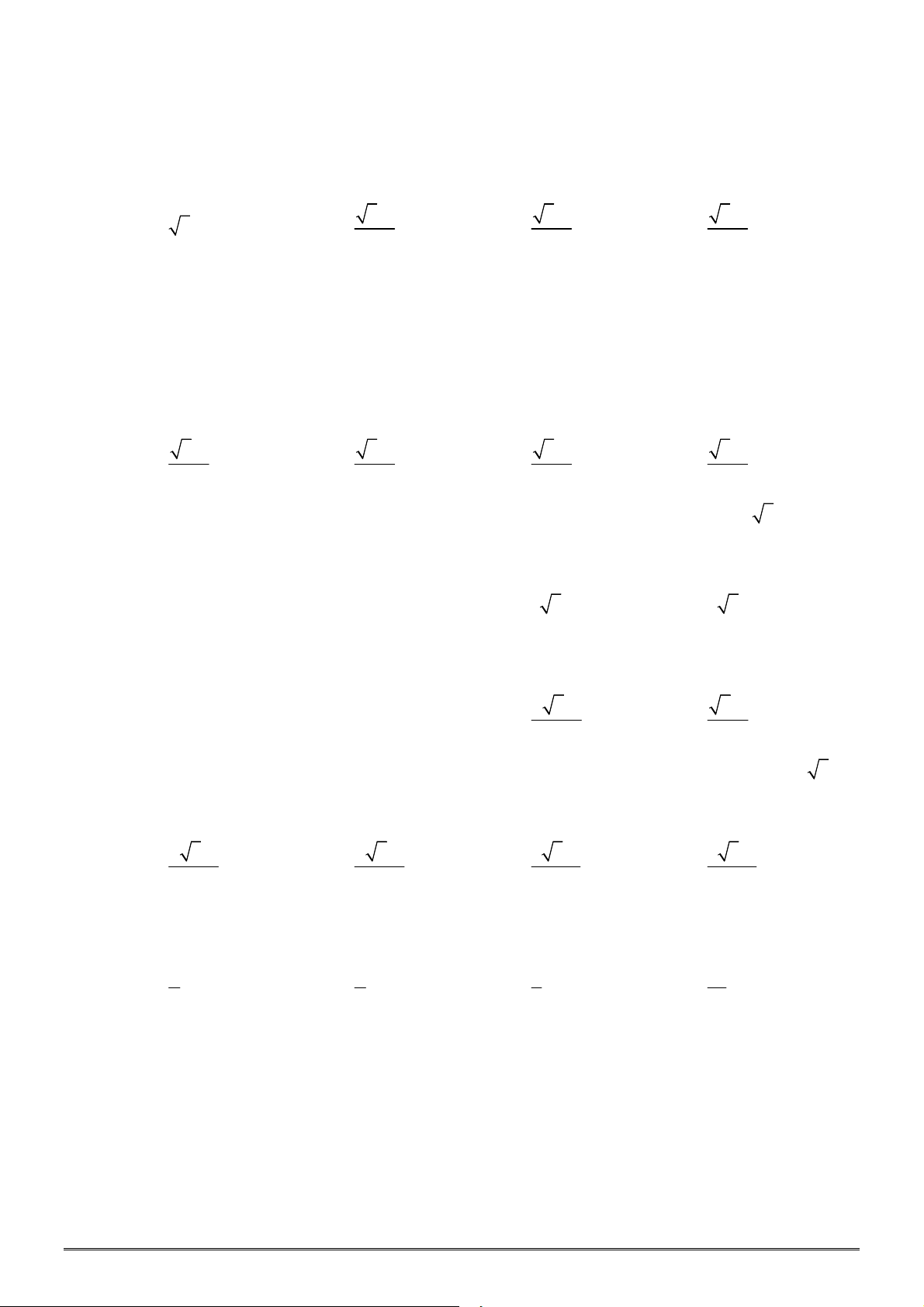
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/24
TRƯỜNG THPT
CHUYÊN NGOẠI NGỮ
NHÓM TOÁN 12
ĐỀ MINH HỌA THI THI HỌC KÌ I NĂM HỌC 2017-2018
MÔN: TOÁN – KHỐI 12
Thời gian làm bài: 90 phút
Câu 1. [2H1-2] Cho hình lăng trụ đứng
.
ABC A B C
có đáy là tam giác vuông cân,
AB AC a
,
2
A C a
. Thể tích của khối lăng trụ đó bằng
A.
3
3
a
. B.
3
3
6
a
. C.
3
3
3
a
. D.
3
3
2
a
.
Câu 2. [2H1-2] Hình hộp chữ nhật
.
ABCD A B C D
có diện tích các mặt
ABCD
,
ADD A
,
CDD C
lần lượt là
15
cm
2
,
20
cm
2
,
12
cm
2
. Thể tích khối hộp chữ nhật đó là
A.
30
cm
3
. B.
60
cm
3
. C.
45
cm
3
. D.
90
cm
3
.
Câu 3. [2H1-2] Cho lăng trụ
.
ABC A B C
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của
C
trên
A B C
là trung điểm của
B C
, góc giữa
CC
với
A B C
bằng
45
. Thể tích khối
lăng trụ
.
ABC A B C
là
A.
3
3
4
a
. B.
3
3
12
a
. C.
3
3
8
a
. D.
3
3
24
a
.
Câu 4. [2H1-2] Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật có
2
AB a
,
3
BC a
. Biết rằng
SAB
là tam giác cân tại
S
và
SAB
vuông góc với
ABCD
; góc giữa
SC
và
ABCD
bằng
60
. Thể tích khối chóp
.
S ABCD
là
A.
3
4
a
. B.
3
3
a
. C.
3
3 3
a
. D.
3
2 3
a
.
Câu 5. [2H1-2] Cho hình chóp
.
S ABC
có
SA
vuông góc với
ABC
và đáy là tam giác vuông tại
B
.
Biết
SA a
,
2
AB a
,
3
AC a
. Thể tích khối chóp
.
S ABC
là
A.
3
2
a
. B.
3
a
. C.
3
2 5
3
a
. D.
3
5
3
a
.
Câu 6. [2H1-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a
,
3
AD a
và
2
SA a
vuông góc với mặt đáy. Gọi
M
,
N
,
E
,
F
lần lượt là trung điểm của
SA
,
SB
,
SC
,
SD
. Thể tích của khối chóp cụt
.
ABCD MNEF
bằng
A.
3
7 3
12
a
. B.
3
7 3
6
a
. C.
3
5 3
8
a
. D.
3
5 3
4
a
.
Câu 7. [2H1-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
,
N
,
P
,
Q
lần
lượt là trung điểm của
SA
,
SB
,
SC
,
SD
. Tỉ lệ
. .
:
S MNPQ S ABCD
V V bằng
A.
1
2
. B.
1
4
. C.
1
8
. D.
1
16
.
Câu 8. [2D1-2] Trong tất cả các hình chữ nhật có cùng chu vi bằng
16
cm thì hình chữ nhật có diện
tích lớn nhất bằng
A.
36
cm
2
. B.
20
cm
2
. C.
16
cm
2
. D.
30
cm
2
.
Câu 9. [2D2-3] Ông
A
gửi
15
triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn
1
quý, với lãi
suất
1,65%
/quý. Hỏi sau bao nhiêu quý thì ông
A
có ít nhất
20
triệu đồng (bao gồm cả vốn
lẫn lãi) từ số vốn ban đầu? (Giả sử lãi suất không thay đổi).
A.
16
quý. B.
18
quý.
C.
17
quý. D.
19
quý.
12

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/24
Câu 10. [2H2-2] Cho hình chóp đều
.
S ABCD
có cạnh đáy bằng
2
a
, góc giữa mặt bên và mặt đáy bằng
45
. Khi đó bán kính mặt cầu ngoại tiếp hình chóp
.
S ABCD
bằng
A.
3
2
a
. B.
2
a
. C.
2
2
a
. D.
3
3
a
.
Câu 11. [2H2-2] Cho
1
S
,
2
S
là hai mặt cầu có bán kính lần lượt là
1
R
,
2
R
. Tính tỉ số diện tích của
mặt cầu
1
S
, và mặt cầu
2
S
biết
1 2
2
R R
.
A.
6
. B.
8
. C.
4
. D.
2
.
Câu 12. [2H2-2] Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
2
a
, đường cao bằng
a
. Thể
tích của khối nón đỉnh
S
, đường tròn đáy là đường tròn ngoại tiếp tam giác
ABC
bằng
A.
3
2
9
a
. B.
3
2
3
a
. C.
3
4
3
a
. D.
3
4
9
a
.
Câu 13. [2H2-2] Cho hình vuông
ABCD
cạnh
4 cm
. Gọi
M
,
N
lần lượt là trung điểm của
AD
,
BC
.
Cho hình vuông đó quay xung quanh trục
MN
ta được khối trụ có thể có thể tích bằng bao
nhiêu?
A.
3
8
cm
3
. B.
3
16
cm
3
. C.
3
8 cm
. D.
3
16 cm
.
Câu 14. [2H2-2] Một khối lập phương có thể tích
3
8 cm
. Khi đó thể tích khối cầu ngoại tiếp hình lập
phương đó bằng?
A.
3
4 3 cm
. B.
3
2 3 cm
. C.
3
8 3 cm
. D.
3
6 3 cm
.
Câu 15. [1H3-2] Cho tứ diện
ABCD
có
AB
,
AC
,
AD
đôi một vuông góc. Tính khoảng cách từ
A
đến
BCD
biết
2 cm
AB AC
,
3 cm
AD
.
A.
3 11
cm
2
. B.
3 2
cm
11
. C.
3 22
cm
11
. D.
3 11
cm
11
.
Câu 16. [1H3-2] Cho hình hộp chữ nhật
.
ABCD A B C D
có
4 cm
AB
,
3 cm
AD
và đường chéo
A C
tạo với mặt phẳng
ABCD
góc
60
. Gọi
M
là trung điểm của
BC
. Khoảng cách giữa
AM
và
A D
là
A.
5 cm
. B.
5 3 cm
. C.
4 cm
. D.
4 3 cm
.
Câu 17. [1H3-2] Cho hình chóp đều
.
S ABCD
có đường cao bằng
a
và thể tích bằng
3
4
3
a
. Tính góc
giữa mặt bên và mặt đáy.
A.
75
. B.
60
. C.
45
. D.
30
.
Câu 18. [2D2-2] Chọn khẳng định sai?
A.
log 0 0 1
x x
. B.
ln 0 1
x x
.
C.
2 2
3 3
log log 0
a b a b
. D.
2 2
log log 0
a b a b
.
Câu 19. [2D2-2] Số nghiệm của phương trình
2
2 9 5
2 1
x x
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 20. [1D4-2] Hàm số
2
ln 1
y x x
có đạo hàm bằng
A.
2
1
1
x x
. B.
2
1
1
x
. C.
2
1
x
x x
. D.
2
1
x
x
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/24
Câu 21. [2D2-3] Đặt
2 3
log 5 , log 2
a b
. Biểu diễn
12
log 100
theo
,
a b
.
A.
2 1
2 1
b a
b
. B.
2 1
2 1
a
b
. C.
2 1
2
a
b
. D.
2 1
2
b a
b
.
Câu 22. [2D2-2] Rút gọn
3
2
log
log
9 4
a
b
được
A.
3 2
a b
. B.
9 4
a b
. C.
2 2
a b
. D.
a b
.
Câu 23. [2D2-3] Tập xác định của hàm số
1
3
log 3 1
y x
là
A.
3;
. B.
10
3;
3
. C.
10
3;
3
. D.
10
;
3
.
Câu 24. [2D2-2] Tổng tất cả các nghiệm của phương trình
2
2
log 1 3
x
là
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 25. [2D2-2] Phương trình
4 3.6 2.9 0
x x x
có hai nghiệm
0
x
và
2
1
x
y
x
, với
0
a b
.
Khi đó
b
a
là
A.
2
. B.
3
. C.
4
. D.
3
2
.
Câu 26. [2D2-2] Phương trình
2017
log 2016 2017
x x
có bao nhiêu nghiệm?
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 27. [2D2-2] Cho
,
a b
là các số dương và
1
a
. Chọn khẳng định đúng.
A.
2
3 2
3
log 1 log
2
a
a
a b b
. B.
2
3 2
1
log 3 log
2
a
a
a b b
.
C.
2
3 2
3
log log
2
a
a
a b b
. D.
2
3 2
3
log log
2
a
a
a b b
.
Câu 28. [2D2-2] Cho hàm số
e
x
y x
. Chọn khẳng định sai.
A. Hàm số đồng biến trên khoảng
0;
. B. Hàm số nghịch biến trên khoảng
; 1
.
C.
min 0
y
. D. Hàm số đạt cực tiểu tại
1
x
.
Câu 29. [2D2-2] Cho hàm số
1
.
2
x
x
y
Khi đó
1
y
bằng
A.
1
2
. B.
1
4
. C.
0
. D.
4
.
Câu 30. [2D2-3] Số nghiệm của phương trình
3 3 3
log log log
2 7 5
x x x
là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 31. [2D1-1] Hàm số nào sau đây đồng biến trên
?
A.
1
x
y
x
. B.
2
3 1
y x x
. C.
3 2
3 3 1
y x x x
. D.
4 2
2 1
y x x
.
Câu 32. [2D1-1] Chọn khẳng định sai?
A. Đồ thị hàm số bậc ba có tâm đối xứng.
B. Đồ thị hàm số
ax b
y
mx n
,
0,
m an bm
có tiệm cận ngang.
C. Đồ thị hàm số bậc ba có tiệm cận đứng.
D. Đồ thị hàm số bậc bốn luôn có điểm cực trị.
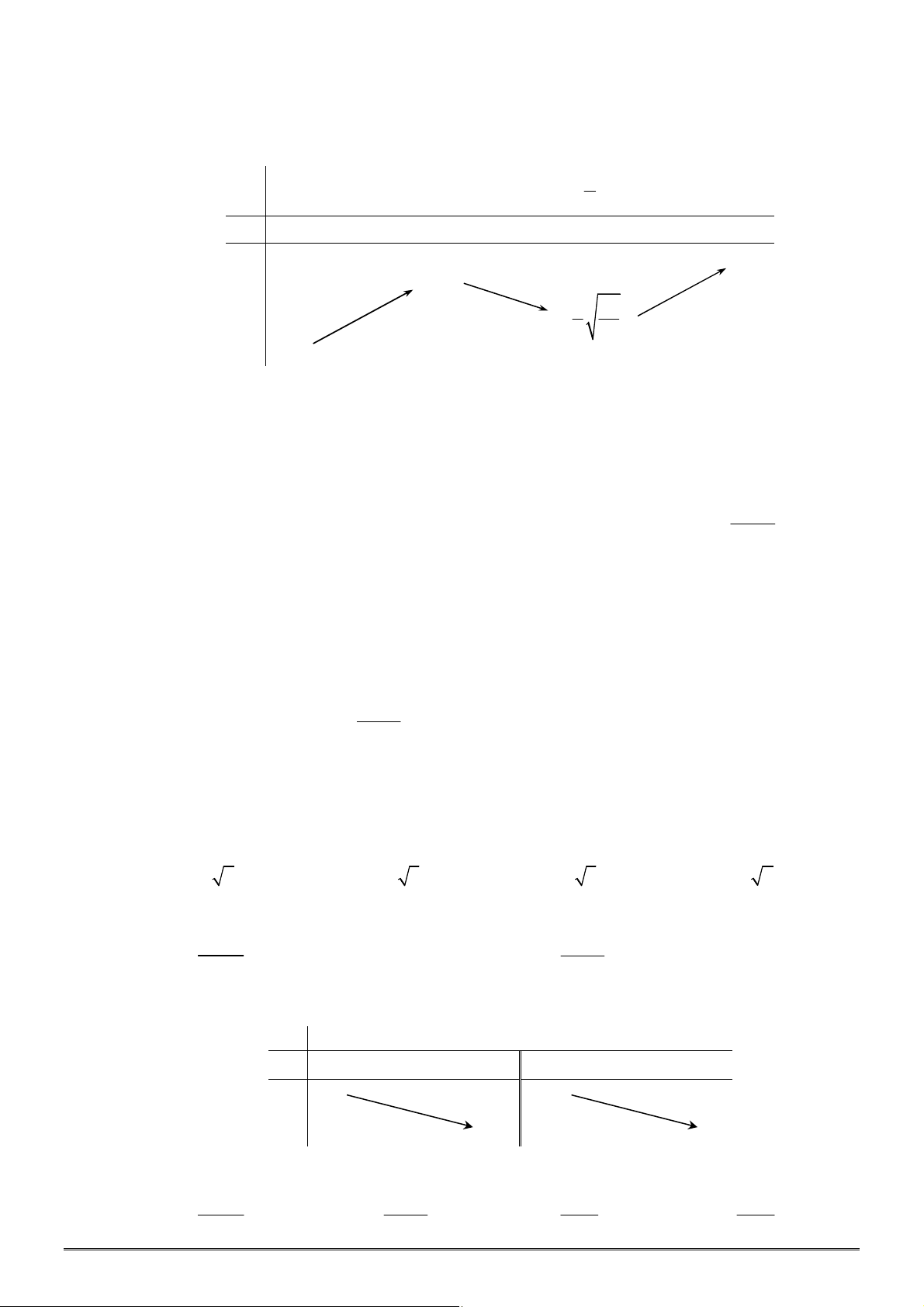
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/24
Câu 33. [2D1-2] Giá trị cực đại của hàm số
4 2
3 3
y x x
bằng
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 34. [2D1-2] Cho hàm số
y f x
xác định, liên tục trên
và có bảng biến thiên như sau:
Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số cắt trục hoành tại ba điểm phân biệt.
B. Hàm số có đúng một cực trị.
C. Hàm số có giá trị lớn nhất bằng
0
.
D. Hàm số đồng biến trên khoảng
1; 2017
.
Câu 35. [2D1-2] Gọi
M
,
m
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3
1
x
y
x
trên đoạn
2; 4
. Khi đó tổng
M m
bằng
A.
7
. B.
13
. C.
14
. D.
6
.
Câu 36. [2D1-2] Tiếp tuyến của đồ thị hàm số
3
2
y x x
tại điểm
0; 2
M có phương trình dạng
y ax b
. Khi đó giá trị của hệ số
b
là
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 37. [2D1-2] Đồ thị hàm số
2 1
2
x
y
x
cắt đường thẳng
3 2
y x
tại điểm duy nhất
A
. Khi đó
tung độ của
A
là
A.
2
. B.
1
. C.
1
. D.
2
.
Câu 38. [2D1-3] Tìm tất cả các giá trị của
m
để đồ thị hàm số
4 2 2
2 1
y x m x
có ba điểm cực trị tạo
thành một tam giác đều.
A.
3
6
m . B.
6
3
m
. C.
3
3
m
. D.
3
2
m
.
Câu 39. [2D1-2] Đồ thị hàm số nào dưới đây có tiệm cận ngang?
A.
2
2
1
x
y
x
. B.
3
2
y x x
. C.
2 1
2
x
y
x
. D.
2
2 2
y x x
.
Câu 40. [2D1-1] Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số
y f x
là hàm số nào sau đây?
A.
2 3
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2
1
x
y
x
. D.
2
1
x
y
x
.
x
0
2
5
y
||
0
y
0
3
3 4
5 25
x
1
y
–
–
y
2
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/24
Câu 41. [2D1-2] Đồ thị hàm số
3 2
3 2
y x x
có tâm đối xứng là điểm
I
. Khi đó hoành độ của
I
là
A.
2
. B.
0
. C.
2
. D.
1
.
Câu 42. [2D1-3] Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
3 1
x x
với
0;3
x . Mệnh đề
nào sau đây sai?
A.
0;3
min 1
y
. B.
0;3
max 19
y
.
C.
0;3
min 0
y
. D. Hàm số đạt giá trị lớn nhất tại
3
x
.
Câu 43. [2D1-2] Có bao nhiêu giá trị nguyên của
m
để phương trình
3
3 1
x x m
có ba nghiệm phân
biệt.
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 44. [2D1-3] Tìm
m
để bất phương trình
2
3 1
x m x
có nghiệm?
A.
1
m
. B.
10
m . C.
1
m
. D.
1 10
m .
Câu 45. [2D1-2] Cho hàm số
2
1
x
y
x
có đồ thị
C
và
1;1
I . Khi đó có bao nhiêu điểm thuộc đồ thị
C
sao cho khoảng cách tới
I
bằng
10
.
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 46. [2D1-3] Phương trình
4 2
2 3
x x k
có
6
nghiệm phân biệt khi và chỉ khi
A.
3 4
k
. B.
0 3
k
. C.
3
k
. D.
4
k
.
Câu 47. [2D1-3] Tìm
m
để hàm số
3 2 2
2 2
2 3 1
3 3
y x mx m x
có hai điểm cực trị
1
x
,
2
x
thỏa
mãn
1 2 1 2
2 0
x x x x
.
A.
1
m
;
1
3
m
. B.
1
m
. C.
2
m
,
1
m
. D.
2
m
.
Câu 48. [2D1-1] Hàm số
3
3 2
y x x
.
A. Đồng biến trên khoảng
0;
. B. Nghịch biến trên khoảng
1;1
.
C. Đồng biến trên khoảng
;1
. D. Nghịch biến trên khoảng
0;2
.
Câu 49. [2D2-1] Cho hàm số
y f x
có đồ thị
C
như hình vẽ sau:
Khẳng định nào sau đây sai?
A. Hàm số nghịch biến trên
.
B. Đồ thị hàm số có một đường tiệm cận.
C. Phương trình của đồ thị
C
có dạng
x
y a
với
1
a
.
D. Đồ thị hàm số cắt trục tung.
Câu 50. [2D2-2] Phương trình
2
3 5
3
2
5
4 2 log
2 6
x x x
x
x x
có hai nghiệm là
1
x
,
2
x
. Khi đó tổng
1 2
x x
bằng
A.
5
. B.
5
2
. C.
5
. D.
5
2
.
----------HẾT----------
O
x
y
1
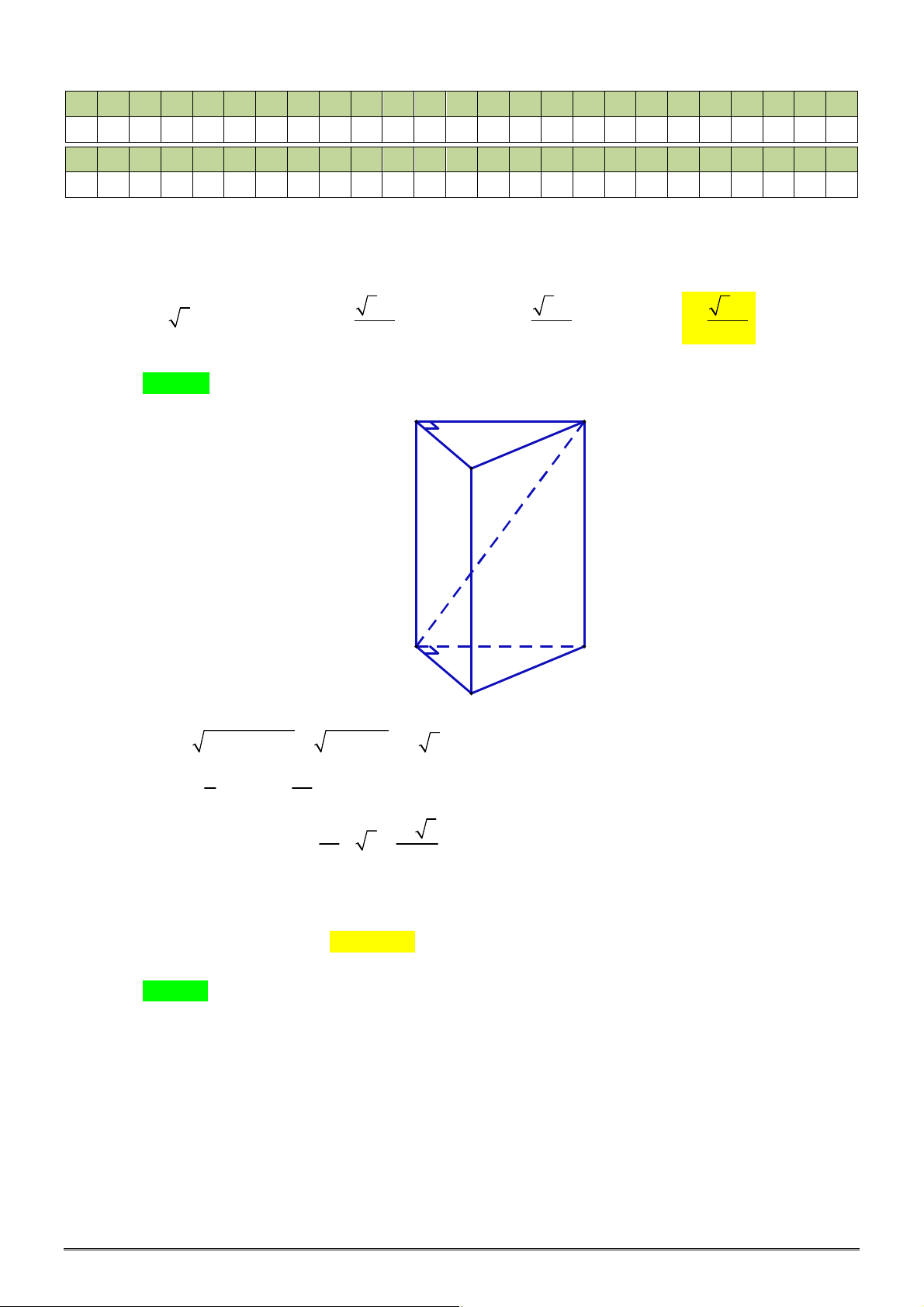
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/24
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
B C
A
D
A
C
C
B
A
C
D
D
A
C
B C
C
C
B A
C
C
A
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
D
C
A
D
C
C
A
D
B
C
C
B C
B D
A
C
B A
A
B B C
D
HƯỚNG DẪN GIẢI
Câu 1. [2H1-2] Cho hình lăng trụ đứng
.
ABC A B C
có đáy là tam giác vuông cân,
AB AC a
,
2
A C a
. Thể tích của khối lăng trụ đó bằng
A.
3
3
a
. B.
3
3
6
a
. C.
3
3
3
a
. D.
3
3
2
a
.
Lời giải
Chọn D.
C
B
A'
C'
B'
A
2 2 2 2
4 3
AA A C AC a a a
.
2
1
.
2 2
ABC
a
S AB AC
.
2 3
.
3
. . 3
2 2
ABC A B C ABC
a a
V S AA a
.
Câu 2. [2H1-2] Hình hộp chữ nhật
.
ABCD A B C D
có diện tích các mặt
ABCD
,
ADD A
,
CDD C
lần lượt là
15
cm
2
,
20
cm
2
,
12
cm
2
. Thể tích khối hộp chữ nhật đó là
A.
30
cm
3
. B.
60
cm
3
. C.
45
cm
3
. D.
90
cm
3
.
Lời giải
Chọn B.
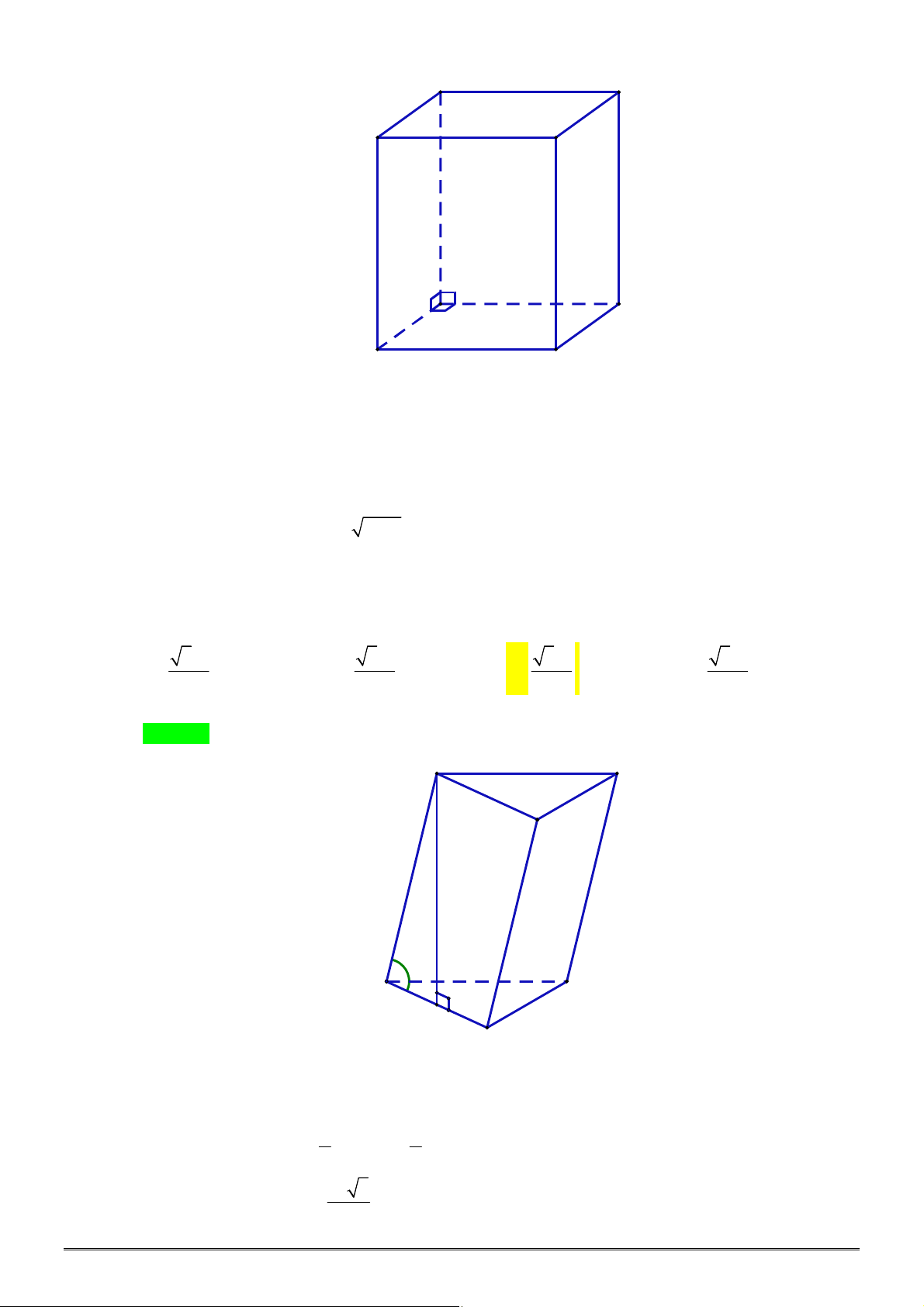
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/24
C'
C
D'
B'
A
D
B
A'
. 15
ABCD
S AB AD
.
. 20
ADD A
S AD AA
.
. 12
CDD C ABB A
S S AB AA
.
2
. . . . . . . . . 15.20.12 3600
ABCD ADD A CDD C
S S S AB AD AD AA AB AA AB AD AA
.
.
. . 3600 60
ABCD A B C D
V AB AD AA
(cm
3
).
Câu 3. [2H1-2] Cho lăng trụ
.
ABC A B C
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của
C
trên
A B C
là trung điểm của
B C
, góc giữa
CC
với
A B C
bằng
45
. Thể tích khối
lăng trụ
.
ABC A B C
là
A.
3
3
4
a
. B.
3
3
12
a
. C.
3
3
8
a
. D.
3
3
24
a
.
Lời giải
Chọn C.
45°
B
A
H
B'
A'
C'
C
Gọi
H
là trung điểm
B C
.
Ta có
CH A B C
nên góc giữa
CC
và
A B C
là góc
CC H
45
CC H
.
.tan .tan45
2 2
a a
CH C H CC H
.
Diện tích đáy là
2
3
4
ABC
a
S
.
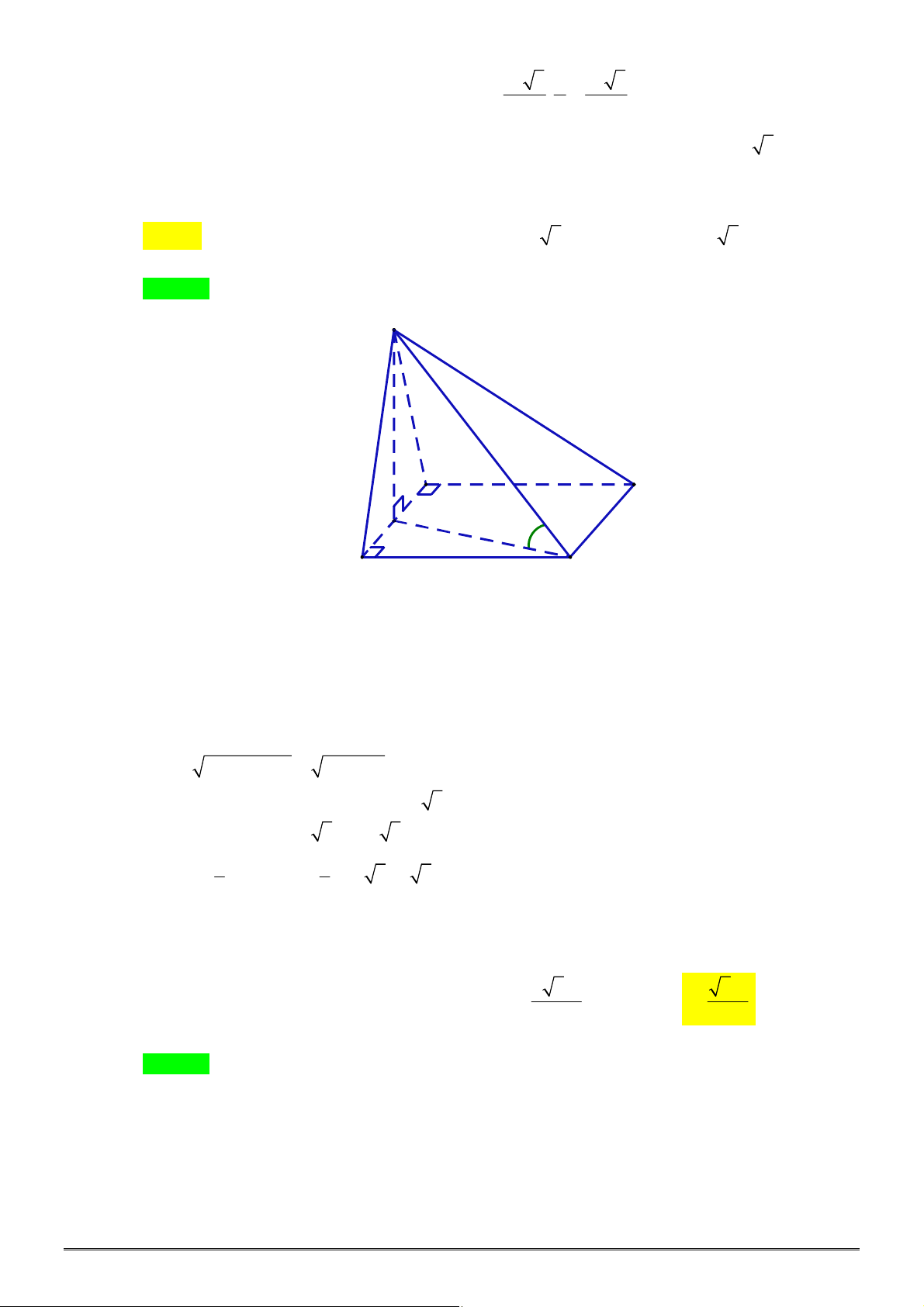
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/24
Thể tích khối lăng trụ là
2 3
.
3 3
. .
4 2 8
ABC A B C ABC
a a a
V S CH
.
Câu 4. [2H1-2] Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật có
2
AB a
,
3
BC a
. Biết rằng
SAB
là tam giác cân tại
S
và
SAB
vuông góc với
ABCD
; góc giữa
SC
và
ABCD
bằng
60
. Thể tích khối chóp
.
S ABCD
là
A.
3
4
a
. B.
3
3
a
. C.
3
3 3
a
. D.
3
2 3
a
.
Lời giải
Chọn A.
60°
H
C
B
D
A
S
Gọi
H
là trung điểm
AB
.
Ta có:
SAB ABCD
SAB ABCD AB SH ABCD
SH AB
.
Góc giữa
SC
và
ABCD
là
SCH
60
SCH
.
2 2 2 2
3 2
CH BC BH a a a
.
.tan 2 .tan 60 2 3
SH CH SCH a a
.
2
. 2 . 3 2 3
ABCD
S AB BC a a a .
2 3
.
1 1
. . .2 3.2 3 4
3 3
S ABCD ABCD
V S SH a a a
.
Câu 5. [2H1-2] Cho hình chóp
.
S ABC
có
SA
vuông góc với
ABC
và đáy là tam giác vuông tại
B
.
Biết
SA a
,
2
AB a
,
3
AC a
. Thể tích khối chóp
.
S ABC
là
A.
3
2
a
. B.
3
a
. C.
3
2 5
3
a
. D.
3
5
3
a
.
Lời giải
Chọn D.
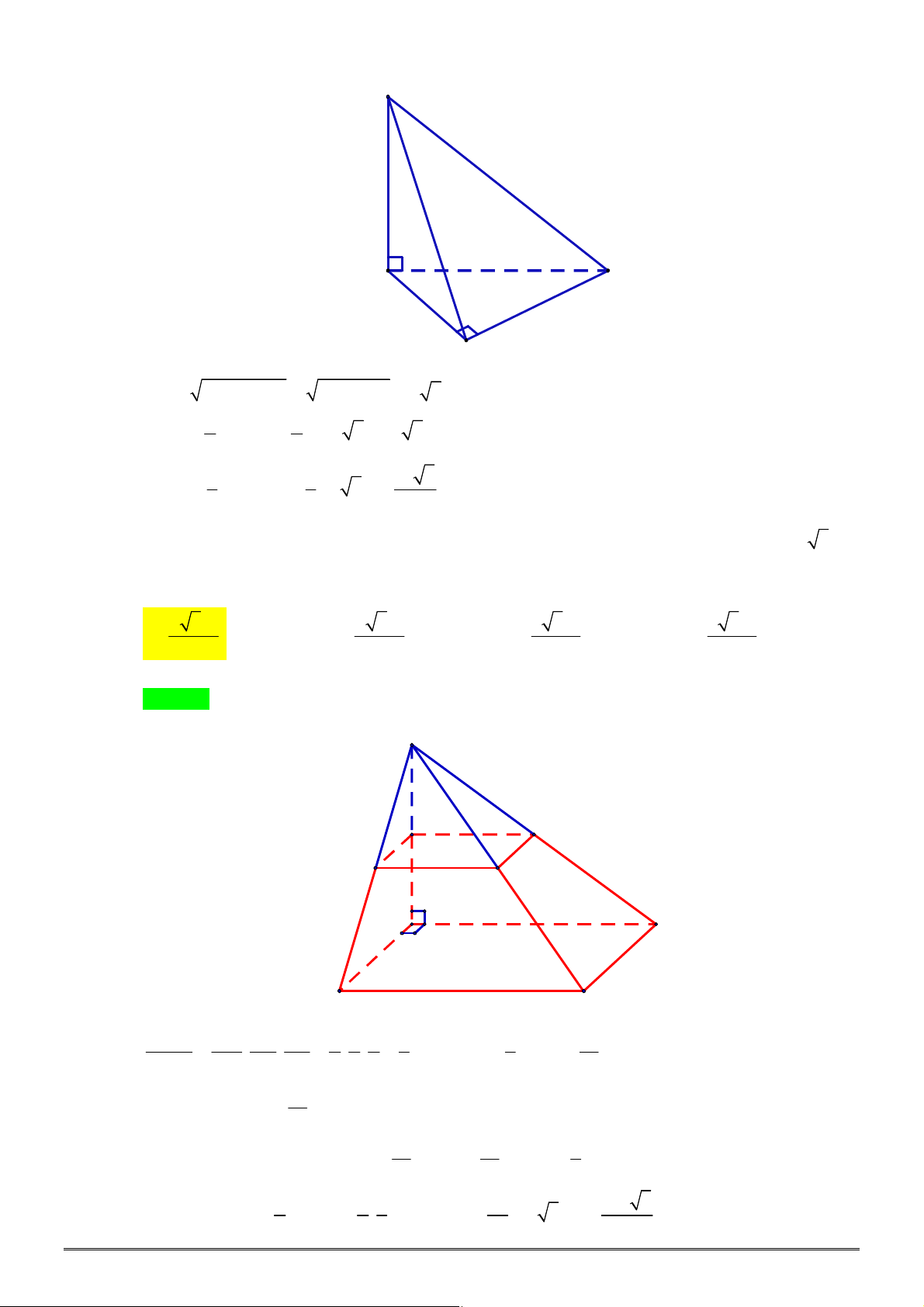
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/24
B
A
C
S
2 2 2 2
9 4 5
BC AC AB a a a
.
2
1 1
. .2 . 5 5
2 2
ABC
S AB BC a a a
.
3
2
.
1 1 5
. . . 5.
3 3 3
S ABC ABC
a
V S SA a a
.
Câu 6. [2H1-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a
,
3
AD a
và
2
SA a
vuông góc với mặt đáy. Gọi
M
,
N
,
E
,
F
lần lượt là trung điểm của
SA
,
SB
,
SC
,
SD
. Thể tích của khối chóp cụt
.
ABCD MNEF
bằng
A.
3
7 3
12
a
. B.
3
7 3
6
a
. C.
3
5 3
8
a
. D.
3
5 3
4
a
.
Lời giải
Chọn A.
F
E
N
M
C
A
D
B
S
.
.
1 1 1 1
. . . .
2 2 2 8
S MNE
S ABC
V
SM SN SE
V SA SB SC
. . .
1 1
8 16
S MNE S ABC S ABCD
V V V .
Tương tự:
. .
1
16
S MEF S ABCD
V V .
Suy ra
. . . . . .
1 1 1
16 16 8
S MNEF S MNE S MEF S ABCD S ABCD S ABCD
V V V V V V .
Vậy
3
. .
7 7 1 7 7 3
. . . . . 3.2
8 8 3 24 12
ABCD MNEF S ABCD
a
V V AB AD SA a a a .
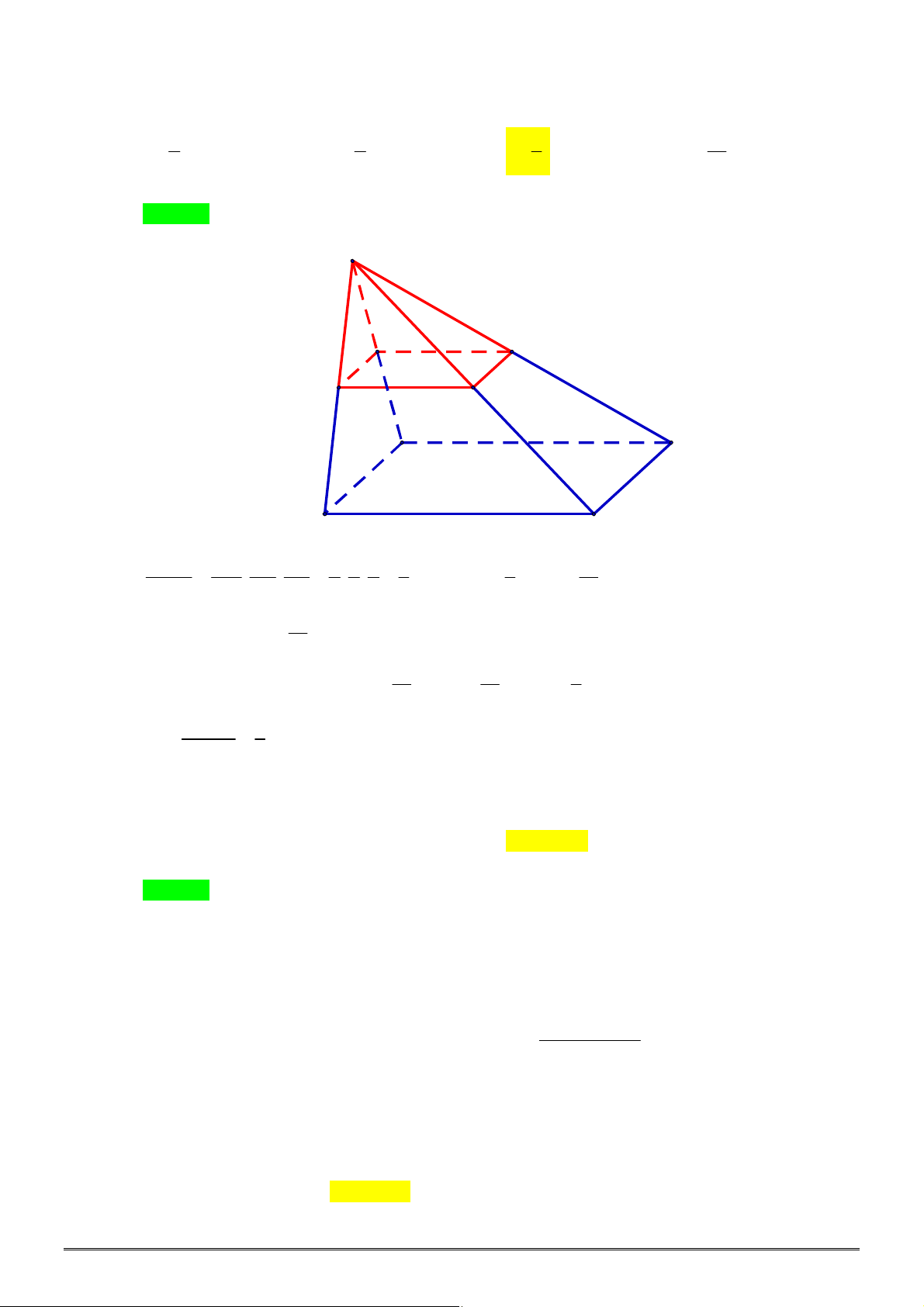
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/24
Câu 7. [2H1-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
,
N
,
P
,
Q
lần
lượt là trung điểm của
SA
,
SB
,
SC
,
SD
. Tỉ lệ
. .
:
S MNPQ S ABCD
V V bằng
A.
1
2
. B.
1
4
. C.
1
8
. D.
1
16
.
Lời giải
Chọn C.
Q
P
N
M
C
B
D
A
S
.
.
1 1 1 1
. . . .
2 2 2 8
S MNP
S ABC
V
SM SN SP
V SA SB SC
. . .
1 1
8 16
S MNP S ABC S ABCD
V V V .
Tương tự:
. .
1
16
S MPQ S ABCD
V V .
Suy ra
. . . . . .
1 1 1
16 16 8
S MNPQ S MNP S MPQ S ABCD S ABCD S ABCD
V V V V V V .
Vậy
.
.
1
8
S MNPQ
S ABCD
V
V
.
Câu 8. [2D1-2] Trong tất cả các hình chữ nhật có cùng chu vi bằng
16
cm thì hình chữ nhật có diện
tích lớn nhất bằng
A.
36
cm
2
. B.
20
cm
2
. C.
16
cm
2
. D.
30
cm
2
.
Lời giải
Chọn C.
Gọi hai kích thước của hình chữ nhật lần lượt là
x
,
y
, 0
x y
.
Chu vi hình chữ nhật:
2 2 16
x y
8
y x
8
x
.
Diện tích hình chữ nhật:
8
S x x
.
Áp dụng bất đẳng thức Cô-si, ta được
2
8
8 16
4
x x
S x x S
.
Vậy diện tích lớn nhất là
16
xảy ra khi
8 4
x x x
.
Câu 9. [2D2-3] Ông
A
gửi
15
triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn
1
quý, với lãi
suất
1,65%
/quý. Hỏi sau bao nhiêu quý thì ông
A
có ít nhất
20
triệu đồng (bao gồm cả vốn
lẫn lãi) từ số vốn ban đầu? (Giả sử lãi suất không thay đổi).
A.
16
quý. B.
18
quý. C.
17
quý. D.
19
quý.
Lời giải
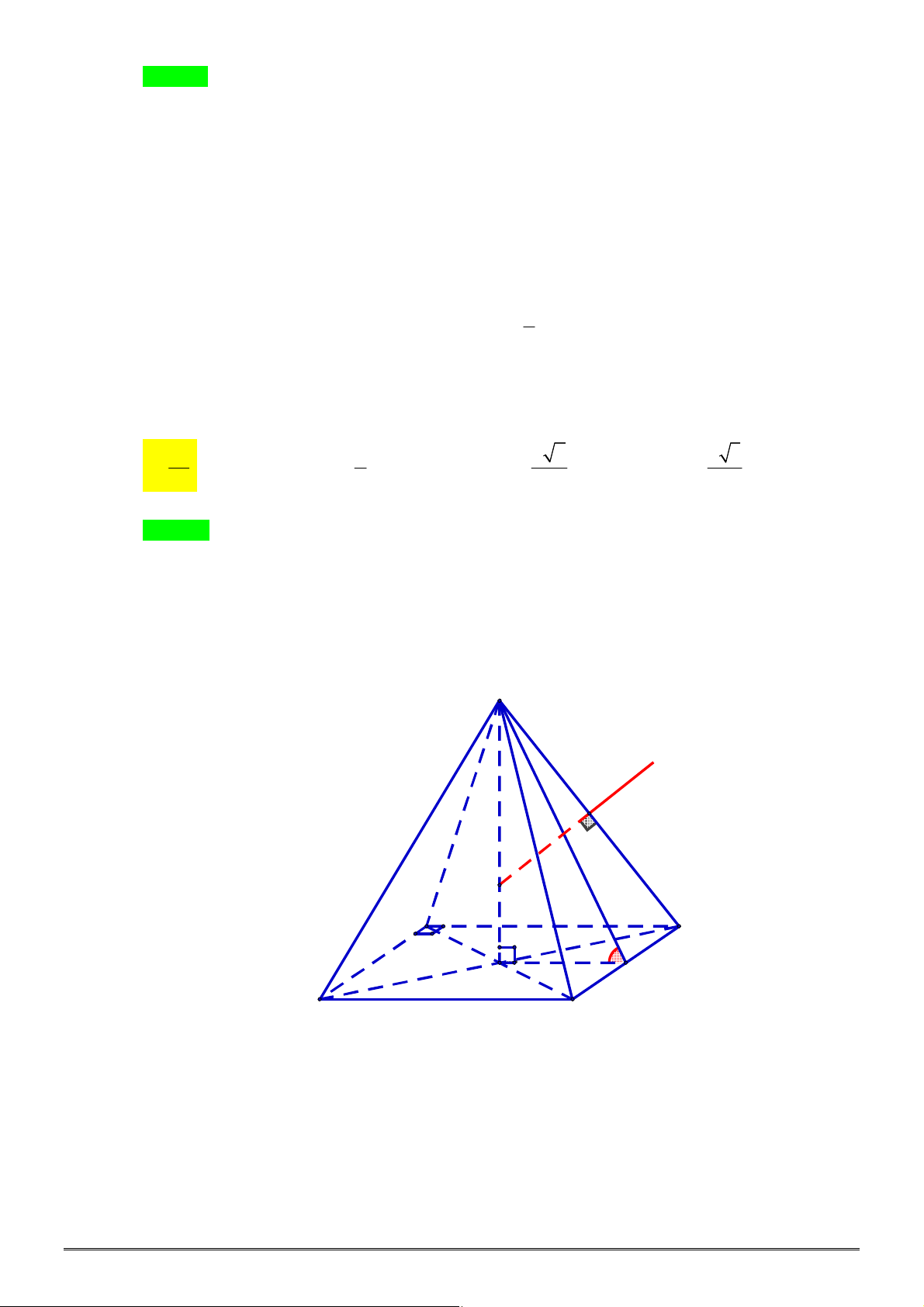
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/24
Chọn B.
15
P
, lãi suất là
1,65% 0,0165
r
.
Sau
1
quý, ông
A
có:
1
P Pr P r
.
Sau
2
quý, ông
A
có:
2
1
P r
.
…
Sau
n
quý, ông
A
có:
1
n
P r
.
Ông
A
muốn nhận được ít nhất
20
triệu đồng (bao gồm cả vốn lẫn lãi) khi số quý (là
n
) là số
nguyên dương nhỏ nhất thỏa:
1,0165
4
1 20 15. 1,0165 20 log 17,58
3
n n
P r n n .
Vậy
18
n
(quý).
Câu 10. [2H2-2] Cho hình chóp đều
.
S ABCD
có cạnh đáy bằng
2
a
, góc giữa mặt bên và mặt đáy bằng
45
. Khi đó bán kính mặt cầu ngoại tiếp hình chóp
.
S ABCD
bằng
A.
3
2
a
. B.
2
a
. C.
2
2
a
. D.
3
3
a
.
Lời giải
Chọn A.
Gọi
M
là trung điểm
CD
.
SCD ABCD CD
SM CD
OM CD
Góc giữa mặt bên
SCD
và
ABCD
là
SMO
45
SMO
.
d
45°
I
N
M
O
C
A
D
B
S
Gọi
N
là trung điểm
SD
.
Trong mặt phẳng
SOD
dựng đường trung trực
d
của đoạn thẳng
SD
.
I d IS ID
d SO I
I SO IA IB IC ID
Suy ra mặt cầu ngoại tiếp chóp
.
S ABCD
có tâm
I
, bán kính
R IS
.
tan
SO OM SMO a
.
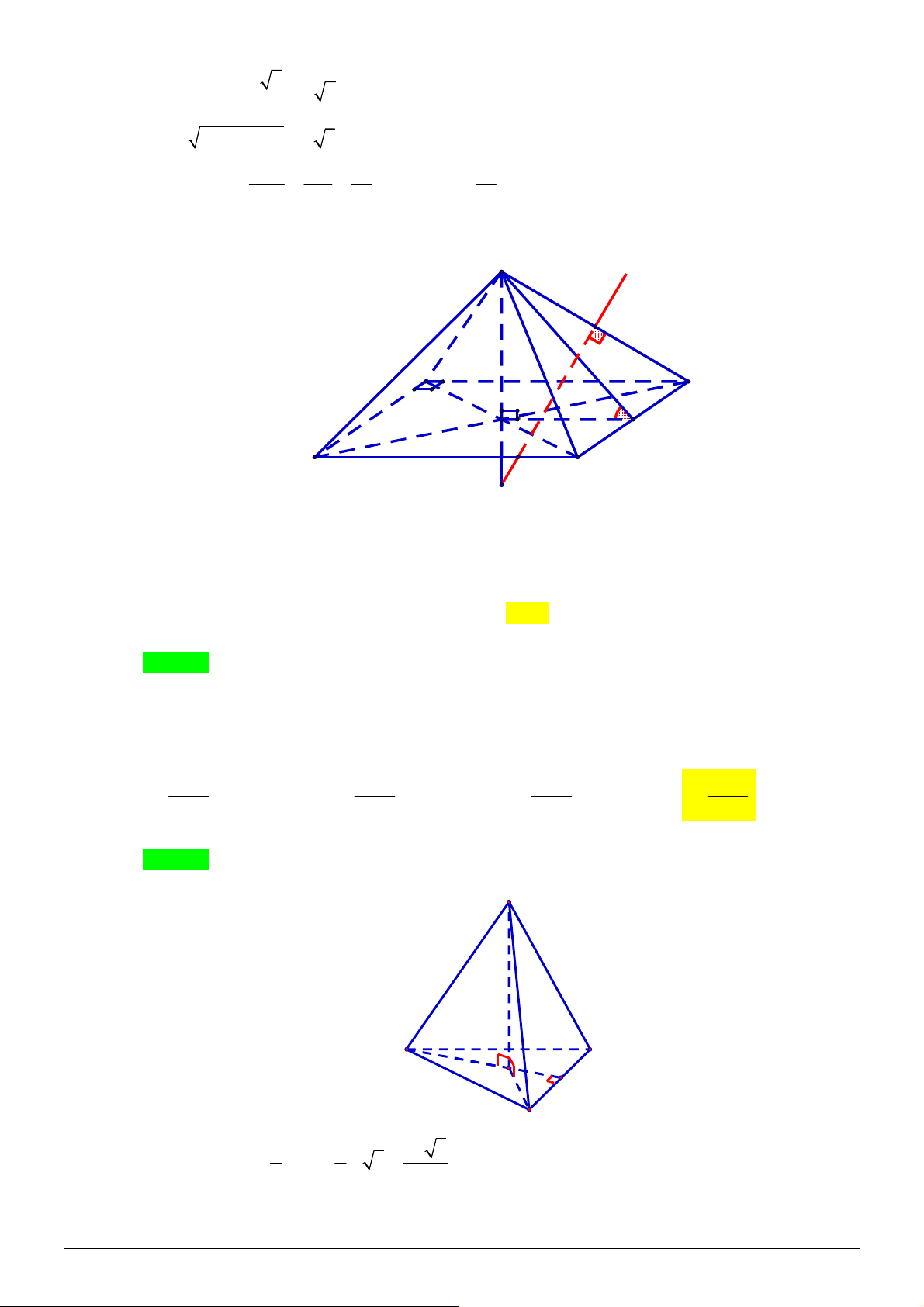
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/24
2 2
2
2 2
BD a
OD a
.
2 2
3
SD SO OD a
.
Vây
2 2
3 3
2 2 2
SD a a
R IS
SO a
. (chú ý:
3
2
a
R SO
nên
I
sẽ nằm ngoài đoạn
SO
).
Hình được vẽ lại như sau:
45°
d
I
N
M
O
C
B
D
A
S
Câu 11. [2H2-2] Cho
1
S
,
2
S
là hai mặt cầu có bán kính lần lượt là
1
R
,
2
R
. Tính tỉ số diện tích của
mặt cầu
1
S
, và mặt cầu
2
S
biết
1 2
2
R R
.
A.
6
. B.
8
. C.
4
. D.
2
.
Lời giải
Chọn C.
Ta có:
2
4
C
S R
nếu
1 2 1 2
2 4
R R S S
.
Câu 12. [2H2-2] Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
2
a
, đường cao bằng
a
. Thể
tích của khối nón đỉnh
S
, đường tròn đáy là đường tròn ngoại tiếp tam giác
ABC
bằng
A.
3
2
9
a
. B.
3
2
3
a
. C.
3
4
3
a
. D.
3
4
9
a
.
Lời giải
Chọn D.
Ta có:
2 2 2 3
. 3
3 3 3
a
r AO AM a .
S
C
A
B
M
O
2
a
a
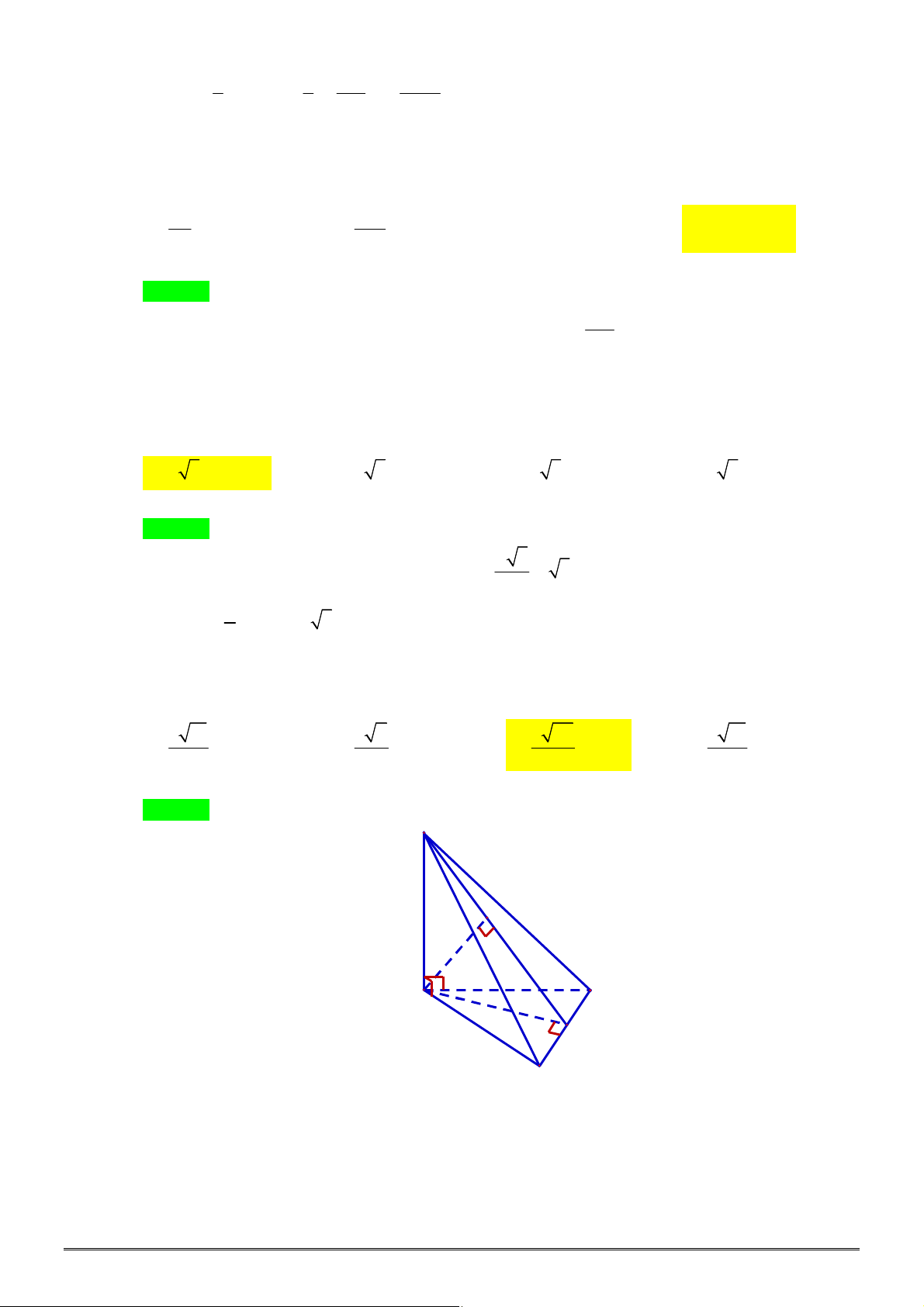
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/24
Vậy
2 3
2
1 1 4a 4
. . . . .
3 3 3 9
a
V r SO a
.
Câu 13. [2H2-2] Cho hình vuông
ABCD
cạnh
4 cm
. Gọi
M
,
N
lần lượt là trung điểm của
AD
,
BC
.
Cho hình vuông đó quay xung quanh trục
MN
ta được khối trụ có thể có thể tích bằng bao
nhiêu?
A.
3
8
cm
3
. B.
3
16
cm
3
. C.
3
8 cm
. D.
3
16 cm
.
Lời giải
Chọn D.
Khi quay xung quanh trục
MN
, thì bán kính trục bằng
2 cm
2
AD
r ,
đường cao
4 cm
h AB
. Vậy
2 2 3
.2 .4 16 cm
V r h
Câu 14. [2H2-2] Một khối lập phương có thể tích
3
8 cm
. Khi đó thể tích khối cầu ngoại tiếp hình lập
phương đó bằng?
A.
3
4 3 cm
. B.
3
2 3 cm
. C.
3
8 3 cm
. D.
3
6 3 cm
.
Lời giải
Chọn A.
3
8 cm 2 cm
hlp
V a . Suy ra bán kính
3
3 cm
2
a
R .
Vậy:
3 3
4
4 3 cm
3
C
V R
.
Câu 15. [1H3-2] Cho tứ diện
ABCD
có
AB
,
AC
,
AD
đôi một vuông góc. Tính khoảng cách từ
A
đến
BCD
biết
2 cm
AB AC
,
3 cm
AD
.
A.
3 11
cm
2
. B.
3 2
cm
11
. C.
3 22
cm
11
. D.
3 11
cm
11
.
Lời giải
Chọn C.
Gọi
M
là trung điểm của
BC AM BC
.
Ta có:
AD AC
AD BC
AD AB
.
Suy ra:
BC AMD
, kẻ
AH DM AH BCD
Khi đó:
,
d A BCD AH
.
A
B
M
2 cm
H
D
3 cm
C
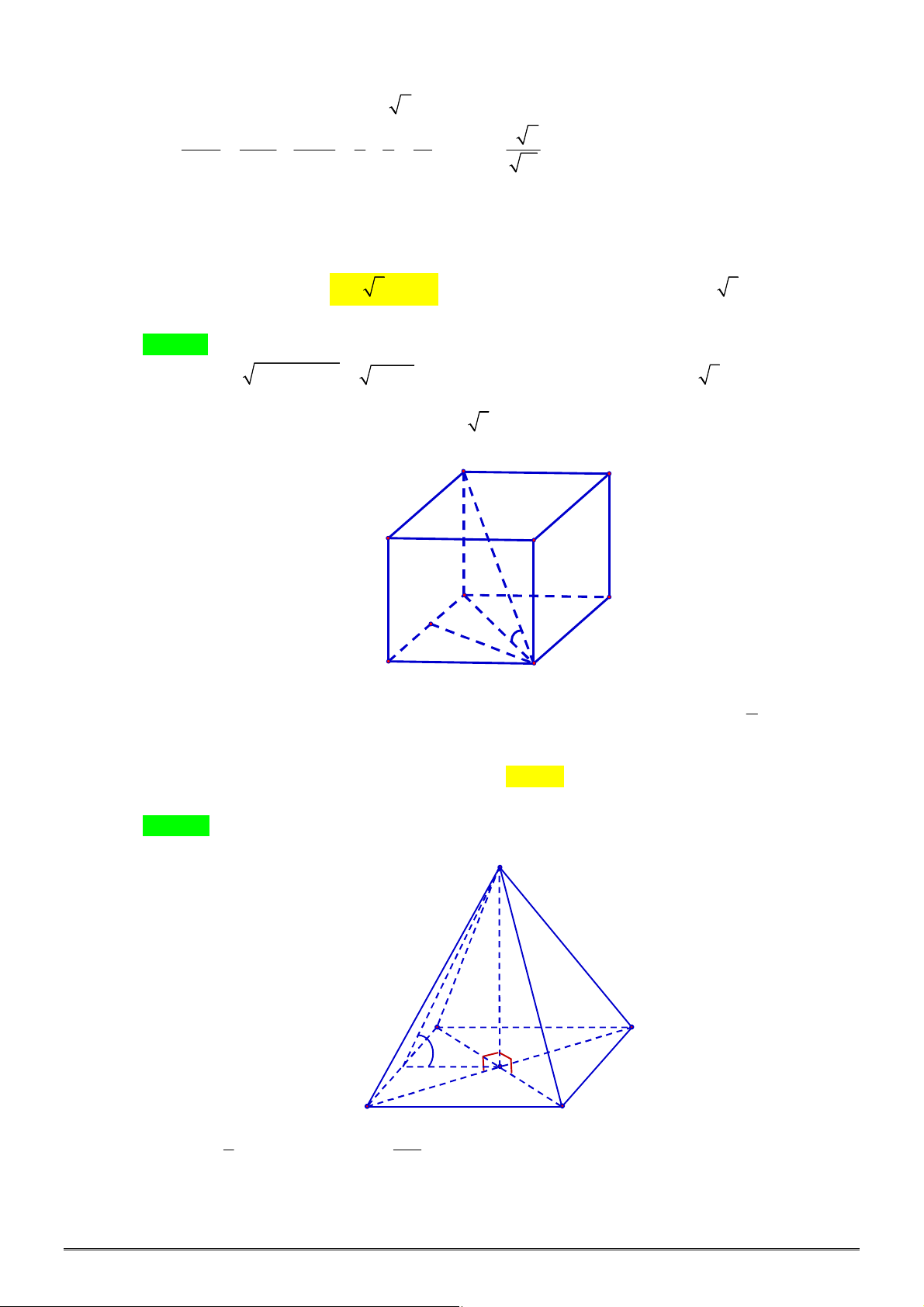
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/24
Ta có:
ABC
vuông cân tại
A
,
.sin 2.sin45 2
AM AC C
Vậy
2 2 2
1 1 1 1 1 11 3 2
cm
D 9 2 18
11
AH
AH A AM
.
Câu 16. [1H3-2] Cho hình hộp chữ nhật
.
ABCD A B C D
có
4 cm
AB
,
3 cm
AD
và đường chéo
A C
tạo với mặt phẳng
ABCD
góc
60
. Gọi
M
là trung điểm của
BC
. Khoảng cách giữa
AM
và
A D
là
A.
5 cm
. B.
5 3 cm
. C.
4 cm
. D.
4 3 cm
.
Lời giải
Chọn B.
Ta có:
2 2
16 9 5 cm
AC AB AD , suy ra:
.tan60 5 3 cm
AA AC
.
Do
, 5 3 cm
AA A D
d AM A D AA
AA AM
.
Câu 17. [1H3-2] Cho hình chóp đều
.
S ABCD
có đường cao bằng
a
và thể tích bằng
3
4
3
a
. Tính góc
giữa mặt bên và mặt đáy.
A.
75
. B.
60
. C.
45
. D.
30
.
Lời giải
Chọn C.
Ta có
2
1 3
. 4
3
ABCD ABCD
V
V SH S S a
SH
.
Đáy
ABCD
là hình vuông nên cạnh bằng
2
a
.
Gọi
M
là trung điểm của
AB
.
S
H
C
D
A
B
a
M
A
D
D
C
B
B
A
C
M
60
4 cm
3 cm

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/24
Ta có
,
SM AB
SAB ABCD SMH
HM AB
.
tan 1 45
SH a
SMH SMH
MH a
.
Câu 18. [2D2-2] Chọn khẳng định sai?
A.
log 0 0 1
x x
. B.
ln 0 1
x x
.
C.
2 2
3 3
log log 0
a b a b
. D.
2 2
log log 0
a b a b
.
Lời giải
Chọn C.
Vì
0
log log
1
a a
b c
b c
a
ở đây cơ số
2
1
3
a
.
Câu 19. [2D2-2] Số nghiệm của phương trình
2
2 9 5
2 1
x x
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C.
Ta có
2
2 9 5 2
5
2 1 2 9 5 0
1
2
x x
x
x x
x
.
Câu 20. [1D4-2] Hàm số
2
ln 1
y x x
có đạo hàm bằng
A.
2
1
1
x x
. B.
2
1
1
x
. C.
2
1
x
x x
. D.
2
1
x
x
.
Lời giải
Chọn B.
Ta có:
2
2
2 2
1
1
1
ln 1
1 1
x
x
x x
x x x
.
Câu 21. [2D2-3] Đặt
2 3
log 5 , log 2
a b
. Biểu diễn
12
log 100
theo
,
a b
.
A.
2 1
2 1
b a
b
. B.
2 1
2 1
a
b
. C.
2 1
2
a
b
. D.
2 1
2
b a
b
.
Lời giải
Chọn A.
12 12 12 12
log 100 2log 10 2 log 2 log 5
.
12
2 2 2
1 1 1
log 2
1
log 12 log 3 log 4 1 2
2
b
b
b
.
12
5 5 5
1 1
log 5
log 12 log 3 log 4
, với
5 2 3
log 3 log 5.log 2
ab
và
5 5
2
log 4 2log 2
a
.
Do đó
12
1
log 5
1 2
1 2
ab
b
ab a
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/24
Vậy
12
2 1
log 100 2
1 2 1 2 2 1
b a
b ab
b b b
.
Câu 22. [2D2-2] Rút gọn
3
2
log
log
9 4
a
b
được
A.
3 2
a b
. B.
9 4
a b
. C.
2 2
a b
. D.
a b
.
Lời giải
Chọn C.
Ta có:
3 3
2 2
2
2
log loglog log
2 2
9 4 3 2
a ab b
a b
.
Câu 23. [2D2-3] Tập xác định của hàm số
1
3
log 3 1
y x
là
A.
3;
. B.
10
3;
3
. C.
10
3;
3
. D.
10
;
3
.
Lời giải
Chọn C.
Điều kiện:
1
3
3 0
log 3 1 0
x
x
.
3 0 3
x x
.
1 1 1
3 3 3
1
log 3 1 0 log 3 1 log
3
x x
3 0
10
3
1
3
3
3
x
x
x
.
Vậy tập xác định của hàm số đã cho là
10
3;
3
D
.
Câu 24. [2D2-2] Tổng tất cả các nghiệm của phương trình
2
2
log 1 3
x
là
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn A.
Ta có
2 2
2
log 1 3 1 8
x x
2
9 3
x x
.
Vậy tổng tất cả các nghiệm của phương trình đã cho là
0
.
Câu 25. [2D2-2] Phương trình
4 3.6 2.9 0
x x x
có hai nghiệm
0
x
và
2
1
x
y
x
, với
0
a b
.
Khi đó
b
a
là
A.
2
. B.
3
. C.
4
. D.
3
2
.
Lời giải
Chọn B.
Biến đổi phương trình đã cho thành:
2
2 2
3. 2 0
3 3
x x
2
1
3
2
2
3
x
x
2
3
0
log 2
x
x
.
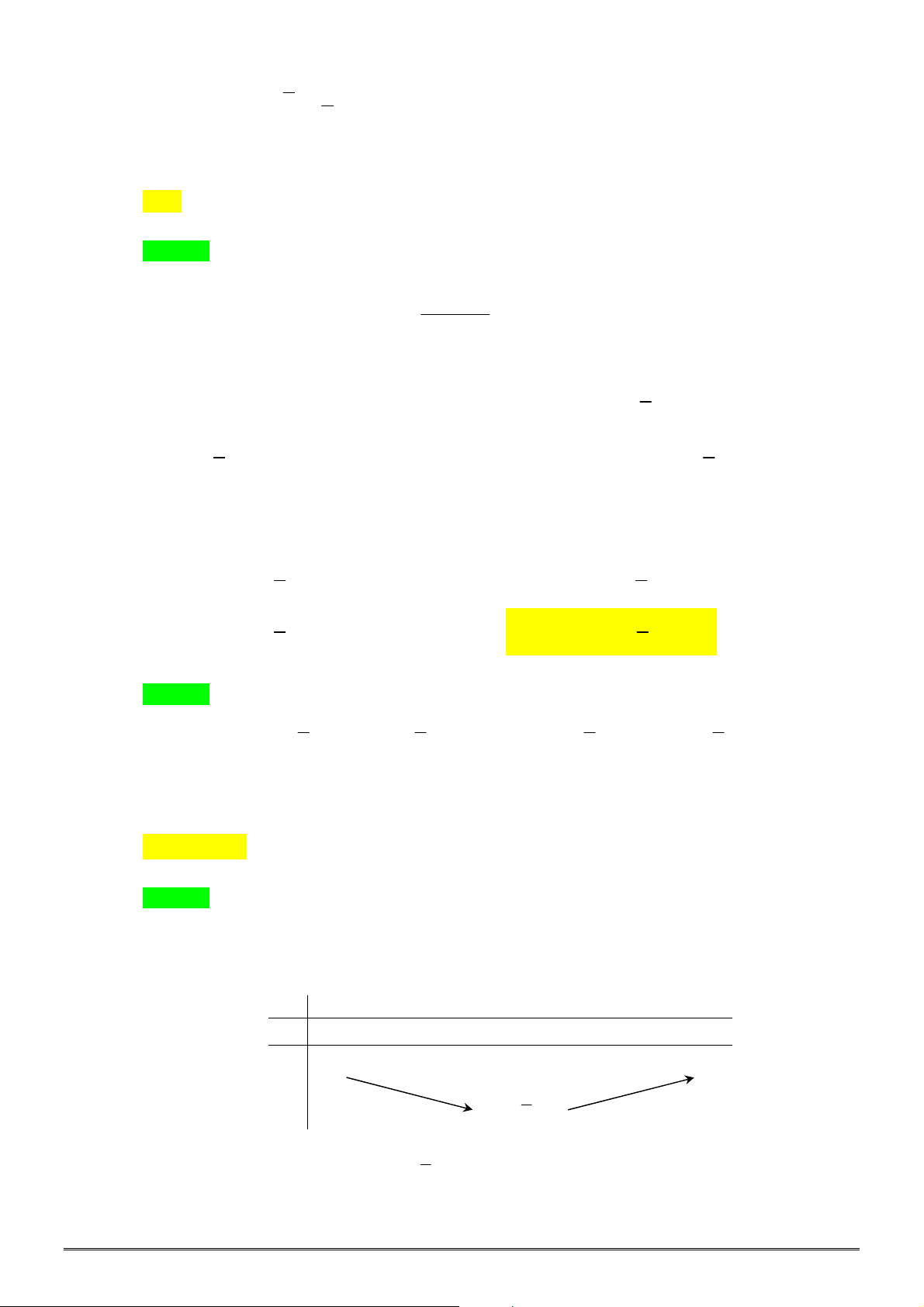
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/24
Từ đó suy ra
2
3
3
2
a
b
a
b
.
Câu 26. [2D2-2] Phương trình
2017
log 2016 2017
x x
có bao nhiêu nghiệm?
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn A.
Điều kiện:
0
x
.
Hàm số
2017
log
f x x
có
1
0, 0
ln2017
f x x
x
nên đồng biến trên
0;
.
Hàm số
2016 2017
g x x
nghịch biến trên
0;
.
Xét hàm số
2017
log 2016 2017
h x x x
liên tục trên khoảng
1
;1
2
.
Ta có
1
. 1 0
2
h h
nên phương trình
0
h x
có nghiệm trên khoảng
1
;1
2
.
Vậy phương trình
2017
log 2016 2017
x x
có nghiệm duy nhất.
Câu 27. [2D2-2] Cho
,
a b
là các số dương và
1
a
. Chọn khẳng định đúng.
A.
2
3 2
3
log 1 log
2
a
a
a b b
. B.
2
3 2
1
log 3 log
2
a
a
a b b
.
C.
2
3 2
3
log log
2
a
a
a b b
. D.
2
3 2
3
log log
2
a
a
a b b
.
Lời giải
Chọn D.
Ta có
2
3 2 3 2
1
log log
2
a
a
a b a b
3 2
1
log log
2
a a
a b
1
3 2log
2
a
b
3
log
2
a
b
.
Câu 28. [2D2-2] Cho hàm số
e
x
y x
. Chọn khẳng định sai.
A. Hàm số đồng biến trên khoảng
0;
. B. Hàm số nghịch biến trên khoảng
; 1
.
C.
min 0
y
. D. Hàm số đạt cực tiểu tại
1
x
.
Lời giải
Chọn C.
Tập xác định của hàm số:
D
.
Đạo hàm:
1 e
x
y x
;
0 1
y x
.
Bảng biến thiên:
Từ bảng biến thiên ta thấy
1
min
e
y
.
x
1
y
0
y
0
1
e

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/24
Câu 29. [2D2-2] Cho hàm số
1
.
2
x
x
y
Khi đó
1
y
bằng
A.
1
2
. B.
1
4
. C.
0
. D.
4
.
Lời giải
Chọn A.
Ta có:
2
2 1 2 ln 2
2
x x
x
x
y
1
1
2
y
.
Câu 30. [2D2-3] Số nghiệm của phương trình
3 3 3
log log log
2 7 5
x x x
là
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn D.
Điều kiện:
0
x
. Khi đó ta xét
3
trường hợp:
Đặt
3
log
t x
ta được phương trình
2 7
2 7 5 1 *
5 5
t t
t t t
.
Nếu
0
t
thì
7
1
5
t
nên
*
vô nghiệm.
Nếu
0
t
thì
*
thành
2 1
(vô lý).
Nếu
0
t
thì
2
1
5
t
nên
*
vô nghiệm.
Vậy phương trình đã cho vô nghiệm.
Câu 31. [2D1-1] Hàm số nào sau đây đồng biến trên
?
A.
1
x
y
x
. B.
2
3 1
y x x
. C.
3 2
3 3 1
y x x x
. D.
4 2
2 1
y x x
.
Lời giải
Chọn C.
Ta có
2
2
3 6 3 3 1 0
y x x x
,
x
nên hàm số đồng biến trên
.
Cách khác
Hàm số ở đáp án A có tập xác định là
\ 0
nên không thỏa.
Hàm số ở đáp án B là hàm số bậc hai có đồ thị là một parabol nên có một điểm cực trị duy nhất.
Hàm số ở đáp án D là hàm số bậc bốn trùng phương nên có ít nhất một cực trị.
Câu 32. [2D1-1] Chọn khẳng định sai?
A. Đồ thị hàm số bậc ba có tâm đối xứng.
B. Đồ thị hàm số
ax b
y
mx n
,
0,
m an bm
có tiệm cận ngang.
C. Đồ thị hàm số bậc ba có tiệm cận đứng.
D. Đồ thị hàm số bậc bốn luôn có điểm cực trị.
Lời giải
Chọn C.
Hàm số bậc ba có tập xác định là
, nên đồ thị không có tiệm cận đứng.
Câu 33. [2D1-2] Giá trị cực đại của hàm số
4 2
3 3
y x x
bằng
A.
3
. B.
1
. C.
2
. D.
0
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/24
Lời giải
Chọn A.
Ta có
3
4 6
y x x
,
3
0
4 6 0
3
2
x
x x
x
.
Vì
2
12 6 0 6 0
y x y
suy ra hàm số đạt cực đại tại
0
x
, khi đó
3
CĐ
y
.
Câu 34. [2D1-2] Cho hàm số
y f x
xác định, liên tục trên
và có bảng biến thiên như sau:
Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số cắt trục hoành tại ba điểm phân biệt.
B. Hàm số có đúng một cực trị.
C. Hàm số có giá trị lớn nhất bằng
0
.
D. Hàm số đồng biến trên khoảng
1; 2017
.
Lời giải
Chọn D.
Dựa vào bảng biến thiên ta suy ra:
* Đồ thị hàm số và trục hoành chỉ có hai điểm chung nên A sai.
* Hàm số có hai cực trị nên B sai.
* Hàm số đạt cực đại tại
0
x
và
0
CĐ
y
nên C sai.
* Hàm số đồng biến trên khoảng
2
;
5
nên cũng đồng biến trên khoảng
1; 2017
.
Câu 35. [2D1-2] Gọi
M
,
m
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3
1
x
y
x
trên đoạn
2; 4
. Khi đó tổng
M m
bằng
A.
7
. B.
13
. C.
14
. D.
6
.
Lời giải
Chọn B.
Ta có hàm số xác định và liên tục trên đoạn
2; 4
.
2
2
2 3
1
x x
y
x
,
2
1 2; 4
0 2 3 0
3 2; 4
x
y x x
x
.
Mà
19
2 7, 3 6, 4
3
y y y
. Suy ra
7, 6 13
M m M m
.
Câu 36. [2D1-2] Tiếp tuyến của đồ thị hàm số
3
2
y x x
tại điểm
0; 2
M có phương trình dạng
y ax b
. Khi đó giá trị của hệ số
b
là
x
0
2
5
y
||
0
y
0
3
3 4
5 25

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/24
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn C.
Ta có
2
3 1 0 1
y x y
.
Phương trình tiếp tuyến của đồ thị hàm số tại điểm
0; 2
M :
0 0 2 2
y y x x
suy
ra
1
2
a
b
.
Câu 37. [2D1-2] Đồ thị hàm số
2 1
2
x
y
x
cắt đường thẳng
3 2
y x
tại điểm duy nhất
A
. Khi đó
tung độ của
A
là
A.
2
. B.
1
. C.
1
. D.
2
.
Lời giải
Chọn C.
Phương trình hoành độ giao điểm
2 1
3 2
2
x
x
x
2
x
.
2 1 2 3 2
x x x
(vì
2
x
không là nghiệm của phương trình)
2
3 6 3 0 1 1
x x x y
.
Câu 38. [2D1-3] Tìm tất cả các giá trị của
m
để đồ thị hàm số
4 2 2
2 1
y x m x
có ba điểm cực trị tạo
thành một tam giác đều.
A.
3
6
m . B.
6
3
m
. C.
3
3
m
. D.
3
2
m
.
Lời giải
Chọn B.
Ta có
3 2
4 4
y x m x
,
3 2
2 2
0
0 4 4 0
x
y x m x
x m
.
Hàm số có ba điểm cực trị khi và chỉ khi
0
m
. Giả sử ba điểm cực trị của đồ thị hàm số là
4 4
0; 1 , ; 1 , ; 1
A B m m C m m
.
Do tính đối xứng nên tam giác
ABC
là tam giác cân tại
A
từ đó để
ABC
là tam giác đều thì
2
2
2 2 2 4 6
6
2 3 3
AB BC AB BC m m m m m
.
Câu 39. [2D1-2] Đồ thị hàm số nào dưới đây có tiệm cận ngang?
A.
2
2
1
x
y
x
. B.
3
2
y x x
. C.
2 1
2
x
y
x
. D.
2
2 2
y x x
.
Lời giải
Chọn C.
Hàm số ở các phương án B và D là các hàm đa thức bậc ba và bậc hai nên đồ thị của nó không
có tiệm cận ngang.
Xét hàm số ở phương án A:
2
2
1
x
y
x
ta có tập xác định
\ 1
D
,
2
2
lim lim
1
x x
x
y
x
;
2
2
lim lim
1
x x
x
y
x
nên đồ thị hàm số không có tiệm cận
ngang.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/24
Xét hàm số ở phương án C:
2 1
2
x
y
x
ta có tập xác định
\ 2
D
,
2 1
lim 2
2
x
x
y
x
suy
ra
2
y
là tiệm cận ngang của đồ thị hàm số.
Câu 40. [2D1-1] Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số
y f x
là hàm số nào sau đây?
A.
2 3
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2
1
x
y
x
. D.
2
1
x
y
x
.
Lời giải
Chọn B.
Dựa vào bảng biến thiên của hàm số, ta suy ra:
Hàm số nghịch biến trên từng khoảng xác định của nó.
Đồ thị hàm số có một tiệm cận đứng là
1
x
và một tiệm cận ngang là
2
y
. Chỉ có hàm số ở
đáp án B thỏa yêu cầu.
Câu 41. [2D1-2] Đồ thị hàm số
3 2
3 2
y x x
có tâm đối xứng là điểm
I
. Khi đó hoành độ của
I
là
A.
2
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn D.
Ta có
2
3 6
y x x
và
6 6
y x
.
Hoành độ tâm đối xứng của đồ thị là nghiệm của phương trình
0 1
y x
.
Câu 42. [2D1-3] Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
3 1
x x
với
0;3
x . Mệnh đề
nào sau đây sai?
A.
0;3
min 1
y
. B.
0;3
max 19
y
.
C.
0;3
min 0
y
. D. Hàm số đạt giá trị lớn nhất tại
3
x
.
Lời giải
Chọn A.
Xét hàm số
3
3 1
f x x x
liên tục trên
. Ta có
0 1 1 0
f f
nên phương trình
0
f x
có ít nhất
1
nghiệm trong khoảng
0;1 0;3
.
Suy ra với
0;3
x đồ thị của hàm số
3
3 1
x x
nằm hoàn toàn phía trên trục hoành và cắt
trục hoành tại ít nhất một điểm.
Vậy giá trị nhỏ nhất của hàm số
3
3 1
x x
với
0;3
x là
0;3
min 0
y
.
Câu 43. [2D1-2] Có bao nhiêu giá trị nguyên của
m
để phương trình
3
3 1
x x m
có ba nghiệm phân
biệt.
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
x
1
y
–
–
y
2
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/24
Chọn C.
Ta có
2
3 3
y x
suy ra
0 1
y x
. Do đó hàm số có
3
CĐ
y
,
1
CT
y
.
Để phương trình
3
3 1
x x m
có ba nghiệm phân biệt thì
2 3
CT CĐ
y m y m
.
Vậy có
4
giá trị nguyên của
m
thỏa yêu cầu bài toán.
Câu 44. [2D1-3] Tìm
m
để bất phương trình
2
3 1
x m x
có nghiệm?
A.
1
m
. B.
10
m . C.
1
m
. D.
1 10
m .
Lời giải
Chọn B.
2
2
3
3 1
1
x
x m x m
x
.
Xét hàm số
2
3
1
x
y
x
có
3
2
1 3
1
x
y
x
suy ra
1
0
3
y x
.
Vậy với
10
m thì bất phương trình đã cho có nghiệm.
Câu 45. [2D1-2] Cho hàm số
2
1
x
y
x
có đồ thị
C
và
1;1
I . Khi đó có bao nhiêu điểm thuộc đồ thị
C
sao cho khoảng cách tới
I
bằng
10
.
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn A.
Gọi
2
;
1
x
M x C
x
.
Ta có
2
2 2
2
2 9
10 1 1 100 1 100
1
1
x
IM x x
x
x
1
.
Thấy ngay phương trình
1
có
4
nghiệm nên có
4
điểm thuộc đồ thị thỏa yêu cầu bài toán.
Câu 46. [2D1-3] Phương trình
4 2
2 3
x x k
có
6
nghiệm phân biệt khi và chỉ khi
A.
3 4
k
. B.
0 3
k
. C.
3
k
. D.
4
k
.
Lời giải
Chọn A.
Xét hàm số
4 2
2 3
y x x
có
3
4 4
y x x
.
0
0
1
x
y
x
suy ra
3
CĐ
y
,
4
CT
y
.
Suy ra đồ thị của hàm số
4 2
2 3
f x x x
.
x
1
3
y
0
y
1
10
1
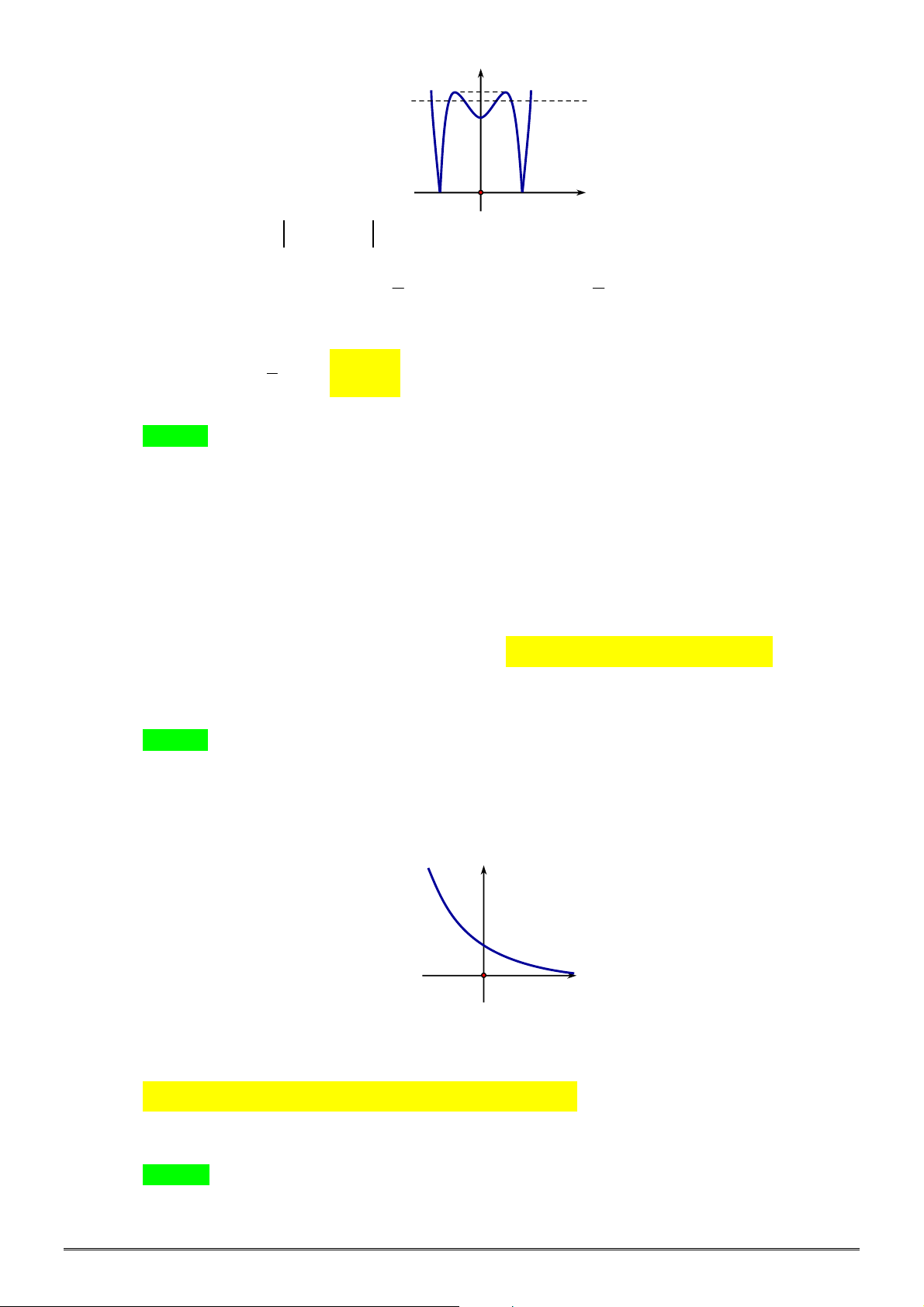
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 23/24
Vậy phương trình
4 2
2 3
x x k
có
6
nghiệm phân biệt khi và chỉ khi
3 4
k
.
Câu 47. [2D1-3] Tìm
m
để hàm số
3 2 2
2 2
2 3 1
3 3
y x mx m x
có hai điểm cực trị
1
x
,
2
x
thỏa
mãn
1 2 1 2
2 0
x x x x
.
A.
1
m
;
1
3
m
. B.
1
m
. C.
2
m
,
1
m
. D.
2
m
.
Lời giải
Chọn B.
Ta có
2 2
2 2 2 3 1
y x mx m
.
Để hàm số có hai điểm cực trị
1
x
,
2
x
thì
2 2
4 3 1 0
m m
.
1
Khi đó
2 2
1 2 1 2
2 0 3 1 2 0 3 2 1 0
x x x x m m m m
.
2
Từ
1
và
2
ta được
1
m
.
Câu 48. [2D1-1] Hàm số
3
3 2
y x x
.
A. Đồng biến trên khoảng
0;
. B. Nghịch biến trên khoảng
1;1
.
C. Đồng biến trên khoảng
;1
. D. Nghịch biến trên khoảng
0;2
.
Lời giải
Chọn B.
Ta có
2
3 3
y x
suy ra
0 1
y x
.
Kết hợp hệ số
1 0
a
suy ra hàm số đã cho nghịch biến trên khoảng
1;1
.
Câu 49. [2D2-1] Cho hàm số
y f x
có đồ thị
C
như hình vẽ sau:
Khẳng định nào sau đây sai?
A. Hàm số nghịch biến trên
.
B. Đồ thị hàm số có một đường tiệm cận.
C. Phương trình của đồ thị
C
có dạng
x
y a
với
1
a
.
D. Đồ thị hàm số cắt trục tung.
Lời giải
Chọn C.
Ta có đồ thị hàm số đã cho có các tính chất như các phương án A, B, D.
O
x
y
1
O
x
y
4
3
y k

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 24/24
Câu 50. [2D2-2] Phương trình
2
3 5
3
2
5
4 2 log
2 6
x x x
x
x x
có hai nghiệm là
1
x
,
2
x
. Khi đó tổng
1 2
x x
bằng
A.
5
. B.
5
2
. C.
5
. D.
5
2
.
Lời giải
Chọn D.
Điều kiện:
2
5 0
2 6 0
x
x x
0
3 5
x
x
.
2 2
3 5 2 6 5 2
3 3 3
2
5
4 2 log 2 2 log 5 log 2 6
2 6
x x x x x x
x
x x x
x x
2
2 6 2 5
3 3
2 log 2 6 2 log 5
x x x
x x x
.
1
Xét hàm số
3
2 log
t
f t t
,
0
t
là hàm số đồng biến trên khoảng
0;
.
Phương trình
1
trở thành
2 2
2 6 5 2 5 5 0
x x x x x
luôn có hai nghiệm là
1
x
,
2
x
.
Khi đó tổng
1 2
5
2
x x
.
----------HẾT----------
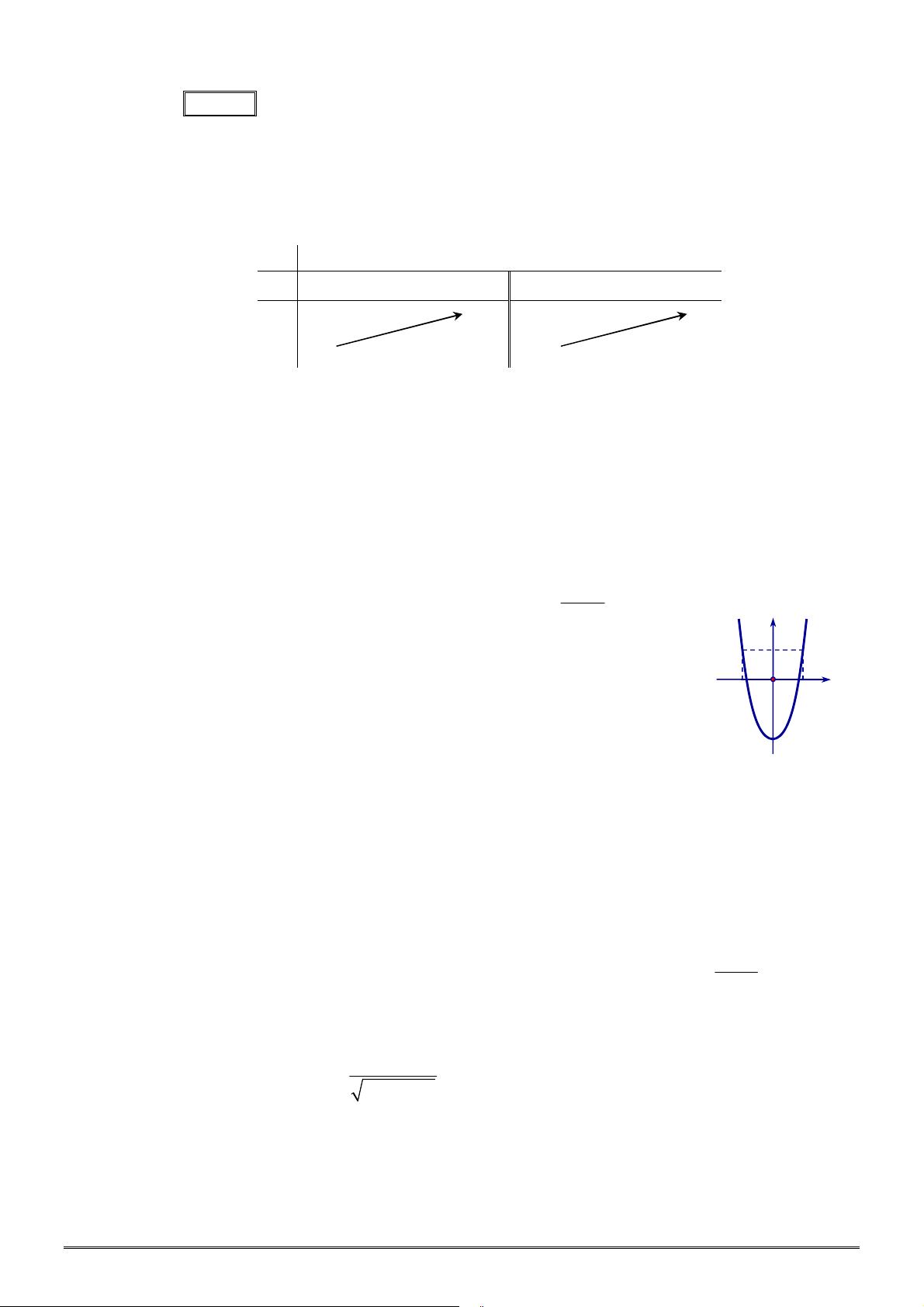
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/27
TRƯỜNG THPT KIM LIÊN – HÀ NỘI ĐỀ ÔN TẬP HỌC KỲ I NĂM HỌC 2017 – 2018
ĐỀ SỐ 1 MÔN TOÁN - LỚP 12
------- ------------------
Câu 1. [2D1-2] Đồ thị hàm số
4 2
20 2016 11
y x x
cắt trục hoành tại mấy điểm?
A.
4
. B.
3
. C.
2
. D.
0
.
Câu 2. [2D1-2] Cho hàm số
y f x
xác định, liên tục trên tập
\ 1
và có bảng biến thiên:
Khẳng định nào dưới đây là sai?
A. Hàm số không có cực trị.
B. Đồ thị hàm số và đường thẳng
25
y
có
1
điểm chung.
C. Đồ thị hàm số có tiệm cận ngang là đường thẳng
2
y
.
D. Hàm số đồng biến trên tập
\ 1
.
Câu 3. [2D1-2] Hàm số nào sau đây nghịch biến trên
?
A.
3 2
3 2
y x x
. B.
3 2
2 2
y x x x
.
C.
4 2
2 2
y x x
. D.
3
2 1
x
y
x
.
Câu 4. [2D1-3] Đường cong trong hình dưới đây là đồ thị của hàm
số nào được liệt kê sau đây?
A.
4 2
2 2
y f x x x
. B.
2
2
y f x x
.
C.
4 2
2 2
y f x x x
. D.
2
2
y f x x
.
Câu 5. [2D1-2] Số điểm cực trị của hàm số
4 3
2 3
y x x
là
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 6. [1D1-2] Giá trị nhỏ nhất của hàm số
3sin5 4cos5
y x x
là
A.
3
. B.
4
. C.
5
. D.
3
.
Câu 7. [2D1-2] Điểm cực đại của đồ thị hàm số
3
12 12
y x x
là
A.
2; 4
. B.
2;28
. C.
4;28
. D.
2;2
.
Câu 8. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
3 1
x
y
x m
có tiệm cận
đứng nằm bên trái trục
Oy
.
A.
0
m
. B.
0
m
. C.
0
m
. D. Đáp án khác.
Câu 9. [2D1-2] Đồ thị hàm số
2
11
2016
x
y
x
có bao nhiêu đường tiệm cận ngang?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 10. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
4 2 2
2016
y x m m x
có
3
điểm cực trị?
A.
1
m
hoặc
0
m
. B.
0 1
m
. C.
1 0
m
. D.
0
m
hoặc
1
m
.
x
1
y
+ +
y
2
2
O
x
y
1
1
2
1
13

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/27
Câu 11. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
1
mx
y
x m
đồng biến trên
khoảng
1;
.
A.
1 1
m
. B.
1
m
. C.
\ 1;1
m
. D.
1
m
.
Câu 12. [2D1-2] Cho hàm số
2
2
3 2
2 3
x x
y
x x
khẳng định nào sau đây sai?
A. Đồ thị hàm số có hai tiệm cận đứng.
B. Đồ thị hàm số có ba đường tiệm cận.
C. Đồ thị hàm số có tiệm cận ngang là đường thẳng
2
y
.
D. Đồ thị hàm số có tiệm cận ngang là đường thẳng
1
2
y
.
Câu 13. [2D1-2] Cho hàm số
4 2
2 2017
f x x x , khẳng định nào sau đây sai?
A.
f x
nghịch biến trên
0;1
. B.
f x
đồng biến trên
0;
.
C.
f x
đồng biến trên
1;0
. D.
f x
nghịch biến trên
; 1
.
Câu 14. [2D1-2] Giá trị nhỏ nhất của hàm số
1
y x
x
bằng bao nhiêu?
A.
2
. B.
0
. C.
2
. D.
1
.
Câu 15. [2D1-2] Cho hàm số
3
3sin 4sin
y x x
. Giá trị lớn nhất của hàm số trên khoảng
;
2 2
bằng
A.
1
. B.
1
. C.
7
. D.
3
.
Câu 16. [2D1-2] Tìm
m
để hàm số
2
2017
y x m x đồng biến trên khoảng
1;2
.
A.
1
m
. B.
3
m
. C.
1
m
. D.
2
m
.
Câu 17. [1D5-3] Một chất điểm chuyển động có phương trình
2 3
6 9 1
s s t t t t
. Thời điểm
t
(giây) tại đó vận tốc
m/s
v của chuyển động đạt giá trị lớn nhất là
A.
3
t
. B.
1
t
. C.
2
t
. D.
4
t
.
Câu 18. [2D1-2] Hàm số
3 2 2
1
1 1
3
y x mx m m x
đạt cực trị tại điểm
1
x
khi
A.
1
m
hoặc
2
m
. B.
1
m
. C.
2
m
. D.
m
.
Câu 19. [2D1-2] Phương trình tiếp tuyến với đồ thị hàm số
4 2
2 1
y x x
tại điểm cực tiểu của đồ thị
hàm số là
A.
1 0
y
. B.
0
y
. C.
1 0
x y
. D.
y x
.
Câu 20. [1D5-3] Cho hàm số
3
3 2
y x x
. Có bao nhiêu tiếp tuyến của đồ thị hàm số song song với
trục hoành?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 21. [2D1-2] Cho hàm số
y f x
có đồ thị như hình vẽ bên.
Khẳng định nào dưới đây là đúng?
A.
max 4
f x
.
B. Hàm số đồng biến trên khoảng
;1
.
C. Giá trị cực tiểu của hàm số bằng
1
.
D.
2;1
min 0
f x
O
x
y
2
2
1
4
1
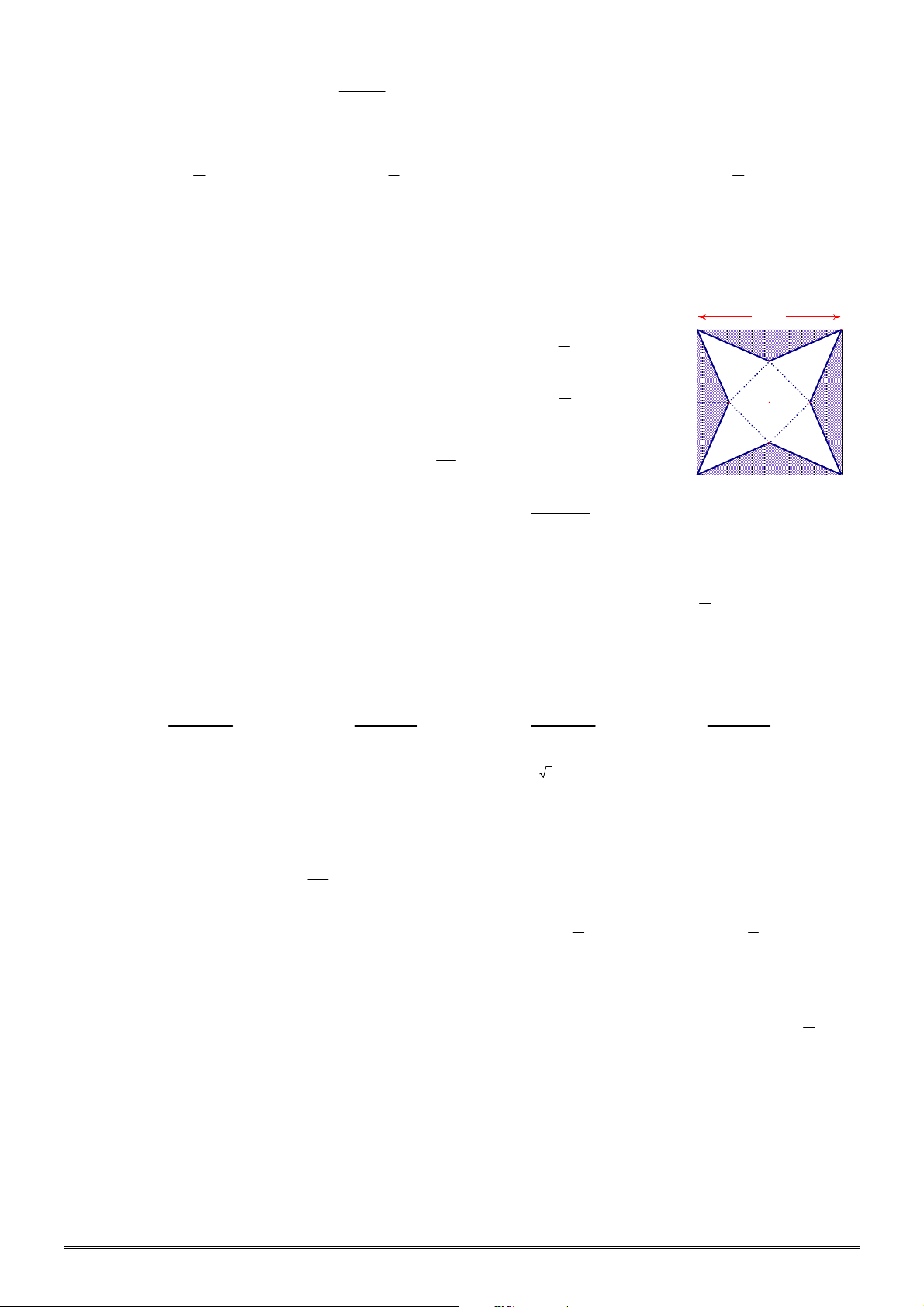
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/27
Câu 22. [2D1-4] Cho hàm số
2 3
2
x
y
x
có đồ thị
C
. Tìm trên
C
những điểm sao cho tiếp tuyến
với
C
tại
M
cắt hai tiệm cận của
C
tại
A
,
B
sao cho
AB
ngắn nhất.
A.
3
0; , 1; 1
2
. B.
5
1; , 3;3
3
. C.
3;3 , 1;1
. D.
5
4; ; 3;3
2
.
Câu 23. [2H1-3] Cho một tấm nhôm hình vuông cạnh
10cm
, tại bốn cạnh tấm nhôm người ta cắt ra
bốn tam giác cân bằng nhau, độ dài đường cao xuất phát từ đỉnh của mỗi tam giác cân bằng
cm
x . Sau đó gập tấm nhôm theo đường chấm chấm (xem hình vẽ bên) để được một khối
chóp tứ giác đều. Tìm
x
để khối chóp nhận được có thể tích lớn nhất.
A.
2
x
. B.
5
2
x
.
C.
1
x
. D.
1
2
x
.
Câu 24. [2D2-2] Tính đạo hàm của hàm số
2
x
x
y
.
A.
1 ln2
4
x
x
. B.
1 ln2
4
x
x
. C.
1 ln 2
2
x
x
. D.
1 ln2
2
x
x
.
Câu 25. [2D2-3] Cho các số thực dương
x
,
y
thỏa mãn
2 2
4 12
x y xy
. Khẳng định nào sau đây đúng?
A.
log 2 8 log log
x y x y
. B.
1
log 2 2log2 log log
2
x y x y
.
C.
log 2log log12 log
x y xy
. D.
2 2
log log4 log12
x y xy
.
Câu 26. [2D2-3] Cho
27
log 5
a
,
8
log 7
b
,
2
log 3
c
. Hãy biểu diễn
12
log 35
theo
a
,
b
và
c
.
A.
3 2
2
b ac
c
. B.
3 3
2
b ac
c
. C.
3 2
3
b ac
c
. D.
3 3
1
b ac
c
.
Câu 27. [2D2-2] Tìm tập xác định
D
của hàm số
3
2 3
1
y x x
.
A.
1;1
D . B.
0;1
D . C.
\ 1;1
D
. D.
1;1 \ 0
D .
Câu 28. [2D2-2] Tìm
x
biết
1
2
1
125
25
x
x
.
A.
1
x
. B.
4
x
. C.
1
4
x
. D.
1
8
x
.
Câu 29. [2D2-3] Hàm số
2
2 1
log
a a
y x
nghịch biến trên khoảng
0;
khi
A.
1
a
và
0 2
a
. B.
1
a
. C.
0
a
. D.
1
a
và
1
2
a
.
Câu 30. [2D2-2] Hàm số
2
e
x
y x
nghịch biến trên khoảng nào trong các phương án sau.
A.
; 2
. B.
2;0
. C.
1;
. D.
;1
.
Câu 31. [2D2-3] Tìm giá trị nhỏ nhất của hàm số
1 3
2 2
x x
f x
.
A.
4
. B.
6
. C.
2
. D.
1
.
x
10 cm

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/27
Câu 32. [2D2-2] Giá trị lớn nhất của hàm số
2
ln ln 1
y x x
trên đoạn
1
;2
2
đạt tại
A.
1
x
. B.
1
2
x
. C.
3
2
x
. D.
3
4
.
Câu 33. [2D2-3] Tính
1 2
.
x x
biết
1
x
,
2
x
thỏa mãn
16
log 2 log 0
x
x
.
A.
1
. B.
1
. C.
0
. D.
4
.
Câu 34. [2D2-2] Tìm
x
biết
2
5 4
1
4
2
x x
.
A.
5 17
2
x
hoặc
5 17
2
x
. B.
5 17 5 17
2 2
x
.
C.
3
x
hoặc
2
x
. D.
2 3
x
.
Câu 35. [2D2-3] Dân số thế được tính theo công thức
.e
ni
S A
trong đó
A
là dân số của năm lấy làm
mốc tính,
S
là dân số sau
n
năm,
i
là tỉ lệ tăn dân số hàng năm. Cho biết năm
2003
Việt Nam
có khoảng
80.902.400
người và tỉ lệ tăng dân số là
1,47%
một năm. Như vậy, nếu tỉ lệ tăng dân
số hàng năm không đổi thì đến năm
2017
số dân của Việt Nam sẽ gần với số nào nhất sau đây?
A.
99.389.200
. B.
99.386.600
. C.
100.861.100
. D.
99.251.200
.
Câu 36. [2H1-1] Có tất cả bao nhiêu loại khối đa diện đều.
A.
3
. B.
5
. C.
6
. D.
7
.
Câu 37. [2D1-4] Cho hàm số
3 2
f x x ax bx c
và giả sử
A
,
B
là hai điểm cực trị của đồ thị
hàm số. Giả sử đường thẳng
AB
đi qua gốc tọa độ. Tìm giá trị nhỏ nhất của
P abc ab c
.
A.
16
25
. B.
1
. C.
9
. D.
25
9
.
Câu 38. [2H1-2] Cho khối hộp
.
ABCD A B C D
có thể tích
V
. Khi đó thể tích khối tứ diện
AB CD
bằng
A.
2
3
V
. B.
3
4
V
. C.
3
V
. D.
6
V
.
Câu 39. [2H2-3] Mặt cầu tâm
O
bán kính
17dm
R
. Mặt phẳng
P
cắt mặt cầu sao cho giao tuyến đi qua
ba điểm
A
,
B
,
C
mà
18dm
AB
,
24dm
BC
,
30dm
CA
. Tính khoảng cách từ
O
đến
P
.
A.
14dm
. B.
7dm
. C.
8dm
. D.
16dm
.
Câu 40. [2H1-3] Để chế tác đồ vật trang trí trong nhà từ khối đá có hình dạng một tứ diện đều cạnh
8dm
.
Ở bốn đỉnh tứ diện, người ta cần cắt đi các tứ diện đều bằng nhau có cạnh bằng
x
, sao cho phần
còn lại của khối đá sau khi cắt có thể tích bằng
3
4
thể tích khối đá ban đầu. Giá trị của
x
là
A.
3 2 dm
. B.
3
3 4 dm
. C.
2 2 dm
. D.
3
2 4 dm
.
Câu 41. [2H1-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt
phẳng
ABCD
, góc tạo bởi đường thẳng
SD
và mặt phẳng
ABCD
bằng
45
. Thể tích khối
chóp
.
S ABCD
bằng.
A.
3
a
. B.
3
2
3
a
. C.
3
3
a
. D.
3
2
a
.
Câu 42. [2H2-2] Cho hình hộp chữ nhật có kích thước
3
,
4
,
5
. Bán kính mặt cầu ngoại tiếp hình hộp là
A.
5 2
. B.
5 2
2
. C.
2 5
. D.
5
.
Câu 43. [2H2-3] Cho hình chóp tứ giác đều
.
S ABCD
có
2
AC a
, góc giữa cạnh bên và mặt đáy bằng
60
. Diện tích mặt cầu ngoại tiếp hình chóp bằng.
A.
2
16
3
a
. B.
2
8
3
a
. C.
2
4
3
a
. D.
2
2
3
a
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/27
Câu 44. [2H1-2] Cho lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
2,
AB a
3
BC a
. Góc giữa đường thẳng
A B
và mặt đáy là
60
. Tính theo
a
thể tích khối lăng trụ
.
ABC A B C
.
A.
3
2 3
a . B.
3
3 3
a . C.
3
3
3
a
. D.
3
3
a .
Câu 45. [2H2-1] Cho mặt cầu
S
có tâm
I
, bán kính
5
và mặt phẳng
P
cắt
S
theo một đường
tròn
C
có bán kính
3
r
. Kết luận nào sau đây sai?
A. Tâm của
C
là hình chiếu vuông góc của
I
trên
P
.
B. Khoảng cách từ
I
đến
P
bằng
4
.
C.
C
là giao tuyến của
S
và
P
.
D.
C
là đường tròn lớn của mặt cầu.
Câu 46. [2H1-3] Cho hình chóp .
S ABC
có đáy
ABC
là tam giác vuông tại
A
, với
2
a
AC ,
BC a
.
Hai mặt phẳng
SAB
và
SAC
cùng tạo với mặt đáy
ABC
góc
60
. Tính khoảng cách từ
điểm
B
tới mặt phẳng
SAC
, biết rằng mặt phẳng
SBC
vuông góc với đáy
ABC
.
A.
3
4
a
.
B.
3
4
a
. C.
4
5
a
. D.
3
a
.
Câu 47. [2H2-3] Một khối cầu thủy tinh có bán kính bằng
4dm
. Người
ta muốn cắt bỏ một chỏm cầu có diện tích mặt cắt là
2
15 dm
để lấy phần còn lại làm bể nuôi cá. Hỏi thể tích
nước tối đa mà bể này chứa là bao nhiêu?
A.
3
175
dm
3
. B.
3
175
dm
4
. C.
3
125
dm
3
. D.
3
175
dm
4
.
Câu 48. [2H2-2] Cho hình chóp .
S ABC
có đáy là tam giác vuông cân tại
B
,
AB a
. Cạnh bên
SA
vuông góc mặt phẳng
ABC
và
SC
hợp với đáy một góc bằng
60
. Thể tích khối cầu ngoại
tiếp hình chóp .
S ABC
.
A.
3
4 2
3
a
. B.
3
8 2
3
a
. C.
3
5 2
3
a
. D.
3
2 2
3
a
.
Câu 49. [2H2-3] Cho hình chóp .
S ABCD
có đáy là hình thang cân
ABCD
với
2
AB a
,
BC CD DA a
và
SA ABCD
. Một mặt phẳng qua
A
vuông góc với
SB
và cắt
,
SB
SC
,
SD
lần lượt tại
M
,
N
,
P
. Tính đường kính khối cầu ngoại tiếp khối đa diện
ABCDMNP
.
A.
3
a
. B.
2
a
. C.
a
. D.
3
2
a
.
Câu 50. [2H2-2] Cho tứ diện
ABCD
có
O
là trung điểm của đoạn thẳng nối trung điểm của hai cạnh
đối diện. Tập hợp các điểm
M
trong không gian thỏa mãn hệ thức
MA MB MC MD a
(với
0
a không đổi) là
A. Mặt cầu tâm
O
bán kính
3
a
r
. B. Mặt cầu tâm
O
bán kính
2
a
r
.
C. Mặt cầu tâm
O
bán kính
r a
. D. Mặt cầu tâm
O
bán kính
4
a
r
.
----------HẾT----------
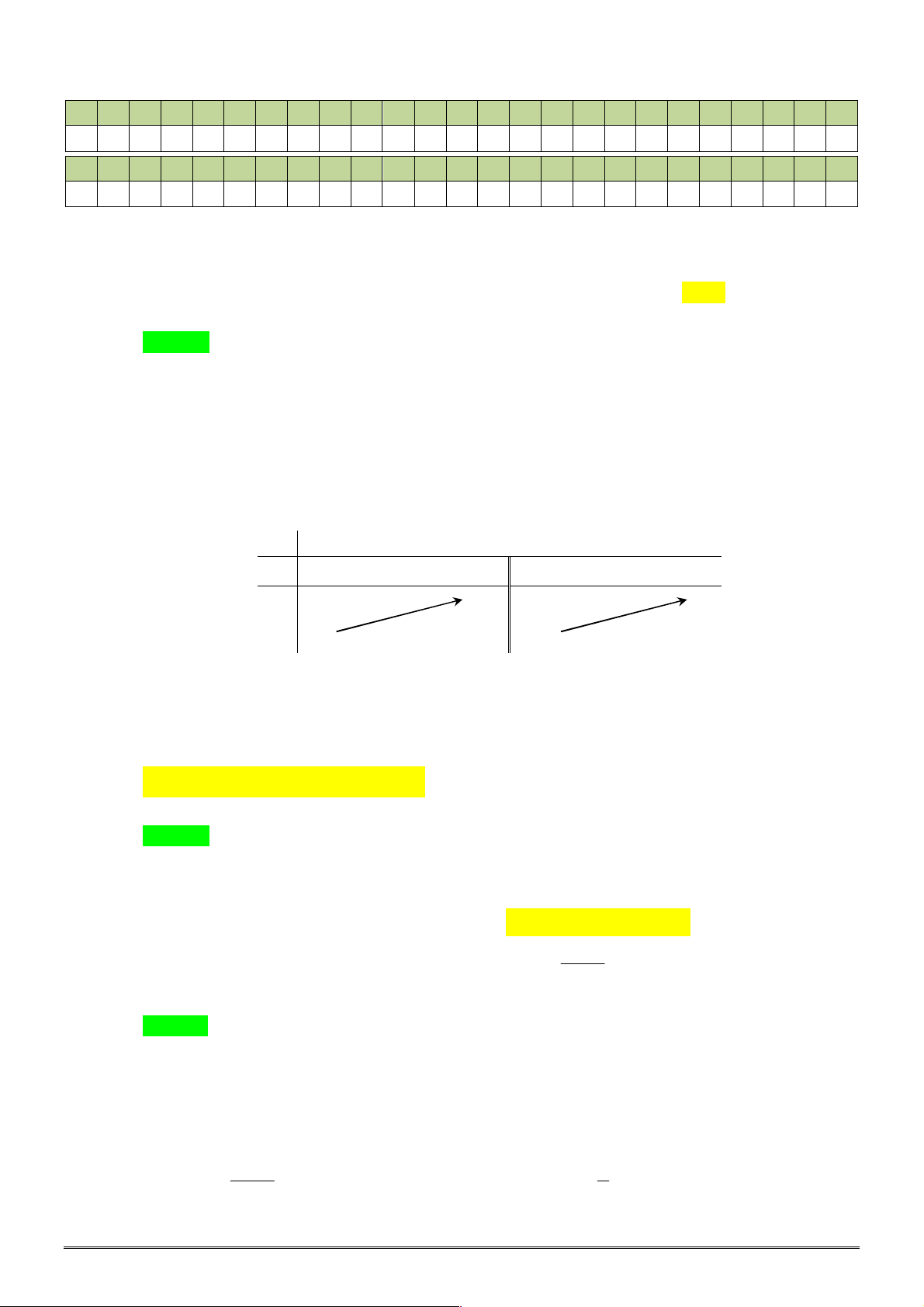
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/27
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
D
B C
D
C
B D
C
C
B C
B A
A
B C
C
A
B D
C
C
D
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B D
C
A
B A
A
A
D
A
B D
C
C
D
C
B A
B D
B A
B B D
HƯỚNG DẪN GIẢI
Câu 1. [2D1-2] Đồ thị hàm số
4 2
20 2016 11
y x x
cắt trục hoành tại mấy điểm?
A.
4
. B.
3
. C.
2
. D.
0
.
Lời giải
Chọn D.
Phương trình hoành độ giao điểm của đồ thị hàm số
4 2
20 2016 11
y x x
và trục hoành là
nghiệm của phương trình
4 2
20 2016 11 0
x x
1
.
Ta thấy phương trình
1
vô nghiệm với.
x
. (vì
2 4
0, 0
x x
với
x
).
Vậy đồ thị hàm số
4 2
20 2016 11
y x x
không cắt trục hoành.
Câu 2. [2D1-2] Cho hàm số
y f x
xác định, liên tục trên tập
\ 1
và có bảng biến thiên:
Khẳng định nào dưới đây là sai?
A. Hàm số không có cực trị.
B. Đồ thị hàm số và đường thẳng
25
y
có
1
điểm chung.
C. Đồ thị hàm số có tiệm cận ngang là đường thẳng
2
y
.
D. Hàm số đồng biến trên tập
\ 1
.
Lời giải
Chọn D.
Dựa vào định nghĩa ta chọn đáp án D.
Câu 3. [2D1-2] Hàm số nào sau đây nghịch biến trên
?
A.
3 2
3 2
y x x
. B.
3 2
2 2
y x x x
.
C.
4 2
2 2
y x x
. D.
3
2 1
x
y
x
.
Lời giải
Chọn B.
Với
3 2 2
3 2 3 6
y x x y x x
. Hàm số nghịch biến trên khoảng
0;2
.
Do đó loại đáp án A.
Với
4 2
2 2
y x x
là hàm trùng phương nên không nghịch biến trên
.
Do đó loại đáp án C.
Với
3
2 1
x
y
x
là hàm nhất biến có tập xác định là
1
\
2
. Do đó loại đáp án D.
x
1
y
+ +
y
2
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/27
Câu 4. [2D1-3] Đường cong trong hình dưới đây là đồ thị của hàm số nào được liệt kê sau đây?
A.
4 2
2 2
y f x x x
. B.
2
2
y f x x
.
C.
4 2
2 2
y f x x x
. D.
2
2
y f x x
.
Lời giải
Chọn C.
Ta thấy hàm số
4 2
2 2
y f x x x
là hàm trùng phương có hệ số
2 0
ab
nên hàm số
có
3
điểm cực trị
loại đáp án A.
Đồ thị hàm số trên hình vẽ đi qua điểm
1;1
M nên loại được đáp án B, D.
Vậy đáp án đúng là C.
Câu 5. [2D1-2] Số điểm cực trị của hàm số
4 3
2 3
y x x
là
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn D.
4 3 3 2 2
2 3 4 6 2 2 3
y x x y x x x x
.
Ta thấy
y
đổi dấu khi
x
qua
0
3
2
x
nên hàm số có
1
điểm cực trị.
Câu 6. [1D1-2] Giá trị nhỏ nhất của hàm số
3sin5 4cos5
y x x
là
A.
3
. B.
4
. C.
5
. D.
3
.
Lời giải
Chọn C.
Ta có
3 4
3sin5 4cos5 5 sin5 cos5 5 5sin 5
5 5
y x x x x x
5 5
y
.
Với
3
cos
5
,
4
sin
5
. Do đó giá trị nhỏ nhất của hàm số là
5
y
.
Câu 7. [2D1-2] Điểm cực đại của đồ thị hàm số
3
12 12
y x x
là
A.
2; 4
. B.
2;28
. C.
4;28
. D.
2;2
.
Lời giải
Chọn B.
3
12 12
y x x
2
3 12; 6
y x y x
.
0 2
y x
.
2 12 0
y
.
D
2 12 0 2 28
C
y y y
.
Vậy điểm cực đại của đồ thị là
2;28
.
O
x
y
1
1
2
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/27
Câu 8. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
3 1
x
y
x m
có tiệm cận
đứng nằm bên trái trục
Oy
.
A.
0
m
. B.
0
m
. C.
0
m
. D. Đáp án khác.
Lời giải
Chọn D.
Tập xác định
\
D m
.
Đồ thị hàm số
3 1
x
y
x m
có tiệm cận đứng nằm bên trái trục
Oy
khi
3 1
lim lim
0
x m x m
x
y
x m
m
1 3 0
0
m
m
1
0
3
m
.
Câu 9. [2D1-2] Đồ thị hàm số
2
11
2016
x
y
x
có bao nhiêu đường tiệm cận ngang?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C.
2
11
1
lim lim 1
2016
1
x x
x
y
x
,
2
11
1
lim lim 1
2016
1
x x
x
y
x
.
Vậy đồ thị hàm số
2
11
2016
x
y
x
có
2
đường tiệm cận ngang là
1
y
.
Câu 10. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
4 2 2
2016
y x m m x
có
3
điểm cực trị?
A.
1
0
m
m
. B.
0 1
m
. C.
1 0
m
. D.
0
1
m
m
.
Lời giải
Chọn C.
Ta có
3 2 2 2
4 2 2
y x m m x x x m m
.
2 2
0
0
0
x
y
x m m
.
Hàm số có
3
điểm cực trị
0
y
có
3
nghiệm phân biệt
2
0 1 0
m m m
.
Câu 11. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
1
mx
y
x m
đồng biến trên
khoảng
1;
.
A.
1 1
m
. B.
1
m
. C.
\ 1;1
m
. D.
1
m
.
Lời giải
Chọn B.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/27
Ta có TXĐ:
\
D m
,
2
2
1
m
y
x m
do đó hàm số đồng biến trên khoảng
1;
thì
2
1 0
1
m
m
1
1
1
1
m
m
m
m
.
Câu 12. [2D1-2] Cho hàm số
2
2
3 2
2 3
x x
y
x x
khẳng định nào sau đây sai?
A. Đồ thị hàm số có hai tiệm cận đứng.
B. Đồ thị hàm số có ba đường tiệm cận.
C. Đồ thị hàm số có tiệm cận ngang là đường thẳng
2
y
.
D. Đồ thị hàm số có tiệm cận ngang là đường thẳng
1
2
y
.
Lời giải
Chọn C.
Ta có TXĐ:
3
\ 1;
2
D
.
2
2
3 2 1
lim lim
2 3 2
x
x
x x
y
x x
do đó đồ thị hàm số có một TCN
1
2
y
.
1
lim
x
y
và
3
2
lim
x
y
nên đồ thị hàm số có hai TCĐ
1
x
,
3
2
x
.
Vậy đồ thị hàm số có ba đường tiệm cận trong đó có một đường tiệm cận ngang là đường thẳng
1
2
y
.Vậy khẳng định sau là C.
Câu 13. [2D1-2] Cho hàm số
4 2
2 2017
f x x x , khẳng định nào sau đây sai?
A.
f x
nghịch biến trên
0;1
. B.
f x
đồng biến trên
0;
.
C.
f x
đồng biến trên
1;0
. D.
f x
nghịch biến trên
; 1
.
Lời giải
Chọn B.
Ta có TXĐ:
D
,
2
4 2
4 1
2 2 2017
x x
f x
x x
0
0
1
x
f x
x
,suy ra hàm số đồng biến trên khoảng
1;0
và
1;
,hàm số nghịch
biến trên các khoảng
; 1
và
0;1
. Vậy khẳng định B sai.
Câu 14. [2D1-2] Giá trị nhỏ nhất của hàm số
1
y x
x
bằng bao nhiêu?
A.
2
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn A.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/27
Ta có TXĐ:
0;D
,
2
2
1
1
2
x
y
x x
x
0 1
y x
suy ra
1
x
. Hàm số nghịch biến trên
0;1
và đồng biến trên
1;
.
Vậy giá trị nhỏ nhất của hàm số là
1 2
y .
Cách khác. Dùng BĐT Cauchy
Câu 15. [2D1-2] Cho hàm số
3
3sin 4sin
y x x
. Giá trị lớn nhất của hàm số trên khoảng
;
2 2
bằng
A.
1
. B.
1
. C.
7
. D.
3
.
Lời giải
Chọn A.
Đặt
sin
x t
, theo giả thiết
;
2 2
x
suy ra
1;1
t .
Khi đó xét hàm số
3
3 4
f t t t
trên khoảng
1;1
.
Có
2
3 12
f t t
suy ra
1
0
2
f t x
sau xét dấu ta được
1
1
2
f
là giá trị lớn nhất của hàm số đã cho trên khoảng.
;
2 2
..
Cách khác.
3 3
; 3 ; 1 sin3 1 1 1
2 2 2 2
x x x y
2
1 sin 3 1 3 2
2 6 3
y x x k k x k k
;
2 2
x
nên
2
0
2 6 3 2 6
k k x
Vậy
;
2 2
max 1
y
đạt được khi
1
sinx
2 6
t x
.
Câu 16. [2D1-2] Tìm
m
để hàm số
2
2017
y x m x đồng biến trên khoảng
1;2
.
A.
1
m
. B.
3
m
. C.
1
m
. D.
2
m
.
Lời giải
Chọn B.
Ta có TXĐ:
D
,
2
3 2
y x mx
suy ra
0
2
0
3
x
m
y
x
.
Dễ thấy nếu
0
m
thì hàm số có hai điểm cực trị.
Để hàm số đồng biến trên khoảng
1;2
thì
2
1;2 0;
3
m
2
0 1 2
3
m
2
2 3
3
m
m
.
Câu 17. [1D5-3] Một chất điểm chuyển động có phương trình
2 3
6 9 1
s s t t t t
. Thời điểm
t
(giây) tại đó vận tốc
m/s
v của chuyển động đạt giá trị lớn nhất là

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/27
A.
3
t
. B.
1
t
. C.
2
t
. D.
4
t
.
Lời giải
Chọn C.
Ta có phương trình vận tốc:
2
3 12 9
v v t t t
.
Bài toán dẫn đến tìm
t
để giá trị vận tốc lớn nhất, có
6 12
v t t
.
Suy ra GTLN của vận tốc là
2 3
v
khi
2
t
.
Câu 18. [2D1-2] Hàm số
3 2 2
1
1 1
3
y x mx m m x
đạt cực trị tại điểm
1
x
khi
A.
1
m
hoặc
2
m
. B.
1
m
. C.
2
m
. D.
m
.
Lời giải
Chọn C.
Ta có TXĐ:
D
,
2 2
2 1
y x mx m m
.
Để hàm số có cực trị thì
2 2
1 0 1
m m m m
.
Theo giả thiết hàm số đạt cực trị tại điểm
1
x
do đó:
2
3 2 0
m m
1
2
m
m
đối chiếu điều kiện suy ra
2
m
là giá trị cần tìm.
Câu 19. [2D1-2] Phương trình tiếp tuyến với đồ thị hàm số
4 2
2 1
y x x
tại điểm cực tiểu của đồ thị
hàm số là
A.
1 0
y
. B.
0
y
. C.
1 0
x y
. D.
y x
.
Lời giải
Chọn A.
Ta có TXĐ:
D
,
3
4 4
y x x
suy ra
0 0
y x
.
Do đó PTTT với đồ thị hàm số tại điểm cực tiểu của đồ thị hàm số là
1 0
y
.
Câu 20. [1D5-3] Cho hàm số
3
3 2
y x x
. Có bao nhiêu tiếp tuyến của đồ thị hàm số song song với
trục hoành?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B.
Dễ thấy tại các điểm cực trị thì tiếp tuyến của đồ thị hàm số song song hoặc trùng với trục hoành.
Do đó
2
3 3
y x
và
0 1
y x
nên hàm số có hai điểm cực trị.
Với
1
x
tiếp điểm
1;0
A . Pttt là
0
y
: Thỏa mãn.
Với
1
x
tiếp điểm
1;4
B . Pttt là
4
y
: Loại do trùng với trục hoành
Vậy có
1
tiếp tuyến của đồ thị hàm số đã cho song song với trục hoành.
Câu 21. [2D1-2] Cho hàm số
y f x
có đồ thị như hình vẽ bên. Khẳng định nào dưới đây là đúng?
O
x
y
2
2
1
4
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/27
A.
max 4
f x
. B. Hàm số đồng biến trên khoảng
;1
.
C. Giá trị cực tiểu của hàm số bằng
1
. D.
2;1
min 0
f x
Lời giải
Chọn D.
A. Sai vì
4
là giá trị cực đại của hàm số chứ không phải là GTLN của hàm số trên
.
B. Sai vì hàm số nghịch biến trên khoảng
; 1
và đồng biến trên khoảng
1;1
.
C. Sai vì
1
là điểm cực tiểu của hàm số chứ không phải là giá trị cực tiểu của hàm số.
D. Đúng vì
0, 2;1
1 2;1 : 1 0
f x x
f
.
Câu 22. [2D1-4] Cho hàm số
2 3
2
x
y
x
có đồ thị
C
. Tìm trên
C
những điểm sao cho tiếp tuyến
với
C
tại
M
cắt hai tiệm cận của
C
tại
A
,
B
sao cho
AB
ngắn nhất.
A.
3
0; , 1; 1
2
. B.
5
1; , 3;3
3
. C.
3;3 , 1;1
. D.
5
4; ; 3;3
2
.
Lời giải
Chọn C.
Ta có
2
2 3 1 1
2 ;
2 2
2
x
y C y
x x
x
C
có tiệm cận đứng là
1
: 2 2 0
x x
và tiệm cận ngang là
2
: 2 2 0
y y
Xét điểm
0 0
0
1
;2 2
2
M x C x
x
. Tiếp tuyến của
C
tại M có phương trình là
0
2
0
0
1 1
2
2
2
y x x
x
x
. Tiếp tuyến này cắt tiệm cận đứng
1
tại điểm
0
1
2;2 1
2
A
x
và cắt tiệm cận ngang
2
tại điểm
0
2 1 ;2
B x .
Ta có:
2
2
0
0
1
2 1 2 2 2 1
2
AB x
x
2
2
0
0
2
2 2
2
x
x
2 2
Đẳng thức xảy ra
2
2
0
0
2
2 2
2
x
x
4
0
2 1
x
2
0
2 1
x
0 0
0 0
3, 3
1; 1
x y
x y
.
Vậy có hai điểm thỏa đề bài có tọa độ là
3;3
và
1;1
.
Câu 23. [2H1-3] Cho một tấm nhôm hình vuông cạnh
10cm
, tại bốn cạnh tấm nhôm người ta cắt ra
bốn tam giác cân bằng nhau, độ dài đường cao xuất phát từ đỉnh của mỗi tam giác cân bằng
cm
x . Sau đó gập tấm nhôm theo đường chấm chấm (xem hình vẽ bên) để được một khối
chóp tứ giác đều. Tìm
x
để khối chóp nhận được có thể tích lớn nhất.
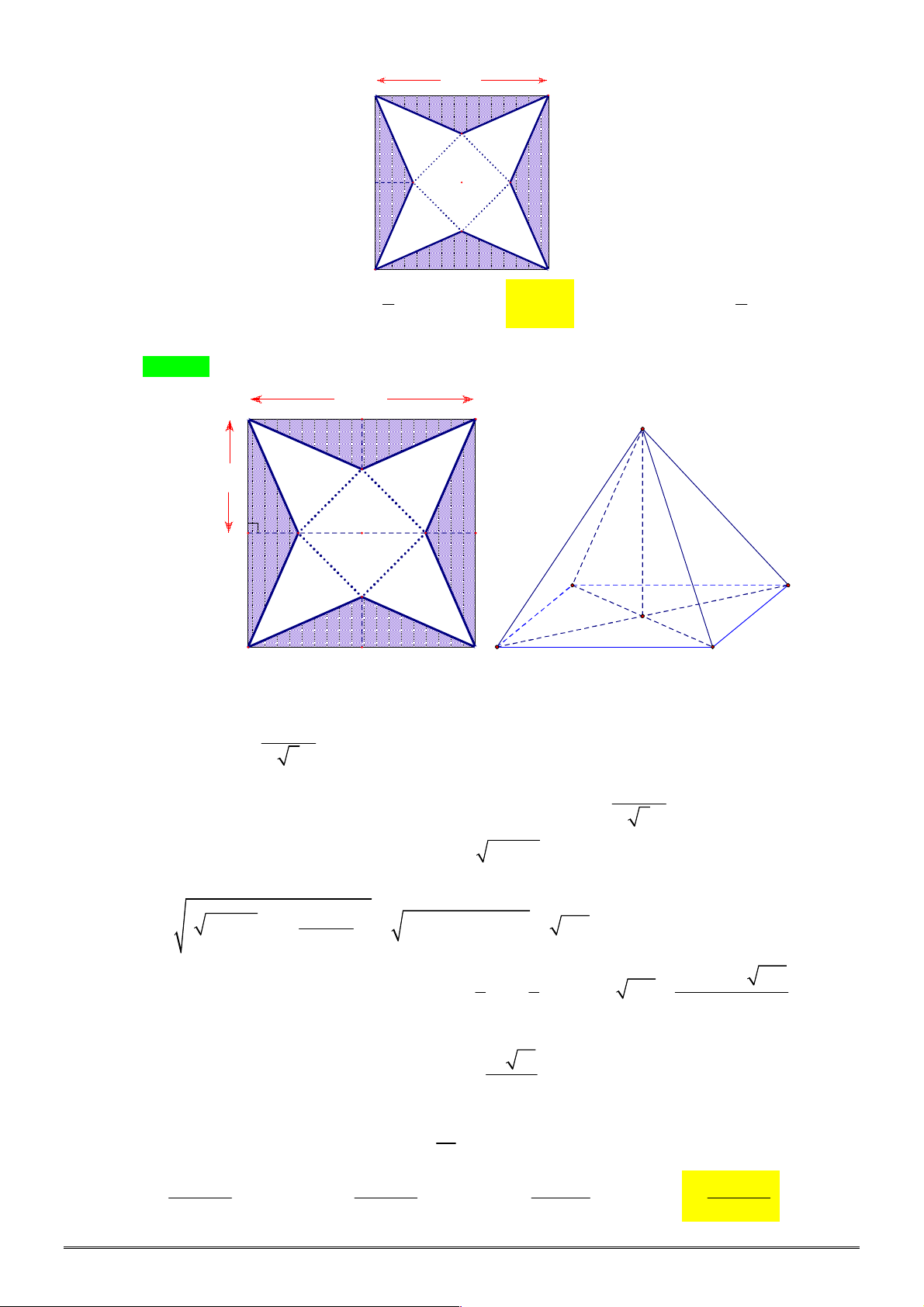
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/27
x
10 cm
A.
2
x
. B.
5
2
x
. C.
1
x
. D.
1
2
x
.
Lời giải
Chọn C.
x
x
x
x
10-2x
5 cm
10 cm
Điều kiện:
0 5 *
x
Hình chóp đều tạo thành có đáy là hình vuông có đường chéo bằng
10 2
x
nên cạnh hình
vuông đó bằng
10 2
2
x
.
Diện tích hình vuông đáy của hình chóp đều tạo thành là
2
2
10 2
2 5
2
x
B x
Cạnh bên của hình chóp đều tạo thành bằng
2 2
5
x
.
Chiều cao của hình chóp đều tạo thành bằng
2
2
2
2 2 2
10 2
5 25 5 10
2
x
h x x x x
Thể tích của khối chóp đều tạo thành là
2
2
2 5 10
1 1
.2 5 10
3 3 3
x x
V Bh x x
Sử dụng chức năng của máy tính cầm tay lần lượt thử các phương án ta thấy khi
1
x
thì thể
tích khối chóp đều tạo thành là lớn nhất
32 10
3
V
.
Câu 24. [2D2-2] Tính đạo hàm của hàm số
2
x
x
y
.
A.
1 ln2
4
x
x
. B.
1 ln2
4
x
x
. C.
1 ln 2
2
x
x
. D.
1 ln2
2
x
x
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/27
Lời giải
Chọn D.
2
2
2 2
2 .2 ln 2 1 ln2
2 2 2
2
x x
x x
x x x
x
x x
x x x
y
.
Câu 25. [2D2-3] Cho các số thực dương
x
,
y
thỏa mãn
2 2
4 12
x y xy
. Khẳng định nào sau đây đúng?
A.
log 2 8 log log
x y x y
. B.
1
log 2 2log2 log log
2
x y x y
.
C.
log 2log log12 log
x y xy
. D.
2 2
log log4 log12
x y xy
.
Lời giải
Chọn B.
Ta có:
2 2
2 2 2
4 12 4 2 16 2 16
x y xy x xy y xy x y xy
2
log 2 log8 2log 2 log16 log log
x y xy x y x y
2log 2 4log2 log log 2log 2 4log2 log log
x y x y x y x y
1
log 2 2log2 log log
2
x y x y
.
Câu 26. [2D2-3] Cho
27
log 5
a
,
8
log 7
b
,
2
log 3
c
. Hãy biểu diễn
12
log 35
theo
a
,
b
và
c
.
A.
3 2
2
b ac
c
. B.
3 3
2
b ac
c
. C.
3 2
3
b ac
c
. D.
3 3
1
b ac
c
.
Lời giải
Chọn B.
Cách 1: Tự luận.
2 8 2 27
2 2 2
12
2 2 2
2
log 8.log 7 log 27.log 5
log 35 log 7 log 5
log 35
log 12 log 3 log 4 2
3 3log 3. 3 3
2 2
c
b a b ac
c c
Cách 2: Sử dụng máy tính cầm tay.
Sử dụng chức năng gán lần lượt gán các biểu thức
27 8 2 12
log 5, log 7, log 3, log 35
vào các biến
, , ,
A B C D
. Sau đó bấm
D
(biểu thức ở các phương án), chừng nào thấy kết quả bằng
0
thì
đó là phương án đúng.
Phương án A. khác
0
, sai.
Phương án B. bằng
0
, đúng.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/27
Phương án C. khác
0
, sai.
Phương án D. khác
0
, sai.
Câu 27. [2D2-2] Tìm tập xác định
D
của hàm số
3
2 3
1
y x x
.
A.
1;1
D . B.
0;1
D . C.
\ 1;1
D
. D.
1;1 \ 0
D .
Lời giải
Chọn D.
Hàm số xác định
2
1 1
1 0
0
0
x
x
x
x
. Vậy
1;1 \ 0
D .
Câu 28. [2D2-2] Tìm
x
biết
1
2
1
125
25
x
x
.
A.
1
x
. B.
4
x
. C.
1
4
x
. D.
1
8
x
.
Lời giải
Chọn C.
Cách 1: Tự luận.
1
1 2
2 2 3 2 2 6
1 1
125 5 5 5 5 2 2 6
25 4
x
x x
x x x
x x x
.
Cách 2: Sử dụng máy tính cầm tay tính giá trị biểu thức
1
2
1
125
25
x
x
lần lượt tại các giá trị
của
x
trong các phương án, khi nào thấy kết quả bằng
0
thì đó là phương án đúng.
Phương án A. khác
0
, sai.
Phương án B. khác
0
, sai.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/27
Phương án C. bằng
0
, đúng.
Phương án D. khác
0
, sai.
Câu 29. [2D2-3] Hàm số
2
2 1
log
a a
y x
nghịch biến trên khoảng
0;
khi
A.
1
a
và
0 2
a
. B.
1
a
. C.
0
a
. D.
1
a
và
1
2
a
.
Lời giải
Chọn A.
Điều kiện để hàm số xác định trên khoảng
0;
là
2
2
2
2
1
2 1 0
1 0
0
2 1 1
2 0
2
a
a a
a
a
a a
a a
a
(*).
Khi điều kiện (*) thỏa thì hàm số nghịch biến trên khoảng
0;
khi:
2
2 1 1
a a
2
2 0 0 2
a a a
Kết hợp với điều kiện (*) ta được kết quả:
1
a
và
0 2
a
.
Câu 30. [2D2-2] Hàm số
2
e
x
y x
nghịch biến trên khoảng nào trong các phương án sau.
A.
; 2
. B.
2;0
. C.
1;
. D.
;1
.
Lời giải
Chọn B.
Ta có:
2 2 2 2 2
e e e 2 e e e 2
x x x x x x
y x x x x x x x
Hàm số nghịch biến khi và chỉ khi:
2 2
0 e 2 0 2 0
x
y x x x x
(Do e 0,
x
x
)
2 0
x
Vậy hàm số nghịch biến trên khoảng
2;0
.
Câu 31. [2D2-3] Tìm giá trị nhỏ nhất của hàm số
1 3
2 2
x x
f x
.
A.
4
. B.
6
. C.
2
. D.
1
.
Lời giải
Chọn A.
Áp dụng bất đẳng thức Cô-si cho hai số dương
1
2
x
và
3
2
x
ta có:
1 3 1 3 2
2 2 2 2 .2 2 2 4
x x x x
f x
.
Đẳng thức xảy ra khi và chỉ khi
1 3
2 2 1 3 2
x x
x x x
.
Do đó
min 4
x
f x
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/27
Câu 32. [2D2-2] Giá trị lớn nhất của hàm số
2
ln ln 1
y x x
trên đoạn
1
;2
2
đạt tại
A.
1
x
. B.
1
2
x
. C.
3
2
x
. D.
3
4
.
Lời giải
Chọn A.
Ta có
2
2
2
1 2 1
1
1
x x
y
x x
x x
;
2
1
1 ;2
2
0 1 0
1
1 ;2
2
x
y x
x
.
1 2
ln
2 5
y
;
2
2 ln
5
y
;
1 ln 2
y .
Do đó:
1
;2
2
max ln2
y
khi
1
x
.
Câu 33. [2D2-3] Tính
1 2
.
x x
biết
1
x
,
2
x
thỏa mãn
16
log 2 log 0
x
x
.
A.
1
. B.
1
. C.
0
. D.
4
.
Lời giải
Chọn A.
Điều kiện:
0,
x
1
x
.
Với điều kiện đó, ta có:
16 2
2
1 1
log 2 log 0 log 0
log 4
x
x x
x
2
2
4 log 0
x
2
log 2
x
hoặc
2
log 2
x
4
x
hoặc
1
4
x
.
Như vậy, phương trình
16
log 2 log 0
x
x
có hai nghiệm
1
1
4
x
và
2
4
x
.
Do đó:
1 2
1
. .4 1
4
x x
.
Câu 34. [2D2-2] Tìm
x
biết
2
5 4
1
4
2
x x
.
A.
5 17
2
x
hoặc
5 17
2
x
. B.
5 17 5 17
2 2
x
.
C.
3
x
hoặc
2
x
. D.
2 3
x
.
Lời giải
Chọn D.
Ta có:
2 2
5 4 5 4 2
2
1 1 1
4 5 4 2
2 2 2
x x x x
x x
2
5 6 0 2 3
x x x
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/27
Câu 35. [2D2-3] Dân số thế được tính theo công thức
.e
ni
S A
trong đó
A
là dân số của năm lấy làm
mốc tính,
S
là dân số sau
n
năm,
i
là tỉ lệ tăn dân số hàng năm. Cho biết năm
2003
Việt Nam
có khoảng
80.902.400
người và tỉ lệ tăng dân số là
1,47%
một năm. Như vậy, nếu tỉ lệ tăng
dân số hàng năm không đổi thì đến năm
2017
số dân của Việt Nam sẽ gần với số nào nhất sau
đây?
A.
99.389.200
. B.
99.386.600
. C.
100.861.100
. D.
99.251.200
.
Lời giải
Chọn A.
Áp dụng công thức
.e
ni
S A
với
80.902.400
A
,
2017 2003 14
n
,
1,47% 0,0147
i
,
ta có số dân Việt Nam đến năm
2017
là
14.0,0147
.e 80902400.e 99389203,38
ni
S A .
Như vậy, số dân Việt Nam đến năm
2017
gần với số
99.389.200
nhất.
Câu 36. [2H1-1] Có tất cả bao nhiêu loại khối đa diện đều.
A.
3
. B.
5
. C.
6
. D.
7
.
Lời giải
Chọn B.
Có
5
loại khối đa diện đều, đó là
Khối đa diện đều loại
3;3
: Tứ diện đều.
Khối đa diện đều loại
4;3
: Khối lập phương.
Khối đa diện đều loại
3;4
: Khối bát diện đều.
Khối đa diện đều loại
5;3
: Khối mười hai mặt đều.
Khối đa diện đều loại
3;5
: Khối hai mươi mặt đều.
Câu 37. [2D1-4] Cho hàm số
3 2
f x x ax bx c
và giả sử
A
,
B
là hai điểm cực trị của đồ thị
hàm số. Giả sử đường thẳng
AB
đi qua gốc tọa độ. Tìm giá trị nhỏ nhất của
P abc ab c
.
A.
16
25
. B.
1
. C.
9
. D.
25
9
.
Lời giải
Chọn D.
Ta có
2
3 2
f x x ax b
Hàm số
f x
có hai cực trị khi và chỉ khi
0
f x
có hai nghiệm phân biệt
phương trình
2
3 2 0
x ax b
có hai nghiệm phân biệt
2
3 0
a b
.
Khi đó,
f x
đạt cực trị tại hai điểm
1
x
,
2
x
là hai nghiệm của
f x
.
Mặt khác:
2
3 2 2
1 1 2 2
3 2
3 9 3 9 9
b a ab
x ax bx c x a x ax b x c
Hay
2
1 1 2 2
3 9 3 9 9
b a ab
f x x a f x x c
.
Do đó, các giá trị cực trị của hàm số là
2 2
1 1 1 1 1 1
1 1 2 2 2 2
3 9 3 9 9 3 9 9
b a ab b a ab
y f x x a f x x c x c
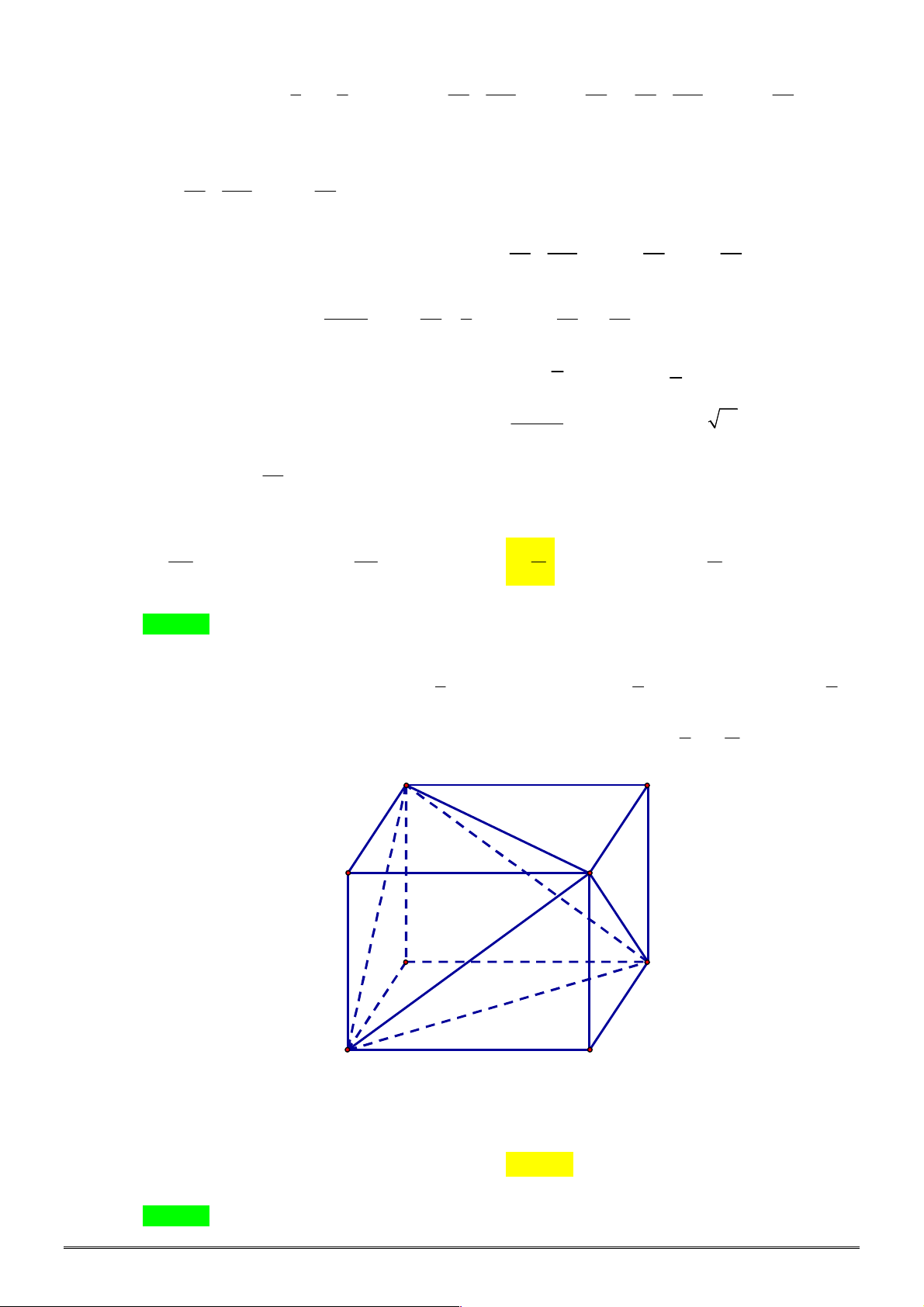
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/27
2 2
2 2 2 2 2 2
1 1 2 2 2 2
3 9 3 9 9 3 9 9
b a ab b a ab
y f x x a f x x c x c
Bởi vậy, đường thẳng đi qua hai điểm cực trị
A
,
B
của đồ thị hàm số
f x
là
2
2 2
3 9 9
b a ab
y x c
.
Vì đường thẳng
AB
đi qua gốc tọa độ nên:
2
2 2
0 .0
3 9 9 9
b a ab ab
c c
.
Nên:
2
2
1 25 25
5
9 9 9 9 9
ab
ab
P abc ab c ab ab
.
Dấu
" "
xảy ra khi và chỉ khi:
2 3
3
5
5
5
3 0 15
; 15 0;
0
b
b
ab
a
a
a b a
a
a
Vậy:
25
min
9
P
.
Câu 38. [2H1-2] Cho khối hộp
.
ABCD A B C D
có thể tích
V
. Khi đó thể tích khối tứ diện
AB CD
bằng
A.
2
3
V
. B.
3
4
V
. C.
3
V
. D.
6
V
.
Lời giải
Chọn C.
Ta có:
1
. ;
3
ABCB ACDD CB C D AA B D ABC
V V V V S d B ABCD
1 1
. ;
6 6
ABCD
S d B ABCD V
Bởi vậy
.
1
4.
6 3
AB CD ABCD A B C D ABCB ACDD CB C D AA B D
V
V V V V V V V V
.
Câu 39. [2H2-3] Mặt cầu tâm
O
bán kính
17dm
R
. Mặt phẳng
P
cắt mặt cầu sao cho giao tuyến đi qua
ba điểm
A
,
B
,
C
mà
18dm
AB
,
24dm
BC
,
30dm
CA
. Tính khoảng cách từ
O
đến
P
.
A.
14dm
. B.
7dm
. C.
8dm
. D.
16dm
.
Lời giải
Chọn C.
A
B
B
D
D
C
A
C
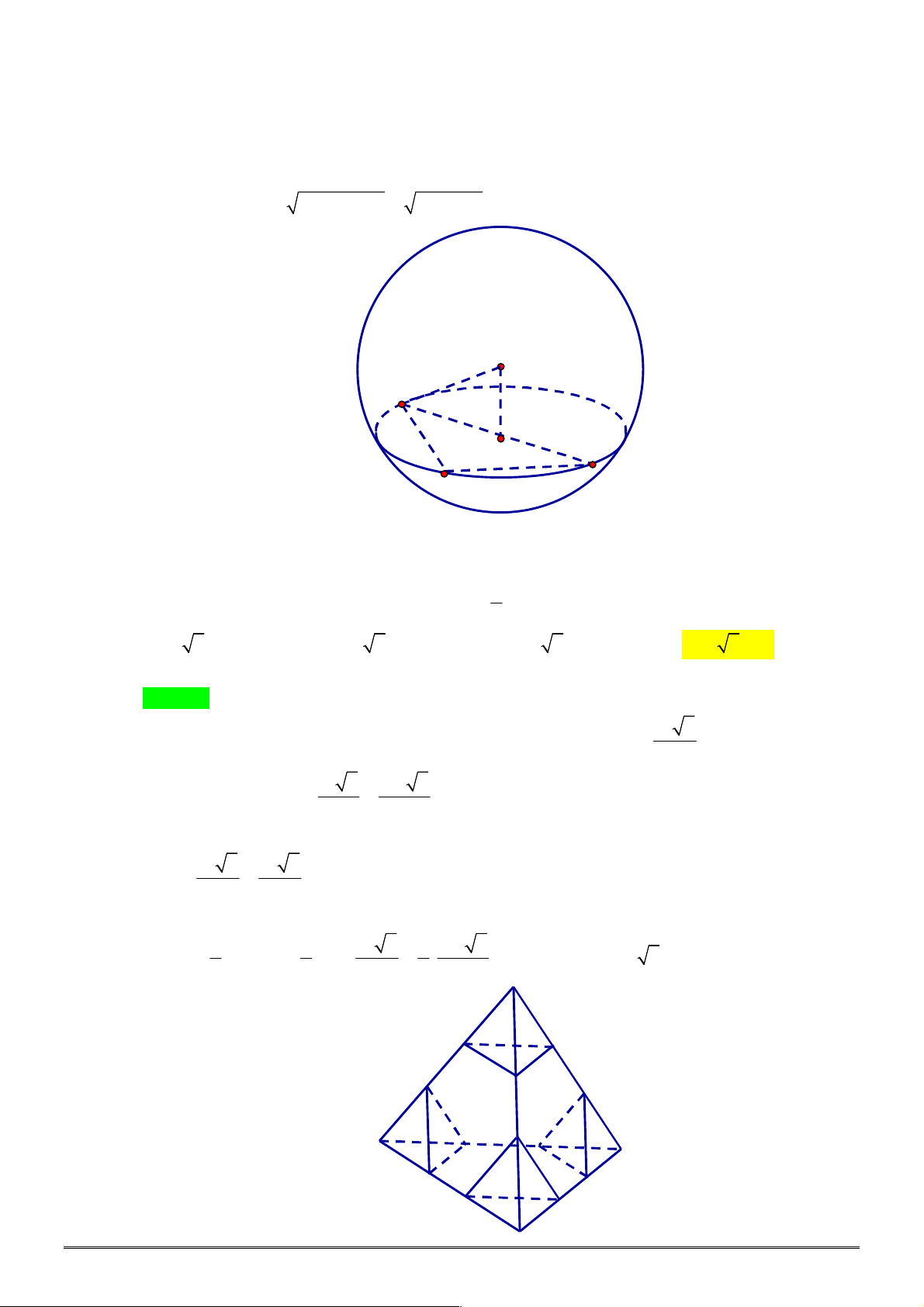
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/27
Vì
2 2 2 2 2 2
18 24 900 30
AB BC CA
nên tam giác
ABC
là tam giác vuông đỉnh
B
.
Gọi
H
là trung điểm
AC
thì
H
là tâm đường tròn ngoại tiếp tam giác
ABC
. Từ đó ta có
OH ABC
, hay
OH P
.
Do đó, khoảng cách từ
O
đến
P
là
2 2 2 2
; 17 15 8 dm
d O P OH OA AH .
Câu 40. [2H1-3] Để chế tác đồ vật trang trí trong nhà từ khối đá có hình dạng một tứ diện đều cạnh
8dm
.
Ở bốn đỉnh tứ diện, người ta cần cắt đi các tứ diện đều bằng nhau có cạnh bằng
x
, sao cho phần
còn lại của khối đá sau khi cắt có thể tích bằng
3
4
thể tích khối đá ban đầu. Giá trị của
x
là
A.
3 2 dm
. B.
3
3 4 dm
. C.
2 2 dm
. D.
3
2 4 dm
.
Lời giải
Chọn D.
Ta có công thức tính thể tích của khối tứ diện đều cạnh
a
là
3
2
12
a
V . Do đó, thể tích của
khối đá ban đầu là
3
3
8 2 128 2
dm
12 3
V .
Thể tích của bốn khối tứ diện đều cạnh
x
cắt ở bốn đỉnh của khối đá ban đầu là
3 3
3
2 2
4. dm
12 3
x x
V
Yêu cầu của đề bài tương đương với:
3
3
3
3 1 2 1 128 2
. 32 2 4 dm
4 4 3 4 3
x
V V V V V x x
O
A
H
C
B
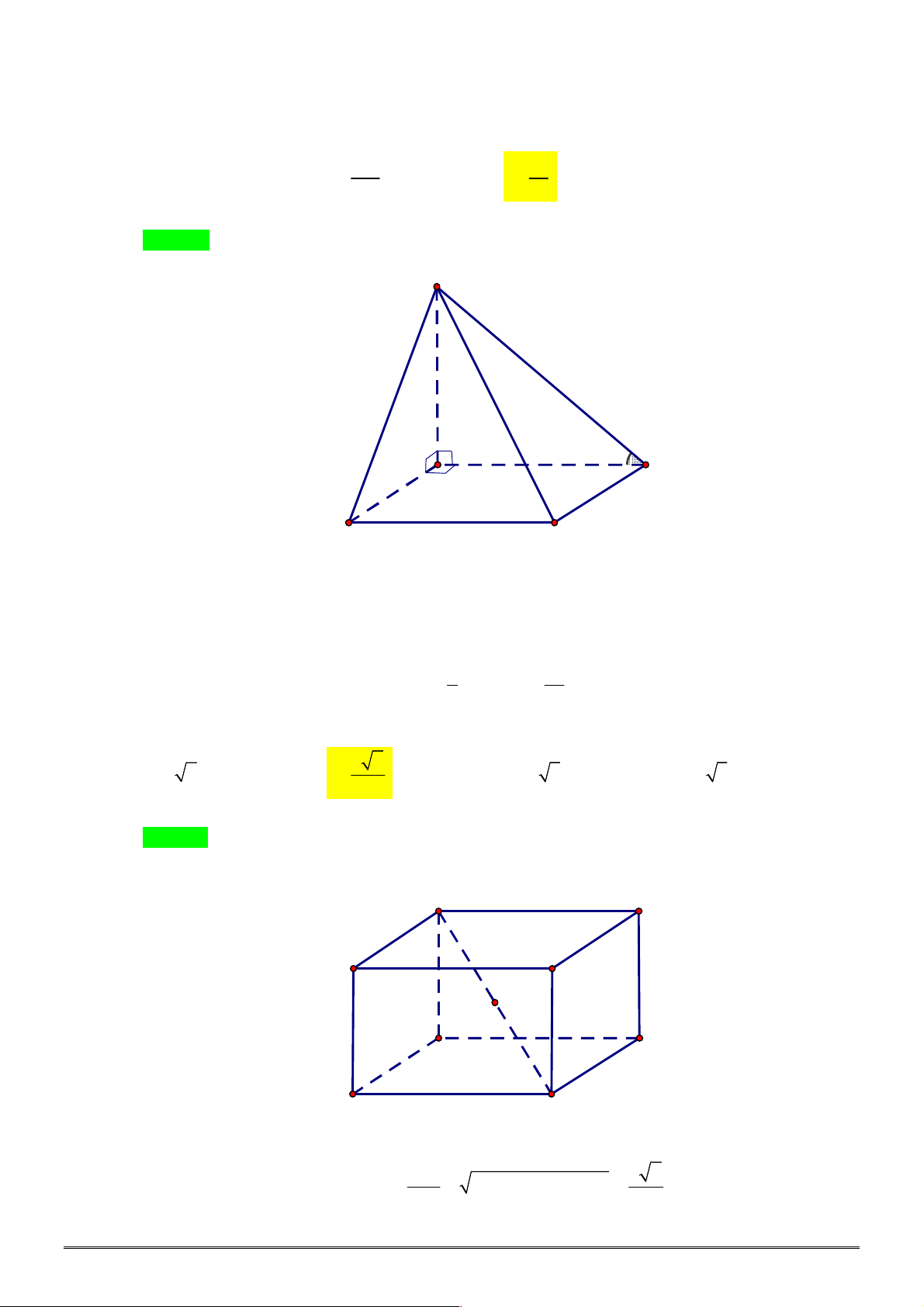
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/27
Câu 41. [2H1-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt
phẳng
ABCD
, góc tạo bởi đường thẳng
SD
và mặt phẳng
ABCD
bằng
45
. Thể tích khối
chóp
.
S ABCD
bằng.
A.
3
a
. B.
3
2
3
a
. C.
3
3
a
. D.
3
2
a
.
Lời giải
Chọn C.
45
A
B
C
D
S
Hình chiếu vuông góc của
SD
lên
ABCD
là
AD
suy ra:
; ; 45
SD ABCD SD AD SDA
Tam giác
SAD
vuông cân tại A nên
SA AD a
.
Thể tích khối chóp
.
S ABCD
là
3
1
.
3 3
SABCD ABCD
a
V S SA
Câu 42. [2H2-2] Cho hình hộp chữ nhật có kích thước
3
,
4
,
5
. Bán kính mặt cầu ngoại tiếp hình hộp là
A.
5 2
. B.
5 2
2
. C.
2 5
. D.
5
.
Lời giải
Chọn B.
Xét hình hộp chữ nhật
.
ABCD A B C D
có
3;
AB
4;
AD
5
AA
O
A'
B'
C'
D'
B
C
D
A
Do các đỉnh
,
B
,
C
,
D
,
A
,
B
D
cùng nhìn đoạn
AC
dưới một góc vuông nên bán kính
mặt cầu ngoại tiếp hình hộp là
2 2 2
5 2
2 2
AC
R AB AD AA
.
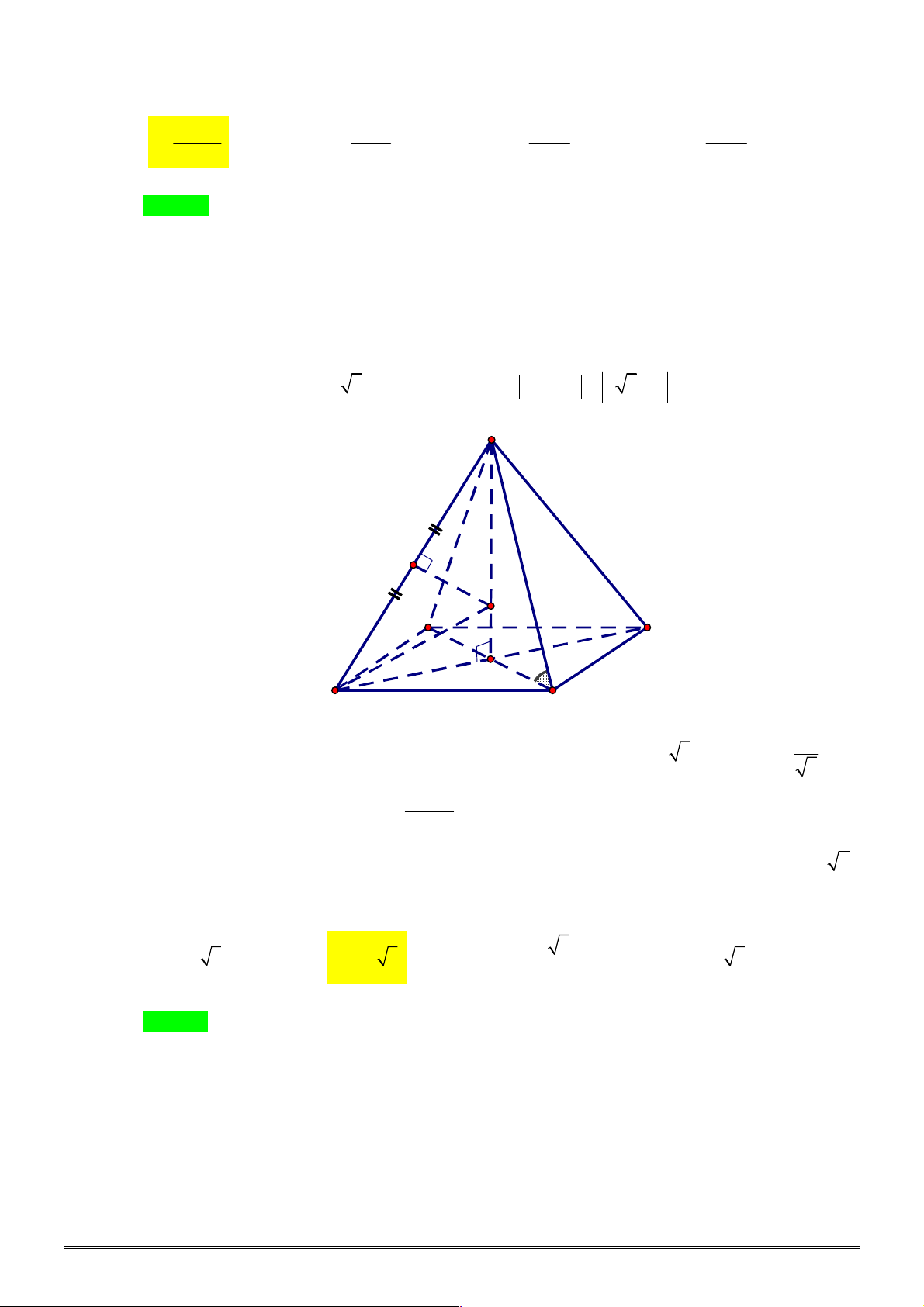
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/27
Câu 43. [2H2-3] Cho hình chóp tứ giác đều
.
S ABCD
có
2
AC a
, góc giữa cạnh bên và mặt đáy bằng
60
. Diện tích mặt cầu ngoại tiếp hình chóp bằng.
A.
2
16
3
a
. B.
2
8
3
a
. C.
2
4
3
a
. D.
2
2
3
a
.
Lời giải
Chọn A.
Gọi
I
là tâm đáy, do tâm
O
của mặt cầu ngoại tiếp hình chóp cách đều các đỉnh của đa giác
đáy nên
O
thuộc
SI
,
O
cách đều hai đỉnh
S
và
B
nên
O
nằm trên đường thẳng
d
là trung
trực trong mặt phẳng
SBD
của cạnh
SB
. Vậy
O d SI
và ta có bán kính mặt cầu ngoại
tiếp hình chóp là
R OS OB
.
Góc giữa cạnh bên
SC
và mặt phẳng đáy là
; 60
SC ABCD SCI
.
Ta có:
.tan60 3
SI IC a
,
BI IC a
,
3
IO SI OS a R
60
M
I
B
C
D
A
S
O
Xét tam giác
OIB
vuông tại
I
ta có:
2 2 2
OB BI OI
2
2 2
3
R a a R
2
3
a
R
.
Diện tích mặt cầu là
2
2
16
4
3
cau
a
S R
.
Câu 44. [2H1-2] Cho lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
2,
AB a
3
BC a
. Góc giữa đường thẳng
A B
và mặt đáy là
60
. Tính theo
a
thể tích khối lăng trụ
.
ABC A B C
.
A.
3
2 3
a . B.
3
3 3
a . C.
3
3
3
a
. D.
3
3
a .
Lời giải
Chọn B.
AB là hình chiếu vuông góc của
A B
lên mặt phẳng đáy
ABC
nên ta có:
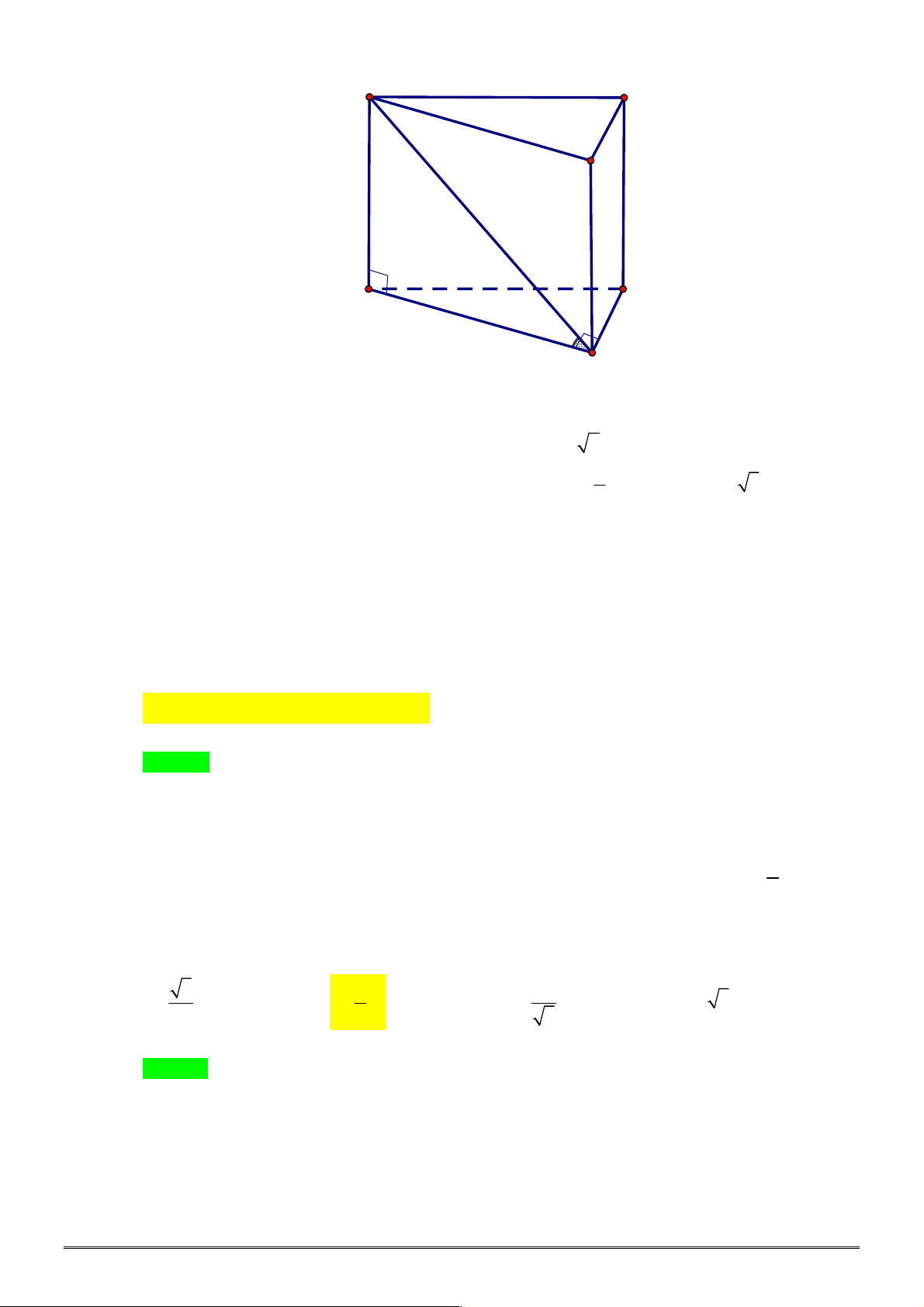
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 23/27
60
A'
B'
C'
A
B
C
; ; 60
A B ABC A B AB ABA
.tan60 6
AA AB a
Thể tích khối lăng trụ
.
ABC A B C
là
3
.
1
. . . 3 3
2
ABC A B C ABC
V S AA AB BC AA a
.
Câu 45. [2H2-1] Cho mặt cầu
S
có tâm
I
, bán kính
5
và mặt phẳng
P
cắt
S
theo một đường
tròn
C
có bán kính
3
r
. Kết luận nào sau đây sai?
A. Tâm của
C
là hình chiếu vuông góc của
I
trên
P
.
B. Khoảng cách từ
I
đến
P
bằng
4
.
C.
C
là giao tuyến của
S
và
P
.
D.
C
là đường tròn lớn của mặt cầu.
Lời giải
Chọn D.
Bán kính của
C
là
3
r
, bán kính mặt cầu
S
là
5
R
nên
r R
. Vậy đường tròn
C
không phải là đường tròn lớn của mặt cầu
S
.
Câu 46. [2H1-3] Cho hình chóp .
S ABC
có đáy
ABC
là tam giác vuông tại
A
, với
2
a
AC ,
BC a
.
Hai mặt phẳng
SAB
và
SAC
cùng tạo với mặt đáy
ABC
góc
60
. Tính khoảng cách từ
điểm
B
tới mặt phẳng
SAC
, biết rằng mặt phẳng
SBC
vuông góc với đáy
ABC
.
A.
3
4
a
.
B.
3
4
a
. C.
4
5
a
. D.
3
a
.
Lời giải
Chọn B.
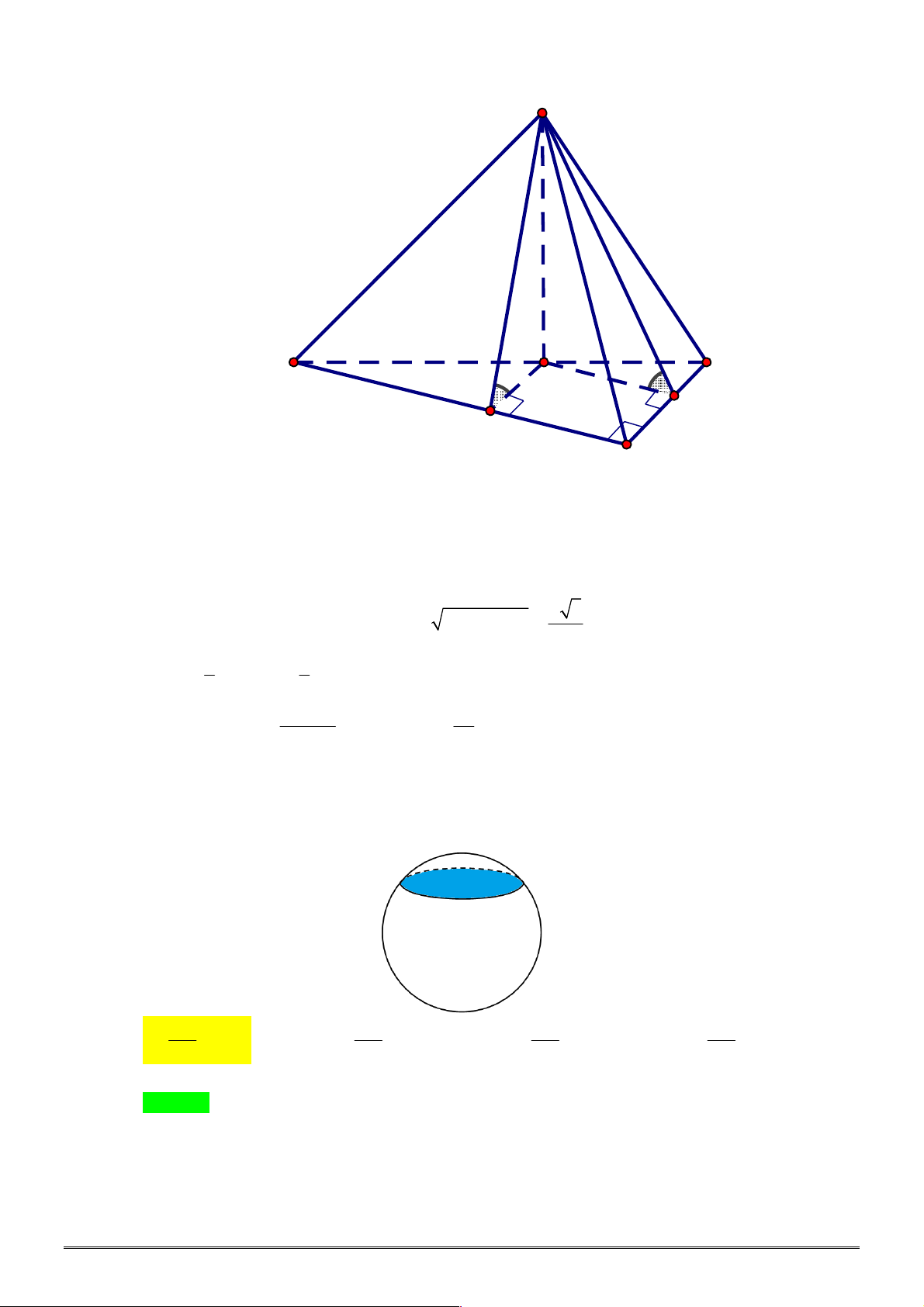
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 24/27
60
60
B
A
C
S
H
N
M
Gọi
H
là hình chiếu của
S
lên mặt phẳng
ABC
và
,
M
N
lần lượt là hình chiếu của
H
lên
,
AB
AC
. Khi đó ta có:
; ; 60
SAB ABC SM HM SMH
và
; ; 60
SAC ABC SN HN SNH
Xét tam giác vuông
ABC
ta có:
2 2
3
2
a
AB BC AC
.
1 1
. ; .
3 3
S ABC ABC SAC
V SH S d B SAC S
. . . . ;
SH AB AC AC SN d B SAC
. 3
; .sin60
4
SH AB a
d B SAC AB
SN
.
Câu 47. [2H2-3] Một khối cầu thủy tinh có bán kính bằng
4dm
. Người ta muốn cắt bỏ một chỏm cầu
có diện tích mặt cắt là
2
15 dm
để lấy phần còn lại làm bể nuôi cá. Hỏi thể tích nước tối đa
mà bể này chứa là bao nhiêu?
A.
3
175
dm
3
. B.
3
175
dm
4
. C.
3
125
dm
3
. D.
3
175
dm
4
.
Lời giải
Chọn A.
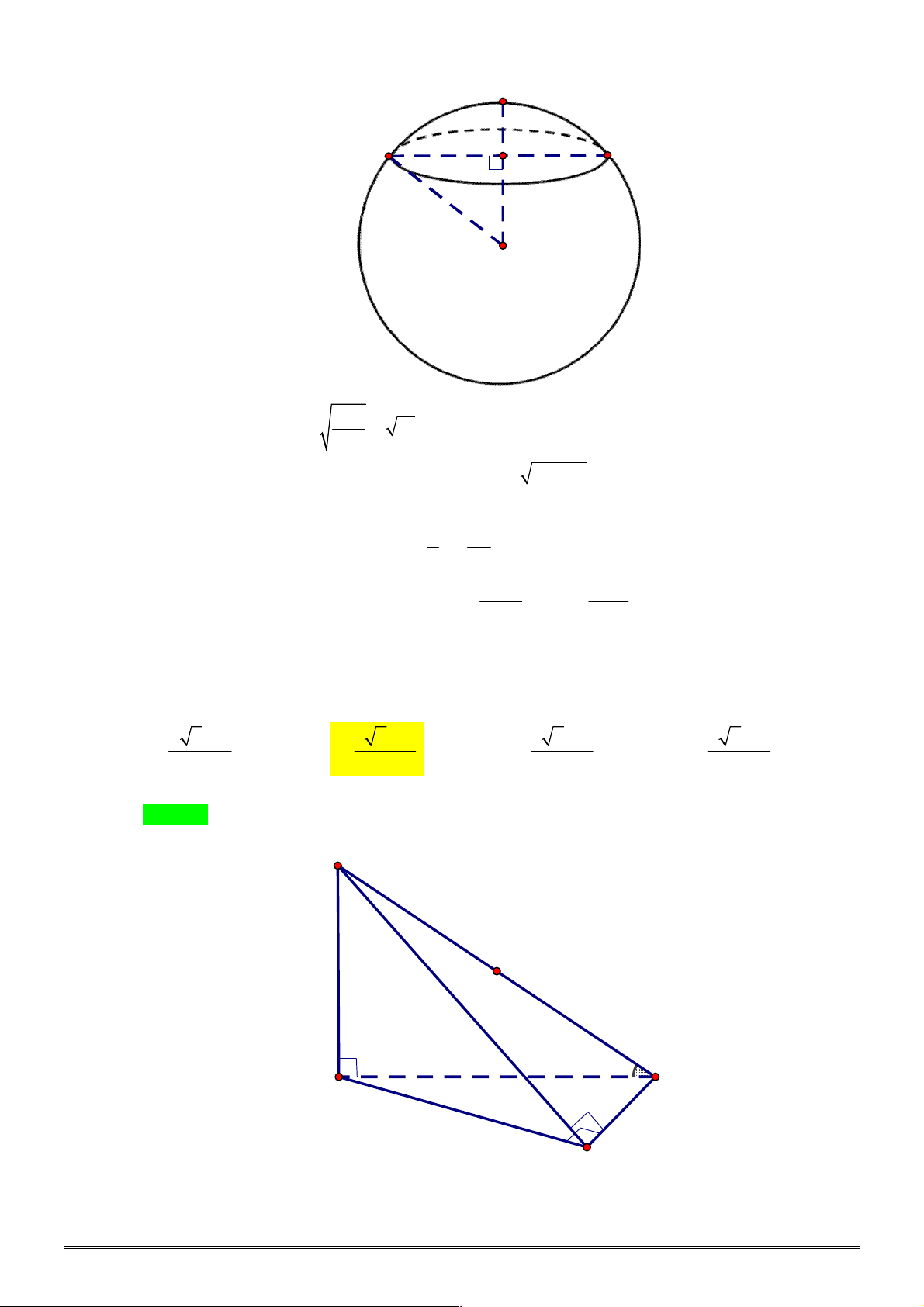
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 25/27
H
O
A
M
Bán kính mặt cắt là
15 dm
tron
S
r
Chiều cao chỏm cầu là
2 2
4 1 3 dm
h MH OM OH R R r
Thể tích chỏm cầu là
2 2 2 3
chom
3 27 dm
3 6
h h
V h R r h
.
Vậy thể tích phần còn lại là
3
cau chom
256 175
27 dm
3 3
V V V
.
Câu 48. [2H2-2] Cho hình chóp .
S ABC
có đáy là tam giác vuông cân tại
B
,
AB a
. Cạnh bên
SA
vuông góc mặt phẳng
ABC
và
SC
hợp với đáy một góc bằng
60
. Thể tích khối cầu ngoại
tiếp hình chóp .
S ABC
.
A.
3
4 2
3
a
. B.
3
8 2
3
a
. C.
3
5 2
3
a
. D.
3
2 2
3
a
.
Lời giải
Chọn B.
60
I
A
B
C
S
Gọi
I
là trung điểm
SC
, do
A
và
B
cùng nhìn đoạn
SC
dưới một góc vuông nên mặt cầu
ngoại tiếp hình chóp là mặt cầu đường kính
SC
.
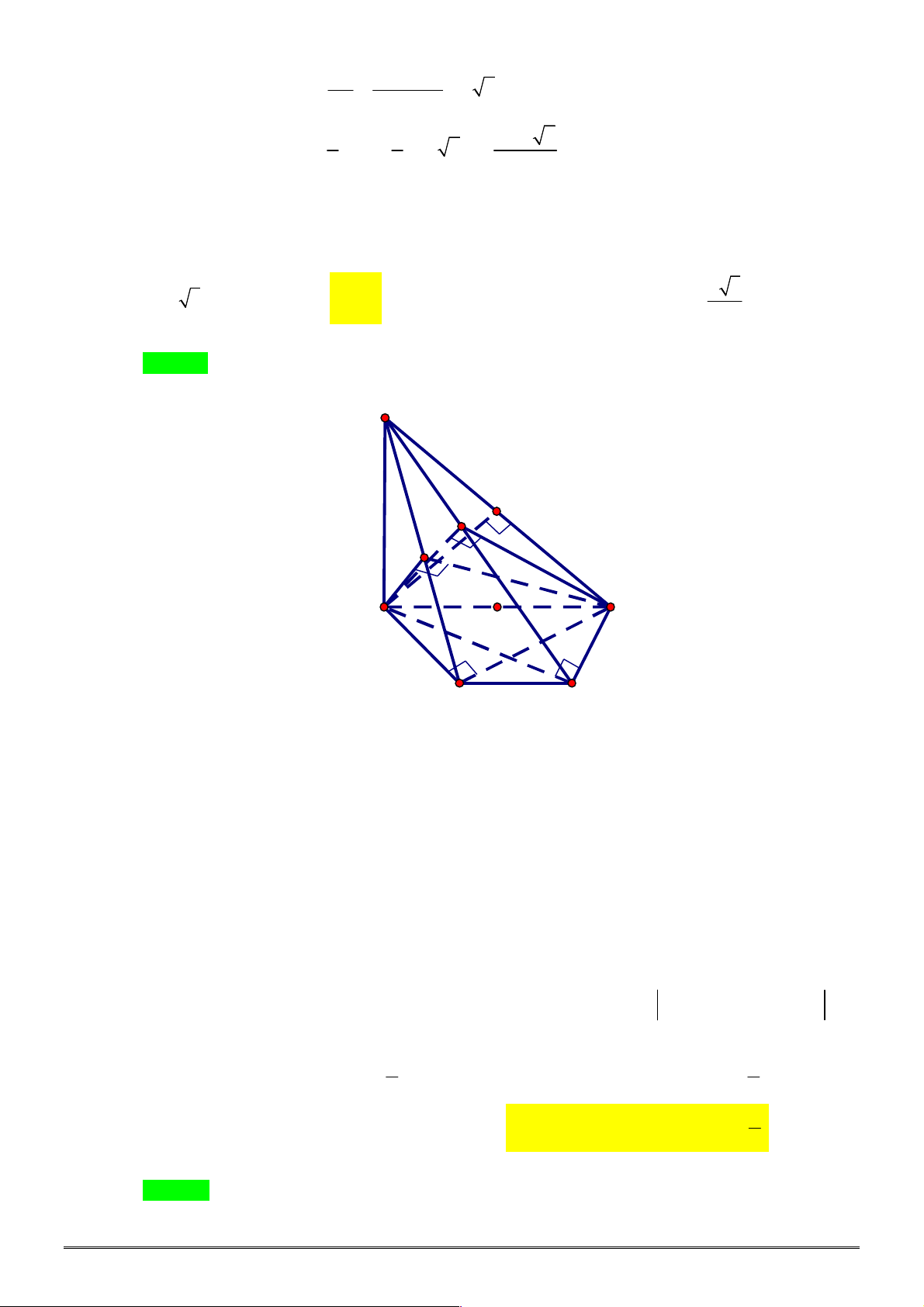
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 26/27
Bán kính mặt cầu là
2
2 2.cos60
SC AC
R a
.
Thể tích khối cầu là
3
3
3
4 4 8 2
2
3 3 3
a
V R a
.
Câu 49. [2H2-3] Cho hình chóp .
S ABCD
có đáy là hình thang cân
ABCD
với
2
AB a
,
BC CD DA a
và
SA ABCD
. Một mặt phẳng qua
A
vuông góc với
SB
và cắt
,
SB
SC
,
SD
lần lượt tại
M
,
N
,
P
. Tính đường kính khối cầu ngoại tiếp khối đa diện
ABCDMNP
.
A.
3
a
. B.
2
a
. C.
a
. D.
3
2
a
.
Lời giải
Chọn B.
O
A
D
C
B
S
N
M
P
Gọi
O
là trung điểm của
AB
, do
2 2 2 2
AB AD DC CB a
nên ta có
O
là tâm đường
tròn ngoại tiếp hình thang
ABCD
.
Ta có:
AM SB
AC BC BC SAC
AN SBC
nên
NB AN
BD AD BD SAD
AP SBD
nên
BP AP
Thấy
,
C
,
D
,
M
,
N
P
cùng nhìn đoạn
AB
dưới một góc vuông nên
,
A
,
B
,
C
,
D
,
M
,
N
P
cùng thuộc mặt cầu đường kính
AB
. Do đó đường kính mặt cầu ngoại tiếp khối đa diện
ABCDMNP
là
2
a
.
Câu 50. [2H2-2] Cho tứ diện
ABCD
có
O
là trung điểm của đoạn thẳng nối trung điểm của hai cạnh
đối diện. Tập hợp các điểm
M
trong không gian thỏa mãn hệ thức
MA MB MC MD a
(với
0
a không đổi) là
A. Mặt cầu tâm
O
bán kính
3
a
r
. B. Mặt cầu tâm
O
bán kính
2
a
r
.
C. Mặt cầu tâm
O
bán kính
r a
. D. Mặt cầu tâm
O
bán kính
4
a
r
.
Lời giải
Chọn D.
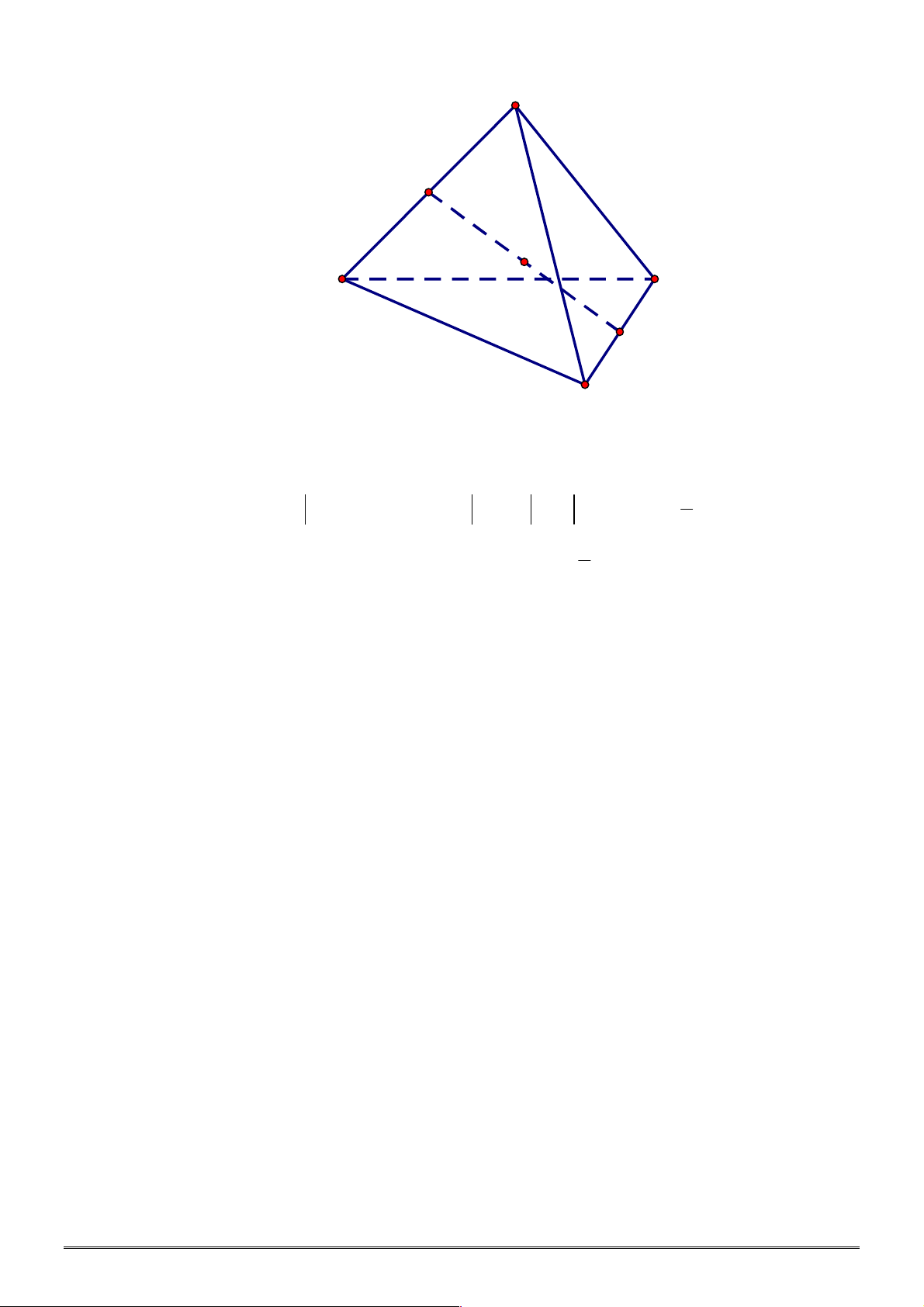
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 27/27
O
F
E
B
C
D
A
Gọi
,
E
F
lần lượt là trung điểm
,
AB
CD
và
O
là trung điểm của
EF
.
2 2 4.
MA MB MC MD ME MF MO
4
4
a
MA MB MC MD a MO a MO
Vậy quỹ tích các điểm
M
là mặt cầu tâm
O
bán kính
4
a
r
.
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/24
TRƯỜNG THPT KIM LIÊN – HÀ NỘI ĐỀ ÔN TẬP HỌC KỲ I NĂM HỌC 2017 – 2018
ĐỀ SỐ 2 MÔN TOÁN - LỚP 12
------- ------------------
Câu 1. [2D1-1] Cho hàm số
4 2
5 2
y x x
. Hàm số nghịch biến trên khoảng nào?
A.
0;
. B.
1;1
. C.
0;1
. D.
;0
.
Câu 2. [2D1-1] Cho hàm số
2 1
1
x
y
x
có đạo hàm
2
3
0, 1
1
y x
x
. Có hai học sinh phát biểu
như sau:
Học sinh
X
: “ Hàm số luôn nghịch biến trên tập xác định”
Học sinh
Y
: “ Hàm số luôn nghịch biến trên từng khoảng xác định”.
Phát biểu nào đúng, phát biểu nào sai?
A.
X
đúng và
Y
sai. B.
X
sai và
Y
đúng. C.
X
và
Y
đều đúng. D.
X
và
Y
đều sai.
Câu 3. [2D1-2] Với các giá trị nào của
m
thì hàm số
3 2
1
2 1
3 2
m
y x x x
luôn đồng biến trên
?
A.
2 2
m
. B.
2 2
m . C. Không có
m
. D.
2
m
.
Câu 4. [2D1-2] Tìm các giá trị của
m
để hàm số
1 2 2
m x m
y
x m
nghịch biến trên khoảng
1;
?
A.
1
m
. B.
2
m
. C.
1
m
hoặc
2
m
. D.
1 2
m
.
Câu 5. [2D1-1] Trong các khẳng định sau về hàm số
4 2
1 1
x 3
4 2
y x
. Khẳng định nào đúng:
A. Hàm số có điểm cực tiểu là
0
x
. B. Hàm số có hai điểm cực đại là
1
x
.
C. Cả
A
và
B
đều đúng. D. Có
A
đúng,
B
sai.
Câu 6. [2D1-2] Cho hàm số
3
2
y x x
. Hệ thức liên hệ giữa giá trị cực đại
Đ
C
y
và giá trị cực tiểu
CT
y
là
A. 2
CT C
Đ
y y
. B.
2
C C
Đ
T
y y
. C.
CT C
Đ
y y
. D.
Đ
CT C
y y
.
Câu 7. [2D1-2] Giá trị của
m
để hàm số
3 2 2
1
1 1
3
y x mx m m x
đạt cực tiểu tại điểm
1
x
là
A.
1
. B.
2
. C.
3
. D. Không có
m
.
Câu 8. [2D1-2] Giá trị của
m
để hàm số
4 2
1 1 2
y mx m x m
chỉ có đúng một cực trị là
A.
1
m
. B.
0
m
. C.
0 1
m
. D.
0
m
hoặc
1
m
.
Câu 9. [2D1-1] Cho hàm số
3 2
3x 3
y x
xác định trên
1;3
. Gọi
M,m
lần lượt là giá trị lớn nhất
và nhỏ nhất của hàm số thì
M + m
bằng
A.
2
. B.
4
. C.
6
. D.
8
.
Câu 10. [2D1-2] Giá trị nhỏ nhất của hàm số
2
4
y x x
trên
1;2
là
A.
1;2
min 0
y
. B.
1;2
min 3 1
y
. C.
1;2
min 2 2
y
. D.
1;2
min 2
y
.
Câu 11. [2D1-3] Các giá trị của
m
để giá trị lớn nhất của hàm số
2
1
x m m
y
x
trên đoạn
0;1
bằng
5
m
là
A.
11 4 5
2
. B.
11 5 5
2
. C.
11 6 5
2
. D. Không có giá trị nào.
14
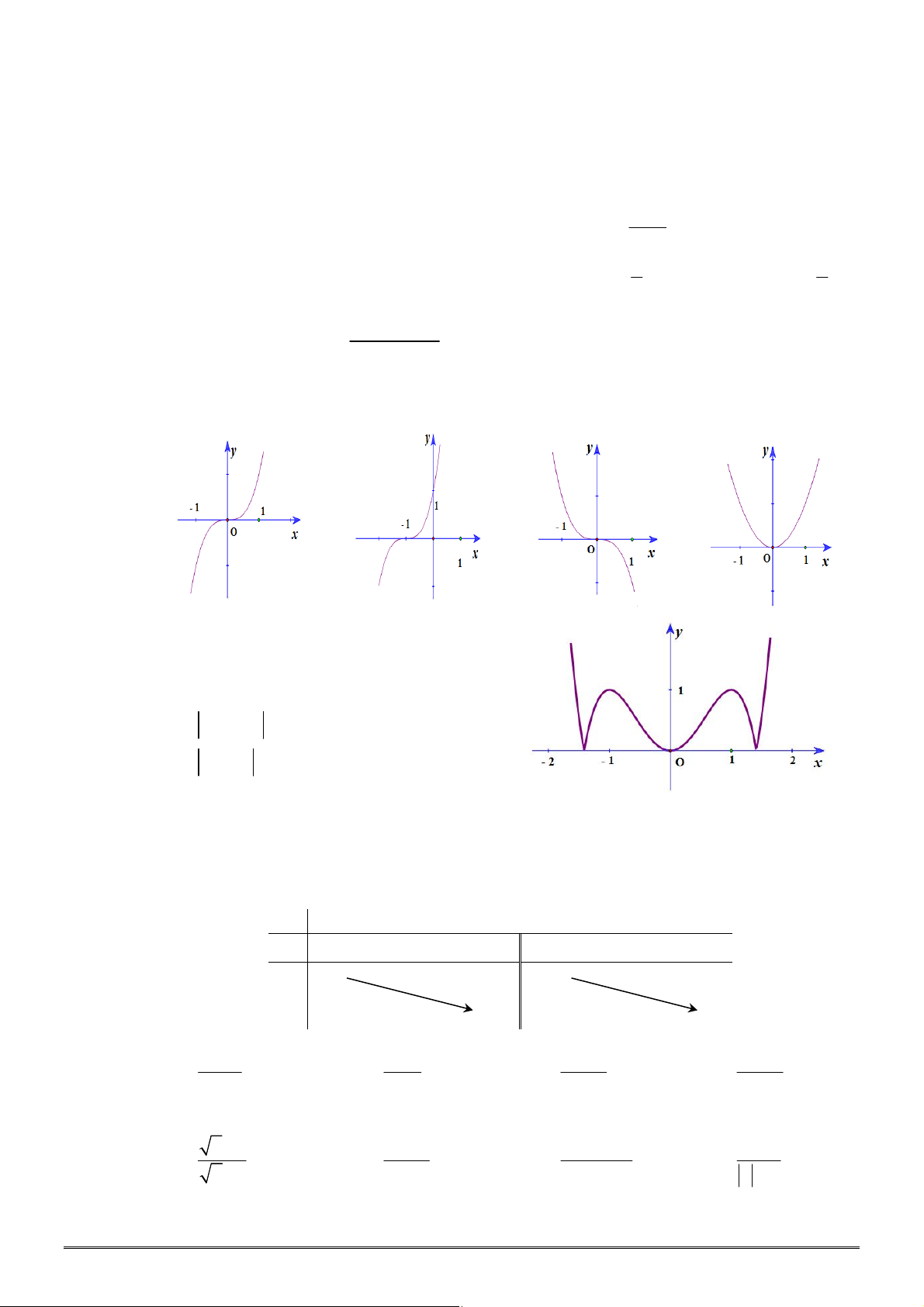
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/24
Câu 12. [2D1-3] Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: nếu mỗi đơn vị diện
tích của mặt hồ có
n
con cá thì trung bình mỗi con cá sau một vụ cân nặng
480 20 gam
P n n . Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ
để sau một vụ thu hoạch được nhiều cá nhất.
A.
10
. B.
16
. C.
26
. D.
12
.
Câu 13. [2D1-1] Phương trình các đường tiệm cận của đồ thị hàm số
3
2
x
y
x
là
A.
1
x
và
2
y
. B.
2
x
và
1
y
. C.
2
x
và
1
2
y
. D.
1
x
và
1
2
y
.
Câu 14. [2D1-2] Đồ thị hàm số
2
2
3 7 6
2 7 3
x x
y
x x
có bao nhiêu đường tiệm cận?
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 15. [2D1-2] Hàm số
3 2
3 3 1
y x x x
có đồ thị là hình nào sau đây?
A. . B. . C. . D. .
Câu 16. [2D1-3] Hình bên là đồ thị của hàm số nào sau đây?
A.
4 2
2
y x x
.
B.
4 2
2
y x x
.
C.
4 2
2
y x x
.
D.
3
3
y x x
.
Câu 17. [2D1-2] Tìm tất cả các giá trị của tham số
m
sao cho phương trình
3 2
3 0
x x m
có ba
nghiệm phân biệt?
A.
0 4
m
. B.
0
m
. C.
4
m
. D.
0 4
m
.
Câu 18. [2D1-2] Hàm số nào sau đây không có bảng biến thiên như hình dưới đây?
A.
2 1
2
x
y
x
. B.
3
2
x
y
x
. C.
2 3
2
x
y
x
. D.
2 3
2
x
y
x
.
Câu 19. [2D1-2] Đồ thị hàm số nào dưới đây có đúng hai đường tiệm cận?
A.
1
1
x
y
x
. B.
2
1
y
x x
. C.
2
5
7
x
y
x x
. D.
1
2
y
x
.
x
2
y
–
–
y
2
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/24
Câu 20. [2D1-2] Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số
3 2
1
2 3 5
3
y x x x
A. Song song với đường thẳng
1
x
. B. Song song với trục hoành.
C. Có hệ số góc dương. D. Có hệ số góc bằng
1
.
Câu 21. [2D1-2] Phương trình tiếp tuyến của đồ thị hàm số
4 2
2 1
y x x
mà vuông góc với đường
thẳng
8 0
x y
là
A.
8 6
y x
. B.
8 10
y x
. C.
8 6
y x
. D.
8
y x
.
Câu 22. [2D1-3] Cho hàm số
1
1
x
y
x
có đồ thị
H
và đường thẳng
: 2
d y x m
. Tìm các giá trị
của
m
để đường thẳng
d
cắt
H
tại hai điểm phân biệt
A
và
B
sao cho độ dài đoạn
AB
ngắn nhất?
A.
1 2
m
. B.
1
m
. C.
0
m
. D.
2
m
.
Câu 23. [2D2-1] Trong các biểu thức sau, biểu thức nào có nghĩa?
A.
5
2
. B.
1
3
8
. C.
3
4
5
. D.
3
0
.
Câu 24. [2D2-2] Các giá trị của
x
thỏa mãn đẳng thức
1
4
4
x x
là
A.
0
x
. B.
0
x
.
C.
0
x
. D. Không có giá trị nào.
Câu 25. [2D2-2] Biến đổi thành dạng lũy thừa với số mũ hữu tỉ của biểu thức
2002
2003
2017
...
a
(với
0
a
) là
A.
1
2017
a
. B.
2001!
2017 !
a
. C.
2002
2017
a
. D.
2002
2017 !
a
.
Câu 26. [2D2-3] Giá trị của biểu thức
log tan1 log tan 2 log tan3 ... log tan89
là
A.
1
. B.
0
. C. Không xác định. D.
44
.
Câu 27. [2D2-3] So sánh giá trị của biểu thức
2 3 2017
log 3.log 4...log 2018
P và
2
1 log 1009
Q ta có:
A.
P Q
. B.
P Q
.
C.
P Q
. D. Không so sánh được.
Câu 28. [2D2-2] Các giá trị của
x
thỏa mãn
2
1
2
log 5 7 0
x x
là
A.
2 3
x
. B.
2
x
hoặc
3
x
. C.
3
x
. D.
2
x
.
Câu 29. [2D2-2] Biểu thức
2
2 2
ln log e ln log e
a a
A a a được đơn giản thành
A.
2
. B.
2
2ln 2
a
. C.
2
ln 2
a
. D.
2
5ln 2
a
.
Câu 30. [2D2-3] Cho hai số dương
a
và
b
. Đặt
2
e e
e ;
2
a b
a b
X Y
. Khi đó:
A.
X Y
. B.
X Y
. C.
X Y
. D.
X Y
.
Câu 31. [2D2-2] Tập xác định của hàm số:
2016
2
1y x
là
A.
. B.
; 1 1;
.
C.
1;1
. D.
\ 1;1
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/24
Câu 32. [2D2-2] Tập xác định của hàm số:
1
2
2017
2y x x là
A.
; 1 2;
. B.
; 1 2;
. C.
1;2
. D.
\ 1;2
.
Câu 33. [2D2-2] Hàm số
2
e
x
y x
đồng biến trong khoảng
A.
;0
. B.
2;
. C.
0;2
. D.
;
.
Câu 34. [2D2-1] Cho
0 1
a
. Khẳng định nào dưới đây là đúng:
A.
1 0
x
a x
. B.
1 0
x
a x
. C.
1 0
x
a x
. D.
1 0 1
x
a x
.
Câu 35. [2D2-1] Cho
1
x
. Khẳng định nào dưới đây là đúng:
A.
log 0 0;1
a
x a . B.
log 0 0
a
x a
.
C.
log 0 0 1
a
x a
. D.
log 0 1
a
x a
.
Câu 36. [2D2-2] Đạo hàm của hàm số
ln 1
y x x
là
A.
ln 1
x
. B.
ln
x
. C.
1
1
x
. D.
1
.
Câu 37. [2D2-4] Một xe máy điện trị giá
10
triệu được bán trả góp
11
lần, mỗi lần trả góp với số tiền là
1
triệu (lần đầu trả sau khi nhận xe được một tháng). Tính lãi suất tiền hàng tháng?
A. 1,62%/
tháng
. B. t2,1% /
háng
. C. t1,1%/
háng
. D. 1,922%/
tháng
.
Câu 38. [2H1-2] Cho
H
là khối chóp tứ giác đều có tất cả các cạnh bằng
a
. Thể tích của
H
bằng
A.
3
3
a
. B.
3
2
6
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Câu 39. [2H1-2] Cho hình hộp chữ nhật
.
ABCD A B C D
. Gọi
E
,
F
lần lượt thuộc cạnh
BB
,
DD
sao cho
1
2
BE EB
,
1
2
DF FD
. Mặt phẳng
AEF
cắt cạnh
CC
tại
K
và chia khối hộp
thành hai khối đa diện là
A. Khối đa diện
A B C D AEKF
và khối đa diện
BCDEKF
.
B. Khối đa diện
A B C D AEKF
và khối đa diện
ABCDEKF
.
C. Khối đa diện
A B C D EKF
và khối đa diện
ABCDEKF
.
D. Khối đa diện
A B C D AEKF
và khối đa diện
ACDEKF
.
Câu 40. [2H1-2] Đáy của một hình hộp đứng là một hình thoi có đường chéo nhỏ bằng
d
và góc nhọn
bằng
. Diện tích của mặt bên bằng
S
. Thể tích của hình hộp đã cho là
A.
cos
2
dS
. B.
sin
2
dS
. C.
1
sin
2
dS
. D.
sin
dS
.
Câu 41. [2H1-3] Cho hình chóp đều
.
S ABCD
. Người ta tăng cạnh đáy của hình chóp lên
k
lần nhưng
muốn giữ nguyên thể tích. Khi đó tỉ số tan của góc giữa cạnh bên và mặt phẳng đáy của hình
chóp đều
.
S ABCD
và hình chóp sau khi tăng cạnh đáy là
A.
3
k
. B.
2
k
. C.
1
. D.
2
.
Câu 42. [2H2-2] Cho hình lập phương
.
ABCD A B C D
cạnh
a
. Tâm và bán kính của mặt cầu đi qua
8
đỉnh của hình lập phương là
A.
2
a
. B.
3
2
a
. C.
2
2
a
. D.
5
2
a
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/24
Câu 43. [2H2-2] Cho ba điểm
A
,
B
,
C
nằm trên mặt cầu, biết rằng góc
ACB
bằng
90
. Trong các
khẳng định sau, khẳng định nào đúng?
A. Có
AB
là một đường kính của mặt cầu.
B. Tam giác
ABC
vuông cân tại
C
.
C. Mặt phẳng
ABC
cắt mặt cầu theo giao tuyến là một đường tròn lớn.
D. Luôn có một đường tròn nằm trên mặt cầu ngoại tiếp tam giác
ABC
.
Câu 44. [2H2-4] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
1
, mặt bên
SAB
là tam giác
đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích
V
của khối cầu ngoại tiếp
hình chóp là
A.
5 15
18
. B.
5 15
54
. C.
4 3
27
. D.
5
3
.
Câu 45. [2H2-1] Cho mặt cầu
;
S I R
và mặt phẳng
.
P
Giả sử
d
là khoảng cách từ tâm
I
của mặt
cầu đến mặt phẳng
.
P
Biết mặt phẳng
P
tiếp xúc mặt cầu. Khẳng định nào sau đây đúng?
A.
2
d R
. B.
R d
. C.
2
d R
. D.
3 3
0
d R
.
Câu 46. [2H2-3] Một mặt cầu
S
ngoại tiếp một hình lập phương cạnh là
3 cm
. Một mặt phẳng
P
cách tâm
I
của hình lập phương một khoảng
1cm
cắt mặt cầu
S
theo một đường tròn. Diện
tích của hình tròn bằng
A.
2
3
. B.
3
5
. C.
5
. D.
5
4
.
Câu 47. [2H2-3] Một khối cầu bán kính bằng
5
dm người ta cắt bỏ hai đầu bằng mặt phẳng vuông góc
với đường kính của khối cầu và cách tâm một khoảng bằng
4
dm để làm một chiếc lu đựng
nước. Tính thể tích của cái lu.
A.
3
500
dm
3
. B.
3
dm
1
22
5
96
. C.
3
952
dm
27
. D.
3
472
dm
3
.
Câu 48. [2H2-3] Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
B
biết
AB BC a
,
2
AD a
,
SA ABCD
và
SA
2
a
. Gọi
E
là trung điểm của
AD
. Kẻ
EK
SD
tại
K
.
Bán kính mặt cầu đi qua sáu điểm
S
,
A
,
B
,
C
,
E
,
K
bằng
A.
a
. B.
3
2
a
. C.
1
2
a
. D.
6
2
a
.
Câu 49. [2H2-4] Một hình chóp tứ giác đều có cạnh đáy bằng
a
và cạnh bên bằng
2
x
. Điều kiện cần
và đủ của
x
để tâm mặt cầu ngoại tiếp hình chóp ở ngoài hình chóp là
A.
2
2 2
a a
x
. B.
2
2 2
a a
x
. C.
2
a
x
. D.
2
a
x
.
Câu 50. [2H2-3] Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp
. .
S ABCD
A.
21
6
a
. B.
21
3
a
. C.
2 21
6
a
. D.
21
6
a
.
----------HẾT----------
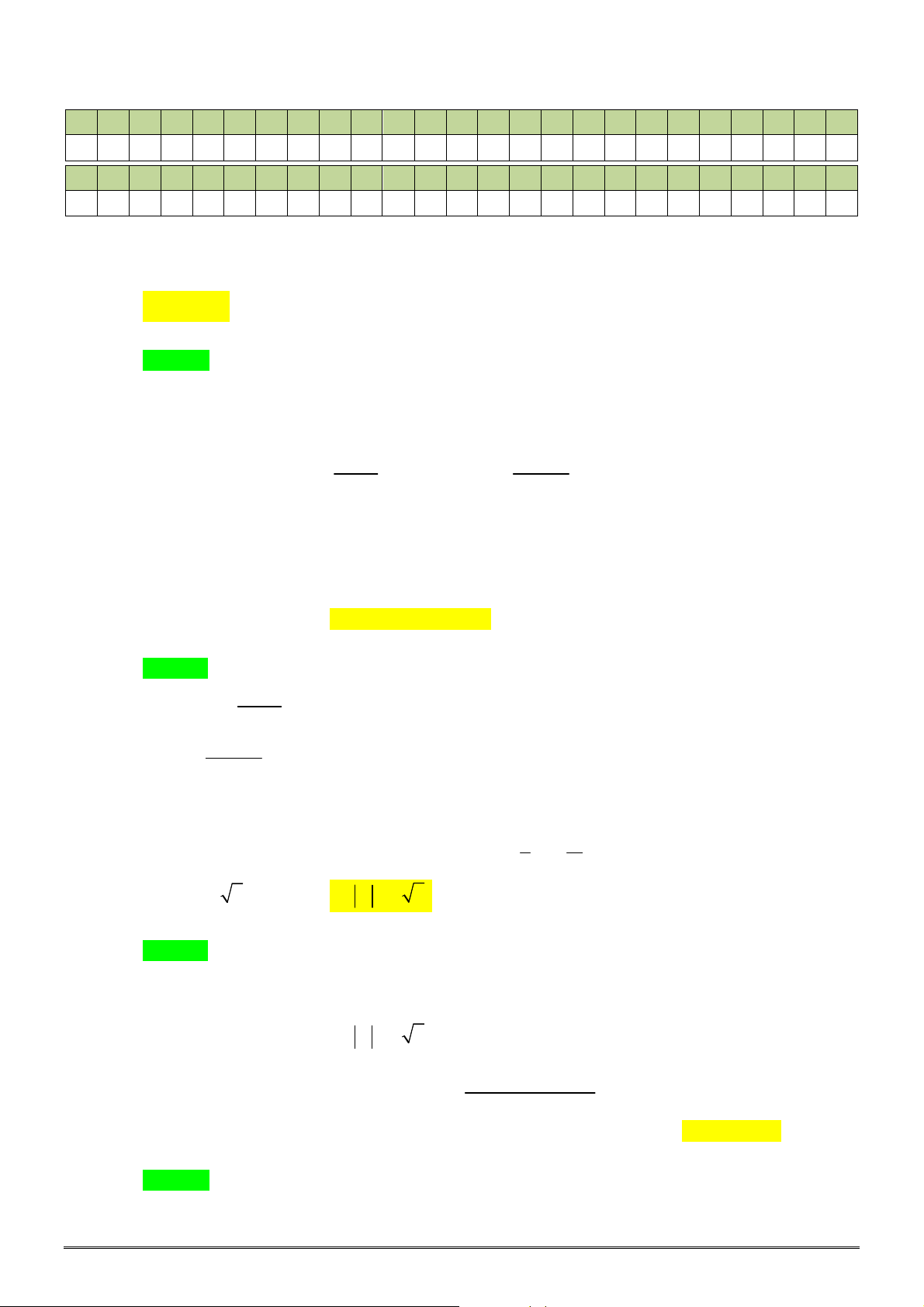
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/24
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
B B D
C
D
D
D
A
B
B D
B B B C
D
B A
B A
D
C
A
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B C
A
B D
D
A
C
C
D
B A
B B A
A
B D
B D
D
D
A
B D
HƯỚNG DẪN GIẢI
Câu 1. [2D1-1] Cho hàm số
4 2
5 2
y x x
. Hàm số nghịch biến trên khoảng nào?
A.
0;
. B.
1;1
. C.
0;1
. D.
;0
.
Lời giải
Chọn A.
Ta có:
3 2
4 10 2 2 5
y x x x x
. Xét
2
0 2 2 5 0 0.
y x x x
Ta có:
0 0
y x
.
Câu 2. [2D1-1] Cho hàm số
2 1
1
x
y
x
có đạo hàm
2
3
0, 1
1
y x
x
. Có hai học sinh phát biểu
như sau:
Học sinh
X
: “ Hàm số luôn nghịch biến trên tập xác định”
Học sinh
Y
: “ Hàm số luôn nghịch biến trên từng khoảng xác định”.
Phát biểu nào đúng, phát biểu nào sai?
A.
X
đúng và
Y
sai. B.
X
sai và
Y
đúng. C.
X
và
Y
đều đúng. D.
X
và
Y
đều sai.
Lời giải
Chọn B.
Hàm số
2 1
1
x
y
x
. TXĐ:
\ 1
D
.
Có
2
3
0, 1
1
y x
x
hàm số nghịch biến trên khoảng
;1
và
1;
hay nghịch
biến trên từng khoảng xác định.
Câu 3. [2D1-2] Với các giá trị nào của
m
thì hàm số
3 2
1
2 1
3 2
m
y x x x
luôn đồng biến trên
?
A.
2 2
m
. B.
2 2
m . C. Không có
m
. D.
2
m
.
Lời giải
Chọn B.
Ta có:
2
2
y x mx
. Để hàm số luôn đồng biến trên
thì
0
y
với
x
.(Dấu
' '
xảy ra
tại hữu hạn điểm trên
)
ĐK:
2
0 8 0 2 2
m m .
Câu 4. [2D1-2] Tìm các giá trị của
m
để hàm số
1 2 2
m x m
y
x m
nghịch biến trên khoảng
1;
?
A.
1
m
. B.
2
m
. C.
1
m
hoặc
2
m
. D.
1 2
m
.
Lời giải
Chọn D.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/24
TXĐ:
\
D m
. Ta có
2
2
2
,
m m
y
x m
để hàm số nghịch biến thì
2
2
2
2
0 0 2 0 1 2
m m
y m m m
x m
.
Suy ra hàm số nghịch biến trên khoảng
;
m
và
;m
.Để hàm số nghịch biến trên
khoảng
1;
thì
1 1
m m
. Vậy
1 2
m
.
Câu 5. [2D1-1] Trong các khẳng định sau về hàm số
4 2
1 1
x 3
4 2
y x
. Khẳng định nào đúng:
A. Hàm số có điểm cực tiểu là
0
x
. B. Hàm số có hai điểm cực đại là
1
x
.
C. Cả
A
và
B
đều đúng. D. Có
A
đúng,
B
sai.
Lời giải
Chọn C.
Ta có:
3 2
1
y x x x x
. Xét
2
0
0 1 0
1
x
y x x
x
Ta có bảng biến thiên:
Vậy hàm số có điểm cực tiểu là
0
x
và có hai điểm cực đại là
1
x
.
Câu 6. [2D1-2] Cho hàm số
3
2
y x x
. Hệ thức liên hệ giữa giá trị cực đại
Đ
C
y
và giá trị cực tiểu
CT
y
là
A. 2
CT C
Đ
y y
. B.
2
C C
Đ
T
y y
. C.
CT C
Đ
y y
. D.
Đ
CT C
y y
.
Lời giải
Chọn D.
Ta có:
2
3 2
y x
. Xét
2
6
0 3 2 0
3
y x x
.
6
y x
hàm số đại cực đại tại
6
3
x
và đạt cực tiểu tại
6
3
x .
Suy ra:
6 4 6
3 9
ĐC
y y
và
6 4 6
3 9
CT CT C
Đ
y y y y
.
Câu 7. [2D1-2] Giá trị của
m
để hàm số
3 2 2
1
1 1
3
y x mx m m x
đạt cực tiểu tại điểm
1
x
là
A.
1
. B.
2
. C.
3
. D. Không có
m
.
Lời giải
Chọn D.
x
1
0
1
y
0
0
0
y
11
4
3
11
4

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/24
Ta có:
2 2
2 1, 2 2
y x mx m m y x m
. Để hàm có đạt cực tiểu tại điểm
1
x
thì
2
1
1 0
3 2 0
2
2 2 0
1 0
1
m
y
m m
m
m
y
m
không có giá trị của
m
.
Câu 8. [2D1-2] Giá trị của
m
để hàm số
4 2
1 1 2
y mx m x m
chỉ có đúng một cực trị là
A.
1
m
. B.
0
m
. C.
0 1
m
. D.
0
m
hoặc
1
m
.
Lời giải
Chọn D.
Ta có:
3 2
4 2 1 2 2 1
y mx m x x mx m
. Để hàm số chỉ có đúng một cực trị thì
0
y
2
2 2 1 0
x mx m
có đúng một nghiệm nên phương trình
2
2 1 0
mx m
vô
nghiệm hoặc có nghiệm
1
0 2 . 1 0
0
m
x m m
m
.
Câu 9. [2D1-1] Cho hàm số
3 2
3x 3
y x
xác định trên
1;3
. Gọi
M,m
lần lượt là giá trị lớn nhất
và nhỏ nhất của hàm số thì
M + m
bằng
A.
2
. B.
4
. C.
6
. D.
8
.
Lời giải
Chọn A.
Ta có:
2
3 6
y x x
. Xét
2
0
0 3 6 0
2
x
y x x
x
.
Suy ra:
2 1, 1 1, 3 3 3, 1 2
y y y M m M m
.
Câu 10. [2D1-2] Giá trị nhỏ nhất của hàm số
2
4
y x x
trên
1;2
là
A.
1;2
min 0
y
. B.
1;2
min 3 1
y
. C.
1;2
min 2 2
y
. D.
1;2
min 2
y
.
Lời giải
Chọn B.
TXĐ:
2;2
D
Ta có:
2
1
4
x
y
x
. Xét
2
2 2
2
0
0 1 0 4
4
4
x
x
y x x
x x
x
0
2
2
x
x
x
. Ta có:
1 3 1, 2 2 2, 2 2
y y y
. Vậy
1;2
min 3 1
y
.
Câu 11. [2D1-3] Các giá trị của
m
để giá trị lớn nhất của hàm số
2
1
x m m
y
x
trên đoạn
0;1
bằng
5
m
là
A.
11 4 5
2
. B.
11 5 5
2
. C.
11 6 5
2
. D. Không có giá trị nào.
Lời giải
Chọn B.
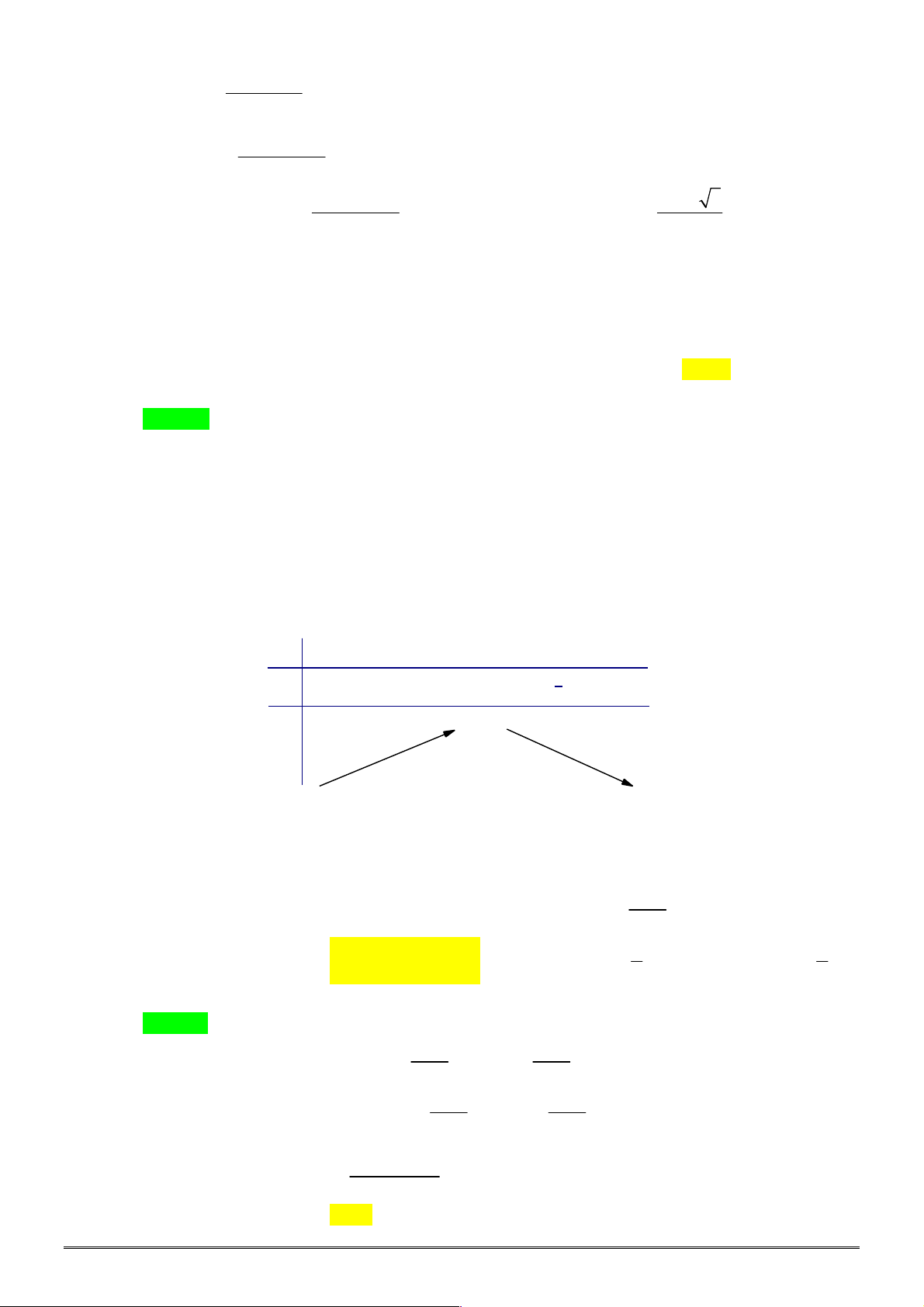
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/24
Ta có
2
2
1
0
1
m m
y
x
hàm số đã cho luôn đồng biến và xác định trên
0;1
.
2
0;1
1
max
2
m m
y
tại
1
x
.
Để
0;1
max 5
y m
2
2
1 11 5 5
5 11 1 0
2 2
m m
m m m m
.
Câu 12. [2D1-3] Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: nếu mỗi đơn vị diện
tích của mặt hồ có
n
con cá thì trung bình mỗi con cá sau một vụ cân nặng
480 20 gam
P n n . Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ
để sau một vụ thu hoạch được nhiều cá nhất.
A.
10
. B.
16
. C.
26
. D.
12
.
Lời giải
Chọn D.
Theo giả thiết: Trọng lượng mỗi con cá trên mỗi đơn vị diện tích sau một vụ là
480 20 ,
P n n
0 24
n .
Nếu trong hồ có
n
con cá thì tổng trọng lượng của chúng là
480 20 gam
T n n n .
Xét hàm số
2
480 20
y x x
, với
0 24
x
. Ta có
480 40
y x
. Cho
0 12 0;24
y x
.
Bảng biến thiên ( Chỉnh đầu mút
trên bbt thành
24
cho em nhé)
2880
12
0
∞
+
+
y
y'
x
0
Vậy
0;24
Max 2880
y tại
12
x
.Vậy phải thả
12
con cá trên một đơn vị diện tích của mặt hồ để
sau một vụ thu hoạch được nhiều cá nhất.
Câu 13. [2D1-1] Phương trình các đường tiệm cận của đồ thị hàm số
3
2
x
y
x
là
A.
1
x
và
2
y
. B.
2
x
và
1
y
. C.
2
x
và
1
2
y
. D.
1
x
và
1
2
y
.
Lời giải
Chọn B.
2
x
là tiệm cận đứng, vì
2 2
3 3
lim ; lim
2 2
x x
x x
x x
.
1
y
là tiệm cận ngang, vì
3 3
lim 1; lim 1
2 2
x x
x x
x x
.
Câu 14. [2D1-2] Đồ thị hàm số
2
2
3 7 6
2 7 3
x x
y
x x
có bao nhiêu đường tiệm cận?
A.
3
. B.
2
. C.
4
. D.
1
.
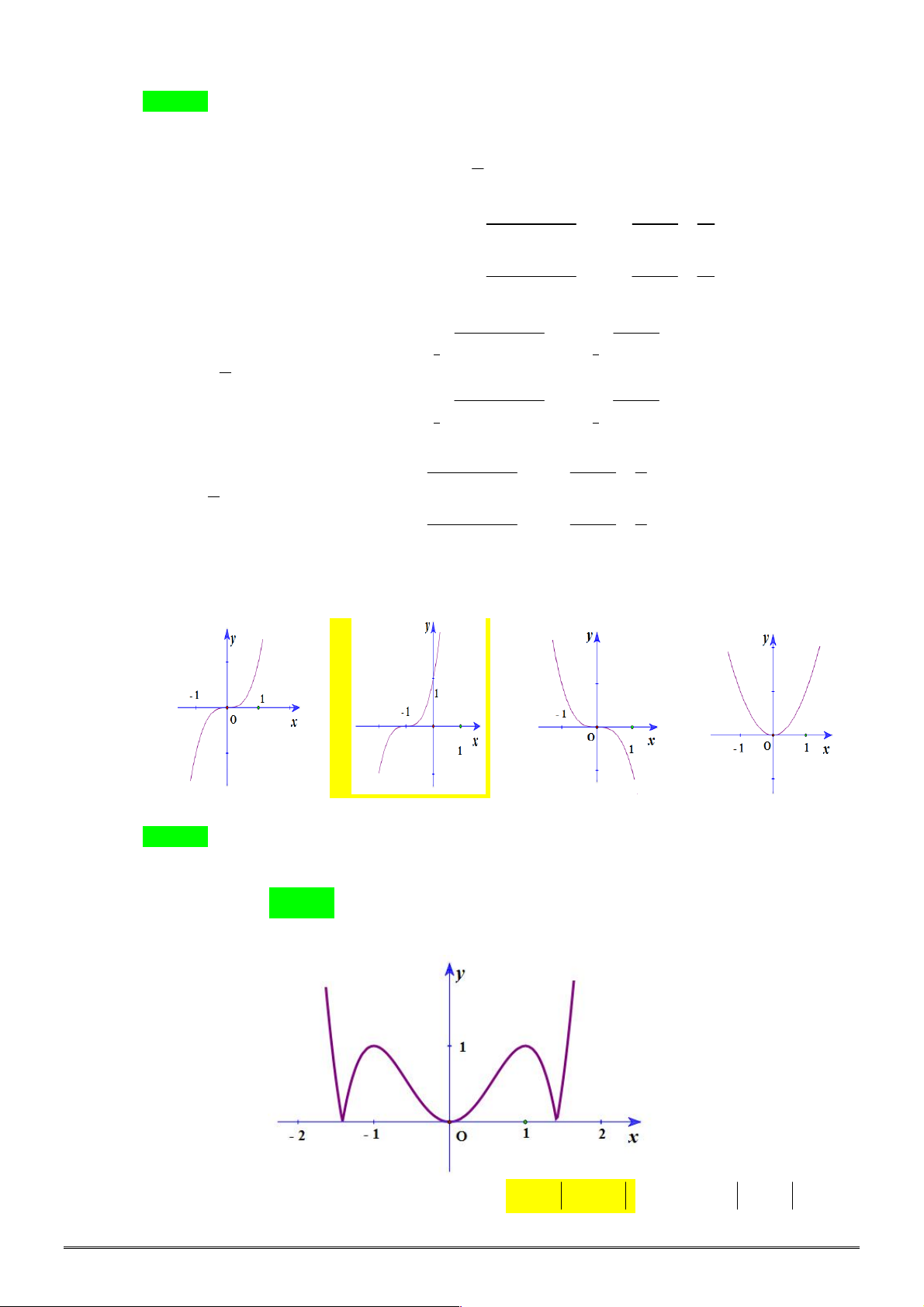
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/24
Lời giải
Chọn B.
Xét phương trình
2
3
2 7 3 0
1
2
x
x x
x
3
x
không là tiệm cận đứng, vì
2
2
3 3
2
2
3 3
3 7 6 3 2 11
lim lim
2 7 3 2 1 5
3 7 6 3 2 11
lim lim
2 7 3 2 1 5
x x
x x
x x x
x x x
x x x
x x x
.
1
2
x
là tiệm cận đứng, vì
2
2
1 1
2 2
2
2
1 1
2 2
3 7 6 3 2
lim lim
2 7 3 2 1
3 7 6 3 2
lim lim
2 7 3 2 1
x x
x x
x x x
x x x
x x x
x x x
.
3
2
y
là tiệm cận đứng, vì
2
2
2
2
3 7 6 3 2 3
lim lim
2 7 3 2 1 2
3 7 6 3 2 3
lim lim
2 7 3 2 1 2
x x
x x
x x x
x x x
x x x
x x x
.
Vậy đồ thị hàm số có 2 đường tiệm cận.
Câu 15. [2D1-2] Hàm số
3 2
3 3 1
y x x x
có đồ thị là hình nào sau đây?
A. . B. . C. . D. .
Lời giải
Chọn B.
Vì lim ; lim
x x
y y
nên loại C và D.
Vì
0 1
y
nên Chọn B.
Câu 16. [2D1-3] Hình bên là đồ thị của hàm số nào sau đây?
A.
4 2
2
y x x
. B.
4 2
2
y x x
. C.
4 2
2
y x x
. D.
3
3
y x x
.
Lời giải
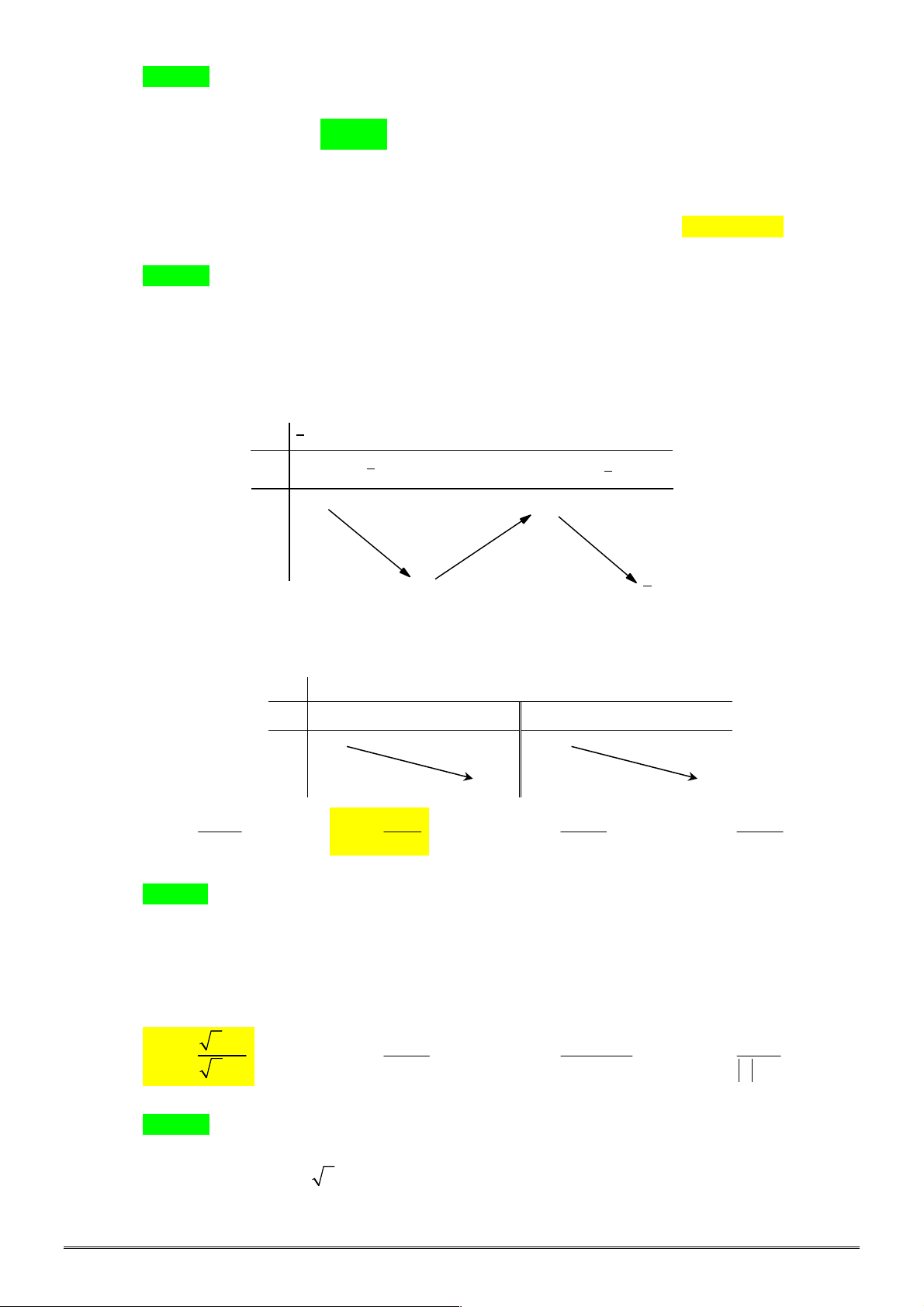
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/24
Chọn C.
Dựa vào đồ thị hàm số, ta thấy 0,y x
nên loại A và B.
Ta thấy,
1 1
y
nên Chọn C.
Câu 17. [2D1-2] Tìm tất cả các giá trị của tham số
m
sao cho phương trình
3 2
3 0
x x m
có ba
nghiệm phân biệt?
A.
0 4
m
. B.
0
m
. C.
4
m
. D.
0 4
m
.
Lời giải
Chọn D.
Ta có
3 2 3 2
3 0 3
x x m x x m
.
Xét hàm số
3 2 2
3 3 6
f x x x f x x x
. Cho
0
0
2
x
f x
x
.
Bảng biến thiên
2
f(
x
)
4
0
0
0
x
f
/
(
x
)
+
∞
+∞
0
∞
+
∞
Từ BBT
Để phương trình đã cho có 3 nghiệm phân biệt
0 4
m
.
Câu 18. [2D1-2] Hàm số nào sau đây không có bảng biến thiên như hình dưới đây?
A.
2 1
2
x
y
x
. B.
3
2
x
y
x
. C.
2 3
2
x
y
x
. D.
2 3
2
x
y
x
.
Lời giải
Chọn B.
Từ BBT
Đồ thị hàm số có tiệm cận đứng là
2
x
và tiệm cận ngang là
2
y
.
Nhận thấy, đáp án A, C, D đều có tiệm cận đứng là
2
x
và tiệm cận ngang là
2
y
.
Đáp án B có tiệm cận đứng là
2
x
và tiệm cận ngang là
1
y
.
Câu 19. [2D1-2] Đồ thị hàm số nào dưới đây có đúng hai đường tiệm cận?
A.
1
1
x
y
x
. B.
2
1
y
x x
. C.
2
5
7
x
y
x x
. D.
1
2
y
x
.
Lời giải
Chọn A.
Xét đáp án A:
Xét phương trình
1 0 1
x x
.
x
2
y
–
–
y
2
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/24
Vì
1 1
1 1
lim ; lim
1 1
x x
x x
x x
đường thẳng
1
x
là tiệm cận đứng của đồ
thị hàm số.
Vì
1
lim 1
1
x
x
x
đường thẳng
1
y
là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số chỉ có 2 đường tiệm cận.
Xét đáp án B:
Xét phương trình
2
0
0
1
x
x x
x
.
Vì
2 2
0 0
1 1
lim ; lim
x x
x x x x
đường thẳng
0
x
là tiệm cận đứng của đồ
thị hàm số.
Vì
2
1
2
1
1
lim
1
lim
x
x
x x
x x
đường thẳng
1
x
là tiệm cận đứng của đồ thị hàm số.
Vì
2 2
1 1
lim 0; lim 0
x x
x x x x
đường thẳng
0
y
là tiệm cận ngang của đồ thị
hàm số.
Vậy đồ thị hàm số chỉ có 3 đường tiệm cận. Loại B.
Xét đáp án C:
Xét phương trình
2
7 0
x x VN
. Do đó đồ thị hàm số không có tiệm cận đứng.
Vì
2
2
5
lim 0
7
5
lim 0
7
x
x
x
x x
x
x x
đường thẳng
0
y
là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số chỉ có 1 đường tiệm cận. Loại C.
Xét đáp án D:
Xét phương trình
2 0
x VN
. Do đó đồ thị hàm số không có tiệm cận đứng.
Vì
1
lim 0
2
1
lim 0
2
x
x
x
x
đường thẳng
0
y
là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số chỉ có 1 đường tiệm cận. Loại D.
Câu 20. [2D1-2] Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số
3 2
1
2 3 5
3
y x x x
A. Song song với đường thẳng
1
x
. B. Song song với trục hoành.
C. Có hệ số góc dương. D. Có hệ số góc bằng
1
.
Lời giải
Chọn B.
Ta có
2
4 3
y x x
. Cho
1
0
3
x
y
x
Dễ thấy
3
x
là điểm cực tiểu của hàm số.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/24
Suy ra
3 0
y
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số song song với trục hoành.
Câu 21. [2D1-2] Phương trình tiếp tuyến của đồ thị hàm số
4 2
2 1
y x x
mà vuông góc với đường
thẳng
8 0
x y
là
A.
8 6
y x
. B.
8 10
y x
. C.
8 6
y x
. D.
8
y x
.
Lời giải
Chọn A.
Vì tiếp tuyến vuông góc với đường thẳng
1
8 0
8
x y y x
suy ra hệ số góc của tiếp
tuyến là
8
k
.
Mà
0
k y x
suy ra
3
0 0 0 0
4 4 8 1 2 1; 2
x x x y M
.
Phương trình tiếp tuyến của đồ thị hàm số tại
1; 2
M
là
8 1 2
y x
hay
8 6
y x
.
Câu 22. [2D1-3] Cho hàm số
1
1
x
y
x
có đồ thị
H
và đường thẳng
: 2
d y x m
. Tìm các giá trị
của
m
để đường thẳng
d
cắt
H
tại hai điểm phân biệt
A
và
B
sao cho độ dài đoạn
AB
ngắn nhất?
A.
1 2
m
. B.
1
m
. C.
0
m
. D.
2
m
.
Lời giải
Chọn D.
Phương trình hoành độ giao điểm:
1
2 1
1
x
x m x
x
1 1 2
x x x m
(vì
1
x
không là nghiệm của phương trình)
2
2 2 1 0 *
x mx m .
Để
d
cắt
H
tại hai điểm phân biệt thì trước hết phương trình
*
phải có hai nghiệm phân
biệt khác
1
2
1 2
2 1 0
1 2
m
m m
m
.
Khi đó
d
cắt
H
tại hai điểm phân biệt
A
và
B
. Giả sử
1 1 2 2
; , ;
A x y B x y
trong đó
1 2
,
x x
là hai nghiệm của phương trình
*
và
1 1
2
y x m
,
2 2
2
y x m
. Theo định lý Vi-et
1 2
1 2
2
. 2 1
x x m
x x m
.
Ta có
2 2 2 2 2
2
1 2 1 2 1 2 2 1 2 1 1
2 4
AB x x y y x x x x x x x x
2 2
2 4 4 2 1 8 2 1
m m m m
.
Xét hàm số
2
2 1
f m m m
, với
;1 2 1 2;m
. Ta có
2 2 0 1
f m m m
.
Bảng biến thiên
m
-2
1 2
1
1 2
f’(m) - - -
0
+
+

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/24
f(m) 0
0
Dựa vào bảng biến thiên của hàm số trên
;1 2 1 2;
và các đáp án của bài suy
ra hàm số đạt GTNN bằng
7
khi
2
m
. Khi đó
2 14
AB
khi
2
m
, từ đó Chọn D.
Bình luận: (Theo quan điểm cá nhân người giải)
Câu này chưa sử dụng giả thiết độ dài đoạn
AB
ngắn nhất, nếu giải theo quan điểm trắc
nghiệm thì ta chỉ cần tới điều kiện
1 2
1 2
m
m
là đã chọn đáp án D nên chỉ dừng lại mức
độ vận dụng thấp.
Học sinh có thể dựa vào BBT và nhầm lẫn GTNN của hàm số đạt tại
1 2
m
và Chọn
A.
Nếu học sinh biến đổi
2
2
8 2 1 8 1 2 16
m m m
và ta kết luận giá trị nhỏ nhất
đạt tại
1
m
thì lưu ý dấu bằng không xảy ra khi
1
m
.
Nếu giải theo quan điểm tự luận thì bài này thuộc loại khó, đáng ở mức độ vận dụng cao.
Câu 23. [2D2-1] Trong các biểu thức sau, biểu thức nào có nghĩa?
A.
5
2
. B.
1
3
8
. C.
3
4
5
. D.
3
0
.
Lời giải
Chọn C.
Đáp án A và B sai vì số mũ không nguyên nên cơ số phải dương, đáp án D sai vì số mũ nguyên
âm nên cơ số khác
0
. Chỉ có biểu thức ở đáp án C có nghĩa.
Câu 24. [2D2-2] Các giá trị của
x
thỏa mãn đẳng thức
1
4
4
x x
là
A.
0
x
. B.
0
x
.
C.
0
x
. D. Không có giá trị nào.
Lời giải
Chọn A.
Vì số mũ là
1
4
(không nguyên) nên cơ số dương suy ra loại đáp án B. Mặt khác đáp án C
không thỏa vì khi đó vế phải âm còn vế trái dương, chỉ có đáp án A thỏa.
Câu 25. [2D2-2] Biến đổi thành dạng lũy thừa với số mũ hữu tỉ của biểu thức
2002
2003
2017
...
a
(với
0
a
) là
A.
1
2017
a
. B.
2001!
2017 !
a
. C.
2002
2017
a
. D.
2002
2017 !
a
.
Lời giải
Chọn B.
Cách 1:
Ta có
2001!
1 1 1 1 1 1 1
20162002
2003
2017 !
2002
2017 2017 2016 2015 2003 2002 2017.2016.2015...2003.20022003
2017
... ...a a a a a
.
Cách 2:

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/24
Đặt
2003
2002 2002
2002
2003 2003 2004
2017 2017 2017
... ... ...
A a A a A a
, cứ thế suy ra
2001!
1
2002.2003....2017
2017 !
2002.2003....2017
2002.2003...2017
A a A a a a .
Câu 26. [2D2-3] Giá trị của biểu thức
log tan1 log tan 2 log tan3 ... log tan89
là
A.
1
. B.
0
. C. Không xác định. D.
44
.
Lời giải
Chọn B.
Ta có:
log tan1 log tan 2 log tan3 ... log tan89 log tan1 .
tan 2 .tan3 ...tan89
log tan1 .tan89 . tan 2 .tan88 ...tan 45 log 1.1..
.1 0
.
Câu 27. [2D2-3] So sánh giá trị của biểu thức
2 3 2017
log 3.log 4...log 2018
P và
2
1 log 1009
Q ta có:
A.
P Q
. B.
P Q
.
C.
P Q
. D. Không so sánh được.
Lời giải
Chọn C.
Áp dụng công thức
log .log log
a b a
b c c
với mọi
,
a b
dương, khác
1
và mọi
0
c
.
Ta có
2 3 2017 2 2
log 3.log 4...log 2018 log 2018 log 2.1009
P
2 2 2
log 2 log 1009 1 log 1009
Q
.
Câu 28. [2D2-2] Các giá trị của
x
thỏa mãn
2
1
2
log 5 7 0
x x
là
A.
2 3
x
. B.
2
x
hoặc
3
x
. C.
3
x
. D.
2
x
.
Lời giải
Chọn A.
Ta có
2
2
1
2
2
5 7 0
log 5 7 0 2 3
2 3
5 7 1
x x x
x x x
x
x x
.
Câu 29. [2D2-2] Biểu thức
2
2 2
ln log e ln log e
a a
A a a được đơn giản thành
A.
2
. B.
2
2ln 2
a
. C.
2
ln 2
a
. D.
2
5ln 2
a
.
Lời giải
Chọn B.
Ta có
2
2 2 2 2 2 2
ln log e ln log e ln 2ln log e log e ln log e
a a a a a
A a a a a a
2 2
2ln 2lne 2ln 2
a a
.
Câu 30. [2D2-3] Cho hai số dương
a
và
b
. Đặt
2
e e
e ;
2
a b
a b
X Y
. Khi đó:
A.
X Y
. B.
X Y
. C.
X Y
. D.
X Y
.
Lời giải
Chọn D.
Ta có
e e 1 1
ln ln e .e lne ln e
ln e .e
2 2 2 2
e e
e e e
2
a b
a b a a
a b
a b
a b
Y e e X
. Dấu đẳng thức xảy ra
khi và chỉ khi
0
a b
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/24
Câu 31. [2D2-2] Tập xác định của hàm số:
2016
2
1y x
là
A.
. B.
; 1 1;
. C.
1;1
. D.
\ 1;1
.
Lời giải
Chọn D.
Theo chú ý sgk- Đại số 12- trang 57:
Tập xác định của hàm số lũy thừa
y x
tùy thuộc vào giá trị của
. Cụ thể,
Với
nguyên dương, tập xác định là
;
Với
nguyên âm hoặc bằng
0
, tập xác định là
\ 0
Với
không nguyên, tập xác định là
0;
.
Hàm số
2016
2
1y x
có
2016
nguyên âm, nên hàm số có nghĩa khi
2
1 0
x
1
x
. Vậy TXĐ:
\ 1;1
D
.
Câu 32. [2D2-2] Tập xác định của hàm số:
1
2
2017
2y x x là
A.
; 1 2;
. B.
; 1 2;
. C.
1;2
. D.
\ 1;2
.
Lời giải
Chọn A.
Hàm số
1
2
2017
2y x x có
1
2017
không nguyên nên
2
1
2 0
2
x
x x
x
. Vậy
TXĐ:
; 1 2;D
.
Câu 33. [2D2-2] Hàm số
2
e
x
y x
đồng biến trong khoảng
A.
;0
. B.
2;
. C.
0;2
. D.
;
.
Lời giải
Chọn C.
Ta có
2 2
e 2 e e
x x x
y x x x
0
e 2 0
2
x
x
x x
x
;
0 0 2
y x
.
Vậy Chọn C.
Câu 34. [2D2-1] Cho
0 1
a
. Khẳng định nào dưới đây là đúng:
A.
1 0
x
a x
. B.
1 0
x
a x
. C.
1 0
x
a x
. D.
1 0 1
x
a x
.
Lời giải
Chọn C.
Với
0 1
a
:
1 0
x
a x
.
Câu 35. [2D2-1] Cho
1
x
. Khẳng định nào dưới đây là đúng:
A.
log 0 0;1
a
x a . B.
log 0 0
a
x a
.
C.
log 0 0 1
a
x a
. D.
log 0 1
a
x a
.
Lời giải
Chọn D.
Ta có
1
x
:
log 0 1
a
x a
.
Câu 36. [2D2-2] Đạo hàm của hàm số
ln 1
y x x
là
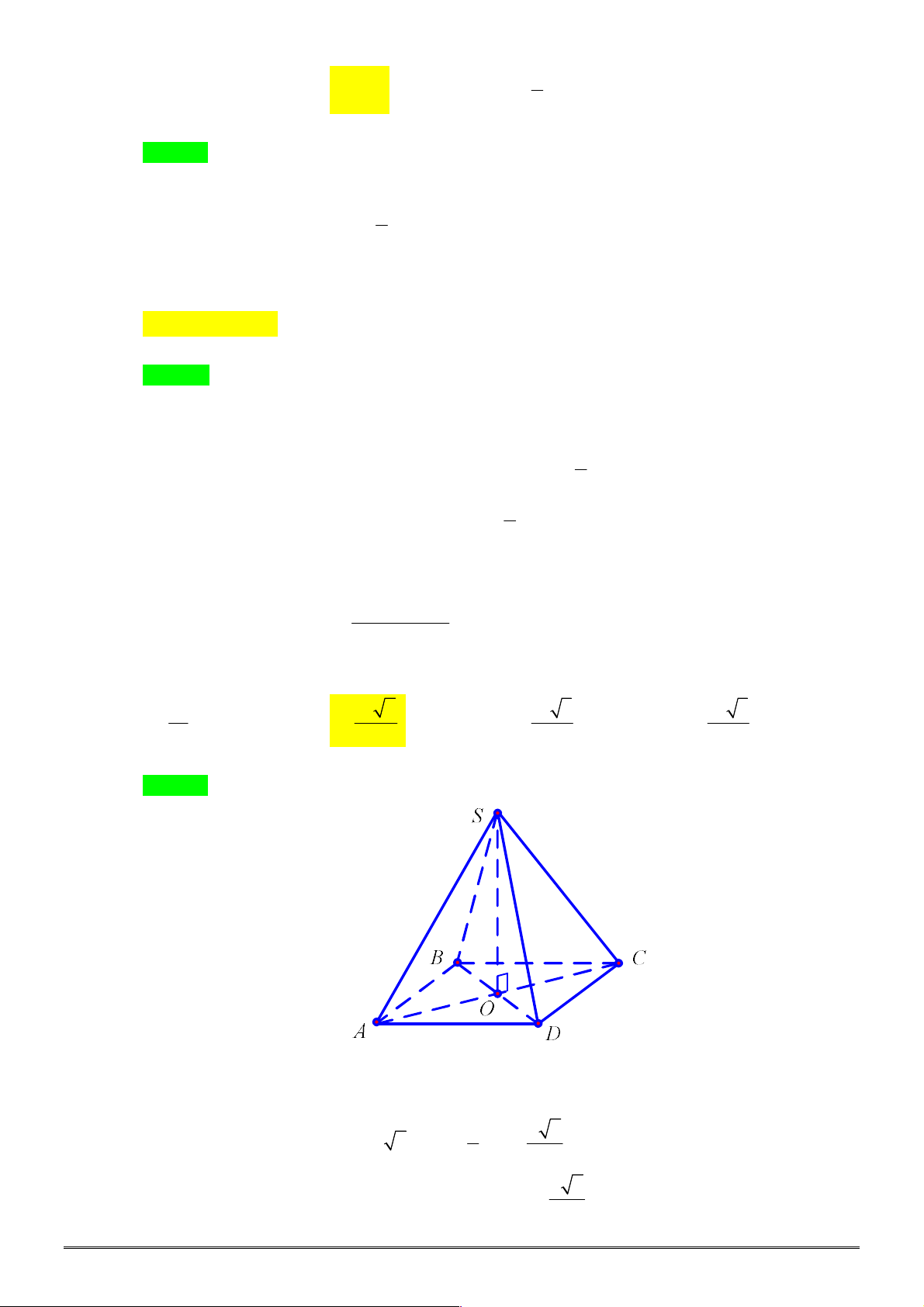
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/24
A.
ln 1
x
. B.
ln
x
. C.
1
1
x
. D.
1
.
Lời giải
Chọn B.
0;D
1
ln 1 ln 1 . ln
y x x x x x
x
.
Câu 37. [2D2-4] Một xe máy điện trị giá
10
triệu được bán trả góp
11
lần, mỗi lần trả góp với số tiền là
1
triệu (lần đầu trả sau khi nhận xe được một tháng). Tính lãi suất tiền hàng tháng?
A. 1,62%/
tháng
. B. t2,1% /
háng
. C. t1,1%/
háng
. D. 1,922%/
tháng
.
Lời giải
Chọn A.
Nếu gọi
:
n
số tháng phải trả,
:
r
là lãi suất hàng tháng,
:
M
số tiền phải trả ban đầu,
i
M
: là số
tiền còn lại phải trả ở tháng thứ
i
,
x
số tiền trả mỗi tháng.
Ta có
1
1
M r M x
;
2 1
1
M r M x
; … ;
1 1
n
n
x
M r
r
Áp dụng công thức lãi kép gửi hàng tháng:
1 1
n
n
x
T r
r
. Tiền giá xe ban đầu sau
11
tháng tăng lên thành
11
11
10000000 1
T r
tương ứng với phương trình sau:
11
11
1 1
1000000 1 1000000 1,62%
r
r r
r
.
Câu 38. [2H1-2] Cho
H
là khối chóp tứ giác đều có tất cả các cạnh bằng
a
. Thể tích của
H
bằng
A.
3
3
a
. B.
3
2
6
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Lời giải
Chọn B.
Vì
H
là khối chóp tứ giác đều có tất cả các cạnh bằng
a
, giả sử
H
là hình chóp
.
S ABCD
như trên. Khi đó
O
là tâm của đáy là hình vuông
ABCD
cạnh
a
,
SO ABCD
.
Ta có
2
ABCD
S a
,
2
AC BD a
,
1 2
2 2
a
OC AC .
Xét tam giác vuông
SOC
:
2 2 2
2
2
a
SO SC OC SO .
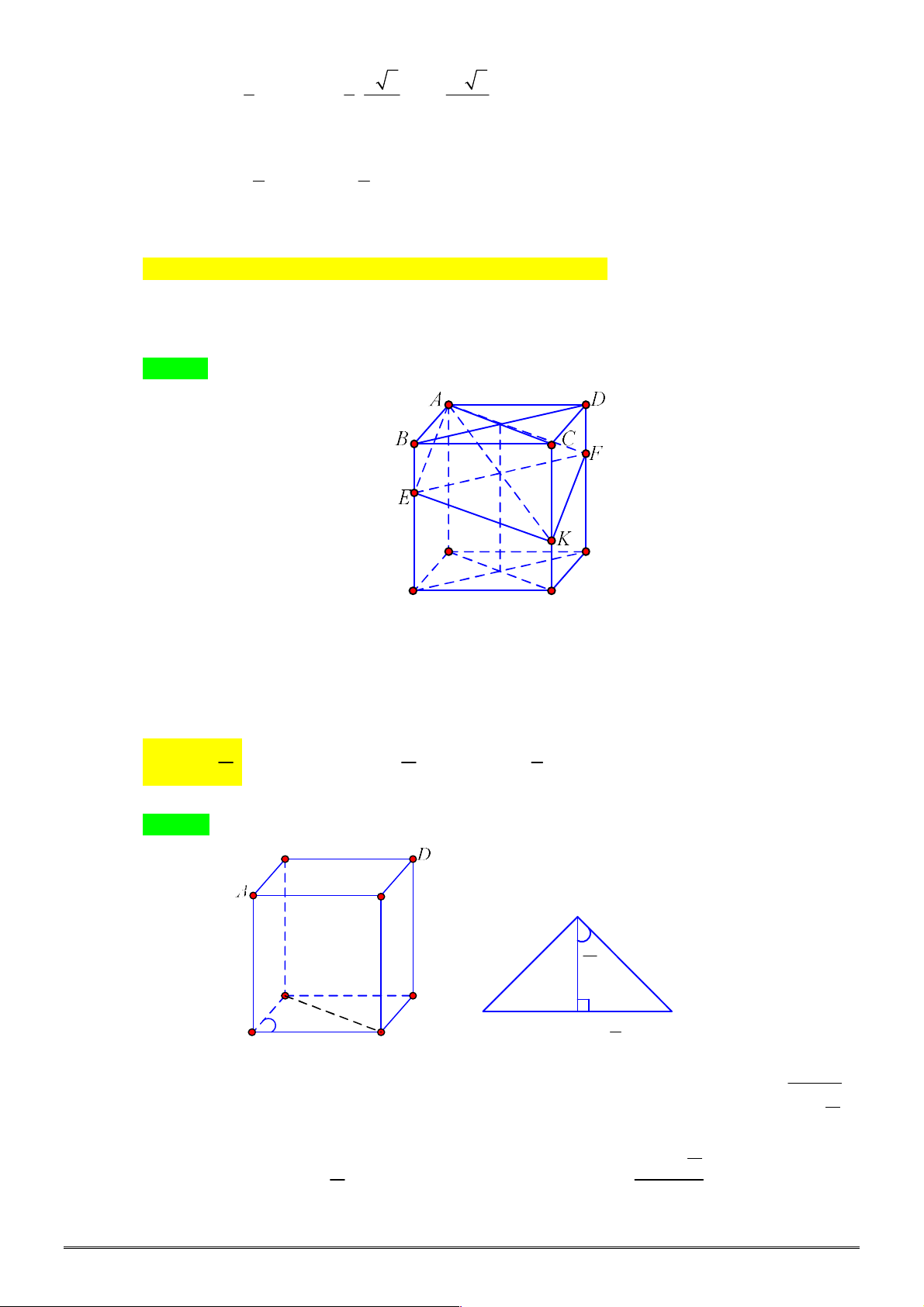
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/24
Do đó
3
2
1 1 2 2
.
3 3 2 6
ABCD
H
a a
V SO S a .
Câu 39. [2H1-2] Cho hình hộp chữ nhật
.
ABCD A B C D
. Gọi
E
,
F
lần lượt thuộc cạnh
BB
,
DD
sao cho
1
2
BE EB
,
1
2
DF FD
. Mặt phẳng
AEF
cắt cạnh
CC
tại
K
và chia khối hộp
thành hai khối đa diện là
A. Khối đa diện
A B C D AEKF
và khối đa diện
BCDEKF
.
B. Khối đa diện
A B C D AEKF
và khối đa diện
ABCDEKF
.
C. Khối đa diện
A B C D EKF
và khối đa diện
ABCDEKF
.
D. Khối đa diện
A B C D AEKF
và khối đa diện
ACDEKF
.
Lời giải
Chọn B.
A
B
C
D
Mặt phẳng
AEF
chia hình hộp chữ nhật
.
ABCD A B C D
thành hai khối đa diện
A B C D AEKF
và khối đa diện
ABCDEKF
.
Câu 40. [2H1-2] Đáy của một hình hộp đứng là một hình thoi có đường chéo nhỏ bằng
d
và góc nhọn
bằng
. Diện tích của mặt bên bằng
S
. Thể tích của hình hộp đã cho là
A.
cos
2
dS
. B.
sin
2
dS
. C.
1
sin
2
dS
. D.
sin
dS
.
Lời giải
Chọn A.
A
B
C
D
S
d
2
2
d
B
C
A
Giả sử hình hộp đứng cho như hình vẽ trên. Ta có cạnh đáy hình thoi là
2sin
2
d
B C C D
,
đường chéo
cot
2
B D d
. Chiều cao của hình hộp đứng
.2sin
2
S
DD
d
.
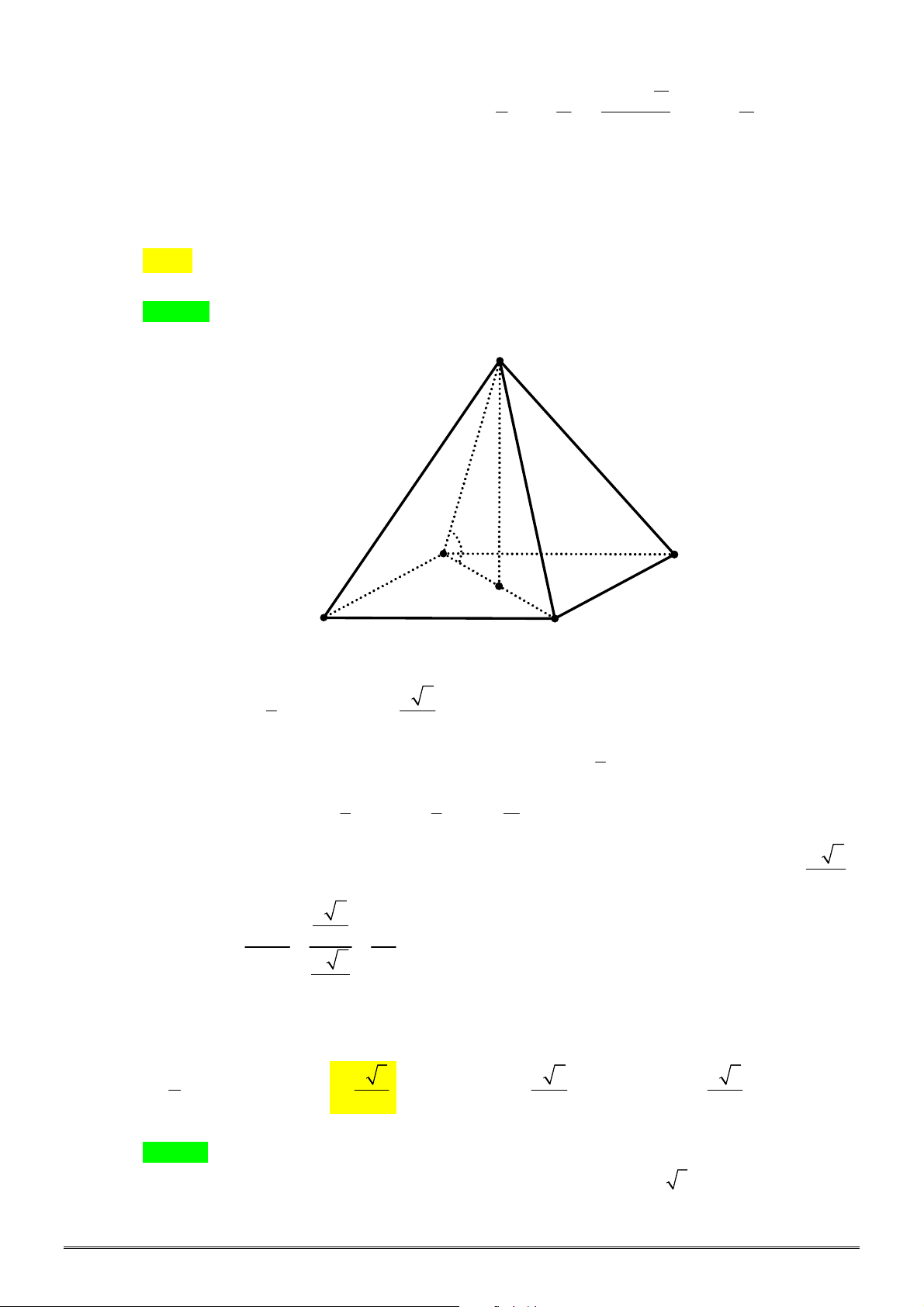
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/24
Vậy thể tích hình hộp đứng:
.2sin
1
2
. cot cos
2 2 2
A B C D
S
V S DD d d dS
d
.
Câu 41. [2H1-3] Cho hình chóp đều
.
S ABCD
. Người ta tăng cạnh đáy của hình chóp lên
k
lần nhưng
muốn giữ nguyên thể tích. Khi đó tỉ số tan của góc giữa cạnh bên và mặt phẳng đáy của hình
chóp đều
.
S ABCD
và hình chóp sau khi tăng cạnh đáy là
A.
3
k
. B.
2
k
. C.
1
. D.
2
.
Lời giải
Chọn A.
a
h
α
C
A
D
B
S
Gọi
là góc giữa cạnh bên và mặt đáy của hình chóp.
Ta có:
2
.
1
.
3
S ABCD
V a h
và
2
tan
h
a
Sau khi tăng cạnh đáy hình chóp lên
k
lần ta có:
2
.
1
.
3
S A B C D
V ka h
.
Vì thể tích không đổi nên
2
2 2
1 1
. .
3 3
h
ka h a h k
h
,
Gọi
là góc giữa cạnh bên và mặt đáy của hình chóp sau khi tăng cạnh khi đó
2
tan
h
ka
.
Từ đó suy ra
3
2
tan .
tan
2
h
k h
a
k
h
h
ka
.
Câu 42. [2H2-2] Cho hình lập phương
.
ABCD A B C D
cạnh
a
. Tâm và bán kính của mặt cầu đi qua
8
đỉnh của hình lập phương là
A.
2
a
. B.
3
2
a
. C.
2
2
a
. D.
5
2
a
.
Lời giải
Chọn B.
Hình lập phương
.
ABCD A B C D
cạnh
a
nên có đường chéo bằng
3
a
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/24
Mặt cầu đi qua
8
đỉnh của hình lập phương nên là mặt cầu ngoại tiếp của hình lập phương nên
mặt cầu có tâm là trung điểm của
AC
và bán kính
3
2
a
R .
Câu 43. [2H2-2] Cho ba điểm
A
,
B
,
C
nằm trên mặt cầu, biết rằng góc
ACB
bằng
90
. Trong các
khẳng định sau, khẳng định nào đúng?
A. Có
AB
là một đường kính của mặt cầu.
B. Tam giác
ABC
vuông cân tại
C
.
C. Mặt phẳng
ABC
cắt mặt cầu theo giao tuyến là một đường tròn lớn.
D. Luôn có một đường tròn nằm trên mặt cầu ngoại tiếp tam giác
ABC
.
Lời giải
Chọn D.
I
B
C
A
Câu 44. [2H2-4] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
1
, mặt bên
SAB
là tam giác
đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích
V
của khối cầu ngoại tiếp
hình chóp là
A.
5 15
18
. B.
5 15
54
. C.
4 3
27
. D.
5
3
.
Lời giải
Chọn B.
d
O
G
H
S
I
B
C
A
Gọi
H
là trung điểm của
AB
. Suy ra
SH ABC
.
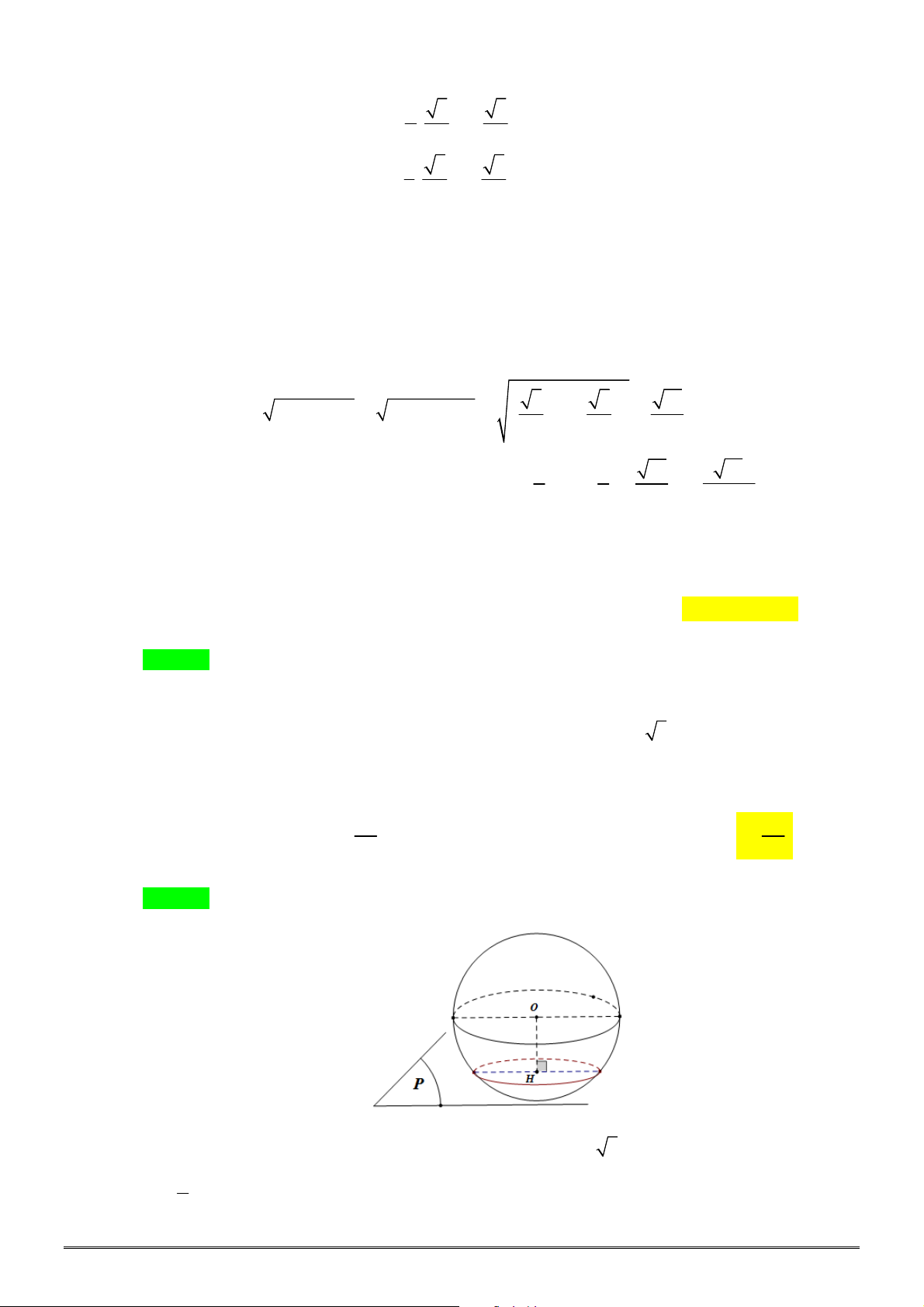
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/24
Gọi
,
O G
lần lượt là trọng tâm tam giác
,
ABC
SAB
.
Trong tam giác đều
ABC
có
2 3
. .1
3 2
OB
3
3
.
Trong tam giác đều
SAB
có
1 3
. .1
3 2
GH
3
6
.
Gọi
d
là đường thẳng đi qua
O
và song song với
SH
.
Khi đó
d
là trục của đường tròn ngoại tiếp tam giác
ABC
.
Trong
SHO
gọi
I
là giao của đường thẳng
d
với đường thẳng đi qua
G
và song song với
CH
.
Do
CH SAB
IG SAB
nên
IG
là trục của đường tròn ngoại tiếp tam giác
SAB
.
Do đó
I
là tâm mặt cầu ngoại tiếp hình chóp
.
S ABC
.
Ta có
R IB
2 2
OI OB
2 2
GH OB
2 2
3 3
3 6
15
6
.
Suy ra thể tích khối cầu ngoại tiếp hình chóp là
3
4
3
V R
3
4 15
3 6
5 15
54
.
Câu 45. [2H2-1] Cho mặt cầu
;
S I R
và mặt phẳng
.
P
Giả sử
d
là khoảng cách từ tâm
I
của mặt
cầu đến mặt phẳng
.
P
Biết mặt phẳng
P
tiếp xúc mặt cầu. Khẳng định nào sau đây đúng?
A.
2
d R
. B.
R d
. C.
2
d R
. D.
3 3
0
d R
.
Lời giải
Chọn D.
Do
P
tiếp xúc mặt cầu nên
3 3
0
d R d R
.
Câu 46. [2H2-3] Một mặt cầu
S
ngoại tiếp một hình lập phương cạnh là
3 cm
. Một mặt phẳng
P
cách tâm
I
của hình lập phương một khoảng
1cm
cắt mặt cầu
S
theo một đường tròn. Diện
tích của hình tròn bằng
A.
2
3
. B.
3
5
. C.
5
. D.
5
4
.
Lời giải
Chọn D.
Mặt cầu
S
ngoại tiếp một hình lập phương cạnh là
3 cm
nên bán kính mặt cầu là
3
cm.
2
R
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/24
Bán kính của đường tròn thiết diện:
2 2
9 5
1
4 2
r R d
Diện tích của hình tròn cần tìm là
2
5
4
S r
Câu 47. [2H2-3] Một khối cầu bán kính bằng
5
dm người ta cắt bỏ hai đầu bằng mặt phẳng vuông góc
với đường kính của khối cầu và cách tâm một khoảng bằng
4
dm để làm một chiếc lu đựng
nước. Tính thể tích của cái lu.
A.
3
500
dm
3
. B.
3
dm
1
22
5
96
. C.
3
952
dm
27
. D.
3
472
dm
3
.
Lời giải
Chọn D.
Tính thể tích
V
của lu bằng thể tích khối cầu bán kính
5 dm
R
- thể tích của hai chỏm cầu có
bán kính
3dm
r
, chiều cao
1 dm
h
.
Suy ra
3
3
2
4 472
2
3 3 3
dm
R h
h
V R
Câu 48. [2H2-3] Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
B
biết
AB BC a
,
2
AD a
,
SA ABCD
và
SA
2
a
. Gọi
E
là trung điểm của
AD
. Kẻ
EK
SD
tại
K
.
Bán kính mặt cầu đi qua sáu điểm
S
,
A
,
B
,
C
,
E
,
K
bằng
A.
a
. B.
3
2
a
. C.
1
2
a
. D.
6
2
a
.
Lời giải
Chọn A.
Ta thấy
;
AB BC AE EC a
; ;
SA ABCD SA AC SB BC SE EC
Ta có:
1
SD EK
Lại có:
2
CE AD
CE SAD CE SD
CE SA
Từ
1
2
:
SD EKC SK KC
R
h
r
S
A
B
C
E
O
D
K
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 23/24
Suy ra 4 điểm
A
,
B
,
E
,
K
cùng nhìn
SC
dưới 1 góc
90
nên mặt cầu đi qua sáu điểm
S
,
A
,
B
,
C
,
E
,
K
có tâm là trung điểm
SC
và bán kính
2
SC
a
.
Câu 49. [2H2-4] Một hình chóp tứ giác đều có cạnh đáy bằng
a
và cạnh bên bằng
2
x
. Điều kiện cần
và đủ của
x
để tâm mặt cầu ngoại tiếp hình chóp ở ngoài hình chóp là
A.
2
2 2
a a
x
. B.
2
2 2
a a
x
. C.
2
a
x
. D.
2
a
x
.
Lời giải
Chọn B.
O
N
M
D
C
B
A
S
Gọi
O
là giao điểm của
AC
và
,
BD SO
là trục đường tròn ngoại tiếp hình vuông
.
ABCD
Trong mặt phẳng
SAO
dựng trung trực của
SA
cắt
SA
tại
M
cắt
SO
tại
N
thì
N
là tâm
mặt cầu ngoại tiếp hình chóp
.
S ABCD
bán kính
R SN
.
Nhận xét:
2
2 2 2
4 0
2
a
SO SA AO x
1
2 2
a
x
Xét tam giác
SMN
và tam giác
SAO
là 2 tam giác đồng dạng, ta có
2
.
2
SN SM SA SM SA
SN
SA SO SO SO
.
Điều kiện cần và đủ để tâm mặt cầu ngoại tiếp hình chóp ở ngoài hình chóp là
2
2 2
2
2
SA
SO SA SO
SO
2
2 2
4 2 4
2
a
x x
0 2
2
a
x
Từ
1
và
2
suy ra
2
2 2
a a
x
.
Câu 50. [2H2-3] Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp
. .
S ABCD
A.
21
6
a
. B.
21
3
a
. C.
2 21
6
a
. D.
21
6
a
.
Lời giải
Chọn D.
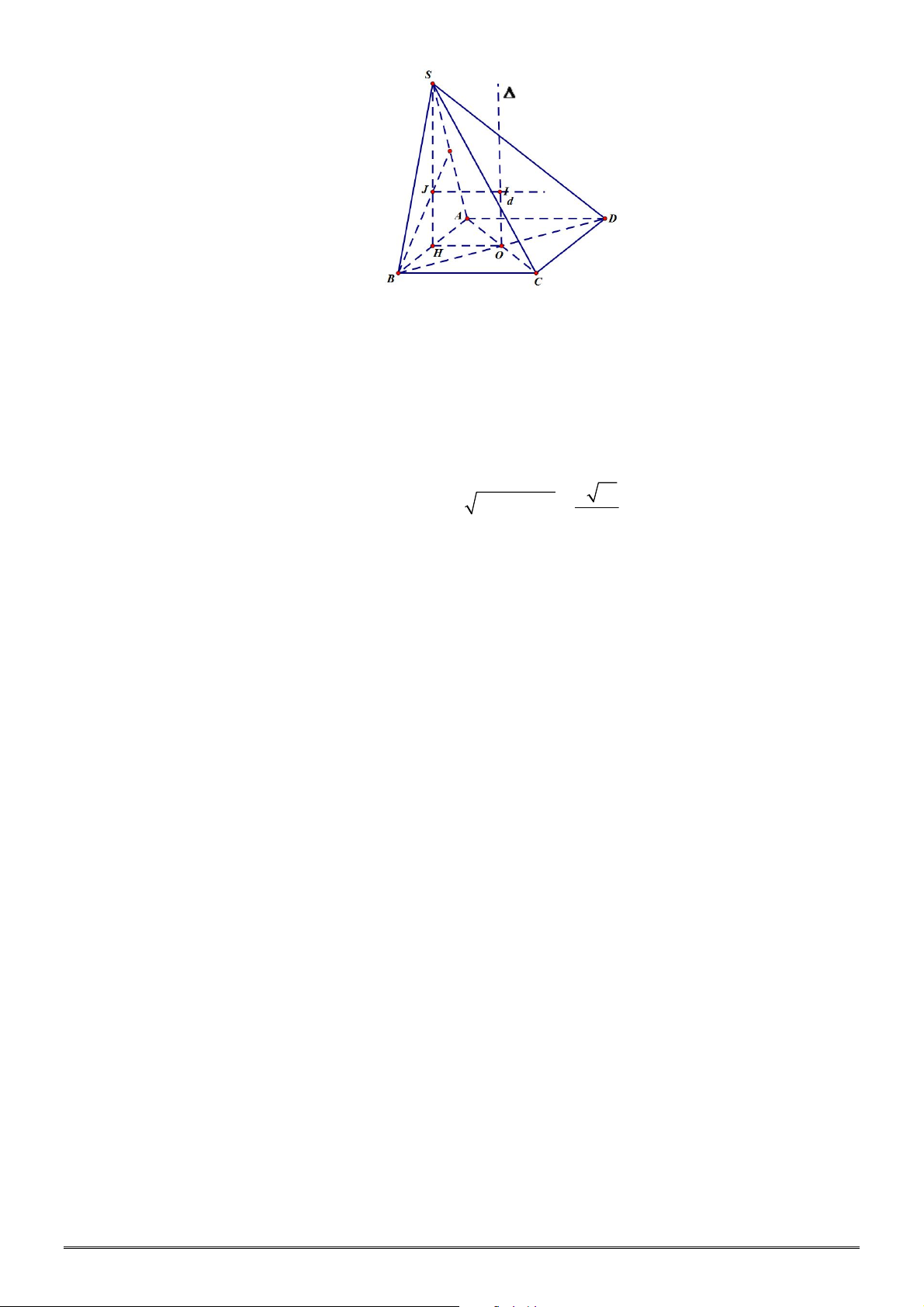
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 24/24
Gọi
O
là tâm của hình vuông
ABCD
suy ra
O
là tâm đường tròn
ngoại tiếp
ABCD
. Kẻ đường thẳng
qua
O
vuông góc
ABCD
,
khi đó
là trục của hình vuông
ABCD
.
Gọi
J
là trọng tâm tam giác
SAB
. Kẻ đường thẳng
d
song song
với
OH
cắt
tại
I
.
Ta có
IA IB IC ID IS
.
Suy ra
I
là tâm mặt cầu ngoài tiếp hình chóp.
Vậy: bán kính mặt cầu cần tìm là
2 2
21
6
a
R IA OI OA .
----------HẾT----------
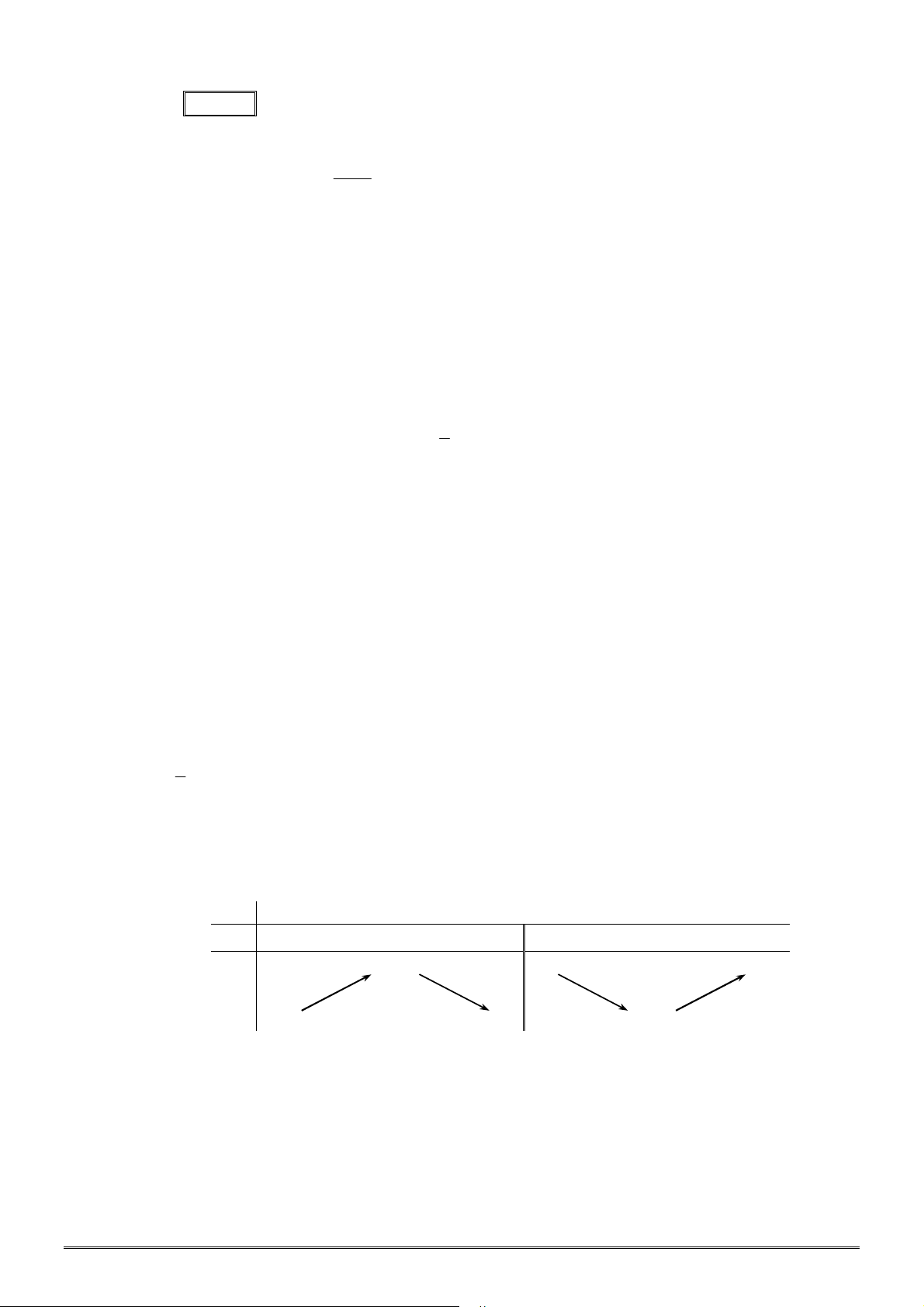
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/25
TRƯỜNG THPT KIM LIÊN – HÀ NỘI ĐỀ ÔN TẬP HỌC KỲ I NĂM HỌC 2017 – 2018
ĐỀ SỐ 3 MÔN TOÁN - LỚP 12
------- ------------------
Câu 1. [2D1-2] Cho hàm số
1
2
x
y
x
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đơn điệu trên
.
B. Hàm số đồng biến trên
\ 2
.
C. Hàm số nghịch biến trên
\ 2
.
D. Hàm số đồng biến trên các khoảng
; 2
và
2;
.
Câu 2. [2D1-2] Hỏi hàm số
3 2
3 4
y x x
nghịch biến trên khoảng nào?
A.
2;0
. B.
; 2
. C.
0;
. D.
.
Câu 3. [2D1-3] Tìm
m
bé nhất để hàm số
3 2
1
4 2016
3
y x mx x đồng biến trên tập xác định?
A.
4
m
. B.
2
m
. C.
2
m
. D.
0
m
.
Câu 4. [2D1-4] Một chất điểm chuyển động theo quy luật
3 2
6
s t t t
. Tính thời điểm
t
(giây) tại
đó vận tốc
v
(m/s) của chuyển động đạt giá trị lớn nhất.
A.
0
t
. B.
6
t
. C.
4
t
. D.
2
t
.
Câu 5. [2D1-2] Số điểm cực trị của hàm số
4 2
1
y x x
là
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 6. [2D1-2] Tìm giá trị cực tiểu
CT
y
của hàm số
3 2
6 9 5
y x x x
.
A.
5
CT
y
. B.
1
CT
y
. C.
3
CT
y
. D.
9
CT
y
.
Câu 7. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
3 2 2
1
1 1
3
y x mx m m x
đạt cực đại tại điểm
1
x
.
A.
1
m
. B.
2
m
. C.
0
m
. D.
4
m
.
Câu 8. [2D1-1] Cho hàm số
y f x
xác định, liên tục trên các khoảng
;1
,
1;
và có bảng
biến thiên như hình dưới. Khẳng định nào sau đây đúng?
A. Hàm số có giá trị cực tiểu bằng
1
.
B. Hàm số có giá trị lớn nhất bằng
1
và giá trị nhỏ nhất bằng
5
.
C. Hàm số đạt cực đại tại
0
x
và đạt cực tiểu tại
2
x
.
D. Hàm số nhiều hơn hai cực trị.
Câu 9. [2D1-2] Hàm số nào sau đây có giá trị nhỏ nhất trên
?
A.
3 2
2
y x x
. B.
3 2
2 5
y x x
.
C.
4 2
2 5
y x x
. D.
4 2
3
y x x
.
x
0
1
2
y
0
0
y
1
5
15
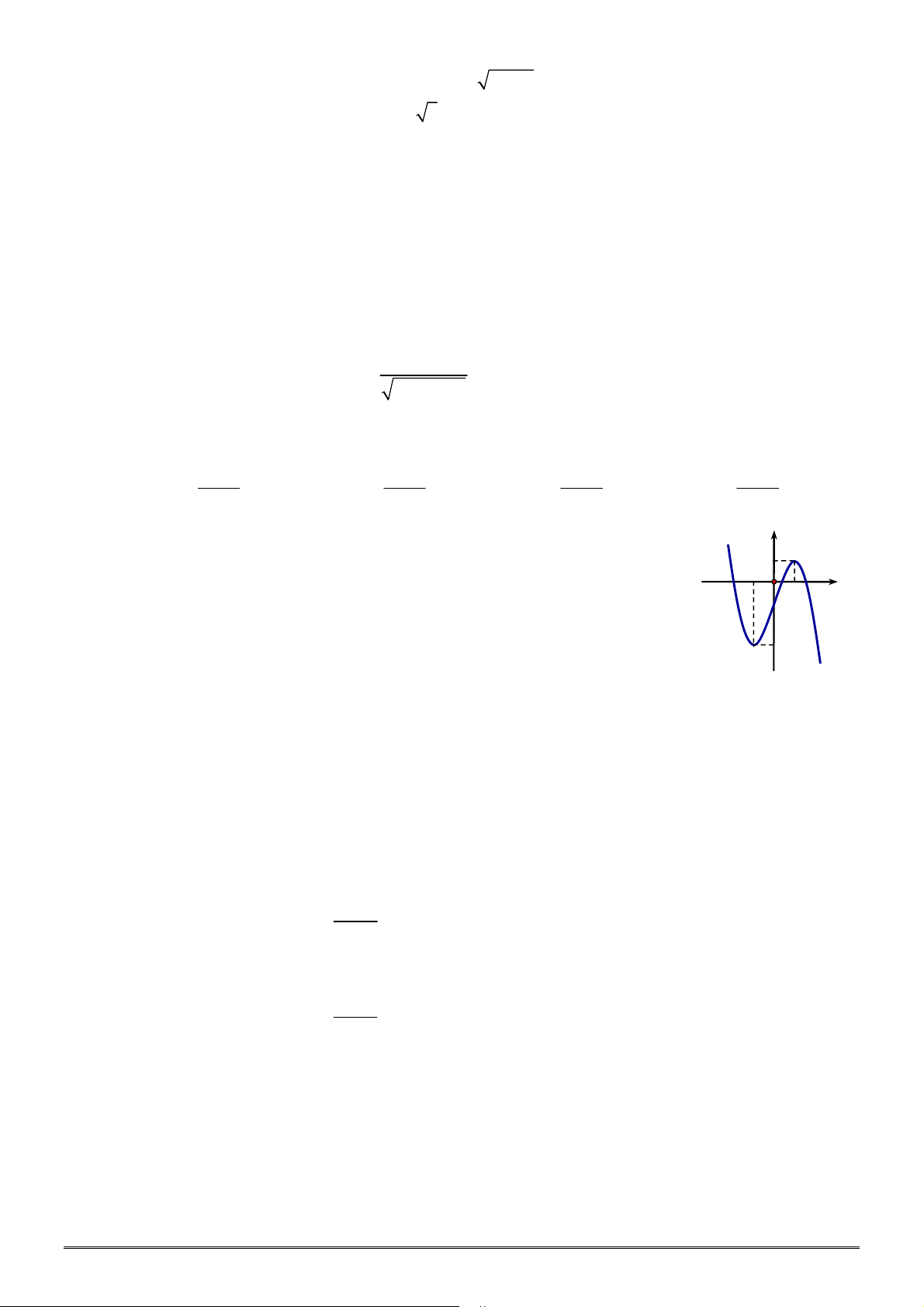
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/25
Câu 10. [2D1-2] Tìm giá trị nhỏ nhất của hàm số
6 3
y x
trên đoạn
1;1
.
A.
1;1
min 3
y
. B.
1;1
min 3
y
. C.
1;1
min 0
y
. D.
1;1
min 1
y
.
Câu 11. [2D1-2] Tìm giá trị
m
để hàm số
3 2
3
y x x m
có giá trị nhỏ nhất trên đoạn
1;1
bằng
0
?
A.
6
m
. B.
0
m
. C.
2
m
. D.
4
m
.
Câu 12. [2H2-3] Một người thợ thủ công pha một khối thạch cao vào nước tạo thành một hỗn hợp có
thể tích
3
330cm
V , sau đó đổ vào khuôn để đúc thành những viên phấn hình trụ có bán kính
đáy
0,5cm
R
và chiều cao
6cm
h
. Biết rằng trong quá trình đúc sự tiêu hao nguyên liệu là
không đáng kể. Hỏi người thợ thủ công đó đúc được bao nhiêu viên phấn?
A.
50
viên. B.
70
viên. C.
24
viên. D.
23
viên.
Câu 13. [2D1-2] Đồ thị của hàm số
2
2 3
2016
x
y
x
có bao nhiêu đường tiệm cận ngang?
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 14. [2D1-2] Đồ thị hàm số nào sau đây có tiệm cận đứng là đường thẳng
1
x
?
A.
2
1
1
x
y
x
. B.
2
3
1
x
y
x
. C.
2
1
1
x
y
x
. D.
2
3
1
x
y
x
.
Câu 15. [2D1-1] Đường cong trong hình bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi
hàm số đó là hàm số nào?
A.
2
1
y x x
. B.
4 2
1
y x x
.
C.
3
3 1
y x x
. D.
3 2
1
y x x
.
Câu 16. [2D1-1] Cho hàm số
4 2
2 3
y x x
. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số có tập xác định là
.
B. lim
x
y
và lim
x
y
.
C. Đồ thị hàm số có ba điểm cực trị.
D. Đồ thị hàm số nhận trục hoành
Ox
làm trục đối xứng.
Câu 17. [2D1-2] Cho hàm số
4 2
2
y x x
. Có bao nhiêu tiếp tuyến của đồ thị hàm số song song với
trục hoành?
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 18. [2D1-1] Cho hàm số
2 1
1
x
y
x
. Khẳng định nào sau đây là khẳng định đúng?
A.
1
lim
x
y
. B.
1
lim
x
y
. C.
1
lim
x
y
. D.
1
lim
x
y
.
Câu 19. [2D1-1] Cho hàm số
2 1
1
x
y
x
. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số không có cực trị.
B.
lim 2
x
y
và
lim 2
x
y
.
C. Đồ thị hàm số không cắt trục tung.
D. Đồ thị hàm số có tâm đối xứng là điểm
1;2
I .
Câu 20. [2D1-1] Cho hàm số
3 2
4 4
y x x x
. Tìm phương trình tiếp tuyến của đồ thị hàm số tại gốc
toạ độ?
A.
y x
. B.
4
y x
. C.
4
y x
. D.
y x
.
O
x
y
1
1
2
3
1
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/25
Câu 21. [2D1-1] Tìm số giao điểm của đồ thị hàm số
2
1 3
y x x x
với trục hoành.
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 22. [2D1-2] Tìm điều kiện của
m
để đường thẳng
y m
cắt đồ thị hàm số
4 2
y x x
tại bốn
điểm phân biệt.
A.
1
0
4
m
. B.
1
0
4
m
. C.
1
4
m
. D.
1
4
m
.
Câu 23. [2D2-1] Cho
,
a b
là hai số thực dương,
m
là một số nguyên còn
n
là một số nguyên dương.
Khẳng định nào dưới đây là khẳng định sai?
A. .
m n m n
a a a
. B.
m
m n
n
a
a
a
. C.
n
m m n
a a
. D.
m
n
m
n
a a
.
Câu 24. [2D2-1] Cho
2 3 2 3
m n
với ,m n
. Khẳng định nào sau đây là khẳng định đúng?
A.
m n
. B.
m n
. C.
m n
. D.
m n
.
Câu 25. [2D2-1] Cho
a
là số thực dương. Rút gọn biểu thức
3 1
3 1
5 3 4 5
.
a
P
a a
A.
2
P a
. B.
1
P a
. C.
1
P
. D.
P a
.
Câu 26. [2D2-3] Một người đầu tư
200
triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
14%
một năm. Hỏi sau ba năm mới rút lãi thì người đó thu được bao nhiêu triệu đồng tiền lãi?
(Giả sử rằng lãi suất hàng năm không thay đổi).
A.
59,92
triệu đồng. B.
96,31
triệu đồng. C.
84
triệu đồng. D.
137,79
triệu đồng.
Câu 27. [2D2-1] Cho
,
a b
là hai số thực dương. Tìm
x
biết
2 2 2
log 2log 4log
x a b
.
A.
2 4
.
x a b
. B.
2 2
.
x a b
. C.
2
.
x a b
. D.
4
.
x a b
.
Câu 28. [2D2-2] Cho các số thực dương
,
x y
thỏa mãn
2 2
7
x y xy
. Khẳng định nào sau đây đúng?
A.
1
log log log
3 2
x y
x y
. B.
2 2
log
log log
7
x y
x y
.
C.
2 2
log log log
3
x y
x y
. D.
2 2
log 2 log log
7
x y
x y
.
Câu 29. [2H1-2] Cho khối hộp
.
ABCD A B C D
có thể tích là
V
. Tính theo
V
thể tích khối tứ diện
AB CD
.
A.
2
3
V
. B.
3
4
V
. C.
3
V
. D.
6
V
.
Câu 30. [2D2-1] Đặt
ln 2
a
,
ln3
b
. Hãy biểu diễn
7
ln21 2ln14 3ln
2
Q theo
a
và
b
.
A. 5
Q a b
. B. 5
Q b a
. C. 6
Q a b
. D.
11 5
Q a b
.
Câu 31. [2D2-1] Trong các khẳng định sau, khẳng định nào sai?
A. Hàm số
log
y x
là hàm số lôgarit.
B. Hàm số
1
3
x
y
là hàm số mũ.
C. Hàm số
x
y
nghịch biến trên
.
D. Hàm số
ln
y x
đồng biến trên khoảng
0;
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/25
Câu 32. [2D2-2] Cho hàm số
2
ln 4
f x x x
. Tìm tập nghiệm của phương trình
0
f x
.
A.
;0 4;
. B.
4
. C.
2
. D.
.
Câu 33. [2D2-2] Cho hàm số
1
.ln
8
2016.e
x
y . Khẳng định nào sau đây là khẳng định đúng?
A.
2 ln 2 0
y y
. B.
3 ln 2 0
y y
. C.
8 ln 2 0
y y
. D.
8 ln 2 0
y y
.
Câu 34. [2D2-2] Tìm tập xác định
D
của hàm số
2
2 2
1
y x x
.
A.
1;1
D . B.
0;1
D . C.
\ 1;1
D
. D.
1;1 \ 0
D .
Câu 35. [2H1-2] Tìm số mặt phẳng đối xứng của hình chóp tứ giác đều.
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 36. [2D2-2] Tìm giá trị của
x
để đồ thị hàm số
2
log
y x
nằm ở phía trên đường thẳng
2
y
.
A.
4
x
. B.
4
x
. C.
4
x
. D.
0 4
x
.
Câu 37. [2D2-2] Số giá trị của
a
để
2
3 2
2 0,25
a a
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 38. [2H2-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
SA ABC
. Tìm tâm
mặt cầu ngoại tiếp hình chóp.
A. Trung điểm
SB
. B. Trung điểm
SC
.
C. Trung điểm
BC
. D. Một đáp án khác.
Câu 39. [2H1-2] Cho lăng trụ đứng .
ABC A B C
có đáy
ABC
là tam giác vuông tại
B
.
2
AB a
,
5
AC a
,
2 3
AA a
. Tính thể tích
V
của khối lăng trụ .
ABC A B C
.
A.
3
2 3
3
a
V . B.
3
3
3
a
V . C.
3
4 3
V a . D.
3
2 3
V a .
Câu 40. [2H1-3] Người ta cắt miếng bìa hình tam giác đều cạnh bằng 2 như hình
dưới và gấp theo các đường kẻ, sau đó dán các mép lại để được hình tứ
diện đều. Tính thể tích
V
của khối tứ diện tạo thành.
A.
2
96
V . B.
2
12
V .
C.
3
96
V . D.
3
16
V .
Câu 41. [2H1-2] Cho hình chóp
.
S ABC
có
M
,
N
và
P
lần lượt là trung điểm các cạnh
AB
,
BC
và
CA
. Gọi
1 .
S ABC
V V ,
2 .
S MNP
V V . Khẳng định nào sau đây là khẳng định đúng?
A.
1 2
2
V V
. B.
1 2
4
V V
.
C.
1 2
8
V V
. D.
1 2
3 8
V V
.
Câu 42. [2H1-3] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
; biết
2
AB AD a
,
CD a
. Góc giữa hai mặt phẳng
SBC
và
ABCD
bằng
60
. Gọi
I
là
trung điểm
AD
, biết hai mặt phẳng
SBI
và
SCI
cùng vuông góc với mặt phẳng
ABCD
.
Tính thể tích
V
của khối chóp
.
S ABCD
.
A.
3
3 5
5
a
V B.
3
3 5
8
a
V C.
3
3 15
8
a
V . D.
3
3 15
5
a
V .

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/25
Câu 43. [2H2-1] Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình chóp nào cũng có mặt cầu ngoại tiếp.
B. Hình hộp đứng nào cũng có mặt cầu ngoại tiếp.
C. Hình lăng trụ tam giác có cạnh bên không vuông góc với đáy có thể nội tiếp một mặt cầu.
D. Hình tứ diện nào cũng có mặt cầu ngoại tiếp.
Câu 44. [2H2-2] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
SA
vuông
góc với mặt phẳng đáy và
SA a
. Tính diện tích
S
của mặt cầu ngoại tiếp hình chóp đã cho.
A.
2
4
S a
. B.
2
3
S a
. C.
2
3
S a
. D.
2
6
S a
.
Câu 45. [2H2-2] Cho mặt cầu tâm
O
bán kính
R
và mặt phẳng
P
cách tâm
O
một khoảng
2
R
.Tìm
bán kính
r
của đường tròn giao tuyến giữa mặt phẳng
P
và mặt cầu đã cho?
A.
3
2
R
r . B.
3
4
R
r . C.
2
2
R
r . D.
2
4
R
r .
Câu 46. [2H1-2] Trong các mệnh đề sau, mệnh đề nào sai?
A. Chỉ có năm loại khối đa diện đều.
B. Hình chóp tam giác đều là hình chóp có bốn mặt là những tam giác đều.
C. Mỗi cạnh của hình đa diện đều là cạnh chung của đúng hai mặt.
D. Mỗi khối đa diện đều là một khối đa diện lồi.
Câu 47. [2H1-3] Trong không gian cho ba điểm cố định
A
,
B
,
C
phân biệt và không thẳng hàng. Tìm
tập hợp các điểm
M
trong không gian sao cho thể tích khối chóp
.
M ABC
là một số dương
không đổi?
A. Hai đường thẳng song song. B. Một mặt cầu.
C. Một mặt phẳng. D. Hai mặt phẳng song song.
Câu 48. [2H2-3] Cho hình chóp
.
S ABCD
có
SA ABCD
,
SA a
. Đáy
ABCD
là hình thang vuông
tại
A
và
B
,
AB BC a
và
2
AD a
. Tính theo
a
thể tích khối cầu ngoại tiếp hình chóp
.
S ACD
.
A.
3
5 5
9
a
V
. B.
3
5 5
6
a
V
. C.
3
5 5
3
a
V
. D.
3
5 5
12
a
V
.
Câu 49. [1H2-2] Cho hình lăng trụ
.
ABCD A B C D
có đáy
ABCD
là hình vuông. Hình chiếu vuông
góc của
A
lên
mp ABCD
là trung điểm
AB
, góc giữa
mp A CD
và
mp ABCD
là
60
.
Thể tích của khối chóp
.
B ABCD
là
3
8 3
3
a
. Tính theo
a
độ dài đoạn thẳng
AC
?
A.
3
2 2
a
. B.
2
a
. C.
2
a
. D.
2 2
a
.
Câu 50. [2H1-4] Cho khối chóp
.
S ABCD
có đáy là hình bình hành và có thể tích là
V
. Gọi
M
là trung
điểm của
SB
,
P
là điểm thuộc cạnh
SD
sao cho
2
SP DP
. Mặt phẳng
AMP
cắt cạnh
SC
tại
N
. Tính thể tích của khối đa diện
ABCDMNP
theo
V
.
A.
23
30
V
. B.
19
30
V
. C.
2
5
V
. D.
7
30
V
.
----------HẾT----------
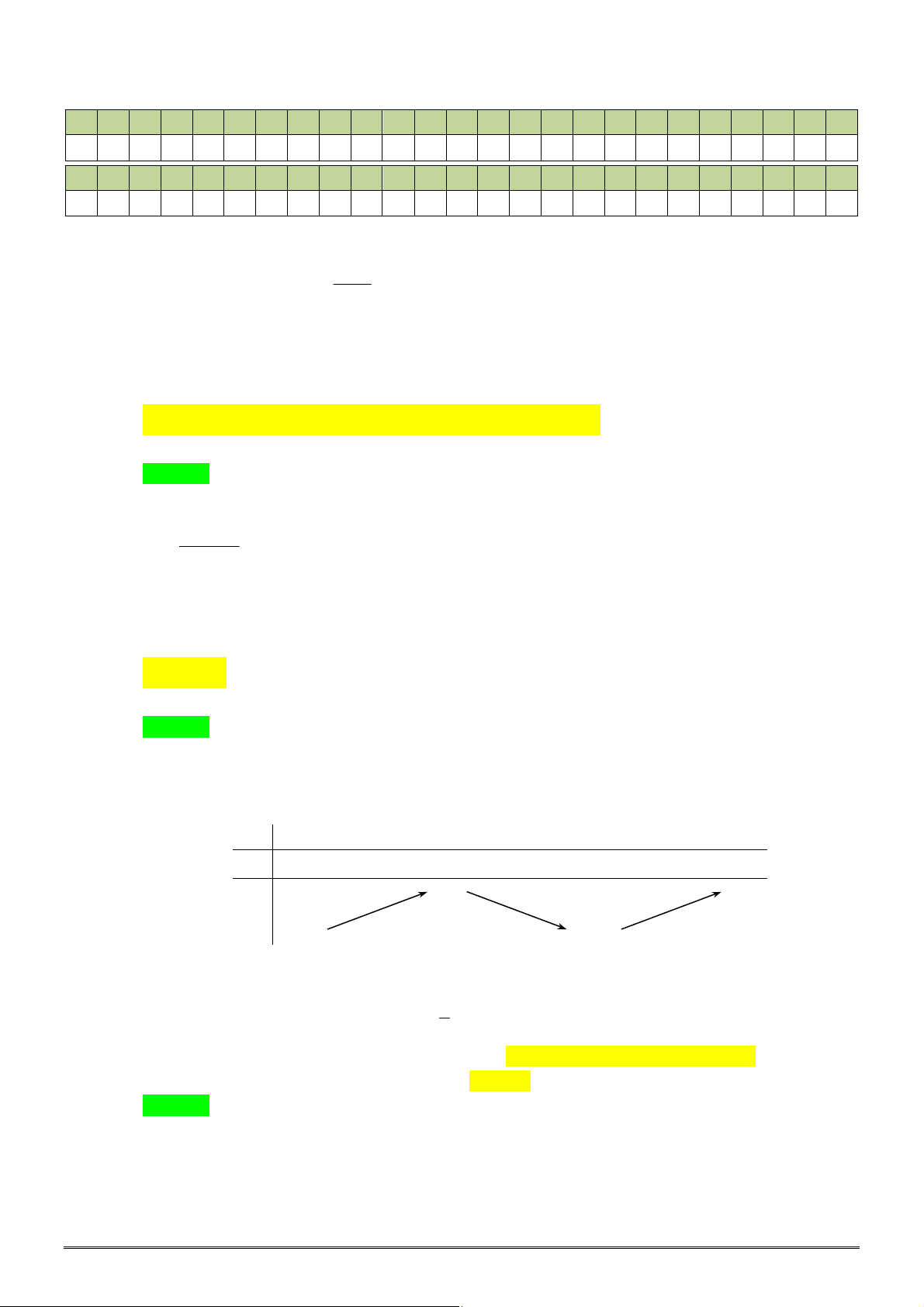
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/25
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
A
C
D
D
A
B C
C
B
D
B B B C
D
A
C
C
B C
A
C
B D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B B A
C
A
C
D
B D
A
B A
B D
B B D
D
B A
B D
B D
A
HƯỚNG DẪN GIẢI
Câu 1. [2D1-2] Cho hàm số
1
2
x
y
x
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đơn điệu trên
.
B. Hàm số đồng biến trên
\ 2
.
C. Hàm số nghịch biến trên
\ 2
.
D. Hàm số đồng biến trên các khoảng
; 2
và
2;
.
Lời giải
Chọn D.
Tập xác định
\ 2
D
.
2
3
0
2
y
x
với mọi
2
x
.
Vậy hàm số đồng biến trên các khoảng
; 2
và
2;
.
Câu 2. [2D1-2] Hỏi hàm số
3 2
3 4
y x x
nghịch biến trên khoảng nào?
A.
2;0
. B.
; 2
. C.
0;
. D.
.
Lời giải
Chọn A.
Tập xác định
D
.
2
0
3 6 3 2 ; 0 3 2 0
2
x
y x x x x y x x
x
.
Vậy hàm số đồng biến trên các khoảng
; 2
và
0;
, nghịch biến trên khoảng
2;0
.
Câu 3. [2D1-3] Tìm
m
bé nhất để hàm số
3 2
1
4 2016
3
y x mx x đồng biến trên tập xác định?
A.
4
m
. B.
2
m
. C.
2
m
. D.
0
m
.
Lời giải
Chọn C.
Tập xác định
D
.
2
2 4
y x mx
.
Hàm đồng biến trên
2
0, 4 0 2 2
y x m m
.
Vậy giá trị
m
nhỏ nhất thỏa mãn bài toán là
2
m
.
x
2
0
y
0
0
y
0
4
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/25
Câu 4. [2D1-4] Một chất điểm chuyển động theo quy luật
3 2
6
s t t t
. Tính thời điểm
t
(giây) tại
đó vận tốc
v
(m/s) của chuyển động đạt giá trị lớn nhất.
A.
0
t
. B.
6
t
. C.
4
t
. D.
2
t
.
Lời giải
Chọn D.
Ta có vận tốc
2
3 12
v t s t t t
.
Thời điểm
t
(giây) tại đó vận tốc
v
(m/s) của chuyển động đạt giá trị lớn nhất nên ta cần tìm
GTLN của hàm số
2
3 12
v t t t
với
0
t
.
Ta có
6 12; 0 6 12 0 2
v t t v t t t
.
Dựa vào bảng biến thiên ta thấy hàm số đạt GTLN tại
2
t
.
Câu 5. [2D1-2] Số điểm cực trị của hàm số
4 2
1
y x x
là
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn D.
Cách 1:
Tập xác định
D
.
3
4 2
y x x
,
3 2
0 4 2 0 2 2 1 0 0
y x x x x x
.
Dựa vào bảng biến thiên ta thấy hàm số có một điểm cực trị.
Cách 2:
Hàm số bậc 4 trùng phương có
. 0
a b
nên hàm số có một điểm cực trị.
Câu 6. [2D1-2] Tìm giá trị cực tiểu
CT
y
của hàm số
3 2
6 9 5
y x x x
.
A.
5
CT
y
. B.
1
CT
y
. C.
3
CT
y
. D.
9
CT
y
.
Lời giải
Chọn A.
Tập xác định
D
.
2
3 12 9
y x x
,
2
1
0 3 12 9 0
3
x
y x x
x
.
t
0
2
v t
+
0
-
v t
0
12
x
0
y
0
y
1
x
1
3
y
0
0
y
9
5
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/25
Từ bảng biến thiên suy ra:
Hàm số đạt cực đại tại
1
x
, giá trị cực đại
1 9
CÑ
y f
.
Hàm số đạt cực tiểu tại
1
x
, giá trị cực tiểu
3 5
CT
y f
.
Câu 7. [2D1-3] Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
3 2 2
1
1 1
3
y x mx m m x
đạt cực đại tại điểm
1
x
.
A.
1
m
. B.
2
m
. C.
0
m
. D.
4
m
.
Lời giải
Chọn B.
Tập xác định
D
.
2 2
2 1
y x mx m m
.
Hàm số đạt cực đại tại
1
x
(giả thiết), suy ra:
2
1
1 0 3 2 0
2
m
y m m
m
.
Thử lại:
Khi
2
1 2 1;
m y x x
2
0 2 1 0 1
y x x x
.
BBT
Khi
2
2 4 3;
m y x x
2
3
0 4 3 0
1
x
y x x
x
.
BBT
Vậy hàm số đạt cực đại tại điểm
1
x
khi
2
m
.
Câu 8. [2D1-1] Cho hàm số
y f x
xác định, liên tục trên các khoảng
;1
,
1;
và có bảng
biến thiên như hình dưới. Khẳng định nào sau đây đúng?
A. Hàm số có giá trị cực tiểu bằng
1
.
B. Hàm số có giá trị lớn nhất bằng
1
và giá trị nhỏ nhất bằng
5
.
C. Hàm số đạt cực đại tại
0
x
và đạt cực tiểu tại
2
x
.
D. Hàm số nhiều hơn hai cực trị.
Lời giải
Chọn C.
x
1
y
0
y
x
1
3
y
0
0
y
C
Đ
CT
x
0
1
2
y
0
0
y
1
5
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/25
Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại
0
x
và đạt cực tiểu tại
2
x
.
Câu 9. [2D1-2] Hàm số nào sau đây có giá trị nhỏ nhất trên
?
A.
3 2
2
y x x
. B.
3 2
2 5
y x x
. C.
4 2
2 5
y x x
. D.
4 2
3
y x x
.
Lời giải
Chọn C.
Xét hàm số
3 2
2
y x x
ta có:
2
3 2
y x x
;
2
0
0 3 2 0
2
3
x
y x x
x
.
BBT
Dựa vào bảng biến thiên ta thấy, hàm số không có giá trị nhỏ nhất trên
.
Xét hàm số
3 2
2 5
y x x
ta có:
2
6 2
y x x
;
2
0
0 6 2 0
1
3
x
y x x
x
.
BBT
Dựa vào bảng biến thiên ta thấy, hàm số không có giá trị nhỏ nhất trên
.
Xét hàm số
4 2
2 5
y x x
ta có:
3
8 2
y x x
;
3 2
0
0 8 2 0 2 4 1 0
1
2
x
y x x x x
x
.
BBT
Dựa vào bảng biến thiên ta thấy, hàm số có giá trị nhỏ nhất trên
.
Xét hàm số
4 2
3
y x x
ta có:
x
2
3
0
y
0
0
y
50
27
2
x
0
1
3
y
0
0
y
5
136
27
x
1
2
0
1
2
y
0
0
0
y
41
8
5
2
41
8
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/25
3
4 2
y x x
;
3 2
0 4 2 0 2 2 1 0 0
y x x x x x
.
BBT
Dựa vào bảng biến thiên ta thấy, hàm số không có giá trị nhỏ nhất trên
.
Câu 10. [2D1-2] Tìm giá trị nhỏ nhất của hàm số
6 3
y x
trên đoạn
1;1
.
A.
1;1
min 3
y
. B.
1;1
min 3
y
. C.
1;1
min 0
y
. D.
1;1
min 1
y
.
Lời giải
Chọn B.
Hàm số xác định và liên tục trên đoạn
1;1
.
3
0, 1,1
2 6 3
y x
x
.
Suy ra hàm số nghịch biến trên
1;1
. Do đó
1,1
1,1
max 1 3
min 1 3
y y
y y
.
Câu 11. [2D1-2] Tìm giá trị
m
để hàm số
3 2
3
y x x m
có giá trị nhỏ nhất trên đoạn
1;1
bằng
0
?
A.
6
m
. B.
0
m
. C.
2
m
. D.
4
m
.
Lời giải
Chọn D.
Hàm số
3 2
3
y x x m
liên tục trên
1;1
.
2
3 6
y x x
,
0 0 2
y x x
Bảng biến thiên:
x
1
0
1
y
0
y
2
m
m
4
m
Dựa vào bảng biến thiên, ta có
1;1
min 1 4
y y m
Mà
1;1
min 0
y
4 0 4
m m
.
Câu 12. [2H2-3] Một người thợ thủ công pha một khối thạch cao vào nước tạo thành một hỗn hợp có
thể tích
3
330cm
V , sau đó đổ vào khuôn để đúc thành những viên phấn hình trụ có bán kính
đáy
0,5cm
R
và chiều cao
6cm
h
. Biết rằng trong quá trình đúc sự tiêu hao nguyên liệu là
không đáng kể. Hỏi người thợ thủ công đó đúc được bao nhiêu viên phấn?
A.
50
viên. B.
70
viên. C.
24
viên. D.
23
viên.
Lời giải
x
0
y
0
y
3
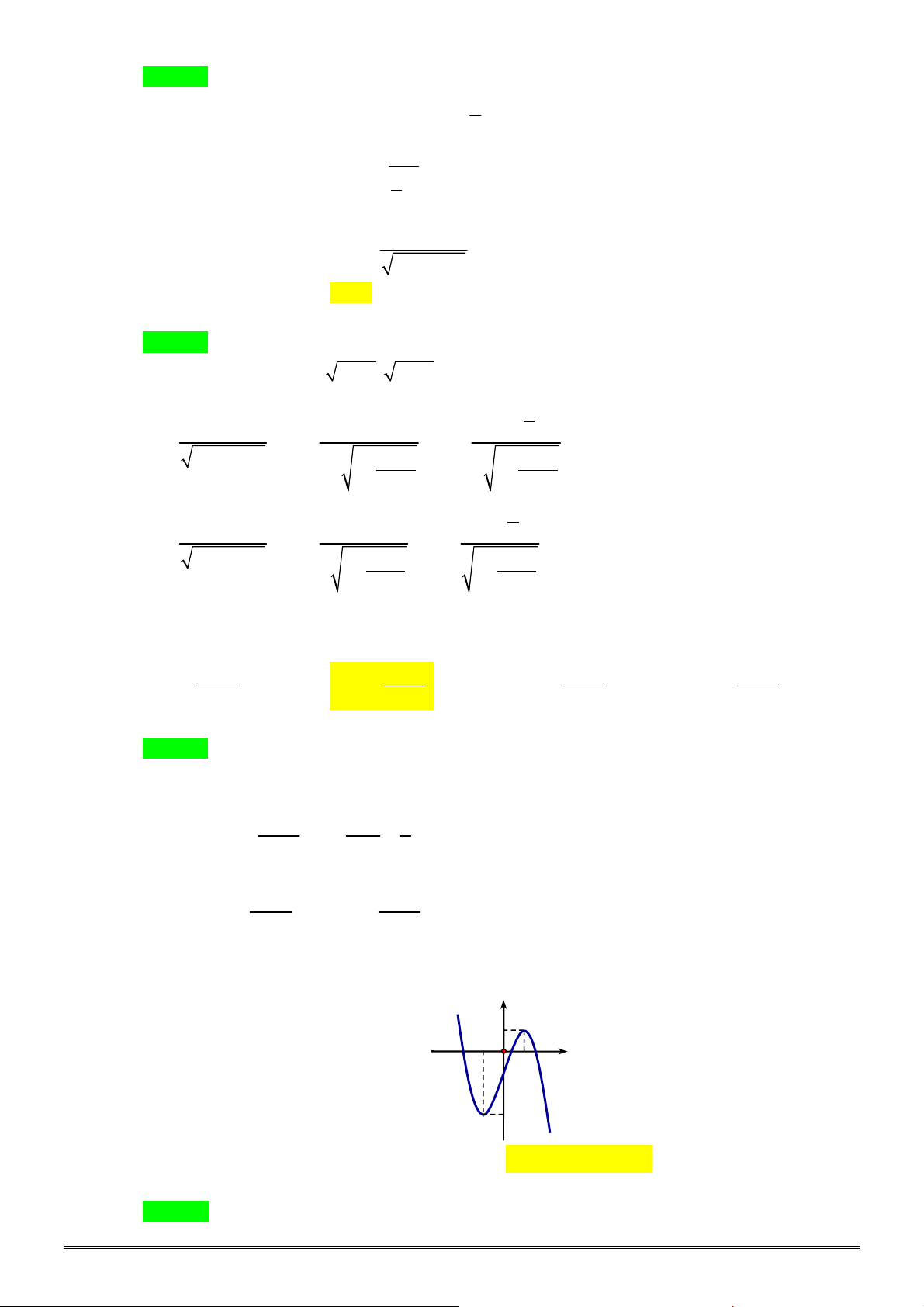
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/25
Chọn B.
Mỗi viên phấn có thể tích
2
3
3
. 0,5 .6 cm
2
V
.
Số viên phấn có thể đúc được là
330
70
3
2
(viên).
Câu 13. [2D1-2] Đồ thị của hàm số
2
2 3
2016
x
y
x
có bao nhiêu đường tiệm cận ngang?
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn B.
Tập xác định
\ 2016; 2016
D
.
2
2 2
3
2
2 3 2 3
lim lim lim 2
2016 2016
2016
1 1
x x x
x x
x
x
x
x x
2
2 2
3
2
2 3 2 3
lim lim lim 2
2016 2016
2016
1 1
x x x
x x
x
x
x
x x
Suy ra đồ thị hàm số có hai đường tiệm cận ngang là
2
y
và
2
y
.
Câu 14. [2D1-2] Đồ thị hàm số nào sau đây có tiệm cận đứng là đường thẳng
1
x
?
A.
2
1
1
x
y
x
. B.
2
3
1
x
y
x
. C.
2
1
1
x
y
x
. D.
2
3
1
x
y
x
.
Lời giải
Chọn B.
Nhận xét: Cả bốn đáp án đều hàm phân thức, nên để
1
x
là tiệm cận đứng thì
1
x
phải là
nghiệm của mẫu. Do đó, ta loại được câu C và D.
Xét câu A,
2
1 1
1 1 1
lim lim
1 1 2
x x
x
x x
suy ra loại A.
Như vậy đáp án là B.
Thật vậy,
2
1
3
lim
1
x
x
x
,
2
1
3
lim
1
x
x
x
nên
1
x
là tiệm cận đứng của đồ thị hàm số.
Câu 15. [2D1-1] Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
2
1
y x x
. B.
4 2
1
y x x
. C.
3
3 1
y x x
. D.
3 2
1
y x x
.
Lời giải
Chọn C.
O
x
y
1
1
2
3
1
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/25
Dựa vào đồ thị, ta thấy đây là đồ thị của hàm số bậc ba
3 2
y ax bx cx d
0
a
nên loại
A, B.
lim
x
y
nên
0
a
. Nên ta Chọn C.
Câu 16. [2D1-1] Cho hàm số
4 2
2 3
y x x
. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số có tập xác định là
.
B. lim
x
y
và lim
x
y
.
C. Đồ thị hàm số có ba điểm cực trị.
D. Đồ thị hàm số nhận trục hoành
Ox
làm trục đối xứng.
Lời giải
Chọn D.
Đồ thị hàm trùng phương
4 2
y ax bx c
0
a
nhận trục tung làm trục đối xứng.
Nên khẳng định sai là câu D.
Câu 17. [2D1-2] Cho hàm số
4 2
2
y x x
. Có bao nhiêu tiếp tuyến của đồ thị hàm số song song với
trục hoành?
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn A.
Trục hoành có phương trình
0
y
.
d
là tiếp tuyến của đồ thị thị hàm số,
d
song song với trục hoành nên
d
có hệ số góc
0
k
và có dạng
y b
0
b
.
Ta có:
0 0
3
0 0 0
0 0
0 0
4 4 0
1 1
x y
k y x x x
x y
d
qua điểm
0;0
A
0
b
(loại).
d
qua điểm
1;1
B
1
b
1
y
.
Vậy chỉ có
1
tiếp tuyến của đồ thị hàm số song song với trục hoành.
Câu 18. [2D1-1] Cho hàm số
2 1
1
x
y
x
. Khẳng định nào sau đây là khẳng định đúng?
A.
1
lim
x
y
. B.
1
lim
x
y
. C.
1
lim
x
y
. D.
1
lim
x
y
.
Lời giải
Chọn C.
1
2 1
lim
1
x
x
x
(vì khi
1
x
thì
2 1 1
x
,
1 0
x
và
1 0
x
).
Câu 19. [2D1-1] Cho hàm số
2 1
1
x
y
x
. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số không có cực trị.
B.
lim 2
x
y
và
lim 2
x
y
.
C. Đồ thị hàm số không cắt trục tung.
D. Đồ thị hàm số có tâm đối xứng là điểm
1;2
I .
Lời giải

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/25
Chọn C.
Tập xác định
\ 1
D
.
2
1
0
1
y x D
x
nên hàm số không có cực trị. (A đúng)
lim 2
x
y
, (B đúng).
2.0 1
0 1
1
x y
x
đồ thị hàm số cắt trục tung tại điểm
0;1
A . (C sai).
Tiệm cận đứng
1
x
, tiệm cận ngang
2
y
Tâm đối xứng của đồ thị là
1;2
I (D đúng).
Câu 20. [2D1-1] Cho hàm số
3 2
4 4
y x x x
. Tìm phương trình tiếp tuyến của đồ thị hàm số tại gốc
toạ độ?
A.
y x
. B.
4
y x
. C.
4
y x
. D.
y x
.
Lời giải
Chọn B.
Điểm
3 2
0;0 : 4 4
O C y x x x
.
2
3 8 4
y x x
.
Phương trình tiếp tuyến của
C
tại
0;0
O có dạng:
0 0 0 4
y y x x
.
Câu 21. [2D1-1] Tìm số giao điểm của đồ thị hàm số
2
1 3
y x x x
với trục hoành.
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn C.
Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là
2
2
2
1
1 0
1 3 0
3 0
3 0
x
x
x x x
x x VN
x x
Vậy đồ thị hàm số
2
1 3
y x x x
cắt trục hoành tại một điểm.
Câu 22. [2D1-2] Tìm điều kiện của
m
để đường thẳng
y m
cắt đồ thị hàm số
4 2
y x x
tại bốn
điểm phân biệt.
A.
1
0
4
m
. B.
1
0
4
m
. C.
1
4
m
. D.
1
4
m
.
Lời giải
Chọn A.
Phương trình hoành độ giao điểm của hai đồ thị là
4 2 4 2
0
x x m x x m
1
.
Đặt
2
0
t x t
, khi đó
1
trở thành
2
0
t t m
2
.
Để
1
có bốn nghiệm phân biệt thì
2
phải có hai nghiệm dương phân biệt. Điều này xảy ra
khi và chỉ khi

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/25
0
1 4 0
1
1
0 1 0 0
4
4
0
0
0
m
m
b
S S m
a
m
P m
c
P
a
.
Câu 23. [2D2-1] Cho
,
a b
là hai số thực dương,
m
là một số nguyên còn
n
là một số nguyên dương.
Khẳng định nào dưới đây là khẳng định sai?
A. .
m n m n
a a a
. B.
m
m n
n
a
a
a
. C.
n
m m n
a a
. D.
m
n
m
n
a a
.
Lời giải
Chọn C.
Ta có
.
n
m m n
a a
nên khẳng định C sai.
Câu 24. [2D2-1] Cho
2 3 2 3
m n
với ,m n
. Khẳng định nào sau đây là khẳng định đúng?
A.
m n
. B.
m n
. C.
m n
. D.
m n
.
Lời giải
Chọn B.
Ta có
0 2 3 1 2 3 2 3
m n
m n
.
Câu 25. [2D2-1] Cho
a
là số thực dương. Rút gọn biểu thức
3 1
3 1
5 3 4 5
.
a
P
a a
A.
2
P a
. B.
1
P a
. C.
1
P
. D.
P a
.
Lời giải
Chọn D.
Ta có
3 1
3 1
3 1 3 1
2
5 3 4 5 5 3 4 5
.
a
a a
P a
a
a a a
.
Câu 26. [2D2-3] Một người đầu tư
200
triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
14%
một năm. Hỏi sau ba năm mới rút lãi thì người đó thu được bao nhiêu triệu đồng tiền lãi?
(Giả sử rằng lãi suất hàng năm không thay đổi).
A.
59,92
triệu đồng. B.
96,31
triệu đồng. C.
84
triệu đồng. D.
137,79
triệu đồng.
Lời giải
Chọn B.
Gọi
A
là số tiền ban đầu và
%
r
là lãi suất một năm.
Sau năm đầu tiên, người đó thu được số tiền cả vốn lẫn lãi là
1
. 1 %
A A r
.
Sau năm thứ hai, người đó thu được số tiền cả vốn lẫn lãi là
2
2 1
. 1 % . 1 % . 1 % . 1 %
A A r A r r A r .
Sau năm thứ ba, người đó thu được số tiền cả vốn lẫn lãi là
2 3 3
3 2
. 1 % . 1 % . 1 % . 1 % 200. 1 0,14 296,3088
A A r A r r A r triệu
đồng.
Vậy số tiền lãi thu được là
296,3088 200 96,3088 96,31
triệu đồng.
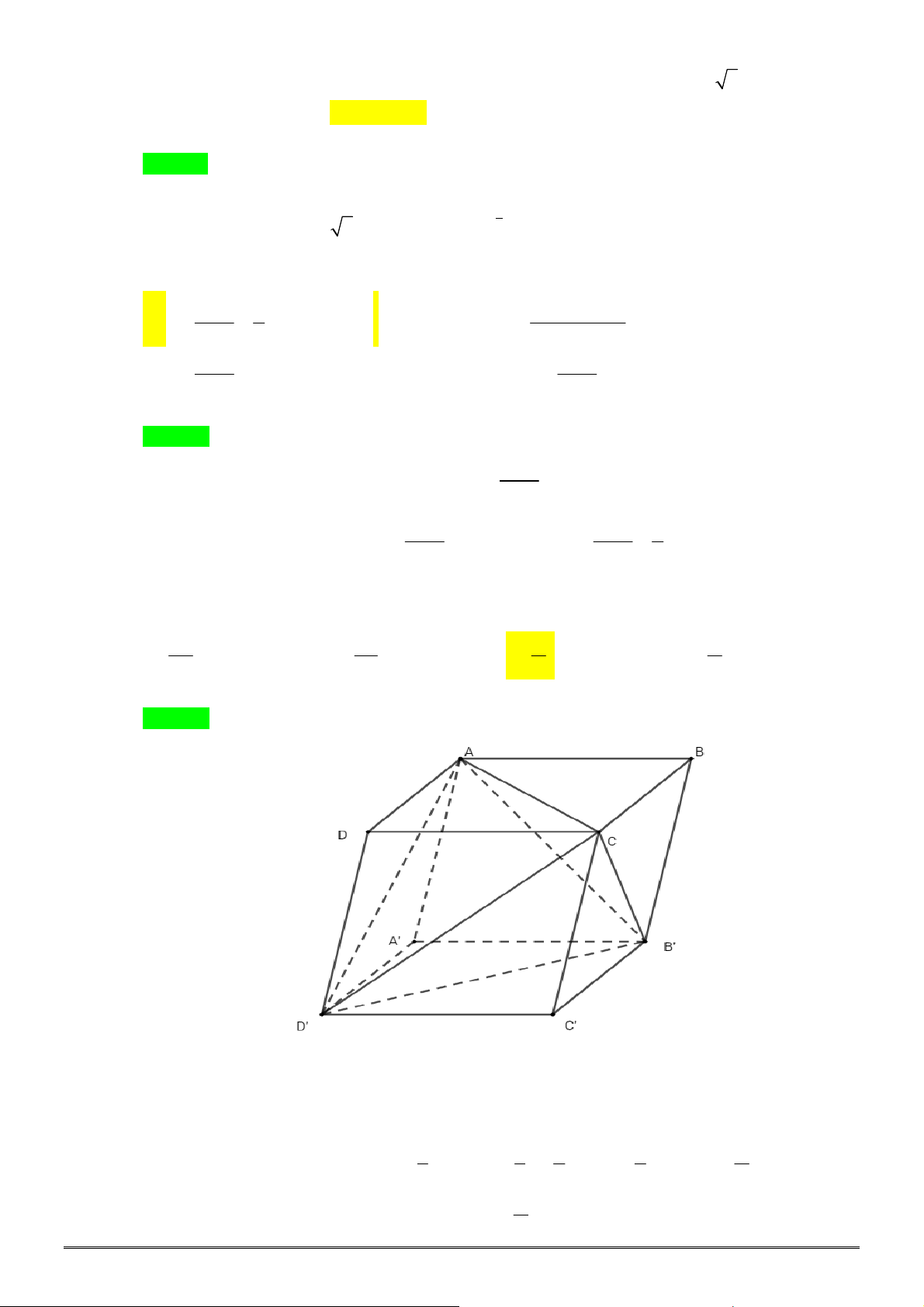
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/25
Câu 27. [2D2-1] Cho
,
a b
là hai số thực dương. Tìm
x
biết
2 2 2
log 2log 4log
x a b
.
A.
2 4
.
x a b
. B.
2 2
.
x a b
. C.
2
.
x a b
. D.
4
.
x a b
.
Lời giải
Chọn B.
Ta có
1
2 2 2 2 2 2 2
2
2 2 2 2 2 2 2 2
log 2log 4log log 4log log log log . .
x a b a b a b a b x a b
Câu 28. [2D2-2] Cho các số thực dương
,
x y
thỏa mãn
2 2
7
x y xy
. Khẳng định nào sau đây đúng?
A.
1
log log log
3 2
x y
x y
. B.
2 2
log
log log
7
x y
x y
.
C.
2 2
log log log
3
x y
x y
. D.
2 2
log 2 log log
7
x y
x y
.
Lời giải
Chọn A.
Ta có
2
2 2 2 2
7 2 9
3
x y
x y xy x xy y xy xy
1
.
Lấy
log
hai vế của
1
, ta có
2
1
log log log log log
3 3 2
x y x y
xy x y
.
Câu 29. [2H1-2] Cho khối hộp
.
ABCD A B C D
có thể tích là
V
. Tính theo
V
thể tích khối tứ diện
AB CD
.
A.
2
3
V
. B.
3
4
V
. C.
3
V
. D.
6
V
.
Lời giải
Chọn C.
Gọi
h
là chiều cao hại từ đỉnh
B
xuống mặt phẳng
ABCD
của khối hộp.
Tứ diện
B ABC
có chiều cao hạ từ đỉnh
B
xuống mặt phẳng
ABC
chính là chiều cao
h
của
khối hộp.
Thể tích khối tứ diện
B ABC
là
1 1 1 1
3 3 2 6 6
ABC ABCD ABCD
V
V h S h S h S
.
Tương tự, ta tính được
6
CB D C D DAC AA B D
V
V V V
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/25
Vậy
4
6 3
AB CD CB D C D DAC AA B D AB BC
V V
V V V V V V V
.
Câu 30. [2D2-1] Đặt
ln 2
a
,
ln3
b
. Hãy biểu diễn
7
ln21 2ln14 3ln
2
Q theo
a
và
b
.
A. 5
Q a b
. B. 5
Q b a
. C. 6
Q a b
. D.
11 5
Q a b
.
Lời giải
Chọn A.
Ta có
7
ln21 2ln14 3ln ln3 ln7 2ln2 2ln7 3ln 7 3ln2 ln3 5ln 2 5
2
Q a b
.
Câu 31. [2D2-1] Trong các khẳng định sau, khẳng định nào sai?
A. Hàm số
log
y x
là hàm số lôgarit.
B. Hàm số
1
3
x
y
là hàm số mũ.
C. Hàm số
x
y
nghịch biến trên
.
D. Hàm số
ln
y x
đồng biến trên khoảng
0;
.
Lời giải
Chọn C.
Ta có:
1
nên hàm số mũ
x
đồng biến trên
.
Câu 32. [2D2-2] Cho hàm số
2
ln 4
f x x x
. Tìm tập nghiệm của phương trình
0
f x
.
A.
;0 4;
. B.
4
. C.
2
. D.
.
Lời giải
Chọn D.
Điều kiện:
2
0
4 0
4
x
x x
x
.
Đạo hàm:
2
2 4
4
x
f x
x x
.
Ta có:
2
2 4
0 0 2
4
x
f x x
x x
(không thỏa mãn điều kiện).
Vậy không có giá trị của
x
nào để
0
f x
.
Câu 33. [2D2-2] Cho hàm số
1
.ln
8
2016.e
x
y . Khẳng định nào sau đây là khẳng định đúng?
A.
2 ln 2 0
y y
. B.
3 ln 2 0
y y
. C.
8 ln 2 0
y y
. D.
8 ln 2 0
y y
.
Lời giải
Chọn B.
Đạo hàm:
1
.ln
8
1
2016.ln .e
8
x
y
.
Ta có:
1
.ln
3
8
1
0 2016.ln .e ln 2 3 ln2
8
x
y A A y y y
.
Vậy
3 ln 2 0
y y
.
Câu 34. [2D2-2] Tìm tập xác định
D
của hàm số
2
2 2
1
y x x
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/25
A.
1;1
D . B.
0;1
D . C.
\ 1;1
D
. D.
1;1 \ 0
D .
Lời giải
Chọn D.
Điều kiện:
2
1 1
1 0
0
0
x
x
x
x
.
Vậy
1;1 \ 0
D .
Câu 35. [2H1-2] Tìm số mặt phẳng đối xứng của hình chóp tứ giác đều.
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn A.
Hình chóp tứ giác đều có bốn mặt phẳng đối xứng (như hình vẽ bên).
M
Q
N
K
O
C
A
B
D
S
Câu 36. [2D2-2] Tìm giá trị của
x
để đồ thị hàm số
2
log
y x
nằm ở phía trên đường thẳng
2
y
.
A.
4
x
. B.
4
x
. C.
4
x
. D.
0 4
x
.
Lời giải
Chọn B.
Điều kiện:
0
x
.
Đồ thị hàm số
2
log
y x
nằm ở phía trên đường thẳng
2
y
khi
2
log 2 4
x x
.
Câu 37. [2D2-2] Số giá trị của
a
để
2
3 2
2 0,25
a a
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn A.
Ta có:
2
2 2
3 2 3 2 3 2 2 2
1
2 0,25 2 2 2 3 2 2
4
a
a a a a a
a a
2
2 2 3 0
a a
(phương trình vô nghiệm).
Vậy không có giá trị của
a
nào để
2
3 2
2 0,25
a a
.
Câu 38. [2H2-2] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
SA ABC
. Tìm tâm
mặt cầu ngoại tiếp hình chóp.
A. Trung điểm
SB
. B. Trung điểm
SC
. C. Trung điểm
BC
. D. Một đáp án khác.
Lời giải
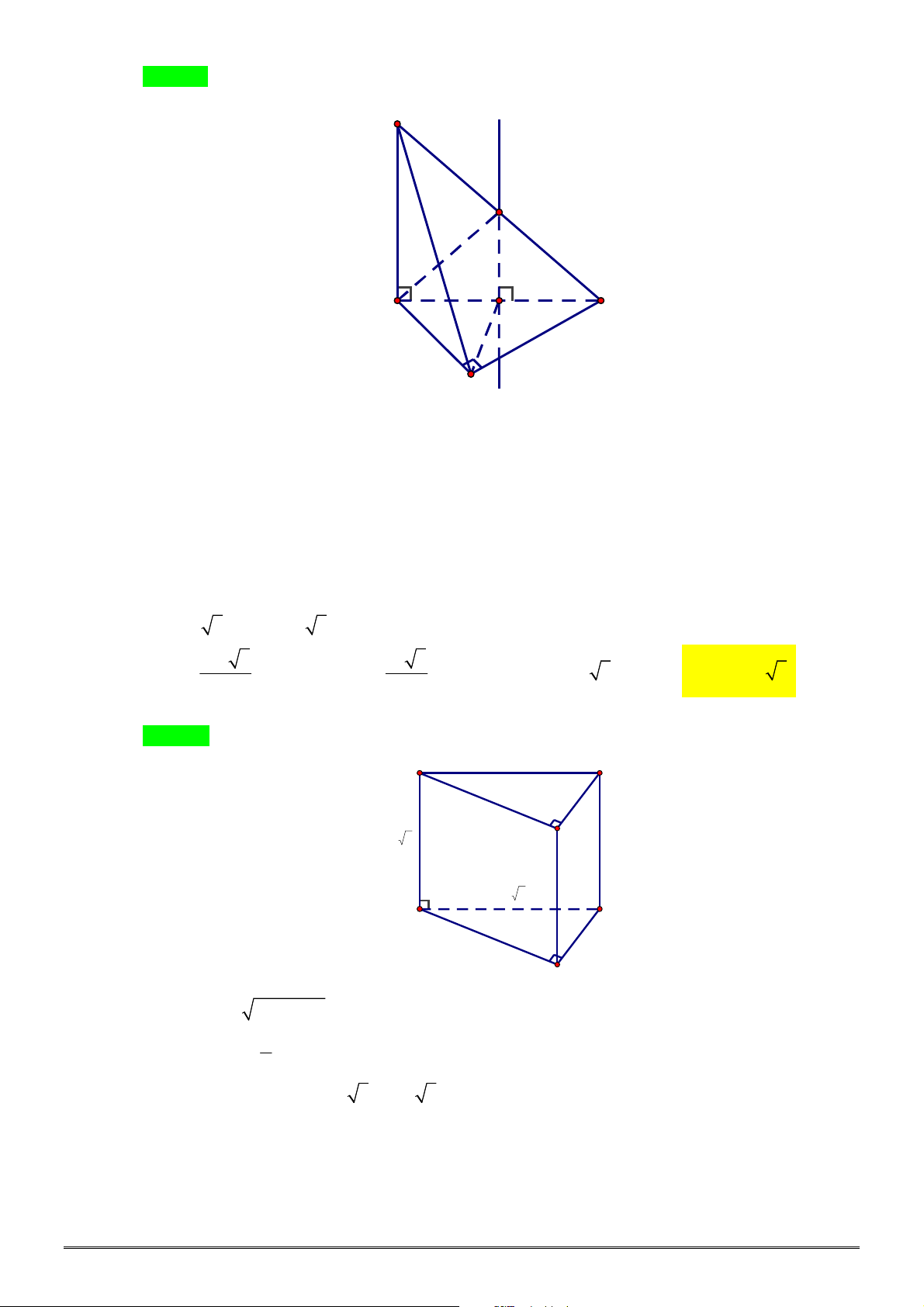
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/25
Chọn B.
d
O
M
A
C
B
S
Gọi
M
là trung điểm
AC
thì
M
là tâm đường tròn ngoại tiếp
ABC
. Qua
M
dựng đường
thẳng
d
vuông góc với
ABC
//
d SA d SAC
.
Gọi
O d SC O
là trung điểm của
SC
.
Mà
SAC
vuông tại
A
nên
SO CO AO
.
Từ đó ta có:
OA OB OC OS
.
Vậy tâm mặt cầu ngoại tiếp hình chóp .
S ABC
là trung điểm của
SC
.
Câu 39. [2H1-2] Cho lăng trụ đứng .
ABC A B C
có đáy
ABC
là tam giác vuông tại
B
.
2
AB a
,
5
AC a
,
2 3
AA a
. Tính thể tích
V
của khối lăng trụ .
ABC A B C
.
A.
3
2 3
3
a
V . B.
3
3
3
a
V . C.
3
4 3
V a . D.
3
2 3
V a .
Lời giải
Chọn D.
2a 3
a 5
2a
C'
B'
A
B
C
A'
Ta có:
2 2
5 4
BC a a a
.
Do đó:
2
1
.2 .
2
ABC
S a a a
.
Vậy
2 3
. .2 3 2 3
ABC
V S AA a a a
.
Câu 40. [2H1-3] Người ta cắt miếng bìa hình tam giác đều cạnh bằng 2 như hình dưới và gấp theo các
đường kẻ, sau đó dán các mép lại để được hình tứ diện đều. Tính thể tích
V
của khối tứ diện
tạo thành.
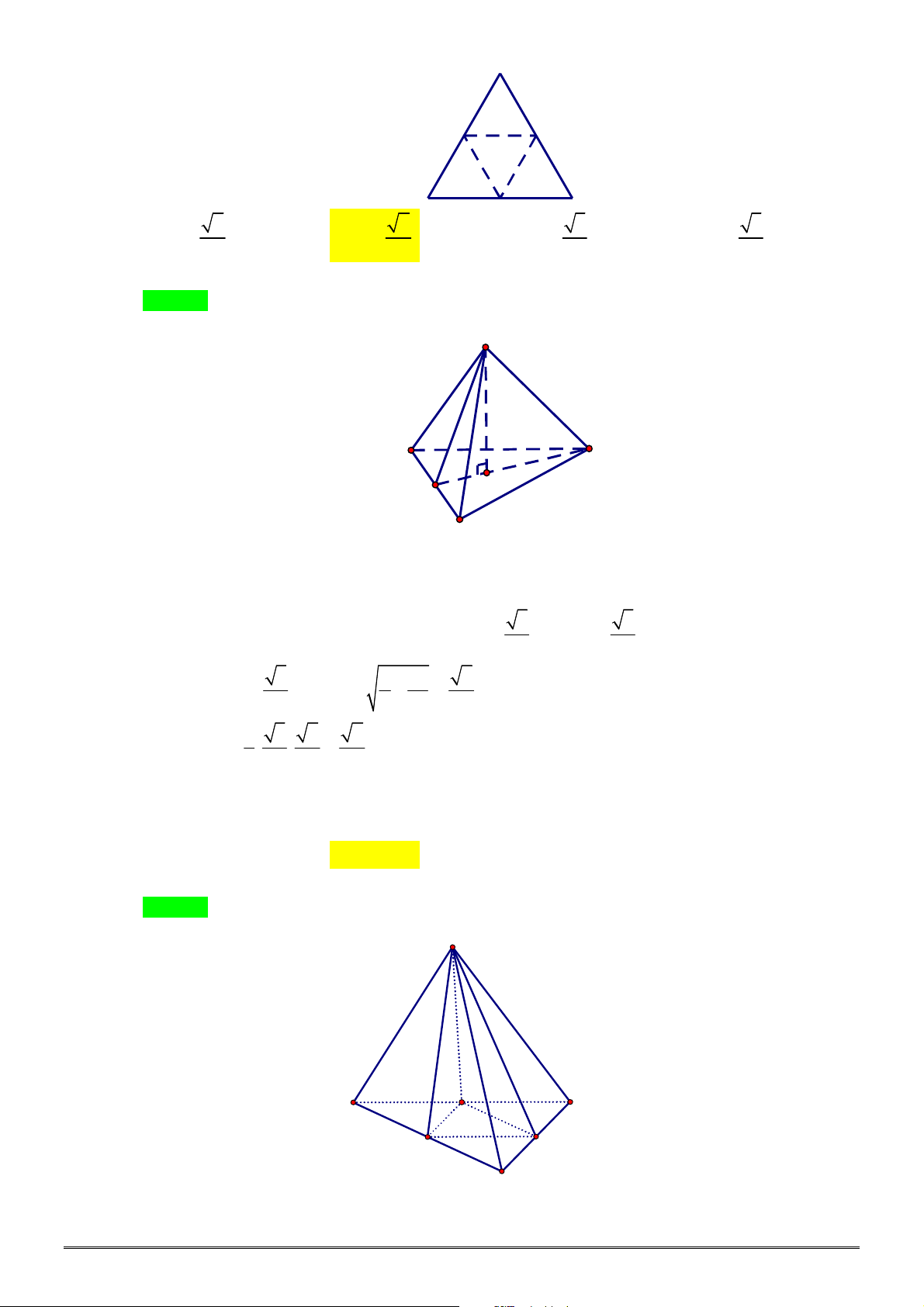
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/25
A.
2
96
V . B.
2
12
V . C.
3
96
V . D.
3
16
V .
Lời giải
Chọn B.
G
M
C
D
B
A
Giả sử khối tứ diện đều được tạo thành như hình bên.
Khi đó tất cả các cạnh của tứ diện đều này có độ dài bằng 1. Gọi
M
là trung điểm của
BC
và
G
là trọng tâm của
BCD
. Ta có:
3
2
MA MD và
3
6
MG .
Suy ra:
3
4
BCD
S
và
3 3 6
4 36 3
AG .
Vậy
.
1 3 6 2
. .
3 4 3 12
A BCD
V .
Câu 41. [2H1-2] Cho hình chóp
.
S ABC
có
M
,
N
và
P
lần lượt là trung điểm các cạnh
AB
,
BC
và
CA
. Gọi
1 .
S ABC
V V ,
2 .
S MNP
V V . Khẳng định nào sau đây là khẳng định đúng?
A.
1 2
2
V V
. B.
1 2
4
V V
. C.
1 2
8
V V
. D.
1 2
3 8
V V
.
Lời giải
Chọn B.
P
M
N
B
A
C
S
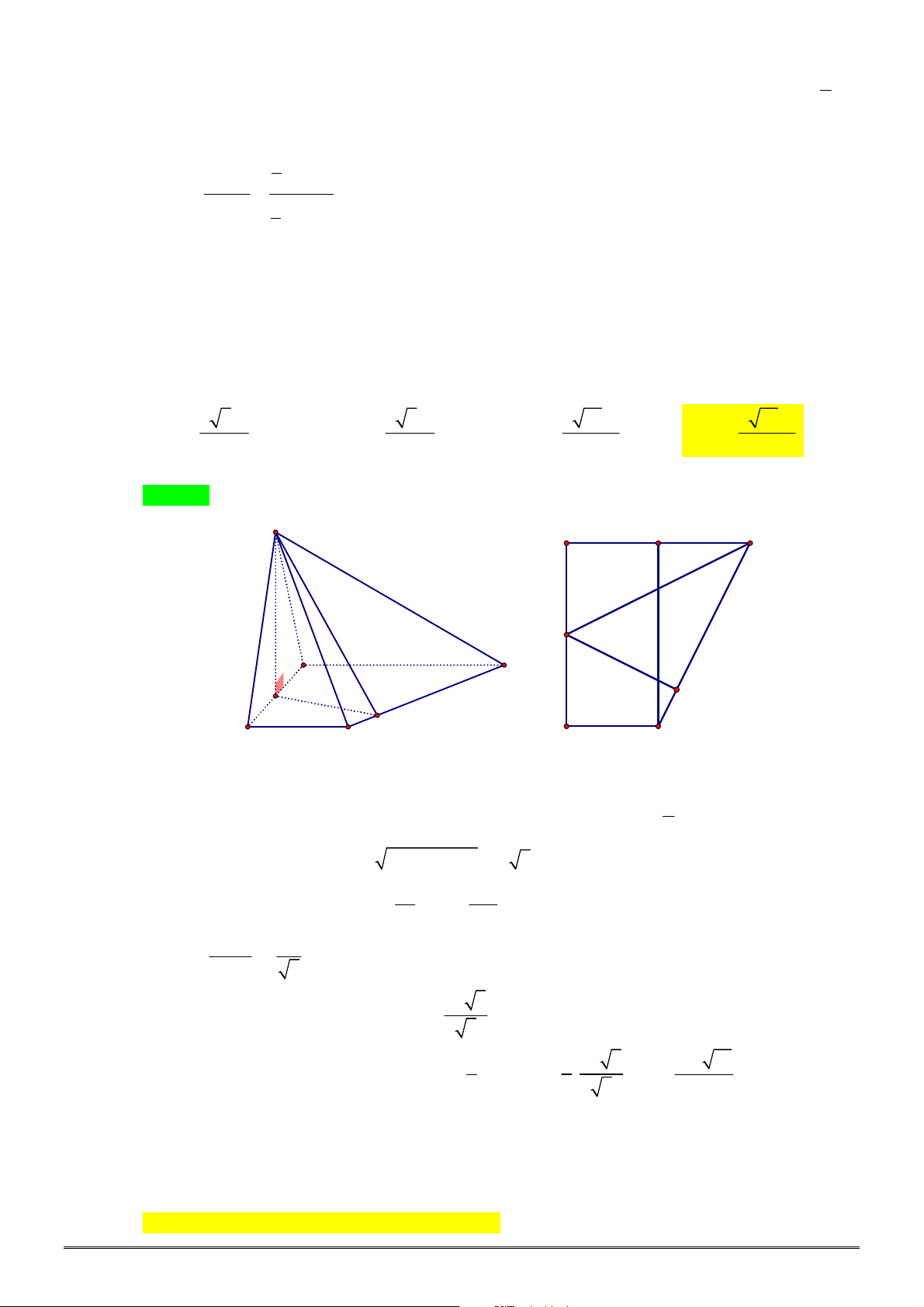
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/25
Đặt
;S ABC
d h
. Có tam giác
MNP
đồng dạng với tam giác
ABC
, tỉ số đồng dạng bằng
1
2
nên 4
ABC MNP
S S
.
Suy ra:
.
.
1
.
3
4
1
.
3
ABC
S ABC
S MNP
MNP
h S
V
V
h S
.
Vậy
1 2
4
V V
.
Câu 42. [2H1-3] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
; biết
2
AB AD a
,
CD a
. Góc giữa hai mặt phẳng
SBC
và
ABCD
bằng
60
. Gọi
I
là
trung điểm
AD
, biết hai mặt phẳng
SBI
và
SCI
cùng vuông góc với mặt phẳng
ABCD
.
Tính thể tích
V
của khối chóp
.
S ABCD
.
A.
3
3 5
5
a
V B.
3
3 5
8
a
V C.
3
3 15
8
a
V . D.
3
3 15
5
a
V .
Lời giải
Chọn D.
I
C
A
B
D
S
H
H
I
C
M
D
A
B
Kẻ
,
IH BC
H BC
. Suy ra:
;
SBC ABCD SHI
60
.
Gọi
M
là trung điểm của
AB
. Khi đó:
2
MC AD a
,
1
2
MB MA AB a
.
BCM
vuông tại
M
2 2
BC MB MC
5
a
.
IBC ABCD ICD IAB
S S S S
2
2 2
3
2
a
a a
2
3
2
a
.
2
IBC
S
IH
BC
3
5
a
.
SIH
vuông tại
I
.tan60
SI IH
3 3
5
a
.
Vậy thể tích khối chóp cần tìm là
.
1
.
3
S ABCD ABCD
V SI S
2
1 3 3
. .3
3
5
a
a
3
3 15
5
a
.
Câu 43. [2H2-1] Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình chóp nào cũng có mặt cầu ngoại tiếp.
B. Hình hộp đứng nào cũng có mặt cầu ngoại tiếp.
C. Hình lăng trụ tam giác có cạnh bên không vuông góc với đáy có thể nội tiếp một mặt cầu.
D. Hình tứ diện nào cũng có mặt cầu ngoại tiếp.
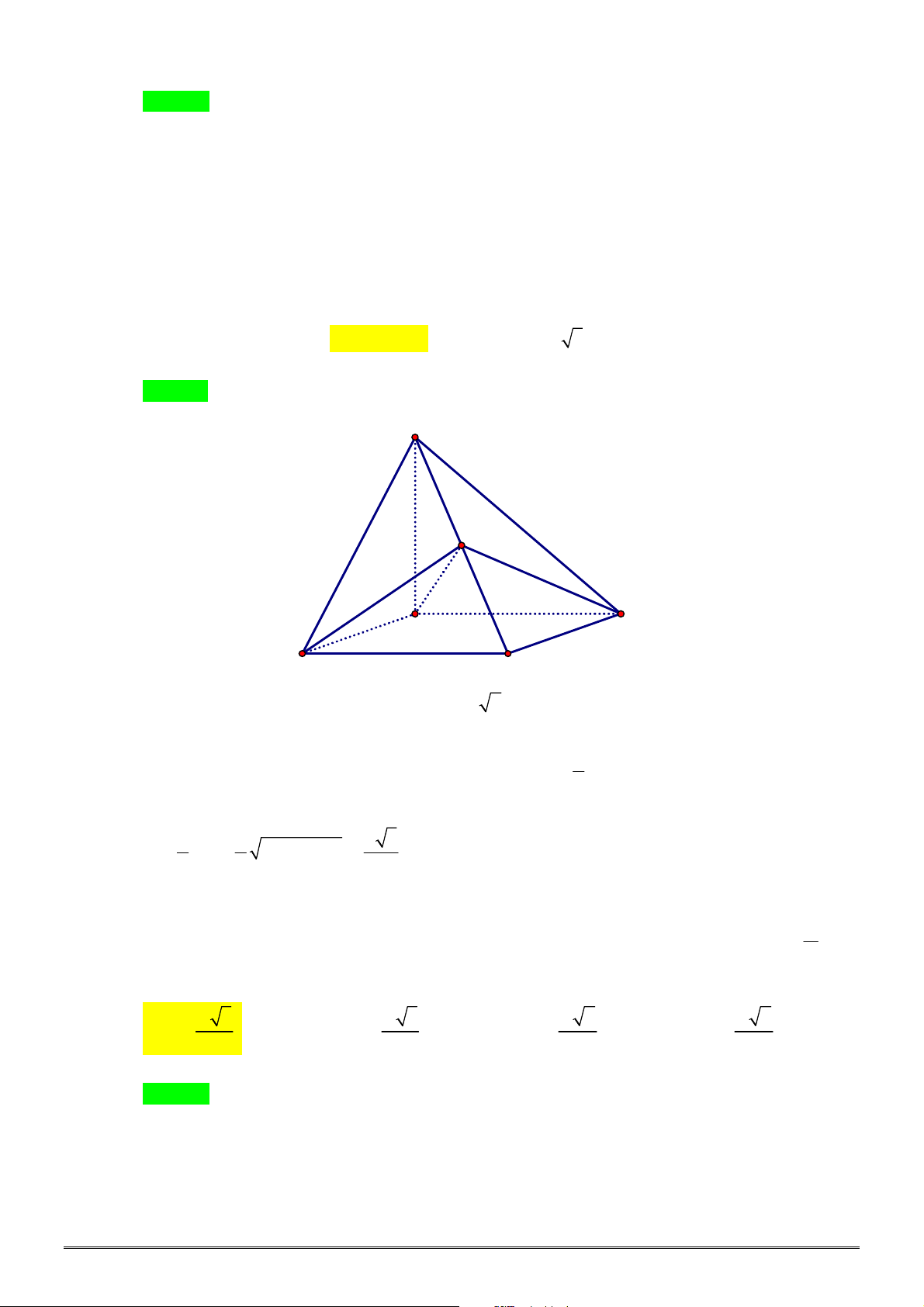
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/25
Lời giải
Chọn D.
Chỉ có hình chóp có đáy là đa giác nội tiếp được đường tròn mới có mặt cầu ngoại tiếp.
Đáp án A sai.
Chỉ những hình lăng trụ đứng có đáy là đa giác nội tiếp được đường tròn mới có mặt cầu ngoại
tiếp.
Đáp án B, C sai.
Hình tứ diện có đáy là tam giác luôn nội tiếp một đường tròn nên luôn có mặt cầu ngoại tiếp.
Đáp án D đúng.
Câu 44. [2H2-2] Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
SA
vuông
góc với mặt phẳng đáy và
SA a
. Tính diện tích
S
của mặt cầu ngoại tiếp hình chóp đã cho.
A.
2
4
S a
. B.
2
3
S a
. C.
2
3
S a
. D.
2
6
S a
.
Lời giải
Chọn B.
I
C
A
D
B
S
Vì
ABCD
là hình vuông cạnh
a
nên
2
AC a
.
Dễ dàng chứng minh được các tam giác
,
SAC
SBC
và
SCD
lần lượt vuông tại
,
A
B
và
D
.
Gọi
I
là trung điểm của
SC
1
2
IA IB IC ID IS SC
.
Do đó: mặt cầu ngoại tiếp hình chóp
.
S ABCD
có tâm là
I
và bán kính
1
2
R SC
2 2
1
2
SA AC
3
2
a
.
Vậy diện tích mặt cầu ngoại tiếp hình chóp
.
S ABCD
là
2
4
S R
2
3
a
Câu 45. [2H2-2] Cho mặt cầu tâm
O
bán kính
R
và mặt phẳng
P
cách tâm
O
một khoảng
2
R
.Tìm
bán kính
r
của đường tròn giao tuyến giữa mặt phẳng
P
và mặt cầu đã cho?
A.
3
2
R
r . B.
3
4
R
r . C.
2
2
R
r . D.
2
4
R
r .
Lời giải
Chọn A.
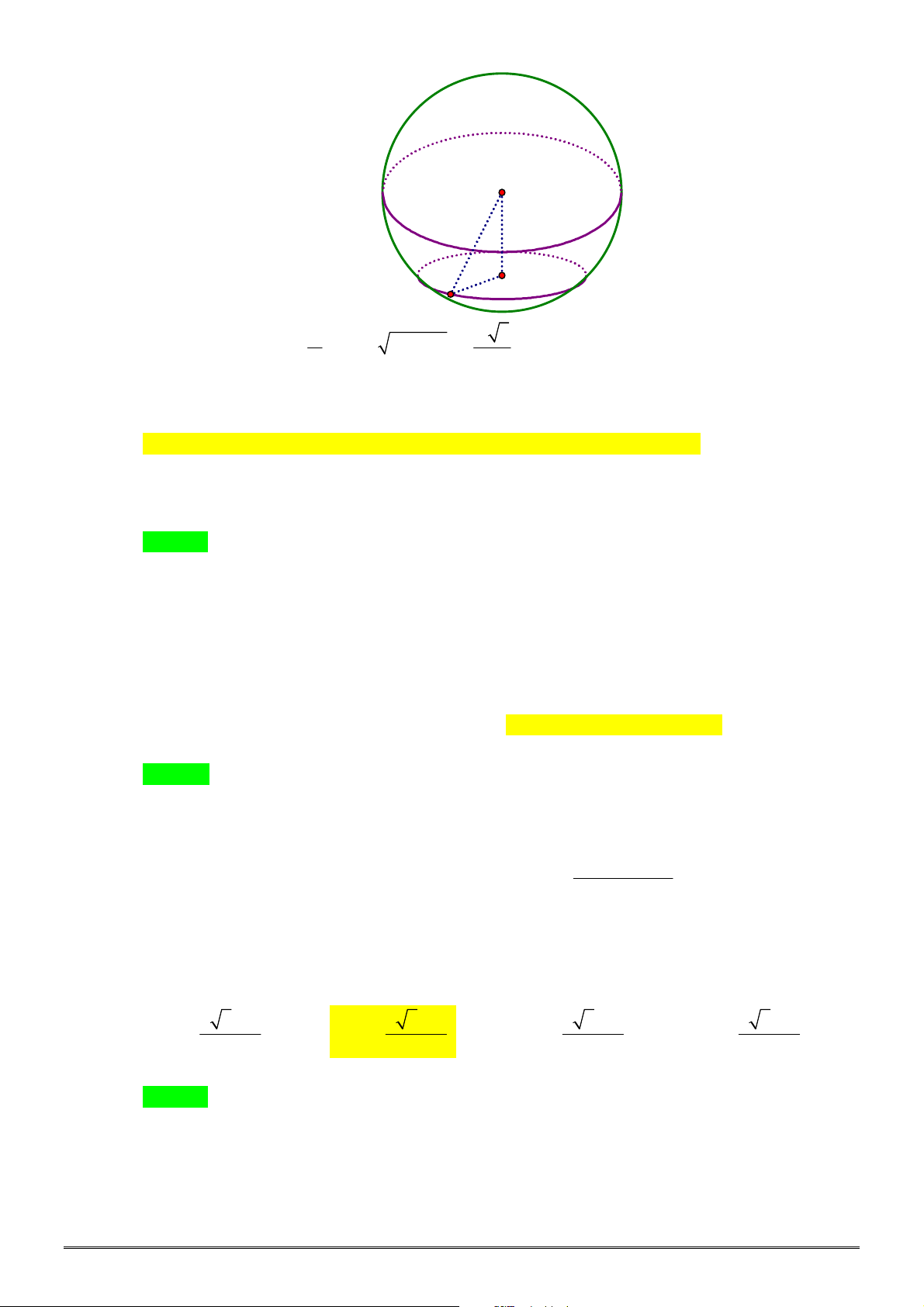
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/25
d
R
r
Đặt:
;
d d O P
2
R
2 2
r R d
3
2
R
.
Câu 46. [2H1-2] Trong các mệnh đề sau, mệnh đề nào sai?
A. Chỉ có năm loại khối đa diện đều.
B. Hình chóp tam giác đều là hình chóp có bốn mặt là những tam giác đều.
C. Mỗi cạnh của hình đa diện đều là cạnh chung của đúng hai mặt.
D. Mỗi khối đa diện đều là một khối đa diện lồi.
Lời giải
Chọn B.
Hình chóp tam giác đều chỉ có mặt đáy phải là tam giác đều, các mặt bên chỉ cần thỏa mãn điều
kiện tam giác cân.
Câu 47. [2H1-3] Trong không gian cho ba điểm cố định
A
,
B
,
C
phân biệt và không thẳng hàng. Tìm
tập hợp các điểm
M
trong không gian sao cho thể tích khối chóp
.
M ABC
là một số dương
không đổi?
A. Hai đường thẳng song song. B. Một mặt cầu.
C. Một mặt phẳng. D. Hai mặt phẳng song song.
Lời giải
Chọn D.
Khối chóp
.
M ABC
có đáy là tam giác
ABC
có diện tích không đổi. Thể tích khối chóp
.
M ABC
không đổi khi
;
M ABC
d không đổi. Khi đó tập hợp các điểm
M
là hai mặt phẳng
song song với
ABC
và cách
ABC
một khoảng bằng
3 .
V M ABC
S ABC
.
Câu 48. [2H2-3] Cho hình chóp
.
S ABCD
có
SA ABCD
,
SA a
. Đáy
ABCD
là hình thang vuông
tại
A
và
B
,
AB BC a
và
2
AD a
. Tính theo
a
thể tích khối cầu ngoại tiếp hình chóp
.
S ACD
.
A.
3
5 5
9
a
V
. B.
3
5 5
6
a
V
. C.
3
5 5
3
a
V
. D.
3
5 5
12
a
V
.
Lời giải
Chọn B.
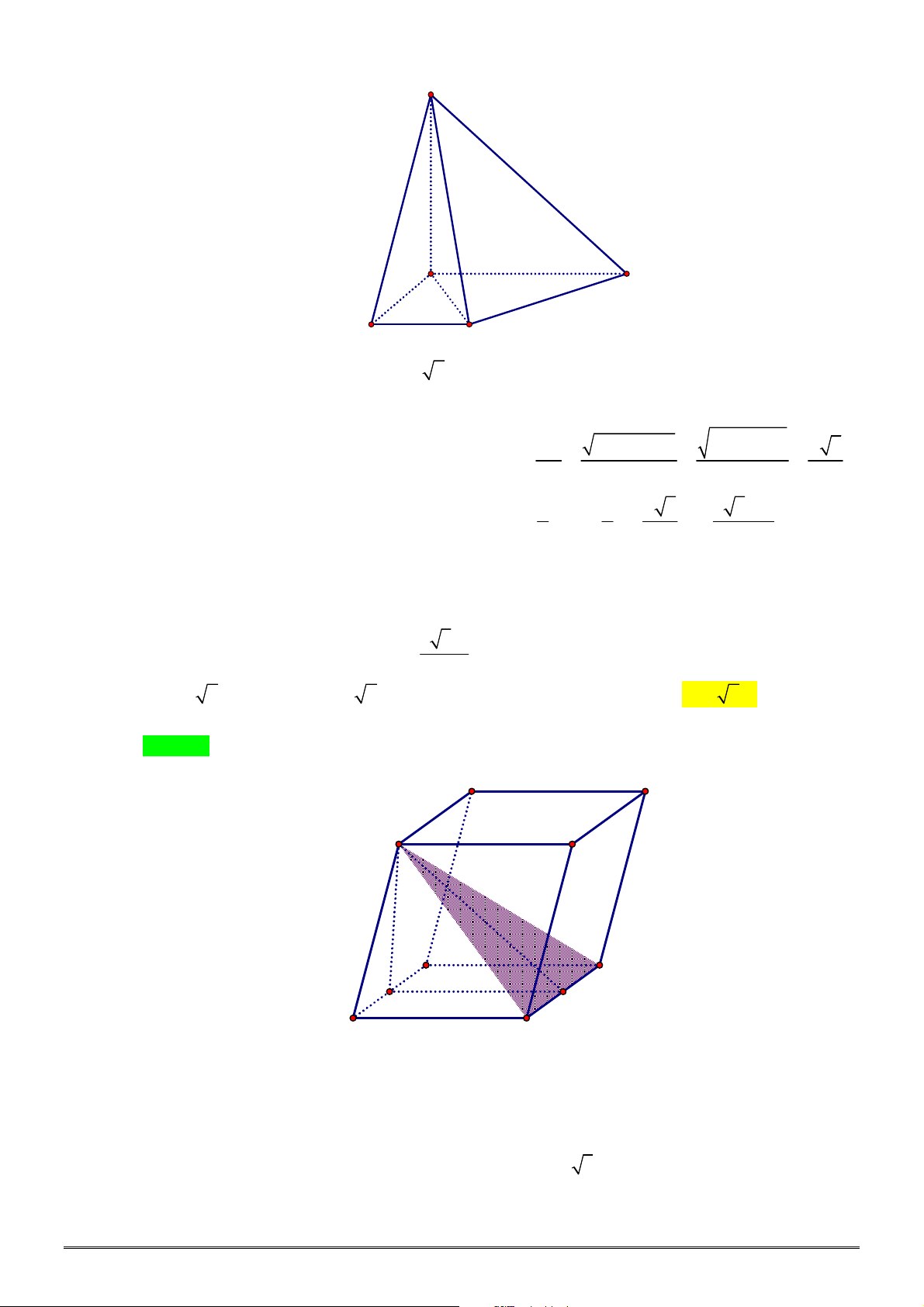
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 23/25
C
A
D
B
S
Xét tam giác
ACD
, có
2
AC CD a
;
2
AD a
. Ta được tam giác
ACD
vuông cân tại
C
.
Có
90
DC SAC SCD
;
90
SAD
. Suy ra mặt cầu ngoại tiếp hình chóp
.
S ACD
có
tâm là trung điểm đoạn thẳng
SD
và bán kính bằng
2
2
2 2
2
5
2 2 2 2
a a
SD SA AD a
.
Thể tích khối cầu ngoại tiếp hình chóp
.
S ACD
:
3
3
3
4 4 5 5 5
.
3 3 2 6
a a
V R
.
Câu 49. [1H2-2] Cho hình lăng trụ
.
ABCD A B C D
có đáy
ABCD
là hình vuông. Hình chiếu vuông
góc của
A
lên
mp ABCD
là trung điểm
AB
, góc giữa
mp A CD
và
mp ABCD
là
60
.
Thể tích của khối chóp
.
B ABCD
là
3
8 3
3
a
. Tính theo
a
độ dài đoạn thẳng
AC
?
A.
3
2 2
a
. B.
2
a
. C.
2
a
. D.
2 2
a
.
Lời giải
Chọn D.
x
M
H
C'
D'
A'
D
B
C
A
B'
Gọi
H
,
M
lần lượt là trung điểm của
AB
,
CD
. Ta có
A H ABCD
;
; ;
A CD ABCD A M HM
A MH
60
.
Đặt
AB x
.
Tam giác
A HM
vuông tại
H
có
.tan60 3
A H HM x
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 24/25
Ta có
2
. .
1 1
. . . 3.
3 3
B ABCD A ABCD ABCD
V V A H S x x
. Từ giả thiết, ta được
3 3
3 8 3
2
3 3
x a
x a
.
Vậy
2 2 2
AC x a
.
Câu 50. [2H1-4] Cho khối chóp
.
S ABCD
có đáy là hình bình hành và có thể tích là
V
. Gọi
M
là trung
điểm của
SB
,
P
là điểm thuộc cạnh
SD
sao cho
2
SP DP
. Mặt phẳng
AMP
cắt cạnh
SC
tại
N
. Tính thể tích của khối đa diện
ABCDMNP
theo
V
.
A.
23
30
V
. B.
19
30
V
. C.
2
5
V
. D.
7
30
V
.
Lời giải
Chọn A.
N
I
O
M
P
C
A
D
B
S
.
I
O
P
M
B
S
D
Q
N
I
O
A
S
C
Gọi
O
là tâm của hình vuông
ABCD
. Trong
SBD
,
SO MP I
. Trong
SAC
,
AI SC N
.
Có
//
OM SP
, theo định lí Ta-let, ta có
2
4
3
1
3
2
SD
IS SP
IO MO
SD
.
Gọi
Q
là trung điểm đoạn thẳng
AN
. Có //
QO SC
, theo định lí Ta-let, ta có:
1 4 2
.
2 2 3 3
SN SI
NC QO
2
5
SN
SC
. Thay xem co dung ko
1 4 2
.
2 2 3 3
SN SI
NC IO
Áp dụng công thức tỉ số thể tích khối chóp tứ giác, được:

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 25/25
.
.
1
. . .
2
S AMNP
S ABCD
V
SA SN SM SP
V SA SC SB SD
1 2 1 2 7
. .
2 5 2 3 30
. Suy ra:
.
7 23 23
1
30 30 30
ABCDMNP
ABCDMNP
S ABCD
V
V
V
V
.
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/22
TRƯỜNG THPT KIM LIÊN – HÀ NỘI ĐỀ ÔN TẬP HỌC KỲ I NĂM HỌC 2017 – 2018
ĐỀ SỐ 4 MÔN TOÁN - LỚP 12
------- ------------------
Câu 1. [2D1-1] Hàm số
3 2
6 9 7
y x x x
đồng biến trên
A. Khoảng
1;3
. B. Đoạn
1;3
.
C. Tập
;1 3;
. D. Các khoảng
;1
,
3;
.
Câu 2. [2D1-1] Cho hàm số
2 1
1
x
y
x
. Kết luận nào sau đây đúng:
A. Hàm số đồng biến trên
\ 1
.
B. Hàm số đồng biến trên các khoảng
;1
,
3;
.
C. Hàm số đồng biến trên tập
;1 1;
.
D. Hàm số nghịch biến trên các khoảng
;1
,
3;
.
Câu 3. [2D1-3] Giá trị của tham số
m
để hàm số
3 2
1
2 2 2 2 5
3
m
y x m x m x
nghịch
biến trên
là
A.
2 3
m
. B.
2
m
. C.
1
m
. D.
2 3
m
.
Câu 4. [2D1-2] Điểm cực đại của hàm số
3 2
3 1
y x x
là
A.
0
x
. B.
2
x
. C.
0;2
. D.
2;6
.
Câu 5. [2D1-2] Giá trị của tham số
m
để hàm số
3
2 1
y x mx
đạt cực tiểu tại
1
x
A.
3
2
m
. B.
3
2
m
. C.
2
3
m
. D.
2
3
m
.
Câu 6. [2D1-2] Hàm số
4 2
3 2 1
y mx m x m
chỉ có cực đại mà không có cực tiểu với:
A.
3
m
. B.
3
m
. C.
3
0
m
m
. D.
3 0
m
.
Câu 7. [2D1-2] Giá trị lớn nhất của hàm số
2
4
y x x
là
A.
2
. B.
0
. C.
4
. D.
1
.
Câu 8. [2D1-2] Giá trị lớn nhất của hàm số
3 1
3
x
y
x
trên đoạn
0;2
là
A.
1
3
. B.
5
. C.
4
. D.
1
3
.
Câu 9. [2D1-1] Số giao điểm của đồ thị hai hàm số
3 2
6 9 1
y x x x
và
1
y x
là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 10. [2D1-3] Tìm
m
để đường thẳng
1
y x m
cắt đồ thị
2 1
1
x
y
x
tại hai điểm phân biệt
A
,
B
và
2 3
AB .
A.
4 3
m . B.
2 10
m . C.
4 10
m . D.
2 3
m .
Câu 11. [2D1-2] Đồ thị hàm số nào sau đây có tiệm cận đứng là đường thẳng
1
x
và tiệm cận ngang
là
2
y
.
A.
2
1
x
y
x
. B.
1
1
x
y
x
. C.
2
1
x
y
x
. D.
2
1
x
y
x
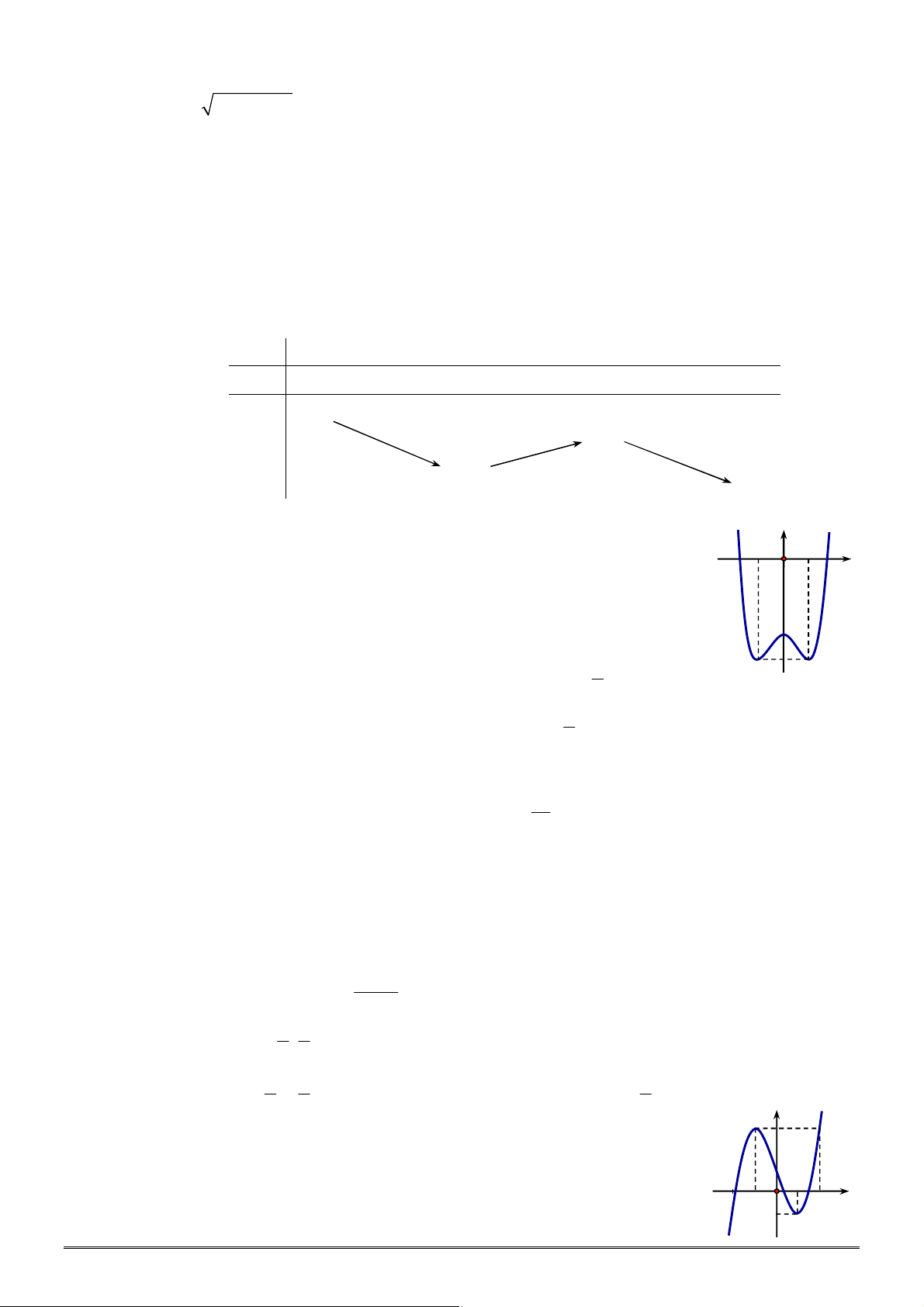
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/22
Câu 12. [2D1-3] Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
2
2 3
y x x x
là
A.
3
. B.
2
. C.
1
. D.
0
Câu 13. [2D1-2] Cho hàm số
3 2
3 1
y x x
. Phương trình tiếp tuyến tại điểm
3;1
A là
A.
9 20
y x
. B.
9 28
y x
. C.
9 20
y x
. D.
9 28
y x
.
Câu 14. [2D1-3] Trong các tiếp tuyến của đồ thị hàm số
3 2
3 2
y x x
, hệ số góc nhỏ nhất của các
tiếp tuyến đó là
A.
3
. B.
3
. C.
4
. D.
0
Câu 15. [2D1-2] Bảng biến thiên trong hình dưới đây là bảng biến thiên của hàm số nào?
A.
3 2
3 1
y x x
. B.
3 2
3 1
y x x
.
C.
3 2
3 1
y x x
. D.
3 2
3 1
y x x
Câu 16. [2D1-2] Đồ thị trong hình dưới đây là đồ thị của hàm số nào?
A.
4 2
3
y x x
. B.
4 2
3
y x x
.
C.
4 2
2 3
y x x
. D.
4 2
3
y x x
.
Câu 17. [2D1-3] Giá trị của tham số
m
để đồ thị của hai hàm số
3
5
2
4
y x x
và
2
y x x m
tiếp xúc là
A.
2
m
. B.
2
m
. C.
2
3
m
. D.
3
m
.
Câu 18. [2D1-2] Giá trị nhỏ nhất của hàm số
2
3sin 4cos 2
y x x
là
A.
2
. B.
6
. C.
19
3
. D. Không tồn tại.
Câu 19. [2D1-3] Xét phương trình
3 2
3 2 0
x x m
. Phát biểu nào sau đây là đúng:
A. Với
7
m
, phương trình trên có ba nghiệm phân biệt.
B. Với
1
m
, phương trình trên có hai nghiệm phân biệt.
C. Với
2 6
m
, phương trình trên có ba nghiệm phân biệt.
D. Phương trình trên có ba nghiệm phân biệt khi
2
m
hoặc
6
m
.
Câu 20. [2D1-2] Đồ thị hàm số
2
2 1
x
y
x
A. Nhận điểm
1 1
;
2 2
làm tâm đối xứng. B. Không có tâm đối xứng.
C. Nhận điểm
1 1
;
2 2
làm tâm đối xứng. D. Nhận điểm
1
;2
2
làm tâm đối xứng.
Câu 21. [2D1-1] Đồ thị hình bên là đồ thị của hàm số nào?
A.
3
3 1
y x x
. B.
3 2
1
y x x
.
C.
3
3 1
y x x
. D.
3
3 1
y x x
.
x
0
2
y
0
0
y
3
1
O
x
y
4
3
1
1
O
x
y
1
1
1
3
2
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/22
Câu 22. [2D1-1] Biết hàm số
2
4 1
1
x x
y
x
có hai cực trị
1
x
,
2
x
. Tích
1 2
.
x x
bằng
A.
2
. B.
5
. C.
1
. D.
4
.
Câu 23. [2D2-1] Biểu thức
a a a a
;
0
a
bằng
A.
13
16
a
. B.
11
64
a
. C.
15
16
a
. D.
15
8
a
.
Câu 24. [2D2-1] Xét mệnh đề: “Với mọi số thực
a
,
x
,
y
, nếu
x y
thì
x y
a a
”. Với điều kiện sau
đây của
a
thì mệnh đề trên đúng.
A.
a
bất kì. B.
0
a
. C.
1
a
. D.
0 1
a
.
Câu 25. [2D2-2] Tỉ lệ tăng dân số hàng năm của một nước là
1,5%
. Năm
2000
, dân số nước này là
212942000
. Dân số nước đó vào năm
2008
xấp xỉ:
A.
239877584
người. B.
240090000
người.
C.
230081000
người. D.
24078100
người.
Câu 26. [2D2-2] Đẳng thức
7 7 7
1
log log log
3 2
a b
a b
, với
, 0
a b
tương đương với:
A.
2 2
7
a b ab
. B.
2 2
14
a b ab
. C.
2 2
5
a b ab
. D.
3 3
7
a b ab
.
Câu 27. [2D2-2] Cho
12
log 27
a
. Khi đó
36
log 24
bằng
A.
9
6 2
a
a
. B.
9
6 2
a
a
. C.
9
6 2
a
a
. D.
9
6 2
a
a
.
Câu 28. [2D2-1] Giá trị của biểu thức
2
8log 7
a
a
,
0, 1
a a
bằng
A.
2
7
. B.
4
7
. C.
8
7
. D.
16
7
.
Câu 29. [2D2-1] Biết
ln 2
a
,
ln3
b
. Biểu diễn
1
ln
12
theo
a
,
b
được kết quả:
A.
2
a b
. B.
2
a b
. C.
2
a b
. D.
2
a b
.
Câu 30. [2D2-1] Biết
log 0
a
, khi đó
a
thỏa mãn:
A.
a
bất kì. B.
0
a
. C.
1
a
. D.
0 1
a
.
Câu 31. [2D2-2] Tập xác định của hàm số
2
1
2
log 1
y x
là
A.
; 1 1;D
. B.
D
.
C.
1;1
D
. D.
; 1 1;D
.
Câu 32. [2D2-3] Đạo hàm của hàm số
2x
1 e
y x là hàm số
A.
2
2 1 e
x
y x . B.
2 1 e
x
x . C.
2
2 1 e
2
x
x
. D.
2
2 e
x
x
.
Câu 33. [2D2-1] Đồ thị của hàm số
2
x
y
A. Nhận trục tung làm tiệm cận đứng.
B. Có trục đối xứng.
C. Đối xứng với đồ thị hàm số
1
2
x
y
qua trục hoành.
D. Nhận trục hoành là tiệm cận ngang.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/22
Câu 34. [2D2-3] Đạo hàm của hàm số
3
2
ln 2
y x
tại điểm
1
x
là
A.
1
3
2
ln 2
3
. B.
1
3
2
ln 2
3
. C.
1
3
1
ln 2
3
. D.
1
3
1
ln 2
3
.
Câu 35. [2D2-1] Cho hàm số
4
y x
. Trong các khẳng định sau, khẳng định nào sai?
A. Tập xác định của hàm số là
0;D
. B. Hàm số nghịch biến trên tập xác định.
C. Đồ thị hàm số qua điểm
1;1
. D. Đồ thị hàm số không có đường tiệm cận.
Câu 36. [2D2-3] Cho hàm số
2
ln 1
y x
. Số nghiệm của phương trình
0
y
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 37. [2D2-3] Số điểm cực trị của hàm số
e
1
x
y
x
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 38. [2D2-3] Giá trị của
x
thỏa mãn đẳng thức
3 5
5 3
x x
là
A.
5 3
3
log log 5
x . B.
5 5
3
log log 3
x .
C.
3 5
5
log log 3
x . D.
3 3
5
log log 5
x .
Câu 39. [2H1-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
3
a
. Biết tam giác
SAB
là tam giác cân tại
S
và nằm trong mặt phẳng vuông góc với đáy, tam giác
SAB
vuông. Thể
tích khối chóp
.
S ABCD
là
A.
3
9 3
a . B.
3
9 3
2
a
. C.
3
9
a
. D.
3
9
2
a
.
Câu 40. [2D1-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật
2
AD a
,
AC a
. Gọi
H
là trọng tâm tam giác
ABD
,
SH
vuông góc với đáy, góc giữa
SD
và mặt phẳng
ABCD
bằng
30
. Thể tích khối chóp
.
S ABCD
là
A.
3
a
. B.
3
2
a
. C.
3
2 35
9
a
. D.
3
5
3
a
.
Câu 41. [2H1-3] Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
2
BC a
. Biết
A C
tạo với mặt đáy một góc
60
. Thể tích khối lăng trụ
.
ABC A B C
là
A.
3
3 3
a . B.
3
6 3
a . C.
3
3 3
2
a
. D.
3
3
2
a
.
Câu 42. [2H1-3] Cho hình lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác đều,
3
AB a
. Biết hình
chiếu của
A
lên mặt phẳng
ABC
trùng với trung điểm của
BC
và cạnh bên bằng
2
a
. Thể
tích khối lăng trụ
.
ABC A B C
là
A.
3
21
8
a
. B.
3
3 21
8
a
. C.
3
14
12
a
. D.
3
14
8
a
.
Câu 43. [2H1-3] Cho khối tứ diện có thể tích là
V
. Gọi
V
là thể tích của khối đa diện có đỉnh là trung
điểm các cạnh của khối tứ diện đã cho. Ta có
V
bằng
A.
3
.
4
V
B.
4
.
5
V
C.
.
2
V
D.
2
.
3
V

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/22
Câu 44. [2H1-2] Cho nửa hình tròn đường kính
3
AB a
quay quanh trục
AB
, ta được khối tròn
xoay có thể tích là
A.
3
2 3
a . B.
3
3
2
a
. C.
3
3
2
a
. D.
3
2 3
3
a
.
Câu 45. [2H1-2] Cho hình lăng trụ đứng có đáy là hình vuông cạnh
a
, chiều cao bằng
2
a
. Diện tích
mặt cầu ngoại tiếp hình lăng trụ đó là
A.
2
6
a
. B.
2
6
4
a
. C.
2
6
4
a
. D.
2
6
a
.
Câu 46. [2H1-1] Tên gọi của khối đa diện đều loại
3;4
là khối:
A. Bát diện đều. B. Lập phương.
C. Hai mươi mặt đều. D. Mười hai mặt đều.
Câu 47. [2H1-3] Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
6
3
a
. Gọi
O
là tâm đáy. Trong các khẳng định sau, khẳng định nào đúng khi nói về mặt cầu ngoại tiếp tứ
diện
.
S ABC
?
A. Mặt cầu có tâm trùng với
O
và bán kính
3
3
a
R .
B. Mặt cầu có tâm trùng với
O
và bán kính
6
6
a
R .
C. Mặt cầu có tâm là trung điểm
SO
và bán kính
3
6
a
R .
D. Mặt cầu có tâm là trung điểm
SO
và bán kính
3
2
a
R .
Câu 48. [2H1-2] Cho hình chóp có đáy là đa giác
n
cạnh. Trong các khẳng định sau, khẳng định nào đúng?
A. Số cạnh của hình chóp bằng
1
n
. B. Số mặt của hình chóp bằng
2
n
.
C. Số đỉnh của hình chóp bằng
2 1
n
. D. Số mặt của hình chóp bằng số đỉnh.
Câu 49. [2H1-3] Cho hình chóp
.
S ABCD
có
SA ABCD
. Đáy
ABCD
là hình thoi,
2
AC a
,
3
BD a
,
I
là trung điểm của
SC
. Bán kính mặt cầu tâm
I
và tiếp xúc với mặt phẳng
SAB
là
A.
3
2
a
. B.
3
4
a
. C.
21
7
a
. D.
2
4
a
.
Câu 50. [2H1-3] Cho hình chóp
.
S ABC
có
SA ABC
,
2
SA a
. Đáy
ABC
là tam giác đều cạnh
a
.
Bán kính mặt cầu tâm
S
và tiếp xúc với đường thẳng
BC
là
A.
3
2
a
. B.
3 5
2
a
. C.
15
2
a
. D.
19
2
a
.
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/22
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
D
D
B 5 B A
D
C
C
A
C
B A
B C
B A
C
A
C
B C
C
A
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
A
B C
D
D
A
D
B
B
B A
A
D
C
D
B C
C
D
A
A
D
C
D
HƯỚNG DẪN GIẢI
Câu 1. [2D1-1] Hàm số
3 2
6 9 7
y x x x
đồng biến trên
A. Khoảng
1;3
. B. Đoạn
1;3
.
C. Tập
;1 3;
. D. Các khoảng
;1
,
3;
.
Lời giải
Chọn D.
Ta có:
2
3 12 9
y x x
.
0
y
1
3
x
x
Vậy hàm số đồng biến trên các khoảng
;1 , 3;
.
Câu 2. [2D1-1] Cho hàm số
2 1
1
x
y
x
. Kết luận nào sau đây đúng:
A. Hàm số đồng biến trên
\ 1
.
B. Hàm số đồng biến trên các khoảng
;1
,
3;
.
C. Hàm số đồng biến trên tập
;1 1;
.
D. Hàm số nghịch biến trên các khoảng
;1
,
3;
.
Lời giải
Chọn D.
TXĐ:
\ 1
D
.
Ta có:
2
3
0 1
1
y x
x
.
Vậy hàm số nghịch biến trên các khoảng
;1 , 1;
.
Câu 3. [2D1-3] Giá trị của tham số
m
để hàm số
3 2
1
2 2 2 2 5
3
m
y x m x m x
nghịch
biến trên
là
A.
2 3
m
. B.
2
m
. C.
1
m
. D.
2 3
m
.
Lời giải
Chọn D.
Ta có:
2
1 4 2 2 2
y m x m x m
x
1
3
y
0
0
y
11
7

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/22
TH
1
:
1
m
ta có:
4 2
y x
, không thỏa.
TH
2
:
1
m
Để hàm số nghịch biến trên
khi 0y x
2
1 0
2 2 1 .2. 2 0
m
m m m
1
2 3
m
m
2 3
m
.
Câu 4. [2D1-2] Điểm cực đại của hàm số
3 2
3 1
y x x
là
A.
0
x
. B.
2
x
. C.
0;2
. D.
2;6
.
Lời giải
Chọn B.
Ta có:
2
3 6
y x x
.
0
y
0
2
x
x
.
6 6
y x
.
Với
0
x
0 6 0
y
nên
0
x
là điểm cực tiểu của hàm số.
Với
2
x
2 6 0
y
nên
2
x
là điểm cực đại của hàm số.
Câu 5. [2D1-2] Giá trị của tham số
m
để hàm số
3
2 1
y x mx
đạt cực tiểu tại
1
x
A.
3
2
m
. B.
3
2
m
. C.
2
3
m
. D.
2
3
m
.
Lời giải
Chọn A.
Ta có:
2
3 2
y x m
;
6
y x
.
Để hàm số đạt cực tiểu tại
1
x
khi
1 0
1 0
y
y
3 2 0
6 0
m
3
2
m
.
Câu 6. [2D1-2] Hàm số
4 2
3 2 1
y mx m x m
chỉ có cực đại mà không có cực tiểu với:
A.
3
m
. B.
3
m
. C.
3
0
m
m
. D.
3 0
m
.
Lời giải
Chọn B.
Xét hàm số:
4 2
3 2 1
y mx m x m
1
.
* Với
0
m
ta có:
2
3 1
y x
.hàm số luôn có một cực tiểu. Do đó
0
m
không thỏa mãn.
* Với
0
m
để hàm số
1
có cực đại mà không có cực tiểu khi
0
0
3
3
3 0
0
m
m
m
m
m m
m
.
Câu 7. [2D1-2] Giá trị lớn nhất của hàm số
2
4
y x x
là
A.
2
. B.
0
. C.
4
. D.
1
.
Lời giải

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/22
Chọn A.
Xét hàm số
2
4
y x x
. Tập xác định
0;4
D .
Ta có
2
2
4 4 2 2
y x x x
với
x D
.
Vậy giá trị lớn nhất của hàm số là
2
, khi
2
x
.
Câu 8. [2D1-2] Giá trị lớn nhất của hàm số
3 1
3
x
y
x
trên đoạn
0;2
là
A.
1
3
. B.
5
. C.
4
. D.
1
3
.
Lời giải
Chọn D.
Xét hàm số
3 1
3
x
y
x
trên
0;2
.
Ta có
2
8
0
3
y
x
3
x
nên hàm số nghịch biến trên
0;2
.
Dó đó hàm số đạt giá trị lớn nhất tại
0
x
và
0;2
1
0
3
max y y
.
Câu 9. [2D1-1] Số giao điểm của đồ thị hai hàm số
3 2
6 9 1
y x x x
và
1
y x
là
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn C.
Phương trình hoành độ giao điểm của hai đồ thị hàm số là
3 2
6 9 1 1
x x x x
3 2 2
6 10 0 6 10 0 0
x x x x x x x
do
2
2
6 10 3 1 0
x x x
.
Do đó có
1
giao điểm.
Câu 10. [2D1-3] Tìm
m
để đường thẳng
1
y x m
cắt đồ thị
2 1
1
x
y
x
tại hai điểm phân biệt
A
,
B
và
2 3
AB .
A.
4 3
m . B.
2 10
m . C.
4 10
m . D.
2 3
m .
Lời giải
Chọn C.
Phương trình hoành độ giao điểm của hai đồ thị hàm số là
2 2
2 1
1 1 2 1 2 2 0
1
x
x m x mx m x x m x m
x
,
1
(với
1
x
).
Yêu cầu bài toán trở thành tìm
m
để
1
có hai nghiệm phân biệt thỏa mãn
1
x
và tọa độ
giao điểm
A
,
B
của chúng thỏa mãn
2 3
AB .
Mà
1
có hai nghiệm phân biệt khi và chỉ khi
2
0 2 4 2 0
m m
6
2 6 0
2
m
m m
m
.
Phương trình
1
có hai nghiệm khác
1
khi:
1 1 2 2 0
m m
1 0
.
Gỉa sử
1 2
,
x x
là các nghiệm của phương trình
1
ta có:
1 2
1 2
2
2
x x m
x x m
*

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/22
1 1 2 2
; 1 ; ; 1
A x x m B x x m
.
2 3
AB
2
1 2
2 12
x x
2
1 2 1 2
4 6
x x x x
**
Thay
*
vào
**
ta được:
2
8 6 0
m m
4 10
m (thỏa).
Câu 11. [2D1-2] Đồ thị hàm số nào sau đây có tiệm cận đứng là đường thẳng
1
x
và tiệm cận ngang
là
2
y
.
A.
2
1
x
y
x
. B.
1
1
x
y
x
. C.
2
1
x
y
x
. D.
2
1
x
y
x
Lời giải
Chọn A.
Xét hàm số:
2
1
x
y
x
có TXĐ:
\ 1
D
.
Ta có:
2 2
lim lim lim 2
1
1
1
x x x
x x
y
x
x
x
.
1 1
2
lim lim
1
x x
x
y
x
;
1 1
2
lim lim
1
x x
x
y
x
.
Nên đồ thị hàm số
2
1
x
y
x
có tiệm cận đứng là đường thẳng
1
x
và tiệm cận ngang là
2
y
.
Câu 12. [2D1-3] Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
2
2 3
y x x x
là
A.
3
. B.
2
. C.
1
. D.
0
Lời giải
Chọn C.
TXĐ:
D
. Nên đồ thị hàm số không có đường tiệm cận đứng.
Ta có:
2
2
2 3
lim lim 2 3 lim 1 1
x x x
y x x x x
x x
.
Xét
2 2
2
2
2 3
lim lim 2 3 lim
2 3
x x x
x x x
y x x x
x x x
2
2
3
2
2 3
lim lim 1
2 3
2 3
1 1
x x
x
x
x x x
x x
nên đồ thị hàm số có một đường tiệm cận
ngang
1
y
.
Câu 13. [2D1-2] Cho hàm số
3 2
3 1
y x x
. Phương trình tiếp tuyến tại điểm
3;1
A là
A.
9 20
y x
. B.
9 28
y x
. C.
9 20
y x
. D.
9 28
y x
.
Lời giải
Chọn B.
Ta có:
2
3 6
y x x
,
2
3 3.3 6.3 9
y
.
Phương trình tiếp tuyến tại
3;1
A có dạng:
3 3 1 9 3 1 9 28
y y x x x
.
Vậy phương trình tiếp tuyến cần tìm là
9 28
y x
.
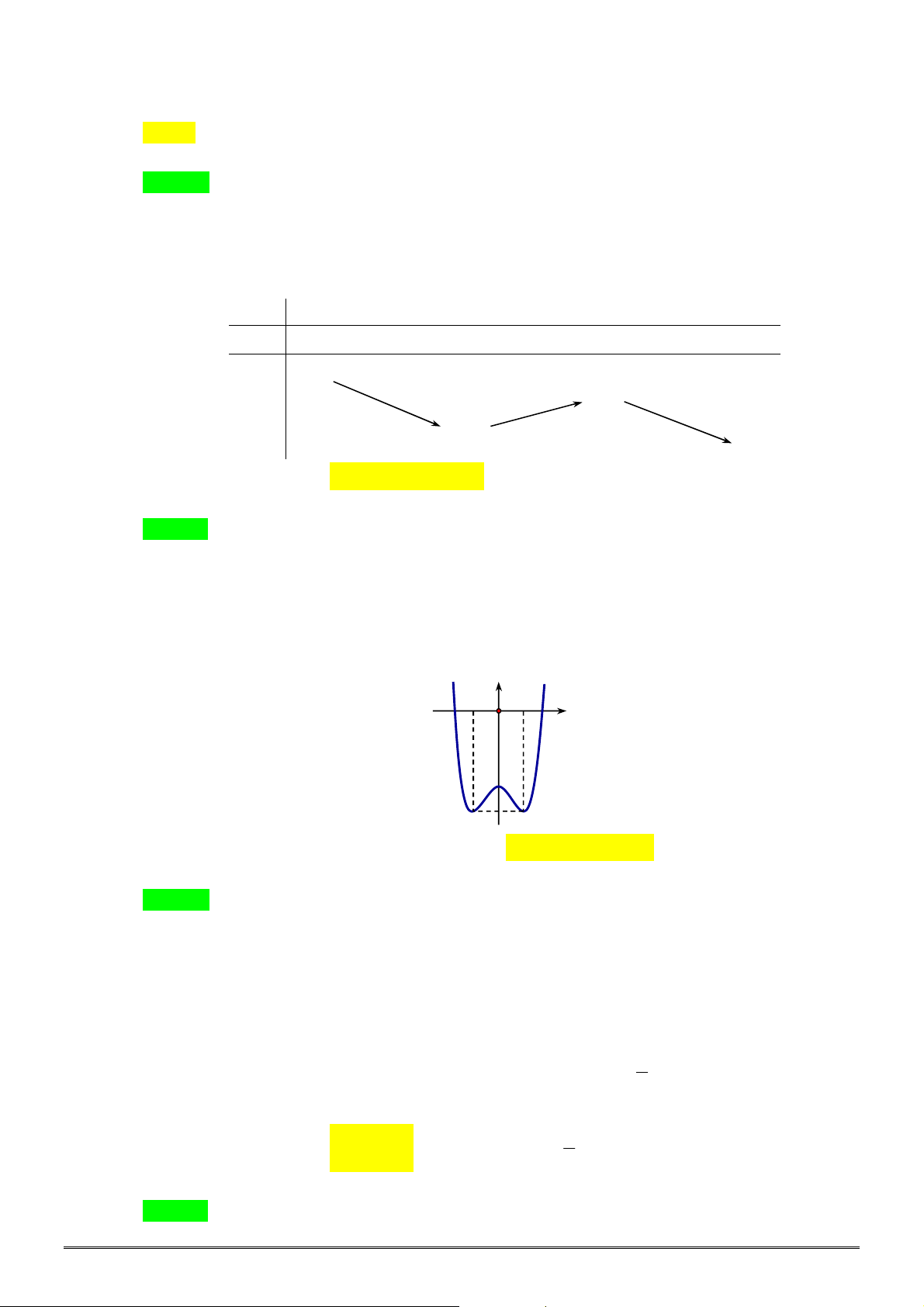
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/22
Câu 14. [2D1-3] Trong các tiếp tuyến của đồ thị hàm số
3 2
3 2
y x x
, hệ số góc nhỏ nhất của các
tiếp tuyến đó là
A.
3
. B.
3
. C.
4
. D.
0
Lời giải
Chọn A.
Gọi
k
là hệ số góc của tiếp tuyến, khi đó
2
2
0 0 0 0
3 6 3 1 3 3
k y x x x x
.
Vậy
min 0
3 1
k x
.
Câu 15. [2D1-2] Bảng biến thiên trong hình dưới đây là bảng biến thiên của hàm số nào?
A.
3 2
3 1
y x x
. B.
3 2
3 1
y x x
. C.
3 2
3 1
y x x
. D.
3 2
3 1
y x x
Lời giải
Chọn B.
Ta có:
lim 0
x
y a
nên loại A và C
Điểm cực đại của đồ thị hàm số là
2; 3
nên hàm số cần tìm có phương trình:
3 2
3 1
y x x
.
Câu 16. [2D1-2] Đồ thị trong hình dưới đây là đồ thị của hàm số nào?
A.
4 2
3
y x x
. B.
4 2
3
y x x
. C.
4 2
2 3
y x x
. D.
4 2
3
y x x
.
Lời giải
Chọn C.
Dựa vào dạng đồ thị của hàm số trùng phương (sgk) nên
0
a
(loại B).
Đồ thị có điểm cực đại là
0; 3
nên loại D.
Đồ thị hàm có hai điểm cực tiểu là
1; 4 ; 1; 4
nên loại A.
Vậy đồ thị đã cho là của hàm số
4 2
2 3
y x x
.
Câu 17. [2D1-3] Giá trị của tham số
m
để đồ thị của hai hàm số
3
5
2
4
y x x
và
2
y x x m
tiếp
xúc là
A.
2
m
. B.
2
m
. C.
2
3
m
. D.
3
m
.
Lời giải
Chọn B.
O
x
y
4
3
1
1
x
0
2
y
0
0
y
3
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/22
Để đồ thị của hai hàm số
3
5
2
4
y x x
và
2
y x x m
tiếp xúc
3 2
2
5
2
4
5
3 2 1
4
x x x x m
x x
có nghiệm
3 2
3 2
2
1
2
4
5
2
1
4
2
12 8 1 0
1
6
m x x x
x x x x m
x
x x
x
Với
1
2
2
x m
.
Với
1 107
6 54
x m .
Câu 18. [2D1-2] Giá trị nhỏ nhất của hàm số
2
3sin 4cos 2
y x x
là
A.
2
. B.
6
. C.
19
3
. D. Không tồn tại.
Lời giải
Chọn A.
TXĐ:
D
.
Xét
2 2
3sin 4cos 2 3cos 4cos 5
y x x x x f x
Đặt
cos 1; 1
t x t
Khi đó:
2
3 4 5
y f t t t
trên
1; 1
.
Xét
2
6 4 0 1; 1
3
y t t
.
Ta có:
2 19
1 6; ; 1 2
3 3
f f f
.
Vậy
1;1
19
3
x t
Max y Max f t
và
1;1
2
x t
Min y Min f t
.
Câu 19. [2D1-3] Xét phương trình
3 2
3 2 0
x x m
. Phát biểu nào sau đây là đúng:
A. Với
7
m
, phương trình trên có ba nghiệm phân biệt.
B. Với
1
m
, phương trình trên có hai nghiệm phân biệt.
C. Với
2 6
m
, phương trình trên có ba nghiệm phân biệt.
D. Phương trình trên có ba nghiệm phân biệt khi
2
m
hoặc
6
m
.
Lời giải
Chọn C.
TXĐ:
D
.
Xét phương trình
3 2 3 2
3 2 0 3 2
x x m x x m
.
Đặt
3 2 2
0 2
3 2 3 6 0
2 6
x y
f x x x f x x x
x y
.
Bảng biến thiên:

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/22
Dựa vào bảng biến thiên ta thấy: với
2 6
m
, phương trình trên có ba nghiệm phân biệt.
Câu 20. [2D1-2] Đồ thị hàm số
2
2 1
x
y
x
A. Nhận điểm
1 1
;
2 2
làm tâm đối xứng.
B. Không có tâm đối xứng.
C. Nhận điểm
1 1
;
2 2
làm tâm đối xứng.
D. Nhận điểm
1
;2
2
làm tâm đối xứng.
Lời giải
Chọn A.
TXĐ:
1
\
2
D
.
Ta có:
2
1
2 1
lim lim lim
1
2 1 2
2
x x x
x
x
x
y
x
x
x
.
1 1
2 2
2
lim lim
2 1
x x
x
y
x
;
1 1
2 2
2
lim lim
2 1
x x
x
y
x
.
Đồ thị hàm số có một đường tiệm cận đứng
1
2
x
và đường tiệm cận ngang
1
2
y
.
Nên đồ thị hàm số nhận
1 1
;
2 2
làm tâm đối xứng.
Câu 21. [2D1-1] Đồ thị hình bên là đồ thị của hàm số nào?
A.
3
3 1
y x x
. B.
3 2
1
y x x
. C.
3
3 1
y x x
. D.
3
3 1
y x x
.
Lời giải
Chọn C.
Dựa vào đồ thị, ta có
0
a
loại B.
Đồ thị hàm số đi qua điểm
0; 1
loại A; D.
Vậy đồ thị trên là đồ thị của hàm số
3
3 1
y x x
.
O
x
y
1
1
1
3
2
2
x
2
0
y
0
0
y
6
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/22
Câu 22. [2D1-1] Biết hàm số
2
4 1
1
x x
y
x
có hai cực trị
1
x
,
2
x
. Tích
1 2
.
x x
bằng
A.
2
. B.
5
. C.
1
. D.
4
.
Lời giải
Chọn B.
Tập xác định
\ 1
D
.
2
2
2 5
; 1
1
x x
y x
x
.
2
0 2 5 0
y x x
.
Vì tam thức trên có
0
ac
nên phương trình
0
y
luôn có hai nghiệm phân biệt.
Tức là hàm số đã cho luôn có hai cực trị
1
x
,
2
x
.
Khi đó
1 2
. 5
x x
.
Câu 23. [2D2-1] Biểu thức
a a a a
;
0
a
bằng
A.
13
16
a
. B.
11
64
a
. C.
15
16
a
. D.
15
8
a
.
Lời giải
Chọn C.
Ta có
1 1 1 1 15
2 4 8 16 16
a a a a a a
.
Câu 24. [2D2-1] Xét mệnh đề: “Với mọi số thực
a
,
x
,
y
, nếu
x y
thì
x y
a a
”. Với điều kiện sau
đây của
a
thì mệnh đề trên đúng.
A.
a
bất kì. B.
0
a
. C.
1
a
. D.
0 1
a
.
Lời giải
Chọn C.
Vì
x y
x y a a
nên
1
a
.
Câu 25. [2D2-2] Tỉ lệ tăng dân số hàng năm của một nước là
1,5%
. Năm
2000
, dân số nước này là
212942000
. Dân số nước đó vào năm
2008
xấp xỉ:
A.
239877584
người. B.
240090000
người.
C.
230081000
người. D.
24078100
người.
Lời giải
Chọn A.
Dân số nước này sau
8
năm là
0,015.8
212942000.e 239877584
S .
Câu 26. [2D2-2] Đẳng thức
7 7 7
1
log log log
3 2
a b
a b
, với
, 0
a b
tương đương với:
A.
2 2
7
a b ab
. B.
2 2
14
a b ab
. C.
2 2
5
a b ab
. D.
3 3
7
a b ab
.
Lời giải
Chọn A.
Ta có:
2
7 7 7 7 7
1
log log log log log
3 2 3
a b a b
a b ab
.
2
2 2
7
3
a b
ab a b ab
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/22
Câu 27. [2D2-2] Cho
12
log 27
a
. Khi đó
36
log 24
bằng
A.
9
6 2
a
a
. B.
9
6 2
a
a
. C.
9
6 2
a
a
. D.
9
6 2
a
a
.
Lời giải
Chọn A.
Ta có:
3
3
12 3
2
3
log 3 3
log 27 log 2
2
log 2 .3
a
a a
a
.
Khi đó:
3
3
3
36
2 2
3
3
log 2 .3
3log 2 1
9
log 24
2log 2 2 6 2
log 2 .3
a
a
.
Câu 28. [2D2-1] Giá trị của biểu thức
2
8log 7
a
a
,
0, 1
a a
bằng
A.
2
7
. B.
4
7
. C.
8
7
. D.
16
7
.
Lời giải
Chọn B.
Ta có:
4
2
8log 7
4log 7 log 7
4
7
a a a
a a a
.
Câu 29. [2D2-1] Biết
ln 2
a
,
ln3
b
. Biểu diễn
1
ln
12
theo
a
,
b
được kết quả:
A.
2
a b
. B.
2
a b
. C.
2
a b
. D.
2
a b
.
Lời giải
Chọn C.
Ta có:
2
1
ln ln 2 .3 2ln2 ln3 2
12
a b
.
Câu 30. [2D2-1] Biết
log 0
a
, khi đó
a
thỏa mãn:
A.
a
bất kì. B.
0
a
. C.
1
a
. D.
0 1
a
.
Lời giải
Chọn D.
Ta có:
0
0
log 0 0 1
10
a
a a
a
.
Câu 31. [2D2-2] Tập xác định của hàm số
2
1
2
log 1
y x
là
A.
; 1 1;D
. B.
D
.
C.
1;1
D
. D.
; 1 1;D
.
Lời giải
Chọn D.
Điều kiện
2
1 0 ; 1 1;x x
.
Vậy tập xác định của hàm số là
; 1 1;D
.
Câu 32. [2D2-3] Đạo hàm của hàm số
2x
1 e
y x là hàm số
A.
2
2 1 e
x
y x . B.
2 1 e
x
x . C.
2
2 1 e
2
x
x
. D.
2
2 e
x
x
.
Lời giải
Chọn A.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/22
Ta có:
2 2 2
e 2 1 e 2 1 e
x x x
y x x
.
Vậy đạo hàm của hàm số đã cho là hàm số
2
2 1 e
x
y x .
Câu 33. [2D2-1] Đồ thị của hàm số
2
x
y
A. Nhận trục tung làm tiệm cận đứng.
B. Có trục đối xứng.
C. Đối xứng với đồ thị hàm số
1
2
x
y
qua trục hoành.
D. Nhận trục hoành là tiệm cận ngang.
Lời giải
Chọn D.
Câu 34. [2D2-3] Đạo hàm của hàm số
3
2
ln 2
y x
tại điểm
1
x
là
A.
1
3
2
ln 2
3
. B.
1
3
2
ln 2
3
. C.
1
3
1
ln 2
3
. D.
1
3
1
ln 2
3
.
Lời giải
Chọn B.
Viết lại hàm số ta được
2
3
ln2
y x
Ta có:
1 1
3 3
2 2
ln 2 1 ln 2
3 3
y x y
x
Vậy đạo hàm của hàm số
3
2
ln 2
y x
tại điểm
1
x
là
1
3
2
ln 2
3
.
Câu 35. [2D2-1] Cho hàm số
4
y x
. Trong các khẳng định sau, khẳng định nào sai?
A. Tập xác định của hàm số là
0;D
. B. Hàm số nghịch biến trên tập xác định.
C. Đồ thị hàm số qua điểm
1;1
. D. Đồ thị hàm số không có đường tiệm cận.
Lời giải
Chọn B.
Do
0
4
nên hàm số đồng biến trên tập xác định.
Câu 36. [2D2-3] Cho hàm số
2
ln 1
y x
. Số nghiệm của phương trình
0
y
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B.
Có
2
2x
1
y
x
,
2
2x
0 0 0
1
y x
x
.
Vậy số nghiệm của phương trình là 1.
Câu 37. [2D2-3] Số điểm cực trị của hàm số
1
x
e
y
x
là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn A.
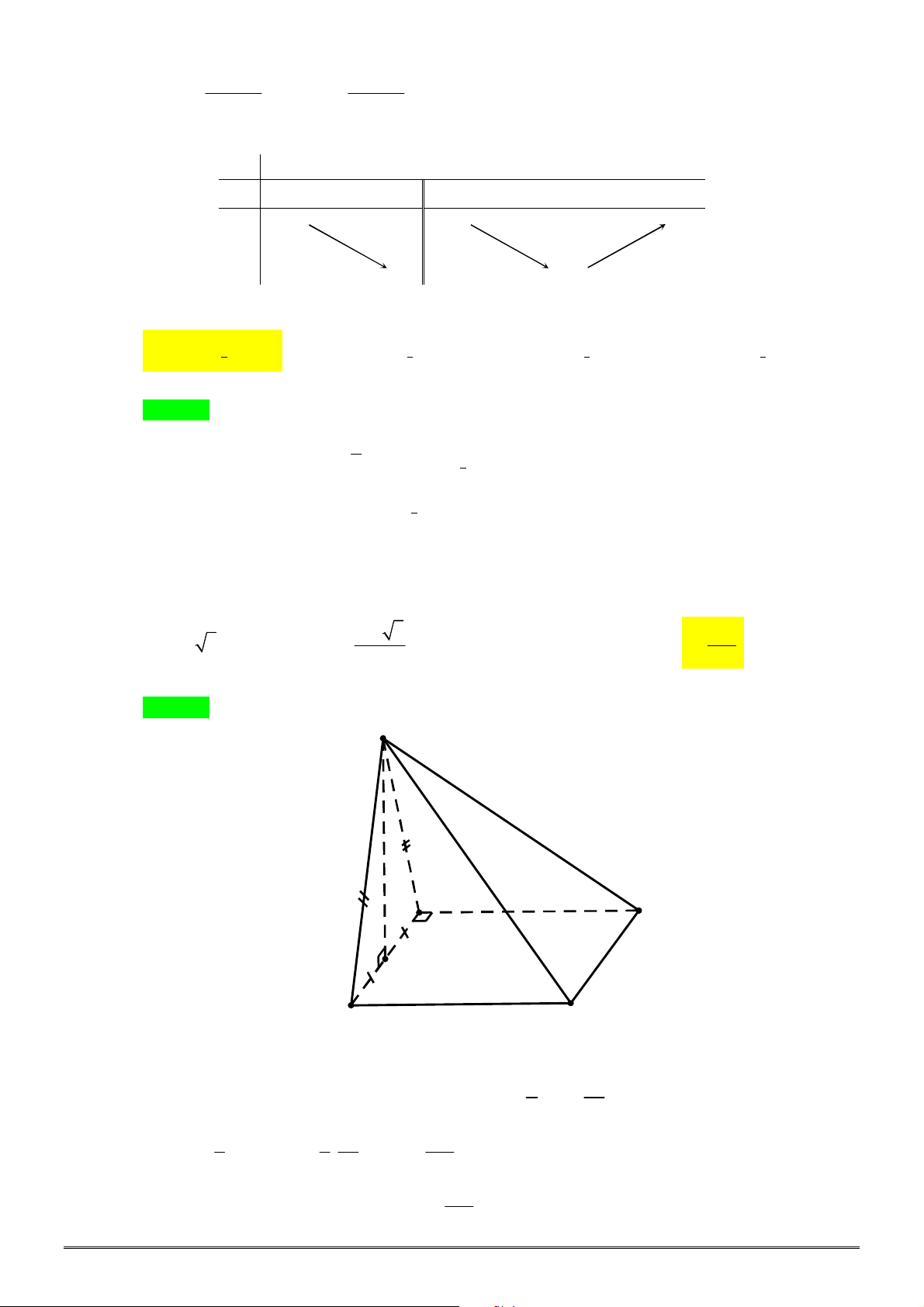
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/22
Có
2
1
x
xe
y
x
,
2
0 0 0
1
x
xe
y x
x
.
Ta có BBT
Câu 38. [2D2-3] Giá trị của
x
thỏa mãn đẳng thức
3 5
5 3
x x
là
A.
5 3
3
log log 5
x . B.
5 5
3
log log 3
x . C.
3 5
5
log log 3
x . D.
3 3
5
log log 5
x .
Lời giải
Chọn A.
Ta có
3 5
3 5 3
3
5
5 3 log 5 log log 5
3
x x
x
x
.
Vậy giá trị cần tìm của
x
là
5 3
3
log log 5
x .
Câu 39. [2H1-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
3
a
. Biết tam giác
SAB
là
tam giác cân tại
S
và nằm trong mặt phẳng vuông góc với đáy, tam giác
SAB
vuông. Thể tích
khối chóp
.
S ABCD
là
A.
3
9 3
a . B.
3
9 3
2
a
. C.
3
9
a
. D.
3
9
2
a
.
Lời giải
Chọn D.
3a
3a
H
C
B
A
D
S
Gọi
H
là trung điểm của
AB
thì
SH ABCD
.
Lại do tam giác
SAB
vuông và cân ở
S
nên
1 3
2 2
a
SH AB
3
2
.
1 1 3 9
. . . . 3
3 3 2 2
S ABCD ABCD
a a
V SH S a (đvtt).
Vậy thể tích của khối chóp
.
S ABCD
là
3
9
2
a
.
x
1
0
y
0
y
1
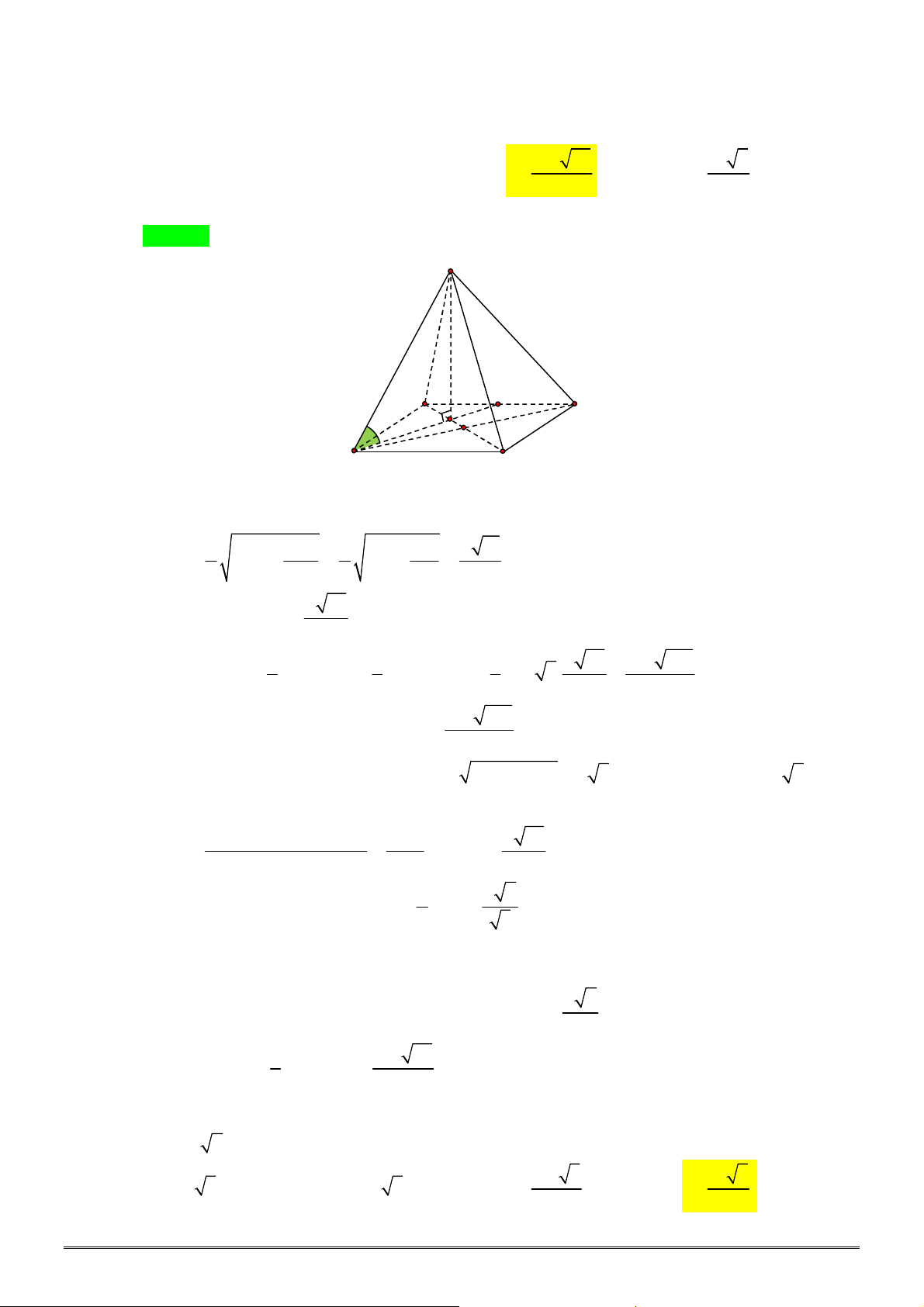
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/22
Câu 40. [2D1-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật
2
AD a
,
AC a
. Gọi
H
là trọng tâm tam giác
ABD
,
SH
vuông góc với đáy, góc giữa
SD
và mặt phẳng
ABCD
bằng
0
30
. Thể tích khối chóp
.
S ABCD
là
A.
3
a
. B.
3
2
a
. C.
3
2 35
9
a
. D.
3
5
3
a
.
Lời giải
Chọn C.
Ta có
-
2 2 2 2 2 2 2
9 4 5
AB CD AC AD a a a
.
-
2 2
2 2
2 2 5 11
4
3 4 3 4 3
AB a a
DH AD a .
-
33
.tan30
9
a
SH HD
Suy ra
3
2
. D D
1 1 1 33 2 165
. . . . . D .2 5.
3 3 3 9 27
S ABC ABC
a a
V SH S SH AB A a (đvtt).
Vậy thể tích của khối chóp
.
S ABCD
là
3
2 165
27
a
.
Tam giác
ADC
vuông tại
D
có
2 2 2
5 . 2 5
ABCD
DC AC AD a S AD DC a
.
DM
là trtung tuyến của tam giác
ABD
:
2 2 2
2
2
2
21 21
4 4 2
AD BD AB
a a
DM DM
H
là trọng tâm
ABD
nên
2 7
3
3
a
DH DM ;
,
SD ABCD SDH
Tam giác
SHD
vuông tại
H
có
7
.tan30
3
a
SH DH .
Khi đó
3
.
1 2 35
.
3 9
S ABCD ABCD
a
V S SH .
Câu 41. [2H1-3] Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
2
BC a
. Biết
A C
tạo với mặt đáy một góc
60
. Thể tích khối lăng trụ
.
ABC A B C
là
A.
3
3 3
a . B.
3
6 3
a . C.
3
3 3
2
a
. D.
3
3
2
a
.
Lời giải
A
B
D
C
H
S
30
O
M
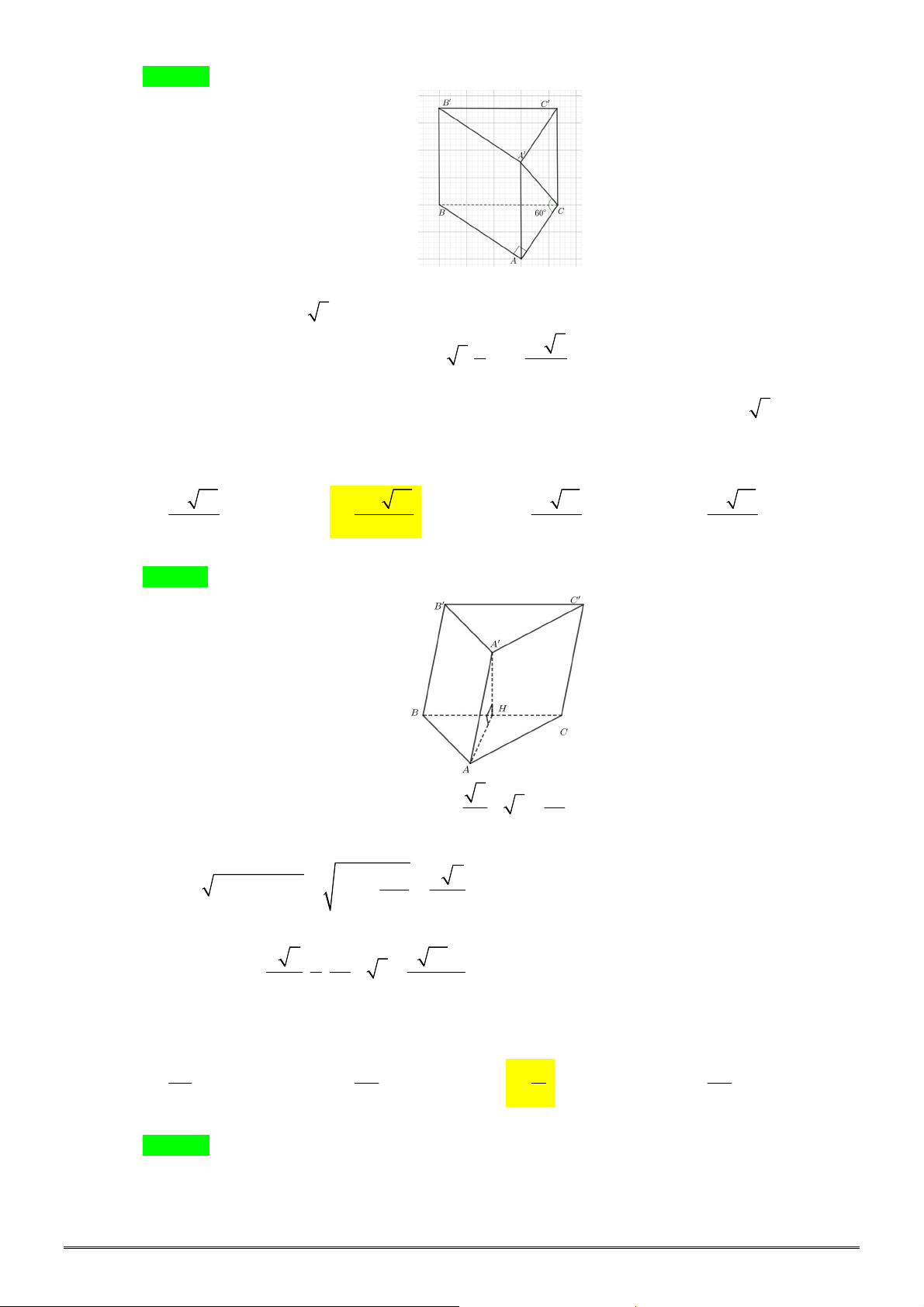
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/22
Chọn D.
Do tam giác
ABC
là tam giác vuông cân tại
A
nên:
2 2
2
AC BC AC a
.
.tan60 3
AA A C a
.
Vậy thể tích lăng trụ là
3
2
1 3
. 3.
2 2
ABC
a
V AA S a a
.
Câu 42. [2H1-3] Cho hình lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác đều,
3
AB a
. Biết hình
chiếu của
A
lên mặt phẳng
ABC
trùng với trung điểm của
BC
và cạnh bên bằng
2
a
. Thể
tích khối lăng trụ
.
ABC A B C
là
A.
3
21
8
a
. B.
3
3 21
8
a
. C.
3
14
12
a
. D.
3
14
8
a
.
Lời giải
Chọn B.
Gọi
H
là trung điểm của
BC
ta có:
3 3
. 3
2 2
a
AH a .
Xét tam giác vuông
AHA
có:
2
2 2 2
9 7
4
4 2
a a
A H AA AH a
.
Thể tích lăng trụ là
3
7 1 3 3 21
. . . . 3
2 2 2 8
ABC
a a a
V HA S a
.
Câu 43. [2H1-3] Cho khối tứ diện có thể tích là
V
. Gọi
V
là thể tích của khối đa diện có đỉnh là trung
điểm các cạnh của khối tứ diện đã cho. Ta có
V
bằng
A.
3
.
4
V
B.
4
.
5
V
C.
.
2
V
D.
2
.
3
V
Lời giải
Chọn C.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/22
Gọi các trung điểm của các cạnh như hình vẽ.
Ta có:
1 1 1 1
. .
2 2 2 8
AMIJ
V V V
.
Tương tự ta cũng có:
1
8
DPJK CPNI BNKM
V V V V
.
Vậy thể tích khối đa diện có đỉnh là trung điểm các cạnh của khối tứ diện đã cho là
1
4.
8 2
V
V V V
.
Câu 44. [2H1-2] Cho nửa hình tròn đường kính
3
AB a
quay quanh trục
AB
, ta được khối tròn xoay
có thể tích là
A.
3
2 3
a . B.
3
3
2
a
. C.
3
3
2
a
. D.
3
2 3
3
a
.
Lời giải
Chọn C.
Khối tròn xoay tạo được là mặt cầu, có bán kính
3
2 2
AB a
R .
Vậy thể tích của mặt cầu là
3
3
3 3
4
2 2
a a
V
.
Câu 45. [2H1-2] Cho hình lăng trụ đứng có đáy là hình vuông cạnh
a
, chiều cao bằng
2
a
. Diện tích
mặt cầu ngoại tiếp hình lăng trụ đó là
A.
2
6
a
. B.
2
6
4
a
. C.
2
6
4
a
. D.
2
6
a
.
Lời giải
Chọn D.
Hình lăng trụ đứng là hình hộp chữ nhật với các kích thước:
a
,
a
,
2
a
.
Bán kính của mặt cầu:
2 2 2
1 6
4
2 2
a
R a a a .
Diện tích mặt cầu ngoại tiếp hình lăng trụ đó là
2
2
6
4 . 6
2
a
S a
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/22
Câu 46. [2H1-1] Tên gọi của khối đa diện đều loại
3;4
là khối:
A. Bát diện đều. B. Lập phương. C. Hai mươi mặt đều. D. Mười hai mặt đều.
Lời giải
Chọn A.
Câu 47. [2H1-3] Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
6
3
a
. Gọi
O
là tâm đáy. Trong các khẳng định sau, khẳng định nào đúng khi nói về mặt cầu ngoại tiếp tứ
diện
.
S ABC
?
A. Mặt cầu có tâm trùng với
O
và bán kính
3
3
a
R .
B. Mặt cầu có tâm trùng với
O
và bán kính
6
6
a
R .
C. Mặt cầu có tâm là trung điểm
SO
và bán kính
3
6
a
R .
D. Mặt cầu có tâm là trung điểm
SO
và bán kính
3
2
a
R .
Lời giải
Chọn A.
Ta có:
2 3 3
. .
3 2 3
a
AO BO CO a .
Xét tam giác vuông
SOA
có:
2
2 2 2
6 3 3
9 9 3
a a
SO SA AO a .
Ta thấy
3
3
a
AO BO CO SO nên mặt cầu ngoại tiếp tứ diện
.
S ABC
có tâm
O
bán
kính
3
3
a
R .
Câu 48. [2H1-2] Cho hình chóp có đáy là đa giác
n
cạnh. Trong các khẳng định sau, khẳng định nào đúng?
A. Số cạnh của hình chóp bằng
1
n
. B. Số mặt của hình chóp bằng
2
n
.
C. Số đỉnh của hình chóp bằng
2 1
n
. D. Số mặt của hình chóp bằng số đỉnh.
Lời giải
Chọn D.
Số cạnh của hình chóp bằng
2 1
n
.
Số mặt của hình chóp bằng
1
n
.
Số đỉnh của hình chóp bằng
1
n
.
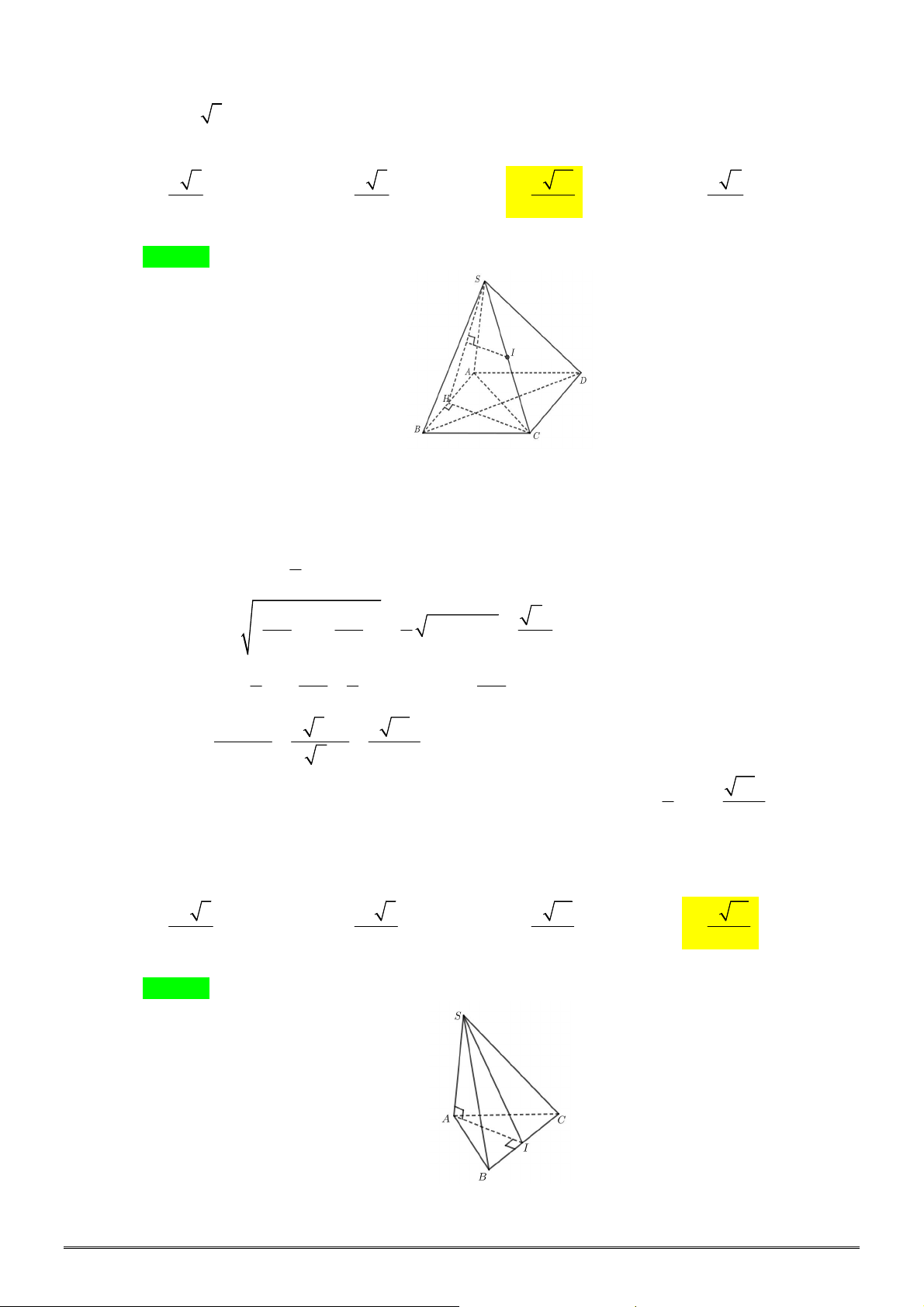
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/22
Câu 49. [2H1-3] Cho hình chóp
.
S ABCD
có
SA ABCD
. Đáy
ABCD
là hình thoi,
2
AC a
,
3
BD a
,
I
là trung điểm của
SC
. Bán kính mặt cầu tâm
I
và tiếp xúc với mặt phẳng
SAB
là
A.
3
2
a
. B.
3
4
a
. C.
21
7
a
. D.
2
4
a
.
Lời giải
Chọn C.
Từ
C
kẻ
CH AB
. Ta có:
CH AB
CH SAB
CH SA
.
Bán kính mặt cầu tâm
I
và tiếp xúc với mặt phẳng
SAB
là khoảng cách từ
I
đến
SAB
.
Mà:
1
,
2
d I SAB CH
.
Ta có:
2 2
2 2
1 7
4 3
2 2 2 2
AC BD a
AB a a
.
Ta có:
1 1
. . . . . .
2 2 2 2
ABC
AC AC
S BD AB HC BD AB HC
.
. 3.2 2 21
2 7
7
BD AC a a a
HC
AB
a
.
Vậy bán kính mặt cầu tâm
I
và tiếp xúc với mặt phẳng
SAB
là
1 21
2 7
a
R HC .
Câu 50. [2H1-3] Cho hình chóp
.
S ABC
có
SA ABC
,
2
SA a
. Đáy
ABC
là tam giác đều cạnh
a
.
Bán kính mặt cầu tâm
S
và tiếp xúc với đường thẳng
BC
là
A.
3
2
a
. B.
3 5
2
a
. C.
15
2
a
. D.
19
2
a
.
Lời giải
Chọn D.
Gọi
I
là trung điểm của
BC
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/22
Ta có:
BC AI
BC SI
BC SA
.
Vậy bán kính mặt cầu tâm
S
và tiếp xúc với đường thẳng
BC
là
2
2 2 2
3 19
4
4 2
a a
SI SA IA a .
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/13 - Mã đề thi 132
SỞ GD VÀ ĐT LONG AN
TRƯỜNG THPT CHUYÊN
LONG AN
ĐỀ THI HỌC KỲ 1
MÔN: TOÁN 12 – Hệ không chuyên
(Thời gian làm bài 90 phút)
Họ và tên thí sinh:..............................................................SBD:.....................
Câu 1. Đồ thị hàm số nào sau đây có ba điểm cực trị?
A.
4 2
2 1
y x x
. B.
4 2
2 1
y x x
. C.
4 2
2 1
y x x
. D.
4 2
2 4 1
y x x
.
Câu 2. Tính đạo hàm của hàm số
2
x
f x
?
A.
1
.2 ln 2
x
f x x
. B.
1
.2
x
f x x
. C.
1
2 ln 2
x
f x
. D.
2 ln 2
x
f x
.
Câu 3. Số nghiệm của phương trình
2
log 1 2
x
là:
A. Kết quả khác. B.
1
. C.
0
. D.
2
.
Câu 4. Tập nghiệm của bất phương trình
2
1 1
3 3
log 2 1 log 1
x x x
là:
A.
1;2
. B.
3;
. C.
2;
. D.
1;
.
Câu 5. Tìm giá trị nhỏ nhất của hàm số
2 1
1
x
y
x
trên đoạn
2;3
?
A.
0
. B.
1
. C.
5
. D.
2
.
Câu 6. Cho lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
2 , 2
BC a AA a
.
Tính thể tích
V
của lăng trụ
.
ABC A B C
.
A.
3
8
3
a
V . B.
3
2
3
a
V . C.
3
2
V a
. D.
3
4
V a
.
Câu 7. Cho hàm số
2 3
1
x
y
x
có đồ thị
C
. Tiếp tuyến của
C
tại điểm có hoành độ bằng
2
cắt
các trục
Ox
và
Oy
tại các điểm
;0
A a
,
0;
B b
. Khi đó, giá trị của
5
P a b
bằng:
A.
17
5
P . B.
0
P
. C.
17
P
. D.
34
P
.
Câu 8. Gọi
1
x
,
2
x
là các nghiệm của phương trình
2
1 3
3
log 3 1 log 3 0
x x
. Khi đó, tích
1 2
x x
:
A.
3
. B.
3
3
. C.
3 1
3
. D.
3
3
.
Câu 9. Hàm số
3 2
1 1 1
3 2 2
y x mx
đạt cực tiểu tại
2
x
khi
m
nhận giá trị nào sau đây?
A.
2
m
. B.
4
m
. C.
1
m
. D.
3
m
.
Câu 10. Số điểm cực đại của hàm số
4
100
y x là:
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 11. Cho khối chóp
.
S ABC
có
SA ABC
,
SA a
, đáy
ABC
là tam giác đều cạnh bằng
a
. Tính
thể tích
V
của khối tứ diện
.
S ABC
.
A.
3
3
4
a
V . B.
3
3
12
a
V . C.
3
3
7
a
V . D.
3
3
3
a
V .
17
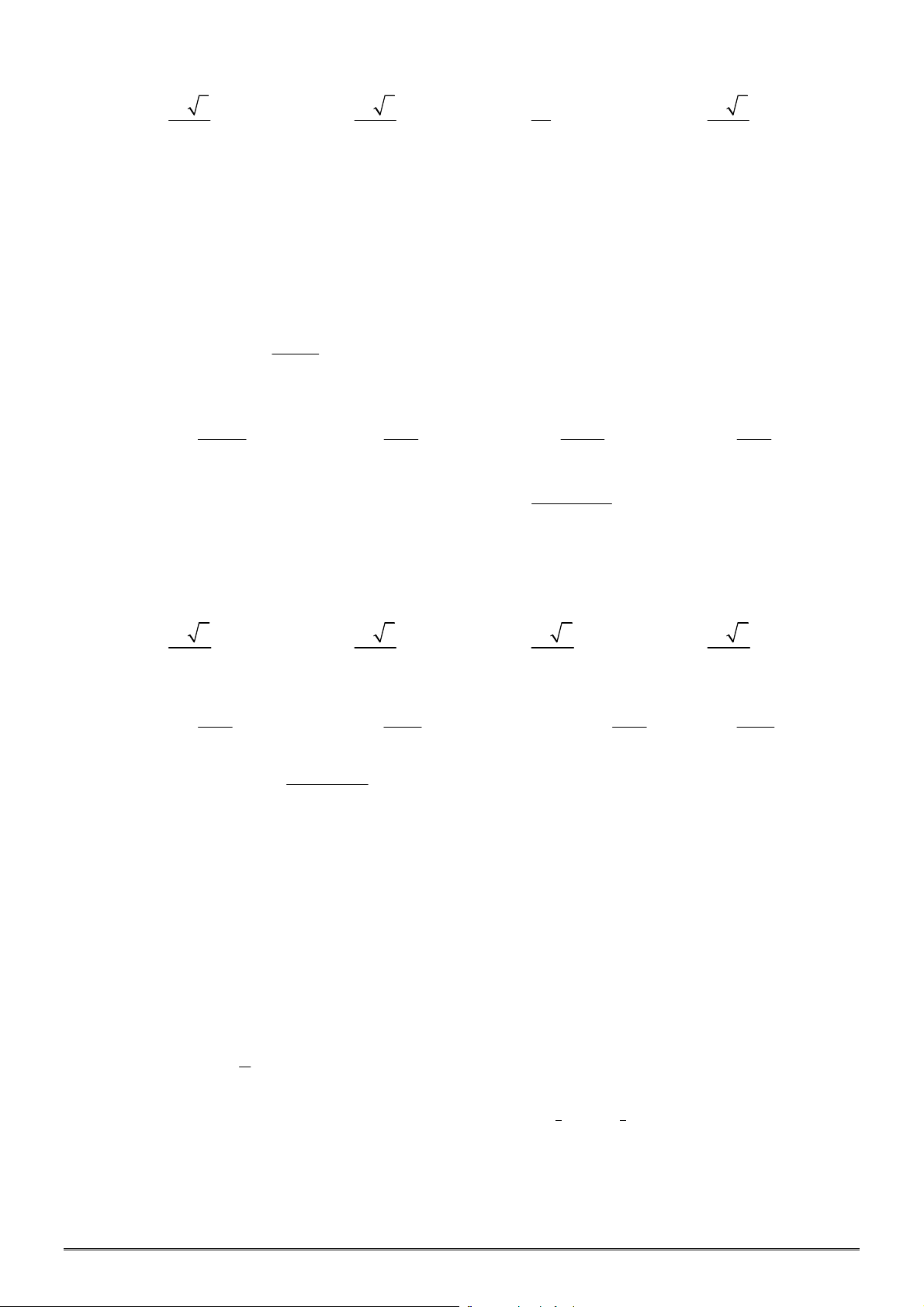
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/13 - Mã đề thi 132
Câu 12. Cho lăng trụ đứng
.
ABC A B C
có tất cả các cạnh bằng
a
. Tính thể tích khối tứ diện
A B AC
?
A.
3
3
4
a
. B.
3
3
12
a
. C.
3
6
a
. D.
3
3
6
a
.
Câu 13. Một người gửi tiền vào ngân hàng
100
triệu đồng thể thức lãi kép, kỳ hạn là
1
tháng với lãi
suất
0,5%
một tháng. Hỏi sau ít nhất bao nhiêu tháng, người đó có nhiều hơn
125
triệu đồng?
A.
44
tháng. B.
45
tháng. C.
47
tháng. D.
46
tháng.
Câu 14. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật với
3
AB a
,
4
BC a
,
12
SA a
và
SA
vuông góc mặt đáy. Tính diện tích mặt cầu ngoại tiếp khối chóp
.
S ABCD
.
A.
25
S
. B.
289
S
. C.
169
S
. D.
144
S
.
Câu 15. Tìm hàm số
ax b
y
cx d
biết rằng đồ thị hàm số cắt trục tung tại điểm
0;1
M vào giao điểm
hai đường tiệm cận của hàm số là
1; 1
I
.
A.
2
2
x
y
x
. B.
1
1
x
y
x
. C.
2 1
1
x
y
x
. D.
1
1
x
y
x
.
Câu 16. Tìm tất cả các tiệm cận đứng của đồ thị hàm số
2
2
3 2
4
x x
y
x
.
A.
2
x
. B.
2, 2
x x
. C.
4
x
. D.
2
x
.
Câu 17. Cho hình chóp đều
.
S ABCD
có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt đáy bằng
60
.
Tính thể tích khối chóp
.
S ABCD
?
A.
3
6
3
a
. B.
3
3
6
a
. C.
3
6
2
a
. D.
3
6
6
a
.
Câu 18. Hàm số nào sau đây có đồ thị nhận đường thẳng
2
x
làm tiệm cận đứng?
A.
1
1
y
x
. B.
2
2
y
x
. C.
1
2
1
y x
x
. D.
5
2
x
y
x
.
Câu 19. Đồ thị hàm số
2
2 3
4 4
x
y
x x
có tiệm cận đứng
x a
và tiệm cận ngang
y b
. Khi đó giá trị
của
2
a b
bằng:
A.
2
. B.
2
. C.
4
. D.
4
.
Câu 20. Cho khối chóp tam giác
.
S ABC
. Gọi
A
,
B
,
C
lần lượt là trung điểm của cạnh
SA
,
SB
,
SC
. Khi đó thể tích khối chóp
.
S ABC
gấp bao nhiêu lần thể tích khối chóp
.
S A B C
?
A.
6
. B.
4
. C.
8
. D.
2
.
Câu 21. Giá trị nhỏ nhất của hàm số
2
2 4
y x x
trên đoạn
2;4
là:
A.
1
. B.
4
. C.
4
. D.
2
.
Câu 22. Cho các số thực dương
,
a b
. Mệnh đề nào sau đây đúng?
A.
2
2 2
1
log log
2
a a
. B.
2 2
1 1
log log
a a
a b a b
.
C.
2 2
2 2
log 2log
a b a b
. D.
3 3
4 4
log log
a b a b
.
Câu 23. Cho hàm số
4 2
2 1
y x x
biết
;
a b
là khoảng nghịch biến dài nhất của hàm số với
,a b
. Tính giá trị của
5
a b
là:
A.
1
. B.
6
. C.
5
. D.
2
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/13 - Mã đề thi 132
Câu 24. Thể tích khối hộp chữ nhật có ba cạnh xuất phát từ một đỉnh lần lượt có độ dài
, ,
a b c
là:
A.
1
6
V abc
. B.
1
3
V abc
. C.
V abc
. D.
4
3
V abc
.
Câu 25. Số nghiệm nguyên của bất phương trình
2
log 2 11 25 1
x x
là:
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 26. Tập xác định của hàm số
1
2
1
y x
là:
A.
D ;1
. B.
D 1;
. C.
D 0;1
. D.
D 1;
.
Câu 27. Chọn phát biểu đúng trong các phát biểu sau?
A. Đồ thị hàm số logarit không nằm bên dưới trục hoành.
B. Đồ thị hàm số mũ với cơ số dương nhỏ hơn 1 thì nằm dưới trên trục hoành.
C. Đồ thị hàm số logarit luôn nằm bên phải trục tung.
D. Đồ thị hàm số mũ với số mũ âm luôn có hai tiệm cận.
Câu 28. Cho hình chóp đều
.
S ABC
có cạnh đáy bằng
a
, góc giữa mặt bên và đáy bằng
60
. Tính diện
tích xung quanh
xq
S
của hình nón có đỉnh
S
và có đường tròn đáy là đường tròn ngoại tiếp tam
giác đáy
ABC
.
A.
2
10
8
xq
a
S
. B.
2
7
6
xq
a
S
. C.
2
3
3
xq
a
S
. D.
2
7
4
xq
a
S
.
Câu 29. Hàm số
1
2
x
y
x
có đồ thị
H
. Tiếp tuyến của
H
tại giao điểm của
H
với trục hoành là:
A.
1 1
3 3
y x
. B.
3
y x
. C.
3
y x
. D.
3 3
y x
.
Câu 30. Cho khối hộp chữ nhật
.
ABCD A B C D
có
8
AD
,
6
CD
,
12
AC
. Tính diện tích toàn
phần của khối trụ có hai đường tròn đáy ngoại tiếp hai hình chữ nhật
ABCD
và
A B C D
.
A.
5 4 11 5
tp
S
. B.
26
tp
S
.
C.
576
tp
S
. D.
10 2 11 5
tp
S
.
Câu 31. Đồ thị hàm số
3 2
3 9 2
y x x x
có tâm đối xứng là:
A.
2; 20
I . B.
1;7
I . C.
2;0
I . D.
1; 9
I
.
Câu 32. Cho hình lăng trụ đứng
.
ABCD A B C D
có đáy
ABCD
là hình thang cân với cạnh
,
AB BC a
2
AD a
. Chiều cao của hình lăng trụ bằng
2
a
. Tính tổng thể tích
V
khối trụ
ngoại tiếp lăng trụ đã cho.
A.
2
3
V a
. B.
2
4
V a
. C.
3
V a
. D.
3
2
V a
.
Câu 33. Cho hàm số
y f x
xác định trên
\ 1
và có bảng biến thiên như hình vẽ dưới đây.
Kết luận nào sau đây là đúng?
A. Hàm số đạt giá trị nhỏ nhất là
4
.
B. Hàm số đạt cực đại tại
1
x
.
C. Đồ thị hàm số có điểm cực tiểu
0
x
.
D. Đồ thị hàm số chỉ có hai tiệm cận.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/13 - Mã đề thi 132
Câu 34. Tìm số các giá trị nguyên của tham số
m
để hàm số
4 2
1 3 10 2
y m x m x
có ba cực trị?
A.
3
. B.
5
. C.
4
. D.
0
.
Câu 35. Gọi
n
,
d
lần lượt số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
2
1
x
y
x
. Tính giá
trị của
2 3
T n d
?
A.
7
T
. B.
4
T
. C.
5
T
. D.
8
T
.
Câu 36. Cho đồ thị hàm số
3 2
3 4
y x x
có hai điểm cực trị là
A
,
B
. Tính diện tích tam giác
OAB
?
A.
4
S
. B.
8
S
. C.
2 5
S . D.
2
S
.
Câu 37. Cho hình vuông
ABCD
có cạnh bằng
4
. Tính tỉ số thể tích của hai khối tròn xoay sinh ra khi
lần lượt quay hình vuông đã cho quanh các đường thẳng chứa cạnh
AB
và đường chéo
AC
của hình vuông?
A.
3 2
. B.
3 2
2
. C.
3
. D.
3
2
.
Câu 38. Cho hàm số
2
2
x
y x x e
. Xác định tổng các nghiệm của phương trình
0
y y
?
A.
3
. B.
3 5
. C.
3
. D.
3 5
.
Câu 39. Cho một tấm nhôm hình chữ nhật
ABCD
có
24 cm
AD
. Ta gấp tấm nhôm theo hai cạnh
MN
,
QP
vào phía trong đến khi
,
AB CD
trùng nhau như hình vẽ dưới đây để được một hình
lăng trụ khuyết hai đáy. Tìm
x
để thể tích khối lăng trụ lớn nhất?
A.
8
x
. B.
10
x
. C.
9
x
. D.
6
x
.
Câu 40. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
2 2
sin cos
2 2
x x
y lần lượt là
m
,
M
. Tính giá trị
.
P M m
?
A.
4 2
P
. B.
3 2
P
. C.
6
P
. D.
6 2
P
.
Câu 41. Cho hình trụ có trục
2 7
OO
,
ABCD
là hình vuông có cạnh bằng 8 sao cho các đỉnh nằm
trên đường tròn đáy và tâm hình vuông trùng với trung điểm
OO
. Thể tích khối trụ là:
A.
25 7
. B.
50 7
. C.
16 7
. D.
25 14
.
Câu 42. Người ta nối trung điểm các cạnh của hình hộp chữ nhật rồi
cắt bỏ các hình chóp tam giác ở các góc của hình hộp như hình
vẽ bên. Hình còn lại là một đa diện có số đỉnh và số cạnh là:
A.
12
đỉnh,
24
cạnh.
B.
10
đỉnh,
24
cạnh.
C.
10
đỉnh,
48
cạnh.
D.
12
đỉnh,
20
cạnh.
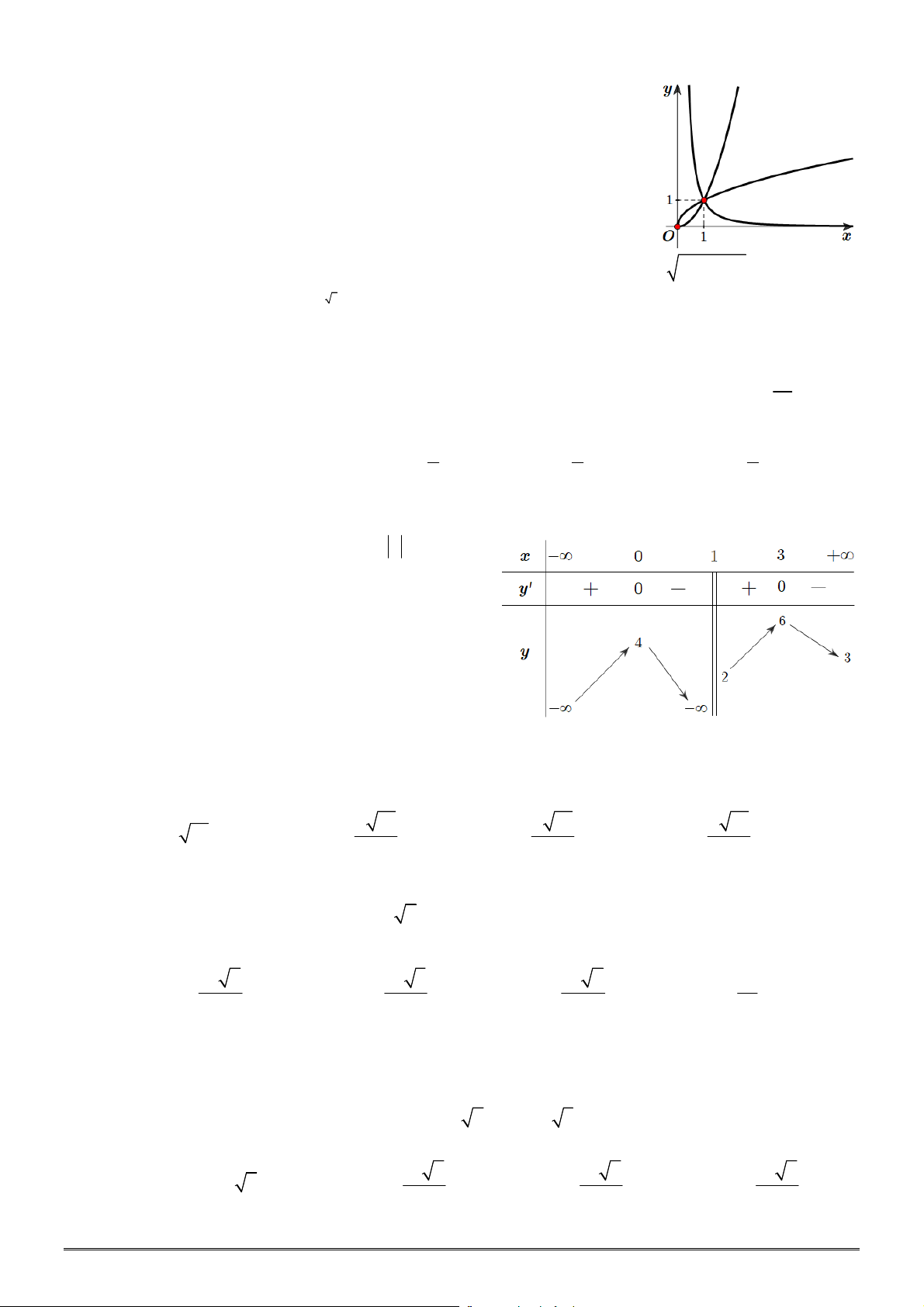
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/13 - Mã đề thi 132
Câu 43. Hình vẽ sau là đồ thị của ba hàm số
y x
,
y x
,
y x
với
điều kiện
0
x
và
,
,
là các số thực cho trước. Mệnh đề
nào dưới đây đúng?
A.
.
B.
.
C.
.
D.
.
Câu 44. Tìm tập hợp các giá trị của tham số
m
để phương trình
2 2
5 5
log 2 log 1 2 0
x x m
có
nghiệm thuộc đoạn
3
1;5
?
A.
2;3
. B.
2;6
. C.
0;5
. D.
1;6
.
Câu 45. Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
3
3
1
3 2x mx
x
nghiệm
đúng với mọi
1
x
?
A.
;1
m . B.
2
;
3
m
. C.
2
;1
3
m
. D.
2
;
3
m
.
Câu 46. Cho hàm số
y f x
xác định trên
\ 1
và có bảng biến thiên như hình vẽ dưới đây.
Hỏi khi đó đồ thị hàm số
y f x
có bao
nhiêu tiệm cận?
A.
4
.
B.
3
.
C.
1
.
D.
2
.
Câu 47. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật có
AB a
,
3
BC a
và
SA ABCD
.
Gọi
G
là trọng tâm tam giác
SAB
. Tính khoảng cách từ
G
đến mặt phẳng
SAC
bằng:
A.
10
a . B.
10
3
a
. C.
10
2
a
. D.
10
10
a
.
Câu 48. Cắt hình nón
N
có đỉnh
S
bởi một mặt phẳng chứa trục hình nón ta được một tam giác
vuông cân có cạnh huyền bằng
2
a
;
BC
là một dây cung của hình tròn đáy của
N
sao cho
mặt phẳng
SBC
tạo với đáy góc
60
. Tính diện tích
S
của tam giác
SBC
.
A.
2
2
2
a
S . B.
2
3
3
a
S . C.
2
2
3
a
S . D.
2
3
a
S .
Câu 49. Cho khối chóp
.
S ABCD
có thể tích bằng 81. Gọi
M
,
N
,
P
,
Q
lần lượt là trọng tâm các mặt
bên
SAB
,
SBC
,
SCD
,
SDA
. Tính thể tích
V
của khối chóp .
S MNPQ
?
A.
18
V
. B.
24
V
. C.
12
V
. D.
54
V
.
Câu 50. Cho hình chóp
.
S ABC
có
SA a
,
2
SB a
,
3
SC a
. Tính thể tích lớn nhất
max
V
của khối
chóp đã cho.
A.
3
max
6.
V a B.
3
max
6
.
2
a
V C.
3
max
6
.
3
a
V D.
3
max
6
.
6
a
V
----------HẾT----------
y x
y x
y x

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/13 - Mã đề thi 132
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C D
D
C C C D
C A
D
B B
B
C
B A
D
D
B C B D
A
C D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
C B A
D
D
D
D
C A
A
A
C
A
D
B A
D
C B B D
C C C
HƯỚNG DẪN GIẢI
Câu 1. Chọn C.
Hàm trùng phương
4 2
0
y ax bx c a
có ba điểm cực trị
. 0
a b
(trái dấu).
Câu 2. Chọn D.
Đạo hàm của
x
y a
là
.ln
x
y a a
.
Câu 3. Chọn D.
ĐKXĐ:
2
1 100 101
1 1 100
1 100 99
PT
x x
x x
x x
PT có 2 nghiệm.
Câu 4. Chọn C.
ĐKXĐ:
2
1
1
1 0
x
x
x
.
BPT
2 2
2
2 1 1 3 2 0
1
x
x x x x x
x
ÑKXÑ
2
x
.
Câu 5. Chọn C.
2
3
0,
1
y x D
x
hàm đồng biến trên TXĐ
2;3
min 2 5
y y
.
Câu 6. Chọn C.
2
3
1
. . 2
2
2
lang tru day
BC
V S h AA a
.
Câu 7. Chọn D.
2
2
2 5
5
: 5 2 7 5 17
2 7
1
x
y
y tt y x x
y
x
.
,
17 17
;0 , 0;17 5 17 34
5 5
Ox Oy
A B P
.
Câu 8. Chọn C.
PT
2
3 3
log 3 1 log 3 0
x x
.
3 1
3 1 3 2 3 1 2 1 2
log log log 3 1 3
x x x x x x
.
Câu 9. Chọn A.
2
2 4 2 0 2
y x mx y m m
.
Do không có đáp án “Không tồn tại
m
” chọn
2
m
.
Câu 10. Chọn D.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/13 - Mã đề thi 132
3
4 0 0
y x x
. Vẽ nhanh trục số thấy
y
chuyển dấu từ âm sang dương khi qua
0 0
x x
là cực tiểu duy nhất, nên không có cực đại.
Câu 11. Chọn B.
2 3
1 1 3 3
. . .
3 3 4 12
SABC ABC
a a
V S SA a .
Câu 12. Chọn B.
2 3
.
3 3
. .
4 4
ABC A B C ABC
a a
V S AA a
.
Tứ diện có 4 đỉnh là 4 đỉnh của lăng trụ tam giác thì có
3
.
1 3
3 12
ABC A B C
a
V V
.
Câu 13. Chọn B.
Công thức lãi kép:
. 1
n
n
T a r
.
1 0,005
125
100. 1 0,005 125 log 44,74
100
n
n
T n
sau ít nhất 45 tháng.
Câu 14. Chọn C.
Hình chóp có cạnh bên vuông góc đáy
2
2
4
day
h
R R
với
2 2
5
,
2 2
day
AB BC a
h SA R
.
2
2 2
5 13
36 4 169
2 2
a a
R a S R
.
Câu 15. Chọn B.
Đồ thị đi qua điểm
0;1
M Loại D.
Đồ thị có tiệm cận đứng
1
I
x x
Loại A.
Đồ thị có tiệm cận ngang
1
I
y y
Loại C.
Câu 16. Chọn A.
Mẫu số có nghiệm
2, 2
x x
mà nghiệm
2
x
là nghiệm của tử nên loại.
Vậy chỉ có
2
x
là tiệm cận đứng.
Câu 17. Chọn D.
Hình chóp đều
.
S ABCD
có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt đáy bằng
60
.
Đường cao
3
2
2 6 1 1 6 6
.tan60 .tan 60 . .
2 2 2 3 3 2 6
day
AC a a a a
h V S h a
.
Câu 18. Chọn D.
Với tiệm cận đứng 2x
hàm số có mẫu là dạng
" 2", "2 "
x x
.
Câu 19. Chọn B.
Nghiệm của mẫu
2
2
4 4 2 0 2
x x x x
(không là nghiệm tử)
2
x
là
TCĐ.
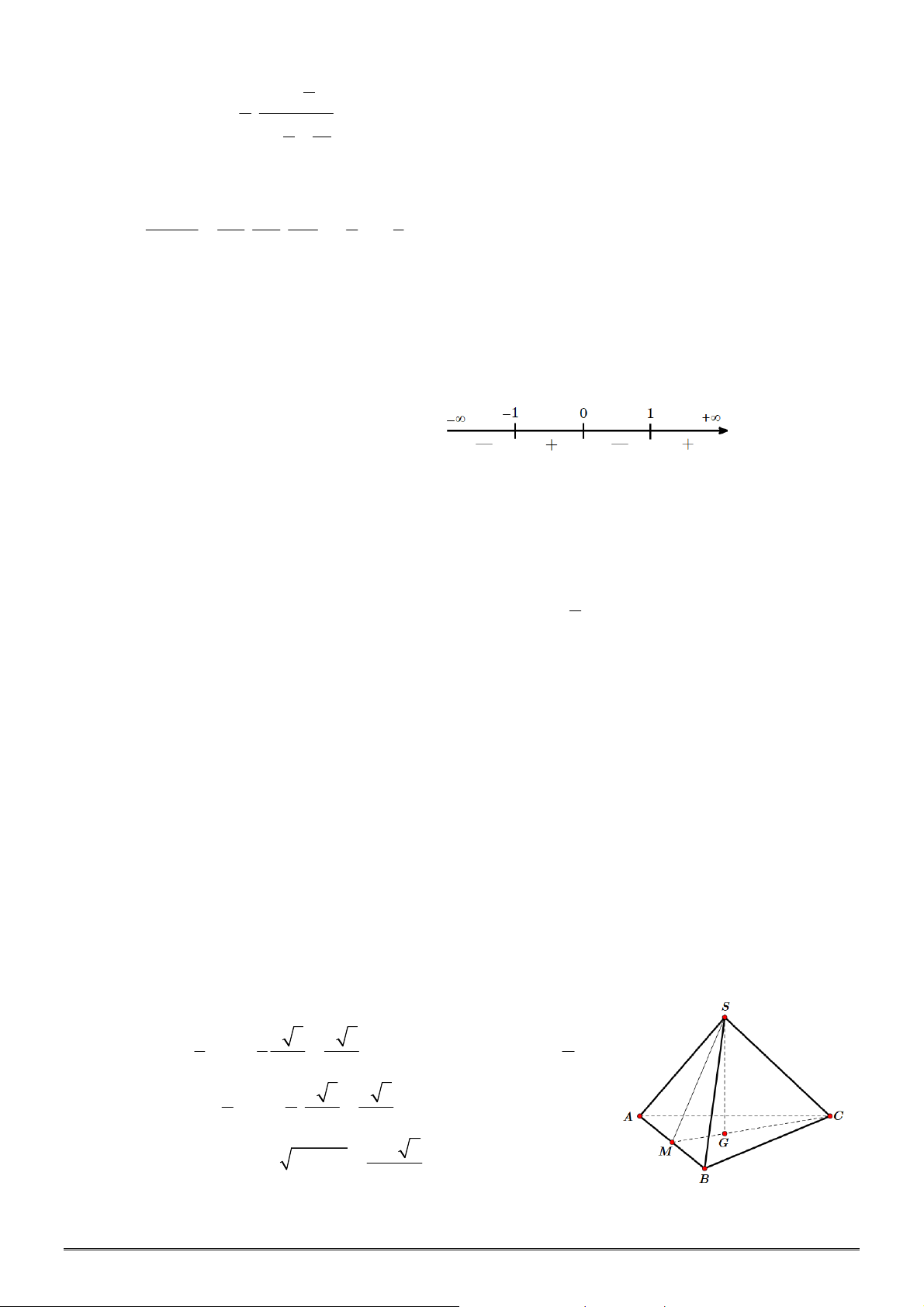
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/13 - Mã đề thi 132
2
3
2
1
lim lim . 0 0
4 4
1
x x
x
y y
x
x x
là TCN
2
2 2
0
a
a b
b
.
Câu 20. Chọn C.
3
.
. .
.
1 1
. . 8
2 8
S A B C
S ABC S A B C
S ABC
V SA SB SC
V V
V SA SB SC
.
Câu 21. Chọn B.
2;4
2 2 0 1 2;4 min 4 4
y x x y
.
Câu 22. Chọn D.
Câu 23. Chọn A.
3
0
4 4 0
1
x
y x x
x
. Dựa vào trục số
0;1
là khoảng nghịch biến cần tìm
0, 1 5 1
a b a b
.
Câu 24. Chọn C.
Câu 25. Chọn D.
ĐKXĐ:
2
2 11 25 0
x x
(luôn đúng)
BPT
2 2
5
2 11 25 10 2 11 15 0 ;3 3
2
x
x x x x x x
.
Câu 26. Chọn D.
Hàm số lũy thừa
y u x
với số mũ không nguyên, hay số mũ âm thì ĐKXĐ là:
0
u x
.
Khi đó
1 0 1;x x
.
Câu 27. Chọn C.
A sai vì đồ thị hàm số logarit
log
a
y x
có thể nằm dưới trục hoành.
B sai vì đồ thị hàm số mũ
x
y a
luôn nằm trên trục hoành và nhận trục
Ox
làm tiệm cận
ngang.
C đúng vì đồ thị hàm số logarit
log
a
y x
luôn nằm bên phải trục tung, nhận trục
Oy
là tiệm
cận đứng.
D sai vì đồ thị hàm số mũ
x
y a
luôn có một tiệm cận duy nhất là trục
Ox
.
Câu 28. Chọn B.
Xác định nhanh góc giữa mặt bên với đáy là
60
SMG
.
1 1 3 3
.tan60
3 3 2 6 2
a a a
MG CM SG h MG
.
2 2 3 3
.
3 3 2 3
a a
R CG CM .
2
2 2
7
. . . .
6
xq
a
S R l R R h
.
Câu 29. Chọn A.
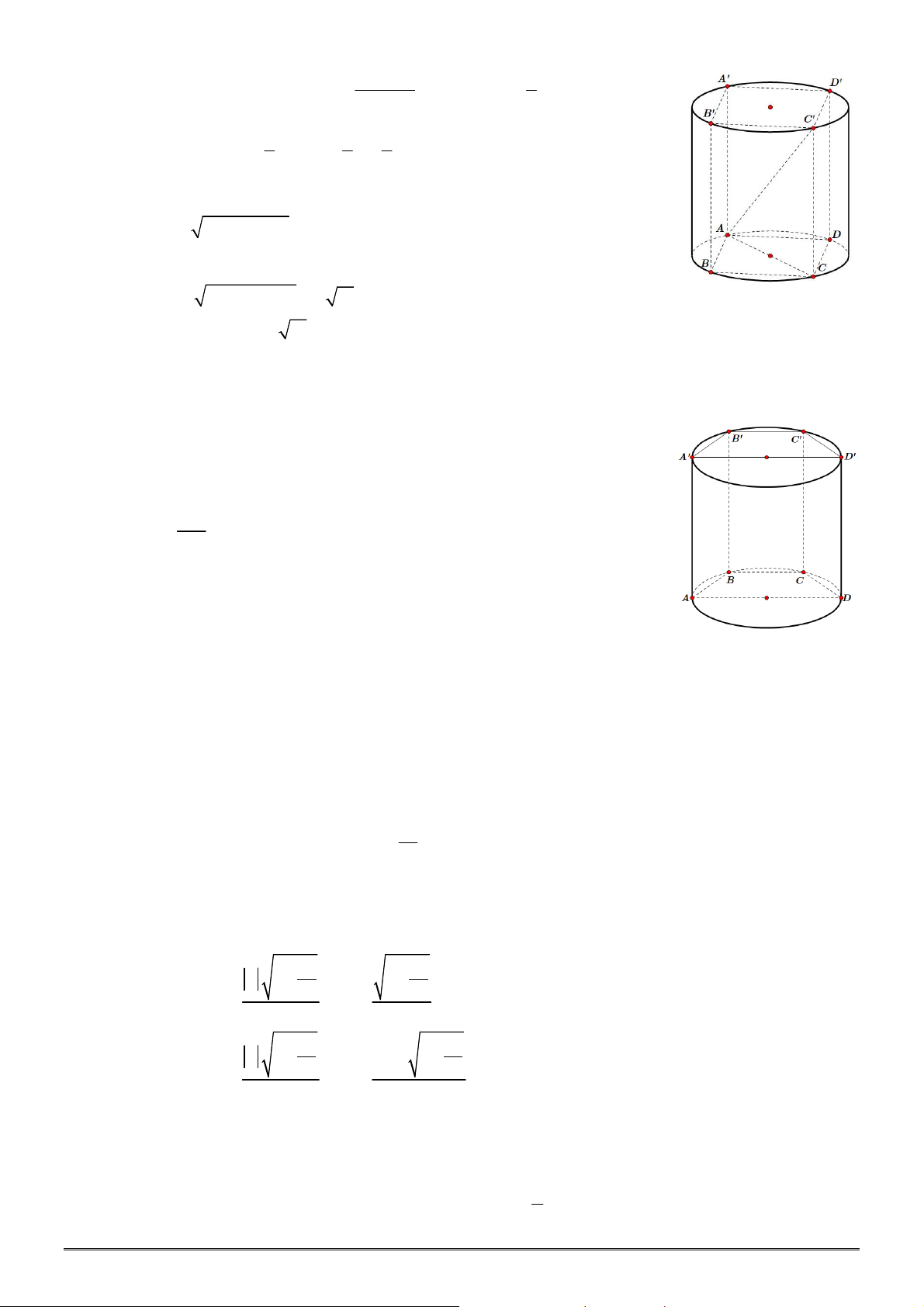
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/13 - Mã đề thi 132
1;0
H Ox A và
2
3 1
1
3
2
y k y
x
.
Suy ra
1 1 1
: 1
3 3 3
tt y x x
.
Câu 30. Chọn D.
2 2
10 5
AC AD CD R
.
2
2 2 2
tp
S R Rh R R h
2 2
2 11
CC AC AC h
.
10 5 2 11
tp
S
.
Câu 31. Chọn D.
2
3 6 9 6 6 0 1 1; 9
y x x y x x
là điểm uốn cũng là tâm đối xứng hàm
bậc ba.
Câu 32. Chọn D.
Hình thang
ABCD
với kích thước như đề bài là nửa lục giác đều.
2
AD
R a
và
2 3
2 . . 2
tru
h a V R h a
.
Câu 33. Chọn D.
A sai vì không tồn tại giá trị
x
để hàm số đạt giá trị
4
.
B sai vì hàm số không xác định tại
1
x
nên không là điểm cực đại.
C sai vì đồ thị hàm số có điểm cực tiểu là
0;1
.
D đúng vì
1
lim 4, lim
x
x
y y
4
y
là TCN,
1
x
là TCĐ Hàm số có 2 tiệm
cận.
Câu 34. Chọn C.
Hàm trùng phương
4 2
0
y ax bx c a
có ba điểm cực trị
. 0
a b
(trái dấu).
1 0
10
1; 0;1;2;3
1 3 10 0
3
m
m
m m
m m
có 4 giá trị
m
.
Câu 35. Chọn A.
0
lim 0
x
y x
là TCN
1
d
.
2 2
1 1
1 1
lim lim lim 1 1
1
x x x
x
x x
y y
x
là TCN.
2 2
1 1
1 1 1
lim lim lim 1 1
1
x x x
x
x x
y y
x
là TCN.
2 2.2 3.1 7
n T
.
Câu 36. Chọn A.
2
0 0;4
1
3 6 0 . 4
2
2 2;0
OAB
x A
y x x S OAOB
x B
.
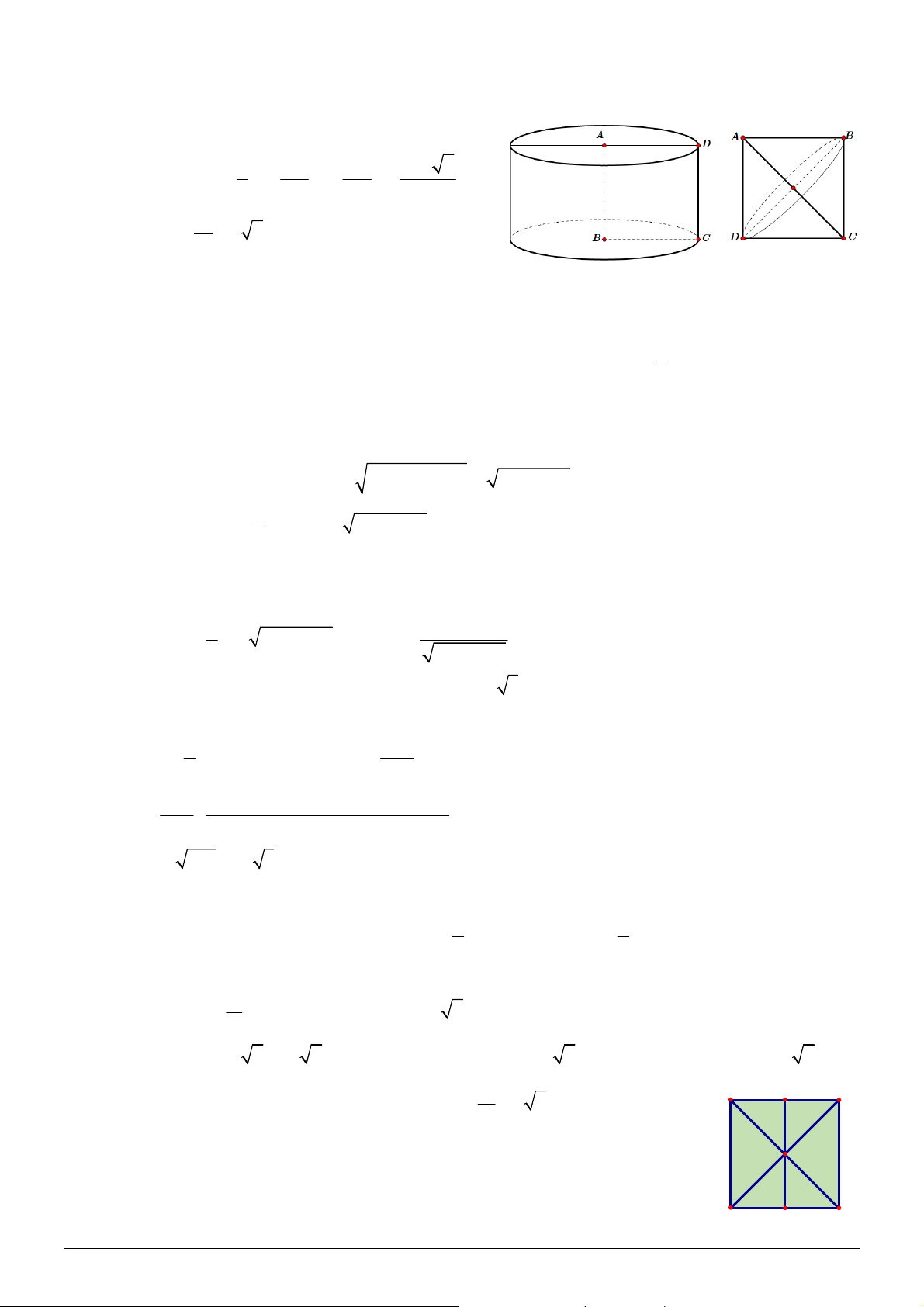
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/13 - Mã đề thi 132
Câu 37. Chọn A.
Quay quanh cạnh
AB
:
2
1
. . 64
tru
V V BC AB
.
Quay quanh đường chéo
AC
:
2
2
2 32 2
2 . . .
3 2 2 3
non
BD AC
V V
.
1
2
3 2
V
V
.
Câu 38. Chọn C.
2 2
2 2 2 4 2
x x x
y x e x x e x x e
.
2 2
1 2
0
2 6 2 0 2 6 2 0 3
x
b
y y x x e x x x x
a
.
Câu 39. Chọn C.
Đáy là tam giác cân có cạnh bên là
cm
x , cạnh đáy là
24 2
NP x
với
12
x
.
Đường cao từ đỉnh
A
:
2
2
12 24 144
A
h x x x với
24 144 0 6
x x
.
1
24 2 . 24 144
2
ANP
S S x x x .
.
ANP
V S AB
, do
AB
không đổi nên
V
đạt GTLN
S x
đạt GTLN trên
6;12
.
Cách 1. Đạo hàm
6;12
1 12
2 24 144 24 2 0 8
2
24 144
SOLVE
For X
S x x x x
x
Chọn luôn A.
Để chắc chắn ta thử lại với
6 0, 8 16 3, 12 0
S S S
(thỏa mãn).
Cách 2. Bất đẳng thức AM – GM (Cauchy).
2 2
2
2
1 1
24 2 24 144 144 12 24 144
4 4.6
S x x x x
3
2
1 144 12 144 12 24 144
4.6 3
x x x
768 16 3
S . Dấu bằng xảy ra
144 12 24 144 8
x x x
.
Câu 40. Chọn D.
2
sin
2
x
t
với
2 2
cos 1 sin
2 2
1;2 2 2
x x
t y f t t
t t
.
Cách 1. Dùng đạo hàm giải.
1;2
2
2
2
1 0 2 2
t
f t t t
t
.
1 3, 2 2 2, 2 3 min 2 2, max 3 . 6 2
f f f m y M y M m
.
Nếu dùng bất đẳng thức Cô–si
2
2 2 2
2
t
t
f t ta chỉ tìm được min.
Câu 41. Chọn B.
,
H K
lần lượt là trung điểm
,
CD AB
. Suy ra
HK
đi qua
A
B
C
D
M
H
K
M
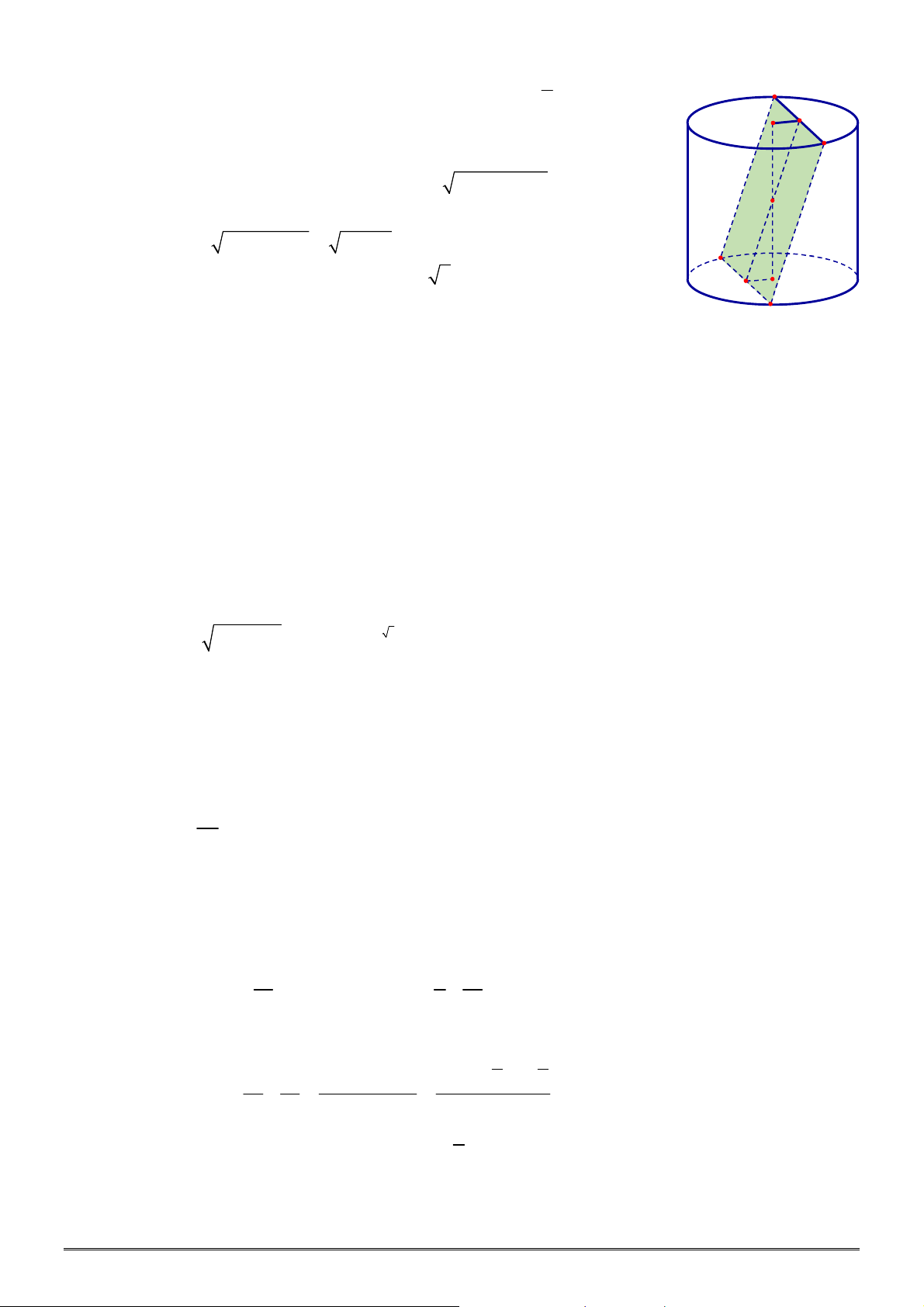
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/13 - Mã đề thi 132
tâm
M
của hình vuông
ABCD
và ta có được
1
4
2
MK AB
Mục tiêu tính bán kính
OA OB R
của hình trụ?
OO
là trục hình trụ suy ra
OO
vuông góc 2 đáy.
Suy ra
OO OK
(
OK
đáy)
2 2
3
OK MK MO
OK
đi qua tâm hình tròn đáy và qua trung điểm dây
AB OK AB
2 2 2 2
3 4 5
OB OK KB R
(
OKB
vuông tại
K
)
Thể tích hình trụ là
2
. . 50 7
V R h
.
Câu 42. Chọn A.
Hình hộp chữ nhật có tất cả 12 cạnh Số đỉnh (trung điểm mỗi cạnh) hình cần biết là 12 đỉnh.
Loại B, C.
Mỗi mặt của hình hộp chữ nhật chứa 4 cạnh của hình cần biết mà hình hộp chữ nhật có 6 mặt.
Số cạnh của hình cần biết là 24 cạnh.
Câu 43. Chọn D.
Đồ thị hàm số lũy thừa
y x
từ trái qua phải, đi xuống số mũ
0
.
Đồ thị hàm số lũy thừa ,
y x y x
từ trái qua phải, đi lên số mũ
, 0
.
Kẻ đường thẳng
1
x m
cắt ,
y x y x
lần lượt tại
,
A B
.
Ta thấy
A B
y y
.
Câu 44. Chọn C.
Đặt
2
5
log 1
t x
với
3 2
5
1 5 1 log 1 4 1 2
x x t
.
Pt
2
2 3
f t
t t m
có nghiệm trên đoạn
1;2
.
Cách 1. Lập bảng biến thiên:
2 2 0 1 1;2
f t t t
. Tính
1 0, 2 5
f f
.
Dựa vào BBT:
0;5
ycbt
m .
Cách 2. Dùng điều kiện có nghiệm.
1 1;2
2
D
b
x
a
và hệ số
2
t
dương nên hàm số đồng biến trên đoạn
1;2
.
Để phương trình
f t m
có nghiệm trên đoạn
1;2
1;2
1;2
min max 1 2 0;5
f t m f t f m f m .
Câu 45. Chọn B.
3 2
3 4
1 2 1
3 2 , 1 3 , 1
f x
mx x x m x x
x x x
(*)
2
3
6 3
2 5 5 5
1 7
2
2 4 2 2 4
2 2
2 0, 1
x
x x
f x x x
x x x x
.
1;
2
* 3 min 1 2
3
m f x f m
.
Câu 46. Chọn B.
A
B
C
D
K
O
O
H
M
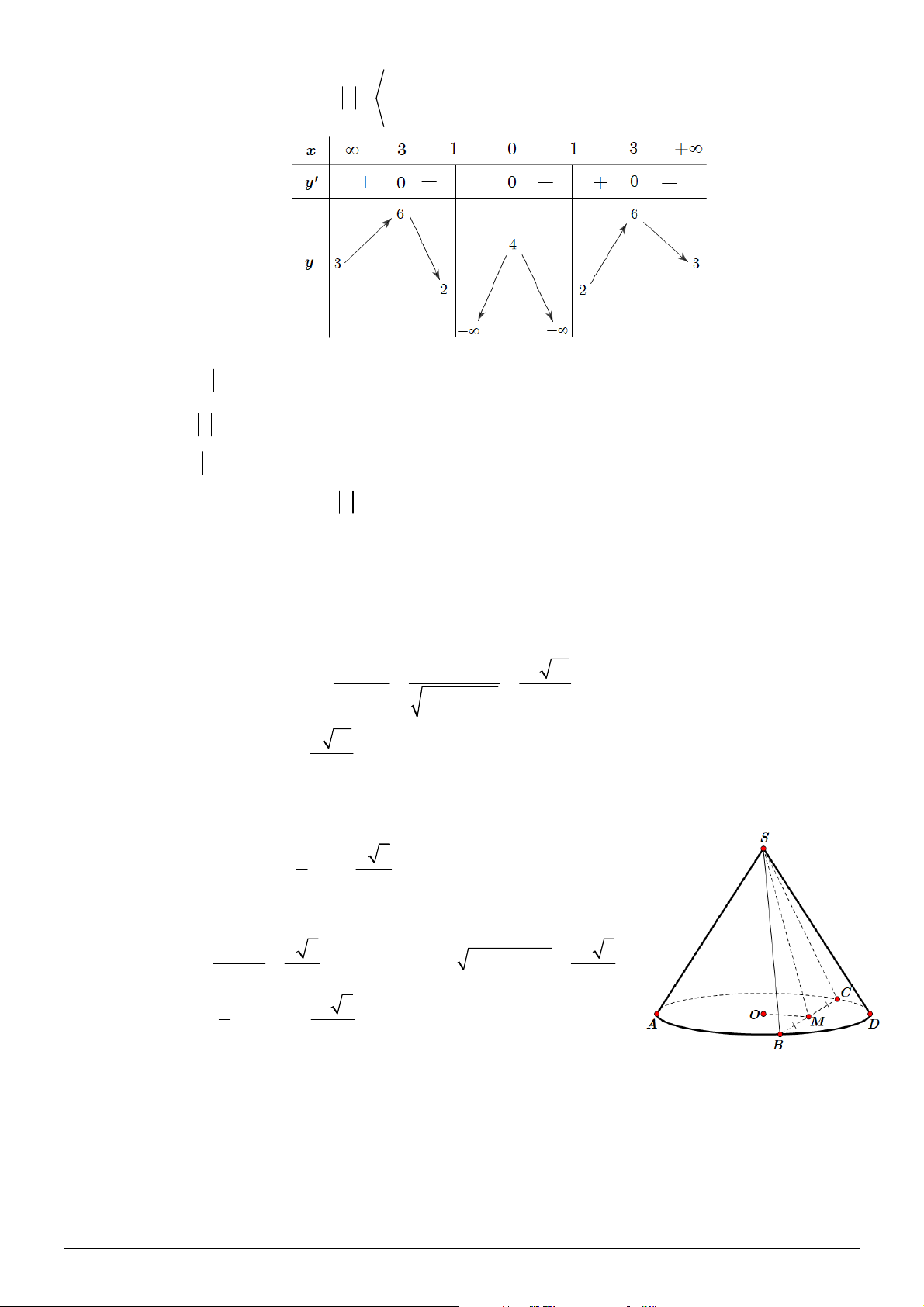
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/13 - Mã đề thi 132
Từ
f x
suy ra đồ thị
f x
:
0
Oy
Oy x
Giöõ nguyeânphaànñoàthòbeânphaûitruïc
Laáyñoáixöùngphaàntreânquatruïc
.
Dựa vào bảng biến thiên:
1
lim 1
x
f x x
là TCĐ.
1
lim 1
x
f x x
là TCĐ.
lim 3 3
x
f x y
là TCN.
Vậy đồ thị hàm số
y f x
có tất cả 3 tiệm cận.
Câu 47. Chọn D.
Gọi
N
trung điểm
SA
thì
BG
cắt
SAC
tại
N
;
1
3
;
d G SAC
GN
BN
d B SAC
(*)
BH AC H AC
mà
BH SA BH SAC
với
H SAC
.
2
2
. .3 3 10
;
10
3
BA BC a a a
d B SAC BH
AC
a a
10
* ;
10
a
d G SAC
.
Câu 48. Chọn C.
SAD
là tam giác vuông đề cập trong đề.
1 2
,
2 2
a
SO OB OA AD SA SB a
.
Gọi
M
là trung điểm của
BC
Góc
,
SBC ñaùy
60
SMO
.
2 2
6 2 3
2 2
sin 60 3 3
SO a a
SM BC MB SB SM
.
2
1 2
.
2 3
SBC
a
S BC SM .
Giải thích thêm. Góc
,
SBC ñaùy
?
Ta có:
SBC
đáy
BC
.
Gọi
M
là trung điểm của
BC
BC OM
mà
BC SO BC SOM BC SM
.
SBC SM BC
ñaùy OM BC
Góc
,
SBC ñaùy SMO
.
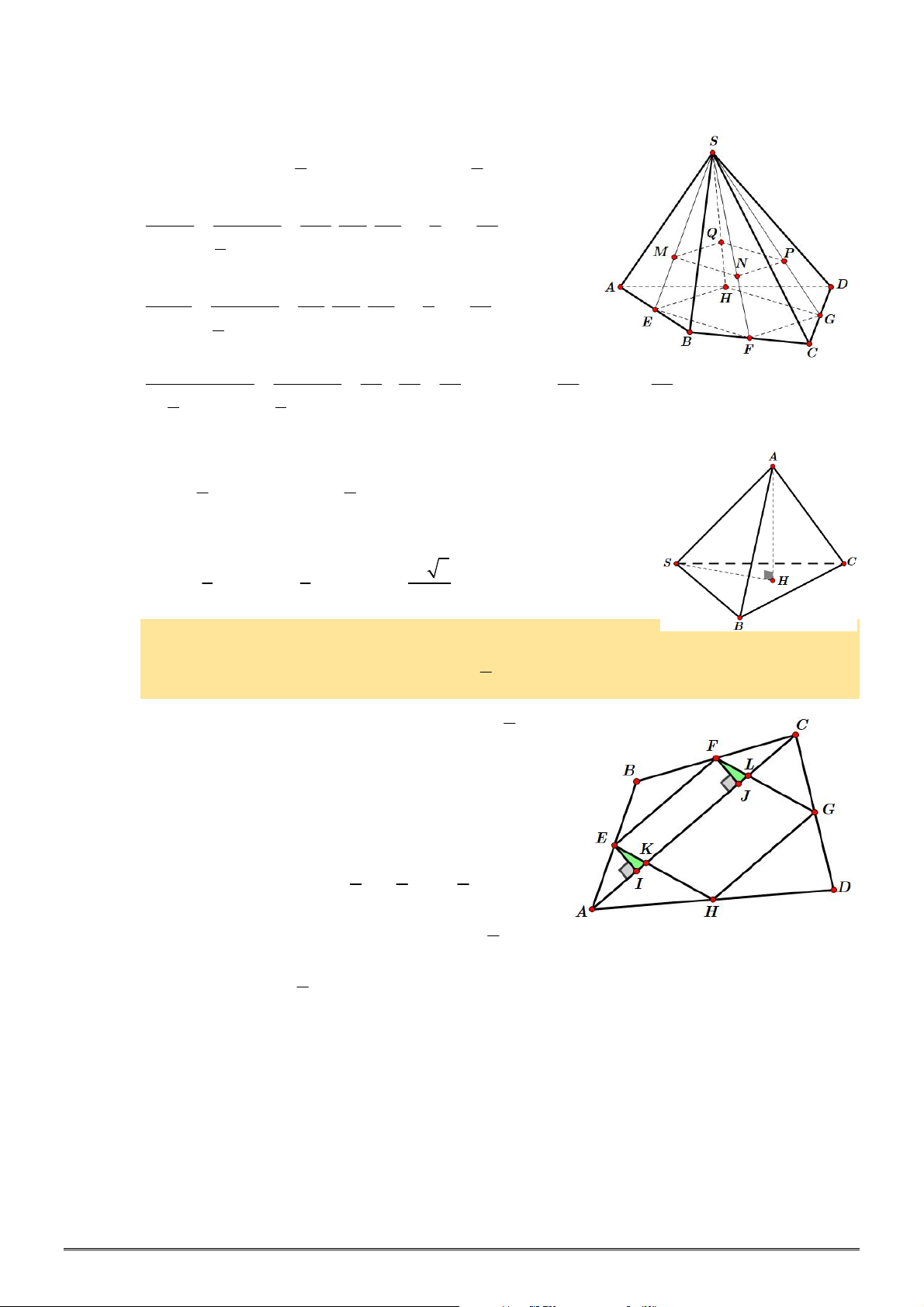
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/13 - Mã đề thi 132
Câu 49. Chọn C.
Ở đây ta lấy tổng quát đáy
ABCD
là một tứ giác.
Gọi
, , ,
E F G H
thứ tự là trung điểm
, , ,
AB BC CD DA
.
Tính chất:
. .
1 1
2 2
EFGH ABCD S EFGH S ABCD
S S V V .
3
. .
.
.
2 8
. .
1
3 27
2
S MQN S MQN
S EHF
S EFGH
V V
SM SQ SN
V SE SH SF
V
.
3
. .
.
.
2 8
. .
1
3 27
2
S PQN S PQN
S GHF
S EFGH
V V
SP SQ SN
V SG SH SF
V
.
. . .
. . .
. .
8 8 16 8 4
12
1 1
27 27 27 27 27
2 2
S MQN S PQN S MNPQ
S MNPQ S EFGH S ABCD
S EFGH S EFGH
V V V
V V V
V V
.
Câu 50. Chọn C.
1 1
. .sin .
2 2
SBC
S SB SC BSC SB SC
.
Gọi
H
là hình chiếu của
A
lên mặt
SBC
thì
AH AS
.
3
max
1 1 6
. . .
3 3 3
SABC SBC
a
V S AH SB SC SA V
.
Tính chất câu 49. Cho tứ giác
ABCD
. Gọi
, , ,
E F G H
lần lượt là trung điểm của
, , ,
AB BC CD DA
.Chứng minh rằng:
1
2
EFGH ABCD
S S ?
Ta có
EF
là đường trung bình
ABC
1
2
EF AC
.
Gọi
,
I J
lần lượt là hình chiếu của
,
E F
lên
AC
.
Gọi
,
K L
lần lượt là giao điểm của
,
EH FG
với
AC
.
IEK JFL IEK EFJK JFL EFJK
S S hai nhau S S S S
1 1 1
. .
2 2 2
EFLK EFJI ABC
S S EF EI AC BH S
(1).
Chứng minh tương tự cho
ADC
1
2
HGLK ADC
S S
(2)
(1) + (2)
1
2
EFGH ABCD
S S .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/26 - Mã đề thi 357
SỞ GIÁO DỤC VÀ ĐÀO TẠO
LÂM ĐỒNG
KIỂM TRA CHẤT LƯỢNG HỌC KỲ 1
Năm học 2017-2018
MÔN: TOÁN 12
Thời gian làm bài 90 phút
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 357
Câu 1. [2H1-2] Cho lăng trụ
.
ABC A B C
. Gọi
O
là tâm của mặt bên
ACC A
. Gọi
1
V
,
2
V
lần lượt là
thể tích của khối chóp
.
O ABC
và khối lăng trụ
.
ABC A B C
. Tính tỷ số
1
2
V
V
.
A.
1
2
1
3
V
V
. B.
1
2
1
4
V
V
. C.
1
2
1
2
V
V
. D.
1
2
1
6
V
V
.
Câu 2. [2D2-1] Cho
x
là số thực dương. Biểu diễn
1
5
4
4
.
P x x
thành dạng lũy thừa với số mũ hữu tỷ.
A.
3
10
P x
. B.
11
4
P x
. C.
7
20
P x
. D.
21
20
P x
.
Câu 3. [2D2-2] Hàm số nào sau đây nghịch biến trên
?
A.
3
x
y
. B.
5
2
x
y
. C.
2 2
3
x
y
. D.
2018
2017
x
y
.
Câu 4. [2D1-2] Biết rằng đồ thị hàm số
2 1
1
x
y
x
và đường thẳng
7
y x
cắt nhau tại hai điểm
1 1
;
A x y
,
2 2
;
B x y
. Tính giá trị của tổng
1 2
S x x
.
A.
6
S
. B.
10
S
. C.
6
S
. D.
8
S
.
Câu 5. [2H2-2] Thiết diện qua trục của hình nón là một tam giác đều cạnh bằng
a
. Tính thể tích
V
của khối nón đã cho.
A.
3
3
24
a
. B.
3
3
12
a
. C.
3
3
8
a
. D.
3
3
48
a
.
Câu 6. [2D1-2] Tìm giá trị nhỏ nhất của hàm số
3 2
5 1
y x x x
trên đoạn
2;0
:
A.
2;0
min 5
y
. B.
2;0
min 1
y
. C.
2;0
min 1
y
. D.
2;0
min 4
y
.
Câu 7. [2D2-2] Tìm nghiệm của phương trình
3
log 2 5 2
x
.
A.
2
x
. B.
13
2
x
. C.
11
2
x
. D.
7
x
.
Câu 8. [2H1-1] Hình nào trong các hình dưới đây không phải hình đa diện?
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 9. [2H2-1] Cho khối trụ có bán kính đáy là
2 3
và chiều cao bằng
3
. Tính diện tích xung quanh
xq
S
của hình trụ.
A.
12 3
xq
S
. B.
4 3 2 3 3
xq
S
.
C.
18 3
xq
S
. D.
6 3
xq
S
.
Hình 1.
Hình 3.
Hình 4.
Hình 2.
18
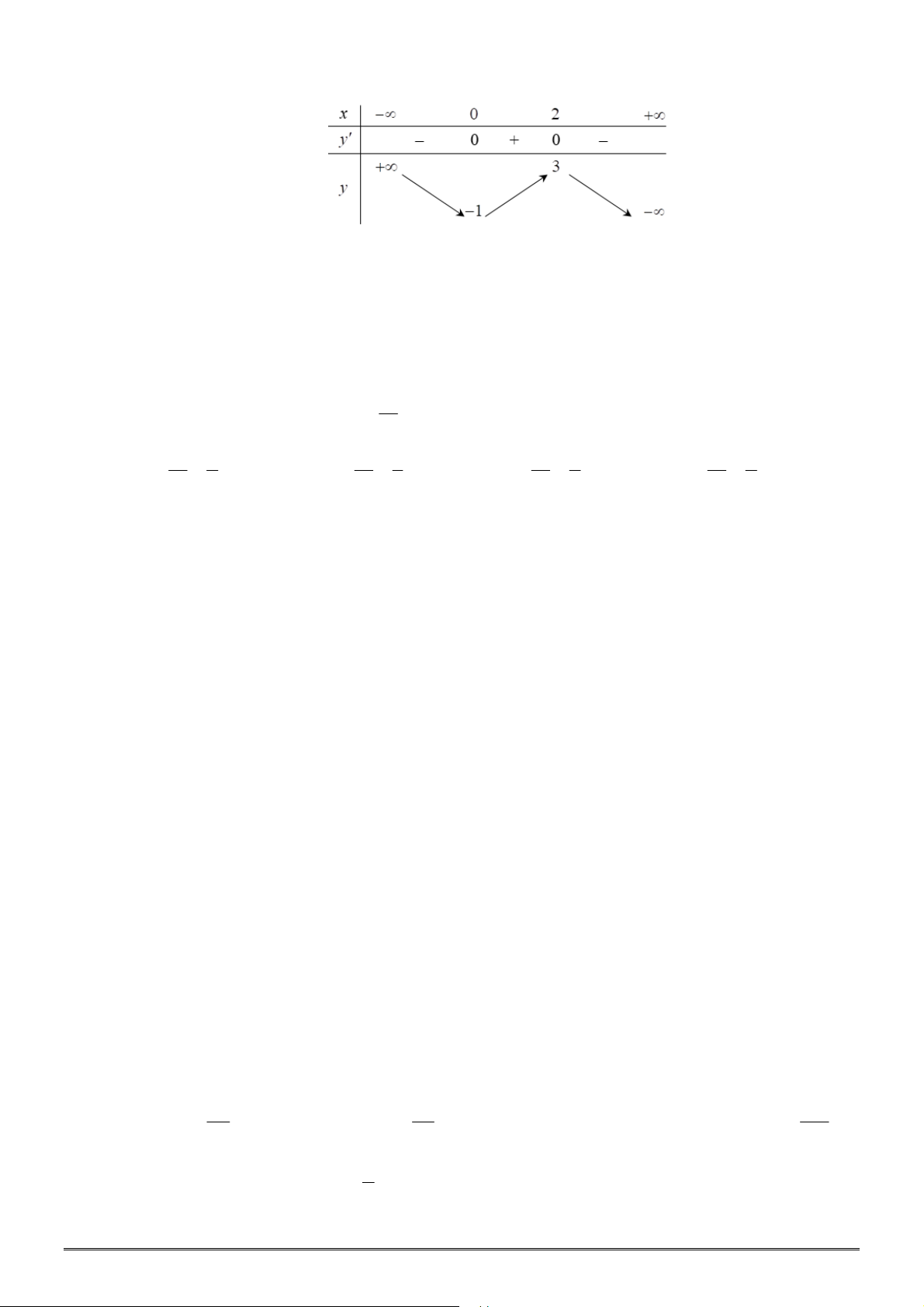
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/26 - Mã đề thi 357
Câu 10. [2D1-1] Cho hàm số
y f x
có bảng biến thiên như hình vẽ.
Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
1; 3
. B. Hàm số nghịch biến trên khoảng
0; 2
.
C. Hàm số đồng biến trên khoảng
0; 2
. D. Hàm số nghịch biến trên khoảng
; 2
.
Câu 11. [2H1-2] Cho hình chóp
.
S ABC
, gọi
M
là trung điểm của
SB
và
D
là điểm đối xứng của
B
qua
C
. Cạnh
SC
cắt mặt phẳng
AMD
tại
N
. Gọi
1
V
,
2
V
lần lượt là thể tích của khối chóp
.
S AMN
và
.
S ABC
. Tính tỉ số
1
2
V
V
.
A.
1
2
2
3
V
V
. B.
1
2
1
3
V
V
. C.
1
2
1
6
V
V
. D.
1
2
1
4
V
V
.
Câu 12. [2H2-1] Cho hình chữ nhật
ABCD
có
3
AB
,
4
AD
. Gọi
M
,
N
lần lượt là trung điểm của
các cạnh
AD
,
BC
. Quay hình chữ nhật
ABCD
quanh trục
MN
, tính thể tích
V
của khối trụ
nhận được.
A.
4
V
. B.
12
V
. C.
48
V
. D.
36
V
.
Câu 13. [2D2-2] Tìm đạo hàm của hàm số
3 2
x
y x .
A.
2 1 3 ln3
x
y x
. B.
2 4
x
y x
.
C.
2 1 3 log2
x
y x
. D.
2 1 3 ln2
x
y x
.
Câu 14. [2D1-2] Cho hàm số
3 2
4 6 5
y x x
. Tính giá trị cực tiểu
CT
y
của hàm số.
A.
0
CT
y
. B.
5
CT
y
. C.
3
CT
y
. D.
1
CT
y
.
Câu 15. [2D1-1] Hàm số
4 2
8 3
y x x
có bao nhiêu điểm cực trị?
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 16. [2H1-1] Khối tứ diện đều có bao nhiêu mặt phẳng đối xứng?
A.
6
. B.
3
. C. Vô số. D.
4
.
Câu 17. [2H2-2] Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lăng trụ đứng có đáy là tam giác nội tiếp được trong một mặt cầu.
B. Hình hộp chữ nhật có ba kích thước phân biệt nội tiếp được trong một mặt cầu.
C. Hình chóp
.
S ABCD
có đáy là hình bình hành nội tiếp được trong một mặt cầu.
D. Hình chóp
.
S ABCD
có đáy là hình chữ nhật nội tiếp được trong một mặt cầu.
Câu 18. [2D2-1] Cho số thực
a
dương, khác 1 và số thực
tùy ý. Mệnh đề nào dưới đây đúng?
A.
1
a
a
. B.
1
a
a
. C.
a a
. D.
1
a
a
.
Câu 19. [2D1-1] Đồ thị hàm số
3
y
x
có bao nhiêu đường tiệm cận?
A.
1
. B.
0
. C.
3
. D.
2
.
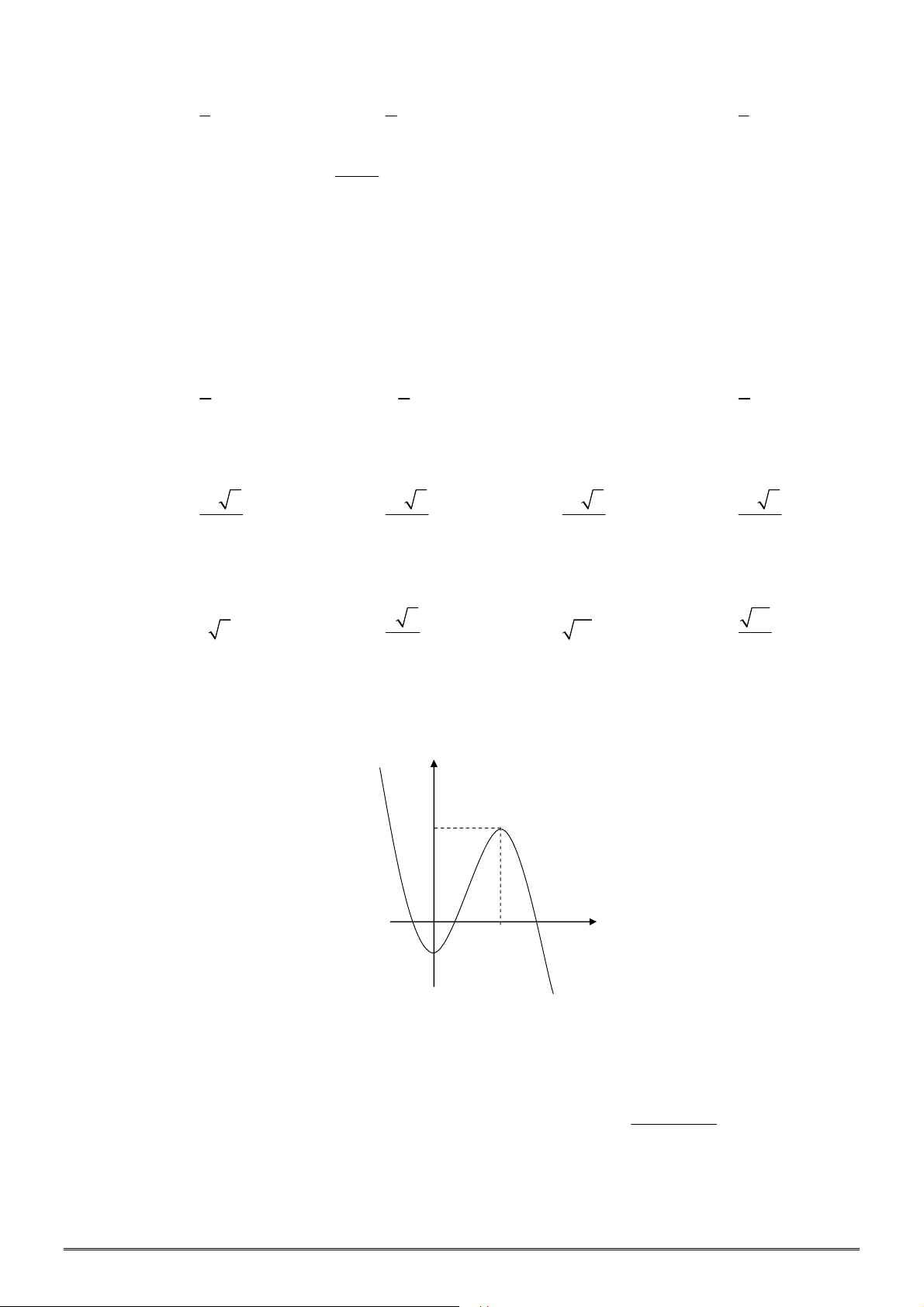
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/26 - Mã đề thi 357
Câu 20. [2H1-1] Viết công thức tính thể tích
V
của khối chóp có diện tích là
S
và chiều cao
h
.
A.
1
3
V S h
. B.
1
.
2
V S h
. C.
.
V S h
. D.
1
.
3
V S h
.
Câu 21. [2D1-2] Cho hàm số
2 1
2
x
y
x
. Gọi
M
là giá trị lớn nhất của hàm số trên đoạn
1;2
. Mệnh
đề nào sau đây đúng?
A.
1;2
M . B.
1;0
M . C.
0;1
M . D.
4;2
M .
Câu 22. [2D1-1] Đồ thị hàm số
3 2
2 1
y x x x
và đường thẳng
1
y x
có bao nhiêu giao điểm?
A.
2
. B.
0
. C.
3
. D.
1
.
Câu 23. [2D2-2] Cho số thực
a
dương và khác
1
. Tính
2
3
log .
a
P a
A.
2
.
3
P
B.
2
.
3
P
C.
6.
P
D.
3
.
2
P
Câu 24. [2H2-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông và cạnh bên
SA
vuông góc với
đáy. Cho biết
SAC
là tam giác vuông cân và
SC a
. Tính thể tích
V
của hình chóp
.
S ABCD
.
A.
3
2
.
8
a
V B.
3
2
.
24
a
V C.
3
2
.
12
a
V D.
3
2
.
3
a
V
Câu 25. [2H2-2] Tính bán kính
R
của mặt cầu ngoại tiếp hình hộp chữ nhật có kích thước lần lượt là
3,4,5
.
A.
5 2
R
. B.
5 2
2
R . C.
15
R . D.
12
2
R .
Câu 26. [2D1-2] Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hãy tìm hàm số
đó.
A.
3 2
3 1
y x x
. B.
3 2
3 1
y x x
. C.
3 2
3 1
y x x
. D.
3 2
2 1
y x x
.
x
y
O
3
2
-1
Câu 27. [2H1-1] Khối nào trong các khối sau là khối đa diện đều loại
3;4
?
A. Khối tứ diện đều. B. Khối bát diện đều .
C. Khối nhị thập diện đều . D. Khối lập phương .
Câu 28. [2D1-3] Tìm tất cả giá trị của tham số
m
để đồ thị hàm số
2
3
4
x
y
x x m
có ba đường tiệm
cận .
A.
4
m
. B.
4
3
m
m
. C.
4
m
. D.
4
3
m
m
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/26 - Mã đề thi 357
Câu 29. [2H1-2] Cho hình hộp đứng
.
ABCD A B C D
có đáy là hình vuông, tam giác
B AC
đều có
cạnh bằng
a
. Tính thể tích
V
của khối hộp đã cho.
A.
3
2
8
a
V . B.
3
3
9
a
V . C.
3
2
4
a
V . D.
3
2
12
a
V .
Câu 30. [2H2-1] Viết công thức tính diện tích xung quanh của hình nón có bán kính đáy là
r
và chiều
cao
h
.
A.
2 2
2
xq
S r r h
. B.
xq
S rh
. C.
2 2
xq
S r r h
. D.
xq
S r r h
.
Câu 31. [2D2-2] Cho phương trình
2
2
2
2
log log 6 0
8
x
x
với điều kiện
0
x
, nếu đặt
2
log
t x
ta
được phương trình nào sau đây?
A.
2
4 2 9 0
t t
. B.
2
2 2 3 0
t t
. C.
2
3 3 0
t
. D.
2
4 2 3 0
t t
.
Câu 32. [2D1-2] Cho hàm số
3 2
3 1 1
y x x . Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số
1
đồng biến trên các khoảng
;0 , 2;
và nghịch biến trên khoảng
0;2
.
B. Hàm số
1
đồng biến trên các khoảng
; 2 , 0;
và nghịch biến trên khoảng
2;0
.
C. Hàm số
1
nghịch biến trên các khoảng
;0 , 2;
và đồng biến trên khoảng
0;2
.
D. Hàm số
1
nghịch biến trên các khoảng
; 2 , 0;
và đồng biến trên khoảng
2;0
.
Câu 33. [2H1-2] Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh
a
và cạnh bên
SA
vuông góc với
đáy,
2
SA a
. Tính thể tích
V
của khối chóp
.
S ABC
?
A.
3
2
6
a
. B.
3
3
6
a
. C.
3
3
12
a
. D.
3
2 3
9
a
.
Câu 34. [2D2-2] Tìm tập xác định
D
của hàm số
3
2
4
4
y x
.
A.
\ 2; 2
D
. B.
D
.
C.
; 2 2;D
. D.
; 2 2;D
.
Câu 35. [2H1-2] Cho hình lăng trụ
.
ABC A B C
có diện tích đáy bằng
2
a
, cạnh bên
AA a
và hợp với
đáy
ABC
một góc
60
. Tính thể tích
V
của khối lăng trụ
.
ABC A B C
.
A.
3
3
2
a
V . B.
3
3
6
a
V . C.
3
2
a
V . D.
3
3
3
a
V .
Câu 36. [2D1-2] Cho hàm số
1
mx m
y
x m
, (
m
là tham số). Tìm giá trị của
m
để
0;2
max 2
y
.
A.
1
m
. B.
3
m
. C.
5
m
. D.
1
3
m
.
Câu 37. [2D1-3] Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ bên. Khẳng định nào sau đây
đúng ?
A.
0, 0, 0, 0.
a b c d
B.
0, 0, 0, 0.
a b c d
C.
0, 0, 0, 0.
a b c d
D.
0, 0, 0, 0.
a b c d
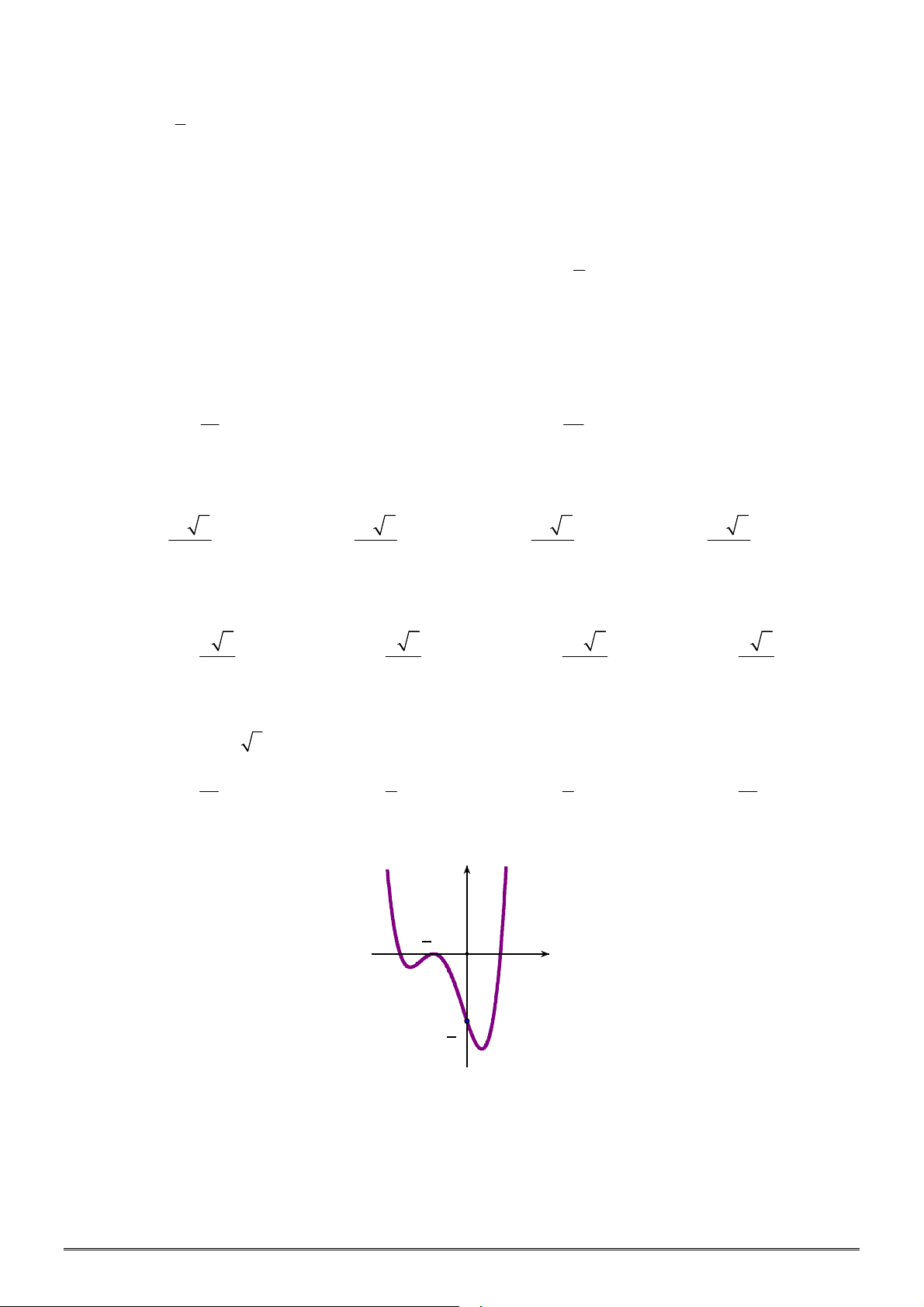
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/26 - Mã đề thi 357
Câu 38. [2D1-3] Gọi
S
là tập hợp các giá trị nguyên của
m
trên đoạn
10;10
để hàm số
3 2
1
2 1 2 2
3
y x m x m x
có cực đại và cực tiểu. Tìm số phần tử của
S
.
A.
20
. B.
19
. C.
18
. D.
21
.
Câu 39. [2D2-2] Tìm tất cả các giá trị của tham số
m
để phương trình
9 2 1 3 2 1 0
x x
m m
có
hai nghiệm thực phân biệt.
A.
0
m
. B.
1
0
m
m
. C.
1
2
0
m
m
. D.
0
m
.
Câu 40. [2D2-2] Tìm giá trị của tham số
m
để phương trình
2 2
3 3
log 2 log 1 4 0
x m x m
có hai
nghiệm thực phân biệt
1 2
;
x x
thỏa điều kiện
1 2
9
x x
.
A.
13
2
m
. B.
3
m
. C.
1
4
m
. D.
2
m
.
Câu 41. [2H1-2]Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy là
a
và tất cả các mặt bên của hình
chóp là các tam giác vuông cân. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
2
8
a
. B.
3
6
18
a
. C.
3
2
12
a
. D.
3
2
24
a
.
Câu 42. [2H2-2]Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy là
a
và cạnh bên hợp với đáy góc
60
. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp.
A.
6
3
a
R . B.
6
2
a
R . C.
2 6
3
a
R . D.
6
6
a
R .
Câu 43. [2D2-2] Cho biết
log 2
a
b
và
log 3
b
c
,
0 1,0 1, 0
a b c
. Tính giá trị của biểu thức
2
log
ab
P b c
.
A.
10
3
P
. B.
7
4
P
. C.
7
3
P
. D.
16
3
P
.
Câu 44. [2D1-3] Cho hàm số
y f x
liên tục trên
và hàm số
y f x
có đồ thị như hình vẽ.
x
y
1
1
2
O
Đặt
2
g x f x x
. Khẳng định nào dưới đây đúng?
A. Hàm số
g x
có một điểm cực đại và một điểm cực tiểu.
B. Hàm số
g x
chỉ có một điểm cực đại.
C. Hàm số
g x
có một điểm cực đại và hai điểm cực tiểu.
D. Hàm số
g x
chỉ có một điểm cực tiểu.
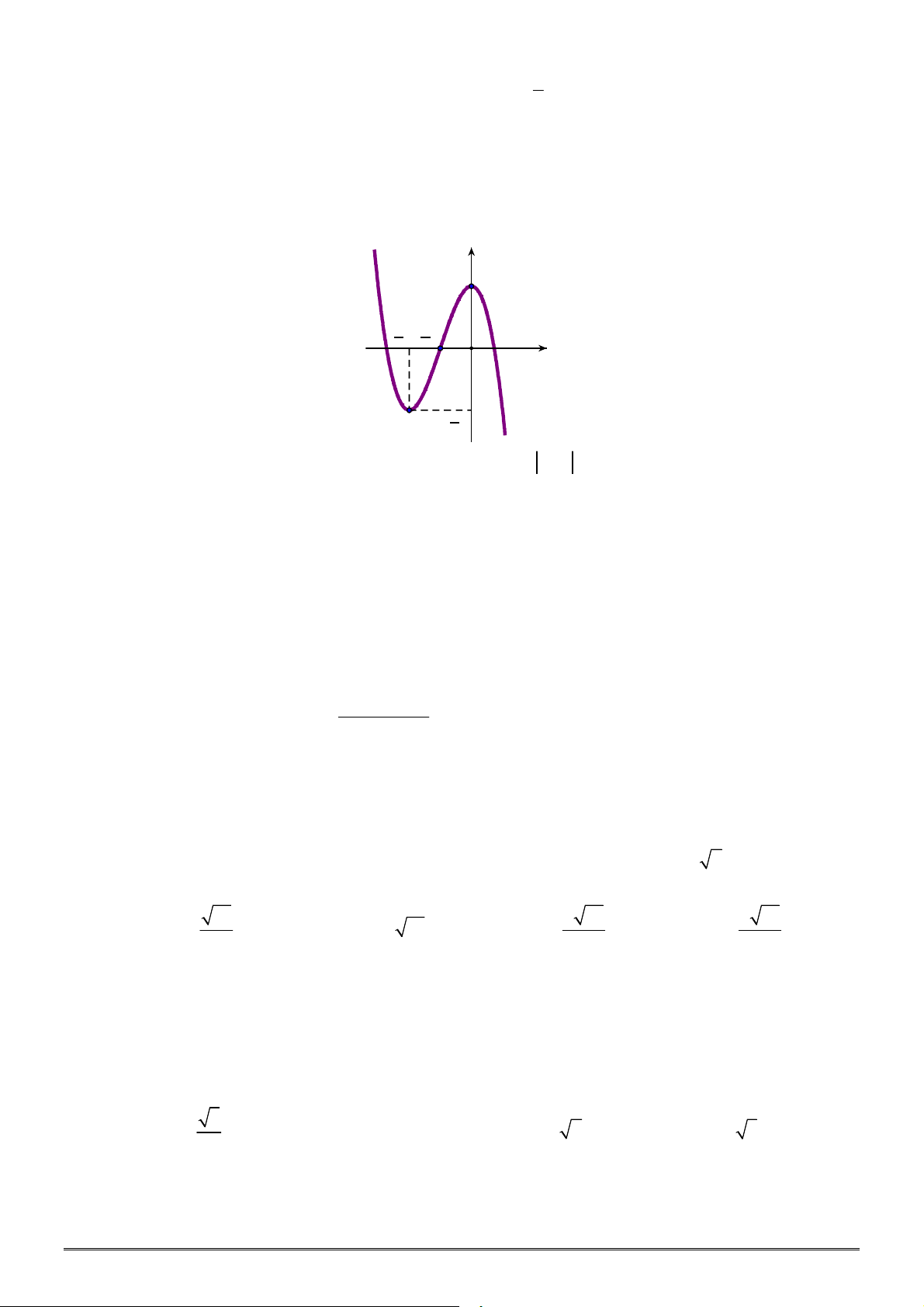
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/26 - Mã đề thi 357
Câu 45. [2D1-2] Tìm giá trị của tham số m để hàm số
3 2 2
1
1 2 1
3
y x mx m x m
đạt cực tiểu
tại điểm
0
2
x
.
A.
3
m
hoặc
1
m
. B.
3
m
hoặc
1
m
.
C.
1
m
D.
3
m
.
Câu 46. [2D1-3] Cho hàm số
2
1 2 2
y x x x
có đồ thị như hình vẽ bên
x
y
2
2
12
O
Tìm tất cả giá trị của tham số m để phương trình
2
1 2 2
x x x m
có 4 nghiệm thực
phân biệt.
A.
0 2
m
. B. Không tồn tại m. C.
2
m
. D.
0 2
m
.
Câu 47. [2D2-3] Sự tăng trưởng của một loài vi khuẩn trong phòng thí nghiệm được tính theo công thức
.3
rt
f t F
trong đó
F
là lượng vi khuẩn ban đầu,
r
là tỉ lệ tăng trưởng
0
r
và
t
là thời
gian(đơn vị: giờ). Biết rằng số lượng vi khuẩn ban đầu là
6
10
con và sau
3
giờ là
6
5.10
con.
Hỏi sau thời gian mấy giờ, số lượng vi khuẩn là
125
triệu con?
A.
75
giờ. B.
9
giờ. C.
6
giờ. D.
60
giờ.
Câu 48. [2D2-3] Cho hàm số
3 2
3
x
x
m m
y
m
, (
m
tham số). Tìm tất cả các giá trị của tham số
m
để
hàm số đồng biến trên
0;1
.
A.
3
2
m
m
. B.
3 1
2
m
m
. C.
1
2
m
m
. D.
3
1
m
m
.
Câu 49. [2H1-3] Cho tứ diện
ABCD
có
2
AB
, tất cả các cạnh còn lại bằng
2 2
. Thể tích
V
của
khối tứ diện
ABCD
A.
10
3
V . B.
2 10
V . C.
4 10
3
V . D.
2 10
3
V .
Câu 50. [2H2-4] Cho mặt cầu
S
có tâm
O
, bán kính bằng
2
. Hai mặt phẳng
P
và
Q
song song
với nhau và cách đều tâm
O
một khoảng cách là
x
0 2
x
lần lượt cắt mặt cầu
S
theo
giao tuyến là hai đường tròn
C
và
C
. Xác định
x
để hình trụ có hai đường tròn đáy là
C
và
C
có diện tích xung quanh lớn nhất.
A.
3
2
x . B.
1
x
. C.
2
x
. D.
3
x .
----------HẾT----------
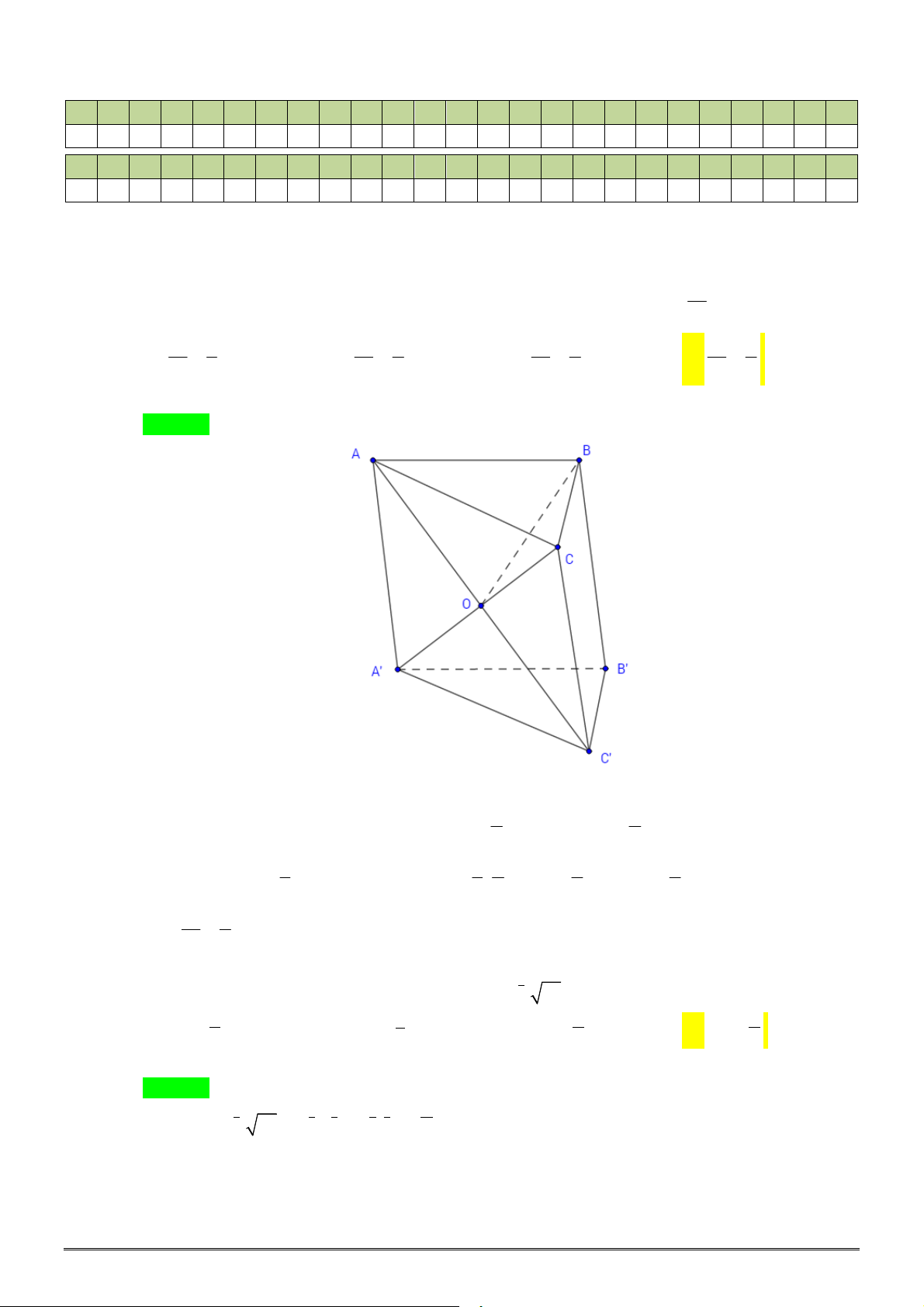
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/26 - Mã đề thi 357
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
D
C C C B D
A
A
C B B
D
C
B A
C D
D
D
C A
D
B B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
B B C C D
B B D
B C B
B
C
B D
A
C A
D
A
B A
D
C
HƯỚNG DẪN GIẢI
Câu 1. [2H1-2] Cho lăng trụ
.
ABC A B C
. Gọi
O
là tâm của mặt bên
ACC A
. Gọi
1
V
,
2
V
lần lượt là
thể tích của khối chóp
.
O ABC
và khối lăng trụ
.
ABC A B C
. Tính tỷ số
1
2
V
V
.
A.
1
2
1
3
V
V
. B.
1
2
1
4
V
V
. C.
1
2
1
2
V
V
. D.
1
2
1
6
V
V
.
Lời giải
Chọn D.
Gọi
h
là khoảng cách từ điểm
C
đến mặt phẳng
ABC
.
Do
O
là trung điểm
AC
nên
1
, ,
2
d O ABC d C ABC
2
h
.
Khi đó, ta có
1
1
,
3
ABC
V d O ABC S
1
3 2
ABC
h
S
1
6
ABC
h S
2
1
6
V
.
Vậy
1
2
1
6
V
V
.
Câu 2. [2D2-1] Cho
x
là số thực dương. Biểu diễn
1
5
4
4
.
P x x
thành dạng lũy thừa với số mũ hữu tỷ.
A.
3
10
P x
. B.
11
4
P x
. C.
7
20
P x
. D.
21
20
P x
.
Lời giải
Chọn D.
Ta có
1
5
4
4
.
P x x
4
1
5
4
.
x x
1 4
4 5
x
21
20
x
.
Câu 3. [2D2-2] Hàm số nào sau đây nghịch biến trên
?
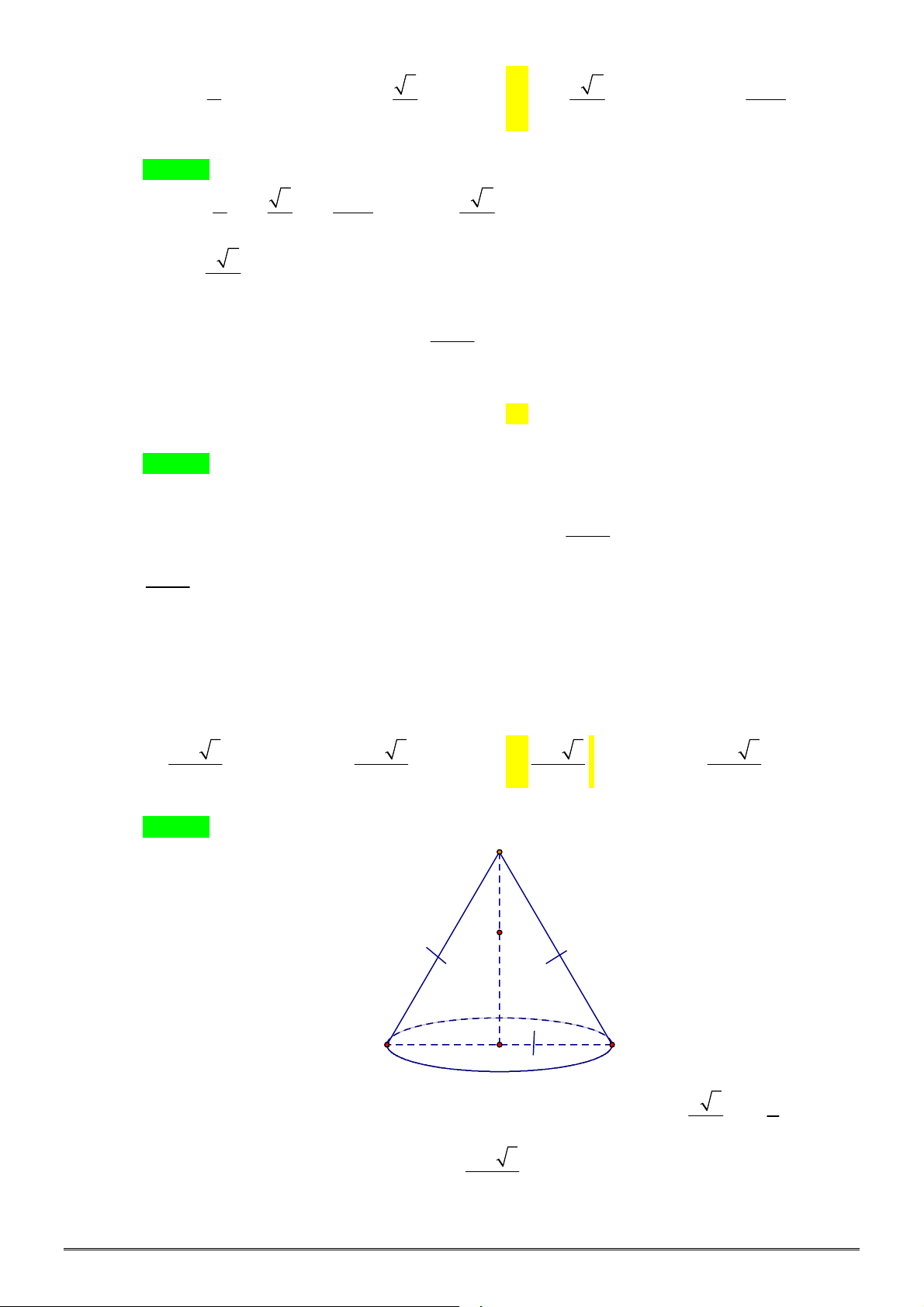
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/26 - Mã đề thi 357
A.
3
x
y
. B.
5
2
x
y
. C.
2 2
3
x
y
. D.
2018
2017
x
y
.
Lời giải
Chọn C.
Ta thấy:
1
3
,
5
1
2
,
2018
1
2017
và
2 2
0 1
3
nên theo tính chất của hàm số mũ ta có hàm
số
2 2
3
x
y
nghịch biến trên
.
Câu 4. [2D1-2] Biết rằng đồ thị hàm số
2 1
1
x
y
x
và đường thẳng
7
y x
cắt nhau tại hai điểm
1 1
;
A x y
,
2 2
;
B x y
. Tính giá trị của tổng
1 2
S x x
.
A.
6
S
. B.
10
S
. C.
6
S
. D.
8
S
.
Lời giải
Chọn C.
Tập xác định:
\ 1
D
.
Phương trình hoành độ giao điểm của đồ thị hàm số
2 1
1
x
y
x
và đường thẳng
7
y x
là:
2 1
7 2 1 1 7
1
x
x x x x
x
(do
1
x
không phải là nghiệm của phương trình)
1
2
2
2
6 8 0
4
x x
x x
x x
. Vậy tổng
1 2
2 4 6
S x x
.
Câu 5. [2H2-2] Thiết diện qua trục của hình nón là một tam giác đều cạnh bằng
a
. Tính thể tích
V
của khối nón đã cho.
A.
3
3
24
a
. B.
3
3
12
a
. C.
3
3
8
a
. D.
3
3
48
a
.
Lời giải
Chọn C.
a
Vì thiết diện qua trục của hình nón là tam giác đều nên hình nón có :
3
2
a
h ;
2
a
r
.
Do đó thể tích của khối nón là:
3
2
3
8
a
V r h
.
Câu 6. [2D1-2] Tìm giá trị nhỏ nhất của hàm số
3 2
5 1
y x x x
trên đoạn
2;0
:
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/26 - Mã đề thi 357
A.
2;0
min 5
y
. B.
2;0
min 1
y
. C.
2;0
min 1
y
. D.
2;0
min 4
y
.
Lời giải
Chọn B.
2
3 2 5
y x x
.
1 2;0
0
5
2;0
3
x
y
x
.
Ta có:
2 1
f
;
1 4
f
;
0 1
f
.
Vậy
2;0
min 1
y
.
Câu 7. [2D2-2] Tìm nghiệm của phương trình
3
log 2 5 2
x
.
A.
2
x
. B.
13
2
x
. C.
11
2
x
. D.
7
x
.
Lời giải
Chọn D.
Điều kiện:
5
2
x
2
3
log 2 5 2 2 5 3 7
x x x
( t/m đk)
Câu 8. [2H1-1] Hình nào trong các hình dưới đây không phải hình đa diện?
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Lời giải
Chọn A.
Hình đa diện (gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai
điều kiện:
a) Hai đa giác phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ
có một cạnh chung.
b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Do đó Hình 1 không phải hình đa diện.
Câu 9. [2H2-1] Cho khối trụ có bán kính đáy là
2 3
và chiều cao bằng
3
. Tính diện tích xung quanh
xq
S
của hình trụ.
A.
12 3
xq
S
. B.
4 3 2 3 3
xq
S
.
C.
18 3
xq
S
. D.
6 3
xq
S
.
Lời giải
Chọn A.
Diện tích xung quanh của hình trụ là:
2 2 .2 3.3 12 3
xq
S Rh
.
Hình 1.
Hình 3.
Hình 4.
Hình 2.
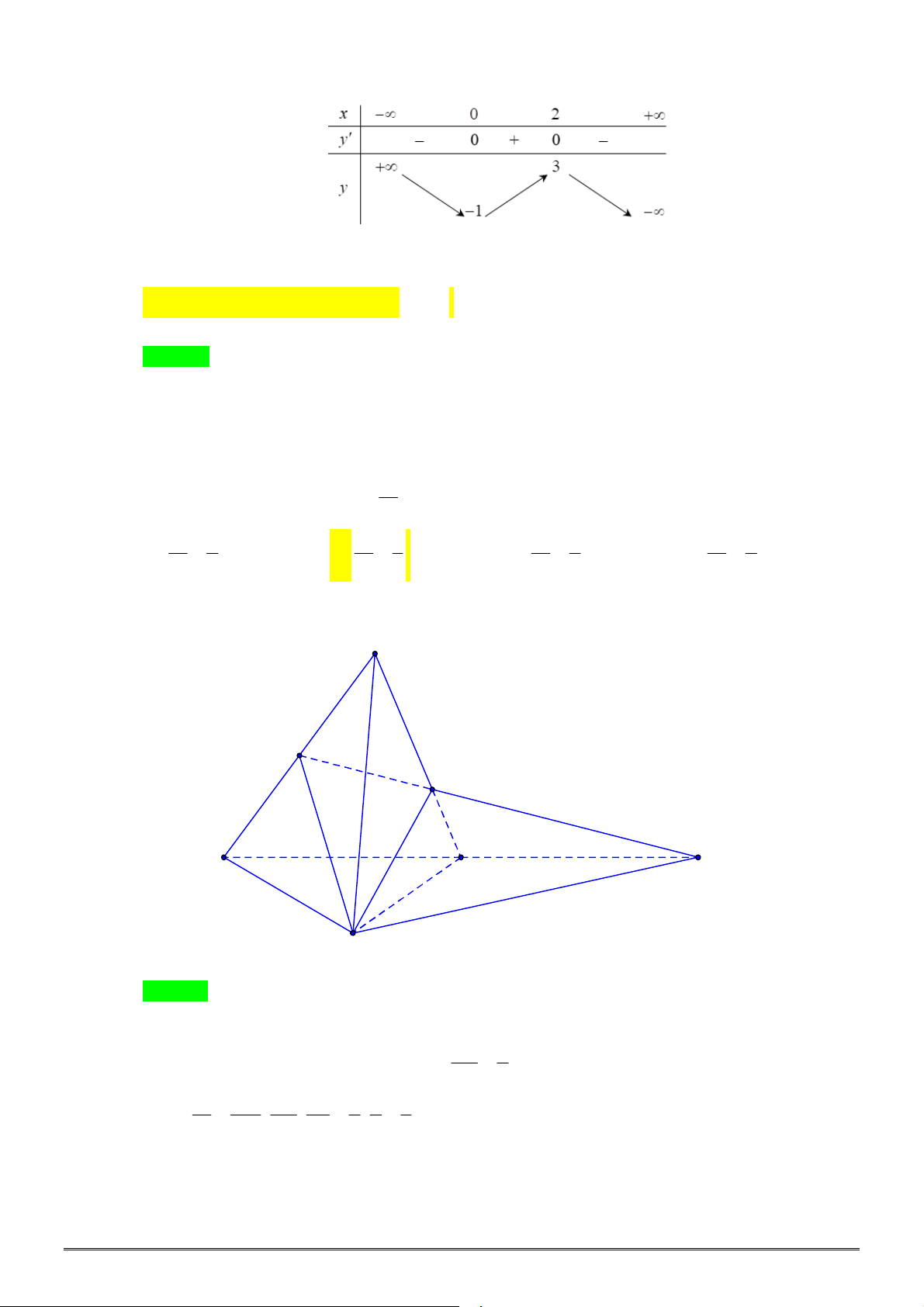
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/26 - Mã đề thi 357
Câu 10. [2D1-1] Cho hàm số
y f x
có bảng biến thiên như hình vẽ.
Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
1; 3
. B. Hàm số nghịch biến trên khoảng
0; 2
.
C. Hàm số đồng biến trên khoảng
0; 2
. D. Hàm số nghịch biến trên khoảng
; 2
.
Lời giải
Chọn C.
Dựa vào bảng biến thiên hàm số đồng biến trên khoảng
0; 2
.
Câu 11. [2H1-2] Cho hình chóp
.
S ABC
, gọi
M
là trung điểm của
SB
và
D
là điểm đối xứng của
B
qua
C
. Cạnh
SC
cắt mặt phẳng
AMD
tại
N
. Gọi
1
V
,
2
V
lần lượt là thể tích của khối chóp
.
S AMN
và
.
S ABC
. Tính tỉ số
1
2
V
V
.
A.
1
2
2
3
V
V
. B.
1
2
1
3
V
V
. C.
1
2
1
6
V
V
. D.
1
2
1
4
V
V
.
Lời giải
N
M
D
S
B
A
C
Chọn B.
Trong mặt phẳng
SBD
có
SC MD N
. Do
SC
và
MD
là trung tuyến của tam giác
SBD
nên
N
là trọng tâm của tam giác, suy ra
2
3
SN
SC
.
Ta có
1
2
1 2 1
2 3 3
V SM SN SA
V SB SC SA
.
Câu 12. [2H2-1] Cho hình chữ nhật
ABCD
có
3
AB
,
4
AD
. Gọi
M
,
N
lần lượt là trung điểm của
các cạnh
AD
,
BC
. Quay hình chữ nhật
ABCD
quanh trục
MN
, tính thể tích
V
của khối trụ
nhận được.
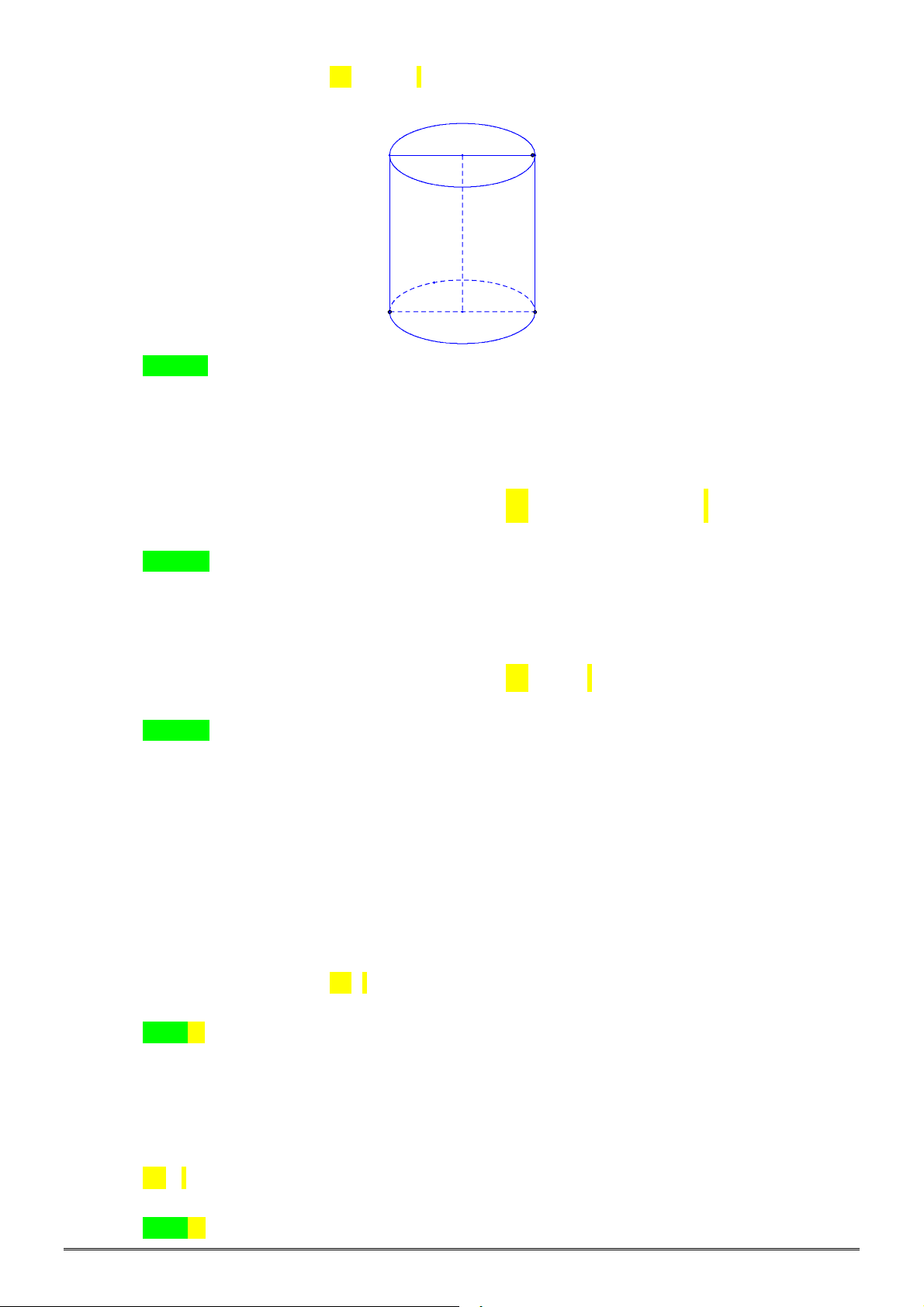
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/26 - Mã đề thi 357
A.
4
V
. B.
12
V
. C.
48
V
. D.
36
V
.
Lời giải
M
A
N
B C
D
Chọn B.
Thể tích của khối trụ bằng
2 2 2
. . 2 3 12
V R h MA AB
.
Câu 13. [2D2-2] Tìm đạo hàm của hàm số
3 2
x
y x .
A.
2 1 3 ln3
x
y x
. B.
2 4
x
y x
.
C.
2 1 3 log2
x
y x
. D.
2 1 3 ln2
x
y x
.
Lời giải
Chọn D.
3 2 3 2 3 . 2 2 3 .2 .ln2 2 1 3 ln2
x x x x x x
y x y x x x x
Câu 14. [2D1-2] Cho hàm số
3 2
4 6 5
y x x
. Tính giá trị cực tiểu
CT
y
của hàm số.
A.
0
CT
y
. B.
5
CT
y
. C.
3
CT
y
. D.
1
CT
y
.
Lời giải
Chọn C.
3 2
4 6 5
y x x
. TXĐ:
D
.
2
0
12 12 0
1
x
y x x
x
.
24 12
y x
.
Ta có:
0 12 0
y
Hàm số đạt cực đại tại
0
x
.
1 12 0
y
Hàm số đạt cực tiểu tại
1
x
và
1 3
CT
y y
.
Câu 15. [2D1-1] Hàm số
4 2
8 3
y x x
có bao nhiêu điểm cực trị?
A.
3
. B.
1
. C.
0
. D.
2
.
Lời giải
Chọn B.
Ta có:
3
4 16
y x x
0
y
3
4 16 0
x x
0
x
là nghiệm duy nhất.
Vậy hàm số có
1
cực trị.
Câu 16. [2H1-1] Khối tứ diện đều có bao nhiêu mặt phẳng đối xứng?
A.
6
. B.
3
. C. Vô số. D.
4
.
Lời giải
Chọn A.
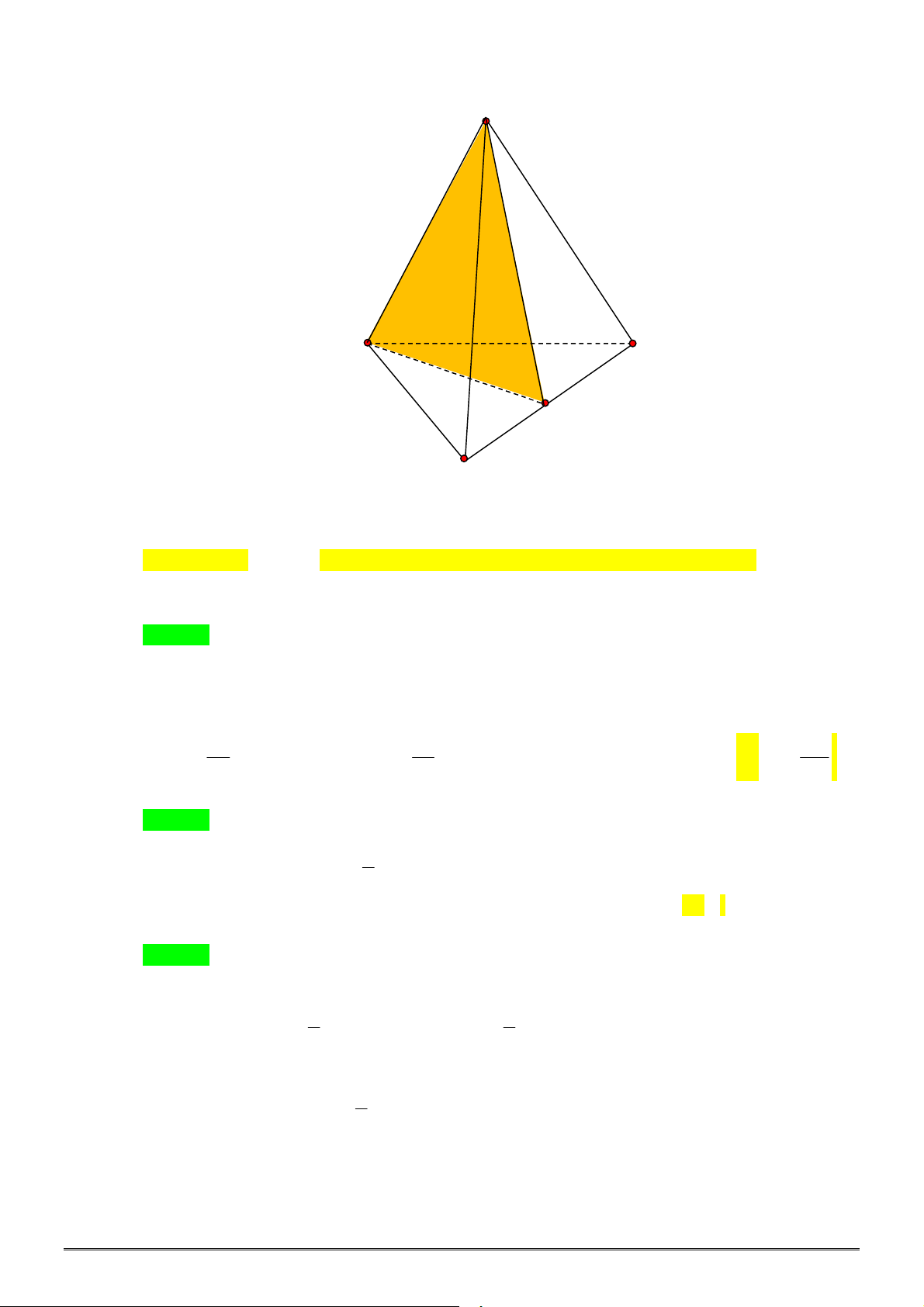
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/26 - Mã đề thi 357
Mặt phẳng đối xứng của tứ diện đều là mặt phẳng chứa một cạnh và trung điểm của cạnh đối
diện. Mà khối tứ diện đều có tất cả
6
cạnh, nên khối tứ diện có
6
mặt phẳng đối xứng.
Câu 17. [2H2-2] Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lăng trụ đứng có đáy là tam giác nội tiếp được trong một mặt cầu.
B. Hình hộp chữ nhật có ba kích thước phân biệt nội tiếp được trong một mặt cầu.
C. Hình chóp
.
S ABCD
có đáy là hình bình hành nội tiếp được trong một mặt cầu.
D. Hình chóp
.
S ABCD
có đáy là hình chữ nhật nội tiếp được trong một mặt cầu.
Lời giải
Chọn C.
Hình bình hành không thể nội tiếp được đường tròn nên hình chóp
.
S ABCD
có đáy là hình
bình hành không thể nội tiếp được trong một mặt cầu.
Câu 18. [2D2-1] Cho số thực
a
dương, khác 1 và số thực
tùy ý. Mệnh đề nào dưới đây đúng?
A.
1
a
a
. B.
1
a
a
. C.
a a
. D.
1
a
a
.
Lời giải
Chọn D.
Câu 19. [2D1-1] Đồ thị hàm số
3
y
x
có bao nhiêu đường tiệm cận?
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải
Chọn D.
Tập xác định
\ 0
D
.
Ta có
0 0
3
lim lim
x x
y
x
,
0 0
3
lim lim
x x
y
x
.
Suy ra đường thẳng
0
x
là tiệm cận đứng.
Ta cũng có
3
lim lim 0
x x
y
x
. Suy ra đường thẳng
0
y
là tiệm cận ngang.
Vậy đồ thị hàm số đã cho có hai đường tiệm cận.
Câu 20. [2H1-1] Viết công thức tính thể tích
V
của khối chóp có diện tích là
S
và chiều cao
h
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/26 - Mã đề thi 357
A.
1
3
V S h
. B.
1
.
2
V S h
. C.
.
V S h
. D.
1
.
3
V S h
.
Lời giải
Chọn D.
Công thức tính thể tích
V
của khối chóp có diện tích là
S
và chiều cao
h
là:
1
.
3
V S h
.
Câu 21. [2D1-2] Cho hàm số
2 1
2
x
y
x
. Gọi
M
là giá trị lớn nhất của hàm số trên đoạn
1;2
. Mệnh
đề nào sau đây đúng?
A.
1;2
M . B.
1;0
M . C.
0;1
M . D.
4;2
M .
Lời giải
Chọn C.
TXĐ:
\ 2
D
.
Ta có
2
5
0
2
y
x
với
x D
nên
0
y
với
1;2
x suy ra hàm số đồng biến trên
đoạn
1;2
. Khi đó
3
2
4
M y
suy ra
0;1
M .
Câu 22. [2D1-1] Đồ thị hàm số
3 2
2 1
y x x x
và đường thẳng
1
y x
có bao nhiêu giao điểm?
A.
2
. B.
0
. C.
3
. D.
1
.
Lời giải
Chọn A.
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số:
3 2 3 2
0
2 1 1 2 0
2
x
x x x x x x
x
Suy ra đồ thi hàm số
3 2
2 1
y x x x
và
1
y x
có 2 giao điểm.
Câu 23. [2D2-2] Cho số thực
a
dương và khác
1
. Tính
2
3
log .
a
P a
A.
2
.
3
P
B.
2
.
3
P
C.
6.
P
D.
3
.
2
P
Lời giải
Chọn D.
2
3
3 3
log log .
2 2
a
a
P a a
Câu 24. [2H2-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông và cạnh bên
SA
vuông góc với
đáy. Cho biết
SAC
là tam giác vuông cân và
SC a
. Tính thể tích
V
của hình chóp
.
S ABCD
.
A.
3
2
.
8
a
V B.
3
2
.
24
a
V C.
3
2
.
12
a
V D.
3
2
.
3
a
V
Lời giải
Chọn B.
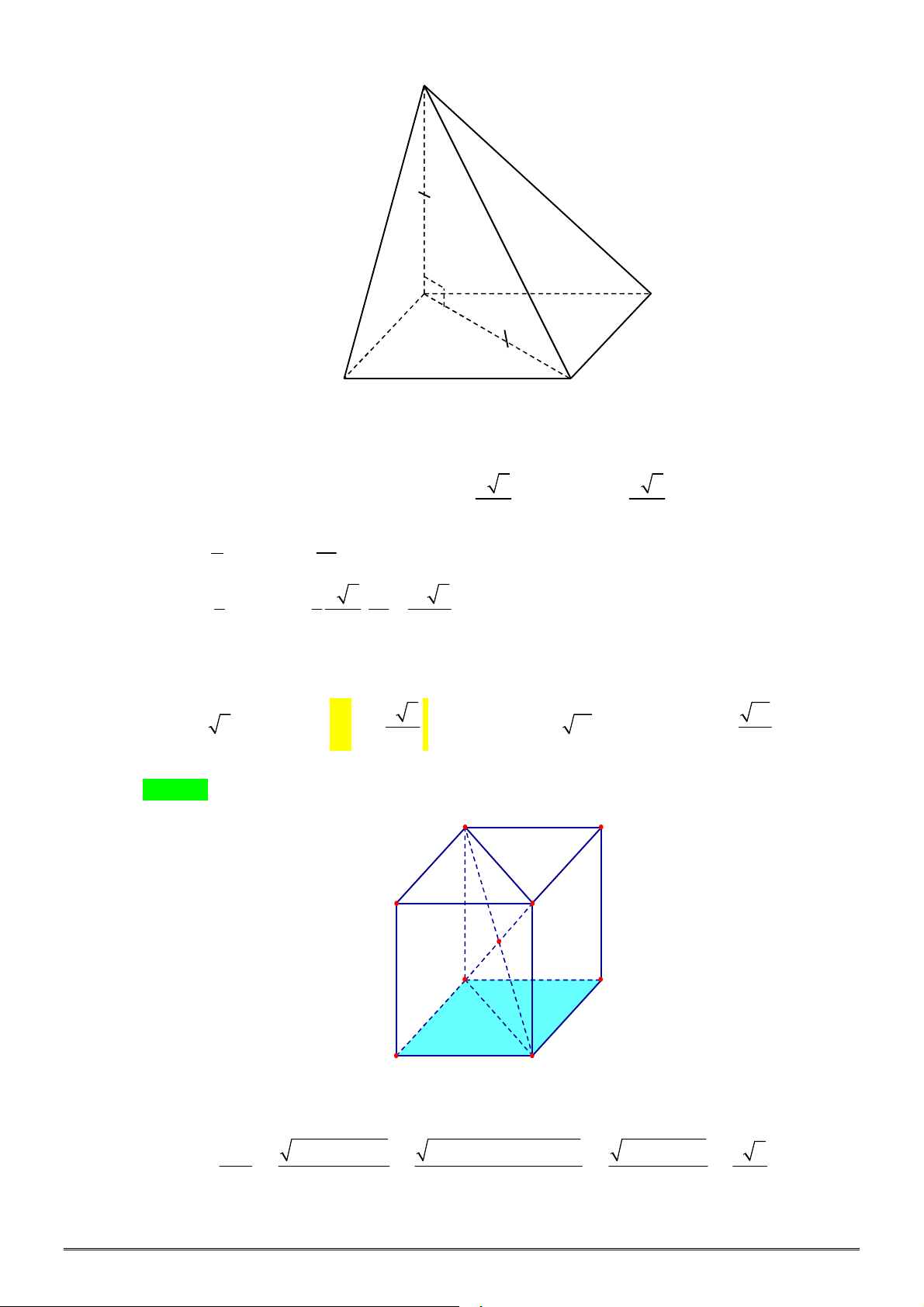
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/26 - Mã đề thi 357
Đặt
SA x AC x
(do
SAC
cân tại
A
)
SA ABCD SA AC SAC
vuông tại
A
2 2 2
SC SA AC
2 2 2
a x x
2
2
a
x
2
2
a
SA AC
2
a
AB
2
4
ABCD
a
S
2 3
.
1 1 2 2
. . .
3 3 2 4 24
S ABCD ABCD
a a a
V SA S
Câu 25. [2H2-2] Tính bán kính
R
của mặt cầu ngoại tiếp hình hộp chữ nhật có kích thước lần lượt là
3,4,5
.
A.
5 2
R
. B.
5 2
2
R . C.
15
R . D.
12
2
R .
Lời giải
Chọn B.
Gọi
I
là giao điểm của
AC
và
A C
. Khi đó,
I
chính là tâm của mặt cầu ngoại tiếp hình hộp
chữ nhật. Bán kính
R
được tính:
R IA
2
AC
2 2
2
AA A C
2 2 2
2
AA A B B C
2 2 2
5 4 3
2
5 2
2
.
A
B
C
D
D
C
B
A
I
B
C
A
D
S
a
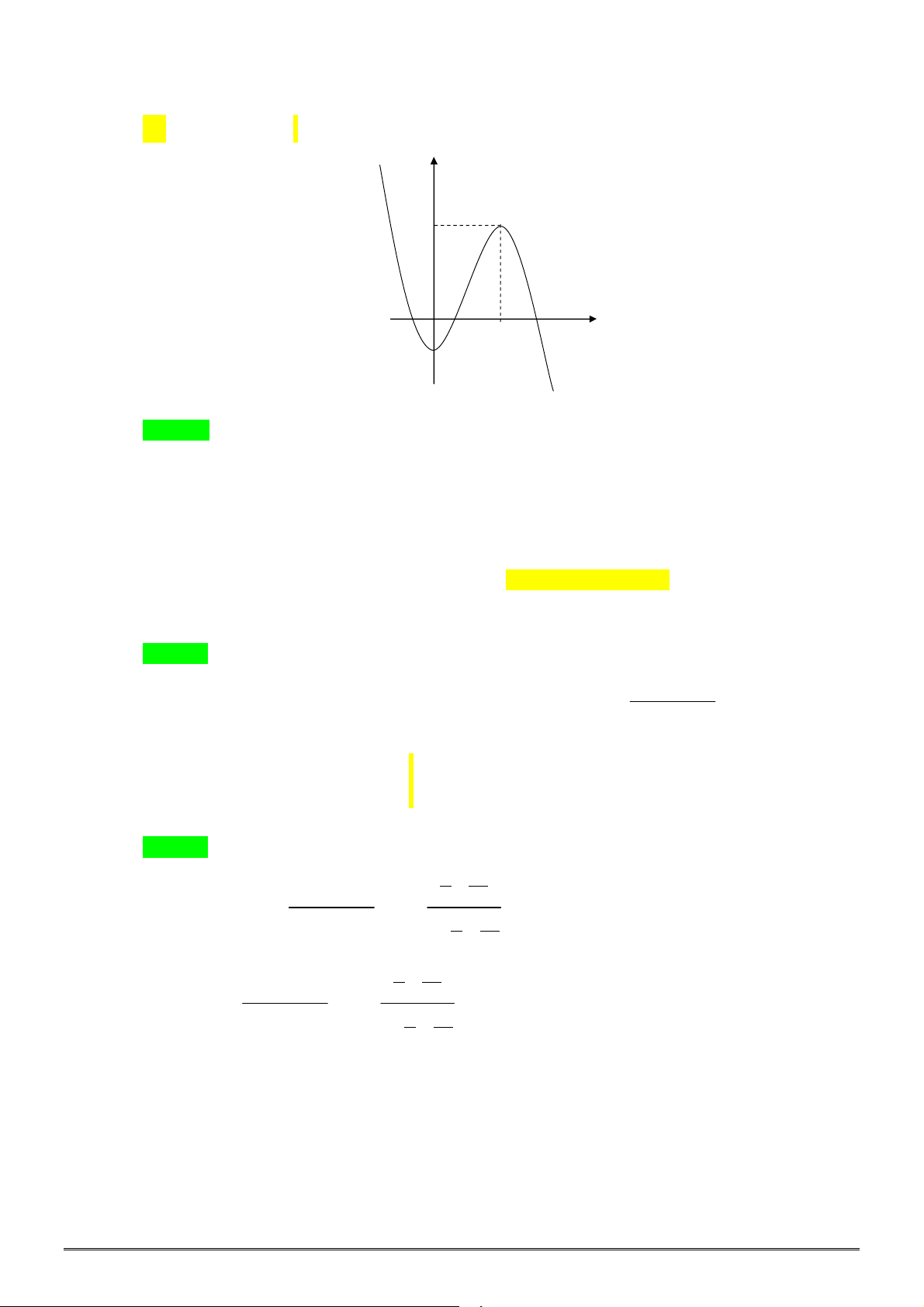
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/26 - Mã đề thi 357
Câu 26. [2D1-2] Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hãy tìm hàm số
đó.
A.
3 2
3 1
y x x
. B.
3 2
3 1
y x x
. C.
3 2
3 1
y x x
. D.
3 2
2 1
y x x
.
x
y
O
3
2
-1
Lời giải
Chọn A.
Dựa vào đồ thị ta có
0
a
, và đồ thị giao với trục
Oy
phía dưới trục hoành nên loại đáp án B
và C.
Dựa vào đồ thị, ta thấy khi
2
x
thì
3
y
nên loại đáp án D.
Câu 27. [2H1-1] Khối nào trong các khối sau là khối đa diện đều loại
3;4
?
A. Khối tứ diện đều. B. Khối bát diện đều .
C. Khối nhị thập diện đều . D. Khối lập phương .
Lời giải
Chọn B.
Câu 28. [2D1-3] Tìm tất cả giá trị của tham số
m
để đồ thị hàm số
2
3
4
x
y
x x m
có ba đường tiệm
cận .
A.
4
m
. B.
4
3
m
m
. C.
4
m
. D.
4
3
m
m
.
Lời giải
Chọn B.
Ta có
2
2
2
1 3
3
lim lim lim 0
4
4
1
x x x
x
x x
y
m
x x m
x x
2
2
2
1 3
3
lim lim lim 0
4
4
1
x x x
x
x x
y
m
x x m
x x
nên đồ thị hàm số có tiệm cận ngang là đường
thẳng
0
y
.
Để đồ thị hàm số có ba đường tiệm cận thì đồ thị hàm số có hai đường tiệm cận đứng . Do đó
phương trình
2
4 0
x x m
phải có hai nghiệm phân biệt khác 3. Điều này xảy ra khi
4 0 4
9 12 0 3
m m
m m
.
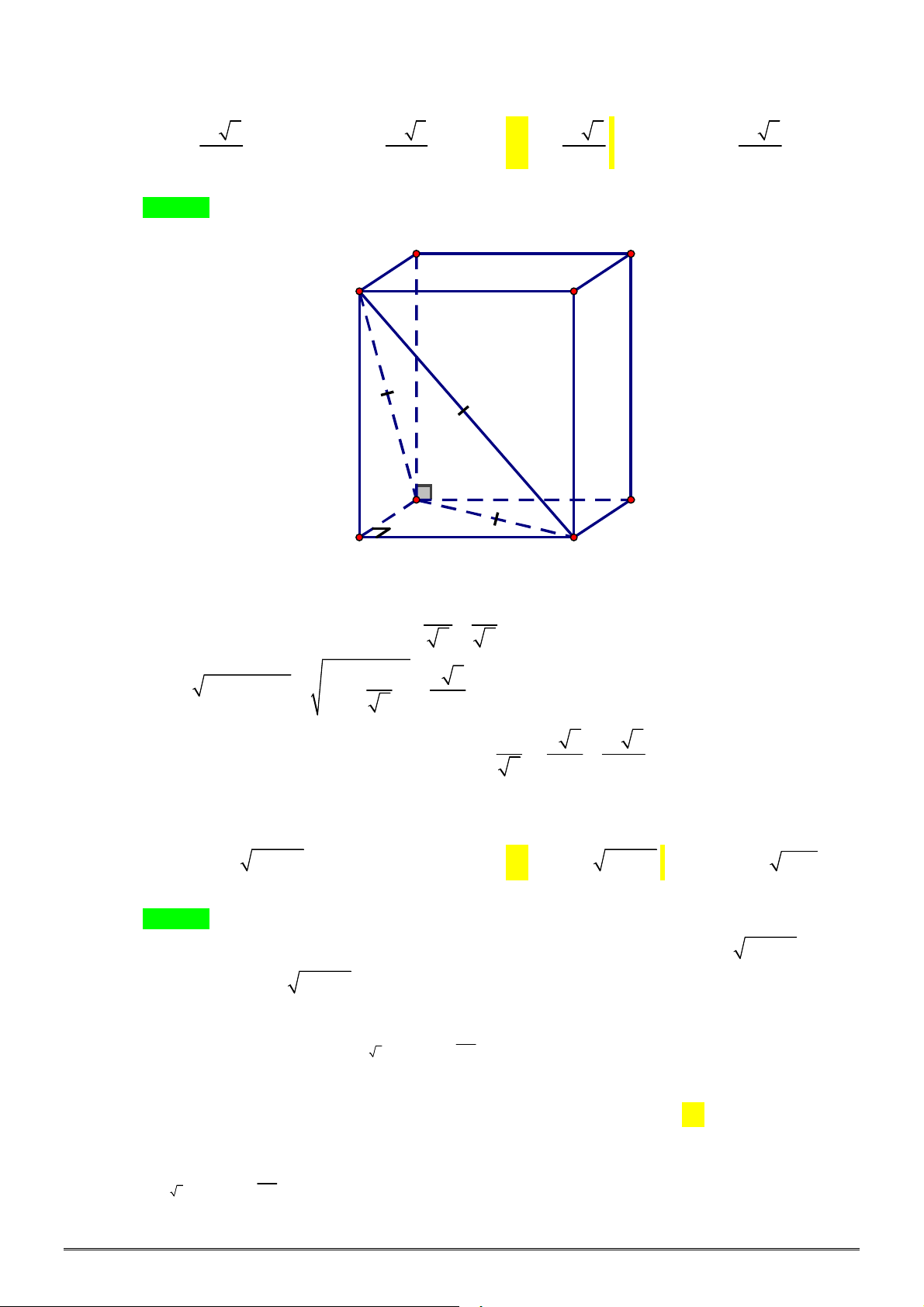
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/26 - Mã đề thi 357
Câu 29. [2H1-2] Cho hình hộp đứng
.
ABCD A B C D
có đáy là hình vuông, tam giác
B AC
đều có
cạnh bằng
a
. Tính thể tích
V
của khối hộp đã cho.
A.
3
2
8
a
V . B.
3
3
9
a
V . C.
3
2
4
a
V . D.
3
2
12
a
V .
Lời giải
Chọn C.
C'
B'
D'
C
A
D
B
A'
.
ABCD A B C D
là hình hộp đứng nên các cạnh bên vuông góc với đáy
ABCD
.
Đáy
ABCD
là hình vuông nên
2 2
AC a
AB
.
2
2 2 2
2
2
2
a a
BB AB AB a
.
Thể tích khối hộp
2
3
2
2 2
. . .
2 4
2
ABCD
a a a
V S BB AB BB
.
Câu 30. [2H2-1] Viết công thức tính diện tích xung quanh của hình nón có bán kính đáy là
r
và chiều
cao
h
.
A.
2 2
2
xq
S r r h
. B.
xq
S rh
. C.
2 2
xq
S r r h
. D.
xq
S r r h
.
Lời giải
Chọn C.
Hình nón có bán kính đáy là
r
và chiều cao
h
nên có độ dài đường sinh là
2 2
l r h
.
Vậy
2 2
xq
S rl r r h
.
Câu 31. [2D2-2] Cho phương trình
2
2
2
2
log log 6 0
8
x
x
với điều kiện
0
x
, nếu đặt
2
log
t x
ta
được phương trình nào sau đây?
A.
2
4 2 9 0
t t
. B.
2
2 2 3 0
t t
. C.
2
3 3 0
t
. D.
2
4 2 3 0
t t
.
Lời giải
2
2
2
2
log log 6 0
8
x
x
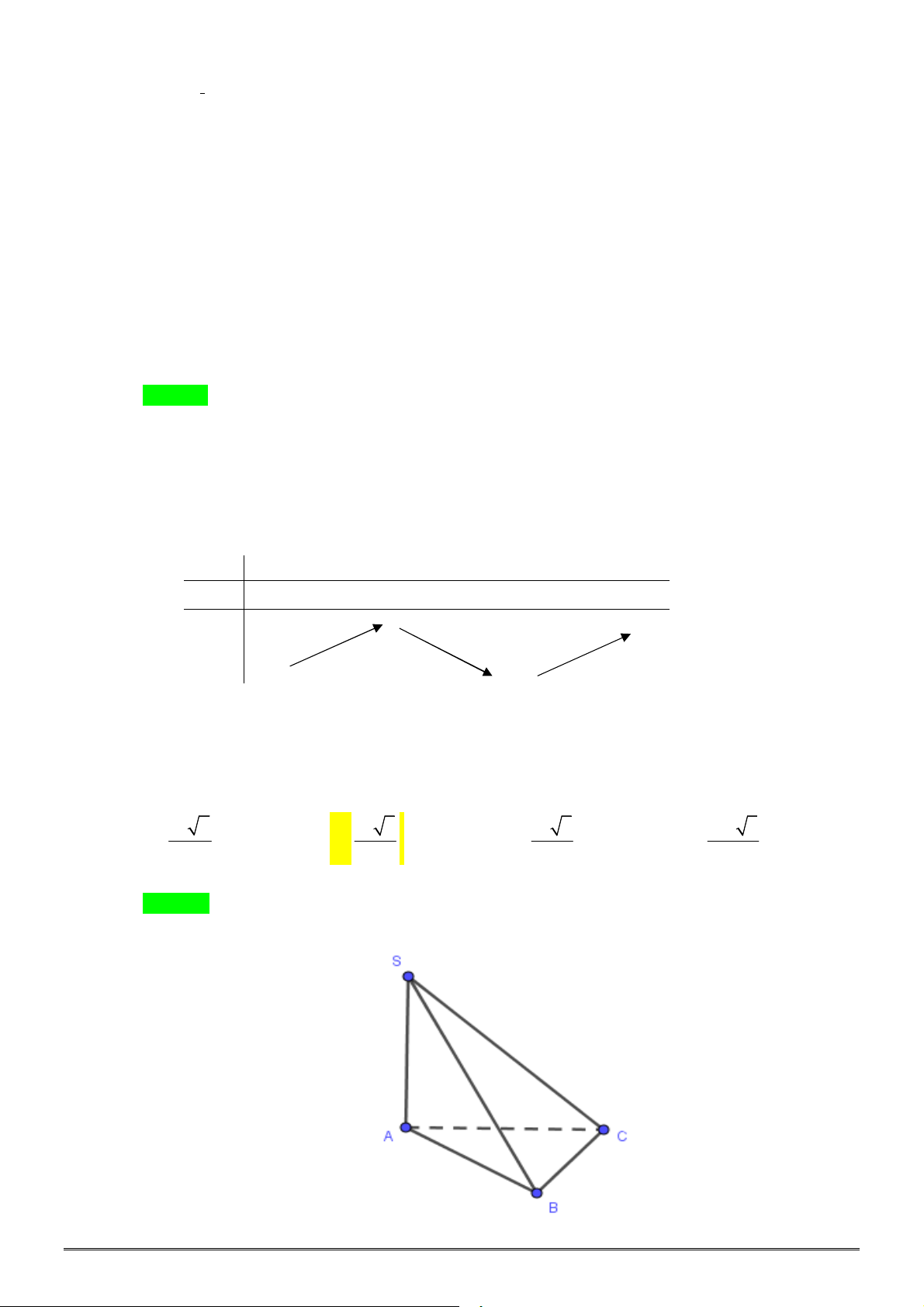
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/26 - Mã đề thi 357
1
2
2 2
2 2
2
log log log 8 6 0
x x
2
2 2
4log 2log 3 0 1
x x
Đặt
2
log
t x
thì phương trình
1
trở thành
2
4 2 3 0
t t
Câu 32. [2D1-2] Cho hàm số
3 2
3 1 1
y x x . Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số
1
đồng biến trên các khoảng
;0 , 2;
và nghịch biến trên khoảng
0;2
.
B. Hàm số
1
đồng biến trên các khoảng
; 2 , 0;
và nghịch biến trên khoảng
2;0
.
C. Hàm số
1
nghịch biến trên các khoảng
;0 , 2;
và đồng biến trên khoảng
0;2
.
D. Hàm số
1
nghịch biến trên các khoảng
; 2 , 0;
và đồng biến trên khoảng
2;0
.
Lời giải
Chọn B.
3 2
3 1
y x x
2
3 6
y x x
2
0 3 6 0
y x x
0
2
x
x
Bảng biến thiên:
x
2
0
y
+
0
-
0
+
y
3
1
Dựa vào bảng biến thiên ta có: hàm số
1
đồng biến trên các khoảng
; 2 , 0;
và
nghịch biến trên khoảng
2;0
.
Câu 33. [2H1-2] Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh
a
và cạnh bên
SA
vuông góc với
đáy,
2
SA a
. Tính thể tích
V
của khối chóp
.
S ABC
?
A.
3
2
6
a
. B.
3
3
6
a
. C.
3
3
12
a
. D.
3
2 3
9
a
.
Lời giải
Chọn C.
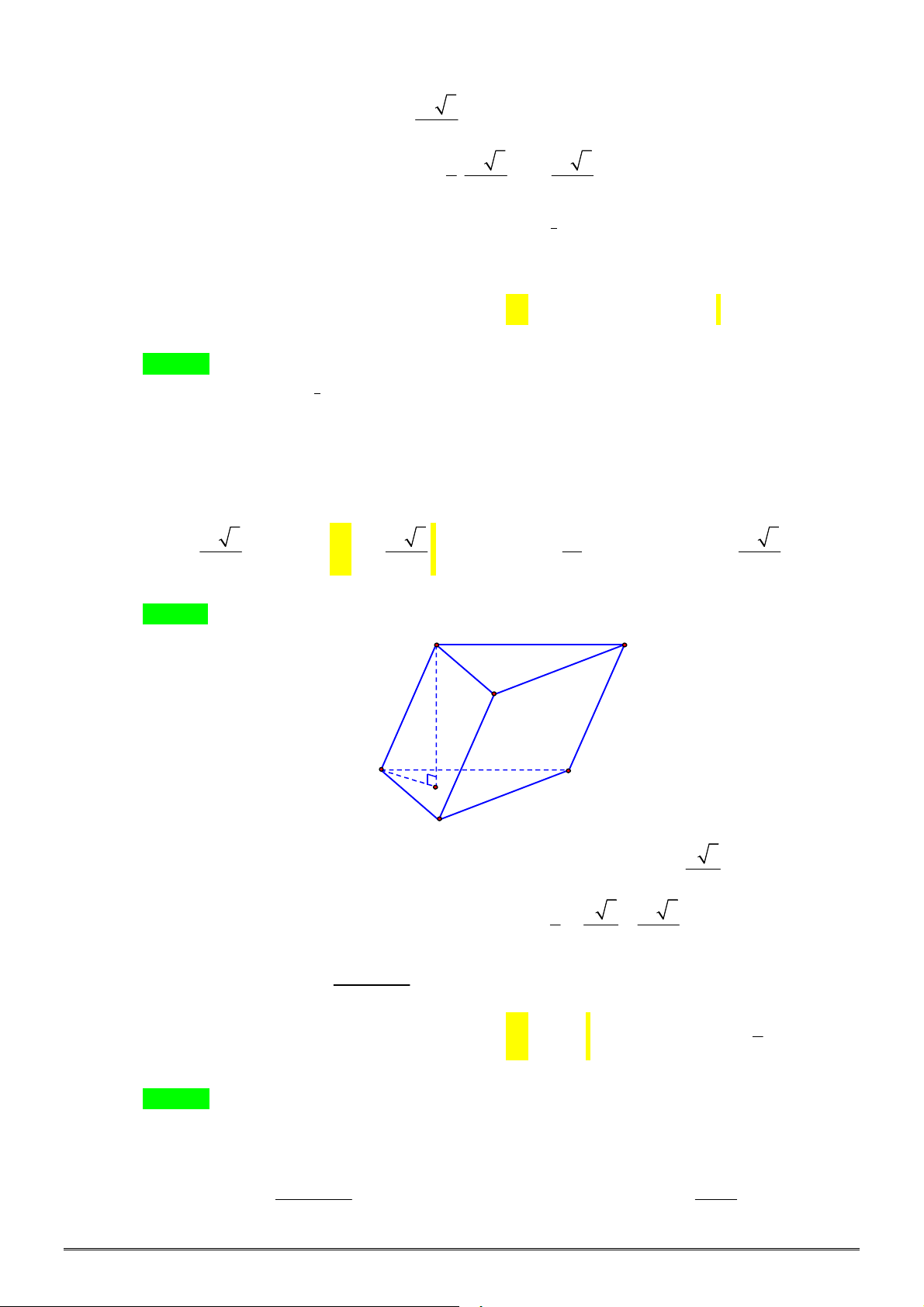
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/26 - Mã đề thi 357
Diện tích tam giác đều
ABC
là
2
3
4
a
S .
Do đó thể tích khối chóp
.
S ABC
là
2 3
1 3 3
. .2 .
3 4 6
a a
V a
Câu 34. [2D2-2] Tìm tập xác định
D
của hàm số
3
2
4
4
y x
.
A.
\ 2; 2
D
. B.
D
.
C.
; 2 2;D
. D.
; 2 2;D
.
Lời giải
Chọn D.
Hàm số
3
2
4
4
y x
là hàm số lũy thừa với số mũ không nguyên nên xác định khi
2
4 0 ; 2 2;x x
. Vậy tập xác định
; 2 2;D
.
Câu 35. [2H1-2] Cho hình lăng trụ
.
ABC A B C
có diện tích đáy bằng
2
a
, cạnh bên
AA a
và hợp với
đáy
ABC
một góc
60
. Tính thể tích
V
của khối lăng trụ
.
ABC A B C
.
A.
3
3
2
a
V . B.
3
3
6
a
V . C.
3
2
a
V . D.
3
3
3
a
V .
Lời giải
Chọn B.
Gọi
H
là hình chiếu của
A
trên đáy
A B C
ta có
3
sin60
2
a
AH AA
.
Vậy thể tích
V
của khối lăng trụ
.
ABC A B C
là:
3
2
1 3 3
3 2 6
a a
V a .
Câu 36. [2D1-2] Cho hàm số
1
mx m
y
x m
, (
m
là tham số). Tìm giá trị của
m
để
0;2
max 2
y
.
A.
1
m
. B.
3
m
. C.
5
m
. D.
1
3
m
.
Lời giải
Chọn C.
Để có GTLN trên đoạn
0;2
cần điều kiện
0
2
m
m
.
Khi đó ta có
2
2
1
0
m m
y
x m
,
0;2
x . Do đó
0;2
1
max 2 2 2 5
2
m
y y m
m
.
A
A
B
C
C
B
H

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/26 - Mã đề thi 357
Câu 37. [2D1-3] Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ bên. Khẳng định nào sau đây
đúng ?
A.
0, 0, 0, 0.
a b c d
B.
0, 0, 0, 0.
a b c d
C.
0, 0, 0, 0.
a b c d
D.
0, 0, 0, 0.
a b c d
Lời giải
Chọn B .
Ta có
3
3 2
y ax bx c
Từ đồ thị của hàm số đã cho, ta có:
+ lim
x
y
0
a
;
+Tung độ giao điểm của đồ thị với trục tung là số âm, hay
0
d
;
+Hàm số có điểm cực trị
1 2 1 2
,
x x x x
và
1 2 1 2
0, 0
x x x x
. Do
1 2
,
x x
là các nghiệm của
phương trình
0
y
nên
1 2 1 2
0, 0
b c
x x x x
a a
0
b
,
0
c
(do
0
a
)
Câu 38. [2D1-3] Gọi
S
là tập hợp các giá trị nguyên của
m
trên đoạn
10;10
để hàm số
3 2
1
2 1 2 2
3
y x m x m x
có cực đại và cực tiểu. Tìm số phần tử của
S
.
A.
20
. B.
19
. C.
18
. D.
21
.
Lời giải
Chọn B .
TXĐ:
.
2
2 2 1 2
y x m x m
.
2
2
2 1 2 4 3 1
m m m m
.
Hàm số có cực đại và cực tiểu
2
1
0 4 3 1 0
4
1
m
m m
m
.
Vì
10; 9;...,9,10
m nên
10; 9;...; 1;2;3;...;10
S
( ) 19
n S
.
Câu 39. [2D2-2] Tìm tất cả các giá trị của tham số
m
để phương trình
9 2 1 3 2 1 0
x x
m m
có
hai nghiệm thực phân biệt.
A.
0
m
. B.
1
0
m
m
. C.
1
2
0
m
m
. D.
0
m
.
Lời giải
Chọn C.
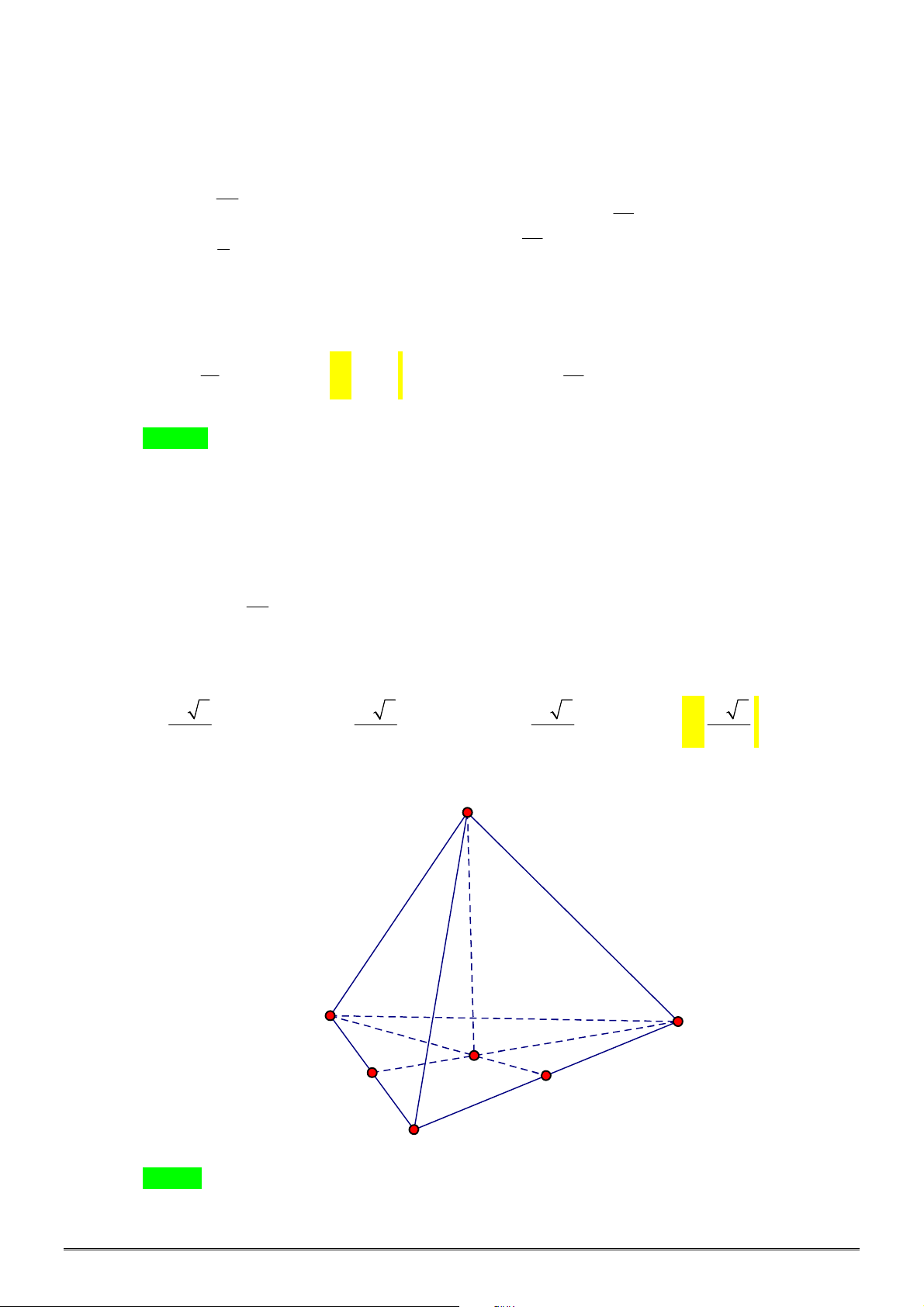
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/26 - Mã đề thi 357
Đặt
3 0
x
t
. Ta có
2
2 1 2 1 0
t m t m
. Theo yêu cầu của đề bài phương trình này
phải có 2 nghiệm dương phân biệt
2
2
0
1 2 1 0
0
0
0 2 1 0 1
1
1
2
2 1 0
0
2
m m
m
m
b
S m m
a
m
m
c
m
P
a
.
Câu 40. [2D2-2] Tìm giá trị của tham số
m
để phương trình
2 2
3 3
log 2 log 1 4 0
x m x m
có hai
nghiệm thực phân biệt
1 2
;
x x
thỏa điều kiện
1 2
9
x x
.
A.
13
2
m
. B.
3
m
. C.
1
4
m
. D.
2
m
.
Lời giải
Chọn B.
Điều kiện
0
x
. Do
1 2
9
x x
nên
3 1 2 3 3 1 3 2
log log 9 log log 2
x x x x
Đặt
3
log
t x
, ta có
2
2 2 1 4 0
t m t m
. Theo yêu cầu của đề bài phương trình này phải
có 2 nghiệm
1 2
;
t t
thỏa
1 2
2
t t
.
Khi đó:
2
2
0
2 4 1 0
0
3
2
3
2 2 2
m m
m
m
b
S
m
m
a
.
Câu 41. [2H1-2]Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy là
a
và tất cả các mặt bên của hình
chóp là các tam giác vuông cân. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
2
8
a
. B.
3
6
18
a
. C.
3
2
12
a
. D.
3
2
24
a
.
Lời giải
G
A
B
C
S
Chọn D
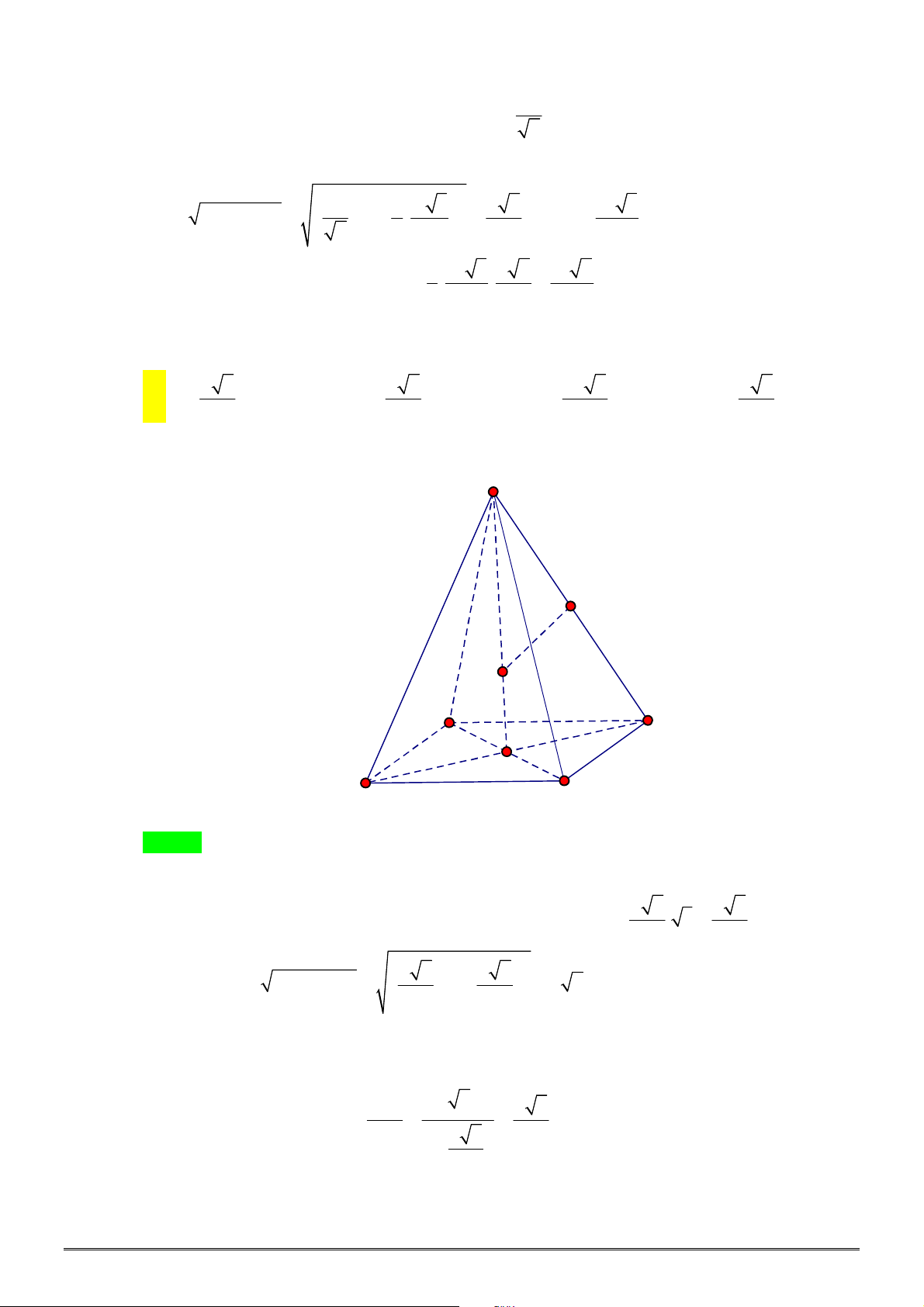
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/26 - Mã đề thi 357
Hình chóp tam giác đều
.
S ABC
có cạnh đáy là
a
và tất cả các mặt bên của hình chóp là các tam
giác vuông cân nên cạnh bên của hình chóp bằng
2
a
.
Gọi
G
là trọng tâm tam giác
ABC
, khi đó
SG ABC
và
2
2
2 2
2 . 3 6
.
3 2 6
2
a a a
SG SA AG
;
2
3
4
ABC
a
S
.
Thể tích khối chóp
.
S ABC
là
2 3
.
1 3 6 2
. .
3 4 6 24
S ABC
a a a
V .
Câu 42. [2H2-2]Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy là
a
và cạnh bên hợp với đáy góc
60
. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp.
A.
6
3
a
R . B.
6
2
a
R . C.
2 6
3
a
R . D.
6
6
a
R .
Lời giải
M
O
C
B
A
D
S
I
Chọn A
Gọi
O AC BD
. Hình chóp
.
S ABCD
đều nên
SO ABCD
.
Góc giữa cạnh bên và mặt đáy bằng
60
nên
2 6
.tan60 . 3
2 2
a a
SO AO .
Cạnh bên
2 2
2 2
6 2
2
2 2
a a
SA SO AO a
Trong mặt phẳng
SAO
, kẻ đường trung trực
Mx
của cạnh
SA
. Khi đó
Mx SO I
là tâm
mặt cầu ngoại tiếp hình chóp.
Bán kính mặt cầu là
2
2
2
6
2 3
6
2.
2
a
SA a
R SI
SO
a
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/26 - Mã đề thi 357
Câu 43. [2D2-2] Cho biết
log 2
a
b
và
log 3
b
c
,
0 1,0 1, 0
a b c
. Tính giá trị của biểu thức
2
log
ab
P b c
.
A.
10
3
P
. B.
7
4
P
. C.
7
3
P
. D.
16
3
P
.
Lời giải
Chọn C .
2 2
1
log log log 2log log
2
ab ab ab ab ab
P b c b c b c
2log log
2.2 3 7
1
log log 2 log log 1 2 3
2 1
2
a b
a a b b
b c
P
a b a b
.
Câu 44. [2D1-3] Cho hàm số
y f x
liên tục trên
và hàm số
y f x
có đồ thị như hình vẽ.
x
y
1
1
2
O
Đặt
2
g x f x x
. Khẳng định nào dưới đây đúng?
A. Hàm số
g x
có một điểm cực đại và một điểm cực tiểu.
B. Hàm số
g x
chỉ có một điểm cực đại.
C. Hàm số
g x
có một điểm cực đại và hai điểm cực tiểu.
D. Hàm số
g x
chỉ có một điểm cực tiểu.
Lời giải
Chọn A.
2
g x f x
;
0 2 0 2
g x f x f x
(*)
Nghiệm của (*) chính là hoành độ giao điểm của đồ thị
y f x
với đường thẳng
2
y
Dựa vào đồ thị
f x
, ta thấy phương trình (*) có hai nghiệm phân biệt
1 2
0, 0
x x
Bảng biến thiên của hàm số
y g x
:
x
y
x
2
1
2
O
y f x
2
y
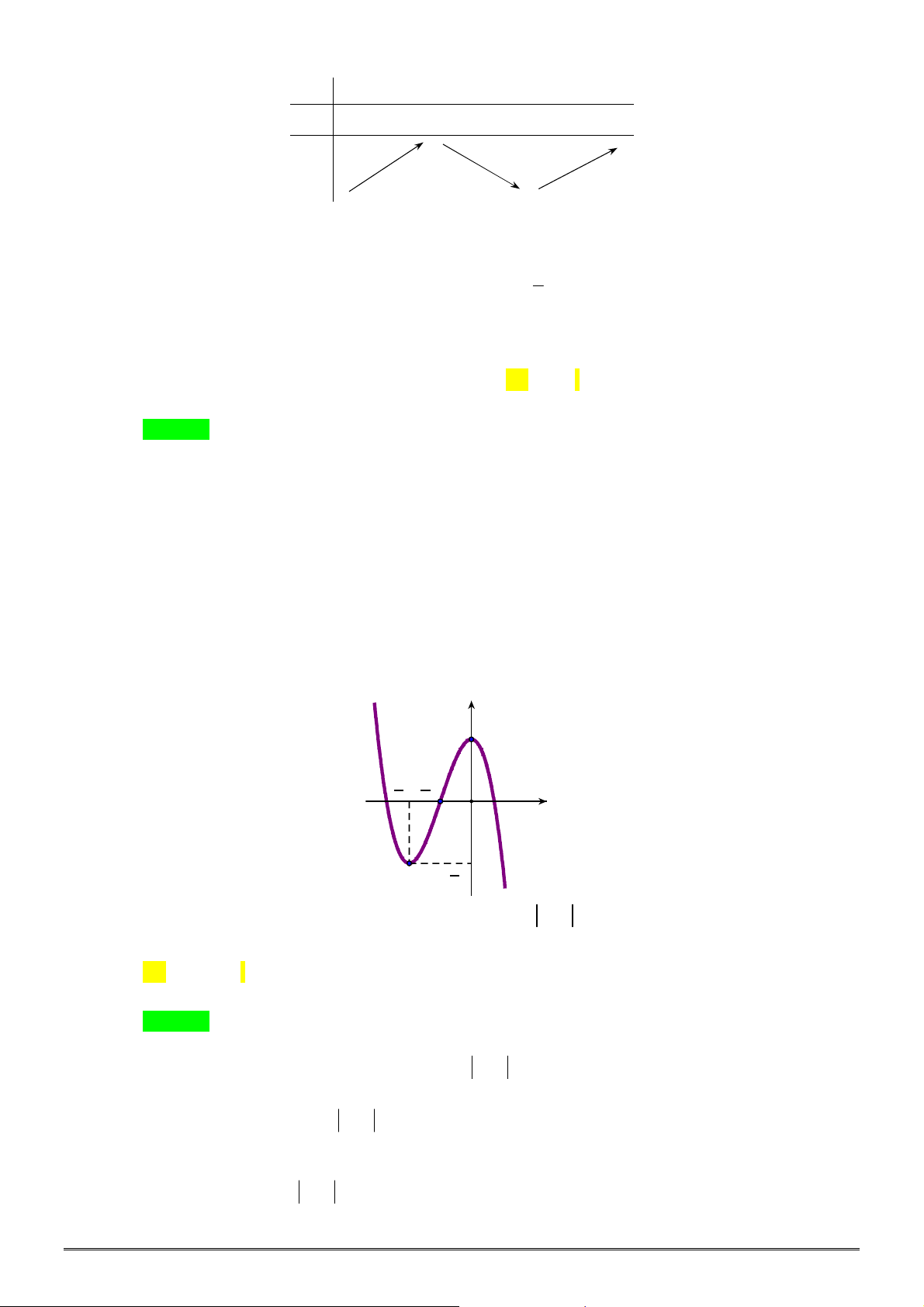
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 23/26 - Mã đề thi 357
Suy ra, hàm số
y g x
có đúng 1 cực đại và 1 cực tiểu.
Câu 45. [2D1-2] Tìm giá trị của tham số m để hàm số
3 2 2
1
1 2 1
3
y x mx m x m
đạt cực tiểu
tại điểm
0
2
x
.
A.
3
m
hoặc
1
m
. B.
3
m
hoặc
1
m
.
C.
1
m
D.
3
m
.
Lời giải
Chọn D.
Tập xác định
D
;
2 2
2 1
y x mx m
;
2 2
y x m
.
Hàm số đạt cực tiểu tại
2
x
thì
2
1
2 0 4 3 0
3
m
y m m
m
Với
1
m
:
2 2. 2 2 2 0
y
nên hàm số đạt cực đại tại
2
x
(không thỏa).
Với
3
m
:
2 2. 2 6 2 0
y
nên hàm số đạt cực tiểu tại
2
x
(thỏa).
Vậy
3.
m
Câu 46. [2D1-3] Cho hàm số
2
1 2 2
y x x x
có đồ thị như hình vẽ bên
x
y
2
2
12
O
Tìm tất cả giá trị của tham số m để phương trình
2
1 2 2
x x x m
có 4 nghiệm thực
phân biệt.
A.
0 2
m
. B. Không tồn tại m. C.
2
m
. D.
0 2
m
.
Lời giải
Chọn A.
Đặt
2
1 2 2
f x x x x
. Khi đó
2
khi 1
1 2 2
khi 1
f x x
x x x
f x x
Suy ra đồ thị hàm số
2
1 2 2
y x x x
trùng với đồ thị hàm số
y f x
khi
x
và
đối xứng với đồ thị hàm số
y f x
qua trục hoành khi
1
x
.
Đồ thị hàm số
2
1 2 2
y x x x
x
g x
g x
0
2
x
0
0
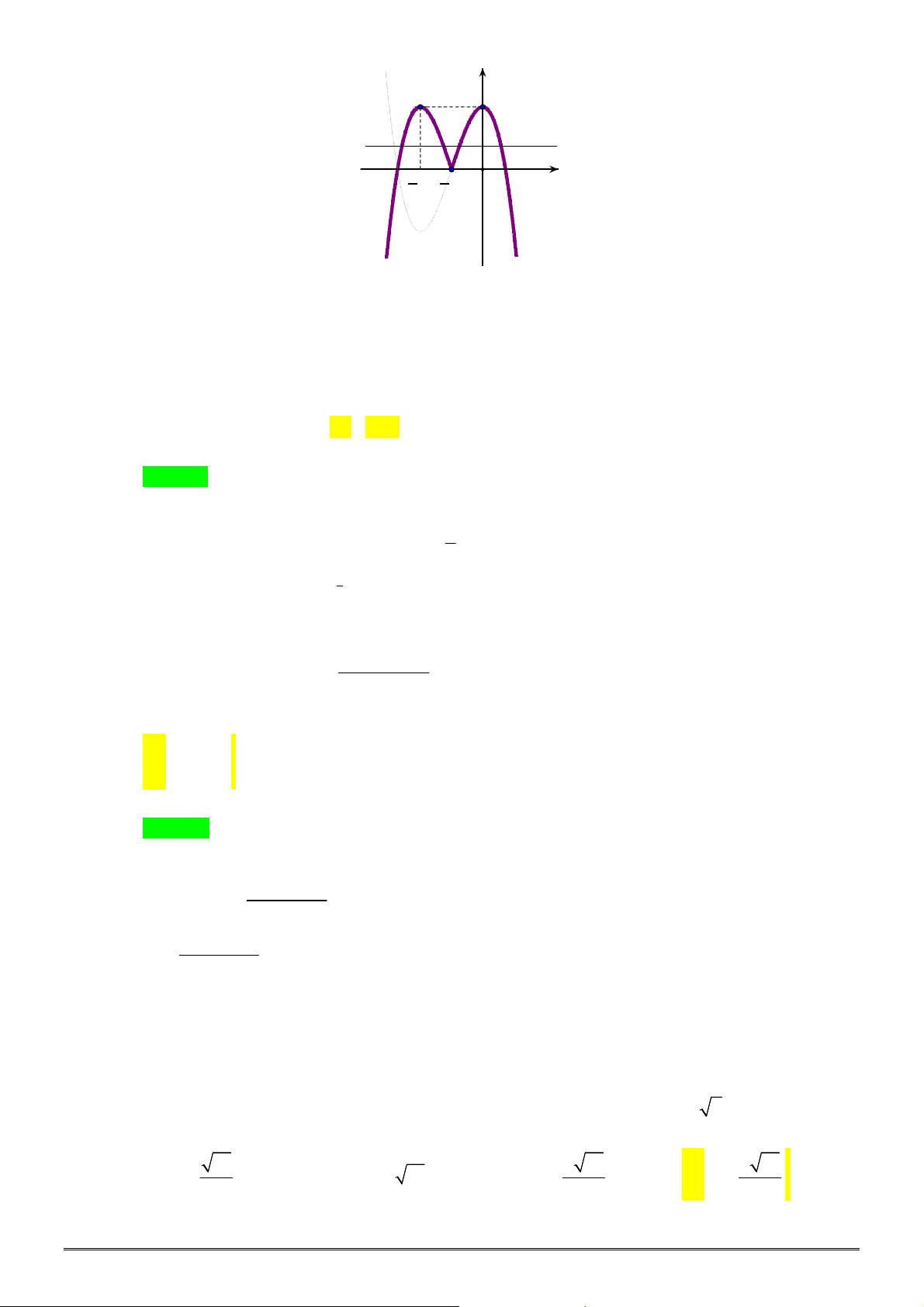
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 24/26 - Mã đề thi 357
x
y
y
= m
2
12 O
Dựa vào đồ thị, suy ra phương trình đã cho có 4 nghiệm khi
0 2
m
.
Câu 47. [2D2-3] Sự tăng trưởng của một loài vi khuẩn trong phòng thí nghiệm được tính theo công thức
.3
rt
f t F
trong đó
F
là lượng vi khuẩn ban đầu,
r
là tỉ lệ tăng trưởng
0
r
và
t
là thời
gian(đơn vị: giờ). Biết rằng số lượng vi khuẩn ban đầu là
6
10
con và sau
3
giờ là
6
5.10
con.
Hỏi sau thời gian mấy giờ, số lượng vi khuẩn là
125
triệu con?
A.
75
giờ. B.
9
giờ. C.
6
giờ. D.
60
giờ.
Lời giải
Chọn B.
Số lượng vi khuẩn ban đầu là
6
10
con và sau
3
giờ là
6
5.10
con
nên:
6 6 3
3 3
1
5.10 10 .3 3 log 5 log 5
3
r
r r .
Mặt khác:
3
1
log 5.
6 6
3
125.10 10 .3 9
t
t
.
Vậy, sau
9
giờ thì số vi khuẩn là
125
triệu con.
Câu 48. [2D2-3] Cho hàm số
3 2
3
x
x
m m
y
m
, (
m
tham số). Tìm tất cả các giá trị của tham số
m
để
hàm số đồng biến trên
0;1
.
A.
3
2
m
m
. B.
3 1
2
m
m
. C.
1
2
m
m
. D.
3
1
m
m
.
Lời giải
Chọn A.
Đặt
3
x
t
, với
0;1 1;3
x t .
Ta được:
2mt m
y g t
t m
. Tập xác định
\
D m
.
2
2
2
m m
y
t m
. Để hàm số ban đầu đồng trên
0;1
thì
g t
đồng biến trên
1;3
2
1;3
1; 3
2 0
0, 1;3
m
m m
m m
y t
3; 1 3
1; 2 2
m m m
m m m
.
Câu 49- 50
Câu 49. [2H1-3] Cho tứ diện
ABCD
có
2
AB
, tất cả các cạnh còn lại bằng
2 2
. Thể tích
V
của
khối tứ diện
ABCD
A.
10
3
V . B.
2 10
V . C.
4 10
3
V . D.
2 10
3
V .
Lời giải
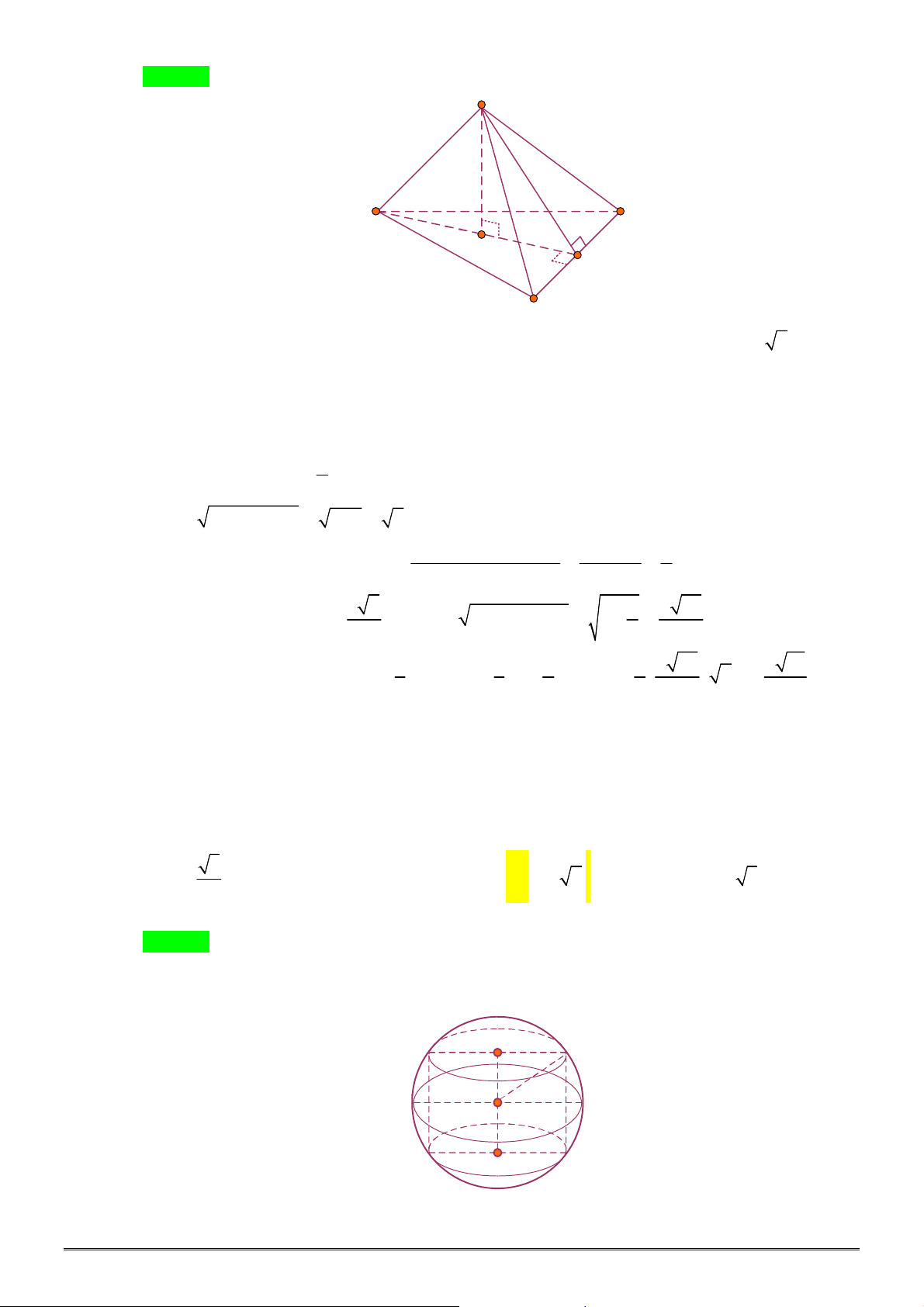
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 25/26 - Mã đề thi 357
Chọn D.
A
B
C
D
H
M
Gọi
M
là trung điểm của
AB
. Do giả thiết ta có
2 2
DA DB BC AC DC
nên tam
giác
DAB
cân tại
D
, ta giác
ABC
cân tại
C
và
ADB ACB
. Khi đó
DM AB
và
CM AB
nên
AB DCM
. Trong mặt phẳng
DCM
kẻ
DH CM
suy ra
DH AB
và
DH ABC
hay
DH
là chiều cao của tứ diện
ABCD
.
Ta có
1
1
2
BM AB
nên trong tam giác vuông
DMB
:
2 2
8 1 7
DM DB BM CM
.
Trong tam giác
DMC
:
2 2 2
7 7 8 3
cos
2 . 2.7 7
DM CM DC
DMC
DM CM
3 7
.cos
7
HM DM DMC
2 2
9 2 70
7
7 7
DH DM HM .
Vậy thể tích tứ diện
ABCD
:
1 1 1 1 2 70 2 10
. . . 7.2
3 3 2 6 7 3
ABC
V DH S DH CM AB .
Câu 50. [2H2-4] Cho mặt cầu
S
có tâm
O
, bán kính bằng
2
. Hai mặt phẳng
P
và
Q
song song
với nhau và cách đều tâm
O
một khoảng cách là
x
0 2
x
lần lượt cắt mặt cầu
S
theo
giao tuyến là hai đường tròn
C
và
C
. Xác định
x
để hình trụ có hai đường tròn đáy là
C
và
C
có diện tích xung quanh lớn nhất.
A.
3
2
x . B.
1
x
. C.
2
x
. D.
3
x .
Lời giải
Chọn C.
Giải sử hình cầu
S
tâm
O
có bán kính
2
R
, hai đáy hình trụ có bán kính
r
như hình vẽ
sau:
M
I
I
O
r
R
x
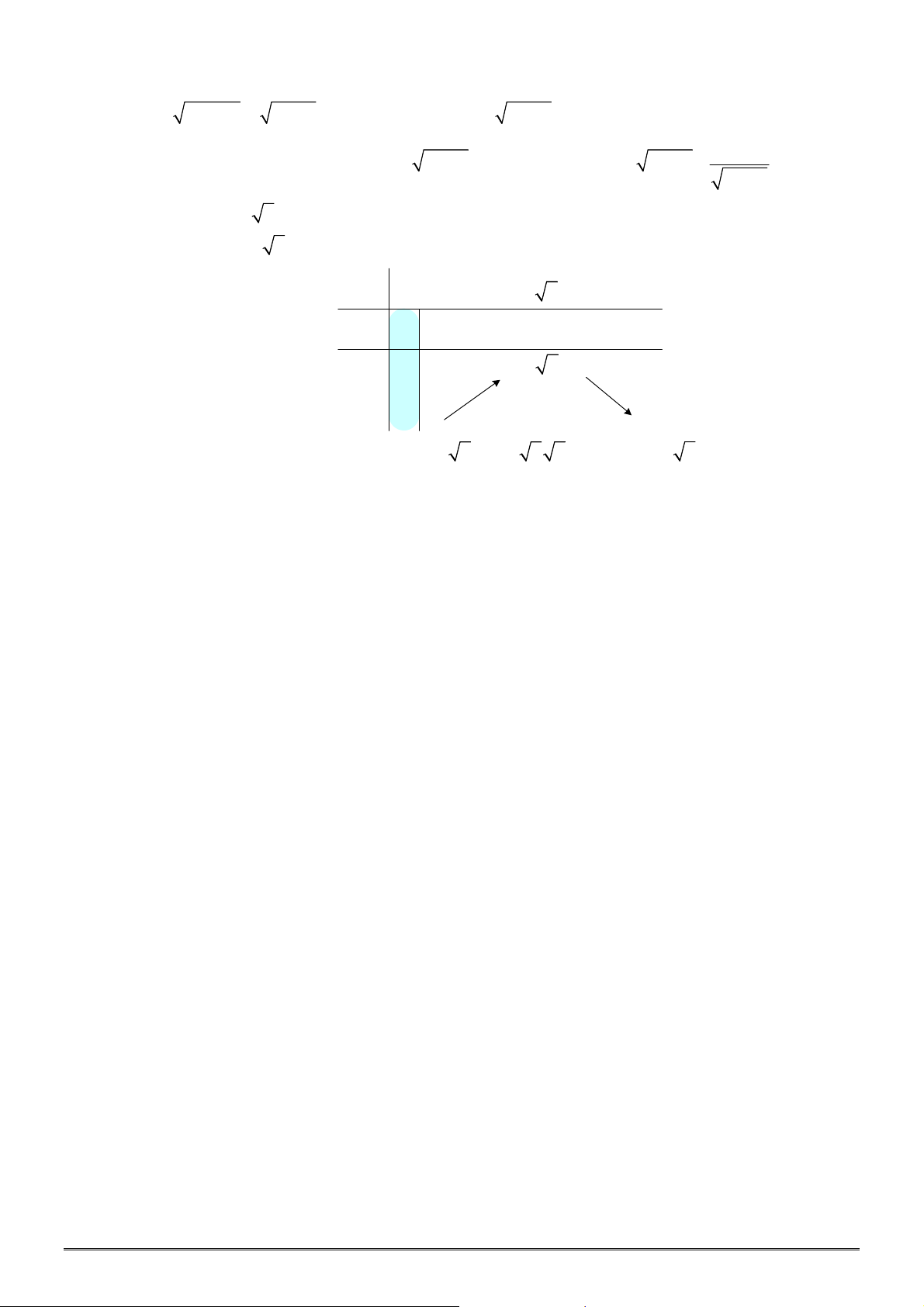
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 26/26 - Mã đề thi 357
Áp dụng công thức tính diện tích xung quanh hình trụ ta có 2
tru
S S rh
với
2
h x
,
2 2 2
4
r R x x
suy ra
2
2 4 4
S rh x x
0 2
x
.
Ta khảo sát hàm số
2
2 4 4
S rh x x
trên
0;2
:
2
2
2
4 4
4
x
S x
x
2
0
2
x
S
x
. Ta có bảng biến thiên sau
x
S
S
0
2
2
0
2
S
0
0
Vậy diện tích hình trụ lớn nhất là
2 4 2 2 8
S S
khi
2
x
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/25 - Mã đề thi 753
ĐẠI HỌC QUỐC GIA HÀ NỘI
TRƯỜNG ĐẠI HỌC NGOẠI NGỮ
TRƯỜNG THPT CHUYÊN NGOẠI NGỮ
ĐỀ KIỂM TRA HỌC KỲ 1 – LỚP 12
Năm học 2017 - 2018
Môn: Toán – Thời gian làm bài 90 phút
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 753
Câu 1. [2D2-2] Đặt
2
log 3
a
,
3
log 5
b
. Biểu diễn
15
log 18
theo
a
,
b
là:
A.
2 1
1
b
a b
. B.
2 1
1
b
b a
. C.
2 1
1
a
b a
. D.
2 1
1
a
a b
.
Câu 2. [2H1-2] Cho hình chóp
.
S ABCD
có
SA
vuông góc với
ABCD
và đáy
ABCD
là hình thoi.
Biết
3
SA a
và
SC
tạo với
ABCD
góc
60
. Tính độ dài
BD
biết thể tích của khối chóp
.
S ABCD
bằng
3
3
a
.
A.
2
BD a
. B.
3
BD a
. C.
2 2
BD a
. D.
2 3
BD a
.
Câu 3. [2D1-1] Hàm số nào trong số bốn hàm số sau đồng biến trên khoảng
0:
?
A.
ln
y x x
. B.
x
y
. C.
1
x
y e
x
. D.
2
1
y x
.
Câu 4. [2H1-2] Cho hình lập phương có diện tích toàn phần bằng
24
2
cm
. Khi đó thể tích của khối lập
phương là?
A.
12
3
cm
. B.
27
3
cm
. C.
8
3
cm
. D.
24
3
cm
.
Câu 5. [2D1-3] Tiếp tuyến với đồ thị hàm số
2 1
1
x
y
x
tại điểm
M
có
0
M
x
cắt hai trục tọa độ lần
lượt tại
A
và
B
. Tính diện tích
S
của tam giác
OAB
.
A.
1
2
. B.
2
. C.
3
. D.
1
4
V
.
Câu 6. [2H2-3] Cho hình chóp
.
S ABC
có
SA
,
SB
,
SC
đôi một vuông góc và
2
SA SB a
,
SC a
.
Tính thể tích
V
của khối cầu ngoại tiếp hình chóp
.
S ABC
.
A.
3
9
2
a
V
. B.
3
36
V a
. C.
3
27
V a
. D.
3
27
2
a
V
.
Câu 7. [1H3-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
,
B
và
SA
vuông
góc với
ABCD
. Biết
2
SA AD a
,
AB BC a
. Tính khoảng cách
h
từ
C
đến
SBD
.
A.
6
6
a
h . B.
3
3
a
h . C.
6
2
a
h . D.
2
2
a
h .
Câu 8. [2D1-2] Hàm số
3
3
1
y x
x
đạt giá trị nhỏ nhất trên
0;
tại
0
x
. Khẳng định nào
ĐÚNG?
A.
0
1
;1
2
x
. B.
0
1
0;
2
x
. C.
0
3
1;
2
x
. D.
0
3
;2
2
x
.
Câu 9. [2D2-3] Tìm giá trị của tham số
m
để phương trình
2
2 2
log log 2 6 0
x m x m
có hai
nghiệm
1
x
,
2
x
thỏa mãn
1 2
16
x x
.
A.
4
m
. B.
11
m
. C.
4
m
. D.
5
m
.
19

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/25 - Mã đề thi 753
Câu 10. [1D5-2] Có bao nhiêu tiếp tuyến của đồ thị hàm số
4 2
2 1
y x x
song song với trục hoành?
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 11. [2H2-2] Khẳng định nào dưới đây là SAI?
A. Hình chóp đều bất kì luôn nội tiếp trong một hình cầu.
B. Hình chóp tam giác bất kì luôn nội tiếp trong một hình nón.
C. Hình lăng trụ tam giác bất kì luôn nội tiếp trong một hình trụ.
D. Hình lăng trụ đều bất kì luôn nội tiếp trong một hình trụ.
Câu 12. [2H2-2] Một hình trụ có thiết diện qua trục là hình vuông chu vi
16cm
. Tính thể tích
V
khối
trụ đã cho.
A.
3
8 cm
V
. B.
3
16
cm
3
V
. C.
3
16 cm
V
. D.
3
32 cm
V
.
Câu 13. [2D2-2] Phương trình
3 3
log 2 1 log 1 0
x x
có bao nhiêu nghiệm?
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 14. [2D2-1] Cho hàm số
log
y x
. Khẳng định nào sau đây khẳng định SAI?
A. Hàm số có tập giá trị là
0;
. B. Hàm số đồng biến trên khoảng
0;
.
C. Hàm số có tập xác định là
0;
. D. Hàm số có tập giá trị là
;
.
Câu 15. [2D2-2] Hàm số
3
ln 1
1
y x
x
đồng biến trên khoảng nào?
A.
1;2
. B.
1
;1
2
. C.
1
;
2
. D.
2;
.
Câu 16. [2D1-3] Tìm tập hợp tất cả các giá trị của tham số
m
để hàm số
3 2
1 1
y x m x mx
đồng biến trên khoảng
0;1
.
A.
;0
. B.
0;
. C.
;0
. D.
0;
.
Câu 17. [2H2-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật và
SA
vuông góc với mặt
đáy. Biết
2
SA a
,
4
BD a
. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp
.
S ABCD
.
A.
5
R a
. B.
2 5
R a
. C.
2 3
R a
. D.
3
R a
.
Câu 18. [2D1-2] Cho hàm số
f x
có tính chất:
0
f x
0; 3
x và
0
f x
1; 2
x .
Khẳng định nào dưới đây là SAI?
A. Hàm số
f x
là hàm hằng trên khoảng
1; 2
.
B. Hàm số
f x
đồng biến trên khoảng
0; 1
.
C. Hàm số
f x
đồng biến trên khoảng
0; 3
.
D. Hàm số
f x
đồng biến trên khoảng
2; 3
.
Câu 19. [2H1-2] Hình lăng trụ có đáy là thập giác lồi có bao nhiêu cạnh?
A.
20
. B.
12
. C.
30
. D.
22
.
Câu 20. [2D1-2] Cho hàm số
y f x
xác định trên
\ 0
, liên tục trên mỗi khoảng xác định và có
bảng biến thiên như hình bên.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/25 - Mã đề thi 753
Tìm tập hợp tất cả các giá trị của tham số thực
m
sao cho phương trình
2 0
m f x
có ba
nghiệm thực phân biệt.
A.
4;2
. B.
; 4
. C.
4;2
. D.
4;2
.
Câu 21. [2D2-1] Cho
a
là số thực dương tùy ý. Mệnh đề nào dưới đây SAI?
A.
3
3
4
2
2 2 2
5
log log
18
a a a
. B.
2
1
log
log 2
a
a .
C.
2
2 2
log 2log
a a
. D.
2 3 2
log log .log 3
a a .
Câu 22. [2D2-2] Tập xác định của hàm số
ln log
y x
là
A.
0;1
. B.
1;
. C.
0;
. D.
0;
.
Câu 23. [2D1-2] Cho hàm số
f x
có đạo hàm liên tục trên
;
a b
và đồ thị hàm số
y f x
được
cho như hình bên. Gọi
n
là số điểm cực trị của hàm số
y f x
trên khoảng
;
a b
thì
n
bằng bao nhiêu?
x
y
21 b
a
O
A.
0.
n
B.
1.
n
C.
3
n
D.
2.
n
Câu 24. [2D1-2] Đồ thị hàm số
3 2
2 3 1
y x x x
và đường thẳng
2
y x
cắt nhau tại điểm
; .
A A
A x y
Tìm
.
A
y
A.
0.
A
y
B.
3.
A
y
C.
2.
A
y
D.
1.
A
y
Câu 25. [2D2-2] Phương trình
1
5 5. 0,2 26
x
x
có hai nghiệm
1
x
,
2
x
. Tính tổng
1 2
S x x
.
A.
13
. B.
26
. C.
1
. D.
0
.
Câu 26. [2D1-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
O
là giao điểm của
AC
và
BD
. Gọi
M
,
N
lần lượt là trung điểm của
SB
,
SC
. Tính tỉ số
.
OBCNM
S ABCD
V
k
V
.
A.
3
16
k . B.
1
8
k
. C.
3
8
k
. D.
1
16
k .
Câu 27. [2D1-2] Cho hàm số
y f x
có
lim 1
x
f x
và
lim 1
x
f x
. Tìm phương trình đường
tiệm cận ngang của đồ thị hàm số
1 2018.
y f x
.
A.
1
y
. B.
2019
y
. C.
1
y
. D.
2017
y
.
x
0
1
y
0
y
1
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/25 - Mã đề thi 753
Câu 28. [2D1-2] Đồ thị hình bên là đồ thị của hàm số nào?
A.
3 2
3 3 1
y x x x
. B.
3
1
3 1
3
y x x
.
C.
3 2
3 3 1
y x x x
. D.
3
3 1
y x x
.
Câu 29. [2D1-1] Cho hàm số
y f x
xác định, liên tục trên
và có bảng biến thiên như hình dưới
đây. Khẳng định nào sau đây là sai:
A. Hàm số có ba điểm cực trị.
B.
0
1
x
được gọi là điểm cực tiểu của hàm số.
C.
0
1
y
được gọi là giá trị cực tiểu của hàm số.
D.
0;2
M được gọi là điểm cực đại của hàm số.
Câu 30. [2D2-1] Tính đạo hàm của hàm số
2
log 5 1
y x
.
A.
5
5 1 ln2
y
x
. B.
1
5 1
y
x
. C.
5
5 1
y
x
. D.
1
5 1 ln2
y
x
.
Câu 31. [2D1-3] Tìm các giá trị của
m
để đồ thị hàm số
3 2 2
1
1 2 1 3
3
y x m x m x
có hai
điểm cực trị cách đều trục tung.
A.
1
m
. B.
1
m
. C.
2
m
. D.
1
m
.
Câu 32. [2D2-2] Cho
3
log 2
a
và
2
1
log
2
b
. Tính
2
3 3 1
4
2log log 3 log
I a b
.
A.
4
I
. B.
5
4
I
. C.
3
2
I
. D.
0
I
.
Câu 33. [2H1-1] Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
,
AC a
và
5
BC a
. Biết góc giữa
AB C
và
ABC
bằng
45
, tính thể tích
V
của khối lăng trụ
đã cho.
A.
3
6
V a
. B.
3
2
V a
. C.
3
5
V a
. D.
3
4
V a
.
Câu 34. [2D2-2] Đặt
3
5
0
1
lim
1
x
x
x
e
a
e
. Tính giá trị của
5 4
P a
.
A.
4
P
. B.
1
P
. C.
3
P
. D.
7
P
.
x
1
0
1
y
0
0
0
y
1
2
1
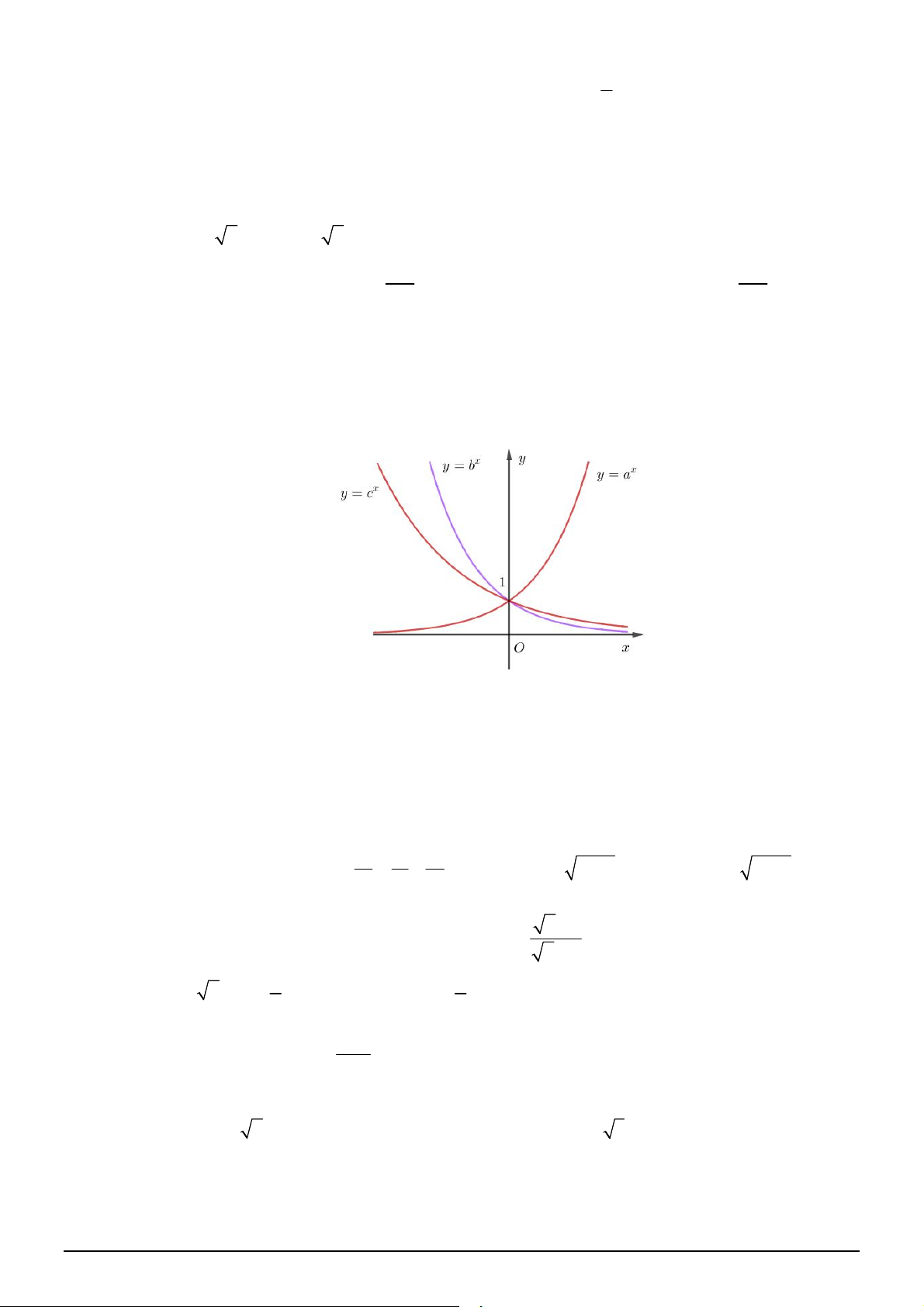
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/25 - Mã đề thi 753
Câu 35. [2D1-2] Cho chuyển thẳng xác định bởi phương trình
4 2
1
3
2
S t t
, trong đó
t
tính bằng
giây
s
,
S
được tính bằng mét
m
. Tính vận tốc của chuyển động tại thời điểm
4
t s
.
A.
232 m/s
v
. B.
140 m/s
v
. C.
116 m/s
v
. D.
280 m/s
v
.
Câu 36. [2H1-2] Cho hình chóp
.
S ABC
có
SA
,
SB
,
SC
đôi một vuông góc. Biết
2
SAB
S a
,
2
2
SBC
S a ,
2
2
SCA
S a . Tính thể tích
V
của khối chóp
.
S ABC
theo
a
?
A.
3
2
V a
. B.
3
4
3
a
V . C.
3
4
V a
. D.
3
2
3
a
V .
Câu 37. [2D2-3] Huyện
A
có
300
nghìn người. Với mức tăng dân số bình quân
1,2%
/năm thì sau
n
năm dân số sẽ vượt lên
330
nghìn người. Hỏi
n
nhỏ nhất bằng bao nhiêu?
A.
9
năm. B.
7
năm. C.
10
năm. D.
8
năm.
Câu 38. [2D2-3] Cho đồ thị các hàm số , ,
x x x
y a y b y c
có hình vẽ bên. Tìm khẳng định ĐÚNG.
A.
a c b
. B.
b c a
. C.
c b a
. D.
a b c
.
Câu 39. [2H2-2] Cho hình trụ
T
có trục
2
OO a
, bán kính đường tròn đáy bằng
a
. Gọi
S
là mặt
cầu tiếp xúc với hai mặt đáy của hình trụ và tiếp xúc với các đường sinh của hình trụ. Gọi
N
là hình nón đỉnh
O
và đáy là hình tròn
O
của hình trụ. Gọi
1
V
,
2
V
,
3
V
là thể tích của khối
trụ
T
, khối cầu
S
và khối nón
N
. Khẳng định nào ĐÚNG?
A.
1 2 3
V V V
. B.
3 1 2
1 1 1
V V V
. C.
2 3 1
.
V V V
. D.
3 1 2
.
V V V
.
Câu 40. [2D1-2] Các đường tiệm cận của đồ thị hàm số
1
2
x
y
x
là:
A.
2
x
;
1
2
y
. B.
4
x
;
1
2
y
. C.
2
x
;
1
y
. D.
4
x
;
1
y
.
Câu 41. [2D1-3] Cho hàm số
1
1
x
y
x
có đồ thị
C
và
A
là một điểm thuộc
C
. Gọi
S
là tổng các
khoảng cách từ
A
đến các đường tiệm cận của
C
. Tìm
min
S
.
A.
min 2 2
S
. B.
min 2
S
. C.
min 2 3
S . D.
min 3
S
.
Câu 42. [2D2-3] Cho phương trình
.2017 2 .2018 2 1 0
x x
x x x
. Tìm khẳng định ĐÚNG?
A. Phương trình có đúng một nghiệm nguyên. B. Phương trình không có nghiệm nguyên.
C. Phương trình có nghiệm nguyên lớn hơn
5
. D. Phương trình có nghiệm nguyên âm.
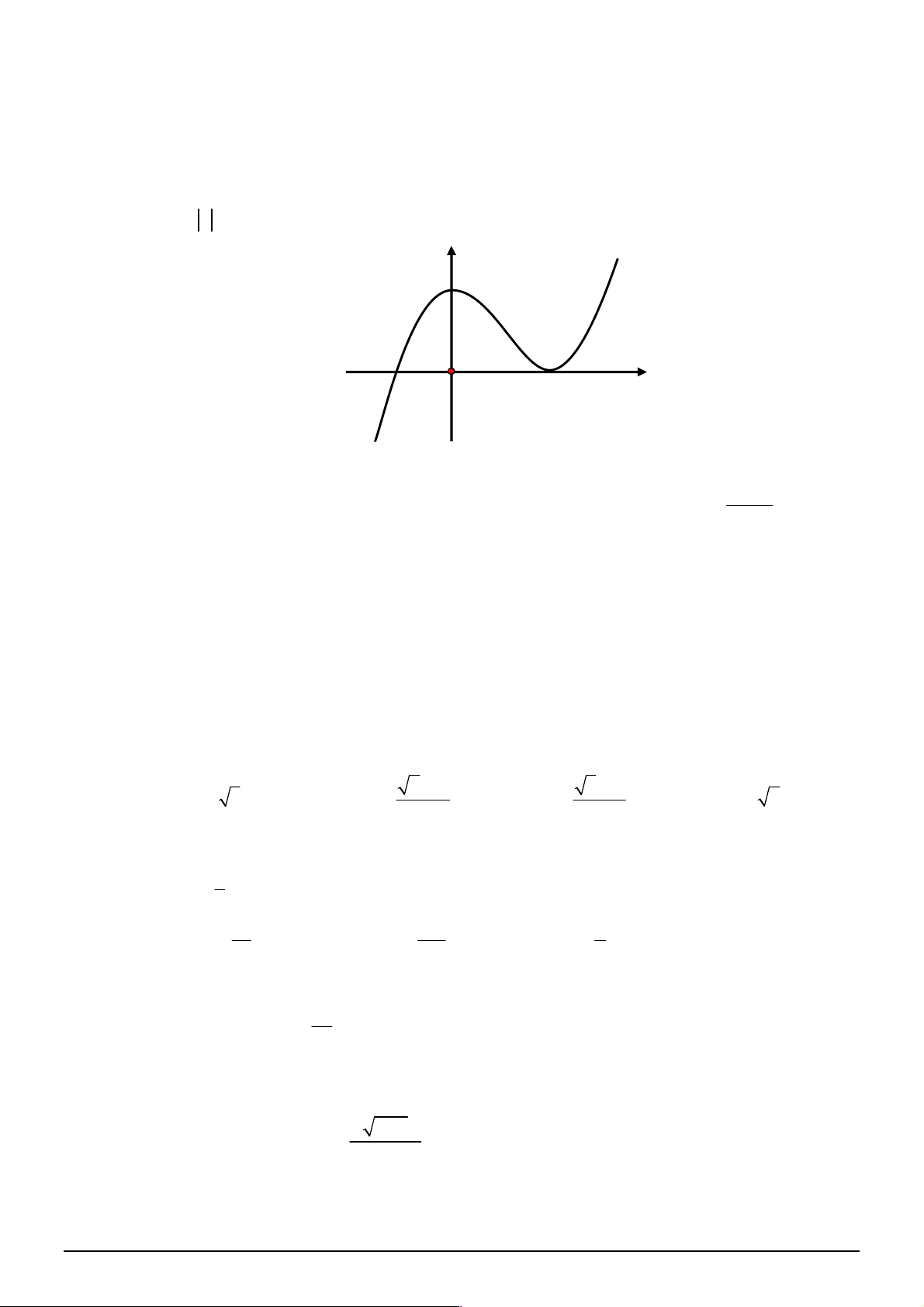
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/25 - Mã đề thi 753
Câu 43. [2H1-3] Cho hình hộp
.
ABCD A B C D
có thể tích
48
đvtt
. Tính thể tích khối tứ diện
BCD B
.
A.
12
đvtt
. B.
6
đvtt
. C.
8
đvtt
. D.
16
đvtt
.
Câu 44. [2D1-3] Cho hàm số
y f x
có đồ thị như hình bên. Trên đoạn
1;3
, đồ thị hàm số
y f x
có mấy điểm cực trị?
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 45. [2D1-2] Tìm tập hợp tất cả các giá trị của tham số
m
để đồ thị hàm sô
2 3
2
x
y
x
cắt đường
thẳng
2
y x m
tại hai điểm phân biệt.
A.
3;
. B.
;1 3;
. C.
1;3
. D.
;1
.
Câu 46. [2D2-1] Tìm tập xác định
D
của hàm số
5
2
2
y x x
.
A.
D
. B.
; 1 2;
. C.
0;D
. D.
\ 1;2
D
.
Câu 47. [2H2-2] Cho hình chóp đều
.
S ABC
cạnh đáy
3
AB a
, góc giữa cạnh bên và mặt đáy bằng
45 .
Tính diện tích xung quanh
xq
S
của hình nón đỉnh
S
và đường tròn đáy là đường tròn
ngoại tiếp tam giác
ABC
.
A.
2
3 3
xq
S a
. B.
2
2
3
xq
a
S
. C.
2
3
3
xq
a
S
. D.
2
3 2
xq
S a
.
Câu 48. [2D1-3] Cho
x
,
y
là hai số thực không âm thỏa mãn
2
x y
. Tìm giá trị nhỏ nhất của biểu
thức
3 2 2
1
1
3
P x x y x
.
A.
17
min
3
P
. B.
115
min
3
P . C.
7
min
3
P
. D.
min 5
P
.
Câu 49. [2H1-3] Cho hình lăng trụ tam giác đều
.
ABC A B C
có
2
AB a
. Biết khoảng cách từ điểm
B
đến
AB C
bằng
3
2
a
. Kí hiệu
là góc giữa hai mặt phẳng
AB C
và
ABC
. Số đo
bằng
A.
30
. B.
60
. C.
90
. D.
45
.
Câu 50. [2D1-3] Đồ thị hàm số
2
1
2
x
y
x x
có bao nhiêu đường tiệm cận?
A.
3
. B.
1
. C.
2
. D.
0
.
----------HẾT----------
O
x
y
4
2
1
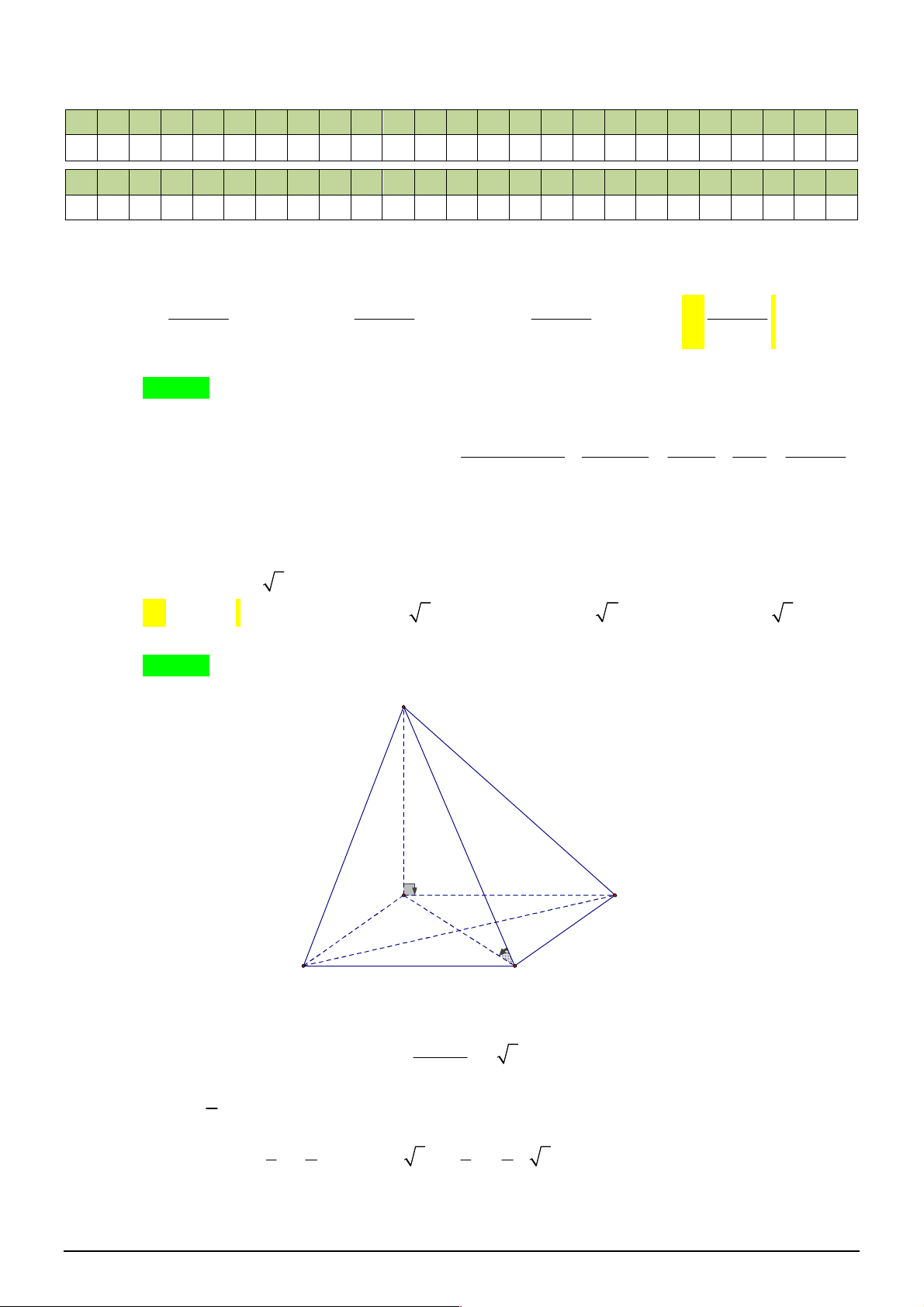
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/25 - Mã đề thi 753
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
A
C
C
A
A
A
A
C
B
B B B A
D
D
A
C
C
D
B B D
B D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
B D
D
A
B C
B B
C
D
D
A
A
D
A
B C
A
B D
D
C
B C
HƯỚNG DẪN GIẢI
Câu 1. [2D2-2] Đặt
2
log 3
a
,
3
log 5
b
. Biểu diễn
15
log 18
theo
a
,
b
là:
A.
2 1
1
b
a b
. B.
2 1
1
b
b a
. C.
2 1
1
a
b a
. D.
2 1
1
a
a b
.
Lời giải
Chọn D.
Ta có:
2 2 3
log 5 log 3.log 5
ab
.
2
15 15 15 15
2 2 3
1 2 1 2 2 1
log 18 log 2.3 log 2 2log 3
log 3 log 5 1 log 5 1 1
a
a ab b a b
.
Câu 2. [2H1-2] Cho hình chóp
.
S ABCD
có
SA
vuông góc với
ABCD
và đáy
ABCD
là hình thoi.
Biết
3
SA a
và
SC
tạo với
ABCD
góc
60
. Tính độ dài
BD
biết thể tích của khối chóp
.
S ABCD
bằng
3
3
a
.
A.
2
BD a
. B.
3
BD a
. C.
2 2
BD a
. D.
2 3
BD a
.
Lời giải
Chọn A.
60°
S
D
C
B
A
3
a
Theo giả thiết ta có:
, 60
SA ABCD SC ABCD SCA
.
Tam giác
SAC
vuông tại
C
:
3
tan60
SA
AC a
.
1
.
2
ABCD
S AC BD
.
Ta có:
3
.
1 1 1 1
. . 3 .3 . . 3. 2
3 2 3 2
S ABCD
V SA AC BD a a a BD BD a
.
Câu 3. [2D1-1] Hàm số nào trong số bốn hàm số sau đồng biến trên khoảng
0:
?
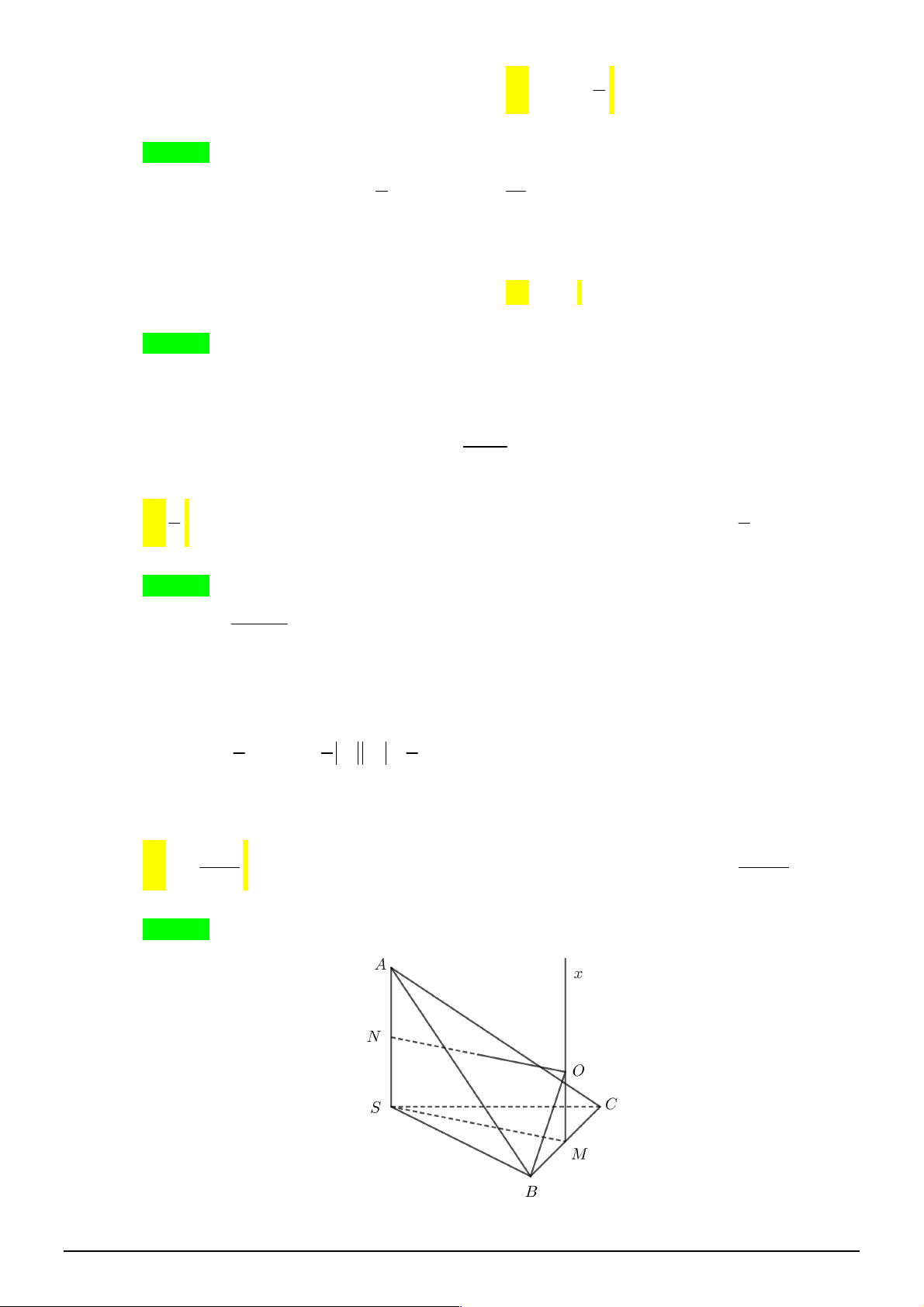
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/25 - Mã đề thi 753
A.
ln
y x x
. B.
x
y
. C.
1
x
y e
x
. D.
2
1
y x
.
Lời giải
Chọn C.
Chọn C vì với hàm số
1
x
y e
x
ta có
2
1
0
x
y e
x
,
0:x
.
Câu 4. [2H1-2] Cho hình lập phương có diện tích toàn phần bằng
24
2
cm
. Khi đó thể tích của khối lập
phương là?
A.
12
3
cm
. B.
27
3
cm
. C.
8
3
cm
. D.
24
3
cm
.
Lời giải
Chọn C.
Vì hình lập phương có sáu mặt là hình vuông nên diện tích mỗi hình vuông là
24:6 4
3
cm
.
Do đó cạnh hình vuông bằng
2
cm
. Vì thế thể tích hình lập phương bằng
2.2.2 8
3
cm
.
Câu 5. [2D1-3] Tiếp tuyến với đồ thị hàm số
2 1
1
x
y
x
tại điểm
M
có
0
M
x
cắt hai trục tọa độ lần
lượt tại
A
và
B
. Tính diện tích
S
của tam giác
OAB
.
A.
1
2
. B.
2
. C.
3
. D.
1
4
V
.
Lời giải
Chọn A.
Ta có:
2
1
0 1
1
y y
x
;
0
M
x
1
M
y
.
Phương trình tiếp tuyến
d
tại điểm
0;1
M là:
1 1 0 1
y x y x
.
Theo đề bài, ta có
A d Ox
1;0
A ;
B d Oy
0;1
B .
Vậy
1 1 1
. .
2 2 2
OAB A B
S OAOB x y
.
Câu 6. [2H2-3] Cho hình chóp
.
S ABC
có
SA
,
SB
,
SC
đôi một vuông góc và
2
SA SB a
,
SC a
.
Tính thể tích
V
của khối cầu ngoại tiếp hình chóp
.
S ABC
.
A.
3
9
2
a
V
. B.
3
36
V a
. C.
3
27
V a
. D.
3
27
2
a
V
.
Lời giải
Chọn A.
Ta có
SBC
vuông tại
S
và
SA SBC
.
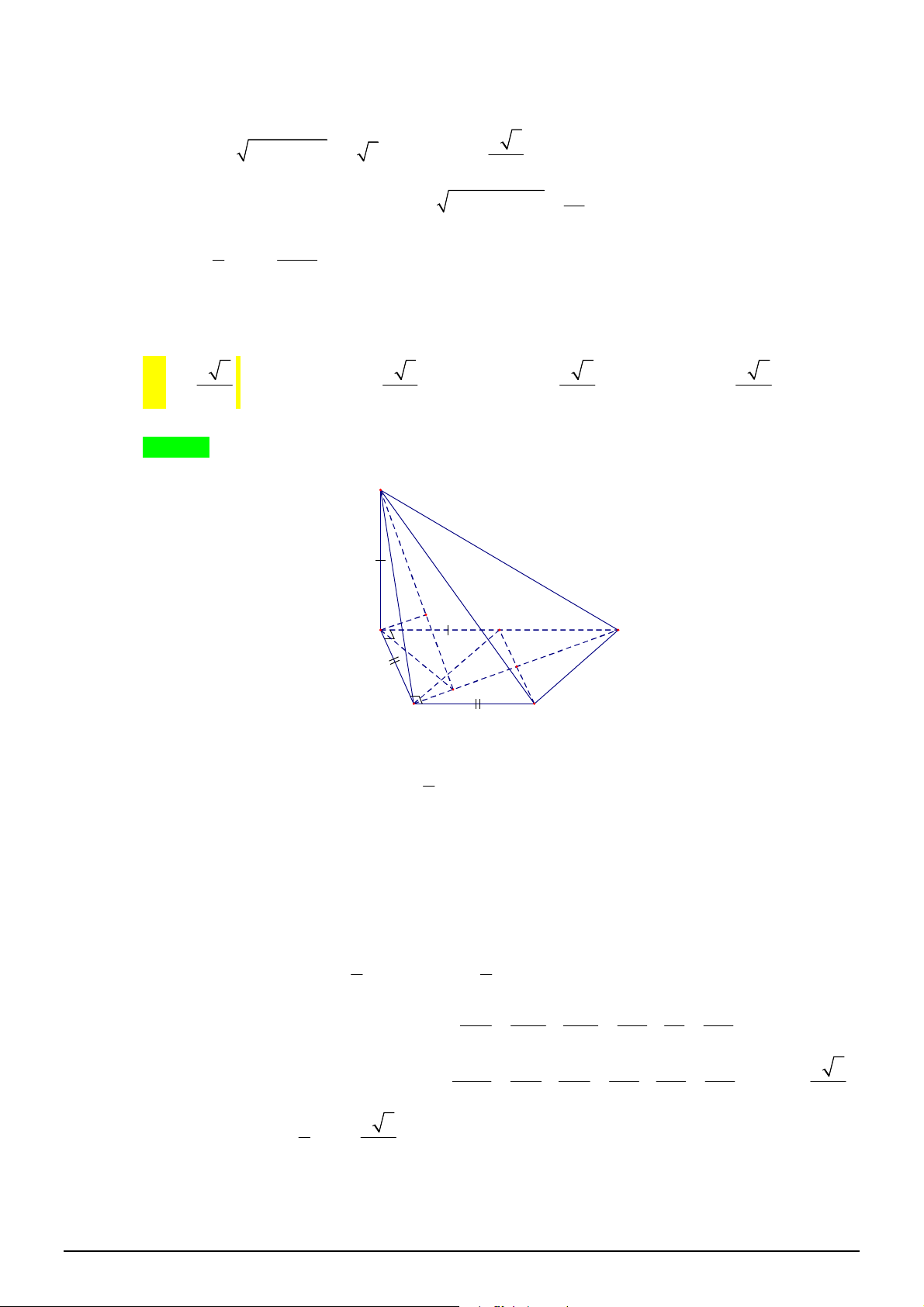
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/25 - Mã đề thi 753
Gọi
M
là trung điểm của
BC
, kẻ
Mx SBC
, kẻ
NO SA
cắt
Mx
tại điểm
O
.
Khi đó
O
là tâm mặt cầu ngoại tiếp khối chóp
.
S ABC
và bán kính
R OB
.
Ta có
2 2
5
BC SB SC a
suy ra
5
2
a
BM .
Ta có
OM SN a
. Do đó
2 2
3
2
a
R BO BM OM .
Vậy
3
3
4 9
3 2
a
V R
.
Câu 7. [1H3-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
,
B
và
SA
vuông
góc với
ABCD
. Biết
2
SA AD a
,
AB BC a
. Tính khoảng cách
h
từ
C
đến
SBD
.
A.
6
6
a
h . B.
3
3
a
h . C.
6
2
a
h . D.
2
2
a
h .
Lời giải
Chọn A.
a
2a
E
A
B
C
D
S
I
H
Gọi
E
là trung điểm
AD
.
Ta có
1
, , ,
2
d C SBD d E SBD d A SBD
.
Trong
ABCD
gọi
I
là hình chiếu vuông góc của
A
lên
BD
.
Ta có
;
BD AI BD SA BD SAI SAI SBD
1
;
SAI SBD SI
2
;
Gọi
H
là hình chiếu vuông góc của
A
lên
SI
, suy ra
AH SI
3
.
Từ
1
,
2
và
3
, suy ra
1 1
,
2 2
d A SBD AH
.
Trong tam giác
ABD
vuông tại
A
, ta có:
2 2 2 2 2 2
1 1 1 1 1 5
4 4
AI DA AB a a a
.
Trong tam giác
SAI
vuông tại
A
, ta có:
2 2 2 2 2 2
1 1 1 1 5 6
4 4 4
AH SA AI a a a
6
3
a
AH .
Vậy
,
d C SBD
1 6
2 6
a
AH .
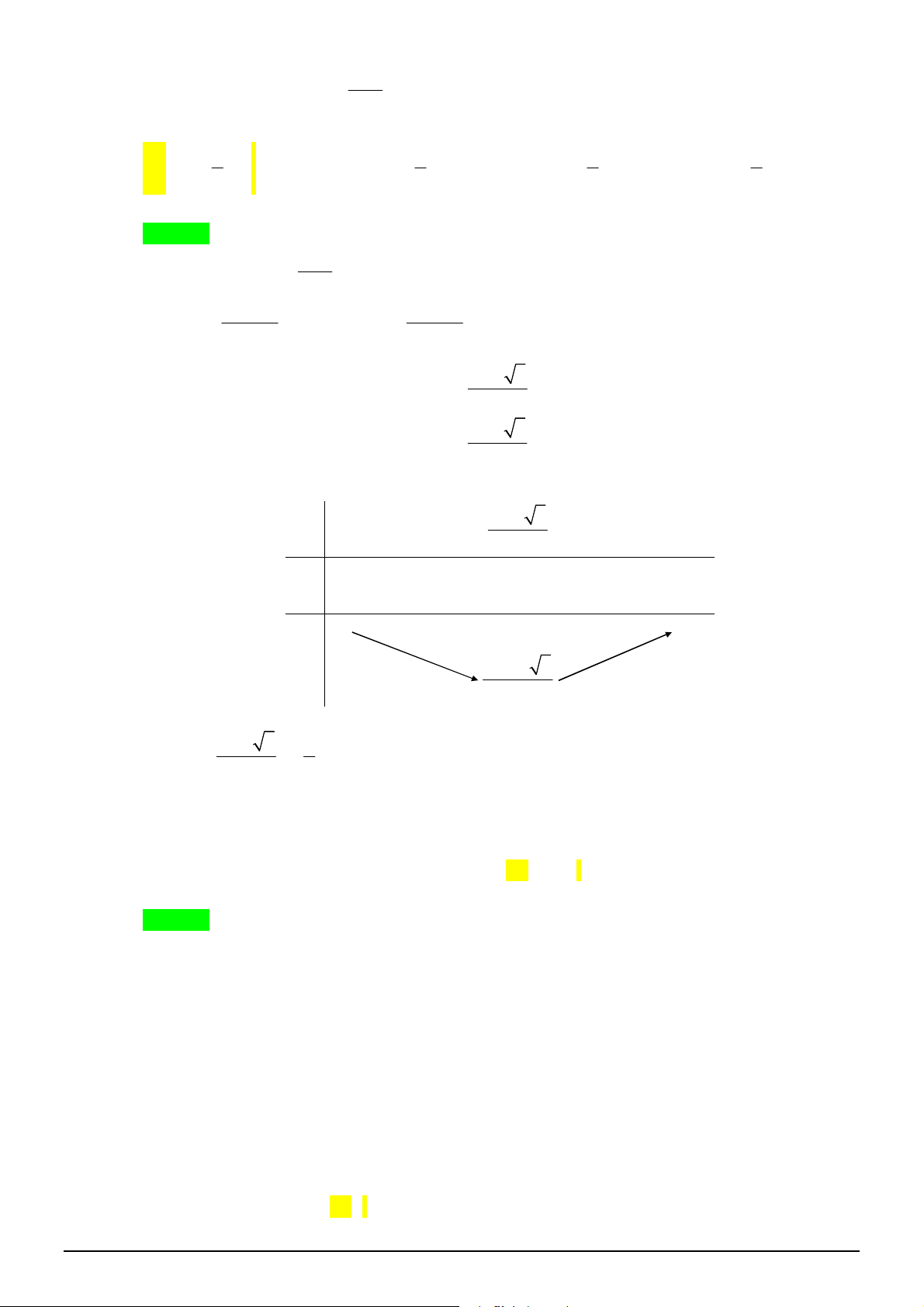
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/25 - Mã đề thi 753
Câu 8. [2D1-2] Hàm số
3
3
1
y x
x
đạt giá trị nhỏ nhất trên
0;
tại
0
x
. Khẳng định nào
ĐÚNG?
A.
0
1
;1
2
x
. B.
0
1
0;
2
x
. C.
0
3
1;
2
x
. D.
0
3
;2
2
x
.
Lời giải
Chọn A.
Xét hàm số
3
3
1
y x
x
trên
0;
, ta có:
2
2
3
3
1
y x
x
;
2
2
2
3
0 3 0 1 1
1
y x x x
x
2
2
1 5
0;
1 1
1 0
2
1 1
1 0
1 5
0;
2
x
x x
x x
x x
x x
x
.
Bảng biến thiên:
Vậy
0
1 5 1
;1
2 2
x
.
Câu 9. [2D2-3] Tìm giá trị của tham số
m
để phương trình
2
2 2
log log 2 6 0
x m x m
có hai
nghiệm
1
x
,
2
x
thỏa mãn
1 2
16
x x
.
A.
4
m
. B.
11
m
. C.
4
m
. D.
5
m
.
Lời giải
Chọn C.
Điều kiện
0
x
. Đặt
2
log
t x
. Phương trình đã cho trở thành
2
2 6 0 *
t mt m .
Chú ý rằng
1 2
16
x x
2 1 2
log 4
x x
2 1 2 2
log log 4
x x
.
Do đó phương trình đã cho có hai nghiệm
1
x
,
2
x
thỏa mãn
1 2
16
x x
khi và chỉ khi phương
trình
*
có hai nghiệm
1
t
,
2
t
thỏa mãn
1 2
4
t t
0
4
S
2
8 24 0
4
m m
m
4
m
.
Vậy
4
m
là giá trị cần tìm.
Câu 10. [1D5-2] Có bao nhiêu tiếp tuyến của đồ thị hàm số
4 2
2 1
y x x
song song với trục hoành?
A.
2
. B.
1
. C.
0
. D.
3
.
x
0
1 5
2
y
–
0
y
3
7 5 5
2
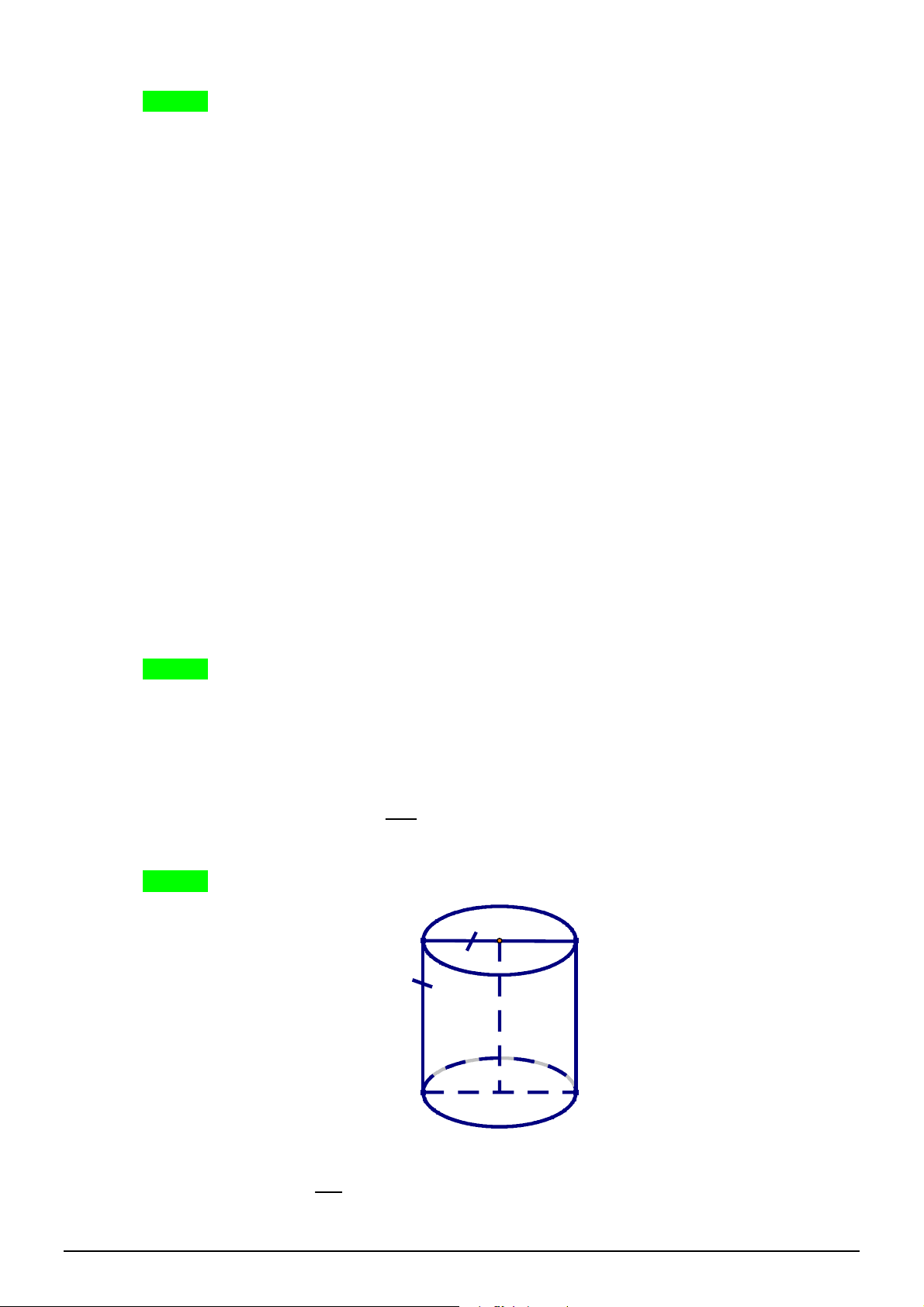
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/25 - Mã đề thi 753
Lời giải
Chọn B.
Tập xác định
D
. Đạo hàm:
3
4 4
y x x
.
Cách 1: Vì tiếp tuyến song song với trục nên tiếp tuyến có hệ số góc bằng
0
0
y
0
x
,
1
x
.
* Với
0
x
1
y
. Phương trình tiếp tuyến của đồ thị hàm số tại điểm
0;1
là
0 1 1
y y x
1
y
. Tiếp tuyến này song song với trục hoành nên nhận.
* Với
1
x
0
y
. Phương trình tiếp tuyến của đồ thị hàm số tại các điểm
1;0
là
0 1 0
y y x
0
y
. Tiếp tuyến này trùng với trục hoành nên loại.
Vậy có đúng
1
tiếp tuyến song song với trục hoành.
Cách 2: Tập xác định
D
. Đạo hàm:
3
4 4
y x x
;
0
y
0
x
,
1
x
.
Tiếp tuyến của đồ thị hàm số song song với trục hoành là các tiếp tuyến tại các điểm cực trị có
tung độ khác
0
.
Mà các điểm cực trị của đồ thị hàm số có toạ độ là
0;1
và
1;0
nên suy ra có đúng
1
tiếp
tuyến thỏa mãn yêu cầu bài toán.
Câu 11. [2H2-2] Khẳng định nào dưới đây là SAI?
A. Hình chóp đều bất kì luôn nội tiếp trong một hình cầu.
B. Hình chóp tam giác bất kì luôn nội tiếp trong một hình nón.
C. Hình lăng trụ tam giác bất kì luôn nội tiếp trong một hình trụ.
D. Hình lăng trụ đều bất kì luôn nội tiếp trong một hình trụ.
Lời giải
Chọn B.
Hình chóp tam giác bất kì luôn nội tiếp trong một hình nón thì các cạnh bên phải bằng nhau.
Đáp án B không đúng trong trường hợp cạnh bên vuông góc với mặt phẳng đáy.
Câu 12. [2H2-2] Một hình trụ có thiết diện qua trục là hình vuông chu vi
16cm
. Tính thể tích
V
khối
trụ đã cho.
A.
3
8 cm
V
. B.
3
16
cm
3
V
. C.
3
16 cm
V
. D.
3
32 cm
V
.
Lời giải
Chọn B.
D
C
B
A
Giả sử ta có hình vẽ, khi đó:
4 16
AB
4
AB
.
Suy ra hình trụ có
2
2
AB
R
,
4
h AD
.
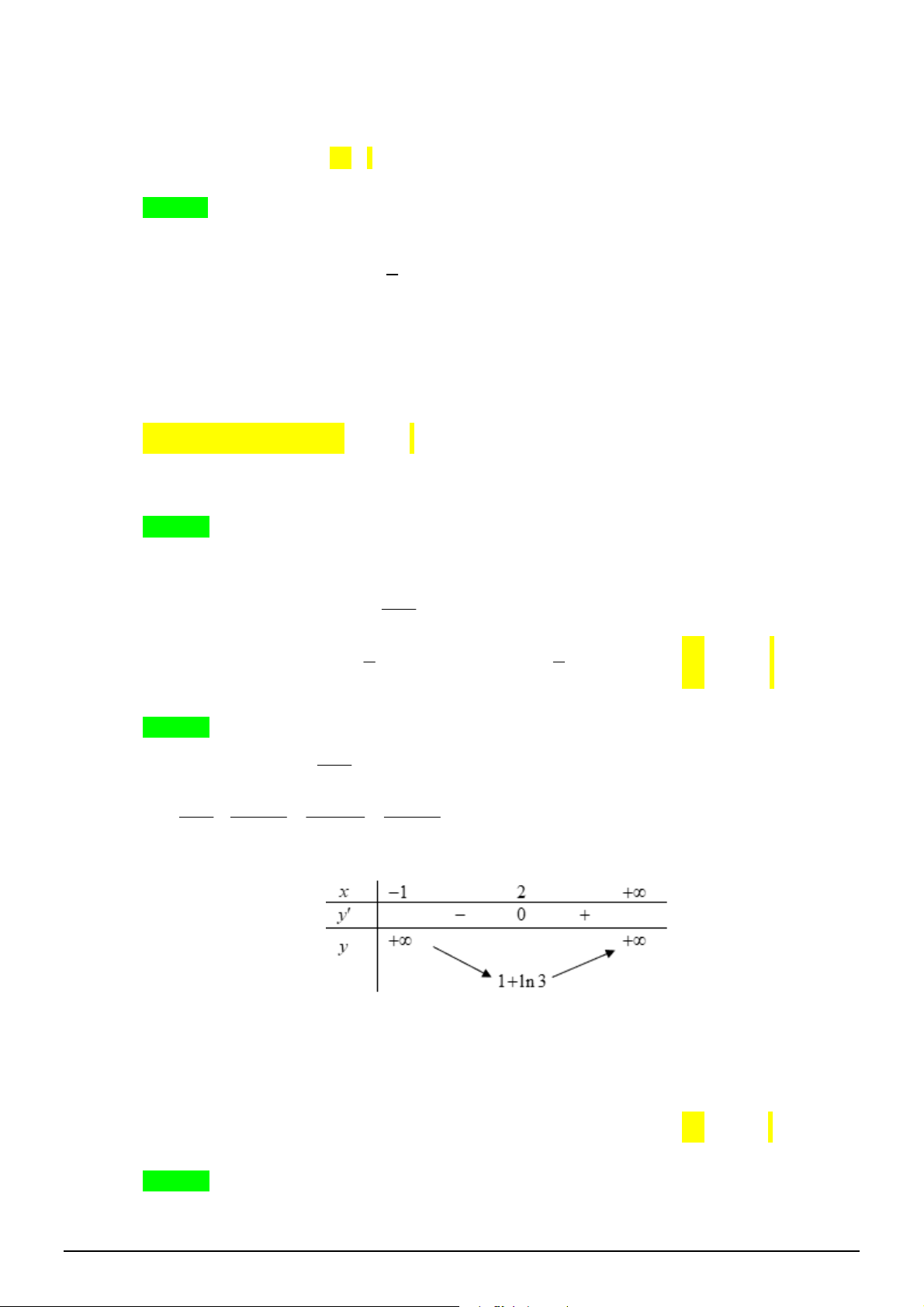
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/25 - Mã đề thi 753
Vậy
2 3
16 cm
V R h
.
Câu 13. [2D2-2] Phương trình
3 3
log 2 1 log 1 0
x x
có bao nhiêu nghiệm?
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải
Chọn B.
Điều kiện:
1
1 0
1
1
2 1 0
2
x
x
x
x
x
Khi đó phương trình đã cho tương đương:
3 3
log 2 1 log 1 2 1 1 2
x x x x x
(loại).
Suy ra phương trình đã cho vô nghiệm.
Câu 14. [2D2-1] Cho hàm số
log
y x
. Khẳng định nào sau đây khẳng định SAI?
A. Hàm số có tập giá trị là
0;
. B. Hàm số đồng biến trên khoảng
0;
.
C. Hàm số có tập xác định là
0;
. D. Hàm số có tập giá trị là
;
.
Lời giải
Chọn A.
Hàm số có tập giá trị là
;
.
Câu 15. [2D2-2] Hàm số
3
ln 1
1
y x
x
đồng biến trên khoảng nào?
A.
1;2
. B.
1
;1
2
. C.
1
;
2
. D.
2;
.
Lời giải
Chọn D.
Hàm số
3
ln 1
1
y x
x
xác định trên khoảng
1;
.
2 2 2
1 3 1 3 2
1
1 1 1
x x
y
x
x x x
;
0 2
y x
.
Ta có bảng biến thiên sau:
Theo bảng biến thên trên ta có hàm số đồng biến trên khoảng
2;
.
Câu 16. [2D1-3] Tìm tập hợp tất cả các giá trị của tham số
m
để hàm số
3 2
1 1
y x m x mx
đồng biến trên khoảng
0;1
.
A.
;0
. B.
0;
. C.
;0
. D.
0;
.
Lời giải
Chọn D.
Hàm số
3 2
1 1
y x m x mx
xác định trên
.
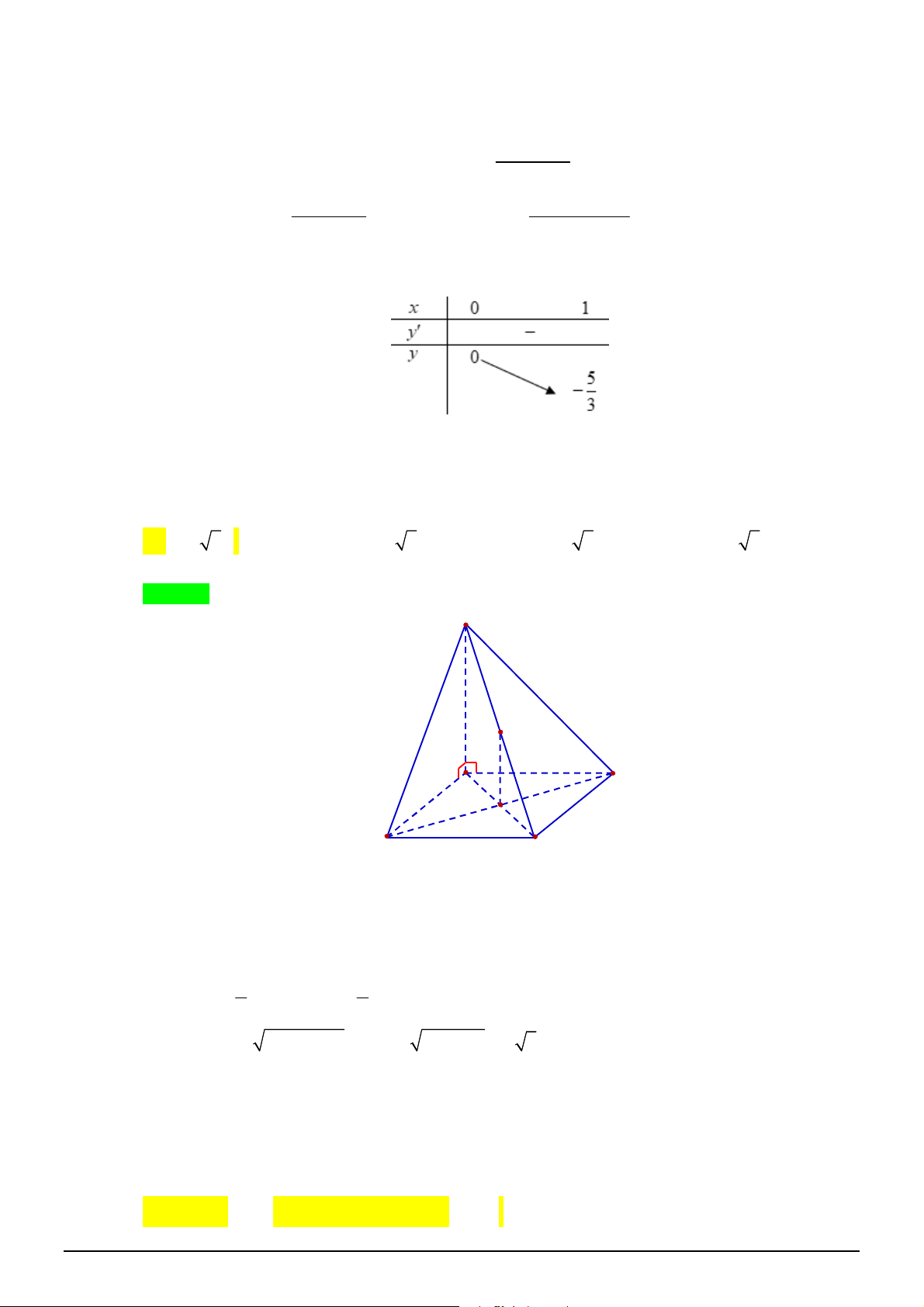
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/25 - Mã đề thi 753
2
3 2 1
y x m x m
Hàm số
3 2
1 1
y x m x mx
đồng biến trên khoảng
0;1
0, 0;1
y x
2
2
3 2
3 2 2 1 0, 0;1 , 0;1
2 1
x x
x x m x x m x
x
Xét hàm số
2
3 2
2 1
x x
g x
x
,
0;1
x ;
2
2
6 6 2
0
2 1
x x
g x
x
,
0;1
x .
Bảng biến thiên của
g x
:
Suy ra hàm số đồng biến trên khoảng
0;1
thì
0
m
.
Câu 17. [2H2-2] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật và
SA
vuông góc với mặt
đáy. Biết
2
SA a
,
4
BD a
. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp
.
S ABCD
.
A.
5
R a
. B.
2 5
R a
. C.
2 3
R a
. D.
3
R a
.
Lời giải
Chọn A.
Gọi
O
là giao điểm của
AC
và
BD
. Suy ra
O
là tâm của hình
chữ nhật
ABCD
.
Kẻ
OI
song song với
SA
cắt
SC
tại
I
.
Suy ra
I
là tâm mặt cầu ngoại tiếp hình chóp
.
S ABCD
.
Ta có
OI
là đường trung bình của
SAC
,
suy ra
1
2
OI SA a
,
1
2
2
OB BD a
.
Ta lại có
2 2
IB OI OB
2 2
4 5
IB a a a
.
Câu 18. [2D1-2] Cho hàm số
f x
có tính chất:
0
f x
0; 3
x và
0
f x
1; 2
x .
Khẳng định nào dưới đây là SAI?
A. Hàm số
f x
là hàm hằng trên khoảng
1; 2
.
B. Hàm số
f x
đồng biến trên khoảng
0; 1
.
C. Hàm số
f x
đồng biến trên khoảng
0; 3
.
S
A
B
C
D
O
I
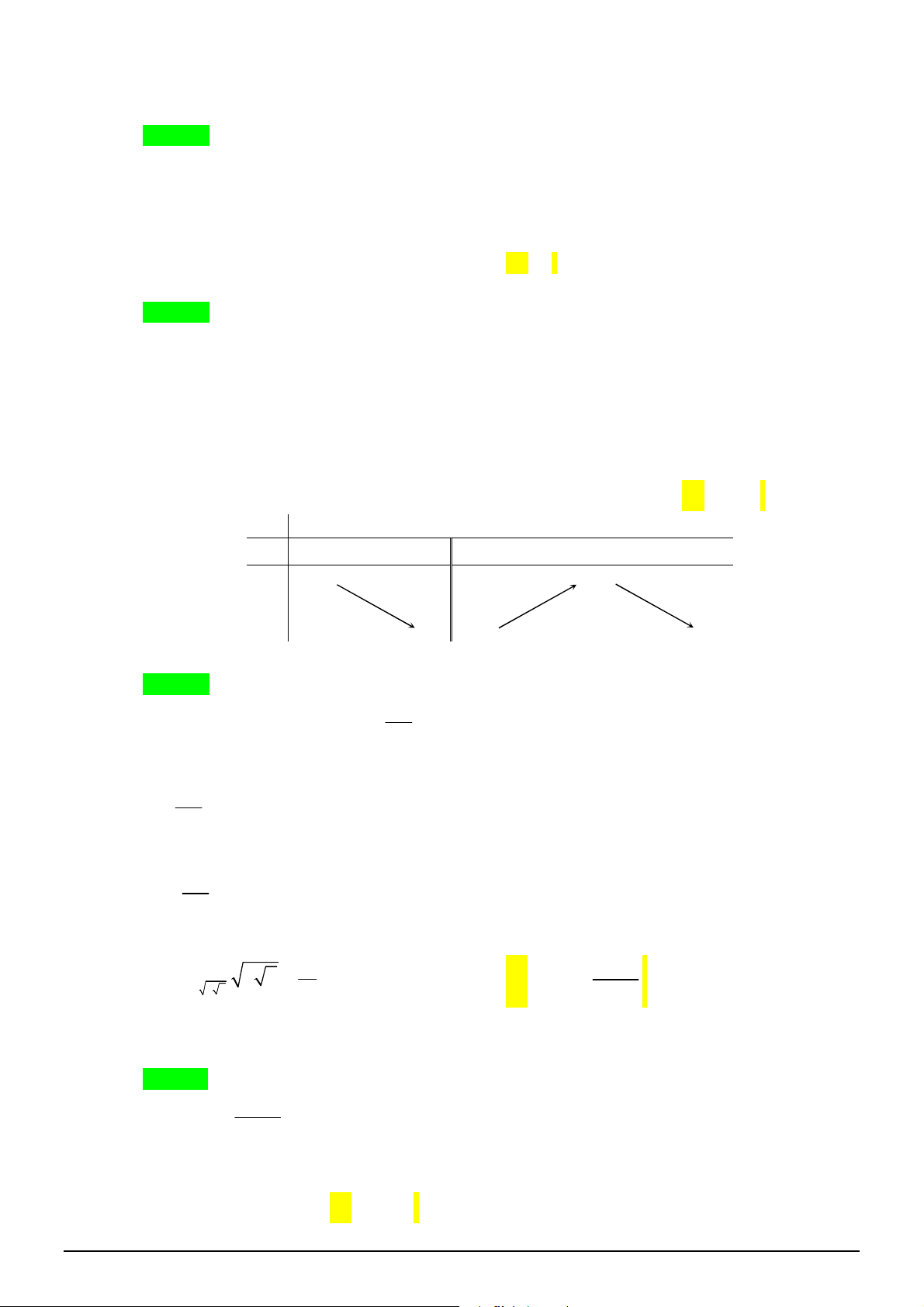
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/25 - Mã đề thi 753
D. Hàm số
f x
đồng biến trên khoảng
2; 3
.
Lời giải
Chọn C.
0
f x
0; 3
x và
0
f x
1; 2
x không phải tại một số hữu hạn điểm thuộc
0; 3
f x
không đồng biến trên khoảng
0; 3
.
Câu 19. [2H1-2] Hình lăng trụ có đáy là thập giác lồi có bao nhiêu cạnh?
A.
20
. B.
12
. C.
30
. D.
22
.
Lời giải
Chọn C.
Số cạnh của lăng trụ có đáy là đa giác lồi
n
cạnh:
3
n
. Suy ra số cạnh hình lăng trụ có đáy là
thập giác lồi là
30
.
Câu 20. [2D1-2] Cho hàm số
y f x
xác định trên
\ 0
, liên tục trên mỗi khoảng xác định và có
bảng biến thiên như hình bên. Tìm tập hợp tất cả các giá trị của tham số thực
m
sao cho
phương trình
2 0
m f x
có ba nghiệm thực phân biệt.
A.
4;2
. B.
; 4
. C.
4;2
. D.
4;2
.
Lời giải
Chọn D.
Ta có
2 0 *
2
m
m f x f x
.
Số nghiệm của phương trình
*
bằng số giao điểm của đồ thị hàm số
y f x
và đường thẳng
2
m
y
.
Dựa vào bảng biến thiên, ta suy ra phương trình
*
có 3 nghiệm thực phân biệt khi:
1 2 4 2
2
m
m
.
Câu 21. [2D2-1] Cho
a
là số thực dương tùy ý. Mệnh đề nào dưới đây SAI?
A.
3
3
4
2
2 2 2
5
log log
18
a a a
. B.
2
1
log
log 2
a
a .
C.
2
2 2
log 2log
a a
. D.
2 3 2
log log .log 3
a a .
Lời giải
Chọn B.
Để
2
1
log
log 2
a
a thì điều kiện là
0 1
a
.
Câu 22. [2D2-2] Tập xác định của hàm số
ln log
y x
là
A.
0;1
. B.
1;
. C.
0;
. D.
0;
.
x
0
1
y
0
y
1
2
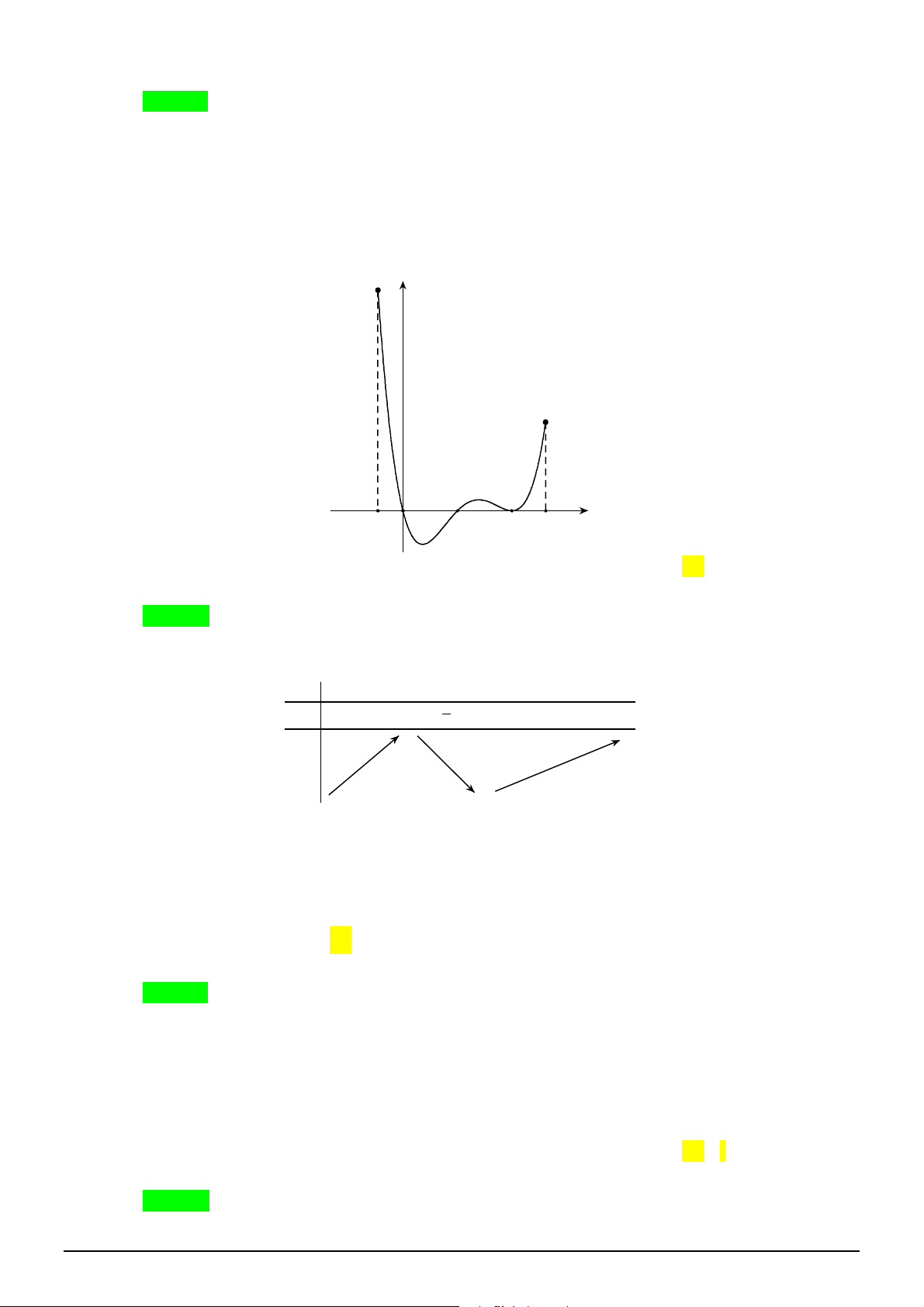
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/25 - Mã đề thi 753
Lời giải
Chọn B.
Hàm số xác định khi
log 0 log log1 1
x x x
.
Vậy tập xác định của hàm số đã cho là
1;D
.
Câu 23. [2D1-2] Cho hàm số
f x
có đạo hàm liên tục trên
;
a b
và đồ thị hàm số
y f x
được
cho như hình bên. Gọi
n
là số điểm cực trị của hàm số
y f x
trên khoảng
;
a b
thì
n
bằng bao nhiêu?
x
y
21 b
a
O
A.
0.
n
B.
1.
n
C.
3
n
D.
2.
n
Lời giải
Chọn D.
Từ đồ thị hàm số
y f x
, ta có bảng biến thiên của hàm số
y f x
như sau:
y
y'
+++ 000
b
x
a
1
2
0
Suy ra hàm số
y f x
có hai cực trị là
0
x
và
1
x
nên
2
n
.
Câu 24. [2D1-2] Đồ thị hàm số
3 2
2 3 1
y x x x
và đường thẳng
2
y x
cắt nhau tại điểm
; .
A A
A x y
Tìm
.
A
y
A.
0.
A
y
B.
3.
A
y
C.
2.
A
y
D.
1.
A
y
Lời giải
Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị là:
3 2
2 3 1 2
x x x x
3 2
2 2 1 0
x x x
1
x
Với
1
x
thì
3
y
. Suy ra
3.
A
y
Câu 25. [2D2-2] Phương trình
1
5 5. 0,2 26
x
x
có hai nghiệm
1
x
,
2
x
. Tính tổng
1 2
S x x
.
A.
13
. B.
26
. C.
1
. D.
0
.
Lời giải
Chọn D.
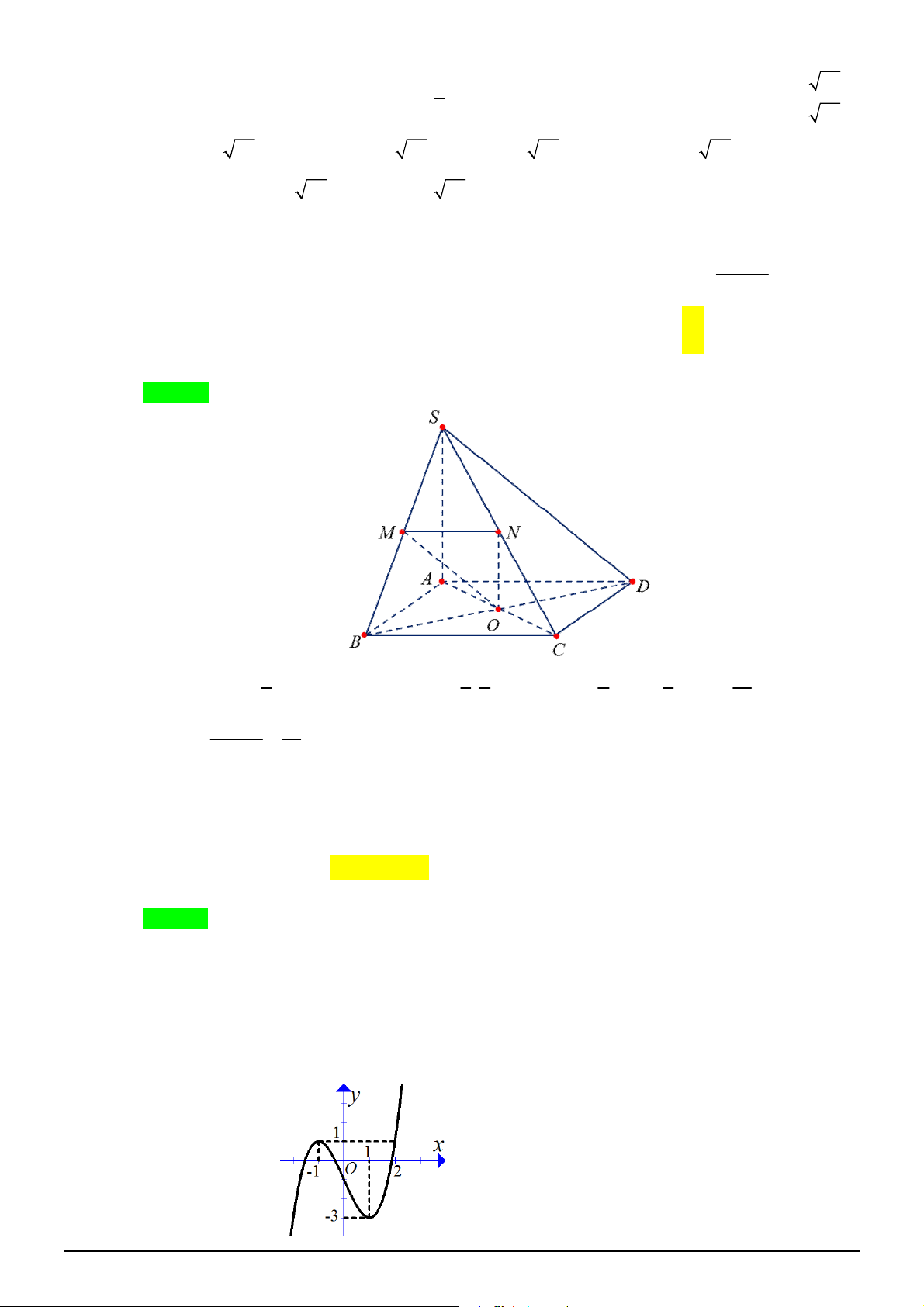
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/25 - Mã đề thi 753
Ta có
1
5 5. 0,2 26
x
x
1
1
5 5. 26
5
x
x
2
5 26.5 1 0
x x
5 13 2 42
5 13 2 42
x
x
.
5
5 13 2 42 log 13 2 42
x
x
,
5
5 13 2 42 log 13 2 42
x
x
.
1 2 5 5 5
log 13 2 42 log 13 2 42 log 1 0
x x
.
Câu 26. [2D1-3] Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
O
là giao điểm của
AC
và
BD
. Gọi
M
,
N
lần lượt là trung điểm của
SB
,
SC
. Tính tỉ số
.
OBCNM
S ABCD
V
k
V
.
A.
3
16
k . B.
1
8
k
. C.
3
8
k
. D.
1
16
k .
Lời giải
Chọn D.
Ta có
.
1 1 1 3 1 1
; . . A; .
3 3 2 4 8 16
OBCNM BCNM SBC SABC S ABCD
V d O BCNM S d SBC S V V
Vậy
.
1
16
OBCNM
S ABCD
V
k
V
.
Câu 27. [2D1-2] Cho hàm số
y f x
có
lim 1
x
f x
và
lim 1
x
f x
. Tìm phương trình đường
tiệm cận ngang của đồ thị hàm số
1 2018.
y f x
.
A.
1
y
. B.
2019
y
. C.
1
y
. D.
2017
y
.
Lời giải
Chọn B.
Ta có
lim 1 2018. 1 2018. 1 2019
x
f x
.
lim 1 2018. 1 2018. 1 2019
x
f x
.
Vậy phương trình đường tiệm cận ngang của đồ thị hàm số
1 2018.
y f x
là
2019
y
.
Câu 28. [2D1-2] Đồ thị hình bên là đồ thị của hàm số nào?

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/25 - Mã đề thi 753
A.
3 2
3 3 1
y x x x
. B.
3
1
3 1
3
y x x
.
C.
3 2
3 3 1
y x x x
. D.
3
3 1
y x x
.
Lời giải
Chọn D.
Từ đồ thị ta có
1
x
,
3
y
Đáp án A:
1
x
1 3 3 1 2
y
( loại ).
Đáp án B:
1
x
1 13
3 1
3 3
y
( loại ).
Đáp án C:
1
x
1 3 3 1 6
y
( loại ).
Câu 29. [2D1-1] Cho hàm số
y f x
xác định, liên tục trên
và có bảng biến thiên như hình dưới
đây. Khẳng định nào sau đây là sai:
A. Hàm số có ba điểm cực trị.
B.
0
1
x
được gọi là điểm cực tiểu của hàm số.
C.
0
1
y
được gọi là giá trị cực tiểu của hàm số.
D.
0;2
M được gọi là điểm cực đại của hàm số.
Lời giải
Chọn D.
Phương án D sai vì
0;2
M được gọi là điểm cực đại của đồ thị hàm số.
Câu 30. [2D2-1] Tính đạo hàm của hàm số
2
log 5 1
y x
.
A.
5
5 1 ln2
y
x
. B.
1
5 1
y
x
. C.
5
5 1
y
x
. D.
1
5 1 ln2
y
x
.
Lời giải
Chọn A.
Ta có:
1 5
. 5 1
5 1 ln 2 5 1 ln2
y x
x x
.
Câu 31. [2D1-3] Tìm các giá trị của
m
để đồ thị hàm số
3 2 2
1
1 2 1 3
3
y x m x m x
có hai
điểm cực trị cách đều trục tung.
A.
1
m
. B.
1
m
. C.
2
m
. D.
1
m
.
Lời giải
Chọn B.
3 2 2
1
1 2 1 3
3
y x m x m x
2 2
2 1 2 1
y x m x m
2
2
1 2 1
m m
Đ
x
1
0
1
y
0
0
0
y
1
2
1
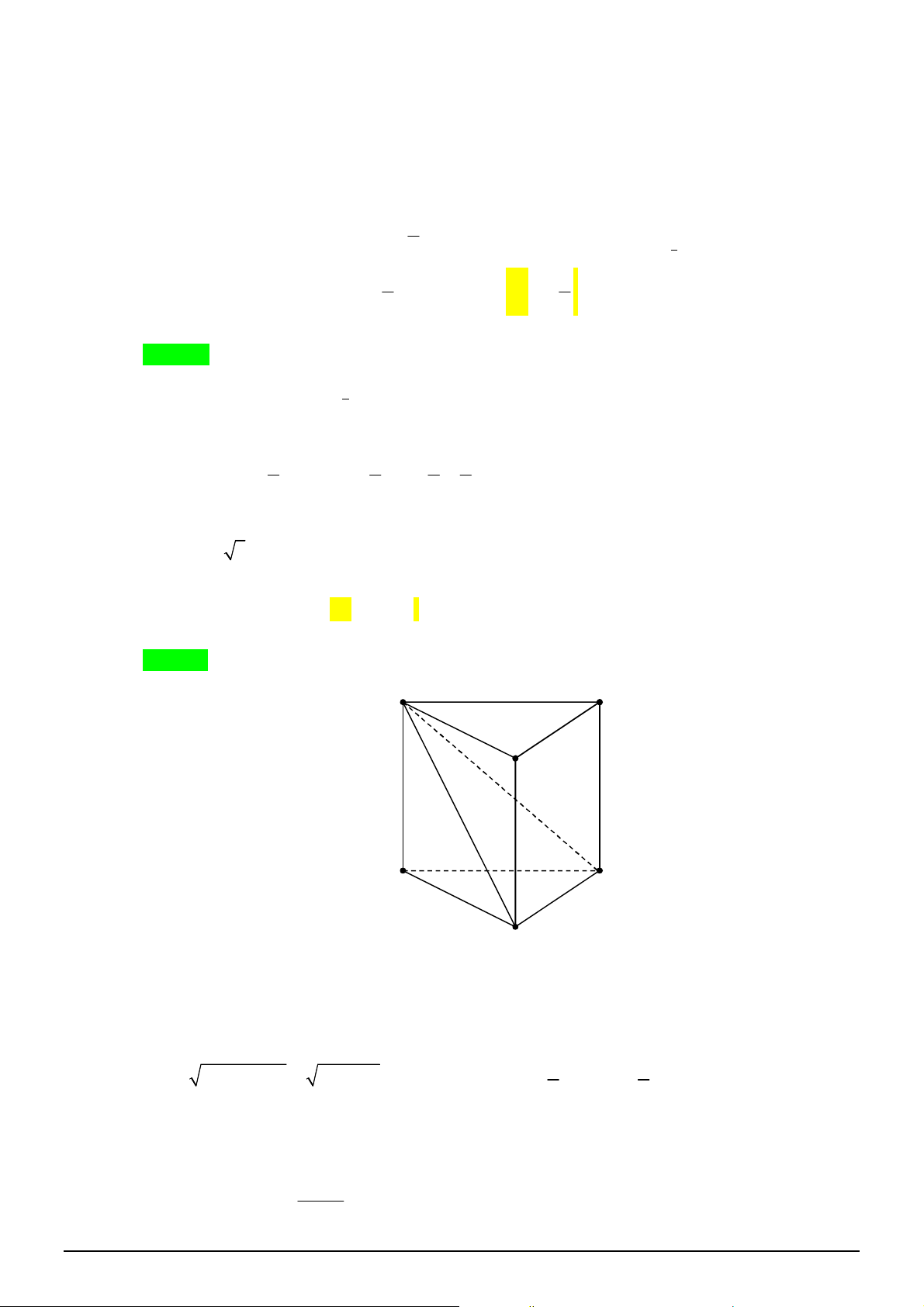
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/25 - Mã đề thi 753
Để đồ thị hàm số có hai điểm cực trị cách đều trục tung thì:
1 2
0
0
0
a
x x
2
2
2
1 0
1 2 1 0
2 1 0
m m
Đ
m
2
2
1 2 1 0
1
1
m m
m L
m N
Câu 32. [2D2-2] Cho
3
log 2
a
và
2
1
log
2
b
. Tính
2
3 3 1
4
2log log 3 log
I a b
.
A.
4
I
. B.
5
4
I
. C.
3
2
I
. D.
0
I
.
Lời giải
Chọn C.
2
3 3 1
4
2log log 3 log
I a b
3 3 3 2
2log log 3 log log
a b
3
1
2log 1 2
2
3
1
2log 3
2
1
2
2
3
2
.
Câu 33. [2H1-1] Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
,
AC a
và
5
BC a
. Biết góc giữa
AB C
và
ABC
bằng
45
, tính thể tích
V
của khối lăng trụ
đã cho.
A.
3
6
V a
. B.
3
2
V a
. C.
3
5
V a
. D.
3
4
V a
.
Lời giải
Chọn B.
Ta có
AB C ABC AC
AB AC
AB AC
; ; 45
AB C ABC AB AB B AB
.
2 2 2 2
5 2
AB BC AC a a a
, ta được
2
1 1
. . . .2
2 2
ABC
S AB AC a a a
.
Tam giác
ABB
vuông cân tại
B
, ta được
2
BB AB a
.
Thể tích khối lăng trụ:
2 3
. 2 . 2
ABC
V BB S a a a
.
Câu 34. [2D2-2] Đặt
3
5
0
1
lim
1
x
x
x
e
a
e
. Tính giá trị của
5 4
P a
.
B
C
A
A
B
C
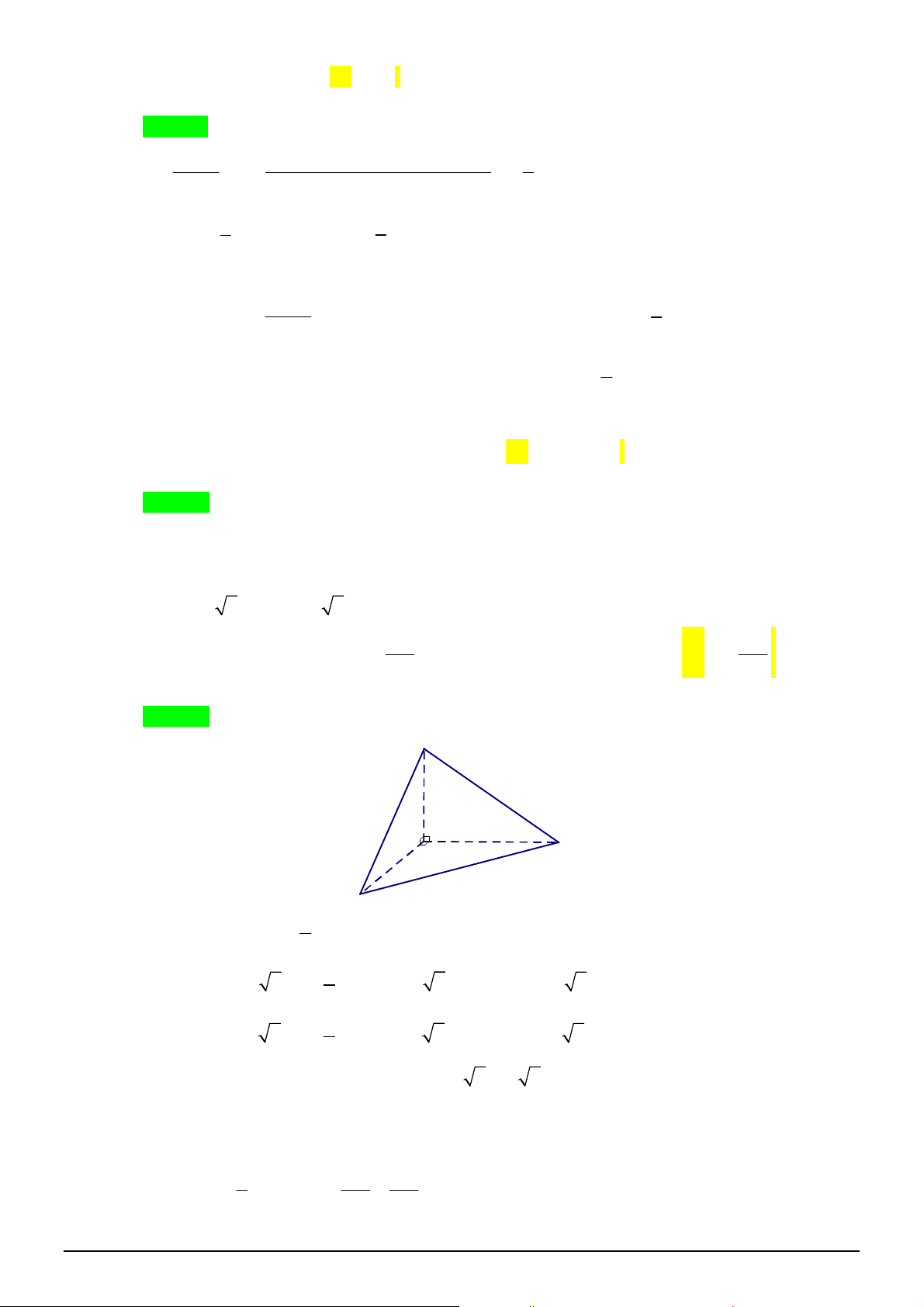
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/25 - Mã đề thi 753
A.
4
P
. B.
1
P
. C.
3
P
. D.
7
P
.
Lời giải
Chọn B.
2
3
5
4 3 2
0 0
1 1
1 3
lim lim
1 5
1 1
x x x
x
x
x x x x x
x x
e e e
e
e
e e e e e
.
Với
3
5
a
, ta được
3
5. 4 1
5
P
.
[phương pháp trắc nghiệm]
Nhập biểu thức
3
5
1
1
x
x
e
e
, CALC
0.00000000000001
x
, được
3
5
a
.
Câu 35. [2D1-2] Cho chuyển thẳng xác định bởi phương trình
4 2
1
3
2
S t t
, trong đó
t
tính bằng
giây
s
,
S
được tính bằng mét
m
. Tính vận tốc của chuyển động tại thời điểm
4
t s
.
A.
232 m/s
v
. B.
140 m/s
v
. C.
116 m/s
v
. D.
280 m/s
v
.
Lời giải
Chọn C.
Ta có
3
2 3
v t S t t t
. Do đó
3
4 2.4 3.4 116 m/s
v .
Câu 36. [2H1-2] Cho hình chóp
.
S ABC
có
SA
,
SB
,
SC
đôi một vuông góc. Biết
2
SAB
S a
,
2
2
SBC
S a ,
2
2
SCA
S a . Tính thể tích
V
của khối chóp
.
S ABC
theo
a
?
A.
3
2
V a
. B.
3
4
3
a
V . C.
3
4
V a
. D.
3
2
3
a
V .
Lời giải
Chọn D.
C
B
A
S
Ta có
2
SAB
S a
2
1
.
2
SA SB a
2
. 2
SA SB a
(1)
2
2
SBC
S a
2
1
. 2
2
SC SB a
2
. 2 2.
SC SB a
(2)
2
2
SCA
S a
2
1
. 2
2
SC SA a
2
. 2 2.
SC SA a
(3)
Từ (1), (2). (3)
2 2 2 6
. . 2 .2 2.2 2 16
SAB SBC SAC
S S S a a a a
2
6
. . 16
SA SB SC a
3
. . 4
SA SB SC a
Mà
3 3
.
1 4 2
. .
6 6 3
S ABC
a a
V SA SB SC .
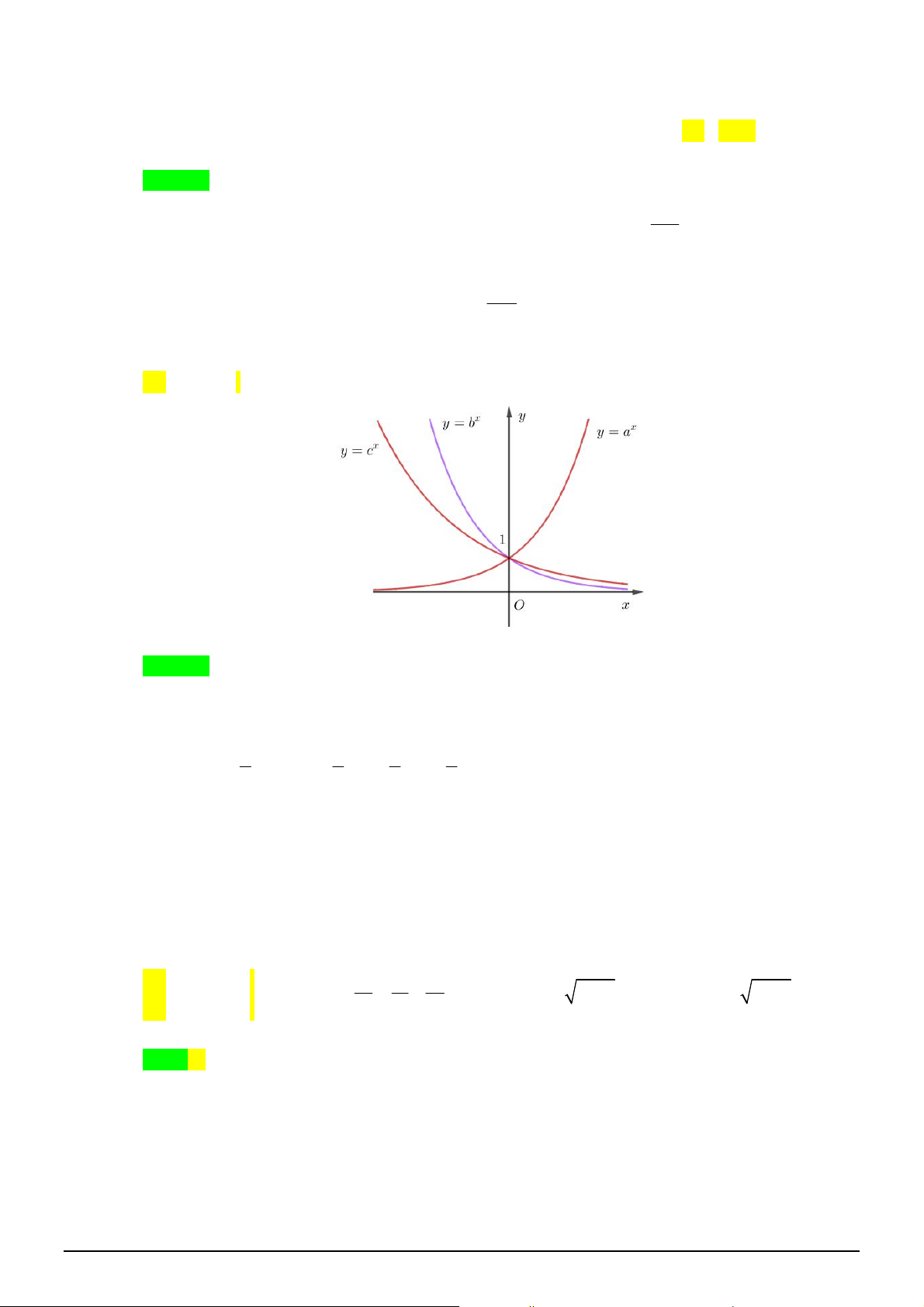
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/25 - Mã đề thi 753
Câu 37. [2D2-3] Huyện
A
có
300
nghìn người. Với mức tăng dân số bình quân
1,2%
/năm thì sau
n
năm dân số sẽ vượt lên
330
nghìn người. Hỏi
n
nhỏ nhất bằng bao nhiêu?
A.
9
năm. B.
7
năm. C.
10
năm. D.
8
năm.
Lời giải.
Chọn D.
Dùng công thức tăng trưởng kép, dân số sau
n
năm là
1,2
300 1
100
n
n
T
(nghìn người). Do đó
theo yêu cầu bài toán
330 300 1,012 330
n
n
T
1,012
330
log 7,99
300
n .
Câu 38. [2D2-3] Cho đồ thị các hàm số , ,
x x x
y a y b y c
có hình vẽ bên. Tìm khẳng định ĐÚNG.
A.
a c b
. B.
b c a
. C.
c b a
. D.
a b c
.
Lời giải.
Chọn A.
Đồ thị các hàm số ,
x x
y b y c
là các hàm số giảm nên
0 , 1
b c
, đồ thị hàm số
x
y a
tăng
nên
1
a
. Hơn nữa với mọi
0
x
, ta có
1
x
x x
b
b c
c
0
x
b b
c c
1
b
c
b c
.
Ta chọn kết quả
.
a c b
Câu 39. [2H2-2] Cho hình trụ
T
có trục
2
OO a
, bán kính đường tròn đáy bằng
a
. Gọi
S
là mặt
cầu tiếp xúc với hai mặt đáy của hình trụ và tiếp xúc với các đường sinh của hình trụ. Gọi
N
là hình nón đỉnh
O
và đáy là hình tròn
O
của hình trụ. Gọi
1
V
,
2
V
,
3
V
là thể tích của khối
trụ
T
, khối cầu
S
và khối nón
N
. Khẳng định nào ĐÚNG?
A.
1 2 3
V V V
. B.
3 1 2
1 1 1
V V V
. C.
2 3 1
.
V V V
. D.
3 1 2
.
V V V
.
Lời giải
Chọn A.
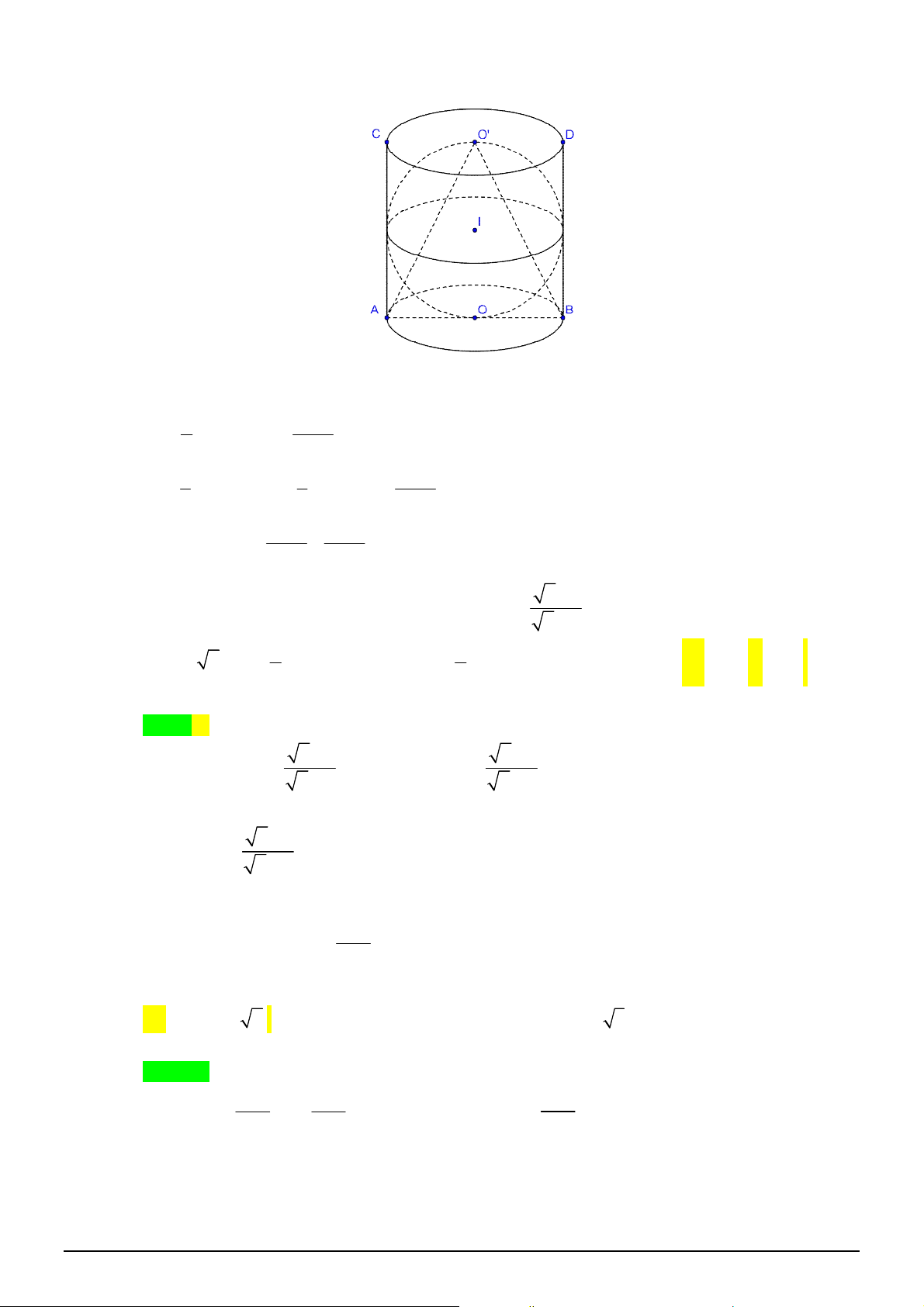
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/25 - Mã đề thi 753
Ta có
2
1
V R h
2 3
1
. 2
V R OO a
.
3
2
4
3
V R
3
2
4
3
a
V
2
3
1
3
V R h
3
2
3
1 2
.
3 3
a
V R OO
.
Suy ra
3 3
3
2 3
4 2
2
3 3
a a
V V a
. Do vậy:
1 2 3
V V V
.
Câu 40. [2D1-2] Các đường tiệm cận của đồ thị hàm số
1
2
x
y
x
là:
A.
2
x
;
1
2
y
. B.
4
x
;
1
2
y
. C.
2
x
;
1
y
. D.
4
x
;
1
y
.
Lời giải
Chọn D.
Ta có
4 4
1
lim lim
2
x x
x
y
x
,
4 4
1
lim lim
2
x x
x
y
x
nên
4
x
là tiệm cận đứng của đồ
thị hàm số.
1
lim lim 1
2
x x
x
y
x
nên
1
y
là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số có các đường tiệm cận là:
4
x
;
1
y
.
Câu 41. [2D1-3] Cho hàm số
1
1
x
y
x
có đồ thị
C
và
A
là một điểm thuộc
C
. Gọi
S
là tổng các
khoảng cách từ
A
đến các đường tiệm cận của
C
. Tìm
min
S
.
A.
min 2 2
S
. B.
min 2
S
. C.
min 2 3
S . D.
min 3
S
.
Lời giải
Chọn A.
* Ta có
1 2
1
1 1
x
y
x x
. Gọi
2
;1
1
A C A a
a
, với
1
a
.
*
C
có tiệm cận đứng (TCĐ):
1 1 0
x x
.
*
C
có tiệm cận ngang (TCN):
1 1 0
y y
.
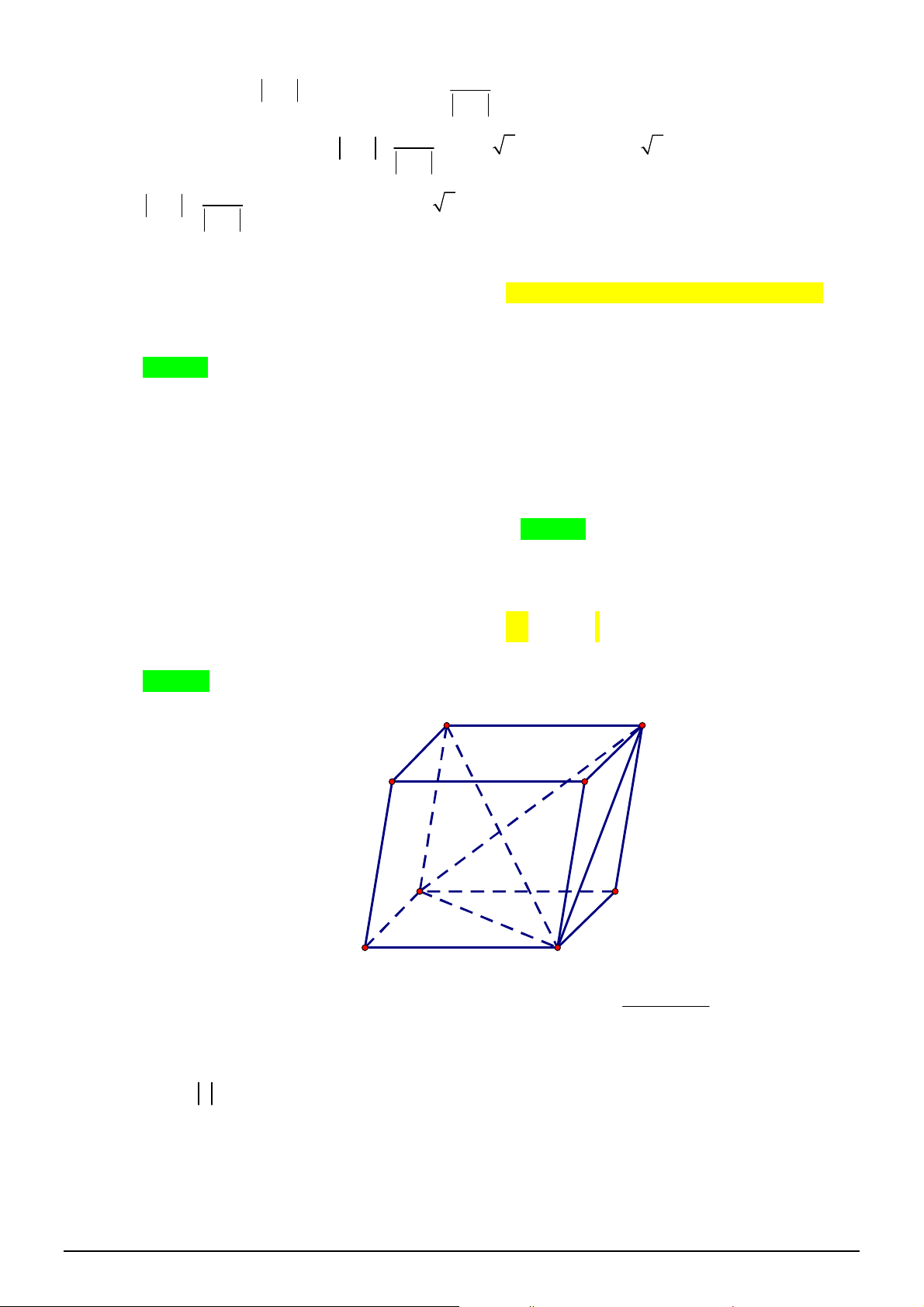
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/25 - Mã đề thi 753
*
1
; 1d A TC
Đ a d
;
2
2
;
1
d A TCN d
a
.
Suy ra
1 2
2
1 2 2
1
AM GM
S d d a
a
min 2 2
S
khi và chỉ khi
2
2
1 1 2 1 2
1
a a a
a
.
Câu 42. [2D2-3] Cho phương trình
.2017 2 .2018 2 1 0
x x
x x x
. Tìm khẳng định ĐÚNG?
A. Phương trình có đúng một nghiệm nguyên. B. Phương trình không có nghiệm nguyên.
C. Phương trình có nghiệm nguyên lớn hơn
5
. D. Phương trình có nghiệm nguyên âm.
Lời giải
Chọn B.
Xét phương trình
.2017 2 .2018 2 1 0 1
x x
x x x , ta có:
* Với
x
nguyên và
0
x
thì vế trái của
1
âm nên phương trình vô nghiệm do đó loại D.
* Với
x
nguyên và
2
x
thì vế trái của
1
dương nên phương trình vô nghiệm do đó loại C.
* Với
1
x
phương trình
1
không thỏa do đó loại A.
Vậy phương trình không có nghiệm nguyên do đó Chọn B.
Câu 43. [2H1-3] Cho hình hộp
.
ABCD A B C D
có thể tích
48
đvtt
. Tính thể tích khối tứ diện
BCD B
.
A.
12
đvtt
. B.
6
đvtt
. C.
8
đvtt
. D.
16
đvtt
.
Lời giải
Chọn C.
B
A
D
C
C'
D'
A'
B'
Ta có:
. ' . .
6
ABCD A B C D ADD A BCC B D BCB
V V V
. '
.
đv
8
6
tt
ABCD A B C D
BCD B D BCB
V
V V
.
Câu 44. [2D1-3] Cho hàm số
y f x
có đồ thị như hình bên. Trên đoạn
1;3
, đồ thị hàm số
y f x
có mấy điểm cực trị?
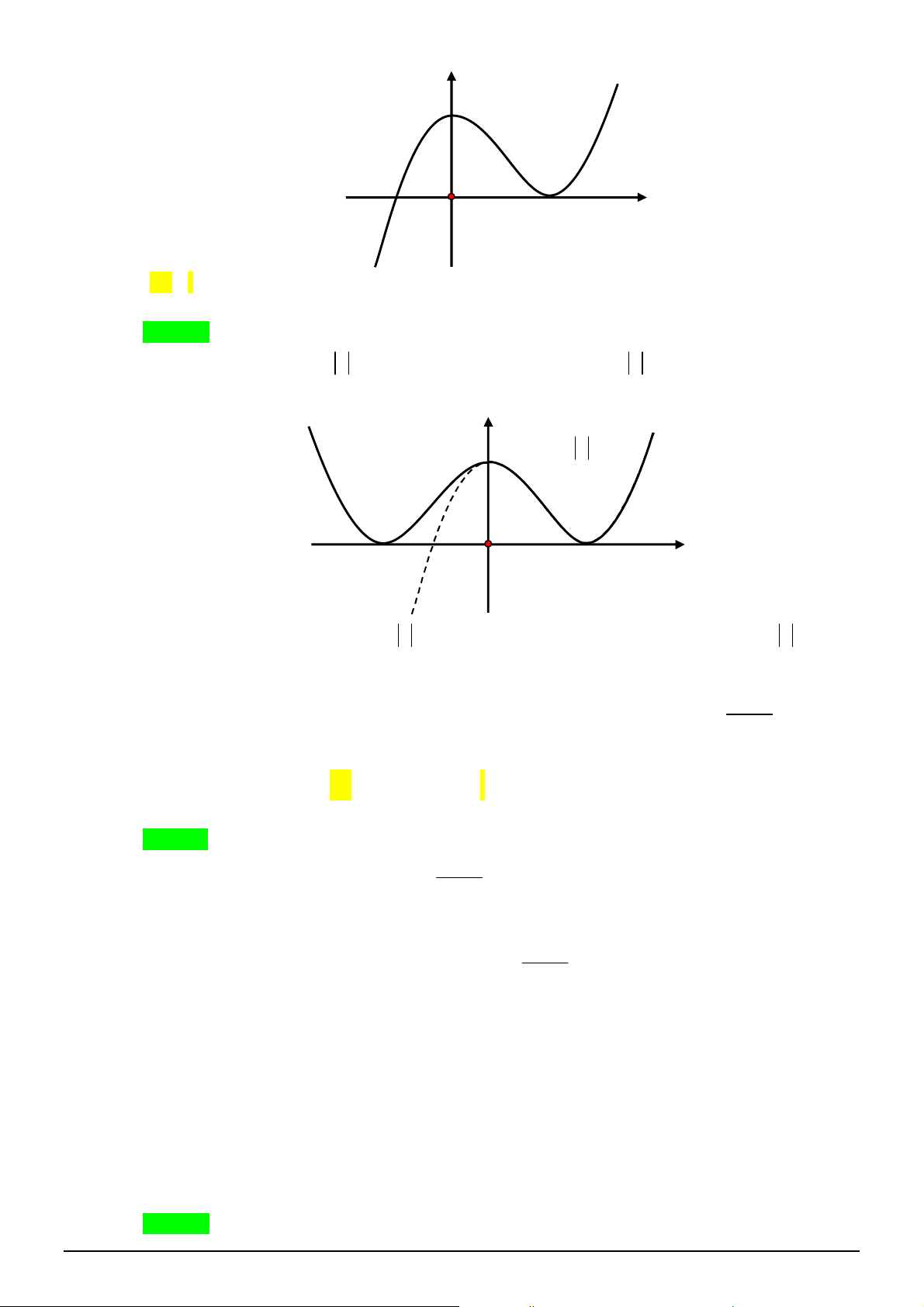
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 23/25 - Mã đề thi 753
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn A.
* Đồ thị hàm số
y f x
được suy từ đồ thị hàm số
y f x
bằng cách giữ lại phần đồ
thị ở bên phải trục
Oy
và kèm thêm phần đối xứng của nó qua trục
Oy
.
* Nhìn vào đồ thị hàm số
y f x
ta thấy trên đoạn
1;3
, đồ thị hàm số
y f x
có hai
điểm cực trị.
Câu 45. [2D1-2] Tìm tập hợp tất cả các giá trị của tham số
m
để đồ thị hàm sô
2 3
2
x
y
x
cắt đường
thẳng
2
y x m
tại hai điểm phân biệt.
A.
3;
. B.
;1 3;
. C.
1;3
. D.
;1
.
Lời giải
Chọn B.
Xét phương trình hoành độ giao điểm:
2 3
2
2
x
x m
x
(điều kiện
2
x
)
2 3 2 2
x x x m
2
2 4 3 0 1
x mx m
Để đường thẳng
2
y x m
cắt đồ thị hàm số
2 3
2
x
y
x
tại hai điểm phân biệt
1
có hai
nghiệm phân biệt khác
2
.
Ta có hệ điều kiện sau:
2
2
4 3 0
2 2 2 4 3 0
m m
m m
1
3
1 0
m
m
1
3
m
m
.
Câu 46. [2D2-1] Tìm tập xác định
D
của hàm số
5
2
2
y x x
.
A.
D
. B.
; 1 2;
. C.
0;D
. D.
\ 1;2
D
.
Lời giải
Chọn D.
O
x
y
4
2
1
2
y f x
O
x
y
4
2
1
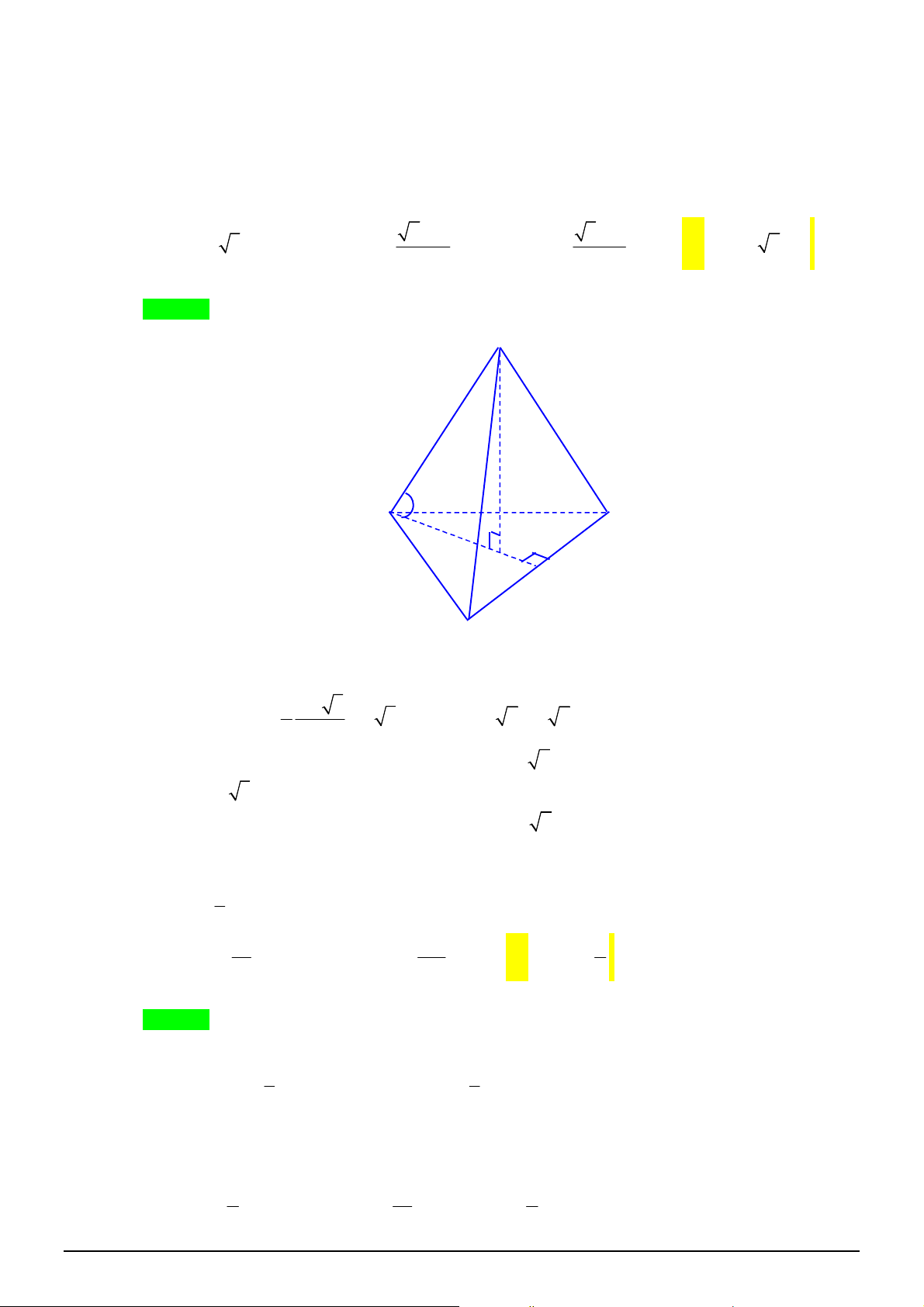
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 24/25 - Mã đề thi 753
Điều kiện xác định của hàm số là
2
2 0
x x
1
2
x
x
.
Câu 47. [2H2-2] Cho hình chóp đều
.
S ABC
cạnh đáy
3
AB a
, góc giữa cạnh bên và mặt đáy bằng
45 .
Tính diện tích xung quanh
xq
S
của hình nón đỉnh
S
và đường tròn đáy là đường tròn
ngoại tiếp tam giác
ABC
.
A.
2
3 3
xq
S a
. B.
2
2
3
xq
a
S
. C.
2
3
3
xq
a
S
. D.
2
3 2
xq
S a
.
Lời giải
Chọn D.
Gọi
G
là trọng tâm tam giác
ABC
. Ta có:
; 45
SA ABC SAG
nên
SGA
vuông cân tại
G
2 3
3
3 2
AB
SG AG a
và
2 6
SA AG a
.
Hình nón thỏa mãn đề bài có đường sinh
6
l SA a
, bán kính đường tròn đáy
3.
r AG a
Diện tích xung quanh của hình nón là:
2
3 2
xq
S rl a
.
Câu 48. [2D1-3] Cho
x
,
y
là hai số thực không âm thỏa mãn
2
x y
. Tìm giá trị nhỏ nhất của biểu
thức
3 2 2
1
1
3
P x x y x
.
A.
17
min
3
P
. B.
115
min
3
P . C.
7
min
3
P
. D.
min 5
P
.
Lời giải
Chọn C.
Ta có:
2
x y
2
y x
; điều kiện:
0 2
x
.
Khi đó:
2
3 2 3 2
1 1
2 1 2 5 5
3 3
P x x x x x x x x
liên tục trên đoạn
0;2
.
2
4 5
P x x x
;
0
P x
2
4 5 0
x x
1 0;2
5 0;2
x
x
.
Do
7
1
3
P
;
0 5
P
;
17
2
3
P
. Vậy
7
min
3
P
.
S
A
B
M
C
G
3
a
45
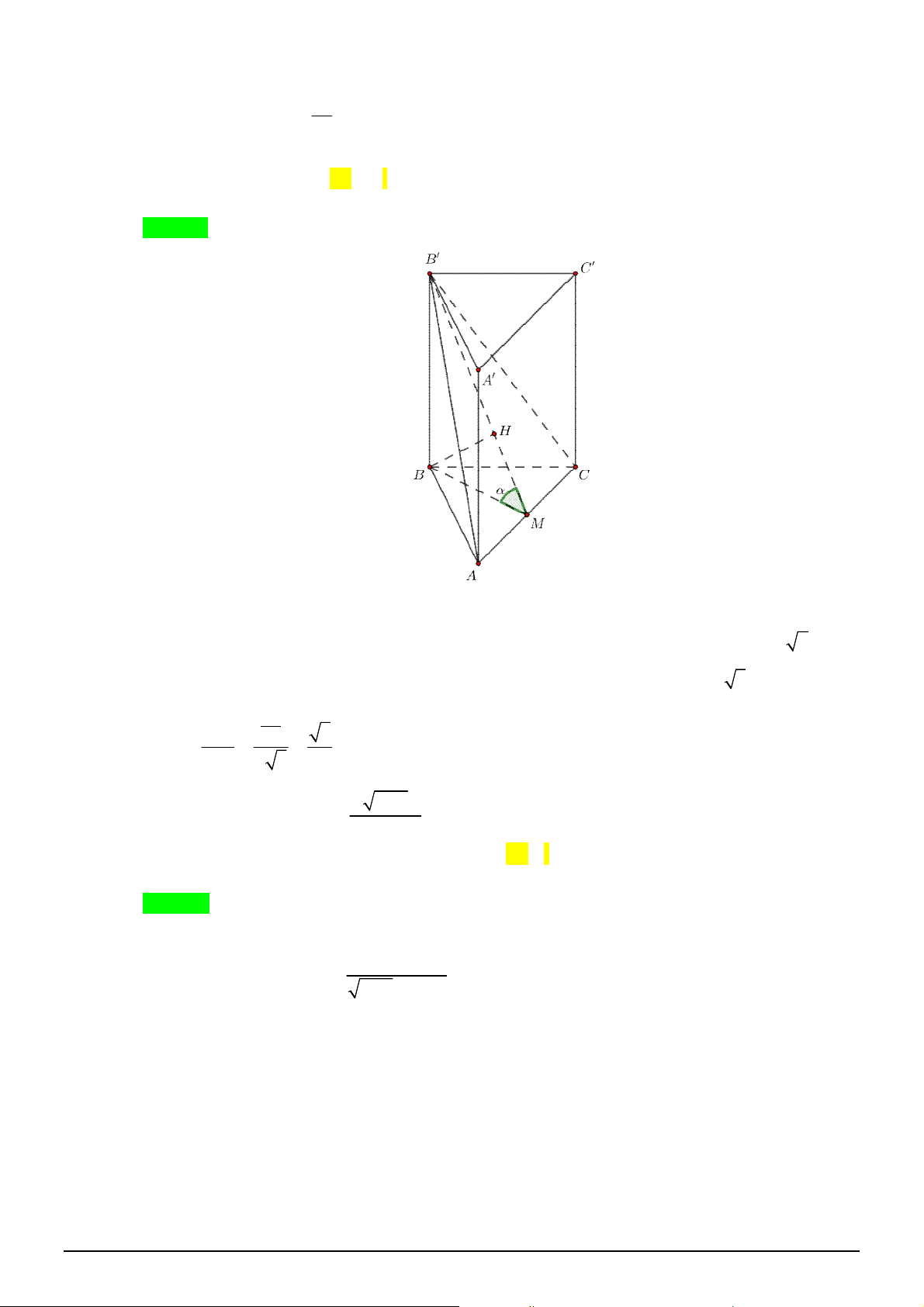
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 25/25 - Mã đề thi 753
Câu 49. [2H1-3] Cho hình lăng trụ tam giác đều
.
ABC A B C
có
2
AB a
. Biết khoảng cách từ điểm
B
đến
AB C
bằng
3
2
a
. Kí hiệu
là góc giữa hai mặt phẳng
AB C
và
ABC
. Số đo
bằng
A.
30
. B.
60
. C.
90
. D.
45
.
Lời giải
Chọn B.
Gọi
M
là trung điểm
AC
, do
ABC
đều nên
AC BM
;
AC BB
AC BB M
.
Trong
BB M
, hạ
BH B M
tại
H
thì
BH AB C
nên
; 2
d B AB C BH a
.
Ta có, góc giữa hai mặt phẳng
AB C
và
ABC
là
BMH
. Mà
3
BM a
, khi đó
3
3
2
sin
2
3
a
BH
BM
a
60
.
Câu 50. [2D1-3] Đồ thị hàm số
2
1
2
x
y
x x
có bao nhiêu đường tiệm cận?
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn C.
Tập xác định
1;D
.
Biến đổi hàm số, ta có
1
1 2
y
x x
.
Do
lim 0
x
y
nên đồ thị hàm số có đường tiệm cận ngang là
0
y
.
1
lim
x
y
nên đồ thị hàm số có đường tiệm cận đứng là
1
x
.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/22 - Mã đề thi 132
UBND TỈNH BẮC NINH
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA ĐỊNH KỲ LẦN 1 NĂM HỌC 2017 – 2018
MÔN TOÁN 12
Thời gian làm bài 90 phút;
Họ, tên thí sinh……………………………Lớp……………………….
Mã đề thi 132
Câu 1. [2D2-2] Đặt
3
log 45
a . Mệnh đề nào dưới đây đúng?
A.
45
2
log 5
a
a
. B.
45
1
log 5
a
a
. C.
45
2
log 5
a
a
. D.
45
2
log 5
a
a
.
Câu 2. [2D1-2] Cho hàm số
3 2
3 9 1
y x x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
3;1
. B. Hàm số nghịch biến trên khoảng
3;1
.
C. Hàm số nghịch biến trên khoảng
; 3
. D. Hàm số nghịch biến trên khoảng
1;
.
Câu 3. [2D1-3] Đồ thị của hàm số
2
2
4 1
x
y
x
có bao nhiêu đường tiệm cận?
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 4. [2H1-1] Cho một hình đa diện. Mệnh đề nào dưới đây sai?
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh. B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C. Mỗi cạnh là cạnh chung của ít nhất ba mặt. D. Mỗi mặt có ít nhất ba cạnh.
Câu 5. [2D1-1] Đồ thị hàm số
2
2
1 2
6 9
x
y
x x
có tiệm cân đứng
x a
và tiệm cận ngang
y b
. Tính
giá trị
2
T a b
.
A.
4
T
. B.
1
T
. C.
8
T
. D.
6
T
.
Câu 6. [2H1-1] Cho lăng trụ đứng
1 1 1
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
C
,
2
AC a
.
Biết tam giác
1
ABC
có chu vi bằng
5
a
. Tính thể tích
V
của khối lăng trụ
1 1 1
.
ABC A B C
.
A.
3
3
2
a
V . B.
3
2
a
V . C.
3
1
3
V a
. D.
3
V a
.
Câu 7. [2D1-2] Tìm giá trị lớn nhất của hàm số
2
4
x
y
x
trên đoạn
1;5
.
A.
1;5
1
max
5
y
. B.
1;5
1
max
4
y
. C.
1;5
5
max
29
y . D.
1;5
2
max
6
y .
Câu 8. [2D1-2] Cho hàm số
f x
có đạo hàm
2
1 3
f x x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại
3
x
. B. Hàm số đạt cực tiểu tại
3
x
.
C. Hàm số đạt cực tiểu tại
1
x
. D. Hàm số đạt cực đại tại
1
x
.
Câu 9. [2D2-1] Cho
0
a
. Hãy viết biểu thức
4 5
4
3
a a
a a
dưới dạng lũy thừa với số mũ hữu tỉ.
A.
23
4
a
B.
3
4
a
. C.
19
4
a
. D.
9
2
a
.
Câu 10. [2D2-2] Tính tổng lập phương các nghiệm của phương trình
2 3 2 3
log .log 1 log log
x x x x
.
A.
5
. B.
35
. C.
13
. D.
125
.
Câu 11. [2D2-1] Cho
a
là số thực dương khác
1
. Mệnh đề nào dưới đây đúng với mọi số dương
x
,
y
.
A.
log log
a a
xy x y
. B.
log log log
a a a
xy x y
.
C.
log log
a a
xy x y
. D.
log log .log
a a a
xy x y
.
20
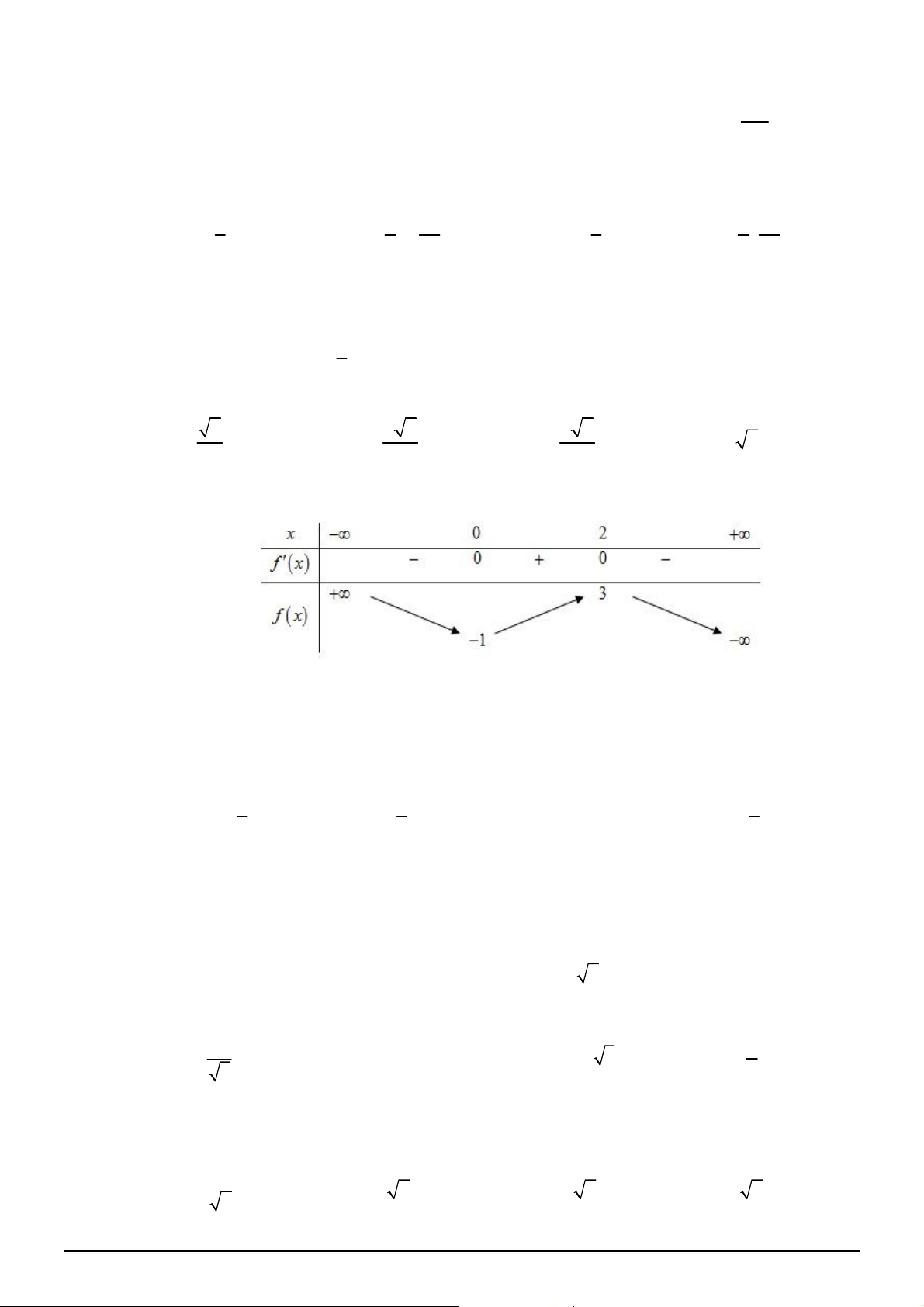
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/22 - Mã đề thi 132
Câu 12. [2D2-1] Tính đạo hàm của hàm số
3
x
y
.
A.
3 .ln3
x
y
. B.
1
.3
x
y x
. C.
3
x
y
. D.
1
.3
ln3
x
y
.
Câu 13. [2D1-1] Tìm điểm cực đại của đồ thị hàm số
3 2
2 5
2 1
3 2
y x x x
.
A.
1
2;
3
M
. B.
1 35
;
2 24
M
. C.
1
2;
3
M
. D.
1 35
;
2 24
M
.
Câu 14. [2H2-2] Tính thể tích của khối hộp chữ nhật
.
ABCD A B C D
có
3
AB
,
4
AD
,
5
AA
.
A.
60
V
. B.
10
V
. C.
20
V
. D.
12
V
.
Câu 15. [2D1-3] Cho hàm số
3 2
1
2 2 1
3
y x x x C
. Biết đồ thị
C
có hai tiếp tuyến cùng vuông
góc với đường thẳng :
d y x
. Gọi
h
là khoảng cách giữa hai tiếp tuyến đó. Tính
h
.
A.
2
3
h . B.
4 2
3
h . C.
2 2
3
h . D.
2
h
.
Câu 16. [2D1-2] Cho hàm số
y f x
có bảng biến thiên như sau:
Tìm tất cả các giá trị của tham số
m
để phương trình
f x m
có ba nghiệm thực phân biệt.
A.
1;3
m . B.
1;m
. C.
1;3
m . D.
;3
m .
Câu 17. [2D2-1] Tìm tập xác định
D
của hàm số
1
3
3 1
y x
.
A.
1
\
3
D
. B.
1
;
3
D
. C.
D
. D.
1
;
3
D
.
Câu 18. [2D1-2] Tìm số giao điểm của đồ thị hàm số
2
1 2
y x x x
với trục hoành.
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 19. [2D1-2] Tìm giá trị cực tiểu
CT
y
của hàm số
4 2
4 3
y x x
.
A.
3
CT
y
. B.
0
CT
y
. C.
2
CT
y . D.
1
CT
y
.
Câu 20. [2D2-1] Trong các hàm số sau, hàm số nào đồng biến trên
?
A.
2
3
x
y
. B.
0,99
x
y . C.
2 3
x
y . D.
2
3
x
y
.
Câu 21. [2H1-2] Cho khối chóp
.
S ABCD
có đáy là hình chữ nhật cạnh
2
AB a
,
AD a
. Hình chiếu
của đỉnh
S
lên mặt đáy là trung điểm cạnh
AB
, cạnh bên
SC
tạo với mặt phẳng đáy một góc
45
. Tính thể tích
V
của khối chóp đã cho.
A.
3
2 2
V a
. B.
3
2
3
a
V . C.
3
2 2
3
a
V . D.
3
2
6
a
V .
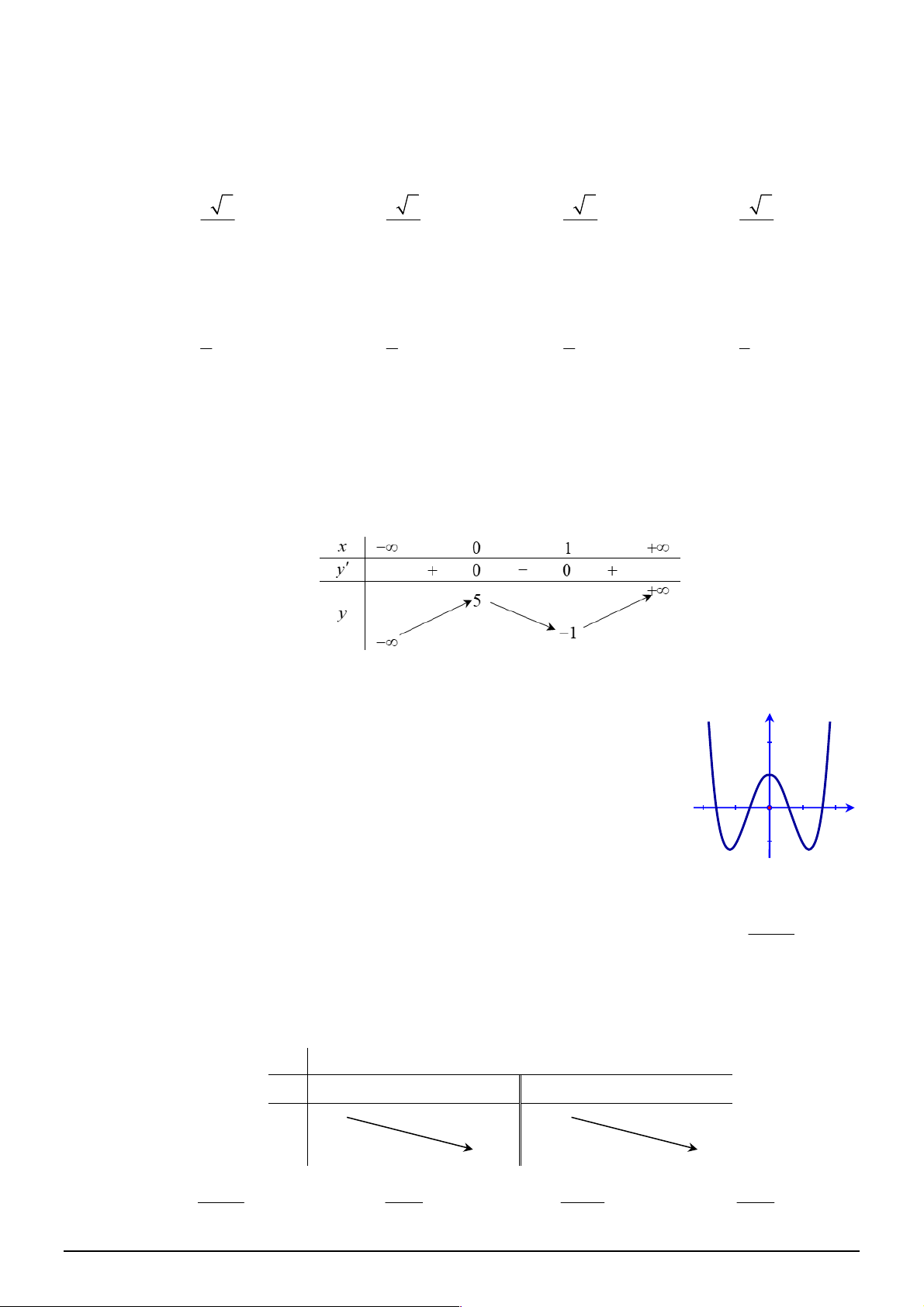
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/22 - Mã đề thi 132
Câu 22. [2D2-2] Cho hàm số
2
ln
f x x x
. Tính
e
f
?
A.
e
. B.
3e
. C.
2e
. D.
2 e
.
Câu 23. [2D1-3] Cho hàm số
3
1
y x mx
(với
m
là tham số). Tìm tất cả các giá trị của
m
để đồ thị
hàm số cắt trục hoành tại ba điểm phân biệt.
A.
3
3 2
2
m . B.
3
3 2
.
2
m C.
3
3 2
2
m . D.
3
3 2
.
2
m
Câu 24. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để hàm số
3 2
2 1 2
y x x m x
nghịch biến trên khoảng
;
.
A.
7
3
m
. B.
7
3
m
. C.
7
3
m
. D.
1
3
m
.
Câu 25. [2D2-1] Tìm tập xác định
D
của hàm số
2
ln 3
y x x
.
A.
; 0 3; D
. B.
; 0 3; D
.
C.
0; 3
D . D.
0; 3
D .
Câu 26. [2D1-1] Cho hàm số
y f x
có bảng biến thiên như hình bên. Mệnh đề nào dưới đây đúng?
A. Hàm số có điểm cực tiểu bằng
0
. B. Hàm số có điểm cực đại bằng
5
.
C. Hàm số có điểm cực tiểu bằng
1
. D. Hàm số có điểm cực tiểu bằng
1
.
Câu 27. [2D1-1] Đường cong ở hình vẽ là đồ thị của một trong bốn hàm
số dưới đây. Hàm số đó là hàm số nào?
A.
4 2
3 1
y x x
. B.
3 2
2 1
y x x
.
C.
3
3 1
y x x
. D.
4 2
3 1
y x x
.
Câu 28. [2D2-2] Gọi
S
là tập nghiệm của phương trình
2 1 1
2 5.2 3 0
x x
. Tìm
S
.
A.
3
1;log 2
S . B.
2
0;log 3
S . C.
2
1;log 3
S . D.
1
S .
Câu 29. [2D1-1] Đường thẳng nào cho dưới đây là tiệm cận ngang của đồ thị hàm số
2 3
1
x
y
x
.
A.
2
x
. B.
2
y
. C.
1
y
. D.
2
y
.
Câu 30. [2D1-2] Bảng sau là bảng biến thiên của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
A.
2 3
2
x
y
x
. B.
1
2
x
y
x
. C.
2 1
2
x
y
x
. D.
4
2
x
y
x
.
x
2
y
–
–
y
2
2
O
y
x
2
1
1
2
2
1
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/22 - Mã đề thi 132
Câu 31. [2D2-3] Ông A gửi vào ngân hàng
100
triệu đồng theo hình thức lãi suất kép. Lãi suất ngân
hàng là
8%
trên năm và không thay đổi qua các năm ông gửi tiền. Sau
5
năm ông cần tiền để
sửa nhà, ông đã rút toàn bộ số tiền và sử dụng một nửa số tiền đó vào công việc, số còn lại ông
tiếp tục gửi ngân hàng với hình thức như trên. Hỏi sau
10
năm ông A đã thu được số tiền lãi là
bao nhiêu? (đơn vị tính là triệu đồng).
A.
81,412.
B.
80,412.
C.
79,412.
D.
100,412.
Câu 32. [2D1-1] Cho đồ thị hàm số
3
: 3
C y f x x x
. Mệnh đề nào dưới đây sai?
A. Đồ thị
C
cắt trục tung tại một điểm.
B. Đồ thị
C
nhận gốc tọa độ
O
là tâm đối xứng.
C. Đồ thị
C
cắt trục hoành tại ba điểm phân biệt.
D. Đồ thị
C
nhận trục
Oy
làm trục đối xứng.
Câu 33. [2D1-2] Cho hàm số
2 1
1
x
y
x
. Phương trình tiếp tuyến tại điểm
2;5
M của đồ thị hàm số
trên là:
A.
3 11
y x
. B.
3 11
y x
. C.
3 11
y x
. D.
3 11
y x
.
Câu 34. [2H1-2] Cho khối chóp
.
S ABC
có
SA
,
SB
,
SC
đôi một vuông góc với nhau và
SA a
,
SB b
,
SC c
. Tính thể tích khối chóp
.
S ABC
.
A.
1
3
V abc
. B.
V abc
. C.
1
2
V abc
. D.
1
6
V abc
.
Câu 35. [2D1-2] Hàm số nào sau đây đồng biến trên khoảng
;
?
A.
3
1
y x
. B.
4
3
y x x
. C.
x
y e
. D.
1
2
x
y
x
.
Câu 36. [2H1-2] Cho khối tứ diện
ABCD
,
M
là trung điểm
AB
. Mặt phẳng
MCD
chia khối tứ diện
ABCD
thành hai khối đa diện nào?
A. Hai khối lăng trụ tam giác. B. Một lăng trụ tam giác và một khối tứ diện.
C. Hai khối tứ diện. D. Hai khối chóp tứ giác.
Câu 37. [2H2-1] Viết công thức thể tích
V
của khối cầu có bán kính
r
.
A.
3
1
3
V r
. B.
3
4
3
V r
. C.
3
V r
. D.
2
4
V r
.
Câu 38. [2H1-2] Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng
6
gần bằng số nào sau đây
nhất?
A.
46
. B.
48
. C.
52
. D.
51
.
Câu 39. [2H1-2] Cho hình chóp tứ giác đều có cạnh đáy bằng
a
và biết diện tích xung quanh gấp đôi
diện tích đáy. Tính thể tích của khối chóp.
A.
3
3
12
a
V . B.
3
3
3
a
V . C.
3
3
2
a
V . D.
3
3
6
a
V .
Câu 40. [2H1-2] Cho hình chóp tam giác đều có cạnh bên là
b
và chiều cao là
h
,
b h
. Tính thể tích
khối chóp đó.
A.
2 2
3
4
V b h h
. B.
2 2
3
12
V b h h
. .C.
2 2
3
4
V b h b
. D.
2 2
3
8
V b h h
.
Câu 41. [2D1-2] Tìm giá trị nhỏ nhất của hàm số
3 2
3 9 2
y x x x
trên đoạn
0;4
.
A.
0;4
min 2
y
. B.
0;4
min 34
y
. C.
0;4
min 25
y
. D.
0;4
min 18
y
.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/22 - Mã đề thi 132
Câu 42. [2H1-1] Nếu tăng chiều cao một khối chóp lên
2
lần và giảm diện tích đáy đi
6
lần thì thể tích
khối chóp đó tăng hay giảm bao nhiêu lần?
A. Tăng
3
lần. B. Giảm
3
lần.
C. Giảm
12
lần. D. Không tăng, không giảm.
Câu 43. [2D2-1] Tìm nghiệm của phương trình:
2
log 2 1 3
x
.
A.
9
2
x
. B.
8
x
. C.
7
2
x
. D.
5
x
.
Câu 44. [2H2-2] Cho tứ diện
ABCD
có
DA
vuông góc với mặt phẳng
ABC
và
AD a
,
2
AC a
;
cạnh
BC
vuông góc với cạnh
AB
. Tính bán kính
r
mặt cầu ngoại tiếp tứ diện
ABCD
.
A.
3
2
a
r . B.
r a
. C.
5
2
a
r . D.
5
r a
.
Câu 45. [2H1-2] Cho hình hộp chữ nhật
.
ABCD A B C D
có tâm
I
. Gọi
V
,
1
V
lần lượt là thể tích của
khối hộp
.
ABCD A B C D
và khối chóp
.
I ABCD
. Tính tỉ số
1
V
k
V
.
A.
1
6
k
. B.
1
12
k . C.
1
8
k
. D.
1
3
k
.
Câu 46. [2H2-1] Viết công thức diện tích xung quanh
xq
S
của hình nón tròn xoay có độ dài đường sinh
l
và bán kính đường tròn đáy
r
.
A.
xq
S rl
. B. 2
xq
S rl
. C.
xq
S rl
. D.
1
2
xq
S rl
.
Câu 47. [2H2-1] Một hình trụ có bán kính đáy
5
r
(cm), chiều cao
7
h
(cm). Tính diện tích xung quanh
của hình trụ.
A.
35
xq
S
(cm
2
). B.
70
xq
S
(cm
2
). C.
70
3
xq
S
(cm
2
). D.
35
3
xq
S
(cm
2
).
Câu 48. [2D1-1] Đồ thị hàm số nào dưới đây đi qua điểm
2; 1
M
?
A.
4 2
4 1
y x x
. B.
3
1
x
y
x
. C.
3
3 1
y x x
. D.
2 3
3
x
y
x
.
Câu 49. [2D2-2] Cho hàm số
1
1
x
y
x
. Gọi
M
là giá trị lớn nhất và
m
là giá trị nhỏ nhất của hàm số
trên đoạn
5; 1
. Tính
M m
.
A.
6.
B.
3
.
2
C.
6
.
5
D.
2
.
3
Câu 50. [2D2-2] Tìm
2017
0
e 1
lim .
x
x
x
A.
0.
B.
1.
C.
2017.
D.
.
----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/22 - Mã đề thi 132
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
B A
C A
B C B C
B
B A
A
D
C C B C D
C C B D
A
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
D
C B A
A
D
B D
A
C B D
D
A
C B A
C A
C B D
D
C
HƯỚNG DẪN GIẢI
Câu 1. [2D2-2] Đặt
3
log 45
a . Mệnh đề nào dưới đây đúng?
A.
45
2
log 5
a
a
. B.
45
1
log 5
a
a
. C.
45
2
log 5
a
a
. D.
45
2
log 5
a
a
.
Lời giải
Chọn D.
Ta có
3 3 3
log 45 log 9.5 2 log 5
a a . Do đó
3 5
1
log 5 2 log 3
2
a
a
.
Lại có
45
5
1
log 5
log 45
5
1
log 9.5
5
1
2log 3 1
1 2
2
1
2
a
a
a
.
Câu 2. [2D1-2] Cho hàm số
3 2
3 9 1
y x x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
3;1
. B. Hàm số nghịch biến trên khoảng
3;1
.
C. Hàm số nghịch biến trên khoảng
; 3
. D. Hàm số nghịch biến trên khoảng
1;
.
Lời giải
Chọn B.
Tập xác định
.
Ta có
2
3 6 9
y x x
. Do đó
2
0 3 6 9 1 3
y x x x x
.
Do hệ số
3 0
a
nên trên khoảng
3;1
thì
0
y
. Vậy hàm số đã cho nghịch biến trên
khoảng
3;1
.
Câu 3. [2D1-3] Đồ thị của hàm số
2
2
4 1
x
y
x
có bao nhiêu đường tiệm cận?
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn A.
Tập xác định
1 1
; ;
2 2
D
.
1
2
lim
x
y
;
1
2
lim
x
y
đồ thị hàm số có 2 đường tiệm cận đứng là hai đường thẳng
1
2
x
và
1
2
x
.
1
lim
2
x
y
;
1
lim
2
x
y
đồ thị hàm số có 2 đường tiệm cận ngang là hai đường thẳng
1
2
y
và
1
2
y
.
Vậy đồ thị của hàm số có
4
đường tiệm cận.
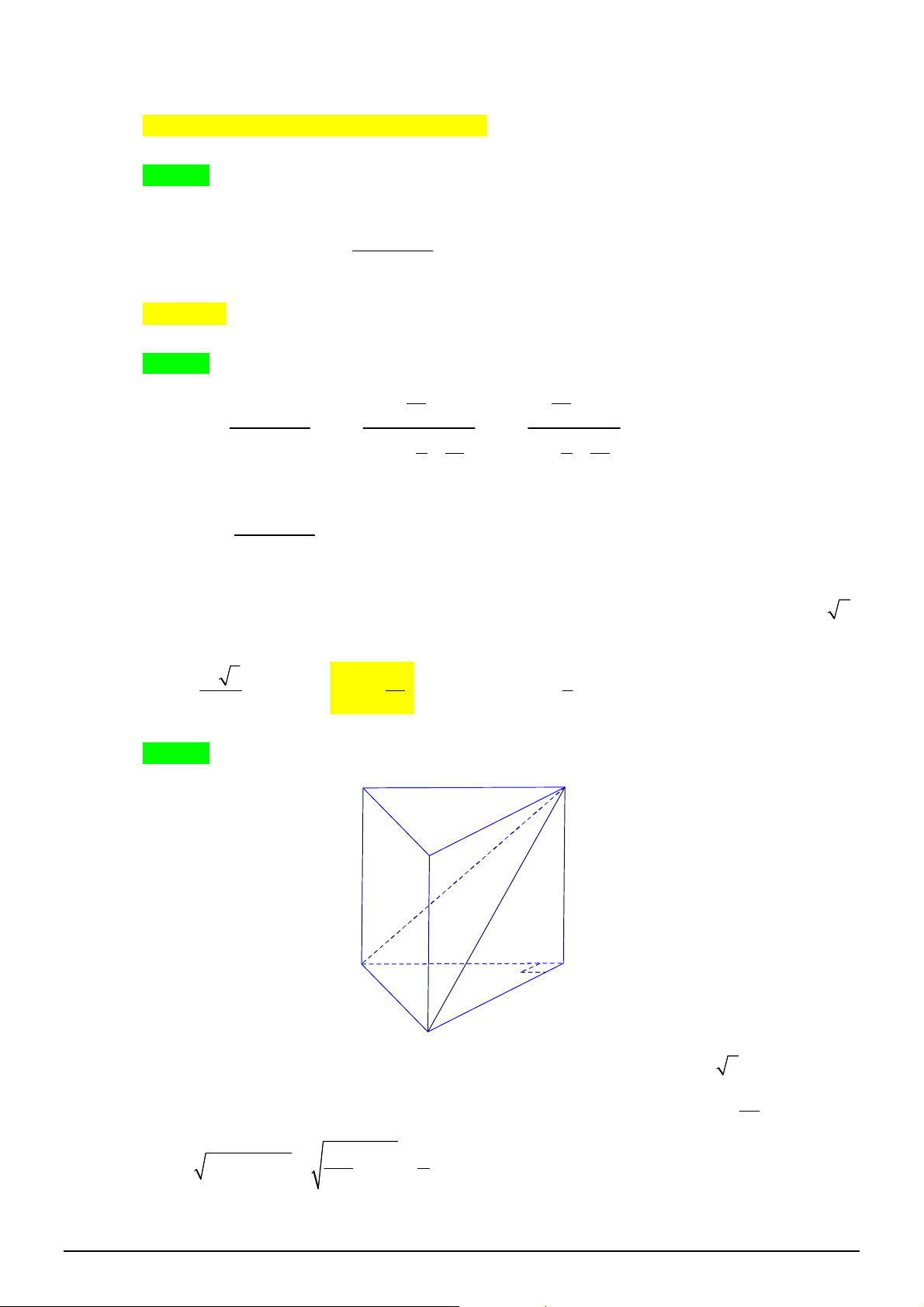
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/22 - Mã đề thi 132
Câu 4. [2H1-1] Cho một hình đa diện. Mệnh đề nào dưới đây sai?
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh. B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C. Mỗi cạnh là cạnh chung của ít nhất ba mặt. D. Mỗi mặt có ít nhất ba cạnh.
Lời giải
Chọn C.
Theo định nghĩa về hình đa diện thì mỗi cạnh là cạnh chung của đúng 2 mặt nên đáp án C.
Câu 5. [2D1-1] Đồ thị hàm số
2
2
1 2
6 9
x
y
x x
có tiệm cân đứng
x a
và tiệm cận ngang
y b
. Tính
giá trị
2
T a b
.
A.
4
T
. B.
1
T
. C.
8
T
. D.
6
T
.
Lời giải
Chọn A.
Ta có
2
2
2 2
2
2
2 2
1 1
2 2
1 2
lim lim lim 2
6 9 6 9
6 9
1 1
x x x
x
x
x x
x x
x
x x x x
nên đường thẳng
2
y
là tiệm cận ngang.
Lại có
2
2
3
1 2
lim
6 9
x
x
x x
nên đường thẳng
3
x
là tiệm cận đứng.
Suy ra
3
a
,
2
b
nên
2 4
T a b
Câu 6. [2H1-1] Cho lăng trụ đứng
1 1 1
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
C
,
2
AC a
.
Biết tam giác
1
ABC
có chu vi bằng
5
a
. Tính thể tích
V
của khối lăng trụ
1 1 1
.
ABC A B C
.
A.
3
3
2
a
V . B.
3
2
a
V . C.
3
1
3
V a
. D.
3
V a
.
Lời giải
Chọn A.
Vì là
1 1 1
.
ABC A B C
lăng trụ đứng và tam giác
ABC
vuông cân tại
C
,
2
AC a
nên
1 1
C B C A
và
2
AB a
. Chu vi tam giác
1
C AB
bằng
1
2 5
C B AB a
1
3
2
a
C B , từ đó ta có
2
2 2 2
1 1
9
2
4 2
a a
CC C B CB a
.
A
1
A
1
B
1
C
C
B
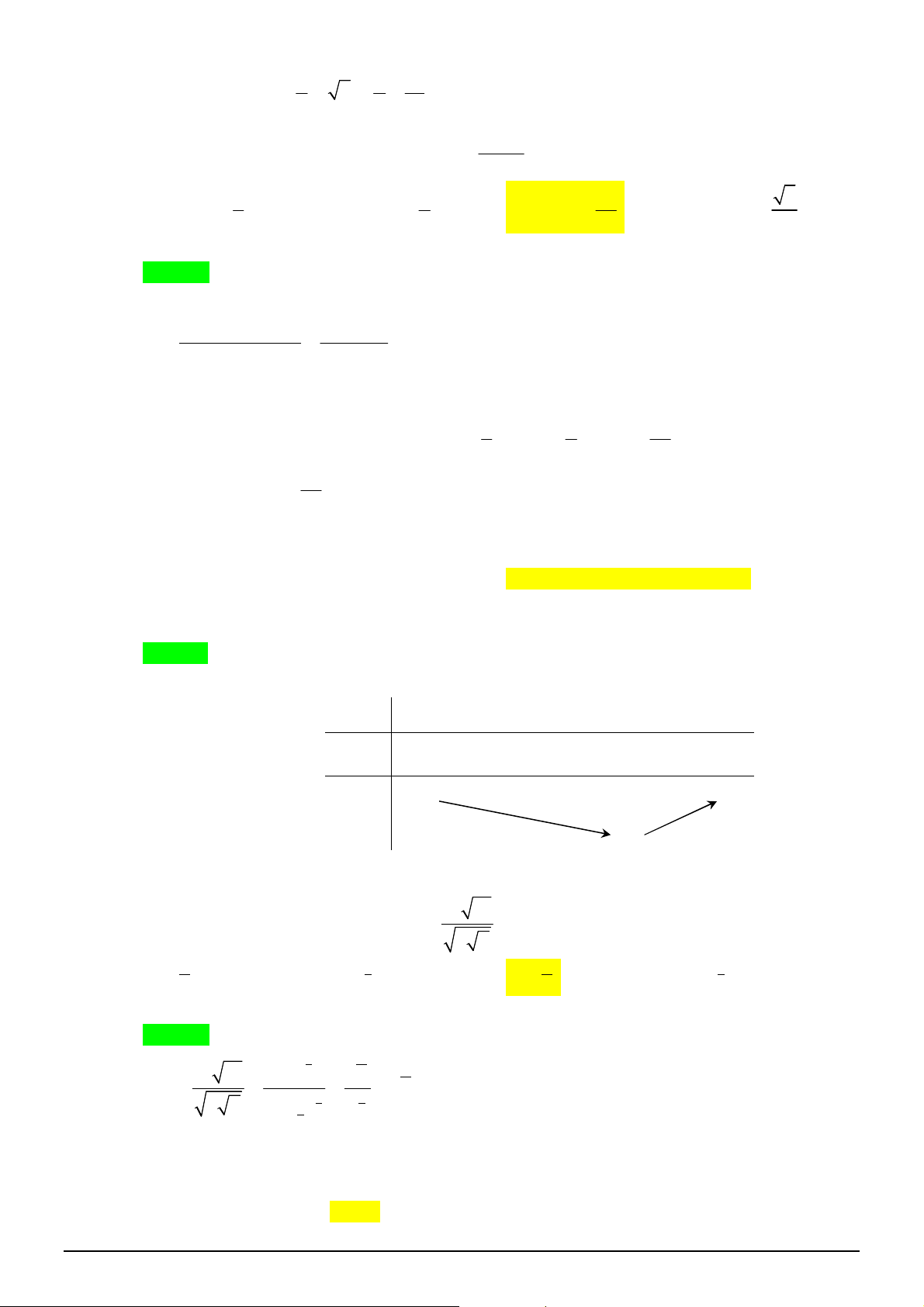
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/22 - Mã đề thi 132
Thể tích
1 1 1
3
2
.
1
2 .
2 2 2
ABC A B C
a a
V a .
Câu 7. [2D1-2] Tìm giá trị lớn nhất của hàm số
2
4
x
y
x
trên đoạn
1;5
.
A.
1;5
1
max
5
y
. B.
1;5
1
max
4
y
. C.
1;5
5
max
29
y . D.
1;5
2
max
6
y .
Lời giải
Chọn C.
Ta có:
D
2
2
2 2
2 2
4 2
4
4 4
x x x
x
y
x x
2
0 4 0 2
y x x
Vì hàm số liên tục trên đoạn
1;5
và
1
1
5
f
,
1
2
4
f
,
5
5
29
f .
Nên suy ra:
1;5
5
max
29
y
.
Câu 8. [2D1-2] Cho hàm số
f x
có đạo hàm
2
1 3
f x x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại
3
x
. B. Hàm số đạt cực tiểu tại
3
x
.
C. Hàm số đạt cực tiểu tại
1
x
. D. Hàm số đạt cực đại tại
1
x
.
Lời giải
Chọn B.
Bảng biến thiên:
Suy ra: Hàm số đạt cực tiểu tại
3
x
.
Câu 9. [2D2-1] Cho
0
a
. Hãy viết biểu thức
4 5
4
3
a a
a a
dưới dạng lũy thừa với số mũ hữu tỉ.
A.
23
4
a
B.
3
4
a
. C.
19
4
a
. D.
9
2
a
.
Lời giải
Chọn C.
Ta có
5 21
19
4 5 44
4 4
4
1 1
3
1
3 2
2
.
.
a a a a a
a
a a
a
a a
.
Câu 10. [2D2-2] Tính tổng lập phương các nghiệm của phương trình
2 3 2 3
log .log 1 log log
x x x x
.
A.
5
. B.
35
. C.
13
. D.
125
.
x
1
3
f x
0
0
f x
CT
y

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/22 - Mã đề thi 132
Lời giải
Chọn B.
Điều kiện
0
x
.
Cách 1.
2 3 2 3
log .log 1 log log
x x x x
.
2 3 2 2 3 2
log .log 2.log 1 log log 2.log
x x x x
.
2
3 2 3 2
log 2. log 1 log 2 log 1 0
x x
.
2
2 2
3
log 1
1
log log 3
log 2
x
x
2
3
x
x
(nhận).
Vậy tổng lập phương các nghiệm là
35
.
Cách 2.
2 3 2 3
log .log 1 log log
x x x x
2 3 2 3
log .log log 1 log 0
x x x x
2 3 3
log . log 1 log 1 0
x x x
2 3
log 1 . log 1 0
x x
2
3
log 1
2
log 1
3
x
x
x x
(nhận).
Vậy tổng lập phương các nghiệm là
35
.
Câu 11. [2D2-1] Cho
a
là số thực dương khác
1
. Mệnh đề nào dưới đây đúng với mọi số dương
x
,
y
.
A.
log log
a a
xy x y
. B.
log log log
a a a
xy x y
.
C.
log log
a a
xy x y
. D.
log log .log
a a a
xy x y
.
Lời giải
Chọn B.
Theo công thức biến đổi lôgarit của một tích ta có
log log log
a a a
xy x y
.
Câu 12. [2D2-1] Tính đạo hàm của hàm số
3
x
y
.
A.
3 .ln3
x
y
. B.
1
.3
x
y x
. C.
3
x
y
. D.
1
.3
ln3
x
y
.
Lời giải
Chọn A.
Sử dụng công thức đạo hàm của hàm số mũ ta có
3 3 .ln3
x x
y
.
Câu 13. [2D1-1] Tìm điểm cực đại của đồ thị hàm số
3 2
2 5
2 1
3 2
y x x x
.
A.
1
2;
3
M
. B.
1 35
;
2 24
M
. C.
1
2;
3
M
. D.
1 35
;
2 24
M
.
Lời giải
Chọn A.
TXĐ:
D
.
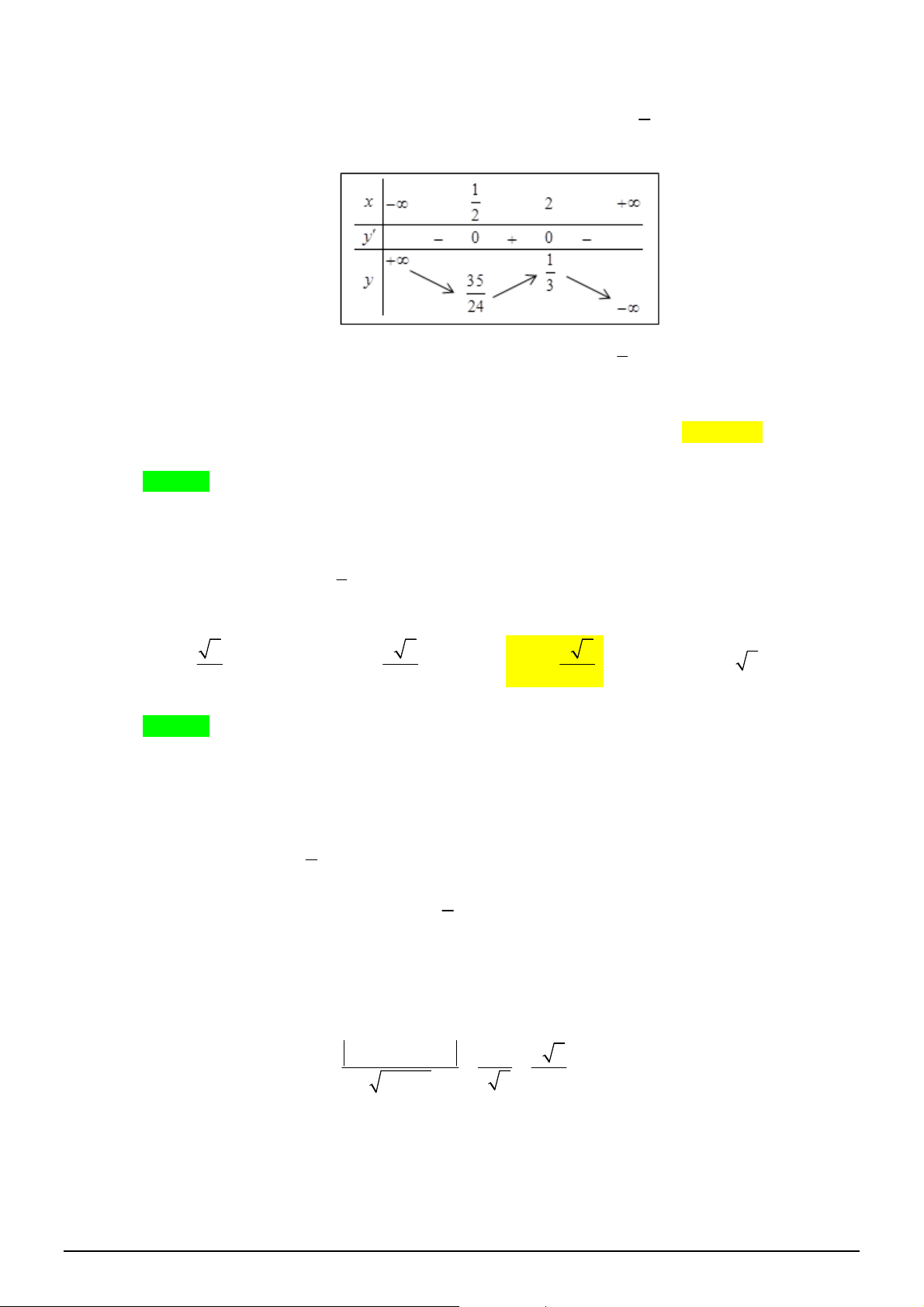
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/22 - Mã đề thi 132
Ta có
3 2
2 5 2
y x x
suy ra
2 2
2
0 2 5 2 0
1
2
x
y x x
x
.
Lập bảng biên thiên
Căn cứ vào BBT ta có điểm cực đại của đồ thị hàm số là
1
2;
3
M
.
Câu 14. [2H2-2] Tính thể tích của khối hộp chữ nhật
.
ABCD A B C D
có
3
AB
,
4
AD
,
5
AA
.
A.
60
V
. B.
10
V
. C.
20
V
. D.
12
V
.
Lời giải
Chọn D.
Theo giả thiết
.
ABCD A B C D
là hình hộp chữ nhật có
3
AB
,
4
AD
,
5
AA
nên ta có
thể tích hình hộp chữ nhật là
. . 3.4.5 60
V AA AB AD
.
Câu 15. [2D1-3] Cho hàm số
3 2
1
2 2 1
3
y x x x C
. Biết đồ thị
C
có hai tiếp tuyến cùng vuông
góc với đường thẳng :
d y x
. Gọi
h
là khoảng cách giữa hai tiếp tuyến đó. Tính
h
.
A.
2
3
h . B.
4 2
3
h . C.
2 2
3
h . D.
2
h
.
Lời giải
Chọn C.
Ta có:
2
4 2
y x x
.
Gọi
0
x
là hoành độ tiếp điểm. Tiếp tuyến của đồ thị hàm số vuông góc với
2 2
0 0 0 0 0
: 4 2 1 4 3 0 1
d y x x x x x x
hoặc
0
3
x
.
Với
0
1
x
0
4
3
y
và
0
1
f x
Phương trình tiếp tuyến
1
7
: 3 3 7 0
3
d y x x y
Với
0
3
x
0
2 3; 2
y A
Vì hai tiếp tuyến
1
d
và
2
d
cùng vuông góc với đường thẳng :
d y x
nên
1 2
//
d d
, do đó
khoảng cách giữa hai tiếp tuyến bằng khoảng cách từ
3; 2
A
đến
1
d
.
1 2 1
2 2
3.3 3 2 7
4 2 2
, ,
3
3 2
3 3
h d d d d A d
.
Câu 16. [2D1-2] Cho hàm số
y f x
có bảng biến thiên như sau:

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/22 - Mã đề thi 132
Tìm tất cả các giá trị của tham số
m
để phương trình
f x m
có ba nghiệm thực phân biệt.
A.
1;3
m . B.
1;m
. C.
1;3
m . D.
;3
m .
Lời giải
Chọn C.
Dựa vào bảng biến thiên ta thấy đáp án C đúng.
Câu 17. [2D2-1] Tìm tập xác định
D
của hàm số
1
3
3 1
y x
.
A.
1
\
3
D
. B.
1
;
3
D
. C.
D
. D.
1
;
3
D
.
Lời giải
Chọn B.
Điều kiện xác định:
1
3 1 0
3
x x
.
Vậy tập xác định của hàm số
1
3
3 1
y x
là
1
;
3
D
.
Câu 18. [2D1-2] Tìm số giao điểm của đồ thị hàm số
2
1 2
y x x x
với trục hoành.
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn C.
Tọa độ giao điểm của đồ thị hàm số
2
1 2
y x x x
với trục hoành có hoành độ là nghiệm
của phương trình:
2
1 2 0
x x x
2
1
1 0
0
2 0
2
x
x
x
x x
x
Ta có các giao điểm là:
0;0
,
1;0
,
2;0
.
Câu 19. [2D1-2] Tìm giá trị cực tiểu
CT
y
của hàm số
4 2
4 3
y x x
.
A.
3
CT
y
. B.
0
CT
y
. C.
2
CT
y . D.
1
CT
y
.
Lời giải
Chọn D.
3
4 8
y x x
.
2
2
0 4 2 0
0
x
y x x
x
.
Cách 1: Bảng biến thiên:
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/22 - Mã đề thi 132
Dựa vào bảng biến thiên, hàm snố đạt cực tiểu tại
2
x
, khi đó giá trị cực tiểu
1
CT
y
.
Cách 2:
2
12 8
y x
.
2 16 0
f
nên hàm số đạt cực tiểu tại
2
x
, khi đó giá trị cực tiểu
1
CT
y .
Câu 20. [2D2-1] Trong các hàm số sau, hàm số nào đồng biến trên
?
A.
2
3
x
y
. B.
0,99
x
y . C.
2 3
x
y . D.
2
3
x
y
.
Lời giải
Chọn C.
Theo tính chất của hàm số mũ, hàm số
x
y a
đồng biến trên
khi
1
a
.
Ta có:
2 3 1
do đó hàm số
2 3
x
y đồng biến trên
.
Câu 21. [2H1-2] Cho khối chóp
.
S ABCD
có đáy là hình chữ nhật cạnh
2
AB a
,
AD a
. Hình chiếu
của đỉnh
S
lên mặt đáy là trung điểm cạnh
AB
, cạnh bên
SC
tạo với mặt phẳng đáy một góc
45
. Tính thể tích
V
của khối chóp đã cho.
A.
3
2 2
V a
. B.
3
2
3
a
V . C.
3
2 2
3
a
V . D.
3
2
6
a
V .
Lời giải
Chọn C.
Ta có diện tích đáy của hình chóp
.
S ABCD
là:
2
2
ABCD
S a
.
Goi
I
là trung điểm của
AB
thì chiều cao của khối chóp
.
S ABCD
là
h SI
và
2
IC a
.
Tam giác
SIC
vuông cân tại
I
có:
2
SI IC a
.
Vậy thể tích khối chóp đã cho là:
3
2 2
3
a
V .
Câu 22. [2D2-2] Cho hàm số
2
ln
f x x x
. Tính
e
f
?
A.
e
. B.
3e
. C.
2e
. D.
2 e
.
Lời giải
x
2
0
2
y
0
0
0
y
1
3
1
A
B
C
D
S
I
45

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/22 - Mã đề thi 132
Chọn B.
Ta có
2 ln
f x x x x
e 2e e 3e
f
.
Câu 23. [2D1-3] Cho hàm số
3
1
y x mx
(với
m
là tham số). Tìm tất cả các giá trị của
m
để đồ thị
hàm số cắt trục hoành tại ba điểm phân biệt.
A.
3
3 2
2
m . B.
3
3 2
.
2
m C.
3
3 2
2
m . D.
3
3 2
.
2
m
Lời giải
Chọn D.
Tập xác định:
D
2
3
y x m
.
Hàm số có 2 cực trị
0
y
có 2 nghiệm phân biệt
0
m
.
Phương trình đường thẳng qua 2 cực trị:
2
1
3
m
y x
.
Đồ thị hàm số cắt trục hoành tại ba điểm phân biệt
Đồ thị hàm số có 2 điểm cực trị nằm về
hai phía trục hoành.
. 0
CĐ CT
y y
2 2
1 . 1 0
3 3
CCĐ T
m m
x x
2
4 2
. 1 0
9 3
CT C CCĐ Đ T
m
x x m x x
3
3
4 3 2
1 0
27 2
m
m .
Câu 24. [2D1-2] Tìm tất cả các giá trị thực của tham số
m
để hàm số
3 2
2 1 2
y x x m x
nghịch biến trên khoảng
;
.
A.
7
3
m
. B.
7
3
m
. C.
7
3
m
. D.
1
3
m
.
Lời giải
Chọn A.
Tập xác định:
D
2
3 4 1
y x x m
.
Hàm số nghịch biến trên
;
0
0,
a
y x
4 3 1 0
m
7
3
m
.
Câu 25. [2D2-1] Tìm tập xác định
D
của hàm số
2
ln 3
y x x
.
A.
; 0 3; D
. B.
; 0 3; D
.
C.
0; 3
D . D.
0; 3
D .
Lời giải
Chọn B.
Hàm số
2
ln 3
y x x
xác định khi
2
0
3 0
3
x
x x
x
.
Câu 26. [2D1-1] Cho hàm số
y f x
có bảng biến thiên như hình bên. Mệnh đề nào dưới đây đúng?
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/22 - Mã đề thi 132
A. Hàm số có điểm cực tiểu bằng
0
. B. Hàm số có điểm cực đại bằng
5
.
C. Hàm số có điểm cực tiểu bằng
1
. D. Hàm số có điểm cực tiểu bằng
1
.
Lời giải
Chọn D.
Dựa vào BBT hàm số có điểm cực tiểu bằng
1
.
Câu 27. [2D1-1] Đường cong ở hình vẽ là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm
số nào?
A.
4 2
3 1
y x x
. B.
3 2
2 1
y x x
. C.
3
3 1
y x x
. D.
4 2
3 1
y x x
.
Lời giải
Chọn D.
Ta thấy đường cong ở hình vẽ là đồ thị của hàm trùng phương nên loại phương án B và C.
Đồ thị cắt trục tung tại điểm có tung độ bằng
1
nên phương án D thỏa mãn, loại phương án A.
Câu 28. [2D2-2] Gọi
S
là tập nghiệm của phương trình
2 1 1
2 5.2 3 0
x x
. Tìm
S
.
A.
3
1;log 2
S . B.
2
0;log 3
S . C.
2
1;log 3
S . D.
1
S .
Lời giải
Chọn C.
Ta có
2
2 1 1 2
log 3
2 3
1 5
2 5.2 3 0 2 2 3 0
12 2
2 2
x
x x x x
x
x
x
.
Câu 29. [2D1-1] Đường thẳng nào cho dưới đây là tiệm cận ngang của đồ thị hàm số
2 3
1
x
y
x
.
A.
2
x
. B.
2
y
. C.
1
y
. D.
2
y
.
Lời giải
Chọn B.
Tập xác định
\ 1
D
.
Ta có:
3
2
2 3
lim lim lim 2
1
1
1
x x x
x
x
y
x
x
và
3
2
2 3
lim lim lim 2
1
1
1
x x x
x
x
y
x
x
.
Suy ra đường thẳng
2
y
là đường tiệm cận ngang của đồ thị hàm số
2 3
1
x
y
x
.
Câu 30. [2D1-2] Bảng sau là bảng biến thiên của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
O
y
x
2
1
1
2
2
1
1

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/22 - Mã đề thi 132
A.
2 3
2
x
y
x
. B.
1
2
x
y
x
. C.
2 1
2
x
y
x
. D.
4
2
x
y
x
.
Lời giải
Chọn A.
Dựa vào bảng biến thiên ta có:
lim lim 2
x x
y y
và
2
lim
x
y
;
2
lim
x
y
.
Vậy đồ thị hàm số có tiệm cận đứng là đường thẳng
2
x
và tiệm cận ngang đường thẳng
2
y
.
Câu 31. [2D2-3] Ông A gửi vào ngân hàng
100
triệu đồng theo hình thức lãi suất kép. Lãi suất ngân
hàng là
8%
trên năm và không thay đổi qua các năm ông gửi tiền. Sau
5
năm ông cần tiền để
sửa nhà, ông đã rút toàn bộ số tiền và sử dụng một nửa số tiền đó vào công việc, số còn lại ông
tiếp tục gửi ngân hàng với hình thức như trên. Hỏi sau
10
năm ông A đã thu được số tiền lãi là
bao nhiêu? (đơn vị tính là triệu đồng).
A.
81,412.
B.
80,412.
C.
79,412.
D.
100,412.
Lời giải
Chọn A.
Áp dụng công thức lãi kép:
1
n
n
T A r
với:
n
T
là số tiền cả vốn lẫn lãi nhận được sau
n
kì hạn.
A
là số tiền gửi ban đầu.
r
là lãi suất trong một kì hạn.
n
số kì hạn.
+ Giai đoạn 1: Sau 5 năm đầu, ông A thu được số tiền cả vốn lẫn lãi là:
5
5
100. 1 8% 146,933
T triệu đồng.
Do đó lãi suất của giai đoạn 1 là:
146,933 100 46,933
triệu đồng.
+ Giai đoạn 2: Sau 5 kế tiếp, ông A thu được số tiền cả vốn lẫn lãi là:
5
10
146,933
. 1 8% 107,946
2
T triệu đồng.
Do đó lãi suất của giai đoạn 2 là:
146,933
107,946 34,479
2
triệu đồng.
Tổng số lãi nhận được của hai giai đoạn là:
46,933 34,479 81,412
triệu đồng.
Câu 32. [2D1-1] Cho đồ thị hàm số
3
: 3
C y f x x x
. Mệnh đề nào dưới đây sai?
A. Đồ thị
C
cắt trục tung tại một điểm.
B. Đồ thị
C
nhận gốc tọa độ
O
là tâm đối xứng.
C. Đồ thị
C
cắt trục hoành tại ba điểm phân biệt.
D. Đồ thị
C
nhận trục
Oy
làm trục đối xứng.
Lời giải
Chọn D.
x
2
y
–
–
y
2
2

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/22 - Mã đề thi 132
Xét phương án A: Cho
0
x
ta được
0
y
C
cắt trục tung tại điểm
0;0
O . Vậy A
đúng.
Xét phương án B: Hàm số đã cho có
;f x f x x
nên nó là hàm số lẻ, do đó đồ thị
nhận gốc tọa độ làm tâm đối xứng. Vậy B đúng.
Xét phương án C: Phương trình hoành độ giao điểm của
C
và
Ox
:
3
0
3 0 3
3
x
x x x
x
nên đồ thị
C
cắt trục hoành tại ba điểm phân biệt. Vậy C đúng.
Xét phương án D: Đây là hàm số lẻ nên đồ thị không thể nhận trục tung làm trục đối xứng. Vậy
D sai.
Câu 33. [2D1-2] Cho hàm số
2 1
1
x
y
x
. Phương trình tiếp tuyến tại điểm
2;5
M của đồ thị hàm số
trên là:
A.
3 11
y x
. B.
3 11
y x
. C.
3 11
y x
. D.
3 11
y x
.
Lời giải
Chọn B.
2 1
1
x
y
x
. TXĐ:
\ 1
D
.
2
3
1
y
x
2 3
y
.
Vậy tiếp tuyến của đồ thị hàm số tại điểm
2;5
M có phương trình là
3 2 5 3 11
y x y x
.
Câu 34. [2H1-2] Cho khối chóp
.
S ABC
có
SA
,
SB
,
SC
đôi một vuông góc với nhau và
SA a
,
SB b
,
SC c
. Tính thể tích khối chóp
.
S ABC
.
A.
1
3
V abc
. B.
V abc
. C.
1
2
V abc
. D.
1
6
V abc
.
Lời giải
Chọn D.
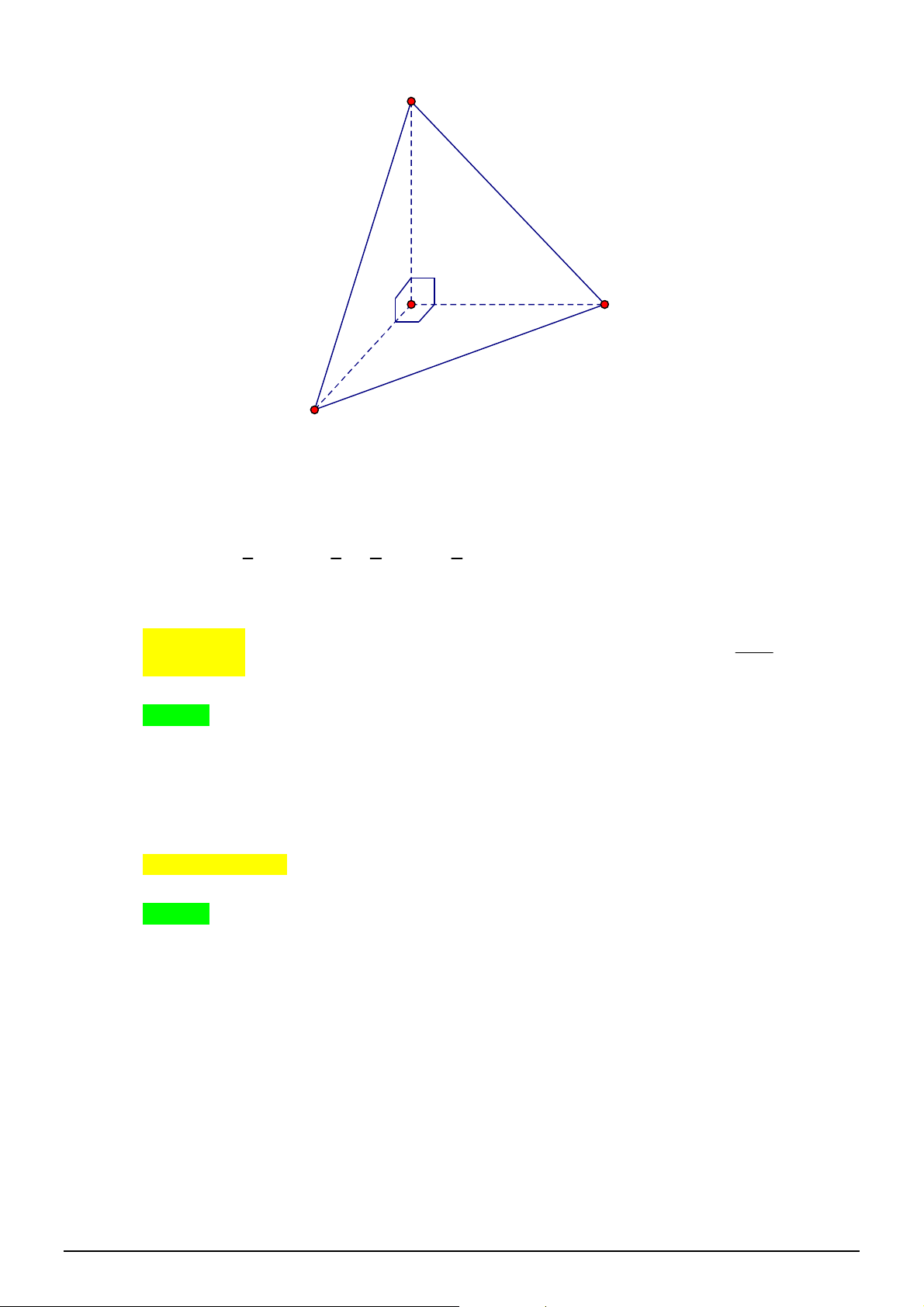
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/22 - Mã đề thi 132
b
c
a
C
B
A
S
Ta có:
SA SB
SA SBC
SA SC
.
SB SC SBC
vuông tại
S
.
Vậy
.
1 1 1 1
. . .
3 3 2 6
S ABC SBC
V SA S SA SB SC abc
.
Câu 35. [2D1-2] Hàm số nào sau đây đồng biến trên khoảng
;
?
A.
3
1
y x
. B.
4
3
y x x
. C.
x
y e
. D.
1
2
x
y
x
.
Lời giải
Chọn A.
Ta có
3
1
y x
2
3 0,y x x
và
0 0
y x
hàm số luôn đồng biến trên
Câu 36. [2H1-2] Cho khối tứ diện
ABCD
,
M
là trung điểm
AB
. Mặt phẳng
MCD
chia khối tứ diện
ABCD
thành hai khối đa diện nào?
A. Hai khối lăng trụ tam giác. B. Một lăng trụ tam giác và một khối tứ diện.
C. Hai khối tứ diện. D. Hai khối chóp tứ giác.
Lời giải
Chọn C.
Mặt phẳng
MCD
chia khối tứ diện
ABCD
thành hai khối tứ diện
MBCD
và
AMCD
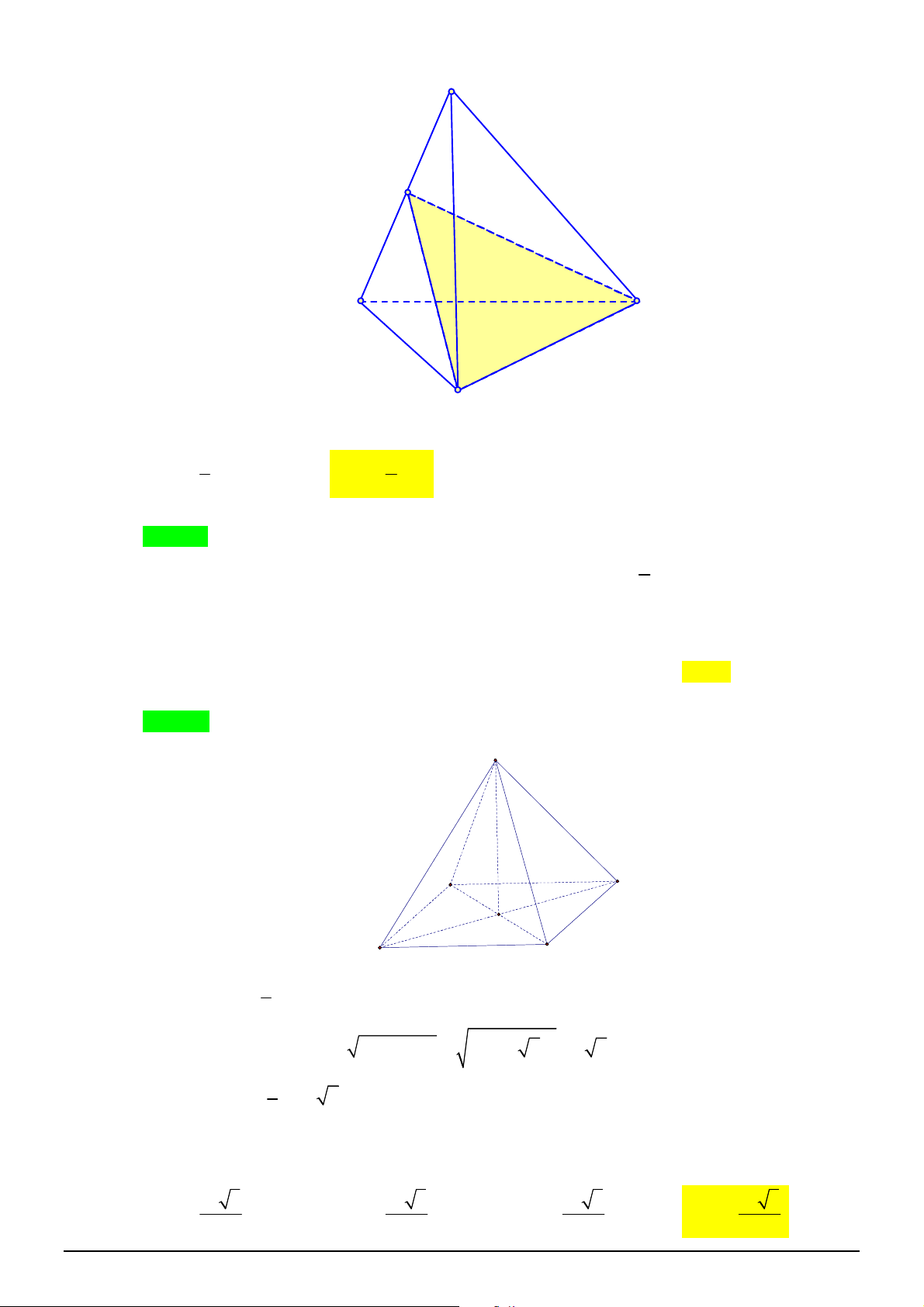
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/22 - Mã đề thi 132
Câu 37. [2H2-1] Viết công thức thể tích
V
của khối cầu có bán kính
r
.
A.
3
1
3
V r
. B.
3
4
3
V r
. C.
3
V r
. D.
2
4
V r
.
Lời giải
Chọn B.
Ta có công thức tính thể tích
V
của khối cầu có bán kính
r
là
3
4
3
V r
.
Câu 38. [2H1-2] Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng
6
gần bằng số nào sau đây
nhất?
A.
46
. B.
48
. C.
52
. D.
51
.
Lời giải
Chọn D.
O
C
A
D
B
S
Ta có
.
1
3
S ABCD ABCD
V S SO
.
Mà
2
6 36
ABCD
S
;
2
2 2 2
6 3 2 3 2
SO SA OA .
Suy ra
.
1
.36.3 2 50,912
3
S ABCD
V .
Câu 39. [2H1-2] Cho hình chóp tứ giác đều có cạnh đáy bằng
a
và biết diện tích xung quanh gấp đôi
diện tích đáy. Tính thể tích của khối chóp.
A.
3
3
12
a
V . B.
3
3
3
a
V . C.
3
3
2
a
V . D.
3
3
6
a
V .
A
B
C
D
M
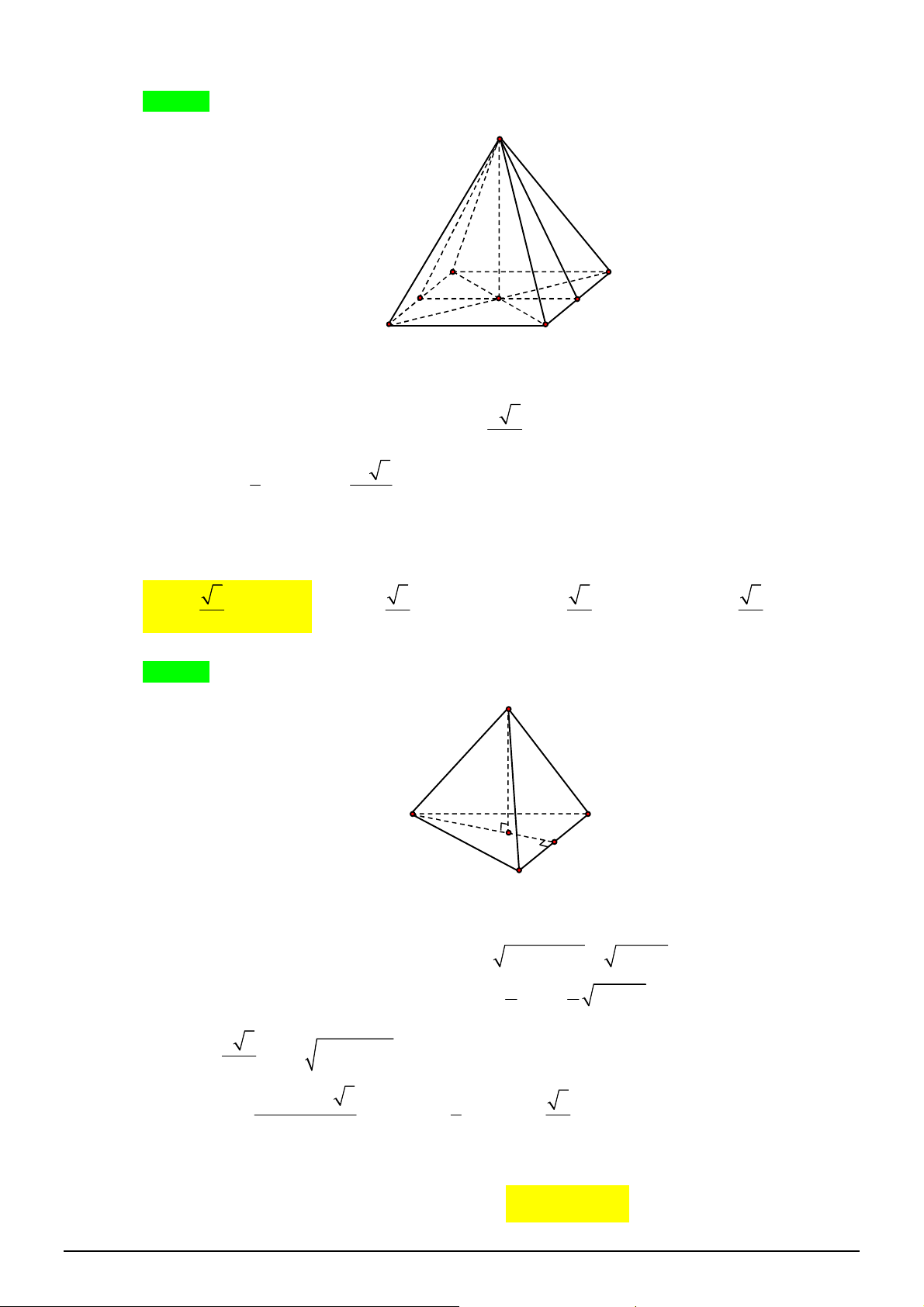
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/22 - Mã đề thi 132
Lời giải
Chọn D.
Giả sử
.
S ABCD
là hình chóp tứ giác đều cạnh
a
,
O
là tâm mặt đáy.
Ta có 2
xq ABCD
S S
2
4 2 .
SAB ABCD
S S SH AB a SH a
.
Khi đó
SHK
là tam giác đều cạnh
a
3
2
a
SO
Vậy
3
.
1 3
.
3 6
S ABCD ABCD
a
V S SO .
Câu 40. [2H1-2] Cho hình chóp tam giác đều có cạnh bên là
b
và chiều cao là
h
,
b h
. Tính thể tích
khối chóp đó.
A.
2 2
3
4
V b h h
. B.
2 2
3
12
V b h h
. .C.
2 2
3
4
V b h b
. D.
2 2
3
8
V b h h
.
Lời giải
Chọn A.
Giả sử
.
S ABC
là hình chóp tam giác đều,
H
là tâm mặt đáy.
Ta có:
Tam giác
SAH
vuông tại
H
có
2 2 2 2
AH SA SH b h
.
Tam giác
ABC
đều có đường cao
2 2
3 3
2 2
AK AH b h
và
2 2
2 3
3
3
AB AK b h
.
Khi đó
2 2
3 3
4
ABC
b h
S
và
2 2
.
1 3
.
3 4
S ABC ABC
V S SH b h h
.
Câu 41. [2D1-2] Tìm giá trị nhỏ nhất của hàm số
3 2
3 9 2
y x x x
trên đoạn
0;4
.
A.
0;4
min 2
y
. B.
0;4
min 34
y
. C.
0;4
min 25
y
. D.
0;4
min 18
y
.
S
A
B
C
H
K
b
h
S
A
B
C
D
O
H
K

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/22 - Mã đề thi 132
Lời giải
Chọn C.
Hàm số
3 2
3 9 2
y x x x
xác định và liên tục trên đoạn
0;4
.
Đạo hàm
2
3 6 9
y x x
. Ta có
0
y
2
3 6 9 0
x x
3 0;4
1 0;4
x
x
.
Ta có:
0 2
y
;
4 18
y
;
3 25
y
. Vậy
0;4
min 25
y
.
Câu 42. [2H1-1] Nếu tăng chiều cao một khối chóp lên
2
lần và giảm diện tích đáy đi
6
lần thì thể tích
khối chóp đó tăng hay giảm bao nhiêu lần?
A. Tăng
3
lần. B. Giảm
3
lần.
C. Giảm
12
lần. D. Không tăng, không giảm.
Lời giải
Chọn B.
Gọi
V
,
h
,
B
lần lượt là thể tích, chiều cao, diện tích đáy của khối chóp ban đầu.
Ta có
1
. .
3
V h B
.
Khối chóp sau khi thay đổi có chiều cao là
2
h
và diện tích đáy là
6
B
.
Thể tích khối chóp sau khi thay đổi là
1
.2 .
3 6
B
V h
1 1
. . .
3 3
h B
1
.
3
V
.
Vậy thể tích khối chóp giảm đi
3
lần.
Câu 43. [2D2-1] Tìm nghiệm của phương trình:
2
log 2 1 3
x
.
A.
9
2
x
. B.
8
x
. C.
7
2
x
. D.
5
x
.
Lời giải
Chọn A.
Điều kiện:
1
2
x
.
Với điều kiện trên,
2
log 2 1 3
x
3
2 1 2
x
9
2
x N
.
Câu 44. [2H2-2] Cho tứ diện
ABCD
có
DA
vuông góc với mặt phẳng
ABC
và
AD a
,
2
AC a
;
cạnh
BC
vuông góc với cạnh
AB
. Tính bán kính
r
mặt cầu ngoại tiếp tứ diện
ABCD
.
A.
3
2
a
r . B.
r a
. C.
5
2
a
r . D.
5
r a
.
Lời giải
Chọn C.
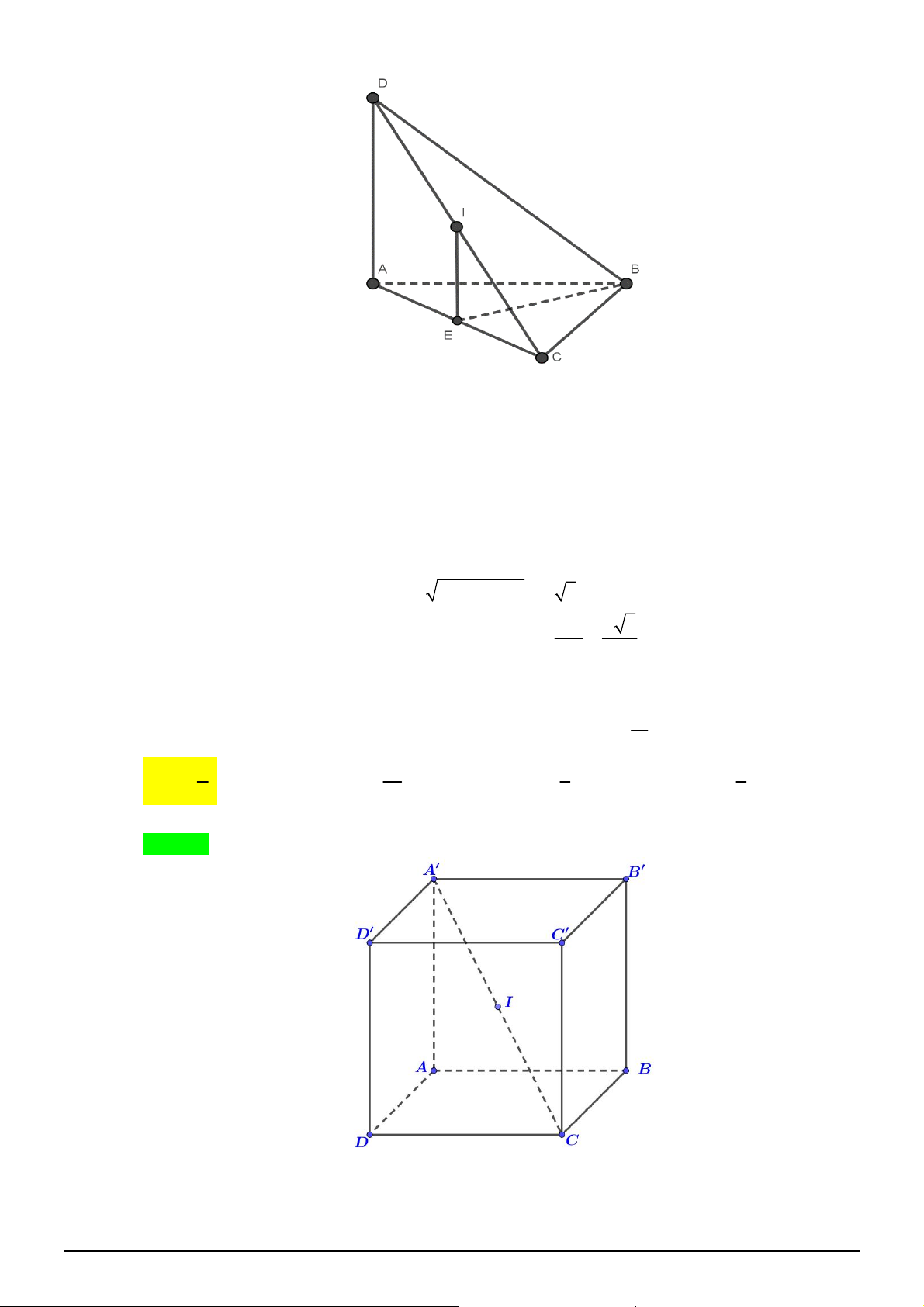
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/22 - Mã đề thi 132
Ta có:
DA BC
DA ABC
DA AC
.
DA BC
BC DB
AB BC
90 1
DBC
.
DA AC
90 2
DAC
.
1
,
2
tứ diện
ABCD
nội tiếp mặt cầu đường kính
DC
.
Xét
ADC
vuông tại
A
, ta có:
2 2
5
CD AD AC a
.
Vậy bán kính mặt cầu ngoại tiếp tứ diện
ABCD
là
5
2 2
CD a
r .
Câu 45. [2H1-2] Cho hình hộp chữ nhật
.
ABCD A B C D
có tâm
I
. Gọi
V
,
1
V
lần lượt là thể tích của
khối hộp
.
ABCD A B C D
và khối chóp
.
I ABCD
. Tính tỉ số
1
V
k
V
.
A.
1
6
k
. B.
1
12
k . C.
1
8
k
. D.
1
3
k
.
Lời giải
Chọn A.
Ta có:
.
.
ABCD A B C D ABCD
V V AA S
.
Lại có:
1
,
2
d I ABCD AA
(vì
I
là trung điểm
A C
).

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/22 - Mã đề thi 132
1 .
1 1 1 1
, . . .
3 3 2 6
I ABCD ABCD ABCD
V V d I ABCD S AA S V
.
Vậy,
1
1
6
V
k
V
.
Câu 46. [2H2-1] Viết công thức diện tích xung quanh
xq
S
của hình nón tròn xoay có độ dài đường sinh
l
và bán kính đường tròn đáy
r
.
A.
xq
S rl
. B. 2
xq
S rl
. C.
xq
S rl
. D.
1
2
xq
S rl
.
Lời giải
Chọn C.
Câu 47. [2H2-1] Một hình trụ có bán kính đáy
5
r
(cm), chiều cao
7
h
(cm). Tính diện tích xung quanh
của hình trụ.
A.
35
xq
S
(cm
2
). B.
70
xq
S
(cm
2
). C.
70
3
xq
S
(cm
2
). D.
35
3
xq
S
(cm
2
).
Lời giải
Chọn B.
Diện tích xung quanh của hình trụ là
2 2 .5.7 70
xq
S rh
(cm
2
).
Câu 48. [2D1-1] Đồ thị hàm số nào dưới đây đi qua điểm
2; 1
M
?
A.
4 2
4 1
y x x
. B.
3
1
x
y
x
. C.
3
3 1
y x x
. D.
2 3
3
x
y
x
.
Lời giải
Chọn D.
Vì thay tọa độ điểm
2; 1
M
vào
2 3
3
x
y
x
ta được
2.2 3
1
2 3
(thỏa mãn).
Câu 49. [2D2-2] Cho hàm số
1
1
x
y
x
. Gọi
M
là giá trị lớn nhất và
m
là giá trị nhỏ nhất của hàm số
trên đoạn
5; 1
. Tính
M m
.
A.
6.
B.
3
.
2
C.
6
.
5
D.
2
.
3
Lời giải
Chọn D.
Ta có
2
2
0 5; 1
1
y x
x
2
5 , 1 0
3
M y m y
Vậy
2
.
3
M m
Câu 50. [2D2-2] Tìm
2017
0
e 1
lim .
x
x
x
A.
0.
B.
1.
C.
2017.
D.
.
Lời giải
Chọn C.
2017 2017
0 0
e 1 e 1
lim lim .2017 2017.
2017
x x
x x
x x
----------HẾT----------
Bấm Tải xuống để xem toàn bộ.




