TOP5 đề ôn tập giữa học kỳ 1 Toán 12 năm học 2017 – 2018 – Lê Văn Đoàn

Tuyển tập 5 đề ôn tập giữa học kỳ 1 Toán 12 năm học 2017 – 2018 do thầy Lê Văn Đoàn biên soạn, mỗi đề gồm 40 câu hỏi trắc nghiệm và 6 bài toán tự luận.Mời bạn đọc đón xem.

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

30 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 1
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN GIỮA KỲ 1 NĂM HỌC 2017 – 2018
TRƯỜNG THPT ............................................................ Khối 12 – Môn thi: TOÁN
(Đề thi gồm 06 trang) Thời gian làm bài: 90 phút, không kể thời gian phát đề
PHẦN 1. TRẮC NGHIỆM
Câu 1. Cho hàm số
3
3 2.
y x x
Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên khoảng
( ;0)

và nghịch biến trên khoảng
(0; ).
B. Hàm số nghịch biến trên khoảng
( ; ).
C. Hàm số đồng biến trên khoảng
( ; ).
D. Hàm số nghịch biến trên khoảng
( ;0)

và đồng biến trên khoảng
(0; ).
Câu 2. Cho hàm số
4 2
2 .
y x x
Mệnh đề nào dưới đây là đúng ?
A. Hàm số đồng biến trên khoảng
( ; 2).

B. Hàm số nghịch biến trên khoảng
( ; 2).

C. Hàm số đồng biến trên khoảng
( .
1;1)
D. Hàm số nghịch biến trên khoảng
( .
1;1)
Câu 3. Cho hàm số
2
2 1.
y x
Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng
( 1;1).
B. Hàm số đồng biến trên khoảng
(0; ).
C. Hàm số đồng biến trên khoảng
( ;0).

D. Hàm số nghịch biến trên khoảng
(0; ).
Câu 4. Có bao nhiêu giá trị nguyên của
m
để hàm số
3 2
(4 9) 5
y x mx m x
nghịch biến
trên
( ; ).
A.
7.
B.
4.
C.
6.
D.
5.
Câu 5. Tìm tập hợp các giá trị thực của tham số
m
sao cho hàm số
1
x
y
x m
nghịch biến trên
khoảng
( ;2).
A.
(1, ).
B.
[1, ).
C.
(2, ).
D.
[2, ).
Câu 6. Cho hàm số
( )
f x
có bảng biến thiên như sau:
x
1
2

y
0
0
y
4
2
2
5
Mệnh đề nào dưới đây đúng ?
A. Hàm số có bốn điểm cực trị. B. Hàm số đạt cực tiểu tại
2.
x
C. Hàm số không có cực đại. D. Hàm số đạt cực tiểu tại
5.
x
Mã đề thi: 101
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 2
Câu 7. Cho hàm số
( )
f x
có đồ thị
( )
f x
của nó trên khoảng
K
như hình vẽ. Khi đó trên
,
K
hàm số
( )
y f x
có bao nhiêu điểm cực đại ?
A.
0.
B.
2.
C.
3.
D.
1.
Câu 8. Hỏi có bao nhiêu giá trị nguyên của
m
để hàm số
3 2 2
2 (2 1) ( 1)
y x m x m x
có hai
điểm cực trị.
A.
4.
B.
5.
C.
3.
D.
6.
Câu 9. Tìm giá trị lớn nhất của hàm số
3 2
2 1
3 2
x x
y x trên đoạn
[0; 2].
A.
[0;2]
1
max
3
y
B.
[0;2]
max
0.
y
C.
[0;2]
max 1.
y
D.
[0;2]
7
max
3
y
Câu 10. Tìm giá trị lớn nhất của hàm số
4 sin 2 cos 2
y x x
trên
3
0;
4
D
A.
max 2 2.
y
D
B.
max 4 2.
y
D
C.
max 2.
y
D
D.
max 4 2.
y
D
Câu 11. Hỏi tham số
m
thuộc khoảng nào sau đây thì giá trị nhỏ nhất của hàm số
2
1
x m m
y
x
trên đoạn
[0;1]
bằng
2.
A.
( ; 2).
m

B.
( 2;4).
m
C.
(4;15).
m
D.
(15; ).
m

Câu 12. Một chất điểm chuyển động theo phương trình
3 2
2 18 2 1,
S t t t
trong đó
t
tính
bằng giây
( )
s
và
S
tính bằng mét
( ).
m
Tính thời gian vận tốc chất điểm đạt giá trị lớn nhất.
A.
5 .
t s
B.
6 .
t s
C.
3 .
t s
D.
1 .
t s
Câu 13. Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
3 2
1
x
y
x
A.
1, 2.
x y
B.
1, 2.
x y
C.
1, 2.
x y
D.
2, 1.
x y
Câu 14. Tìm số đường tiệm cận của đồ thị hàm số
3
2
3 4
16
x x
y
x
A.
2.
B.
3.
C.
1.
D.
0.
Câu 15. Hỏi đồ thị hàm số
2
2 1 3 1
x x
y
x x
có tất cả bao nhiêu đường tiệm cận ?
A.
0.
B.
1.
C.
2.
D.
3.
Câu 16. Đồ thị (C) trong hình sau là đồ thị hàm số nào trong 4 hàm số được liệt kê ở 4 phương án
dưới đây ?
A.
3
3 1.
y x x
B.
3
3 1.
y x x
C.
4 2
1.
y x x
D.
2
1.
y x x
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 3
Câu 17. Đồ thị sau đây là đồ thị của hàm số nào ?
A.
2
1
x
y
x
B.
1
1
x
y
x
C.
3
1
x
y
x
D.
2 1
1
x
y
x
Câu 18. Đồ thị hình bên dưới là của hàm số nào ?
A.
4 2
3 3.y x x
B.
4 2
1
3 3.
4
y x x
C.
4 2
2 3.y x x
D.
4 2
2 3.y x x
Câu 19. Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ. Hỏi mệnh đề nào dưới đây đúng.
A.
0, 0, 0, 0.a b c d
B.
0, 0, 0, 0.a b c d
C.
0, 0, 0, 0.a b c d
D.
0, 0, 0, 0.a b c d
Câu 20. Tìm tọa độ giao điểm của đồ thị
4
( ) :
1
x
C y
x
và đường thẳng
: 1.y x
A.
1
(0;1).M B.
2
(2;3).M C.
3
(1;2).M D.
4
(1;3).M
Câu 21. Cho đồ thị hàm số
3
3 1y x x
như hình bên dưới. Tìm tất cả các giá trị thực của tham
số m sao cho phương trình
3
3 0x x m có ba nghiệm thực phân biệt.
A. 2 3.m
B. 2 2.m
C. 2 2.m
D. 1 3.m
Câu 22. Tiếp tuyến của đồ thị hàm số
4
1
y
x
tại điểm có tung độ
0
2y có phương trình là
A. 2.y x B. 2.y x C. 1.y x D. 3.y x
Câu 23. Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau ?
A. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
B. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
C. Mỗi mặt có ít nhất ba cạnh.
D. Mỗi cạnh là cạnh chung của ít nhất ba mặt.
y
x
O
1
3
1
1
1
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 4
Câu 24. Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng ?
A.
4
mặt phẳng. B.
3
mặt phẳng. C.
6
mặt phẳng. D.
9
mặt phẳng.
Câu 25. Cho khối chóp
.
S ABC
có
SA
vuông góc với đáy,
4,
SA
6,
AB
10
BC
và
8.
CA
Tính thể tích
V
của khối chóp.
A.
40.
V
B.
192.
V
C.
32.
V
D.
24.
V
Câu 26. Cho khối chóp
.
S ABCD
có đáy là hình chữ nhật,
( ),
SA ABCD
3 ,
AB a
2 ,
AD a
5 .
SB a
Tính thể tích
V
của khối chóp
.
S ABCD
theo
.
a
A.
2
8 .
V a
B.
3
24 .
V a
C.
3
10 .
V a
D.
3
8 .
V a
Câu 27. Cho khối chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
2 .
a
Tính thể tích
V
của khối chóp
. .
S ABC
A.
3
13
12
a
V
B.
3
11
12
a
V
C.
3
11
6
a
V
D.
3
11
4
a
V
Câu 28. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a
SA
vuông góc với mặt phẳng
đáy và cạnh bên
SD
hợp với đáy một góc
60 .
Tính thể tích
V
của khối chóp
. .
S ABCD
A.
3
3 .
V a
B.
3
3
6
a
V
C.
3
2 3
3
a
V
D.
3
3
3
a
V
Câu 29. Cho hình chóp
.
S ABCD
có đáy là hình thang
ABCD
vuông tại
A
và
D
có
2 2 ,
AB AD CD
)
(
.
SA AB
D
C
Góc giữa
SC
và đáy bằng
60 .
Biết khoảng cách từ
B
đến
(
)
SCD
là
42
7
a
Tính
.
3
S ABCD
V
k
a
A.
3
2
k
B.
6
3
k
C.
6
2
k
D.
3
3
k
Câu 30. Cho hình chóp đều
.
S ABC
có
,
AB a
mặt bên hợp với đáy một góc
60
.
Tính thể tích
V
của khối chóp
. .
S ABC
A.
3
3
12
V
a
B.
3
3
72
a
V
C.
3
3
24
a
V
D.
3
3
6
a
V
Câu 31. Cho hình chóp đều
. ,
S ABCD
đáy
ABCD
là hình vuông cạnh
,
a
các cạnh bên tạo với đáy góc
45 .
Tính diện tích toàn phần
tp
S
của hình chóp trên theo
.
a
A.
2
tp
( 3 1) .
S a
B.
2
tp
2 3 .
S a
C.
2
tp
4 .
S a
D.
2
tp
( 3 1) .
S a
Câu 32. Cho hình chóp
.
S ABCD
có thể tích bằng
18,
đáylà hình bình hành. Điểm
M
cạnh
SD
thỏa
2 .
SM MD
Mặt phẳng
( )
ABM
cắt
SC
tại
.
N
Tính thể tích
V
khối chóp
. .
S ABNM
A.
9.
V
B.
10.
V
C.
12.
V
D.
6.
V
Câu 33. Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
3.
a
Gọi
,
M N
lần lượt là trung
điểm của
, .
SB SC
Tính thể tích
V
của khối chóp
. ,
S AMN
biết mặt phẳng
( )
AMN
vuông
góc với mặt phẳng
( ).
SBC
A.
3
15
32
a
V
B.
3
3 15
32
a
V
C.
3
3 13
64
a
V
D.
3
3 13
32
a
V
Câu 34. Cho khối lăng trụ đứng
.
ABC A B C
có
,
BB a
đáy
ABC
là tam giác vuông cân tại
B
và
2.
AC a
Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
.
V a
B.
3
3
a
V
C.
3
6
a
V
D.
3
2
a
V
Câu 35. Cho lăng trụ tam giác đều
.
ABC A B C
có cạnh đáy bằng
a
và
.
AB BC
Tính thể tích
V
của khối lăng trụ.
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 5
A.
3
6 .
V a
B.
3
7
8
a
V
C.
3
6
8
a
V
D.
3
6
4
a
V
Câu 36. Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
,
A
,
AC a
60 .
ACB
Đường thẳng
BC
tạo với
( )
ACC A
một góc
30 .
Tính thể tích
V
của khối
lăng trụ
. .
ABC A B C
A.
3
6 .
V a
B.
3
3
3
a
V
C.
3
3 .
V a
D.
3
3 .
V a
Câu 37. Cho hình lăng trụ tam giác đều
.
ABC A B C
có
,
AB a
đường thẳng
AB
tạo với mặt
phẳng
( )
BCC B
một góc
30 .
Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
6
4
a
V
B.
3
6
12
a
V
C.
3
3
4
a
V
D.
3
4
a
V
Câu 38. Cho lăng trụ tam giác
.
ABC A B C
có đáy là tam giác vuông cân, cạnh huyền
2 .
AC a
Hình chiếu của
A
lên mặt phẳng
( )
A B C
là trung điểm
I
của
,
A B
góc giữa cạnh bên và
mặt đáy bằng
60 .
Tính thể tích
V
của khối lăng trụ
. .
ABC A B C
A.
3
6
6
a
V
B.
3
3
4
a
V
C.
3
2 .
V a
D.
3
6
2
a
V
Câu 39. Xét hình chóp
.
S ABC
thỏa mãn
,
SA a
2 ,
SB a
3
SC a
với
a
là hằng số dương cho
trước. Tìm giá trị lớn nhất
max
V
của thể tích khối chóp
. ?
S ABC
A.
3
6 .
V a
B.
3
2 .
V a
C.
3
.
V a
D.
3
3 .
V a
Câu 40. Một hình chóp tam giác đều có cạnh bên bằng
b
và cạnh bên tạo với mặt phẳng đáy một góc
.
Tính thể tích
V
của hình chóp đó.
A.
3 2
3
cos sin .
4
V b
B.
3 2
3
sin cos .
4
V b
C.
3 2
3
cos sin .
4
V b
D.
3
3
cos sin .
4
V b
PHẦN 2. TỰ LUẬN
Bài 1. Tìm tham số
m
để hàm số
3 2
( 1) ( 1) 2 2.
y m x m x x
a) Nghịch biến trên tập xác định của nó ? b) Đồng biến biến trên khoảng
(0; )

?
Bài 2. Biết
1 73
(1; 3), ;
3 27
M N
là hai điểm cực trị của đồ thị hàm số
3 2
.
y ax bx cx d
Tính
giá trị của biểu thức tại
5.
x
Bài 3. Tìm tham số
m
để đồ thị hàm số
4 2
2( 1)
y x m x m
có ba điểm cực trị
, ,
A B C
sao
cho
,
OA BC
trong đó
O
là gốc tọa độ và
A
là điểm cực trị thuộc trục tung.
Bài 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2 2
2 2 8 4 .
y x x x x
Bài 5. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
3
, ,
2
a
a SD hình chiếu vuông
góc của
S
trên mặt phẳng
( )
ABCD
là trung điểm
H
của cạnh
.
AB
Tính theo
a
thể tích
khối chóp
.
S ABCD
và khoảng cách từ điểm
A
đến mặt phẳng
( ).
SBD
Bài 6. Cho lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
,
A I
là trung điểm
của
, 6,
BC BC a
mặt phẳng
( )
A BC
tạo với mặt phẳng
( )
ABC
một góc bằng
60 .
Tính
thể tích khối lăng trụ
.
ABC A B C
và khoảng cách giữa hai đường thẳng
, .
AB A I
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 6
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN GIỮA KỲ 1 NĂM HỌC 2017 – 2018
TRƯỜNG THPT ............................... Khối 12 – Môn thi: TOÁN
(Đề thi gồm 06 trang) Thời gian làm bài: 90 phút, không kể thời gian phát đề
PHẦN 1. TRẮC NGHIỆM
Câu 1. Bảng biến thiên dưới đây là của một hàm số trong bốn hàm số được liệt kê ở bốn phương án
A, B, C, D
dưới đây. Hỏi hàm số đó là hàm số nào ?
x
0
2

y
0
0
y

1
3
A.
3 2
3 1.
y x x
B.
3 2
3 1.
y x x
C.
3 2
3 1.
y x x
D.
3 2
3 1.
y x x
Câu 2. Bảng biến thiên dưới đây là của một hàm số trong bốn hàm số được liệt kê ở bốn phương án
A, B, C, D
dưới đây. Hỏi hàm số đó là hàm số nào ?
x
1
0
1

y
0
0
0
y
3
3
1
A.
4 2
2 4 1.
y x x
B.
4 2
2 4 1.
y x x
C.
4 2
2 4 1.
y x x
D.
4 2
2 4 1.
y x x
Câu 3. Hàm số nào sau đây có bảng biến thiên như hình bên dưới ?
x
2

y
y
1

1
A.
1
2
x
y
x
B.
2 1
2
x
y
x
C.
2 5
2
x
y
x
D.
3
2
x
y
x
Câu 4. Có bao nhiêu giá trị nguyên của tham số
m
sao cho hàm số
2
1
mx x m
y
x
đồng biến
trên từng khoảng xác định của nó.
A.
3.
B.
1.
C.
5.
D.
7.
Mã đề thi: 102
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 7
Câu 5. Có bao nhiêu giá trị nguyên của tham số m sao cho hàm số
9
( )
mx
f x
x m
luôn nghịch biến
trên khoảng
( ;1).
A. 2. B. 3. C. 5. D. 9.
Câu 6. Cho hàm số
( )y f x
xác định, liên tục trên và có bảng biến thiên:
x
0 1
y
0
y

0
1
Hỏi khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1.
D. Hàm số đạt cực đại tại 0x và đạt cực tiểu tại 1.x
Câu 7. Cho hàm số
( )y f x
có đồ thị như hình vẽ bên dưới. Hàm số
( )f x
đạt cực tiểu tại điểm nào
dưới đây ?
A.
1.x
B.
1.x
C.
2.x
D. 0.x
Câu 8. Tìm tất cả các giá trị thực của tham số
m
để đồ thị của hàm số
3 2 3
3 4y x mx m
có hai
điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4, với O là gốc tọa độ.
A.
4
1
2
m hoặc
4
1
2
m B. 1m hoặc 1.m
C. 1.m D. 0.m
Câu 9. Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số
3 1
3
x
y
x
trên đoạn [0;2].
Tính tổng
.S M m
A. 4.S B.
8
5
S
C.
14
3
S
D.
14
3
S
Câu 10. Cho hàm số
3
sin cos 2 sin 2.y x x x
Tìm giá trị nhỏ nhất
m
của hàm số đã cho trên
khoảng
;
2 2
A.
23
27
m
B.
1
27
m
C. 5.m D. 1.m
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 8
Câu 11. Tìm các giá trị của
m
để giá trị nhỏ nhất của hàm số
3 2
3y x x m
trên đoạn [ 1;1]
bằng 0.
A.
4.m
B.
2.m
C.
6.m
D. 0.m
Câu 12. Một chuyển động theo quy luật
2 3
1
9 ,
2
s t t
với
t
(giây) là khoảng thời gian từ lúc vật bắt
đầu chuyển động và
s
(mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi
trong khoảng thời gian
10
giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật là
bao nhiêu ?
A. 54 ( / ).m s B. 216 ( / ).m s C. 30 ( / ).m s D. 400 ( / ).m s
Câu 13. Cho hàm số
2 3
3 6
x
y
x
có đồ thị
( ).C
Khẳng định nào là sai ?
A.
( )C
có tiệm cận đứng
2.x
B.
( )C
có tiệm cận ngang
2
3
y
C.
( )C
có tâm đối xứng
2
2;
3
I
D.
( )C
đi qua điểm
1
1;
9
A
Câu 14. Cho hàm số
( )f x
có đồ thị như hình vẽ bên. Tiệm cận đứng và tiệm cận ngang của đồ thị lần
lượt là:
A.
1x
và
2.y
C.
1x
và
2.y
B.
1x
và
2.y
D.
1x
và
2.y
Câu 15. Hỏi đồ thị hàm số
2
1
4 3
x
y
x x
có bao nhiêu đường tiệm cận ?
A. 1. B. 2. C. 3. D. 4.
Câu 16. Đồ thị hình bên dưới là của hàm số nào ?
A.
1
1 2
x
y
x
B.
1
2 1
x
y
x
C.
3 2
2 1
x
y
x
D.
1 2
1
x
y
x
Câu 17. Gọi
, A B
là giao điểm của đồ thị hàm số
2 1
1
x
y
x
và đường thẳng
: 1.d y x
Tính độ
dài đoạn thẳng .AB
A. 2.AB B.
2 2.AB
C.
2.AB
D.
2 3.AB
O
x
y
3
2
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 9
Câu 18. Đồ thị hàm số
3 2
2018 2017 1y x mx x có dạng nào sau đây ?
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 19. Cho đồ thị như hình vẽ là đồ thị của hàm số nào sau đây ?
A.
4 2
1
2 2.
4
y x x
B.
4 2
1
2 2.
4
y x x
C.
4 2
1
2 2.
4
y x x
D.
4 2
8 2.y x x
Câu 20. Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng
A.
0, 0, 0, 0.a b c d
B.
0, 0, 0, 0.a b c d
C.
0, 0, 0, 0.a b c d
D.
0, 0, 0, 0.a b c d
Câu 21. Đồ thị hình bên dưới là của hàm số
3 2
3 4y x x
. Tìm các giá trị của m để phương
trình
3 2
3 0x x m
có hai nghiệm phân biệt ?
A.
4m
hoặc
0.m
B.
4.m
C. 0 4.m
D.
0.m
Câu 22. Phương trình tiếp tuyến của đồ thị (C) hàm số
4 2
2y x x tại điểm có hoành độ
0
2x là
A. 24 40.y x B. 8 3.y x C. 24 16.y x D. 8 8.y x
Câu 23. Cho hình chóp .S ABCD có đáy ABCD là hình thoi tâm O và có thể tích bằng 8. Tính thể
tích V của khối chóp . .S OCD
Hình 1 Hình 2 Hình 3 Hình 4
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 10
A.
3.
V
B.
4.
V
C.
5.
V
D.
2.
V
Câu 24. Hình nào dưới đây không phải là một khối đa diện ?
A. B. C. D.
Câu 25. Cho khối chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
.
a
Hai mặt bên
( )
SAB
và
( )
SAC
cùng vuông góc với đáy. Tính thể tích
V
khối chóp
. ,
S ABC
biết
3.
SC a
A.
3
2 6
9
a
V
B.
3
6
12
a
V
C.
3
3
2
a
V
D.
3
3
4
a
V
Câu 26. Khối chóp tam giác đều có thể tích
3
2 ,
V a
cạnh đáy bằng
2 3.
a
Tính chiều cao
h
của khối
chóp đó.
A.
6.
h a
B.
6
3
a
h
C.
2 3
3
a
h
D.
3
a
h
Câu 27. Cho khối chóp
.
S ABCD
có
ABCD
là hình vuông cạnh
3 .
a
Tam giác
SAB
cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Tính thể tích
V
của khối chóp
. ,
S ABCD
biết góc giữa
SC
và mặt phẳng
( )
ABCD
bằng
60 .
A.
3
9 3 .
V a
B.
3
18 15 .
V a
C.
3
18 3 .
V a
D.
3
9 15
2
a
V
Câu 28. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật, biết
, 3.
AB a AD a
Hình
chiếu
S
lên đáy là trung điểm
H
cạnh
,
AB
góc tạo bởi
SD
và đáy là
60 .
Tính thể tích
V
khối chóp
. .
S ABCD
A.
3
5
5
a
V
B.
3
13
2
a
V
C.
3
15
2
a
V
D.
3
2
a
V
Câu 29. Cho hình chóp
.
S ABC
có
( )
SA ABC
và tam giác
SBC
đều cạnh
a
và nằm trong mặt
phẳng hợp với mặt phẳng đáy một góc
60 .
Tính thể tích
V
của khối chóp
. .
S ABC
A.
3
3 3
16
a
V
B.
3
3
16
a
V
C.
3
3
8
a
V
D.
3
3
32
a
V
Câu 30. Cho hình chóp
.
S ABC
có đáy là tam giác vuông cân ở
,
B
2,
AC a
( ),
SA ABC
.
SA a
Gọi
G
là trọng tâm của tam giác
,
SBC
mặt phẳng
( )
đi qua
AG
và song song
với
BC
cắt
,
SC SB
lần lượt tại
, .
M N
Tính thể tích
V
của khối chóp
. .
S AMN
A.
3
2
27
a
V
B.
3
2
9
a
V
C.
3
4
27
a
V
D.
3
4
9
a
V
Câu 31. Tổng diện tích các mặt của
1
hình lập phương bằng
150.
Tính thể tích
V
khối lập phương đó.
A.
200.
V
B.
625.
V
C.
100.
V
D.
125.
V
Câu 32. Cho hình lập phương
.
ABCD A B C D
cạnh
.
a
Gọi
E
và
E
lần lượt là trung điểm
,
CD
.
A B
Tính thể tích
V
của khối đa diện
ABEDD A E
theo
.
a
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 11
A.
3
6
V
a
B.
3
2
a
V
C.
3
4
a
V
D.
3
3
a
V
Câu 33. Cho khối lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác cân với
,
AB AC a
120 .
BAC
Mặt phẳng
( )
AB C
tạo với đáy một góc
60 .
Tính thể tích
V
của khối lăng
trụ đã cho.
A.
3
3
8
a
V
B.
3
9
8
a
V
C.
3
8
a
V
D.
3
3
4
a
V
Câu 34. Cho lăng trụ đứng tam giác
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
với
,
BA BC a
biết
A B
hợp với đáy
ABC
một góc
60 .
Tính thể tích
V
của khối lăng trụ
. .
ABC A B C
A.
3
3
6
a
V
B.
3
2 .
V a
C.
3
3
2
a
V
D.
3
2
a
V
Câu 35. Cho hình lăng trụ đều
.
ABC A B C
có
,
AB a
3
2
a
AA
Gọi
G
là trọng tâm tam giác
.
A BC
Tính thể tích
V
của tứ diện
GABC
theo
.
a
A.
3
3
12
a
V
B.
3
3 3
8
a
V
C.
3
3
24
a
V
D.
3
3
16
a
V
Câu 36. Cho hình lăng trụ tam giác
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
,
A
,
AB a
3.
AC a
Hình chiếu vuông góc của
A
lên
( )
ABC
là trung điểm của
.
BC
Góc giữa
AA
và
( )
ABC
bằng
60 .
Tính thể tích
V
của khối lăng trụ
. .
ABC A B C
A.
3
2
a
V
B.
3
3
2
a
V
C.
3
3
2
a
V
D.
3
3 3
2
a
V
Câu 37. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi tâm
,
O
,
AB a
60 ,
BAD
( )
SO ABCD
và mặt phẳng
( )
SCD
tạo với mặt đáy một góc
60 .
Tính thể tích
V
của khối
chóp
. .
S ABCD
A.
3
3
24
a
V
B.
3
3
8
a
V
C.
3
3
12
a
V
D.
3
3
48
a
V
Câu 38. Một công ty sản xuất gỗ muốn thiết kế các thùng đựng hàng bên trong dạng hình lăng trụ tứ
giác đều không nắp có thể tích là
2
62,5dm .
Để tiết kiệm vật liệu làm thùng, người ta cần thiết
kế thùng sao cho có tổng
S
diện tích xung quanh và diện tích mặt đáy là nhỏ nhất. Tìm
.
S
A.
2
106,25dm .
S
B.
2
75dm .
S
C.
2
50 5dm .
S
D.
2
45dm .
S
Câu 39. Cho khối chóp
.
S ABC
có đường cao
2 ,
SA a
tam giác
ABC
vuông ở
C
có
2 ,
AB a
góc
30 .
CAB
Gọi
H
là hình chiếu của
A
trên
.
SC
Gọi
B
là điểm đối xứng của
B
qua mặt
phẳng
( ).
SAC
Tính thể tích
V
của khối chóp
. .
H AB B
A.
3
2 3
7
a
V
B.
3
2 3
7
a
V
C.
3
6 3
7
a
V
D.
3
3
7
a
V
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 12
Câu 40. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi tâm
I
có cạnh bằng
,
a
60 .
BAD
Gọi
H
là trung điểm của
IB
và
SH
vuông góc với
( ).
ABCD
Góc giữa
SC
và
( )
ABCD
bằng
45 .
Tính thể tích
V
của khối chóp
. .
S AHCD
A.
3
35
32
a
V
B.
3
39
24
a
V
C.
3
39
32
a
V
D.
3
35
24
a
V
PHẦN 2. TỰ LUẬN
Bài 1. Tìm tham số
m
để hàm số
4
( )
mx
y f x
x m
a) Đồng biến trên từng khoảng xác định của nó ?
b) Luôn nghịch biến trên nửa khoảng
( ;1)

?
Bài 2. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
3 2
1
1
3
y x mx x m có hai
cực trị
1 2
,
x x
thỏa mãn điều kiện
2 2
1 2 1 2
4 2.
x x x x
Bài 3. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
4 2
(3 1) 3
y x m x
có ba
điểm cực trị tạo thành tam giác cân và độ dài cạnh đáy bằng
2
3
độ dài cạnh bên.
Bài 4. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
4 2 2 2
2 1
y x m x m
có ba
điểm cực trị
, ,
A B C
sao cho bốn điểm
, , ,
A B C O
là bốn đỉnh một hình thoi với
O
là gốc
tọa độ.
Bài 5. Cho hình chóp
. ,
S ABC
đáy
ABC
là tam giác đều cạnh
2 ,
a SA
vuông góc với đáy, góc giữa
đường thẳng
SB
và mặt phẳng đáy
(
)
ABC
bằng
60 .
Gọi
I
trung điểm của
,
BC H
là hình
chiếu vuông góc của
A
trên
.
SI
Tính thể tích khối chóp
.
S ABC
và khoảng cách từ
G
là tâm
đường tròn ngoại tiếp tam giác
ABC
đến mặt phẳng
( ).
ABH
Bài 6. Cho lăng trụ tam giác đều
.
ABC A B C
có
2,
AA a
đường thẳng
B C
tạo với mặt
phẳng
( )
ABB A
một góc
45 .
Tính theo
a
thể tích khối lăng trụ đã cho và khoảng cách giữa
hai đường thẳng
AB
và
.
BC
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 13
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN GIỮA KỲ 1 NĂM HỌC 2017 – 2018
TRƯỜNG THPT ............................... Khối 12 – Môn thi: TOÁN
(Đề thi gồm 06 trang) Thời gian làm bài: 90 phút, không kể thời gian phát đề
PHẦN 1. TRẮC NGHIỆM
Câu 1. Hàm số nào sau đây đồng biến trên ( ; ). 
A.
4
.y x B.
1
y
x
C.
3 2
3 .y x x D.
3 2
2 5 .y x x x
Câu 2. Cho hàm số
2
1
x
y
x
Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng ( ; 1).
B. Hàm số đồng biến trên khoảng ( ; 1).
C. Hàm số nghịch biến trên khoảng ( ; ). 
D. Hàm số nghịch biến trên khoảng ( 1; ). 
Câu 3. Hàm số
2
2
1
y
x
nghịch biến trên khoảng nào dưới đây ?
A. (0; ). B. ( 1;1). C. ( ; ).  D. ( ; 0).
Câu 4. Có bao nhiêu giá trị nguyên của m để hàm số
3 2
1
( 2) ( 2) (3 1)
3
y m x m x m x
đồng
biến trên ( ; ). 
A. 1. B. 2. C. 5. D. Vô số.
Câu 5. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
tan 2
tan 2
x
y
m x
đồng biến trên
khoảng 0;
4
A. 1.m B. 1 2.m C. 1 2.m D. 1 2.m
Câu 6. Tìm giá trị cực đại
y
CĐ
của hàm số
3
3 2.y x x
A.
4.y
CĐ
B.
1.y
CĐ
C.
0.y
CĐ
D.
1.y
CĐ
Câu 7. Cho hàm số
( )y f x
có đạo hàm trên
và đồ thị hàm số ( )y f x
trên
như hình bên
dưới. Tìm khẳng định đúng ?
A.
( )y f x
có 1 điểm cực đại và 1 điểm cực tiểu.
B.
( )y f x
có 2 điểm cực đại và 2 điểm cực tiểu.
C.
( )y f x
có 1 điểm cực đại và 2 điểm cực tiểu.
D.
( )y f x
có 2 điểm cực đại và 1 điểm cực tiểu.
Mã đề thi: 103
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 14
Câu 8. Hỏi tham số
m
thuộc khoảng nào sau đây thì đồ thị hàm số
4 2
2 1y x mx
có ba điểm
cực trị (0;1), , A B C thỏa 4.BC
A. ( ; 4).m  B. ( 4;0).m C. (0;10).m D. (10; ).m 
Câu 9. Tính giá trị nhỏ nhất của hàm số
2
4
3y x
x
trên khoảng (0; ).
A.
3
(0; )
min 3 9.y
B.
(0; )
min 7.y

C.
(0; )
33
min
5
y

D.
3
(0; )
min 2 9.y
Câu 10. Tìm giá trị lớn nhất M của hàm số
2
sin 1
sin sin 1
x
y
x x
A. 1.M B. 2.M C. 1.M D.
3
2
M
Câu 11. Cho hàm số
3 2
3 6.y x m x
Hỏi các giá trị của tham số
m
thuộc khoảng nào sau đây
thì giá trị lớn nhất của hàm số trên đoạn [0; 3] bằng 42.
A. ( ; 5). B. ( 5; 0). C. ( 5;5). D. (5; ).
Câu 12. Một đường dây điện được nối từ một nhà máy điện ở
A
đến một hòn đảo ở
C
như hình vẽ.
Khoảng cách từ
C
đến
B
là
1
km. Bờ biển c hạy thẳng từ
A
đến
B
với khoảng cách là
4
km. Tổng chi phí lắp đặt cho
1
km dây điện trên biển là
40
triệu đồng, còn trên đất liền là
20
triệu
đồng. Tính tổng chi phí nhỏ nhất để hoàn thành công việc trên (làm tròn đến hai chữ số sau dấu
phẩy).
A. 106,25 triệu đồng.
B. 120 triệu đồng.
C. 164, 92 triệu đồng.
D. 114,64 triệu đồng.
Câu 13. Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số
1
3
3
y
x
A.
3.y
B.
3.x
C.
3.x
D.
3.y
Câu 14. Tìm các giá trị của tham số thực m để hàm số
2
6
4
x x m
y
x m
không có tiệm cận đứng ?
A.
2.m
B. {0;8}.m C.
16.m
D.
1.m
Câu 15. Tìm các hệ số thực
, , a b c
để hàm số
2ax
y
cx b
có đồ thị như hình vẽ.
A.
2, 2, 1.a b c
B.
1, 1, 1.a b c
C.
1, 2, 1.a b c
D.
1, 2, 1.a b c
Câu 16. Đồ thị hàm số
2 3
5 4
x x
y
x x
có mấy tiệm cận ?
A. 4. B. 2. B. 3. D. 5.
Câu 17. Đồ thị sau là của hàm số nào ?
A
B
C
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 15
A.
1
1
x
y
x
B.
2
1
x
y
x
C.
1
2
x
y
x
D.
2
1
x
y
x
Câu 18. Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
A.
3 1
2
x
y
x
B.
2
( 3).y x x
C.
2
( 3).y x x
D.
2 2
( 2) .y x
Câu 19. Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
A.
4 2
2 1.y x x
B.
4 2
2 1.y x x
C.
4 2
2 1.y x x
D.
4 2
2 1.y x x
Câu 20. Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng.
A.
0, 0, 0, 0.a b c d
B.
0, 0, 0, 0.a b c d
C.
0, 0, 0, 0.a b c d
D.
0, 0, 0, 0.a b c d
Câu 21. Đồ thị trong hình bên dưới là đồ thị của hàm số
4 2
4 .y x x
Dựa vào đồ thị bên hãy tìm
tất cả các giá trị thực của tham số m sao cho phương trình
4 2
4 2 0x x m
có đúng 2
nghiệm phân biệt ?
A. 0m hoặc 4.m
B. 0.m
C. 2m hoặc 6.m
D. 2.m
Câu 22. Viết phương trình tiếp tuyến của đồ thị hàm số
2 1
2
x
y
x
Biết tiếp tuyến có hệ số góc là 5.
-4 -3 -2 -1 1 2 3 4
-4
-3
-2
-1
1
2
3
4
x
y
O
x
y
2
1
3
1
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 16
A.
5 2
y x
và
5 22.
y x
B.
5 2
y x
và
5 22.
y x
C.
5 2
y x
và
5 22.
y x
D.
5 2
y x
và
5 22.
y x
Câu 23. Gọi
,
M N
là giao điểm của đường thẳng
1
y x
và đường cong
2 4
1
x
y
x
Khi đó,
hãy tìm tọa độ trung điểm
I
của đoạn thẳng
.
MN
A.
(1;2).
I
B.
( 2; 3).
I
C.
(1;3).
I
D.
(2;3).
I
Câu 24. Một hình đa diện có các mặt là các tam giác thì số mặt
M
và số cạnh
C
của đa diện đó thỏa mãn
điều kiện nào sau đây.
A.
3 2 .
C M
B.
3 2 .
M C
C.
2 .
C M
D.
2 .
C M
Câu 25. Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng ?
A.
4
mặt phẳng. B.
1
mặt phẳng. C.
2
mặt phẳng. D.
3
mặt phẳng.
Câu 26. Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật có
,
AB a
3.
BC a
Hai mặt phẳng
( )
SAB
và
( )
SAD
cùng vuông góc với đáy,
60 .
SCA
Tính thể tích
V
khối chóp
. .
S ABCD
A.
3
.
V a
B.
3
2 .
V a
C.
3
3 .
V a
D.
3
2 3 .
V a
Câu 27. Cho hình chóp
.
S ABC
có đáy là tam giác vuông cân tại
, 2
A BC a
và
SBC
là tam giác
vuông cân tại
S
và nằm trong mặt phẳng vuông góc đáy. Tính thể tích khối chóp
. .
S ABC
A.
3
.
V a
B.
3
2
3
a
V
C.
3
2
3
a
V
D.
3
3
a
V
Câu 28. Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là
3.
a
Tính thể tích
V
của khối chóp đó.
A.
3
2 2
.
3
V a
B.
3
4 2
.
3
V a
C.
3
2
.
6
V a
D.
3
2
.
9
V a
Câu 29. Hình chóp tứ giác
.
S ABCD
có đáy là hình chữ nhật cạnh
,
AB a
2,
AD a
( ),
SA ABCD
góc giữa
SC
và đáy bằng
60 .
Tính thể tích
V
của khối chóp
. .
S ABCD
A.
3
3 2 .
V
a
B.
3
6 .
V a
C.
3
3 .
V a
D.
3
2 .
V a
Câu 30. Cho khối chóp
.
S ABCD
có đáy là hình vuông cạnh
,
a
SA
vuông góc với đáy và
SC
tạo với
mặt phẳng
( )
SAB
một góc
30 .
Tính thể tích
V
của khối chóp.
A.
3
6
3
a
V
B.
3
2
3
a
V
C.
3
2
3
a
V
D.
3
2 .
V a
Câu 31. Cho khối chóp
.
S ABC
có đáy là tam giác cân tại
,
A
2 ,
BC a
120
,
BAC
( )
SA ABC
và mặt
( )
SBC
hợp với đáy một góc
45
.
Tính thể tích
V
của khối chóp
. .
S ABC
A.
3
3
a
V
B.
3
.
2
V a
C.
3
2
a
V
D.
3
9
a
V
Câu 32. Cho hình hộp
.
ABCD A B C D
có thể tích
3
16cm .
Gọi
, ,
M N K
lần lượt là trung điểm của
,
BC
, .
CD D A
Tính thể tích
V
của khối tứ diện
.
AMNK
A.
3
6cm .
V
B.
3
4cm .
V
C.
3
2cm .
V
D.
3
8
cm .
3
V
Câu 33. Cho hình chóp tứ giác đều
. ,
S ABCD
cạnh đáy
2 3,
AB a
mặt bên tạo với đáy góc
60 .
Tính thể tích
V
của khối chóp
. .
S ABCD
A.
3
8 .
V a
B.
3
12 .
V a
C.
3
9 .
V a
D.
3
12 3 .
V a
Câu 34. Cho hình hộp đứng
.
ABCD A B C D
có đáy
ABCD
là hình thoi cạnh
a
và
60 ,
BAD
AB
hợp với đáy
( )
ABCD
một góc
30 .
Tính thể tích
V
của khối hộp.
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 17
A.
3
2
a
V
B.
3
3
2
a
V
C.
3
6
a
V
D.
3
2
6
a
V
Câu 35. Cho lăng trụ tam giác
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
,
A
cạnh
2 2.
AC
Biết
AC
tạo với mặt phẳng
( )
ABC
một góc
60
và
4.
AC
Tính thể tích
V
của khối đa diện
.
ABCB C
A.
8
3
V
B.
16
3
V
C.
8 3
3
V
D.
16 3
3
V
Câu 36. Cho hình chóp đều
.
S ABCD
có cạnh đáy bằng
2,
khoảng cách từ tâm của đáy đến mặt bên
bằng
2
2
Tính thể tích
V
của khối chóp.
A.
4.
V
B.
1
3
V
C.
2
3
V
D.
4
3
V
Câu 37. Cho hình lăng trụ tứ giác đều
.
ABCD A B C D
có cạnh đáy bằng
.
a
Biết đường chéo của
mặt bên là
3.
a
Tính thể tích
V
của khối lăng trụ
. .
ABCD A B C D
A.
3
3 .
V a
B.
3
2 .
V a
C.
3
2
3
a
V
D.
3
2 .
V a
Câu 38. Cho lăng trụ tam giác
. ,
ABC A B C
có đáy
ABC
là tam giác đều cạnh
,
a
hình chiếu của
A
xuống
( )
ABC
là tâm
O
đường tròn ngoại tiếp tam giác
.
ABC
Biết
AA
hợp với đáy
( )
ABC
một góc
60 .
Tính thể tích
V
của khối lăng trụ
. .
ABC A B C
A.
3
3
12
a
V
B.
3
3 3
4
a
V
C.
3
3
4
a
V
D.
3
3
36
a
V
Câu 39. Cho hình hộp chữ nhật
.
ABCD A B C D
có tổng diện tích của tất cả các mặt là
36,
độ dài
đường chéo
AC
bằng
6.
Hỏi thể tích của khối hộp lớn nhất
max
V
là bao nhiêu ?
A.
max
8.
V
B.
max
8 2.
V
C.
max
16 2.
V
D.
max
24 3.
V
Câu 40. Cho chóp đều
.
S ABCD
có khoảng cách từ
A
đến
( )
SCD
bằng
2 .
a
Tính giá trị nhỏ nhất
min
V
của thể tích khối chóp
.
S ABCD
theo
.
a
A.
3
min
4 .
V a
B.
3
min
2 .
V a
C.
3
min
3 3 .
V a
D.
3
min
2 3 .
V a
PHẦN 2. TỰ LUẬN
Bài 1. Biết hàm số
sin cos
y a x b x x
đạt cực trị tại điểm
3
x
và
x
với
(0;2 ).
x
Tính giá trị biểu thức
3.
T a b
Bài 2. Đồ thị hàm số
4 2
2 4
y x mx
có ba điểm cực trị nằm trên các trục tọa độ. Tìm
.
m
Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
( 6) 4
y x x
trên đoạn
[0;3].
Bài 4. Cho hình chóp
.
S ABCD
có đáy
ABCD
là một tứ giác lồi và
ABD
đều cạnh
,
a BCD
là tam giác cân tại
, 120 ,
o
C BCD SA a
và
( ).
SA ABCD
Tính thể tích khối chóp
.
S ABCD
và khoảng cách từ điểm
C
đến mặt phẳng
( )
SBD
theo
.
a
Bài 5. Cho hình lăng trụ tam giác đều
.
ABC A B C
có tất cả các cạnh đều bằng 3a. Các điểm M, N
lần lượt thuộc các cạnh bên
,
BB CC
sao cho
2 , 2 .
B M BM CN NC
Tính thể tích
khối tứ diện
ACMN
và khoảng cách từ điểm
A
đến mặt phẳng
( )
AMN
theo
.
a
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 18
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN GIỮA KỲ 1 NĂM HỌC 2017 – 2018
TRƯỜNG THPT ............................... Khối 12 – Môn thi: TOÁN
(Đề thi gồm 06 trang) Thời gian làm bài: 90 phút, không kể thời gian phát đề
PHẦN 1. TRẮC NGHIỆM
Câu 1. Cho hàm số
( )
y f x
có bảng xét dấu đạo hàm như sau:
x
1
0
2

y
0
0
Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên khoảng
( 2;0).
B. Hàm số đồng biến trên khoảng
( ;0).

C. Hàm số nghịch biến trên khoảng
(0;2).
D. Hàm số đồng biến trên khoảng
( ;2).

Câu 2. Cho hàm số
( )
f x
xác định, liên tục trên
và có đồ thị của hàm số
( )
f x
là đường cong như
hình vẽ bên dưới. Hỏi khẳng định nào sau đây là đúng ?
A. Hàm số
( )
f x
đồng biến trên khoảng
(0;2).
B. Hàm số
( )
f x
nghịch biến trên khoảng
( 2;2).
C. Hàm số
( )
f x
đồng biến trên khoảng
( ; 1).

D. Hàm số
( )
f x
nghịch biến trên khoảng
( ;0).

Câu 3. Trên khoảng nào sau đây, hàm số
2
2
y x x
đồng biến ?
A.
(1; ).

B.
(
1;2)
.
C.
(
0;1)
.
D.
( ;1).

Câu 4. Tìm các giá trị thực của tham số
m
sao cho hàm số
sin
y x mx
luôn đồng biến trên
.
A.
1.
m
B.
1.
m
C.
1 1.
m
D.
1.
m
Câu 5. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
3 2
3 4
y x x mx
nghịch
biến trên khoảng
(0; ).

A.
0.
m
B.
0.
m
C.
0.
m
D.
0.
m
Câu 6. Cho hàm số
( )
y f x
có đồ thị như hình vẽ bên dưới. Hỏi đồ thị hàm số
( )
y f x
có bao
nhiêu điểm cực trị ?
A.
1.
B.
2.
C.
3.
D.
4.
Mã đề thi: 104
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 19
Câu 7. Biết rằng đồ thị của hàm số
3 2
3 5
y x x
có hai điểm cực trị
A
và
.
B
Tính diện tích
S
của tam giác
OAB
với
O
là gốc tọa độ.
A.
9.
S
B.
10
3
S
C.
5.
S
D.
10.
S
Câu 8. Tìm tất cả các giá trị thực của tham số
m
để đồ thị của hàm số
4 2
2
y x mx
có ba điểm
cực trị tạo thành tam giác có diện tích nhỏ hơn
1.
A.
0.
m
B.
1.
m
C.
3
0 4.
m
D.
0 1.
m
Câu 9. Gọi
,
M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
( ) 4 .
f x x x
Tính
.
S M m
A.
2 2.
S
B.
2 2 2.
S
C.
4.
M m
D.
2 2 2.
S
Câu 10. Cho hàm số
( )
y f x
có đồ thị trên đoạn
[ 2;4]
như hình vẽ. Tìm
2;4
max ( ) .
f x
A.
2;4
max ( ) 2.
f x
B.
2;4
max ( ) (0) .
f x f
C.
2;4
max ( ) 3.
f x
D.
2;4
max ( ) 1.
f x
Câu 11. Cho hàm số
3 2 2
( 1) .
y x mx m m x
Gọi
S
là tập hợp các giá trị của tham số
m
sao cho giá trị nhỏ nhất của hàm số trên đoạn
[ 1;1]
bằng
6.
Tính tổng các phần tử của
.
S
A.
2.
B.
0.
C.
2 6.
D.
1.
Câu 12. Cho tam giác vuông có tổng một cạnh góc vuông và cạnh huyền bằng
2.
Tìm độ dài ba cạnh
của tam giác sao cho diện tích của tam giác lớn nhất.
A.
2 2 3 4
; ;
3 3 3
B.
2 4
; 1;
3 3
C.
3 4
; ; 1.
5 5
D.
2 2 4
; ;
3 3 3
Câu 13. Cho hàm số
( )
f x
xác định, liên tục trên
\ { 1}
D
và có bảng biến thiên như sau:
x
1
1

( )
f x
0
( )
f x
2


0
Khẳng định nào sau đây là sai ?
A. Hàm số không có đạo hàm tại
1.
x
B. Hàm số đã cho đạt cực tiểu tại
1.
x
C. Đồ thị hàm số không có tiệm cận ngang.
D. Đồ thị hàm số không có tiệm cận đứng.
Câu 14. Đồ thị hàm số
2
2
4
x
y
x
có mấy tiệm cận ?
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 20
A. 0. B. 3. C. 1. D. 2.
Câu 15. Cho hàm số
2
1 1
2
x x
y
x x
Chọn khẳng định đúng ?
A. Đồ thị hàm số có một tiệm cận ngang là đường thẳng 0.y
B. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng 1y và 1.y
C. Đồ thị hàm số có một tiệm cận ngang là đường thẳng 1.y
D. Đồ thị hàm số có một tiệm cận ngang là đường thẳng 1.y
Câu 16. Cho hàm số
4
.
1
ax
y
bx
Hãy xác định hệ số a và
,b
biết rằng đồ thị hàm số có đường tiệm
cận ngang là
2y
và tiệm cận đứng là đường thẳng
1.x
A.
1.a b
B.
3a
và
1.b
C.
1a
và
2.b
D.
2a
và
1.b
Câu 17. Đồ thị sau đây là của hàm số nào ?
A.
3
3 1.y x x
B.
3 2
3 1.y x x
C.
3
3 1.y x x
D.
3 2
3 1.y x x
Câu 18. Đồ thị sau đây là của hàm số nào ?
A.
4 2
3 3.y x x
B.
4 2
1
3 3.
4
y x x
C.
4 2
2 3.y x x
D.
4 2
2 3.y x x
Câu 19. Đồ thị sau đây là của hàm số nào ?
A.
2 1
1
x
y
x
B.
2
1
x
y
x
C.
1
1
x
y
x
D.
2
1
x
y
x
Câu 20. Cho hàm số
3 2
y ax bx cx d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng.
A.
0, 0, 0, 0.a b c d
B.
0, 0, 0, 0.a b c d
C.
0, 0, 0, 0.a b c d
D.
0, 0, 0, 0.a b c d
2
1
O
3
-1
1
-1
-2
-4
O
-3
-1
1
4
2
-2
1
1
O
-2
O
x
y
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 21
Câu 21. Cho hàm số
2 3
2
x
y
x
có đồ thị
( )
C
và đường thẳng
: .
d y x m
Tìm tất cả các giá trị
của tham số
m
để đường thẳng
d
cắt đồ thị
( )
C
tại
2
điểm phân biệt ?
A.
2.
m
B.
6.
m
C.
2.
m
D.
2
m
hoặc
6.
m
Câu 22. Cho hàm số
( )
f x
liên tục trên
và có bảng biến thiên như sau:
x
0
2

y
0
0
y

3
1
Tìm tất cả các giá trị của tham số thực
m
để phương trình
( ) 2 1
f x m
có
3
nghiệm thực
phân biệt.
A.
1 3.
m
B.
1 1
2 2
m
C.
0 2.
m
D.
1 1.
m
Câu 23. Khối lập phương là khối đa diện đều loại nào ?
A.
{5;3}.
B.
{3;4}.
C.
{4;3}.
D.
{3;5}.
Câu 24. Cho hình chóp
.
S ABC
có đáy là tam giác vuông cân tại
A
và
2.
AB AC a
Tam giác
SBC
có diện tích bằng
2
2
a
và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích
V
của khối chóp
. .
S ABC
A.
3
4
3
a
V
B.
3
3
a
V
C.
3
2 .
V a
D.
3
2
3
a
V
Câu 25. Cho hình chóp tứ giác đều
. ,
S ABCD
đáy
ABCD
có diện tích
2
16cm ,
diện tích một mặt bên
là
2
8 3cm .
Tính thể tích
V
của khối chóp
. .
S ABCD
A.
3
32 2
cm .
3
V
B.
3
32 13
cm .
3
V
C.
3
32 11
cm .
3
V
D.
3
32 15
cm .
3
V
Câu 26. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
,
B
,
AB a
3,
BC a
SA
vuông góc với mặt phẳng đáy. Biết góc giữa
SC
và
( )
ABC
bằng
60 .
Tính thể tích
V
của
khối chóp
. .
S ABC
A.
3
3 .
V a
B.
3
3 .
V a
C.
3
.
V a
D.
3
3
3
a
V
Câu 27. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
,
a SA
vuông góc với mặt đáy,
SD
tạo
với mặt phẳng
( )
SAB
một góc bằng
30 .
Tính thể tích
V
của khối chóp
. .
S ABCD
A.
3
6
18
a
V
B.
3
3 .
V a
C.
3
6
3
a
V
D.
3
3
3
a
V
Câu 28. Cho khối chóp
.
S ABCD
có đáy là hình chữ nhật,
,
AB a
3,
AD a
SA
vuông góc với
đáy và mặt phẳng
( )
SBC
tạo với mặt phẳng đáy một góc
60 .
Tính thể tích
V
của khối chóp
. .
S ABCD
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 22
A.
3
3
a
V
B.
3
3
3
a
V
C.
3
.
V a
D.
3
3 .
V a
Câu 29. Cho khối tứ diện đều
ABCD
có cạnh bằng
.
a
Gọi
,
B C
lần lượt là trung điểm của các
cạnh
AB
và
.
AC
Tính thể tích
V
của khối tứ diện
AB C D
theo
.
a
A.
3
3
48
a
V
B.
3
2
48
a
V
C.
3
24
a
V
D.
3
2
24
a
V
Câu 30. Cho hình chóp
.
S ABC
có
60 ,
ASB CSB
90 ,
ASC
,
SA SB a
3 .
SC a
Tính
thể tích
V
của khối chóp
.
S ABC
theo
.
a
A.
3
2
4
a
V
B.
3
2
12
a
V
C.
3
6
6
a
V
D.
3
6
18
a
V
Câu 31. Cho khối lăng trụ
.
ABC A B C
có thể tích bằng
.
V
Gọi
,
I K
lần lượt là trung điểm của
, .
Hãy tính thể tích
V
của khối đa diện
ABCIKC
theo
V
?
A.
3
5
V
V
B.
3
V
V
C.
2
3
V
V
D.
4
5
V
V
Câu 32. Tính theo
a
thể tích
V
của khối lập phương
. ,
ABCD A B C D
biết
.
AC a
A.
3
3 3 .
V a
B.
3
3
3
a
V
C.
3
27
a
V
D.
3
3
9
a
V
Câu 33. Tính thể tích
V
của khối có
4
mặt tam giác cân bằng nhau,
4
mặt là hình chữ nhật và đáy
cũng là hình chữ nhật với các kích thước cùng đơn vị đo được cho như hình.
A.
5400 ( t).
v
t
V
đ
B.
1800 ( t).
v
t
V
đ
C.
128(9 73)
( tt).
3
v
V
đ
D.
128(3 73) ( tt).
v
V
đ
Câu 34. Cho hình lăng trụ đứng
.
ABC A B C
có đáy là tam giác vuông cân đỉnh
,
A
mặt bên là
BCC B
hình vuông, khoảng cách giữa
AB
và
CC
bằng
.
a
Tính thể tích
V
của khối lăng
trụ
. .
ABC A B C
A.
3
2
3
a
V
B.
3
2 .
V a
C.
3
2
2
a
V
D.
3
.
V a
Câu 35. Cho hình lăng trụ tam giác đều
.
ABC A B C
có
3.
AA a
Gọi
I
là giao điểm của
AB
và
.
A B
Cho biết khoảng cách từ điểm
I
đến mặt phẳng
( )
BCC B
bằng
3
2
a
Tính thể tích
V
của khối lăng trụ
.
ABC A B C
theo
.
a
A.
3
3 .
V a
B.
3
.
V a
C.
3
3
4
a
V
D.
3
4
a
V
Câu 36. Cho hình chóp
.
S ABCD
có đáy là hình bình hành và có thể tích bằng
8.
Gọi
,
M N
lần lượt
là trung điểm của các cạnh
,
AB
.
AD
Tính thể tích
V
của khối tứ diện
.
SCMN
A.
4.
V
B.
5.
V
C.
2.
V
D.
3.
V
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 23
Câu 37. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi và
4, 2.
AC BD
Mặt chéo
SBD
nằm trong mặt phẳng vuông góc với mặt phẳng
( )
ABCD
và
3, 1.
SB SD
Tính thể
tích
V
của khối chóp
. .
S ABCD
A.
2 3
3
V
B.
2 3.
V
C.
8 3
3
V
D.
4 3
3
V
Câu 38. Lăng trụ tam giác
.
ABC A B C
có đáy tam giác đều diện tích bằng
3,
góc giữa cạnh bên
và đáy bằng
30 .
Hình chiếu của
A
lên mặt phẳng
(
)
ABC
là trung điểm
I
của
.
BC
Tính
thể tích
V
khối lăng trụ.
A.
9
8
V
B.
3
3
V
C.
3 3.
V
D.
3.
V
Câu 39. Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích
thước
, , (dm).
x y z
Biết tỉ số hai cạnh đáy là
: 1 : 3
x y
và thể tích của khối hộp bằng
18
lít. Để tốn ít vật liệu nhất thì các kích thước
, ,
x y z
của nó bằng bao nhiêu ?
A.
3
2, 6,
2
x y z
B.
1, 3, 6.
x y z
C.
3 9 3
, ,
2 2 2
x y z
D.
1 3
, , 24.
2 2
x y z
Câu 40. Khối chóp
.
S ABCD
có đáy
ABCD
là hình thoi cạnh
.
a
Biết
,
SA SB SC a
cạnh
SD
thay đổi. Tính thể tích lớn nhất
max
V
của khối chóp
. .
S ABCD
A.
3
max
8
a
V
B.
3
max
4
a
V
C.
3
max
3
8
a
V
D.
3
max
2
a
V
PHẦN 2. TỰ LUẬN
Bài 1. Cho
( )
1
n
f x x m
x
Tìm
,
m n
để hàm số đạt cực đại tại
2
x
và
( 2) 2.
f
Bài 2. Tìm giá trị cực đại
y
C
Đ
của hàm số
2 cos
y x x
trên khoảng
(0; ).
Bài 3. Tìm
m
để hai điểm cực đại và cực tiểu của đồ thị hàm số
3 2
3 2
y x x mx m
nằm
về hai phía so với trục hoành ?
Bài 4. Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
, 2 2 2 .
B BC AB AD a
Gọi
E
là điểm đối xứng với
A
qua
,
D M
là trung điểm của
.
BC
Biết rằng cạnh bên
SB
vuông góc với mặt phẳng đáy, góc giữa 2 mặt phẳng
( )
SCE
và mặt phẳng
( )
ABCD
bằng
45 .
o
Tính thể tích khối chóp
.
S AMCE
và khoảng cách giữa 2 đường thẳng
, .
AM SD
Bài 5. Cho lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
, , 2 ,
B AB a AA a
3 .
A C a
Gọi M là trung điểm của đoạn thẳng
,
A C I
là giao điểm của AM và
.
A C
Tính
theo a thể tích khối tứ diện IABC và khoảng cách từ điểm A đến mặt phẳng (IBC).
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 24
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN GIỮA KỲ 1 NĂM HỌC 2017 – 2018
TRƯỜNG THPT ............................... Khối 12 – Môn thi: TOÁN
(Đề thi gồm 06 trang) Thời gian làm bài: 90 phút, không kể thời gian phát đề
PHẦN 1. TRẮC NGHIỆM
Câu 1. Cho hàm số
3
3 2.
y x x
Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên khoảng
( ;0)

và nghịch biến trên khoảng
(0; ).
B. Hàm số nghịch biến trên khoảng
( ; ).
 
C. Hàm số đồng biến trên khoảng
( ; ).
 
D. Hàm số nghịch biến trên khoảng
( ;0)

và đồng biến trên khoảng
(0; ).
Câu 2. Cho hàm số
4 2
2 .
y x x
Mệnh đề nào dưới đây là đúng ?
A. Hàm số đồng biến trên khoảng
( ; 2).

B. Hàm số nghịch biến trên khoảng
( ; 2).

C. Hàm số đồng biến trên khoảng
( .
1;1)
D. Hàm số nghịch biến trên khoảng
( .
1;1)
Câu 3. Cho hàm số
( )
f x
xác định, liên tục trên
và có đồ thị hàm số
( )
y f x
là đường cong
trong hình bên dưới. Hỏi mệnh đề nào dưới đây đúng ?
A. Hàm số
( )
f x
đồng biến trên khoảng
(
1;2)
.
B. Hàm số
( )
f x
nghịch biến trên khoảng
(
0;2).
C. Hàm số
( )
f x
đồng biến trên khoảng
(
2;1).
D. Hàm số
( )
f x
nghịch biến trên khoảng
(
1;1).
Câu 4. Cho hàm số
sin 3 cos .
y x x mx
Tìm tất cả các giá trị thực của tham số
m
sao cho
hàm số đồng biến trên
.
A.
2.
m
B.
2.
m
C.
2.
m
D.
1.
m
Câu 5. Tìm tất cả các giá trị của tham số
m
để hàm số
3 2
2 3(2 1) 6 ( 1) 1
y x m x m m x
đồng biến trên
(2; ).
A.
1.
m
B.
1.
m
C.
2.
m
D.
1.
m
Câu 6. Gọi
,
A B
là các điểm cực tiểu của đồ thị hàm số
4 2
2 1.
y x x
Tính diện tích
S
của tam
giác
AOB
với
O
là gốc tọa độ.
A.
3.
S
B.
2.
S
C.
1.
S
D.
4.
S
Câu 7. Cho hàm số
4 2
2017 2018
y x mx m n
với
,
m n
là các số thực dương và
.
m n
Hỏi
đồ thị hàm số đã cho có bao nhiêu điểm cực tiểu ?
A.
2.
B.
1.
C.
3.
D.
0.
Mã đề thi: 105
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 25
Câu 8. Hỏi
m
thuộc khoảng nào thì hàm số
3 2 2
3 3( 1)
y x mx m x
đạt cực tiểu tại
2.
x
A.
( ; 3).

B.
( 3;0).
C.
(0;6).
D.
(6; ).

Câu 9. Tìm giá trị nhỏ nhất của hàm số
2
3
1
x
y
x
trên đoạn
[2; 4].
A.
[2;4]
min 6.
y
B.
[2;4]
min 2.
y
C.
[2;4]
min 3.
y
D.
[2;4]
19
min
3
y
Câu 10. Cho hàm số
( )
y f x
xác định và liên tục trên khoảng
( 3;2),
3
lim ( ) 5,
x
f x

2
lim ( ) 3
x
f x
và có bảng biến thiên như sau:
x
3
1
1
2
y
0
0
y
0
3
5
2
Mệnh đề nào dưới đây sai ?
A. Hàm số không có giá trị nhỏ nhất trên khoảng
( 3;2).
B. Giá trị cực đại của hàm số bằng
0.
C. Giá trị lớn nhất của hàm số trên khoảng
( 3;2)
bằng
0.
D. Giá trị cực tiểu của hàm số bằng
2.
Câu 11. Tìm tất cả các giá trị của tham số thực
m
để giá trị nhỏ nhất của hàm số
3 2
3 6
y x mx
trên đoạn
[0;3]
bằng
2.
A.
2.
m
B.
31
27
m
C.
3
2
m
D.
1.
m
Câu 12. Một vùng đất hình chữ nhật
ABCD
có
25
AB km
,
20
BC km
và
M
,
N
lần lượt là
trung điểm của
AD
,
BC
. Một người cưỡi ngựa xuất phát từ
A
đi đến
C
bằng cách đi thẳng
từ
A
đến một điểm
X
thuộc đoạn
MN
rồi lại đi thẳng từ
X
đến
.
C
Vận tốc của ngựa khi
đi trên phần
ABNM
là
15 / ,
km h
vận tốc của ngựa khi đi trên phần
MNCD
là
30 /
km h
.
Thời gian ít nhất để ngựa di chuyển từ
A
đến
C
là mấy giờ ?
A.
2 5
3
B.
41
4
C.
4 29
6
D.
5
3
Câu 13. Cho hàm số
( )
y f x
xác định trên
\ {1},
D
liên tục trên mỗi khoảng xác định và có
bảng biến thiên:
x
0
1
( )
f x
0
( )
f x
2
0
5
3
Hỏi mệnh đề nào dưới đây đúng ?
A. Đồ thị hàm số có hai tiệm cận ngang là
0, 5
y y
và tiệm cận đứng là
1.
x
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 26
B. Giá trị cực tiểu của hàm số là
CT
3.
y
C. Giá trị cực đại của hàm số là
CD
5.
y
D. Hàm số có giá trị lớn nhất bằng
5.
Câu 14. Biết các đường tiệm cận của đường cong
2
6 1 2
( ) :
5
x x
C y
x
và trục tung cắt nhau
tạo thành một đa giác
( ).
H
Mệnh đề nào dưới đây đúng ?
A.
( )
H
là một hình vuông có diện tích bằng
25.
B.
( )
H
là một hình chữ nhật có diện tích bằng
8.
C.
( )
H
là một hình vuông có diện tích bằng
4.
D.
( )
H
là một hình chữ nhật có diện tích bằng
10.
Câu 15. Số đường tiệm cận của đồ thị hàm số
2
4
x
y
x
là bao nhiêu ?
A.
4.
B.
3.
C.
1.
D.
2.
Câu 16. Cho hàm số
1
2
ax
y
bx
Tìm
S a b
để đồ thị hàm số có
1
x
là tiệm cận đúng và
1
2
y là tiệm cận ngang.
A.
3.
S
B.
3.
S
C.
1.
S
D.
8.
S
Câu 17. Hàm số
3 2
6 9 1
y x x x
có đồ thị nào sau đây ?
A. B. . C. . D. .
Câu 18. Cho đồ thị như hình vẽ dưới đây. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau ?
A.
4 2
1
2 2.
4
y x x
B.
4 2
1
2 2.
4
y x x
C.
4 2
1
2 1.
4
y x x
D.
4 2
1
2 .
4
y x x
Câu 19. Đồ thị trong hình bên dưới là của hàm số nào ?
A.
3
3 1.
y x x
B.
4 2
3 .
y x x
C.
2 3
1
x
y
x
D.
2 1
1
x
y
x
2
2
4
2
-3
1
3
1
O
4
2
2
3
1
-1
3
O
2
2
4
-3
1
3
1
O
2
2
4
2
-3
1
3
1
O
2
2
2-2
O
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 27
x
y
0
Câu 20. Cho hàm số
4 2
y ax bx c
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng ?
A.
0, 0, 0.a b c
B.
0, 0, 0.a b c
C.
0, 0, 0.a b c
D.
0, 0, 0.a b c
Câu 21. Cho hàm số
ax b
y
cx d
có đồ thị như hình vẽ dưới. Mệnh đề nào dưới đây đúng ?
A.
0, 0, 0, 0.a b c d
B.
0, 0, 0, 0.a b c d
C.
0, 0, 0, 0.a b c d
D.
0, 0, 0, 0.a b c d
Câu 22. Cho hàm số
2
( 2)( 1)y x x có đồ thị ( ).C Mệnh đề nào dưới đây đúng ?
A. ( )C cắt trục hoành tại hai điểm. B. ( )C cắt trục hoành tại một điểm.
C. ( )C không cắt trục hoành. D. ( )C cắt trục hoành tại ba điểm.
Câu 23. Tìm tất cả các giá trị của tham số m để đồ thị hàm số
4 2
2 2y x mx m
cắt trục
Ox
tại
4
điểm phân biệt ?
A. (2; ).m  B. ( ;1).m
C. ( ; 1) (2; ).m  D. (0; ).m 
Câu 24. Cho hàm số ( )y f x xác định trên \{0}, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau:
x

0
1
y
0
y
1

2

Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình ( )f x m có ba
nghiệm thực phân biệt.
A. [ 1;2]. B. ( 1;2). C. ( 1;2]. D. ( ;2].
Câu 25. Mặt phẳng ( )AB C
chia khối lăng trụ .ABC A B C
thành các khối đa diện nào ?
O
x
y
O
x
y
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 28
A. Một khối chóp tam giác và một khối chóp ngũ giác.
B. Một khối chóp tam giác và một khối chóp tứ giác.
C. Hai khối chóp tam giác.
D. Hai khối chóp tứ giác.
Câu 26. Cho hình chóp
. ,
S ABC
có đáy
ABC
là tam giác vuông cân tại
,
A
,
AB a
các cạnh bên
.
SA SB SC a
Tính thể tích
V
của khối
. .
S ABC
A.
3
12
a
V
B.
3
2
12
a
V
C.
3
2
4
a
V
D.
3
2
6
a
V
Câu 27. Cho hình chóp đều
.
S ABCD
có chiều cao bằng
2
a
và độ dài cạnh bên bằng
6.
a
Tính thể
tích
V
của khối chóp
. .
S ABCD
A.
3
8 2
3
a
V
B.
3
10 2
3
a
V
C.
3
8 3
3
a
V
D.
3
10 3
3
a
V
Câu 28. Cho khối chóp
.
S ABC
có đáy là tam giác vuông tại
,
A
( ),
SB ABC
,
AB a
30 ,
ACB
góc giữa đường thẳng
SC
và mặt phẳng
ABC
là
60 .
Tính thể tích
V
khối chóp
. .
S ABC
A.
3
3 .
V a
B.
3
.
V a
C.
3
2 .
V a
D.
3
3
2
a
V
Câu 29. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
.
a
Cạnh bên
SA
vuông góc với mặt
phẳng đáy, cạnh bên
SC
tạo với
( )
SAB
một góc
30 .
Tính thể tích của khối chóp
. .
S ABCD
A.
3
3
3
a
V
B.
3
2
4
a
V
C.
3
2
2
a
V
D.
3
2
3
a
V
Câu 30. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật, mặt bên
( )
SAD
là tam giác đều
cạnh
2
a
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích
V
của khối
chóp
. ,
S ABCD
biết rằng mặt phẳng
( )
SBC
tạo với mặt phẳng đáy một góc
30 .
A.
3
3
2
a
V
B.
3
2 3 .
V a
C.
3
2 3
3
a
V
D.
3
4 3
3
a
V
Câu 31. Cho khối chóp
.
S ABCD
có đáy là hình vuông cạnh
,
a SA
vuông góc với đáy và khoảng
cách từ
A
đến mặt phẳng
( )
SBC
bằng
2
2
a
Tính thể tích
V
của khối chóp đã cho.
A.
3
2
a
V
B.
3
.
V a
C.
3
3
3
9
a
V
D.
3
3
a
V
Câu 32. Hình chóp
.
S ABC
có
, ,
M N P
lần lượt trung điểm của
SA SB SC
Gọi
1
V
là thể tích
khối
.
MNP ABC
và
2
V
là thể tích khối
. .
S ABC
Tính tỉ số
1
2
V
V
A.
1
2
1
8
V
V
B.
1
2
8.
V
V
C.
1
2
7
8
V
V
D.
1
2
8
7
V
V
Câu 33. Cho khối lăng trụ
. .
ABC A B C
Gọi
,
M N
lần lượt là trung điểm của hai cạnh
AA
và
.
BB
Mặt phẳng
(
)
C MN
chia khối lăng trụ đã cho thành hai phần. Gọi
1
V
là thể tích khối
.
C MNB A
và
2
V
là thể tích khối
. .
ABC MNC
Tính tỉ số
1
2
V
V
A.
1
2
2
3
V
V
B.
1
2
2.
V
V
C.
1
2
1
2
V
V
D.
1
2
3
2
V
V
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 29
Câu 34. Cho hình lập phương .ABCD A B C D
có diện tích tam giác ACD
bằng
2
3 .a Tính thể
tích V của hình lập phương.
A.
3
3 3 .V a B.
3
2 2 .V a C.
3
.V a D.
3
8 .V a
Câu 35. Cho hình lập phương .ABCD A B C D
có khoảng cách từ C
đến mặt phẳng
( )A BD
bằng
4 3
2
a
Tính theo a thể tích V của khối lập phương
. .ABCD A B C D
A.
3
8 .V a B.
3
3 3 .V a C.
3
8 3 .V a D.
2
216 .V a
Câu 36. Tính thể tích V của vật thể với các kích thước được cho trong hình vẽ dưới đây ?
A.
3
6600cm .V
B.
3
5700cm .V
C.
3
6400cm .V
D.
3
7800cm .V
Câu 37. Cho khối lăng trụ đứng .ABC A B C
có đáy ABC là tam giác cân với ,AB AC a
120 .BAC Mặt phẳng
( )AB C
tạo với đáy một góc 60 . Tính thể tích V của khối lăng
trụ . .ABC A B C
A.
3
3
8
a
V
B.
3
9
8
a
V
C.
3
8
a
V
D.
3
3
4
a
V
Câu 38. Một hình lăng trụ có đáy là tam giác đều cạnh bằng ,a cạnh bên bằng b và tạo với mặt phẳng
đáy một góc . Tính thể tích V của khối chóp có đáy là đáy của lăng trụ và đỉnh là một điểm
bất kì trên đáy còn lại.
A.
2
3
sin .
12
V a b
B.
2
3
sin .
4
V a b
C.
2
3
cos .
12
V a b
D.
2
3
cos .
4
V a b
Câu 39. Cho một tấm nhôm hình chữ nhật ABCD có 24 cm.AD Ta gấp tấm nhôm theo hai cạnh
MN và QP vào phía trong đến khi AB và CD trùng nhau như hình vẽ dưới đây để được
một hình lăng trụ khuyết hai đáy. Tìm x AN PD để thể tích khối lăng trụ lớn nhất ?
A. 9 cm.x B. 8 cm.x C. 10 cm.x D. 6 cm.x
Câu 40. Một hình chóp tứ giác đều có tổng độ dài của đường cao và bốn cạnh đáy là 33. Hỏi độ dài
cạnh bên ngắn nhất là bao nhiêu ?
A.
33
17
B. 33. C. 11 3. D.
33
2
24cm
B
A
M
Q
C
N
P
D
M
Q
N
P
B C
A D
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Trang 30
PHẦN 2. TỰ LUẬN
Bài 1. Tìm giá trị cực đại
y
C
Đ
(nếu có) của hàm số
2
2 1.
y x x
Bài 2. Tìm tất cả các giá trị thực của tham số
m
để đồ thị của hàm số
4 2
2 1
y x mx
có ba điểm
cực trị là ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng
1.
Bài 3. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
4 2 2
2 2 1
y x mx m
có giá trị
cực tiểu bằng
2.
Bài 4. Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số
2
2 5 .
y x x
Bài 5. Cho hình chóp
.
S ABC
có
SAB
đều cạnh
,
a
ABC
cân tại
.
C
Hình chiếu của đỉnh
S
trên mặt phẳng
( )
ABC
là trung điểm của cạnh
;
AB
góc hợp bởi cạnh
SC
và mặt phẳng đáy
bằng
30 .
o
Tính thể tích khối chóp
.
S ABC
và khoảng cách giữa hai đường thẳng
SA
và
BC
theo
.
a
Bài 6. Cho hình lăng trụ
.
ABC A B C
có
0
10
, 2, , 135 .
4
a
AA AC a BC a ACB
Hình
chiếu vuông góc của
C
trên mặt phẳng (ABC) trùng với trung điểm M của AB. Tính theo a
thể tích khối lăng trụ
.
ABC A B C
và góc tạo bởi đường thẳng
C M
với mặt phẳng
( ).
ACCA
| 1/30
| | Tải xuống

Có thể bạn quan tâm:

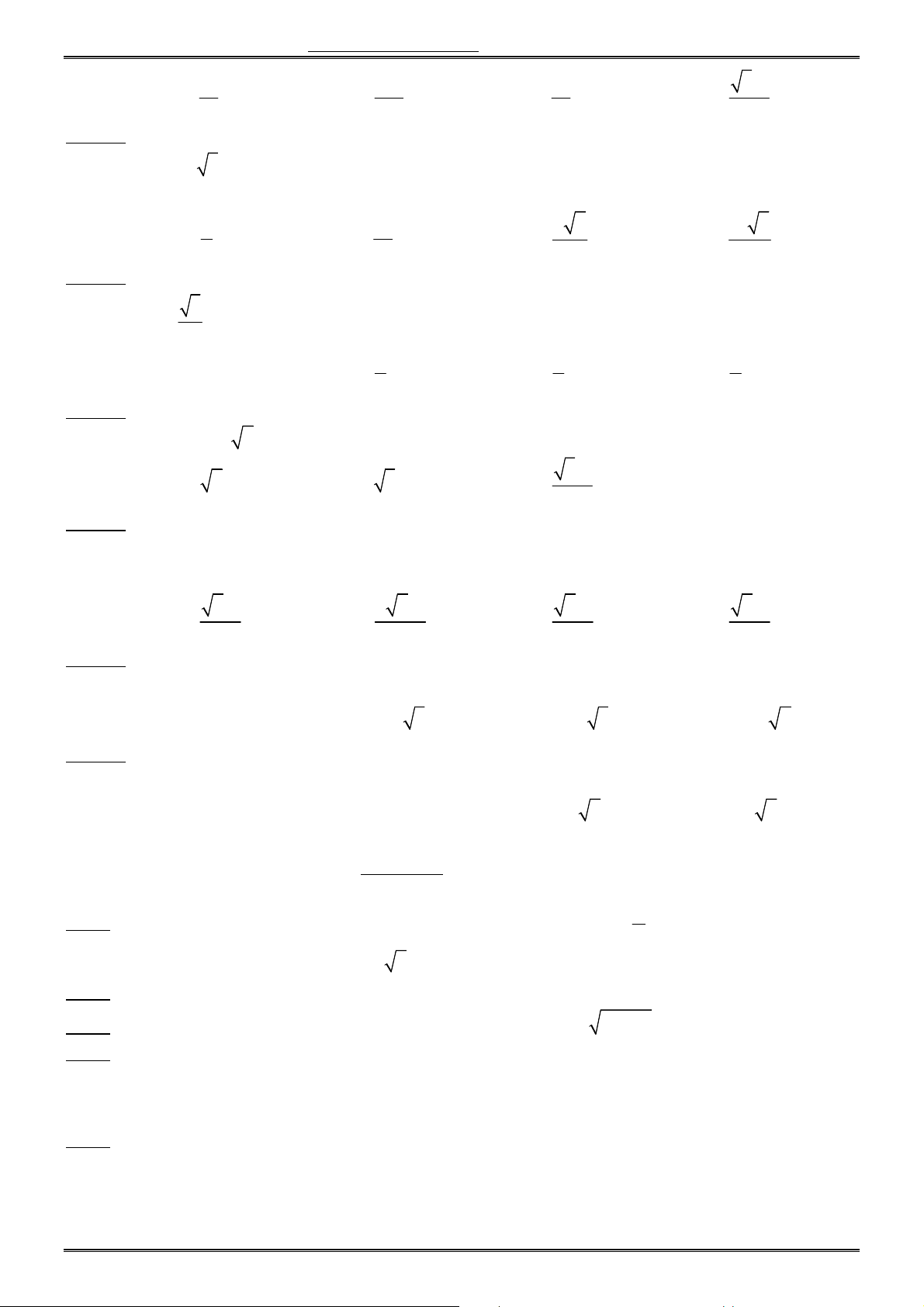
Preview text:

Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN GIỮA KỲ 1 NĂM HỌC 2017 – 2018
TRƯỜNG THPT ............................................................
Khối 12 – Môn thi: TOÁN
(Đề thi gồm 06 trang)
Thời gian làm bài: 90 phút, không kể thời gian phát đề Mã đề thi: 101
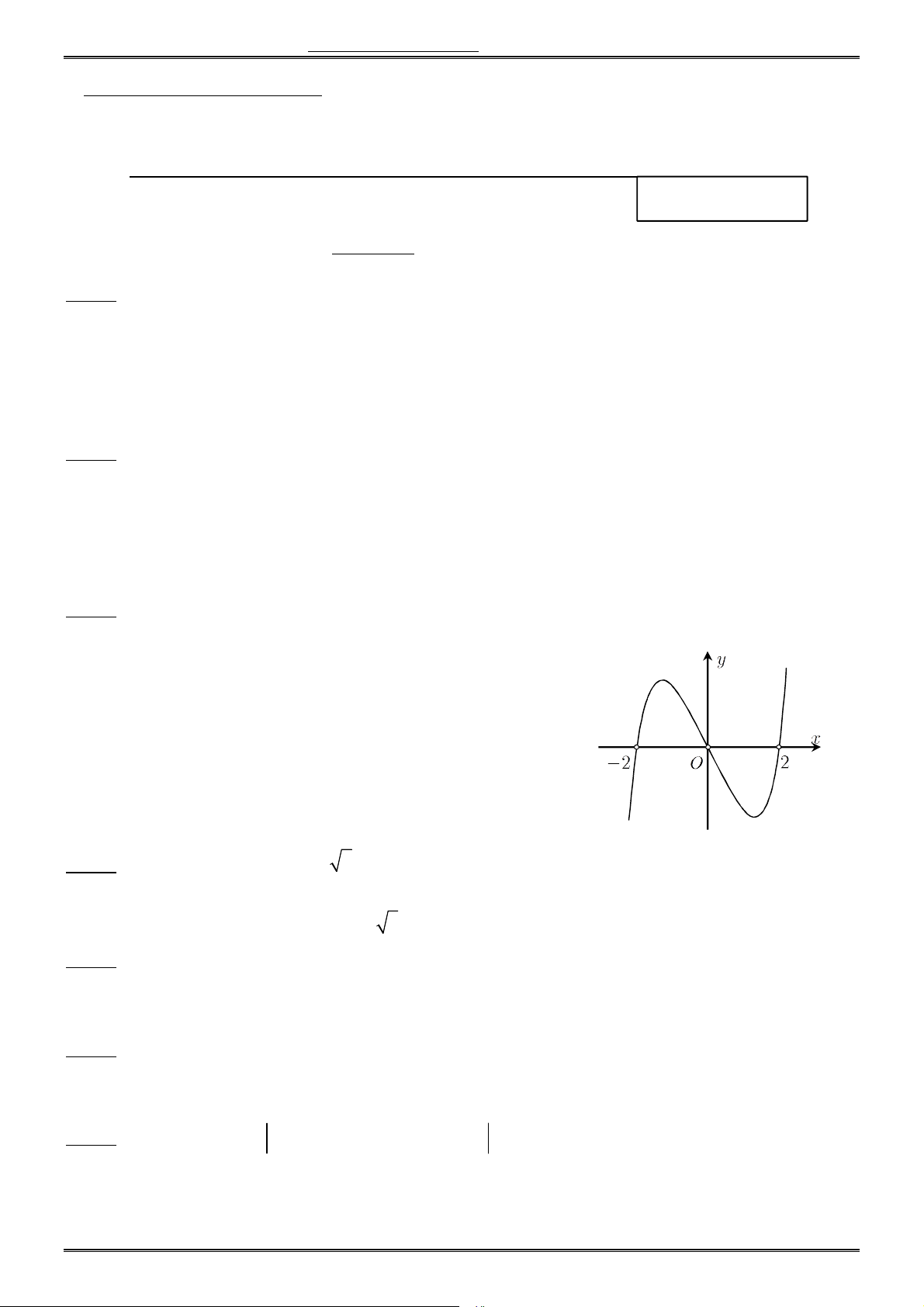
PHẦN 1. TRẮC NGHIỆM Câu 1. Cho hàm số 3
y x  3x  2. Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên khoảng ( ;
 0) và nghịch biến trên khoảng (0; )  .
B. Hàm số nghịch biến trên khoảng ( ;   )  .
C. Hàm số đồng biến trên khoảng ( ;   )  .
D. Hàm số nghịch biến trên khoảng ( ;
 0) và đồng biến trên khoảng (0; )  . Câu 2. Cho hàm số 4 2
y x  2x . Mệnh đề nào dưới đây là đúng ?
A. Hàm số đồng biến trên khoảng ( ;  2  ).
B. Hàm số nghịch biến trên khoảng ( ;  2  ).
C. Hàm số đồng biến trên khoảng ( 1  ;1).
D. Hàm số nghịch biến trên khoảng ( 1  ;1). Câu 3. Cho hàm số 2
y  2x  1. Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng ( 1  ;1).
B. Hàm số đồng biến trên khoảng (0;  )  .
C. Hàm số đồng biến trên khoảng ( ;  0).
D. Hàm số nghịch biến trên khoảng (0;  )  .
Câu 4. Có bao nhiêu giá trị nguyên của m để hàm số 3 2 y x
  mx  (4m  9)x  5 nghịch biến trên ( ;   )  . A. 7. B. 4. C. 6. D. 5. x  1
Câu 5. Tìm tập hợp các giá trị thực của tham số m sao cho hàm số y  nghịch biến trên x m khoảng ( ;  2).
A. (1, ). B. [1,  )  . C. (2,  )  . D. [2,  )  .
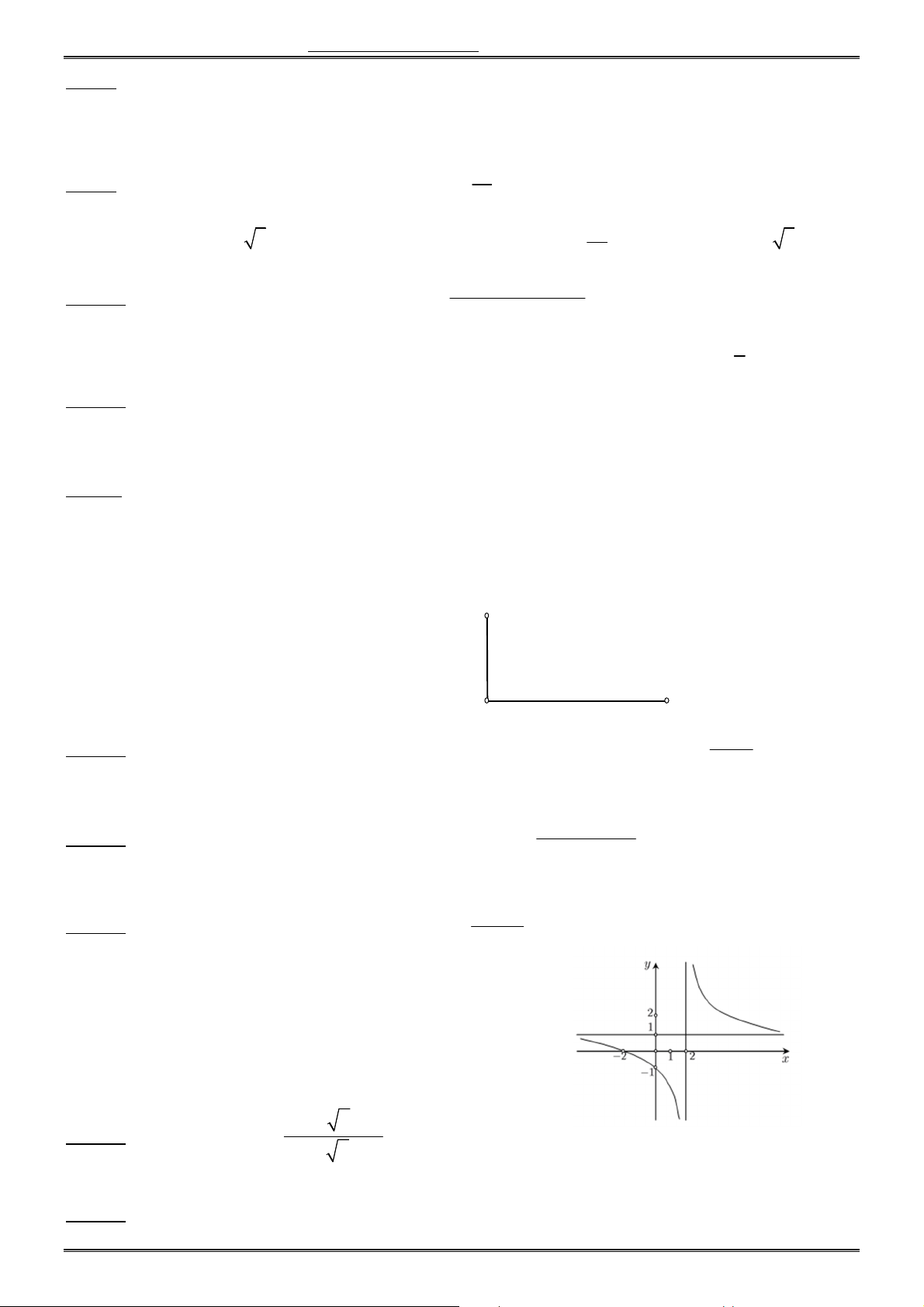
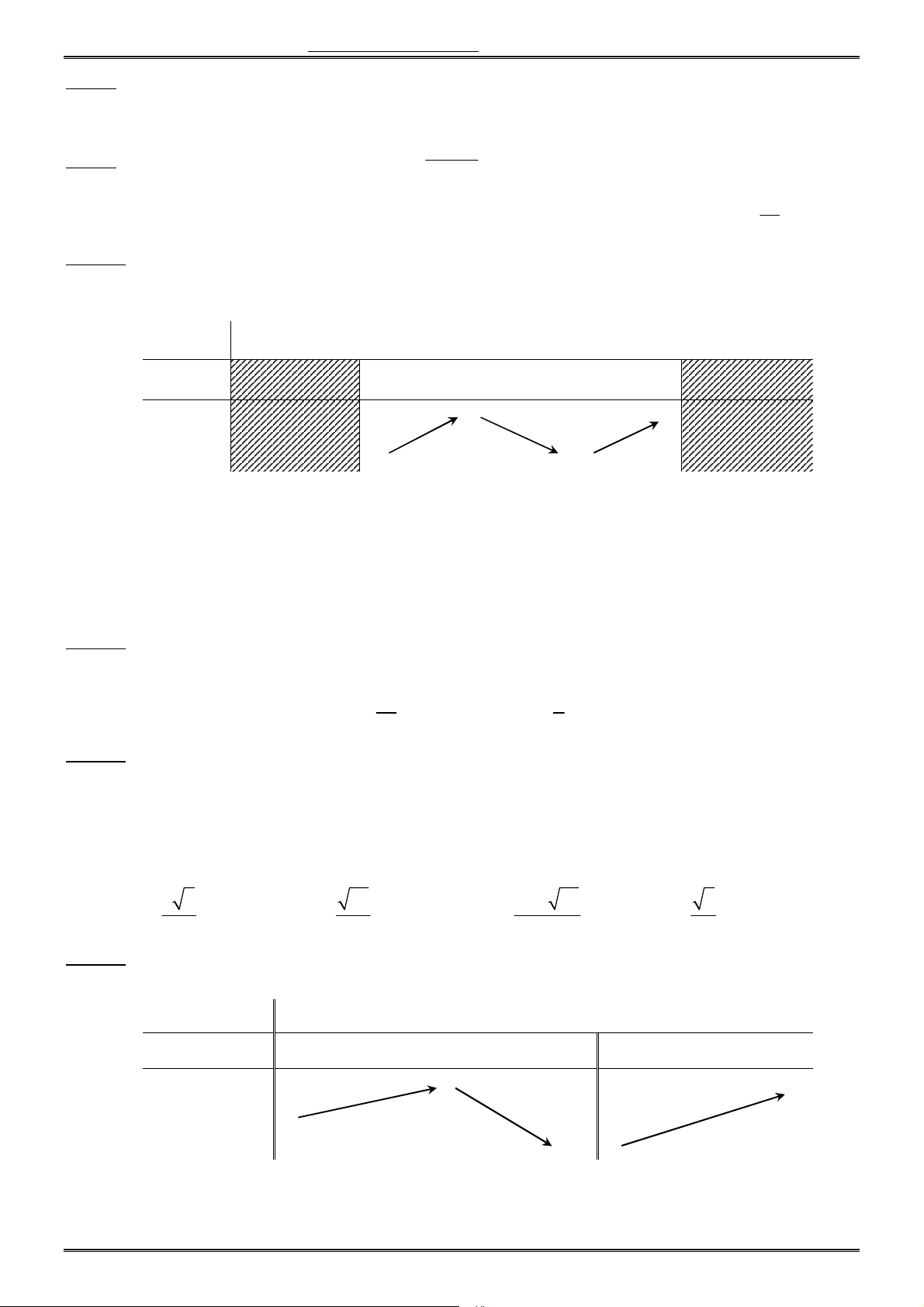
Câu 6. Cho hàm số f (x) có bảng biến thiên như sau: x  1 2  y  0  0  y 4 2 2 5
Mệnh đề nào dưới đây đúng ?
A. Hàm số có bốn điểm cực trị.
B. Hàm số đạt cực tiểu tại x  2.
C. Hàm số không có cực đại.
D. Hàm số đạt cực tiểu tại x  5. Trang 1
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
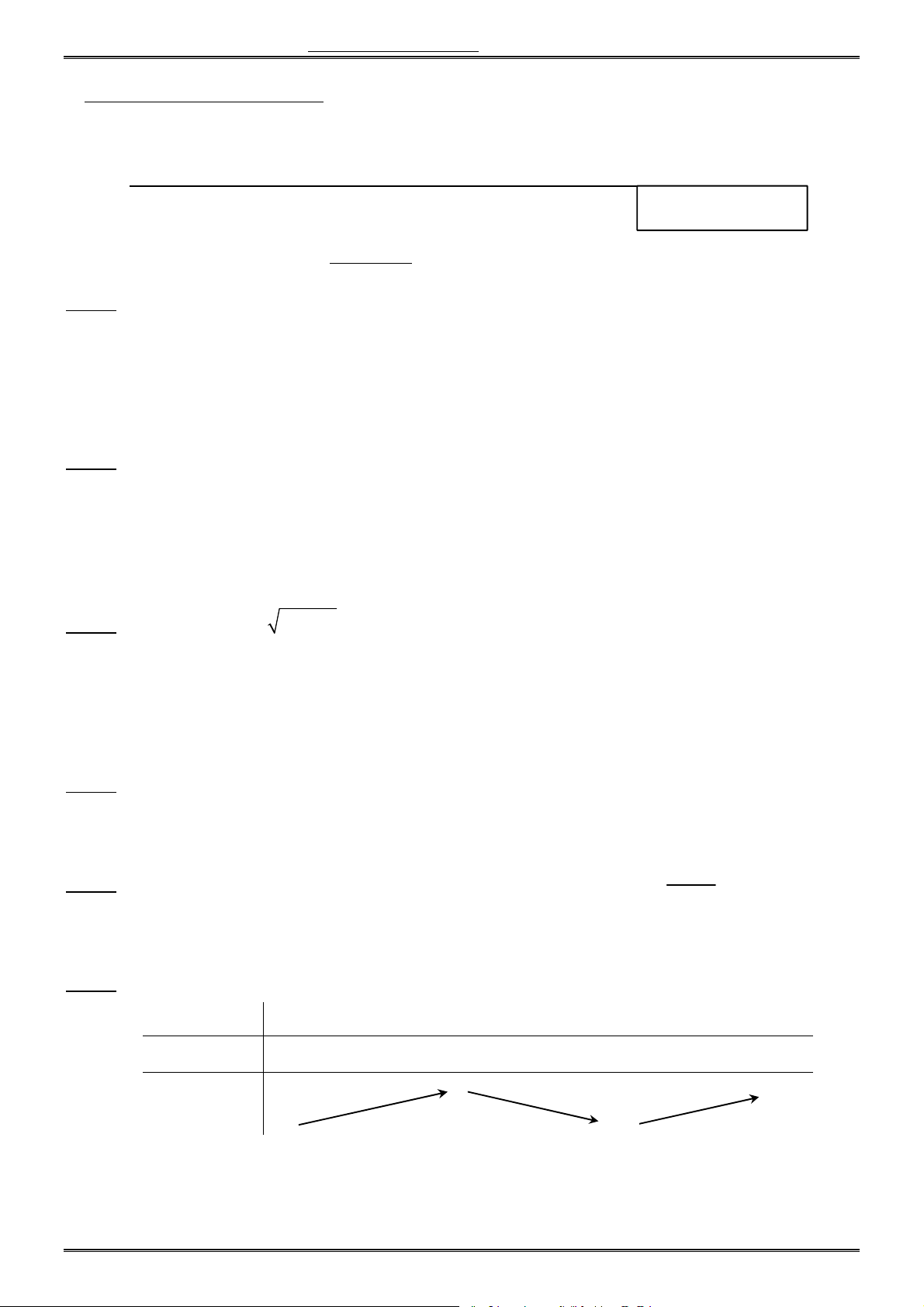
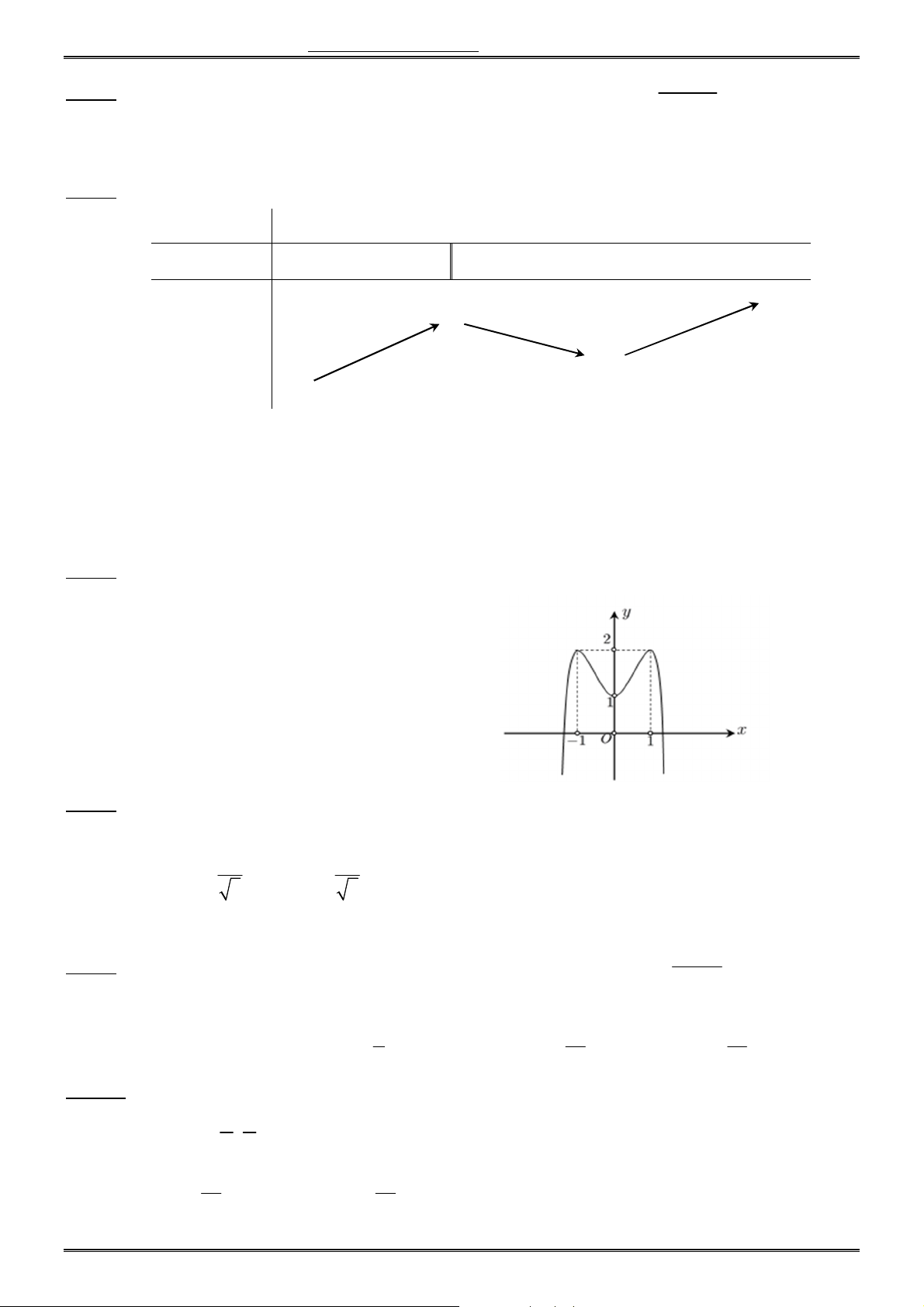
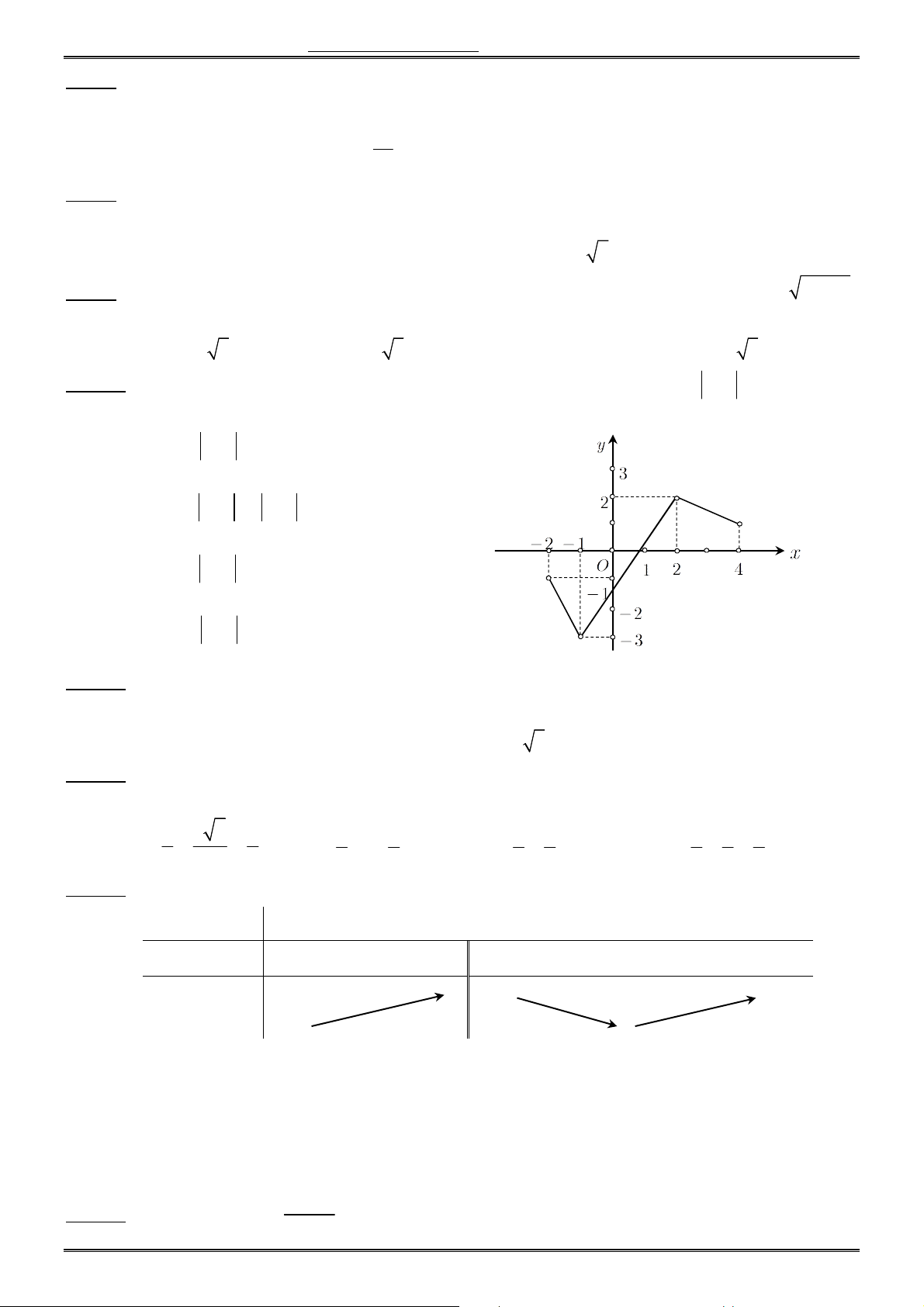
Câu 7. Cho hàm số f (x) có đồ thị f (
x) của nó trên khoảng K như hình vẽ. Khi đó trên K, hàm số
y f (x) có bao nhiêu điểm cực đại ? A. 0. B. 2. C. 3. D. 1.
Câu 8. Hỏi có bao nhiêu giá trị nguyên của m để hàm số 3 2 2
y  2x  (2m  1)x  (m  1)x có hai điểm cực trị. A. 4. B. 5. C. 3. D. 6. 3 2 x x
Câu 9. Tìm giá trị lớn nhất của hàm số y  
 2x 1 trên đoạn [0;2]. 3 2 1 7
A. max y   
B. max y  0.
C. max y  1. D. max y   [0;2] 3 [0;2] [0;2] [0;2] 3  3
Câu 10. Tìm giá trị lớn nhất của hàm số y  4 sin x  2 cos 2x trên D  0;    4   
A. max y  2 2.
B. max y  4 2. C. max y  2.
D. max y  4  2. D D D D 2
x m m
Câu 11. Hỏi tham số m thuộc khoảng nào sau đây thì giá trị nhỏ nhất của hàm số y x  1
trên đoạn [0;1] bằng 2. A. m  ( ;  2  ). B. m  ( 2  ; 4).
C. m  (4;15).
D. m  (15;  )  .
Câu 12. Một chất điểm chuyển động theo phương trình S   3 t  2 2
18t  2t  1, trong đó t tính
bằng giây (s) và S tính bằng mét (m). Tính thời gian vận tốc chất điểm đạt giá trị lớn nhất.
A. t  5s.
B. t  6s.
C. t  3s.
D. t  1s. 3  2x
Câu 13. Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y   x  1
A. x  1, y  2. B. x  1, y  2.
C. x  1, y  2.
D. x  2, y  1. 3 x  3x  4
Câu 14. Tìm số đường tiệm cận của đồ thị hàm số y   2 x  16 A. 2. B. 3. C. 1. D. 0.
2x  1  3x  1
Câu 15. Hỏi đồ thị hàm số y
có tất cả bao nhiêu đường tiệm cận ? 2 x x A. 0. B. 1. C. 2. D. 3.
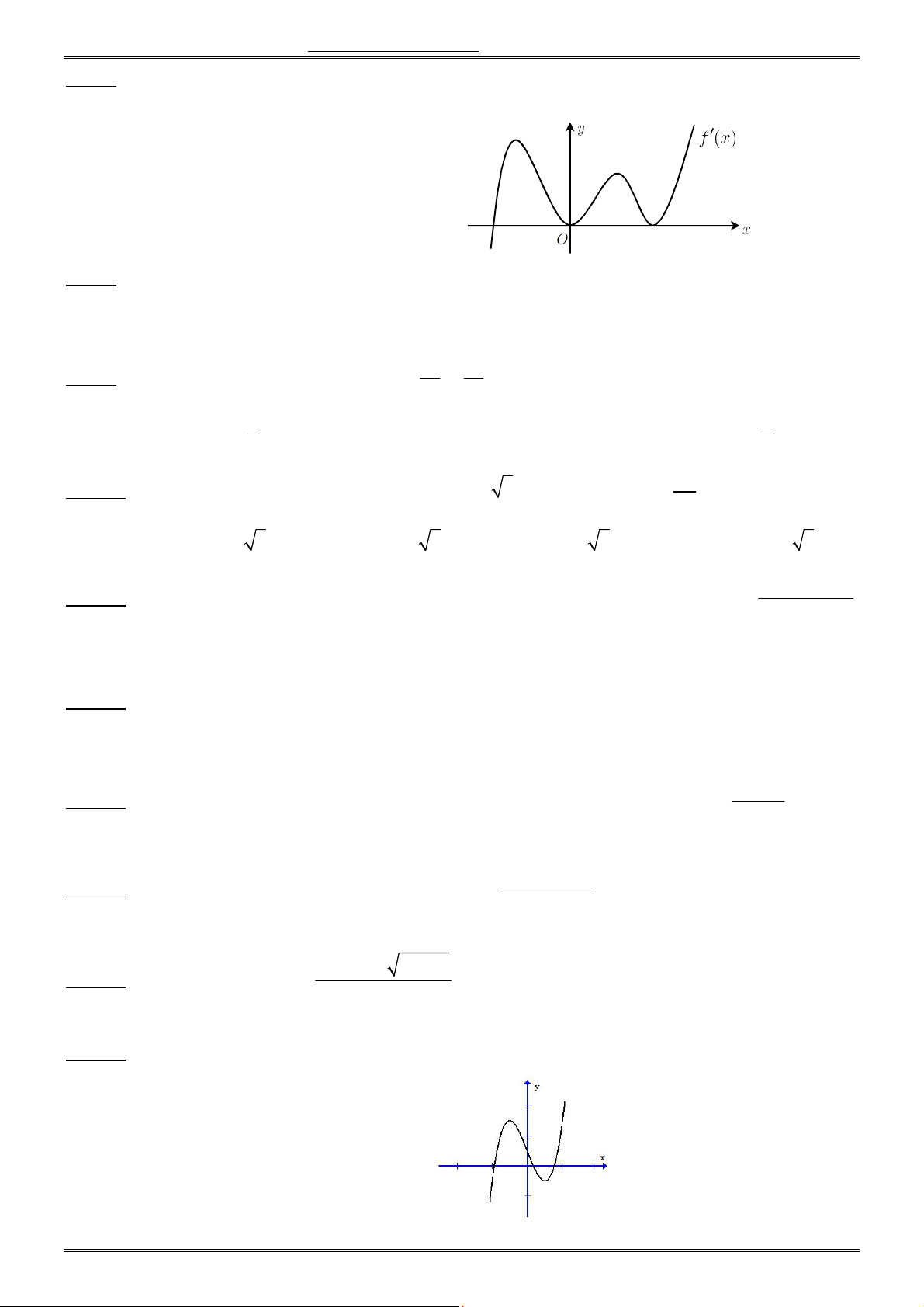
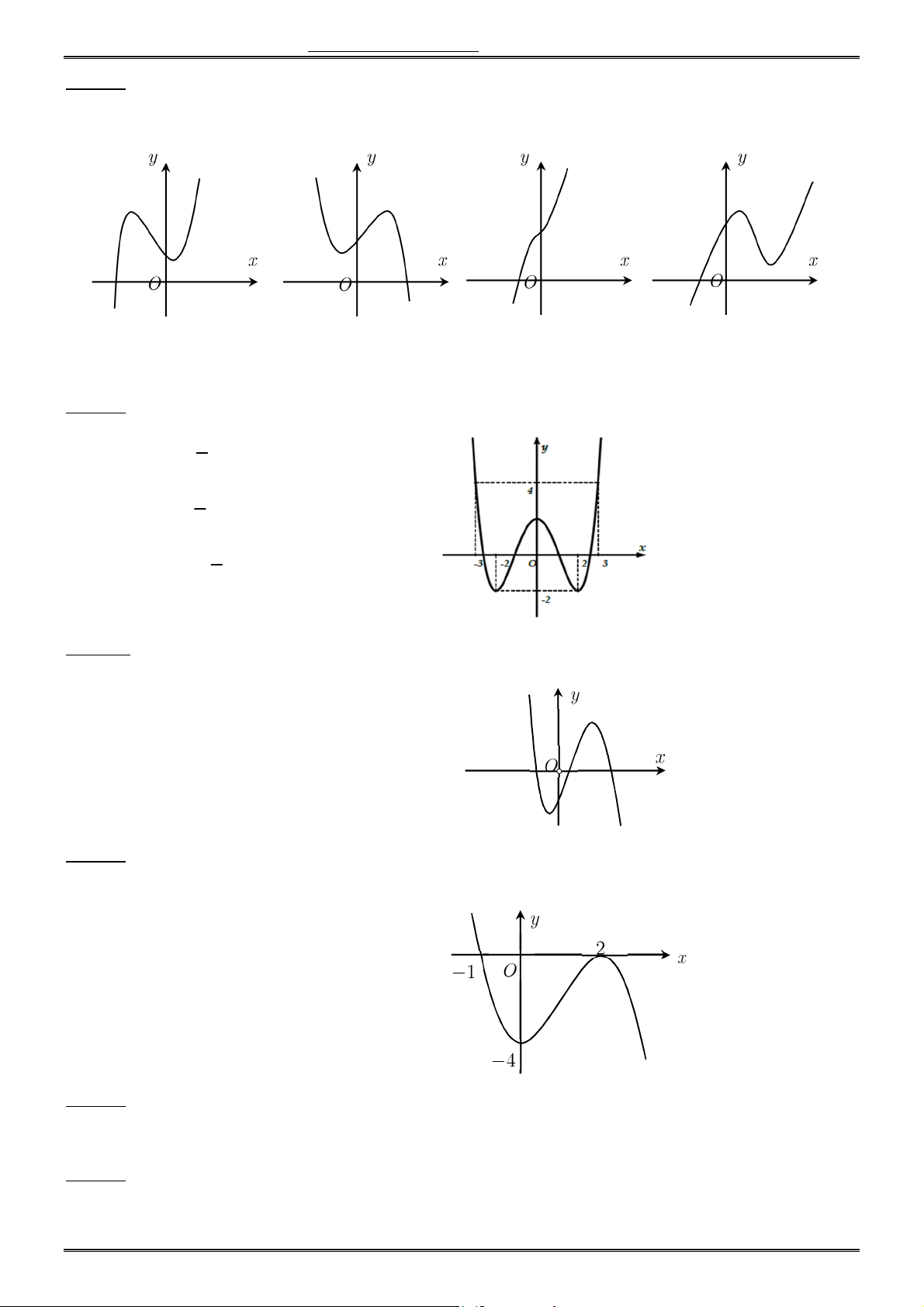
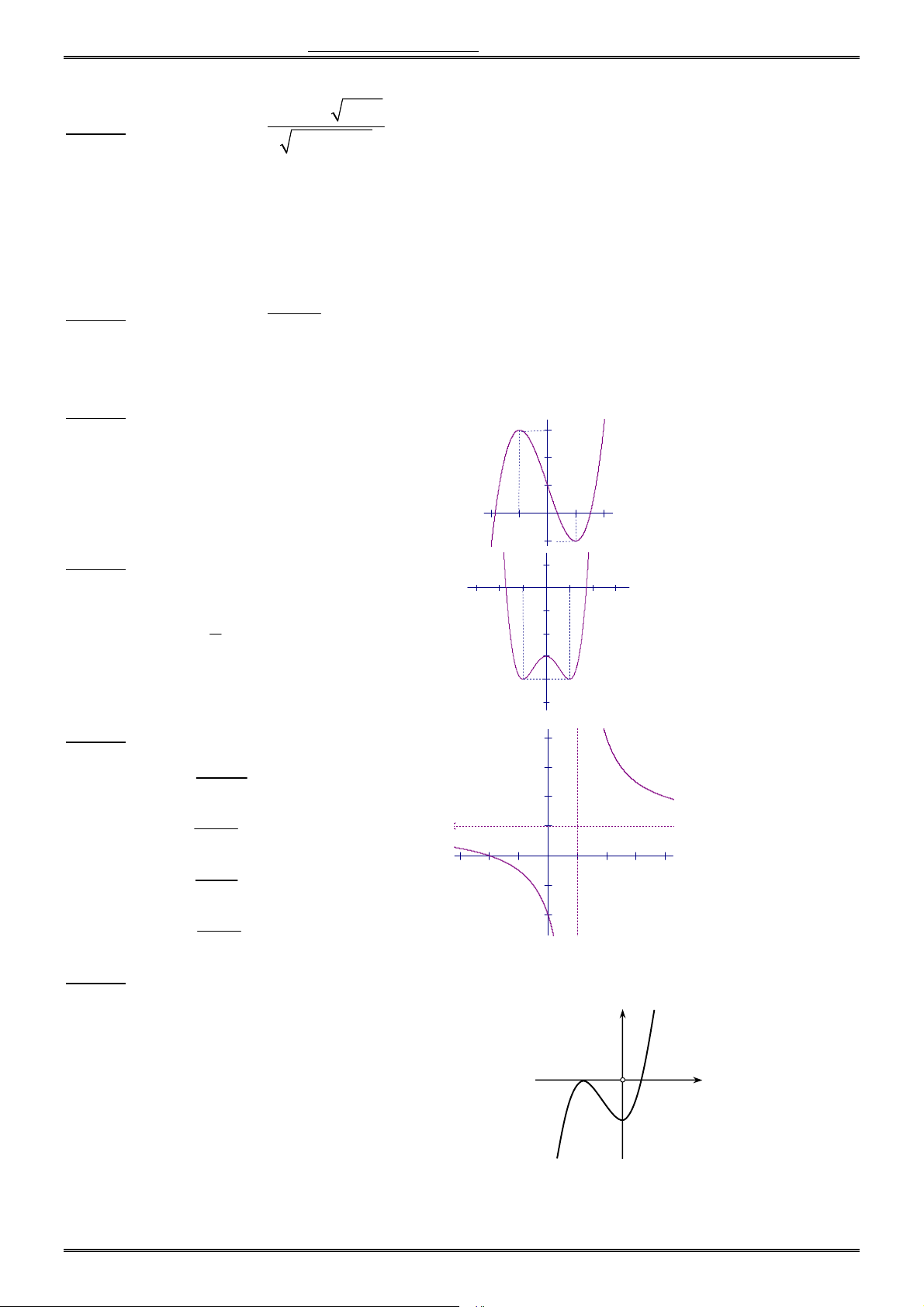
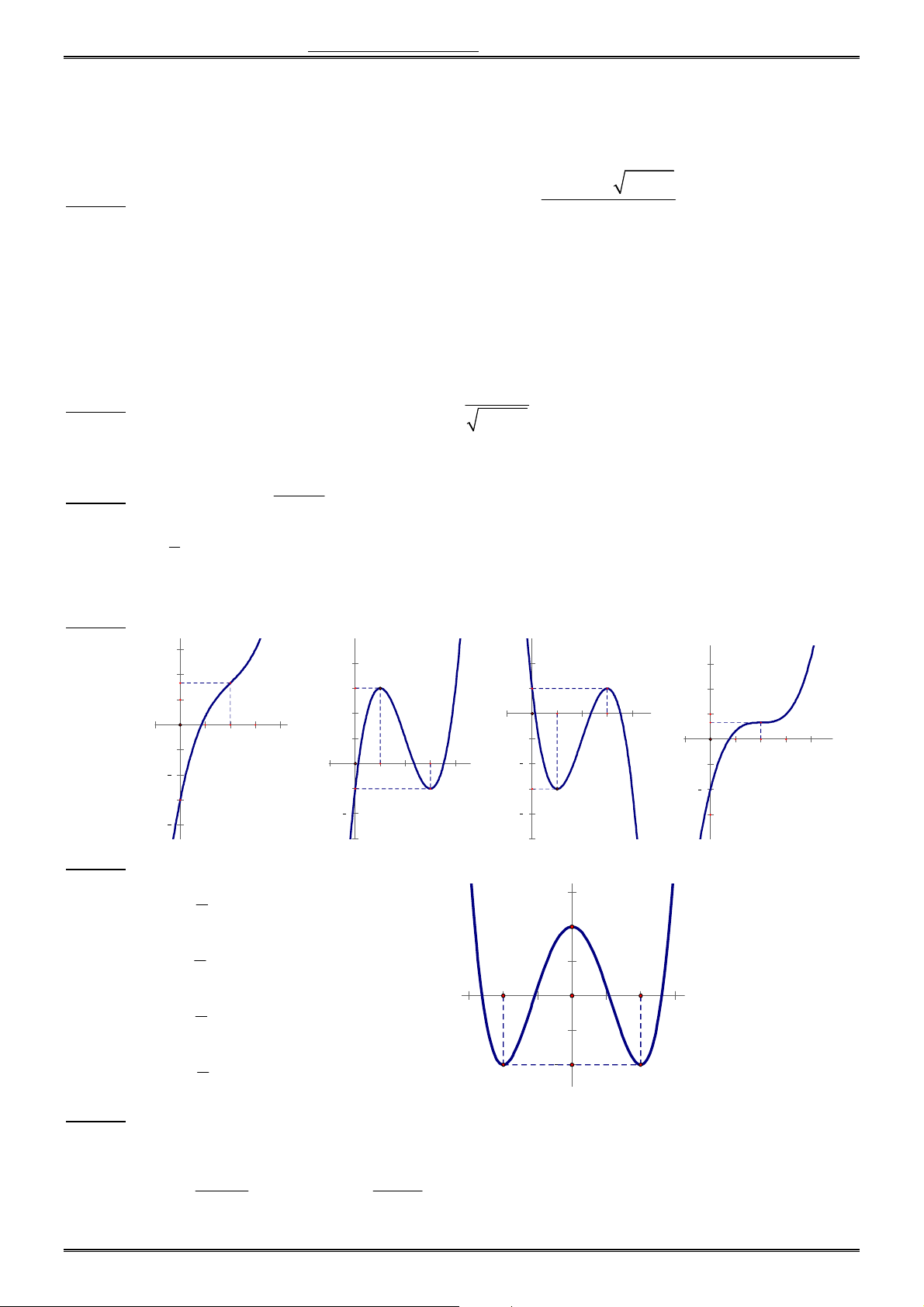
Câu 16. Đồ thị (C) trong hình sau là đồ thị hàm số nào trong 4 hàm số được liệt kê ở 4 phương án dưới đây ? A. 3 y x   3x  1. B. 3
y x  3x  1. C. 4 2
y x x  1. D. 2 y x   x  1. Trang 2
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
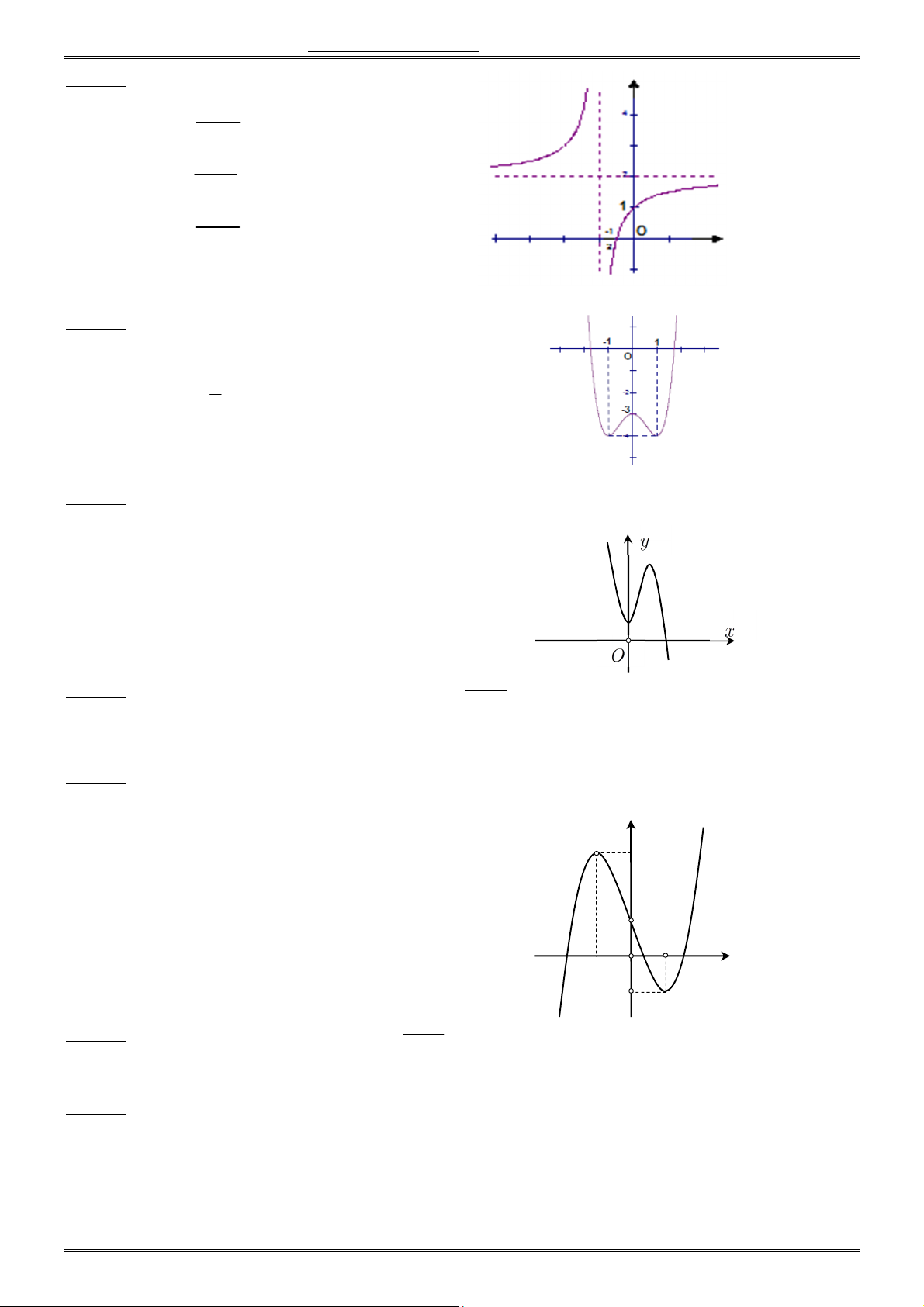
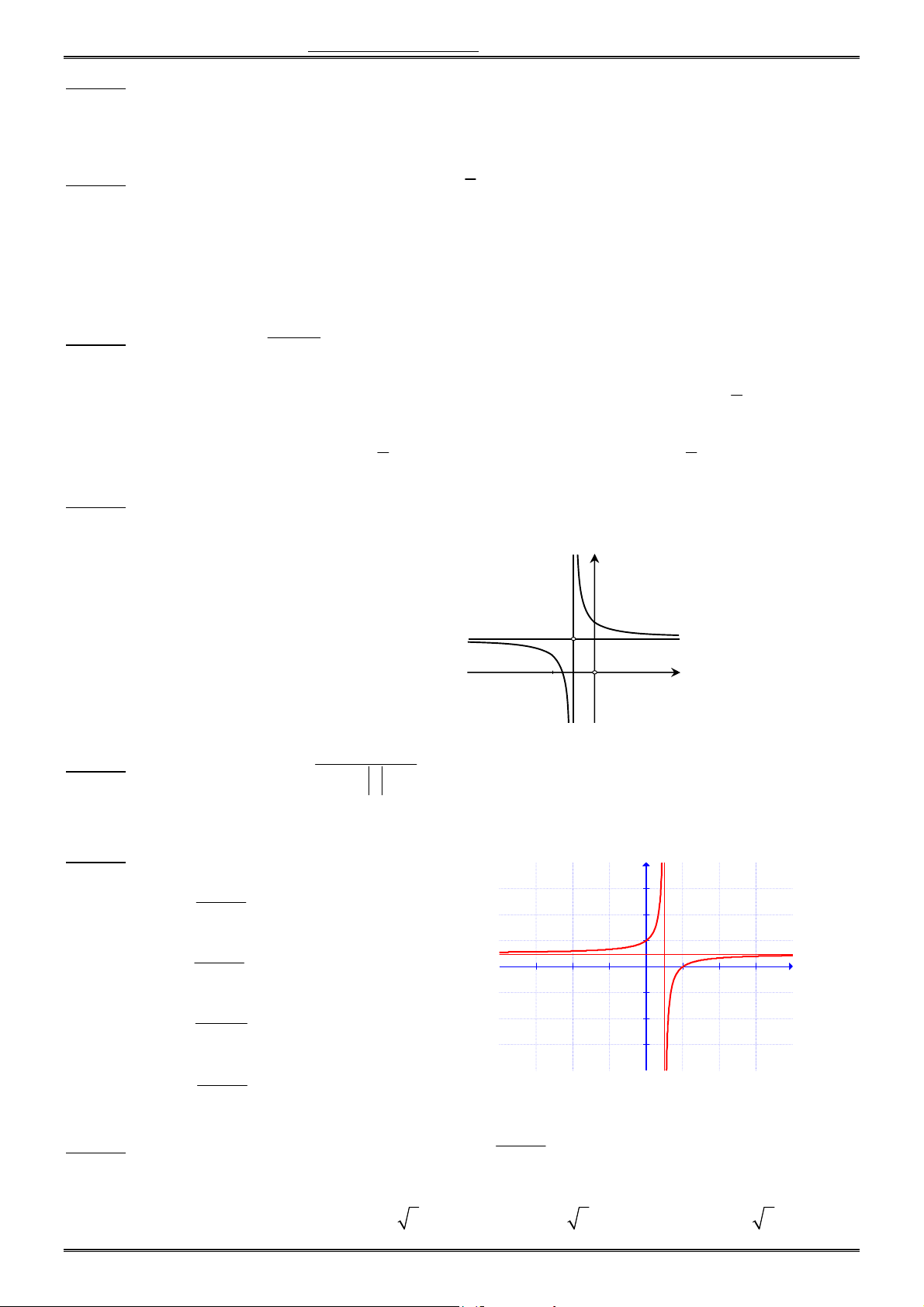
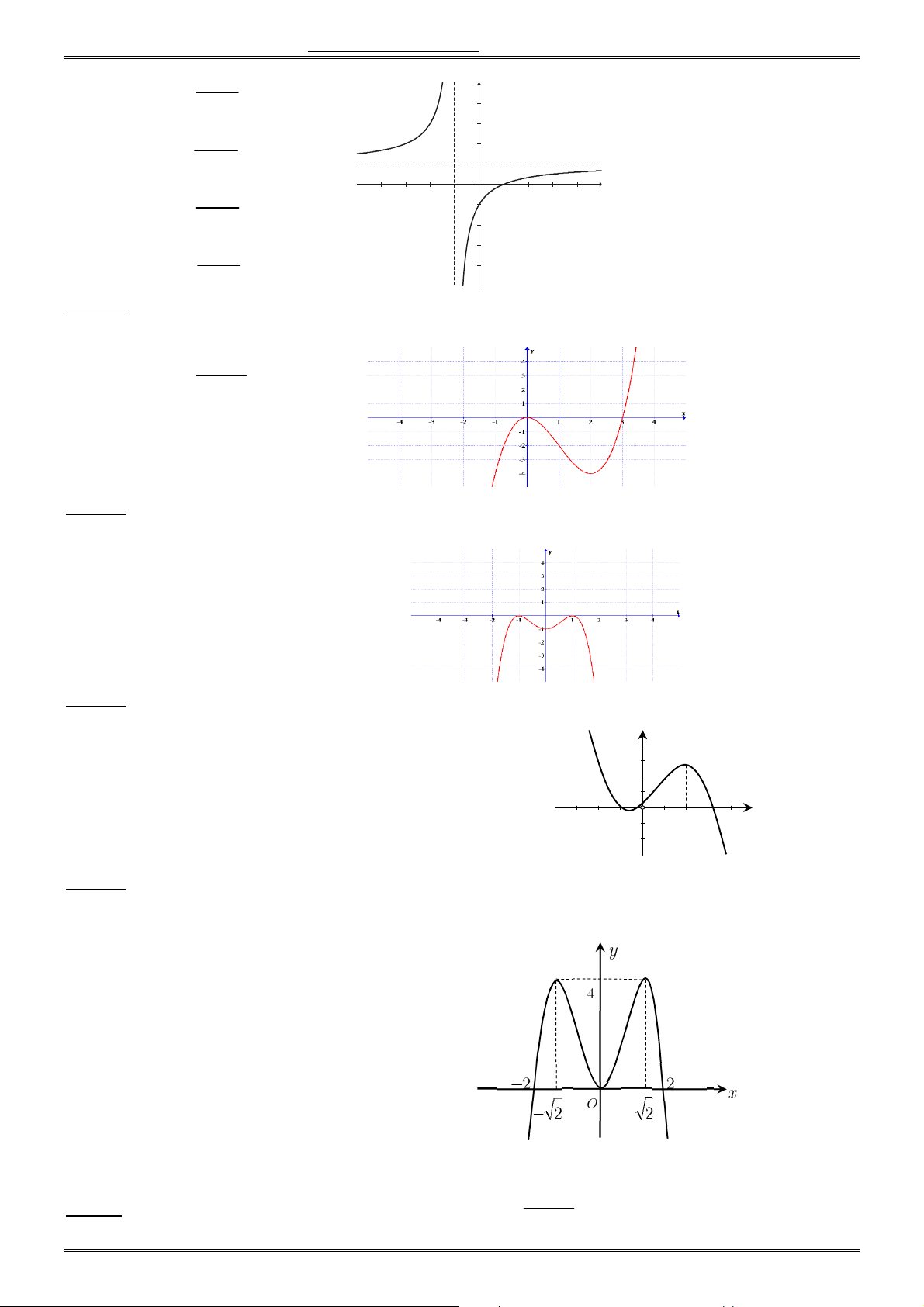
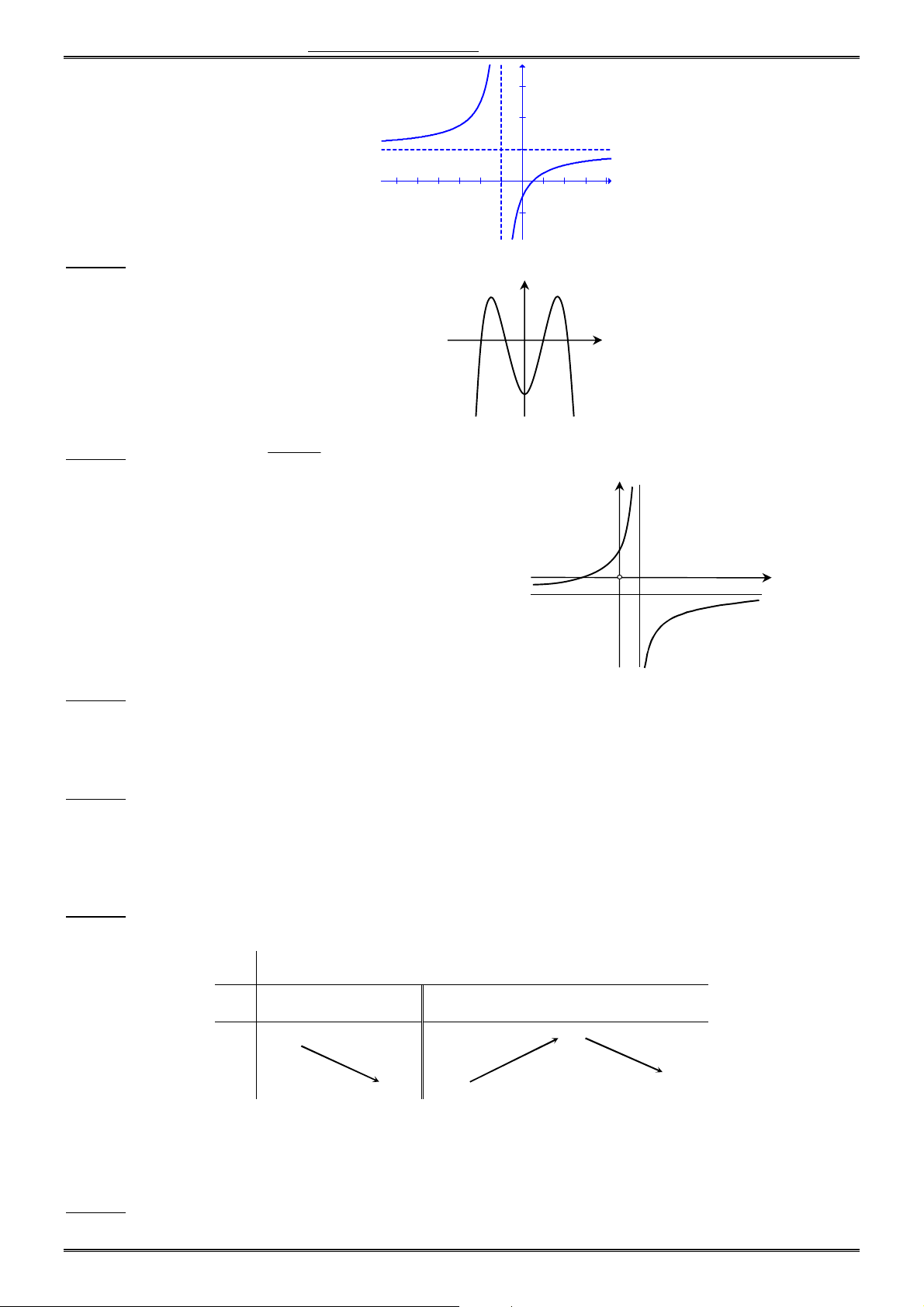
Câu 17. Đồ thị sau đây là đồ thị của hàm số nào ? x  2 A. y   x  1 x  1 B. y   x  1 x  3 C. y   1  x 2x  1 D. y   x  1
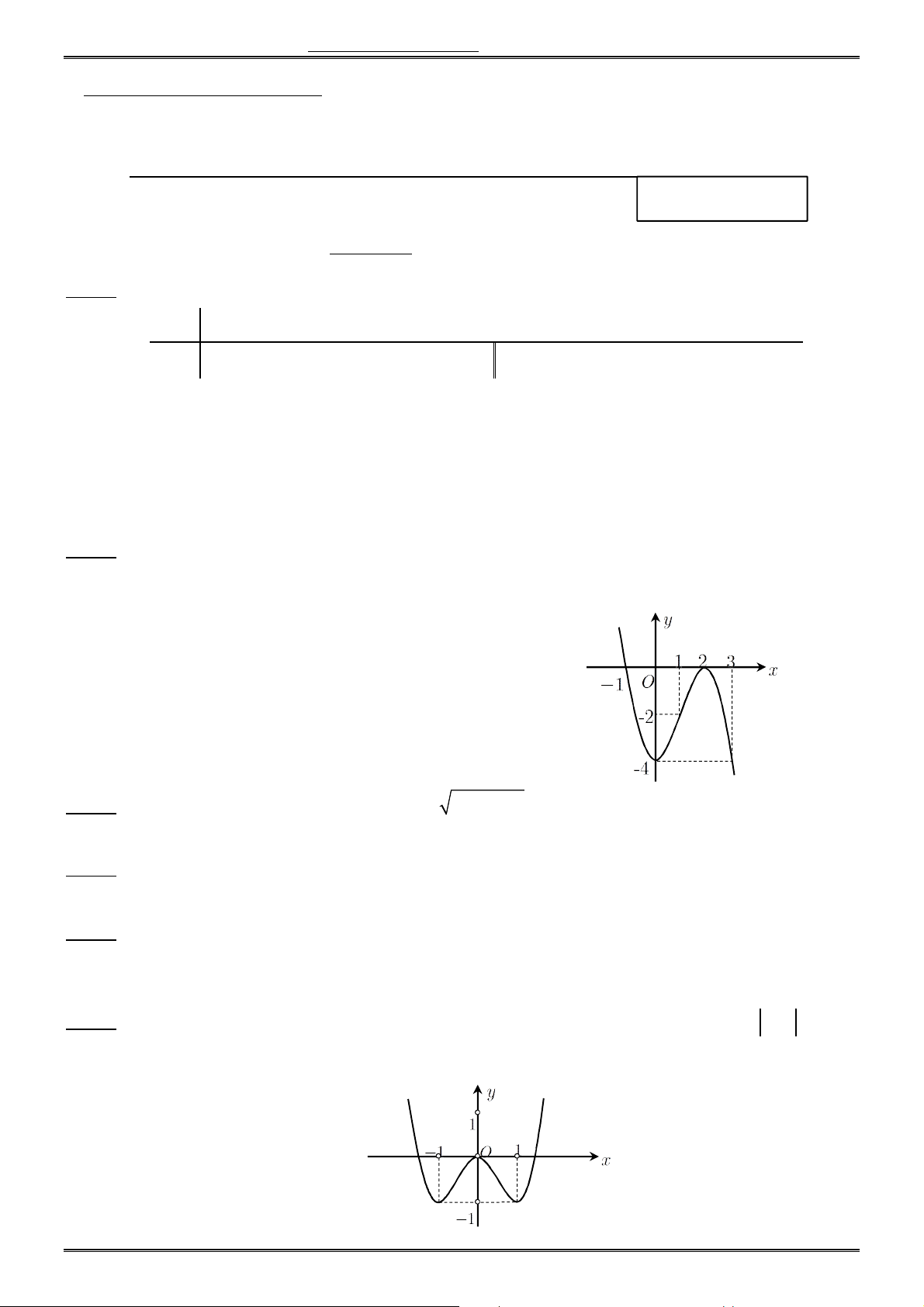
Câu 18. Đồ thị hình bên dưới là của hàm số nào ? A. 4 2
y x  3x  3. 1 B. 4 2
y   x  3x  3. 4 C. 4 2
y x  2x  3. D. 4 2
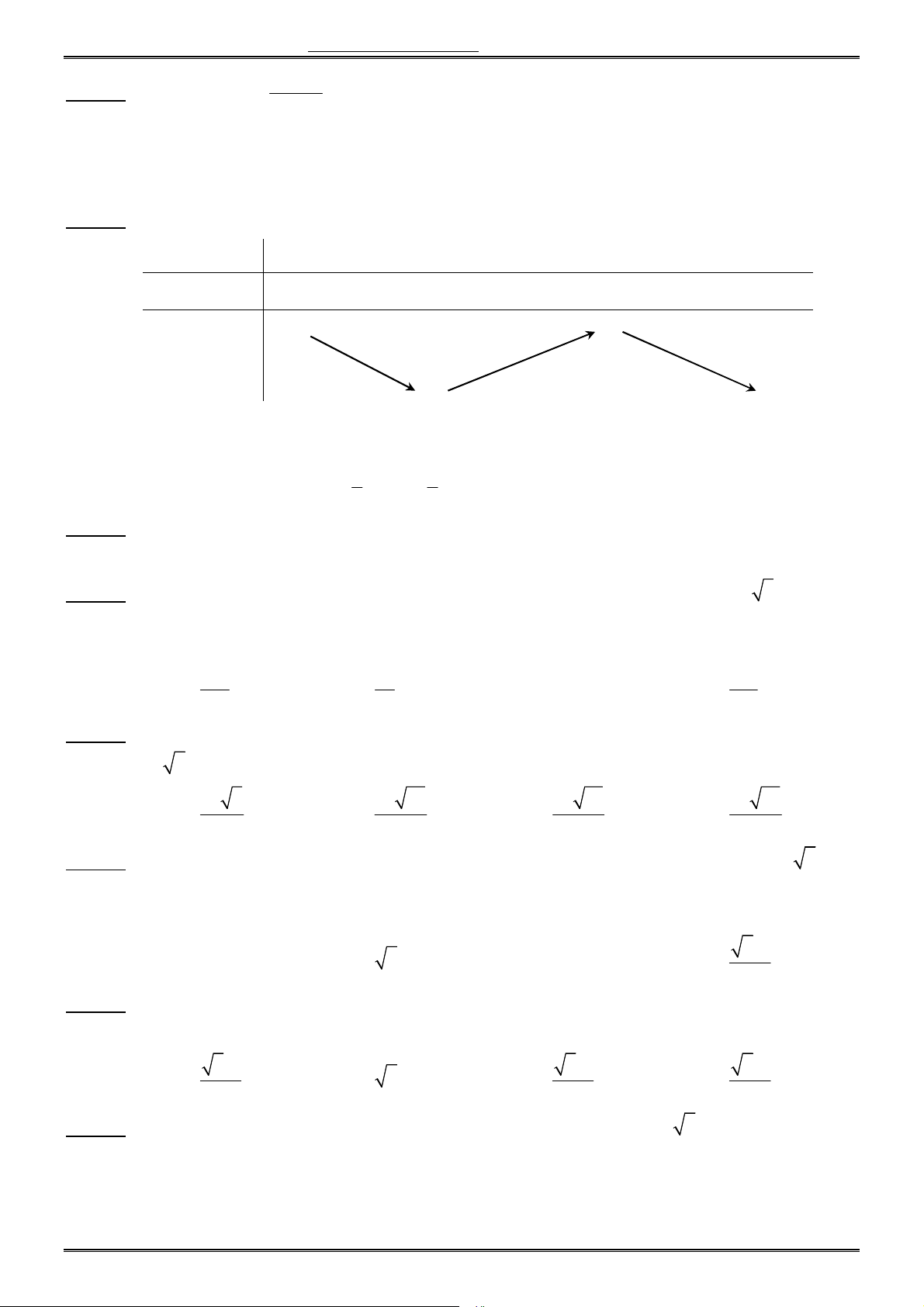
y x  2x  3. Câu 19. Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ. Hỏi mệnh đề nào dưới đây đúng.
A. a  0, b  0, c  0, d  0.
B. a  0, b  0, c  0, d  0.
C. a  0, b  0, c  0, d  0.
D. a  0, b  0, c  0, d  0. 4x
Câu 20. Tìm tọa độ giao điểm của đồ thị (C ) : y
và đường thẳng  : y x  1. x  1
A. M (0;1).
B. M (2; 3).
C. M (1;2).
D. M (1; 3). 1 2 3 4
Câu 21. Cho đồ thị hàm số 3
y x  3x  1 như hình bên dưới. Tìm tất cả các giá trị thực của tham
số m sao cho phương trình 3
x  3x m  0 có ba nghiệm thực phân biệt. y A. 2
  m  3. 3 B. 2
  m  2. 1
C. 2  m  2. 1 x 1  O D. 1
  m  3. 1  4
Câu 22. Tiếp tuyến của đồ thị hàm số y
tại điểm có tung độ y  2 có phương trình là x  1 0
A. y x  2.
B. y x   2.
C. y x  1.
D. y x   3.
Câu 23. Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau ?
A. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
B. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
C. Mỗi mặt có ít nhất ba cạnh.
D. Mỗi cạnh là cạnh chung của ít nhất ba mặt. Trang 3
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Câu 24. Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng ?
A. 4 mặt phẳng.
B. 3 mặt phẳng.
C. 6 mặt phẳng. D. 9 mặt phẳng.
Câu 25. Cho khối chóp S.ABC có SA vuông góc với đáy, SA  4, AB  6, BC  10 và CA  8.
Tính thể tích V của khối chóp.
A. V  40.
B. V  192.
C. V  32. D. V  24.
Câu 26. Cho khối chóp S.ABCD có đáy là hình chữ nhật, SA  (ABCD), AB  3a, AD  2 , a
SB  5a. Tính thể tích V của khối chóp S.ABCD theo . a A. 2
V  8a . B. 3
V  24a . C. 3
V  10a . D. 3
V  8a .
Câu 27. Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a. Tính thể tích
V của khối chóp S.ABC. 3 13a 3 11a 3 11a 3 11a A. V   B. V   C. V   D. V   12 12 6 4
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng
đáy và cạnh bên SD hợp với đáy một góc 60. Tính thể tích V của khối chóp S.ABCD. 3 3a 3 2 3a 3 3a A. 3
V  3a . B. V   C. V   D. V   6 3 3
Câu 29. Cho hình chóp S.ABCD có đáy là hình thang ABCD vuông tại A và D có
AB  2AD  2CD, SA  (ABCD). Góc giữa SC và đáy bằng 60. Biết khoảng cách từ B a 42 V đến (SCD) là  Tính S .ABCD k   7 3 a 3 6 6 3 A. k   B. k   C. k   D. k   2 3 2 3
Câu 30. Cho hình chóp đều S.ABC có AB  ,
a mặt bên hợp với đáy một góc 60. Tính thể tích V
của khối chóp S.ABC . 3 3a 3 3a 3 3a 3 3a A. V   B. V   C. V   D. V   12 72 24 6
Câu 31. Cho hình chóp đều S.ABC ,
D đáy ABCD là hình vuông cạnh a, các cạnh bên tạo với đáy góc 45 .
 Tính diện tích toàn phần S của hình chóp trên theo a. tp A. 2
S  ( 3  1)a . B. 2
S  2 3a . C. 2
S  4a . D. 2
S  ( 3  1)a . tp tp tp tp
Câu 32. Cho hình chóp S.ABCD có thể tích bằng 18, đáylà hình bình hành. Điểm M  cạnh SD
thỏa SM  2MD. Mặt phẳng (ABM ) cắt SC tại N . Tính thể tích V khối chóp S.ABNM . A. V  9. B. V  10. C. V  12. D. V  6.
Câu 33. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a 3. Gọi M, N lần lượt là trung
điểm của SB, SC. Tính thể tích V của khối chóp S.AMN , biết mặt phẳng (AMN ) vuông
góc với mặt phẳng (SBC ). 3 15a 3 3 15a 3 3 13a 3 3 13a A. V   B. V   C. V   D. V   32 32 64 32
Câu 34. Cho khối lăng trụ đứng ABC .AB C
  có BB  a, đáy ABC là tam giác vuông cân tại B
và AC a 2. Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a 3 a A. 3
V a . B. V   C. V   D. V   3 6 2
Câu 35. Cho lăng trụ tam giác đều ABC .AB C
  có cạnh đáy bằng a và AB  BC . Tính thể tích
V của khối lăng trụ. Trang 4
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 3 7a 3 6a 3 6a A. 3
V  6a . B. V   C. V   D. V   8 8 4
Câu 36. Cho hình lăng trụ đứng ABC .AB C
  có đáy ABC là tam giác vuông tại ,
A AC a, 
ACB  60. Đường thẳng BC  tạo với (ACC A
 ) một góc 30. Tính thể tích V của khối
lăng trụ ABC .AB C  . 3 3a A. 3
V  6a . B. V   C. 3
V  3a . D. 3
V  3a . 3
Câu 37. Cho hình lăng trụ tam giác đều ABC .AB C   có AB  ,
a đường thẳng AB tạo với mặt phẳng (BCC B
 ) một góc 30. Tính thể tích V của khối lăng trụ đã cho. 3 6a 3 6a 3 3a 3 a A. V   B. V   C. V   D. V   4 12 4 4
Câu 38. Cho lăng trụ tam giác ABC .AB C
  có đáy là tam giác vuông cân, cạnh huyền AC  2a.
Hình chiếu của A lên mặt phẳng (AB C
 ) là trung điểm I của AB , góc giữa cạnh bên và
mặt đáy bằng 60. Tính thể tích V của khối lăng trụ ABC .AB C  . 3 6a 3 3a 3 6a A. V   B. V   C. 3
V  2a . D. V   6 4 2
Câu 39. Xét hình chóp S.ABC thỏa mãn SA a, SB  2a, SC  3a với a là hằng số dương cho
trước. Tìm giá trị lớn nhất V
của thể tích khối chóp S.ABC ? max A. 3
V  6a . B. 3
V  2a . C. 3
V a . D. 3 V  3a .
Câu 40. Một hình chóp tam giác đều có cạnh bên bằng b và cạnh bên tạo với mặt phẳng đáy một góc .
Tính thể tích V của hình chóp đó. 3 3 A. 3 2 V b cos sin . B. 3 2
V b sin cos . 4 4 3 3 C. 3 2
V b cos sin . D. 3 V b cos sin . 4 4 PHẦN 2. TỰ LUẬN
Bài 1. Tìm tham số m để hàm số 3 2
y  (m  1)x  (m  1)x  2x  2.
a) Nghịch biến trên tập xác định của nó ? b) Đồng biến biến trên khoảng (0;  )  ? 1 73  
Bài 2. Biết M(1;3), N  ;  
y ax bx cx d
là hai điểm cực trị của đồ thị hàm số 3 2 . Tính 3 27
giá trị của biểu thức tại x  5.
Bài 3. Tìm tham số m để đồ thị hàm số 4 2
y x  2(m  1)x m có ba điểm cực trị ,
A B, C sao
cho OA BC, trong đó O là gốc tọa độ và A là điểm cực trị thuộc trục tung.
Bài 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 2
y x  2x  2  8x  4x . 3a
Bài 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD  , hình chiếu vuông 2
góc của S trên mặt phẳng (ABCD) là trung điểm H của cạnh AB. Tính theo a thể tích
khối chóp S.ABCD và khoảng cách từ điểm A đến mặt phẳng (SBD).
Bài 6. Cho lăng trụ đứng ABC .AB C
  có đáy ABC là tam giác vuông cân tại ,
A I là trung điểm
của BC, BC a 6, mặt phẳng (ABC ) tạo với mặt phẳng (ABC ) một góc bằng 60. Tính
thể tích khối lăng trụ ABC .AB C
  và khoảng cách giữa hai đường thẳng A ,
B AI. Trang 5
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN GIỮA KỲ 1 NĂM HỌC 2017 – 2018
TRƯỜNG THPT ...............................
Khối 12 – Môn thi: TOÁN
(Đề thi gồm 06 trang)
Thời gian làm bài: 90 phút, không kể thời gian phát đề Mã đề thi: 102
PHẦN 1. TRẮC NGHIỆM
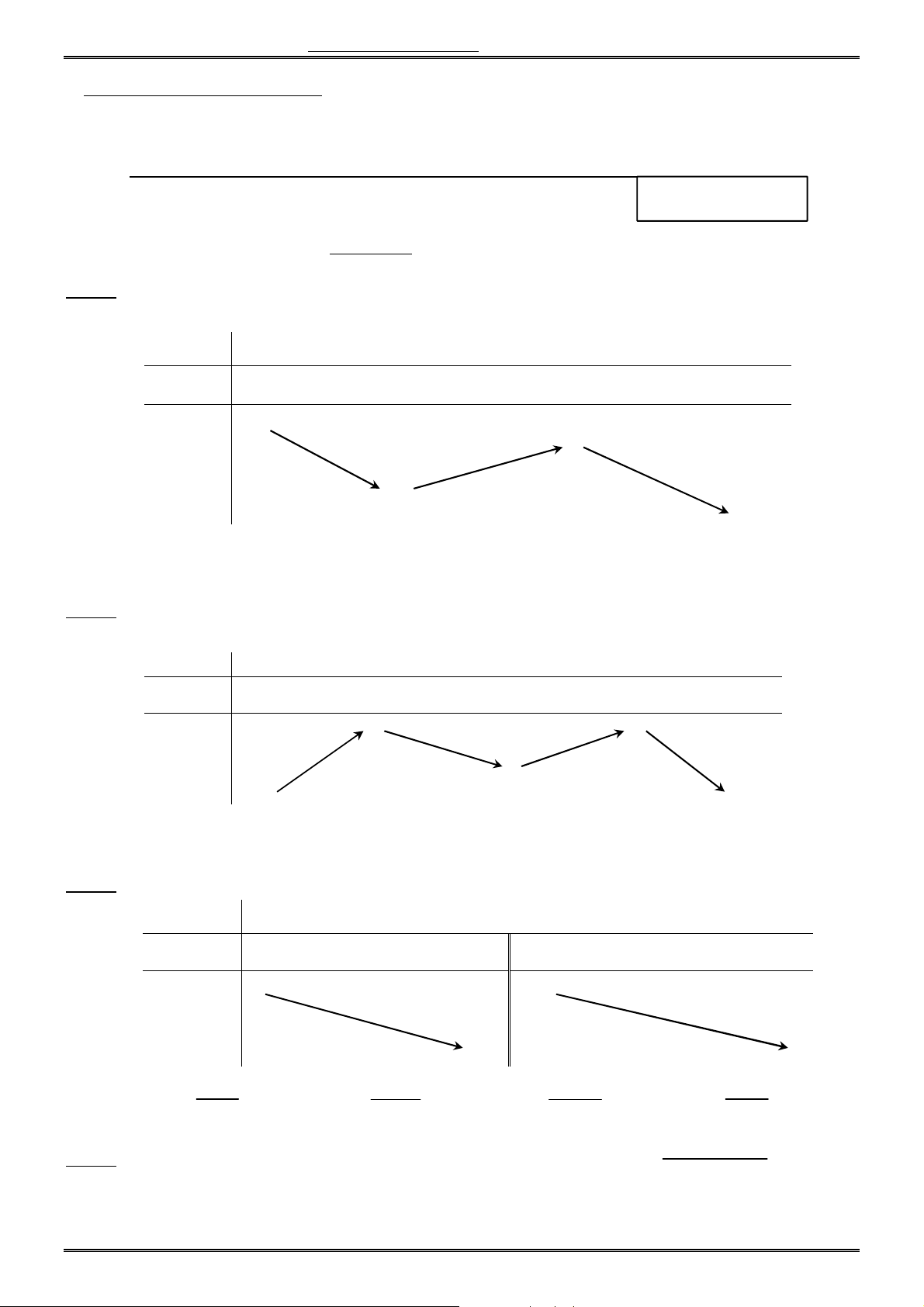
Câu 1. Bảng biến thiên dưới đây là của một hàm số trong bốn hàm số được liệt kê ở bốn phương án
A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? x  0 2  y  0  0   y 3 1   A. 3 2
y x  3x  1. B. 3 2 y x   3x  1. C. 3 2
y x  3x  1. D. 3 2 y x   3x  1.
Câu 2. Bảng biến thiên dưới đây là của một hàm số trong bốn hàm số được liệt kê ở bốn phương án
A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? x  1 0 1  y  0  0  0  3 3 y 1   A. 4 2
y  2x  4x  1. B. 4 2 y  2
x  4x  1. C. 4 2 y  2
x  4x 1. D. 4 2 y  2
x  4x  1.
Câu 3. Hàm số nào sau đây có bảng biến thiên như hình bên dưới ? x  2  y 1  y  1 x  1 2x  1 2x  5 x  3 A. y   B. y   C. y   D. y   x  2 x  2 x  2 x  2 2
mx x m
Câu 4. Có bao nhiêu giá trị nguyên của tham số m sao cho hàm số y  đồng biến x  1
trên từng khoảng xác định của nó. A. 3. B. 1. C. 5. D. 7. Trang 6
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 mx  9
Câu 5. Có bao nhiêu giá trị nguyên của tham số m sao cho hàm số f (x )  luôn nghịch biến x m trên khoảng ( ;  1). A. 2. B. 3. C. 5. D. 9.
Câu 6. Cho hàm số y f (x) xác định, liên tục trên  và có bảng biến thiên: x  0 1  y   0   0 y 1 
Hỏi khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1.
D. Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1.
Câu 7. Cho hàm số y f (x) có đồ thị như hình vẽ bên dưới. Hàm số f (x ) đạt cực tiểu tại điểm nào dưới đây ? A. x  1. B. x  1. C. x  2.
D. x  0.
Câu 8. Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số 3 2 3
y x  3mx  4m có hai
điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4, với O là gốc tọa độ. 1 1 A. m   hoặc m  
B. m  1 hoặc m  1. 4 2 4 2
C. m  1.
D. m  0. 3x  1
Câu 9. Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số y  trên đoạn [0;2]. x  3
Tính tổng S M m. 8 14 14 A. S  4. B. S   C. S    D. S   5 3 3 Câu 10. Cho hàm số 3
y  sin x  cos 2x  sin x  2. Tìm giá trị nhỏ nhất m của hàm số đã cho trên      khoảng   ;     2 2  23 1 A. m   B. m  
C. m  5.
D. m  1. 27 27 Trang 7
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Câu 11. Tìm các giá trị của m để giá trị nhỏ nhất của hàm số 3 2 y x
  3x m trên đoạn [1;1] bằng 0. A. m  4. B. m  2. C. m  6. D. m  0. 1
Câu 12. Một chuyển động theo quy luật 2 3
s  9t t , với t (giây) là khoảng thời gian từ lúc vật bắt 2
đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi
trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật là bao nhiêu ?
A. 54 (m/s).
B. 216 (m/s).
C. 30 (m/s).
D. 400 (m/s). 2x  3
Câu 13. Cho hàm số y
có đồ thị (C ). Khẳng định nào là sai ? 3x  6 2
A. (C ) có tiệm cận đứng x  2  .
B. (C ) có tiệm cận ngang y   3  2    1  
C. (C ) có tâm đối xứng I   2;   C A 1  ;    D. ( ) đi qua điểm  3  9
Câu 14. Cho hàm số f (x) có đồ thị như hình vẽ bên. Tiệm cận đứng và tiệm cận ngang của đồ thị lần lượt là: y
A. x  1 và y  2.
C. x  1 và y  2. 3
B. x  1 và y  2.  2 O x
D. x  1 và y  2. x  1
Câu 15. Hỏi đồ thị hàm số y
có bao nhiêu đường tiệm cận ? 2 x  4 x  3 A. 1. B. 2. C. 3. D. 4.
Câu 16. Đồ thị hình bên dưới là của hàm số nào ? y 1  x 3 A. y   1  2x 2 1  x 1 B. y   x 2x  1 -3 -2 -1 1 2 3 -1 3  2x C. y   -2 2x  1 -3 1  2x D. y   x  1 2x  1 Câu 17. Gọi ,
A B là giao điểm của đồ thị hàm số y
và đường thẳng d : y x  1. Tính độ x  1
dài đoạn thẳng AB. A. AB  2. B. AB  2 2. C. AB  2.
D. AB  2 3. Trang 8
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Câu 18. Đồ thị hàm số 3 2
y  2018x mx  2017x  1 có dạng nào sau đây ? Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 19. Cho đồ thị như hình vẽ là đồ thị của hàm số nào sau đây ? 1 A. 4 2
y x  2x  2. 4 1 B. 4 2
y x  2x  2. 4 1 C. 4 2
y   x  2x  2. 4 D. 4 2
y x  8x  2. Câu 20. Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng
A. a  0, b  0, c  0, d  0.
B. a  0, b  0, c  0, d  0.
C. a  0, b  0, c  0, d  0.
D. a  0, b  0, c  0, d  0. 3 2
Câu 21. Đồ thị hình bên dưới là của hàm số y  x  3x  4 . Tìm các giá trị của m để phương trình 3 x  2
3x m  0 có hai nghiệm phân biệt ?
A. m  4 hoặc m  0.
B. m  4.
C. 0  m  4.
D. m  0.
Câu 22. Phương trình tiếp tuyến của đồ thị (C) hàm số 4 2
y x  2x tại điểm có hoành độ x  2 là 0
A. y  24x  40.
B. y  8x  3.
C. y  24x  16.
D. y  8x  8.
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và có thể tích bằng 8. Tính thể
tích V của khối chóp S.OCD. Trang 9
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
A. V  3.
B. V  4.
C. V  5. D. V  2.
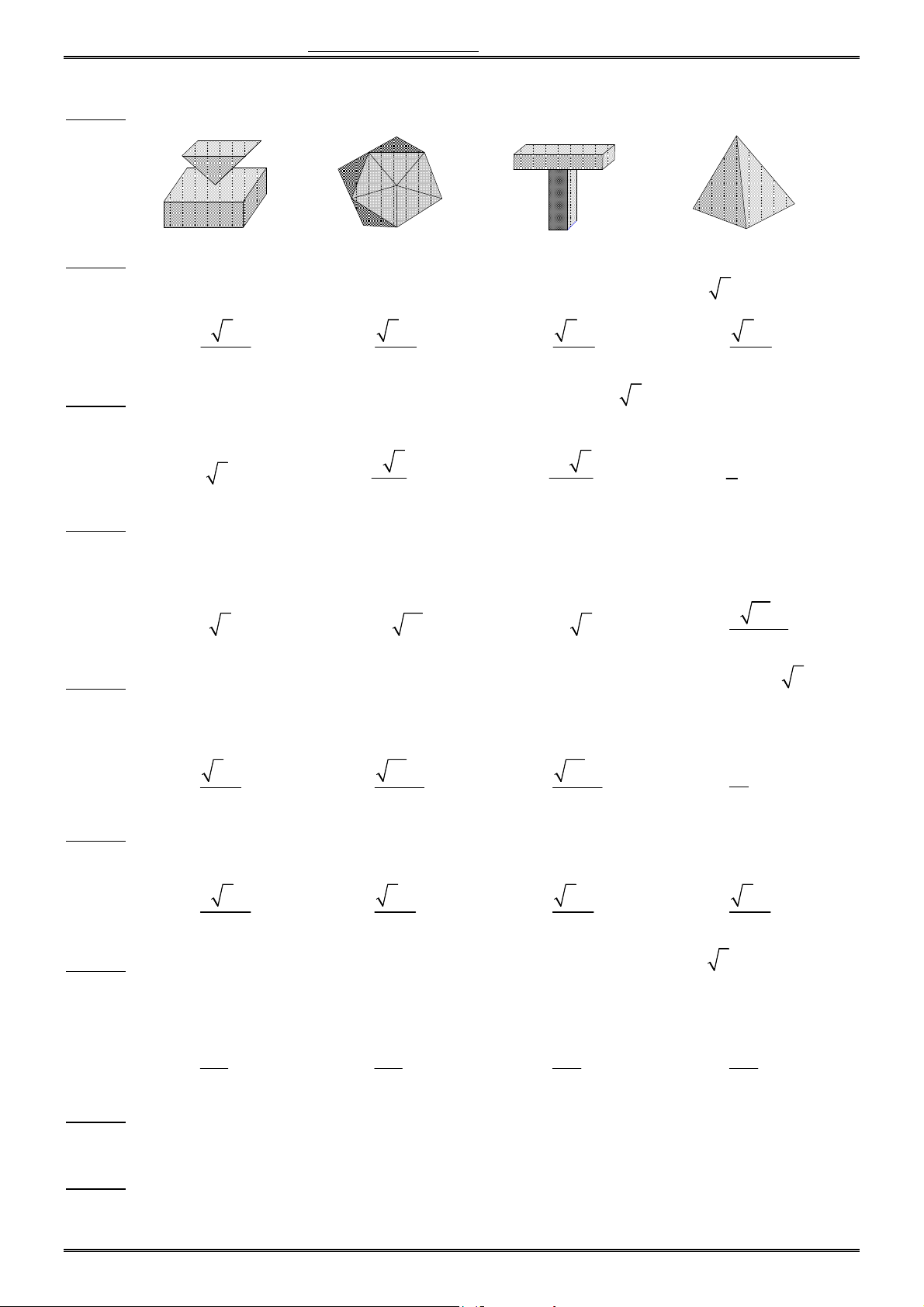
Câu 24. Hình nào dưới đây không phải là một khối đa diện ? A. B. C. D.
Câu 25. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh .
a Hai mặt bên (SAB) và (SAC )
cùng vuông góc với đáy. Tính thể tích V khối chóp S.ABC, biết SC a 3. 3 2 6a 3 6a 3 3a 3 3a A. V   B. V   C. V   D. V   9 12 2 4
Câu 26. Khối chóp tam giác đều có thể tích 3
V  2a , cạnh đáy bằng 2a 3. Tính chiều cao h của khối chóp đó. a 6 2a 3 a
A. h a 6. B. h   C. h   D. h   3 3 3
Câu 27. Cho khối chóp S.ABCD có ABCD là hình vuông cạnh 3a. Tam giác SAB cân tại S và nằm
trong mặt phẳng vuông góc với đáy. Tính thể tích V của khối chóp S.ABC , D biết góc giữa
SC và mặt phẳng (ABCD) bằng 60. 3 9 15a A. 3
V  9 3a . B. 3
V  18 15a . C. 3
V  18 3a . D. V   2
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, biết AB a, AD a 3. Hình
chiếu S lên đáy là trung điểm H cạnh AB, góc tạo bởi SD và đáy là 60. Tính thể tích V
khối chóp S.ABCD. 3 5a 3 13a 3 15a 3 a A. V   B. V   C. V   D. V   5 2 2 2
Câu 29. Cho hình chóp S.ABC có SA  (ABC ) và tam giác SBC đều cạnh a và nằm trong mặt
phẳng hợp với mặt phẳng đáy một góc 60. Tính thể tích V của khối chóp S.ABC . 3 3 3a 3 3a 3 3a 3 3a A. V   B. V   C. V   D. V   16 16 8 32
Câu 30. Cho hình chóp S.ABC có đáy là tam giác vuông cân ở B, AC a 2, SA  (ABC ),
SA a. Gọi G là trọng tâm của tam giác SBC, mặt phẳng () đi qua AG và song song
với BC cắt SC, SB lần lượt tại M, N . Tính thể tích V của khối chóp S.AMN . 3 2a 3 2a 3 4a 3 4a A. V   B. V   C. V   D. V   27 9 27 9
Câu 31. Tổng diện tích các mặt của 1 hình lập phương bằng 150. Tính thể tích V khối lập phương đó.
A. V  200.
B. V  625.
C. V  100.
D. V  125.
Câu 32. Cho hình lập phương ABC . D AB CD   cạnh .
a Gọi E và E lần lượt là trung điểm CD,
AB . Tính thể tích V của khối đa diện ABEDD A
 E theo . a Trang 10
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 3 a 3 a 3 a 3 a A. V   B. V   C. V   D. V   6 2 4 3
Câu 33. Cho khối lăng trụ đứng ABC .AB C
  có đáy ABC là tam giác cân với AB AC a, 
BAC  120. Mặt phẳng (AB C  )
 tạo với đáy một góc 60. Tính thể tích V của khối lăng trụ đã cho. 3 3a 3 9a 3 a 3 3a A. V   B. V   C. V   D. V   8 8 8 4
Câu 34. Cho lăng trụ đứng tam giác ABC .AB C
  có đáy ABC là tam giác vuông cân tại B với
BA BC a, biết AB hợp với đáy ABC một góc 60. Tính thể tích V của khối lăng trụ
ABC .AB C  . 3 3a 3 3a 3 a A. V   B. 3
V  2a . C. V   D. V   6 2 2 3a
Câu 35. Cho hình lăng trụ đều ABC .AB C   có AB  , a AA 
 Gọi G là trọng tâm tam giác 2
ABC . Tính thể tích V của tứ diện GABC theo a. 3 3a 3 3 3a 3 3a 3 3a A. V   B. V   C. V   D. V   12 8 24 16
Câu 36. Cho hình lăng trụ tam giác ABC .AB C
  có đáy ABC là tam giác vuông tại , A AB  , a
AC a 3. Hình chiếu vuông góc của A lên (ABC) là trung điểm của BC. Góc giữa AA
và (ABC) bằng 60. Tính thể tích V của khối lăng trụ ABC .AB C  . 3 a 3 a 3 3 3a 3 3a 3 A. V   B. V   C. V   D. V   2 2 2 2 
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB  , a BAD  60 , 
SO  (ABCD) và mặt phẳng (SCD) tạo với mặt đáy một góc 60 .
 Tính thể tích V của khối chóp S.ABC . D 3 3a 3 3a 3 3a 3 3a A. V   B. V   C. V   D. V   24 8 12 48
Câu 38. Một công ty sản xuất gỗ muốn thiết kế các thùng đựng hàng bên trong dạng hình lăng trụ tứ
giác đều không nắp có thể tích là 2
62,5dm . Để tiết kiệm vật liệu làm thùng, người ta cần thiết
kế thùng sao cho có tổng S diện tích xung quanh và diện tích mặt đáy là nhỏ nhất. Tìm S. A. 2
S  106,25dm . B. 2 S  75dm . C. 2 S  50 5dm . D. 2 S  45dm .
Câu 39. Cho khối chóp S.ABC có đường cao SA  2a, tam giác ABC vuông ở C có AB  2a, góc  CAB  30 .
 Gọi H là hình chiếu của A trên SC. Gọi B là điểm đối xứng của B qua mặt
phẳng (SAC ). Tính thể tích V của khối chóp H .AB B  . 3 2 3a 3 2 3a 3 6 3a 3 3a A. V   B. V   C. V   D. V   7 7 7 7 Trang 11
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I có cạnh bằng a, BAD  60 . 
Gọi H là trung điểm của IB và SH vuông góc với (ABCD). Góc giữa SC và (ABCD) bằng 45 .
 Tính thể tích V của khối chóp S.AHC . D 3 35a 3 39a 3 39a 3 35a A. V   B. V   C. V   D. V   32 24 32 24 PHẦN 2. TỰ LUẬN mx  4
Bài 1. Tìm tham số m để hàm số y f (x)  x m
a) Đồng biến trên từng khoảng xác định của nó ?
b) Luôn nghịch biến trên nửa khoảng ( ;  1) ? 1
Bài 2. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y  3 x  2
mx x m  1 có hai 3
cực trị x , x thỏa mãn điều kiện 2 2
x x  4x x  2. 1 2 1 2 1 2
Bài 3. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 4 2
y x  (3m  1)x  3 có ba 2
điểm cực trị tạo thành tam giác cân và độ dài cạnh đáy bằng độ dài cạnh bên. 3
Bài 4. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 4 2 2 2
y  2x m x m  1 có ba điểm cực trị ,
A B, C sao cho bốn điểm ,
A B, C , O là bốn đỉnh một hình thoi với O là gốc tọa độ.
Bài 5. Cho hình chóp S.ABC, đáy ABC là tam giác đều cạnh 2a, SA vuông góc với đáy, góc giữa
đường thẳng SB và mặt phẳng đáy (ABC ) bằng 60. Gọi I trung điểm của BC, H là hình
chiếu vuông góc của A trên SI. Tính thể tích khối chóp S.ABC và khoảng cách từ G là tâm
đường tròn ngoại tiếp tam giác ABC đến mặt phẳng (ABH ).
Bài 6. Cho lăng trụ tam giác đều ABC .AB C
  có AA  a 2, đường thẳng B C  tạo với mặt phẳng (ABB A
 ) một góc 45. Tính theo a thể tích khối lăng trụ đã cho và khoảng cách giữa
hai đường thẳng AB và BC . Trang 12
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN GIỮA KỲ 1 NĂM HỌC 2017 – 2018
TRƯỜNG THPT ...............................
Khối 12 – Môn thi: TOÁN
(Đề thi gồm 06 trang)
Thời gian làm bài: 90 phút, không kể thời gian phát đề Mã đề thi: 103
PHẦN 1. TRẮC NGHIỆM
Câu 1. Hàm số nào sau đây đồng biến trên ( ;   )  . 1 A. 4
y x .
B. y    C. 3 2
y x  3x . D. 3 2
y x  2x  5x. x x  2
Câu 2. Cho hàm số y
 Mệnh đề nào dưới đây đúng ? x  1
A. Hàm số nghịch biến trên khoảng ( ;  1  ).
B. Hàm số đồng biến trên khoảng ( ;  1  ).
C. Hàm số nghịch biến trên khoảng ( ;   )  .
D. Hàm số nghịch biến trên khoảng (1;  )  . 2
Câu 3. Hàm số y
nghịch biến trên khoảng nào dưới đây ? 2 x  1 A. (0;  )  . B. ( 1  ;1). C. ( ;   )  . D. ( ;  0). 1
Câu 4. Có bao nhiêu giá trị nguyên của m để hàm số 3 2
y  (m  2)x  (m  2)x  (3m  1)x đồng 3 biến trên ( ;   )  . A. 1. B. 2. C. 5. D. Vô số. tan x  2
Câu 5. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y  đồng biến trên m tan x  2     khoảng 0;     4 
A. m  1. B. 1
  m  2.
C. 1  m  2.
D. 1  m  2. 3
Câu 6. Tìm giá trị cực đại y của hàm số y x  3x  2. CĐ A. y  4. B. y  1. C. y  0. D. y  1  . CĐ CĐ CĐ CĐ
Câu 7. Cho hàm số y f (x) có đạo hàm trên  và đồ thị hàm số y f (
x) trên  như hình bên
dưới. Tìm khẳng định đúng ?
A. y f (x) có 1 điểm cực đại và 1 điểm cực tiểu.
B. y f (x) có 2 điểm cực đại và 2 điểm cực tiểu.
C. y f (x) có 1 điểm cực đại và 2 điểm cực tiểu.
D. y f (x) có 2 điểm cực đại và 1 điểm cực tiểu. Trang 13
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Câu 8. Hỏi tham số m thuộc khoảng nào sau đây thì đồ thị hàm số 4 2
y x  2mx  1 có ba điểm cực trị ( A 0;1), ,
B C thỏa BC  4. A. m  ( ;  4  ). B. m  ( 4  ; 0).
C. m  (0;10).
D. m  (10;  )  . 4
Câu 9. Tính giá trị nhỏ nhất của hàm số y  3x  trên khoảng (0;  )  . 2 x 33 A. 3 min y  3 9. B. min y  7. C. min y   D. 3 min y  2 9. (0;) (0;) (0;) 5 (0;) sin x  1
Câu 10. Tìm giá trị lớn nhất M của hàm số y   2
sin x  sin x  1 3 A. M  1. B. M  2. C. M  1. D. M   2 Câu 11. Cho hàm số 3 2
y x  3m x  6. Hỏi các giá trị của tham số m thuộc khoảng nào sau đây
thì giá trị lớn nhất của hàm số trên đoạn [0; 3] bằng 42. A. ( ;  5  ). B. ( 5  ; 0). C. ( 5  ;5). D. (5; )  .
Câu 12. Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như hình vẽ.
Khoảng cách từ C đến B là 1 km. Bờ biển c
hạy thẳng từ A đến B với khoảng cách là 4
km. Tổng chi phí lắp đặt cho 1 km dây điện trên biển là 40 triệu đồng, còn trên đất liền là 20 triệu
đồng. Tính tổng chi phí nhỏ nhất để hoàn thành công việc trên (làm tròn đến hai chữ số sau dấu phẩy).
A. 106, 25 triệu đồng. C
B. 120 triệu đồng.
C. 164, 92 triệu đồng. B A
D. 114, 64 triệu đồng. 1
Câu 13. Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số y  3   x  3 A. y  3. B. x  3. C. x  3  .
D. y  3. 2
x  6x m
Câu 14. Tìm các giá trị của tham số thực m để hàm số y
không có tiệm cận đứng ? 4x m A. m  2.
B. m  {0; 8}. C. m  16. D. m  1. ax  2
Câu 15. Tìm các hệ số thực a, b, c để hàm số y
có đồ thị như hình vẽ. cx b
A. a  2, b  2, c  1.
B. a  1, b  1, c  1.
C. a  1, b  2, c  1.
D. a  1, b  2, c  1. x  2 x  3
Câu 16. Đồ thị hàm số y
có mấy tiệm cận ? x  5 x  4 A. 4. B. 2. B. 3. D. 5.
Câu 17. Đồ thị sau là của hàm số nào ? Trang 14
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 x  1 A. y   y x  1 4 3 x  2 B. y   2 x  1 1 x x  1 -4 -3 -2 -1 1 2 3 4 C. y   -1 x  2 -2 x  2 -3 D. y   -4 x  1
Câu 18. Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? 3x  1 A. y   x  2 B. 2
y x (x  3). C. 2 y x  (x  3). D. 2 2
y  (x  2) .
Câu 19. Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? A. 4 2 y x   2x  1. B. 4 2 y x   2x  1. C. 4 2
y x  2x  1. D. 4 2
y x  2x  1. Câu 20. Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng.
A. a  0, b  0, c  0, d  0. y
B. a  0, b  0, c  0, d  0. 1
C. a  0, b  0, c  0, d  0.  1 O 2 3 x
D. a  0, b  0, c  0, d  0. 4 2
Câu 21. Đồ thị trong hình bên dưới là đồ thị của hàm số y x
  4x . Dựa vào đồ thị bên hãy tìm
tất cả các giá trị thực của tham số m sao cho phương trình 4 x  2
4x m  2  0 có đúng 2 nghiệm phân biệt ?
A. m  0 hoặc m  4. B. m  0.
C. m  2 hoặc m  6.
D. m  2. 2x  1
Câu 22. Viết phương trình tiếp tuyến của đồ thị hàm số y
 Biết tiếp tuyến có hệ số góc là 5. x  2 Trang 15
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
A. y  5x  2 và y  5x  22.
B. y  5x  2 và y  5x  22.
C. y  5x  2 và y  5x  22.
D. y  5x  2 và y  5x  22. 2x  4
Câu 23. Gọi M , N là giao điểm của đường thẳng y x  1 và đường cong y   Khi đó, x  1
hãy tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I (1;2).
B. I (2;3).
C. I (1; 3).
D. I (2; 3).
Câu 24. Một hình đa diện có các mặt là các tam giác thì số mặt M và số cạnh C của đa diện đó thỏa mãn
điều kiện nào sau đây.
A. 3C  2M .
B. 3M  2C .
C. 2C M .
D. C  2M .
Câu 25. Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng ?
A. 4 mặt phẳng.
B. 1 mặt phẳng.
C. 2 mặt phẳng. D. 3 mặt phẳng.
Câu 26. Cho hình chóp S.ABCD có đáy là hình chữ nhật có AB  ,
a BC a 3. Hai mặt phẳng (SAB) 
và (SAD) cùng vuông góc với đáy, SCA  60. Tính thể tích V khối chóp S.ABCD. A. 3
V a . B. 3
V  2a . C. 3
V  3a . D. 3
V  2 3a .
Câu 27. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại ,
A BC  2a và SBC là tam giác
vuông cân tại S và nằm trong mặt phẳng vuông góc đáy. Tính thể tích khối chóp S.ABC . 3 2a 3 2a 3 a A. 3
V a . B. V   C. V   D. V   3 3 3
Câu 28. Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là a 3.
Tính thể tích V của khối chóp đó. 2 2 4 2 2 2 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V a . 3 3 6 9
Câu 29. Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB  ,
a AD a 2,
SA  (ABCD), góc giữa SC và đáy bằng 60. Tính thể tích V của khối chóp S.ABCD. A. 3
V  3 2a . B. 3
V  6a . C. 3
V  3a . D. 3 V  2a .
Câu 30. Cho khối chóp S .ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SC tạo với
mặt phẳng (SAB) một góc 30. Tính thể tích V của khối chóp. 3 6a 3 2a 3 2a A. V   B. V   C. V   D. 3
V  2a . 3 3 3 
Câu 31. Cho khối chóp S.ABC có đáy là tam giác cân tại , A BC  2 ,
a BAC  120, SA  (ABC )
và mặt (SBC ) hợp với đáy một góc 45 .
 Tính thể tích V của khối chóp S.ABC. 3 a 3 a 3 a A. V   B. 3
V  2a . C. V   D. V   3 2 9
Câu 32. Cho hình hộp ABC . D AB CD   có thể tích 3
16cm . Gọi M, N, K lần lượt là trung điểm của BC, C , D D A
 . Tính thể tích V của khối tứ diện AMNK. 8 A. 3 V  6cm . B. 3 V  4cm . C. 3 V  2cm . D. 3 V  cm . 3
Câu 33. Cho hình chóp tứ giác đều S.ABC ,
D cạnh đáy AB  2a 3, mặt bên tạo với đáy góc 60 . 
Tính thể tích V của khối chóp S.ABC . D A. 3
V  8a . B. 3
V  12a . C. 3
V  9a . D. 3 V  12 3a . 
Câu 34. Cho hình hộp đứng ABCD.AB CD
  có đáy ABCD là hình thoi cạnh a và BAD  60,
AB hợp với đáy (ABCD) một góc 30 . Tính thể tích V của khối hộp. Trang 16
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 3 a 3 3a 3 a 3 2a A. V   B. V   C. V   D. V   2 2 6 6
Câu 35. Cho lăng trụ tam giác ABC .AB C
  có đáy ABC là tam giác vuông cân tại , A cạnh
AC  2 2. Biết AC  tạo với mặt phẳng (ABC) một góc 60 và AC   4. Tính thể tích V
của khối đa diện ABCB C  . 8 16 8 3 16 3 A. V   B. V   C. V   D. V   3 3 3 3
Câu 36. Cho hình chóp đều S.ABCD có cạnh đáy bằng 2, khoảng cách từ tâm của đáy đến mặt bên 2 bằng
 Tính thể tích V của khối chóp. 2 1 2 4
A. V  4. B. V   C. V   D. V   3 3 3
Câu 37. Cho hình lăng trụ tứ giác đều ABCD.AB CD
  có cạnh đáy bằng a. Biết đường chéo của
mặt bên là a 3. Tính thể tích V của khối lăng trụ ABCD.AB CD  . 3 2a A. 3
V  3a . B. 3
V  2a . C. V   D. 3
V  2a . 3
Câu 38. Cho lăng trụ tam giác ABC .AB C
 , có đáy ABC là tam giác đều cạnh a, hình chiếu của
A xuống (ABC) là tâm O đường tròn ngoại tiếp tam giác ABC . Biết AA hợp với đáy
(ABC) một góc 60. Tính thể tích V của khối lăng trụ ABC .AB C  . 3 3a 3 3 3a 3 3a 3 3a A. V   B. V   C. V   D. V   12 4 4 36
Câu 39. Cho hình hộp chữ nhật ABCD.AB CD
  có tổng diện tích của tất cả các mặt là 36, độ dài
đường chéo AC  bằng 6. Hỏi thể tích của khối hộp lớn nhất V là bao nhiêu ? max A. V  8. B. V  8 2. C. V  16 2. D. V  24 3. max max max max
Câu 40. Cho chóp đều S.ABCD có khoảng cách từ A đến (SCD) bằng 2a. Tính giá trị nhỏ nhất V min
của thể tích khối chóp S.ABCD theo a. 3 A. V  4a . B. 3 V  2a . C. 3 V  3 3a . D. 3 V  2 3a . min min min min PHẦN 2. TỰ LUẬN
Bài 1. Biết hàm số y a sin x b cos x x đạt cực trị tại điểm x
và x với x  (0;2). 3
Tính giá trị biểu thức T a b 3.
Bài 2. Đồ thị hàm số 4 2
y x  2mx  4 có ba điểm cực trị nằm trên các trục tọa độ. Tìm . m
Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y  (x  6) x  4 trên đoạn [0;3].
Bài 4. Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi và A
BD đều cạnh a, BCD  là tam giác cân tại ,  120o C BCD
, SA a và SA  (ABCD). Tính thể tích khối chóp
S.ABCD và khoảng cách từ điểm C đến mặt phẳng (SBD) theo a.
Bài 5. Cho hình lăng trụ tam giác đều ABC .AB C
  có tất cả các cạnh đều bằng 3a. Các điểm M, N
lần lượt thuộc các cạnh bên BB , CC  sao cho B M
 2BM, CN  2NC . Tính thể tích
khối tứ diện ACMN và khoảng cách từ điểm A đến mặt phẳng (AMN ) theo a. Trang 17
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN GIỮA KỲ 1 NĂM HỌC 2017 – 2018
TRƯỜNG THPT ...............................
Khối 12 – Môn thi: TOÁN
(Đề thi gồm 06 trang)
Thời gian làm bài: 90 phút, không kể thời gian phát đề Mã đề thi: 104
PHẦN 1. TRẮC NGHIỆM
Câu 1. Cho hàm số y f (x) có bảng xét dấu đạo hàm như sau: x  1 0 2 
y  0   0 
Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên khoảng ( 2  ; 0).
B. Hàm số đồng biến trên khoảng ( ;  0).
C. Hàm số nghịch biến trên khoảng (0;2).
D. Hàm số đồng biến trên khoảng ( ;  2).
Câu 2. Cho hàm số f (x) xác định, liên tục trên  và có đồ thị của hàm số f (
x) là đường cong như
hình vẽ bên dưới. Hỏi khẳng định nào sau đây là đúng ?
A. Hàm số f (x) đồng biến trên khoảng (0;2).
B. Hàm số f (x) nghịch biến trên khoảng ( 2  ;2).
C. Hàm số f (x) đồng biến trên khoảng ( ;  1  ).
D. Hàm số f (x) nghịch biến trên khoảng ( ;  0).
Câu 3. Trên khoảng nào sau đây, hàm số 2 y x
 2x đồng biến ? A. (1; )  . B. (1;2). C. (0;1). D. ( ;  1).
Câu 4. Tìm các giá trị thực của tham số m sao cho hàm số y  sin x mx luôn đồng biến trên .  A. m  1  .
B. m  1. C. 1
  m  1. D. m  1  .
Câu 5. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2 y x
  3x mx  4 nghịch
biến trên khoảng (0;  )  .
A. m  0.
B. m  0.
C. m  0.
D. m  0.
Câu 6. Cho hàm số y f (x) có đồ thị như hình vẽ bên dưới. Hỏi đồ thị hàm số y f (x) có bao nhiêu điểm cực trị ? A. 1. B. 2. C. 3. D. 4. Trang 18
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Câu 7. Biết rằng đồ thị của hàm số 3 2 y x
 3x  5 có hai điểm cực trị A và B. Tính diện tích S
của tam giác OAB với O là gốc tọa độ. 10
A. S  9. B. S  
C. S  5.
D. S  10. 3
Câu 8. Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số 4 2
y x  2mx có ba điểm
cực trị tạo thành tam giác có diện tích nhỏ hơn 1.
A. m  0.
B. m  1. C. 3 0  m  4.
D. 0  m  1.
Câu 9. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
f (x)  x  4  x .
Tính S M m. A. S  2 2.
B. S  2 2  2.
C. M m  4.
D. S  2 2  2.
Câu 10. Cho hàm số y f (x) có đồ thị trên đoạn [ 2
 ;4] như hình vẽ. Tìm max f(x) .     2;4
A. max f (x)  2.     2;4
B. max f (x)  f (0) .     2;4
C. max f (x)  3.     2;4
D. max f (x)  1.     2;4 Câu 11. Cho hàm số 3 2 2 y x
  mx  (m m  1)x. Gọi S là tập hợp các giá trị của tham số m
sao cho giá trị nhỏ nhất của hàm số trên đoạn [ 1
 ;1] bằng 6. Tính tổng các phần tử của S. A. 2. B. 0. C. 2 6. D. 1.
Câu 12. Cho tam giác vuông có tổng một cạnh góc vuông và cạnh huyền bằng 2. Tìm độ dài ba cạnh
của tam giác sao cho diện tích của tam giác lớn nhất. 2 2 3 4 2 4 3 4 2 2 4 A. ; ;  B. ; 1;  C. ; ; 1. D. ; ;  3 3 3 3 3 5 5 3 3 3
Câu 13. Cho hàm số f (x ) xác định, liên tục trên D   \ {1} và có bảng biến thiên như sau: x  1 1  f (  x)   0  f (x ) 2    0
Khẳng định nào sau đây là sai ?
A. Hàm số không có đạo hàm tại x  1.
B. Hàm số đã cho đạt cực tiểu tại x  1.
C. Đồ thị hàm số không có tiệm cận ngang.
D. Đồ thị hàm số không có tiệm cận đứng. x  2
Câu 14. Đồ thị hàm số y  có mấy tiệm cận ? 2 x  4 Trang 19
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 A. 0. B. 3. C. 1. D. 2.
x  1  1  x
Câu 15. Cho hàm số y
 Chọn khẳng định đúng ? 2 x x  2
A. Đồ thị hàm số có một tiệm cận ngang là đường thẳng y  0.
B. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng y  1 và y  1.
C. Đồ thị hàm số có một tiệm cận ngang là đường thẳng y  1  .
D. Đồ thị hàm số có một tiệm cận ngang là đường thẳng y  1. ax  4
Câu 16. Cho hàm số y
. Hãy xác định hệ số a và b, biết rằng đồ thị hàm số có đường tiệm bx  1
cận ngang là y  2 và tiệm cận đứng là đường thẳng x  1.
A. a b  1.
B. a  3 và b  1. C. a  1 và b  2. D. a  2 và b  1.
Câu 17. Đồ thị sau đây là của hàm số nào ? 3 A. 3
y x  3x  1. 2 B. 3 2 y x   3x  1. 1 C. 3
y x  3x  1. -1 1 O D. 3 2 y x
  3x  1. -1
Câu 18. Đồ thị sau đây là của hàm số nào ? -1 1 A. 4 2
y x  3x  3. O 1 B. 4 2
y   x  3x  3. -2 4 -3 C. 4 2
y x  2x  3. -4 D. 4 2
y x  2x  3.
Câu 19. Đồ thị sau đây là của hàm số nào ? 4 2x  1 A. y   x  1 2 x  2 B. y   1 x  1 -2 O 1 x  1 C. y   x  1 x  2 -2 D. y   1  x
Câu 20. Cho hàm số  3  2 y ax
bx cx d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng.
A. a  0, b  0, c  0, d  0. y
B. a  0, b  0, c  0, d  0. O x
C. a  0, b  0, c  0, d  0.
D. a  0, b  0, c  0, d  0. Trang 20
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 2x  3
Câu 21. Cho hàm số y
có đồ thị (C ) và đường thẳng d : y x m. Tìm tất cả các giá trị x  2
của tham số m để đường thẳng d cắt đồ thị (C ) tại 2 điểm phân biệt ? A. m  2. B. m  6. C. m  2.
D. m  2 hoặc m  6.
Câu 22. Cho hàm số f (x) liên tục trên  và có bảng biến thiên như sau: x  0 2  y  0  0   3 y 1 
Tìm tất cả các giá trị của tham số thực m để phương trình f (x)  2m  1 có 3 nghiệm thực phân biệt. 1 1
A. 1  m  3. B.   m  
C. 0  m  2.
D. 1  m  1. 2 2
Câu 23. Khối lập phương là khối đa diện đều loại nào ? A. {5;3}. B. {3; 4}. C. {4; 3}. D. {3;5}.
Câu 24. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A và AB AC a 2. Tam giác
SBC có diện tích bằng 2
2a và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích
V của khối chóp S.ABC. 3 4a 3 a 3 2a A. V   B. V   C. 3
V  2a . D. V   3 3 3
Câu 25. Cho hình chóp tứ giác đều S.ABC ,
D đáy ABCD có diện tích 2
16cm , diện tích một mặt bên là 2
8 3cm . Tính thể tích V của khối chóp S.ABCD. 32 2 32 13 32 11 32 15 A. 3 V  cm . B. 3 V  cm . C. 3 V  cm . D. 3 V  cm . 3 3 3 3
Câu 26. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  ,
a BC a 3, SA
vuông góc với mặt phẳng đáy. Biết góc giữa SC và (ABC) bằng 60. Tính thể tích V của
khối chóp S.ABC . 3 3a A. 3
V  3a . B. 3
V  3a . C. 3
V a . D. V   3
Câu 27. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt đáy, SD tạo
với mặt phẳng (SAB) một góc bằng 30. Tính thể tích V của khối chóp S.ABCD. 3 6a 3 6a 3 3a A. V   B. 3
V  3a . C. V   D. V   18 3 3
Câu 28. Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB  ,
a AD a 3, SA vuông góc với
đáy và mặt phẳng (SBC ) tạo với mặt phẳng đáy một góc 60. Tính thể tích V của khối chóp S.ABCD. Trang 21
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 3 a 3 3a A. V   B. V   C. 3
V a . D. 3
V  3a . 3 3
Câu 29. Cho khối tứ diện đều ABCD có cạnh bằng .
a Gọi B , C  lần lượt là trung điểm của các
cạnh AB và AC . Tính thể tích V của khối tứ diện AB CD  theo . a 3 3a 3 2a 3 a 3 2a A. V   B. V   C. V   D. V   48 48 24 24   
Câu 30. Cho hình chóp S.ABC có ASB CSB  60 ,
ASC  90 , SA SB a, SC  3a. Tính
thể tích V của khối chóp S.ABC theo . a 3 2a 3 2a 3 6a 3 6a A. V   B. V   C. V   D. V   4 12 6 18
Câu 31. Cho khối lăng trụ ABC.AB C
  có thể tích bằng V . Gọi I, K lần lượt là trung điểm của
AA , BB . Hãy tính thể tích V  của khối đa diện ABCIKC  theo V ? 3V V 2V 4V A. V    B. V    C. V    D. V    5 3 3 5
Câu 32. Tính theo a thể tích V của khối lập phương ABCD.AB CD
 , biết AC   a. 3 3a 3 a 3 3a A. 3
V  3 3a . B. V   C. V   D. V   3 27 9
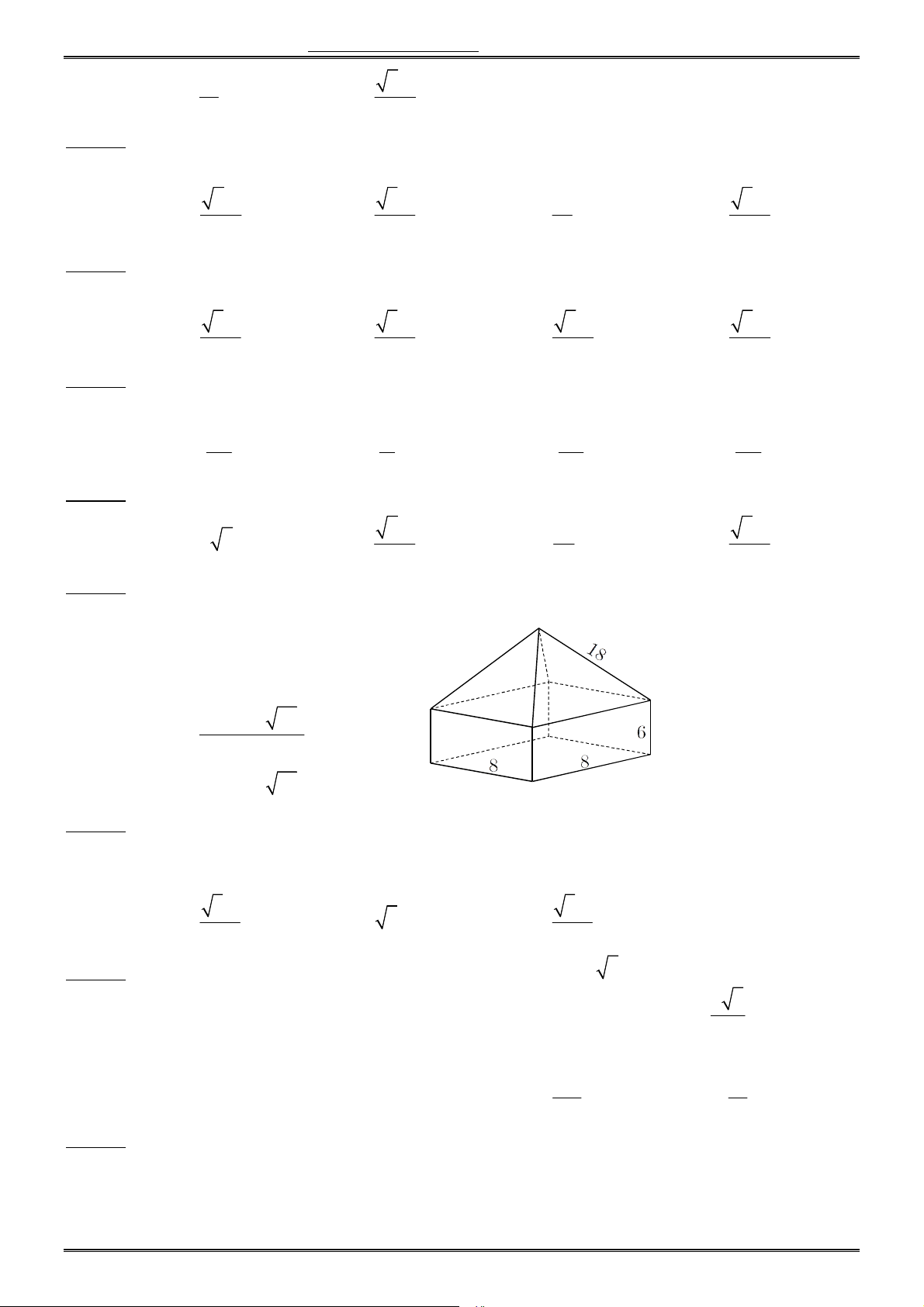
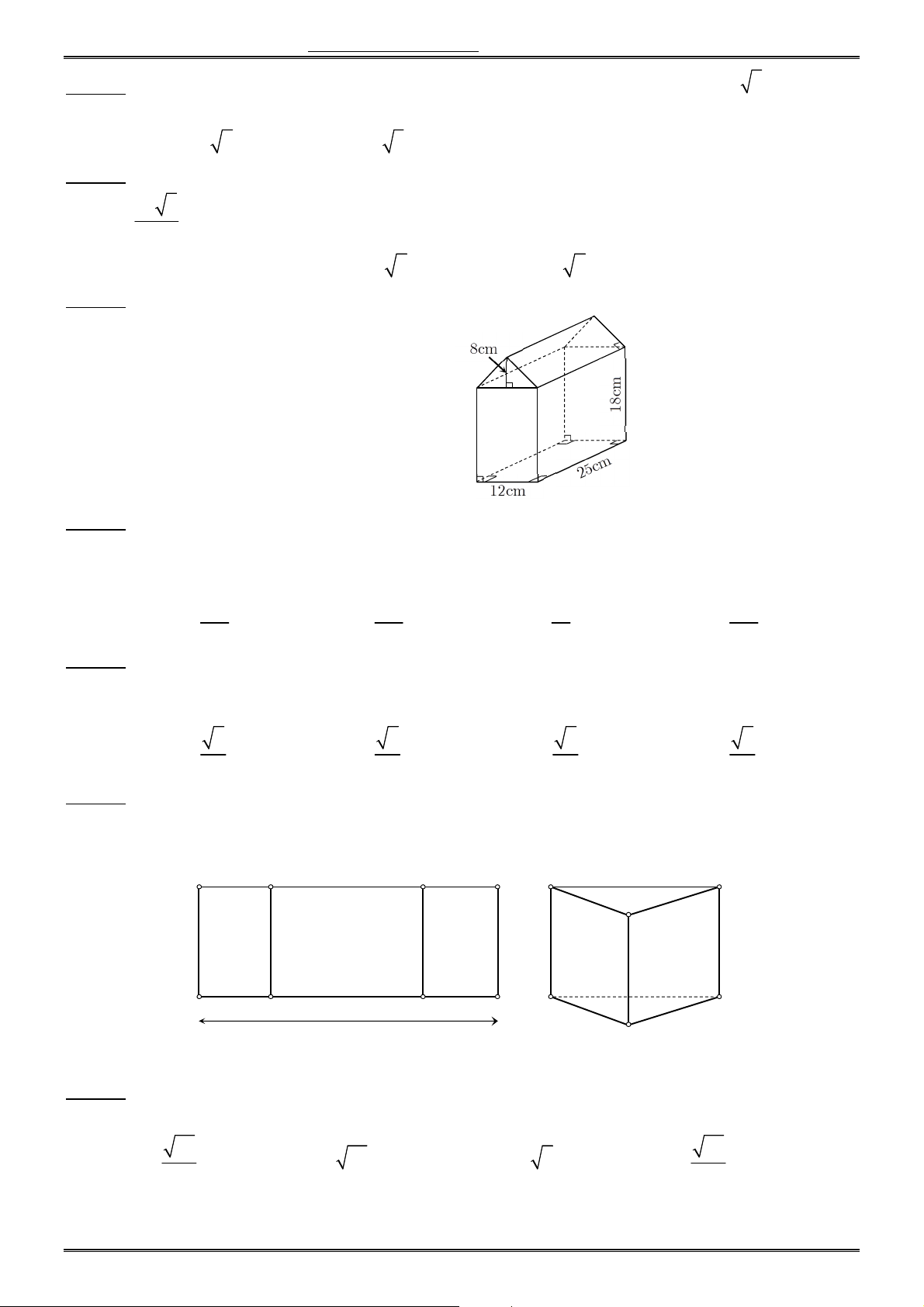
Câu 33. Tính thể tích V của khối có 4 mặt tam giác cân bằng nhau, 4 mặt là hình chữ nhật và đáy
cũng là hình chữ nhật với các kích thước cùng đơn vị đo được cho như hình.
A. V  5400 ( v đ t t ).
B. V  1800 ( v đ t t ). 128(9  73) C. V  ( v đ tt). 3
D. V  128(3  73) ( v đ tt).
Câu 34. Cho hình lăng trụ đứng ABC .AB C
  có đáy là tam giác vuông cân đỉnh , A mặt bên là BCC B
  hình vuông, khoảng cách giữa AB và CC  bằng a. Tính thể tích V của khối lăng
trụ ABC .AB C  . 3 2a 3 2a A. V   B. 3
V  2a . C. V   D. 3
V a . 3 2
Câu 35. Cho hình lăng trụ tam giác đều ABC .AB C
  có AA  a 3. Gọi I là giao điểm của ABa 3
và AB. Cho biết khoảng cách từ điểm I đến mặt phẳng (BCC B  ) bằng  Tính thể tích 2
V của khối lăng trụ ABC .AB C
  theo a. 3 3a 3 a A. 3
V  3a . B. 3
V a . C. V   D. V   4 4
Câu 36. Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích bằng 8. Gọi M, N lần lượt
là trung điểm của các cạnh AB, A .
D Tính thể tích V của khối tứ diện SCMN.
A. V  4.
B. V  5.
C. V  2.
D. V  3. Trang 22
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình thoi và AC  4, BD  2. Mặt chéo SBD
nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD) và SB  3, SD  1. Tính thể
tích V của khối chóp S.ABC . D 2 3 8 3 4 3 A. V  
B. V  2 3. C. V   D. V   3 3 3
Câu 38. Lăng trụ tam giác ABC .AB C
  có đáy tam giác đều diện tích bằng 3, góc giữa cạnh bên
và đáy bằng 30. Hình chiếu của A lên mặt phẳng (ABC ) là trung điểm I của BC . Tính
thể tích V khối lăng trụ. 9 3 A. V   B. V  
C. V  3 3.
D. V  3. 8 3
Câu 39. Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước x, ,
y z (dm). Biết tỉ số hai cạnh đáy là x : y  1 : 3 và thể tích của khối hộp bằng 18
lít. Để tốn ít vật liệu nhất thì các kích thước x, y, z của nó bằng bao nhiêu ? 3
A. x  2, y  6, z  
B. x  1, y  3, z  6. 2 3 9 3 1 3 C. x
, y  , z  
D. x  , y  , z  24. 2 2 2 2 2
Câu 40. Khối chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Biết SA SB SC a, cạnh SD
thay đổi. Tính thể tích lớn nhất V
của khối chóp S.ABC . D max 3 a 3 a 3 3a 3 a A. V   B. V   C. V   D. V   max 8 max 4 max 8 max 2 PHẦN 2. TỰ LUẬN n
Bài 1. Cho f (x )  x m
 Tìm m, n để hàm số đạt cực đại tại x  2 và f ( 2  )  2  . x  1
Bài 2. Tìm giá trị cực đại y của hàm số y x  2 cos x trên khoảng (0; ) . CĐ
Bài 3. Tìm m để hai điểm cực đại và cực tiểu của đồ thị hàm số y  3 x  2
3x mx m  2 nằm
về hai phía so với trục hoành ?
Bài 4. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và ,
B BC  2AB  2AD  2a.
Gọi E là điểm đối xứng với A qua D, M là trung điểm của BC . Biết rằng cạnh bên SB
vuông góc với mặt phẳng đáy, góc giữa 2 mặt phẳng (SCE ) và mặt phẳng (ABCD) bằng
45o. Tính thể tích khối chóp S.AMCE và khoảng cách giữa 2 đường thẳng AM, SD.
Bài 5. Cho lăng trụ đứng ABC .AB C
  có đáy ABC là tam giác vuông tại , B AB  ,
a AA  2a,
AC  3a. Gọi M là trung điểm của đoạn thẳng AC , I là giao điểm của AM và AC. Tính
theo a thể tích khối tứ diện IABC và khoảng cách từ điểm A đến mặt phẳng (IBC). Trang 23
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN GIỮA KỲ 1 NĂM HỌC 2017 – 2018
TRƯỜNG THPT ...............................
Khối 12 – Môn thi: TOÁN
(Đề thi gồm 06 trang)
Thời gian làm bài: 90 phút, không kể thời gian phát đề Mã đề thi: 105
PHẦN 1. TRẮC NGHIỆM Câu 1. Cho hàm số 3
y x  3x  2. Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên khoảng ( ;
 0) và nghịch biến trên khoảng (0; )  .
B. Hàm số nghịch biến trên khoảng ( ;   )  .
C. Hàm số đồng biến trên khoảng ( ;   )  .
D. Hàm số nghịch biến trên khoảng ( ;
 0) và đồng biến trên khoảng (0; )  . Câu 2. Cho hàm số 4 2
y x  2x . Mệnh đề nào dưới đây là đúng ?
A. Hàm số đồng biến trên khoảng ( ;  2).
B. Hàm số nghịch biến trên khoảng ( ;  2).
C. Hàm số đồng biến trên khoảng ( 1  ;1).
D. Hàm số nghịch biến trên khoảng ( 1  ;1).
Câu 3. Cho hàm số f (x) xác định, liên tục trên  và có đồ thị hàm số y f (x) là đường cong
trong hình bên dưới. Hỏi mệnh đề nào dưới đây đúng ?
A. Hàm số f (x) đồng biến trên khoảng (1;2).
B. Hàm số f (x) nghịch biến trên khoảng (0;2).
C. Hàm số f (x) đồng biến trên khoảng  ( 2;1).
D. Hàm số f (x) nghịch biến trên khoảng  ( 1;1).
Câu 4. Cho hàm số y  sin x  3 cos x mx. Tìm tất cả các giá trị thực của tham số m sao cho
hàm số đồng biến trên . 
A. m  2.
B. m  2.
C. m  2.
D. m  1.
Câu 5. Tìm tất cả các giá trị của tham số m để hàm số 3 2
y  2x  3(2m  1)x  6m(m  1)x  1 đồng biến trên (2;  )  . A. m  1. B. m  1. C. m  2.
D. m  1. Câu 6. Gọi ,
A B là các điểm cực tiểu của đồ thị hàm số 4 2
y x  2x  1. Tính diện tích S của tam
giác AOB với O là gốc tọa độ.
A. S  3.
B. S  2.
C. S  1.
D. S  4. Câu 7. Cho hàm số 4 2
y  2017x  2018mx m n với m, n là các số thực dương và m n. Hỏi
đồ thị hàm số đã cho có bao nhiêu điểm cực tiểu ? A. 2. B. 1. C. 3. D. 0. Trang 24
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Câu 8. Hỏi m thuộc khoảng nào thì hàm số 3 2 2 y x
  3mx  3(m  1)x đạt cực tiểu tại x  2. A. ( ;  3). B. ( 3  ; 0). C. (0; 6). D. (6; )  . 2 x  3
Câu 9. Tìm giá trị nhỏ nhất của hàm số y  trên đoạn [2; 4]. x  1 19
A. min y  6.
B. min y  2.
C. min y  3. D. min y   [2;4] [2;4] [2;4] [2;4] 3
Câu 10. Cho hàm số y f (x) xác định và liên tục trên khoảng ( 3
 ;2), lim f (x)  5, x 3 
lim f (x)  3 và có bảng biến thiên như sau: x 2  x  3 1 1 2  y   0  0  0 3 y 5 2
Mệnh đề nào dưới đây sai ?
A. Hàm số không có giá trị nhỏ nhất trên khoảng (3;2).
B. Giá trị cực đại của hàm số bằng 0.
C. Giá trị lớn nhất của hàm số trên khoảng (3;2) bằng 0.
D. Giá trị cực tiểu của hàm số bằng 2.
Câu 11. Tìm tất cả các giá trị của tham số thực m để giá trị nhỏ nhất của hàm số 3 2
y x  3mx  6
trên đoạn [0; 3] bằng 2. 31 3 A. m  2. B. m   C. m   D. m  1. 27 2
Câu 12. Một vùng đất hình chữ nhật ABCD có AB  25km , BC  20km và M , N lần lượt là
trung điểm của AD , BC . Một người cưỡi ngựa xuất phát từ A đi đến C bằng cách đi thẳng
từ A đến một điểm X thuộc đoạn MN rồi lại đi thẳng từ X đến C. Vận tốc của ngựa khi
đi trên phần ABNM là 15km/h, vận tốc của ngựa khi đi trên phần MNCD là 30km/h .
Thời gian ít nhất để ngựa di chuyển từ A đến C là mấy giờ ? 2 5 41 4  29 5 A. B. C. D. 3 4 6 3
Câu 13. Cho hàm số y f (x) xác định trên D   \ {1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên: x  0 1  f (x )  0   2 5 0 f (x )  3
Hỏi mệnh đề nào dưới đây đúng ?
A. Đồ thị hàm số có hai tiệm cận ngang là y  0, y  5 và tiệm cận đứng là x  1. Trang 25
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
B. Giá trị cực tiểu của hàm số là y  3. CT
C. Giá trị cực đại của hàm số là y  5. CD
D. Hàm số có giá trị lớn nhất bằng 5. 2
6x  1  x  2
Câu 14. Biết các đường tiệm cận của đường cong (C ) : y  và trục tung cắt nhau x  5
tạo thành một đa giác (H). Mệnh đề nào dưới đây đúng ?
A. (H ) là một hình vuông có diện tích bằng 25.
B. (H ) là một hình chữ nhật có diện tích bằng 8.
C. (H ) là một hình vuông có diện tích bằng 4.
D. (H ) là một hình chữ nhật có diện tích bằng 10. x
Câu 15. Số đường tiệm cận của đồ thị hàm số y  là bao nhiêu ? 2 x  4 A. 4. B. 3. C. 1. D. 2. ax  1
Câu 16. Cho hàm số y
 Tìm S a b để đồ thị hàm số có x  1 là tiệm cận đúng và bx  2 1
y  là tiệm cận ngang. 2 A. S  3. B. S  3. C. S  1. D. S  8. Câu 17. Hàm số 3 2
y x  6x  9x  1 có đồ thị nào sau đây ? 4 2 2 3 1 2 1 2 1 O 3 1 O 2 3 1 O 2 3 1 2 O 3 1 2 -1 -3 2 -3 2 4 -3 A. 4 B. . C. . D. 4 .
Câu 18. Cho đồ thị như hình vẽ dưới đây. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau ? 1 A. 4 2
y x  2x  2. 4 2 1 B. 4 2
y x  2x  2. 4 O 1 -2 2 C. 4 2
y x  2x  1. 4 1 D. 4 2
y x  2x . 2 4
Câu 19. Đồ thị trong hình bên dưới là của hàm số nào ? A. 3
y x  3x  1. B. 4 2 y x   3x . 2x  3 2x  1 C. y   D. y   x  1 x  1 Trang 26
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 y x 0 Câu 20. Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng ? y
A. a  0, b  0, c  0.
B. a  0, b  0, c  0. x O
C. a  0, b  0, c  0.
D. a  0, b  0, c  0. ax b
Câu 21. Cho hàm số y
có đồ thị như hình vẽ dưới. Mệnh đề nào dưới đây đúng ? cx d y
A. a  0, b  0, c  0, d  0.
B. a  0, b  0, c  0, d  0. x O
C. a  0, b  0, c  0, d  0.
D. a  0, b  0, c  0, d  0. Câu 22. Cho hàm số 2
y  (x  2)(x  1) có đồ thị (C ). Mệnh đề nào dưới đây đúng ?
A. (C ) cắt trục hoành tại hai điểm.
B. (C ) cắt trục hoành tại một điểm.
C. (C ) không cắt trục hoành.
D. (C ) cắt trục hoành tại ba điểm.
Câu 23. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y  4 x  2
2mx m  2 cắt trục Ox
tại 4 điểm phân biệt ? A. m  (2;  )  . B. m  ( ;  1). C. m  ( ;  1  )  (2; )  . D. m  (0;  )  .
Câu 24. Cho hàm số y f (x) xác định trên \
 {0}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: x  0 1  y  0   2 y 1  
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f (x)  m có ba nghiệm thực phân biệt. A. [1;2]. B. (1;2). C. ( 1  ;2]. D. ( ;  2].
Câu 25. Mặt phẳng (AB C
 ) chia khối lăng trụ ABC.AB C
  thành các khối đa diện nào ? Trang 27
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
A. Một khối chóp tam giác và một khối chóp ngũ giác.
B. Một khối chóp tam giác và một khối chóp tứ giác.
C. Hai khối chóp tam giác.
D. Hai khối chóp tứ giác.
Câu 26. Cho hình chóp S.ABC, có đáy ABC là tam giác vuông cân tại , A AB  , a các cạnh bên
SA SB SC a. Tính thể tích V của khối S.ABC. 3 a 3 2a 3 2a 3 2a A. V   B. V   C. V   D. V   12 12 4 6
Câu 27. Cho hình chóp đều S.ABCD có chiều cao bằng a 2 và độ dài cạnh bên bằng a 6. Tính thể
tích V của khối chóp S.ABCD. 3 8 2a 3 10 2a 3 8 3a 3 10 3a A. V   B. V   C. V   D. V   3 3 3 3 
Câu 28. Cho khối chóp S.ABC có đáy là tam giác vuông tại ,
A SB  (ABC ), AB  , a ACB  30 , 
góc giữa đường thẳng SC và mặt phẳng ABC là 60. Tính thể tích V khối chóp S.ABC. 3 3a A. 3
V  3a . B. 3
V a . C. 3
V  2a . D. V   2
Câu 29. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt
phẳng đáy, cạnh bên SC tạo với (SAB) một góc 30. Tính thể tích của khối chóp S.ABCD. 3 3a 3 2a 3 2a 3 2a A. V   B. V   C. V   D. V   3 4 2 3
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên (SAD) là tam giác đều
cạnh 2a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp S.ABC ,
D biết rằng mặt phẳng (SBC ) tạo với mặt phẳng đáy một góc 30. 3 3a 3 2 3a 3 4 3a A. V   B. 3
V  2 3a . C. V   D. V   2 3 3
Câu 31. Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và khoảng a 2
cách từ A đến mặt phẳng (SBC ) bằng
 Tính thể tích V của khối chóp đã cho. 2 3 a 3 3 3a 3 a A. V   B. 3
V a . C. V   D. V   2 9 3
Câu 32. Hình chóp S.ABC có M, N, P lần lượt trung điểm của S ,
A SB, SC. Gọi V là thể tích 1 V
khối MNP.ABC và V là thể tích khối S.ABC . Tính tỉ số 1  2 V2 V 1 V V 7 V 8 A. 1   B. 1  8. C. 1   D. 1   V 8 V V 8 V 7 2 2 2 2
Câu 33. Cho khối lăng trụ ABC.AB C
 . Gọi M, N lần lượt là trung điểm của hai cạnh AA và
BB . Mặt phẳng (C M
N) chia khối lăng trụ đã cho thành hai phần. Gọi V là thể tích khối 1 V C .MNB A
  và V là thể tích khối ABC.MNC . Tính tỉ số 1  2 V2 V 2 V V 1 V 3 A. 1   B. 1  2. C. 1   D. 1   V 3 V V 2 V 2 2 2 2 2 Trang 28
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789
Câu 34. Cho hình lập phương ABCD.AB CD
  có diện tích tam giác ACD  bằng 2 3a . Tính thể
tích V của hình lập phương. A. 3
V  3 3a . B. 3
V  2 2a . C. 3
V a . D. 3
V  8a .
Câu 35. Cho hình lập phương ABCD.AB CD
  có khoảng cách từ C  đến mặt phẳng (ABD) bằng
4a 3  Tính theo a thể tích V của khối lập phương ABC . D AB CD  . 2 A. 3
V  8a . B. 3
V  3 3a . C. 3
V  8 3a . D. 2
V  216a .
Câu 36. Tính thể tích V của vật thể với các kích thước được cho trong hình vẽ dưới đây ? A. 3 V  6600cm . B. 3 V  5700cm . C. 3 V  6400cm . D. 3 V  7800cm .
Câu 37. Cho khối lăng trụ đứng ABC .AB C
  có đáy ABC là tam giác cân với AB AC a, 
BAC  120. Mặt phẳng (AB C  )
 tạo với đáy một góc 60. Tính thể tích V của khối lăng
trụ ABC .AB C  . 3 3a 3 9a 3 a 3 3a A. V   B. V   C. V   D. V   8 8 8 4
Câu 38. Một hình lăng trụ có đáy là tam giác đều cạnh bằng a, cạnh bên bằng b và tạo với mặt phẳng
đáy một góc . Tính thể tích V của khối chóp có đáy là đáy của lăng trụ và đỉnh là một điểm
bất kì trên đáy còn lại. 3 3 3 3 A. 2 V a b sin . B. 2 V a b sin . C. 2 V a b cos . D. 2 V a b cos . 12 4 12 4
Câu 39. Cho một tấm nhôm hình chữ nhật ABCD có AD  24 cm. Ta gấp tấm nhôm theo hai cạnh
MN và QP vào phía trong đến khi AB và CD trùng nhau như hình vẽ dưới đây để được
một hình lăng trụ khuyết hai đáy. Tìm x AN PD để thể tích khối lăng trụ lớn nhất ? B M Q C M Q B C A N P D N P 24cm A D
A. x  9 cm.
B. x  8 cm.
C. x  10 cm.
D. x  6 cm.
Câu 40. Một hình chóp tứ giác đều có tổng độ dài của đường cao và bốn cạnh đáy là 33. Hỏi độ dài
cạnh bên ngắn nhất là bao nhiêu ? 33 33 A. B. 33. C. 11 3. D. 17 2 Trang 29
Biªn so¹n vµ gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 PHẦN 2. TỰ LUẬN
Bài 1. Tìm giá trị cực đại y (nếu có) của hàm số 2
y x  2x  1. CĐ
Bài 2. Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số 4 2
y x  2mx  1 có ba điểm
cực trị là ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng 1.
Bài 3. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 4 2 2
y x  2mx  2m  1 có giá trị cực tiểu bằng 2.
Bài 4. Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số 2
y  2x  5  x .
Bài 5. Cho hình chóp S.ABC có SA
B đều cạnh a, A
BC cân tại C. Hình chiếu của đỉnh S
trên mặt phẳng (ABC ) là trung điểm của cạnh AB; góc hợp bởi cạnh SC và mặt phẳng đáy
bằng 30o. Tính thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng SA và BC theo a. a 10 
Bài 6. Cho hình lăng trụ ABC .AB C   có 0 AA 
, AC a 2, BC a, ACB  135 . Hình 4
chiếu vuông góc của C  trên mặt phẳng (ABC) trùng với trung điểm M của AB. Tính theo a
thể tích khối lăng trụ ABC .AB C
  và góc tạo bởi đường thẳng C M  với mặt phẳng (ACCA )  . Trang 30