

Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI THPT
THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC 2021 – 2022 MÔN VẬT LÝ ĐỀ CHÍNH THỨC
Ngày thi thứ nhất: 28 tháng 12 năm 2021
(Đề thi có 3 trang)
Thời gian làm bài: 180 phút (không kể thời gian phát đề) Bài 1. (3,5 điểm)
Một khối gỗ nhỏ đặt trên một mặt dốc phẳng mà góc nghiêng 𝛼 giữa mặt dốc so với phương ngang
thay đổi được (0 < 𝛼 < 90o). Coi hệ số ma sát nghỉ và ma sát trượt giữa khối gỗ với mặt dốc là 𝜇.
1. Xác định điều kiện của 𝛼 theo 𝜇 để khối gỗ có thể tự trượt xuống không vận tốc đầu.
2. Giữ cho góc nghiêng 𝛼 = 𝛼!, truyền vận tốc ban đầu 𝑣$!
$⃗ hướng lên dọc theo mặt dốc để khối
gỗ trượt lên đến điểm cao nhất, sau đó trượt xuống về điểm xuất phát. Xác định thời gian 𝑇
trong chuyển động này của khối gỗ.
3. Sau đó, bằng cách phun lên mặt dốc và khối gỗ một lớp sơn đặc biệt rất mỏng sao cho ma sát
giữa khối gỗ và mặt dốc có thể bỏ qua, rồi truyền vận tốc ban đầu cho khối gỗ như câu 2. Tính
thời gian 𝑇! trong chuyển động này của khối gỗ.
4. Xét tỷ lệ 𝐾 = "! theo 𝑥 với 𝑥 = #$%&!. Không tính toán, từ lập luận hãy xác định giá trị của 𝐾 " '
khi 𝑥 rất lớn. Phác họa dáng điệu đồ thị biểu diễn 𝐾 theo 𝑥. Bài 2. (4,0 điểm)
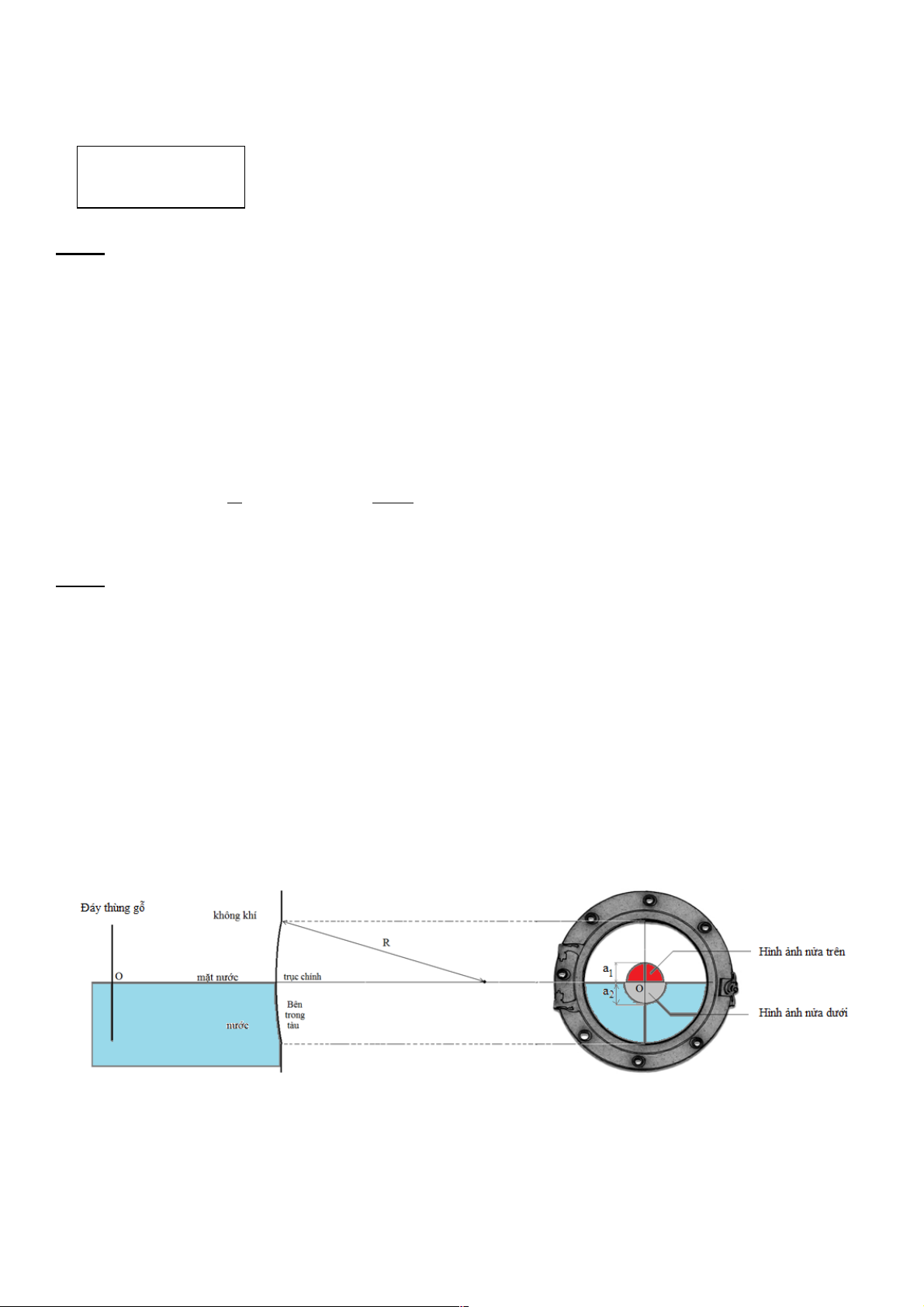
Porthole là những ô cửa sổ tròn được cố định trên mạn tàu, cho người bên trong quan sát hình ảnh
bên ngoài tàu. Đó là một tấm kính cong chịu lực, coi như một phần mặt cầu bán kính 𝑅 = 65 cm, bề
dày tấm kính có thể bỏ qua. Hình dưới đây mô tả hình dạng, kích thước của porthole trên tàu.
Một hành khách thông qua porthole đang quan sát đáy một thùng gỗ có dạng hình tròn phẳng, đường
kính 𝑎 = 50 cm đang chìm một nửa trong nước. Mắt người này đặt trên trục chính của porthole (trục
chính vuông góc với đáy thùng gỗ) và tàu đang ở trạng thái sao cho mặt nước nằm ngang chia đôi
porthole thành hai phần bằng nhau như Hình a.
Hình b thể hiện hình ảnh của đáy thùng gỗ ngắm được qua porthole, theo đó các hình ảnh nửa trên
(trong không khí) và nửa dưới (trong nước) là các hình bán nguyệt có bán kính lần lượt là 𝑎( và 𝑎).
Lấy chiết suất của không khí là 1, của nước là 4/3. Coi các tia sáng xuất phát từ đáy thùng gỗ đến
mắt là những tia đi gần trục chính của porthole. Hình a Hình b
1. Xác định vị trí tâm 𝑂 của đáy thùng gỗ và vị trí đặt mắt trên trục chính của porthole để
𝑎( = 2,5 cm và 𝑎) = 3,0 cm.
2. Để hai ảnh của đáy thùng gỗ ngắm được qua nửa trên và nửa dưới của porthole bằng nhau,
người này đã dời mắt một đoạn Δ𝑦 trên trục chính của porthole. Tính Δ𝑦 và hướng dịch chuyển của mắt. Bài 3. (4,0 điểm)
Để giải thích đơn giản cho một nhận xét thực tế: Càng lên cao không khí càng loãng. Người ta đưa ra
mô hình sau về bầu khí quyển trên mặt đất:
Coi không khí là khí lý tưởng lưỡng nguyên tử, có khối lượng mol 𝜇 = 29 g⁄mol, khối lượng riêng 𝜌.
Bỏ qua sự thay đổi theo độ cao, gia tốc trọng trường luôn có giá trị 𝑔.
1. Tính khối lượng riêng của khí quyển tại nơi ngang mặt nước biển có áp suất 𝑝! = 762 mmHg
và nhiệt độ 𝑡! = 34°C.
2. Chứng minh rằng độ thay đổi áp suất 𝑝 theo độ cao ℎ được mô tả bởi: *+ = −𝜌𝑔. *,
3. Khi lên cao, sự giảm của áp suất không khí được coi như quá trình giãn nở đoạn nhiệt thuận
nghịch. Cho biết độ thay đổi tỷ đối giữa áp suất 𝑝 và nhiệt độ 𝑇 liên hệ bởi: *+ = 𝐵 *". Tính + " giá trị của 𝐵.
4. Từ các dữ kiện trên, tính độ thay đổi của khối lượng riêng theo độ cao *- để làm sáng tỏ nhận *,
xét: Càng lên cao không khí càng loãng.
Bài 4. (4,0 điểm) Việc đo đạc hiệu điện thế có giá trị lớn, lên đến hàng trăm kV, nhận được sự quan
tâm và nghiên cứu bởi các nhà Vật lý Kỹ thuật Khí tượng. Một trong những mạch Cơ – Điện để đo
đạc phổ biến là vôn kế Abraham, một dạng điện kế tĩnh điện, có mô hình cấu tạo gồm:
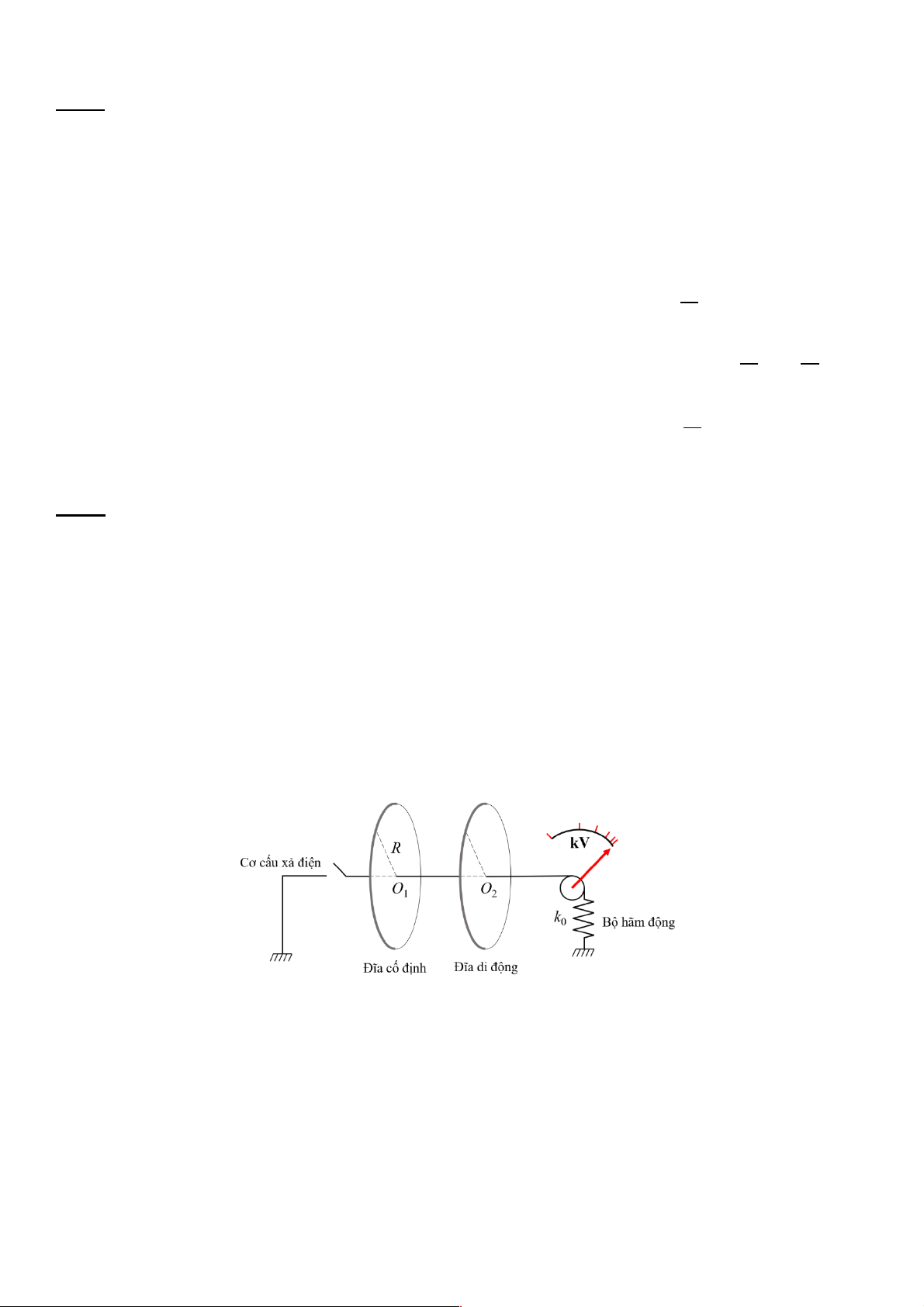
Trong một buồng chân không, bố trí hai đĩa kim loại tròn phẳng, giống hệt nhau cùng bán kính 𝑅,
được đặt đồng trục nằm ngang (các tâm 𝑂( và 𝑂) cùng nằm trên một trục nằm ngang qua các tâm và
vuông góc với mặt của hai đĩa). Đĩa 𝑂( được giữ cố định, đĩa 𝑂) có thể di chuyển không ma sát như hình dưới.
Nối tâm 𝑂) với một lò xo có độ cứng 𝑘 bằng một dây mảnh nhẹ không co dãn, cách điện, qua một ròng
rọc nhẹ, cố định và không ma sát. Khi các bản không tích điện, lò xo không biến dạng, tâm 𝑂( và 𝑂)
cách nhau đoạn 𝑂(𝑂) = 𝑎 ≪ 𝑅. Khi mắc hai bản của vôn kế vào một hiệu điện thế cần đo, coi như
điện tích trên hai đĩa luôn cùng độ lớn và phân bố đều trên bề mặt. Bỏ qua hiệu ứng biên của trường
điện. Hằng số điện là 𝜀!.
1. Khi hiệu điện thế giữa hai đĩa là 𝑈, tâm 𝑂( và 𝑂) cách nhau đoạn 𝑥. Xác định lực tĩnh điện tác
dụng lên đĩa 𝑂) theo 𝑅, 𝜀!, 𝑈 và 𝑥, nhận xét chiều dịch chuyển của 𝑂).
2. Viết biểu thức liên hệ độ biến dạng ∆𝑥 của lò xo theo 𝑅, 𝜀!, 𝑘, 𝑈 và 𝑎.
3. Trường hợp ∆𝑥 ≪ 𝑎, xác định độ biến dạng ∆𝑥 theo 𝑅, 𝜀!, 𝑘, 𝑈 và 𝑎.
4. Xét một vôn kế Abraham với các thông số: 𝑅 = 1,32 m, 𝑎 = 5,46 cm, 𝑘 = 120 kN m ⁄ .
Lấy 𝜀! = 8,8542 ∙ 10.() C)/Nm).
a. Biết rằng bộ chỉ thị của vôn kế Abraham chỉ phát hiện được các dịch chuyển cỡ vài mm.
Hãy đánh giá tính khả dụng của vôn kế Abraham khi đo hiệu điện thế 𝑈 = 100 kV.
b. Giả sử cấu tạo của vôn kế chỉ cho phép khoảng cách 𝑥 thỏa 𝑥 ≥ 0,65𝑎. Xác định giá trị hiệu
điện thế tối đa mà vôn kế này đo được. Bài 5. (4,5 điểm)
Nếu bỏ qua các hiện tượng như thay đổi nhiệt độ và quá trình biến đổi trạng
thái của tuyết, mô hình đơn giản sau đây có thể dùng để mô tả chuyển động
của quả cầu tuyết lăn không trượt trên mặt dốc phủ tuyết đồng đều:
Giả thiết rằng khối lượng riêng của tuyết tại mọi nơi đều bằng 𝜌. Xét một
quả cầu tuyết lăn không trượt trên mặt dốc chính có góc nghiêng 𝛼 không
đổi so với mặt phẳng ngang. Khi quả cầu lăn không trượt trên mặt dốc đầy
tuyết, các lớp tuyết trên dốc bám dần vào quả cầu làm cho khối lượng và
bán kính của quả cầu tăng lên dần. Giả sử tốc độ tăng bán kính của quả cầu
tuyết tỷ lệ với tốc độ chuyển động của khối tâm quả cầu với hệ số 𝑘 > 0.
Tại thời điểm 𝑡, bán kính quả cầu là 𝑅.
1. Chứng minh rằng moment quán tính của quả cầu đối với trục qua tâm là /0 𝜌𝑅1. (1
2. Viết biểu thức liên hệ giữa tốc độ tăng khối lượng quả cầu tuyết với tốc độ chuyển động của
khối tâm và bán kính quả cầu tuyết.
3. Viết biểu thức liên hệ giữa gia tốc khối tâm quả cầu tuyết, tốc độ khối tâm quả cầu tuyết và bán kính của nó.
4. Sau khoảng thời gian đủ lâu, người ta thấy rằng gia tốc của khối tâm quả cầu tuyết là không
đổi. Hãy xác định gia tốc không đổi này.
Gợi ý: ∑ 𝐹⃗ = *+⃗ và ∑ 𝑀 $⃗ = *45⃗ *3 *3 ------- HẾT-------
Họ và Tên thí sinh:…………………………………………………. Số báo danh……………………
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI THPT
THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC 2021 – 2022 MÔN VẬT LÝ Đ ÁP ÁN ĐỀ NG HỊ
Ngày thi thứ nhất: 28 tháng 12 năm 2021
Thời gian làm bài: 180 phút (không kể thời gian phát đề) Bài 1. (3.5 điểm)
1. Điều kiện 𝑃 sin 𝛼 ≥ 𝐹!"#$!%& = 𝐹!"' → 𝑃 sin 𝛼 ≥ 𝜇𝑃 cos 𝛼 → tan 𝛼 ≥ 𝜇 ............... (0.5 điểm)
2. Vì vật đi lên cao nhất, rồi trượt xuống → tan 𝛼 > 𝜇 ................................................. (0.25 điểm)
Gia tốc lên và xuống: 𝑎( = −𝑔(sin 𝛼 + 𝜇 cos 𝛼) và 𝑎) = 𝑔(sin 𝛼 − 𝜇 cos 𝛼) ...... (0.5 điểm) Thời gian đi lên: 𝑡 ( ( = *$+! = +!
............................................................ (0.5 điểm) %" , -./ 012 34- 0 Thời gian đi xuống: 𝑡 ( ) = +! = +!
............................. (0.5 điểm) √%"%#
, 6(-./ 012 34- 0)(-./ 0$2 34- 0) Tổng thời gian 𝑇 = +! 8 ( + (
9 ............................................ (0.25 điểm) , -./ 012 34- 0 6-./#0$2#34-#0
3. Khi khử ma sát → 𝜇 = 0 → 𝑇* = )+! ................................................................... (0.25 điểm) , -./ 0
4. Khi 𝑥 = 9:/ 0 rất lớn thì 𝜇 → 0 hoặc 𝛼 → 90° → 𝑇 = 𝑇 2
* → 𝐾 = 1 ........................ (0.5 điểm) Ta có: 𝐾 = ;! = )
với 𝑥 > 1 ...................................................................... (0.5 điểm) ; ""1 " "$ " % &"'%#
Phác họa: Đúng dáng điệu, không qua gốc tọa độ và có tiệm cận 𝐾 = 1 ............. (0.25 điểm) 𝐾 1 𝑥 Bài 2. (4.0 điểm)
1. Gọi 𝑥 là khoảng cách từ đáy thùng đến porthole; 𝑦 là khoảng cách từ mắt đến porthole
Nửa thị trường bên trên toàn bộ là không khí, tia sáng truyền thẳng ....................... (0.5 điểm)
Tam giác đồng dạng: < = %" = ),? → 𝑥 = 9𝑦 ..................................................... (0.5 điểm) &1< %/) )?
Nửa thị trường bên dưới, sơ đồ tạo ảnh: @ABB (DE&,#EF/G) ;HIH (#EF/G,JE$K? L!)
𝐴𝐶 D⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯F 𝐴(𝐶( D⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯F 𝐴)𝐶) ............................................. (0.25 điểm)
Khoảng cách từ 𝐴(𝐶( đến porthole: 𝑥( = & = G 𝑥 và 𝐴 # F
(𝐶( = 𝐴𝐶 ........................... (0.25 điểm)
Thấu kính phân kỳ có: ( = (𝑛 − 1) ( → 𝑓 = J = −195 cm ............................... (0.25 điểm) M J #$(
Công thức thấu kính → ( + ( = ( → 𝑥
= − (N?& cm .................... (0.25 điểm) & ) = & # &" M &(#$()1#J )K*1&
Tỷ lệ ảnh-vật |𝑘| = O#P# = || → 𝐴
% = K?** .............................. (0.5 điểm) OP & )𝐶) = #J " &(#$()1#J ) )K*1&
→ 𝑥 = F?? ≈ 151,667 cm và 𝑦 = F?? ≈ 16,852 cm ............................................. (0.5 điểm) G )R
2. Khi hai ảnh bằng nhau, góc nhắm của mắt như nhau ở nửa trên và dưới ................ (0.25 điểm)
→ %/) = O#P# (với 𝑥 = F?? cm không thay đổi) ................................................... (0.25 điểm) &1< ||1< G
→ 𝑦 = 65 cm → Vậy mắt cần dịch ra xa porthole đoạn ∆𝑦 = 48,15 cm ................ (0.5 điểm)
(Học sinh có thể giải bằng cách sử dụng công thức lưỡng chất cầu vẫn được điểm tối đa) Bài 3. (4.0 điểm)
1. Định luật Clapeyron-Mendeleev/ Phương trình trạng thái khí lý tưởng: ................. (0.25 điểm)
𝑝𝑉 = 𝑛𝑅𝑇 → 𝑝𝜇 = 𝜌𝑅𝑇 .......................................................................................... (0.25 điểm) Ta có: 𝜌* = S!2 = S!2 = 1,152 ~ 1,154 g 𝑙
⁄ ................................................. (0.25 điểm) J;! J('!1)RG)
2. Để một lớp không khí mỏng cân bằng tại (ℎ → ℎ + 𝑑ℎ) thì: .................................. (0.25 điểm)
𝑆_𝑝T − 𝑝(T1UT)` = (𝜌𝑆𝑑ℎ)𝑔 → US = −𝜌𝑔 ............................................................ (0.5 điểm) UT
3. Vì khí lý tưởng lưỡng nguyên tử nên chỉ số đoạn nhiệt 𝛾 = 1,4 .............................. (0.25 điểm)
Đoạn nhiệt thuận nghịch: 𝑝𝑉V = 𝑐𝑜𝑛𝑠𝑡 → 𝑝($V𝑇V = 𝑐𝑜𝑛𝑠𝑡 .................................. (0.5 điểm)
→ (1 − 𝛾) US + 𝛾 U; = 0 ↔ US = V U; = 𝐵 U;. Vậy hệ số 𝐵 = R ......................... (0.25 điểm) S ; S V$( ; ; )
4. Ta có: UW = 2 h( US − S U;i = 2 hUS − S U;i .......................................................... (0.5 điểm) UT J ; UT ;# UT J; UT ; UT
Mà lại có: US = R S U; ................................................................................................ (0.25 điểm) UT ) ; UT
→ UW = 2 h? USi ........................................................................................................ (0.25 điểm) UT J; R UT
Vì 𝑇 > 0 và US = −𝜌𝑔 < 0 nên UW < 0 .................................................................. (0.5 điểm) UT UT Bài 4. (4.0 điểm)
1. Vì 𝑥 đủ nhỏ so với 𝑅, nên vùng không gian giữa hai đĩa được xem như là điện trường tổng hợp tạo bởi
hai mặt phẳng rộng vô hạn, là điện trường đều, có độ lớn: 𝐸 = X ..................... (0.25 điểm) &
(Học sinh có thể mô tả đây là điện trường trong lòng tụ điện phẳng, chân không)
Điện trường do mỗi đĩa gây ra: 𝐸( = 𝐸) = Y = X ................................................. (0.25 điểm) ) )&
Điện tích mỗi đĩa có độ lớn: 𝑄( = 𝑄) = 𝐶𝑈 = Z![J# 𝑈) ......................................... (0.5 điểm) &
Lực hút: 𝐹Y = 𝑄𝐸 = Z![J#X# → Đĩa 𝑂 )
) dịch chuyển lại gần 𝑂( .............................. (0.5 điểm)
2. Khi đĩa 𝑂) cân bằng: 𝑘*∆𝑥 = Z![J#X# = Z![J#X# .................................................... (0.5 điểm) ) )(%$∆&)# $)
3. Với giả thiết ∆𝑥 ≪ 𝑎 thì ( = ( h1 − ∆&i
≈ ( h1 + )∆&i ........................... (0.5 điểm) (%$∆&)# %# % %# % → ∆𝑥 = %
................................................................................................. (0.5 điểm) )] (!)* +!,-#.#$(^
4. a. Từ dữ kiện và giả thiết ∆𝑥 ≪ 𝑎: ∆𝑥 = %
= 0,695 mm ..................... (0.25 điểm) )] (!)* +!,-#.#$(^
Giả thiết phù hợp, nhưng điện kế này không đo được dưới 𝟏𝟎𝟎 𝐤𝐕 ..................... (0.25 điểm)
b. Từ dữ liệu: & ≥ 65% → ∆𝑥 ≤ 0,35𝑎 → Không thể tính gần đúng, do đó: ......... (0.25 điểm) % 𝑘 `!%*
*∆𝑥 = Z![J#X# → 𝑈 < w ((_G
= 345,238 kV ............................................... (0.25 điểm) ) F***[ Z!J# Bài 5. (4.5 điểm)
1. Trong quả cầu đặc, vi phân trong tọa độ cầu: 𝑑𝑚 = 𝜌𝑟) sin 𝜃 𝑑𝑟𝑑𝜑𝑑𝜃 ................. (0.25 điểm)
𝑑𝐼 = (𝑟 sin 𝜃))𝑑𝑚 = 𝜌𝑟FsinG𝜃𝑑𝑟𝑑𝜑𝑑𝜃 ................................................................. (0.25 điểm)
Moment quán tính quả cầu: 𝐼 = 𝜌 ∫J 𝑟F𝑑𝑟 ∫[ sinG𝜃 𝑑𝜃 ∫)[ 𝑑𝜑 = _[ 𝜌𝑅? ............. (0.5 điểm) * * * (?
(Nếu học sinh phân hoạch theo các khác, đúng vẫn được trọn điểm)
Nếu học sinh áp dụng: 𝐼 = ) 𝑚𝑅) và 𝑚 = F 𝜌𝑅G rồi rút ra kết quả ........................ (0.5 điểm) ? G
2. Theo giả thiết ta có: UJ = 𝑘𝑣 .................................................................................... (0.25 điểm) U'
Lại có: 𝑚 = F 𝜋𝜌𝑅G → U! = 4𝜋𝜌𝑅) UJ = 4𝜋𝜌𝑅)𝑘𝑣 .............................................. (0.25 điểm) G U' U'
3. Định luật II Newton: 𝑚𝑔 sin 𝛼 − 𝑓 !"# = 𝑚𝑎 + 𝑣 U! ............................................ (0.5 điểm) U'
Chuyển động quay tâm: 𝑓 !"#𝑅 = 𝐼𝛾 + 𝜔 Ua .......................................................... (0.5 điểm) U'
Chuyển động lăn không trượt: 𝑣 = 𝑅𝜔 → 𝑎 = 𝑅𝛾 + 𝜔 UJ ....................................... (0.5 điểm) U'
Thay vào, rút gọn 𝑎 = ? 𝑔 sin 𝛼 − )G +# .................................................................... (0.5 điểm) R R J
4. Theo giả thiết 𝑎 = 𝑐𝑜𝑛𝑠𝑡: → 𝑎 = ? 𝑔 sin 𝛼 ............................................................ (0.5 điểm) ?G
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI THPT
THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC 2021 – 2022 MÔN VẬT LÝ ĐỀ CHÍNH THỨC
Ngày thi thứ hai: 29 tháng 12 năm 2021 (Đề thi có 4 trang)
Thời gian làm bài: 180 phút (không kể thời gian phát đề) Bài 1. (4,0 điểm) i
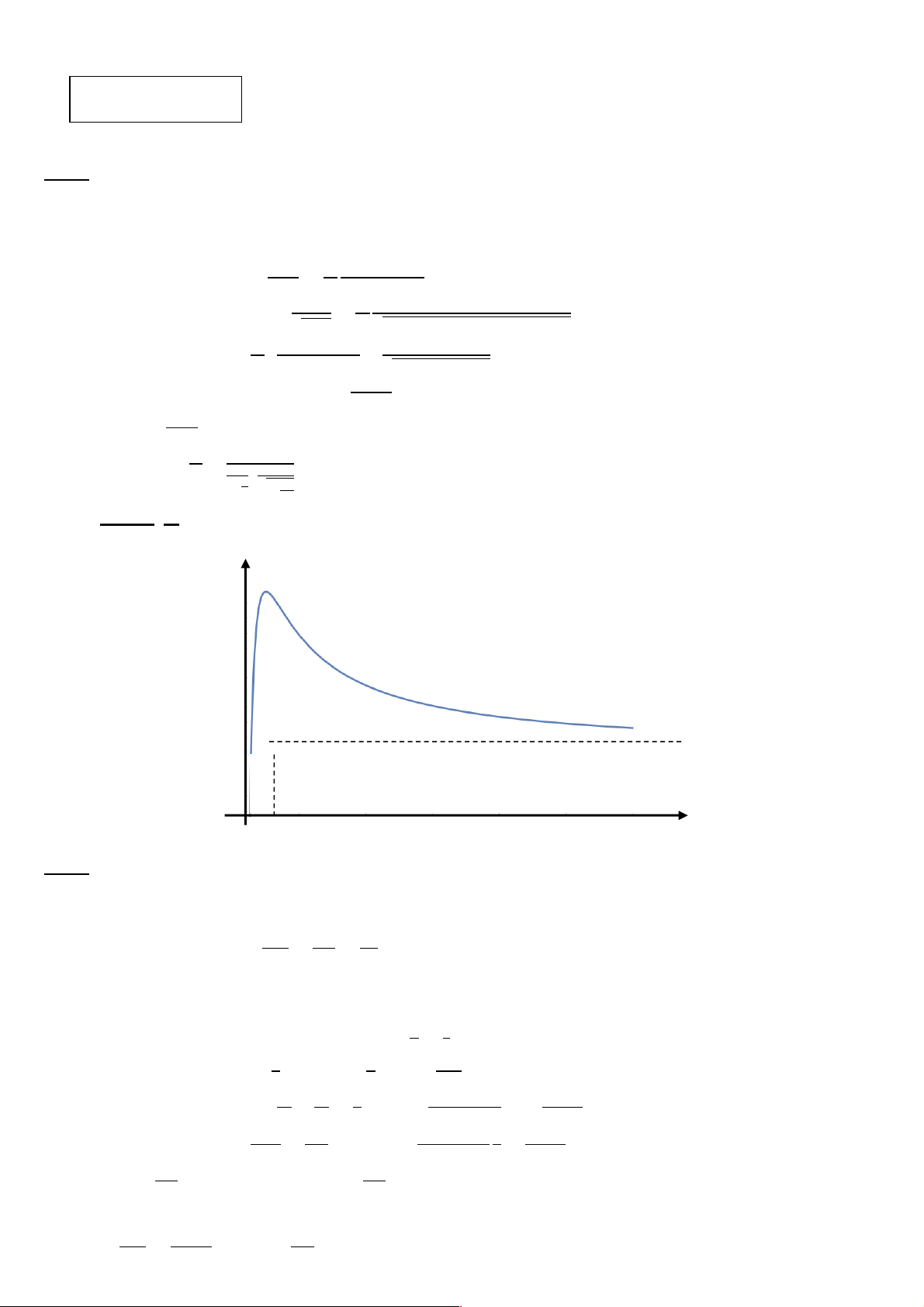
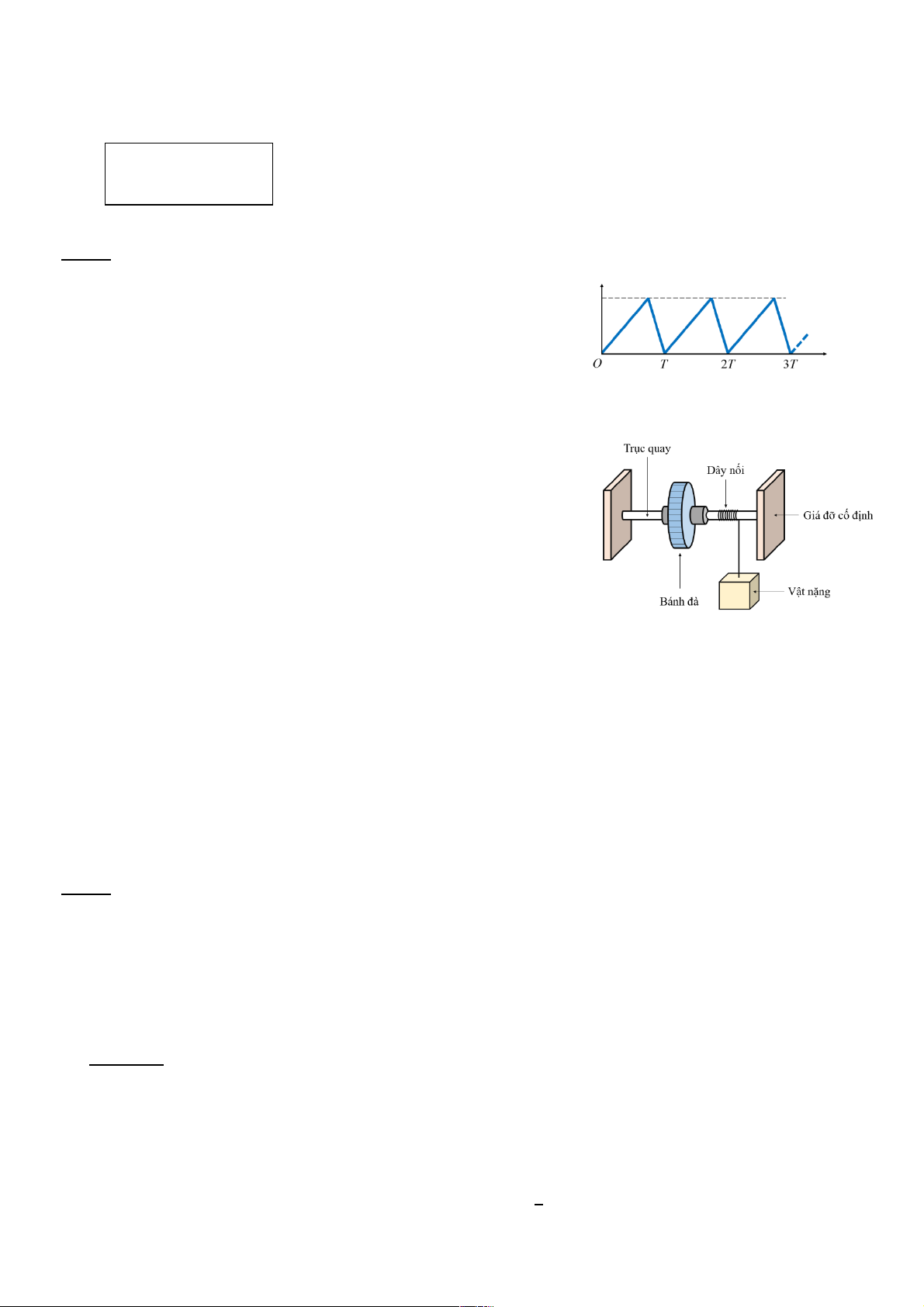
1.1. Một dòng điện chạy trong dây dẫn kim loại mà đồ thị biểu I0
diễn cường độ theo thời gian có dạng răng cưa với giá trị cực
đại 𝐼! và chu kỳ 𝑇 như hình bên. t
a. Xác định giá trị hiệu dụng 𝐼 của dòng điện này.
b. Xét dòng điện xoay chiều hình sin cùng giá trị cực đại và chu kỳ với dòng điện răng cưa trên.
Tính tỷ số giữa số electron dịch chuyển qua dây dẫn trong một chu kỳ của hai dòng điện này.
1.2. Để đo moment quán tính của một bánh đà hoặc một đĩa
nặng đồng chất đối với trục vuông góc qua khối tâm, người ta
bố trí thí nghiệm như hình bên.
Bánh đà cần đo moment quán tính được gắn vào trục quay nhẹ
cố định nằm ngang. Một sợi dây mảnh, nhẹ, không co dãn một
đầu gắn với vật nặng khối lượng 𝑚, đầu còn lại gắn vào một chốt
trên trục qua rồi thực hiện theo tiến trình sau:
- Quấn dây nối quanh trục của bánh đà sao cho các vòng sát nhau và không chồng lên nhau.
- Thả vật nặng không vận tốc đầu và bắt đầu đếm số vòng quay của bánh đà, khi vật nặng đi
xuống quãng đường ℓ thì dây bị bung và rời khỏi trục quay, số vòng quay đếm được là 𝑛".
- Khi dây bị bung ra và rời khỏi trục thì bắt đầu bấm đồng hồ và đếm số vòng quay cho tới khi
bánh đà dừng lại và bấm dừng đồng hồ. Thời gian đo được là 𝑡, số vòng quay đếm được là 𝑛#.
Coi như tổng moment cản đối với trục quay không đổi. Bán kính tiết diện của trục quay là 𝑅, và
gia tốc trọng trường là 𝑔.
Xác định moment quán tính của vật cần đo đối với trục quay theo 𝑚, ℓ, 𝑡, 𝑛", 𝑛#, 𝑅 và 𝑔. Bài 2. (4,0 điểm)
Việc tìm hiểu bản chất tự nhiên, mô tả đặc tính của hạt cơ bản như khối lượng, điện tích, năng lượng
hay quá trình biến đổi hạt nhân là nghiên cứu cơ bản của Vật lý. Một hạt cơ bản rất gần gũi với học
sinh phổ thông là electron. Một mô hình tính toán cổ điển về electron thường được sử dụng trong
Vật lý sơ cấp là xem electron như một quả cầu điện môi bán kính 𝑅, tích điện đều với mật độ điện khối 𝜌.
Chuyển động tự quay của electron được xem như quay đều quanh trục qua tâm với tốc độ góc 𝜔. Cho biết:
- Hằng số điện 𝜀!, khối lượng của electron 𝑚 và điện tích của electron 𝑒.
- Bán kính của electron không vượt quá thang đo femto-mét (fm).
- Trong tọa độ cầu (𝑟, 𝜑, 𝜃), vi phân thể tích có dạng: 𝑑𝑉 = 𝑟# sin 𝜃 𝑑𝑟𝑑𝜑𝑑𝜃.
- Vi phân moment từ do mỗi điện tích 𝑑𝑞 rất nhỏ chuyển động tròn trên quỹ đạo có bán kính 𝑅 với vận tốc góc 𝜔
:⃗ không đổi được xác định: 𝑑𝑀
:⃗ = " 𝑅#𝜔:⃗𝑑𝑞. #
1. Mỗi vật tích điện đều chứa năng lượng dưới dạng năng lượng điện trường. Cho biết năng lượng
điện trường dự trữ trong electron có dạng: 𝑊 = 𝐴 ∙ $!%", với 𝐴 là một hệ số không có thứ nguyên.
a. Tính giá trị của 𝐴.
b. Một học sinh nhận định: “Năng lượng điện trường dự trữ trong electron chính bằng động năng
tự quay quanh trục của nó.”. Hãy ước tính tốc độ của các điểm trên “xích đạo” của electron,
từ đó nhận xét về nhận định của bạn học sinh này.
2. Spin là cách viết đơn giản của cụm từ “spin angular mometum”, nghĩa là moment động lượng spin.
Spin cũng là đặc tính tự nhiên của các hạt cơ bản, bao gồm các hạt như electron, proton và neutron.
Spin của electron, ký hiệu là 𝑆::⃗', thể hiện tính chất chuyển động quay của electron.
a. Biết moment từ 𝑀
:::⃗' của electron có độ lớn: 𝑀' = 𝑁 ∙ 𝜌𝜔𝑅(, trong đó là một hệ số không có
thứ nguyên. Tính giá trị của 𝑁.
b. Một bạn học sinh cho rằng: “Moment từ của electron chính là spin của nó.”. Hãy chứng tỏ
rằng nhận định của học sinh là không chính xác, từ đó hãy đề xuất liên hệ giữa 𝑀 :::⃗ ::⃗ ' và 𝑆'. Bài 3. (4,0 điểm)
“Tên lửa nước” là mô hình được thiết kế rất đơn giản. Nhưng để tên lửa bay một cách tối ưu, tức là có
thể bay lâu, cao hoặc xa hơn, học sinh cần hiểu rõ nhiều về các yếu tố Vật lý.
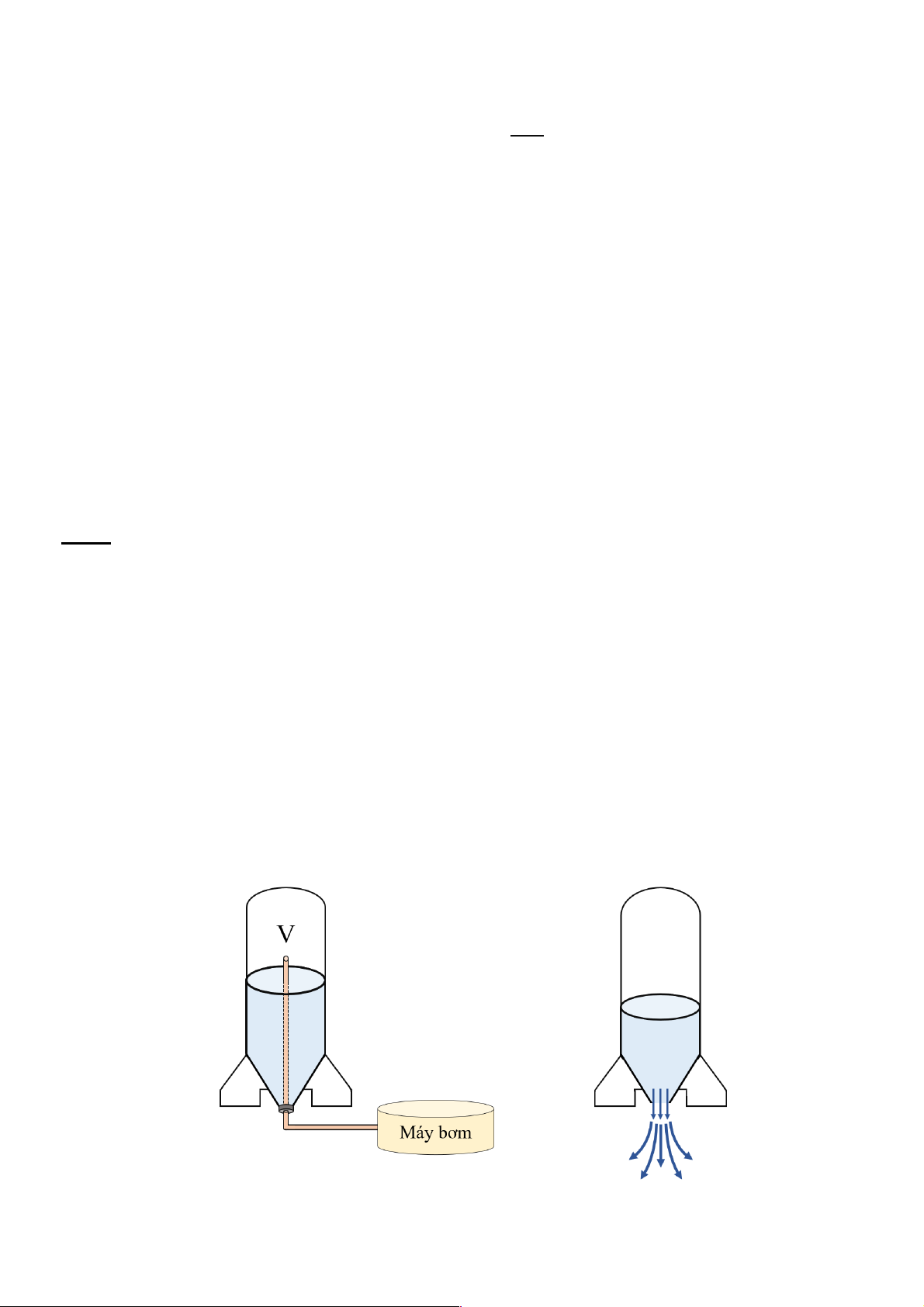
Nguyên lý hoạt động của tên lửa được mô tả như Hình a và Hình b:
- Giai đoạn chuẩn bị: Bên trong thân tên lửa gồm nước ở bên dưới và khí ở bên trên như Hình a.
Khí được bơm thêm vào, làm tăng áp đến khi đủ mạnh để làm bung chốt.
- Giai đoạn chuyển động: Sự chênh lệch áp suất làm đẩy nước ra ngoài qua vòi phun, giúp cho
tên lửa chuyển động nhờ phản lực như Hình b.
Bỏ qua áp suất do sự chênh lệch độ cao. Nước có khối lượng riêng 𝜌. Xem như nước trong tên lửa là
chất lỏng lý tưởng: không nén, không có độ nhớt, không xoáy khi phun. Coi nhiệt độ khí trong tên lửa
và bên ngoài khí quyển luôn bằng nhau và không đổi trong quá trình khảo sát. Không khí được xem
như một chất khí lý tưởng và bỏ qua sự bay hơi của nước. Hình a Hình b
1. Giai đoạn chuẩn bị: Khi chưa bơm, phần khí trong tên lửa có dung tích 𝑉 và có áp suất 𝑝! giống
khí quyển bên ngoài. Khí trong bình được bơm thêm vào, mỗi lần bơm được một lượng không khí
có thể tích 𝑣 = 0,5𝑉. Áp suất do chốt khóa gây ra tại vòi phun là 3𝑝!. Xác định số lần bơm tối
thiểu để tên lửa được phóng lên.
2. Giai đoạn chuyển động: Tại thời điểm 𝑡, tên lửa đang chuyển động được gia tốc do phóng một
lượng nước khối lượng 𝑑𝑚 ra ngoài trong thời gian 𝑑𝑡 qua vòi phun có tiết diện 𝑆, áp suất của khí
trong tên lửa là 𝑝 và đang giảm dần.
a. Chứng minh rằng độ lớn lực đẩy tác dụng lên tên lửa khi gia tốc có dạng: 𝐹) = 𝑣 *+, với 𝑣 là *)
tốc độ tương đối của lượng nước phóng ra so với tên lửa.
b. Xác định biểu thức lực đẩy 𝐹) theo 𝑝, 𝑝! và 𝑆.
c. Viết biểu thức có thể dùng để xác định thời gian xả nước theo 𝜌, 𝑝!, 𝑉 và 𝑆. Cho biết: ∫ !"
= & √𝑥 − 𝑎 + & arctan -"$% "!√"$% %" √%" % Bài 4. (4,0 điểm)
Để đo bề dày của các bản trong suốt có bề dày rất mỏng, người ta thường ứng dụng thí nghiệm giao
thoa ánh sáng. Phép đo bề dày rất mỏng của một bản mặt trong suốt được bố trí như sau:
Hai khe hẹp 𝑆", 𝑆# song song cùng nằm trong mặt phẳng (𝐾) cố định thẳng đứng, cách nhau đoạn 𝑎.
Một khe hẹp 𝑆 phát ánh sáng đơn sắc bước sóng 𝜆 đặt song song, cách đều hai khe 𝑆", 𝑆#. Sau (𝐾) đặt
một màn chắn sáng (𝐿) song song và cách mặt phẳng chứa hai khe đoạn 𝑑 thì trên màn thu được một
hệ vân giao thoa gồm các vân sáng và vân tối xen kẽ cách đều nhau.
Sau đó đặt bản trong suốt cần đo bề dày ngay sau khe 𝑆", kết quả là toàn bộ hệ vân dịch chuyển một
đoạn ℓ. Coi bản trong suốt này là một bản mặt song song rất mỏng, bề dày 𝑒, chiết suất đối với ánh
sáng sử dụng trong phép đo là 𝑛.
1. Xác định độ dịch chuyển ℓ theo 𝜆, 𝑑, 𝑎, 𝑛 và 𝑒.
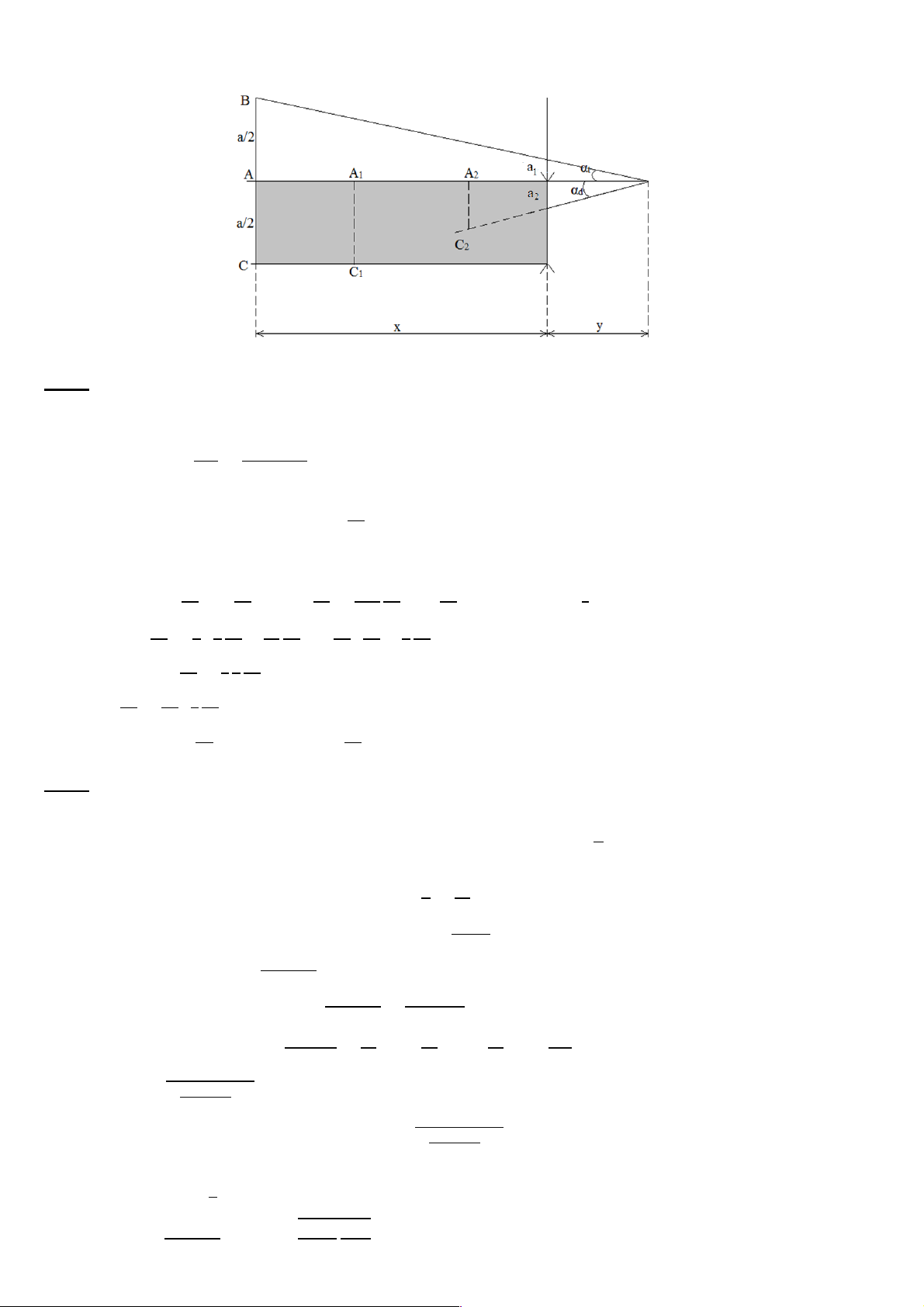
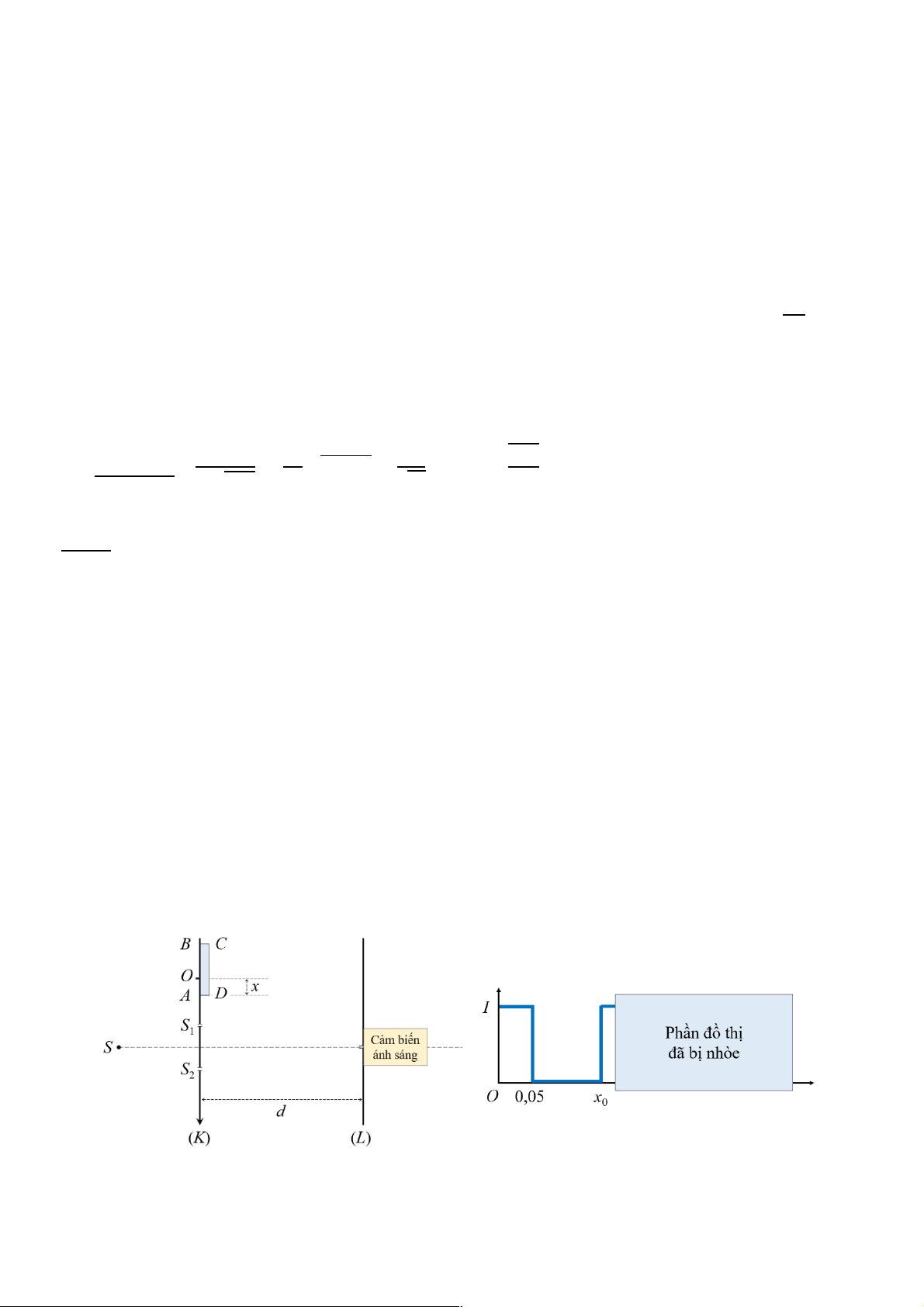
2. Thiết lập hệ thống với 𝑎 = 0,1 mm, 𝜆 = 750 nm, bản 𝐴𝐵𝐶𝐷 có bề dày 𝐵𝐶 = 𝑒 ≤ 3,4 µm,
𝐴𝐵 = 0,5 mm và 𝑛 = 1,5. Gọi 𝑂 là một vị trí cố định trên (𝐾), khoảng cách từ 𝑂 đến 𝐴 là 𝑥.
Nhờ hệ thống cơ vi động, bản 𝐴𝐵𝐶𝐷 tịnh tiến dọc xuống như Hình a. i x (mm) Hình a Hình b
Ngay vị trí vân sáng trung tâm trên màn (𝐿) đặt một tấm cảm biến ánh sáng kích thước nhỏ.
Cảm biến này được nối với hệ thống mạch điện hoạt động theo nguyên tắc: Dòng điện luôn
được duy trì ổn định với giá trị không đổi 𝐼 đến khi tại vị trí cảm biến là một vân tối thì dòng điện bằng không.
Hình b biểu diễn sự phụ thuộc dòng điện 𝐼 theo 𝑥 nhưng do sơ suất, đồ thị đã bị nhòe một phần.
a. Xác định giá trị 𝑥, trên đồ thị và bề dày 𝑒 của bản.
b. Vẽ lại toàn bộ đồ thị hoàn chỉnh khi không bị nhòe. Bài 5. (4,0 điểm)
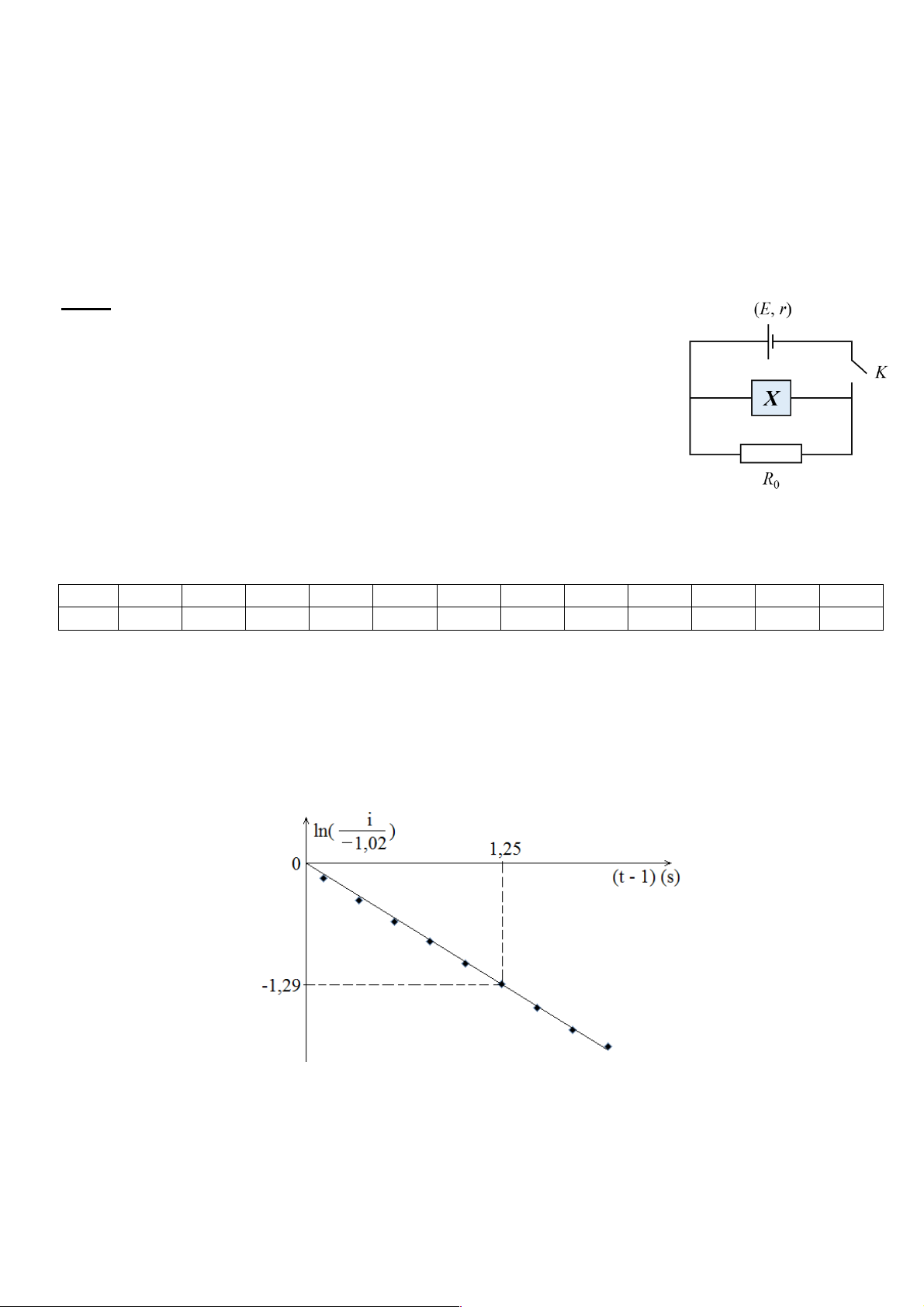
Cho mạch điện gồm 3 nhánh song song như hình bên:
- Nhánh trên cùng là nguồn điện không đổi có suất điện động 𝐸 = 12,00 V
và điện trở trong 𝑟 = 1,16 Ω.
- Nhánh giữa có phần tử 𝑋 là một trong các linh kiện: điện trở không đổi,
tụ điện hoặc cuộn dây.
- Nhánh dưới có điện trở 𝑅! = 6,00 Ω.
Điện trở của dây dẫn và khóa 𝐾 không đáng kể. Lúc 𝑡 = 0, khóa 𝐾 đang đóng và dòng điện trong
mạch đang ở trạng thái ổn định. Sau đó, tại thời điểm 𝑡 = 𝑡!, ngắt khóa 𝐾. Bằng các dụng cụ đo thích
hợp, nhận được giá trị cường độ dòng điện qua điện trở 𝑅! ở các thời điểm tương ứng như sau: 𝑡 (s) 0,00 0,25 0,50 0,75 1,00 1,25 1,50 1,75 2,00 2,25 2,50 2,75 𝑖 (A) 1,46 1,46 1,46
1,46 – 1,02 – 0,78 – 0,60 – 0,47 – 0,36 – 0,28 – 0,21 – 0,16
1. Từ bảng số liệu, hãy lập luận và cho biết 𝑋 là loại linh kiện nào?
2. Thiết lập hệ thức cường độ dòng điện qua điện trở 𝑅! sau khi ngắt khóa 𝐾 theo thời gian.
3. Sau khi tuyến tính hóa bảng số liệu, thu được đồ thị như hình dưới. Hãy thực hiện yêu cầu sau:
- Nếu 𝑋 là điện trở không đổi, hãy tính giá trị điện trở 𝑅-.
- Nếu 𝑋 là tụ điện, hãy tính giá trị điện dung 𝐶-.
- Nếu 𝑋 là cuộn dây, hãy tính điện giá trị trở 𝑟- và hệ số tự cảm 𝐿-. ------- HẾT-------
Họ và Tên thí sinh: ............................................................... Số báo danh: ..........................
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI THPT
THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC 2021 – 2022 MÔN VẬT LÝ Đ ÁP ÁN ĐỀ NG HỊ
Ngày thi thứ hai: 29 tháng 12 năm 2021
Thời gian làm bài: 180 phút (không kể thời gian phát đề) Bài 1. (4.0 điểm)
1. a. Ta có: 𝑖! = "! 𝑡 (0 < 𝑡 < 𝑎) và 𝑖
- (0 < 𝑡 < 𝑇 − 𝑎) .............. (0.5 điểm) # $ = 𝐼% *1 − & '(# "
Nhiệt lượng tỏa ra: 𝑄 = 𝑅 *∫# 𝑖$ '(# $ ' ! 𝑑𝑡 + ∫
𝑖 𝑑𝑡- = )"! ....................................... (0.5 điểm) % $ % *
→ 𝐼 = "! .................................................................................................................. (0.25 điểm) √* b.
Khi dùng dòng răng cưa: 𝑁! = 𝑆,-.(/0á2 = "!' .............................................. (0.25 điểm) $
Dòng sine: 𝑖 = 𝐼% sin *$3 𝑡 + 𝜑- .............................................................................. (0.25 điểm) '
Khi dùng dòng hàm sine: 𝑁 '
$ = ∫ 𝑖𝑑𝑡 = "!' ............................................................ (0.25 điểm) % 3
Tỷ lệ số hạt giữa dòng răng cưa so với dòng hàm sine: 4# = 3 ................................ (0.25 điểm) 4" $
Học sinh xét trường hợp riêng của 𝝋: 𝜑 là một giá trị xác định .......................... (0.5 điểm)
2. 𝑀 = 𝑐𝑜𝑛𝑠𝑡 → Công cản 𝑊 cho mỗi vòng không đổi
Bảo toàn năng lượng quá trình đầu tiên: 𝑚𝑔𝑙 = ! 𝑚𝑣$ + ! 𝐼𝜔$ + 𝑊𝑛 $ $
! ................. (0.25 điểm)
Bảo toàn năng lượng quá trình thứ hai: ! 𝐼𝜔$ = 𝑊𝑛 $
$ ............................................. (0.25 điểm)
𝑀 = 𝑐𝑜𝑛𝑠𝑡 → 𝛾 = 𝑐𝑜𝑛𝑠𝑡 → 𝜔 = 536" .................................................................... (0.5 điểm) &
Lại có 𝑣 = 𝜔𝑅 → Moment quán tính: 𝐼 = 6" 𝑚 * 89&" − 𝑅$- ............................ (0.25 điểm) 6 " #76" :3"6" Bài 2. (4.0 điểm)
1. a. Xét một quả cầu bán kính 𝑟: 𝑞 = 53 𝜌𝑟*............................................................ (0.25 điểm) *
Xét một lớp điện tích trong khoảng 𝑟 → 𝑟 + 𝑑𝑟: 𝑑𝑞 = 4𝜋𝜌𝑟$𝑑𝑟 ............................ (0.25 điểm)
Năng lượng của quả cầu: 𝑊 = ∫) ! <=< = 53 @")$ → 𝐴 = 53 ............................. (0.5 điểm) % 53;! > !? ;! !?
(Học sinh tính tổng năng lượng điện trường bên trong và bên ngoài quả cầu vẫn được trọn điểm)
(Nếu học sinh sử dụng công thức: 𝑊 = * AB" và 𝑄 = 53 𝜌𝑅* rồi ra kết quả ........ (0.5 điểm)) ? )" *
b. 𝑊 = 𝐴 @")$ → 𝑊 = 𝐴 C" ................................................................................. (0.25 điểm) ;! ;!)
Động năng quay quanh trục của quả cầu: 𝑊D = ! 𝐼𝜔$ = ! 𝑚𝑣$ ............................. (0.25 điểm) $ ?
Ước tính được giá trị: 𝑣 = O𝐴 𝑒" > 𝑐 (ước tính khoảng 4𝑐 ~ 33𝑐) .................... (0.5 điểm) ;!𝑚𝑅
Đây là nhận định sai, vì không thể có tốc độ lớn hơn tốc độ ánh sáng .................... (0.25 điểm)
2. a. Khoảng cách từ 𝑑𝑞 ở tọa độ (𝑟, 𝜑, 𝜃) đến trục quay: 𝑟 sin 𝜃............................ (0.25 điểm) Moment từ: 𝑀 ) 3 $3
C = ! 𝜌𝜔 ∫ 𝑟5𝑑𝑟 ∫ sin*𝜃 𝑑𝜃 ∫
𝑑𝜑 = 53 𝜌𝜔𝑅? → 𝑁 = 53 ......... (0.5 điểm) $ % % % !? !? b. 𝑀
T⃗C = 𝑁 ∙ 𝜌𝜔T⃗𝑅? = −𝑁 ∙ 𝜔T⃗𝑒𝑅$ ........................................................................... (0.25 điểm)
Theo giả thiết: 𝑆⃗C = 𝐼𝜔T⃗ = $ 𝑚𝜔T⃗𝑅$ .......................................................................... (0.25 điểm) ? Nếu 𝑀
T⃗C = 𝑆T⃗C ↔ −3𝑒 = 2𝑚 → Sai → 𝑀T⃗C = −𝐾 C 𝑆⃗
E C, 𝐾 = 𝑐𝑜𝑛𝑠𝑡 > 0 ................. (0.5 điểm) Bài 3. (4.0 điểm)
1. Để khí trong tên lửa nén đủ mạnh để làm bung chốt: 𝑝 ≥ 4𝑝% ................................ (0.25 điểm) F )
Ta có: F!G + !(4%" = FG ............................................................................................ (0.25 điểm) ' ' '
→ 𝑝 = 𝑝% *1 + 4- ≥ 4𝑝 $
% → Cần bơm tối thiểu 6 lần .............................................. (0.5 điểm)
2. a. Bảo toàn động lượng cho cả hệ: 𝑚𝑣T%
T⃗ = (𝑚 − 𝑑𝑚)(𝑣T% T⃗ + 𝑑𝑣T%
T⃗) + 𝑢T⃗𝑑𝑚 .......... (0.5 điểm) → 0T⃗ = 𝑚𝑑𝑣T%
T⃗ + 𝑑𝑚[𝑢T⃗ − (𝑣T%
T⃗ + 𝑑𝑣T%T⃗)] ...................................................................... (0.25 điểm) → `𝐹
TT⃗&` = 𝑚 b=JK⃗b = 𝑣 =E ............................................................................................ (0.25 điểm) =& =&
b. Ta có: 𝑝 = 𝑝% + ! 𝜌𝑣$ → 𝑣 = O$(F(F!) ............................................................ (0.5 điểm) $ @
Lại có: =G = 𝑆𝑣 → =E = 𝜌𝑆𝑣 ................................................................................... (0.5 điểm) =& =&
→ 𝐹& = 𝜌𝑆𝑣$ = 2𝑆(𝑝 − 𝑝%) .................................................................................... (0.25 điểm)
3. Đẳng nhiệt: 𝑝𝑉 = 𝑐𝑜𝑛𝑠𝑡 → 𝑝𝑆𝑣 + 𝑉 =F =F A = 0 → 𝑑𝑡 = − F!G O@
.............. (0.25 điểm) =& M $ F"N(F(F!) Thời gian: 5F @ 𝑡 = F!G O@ ∫ ! =F = G O
*√* + 3- ......................................... (0.5 điểm) M $ F! F"N(F(F!) M $F! 5 O Bài 4. (4.0 điểm)
1. Ban đầu: ∆𝛿 = 𝑑! − 𝑑$ = P# ................................................................................... (0.25 điểm) =
Tọa độ của mỗi vân: P# = 𝑘𝜆 → 𝑥 = 𝑘 Q= ............................................................... (0.25 điểm) = #
Khi đặt bản mặt song song tại 𝑆 D D
!: ∆𝛿D = 𝑑! − 𝑑$ = P# + 𝑒(𝑛 − 1) ....................... (0.25 điểm) =
Tọa độ của mỗi vân: P# + 𝑒(𝑛 − 1) = 𝑘𝜆 → 𝑥D = 𝑘 Q= − 𝑒(𝑛 − 1) = ..................... (0.25 điểm) = # #
→ ℓ = 𝑒(𝑛 − 1) = và dịch về phía khe 𝑆 #
! ................................................................ (0.5 điểm)
2. Khi 𝑥 = 0,05 mm, tại cảm biến: vân sáng thành vân tối → 𝐴 vừa tới 𝑆! ................ (0.5 điểm)
→ 𝑂𝑆! = 0,05 mm và độ dịch ℓ = *𝑘 + !- 𝑖 .......................................................... (0.5 điểm) $
Tại cảm biến là vân sáng: bản không che khe nào hoặc che đồng thời hai khe ....... (0.25 điểm)
Tại cảm biến là vân tối: bản chỉ che khe 𝑆! hoặc chỉ che khe 𝑆$ ............................. (0.25 điểm)
Khi 𝑥 = 𝑥0, tại cảm biến: vân tối thành vân sáng → 𝐴 vừa tới 𝑆$ ........................... (0.25 điểm)
→ 𝑥0 = 𝑂𝑆$ = 𝑂𝑆! + 𝑆!𝑆$ = 0,15 mm .................................................................. (0.25 điểm)
→ 𝑒 = 2,25 µm ......................................................................................................... (0.5 điểm) Bài 5. (4.0 điểm)
1. Lập luận đúng từ bảng số liệu → X là cuộn dây. r Khi chưa ngắt khóa K: 𝐼 W = 6,57 Ω PR = :,TO = V − 1,46 → p U& U7 '(& 𝐼 ')(
PR = 1,33 A...........(0.5 điểm + 0.5 điểm) &
2. Sau khi ngắt khóa K, dòng điện qua cuộn dây bắt đầu giảm nên xuất hiện suất điện động tự cảm duy trì
dòng điện phóng qua Ro theo chiều ngược lại nên lúc này giá trị cường độ dòng điện i sẽ là âm. Xét ở một
thời điểm t, cường độ dòng điện qua cuộn dây đang có độ lớn là ix, sau khoảng thời gian dt, cường độ dòng điện
qua cuộn dây lúc này có độ lớn là ix + dix (dix < 0). Khi đó suất điện động tự cảm:
𝐸$% = −𝐿. &'! > 0 .................................................................................................................(0.5 điểm) &$
Áp dụng định luật Ohm rút ra: −𝐿. =X* = (𝑅 + 𝑟 X*
= − )7>, ∫& 𝑑𝑡.......................................................(0.5 điểm) =& =)𝑖P → ∫ =X* "*+ X* Y &+
→ 𝑖 = −1,33𝑒(-).*(&(& /
+) (𝐴, 𝑠).............................................................................(0.5 điểm) 3. Ta có ∫'
&' = − -./" ∫$ 𝑑𝑡 → ln 1 ' 2 = − -./" (𝑡 − 1).............................................(0.5 điểm) (),+, ' 0 ) (),+, 0
𝑦 = ln * X - , 𝑥 = 𝑡 − 1 → 𝑦 = − )7>, . 𝑥.............................................................(0.5 điểm) (!,%$ Y
Từ đồ thị ta tính được: L = 12,18 H ...............................................................................(0.5 điểm)




