





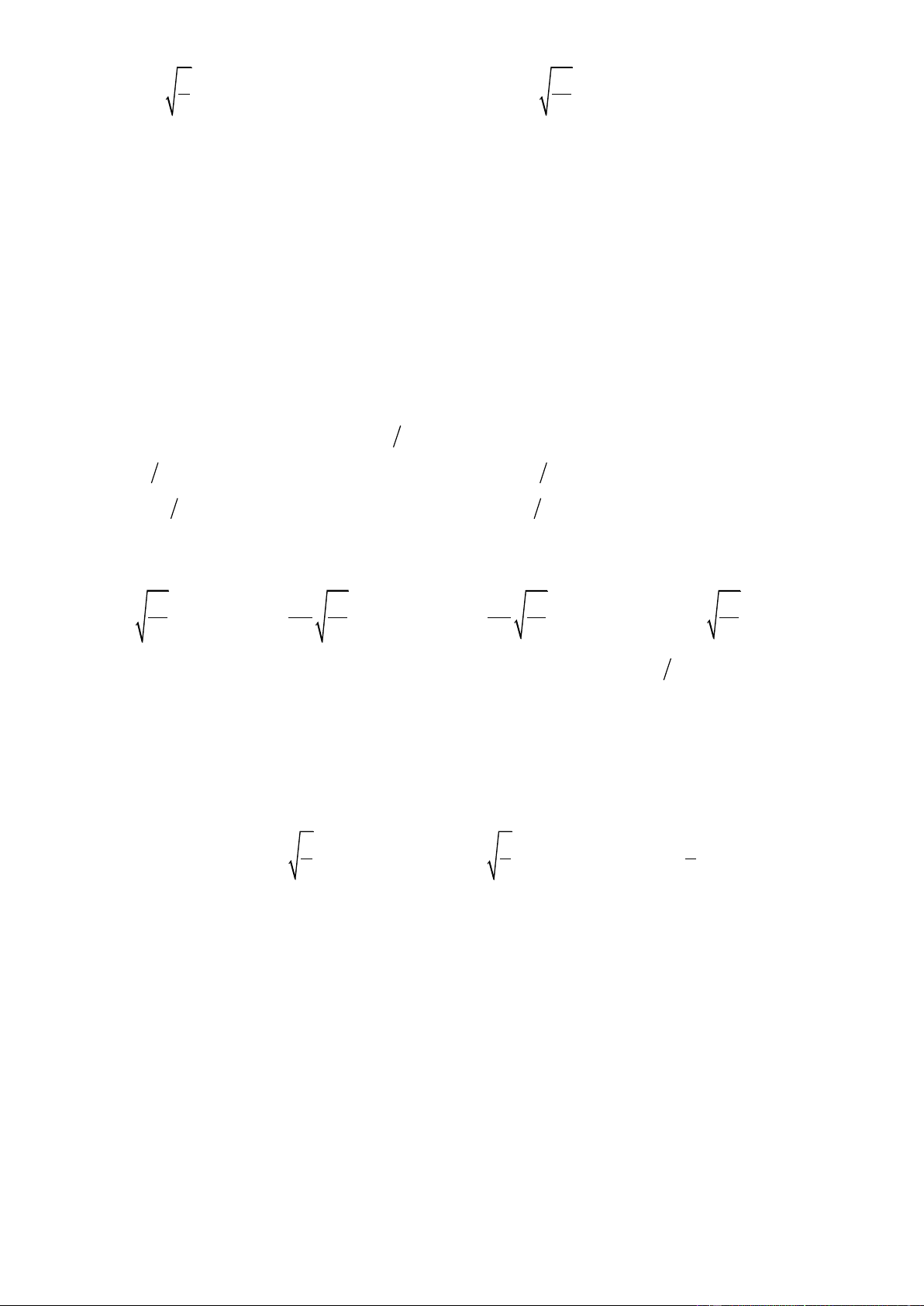




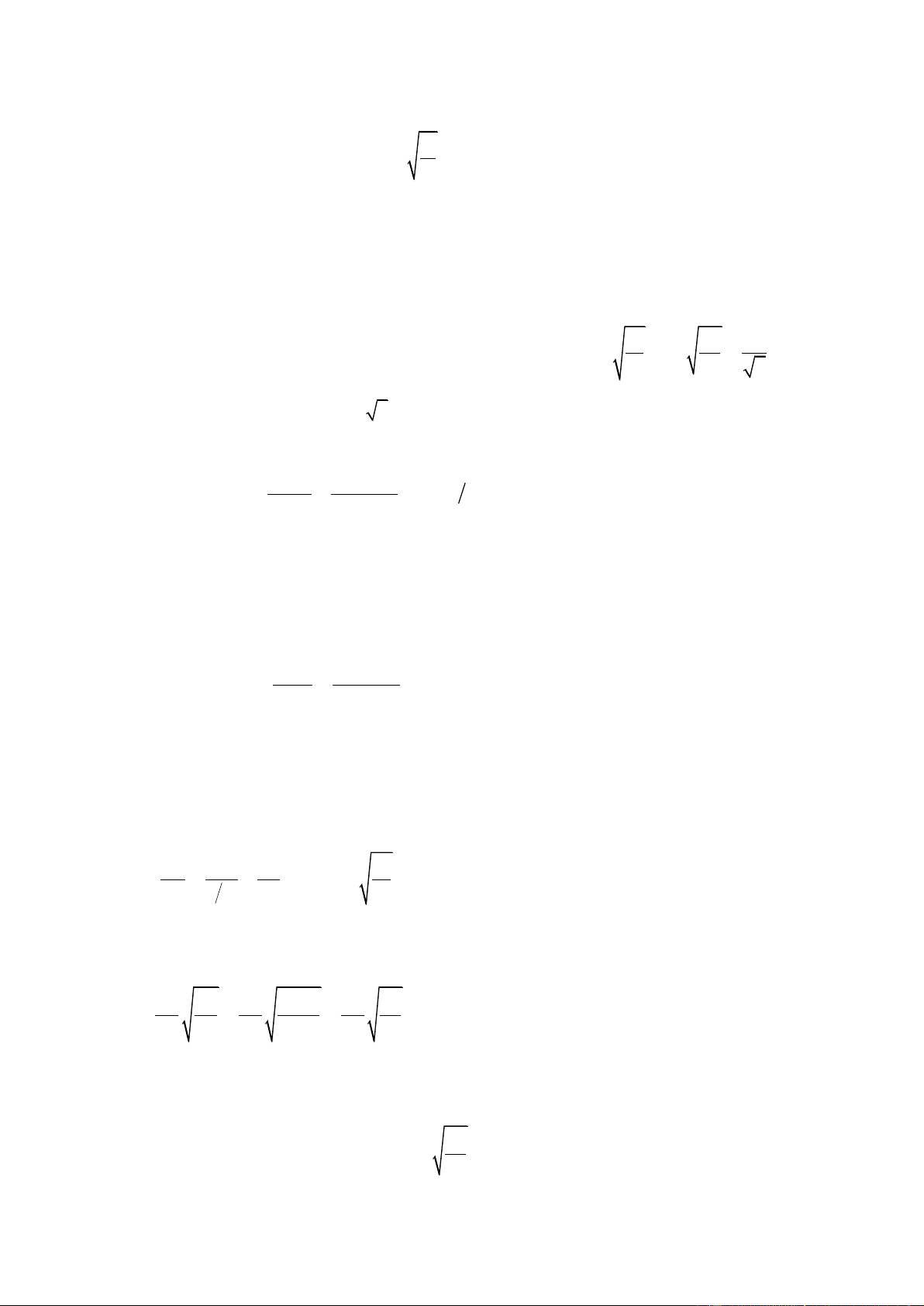
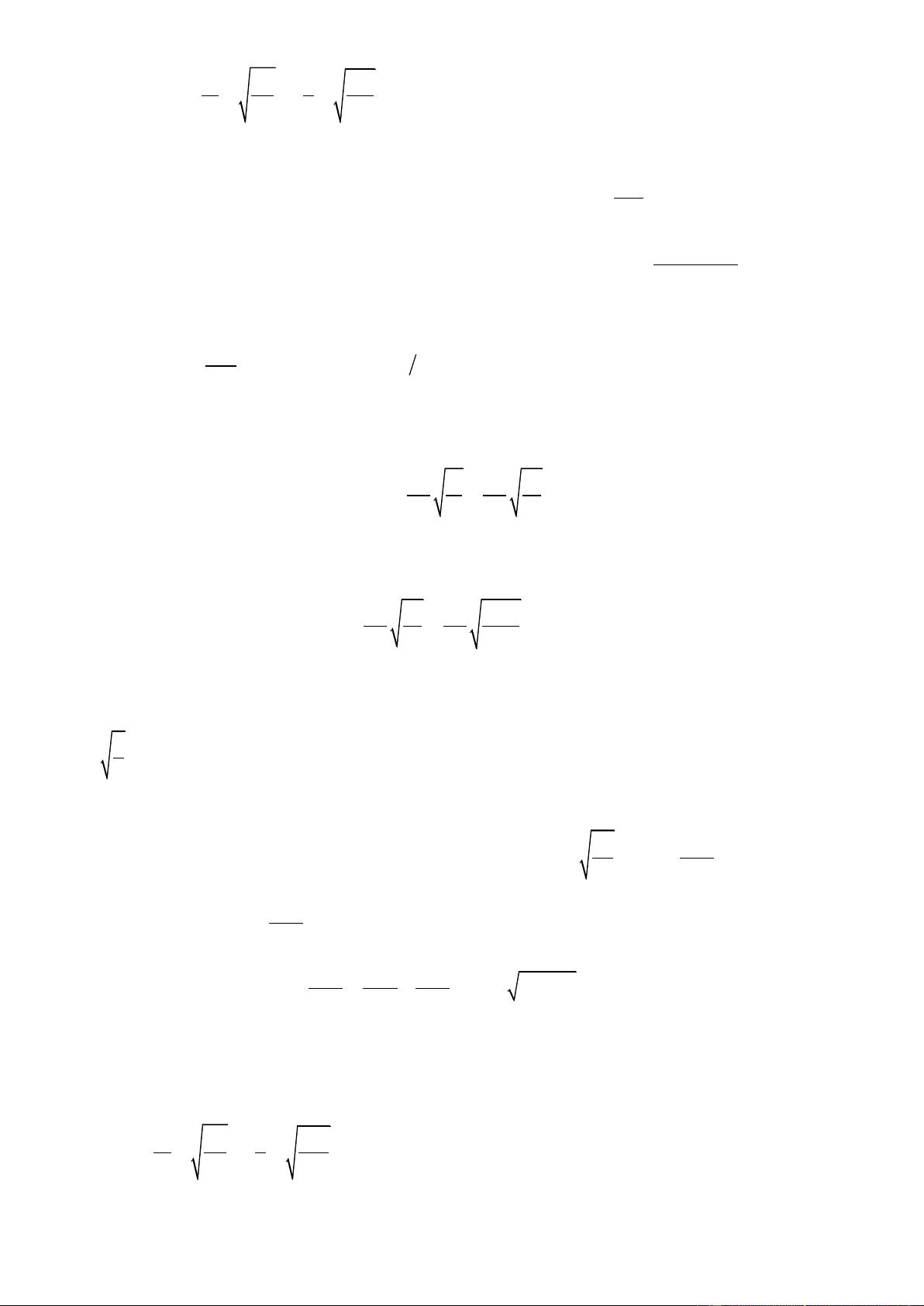

Preview text:
BÀI TẬP TRẮC NGHIỆM NHẬN BIẾT
VỀ DAO ĐỘNG ĐIỀU HÒA VÀ CON LẮC LÒ XO 1.1. Phương pháp
Chúng ta cần nhớ lại các kiến thức ở phần lý thuyết đã học, các điểm cần lưu ý là:
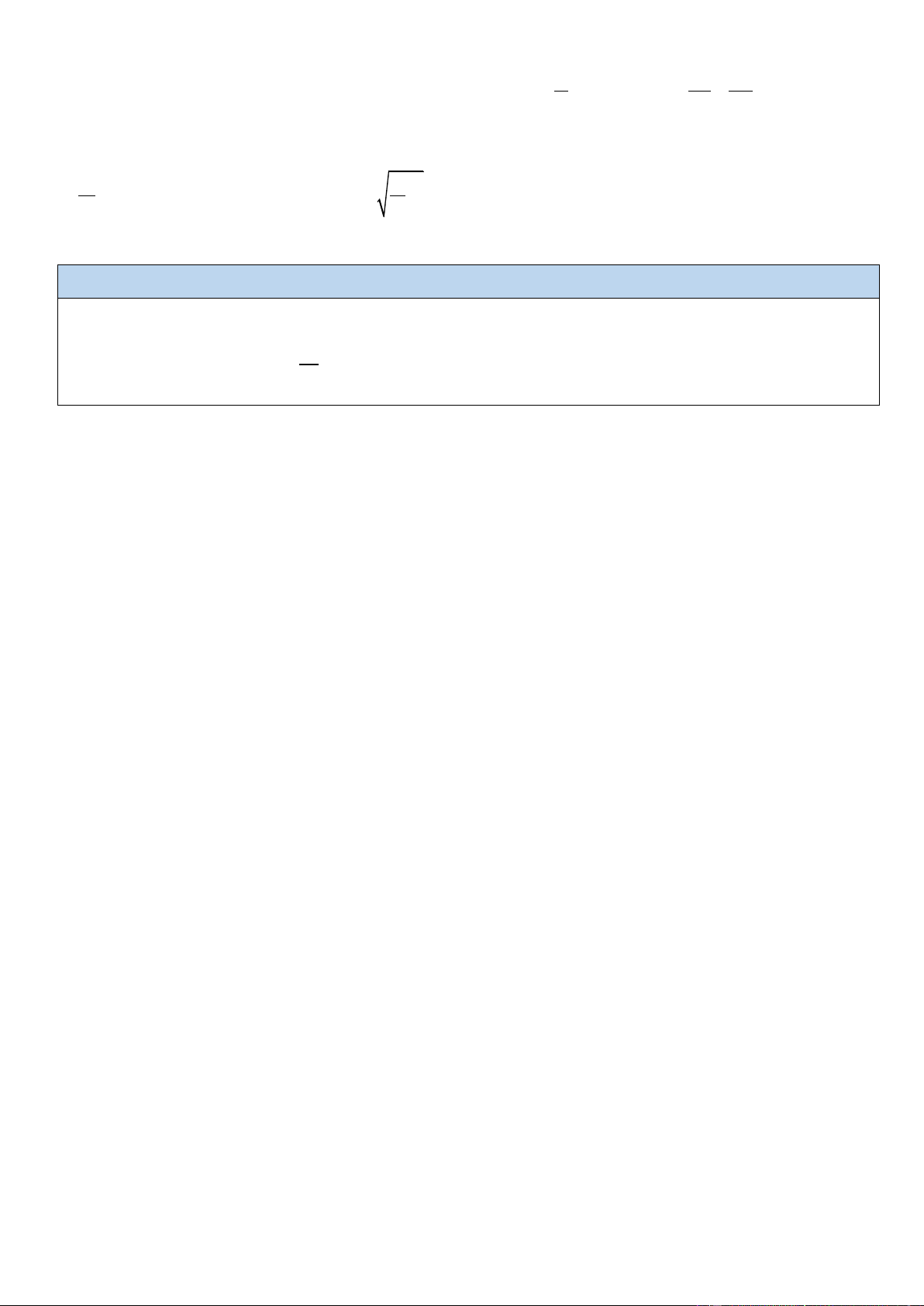
- Giả sử con lắc lò xo dao động điều hòa với phương trình x = Ac (
os t + ) . Tần số góc của con k lắc lò xo là = (rad s) . m
- Đối với trường hợp con lắc lò xo thẳng đứng ta luôn có mg = k l 0 Trong đó l
là độ biến dạng của lò xo khi vật ở vị trí cân bằng. Từ đó ngoài cách tính tần số góc khi biết o
khối lượng m của vật và độ cứng k của lò xo thì ta còn có thể tính được tần số góc khi biết độ biến dạng
của lò xo khi vật ở vị trí cân bằng bởi công thức: k = g l 1 g 0 m = T = 2 f = l g 2 l 0 0 mg = k l 0
- Chu kì của con lắc lò xo tỉ lệ với căn bậc hai của khối lượng m tỉ lệ nghịch với căn bậc hai của k,
chỉ phụ thuộc vào m và k. Chú ý
Dưới đây là những bài toán hết sức cơ bản về con lắc lò xo, dao động điều hòa, mức độ nhận biết và là kiến
thức nền tảng, vậy nên bạn đọc không được chủ quan mà phải nắm chắc kiến thức phần này.
1.2. Ví dụ minh họa
Ví dụ 1: Một vật nhỏ dao động theo phương trình x = 5 cos(t + 0, 5 ) (cm) . Pha ban đầu của dao động là: A. B. 0, 5 C. 0, 25 D. 1, 5 Lời giải
Phương trình dao động điều hòa có dạng x = A cos(t + ) thì là pha ban đầu của dao động. Đáp án B.
Ví dụ 2: Con lắc lò xo có khối lượng vật nhỏ là m dao động điều hòa theo phương ngang với phương
trình x = A cos t . Mốc tính thế năng ở vị trí cân bằng. 1 1 A. 2 m A B. 2 m A . C. 2 2 m A . D. 2 2 m A . 2 2 Lời giải 1
Cơ năng của con lắc là: cơ năng của con lắc là 2 2 m A . 2 Đáp án D. Trang 1
Ví dụ 3: Một con lắc lò xo gồm một vật nhỏ khối lượng m và lò xo có độ cứng k. Con lắc dao động điều
hòa với tần số góc là: m k m k A. 2 . B. 2 . C. . D. . k m k m Lời giải k
Con lắc dao động điều hòa với tần số góc là = . m Đáp án D. Ví dụ 4:Hai
dao động có phương trình lần lượt là x = 5cos(2t + 0,75 ) (cm) và 1
x = 10 cos(2 t + 0, 5 ) (cm). Độ lệch pha của hai dao động này có độ lớn bằng: 2 A. 0, 25 . B. 1, 25 . C. 0, 5 . D. 0, 75 . Lời giải
Độ lệch pha của hai dao động được xác định bằng hiệu số pha của hai dao động, có độ lớn là
= (2t + 0,75 ) − (2t + 0,5 ) = 0,25. Đáp án A.
Ví dụ 5: Một chất điểm dao động theo phương trình x = 6 cost (cm). Dao động của chất điểm có biên độ là: A. 2 cm. B. 6 cm. C. 3 cm. D. 12 cm. Lời giải
Dao động x = 6 cost của chất điểm có biên độ là 6 cm. Đáp án B.
Ví dụ 6: Một vật nhỏ khối lượng 100g dao động theo phương trình x = 8 cos10t ( x tính bằng cm, t tính
bằng s). Động năng cực đại của vật bằng: A. 32mJ. B. 64mJ. C. 16mJ. D. 128mJ. Lời giải
Động năng cực đại của vật chính là cơ năng trong dao động, ta có: 2 2 1 0,1.10 .0, 08 2 2 W = m A = = 32mJ. 2 3 Đáp án A.
Ví dụ 7: Một vật dao động với phương trình x = 5cos 4 t + .
Tại thời điểm t = 1s hãy xác định li độ 6 của dao động A. 2,5cm. B. 5cm. C. 2, 5 3 cm. D. 2, 5 2 cm. Lời giải Trang 2
Tại thời điểm t = 1s ta có x = 5cos 4 .1+ = 2,5 3. 6 Đáp án C.
Ví dụ 8: Khi gắn quả nặng m1 vào lò xo, nó dao động với chu kì T1 = 1,2s. Khi gắn quả nặng m2 vào lò
xo, nó dao động với chu kì T2 = 1,6s. Khi gắn đồng thời m1 và m2 vào lò xo đó, chúng dao động với chu kì bao nhiêu? A. 2 s. B. 3 s. C. 8 s. D. 5 s. Lời giải
Chỉ cần nhận xét đơn giản là chu kì tỉ lệ thuận với m nên khối lượng m tỉ lệ thuận với 2 T . Từ đây khi gắn đồng thời m = +
1 và m2 vào thì chu kì lúc này được xác định bởi 2 2 2 T T T 1 2
Nếu không quen với cách giải thích này ta có thể làm như sau: m1 T = 2 1 k m m m 2 2 2 1 2 2 2 T = 2 T = (2 ) + = T + T 2 1 2 k k k m + m 1 2 T = 2 k
Thay số ta được T = 2s. Đáp án A. Nhận xét
Nếu đề bài hỏi khi treo vật có khối lượng m − m với m m thì lập luận tương tự ta có chu kì lúc đó 1 2 1 2 được xác định bởi 2 2 2
T = T + T 1 2
Ví dụ 9: Viên bi m1 gắn vào lò xo có độ cứng k thì hệ dao động với chu kì T1 = 0,3s. Viên bi m2 gắn vào
lò xo có độ cứng k thì hệ dao động với chu kì T = +
2 = 0,4s. Hỏi nếu vật có khối lượng m 4m 3m vào lò 1 2
xo có độ cứng k thì hệ có chu kì dao động là bao nhiêu? A. 0,4 s. B. 0,916 s. C. 0,6 s. D. 0,7 s. Lời giải
Vì khối lượng m tỉ lệ thuận với 2
T nên ta có khi treo vật có khối lượng m = 4m + 3m vào lò xo k thì hệ 1 2
có chu kì dao động được xác định bởi 2 2 2
T = 4T + 3T . Thay số vào ta tính được T = 0,916 s. 1 2 Đáp án B.
Ví dụ 10: Một vật dao động điều hòa với tần số góc = 10 rad s , khi vật có li độ là 3 cm thì tốc độ là 40
cm/s. Hãy xác định biên độ của dao động? A. 4 cm. B. 5 cm. C. 6 cm. D. 3 cm. Trang 3 Lời giải
Đề cho li độ và vận tốc nên ta nhớ đến công thức độc lập thời gian giữa x và v . 2 2 40 Ta có 2 2 A = x + = 3 + = 5 cm. 2 2 10 Đáp án B.
Ví dụ 11: Một vật dao động điều hòa với biên độ A = 5 cm, khi vật có li độ 2,5cm thì tốc độ của vật là
5 3 cm/s. Hãy xác định vận tốc cực đại của dao động? A. 10 m/s. B. 8 m/s. C. 10 cm/s. D. 8 cm/s. Lời giải 2 2 x v
Vì x và v vuông góc với nhau nên ta có công thức độc lập: + =1 A v max Từ đó suy ra v = 10 cm/s. max Đáp án C.
Ví dụ 12: Một vật dao động điều hòa với gia tốc cực đại là 200 cm/s2 và tốc độ cực đại là 20cm/s. Hỏi khi
vật có gia tốc là 100 cm/s2 thì tốc độ dao động của vật lúc đó là A. 10 cm/s. B. 10 2 cm/s. C. 5 3 cm/s. D. 10 3 cm/s. Lời giải
Đề bài cho gia tốc hỏi vận tốc nên ta nhớ ngay đến công thức độc lập thời gian giữa a và v là: 2 2
a v +
=1. Thay số vào ta tính được v = 10 3 . a v max max Đáp án D.
Ví dụ 13: Có ba lò xo giống nhau được đặt trên mặt phẳng ngang, lò xo thứ nhất gắn vật nặng m = 0,1kg; 1
vật nặng m = 300g được gắn vào lò xo thứ 2; vật nặng m = 0,4kg gắn vào lò xo 3. Cả ba vật đều có thể 2 3
dao động không ma sát trên mặt phẳng ngang. Ban đầu kéo cả 3 vật ra một đoạn bằng nhau rồi buông tay
không vận tốc đầu cùng một lúc. Hỏi vật nặng nào về vị trí cân bằng đầu tiên? A. vật 1. B. vật 2. C. vật 3.
D. 3 vật về cùng lúc. Lời giải
Vì ban đầu kéo cả 3 vật ra một đoạn bằng nhau nên muốn biết vật nào về vị trí cân bằng đầu tiên thì ta
phải so sánh chu kì của 3 vật. Vật nào có chu kì càng nhỏ thì dao động càng nhanh và ngược lại. Khi độ
cứng của lò xo giống nhau thì chu kì tỉ lệ thuận với căn bậc hai của khối lượng, mà m m m nên 1 2 3
T T T , do đó vật 1 sẽ về vị trí cân bằng trước vật 2 và vật 3. 1 2 3 Đáp án A.
Ví dụ 14: Ba con lắc lò xo có độ cứng lần lượt là k;2k;3k. Được đặt trên mặt phẳng ngang và song song
với nhau. Con lắc 1 gắn vào điểm A; con lắc 2 gắn vào điểm B; con lắc 3 gắn vào điểm C. Biết AB = BC, Trang 4
lò xo 1 gắn vật m = m ; lò xo 2 gắn vật m = 2m , lò xo 3 gắn vật m . Ban đầu kéo lò xo 1 đoạn là a; lò 1 2 3
xo 2 một đoạn là 2a; lò xo 3 một đoạn là A , rồi buông tay cùng một lúc. Hỏi ban đầu phải kéo vật 3 ra 3
một đoạn là bao nhiêu và khối lượng m là bao nhiêu để trong quá trình dao động thì 3 vật luôn thẳng 3 hàng?
A. 3m; 3a.
B. 3m; 6a.
C. 6m; 6a.
D. 9m; 9a. Lời giải
Trước hết, để trong quá trình dao động 3 vật luôn thẳng hàng thì tần số góc của 3 vật phải bằng nhau. Ta k 2k 3k có = = = = m = 3m 1 2 3 3 m 2m 3m
Tiếp theo, vì AB = BC và trong quá trình dao động 3 vật luôn thẳng hàng nên ta có O m chính là đường 2 2
trung bình của hình thang O O m m . 1 3 3 1 a + A Từ đó ta có: 3 2a = A = 3 . a 3 2 Đáp án A.
Ví dụ 15: Một con lắc lò xo gồm lo xo nhẹ có độ cứng 100 N/m và vật nhỏ có khối lượng m. Con lắc dao
động điều hòa theo phương ngang vớ T
i chu kì T. Biết ở thời điểm t vật có li độ 5cm, ở thời điểm t + vật 4
có vận tốc 50 cm/s. Giá trị của m bằng: A. 0,5kg. B. 1,2kg. C. 0,8kg. D. 1,0kg. Lời giải T Vì t = t +
nên nếu ta giả sử x = A cos t thì 1 ( 1) 2 1 4 T 2 T
x = Acos t + = Acos t + . = Acos t + = −Asin t 2 1 1 1 ( 1) 4 T 4 2 x x
Từ đó ta có sin (t + cos t = +
=1 x + x = A x = A − x 1 ) ( 1) 2 2 2 2 1 2 2 2 2 2 2 2 2 2 1 2 1 2 A A Trang 5 2 2 x x
Hoặc ta có thể nhận xét nhanh là vì x và x lệch nhau về góc là nên ta có luôn 1 2 + =1 1 2 2 2 2 A A Vậy là ta đã tính xong 2 2
A − x , thay vào biểu thức độc lập thời gian ta có ngay: 2 2 v k 2 2 2 2
= A − x = x v = x v = x .
Thay số ta có m = 1 kg. 2 1 2 1 2 1 m Đáp án D. Phân tích
Đề bài cho liên quan đến li độ và tốc độ, ta nhớ ngay đến biểu thức độc lập thời gian giữa v và x. Ta có v2 2 v vậy ta sẽ tìm x 2 2 2 + = 2 rồi dùng x A 2 Trang 6
1.3. Bài tập tự luyện
Câu 1: Gọi k là độ cứng của lò xo, m là khối lượng của vật nặng. Bỏ qua ma sát khối lượng của lò xo và
kích thước vật nặng. Công thức chu kỳ của dao động? k m A. T = 2 . B. T = 2 . m k m
C. T = 2 k . m D. T = 2 . k
Câu 2: Hãy tìm nhận xét đúng về con lắc lò xo.
A. Con lắc lò xo có chu kỳ tăng lên khi biên độ dao động tăng lên.
B. Con lắc lò xo có chu kỳ không phụ thuộc vào gia tốc trọng trường.
C. Con lắc lò xo có chu kỳ giảm xuống khi khối lượng vật nặng tăng lên.
D. Con lắc lò xo có chu kỳ phụ thuộc vào việc kéo vật nhẹ hay mạnh trước khi buông tay cho vật dao động.
Câu 3: Gọi k là độ cứng của lò xo, m là khối lượng của vật năng. Bỏ qua ma sát khối lượng của lò xo và
kích thước vật nặng. Nếu độ cứng của lò xo tăng gấp đôi, khối lượng vật dao động không thay đổi thì chu
kỳ dao động thay đổi như thế nào? A. Tăng 2 lần.
B. Tăng 2 lần. C. Giảm 2 lần. D. Giảm 2 lần.
Câu 4: Một con lắc lò xo treo thẳng đứng dao động với biên độ 10 cm, chu kỳ 1s. Khối lượng của quả nặng 400g, lấy 2 = 10, cho 2
g = 10 m s . Độ cứng của lò xo là bao nhiêu?
A. 16 N m.
B. 20 N m.
C. 32 N m. D. 40 N m.
Câu 5: Một con lắc lò xo dao động với chu kỳ T = 0,4 s. Nếu tăng biên độ dao động của con lắc lên 4
lần thì chu kỳ dao động của vật có thay đổi như thế nào? A. Tăng lên 2 lần.
B. Giảm 2 lần.
C. Không đổi. D. Đáp án khác.
Câu 6: Con lắc lò xo dao động điều hòa với chu kì T = 0,4 s. Độ cứng của lò xo là 100 N m , tìm khối lượng của vật? A. 0,2 kg. B. 0,4 kg. C. 0,4 g. D. Đáp án khác.
Câu 7: Một con lắc lò xo dao động với chu kỳ T = 0,4 s. Nếu tăng khối lượng của vật lên 4 lần thì T thay đổi như thế nào? A. Tăng lên 2 lần. B. Giảm 2 lần. C. Không đổi. D. Đáp án khác.
Câu 8: Một con lắc lò xo gồm viên bi nhỏ có khối lượng m và lò xo khối lượng không đáng kể có độ
cứng k, dao động điều hòa theo phương thẳng đứng tại nơi có gia tốc rơi tự do là g. Khi viên bi ở vị trí
cân bằng, lò xo dãn một đoạn l. Công thức tính chu kỳ dao động điều hòa của con lắc là: l l A. T 2 = . B. T = 2 . g g Trang 7 g g C. T = 2 . D. T = 2 . l l
Câu 9: Một con lắc lò xo gồm vật có khối lượng m và lò xo có độ cứng k, dao động điều hòa. Nếu tăng
độ cứng k lên 2 lần và giảm khối lượng m đi 8 lần thì tần số dao động của vật sẽ? A. Tăng 2 lần. B. Tăng 4 lần. C. Tăng 2 lần. D. Giảm 2 lần.
Câu 10: Một con lắc lò xo gồm một vật có khối lượng m và lò xo có độ cứng k không đổi, dao động điều
hòa. Nếu khối lượng m = 400g thì chu kỳ dao động của con lắc là 2s. Để chu kỳ của con lắc là 1s thì khối lượng m bằng A. 200g. B. 0,1kg. C. 0,3kg. D. 400g.
Câu 11: Một vật treo vào lò xo có khối lượng không đáng kể, chiều dài tự nhiên l độ cứng k, treo thẳng 0
đứng vào vật m = 100g vào lò xo thì chiều dài của nó là 31 cm. Treo thêm vật m = 100 g vào lò xo thì 1 2
cheièu dài của lò xo là 32 cm. Cho 2
g = 10m s , độ cứng của lò xo là:
A. 10 N m. B. 0,10 N . m C. 1000 N . m D. 100 N . m
Câu 12: Một con lắc lò xo dao động điều hòa theo phương thẳng đứng, tại nơi có gia tốc rơi tự do bằng g.
Ở vị trí cân bằng lò xo dãn ra một đoạn l
. Tần số dao động của con lắc được xác định theo công thức: l 1 l 1 g g A. 2 . B. . C. . D. 2 . g 2 g 2 l l
Câu 13: Một vật treo vào lò xo làm nó dãn ra 4cm. Lấy 2 = 10 , cho 2
g = 10m s . Tần số dao động của vật là A. 2,5 Hz/ B. 5,0 Hz. C. 4,5 Hz. D. 2,0 Hz.
Câu 14: Gọi k là độ cứng của lò xo, m là khối lượng của vật nặng. Bỏ qua ma sát khối lượng của lò xo và
kích thước vật nặng. Nếu độ cứng của lò xo tăng gấp đôi, khối lượng vật dao động tăng gấp ba thì chu kỳ dao động tăng gấp: 3 2 3 A. 6 lần. B. lần. C. lần. D. lần 2 3 2
Câu 15: Khi gắn quả nặng m vào lò xo, nó dao động điều hòa với chu kỳ T = 1,2s. Khi gắn quả nặng 1 1
m vào lò xo trên nó dao động với chu kỳ 1,6s. Khi gắn đồng thời hai vật m và m thì chu kỳ dao động 2 1 2 của chúng là A. 1,4 s. B. 2,0 s. C. 2,8 s. D. 4,0 s.
Câu 16: Trong dao động điều hòa của con lắc lò xo. Nếu muốn số dao động trong 1 giây tăng lên 2 lần thì
độ cứng của lò xo phải:
A. Tăng 2 lần. B. Giảm 4 lần. C. Giảm 2 lần. D. Tăng 4 lần.
Câu 17: Một con lắc lò xo gồm một vật có khối lượng m và lò xo có độ cứng k không đổi, dao động điều
hòa. Nếu khối lượng m = 200g thì chu kỳ dao động của con lắc là 2s. Để chu kỳ con lắc là 1s thì khối lượng m bằng Trang 8 A. 200g. B. 100g. C. 50g. D. 400 g.
Câu 18: Khi gắn một vật có khối lượng m = 4kg vào một lò xo có khối lượng không đáng kể, nó dao
động với chu kỳ T = 1s, khi gắn một vật khác khối lượng m vào lò xo trên nó dao động với chu kỳ 1 2
T = 0,5s. Khối lượng m bằng 2 2 A. 0,5 kg. B. 2kg. C. 1kg. D. 3kg.
Câu 19: Viên bi m gắn vào lò xo K thì hệ dao động với chu kỳ T = 0,6s. Viên bi m gắn vào lò xo K 1 1 2
thì hệ dao động với chu kỳ T = 0,8s. Hỏi nếu gắn cả 2 viên bi m và m với nhau và gắn vào lò xo K thì 2 1 2
hệ có chu kỳ dao động là A. 0,6s. B. 0,8s. C. 1s. D. 0,7s.
Câu 20: Lần lượt treo vật m , vật m vào một con lắc lò xo có độ cứng k = 40 N m và kích thích chúng 1 2
dao động trong cùng một khoảng thời gian nhất định, m thực hiện 20 dao động và m thực hiện được 10 1 2
dao động. Nếu cùng treo cả hai vật vào lò xo thì chu kỳ dao động của hệ bằng . Khối lượng m , m là: 2 1 2 A. 0,5kg; 2kg. B. 2kg; 0,5kg. C. 50g; 200g. D. 200g; 50g.
Câu 21: Con lắc lò xo gồm một vật nặng khối lượng m = 1kg , một lò xo có khối lượng không đáng kể và
độ cứng k = 100 N m thực hiện dao động điều hòa. Tại thời điểm t = 2s, li độ và vận tốc của vật lần lượt
bằng x = 6cm và = 80 cm s. Biên độ dao động của vật là: A. 6 cm. B. 7 cm. C. 8 cm. D. 10 cm.
Câu 22: Nếu gắn vật m = 0,3 kg vào lò xo k thì trong khoảng thời gian t vật thực hiện được 6 dao động, 1
gắn thêm gia trọng m vào lò xo k thì cũng khoảng thời gian t vật thực hiện được 3 dao động, tìm m ? A. 0,3 kg. B. 0,6 kg. C. 0,9 kg. D. 1,2 kg.
Câu 23: Gắn vật m = 400g vào lò xo K thì trong khoảng thời gian t lò xo thực hiện được 4 dao động, nếu
bỏ bớt khối lượng của m đi khoảng m thì cũng trong khoảng thời gian trên lò xo thực hiện 8 dao động,
tìm khối lượng đã được bỏ đi? A. 100g. B. 200g. C. 300g. D. 400g.
Câu 24: Một con lắc lò xo gồm lò xo có độ cứng 30 N m và viên bi có khối lượng 0,3kg dao động điều
hòa. Tại thời điểm t, vận tốc và gia tốc của viên bi lần lượt là 20cm s và 2
200cm s . Biên độ dao động của viên bi? A. 2 cm. B. 4 cm. C. 2 2 cm. D. 3 cm.
Câu 25: Con lắc lò xo gồm một vật nặng khối lượng m = 1kg . Một lò xo có khối lượng không đáng kể và
độ cứng k = 100 N m thực hiện dao động điều hòa. Tại thời điểm t = 1s, li độ và vận tốc của vật lần
lượng bằng x = 3 cm và = 0,4m .
s Biên độ dao động của vật là A. 3 cm. B. 4 cm. C. 5 cm. D. 6 cm.
Câu 26: Một phút vật nặng gắn vào đầu một lò xo thực hiện đúng 120 chu kỳ dao động. Với biên độ 8cm.
Giá trị lớn nhất của gia tốc là: Trang 9 A. 2 1263m s . B. 2 12,63m s . C. 2 1,28m s . D. 2 0,128m s .
Câu 27: Con lắc lò xo có độ cứng K = 100 N m được gắn vật có khối lượng m = 0,1kg , kéo vật ra khỏi
vị trí cân bằng một đoạn 5 cm rồi buông tay cho vật dao động. Tính V
vật có thể đạt được. max
A. 50 m s
B. 500 m s
C. 25 m s D. 0,5 m s
Câu 28: Một vật khối lượng m = 0,5 kg được gắn vào một lò xo có độ cứng k = 200 N m và dao động
điều hòa với biên độ A = 0,1m. Vận tốc của vật khi xuất hiện li độ 0,05m là: A. 17,32cm . s B. 17,33cm . s C. 173,2cm . s D. 5 m . s
Câu 29: Con lắc lò xo có độ cứng K = 50 N m gắn thêm vật có khối lượng m = 0,5 kg rồi kích thích
cho vật dao động. Tìm khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ cực đại đến vị trí cân bằng A. . s B. . s C. . s D. . s 5 4 20 15
Câu 30: Con lắc lò xo gồm hòn bi có m = 400g và lò xo có k = 80 N m dao động điều hòa trên một
đoạn thẳng dài 10 cm. Tốc độ của hòn bi khi qua vị trí cân bằng là A. 1,41 m . s B. 2,00 m . s C. 0,25 m . s D. 0,71 m . s
Câu 31: Một con lắc lò xo, gồm lò xo nhẹ có độ cứng 50 N m, vật có khối lượng 2 kg, dao động điều
hòa theo phương thẳng đứng. Tại thời điểm vật có gia tốc 2
75 cm s thì nó có vận tốc 15 3 cm s. Biên độ dao động là A. 5 cm. B. 6 cm. C. 9 cm. D. 10 cm.
Câu 32: Một con lắc lò xo gồm lò xo có độ cứng 20 N m và viên bi có khối lượng 0,2 kg dao động điều
hòa. Tại thời điểm t, vận tốc và gia tốc của viên bi lần lượt là 20cm s và 2
2 3 m s . Biên độ dao động của viên bi là A. 4 cm. B. 2 cm. C. 4 3 cm. D. 10 3 cm.
Câu 33: Con lắc lò xo gồm vật nặng khối lượng m = 1kg , một lò xo có khối lượng không đáng kể và độ
cứng k = 100 N m thực hiện dao động điều hòa. Tại thời điểm t = 2s, li độ và vận tốc của vật lần lượt
bằng x = 6 cm và = 80cm s. Biên độ dao động của vật là: A. 4 cm. B. 6 cm. C. 5 cm. D. 10 cm.
Câu 34: Cho dao động điều hòa sau: x = 10cos 3 t + c . m 4
Tại thời điểm t = 1s thì li độ của vật là bao nhiêu? A. 5 2 cm. B. −5 2 cm. C. 5 cm. D. 10 cm.
Câu 35: Cho dao động điều hòa sau x = 3cos 4 t −
cm. Hãy xác định vận tốc cực đại của dao động? 6 Trang 10 A. 12 cm . s B. 12 cm . s
C. 12 + 3 cm . s D. Đáp án khác
Câu 36: Cho dao động điều hòa sau x = co (
s 8 t + ) cm. Xác định tốc độ của vật khi vật qua vị trí cân bằng. A. 8 cm . s B. 16 cm . s C. 4 cm . s D. 20 cm . s
Câu 37: Một chất điểm dao động điều hòa theo phương trình x = 3cos t + cm, pha dao động của 2
chất điểm tại thời điểm t = 1s là A. 0 cm. B. 1,5 cm. C. 1,5 rad. D. 0,5 Hz.
Câu 38: Một vật dao động nằm ngang trên quỹ đạo dài 10 cm, tìm biên độ dao động. A. 10 cm. B. 5 cm. C. 8 cm. D. 4 cm.
Câu 39: Một vật dao động theo phương trình:
x = 0,04cos 10 t − ( ) m . 4
Tính tốc độ cực đại và gia tốc cực đại của vật. A. 2 4 m ;
s 40 m s . B. 2 0,4 m ;
s 40 m s . C. 2 40 m ;
s 4 m s . D. 2 0,4 m ; s 4 m s .
Câu 40: Một vật dao động điều hòa có phương trình dao động x = 5co (
s 2 t ) cm. Xác định gia tốc của
vật khi x = 3 cm. Biết 2 = 10. A. 2 1 − 2m s . B. 2 1 − 20 cm s . C. 2 1,2 m s . D. 2 6 − 0 m s .
Câu 41: Vật dao động điều hòa trên trục Ox quanh vị trí cân bằng là gốc tọa độ. Gia tốc của vật có phương trình: 2 a = −400 .
x Số dao động toàn phần vật thực hiện được trong mỗi giây là A. 20. B. 10. C. 40. D. 5.
Câu 42: Một vật dao động điều hòa với biên độ bằng 0,05m, tần số 2,5 Hz. Gia tốc cực đại của vật bằng A. 2 12,3 m s . B. 2 6,1 m s . C. 2 3,1 m s . D. 2 1,2 m s .
Câu 43: Vật dao động điều hòa với phương trình x = 20cos 2 t − (c )
m . Gia tốc của vật tại thời điểm 2 1 t = s là 2 A. 2 0 m s . B. 2 2 m s . C. 2 9,8 m s . D. 2 10 m s .
Câu 44: Một vật dao động điều hòa, khi vật có li độ x = 4cm thì vận tốc = 40 3 cm s; khi vật có li 1 1
độ x = 4 2 cm thì vận tốc = 40 2 cm s. Chu kỳ dao động của vật là: 2 2 Trang 11 A. 0,1s. B. 0,8s. C. 0,2s. D. 0,4s.
Câu 45: Một vật dao động điều hòa, khi vật có li độ x = 4cm thì vận tốc = 40 3 cm s ; khi vật có 1 ( ) 1
li độ x = 4 3 cm thì vận tốc = 40 cm s . Độ lớn tốc độ góc? 2 ( ) 2 A. 5 rad . s B. 20 rad . s C. 10 rad . s D. 4 rad . s
Câu 46: Một vật dao động điều hòa, tại thời điểm t thì vật có li độ x = 2,5cm , tốc độ = 50 3 cm s. 1 1 1
Tại thời điểm t thì vật có độ lớn li độ là x = 2,5 3 cm thì tốc độ là = 50 cm s. Hãy xác định độ lớn 2 2 2 biên độ A. A.10 cm. B. 5 cm. C. 4 cm. D. 5 2 cm.
Câu 47: Một vật dao động điều hòa có phương trình li độ x = Asin(t + ). Biểu thức gia tốc của vật là A. 2 a = − . x B. 2 a = − . C. 2 a = − .
x sin(t + ). D. 2 a = − . A
Câu 48: Một vật dao động điều hòa với chu kì T = 3,14s . Xác định pha dao động của vật khi nó qua vị trí
x = 2 cm với vận tốc = 0,04 m . s A. . B. . C. . D. − . 3 4 6 4
Câu 49: Một chất điểm dao động điều hòa. Khi đi qua vị trí cân bằng, tốc độ của chất điểm là 40cm s,
tại vị trí biên gia tốc có độ lớn 2
200cm s . Biên độ dao động của chất điểm là A. 0,1 m. B. 8 cm. C. 5 cm. D. 0,8 m.
Câu 50: Một vật dao động điều hòa, khi vật có li độ 4cm thì tốc độ là 30 (cm )
s , còn khi vật có li độ
3cm thì vận tốc là 40 (cm )
s . Biên độ và tần số dao động là:
A. A = 5c , m f = 5 z H .
B. A = 12c , m f = 12 z H .
C. A = 12c , m f = 10 z H .
D. A = 10c , m f = 10 z H . ĐÁP ÁN 1-B 2-B 3-D 4-A 5-C 6-B 7-A 8-A 9-B 10-B 11-D 12-C 13-A 14-B 15-B 16-D 17-C 18-C 19-C 20-A 21-D 22-C 23-C 24-C 25-C 26-B 27-D 28-C 29-C 30-D 31-B 32-A 33-D 34-B 35-B 36-A 37-C 38-B 39-B 40-B 41-B 42-A 43-A 44-C 45-C 46-B 47-A 48-D 49-B 50-A Trang 12
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Đáp án B. m
Chu kỳ dao động của con lắc lò xo là: T = 2 . k
Câu 2: Đáp án B.
Nhìn vào công thức tính chu kỳ dao động của con lắc lò xo thì chu kỳ của con lắc lò xo không phụ thuộc
vào gia tốc trọng trường.
Câu 3: Đáp án D. m m T
Độ cứng của lò xo tăng gấp đôi khi chu kỳ mới của con lắc sẽ là: 1 T = 2 = 2 = . 2 k 2k 2 2
Vậy chu kỳ mới của con lắc lò xo giảm 2 lần.
Câu 4: Đáp án A. 2 Độ 4 m 4.10.0,4
cứng của lò xo là: K = = = 16 N m . 2 2 ( ) T 1
Câu 5: Đáp án C.
Vì chu kỳ dao động của con lắc lò xo không phụ thuộc vào biên độ dao động của con lắc nên khi biên độ
dao động của con lắc tăng 4 lần thì chu kỳ của con lắc vẫn không đổi.
Câu 6: Đáp án B. 2 2 T .K 0,4 .100
Khối lượng của vật là: m = = = 0,4 kg . 2 ( ) 4 4.10
Câu 7: Đáp án A.
Nếu tăng khối lượng của vật lên 4 lần thì T sẽ tăng lên 2 lần.
Câu 8: Đáp án A.
Khi viên bi ở vị trí cân bằng thì: mg g g l l = = = T = 2 . 2 k k m g
Câu 9: Đáp án B.
Khi tăng độ cứng lên 2 lần và giảm khối lượng đi 8 lần thì tần số dao động của vật sẽ là: 1 k 1 2k 1 k 2 1 1 f = = = .4 = 4 f . 1 2 m 2 m / 8 2 m 2 1 1
Vậy tần số tăng lên 4 lần.
Câu 10: Đáp án B. m
Ban đầu khi con lắc có khối lượng m thì: 1 T = 2 . 1 k
Sau đó thì ta có chu kỳ sẽ là: Trang 13 T m 2 0,4 Lập tỉ lệ ta được: 1 1 = = m = 0,1k . g 2 T m 1 m 2 2 2
Câu 11: Đáp án D. m g
Ban đầu treo vật m thì lò xo lệch khỏi vị trí cân bằng một đoạn là: 1 l = 1 1 k (m +m g 1 2 )
Sau khi treo thêm vật m thì lò xo lệch khỏi vị trí cân bằng một đoạn là: l = 2 2 k
Vì sau khi treo thêm vật m thì chiều dài lò xo lúc này lớn hơn chiều dài lò xo lúc ban đầu 1cm nên ta có: 2 m g 2 l − l =
= 0,01m k = 100 N m . 2 1 ( ) k
Câu 12: Đáp án C
Tần số dao động của con lắc được tính theo công thức: 1 k 1 g f = = . 2 m 2 l
Câu 13: Đáp án A.
Tần số dao động của vật là: 1 g 1 10 f = = = 2,5 z H . 2 l 2 0,04
Câu 14: Đáp án B.
Độ cứng của vật dao động gấp đôi, khối lượng của vật dao động tăng gấp 3 lần thì chu kỳ dao động tăng 3 gấp lần. 2
Câu 15: Đáp án B. 2 m T .k
Khi gắn quả nặng m thì con lắc dao động với chu kỳ T thì: 1 1 T = 2 m = . 1 1 1 1 2 k 4 2 T .k Tương tự ta cũng có: 2 m =
. Nên từ đó ta gắn đồng thời cả hai vật với nhau thì ta sẽ có chu kỳ là: 2 2 4 2 2 2 T .k T .k T .k 1 2 2 2 = +
T = T + T = 2s. 2 2 2 1 2 4 4 4
Câu 16: Đáp án D.
Để số dao động trong 1 giây tăng lên 2 lần thì độ cứng của lò xo phải tăng 4 lần.
Câu 17: Đáp án C. T m 2 200 Ta có tỉ lệ: 1 1 = = m = 50 . g 2 T m 1 m 2 2 2
Câu 18: Đáp án C. Trang 14
Làm tương tự như câu 17 lập tỉ lệ sau đó ta suy ra được m = 1k . g 2
Câu 19: Đáp án C.
Nếu gắn cả hai viên bi vào lò xo thì chu kỳ của con lức lò xo là: 2 2 2 2
T = T + T = 0,6 + 0,8 = 1s. 1 2
Câu 20: Đáp án A.
Nếu cùng treo cả hai vật đó vào lò xo thì chu kỳ của con lắc là: 2 2 2
T = T + T = s . 1 2 ( ) 2 T t / N N 10 1 Lại có: 1 1 2 = = = = T = 2T 2 1 T t / N N 20 2 2 2 1 2 T + (2T )2 2 2 = T = 1 1 1 2 2 m = 0,5k ; g m = 2k . g 1 2
Câu 21: Đáp án D.
Tần số góc dao động của con lắc là: k 100 = = = 10(rad ) s . m 1
Biên độ dao động của vật là: 2 2 80 2 2 2 A = x + = 6 +
= 100 A = 10c . m 10
Câu 22: Đáp án C. m T 0,3 1 Ta có tỉ lệ: 1 1 =
= m = 0,9 k . g m T 0,3+ m 4 2 2
Câu 23: Đáp án C. 2 m 8 0,4 Ta có: = = 4 m = 0,3 (kg) m− m 4 0,4 − m
Câu 24: Đáp án C. k
Tần số góc dao động của lò xo: = = 10(rad ) s . m
Biên độ dao động của con lắc lò xo là: 2 2 2 a 2 2 A = x + = + 2 2 2 200 20 = + = 2 2 cm . 2 ( ) 10 10
Câu 25: Đáp án C. Trang 15
Câu 26: Đáp án B. 60
Chu kỳ dao động của con lắc lò xo là: T = = 0,5s. 120
Giá trị lớn nhất của gia tốc là: a = A = 8.(4 )2 2 = 1263,3 ( 2 1 cm s ) = 12,63( 2 m s . max )
Câu 27: Đáp án D.
Tần số dao động của vật là: k 100 = = = 10 10 (rad ) s . m 0,1
Vận tốc lớn nhất mà vật có thể đạt được:
= A = 50 10 cm s = 0,5 m s . max ( ) ( )
Câu 28: Đáp án C.
Tần số dao động của vật là: k 200 = = = 20(rad ) s . m 0,5
Vận tốc của vật khi xuất hiện li độ 0,05m là: 2 = = 173,2 cm s . max ( ) 2
Câu 29: Đáp án C.
Tần số dao động của con lắc là: k 50 = = = 10(rad ) s m 0,5
Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ cực đại đến vị trí cân bằng là: T / 5 t = = = ( )s. 4 4 20
Câu 30: Đáp án D.
Tần số dao động của con lắc là: k 80 = = = 10 2 (rad ) s . m 0,4
Vật dao động điều hòa trên một đoạn thẳng dài 10cm thì biên độ dao động của vật là 5cm. Vậy tốc độ của
hòn bi khi qua vị trí cân bằng là: = = .
A = 5.10 2 = 50 2 cm s = 0,71 m s . max ( ) ( )
Câu 31: Đáp án B.
Tần số góc của dao động này là: Trang 16 k 50 = = = 5(rad ) s . m 2
Áp dụng công thức liên hệ độc lập với thời gian: 2 2 2 2 2 2 a 75 15 3 2 A = + = + = 36 2 2 5 5 A = 6(c ) m .
Câu 32: Đáp án A.
Tần số góc của dao động là: k 20 = = = 10(rad ) s . m 0,2
Biên độ dao động của con lắc là: 2 2 2 2 a 200 3 20 2 A = + = + = 16 2 2 10 10 A = 4(c ) m .
Câu 33: Đáp án D.
Tần số góc của dao động là: k 100 = = = 10(rad ) s . m 1
Biên độ dao động của con lắc là: 2 2 80 2 2 2 A = x + = 6 + = 100 A = 10 (c ) m . 10
Câu 34: Đáp án B.
Li độ của vật ở thời điểm t = 1slà: x = 10cos 3 .1+ = 5 − 2 c . m 4
Câu 35: Đáp án B.
Vận tốc cực đại của dao động là: = .
A = 3.4 = 12 cm s . max ( )
Câu 36: Đáp án A.
Tốc độ của vật khi qua vị trí cân bằng là: = .
A = 1.8 = 8 (cm ) s .
Câu 37: Đáp án C.
Pha dao động của chất điểm tại thời điểm t = 1s là: Trang 17
= t + = .1+ = 1,5. 2 2
Câu 38: Đáp án B.
Vật dao động trên quỹ đạo dài 10cm thì biên độ dao động của vật là: A = 5c . m
Câu 39: Đáp án B.
Tốc độ cực đại của dao động là:
= A = 0,04.10 = 0,4 (m ) s .
Gia tốc cực đại của dao động là: a = A = 0,04.(10 )2 2 = 40 m s . max ( )
Câu 40: Đáp án B.
Gia tốc của vật khi x = 3cm là:
a = x = ( )2 2 = ( 2 3. 2 120 cm s ).
Câu 41: Đáp án B. 1 20
Số dao động toàn phân vật thực hiện được trong mỗi giây là: N = = = = 10. T 2 2
Câu 42: Đáp án A.
Gia tốc cực đại của vật bằng: a
= A = 0,05.(2,5.2 )2 2 = 12,5( 2 m s . max )
Câu 43: Đáp án A. 1
Gia tốc của vật tại thời điểm t − s là: 2 a = − x = − ( )2 t − = ( 2 2. 2 .20cos 2 0 m s ). 2
Câu 44: Đáp án C.
Áp dụng công thức liên hệ ta có: 2 2 2 1 2 2 x + = x + 1 2 2 40 3 4 + = (4 2) 2 2 40 2 2 + = 10 (rad ) s T = 0,2s.
Câu 45: Đáp án C.
Giải tương tự câu 47 thì ta suy ra được = 10 (rad ) s . Trang 18
Câu 46: Đáp án B. 50 3 50 2 ( )2 2 2 Ta có: 2,5 + = 2,5 3 + 2 ( ) 2 = 20(rad ) s .
Vậy biên độ dao động của vật là: 2 2 2 A = x +
= 25 A = 5 cm . 2 ( )
Câu 47: Đáp án A.
Biểu thức gia tốc của vật là: 2 a = − . x
Câu 48: Đáp án D. 2
Tần số góc của dao động là: = = 2(rad ) s . T 2
Biên độ dao động của vật là: 2 A = x + = 2 2 cm 2 ( )
Vì vật đang qua vị trí có x = 2cm và vận tốc = 0,04m s nên pha dao động của vật lúc này là: = − (rad). 4
Câu 49: Đáp án B
Theo đề cho thì ta có vận tốc lớn nhất và gia tốc lớn nhất lần lượt là: = . A = 40 cm s max ( ) 200 = = 5 rad s . 2 a = . A = 200 ( 2 cm s 40 max ) ( ) 40
Vậy biên độ dao động của chất điểm là: A = = 8c . m 5
Câu 50: Đáp án A. 2 Dùng công thức: 2 2 A = x + 2 = 10 (rad )
s ; A = 5c . m Trang 19




