


































































Preview text:
TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN - TỈNH NINH THUẬN GV: VŨ NGỌC HUY TO T ÁN O 10 BỘ ĐỀ CHK1 1 Bài tâp trắc nghiệm 2 Bài tập tự luận π
TÀI LIỆU ÔN TẬP CUỐI HỌC KÌ 1 CHO 3 BỘ SÁCH MỤC LỤC
Đề số 1: TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN NINH THUẬN 3
Đề số 2: TRƯỜNG THPT GIỒNG ÔNG TỐ
. . . . . . . . . . . . . 8
Đề số 3: TRƯỜNG THPT BÀ ĐIỂM
. . . . . . . . . . . . . . . . . 14
Đề số 4: TRƯỜNG THPT BÌNH PHÚ
. . . . . . . . . . . . . . . . . 16
Đề số 5: TRƯỜNG THPT BÌNH TÂN
. . . . . . . . . . . . . . . . . 18
Đề số 6: TRƯỜNG THPT HÀN THUYÊN
. . . . . . . . . . . . . . 23
Đề số 7: TRƯỜNG THPT LÊ HỒNG PHONG
. . . . . . . . . . . . 29
Đề số 8: TRƯỜNG THPT LÊ QÚY ĐÔN
. . . . . . . . . . . . . . . 31
Đề số 9: TRƯỜNG THPT MARIE-CURIE
. . . . . . . . . . . . . . 33
Đề số 10: TRƯỜNG THPT NGUYỄN AN NINH . . . . . . . . . . 35
Đề số 11: TRƯỜNG THPT NGUYỄN CHÍ THANH . . . . . . . . . 37
Đề số 12: TRƯỜNG THPT NGUYỄN CÔNG TRỨ . . . . . . . . . 39
Đề số 13: TRƯỜNG THPT NGUYỄN DU
. . . . . . . . . . . . . . 41
Đề số 14: TRƯỜNG THPT NGUYỄN HỮU TIẾN . . . . . . . . . . 43
Đề số 15: TRƯỜNG NGUYỄN KHUYẾN & LÊ THÁNH TÔNG . 45
Đề số 16: TRƯỜNG THPT NGUYỄN THÁI BÌNH . . . . . . . . . 47
Đề số 17: TRƯỜNG THPT NGUYỄN THỊ DIỆU . . . . . . . . . . 52
Đề số 18: TRƯỜNG THPT PHẠM PHÚ THỨ
. . . . . . . . . . . . 54
Đề số 19: TRƯỜNG THPT PHỔ THÔNG NĂNG KHIẾU . . . . . 56
Đề số 20: TRƯỜNG THPT TAM PHÚ
. . . . . . . . . . . . . . . . 59
Đề số 21: TRƯỜNG THPT TẠ QUANG BỬU
. . . . . . . . . . . . 61
Đề số 22: TRƯỜNG THPT TÂY THẠNH
. . . . . . . . . . . . . . 63
Đề số 23: TRƯỜNG THPT THỦ ĐỨC
. . . . . . . . . . . . . . . . 65
Đề số 24: TRƯỜNG THỰC HÀNH SÀI GÒN
. . . . . . . . . . . . 73
Đề số 25: TRƯỜNG THPT TRẦN KHAI NGUYÊN . . . . . . . . . 75
Đề số 26: TRƯỜNG THPT TRẦN PHÚ
. . . . . . . . . . . . . . . 78
Đề số 27: TRƯỜNG THPT TRẦN QUANG KHẢI . . . . . . . . . 80
Đề số 28: TRƯỜNG THPT VÕ THỊ SÁU
. . . . . . . . . . . . . . . 82
Đề số 29: TRƯỜNG THPT GÒ VẤP
. . . . . . . . . . . . . . . . . 84
Đề số 30: TRƯỜNG THPT HÙNG VƯƠNG
. . . . . . . . . . . . . 87
Đề số 31: TRƯỜNG THPT NGUYỄN THỊ MINH KHAI . . . . . . 89
Đề số 32: TRƯỜNG THPT NGUYỄN THƯỢNG HIỀN . . . . . . . 90
Đề số 33: TRƯỜNG THPT TRƯỜNG CHINH - ĐỀ 3 . . . . . . . . 92
Đề số 34: TRƯỜNG THPT TRƯỜNG CHINH - ĐỀ 4 . . . . . . . . 94
Đề số 35: TRƯỜNG THPT TRẦN HƯNG ĐẠO
. . . . . . . . . . . 96
Đề số 36: TRƯỜNG THPT NGUYỄN KHUYẾN . . . . . . . . . . 101
Đề số 37: TRƯỜNG THPT NGUYỄN TẤT THÀNH . . . . . . . . 103
Đề số 38: TRƯỜNG THPT TRƯỜNG CHINH - ĐỀ 1 . . . . . . . . 105
Đề số 39: TRƯỜNG THPT TRƯỜNG CHINH - ĐỀ 2 . . . . . . . . 107
Đề số 40: TRƯỜNG THPT TRƯNG VƯƠNG
. . . . . . . . . . . . 110
Đề số 41: TRƯỜNG THPT BÌNH HƯNG HÒA
. . . . . . . . . . . 112
Đề số 42: TRƯỜNG THPT PHÚ NHUẬN
. . . . . . . . . . . . . . 113 1 GV: VŨ NGỌC HUY
Đề số 43: TRƯỜNG THPT NGUYỄN HỮU CẦU . . . . . . . . . . 114 2 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ CUỐI HỌC KÌ I KHỐI 10/2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN NINH THUẬN
Thời gian làm bài: 90 phút Chương trình chuẩn
PHẦN 1 - TRẮC NGHIỆM I. Phần trắc nghiệm
Câu 1: Cho hàm số bậc hai y = ax2 + bx + c, (a 6= 0) có bảng biến thiên như hình dưới. Hàm
số nghịch biến trên khoảng nào sau đây? x −∞ −2 +∞ +∞ +∞ y −1 A. (−∞; 0). B. (−2; +∞). C. (−∞; −2). D. (−∞; −1). ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 2:
Cho hai tập A, B minh họa bằng biểu đồ Ven (như hình vẽ bên).
Phần tô đậm trong hình là tập nào sau đây? A. A ∪ B. B. A \ B. C. A ∩ B. D. B \ A. A B ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 3: Cặp số (x; y) nào sau đây không phải là nghiệm của bất phương trình 3x − 2y + 1 ≥ 0? A. (0; 1). B. (3; 5). C. (1; 0). D. (0; −1). ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 4: Điều kiện cần và đủ để 3 điểm phân biệt A, B, C thẳng hàng là # » # » # » # »
A. AB và AC cùng phương.
B. AB và AC cùng hướng. # » # » # » # »
C. AB và AC ngược hướng.
D. AB và AC là hai vectơ bằng nhau. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 5: Khẳng định nào sau đây đúng?
A. cos(1800 − β) = cos β.
B. sin(900 − β) = cos β.
C. sin(900 − β) = sin β.
D. sin(1800 − β) = − sin β. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
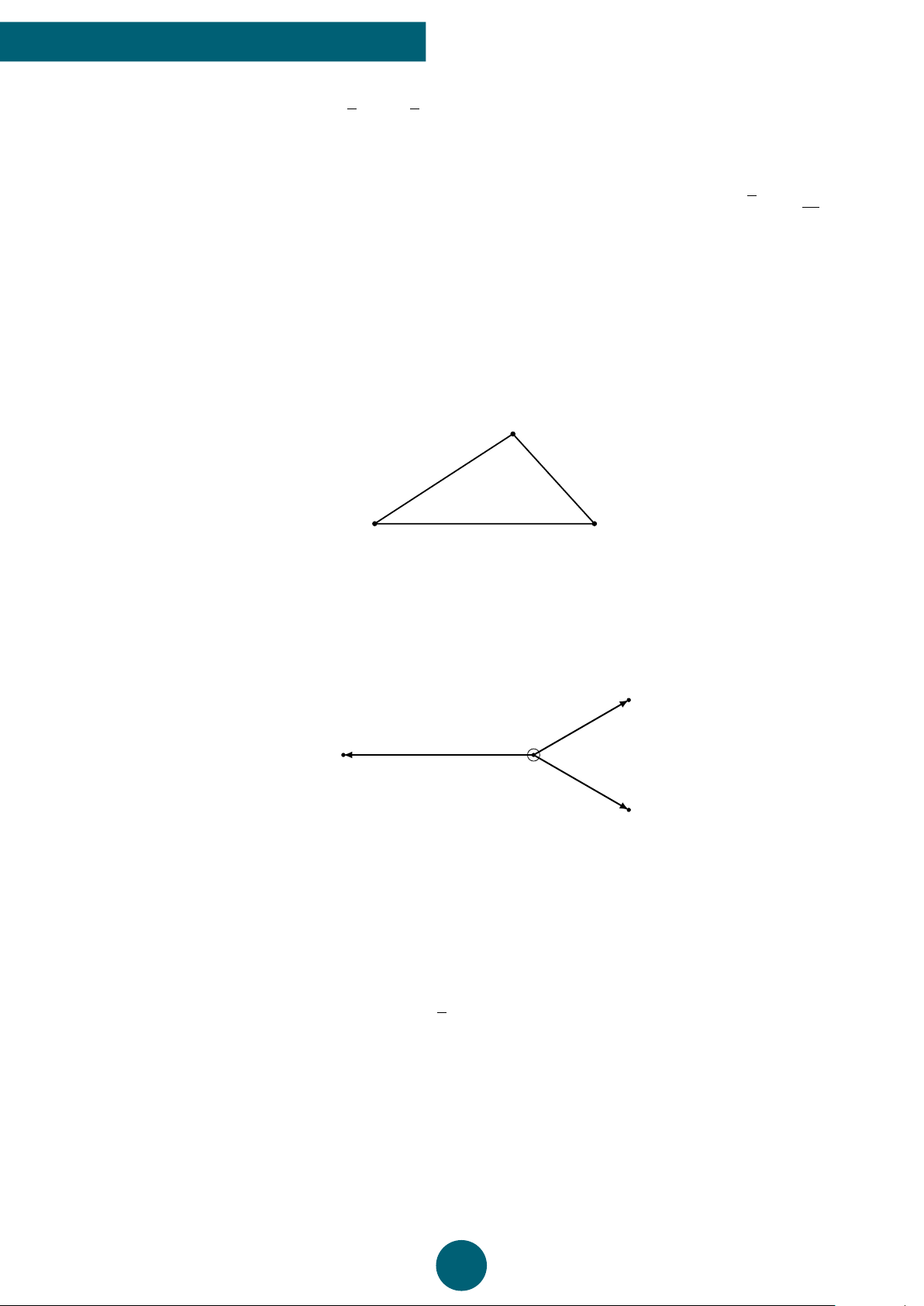
Câu 6: Cho ba điểm A, B, C thẳng hàng (như hình vẽ dưới). Khẳng định nào sau đây đúng?# » 3# » # » 5 # » # » 5 # » # » 2 # » A. AC = BC. B. AB = BC. C. AB = AC. D. CB = CA. 2 2 3 3 3 GV: VŨ NGỌC HUY A C B ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . #» #» #» #»
Câu 7: Cho hai véc-tơ a , b tùy ý. Tích vô hướng của hai véc-tơ a , b bằng #» #» #» #» #» #» Ä #» #»ä A. a · b = | #» a | b . B. a · b = | #» a | b cos a , b . #» #» #» #» #» #» Ä #» #»ä C. a · b = − | #» a | b . D. a · b = | #» a | b sin a , b . ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 8: Với điều kiện nào của m thì f (x) = (m + 1)x2 + mx + 3 là một tam thức bậc hai? A. m = 0. B. m 6= 1. C. m ≥ −1. D. m 6= −1. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
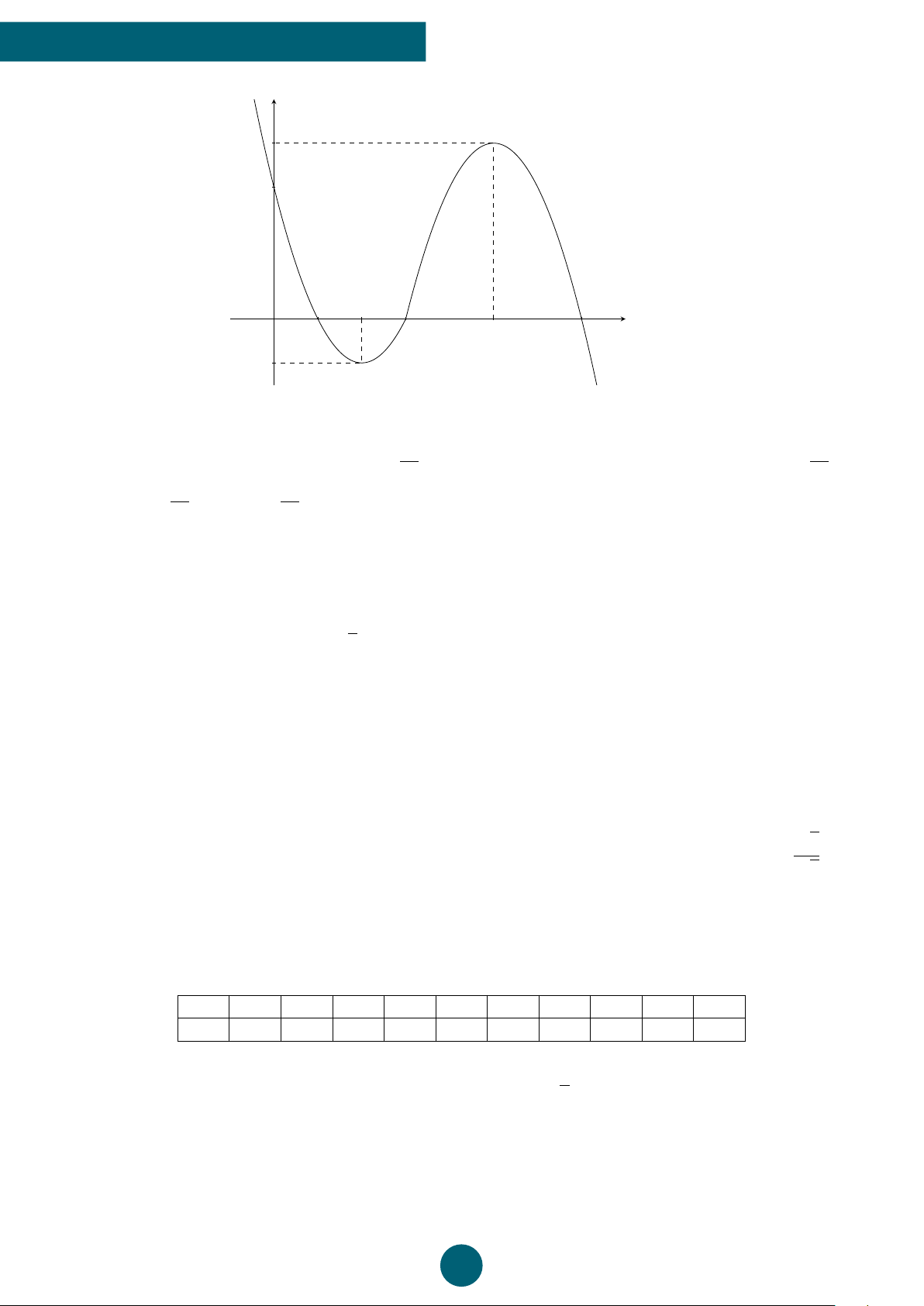
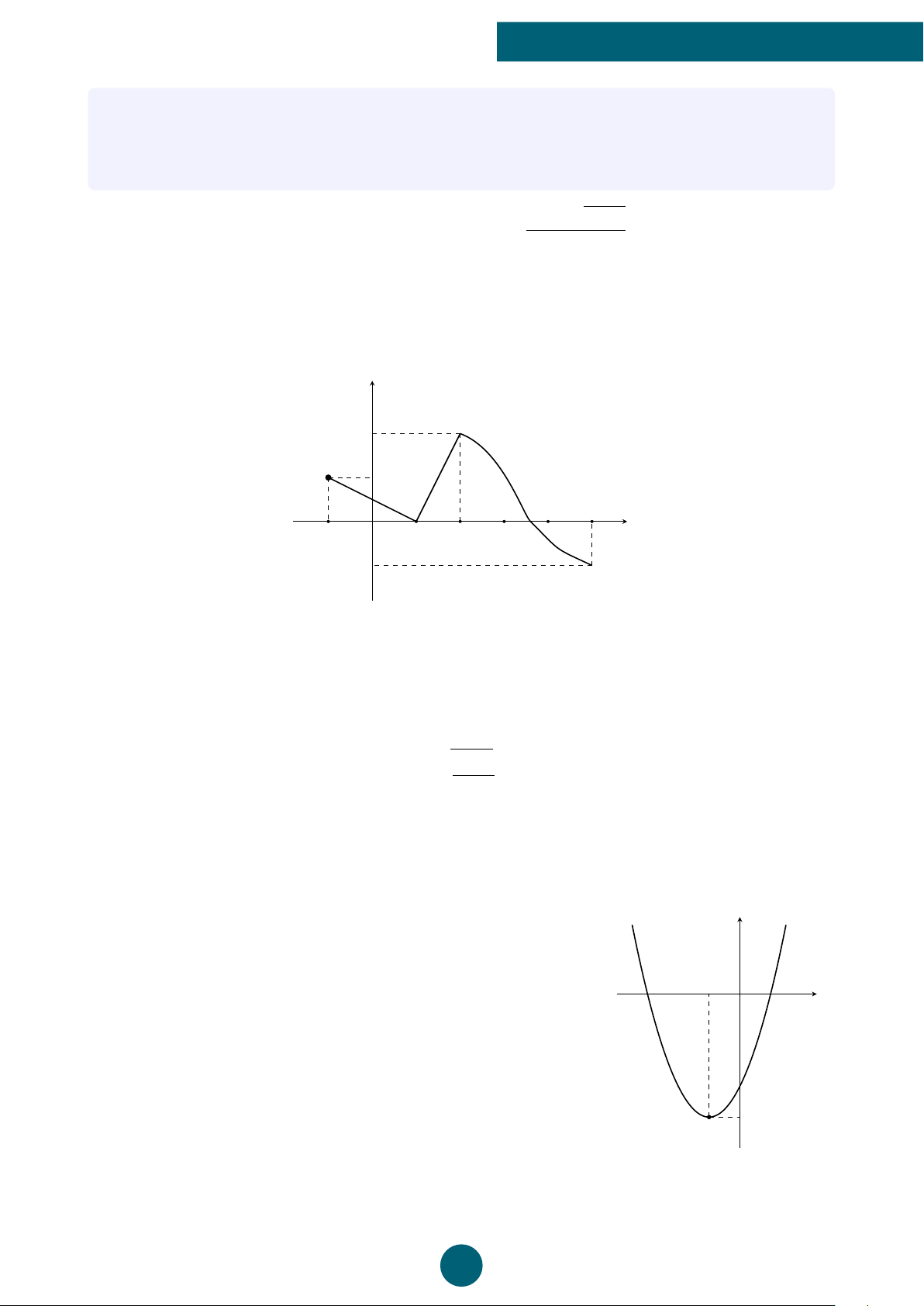
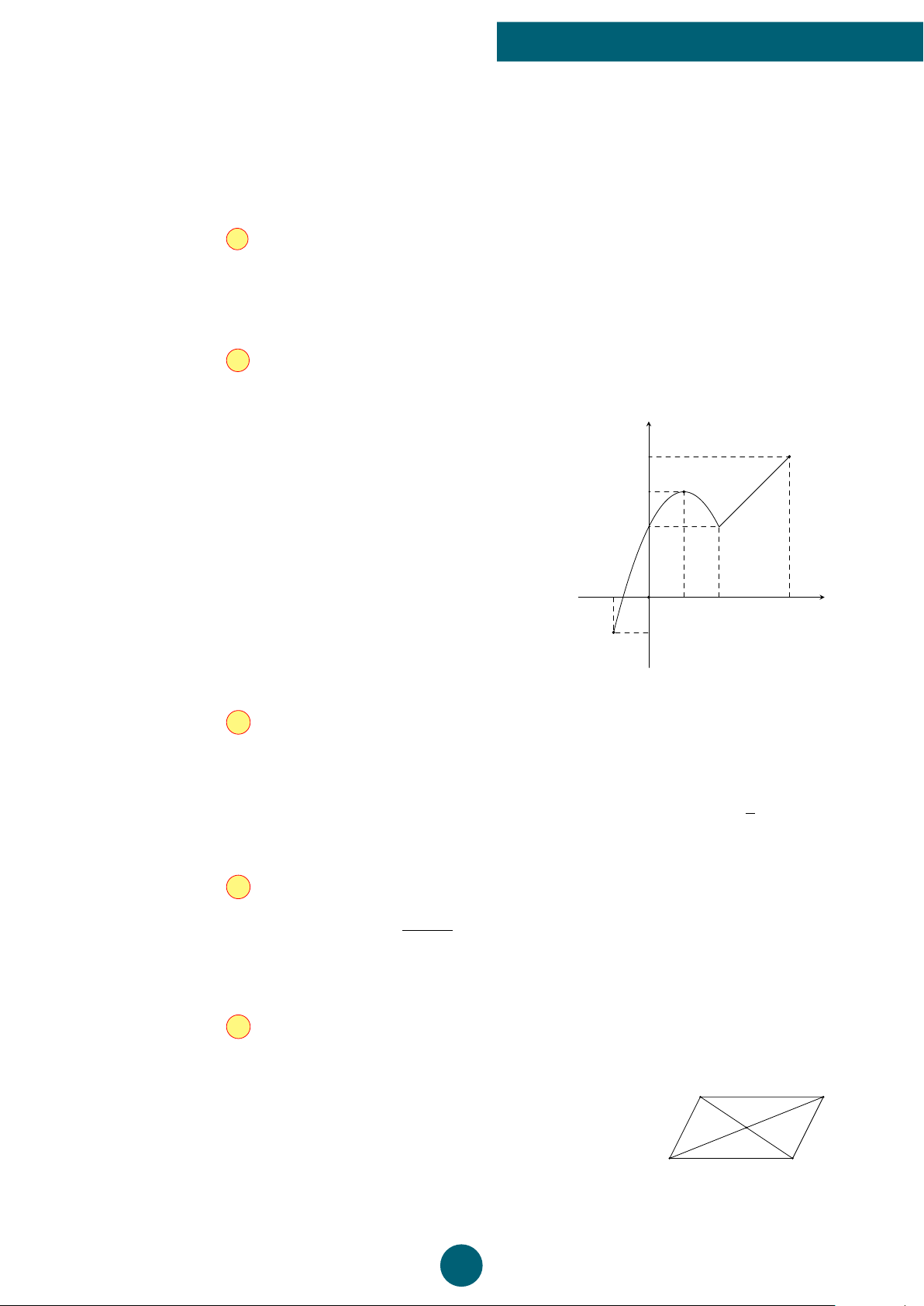
Câu 9: Cho hàm số y = f (x) có tập xác định là [−3; 3] y
và đồ thị của nó được biểu diễn bởi hình bên. Hàm số 4
đồng biến trên khoảng nào sau đây? A. (0; 3). B. (−3; 0). C. (−1; 3). D. (−1; 0). 1 x −3 −1O 3 −1 ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 10: Tập nghiệm của bất phương trình x2 − x − 6 ≤ 0 là A. S = [−3; 2].
B. S = (−∞; −2] ∪ [3; +∞). C. S = (−2; 3). D. S = [−2; 3]. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 11: Cho tam giác ABC có AB = 2a, góc A = 30◦ góc C = 45◦. Độ dài cạnh BC bằng √ √ √ a 2 √ A. 2a 2. B. a 3. C. . D. a 2. 2 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 12: Cho ABCD là hình bình hành tâm O. Khẳng định nào sau đây sai? # » # » # » # » # » # » A. AB + AC = AD. B. AB + AD = AC. # » # » # » # » # » # » # » #» C. AB + AD = 2AO.
D. OA + OB + OC + OD = 0 . ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √ √
Câu 13: Tập xác định của hàm số y = x + 2 − 6 − 2x là A. D = [2; 3]. B. D = [−3; −2]. C. D = [−2; 3]. D. D = [−3; 2]. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 GV: VŨ NGỌC HUY
Câu 14: Cho tam giác ABC có BC = 10, AC = 8, ’
ACB = 30◦. Diện tích tam giác ABC bằng √ √ A. 20. B. 40. C. 20 2. D. 20 3. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
®2x2 − 3x + 1 khi x < −1
Câu 15: Cho hàm số f (x) = √
. Giá trị của P = f (−1) + f (2) − x + 2 khi x ≥ −1 3 f (−2) là A. −35. B. −25. C. −42. D. 30. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
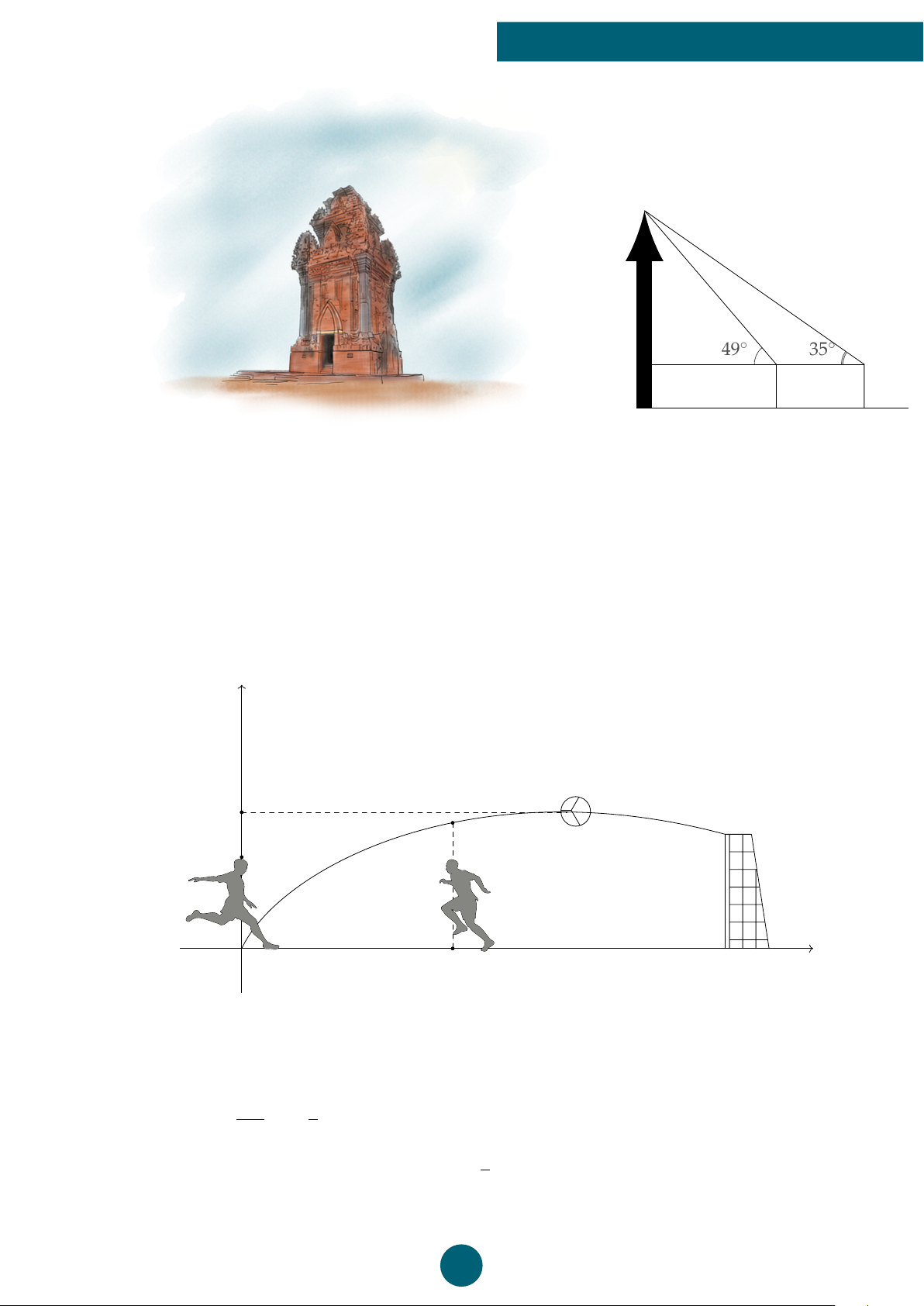
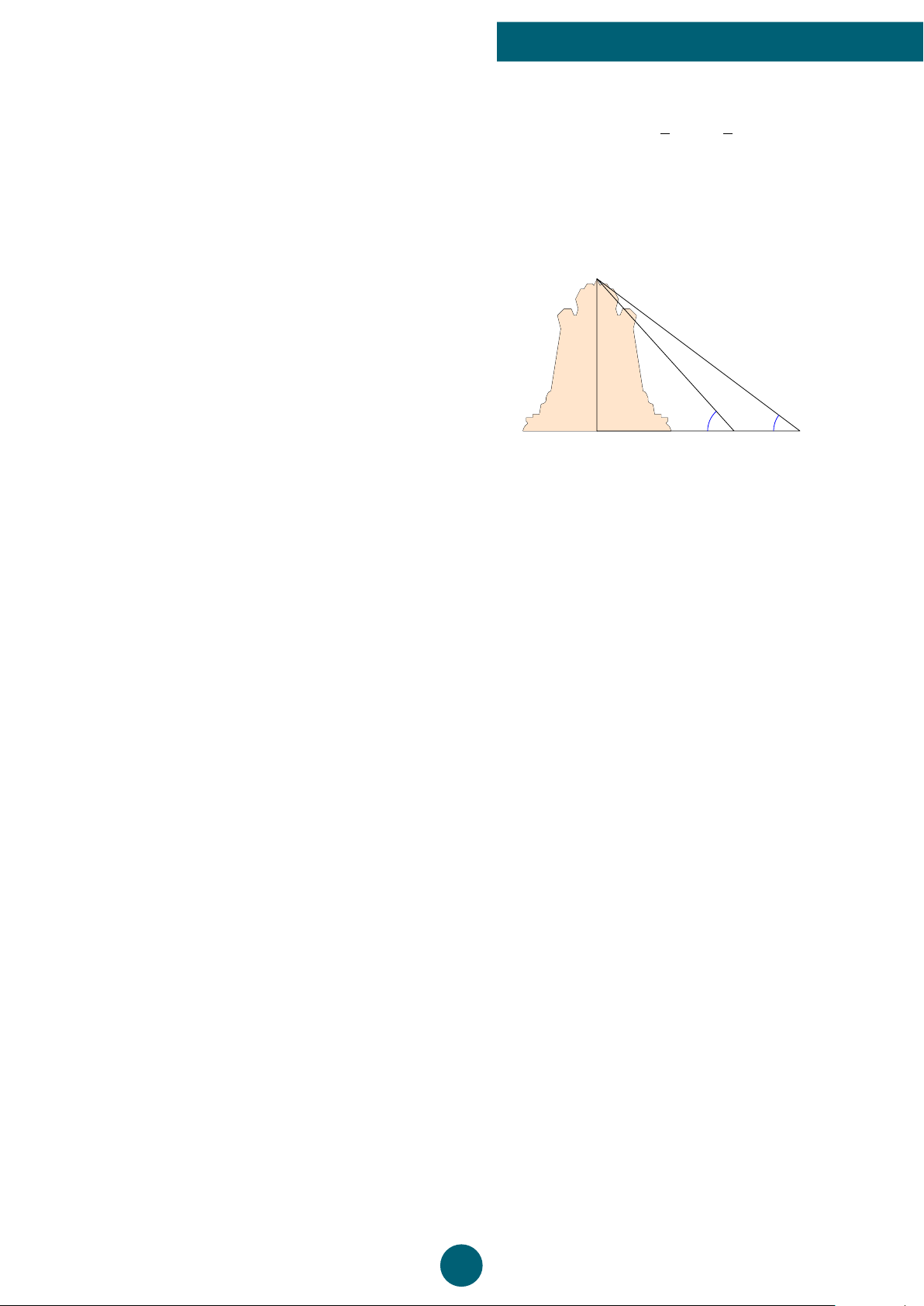
Câu 16: Từ một đỉnh tháp chiều cao CD, người ta nhìn hai điểm A và B trên mặt đất dưới các
góc nhìn là 72◦120 và 34◦260. Ba điểm A, B, D thẳng hàng. Tính chiều cao của tháp biết khoảng cách AB = 91 m. A. 81,38 m. B. 82,83 m. C. 71,27 m. D. 91,12 m. C h 71◦120 34◦260 D A 91 m B ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √
Câu 17: Cho tam giác ABC vuông tại A có AB = a, AC = a 3, gọi H là chân đường cao hạ # » # »
từ A. Tích vô hướng của BH · AC bằng √ a2 3a2 3a2 3a2 A. . B. . C. . D. . 4 4 2 4 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 18: Cho tam thức bậc hai f (x) = 2x2 + bx + c biết f (x) > 0 ⇔ x ∈ (−∞; x1) ∪ (x2; +∞) 3
và |x1 − x2| = . Khi đó giá trị của biểu thức b2 − 8c bằng 2 A. 8. B. 10. C. 9. D. 11. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 19: Cho hàm số y = ax2 + bx + c(a 6= 0) có đồ thị là parabol (P). Biết đồ thị của hàm số
đi qua điểm A(0; 3) và có đỉnh I(1; 1). Tính tổng S = a2 + b2 + c2. A. 4. B. 25. C. 20. D. 29. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 GV: VŨ NGỌC HUY
Câu 20: Cho ABCD là hình bình hành tâm O. Gọi M là trung điểm của OD. Khẳng định nào sau đây đúng? # » 1 # » 1 # » # » 1 # » 3 # » A. AM = AB + AD. B. AM = AB + AD. 3 2 4 4 # » 1 # » 1 # » # » 1 # » 3 # » C. AM = AB + AD. D. AM = − AB + AD. 3 2 8 8 ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ĐÁP ÁN 1. C 2. B 3. A 4. C 5. B 6. C 7. B 8. D 9. A 10. D 11. D 12. A 13. C 14. A 15. C 16. A 17. D 18. C 19. D 20. B PHẦN 2 - TỰ LUẬN
Bài 1: Cho tam giác ABC có AB = 3a, AC = 4a, ’
BAC = 60◦. Gọi M là trung điểm của BC và
I là trung điểm của AM. # » # » # » #»
a) Chứng minh rằng: 2I A + IB + IC = 0 .
b) Tính cạnh BC, diện tích tam giác ABC và độ dài đường cao AH của tam giác ABC. # » # »
c) Tính tích vô hướng BA · CB. ý Lời giải. # » # » # » #» a) 2I A + IB + IC = 0 . √ b) BC = a 13. √
Diện tích tam giác ABC: S4ABC = 3 3a2. √ 6a 39 Độ dài đường cao AH = . 13 # » # »
c) Tích vô hướng BA · CB = −3a2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
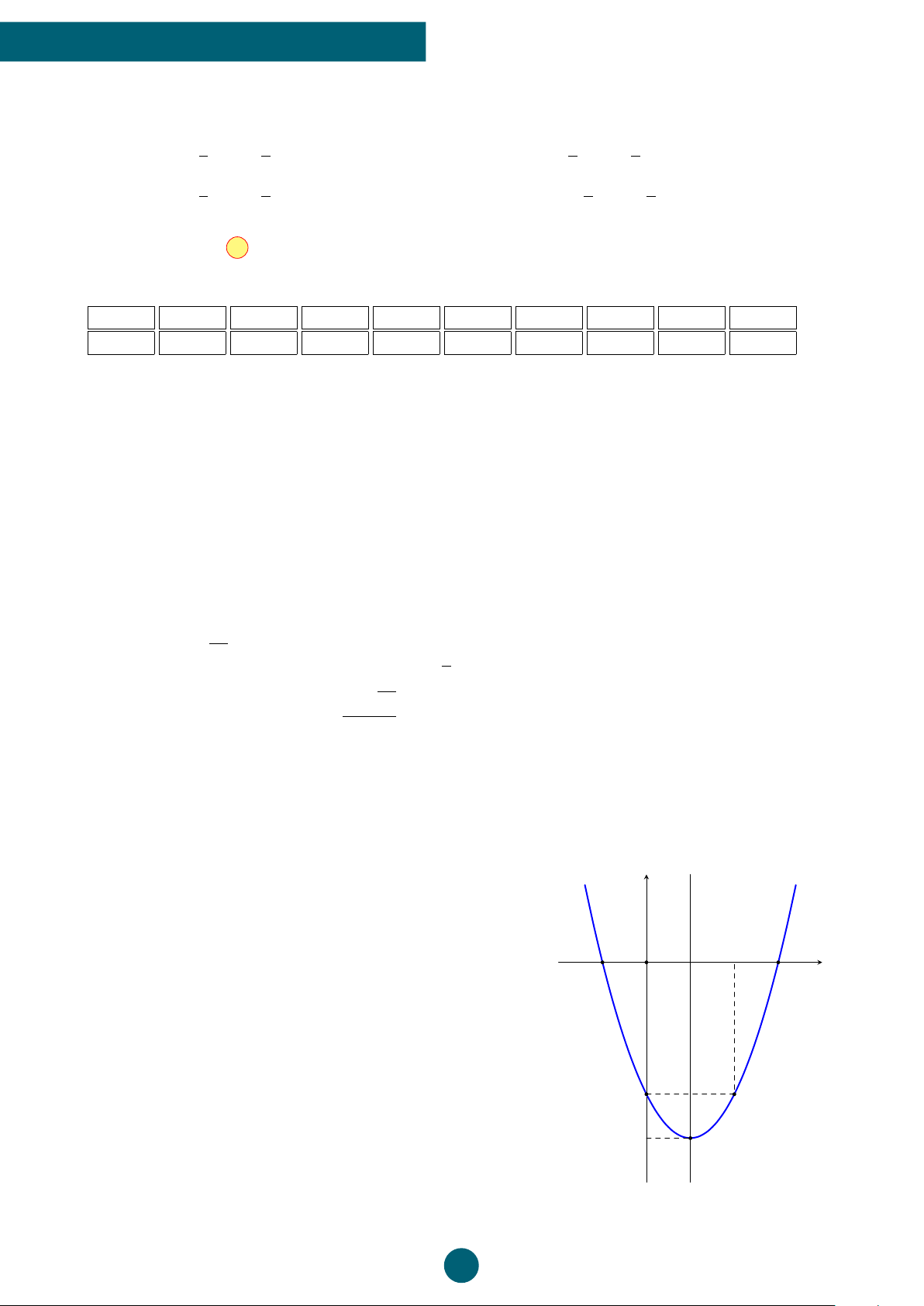
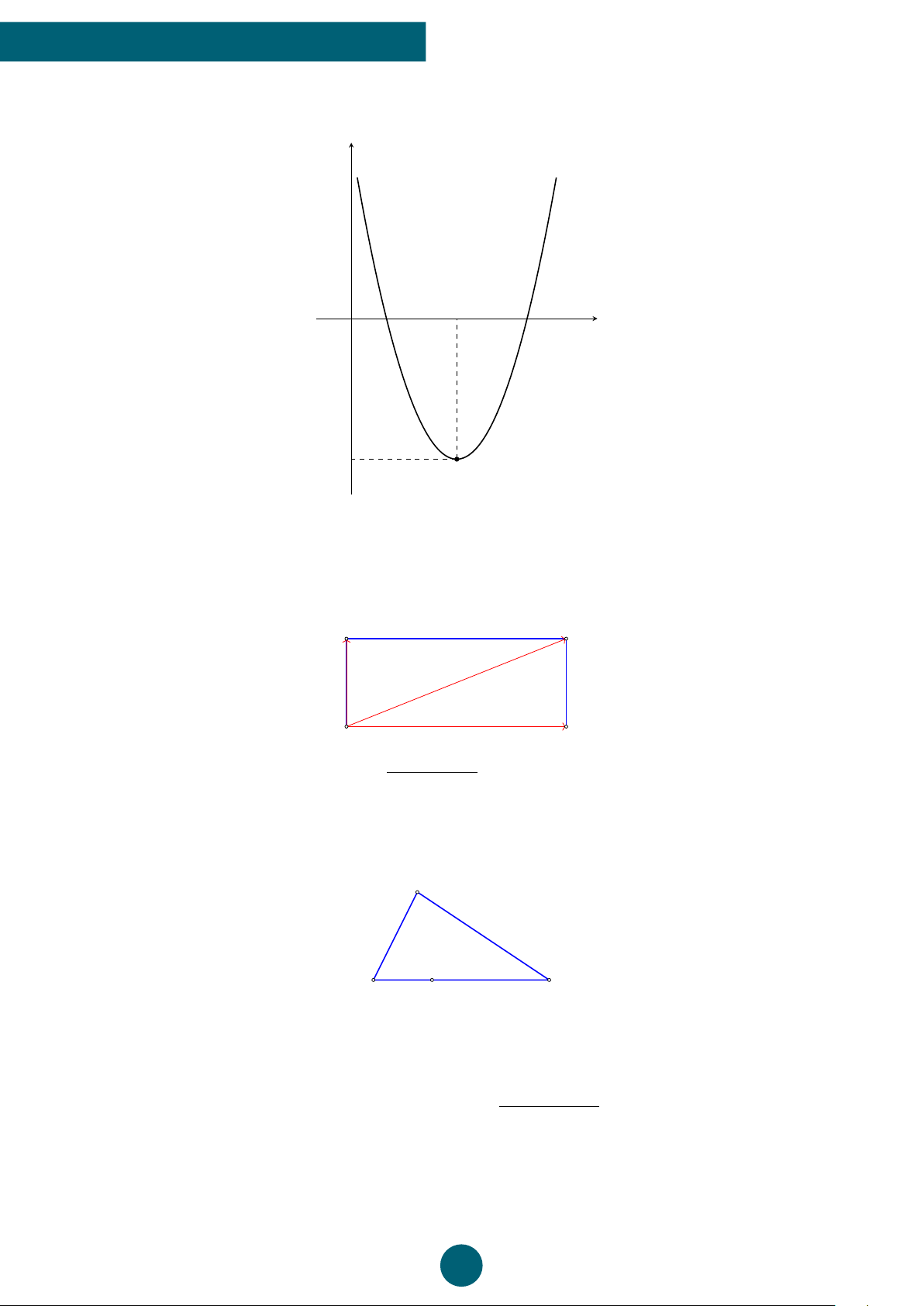
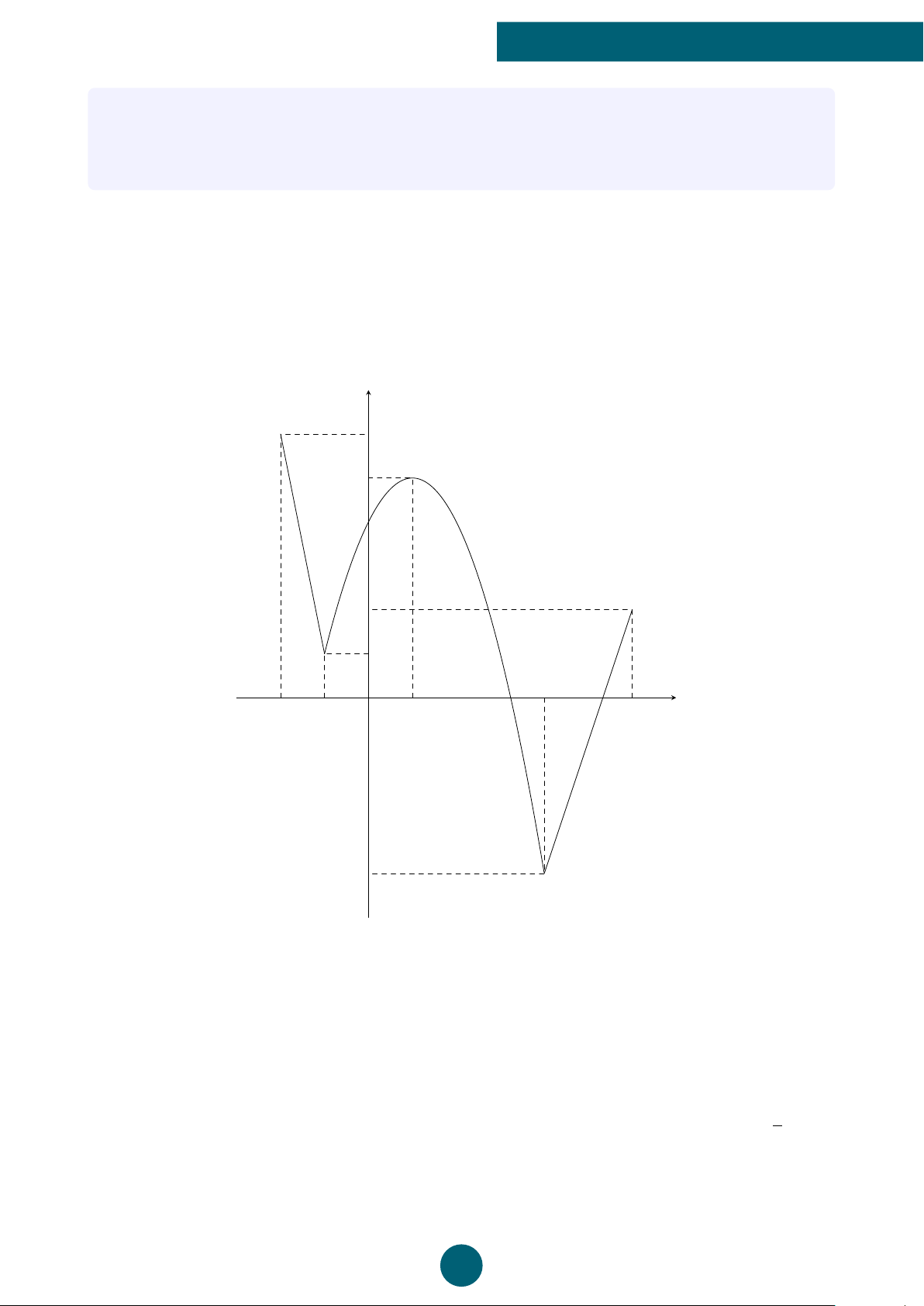
Bài 2: Vẽ đồ thị hàm số bậc hai y = x2 − 2x − 3. ý Lời giải.
Ta có a = 1, b = −2, c = −3, ∆ = (−2)2 − 4 · 1 · (−3) = y x = 1 16.
• Tọa độ đỉnh I(1; −4). B C
• Trục đối xứng x = 1. −1 O x 2 33
• Giao điểm của parabol với trục tung là A(0; −3). − x2
• Giao điểm của parabol với trục hoành là B(−1; 0) − 2x và C(3; 0). = A y
• Điểm đối xứng với điểm A(0; −3) qua trục đối −3 D xứng x = 1 là D(2; −3). −4 I
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận
được đồ thị hàm số y = x2 − 2x − 3.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 GV: VŨ NGỌC HUY
Bài 3: Tìm các giá trị của tham số m để bất phương trình x2 − 2(m + 1)x + 5m − 1 < 0 vô nghiệm. ý Lời giải.
Ta có f (x) = x2 − 2(m + 1)x + 5m − 1 < 0 vô nghiệm
⇔ f (x) = x2 − 2(m + 1)x + 5m − 1 ≥ 0 ∀x ∈ R
⇔ ∆0 = m2 − 3 + 2 ≤ 0
⇔ m ∈ [1; 2]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
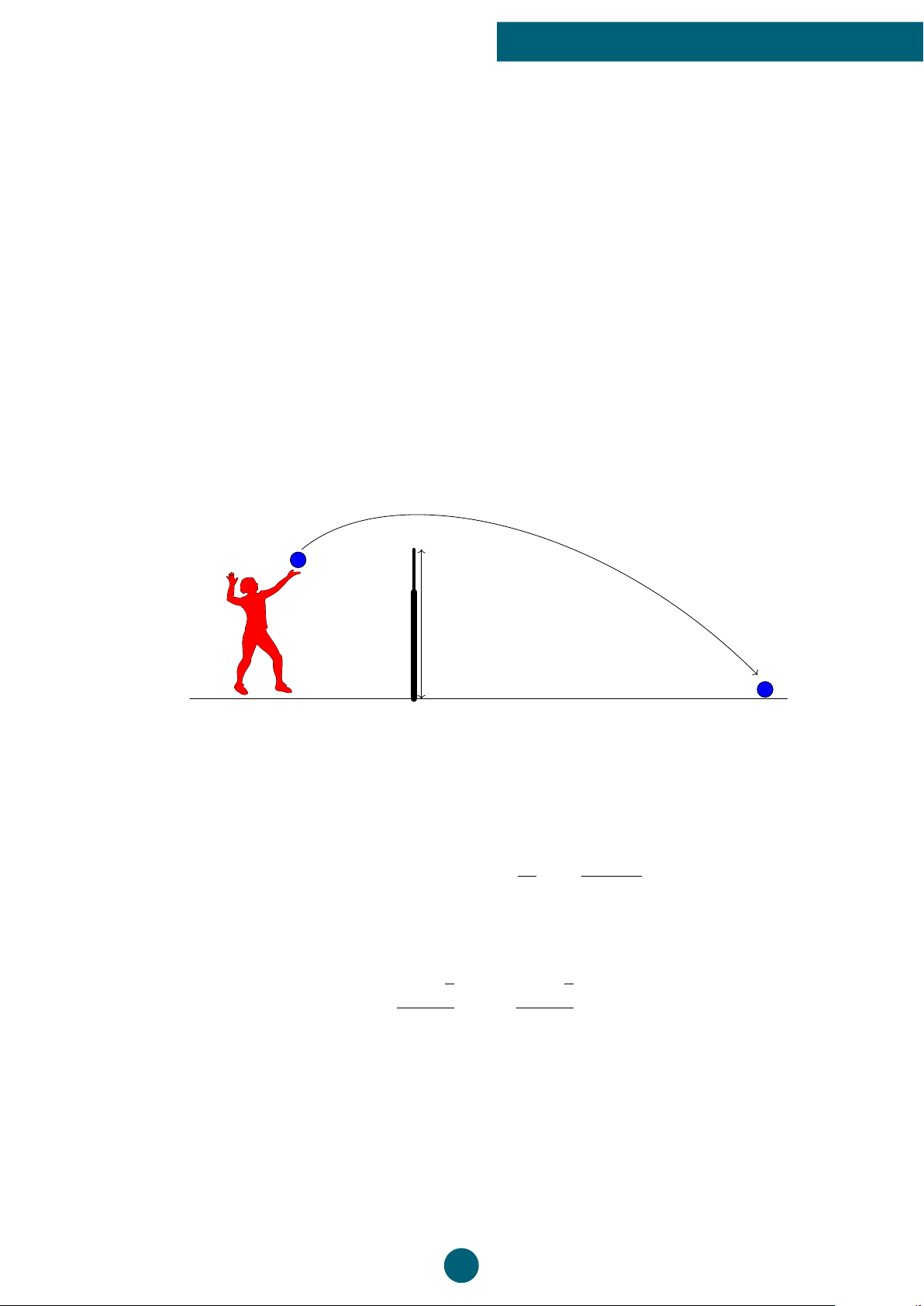
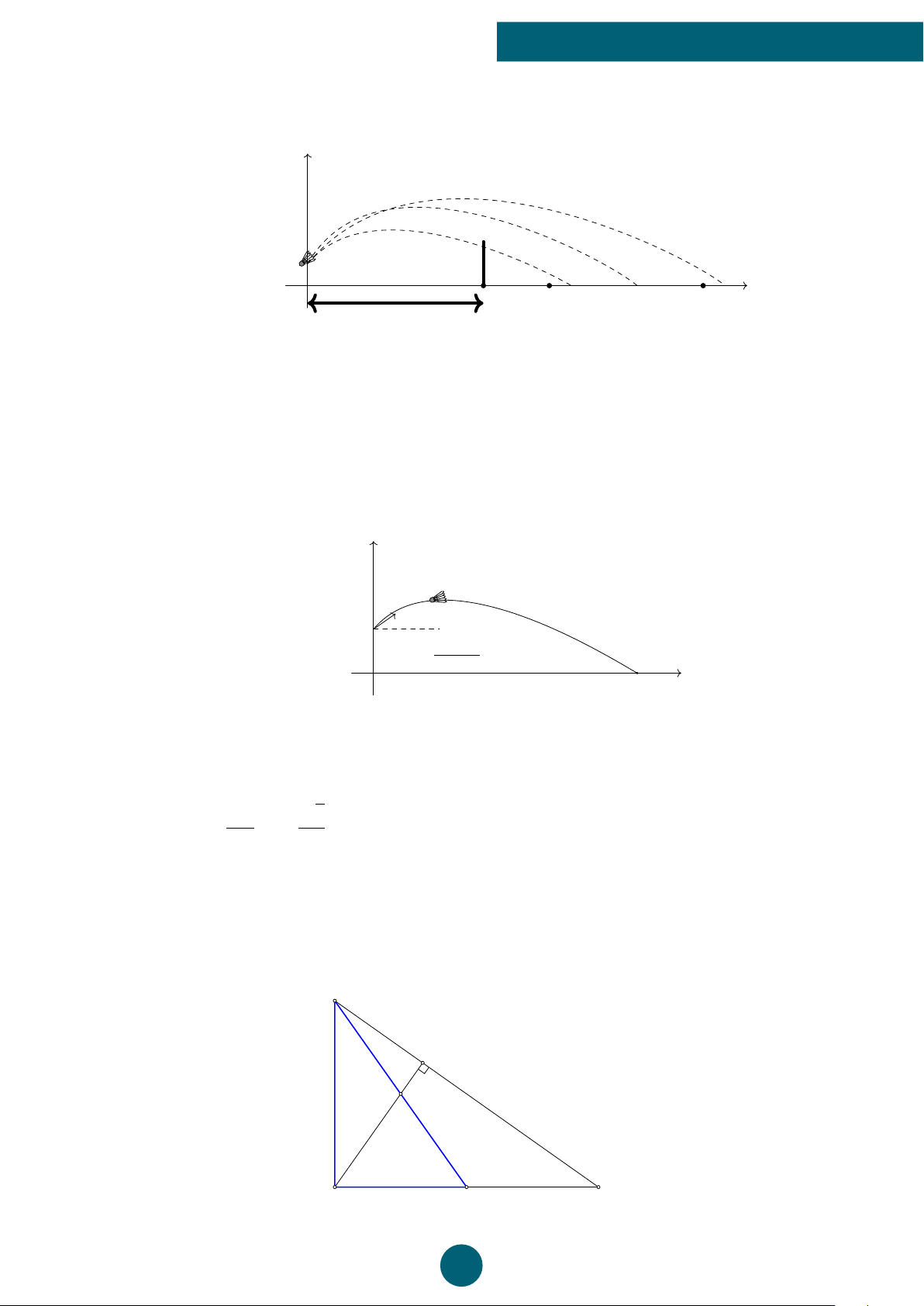
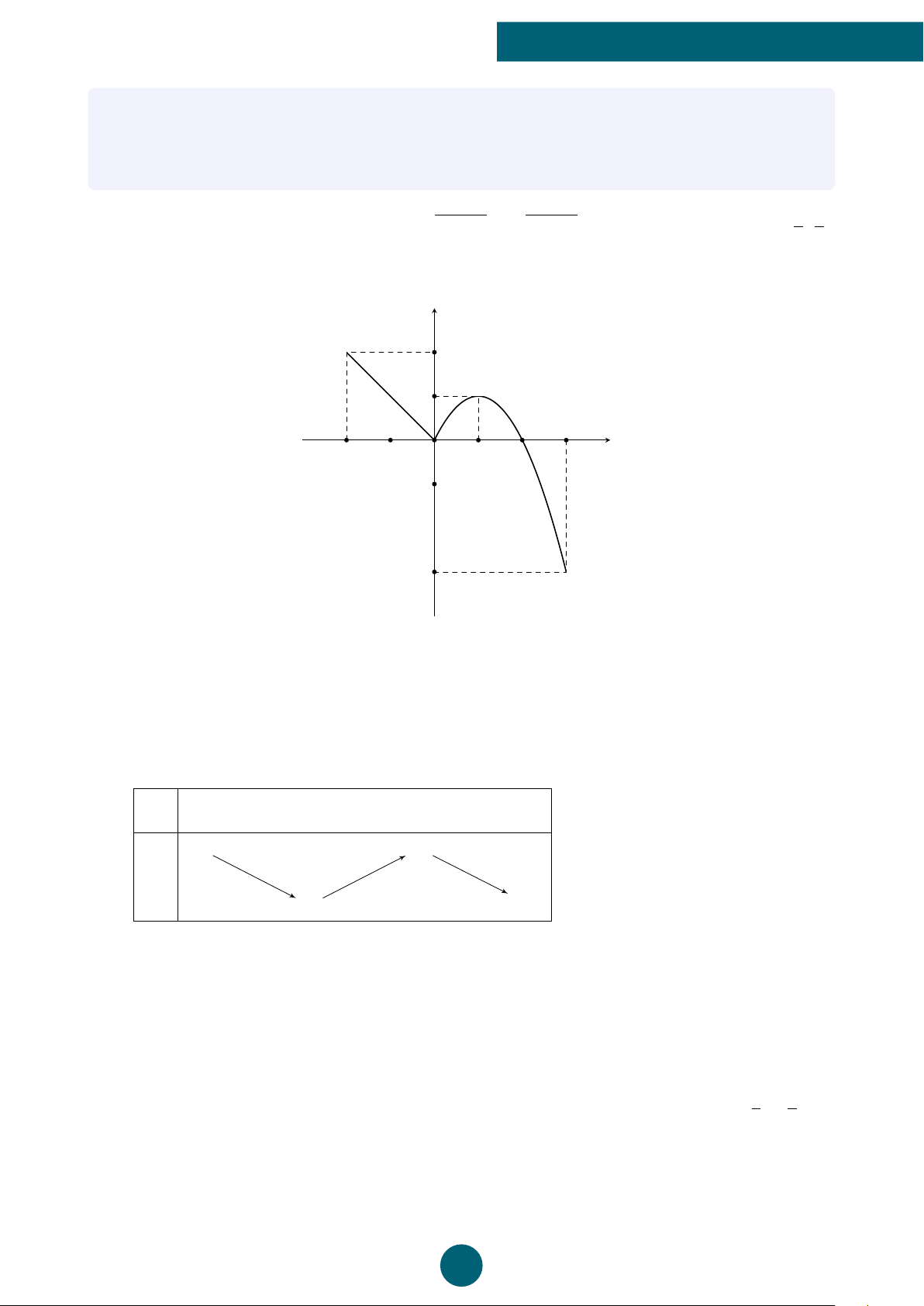
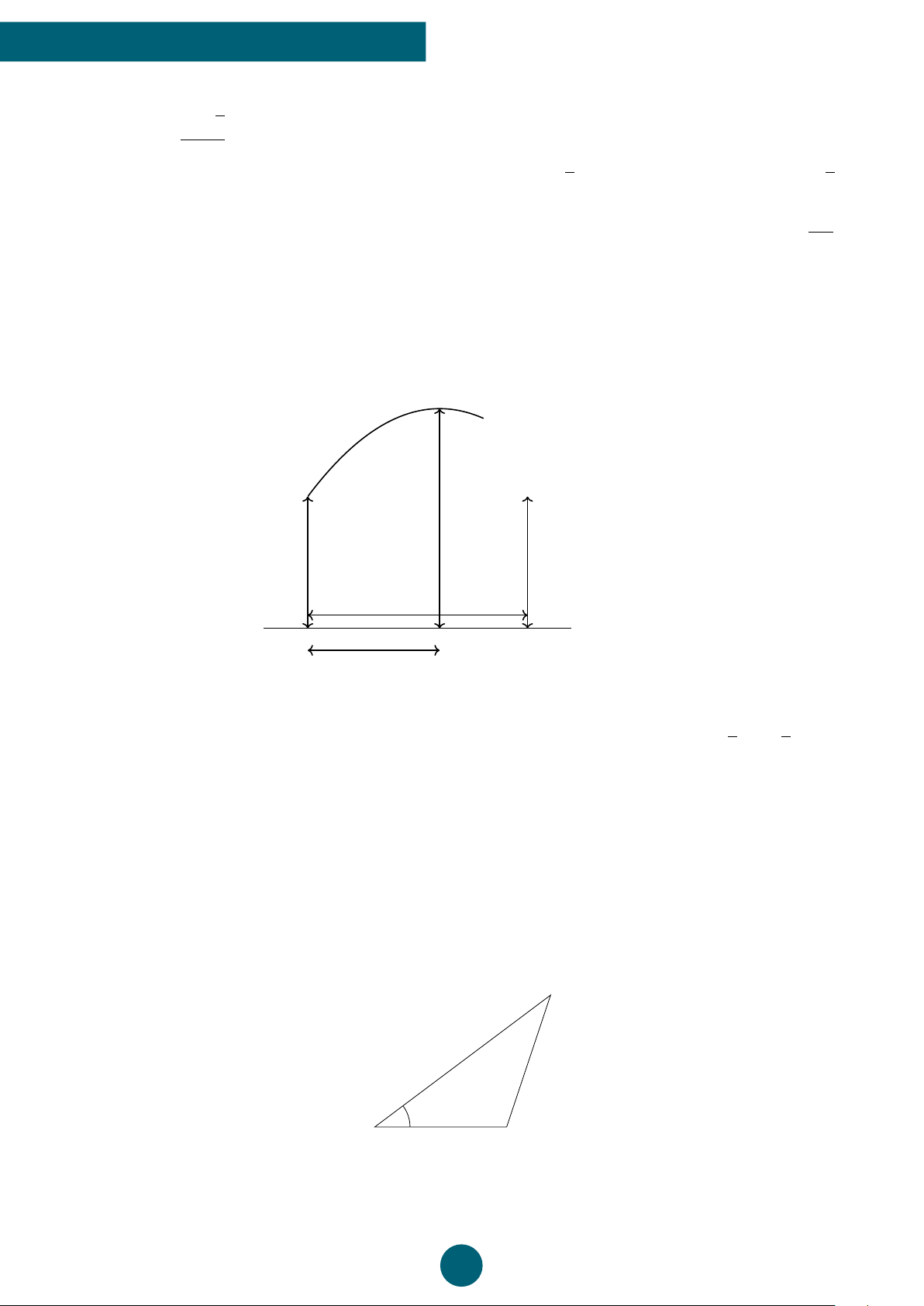
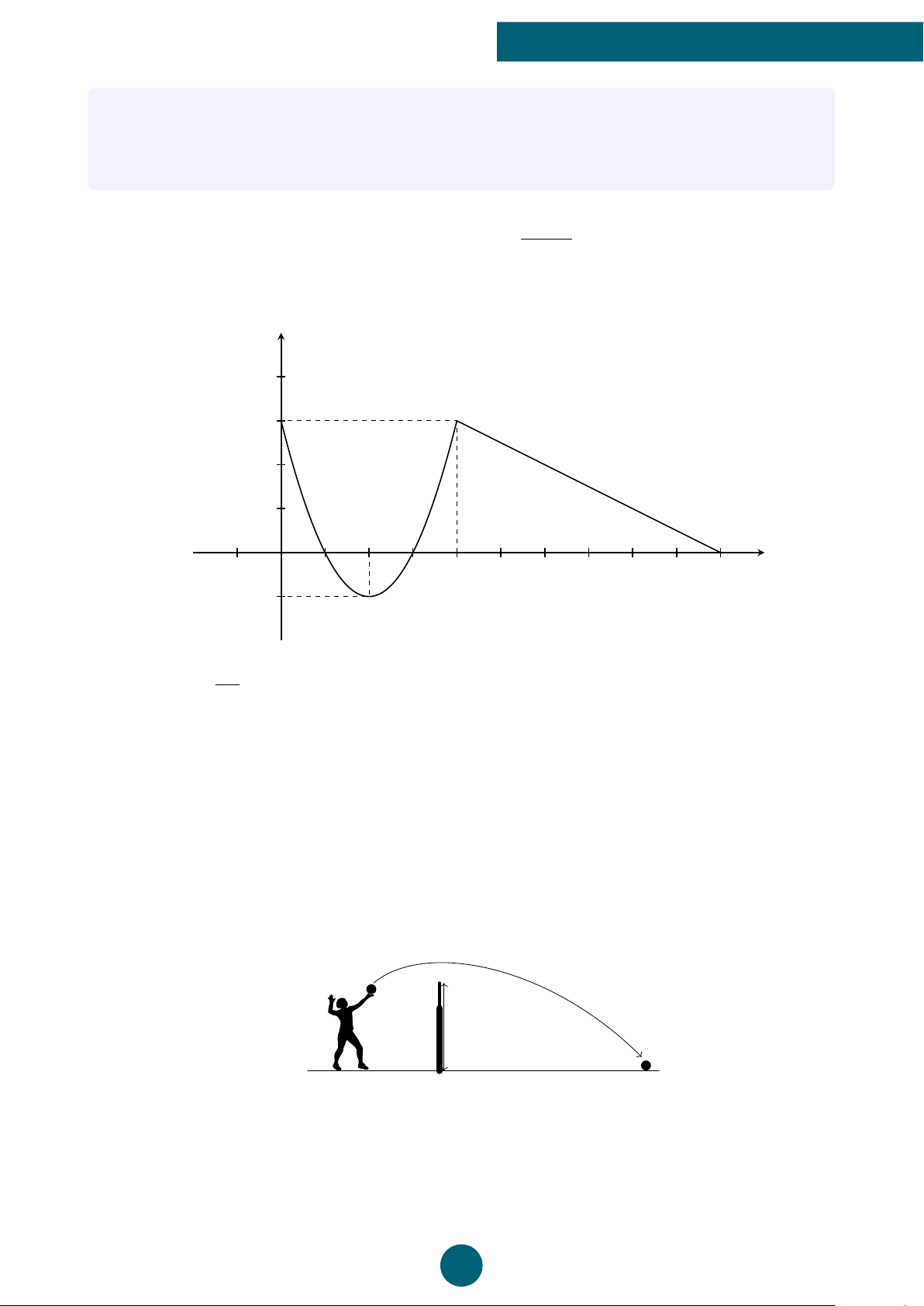
Bài 4: Một vận động viên bóng chuyền đánh bóng qua lưới, biết quỹ đạo chuyển động của
bóng là một cung parabol (P) được mô phỏng bởi phương trình h(t) = −0, 4t2 + 2t + 0, 4,
trong đó h là chiều cao của bóng tính bằng mét và t là thời gian bóng di chuyển tính bằng giây.
a) Tìm thời gian để bóng đạt độ cao lớn nhất.
b) Tìm khoảng thời gian mà bóng cao hơn lưới, biết rằng chiều cao của lưới bằng 2, 4 m. 2,4 m ý Lời giải. b 2
a) Thời gian để bóng đạt độ cao lớn nhất là t = − = − = 2,5 (s). 2a −0,4 · 2
b) Khoảng thời gian mà bóng cao hơn lưới là
− 0,4t2 + 2t + 0,4 > 2, 4 ⇔ 0,4 − 2t + 2 < 0 √ √ 5 − 5 5 + 5 ⇔ 1,38 ≈ < t < ≈ 3,62 2 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ GIỮA HỌC KÌ I KHỐI 10/2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT GIỒNG ÔNG TỐ
Thời gian làm bài: 90 phút
PHẦN TRẮC NGHIỆM (7 Điểm)
Câu 1: Để điều tra các con trong mỗi gia đình của một chung cư gồm 100 gia đình. Người ta
chọn ra 20 gia đình ở tầng 4 và thu được mẫu số liệu sau đây: 2, 4, 2, 1, 3, 5, 1, 1, 2, 3, 1, 2, 2, 3,
4, 1, 1, 2, 3, 2, 4. Có bao nhiêu giá trị khác nhau trong mẫu số liệu trên? A. 4. B. 10 . C. 5 . D. 20. D
Câu 2: Tam giác ABC có AB = 2, AC = 1 và “
A = 60◦. Tính độ dài BC. √ √ A. BC = 1 . B. BC = 2. C. BC = 3 . D. BC = 2. C #» #»
Câu 3: Cho hai vectơ a và b không cùng phương. Hai vectơ nào sau đây không cùng phương? 1 #» #» #» #» 1 #» #» 1 #» #»
A. − a − b và 2 a + b . B. a − b và − a + b . 2 2 2 #» #» 1 #» #» 1 #» #» #» #»
C. −3 a + b và − a + 6 b . D. a + b và a − 2 b . 2 2 A
Câu 4: Bạn Nam để dành 800 nghìn đồng. Trong đợt quyên góp ủng hộ miền Trung sau đợt
lũ lụt, bạn Nam đã đóng góp x tờ 20 nghìn và y tờ 50 nghìn. Bất phương trình thể hiện mối
liên hệ giữa x với y là A. 50x + 20y ≤ 800. B. 50x + 20y ≥ 800 . C. 20x + 59y ≥ 800. D. 20x + 50y ≤ 800 . D
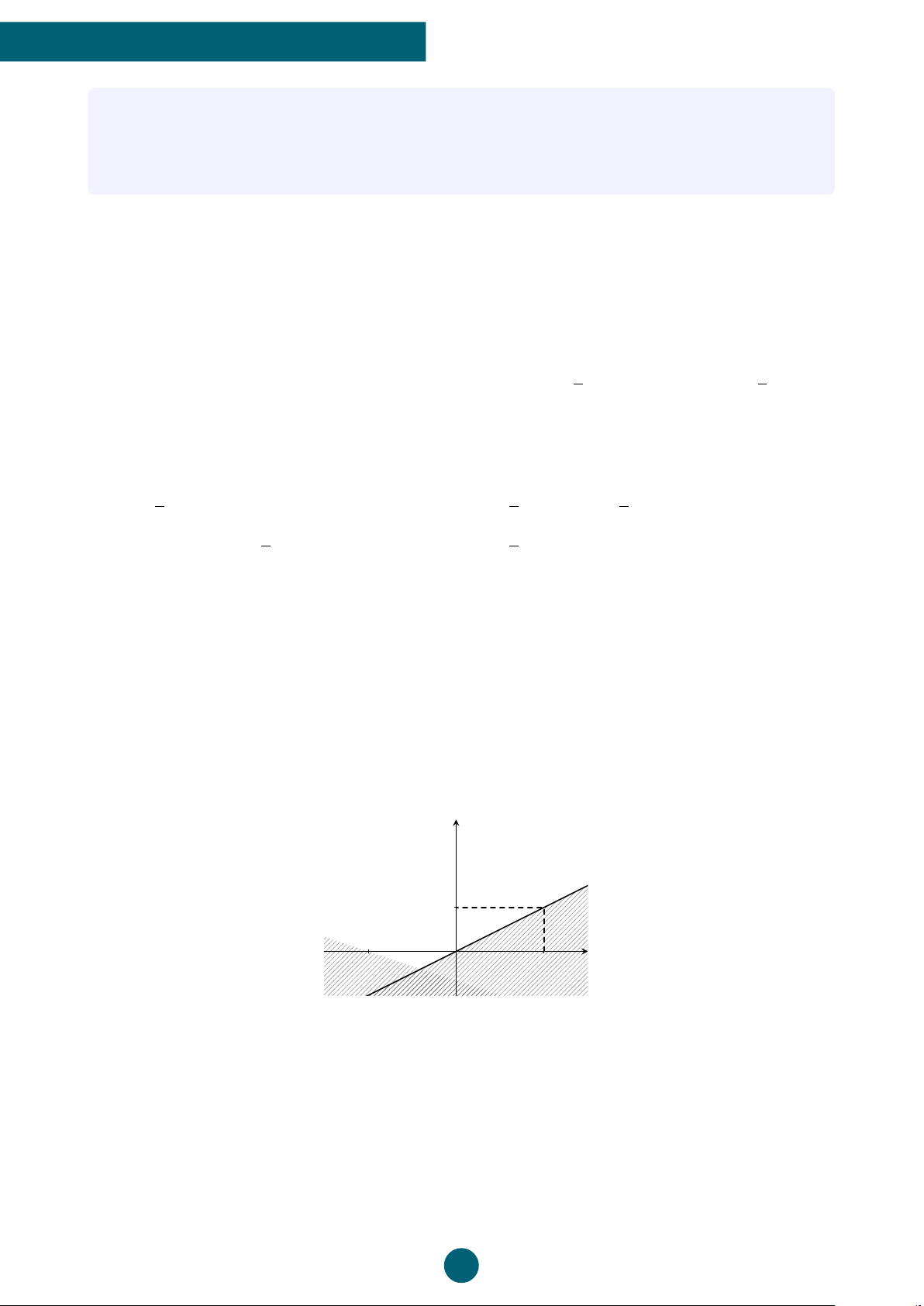
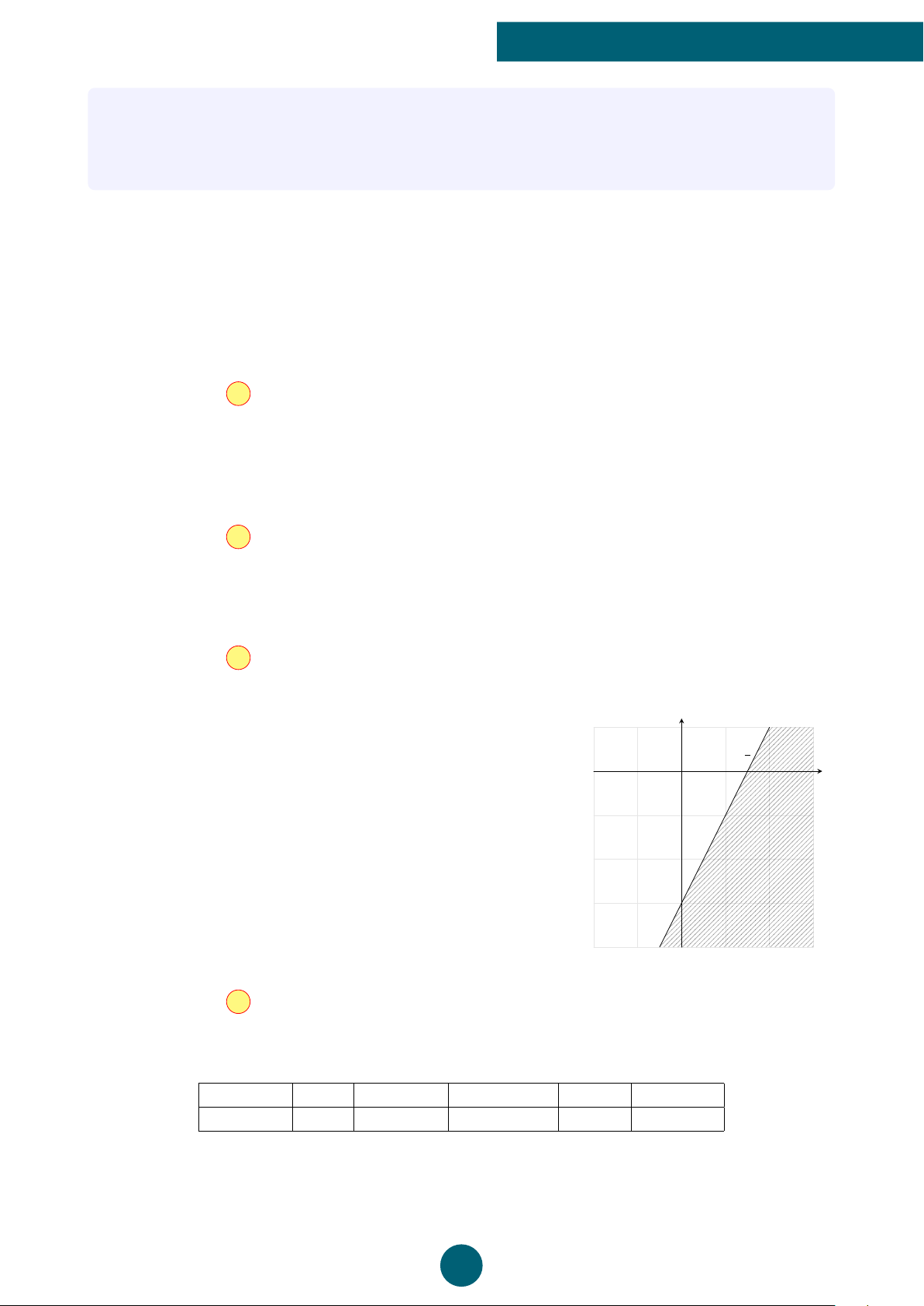
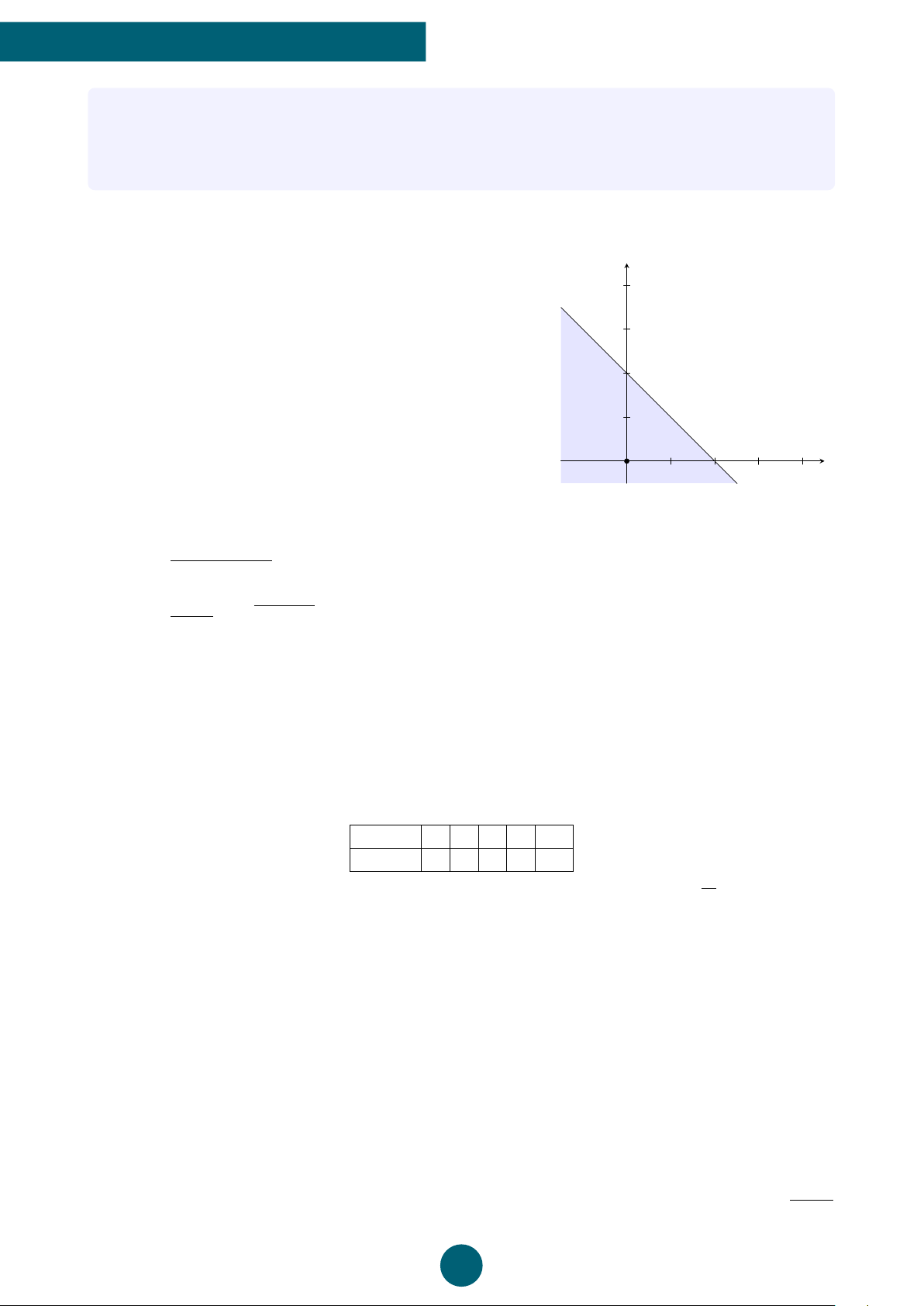
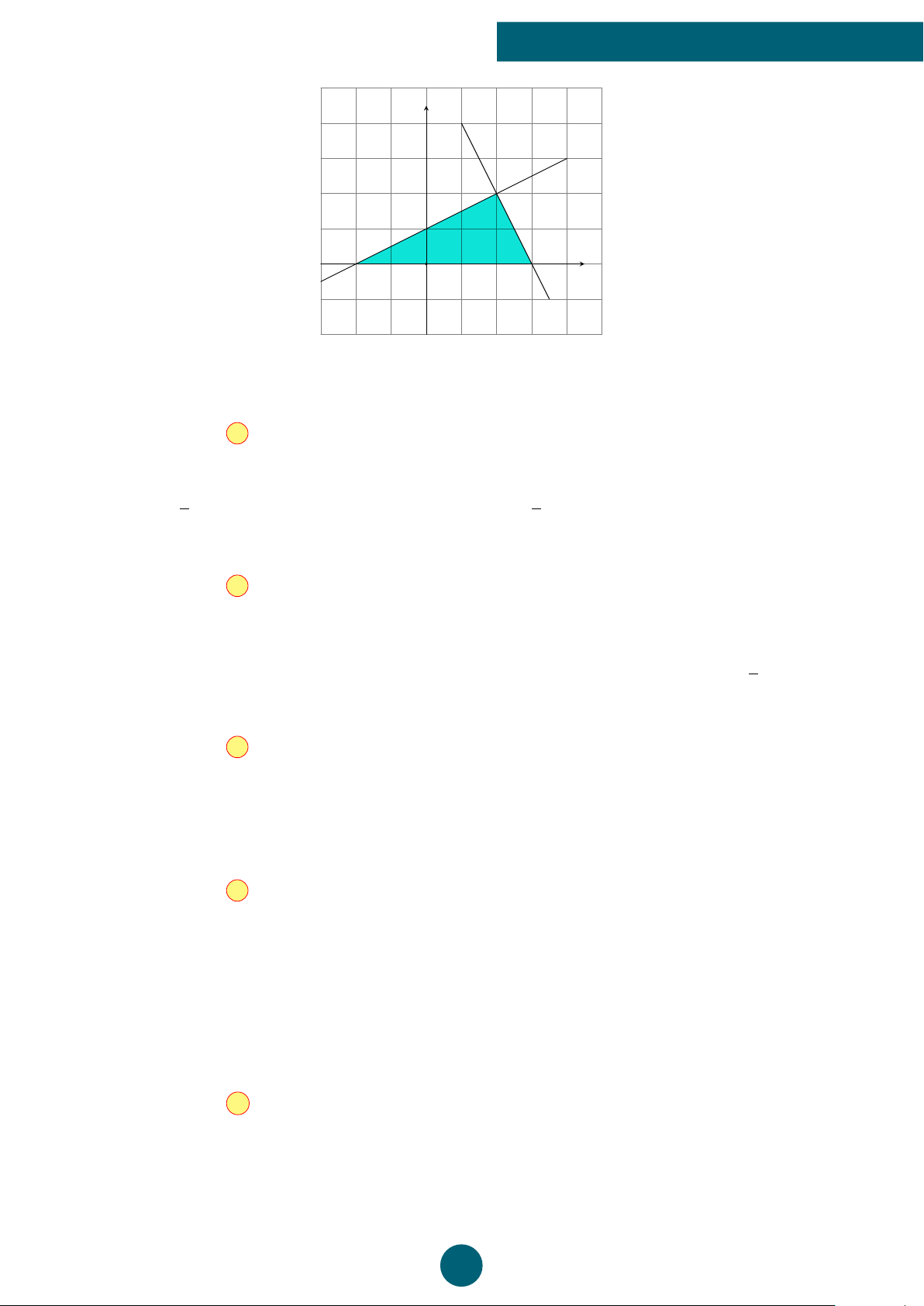
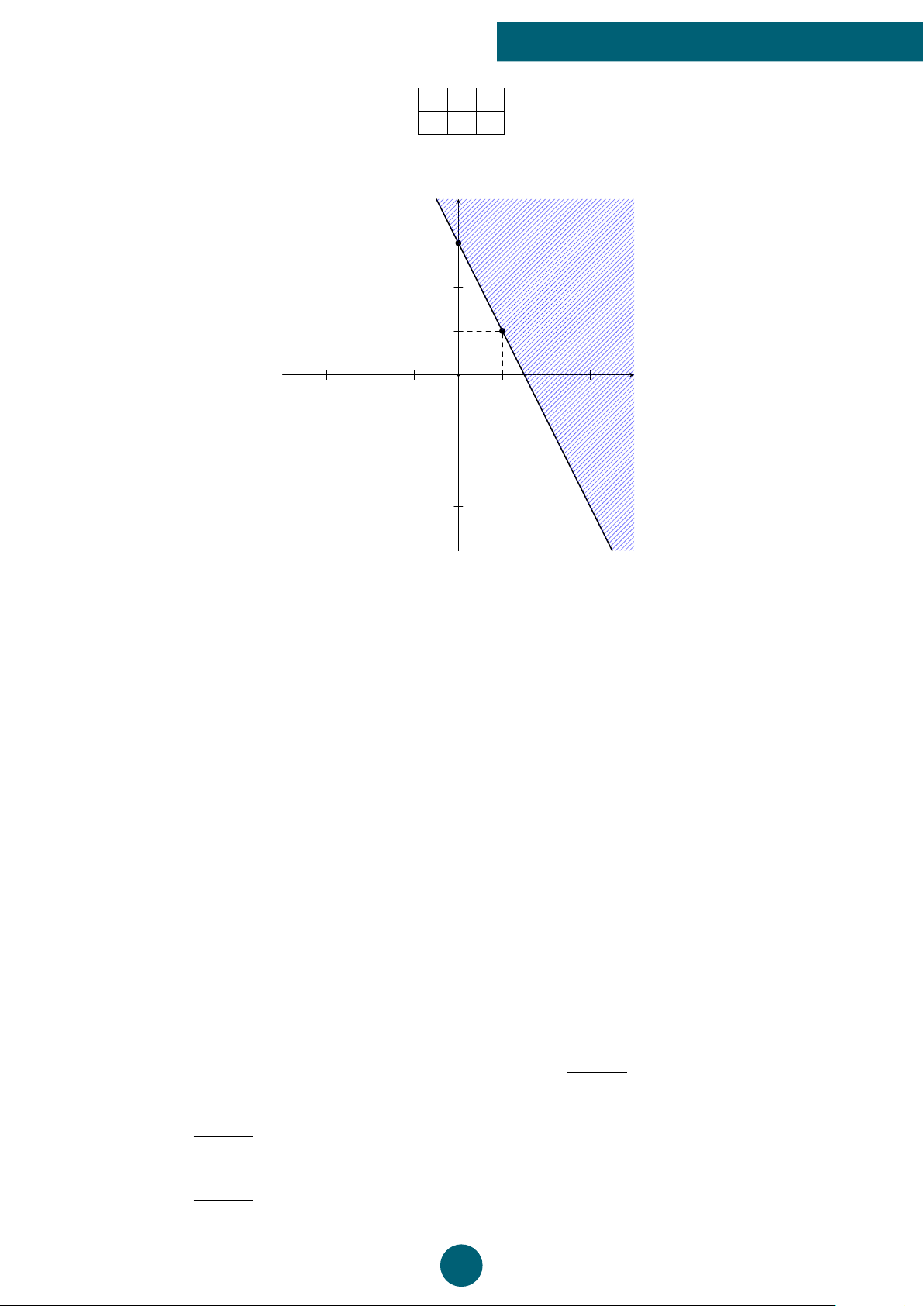
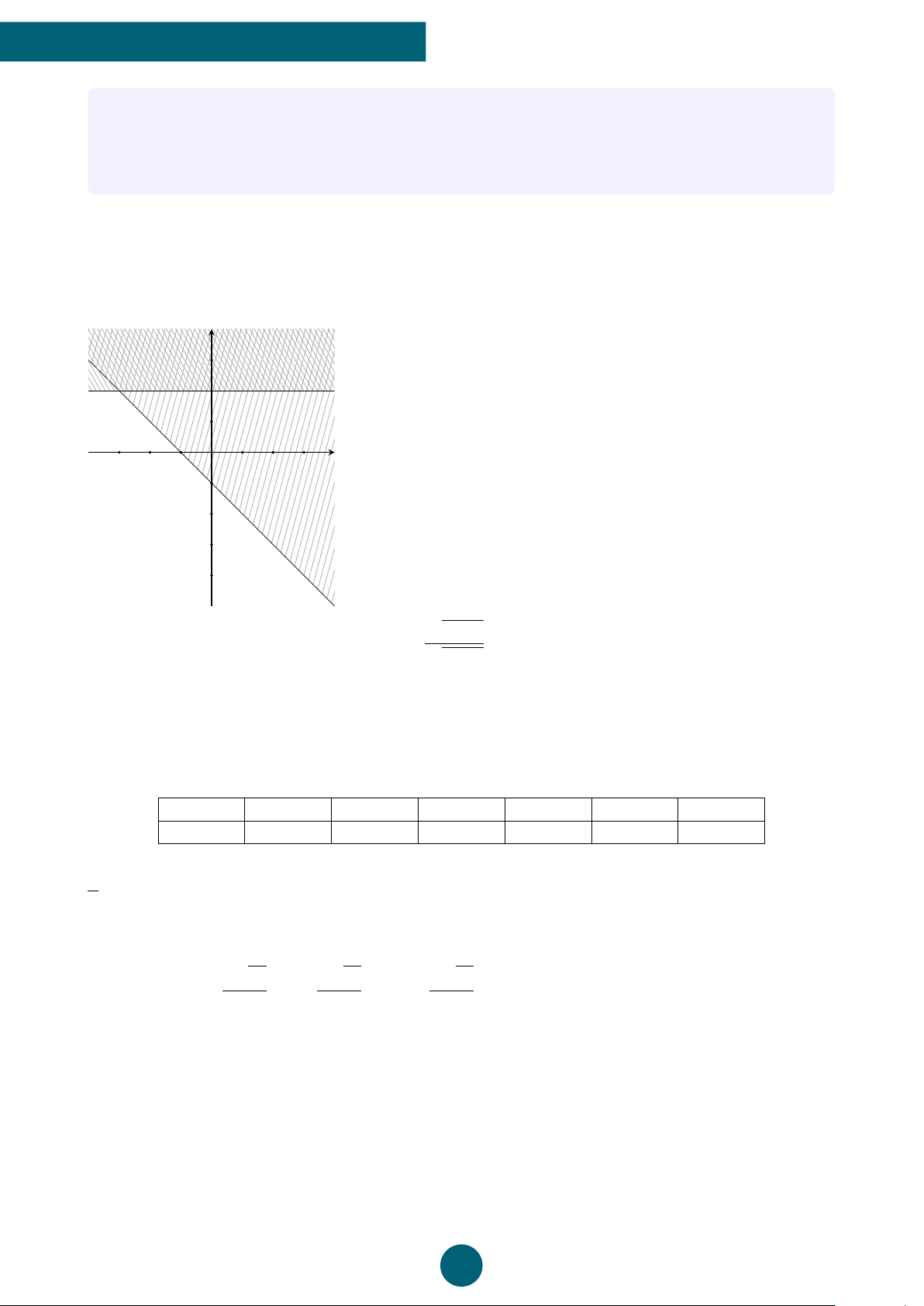
Câu 5: Phần không tô đậm trong hình vẽ dưới đây (không chứa biên) biểu diễn tập nghiệm
của hệ bất phương trình nào trong các hệ bất phương trình sau? y 1 x −2 O 2 ®x − 2y ≤ 0 ®x − 2y < 0 ®x − 2y > 0 ®x − 2y ≤ 0 A. . B. . C. . D. . x + 3y ≤ −2 x + 3y > −2 x + 3y < −2 x + 3y ≥ −2 B
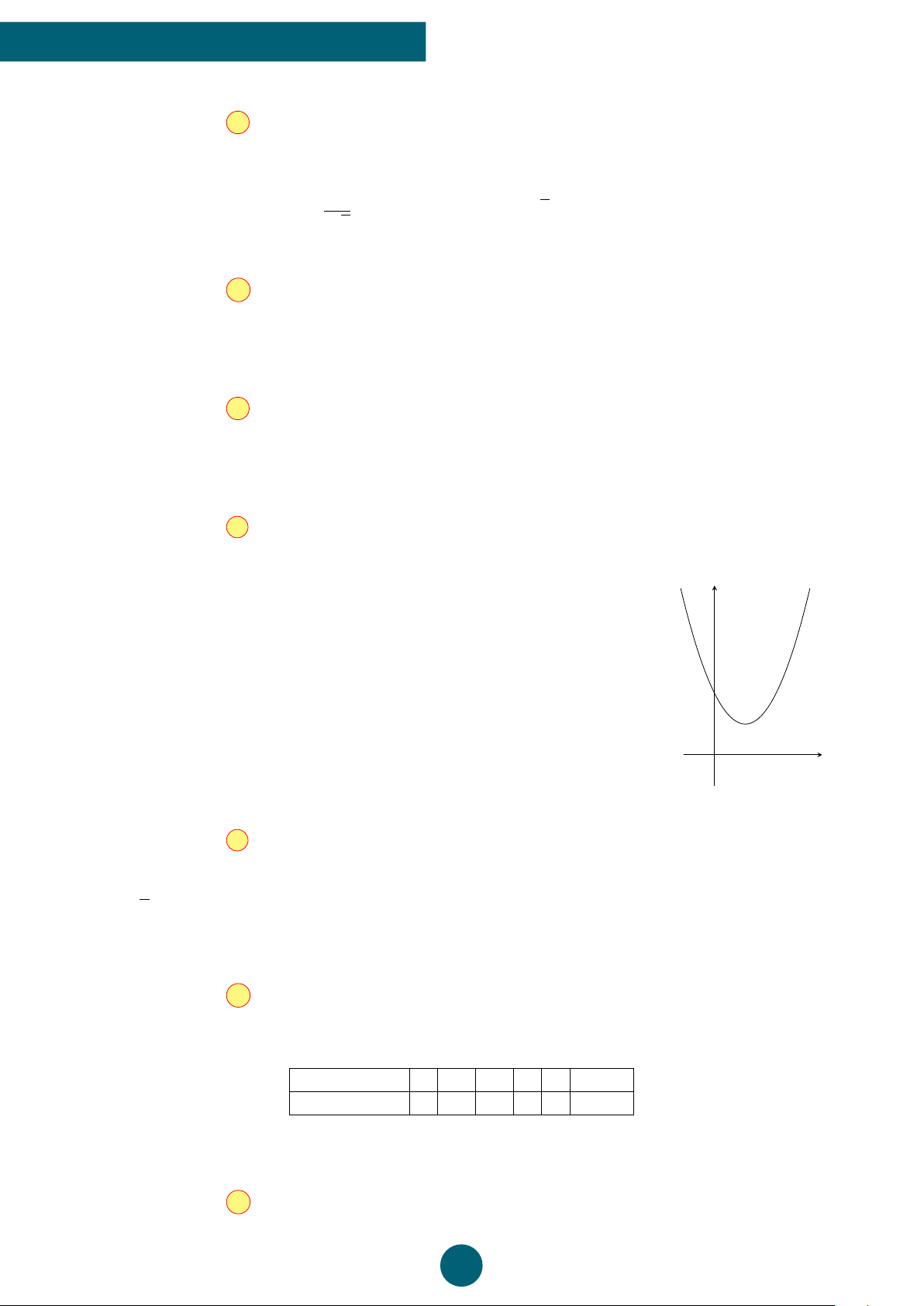
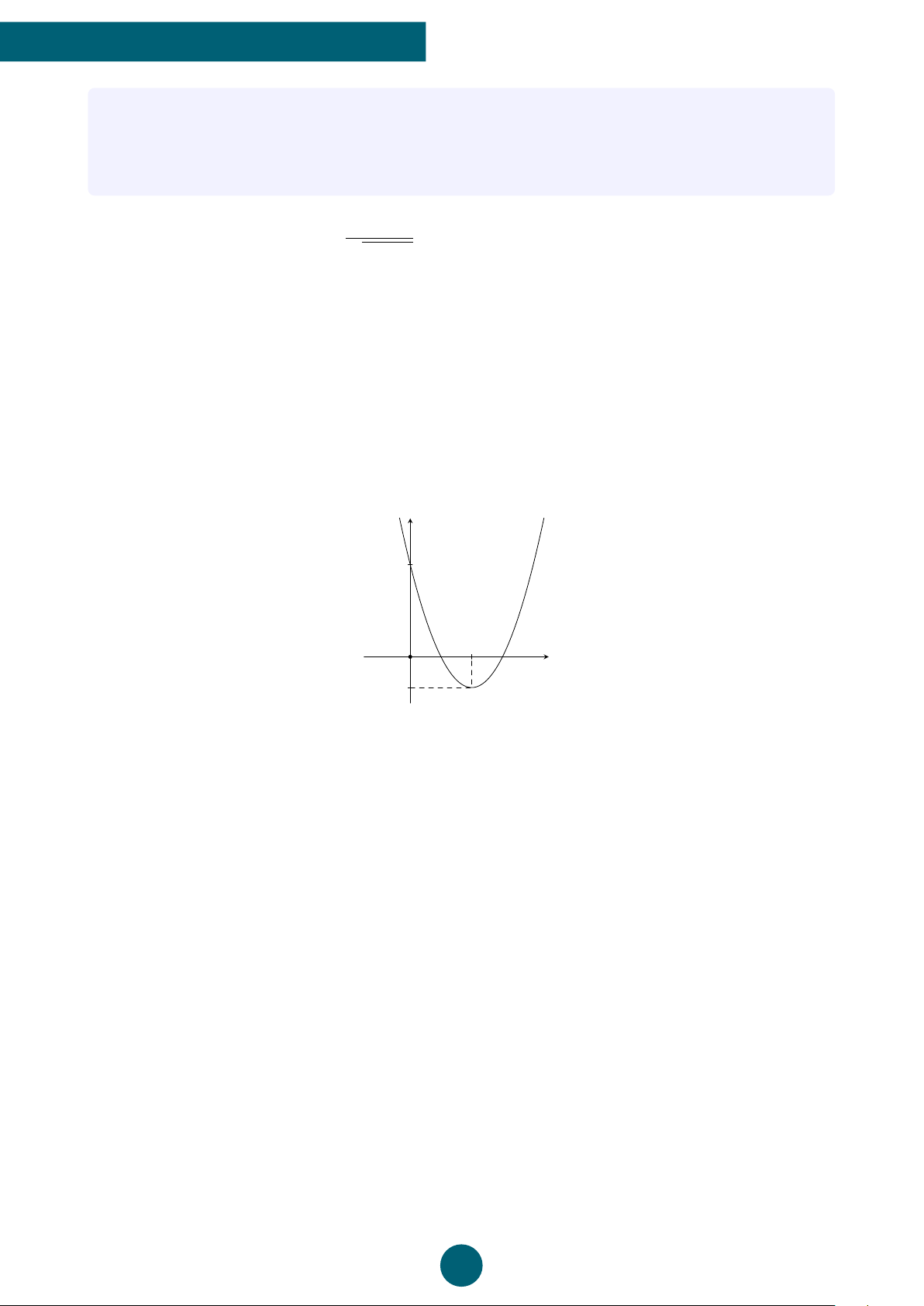
Câu 6: Cho hàm số y = ax2 + bx + c có đồ thị như hình bên. Khẳng định nào sau đây là đúng
A. a > 0, b < 0, c > 0.
B. a < 0, b < 0, c > 0 .
C. a > 0, b > 0, c > 0 .
D. a > 0, b < 0, c < 0. A 8 GV: VŨ NGỌC HUY y x O cos 750◦ + sin 420◦
Câu 7: Giá trị của biểu thức A = bằng
sin(−330)◦ − cos(−390◦) √ √ 1 − 3 √ 2 3 √ A. √ . B. −3 − 3. C. √ . D. 2 − 3 3. 3 3 − 1 B
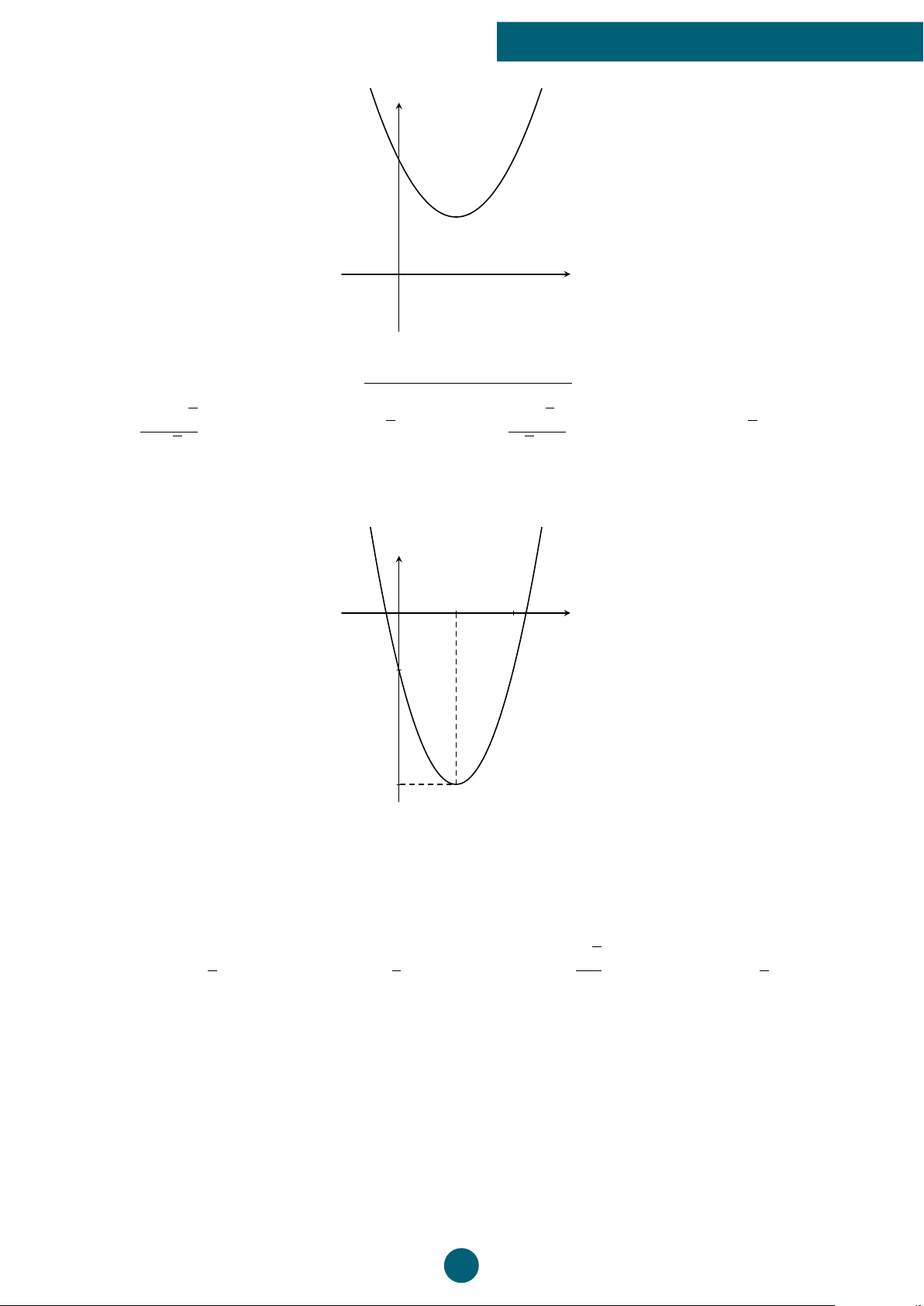
Câu 8: Đồ thị trong hình vẽ là đồ thị của hàm số nào? y 1 2 x O −1 −3
A. y = −2x2 − 4x − 1 .
B. y = 2x2 − 4x − 1 . C. y = 2x2 − 4x + 1 .
D. y = x2 − 4x − 1 . B
Câu 9: Tam giác ABC có AB = 8 cm, AC = 18 cm và có diện tích là 64 cm2. Giá trị của sin A bằng √ 8 4 3 3 A. sin A = . B. sin A = . C. sin A = . D. sin A = . 9 5 2 8 A
Câu 10: Tập hợp D = (−∞; 2] ∩ (−6; +∞) là tập nào sau đây? A. (−∞; ∞) . B. (−∞; 6]. C. [−6; 2]. D. (−6; 2] . D
Câu 11: Hãy chọn mệnh đề đúng.
A. Z ⊂ N.
B. R ⊂ Q.
C. Q ⊂ Z.
D. Z ⊂ Q. D # » # »
Câu 12: Trên đường thẳng MN lấy điểm P sao cho MN = −3MP. Điểm P được xác định
đúng trong hình vẽ nào sau đây? 9 GV: VŨ NGỌC HUY M P N N M P Hình 1 Hình 2 N M P M P N Hình 3 Hình 4 A. Hình 3 . B. Hình 2 . C. Hình 4 . D. Hình 1 . A √
Câu 13: Khi sử dụng máy tính bỏ túi 10 chữ số thập phân ta được 8 = 2,828427125. Giá trị √ gần đúng của
8 chính xác đến hàng phần trăm là A. 2,84. B. 2,81. C. 2,82. D. 2,83. D 1
Câu 14: Điểm nào sau đây thuộc đồ thị hàm số y = ? x − 1 A. M3(2; 0). B. M4(0; −2). C. M1(2; 1). D. M2(1; 1). C
Câu 15: Liệt kê các phần tử của tập hợp X = {x ∈ N|x − 5 ≤ −4x}. A. ∅. B. {0; 1; 2}. C. {0; 1}. D. {−1; 0; 1}. D
Câu 16: Bảng biến thiên của hàm số y = −2x2 + 4x + 1 là bảng nào sau đây? x −∞ 2 +∞ x −∞ 1 +∞ −∞ −∞ −∞ −∞ y y 1 3 A. . B. . x −∞ 1 +∞ x −∞ 2 +∞ 3 1 y y −∞ −∞ −∞ −∞ C. . D. . C #» #» #» #» #»
Câu 17: Cho hai vectơ a và b thõa mãn | #»
a | = 3, | b | = 2 và a · b = −3. Xác định góc α #» #» giữa hai vectơ a và b A. α = 60◦. B. α = 30◦. C. α = 120◦. D. α = 45◦. C # » # »
Câu 18: Cho tam giác ABC vuông tại A và có AB = c, AC = b. Tính BA · BC. # » # » # » # »
A. BA · BC = b2 − c2. B. BA · BC = b2. # » # » # » # » C. BA · BC = b2 + c2. D. BA · BC = c2. C
Câu 19: Điểm I(−2; 1) là đỉnh của Parabol nào sau đây?
A. y = −x2 − 4x + 3. B. y = x2 + 4x − 5. C. y = x2 + 4x + 5. D. y = 2x2 + 4x + 1. C
Câu 20: Cho a = 46,7543 và độ chính xác d = 0,01. Số quy tròn của a là A. 46,75. B. 46,7. C. 46,8. D. 46,76. A 10 GV: VŨ NGỌC HUY Ä # » # »ä
Câu 21: Tam giác ABC vuông ở A và có BC = 2AC. Tính cos AC, CB Ä # » # »ä 1 Ä # » # »ä 1 A. cos AC, CB = − . B. cos AC, CB = . 2 √ 2 √ Ä # » # »ä 3 Ä # » # »ä 3 C. cos AC, CB = . D. cos AC, CB = − . 2 2 C
Câu 22: Gọi O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD. Đẳng thức nào sau đây là sai? # » # » # » # » # » # » # » # » A. AB = DC. B. OA = OC. C. OB = DO. D. CB = DA. B
Câu 23: Tam giác ABC vuông cân tại A, có AB = a. Tính bán kính r của đường tròn nội tiếp tam giác ABC. a a a a A. r = √ . B. r = √ . C. r = . D. r = . 2 2 + 2 2 3 B
Câu 24: Cho Parabol (P) : ax2 + bx + 2 (a 6= 0). Biết rằng parabol đó đi qua hai điểm A(1; 5) và B(−2; 8) A. y = 2x2 + x + 2. B. y = x2 − 4x + 2. C. y = −x2 + 2x + 2. D. y = x2 − 3x + 2. A # » # » # » # »
Câu 25: Cho bốn điểm A, B, C, D phân biệt. Khi đó AB − DC + BC − AD bằng vectơ nào sau đây? # » #» # » # » A. 2DC. B. 0 . C. AC. D. BD. B x2 + 1 khi x > 2
Câu 26: Cho hai hàm số f (x) = 2x2 + 3x + 1 và g(x) =
2x − 1 khi − 2 ≤ x ≤ 2 . Tính các 6 − 5x khi x < −2
giá trị f (−1) và g(−3), g(2), g(3).
A. f (−1) = 0, g(−3) = 21, g(2) = 3, g(3) = 10.
B. f (−1) = 1, g(−3) = 32, g(2) = 5, g(3) = 17.
C. f (−1) = −1, g(−3) = 34, g(2) = 3, g(3) = 8.
D. f (−1) = −1, g(−3) = 12, g(2) = 41, g(3) = 7. A
Câu 27: Cho tam giác ABC. Gọi M là điểm trên cạnh BC sao cho MB = 3MC. Khi đó, biểu # » # » # »
diễn AM theo AB và AC ta được # » 1 # » 1 # » # » 1 # » 3 # » A. AM = AB + AC. B. AM = AB + AC. 4 6 4 4 # » 1 # » # » # » 1 # » 1 # » C. AM = AB + 3AC. D. AM = AB + AC. 4 2 6 C
Câu 28: Cho hàm số y = ax2 + bx + c (a > 0). Khẳng định nào sau đây là sai? Å b ã
A. Hàm số đồng biến trên − ; +∞ . 2a b
B. Đồ thị của hàm số có trục đối xứng là đường thẳng x = − . 2a
C. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt. Å b ã
D. Hàm số nghịch biến trên khoảng −∞; − . 2a 11 GV: VŨ NGỌC HUY C x + 1
Câu 29: Tập xác định của hàm số y = là x − 1 A. R \ {1}. B. (1; +∞). C. R \ {−1}.
D. R \ {−1; 1}. A # » # »
Câu 30: Cho hình vuông ABCD cạnh a, tâm O. Khi đó, OA − BO bằng √ a A. 2a. B. 2a. C. . D. a. 2 D
Câu 31: Cho tập hợp A = [9; +∞). Hãy viết lại tập hợp A đưới dạng nêu tính chất đặc trưng.
A. A = {x ∈ R|9 ≤ x ≤ +∞}.
B. A = {x ∈ R|x ≤ 9}.
C. A = {x ∈ R|x ≥ 9}.
D. A = {x ∈ R|x < 9}. C
Câu 32: Hệ nào sau đây không phải là hệ bất phương trình bậc nhất hai ẩn? ®5x + y − 9 = 0 ®3x + y − 1 ≤ 0 A. . B. . 4x − 7y + 3 = 0 2x − y + 2 ≥ 0 x + y − 3 ≤ 0 ® y − 1 < 0 − 2x + y + 3 ≥ 0 C. . D. . x + 2 ≥ 0 x ≥ 0 7 ≥ 0 A
Câu 33: Cho tam giác ABC có BC = a, AC = b, AB = c, R là bán kính đường tròn ngoại tiếp
tam giác ABC. Tìm công thức sai a a c sin A A. = 2R. B. sin A = . C. sin C = . D. b sin B = 2R. sin A 2R a D
Câu 34: Cho tam giác ABC có BC = a, AC = b, AB = c. Chọn công thức sai a2 + b2 − c2 1 A. cos C = . B. S = bc sin A. 2ab 2 1 c2 + b2 − a2 C. S = ab cos C. D. cos A = . 2 2bc C
Câu 35: Trong các hàm số sau, hàm số nào đồng biến trên R? A. y = −2(2x − 3). B. y = 1 − 2x. C. y = x2 + 2x − 1. D. y = 3x + 2. D PHẦN 2 - TỰ LUẬN 1
Bài 1 (1 điểm): Tìm tập xác định của hàm số y = . x2 − 2x − 3
ĐS: D = R \ {−1; 3}.
Bài 2 (0,5 điểm): Một quả bóng được cầu thủ sút lên rồi rơi xuống theo quỹ đạo là một
parabol. Biết rằng ban đầu quả bóng được sút lên từ độ cao 1 m, sau đó 1 giây nó đạt độ cao
10 m và sau 3,5 giây nó ở độ cao 6,25 m. Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét? ĐS: 13 m.
Bài 3 (1 điểm): Cho hình bình hành ABCD có E, N lần lượt là trung điểm của BC, AE. Tìm # » # » # » 5 3
các số p và q sao cho DN = pAB + qAC. ĐS: p = ; q = − 4 4 12 GV: VŨ NGỌC HUY #»
Bài 4 (0,5 điểm): Tính công sinh bởi một lực F có độ lớn 60 N kéo một vật dịch chuyển một #» Ä #» #»ä
vectơ d có độ dài 200 m. Cho biết F , d = 60◦. ĐS: A = 6000 J. 13 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT BÀ ĐIỂM
Thời gian làm bài: 90 phút
Bài 1: Cho hai tập hợp A = [−3; 8) và B = (−∞; 5]. Tìm A ∩ B, A ∪ B, A \ B, B \ A.
ĐS: A ∩ B = [−3; 5], A ∪ B = (−∞; 8), A \ B = (5; 8), B \ A = (−∞; −3). ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 2: Trong năm học 2022- 2023, trường THPT Bà Điểm mở lớp luyện thi IELTS và tiếng
Trung. Lớp 10A có 20 bạn đăng ký học tiếng Trung, 15 bạn đăng ký học IELTS, 3 bạn đăng ký
học cả 2 môn này, và 18 bạn không đăng ký học môn nào trong 2 môn trên.
a) Lớp 10A có bao nhiêu học sinh đăng ký ít nhất một trong hai môn nêu trên?
b) Tính sĩ số lóp 10A?
ĐS: a) 32 học sinh; b) 50 học sinh ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 3: Một xưởng có máy cắt và máy tiện dùng để sản xuất trục sắt và đinh ốc. Sản xuất 1 tấn
trục sắt thì lần lượt máy cắt chạy trong 3 giờ và máy tiện chạy trong 1 giờ, tiền lãi là 2 triệu.
Sản xuất 1 tấn đinh ốc thì lần lượt máy cắt và máy tiện chạy trong 1 giờ tiền lãi là 1 triệu. Một
máy không thể sản xuất cả 2 loại. Máy cắt làm không quá 6 giờ/ngày, máy tiện làm không
quá 4 giờ/ngày. Một ngày xưởng nên sản xuất bao nhiêu tấn mỗi loại để tiền lãi cao nhất.
ĐS: Một ngày xưởng sản xuất 1 tấn trục sắt và 3 tấn đinh ốc thì thu được tiền lãi cao nhất là 5 triệu ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √ 3x + 1
Bài 4: Tìm tập xác định của hàm số sau: y = 2x − 4 − √ . ĐS: D = [2; 5) 15 − 3x ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 5: Tìm hàm số y = ax2 + bx + c(a 6= 0), biết rằng đồ thị (P) của hàm số đi qua điểm
M(3; 1) và (P) có đỉnh I(2; −1).
ĐS: a = 2, b = −8, c = 7 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 6: Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh
nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào
một chiếc là 27 triệu đồng và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe
mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng
tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng
nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200
chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm
giá, lợi nhuận thu được sẽ là cao nhất.
ĐS: 30,5 triệu đồng. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 GV: VŨ NGỌC HUY 1
Bài 7: Cho tam giác ABC có AB = 8, AC = 10, cos A = − . Tính BC, S, h 5 c, R. √ √ √ 35 6
ĐS: BC = 14, S = 16 6, hc = 4 6, R = . 12 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
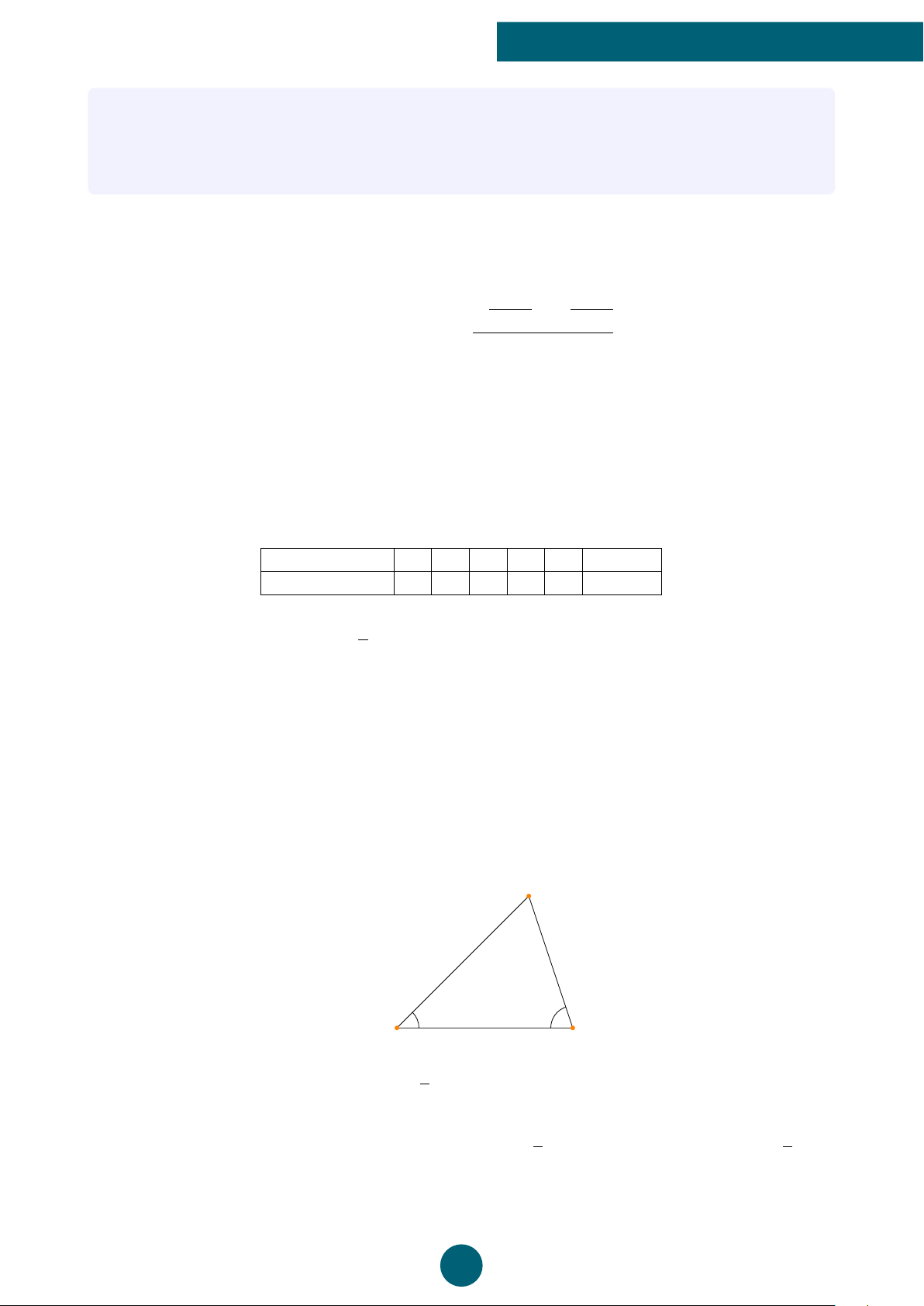
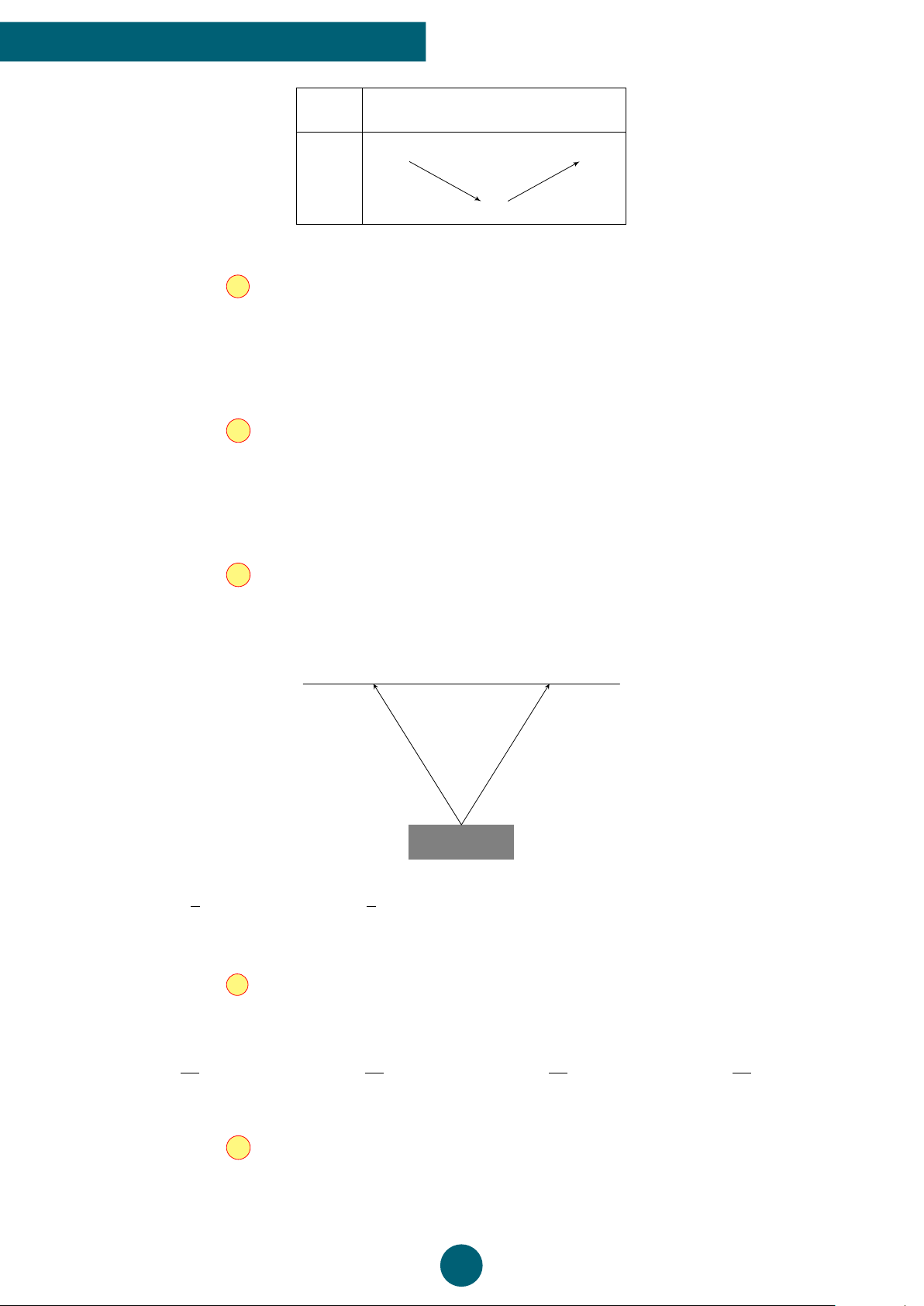
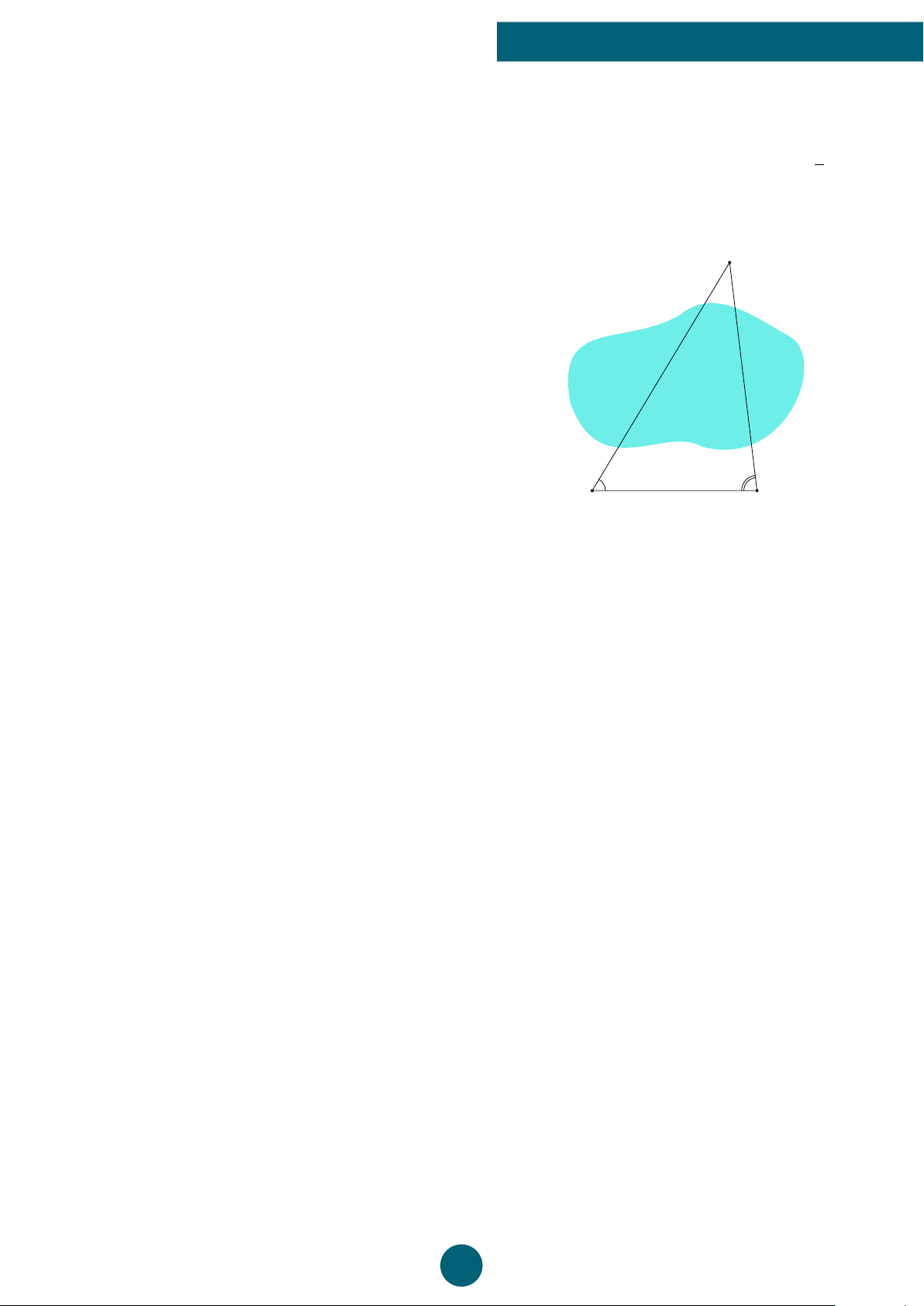
Bài 8: Tính khoảng cách từ điểm A trên bờ đến điểm C là gốc cây giữa đầm lầy. Biết AB = 40 m, ’ CAB = α = 45◦; ’
CBA = β = 70◦ (làm tròn kết quả đến 2 chữ số thập phân). C α β 40 A B ĐS: AC = 41,47 m. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 9: Cho hình bình hành ABCD và M là một điểm tùy ý. Chứng minh rằng: # » # » # » # » #» MA − MB + MC − MD = 0 . ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » # »
Bài 10: Tam giác ABC có AB = 3; BC = 4; b B = 45◦. Tính AB · BC. # » # » √ ĐS: AB · BC = −6 2. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT BÌNH PHÚ
Thời gian làm bài: 90 phút
Bài 1: Cho các tập hợp A = {2; 4; 6; 8}, B = {2; 3; 4; 5; 6; 7}, C = (2; 4). Tìm A ∩ B, A ∩ C, A ∪ B và A \ B.
ĐS: A ∩ B = {2; 4; 6}, A ∩ C = ∅, A ∪ B = {2; 3; 4; 5; 6; 7; 8}, A \ B = {8}. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 2: 2
a) Tính cos α, biết rằng sin α =
với 90◦ < α < 180◦. 3
b) Cho 4ABC có AB = 6, AC = 8, “
A = 60◦. Tính BC, diện tích và bán kính đường tròn ngoại tiếp tam giác ABC. √ √ 5 √ √ 2 39
ĐS: a) cos α = − ; b) BC = 2 13, S = 12 3, . 3 3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 3: Một cửa hàng điện lạnh dự định kinh doanh hai loại máy điều hòa, điều hòa hai chiều
và điều hòa một chiều với số vốn ban đầu không vượt quá 1,2 tỉ đồng (1 200 triệu đồng). Điều hòa 2 chiều Điều hòa 1 chiều Giá mua vào 20 triệu đồng/1 máy 10 triệu đồng/1 máy
Lợi nhuận dự kiến 3,5 triệu đồng/1 máy 2 triệu đồng/1 máy
Cửa hàng ước tính rằng tổng nhu cầu của thị trường sẽ không vượt quá 100 máy cả hai loại.
Nếu là chủ cửa hàng thì em cần đầu tư kinh doanh mỗi loại bao nhiêu máy đề lợi nhuận thu được là lớn nhất.
ĐS: Điều hòa 2 chiều:20 máy; Điều hòa 1 chiều: 80 máy. Lợi nhuận: 230 triệu đồng. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 4:
a) Vẽ parabol (P) : y = x2 − 4x + 3.
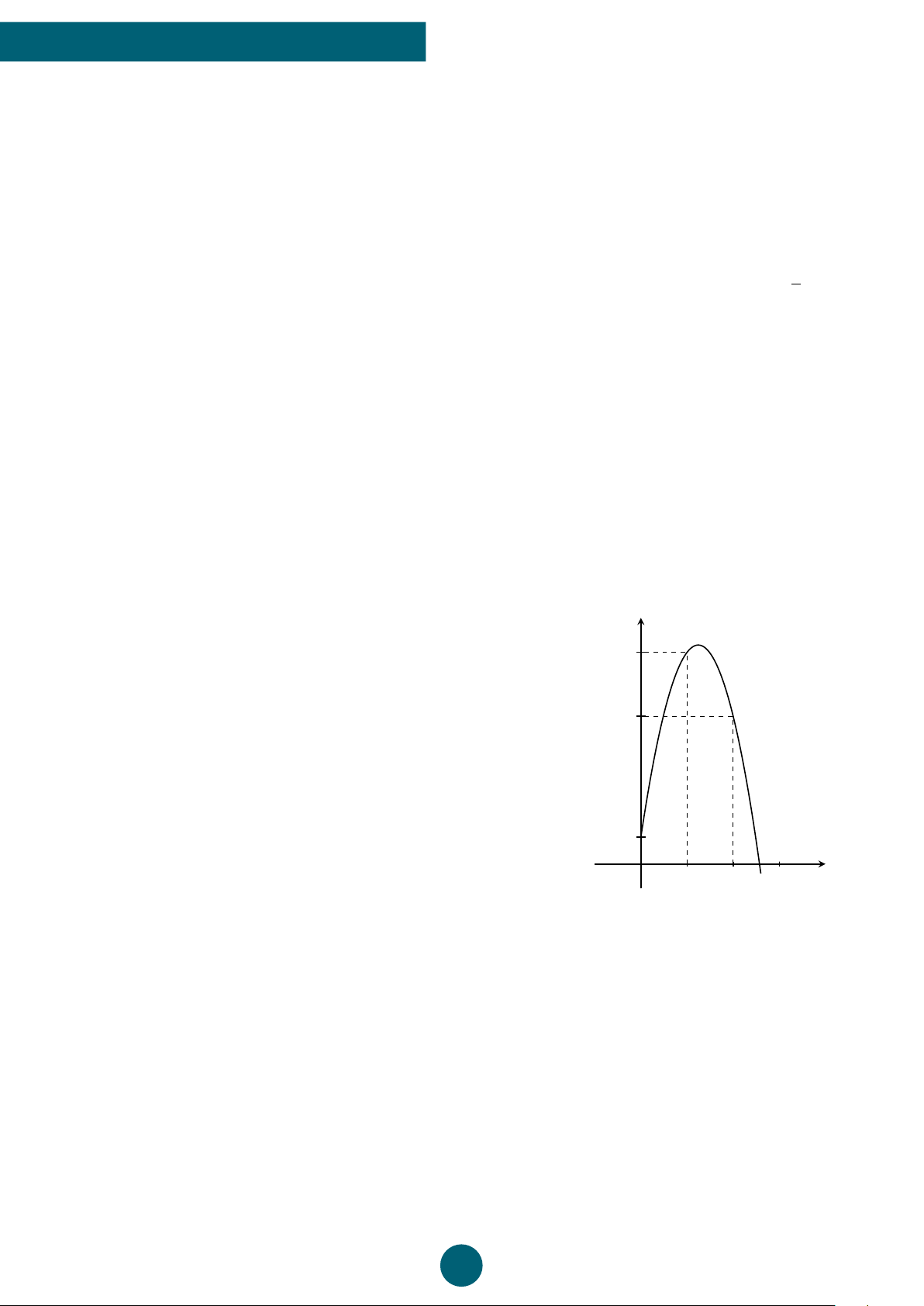
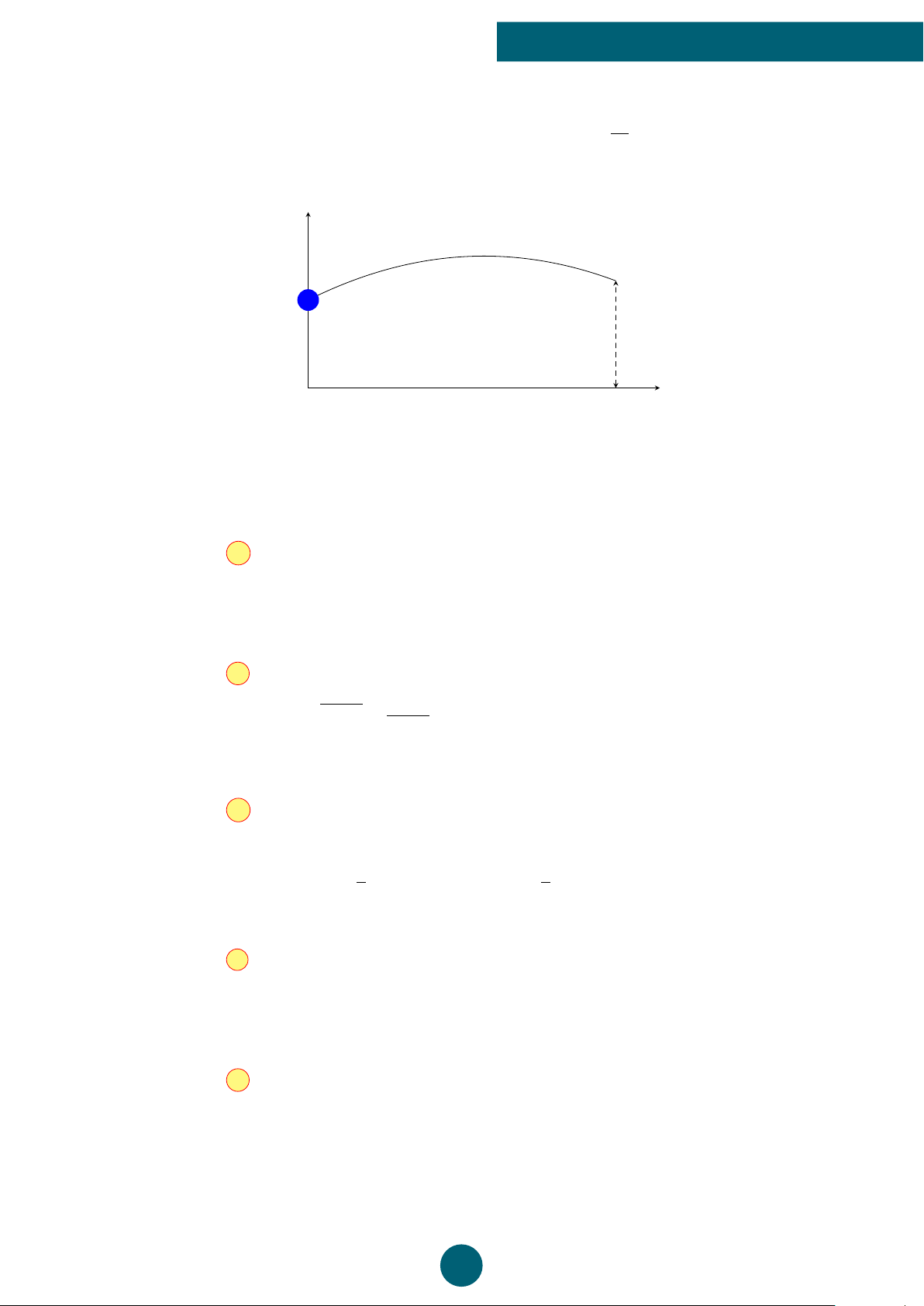
b) Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ
đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ Oxy, trong đó x
là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên và y là độ cao (tính bằng
mét) của quả bóng. Giả thiết rằng quả bóng được đá từ một nóc nhà cao 3 m. Sau đó 1
giây, quả bóng đạt độ cao 6 m và 4 giây sau khi đá lên, nó ở độ cao bằng với độ cao từ
vị trí xuất phát (xem hình vẽ bên dưới ). 16 GV: VŨ NGỌC HUY y 6 A 3 B O x 1 4
Xác định độ cao lớn nhất của quả bóng. ĐS: b) 7 m. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 5: Cho tam giác ABC vuông tại B, gọi M, N lần lượt là trung điểm c¸ủa các cạnh AB và AC. # » # » # »
a) Chứng minh rằng: BC = 2AN − 2AM. # » # »
b) Gọi H là điểm trên cạnh AC sao cho AH · AC = AB2. Chứng minh BH ⊥ AC. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 6: Một nhà nghiên cứu ghi lại số tuổi của 20 bệnh nhân. Kết quả thống kê ở bảng số liệu chi tiết sau đây: 21 17 20 18 20 17 15 13 15 20 15 12 18 17 15 16 21 15 12 18
a) Lập bảng phân bố tần số. Tính số tuổi trung bình của các bệnh nhân?
b) Tìm mốt và tứ phân vị của mẫu số liệu.
ĐS: a) Số tuổi trung bình: 16,75; mốt: 15; b) Q1 = 15, Q2 = 17, Q3 = 19. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ GIỮA HỌC KÌ I KHỐI 10/2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT BÌNH TÂN
Thời gian làm bài: 90 phút
PHẦN 1 - TRẮC NGHIỆM
Câu 1: Cho mệnh đề ∀x ∈ R : x3 + x > 0. Phủ định mệnh đề này là
A. ∃x ∈ R : x3 + x < 0.
B. ∃x ∈ R : x3 + x ≤ 0.
C. ∃x ∈ R : x3 + x = 0.
D. ∀x ∈ R : x3 + x ≤ 0. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √ 2 x − 2 − 3 khi x ≥ 2
Câu 2: Cho hàm số f (x) = x − 1 . Tính P = f (2) + f (−2). x2 + 2 khi x < 2 7 A. P = 3. B. P = 2. C. P = . D. P = 6. 2 ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 3: Cho hàm số bậc hai có bảng biến thiên như sau x −∞ 1 +∞ 21 y −∞ −∞
Hàm số này nghịch biến trên A. (1; +∞). B. (−∞; 21). C. (−∞; 1). D. (−21; +∞). ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . #»
Câu 4: Cho hai vectơ tùy ý, khác 0 . Khẳng định nào dưới đây đúng? #» #» #» #» #» #» A. a · b = | #» a || b |. B. a · b = −| #» a || b |. #» #» #» #» #» #» #» #» #» #» C. a · b = | #» a || b | sin( a , b ). D. a · b = | #» a || b | cos( a , b ). ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 5: Cho 3 điểm A, B, C phân biệt tùy ý. Khẳng định nào sau đây là đúng? # » # » # » # » # » # » # » # » # » # » # » # » A. AB − AC = BC. B. AB + BC = CA. C. AB − AC = CB. D. AB + AC = BC. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 GV: VŨ NGỌC HUY #» #» #» #» #»
Câu 6: Cho hai vectơ a , b tùy ý, khác 0 . Hai vectơ a , b được gọi là đối nhau nếu
A. Chúng ngược hướng.
B. Chúng cùng phương và cùng độ dài.
C. Chúng cùng hướng và cùng độ dài.
D. Chúng ngược hướng và cùng độ daì. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 7: Cho tam giác ABC. Chọn khẳng định đúng?
A. AB2 = AC2 + BC2 + 2AC · BC · tan A.
B. AB2 = AC2 + BC2 − 2AC · BC · cos C.
C. AB2 = AC2 + BC2 + 2AC · BC · cos C.
D. AB2 = AC2 + BC2 − 2AC · BC · cot A. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 8: Cặp số (x; y) nào sau đây là một nghiệm của bất phương trình 2022x − 2023y > 0? A. (−1; 0). B. (1; 1). C. (1; 0). D. (0; 1). ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 9: Phần tô đen trong hình bên là biểu diễn của tập hợp nào dưới đây? A B A. A ∪ B. B. A ∩ B. C. A \ B. D. B \ A. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 10: Thống kê số bàn thắng trong các trận đấu tại WORLD CUP 2022 tính đến ngày
20/11/2022 được ghi lại trong bảng tần số sau: Số bàn thắng 0 1 2 3 4 5 6 7 8 Số trận 5 6 12 5 1 4 1 1 1
Mốt của bảng số liệu là A. 2. B. 12. C. 1. D. 8. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ĐÁP ÁN 1. B 2. A 3. A 4. D 5. C 6. D 7. B 8. C 9. A 10. A PHẦN 2 - TỰ LUẬN Å 2 ò Bài 1: ĐS: D = −∞; 3 ý Lời giải. 2
Điều kiện −3x + 2 ≥ 0 ⇔ x ≤ . 3 √ Å 2 ò
Vậy tập xác định của hàm số y = −3x + 2 là D = −∞;
. . . . . . . . . . . . . . . . . . . . . . . . . . . 3 19 GV: VŨ NGỌC HUY
Bài 2: ý Lời giải. y y = x2 − 6x + 5 3 x O −4
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » # »
Bài 3: |AB + AD| theo a. ĐS: 13a ý Lời giải. B C A D # » # » # » √ Ta có |AB + AD| = |AC| = AC =
AB2 + BC2 = 13a. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 4: ĐS: ý Lời giải. A B C I # » # » # » # » # » # » # » # » # » #»
Ta có 2AB + AC = 2(AI + IB) + (AI + IC) = 3AI
(do 2IB + IC = 0 ). . . . . . . . . . . . . .
Bài 5: Trong mặt phẳng tọa độ Oxy, chọn điểm có tọa độ (0; y0) là điểm xuất phát thì phương −g · x2
trình quỹ đạo của cầu lông khi rời khỏi vợt là y =
+ tan(α) · x + y0; trong đó: 2 · v2 · cos2 0 α
• g là gia tốc trọng trường; α là góc phát cầu (so với phương ngang của mặt đất);
• v0 là vận tốc ban đầu của cầu; y0 là khoảng cách từ vị trí phát cầu đến mặt đất. 20 GV: VŨ NGỌC HUY y hỏng hợp lệ hỏng 1,524 m x O lưới phân cách điểm biên trong điểm biên ngoài 4 m Hình 10
Một người đang tập chơi cầu lông, có khuynh hướng phát cầu góc 30◦ (so với mặt đất) biết
cầu rời mặt vợt ở độ cao 0, 8 m so với mặt đất và vận tốc xuất phát của cầu là 8 m/s (bỏ qua
sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng thẳng đứng, lấy g là 9, 8
m/s2. Người ấy phát cầu như thế có bị xem là hỏng không? Vì sao? (biết điểm biên trong và
biên ngoài lần lượt cách O là 9, 58 m và 9, 94 m) y α = 30◦ y0 = 0,8 m −g · x2 y = + tan(α) · x + y◦ 2v2◦ · cos2 α x O điểm chạm đất ĐS: ý Lời giải.
Với g = 9,8 m/s2, góc phát cầu α = 30◦, vận tốc ban đầu v0 = 8 m/s, phương trình quỹ đạo √ 49 3 của cầu là y = − x2 + x + 0,8 = 0 ta được x 480 3 1 ≈ 6,81 và x2 ≈ −1,15.
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm
đất là 6,81 m. Vậy người chơi phát cầu là hỏng vì cầu chạm đất nằm ngoài khoảng biên trong
và biên ngoài. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 6: ĐS: ý Lời giải. C I M A B N 21 GV: VŨ NGỌC HUY Ta có # » # » 1 # » # » # » # » AM · CN = (AC + AB) · (CA + 2AB) 2 1 # » # » # » # » 1 # » # » =
AC · CA + AC · AB + AB · CA + AB2 2 2 1 √ √ =
· a 2 · a 2 · (−1) + 0 + 0 + a2 = 0. 2
Vậy AM ⊥ CN. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
——————Hết————- 22 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ GIỮA HỌC KÌ I KHỐI 10/2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT HÀN THUYÊN
Thời gian làm bài: 90 phút
PHẦN 1 - TRẮC NGHIỆM
Câu 1: Cho tam giác ABC, trọng tâm là G. Phát biểu nào sau đây là đúng? # » # » # » # » # » # » A. GA + GB + GC = 0.
B. |GA| + |GB| + |GC| = 0. # » # » # » # » # » # » C. |AB + BC| = AC. D. AB + BC = |AC|. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 2: Cho tam giác ABC có AB = c, AC = b, CB = a. Chọn mệnh đề sai ?
A. b2 = a2 + c2 − 2ac · cos B.
B. a2 = b2 + c2 − 2bc · cos A.
C. c2 = b2 + a2 − 2ba · cos C.
D. c2 = a2 + b2 − 2ab · cos B. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 3: Trong các tập hợp sau, tập hợp nào là con của tập hợp A = {1; 2; 3; 4; 5}? A. A3 = {4; 5}. B. A2 = {0; 1; 3}. C. A4 = {0}. D. A1 = {1; 6}. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 4:
Miền nghiệm của bất phương trình nào sau đây được biểu y
diễn bởi nửa mặt phằng không bị gạch trong hình vẽ sau? A. x − y ≥ 3. B. 2x − y ≥ 3. 3 O 2 C. 2x + y ≤ 3. D. 2x − y ≤ 3. x −3 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 5: Điểm kiểm tra học kì của một học sinh được thống kê trong bảng dữ liệu sau: Điểm
kiểm tra học kì của một học sinh được thống kê trong bảng dữ liệu sau: Môn học Toán Ngữ Văn Tiếng Anh Vật Lý Hóa Học Điểm 95 78 84 85 92
Phương sai và độ lệch chuẩn của bảng số liệu trên lần lượt sấp xỉ bằng A. 34.5 và 5.9. B. 84 và 81. C. 36.6 và 6.1. D. 6.1 và 37.2. ý Lời giải. 23 GV: VŨ NGỌC HUY
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 6: Cho tam giác ABC có “
A = 30◦, BC = 5. Tính bán kính đường tròn ngoại tiếp tam giác ABC. 10 √ A. 10. B. √ . C. 10 3. D. 5. 3 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 7: Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là
A. Độ lệch chuẩn. B. Số trung vị. C. Mốt. D. Số trung bình. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 8: Parabol y = 2x2 − 4x + 1 có đỉnh là A. I(2; 1). B. I(1; −1). C. I(−2; 17). D. I(−1; 7). ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 9:
Cho hàm số y = ax2 + bx + c có đồ thị như hình bên. Khẳng định nào y sau đây đúng?
A. a < 0, b < 0, c > 0.
B. a > 0, b < 0, c > 0.
C. a > 0, b > 0, c > 0.
D. a > 0, b < 0, c < 0. x O ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 10: Bất phương trình nào là bất phương trình bậc nhất hai ẩn? y A. + 10y ≥ 4. B. 3x + 4y2 ≤ 7. x
C. x3 + 2x + 4y > 100. D. x + 3y > 7. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 11: Tiền thưởng (triệu đồng) của cán bộ và nhân viên trong một công ty được cho trong
bảng dưới đây. Tính tiền thưởng trung bình Tiền thưởng 2 3 4 5 6 Cộng Tần số 5 15 10 6 4 40 A. 3625000 đồng. B. 3745000 đồng. C. 3715000 đồng. D. 3725000 đồng. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 GV: VŨ NGỌC HUY
Câu 12: Khoảng tứ phân vị của tập hợp số dữ liệu 4; 7; 9; 11; 12; 20 là A. 10. B. 11. C. 5. D. 9. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 13: Khẳng định nào sau đây là sai? sin x A. cot x = . B. tan x · cot x = 1. cos x 1 C. sin2 x + cos2 x = 1. D. cot2 x + 1 = . sin2 x ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ®x + 3y − 2 ≥ 0
Câu 14: Cho hệ bất phương trình
. Trong các điểm sau, điểm nào thuôc miền 2x + y + 1 ≤ 0
nghiệm của hệ bất phương trinh? A. Q(−1; 0). B. N(−1; 1). C. M(0; 1). D. P(1; 3). ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 15: # »
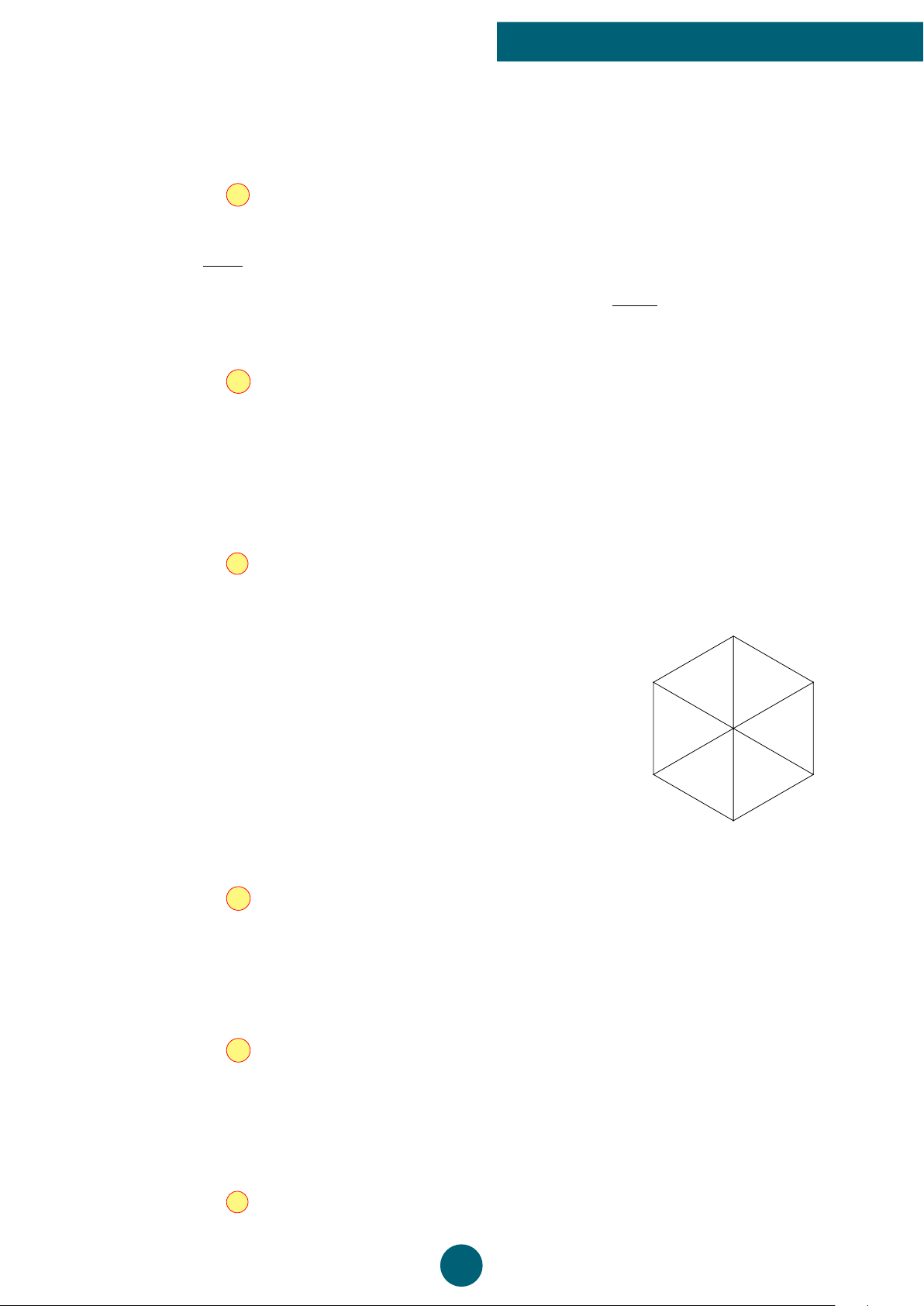
Cho lục giác đều ABCDEF tâm O (như hình vẽ ). Vectơ OB ngược A
hướng với vectơ nào sau đây? # » # » # » # » A. CD. B. EB. C. BC. D. OC. F B O E C D ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 16: Cho các tập hợp A = {x ∈ R | −5 ≤ x < 1} và B = {x ∈ R | −3 < x ≤ 3}. Tìm tập hợp A ∪ B. A. A ∪ B = [−5; 3]. B. A ∪ B = (−3; 1). C. A ∪ B = (−3; 3]. D. A ∪ B = [−5; 1). ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 17: Tam giác ABC có các cạnh a, b, c thỏa mãn điều kiện (a + b + c)(a + b − c) = 2ab. Tính số đo của góc C. A. 45◦. B. 90◦. C. 120◦. D. 30◦. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 GV: VŨ NGỌC HUY
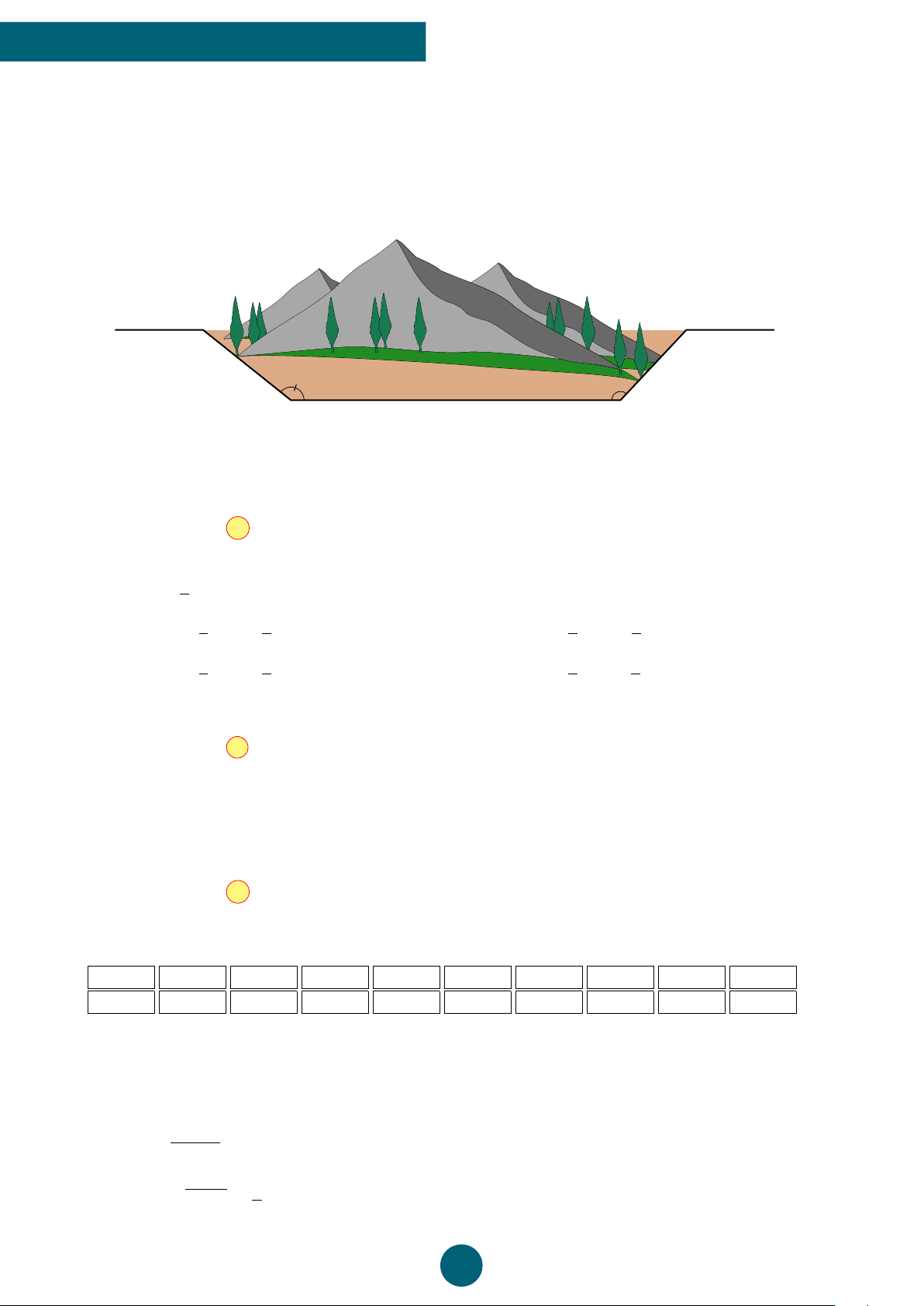
Câu 18: Do tránh núi, đường giao thông hiện tại phải đi vòng như hình dưới. Để rút ngắn
khoảng cách người ta dự tính làm đường hầm xuyên núi, nối thẳng từ A tới E. Hỏi độ dài
đường mới sẽ giảm bảo bao nhiêu kilômét so với đường cũ? (Làm tròn đến chữ số hàng đơn
vị). Biết AB = 10 km , BD = 8 km, DE = 14 km, góc ABD = 110◦, góc BDE = 130◦. E A 14 km 10 km 130◦ 110◦ 8 km D C A. ≈ 22 km. B. ≈ 24 km. C. ≈ 10 km. D. ≈ 12 km. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 19: Cho tam giác ABC, điểm I là trung điểm của AB, N là một điểm trên cạnh AC sao 1 cho N A =
NC. Gọi M là trung điểm của I N, mệnh đề nào sau đây là đúng? 2 # » 1 # » 1 # » # » 1 # » 1 # » A. AM = CA + AB. B. AM = AC + AB. 2 4 6 4 # » 1 # » 1 # » # » 1 # » 1 # » C. AM = CA + AB. D. AM = AB − AC. 6 4 6 4 ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 20: An chèo thuyền qua một dòng sông về hướng Đông với vận tốc 7,5 km/h. Dòng
nước chảy về hướng Bắc với vận tốc 3,6 km/h. Tính gần đúng vận tốc của thuyền. A. 8,3 km/h. B. 10,4 km/h. C. 7,9 km/h. D. 5,2 km/h. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ĐÁP ÁN 1. A 2. D 3. A 4. D 5. C 6. D 7. C 8. B 9. B 10. D 11. D 12. C 13. A 14. B 15. A 16. A 17. B 18. C 19. B 20. C PHẦN 2 - TỰ LUẬN
Bài 1: Tìm tập xác định của các hàm số sau: 3x a) y = . 1 − x2 √ 2 b) y = 3 − x + . x 26 GV: VŨ NGỌC HUY
ĐS: a) D = R \ {±1}; b) D = (−∞; 3] \ {0} ý Lời giải.
a) Hàm số xác định khi 1 − x2 6= 0 ⇔ x 6= ±1. Vậy D = R \ {±1}. ®3 − x ≥ 0
b) Hàm số xác định khi ⇔ 0 6= x ≤ 3. x 6= 0 Vậy D = (−∞; 3] \ {0}.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 − 2 cos2 x Bài 2: Chứng minh = sin x + cos x. ĐS: sin x − cos x ý Lời giải. Ta có 1 − 2 cos2 x sin x − cos x sin2 x + cos2 x − 2 cos2 x = sin x − cos x sin2 x − cos2 x = sin x − cos x
(sin x − cos x)(sin x + cos x) = sin x − cos x = sin x + cos x.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » # » # » # » # »
Bài 3: Cho 5 điểm A, B, C, D, E. Chứng minh rằng DE + AB + BC − DC = AE. ĐS: ý Lời giải. # » # » # » # » # » # » # » # » # » # »
Ta có DE + AB + BC − DC = DE − DC + AC = AC + CE = AE. . . . . . . . . . . . . . . . . . . . . . . .
Bài 4: Cho tam giác ABC có AB = 12 cm, BC = 13 cm, AC = 18 cm. Tính tích vô hướng # » # » 11 BA · CB. ĐS: 2 ý Lời giải. AB2 + BC2 − AC2 11
Áp dụng định lý cosin trong tam giác ABC có cos B = = − . 2AB · BC 312 # » # » # » # » 11
Ta có BA · CB = −BA · BC = −BA · BC · cos B =
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
Bài 5: Một của hàng buôn giày nhập một đôi với giá 60 (nghìn đồng). Cửa hàng ước tính rằng
nếu đôi giày được bán với giá x (nghìn đồng) thì mỗi tháng khách hàng sẽ mua (150 − x)
đôi. Hỏi cửa hàng bán một đôi giày với giá bao nhiêu thì thu được nhiều lãi nhất? ĐS: 105 (nghìn đồng) ý Lời giải.
Số tiền để nhập giày là: 60 · (150 − x) (nghìn đồng).
Số tiền mà khách mua là: x(150 − x) (nghìn đồng).
Do đó, số tiền lãi là x(150 − x) − 60(150 − x) = −x2 + 210x − 9000. 27 GV: VŨ NGỌC HUY
x(150 − x) − 60(150 − x) = −x2 + 210x − 9000 Ä ä = − x2 − 210x + 9000 Ä ä
= − x2 − 210x + 11025 − 2025 Ä ä
= − x2 − 210x + 11025 + 2025
= 2025 − (x − 105)2 ≤ 2025.
Dấu “= ”xảy ra khi x = 105.
Vậy số tiền lãi lớn nhất là 2025 (nghìn đồng) khi bán đôi giày với giá 105 (nghìn đồng). . 28 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT LÊ HỒNG PHONG
Thời gian làm bài: 90 phút
Bài 1: Cho các tập hợp A = (−∞; 2), B = (−3; +∞), C = (1; 4). Tìm (A ∩ B) ∪ C. ĐS: (−3; 4) ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x + y ≤ 4
Bài 2: Biểu diễn miền nghiệm của hệ bất phương trình x ≥ 1
trên mặt phẳng Oxy. ĐS: y ≥ 1 y 4 x + y+− 0 4 = = 0 1 −1y − 1 = 0 1 x x O 1 4 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 3: Cho parabol (P) : y = x2 + ax + b. Tìm a , b biết (P) có trục đối xứng là d : x = 2 và qua điểm A(0; 3). ĐS: a = −4; b = 3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ®x2 − 4x + 3 khi x ≤ 3
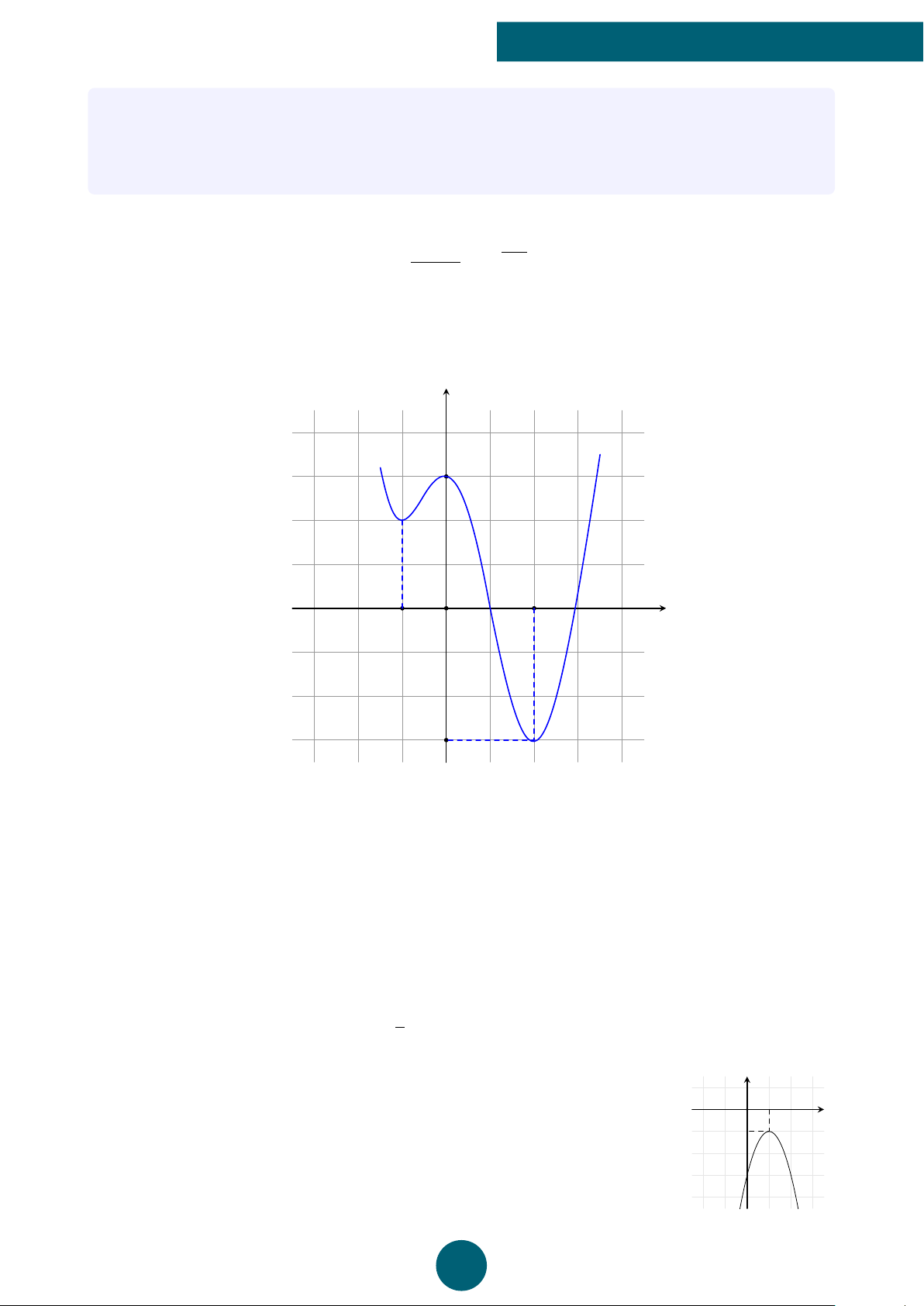
Bài 4: Cho hàm số f (x) =
− x2 + 10x − 21 khi x > 3.
a) Vẽ đồ thị hàm số f (x).
b) Tìm tất cả các giá trị của tham số m sao cho phương trình f (x) = m có 2 phân biệt. 29 GV: VŨ NGỌC HUY y 4 3 2 x O 1 3 5 7 −1 ĐS: a) ; b)m = −1 hoặc m = 4 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 5
Bài 5: Cho 90◦ < α < 180◦ và sin α =
. Tính cos α, tan α, cot α.
ĐS: cos α = − ; 13 13 12 5 tan α = − ; cot α = − 5 12 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 6: Cho hình thang ABCD có “ A = b B = 90◦, BC = a, AD = 2a. # » # » 1 # »
a) Chứng minh AC = AB + AD. 2
b) Gọi G là trong tâm tam giác ACD. Tính AB theo a biết AG ⊥ BD. ĐS: AB = a ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 7: Cho tam giác ABC nội tiếp đường tròn (O, R), phân giác trong góc A cắt đường tròn
tại D (D khác A). Biết “ A = 75◦, b
B = 45◦, tính tỉ số diện tích tam giác ABD và tam giác ACD. √3 ĐS: √2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 8: Điểm chuẩ vào lớp 10 của trường có điểm chuẩn cao nhất trong từng quận huyện ở
Thành phố Hồ Chí Minh năm 2021 − 2022 như sau 24,1 25,3 20 25 25,2 24,7 20,7 25,9 23,5 22,4 22,9 25,8 24 25,6 26,3 25,3 21,4 18,8 16 21,8 25,1 18,9
Tính số trung bình, tứ phân vị, mốt, độ lệch chuẩn, khoảng biến thiên, khoảng tứ phân vị và
tìm các giá trị bất thường của mẫu số liệu trên.
ĐS: a) x = 23,123; độ lệch chuẩn 2,737; ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT LÊ QÚY ĐÔN
Thời gian làm bài: 90 phút 2x + 3y ≤ 12
Bài 1: Biểu diễn miền nghiệm của hệ bất phương trình x ≥ 0 ĐS: y ≥ 0. y 4 2x + 3y+−12=0 x O 6 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √ 1
Bài 2: Tìm tập xác định D của hàm số f (x) = 4 − x + . ĐS: (−∞; 4] \ {0} x ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 3: Xét sự biến thiên của hàm số y = x2 − 4x + 5 trên (−∞; 2). ĐS: hàm số nghịch biến trên (−∞; 2) ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 4: Cho hàm số y = ax2 + bx + 3 có đồ thị (P). Tìm a, b biết (P) có đỉnh I(2; −1). ĐS: y = x2 − 4x + 3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 5: 31 GV: VŨ NGỌC HUY
Tại một khu hội chợ người ta thiết kế cổng chào có hình y
parabol hướng bề lõm xuống dưới. Giả sử lập một hệ
trục tọa độ Oxy sao cho một chân cổng đi qua gốc O
như hình vẽ (x và y tính bằng mét). Chân kia của cổng ở
vị trí (4; 0). Biết một điểm M trên cổng có tọa độ (1; 3). M 3
Hỏi chiều cao của cổng (vị trí cao nhất của cổng tới mặt đất) là bao nhiêu mét? x O 1 4 ĐS: 4 m ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » # » # » # »
Bài 6: Cho hình bình hành ABCD và điểm M tùy ý. Chứng minh MA + MC = MB + MD. ĐS: ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 7: Cho hình thang vuông ABCD có hai đáy AB = a, CD = b và chiều cao AD = h. Gọi
M là trung điểm cạnh BC. Biết rằng h2 = a2 + ab. Tính góc giữa AM và BD. ĐS: 90◦ ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » # » # »
Bài 8: Cho ba lực F1 = MA, F2 = MB, F3 = MC cùng tác động vào một vật tại điểm M và
vật đứng yên. Cho biết cường độ của F1, F2 đều bằng 50N và góc ’
AMB = 60◦. Tính cường độ √ của lực F3. ĐS: 50 3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 9: Theo dõi số vụ va chạm giao thông mỗi ngày tại một giao lộ, kết quả được ghi lại ở bảng sau Số vụ va chạm 0 1 2 3 4 5 Số ngày 4 9 2 7 3 1
Tính số trung bình, tứ phân vị và mốt của bảng kết quả trên.
ĐS: x = 1,96; Q1 = 1; Q2 = 1,5; Q3 = 7; M0 = 1 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT MARIE-CURIE
Thời gian làm bài: 90 phút √ x2 − x − 2
Bài 1: (1 điểm). Tìm tập xác định của hàm số f (x) = .
x2 − 5x + 6 ĐS: D = (2;+∞) \ {3}. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 2: (0.5 điểm). Cho hàm số y = f (x) xác định trên đoạn [−1; 5] và có đồ thị như hình vẽ. y 2 1 O 4 5 x −1 1 2 3 −1
Hãy xác định các khoảng đồng biến, nghịch biến của hàm số y = f (x) trên khoảng (−1; 5).
ĐS: Hàm số đồng biến trên (1; 2), hàm số nghịch biến trên các khoảng (−1; 1) và (2; 5). ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 khi x < −1
Bài 3: (0.5 điểm). Cho hàm số f (x) = x + 1 √
. Tính giá trị của biểu thức 3 x + 4 khi x ≥ −1 A = f (0) + f (−3). ĐS: A = 5 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
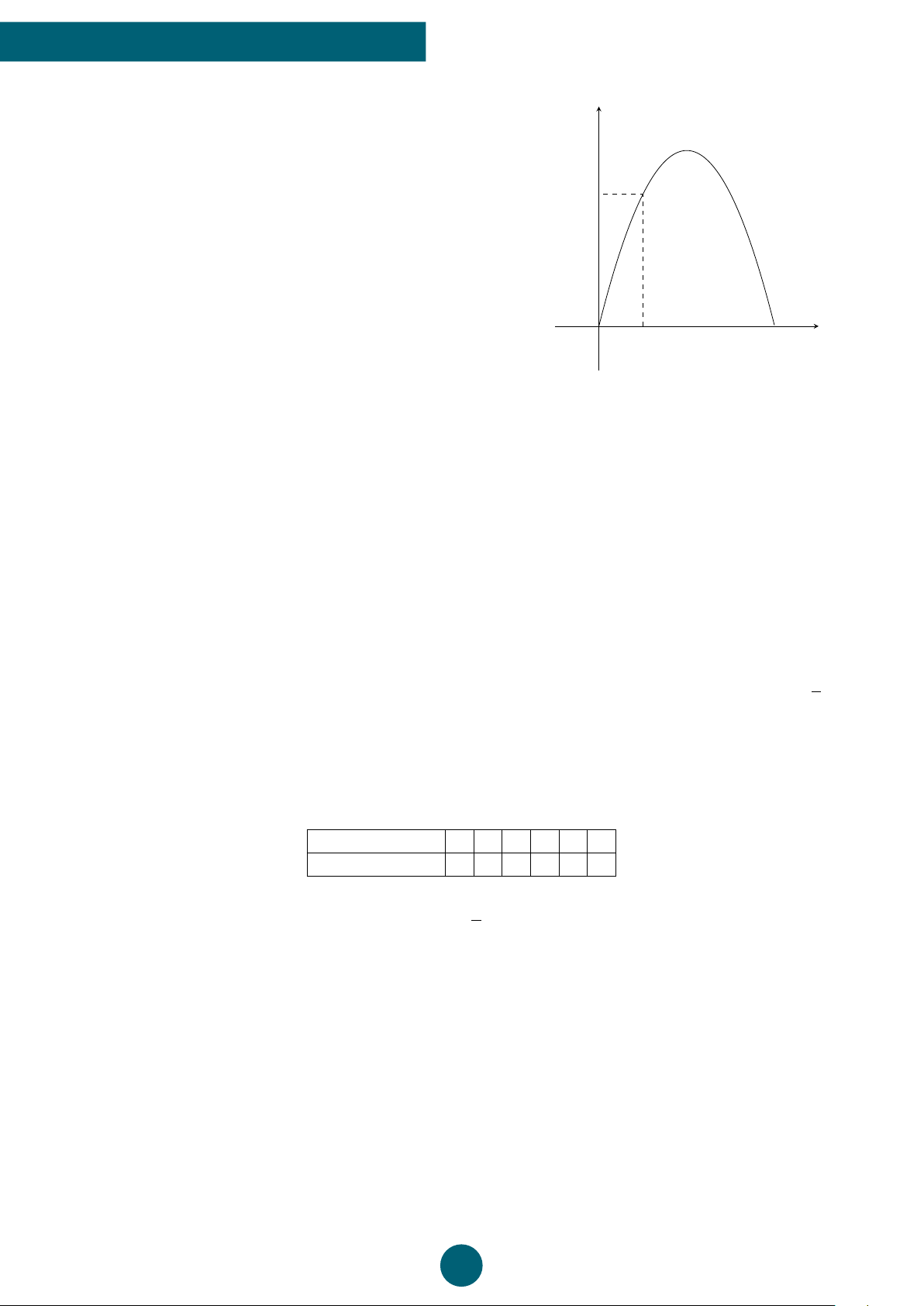
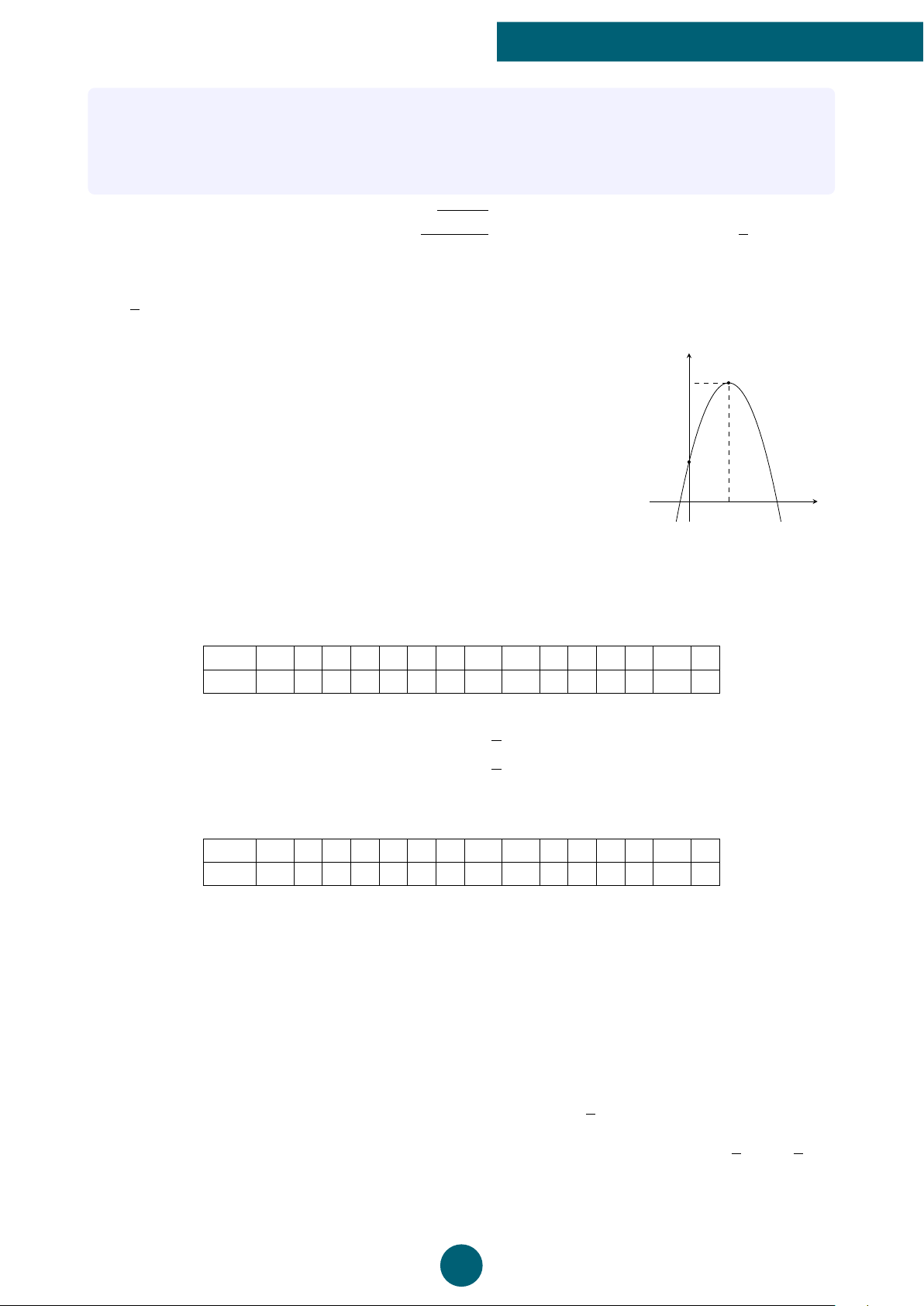
Bài 4: (3 điểm). Cho hàm số f (x) = ax2 + 2x + c với a 6= 0 có đồ thị (P) như hình vẽ bên. y a) Xác định dấu của a.
b) Xác định trục đối xứng của đồ thị (P). −1 x −3 O 1
c) Tìm giao điểm của (P) với hai trục tọa độ.
d) Lập bảng biến thiên của hàm số. −3
e) Tính giá trị T = f (2) − f (−4). −4
ĐS: a) a > 0 b) x = −1,
c) A(0, −3), B(−3, 0) và C(1, 0), e) T = 10 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 GV: VŨ NGỌC HUY
Bài 5: (1 điểm). Tuổi thọ của 30 bóng đèn thắp thử (đơn vị: giờ) được cho bởi bảng số liệu thống kê dưới đây 1180 1150 1190 1170 1180 1170 1160 1170 1160 1150 1190 1180 1170 1170 1170 1190 1170 1170 1170 1180 1170 1160 1160 1160 1170 1160 1180 1180 1150 1170
a) Lập bảng phân bố tần số.
b) Tính số trung bình của mẫu số liệu trên.
c) Tính mốt và trung bị của mẫu số liệu.
ĐS: a) b) x = 1170, c)Mo = 1170, Me = 1170 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 6: (3 điểm). Cho hình vuông ABCD tâm O có AB = 3. # » # » a) Tính BO · BC # » # » b) Tính |AO + AB|.
c) Gọi M là điểm trên cạnh CD thỏa mãn MD = 2MC và N là trung điểm của AM. Hãy # » # » # »
phân tích vectơ DN theo hai vectơ AC và BC. √ 3 10 # » 5 # » 1 # » ĐS: a) 9, b) , c)DN = − BC + AC 2 6 3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x ≥ 0
Bài 7: (1 điểm). Tìm miền nghiệm của hệ bất phương trình y ≤ 0 2x − 3y − 6 ≤ 0. ĐS: ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT NGUYỄN AN NINH
Thời gian làm bài: 90 phút
Bài 1: Cho 4 cặp số (−1; −3),(1; 2), (−2; 0), (4; −1) và cho bất phương trình 2x − 3y + 4 ≤ 0 (1).
Hãy liệt kê những cặp số là nghiệm của bất phương trình (1) và những cặp số không là
nghiệm của bất phương trình (1). ĐS:
• (1; 2), (−2; 0) là nghiệm của bất phương trình (1).
• (−1; −3), (4; −1) không là nghiệm của bất phương trình (1). ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 2:
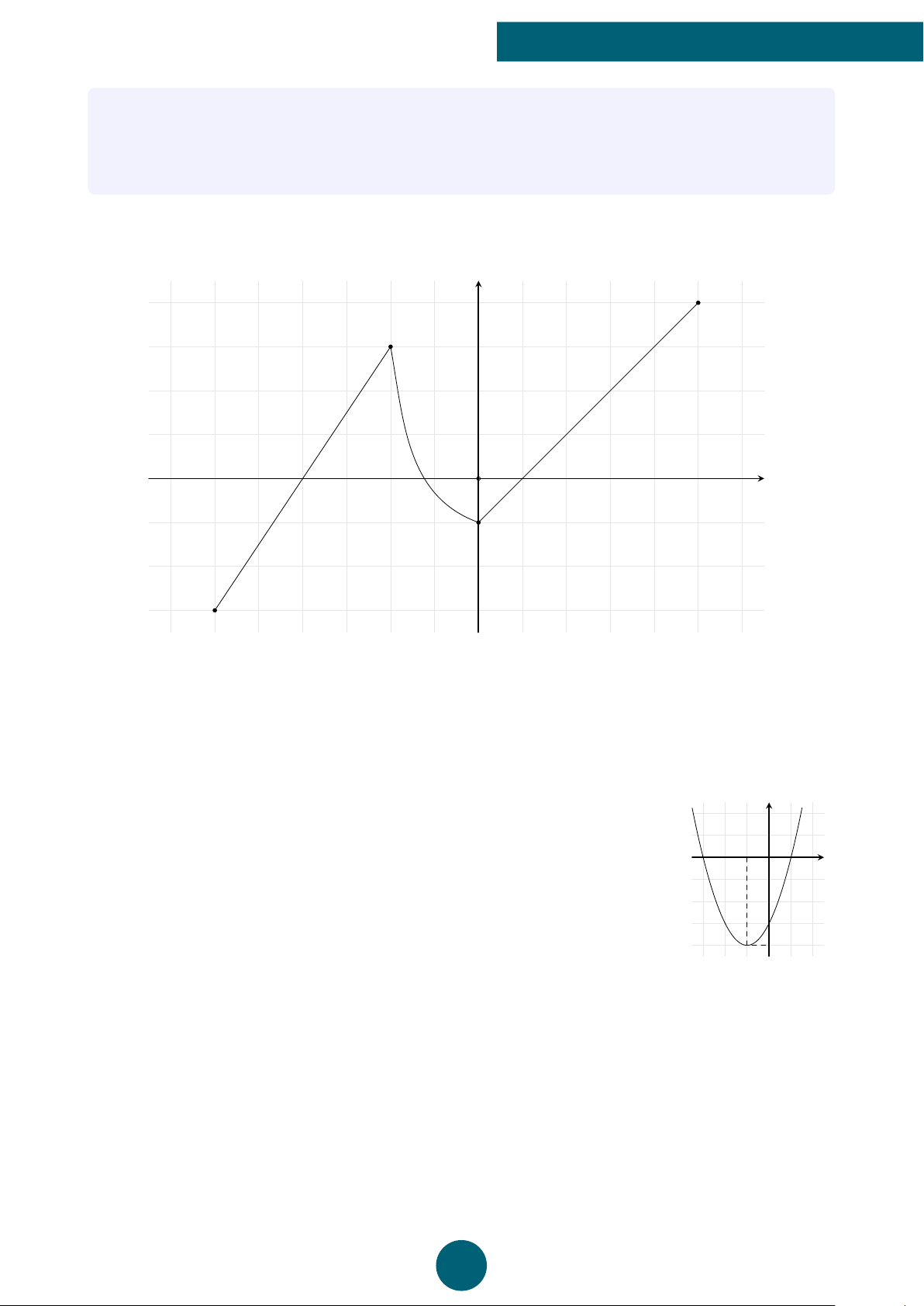
Cho hàm số y = f (x) có đồ thị như hình vẽ bên dưới y 6
a) Tìm tập xác định và tập giá trị của hàm số; 5
b) Tính f (−1), f (6). 1 1 O 4 − x 2 −1 1 6 −4 ĐS:
a) Tập xác định D = [−2; 6]; tập giá trị I = [−4; 6].
b) f (−1) = 1, f (6) = 2. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Bài 3: Cho hàm số y = −3x2 − 4x +
có đồ thị là parabol (P). 3
a) Tìm tọa độ đỉnh S và trục đối xứng của parabol (P);
b) Tìm tọa độ giao điểm của đồ thị (P) với trục hoành. ĐS: Å 2 ã 2 a) Đỉnh S − ; 3
và trục đối xứng x = − ; 3 3 Å 1 ã Å 5 ã b) A ; 0 và B − ; 0 . 3 3 35 GV: VŨ NGỌC HUY ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . #» # » # » # » #» #»
Bài 4: Cho hình bình hành ABCD tâm O. Rút gọn a = OA + BO − CD. ĐS: a = 0 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 # »
Bài 5: Cho tam giác ABC. Điểm I trên cạnh AC sao cho CI = CA. Phân tích BI theo 2 vecto 4 # » # » # » 3 # » # » AB và AC. ĐS: BI = AC − AB. 4 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √ Å 5 ò
Bài 6: Tìm tập xác định của hàm số f (x) = 5 − 3x.
ĐS: tập xác định D = −∞; . 3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 7: Cho hàm số bậc hai y = f (x) = ax2 + bx + c có f (2) = 11, f (−5) = 144 và đồ thị của
hàm số đi qua điểm A(0; −1). Xác định giá trị của các hệ số a, b, c.
ĐS: a = 5, b = −4,c = −1. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » # »
Bài 8: Cho tam giác ABC vuông tại A có AC = 2022a. Tính AC · CB theo a. # » # »
ĐS: AC · CB = −20222a2. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 9:
Từ vị trí A người ta quan sát một cây cao (hình vẽ). Biết AH = 4 m, HB = 20 m, ’ BAC = 45◦. Chiều cao của C
cây bằng bao nhiêu? (Độ dài cạnh lấy tròn đến phần
nguyên, góc lấy tròn đến phút). A 45◦ 4 H 20 B ĐS: 17,3 m. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 10: Trong một cuộc thi gói bánh vào dịp năm mới, mỗi đội chơi được sử dụng tối đa 20 kg
gạo nếp, 2 kg thị ba chỉ, 5 kg đậu xanh để gói bánh chưng và bánh tét. Để gói một cái bánh
chưng cần 0,4 kg gạo nếp, 0,05 kg thịt và 0,1 kg đậu xanh; để gói một cái bánh tét cần 0,6 kg
gạo nếp, 0,075 kg thịt và 0,15 kg đậu xanh. Mỗi cái bánh chưng nhận được 5 điểm thưởng,
mỗi cái bánh tét nhận được 7 điểm thưởng. Hỏi điểm thưởng cao nhất có thể đạt được là bao nhiêu? ĐS: 200 điểm. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT NGUYỄN CHÍ THANH
Thời gian làm bài: 90 phút Bài 1:
a) Biểu diễn miền nghiệm của bất phương trình x + 2y − 8 ≤ 0 trên mặt phẳng toạ độ Oxy. √ √ 4 − x + x + 2
b) Tìm tập xác định của hàm số y = f (x) = . x2 − 5x + 6
c) Vẽ đồ thị hàm số (P) : y = x2 − 2x + 2.
ĐS: b) D = [−2; 2) ∪ (2; 3) ∪ (3; 4]. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 2: Sản lượng lúa (tạ) của 40 thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng tần số sau: Sản lượng (x) 20 21 22 23 24 Tần số (n) 5 8 11 10 6 N = 40
Tìm năng suất lúa trung bình, tứ phân vị, mốt và phương sai của bảng số liệu trên.
ĐS: x = 22,1; Q1 = 21; Q2 = 22; Q3 = 23; Mo = 22; S2 ≈ 1,54. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 3:
a) Trên biển một con thuyền thả neo ở vị trí A. Một người đứng ở vị trí K trên bờ biển
muốn đo khoảng cách từ người đó đến con thuyền, người đó đã chọn một điểm H trên
bờ với K và đo được KH = 380 m, ’ AKH = 50◦, ’
AHK = 45◦. Khoảng cách KA từ người
đó đến con thuyền bằng bao nhiêu? (làm tròn đến hàng đơn vị) A 50◦ 45◦ H 380 m K √
b) Cho tam giác ABC có cạnh a = 2 3 cm, b = 2 cm và b
C = 30◦. Tính diện tích tam giác
ABC, bán kính đường tròn ngoại tiếp và nội tiếp tam giác ABC. √ √
ĐS: a) KA = 270 m; b) S =
3 cm2; R = 2 cm; r = −3 + 2 3 cm. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 GV: VŨ NGỌC HUY Bài 4: # »
a) Cho tứ giác ABCD. Gọi P, Q lần lượt là trung điểm của AD, BC. Chứng minh AB − # » # » CD = 2PQ. #» # » #» # » #» # »
b) Cho ba lực F 1 = MA, F 2 = MB và F 3 = MC cùng tác động vào một vật tại điểm M #» #»
và vật đứng yên. Cho biết độ lớn của F 1, F 2 đều là 200 N và ’ AMB = 60◦. Tìm độ lớn #» của lực F 3. #» √ ĐS: b) F = 200 3 N. 3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 5: Một phân xưởng cần sản xuất ra hai loại sản phẩm. Để sản xuất 1 kilogam sản phẩm
loại I cần sử dụng máy trong 20 giờ và tiêu tốn 2 kilogam nguyên liệu. Để sản xuất 1 kilogam
sản phẩm loại II cần sử dụng máy trong 10 giờ và tốn 3 kilogam nguyên liệu. Biết rằng 1
kilogam sản phẩm loại I thu lãi được 50000 đồng, 1 kilogam sản phẩm Ioại II thu lãi được
40000 đồng, có thể sử dụng máy tối đa 1200 giờ và có 300 kilogam nguyên liệu. Hỏi phân
xưởng đó nên sản xuất mỗi loại sản phẩm bao nhiêu kilogam để thu lãi cao nhất?
ĐS: Loại I: 15 kg; Loại II: 90 kg ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 6:
Khi một quả bóng được đá lên, nó sẽ bay theo quỹ đạo của h
một cung parabol trong mặt phẳng tọa độ Oth như hình bên,
trong đó t là thời gian kể từ khi quả bóng được đá lên (tính 8,6
bằng giây), h là độ cao (tính bằng mét) của quả bóng. Giả
sử quả bóng được đá lên từ độ cao 1,1 m. Sau 1 giây nó đạt
độ cao 8,6 m. Sau 2 giây, nó đạt độ cao 6 m. Hỏi độ cao lớn 6
nhất mà quả bóng đạt được là bao nhiêu? (làm tròn đến hàng phần chục). 1,1 O 1 2 3 t ĐS: 8,90 m ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT NGUYỄN CÔNG TRỨ
Thời gian làm bài: 90 phút ®x ≥ 2
Bài 1: Hãy liệt kê 2 nghiệm của hệ bất phương trình 2x + y − 8 ≤ 0. ĐS: (2; 4), (2; 3). ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
Bài 2: Tập xác định của hàm số y = √ . x − 2 ĐS: D = (2; +∞). ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » # »
Bài 3: Cho tam giác ABC đều cạnh a. Tính AB · BC. # » # » 1 ĐS: AB · BC = a2. 2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √
Bài 4: Qui tròn số ¯a =
5 = 2,236067977 . . . với độ chính xác đến hàng phần trăm. √ ĐS: ¯a = 5 = 2,24 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 5: Cho hai tâp hợp A = [−3; 4] và B = (−∞; 1). Tìm A ∩ B, A ∪ B, B \ A, CRA. ĐS: • A ∩ B = [−3; 1); • A ∪ B = (−∞; 4]; • B\A = (−∞; −3);
• CRA = (−∞; −3) ∪ (4; +∞). ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 6: Cho tam giác ABC có b B = 60◦, b
C = 45◦ và AB = 5. Tính độ dài cạnh AC (qui tròn kết
quả đến hàng phần trăm). ĐS: 6,12. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 7: Quy tròn số ¯a = 7216, 4 đến hàng đơn vị, ta được số gần đúng a = 7216. Tìm sai số
tuyệt đối ∆a và sai số tương đối δa của số gần đúng a. 1
ĐS: ∆a = 0,4; δa = . 18040 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 GV: VŨ NGỌC HUY Bài 8:
Cho parabol (P) : y = ax2 + bx + c, (a 6= 0) như hình vẽ. Xác định y
các hệ số a, b, c của (P) : y = ax2 + bx + c (a 6= 0). −2 −1 x O −1 −2
ĐS: a = 1, b = 2, c = −1. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . #»
Bài 9: Một vật trượt trên sàn dưới tác dụng của một lực không đổi F có độ lớn 20 N, hợp với #»
hướng chuyển động của vật một góc 30◦. Tính công A sinh ra bởi lực F biết vật di chuyển
được một quãng đường bằng 20 m. √ ĐS: 200 3 J. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 10: Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 ha. Nếu
trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì
cần 30 ngày công và thu được 50 triệu đồng. Bác Năm cần trồng bao nhiêu ha cho mỗi loại
cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày
công cho việc trồng ngô và đậu xanh.
ĐS: 6 ha ngô và 2 ha đậu xanh. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT NGUYỄN DU
Thời gian làm bài: 90 phút √1 − 3x Å 1 ò
Bài 1: Tìm tập xác định của hàm số y = . ĐS: D = −∞; \ − 5 . x + 5 3
Bài 2: Hàm số y = (3 − 4m)x − 2 nghịch biến trên R với giá trị nào của tham số m? ĐS: 3 m > . 4 Bài 3: y
Hàm số y = ax2 + bx + 2 (a 6= 0) có đồ thị như hình bên. Hãy xác
định các giá trị a và b. 6 2 O x 2
ĐS: a = −1 và b = 4.
Bài 4: Nhà sản xuất công bố chiều dài và chiều rộng của một tấm thép hình chữ nhật là
100 ± 0,4 cm và 60 ± 0,4 cm. Tính diện tích của tấm thép.
ĐS: 6 000 ± 64,16 cm2.
Bài 5: Kết quả bài thi môn Toán của các bạn học sinh tổ 1 và tổ 2 cho ở bảng sau Tổ 1 7 7 6 8 9 7 7 10 9 8 6 8 7 8 9 Tổ 2 10 9 8 9 5 7 8 6 10 7 8 8 9 10 6
Hãy tìm số trung bình, tứ phân vị và mốt của kết quả bài thi ở mỗi tổ theo mẫu số liệu trên. Tổ 1:
x = 7,7 (Q1; Q2; Q3) = (7; 8; 9) Mo = 7
ĐS: Tổ 2: x = 8,0 (Q1;Q2;Q3) = (7;8;9) Mo = 8.
Bài 6: Kết quả bài thi môn Toán của các bạn học sinh tổ 1 và tổ 2 cho ở bảng sau Tổ 1 7 7 6 8 9 7 7 10 9 8 6 8 7 8 9 Tổ 2 10 9 8 9 5 7 8 6 10 7 8 8 9 10 6
Hãy tìm phương sai và độ lệch chuẩn kết quả bài thi của mỗi tổ từ đó so sánh độ ổn định kết Tổ 1: S2 = 1,26 S = 1,12 quả bài thi của 2 tổ.
ĐS: Tổ 2: S2 = 2,27 S = 1,51.
Bài 7: Tính góc lớn nhất của tam giác ABC biết các cạnh lần lượt là a = 8, b = 12 và c = 5. ĐS: ’ ABC ≈ 133◦25’57”. # » 1 # » # » # »
Bài 8: Cho tam giác ABC và các điểm M, N thỏa mãn MB =
BC, AN = 3NB. Hãy biểu thị 2 # » # » # » # » 1 # » 1 # »
véc-tơ MN theo hai véc-tơ AB và BC. ĐS: MN = − AB + BC. 4 2 Bài 9: 41 GV: VŨ NGỌC HUY #» # » #» # » #» # » #» A Cho ba lực F F1
1 = M A, F2 = MB và F 3 = MC cùng tác #»
động vào một vật tại điểm M và vật đứng yên. Cho biết F3 #» #» #» F2 độ lớn của F C M
1, F2 đều bằng 90 N và góc ’ AMB = 60◦. Tính #» độ lớn của lực F 3. B #» √ ĐS: F = 90 3 N. 3 # » # »
Bài 10: Cho hình chữ nhật ABCD có tâm O và cho AB = 3a, AD = 4a. Tính AB · AO. ĐS: # » # » 9a2 AB · AO = . 2 42 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT NGUYỄN HỮU TIẾN
Thời gian làm bài: 90 phút
Bài 1: Tìm tập xác định của các hàm số sau √ x − 77 8 − 4x a) y = √ . b) y = . √ 6 − 2x 1 − x − 2 ĐS: a) D = (−∞; 3) b) D = 2 .
Bài 2: Cho hàm số y = −x2 + 2x + 2.
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số.
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [2; 3]. y 3 2 ĐS: a) O x 1 b) max y = 2 và min y = −1. [2;3] [2;3]
Bài 3: Xác định parabol (P) : y = ax2 + bx + 5 biết (P) có trục đối xứng x = 2 và (P) cắt trục
hoành tại điểm có hoành độ bằng −1.
ĐS: (P) : y = −x2 + 4x + 5.
Bài 4: Thống kê thời gian học tập tại nhà của 28 học sinh ngẫu nhiên, ta được kết quả như sau Thời gian (h) 0 1 2 3 4 5 6 7 Số học sinh 2 4 8 5 5 3 1 0
a) Tính thời gian trung bình học tập tại nhà của 28 học sinh này. (Kết quả lấy 2 chữ số thập phân).
b) Tìm số trung vị của mẫu số liệu trên. ĐS: a) x = 2,7 h b) Mo = 2,5 h.
Bài 5: Cho hình vuông ABCD có tâm O và cạnh AB = a. Gọi M là trung điểm của cạnh BC
và K là một điểm tùy ý. # » # » # » # » # »
a) Chứng minh rằng K A + KB + KC + KD = 4KO. # » # » b) Tính AB + AC. # » # » √ ĐS: b) AB + AC = 4a 5. 3
Bài 6: Cho tam giác ABC có cạnh AB = 4a, AC = 5a và cos A = . 5 # » # »
a) Tính tích vô hướng AB · AC. # » # »
b) Gọi H là trực tâm của 4ABC và M là trung điểm của cạnh BC. Tính MH · MA. 43 GV: VŨ NGỌC HUY # » # » # » # » ĐS: a) AB · AC = 12a2 b) MH · MA = 17a2.
Bài 7: Cho tam giác ABC có b = 8 cm, c = 5 cm và “ A = 60◦.
a) Tính độ dài đường cao ha của tam giác ABC.
b) Tính bán kính R của đường tròn ngoại tiếp tam giác ABC. √ √ 20 3 7 3 ĐS: a) ha = cm b) R = cm. 7 3 Bài 8: A
Người ta định lát gạch tổ ong trên mảnh đất hình tứ giác ABCD
như mô hình bên cạnh. Biết rằng AB = 6 m, BC = CD = 4 m, D ’ ABC = 100◦, ’
BCD = 120◦ và giá lát gạch là 400 nghìn đồng trên 6
một mét vuông bao gồm cả công thợ. Hỏi người ta cần bao nhiêu 4
tiền để lát gạch cả mảnh đất đó? B C 4 1 √ Ä ĐS: T =
24 3 sin 70◦ + 16 sin 120◦ä · 400 000 ≈ 10 583 739 đồng. 2 44 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG NGUYỄN KHUYẾN & LÊ THÁNH TÔNG
Thời gian làm bài: 90 phút
Bài 1: (1 điểm). Cho A = {0; 2; 4; 6; 8}, B = {0; 3; 6; 9} và E = {0; 1; 2; 3; 4; 5; 6; 8; 9}. Xác định
các tập hợp sau: A ∩ B, A ∪ B, A \ B, CEB.
ĐS: A ∩ B = {0; 6}, A ∪ B = {0; 2; 3; 4; 6; 8; 9}, A \ B = {2; 4; 8}, CEB = {1; 2; 4; 5; 8}. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 2: (1 điểm). Cho bất phương trình bậc nhất hai ẩn 2x − 3y + 5 ≤ 0 và x + 2y − 3 ≥ 0.
Cặp số nào sau đây thỏa mãn đồng thời cả hai bất phương trình đã cho? Vì sao? a) (1; 3). b) (−2; 2).
ĐS: a)Thỏa mãn; b) Không thỏa mãn ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 3: (1 điểm). Cho hình bình hành ABCD có ’
ABC = 120◦ và AB = 2, AD = 4. Tính tích # » # » # » # » vô hướng AB · AD ĐS: AB · AD = 4 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 4: (1 điểm). Gọi I là trung điểm đoạn thẳng AB cho trước và O là điểm tùy ý. Chứng # » # » # » minh rằng OA + OB = 2OI. ĐS: ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 5: (1 điểm). Điểm kiểm tra thường xuyên môn Toán của các học sinh tổ 1 trong lớp 10A
được thống kê lại ở bảng sau Điểm 5 6 7 8 10 Số học sinh 1 4 3 6 1
Hãy tìm số trung vị và số trung bình của mẫu số liệu trên. ĐS: Me = 7 và x = 7,2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 6: (1 điểm). √2
a) Tìm tập xác định của hàm số y = f (x) = x3 + . x2 − 1 √ 1
b) Tìm các giá trị của tham số m để tập xác định của hàm số y = g(x) = x − 1 + √m − x
chứa đúng năm số nguyên.
ĐS: a) D = R \ {−1; 1}; b) 5 < m ≤ 6. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 GV: VŨ NGỌC HUY
Bài 7: (1.5 điểm). Cho parabol (P) : y = f (x) = x2 − 2x + m.
a) Chỉ ra đỉnh và các khoảng đồng biến, nghịch biến của parabol (P).
b) Tìm m để parabol (P) cắt trục hoành tại hai điểm phân biệt có hoành độ x1, x2 thỏa x2 + x2 = 10. 1 2
ĐS: a) Đồng biến trên (1; +∞) và nghịch biến (−∞; 1); Đỉnh I(1; m − 1) b) m = −3. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 8: (1.5 điểm).
a) Cho tam giác ABC có AB = 3a, AC = 5a và BC = 7a. Chứng minh rằng tam giác ABC có một góc tù. b) Cho tam giác ABC có ’ ABC = 108◦, ’
ACB = 58◦, BC = 42. Tính chiều cao hạ từ A của tam giác ABC. 1 ĐS: a) cos ’ ABC = − . b) h = AH ≈ 140. 2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 9: (1 điểm). Một phần công viên của thị trấn X có hình dạng là tam giác đều ABC cạnh
bằng 12m. Người ta muốn sử dụng phần diện tích đất hình chữ nhật MNPQ (có M, N thuộc
cạnh BC; P, Q lần lượt thuộc cạnh AB, AC) để xây dựng một hồ nước. Tìm diện tích lớn nhất
của hình chữ nhật MNPQ đó. √
ĐS: Diện tích lớn nhất của hình chữ nhật là 18 3 đạt được khi BM = 3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT NGUYỄN THÁI BÌNH
Thời gian làm bài: 90 phút √
Câu 1: Tập xác định D của hàm số y = 3x − 1 là ï 1 ã Å 1 ã A. D = ; +∞ . B. D = ; +∞ . C. D = [0; +∞). D. D = (0; +∞). 3 3
Câu 2: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? A. x + 3y ≤ 2.
B. (3x − y)(x + 2y) ≥ 5. C. y3 − 2 ≤ 0. D. x2 + y > 3. #» #» #»
Câu 3: Cho a và b là hai vectơ đều khác vectơ 0 và có tích vô hướng bằng 0. Góc giữa hai vectơ này bằng A. 0◦. B. 60◦. C. 90. D. 180◦.
Câu 4: Cho góc α là góc nhọn. Mệnh đề nào sai trong các mệnh đề sau?
A. cot α > 0.
B. cos α > 0.
C. sin α > 0.
D. tan α < 0.
Câu 5: Cho số đúng a = 1, 49 và số gần đúng a = 1, 5. Sai số tuyệt đối của số gần đúng a là A. 0,1. B. 0,05. C. 0,01. D. 0,5.
Câu 6: Hàm số nào sau đây là hàm số bậc hai?
A. y = 2022x3 − 5x + 1.
B. y = 2x2 + x − 2018. 2x − 1 C. y = . D. y = −x4 + 2. x + 3 # » # » # »
Câu 7: Cho hình bình hành ABCD. Tìm vectơ AB + AD − AC. # » # » # » #» A. 2AC. B. −AC. C. AC. D. 0 . ®3x + 4y − 1 > 0
Câu 8: Cặp số (x; y) nào sau đây không là nghiệm của hệ bất phương trình ? x + 2y − 3 ≤ 0 A. (3, 0). B. (−1; 2). C. (0; 0). D. (2; 0).
Câu 9: Cho hàm số f (x) = −3x2 + 2x − 1. Tính f (2)? A. f (2) = −6. B. f (2) = −9. C. f (2) = 0. D. f (2) = 2.
Câu 10: Điểm nào sau đây thuộc đồ thị hàm số y = −x2 − 2x + 1. A. I(2; 2). B. M(1; 0). C. M(−3; 6). D. M(0; 1). #»
Câu 11: Từ hai điểm phân biệt A, B xác định được bao nhiêu vectơ khác 0 ? A. 4. B. 2. C. 1. D. 3.
Câu 12: Cho các điểm phân biệt A, B, C. Đẳng thức nào sau đây đúng? # » # » # » # » # » # » # » # » # » # » # » # » A. AB = BC + CA. B. AB = AC + CB. C. AB = BC + AC. D. AB = CA + CB.
Câu 13: Tọa độ giao điểm của parabol (P) : y = x2 + 5x + 4 với trục hoành:
A. (0; −1); (−4; 0).
B. (−1; 0); (0; −4).
C. (−1; 0); (−4; 0).
D. (0; −1); (0; −4).
Câu 14: Cho tam giác ABC có a = 5, A = 60◦. Tính bán kính đường tròn ngoại tiếp tam giác ABC. √ √ 5 5 3 10 3 √ A. . B. . C. . D. 5 3. 3 3 3 47 GV: VŨ NGỌC HUY
Câu 15: Cho hàm số y = ax2 + bx + c(a 6= 0) có đồ thị (P). Tọa độ đỉnh của (P) là Å b ∆ ã Å b ∆ ã Å b ∆ ã Å b ∆ ã A. I − ; − . B. I − ; . C. I ; . D. I − ; − . 2a 4a 2a 4a 2a 4a a 4a
Câu 16: Bảng thống kê số lớp và số học sinh theo từng khối ở một trường THPT. Khối 10 11 12 Số lớp 12 13 12 Số học sinh 385 553 470
Hiệu trưởng trường đó cho biết sĩ số học sinh của mỗi lớp lớn hơn 30 và không vượt quá 40
em. Khối lớp bị thống kê sai là A. Khối 10. B. Khối 11. C. Khối 10,12. D. Khối 12.
Câu 17: Cho tam giác ABC có BC = a, AC = b và AB = c. Khẳng định nào sau đây đúng? b2 + c2 + a2 b2 + c2 − a2 A. cos A = . B. cos A = . bc 2bc b2 + c2 − a2 b2 + c2 + a2 C. cos A = . D. cos A = . bc 2bc
Câu 18: Cho bảng biến thiên của hàm số y = f (x) x −∞ 1 +∞ +∞ +∞ y 1
Hàm số nào sau đây có bảng biến thiên như trên? A. y = −x2 + 2x + 1. B. y = x2 + 1. C. y = −x2 − 1. D. y = x2 − 2x + 2. Câu 19:
Cho hàm số y = f (x) xác định trên đoạn [−3; 2] và có đồ thị y
như hình vẽ bên. Khẳng định nào dưới đây là khẳng định đúng? 4
A. Hàm số nghịch biến trên khoảng (−3; −1).
B. Hàm số nghịch biến trên khoảng (1; 2). 2
C. Hàm số nghịch biến trên khoảng (−1; 1).
D. Hàm số đồng biến trên khoảng (−1; 1). − − x 3 1 O 1 2
Câu 20: Cho tập hợp A = {x ∈ N | x < 4}. Tìm mệnh đề đúng? A. A = {0; 1; 2; 3}. B. A = {1; 2; 3}. C. A = {0; 1; 2; 3; 4}. D. A = {4}.
Câu 21: Cặp số nào sau đây là nghiệm của bất phương trình 2x − y + 1 < 0? A. (3; 5). B. (0; −1). C. (1; 4). D. (2; −1).
Câu 22: Cho tập hợp A = {x ∈ R | 2x + 6 ≥ 0}. Tìm mệnh đề đúng? A. A = (−∞; −3]. B. A = (−∞; −3). C. A = [−3; +∞). D. A = (−3; +∞).
Câu 23: Số quy tròn của số gần đúng a = 2, 235 với độ chính xác d = 0, 002 là A. 2,2. B. 2,23. C. 2,235. D. 2,24. 48 GV: VŨ NGỌC HUY Câu 24:
Cho miền nghiệm (phần không gạch y
chéo) của bất phương trình bậc nhất
hai ẩn như hình vẽ. Bất phương trình 4
nào sau đây nhận miền nghiệm trên làm tập nghiệm? 3 A. 2x + 3y < 8. B. 3x + 2y > 8. C. 3x + 2y < 8. D. 2x + 3y > 8. 2 1 x −3 −2 −1 O 1 2 3 4
Câu 25: Tam giác ABC có a = 8, c = 3, b
B = 60◦. Độ dài cạnh b bằng bao nhiêu? √ √ A. 49. B. 97. C. 61. D. 7.
Câu 26: Cho hai tập hợp A = [−5; 3), B = (1; +∞). Khi đó A ∩ B là tập nào sau đây? A. (1; 3]. B. (1; 3). C. [5; +∞). D. [−5; 1].
Câu 27: Tỷ lệ phần trăm về hạnh kiểm của học sinh trường A được biểu diễn bởi biểu đồ sau: Trung bình 5% Khá Khá Tốt 43.8% Trung bình Yếu Tốt 49.1%
Số học sinh đạt hạnh kiểm yếu chiếm bao nhiêu phần trăm? A. 3, 1%. B. 4%. C. 3%. D. 2, 1%. Câu 28:
Parabol dưới đây là đồ thị của hàm số nào? y
A. y = −x2 − 2x + 1. B. y = x2 − 2x − 1. C. y = x2 + 2x − 1.
D. y = −2x2 + 2x − 1. −2 −1 x O −1 −2 Câu 29: 49 GV: VŨ NGỌC HUY
Phần không tô đậm trong hình vẽ dưới đây (không chứa y
biên), biểu diễn tập nghiệm của hệ bất phương trình nào
trong các hệ bất phương trình sau? ®x − y > 0 ®x − y < 0 A. . B. . 2x − y < 1 2x − y < 1 1 ®x − y < 0 ®x − y > 0 C. . D. . 2x − y > 1 2x − y > 1 x O 1
Câu 30: Cho tam giác ABC có A = 60◦, AB = 7 cm, AC = 5 cm. Tính diện tích tam giác đã cho. √ √ √ √ 35 3 35 3 5 3 35 3 A. cm2. B. cm2. C. cm2. D. cm2. 2 4 4 2
Câu 31: Cho hình bình hành ABCD, giao điểm của hai đường chéo là O. Tìm mệnh đề sai trong các mệnh đề sau: # » # » # » # » # » # » A. CO − OB = BA. B. AB − BC = DB. # » # » # » # » # » # » # » #»
C. DA − DB = OD − OC. D. DA + DB + DC = 0 . Câu 32:
Cho hàm số f (x) = ax + b có đồ thị như hình vẽ bên. Khẳng định y nào sau đây là đúng
A. f (1) > f (−2023).
B. f (2022) < f (2023).
C. f (2022) > f (2023). D. f (1) < f (2023). 2 x O 2
Câu 33: Cho hai tập hợp A = [−2; 3) và B = [m; m + 5). Tìm tất cả các giá trị thực của tham số m đề A ∩ B 6= ∅.
A. −7 < m ≤ −2. B. −2 < m ≤ 3. C. −7 < m < 3. D. −2 ≤ m < 3. Câu 34:
Hai trạm quan sát ở hai thành phồ Đà Nẵng và Nha Trang Vệ tinh
đồng thời nhìn thấy một vệ tinh với góc nâng lần lượt là 75◦
và 60◦. Vệ tính cách trạm quan sát tại thành phố Đà Nẵng 637
km. Khoảng cách giữa hai thành phố gần với giá trị nào sau đây? 75◦ A. 510 km. B. 530 km. C. 520 km. D. 540 km. 60◦ Đà Nẵng Nha trang
Câu 35: Cho hàm số y = −2x2 + bx + c, có đồ thị là parabol (P) và có đỉnh I(1; 3). Khi đó b + c bằng A. 3. B. 4. C. 6. D. 5.
Câu 36: Ông An dự định trồng lúa và khoai lang trên một mảnh đất có diện tích 10 ha. Nếu
trồng 1 ha lúa thì cần 10 ngày công và thu được 20 triệu đồng. Nếu trồng 1 ha khoai lang thì
cần 30 ngày công và thu được 30 triệu đồng. Biết rằng, Ông An chỉ có thể sử dụng không quá 50 GV: VŨ NGỌC HUY
180 ngày cho công việc tròng lúa và khoai lang. Số tiền nhiểu nhất Ông An thu được từ trồng
hai loại cây nói trên là bao nhiêu? A. 240 triệu đồng. B. 180 triệu đồng. C. 260 triệu đồng. D. 200 triệu đồng. Câu 37: − 2x + y ≤ 2 Cho hệ bất phương trình
− x + 2y ≥ 4 có miền nghiệm là y x + y ≤ 5
miền được tô màu (miền tam giác ABC có tọa độ các đỉnh
là A(0; 2), B(2; 3), C(1; 4), bao gồm cả các cạnh như hình vẽ 5
bên. Giá trị nhỏ nhất Fmin của biểu thức F(x; y) = −x + y trên C
miền xác định bởi hệ trên là 4 A. F B min = 4.
B. Fmin = 3. C. Fmin = 1. D. Fmin = 2. 3 2 A x O 1 2
Câu 38: Một xưởng sản xuất định lựa chọn hai loại máy chế biến loại I và loại II. Máy loại I
mỗi ngày 1 máy chế biến được 300 kilogam sản phẩm, máy loại II mỗi ngày 1 máy chế biến
được 450 kilogam sản phẩm. Biết để có lãi mỗi ngày xưởng phải sản xuất được nhiều hơn 50
tấn sản phẩm. Hỏi xưởng nên lựa chọn số lượng máy như thế nào trong các phương án dưới
đây để đảm bảo có lãi?
A. 80 máy chế biến loại I và 50 máy chế biến loại II.
B. 50 máy chế biến loại I và 80 máy chế biến loại II.
C. 65 máy chế biến loại I và 65 máy chế biến loại II.
D. 70 máy chế biến loại I và 60 máy chế biến loại II.
Câu 39: Cho hình thoi ABCD tâm O có cạnh bằng 2a và ABD = 60◦. Gọi I là điểm thỏa mãn # » # » #» # » # »
2IC + ID = 0 . Tính tích vô hướng AO · BI. # » # » a2 # » # » a2 # » # » # » # » A. AO · BI = − . B. AO · BI = . C. AO · BI = 2a2. D. AO · BI = −a2. 4 4 Câu 40:
Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc thời gian y
t(h) có đồ thị là một phần của parabol có đỉnh I(2; 9) và trục đối xứng 9
song song với trục tung như hình vẽ. Vận tốc của vật tại thời điểm 2 giờ 30
phút sau khi vật bắt đầu chuyển động gần bằng giá trị nào nhất trong các giá trị sau? 6 A. 8, 7 (km/h). B. 8, 6 (km/h). C. 8, 8 (km/h). D. 8, 5 (km/h). x O 2 3 51 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT NGUYỄN THỊ DIỆU
Thời gian làm bài: 90 phút
Bài 1 (1 điểm): Cho hai tập hợp A = (−2; 5], B = (1; +∞). Xác định các tập hợp A ∩ B,
A ∪ B, A\B, CRB. ĐS: A ∩ B = (1; 5], A ∪ B = (−2; +∞), A\B = (−2; 1], CRB = (−∞; 1]. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √x − 2
Bài 2 (1 điểm): Tìm tập xác định của hàm số y = .
ĐS: D = [2; +∞) \ {3}. 3x2 − 10x + 3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 3 (2,5 điểm):
a) Xác định các hệ số a, b của parabol (P) : y = ax2 + bx + 2, biết rằng (P) qua A(3; −1)
và có trục đối xứng là đường thẳng x = 1.
b) Lập bảng biến thiên và vẽ đồ thị hàm số y = −x2 + 2x + 2
c) Tìm tọa độ giao điểm của đường thẳng d : y = 5x − 2 và parabol (P) : y = −x2 + 2x + 2.
ĐS: a) a = −1; b = 2; c) (1; 3), (−4; −22). ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 4 (1 điểm): Tính giá trị nhỏ nhất của biểu thức F(x; y) = 12x − 15y với (x; y) thỏa mãn x + 3y + 3 ≥ 0 hệ bất phương trình: x − 2y + 3 ≥ 0
ĐS: Giá trị nhỏ nhất F(−3; 0) = −36. x + y − 3 ≤ 0. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 5 (2 điểm): Cho tam giác ABC có AB = 8, AC = 5, ’
BAC = 40◦. Tính độ dài cạnh BC,
bán kính đường tròn ngoại tiếp, diện tích và độ dài đường cao AH của tam giác ABC. (Kết
quả làm tròn đến hàng phần trăm)
ĐS: BC = 5,26; R = 4,1; S = 12,86; AH = 4,88. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 6 (1,5 điểm): Cho hình bình hành ABCD có tâm O. # » # » # » # » # »
a) Với M là điểm tùy ý, chứng minh rằng MA + MB + MC + MD = 4MO. # » # » #» # » # » #»
b) Gọi I, J lần lượt là điểm trên các đoạn BC, BD sao cho BC + 5IB = 0 , 2JB + JO = 0 .
Chứng minh rằng ba điểm A, I, J thẳng hàng. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 7 (1 điểm): Một cảnh sát giao thông ghi lại tốc độ (đơn vị: km/h) của 25 xe qua trạm như sau: 40 35 50 60 55 35 60 45 60 50 55 50 40 45 45 40 50 60 45 35 55 45 60 45 45 52 GV: VŨ NGỌC HUY
a) Lập bảng phân bố tần số và xác định số trung vị, mốt của bảng số liệu trên.
b) Tính tốc độ trung bình của 25 xe qua trạm.
ĐS: a) Q2 = 45, Mo = 45; b) x = 48,2. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT PHẠM PHÚ THỨ
Thời gian làm bài: 90 phút
Bài 1: Biểu diễn miền nghiệm của bất phương trình x − y − 2 < 0 trên mặt phẳng tọa độ Oxy. y 4 3 2 1 ĐS: O 1 2 3 4 x
Bài 2: Tìm tập xác định của các hàm số sau 3x + 1 a) y = ; x2 − 10x + 9 2 √ b) y = − 5x + 15. x − 7
ĐS: a) D = R \ {1; 9}; b) D = [−3; +∞) \ {7}
Bài 3: Khảo sát sự biến thiên và vẽ đồ thị hàm số y = x2 − 6x + 5.
ĐS: Hàm số nghịch biến trên (−∞; 3), đồng biến trên (3; +∞)
Bài 4: Xác định parabol (P) : y = ax2 + bx − 3 biết (P) có đỉnh I(−1; −4).
ĐS: (P) : y = 4x2 + 8x − 3
Bài 5: Hãy tìm số trung bình và mốt của mẫu số liệu sau Giá trị 6 7 8 9 10 Tần số 5 8 4 2 1 ĐS: X = 7,3, M0 = 7 Bài 6: # » # » # » # » # » # »
a) Cho 6 điểm bất kì A, B, C, H, K, I. Chứng minh rằng AB − HC − IK = CI − H A + KB.
b) Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của BC và CD. Chứng minh rằng # » # » # » # » # » 2(AB + N A + AM + DA) = 3DB. # » # »
Bài 7: Cho hình chữ nhật ABCD có AB = 4a, AD = 3a. Tính độ dài vectơ 2AB − AC. # » # » ĐS: 2AB − AC = 5a
Bài 8: Cho tam giác ABC vuông tại B có BA = 6, BC = 8. Gọi M là điểm thưộc cạnh AC sao # » # »
cho MA = 2MC. Tính tích vô hướng MA · MC. # » # » −200 ĐS: MA · MC = 9 54 GV: VŨ NGỌC HUY
Bài 9: Một rạp chiếu phim có sức chứa 1000 người. Với giá vé là 40 nghìn đồng, trung bình
sẽ có khoảng 300 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu
phim đã khảo sát thị trường và thấy rằng nếu giá vé cứ giảm 10 nghìn đồng thì sẽ có thêm
100 người đến rạp mỗi ngày. Tìm công thức của hàm số R(x) mô tả doanh thu từ tiền bán vé
mỗi ngày của rạp chiếu phim khi giá vé là x nghìn đồng. x2 ĐS: 23000x − 20 55 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT PHỔ THÔNG NĂNG KHIẾU
Thời gian làm bài: 90 phút 1
Bài 1: Cho hàm số y = f (x) = √ . 2x − 4
a) Tìm tập xác định của hàm số.
b) Xét tính biến thiên của hàm số đã cho trên tập xác định.
ĐS: a) D = (2; +∞); b) Hàm số nghịch biến trên tập xác định.
Bài 2: Cho hàm số y = f (x) = ax2 + bx + c có đồ thị như hình vẽ y 3 2 x O −1 a) Tìm a, b, c.
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [0; 3].
ĐS: a) a = 1, b = −4, c = 3; b) ymin = −1, ymax = 3
Bài 3: Tháp Bánh Ít là một trong số ít những quần thể kiến trúc, văn hoá Chăm còn sót lại
ở Việt Nam, được xây dựng vào khoảng cuối thế kỉ XI - đến đầu thế kỉ XII nằm trên ngọn
đồi tại thôn Đại Lộc, xã Phước Hiệp, huyện Tuy Phước, tỉnh Bình Định. Theo dòng thời gian,
tháp Bánh Ít đã mang trong mình những dấu ấn lịch sử của Vương quốc Chăm Pa cổ đại.
Trong một lần di dã ngoại các bạn học sinh trường Phổ thông Năng Khiếu đã thực hiện phép
đo ngọn tháp bằng cách đặt hai giác kế (công cụ dùng để đo góc) tại hai điểm A, B trên mặt
đất cách nhau 12 m cùng thẳng hàng với chân C của tháp. Chân của giác kế có chiều cao
h = 1,3 m. Gọi D là đỉnh tháp, các điểm C1, A1, B1 thẳng hàng (như hình v¯e). Các bạn nhận thấy ◊ DA1C1 = 49◦ và ÷
DB1C1 = 35◦. Hãy tính chiều cao CD của ngọn tháp. 56 GV: VŨ NGỌC HUY D 49◦ A1 35◦ B1 C1 1,3 m 12 m C A 12 m B ĐS: 22,8 m.
Bài 4: Trong trận chung kết WC2022, L.Messi đã có cơ hội thực hiện cú sút phạt trực tiếp
trước khung thành đội Pháp. Các cầu thủ Pháp lập thành hàng rào chắn cách điểm đá phạt 9
m và cầu thủ cao nhất trong hàng rào là 2 m. Giả định rằng quỹ đạo quả bóng sau khi Messi
thực hiẹn cú sút là một Parabol (như hình vẽ) và nó đạt được chiều cao cực đại là 3 m sau khi
rời chân Messi 14 m. Hỏi cú đá phạt này của Messi có đưa bóng đi qua điểm cao nhất của
hàng rào hay không? Tại sao? y B 3 2 x O 9 20 3 3 ĐS: (P) : y = −
x2 + x. Bóng vượt qua được rào cản, vì chiều cao quả bóng khi đó là 196 7 2,62 m. √
Bài 5: Cho tam giác ABC có AB = 2, AC = 2 2 và ’
BAC = 135◦. Gọi M là điểm nằm trên cạnh BC sao cho BC = 3CM. 57 GV: VŨ NGỌC HUY # » # »
a) Tính AB · AC. Tính độ dài đoạn thẳng BC. # » # » # »
b) Biểu diễn AM theo AB, AC. Tính AM. # » # »
c) Gọi N là điểm thỏa mãn AN = xAC, x ∈ R. Tìm x sao cho BN ⊥ AM. √ # » # » √ # » 1 # » 2 # » 2 5
ĐS: a) AB · AC = −4, BC = 2 5; b) AM = AB + AC, AM = ; c)x = 0,5. 3 3 3 58 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY TRƯỜNG THPT TAM PHÚ
Thời gian làm bài: 90 phút √ √ ï 1 5ò
Bài 1: Tìm tập xác định của hàm số y = 4x − 2 + 5 − 2x. ĐS: D = ; 2 2
Bài 2: Cho hàm số y = f (x) có đồ thị trên [−2; 3] như sau: y 2 1 3 x −2 O 1 2 −1 −3
a) Lập bảng biến thiên của hàm số trên [−2; 3].
b) Cho biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên [0; 3]. ĐS: max = 2, min = −3 ý Lời giải. x −2 0 1 3 2 1 y 0 −3 a)
b) Trên đoạn [0; 3] giá trị lớn nhất của hàm số là 2, giá trị nhỏ nhất của hàm số là −3.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 3: (2 điểm) Cho hàm số y = 2x2 + 4x − 1 có đồ thị (P). a) Vẽ đồ thị (P). Å 1 5 ã
b) Tìm tọa độ giao điểm của (P) và đường thẳng d : y = −x − 3. ĐS: − ; − và 2 2 (−2; −1)
Bài 4: Cho tam giác ABC biết CA = 8,2 và b C = 110◦, b
B = 25◦. Tính độ dài cạnh BC và diện tích tam giác ABC.
ĐS: BC ≈ 13,7, SABC ≈ 52,9 59 GV: VŨ NGỌC HUY # » # »
Bài 5: Cho tam giác ABC có AB = 5; BC = 9; ’ ABC = 30◦. Tính AB · BC. ĐS: √ # » # » 45 3 AB · BC = 2 √ # » # » √
Bài 6: Cho tam giác ABC vuông cân đỉnh C biết AB = 4 2. Tính AB + AC. ĐS: 4 5 Ä #» #»ä #» #» #» −1
Bài 7: Tính cos a , b biết | #»
a | = 20, | b | = 160 và a · b = −80. ĐS: 40
Bài 8: Trong lúc chơi bóng rổ, bạn Bình phát hiện ra quỹ đạo ném xiên của quả bóng là một
parabol. Trong một lần ném, quả bóng đạt độ cao 3m tại điểm A và tiếp tục đạt vị trí cao nhất
so với mặt đất là 5m tại điểm I. Gọi O, H lần lượt là chân đường vuông góc của A và I lên
mặt đất (AO = 3m, I H = 5m). Biết OH = 3m (tham khảo hình vẽ). I A M 5m 3m 3m 5m O 3m H D
a) Nếu chọn điểm O làm gốc tọa độ, em hãy giúp bạn Bình lập phương trình quỹ đạo của 2 4 quả bóng khi đó. ĐS: y = − x2 + x + 3 9 3
b) Trong mặt phẳng quỹ đạo của quả bóng, nếu tâm rổ đặt tại vị trí điểm M cách mặt đất
3m. D là chân đường vuông góc của M lên mặt đất và OD = 5m thì trái bóng bạn Bình
ném như trên có vào rổ không? Tại sao? ĐS: Không
Bài 9: Một công ty du lịch lữ hành mở hai tuyến đường du lịch từ vị trí A đến vị trí B. Tuyến
thứ nhất, đi từ A đến B bằng phương tiện cáp treo. Tuyến thứ hai, họ muốn đi bộ từ A đến C
rồi mới dùng cáp treo đi từ C đến B. Tính độ dài cáp treo từ C đến B biết chiều dài cáp treo
từ A đến B là 1672m, quãng đường người du lịch đi bộ từ A đến C là 950 m và ’ BAC = 32◦. ĐS: 1002 B 1672m 32◦ A 950m C 60 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT TẠ QUANG BỬU
Thời gian làm bài: 90 phút
Bài 1: Tìm tập xác định của các hàm số sau √ a) y = 5 − 2x. 1 b) y = . 2x + 6 Å 5 ò ĐS: a) −∞; ; b) R \ {−3} 2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 2: Dự báo thời tiết ngày 01/5/2021 tại Thành phố Hồ Chí Minh được cho trong bảng sau Giờ 1 4 7 10 13 16 19 22 Nhiệt độ (◦C) 28 27 28 32 31 29 28 27
Biết rằng bảng dữ liệu dự báo thời tiết là một hàm số, hãy tìm tập xác định của hàm số đó?
ĐS: {1; 4; 7; 10; 13; 16; 19; 22} ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 3:
a) Cho các tập hợp A = {0; 2; 4; 6; 8}, B = {0; 3; 6; 9}. Xác định các tập hợp A \ B, B ∩ A.
b) Cho các tập C = [−2; 1), D = (0; 3]. Xác định các tập hợp C ∩ D, D \ C.
ĐS: a) A \ B = {2; 4; 8}; B ∩ A = {0; 6} ; b) C ∩ D = (0; 1); D \ C = [1; 3] ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3x + y ≤ 5 x + 2y ≤ 4
Bài 4: Biểu diễn miền nghiệm của hệ bất phương trình x ≥ 0 y ≥ 0. Å 6 7ã Å 5 ã
ĐS: Miền nghiệm là miền tứ giác OABC với O(0; 0), A(0; 2), B ; , C ; 0 kể cả biên. 5 5 3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 5: Cho hàm số y = f (x) = −x2 + 4x − 3.
a) Lập bảng biến thiên của hàm số đã cho.
b) Vẽ đồ thị hàm số đã cho. ĐS: ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61 GV: VŨ NGỌC HUY
Bài 6: Các nhà khảo cổ học tìm được một mảnh chiếc đĩa cổ hình tròn bị vỡ. Để xác định
đường kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên vành đĩa và tiến hành đo đạc thu
được kết quả như sau BC = 28 cm; ‘
BAC = 120◦ (Hình vẽ). Tính đường kính của chiêc đĩa
(làm tròn kết quả đển hàng phần nghìn). B C A ĐS: 16,166 cm ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 7: Tính diện tích một lá cờ hình tam giác cân. Biết lá cờ đó có chiều dài cạnh bên là 32 cm
và góc ở đáy có số đo là 48◦ (làm tròn kết quả đến hàng phần nghìn). ĐS: 509,195 cm2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 8: Cho tam giác ABC có trung tuyến AM. Gọi I là trung điểm của AM và K là điểm trên 1 cạnh AC sao cho AK = AC. 3 # » 1 # » 1 # » a) Chứng minh BI = BA + BC. 2 4 # » # » # »
b) Tính BK theo BA, BC.
c) Chứng minh ba điểm B, I, K thẳng hàng. # » 1 # » 1 # » # » 2 # » 1 # » ĐS: a) BI = BA + BC ; b) BK =
BA + BC ; c) Ba điểm B, I, K thẳng hàng. 2 4 3 3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 9: Cho tam giác đều ABC có cạnh bằng 2 và có đường cao AH. Tính các tích vô hướng. # » # » a) AB · AC. # » # » b) AH · BC. # » # » # » # »
ĐS: a) AB · AC = 2 ; b) AH · BC = 0 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT TÂY THẠNH
Thời gian làm bài: 90 phút
Bài 1: Cho hai tập hợp A = (−∞; 3] và B = (−1; 4]. Tìm A ∩ B, A ∪ B, CRA, A \ B.
ĐS: A ∩ B = (−1; 3]; A ∪ B = (−∞; 4]; CRA = (3; +∞); A \ B = (−∞; −1] ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 2: Cho hàm số y = f (x) xác định trên [−2; 6] và có đồ thị như hình dưới đây. Tìm các
khoảng đồng biến, nghịch biến của hàm số y = f (x). y 6 5 2 1 4 − − x 2 1 O 1 6 −4
ĐS: Các khoảng đồng biến là (−1; 1), (4; 6); các khoảng nghịch biến là (−2; −1), (1; 4) ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 3: Khảo sát sự biến thiên và vẽ đồ thị (P) của hàm số y = −x2 + 2x − 1. ĐS: ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Bài 4: Xác định parabol (P) : y = ax2 + bx + 2(a 6= 0), biết (P) có trục đối xứng x = và cắt 2
trục hoành tại điểm M có hoành độ bằng 1 . ĐS: y = x2 − x + 2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63 GV: VŨ NGỌC HUY
Bài 5: Một gia đình sản xuất gạo, do điều kiện nhà xưởng nên mỗi đợt gia đình đó sản xuất
được x kg gạo. Biết rằng mỗi kg bán được với giá 350 − 5x (nghìn đồng) và chi phí sản xuất
x kg gạo là x2 + 5x + 1000 (nghìn đồng). Hỏi gia đình đó phải sản xuất được bao nhiêu kg
gạo đề đạt được lợi nhuận tối đa? ĐS: x = 35 kg ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 6: Tìm số trung bình, mốt và tứ phân vị của mẫu số liệu sau đây 155 165 150 155 165 170 165 150 155 160
ĐS: x = 159; M0 = 155; M0 = 165; Q1 = 155; Q2 = 157,5; Q3 = 165 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 7: Cho tam giác ABC có BC = 10, AB = 5, b
B = 60◦. Tính diện tích và bán kính đường √ 25 3
tròn ngoại tiếp của tam giác ABC. ĐS: S = , R = 5 2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » 1 # »
Bài 8: Cho tam giác ABC có D là điểm đối xứng của A qua B và điểm M thỏa BM = BC. 2 # » # » # » # » 3 # » 1 # »
Phân tích DM theo hai vectơ AB và AC. ĐS: DM = − AB + AC 2 2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 9: Cho tam giác ABC có AB = 3, BC = 6, AC = 8. Gọi I là điểm trên cạnh AC sao cho # » # » # » # » # » # » 91 # » # » 597
2I A = 3IC. Tính CB · AC và BI · AI. ĐS: CB · AC = − , BI · AI = 2 50 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 10: Cho hình chữ nhật ABCD có AB = 3, AD = 4. Gọi M là điểm thỏa điều kiện # » # » 16
AM = kAB. Tìm số thực k để AC vuông góc với DM. ĐS: k = 9 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ GIỮA HỌC KÌ I KHỐI 10/2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT THỦ ĐỨC
Thời gian làm bài: 90 phút # » # » # » # »
Câu 1: Cho tam giác ABC và điểm M thỏa mãn |MB − MC| = |BM − BA|. Tập hợp điểm M là
A. Đường trung trực của đoạn BC.
B. Đường thẳng AB.
C. Đường tròn tâm A bán kính BC.
D. Đường thẳng qua A và song song với BC. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 2: Cho tam giác ABC, đặt AB = c, AC = b, BC = a. Gọi R, r và p lần lượt là bán kính
đường tròn ngoại tiếp, đường tròn nội tiếp và nửa chu vi 4ABC. Kí hiệu S là diện tích
4ABC. Hệ thức nào sau đây sai? S A. c = 2R · sin C. B. p = . rabc
C. c2 = a2 + b2 − 2ab cos C. D. S = . 4r ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ®x2 + 3x khi x ≥ 0
Câu 3: Cho hàm số f (x) =
. Giá trị của f (−1) bằng 3 − x khi x < 0 A. 5. B. 2. C. 4. D. −2. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 4:
Hàm số bậc hai nào trong các hàm số sau có đồ thị như hình vẽ y dưới đây? 4 A. y = x2 − 4x. B. y = x2 − 4x + 4. C. y = −x2 + 4x + 4. D. y = −x2 + 4x. x O 2 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 5: Hàm số nào có bảng biến thiên như trong hình vẽ? A. y = x2 − 2x + 5. B. y = 2x2 − 8x + 5. C. y = (x − 2)2 + 1. D. y = −x2 + 4x + 5. 65 GV: VŨ NGỌC HUY x −∞ 2 +∞ +∞ +∞ y 1 ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 6: Cho hai tập hợp M = [−3; 6) và N = (0; 7]. Tìm M ∩ N. A. M ∩ N = (−3; 7]. B. M ∩ N = [0; 7]. C. M ∩ N = [−3; 0). D. M ∩ N = (0; 6). ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 7: Phủ định của mệnh đề "∀n ∈ N, n(n + 1) là số chẵn" là
A. ∃n ∈ N, n(n + 1) là số chẵn.
B. ∀n ∈ N, n(n + 1) không là số chẵn.
C. ∃n ∈ N, n(n + 1) không là số lẻ.
D. ∃n ∈ N, n(n + 1) là số lẻ. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 8: Một vật có khối lượng m được treo cố định trên trần nhà bằng 2 sợi dây không dãn có #» #»
độ đài bằng nhau. Biết rằng lực căng dây T 1 và T 2 có độ lớn bằng nhau bằng 600N và hợp
với nhau một góc 60◦ như hình vẽ bên dưới. # » # » T2 T1 60◦ #» #»
Độ lớn hợp lực của 2 lực căng dây T 1 và T 2 là √ √ A. 1200 3N. B. 600 3N. C. 1200N. D. 600N. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 9: Cho hình chữ nhật ABCD tâm là O, AD = 3 và AB = 5. Gọi M là điểm thỏa mãn # » # »
AM = mAB vơi m ∈ R. Tìm m để 4AOM vuông tại O. 17 17 17 13 A. m = . B. m = . C. m = . D. m = . 25 15 9 20 ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 10: Một vận động viên ném một quả bóng vào rổ. Rổ ở độ cao 3,05 m và cách vận động
viên 7 m theo phương ngang. Quả bóng rời tay vận động viên ở độ cao 2,1 m và có tốc độ là 66 GV: VŨ NGỌC HUY
v(m/s). Nếu gốc tọa độ được đặt tại chân vận động viên thì quỹ đạo của quả bóng khi rời 10
tay vận động viên là một đường cong cho bởi hàm số sau y = − · x2 + x + 2,1, trong đó x v2
là quãng đường tính bằng mét mà bóng đi được theo phương ngang (tham khảo hình vẽ bên
dưới) và y là độ cao của quả bóng tính bằng mét. y Rổ 2,1 m 3,05 m x O 7 m
Biết vận động viên ghi được điểm. Tìm độ cao lớn nhất mà bóng có thể đạt được (làm tròn
đến 1 số thập phân sau dấu phẩy). A. 4,1 m. B. 3,5 m. C. 4,5 m. D. 5,2 m. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 11: Đồ thị hàm số y = −x2 − 4x + 2022 có đỉnh là A. I(2; −2026). B. I(−2; −2026). C. I(−2; 2026). D. I(2; 2026). ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √ x + 2
Câu 12: Tập xác định y = x + 1 + x A. (−1; +∞) \ {0}. B. R \ {0}. C. (−1; +∞). D. [−1; +∞) \ {0}. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 13: Cho tam giác ABC có AB = 6, BC = 8, ’
ABC = 120◦. Diện tích S tam giác ABC bằng √ √ A. 13,9. B. 12 3. C. 24 3. D. 21. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 14: Tìm m để đồ thị hàm số y = x2 − (m + 1)x + 4m − 5 nhận x = 2 là trục đối xứng. A. m = 1. B. m = −3. C. m = 3. D. m = −5. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 15: Trong các tập hợp sau tập hợp nào có hai phần tử?
A. x ∈ Rx2 − x + 6 = 0 .
B. x ∈ Z2x2 − 5x + 2 = 0 .
C. n ∈ Nn2 ≤ 1 .
D. {n ∈ N|n ≤ 2}. ý Lời giải. 67 GV: VŨ NGỌC HUY
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 16: Hàm số y = x2 − 4x + 11 nghịch biến trên khoảng A. (2; +∞). B. (7; +∞). C. (−∞; 2). D. (4; +∞). ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 17: Tìm tất cả các giá trị của tham số m để hàm số y = m2 − 1 x3 + (m + 1)x2 + 5x − 3 là hàm số bậc hai. A. m 6= ±1. B. m 6= −1. C. m = 1. D. m ∈ R. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » # » # »
Câu 18: Cho ba điểm A, B, C phân biệt thỏa mãn 3OC = 2OA + OB với mọi điểm O. Mệnh
đề nào sau đây là đúng?
A. Ba điểm A, B, C thẳng hàng.
B. Ba điểm A, B, C tạo thành tam giác vuông.
C. Ba điểm A, B, C tao thành tam giác cân.
D. C là trung điểm của AB. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 19: Khẳng định nào sau đây là sai? # » # » # »
A. Nếu G là trọng tâm cùa tam giác ABC thì GA + GB = CG. # » # »
B. Với 3 điểm I, J, K bất kỳ ta có I J + JK = IK. # » # » # »
C. Nếu AB + AD = AC thì ABCD là hình bình hành. # » # » # »
D. Nếu I là trung điểm của AB thì với mọi điểm M ta có MA + MB = 2MI. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 20: Cho các điểm A, B, O. Khẳng định nào sau đây là đúng? # » # » # » # » # » # » # » # » # » # » # » A. AB = OA + OB. B. AB = OB − OA. C. AB = OA − OB. D. AB = AO − OB. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » # »
Câu 21: Cho hình vuông ABCD có độ dài cạnh bằng 10. Tính giá trị AB · CD A. 100. B. 10. C. 0. D. −100. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . #» # » # » # » # »
Câu 22: Cho 4 điểm phân biệt A, B, C, D. Thu gọn u = AD − AB − BC − CA ta được kết quả là #» #» #» # » #» # » #» # » A. u = 0 . B. u = CD. C. u = DB. D. u = AD. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68 GV: VŨ NGỌC HUY ®x − y < 3
Câu 23: Cho hệ bất phương trình
. Điểm nào sau đây thuộc miền nghiệm của x + 2y ≥ −2
hệ bất phương trình đã cho? A. (3; 0). B. (1; 0). C. (2; −1). D. (−2; −3). ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 24: Tìm a để hàm số y = −x2 + 2x + 3 − 2a đạt giá trị lớn nhất bằng 2022. A. a = −1001. B. a = 1009. C. a = −1009. D. a = 1001. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 25:
Cho hàm số f (x) với tập xác định là đoạn [−1; 4] có đồ thị y như hình vẽ bên dưới
Khẳng định nào sau đây là sai? 4
A. Hàm số f (x) đạt giá trị lớn nhất là 3. 3
B. Hàm số f (x) đồng biến trên khoảng (2; 4).
C. Hàm số f (x) đạt giá trị nhỏ nhất là −1. 2
D. Hàm số f (x) nghịch biến trên khoảng (1; 2). −1 x O 1 2 4 −1 ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » # »
Câu 26: Cho ba điểm phân biệt A, B, C. Nếu AB = −3BC thì đẳng thức nào dưới đây đúng?# » # » # » # » #» # » 2 # » A. AC = 2BC. B. AB = −3BC. C. AB + 3CB = 0 . D. AC = AB. 3 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x + 1
Câu 27: Tập xác định của hàm số y = là x2 + 1 A. R. B. R \ {−1}. C. R \ {±1}. D. (−1; +∞). ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 28:
Cho hình bình ABCD có tâm O. Các cặp véc-tơ nào sau đây là véc-tơ D C đối nhau? # » # » # » # » A. AD và BC. B. OD và BO. O # » # » # » # » C. CD và BA. D. AO và CO. A B ý Lời giải. 69 GV: VŨ NGỌC HUY
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 29: Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh AD. Trên cạnh BC lấy
điểm N sao cho BC = 3BN. Chọn khẳng định đúng. # » 2 # » 1 # » # » # » 1 # » A. MN = AB − AD. B. MN = AB − AD. 3 2 6 # » 1 # » # » # » 1 # » 1 # » C. MN = AB − AD. D. MN = AB − AD. 6 2 3 ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 30: Tập giá trị của hàm số y = 7x2 − 14x + 23 là A. [16; +∞). B. (16; +∞). C. [1; +∞). D. R. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 31: Trong các phát biểu sau, có bao nhiêu phát biểu là mệnh đề đúng?
(I) Hà Nội là Thủ đô của Việt Nam.
(II) Số 16 là một số chính phương.
(III) x = 1 có phải là nghiệm của phương trình x2 − 1 = 0 không?
(IV) Phương trình 3x2 − 5x + 2 = 0 có nghiệm nguyên. (V) 5 < 7 − 3. A. 3. B. 2. C. 4. D. 5. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 32: Bất phương trình nào sau đây không phải là bất phương trình bậc nhất hai ẩn? x y A. (x + 3)y + 1 ≤ 0. B. − + 10 < 0. 2 13
C. 2x − 13y + 5 < 0.
D. x − 5y − 13 ≥ 0. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Câu 33: Cho tam giác ABC có AB = AC = 1, ’
BAC = 120◦, M ∈ AB sao cho AM = . Khi 3 # » # » đó AM · AC bằng 1 3 1 3 A. . B. − . C. − . D. − . 2 8 6 2 ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 34: Tìm giá trị nhỏ nhất của biểu thức F(x, y) = 10x − 30y với (x; y) là nghiệm của hệ
bất phương trình có miền nghiệm là phần được tô đậm trong hình vẽ dưới đây. 70 GV: VŨ NGỌC HUY y 2 − x 2 O 2 3 A. −20. B. −40. C. −60. D. 30. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 35: Cho tam giác ABC có AB = 3, AC = 6 va ’
BAC = 120◦. Giá trị của tích vô hướng # » # » AB · AC bằng √ √ A. −9 3. B. −9. C. 9 3. D. −9. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 36: Cho tam giác ABC đều có trọng tâm G. Gọi M là trung điểm BC. Khẳng định nào sau đây là đúng? # » # » # » # » # » # » # » # » 1 # » A. AM = 3AG. B. GA = −2GM.
C. GA = GB = GC. D. MB = BC. 2 ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 37: Miền nghiệm của bất phương trình 4x − 3y < 3 là nửa mặt phẳng không chứa điểm A. (−5; −3). B. (1; −2). C. (−3; 2). D. (−1; 1). ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Dựa vào thông tin dưới đây để trả lời từ câu 38 đến câu 40.
Một cửa hàng làm bánh mì thuê mặt bằng mỗi tháng hết 5 triệu đồng. Chi phí làm một chiếc
bánh mì là 10000 đồng. Gọi x số bánh mì cửa hàng làm trong tháng đó.
Câu 38: Công thức tính chi phí của cửa hàng trong một tháng đó là
A. C(x) = 500 + x (nghìn đồng).
B. C(x) = 5000 − 10x (nghìn đồng).
C. C(x) = 5000 + 10x (nghìn đồng).
D. C(x) = 1000 + 50x (nghìn đồng). ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 39: Giả sử r(x) = −0,0005x2 + 18x (đơn vị nghìn đồng) là số tiền cửa hàng thu được
khi bán được x bánh mì. Lập công thức tính lợi nhuận trong tháng của cửa hàng khi bán hết
được x bánh mì. (Biết lợi nhuận bằng doanh thu trừ chi phí)
A. p(x) = −0, 0005x2 + 8x − 5000.
B. p(x) = −0, 0005x2 + 18x. 71 GV: VŨ NGỌC HUY
C. p(x) = 0, 0005x2 − 8x + 5000.
D. p(x) = −0, 0005x3 + 8x + 5000. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 40: Tìm số bánh mì x sao cho lợi nhuận của cửa hàng trong tháng là lớn nhất. A. x = 9000. B. x = 8000. C. x = 10000. D. x = 7000. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ĐÁP ÁN 1. C 2. D 3. C 4. D 5. C 6. D 7. D 8. B 9. A 10. A 11. C 12. D 13. B 14. C 15. C 16. C 17. C 18. A 19. C 20. B 21. D 22. D 23. B 24. C 25. A 26. D 27. A 28. D 29. B 30. A 31. A 32. A 33. C 34. B 35. B 36. B 37. B 38. C 39. A 40. B 72 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THỰC HÀNH SÀI GÒN
Thời gian làm bài: 90 phút Bài 1: √
a) Tìm tập xác định của hàm số sau y = f (x) = 3x + 2.
b) Tìm các khoảng đồng biến, nghịch biến của hàm số có đồ thị như sau: y 4 3 2 1 2 − O x 1 1 3 4 5 6 7 8 9 10 −1 ï −2 ã ĐS: a) D =
; +∞ ; b) f (x) đồng biến trên (2; 4) và nghịch biến trên (0; 2) và (4; 10). 3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 2: Lập bảng biến thiên và vẽ đồ thị của hàm số y = f (x) = −x2 + 5x − 4. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 3: Trong hình vẽ minh họa bên dưới, một vận động viên bóng chuyền đứng cách phía
sau vạch quy định 1 m đang tập phát bóng. Độ cao h (m) của quả bóng sau thời gian t giây
tính từ lúc bắt đầu phát bóng được cho bởi hàm số h = −4,9t2 + 3,82t + 1,7. 2,43 m
a) Khi nào quả bóng đạt được độ cao cao nhất (làm tròn kết quả đến chữ số thập phân thứ hai)? 73 GV: VŨ NGỌC HUY
b) Quả bóng đến lưới lúc t = 0,6 giây. Liệu bóng có qua lưới không? Hãy giải thích, biết
chiều cao lưới là 2,43 m (làm tròn kết quả đến hàng phần trăm).
ĐS: a) 0,39 giây; b) h(0, 6) = 2,228 < 2,43 nên bóng không qua lưới. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 4: Một vận động viên A tham gia tập luyện chạy cự ly 100 mét. Kết quả sau 20 ngày
luyện tập được trình bày theo bảng dưới đây:
Thời gian chạy 20 ngày của vận động viên A 14 13 12 15 12 15 16 14 12 18 13 16 12 15 16 14 12 30 28 13
a) Tìm số trung bình, tứ phân vị và mốt của mẫu số liệu trên.
b) Huấn luyện viên muốn gửi bài báo cáo thành tích cho ban huấn luyện. Trong các tham
số trên, huấn luyện viên chọn tham số nào để phản ánh đúng khả năng của vận động viên A? Giải thích.
ĐS: a) x = 15,5; Q1 = 12,5; Q2 = 14; Q3 = 16; M0 = 12; b) Số trung bình.
Bài 5: Cho hình thoi ABCD có O là giao điểm của hai đường chéo, AB = 2a và ’ BAD = 60◦.
Trên đoạn thẳng AB lấy điểm M sao cho MB = 2MA. Gọi N là trung điểm của đoạn thẳng AO. # » # »
a) Tính tích vô hướng AM · AN. # » # » # » # »
b) Gọi I là trung điểm của đoạn thẳng MN. Phân tích các vectơ AI, CI theo AB và AC. # » # »
c) Đường thẳng MN cắt BC tại P. Biết PB = kPC, tìm k. 1 # » 1 # » 1 # » # » 1 # » 7 # » 2 ĐS: a) a2; b) AI = AB + AC; CI = AB − AC; c) k = . 2 6 8 6 8 3
Bài 6: Khi đo chiều dài của một cây cầu, các kỹ sư thu được kết quả là a = 372,7362 m ±
0,001 m. Tìm số quy tròn của số gần đúng 372,7362. ĐS: a = 372,74. 74 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT TRẦN KHAI NGUYÊN
Thời gian làm bài: 90 phút
Bài 1: Phát biểu mệnh đề phủ định của mệnh đề sau:
P : “2023 chia hết cho 5”.
Q : “∃x ∈ R, x2 − 1 ≤ 0”.
ĐS: P: “2023 không chia hết cho 5”; Q: “∀x ∈ R, x2 − 1 > 0”. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 2: Cho các tập hợp A = {3; 5; 7; 9; 11}, B = {3; 4; 5; 6}, C = {5; 6; 7; 8}. Hãy xác định tập hợp (A ∪ B) ∩ C.
ĐS: (A ∪ B) ∩ C = {5; 6; 7}. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 3: Một nhà máy sản xuất có 24 tấn nguyên liệu loại A và 18 tấn nguyên liệu loại B để sản
xuất hai loại sản phẩm X và Y. Để sản xuất 1 tấn sản phẩm X cần dùng 6 tấn nguyên liệu A
và 2 tấn nguyên liệu B. Để sản xuất 1 tấn sản phẩm Y cần dùng 3 tấn nguyên liệu A và 6 tấn
nguyên liệu B. Biết khi bán 1 tấn sản phẩm X lãi được 12 triệu đồng, bán 1 tấn sản phẩm Y
lãi được 10 triệu đồng. Hãy lập kế hoạch sản xuất của nhà máy để thu được tiền lãi cao nhất.
ĐS: Nhà máy cần sản xuất 3 tấn sản phẩm X và 2 tấn sản phẩm Y để thu được tiền lãi cao nhất. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 4: Lập bảng biến thiên của hàm số y = 2x2 + 4x + 5. Hàm số này có giá trị lớn nhất hay
giá trị nhỏ nhất? Tìm giá trị đó.
ĐS: GTNN bằng 3 tại x = −1 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 5: Tính khoảng cách AB giữa hai nóc tòa nhà cao ốc. Cho biết khoảng cách từ hai điểm
đó đến một vệ tinh viễn thông lần lượt là 370 km, 330 km và góc nhìn từ vệ tinh đến A và B
là 18◦ (kết quả làm tròn một chữ số thập phân). 75 GV: VŨ NGỌC HUY 18◦ 370 km 330 km A B ĐS: 116,4 km ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » # » #» # » # » #»
Bài 6: Cho tam giác ABC, lấy các điểm M, N, P sao cho MA + 2MB = 0 ; 4NB + NC = 0 ; # » # » #» 2PA − PC = 0 . # » # » # » # »
a) Biểu thị mỗi vectơ PM, PN theo hai vectơ AB, AC.
b) Chứng minh ba điểm M, N, P thẳng hàng. # » 2 # » # » # » 4 # » 6 # » ĐS: a) PM = AB + AC; PN = AB + AC. 3 5 5 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √ # » # » # » # »
Bài 7: Cho hình chữ nhật có tâm O và cho AB = 5a, AD = 5a 3. Tính CB · CD và CD · CO. # » # » # » # » 25
ĐS: CB · CD = 0; CD · CO = . 2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 8: Cho số gần đúng a = 8712 với độ chính xác d = 100. Hãy viết số quy tròn của số a và
ước lượng sai số tuyệt đối của số quy tròn.
ĐS: Số quy tròn của a là 9000; ∆a = 288. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 9: Thu thập theo tháng (đơn vị: triệu đồng) của các công nhân trong một công ty nhỏ được cho như sau: 6 8 7 8 10 6 6 9 10 8
a) Tìm khoảng biến thiên và phương sai của mẫu số liệu trên. 76 GV: VŨ NGỌC HUY
b) Tìm khoảng tứ phân vị của mẫu số liệu trên.
ĐS: a) R = 4; S2 = 2,16; b) ∆Q = 3. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT TRẦN PHÚ
Thời gian làm bài: 90 phút
Bài 1: Biểu diễn miền nghiệm của bất phương trình: 2x − 5y − 10 < 0. ĐS: Miền nghiệm của
bất phương trình là nửa mặt phẳng không kể bờ ∆ : 2x − 5y − 10 = 0 có chứa gốc toạ độ O x 1
Bài 2: Tìm tập xác định của hàm số sau: y = √ − . ĐS: 12x2 + 3 x2 − 3x − 18 D = R \ {−3; 6} −3
Bài 3: Xét tính đồng biến, nghịch biến của hàm số f (x) =
trên khoảng (5; +∞). ĐS: 2x − 10
Hàm số đồng biến trên khoảng (5; +∞)
Bài 4: Khảo sát sự biến thiên và vẽ đồ thị hàm số (P) : y = x2 + 6x + 8. ĐS: Hàm số nghịch
biến trên khoảng (−∞; −3) và đồng biến trên khoảng (−3; +∞)
Bài 5: Cầu Ponte Luis ở Porto (Bồ Đào Nha) có hình dạng đường cong parabol có bề lõm quay
xuống dưới để giúp giảm lực mà cây cầu phải gánh. Giả sử ta lập một hệ trục tọa độ Oxy sao
cho một chân cầu đi qua gốc O như hình vẽ (x, y tính bằng mét), chân kia của cầu ở vị trí
(6; 0). Biết một điểm A trên cầu có tọa độ là (2; 4). Tìm hàm số bậc hai có đồ thị chứa cung parabol nói trên. y A 4 x O 2 6 −1 ĐS: y = x2 + 3x 2
Bài 6: Để biết ha loại hoa hồng đỏ (HĐ) và hoa hồng trắng (HT) phát triển như thế nào sau
khi gieo hạt, bạn Mai gieo 6 hạt hoa hồng đỏ và 6 hạt hoa hồng trắng vào 12 chậu riêng biệt
va cung cấp cho chúng lượng nước, ánh sáng như nhau. Sau 1 năm, 12 hạt đã nảy mầm và
phát triển thành 12 cây con. Bạn Mai đo chiều cao từ rễ đến ngọn của mỗi cây (đơn vị mm) và
ghi kết quả là mẫu số liệu sau: Cây HĐ1 HĐ2 HĐ3 HĐ4 HĐ5 HĐ6 Chiều cao 110 101 93 103 104 97 Cây HT1 HT2 HT3 HT4 HT5 HT6 Chiều cao 85 90 87 92 100 105 78 GV: VŨ NGỌC HUY
a) Hãy tính phương sai của hai mẫu số liệu lấy từ hoa hồng đỏ và hoa hồng trắng? (làm
tròn đến hàng phần chục)
b) Theo em, cây hoa hồng loại nào phát triển đồng đều hơn? Vì sao?
ĐS: a) 28,8 và 50,5; b) Hoa hồng đỏ √
Bài 7: Cho tam giác ABC có A là góc nhọn và AB = 7; AC = 8 và diện tích S = 14 3. Tính √
số đo góc A và độ dài cạnh BC. ĐS: “ A = 60◦, BC = 57
Bài 8: Cho hình thang vuông ABCD vuông tại A và B có AD = 2AB = 2a. Gọi M là trung # » 1 # » # »
điểm của cạnh AC, N là trung điểm của cạnh AD. Chứng minh: CN = AD − AC và tính 2 # » # » # » # » √ 2MN + BC theo a. ĐS: 2MN + BC = a 5
Bài 9: Cho tam giác MNP có MP = 6, NP = 8, b
P = 150◦. Gọi E là trung điểm của cạnh MN # » # » # » # » √
và F là một điểm trên cạnh NP = 4NF. Tính MF · PE? ĐS: MF · PE = 6 + 3 3 79 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT TRẦN QUANG KHẢI
Thời gian làm bài: 90 phút Bài 1:
a) Cho tập hợp A = x ∈ R | x2 − 5x − 6 = 0 ; B = {1; −1}. Xác định tập hợp A\B.
b) Biết D = {x ∈ R | 1 ≤ x ≤ 5}; E = {x ∈ R | 3 < x ≤ 6}. Tìm D ∩ E và D ∪ E.
ĐS: a) A\B = 6; b)D ∩ E = (3; 5]; D ∪ E = [1; 6]
Bài 2: Tìm tập xác định của các hàm số sau 8x + 3 1 a) y = f (x) = b) y = g(x) = √ x2 − 4 6 − 3x
ĐS: a) D = R \ 2; −2; b) D = (−∞; 2)
Bài 3: Cho hàm số bậc hai y = f (x) = ax2 + bx + c có f (0) = 1, f (1) = −4, f (2) = −7. Hãy
xác định giá trị của các hệ số a, b và c.
ĐS: a = 1; b = −6; c = 1
Bài 4: Cho hàm số bậc hai y = −x2 + 2x + m. Hãy xác định giá trị của m để hàm số đạt giá trị lớn nhất bằng 5. ĐS: m = 4
Bài 5: Cho hình vuông ABCD có cạnh bằng 4. #» # » # »
a) Tính độ dài của vecto a = AB + AD # » # »
b) Tính tích vô hướng BA · BC. √ ĐS: a) 2; b) 0
Bài 6: Cho tứ giác ABCD. Gọi M và N lần lượt là trung điểm các cạnh AB và CD. # » # » # »
a) Chứng minh rằng AC + BD = 2MN. 2
b) Gọi K là điểm trên cạnh AC sao cho AK =
AC, I là trung điểm của MK. 3 # » 1 # » 1 # » Chứng minh rằng AI = AB + AC. 4 3 ĐS: #»
Bài 7: Một người dùng một lực F có độ lớn 100N để kéo một thùng hàng dịch chuyển một #» #»
đoạn 15m. Biết lực F hợp với hướng dịch chuyển một góc 60◦. Tính công sinh bởi lực F ? ĐS: 750 N
Bài 8: Xoài cát Hòa Lộc là loại xoài đặc sản nổi tiếng của vùng đồng bẳng sông Cửu Long.
Một năm xoài có hai mùa, mùa thuận là từ tháng 3 đến tháng 5, mùa nghịch là từ tháng 10
đến tháng 12. Xoài có thể ra trái sau 24 tháng trồng. Năm 2005, Cục Sở hữu trí tuệ thuộc Bộ
Khoa học và Công nghệ cấp văn bằng bảo hộ độc quyền Nhãn hiệu tập thể cho sản phẩm
Xoài cát Hòa Lộc. Xoài cát Hòa Lộc được xuất khẩu sang các nước Pháp, Mỹ, Canada....
Bạn Hoa chọn ngẫu nhiên 10 trái xoài cát Hòa Lộc và ghi lại khối lượng ở bảng sau (đơn vi: gam) 450 510 510 600 480 420 510 450 650 540 80 GV: VŨ NGỌC HUY
a) Em hãy tính khối lượng trung bình x của một trái xoài ở bảng trên. Nếu bạn Hoa muốn
mua 3 kg xoài thì sẽ được khoảng bao nhiêu trái ?
b) Em hãy tìm mốt Mo của khối lượng xoài ở mẫu số liệu trên.
ĐS: a) x = 512, 5 trái; b)MO = 510
Bài 9: Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong hội chợ Tết.
Cần 2 giờ để vẽ tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ tấm thiệp loại lớn có
giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít
nhất 12 tấm. Hãy cho biết bạn ấy phải vẽ bao nhiêu tấm thiệp mỗi loại để có nhiều tiền nhất?
ĐS: 6 tấm thiệp nhỏ và 6 tấm thiệp lớn 81 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT VÕ THỊ SÁU
Thời gian làm bài: 90 phút
Câu 1: Lập bảng biến thiên và vẽ đồ thị hàm số y = x2 − 4x + 3.
Câu 2: Tìm hàm số bậc hai y = ax2 + bx + c, biết rằng đồ thị hàm số là parabol (P) cắt trục
tung tại điểm có tung độ là 4, đi qua điểm A(3; 7) và có trục đối xứng là đường thẳng x = 2. ĐS: y = −x2 + 4x + 4 √
Câu 3: Sử dụng máy tính cầm tay tìm số gần đúng cho
3 với độ chính xác 0, 0003. ĐS: a = 1, 732
Câu 4: Điểm kiểm tra thường xuyên của một nhóm gồm 11 học sinh lần lượt:
4; 7; 8; 9; 6; 8; 8; 7; 9; 6; 7 79
. Tìm số trung bình và số trung vị của mẫu số liệu. ĐS: x = , M 11 e = 7
Câu 5: Hai chiếc tảu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau
một góc 60◦. Tàu B chạy với tốc độ 50km/h, tàu C với tốc độ 20km/h. Hỏi sau 2 giờ hai tàu √ cách nhau bao nhiêu km ? ĐS: 20 19 B 50 km/h 60◦ A 20 km/h C
Câu 6: Cho hình bình hành ABCD. Gọi M là trung điểm của AB. # » 1 # » # » 1 # » # » 1 # »
a) Gọi N, P là hai điểm thoả AN = AC; AP =
AD. Chứng minh rằng MN = − AB + 6 4 3 1 # » AD. 6
b) Chứng tỏ ba điểm M, N, P thẳng hàng. 82 GV: VŨ NGỌC HUY
Câu 7: Cho hình thoi ABCD tâm O có cạnh bằng a và ’
ABD = 60◦. Gọi I là điểm thỏa mãn # » # » #» # » # » 59
2IC + ID = 0 . Tính tích vô hướng AO · BI. ĐS: a2 16 p(2x + 6)(x + 1) 3
Câu 8: Tìm tập xác định của hàm số: f (x) = √ − . ĐS: x + 1 − 1 |x| − 1 D = (−1; ∞) \ {1} 83 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY TRƯỜNG THPT GÒ VẤP
Thời gian làm bài: 90 phút
Bài 1: Cho A = (−∞; 3), B = (1; 5] và C = [−2; 4]. a) Tìm A ∩ B, A \ B.
b) Tìm B ∪ C, A ∩ C. ý Lời giải.
a) A ∩ B = (1; 3), A \ B = (−∞; 1].
b) B ∪ C = [−2; 5], A ∩ C = [−2; 3).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
Bài 2: Tìm tập xác định của hàm số y = √ . (x + 2) x + 1 ý Lời giải. ®x + 2 6= 0 ®x 6= −2 Hàm số xác định⇔ ⇔ ⇔ x > −1. x + 1 > 0 x > −1
Vậy tập xác định của hàm số là D = (−1; +∞). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2x − 1
Bài 3: Xét sự đồng biến và nghịch biến của hàm số y = f (x) = trên khoảng x + 2 (−∞; −2). ý Lời giải. 5 y = f (x) = 2 − . x + 2 5 5 5
∀x1, x2 ∈ (−∞; −2) : x1 < x2, ta có f (x1) − f (x2) = 2 − − 2 + = − x1 + 2 x2 + 2 x2 + 2 5 . x1 + 2 5 5
Lại có x1 < x2 ⇒ x1 + 2 < x2 + 2 ⇒ > ⇒ f (x x
1) − f (x2) < 0 ⇒ f (x1) < 1 + 2 x2 + 2 f (x2).
Vậy hàm số đồng biến trên (−∞; −2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 4: Xác định parabol (P) : y = ax2 + bx + 2, biết rằng (P) đi qua điểm M(1; 5) và có trục 1
đối xứng là đường thẳng x = − . 4 ý Lời giải.
M ∈ (P) ⇒ a + b + 2 = 5 ⇒ a + b = 3. (1) 1 b 1
(P) có trục đối xứng là đường thẳng x = − ⇒ − = − ⇒ 2a − 4b = 0. (2) 4 2a 4 ®a + b = 3 ®a = 2 Từ (1) và (2) ⇒ ⇔ 2a − 4b = 0 b = 1.
Vậy (P) : y = 2x2 + x + 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 5: Trong mặt phẳng với hệ trục tọa độ Oxy, hãy xác định miền nghiệm của bất phương
trình: −x + 4y ≤ 3(y − x + 1). ý Lời giải.
−x + 4y ≤ 3(y − x + 1) ⇔ 2x + y − 3 ≤ 0.
Ta vẽ đường thẳng 2x + y − 3 = 0 ⇔ y = −2x + 3. Bảng giá trị 84 GV: VŨ NGỌC HUY x 0 1 y 3 1 Ta có đồ thị như sau y 3 2 1 x O −3 −2 −1 1 2 3 −1 −2 −3
Chọn điểm O(0; 0) thay vào bất phương trình 2x + y − 3 ≤ 0 ta được
2 · 0 + 0 − 3 ≤ 0 ⇔ −3 ≤ 0 (đúng)
Suy ra điểm O(0; 0) thuộc miền nghiệm của bất phương trình 2x + y − 3 ≤ 0
Vậy miền nghiệm của bất phương trình −x + 4y ≤ 3(y − x + 1) là những phần không bị gạch
kể cả đường thẳng đó. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 6: Mẫu số liệu tuổi của 16 nhân viên trong công ty X như sau: 18 30 20 22 21 40 47 22 20 19 25 30 44 40 35 47
Tìm số trung bình và tứ phân vị của mẫu số liệu trên. ý Lời giải.
Sấp xếp lại mẫu số liệu theo thứ tự không giảm, ta được: 18 19 20 20 21 22 22 25 30 30 35 40 40 44 47 47 Số trụng bình là
18 + 19 + 20 + 20 + 21 + 22 + 22 + 25 + 30 + 30 + 35 + 40 + 40 + 44 + 47 + 47 x = = 30. 16 25 + 30
Vì n = 16 là số chẵn nên giá trị tứ phân vị thứ hai là Q2 = = 27,5. 2
Tứ phân vị thứ nhất là trung vị của mẫu: 18 19 20 20 21 22 22 25. 20 + 21 Do đó Q1 = = 20,5. 2
Tứ phân vị thứ ba là trung vị của mẫu: 30 30 35 40 40 44 47 47. 40 + 40 Do đó Q3 =
= 40. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 85 GV: VŨ NGỌC HUY
Bài 7: Khi một vật được ném lên thì chiều cao h (m) so với mặt đất theo thời gian t (giây)
được tính bởi hàm số h(t) = −5t2 + v0t + h0 với v0 là vận tốc ban đầu, h0 (m) là độ cao ban
đầu của vật. Một quả bóng được cầu thủ Messi đá lên từ mặt đất với vận tốc ban đầu là 20 (m/s). Hỏi
a) Độ cao lớn nhất của quả bóng so với mặt đất?
b) Sau bao lâu thì bóng chạm đất? ý Lời giải.
Ta có h0 = 0 (m) và v0 = 20 (m/s) ⇒ h(t) = −5t2 + 20t. 20
a) Quả bóng có độ cao lớn nhất so với mặt đất sau khi nó di chuyển được t1 = − = 2 · (−5) 2 giây.
Vậy độ cao lớn nhất của quả bóng so với mặt đất là h1 = −5t2 + 20t 1 1 = 20 m. ñt2 = 4 (nhận)
b) Ta có h2 = 0 ⇒ −5t2 + 2 20t2 = 0 ⇔ t2 = 0(loại).
Vậy sau 4 giây thì bóng chạm đất.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 8: Cho tam giác ABC có a = 6, b = 5, c = 8. Tính cos A và diện tích của tam giác ABC. ý Lời giải. 53
Ta có a2 = b2 + c2 − 2bc cos A ⇒ cos A = . 80 a + b + c 19 Ta có p = = . 2 2 √ 3 399
Vậy SABC = pp(p − a)(p − b)(p − c) =
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 # » # »
Bài 9: Cho hình thoi ABCD có đường chéo AC = 2a, BD = 4a. Tính CA + AD. ý Lời giải. # » # » # » Ta có CA + AD = CD = CD. A
Gọi O là giao điểm của AC và BD √ √ ⇒ OC = a, OD = 2a ⇒ CD = OC2 + OD2 = a 5. O # » # » √ B D Vậy CA + AD = a 5. C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . #»
Bài 10: Một người dùng một lực F tạo với mặt đất một góc 45◦ và có độ lớn là 20 N để kéo #»
một vật dịch chuyển theo đường thẳng một đoạn 80 m. Tính công sinh bởi lực F . #» F 45◦ 80 m ý Lời giải. #» √
Công sinh bởi lực F là A = |F| · s · cos α = 20 · 80 · cos 45◦ = 800 2 J. . . . . . . . . . . . . . . . . . . . 86 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT HÙNG VƯƠNG
Thời gian làm bài: 90 phút √
Bài 1: Tìm tập xác định của hàm số y = f (x) = x2 + x + 1 + x − 2022. ĐS: D = [2022; +∞).
Bài 2: Cho hàm số y = f (x) = −x2 + 2x + 3.
a) Lập bảng biến thiên của hàm số.
b) Dựa vào bảng biến thiên, tìm khoảng đồng biến và khoảng nghịch biến của hàm số. x −∞ 1 +∞ 4 y −∞ −∞ ĐS: a)
; b) Hàm số đồng biến trên (−∞; 1) và nghịch biến trên (1; +∞).
Bài 3: Cho tam giác ABC có AB = 10 cm, BC = 8 cm, AC = 12 cm.
a) Tính diện tích S của tam giác ABC.
b) Tính bán kính đường tròn nội tiếp r của tam giác ABC. √ √
ĐS: a) S = 15 7; b) r = 7.
Bài 4: Cho hình vuông ABCD tâm O và độ dài cạnh bằng a. Ä # » # »ä # » # »
a) Xác định và tính góc AB, AC .
b) Tính tích vô hướng AB · OC. Ä # » # »ä # » # » a2 ĐS: a) AB, AC = ’
BAC = 45◦; b) AB · OC = . 2
Bài 5: Bảng sau đây cho biết sức chứa dành cho khán giả của các sân vận động được sử dụng
trong nhiều sự kiện thể thao tại Việt Nam (số liệu gần đúng). Sân Thống Hòa Hàng Đồng Lạch Thiên Cần Mỹ vận Tự Do Nhất Xuân Đẫy Nai Tray Trường Thơ Đình động Sức 15 000 16 000 20 500 22 500 30 000 30 000 30 000 30 000 40 190 chứa (Nguồn: Wikipedia)
Tìm số trung bình, mốt và tứ phân vị của mẫu số liệu trên. 234190 ĐS: x = ; M 9
0 = 30 000; Q1 = 18 250; Q2 = 30 000; Q3 = 30 000. 87 GV: VŨ NGỌC HUY Bài 6:
Một ô tô muốn đi từ A đến C, nhưng
giữa A và C là một ngọn núi cao nên
ô tô phải đi đường tránh thành hai A C
đoạn từ A đến B rồi từ B đến C, các
đoạn đường tạo thành tam giác ABC
có độ dài AB = 15 km, BC = 20 km và ’
ABC = 60◦. Để rút ngắn khoảng
cách và tránh sạt lở núi, người ta dự
định làm đường hầm xuyên núi nối B
thẳng từ A đến C. Hỏi quãng đường
từ A đến C dài bao nhiêu? (Kết quả
làm tròn đến chữ số thập phân thứ hai). √
ĐS: AC = 5 13 km ≈ 18,03 km. Bài 7:
Khi một quả bóng được đá lên nó sẽ đạt độ cao nào y
đó rồi rơi xuống đất. Biết quỹ đạo của quả bóng là 10
một đường parabol trong mặt phẳng tọa độ Oth có S
phương trình h = at2 + bt + c với a < 0, trong đó t là 9
thời gian (tính bằng giây) kể từ khi quả bóng được đá
lên và h là độ cao (tính bằng mét) của quả bóng. Giả 8
thiết rằng quả bóng được đá lên từ độ cao 1 m và sau 7
1 giây thì nó đạt được độ cao 6,5 m, sau 4 giây thì nó B 6,5
đạt được độ cao 5 m. Hãy xác định độ cao cao nhất 6
mà quả bóng đã đạt được. C 5 4 3 2 1 A x O −1 1 2 3 4 5 −1 55 ĐS: m ≈ 9,17 m. 6 88 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
Thời gian làm bài: 90 phút Bài 1: √x − 1
a) Tìm tập xác định của hàm số y = f (x) =
. ĐS: Tập xác định D = [1; +∞) \ {2} x − 2 2x − 1
b) Xét tính đơn điệu của hàm số y = f (x) =
trên khoảng (−∞; −1). ĐS: Hàm số x + 1
đồng biến trên khoảng (−∞; −1)
Bài 2: Cho hàm số bậc hai y = f (x) = x2 + mx + n. Tìm m, n biết đồ thị hàm số là một parabol có đỉnh S(1; 4). ĐS: m = −2, n = 5
Bài 3: Điểm số bài kiểm tra cuối học kỳ I của các bạn học sinh trong một nhóm học tập là 6;
10; 6; 8; 7; 10. Tính số trung bình, trung vị của mẫu số liệu (Làm tròn đến 2 chữ số sau dấu phẩy).
ĐS: Số trung bình x ≈ 7,83, Số trung vị Me = 7,5
Bài 4: Một bạn học sinh lớp 10 muốn làm 2 loại sản phẩm A và B để tham gia hội Xuân. Biết
rằng mỗi sản phẩm loại A cần 100 ngàn đồng tiền nguyên liệu, 2 giờ công và bán được 450
ngàn đồng; mỗi sản phẩm loại B cần 200 ngàn đồng tiền nguyên liệu, 3 giờ công và bán được
750 ngàn đồng. Bạn có 700 ngàn đồng tiền vốn và có 12 giờ chuẩn bị. Hỏi bạn ấy cần làm bao
nhiêu sản phẩm mỗi loại để số tiền thu được là lớn nhất? ĐS: Lợi nhuận lớn nhất bằng 2 850
ngàn đồng đạt khi làm 3 sản phẩm loại A và 2 sản phẩm loại B
Bài 5: Cho 4ABC. Đặt a = BC, b = AC, c = AB, p là nửa chu vi tam giác, R là bán kính
đường tròn ngoại tiếp tam giác.
a) Chứng minh p = R · (sin A + sin B + sin C).
b) Biết b = 3, a = 5, ’
BCA = 60◦. Tính c, S4ABC (Làm tròn đến 2 chữ số sau dấu phẩy).√ √ 15 3 ĐS: c = 19, S4ABC = 4
Bài 6: Cho hình vuông ABCD cạnh a, tâm O. √ # » # » # » # » # » # » a2 2 # » # »
a) Tính các tích vô hướng AB · AC, AC · BD theo a. ĐS: AB · AC = , AC · BD = 0 2 # » # »
b) Chứng minh 2MA · MC = 2MO2 − a2 (với M là điểm tùy ý). # » # » # » # » 1 1
c) Gọi I, J là hai điểm di động thỏa AI = mAB, D J = (1 − n)DA, + = 1. Chứng m n
minh đường thẳng I J luôn đi qua một điểm cố định. 89 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT NGUYỄN THƯỢNG HIỀN
Thời gian làm bài: 90 phút
Bài 1: Cho tập hợp A = {x ∈ N(x − 1)(x2 − x − 2) = 0}. Viết tập hợp A dưới dạng liệt kê
các phần tử và viết tất cả các tập hợp con của tập hợp A. ĐS: A = {1; 2} √ √ x + 1 + 4 − x
Bài 2: Tìm tập xác định của hàm số f (x) = . ĐS: Tập xác định −x2 − 2x + 3 D = [−1; 4] \ {1} Bài 3:
Cho hàm số xác định trên đoạn [−3; 2] như hình bên, hãy xác định y 4
các khoảng biến thiên và tập giá trị của hàm số đó trên đoạn [−3; 2]. 3 x −3 −2 − O 1 −2
ĐS: Hàm số đồng biến trên khoảng (−3; −1) và (0; 2).
Hàm số nghịch biến trên khoảng (−1, 0).
Tập giá trị của hàm số trên đoạn [−3; 2] là T = [−2; 4].
Bài 4: Cho hàm số bậc hai y = ax2 + bx + c (a 6= 0) có đồ thị là parabol (P). Biết rằng (P) có
đỉnh I(1; 3) và cắt trục tung tại điểm có tung độ là 4. Xác định a, b, c. ĐS: a = 1, b = −2, c = 4
Bài 5: Kết quả điểm thi GHK1 môn Toán của lớp 10A được cho bởi bảng sau Điểm 5 6 7 8 9 10 Số lượng 2 5 9 12 10 2
Tìm số điểm trung bình môn Toán của lớp 10A. Xác định độ lệch chuẩn của mẫu số liệu trên
và nêu ý nghĩa của nó. ĐS: Điểm trung bình x = 7,725, Độ lệch chuẩn S ≈ 1,2447. Độ lệch
chuẩn ở mức thấp, cho thấy mức độ chênh lệch điểm thi GHK1 môn Toán không đáng kể. Bài 6:
Một máy bay có véc-tơ vận tốc chỉ theo hướng bắc, vận tốc gió là một B 70 km/h
véc-tơ theo hướng đông như hình bên. Tính độ dài véc-tơ tổng của hai C véc-tơ nói trên. km/h 350 A √ ĐS: 70 26 km/h 90 GV: VŨ NGỌC HUY
Bài 7: Cho tam giác ABC có M là trung điểm của đoạn AB, điểm N thuộc cạnh AC sao cho # » 1 # » 1 # »
NC = 2N A và gọi K là trung điểm của MN. Chứng minh rằng AK = AB + AC. 4 6 Ä # » # »ä Ä # » # »ä
Bài 8: Cho tam giác ABC có AB = 5a; AC = 8a; ’
BAC = 60◦. Tính AB + AC · 2AC − AB theo a. ĐS: Bài 9:
Để đo chiều ca của tháp Cánh Tiên (tháp cổ Chăm D
Pa ở tỉnh Bình Định), một bạn chon hai vị trí A và B
trên mặt đất sao cho ba điểm A, B, C thẳng hàng,
với C là chân tháp và CD = h là chiều cao của tháp.
Bạn đóđo được AB = 8 m, ’ CAD = 63◦; ’ CBD = 48◦
(tham khảo hình vẽ bên). Tính chiều cao của tháp. 48◦ 63◦ B C A 8 m
ĐS: Chiều cao tháp bằng 10,43 m.
Bài 10: Nhà bạn An định làm bánh bán dịp Noel 2022 với hai sản phẩm bánh Sago và bánh
Hano. Biết để sản xuất ra 1 kg bánh Sago cần 5 kg nguyên liệu I và 4 kg nguyên liệu I I; để
sản xuất 2 kg bánh Hano cần 4 kg nguyên liệu I và 4 kg nguyên liệu I I. Biết giá của 1 kg
nguyên liệu I là 10 nghìn đồng, giá của 1 kg nguyên liệu I I là 20 nghìn đồng. Giá bán của
1 kg bánh Sago là 270 nghìn đồng và 1 kg bánh Hano là 125 nghìn đồng. Biết chi phí vận
chuyển là 200 nghìn đồng và nhà An hiện chỉ có 175 kg nguyên liệu I và 150 kg nguyên liệu
I I. Hỏi nhà bạn An cần làm bao nhiêu bánh Sago và bánh Hano để thu được lợi nhuận lớn
nhất và số tiền lời lớn nhất thu được là bao nhiêu. ĐS: 25 kg bánh Sago và 25 kg bánh Hano
để thu lợi lớn nhất. Số tiền lớn nhất thu được là 9 675 nghìn đồng. 91 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT TRƯỜNG CHINH - ĐỀ 3
Thời gian làm bài: 90 phút
Bài 1: Cho A = (−2; 4) và B = (−∞; 3]. Tìm A ∩ B, A ∪ B, A \ B, B \ A. ĐS:
A ∩ B = (−2; 3], A ∪ B = (−∞; 4), A \ B = (3; 4), B \ A = (−∞; −2] ®x − 2y + 4 ≥ 0
Bài 2: Biểu diễn miền nghiệm của hệ bất phương trình: ĐS: 3x + y − 6 ≤ 0. y 3 2 1 x − 2y + 4 = 0 O −4 −3 −2 −1 1 2 3 4 x 3 −1 x+ −2 y− −3 6= − 0 4 √ |x − 2| − 5 + 2x ï 5 ã ß 3™
Bài 3: Tìm tập xác định của hàm số y = . ĐS: − ; +∞ \ 3 − 2x 2 2
Bài 4: Tìm các số b, c sao cho đồ thị hàm số y = x2 + bx + c là một parabol có đỉnh I(2; 5). ĐS: b = −4, c = 9
Bài 5: Điểm kiểm tra giữa học kì 9 môn của bạn An như sau: 7; 8; 5; 6; 8; 7; 5; 9; 8.
Tìm số trung bình, trung vị, tứ phân vị, khoảng biến thiên của mẫu số liệu trên. ĐS: x = 7;
Me = 7; Q1 = 5,5; Q2 = 7; Q3 = 8; R = 4
Bài 6: Cho tam giác ABC có AB = 5, AC = 6, BC = 8. Tính góc A, diện tích tam giác ABC,
độ dài đường cao BK, bán kính đường tròn nội tiếp tam giác ABC. ĐS: √ √ √ 3 399 399 3 399 “ A ≈ 92◦520, S = , BK = , r = 4 4 38 Bài 7: # » # » # » # »
a) Cho tứ giác ABCD. Chúng minh rằng: AC + BD = AD − CB. # » 2 # »
b) Cho tam giác ABC có M là trung điểm cạnh AB. Điểm N thoả điều kiện BC = BN. 5 # » # » # » # » 1 # » # »
Tính vecto MN theo hai vecto CA, CB.
ĐS: MN = − CA − 2CB 2 # » # »
c) Cho hình chữ nhât ABCD có AD = 6, AB = 8. Tính tích vô hướng AB · AC. ĐS: 64 Bài 8: 92 GV: VŨ NGỌC HUY #» #»
a) Trong Vật lí, tích vô hướng của F và d biểu diễn công A sinh bởi lực F khi thực hiện #» #»
độ dịch chuyển d . Một người dùng một lực F có cường độ 15 N kéo một chiếc xe đi #» #»
quãng đường dài 30 m. Tính công sinh bởi lực F , biết rằng góc giữa vecto F và hướng √ di chuyển là 30◦. ĐS: 225 3 J b)
Để đo khoảng cách từ vị trí A đến vị trí B ở hai B
bên bờ hồ, bạn An đi dọc bờ hồ từ vị trí A đến vị
trí C và tiến hành đo các góc BAC và BCA. Biết AC = 25 m, ’ BAC = 58,95◦, ’ BCA = 83,15◦ ( tham
khảo hình bên). Hỏi, khoảng cách từ vị trí A đến
vị trí B là bao nhiêu mét? ĐS: 40,41 m 58,95◦ 83,15◦ A 25 m C
c) Một người bán nước giải khát đang có 48 g bột cam, 18 l nước và 420 g đường để pha
chế hai loại nước cam A và B. Để pha chế 1 l nước cam loại A cần 30 g đường, 1 l nước
và 1 g bột cam, để pha chế 1 l nước cam loai B cần 10 g đường 1 l nước và 4 g bột cam.
Mỗi lít nước cam loại A bán được 30 nghìn đồng, mỗi lít nước cam loại B bán đựợc 40
nghìn đồng. Người đó nên pha chế bao nhiêu lít nước cam mỗi loại để có doanh thu cao nhất?
ĐS: 8 lít loại A và 10 lít loại B 93 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT TRƯỜNG CHINH - ĐỀ 4
Thời gian làm bài: 90 phút
Bài 1: Cho tập họp A = (−2; +∞) và B = (−∞; 2]. Tìm A ∪ B, A ∩ B, A \ B, CRA. ĐS:
A ∪ B = R; A ∩ B = (−2; 2]; A \ B = (2; +∞); CRA = (−∞; −2] ®x + y + 1 ≤ 0
Bài 2: Biểu diễn miền nghiệm của hệ bất phương trình sau: ĐS: y ≤ 2. y 3 y = 2 1 −3 −2 −1 1 2 3 x O −1 −2 x + − y 3 + 1 = −4 0 √x + 3
Bài 3: Tìm tập xác định của hàm só: y = √ . ĐS: [−3; 2) 2 − x
Bài 4: Xác định công thức của P : y = 2x2 + bx + c, biết (P) có đỉnh I(−1; 3). ĐS: b = 4; c = 5
Bài 5: Một cửa hàng trà sữa vừa khai trương, thống kê lượng khách tới quán trong 7 ngày
đầu và thu được mẩu số liệu sau: Ngày 1 Ngày 2 Ngày 3 Ngày 4 Ngày 5 Ngày 6 Ngày 7 575 454 400 325 351 333 412
Tìm số trung bình, trung vị, khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu. ĐS:
x ≈ 407,14; Me = 400; R = 250; ∆Q = 121
Bài 6: Cho tam giác ABC có AB = 2, BC = 3, AC = 4. Tính số đo góc B, tính diện tích, bán
kính đường tròn ngoại tiếp và đường cao AH của tam giác ABC. ĐS: √ √ √ 3 15 8 15 3 15 b B ≈ 46◦340, S = , R = , AH = 4 15 8
Bài 7: Cho tam giác ABC. Gọi K, H lần lượt là trung điểm BC, AK. Điểm M tùy ý. # » # » # » # »
a) Chứng minh rằng: AM + BC = AC + BM. # » # » # » # »
b) Chứng minh rằng: 2MA + MB + MC = 4MH. # » # »
c) Tính BC · BK biết BC = 8. ĐS: 32 Bài 8: 94 GV: VŨ NGỌC HUY #»
a) Một người dùng một lực F có cường độ 30 N kéo một chiếc xe đi quãng đường đài #» #»
60 m. Tính công sinh bởi lực F , biết rằng góc giữa vectơ F và hướng di chuyển là 45◦. √ ĐS: 900 2 J b)
Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. D
Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng
hàng. Ta đo được AB = 24 m, ’ CAD = 63◦; ’ CBD = 48◦. Tính
chiều cao h của khối tháp? ĐS: h ≈ 61,4 m 48◦ 63◦ C A 24 m B
c) Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít
nước và 210 g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần
30 g đường, 1 lít nước và 1 g hương liệu, pha chế 1 lít nước táo cần 10 g đường, 1 lít
nước và 4 g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, Mỗi lít nước táo
nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để số
điểm thưởng là lớn nhất.
ĐS: 4 lít nước cam và 5 lít nước táo 95 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ GIỮA HỌC KÌ I KHỐI 10/2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT TRẦN HƯNG ĐẠO
Thời gian làm bài: 90 phút
PHẦN 1 - TRẮC NGHIỆM
Câu 1: Cho các điểm phân biệt A, B, C. Đẳng thức nào sau đây đúng? # » # » # » # » # » # » # » # » # » # » # » # » A. AB = AC + CB. B. AB = BC − AC. C. AB = CA + BC. D. AB = CB − AC. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ® − 2x + 6 khi x ≤ 1
Câu 2: Đồ thị của hàm số y = f (x) =
đi qua điểm nào sau đây? 4 khi x > 1 A. M (0; 6). B. P (2; −3). C. N (1; −4). D. Q (0; 4). ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 3: Cho tam giác ABC có AB = 4, BC = 8, b
B = 60◦. Tính độ dài cạnh AC. √ √ √ √ A. 4 7. B. 2 3. C. 2 7. D. 4 3. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 4: Cho tam giác ABC có “ A = 15◦, c = 3, b
B = 45◦. Bán kính đường tròn ngoại tiếp của tam giác ABC là √ √ √ √ A. R = 3 3. B. R = 3. C. R = 2 3. D. R = 4 3. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 5: Cho hàm số y = f (x) có tập xác định [−1; 9] và đồ thị của nó như hình dưới đây. y 6 5 4 3 2 1 5 − x 2 −1 O 1 2 3 4 6 7 8 9 −2
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên (4; 9).
B. Hàm số đồng biến trên (−1; 5).
C. Hàm số nghịch biến trên (1; 5).
D. Hàm số nghịch biến trên (1; 6). 96 GV: VŨ NGỌC HUY ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x − 3
Câu 6: Tập xác định của hàm số y = là x2 − 4x + 3 A. D = R \ {3}. B. D = R \ {1}.
C. D = R \ {−3; −1}.
D. D = R \ {3; 1}. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 7: Mệnh đề phủ định của mệnh đề P : 00∀x ∈ R, x2 ≥ 000 là
A. P : 00∃x ∈ R, x2 < 000.
B. P : 00∀x ∈ R, x2 < 000.
C. P : 00∀x ∈ R, x2 ≤ 000.
D. P : 00∃x ∈ R, x2 6= 000. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 8: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? A. x2 + 4y2 ≤ 6. B. xy + x + y > 0. C. 2x − 3y ≥ −2. D. x + y2 ≥ 2. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 9: Cho tập hợp A = {x ∈ R|x ≤ 3}. Hãy viết tập hợp A dưới dạng khoảng, đoạn, nửa khoảng A. A = (−∞; 3). B. A = (−∞; 3]. C. A = (3; +∞). D. A = [3; +∞). ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 10: Cho hai tập hợp A = (−6; 0) và B = (3; +∞). Khẳng định nào sau đây đúng? A. A ∪ B = (0; +∞). B. A ∩ B = (−3; 0].
C. A ∩ B = (−6; −3).
D. A ∪ B = (−6; +∞). ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ®x − y ≤ −3
Câu 11: Cho hệ bất phương trình bậc nhất hai ẩn
. Điểm nào sau đây thuộc 2y ≥ −4
miền nghiệm của hệ bất phương trình đã cho? A. P(−3; 1). B. N(−2; 1). C. O(0; 0). D. M(3; −1). ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 12: 97 GV: VŨ NGỌC HUY
Miền không tô đậm ở hình vẽ dưới đây là biểu diễn miền nghiệm của y bất phương trình nào? A. 2x − y + 4 ≤ 0. B. 2x − y + 4 ≥ 0. 4 C. 2x + y + 4 ≥ 0. D. 2x + y + 4 ≤ 0. − x 2 O ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 13: Trong các cặp số sau đây, cặp số (x; y) nào sau đây thuộc miền nghiệm của bất
phương trình 2x − 3y + 5 > 0? A. (−3; 2). B. (−5; 0). C. (0; 0). D. (−2; 1). ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 14: Phương trình trục đối xứng của parabol y = 2x2 − 6x + 1 là 3 1 3 A. x = − . B. x = 3. C. x = . D. x = . 2 2 2 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √ √
Câu 15: Cho biết 3 3 = 1,44224957.... Số gần đúng của 3 3 với độ chính xác d = 0,0001 là A. 1,4421. B. 1,4422. C. 1,442. D. 1,44. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 16: Hệ bất phương trình nào sau đây không phải là hệ bất phương trình bậc nhất hai ẩn? ®x > 3 ®x − 2y ≤ 3 ®3x + y < 4 ®y > 0 A. . B. . C. . D. . y ≤ −4 x + 2y ≥ 4 x2 + y > 3 x + y ≤ 0 ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 17: Câu nào sau đây không phải là mệnh đề? A. 2 + 1 > 10.
B. Bạn bao nhiêu tuổi rồi?. √ C. 2 là một số vô tỉ.
D. 5 là một số lẻ. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 18: Tam giác ABC có BC = a, AC = b, AB = c và bán kính đường tròn ngoại tiếp R.
Đẳng thức nào sau đây đúng? a + b + c abc abc a + b + c A. S = . B. S = . C. S = . D. S = . 4R 2R 4R 2R ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98 GV: VŨ NGỌC HUY
Câu 19: Cho số gần đúng a = 2048 với độ chính xác d = 50. Số quy tròn của a bằng bao nhiêu? A. 2000. B. 2040. C. 2050. D. 2100. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » # »
Câu 20: Trên đường thẳng MN lấy điểm P sao cho MN = −3MP. Điểm P được xác định
đúng trong hình vẽ nào sau đây? M P N N M P Hình 1 Hình 2 N M P M P N Hình 3 Hình 4 A. Hình 1. B. Hình 4. C. Hình 2. D. Hình 3. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ĐÁP ÁN 1. A 2. D 3. A 4. D 5. C 6. D 7. C 8. B 9. B 10. D 11. D 12. C 13. A 14. B 15. A 16. A 17. B 18. C 19. B 20. C PHẦN 2 - TỰ LUẬN
Bài 1: Xác định hàm số y = ax2 + bx + c (a 6= 0) biết đồ thị của hàm số là một parabol có
đỉnh I(1; 1) và đi qua điểm A(2; 3). ĐS: y = 2x2 − 4x + 3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 2: Một cổng chào của sân vận động tỉnh A có hình dạng là một parabol hướng bề lõm
xuống dưới. Giả sử ta gắn hệ tọa độ Oxy sao cho một chân cổng đi qua gốc tọa độ O như
hình vẽ (x, y tính bằng mét), chân kia của cổng ở vị trí có tọa độ (4; 0). Biết một điểm M trên
cổng có tọa độ (3; 12). Tính chiều cao của cổng ở vị trí cao nhất. ĐS: 16m ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 3: Lớp 10A tham gia cuộc thi thiết kế thiệp mừng ngày Nhà giáo Việt Nam 20-11 do
Đoàn thanh niên phát động và các tấm thiệp sẽ được nhà trường mua lại tặng các thầy cô
giáo. Cần 1 giờ để hoàn thành một tấm thiệp nhỏ có giá 15 nghìn đồng và 3 giờ để hoàn thành
tấm thiệp loại lớn có giá 40 nghìn đồng. Mỗi lớp chỉ có 6 giờ để thiết kế và chỉ được dự thi
không quá 4 thiệp. Hãy cho biết lớp 10A cần làm bao nhiêu tấm thiệp mỗi loại để được tiền nhiều nhất?
ĐS: 3 thiệp loại nhỏ, 1 thiệp loại lớn ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 4: # » # » # » # » # »
a) Cho các điểm A, B, C, D, E. Chứng minh AD + BC − EC − BD = AE. 99 GV: VŨ NGỌC HUY
b) Cho 4ABC vuông tại A có AB = 3, AC = 4. Gọi H là trung điểm cạnh BC. Tính độ dài # » # » véc-tơ HB − HC. ĐS: a) b) 5 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 5: # » # »
a) Cho 4ABC có AB = 2, BC = 4, ’
ABC = 60◦. Tính tích vô hướng BA · BC. # » # »
b) Cho hình vuông ABCD có tâm O có độ dài cạnh bằng a. Tính tích vô hướng AB · OC. 1 ĐS: a) −4; b) 2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 6: Cho tam giác ABC vuông tại B có AB = 3a và BC = 4a. Gọi M là điểm thỏa mãn # » # » # » #» √ # » # »
MA + MB − MC = 0 và N là trung điểm của AC. Tính 2MA + MB theo a. ĐS: 3 17 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ GIỮA HỌC KÌ I KHỐI 10/2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT NGUYỄN KHUYẾN
Thời gian làm bài: 90 phút Bài 1: x √
a) Tìm tập xác định của hàm số y = − −x.
ĐS: D = (−∞; 0]\{−1}. 1 − x2
b) Cho hàm số y = f (x) xác định trên khoảng (−∞, +∞) có đồ thị như hình vẽ dưới đây.
Hàm số đồng biến trên khoảng nào? y 3 2 x −1 O −3
ĐS: Hàm số đồng biến trên (−1; 0) và (2; +∞). ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 2:
a) Xác định parabol (P) : y = ax2 + bx + 2, biết rằng (P) đi qua điểm M(1; 5) và có trục 1
đối xứng là đường thẳng x = − .
ĐS: (P) : y = 2x2 + x + 2. 4 y O 1 x −1 −3
b) Lập bảng biến thiên vẽ đồ thị hàm số y = −2x2 + 4x − 3. ĐS: 101 GV: VŨ NGỌC HUY c)
Cổng của một công viên có khoảng trống phía trong cổng dạng
parabol với chiều cao, độ rộng như hình vẽ. Cần đưa hàng hóa
qua cổng này bằng xe tải có chiều cao là 5 m và rộng 4 m. Xe có
qua được cổng không? Vì sao? 8 m 6 m
ĐS: Xe không đi qua được. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 3: Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất A và 9 kg
chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và
0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg
chất A và 1,5 kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua
nguyên liệu là ít nhất? Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10
tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.
ĐS: 5 tấn nguyên liệu loại A và 4 tấn loại B thì giá thành nhỏ nhất là 32 triệu. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 4:
a) Cho hình chữ nhật ABCD có AB = 2a và AB = 2BC. Gọi M là trung diểm AD. Tính # » # » # » # »
theo a các độ dài |AB + AD| và |MB + MC|.
b) Cho hình vuông ABCD có cạnh bằng 5. Tính tích vô hướng . # » # » c) DA · BD
d) Cho tam giác ABC. Gọi M là điểm trên cạnh BC sao cho MB = 4MC. Chứng minh # » 1 # » 4 # » AM = AB + AC. 5 5 ĐS: # » # » √ # » # » a) |AB + AD| = a 5. |MB + MC| = 4a. √ # » # » 25 2 b) DA · BD = − . 2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # » # » #» # » # »
Bài 5: Cho tam giác ABC. Gọi P, Q, R là các điểm thỏa hệ thức 3PB + 4PC = 0 , 2RA + RB = #» # » # » #»
0 , 3QA − 2QC = 0 . Chứng minh P, Q, R thẳng hàng . ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT NGUYỄN TẤT THÀNH
Thời gian làm bài: 90 phút
Bài 1: Cho hàm số y = f (x) có đồ thị như hình vẽ. Dựa vào đồ thị, tìm tập xác định, tập giá
trị và các khoảng đồng biến, nghịch biến của hàm số.(Hs không cần vẽ hình) y 4 3 y = f (x) x −6 −2 O 1 5 −1 −3
ĐS: Tập xác định D = [−6; 5], tập giá trị T = [−3; 4], hàm số đồng biến trên (−6; −2) và
(0; 5), hàm số nghịch biến trên (−2; 0). ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 2: Vẽ đồ thị của hàm số y = x2 + 2x − 3. Tìm tập giá trị và các khoảng đồng biến, nghịch biến của hàm số. y −1 x −3 O 1 −3 −4
ĐS: Đồ thị hàm số
Tập giá trị T = [−4; +∞), hàm số nghịch biến trên (−∞; −1) và nghịch biến trên (−1; +∞). ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 3: Tìm các số a, b, c, biết đồ thị hàm số y = ax2 + bx + c qua A(0; −3) và có đỉnh S(−2; 1).
ĐS: a = −1; b = −4; c = −3 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 4: Một công ty sản xuất hai loại sơn nội thất và sơn ngoài trời. Nguyên liệu để sản xuất
gồm hai loại A, B với trữ lượng là 12 tấn và 8 tấn tương ứng. Để sản xuất 1 tấn sơn nội thất
cần 5 tấn nguyên liệu A và 1 tấn nguyên liệu B. Để sản xuất 1 tấn sơn ngoài trời cần 2 tấn 103 GV: VŨ NGỌC HUY
nguyên liệu A và 2 tấn nguyên liệu B. Qua điều tra thị trường, công ty thấy nhu cầu sơn nội
thất không hơn sơn ngoài trời quá 1 tấn. Giá bán 1 tấn sơn nội thất là 2000 USD, giá bán 1 tấn
sơn ngoài trời là 3000 USD. Hỏi cần sản xuất mỗi loại sơn bao nhiêu tấn đề có doanh thu lớn nhất?
ĐS: Để đạt doanh thu lớn nhất cần sản xuất 1 tấn sơn nội thất và 3, 5 tấn sơn ngoài trời. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 5: Cho hình vuông ABCD tâm I, AD = 3. G là trọng tâm 4BCD. # » # » # » # » # » # » # » # »
a) Tính |AD + DC|; |GB + GD|; I A · GD; AD · DB. # » # » # » # »
b) Chứng minh rằng AD − BG − 2CG = 6IG. # » # » 3
c) Tìm tất cả các điểm M thỏa mãn điều kiện GI · I M = . 4 ĐS: # » # » √ # » # » √ # » # » # » # »
a) |AD + DC| = 3 2; |GB + GD| =
2; I A · GD = 1; AD · DB = −9. Å # » # » 3 ã
c) M chạy trên đường thẳng qua E E ∈ IG và GI · IE = , vuông góc với IG. 4 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT TRƯỜNG CHINH - ĐỀ 1
Thời gian làm bài: 90 phút
Bài 1: Cho hai tập hợp A = (−1; 7), B = [−2; 5). Tìm A ∪ B; A ∩ B; A \ B; CRA. ĐS:
A ∪ B = [−2; 7), A ∩ B = (−1; 5), A \ B = [5; 7), CRA = (−∞; −1] ∪ [7; +∞) ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 2: Biểu diễn miền nghiệm của hệ bất phương trình sau trên mặt phẳng tọa độ Oxy: ®3x + y − 4 < 0 x − y + 5 < 0 . ĐS: ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √ x + 4 Å 3 ã
Bài 3: Tìm tập xác định của hàm số y = x + 1 + √ . ĐS: D = ; +∞ 2x − 3 2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 4: Cho hàm số y = −x2 + 6x − 5.
a) Tìm tọa độ đỉnh, lập bảng biến thiên và chỉ ra các khoảng đơn điệu của hàm số trên.
b) Hàm số đạt giá trị nhỏ nhất hay giá trị lớn nhất? Tìm giá trị đó.
ĐS: a) Đỉnh I(3; 4), đồng biến trên (−∞; 3), nghịch biến trên (3; +∞).
b) Hàm số đạt GTLN bằng 4 khi x = 3. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 5: Một hộ gia đình có sản lượng điện sử dụng trong 12 tháng của năm 2021 như sau: Tháng 1 2 3 4 5 6 7 8 9 10 11 12 Điện năng (kWh) 447 458 396 415 459 510 366 451 430 447 380 415
Hãy tìm số trung bình, tứ phân vị, khoảng tứ phân vị và khoảng biến thiên của mẫu số liệu trên.
ĐS: x ≈ 431, 16; Q1 = 405, 5; Q2 = 438, 5; Q3 = 454, 5; ∆Q = 49; R = 144 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 6: Cho tam giác ABC có AB = 9, AC = 8, BC = 7. Tính diện tích tam giác ABC, đường
cao AH, bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp của tam giác ABC. √ √ √ 24 5 21 5 √ ĐS: SABC = 12 5; AH = ; R = ; r = 5 7 10 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 7: Cho tam giác đều ABC cạnh a. Gọi E, F lần lượt là trung điểm của AC và BC; I là trọng tâm của tam giác ABC. #» #» # » # »
a) Tính độ dài vectơ v biết v = BC + BC. 105 GV: VŨ NGỌC HUY # » 1 # » 1 # »
b) Chứng minh rằng I F = − BA + BC. 3 6 # » # » c) Tính I A · AB. √ a2 ĐS: a) a 3; c) − 2 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 8:
a) Hai chiếc xe cùng xuất phát ở vị trí A, đi theo hai hướng tạo với nhau ’ BAC = 30◦ (tham
khảo hình vẽ). Sau 1 giờ, xe thứ nhất chạy được 35 (km), xe thứ hai chạy được 50 (km).
Hỏi khoảng cách giữa 2 xe sau khi chạy được 1 giờ là bao nhiêu? B xe 1 30◦ A C xe 2 #» # » #» # » #» # »
b) Cho 3 lực F1 = MA, F2 = MB và F3 = MC (như hình vẽ) cùng tác động vào một vật tại #» #»
điểm M và vật đứng yên. Cường độ của F1, F2 đều là 50 (N), ’ AMB = 60◦. Tìm độ lớn #» #»
của lực F3. (Biết rằng vật đứng yên khi tổng các vectơ lực tác động vào vật bằng 0 ) A #» F #» 1 F3 M C #» F2 B
c) Người ta dự định dùng hai nguyên liệu là mía và củ cải đường để chiết xuất ít nhất 140
(kg) đường kính và 9 (kg) đường cát. Từ mỗi tấn mía giá 4 (triệu đồng) có thể chiết xuất
được 20 (kg) đường kính và 0, 6 (kg) đường cát. Từ mỗi tấn củ cải đường giá 3 (triệu
đồng) chiết xuất được 10 (kg) đường kính và 1, 5 (kg) đường cát. Hỏi phải dùng bao
nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất, biết cơ sở cung
cấp nguyên liệu chỉ cung cấp không quá 10 tấn mía và không quá 9 tấn củ cải đường. √
ĐS: a) BC ≈ 26, 34; b) 50 3 ≈ 86, 6 (N), c) 2, 5 tấn mía, 9 tấn củ cải đường ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT TRƯỜNG CHINH - ĐỀ 2
Thời gian làm bài: 90 phút ï 5 ã Å 5 ã
Bài 1: Cho hai tập hợp A = −3;
, B = (−2; 4]. Tìm A ∩ B, A \ B. ĐS: A ∩ B = −2; , 2 2 A \ B = [−3; −2] ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 2: Giải hệ bất phương trình bậc nhất hai ẩn: ®2x − y + 4 ≥ 0 2x − 3y ≤ 0 . ĐS: ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √ 2 − 3 − x 1
Bài 3: Tìm tập xác định của hàm số y = + √
. ĐS: D = (−4; 3) \ {−2; 2} x2 − 4 x + 4 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 4: Cho hàm số y = −x2 − 6x + 7.
a) Tìm tọa độ đỉnh, lập bảng biến thiên và chỉ ra các khoảng đơn điệu của hàm số trên.
b) Hàm số đạt giá trị nhỏ nhất hay giá trị lớn nhất? Tìm giá trị đó.
ĐS: a) Đỉnh I(−3; 16), đồng biến trên (−∞; −3), nghịch biến trên (−3; +∞).
b) Hàm số đạt GTLN bằng 16 khi x = −3. ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 5: Cho biết điểm kiểm tra thường xuyên môn Lịch sử của 12 học sinh như sau:
7; 7; 9; 8; 10; 10; 5; 8; 9; 9; 7; 10
a) Tìm các tứ phân vị của mẫu.
b) Viết công thức và tính phương sai của mẫu.
ĐS: a) Q1 = 7; Q2 = 8, 5; Q3 = 9, 5; b) S2 = 2, 1875 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 6: Cho tam giác ABC có AB = 4, BC = 5, b
B = 60◦. Tính độ dài cạnh AC, diện tích tam
giác ABC, bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp của tam giác ABC. √ √ √ ĐS: AC = 21; SABC = 5 3; R = 7; r ≈ 1, 91 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 7: Cho hình vuông MNPQ tâm O có cạnh bằng 3a. #» # » # »
a) Dựng và tính độ dài vectơ v = MN − PN. 107 GV: VŨ NGỌC HUY # » # » # »
b) Gọi K là trung điểm của OP. Phân tích NK theo hai vectơ N M và NP. # » # »
c) Tính tích vô hướng MP · N M. √ # » 1 # » 3 # » ĐS: a) 3a 2; b) NK = N M + NP, c) 9a2 4 4 ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bài 8:
a) Tại một đài kiểm lâm, người ta phát hiện có một đám cháy. Cách đài kiểm lâm 50 (m) có
một bồn nước. Bằng máy trắc địa, người ta đo được góc nhìn từ bồn nước tới đài kiểm
lâm và đám cháy là 97◦; góc nhìn từ đài kiểm lâm tới bồn nước và đám cháy là 34◦. Tính
khoảng cách từ bồn nước tới đám cháy. Bồn nước 97◦ 50 m Đài kiểm lâm 34◦ b) 108 GV: VŨ NGỌC HUY
Một người chạy bộ trong thời gian 2 giờ với vận tôc v (km/h) phụ v
thuộc thời gian t (h) có đồ thị là một phần parabol với đỉnh I(1; 8) 8
và trục đối xứng song song trục tung như hình bên. Tính vận tốc
tức thời tại phút 90 kể từ lúc bắt đầu chạy.
c) Một công ty, trong một tháng cần sản xuất ít nhất 12 viên kim cương
to và 9 viên kim cương nhỏ. Từ 1 tấn carbon loại I (giá 100 triệu
đồng) có thể chiết xuất được 6 viên kim cương to và 3 viên kim
cương nhỏ. Từ 1 tấn carbon loại II (giá 40 triệu đồng) có thể chiết
xuất được 2 viên kim cương to và 2 viên kim cương nhỏ. Mỗi viên
kim cương to có giá 20 triệu đồng, mỗi viên kim cương nhỏ có giá
10 triệu đồng. Hỏi trong một tháng công ty này thu về được nhiều
nhất là bao nhiêu tiền? Biết rằng mỗi tháng chỉ có thể sử dụng tối
đa 4 tấn carbon mỗi loại. O 1 t
ĐS: a) ≈ 37; b) 7, 5 (km/h), c) 113, 3 (triệu đồng) ý Lời giải.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ CUỐI HỌC KÌ I KHỐI 10/2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT TRƯNG VƯƠNG
Thời gian làm bài: 90 phút
Bài 1: Tìm tập xác định của các hàm số sau x a) f (x) + √ . 2x − 7 √ 3x b) f (x) = x − 1 + . x2 + 4 ï 7 ã ĐS: a) D = ; +∞ ; b) D = [1; +∞) 2
Bài 2: Cho hàm số xác định trên [−1; 8] và có đồ thị như hình vẽ. Tìm tập giá trị, khoảng
đồng biến, nghịch biến của hàm số. y 5 4 3 2 1 x −1 1 2 3 4 5 6 7 8 −1 −2
Bài 3: Tìm m để hàm số y = (2m + 1)x2 − 5mx + m + 2 có giá trị nhỏ nhất bằng −1. ĐS: m = 2.
Bài 4: Tìm công thức hàm số bậc hai biết đồ thị hàm số có trục đối xứng là đường thẳng
x = 2, cắt trục tung tại điểm có tung độ bằng 3 và một trong hai giao điểm với trục hoành có hoành độ là 5. −3 12 ĐS: y = x2 + + 3. 5 5
Bài 5: Kết quả nhảy xa (đơn vị: mét) của hai bạn An và Bình sau 5 lần được thống kê ở bảng dưới đây: An 2,4 2,6 2,3 2,5 2,7 Bình 2,4 2,5 2,5 2,5 2,6
a) Kết quả trung bình của hai bạn có bằng nhau hay không?
b) Tính phương sai và độ lệch chuẩn của mẫu số liệu thống kê kết quả 5 lần nhảy xa của
mỗi bạn. Từ đó cho biết bạn nào có kết quả nhảy xa ổn định hơn. 1 1 1 1
ĐS: a) Bằng nhau; b) s2 = ; s2 = ; √ ; √ . A σ σ 50 B 250 A = B = 5 2 5 10
Bài 6: Cho tứ giác ABCD, gọi M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng 110 GV: VŨ NGỌC HUY # » # » # » # » # » # » # » a) AB + DC = AC + DB. b) BC + AD = 2MN.
Bài 7: Cho tam giác đều ABC có cạnh bằng a. # » # » # » # »
a) Hãy tính độ dài của các vectơ sau: AB − AC; AB + AC. # » # » # » # »
b) Cho E là trung điểm của AC, hãy tính các tích vô hướng: AB · AC; BA · EB. √ a2 −3a2 ĐS: a) a, a 3; b) , . 2 4 111 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT BÌNH HƯNG HÒA
Thời gian làm bài: 90 phút
Bài 1: Tìm tập xác định của các hàm số sau: 1 + x √ x a) b) 2x + 4 + √ x2 − 5x 6 − x
ĐS: a) D = R \ {0; 5}; b) D = [−2; 6).
Bài 2: Lập bảng biến thiên và vẽ đồ thị hàm số y = x2 − 4x + 1.
Bài 3: Xác định parabol (P) : y = ax2 + bx + c biết (P) có đỉnh S(1; 6) và đi qua điểm 1 2 17 A(−2; 3). ĐS: y = − x2 + x + . 3 3 3
Bài 4: Điểm số bài kiểm tra môn Toán của các bạn học sinh tổ 1 lớp 10C được ghi lại như sau: 10 7 8 8 5 6 9 6 8
Hãy tìm số trung bình, tứ phân vị và mốt của mẫu số liệu trên. ĐS: 67 x = ; Q 9
2 = 8; Q1 = 6; Q3 = 8, 5; M0 = 8. # » # » # » # » # »
Bài 5: Cho bốn điểm A, B, C và D. Chứng minh rằng 2AD + CA − AB = BD + CD.
Bài 6: Cho hình chữ nhật ABCD tâm O và AD = 3a, CD = a. Tính tích vô hướng của # » # » 9 AD · AO. ĐS: . 2
Bài 7: Bác An muốn trồng một vườn hoa trên mảnh đất hình chữ nhật và làm hàng rào bao
quanh. Bác An chỉ có đủ vật liệu để làm 60 m hàng rào. Tìm kích thước của vườn hoa hình
chữ nhật có diện tích lớn nhất mà bác An có thể làm hàng rào bao quanh. ĐS: 900 m2. # » # » # » 1 # »
Bài 8: Cho tam giác ABC và hai điểm M, N thỏa mãn AM = 3MC, BN = NC. Gọi E là 2
giao điểm của AN và BM. Tính diện tích tam giác ABC biết diện tích tam giác EBN bằng 2. 1 ĐS: . 30 112 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ THI HK1 NĂM HỌC 2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT PHÚ NHUẬN
Thời gian làm bài: 90 phút
Bài 1: Nhiệt độ của Hà Nội trong 10 ngày liên tiếp được ghi lại trong bảng sau 33 34 36 31 34 30 33 34 35 34
Tính số trung bình, số trung vị, khoảng biến thiên và phương sai của bảng trên. 71
ĐS: x = 33, 4; Me = 34; R = 6; s2 = = 2,84 25
Bài 2: Một bác nông dân cần trồng lúa và khoai trên diện tích đất gồm 6 ha, với lượng phân
bón dự trữ là 100 kg. Để trồng 1 ha lúa cần sử dụng 20 kg phân bón với lợi nhuận là 30 triệu
đồng, để trồng 1 ha khoai cần sử dụng 10 kg phân bón với lợi nhuận là 20 triệu đồng. Để đạt
lợi nhuận cao nhất, bác nông dân đã trồng x ha lúa và y ha khoai (x, y ≥ 0). Tìm giá trị của x. ĐS: x = 4.
Bài 3: Tìm parabol (P) : y = ax2 + bx + c, biết rằng (P) đi qua ba điểm A(1; −1); B(2; 3); C(−1; −3).
ĐS: (P) : y = x2 + x − 3 .
Bài 4: Cho parabol (P) : y = x2 + 6x + 8.
a) Xác định tọa độ đỉnh, trục đối xứng của parabol (P), tọa độ giao điểm của parabol (P) với trục hoành.
b) Lập bảng biến thiên, vẽ đồ thị hàm số y = x2 + 6x + 8.
c) Dựa vào đồ thị trên tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số f (x) = x2 + 6x + 8 trên đoạn [−4; 0]
ĐS: a) (−3; −1), x = −3, (−2; 0) và (−4; 0); c) GTNN = −1, GTLN = 8.
Bài 5: Cho 4ABC có AB = 6, AC = 10 và “
A = 1200. Tính độ dài cạnh BC và đường cao kẻ từ A của 4ABC. √ 15 3 ĐS: BC = 14; ha = . 7
Bài 6: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của BC và AD. Chứng # » # » # » # » minh rằng AM + AN = AB + AD. 2
Bài 7: Cho 4ABC đều cạnh a. Gọi M là điểm trên cạnh BC sao cho BM = BC và N là điểm 3 # » # » thỏa 5AN = 4AC. # » # »
a) Tính AB · AC theo a. # » # » # » # »
b) Phân tích BN, AM theo các vecto AB và AC.
c) Chứng minh AM⊥BN. 1 # » # » 4 # » # » 1 # » 2 # »
ĐS: a) a2; b) BN = −AB + AC, AM = AB + AC. 2 5 3 3 113 GV: VŨ NGỌC HUY
THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ HỌC KÌ I KHỐI 12/2022-2023 GV: VŨ NGỌC HUY
TRƯỜNG THPT NGUYỄN HỮU CẦU
Thời gian làm bài: 90 phút
PHẦN 1 - TRẮC NGHIỆM
Câu 1: Giá trị nhỏ nhất của hàm số y = 3x + 4 trên khoảng (0; +∞) là: √ x2 √ A. 33. B. 3 3 9. C. 7. D. 2 3 9. 5 ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 2: Khối chóp có thể tích bằng 15 , diện tích đáy bằng 3 . Chiều cao h của khối chóp bằng. A. h = 10. B. h = 15. C. h = 3. D. h = 5. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Ä ä1−3x
Câu 3: Nghiệm của phương trình 1 = 243 là 3 A. x = −2. B. x = 2. C. x = 3. D. x = −3. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 4: Hàm số nào sau đây đồng biến trên R ? √ x
A. y = x4 + 2x2 + 1. B. y = 5 . C. y = (ln 2)x. D. y = x − 2 . 2 x ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 5: Một hình nón có chiều cao h = 5 và góc ở đỉnh bằng 60◦. Diện tích xung quanh hình nón bằng:√ √ A. 50π 3. B. 25π 3. C. 50π . D. 25π . 3 3 ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 6: Cho hàm số y = f (x) có bảng biến thiên như sau:
Khẳng định nào sau đây sai
A. Hàm số đạt cực đại tại x = 1.
B. Hàm số đạt cực tiểu tại x = 2.
C. Hàm số tăng trên khoảng (3; 5).
D. Hàm số giảm trên khoảng (0; 1). ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 7: Cho hàm số y = f (x) có bảng xét dấu của hàm số f 0(x) như sau:
Hỏi hàm số f (x) có mấy điểm cực trị? A. 4. B. 1. C. 2. D. 3. ý Lời giải. 114 GV: VŨ NGỌC HUY
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 8: Cho lăng trụ có diện tích đáy bằng 5. Cạnh bên bằng 3 và tạo với đáy một góc 45◦.
Thể tích V của khối lăng trụ bằng: √ √ A. V = 15. B. V = 5. C. V = 15 2. D. V = 5 2. 2 2 2 2 ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 9: Cho hàm số y = x+1. Tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng 3 có hệ x−1 số góc bằng A. − 1. B. 2. C. 1. D. −2. 2 2 ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 10: Khối trụ có thể tích bằng 2πa3 và chiều cao bằng 2a. Bán kính đáy R bằng: √ √ A. R = a. B. R = 2a. C. R = a 2. D. R = a 3. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 11: Hàm số y = ax+b có đồ thị như hình vẽ. Khẳng định nào sau đây sai? cx+d
A. Đồ thị hàm số có tiệm cận ngang là y = 2.
B. Hàm số đồng biến trên R\{−1}.
C. Đồ thị hàm số có tâm đối xứng là điểm (−1; 2).
D. Đồ thị hàm số có tiệm cận đứng là x = −1. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 12: Lăng trụ đứng có đáy là tam giác đều cạnh bằng 3. Chiều cao lăng trụ bằng 4. Diện
tích S của mặt cầu ngoại tiếp lăng trụ bằng A. S = 24π. B. S = 25π. C. S = 9π. D. S = 28π. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 13: Bất phương trình log (x +
x có tập nghiệm là nửa khoảng (a 3 2) ≤ 1 − log3 ; b]. Khi đó, tồng a + b bằng A. 2. B. 4. C. 1. D. −2. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 14: Đồ thị hàm số nào sau đây có dạng đường cong như hình sau?
A. y = x4 − 2x2 − 1.
B. y = −x4 + 2x2 − 1.
C. y = −x3 − 3x2 − 1.
D. y = −x3 + 3x2 − 1. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115 GV: VŨ NGỌC HUY
Câu 15: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x−1 trên đoạn [0; 2] bằng 2x+1 A. − 1. B. 1. C. −1. D. − 4. 5 5 5 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 16: Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 2x−3 có phương trình lần x−1 lượt là A. x = 3, y = 3. B. x = 1, y = 3. C. x = 3, y = 2. D. x = 1, y = 2. 2 2 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 17: Thể tích V của khối cầu có bán kính bằng 6 là A. V = 108π. B. V = 288π. C. V = 144π. D. V = 36π. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √
Câu 18: Cho a, b > 0 và log b = a + b bằng a 3. Giá trị của log√ log b a A. 7. B. 2. C. 8. D. 13. 6 3 3 6 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 19: Nghiệm của phương trình log1 (3x − 1) = −3 là 2 A. 3. B. 7. C. 10. D. 2. 3 3 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 20: Tiếp tuyến với đồ thị hàm số y = x5 − 5x4 + 4 tại giao điểm của đồ thị với trục tung có phương trình là A. y = 4. B. y = −80x + 4. C. y = −15x + 4. D. y = 0. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 21: Cho mặt cầu tâm O, bán kính R = 7. Một đường thẳng d cắt mặt cầu theo một dây
cung có độ dài bằng 4 . Khoảng cách h từ tâm O đến đường thẳng d bằng √ √ √ √ A. h = 3 5. B. h = 65 . C. h = 53. D. h = 57 . 2 2 ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √
Câu 22: Với 0 < a 6= 1 thì log√ 3 (a a) bằng a A. 4. B. 9. C. 1. D. 3. 3 2 2 4 ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116 GV: VŨ NGỌC HUY 2
Câu 23: Tập xác định của hàm số y = (x − 2) 3 là A. (2; +∞). B. R\{2}. C. R. D. (−∞; 2). ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 24: Một hình nón đỉnh S có đáy là đường tròn có bán kính bằng 3 và chiều cao bằng 5 .
Diện tích mặt cầu tâm S và chứa đường tròn đáy của hình nón bằng. A. S = 100π. B. S = 36π. C. S = 136π. D. S = 64π. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √
Câu 25: Một khối hộp chữ nhật ABCD · A0B0C0D0 có AB = 1, BC = 2, A0C = 21. Thể tích V của khối hộp bằng √ √ A. V = 4. B. V = 3 5. C. V = 2 21. D. V = 8. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 26: Tiệm cận ngang của đồ thị hàm số y = 1−2x là đường thẳng x−2 A. y = 2. B. y = −2. C. y = −1. D. y = 1. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 27: Thể tích V của khối nón có đường sinh bằng 5 và bán kính đáy bằng 4 là: A. V = 80π . B. V = 100 3 π. C. V = 36π. D. V = 16π. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 28: Đồ thị hàm số y = (a+2)x+1 nhận điểm I(4; 3) làm tâm đối xứng. Khi đó tổng a + b x−b+3 bằng A. −7. B. 8. C. −8. D. 7. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 29: Cho hàm số y = f (x) có đồ thị như hình vẽ. Tìm tất cả các giá trị của m để phương
trình f (x) = m − 2 có đúng hai nghiệm. A. −4 ≤ m ≤ −3.
B. m > −1 ∨ m = −2.
C. m ≥ −2 ∨ m = −2.
D. −2 < m < −1. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 30: Đường cong trong hình sau là đồ thị của hàm số nào?
A. y = − 1 x3 + 2x2 − 3x + 1.
B. y = 1 x3 − 3x2 + 9 x + 1. 3 2 2
C. y = 1 x3 − 2x2 + 3x + 1.
D. y = 1 x3 + 3 x2 − 9 x + 1. 3 2 2 2 ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117 GV: VŨ NGỌC HUY
Câu 31: Cho hàm số y = − x3 + (m − 3)x2 − (m + 27) + m2 − 2. Có bao nhiêu giá trị nguyên 3
của tham số m để hàm số nghịch biến trên R ? A. 12. B. 6. C. 10. D. 8. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 32: Cho hàm số y = ax, y = log x
x có đồ thị như hình vẽ. Khẳng định nào b , y = logc sau đây đúng?
A. a < b < c < 1.
B. c < 1 < a < b.
C. 1 < b < a < c. D. b < 1 < a < c . ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 33: Cho tứ diện ABCD có thể tích V. Gọi M, N, K lần lượt là trung điểm AB, CD, AD và
H là trọng tâm tam giác ACD. Thể tích tứ diện MNHK tính theo V là: A. 1 V. B. 1 V. C. 1 V. D. 1 V. 18 12 36 24 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 34: Đồ thị hàm số y = x + 16 đạt cực đại tại điểm (x x
1; y1) và đạt cực tiểu tại điểm
(x2; y2). Khi đó, giá trị của y2 − y1 bằng A. −16. B. −8. C. 8. D. 16. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 35: Cho ba số a, b, c thỏa 2a = 3b · 5c. Khi đó a = xb + yc. Giá trị của x bằng y A. x = log = log = log = log y 2 5. B. xy 2 3. C. xy 5 3. D. xy 3 5. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 36: Phương trình 4x − 5 · 2x + 2 = 0 có hai nghiệm x1, x2. Khi đó tổng x1 + x2 bằng A. 1. B. 2. C. 5. D. 0. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 37: Hàm số y = x4 − 2(m + 1)x2 + m2 − 4 có 3 điểm cực trị khi và chỉ khi A. m ≥ −1. B. m > 1. C. m ≤ 1. D. m > −1. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 38: Cho A là tập hợp các số tự nhiên lớn hơn 5. Chọn viết đúng. A. m = −11. B. m = 16. C. m = −16. D. m = 11. ý Lời giải. 118 GV: VŨ NGỌC HUY
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 39: Cho hàm số y = f (x) = −x4 + 2x2 + 2 có đồ thị như hình vẽ. Hỏi phương trình
log ( f (x)) = x có bao nhiêu nghiệm? 2 A. 3. B. 5. C. 7. D. 2. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 40: Biết 4a − 2a+b − 2 · 4b = 0. Khi đó hiệu a − b bằng A. 1. B. 2. C. 3. D. 4. ý Lời giải.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 41: Cho hình hộp ABCD · A1B1C1D1 có thể tích là V. Gọi I là tâm hình hộp, O là giao
điểm của AC và BD, M là trung điểm DD1, G là trọng tâm tam giác B1C1D1. Thể tích tứ diện GMIO tính theo V là: A. 1 V. B. 1 V. C. 1 V. D. 1 V. 96 36 72 48 ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 42: Có bao nhiêu giá trị nguyên m ∈ [−10; 10] để phương trình ln(x + m) + m = ex có hai nghiệm phân biệt? A. 8. B. 9. C. 16. D. 18. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 43: Cho hàm số y = f (x) = x3 − 3x2 + 2 có đồ thị như hình vẽ
Hỏi phương trình f x2 + 2x + 1 = 1 có mấy nghiệm? A. 3. B. 6. C. 8. D. 4. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 44: Cho hàm số f (x) = x3 − 3x2 + 2. Hỏi hàm số g(x) = f [x f (x)] có mấy điểm cực trị? A. 5. B. 7. C. 9. D. 11. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √ √
Câu 45: Cho tứ diện ABCD.AB = AC = a, AD = 2a, DB = DC = a 5, BC = a 2. Bán
kính R của mặt cầu ngoại tiếp tứ diện bằng √ √ √ √ A. R = 3a 2. B. R = a 6. C. R = a 6. D. R = a 14. 4 2 2 ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 46: Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = f (x − 1)2 + m có đúng 3 điểm cực trị. 119 GV: VŨ NGỌC HUY A. 4. B. 2. C. 5. D. 3. ý Lời giải.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 47: Cho tứ diện SABC có SB ⊥ (ABC), SB = 3a. Tam giác ABC có BC = 2a, góc
A = 120◦. Bán kính R của mặt cầu ngoại tiếp tứ diện SABC bằng: √ √ √ √ A. R = a 43. B. R = a 129. C. R = a 43. D. R = a 129. 3 3 6 6 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 48: Cho hàm số y = f (x) có đồ thị như hình vẽ
Có bao nhiêu giá trị nguyên của m để phương trình | f (|x|)| = m có đúng 6 nghiệm phân biệt? A. 3. B. 4. C. 2. D. 1. ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 49: Cho hình chóp SABCD có đáy ABCD là hình thoi tâm O, cạnh a, góc ABC =
60◦, SO ⊥ ( ABCD ) và tam giác SAC đều. Gọi M là trung điểm SA, tính tang của góc tạo bởi CM và mặt phẳng (SCD) A. 2 √ . B. 2. C. 1 √ . D. 1. 5 5 2 ý Lời giải.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √
Câu 50: Cho hai số dương a, b thỏa log a = b = 3 log2
log 4(a + b). Giá trị của ab bằng A. ab = 64. B. ab = 36. C. ab = 144. D. ab = 12. ý Lời giải.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
Document Outline
- bia-CHK1-K10
- CHK1-K10




