
























































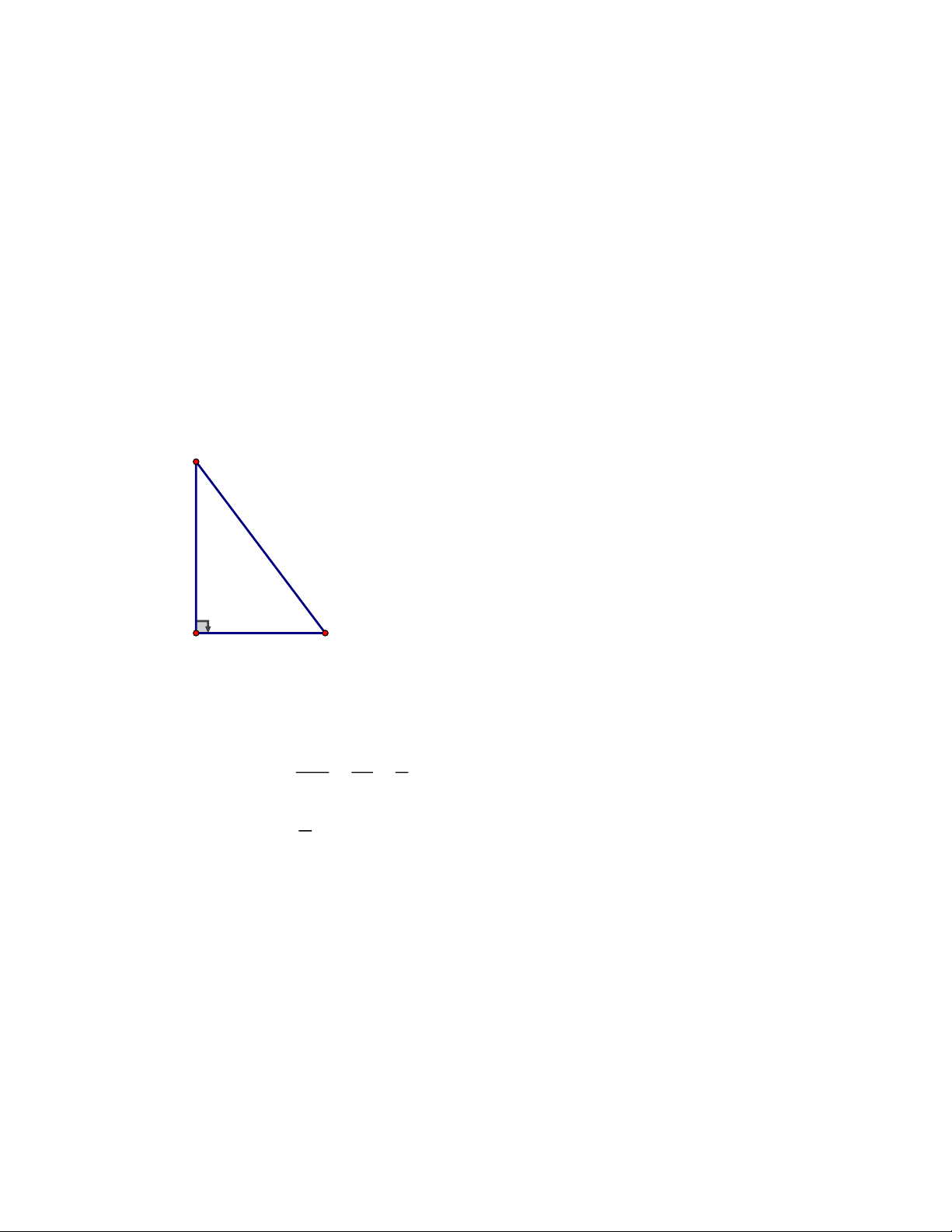




Preview text:
BỘ ĐỀ CÂU CUỐI HÌNH HỌC TUYỂN SINH VÀO LỚP 10
MÔN TOÁN THPT CÁC TỈNH TRÊN CẢ NƯỚC NĂM HỌC 2020-2021
PHẦN 1: CHỨNG MINH 3 ĐIỂM THẲNG HÀNG, ĐỒNG QUY CẦN THƠ
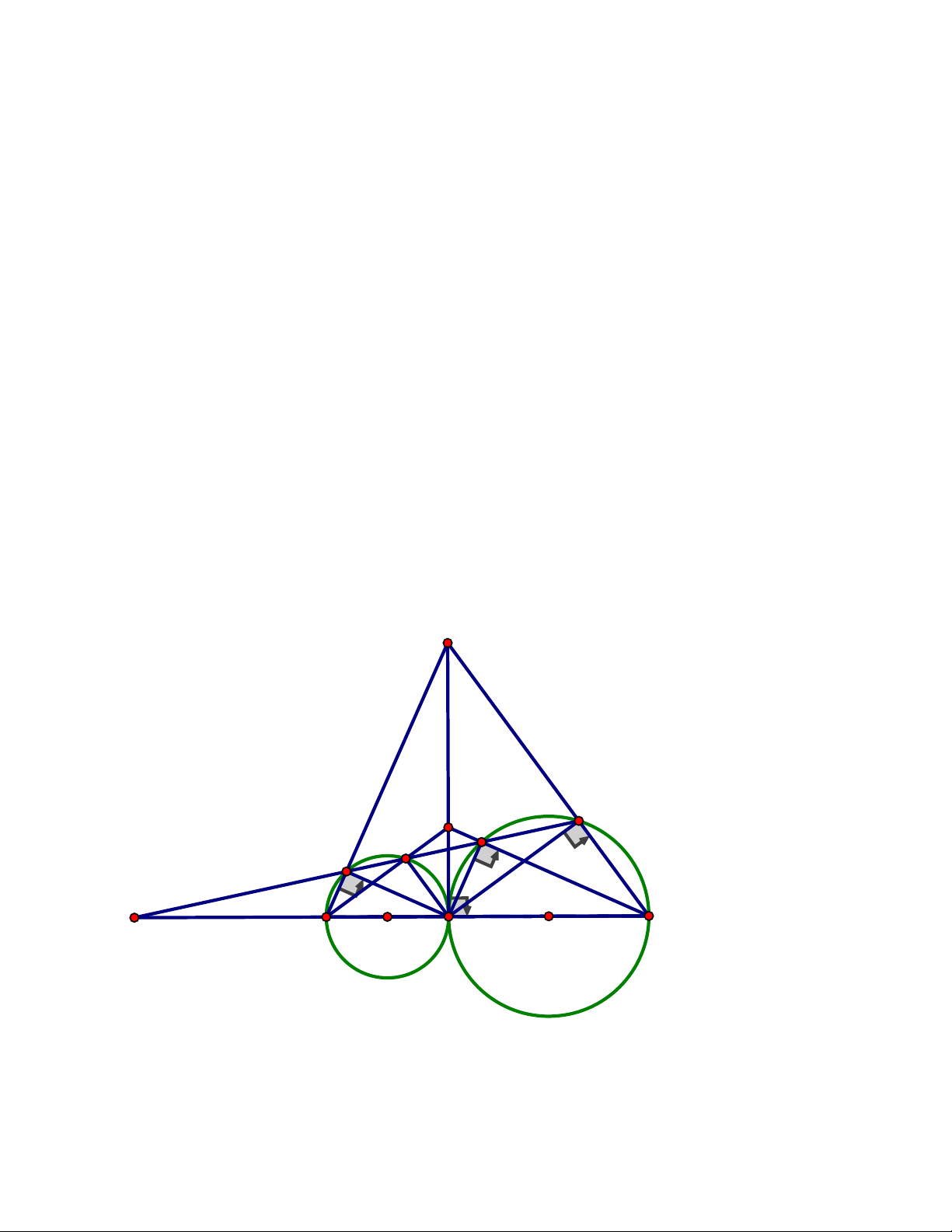
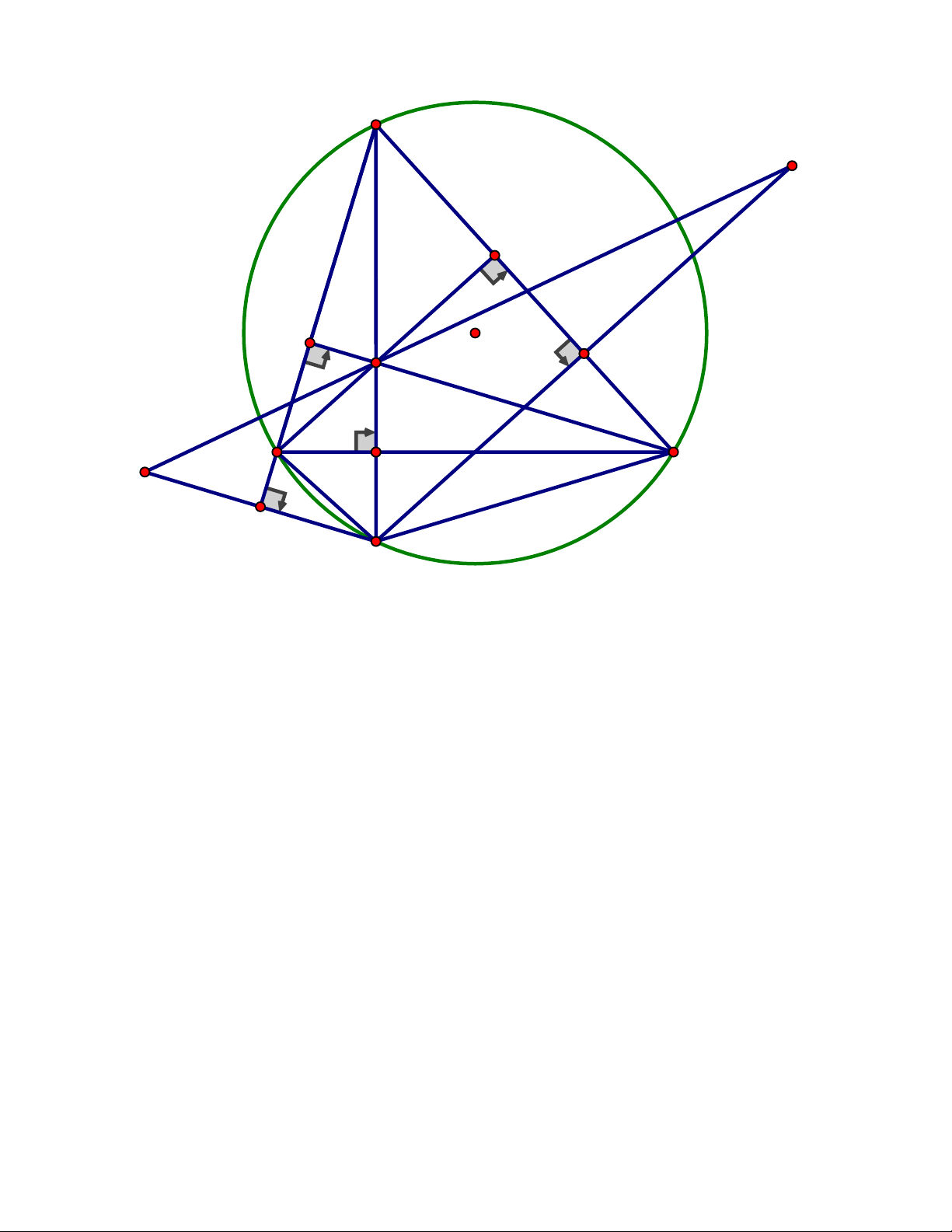
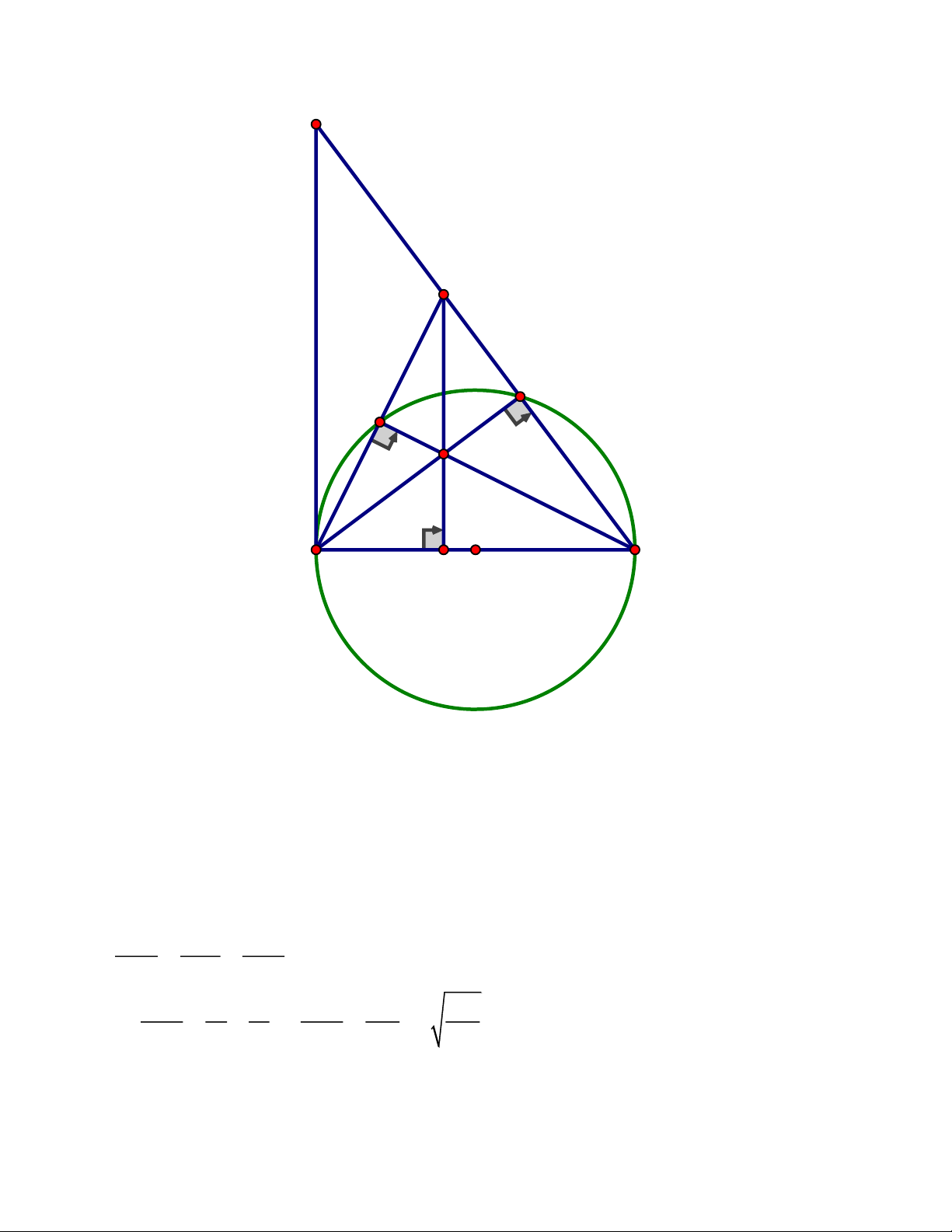
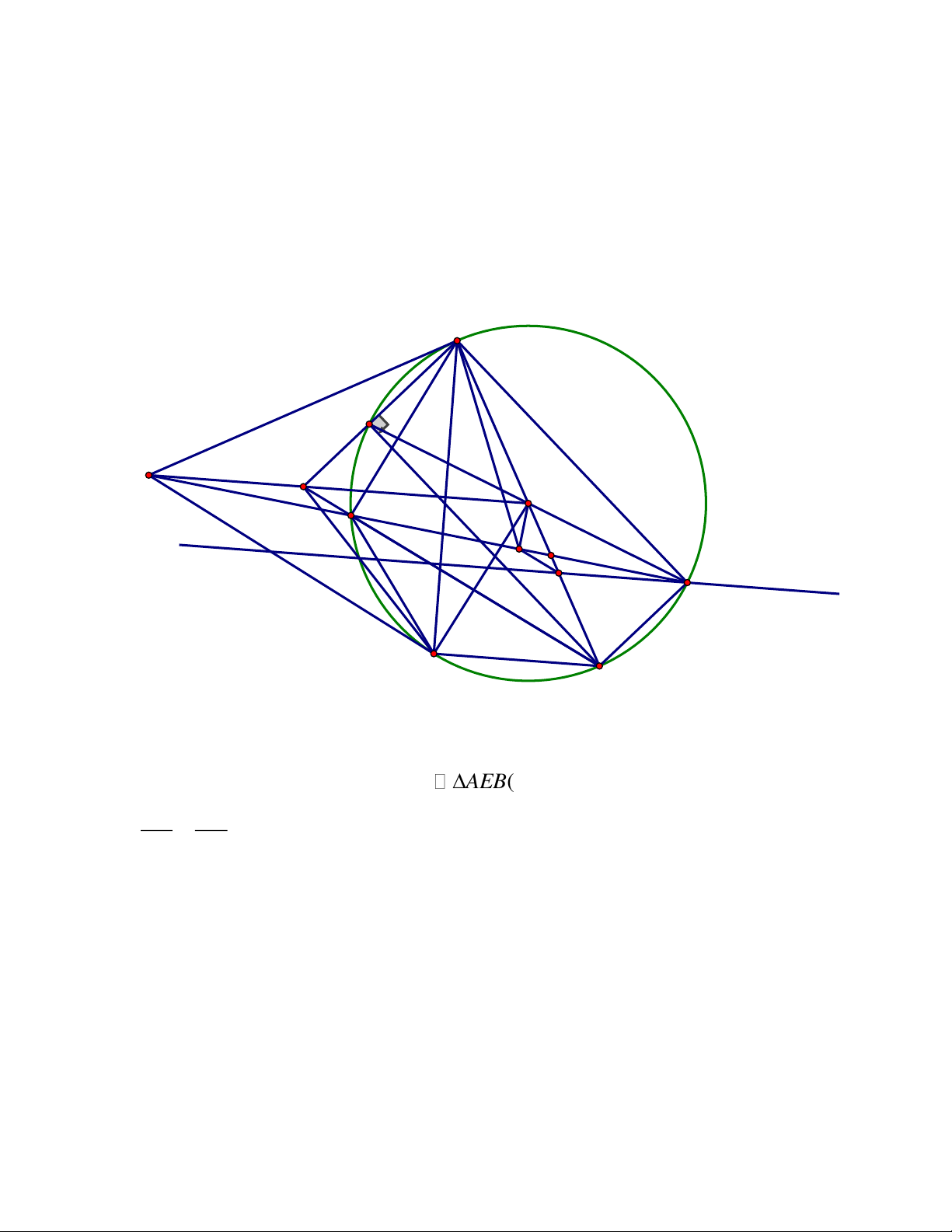
Câu 4. (2,5 điểm) Cho tam giác ABC có ba góc nhọn và AB A .
C Vẽ đường cao AH ,
đường tròn đường kính HB cắt AB tại D và đường tròn đường kính HC cắt AC tại E
a) Chứng minh rằng tứ giác ADHE nội tiếp
b) Gọi I là giao điểm của hai đường thẳng DE và BC.Chứng minh 2 IH I . D IE
c) Gọi M , N lần lượt là giao điểm của đường thẳng DE với đường tròn đường kính
HB và đường tròn đường kính HC. Chứng minh rằng giao điểm của hai đường
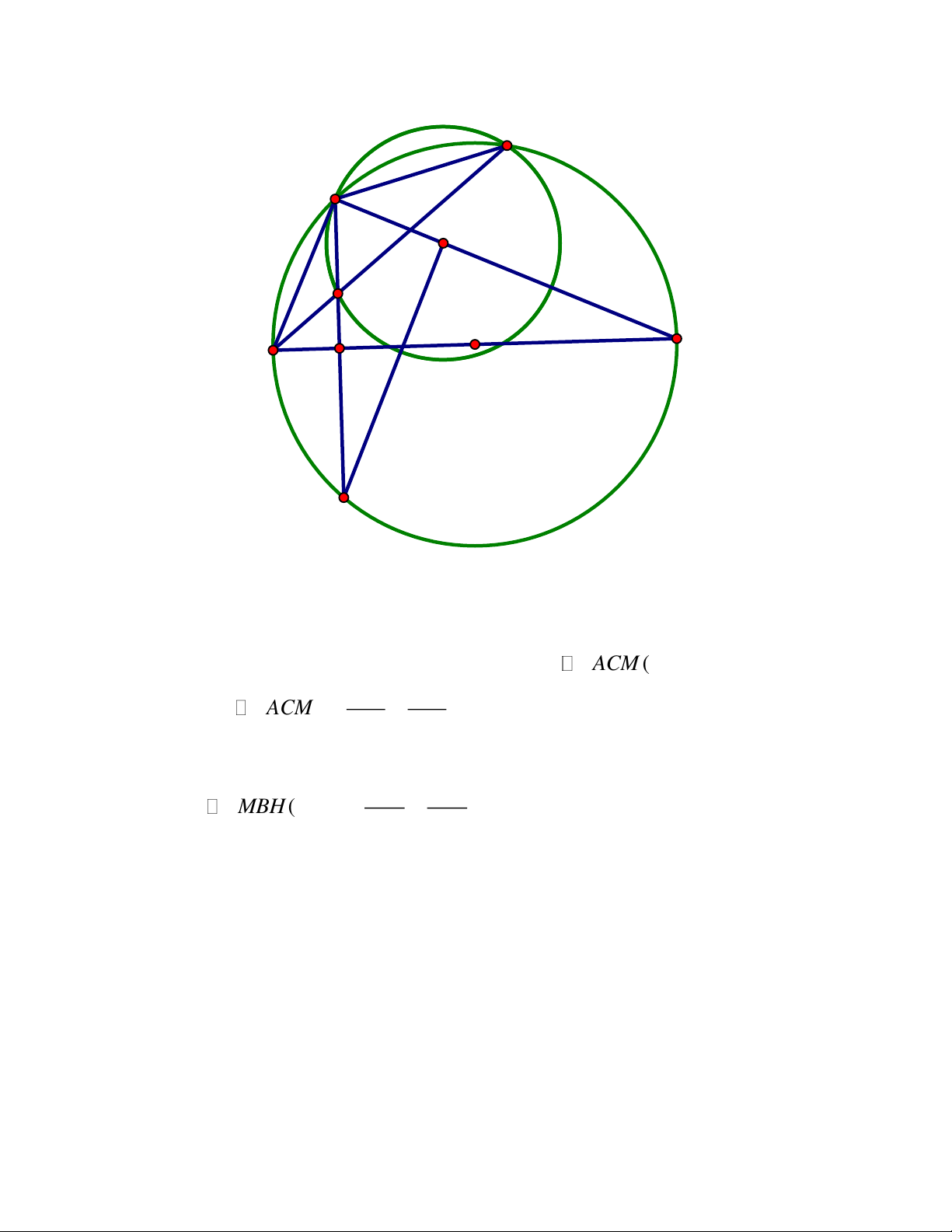
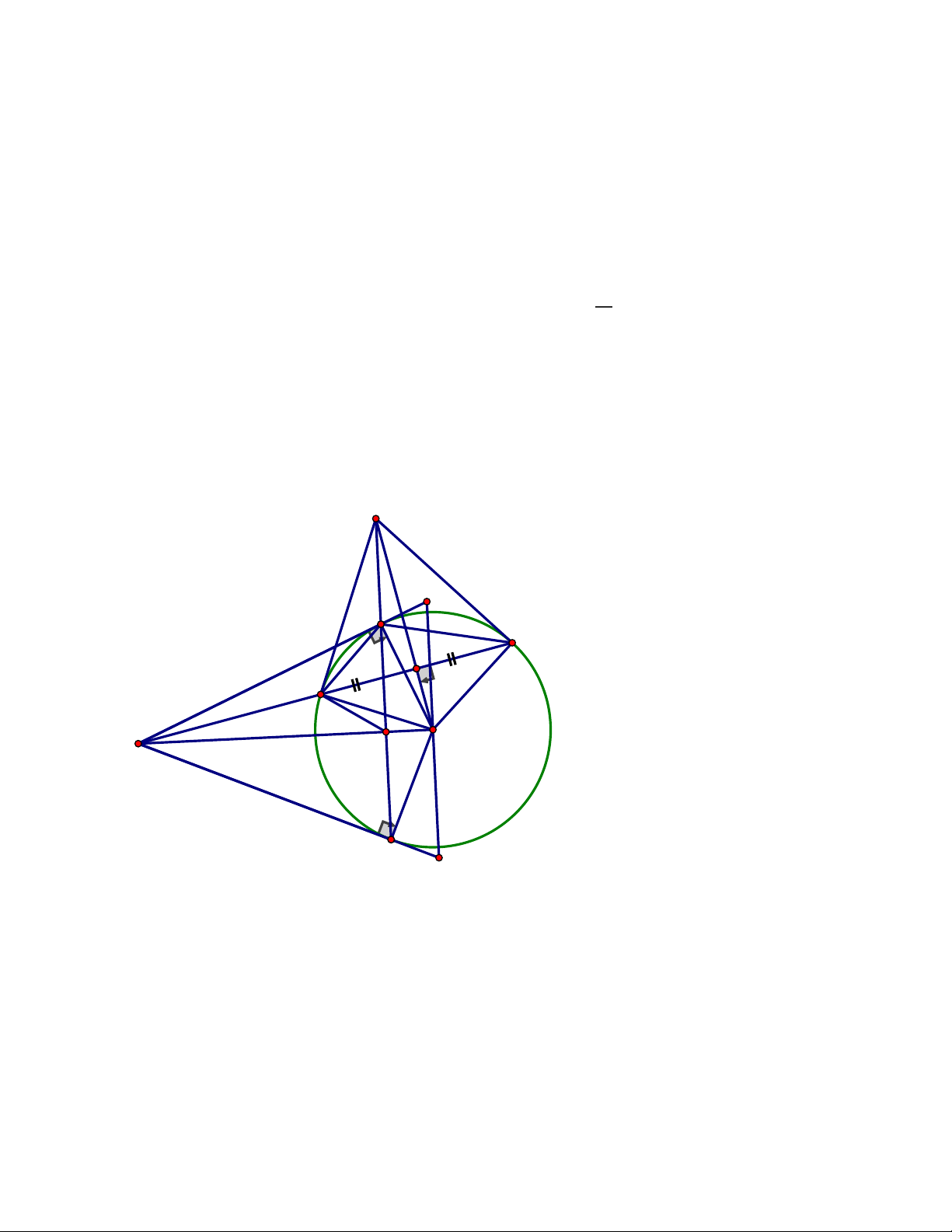
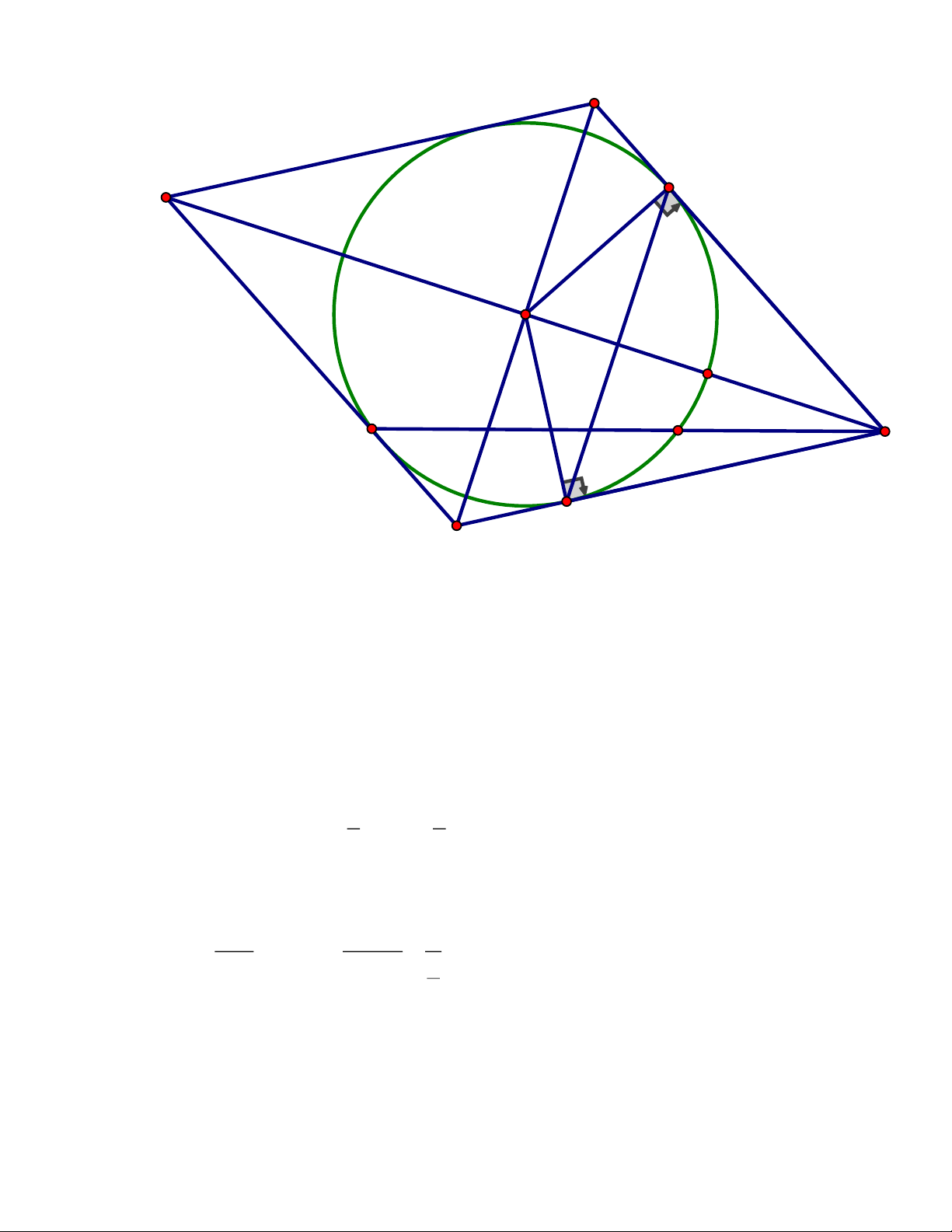
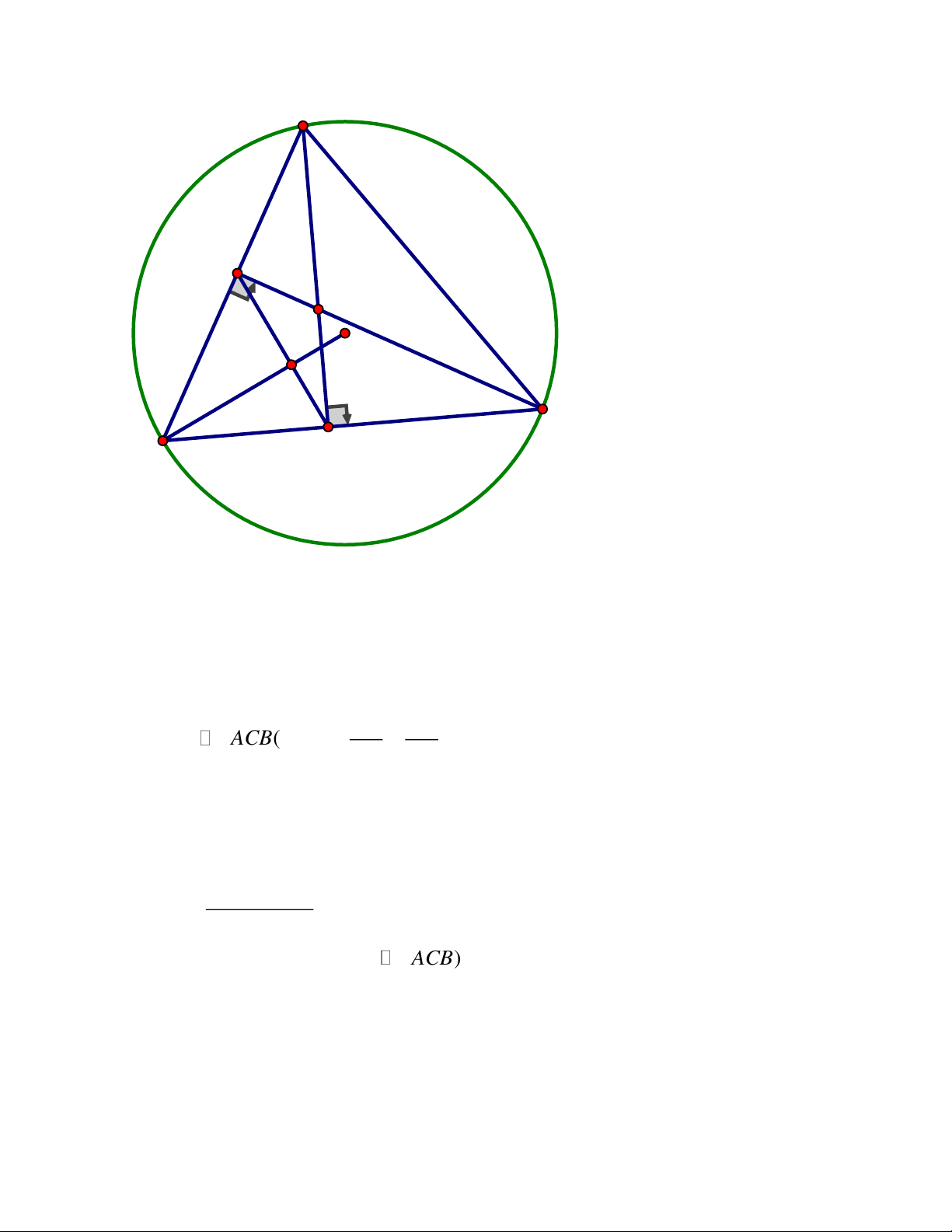
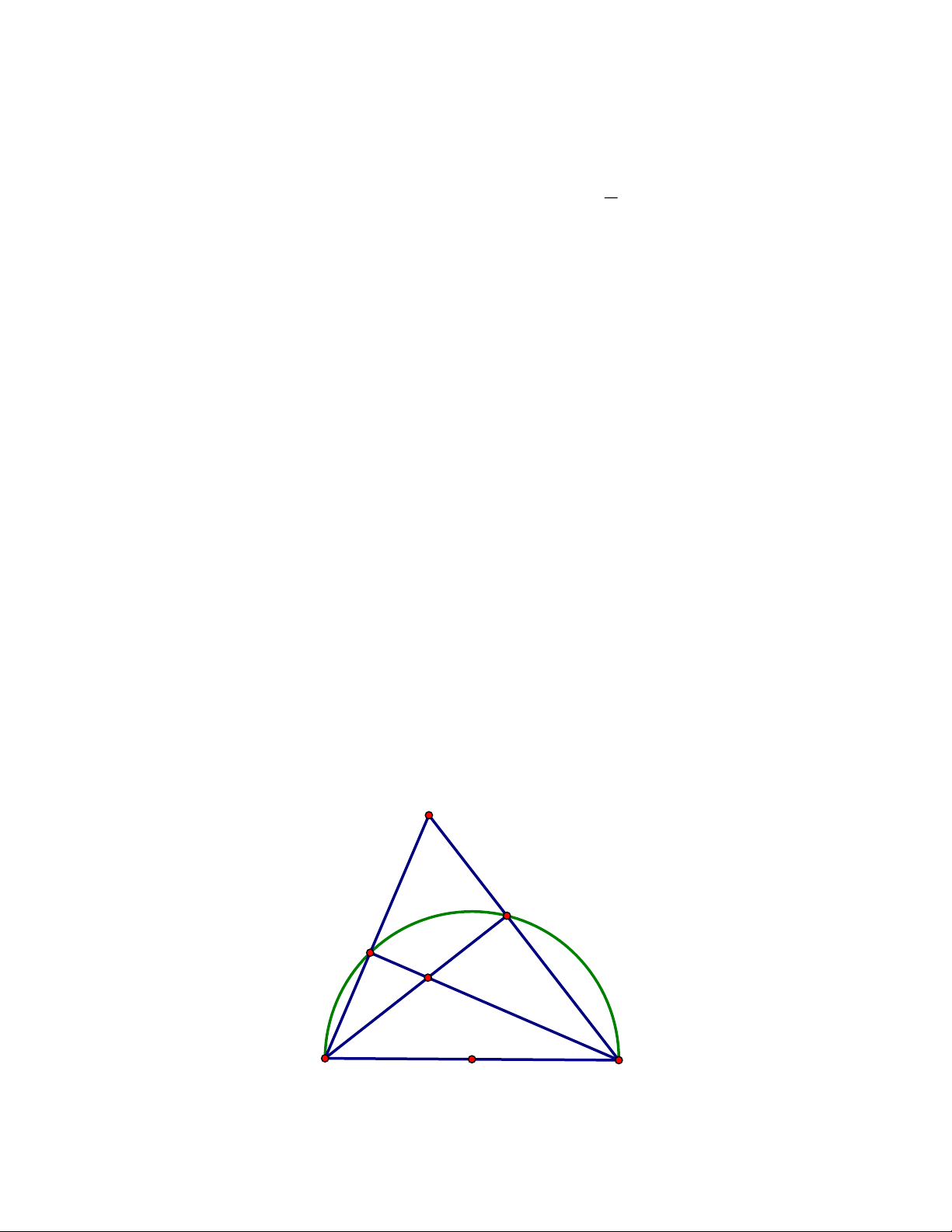
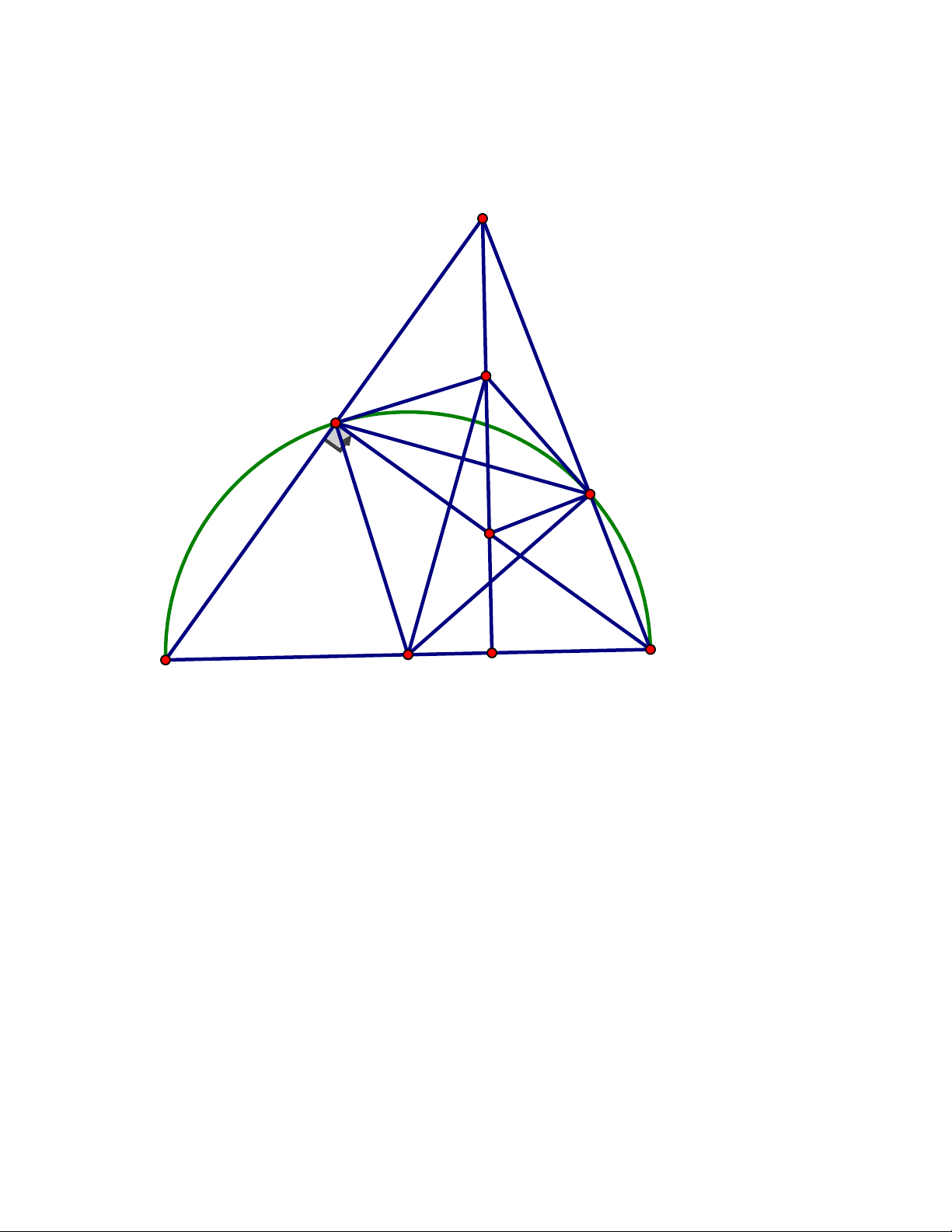
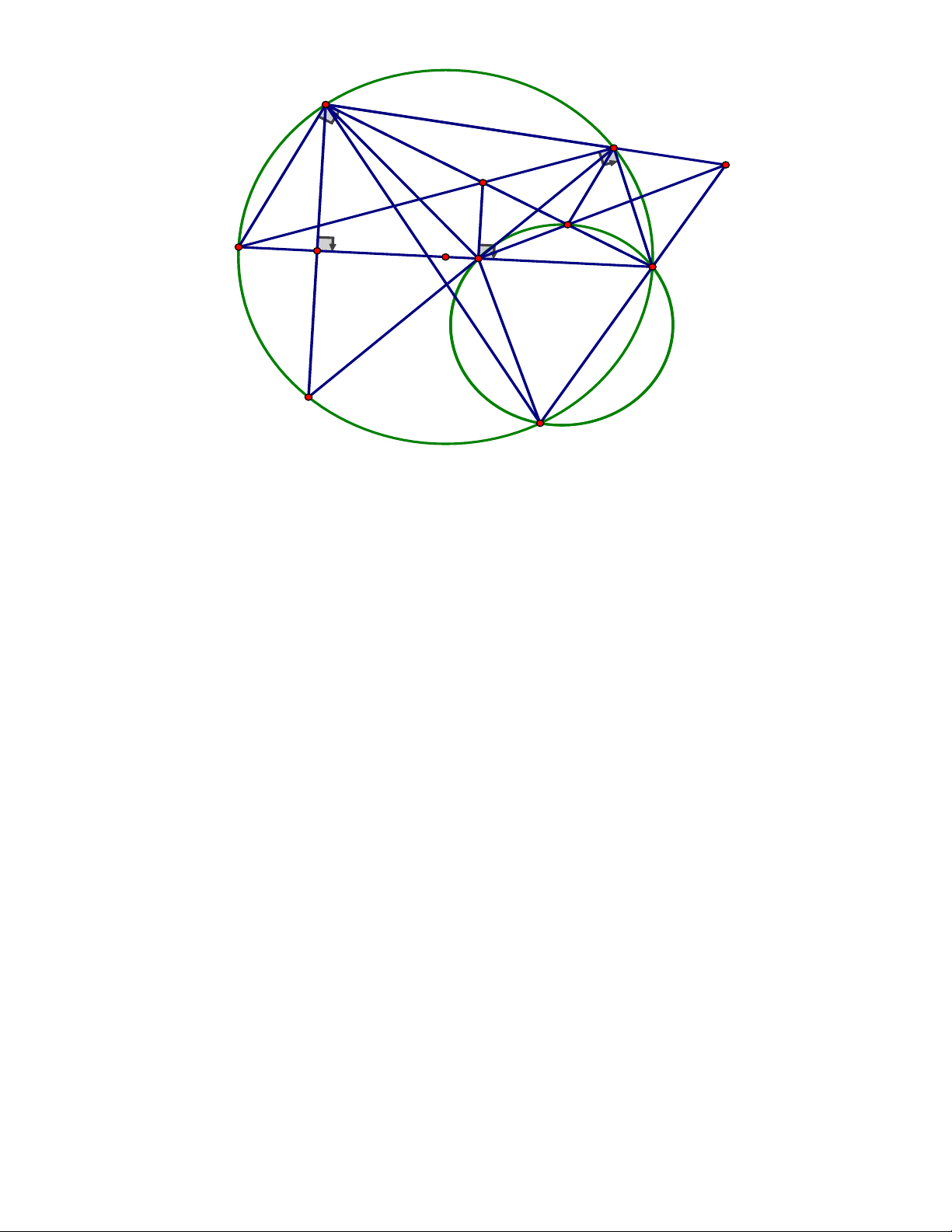
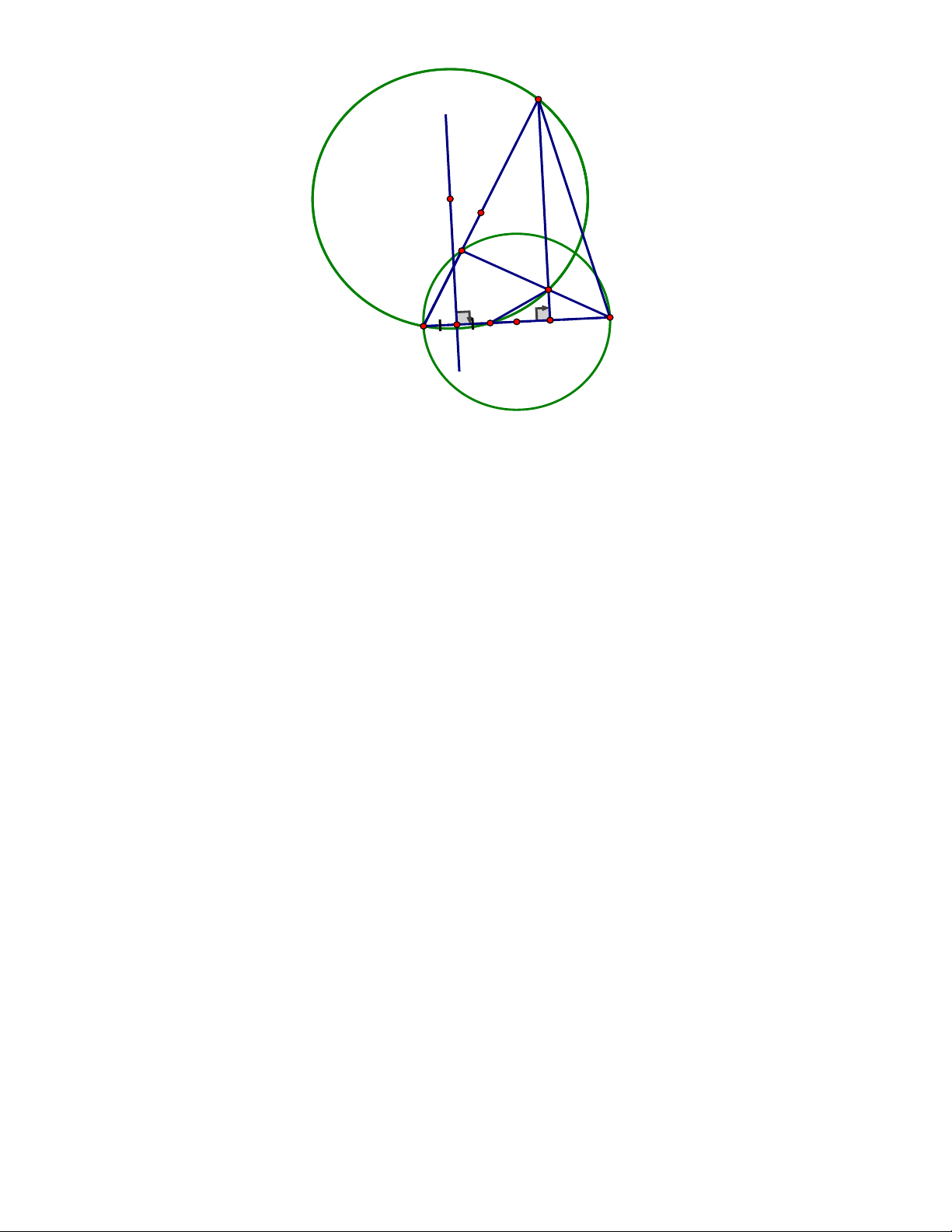
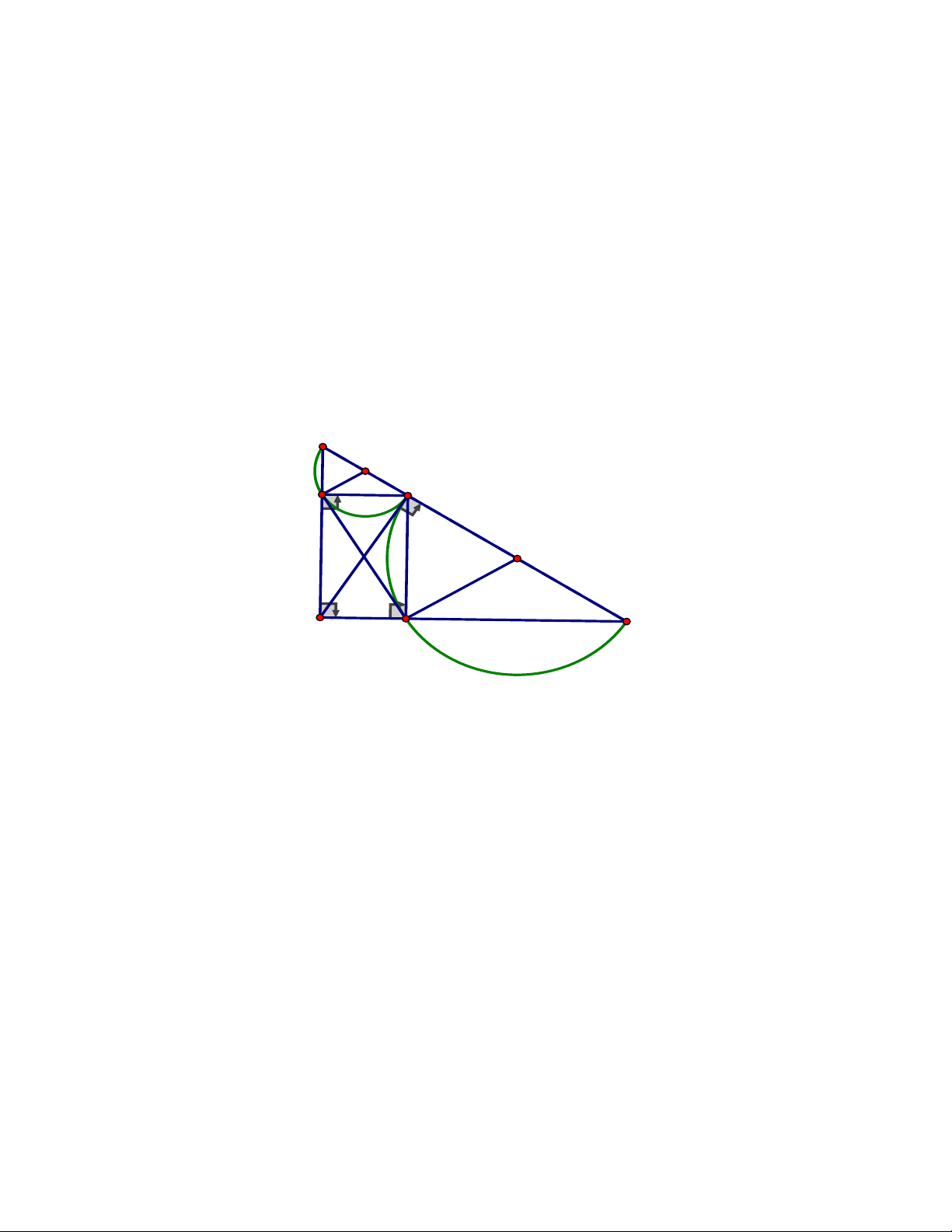
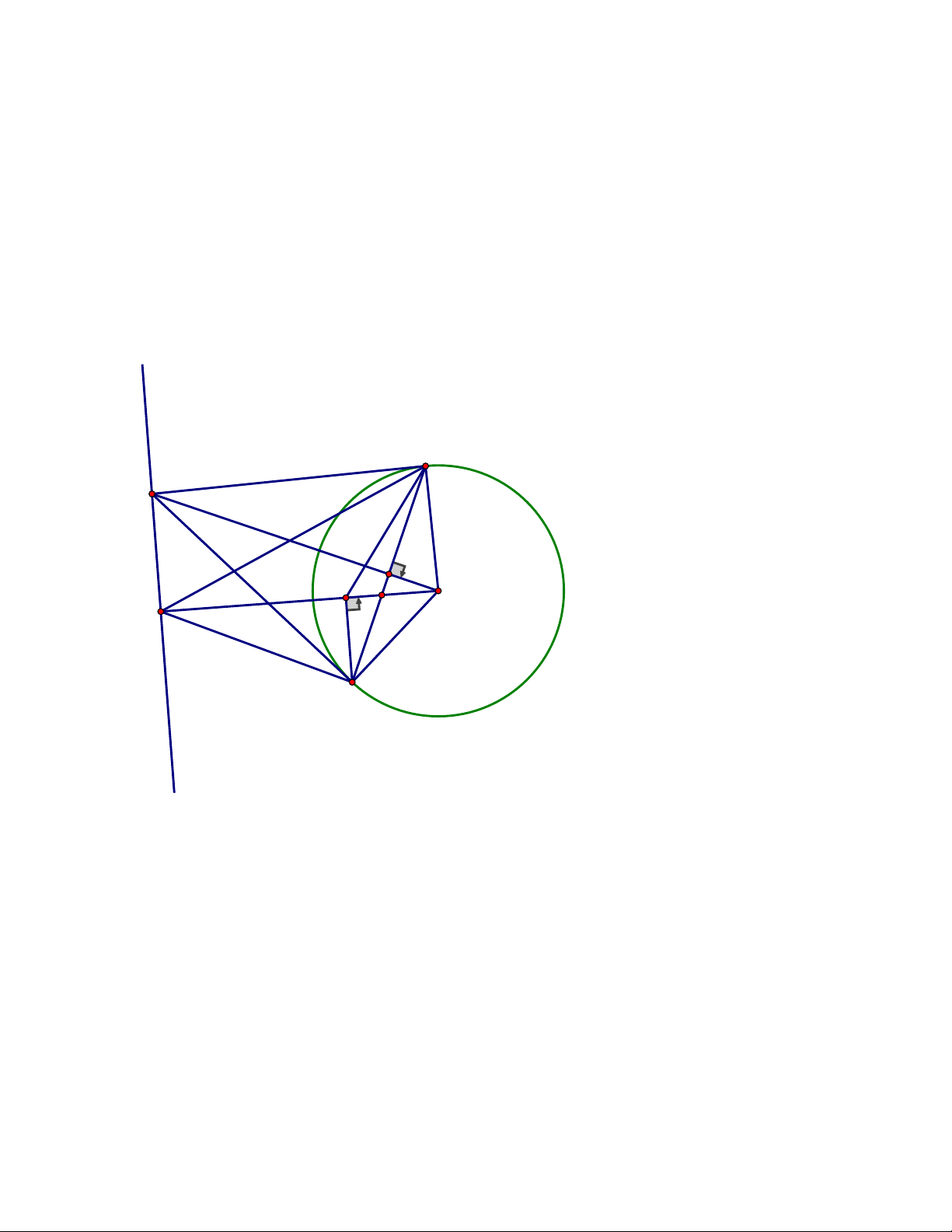
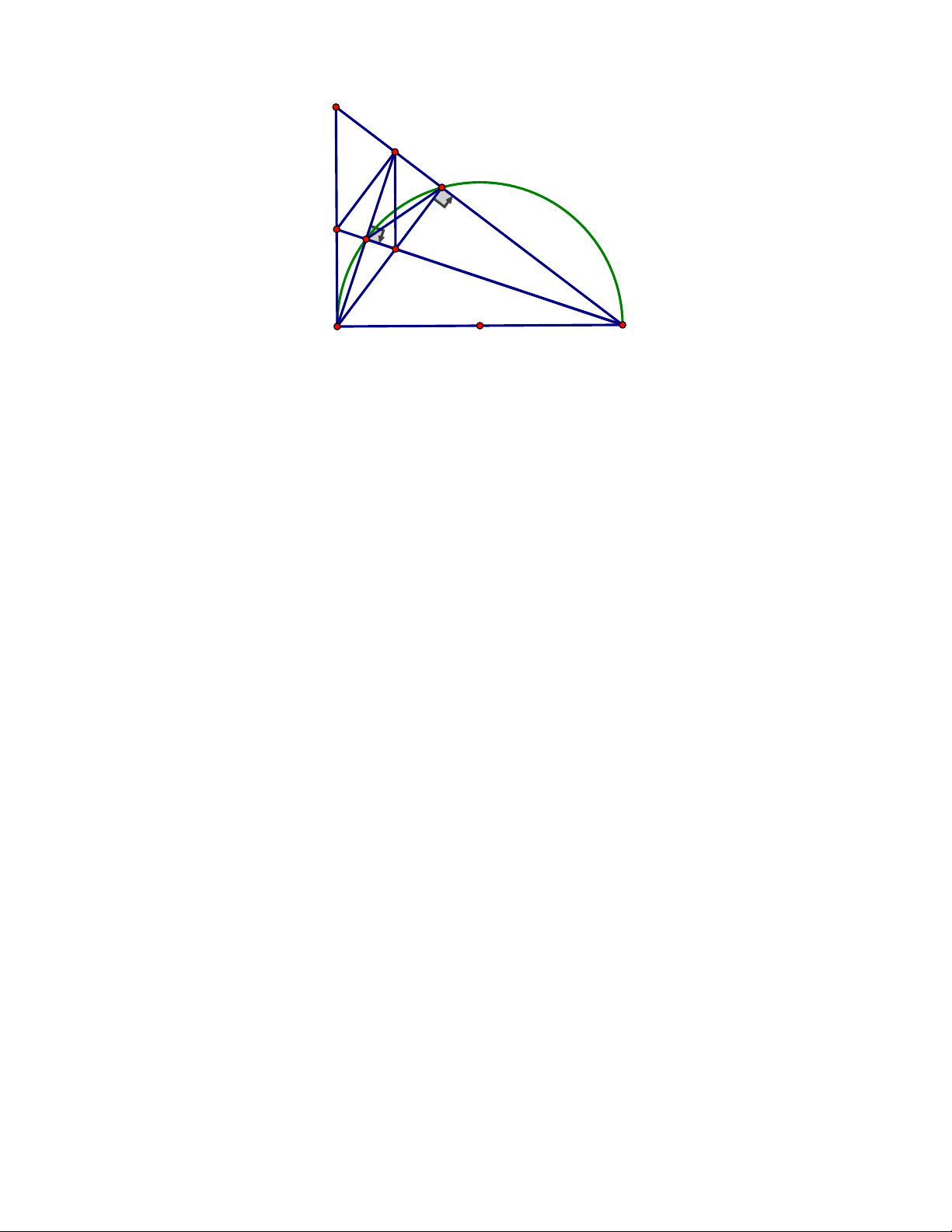
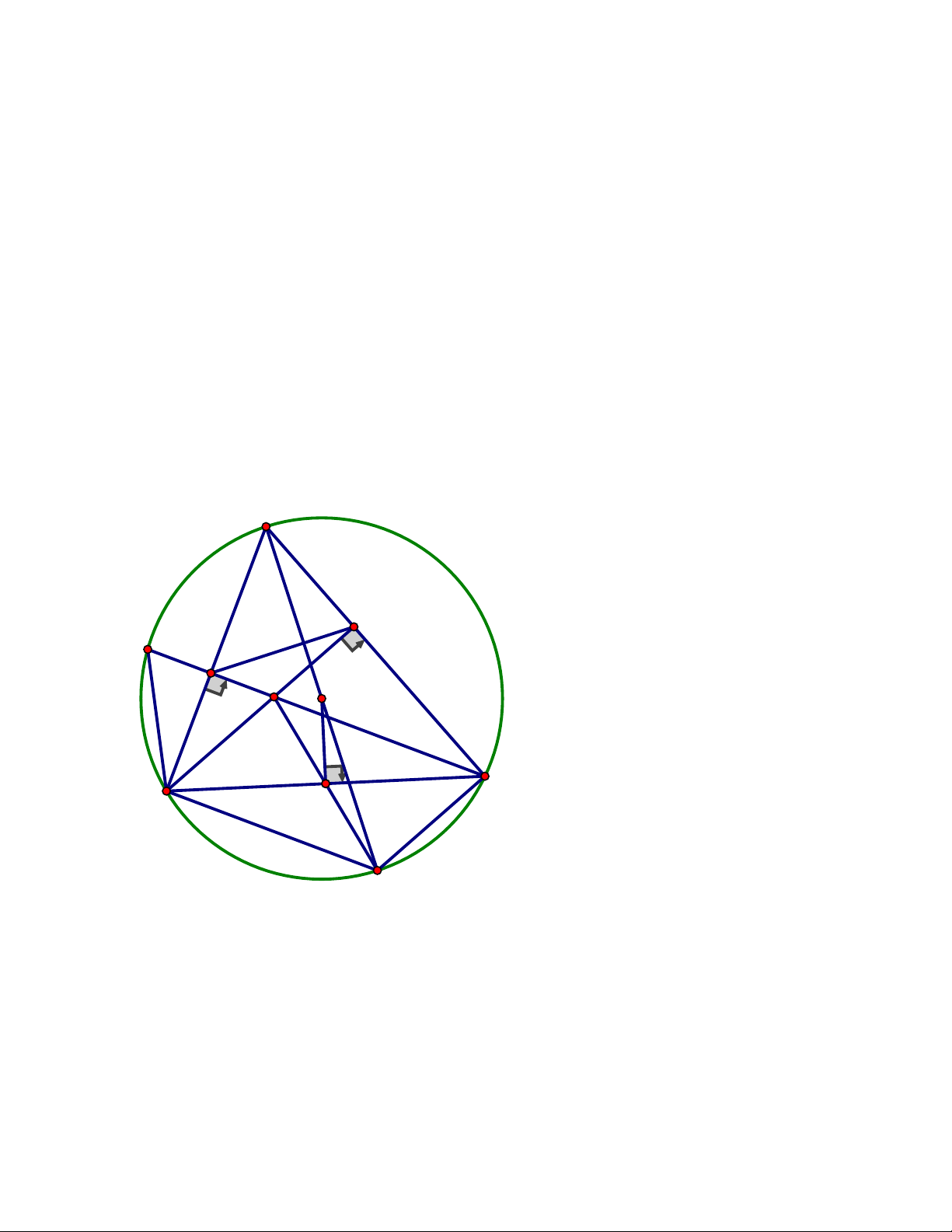
thẳng BM và CN nằm trên đường thẳng AH. ĐÁP ÁN Câu 4. A K N E M D C I B H
a) Chứng minh rằng tứ giác ADHE nội tiếp
Ta có: BDH là góc nội tiếp chắn nửa đường tròn đường kính 0
BH BDH 90
CEH là góc nội tiếp chắn nửa đường tròn đường kính 0
CH CEH 90
Xét tứ giác ADHE ta có: 0 0 0
ADH AEH 90 90 180 ADHE là tứ giác nội tiếp Trang 1 b) Chứng minh: 2 IH I . D IE
Ta có: ADHE là tứ giác nội tiếp (cmt) D AH D
EH (cùng chắn DH)
Hay BAH IEH ,lại có BAH BHD (cùng phụ với D BH )
BHD IEH BAH hay BHD IEH Xét I DH và I HE ta có: I
chung; IHD IEH (cmt) ID IH 2 I DH I
HE(g.g) I .
D IE IH (dfc ) m IH IE
c) Chứng minh giao điểm hai đường thẳng BM ,CN nằm trên đường thẳng AH
Gọi giao điểm của BM và CN là K Ta có: B
MH là góc nội tiếp chắn nửa đường tròn đường kính BH 0 B MH 90
Hay MH BK , chứng minh tương tự NH KC
Vì ADHE là tứ giác nội tiếp (cmt) nên DAH DEH (cùng chắn cung DH ) hay BAH MEH
Vì BDMH là tư giác nội tiếp đường tròn đường kính B , D MH
HME DBH (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện)
Hay EMH ABH mà 0 0
BAH ABH 90 MBH HME 90 0
MHE 90 hay MH HE
Mà HE AC MH / / AC
Lại có: MH BK cmt BK AC , chứng minh tương tự: CK AB
K là trực tâm A
BC K AH(dfc ) m ĐỒNG NAI
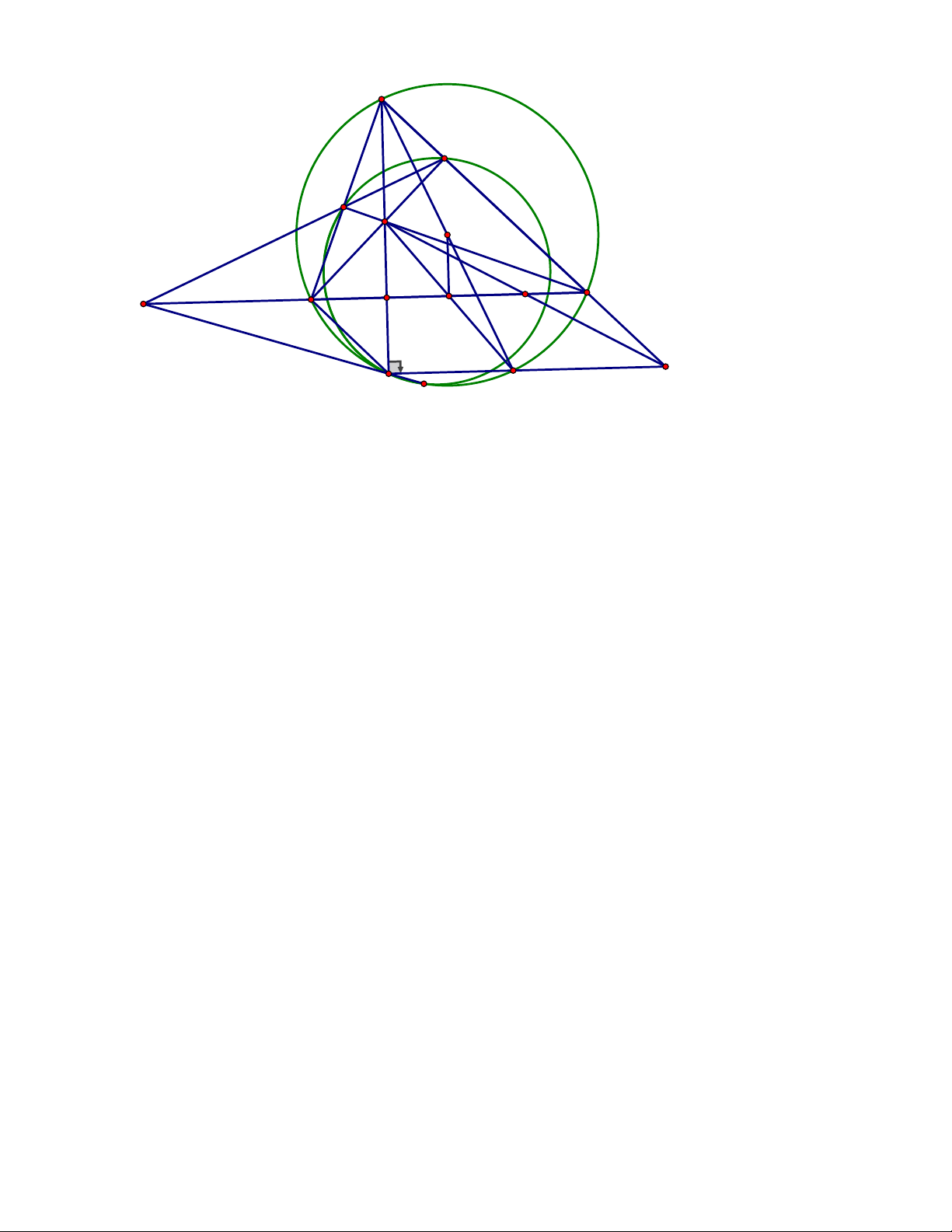
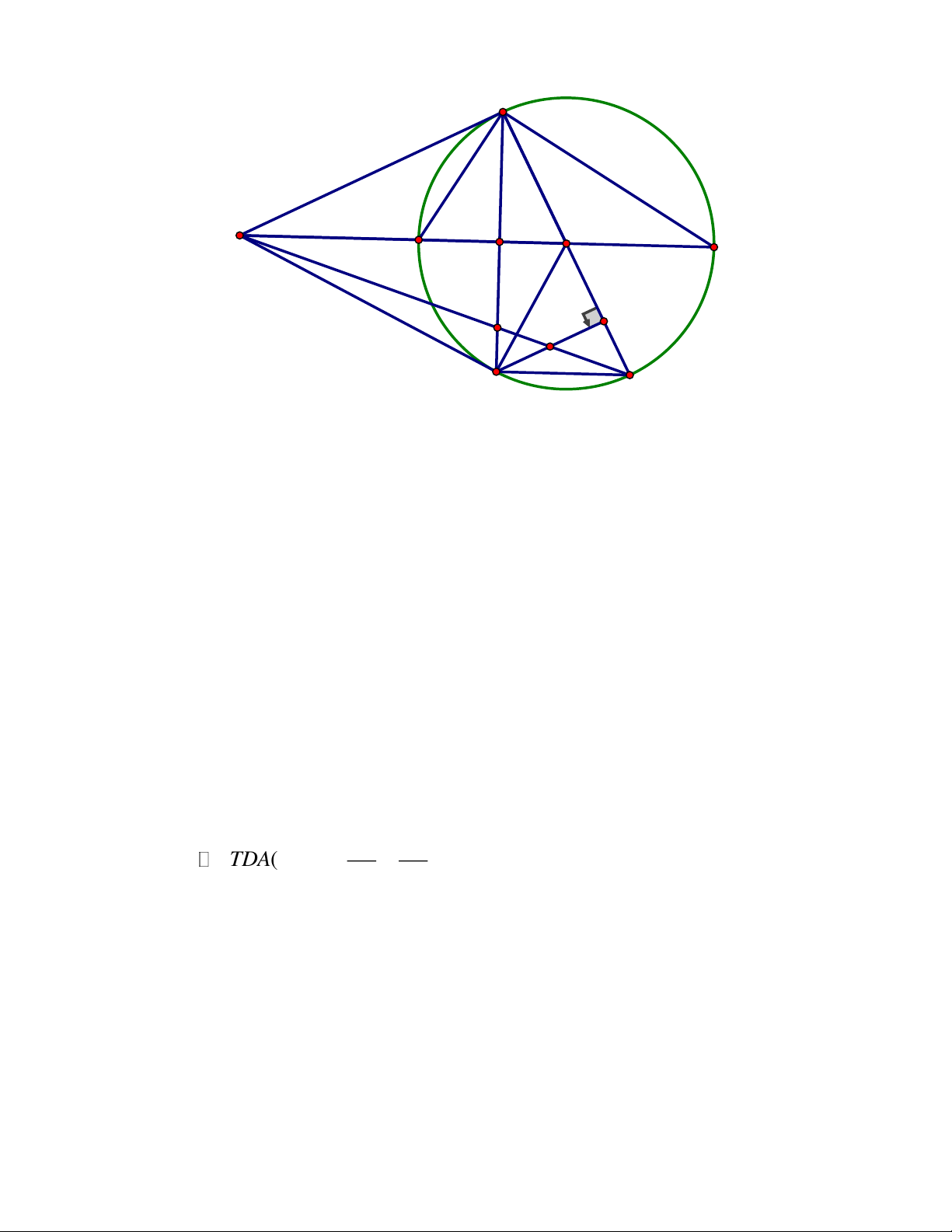
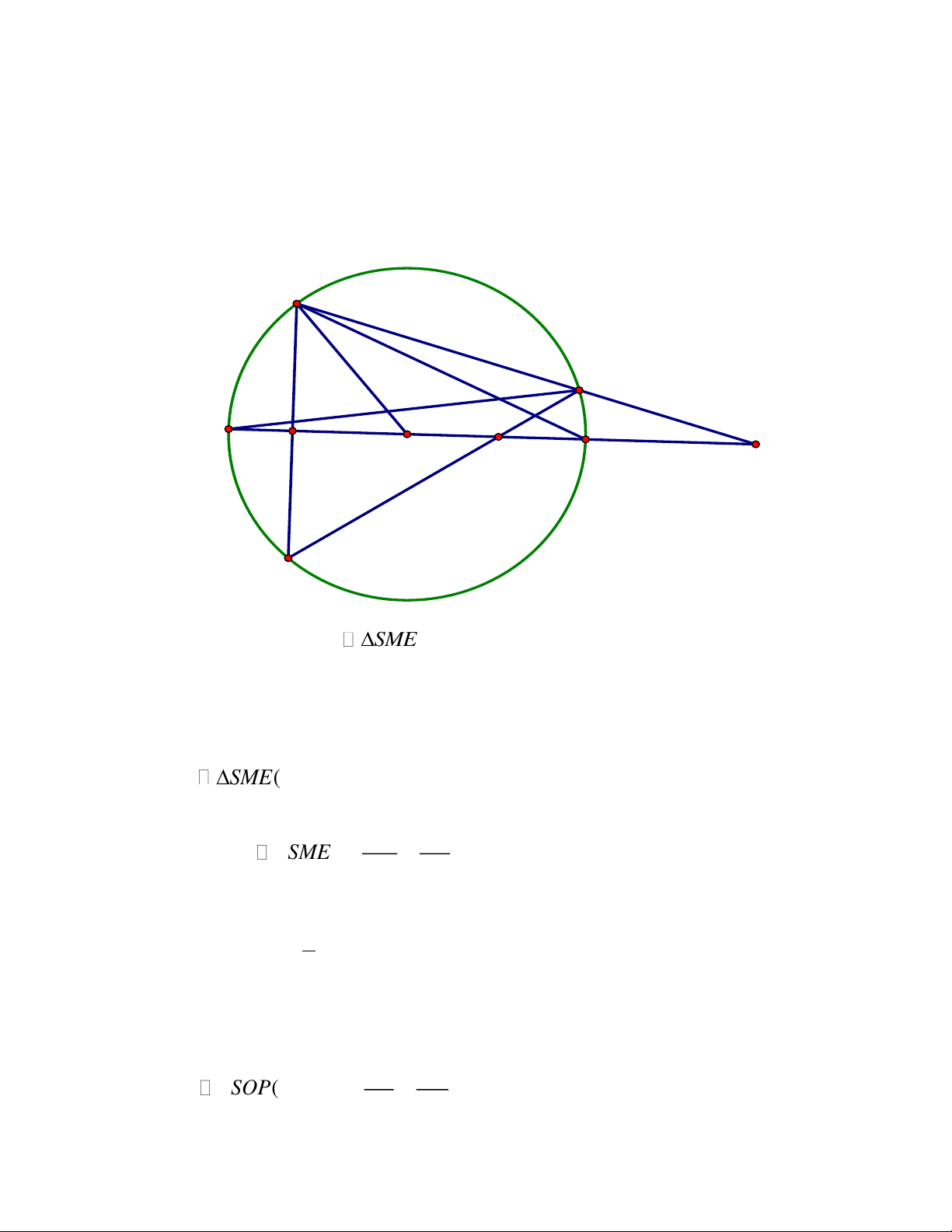
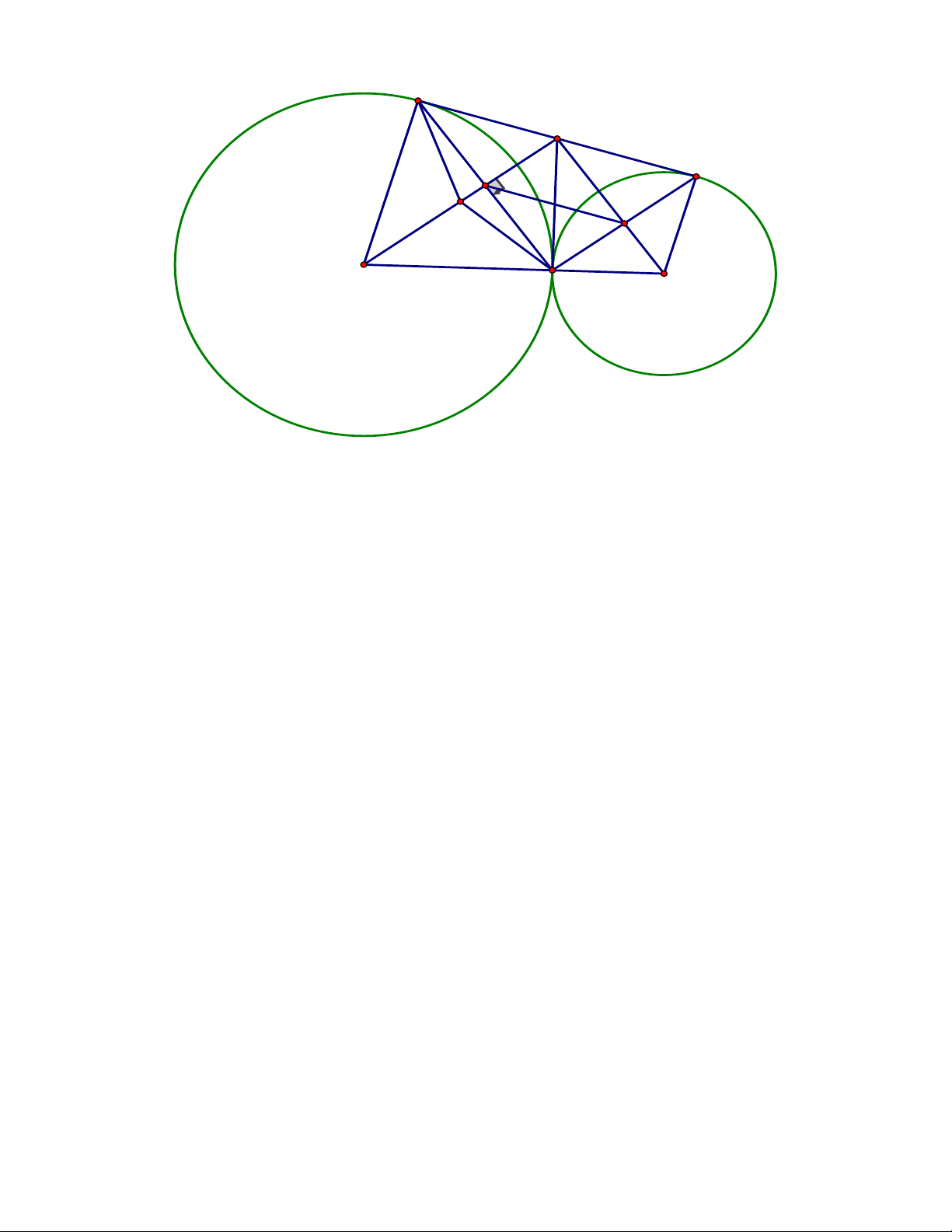
Câu 5. (2,75 điểm) Cho tam giác nhọn ABC nội tiếp đường tròn O có hai đường cao
BE,CF cắt nhau tại trực tâm H, AB A .
C Vẽ đường kính AD của O. Gọi K là giao
điểm của đường thẳng AH với đường tròn O, K khác . A Gọi ,
L P lần lượt là giao điểm
của đường thẳng AH với đường tròn O, K khác . A Gọi ,
L P lần lượt là giao điểm của
hai đường thẳng BC và EF, AC và KD
1) Chứng minh tứ giác EHKP nội tiếp đường tròn và tâm I của đường tròn này
thuộc đường thẳng BC
2) Gọi M là trung điểm của đoạn thẳng BC.Chứng minh AH 2OM
3) Gọi T là giao điểm của đường tròn O với đường tròn ngoại tiếp tam giác
EFK,T khác K.Chứng minh rằng ba điểm ,
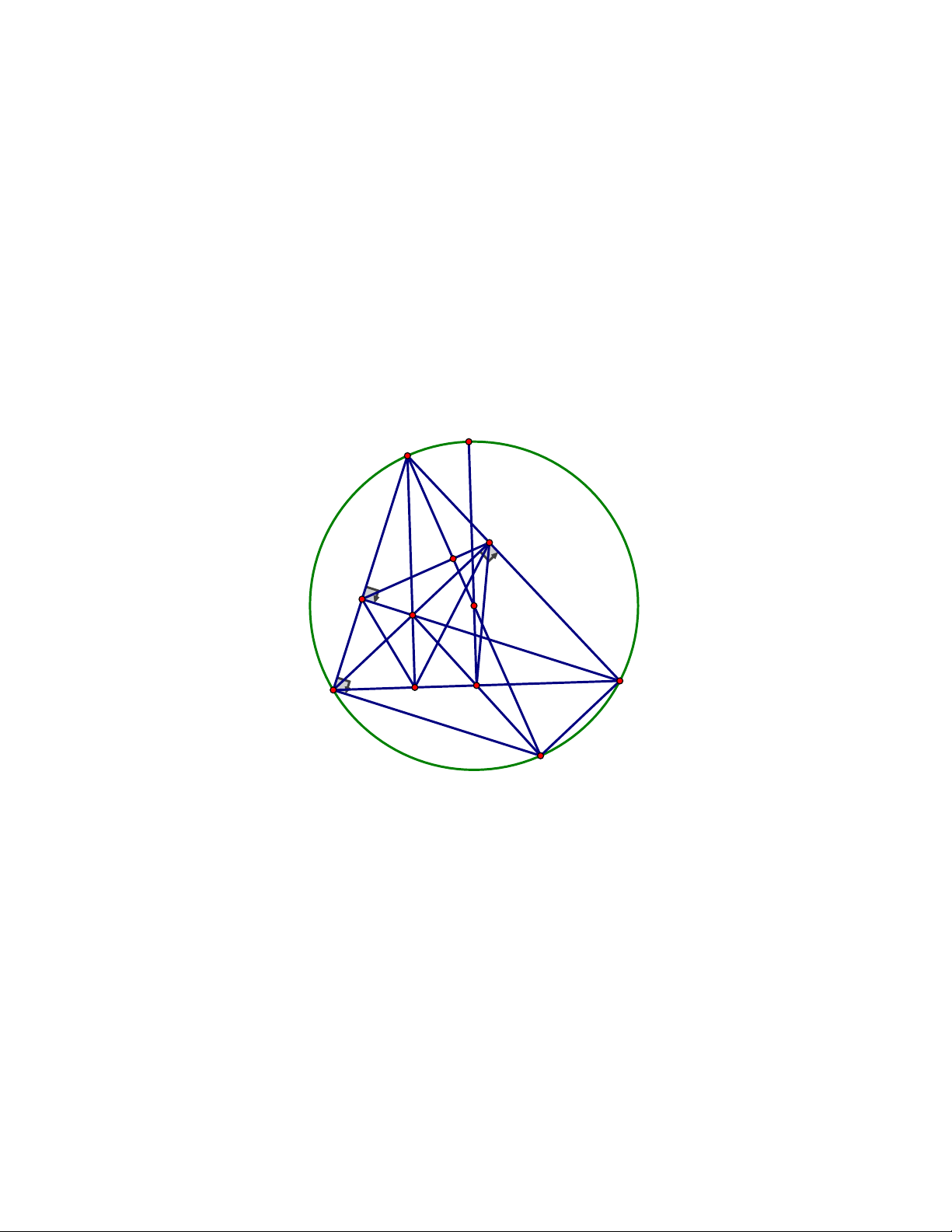
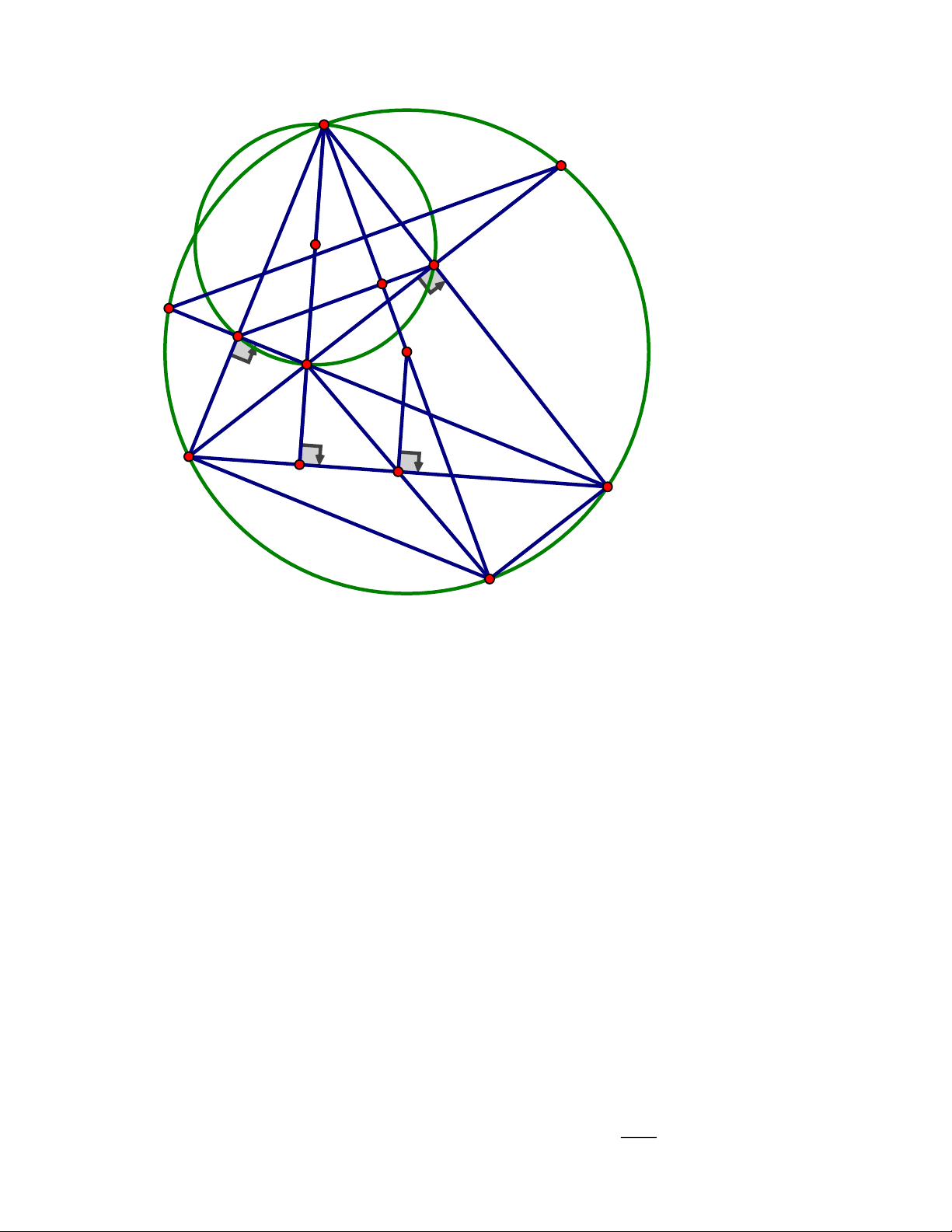
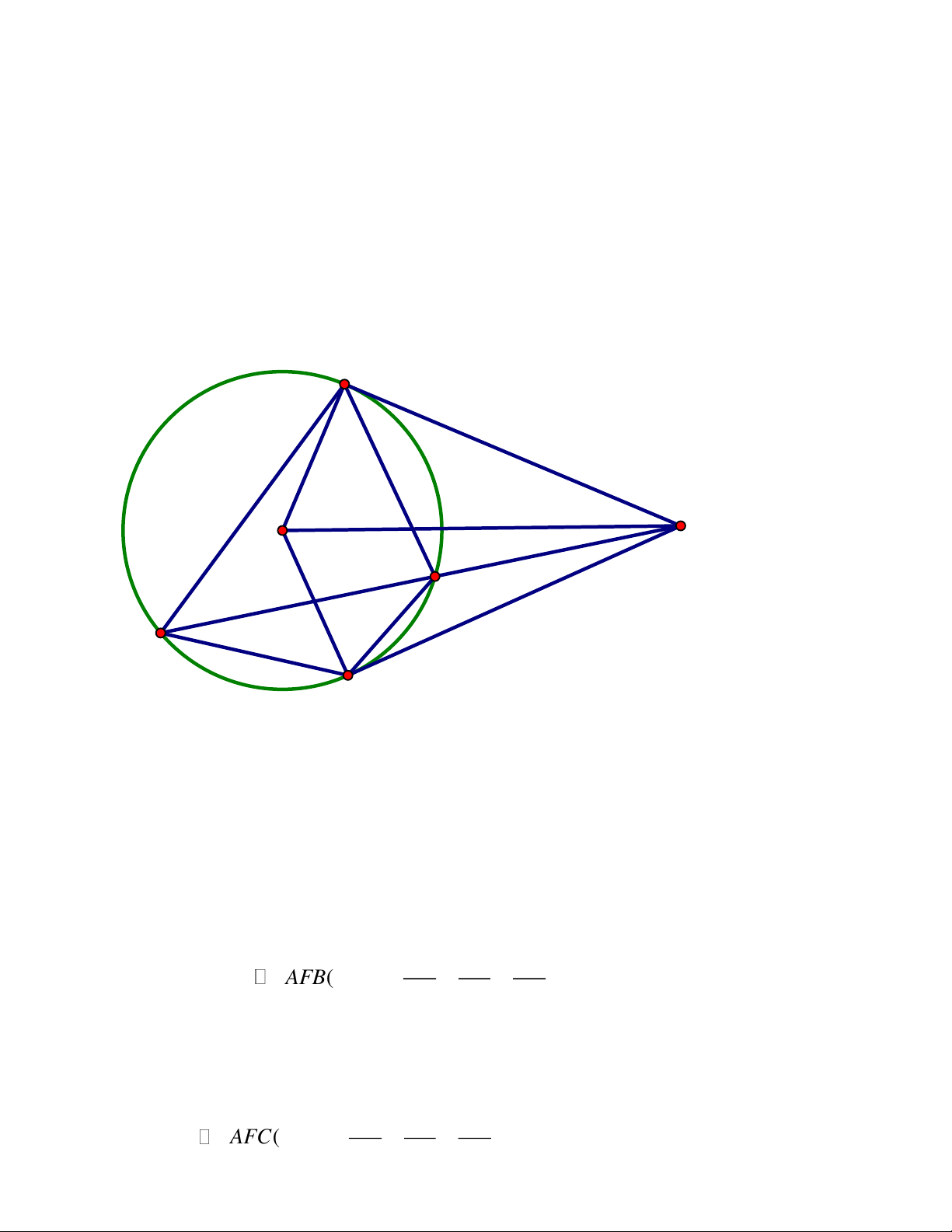
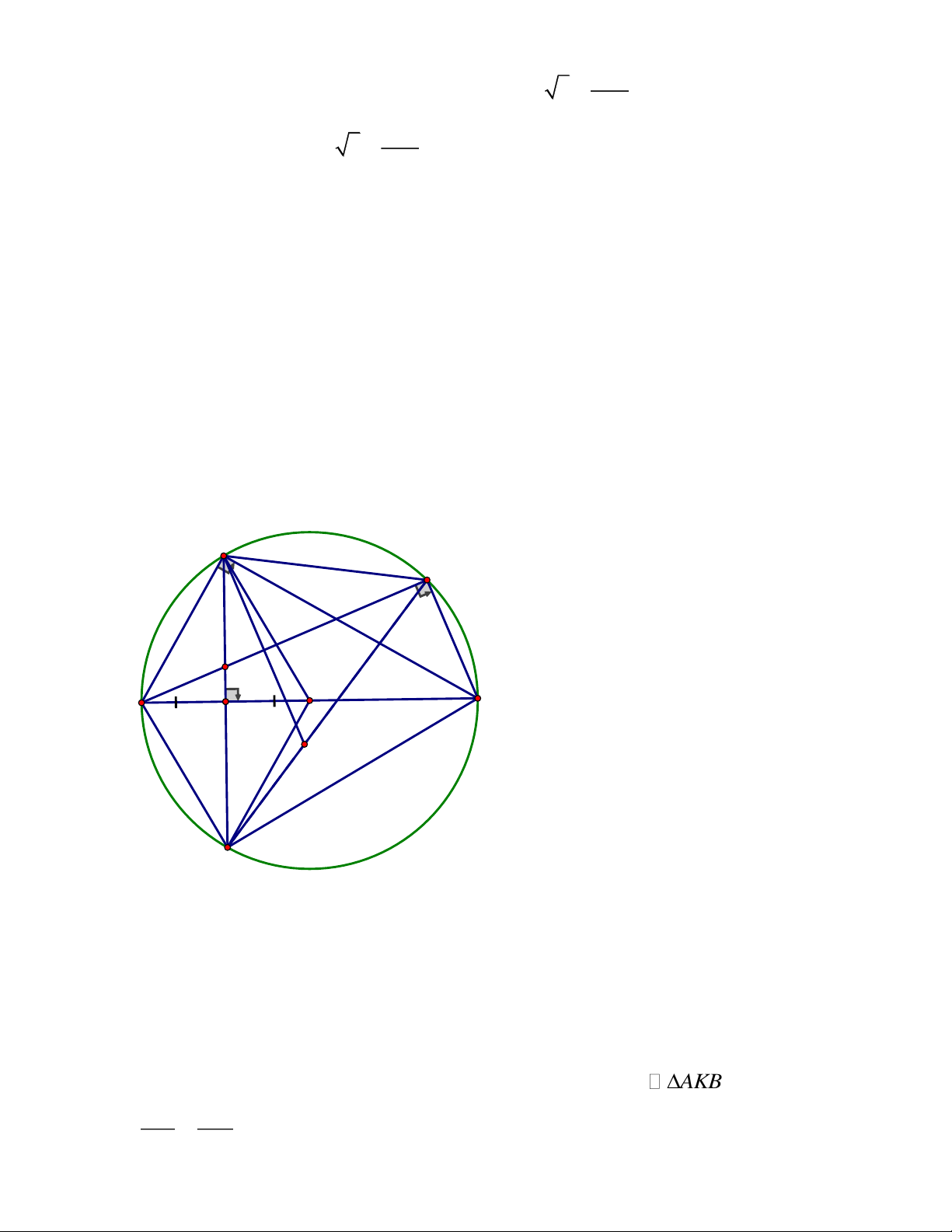
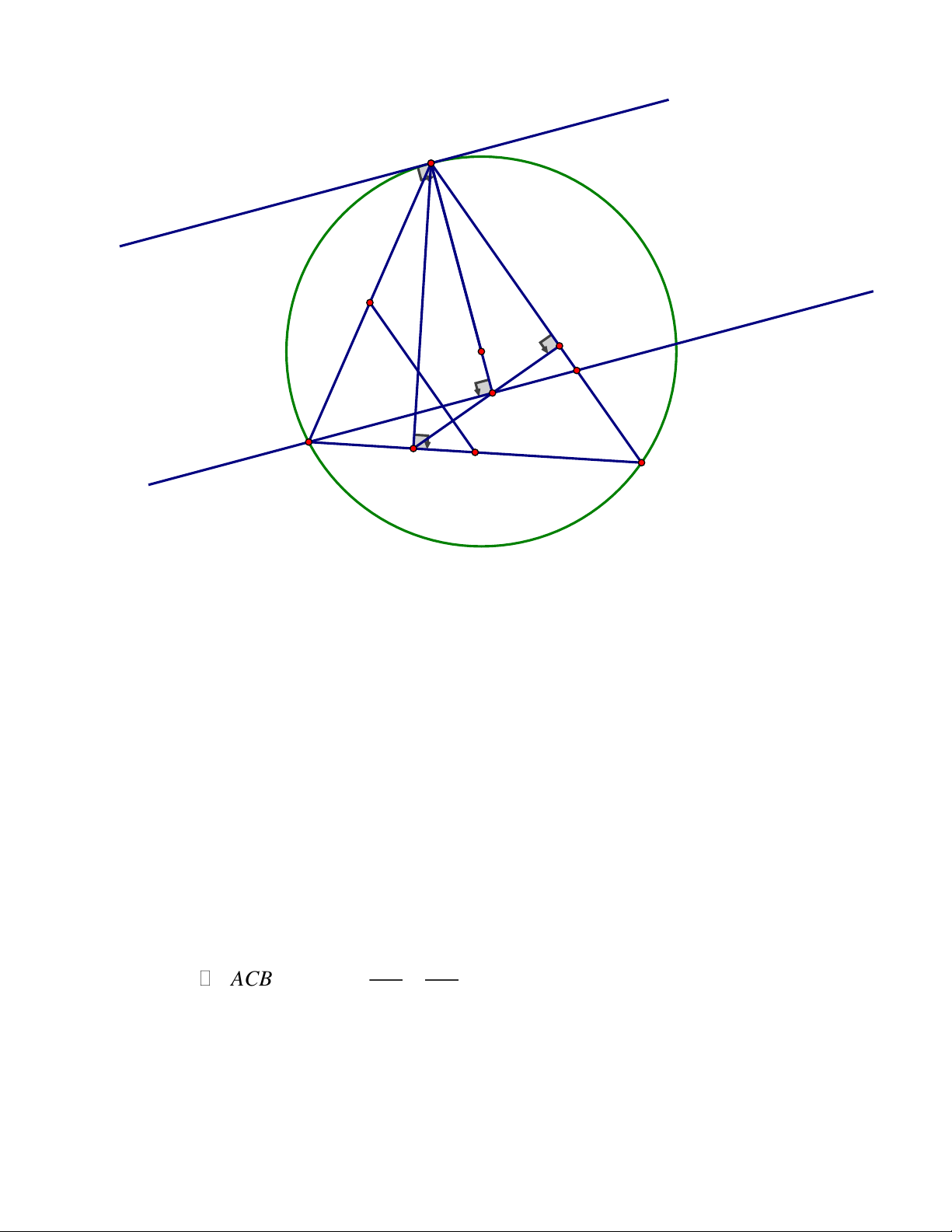
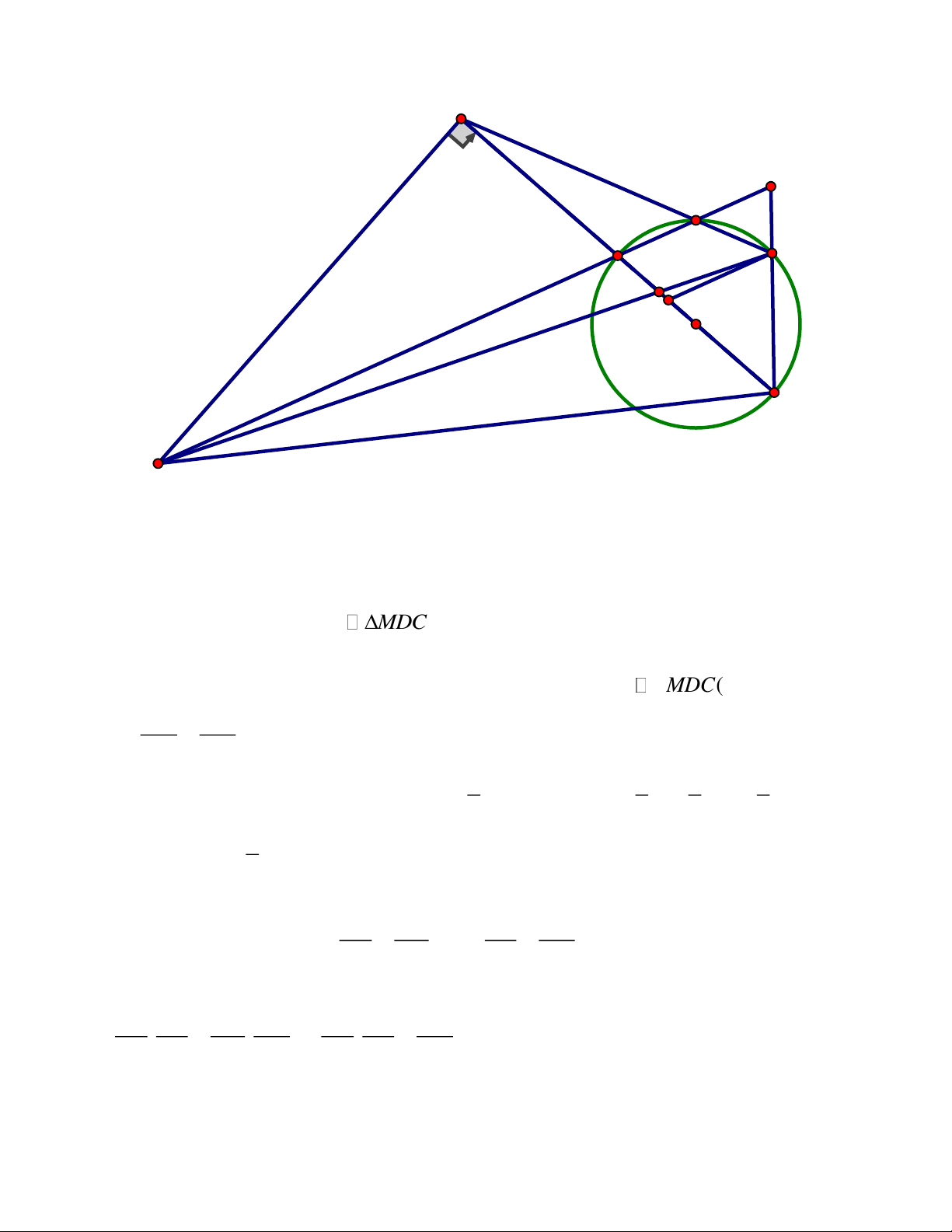
L K,T thẳng hàng. ĐÁP ÁN Câu 5. Trang 2 A E F H O L B C J M I P K D T'
1) Chứng minh EHKP là tứ giác nội tiếp
Ta có: BE là đường cao của A
BC BE AC hay 0 BEC H EC 90 A
KD là góc nội tiếp chắn nửa đường tròn 0 A KD 90
Xét tứ giác EHKP có: 0 0 0 H EP H
KP 90 90 180 , mà hai góc này đối diện
nên EHKP là tứ giác nội tiếp (đpcm) Có 0 H
KP 90 là góc nội tiếp chắn cung HP HP là đường kính của đường tròn
ngoại tiếp tứ giác EHKP Tâm I của đường tròn này là trung điểm của HP
Gọi J là giao điểm của AK và BC
Ta có: HBJ HAC (cùng phụ với A CB) K BC K
AC (hai góc nôi tiếp cùng chắn cung KC) hay J BK H AC H BJ J BK H
AC BJ là phân giác của HBK
Ta có: AH là đường cao của A
BC AH BC J BJ là đường cao B HK Xét B
HK ta có: BJ vừa là đường cao, vừa là đường phân giác từ đỉnh B của tam giác B
HK cân tại B và BJ là đường trung tuyến của B
HK J là trung điểm của HK
Gọi I ' là giao điểm của BC và HP
Ta có: AJ BC Jmà KP AH K BC / /KP hay JI '/ /KP Xét H
KP ta có: J là trung điểm của HK(cmt);IJ / /KP(cmt) I 'J là đường trung bình của H
KP I 'là trung điểm của HP I I ' hay I BC(dfcm)
2) Chứng minh AH 2OM Ta có: 0 A BD A CD AB BD
90 (góc nội tiếp chắn nửa đường tròn) AC CD Trang 3
AB EF(gt) CF / / BD BH / /CD Mà hay
BDCH là hình bình hành
BE AC(gt) BE / /CD CH / / BD
BC cắt HD tại trung điểm mỗi đường, lại có M là trung điểm của BC(gt)
M cũng là trung điểm của . HD Xét A HDta có: ,
O M lần lượt là trung điểm của A ,
D HD OM là đường trung bình A HD OM / / AH
AH 2OM (dfcm) 1 OM AH 2 3) Chứng minh ,
L K,T thẳng hàng
Gọi T ' là giao điểm của tia LK với đường tròn O
Xét tứ giác BFEC ta có: 0 BFC B
EC 90 . mà đỉnh F, E là các đỉnh kề nhau
Nên BFEC là tứ giác nội tiếp LFB LCE (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện) Xét L FB và L CE ta có: L chung; LF LB L FB L
CE(cmt) L FB L
CE(g.g)
LE.LF L . B LC LC LE
Ta có tứ giác BCT ' K nội tiếp đường tròn O L KB L
CT '(góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện) Xét L BK và L
CT 'ta có: L chung; LKB LCT '(cmt) L BK L
T 'C(g g) LB LK LF LK L .
B LC LK.LT ' LE.LF LK.LT ' L . B LC LT ' LC LT ' LE Xét L FK và L
T 'E ta có: LF LK ELT ' chung; L FK L
T 'E(c g c) LFK LET ' LT ' LE
EFKT 'là tứ giác nội tiếp (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện)
T 'thuộc đường tròn ngoại tiếp tam giác EFK
T T ' ,
L K,T thẳng hàng.(đpcm) HÀ NỘI Bài IV. (3,0 điểm)
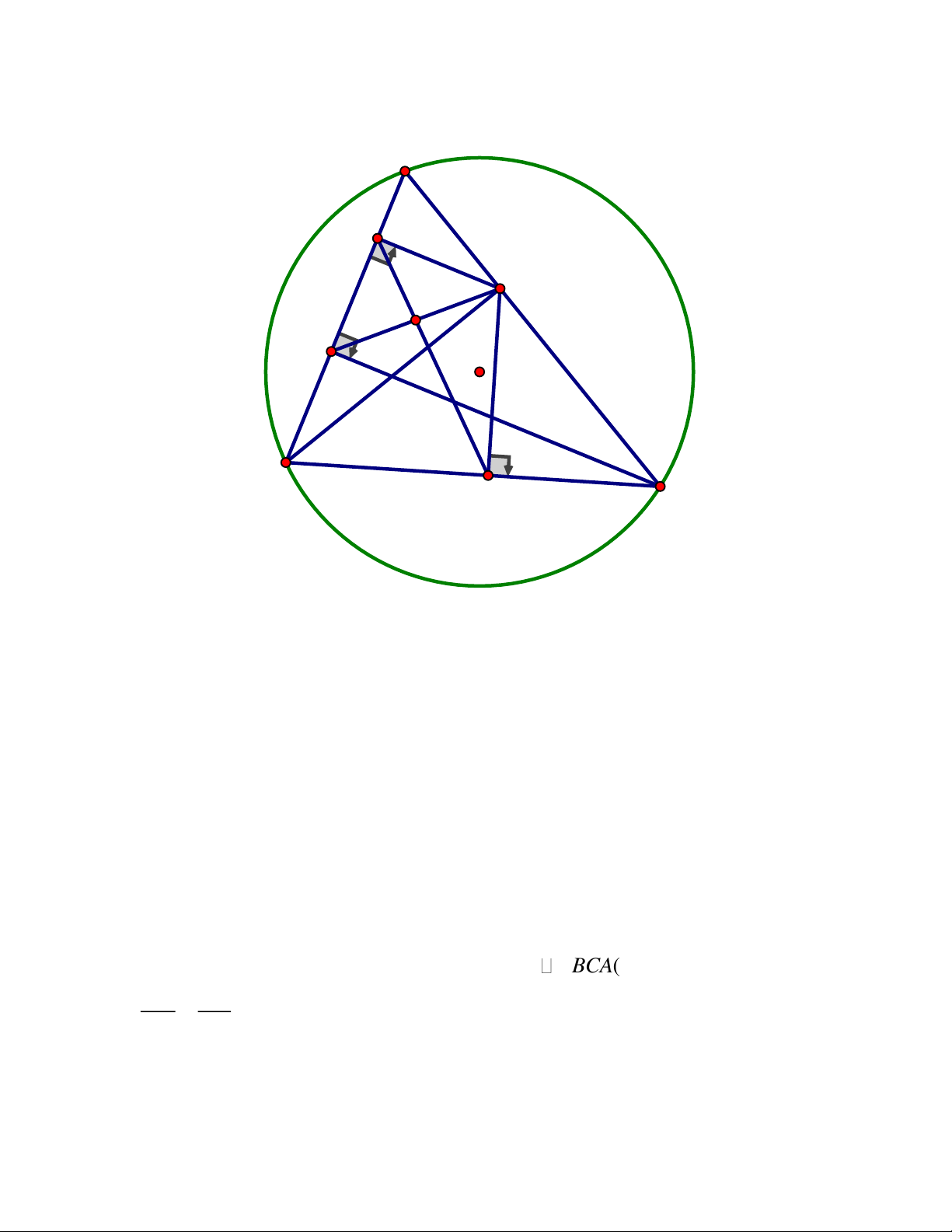
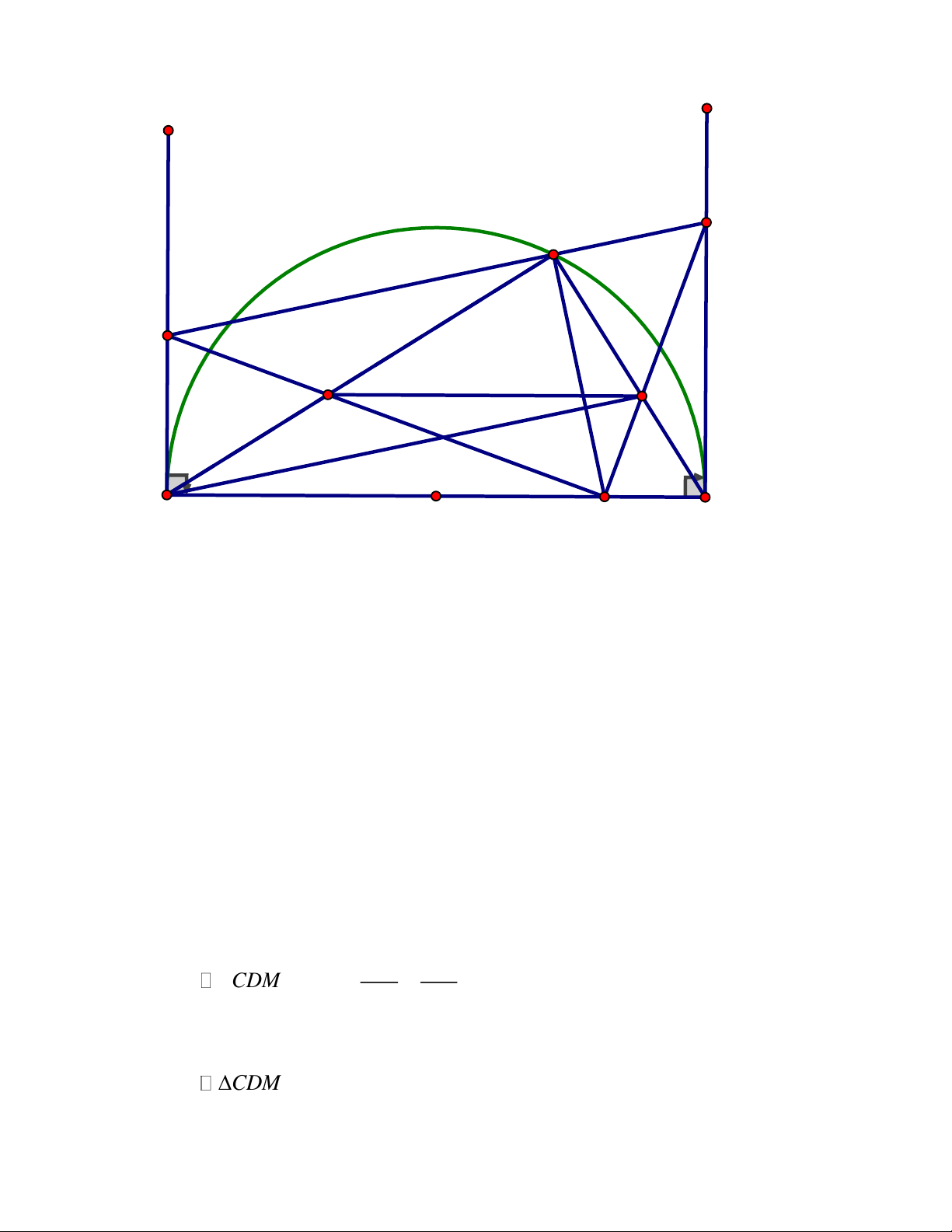
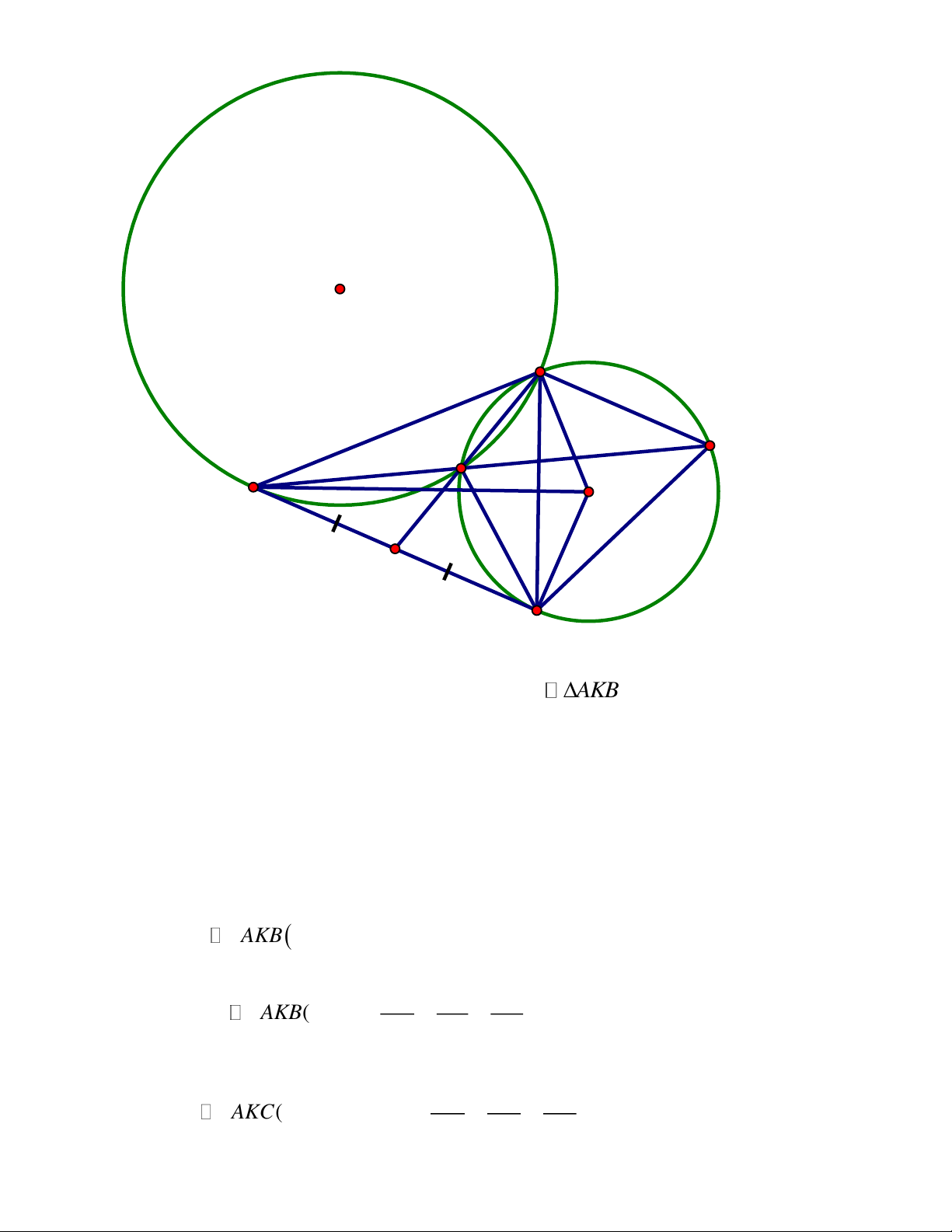
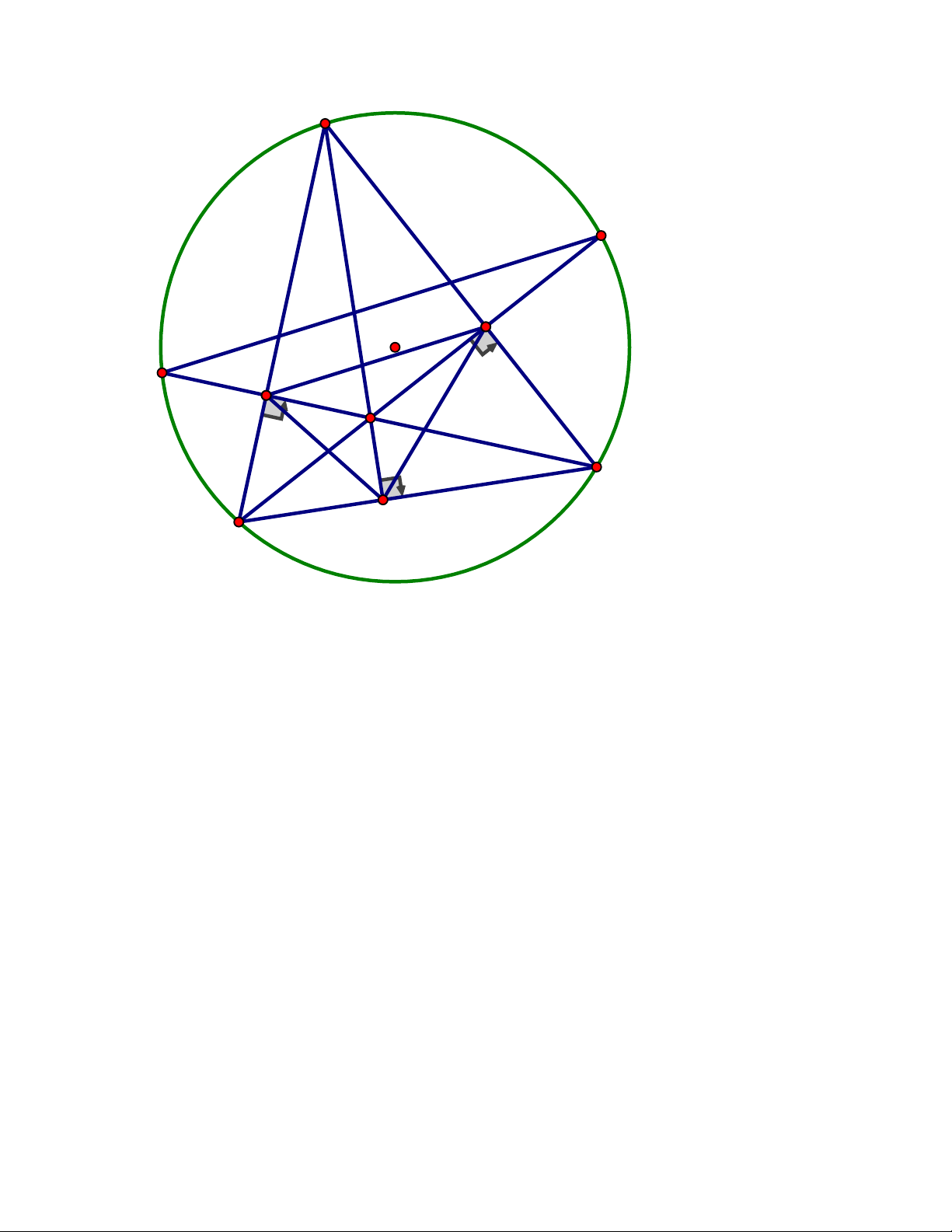
Cho tam giác ABC có ba góc nhọn và đường cao BE.Gọi H và K lần lượt là
chân các đường vuông góc kẻ từ điểm E đến đường thẳng A , B BC
1) Chứng minh tứ giác BHEK là tứ giác nội tiếp
2) Chứng minh BH.BA BK.BC
3) Gọi F là chân đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung
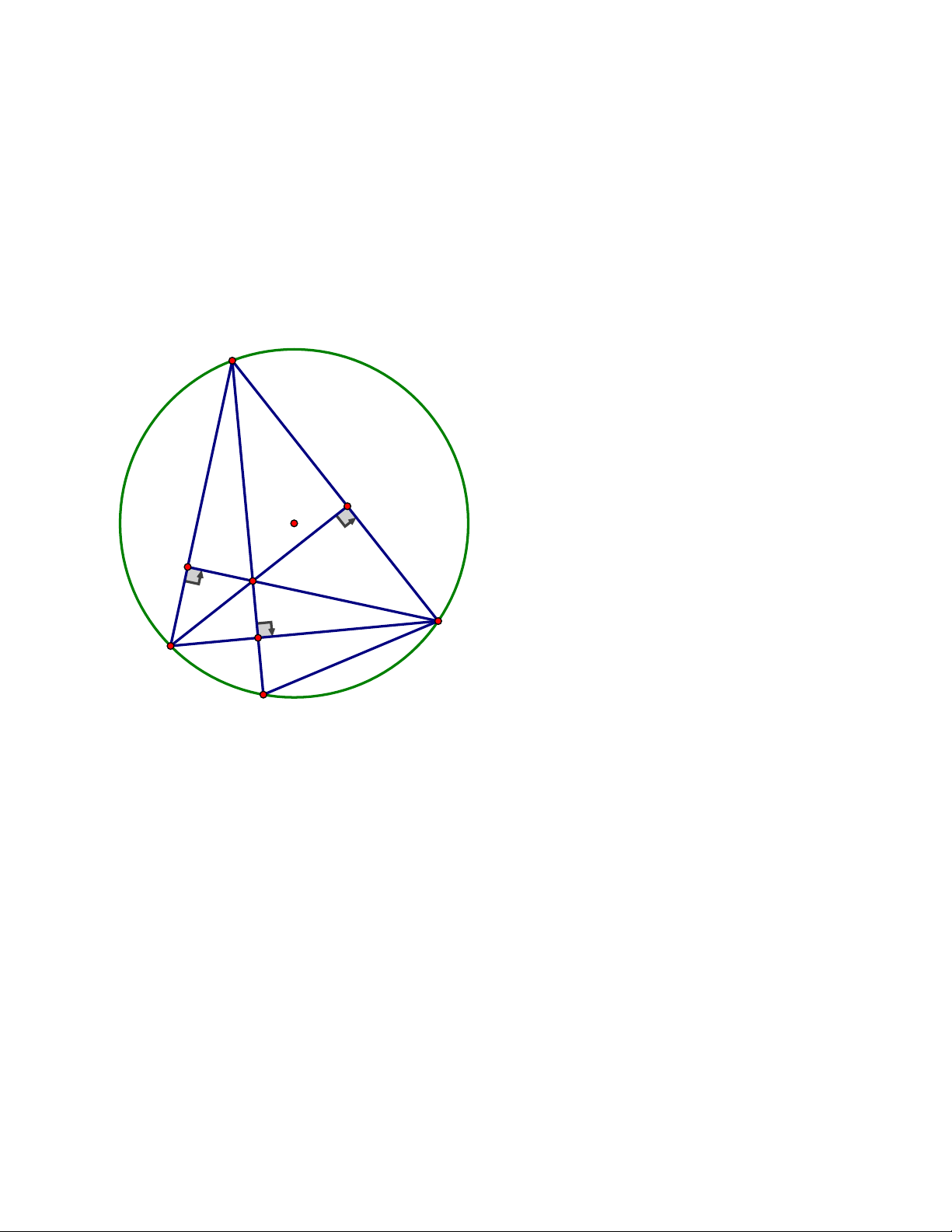
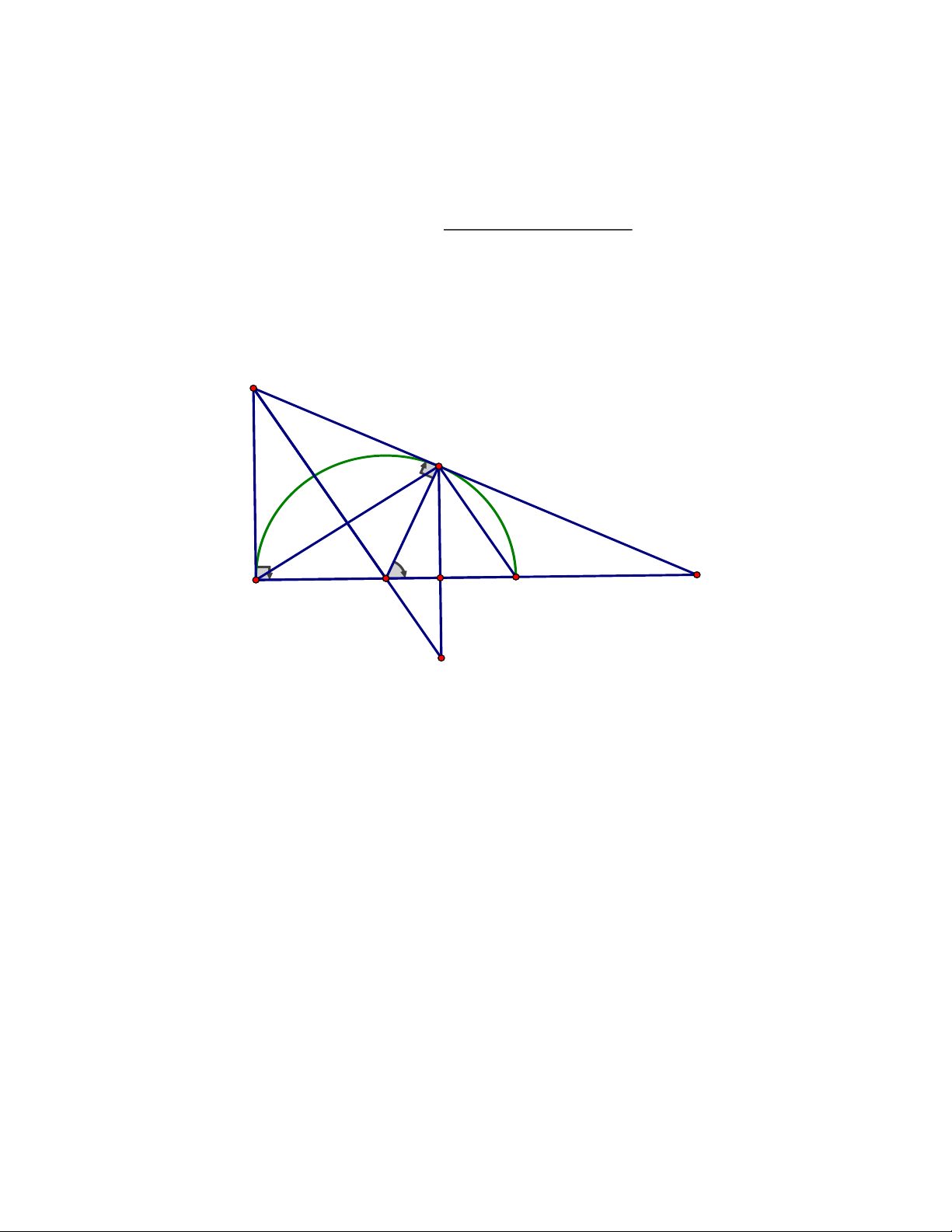
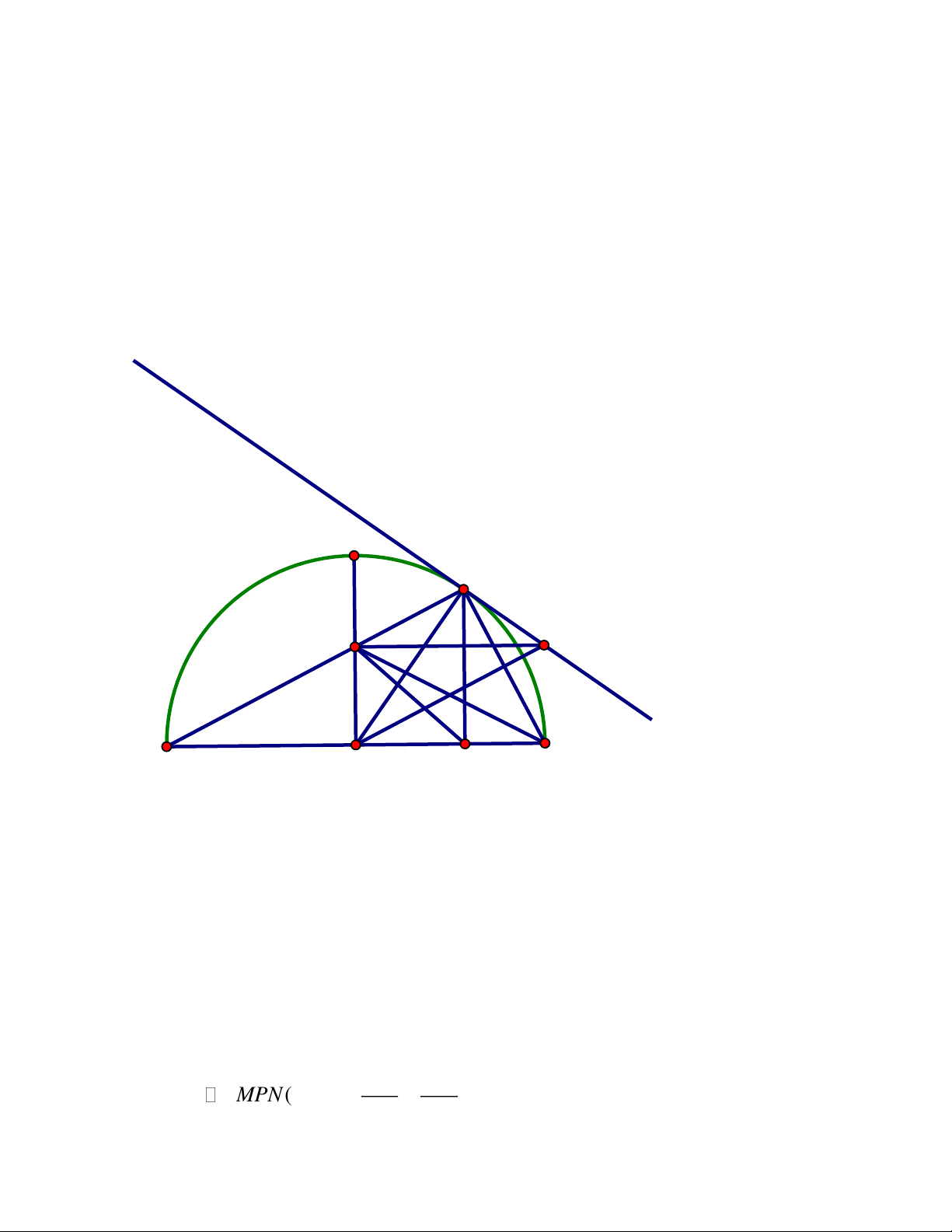
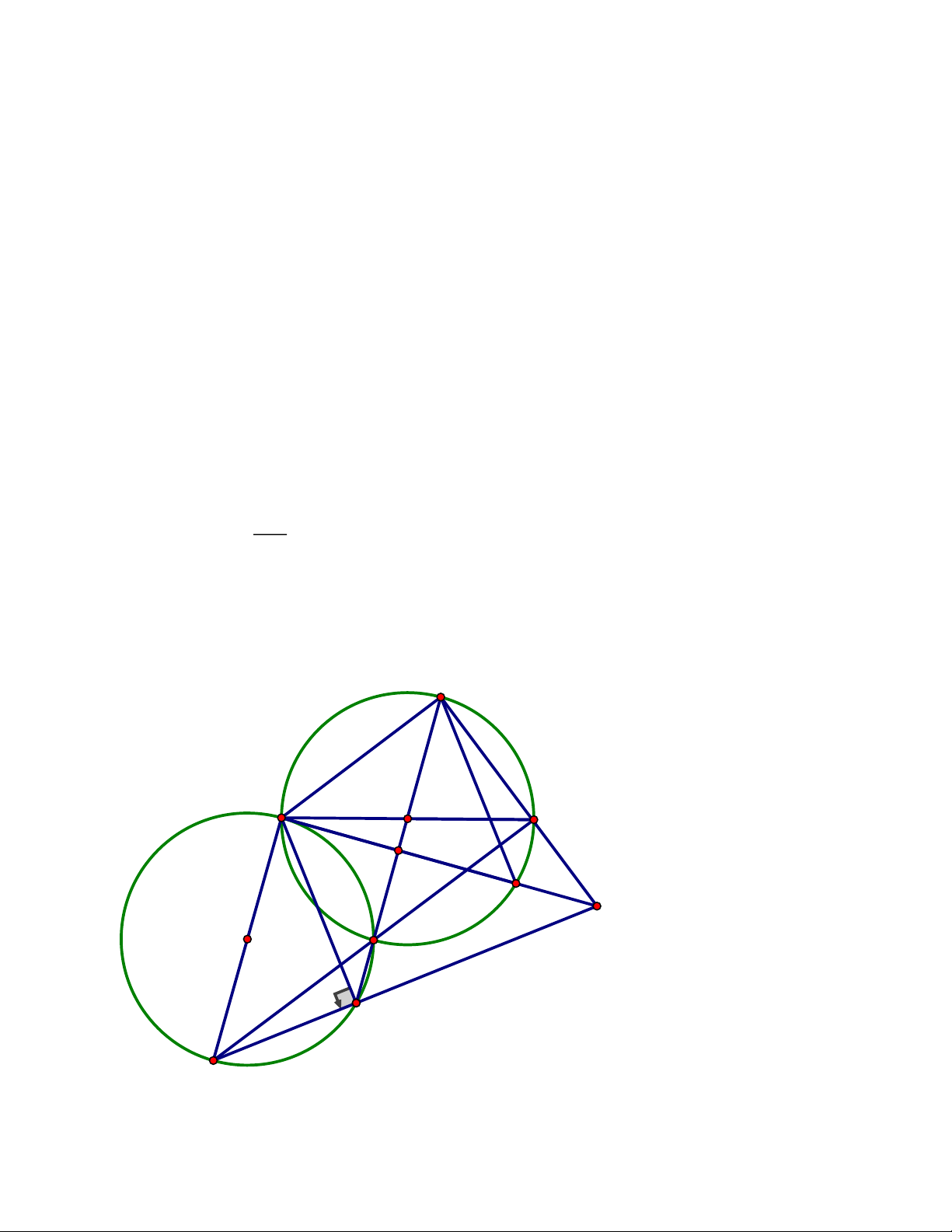
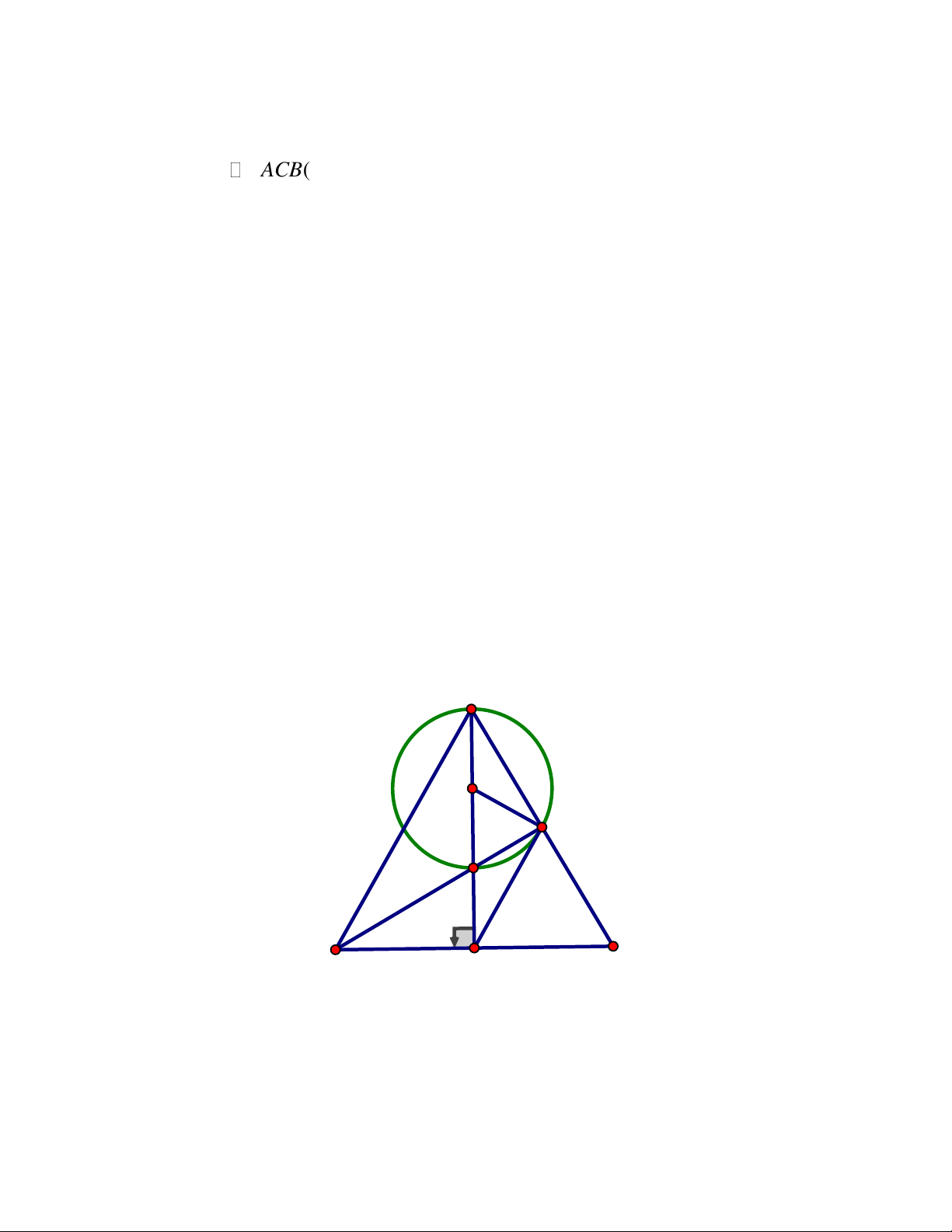
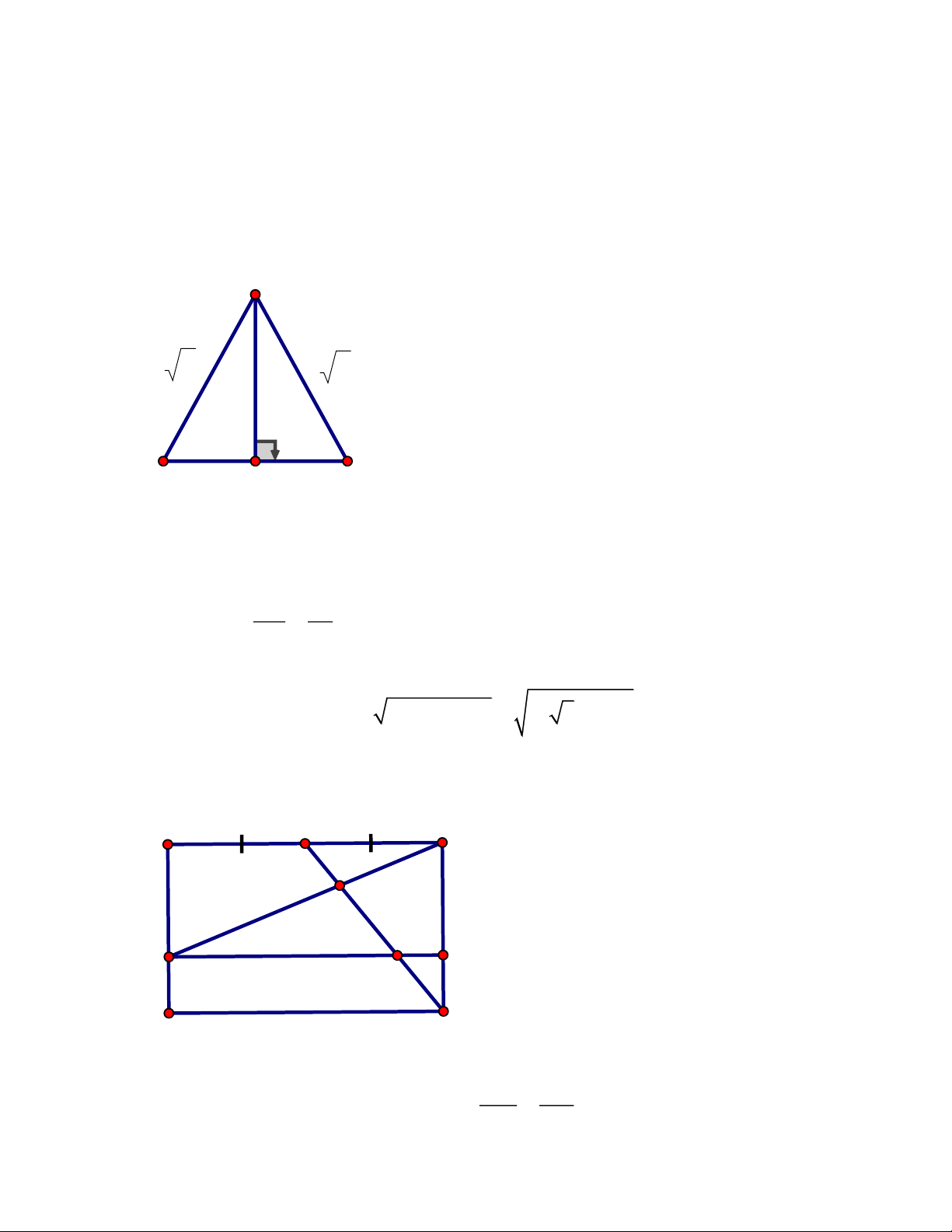
điểm của đoạn thẳng EF.Chứng minh ba điểm H, I, K là ba điểm thẳng hàng Trang 4 ĐÁP ÁN Bài IV. A H 1 2 1 E I 2 1 O F B K C
1) Chứng minh BHEK là tứ giác nội tiếp Ta có : 0 BHE
doEH AB 0 90 ,
BKE 90 do EK BC Tứ giác BHEK có 0 0 0
BHE BKE 90 90 180 nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng 0 180 )dfcm
2) Chứng minh BH.BA BK.BC
Theo câu a) tứ giác BHEK nội tiếp nên BKH BEH (cùng chắn cung BH ) Ta có: 0
BEH EBH 90 (do B HE vuông tại H) 0
BAE EBH 90 (do A
BE vuông tại E) nên BEH BAE (cùng phụ với EBH )
Mà BKH BEH (cmt) nên BKH BAE BEH Xét B HK và B CAcó:
ABC chung; BKH BAE BAC(cmt) B HK B C ( A g.g) BH BK
(hai cặp cạnh tương ứng tỉ lệ) BH.BA B . C BK BC BA
a) Chứng minh H , I , K thẳng hàng
Gọi I ' là giao điểm của HK và EF
Xét tứ giác BFEC có : 0
BFC BEC 90 (gt) nên là tứ giác nội tiếp (tứ giác có 2 đỉnh
kề nhau nhìn 1 cạnh dưới các góc bằng nhau) B F (cùng chắn EC) 1 1 Trang 5
Ta có: EH / /CF (cùng vuông góc với AB) F E (so le trong) do đó B E 1 1 1 1 1
Theo câu a, tứ giác BHEK nội tiếp nên B H (cùng chắn EK )2 1 1
Từ (1) và (2) ta suy ra H E 1 1 I
'HE có H E nên là tam giác cân I 'H I 'E 3 1 1 Lại có: 0
H H BHE 90 ; 0
F E 90 (do H FE vuông tại H) 1 2 2 1
Nên H F hay tam giác I ' HF cân tại I ' I ' H I ' F 4 2 2
Từ 3 và 4 I ' E I ' F hay I là trung điểm EF
Do đó I ' I nên ba điểm H, I, K thẳng hàng (đpcm)
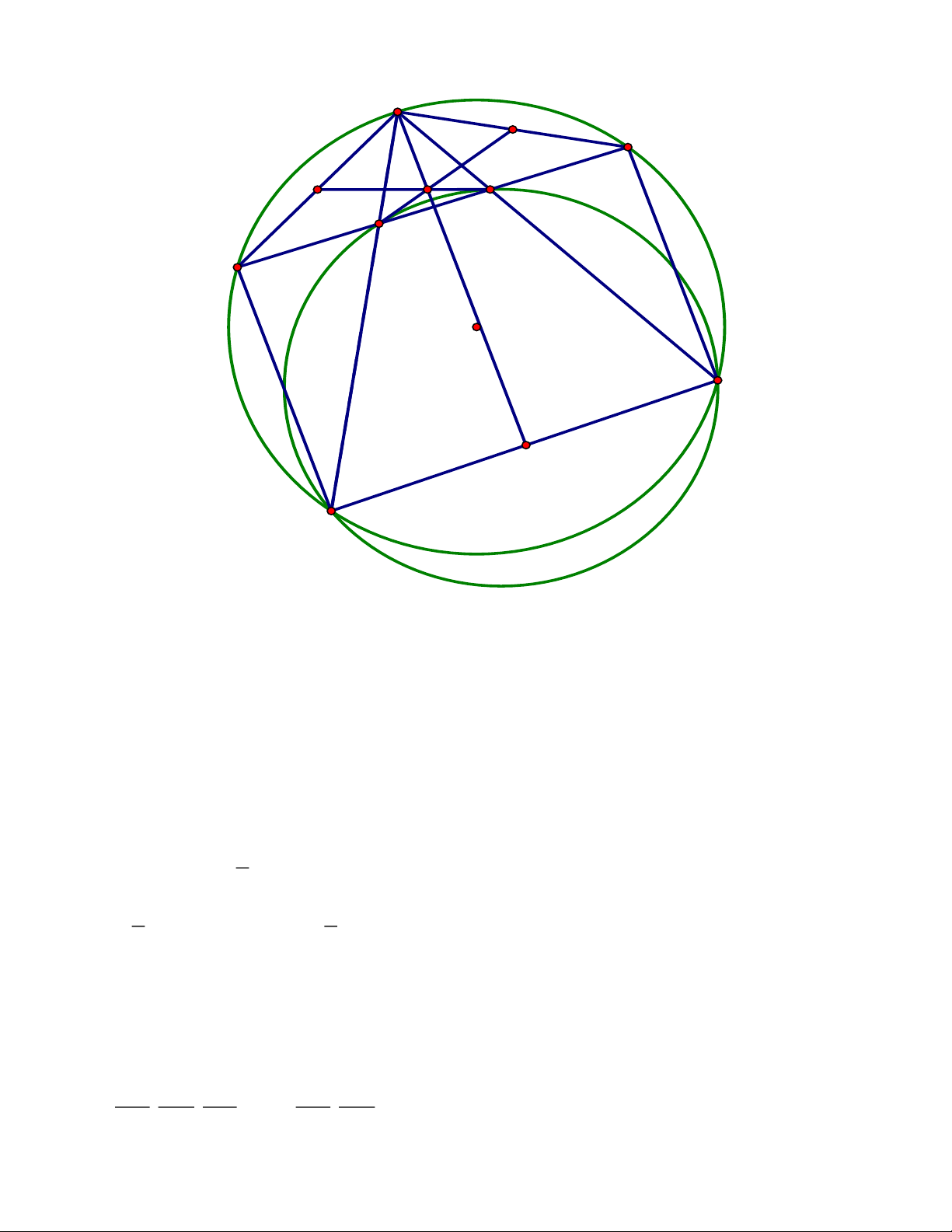
CHUYÊN KHOA HỌC TỰ NHIÊN (HÀ NỘI) Câu III. (3 điểm)
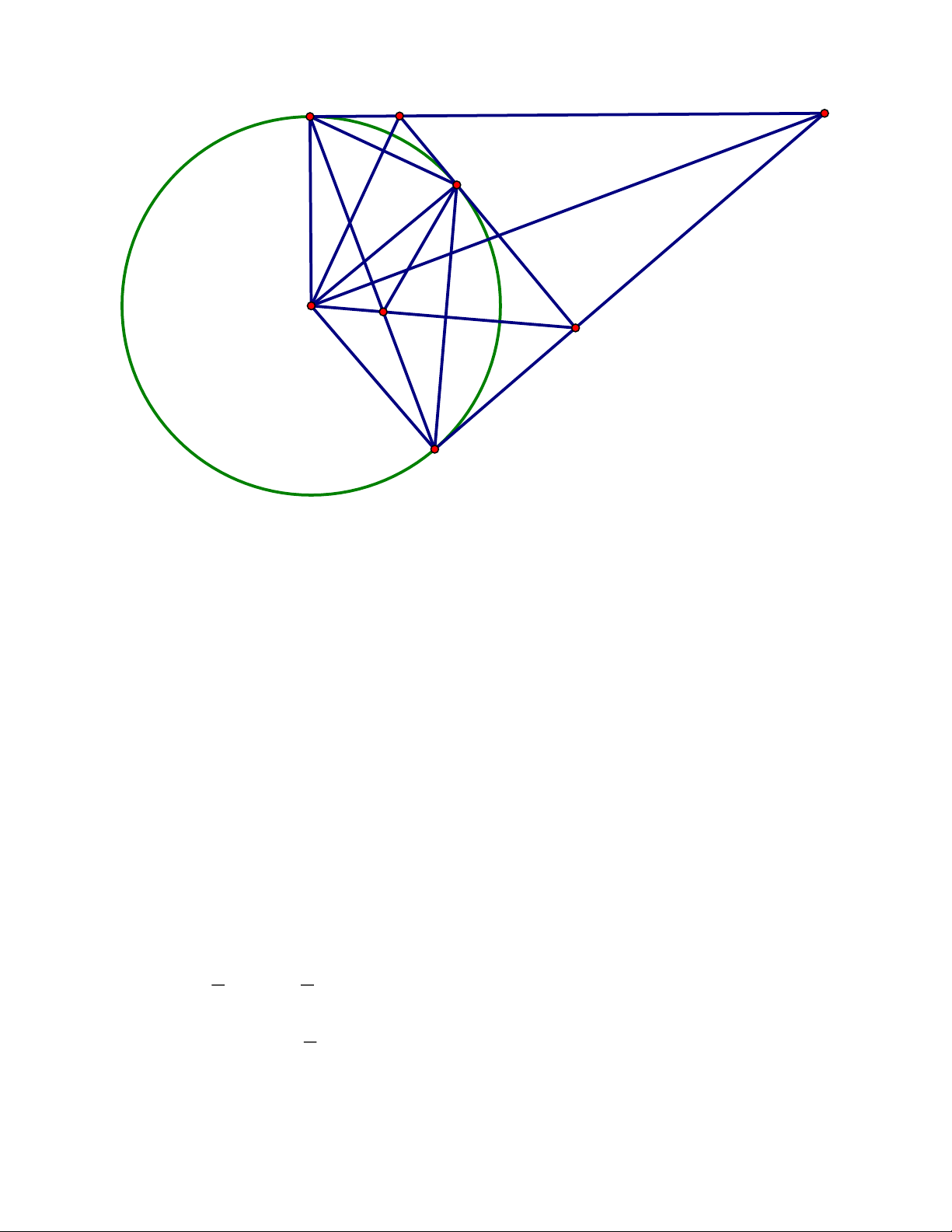
Cho tam giác ABC có BAC là góc nhỏ nhất trong ba góc của tam giác và nội tiếp đường
tròn (O). Điểm D thuộc cạnh BC sao cho AD là phân giác BAC.Lấy các điểm M , N
thuộc (O) sao cho đường thẳng CM , BN cùng song song với đường thẳng AD
1) Chứng minh rằng AM AN
2) Gọi giao điểm của đường thẳng MN với các đường thẳng AC, AB lần lượt là
E, F. Chứng minh rằng bốn điểm ,
B C, E, F cùng thuộc một đường tròn
3) Gọi P,Q theo thứ tự là trung điểm của các đoạn thẳng AM , AN. Chứng minh
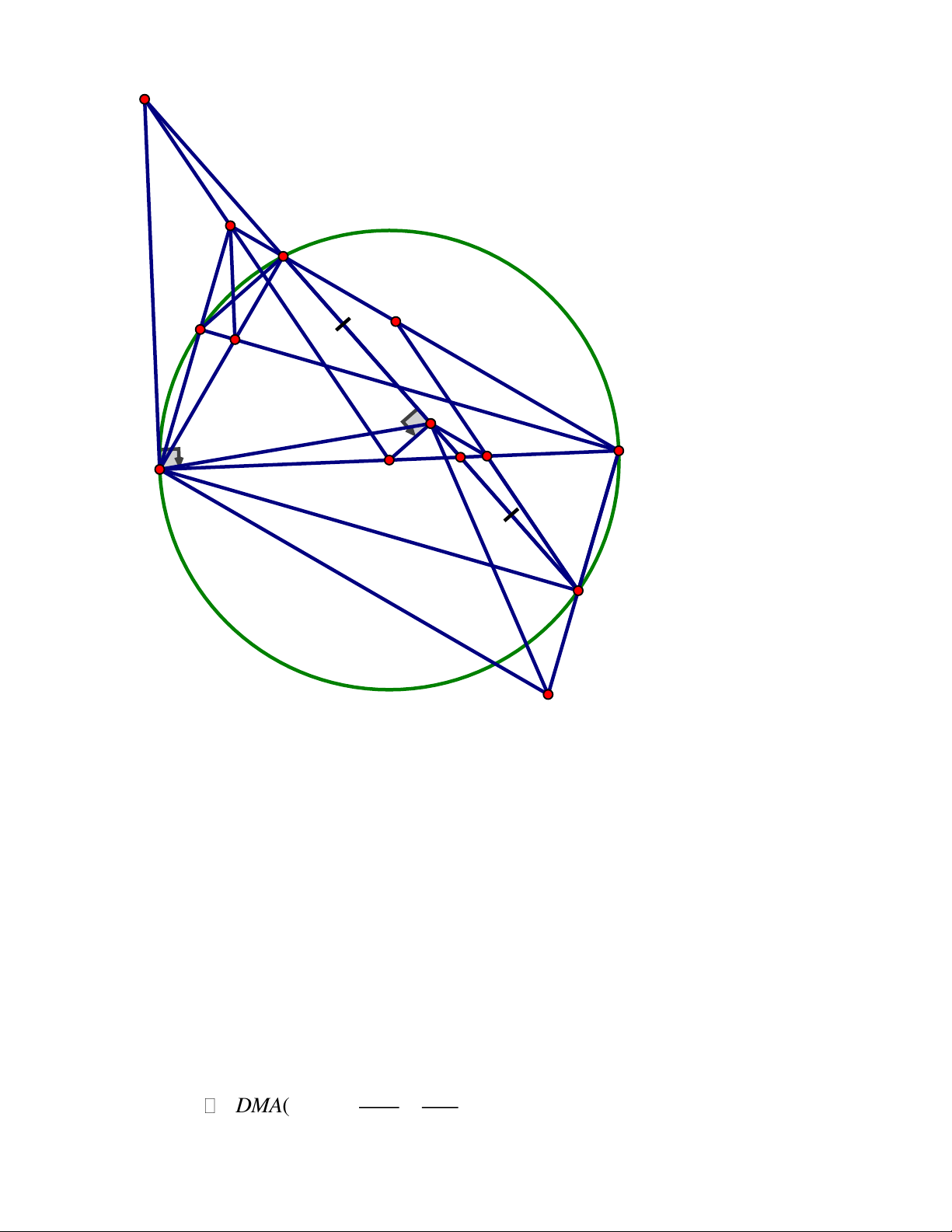
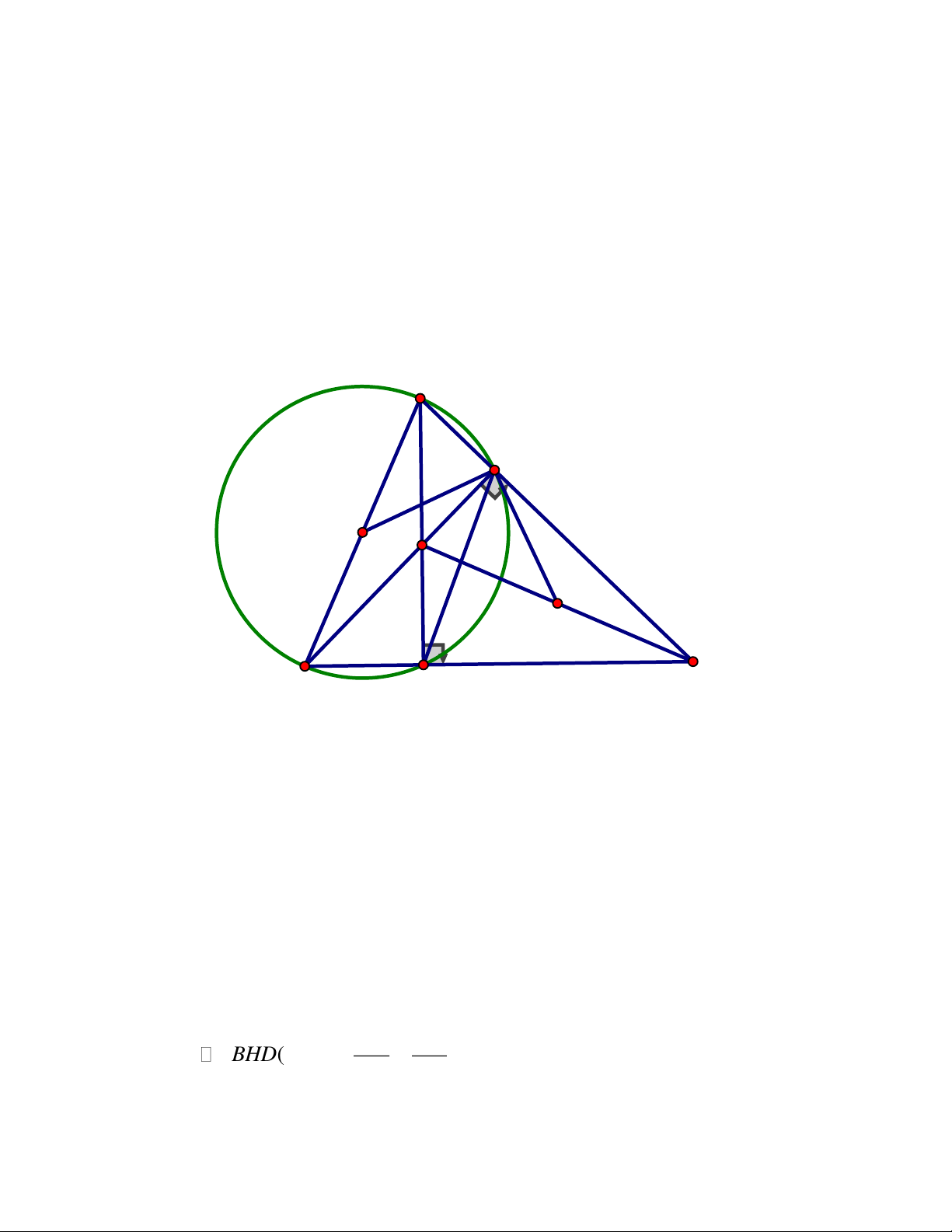
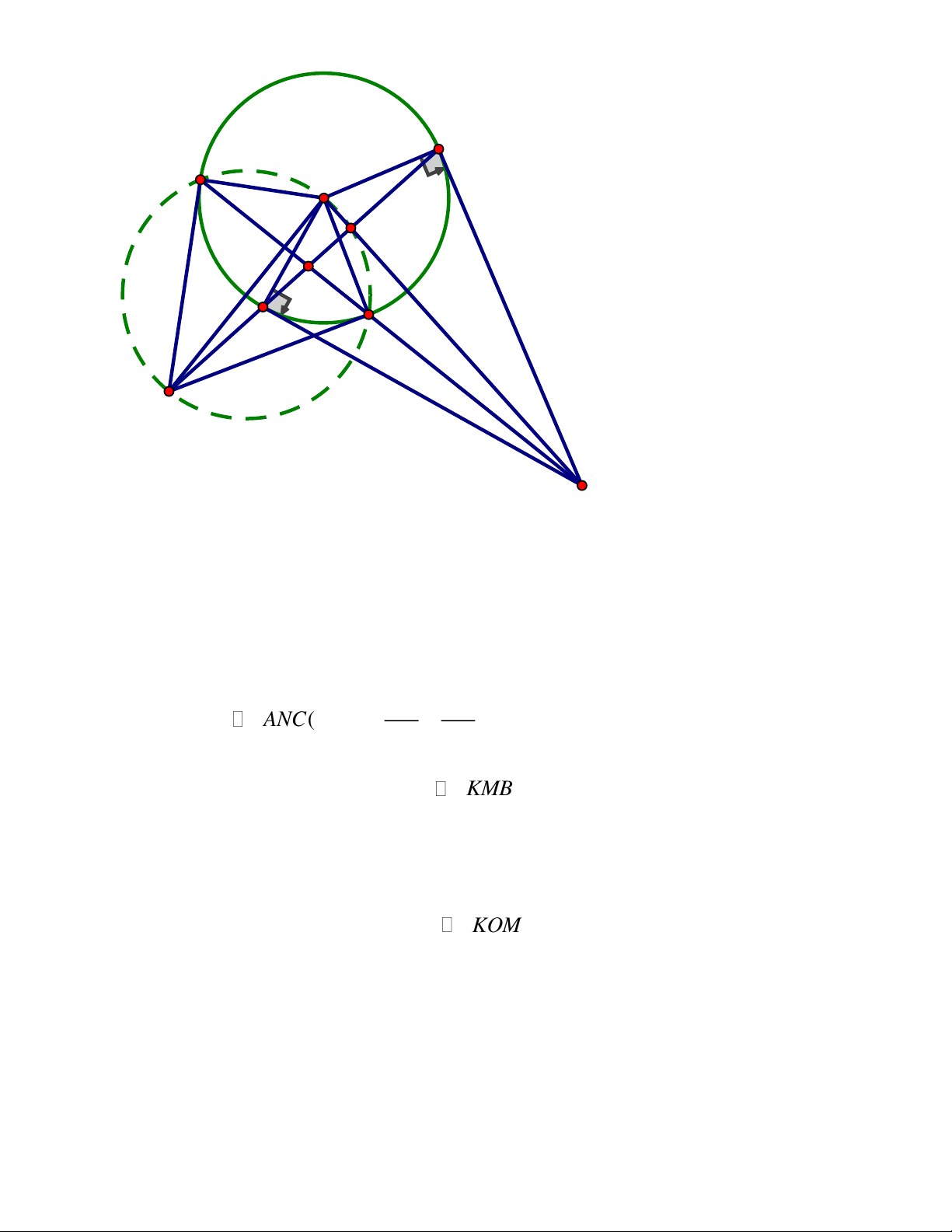
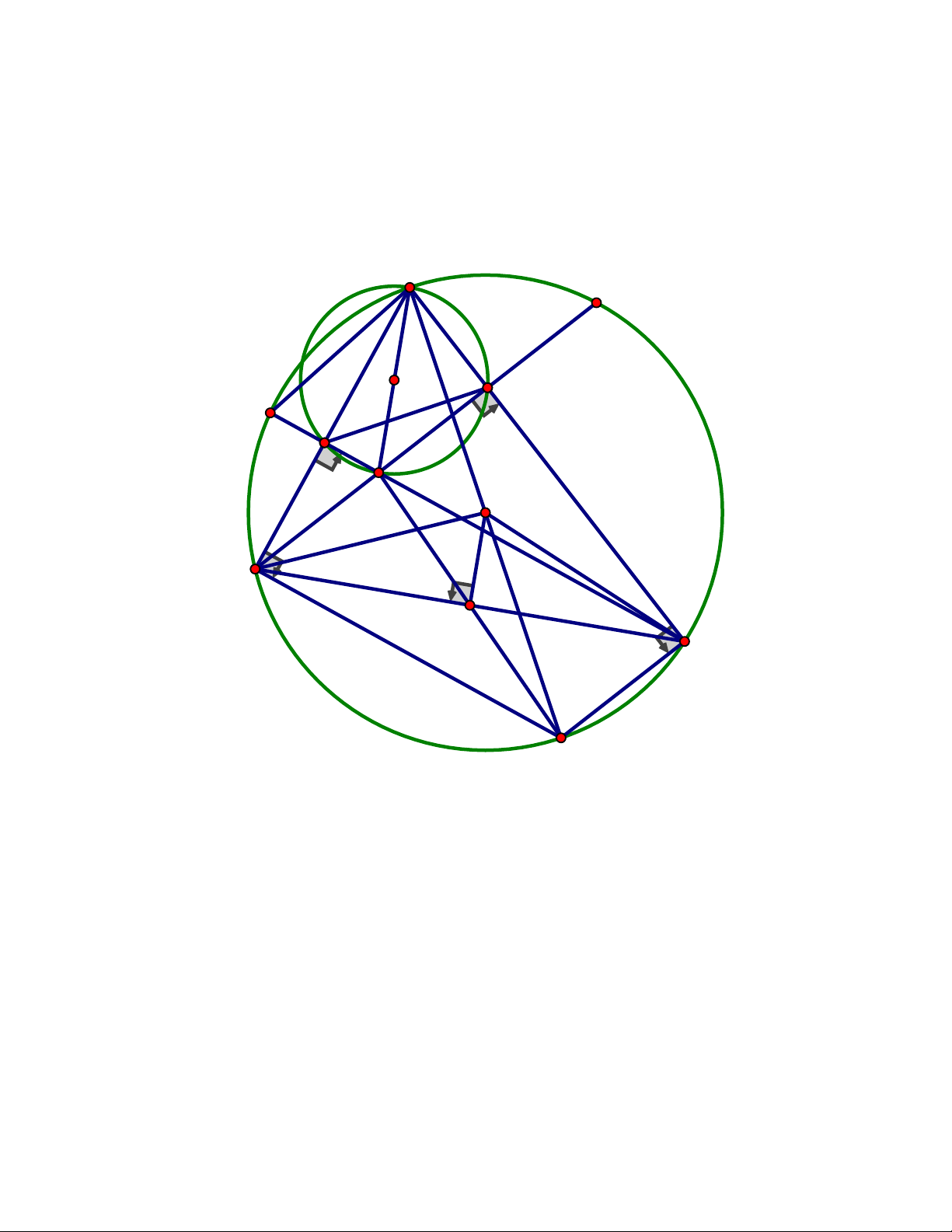
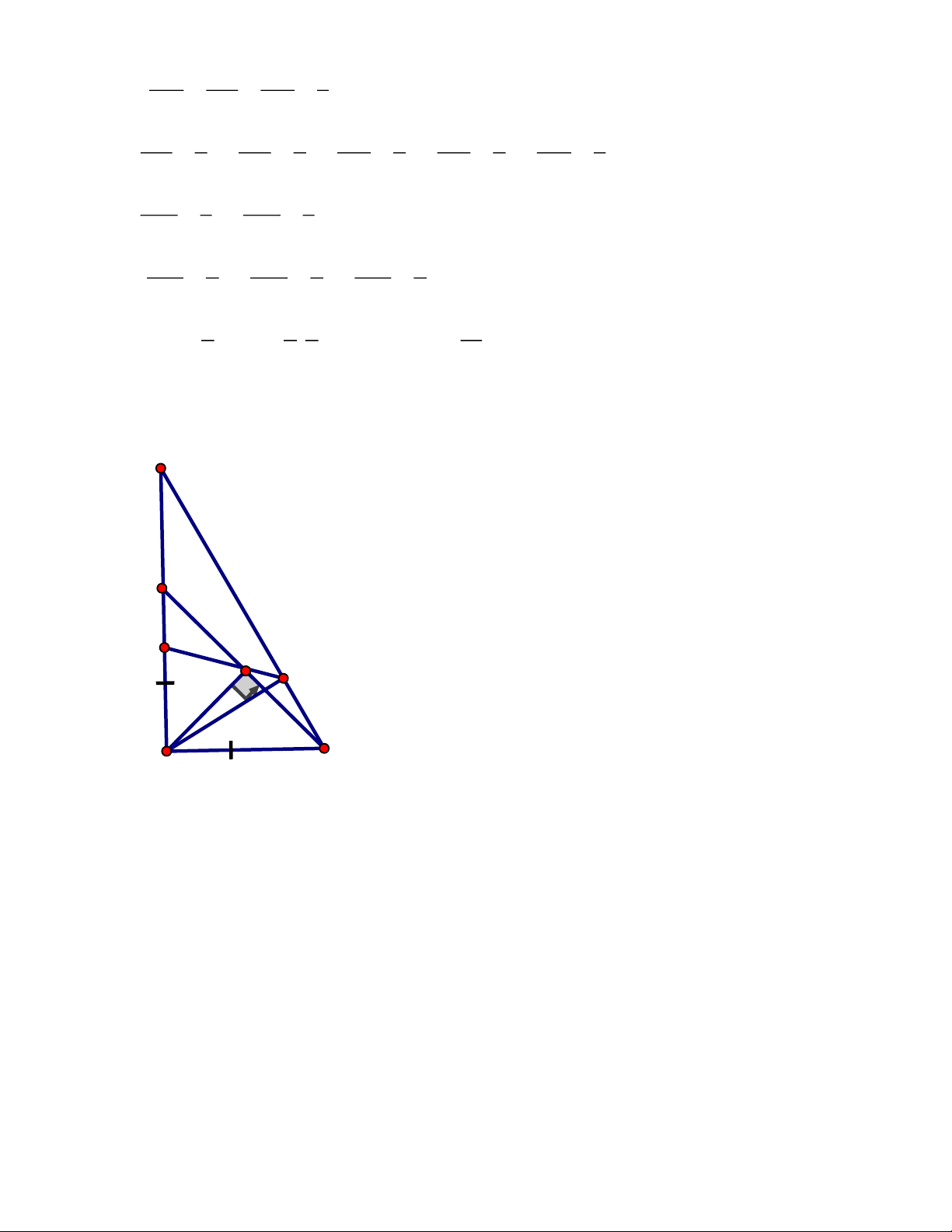
rằng các đường thẳng EQ, FP, AD đồng quy. ĐÁP ÁN Câu III. Trang 6 A P M Q K E F N O C D B
1) Chứng minh rằng AM AN
Ta có: NBA DAB (so le trong do BN / / AD)
DAB DAC(gt) ; DAC ACM (so le trong do CM / / AD)
NBA MCA sd AN sd AM (trong một đường tròn, hai góc nội tiếp bằng nhau
thì chắn hai cung bằng nhau).
Vậy AM AN (trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau)
2) Chứng minh rằng 4 điểm ,
B C, E, F cùng thuộc một đường tròn. 1 Ta có: AEF
sdAN sdCM(góc có đỉnh ở bên trong đường tròn) 2 1 sd AM 1
sdCM sd AC ABC (góc nội tiếp bằng nửa số đo cung bị chắn) 2 2
Vậy tứ giác BCEF là tứ giác nội tiếp (tứ giác có góc ngoài và góc trong tại đỉnh đối diện
bằng nhau) hay B,C, E,F cùng thuộc một đường tròn.
3) Chứng minh các đường thẳng EQ, FP, AD đồng quy
Áp dụng định lý Mê-lê-na-uýt trong tam giác AHN, cát tuyến EKQ , ta có: EN KH QA EN KH . . 1 .
1(do Q là trung điểm của AN(gt)nên QA QN) EH KA QN EH KA Trang 7 EN KA I EH KH
Gọi AD PE K
' .Ta đi chứng minh K ' K
Áp dụng định lý Mê-lê-na-uýt trong tam giác AHM , cát tuyến PKF ta có: FM K ' H PA FM K 'H . . 1 .
1(Do P là trung điểm của AM gt nên FH K ' A PM FH K ' A PA PM ) FM K ' A II FH K ' H EN FM FM FH FM FH HM Ta sẽ chứng minh * EH FH EN EH EN (tính chất dãy tỉ EH HN số bằng nhau) HM DC
Vì BN / / AD / /CM nên áp dụng định lý Ta – let ta có: HN DB DC AC HM AC Lại có :
(định lý đường phân giác), do đó: 1 DB AB HN AB Xét AEF và ABC
có: AEF ABC(cmt), BAC chung AC AF AEF ABC g.g 2 AB AE HM AF Từ (1) và (2) 3 HN AE AF HF
Tiếp tục áp dụng định lý đường phân giác trong tam giác AEF ta có: 4 AE HE HM HF EN FM Từ (3) và (4) ta suy ra
, do đó * được chứng minh, tức là III HN HE EH FH KA K ' A
Từ I , II , III suy ra
, do đó K K ' KH K ' H
Vậy EQ, FP, AD đồng quy tại K KHÁNH HÒA
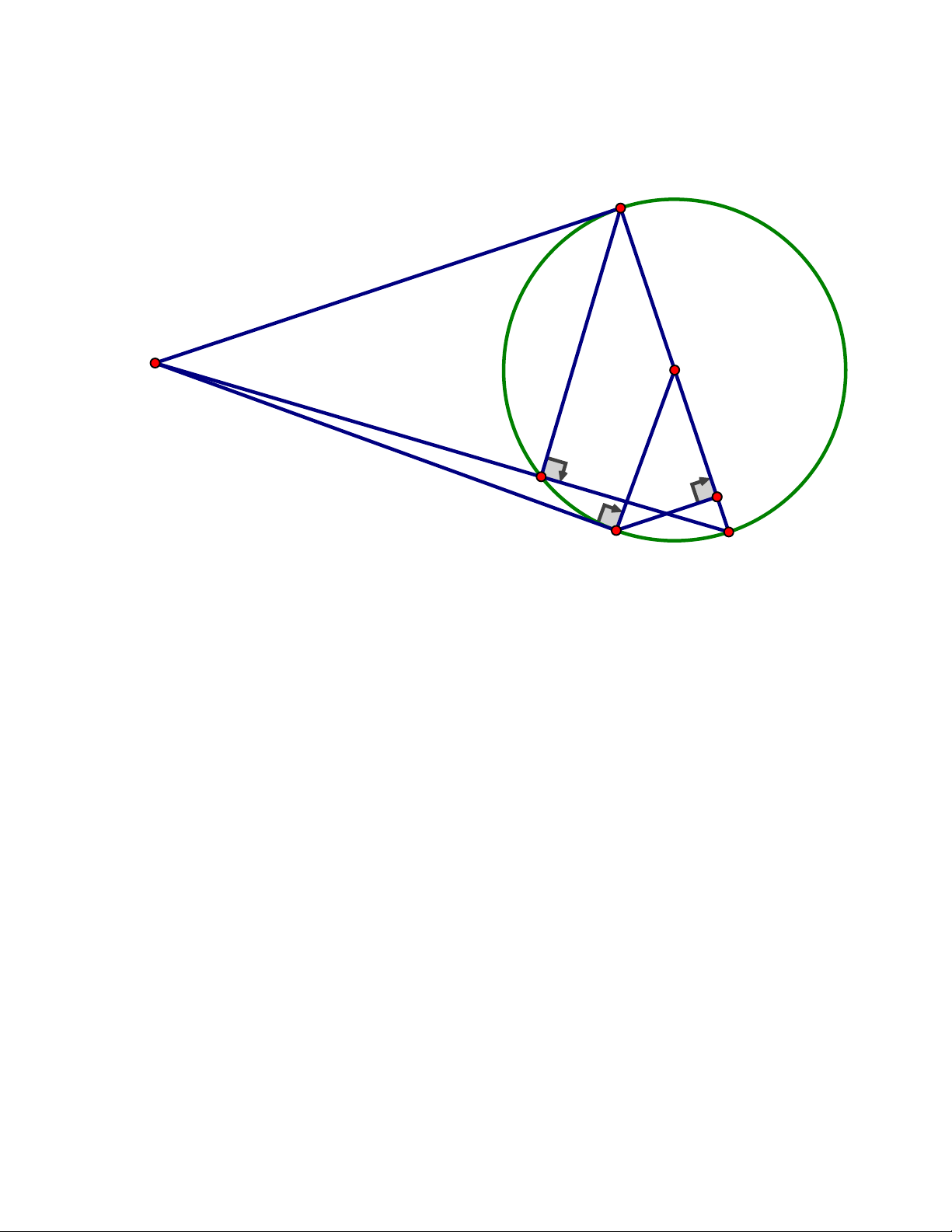
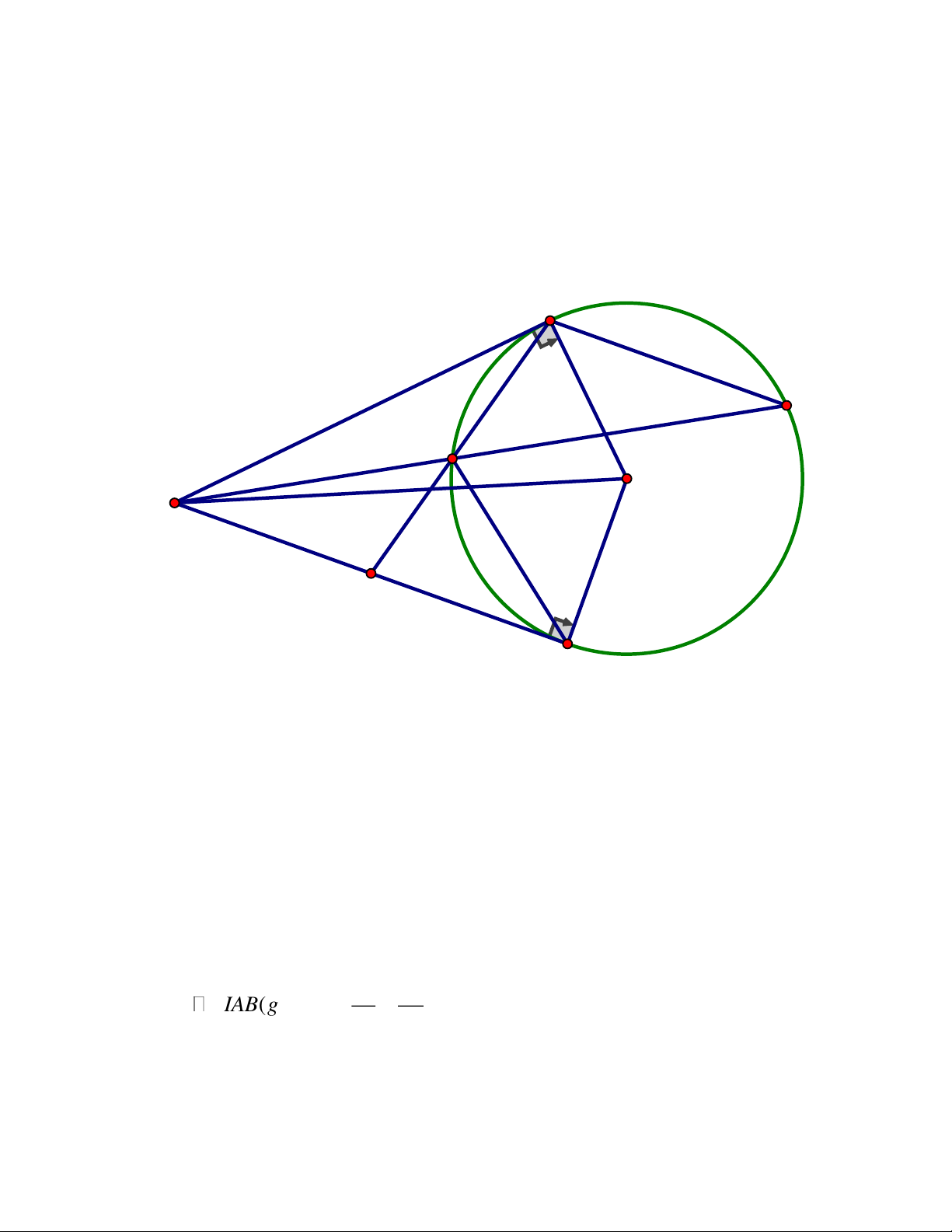
Câu 4. (3,00 điểm) Cho đường tròn O và một điểm I nằm ngoài đường tròn. Qua I kẻ
hai tiếp tuyến IM và IN với đường tròn O. Gọi K là điểm đối xứng với M qua O.
Đường thẳng IK cắt đường tròn O tại H
a) Chứng minh tứ giác IMON nội tiếp đường tròn
b) Chứng minh IM .IN IH.IK
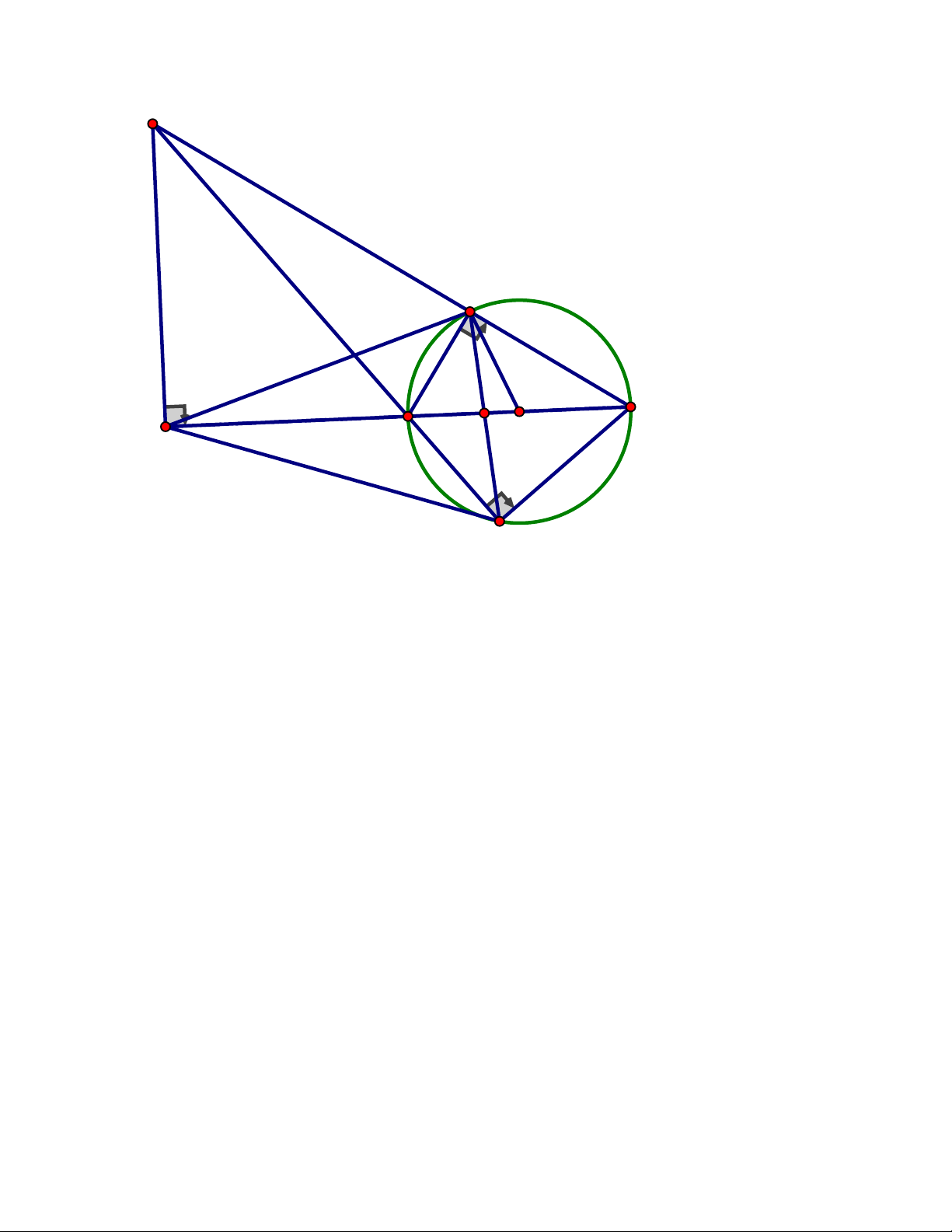
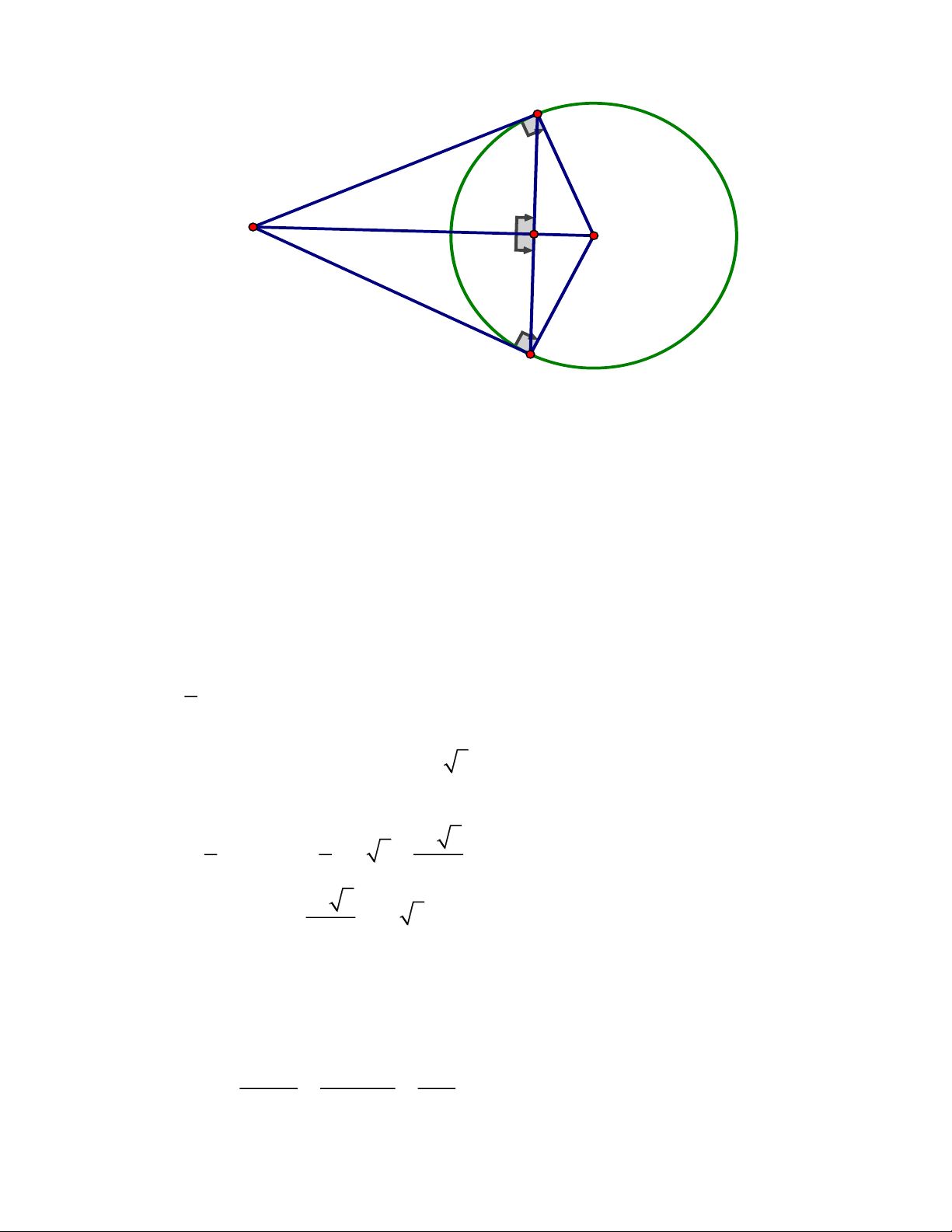
c) Kẻ NP vuông góc với MK. Chứng minh đường thẳng IK đi qua trung điểm của . NP Trang 8 ĐÁP ÁN Câu 4. M O I H P K N
a) Chứng minh IMON là tứ giác nội tiếp
Ta có: IM , IN là các tiếp tuyến của O tại 0
M , N IMO INO 90
Xét tứ giác IMON ta có: 0 0 0
IMO INO 90 90 180
Mà hai góc này là hai góc đối diện nên IMON là tứ giác nội tiếp đường tròn
b) Chứng minh IM .IN IH.IK
Ta có: K là điểm đối xứng của M qua O O là trung điểm của MK và MK là đường kính của (O) Ta có: MHK 0
là góc nội tiếp chắn nửa đường tròn (O) MHK 90 hay MH HK
Áp dụng hệ thức lượng vào I
MK vuông tại M có đường cao MH Ta có: 2
IM IH.IK
Mà IM IN (tính chất hai tiếp tuyến cắt nhau) 2
IM IN.IM IH.IK(dfcm)
c) Chứng minh đường thẳng IK đi qua trung điểm của NP
Gọi IK NP J
IK M E Trang 9
Ta có: IM IN (cmt) nên tam giác IMN cân tại I INM IMN (hai góc đáy tam giác cân)
Lại có: MNP IMN (so le trong do NP / /MI cùng vuông góc với MK )
INM MNP(cùng bằng IMN) NE là phân giác trong INJ
Lại có : MNK là góc nội tiếp chắn nửa đường tròn O nên 0 MNK 90 , do đó
NK NE nên NK là phân giác ngoài của INJ NI EI KI
Áp dụng tính chất đường phân giác ta có: NJ EJ KJ EI MI KI MI
Áp dụng định lý Ta let do NP / /MI ta có: ; EJ NJ KJ JP MI MI Từ đó suy ra
NJ JP J là trung điểm của NP NJ JP
Vậy đường thẳng IK đi qua trung điểm của NP(dfc ) m THÁI NGUYÊN
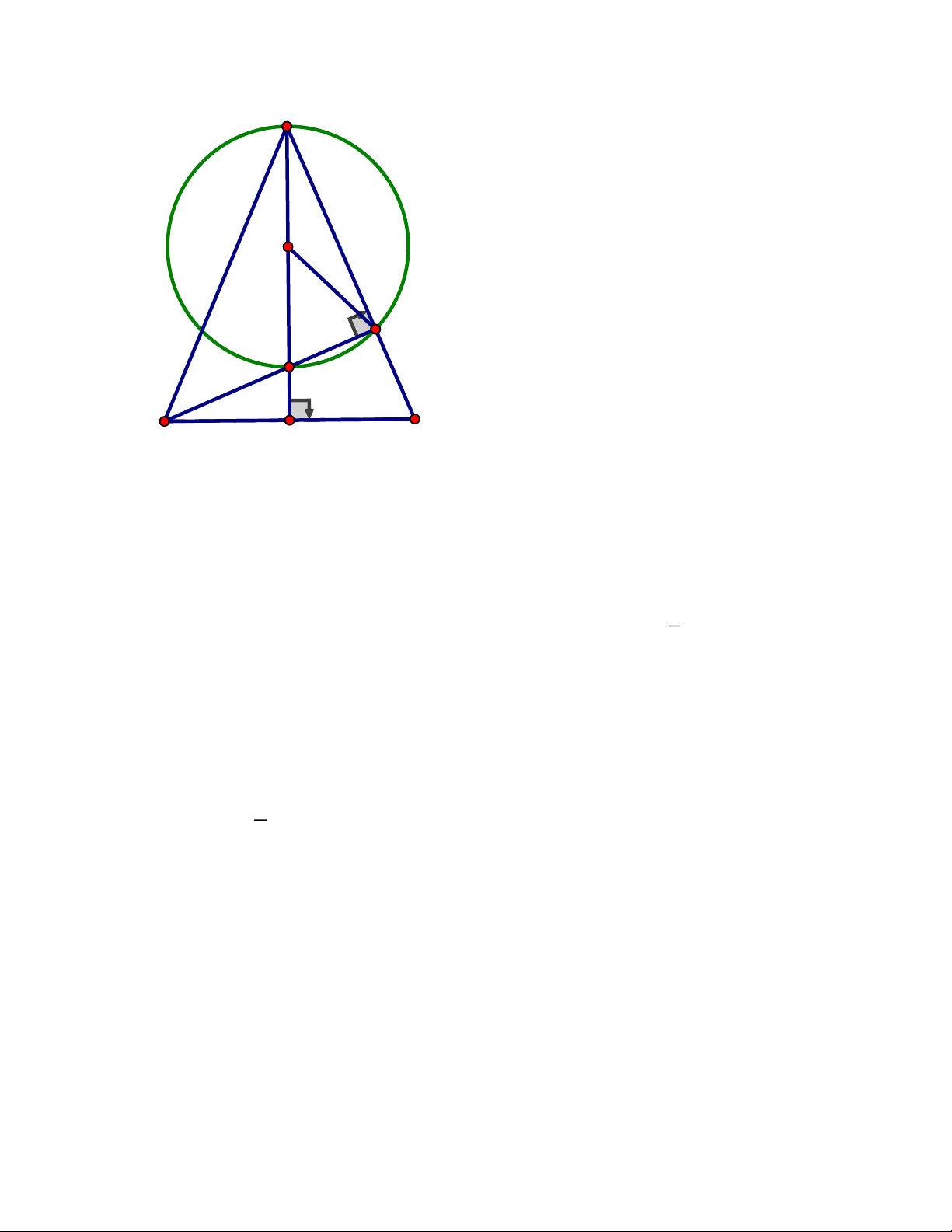
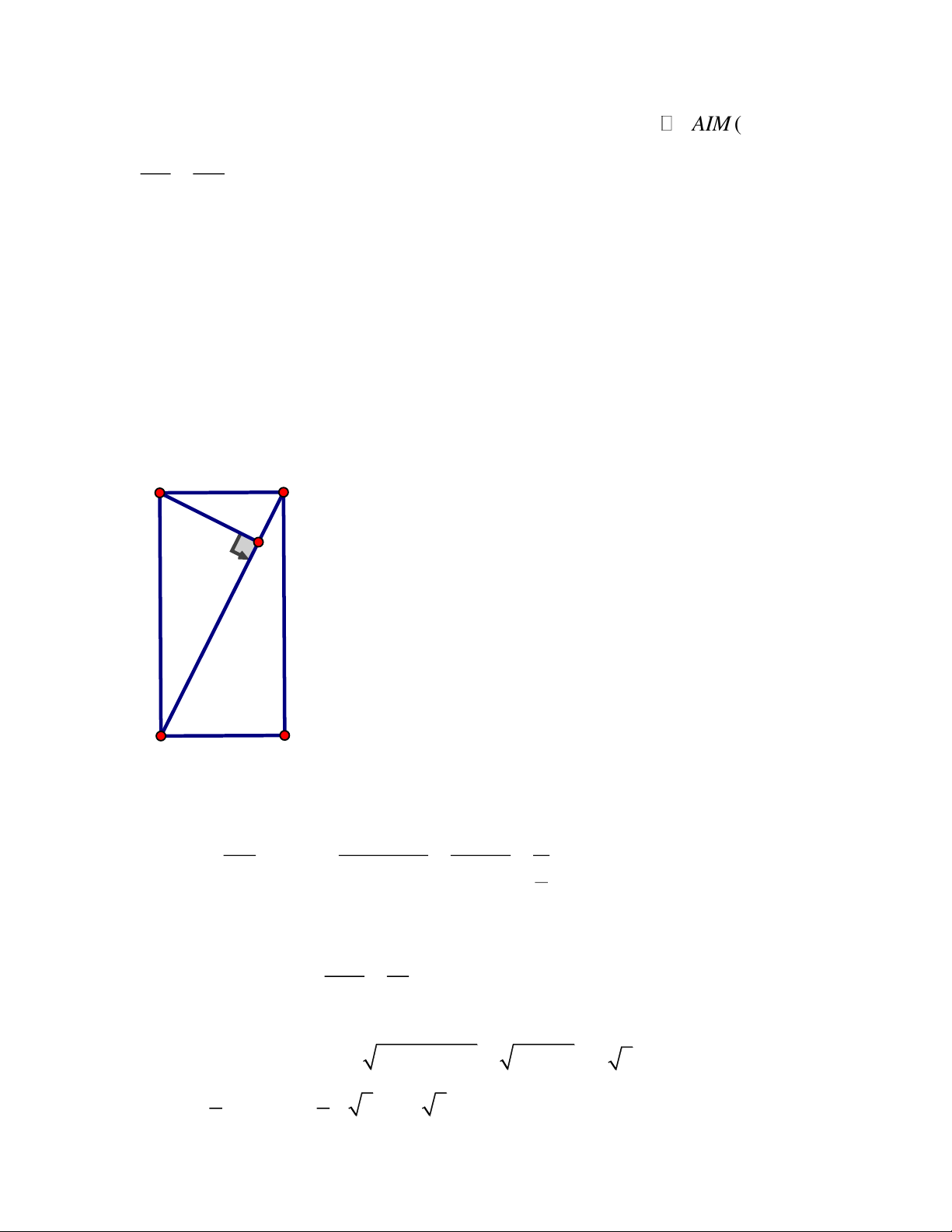
Câu 9. Cho tam giác ABC cân tại ,
A các đường cao AM , BN cắt nhau tại H.Chứng
minh MN là tiếp tuyến của đường tròn đường kính AH
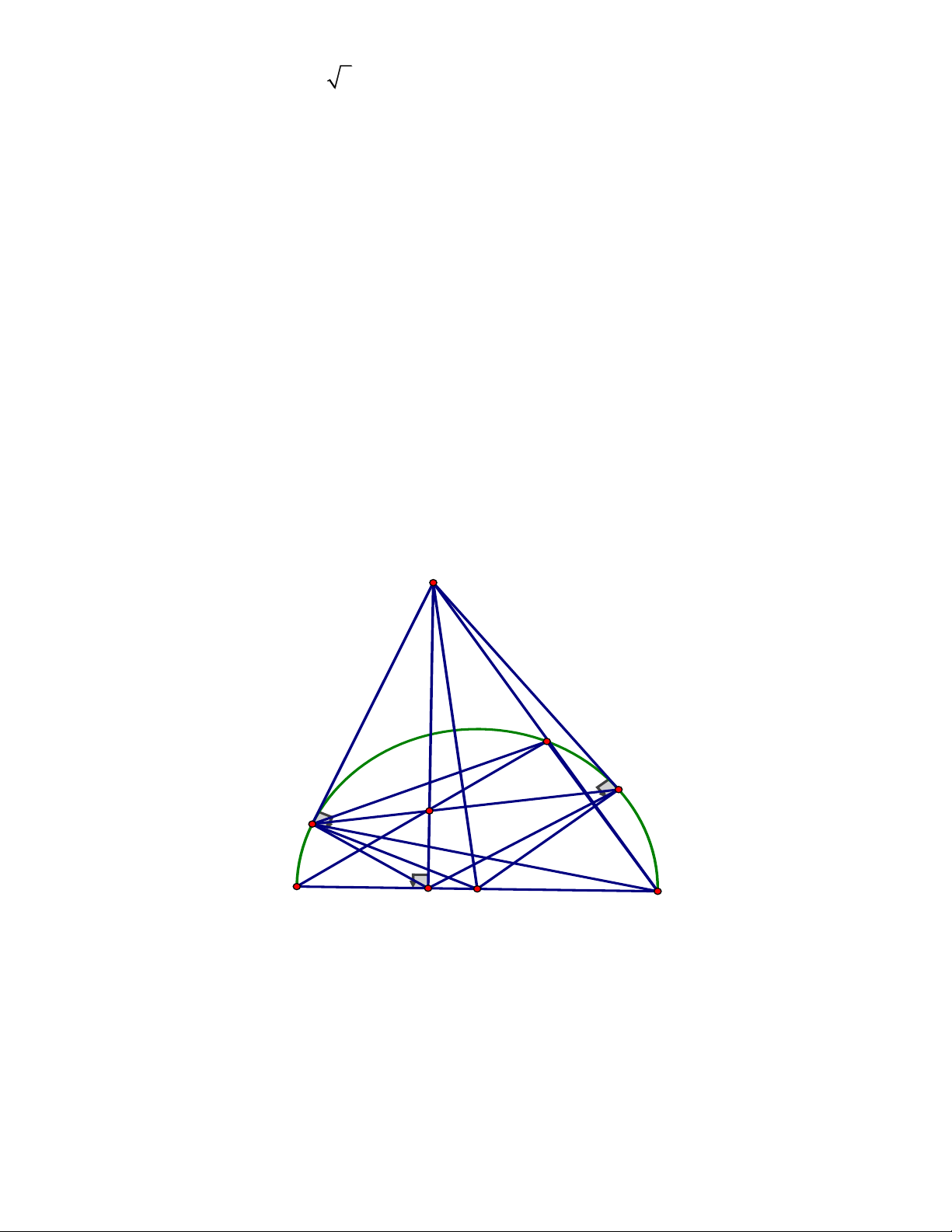
Câu 10. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn O , các đường cao A ,
D BE,CF cắt nhau tại H.Đường thẳng AD cắt đường tròn O tại M khác A
a) Chứng minh tam giác BHM cân
b) Gọi P,Q lần lượt là điểm đối xứng với M qua AB và .
AC Chứng minh ba điểm
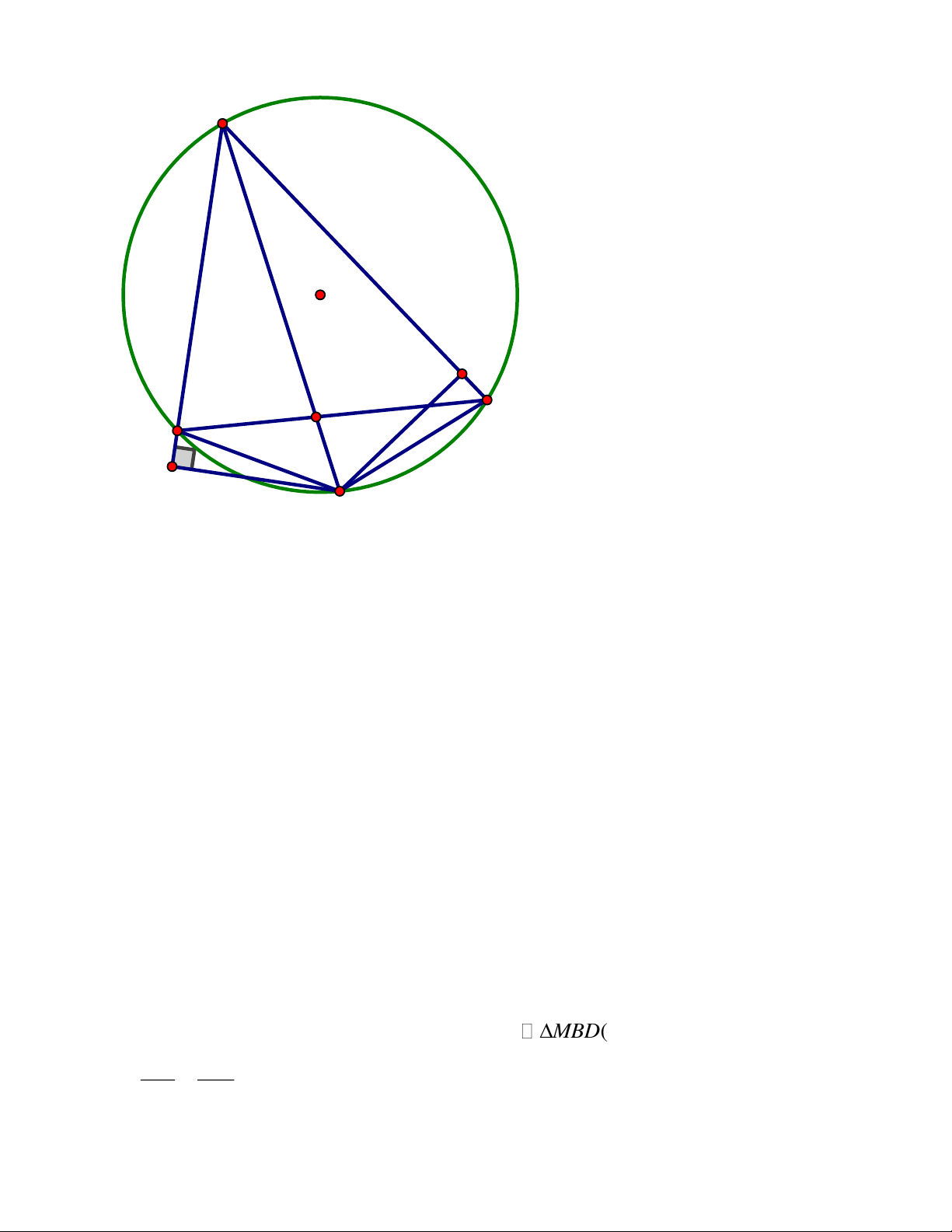
P, H ,Q thẳng hàng. ĐÁP ÁN Câu 9. Trang 10 A O N H B M C
Gọi O là trung điểm của AH O là tâm của đường tròn đường kính AH
Ta có: BN là đường cao của 0 A
BC BN AC HNA 90 A NH vuông tại
N N O* 1 Xét A
NH vuông tại N có đường trung tuyến ON ON OH AH (đường trung 2
tuyến ứng với cạnh huyền trong tam giác vuông). O
NH cân tại O ONH OHN 1 Vì ABC
cân tại A, có đường cao AM M là trung điểm BC Xét B
CN vuông tại N có đường trung tuyến NM 1
MN BM BC (đường trung tuyến ứng với cạnh huyền) 2 MBN MNB 2
Mặt khác BHM OHN (hai góc đối đỉnh) 0
OHN HBM 90 3 Từ (1), (2), (3) suy ra 0
MBN HNO 90 hay MN ON **
Từ *,** MN là tiếp tuyến của đường tròn đường kính AH. Câu 10. Trang 11 A Q E F J H O B D C P I M
a) Chứng minh B HM cân C F AB Ta có: A ,
D CF là hai đường cao của 0 A BC AFC A DC 90 AD BC
Xét tứ giác ACDF có : 0 A FC E
DC 90 , Mà đỉnh F,D là hai đỉnh kề nhau nên
ACDF là tứ giác nội tiếp DAC DFC (cùng chắn DC) hay M AC D FC 1
Xét đường tròn Ota có: MBC MAC 2 (hai góc nội tiếp cùng chắn MC)
Xét tứ giác BFHD có: 0 0 0
BFH BDH 90 90 180 BFHD là tứ giác nội tiếp
HFD HBD (hai góc nội tiếp cùng chắn HD) hay CFD H BD 3 Từ (1), (2), (3) suy ra H BD C BM hay H BD D
BM BD là đường phân giác của B HM Xét H
BM ta có: BD vừa là đường cao, vừa là đường phân giác B
HM cân tại B (dfc ) m
b) Chứng minh P, H ,Q thẳng hàng Trang 12
Gọi I là giao điểm của AB và PM , J là giao điểm của AC và AB PM I MQ AC MQ J
Xét tứ giác IBDM có: 0 0 0
BIM BDM 90 90 180 mà hai góc này là hai góc đối
diện nên IBDM là tứ giác nội tiếp IMB IDB (hai góc nội tiếp cùng chắn IB)
Xét tứ giác MDJC ta có: 0
MDC MJC 90 mà hai góc này kề nhau nên MDJC là tứ
giác nội tiếp JDC JMC (hai góc nội tiếp cùng chắn JC)
Tứ giác ABMC là tứ giác nội tiếp đường tròn O IBM ACM (góc ngoài tại 1
đỉnh bằng góc trong tại đỉnh đối diện) 1 Ta có: B IM vuông tại 0
I IBM IMB 90 2 J MC vuông tại 0
J JMC JCM 90 3 Từ
1 ,2,3 BMI BDI JDC JMC BDI, JDC là hai góc đối đỉnh nên I , , D J thẳng hàng. Ta có: B
HD là tam giác cân tại Bcmt có đường cao BD đồng thời là đường trung
tuyến D là trung điểm của HM . Xét P HM có: ,
D I lần lượt là trung điểm của MH, MP DI là đường trung bình của P HM
DI / /PH PH / /IJ 4 Xét MHQ ta có: ,
D J lần lượt là trung điểm của MH , MQ
DJ là đường trung bình M
HQ DJ / /HQ HQ / /JI 5
Từ (4) và 5 P, H ,Q thẳng hàng.
PHẦN 2: CỰC TRỊ HÌNH HỌC BẮC GIANG
Câu 4. (2,0 điểm) Cho đường tròn tâm O, bán kính R 3c . m Gọi ,
A B là hai điểm phân
biệt cố định trên đường tròn ;
O R ( AB không là đường kính). Trên tia đối của tia BA
lấy một điểm M ( M khác B) . Qua M kẻ hai tiếp tuyến MC, MD với đường tròn đã cho
(C, D là hai tiếp điểm)
a) Chứng minh tứ giác OCMD nội tiếp trong một đường tròn
b) Đoạn thẳng OM cắt đường tròn ; O R tại điểm .
E Chứng minh rằng khi 0
CMD 60 thì E là trọng tâm của tam giác MCD
c) Gọi N là điểm đối xứng của M qua O. Đường thẳng đi qua O vuông góc với
MN cắt các tia MC, MD lần lượt tại các điểm P và Q. Khi M di động trên tia đối của tia ,
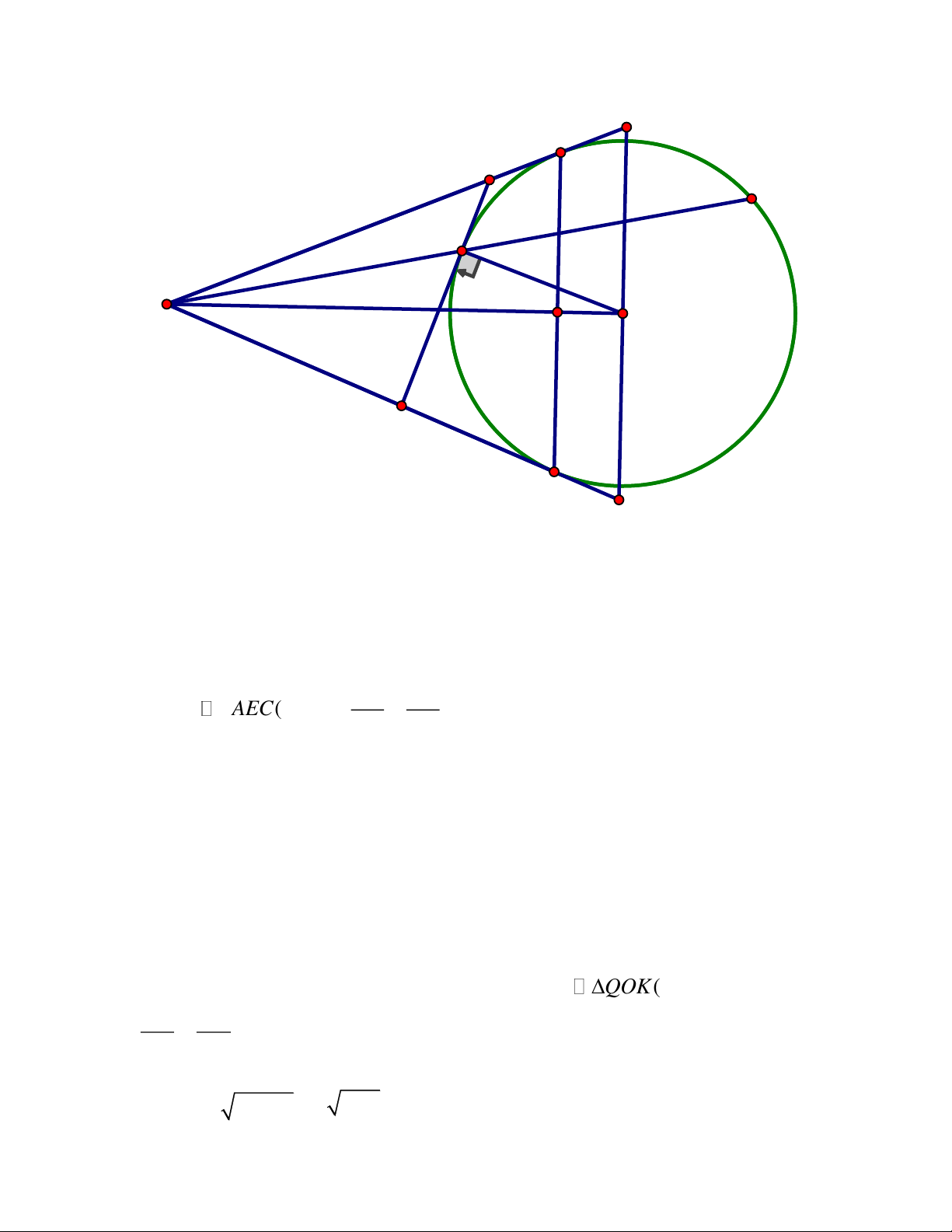
BA tìm vị trí của điểm M để tứ giác MPNQ có diện tích nhỏ nhất ĐÁP ÁN Trang 13 Câu 4. Q D N O E A B M P C
a) Chứng minh tứ giác OCMD nội tiếp
Xét đường tròn tâm O có MC,MD 0
là các tiếp tuyến OCM ODM 90 Tứ giác OCMD có: 0 0 0
OCM ODM 90 90 180 OCMD là tứ giác nội tiếp
b) Chứng minh E là trọng tâm M CD
Xét đường tròn (O) có MC,MD là hai tiếp tuyến cắt nhau tại M nên MC MD và
MO là tia phân giác của CMD 1 1 0 0 0
Mà CMD 60 OMD CMD .60 30 2 2 Xét ODM vuông có 0
OD R 3c , m OMD 30 Ta có: OD OD 3 sin DMO OM
6 cm EM OM OE 6 3 3 cm 0 OM sin 30 1 2 MD MC Lại có:
nên OM là đường trung trực của đoạn DC. Gọi I là giao điểm O
D OC R
của OM và DC OM DC tại I Trang 14
Theo hệ thức lượng trong tam giác ODM vuông ta có: 2 2 OD 3 3 2
OD OI.OM OI 3 9
IM OM OI 6 OM 6 2 2 2 ME 3 2 2 Từ đó ta có:
ME MI MI 9 3 3 2
Xét tam giác MCD có MC MD và 0
CMD 60 nên M
CD là tam giác đều có MI là 2
đường phân giác nên MI cũng là trung tuyến. Lại có ME MI (cmt) nên E là trọng 3
tâm tam giác MCD(dfc ) m
c) Tìm vị trí của M để S min MNPQ
Vì N đối xứng với M qua O nên OM ON
Xét hai tam giác vuông O QM , O
PM có cạnh OM chung, OMQ OMP Suy ra O QM O PM (g. .
c g) OP OQ
Diện tích tứ giác MPNQ là : 1 1 1 S
MN.PQ .2OM.2OQ 4. OM.OQ 4S 4.O . D MQ 4 . R MQ MPNQ 2 2 2 OQM Xét OQM
vuông tại O có OD là đường cao, theo hệ thức lượng trong tam giác vuông ta có: 2 2 OD D .
Q DM R D . Q DM
Áp dụng bất đằng thức Cô si ta có: 2
QM DQ DM 2 D .
Q DM 2 R 2R Hay QM
2R QD DM R min Từ đó S nhỏ nhất là 2
8R MQ 2R MPNQ Khi đó: Xét M DB & M
AD có: DMB chung; MDB MAD (cùng chắn BD) MD MB 2 2 M DB M
AD(g g) MD M . A MB M . A MB R MA MD Đặt AB ,
a MB x ( a không đổi, a, x 0) Ta có:
a a R M .
A MB R x x a 2 2 4 2 2 2 2
R x ax R 0 x do x 0 2
Vậy điểm M thuộc tia đối của tia AB và cách B một khoảng bằng 2 2
a a 4R MB
không đổi thì tứ giác MPNQ có diện tích nhỏ nhất là 2 8R 2 BẠC LIÊU Câu 4. (6,0 điểm) Trang 15
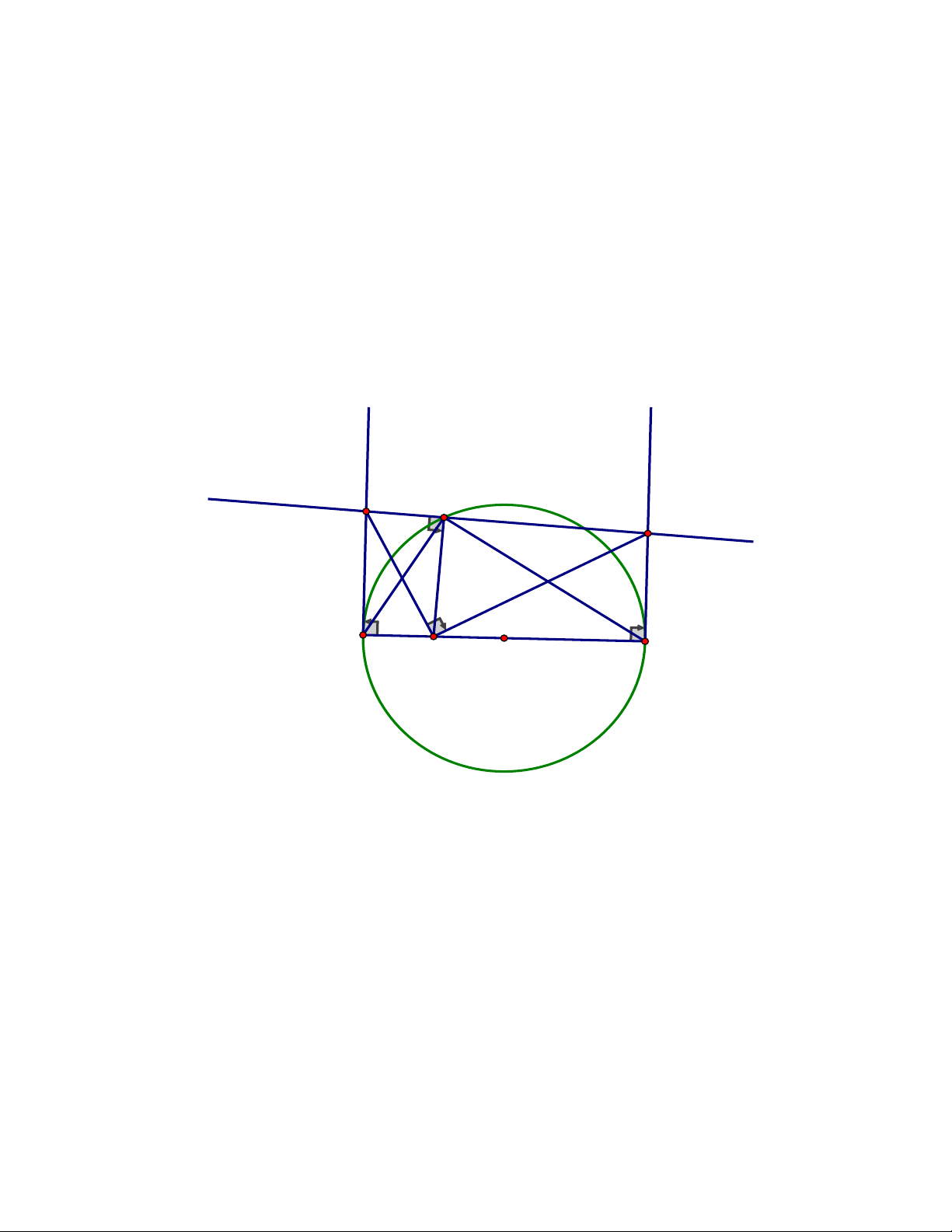
Cho đường tròn tâm O đường kính AB 2 .
R Gọi I là trung điểm của đoạn thẳng O ,
A E là điểm thay đổi trên đường tròn O sao cho E không trùng với Avà . B Dựng
đường thẳng d và d lần lượt là các tiếp tuyến của đường tròn Otại Avà B. Gọi d 1 2
đường thẳng qua E và vuông góc với EI.Đường thẳng d cắt d ,d lần lượt tại M , N 1 2
a) Chứng minh tứ giác AMEI nội tiếp b) Chứng minh I
AE đồng dạng với N B .
E Từ đó chứng minh I . B NE 3I . E NB
c) Khi điểm E thay đổi, chứng minh tam giác MNI vuông tại I và tìm giá trị nhỏ
nhất của diện tích tam giác MNI theo R ĐÁP ÁN Câu 4. d1 d2 d M E N A I O B
a) Chứng minh tứ giác AMEI nội tiếp
Vì d là tiếp tuyến của O tại Anên 0 IAM 90 1
Vì d EI tại E nên 0 IEM 90
Xét tứ giác AMEI có 0 0 0
IAM IEM 90 90 180
Vậy tứ giác AMEI là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 0 180 )
b) Chứng minh I
AE đồng dạng với N B .
E Từ đó chứng minh I . B NE 3I . E NB
Vì AEB là góc nội tiếp chắn nửa đường tròn nên 0 AEB 90 Ta có: 0 0
AEI IEB AEB 90 ; BEN IEB IEN 90 do d IE
AEI BEN (cùng phụ với IEB) Trang 16 Xét I AE và N
BEcó: AEI BEN cmt;IAE NBE (góc nội tiếp và góc tạo bởi
tiếp tuyến và dây cung cùng chắn BE) IE IA I AE N
BE(g.g)
(hai cạnh tương ứng) I .
A NE IE.NB (1) NE NB
Mà I là trung điểm của O (
A gt) OA 2IA
Lại có O là trung điểm của AB AB 2OA 4IA
IB AB IA 4IA IA 3IA. Khi đó ta có: 1 3I .
A NE 3IE.NB (nhân cẩ 2 vế với 3) I .
B NE 3IE.NB(dfcm)
c) Chứng minh M
NI vuông tại I và tìm GTNN của S theo R MNI
Xét tứ giác BNEI có: 0
IEN 90 (do d IE tại E) 0
IBN 90 (do d là tiếp tuyến của đường tròn (O) tại B) 2 0 0 0
IEN IBN 90 90 180
Tứ giác BNEI là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 0 180 )
INE IEB ABE (hai góc nội tiếp cùng chắn cung IE)
Lại có : Tứ giác AMEI là tứ giác nội tiếp (ý a)
IME IAE BAE (hai góc nội tiếp cùng chắn cung IE)
Xét tam giác MNI có: 0
INE IME ABE BAE 90 (do 0
AEB 90 (cmt) nên AEB vuông tại E) M
NI vuông tại I (tam giác có tổng hai góc nhọn bằng 0 90 ) 1 Ta có: S IM.IN M NI 2 Đặt AIM 0 0 0 90 BIN 90 AI AI Xét A
IM vuông ta có: cos IM IM cos BI BI BI Xét B
IN vuông ta có: cos 0 90 IN IN cos 0 90 sin 1 1 AI BI AI.BI S IM.IN . . M NI 2 2 cos sin sin.cos 1 R 3 3R
Ta có: AB 4AI (cmt) AI AB , BI AB 4 2 4 2 2 3R 4 S M NI sin.cos Trang 17 2 3R Do
không đổi nên diện tích tam giác MNI đạt giá trị nhỏ nhất sin.cos đạt 4 giá trị lớn nhất. Vì 0 0
0 90 nên sin ,cos 0. Áp dụng BĐT Cô – si ta có: 2 2 sin cos 1 sin.cos 2 2 2 2 3R 1 3R S : .Dấu " " xảy ra A MI 4 2 2 sin cos 1 0 sin cos 45 2 2 sin cos 2 2 3R
Vậy giá trị nhỏ nhất của diện tích tam giác MNI là , đạt được khi 0 AIM 45 . 2 HÀ NAM
Câu 4. (4,0 điểm) Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn ; O R . Hai
đường cao BE,CF của tam giác ABC cắt nhau tại H. Đường thẳng AH cắt BC tại D và cắt đường tròn ;
O R tại điêm thứ hai là M
1) Chứng minh tứ giác AEHF nội tiếp
2) Chứng minh BC là tia phân giác của EBM
3) Gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF . Chứng minh IE là tiếp tuyến
của đường tròn ngoại tiếp B CE 4) Khi hai điểm ,
B C cố định và điểm Adi động trên đường tròn ; O R nhưng vẫn
thỏa mãn điều kiện tam giác ABC có ba góc nhọn. Chứng minh OA EF. Xác
định vị trí của điểm A để tổng DE EF FDđạt giá trị lớn nhất. ĐÁP ÁN Câu 4. A' A E I K F O H C D N B P M Trang 18
1) Chứng minh AEHF là tứ giác nội tiếp
Ta có: BE,CF là các đường cao của ABC BE AC E 0 C F AB F AFC AEB 90
Xét tứ giác AEHF ta có : 0 0 0
AEH AFH 90 90 180 AEHF là tứ giác nội tiếp
2) Chứng minh BC là tia phân giác của BEM 0 D AC A CD 90 Ta có:
DAC EBC (cùng phụ góc DAC) 0 E BC E CB 90 Hay M AC E BC Lại có: M AC M
BC (cùng chắn cung MC)
MBC EBC MAC BC là phân giác của E BM (dfcm)
3) Chứng minh IE là tiếp tuyến của đường tròn ngoại tiếp B CE Ta có : 0 AEH
90 là góc nội tiếp chắn cung AH
AH là đường kính của đường tròn ngoại tiếp tứ giác AEHF
I là trung điểm của AH Ta có: BEC là tam giác vuông tại E
Đường tròn ngoại tiếp BEC
có tâm là trung điểm của BC
Gọi N là trung điểm của BC N là tâm đường tròn ngoại tiếp BEC 1
NB NE BC (tính chất tiếp tuyến của tam giác vuông) 2 B
NE cân tại N N BE N EB hay D BE N EB 1
Ta có IE là đường trung tuyến của AEH
vuông tại E EI IH AH I EH 2
cân tại I IEH IHE mà IHE BHD (hai góc đối đỉnh) IEH BHD Lại có : 0 0 H BD B
HD 90 I EH B EN 90
Hay IE EN IE là tiếp tuyến của đường tròn ngoại tiếp B EC(dfcm)
4) Xác định vị trí điểm A………
Gọi EF OA K
Kẻ đường kính AP Khi đó ta có A
CP là góc nội tiếp chắn nửa đường tròn 0 A CP 90 0 0 A PC P
AC 90 hay O AC A PC 90
Xét tứ giác BCEF có: 0
BFC BEC 90 , mà hai đỉnh E, F kề nhau BCEF là tứ giác
nội tiếp FBC AEF (góc ngoài bằng góc trong tại đỉnh đối diện) Hay A BC A EB mà A PC A
BC (cùng chắn ccung AC) Trang 19 0 A EF A PC A PC O AE A EF E AO 90
Hay AO EF K(dfcm)
Chứng minh tương tự ta có: OB F , D OC ED 1 Ta có: S O .
A EF (tứ giác có hai đường chéo vuông góc) OEAF 2 1 1 Tương tự: S O . B FD ; S OC.DE OFBD 2 ODCE 2 1 1 1 S S S O . A EF O . B FD OC.DE OEAF OFBD ODCE 2 2 2 1 S
REF FE DE 2SABC
EF FE DE ABC 2 R
Kéo dài ON cắt (O) tại A' A' N BC do ON BC 1 1 Khi đó ta có: S A . D BC A' N.BC ABC 2 2
Đặt BC a
Áp dụng định lý Pytago trong tam giác vuông ONC ta có: 2 a 2 2 2
ON OC CN R 4 2 2 a a a 2 2
A'N OA' ON R R S
R R 4 ABC 2 4 2 a 2
a R R 4
EF FD DE R
Dấu " " xảy ra A A', khi đó điểm Alà điểm chính giữa của cung lớn BC HÀ NAM (CHUYÊN) Câu 4. (3,5 điểm)
Cho đường tròn O, đường kính ABcố định. Điểm H cố định nằm giữa hai điểm
Avà O sao cho AH OH. Kẻ dây cung MN vuông góc với AB tại H. Gọi C là điểm
tùy ý thuộc cung lớn MN sao cho C không trùng với M , N và .
B Gọi K là giao điểm của AC và MN.
1) Chứng minh tứ giác BCKH nội tiếp
2) Chứng minh tam giác AMK đồng dạng với tam giác ACM
3) Cho độ dài đoạn thẳng AH .
a Tính AK.AC H . A HB theo a
4) Gọi I là tâm đường tròn ngoại tiếp tam giác MKC.Xác định vị trí của điểm C để
độ dài đoạn thẳng IN nhỏ nhất ĐÁP ÁN Trang 20 Câu 4. C M I K B A H O N a) Có 0
AH MN KHB 90 mà 0 KCB 90
Tứ giác BCKH có 0 0 0
KHB KCB 90 90 180 BCKH là tứ giác nội tiếp b) Xét A MK và A CM có:
A chung; AMK ACM (cùng chắn AM ) A MK A
CM (g.g) AK AM c) 2 AM K ACM
AK.AC AM 1 AM AC Xét A MH và M
BH có: H H 0
90 ;MAH H
MB (cùng phụ HM ) A 1 2 HA HM 2 A MH M
BH (g.g) H .
A HB HM 2 HM BH Từ (1) và (2) ta có: 2 2 2 2
AK.AC H .
A HB AM HM AH a
d) Vì AM là tiếp tuyến của I (do AMK MC (
A cmt) mà 1 góc là góc nội tiếp , 1
góc là góc tạo bởi tiếp tuyến dây cung) I MB Ta có: NI
khoảng cách từ N xuống BM nhỏ nhất. min
NI BM, do đó khoảng cách từ N đến tâm I nhỏ nhất thì C là giao điểm của
I;IM và (O)
Vậy C là hình chiếu của N trên BM HẢI DƯƠNG Câu 4. (3,0 điểm) Trang 21 Cho ABC
có ba góc nhọn nội tiếp đường tròn ; O R . Gọi ,
D E, F là chân các đường
cao lần lượt thuộc các cạnh BC,C ,
A AB và H là trực tâm của ABC .Vẽ đường kính AK
a) Chứng minh tứ giác BHCK là hình bình hành
b) Trong trường hợp ABC
không cân, gọi M là trung điểm của BC.Hãy chứng
minh FC là phân giác của DFE và 4 điểm M , ,
D F, E cùng nằm trên một đường tròn.
c) Khi BC và đường tròn ;
O R cố định, điểm Athay đổi trên đường tròn sao cho ABC
luôn nhọn, đặt BC .
a Tìm vị trí của điểm Ađể tổng
P DE EF DF lớn nhất và tìm giá trị lớn nhất đó theo a và R ĐÁP ÁN Câu 4. A' A I E F H O C B D M K
a) Chứng minh tứ giác BHCK là hình bình hành
Ta có: ABK là góc nội tiếp chắn nửa đường tròn (O) 0
ABK 90 hay AB BK
Mà CF AB(gt) CF / / BK hay CH / / BK 1
Ta có: ACK là góc nội tiếp chắn nửa đường tròn (O) 0
ACK 90 hay AC CK
Mà BE AC(gt) BE / /CK hay BH / /CK 2
Từ (1) và (2) suy ra tứ giác BHCK là hình bình hành
b) Chứng minh FC là phân giác DFE
Xét tứ giác BFHD ta có: 0 0 0
BFD BHD 90 90 180 , mà hai góc này ở vị trí đối
diện nên BFHD là tứ giác nội tiếp HFD HBD (hai góc nội tiếp cùng chắn HD)3 Trang 22
Xét tứ giác AEHF có 0 0 0
AEH AFH 90 90 180 , mà hai góc này ở vị trí đối diện
nên AEHF là tứ giác nội tiếp HFE HAE (hai góc nội tiếp cùng chắn HE) (4)
Xét tứ giác AEDB ta có: 0
AEB ADB 90 AEDB là tứ giác nội tiếp (dhnb) DAE DBE 5
Từ 3,4,5 EAD EFH HFD HBD
Hay EFC CFD FC là phân giác của DFE (dfc ) m Xét EBC 1
vuông tại E có đường trung tuyến EM EM BM BC 2 EBM
cân tại M MEB EBM EMC MEB EBM 2EBM (góc ngoài
của tam giác). Lại có EFD 2HFD 2HBD 2EBM cmt
EMC EFD 2EBM EFDM là tứ giác nội tiếp E,F, , D M cùng thuộc một đường tròn.
c) Tìm vị trí điểm A…….
Gọi EF OA I
Ta có: FAI BCK (hai góc nội tiếp cùng chắn cung BK ) Xét tứ giác BFEC 0
có BEC BFC 90 (gt), do đó tứ giác BFEC là tứ giác nội tiếp (tứ
giác có 2 đỉnh kề cùng nhìn 1 cạnh dưới các góc bằng nhau)
AFI ACB (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp ) 0
FAI AFI BCK ACB ACK 90 (góc nội tiếp chắn nửa đường tròn) OA EF
Chứng minh tương tự ta có : OB F , D OC ED 1 Ta có: S O .
A EF (tứ giác có hai đường chéo vuông góc) OEAF 2 1 1 S O . B FD ; S OC.DE OFBD 2 ODCE 2 1 1 1 S S S O . A EF O . B FD OC.DE OEAF OFBD ODCE 2 2 2 1 1 1 S . . R EF . . R FD . . R DE ABC 2 2 2 2SABC
EF FD DE R
Kéo dài OM cắt O tại A' A'M BC (do OM BC) Trang 23 1 1 Khi đó ta có: S A . D BC A'M .BC ABC 2 2
Áp dụng định lý Pytago trong tam giác vuông OMC ta có: 2 a 2 2 2
OM OC CM R 4 2 2 a a a 2 2
A'M OA' OM R R S
R R 4 ABC 2 4 2 a 2
a R R 4
EF FD DE R
Dấu " " xảy ra A A', khi đó điểm Alà điểm chính giữa của cung lớn BC
Vậy P DE EF DF đạt giá trị lớn nhất khi điểm Alà điểm chính giữa của cung lớn BC LAI CHÂU Câu 5. (3,0 điểm)
Cho điểm A nằm ngoài đường tròn O.Từ Akẻ hai tiếp tuyến A , B AC và cát
tuyến ADE không đi qua tâm tới đường tròn đó ( ,
B C là hai tiếp điểm, D nằm giữa A và
E). Gọi H là giao điểm của AO và BC
a) Chứng minh tứ giác ABOC là tứ giác nội tiếp
b) Chứng minh AH.AO A . D AE
c) Tiếp tuyến tại D của đường tròn O cắt A ,
B AC theo thứ tự tại I , K.Qua điểm
O kẻ đường thẳng vuông góc với OA cắt AB tại P và cắt AC tại Q. Chứng minh
rằng : IP KQ PQ ĐÁP ÁN Câu 5. Trang 24 P B I E D A H O K C Q
a) Chứng minh ABOC là tứ giác nội tiếp Ta có: 0 0 0
B C 90 90 180 ABOC là tứ giác nội tiếp
b) Chứng minh AH.AO A . D AE Xét A CD và AEC
có: A chung; ACD AEC (cùng chắn CD) AC AD 2 A CD A
EC(g.g)
AE.AD AC (1) AE AC
Áp dụng hệ thức lượng ta có: 2
AH.AO AC 2
Từ (1) và (2) AH.AO A . D AE
c) Chứng minh rằng : IP KQ PQ 0 0
PIK IKQ P Q 360 2PIQ 2OKQ 2P 360 0
PIQ OKQ P 180 0
Lại có: PIO IOP P 180 OKQ IOP Xét P IO và QOK có:
IPO OKQ ( PAQ
cân); IOP OKQ(cmt) P IO Q
OK(g.g) PI PO 2
PI.QK P . O QO OP QO QK
Áp dụng bất đẳng thức Cô – si ta có: 2
IP QK 2 I .
P QK 2 OP PQ
Vậy IP KQ PQ Trang 25 THÁI BÌNH
Câu 4. (3,5 điểm) Qua điểm M nằm bên ngoài đường tròn ;
O R , kẻ hai tiếp tuyến M , A MB ( ,
A B là hai tiếp điểm). Vẽ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D)
a) Chứng minh tứ giác MAOB nội tiếp và MO AB b) Chứng minh M . A AD M . D AC
c) Gọi I là trung điểm của dây cung CD và E là giao điểm của hai đường thẳng AB R
và OI. Tính độ dài đoạn thẳng OE theo R khi OI 3
d) Qua tâm O kẻ đường thẳng vuông góc với OM cắt các đường thẳng M , A MB lần
lượt tại P, Q. Tìm vị trị của điểm M để diện tích tam giác MPQ đạt giá trị nhỏ nhất. ĐÁP ÁN Câu 4. E A P D I C M O H Q B
a) Chứng minh tứ giác MAOB nội tiếp và MO AB Vì M ,
A MB là các tiếp tuyến của (O) nên 0
OAM OBM 90
Xét tứ giác MAOB có: 0 0 0 O AM O
BM 90 90 180
MAOB là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng 0 180 )
Vì OA OB R O thuộc trung trực của AB
MA MB (tính chất 2 tiếp tuyến cắt nhau) M thuộc trung trực của . AB
MOlà trung trực của đoạn thẳng AB
Vậy MO AB(dfcm) Trang 26
b) Chứng minh M . A AD M . D AC Xét M AC và M DAcó: A
MDchung; MAC MDA(cùng chắn cung AC) MA AC M AC M D ( A g.g) M . A AD M . D AC(dfc ) m MD AD
c) Tính độ dài đoạn thẳng OE theo R
Gọi AB OM H, theo ý a) ta có OM AB tại H
Áp dụng hệ thức lượng trong tam giác vuông OAM , đường cao AH ta có: 2
OA OH.OM OC OM
Mà OA OC R nên 2
OC OH.OM OH OC OC OM Xét O CH và O MC có: C OM chung; (cmt) OH OC O CH O MC( . c g.c) O CH O MC O
MI (1) (hai góc tương ứng)
Vì I là trung điểm của CD(gt) nên OI CD (đường kính dây cung) O MI vuông tại 0
I OMI MOI 90 0
Lại có: OEH EOH 90 (do O EH vuông tại H)
Mà MOI EOH nên O MI O EH 2 Từ (1) và (2) suy ra O CH O EH O MI
Tứ giác OECH là tứ giác nội tiếp (Tứ giác có 2 đỉnh liên tiếp cùng nhìn một cạnh
dưới các góc bằng nhau) 0
OCE OHE 90 (hai góc nội tiếp cùng chắn cung OE) O
CEvuông tại C, có đường cao CI
Áp dụng hệ thức lượng trong tam giác vuông OCE ta có: 2 2 OC R 2
OC OI.OE OE 3R OI R 3 R Vậy khi OI thì OE 3R 3
d) Tìm vị trí điểm M……….
Đặt OM x x R.Áp dụng hệ thức lượng trong tam giác vuông OM , P đường cao OA ta có: 1 1 1 1 1 1 2 2 2 2 2 2 OA OM OP R x OP 1 1 1 xR OP 2 2 2 2 2 OP R x x R Trang 27
Xét tam giác MPQ có đường cao MO đồng thời là đường phân giác (tính chất hai tiếp
tuyến cắt nhau) nên M
PQ là tam giác cân tại M, do đó đường cao MO cũng đồng thời 2xR
là đường trung tuyến PQ 2OP 2 2 x R 2 1 1 2xR x Khi đó S M . O PQ . x . R MPQ 2 2 2 2 2 2 x R x R 2 2 2 2 2 x
x R R R 2 2 Ta có: x R 2 2 2 2 2 2 x R x R x R
Áp dụng bất đẳng thức Cô si, ta có: 2 2 R R 2 2 2 2 x R 2 x R . 2R 2 2 2 2 x R x R Khi đó 2 S .
R 2R 2R MPQ 2 R 2 2 2 2 2 Dấu " " xảy ra x R
x R R x R 2(tm) 2 2 x R
Vậy diện tích tam giác MPQ đạt giá trị nhỏ nhất bằng 2
2R M cách tâm O một khoảng bằng R 2 THANH HÓA Câu IV.(3 điểm)
Cho tam giác nhọn ABC nội tiếp đường tròn O . Các đường cao B , D CE (D
thuộc AC, E thuộc AB) của tam giác kéo dài lần lượt cắt đường tròn (O) tại các điểm M
và N (M khác B, N khác C)
1. Chứng minh tứ giác BCDE nội tiếp được trong một dường tròn
2. Chứng minh MN song song với DE
3. Khi đường tròn (O) và dây BC cố định, điểm A di động trên cung lớn BC sao cho
tam giác ABC nhọn, chứng minh bán kính đường tròn ngoại tiếp tam giác ADE
không đổi và tìm vị trí của điểm A để diện tích tam giác ADE đạt giá trị lớn nhất. ĐÁP ÁN Câu IV. Trang 28 A M I G D N O E H B P K C F
1) Chứng minh tứ giác BCDE nội tiếp Vì B ,
D CE là các đường cao của ABC nên 0
BD AC,CE AB BDC BEC 90
Suy ra tứ giác BCDE là tứ giác nội tiếp (Tứ giác có hai đỉnh kề cùng nhìn 1 cạnh dưới các góc bằng nhau
2) Chứng minh MN song song với DE
Vì BCDE là tứ giác nội tiếp (cmt) BDE BCE (cùng chắn cung BE)
Mà BCE BCN BMN (hai góc nội tiếp cùng chắn BN )
BDE BMN , mà hai góc này ở vị trí đồng vị nên MN / /DE
3) Tìm vị trí A để S lớn nhất. ADE
Gọi BD CE H
Xét tứ giác AEHDcó 0 0 0
AEH ADH 90 90 180 AEHD là tứ giác nội tiếp Lai có 0
AEH 90 nên là góc nội tiếp chắn nửa đường tròn, do đó tứ giác AEHDnội
tiếp đường tròn đường kính AH , tâm I là trung điểm của AH AH
Suy ra đường tròn ngoại tiếp tam giác ADE là đường tròn I; 2 Trang 29
Kẻ đường kính AF và gọi K là trung điểm của BC Vì A
BF, ACF là các góc nội tiếp chắn nửa đường tròn (O) nên 0 ABF A CF 90 Ta có: CF AB BF AB
CF / /BH ; CH / /BF BH AB CH BF
Tứ giác BHCF là hình bình hành
Hai đường chéo BC,HF cắt nhau tại trung điểm mỗi đường mà K là trung điểm BC
(theo cách vẽ) nên K cũng là trung điểm của HF
Khi đó OK là đường trung bình của A 1 HF nên OK
AH (tính chất đường trung 2
bình) , suy ra đường tròn ngoại tiếp A
DE là đường tròn I;OK
Mà O và BC cố định, do đó ,
O K cố định nên OK không đổi
Vậy bán kính đường tròn ngoại tiếp A
DE bằng OK không đổi 1 Ta có: B
AC sd cung BC mà BC cố định nên sđ cung BC không đổi. 2
Do đó BAC không đổi Xét A DE và A
CBcó: BAC chung;
AED ACB (góc ngoài và góc trong tại đỉnh đối diện của tứ giác BCDE) A ED A AD
CB(g.g) theo tỉ số k AB 2 S AD Do đó ta có: AED 2 k S AB ACB AD
Xét tam giác vuông ABDcó: cos BAC AB SAED 2 2 cos BAC cos BAC.S , mà cos BAC không đổi nên S AED ABC S AED ABC
đạt giá trị lớn nhất thì S max ABC
Kéo dài AH cắt BC tại P nên AP 1 BC và S A . P BC ABC 2
Do BC không đổi (giả thiết) nên S
không đổi AP lớn nhất ABC
Khi đó Aphải là điểm chính giữa của cung lớn BC Vậy S
đạt giá trị lớn nhất khi A là điểm chính giữa của cung lớn BC AED PHẦN 3: CÒN LẠI Trang 30 AN GIANG Câu 4. (2,0 điểm)
Cho tam giác ABC có ba góc đều nhọn và nội tiếp trong đường tròn O. Vẽ các
đường cao AA', BB',CC ' cắt nhau tại H
a) Chứng minh rằng tứ giác AB' HC ' là tứ giác nội tiếp
b) Kéo dài AA' cắt đường tròn O tại điểm .
D Chứng minh rằng tam giác CDH cân ĐÁP ÁN Câu 4. A B' O C' H C B A' D
a) Chứng minh AB' HC ' là tứ giác nội tiếp Ta có: 0 0
BB' AC AB' H 90 ,CC ' AB AC ' H 90
Tứ giác AB' HC ' có: 0 0 0
AB ' H AC ' H 90 90 180 AB ' HC ' là tứ giác nội tiếp
b) Chứng minh C DH cân Ta có: 0 0
BAA' ABA' 90 ;
BCC ' ABA' 90 BAA' B CC ' Lại có: B AA' B
CD(cùng chắn BD)
BCC ' BCD BAA' Xét C
DH có CA'vừa là đường cao, vừa là đường trung tuyến nên là tam giác cân BÀ RỊA VŨNG TÀU
Bài 4. (3,5 điểm) Cho nửa đường tròn Ocó đường kính .
AB Lấy điểm C thuộc cung
AB sao cho AC BC (C khác ,
A C B).Hai tiếp tuyến của nửa đường tròn O tại A
và C cắt nhau ở M . Trang 31
a) Chứng minh tứ giác AOCM nội tiếp
b) Chứng minh AOM ABC
c) Đường thẳng đi qua C và vuông góc với AB cắt MO tại H. Chứng minh CM CH
d) Hai tia AB và MC cắt nhau tại P, đặt COP 2
PA PC.PM sin
Chứng minh giá trị của biểu thức là một hằng số SMCP ĐÁP ÁN Bài 4. M C α P N A O B H
a) Chứng minh tứ giác AOCM nội tiếp Vì M ,
A MB là các tiếp tuyến của O nên 0
MAO MCO 90
Xét tứ giác AOCM có : 0 0 0
MAO MCO 90 90 180 Tứ giác AOCM là tứ giác nội tiếp. b) Chứng minh A OM A BC
Vì AOCM là tứ giác nội tiếp cmt nên AOM A
CM (hai góc nội tiếp cùng chắn
AM ) . Lại có: ACM ABC (cùng chắn AC ) A OM A BC
c) Chứng minh CM CH
Gọi CH AB N
Theo ý b, ta có: AOM A BC
Mà hai góc này ở vi trí đồng vì nên OM / /BC
BC / /MH CHM BCH BCN 1 (so le trong) Ta lại có: 0 BCN AB
C 90 ( do BCN vuông tại N) 0 C AB A
BC 90 (phụ nhau) B CN C
AB(cùng phụ với ABC ) Lại có: C AB C AO C MO C
MH (hai góc nội tiếp cùng chắn cung OC) Trang 32
BCN CMH 2
Từ (1) và (2) suy ra CHM CMH C
MH cân tại C CH CM (dfc ) m
d) Chứng minh giá trị biểu thức … là một hằng số Xét P OC và P
MAcó: APM chung; PCO PM A 0 90 P OC P M ( A g.g) PC PO 1
PC.PM P .
O PA . Lại có: S CN.A . P Khi đó ta có: PA PM ACP 2 2 PA PC PM 2 . sin PA P . O PAsin S 1 ACP CN.AP 2 P .
A PA POsin 2. . OA sin 1 CN CN.AP 2 CN CN OA 1 Xét O
CN vuông ta có: sin OC OA CN sin 2
PA PC.PM sin 1 2sin. 2 S sin MCP 2
PA PC.PM sin Vậy
2 constast dfcm SMCP BẮC GIANG
Câu 4. (2,0 điểm) Cho đường tròn tâm O, bán kính R 3c . m Gọi ,
A B là hai điểm phân
biệt cố định trên đường tròn ;
O R ( AB không là đường kính). Trên tia đối của tia BA
lấy một điểm M ( M khác B) . Qua M kẻ hai tiếp tuyến MC, MD với đường tròn đã cho
(C, D là hai tiếp điểm)
d) Chứng minh tứ giác OCMD nội tiếp trong một đường tròn
e) Đoạn thẳng OM cắt đường tròn ; O R tại điểm .
E Chứng minh rằng khi 0
CMD 60 thì E là trọng tâm của tam giác MCD
f) Gọi N là điểm đối xứng của M qua O. Đường thẳng đi qua O vuông góc với
MN cắt các tia MC, MD lần lượt tại các điểm P và Q. Khi M di động trên tia đối của tia ,
BA tìm vị trí của điểm M để tứ giác MPNQ có diện tích nhỏ nhất ĐÁP ÁN Câu 4. Trang 33 Q D N O E A B M P C
d) Chứng minh tứ giác OCMD nội tiếp
Xét đường tròn tâm O có MC,MD 0
là các tiếp tuyến OCM ODM 90 Tứ giác OCMD có: 0 0 0
OCM ODM 90 90 180 OCMD là tứ giác nội tiếp
e) Chứng minh E là trọng tâm M CD
Xét đường tròn (O) có MC,MD là hai tiếp tuyến cắt nhau tại M nên MC MD và
MO là tia phân giác của CMD 1 1 0 0 0
Mà CMD 60 OMD CMD .60 30 2 2 Xét ODM vuông có 0
OD R 3c , m OMD 30 Ta có: OD OD 3 sin DMO OM
6 cm EM OM OE 6 3 3 cm 0 OM sin 30 1 2 MD MC Lại có:
nên OM là đường trung trực của đoạn DC. Gọi I là giao điểm O
D OC R
của OM và DC OM DC tại I
Theo hệ thức lượng trong tam giác ODM vuông ta có: Trang 34 2 2 OD 3 3 2
OD OI.OM OI 3 9
IM OM OI 6 OM 6 2 2 2 ME 3 2 2 Từ đó ta có:
ME MI MI 9 3 3 2
Xét tam giác MCD có MC MD và 0
CMD 60 nên M
CD là tam giác đều có MI là 2
đường phân giác nên MI cũng là trung tuyến. Lại có ME MI (cmt) nên E là trọng 3
tâm tam giác MCD(dfc ) m
f) Tìm vị trí của M để S min MNPQ
Vì N đối xứng với M qua O nên OM ON
Xét hai tam giác vuông O QM , O
PM có cạnh OM chung, OMQ OMP Suy ra O QM O PM (g. .
c g) OP OQ
Diện tích tứ giác MPNQ là : 1 1 1 S
MN.PQ .2OM.2OQ 4. OM.OQ 4S 4.O . D MQ 4 . R MQ MPNQ 2 2 2 OQM Xét OQM
vuông tại O có OD là đường cao, theo hệ thức lượng trong tam giác vuông ta có: 2 2 OD D .
Q DM R D . Q DM
Áp dụng bất đằng thức Cô si ta có: 2
QM DQ DM 2 D .
Q DM 2 R 2R Hay QM
2R QD DM R min Từ đó S nhỏ nhất là 2
8R MQ 2R MPNQ Khi đó: Xét M DB & M
AD có: DMB chung; MDB MAD (cùng chắn BD) MD MB 2 2 M DB M
AD(g g) MD M . A MB M . A MB R MA MD Đặt AB ,
a MB x ( a không đổi, a, x 0) Ta có:
a a R M .
A MB R x x a 2 2 4 2 2 2 2
R x ax R 0 x do x 0 2
Vậy điểm M thuộc tia đối của tia AB và cách B một khoảng bằng 2 2
a a 4R MB
không đổi thì tứ giác MPNQ có diện tích nhỏ nhất là 2 8R 2 BẮC CẠN
Câu 5. (3,0 điểm) Cho nửa đường tròn Ođường kính MN, điểm P thuộc nửa đường
tròn PM PN .Kẻ bán kính OK vuông góc với MN cắt dây MP tại E. Gọi d là tiếp Trang 35
tuyến tại P của nửa đường tròn. Đường thẳng đi qua E và song song với MN cắt d ở F. Chứng minh rằng:
a) Tứ giác MPEO nội tiếp đường tròn b) M . E MP M . O MN c) OF / /MP
d) Gọi I là chân đường cao hạ từ P xuống MN. Hãy tìm vị trí điểm P để IE vuông góc với MP ĐÁP ÁN Câu 5. d K P E F M N x I O
a) Tứ giác NPEO nội tiếp đường tròn Vì M
PN là góc nội tiếp chắn nửa đường tròn nên 0 0 M
PN 90 E PN 90
Xét tứ giác NPEO có 0 0 0
EPN EON 90 90 180 NPEO là tứ giác nội tiếp b) M . E MP M . O MN Xét M OE và M PN có: 0
PMN chung; MOE MPN 90 MO ME M OE M
PN(g.g)
ME.MP M . O MN dfcm MP MN
c) OF song song với MP Trang 36
Vì EF / /MN (gt) mà MN OK nên 0
EF OK OEF 90 OPF OEPF là tứ giác nội tiếp
Lại có NPEO là tứ giác nôi tiếp (cmt) 5điểm , O E, ,
P F, N cùng thuộc một đường
tròn nên tứ giác OEFN cũng là tứ giác nội tiếp 0
EON EFN 180 mà 0 0
EON 90 (gt) EFN 90
Xét tứ giác OEFN có: 0
EON OEF EFN 90 OEFN là hình chữ nhật (tứ giác có 3 góc vuông) 0
ONF 90 NF là tiếp tuyến của Otại N
FNP NMP (cùng chắn NP)
Mà NMP OMP OPM (do O
MP cân tại O)
FNP OPM OPE
Mà FNP FOP (hai góc nội tiếp cùng chắn FP). OPE FOP
Mà 2 góc này ở vị trí so le trong nên OF / /MP
d) Tìm vị trí điểm P……
Đặt OI x, MN 2R IN R x0 x R
Áp dụng hệ thức lượng trong tam giác vuông MPN ta có: 2
PI MI NI R xR x 2 2 2 2 .
R x PI R x
Ta có: OK / / PI (cùng vuông góc với MN ) nên áp dụng định lý Ta let ta có: 2 2 OE MO OE R R R x OE 2 2 PI MI R x R x R x
Để IE MPthì IE / /PN (do MP PN) , khi đó OIE INP (hai góc đồng vị ) 2 2 OE R R x
Xét tam giác OIE có: tanOIE OI
x R x 2 2 IP R x
Xét tam giác vuông IPN có tan INP IN R x Trang 37
Vì OIE INP tan O IE tan I NP 2 2 2 2 R R x R x
x R x
R R x x R x R x 2 2 2 2
R Rx xR x x 2Rx R 0
x R R 2 R 2 1 (tm) 1
x R 2 1 OI
x R R 2 0(ktm) 2 R R R x 2 2 2 2 2 2 1 R 2 2 2 2 2 2 tan INP R x
R R 2 1 R 2 2 2 2 1 2 1 2 1
tan MNP tan INP 2 1
Vậy khi điểm P nằm trên đường tròn O thỏa mãn tan MNP
2 1 thì IE MP BẮC NINH Câu 3. (2,0 điểm)
Cho tam giác ABC vuông tại .
A Trên cạnh AC lấy điểm M khác C sao cho AM M .
C Vẽ đường tròn tâm O đường kính MC, đường tròn này cắt BC tại E
E Cvà cắt đường thẳng BM tại DD M
a) Chứng minh ADCB là một tứ giác nội tiếp
b) Chứng minh ABM AEM và EM lầ tia phân giác của góc AED
c) Gọi G là giao điểm của ED và .
AC Chứng minh rằng C . G MA C . A GM ĐÁP ÁN Câu 3. Trang 38 B E G C A M O D
a) ADCB là tứ giác nội tiếp
Xét đường tròn Ota có: MDC là góc nội tiếp chắn nửa đường tròn 0 0
MDC 90 hay BDC 90
Xét tứ giác ADCB có 0 B AC B DC 90 mà ,
A D là 2 đỉnh kề nhau
Nên ADCB là tứ giác nội tiếp
b) Chứng minh ABM AEM và EM lầ tia phân giác của góc AED
Xét đường tròn Ota có: MEC là góc nội tiếp chắn nửa đường tròn 0 0
MEC 90 BEM 90 (hai góc kề bù)
Xét tứ giác ABEM ta có: 0 0 0
BAM BEM 90 90 180 ABEM là tứ giác nội tiếp
ABM AEM (cùng chắn cung AM )
Ta có: MED MCD (hai góc nội tiếp cùng chắn MD của (O)) 1
Vì ADCB là tứ giác nội tiếp (cmt) ACD ABD (hai góc nội tiếp cùng chắn AD) (2)
Lại có ABM AEM (cmt) hay ABD AEM (3)
Từ (1), (2), (3) AEM MED ME là phân giác của AED(dfcm) Trang 39
c) Chứng minh rằng C . G MA C . A GM AE AM Xét AEG
ta có: EM là phân giác trong của tam giác (cmt) (tính chất EG MG AE AM đường phân giác)
(tính chất đường phân giác) EG MG
Lại có : ME EC(cmt) EC là đường phân giác ngoài tại đỉnh E của AEG AE AC
(tính chất đường phân giác) EG CG AM AC AG
AM .CG AC.MG(dfcm) MG CG EG BẾN TRE Câu 8. (2,0 điểm)
Cho tam giác nhọn ABC nội tiếp đường tròn O và có các đường cao BE,CF cắt nhau
tại H E AC, F AB
a) Chứng minh tứ giác AEHF nội tiếp
b) Chứng minh AH BC c) Gọi ,
P G là hai giao điểm của đường thẳng EF và đường tròn (O) sao cho điểm
E nằm giữa hai điểm P và điểm F.Chứng minh AO là đường trung trực của đoạn thẳng PG ĐÁP ÁN Câu 8. A P I E F Q O H B D C K
a) Chứng minh tứ giác AEHF nội tiếp Ta có: 0 0
CF AB AFC 90 , BE AC AEB 90 Trang 40 Tứ giác AFHE có 0 0 0
AFH AEH 90 90 180 Tứ giác AFHE nội tiếp
b) Chứng minh AH BC
Kéo dài AH cắt BC tại D
Do BE,CF là các đường cao trong tam giác và BE CF H nên H là trực tâm của ABC
AD là đường cao trong A
BC AD BC AH BC(dfc ) m
c) Chứng minh AO là đường trung trực của đoạn thẳng PG
Xét tứ giác BFEC có 0
BFC BEC 90 nên là tứ giác nội tiếp (hai đỉnh kề nhau cùng
nhìn cạnh đối diện dưới các góc bằng nhau)
AFE ACB(cùng bù với BFE) 1
Kẻ đường kính AA', Gọi I là giao điểm của AO và PG
Tứ giác BACA'nội tiếp nên BAA' BCA' (cùng chắn BA')2
Từ (1) và (2) suy ra : AFE BAA' ACB BC ' A Mà 0
ACB BCA' A'CA 90 (góc nội tiếp chắn nửa đường tròn) Nên 0
AFE BAA' 90 hay 0
AFI FAI 90 0
AIF 90 AO PG tại I.
I là trung điểm của PG (tính chất đường kính dây cung)
Nên AO là đường trung trực của PG BÌNH ĐỊNH
Bài 4. (3,5 điểm)
Cho đường tròn tâm O, đường kính ABvà d là một tiếp tuyến của đường tròn
Otại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OBlấy điểm N
(khác O và B).Đường thẳng MN cắt đường tròn O tại hai điểm C và D sao cho C nằm giữa M và .
D Gọi H là trung điểm của đoạn thẳng CD
a) Chứng minh tứ giác AOHM nội tiếp trong một đường tròn
b) Kẻ đoạn DK song song với MO(K nằm trên đường thẳng AB). Chứng minh rằng MDK BAH và 2
MA MC.MD
c) Đường thẳng BC cắt đường thẳng OM tại điểm I. Chứng minh rằng đường thẳng
AI song song với đường thẳng BD ĐÁP ÁN Bài 4. Trang 41 M C I F J H N K B A O D E
a) Chứng minh AOHM là tứ giác nội tiếp
Ta có: MAlà tiếp tuyến của O 0 MAO 90
H là trung điểm của CD OH CD H (đường kính – dây cung) 0
OHC OHM 90
Xét tứ giác AOHM có: 0 0 0
MAO OHM 90 90 180 mà hai góc này đối diện nên
AOHM là tứ giác nội tiếp (đpcm) b) Chứng minh M DH B AH và 2
MA MC.MD
Ta có: DK / /MO(gt) M DK D
MO (hai góc so le trong)
Vì AOHM là tứ giác nội tiếp (cm câu a) HMO HAO (cùng chắn OH )
Hay BAD DMO BAH MDK DMO(dfcm) Xét A MC và D
MAta có: M chung; MDA MAC (cùng chắn AC) AM MC 2 A MC D M ( A g.g)
MA MC.MD(dfcm) DM MA
c) Chứng minh AI / / BD Trang 42
Gọi E là giao điểm của MO và .
BD Kéo dài DK cắt BC tại F
Xét tứ giác AHKDcó HAK KDH (câu b)
AHKD là tứ giác nội tiếp (hai đỉnh kề cùng nhìn cạnh đối diện dưới các góc bằng nhau) D AK D
HK (góc nội tiếp cùng chắn DK) Mà D AK D
CB (cùng chắn DB) nên DHK DCB
Hai góc này ở vị trí đồng vị nên HK / /CB HK / /CF
Trong tam giác DCF, HK / /CF, H là trung điểm CD nên K là trung điểm FD
DK KF . Lại có: DK / /MO DK FK BK DF / /IE OE OI BO
Mà DK FK (cmt) OE OI
Xét tứ giác AIBE có hai đường chéo IE và AB cắt nhau tại trung điểm O của mỗi
đường nên AIBE là hình bình hành AI / /BE AI / /BD(dfc ) m BÌNH DƯƠNG Bài 5. (3,5 điểm)
Cho đường tròn O;3cm có đường kính ABvà tiếp tuyến .
Ax Trên Ax lấy điểm
C sao cho AC 8c ,
m BC cắt đường tròn O tại .
D Đường phân giác của góc CAD cắt
đường tròn Otại M và cắt BC tại N
1) Tính độ dài đoạn thẳng AD
2) Gọi E là giao điểm của AD và .
MB Chứng minh tứ giác MNDE nội tiếp được trong đường tròn.
3) Chứng minh tam giác ABN là tam giác cân
4) Kẻ EF vuông góc AB F AB. Chứng minh N, E, F thẳng hàng. ĐÁP ÁN Bài 5. Trang 43 C N D M E A F B O
1) Tính độ dài đoạn thẳng AD
Vì ADB nội tiếp nửa đường tròn (O) nên 0
ADB 90 AD BD hay AD BC
Ta có: Ax là tiếp tuyến của O tại Anên Ax AB hay AB AC
AB là đường kính của O;3cm nên AB 2.3 6(cm) Do đó ABC
vuông tại A có đường cao AD
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có: 1 1 1 2 2 2 AD AB AC 1 1 1 1 25 576 4,8( ) cm 2 2 2 2 AD 6 8 AD 576 25
Vậy AD 4,8cm
2) Chứng minh MNDE là tứ giác nội tiếp Ta có : 0
AD BC(cmt) EDN 90 Trang 44
Tương tự ta có AMB là góc nội tiếp chắn nửa đường tròn Onên 0 AMB 90
AM BM hay 0
AN BM EMN 90
Xét tứ giác MNDE có 0 0 0
EDN EMN 90 90 180
Vậy tứ giác MNDE là tứ giác nội tiếp . 3) Chứng minh ABN là tam giác cân
Ta có: CAN ABM (góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn AM )
MAD MBD (hai góc nội tiếp cùng chắn MD)
Mà CAN MAD(gt) ABM MB ,
D do đó BM là tia phân giác của ABN Xét ABN
có BM là đường cao đồng thời là đường phân giác nên tam giác ABN cân tại B(dfcm)
4) Chứng minh N, E, F thẳng hàng Xét ABN
có AD BN (cmt);
BM AN (cmt);
AD BM E(gt)
E là trực tâm của tam giác ABN
Do đó NE là đường cao thứ ba của tam giác ABN nên NE AB
Lại có : EF AB(gt)
Qua điểm E nằm ngoài đường thẳng AB kẻ được hai đường thẳng EF, NE cùng
vuông góc với AB NE EF (Tiên đề Ơ clit)
Vậy N, E, F thẳng hàng (đpcm) BÌNH PHƯỚC Câu 5. (2,5 điểm)
Từ một điểm T ở bên ngoài đường tròn O , Vẽ hai tiếp tuyến T , A TB với đường tròn ( ,
A B là hai tiếp điểm). Tia TO cắt đường tròn O tại hai điểm phân biệt C và D (C
nằm giữa T và O) và cắt đoạn thẳng AB tại điểm F
a) Chứng minh : Tứ giác TAOB nội tiếp b) Chứng minh: T .
C TD TF.TO
c) Vẽ đường kính AG của đường tròn O. Gọi H là chân đường vuông góc kẻ từ
điểm B đến A ,
G I là giao điểm của TG và BH. Chứng minh I là trung diểm của BH ĐÁP ÁN Câu 5. Trang 45 A T O C F D K I H G B
a) Chứng minh tứ giác TAOH nội tiếp Ta có: T ,
A TB là hai tiếp tuyến của O tại A, B (gt) T A OA 0
TAO TBO 90 T B OB
Xét tứ giác TAOB ta có: 0 0 0
TAO TBO 90 90 180 , mà hai góc này là hai góc đối
diện nên TAOB là tứ giác nội tiếp
b) Chứng minh: T .
C TD TF.TO
Ta có: OA OB R O thuộc đường trung trực của AB
TA TB (tính chất hai tiếp tuyến cắt nhau) T thuộc đường trung trực của AB
TO là đường trung trực của AB TO AB F
Áp dụng hệ thức lượng cho T
AO vuông tại Acó đường cao AF ta có: 2
TA TF.TO (1) Xét T AC và T DAta có:
T chung; TDA TAC (góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn AC) TA TC 2 T AC T D ( A g.g)
TA TC.TD 2 TD TA
Từ (1) và (2) TF TO TC TD 2 . .
TA dfcm
c) Chứng minh I là trung điểm của BH
Gọi AB TG K
AT OA AT AG Ta có:
BH / / AT ABH TAB (so le trong) BH AG
Mà TA TB (tính chất hai tiếp tuyến cắt nhau) nên T AB cân tại T
TAB TBA ABH TBA BK là phân giác của TBH Ta có: 0
ABG 90 (góc nội tiếp chắn nửa đường tròn) BA BG hay BK BG
Do đó BG là phân giác ngoài của TBH Trang 46 BI KI GI
Áp dụng định lý đường phân giác ta có: BT KT GT KI BI GI IH Lại có ; (định lý Ta – lét ) KT AT GT AT BI IH Do đó BI IH AT AT
Vậy I là trung điểm của BH (dfcm) BÌNH THUẬN Bài 5. (4,0 điểm)
Cho nửa đường tròn O đường kính AB 2 .
R Trên đoạn thẳng OB lấy điểm M
(M khác O và B).Đường thẳng vuông góc với MN tại N cắt các tiếp tuyến Ax, By của
nửa đường tròn O lần lượt ở C và D ( Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB)
a) Chứng minh tứ giác ACNM nội tiếp
b) Chứng minh AN.MD N . B CM
c) Gọi E là giao điểm của AN và CM . Đường thẳng qua E và vuông góc với , BD
cắt MD tại F.Chứng minh N, F, B thẳng hàng d) Khi 0
ABN 60 , tính theo R diện tích của phần nửa hình tròn tâm O bán kính R nằm ngoài ABN ĐÁP ÁN Bài 5. Trang 47 y x D N 1 1 C E F 1 1 A B O M
a) Chứng minh tứ giác ACNM nội tiếp
Vì AC là tiếp tuyến của O tại A nên 0 MAC 90
Vì MN CD tại N nên 0 M NC M ND 90
Xét tứ giác ACNM có: 0 0 0
MAC MNC 90 90 180
ACNM là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng 0 180 )
b) Chứng minh AN.MD N . B CM
Vì BD là tiếp tuyến của O tại B nên 0 M BD 90
Xét tứ giác BMND có: 0 0 0 M BD M
ND 90 90 180
BMND là tứ giác nội tiếp M DN M
BN (cùng chắn cung MN) A BN M DC
Vì ACNM là tứ giác nội tiếp (câu a) M AN M
CN (cùng chắn cung MN)
BAN MCD Xét ABN và C DN có: A BN M
DC(cmt); B AN M CD(cmt) AN NB A BN CDM (g.g)
AN.MD N . B CM (dfcm) CM MD
c) Chứng minh N, F, B thẳng hàng.
Gọi E BN DM , ta chứng minh EF BD Vì A BN C
DM (cmt) nên ANB CMD mà 0
ANB 90 (góc nội tiếp chắn nửa đường tròn) 0 0
CMD 90 ENF EMF 90
Xét tứ giác MENF có 0 0 0
ENF EMF 90 90 180 Trang 48
MENF là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng 0 180 ).
N E (hai góc nội tiếp cùng chắn cung MF) 1 1
Mà N D (hai góc nội tiếp cùng chắn cung BM) E D 1 1 1 1 1 0 Vì B
DM vuông tại B nên D BMD 90 (hai góc nhọn trong tam giác vuông phụ 1 nhau) 0 0 0 0 0
Mà BMD CMD M 180 M B
MD 180 C
MD 180 90 90 1 1 D M 2 1 1
Từ (1) và (2) suy ra E M mà hai góc này ở vị trí so le trong nên 1 1
EF / / AM hay EF / / AB . Lại có AB BD(gt) EF BD
Vậy đường thẳng qua E vuông góc với BD cắt MD tại F BN (dfcm) d) Khi 0, ABN
60 , tính theo R diện tích …..
Xét tam giác vuông ABN 0
vuông tại N có AB 2R, ABN 60 (gt) ta có: 0 AN A . B sin A BN 2 .
R sin 60 R 3 0 BN A . B cos A BN 2 . R cos60 R 2 1 1 R 3 S
AN.BN R 3.R ABN 2 2 2 1 2
Diện tích nửa hình tròn tâm ;
O R là S R r 2
Vậy diện tích của phần nửa hình tròn tâm O, bán kính R nằm ngoài ABN là: 2 2 1 R 3 R 2
S S S R r ABN 3 2 2 2 CÀ MAU Bài 6.
Câu 1.Cho tam giác ABC có các góc đều nhọn. Vẽ các đường cao B , D CE của tam giác
ABC.Gọi H là giao điểm của B , D CE
a) Chứng minh tứ giác ADHE nội tiếp được đường tròn
b) Chứng minh rằng: D . E AC B . C AE
c) Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.Chứng minh rằng OA DE ĐÁP ÁN Bài 6. Câu 1. Trang 49 B E H O F C D A
a) Theo giả thiết, ta có: 0
AEH ADH 90 tứu giác ADHE nội tiếp đường tròn 0
b) Vì BDC BEC 90 (gt) và cùng nhìn cạnh BC nên BEDC là tứ giác nội tiếp 0 0
BED BCD 180 BCA BCD 180 BED DEA Xét AED và A
CB có: DAE chung; DEA BC ( A cmt) AE AC A ED A
CB(g.g)
DE.AC BC.AE(dfcm) DE BC
c) Gọi OA ED F Ta có: 0 0
AFD 180 FAD FDA 180 OAC EDA 1 Xét O
AC có OA OC O AC cân tại O 0 180 AOC 0 OAC 90 ABC 2 2
Lại có: EDA ABC (do AE D ACB )3 0 0 0
Từ (1), (2), (3) AFD 180 90 ABC ABC 90
AF FD hay AO ED(dfcm) CAO BẰNG Câu 4. (2.0 điểm) Trang 50
Qua điểm Anằm ngoài đường tròn O vẽ hai tiếp tuyến AB và AC của đường
tròn (B,C là các tiếp điểm)
a) Chứng minh ABOC là tứ giác nội tiếp
b) Kẻ đường thẳng qua diểm A cắt đường tròn O tại hai điểm E và F sao cho E
nằm giữa A và F. Chứng minh B .
E CF BF.CE ĐÁP ÁN Bài 4. B O A E F C
a) AB là tiếp tuyến với O nên 0
OB AB OBA 90
AC là tiếp tuyến với O nên 0
OC AC OCA 90 Tứ giác ABOC có 0 0 0
OBA ACO 90 90 180
Do đó ABOC là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng 0 180 ) b) Xét ABE và AFB
có: A chung ; ABE AFC (cùng chắn cung BE) AB BE AE A BE A
FB(g.g)
(các cặp cạnh tương ứng tỉ lệ) AF BF AF A .
B BF AF.BE và 2
AB AE.AF Xét A CE và AFC có:
A chung; ACE AFC (góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn CE) AC CE AE ACE AF
C(g.g)
(các cặp cạnh tương ứng tỉ lệ) AF CF AC Trang 51 A . C CE A . E CF . Ta có: A .
B BF AF.BE ;
AC.CE AE.CF A .
B BF.AC.CE AF.BE.AE.CF 2
AB .BF.CE AE.AF.BE.CF Mà 2
AB AE.AF (cmt) BF.CE BE.CF (dfcm) ĐẮK LẮK Câu 4. (3,0 điểm)
Cho hai đường tròn bằng nhau ;
O R và (O'; R) cắt nhau tại hai điểm A và B sao cho AB .
R Kẻ đường kính AC của đường tròn O. Gọi E là một điểm bất kỳ trên
cung nhỏ BC(E ;
B C) , CB và EB lần lượt cắt đường tròn O tại các điểm thứ hai là D và F a) Chứng minh 0 AFD 90
b) Chứng minh AE AF
c) Gọi P là giao điểm của CE và .
FD Gọi Q là giao điểm của AP và EF. Chứng
minh AP là đường trung trực của EF AP d) Tính tỉ số AQ ĐÁP ÁN Câu 4. F A O' D Q P O B E C 1) Chứng minh 0 AFD 90 Trang 52
Ta có: ABC là góc nội tiếp chắn nửa đường tròn ; O R 0 0 A
BC 90 A
BD 90 (hai góc kề bù)
Mà ABD là góc nội tiếp chắn nửa đường tròn nên AD là đường kính O '; R
Lại có : AFD là góc nội tiếp chắn cung 0
AD AFD 90 dfcm
2) Chứng minh AE AF
Ta có: AEB ACB (hai góc nội tiếp cùng chắn cung AB của O ) hay AE F ACD 1 A FB A
DB(hai góc nội tiếp cùng chắn cung ABcủa O')
Hay AFE ADC 2
Ta có: AD AC 2R A
DC cân tại A ACD ADC 3
Từ (1), (2), (3) AEF AFE A
EF là tam giác cân AE AF
3) Chứng minh AP là đường trung trực của EF
Ta có: AE AF cmt A thuộc đường trung trực của EF. 4 Xét AEP và AFP ta có: 0
AE AF (cmt); AEP AFD 90 ; AP chung A EP A
FP(ch cgv) PE PF (hai cạnh tương ứng bằng nhau)
Pthuộc đường trung trực của EF 5
Từ (4) và (5) suy ra AP là đường trung trực của EF dfcm AQ 4) Tính tỉ số AP
Ta có: AP là đường trung trực của EF (cmt) AP EF Q
Áp dụng hệ thức lượng cho AFP
vuông tại F có đường cao FQ ta có: 2 2 AF AQ AQ 2 AF A . Q AP AP 2 AQ AP AF Xét AFQ vuông tại Q ta có: AQ AQ AB 1 sin A FQ sin A DB AF AF AD 2 2 AQ 1 AQ 1 AQ 1 . Vậy AF 4 AP 4 AP 4 ĐẮK NÔNG Bài 4. (3,0 điểm) Trang 53
Cho tam giác ABC có ba góc nhọn. Hai đường cao của tam giác ABC là , AD
BE cắt nhau tại H D BC, E AC
a) Chứng minh: CDHE là tứ giác nội tiếp một đường tròn b) Chứng minh: H . A HD H . B HE
c) Gọi điểm I là tâm đường tròn ngoại tiếp tứ giác CDHE. Chứng minh IE là tiếp
tuyến của đường tròn đường kính AB ĐÁP ÁN Bài 4. A E O H I B C D
a) Chứng minh tứ giác CDHE nội tiếp Ta có: A ,
D BE là hai đường cao của AD BC D 0 A
BC(gt)
ADC BEC 90 BE AC E
Xét tứ giác CDHE ta có: 0 0 0
HDC HEC 90 90 180 CDHE là tứ giác nội tiếp
b) Chứng minh H . A HD H . B HE Xét H AE và H BDta có:
AHE BHD (đối đỉnh); 0
AEH BDH 90 AH HE A HE B
HD(g.g)
AH.DH BH.EH dfcm BH HD
c) Chứng minh IE là tiếp tuyến ……….
Xét tứ giác ABDE ta có: 0
ADB AEB 90 , mà hai đỉnh ,
D E là hai đỉnh liên tiếp của
tứ giác ABDE là tứ giác nội tiếp Trang 54 Lại có: AEB vuông tại E , A , B ,
D E cùng thuộc đường tròn tâm O đường kính AB
Ta có: ABDE là tứ giác nội tiếp (cmt) EDC BAE (góc ngoài tại 1 đỉnh bằng góc
trong tại đỉnh đối diện ) (1)
Ta có: I là tâm đường tròn ngoại tiếp tứ giác CDHE I là trung điểm của HC E 1
CH vuông tại E có đường trung tuyến EI EI HI
HC (đường trung tuyến 2
ứng với cạnh huyền của tam giác vuông) H
EI cân tại I IEH IHE (tính chất tam giác cân) hay I EH E HC (2)
Tứ giác CDHE là tứ giác nội tiếp (cmt) CDE CHE (cùng chắn EC) (3)
Từ (1), (2), (3) suy ra EDC BAE HEI A
OE cân tại O OA OE OEB OBE (tính chất tam giác cân)
Hay BAE OEA mà 0 0
OBE BAE 90 OEB HEI 90 OE EI EI
là tiếp tuyến của đường tròn đường kính AB(dfcm) ĐIỆN BIÊN
Câu 4. (3 điểm) Trên nửa đường tròn đường kính , AB bán kính .
R Lấy hai điểm I ,Q sao cho I thuộc cung .
AQ Gọi C là giao điểm của hai tia AI , B ,
Q H là giao điểm của hai
dây AQ và BI. Chứng minh rằng:
1) Tứ giác CIHQ là tứ giác nội tiếp
2) CI.AI HI.BI
3) AI.AC B .
Q BC luôn không đổi. ĐÁP ÁN Bài 4. C Q I H A O B
1) Tứ giác CIHQ nội tiếp Trang 55 Vì A IB, A
QB là các góc nội tiếp chắn nửa đường tròn (O) nên 0 0 AIB A
QB 90 CIH CQH 90 Xét tứ giác CIHQ 0 0 0
có: CIH CQH 90 90 180 nên CIHQ là tứ giác nội tiếp
2) Chứng minh CI.AI HI.BI 0 Xét A HI và B
CI có: HAI CBI (cùng chắn cung IQ); AIH BIC 90 HI AI A HI B
CI (g.g)
(hai cặp cạnh tương ứng tỉ lệ) CI BI
CI.AI HI.BI(dfcm)
3) Chứng minh AI.AC B .
Q BC luôn không đổi Ta có:
AI.AC B .
Q BC AC. AC IC B .
Q BQ QC 2 2
AC AC.IC BQ B . Q QC 2 2 2
AQ QC AC.IC BQ B . Q QC 2 2
AQ BQ QC.QC BQ AC.IC 2
AB QC.BC AC.IC Xét A QC và B IC có: ICQ 0
chung; AQC BIC 90 A QC B
IC(g.g)
AC.IC QC.BC QC.BC AC.IC 0
Vậy AI AC BQ BC AB R2 2 2 . . 2
4R luôn không đổi (đpcm) ĐỒNG THÁP Câu 6. (2,0 điểm)
Cho đường tròn Ovà một điểm Anằm ngoài O. Vẽ các tiếp tuyến AM, AN
với O(M , N là các tiếp điểm)
1) Chứng minh tứ giác AMON là tứ giác nội tiếp 2) Biết rằng 0 OA 10c ,
m MAN 60 .Tính phần diện tích của tứ giác AMON nằm
bên ngoài đường tròn O ĐÁP ÁN Câu 6. Trang 56 M A I O N
1) Chứng minh tứ giác AMON là tứ giác nội tiếp
Ta có: AM , AN là các tiếp tuyến tại M , N của O OM AM 0
AMO ANO 90 O N AN
Xét tứ giác AMON ta có: 0 0 0
AMO ANO 90 90 180 AMON là tứ giác nội tiếp
2) Tính phần diện tích …………..
Ta có: AM , AN là hai tiếp tuyến cắt nhau tại A
AO là phân giác của M
AN (tính chất hai tiếp tuyến cắt nhau) 1 0 MAO MAN 30 2 Xét A
MO vuông tại M ta có: 0 AM .
AO cos MAO 10.cos30 5 3(cm) 0 OM R .
AO sin MAO 10.sin 30 5cm 1 1 25 3 S
OM .AM .5.5 3 cm AMO 2 2 2 2 25 3 2 S 2S 2. 25 3cm AMON AMO 2
Ta có: AMON là tứ giác nội tiếp (cmt) 0
MAN MON 180 (tính chất tứ giác nội tiếp) 0 0 0 0
MON 180 MAN 180 60 120 Mà M
ON là góc ở tâm chắn cung 0
MN sd MN 120 2 2
.R .n .5 .120 25 S cm quat MON 2 ( ) 360 360 3 Trang 57 25
Nên diện tích phần cần tìm là 2 S S S 25 3 (cm ) AMON quat 3 25
Vậy diện tích cần tìm là 2 25 3 (cm ) 3 GIA LAI Câu 5. (3,0 điểm)
Cho đường tròn tâm O, đường kính AB 2 .
R Gọi C là trung điểm của đoạn thẳng
OA, qua C kẻ dây cung MN vuông góc với .
OA Gọi K là điểm tùy ý trên cung nhỏ BM
(K không trùng với B và M ), H là giao điểm của AK và MN
a) Chứng minh tứ giác BCHK là tứ giác nội tiếp b) Chứng minh 2
AH.AK R
c) Trên đoạn thẳng KN lấy điểm I sao cho KI KM .Chứng minh NI KB ĐÁP ÁN Câu 5. M K H O A C B I N a) Ta có: 0
AKB 90 (góc nội tiếp chắn nửa đường tròn); 0
BCH 90 MC AB Do đó 0
HKB BCH 180 . Vậy tứ giác BCHK nội tiếp b) Chứng minh 2
AK.AH R
Ta có: MC là đường trung trực của OA nên MA MO và OM OA , R nên
OM OA MA R O AM dều, 0 M OA 60 Xét A CH và A KBcó: 0 C K 90 , A chung A CH A KB AC AH
AK.AH A . B AC AK AB Trang 58
Mặt khác tam giác AMB vuông tại M có MC là đường cao ứng với cạnh huyền nên 2 2
AC.AB MA R (hệ thức lượng) . Vậy 2
AK.AH R
c) Ta có:Tứ giác OMAN có hai đường chéo OA và MN vuông góc nhau tại trung
điểm C mỗi đường nên là hình thoi. Do đó 0 M ON 2 M OA 120 1 Từ đó 0 MKN
MON 60 ( góc nội tiếp và góc ở tâm cùng chắn cung MN) 2
Mặt khác MK KI M
KI đều MK MI KI
Ta có: BC là trung trực của MN nên BM BN, và 0
MNB MAB 60 (góc nội tiếp
cùng chắn cung BM), do đó B MN đều, suy ra 0
BMN 60 , MB MN Ta có: 0
KMN KMB BMN KMB 60 1 Ta lại có: 0
KMN NMI KMI NMI 60 2
Từ (1), (2) suy ra KMB NMI , vì MN M ,
B MI MK nên M NI M BK( . c g.c)
Vậy NI BK HÀ GIANG Câu 4. (3,5 điểm)
Cho đường tròn Ovà điểm Anằm bên ngoài đường tròn O.Qua điểm Adựng
hai tiếp tuyến AM , AN đến đường tròn O với M , N là các tiếp điểm. Một đường thẳng
d đi qua Acắt đường tròn O tại hai điểm B và C (AB AC, đường thẳng d không đi qua tâm O)
a) Chứng minh tứ giác AMON là tứ giác nội tiếp b) Chứng minh 2 AN A . B AC
c) Hai tiếp tuyến của đường tròn O tại B và C cắt nhau tại K. Chứng minh rằng
điểm K luôn thuộc một đường thẳng cố định khi đường thẳng d thay đổi và đường
thẳng d thỏa mãn điều kiện đề bài ĐÁP ÁN Câu 4. Trang 59 M C O E D N B A K
a) Vì AM , AN là tiếp tuyến tại M, N của O 0
AMO ANO 90 Tứ giác
AMON nội tiếp đường tròn đường kính AO(dfc ) m b) Dễ chứng mnh A MO A
NO(cạnh huyền – cạnh góc vuông) AM AN Xét ABN và A NC ta có:
BAN chung; BNA BCN NCA(tính chất góc tạo bởi tiêp tuyến dây cung) AB AN Suy ra AB N ANC (g.g) 2 A .
B AC AN (dfcm) AN AC
c) Gọi KM cắt (O) tại N '
Vì tứ giác MBN 'C nội tiếp 2 K BN ' K
MB KN '.KM KB
Gọi KO cắt BC tại E Dễ thấy 0
OEA 90 ONA OMA 5 điểm ,
O M , N, E, Acùng thuộc một đường tròn (1)
Áp dụng hệ thức lượng trong K
BO vuôn tại B, đường cao BE,ta có: 2 K .
E KO KB KN '.KM K N 'E K OM 0
OM 'N O MK N
'EK 180 OEN ' 0
OMN ' OEN ' 180
Tứ giác MOEN 'nội tiếp hay 5 điểm M, ,
O E, N ', A cùng thuộc một đường tròn, kết
hợp với (1) suy ra N N ' hay K MN cố định
CHUYÊN ĐẠI HỌC SƯ PHẠM (HÀ NỘI) Bài 4. (3,0 điểm)
Cho đường tròn Ovà một điểm nằm ngoài đường tròn. Kẻ tiếp tuyến ABvới
đường tròn O(B là tiếp điểm) và đường kính BC.Trên đoạn thẳng CO lấy điểm I ( I Trang 60
khác C và O). Đường thẳng IAcắt Otại hai điểm D và E ( D nằm giữa A và E). Gọi
H là trung điểm của đoạn thẳng DE a) Chứng minh A . B BE B . D AE
b) Đường thẳng d đi qua điểm E song song với ,
AO d cắt BC tại điểm K.Chứng minh HK / /CD
c) Tia CD cắt AO tại điểm ,
P tia EO cắt BP tại điểm F.Chứng minh tứ giác
BECF là hình chữ nhật ĐÁP ÁN Bài 4. B F P A O D H I d K E Q C
a) Chứng minh A . B BE B . D AE Xét ABD và AEB
có: A chung; ABD AEB (góc nội tiếp và góc tạo bởi tiếp tuyến
và dây cung cùng chắn BD) A BD A
EB(g.g) AB BD
(hai cặp cạnh tương ứng tỉ lệ ) A . B BE B . D AE(dfc ) m AE BE
b) Chứng minh HK / /CD
Vì H là trung điểm của DE(gt) nên OH DE (tính chất đường kính và dây cung) 0 0
OHD 90 OHA 90
Xét tứ giác OBAH có : 0 0
OHA 90 (cmt);OBA 90 (do AB là tiếp tuyến của O) 0 0 0
OHA OBA 90 90 180 OBAH là tứ giác nội tiếp
OAH OBH (hai góc nội tiếp cùng chắn cung OH)
Mà OAH HEK (so le trong do d / /O ) A
OBH HKE HBK Tứ giác BEKH là tứ giác nội tiếp (Tứ giác có hai đỉnh kề
nhau cùng nhìn một cạnh dưới các góc bằng nhau). Trang 61
HKB HEB DEB(hai góc nội tiếp cùng chắn cung HB)
Mà DEB DCB (hai góc nội tiếp cùng chắn BD) HKB DCB (hai góc nội tiếp
cùng chắn cung BD) HKB DCB DEB. Lại có hai góc này ở vị trí đồng vị bằng nhau
HK / /CD(dfc ) m
c) Chứng minh BECF là hình chữ nhật
Kẻ tiếp tuyến AQ với đường tròn O Q B
Xét tứ giác OBAQ có: 0 0 0
OBA OQA 90 90 180 OBAQ là tứ giác nội tiếp (Tứ
giác có tổng hai góc đối bằng 0 180 )
OBQ OAQ PAQ (hai góc nội tiếp cùng chắn cung OQ)
Lại có: OBQ CBQ CDQ (hai góc nội tiếp cùng chắn cung CQ)
PAQ CDQ OBQ Tứ giác APDQlà tứ giác nội tiếp (Tứ giác có góc ngoài
bằng góc trong tại đỉnh đối diện) ADP AQP (hai góc nội tiếp cùng chắn AP)
Mà ADP CDE (đối đỉnh) CDE CBE (hai góc nội tiếp cùng chắn CE) AQP CBE 1 Xét ABP và A
QP có: APchung; BAP QAP (tính chất hai tiếp tuyến cắt nhau);
AB AQ ( tính chất hai tiếp tuyến cắt nhau) A BP A QP( . c g.c) ABP AQC (2)(hai góc tương ứng)
Từ (1) và (2) CBE ABP AQP 0
CBE CBF ABP CBF EBF ABC 90
EBF là góc nội tiếp chắn nửa đườn tròn (O) nên EF là đường kính của O
O là trung điểm của EF
Xét tứ giác BECF có hai đường chéo BC, EF cắt nhau tại trung điểm mỗi đường BECF 0
là hình bình hành. Lại có: EBF 90 (cmt) nên BECF là hình chữ nhật dfcm HÀ TĨNH
Câu 5. (2,0 điểm) Cho đường tròn tâm O, đường kính MN, điểm I thay đổi trên đoạn OM Trang 62
( I khác M). Đường thẳng qua I vuông góc với MN cắt O tại P và .
Q Trên tia đối của
tia NM lấy điểm S cố định. Đoạn PS cắt O tại E, gọi H là giao điểm của EQ và MN
a) Chứng minh tam giác SPN và tam giác SME đồng dạng
b) Chứng minh độ dài đoạn OH không phụ thuộc vào vị trí của điểm I. ĐÁP ÁN Câu 5. P E M I O H N S Q
a) Chứng minh S PN S ME Ta có : bốn điểm ,
P E, M , N cùng thuộc (O) nên tứ giác PENM nội tiếp
EPN EMN (góc nội tiếp cùng chắn cung EN) Xét S PN và S
ME có : S chung; EPN EMS(cmt) S PN S
ME(g.g) (dfc ) m
b) Chứng minh độ dài đoạn OH không phụ thuộc vào I SP SN Từ câu a, SP N SM E
(hai cặp cạnh tương ứng tỉ lệ) SM SE .
SP SE SM .SN 1 1
Ta có: PEH PEQ
sd PQ sd PM POM 2 0 0
PEH SEH 180 ; POM POS 180 SEH POS Xét S EH và S
OP có: SEH POS(cmtt);S chung SE SH SEH SO
P(g g)
(Hai cặp cạnh tương ứng tỉ lệ) SO SP Trang 63 SE.SP . SO SH 2 SM .SN Từ (1) và (2) suy ra .
SO SH SM .SN SH SO
Mà S, M , N,O cố định nên SM , SN, SO không đổi SH không đổi
OH SO SH không đổi
Vậy độ dài OH không phụ thuộc vào vị trí điểm I (dfc ) m HẢI PHÒNG Bài 4. (3,5 điểm)
1. Qua điểm Anằm ngoài đường tròn O vẽ hai tiếp tuyến AB và AC của đường
tròn (B và C là các tiếp điểm). Gọi E là trung điểm của đoạn thẳng AC, F là giao
điểm thứ hai của đường thẳng EB với đường tròn (O), K là giao điểm thứ hai của
đường thẳng AF với đường tròn O. Chứng minh
a) Tứ giác ABOC là tứ giác nội tiếp và tam giác ABF đồng dạng với tam giác AKB
b) BF.CK CF.BK c) F CE C
BE và EAlà tiếp tuyến của đường tròn ngoại tiếp ABF ĐÁP ÁN Bài 4. Trang 64 B K F O A E C
a) Tứ giác ABOC là tứ giác nội tiếp và A BF A KB O B AB Ta có: A ,
B AC là hai tiếp tuyến của O tại B,C ABO ACO O B AC 0 90
Xét tứ giác ABOC ta có: 0 0 0
ABO ACO 90 90 180 mà hai góc này đối nhau
nên ABOC là tứ giác nội tiếp dfcm Xét ABF và A
KBta có: Achung; AKB ABF (cùng chắn BF) A BF A
KBg gdfcm
b) Chứng minh BF.CK CF.BK AB BF AF Ta có: A BF A KB(cmt)
(các cặp cạnh tương ứng tỉ lệ ) AK KB AB Xét A CF và A
KC có: Achung; AKC ACF (cùng chắn CF) A CF A KC(g AC CF AF g)dfcm
(các cặp cạnh tương ứng tỉ lệ) AK KC AC
Mà AB AC (tính chất hai tiếp tuyến cắt nhau) Trang 65 AB AC BF CF BF.KC . KB CF (dfcm) AK AK KB KC
c) Chứng minh EA là tiếp tuyến……
Ta có: BKC BCE (góc nội tiếp và góc tiếp tuyến dây cung cùng chắn BC)
Lại có: BFCK là tứ giác nội tiếp đường tròn O
EFC BKC (góc ngoài tại 1 điểm bằng góc trong tại đỉnh đối diện)
EFC BCE BKC Xét F CE và C
BEta có: E chung; EFC ECB(cmt) F CE C
BE(g.g)(dfc ) m FE CE Vì 2 2 F CE CBE (cmt)
CE FE.BE AE CE BE EA EF EB EA EA EF Xét AEF và BEA ta có: AEB chung; (cmt) A EF B E (
A c g c) EB EA
FAE ABE (hai góc tương ứng)
Mà ABE là góc nội tiếp chắn cung BF của đường tròn ngoại tiếp ABF
FAE được tạo bởi dây cung AF và AE ( E nằm ngoài đường tròn)
AE là tiếp tuyến của đường tròn ngoại tiếp A BF(dfc ) m HẬU GIANG
Câu IV. (2,0 điểm) Cho đường tròn O có bán kính R 2a và điểm Anằm
ngoài đường tròn O.Kẻ đến O hai tiếp tuyến AM , AN (với M , N là các tiếp điểm.
1) Chứng minh bốn điểm ,
A M , N,O cùng thuộc một đường tròn C .Xác định
tâm và bán kính của đường tròn C
2) Tính diện tích S của tứ giác AMON theo a, biết rằng OA 3a
3) Gọi M ' là điểm đối xứng với M qua O và P là giao điểm của đường thẳng
AO và O, P nằm bên ngoài đoạn .
OA Tính sin MPN ĐÁP ÁN Câu IV. Trang 66 M O A P E I M' N
1) Xác định tâm và bán kính
Gọi I là trung điểm của OA 0
Ta có: OMA 90 ( AM là tiếp tuyến với O ) A MO vuông tại M
Có MI là trung tuyến MI IO IA 1 0
ONA 90 ( AN là tiếp tuyến của O) A NOvuông tại N
Có NI là trung tuyến nên NI IO IA2
Từ (1) và (2) suy ra IO IA IM IN nên 4 điểm ,
A M , N,O cùng thuộc đường tròn OA
C tâm I bán kính R (dfcm) 2
2) Tính diện tích S……..
Gọi E là giao điểm của MN và OA
Ta có: OM ON R và AM AN (tính chất hai tiếp tuyến cắt nhau)
OAlà đường trung trực của MN OA MN tại trung điểm E của MN
Tam giác OMA vuông tại M, theo định lý Pytago ta có:
AM OA OM a2 a2 2 2 2 2 3 2
5a AM a 5
Tam giác AMO vuông tại M có ME là đường cao nên: OM .AM 2 . a a 5 2a 5
ME.OA OM .AM ME OA 3a 3 2a 5 4a 5
MN 2ME 2. 3 3 Trang 67
Tứ giác OMAN có hai đường chéo O , A MN vuông góc nên: 1 1 4a 5 2 S . . OA MN .3 . a 2a 5 OMAN 2 2 3 Vậy 2 S 2a 5 OMAN 3) Tính sin MPN
Nối M ' với N ta có: MPN MM ' N (hai góc nội tiếp cùng chắn MN )
sin MPN sin MM 'N Tam giác MNM 'có 0
MNM ' 90 (góc nội tiếp chắn nửa đường tròn) nên là tam giác vuông tại N MN 4a 5 5
sin MM 'N : 4a MM ' 3 3 5 Vậy sin MPN 3
THÀNH PHỐ HỒ CHÍ MINH Bài 8. Cho đường tròn tâm ;
O bán kính R và điểm Anằm ngoài đường tròn sao cho OA 2 .
R Từ A kẻ hai tiếp tuyến A ,
D AE đến đường tròn O(D, E là hai tiếp điểm)
Lấy điểm M nằm trên cung nhỏ DE sao cho MD M .
E Tiếp tuyến của đường tròn O tại M cắt A ,
D AE lần lượt tại I, J. Đường thẳng DE cắt OJ tại F
a) Chứng minh OJ là đường trung trực của đoạn thẳng ME và OMF OEF
b) Chứng minh tứ giác ODIM nội tiếp và 5 điểm I , , D ,
O F, M cùng nằm trên một đường tròn MF
c) Chứng minh JOM IOAvà sin IOA IO ĐÁP ÁN Bài 8. Trang 68 D I A M O F J E
a) Chứng minh OJ là đường trung trực đoạn thẳng ME và OMF OEF
Ta có: AE, JI là các tiếp tuyến của đường tròn O tại E, M
Mà AE JI J nên JE JM ( tính chất hai tiếp tuyến cắt nhau)
Lại có: OE OM R nên OJ là đường trung trực của đoạn ME(dfcm) Xét O EF và O
MF có: OF chung; EOF MOF (tính chất hai tiếp tuyến cắt nhau);
OE OM R O EF O MF( . c g.c)
OMF OEF (hai góc tương ứng ) (đpcm)
b) Chứng minh ODIM là tứ giác nội tiếp và I, , D ,
O F, M cùng nằm trên một đường tròn
Vì AD là tiếp tuyến với O tại D nên 0 0
AD OD ODA 90 ODI 90
MI là tiếp tuyến với O tại B nên 0
OM MI OMI 90 Tứ giác ODIM có: 0 0 0
ODI OMI 90 90 180 nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng 0
180 ) . Vậy tứ giác ODIM là tứ giác nội tiếp
Theo câu a, EOF MOF EOM 2MOF 1 1
MOF EOM sd cung ME (góc ở tâm bằng số đo cung bị chắn) 2 2 1
Nên MOF MDF sd cungME 2
Xét tứ giác OFMD có MOF MDF (cmt) nên là tứ giác nội tiếp (tứ giác có hai đỉnh kề
cùng nhìn cạnh đối diện các góc bằng nhau), do đó các điểm ,
O F, M , D cùng thuộc một đường tròn Trang 69
Mà tứ giác ODIM nội tiếp (cmt) nên các điểm , O ,
D I , M cùng thuộc một đường tròn. Vậy 5 điểm , O ,
D I, M , F cùng thuộc một đường tròn
c) Chứng minh JOM IOA…….. Xét M OI và DOI
có: OM OD R,OI chung; IM ID (tính chất hai tiếp tuyến
cắt nhau) MOI DOI c c c MIO DIO (2 góc tương ứng)
Tứ giác OFMI nội tiếp (cmt) 0
OFM MIO 180 (tính chất tứ giác nội tiếp)
Mà MIO DIO cmt nên 0
OFM DIO 180 Lại có 0
OIA DIO 180 OFM OIA
Xét tứ giác OEAD có 0 0 0
OEA ODA 90 90 180 nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng 0 180 )
OED OAD (hai góc nội tiếp cùng chắn OD)
Mà OED OEF OMF (theo câu b) nên OMF OAD OAI Xét O FM và O IA có: OFM (
OIA cmt);OMF OAI cmt O FM O I ( A g.g)
FOM IOA(hai góc tương ứng) JOM IOAdfcm JM
sin IOA sin JOM 1 OJ
Tứ giác OFMI nội tiếp (cmt) JFM MIO (góc ngoại tại 1đỉnh và góc trong tại đỉnh đối diện) Xét tam giác J FM và J IOcó:
J chung; JFM MIO JIO cmt J FM J
IO(g.g) JM MF
(hai cặp cạnh tương ứng tỉ lệ ) 2 OJ IO MF
Từ (1) và (2) suy ra IOA (dfcm) IO
PHỔ THÔNG NĂNG KHIẾU (THÀNH PHỐ HỒ CHÍ MÌNH)
Câu 5. (3,0 điểm) Cho tam giác ABC nội tiếp đường tròn T có tâm O, có AB AC, và 0
BAC 90 . Gọi M là trung điểm của đoạn thẳng .
AC Tia MO cắt đường tròn T tại điểm .
D Đường thẳng BC lần lượt cắt các đường thẳng AO và AD tại các điểm N, P
a) Chứng minh rằng tứ giác OCMN nội tiếp và BDC 4.ODC
b) Tia phân giác của BDP cắt đường thẳng BC tại điểm .
E Đường thẳng ME cắt
đường thẳng AB tại điểm F.Chứng minh rằng CA CP và ME DB DE
c) Chứng minh rằng tam giác MNE cân. Tính tỉ số DF Trang 70 ĐÁP ÁN Câu 5. A M C B I E P N F O D
a) Chứng minh OCMN là tứ giác nội tiếp và BDC 4ODC
*) Ta có : AB AC(gt) A thuộc đường trung trực của BC
OB OC (cùng bằng bán kính) O thuộc trung trực của BC
Khi đó ta có OA là trung trực của BC 0
OA BC ONC 90
Vì M là trung điểm của AC (gt) nên OM AC (quan hệ vuông góc giữa đường kính và dây cung) 0 ONC 90 Xét tứ giác OCMN 0
có ONC OMC 90 (cmt), suy ra OCMN là tứ giác nội tiếp (Tứ
giác có 2 đỉnh kề một cạnh cùng nhìn cạnh đối dưới các góc bằng nhau) *)Xét A
CD có DM AC do OM AC DM là đường cao đồng thời là đường trung tuyến suy ra A
CD cân tại D nên DM cũng là đường phân giác của ADC
ADC 2ODC (1) Trang 71
Ta có : AB AC(gt) nên sd AB sd AC (trong một đường tròn hai dây bằng nhau căng
hai cung bằng nhau) ADB ADC (trong 1 đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau)
ADlà phân giác của BDC BDC 2ADC (2)
Từ (1) và (2) suy ra BDC 4.ODC (dfc ) m
b) Phân giác góc BDP cắt BC tại E, ME cắt AB tại F. Chứng minh CA CP và
ME vuông góc với DB
Ta có : sd AB sd AC(cmt)
sd AB sd BD sd AC sd BD
sd AD sd AC sd BD
sdCD sd AC sd BD
doADCDsdADsdCD 1 Lại có : DAC
sdCD (góc nội tiếp chắn cung CD ) 2 1 APC
sdACsdBD(góc có đỉnh nằm phía trong đường tròn chắn cung 2 AC, BD) DAC APC
hay PAC APC Suy ra A
CP cân tại C (tam giác có hai góc bằng nhau) CA CP(dfc ) m
Ta có : APC DPB (hai góc đối đỉnh )
PAC DBP (hai góc nội tiếp cùng chắn cung CD)
Mà APC PAC (do tam giác ACP cân tại C) (cmt)
DPB DBP B
DP cân tại D, do đó phân giác DE đồng thời là đường cao nên DE BC
Xét tứ giác CDEM có 0
CED CMD 90 Tứ giác CDEM là tứ giác nội tiếp (tứ
giác có 2 đỉnh kề nhau cùng nhìn cạnh đối diện dưới các góc bằng nhau)
MEC MDC ADM (hai góc nội tiếp cùng chắn cung MC)
Mà MEC BEF (đối đỉnh) BEF ADM 3 Ta có: 0
ADM DAM 90 (do tam giác ADM vuông tại M) 0
ADE DPE 90 (do tam giác DEP vuông tại D)
Mà DAM APC DPE nên ADM ADE EDB (4) Trang 72
Từ (3) và (4) BEF EDB
Gọi EF BD I. Ta có: 0
DEI EDB DEI BEF DEB 90 D
EI vuông tại I DI IE hay ME DB(dfcm) DE
c) Chứng minh tam giác MNE cân. Tính DF 1 1 1 Ta có: DBA
sd AD lớn sdCD sd AC sdCD sd AB CPD (góc có 2 2 2
đỉnh ở bên trong đường tròn) 0 0
180 DBA 180 CPD
DBF DPE BDE BD là tia phân giác của EBF * BEF
cân tại B (phân giác BI đồng thời là đường cao)
BEF BFE 5 (góc ở đáy tam giác cân)
Ta có: ANM ACO (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp
OCMN ) mà ACO OAC OAB nên ANM OAB , hai góc này lại ở vị trí so le trong
MN / / AF NME BFE (hai góc so le trong ) (6)
Từ (5) và (6) suy ra BEF NME NEM Suy ra M
NE cân tại N (dfc ) m Vì BEF
cân tại B(cmt) nên BE BF Xét B DE và B
DF có: BE BF(cmt);BD chung; EBD FBD(theo *) B DE B DF( .
c g.c) DE DF (hai cạnh tương ứng) DE Vậy 1. DF HÒA BÌNH
Câu IV. (2,0 điểm) Cho tam giác nhọn ABC AB AC có các đường cao , AD
BE,CF cắt nhau tại H
1) Chứng minh rằng: Tứ giác AEHF là tứ giác nội tiếp
2) Chứng minh rằng ADE ADF
3) Chứng minh rằng: Đường tròn ngoại tiếp tam giác EDF đi qua trung điểm M của cạnh BC ĐÁP ÁN Câu IV. Trang 73 A E F H C B D M
1) Chứng minh tứ giác AEHF nội tiếp 0 BE AC AEH 90
Xét tứ giác AEHF có: 0 C F AB AFH 90 0 0 0
AEH AFH 90 90 180 AEHF là tứ giác nội tiếp
2) Chứng minh ADE ADF 0 AD BC B DH 90
Xét tứ giác BDHF có: 0 CF AB BFH 90 0 0 0
BDH BFH 90 90 180
BDHF là tứ giác nội tiếp HDF HBF (cùng chắn cung HF) A DF A BE (1) 0 AD BC H DC 90
Tương tự xét tứ giác CDHE có: 0 BE AC H EC 90 0 0 0
HDC HEC 90 90 180
CDHE là tứ giác nội tiếp HDE HCE (cùng chắn HE) ADE ACF (2) Ta lại có: 0
ABE BAC 90 (do A BE vuông tại E) 0
ACF BAC 90 (do A
CF vuông tại F )
ABE ACF (cùng phụ với BAC) 3 Từ (1), (2), (3) A DE A DF(dfcm) Trang 74
3) Chứng minh đường tròn ngoại tiếp E
DF đi qua trung điểm M của cạnh BC
Gọi M là trung điểm của BC,ta sẽ chứng minh tứ giác DMEF nội tiếp
Xét tam giác BEC vuông tại E có trung tuyến EM ứng với cạnh huyền BC 1
ME BC MB MC (định lý đường trung tuyến trong tam giác vuông) 2 M
BE cân tại M MBE MEB E MC M EB M BE 2 M
BE 2DBH *(góc ngoài của tam giác)
Vì BDHF là tứ giác nội tiếp (cmt) DBH DFH (cùng chắn DH ) 5
Vì AEHF là tứ giác nội tiếp cmt HFE HAE
3 (cùng chắn HE) 0
Mà DBH ACB 90 ( B CE vuông tại E) 0
HAE ACB 90 (do A CD vuông tại D) DBH HAE
4(cùng phụ với ACB) 4
Từ (3) và (4) HFE DBH (6)
Từ (5) và (6) DFE DFH HFE DBH DBH 2DBH 2 *
Từ * và 2 * EMC DFE
DMEF là tứ giác nội tiếp (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện)
Vậy đường tròn ngoại tiếp tam giác DEF đi qua trung điểm M của BC(dfcm) HÒA BÌNH (CHUYÊN)
Câu III. (3,0 điểm)
Cho đường tròn tâm O và dây AB cố định, gọi M là điểm chính giữa của cung
AB và N là một điểm bất kỳ trên dây AB (N khác A, N khác B). Tia MN cắt đường tròn (O) tại E.
1) Chứng minh rằng : Tam giác MNA đồng dạng với tam giác MAE
2) Chứng minh rằng: M .
B BE BN.ME
3) Chứng minh rằng: BM là tiếp tuyến của đường tròn ngoại tiếp tam giác BNE
4) Chứng minh rằng : Khi N di động trên AB thì tổng bán kính của đường tròn
ngoại tiếp tam giác BNE và đường tròn ngoại tiếp tam giác ANE không đổi ĐÁP ÁN Câu III. Trang 75 M' O1 E O O2 N K B A N N2 1 M
1) Vì M là điểm chính giữa AB sd AM sd MB MAB AEM (góc nội tiếp
cùng chắn hai cung bằng nhau) Xét M NAvà M
EA có: M chung; MAN ME ( A cmt) M NA M
AE(g.g) 2) Xét B ME và N MB có:
M chung; ABM MEA (cùng chắn hai cung AM MB) B ME N MB(g ME MB g)
(hai cặp cạnh tương ứng tỉ lệ) BE BN M .
B BE ME.BN (dfcm)
3) Ta có: MBA MEB (chứng minh câu 2)
Mà xét đường tròn ngoại tiếp E
NB thì MEB là góc nội tiếp MBAlà góc tạo bởi tiếp
tuyến – dây cung MB là tiếp tuyến đường tròn ngoại tiếp B NE
4) Vẽ đường kính MM ' cắt AB tại K
Áp dụng định lý Ta let và tam giác đồng dạng ta có: AO AM ' BO M ' B 2 1 ;
mà AK BK (tính chất đường kính – dây cung) AN AK BN BK 1 2
AM ' BM ' (MM ' là đường kính, M chính giữa) Trang 76 AO BO AO BO AM ' 2 1 2 1
AO BO AK (không đổi) AN BN AN BN AK 2 1 1 2 1 2 HÒA BÌNH (CHUYÊN 2) Câu IV. (2,0 điểm) Cho đường tròn ;
O R và dây cung BC 2 .
R Gọi Alà điểm chính giữa của cung
nhỏ BC, M là điểm tùy ý trên cung lớn BC CM BM 0.Qua C kẻ tiếp tuyến d tới
O.Đường thẳng AM cắt d và BC lần lượt tại Q và N.Các đường thẳng MBvà AC cắt nhau tại . P
1) Chứng minh : PQCM là tứ giác nội tiếp
2) Chứng minh rằng: PQ song song với BC 1 1 1
3) Tiếp tuyến tại A của O cắt d tại .
E Chứng minh rằng : CN CQ CE
4) Xác định vị trí của M sao cho bán kính đường tròn ngoại tiếp M BN lớn nhất Câu IV. L M F K O C B N A E P Q
Ý 1. PQCM là tứ giác nội tiếp
Ta có Alà điểm chính giữa cung BC sd BA sd AC
PMQ PCQ (hai góc nội tiếp chắn hai cung bằng nhau)
Mà 2 góc này cùng nhìn PQ PMCQ là tứ giác nội tiếp
Ý 2. PQ song song với BC Trang 77
Ta có: QPC QMC (MPQC là tứ giác nội tiếp ) (1)
QMC BCP (góc nội tiếp cùng chắn hai cung bằng nhau ) 2
Từ (1) và (2) suy ra QPC BCP
Mà hai góc này ở vị trí so le trong nên BC / / PQ Ý 3.
Dễ chứng minh : AE / / BC và AE CE CE AE QE Ta có: (hệ quả Ta let) CN CN QC CE CE QE CE 1 1 1 1 1 CE. 1 CN CQ QC CQ CN CQ CN CQ CE Ý 4.
Ta có : ABN BMN (góc nội tiếp chắn 2 cung bằng nhau)
AB là tiếp tuyến của đường tròn BMN
Kẻ đường kính AL của O . Gọi K là giao điểm đường trung trực của đoạn BN và BL
E là tâm đường tròn BMN
Tương tự dựng F là tâm CMN
Dễ dàng chứng minh được B LC, B EN, C FN cân
LENF là hình bình hành R R LC (không đổi) MBN MCN EB NB
Ta có: MC MB NC NB mà EBN FC
N (g.g) 1 FC NC
EB FC 2EB EB FC 2 R LC ABN LC R MBN 2
Dấu " " xảy ra khi M L là điểm chính giữa của cung lớn BC
HƯNG YÊN (KHÔNG CÓ) KIÊN GIANG
Bài 4. (2,0 điểm) Cho tam giác nhọn ABC có 0
A 60 ,nội tiếp đường tròn tâm O. Kẻ
hai đường cao BD,CE D AC, E AB
a) Chứng minh tứ giác BCDE nội tiếp trong một đường tròn b) Chứng minh A . E AB A . C AD
c) Tính diện tích tam giác ADE, biết diện tích tam giác ABC là 2 100cm ĐÁP ÁN Bài 4 Trang 78 A D E O C B
a) Chứng minh tứ giác BCDE nội tiếp 0
BD AC BDC 90 Vì B ,
D CE là hai đường cao của ABC(gt) 0 C
E AB BEC 90 Xét tứ giác BCDE 0
có BDC BEC 90 (cmt) nên BCDE là tứ giác nội tiếp (tứ giác
có 2 đỉnh kề nhau cùng nhìn một cạnh dưới các góc bằng nhau)
b) Chứng minh A . E AB A . C AD Xét A DE và ABC
có: BAC chung; AED ACD (góc ngoài và góc trong tại đỉnh đối
diện của tứ giác nội tiếp BCDE) AE AD A DE A
BC(g.g)
(hai cặp cạnh tương ứng tỉ lệ) AC AB
Vậy AE.AB AC.AD(dfc ) m c) Tính S ADE Ta có: A DE A AE
BC(cmt) theo tỉ số k AC AE 1
Xét tam giác AEC vuông tại E ta có: 0 k
cos EAC cos60 AC 2 2 S 1 1 1 1 Do đó ta có: ADE 2 k S S .100 25 cm ADE ABC 2 S 2 4 4 4 ABC Vậy 2 S 25cm ADE KON TUM Trang 79
Câu 5. (2,5 điểm) Từ điểm Aở ngoài đường tròn (O),, kẻ hai tiếp tuyến A , B AC tới
đường tròn (B,C là các tiếp điểm). Một đường thẳng d đi qua Acắt đường tròn (O) tại
hai điểm E và F(AE AF và d không đi qua tâm O)
a) Chứng minh ABOC là tứ giác nội tiếp
b) Gọi H là giao điểm của AO và BC.Chứng minh AH.AO A . E AF
c) Gọi K là giao điểm của BC và EF. M là trung điểm EF AK AK Chứng minh 2 AE AF ĐÁP ÁN Câu 5. B O A H E M F C
a) Chứng minh ABOC là tứ giác nội tiếp AB OB Ta có: A ,
B AC là các tiếp tuyến của (O) nên 0 A BO A CO 90 AC OC
Xét tứ giác ABOC ta có: 0 0 0 A BO A
CO 90 90 180 mà hai góc này ở vị trí
đối diện nên ABOC là tứ giác nội tiếp
b) Chứng minh AH.AO A . E AF
Ta có: OB OC R O đường trung trực của BC
AB AC (tính chất hai tiếp tuyến cắt nhau)
Mà AO BC H , Áp dụng hệ thức lượng cho ABO
vuông tại B có đường cao BH, ta có: 2
AB AH.AO Xét AEC và ACF ta có:
A chung; AFC ACE (cùng chắn cung EC) AE AC A EC A
CF(g.g)
AC AE.AF AC AF Trang 80
Mà AB AC(cmt) AH.AO A . E AF(dfc ) m AK AK c) Chứng minh 2 AE AF 0 Xét A KH và A
OM có: A chung; H M 90 AH AK A KH A
OM (g.g)
AK.AM AH.AO AM AO 2
AM .AK AB (phương tích) Xét AEB và ABF
có: Achung; B F (cùng chắn BE) AE AB 2 A EB A
BF(g.g)
AE.AF AB AB AF AK AF
AM.AK AE.AF 1 AE AM AK AE
Chứng minh tương tự : 2 AF AM
Cộng (1), (2) vế theo vế: AK AK AE AF
AM EM AM MF AF AE AM AM AM 2 AM
(Do ME MF ) 2 AM AK AK Vậy 2 AE AF LÂM ĐỒNG
Câu 10. Cho tam giác nhọn ABC có AH , BK ,CQ là ba đường cao
Q AB,K AC,H BC.Chứng minh HAlà tia phân giác của góc QHK
Câu 12. Cho đường tròn ;
O R cố định đi qua hai điểm B và C cố định (BC khác
đường kính). Điểm M di chuyển trên đường tròn O ( d không trùng với B và C). G là trọng tâm M B .
C Chứng minh rằng điểm G chuyển động trên một đường tròn cố định. ĐÁP ÁN Câu 10. Trang 81 A K Q I C B H
Ta gọi I là giao điểm của AH và BK, CQ 0 0 0
Vì IQB IHB 90 90 180 BQIH là tứ giác nội tiếp
ABI QHI (cùng chắn QI) 1 Xét tứ giác BQKC 0
có BQC BKC 90 cùng nhìn BC BQKC là tứ giác nội tiếp ABI QCK 2
Xét tứ giác IHCK có 0 0 0
H K 90 90 180 IHCK là tứ giác nội tiếp QCK KHI (3)
Từ (1) , (2), 3 QHI KHI HA là tia phân giác của QHK Câu 12. Trang 82 B I C K G O M
Gọi I là trung điểm BC, từ G kẻ GK / /OM K IO Xét I
OM có GK / /OM nên theo hệ quả Ta let IK GK IG 1
(do G là trọng tâm) IO OM IM 3 GK 1 R IK GK 1 và OM 3 3 OM 3
Mà I cố định (do ,
B C cố định), O cố định K cố định R
Vậy G di động trên đường tròn tâm K, bán kính 3 LẠNG SƠN Câu 4. (3,5 điểm)
Cho nửa đường tròn O đường kính .
AB Trên nửa đường tròn O lấy điểm C
sao cho CA C .
B Trên đoạn thẳng OB lấy điểm M sao cho M nằm giữa O và . B
Đường thẳng đi qua M vuông góc với AB cắt tia AC tại N, cắt BC tại . E
a) Chứng minh tứ giác ACEM nội tiếp trong một đường tròn
b) Tiếp tuyến của nửa đường tròn O tại C cắt đường thẳng MN tại F.Chứng minh C EF cân Trang 83
c) Gọi H là giao điểm của NB với nửa đường tròn O. Chứng minh HF là tiếp
tuyến của nửa đường tròn O ĐÁP ÁN Câu 4. N F C 2 1 H 2 E 1 1 A O B M
a) Chứng minh tứ giác ACEM nội tiếp đường tròn 0 Ta có: 0 A
CB 90 (góc nội tiếp chắn nửa đường tròn); AME 90 (do EM AB) Tứ giác ACEM có 0 0 0 ACE A
ME 90 90 180 nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng 0 180 )(dfcm)
b) Chứng minh C EF cân
CF là tiếp tuyến của O nên 0 0
OC CF OCF 90 C C 90 1 1 2 Tam giác EMB 0
vuông tại M nên B E 90 mà E E (đối đỉnh) 1 1 1 2 Nên 0 B E 90 2 1 2
Tam giác OBC cân tại O nên B C 3 1 1
Từ (1), (2), (3) suy ra C E C
EF cân tại F(dfc ) m 2 2
c) Chứng minh HF là tiếp tuyến
Tứ giác ABHC nội tiếp nên N HC C AB
Tứ giác ACEM nội tiếp nên E CAM CAB (tính chất) 2 Trang 84
Nên NHC E NEC 2
Tứ giác CNHE có NHC NEC(cmt) nên là tứ giác nội tiếp (hai đỉnh liên tiếp cùng
nhìn cạnh đối diện dưới các góc bằng nhau) 0 0 0 0 0
NHE NCE 180 NHE 180 N
CE 180 90 90 N HEvuông tại H Theo câu b, C
EF cân tại F nên FE FC(4) 0 0 Ta có: CNF E 90 , N
CF C 90 2 2
Mà E C (cmt) CNF NCF N
CF cân tại F FC FN 5 2 2
Từ (4) và (5) suy ra FC FN FE hay F là trung điểm EN 1
Tam giác HNE vuông tại H có HF là trung tuyến nên HF EN CF 2 Xét O CF và OHF
có: OC OH R;OF chung; FC FH (cmt) OC F OHF
.c .cc OHF OCF mà 0 OCF 90 nên 0 OHF 90
OH HF FH là tiếp tuyến của Odfcm LÀO CAI Câu 5. (3,0 điểm)
Cho tam giác ABC có ba góc nhọn AB AC nội tiếp đường tròn tâm . O Kẻ
đường thẳng d là tiếp tuyến tại Acủa đường tròn O.Gọi d ' là đường thẳng qua B và
song song với d;d ' cắt các đường thẳng A ,
O AC lần lượt tại E, .
D Kẻ AF là đường cao
của tam giác ABC F BC
a) Chứng minh rằng tứ giác ABFE nội tiếp b) Chứng minh rằng 2 AB A . D AC
c) Gọi M , N lần lượt là trung điểm của A , B B .
C Chứng minh rằng MN EF ĐÁP ÁN Câu 5. Trang 85 d A 1 2 M d' H 1 D 2 E 1 1 B F N C
a) Chứng minh rằng tứ giác ABFE nội tiếp O A d Ta có: 0 0
AF BC AFB 90 ;
OA d ' AEB 90 d '/ /d Tứ giác ABFE có 0
AFB AEB 90 nên là tứ giác nội tiếp (tứ giác có hai đỉnh kể nhau
cùng nhìn cạnh đối diện dưới các góc bằng nhau) dfcm b) Chứng minh rằng 2 AB A . D AC
Ta có: d / /d ' B A (so le trong) 1 1
Mà A C (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn AB) 1 1
B C A 1 1 1 Xét ABD và A
CBcó: A chung; B C 1 1 AB AD ABD ACB g g
(các cặp cạnh tương ứng tỉ lệ) AC AB 2
AB AC.AD(dfcm)
c) Chứng minh MN EF
Gọi H là giao điểm của EF với AC
Ta có: E E (đối đỉnh) 1 2 Trang 86
Tứ giác ABFE nội tiếp nên E A (góc nội tiếp cùng chắn cung BF ) 2 2
E A E 1 2 2 Lại có A BD A
CB(cmt) ADB ABC (góc tương ứng) 0
ADB E ABC A 90 1 2 0
EHD 180 ADB E 180 90 90 1 0 0 0
FE AC 1
Mà MN là đường trung bình của ABC
nên MN / / AC 2
Từ (1) và (2) suy ra EF MN (dfc ) m LONG AN
Câu 5. (2,5 điểm) Cho tam giác ABC cân tại A 0
BAC 90 , các đường cao AD và BE cắt
nhau tại H.Gọi O là tâm đường tròn ngoại tiếp tam giác AHE
a) Chứng minh bốn điểm C, ,
D H, E cùng thuộc một đường tròn
b) Chứng minh BC 2DE
c) Chứng minh DE là tiếp tuyến của đường tròn O. ĐÁP ÁN Câu 5. A O E H B D C
a) Chứng minh bốn điểm C, ,
D H, E cùng thuộc một đường tròn Ta có: A ,
D BE là các đường cao của A BC(gt) Trang 87 0 BE AC BEC 90 0 HEC 90 hay 0 AD BC ADC 90 0 HDC 90
Xét tứ giác DCEH ta có: 0 0 0
HEC HDC 90 90 180 , mà hai góc này ở vị trí đối
diện nên DCEH là tứ giác nội tiếp hay 4 điểm C, ,
D H, E cùng thuộc một đường tròn
b) Chứng minh BC 2DE
Ta có: AD là đường cao của ABC
cân tại A nên AD cũng là đường trung tuyến của ABC
(tính chất tam giác cân) D là trung điểm của BC 1 Xét BEC
vuông tại E có đường trung tuyến ED ED
BC BC 2ED(dfcm) 2
c) Chứng minh DE là tiếp tuyến của đường tròn O Ta có: A
HEvuông tại E (gt) Tâm đường tròn ngoại tiếp A
HE là trung điểm của
cạnh huyền AH O là trung điểm của AH
OE là đường trung tuyến ứng với cạnh huyền của AEH vuông tại E 1
OE OH AH O
EH cân tại O OEH OHE 2 1 Ta có: B
DEcân tại D DE BD BC DEB EBD (tính chất tam giác cân) 2 Ta có: B HDvuông tại 0
D HBD BHD 90 mà OHE BHD (hai góc đối đỉnh) 0 0 0
BDH OHE 90 BED OHE 90 BED OEH 90 0
OED 90 BE OE
DE là tiếp tuyến của O tại E(dfc ) m NAM ĐỊNH
Bài 4. (3,0 điểm) Cho tam giác nhọn ABC nôi tiếp đường tròn ;
O R . Hai đường cao B ,
D CE của tam giác ABC cắt nhau tại H.Các tia B ,
D CE cắt đường tròn ; O R lần
lượt tại điểm thứ hai la P,Q
1) Chứng minh tứ giác BCDE nội tiếp và cung AP bằng cung AQ
2) Chứng minh E là trung điểm của HQ và OA DE Trang 88 3) Cho góc CAB bằng 0 60 , R 6c .
m Tính bán kính đường tròn ngoại tiếp tam giác AED ĐÁP ÁN Bài 4. A P D J Q E H O B M C F
1) Chứng minh tứ giác BCDE nội tiếp và cung AP cung AQ
Ta có: BD,CE là các đường cao của ABC BD AC D 0 C E AB BEC BDC 90 E
Xét tứ giác BEDC ta có: 0
BEC BDC 90 mà hai đỉnh E, D là hai đỉnh kề nhau
Nên BEDC là tứ giác nội tiếp
Vì BEDC là tứ giác nội tiếp nên E BD E
CD(hai góc nội tiếp cùng chắn ED) A BP A CQ Lại có: A BP, A
CQ lần lượt là tứ giác nội tiếp chắn các cung
AP, AQ cung AP cung AQ
2) Chứng minh E là trung điểm HQ….. Trang 89
Xét tứ giác AEHDta có: 0 0 0 AEH A
DH 90 90 180 , mà hai góc này ở vị trí
đối diện nên AEHDlà tứ giác nội tiếp EAH EDH (cùng chắn cung EH )
Vì BEDC là tứ giác nội tiếp (cmt) EDC ECB (cùng chắn cung EB) A EH E CB E DH hay E AH E
AQ BCQ
Lại có : QAB QCB (hai góc nội tiếp cùng chắn cung QB)
EAH EAQ BCQ AE là tia phân giác của Q AH Xét Q
AH ta có: AE vừa là đường cao, vừa là đường phân giác nên Q AH cân tại A.
AE cũng là đường trung tuyến E là trung điểm HQ(dfcm)
Kéo dài AO cắt đường tròn (O) tại F Khi đó ta có: A
BC AFC (cùng chắn cung AC)
Vì BCDE là tứ giác nội tiếp (cmt) A DE A
BC (góc ngoài tại một đỉnh bằng góc
trong tại đỉnh đối diện ) ADB AFC ABC Ta có 0
ACF 90 (góc nội tiếp chắn nửa đường tròn) 0 0
CAF AFC 90 FAC ADE 90 hay 0 D AO A
DE 90 AO DE(dfcm)
3) Tính bán kính đường tròn ngoại tiếp tứ giác AED
Theo chứng minh b, ta có: AEDH là tứ giác nội tiếp
Nên Đường tròn ngoại tiếp AED
là đường tròn ngoại tiếp tứ giác AEDH Ta có: 0 AEH
90 và là góc nội tiếp chắn cung AH nên AH là đường kính của đường
tròn ngoại tiếp tứ giác AEDH
Gọi J là tâm đường tròn ngoại tiếp A
DE J là trung điểm của AH.Gọi M là trung điểm của BC. FC AC Ta có:
FC / /BD hay BH / /FC DB AC CE AB
CE / /BF hay BF / /CH BF AB
BHCF là hình bình hành nên BC,HF cắt nhau tại trung điểm mỗi đường
Mà M là trung điểm của BC M cũng là trung điểm của HF Xét A HF ta có: ,
O M lần lượt là trung điểm của AE, HF Trang 90 OM / / AH
OM là đường trung bình của AHF 1 OM AH 2 Ta có : B
OC là góc ở tâm chắn cung BC BAC
là góc ở tâm chắn cung BC BAC
là góc nội tiếp chắc cung BC 0 0 BOC 2 B AC 2.60 120 O
BC cân tại O có đường trung tuyến OM OM cũng là phân giác của BOC 0 BOM 60 Xét O BM ta có: 0 OM O . B cos BO
M 6.cos 60 3(cm)
AH 2OM 2.3 6cm 1
Vậy bán kính của đường tròn ngoại tiếp A
DE là : AJ AH 3cm 2 NGHỆ AN
Câu 4. (3,0 điểm) Cho tứ giác ABCD AD BC nội tiếp đường tròn tâm O đường kính .
AB Hai đường chéo AC và BD cắt nhau tại .
E Gọi H là hình chiếu của E trên AB
a) Chứng minh ADEH là tứ giác nội tiếp
b) Tia CH cắt đường tròn O tại điểm thứ hai là K.Gọi I là giao điểm của DK và . AB Chứng minh 2
DI AI.BI
c) Khi tam giác DAB không cân, gọi M là trung điểm của EB,tia DC cắt tia HM
tại N. Tia NB cắt đường tròn ngoại tiếp tam giác HMB tại điểm thứ hai là F.
Chứng minh F thuộc đường tròn (O) ĐÁP ÁN Câu 4. Trang 91 D C E N A M I H B O K F
a) Chứng minh ADEH là tứ giác nội tiếp Ta có: 0 A
DB 90 (góc nôi tiếp chắn nửa đường tròn) 0 EH AB A HE 90 Tứ giác ADEH có: 0 0 0 A DE A
HE 90 90 180 nên là tứ giác nội tiếp (đpcm) b) Chứng minh 2
DI AI.BI
Tứ giác ADCK nội tiếp nên A DK A
CK (hai góc nội tiếp cùng chắn AK) 1
Xét tứ giác ECBH có: 0 ECB A
CB 90 (góc nội tiếp chắn nửa đường tròn) 0 E
HB 90 doEH AB 0 0 0
ECB EHB 90 90 180
Do đó tứ giác ECBH nội tiếp (tứ giác có tổng hai góc đối bằng 0 180 )
ECH EBH (hai góc nội tiếp cùng chắn cung EH ) ACK D BA (2)
Từ (1) và (2) suy ra ADK DBA ADI DBA Lại có 0
DBA DAB 90 nên 0
ADI DAB 90 hay 0
ADI DAI 90 0 DIA
ADI DAI 0 0 0 180 180 90 90
DI AB nên DI là đường cao trong tam giác vuông ADB 2 DI I .
A IB (theo hệ thức lượng) ( dfc ) m
c) Chứng minh F thuộc đường tròn (O)
Theo câu b, DK BAtại I nên AB là đường trung trực của DK
DA AK sd cung AD sd cung AK D CA A
CK CA là tia phân giác của góc DCH
DCH 2ECH (3) Trang 92
Tam giác EHB vuông tại H có M là trung điểm EB nên HM là đường trung tuyến
MH MB M HB cân tại M DMH MHB MBH
2MBH 2EBH 4 Tứ giác ECBH có 0 0 0
ECB EHB 90 90 180 nên là tứ giác nội tiếp
Suy ra ECH EBH 5
Từ (3), (4), (5) suy ra DCH DMH DCMH là tứ giác nội tiếp
NCM NHD (tính chất) Xét NCM và N
HDcó: N chung; NCM NHD(cmt) NC NM NC M NHD (g.g)
(hai cặp cạnh tương ứng tỉ lệ) NH ND
NC.ND NM .NH 6
Tứ giác HMBF nội tiếp nên NMB NFH (tính chất ) Xét N MB và N
FH có: N chung;NMB NFC N MB N
FH (g.g) NM NB
(hai cặp cạnh tương ứng tỉ lệ) NM .NH N . B NF (7) NF NH NC NB
Từ 6 & 7suy ra NC.ND NF.NB NF ND NC NB Xét N BC và N
DF có: N chung; (cmt) N BC N DF( . c g.c) NF ND
NCB NFD BFD (các góc tương ứng) Mà 0
NCB DCB 180 (kề bù) nên 0
BFD DCB 180
Do đó tứ giác DCFB nội tiếp nên F nằm trên đường tròn Odfcm NINH BÌNH Câu 4. (3,5 điểm) 1. Cho ABC
nhọn nội tiếp đường tròn tâm .
O Hai đường cao BE,CF của ABC cắt nhau tại H
a) Chứng minh tứ giác BFEC nội tiếp đường tròn
b) Chứng minh rằng AF.AB A . E AC
c) Kẻ đường kính AD của đường tròn tâm .
O Chứng minh tứ giác BHCD là hình bình hành ĐÁP ÁN Câu 4. 1) Trang 93 A E F H O B C D
a) Ta có: BE là đường cao nên 0
BE AC BEC 90
CF là đường cao nên 0
CF AB BFC 90
Xét tứ giác BFEC có: 0
BEC BFC 90 nên BFEC là tứ giác nội tiếp (hai đỉnh kề một
cạnh cùng nhìn cạnh đối diện dưới các góc bằng nhau)
Vậy tứ giác BFEC nội tiếp
b) Theo câu a, BFEC là tứ giác nội tiếp nên BFE BCE 180 (tính chất) Mà 0
BFE AFE 180 (kề bù) nên BCE BCA AFE Xét AFE và A
CBcó: Achung; AFE ACBmt A FE A
CB(g.g) AF AE
(hai cặp cạnh tương ứng tỉ lệ) AF.AB AE.AC(dfc ) m AC AB
c) Chứng minh BHCD là hình bình hành
AD là đường kính nên 0
ACD ABD 90 (góc nội tiếp chắn nửa đường tròn)
DC AC,DB AB DC AC DB AB Ta có: DC / /BH ; DB / /CH BH AB CH AB
Tứ giác BHCD có DC / /BH, DB / /HC nên là hình bình hành (đpcm) NINH THUẬN Bài 4. (4,0 điểm) Trang 94
Cho đường tròn tâm O đường kính AB 2 .
R Vẽ dây cung CD vuông góc với
AB tại I (I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC(E khác B và C), AE cắt CD tại F .
a) Chứng minh tứ giác BEFI nội tiếp trong một đường tròn.
b) Tính độ dài cạnh AC theo R và 0 A CD khi B AC 60 .
c) Chứng minh khi điểm E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp tam
giác CEF luôn thuộc một đường thẳng cố định. ĐÁP ÁN Bài 4. E C J F A B I O D
a) Chứng minh tứ giác BEFI nội tiếp
Xét đường tròn Ocó 0 AEB
90 (góc nội tiếp chắn nửa đường tròn) Lại có: 0 F
IB 90 (do CD AB tại I )
Xét tứ giác BEFI có 0 0 0
FEB FIB 90 90 180 BEFI là tứ giác nội tiếp
b) Tính độ dài cạnh AC theo R Xét đường tròn (O) có 0
ACB 90 (góc nội tiếp chắn nửa đường tròn)
Xét tam giác ABC vuông tại C ta có: 0 0 0 0
ABC 90 BAC 90 60 30 AC 1 0 Ta có: cos B AC AC A . B cos B AC 2 . R cos 60 2 . R R AB 2 Trang 95
Xét đường tròn Ocó AB CD tại I nên I là trung điểm của dây CD (tính chất đường
kính – dây cung) hay AB là đường trung trực đoạn ,
CD suy ra AC AD
Do đó cung AC cung AD Xét đường tròn (O) có 0 A CD A
BC 30 (hai góc nội tiếp chắn hai cung AC và AD bằng nhau) nên 0 ACD 30 Vậy 0 0
AC R, A
CD 30 khi B AC 60
c) Chứng minh tâm đường tròn ngoại tiếp C
EF thuộc đường thẳng cố định
Xét đường tròn Ocó C EA A
CD (hai góc nội tiếp chắn hai cung bằng nhau C , A AD)
Xét đường tròn ngoại tiếp tam giác CEF có C EF A CF Mà C
EF là góc nội tiếp chắn cung CF AC là tiếp tuyến của đường tròn ngoại tiếp tam giác CEF
Gọi J là tâm đường tròn ngoại tiếp C
EF, JC AC tại C (do AC là tiếp tuyến) 0
Lại có ACB 90 (cmt) hay AC BC J BC
Hay tâm đường tròn ngoại tiếp tam giác CEF luôn thuộc đường thẳng BC cố định. PHÚ THỌ
Câu 3. (3,0 điểm) Cho ABC
có 3 góc nhọn nội tiếp đường tròn O. Tia phân giác
BAC cắt cạnh BC tại D và cắt đường tròn O tại M .Gọi K là hình chiếu của M trên A ,
B T là hình chiếu của M trên AC. Chứng minh rằng:
a) AKMT là tứ giác nội tiếp b) 2 2
MB MC M . D MA
c) Khi đường tròn O và ;
B C cố định, điểm A thay đổi trên cung lớn BC thì tổng AB AC có giá trị không đổi. MK MT ĐÁP ÁN Câu 3. Trang 96 A O T B C D K M
a) Chứng minh AKMT là tứ giác nội tiếp MK AB K Ta có: 0
(gt) AKM ATM 90 MT AC T
Xét tứ giác AKMT có: 0 0 0
AKM ATM 90 90 180 AKMT là tứ giác nội tiếp b) Chứng minh 2 2
MB MC M . D MA Xét O ta có:
MAB là góc nội tiếp chắn cung BM ; MAC là góc nội tiếp chắn cung MC
Lại có: MAlà tia phân giác của BAC(gt) MAB MAC sd BM sdCM (hai góc
nội tiếp bằng nhau chắn hai cung bằng nhau) Ta có : M
BC là góc nội tiếp chắn MC BAM
là góc nội tiếp chắn cung BM M AB M BC M
BD (hai góc nội tiếp chắn hai cung bằng nhau) Xét M ABvà M BD ta có: AMB chung ; M AB M
BD(cmt) M AB M
BD(g.g) MA MB 2 MB M . D MA MB MD Trang 97
Lại có: sd BM sdCM (cmt) MB MC (hai cung bằng nhau chắn hai dây bằng nhau) Vậy 2 2
MB MC M . D M ( A dfcm)
c) Khi đường tròn (O) và B, C cố định………
Đặt BAM CAM . Xét A KM và A TM có:
AM chung; KAM TAM A KM A
TM (cạnh huyền – góc nhọn)
MK MT (hai cạnh tương ứng)
Giả sử, AB AC, khi đó ta có: AB AC AK BK AT TC
AK AT BK TC MK MT MK MK MK Xét B MK và C
MT có: MB MC,MK MT(cmt) B MK C
MT (cạnh huyền – cạnh góc vuông)
BK TC (hai cạnh tương ứng) AB AC AK AT MK MT MK
Xét tam giác AKM vuông tại K có: AK AM.cos, MK AM.sin
Xét tam giác vuông AMT vuông tại T có: AT AM.cos AB AC
AM .cos AM .cos 2cos 2cot MK MT AM .sin sin
Vì đường tròn (O) và BC cố định nên số đo cung BC không đổi 1
BAC 2 số đo cung BC không đổi (góc nội tiếp bằng nửa số đo cung bị chắn) 2
không đổi 2cot không đổi AB AC Vậy 1
2cot không đổi, với
số đo cung BC không đổi. MK MT 4 PHÚ YÊN
Câu 16. (2,00 điểm) Cho đường tròn O , đường kính .
AB Trên (O) lấy điểm C sao cho
AC BC .Trên đoạn thẳng OB lấy điểm I cố định (I khác O, B). Đường thẳng qua
I vuông góc với AB cắt BC tại E, cắt AC tại F
a) Chứng minh rằng: ACEI là tứ giác nội tiếp
b) Gọi M là giao điểm của đường tròn ngoại tiếp tam giác AEF với AB (M khác A).
Chứng minh rằng tam giác EBM cân
c) Chứng minh rằng khi C di chuyển trên O thì tâm đường tròn ngoại tiếp tam giác
AEF chạy trên một đường thẳng cố định ĐÁP ÁN Câu 16. Trang 98 F C E B A M O I
a) Chứng minh rằng tứ giác ACEI là tứ giác nội tiếp Vì A
CB là góc nôi tiếp chắn nửa đường tròn nên 0 0 A
CB 90 A CE 90
Xét tứ giác ACEI có: 0 0 0
ACE AIE 90 90 180 Tứ giác ACEI là tứ giác nội tiếp
b) Chứng minh rằng EBM cân
Vì tứ giác AMEF là tứ giác nội tiếp (các điểm ,
A M , E, F cùng thuộc đường tròn ngoại tiếp AEF ) E MI A
FE AFI(1) (góc ngoài và góc trong tại đỉnh đối diện của
tứ giác nội tiếp). Ta lại có: 0
AFI FAI 90 (do A
FI vuông tại I ) 0 0
ABC CAB 90 ABC FAI 90 ( A BC vuông tại C)
AFI ABC (cùng phụ với FAI ) AFI EBI 2
Từ 1 và 2 EMI EBI EBM cân tại E
c) Chứng minh tâm đường tròn ngoại tiếp tam giác AEF chạy trên một đường thẳng cố định Ta có: EBM
cân tại E (cmt), mà EI BM nên I là trung điểm của BM ( đường cao
đồng thời là đường trung tuyến) M là điểm đối xứng với B qua I và IM IB Mà I , ,
A B cố định IB không đổi nên IM không đổi.
Lại có I cố định nên M cố định
Đường tròn ngoại tiếp tam giác AEF đi qua điểm M, nên tâm đường tròn nội tiếp AEF
thuộc đường trung trực của AM Vì ,
A M cố định nên trung trực của AM là cố định
Vậy tâm đường tròn ngoại tiếp tam giác AEF thuộc trung trực của AM cố định, với M
là điểm đối xứng với B qua I Trang 99 QUẢNG BÌNH
Câu 5. (3,5 điểm) Cho tam giác ABC vuông ở A AB AC có đường cao AH
H BC.Trên nửa mặt phẳng bờ BC chứa điểm ,
A vẽ nửa đường tròn O , 1 đường
kính BH cắt AB tại I ( I khác B) và nửa đường tròn O HC AC 2 đường kính cắt tại K
(K khác C). Chứng minh rằng:
a) Tứ giác AKHI là hình chữ nhật
b) Tứ giác BIKC là tứ giác nội tiếp
c) IK là tiếp tuyến chung của hai nửa đường tròn O O2 1 và ĐÁP ÁN Câu 5. B
O1 H I O2 A K C
a) Xét tứ giác AHKI có 0 0
AKH HKD 90 ; AIH BIH 90 Và theo giả thiết: 0
IAK 90 nên AKHI là hình chữ nhật
b) Vì AKHI là hình chữ nhật nên AIK AHK
Hơn nữa, ta có: AHK HCK (cùng chắn cung HK của nửa đường tròn O2
Do đó AIK HCK tứ giác BIKC là tứ giác nội tiếp c) Ta có: 0
O IK O IH HIK O HI HAK BCA HAK 90 1 1 1 Tương tự 0
ta cũng có: O KI 90 . 2
Từ đó ta có: IK là tiếp tuyến chung của hai đường tròn O O2 1 và QUẢNG NAM Câu 4. (3,5 điểm)
Cho đường tròn O, A là điểm cố định nằm ngoài đường tròn (O). Vẽ đường
thẳng d vuông góc với OA tại ,
A lấy điểm M tùy ý trên d ( M khác A). Vẽ hai tiếp tuyến Trang 100 M ,
B MC của đường tròn O(B,C là hai tiếp điểm; B và M khác phía với đường thẳng ) OA
a) Chứng minh tứ giác MBOC nội tiếp trong đường tròn
b) Hạ BK vuông góc với OA tại K, gọi H là giao điểm của BC và OM .Chứng minh K . A OH K . B HB
c) Chứng minh rằng khi M thay đổi trên d thì đường thẳng BC luôn đi qua điểm cố định ĐÁP ÁN Câu 4. d C M H K A I B
a) Chứng minh tứ giác MBOC nội tiếp Vì M , B MC 0
là hai tiếp tuyến nên OCM OBM 90 Tứ giác MCOB có 0 0 0
OCM OBM 90 90 180 MCOB là tứ giác nội tiếp
b) Chứng minh K . A HO K . B HB Ta có: M ,
B MC là hai tiếp tuyến của (O) MB MC (tính chất tiếp tuyến cắt nhau)
M đường trung trực của BC 1
Có OB OC R O thuộc trung trực của BC (2)
Từ (1) và (2) OM là đường trung trực của BC OM BC tại H 0 BHO 90
Vì tứ giác MBOC nội tiếp trong đường tròn (câu a)
M C (cùng chắn cung OB) 1 1 Mà B
OC cân tại O (vì OB OC) B C 4 1 1
(tính chất tam giác cân) Trang 101 0
Ta có: MAO 90 (do d OA tại A) 0
MBO 90 (do MB là tiếp tuyến của (O)) 0
MAO MBO 90
Xét tứ giác MAOB có hai đỉnh A và B kề nhau cùng nhìn OM dưới một góc 0 90 )
MAOB là tứ giác nội tiếp A M (cùng chắn cung OB ) (5) 1 1
Từ 3,4,5 A B 1 1 Xét K BAvà HOB có: 0
BKA BHO 90 do BK ,
OA BC OM ; A B (cmt) 1 1 KA KB KBA H
OB(g.g) . KA HO . KB HB(dfcm) HB HO
c) Chứng minh rằng khi M thay đổi trên d thì đường thẳng BC luôn đi qua điểm cố định
Gọi giao điểm của OA và BC là I Xét O MAvà O
IH có: O chung; 0 A H 90 OM OI 2 2 O MA O
IH (g.g)
OM .OH OI.OA OB R (hệ thức OA OH lượng) 2 R OI
. Do (O), điểm Acố định suy ra OA là khoảng cách từ O đến d không đổi, R OA
không đổi nên OI không đổi, I thuộc OA cố định, do đó I là điểm cố định. QUẢNG NGÃI Bài 4. (3,5 điểm)
Cho nửa đường tròn tâm O, đường kính AB và điểm M bất kỳ trên nửa đường tròn đó M ,
A M B . Trên nửa mặt phẳng bờ ABchứa nửa đường tròn, kẻ tiếp tuyến .
Ax Tia BM cắt Ax tại I, tia phân giác của góc IAM cắt nửa đường tròn tại E và
cắt tia BM tại F. Tia BE cắt AM tại K và cắt Ax tại H
a) Chứng minh tứ giác EFMK nội tiếp đường tròn b) Chứng minh ABF là tam giác cân
c) Chứng minh tứ giác AFKH là hình thoi
d) Xác định vị trí của điểm M để tứ giác AKFI nội tiếp được đường tròn. ĐÁP ÁN Bài 4. Trang 102 I F M H E K A O B
a) Chứng minh tứ giác EFMK nội tiếp đường tròn
Xét đường tròn Ota có: 0
AEB 90 (góc nội tiếp chắn nửa đường tròn) 0 FEK 90 0
AMB 90 (góc nội tiếp chắn nửa đường tròn) 0 FMK 90 Tứ giác EFMK có 0 0 0
FEK FMK 90 90 180 nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng 0 180 )
Vậy tứ giác EFMK nội tiếp đường tròn (đpcm)
b) Chứng minh ABF là tam giác cân
Tứ giác AEMB nội tiếp nên EAM EBM (cùng chắn EM )
Mà AF là tia phân giác của IAM nên IAF FAM EAM EBM FAI Mà 0 0
FAI FAB IAB 90 ; EBM EFB 90
Nên FAB EFB AFB
Tam giác ABF có FAB AFB nên ABF cân tại B
c) Chứng minh tứ giác AKFH là hình thoi
Tam giác ABF cân tại B (cmt) nên BE vừa là đường cao, vừa là đường trung tuyến
Nên E là trung điểm AF
Tam giác AHK có AE vừa là đường cao vừa là đường phân giác nên A HK cân tại A
AE cũng là đường trung tuyến A
HK E là trung điểm HK
Tứ giác AKFH có hai đường chéo, AF, HK cắt nhau tại trung điểm mỗi đường nên là
hình bình hành, mà HK AF nên tứ giác AKFH là hình thoi dfcm
d) Xác định vị trí của điểm M để tứ giác AFKI nội tiếp được đường tròn
AKFH là hình thoi nên FK / / AH FK / / AI nên tứ giác AKFI là hình thang
Để tứ giác AKFI là tứ giác nội tiếp thì 0
AKF AIF 180 Trang 103 Mà 0
AKF KAI 180 (kề bù) nên AIF KAI hay AIM MAI
Do đó tam giác AMI vuông cân nên 0 0
MAI 45 MAB 45 0 0
sd cungMB 2MAB 2.45 90 M là điểm chính giữa của cung . AB QUẢNG NINH Câu 4. (3,5 điểm) Cho đường tròn ;
O R và Alà một điểm nằm bên ngoài đường tròn. Từ điểm A
kẻ hai tiếp tuyến A ,
B AC với đường tròn O(B,C là hai tiếp điểm). Gọi H là giao điểm
của AO và BC.Kẻ đường kính BD của đường tròn O, AD cắt đường tròn tại điểm thứ hai là E
a) Chứng minh ABOC là tứ giác nội tiếp
b) Tính độ dài AH , biết R 3c , m AB 4cm c) Chứng minh A .
E AD AH.AO
d) Tia CE cắt AH tại F. Chứng tỏ F là trung điểm của AH ĐÁP ÁN Câu 4. B F A O H E D C
a) Chứng minh ABOC là tứ giác nội tiếp
Xét đường tròn Ocó A ,
B AC là các tiếp tuyến 0 0
ABO 90 ; ACO 90
Xét tứ giác ABOC có 0 0 0
ABO ACO 90 90 180 ABOC là tứ giác nội tiếp
b) Tính độ dài AH biết R 3c ,
m AB 4cm
Xét đường tròn Ocó A ,
B AC là hai tiếp tuyến cắt nhau tại A Trang 104
Suy ra AB AC (tính chất) mà OB OC R AO là đường trung trực của đoạn thẳng BC
Do đó OA BC tại H
Xét tam giác ABO vuông tại ,
B theo định lý Pytago ta có: 2 2 2 2 2
AO AB OB 4 3 25 OA 25 5cm Xét ABO
vuông tại B có BH là đường cao, theo hệ thức lượng trong tam giác vuông, ta 2 2 AB 4 2
có: AB AH .AO AH
3,2(cm) Vậy AH 3,2cm AO 5 c) Xét ABO
vuông tại B có BH là đường cao, theo hệ thức lượng trong tam giác vuông, ta có: 2
AB AH.AO(1) Xét AEB và ABD
có: BAE chung; ABE BDE (cùng chắn BE) AE AB 2 A EB A
BD(g g)
AE.AD AB 2 AB AD
Từ (1) và (2) suy ra : A .
E AD AH.AO
d) Chứng tỏ F là trung điểm của AH Xét đường tròn (O) có 0
BCD 90 (góc nội tiếp chắn nửa đường tròn) BC CD
Lại có: AO BC CD / / AO ADC OAD (so le trong)
Xét O có ACE EDC (góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn EC)
Suy ra ACE FAE CDE Xét AFE và C
FAcó: AFE chung; ACE FAE(cmt) A FE C F ( A g g) AF FE 2
FA FC.FE(*) CF FA AE AO
Theo câu b ta có: AE.AD AH.AO AH AD A EH A
OD(c g c) AHE ADO
Suy ra tứ giác EHOD là tứ giác nội tiếp (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối
diện) HED BOA (cùng phụ với AOD)
Xét đường tròn Ocó CED CBD (hai góc nội tiếp cùng chắn CD) 0
Lại có: BOH HBO 90 (do B
HO vuông tại H) Nên 0 0
EHD CED 90 HEC 90 hay EH FC Trang 105
Xét tam giác HFC vuông tại H có HE là đường cao, theo hệ thức lượng trong tam giác vuông ta có: 2 FH F . E FC * * Từ (*) và (**) suy ra 2 2
FA FH FA FH F là trung điểm AH QUẢNG TRỊ Câu 5. (3,0 điểm)
Cho tam giác ABC nhọn AB AC nội tiếp đường tròn O; R. Các đường cao
BD và CE D AC, E AB của tam giác ABC cắt nhau tại H. Gọi I là giao điểm thứ
hai của CE và đường tròn O. Chứng minh rằng:
a) AEHDlà tứ giác nội tiếp b) AHB AIB c) 2 2 2
AH BC 4R ĐÁP ÁN Câu 5. A D I E H O M C B A' a) Ta có: 0 0 0 A DH A
EH 90 90 180 tứ giác AEHDnội tiếp
b) Ta có : AIC ABC (tứ giác AIBC nội tiếp cùng chắn cung AC) 0 B EC B
DC 90 (gt) BEDC là tứ giác nội tiếp
EBC EDA (góc trong tại 1 đỉnh bằng góc ngoài tại đỉnh đối diện) EIA AHE (1)
Mặt khác ADE AHE (do tứ giác AEHDnội tiếp) Trang 106
Tương tự ta có: BIC BAC(AIBC là tứ giác nội tiếp)
BAC DHC(HEAD là tứ giác nội tiếp); DHC IHB (đối đỉnh)
Nên BIC IHB 2
Từ (1) và (2) suy ra AIB AHB
c) Kẻ đường kính AOA', chứng minh được BHCA' là hình bình hành nên HA' đi 1
qua trung điểm M của BC OM 1 AH mà BM BC O MI vuông tại I 2 2
(OM BC - tính chất đường kính dây cung)
Áp dụng định lý Pytago và các biến đổi ta có:
BC BM 2 2 2 BM 2 2 BO OM 2 2 2 4 4 4R 4OM
Mà AH OM 2 2 2 2 4OM 2 2 2 2 2 2
AH BC 4OM 4R 4OM 4R SÓC TRĂNG
Bài 5. (3,0 điểm) Cho tam giác ABC vuông tại A. Gọi M là trung điểm AC và O là trung điểm của .
MC Vẽ đường tròn tâm O, bán kính .
OC Kẻ BM cắt O tại D, đường
thẳng AD cắt O tại E
a) Chứng minh ABCD là tứ giác nội tiếp b) Chứng minh M AB M
DC và tính tích M . B MD theo AC
c) Gọi F là giao điểm của CE với BD và N là giao điểm của BE với AC Chứng minh M . B N .
E CF MF.N . B CE ĐÁP ÁN Bài 5. Trang 107 A D F M N E G O C B
a) Chứng minh ABCD là tứ giác nội tiếp Ta có: 0
MDC 90 (góc nội tiếp chắn nửa đường tròn (O)) 0
BDC BAC 90 ABCDlà tứ giác nội tiếp (tứ giác có 2 đỉnh liên tiếp cùng nhìn
1 cạnh dưới các góc bằng nhau)
b) Chứng minh M AB M
DC và tính tích M . B MD theo AC Xét M AB và M DC có: A MB D MC (đối đỉ 0 nh); MAB M
DC 90 M AB M
DC(g.g) MA MB
(hai cạnh tương ứng) M . B MD M . A MC MD MC 1 1 1 1
Mà M là trung điểm AC 2
nên MA MC AC M . A MC AC. AC AC 2 2 2 4 1 2 Vậy M . B MD AC 4
c) Chứng minh M . B N .
E CF MF.N . B CE NB MB CE EG
Kẻ EG / / BF (G AC) 1 và
2 (định lý Ta – let ) NE EG CF MF
Nhân hai vế của 1 và 2 ta được: NB CE MB EG NB CE MB . . . NE CF EG MF NE CF MF M .
B NE.CF MF.N . B CE(dfcm) SƠN LA Trang 108
Câu 6. (3,0 điểm) Từ điểm A bên ngoài đường tròn tâm O vẽ các cát tuyến A , B AC (B,
C là các tiếp điểm). Gọi H là giao điểm của OA và BC
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn .
b) Tính diện tích tam giác ABC trong trường hợp bán kính đường tròn (O) bằng R và AO 3R
c) Dây cung EF thay đổi nhưng luôn đi qua H.Chứng minh AO là tia phân giác của góc EAF ĐÁP ÁN Câu 6. F B H O A E C
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn Ta có: A ,
B AC là các tiếp tuyến của đường tròn (O) AB OB 0
ABO ACO 90 AC OC
Xét tứ giác ABOC có: 0 0 0
ABO ACO 90 90 180 ABOC là tứ giác nội tiếp
b) Tính diện tích tam giác ABC
Ta có: OB OC R O thuộc đường trung trực của BC
AB AC (tính chất hai tiếp tuyến cắt nhau) A thuộc đường trung trực của BC
AO là đường trung trực của BC AO BC H
H là trung điểm của BC (tính chất đường kính dây cung)
Áp dụng định lý Pytago vào ABO vuông tại B ta có: Trang 109 2 2 2 2 AB
AO OB 9R R 2 2R
Áp dụng hệ thức lượng cho ABO
vuông tại B, đường cao BH ta có: . OB AB 2 2 . R R 2 2R BH AO 3R 3 2 2 AB 8R 8R 4 2R AH
BC 2BH AO 3R 3 3 2 1 1 8R 4 2R 16 2R S AH.BC . . (dvdt) ABC 2 2 3 3 9 2 16 2R
Vậy khi OA 3R thì S (dvdt) ABC 9
c) Chứng minh AO là tia phân giác của EAF
Ta có : ABOC là tứ giác nội tiếp (theo câu a) 4điểm , A , B ,
O C cùng thuộc đường tròn đường kính AO H . A HO H . B HC 1 Ta có 4 điểm E, ,
B F,C cùng thuộc một đường tròn H . E HF H . B HC (phương tích ) (2) HA HF Từ (1) và (2) suy ra .
HA HO HE.HF HE HO Xét H EO và H AF có: HA HF
(cmt); EHO AHF (đối đỉnh) H EO H AF( . c g.c) HE HO
HEO HAF (hai góc tương ứng)
FEO CAF AEOF là tứ giác nội tiếp (hai đỉnh liên tiếp A, E cùng nhìn cạnh OF
dưới các góc bằng nhau)
Xét đường tròn ngoại tiếp AEOF có OE OF (vì OE OF) EAO FAO
AO là tia phân giác của EAF(dfc ) m TÂY NINH
Câu 5.(1,0 điểm) Cho tam giác cân ABC.Biết AB AC a 5, BC 2 . a Gọi M là
trung điểm BC, tính theo a độ đoạn thẳng AM
Câu 9.(1,0 điểm) Cho hình chữ nhật ABCD có diện tích bằng 2020.Gọi M là trung
điểm của AB và N là điểm trên cạnh AD sao cho AN 2N .
D Hai đoạn CM và BN cắt
nhau tại K. Tính diện tích của tam giác KBC Trang 110
Câu 10.(1,0 điểm) Cho tam giác ABC vuông tại A có 0
ABC 60 và đường cao AH (H
thuộc cạnh BC). Trên cạnh AC lấy D sao cho AD A .
B Gọi I là trung điểm , BD đường
thẳng HI cắt AC tại E. Tính AEH ĐÁP ÁN Câu 5. A a 5 a 5 B M C 2a ABC
cân mà MB MC AM BC BC 2a
BM MC a 2 2 Xét A
MC vuông tại M, áp dụng định lý Pytago ta có:
AC AM MC AM
AC MC a 2 2 2 2 2 2 2 5 a 2a Câu 9. M A B K E N F D C MK MB
Kẻ NE / / DC E BC ; NE MC F KF NF Trang 111 EF EC ND 1 Có: MB BC AD 3 EF 1 EF 1 NE 5 NF 5 NF 5 AB 6 NE 6 NF 6 AB 6 MB 3 MK 3 MK 3 KF 5 MF 8 MF 2 MK 1 KC 3 Mà MC 3 MC 4 MC 4 3 3 1 3 S .S . S S .2020 378,75 KBC 4 BMC 4 4 ABCD KBC 16 Câu 10. C D E I H A B Xét ABD
vuông tại A mà AB AD A
BDvuông cân tại A
Lại có: I là trung điểm của BD Trong A
BD có AI là đường trung tuyến, đồng thười AI cũng là đường cao 0 AIB 90 0
mà AHB 90 ( AH là đường cao) 0
AIB AHB 90
Xét tứ giác AIHB có 2 đỉnh H và I kề nhau cùng nhìn cạnh AB dưới 1 góc vuông
Nên tứ giác AIHB là tứ giác nội tiếp 0
AHI ABI 45 (cùng chắn cung AI) 0
Mà AHC 90 ( AH BC) AHI EHC AHC 0 0 0
EHC AHC AHI 90 45 45 1 ABC vuông tại 0
A ABC ACB 90 (hai góc phụ nhau) Trang 112 0 0 0 0
ACB 90 ABC 90 60 30 hay 0 ECH 30 (2)
Ta có: AEH là góc ngoài của E
HC AEH EHC ECH (3) Từ 0 0 0
1 , 2 , 3 AEH 45 30 75 THỪA THIÊN HUẾ Câu 5. (3,0 điểm)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm .
O Gọi M là một
điểm bất kỳ trên cung nhỏ AC sao cho BCM nhọn (M không trùng A và C). Gọi E và F
lần lượt là chân các đường vuông góc kẻ từ M đến BC và .
AC Gọi P là trung điểm của
AB,Q là trung điểm của FE.Chứng minh rằng :
a) Tứ giác MFEC nội tiếp
b) Tam giác FEM và tam giác ABM đồng dạng 0 c) M . A MQ M .
P MF và PQM 90 ĐÁP ÁN Câu 5. M A F
AMF=A1;FMP=A2;PMB=A3 BMQ=A4 Q P O C E B
a) Tứ giác MFEC là tứ giác nội tiếp Trang 113 Ta có: 0 0
MF AC MFC 90 , ME BC MEC 90 Tứ giác MFEC có 0
MFC MEC 90 nên là tứ giác nội tiếp (hai đỉnh kề một cạnh
cùng nhìn cạnh đối diện dưới các góc bằng nhau).
b) Tam giác FEM và tam giác ABM đồng dạng
Theo câu a, tứ giác MFEC nội tiếp nên 0
EFM ECM 180 1
Tứ giác ABCM nội tiếp nên 0
BAM BCM 180 2
Từ (1) và (2) suy ra BAM EFM (cùng bù với BCM )
FEM FCM (hai góc nội tiếp cùng chắn FM )3
FCM ABM (cùng chắn AM )4
Từ (3) và (4) suy ra FEM ABM Xét FEM và ABM có:
BAM EFM (cmt); FEM ABM (cmt) FEM ABM
(g.g)dfcm c) M . A MQ M . P MF và 0 P MQ 90 FE MF Từ câu b ta có: F EM A BM
(các cặp cạnh tương ứng tỉ lệ) AB MA 2FQ MF FQ MF AM FM 2AP MA AP MA AP FQ Xét M AP và M FQ có: AM FM
; MAP MFQcmt M AP M
FQ .cg.c AP FQ MA MP
(2 cặp cạnh tương ứng tỉ lệ) M . A MQ M . P MF dfcm MF MQ Lại có: M AP M
FQ(cmt) AMP FMQ (hai góc tương ứng)
M M M M M M M M AMF PMQ 1 2 2 3 4 1 3 4 Xét M AF và M PQ có: MA MP
AMF PMQ(cmt); (cmt) M FA M PQ( . c g.c) MF MQ
MFA MQP (hai góc tương ứ 0
ng) mà MFA 90 nên 0
MQP 90 dfcm TIỀN GIANG Bài V. (3 điểm)
1. Cho tam giác ABC vuông tại ,
A biết AB 6c , m BC 10c .
m Tính giá trị của biểu
thức P 5sin B 3 Trang 114
2. Cho hai đường tròn ;
O R và O ';r tiếp xúc ngoài tại ,
A với R r. Kẻ BC là
tiếp tuyến chung ngoài của hai đường tròn với B O,C O ', tiếp tuyến
chung trong tại Acủa hai đường tròn cắt BC tại M
a) Chứng minh 4 điểm ; O ;
B M; A cùng thuộc một đường tròn
b) Gọi E là giao điểm của OM và A ,
B F là giao điểm của O'M và . AC Chứng
minh tứ giác AEMF là hình chữ nhật
c) Chứng minh rằng tam giác MEF đồng dạng với tam giác MO'O
d) Cho biết R 16cm và r 9c .
m Tính diện tích tứ giác OBCO' ĐÁP ÁN Bài V. 1. C 10 cm A 6cm B
Áp dụng định lý Pytago ta có: 2 2 2 2 2 2 2 2
AB AC BC AC BC AB 10 6 64 AC 8 4
AC 8 sin B BC 10 5 4
P 5sin B 3 5. 3 7 5 Vậy P 7 2. Trang 115 B 1 M E C 2 I 1 F 1 2 1 O A O'
a) Chứng minh bốn điểm , O ,
B M , A cùng thuộc một đường tròn
Gọi I là trung điểm của OM ta có: 0
OBM 90 (BM là tiếp tuyến với O tại B) O
BM vuông tại B
IO IM IB
1 (trung tuyến ứng với cạnh huyền trong tam giác vuông bằng nửa cạnh huyền) 0
OAM 90 ( AM là tiếp tuyến với O tại ) A O AM vuông tại A
IO IM IA2 (trung tuyến ứng với cạnh huyền trong tam giác vuông bằng nửa cạnh huyền)
Từ 1 và 2 IO IM IB IA Vậy bốn điểm , O ,
B M , A cùng thuộc đường tròn tâm I đường kính OM dfcm
b) Chứng minh AEMF là hình chữ nhật
Ta có: OA OB R
MA MB (tính chất hai tiếp tuyến cắt nhau) OM là đường trung trực của đoạn AB 0
OM AB MEA 90 Tương tự 0
O'M CA MFA 90
MA MB M
AB cân tại M A B 1 1 1
MC MA M
CAcân tại M A C 2 2
Từ (1) và (2) suy ra A A B C BAC B C 1 2 1 2 1 2 0
Mà BAC B C 180 (tổng 3 góc trong tam giác) 1 2 0
BAC B C 90 1 2 Trang 116
Tứ giác AEMF có ba góc vuông nên là hình chữ nhật dfcm
c) Chứng minh M EF M O'O
Theo câu b, tứ giác AEMF là hình chữ nhật nên F A 3 1 1
Mà tứ giác OAMB nội tiếp (câu a) nên O A ( cùng chắn cung BM) (4) 1 1
Từ 3 và 4 suy ra F O 1 1 Xét M EF và M
O'Ocó: M chung; F O (cmt) 1 1 M EF M
O'O(g g)
d) Tính diện tích tứ giác OBCO '
Tứ giác AEMF là hình chữ nhật nên 0 EMF 90 O MO'vuông tại M
MAlà đường cao trong tam giác vuông OMO ' nên: 2 MA A .
O AO' 16.9 144 MA 12cm
MA MB 12cm BC 24cm
Ta có: O'C BC,OB BC OB / /O'C
Tứ giác OBCO ' có OB / /O'C và 0
OBC 90 nên là hình thang vuông 1 S
OB O C BC cm OBCO 1 ' . .16 9.24 300 2 ' 2 2 Vậy 2 S 300cm OBCO ' TRÀ VINH Đề 1.
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O). Các đường cao A ,
D BE,CF cắt nhau tại H
1) Chứng minh tứ giác BDHF nội tiếp đường tròn
2) BE và CF cắt đường tròn O lần lượt tại M , N.Chứng minh MN / /EF
3) Chứng minh H là tâm của đường tròn nội tiếp tam giác DEF Đề 2
Từ một điểm M ở ngoài đường tròn O , vẽ hai tiếp tuyến M , A MB đến đường tròn ( ,
A B là hai tiếp điểm). Qua Avẽ đường thẳng song song với ,
MB cắt đường tròn tại
E, đoạn thẳng ME cắt đường tròn tại F. Hai đường thẳng AF và MB cắt nhau tại I. Chứng minh
1) Tứ giác MAOB nội tiếp đường tròn 2) 2
IB IF.IA 3) IM IB ĐÁP ÁN Đề 1. Trang 117 A M 1 O E 1 1 2 N 1 2 F H 1 C 1 D B
1) Chứng minh tứ giác BDHF nội tiếp 0
AD BC BFH 90 Ta có: 0 C
F AB BDH 90
Xét tứ giác BDHF có 0 0 0
BFH BDH 90 90 180
Tứ giác BDHF là tứ giác nội tiếp
2) Chứng minh MN / /EF BE AC
Xét tứ giác BCEF có: 0
BEC BFC 90 CF AB
BCEF là tứ giác nội tiếp (tứ giác có hai đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc
bằng nhau) C E (hai góc nội tiếp cùng chắn BF ) 1 1 Lại có C M
(hai góc nội tiếp cùng chắn cung BN ) M E C 1 1 1 1 1
Mà hai góc này ở vị trí đồng vị nên MN / / EF (dfcm)
3) Chứng minh H là tâm đường tròn nội tiếp D EF AD BC
Xét tứ giác CDHE có: 0
CDH CEH 90 BE AC 0 0 0
CDH CEH 90 90 180 CDHE là tứ giác nội tiếp Trang 118
E C (hai góc nội tiếp cùng chắn DH) 2 1
Lại có C E (cmt) E E EH là tia phân giác của DEF 1 1 1 1 2
Chứng minh hoàn toàn tương tự ta có FH là phân giác của DFE 2
Vậy H là tâm đường tròn nội tiếp tam giác DEF (dfcm) Đề 2. A E F O M I B
1) Tứ giác MAOB nội tiếp đường tròn O A MA Ta có M ,
A MB là các tiếp tuyến tại ,
A B của O 0
MAO MBO 90 O B MB
Xét tứ giác MAOB có 0 0 0
MAO MBO 90 90 180 , mà hai góc này đối diện nên
MAOB là tứ giác nôi tiếp 2) 2
IB IF.IA Xét I BF và I ABcó: A IBchung
IAB IBF (góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn BF ) IB IF 2 I BF I
AB(g g)
IB IF.I ( A dfcm) IA IB
3) Chứng minh IM IB
Ta có: AE / /MB(gt) AEM EMB (hai góc so le trong)
Hay AEM FMI Trang 119
Lại có: AEI MAI (cùng chắn AF ) M AI I MF A EM Xét M IF và A
IM có: MIA chung; IMF MAI(cmt) M IF A
IM (g.g) MI IF 2 MI I . A IF AI IM 2 2
MI IB I .
A IF MI IB(dfcm) TUYÊN QUANG
Câu 32.(1,0 điểm) Cho hình chữ nhật ABCD có AB cm 0 4
, ADB 30 .Gọi H là
chân đường cao kẻ từ Axuống đường thẳng .
BD Tính độ dài đoạn thẳng BD và diện tích tam giác ABH ĐÁP ÁN Câu 32. 4 cm A B H 300 D C
Xét tam giác vuông ABDcó: AB AB 4 4 sin A DB BD 8(c ) m 0 BD sin A DB sin30 1 2
Áp dụng hệ thức lượng trong tam giác ABDvuông tại A, ta có: 2 2 AB 4 2
AB BH.BD BH 2cm BD 8
Áp dụng định lý Pytago trong tam giác vuông ABH ta có: 2 2 2 2 2 2 2
AB AH BH AH AB BH 4 2 2 3(cm) 1 1 S
AH.BH .2 3.2 2 3 cm ABH 2 2 2 Trang 120
Vậy BD cm S 2 8 , 2 3 cm ABH VĨNH LONG Bài 6. (2,5 diểm)
Cho nửa đường tròn tâm O đường kính .
AB Vẽ đường thẳng d vuông góc với OA
tại M M O, A.Trên d lấy điểm N sao cho N nằm bên ngoài nửa đường tròn (O). Kẻ
tiếp tuyến NE với nửa đường tròn O(E là tiếp điểm, E và Anằm cùng một phía đối
với đường thẳng d )
a) Chứng minh tứ giác OMEN nội tiếp được đường tròn
b) Nối NB cắt nửa đường tròn O tại C. Chứng minh 2
NE NC.NB
c) Gọi H là giao điểm của AC và d . F là giao điểm của tia EH và nửa đường tròn O
Chứng minh NEF NOF ĐÁP ÁN Bài 6. N C F E H A M O B
a) Chứng minh tứ giác OMEN nội tiếp Ta có: 0
d OA NMO 90 NE 0
là tiếp tuyến của O tại E nên OE NE NEO 90 Tứ giác OMEN có 0
NMO NEO 90 nên tứ giác OMEN là tứ giác nội tiếp (hai đỉnh
kề cùng 1 cạnh cùng nhìn cạnh đối diện dưới các góc bằng nhau.(đpcm) b) Chứng minh 2
NE NC.NB
Nối E với C, E với B Trang 121 Xét N EC và N BE có: N chung; N BE N
EC (cùng chắn EC) NE NC NE C NB
E(g.g)
(các cặp cạnh tương ứng tỉ lệ) NB NE Vậy 2 NE . NB NC
c) Chứng minh NEF NOF Xét NCH và N MB có: NC NH N chung; 0
NCH NMB 90 NC H NM
B(g.g) (hai cặp cạnh NM NB
tương ứng tỉ lệ) N .
C NB NH.NM mà NE NH 2 2 NE .
NB NC(cmt) NE NH .NM NM NE Xét N EH và N ME có: NE NH N chung; (cmt) NEH NM E( .
c g.c) NHE NEM (góc tương NM NE ứng ) (1)
Kẻ tiếp tuyến NF ' với nửa đường tròn (O) NF ' NM Do NE N
F ' (tính chất hai tiếp tuyến cắt nhau) 2
NF ' NH.NM NH NF ' NF ' NM Xét N
F 'H và N
MF ' có: N chung; (cmt) NF ' H NM F '( . c g.c) NH NF '
NHF ' NF 'M (các góc tương ứng) (2)
Lại có tứ giác OMEN nội tiếp (câu a) nên 4 điểm ,
O M , E, N cùng thuộc một đường tròn(3) Tứ giác OENF ' có 0 0 0
OEN OF ' N 90 90 180 nên là tứ giác nội tiếp,do đó 4 điểm ,
O E, N, F ' cùng thuộc một đường tròn (4)
Từ (3) và (4) suy ra 5 điểm ,
O M , E, N, F ' cùng thuộc một dường tròn suy ra tứ giác
MENF ' nội tiếp nên 0
NEM NF ' M 180 5 Từ (1), (2), (5) suy ra 0
NHE NHF ' NEM NF 'M 180
E,H,F ' thẳng hàng hay F 'là giao điểm của EH với nửa đường tròn (O)
F F ' Tứ giác NEOF nội tiếp
NEF NOF (cùng chắn cung NF) VĨNH PHÚC
Câu 7. (3,0 điểm) Cho đường tròn (O) và điểm A nằm ngoài đường tròn O.Từ điểm
Akẻ hai tiếp tuyến AB và AC đến O(B,C là các tiếp điểm). Kẻ đường kính BD của Trang 122
đường tròn O.Đường thẳng đi qua O vuông góc với đường thẳng AD và cắt A , D BC
lần lượt tại K, .
E Gọi I là giao điểm của OA và BC.
a) Chứng minh rằng các tứ giác ABOC, AIKE nội tiếp đường tròn
b) Chứng minh rằng OI.OA OK.OE
c) Biết OA 5c ,
m đường tròn O có bán kính R 3c .
m Tính độ dài đoạn thẳng BE ĐÁP ÁN Câu 7. B I A O K C D E
a) Chứng minh rằng các tứ giác ABOC, AIKE nội tiếp đường tròn Vì A ,
B AC là các tiếp tuyến của O nên 0
OBA OCA 90 0 0 0 O BA O
CA 90 90 180 OBAC là tứ giác nội tiếp
Vì OB OC R, AB AC (tính chất hai tiếp tuyến cắt nhau)
OAlà trung trực của BC OA BC tại I
Xét tứ giác AIKE có : 0
AIE AKE 90
AIKE là tứ giác nội tiếp (tứ giác có hai đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau)
b) Chứng minh OI.OA OK.OE
Vì AIKE là tứ giác nội tiếp cmt O IK O
EA (góc và góc trong tại đỉnh đối diện). Xét O IK và O EAcó: A
OE chung;OIK OE ( A cmt) O IK O E ( A g.g) Trang 123 OI OK
OI.OA OK.OE(dfcm) OE OA
c) Tính độ dài đoạn thẳng BE
Vì OA là trung trực của BC(cmt) OA BC Xét O
AB vuông tại B, đường cao BI ta có: 2 2 OB 3 9 2
OB OI.OA OI
cm (hệ thức lượng trong tam giác vuông) OA 5 5 2 9 144 144 2 2 2 2
BI OB OI 3
(Định lý Pytago) BI 2,4(cm) 5 25 25
Ta có BD là đường kính của O;3cm nên BD 6cm
Áp dụng định lý Pytago trong tam giác vuông OAB ta có: 2 2 2 2 2
AB OA OB 5 3 16 AB 4cm
Áp dụng định lý Pytago trong tam giác ABDta có: 2 2 2 2 2
AD AB BD 4 6 52 AD 52 2 13 cm Xét ODK và A DB có: ADB 0
chung; OKD ABD 90 OD AD O DK A
DB(g.g) OK AB O . D AB 3.4 6 OK (cm) AD 2 13 13
Áp dụng hệ thức lượng trong tam giác vuông OAK ta có : 2 6 289 17 2 2 2 2
AK OA OK 5 AK cm 13 13 13 0 Xét O AK và O BI có: I OK chung; O KA O IE 90 OK OI O AK O
EI(g.g)
(hai cặp cạnh tương ứng tỉ lệ) AK EI 17 9 . AK.OI 13 5 EI 5,1(cm) OK 6 13
Vậy BE BI IE 2, 4 5,1 7,5(c ) m YÊN BÁI (KHÔNG CÓ)
-----------------------------------------END----------------------------------------
-NGUYỄN ĐÌNH PHÚC (TP.HCM)- Trang 124