Ứng dụng tích phân bội trong bài toán lưu lượng và lực nâng Môn Quản trị TCDN | Trường Học Viện nông nghiệp Việt Nam

1) Bài 1.
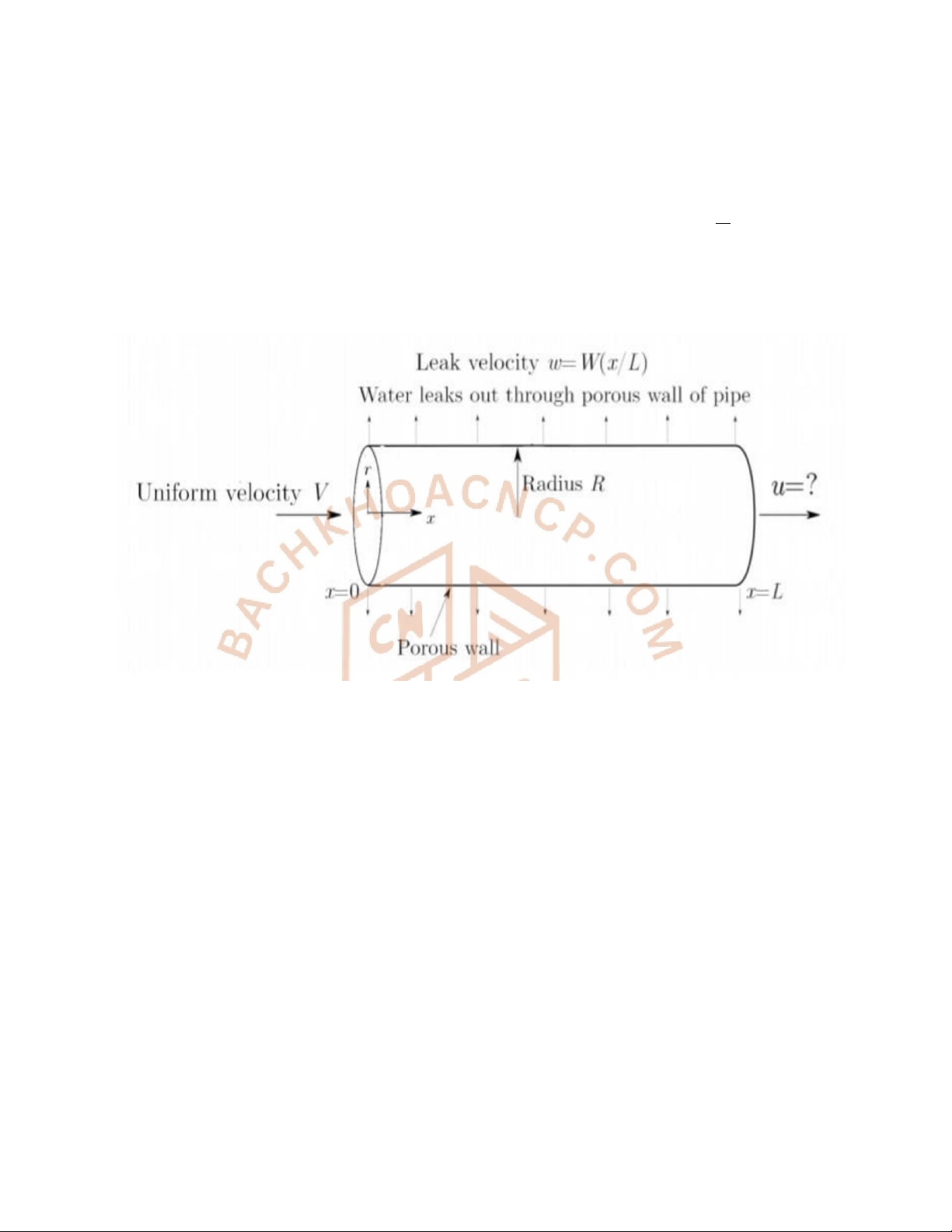
Có một ống nước hình trụ có bán kính R=0.2m và chiều dài L=10m. Nước chảy
qua đường ống với vận tốc v(r) được mô tả bởi hàm số v (r )=2−r2( m ) với 0 ≤ r s ≤ R.
Tính lưu lượng nước Q chảy qua đường ống trong 1 giây.
Phân tích bài toán: Theo đề bài, ta cần tính toán lưu lượng nước Q chảy qua đường
ống trong 1 giây, sử dụng tích phân mặt loại hai.
Thiết lập mô hình toán học:
Lưu lượng nước Q được tính bằng tích phân mặt loại hai như sau: ❑
Q=∬v (r ) dA S Trong đó:
Q là lưu lượng nước (m ¿¿ 3/ s)¿
S là bề mặt của đường ống (mặt trụ).
v(r) là vận tốc nước tại điểm có khoảng cách từ r từ tâm đường ống (m/s).
dA là diện tích phần tử mặt nhỏ trên bề mặt S. Chia nhỏ và tính toán:
Ta có thể chia nhỏ bề mặt S thành các phần tử mặt nhỏ hình chữ nhật có diện tích
dA = dr dz, với dr là chiều dài vi sai theo phương trục r và dz là chiều dài vi sai theo phương trục z.
Vận tốc nước tại điểm có khoảng cách r từ tâm đường ống được mô tả bởi hàm số
v (r )=2−r2
Do đó, lưu lượng nước Q được tính toán như sau: R L R L
Q=∫∫ v (r ) dr dz=∫∫ 2−r2 dr dz 0 0 0 0
Tích phân từng phần 2 lần: R r 3 L Q=∫2 r − ∣ dz 0 3 0 R L3 L3 z R ¿∫ ∣ 2 L− dz=2 Lz− 3 3 0 0
¿ 2 LR− L3 R 3
Thay số R=0.2 và L=10 vào biểu thức Q, ta được: 103 .0,2 3 Q=2.10.0,2− =62,67 m / s 3
Kết luận: Vậy lượng nước Q chảy qua đường ống trong một giây xấp xỉ 62,67 m3/ s 2) Bài 2. Giả sử:
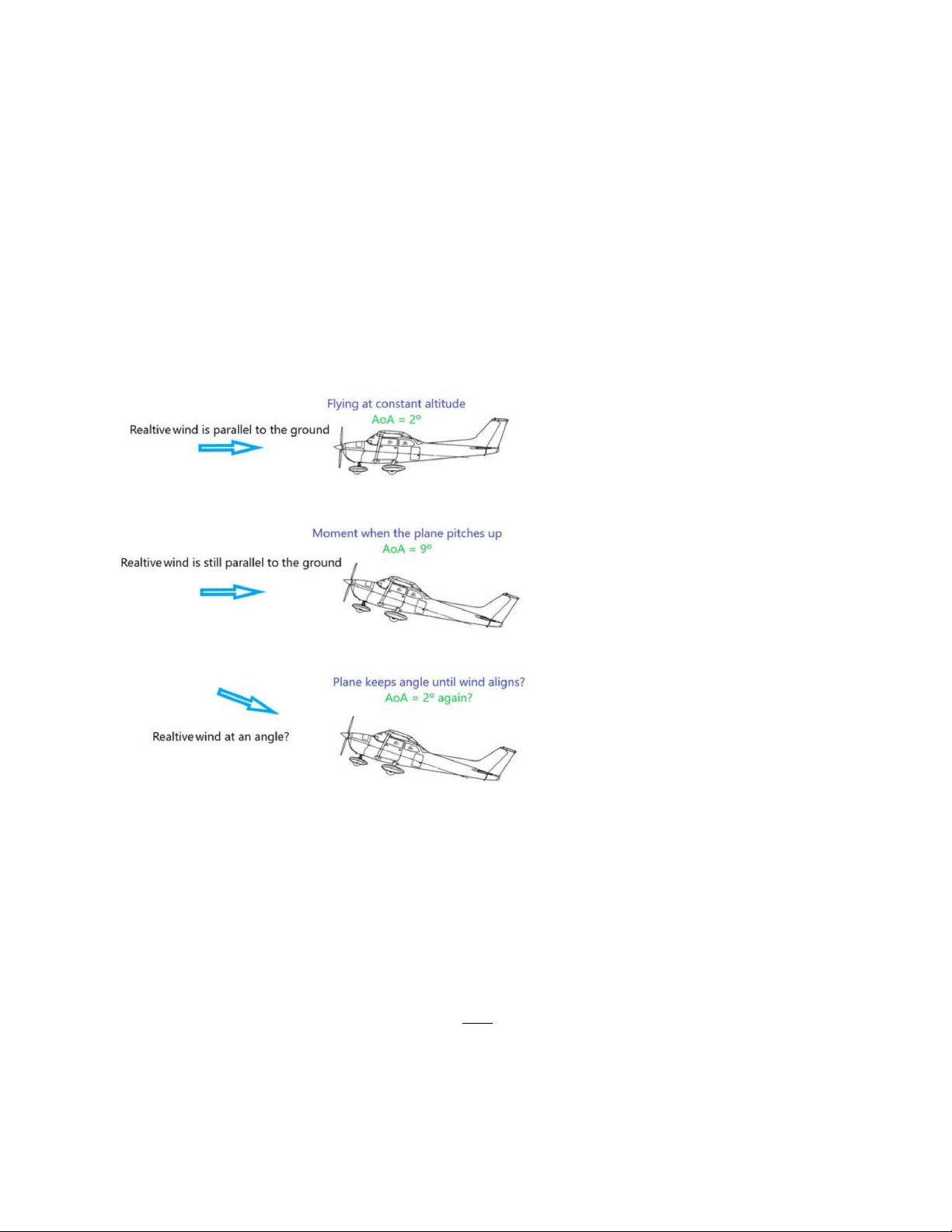
Cánh máy bay hình thang có diện tích bề mặt S = 20 m² và dây cung AB dài l = 5
m. Cánh máy bay di chuyển trong không khí với vận tốc v = 100 m/s theo hướng AB.
Góc nghiêng của cánh máy bay so với phương ngang là α = 15°. Mật độ không khí ρ = 1.2 kg/m³.
Tính toán lực nâng FL tác dụng lên cánh máy bay.
Phân tích bài toán: theo đề bài, ta cần tính toán lực nângFL tác dụng lên cánh máy
bay, sử dụng khái niệm thông lượng và tích phân mặt loại hai.
Thiết lập mô hình toán học: Lực nâng FLtác dụng lên cánh máy bay được tính
bằng tích phân mặt loại hai như sau: ❑ pv2 F =∬ sinαdA L 2 S Trong đó:
FLlà lực nâng tác dụng lên cánh máy bay (N).
p là mật độ không khí (kg/m³).
v là vận tốc cánh máy bay (m/s).
α là góc nghiêng của cánh máy bay so với phương ngang (rad).
dA là diện tích phần tử mặt nhỏ trên bề mặt S. Chia nhỏ và tính toán:
Ta có thể chia nhỏ bề mặt S thành các phần tử mặt nhỏ hình tam giác có diện tích
dA = ½ * dr * dz, với dr là chiều dài vi sai theo phương trục r và dz là chiều dài vi sai theo phương trục z.
Góc nghiêng của cánh máy bay tại điểm có khoảng cách r từ tâm đường ống được
mô tả bởi hàm α(r) = 15° = π/12.
Do đó, lực nâng F đượ L c tính toán như sau:
Kết luận: Lực nâng FLtác dụng lên cánh máy bay xấp xỉ 31058.29 N. 3) Bài 3:
Xác định khối lượng của một quả cầu kim loại rỗng có dạng nửa hình cầu với bán
kính R bằng 2 mét. Mật độ khối lượng của quả cầu thay đổi tuyến tính theo khoảng cách
từ tâm đến mặt phẳng, với p(x, y, z) = k(r), trong đó k là hằng số và r là khoảng cách từ
điểm (x, y, z) đến tâm của quả cầu.
• Quả cầu kim loại rỗng có dạng nửa hình cầu với bán kính R = 2 mét.
• Mật độ khối lượng của quả cầu thay đổi tuyến tính theo khoảng cách từ tâm đến mặt phẳng.
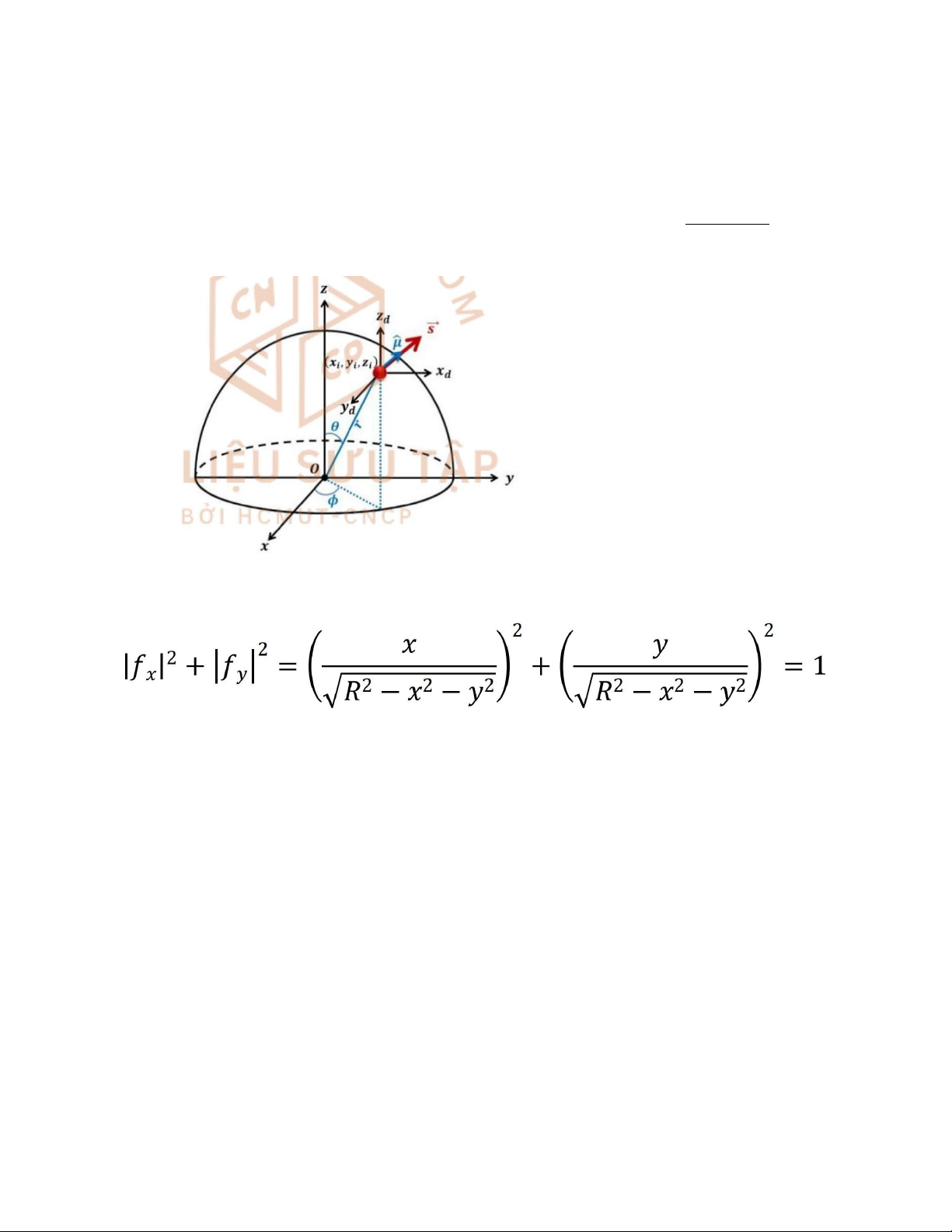
• Phương trình mô tả mặt phẳng của nửa hình cầu là z=√ R2−x2− y2
• Hằng số k thể hiện mật độ khối lượng trung bình của quả cầu.
Tính toán yếu tố Jacobian: Trong đó:
M là khối lượng của quả cầu kim loại (kg).
p(x, y, z) = k(r) là hàm mật độ khối lượng (kg/m³).
S là mặt phẳng của nửa hình cầu.
∣f ∣2 +∣f ∣2=1 là yếu tố Jacobian. x y
dA là phần tử diện tích vô cùng nhỏ trên mặt phẳng S.
Chuyển đổi sang hệ tọa đồ cầu:
+ Do tính đối xứng của nửa hình cầu, ta có thể sử dụng hệ tọa độ cầu để đơn giản hóa tích phân.
+ Thay đổi biến x, y, z thành θ, φ, r.
Biểu diễn dA theo hệ tọa độ cầu: dA=r 2sin (φ )d θd φ .
Thiết lập ranh giới tích phân:
+ 0 ≤ θ ≤ 2π (cho toàn bộ góc quay)
+ 0 ≤ φ ≤ π/2 (cho nửa hình cầu)
+ 0 ≤ r ≤ R (cho bán kính của nửa hình cầu)
Đánh giá tích phân mặt: π 2 π 2 R
M =∫∫∫k (r ) r2 sin ( φ¿¿¿) dθd φdr ¿¿¿ 0 0 0 π 2 R
¿ 2 π k ∫∫r3 sin (φ) d θd φ 0 0 π π 2 k R4 π ¿ ∫ k R4 sin (φ) d θ= 4 2 0 π k R4
Kết luận: Khối lượng M của quả cầu kim loại rỗng là 2