




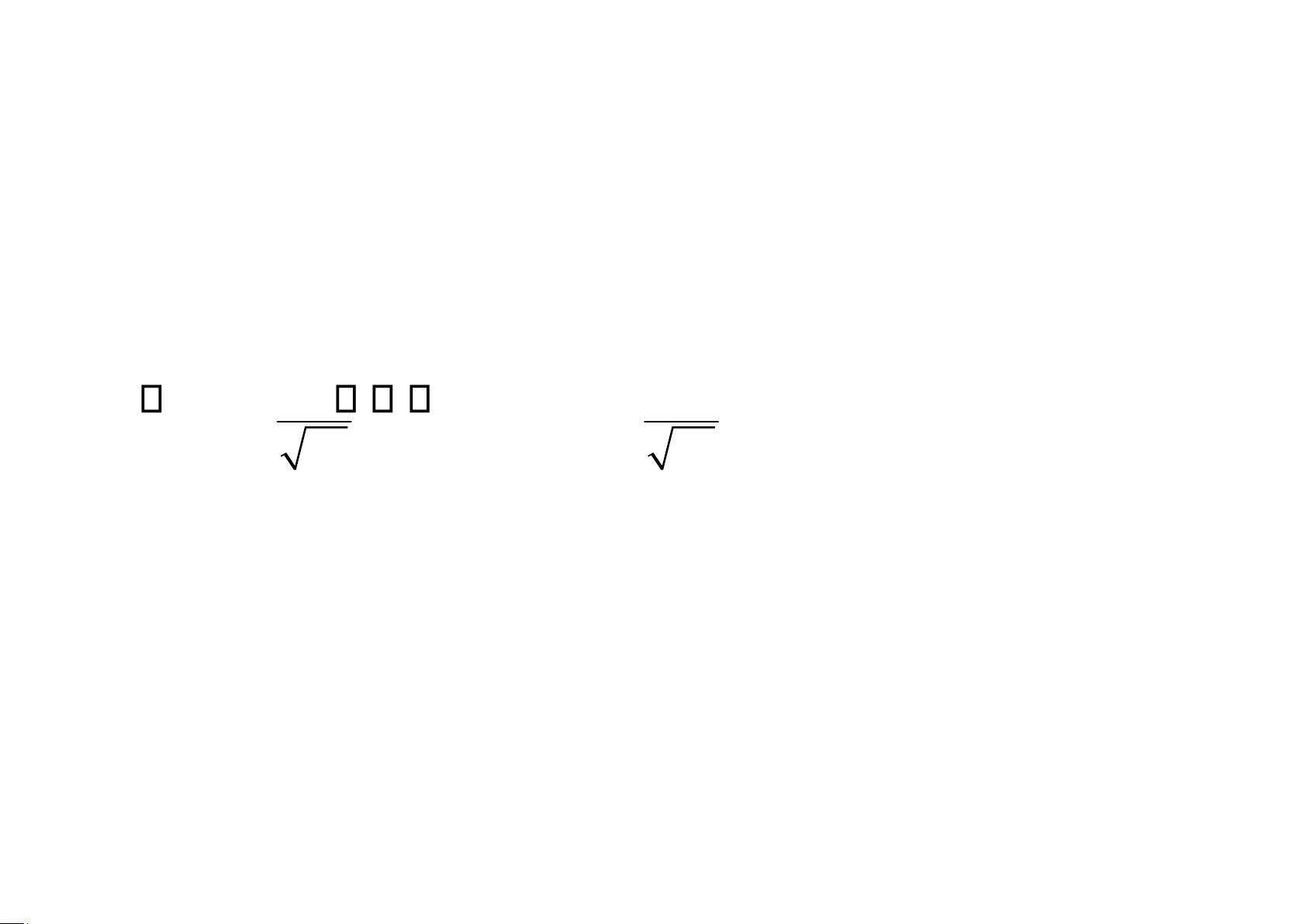
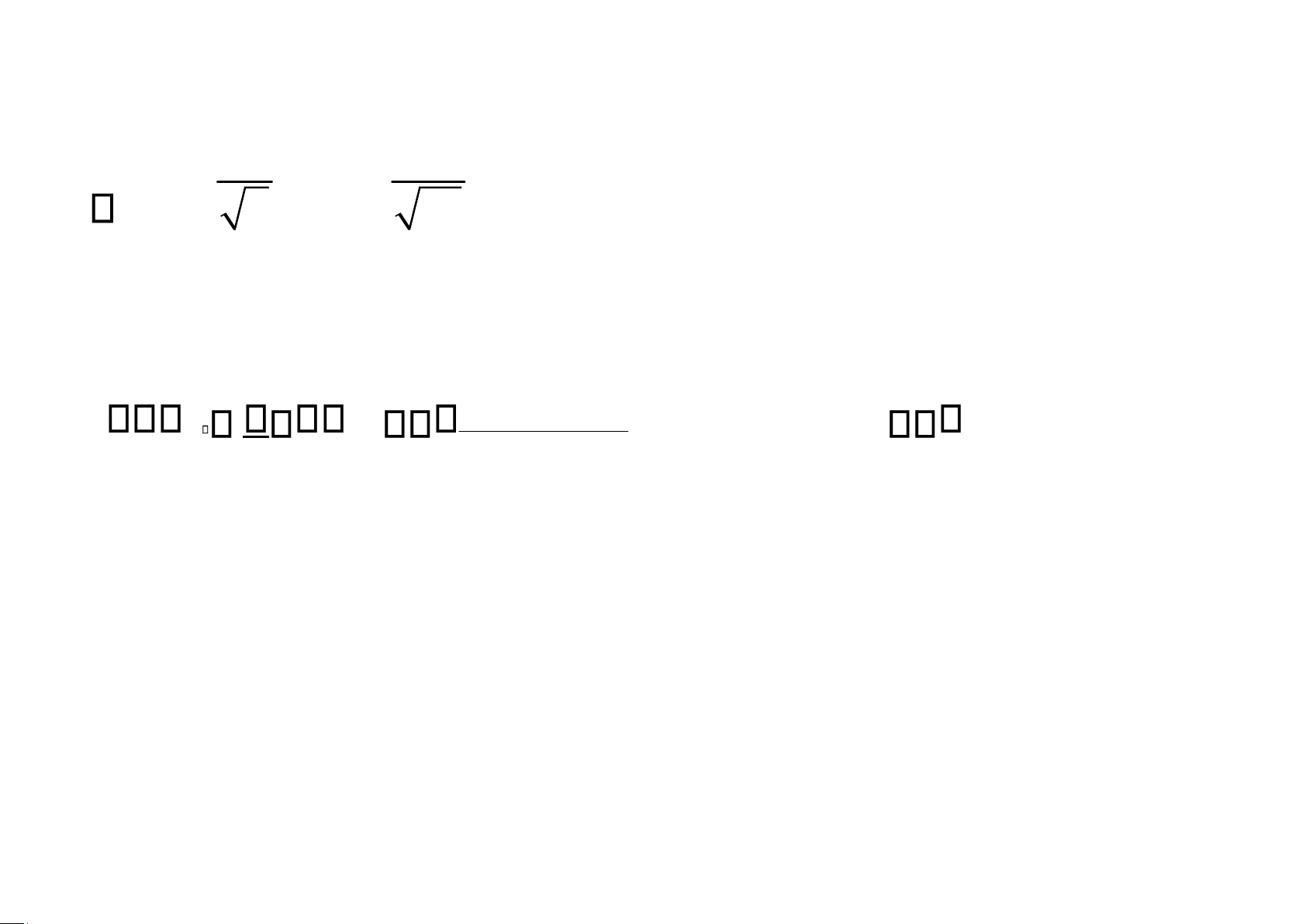


Preview text:
lOMoAR cPSD| 58478860
§6: BÀI TOÁN ƯỚC LƯỢNG TRUNG BÌNH Các nội dung chính:
• Ước lượng điểm và ước lượng khoảng.
• Ước lượng khoảng cho một kỳ vọng. lOMoAR cPSD| 58478860
ĐẶT VẤN ĐỀ X là chiều cao
trung bình của nam thanh niên
Việt Nam từ độ tuổi 22-26. Hãy
ước lượng giá trị của . +) Thực hành: - Lấy mẫu. - Tính:
*) trung bình mẫu x®ước lượng điểm của
*) khoảng (a,b) chứa ®ước lượng khoảng của 1.1ƯỚC LƯỢNG ĐIỂM: lOMoAR cPSD| 58478860
ĐỊNH NGHĨA 1.1 Ước lượng điểm của một tham số ˆ
tổng thể nào đó là một giá trị đơn của một thống kê ˆ .
VD 1.1:Giả sử X là biến ngẫu nhiên với trung bình tổng thể . Lấy mẫu . Khi đó,
là ước lượng điểm của lOMoAR cPSD| 58478860
Cùng một mẫu ngẫu nhiên cùng cỡ,có thể xây dựng
nhiều thống kê ˆ khác nhau để ước lượng tham số ˆ
tổng thể . Để đưa ra kết luận về chất lượng ta dựa vào các tiêu chuẩn:
- Ước lượng không chệch - Ước lượng hiệu quả:
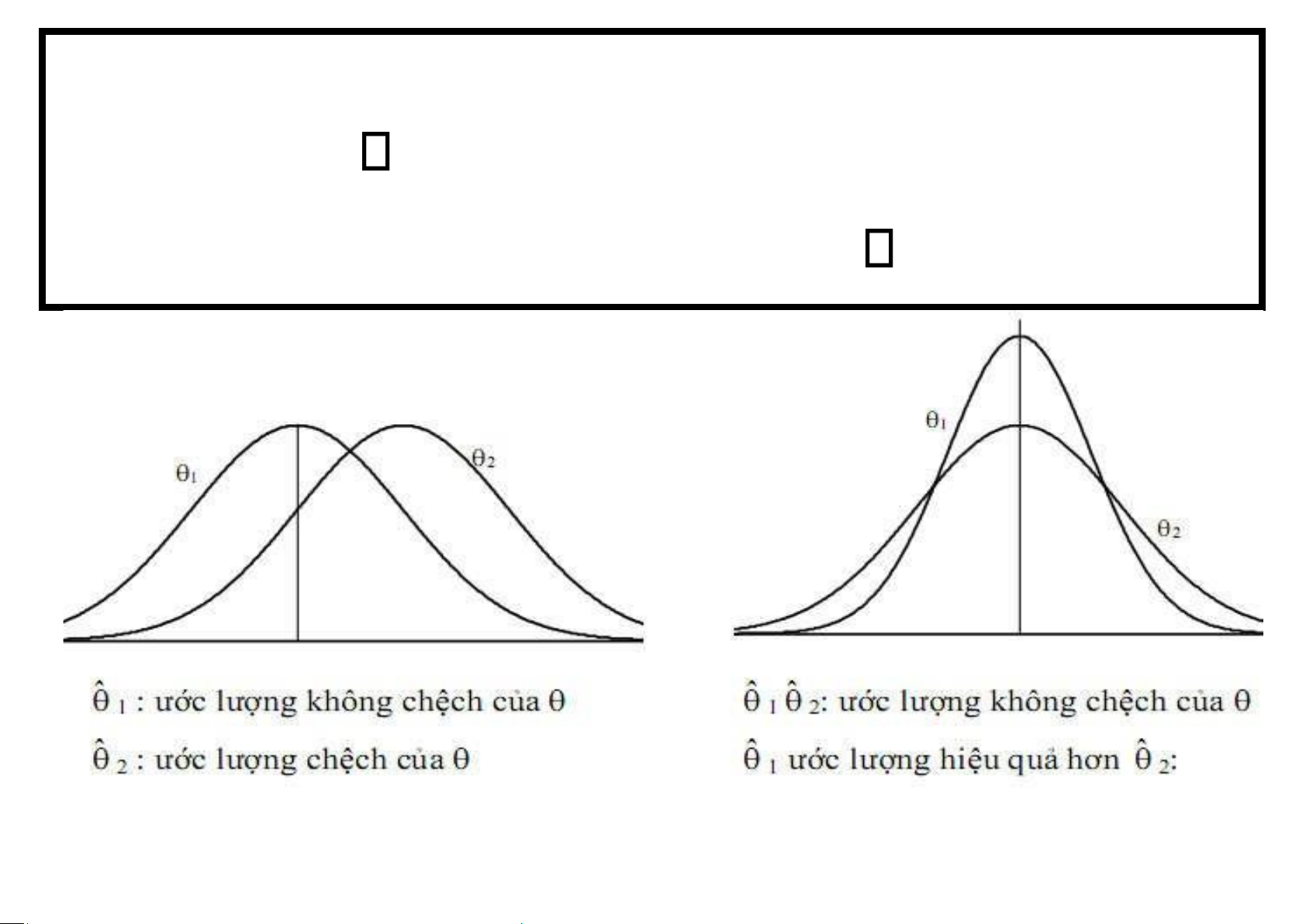
a) Ước lượng không chệch: lOMoAR cPSD| 58478860
ĐỊNH NGHĨA 1.2Thống kê ˆ được gọi là ước lượng
không chệch của tham số nếu thỏa mãn: ˆ E ˆ Nhận xét:
x là ước lượng không chệch của
s2 là ước lượng không chệch của 2
b) Ước lượng hiệu quả: lOMoAR cPSD| 58478860
ĐỊNH NGHĨA 1.2 Xét tất cả các ước lượng không chệch
của tham số , ước lượng có phương sai nhỏ nhất
được gọi là ước lượng hiệu quả của . HẠN CHẾ: lOMoAR cPSD| 58478860
* Khi kích thước mẫu bé thì ước lượng điểm sai lệch
khá nhiều so với giá trị tham số cần ước lượng
* không thể đánh giá được khả năng mắc sai lầm khi ước lượng
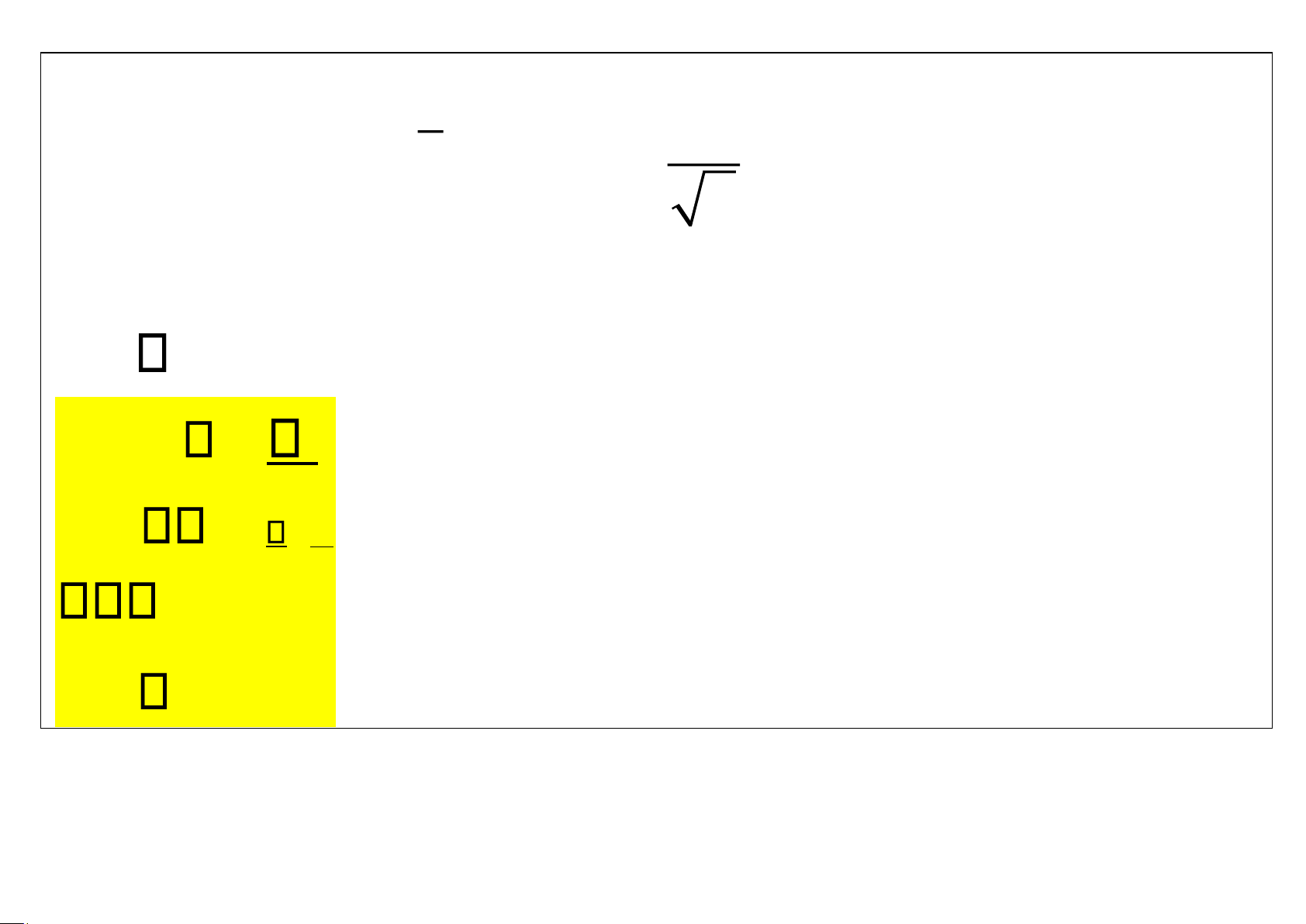
1.2. ƯỚC LƯỢNG KHOẢNG:
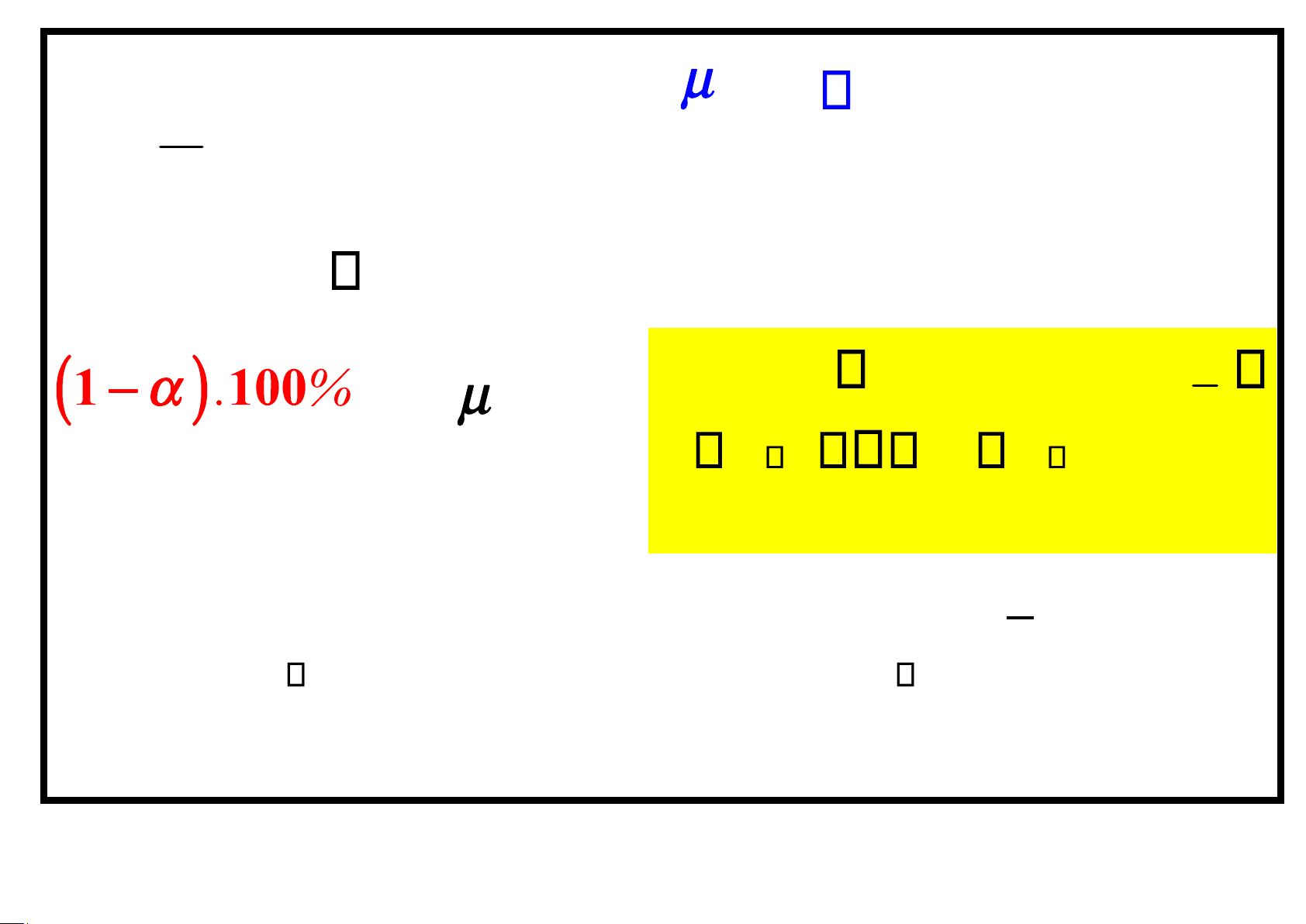
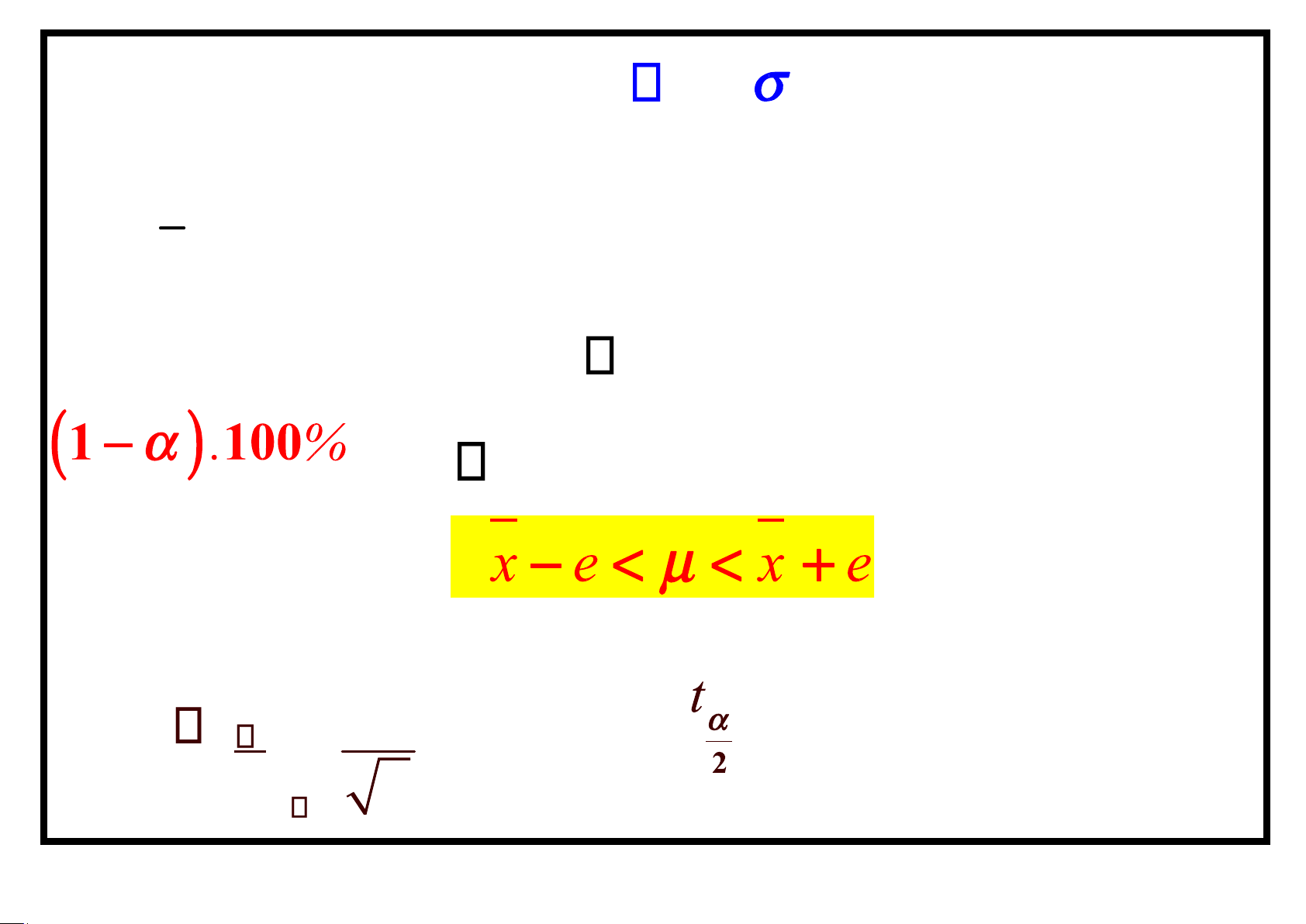
Ước lượng khoảng của tham số tổng thể là một khoảng có dạng ˆL ˆU sao cho: lOMoAR cPSD| 58478860 P( ˆL ˆU ) 1 ˆ ˆ
*)( L , U ) gọi là khoảng tin cậy (1 ).100% *)1
gọi là độ tin cậy của ước lượng *) ˆU
ˆL gọi là độ dài khoảng tin cậy
a. Ước lượng cho một trung bình: lOMoAR cPSD| 58478860
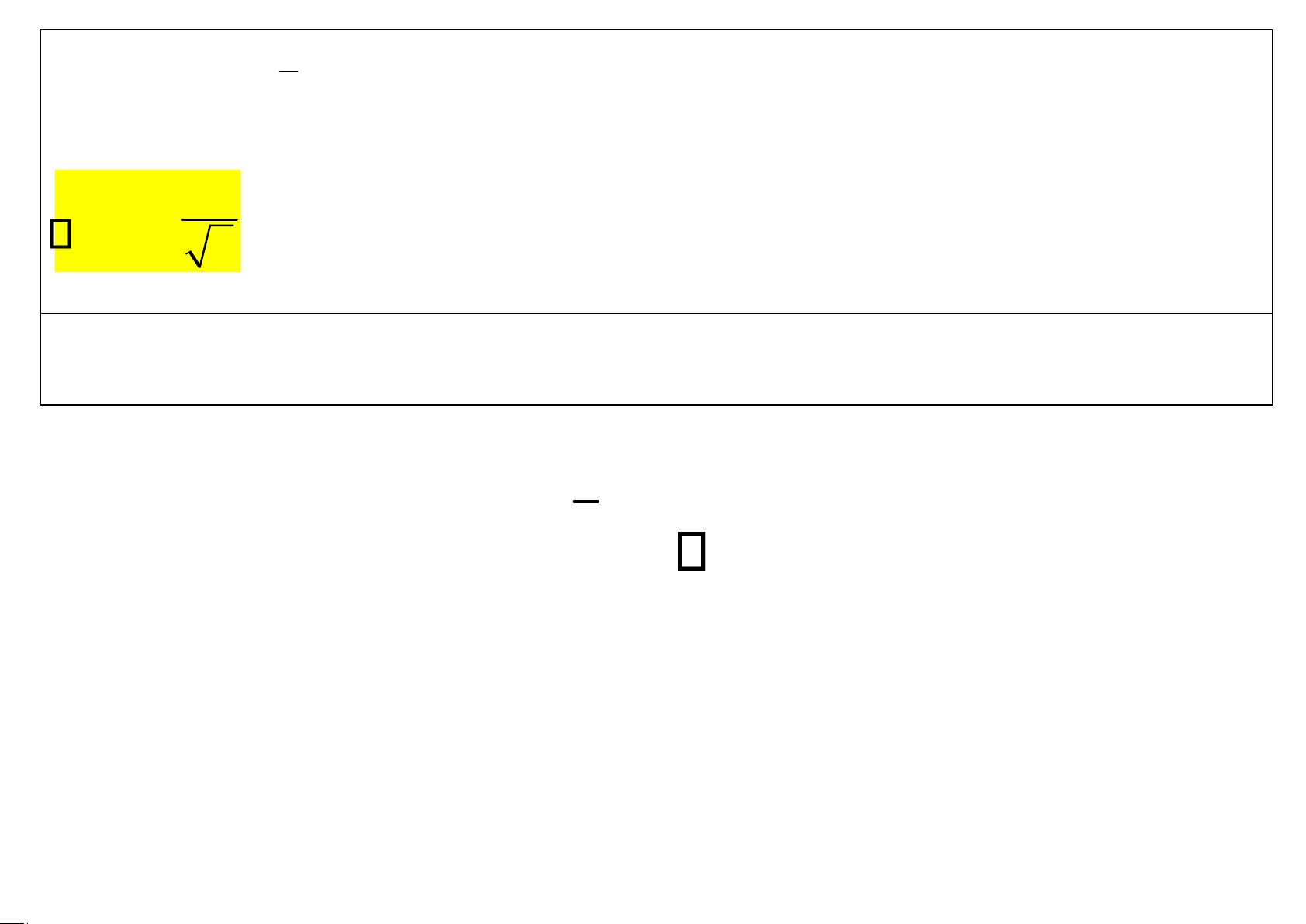
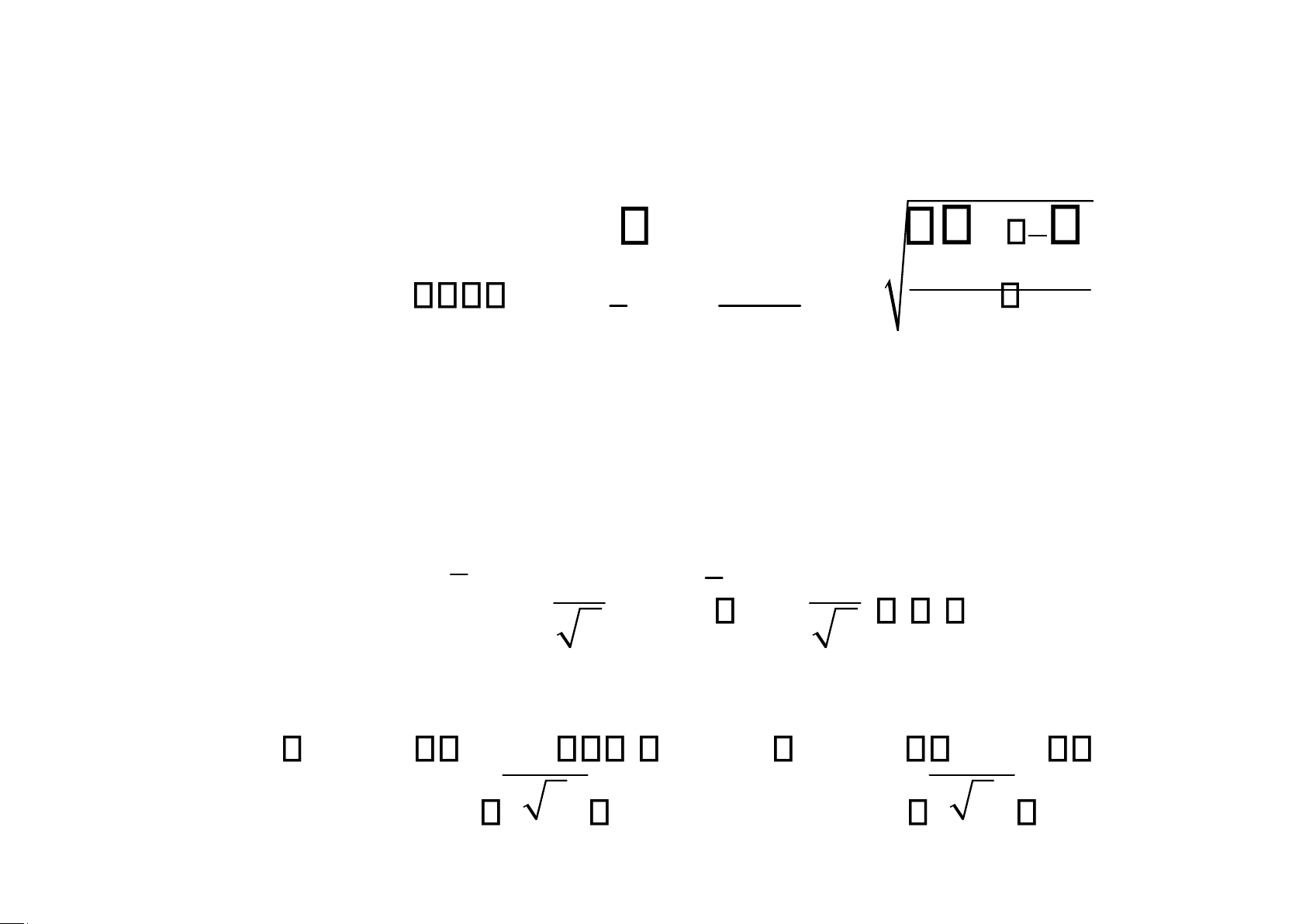
TH1. Khoảng tin cậy cho , khi đã biết:
Nếu X là trung bình của một mẫu ngẫu nhiên cỡ n từ
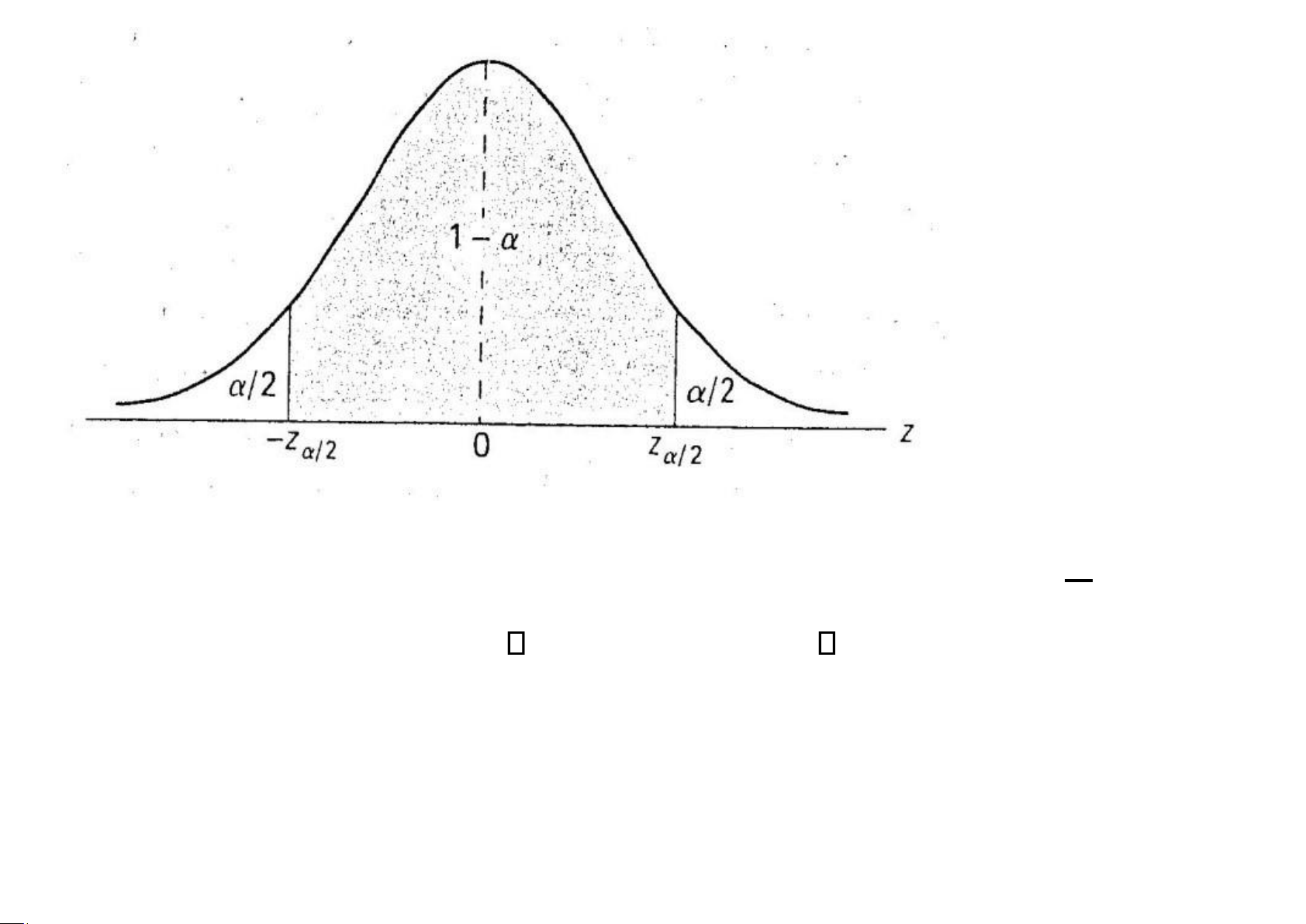
tổng thể với 2 đã biết, thì khoảng tin cậy cho là: x z / 2 x z /2 n n a
trong đó z /2 được xác định bởi P(Z>z /2) = ; 2
Khi đó: P(- zα/2< Z < zα/2) = 1-a . lOMoAR cPSD| 58478860 a Tra bảng A3: P(Zz /2) = 1 - 2 lOMoAR cPSD| 58478860 s
Sai số ước lượng: |x - m|
VD 1.2:Hàm lượng kẽm trung bình thu được khi đo ở
36 địa điểm khác nhau trên một dòng sông là 2,6
gam/ml. Biết rằng độ lệch chuẩn của tổng thể là 0,3. Hãy lOMoAR cPSD| 58478860
tìm khoảng tin cậy 95% cho hàm lượng kẽm trung bình trong dòng sông đó. Lời giải:
- Từ giả thiết: n = 36, x = 2.6, s= 0.3, a)100% = 95% a= 0.05.
- Đây là bài toán ước lượng cho 1 kỳ vọng, s đã biết - Khoảng tin cậy 95% cho m là s s x z a/2 m x za/2 n n lOMoAR cPSD| 58478860 Do a/ 2 = 0.025 nên P(Z > za/2) = 0.025
Suy ra P(Z < za/2) = 1 - a/2= 0.975 Tra bảng A3: za/2 = 1.96.
2.6 (1.96) 0.3 m 2.6 (1.96) 0.3 36 36 2.5 lOMoAR cPSD| 58478860 s ỊNH LÝ 1.1:Để |x - m| n
(1 – )100% , thì cỡ mẫu tối thiểu cần dùng là: z 2( là
m tròn đến số nguyên tiếp theo). n e/2 lOMoAR cPSD| 58478860
Định lý: Nếu x được sử dụng để ước lượng điểm cho m, thì với độ tin cậy
(1 – a )100% ta cho rằng sai số của ước lượng không vượt quá: s =za/2 n 14
Downloaded by Lam Lam (mynmy9x@gmail.com)
VD 1.2:( tiếp) Nếu ta muốn với khoảng tin cậy 95% ,
sai số của ước lượng x cho không vượt quá 0,05, thì
cỡ mẫu tối thiểu phải là bao nhiêu? lOMoAR cPSD| 58478860 Sai so? s =za/2 =1.96. 0.3 = 0.098 n 36 n = z = (1.96)(0.3) =138.3 /2 2 0.05 2 lOMoAR cPSD| 58478860
TH2. Khoảng tin cậy cho khi chưa biết (cỡ mẫu nhỏ n < 30)
Nếu x,s là trung bình và độ lệch chuẩn mẫu từ tổng thể
có phân phối chuẩn với chưa biết, khoảng tin cậy cho là: s với e t
trong đóđược xác định bởi ,n 1 n lOMoAR cPSD| 58478860 2 a
P(T > ta)= , với n–1 bậc tự do. 2 2 lOMoAR cPSD| 58478860 16
Chú ý:Tra bảng A.4 để tính t /2.
VD 1.3:Số lít axit sunfuric trong các bình đựng được xác
định thông qua 7 thùng là
9,8 10,2 10,4 9,8 10,0 10,2 và 9,6 Tìm
khoảng tin cậy 95% cho lượng axit sunfuric trung bình
trong các bình chứa, giả thiết các giá trị đo có phân phối chuẩn. lOMoAR cPSD| 58478860 Lời giải
- Đặt X là biến ngẫu nhiên với số liệu thực nghiệm như trên. xi xi x 2 - Từ giả thiết: a= 0.05, =n 7, x= =10.0, s= 1 = 0.283 n n
- Đây là bài toán ước lượng một kỳ vọng khi chưa biết s , cỡ mẫu n <30.
- Sử dụng Bảng A.4, ta tìm được t0.025 = 2.447 với số bậc tự do là 6. - Do
đó khoảng tin cậy 95% cho mlà x ta/2 s m x ta/2 s n n 10.0 (2.477) 0.283 m 10.0 (2.477) 0.283 7 7