Vở bài học môn Toán 12 phần Hình học

Vở bài học môn Toán 12 phần Hình học được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

18 9 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 1

HỌC SINH: ………………………………………………

LỚP:…………………………………..

HÌNH

HỌC

TOÁN

VỞ BÀI HỌC

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 2

HÌNH HỌC 12-CHƯƠNG I

BÀI 1: KHÁI NIỆM VỀ KHỐI ĐA DIỆN

A. KHỞI ĐỘNG

H1: Rubic này có hình dạng gì?

……………………………………………………………………………………………………

B – HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC:

I.KHỐI LĂNG TRỤ VÀ KHỐI CHÓP

a) Tiếp cận:

H1: Hãy nêu tên các hình sau:

……………………………………………………………………………………………………

H2: Quan sát và dự đoán tên các hình vẽ sau:

Vậy thế nào là khối lăng trụ? Khối chóp?

b) Hình thành kiến thức :

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 3

Lưu ý:

Tên của khối lăng trụ hay khối chóp được đặt theo tên của hình lăng trụ hay hình chóp giới hạn

nó.

Ta gọi đỉnh, cạnh, mặt bên, mặt đáy, cạnh bên, cạnh đáy,… của một hình lăng trụ (hình chóp,

hay hình chóp cụt) theo thứ tự là đỉnh, cạnh, mặt bên, mặt đáy, cạnh bên, cạnh đáy,…của khối

lăng trụ (khối chóp, hay khối chóp cụt) tương ứng.

Điểm không thuộc khối lăng trụ được gọi là điểm ngoài của khối lăng trụ, điểm thuộc khối lăng

trụ nhưng không thuộc hình lăng trụ ứng với khối lăng trụ đó được gọi là điểm trong của khối

lăng trụ. Điểm trong hay điểm ngoài của khối chóp, khối chóp cụt cũng được định nghĩa tương

tự.

c) Ví dụ:

Hình 1

Hình 2

II. KHÁI NIỆM VỀ HÌNH ĐA DIỆN VÀ KHỐI ĐA DIỆN

1. Khái niệm về hình đa diện:

( HÌNH 1) ( HÌNH 2) ( HÌNH 3)

Khối lăng trụ ( khối chóp, khối chóp cụt ) là phần không gian được giới hạn bởi một hình

lăng trụ ( hình chóp, hình chóp cụt ), kể cả hình lăng trụ ( hình chóp, hình chóp cụt ) ấy.

Hình đa diện là hình được tạo bởi một số hữu

hạn các đa giác thoả mãn hai tính chất:

+ Hai đa giác phân biệt chỉ có thể hoặc không

có điểm chung nào hoặc chỉ có một đỉnh chung

hoặc chỉ có một cạnh chung.

+ Mỗi cạnh của đa giác nào cũng là cạnh chung

của đúng hai đa giác.

Lưu ý: -Mỗi đa giác như thế gọi là một mặt

của hình đa diện

-Các định, cạnh của các đa giác ấy cũng là

các định, cạnh của hình đa diện

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 4

➢VD1:

Câu hỏi 1: Trong các hình 1, 2, 3, hình nào là hình đa diện? vì sao?

Câu hỏi 2: Hình lập phương có bao nhiêu cạnh, bao nhiêu đỉnh?

Hình 4 có bao nhiêu cạnh, bao nhiêu đỉnh?

……………………………………………………………………………………………………

2. Khái niệm về khối đa diện:

c)Ví dụ:

➢VD3:Cho khối chóp S.ABCD có O là giao điểm AC và

BD,

I là trung điểm SO, M là trung điểm SA, N đối xứng với I

qua M. Hãy chỉ ra trong các điểm O, I, M, N, điểm nào là

điểm trong, điểm nào là điểm ngoài của khối chóp S.ABCD?

……………………………………………………………………………………………………

➢VD4:Trong các hình sau, hình nào là khối đa diện?

Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện

đó.

Lưu ý:

-Những điểm không thuộc khối đa diện được

gọi là điểm ngoài của khối đa diện.

-Những điểm thuộc khối đa diện nhưng không

thuộc hình đa diện giới hạn khối đa diện ấy

được gọi là điểm trong của khối đa diện.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 5

Hình a Hình b Hình c

Hình d Hình e

Hình f

➢VD5:Trong các mệnh đề sau, mệnh đề nào đúng?

A. Mỗi hình đa diện có ít nhất bốn đỉnh.

B. Mỗi hình đa diện có ít nhất ba cạnh.

C. Số đỉnh của một hình đa diện lớn hơn hoặc bằng số cạnh của nó.

D. Số mặt cảu một hình đa diện lớn hơn hoặc bằng số cạnh của nó.

III. HAI ĐA DIỆN BẰNG NHAU:

1. Phép dời hình trong không gian

a)Phép tịnh tiến theo

vectơ : Trong không

gian cho vectơ .

Phép biến hình mỗi

điểm M thành điểm M’

b) Phép đối xứng qua mặt phẳng (P),

là phép biến hình biến mỗi điểm thuộc

(P) thành chính nó, biến mỗi điểm M

không thuộc (P) thành điểm M’ sao

cho (P) là mặt phẳng trung trực của

MM’.

c) Phép đối xứng tâm O, là phép biến hình

biến điểm O thành chính nó, biến mỗi

điểm M khác O thành điểm M’ sao cho O

là trung điểm của MM’.

d) Phép đối xứng qua đường

thẳng (hay phép đối xứng qua

trục ), là phép biến hình biến

mỗi điểm thuộc đường thẳng

thành chính nó, biến mỗi điểm M

Trong không gian, quy tắc đặt

tương ứng mỗi điểm M với mỗi

điểm M’ xác định duy nhất được

gọi là phép biến hình trong không

gian.

Phép biến hình trong không gian

được gọi là phép dời hình nếu nó

bảo toàn khoảng cách giữa hai

điểm tùy ý.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 6

2. Hai hình bằng nhau:

Định nghĩa: Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.

Đặc biệt: Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.

IV/ PHÂN CHIA VÀ LẮP GHÉP KHỐI ĐA DIỆN:

a) Tiếp cận: Quan sát các hình sau và trả lời câu hỏi tương ứng.

H: Ta có thể phân chia mô hình trên thành những khối hình hộp hay không?

H: Tìm mối liên hệ giữa

hình a và hình b

Quan sát các mảnh ghép

trong các mô hình trên hãy cho biết chúng có bao nhiêu

điểm trong chung với nhau?

……………………………………………………………………………………………………

b) Hình thành kiến thức: Nếu khối đa điện (H) là hợp của hai khối đa diện

( )

và

( )

sao

cho

( )

và

( )

không có chung điểm trong nào thì ta nói có thể chia khối đa diện (H)

thành hai khối đa diện

( )

và

( )

, hay có thể lắp ghép hai khối đa điện

( )

và

( )

thành khối đa diện (H).

c) Ví dụ:

➢VD1: Cho khối tứ diện ABCD. Trên đoạn AD lấy điểm I khác A và D. Mặt phẳng (IBC)

chia khối tứ diện đã cho thành những khối tứ diện nào?

Hình 1

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 7

……………………………………………………………………………………………………

…………………………………………………………………………………………………

➢VD2: Sử dụng đúng hai mặt phẳng khác nhau để chia khối tứ diện thành bốn khối tứ diện.

……………………………………………………………………………………………………

…………………………………………………………………………………………………

C) HOẠT ĐỘNG LUYỆN TẬP VÀ VẬN DỤNG:

Bài tập tự luận:

Bài 1. Hãy phân chia khối lăng trụ thành ba khối tứ diện.

Bài 2. ( Bài tập 3/sgk/trang 12) Hãy phân chia một khối lập phương thành năm khối

tứ diện

Bài tập trắc nghiệm:

Câu 1: [ Mức độ 1] Số các đỉnh hoặc số các mặt bất kì hình đa diện nào cũng:

A. lớn hơn 4. B. lớn hơn hoặc bằng 5.

C. lớn hơn 5. D. lớn hơn hoặc bằng 4.

Câu 2: [ Mức độ 1] Vật thể nào dưới đây không phải là khối đa diện?

A. . B. . C. . D.

Câu 3: [ Mức độ 1] Hình đa diện bên có bao nhiêu cạnh?

. B.

. C.

23.

24.

Câu 4: [ Mức độ 1] Gọi

là số hình đa diện trong bốn hình trên. Tìm

.ABC A B C

  

. ' ' ' 'ABCD A B C D

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 8

4n =

. B.

2n =

. C.

1n =

. D.

3n =

Câu 6: [ Mức độ 1] Cho khối chóp ngũ giác

.S ABCDE

. Mặt phẳng

( )

SAD

chia khối chóp đó thành

A. Hai khối chóp tứ giác.

B. Một khối tứ diện và một khối lăng trụ.

C. Một khối tứ diện và một khối chóp tứ giác.

D. Hai khối tứ diện.

Câu 7: [ Mức độ 1] Trong các mệnh đề sau, mệnh đề nào đúng?

Số các cạnh của hình đa diện luôn luôn:

A. lớn hơn

. B. lớn hơn

C. lớn hơn hoặc bằng

. D. lớn hơn hoặc bằng

Câu 8: [ Mức độ 1] Hình lập phương có tất cả bao nhiêu mặt phẳng đối xứng?

mặt phẳng. B.

mặt phẳng.

mặt phẳng. D.

mặt phẳng.

Câu 9: [ Mức độ 2] Một hình đa diện có các mặt là những tam giác thì số mặt

và số cạnh

của đa

diện đó thoả mãn

32CM=

. B.

2CM=+

. C.

MC

. D.

32MC=

Câu 10: [ Mức độ 2] Cho một đa diện có

đỉnh và mỗi đỉnh là đỉnh chung của đúng

cạnh. Chọn

mệnh đề đúng trong các mệnh đề sau:

là một số chẵn. B.

chia cho

dư

chia hết cho

. D.

là một số lẻ.

Câu 11: [ Mức độ 2] Biết rằng khối đa diện mà mỗi mặt đều là hình ngũ giác. Gọi

là số cạnh của khối

đa diện đó, lúc đó ta có:

là số chia hết cho 3. B.

là số chẵn.

là số lẻ. D.

là số chia hết cho

Câu 12: [ Mức độ 2] Trong các mệnh đề sau, mệnh đề nào đúng?

A. Số đỉnh và số mặt của một hình đa diện luôn bằng nhau.

B. Tồn tại hình đa diện có số đỉnh và số mặt bằng nhau.

C. Tồn tại một hình đa diện có số cạnh bằng số đỉnh.

D. Tốn tại một hình đa diện có số cạnh và mặt bằng nhau.

Câu 13: [ Mức độ 2] Mặt phẳng

( )

AB C



chia khối lăng trụ

.ABC A B C

  

thành các khối đa diện nào?

A. Một khối chóp tam giác và một khối chóp tứ giác.

B. Hai khối chóp tam giác.

C. Một khối chóp tam giác và một khối chóp ngũ giác.

D. Hai khối chóp tứ giác.

Câu 14: [ Mức độ 3] Một hình lập phương có cạnh

4cm

. Người ta sơn đỏ mặt ngoài của hình lập phương

rồi cắt hình lập phương bằng các mặt phẳng song song với các mặt của hình lập phương thành

hình lập phương nhỏ có cạnh

1cm

. Có bao nhiêu hình lập phương có đúng một mặt được sơn

đỏ?

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 9

. B.

. C.

. D.

Câu 15: [ Mức độ 3] Cho tứ diện

.ABCD

Lấy một điểm

giữa

và

điểm

giữa

và

bằng

mặt phẳng:

( )

MCD

và

( )

NAB

, ta chia khối đa diện thành

khối tứ diện

,,,AMCN AMND AMCD BMCN

. B.

, , ,AMCN AMND BMCN BMND

, , ,AMCD AMND BMCN BMND

. D.

, , ,BMCD BMND AMCN AMDN

Câu 16: [Mức độ 1] Hình nào trong các hình sau không phải là hình đa diện?

A. Hình chóp. B. Hình vuông. C. Hình lập phương. D. Hình lăng trụ.

Câu 17: [Mức độ 1] Cho khối chóp có là

– giác

( )

3;n n N

. Mệnh đề nào sau đây đúng?

A. Số cạnh của khối chóp bằng

1.n +

. B. Số mặt của khối chóp bằng

2.n

C. Số đỉnh của khối chóp bằng

1.n +

. D. Số mặt của khối chóp bằng số đỉnh của nó.

Câu 18: [Mức độ 1] Hình nào dưới đây không phải là một khối đa diện?

A. . B. . C. D.

Câu 19: [Mức độ 2] Cho đa diện

( )

có tất cả các mặt đều là tam giác. Khẳng định nào sau đây đúng?

A Tổng các mặt của

( )

luôn là một số chẵn.

B. Tổng các mặt của

( )

luôn gấp đôi tổng số đỉnh của

( )

C. Tổng số các cạnh của

( )

là một số không chia hết cho 3.

D. Tổng số các cạnh của

( )

luôn gấp đôi tổng số các mặt của

( )

Câu 20: [Mức độ 1] Cho khối lăng trụ tam giác đều

. ' ' 'ABC A B C

. Về phía ngoài khối lăng trụ này ta

ghép thêm một khối lăng trụ tam giác đều bằng với khối lăng trụ đã cho, sao cho hai khối lăng

trụ có chung một mặt bên. Hỏi khối đa diện mới lập thành có mấy cạnh?

A. 9. B. 12. C. 15. D. 18

Câu 21: [Mức độ 1] Phân chia khối lăng trụ

.ABC A B C

  

bởi hai mặt phẳng

( )

AB D



và

( )

AB D



được các khối nào sau đây?

A. Khối chóp tứ giác

.A BDD B



và khối tứ diện

ABDB



B. Khối chóp tứ giác

.A BDD B



và khối tứ diện

ADD B



C. Khối chóp tứ giác

.A BDD B



và khối tứ diện

AA B D

  

D. Ba khối tứ diện

ABDB



ADD B



và

.AA B D

  

Câu 22: [Mức độ 1] Một hình hộp đứng có đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt

phẳng đối xứng?

mặt phẳng. B.

mặt phẳng. C.

mặt phẳng. D.

mặt phẳng.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 10

Câu 23: [Mức độ 1] Hình đa diện nào dưới đây không có tâm đối xứng?

A. Tứ diện đều. B. Bát diện đều. C. Hình lập phương. D. Lăng trụ lục giác đều.

Câu 24: [Mức độ 1] Một hình chóp có

cạnh có bao nhiêu mặt?

. B.

. C.

. D.

Câu 25: [Mức độ 2] Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối

xứng?

A. 3 mặt phẳng. B. 4 mặt phẳng. C. 6 mặt phẳng

D. 9 mặt phẳng.

……………………………………………………………………………………………………

…………………………………………………………………………………………………

……………………………………………………………………………………………………

…………………………………………………………………………………………………

……………………………………………………………………………………………………

…………………………………………………………………………………………………

……………………………………………………………………………………………………

…………………………………………………………………………………………………

……………………………………………………………………………………………………

…………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 11

HÌNH HỌC 12 – CHƯƠNG 1

§2. KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA DIỆN ĐỀU

A. PHẦN KIẾN THỨC CHÍNH

I. ĐỊNH NGHĨA CỔ ĐIỂN

1. Định nghĩa

* VD MỞ ĐẦU:

Câu hỏi:

1. Lấy hai điểm

,MN

thuộc khối lập phương. Có nhận xét gì về vị trí của đoạn thẳng

và

khối lập phương?

……………………………………………………………………………………………………

2. Xét hình vẽ dưới đây. Có nhận xét gì về vị trí của đoạn thẳng

và khối đa diện

( )

……………………………………………………………………………………………………

- VD về khối đa diện lồi:

- VD về khối đa diện không phải là đa diện lồi:

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 12

- VD về khối đa diện đều:

* ĐN:

- Khối đa diện

( )

được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của

( )

luôn

thuộc

( )

. Khi đó đa diện xác định

( )

được gọi là đa diện lồi.

- Khối Đa diện đều là khối đa diện lồi có tính chất sau đây:

a) Mỗi mặt của nó là một đa giác đều

cạnh.

b) Mỗi đỉnh của nó là đỉnh chung của đúng

mặt.

Khối đa diện đều như vậy được gọi là khối đa diện đều loại

 

;.pq

* Chú ý:

- Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối

với mỗi mặt phẳng chứa một mặt của nó.

2. Ví dụ

*VD1:

Hình 1

Hình 2

Hình 3

Hình 4

- Trong các hình trên, các hình biểu diễn của khối đa diện lồi là hình: ………………………….

- Trong các hình trên, các hình biểu diễn của khối đa diện không phải đa diện lồi là hình: ……

*VD2:

Gọi tên các khối đa diện đều sau:

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 13

……………

……………..

……………

……………..

…………….

*VD3:

Trong các khối đa diện đều sau hãy xác định số cạnh ở mỗi mặt và mỗi đỉnh của nó là đỉnh chung

của bao nhiêu mặt ?

……………

……………..

……………

……………..

…………….

II. TÍNH CHẤT

1. Định lý

* ĐL: chỉ có năm loại khối đa diện đều. Đó là loại

 

3;3

, loại

 

4;3

, loại

 

3;4

, loại

 

5;3

, loại

 

3;5

Loại

 

3;3

: khối tứ diện đều;

 

4;3

: khối lập phương;

 

3;4

: khối bát diện đều;

 

5;3

: khối mười

hai mặt đều;

 

3;5

: khối hai mươi mặt đều.

2. Ví dụ

*VD1:

Cho các đa diện sau: tứ diện đều, hình chóp tứ giác đều, lăng trụ tam giác đều, lập phương, bát

diện đều.

- Trong các đa diện trên, đa diện đều gồm:………………………………………………………

- Trong các đa diện trên, đa diện không phải đa diện đều gồm:…………………………………

*VD2:

Hoàn thành bảng sau:

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 14

Tên đa diện

Loại

Số mặt

Số đỉnh

Số cạnh

Tứ diện đều

…………

…………..

………….

……………

………………………

 

4;3

…………..

………….

……………

………………………

…………..

……………

………………………

…………..

……………

………………………

…………..

……………

*VD3:

Tính diện tích toàn phần của đa diện đều trên (hình vẽ) biết cạnh của đa diện đó là

10 .cm

……………………………………………………………………………………………………

B. LUYỆN TẬP

I. Chữa bài tập SGK

Bài 1 trang 18 -SGK:

Cắt bìa theo mẫu dưới đây (h.123), gấp theo đường kẻ, rồi dán các mép lại để được các hình tứ diện đều,

hình lập phương và hình bát diện đều.

II. Bài tập trắc nghiệm

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 15

Câu 1. [Mức độ 1] Khẳng định nào sau đây là đúng?

A. Tâm các mặt của một hình lập phương là các đỉnh của một hình lập phương.

B. Tâm các mặt của một hình tứ diện đều là các đỉnh của một hình tứ diện đều.

C. Tâm các mặt của một hình tứ diện đều là các đỉnh của một hình lập phương.

D. Tâm các mặt của một hình lập phương là các đỉnh của một hình tứ diện đều.

Câu 2. [Mức độ 1] Khối bát diện đều là khối đa diện đều loại nào ?

 

3;4

. B.

 

3;3

. D.

 

4;3

. C.

 

5;3

Câu 3. [Mức độ 2] Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ

Khối tứ diện

đều

Khối lập

phương

Bát diện đều

Hình 12 mặt đều

Hình 20

mặt đều

Mệnh đề nào sau đây đúng?

A. Mọi khối đa diện đều có số mặt là những số chia hết cho 4.

B. Khối lập phương và khối bát diện đều có cùng số cạnh.

C. Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.

D. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh.

Câu 4. [Mức độ 2] Số mặt phẳng đối xứng của khối đa diện đều

 

4;3

là

Câu 5. [Mức độ 2] Cho hình đa diện đều loại

 

4;3

cạnh

. Gọi

là tổng diện tích tất cả các mặt của

hình đa diện đó. Mệnh đề nào dưới đây đúng?

4.Sa=

6.Sa=

8.Sa=

10 .Sa=

BÀI TẬP VẬN DỤNG

Câu 1. [Mức độ 1] Trong các hình sau, hình nào không phải là đa diện lồi

A.Hình 1

B.Hình 2

C.Hình 3

D.Hình 4

Câu 2. [Mức độ 1] Trong các hình dưới đây, hình nào không phải là đa diện lồi?

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 16

A. Hình

( )

. B. Hình

( )

. C. Hình

( )

III

. D. Hình

( )

Câu 3. [Mức độ 2] Tâm tất cả các mặt của một hình lập phương là các đỉnh của hình nào trong các hình

sau đây?

A. Bát diện đều. B. Tứ diện đều. C. Lục giác đều. D. Ngũ giác đều.

Câu 4. [Mức độ 2] Chọn khẳng định đúng

A. Tâm tất cả các mặt của một hình lập phương là các đỉnh của một hình lập phương.

B. Tâm tất cả các mặt của một hình tứ diện đều là các đỉnh của một hình tứ diện đều.

C. Tâm tất cả các mặt của một hình tứ diện đều là các đỉnh của một hình lập phương.

D. Tâm tất cả các mặt của một hình lập phương là các đỉnh của một hình tứ diện đều.

Câu 5. [Mức độ 3] Trung điểm các cạnh của một tứ diện đều tạo thành

A. Các đỉnh của một hình tứ diện đều.

B. Các đỉnh của một hình bát diện đều.

C. Các đỉnh của một hình mười hai mặt đều.

D. Các đỉnh của một hình hai mươi mặt đều.

Câu 6. [Mức độ 2] Trong các mệnh đề sau, mệnh đề nào sai?

A. Tồn tại khối tứ diện là khối đa diện đều.

B. Tồn tại khối lăng trụ đều là khối đa diện đều.

C. Tồn tại khối hộp là khối đa diện đều.

D. Tồn tại khối chóp tứ giác đều là khối đa diện đều.

Câu 7. [Mức độ 2] Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ

Khối tứ diện

đều

Khối lập

phương

Bát diện đều

Hình 12 mặt

đều

Hình 20 mặt đều

Mệnh đề nào sau đây đúng?

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 17

A. Mọi khối đa diện đều có số mặt là những số chia hết cho 4.

B. Khối lập phương và khối bát diện đều có cùng số cạnh.

C. Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.

D. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh.

Câu 8. [Mức độ 2] Khối đa diện đều loại

 

5;3

, diện tích một mặt của khối đa diện đó là

. Tổng

diện tích các mặt của khối đa diện đó bằng:

36m

. B.

24m

. C.

18m

. D.

60m

Câu 9. [Mức độ 2] Cho hình bát diện đều cạnh

. Gọi

là tổng diện tích tất cả các mặt của hình bát

diện đó. Tính

23Sa=

. B.

43Sa=

. C.

8Sa=

. D.

3Sa=

Câu 10. [Mức độ 1] Trong các khối đa diện sau: Khối tứ diện, khối lập phương, khối chóp tứ giác, khối

hộp, có mấy khối đa diện lồi?

. B.

. C.

. D.

Câu 11. [Mức độ 1] Khối đa diện

( )

được gọi là khối đa diện lồi nếu

A. Đoạn thẳng nối hai điểm bất kỳ của

( )

nằm về hai phía đối với

( )

B. Đoạn thẳng nối hai điểm bất kỳ của

( )

không thuộc

( )

C. Miền trong của nó luôn nằm về 2 phía đối với mỗi mặt phẳng chứa 1 mặt của nó.

D. Đoạn thẳng nối hai điểm bất kỳ của

( )

luôn thuộc

( )

Câu 12. [Mức độ 1] Chọn khẳng định nào đúng?

A. Khối đa diện đều loại

 

;pq

là khối đa diện đều có

mặt,

đỉnh.

B. Khối đa diện đều loại

 

;pq

là khối đa diện lồi thỏa mãn mỗi mặt của nó là đa giác đều

cạnh và mỗi đỉnh của nó là đỉnh chung của đúng

mặt.

C. Khối đa diện đều loại

 

;pq

là khối đa diện đều có

cạnh,

mặt.

D. Khối đa diện đều loại

 

;pq

là khối đa diện lồi thỏa mãn mỗi đỉnh của nó là đỉnh chung của

đúng

mặt và mỗi mặt của nó là một đa giác đều

cạnh.

Câu 13. [Mức độ 1] Một hình lăng trụ có

cạnh thì có tất cả bao nhiêu đỉnh?

. B.

. C.

. D.

Câu 14. [Mức độ 2] Trong các mệnh đề sau, mệnh đề nào đúng?

A. Khối chóp tứ giác đều là khối đa diện đều loại

 

3;3

B. Khối bát diện đều không phải là khối đa diện lồi.

C. Lắp ghép hai khối hộp luôn được một khối đa diện lồi.

D. Tồn tại hình đa diện có số đỉnh bằng số mặt.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 18

Câu 15. [Mức độ 2] Một người thợ thủ công làm mô hình lồng đèn bát diện đều, mỗi cạnh của bát diện

đó được làm từ các que tre độ dài

8cm

. Hỏi người đó cần ít nhất bao nhiêu mét que tre để làm

100 cái đèn (giả sử mối nối giữa các que tre có độ dài không đáng kể)?

9600

. B.

. C.

6400

. D.

……………………………………………………………………………………………………

…………………………………………………………………………………………………

……………………………………………………………………………………………………

…………………………………………………………………………………………………

……………………………………………………………………………………………………

…………………………………………………………………………………………………

……………………………………………………………………………………………………

…………………………………………………………………………………………………

……………………………………………………………………………………………………

…………………………………………………………………………………………………

……………………………………………………………………………………………………

…………………………………………………………………………………………………

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 19

HÌNH HỌC 12 – CHƯƠNG 1

§3. KHÁI NIỆM VỀ THỂ TÍCH KHỐI ĐA DIỆN

A. PHẦN KIẾN THỨC CHÍNH

I. ĐỊNH NGHĨA CỔ ĐIỂN

1. Định nghĩa

* VD MỞ ĐẦU: Cho khối lập phương có cạnh bằng

1cm

(có thể tích

1cm

). Các khối đa diện được ghép

từ các khối lập phương có cạnh bằng

1cm

(hình vẽ).

a) So sánh thể tích hai khối lập phương (hình vẽ).

b) Tính thể tích

của khối đa diện (hình vẽ).

……………………………………………………………………………………………………

* Định nghĩa: Thể tích của khối đa diện (H) là một số dương duy nhất V

(H)

thoả mãn các tính chất sau:

a) Nếu (H) là khối lập phương có cạnh bằng 1 thì V

(H)

= 1.

b) Nếu hai khối đa diện (H

), (H

) bằng nhau thì V

(H1)

=V(

c) Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H

), (H

) thì V

(H)

= V

(H1)

+ V

(H2)

* Chú ý:

• V

(H)

cũng được gọi là thể tích của hình đa diện giới hạn khối đa diện (H).

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 20

• Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị.

2. Ví dụ

*VD1: Một bậc tam cấp được xếp từ các khối đá hình lập phương có cạnh bằng bằng

1cm

như hình vẽ.

Hãy tính thể tích của khối tam cấp?

……………………………………………………………………………………………………

*VD2: Cho khối lập phương

.ABCD A B C D

   

có cạnh bằng

( )

1 m

.Tính thể tích khối lăng trụ

..ABC A B C

  

……………………………………………………………………………………………………

II. TÍNH CHẤT

1. Định lý

* Định lý: Thể tích của một khối hộp chữ nhật bằng tích ba kích thước của nó.

V abc



* Định lý: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là

V Bh=

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 21

* Định lý: Thể tích khối chópcó diện tích đáy B và chiều cao h là

V Bh=

* Hệ quả: Thể tích của một khối lập phương cạnh a là

.Va

2. Ví dụ

*VD1: Cho hình hộp chữ nhật

.ABCD A B C D

   

có đáy là hình vuông, cạnh bên bằng

và đường chéo

.Tínhthểtích hình hộp chữ nhật này.

……………………………………………………………………………………………………

*VD2: Cho lăng trụ tam giác

. ' ' 'ABC A B C

có đáy là tam giác đều cạnh

, góc giữa cạnh bên và mặt

đáy bằng

. Hình chiếu của

lên

( )

ABC

là trung điểm

của

. Tính thể tích khối lăng

trụ.

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 22

……………………………………………………………………………………………………

*VD3: Cho hình chóp tam giác

.S ABC

có đáy

ABC

là tam giác vuông tại

AB a=

60ACB =

, cạnh

bên

vuông góc với mặt đáy và

hợp với mặt đáy một góc

45

. Tính thể tích

của khối

chóp

.S ABC

……………………………………………………………………………………………………

*VD4: Cho hình chóp S.ABCD có đáy là hình vuông ABCD. Mặt bên SAB là tam giác đều có đường cao

23SH a=

và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp

S.ABCD.

……………………………………………………………………………………………………

*VD4: Cho hình lăng trụ tam giác

. ' ' 'ABC A B C

.Gọi

và

lần lượt lừ trung điểm của các cạnh

'AA

và

'BB

.Đường thẳng

cắt đường thẳng

''CA

tại



. Đường thẳng

cắt đường thẳng

''CB

tại

.Gọi

là thể tích khối lăng trụ

. ' ' 'ABC A B C

a) Tính thể tích khối chóp

.C ABFE

theo

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 23

b) Gọi khối đa diện

( )

là phần còn lại của khối lăng trụ

. ' ' 'ABC A B C

sau khi cắt bỏ đi khối

chóp

.C ABFE

.Tính tỉ số thể tích của

( )

và của khối chóp

. ' ' 'C C E F

……………………………………………………………………………………………………

B. LUYỆN TẬP

I. Chữa bài tập SGK

Bài 1 trang 25 – SGK: Tính thể tích khối tứ diện đều cạnh a.

Bài 2 trang 25 – SGK: Tính thể tích khối bát điện đều cạnh a.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 24

Bài 4 trang 25- SGK: Cho hình chóp

.S ABC

. Trên các tia

, , SA SB SC

lần lượt lấy 3 điểm

', ', 'A B C

khác

. Chứng minh:

S A B C

S ABC

SA SB SC

V SA SB SC

. ' ' '

' ' '

..=

Chú ý: Công thức (1) chỉ vận dụng với chóp tam giác.

Hai trong 3 điểm

', ', 'A B C

có thể trùng với

,,A B C

. Khi đó ta có :

Nếu

'AA

ta có

S A B C

S ABC

SB SC

V SB SC

. ' ' '

Nếu

'AA

và

'BB

ta có

S A B C

S ABC

V SC

. ' ' '

Bài 5 trang 26- SGK: Cho

ABC

vuông cân ở

và

AB a

. Trên đường thẳng qua

và vuông góc với

ABC

lấy điểm

sao cho

CD a

. Mặt phẳng qua

vuông góc với

cắt

tại

và cắt

tại

. Tính thể tích khối tứ diện

CDFE

theo

II. Bài tập trắc nghiệm

Câu 1. [Mức độ 1] Thể tích hình lập phương cạnh

là

. B.

. C.

. D.

Câu 2. [Mức độ 1] Cho khối chóp có đáy là hình vuông cạnh

và chiều cao bằng

. Thể tích của

khối chóp đã cho bằng

. B.

. C.

. D.

Câu 3. [Mức độ 1] Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh

, cạnh bên

vuông góc với

đáy và thể tích của khối chóp đó bằng

. Tính cạnh bên

A. B. C. D.

Câu 4. [Mức độ 2] Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều cạnh

và

'2AA a=

.Thể tích của khối lăng trụ đã cho bằng

. B.

. C.

. D.

Câu 5. [Mức độ 2] Hình chóp

.S ABCD

đáy hình thoi,

2AB a=

, góc

BAD

bằng

120

. Hình chiếu vuông

góc của

lên

( )

ABCD

là

giao điểm của 2 đường chéo, biết

. Khi đó thể tích khối chóp

.S ABCD

là



Câu 6. [Mức độ 2] Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

, mặt bên

SAB

là tam

giác cân tại

và nằm trong mặt phẳng vuông góc với đáy; góc giữa

và mặt phẳng đáy bằng

. Tính thể tích khối chóp

.S ABCD

bằng:

3.a

2 3.a

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 25

. B.

. C.

. D.

Câu 7. [Mức độ 3] Cho hình chóp đều

.S ABC

, góc giữa mặt bên và mặt phẳng đáy

( )

ABC

bằng

khoảng cách giữa hai đường thẳng

và

bằng

. Thể tích của khối chóp

.S ABC

theo

bằng

. B.

. C.

. D.

Câu 8. [Mức độ 3] Cho hình lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình thoi cạnh

60ABC =

Chân đường cao hạ từ



trùng với tâm

của đáy

ABCD

; góc giữa mặt phẳng

( )

BB C C



với

đáy bằng

60

. Thể tích lăng trụ bằng:

. B.

. C.

. D.

Câu 9. [Mức độ 3] Cho hình chóp

.S ABCD

có đáy là hình thang vuông tại

và

AB AD a==

2CD a=

. Hình chiếu của đỉnh

lên mặt

( )

ABCD

trùng với trung điểm của

. Biết thể tích

tứ diện

SBCD

bằng

. Khoảng cách từ đỉnh

đến mặt phẳng

( )

SBC

là?

. B.

Câu 10. [Mức độ 4] Cho tứ diện

ABCD

có các cạnh

,,AB AC AD

đôi một vuông góc nhau;

6AB a=

7AC a=

và

4AD a=

. Gọi

,,M N P

tương ứng là trung điểm các cạnh

,,BC CD DB

. Tính thể

tích

của khối tứ diện

AMNP

7Va=

. B.

V =

. C.

V =

. D.

14Va=

C. BÀI TẬP T LUYỆN (phần này không làm PPT)

Câu 1.[Mức độ 1] Cho hình lăng trụ đứng có diện tích đáy là

3,a

độ dài cạnh bên bằng

. Thể tích

khối lăng trụ này bằng

. B.

. C.

. D.

Câu 2. [Mức độ 1] Cho khối chóp

.S ABC

có

vuông góc với đáy,

= 4SA

= 6AB

= 10BC

và

= 8CA

. Tính thể tích

của khối chóp

.S ABC

= 32V

. B.

= 192V

. C.

= 40V

. D.

= 24V

Câu 3. [Mức độ 2] Cho một hình chóp tam giác đều có cạnh đáy bằng

, góc giữa cạnh bên và mặt

phẳng đáy bằng

45 .

Thể tích khối chóp đó là

Câu 4. [Mức độ 2] Cho hình chóp

.S ABCD

đáy hình chữ nhật,

vuông góc đáy,

, 2AB a AD a==

Góc giữa

và đáy bằng

. Thể tích khối chóp là



Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 26

Câu 5.[Mức độ 2] Cho hình chóp

.S ABC

có

AC a=

2BC a=

120ACB =

, cạnh bên

vuông

góc với đáy. Đường thẳng

tạo với mặt phẳng

( )

SAB

góc

. Tính thể tích của khối chóp

.S ABC

105

. B.

105

. C.

105

. D.

105

Câu 6. [Mức độ 2] Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

. Biết

SAB

là tam giác

đều và nằm trong mặt phẳng vuông góc với mặt phẳng

( )

ABC

. Tính thể tích khối chóp

.S ABC

biết

AB a=

3AC a=



Câu 7. [Mức độ2] Lăng trụ đứng

. ’ ’ ’ABC A B C

có đáy

ABC

là tam giác vuông tại

, 2 , A BC a AB a==

Mặt bên

( )

’’BB C C

là hình vuông. Khi đó thể tích lăng trụ là

. B.

. C.

23a

. D.

Câu 8.[Mức độ 3] Cho hình lăng trụ

. ' ' 'ABC A B C

có đáy

ABC

là tam giác đều cạnh bằng

. Hình chiếu

vuông góc của

trên

( )

ABC

là trung điểm của

. Mặt phẳng

( )

''AA C C

tạo với đáy một góc

bằng

45

. Tính thể tích V của khối lăng trụ

. ' ' 'ABC A B C

V =

. B.

V =

. C.

V =

. D.

V =

Câu 9. [Mức độ 3] Cho hình chóp tứ giác

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

. Tam

giác

SAD

cân tại

và mặt bên

( )

SAD

vuông góc với mặt phẳng đáy. Biết thể tích khối chóp

.S ABCD

bằng

. Tính khoảng cách

từ

đến mặt phẳng

( )

SCD

ha=

. B.

ha=

. C.

ha=

. D.

ha=

Câu 10. [Mức độ 4] Cho hình chóp

.S ABCD

có đáy là hình bình hành. Gọi

là thể tích của khối chóp

.S ABCD

và

lần lượt là trung điểm của các đoạn thẳng

. Thể tích của

khối tứ diện

AMNP

bằng

. B.

. C.

. D.

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 27

HÌNH HỌC 12– CHƯƠNG 2

§1. KHÁI NIỆM VỀ MẶT TRÒN XOAY

I. SỰ TẠO THÀNH MẶT TRÒN XOAY

Quan sát các hình ảnh sau

Nếu dùng một mặt phẳng song song với đáy cắt những đồ vật này thì thiết diện tạo được là hình

gì?...........................................................................................................................................

I. SỰ TẠO THÀNH MẶT TRÒN XOAY

Trong không gian, cho mặt phẳng

( )

chứa đường thẳng



và đường

( )

. C

Khi quay

( )

quay

quanh



một góc

360

thì:

 Mỗi điểm

( )

MC

vạch ra một đường tròn tâm

O

và nằm trên mặt phẳng vuông góc với

.

 Đường

( )

sẽ tạo nên một hình được gọi là mặt tròn xoay.

+ Đường

( )

: Đường sinh của mặt tròn xoay.

+ Đường thẳng



: Trục của mặt tròn xoay.

ĐỒ VẬT NÀO SAU ĐÂY CÓ BỀ MẶT NGOÀI LÀ MẶT TRÒN XOAY?

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 28

II. MẶT NÓN TRÒN XOAY

1. ĐỊNH NGHĨA

Trong mp

( )

, cho hai đường thẳng

( )

và



cắt nhau tại điểm

và tạo thành góc nhọn



( )

0 90





Quay

( )

xung quanh



một góc

360

Đường thẳng

( )

sinh ra một hình gọi là mặt nón tròn xoay.

+ Đỉnh

+ Đường thẳng



: Trục

+ Đường thẳng

( )

: Đường sinh

+ Góc ở đỉnh



2.HÌNH NÓN TRÒN XOAY VÀ KHỐI NÓN TRÒN XOAY

a) Hình nón tròn xoay:

Hỏi: Khi quay

OIM

quanh

, cạnh

và

tạo thành hình gì?



tạo thành hình tròn tâm

, bán kính

– gọi là mặt đáy.

tạo thành một phần nón tròn xoay – gọi là mặt xung quanh.

Vậy hình nón hợp của hai phần: Mặt đáy và mặt xung quanh

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 29

Cho

OIM

vuông tại

Khi quay

OMI

xung quanh cạnh góc vuông

thì đường gấp khúc

OMI

tạo thành một hình gọi là hình nón tròn xoay.

* Gồm hai phần:

– Mặt đáy: Là hình tròn

( )

, IMI

– Phần mặt xung quanh: Là phần mặt tròn xoay sinh bởi

quay xung quanh

* Đặc điểm: – Đỉnh:

– Đường cao:

– Đường sinh:

b) Khối nón tròn xoay:

Phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình nón đó được gọi là khối

nón tròn xoay.

– Điểm ngoài: điểm không thuộc khối nón.

– Điểm trong: điểm thuộc khối nón nhưng không thuộc hình nón.

3. DIỆN TÍCH XUNG QUANH CỦA HÌNH NÓN TRÒN XOAY

a) Hình chóp nội tiếp hình nón tròn xoay

Một hình chóp được gọi là nội tiếp một hình nón nếu

 đáy của hình chóp là đa giác nội tiếp đường tròn đáy của hình nón

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 30

 và đỉnh của hình chóp là đỉnh của hình nón

Khi đó ta nói hình nón ngoại tiếp hình chóp

* Định nghĩa: Diện tích xung quanh của hình nón tròn xoay là giới hạn của diện tích xung quanh

của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.

b) Công thức tính diện tích xung quanh của hình nón tròn xoay:

S rl



trong đó:

: bán kính đáy

: độ dài đường sinh

Ghi nhớ: Tổng của diện tích xung quanh và diện tích đáy gọi là diện tích toàn phần

đátp xq y

S S S rl r



= + = +

4. THỂ TÍCH KHỐI NÓN TRÒN XOAY

a) Định nghĩa:

Thể tích khối nón tròn xoay là giới hạn của thể tích khối chóp đều nội tiếp khối nón đó khi số

cạnh đáy tăng lên vô hạn

b) Công thức tính thể tích khối nón tròn xoay:

V B h r h



Trong đó: r: bán kính

h: chiều cao

Ví dụ 1: Cho tam giác

ABC

vuông tại

3AB a=

và

2.BC a=

Khi quay tam giác

ABC

quanh trục

ta được một hình nón tròn xoay.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 31

a) Tính thể tích khối nón.

b) Tính diện tích xung quanh của hình nón.

……………………………………………………………………………………………………

Ví dụ 2: Cắt hình nón đỉnh

bới một mặt phẳng đi qua trục của hình nón ta được một tam giác vuông cân

có cạnh huyền bằng

là dây cung của đường tròn đáy hình nón sao cho mặt phẳng

( )

IBC

tạo với mặt phẳng chứa đáy hình nón một góc

60

. Tính theo

diện tích

của tam giác

IBC

……………………………………………………………………………………………………

BÀI TẬP TRẮC NGHIỆM

Câu 1: Cho đường thẳng

cắt và không vuông góc với



quay quanh



thì ta được

A. Hình nón tròn xoay. B. Mặt nón tròn xoay. C. Khối nón tròn xoay. D. Mặt trụ tròn xoay.

Câu 2: Cho tam giác

ABC

vuông tại

. Khi quay tam giác

ABC

(kể cả các điểm trong) quanh cạnh

ta được

A. Khối nón. B. Mặt nón. C. Khối trụ. D. Khối cầu

Câu 3: Mặt phẳng chứa trục của một hình nón cắt hình nón theo thiết diện là:

A. Một hình chữ nhật. B. Một tam giác cân. C. Một đường elip. D. Một đường tròn.

Câu 4: Hình

ABCD

(như hình bên) khi quay quanh

thì tạo ra:

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 32

A. Một hình trụ. B. Một hình nón. C. Một hình nón cụt. D. Hai hình nón.

Câu 5: Gọi

lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Đẳng thức

luôn đúng là

lh=

. B.

Rh=

. C.

2 2 2

l h R=+

. D.

2 2 2

R h l=+

Câu 6: Trong không gian cho tam giác

ABC

vuông tại

AB a=

và

3AC a=

. Tính độ dài đường

sinh

của hình nón có được khi quay tam giác

ABC

xung quanh trục

la=

. B.

3la=

. C.

2la=

. D.

2la=

Câu 7: Cho hình nón có thiết diện qua đỉnh

tạo với đáy góc

là tam giác đều cạnh bằng

4cm

. Thể

tích của khối nón đó là:

9 cm



. B.

4 3 .cm



3 cm



7 cm



Câu 8 : Cho khối nón tròn xoay có đường cao

ha=

và bán kính đáy

r =

. Một mặt phẳng

( )

đi

qua đỉnh của khối nón và có khoảng cách đến tâm

của đáy bằng

. Diện tích thiết diện tạo

bởi

( )

và hình nón là:

. B.

. C.

. D.

Câu 9: Một khối nón có bán kính đáy bằng

2 cm

, chiều cao bằng

3cm

. Một mặt phẳng đi qua đỉnh và

tạo với đáy một góc

chia khối nón làm

phần. Tính thể tích

phần nhỏ hơn (Tính gần

đúng đến hàng phần trăm).

1,42cmV 

. B.

2,36cmV 

. C.

1,53cmV 

. D.

2,47cmV 

Câu 10: Một cái phễu có dạng hình nón. Người ta đổ một lượng nước vào phễu sao cho chiều cao của

lượng nước trong phễu bằng một phần ba chiều cao của phễu. Hỏi nếu bịt miệng phễu rồi lật

ngược phễu lên thì chiều cao của nước bằng bao nhiêu? Biết chiều cao của phễu là

cm.

0,5

cm. B.

0,216

cm. C.

0,3

cm. D.

0,188

cm.

C. 3 . πcm

D. 7 . πcm

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 33

HÌNH HỌC 12– CHƯƠNG 2

§1. KHÁI NIỆM VỀ MẶT TRÒN XOAY

A. NHẮC LẠI LÝ THUYẾT

1. Định nghĩa mặt nón

• Trong mặt phẳng (P) cho hai đường thẳng



và  ct nhau tại điểm  và tạo thành góc



với

0 90





. Khi quay mặt phẳng (P) quanh  thì đường thẳng



sinh ra một sinh ra một mặt

trn xoay đưc gọi là mặt nón trn xoay đỉnh . Người ta gọi tt mặt nón trn xoay là mặt nón.

•



gọi là trục của mặt nón.

•

gọi là đường sinh của mặt nón.

•

gọi là đỉnh của mặt nón.

Góc



gọi là góc ở đỉnh của mặt nón

2. Hình nón và khối nón

Cho mặt nón

với trục

,

đỉnh

và góc ở đỉnh



Gọi

( )

là mặt phẳng vuông góc với



tại điểm

khác

(như hình bên). Mặt phẳng

( )

cắt mặt nón theo đường tròn

( )

có tâm

Lại gọi

( )

là mặt phẳng vuông góc với



tại

Khi đó

Phần mặt nón

giới hạn bởi hai mặt phẳng

( )

và

( )

cùng với hình tròn xác định bởi

( )

được gọi là hình nón.

Hình nón cùng với phần bên trong của nó gọi là khối nón

3. Diện tích hình nón và thể tích khối nón

Diện tích xung quanh của hình nón bằng một nửa tích số của độ dài đường trn đáy và độ

dài đường sinh:

S rl



Thể tích khối nón bằng một phần ba tích số diện tích hình trn đáy và chiều cao:

V r h



Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 34

Ví dụ 1: Một khối nón có thiết diện qua trục là tam giác vuông cân cạnh có cạnh huyền bằng

. Tính

diện tích xung quanh, diện tích toàn phần, diện tích thiết diện và thể tích của khối nón đó

……………………………………………………………………………………………………

Bài 3 ( SGK/39). Cho hình nón tròn xoay có đường cao

( )

20h cm=

, bán kính đáy

( )

25r cm=

a. Tính diện tích xung quanh của hình nón đã cho .

b. Tính thể tích của khối nón được tạo thành bởi hình nón đó.

c. Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa

thiết diện là

( )

12 cm

. Tính diện tích thiết

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 35

……………………………………………………………………………………………………

Bài 6 ( SGK/ 39). Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam

giác đều cạnh

. Tính diện tích xung quanh và thể tích của hình nón đó.

……………………………………………………………………………………………………

Ví dụ 2: Cho hình nón đỉnh

, đường cao

và có độ dài đường sinh bằng

3cm

, góc ở đỉnh bằng

Gọi

là điểm thuộc đoạn

thỏa mãn

IO IK=

, cắt hình nón bằng mặt phẳng

()P

qua

và vuông góc với

, khi đó thiết diện tạo thành có diện tích là

. Tính

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 36

BÀI TẬP TRẮC NGHIỆM

Câu 1: Cho khối nón có chiều cao

5h =

và bán kính đáy

3r =

. Thể tích của khối nón đã cho bằng

45 .V



5.V



15V



. D.

20V



Câu 2: Cho khối nón có thể tích



và chiều cao

4h =

. Tìm bán kính  của khối nón đã cho bằng

r = .

r =

. D.

Câu 3: Cho khối nón có thể tích



và bán kính đáy

4r =

. Tìm chiều cao

của khối nón đã cho

bằng

h =

Câu 4: Một hình nón có chiều cao bằng

3 a

và bán kính đáy bằng

. Diện tích xung quanh của hình

nón bằng

2 a



. B.

3.a



. D.

3.a



Câu 5: Cạnh bên của một hình nón bằng

2.a

Thiết diện qua trục của nó là một tam giác cân có góc ở

đỉnh bằng

120 .

Diện tích toàn phần của hình nón bằng

6 a



. B.

( )



. C.

( )

2 3 3a



. D.

( )

3 2 3a



Câu 6: Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác vuông

cân có cạnh góc vuông bằng

. Tính thể tích

của khối nón được tạo nên bởi hình nón đã cho.



. B.



. D.



Câu 7. Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác vuông

cân có cạnh góc vuông bằng

. Tính thể tích

của khối nón được tạo nên bởi hình nón đã

cho.



. B.



. D.



Câu 8. Cho hình nón có thiết diện qua đỉnh

tạo với đáy góc

là tam giác đều cạnh bằng

4cm

. Thể

tích của khối nón đó là:

9 cm



. B.

43cm



. C.

3 cm



. D.

7 cm



Câu 9: Một hình nón có chiều cao

, bán kính đáy

. Một phẳng phẳng đi qua đỉnh và tạo với mặt

đáy góc

. Tính diện tích thiết diện.

. B.

. C.

. D.

Câu 10: Bạn Hoàn có một tấm bìa hình tròn như hình vẽ, Hoàn muốn biến hình tròn đó thành một hình

cái phễu hình nón. Khi đó Hoàn phải cắt bỏ hình quạt tròn

AOB

rồi dán hai bán kính

và

lại với nhau (diện tích chỗ dán nhỏ không đáng kể). Gọi

là góc ở tâm hình quạt tròn dùng làm

phễu. Tìm

để thể tích phễu lớn nhất?

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 37



. B.



. C.



. D.



Câu 11: Tại trung tâm một thành phố người ta tạo điểm nhấn bằng cột trang trí hình nón có kích thước

như sau: chiều dài đường sinh

10ml =

, bán kính đáy

5mR =

. Biết rằng tam giác

SAB

là thiết

diện qua trục của hình nón và

là trung điểm

. Trang trí một hệ thống đèn điện tử chạy từ

đến

trên mặt nón. Xác định giá trị ngắn nhất của chiều dài dây đèn điện tử.

10m

. B.

15m

. C.

5 5 m

. D.

5 3 m

Câu 12: Cho hình nón tròn xoay có đỉnh

và đáy là đường tròn

( ; )C O R

có thể tích V, với

( 0)R a a=

3 , 'SO a O SO=

thỏa mãn

(0 3 )OO x x a



=  

. Mặt phẳng

()



vuông góc

với

tại

cắt hình nón tròn xoay theo giao tuyến là đường tròn

( ')C

. Khi khối nón đỉnh

, đáy là đường tròn

( ')C

đạt giá trị lớn nhất là

, tính tỉ số giữa thể tích khối nón đỉnh

và

khối nón đỉnh

. B.

. C.

. D.

Câu 13: Cho hình nón có đỉnh

, đáy là đường tròn tâm

sao cho

5SO a=

, một mặt phẳng

()



cắt

mặt nón theo hai đường sinh

, SA SB

. Biết khoảng cách từ

đến mặt phẳng

()



bằng

và

diện tích tam giác

SAB

bằng

360

. Thể tích khối nón bằng:

1325 5



. B.

265 5



. C.

1325 5

. D.

265 5

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 38

HÌNH HOC 12 – CHƯƠNG 2

§1. MẶT TRÒN XOAY

III. MẶT TRỤ TRÒN XOAY.

1. Định nghĩa

Trong mặt phẳng

󰇛



󰇜

cho hai đường thẳng  và  song song với nhau,

cách nhau một khoảng bằng . Khi quay mặt phẳng 󰇛󰇜 xung quanh

 thì đường thẳng  sinh ra một mặt tròn xoay được gọi là mặt trụ

tròn xoay (gọi tắt là mặt trụ)

  gọi là trục của mặt trụ.

  là đường sinh của mặt trụ.

  là bán kính của mặt trụ.

2. Hình trụ tròn xoay, khối trụ tròn xoay.

a) Xét hình chữ nhật  Khi quay hình đó xung quanh đường thẳng chứa một cạnh (chẳng

hạn cạnh ) thì đường gấp khúc  tạo thành một hình được gọi là hình trụ tròn xoay

(gọi tắt là hình trụ).

 Hai đáy là hai đường tròn 󰇛󰇜 và 󰇛󰇜.

 Đường sinh là đoạn .

 Mặt xung quanh là mặt do đoạn  tạo thành khi quay.

 Chiều cao .

b) Khối trụ tròn xoay là phần không gian được giới hạn bởi một hình trụ và kể cả hình trụ đó.

3. Công thức tính diện tích hình trụ, thể tích khối trụ.

a) Diện tích xung quanh của hình trụ







b) Diện tích toàn phần của hình trụ









 



 



c) Thể tích của khối trụ 



󰉧  



.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 39

4. Các ví dụ:

*VD1:

Cho hình trụ có hình tròn đáy có bán kính  có chiều cao 



 Tính diện tích xung

quanh, diện tích toàn phần của hình trụ và thể tích của khối trụ theo 

……………………………………………………………………………………………………

*VD2:

Cho hình trụ có hình tròn đáy có bán kính  có thiết diện qua trục là một hình vuông Tính diện

tích xung quanh, diện tích toàn phần của hình trụ và thể tích của khối trụ theo 

……………………………………………………………………………………………………

*VD3:

Cho một hình trụ tròn xoay và hình vuông  cạnh  có hai đỉnh liên tiếp   nằm trên đường

tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt

phẳng 󰇛󰇜 tạo với đáy hình trụ một góc  Tính diện tích xung quanh của hình trụ theo 

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 40

……………………………………………………………………………………………………

*VD4:

Cho một bể bơi mini có dạng hình trụ như hình bên. Giả sử bán kính của bể bơi là 1m, chiều cao

của bể bơi là 0,5m. Hỏi muốn bơm nước đầy bể bơi thì cần bao nhiêu 



nước?

……………………………………………………………………………………………………

…………………………………………………………………………………………………

B. LUYỆN TẬP

Bài tập trắc nghiệm

Câu 1. [Mức độ 1] Cho hình trụ 󰇛󰇜 có chiều cao , độ dài đường sinh  bán kính đáy . Kí hiệu 



là

diện tích xung quanh của

󰇛



󰇜

 Khẳng định nào sau đây là đúng?

S rh



. B.

S rl



. C.

S r h



. D.

S rl



Câu 2. [Mức độ 1] Cho hình trụ 󰇛󰇜 có chiều cao , độ dài đường sinh  bán kính đáy . Kí hiệu 



là

diện tích toàn phần của

󰇛



󰇜

 Khẳng định nào sau đây là đúng?

S rh



. B.

S rl r



. C.

S rl r



. D.

S rl r



Câu 3.[Mức độ 1] Cho hình trụ 󰇛󰇜 có chiều cao , độ dài đường sinh  bán kính đáy . Kí hiệu  là thể

tích của khối trụ

󰇛



󰇜

 Khẳng định nào sau đây là đúng?

V rh



. B.

V r h



. C.

V rl



. D.

2V r h



Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 41

Câu 4.[Mức độ 2] Một hình trụ bán kính đáy  cm, chiều cao  cm. Diện tích xung quanh của

hình trụ này là

( )

35 cm



. B.

( )

70 cm



( )



. D.

( )



Câu 5.[Mức độ 2] Một hình trụ bán kính đáy  , độ dài đường sinh . Diện tích toàn phần của

hình trụ này là

6 a



. B.

2 a



. C.

4 a



. D.

5 a



Câu 6.[Mức độ 2] Quay hình vuông  cạnh  xung quanh một cạnh. Thể tích của khối trụ được tạo

thành là



. B.

2 a



. C.



. D.

3 a



Câu 7.[Mức độ 2] Khối trụ có chiều cao  cm và bán kính đáy  cm thì có thể tích bằng

( )

12 cm



. B.

( )

4 cm



. C.

( )

6 cm



. D.

( )

18 cm



Câu 8.[Mức độ 2] Một lon sữa hình trụ có đường kính đáy bằng chiều cao và bằng   Thể tích thực

của lon sữa đó bằng

( )

2 dm



. B.

( )



. C.

( )



. D.

( )



Câu 9.[Mức độ 2] Cho hình vuông  cạnh   Gọi  lần lượt là trung điểm của  và .

Quay hình vuông  xung quanh . Diện tích xung quanh của hình trụ tạo thành là

( )

64 cm



. B.

( )

32 cm



. C.

( )

96 cm



. D.

( )

126 cm



Câu 10.[Mức độ 2] Cho hình chữ nhật  có  và góc 



. Quay hình chữ nhật này

xung quanh cạnh  Diện tích xung quanh của hình trụ được tạo thành là

3 a



. B.

23a



. C.



. D.

3 a



C. BÀI TẬP T LUYỆN

MỨC NHẬN BIẾT – THÔNG HIỂU

A. A. DẠNG 1. DIỆN TÍCH XUNG QUANH, DIỆN TÍCH TOÀN PHẦN, CHIỀU CAO, BÁN KÍNH ĐÁY, THIẾT DIỆN

Câu 1. (Đề Tham Khảo 2020 Lần 2) Diện tích xung quanh của hình trụ có độ dài đường sinh

và bán

kính đáy

bằng

4 rl



. B.



. C.



. D.

2 rl



Câu 2. (Mã 101 - 2020 Lần 1) Cho hình trụ có bán kính đáy

8R =

và độ dài đường sinh

3l =

. Diện tích

xung quanh của hình trụ đã cho bằng:



. B.

192



. C.



. D.



Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 42

Câu 3. (Mã 102 - 2020 Lần 1) Cho hình trụ có bán kính đáy và độ dài đường sinh . Diện tích

xung quanh của hình trụ đã cho bằng

A. . B. . C. . D. .

Câu 4. (Mã 103 - 2020 Lần 1) Cho hình trụ có bán kính đáy

5r =

và độ dài đường sinh

3l =

. Diện tích

xung quanh của hình trụ đã cho bằng



Câu 5. (Mã 104 - 2020 Lần 1) Cho hình trụ có bán

và độ dài đường sinh

3l =

. Diện tích xung quanh

của hình trụ đã cho bằng



. B.

147



. C.



. D.



Câu 6. (Đề Minh Họa 2020 Lần 1) Cho hình trụ có bán kính đáy bằng

. Biết rằng khi cắt hình trụ đã

cho bởi một mặt phẳng qua trục, thiết diện thu được là một hình vuông. Diện tích xung quanh của hình trụ

đã cho bằng



. B.



. C.



. D.



Câu 7. (Đề Minh Họa 2017) Trong không gian, cho hình chữ nhật

ABCD

có

1AB =

và

2AD =

. Gọi

,MN

lần lượt là trung điểm của

và

. Quay hình chữ nhật

ABCD

xung quanh trục

, ta được

một hình trụ. Tính diện tích toàn phần

của hình trụ đó.



. B.



. C.



. D.



Câu 8. (Mã 105 2017) Cho hình trụ có diện tích xung quanh bằng



và độ dài đường sinh bằng

đường kính của đường tròn đáy. Tính bán kính

của đường tròn đáy.



. B.

5r =

. C.



. D.

r =

Câu 9. (Chuyên Lam Sơn Thanh Hóa 2019) Cho khối trụ

( )

có bán kính đáy

1R =

, thể tích



Tính diện tích toàn phần của hình trụ tương ứng

12S



. B.

11S



. C.

10S



. D.



Câu 10. (THPT Lê Quy Đôn Điện Biên 2019) Tính diện tích xung quanh của hình trụ biết hình trụ có

bán kính đáy là

và đường cao là

2 a



. B.



. C.



. D.

23a



B. DẠNG 2. THỂ TÍCH

Câu 11. (Mã 102 - 2020 Lần 2) Cho khối trụ có bán kính đáy bằng

5r =

và chiều cao

3h =

. Thể tích

của khối trụ đã cho bằng



. B.



. C.



. D.



Câu 12. (Mã 103 - 2020 Lần 2) Cho khối trụ có bán kính

3r =

và chiều cao

4h =

. Thể tích khối trụ đã

cho bằng



. B.



. C.



. D.



4r =

3l =



Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 43

Câu 13. (Mã 101 - 2020 Lần 2) Cho khối trụ có bán kính đáy

4r =

và chiều cao

3h =

. Thể tích của

khối trụ đã cho bằng



. B.



. C.



. D.



Câu 14. (Mã 104 - 2020 Lần 2) Cho khối trụ có bán kính đáy

3r =

và chiều cao

5h =

. Thể tích của

khối trụ đã cho bằng



. B.



. C.



. D.



Câu 15. (Mã 103 2018) Thể tích của khối trụ tròn xoay có bán kính đáy

và chiều cao

bằng



. B.



. C.



. D.

2 rh



Câu 16. (Mã 123 2017) Tính thể tích V của khối trụ có bán kính

4r =

và chiều cao

42h =

32V



. B.

64 2V



. C.

128V



. D.

32 2V



Câu 17. (Chuyên Lê Hồng Phong Nam Định 2019) Thể tích khối trụ có bán kính đáy

ra=

và chiều

cao

2ha=

bằng

42a



. B.



. C.

2 a



. D.



Câu 18. (Chuyên Lê Quý Đôn Điện Biên 2019) Thiết diện qua trục của một hình trụ là một hình vuông

có cạnh bằng

. Tính theo

thể tích khối trụ đó.



. B.

2 a



. C.

4 a



. D.



Câu 19. (THPT Lê Quý Đôn Đà Nẵng 2019) Cho hình chữ nhật

ABCD

có

2 2 . AB BC a==

Tính thể

tích khối tròn xoay khi quay hình phẳng

ABCD

quanh trục

.AD

4 a



. B.

2 a



. C.

8 a



. D.



Câu 20. (Chuyên Bắc Giang 2019) Cho hình trụ có diện tích toàn phần là



và có thiết diện cắt bởi

mặt phẳng qua trục là hình vuông. Tính thể tích khối trụ?



. B.



. C.



. D.



MỨC VẬN DỤNG 1. Diện tích xung quanh, diện tích toàn phần, chiều cao, bán kính đáy, thiết diện

Câu 21. (Mã 103 - 2019) khoảng bằng 1, thiết diện thu được có diện tích bằng

12 2

. Diện tích xung

quanh của hình trụ đã cho bằng

6 10



. B.

6 34



. C.

3 10



. D.

3 34



Câu 22. (Mã 101 - 2019) Cho hình trụ có chiều cao bằng

. Cắt hình trụ đã cho bởi mặt phẳng song

song với trục và cách trục một khoảng bằng

, thiết diện thu được có diện tích bằng

. Diện tích xung

quanh của hình trụ đã cho bằng

10 3



. B.

5 39



. C.

20 3



. D.

10 39



Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 44

Câu 23. (Mã 102 - 2019) Cho hình trụ có chiều cao bằng

. Cắt hình trụ đã cho bởi một mặt phẳng

song song với trục và cách trục một khoảng bằng

, thiết diện thu được có diện tích bằng

. Diện tích

xung quanh của hình trụ đã cho bằng

16 2



. B.



. C.

12 2



. D.

24 2



Câu 24. Cắt hình trụ

( )

bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện

tích bằng

30cm

và chu vi bằng

26 cm

. Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy

của hình trụ

( )

. Diện tích toàn phần của

( )

là:

( )

23 cm



. B.

( )



. C.

( )



. D.

( )

69 cm



Câu 25. Một hình trụ có bán kính đáy bằng

cm và có chiều cao là

cm. Một đoạn thẳng

có

chiều dài là

100

cm và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách

từ đoạn thẳng

đó đến trục hình trụ.

50d =

cm. B.

50 3d =

cm. C.

25d =

cm. D.

25 3d =

cm.

C. D. DẠNG 2. THỂ TÍCH

Câu 26. (Đề Tham Khảo 2020 Lần 2) Cho hình trụ có chiều cao bằng 6a. Biết rằng khi cắt hình trụ đã

cho bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 3a, thiết diện thu được là một

hình vuông. Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng

216 a



. B.

150 a



. C.

54 a



. D.

108 a



Câu 27. (Đề Tham Khảo 2019) Một khối đồ chơi gồm hai khối trụ

( ) ( )

,HH

xếp chồng lên nhau, lần

lượt có bán kính đáy và chiều cao tương ứng là

1 1 2 2

, , ,r h r h

thỏa mãn

2 1 2 1

r r h h==

(tham khảo hình

vẽ). Biết rằng thể tích của toàn bộ khối đồ chơi bằng

30cm

, thể tích khối trụ

( )

bằng

24cm

. B.

15cm

. C.

20cm

. D.

10cm

Câu 28. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hình trụ có chiều cao bằng

. Biết hai

điểm

,AC

lần lượt nằm trên hai đáy thỏa

10AC a=

, khoảng cách giữa

và trục của hình trụ bằng

Thể tích của khối trụ đã cho là

128 a



. B.

320 a



. C.

80 a



. D.

200 a



Câu 29. (Sở Hà Nội 2019) Hỏi nếu tăng chiều cao của khối trụ lên

lần, bán kính của nó lên

lần thì

thể tích của khối trụ mới sẽ tăng bao nhiêu lần so với khối trụ ban đầu?

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 45

. B.

. C.

. D.

Câu 30. (Chuyên ĐHSPHN - 2018) Cần đẽo thanh gỗ hình hộp có đáy là hình vuông thành hình trụ có

cùng chiều cao. Tỉ lệ thể tích gỗ cần phải đẽo đi ít nhất (tính gần đúng) là

30%

. B.

50%

. C.

21%

. D.

11%

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 46

HÌNH HOC 12 – CHƯƠNG 2

§1. MẶT TRÒN XOAY

I. TÓM TẮT KIẾN THỨC VỀ HÌNH NÓN, KHỐI NÓN.

1. Hình nón tròn xoay

Hình thành: Cho  vuông tại  quay quanh trục , ta được mặt nón như hình trên

với:







2. Khối nón tròn xoay

- Khối nón tròn xoay là phần không gian được giới hạn bởi hình nón tròn xoay kể cả hình nón đó.

- Các yếu tố của hình nón cũng là của khối nón tương ứng.

3. Các yếu tố của hình nón

Trục của hình nón: 

Đường cao: .

Bán kính đáy: 

Đường sinh: 

Góc ở đỉnh: 





Thiết diện qua trục là  cân tại 

Góc giữa đường sinh và mặt đáy: 











4. Một số công thức.

Chu vi đáy: 

Diện tích đáy: 









Thể tích: 





















(liên tưởng đến thể tích khối chóp).

Diện tích xung quanh: 





Diện tích toàn phần: 







 



 



Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 47

5. Bài tập trắc nghiệm

Dạng 1: Xác định các yếu tố cơ bản của khối nón. Tính diện tích, thể tích.

Câu 1.[Mức độ 1] Cho khối nón có chiều cao      . Thể tích của khối nón đã

cho là

3 a



. B.



. C.



. D.

3 a



Câu 2.[Mức độ 1] Cho hình nón có đường sinh      .

Diện tích xung quanh của hình nón đã cho là

24 a



. B.

12 a



. C.

4 a



. D. 



Câu 3.[Mức độ 1] Cho hình nón có đường sinh      .

Diện tích toàn phần của hình nón đã cho bằng



. B.



. C.



. D.



Câu 4.[Mức độ 1] Cho hình nón có đường sinh bằng  và đường kính bằng 6a.

Chiều cao của hình nón đã cho bằng

. B.

2 34a

. C.

109a

. D.

91a

Câu 5.[Mức độ 2] Trong không gian, cho tam giác  vuông tại  có . Khi quay tam

giác  quanh cạnh góc vuông  thì đường gấp khúc  tạo thành một hình nón. Diện tích

xung quanh của hình nón đó bằng

10 a



. B.

5 a



. C.

5 a



. D.

25a



Câu 6.[Mức độ 2] Cắt một hình nón bởi một mặt phẳng qua trục của nó ta được thiết diện là một tam giác

đều có cạnh bằng . Thể tích của khối nón được tạo nên bởi hình nón đã cho bằng

2 a



. B.

3 a



. C.



. D.



Câu 7.[Mức độ 2] Cho hình chóp tứ giác đều có cạnh đáy bằng  và cạnh bên bằng . Tính diện tích

xung quanh của hình nón có đỉnh trùng với đỉnh hình chóp và đường tròn đáy ngoại tiếp đáy hình

chóp đã cho.

2 a



. B.

22a



. C.

3 a



. D.

4 a



Dạng 2: Thiết diện của khối chóp.

1TRƯỜNG HỢP 1: Thiết diện qua trục của hình nón: 

󰇛



󰇜

đi qua trục của hình nón và cắt mặt nón

theo 2 đường sinh  Thiết diện là tam giác cân.

. Cách vẽ hình: trên hình vẽ thiết diện là tam giác .

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 48

Thiết diện qua trục của hình nón thông thường hay gặp ở một số dạng như:

• Thiết diện qua trục là một tam giác vuông.

• Thiết diện qua trục là một tam giác vuông cân.

• Thiết diện qua trục là một tam giác đều.

• Thiết diện qua trục có góc ở đỉnh bằng số độ cho trước ( hay ).

• …..

2TRƯỜNG HỢP 2: Thiết diện qua đỉnh của hình nón: 

󰇛



󰇜

đi qua đnh của hình nón và cắt mặt nón

theo 2 đường sinh  Thiết diện cũng là tam giác cân.

. Cách vẽ hình: trên hình vẽ thiết diện là tam giác .

 Lưu ý: Khi vẽ thiết diện qua đỉnh, nếu kẻ  thì theo tính chất đường kính và dây cung

của đường tròn (đường kính vuông góc với dây cung thì đi qua trung điểm của dây cung và

ngược lại), thì  chính là trung điểm của . Khi đó góc giữa mặt phẳng

󰇛



󰇜

với đường tròn

đáy chính là 



Thiết diện qua đỉnh của hình nón thông thường hay gặp ở một số dạng như:

• Thiết diện qua đỉnh là một tam giác vuông.

• Thiết diện qua đỉnh là một tam giác vuông cân.

• Thiết diện qua đỉnh là một tam giác đều.

• Thiết diện qua đỉnh có góc tạo bởi thiết diện và trục là số cho trước ( hay ).

• Thiết diện qua đỉnh của hình nón có khoảng cách từ tâm đáy tới mặt phẳng chứa thiết diện là



󰇛

󰇜

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 49

• Thiết diện là một tam giác cân đồng thời tạo với mặt phẳng đường tròn đáy góc cho trước.

• …

3TRƯỜNG HỢP 3: Thiết diện vuông góc với trục của hình nón và song song với đường tròn đáy hình

nón: 󰇛󰇜 vuông góc vi trục hình nón  giao tuyến là một đường tròn.

. Cách vẽ hình: trên hình vẽ, thiết diện là đường tròn tâm .

Câu 1.[Mức độ 2] Cho hình nón có thiết diện qua trục là tam giác vuông có cạnh huyền bằng 



. Diện

tích xung quanh 



của hình nón đó bằng

A. 













. B. 













. C. 















. D.













Câu 2.[Mức độ 2] Diện tích toàn phần của hình nón có khoảng cách từ tâm của đáy đến đường sinh bằng



 và thiết diện qua trục là tam giác đều bằng

A. . B. . C. . D..

Câu 3.[Mức độ 2] Cho một khối nón có bán kính đáy là cm, góc giữa đường sinh và mặt đáy là . Tính

diện tích thiết diện của khối nón cắt bởi mặt phẳng đi qua hai đường sinh vuông góc với nhau.

A. 

󰇛



󰇜

. B. 

󰇛



󰇜

. C.







󰇛



󰇜

. D.

󰇛



󰇜

Câu 4.[Mức độ 2] Cho hình nón tròn xoay có chiều cao  và bán kính đáy . Một thiết diện

đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là 12. Tính diện

tích của thiết diện đó.

500

. B.

300

. C.

406

. D.

400

Câu 5.[Mức độ 3] Mặt phẳng trung trực của đường cao của một khối nón chia nó ra thành hai khối. Tỉ số

thể tích của khối bé chia khối lớn bằng





. B.





. C.





. D.







5. Bài tập trắc nghiệm.

MỨC VẬN DỤNG: NHẬN BIẾT – THÔNG HIỂU tích xung quanh, diện tích toàn phần,

chiều cao, bán kính đáy, thiết diện

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 50

Câu 1. (Đề Minh Họa 2020 Lần 1) Diện tích xung quanh của hình nón có độ dài đường sinh

và bán

kính đáy

bằng

4 rl



. B.

2 rl



. C.



. D.



Câu 2. (Mã 102 - 2020 Lần 2) Cho hình nón có bán kính đáy

2r =

và độ dài đường sinh

7l =

. Diện

tích xung quanh của hình nón đã cho bằng



. B.



. C.



. D.



Câu 3. (Mã 101 - 2020 Lần 2) Cho hình nón có bán kính đáy

2r =

và độ dài đường sinh

5l =

. Diện

tích xung quanh của hình nón đã cho bằng



. B.



. D.



Câu 4. (Mã 104 - 2020 Lần 2) Cho hình nón có bán kính đáy

2r =

và độ dài đường sinh

7l =

. Diện

tích xung quanh của hình nón đã cho bằng



. B.



. C.



. D.



Câu 5. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Gọi

,,l h r

lần lượt là độ dài đường sinh, chiều

cao và bán kính mặt đáy của hình nón. Diện tích xung quanh

của hình nón là:

S r h



. B.

S rl



. C.

S rh



. D.

S rl



Câu 6. (THPT Lê Quy Đôn Điện Biên 2019) Một hình nón có thiết diện qua trục là một tam giác

vuông cân có cạnh góc vuông bằng

Tính diện tích xung quanh của hình nón.



. B.



. C.



. D.



Câu 7. (THPT Lương Thế Vinh Hà Nội 2019) Cho hình nón có bán kính đáy bằng

và độ dài

đường sinh bằng

. Diện tích xung quanh của hình nón đó bằng

4 a



. B.

3 a



. C.

2 a



. D.

Câu 8. (Sở Vĩnh Phúc 2019) Cho hình nón có diện tích xung quanh bằng

3 a



, bán kính đáy bằng

. Tính độ dài đường sinh của hình nón đó

22a

. B.

. C.

. D.

Câu 9. (THPT - Yên Định Thanh Hóa 2019) Cho khối nón

( )

có thể tích bằng



và chiều cao là

.Tính bán kính đường tròn đáy của khối nón

( )

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 51

Câu 10. (THPT Trần Nhân Tông - QN -2018) Trong không gian, cho tam giác

ABC

vuông tại cân

, gọi

là trung điểm của

2BC =

.Tính diện tích xung quanh của hình nón, nhận được

khi quay tam giác

ABC

xung quanh trục



. B.



. C.



. D.



BÀI TẬP VẬN DỤNGDạng 2. BThể tích

Câu 1. (Mã 103 - 2019) Thể tích của khối nón có chiều cao

và có bán kính đáy

là

2 rh



. B.



. C.



. D.



Câu 2. (Đề Tham Khảo 2020 Lần 2) Cho khối nón có chiều cao

3h =

và bán kính đáy

4r =

. Thể

tích của khối nón đã cho bằng



. B.



. C.



. D.



Câu 3. (Mã 101 - 2020 Lần 1) Cho khối nón có bán kính đáy

5r =

và chiều cao

2h =

. Thể tích khối

nón đã cho bằng:



. B.



. C.



. D.



Câu 4. (Mã 102 - 2020 Lần 1) Cho khối nón có bán kính đáy và chiều cao . Thể tích của

khối nón đã cho bằng

A. . B. . C. . D. .

Câu 5. (Mã 103 - 2020 Lần 1) Cho khối nón có bán kính

2r =

chiều cao

5h =

. Thể tích của khối

nón đã cho bằng



. B.



. C.



. D.



Câu 6. (Mã 104 - 2020 Lần 1) Cho khối nón có bán kính đáy

2r =

và chiều cao

4h =

. Thể tích của

khối nón đã cho bằng



. B.



. C.



. D.



Câu 7. (Mã 110 2017) Cho khối nón có bán kính đáy

3r =

và chiều cao

4h =

. Tính thể tích

của

khối nón đã cho.

12V



16 3V



16 3



Câu 8. (Mã 101 - 2019) Thể tích của khối nón có chiều cao

và bán kính đáy

là



. B.

2 rh



. C.



. D.



Câu 9. (Mã 104 2019) Thể tích khối nón có chiều cao

và bán kính đáy

là

4r =

2h =



Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 52



. B.



. C.

2 rh



. D.



Câu 10. (Mã 102 - 2019) Thể tích của khối nón có chiều cao

và bán kính đáy

là



. B.



. C.

2 rh



. D.



MỨC VẬN DỤNG

Dạng 2. DẠNG 2. DIỆN TÍCH XUNG QUANH, DIỆN TÍCH TOÀN PHẦN, CHIỀU CAO, BÁN KÍNH ĐÁY,

THIẾT DIỆN

Câu 1. (Đề Tham Khảo 2020 Lần 2) Trong không gian, cho tam giác

ABC

vuông tại

AB a=

và

2AC a=

. Khi quay tam giác

ABC

quanh cạnh góc vuông

thì đường gấp khúc

ACB

tạo

thành một hình nón. Diện tích xung quanh hình nón đó bằng

5 a



. B.

5 a



. C.

25a



. D.

10 a



Câu 2. (Mã 101 - 2020 Lần 1) Cho hình nón có bán kính đáy bằng

và góc ở đỉnh bằng

60

. Diện tích

xung quanh của hình nón đã cho bằng



. B.

16 3



. C.



. D.



Câu 3. (Mã 102 - 2020 Lần 1) Cho hình nón có bán kính bằng 5 và góc ở đỉnh bằng . Diện tích

xung quanh của hình nón đã cho bằng

A. . B. . C. . D. .

Câu 4. (Mã 103 - 2020 Lần 1) Cho hình nón có bán kính bằng 3 và góc ở đỉnh bằng

. Diện tích xung

quanh của hình nón đã cho bằng



. B.



. C.



. D.

12 3



Câu 5. (Mã 104 - 2020 Lần 1) Cho hình nón có bán kính đáy bằng 4 và góc ở đỉnh bằng

. Diện tích

xung quanh của hình nón đã cho bằng

64 3



. B.



. C.



. D.

32 3



Câu 6. (Mã 123 2017) Cho một hình nón có chiều cao

ha=

và bán kính đáy

2ra=

. Mặt phẳng

()P

đi

qua

cắt đường tròn đáy tại

và

sao cho

23AB a=

. Tính khoảng cách

từ tâm của

đường tròn đáy đến

()P

d =

da=

60



100 3



50 3



100



Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 53

Câu 7. (KSCL THPT Nguyễn Khuyến 2019) Cho hình nón đỉnh

, đường cao SO,

và

là hai

điểm thuộc đường tròn đáy sao cho khoảng cách từ

đến

( )

SAB

bằng

và

30 , 60SAO SAB==

. Độ dài đường sinh của hình nón theo

bằng

23a

Câu 8. (THPT Cẩm Giàng 2 2019) Cho một hình nón có bán kính đáy bằng

và góc ở đỉnh bằng

60

Tính diện tích xung quanh của hình nón đó.



. B.



. C.



. D.



Câu 9. (THPT Cẩm Giàng 2 2019) Cho đoạn thẳng

có độ dài bằng

, vẽ tia

về phía điểm

sao cho điểm

luôn cách tia

một đoạn bằng

. Gọi

là hình chiếu của

lên tia

khi tam giác

AHB

quay quanh trục

thì đường gấp khúc

AHB

vẽ thành mặt tròn xoay có

diện tích xung quanh bằng:



. B.

( )



. C.

( )



. D.

( )



Câu 10. (HSG Bắc Ninh 2019) Cho hình nón có chiều cao

20h =

, bán kính đáy

25r =

. Một thiết diện

đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là

Tính diện tích

của thiết diện đó.

500S =

. B.

400S =

. C.

300S =

. D.

406S =

BÀI TẬP VẬN DỤNG

Dạng 3. DẠNG 2. THỂ TÍCH

Câu 1. (Đề Minh Họa 2020 Lần 1) Cho hình nón có chiều cao bằng

. Một mặt phẳng đi qua

đỉnh hình nón và cắt hình nón theo một thiết diện là tam giác đều có diện tích bằng

. Thể

tích của khối nón được giới hạn bởi hình nón đã cho bằng

32 5



. B.



. C.

32 5



. D.



Câu 2. (KSCL THPT Nguyễn Khuyến 2019) Tính thể tích của hình nón có góc ở đỉnh bằng

và

diện tích xung quanh bằng

6.a



. B.

3Va



. C.



. D.



Câu 3. (Chuyên Thái Nguyên 2019) Cho tam giác

ABC

vuông tại

, cạnh

6AB =

8AC =

và

là

trung điểm của cạnh

. Khi đó thể tích của khối tròn xoay do tam giác

BMC

quanh quanh

là



106



. C.



. D.



Câu 4. (Chuyên Lê Quý Đôn Điện Biên 2019) Cho hình nón có bán kính đáy bằng

cm, góc ở đỉnh

bằng

60

. Tính thể tích của khối nón đó.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 54



. B.

83cm



. C.



. D.



Câu 5. (Việt Đức Hà Nội 2019) Cho tam giác

ABC

vuông tại

6 , 8AB cm AC cm==

. Gọi

là

thể tích khối nón tạo thành khi quay tam giác

ABC

quanh cạnh

và

là thể tích khối nón

tạo thành khi quay tam giác

ABC

quanh cạnh

. Khi đó, tỷ số

bằng:

. B.

. C.

. D.

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 55

HÌNH HOC 12 – CHƯƠNG 2

§1. MẶT TRÒN XOAY

I. TÓM TẮT KIẾN THỨC VỀ HÌNH TRỤ, KHỐI TRỤ.

1. Hình trụ tròn xoay.

Xét hình chữ nhật  Khi quay hình đó xung quanh đường thẳng chứa một cạnh, chẳng hạn

 thì đường gấp khúc  tạo thành một hình được gọi là hình trụ tròn xoay.

– Hai đáy 󰇛󰇜󰇛󰇜

– Đường sinh: 

– Chiều cao: 

2. Khối trụ tròn xoay.

Khối trụ tròn xoay là phần không gian được giới hạn bởi một hình trụ tròn xoay kể cả hình trụ đó.

Khối trụ tròn xoay được gọi tắt là khối trụ.

3. Một số công thức về hình nón, khối nón.

- Diện tích đáy của hình trụ : 









- Diện tích xung quanh của hình trụ :



.

- Diện tích toàn phần của hình trụ: 







 



 



- Chu vi một đáy của hình trụ: .

- Thể tích khối trụ : 



.

II. BÀI TẬP TỰ LUẬN.

Dạng 1: Xác định các yếu tố cơ bản của khối trụ. Tính diện tích, thể tích.

III. BÀI TẬP TRẮC NGHIỆM.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 56

Câu 1: [Mức độ 1] Cho hình trụ có bán kính đáy  và độ dài đường sinh là  Thể tích khối trụ được tính

theo công thức

A. 









 B. 



 C. 









 D. 





Câu 2: [Mức độ 1] Cho hình trụ có bán kính đáy  và độ dài đường sinh . Diện tích xung

quanh của hình trụ đã cho bằng

A. . B. . C. . D. .

Câu 3: [Mức độ 1] Thể tích của khối trụ có bán kính đáy  và chiều cao 



 bằng

A.  B. 



 C. 



 D. 

Câu 4: [Mức độ 1] Diện tích toàn phần của hình trụ có chiều cao  và bán kính  bằng

A. . B. . C. . D. .

Câu 5: [Mức độ 2] Khối trụ

󰇛



󰇜

có bán kính đáy bằng 

và thể tích bằng . Tính diện tích xung quanh





của hình trụ

󰇛



󰇜

A. 



. B. 



. C. 



. D. 



.

Câu 6: [Mức độ 2] Cho khối trụ 󰇛󰇜 có bán kính đáy bằng  và diện tích toàn phần bằng 



 Tính

thể tích  của khối trụ 󰇛󰇜

A. 



. B. 



. C. 



. D. 



Câu 7: [Mức độ 2] Cho hình trụ có hai đường tròn đáy là 󰇛󰇜 và 󰇛

󰆒

󰇜

󰆒

 Gọi  là một

đường kính của đường tròn 󰇛󰇜 Biết rằng tam giác 

󰆒

 đều. Tính tỉ số

















. B.









 C.





. D.









.

Câu 8: Một hình trụ có bán kính đáy bằng

2cm

và có thiết diện qua trục là một hình vuông. Diện tích

xung quanh của hình trụ là

8 cm



. B.

4 cm



. C.

32 cm



. D.

16 cm



Vì thiết diện qua trục là hình vuông nên ta có

24h l r cm= = =

2 2 .2.4 16

S rl cm

  

= = =

Câu 9: [Mức độ 2] Một thùng đựng thư được thiết kế như hình vẽ bên, phần phía trên là nửa hình trụ.

Thể tích của thùng đựng thư bằng

A.  

B.   

C.  

D.  

Câu 10: [Mức độ 2] Trong không gian, cho hình thang  vuông tại  và  có độ dài các cạnh là

   Tính thể tích  của vật thể tròn xoay khi quay hình thang trên

quanh trục 

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 57

Câu 11: [Mức độ 3] Từ một tấm tôn hình chữ nhật kích thước 80cm x 360cm, người ta làm các thùng

đựng nước hình trụ có chiều cao bằng 80cm, theo hai cách sau (xem hình minh họa dưới đây):

C1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.

C2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của

một thùng.

Kí hiệu 



là thể tích của thùng gò được theo cách 1 và 



là tổng thể tích của hai thùng gò

được theo cách 2. Tính tỉ số











Dạng 2: Thiết diện.

Câu 1: [Mức độ 2] Một hình trụ có bán kính đáy bằng

, mặt phẳng qua trục cắt hình trụ theo một

thiết diện có diện tích bằng

. Tính diện tích xung quanh của hình trụ?

4 a



. B.

8 a



. C.

16 a



. D.

2 a



Câu 2: Một khối trụ có bán kính đáy

7r cm=

. Khoảng cách hai đáy bằng

10cm

. Khi cắt khối trụ bởi một

mặt phẳng song song với trục cách trục

5cm

thì diện tích của thiết diện là:

34S cm=

. B.

40 6S cm=

. C.

21 31S cm=

. D.

38S cm=

Câu 3: [Mức độ 2] Cho hình trụ có chiều cao bằng

. Cắt hình trụ đã cho bởi mặt phẳng song song

với trục và cách trục một khoảng bằng

, thiết diện thu được có diện tích bằng

. Diện tích

xung quanh của hình trụ đã cho bằng

10 3



. B.

5 39



. C.

20 3



. D.

10 39



Câu 4: [Mức độ 2] Một hình trụ tròn xoay có hai đáy là hai đường tròn

󰇛



󰇜

và

󰇛



󰆒



󰇜

. Biết rằng tồn

tại dây cung  của đường tròn

󰇛



󰇜

sao cho tam giác 

󰆒

 đều và góc giữa hai mặt

phẳng

󰇛



󰆒



󰇜

và mặt phẳng chứa đường tròn

󰇛



󰇜

bằng . Tính diện tích xung quanh của

hình trụ đã cho.

4 R



. B.

23R



. C.



. D.



Câu 5: [Mức độ 3] Cho hình thang  vuông tại  và  với 





 Quay hình thang và

miền trong của nó quanh đường thẳng chứa cạnh  Tính thể tích  của khối tròn xoay được tạo

thành.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 58



. B.



. C.



. D.



Câu 6:[Mức độ 3] Cho hình lăng trụ tứ giác đều

.ABCD A B C D

   

có cạnh đáy bằng a

và cạnh bên bằng 4a. Thể tích của khối trụ nội tiếp trong hình lăng trụ là:

4 a



. B.

8 a



. C.

2 a



. D.



III. BÀI TẬP T LUYỆN ( phần này không làm PPT )

MỨC NHẬN BIẾT – THÔNG HIỂU

A. A. DẠNG 1. DIỆN TÍCH XUNG QUANH, DIỆN TÍCH TOÀN PHẦN, CHIỀU CAO, BÁN KÍNH ĐÁY, THIẾT DIỆN

Câu 1. (THPT - YÊN Định Thanh Hóa 2019) Cắt một khối trụ bởi một mặt phẳng qua trục của nó ta

được thiết diện là một hình vuông có cạnh bằng

. Tính diện tích toàn phần của khối trụ.



. B.



. C.



. D.



Câu 2. (Chuyên Lê Hồng Phong Nam Định 2019) Một hình trụ có diện tích xung quanh bằng

4 a



và bán kính đáy là

. Tính độ dài đường cao của hình trụ đó.

. B.

. C.

. D.

Câu 3. (Chuyên Thái Nguyên 2019) Một hình trụ có bán kính đáy bằng

2cm

và có thiết diện qua trục

là một hình vuông. Diện tích xung quanh của hình trụ là

8 cmp

. B.

4 cmp

. C.

32 cmp

. D.

16 cmp

Câu 4. (THPT Gia Lộc Hải Dương Năm 2019) Cắt một hình trụ bởi một mặt phẳng qua trục của nó,

ta được thiết diện là một hình vuông có cạnh bằng

. Tính diện tích toàn phần của hình trụ đã

cho.



. B.



. C.

9 a



. D.



Câu 5. (THPT Yên Phong 1 Bắc Ninh 2019) Trong không gian cho hình chữ nhật

ABCD

có

1, 2AB AD==

. Gọi

,MN

lần lượt là trung điểm của

và

. Quay hình chữ nhật đó xung

quanh trục

ta được một hình trụ. Tính diện tích toàn phần

của hình trụ đó.



10 .



Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 59

Câu 6. (Đồng Tháp - 2018) Hình trụ có bán kính đáy bằng

và chiều cao bằng

. Khi đó diện tích

toàn phần của hình trụ bằng

( )

2 3 1a



−

. B.

( )

13a



. C.



. D.

( )

2 1 3a



Câu 7. (THPT Kinh Môn - HD - 2018) Cho lập phương có cạnh bằng

và một hình trụ có hai đáy là

hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi

là diện tích

mặt của hình

lập phương,

là diện tích xung quanh của hình trụ. Hãy tính tỉ số

. B.



. C.



. D.



Câu 8. (Chuyên Hùng Vương - Gia Lai - 2018) Một hình trụ có bán kính đáy

5cmr =

, chiều cao

7cmh =

. Tính diện tích xung quanh của hình trụ.

( )

35π cmS =

. B.

( )

70π cmS =

. C.

( )

π cm

S =

. D.

( )

π cm

S =

Câu 9. (Chuyên ĐH Vinh - 2018) Cắt một hình trụ bằng một mặt phẳng qua trục của nó, ta được thiết

diện là một hình vuông cạnh

. Diện tích xung quanh của hình trụ bằng

2 a



. B.

8 a



. C.

4 a



. D.

16 a



Câu 10. (THPT Kiến An - Hải Phòng - 2018) Tính diện tích xung quanh của một hình trụ có chiều

cao

20 m

, chu vi đáy bằng

50 m

. B.

50 m



. C.

100 m



. D.

100 m

Câu 11. (Hồng Lĩnh - Hà Tĩnh - 2018)

Cho hình chữ nhật

ABCD

có

AB a=

2AD a=

. Thể tích của

khối trụ tạo thành khi quay hình chữ nhật

ABCD

quanh cạnh

bằng

4 a



. B.



. C.

. D.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 60

Câu 12. (Chuyên Bắc Ninh - 2018) Trong không gian, cho hình chữ nhật

ABCD

có

1AB =

và

2AD =

. Gọi

lần lượt là trung điểm của

và

. Quay hình chữ nhật đó xung

quanh trục

, ta được một hình trụ. Tính thể tích

của khối trụ tạo bởi hình trụ đó



. B.



. C.



. D.



Câu 13. (THPT Trần Phú - Đà Nẵng - 2018) Cho khối trụ có chu vi đáy bằng

4 a



và độ dài đường

cao bằng

. Thể tích của khối trụ đã cho bằng



. B.



. C.

4 a



. D.

16 a



Câu 14. (THPT Hà Huy Tập - 2018) Cho một khối trụ có diện tích xung quanh của khối trụ bằng



. Tính thể tích của khối trụ biết khoảng cách giữa hai đáy bằng

160



. B.

400



. C.



. D.



Câu 15. (Hà Nội - 2018) Cho khối trụ có bán kính hình tròn đáy bằng

và chiều cao bằng

. Hỏi nếu

tăng chiều cao lên 2 lần và tăng bán kính đáy lên 3 lần thì thể tích của khối trụ mới sẽ tăng lên

bao nhiêu lần?

lần. B.

lần. C.

lần. D.

lần.

Câu 16. (THPT Lương Thế Vinh 2018). Cho hình trụ có diện tích toàn phần là



và có thiết diện cắt

bởi mặt phẳng qua trục là hình vuông. Tính thể tích khối trụ?



. B.



. C.



. D.



Câu 17. (Chuyên Phan Bội Châu - Nghệ An - 2018) Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo

thiết diện là hình vuông cạnh

. Thể tích khối trụ đó bằng



. B.



. C.



. D.



Câu 18. (SGD&ĐT BRVT - 2018) Thiết diện qua trục của một hình trụ là hình vuông có cạnh là

.Thể tích khối trụ được tạo nên bởi hình trụ này là:

2 a



. B.



. C.

8 a



. D.



Câu 19. (THPT Kinh Môn - Hải Dương - 2018) Cho một khối trụ

( )

có bán kính đáy bằng

. Biết

thiết diện của hình trụ qua trục là hình vuông có chu vi bằng

. Thể tích của khối trụ sẽ bằng



. B.



. C.



. D.



Câu 20. (THPT Gang Thép - 2018)Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là

hình chữ nhật

ABCD

có

và

thuộc hai đáy của khối trụ. Biết

4AB a=

5AC a=

Tính thể tích của khối trụ:

12Va



. B.

16Va



. C.

4Va



. D.

8Va



MỨC VẬN DỤNG1. Diện tích xung quanh, diện tích toàn phần, chiều cao, bán kính đáy, thiết

diện

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 61

Câu 21. (THPT Lê Quy Đôn Điện Biên 2019) Một hình trụ tròn xoay có hai đáy là hai đường tròn

( )

,OR

và

( )

,OR



. Biết rằng tồn tại dây cung

của đường tròn

( )

,OR

sao cho tam giác

O AB



đều và góc giữa hai mặt phẳng

( )

O AB



và mặt phẳng chứa đường tròn

( )

,OR

bằng

60

. Tính diện tích xung quanh của hình

trụ đã cho.

4 R



. B.

23R



. C.



. D.



Câu 22. (Chuyên Sơn La 2019) Cho khối trụ có bán kính đáy bằng

( )

4 cm

và chiều cao

( )

5 cm

. Gọi

là một dây cung đáy dưới sao cho

( )

43AB cm=

. Người ta dựng mặt phẳng

( )

đi qua

hai điểm

và tạo với mặt phẳng đáy hình trụ một góc



như hình vẽ. Tính diện tích

thiết diện của hình trụ cắt bởi mặt phẳng

( )

8 4 3 3



−

. B.

( )

4 4 3



−

( )

4 4 3 3



−

. D.

( )

8 4 3



−

phương. Gọi

lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình

trụ. Tính

S S S=+

( )

4 2400S



. B.

( )

2400 4S



. C.

( )

2400 4 3S



. D.

( )

4 2400 3S



Câu 24. (Chuyên Quốc Học Huế 2018) Một hình trụ có diện tích xung quanh bằng



, thiết diện qua

trục là hình vuông. Một mặt phẳng

( )



song song với trục, cắt hình trụ theo thiết diện là tứ

giác

ABB A



, biết một cạnh của thiết diện là một dây cung của đường tròn đáy của hình trụ và

căng một cung

120

. Tính diện tích thiết diện

ABB A



. B.

. C.

. D.

Câu 25. (Chuyên Lương Thế Vinh - Đồng Nai - 2018) Ba chiếc bình hình trụ cùng chứa

lượng

nước như nhau, độ cao mực nước trong bình

gấp đôi bình

và trong bình

III

gấp đôi bình

. Chọn nhận xét đúng về bán kính đáy

của ba bình

6yx=−

III

theo thứ tự lập thành cấp số nhân công bội

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 62

theo thứ tự lập thành cấp số nhân công bội

B. D. DẠNG 2. THỂ TÍCH

Câu 26. (Chuyên ĐHSPHN - 2018) Cần đẽo thanh gỗ hình hộp có đáy là hình vuông thành hình trụ có

cùng chiều cao. Tỉ lệ thể tích gỗ cần phải đẽo đi ít nhất (tính gần đúng) là

30%

. B.

50%

. C.

21%

. D.

11%

Câu 27. Một khối gỗ hình trụ có đường kính

0,5m

và chiều cao

( )

. Người ta đã cắt khối gỗ, phần

còn lại như hình vẽ bên có thể tích là

. Tính



( )

. B.



( )

. C.



( )

. D.



( )

Câu 28. (Sở Hưng Yên - 2020) Cho hình trụ có

,OO



là tâm hai đáy. Xét hình chữ nhật

ABCD

có

,AB

cùng thuộc

( )

và

,CD

cùng thuộc

( )



sao cho

3AB a=

2BC a=

đồng thời

( )

ABCD

tạo với mặt phẳng đáy hình trụ góc

60

. Thể tích khối trụ bằng



. B.



. C.



. D.

23a



Câu 29. (Sở Hà Tĩnh - 2020) Cho khối trụ có hai đáy là

( )

và

( )



,AB CD

lần lượt là hai đường

kính của

( )

và

( )



, góc giữa

và

bằng

30

6AB =

. Thể tích khối tứ diện

ABCD

bằng

. Thể tích khối trụ đã cho bằng

180



. B.



. C.



. D.



Câu 30. (Lý Nhân Tông - Bắc Ninh - 2020) Từ một tấm tôn hình chữ nhật kích thước

50cm

240cm

người ta làm các thùng đựng nước hình trụ có chiều cao bằng

50cm

, theo hai cách sau (xem

hình minh họa dưới đây):

• Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 63

• Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh

của một thùng.

Kí hiệu

là thể tích của thùng gò được theo cách 1 và

là tổng thể tích của hai thùng gò được

theo cách 2. Tính tỉ số

. B.

. C.

. D.

Câu 31. (Tiên Du - Bắc Ninh - 2020) Cho hình trụ có hai đáy là hình tròn tâm

và



, chiều cao

3ha=

. Mặt phẳng đi qua tâm

và tạo với



một góc

30

, cắt hai đường tròn tâm

và



tại bốn điểm là bốn đỉnh của một hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng

. Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng



. B.

3 a



. C.



. D.



……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 64

HÌNH HỌC 12 – CHƯƠNG 2

§2. MẶT CẦU

A. PHẦN KIẾN THỨC CHÍNH

I. Mặt cầu và các khái niệm liên quan đến mặt cầu

I.1. Mặt cầu

Quan sát một số hình ảnh:

Định nghĩa mặt cầu: Tập hợp các điểm  trong không gian cách điểm  cố định một khoảng  gọi là mặt

cầu tâm , bán kính , kí hiệu là: 

󰇛



󰇜

. Khi đó 

󰇛



󰇜



󰇝



󰇞

Chú ý:

* Nếu 2 điểm , nằm trên mặt cầu 

󰇛



󰇜

thì đoạn thẳng  được gọi là dây cung của mặt cầu

󰇛



󰇜

. Dây

cung  đi qua tâm  được gọi là một đường kính của mặt cầu

󰇛



󰇜

* Một mặt cầu hoàn toàn được xác định nếu biết tâm và bán kính của nó hoặc

biết một đường kính của mặt cầu đó.

Ví dụ (Bài 1/ 49). Tìm tập hợp các điểm  trong không gian luôn nhìn đoạn

thẳng  cố định dưới một góc vuông.

Giải: Tập hp các điểm  trong không gian luôn nhìn đoạn thẳng  cố định

dưới một góc vuông là mặt cầu đường kính .

I.2. Vị trí tương đối của một điểm đối vi mặt cầu

Câu hỏi: Cho mặt cầu

󰇛



󰇜

và một điểmbất kì. Quan sát hình vẽ hãy cho biết

trong không gian, có bao nhiêu vị trí tương đối giữa điểm  và mặt cầu 

󰇛



󰇜

Trả lời: Có 3 vị trí tương đối

Kết luận: Cho mặt cầu

󰇛



󰇜

và một điểmbất kì. Khi đó:

Nếu 

󰇛



󰇜

. Khi đó  gọi là bán kính mặt cầu. Nếu 

và  là hai bán kính sao cho 

󰇍





󰇍



thì đoạn thẳng gọi là một

đường kính của mặt cầu.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 65

Nếu nằm trong mặt cầu.

Nếu  nằm ngoài mặt cầu.

 Khối cầu 

󰇛



󰇜

là tập hợp tất cả các điểm  sao cho .

Định nghãi khối cầu: Tập hợp các điểm thuộc mặt cầu 

󰇛



󰇜

cùng với các

điểm nằm trong mặt cầu đó được gọi là khối cầu tâm  bán kính .

I.3. Biểu diễn mặt cầu:

Hình biểu diễn của mặt cầu là một hình tròn.

Để trực quan người ta vẽ thêm hình biểu diễn của một số đường tròn nằm trên

mặt cầu đó.

II. Vị trí tương đối của mặt phng và mặt cầu (Hưng dẫn tự học)

Cho mặt cầu

󰇛



󰇜

và một 

󰇛



󰇜

. Gọi  là khoảng cách từ tâm  của mặt cầu đến 

󰇛



󰇜

và  là

hình chiếu của  trên 

󰇛



󰇜

.

Nếu 

󰇛



󰇜

cắt mặt cầu 

󰇛



󰇜

theo giao tuyến là đường tròn nằm trên 

󰇛



󰇜

có tâm

là  và bán kính 



 







 



(hình a).

Đặc biệt khi  mặt phẳng

󰇛



󰇜

cắt mặt cầu theo một đường tròn lớn có bán kính  và

󰇛



󰇜

được gọi là mặt phẳng kính

Nếu 

󰇛



󰇜

không cắt mặt cầu 

󰇛



󰇜

(hình b).

Nếu 

󰇛



󰇜

có một điểm chung duy nhất. Ta nói mặt cầu 

󰇛



󰇜

tiếp xúc 

󰇛



󰇜

Điểm : Tiếp điểm của mặt cầu 

󰇛



󰇜

và mặt phẳng

󰇛



󰇜

󰇛



󰇜

: Mặt phẳng tiếp xúc hay tiếp diện của mặt cầu.

Vậy: +

󰇛



󰇜

tiếp xúc với mặt cầu 

󰇛



󰇜

tại điểm  

󰇛



󰇜

vuông góc  tại điểm .

󰇛



󰇜

tiếp xúc với mặt cầu 

󰇛



󰇜



󰇛

󰇛󰇜

󰇜

. (hình c)

Hình a Hình b Hình c

III. Vị trí tương đối của đường thng và mặt cầu (Hưng dẫn tự học)

Cho mặt cầu

󰇛



󰇜

và một đường thẳng . Gọi  là hình chiếu của  trên đường thẳng vàlà

khoảng cách từ tâmcủa mặt cầu đến đường thẳng . Khi đó:

Nếu không cắt mặt cầu

󰇛



󰇜

Nếu cắt mặt cầu

󰇛



󰇜

tại hai điểm phân biệt.

Nếu và mặt cầu tiếp xúc nhau (tại một điểm duy nhất). Do đó: điều kiện cần và đủ để

đường thẳngtiếp xúc với mặt cầu là

󰇛



󰇜

. Khi đó H được gọi là tiếp điểm và  được

gọi là tiếp tuyến của mặt cầu S.

d =

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 66

Đặc biệt, khi  thì đường thẳng  đi qua tâm  và cắt mặt cầu tại hai điểm . Khi đó  là đường

kính của mặt cầu.



 và

󰇛



󰇜

không có điểm chung



 tiếp xúc

󰇛



󰇜

tại 



 cắt

󰇛



󰇜

tại 2 điểm PB

Nhận xt:

a) Qua một điểm  nằm trên mặt cầu 

󰇛



󰇜

có vô số tiếp tuyến của mặt cầu đó. Tất cả các tiếp

tuyến này đều vuông góc với bán kính  của mặt cầu tại  và đều nằm trên mặt phẳng tiếp xúc với mặt

cầu tại điểm  đó.

b) Qua một điểm  nằm ngoài mặt cầu 

󰇛



󰇜

có vô số tiếp tuyến với mặt cầu đã cho. Các tiếp

tuyến này tạo thành một mặt nón đỉnh . Khi đó độ dài các đoạn thẳng kẻ từ  đến các tiếp điểm đều bằng

nhau.

Ch ý.

+ Mặt cầu nội tiếp hình đa diện nếu mặt cầu đó tiếp xúc với tất cả các mặt của hình đa diện.

+ Mặt cầu ngoại tiếp hình đa diện nếu tất cả các đỉnh của hình đa diện đều nằm trên mặt cầu. Khi

mặt cầu nội tiếp (ngoại tiếp) hình đa diện, người ta cũng nói hình đa diện ngoại tiếp (nội tiếp) mặt cầu.

IV. Công thức tính diện tích và thể tích mặt cầu

• Diện tích mặt cầu: 







• Thể tích mặt cầu: 













Ví dụ:

Ví dụ 1: Một mặt cầu

󰇛



󰇜

có bán kính bằng . Tính diện tích 



, thể tích 



của mặt cầu

󰇛



󰇜

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 67

……………………………………………………………………………………………………

Ví dụ 2: Cho khối cầu

󰇛



󰇜

có thể tích bằng  (



). Diện tích mặt cầu bằng bao nhiêu?

……………………………………………………………………………………………………

Ví dụ 3: Thể tích của khối cầu có diện tích mặt cầu bằng .

……………………………………………………………………………………………………

B. LUYỆN TẬP

I. Chữa bài tập SGK

Bài 2 /49. Cho hình chop đều có tất cả các cạnh đều bằng . Hãy xác định tâm và bán kính

mặt cầu ngoại tiếp hình chop đó.

Gọi  là tâm của đáylà trục của đường tròn ngoại tiếp đa giác đáy.

Trong mặt phẳng xác định bởivà một cạnh bên 

󰇛



󰇜

, ta vẽ đường

trung trực của cạnh và cắt  tại  là tâm của mặt cầu.

Ta có: 











Bán kính là 

































Bài 3 /49. Tìm tập hợp tâm mặt cầu luôn chứa một đường tròn cố định

cho trước

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 68

Gọi là tâm của mặt cầu chứa đường tròn

󰇛



󰇜

cố định cho trước, như vậy  phải cách đều tất cả các điểm

thuộc đường tròn

󰇛



󰇜

, suy ra  nằm trên đường thẳng đi qua tâm  của đường tròn

󰇛



󰇜

và vuông góc với

mặt phẳng

󰇛



󰇜

chứa đường tròn

󰇛



󰇜

Bài 4 /49. Tìm tập hợp tâm những mặt cầu luôn cùng tiếp xúc với ba cạnh của một tam giác cho trước.

Cho , gọi 󰇛󰇜 là đường tròn nội tiếp , O là tâm đường tròn nội tiếp của 󰇛󰇜 󰇛󰇜 tiếp xúc ba

cạnh của .

Gọi I là tâm mặt cẩu

󰇛



󰇜

chứa đường tròn 󰇛󰇜. Suy ra

󰇛



󰇜

tiếp xúc ba

cạnh của , I cách đều tất cả các điểm M nằm trên 󰇛󰇜

Vậy tâm I nằm trên trục đường tròn nội tiếp 󰇛󰇜 (là đường thẳng đi qua

O và vuông góc với mặt phẳng chứa 󰇛󰇜).

Bài 7 /49. Cho hình hộp chữ nhật  có 



a. Hãy xác định tâm và bán kính mặt cầu đi qua 8 đỉnh của hình

hộp chữ nhật.

b. Tính bán kính của đường tròn là giao tuyến của mặt phẳng

󰇛



󰇜

với mặt cầu trên.

Giải:

a. Gọi 







lần lượt là tâm đường tròn ngoại tiếp hai đáy hình hộp chữ nhậy. Suy ra 







là trục

đường tròn ngoại tiếp hai đa giác đáy.

Gọi  là trung điểm của 







. Suy ra:

-Trung điểm  của 







là tâm mặt cầu ngoại tiếp lăng trụ.

-Bán kính:









 











 󰇡











󰇢





















.(bằng một nửa đường chéo của hình

hộp chữ nhật)

Ghi nh: Gọi  là đường chéo hình hộp chữ nhật,  lần lượt là chiều dài, chiều rộng của đáy,  là chiều

cao của hình hộp 







 



 



Đối với hình lập phương cạnh 



b. Bán kính đường tròn giao tuyến của mặt phẳng

󰇛



󰇜

với mặt cầu trên là









 











 



 





















 













 





Bài 10 /49. Cho hình chóp  có 4 đỉnh đều nằm trên một mặt cầu,  và 3 cạnh

đôi môt vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.

Giải:

Hình chóp có 3 cạnh đôi môt vuông góc, lần lượt có độ dài là  sẽ nội tiếp cùng một

mặt cầu với hình hộp chữ nhật có 3 kích thước là . Suy ra bán kính mặt cầu ngoại tiếp khối chóp

là 

















Diện tích mặt cầu 









󰇛





 



 



󰇜

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 69

Thể tích khối cầu 





















󰇛





 



 



󰇜







 



 





II. Bài tập trắc nghiệm

Câu 1. [Mức độ 1]Cho mặt cầu 󰇛󰇜. Chọn khẳng định đng.

A. 󰇛󰇜󰇝󰇞. B. 󰇛󰇜󰇝󰇞.

C. 󰇛󰇜󰇝󰇞. D. 󰇛󰇜󰇝󰇞.

Câu 2. [Mức độ 1]Chọn phát biểu sai.

A. Một mặt cầu được xác định nếu biết đường kính của nó.

B. Một mặt cầu được xác định nếu biết dây cung của nó.

C. Một mặt cầu được xác định nếu tâm và một điểm thuộc mặt cầu đó.

D. Một mặt cầu được xác định nếu biết tâm và bán kính của nó.

Câu 3. [Mức độ 1]Gọi

󰇛



󰇜

là mặt cầu tâm , bán kính ;  là khoảng cách từ 

đến mặt phẳng

󰇛



󰇜

với

. Khi đó, số điểm chung giữa

󰇛



󰇜

và

󰇛



󰇜

là:

A. 2. B. vô số. C. 1. D. 0.

Câu 4. [Mức độ 1]] Khối cầu có bán kính  có thể tích bằng bao nhiêu?

A. . B. . C. . D. .

Câu 5. [Mức độ 1]Thể tích của khối cầu có diện tích mặt cầu bằng .

A.  B.  C.









Câu 6. [Mức độ 1] Một hình cầu có thể tích bằng





ngoại tiếp một hình lập phương.

Thể tích của khối lập phương đó là









. B. . C.





. D.









Câu 7. [Mức độ 1]Cho mặt cầu 󰇛󰇜và mặt phẳng

󰇛



󰇜

. Gọi  là khoảng cách từ  đến mặt phẳng

󰇛



󰇜

Chọn phát biểu đng.

A. Nếu  và  thì mặt phẳng

󰇛



󰇜

cắt mặt cầu 󰇛󰇜.

B. Nếu và  thì mặt phẳng

󰇛



󰇜

tiếp xúc mặt cầu 󰇛󰇜.

C. Nếu và  thì mặt phẳng

󰇛



󰇜

và mặt cầu 󰇛󰇜 không có điểm chung.

D. Nếu  và  thì mặt phẳng

󰇛



󰇜

cắt mặt cầu 󰇛󰇜 theo đường tròn giao tuyến có bán

kính là .

Câu 9. [Mức độ 1]Trong các mệnh đề sau mệnh đề nào đúng?

A. Mọi hình hộp đều có mặt cầu ngoại tiếp.

B. Mọi hình hộp đứng đều có mặt cầu ngoại tiếp.

C. Mọi hình hộp có một mặt bên vuông góc với đáy đều có mặt cầu ngoại tiếp.

D. Mọi hình hộp chữ nhật đều có mặt cầu ngoại tiếp.

Câu 10. [Mức độ 2]Tính bán kính của mặt cầu ngoại tiếp một hình lập phương có cạnh bằng .

A. 







. B. . C. 



. D. 



.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 70

Câu 11. [Mức độ 2]ba điểm phân biệt  không thẳng hàng. Tập hợp tâm  của các mặt cầu thỏa

mãn điều kiện đi qua hai điểm là:

A. Đường thẳng trung trực của . B. Đường tròn đường kính .

C. Đường tròn ngoại tiếp . D. Mặt phẳng trung trực của .

Câu 12. [Mức độ 2]Cho hình lập phương 















cạnh .  là tâm của hình lập phương. Xét

mặt cầu

󰇛



󰇜

tâm  bán kính





. Khẳng định nào sau đây đng?

A. Điểm  nằm trên

󰇛



󰇜

. B. Điểm  nằm ngoài

󰇛



󰇜

C. Điểm  nằm trong

󰇛



󰇜

. D. Điểm  nằm trong

󰇛



󰇜

Câu 13. [Mức độ 2]

Thể tích của khối cầu ngoại tiếp bát diện đều có cạnh bằng  là:

















. C.









. D.











Câu 14. [Mức độ 2]Cho hình lăng trụ tam giác đềucó tất cả các cạnh đều bằng .

Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ.

A. . B. 





. C. 





. D. 





Câu 15. [Mức độ 3] Cho hình chóp  có đáy là hình thoi cạnh , 



, tam giác 

đều và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp

.







 B.







 C.







 D.









Câu 16. [Mức độ 3]Cho hình chóp  có đáy  là hình thoi cạnh , 



 và 

. Mặt cầu ngoại tiếp hình chóp  có bán kính bằng









và . Thể tích khối chóp

là











. B.











. C.











. D.





.

Câu 17. [Mức độ 3]Cho hình chóp  có đáy  là tam giác vuông tại . Biết 

󰇛



󰇜

, 

, 







, góc giữa

󰇛



󰇜

và

󰇛



󰇜

bằng 



. Vị trí tương đối giữa mặt cầu tâm , bán

kính









với mặt phẳng

󰇛



󰇜

là:

A. Tiếp xúc. B. Không có điểm chung.

C. Cắt nhau theo giao tuyến là một đường tròn. D. Cắt nhau theo giao tuyến là đường tròn lớn.

Câu 18. [Mức độ 3] Cho hình chóp  có đáy  là tam giác vuông tại . Biết 

󰇛



󰇜

, 

, góc giữa

󰇛



󰇜

và

󰇛



󰇜

bằng 



. Mặt cầu 

󰇛



󰇜

cắt mặt phẳng

󰇛



󰇜

theo giao tuyến là

một đường tròn

󰇛



󰇜

. Tính bán kính của

󰇛



󰇜

A. 









. B. 





. C. 









. D. 





Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 71

Câu 19. [Mức độ 4] Cho hình chóp  có đáy là hình chữ nhật , 



,

cạnh bên  vuông góc với mặt phẳng đáy, góc giữa đường thẳng  và mặt phẳng đáy

bằng 



. Diện tích mặt cầu ngoại tiếp hình chóp là.







. B.







. C. 



. D. 



BÀI TẬP TỰ LUYỆN

Câu 1. [Mức độ 1]Tính diện tích mặt cầu biết bán kính mặt cầu đó là 





A. . B. . C. 



. D. .

Câu 2. [Mức độ 1]Diện tích của mặt cầu có thể tích là









bằng

A. 



. B. 



. C. 



. D. .

Câu 3. [Mức độ 1]Cho mặt cầu 󰇛󰇜 và đường thẳng . Gọi  là hình chiếu vuông góc của  lên

đường thẳng . Chọn khẳng định sai.

A. Nếu thì đường thẳng  cắt mặt cầu 󰇛󰇜 tại hai điểm phân biệt.

B. Nếu  thì đường thẳng  và mặt cầu 󰇛󰇜 không có điểm chung.

C. Nếu  thì đường thẳng  tiếp xúc với mặt cầu 󰇛󰇜 tại .

D. Nếu  thì đường thẳng  cắt mặt cầu 󰇛󰇜 tại hai điểm phân biệt.

Câu 4. [Mức độ 1] Một khối cầu có bán kính  thì có thể tích  bằng bao nhiêu?





B. 







. C. 







. D. 







Câu 5. [Mức độ 1] Diện tích của mặt cầu có bán kính  bằng 

󰇛



󰇜







. Một hình hộp chữ

nhật có ba kích thước là . Gọi 󰇛󰇜 là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó.

Tâm của mặt cầu 󰇛󰇜 là:

A. Một đỉnh bất kì của hình hộp chữ nhật.

B. Tâm của một mặt bên của hình hộp chữ nhật.

C. Trung điểm của một cạnh của hình hộp chữ nhật.

D. Tâm của hình hộp chữ nhật.

Câu 6. [Mức độ 1]Cho mặt cầu

󰇛



󰇜

có tâm  bán kính  và mặt phẳng

󰇛



󰇜

cắt

󰇛



󰇜

theo một đường

tròn

󰇛



󰇜

có bán kính . Kết luận nào sau đây là sai?

A. Tâm của

󰇛



󰇜

là hình chiếu vuông góc của  trên

󰇛



󰇜

󰇛



󰇜

là giao tuyến của

󰇛



󰇜

và

󰇛



󰇜

C. Khoảng cách từ  đến

󰇛



󰇜

bằng 4.

󰇛



󰇜

là đường tròn lớn của mặt cầu

󰇛



󰇜

Câu 7. [Mức độ 2] Cho hình lăng trụ đứng  có đáy  là tam giác vuông tại 





, góc 







. Thể tích khối cầu ngoại tiếp hình lăng trụ bằng:









. B.











. C.









. D. 



Câu 8. [Mức độ 2] Cho hình chóp , 

󰇛



󰇜

. Tam giác  vuông tại ,

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 72

. Bán kính mặt cầu ngoại tiếp khối chóp.













. C. . D. .

Câu 9. [Mức độ 2]Tính bán kính mặt cầu tiếp xúc với tất cả các cạnh của một hình lập phương cạnh .







. B.







. C.





. D.







Câu 10. [Mức độ 2] Cho hình chóp tứ giác đều có tất cả các cạnh bằng 



 Tính thể tích  của

khối cầu ngoại tiếp khối chóp trên.

A. 













. B. 



C. 









. D. 









Câu 11. [Mức độ 2] Cho hình hộp chữ nhật có kích thức     .

Tính diện tích mặt cầu ngoại tiếp hình hộp.

A. . B. . C. . D. .

Câu 12. [Mức độ 2]Cho hình chóp  có đáy  là hình chữ nhật với độ dài đường chéo bằng



, cạnh  có độ dài bằng  và vuông góc với mặt phẳng đáy. Tính bán kính mặt cầu ngoại

tiếp hình chóp  ?









. B.









. C.









. D.









Câu 13. [Mức độ 3] Cho hình chóp tam giác đều  có đáy  là tam giác đều cạnh  cạnh









 Gọi  là điểm đối xứng của  qua  Tính bán kính  của mặt cầu ngoại tiếp

hình chóp .

A. 









. B. 









. C. 









. D. 









Câu 14. [Mức độ 3]Cho hình chóp  có đáy  là tam giác đều cạnh . 

󰇛



󰇜

và 



.

Vị trí tương đối giữa mặt cầu tâm , bán kính









với mặt phẳng

󰇛



󰇜

là:

A. Tiếp xúc. B. Không có điểm chung.

C. Cắt nhau theo giao tuyến là một đường tròn. D. Cắt nhau theo giao tuyến là đường tròn lớn.

Câu 15. [Mức độ 3] Cho hình lăng trụ đứng  có đáy  là tam giác vuông cân tại

. Góc giữa đường chéo  của mặt bên  với mặt đáy bằng 



. Tính bán

kính mặt cầu ngoại tiếp hình lăng trụ.







. B.









. C.







. D.









Câu 16. [Mức độ 4] Một quả bóng nổi trên mặt hồ khi đóng băng. Khi lấy bóng lên (không làm vỡ bóng)

bóng để lại một lỗ trũng bề ngang  đo ở bề mặt trên cùng và sâu . Bán kính 

󰇛



󰇜

của quả bóng là:

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 73

A. 











. B. 











. C. 











. D. 











Câu 17. [Mức độ 4] Cho hình chóp có đáy  là hình vuông cạnh , tam giác  đều

và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp khối .













. B.













. C.













. D.













Câu 19. [Mức độ 4] Cho hình chóp  có đáy  là hình chữ nhật,  tam

giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi  lần lượt là trung điểm các

cạnh  Tính bán kính  của mặt cầu ngoại tiếp hình chóp .

A. 









. B. 









. C. 









. D. 









Câu 20. [Mức độ 4] Cho hình nón

󰇛



󰇜

có góc ở đỉnh bằng 



 độ dài đường sinh bằng . Dãy hình

cầu

󰇛





󰇜



󰇛





󰇜



󰇛





󰇜



󰇛





󰇜

thỏa mãn:

󰇛





󰇜

tiếp xúc với mặt đáy và các đường sinh của

hình nón

󰇛



󰇜



󰇛





󰇜

tiếp xúc ngoài với

󰇛





󰇜

và tiếp xúc với các đường sinh của hình nón

󰇛



󰇜



󰇛





󰇜

tiếp xúc ngoài với

󰇛





󰇜

và tiếp xúc với các đường sinh của hình nón

󰇛



󰇜

. Tính tổng thể

tích các khối cầu

󰇛





󰇜



󰇛





󰇜



󰇛





󰇜



󰇛





󰇜

 theo .











 B.











 C.











 D.













……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 74

HÌNH HỌC 12- CHƯƠNG 3

§1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN

A. PHẦN KIẾN THỨC CHÍNH

I. TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ

1. Hệ tọa độ

Trong không gian, cho ba trục

' ' '

x Ox, y Oy, z Oz

vuông góc với nhau từng đôi một, với các vectơ

đơn vị

và

2 2 2

1i j k= = =

0i .j j.k k.i= = =

Trong đó:

x Ox

là trục hoành

y Oy

là trục tung

z Oz

là trục cao

là gốc tọa độ

Không gian với hệ trục tọa độ

Oxyz

còn

được gọi là không gian

Oxyz

2. Tọa độ của điểm

Trong không gian

Oxyz

, điểm

có tọa độ là bộ ba số (x;y;z) khi và chỉ khi

OM xi y j zk= + +

Ta viết:

( )

M x; y;z=

hoặc

( )

M x; y;z

*Ví dụ: Cho vectơ

45OM i j k.= − + −

Hãy tìm tọa độ điểm

.........................................................................................................................................................

3. Tọa độ của vectơ

Trong không gian

Oxyz

, vectơ

có tọa độ là bộ ba số

1 2 3

(a ;a ;a )

khi và chỉ khi

1 2 3

a a i a j a k.= + +

Ta viết:

1 2 3

a (a ;a ;a )=

hoặc

1 2 3

a(a ;a ;a )

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 75

Chú ý: Trong không gian

Oxyz

, ta có:

( ) ( )

M x; y;z OM x; y;z=  =

*Ví dụ: Cho vectơ

3 4 5a i j k.= − + −

Hãy tìm tọa độ điểm

.........................................................................................................................................................

II. Biểu thức tọa dộ của các php toán vectơ

a. Định lý

Trong không gian

Oxyz

cho

1 2 3 1 2 3

a ( a ;a ;a ),b (b ;b ;b )==

. Ta có:

1 1 2 2 3 3

a ) a b ( a b ,a b ,a b )

b ) a b (a b ,a b ,a b )

+ = + + +

− = − − −

1 2 3 1 2 3

c ) ka k( a ;a ;a ) ( ka ;ka ;ka )==

( k )

b. Hệ quả

Trong không gian

Oxyz

cho

1 2 3 1 2 3

a ( a ;a ;a ),b (b ;b ;b )==

. Ta có:

a b a b





=  =







* Xét vectơ

có tọa độ là

( )

000;;

0* b ,

→



cùng phương

kR  

1 1 2 2 3 3

a kb , a kb , a kb= = =

* Trong không gian

Oxyz

cho hai điểm

A A A B B B

A( x ; y ;z );B( x ; y ;z )

thì:

B A B A B A

AB ( x x , y y ,z z )= − − −

Nếu

là trung điểm của đoạn

thì

2 2 2

A B A B A B

x x y y z z

M , ,

+ + +







c. Ví dụ.

Cho

1 2 3 3 0 5a ( ; ; ); b ( ; ; )= − = −

a. Tìm tọa độ của

biết

23x a b=−

b. Tìm tọa độ của

biết

3 2 0a b x− + =

.........................................................................................................................................................

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 76

.........................................................................................................................................................

B. Bài tập trắc nghiệm (Chiếu PPT).

Câu 1: [Mức độ 1] Trong không gian Oxyz với hệ tọa độ

( )

O;i; j;k

cho

3OA i k= − +

. Tọa độ điểm A

là

( )

1 0 3;;−

. B.

( )

0 1 3;;−

. C.

( )

1 3 0;;−

( )

13;−

Câu 2: [Mức độ 1] Trong không gian Oxyz, cho điểm

( )

1 2 3M ; ;−

. Tọa độ hình chiếu của M trên trục

Ox là

( )

1 2 0;;−

. B.

( )

1 0 0;;−

. C.

( )

0 0 3;;

( )

0 2 0;;

Câu 3: [Mức độ 2] Trong không gian Oxyz, cho vectơ

34OM i j k= − +

. Gọi M’ là hình chiếu vuông

góc của M trên mp(Oxy). Khi đó tọa độ của điểm M’ là

( )

1 3 4;;−

. B.

( )

1 4 3;;−

. C.

( )

0 0 4;;

. D.

( )

1 3 0;;−

Câu 4: [Mức độ 2] Trong không gian Oxyz, cho hình bình hành ABCD, biết

( ) ( ) ( )

1 0 0 0 0 1 2 11A , , ; B , , ; C , ,

. Tọa độ điểm D là

( )

3 1 0,,

. B.

( )

3 1 0;;−

. C.

( )

3 1 0;;−

. D.

( )

1 3 0;;

Câu 5: [Mức độ 2] Cho ba điểm

( ) ( )

2 11 3 2 1A , , ; B , ,− − −

. Tìm điểm N trên trục x’Ox cách đều A và

( )

400;;

. B.

( )

400;;−

( )

1 4 0;;

. D.

( )

2 0 4;;

Câu 6: [Mức độ 3] Trong không gian với hệ tọa độ Oxyz, cho A(2; 0; 0), B(0; 3; 1), C(-3; 6; 4). Gọi M

là điểm nằm trên đoạn BC sao cho

2MC MB=

. Độ dài đoạn AM là

--A.

. B.

. C.

. D.

C. BÀI TẬP TỰ LUYỆN

Câu 7: [Mức độ 2] Trong không gian với hệ tọa độ

Oxyz

, cho hai vectơ

( )

1 1 2a ; ;=−

( )

3 0 1b ; ;= − −

và điểm

( )

0 2 1A ; ;

. Tọa độ điểm

thỏa mãn

2AM a b=−

là

( )

5 1 2M ; ;−

. B.

( )

3 2 1M ; ;−

. C.

( )

1 4 2M ; ;−

. D.

( )

5 4 2M ; ;−

Câu 8: [Mức độ 2] Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

( )

3 4 2A ; ;−

( )

5 6 2B ; ;−

( )

4 7 1C ; ;−−

. Tọa độ điểm

thỏa mãn

23AD AB AC=+

là

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 77

( )

10 17 7D ; ;−−

. B.

( )

10 17 7D ; ;−

. C.

( )

10 17 7D ; ;−

. D.

( )

10 17 7D ; ;−−

Câu 9: [Mức độ 2] Trong không gian Oxyz, cho tam giác ABC có tọa độ các đỉnh

4 2 3A( ; ; )

1 2 9B( ; ; )−−

và

12C( ; ;z )−

. Xác định giá trị

để tam giác ABC cân tại A.

=−







. B.





=−



. C.







. D.

=−





=−



Câu 10: -[Mức độ 3] Trong không gian Oxyz, điểm M nằm trên mặt phẳng

(O y )x

, cách đều ba điểm

( ) ( ) ( )

2 3 1 0 4 3 3 2 2A , , ,B ; ; ,C ; ;−−

có tọa độ là

17 49

25 50

;;







. B.

( )

3 6 7;;−−

( )

1 13 14;;−−

. D.

4 13

7 14

;;







……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 78

HÌNH HỌC 12- CHƯƠNG 3

§1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN

III. TÍCH VÔ HƯỚNG

1. Biểu thức tọa độ của tích vô hướng

* VD MỞ ĐẦU: Cho các vectơ

( )

1 2 3

a a ;a ;a=

và

( )

1 2 3

b b ;b ;b=

a) Hãy biểu diễn hai vectơ

a,b

theo ba vectơ đơn vị

i , j,k

b) Tính tích vô hướng của hai vectơ

a,b

theo

1 2 3 1 2 3

a ,a ,a ,b ,b ,b

…………………………………………………………………………………………………….

* Định lí: Trong không gian Oxyz tích vô hướng của hai vectơ

( )

1 2 3

a a ; a ; a=

và

( )

1 2 3

b b ; b ; b=

được xác định bởi công thức

1 1 2 2 3 3

a.b a b a b a b .= + +

Ví dụ 1: Trong không gian

Oxyz

, cho

( )

1 2 1a ; ;=−

và

2 3 5b i j k= − + −

. Tính tích vô hướng

của hai vectơ

a,b

…………………………………………………………………………………………………….

2. Ứng dụng

a) Độ dài của một vectơ

Cho vectơ

( )

1 2 3

a a ; a ; a ,=

ta có

222

1 2 3

a a a a .= + +

b) Khoảng cách giữa hai điểm

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 79

Cho hai điểm

( )

A A A

A x ; y ; z

và

( )

B B B

B x ; y ; z .

Ta có

( ) ( ) ( )

2 2 2

B A B A B A

AB x x y y z z .= − + − + −

c) Góc giữa hai vectơ

Gọi



là góc giữa hai vectơ

( )

1 2 3

a a ; a ; a=

và

( )

1 2 3

b b ; b ; b=

với

và

khác vectơ

thì

( )

1 1 2 2 3 3

2 2 2 2 2 2

1 2 3 1 2 3

a b a b a b

cos cos a,b .

a a a . b b b

 = =

+ + + +

* Chú ý:

1 1 2 2 3 3

0a b a b a b a b .⊥  + + =

Ví dụ 2: Trong không gian

Oxyz

cho hai điểm

( ) ( )

3 0 1 1 1 2a ; ; ,b ; ;= = − −

. Hãy tính

ab+

…………………………………………………………………………………………………….

Ví dụ 3: Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

( )

1 2 3A ; ;−

( )

0 1 1B ; ;−

và

( )

4 2 1C ; ;−

. Tính độ dài các đoạn thẳng

AB,AC

và côsin của góc

BAC

…………………………………………………………………………………………………….

Ví dụ 4: Trong không gian

Oxyz

cho hai điểm

( ) ( )

3 1 2 1 2 1A ; ; , B ; ; .−−

Tìm tọa độ điểm

trên trục

sao cho tam giác

ABC

vuông tại

…………………………………………………………………………………………………….

3. Bài tập trắc nghiệm.

Câu 1: Trong không gian với hệ trục tọa độ

Oxyz

cho hai vectơ

( )

11a ; ;m=−

( )

1 0 1b ; ;=

. Vectơ

vuông

góc với

khi

2m =−

. B.

0m =

. C.

1m =

. D.

1m =−

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 80

Câu 2: Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

( )

3 2 1A ; ;

( )

1 3 2B ; ;−

;

( )

2 4 3C ; ;−

. Tích vô

hướng

AB.AC

là

. B.

6−

. C.

. D.

2−

Câu 3: Trong không gian

Oxyz,

cho vectơ

( ) ( )

2 2 4 1 1 1a ; ; , b ; ; .= − − = −

Mệnh đề nào dưới đây sai?

( )

333a b ; ;+ = − −

. B.

và

cùng phương. C.

3b =

. D.

ab⊥

Câu 4: Trong không gian Oxyz, cho

a, b

có độ dài lần lượt là 1 và 2. Biết

3ab+=

khi đó góc giữa

vectơ

a,b

là



. B.



. C.

. D.



−

Câu 5: Trong không gian

Oxyz

cho các điểm

( ) ( ) ( )

5 1 5 4 3 2 3 2 1A ; ; ; B ; ; ; C ; ;−−

. Điểm

( )

I a;b;c

là

tâm đường tròn ngoại tiếp tam giác

ABC

. Tính

2a b c++

. B.

. C.

. D.

9.−

Câu 6: Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

có

( )

1 0 0A ; ;

( )

0 0 1B ; ;

( )

2 1 1C ; ;

Diện tích của tam giác

ABC

bằng

. B.

. C.

. D.

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 81

HÌNH HỌC 12- CHƯƠNG 3

§1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN

IV. Phương trình mặt cầu

1. Bài toán mở đầu

Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

I a;b;c

và số dương

. Tìm điều kiện để

điểm

( )

M x; y;z

nằm trên mặt cầu

( )

tâm

có bán kính

…………………………………………………………………………………………………….

Nhận xét: Mọi điểm

nằm trên mặt cầu

( )

đều có tọa độ thỏa mãn phương trình

(*)

Phương trình

( )

như trên được gọi là phương trình của mặt cầu

( )

2. Định lí: Trong không gian

Oxyz ,

mặt cầu

( S )

có tâm

( )

I a; b; c=

bán kính

có phương trình là:

( )

x a y b z c r− + − + − =

* Ví dụ 1: Viết phương trình mặt cầu tâm

( )

1 2 3I ; ;=−

bán kính

5r.=

…………………………………………………………………………………………………….

* Ví du 2: Tìm tọa độ tâm

và bán kính

của mặt cầu

( S )

, biết:

( ) ( ) ( )

2 2 2

3 4 2 16x y z− + + + − =

( ) ( ) ( )

2 2 2

1 5 3 25x y z+ + − + + =

…………………………………………………………………………………………………….

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 82

3. Nhận xét

Phương trình mặt cầu

( )

x a y b z c r− + − + − =

có thể viết dưới dạng

2 2 2

2 2 2 0x y z ax by cz d+ + − − − + =

với

2 2 2 2

d a b c r= + + −

Ngược lại những phương trình có dạng

2 2 2

2 2 2 0x y z ax by cz d+ + − − − + =

là phương trình

mặt cầu khi và chỉ khi

2 2 2

0a b c d+ + − 

Khi đó mặt cầu có tâm

( )

I a;b;c

và bán kính

2 2 2

r a b c d= + + −

* Ví dụ 3: Trong không gian

Oxyz

, phương trình nào sau là phương trình mặt cầu? Nếu là

phương trình của một mặt cầu, xác định tọa độ tâm và tính bán kính của nó.

2 2 2

4 6 2 14 0x y z x y z+ + − + + + =

2 2 2

8 2 2 62 0x y z xy y z+ + − + + + =

2 2 2

3 2 4 6 2 6 0x y z x y z+ + − + + − =

2 2 2

4 8 2 6 0x y z x y z+ + − + + − =

…………………………………………………………………………………………………….

4. Bài tập trắc nghiệm.

Câu 1: Trong không gian

Oxyz

, mặt cầu

( S )

2 2 2

2 2 6 2 0x y z x y z+ + + − + + =

đi qua điểm nào sau

đây?

A. Điểm

( )

1 1 2Q ; ;−

. B. Điểm

( )

2 3 7M ; ;−

. C. Điểm

( )

1 3 2N ; ;−

. D. Điểm

( )

1 3 0P ; ;

Câu 2: Trong không gian

Oxyz

, mặt cầu tâm

( )

1 2 3I ; ;−

bán kính

2r =

có phương trình là

( ) ( ) ( )

2 2 2

1 2 3 4x y z− + + + − =

. B.

( ) ( ) ( )

2 2 2

1 2 3 4x y z+ + − + + =

( ) ( ) ( )

2 2 2

1 2 3 2x y z− + + + − =

. D.

( ) ( ) ( )

2 2 2

1 2 3 2x y z+ + − + + =

Câu 3: Trong không gian

Oxyz

cho hai điểm

( )

1 2 3I ; ;−

và

( )

1 0 3A ; ;

. Mặt cầu

( S )

tâm

và đi qua điểm

có phương trình là

( ) ( ) ( )

2 2 2

1 2 3 2x y z− + + + − =

. B.

( ) ( ) ( )

2 2 2

1 2 3 4x y z+ + − + + =

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 83

( ) ( ) ( )

2 2 2

1 2 3 4x y z− + + + − =

. D.

( ) ( ) ( )

2 2 2

1 2 3 2x y z+ + − + + =

Câu 4: Trong không gian

Oxyz

cho hai điểm

( )

2 1 0A ; ;−

và

( )

0 3 4B ; ;−

. Mặt cầu đường kính

có

phương trình là

( ) ( ) ( )

2 2 2

1 1 2 3x y z− + − + − =

. B.

( ) ( ) ( )

2 2 2

1 1 2 3x y z− + − + + =

( ) ( ) ( )

2 2 2

1 1 2 9x y z− + − + − =

. D.

( ) ( ) ( )

2 2 2

1 1 2 9x y z− + − + + =

Câu 5: Trong không gian

Oxyz

, phương trình nào sau đây là phương trình mặt cầu?

2 2 2

2 2 2 4 8 0x y z x y+ + + + =

. B.

2 2 2

2 2 4 2 1 0x y z x y z+ + − + − − =

2 2 2

2 2 2 0x y z x y+ + − + + =

. D.

2 2 2

50x y z x y+ − − + − =

Câu 6: Trong không gian

Oxyz

cho mặt cầu

( )

có phương trình

2 2 2

2 4 6 5 0x y z x y z+ + − − − + =

Diện tích của mặt cầu

( S )

là

12

. B.

9

. C.

36

. D.

24

Câu 7: Trong không gian

Oxyz

cho ba điểm

( ) ( ) ( )

1 3 1 2 1 1 4 1 7A ; ; ,B ; ; ;C ; ;−−

. Bán kính

của mặt cầu

đi qua bốn điểm

O,A,B,C

là

r =

. B.

r =

. C.

115

r =

. D.

r =

Câu 8: Tìm tất cả các giá trị thực của tham số

để phương trình

( ) ( ) ( )

2 2 2

2 1 2 2 3 2 2 1 11 0x y z m x m y m z m+ + − − + − + + + − =

là phương trình của một mặt cầu.

0m 

hoặc

1m 

. B.

01m

. C.

1m −

hoặc

2m 

. D.

12m−  

Câu 9: Trong không gian

Oxyz

cho mặt cầu

( )

có phương trình

( ) ( )

2 2 2

2 2 3 6 2 7 0x y z m x my m z+ + − − + + − − =

Gọi

là bán kính của mặt cầu

( )

thì giá trị nhỏ nhất của

bằng

. B.

377

. C.

377

. D.

377

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 84

HÌNH HỌC 12 – CHƯƠNG 3: PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN

§1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN

A. PHẦN KIẾN THỨC CHÍNH

1. Biểu thức tọa độ của các php toán vectơ

Cho

( ) ( )( )

1 2 3 1 2 3

a a ;a ;a ,b b ;b ;b k= = 

•

( )

1 1 2 2 3 3

a b a b ;a b ;a b =   

•

( )

1 2 3

ka ka ;ka ;ka=

•

a b a b





=  =







•

cùng phương

( )

0bb



a kb=

( )

2 2 1 2 3

1 2 3

a kb

a kb , b ,b ,b

b b b

a kb





 =  = = 







• Toạ độ trung điểm

của đoạn thẳng

2 2 2

A B A B A B

x x y y z z

M ; ;

+ + +







• Toạ độ trọng tâm

của tam giác

ABC

3 3 3

A B C A B C A B C

x x x y y y z z z

G ; ;

+ + + + + +







2. Tích vô hưng của 2 vectơ và ứng dụng

Cho

( ) ( )

1 2 3 1 2 3

a a ;a ;a ,b b ;b ;b==

•

1 1 2 2 3 3

a.b a .b a .b a .b= + +

•

222

1 2 3

a a a a= + +

•

2 2 2

B A B A B A

AB AB ( x x ) ( y y ) ( z z )= = − + − + −

•

1 1 2 2 3 3

2 2 2 2 2 2

1 2 3 1 2 3

a b a b a b

a.b

cos(a,b )

a . b

a a a . b b b

+ + + +

B. LUYỆN TẬP

I. Bài tập tự luận sách giáo khoa

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 85

Câu 1: (Bài 1b/68) Trong không gian

Oxyz

, cho hai vectơ

( )

2 5 3a ; ;=−

;

( )

0 2 1b ; ;=−

;

( )

1 7 2c ; ;=

Tính tọa độ vectơ

42e a b c= − −

Câu 2: (Bài 3/68) Trong không gian

Oxyz

, cho hình hộp

ABCD.A' B' C' D'

có

( )

1 0 1A ; ;

( )

2 1 2B ; ;

( )

1 1 1D ; ;−

( )

4 5 5C' ; ;−

. Tìm tọa độ các đỉnh còn lại của hình hộp.

Câu 3: Trong không gian

Oxyz

, cho 3 điểm:

( )

1 2 4A ; ;−

( )

1 1 4B ; ;−

( )

0 0 4C ; ;

. Tính

a) Độ dài các đoạn thẳng

BA;BC

BA.BC

c) Số đo của góc

ABC

II. Bài tập trắc nghiệm

Câu 4: [Mức độ 2] Trong không gian

Oxyz

, cho

( )

1 3 2u ; ;= − −

và

( )

2 5 1v ; ;=−

. Tìm tọa độ của véc

tơ

23a u v=−

( )

8 9 1a ; ; .= − −

( )

8 9 1a ; ; .= − −

( )

8 9 1a ; ; .= − −

( )

8 9 1a ; ; .= − − −

Câu 5: [Mức độ 1] Trong không gian

Oxyz

, cho

( )

1 2 3a ; ;=−

( )

2 4 6b ; ;= − −

. Khẳng định nào sau đây

là đng?

2ab=

. B.

2ba=−

. C.

2=−ab

. D.

2ba=

Câu 6: [Mức độ 2] Trong không gian

Oxyz

, cho tam giác

ABC

có

( ) ( ) ( )

1 2 1 2 3 2 1 0 1 A ; ; ; B ; ; ; C ; ; .−−

Tìm tọa độ đỉnh

sao cho

ABCD

là hình bình hành?

( )

0 1 2D ; ;

. B.

( )

0 1 2D ; ;−

. C.

( )

0 1 2D ; ;−

. D.

( )

0 1 2D ; ;−−

Câu 7: [Mức độ 2] Trong không gian

Oxyz

, cho hình hộp

ABCD.A B C D

   

. Biết tọa độ các đỉnh

( )

3 2 1A ; ;−

( )

4 2 0C ; ;

( )

2 1 1B ; ;



−

( )

3 5 4D ; ;



. Tìm tọa độ đỉnh



của hình hộp.

( )

3 3 1A' ; ;−

. B.

( )

333A' ; ;−

. C.

( )

333A' ; ;−−−

. D.

( )

3 3 3A' ; ;−−

Câu 8: [Mức độ 1] Trong không gian

Oxyz

, cho

( )

1 3 2 u ; ;=−

( )

3 1 2v ; ;= − −

. Khi đó

u.v

bằng

. B.

. C.

. D.

2−

Câu 9:

[Mức độ 2] Trong không gian

Oxyz

, cho

( )

2 1 2a ; ;= − −

( )

0 1 1b ; ;=−

. Góc giữa hai vectơ

a; b

bằng

. B.

120

. C.

. D.

135

Câu 10: [Mức độ 3] Trong không gian

Oxyz

, cho ba điểm

( ) ( ) ( )

2 3 1 1 1 1 1 1 2M ; ; , N ; ; , P ;m ;− − −

. Tìm

để tam giác

MNP

vuông tại

N ?

2 m .=

4 m .=−

6m .=−

0m .=

C. BÀI TẬP T LUYỆN

Câu 11: [Mức độ 2] Trong không gian

Oxyz

, cho ba vectơ

( )

1 2 3a ; ;=

( )

2 2 1b ; ;=−

( )

4 0 4c ; ;=−

Tọa độ vectơ

2d a b c= − +

là

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 86

( )

7 0 4d ; ;= − −

. B.

( )

704d ; ;=−

. C.

( )

7 0 4d ; ;=−

. D.

( )

704d ; ;=

Câu 12: [Mức độ 1] Trong không gian

Oxyz

, cho hai điểm

( )

2 3 1A ; ;−

và

( )

419B ; ;−

. Trung điểm

của đoạn thẳng

có tọa độ là

( )

1 2 4;;−

. B.

( )

2 4 8;;−

. C.

( )

6 2 10;;−−

. D.

( )

1 2 4;;−−

Câu 13: [Mức độ 2] Trong không gian

Oxyz

, cho ba điểm

( ) ( ) ( )

3 2 1 1 1 2 1 2 1A ; ; ,B ; ; ,C ; ;−−

. Tìm tọa độ

điểm M thỏa mãn

2OM AB AC=−

( )

2 6 4M ; ; −−

( )

2 6 4M ; ; −

( )

2 6 4M ; ; −−

. D.

( )

5 5 0M ; ;

Câu 14: [Mức độ 2] Trong không gian

Oxyz

, cho

( )

1 2 4A ; ;−

( )

1 1 4B ; ;−

( )

0 0 4C ; ;

. Tính số đo của

góc

ABC

. B.

135

. C.

120

. D.

Câu 15: [Mức độ 2] Trong không gian

Oxyz

, cho ba điểm

( ) ( ) ( )

1 2 0 2 2 3 1 0 2A ; ; ;B ; ; ;C ; ;− − − −

. Mệnh

đề nào sau đây đúng?

30 BAC =

. B.

60 BAC =

. C.

90 BAC =

. D.

120BAC =

Câu 16: [Mức độ 2] Trong không gian

Oxyz

, cho bốn điểm

( )

1 0 0A ; ; ,

( )

0 1 0B ; ; ,

( )

0 0 1C ; ;

( )

2 1 1D ; ;−−

. Tính góc giữa hai đường thẳng

và

135

. B.

. C.

. D.

Câu 17: [Mức độ 3] Cho ba điểm

( )

1 3 1 A ; ;−

( )

2 6 1B ; ;−

và

( )

492C ; ;−−

. Tìm điểm

trên trục

sao cho vectơ

u MA MB MC=++

có độ dài nhỏ nhất.

( )

1 0 0M ; ;

. B.

( )

400M ; ;

. C.

( )

3 0 0M ; ;

. D.

( )

200M ; ;

Câu 18: [Mức độ 3] Trong không gian

Oxyz

, cho ba điểm

( )

0 0 1A ; ;−

( )

1 1 0B ; ;−

( )

1 0 1C ; ;

. Tìm tọa

độ điểm

sao cho

2 2 2

32MA MB MC+−

đạt giá trị nhỏ nhất.

M ; ;



−





. B.

M ; ;



−





. C.

M ; ;



−−





. D.

M ; ;



−−





……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 87

HÌNH HỌC 12- CHƯƠNG 3

§1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN

TIẾT 5. BÀI TẬP PHƯƠNG TRÌNH MẶT CẦU

A. Kiến thức cần nh

1) Phương trình mặt cầu (S) dạng 1:

Để viết phương trình mặt cầu

( S ),

ta cần tìm tâm

I(a;b;c )

và bán kính

Khi đó:

2 2 2 2

Tâm: I( a;b;c )

( S ): ( S ): ( x a ) ( y b ) ( z c ) R .

Bán kín h:



 − + − + − =





2) Phương trình mặt cầu (S) dạng 2:

Cho

2 2 2

2 2 2 0( S ): x y z ax by cz d .+ + − − − + =

Với

2 2 2

0a b c d+ + − 

là phương trình mặt

cầu dạng

tâm

I(a;b;c ),

bán kính:

2 2 2

0R a b c d= + + − 

B. Bài tập

Dạng 1. Tìm tâm và bán kính của mặt cầu.

Câu 1: Trong không gian

Oxyz

, cho mặt cầu có phương trình:

2 2 2

2 6 6 0x y z x y+ + + − − =

. Tọa độ tâm

và bán khính của mặt cầu đó.

( )

1 3 0 4I ; ; ;R−=

. B.

( )

1 3 0 4I ; ; ;R−=

. C.

( )

1 3 0 16I ; ; ;R−=

. D.

( )

1 3 0 16I ; ; ;R−=

Câu 2: Trong không gian

Oxyz

, cho mặt cầu

( )

2 2 2

2 4 2 0S : x y z x y z m+ + + + − − =

. Tìm

để bán

kính cầu mặt cầu bằng

10m =

. B.

4m =

. C.

23m =

. D.

10m =

Câu 3: Trong không gian

Oxyz

, tìm tất cả các giá trị của

để phương trình

2 2 2

4 2 2 0x y z x y z m+ + + − + + =

là phương trình của một mặt cầu.

6m 

. B.

6m 

. C.

6m 

. D.

6m 

Dạng 2. Vị trí tương đối của điểm vi mặt cầu.

Câu 4: Trong không gian

Oxyz

, cho mặt cầu

2 2 2

1 2 3 9( S ):( x ) ( y ) ( z ) .− + − + − =

Điểm nào sau đây

nằm ngoài mặt cầu

(S)

1 2 5M( ; ; )−

. B.

032N( ; ; )

. C.

1 6 1P( ; ; )−−

. D.

2 4 5Q( ; ; ).

Câu 5: Trong không gian

Oxyz

, cho mặt cầu

2 2 2

6 4 2 0( S ):x y z x y z+ + − − − =

. Điểm nào sau đây

thuộc mặt cầu (S)?

( )

0 1 1M ; ;−

. B.

( )

032N ; ;

. C.

( )

1 6 1P ; ;−−

. D.

( )

1 2 0Q ; ;

Câu 6: Trong không gian với hệ tọa độ

Oxyz

, mặt cầu có phương trình nào sau đây đi qua gốc tọa độ?

2 2 2

2 4 2 0x y z x y+ + + − − =

. B.

2 2 2

4 6 2 0x y z y z+ + − + − =

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 88

2 2 2

2 6 0x y z x z+ + + + =

. D.

2 2 2

2 4 6 2 0x y z x y z+ + + − + − =

Dạng 3. Viết phương trình mặt cầu.

Câu 7: Trong không gian

Oxyz

, mặt cầu tâm

( )

2 1 1I ; ;−

qua điểm

( )

0 1 0A ; ;−

là

( )

19x y z+ + + =

. B.

( ) ( ) ( )

2 2 2

2 1 1 9x y z− + + + + =

( ) ( ) ( )

2 2 2

2 1 1 9x y z+ + − + − =

. D.

( )

19x y z+ − + =

Câu 8: Trong không gian

Oxyz

, cho hai điểm

( ) ( )

6 2 5 4 0 7M ; ; ,N ; ;−−

. Viết phương trình mặt cầu

đường kính

MN.

( ) ( ) ( )

2 2 2

1 1 1 62x y z− + − + − =

. B.

( ) ( ) ( )

2 2 2

5 1 6 62x y z− + − + + =

( ) ( ) ( )

2 2 2

1 1 1 62x y z+ + + + + =

. D.

( ) ( ) ( )

2 2 2

5 1 6 62x y z+ + + + − =

Câu 9: Trong không gian

Oxyz,

mặt cầu

( )

có tâm

( )

2 1 1I ; ; ,−

tiếp xúc với mặt phẳng tọa độ

( )

Oyz .

Phương trình của mặt cầu

( )

là

( ) ( ) ( )

2 2 2

2 1 1 4x y z+ + + + − =

. B.

( ) ( ) ( )

2 2 2

2 1 1 1x y z− + − + + =

( ) ( ) ( )

2 2 2

2 1 1 4x y z− + − + + =

. D.

( ) ( ) ( )

2 2 2

2 1 1 2x y z+ + − + + =

Câu 10: Trong không gian

Oxyz

, cho

( ) ( ) ( )

1 0 0 0 0 2 0 3 0A ; ; ,B ; ; ,C ; ;−−

. Tính bán kính mặt cầu ngoại

tiếp tứ diện

OABC

là

. B.

. C.

. D.

Câu 11: Trong không gian

Oxyz

, cho điểm

( ) ( )

1 1 2 3 2 3A ; ; ,B ; ;−

. Mặt cầu

( )

có tâm

thuộc

và

đi qua hai điểm

A,B

có phương trình.

2 2 2

8 2 0x y z x+ + − + =

. B.

2 2 2

8 2 0x y z x+ + + + =

2 2 2

4 2 0x y z x+ + − + =

. D.

2 2 2

8 2 0x y z x+ + − − =

Dạng 4. Các bài toán cực trị liên quan đến điểm và mặt cầu.

Câu 12: Trong không gian Oxyz, cho mặt cầu

( ) ( ) ( ) ( )

2 2 2

1 2 1 9S : x y z− + − + + =

và hai điểm

( ) ( )

4 3 1 3 1 3A ; ; ,B ; ; ;M

là điểm thay đổi trên

( )

. Gọi

m,n

là giá trị lớn nhất, nhỏ nhất của biểu

thức

2P MA MB .=−

Xác định

mn−

A. 64. B. 48. C. 68. D. 60.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 89

HÌNH HỌC 11 – CHƯƠNG 3

§2. PHƯƠNG TRÌNH MẶT PHẲNG

A. PHẦN KIẾN THỨC CHÍNH

I. Vectơ pháp tuyến của mặt phng

➢ Định nghĩa. Cho mặt phẳng

( )



. Nếu vectơ

có giá vuông góc với

( )



thì được gọi là vectơ pháp

tuyến (VTPT) của

( )



➢ Nhận xét. Nếu vectơ

là VTPT của

( )



thì

( )

k 

cũng là VTPT của

( )



➢ Chú ý. Nếu hai vectơ

và

không cùng phương và có giá song song hoặc nằm trên mặt

phẳng

( )



thì

,n a b





là VTPT của mặt phẳng

( )



Tích có hưng của hai vectơ

Cho hai vectơ

( )

1 2 3

;;a a a a=

và

( )

1 2 3

;;b b b b=

. Tích có hướng của hai vectơ

và

là

( )

2 3 3 1

2 3 3 2 3 1 3 1 1 2 1 2

2 3 3 1

, ; ; ; ;

a a a a

n a b a b a b a b b a a b b a

b b b b





= = = − − −







Nhận xét. Cho mặt phẳng

( )



đi qua ba điểm

. Khi đó mp

( )



có một VTPT là

,n AB AC





➢ Ví dụ 1. Trong không gian

Oxyz

cho ba điểm không thẳng hàng

( )

0;1;2A

( )

1; 1;1B −

và

( )

4;3;2C −

a) Tìm tọa độ một VTPT của mặt phẳng đi qua ba điểm

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 90

……………………………………………………………………………………………………

II. Phương trình tổng quát của mặt phng

Trong không gian

Oxyz

cho mặt phẳng

( )



qua điểm

( )

0 0 0 0

;;M x y z

và có VTPT

( )

;;n A B C=

Với

( )

;;M x y z

bất kì, ta có

( )

( ) ( ) ( ) ( )

( )

0 0 0

M n MM

A x x B y y C z z

Ax By Cz Ax By Cz

Ax By Cz D



  =

 − + − + − =

 + + − − − =

 + + + =

trong đó,

( )

0 0 0

D Ax By Cz= − + +

và

2 2 2

0A B C+ + 

➢ Định nghĩa. Phương trình

( )

được gọi là phương trình tổng quát của mặt phẳng

( )



nhận

( )

;;n A B C=

làm vectơ pháp tuyến.

➢ Ví dụ 1. Trong không gian

Oxyz

cho ba điểm không thẳng hàng

( )

0;1;2A

( )

1; 1;1B −

và

( )

4;3;2C −

a) Tìm tọa độ một VTPT của mặt phẳng đi qua ba điểm

b) Viết phương trình tổng quát của mặt phẳng

( )



Lời giải.

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 91

……………………………………………………………………………………………………

➢ Ví dụ 2. Trong không gian

Oxyz

cho

( )

: 3 1 0Q x y− + =

. Tọa độ một VTPT của mặt phẳng

( )

là

( )

1; 3;1−

. B.

( )

3;1;0−

. C.

( )

1; 3;0−

. D.

( )

2;6; 2−−

……………………………………………………………………………………………………

➢ Ví dụ 3. Trong không gian

Oxyz

, phương trình nào sau đây không phải là phương trình tổng

quát của mặt phẳng?

20xy−=

. B.

10z +=

( )

2 1 2 0mx m y z+ − − − =

. D.

2 3 4 0Ax Ay Az+ + − =

……………………………………………………………………………………………………

2. Các trường hợp riêng

Trong không gian

Oxyz

cho mặt phẳng

( )

:0Ax By Cz D



+ + + =

( )

+ Nếu

0D =

thì mặt phẳng

( )



đi qua gốc tọa độ.

+ Nếu

0A =

thì mặt phẳng

( )



song song hoặc chứa trục

+ Nếu

0B =

thì mặt phẳng

( )



song song hoặc chứa trục

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 92

+ Nếu

0C =

thì mặt phẳng

( )



song song hoặc chứa trục

II. PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG

2. Các trường hợp riêng

Trong không gian

Oxyz

cho mặt phẳng

( )

: z 0Ax By C D



+ + + =

(1)

c)Nếu hai trong ba hệ số

bằng 0

+ Nếu

0AB==

và

0C 

thì

( )



song song hoặc trùng với mặt phẳng

( )

Oxy

+ Nếu

0AC==

và

0B 

thì

( )



song song hoặc trùng với mặt phẳng

( )

Oxz

+ Nếu

0BC==

và

0A 

thì

( )



song song hoặc trùng với mặt phẳng

( )

Oyz

➢ Nhận xt:

Nếu cả bốn hệ số

đều khác 0 thì phương trình

z 0 1

x y z

Ax By C D

a b c

+ + + =  + + =

(2).

Với

=−

Ta gọi phương trình (2) là phương trình mặt phẳng theo đoạn chắn.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 93

C. LUYỆN TẬP VÀ VẬN DỤNG

BÀI TẬP TRẮC NGHIỆM

Dạng 1. Tìm vc tơ pháp tuyến của mặt phng

Bài 1. Trong không gian

Oxyz

, cho mặt phẳng

( )

:3 1 0Qy+=

. Tọa độ một VTPT của mặt phẳng

( )

là:

( )

3;1;0

. B.

( )

0;0;3

. C.

( )

3;0;0

. D.

( )

0;3;0

Bài 2. Trong không gian

Oxyz

, cho mặt phẳng

3 2z 1 0xy− + + + =

. Tọa độ một VTPT của mặt phẳng là:

( )

3;2;1

. B.

( )

1;3;2

. C.

( )

2; 6; 4−−

. D.

( )

1;3;1−

Bài 3. Trong không gian

Oxyz

, mặt phẳng

( )

chứa

( )

0;2;1b =

và song song

( )

1;2;3a =−

. Mặt phẳng

( )

có VTPT là:

( )

2;1; 4n =−

. B.

( )

4;1; 2n = − −

. C.

( )

1; 4;2n =−

. D.

( )

1;2; 4n =−

Dạng 2. Viết phương trình mặt phng khi biết một điểm và VTPT

Bài 4. Viết phương tình tổng quát của mặt phẳng đi qua điểm

( )

1;2;0N −

và có VTPT

( )

2;2; 4a =−

2 2 4 4 0x y z+ − + =

. B.

2 2 0x y z− − + − =

2 2 0x y z+ − + =

. D.

2 2 4 2 0x y z+ − − =

Bài 5. Viết phương tình tổng quát của mặt phẳng đi qua điểm

( )

1;0;2N −

và vuông góc với vec tơ

( )

2;4; 6a =−

2 4 6 5 0x y z+ − + =

. B.

2 3 5 0x y z− − − + =

2 3 7 0x y z+ − + =

. D.

2 3 10 0x y z+ − + =

Dạng 3. Viết phương trình mặt phng theo đoạn chắn

Bài 6. Trong không gian

Oxyz

, cho ba điểm

( ) ( ) ( )

1;0;0 ; 0; 2;0 ; 0;0;5A B C−

. Mặt phẳng đi qua 3 điểm

,,A B C

có phương trình là:

2 5z 0xy− + =

. B.

2 5 1 0x y z− + − =

1 2 5

x y z

+ + =

−

. D.

1 2 5

x y z

+ + =

−

Bài 7. Trong không gian

Oxyz

, mặt phẳng đi qua

( )

1;2;3G

và cắt các trục

;Ox

;Oy

tại điểm

với

là trọng tâm

ABC

có phương trình là:

2 3z 0xy+ + =

. B.

1 2 3

x y z

+ + =

. C.

1 2 3

x y z

+ + =

. D.

3 6 9

x y z

+ + =

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 94

III. ĐIỀU KIỆN ĐỂ HAI MẶT PHẲNG SONG SONG, VUÔNG GÓC

1. Lý thuyết

Cho hai mặt phẳng

1 1 1 1 1

( ): 0A x B y C z D



+ + + =

và

2 2 2 2

( ): 2 0A x B y C z



+ + + =

( ) ( )

n kn

D kD





( ) ( )

n kn

D kD







( )



cắt

( )



n kn

( )



vuông góc

( )



.0nn=

2. Các ví dụ minh họa

➢ Ví dụ 1. Cho hai mặt phẳng

( )



và

( )



có phương trình

( )

: 2 3 1 0x y z



− + + =

( )

:2 4 6 1 0x y z



− + + =

Có nhận xét gì về vectơ pháp tuyến của chúng?

……………………………………………………………………………………………………

➢ Ví dụ 2. Viết phương trình mặt phẳng

( )



đi qua điểm

( )

1; 2;3 M −

và song song với mặt

phẳng

( )

:2 3 5 0x y z



− + + =



……………………………………………………………………………………………………

➢ Ví dụ 3. Viết phương trình mặt phẳng

( )



đi qua hai điểm

( )

3;1; 1 , A −

( )

2; 1;4B −

và vuông

góc với mặt phẳng

( )



có phương trình:

2 3 1 0x y z− + − =

……………………………………………………………………………………………………





󰇍











󰇍



Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 95

……………………………………………………………………………………………………

3. Các bài tập trc nghiệm

Bài 1. Trong không gian

Oxyz

cho mặt phẳng

( )

phương trình:

2 3 4 20 0x y z− + + =

và

( )

:4 13 6 40 0Q x y z− − + =

 Vị trí tương đối của

( )

và

( )

là:

A. Song song. B. Trùng nhau.

C. Cắt nhưng không vuông góc. D. Vuông góc.

Bài 2. Chọn ngẫu nhiên một số có

chữ số. Gọi

là xác suất để tổng các chữ số của số đó là một số lẻ.

Khi đó

bằng:

( )

:2 5 0P x y z− + − =

và

( )

: 4 2 2 10 0Q x y z− + − + =

( )

: 3 0R x y z− + − =

và

( )

:2 2 2 6 0S x y z− + + =

( )

:0T x y z− + =

và

( )

2 2 2

x y z

K −+=

( )

:3 2 3 0X x y z− + − =

và

( )

:6 2 6 0Z x y− − =

Bài 3. Trong không gian

Oxyz

cho hai mặt phẳng

( )

: 3 2 1 0P x y z− + + =

và

( ) ( ) ( ) ( )

: 2 1 1 2 2 4 14 0m x m m y m zQ − + − + − + =

 Mặt phẳng

( ) ( )

PQ⊥

khi

bằng bao

nhiêu?

m =−

. B.

m = − −

. C.

2m =

. D.

m =

Bài 4. Trong không gian

Oxyz

cho hai mặt phẳng

( )

:2 3 0P x y z− − − =

và

( )

: 2 0xzQ − − =

 Tính góc

giữa hai mặt phẳng

( )

và

( )

30

. B.

45

. C.

60

. D.

90

Bài 5. Trong không gian

Oxyz

, cho tứ diện

ABCD

có

( )

0;2;0 ;A

( )

2;0;0 ;B

( )

0;0; 2 ;C

( )

0; 2;0D −

. Số

đo góc của hai mặt phẳng

( )

ABC

và

( )

ACD

là?

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 96

30

. B.

45

. C.

60

. D.

90

Bài 6. Trong không gian

Oxyz

, mặt phẳng

( )



đi qua điểm

( )

2; 1;1A −

và vuông góc hai mặt phẳng

( )

:2 1 0P x z− + =

và

( )

:0Qy=

. Phương trình của mặt phẳng

( )



là:

2 4 0xy+ − =

. B.

2 4 0xz+ − =

. C.

20x y z+ + =

. D.

20x y z− + =

Bài 7. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

( )

2;0; 1 ;P −

( )

1; 1;3Q −

và mặt phẳng

( )

:3 2 5 0P x y z+ − + =

. Gọi

( )



là mặt phẳng đi qua

và vuông góc với

( )

. Phương

trình của

( )



là

7 11 3 0x y z− + + − =

. B.

7 11 1 0x y z− + − =

7 11 15 0x y z− + + + =

. D.

7 11 1 0x y z− − + =

……………………………………………………………………………………………………

…………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 97

HH12 – CHƯƠNG 3

§2. PHƯƠNG TRÌNH MẶT PHẲNG

A. PHẦN KIẾN THỨC CHÍNH

I. ĐỊNH NGHĨA CỔ ĐIỂN

1.Khoảng cách từ một điểm đên mặt phng.

Trong không gian

Oxyz

cho điểm

( )

0 0 0

;;M x y z

và mặt phẳng

( )

:0Ax By Cz D



+ + + =

. Khi đó khoảng cách từ điểm

đến mặt phẳng

( )



là:

( )

0 0 0

2 2 2

Ax By Cz D

A B C



+ + +

B. LUYỆN TẬP

I. Các ví dụ

➢

VD1: Tính khoảng cách từ điểm

( )

1;3; 2M −

đến

( )

:2 2 1 0x y z



− + + =

…………………………………………………………………………………………………….

➢

VD2: Tính khoảng cách giữa hai mặt phẳng song song

( )

và

( )

biết:

( )

: 3 1 0P x y z+ + − =

;

( )

: 3 3 0Q x y z+ + + =

Lời giải

…………………………………………………………………………………………………….

II. Bài tập trắc nghiệm

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 98

Câu 1: [Mức độ 1] Tính khoảng cách từ điểm

( )

1;2;1M

đến

( )

: 3 15 0x y zP − + + =

. B.

. C.

. D.

Câu 2: [Mức độ 1] Trong không gian

Oxyz

, khoảng cách giữa hai mặt phẳng song song:

( )

: 2 2 10 0P x y z+ + − =

và

( )

: 2 2 3 0Q x y z+ + − =

. B.

. C.

. D.

Câu 3: [Mức độ 2] Trong không gian

Oxyz

, Mặt cầu

( )

có tâm

( )

2;1;3I

và tiếp xúc với mặt phẳng

( )

: 2 2 2 0P x y z+ + + =

, phương trình mặt cầu là:

( ) ( ) ( )

2 2 2

1 2 3 16x y z− + − + − =

. B.

( ) ( ) ( )

2 2 2

1 2 3 4x y z− + − + − =

( ) ( ) ( )

2 2 2

1 2 3 16x y z+ + + + + =

. D.

( ) ( ) ( )

2 2 2

1 2 3 4x y z+ + + + + =

Câu 4: [Mức độ 2] Trong không gian

Oxyz

,cho điểm

( )

2;3;5I

phương trình mặt cầu tâm

và tiếp xúc

với mặt phẳng

( )

Oxy

là:

( ) ( ) ( )

2 2 2

2 3 5 5x y z− + − + − =

. B.

( ) ( ) ( )

2 2 2

2 3 5 10x y z− + − + − =

( ) ( ) ( )

2 2 2

2 3 5 25x y z+ + + + + =

. D.

( ) ( ) ( )

2 2 2

2 3 5 25x y z− + − + − =

Câu 5: [Mức độ 2] Trong không gian

Oxyz

, điểm

thuộc trục

và cách đều hai mặt phẳng

( )

: 1 0P x y z+ − + =

và

( )

: 5 0Q x y z− + − =

có toạ độ là:

( )

0; 3;0M −

. B.

( )

0;3;0M

. C.

( )

0; 2;0M −

. D.

( )

0;1;0M

Câu 6: [Mức độ 2] Trong không gian

Oxyz

, mặt phẳng

( )

:2 2 6 0P x y z+ − + =

cắt mặt cầu

( ) ( ) ( ) ( )

2 2 2

: 1 2 3 25S x y z− + − + − =

theo một giao tuyến là đường tròn

( )

. Diện tích của hình

tròn

( )

là:



. B.



. C.



. D.



Câu 7: [Mức độ 3] Trong không gian

Oxyz

, cho hai điểm

( )

2; 2;4A −

( )

3;3; 1B −−

và mặt phẳng

( )

:2 2 8 0P x y z− + − =

. Xét

thay đổi và

( )

MP

, giá trị nhỏ nhất của

23AM BM+

bằng:

145

. B.

135

. C.

105

. D.

108

Câu 8: [Mức độ 3] Trong không gian

Oxyz

, mặt phẳng

( )

đi qua

( )

1;7;2A

và cách

( )

2;4; 1M −−

một

khoảng cách lớn nhất có phương trình là:

( )

:3 3 3 10 0P x y z+ + − =

. B.

( )

: 1 0P x y z+ + + =

( )

: 10 0P x y z+ + − =

. D.

( )

: 10 0P x y z+ + + =

C. BÀI TẬP T LUYỆN

Câu 9: [2H3-2.6-1] (SGD Vĩnh Phc-2019-2020) Trong không gian

Oxyz

, khoảng cách từ điểm

( )

1; 4;5M −

đến mặt phẳng

( )

Oxz

bằng

. B.

. C.

. D.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 99

Câu 10: [2H3-2.6-1] (Chuyên Hà Giang - Năm 2019 - 2020) Cho mặt phẳng

( )

:2 2 6 0x y z



− + − =

và điểm

( )

2; 3;5M −

. Khoảng cách từ

đến mặt phẳng

( )



là

. B.

. C.

. D.

Câu 11: [2H3-2.6-2] (THPT Lê Văn Thịnh - Bắc Ninh - Năm 2019 - 2020) Trong không gian với hệ

trục toạ độ

Oxyz

, cho hai mặt phẳng

( )



2 2 4 0x y z− − + =

và

( )



2 2 7 0x y z− − + =

. Tính

khoảng cách giữa hai mặt phẳng

( )



và

( )



. B.

. C.

. D.

Câu 12: [2H3-2.6-2] (SGD Sơn La - Năm 2019-2020) Cho mặt phẳng

( )

: 2 3 0P x y z− + − =

và điểm

( )

;1;2Mm

với

m

. Tìm tất cả cá giá trị của

sao cho khoảng cách từ điểm

đến mặt

phẳng

( )

bằng

9;m =−

15m =−

. B.

9;m =

15m =

. C.

9;m =−

15m =

. D.

9;m =

15m =−

Câu 13: [2H3-2.6-2] (Chuyên Quang Trung - Lần 01 - Năm 2019 - 2020) Trong không gian với hệ trục

tọa độ

Oxyz

, khoảng cách từ tâm mặt cầu

2 2 2

4 4 4 1 0x y z x y z+ + − − − − =

đến mặt phẳng

( )

: 2 2 10 0P x y z+ + − =

bằng

. B.

. C.

. D.

Câu 14: [2H3-2.6-3] (Chuyên Nguyễn Trãi - Hải Dương - Năm 2019-2020) Cho hai điểm

( )

2;1; 1 ,A −

( )

0;3;1B

. Biết tập hợp các điểm

( )

: 3 0M x y z



 + + + =

thỏa mãn

24MA MB−=

là đường

tròn có bán kính

. Tính

27r =

. B.

6r =

. C.

26r =

. D.

5r =

Câu 15: [2H3-2.6-3] (Chuyên Nguyễn Trãi - Hải Dương - Năm 2019-2020) Cho mặt phẳng

( )



đi

qua hai điểm

( )

4;0;0M

và

( )

0;0;3N

sao cho mặt phẳng

( )



tạo với mặt phẳng

( )

Oyz

một góc

bằng

. Tính khoảng cách từ điểm gốc tọa độ đến mặt phẳng

( )



. B.

. C.

. D.

Câu 16: [2H3-2.7-2] (Chuyên Phan Bội Châu - Nghệ An - Lần 2 - Năm 2019-2020) Trong không gian

Oxyz

, cho mặt cầu

( )

2 2 2

: 25S x y z+ + =

và mặt phẳng

( )

: 2 2 12 0P x y z+ + − =

. Tính bán kính

đường tròn giao tuyến của

( )

và

( )

16.

Câu 17: [2H3-2.7-2] (Vted - Đề 05 - Năm 2019-2020) Trong không gian

Oxyz

, mặt cầu

( ) ( )

: 2 9S x y z+ + − =

cắt mặt phẳng

( )

Oxy

theo giao tuyến là một đường tròn có bán kính

bằng

. B.

. C.

. D.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 100

Câu 18: [2H3-2.7-2] (THPT Đào Duy Từ - Năm 2019 - 2020) Đường tròn giao tuyến của mặt cầu

( ) ( ) ( ) ( )

2 2 2

: 3 2 3 25S x y z− + − + − =

khi cắt bởi mặt phẳng

( )

Oxy

có chu vi bằng



. B.



. C.



. D.



Câu 19: [2H3-2.7-2] (THPT Hoàng Văn Thụ - Nam Định - Lần 2 - Năm 2019 - 2020) Trong không

gian với hệ tọa độ

,Oxyz

cho mặt phẳng

( ): 1 0P x y z+ + + =

. Viết phương trình mặt cầu có tâm

(1;1;0)I

và tiếp xúc với

()mp P

2 2 2

( 1) ( 1) 3.x y z− + − + =

2 2 2

( 1) ( 1) 3.x y z− + − + =

2 2 2

( 1) ( 1) 3.x y z+ + + + =

2 2 2

( 1) ( 1) 3.x y z+ + + + =

Câu 20: [2H3-2.9-2] (THPT Lương Thế Vinh – Hà Nội – Lần 01 – Năm 2019 - 2020) Trong không

gian

Oxyz

, cho

( )

1;2;5 ,A

( )

3;4;1 ,B

( )

2;3; 3 ,C −

là trọng tâm tam giác

ABC

và

là điểm

trên mặt phẳng

( )

Oxz

. Độ dài

ngắn nhất bằng:

. B.

. C.

. D.

Câu 21: [2H3-2.9-3] (THPT Cam Lộ-Quảng Trị-2019-2020) Cho mặt phẳng

( )

:2 2 2 15 0P x y z+ − + =

và mặt cầu

( )

2 2 2

: 2 2 1 0S x y z y z+ + − − − =

. Khoảng cách nhỏ nhất từ một điểm thuộc mặt

phẳng

( )

đến một điểm thuộc mặt cầu

( )

là:

. B.

. C.

. D.

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 101

HH12 – CHƯƠNG 3

§2. PHƯƠNG TRÌNH MẶT PHẲNG

A. PHẦN KIẾN THỨC CHÍNH

I. ĐỊNH NGHĨA CỔ ĐIỂN

1.Tích có hưng của hai vectơ

Trong không gian

Oxyz

cho hai vectơ

( )

1 2 3

;;a a a a=

và

( )

1 2 3

;;b b b b=

. Khi đó

( )

2 3 3 2 3 1 1 3 1 2 2 1

, ; ;a b a b a b a b a b a b a b



= − − −



2. Phương trình mặt phng.

Trong không gian

Oxyz

mặt phẳng

( )

đi qua điểm

( )

0 0 0

;;M x y z

và có một vec tơ pháp tuyến

( )

,,n A B C

có phương trình dạng:

( ) ( ) ( ) ( )

0 0 0

:0P A x x B y y C z z− + − + − =

3. Vị trí tương đối của hai mặt phng.

Trong không gian

Oxyz

, cho hai mặt phẳng

( )



( )



lần lượt có phương trình

( )

1 1 1 1 1

:0A x B y C z D



+ + + =

( )

2 2 2 2 2

:0A x B y C z D



+ + + =

, với

Gọi

( )

1 1 1

;;n A B C

là VTPT

( )

1 1 1 1

:0A x By C z D



+ + + =

;

( )

2 2 2

;;n A B C

là VTPT

( )

2 2 2 2 2

:0A x B y C z D



+ + + =

( )

2 2 2

0 1;2

k k k

A B C k+ +  =

Khi đó:

( ) ( )

( )

1 1 1 1

1 2 2 2 2 2

2 2 2 2

. . . 0

n kn

A B C D

D kD







   = = = 







( ) ( )

( )

1 1 1 1

1 2 2 2 2

2 2 2 2

|| . . 0

n kn

A B C D

A B C

A B C D







  = =  









( ) ( )

1 1 1 1

2 2 2 2

A B C D



  = = =

( )



cắt

( )



1 1 1 2 2 2

: : : :A B C A B C

THđặc biệt:

( ) ( )

1 2 1 2 1 2 1 2

0A A B B C C



⊥  + + =

4. Góc giữa hai mặt phng.

Trong không gian

Oxyz

, cho hai mặt phẳng

( )



( )



lần lượt có phương trình

( )

1 1 1 1 1

:0A x B y C z D



+ + + =

( )

2 2 2 2 2

:0A x B y C z D



+ + + =

, với

Gọi

( )

1 1 1

;;n A B C

là VTPT

( )

1 1 1 1

:0A x By C z D



+ + + =

;

( )

2 2 2

;;n A B C

là VTPT

( )

2 2 2 2 2

:0A x B y C z D



+ + + =

( )

2 2 2

0 1;2

k k k

A B C k+ +  =

Góc giữa hai mặt phằng

( )



( )



và, kí hiệu

( ) ( )

( )



là góc.

Từ đó suy ra

( ) ( )

( )







Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 102

và có công thức tính như sau:

( ) ( )

( )

( ) ( )

( )

( ) ( )

1 2 1 2 1 2

2 2 2 2 2 2

1 1 1 2 2 2

cos , cos ;

A A B B C C

A B C A B C



= = =

+ + + +

B. LUYỆN TẬP

I. Các ví dụ

➢

VD1: Cho ba điểm

( )

5;1;3A

( )

1;6;2B

( )

5;0;4C

. Tìm vectơ pháp tuyến của mặt phẳng

( )

song song với

( )

ABC

…………………………………………………………………………………………………….

➢

VD2: Cho ba điểm

( )

2; 1;1A −

( )

1;0;3B

( )

0; 2;1P −

. Viết phương trình mặt phẳng

( )

đi

qua trọng tâm

của

ABC

và vuông góc với

…………………………………………………………………………………………………….

➢

VD3: Tìm

mn+

để

( )

:2 3 5 0P x my z+ + − =

song song với

( )

: 8 6 2 0Q nx y z− + + =

…………………………………………………………………………………………………….

➢

VD4: Tính góc giữa hai mặt phẳng:

( )

: 2 2 0P x y z− − + =

và

( )

:2 1 0Q x y z− + + =

…………………………………………………………………………………………………….

➢

VD5: Tìm

để điểm

( )

; 1;1 2A m m m−+

thuộc mặt phẳng

( )

:2 1 0P x y z− − + =

…………………………………………………………………………………………………….

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 103

…………………………………………………………………………………………………….

II. Bài tập trắc nghiệm

Câu 1: [Mức độ 1] Toạ độ vecto pháp tuyến của mặt phẳng có cặp vecto chỉ phương

( )

2;1;2a =

( )

3;2;1b =

là:

( )

5;8; 1−

. B.

( )

5; 8;1−

. C.

( )

5; 8; 1−−

. D.

( )

5;8;1

Câu 2: [Mức độ 1] Toạ độ vectơ pháp tuyến của mặt phẳng đi qua ba điểm

( )

1;0;2A

( )

1;1;1B

( )

2;3;0C

là?

( )

1;1; 1−

. B.

( )

1; 1; 1−−

. C.

( )

1;1;1

. D.

( )

1;1; 2−

Câu 3: [Mức độ 2] Phương trình mặt phẳng trung trực của đoạn thẳng

với

( )

1; 2;3 ;A −

( )

3;2;1B −

là?

2 2 0x y z− + =

. B.

2 2 1 0x y z− + + =

. C.

2 2 2 1 0x y z+ + + =

. D.

2 1 0x y z+ − − =

Câu 4: [Mức độ 2] Viết phương trình mặt phẳng

( )

biết

( )

đi qua

( )

1; 3;4A −

và

( )

song song với

( )

:6 5 7 0Q x y z− + + =

6 5 25 0x y z− + + =

. B.

6 5 7 0x y z− + − =

6 5 25 0x y z− + − =

. D.

6 5 17 0x y z− + + =

Câu 5: [Mức độ 2] Mặt phẳng

( )

qua

( )

1;2;3G

cắt các trục toạ độ tại

sao cho

là trọng

tâm của tam giác

ABC

có phương trình là

18 0ax by cz+ + − =

. Gía trị của

abc++

bằng

. B.

. C.

. D.

Câu 6: [Mức độ 2] Cho hai mặt phẳng

( )

:2 2 0P x y mz+ + − =

và và

( )

: 2 8 0Q x ny z+ + + =

song song

với nhau.Tính tổng

mn+

bằng

4,25

. B.

4,5

. C.

2,5

. D.

2,25

Câu 7: [Mức độ 2] Trong không gian

Oxyz

cho mặt phẳng

( )

: 2 2 0m x y m z



− + − + =

và

( )

: 2 1 0x m y z



+ − + =

( )

m

. Tìm

để

( ) ( )



⊥

1m =

. B.

2m =

. C.

3m =

. D.

2m =

Câu 8: [Mức độ 2] Tính góc giữa hai mặt phẳng:

( )

: 4 0P x z+ − =

và

( )

Oxy

. B.

. C.

. D.

Câu 9: [Mức độ 2] Điểm

( )

,1;6Mm

thuộc mặt phẳng

( )

: 2 5 0P x y z− + − =

khi đó

thuộc khoảng

nào trong các khoảng sau đây?

( )

0;2

. B.

( )

2;0−

. C.

( )

2;4

. D.

( )

2;3

C. BÀI TẬP T LUYỆN

Câu 10: [2H3-2.1-1] (THPT Ngô Quyền - Hà Nội - Lần 01 - Năm 2018 - 2019) Toạ độ một vectơ pháp

tuyến của mặt phẳng

( )



đi qua ba điểm

( )

2;0;0M

( )

0; 3;0N −

( )

0;0;4P

là

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 104

( )

2; 3;4−

. B.

( )

6;4; 3−−

. C.

( )

6; 4;3−−

. D.

( )

6;4;3−

Câu 11: [2H3-2.1-2] (THPT Cụm Trần Kim Hưng - Hưng Yên - Năm 2018 - 2019) Trong không gian

với hệ tọa độ

Oxyz

, cho điểm

( )

3 1 3A −−;;

( )

1 3 1B − ;;

và

( )

là mặt phẳng trung trực của đoạn

thẳng

. Một vectơ pháp tuyến của

( )

có tọa độ là:

( )

1 3 1− ;;

. B.

( )

11 2− ;;

. C.

( )

3 1 3−−;;

. D.

( )

1 2 1−;;

Câu 12: [2H3-2.4-1] Trong không gian

Oxyz

, mặt phẳng

( )

: 3 0P x y z+ + − =

đi qua điểm nào dưới

đây?

( )

1; 1; 1M − − −

( )

1;1;1N

( )

3;0;0P −

( )

0;0; 3Q −

Câu 13: [2H3-2.5-1] (Chuyên Phan Bội Châu - Nghệ An - Lần 4 - 2018 - 2019) Trong không gian

Oxyz

, cho hai mặt phẳng

( )

: 2 1 0P x y z− − + =

( )

: 2 7 0Q x y z+ + + =

. Tính góc giữa hai mặt

phẳng đó.

. B.

. C.

120

. D.

Câu 14: [2H3-2.3-1] (THPT Trần Ph - Hải Phòng - Lần 03 - Năm - 2018 -2019) Trong không gian

,Oxyz

cho hai mặt phẳng

( )

: – 2 2 – 3 0P x y z+=

và

( )

: – 2 1 0Q mx y z+ + =

. Với giá trị nào của

thì hai mặt phẳng đó vuông góc với nhau?

1m =

. B.

1m =−

. C.

6m =−

. D.

6m =

Câu 15:

. 0 2 4 0 6n n m m=  − − =  =

. [2H3-2.11-2] (THPT Trần Ph - Hà Tĩnh - Năm 2019 -

2020) Trong không gian

Oxyz

. Cho hai điểm

( )

2; 1;5A −

và

( )

0;1;3 .B

Mặt phẳng trung trực

của đoạn thẳng

có phương trình là

3 3 0x y z+ − + =

. B.

50x y z− + − =

. C.

60x y z− + + =

. D.

3 5 1 0x y z+ − − =

Câu 16: [2H3-2.11-2] (Love book - Đề số 15 - Năm 2018 - 2019) Cho ba điểm

(0;2;0);M

(0;0;1);N

(3;2;1)A

. Lập phương trình mặt phẳng

()MNP

. biết điểm

là hình chiếu vuông góc của điểm

lên trục

2 1 3

x y z

+ + =

3 2 1

x y z

+ + =

211

x y z

+ + =

3 2 1

x y z

+ + =

Câu 17: [2H3-2.5-2] (THPT Nguyễn Khuyến-Lần 5-2018-2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

( )

2;1;2H

là hình chiếu vuông góc của gốc tọa độ

xuống mặt phẳng

( )

, số đo góc giữa mặt

( )

và mặt phẳng

( )

: 11 0Q x y+ − =

Câu 18: [2H3-2.3-2] (Chuyên Quang Trung - Bình Phưc - Lần 05 - Năm 2018 - 2019) Trong không

gian

Oxyz

, cho

( )

0;1;1 , A

( )

1;0;0B

và mặt phẳng

( )

: 3 0P x y z+ + − =

( )

là mặt phẳng song

song với

( )

đồng thời đường thẳng

cắt

( )

tại

sao cho

2CA CB=

. Mặt phẳng

( )

có

phương trình là:

x y z+ + − =

hoặc

0x y z+ + =

. B.

0x y z+ + =

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 105

x y z+ + − =

. D.

20x y z+ + − =

hoặc

0x y z+ + =

Câu 19: [2H3-2.4-2] (THPT Sơn Tây- Hà Nội- Lần 02- Năm 2018- 2019) Trong không gian với hệ tọa

độ

Oxyz

, cho mặt phẳng

( )

: 2 2 3 0P x y z− + + =

và điểm

( )

1; 2;3A −

. Gọi

( ) ( )

;;M a b c P

sao

cho

4AM =

. Tính

abc++

. B.

. C.

. D.

Câu 20: [2H3-2.4-3] (Chuyên Lê Hồng Phong - Nam Định - Lần 01 - Năm 2018 - 2019) Trong không

gian với hệ tọa độ

Oxyz

, cho mặt phẳng

( )

: 2 0P x y z+ − + =

và hai điểm

( )

3;4;1 ;A

( )

7; 4; 3B −−

. Điểm

( )( )

; ; 2M a b c a 

thuộc

( )

sao cho tam giác

ABM

vuông tại

và có

diện tích nhỏ nhất. Khi đó giá trị biểu thức

T a b c= + +

bằng:

6T =

. B.

8T =

. C.

4T =

. D.

0T =

Câu 21: [2H3-2.3-3] (ĐTD - ĐỀ 01 - NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

–3;2;4M

, gọi

lần lượt là hình chiếu của

trên

. Mặt phẳng nào sau

đây song song với

( )

mp ABC

4 6 3 12 0x y z− − + =

. B.

3 6 4 12 0x y z− − + =

4 6 3 12 0x y z− − − =

. D.

6 4 3 12 0x y z− − − =

Câu 22: [2H3-2.5-3] (SGD Đà Nẵng - Năm 2018 - 2019) Trong không gian

Oxyz

, cho hai điểm

( )

1;0;0A

( )

0;0;1B

và mặt phẳng

( )

:2 2 5 0P x y z− − + =

. Tọa độ điểm

trên trục

sao

cho mặt phẳng

( )

ABC

hợp với mặt

( )

một góc

45

là

0; ;0



−





. B.

0; ;0







. C.

0; ;0







. D.

0; ;0



−





……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 106

Chương 3: PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN

Bài 2: PHƯƠNG TRÌNH MẶT PHẲNG (tiết 5)

A. PHẦN KIẾN THỨC CHÍNH

. Trong không gian

Oxyz

cho điểm

( )

0 0 0

;;M x y z

và mặt phẳng

( )

:0P Ax By Cz D+ + + =

. Khi đó khoảng cách từ điểm

đến mặt phẳng

( )

là:

( )

0 0 0

2 2 2

Ax By Cz D

d M P

A B C

+ + +

2. Cho mặt phẳng

( )

:0P Ax By Cz D+ + + =

và mặt cầu

( ) ( ) ( ) ( )

2 2 2

:.C x a y b z c R− + − + − =

Khi đó mặt cầu

( )

có tâm

( )

;;I a b c

và bán kính

+) Nếu

( )

,d M P R

suy ra

( )

và

( )

không có điểm chung.

+) Nếu

( )

,d M P R=

suy ra

( )

và

( )

tiếp xúc nhau.

+) Nếu

( )

,d M P R

suy ra

( )

và

( )

cắt nhau.

3.Mặt phẳng

( )

(Hình 7.5) đi qua ba điểm

( )

;0;0 ,Ma

( )

0; ;0 ,Nb

( )

0;0;Pc

trong đó

, a

đều khác

có phương trình

( )

x y z

a b c

+ + =

. được gọi phương trình mặt phẳng theo đoạn

chắn.

B. LUYỆN TẬP

I. Các ví dụ minh hoạ

Câu 1: Trong không gian

Oxyz

cho mặt phẳng

( )

: 2 2 1 0P x y z− + − =

. Viết phương trình mặt phẳng

( )

song song và cách mặt phẳng

( )

một khoảng bằng 5.

Lời giải

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 107

………………………………………………………………………………………………………………..

Câu 2: Trong không gian

Oxyz

cho hai mặt phẳng

( )

:3 4 2 0P x y z− + + =

và

( )

:3 4 8 0 Q x y z− + + =

Viết phương trình mặt phẳng

( )

song song và cách đều hai mặt phẳng

( )

và

( )

………………………………………………………………………………………………………………..

Câu 3: . Trong không gian

Oxyz

cho mặt phẳng

( )

:2 2 1 0P x y z− + + =

và mặt cầu

( ) ( ) ( ) ( )

2 2 2

: 1 2 3 4.C x y z− + − + − =

Hãy xét vị trí tương đối giữa

( )

và

( )

………………………………………………………………………………………………………………..

Câu 4: Trong không gian

Oxyz

cho mặt phẳng

( )

:2 2 6 0P x y z− + + =

và mặt cầu

( ) ( ) ( ) ( )

2 2 2

: 1 2 3 25.C x y z− + − + − =

Biết

( )

và

( )

cắt nhau theo giao tuyến là một đường

tròn. Tính bán kính đường tròn đó.

………………………………………………………………………………………………………………..



 



Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 108

………………………………………………………………………………………………………………..

Câu 5: Trong không gian

Oxyz

cho mặt phẳng

( )

: 2 2 1 0.P x y z+ − − =

Viết phương trình mặt cầu

( )

tâm

( )

1; 1;2I −

và tiếp xúc với

( )

………………………………………………………………………………………………………………..

Câu 6: Cho hai điểm

( ) ( )

3;5; 1 , B 1;1;3A −

. Tìm tọa độ điểm

thuộc

( )

Oxy

sao cho

MA MB+

nhỏ

nhất?

………………………………………………………………………………………………………………..

Câu 7: Trong không gian

Oxyz

, cho hai điểm

( )

2; 2; 1M

8 4 8

; ;

3 3 3

−







. Viết phương trình mặt cầu có

tâm là tâm của đường tròn nội tiếp tam giác

OMN

và tiếp xúc với mặt phẳng

( )

Oxz

………………………………………………………………………………………………………………..

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 109

………………………………………………………………………………………………………………..

Câu 8: Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

2;4;2M −

. Viết phương trình mặt phẳng

( )

đi qua

điểm

lần lượt là hình chiếu của

trên các trục tọa độ

………………………………………………………………………………………………………………..

II. Bài tập trắc nghiệm

Câu 9: Trong không gian

Oxyz

, phương trình mặt phẳng

( )

đi qua điểm

( )

1;3; 2M −

, cắt các tia

lần lượt tại

sao cho

1 2 4

OA OB OC

là:

2 1 0x y z− − − =

2 4 1 0x y z+ + + =

4 2 1 0.x y z+ + + =

4 2 8 0.x y z+ + − =

Câu 10: Viết phương trình mặt phẳng

( )

qua

( )

1;2;1M

lần lượt cắt các tia

, Ox

, Oy

tại các điểm

, , A B C

sao cho hình chop

.O ABC

đều.

0.x y z− + =

4 0x y z+ + − =

. C.

40x y z− + − =

. D

1 0.x y z+ + − =

Câu 11: Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

( )

2;3;4A −

( )

8; 5;6B −

. Hình chiếu

vuông góc của trung điểm

của đoạn

trên mặt phẳng

( )

Oyz

là điểm nào dưới đây.

( )

0; 1;5M −

. B.

( )

0;0;5Q

. C.

( )

3;0;0P

. D.

( )

3; 1;5N −

Câu 12: Trong không gian tọa độ

Oxyz

, cho mặt cầu

( )

có đường kính

, với

( )

6;2; 5A −

( )

4;0;7B −

. Viết phương trình mặt phẳng

( )

tiếp xúc với mặt cầu

( )

tại

( )

:5 – 6 62 0P x y z+ + =

. B.

( )

:5 – 6 62 0P x y z+ − =

( )

:5 – 6 62 0P x y z− − =

. D.

( )

:5 6 62 0P x y z+ + + =

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 110

Câu 13: Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

( )

: 2 2 2 0P x y z− + − =

và điểm

( )

1; 2; 1I −−

. Viết phương trình mặt cầu

( )

có tâm

và cắt

mặt phẳng

( )

theo giao tuyến là đường tròn có bán kính bằng

( ) ( ) ( ) ( )

2 2 2

: 1 2 1 25.S x y z+ + − + + =

( ) ( ) ( ) ( )

2 2 2

: 1 2 1 16.S x y z+ + − + + =

( ) ( ) ( ) ( )

2 2 2

: 1 2 1 34.S x y z− + + + − =

( ) ( ) ( ) ( )

2 2 2

: 1 2 1 34.S x y z+ + − + + =

Câu 14: . Trong không gian

Oxyz

, cho điểm

( )

2; 1; 1H

. Gọi

( )

là mặt phẳng đi qua

và cắt các trục

tọa độ tại

sao cho

là trực tâm tam giác

ABC

. Phương trình mặt phẳng

( )

là

2 6 0x y z+ + − =

. B.

2 6 0x y z+ + − =

. C.

2 2 6 0x y z+ + − =

. D.

2 6 0x y z+ + + =

C. BÀI TẬP T LUYỆN

Câu 15: [2H3-2.6-1] (THPT Thạch Thành I-Thanh Hóa-Năm 2018-2019) Trong không gian

Oxyz

khoảng cách từ điểm

( )

0;0;5A

đến mặt phẳng

( )

: 2 2 3 0P x y z+ + − =

bằng:

. B.

. C.

. D.

Câu 16: [2H3-2.6-2] (Vted - Đề số 09 - Năm 2018 - 2019) Trong không gian

Oxyz

, phương trình mặt

phẳng

song song và cách mặt phẳng

: 2 2 3 0Q x y z

một khoảng bằng 1; đồng thời

không qua

là

2 2 1 0x y z+ + + =

220x y z+ + =

2 2 6 0x y z+ + − =

2 2 3 0x y z+ + + =

Câu 17: [2H3-2.12-1] (Chuyên Quang Trung - Bình Phưc - Lần 05 - Năm 2018 - 2019) Trong không

gian

Oxyz

, mặt phẳng đi qua

điểm

( )

1;0;0A

( )

0;2;0B

( )

0;0;3C

có phương trình là

1 2 3

x y z

+ + =

. B.

1 2 3

x y z

+ + =

. C.

1 2 3

x y z

+ + = −

. D.

113

x y z

+ + =

Câu 18: [2H3-2.12-2] (THPT Trần Ph - Hải Phòng - Lần 03 - Năm - 2018 -2019) Trong không gian

,Oxyz

cho điểm

(8; 2;4)M −

. Gọi

, , A B C

lần lượt là hình chiếu của

trên các trục

,Ox

,Oy

. Phương trình mặt phẳng đi qua ba điểm

và

là

4 2 8 0.+ − − =x y z

4 2 18 0.− + − =x y z

4 2 8 0.+ + − =x y z

4 2 8 0.− + − =x y z

Câu 19: [2H3-2.12-2] (Vted - Đề số 12 - Năm 2018 - 2019) Trong không gian , cho điểm

( )

1;4;3G

. Viết phương trình mặt phẳng cắt các trục tọa độ

,Ox

,Oy

lần lượt tại

sao cho

là trọng tâm của tứ diện

OABC

A. . B. .

C. . D. .

Câu 20: [2H3-2.6-2] (Vted - Đề số 20 - Năm 2018-2019) Trong không gian

Oxyz

, cho ba điểm

( )

;0;0 ,Aa

( )

0; ;0 ,Bb

( )

0;0;Cc

với

,,abc

là các số thực dương thay đổi thỏa mãn

3abc+ + =

. Khoảng cách từ gốc tọa độ

đến mặt phẳng

( )

ABC

có giá trị lớn nhất bằng

. B.

. C.

. D.

Oxyz

3 12 9

x y z

+ + =

4 16 12

x y z

+ + =

3 12 9 78 0x y z+ + − =

4 16 12 104 0x y z+ + − =

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 111

Câu 21: [2H3-2.6-3] (Vted - Đề số 13 - Năm 2018 - 2019) Trong không gian

,Oxyz

cho ba điểm

(1;0;0),A

(0;1;0),B

(0;0;1)C

. Số mặt phẳng đi qua gốc tọa độ

và cách đều ba điểm

là

. B.

. C.

. D.

Câu 22: [2H3-2.12-3] (ĐTD - Đề 18 - Năm 2018-2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

điểm

( )

3;4;5M

. Gọi

( )

là mặt phẳng qua

sao cho

( )

cắt các trục tọa độ tại các điểm

sao cho khoảng cách từ gốc tọa độ tới

( )

là lớn nhất. Thể tích khối tứ diện

OABC

là?

6250

3125

144

Câu 23: [2H3-2.8-1] (Chuyên Vinh - Lần 3 - Năm 2018 - 2019) Trong không gian

Oxyz

, cho điểm

( )

1;2;5I

và mặt phẳng

( )

: 2 2 2 0− + + =x y z



. Phương trình mặt cầu tâm

và tiếp xúc với

( )



là

( ) ( ) ( )

2 2 2

1 2 5 3− + − + − =x y z

. B.

( ) ( ) ( )

2 2 2

1 2 5 3+ + + + + =x y z

( ) ( ) ( )

2 2 2

1 2 5 9− + − + − =x y z

. D.

( ) ( ) ( )

2 2 2

1 2 5 9+ + + + + =x y z

Câu 24: [2H3-2.8-2] (THPT Yên Dũng 2 - Bắc Giang - Lần 04 - Năm 2018 - 2019) Trong không gian

với hệ tọa độ

Oxyz

, cho mặt cầu

( )

có tâm

( )

1;2;0I −

. Biết mặt phẳng

( )

:3 10 0+ − − =P x y z

cắt

( )

theo giao tuyến là đường tròn bán kính bằng 2, tính bán kính

của mặt cầu

( )

. B.

. C.

. D.

Câu 25: [2H3-2.8-4] (ĐTD - Đề tuần 16 - Năm 2018-2019) Trong không gian với hệ tọa độ

Oxyz

, cho

mặt phẳng

( )

: 2 4 0P x y z+ + − =

. Có tất cả bao nhiêu mặt cầu có tâm nằm trên mặt phẳng

( )

và tiếp xúc với ba trục tọa độ

',x Ox

',y Oy

'z Oz

A. 8 mặt cầu B. 4 mặt cầu C. 3 mặt cầu D. 1 mặt cầu

……………………………………………………………………………………………………

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 112

HÌNH HỌC 12 – CHƯƠNG 3

§2. PHƯƠNG TRÌNH ĐƯỜNG THẲNG

Câu hỏi: Nhắc lại phương trình tham số của đường thẳng trong mặt phẳng Oxy?

……………………………………………………………………………………………………..

I. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG

1. Vectơ ch phương của đường thng

Cho đường thẳng . Vectơ

0u 

gọi là vectơ chỉ phương của đường thẳng  nếu giá của nó

song song hoặc trùng với .

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 113

Chú ý:

+ Nếu

là vectơ chỉ phương của  thì

( )

k.u k 0

cũng là vectơ chỉ phương của .

+ Nếu đường thẳng  đi qua hai điểm A, B thì

là một vectơ chỉ phương.

2. Phương trình tham số của đường thng

Định lí:

Cho đường thẳng  đi qua

( )

0 0 0

;;M x y z

và có vectơ chỉ phương là

( )

;;u a b c=

. Điều kiện cần

và đủ để điểm

( )

;;M x y z

nằm trên  là có một số thực

sao cho

x x at

y y bt

z z ct











Định nghĩa:

Phương trình tham số của đường thẳng  đi qua

( )

0 0 0

;;M x y z

và có vectơ chỉ phương là

( )

;;u a b c=

là phương trình có dạng

( )

, 1

x x at

y y bt t

z z ct





= + 







Trong đó t là tham số.

Chú ý:

Nếu

,,abc

đều khác

thì người ta còn có thể viết phương trình của đường thẳng  dưới dạng

chính tắc như sau:

0 0 0

x x y y z z

a b c

− − −

Nhận xét:

Để viết được phương trình đường thẳng cần biết một điểm thuộc đường thẳng và một véc tơ chỉ

phương của đường thẳng đó.

Ví dụ 1. Trong không gian Oxyz, phương trình tham số của đường thẳng đi qua điểm

( )

2; 1;3M −

và có

vectơ chỉ phương

( )

1;2; 4u −

là

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 114

= − +





= − −







. B.





=−





= − +



. C.

= − +









= − −



. D.





= − +





=−



……………………………………………………………………………………………………..

Ví dụ 2. Trong không gian Oxyz, phương trình chính tắc của đường thẳng đi qua điểm

( )

2; 1;3M −

và có

vectơ chỉ phương

( )

1;2; 4u −

là

1 2 4

2 1 3

x y z+ + −

−

. B.

124

2 1 3

x y z− − +

−

2 1 3

1 2 4

x y z+ − +

−

. D.

2 1 3

1 2 4

x y z− + −

−

……………………………………………………………………………………………………..

Ví dụ 3. Trong không gian Oxyz, cho điểm

( )

1;2;3A

và mặt phẳng

( )

có phương trình

3 4 7 2 0x y z− + + =

. Đường thẳng đi qua

và vuông góc với mặt phẳng

( )

có phương trình

là

( )

4 2

y t t





= − + 







. B.

( )

2 4

y t t





= − 







( )

2 4

y t t

=−





= − 







. D.

( )

2 3

y t t

=−





= + 







……………………………………………………………………………………………………..

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 115

Chú ý: Cho đường thẳng

: ,

x x at

d y y bt t

z z ct





= + 







Md

khi và chỉ khi tồn tại một số

sao cho

( )

0 0 0

;;M x at y bt z ct+ + +

Ví dụ 4. Trong không gian Oxyz, cho điểm

( )

4;3;6A

và

( )

: 1

d y t t





= − 





= − +



Tìm tọa độ của điểm

Md

sao cho

5AM =

biết hoành độ điểm

là số nguyên.

( )

4; 1;3M −

. B.

( )

0;3; 5M −

( )

2;1; 1M −

. D. không có

……………………………………………………………………………………………………..

II. ĐIỀU KIỆN ĐỂ HAI ĐƯỜNG THẲNG SONG SONG, CẮT NHAU, CHÉO NHAU:

Cho đường thẳng

x x a t

d y y bt

z z c t











đi qua điểm

( )

1 1 1

;;M x y z

, có véc tơ chỉ phương là

( )

1 1 1 1

;;u a b c=

và đường thẳng . có véc tơ chỉ phương là

( )

2 2 2 2

;;u a b c=

1. Điều kiện để hai đường thng song song:

/ / '

u k u















Đặc biệt:

u k u















Ví dụ 1. Chứng minh hai đường thẳng sau đây song song:

d y t









=−



và

2 2 '

': 3 4 '

5 2 '

d y t









=−



……………………………………………………………………………………………………..

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 116

……………………………………………………………………………………………………..

Ví dụ 2. Chứng minh hai đường thẳng sau đây trùng nhau:

d y t

=−









=−



và

2 3 '

': 5 3 '

3 6 '

d y t

=−









=−



……………………………………………………………………………………………………..

2. Điều kiện để hai đường thng cắt nhau:

Hai đường thẳng và

cắt nhau khi và chỉ khi hệ phương trình ẩn

và

sau có đúng một

nghiệm

( )

1 1 2 2

x a t x a t

y b t y b t I

z c t z c t

+ = +





+ = +





+ = +



Chú ý: Giả sử hệ (I) có nghiệm

( )

;tt

. Để tìm giao điểm

của

và

ta có thể thay

vào phương trình tham số của

hoặc

vào phương trình tham số của

Ví dụ 3. Tìm giao điểm của hai đường thẳng sau:

: 2 3

d y t









=−



và

2 2 '

': 2 '

1 3 '

d y t

=−





= − +







……………………………………………………………………………………………………..

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 117

3. Điều kiện để hai đường thng chéo nhau:

Cho đường thẳng

x x a t

d y y bt

z z c t











đi qua điểm

( )

1 1 1

;;M x y z

, có véc tơ chỉ phương là

( )

1 1 1 1

;;u a b c=

và đường thẳng

': '

x x a t

d y y b t

z z c t











có véc tơ chỉ phương là

( )

2 2 2 2

;;u a b c=

Chú ý: Hai đường thẳng

và

chéo nhau khi và chỉ khi

và

không cùng phương và hệ

phương trình

1 1 2 2

x a t x a t

y b t y b t

z c t z c t

+ = +





+ = +





+ = +



vô nghiệm

Ví dụ 4. Xét vị trí tương đối của hai đường thẳng sau:

: 1 3

d y t





= − +







và

1 3 '

': 2 2 '

1 2 '

d y t





= − +





= − +



……………………………………………………………………………………………………..

Củng cố bài học:

Bài học hôm nay các em cần nhớ các nội dung sau

1. Phương trình tham số, phương trình chính tắc của đường thẳng.

2. Các vị trí tương đối của hai đường thẳng.

Sơ đồ tư duy:

d đi qua điểm

, có véc tơ chỉ phương là

, d’ có véc tơ chỉ phương là

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 118

''M d d d  

Xét

và

' / / 'M d d d

Xét

và

1 nghiệm

d

cắt

Xét hệ

1 1 2 2

x a t x a t

y b t y b t

z c t z c t

+ = +





+ = +





+ = +



vô nghiệm

d

chéo nhau

B. LUYỆN TẬP

I. BÀI TẬP SGK.

Bài 1 trang 89 – SGK: Viết phương trình tham số của đường thẳng (d) trong mỗi trường hợp sau:

a) (d) đi qua điểm

M(5,4;1)

và có vectơ chỉ phương

a (2; 3;1)=−

b) (d) đi qua điểm

A(2; 1;3)−

và vuông góc với mặt phẳng

( ): 5 0x y z



+ − + =

c) (d) đi qua điểm

(2;0; 3)B −

và song song với đường thẳng

: 3 3





 = − +







d) (d) đi qua hai điểm

(1;2;3)P

và

(5;4;4)Q

Bài 3 trang 90 – SGK: Xét vị trí tương đối của các cặp đường thẳng

và d' cho bởi các phương trình

x 3 2t

d : y 2 3t

z 6 4t

= − +





= − +







và

x 5 t

d : y 1 4t

z 20 t







= − −







x 1 t

d : y 2 t

z 3 t









=−



và

x 1 2t

d : y 1 2t

z 2 2t











= − +





=−



Bài 5 trang 90 – SGK: Tìm số giao điểm của đường thẳng

với mặt phẳng

()



trong các trường hợp

x 12 4t

d : y 9 3t và ( ):3x 5y z 2 0

z 1 t







= + + − − =







Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 119

x 1 t

d : y 2 t

z 1 2t





=−







và

( ): x 3y z 1 0



+ + + =

: 1 2

d y t









=−



và

( ): 4 0x y z



+ + − =

Bài 6 trang 90 – SGK: Tính khoảng cách giữa đường thẳng

: 1 3

= − +





 = − +





= − +



và mặt phẳng

( ):2 2 3 0x y z



− + + =

Bài 7 trang 91- SGK: Cho điểm

A(1;0;0)

và đường thẳng

x 2 t

d : y 1 2t











a) Tìm tọa độ điểm

là hình chiếu vuông góc của điểm

trên đường thẳng

b) Tìm tọa độ điểm

đối xứng với

qua đường thẳng

Bài 8 trang 91- SGK: Cho điểm

M(1;4;2)

và mặt phẳng

: x y z 1 0



+ + − =

a) Tìm tọa độ điểm

là hình chiếu vuông góc của điểm

trên mặt phẳng



b) Tìm tọa độ điểm M' đối xứng với

qua mặt phẳng



c) Tính khoảng cách từ điểm

đến mặt phẳng



Bài 10 trang 91- SGK: Giải bài toán sau đây bằng phương pháp tọa độ:

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Tính khoảng cách từ đỉnh

đến các

mặt phẳng (A'BD) và (B'D'C).

II. BÀI TẬP TRẮC NGHIỆM

Câu 1: Trong không gian

,Oxyz

đường thẳng

1 5 2

3 2 5

x y z

− − +

−

có một véc tơ chỉ phương là

( )

1;5; 2u −

. B.

( )

3; 2 ; 5u −

. C.

( )

3; 2 ; 5u −−

. D.

( )

2; 3; 5u −

Câu 2: Trong không gian

Oxyz

, cho đường thẳng

4 2 1

2 5 1

x y z

− − +

−

. Điểm nào dưới

đây thuộc

( )

4;2;1M

. B.

( )

2;5;1Q

. C.

( )

4;2; 1N −

. D.

( )

2; 5;1P −

Câu 3: Phương trình tham số của đường thẳng

đi qua điểm

( )

1; 1;2A −

và có vectơ chỉ phương

( )

1;2; 3u =−

là

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 120

d y t





=−





= − +



. B.

d y t





= − −







. C.

: 1 3

d y t





= − +





=−



. D.

: 1 2

d y t





= − +





=−



Câu 4: Trong không gian, cho điểm

( )

1; 2; 3A

và mặt phẳng

( )

: 2 0P x z− + =

. Đường thẳng đi qua

và vuông góc với mặt phẳng

( )

có phương trình là.

=−









=−



. B.

=−











. C.









=−



. D





=−







Câu 5: Trong không gian

Oxyz

, cho ba điểm

( )

1;2;0A

( )

1;1;2B

và

( )

2;3;1C

. Đường thẳng đi qua

và song song với

có phương trình là

1 2 1

x y z−−

−

. B.

3 4 3

x y z−−

. C.

3 4 3

x y z++

. D.

1 2 1

x y z++

−

Câu 6: Trong không gian

Oxyz

, cho điểm

(1;0;2)A

và đường thẳng

1 1 2

x y z

−+

. Viết phương

trình đường thẳng



đi qua

, vuông góc và cắt

1 3 1

x y z−−

 = =

−

. B.

1 1 1

x y z−−

 = =

2 2 1

x y z−−

 = =

. D.

1 1 1

x y z−−

 = =

−

Câu 7: Trong không gian với hệ trục tọa độ

Oxyz

, cho hai đường thẳng

d y t

=−









= − +



và

: 2 2

d y t

=−











. Khẳng định nào sau đây đng ?

và

chéo nhau. B.

dd

. C.

dd⊥

. D.

Câu 8: Trong không gian

Oxyz

, cho hai đường thẳng

d y t





=−







và

d y t



=−







= − +









. Mệnh đề nào

sau đây đúng?



⊥

. B.

//dd



. C.

và



chéo nhau. D.





Câu 9: Trong không gian

Oxyz

, cho điểm

( )

8; 4;3M −

và đường thẳng

: 2 2

d y t





= − −







. Gọi

là hình

chiếu vuông góc của

lên

. Khi đó tọa độ của điểm

là

( )

7; 6;2H −

. B.

( )

9; 2;4H −

. C.

( )

2;0; 1H −−

. D.

( )

1; 2;1H −

C. BÀI TẬP T LUYỆN (phần này không làm PPT)

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 121

Dạng 1: Véc tơ chỉ phương.

Câu 10: [Mức độ 1] Cho

: 2 2

d y t





=−







( )

t 

. Điểm nào sau đây không thuộc đường thẳng

( )

0;4;2M

. B.

( )

1;2;3N

. C.

( )

1;–2;3P

. D.

( )

2;0;4Q

Câu 11: [Mức độ 2] Trong không gian với hệ tọa độ

Oxyz

, đường thẳng

1 2 3

x y z

−+

đi qua

những điểm nào sau đây?

( )

2;2;0A −

. B.

( )

2;2;0B

. C.

( )

3;0;3C −

. D.

( )

3;0;3D

Câu 12: [Mức độ 3] Trong hệ trục vuông góc

,Oxyz

cho hai đường thẳng cắt nhau có phương trình lần

lượt là

1 2 2

x y z

−+

−

2 1 2

x y z

+−

−

. Một trong hai đường phân giác của các góc

tạo bởi

có phương trình là

1 3 4

x y z+−

−

. B.

2 4 .





= − +





=−



. C.

1 3 2

x y z−+

. D.





= − +





=−



Câu 13: [Mức độ 4] Trong không gian

( )

Oxy

cho tam giác

ABC

có

( )

2;3;3A

, phương trình đường

trung tuyến kẻ từ

là

3 3 2

1 2 1

x y z− − −

−−

, phương trình đường phân giác trong góc

là

2 4 2

2 1 1

x y z− − −

−−

. Biết rằng

( )

; ; 1u m n=−

là một véc tơ chỉ phương của đường thẳng

Tính giá trị biểu thức

T m n=+

1T =

. B.

5T =

. C.

2T =

. D.

10T =

Dạng 2: Phương trình đường thẳng đi qua 1 điểm, tìm véc tơ chỉ phương.

Câu 14: [Mức độ 1] Phương trình tham số của đường thẳng

( )

đi qua hai điểm

( )

1;2; 3A −

và

( )

3; 1;1B −

là





= − +





= − −



. B.





= − −





= − +



. C.

= − +





= − −







. D.

= − +





=−





= − +



Câu 15: [Mức độ 2] Trong không gian

Oxyz

, cho mặt phẳng

( )

:2 3 2z 2 0P x y+ + + =

và

( )

: 3 2z 1 0Q x y− + + =

. Phương trình đường thẳng đi qua gốc tọa độ

và song song với hai

mặt phẳng

( )

là

12 2 9

x y z

−

. B.

9 12 2

x y z

−−

. C.

12 2 9

x y z

−−

. D.

9 12 2

x y z

−

Lời giải

Chọn C [Mức độ 3] Trong không gian với hệ toạ độ

Oxyz

, cho đường thẳng



là giao tuyến

của hai mặt phẳng

( )

: 1 0Pz−=

và

( )

: 3 0Q x y z+ + − =

. Gọi

là đường thẳng nằm trong mặt

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 122

phẳng

( )

, cắt đường thẳng

1 2 3

1 1 1

x y z− − −

−−

và vuông góc với đường thẳng



. Phương

trình của đường thẳng

là











. B.

=−











. C.











. D.





=−







Câu 16: [Mức độ 3] Trong không gian với hệ tọa độ

Oxyz

, cho các điểm

( )

2;0;0A

;

( )

0;3;0B

;

( )

0;0;4C

. Gọi

là trực tâm tam giác

ABC

. Tìm phương trình tham số của đường thẳng









=−



. B.











. C.











. D.











Dạng 3: Phương trình đường thẳng đi qua 1 điểm, và thỏa mãn điều kiện cho trước.

Câu 17: [Mức độ 1] Phương trình tham số của đường thẳng

( )

đi qua hai điểm

( )

1;2; 3A −

và

( )

3; 1;1B −

là





= − +





= − −



. B.





= − −





= − +



. C.

= − +





= − −







. D.

= − +





=−





= − +



Câu 18: [Mức độ 2] Trong không gian

Oxyz

, cho hai đường thẳng

2 2 3

2 1 1

x y z

− + −

−

và

: 1 2

d y t

=−









= − +



. Đường thẳng



đi qua điểm

( )

1; 2; 3A

, vuông góc với

và cắt

có phương

trình là

1 2 3

1 3 5

x y z− − −

− − −

. B.

1 2 3

1 3 5

x y z− − −

1 2 3

1 3 5

x y z− − −

−

. D.

1 2 3

1 3 5

x y z− − −

−−

Câu 19: [Mức độ 3] Trong không gian

Oxyz

, cho tam giác

ABC

có

( )

2;3;3A

, phương trình đường

trung tuyến kẻ từ

là

3 3 2

1 2 1

x y z− − −

−−

, phương trình đường phân giác trong của góc

là

2 4 2

2 1 1

x y z− − −

−−

. Đường thẳng

có một véc-tơ chỉ phương là

( )

2;1; 1u =−

. B.

( )

1; 1;0u =−

. C.

( )

0;1; 1u =−

. D.

( )

1;2;1u =

Câu 20: [Mức độ 3] Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

2;1;0M

và đường thẳng

2 1 1

x y z−+

 = =

−

. Viết phương trình của đường thẳng

đi qua điểm

, cắt và vuông góc

với



1 4 1

x y z

−−

. B.

2 4 1

x y z

−−

−

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 123

1 4 2

x y z

−−

. D.

1 4 1

x y z

−−

−

Dạng 4: Phương trình đường thẳng đi qua 1 điểm, và thỏa mãn điều kiện cắt, vuông góc với đường

thẳng cho trước.

Câu 21: [Mức độ 2] Trong không gian với hệ tọa độ Descartes

Oxyz

, cho điểm

( )

0; 1; 2−M

và hai

đường thẳng

1 2 3

1 1 2

− + −

−

x y z

1 4 2

2 1 4

+ − −

−

x y z

. Phương trình đường thẳng đi

qua

, cắt cả

và

là

−

x y z

. B.

3 3 4

+−

−

x y z

. C.

9 9 16

+−

−

x y z

. D.

9 9 16

+−

−

x y z

Câu 22: [Mức độ 3] Trong không gian với hệ tọa độ

,Oxyz

cho hai đường thẳng

2 1 1

x y z

−+

−

và

d y t

= − +











. Phương trình đường thẳng vuông góc với

( )

:7 4 0P x y z+ − =

và cắt hai đường

thẳng

, dd

là

2 1 1

x y z−+

. B.

7 1 4

x y z−+

−

. C.

7 1 4

x y z+−

−−

. D.

7 1 4

x y z−+

Câu 23: [Mức độ 3] Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

1;0;2A

và đường thẳng

d y t









= − +



. Phương trình đường thẳng



đi qua

, vuông góc và cắt đường thẳng

là

1 3 2

x y z−−

 = =

−

. B.

1 1 1

x y z−−

 = =

−

2 4 3

x y z−−

 = =

−

. D.

1 3 1

x y z−−

 = =

−

Câu 24: và đường thẳng

có phương trình:

1 1 2

x y z−+

. Viết phương trình đường thẳng



đi qua

, vuông góc và cắt

1 1 1

x y z−−

 = =

. B.

1 1 1

x y z−−

 = =

−

2 1 1

x y z−−

 = =

. D.

1 3 1

x y z−−

 = =

−

Dạng 5: Phương trình đường thẳng cắt 2 đường thẳng và thỏa mãn 2 điều kiện cho trước.

Câu 25: [Mức độ 2] Trong không gian với hệ tọa độ

,Oxyz

cho hai đường thẳng

1 1 2

x y z

a ==

−

2 1 1

x y z

−−

và mặt phẳng

( )

: 0.xyP z− − =

Viết phương trình của đường thẳng

song

song với

( )

, cắt

và

lần lượt tại

và

mà

2.MN =

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 124

7 4 7 4 7 8

3 8 5

x y z

+ − +

−

. B.

7 4 7 4 7 8

3 8 5

x y z

− − +

−

7 1 7 4 7 8

3 8 5

x y z

− + +

−

. D.

7 4 7 4 7 8

3 8 5

x y z

− + +

−

Câu 26: [Mức độ 2] Trong không gian với hệ tọa độ

,Oxyz

cho mặt phẳng phẳng

( )

:2 5 0P x y z− − =

và

hai đường thẳng

1 1 3

1 1 1

x y z

− + −

−

;

2 1 1

x y z

−

−−

Viết phương trình đường thẳng



nằm trên mặt phẳng

( )

sao cho



cắt hai đường thẳng

4 1 3

x y z−−

 = =

. B.

4 1 3

x y z−−

 = =

3 1 1

4 1 3

x y z− − −

 = =

−

3 1 1

4 1 3

x y z− − −

 = =

Câu 27: [Mức độ 3] Trong không gian với hệ tọa độ

Oxyz

, cho hai đường thẳng

3 2 1

1 1 2

x y z

+ − −

−

2 1 1

x y z

− − +

và mặt phẳng

( )

: 3 2 5 0P x y z+ + − =

. Đường thẳng vuông góc với

( )

, cắt cả

và

có phương trình là:

3 2 1

1 3 2

x y z+ + −

. B.

1 3 2

x y z +

4 3 1

1 3 2

x y z+ − +

. D.

7 6 7

1 3 2

x y z+ − +

Câu 28: [Mức độ 3] Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

( )

:2 10 0P x y z− + − =

và

đường thẳng

2 1 1

x y z

+ − −

−

. Đường thẳng

cắt

( )

và

lần lượt tại

và

sao

cho

( )

1;3;2A

là trung điểm

. Tính độ dài đoạn

4 33MN =

. B.

2 26,5MN =

. C.

4 16,5MN =

. D.

2 33MN =

Câu 29: [Mức độ 4] Trong không gian với hệ trục toạ độ

,Oxyz

cho mặt phẳng

( )

: 2 0P x y z+ − + =

và

hai đường thẳng

d y t











;

': 1 .

d y t



=−













=−



Biết rằng có 2 đường thẳng có các đặc điểm: song

song với

( )

; cắt

, dd



và tạo với

góc

30 .

Tính cosin góc tạo bởi hai đường thẳng đó.

. B.

. C.

. D.

Khi đó

( )

cos ,

  =

Dạng 6: Phương trình đường thẳng giao tuyến của 2 mặt phẳng.

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 125

Câu 30: [Mức độ 2] Trong không gian với hệ trục tọa độ

Oxyz

, gọi

( )



là mặt phẳng chứa đường thẳng

1 1 2

x y z−−

 = =

−

và vuông góc với mặt phẳng

( )

: 2 1 0x y z



+ + + =

. Khi đó giao tuyến của

hai mặt phẳng

( )



( )



có phương trình

1 5 2

x y z−+

−

. B.

1 5 2

x y z+−

−

1 1 1

x y z+

−

. D.

1 1 1

x y z+−

Câu 31: [Mức độ 3] Cho hai điểm

( )

3;3;1A

( )

0; 2;1B

, mặt phẳng

( )

: 7 0P x y z+ + − =

. Đường thẳng

nằm trên

( )

sao cho mọi điểm của

cách đều hai điểm

có phương trình là





=−







. B.











. C.

=−





=−







. D.





=−







Câu 32: [Mức độ 3] Trong không gian với hệ tọa độ

Oxyz

, gọi

( )



là mặt phẳng chứa đường thẳng



có phương trình

1 1 2

x y z−−

và vuông góc với mặt phẳng

( )

: 2 1 0x y z



+ − − =

. Giao

tuyến của

( )



và

( )



đi qua điểm nào trong các điểm sau.

( )

1;2;1C

. B.

( )

2;1;0D

. C.

( )

0;1;0B

. D.

( )

2;1;1A

Dạng 7: Phương trình đường thẳng vuông góc chung của 2 đường thẳng chéo nhau.

Câu 33: [Mức độ 2] Trong không gian với hệ tọa độ

Oxyz

, cho hai đường thẳng

4 1 5

3 1 2

x y z− − +

 = =

−−

và

1 3 1

x y z−+

 = =

. Giả sử

M 

N 

sao cho

là đoạn

vuông góc chung của hai đường thẳng



và



. Tính

( )

5; 5;10MN =−

. B.

( )

2; 2;4MN =−

. C.

( )

3; 3;6MN =−

. D.

( )

1; 1;2MN =−

Câu 34: [Mức độ 3] Trong không gian với hệ tọa độ

Oxyz

, cho hai đường thẳng

2 1 1

x y z

−+

−

và

1 1 3

1 7 1

x y z

+ − −

−

. Đường vuông góc chung của

và

lần lượt cắt

tại

và

Tính diện tích

của tam giác

OAB

S =

. B.

6S =

. C.

S =

. D.

S =

Dạng 8: Phương trình đường thẳng hình chiếu vuông góc lên mặt phẳng.

Câu 35: [Mức độ 2] Trong không gian với hệ tọa độ

Oxyz

cho đường thẳng

3 1 1

2 1 3

x y z

+ − −

−

Hình chiếu vuông góc của

trên mặt phẳng

( )

Oyz

là một đường thẳng có vectơ chỉ phương là

( )

0;1;3u =

. B.

( )

0;1; 3u =−

. C.

( )

2;1; 3u =−

. D.

( )

2;0;0u =

Trên con đường thành công không có dấu chân của kẻ lười biếng

Trang 126

Câu 36: [Mức độ 3] Trong không gian với hệ tọa độ

,Oxyz

cho đường thẳng

12 9 1

4 3 1

x y z

− − −

và

mặt thẳng

( )

:3 5 2 0P x y z+ − − =

. Gọi

là hình chiếu của

lên

( )

Phương trình tham số

của

là

2 61

=−









=−



. B.

2 61





=−







. C.

2 61





=−





= − +



. D.

2 61





=−







Dạng 9: Phương trình đường thẳng liên quan đến Min - Max.

Câu 37: [Mức độ 2] Trong không gian với hệ tọa độ

Oxyz

, cho

( )

: 2 2 5 0P x y z− + − =

( )

3;0;1A −

( )

1; 1;3B −

. Viết phương trình đường thẳng

đi qua

, song song với

( )

sao cho khoảng

cách từ

đến

là lớn nhất.

1 1 2

x y z+−

−

. B.

3 2 2

x y z+−

−

. C.

1 2 2

x y z−−

−

. D.

2 6 7

x y z+−

−−

Câu 38: [Mức độ 3] Trong không gian

Oxyz

, cho ba điểm

( )

0;0; 1A −

( )

1;1;0B −

( )

1;0;1C

. Tìm điểm

sao cho

2 2 2

32MA MB MC+−

đạt giá trị nhỏ nhất.

; ; 1



−





. B.

; ;2



−





. C.

; ; 1



−−





. D.

; ; 1



−−





……………………………………………………………………………………………………..

Bấm Tải xuống để xem toàn bộ.

| 1/126

| | Tải xuống

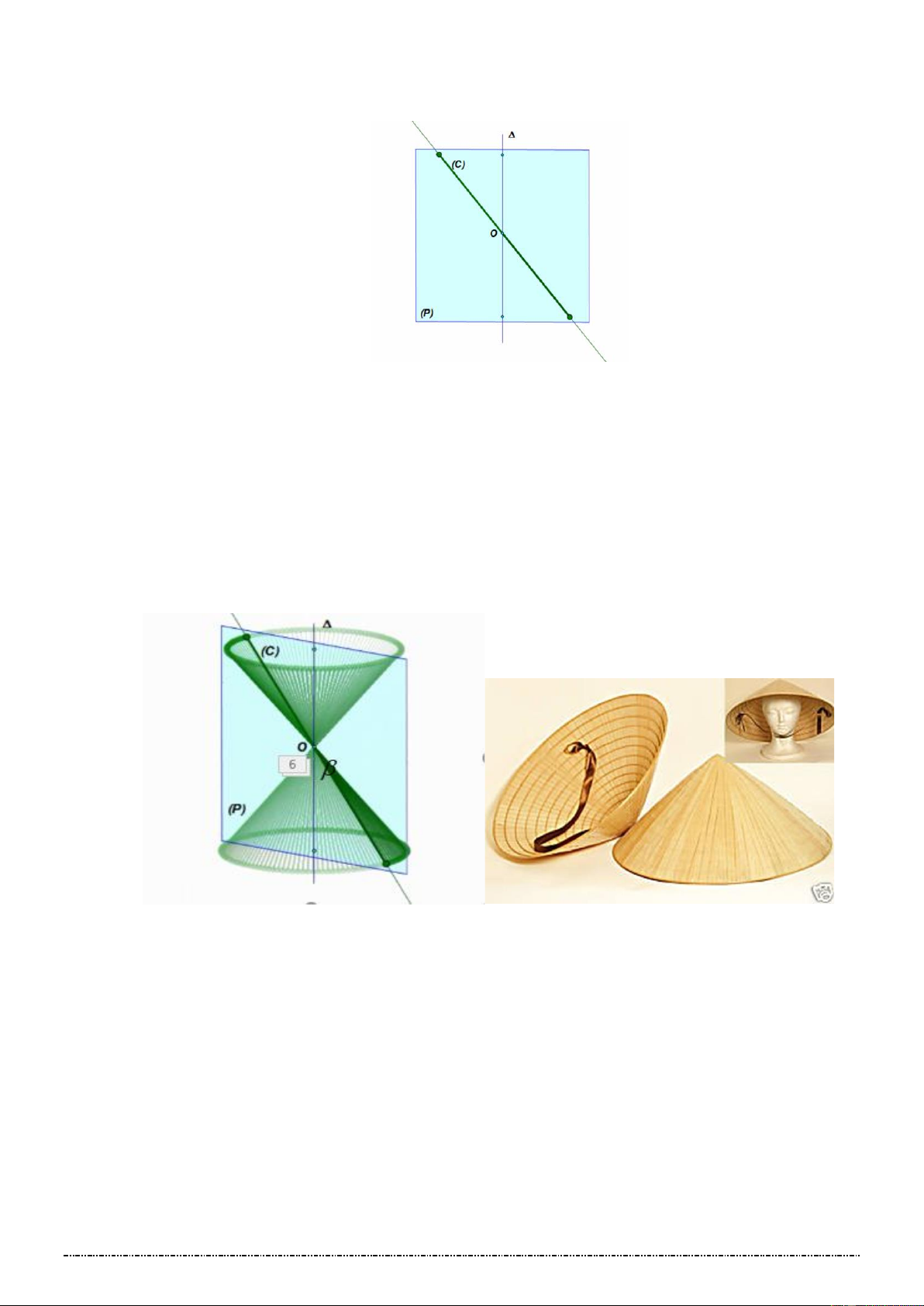
Preview text:

Trên con đường thành công không có dấu chân của kẻ lười biếng
HỌC SINH: ……………………………………………… LỚP:……
…………………………….. TOÁN 12 VỞ BÀI HỌC HÌNH HỌC Trang 1
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HỌC 12-CHƯƠNG I
BÀI 1: KHÁI NIỆM VỀ KHỐI ĐA DIỆN A. KHỞI ĐỘNG
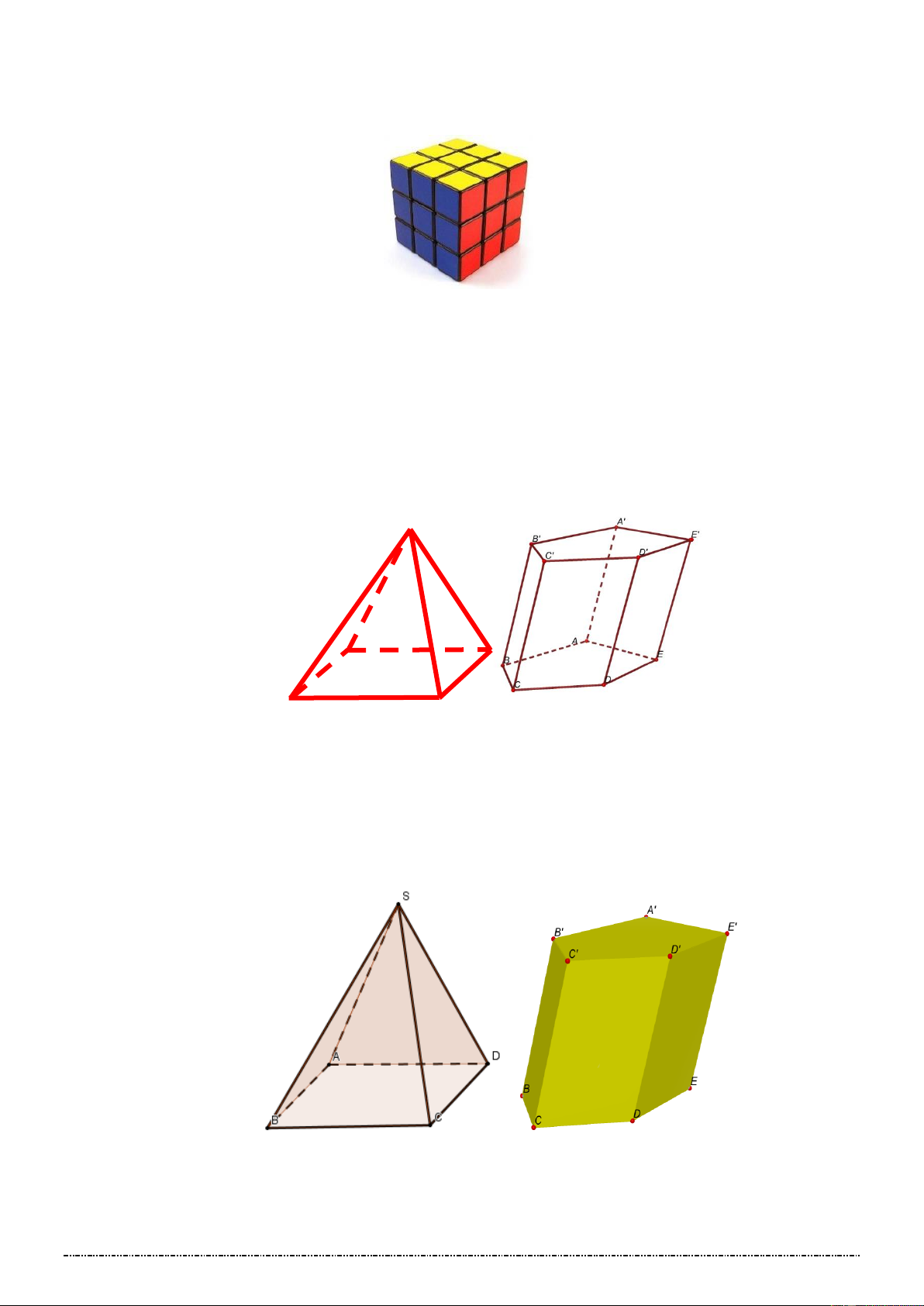
H1: Rubic này có hình dạng gì?
……………………………………………………………………………………………………
……………………………………………………………………………………………………
B – HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC:
I.KHỐI LĂNG TRỤ VÀ KHỐI CHÓP a) Tiếp cận:
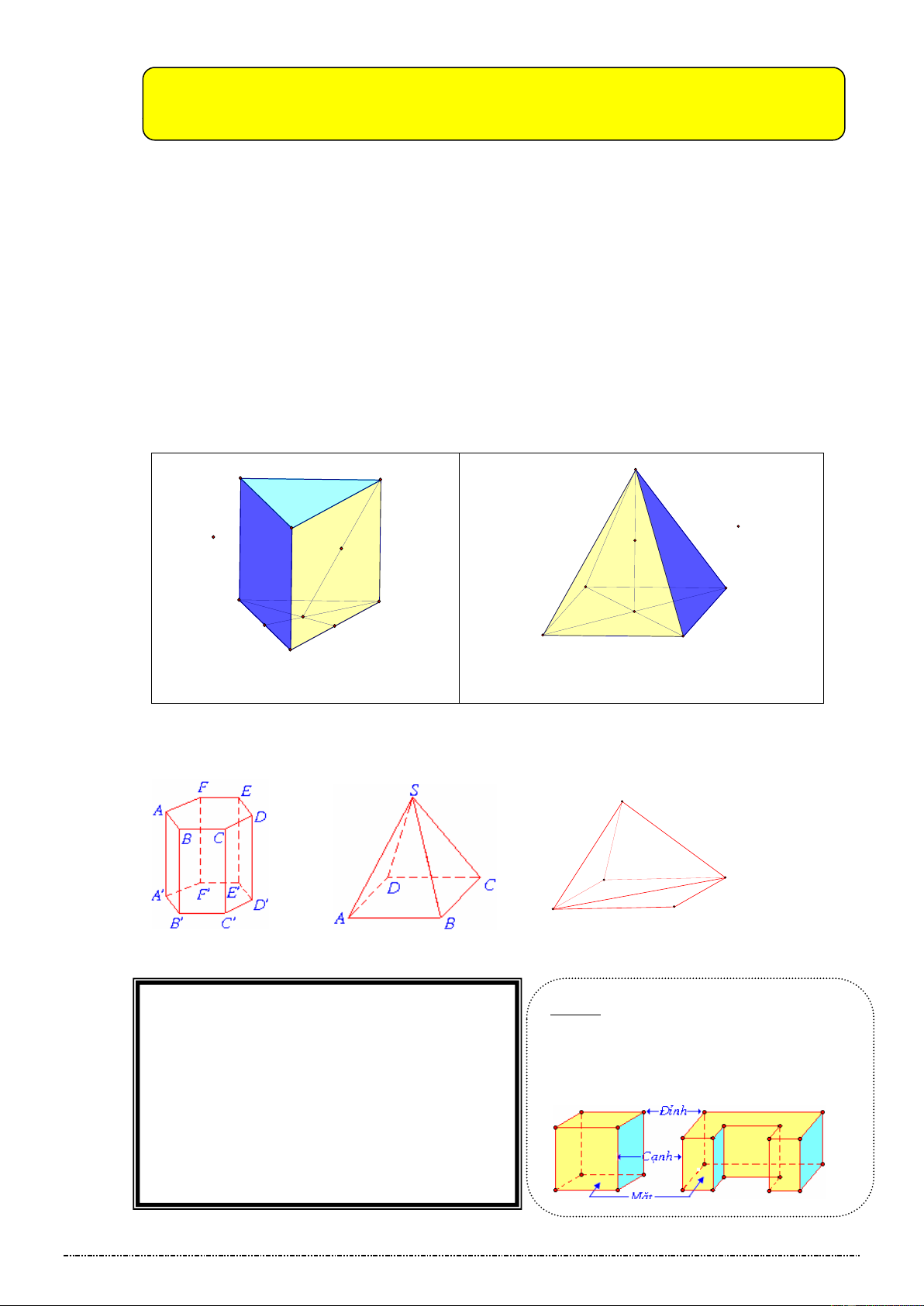
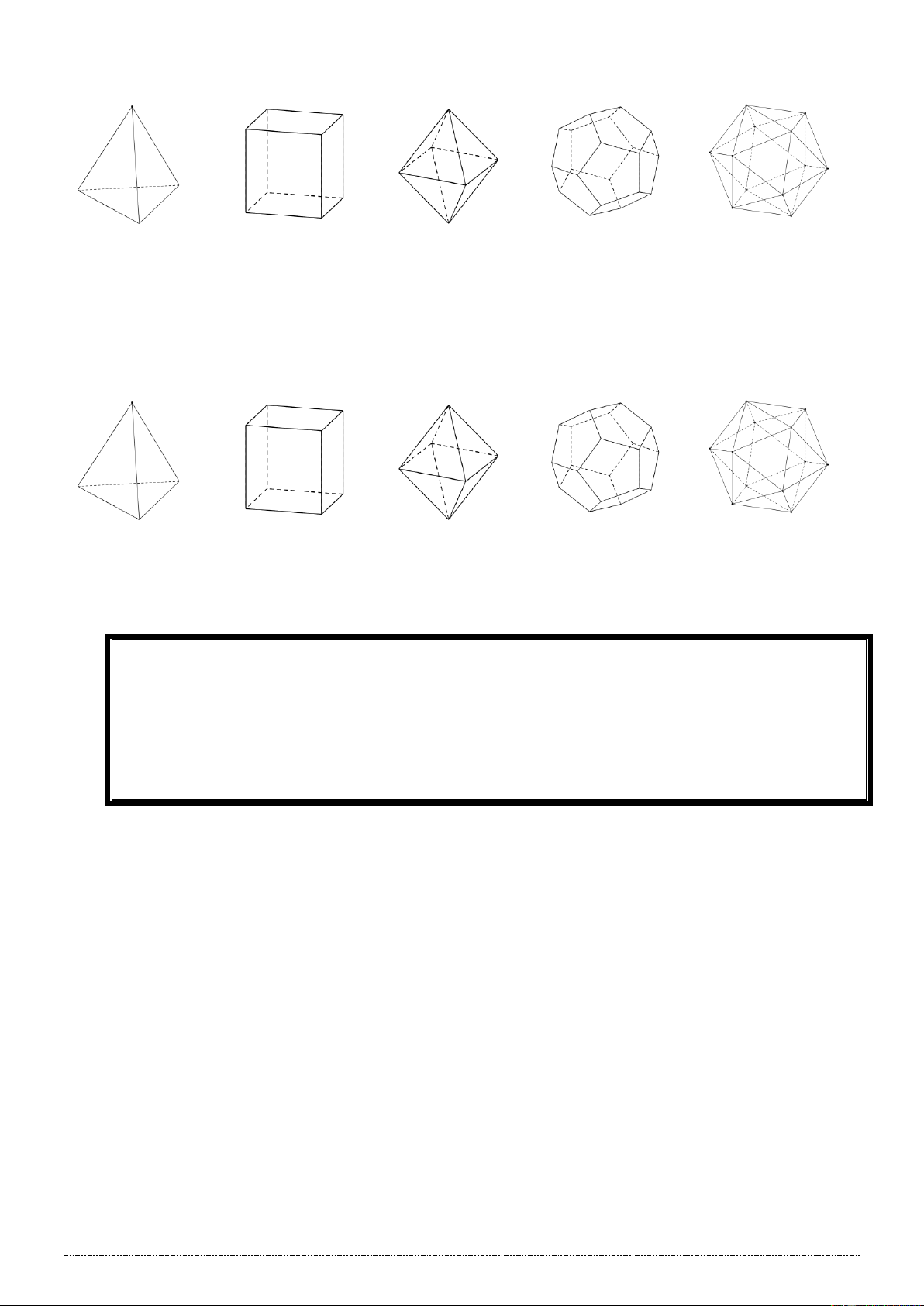
H1: Hãy nêu tên các hình sau:
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
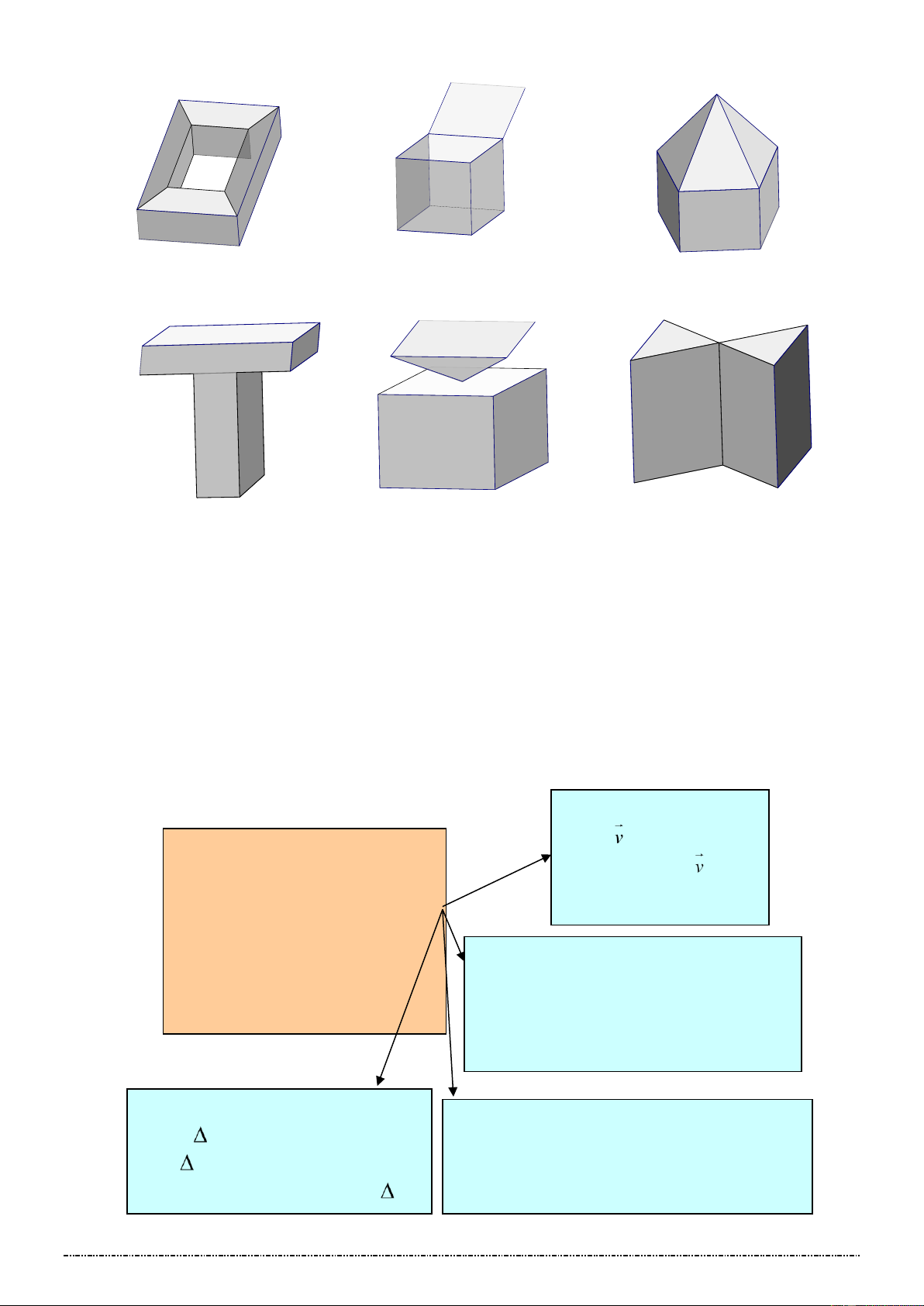
H2: Quan sát và dự đoán tên các hình vẽ sau:
Vậy thế nào là khối lăng trụ? Khối chóp?
b) Hình thành kiến thức : Trang 2
Trên con đường thành công không có dấu chân của kẻ lười biếng
Khối lăng trụ ( khối chóp, khối chóp cụt ) là phần không gian được giới hạn bởi một hình Lưu ý:
lăng trụ ( hình chóp, hình chóp cụt ), kể cả hình lăng trụ ( hình chóp, hình chóp cụt ) ấy.
Tên của khối lăng trụ hay khối chóp được đặt theo tên của hình lăng trụ hay hình chóp giới hạn nó.
Ta gọi đỉnh, cạnh, mặt bên, mặt đáy, cạnh bên, cạnh đáy,… của một hình lăng trụ (hình chóp,
hay hình chóp cụt) theo thứ tự là đỉnh, cạnh, mặt bên, mặt đáy, cạnh bên, cạnh đáy,…của khối
lăng trụ (khối chóp, hay khối chóp cụt) tương ứng.
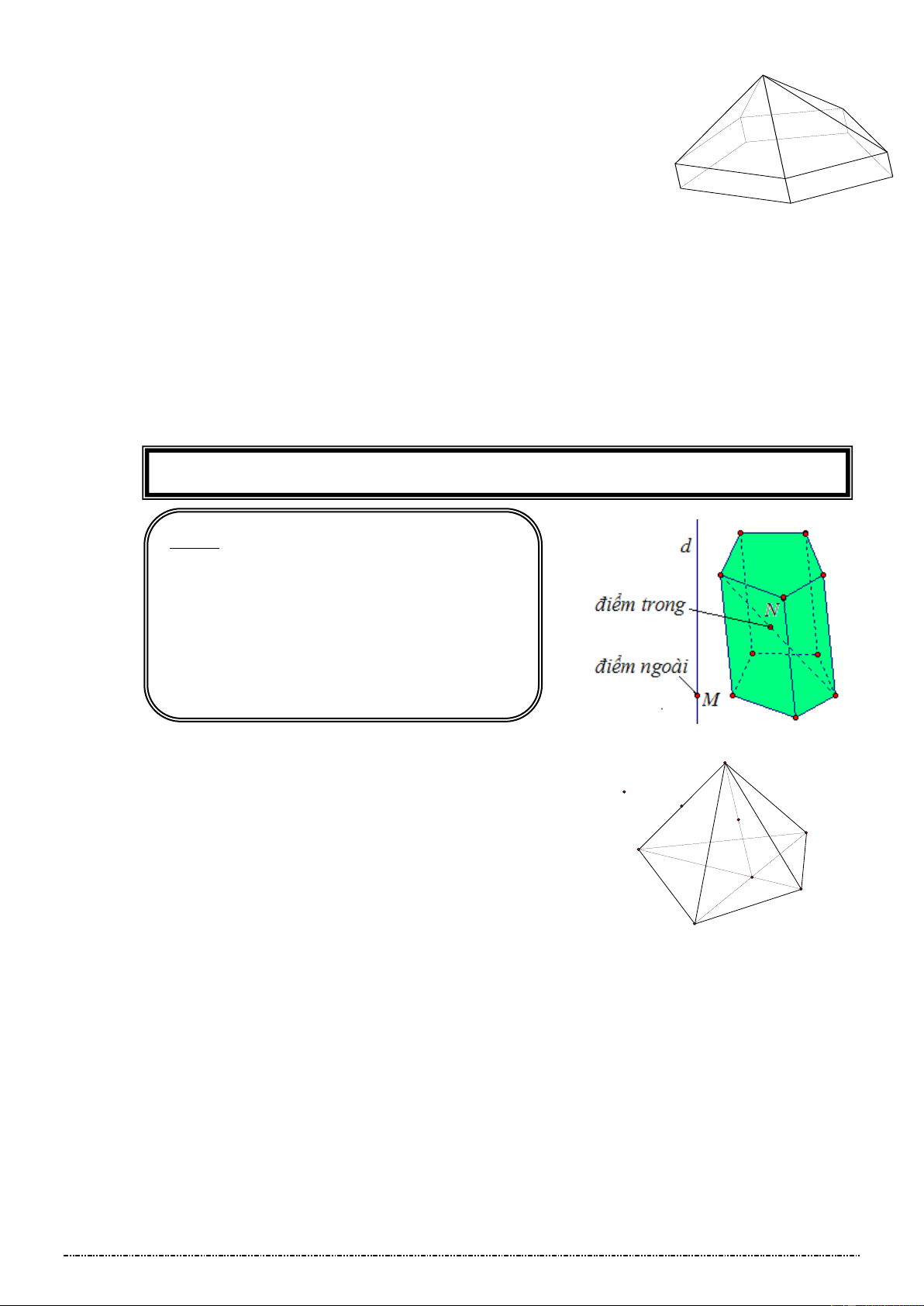
Điểm không thuộc khối lăng trụ được gọi là điểm ngoài của khối lăng trụ, điểm thuộc khối lăng
trụ nhưng không thuộc hình lăng trụ ứng với khối lăng trụ đó được gọi là điểm trong của khối
lăng trụ. Điểm trong hay điểm ngoài của khối chóp, khối chóp cụt cũng được định nghĩa tương tự. c) Ví dụ: A' S B' C' F J E I A B A B O G D C C Hình 1 Hình 2
II. KHÁI NIỆM VỀ HÌNH ĐA DIỆN VÀ KHỐI ĐA DIỆN
1. Khái niệm về hình đa diện: S C D B A
( HÌNH 1) ( HÌNH 2) ( HÌNH 3)
Hình đa diện là hình được tạo bởi một số hữu
Lưu ý: -Mỗi đa giác như thế gọi là một mặt
hạn các đa giác thoả mãn hai tính chất: của hình đa diện
+ Hai đa giác phân biệt chỉ có thể hoặc không
-Các định, cạnh của các đa giác ấy cũng là
có điểm chung nào hoặc chỉ có một đỉnh chung
các định, cạnh của hình đa diện
hoặc chỉ có một cạnh chung.
+ Mỗi cạnh của đa giác nào cũng là cạnh chung
của đúng hai đa giác. Trang 3
Trên con đường thành công không có dấu chân của kẻ lười biếng ➢VD1:
Câu hỏi 1: Trong các hình 1, 2, 3, hình nào là hình đa diện? vì sao?
Câu hỏi 2: Hình lập phương có bao nhiêu cạnh, bao nhiêu đỉnh?
Hình 4 có bao nhiêu cạnh, bao nhiêu đỉnh?
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
2. Khái niệm về khối đa diện:
Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó. Lưu ý:
-Những điểm không thuộc khối đa diện được
gọi là điểm ngoài của khối đa diện.
-Những điểm thuộc khối đa diện nhưng không
thuộc hình đa diện giới hạn khối đa diện ấy
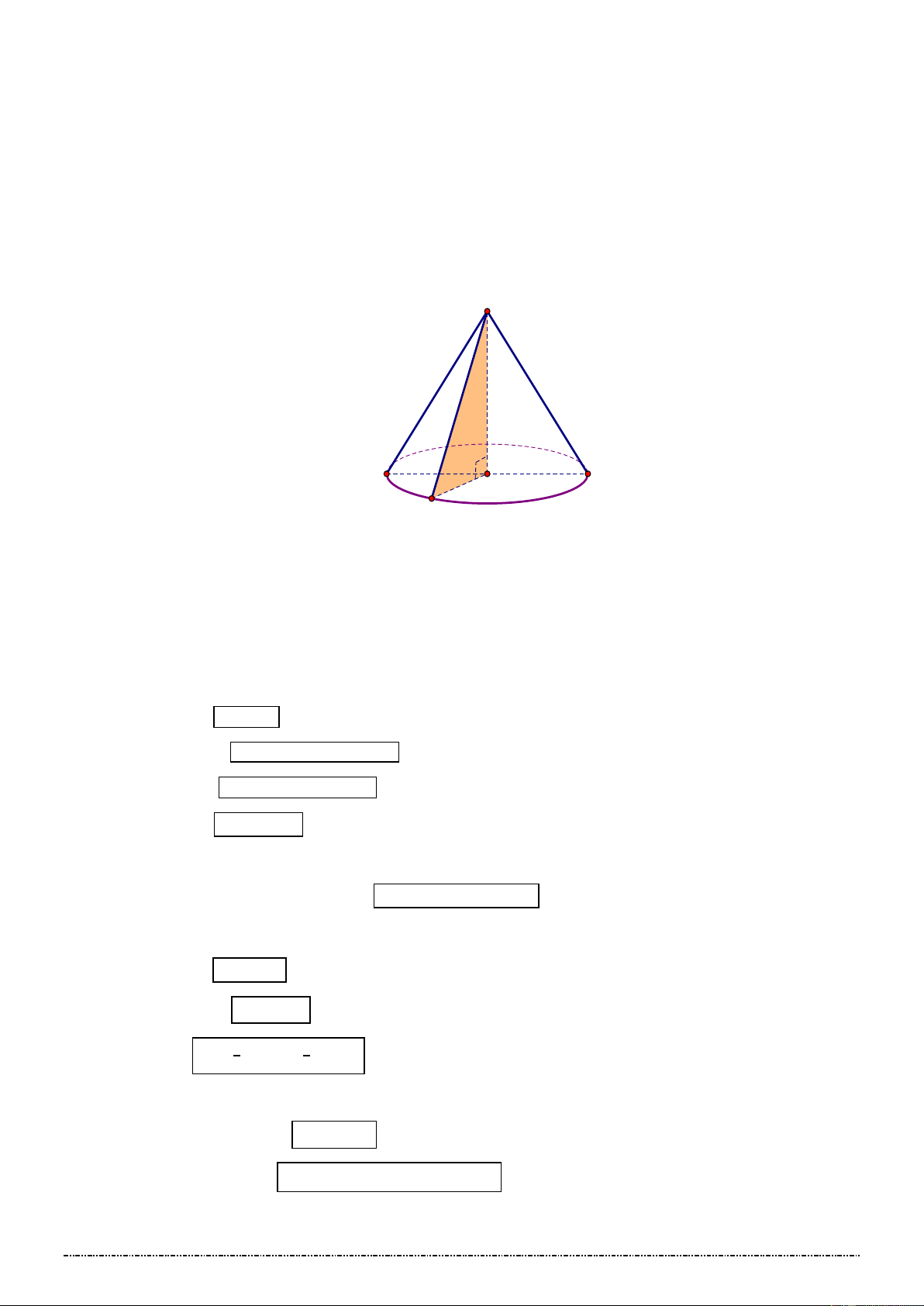
được gọi là điểm trong của khối đa diện. c)Ví dụ: S
➢VD3:Cho khối chóp S.ABCD có O là giao điểm AC và N BD, M I
I là trung điểm SO, M là trung điểm SA, N đối xứng với I D
qua M. Hãy chỉ ra trong các điểm O, I, M, N, điểm nào là A
điểm trong, điểm nào là điểm ngoài của khối chóp S.ABCD? O C B
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
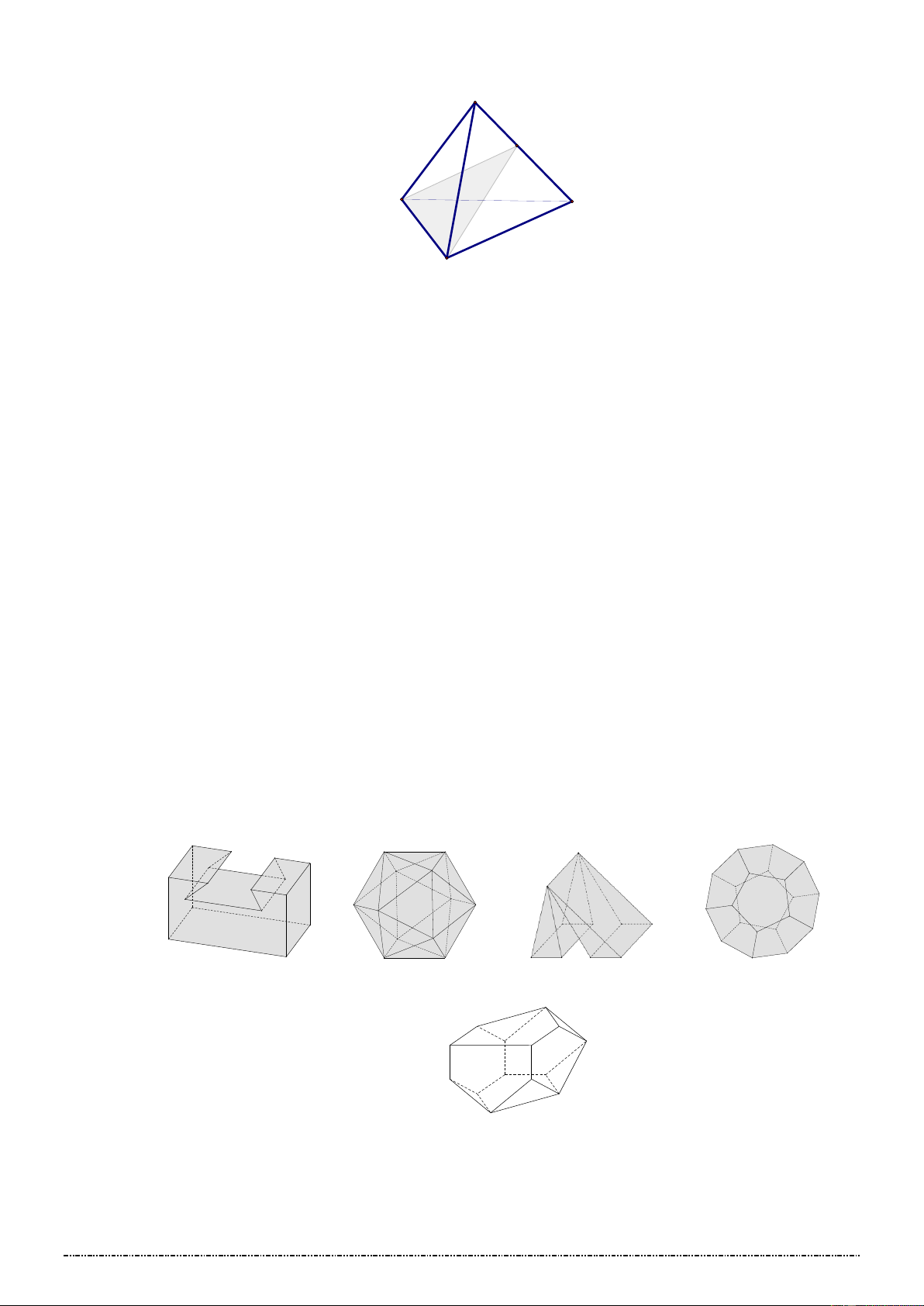
➢VD4:Trong các hình sau, hình nào là khối đa diện? Trang 4
Trên con đường thành công không có dấu chân của kẻ lười biếng Hình a Hình b Hình c Hình d Hình e Hình f
➢VD5:Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mỗi hình đa diện có ít nhất bốn đỉnh.
B. Mỗi hình đa diện có ít nhất ba cạnh.
C. Số đỉnh của một hình đa diện lớn hơn hoặc bằng số cạnh của nó.
D. Số mặt cảu một hình đa diện lớn hơn hoặc bằng số cạnh của nó.
III. HAI ĐA DIỆN BẰNG NHAU:
1. Phép dời hình trong không gian
a)Phép tịnh tiến theo vectơ : Trong không
Trong không gian, quy tắc đặt
tương ứng mỗi điểm M với mỗi gian cho vectơ .
điểm M’ xác định duy nhất được
Phép biến hình mỗi
gọi là phép biến hình trong không
điểm M thành điểm M’ gian.
b) Phép đối xứng qua mặt phẳng (P),
Phép biến hình trong không gian
là phép biến hình biến mỗi điểm thuộc
được gọi là phép dời hình nếu nó
(P) thành chính nó, biến mỗi điểm M
bảo toàn khoảng cách giữa hai
không thuộc (P) thành điểm M’ sao điểm tùy ý.
cho (P) là mặt phẳng trung trực của MM’.
d) Phép đối xứng qua đường
c) Phép đối xứng tâm O, là phép biến hình thẳng
(hay phép đối xứng qua
biến điểm O thành chính nó, biến mỗi trục
), là phép biến hình biến
điểm M khác O thành điểm M’ sao cho O
mỗi điểm thuộc đường thẳng
là trung điểm của MM’.
thành chính nó, biến mỗi điểm M Trang 5
Trên con đường thành công không có dấu chân của kẻ lười biếng
2. Hai hình bằng nhau:
Định nghĩa: Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
Đặc biệt: Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.
IV/ PHÂN CHIA VÀ LẮP GHÉP KHỐI ĐA DIỆN:
a) Tiếp cận: Quan sát các hình sau và trả lời câu hỏi tương ứng. Hình 1
H: Ta có thể phân chia mô hình trên thành những khối hình hộp hay không?
H: Tìm mối liên hệ giữa hình a và hình b Quan sát các mảnh ghép
trong các mô hình trên hãy cho biết chúng có bao nhiêu
điểm trong chung với nhau?
……………………………………………………………………………………………………
……………………………………………………………………………………………………
b) Hình thành kiến thức: Nếu khối đa điện (H) là hợp của hai khối đa diện ( H và ( H sao 2 ) 1 ) cho ( H và ( H
không có chung điểm trong nào thì ta nói có thể chia khối đa diện (H) 2 ) 1 )
thành hai khối đa diện ( H và ( H
, hay có thể lắp ghép hai khối đa điện ( H và ( H2 ) 1 ) 2 ) 1 ) thành khối đa diện (H). c) Ví dụ:
➢VD1: Cho khối tứ diện ABCD. Trên đoạn AD lấy điểm I khác A và D. Mặt phẳng (IBC)
chia khối tứ diện đã cho thành những khối tứ diện nào? Trang 6
Trên con đường thành công không có dấu chân của kẻ lười biếng A I B D C
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………
➢VD2: Sử dụng đúng hai mặt phẳng khác nhau để chia khối tứ diện thành bốn khối tứ diện.
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………
C) HOẠT ĐỘNG LUYỆN TẬP VÀ VẬN DỤNG:
Bài tập tự luận:
Bài 1. Hãy phân chia khối lăng trụ AB . C A B  C
  thành ba khối tứ diện.
Bài 2. ( Bài tập 3/sgk/trang 12) Hãy phân chia một khối lập phương ABC .
D A' B 'C 'D ' thành năm khối tứ diện
Bài tập trắc nghiệm: Câu 1:
[ Mức độ 1] Số các đỉnh hoặc số các mặt bất kì hình đa diện nào cũng: A. lớn hơn 4.
B. lớn hơn hoặc bằng 5. C. lớn hơn 5.
D. lớn hơn hoặc bằng 4. Câu 2:
[ Mức độ 1] Vật thể nào dưới đây không phải là khối đa diện? A. . B. . C. . D. Câu 3:
[ Mức độ 1] Hình đa diện bên có bao nhiêu cạnh? A. 21 . B. 22 . C. 23. D. 24. Câu 4:
[ Mức độ 1] Gọi n là số hình đa diện trong bốn hình trên. Tìm n . Trang 7
Trên con đường thành công không có dấu chân của kẻ lười biếng A. n = 4 . B. n = 2 . C. n = 1 . D. n = 3 . Câu 6:
[ Mức độ 1] Cho khối chóp ngũ giác S.ABCDE . Mặt phẳng (SAD) chia khối chóp đó thành
A. Hai khối chóp tứ giác.
B. Một khối tứ diện và một khối lăng trụ.
C. Một khối tứ diện và một khối chóp tứ giác.
D. Hai khối tứ diện. Câu 7:
[ Mức độ 1] Trong các mệnh đề sau, mệnh đề nào đúng?
Số các cạnh của hình đa diện luôn luôn: A. lớn hơn 6 . B. lớn hơn 7 .
C. lớn hơn hoặc bằng 8 .
D. lớn hơn hoặc bằng 6 . Câu 8:
[ Mức độ 1] Hình lập phương có tất cả bao nhiêu mặt phẳng đối xứng? A. 8 mặt phẳng. B. 9 mặt phẳng. C. 10 mặt phẳng. D. 12 mặt phẳng. Câu 9:
[ Mức độ 2] Một hình đa diện có các mặt là những tam giác thì số mặt M và số cạnh C của đa diện đó thoả mãn
A. 3C = 2M .
B. C = M + 2 .
C. M  C .
D. 3M = 2C .
Câu 10: [ Mức độ 2] Cho một đa diện có m đỉnh và mỗi đỉnh là đỉnh chung của đúng 3 cạnh. Chọn
mệnh đề đúng trong các mệnh đề sau:
A. m là một số chẵn.
B. m chia cho 3 dư 2 .
C. m chia hết cho 3 .
D. m là một số lẻ.
Câu 11: [ Mức độ 2] Biết rằng khối đa diện mà mỗi mặt đều là hình ngũ giác. Gọi C là số cạnh của khối
đa diện đó, lúc đó ta có:
A. C là số chia hết cho 3.
B. C là số chẵn.
C. C là số lẻ.
D. C là số chia hết cho 5.
Câu 12: [ Mức độ 2] Trong các mệnh đề sau, mệnh đề nào đúng?
A. Số đỉnh và số mặt của một hình đa diện luôn bằng nhau.
B. Tồn tại hình đa diện có số đỉnh và số mặt bằng nhau.
C. Tồn tại một hình đa diện có số cạnh bằng số đỉnh.
D. Tốn tại một hình đa diện có số cạnh và mặt bằng nhau.
Câu 13: [ Mức độ 2] Mặt phẳng ( AB C
 ) chia khối lăng trụ ABC.A B  C
  thành các khối đa diện nào?
A. Một khối chóp tam giác và một khối chóp tứ giác.
B. Hai khối chóp tam giác.
C. Một khối chóp tam giác và một khối chóp ngũ giác.
D. Hai khối chóp tứ giác.
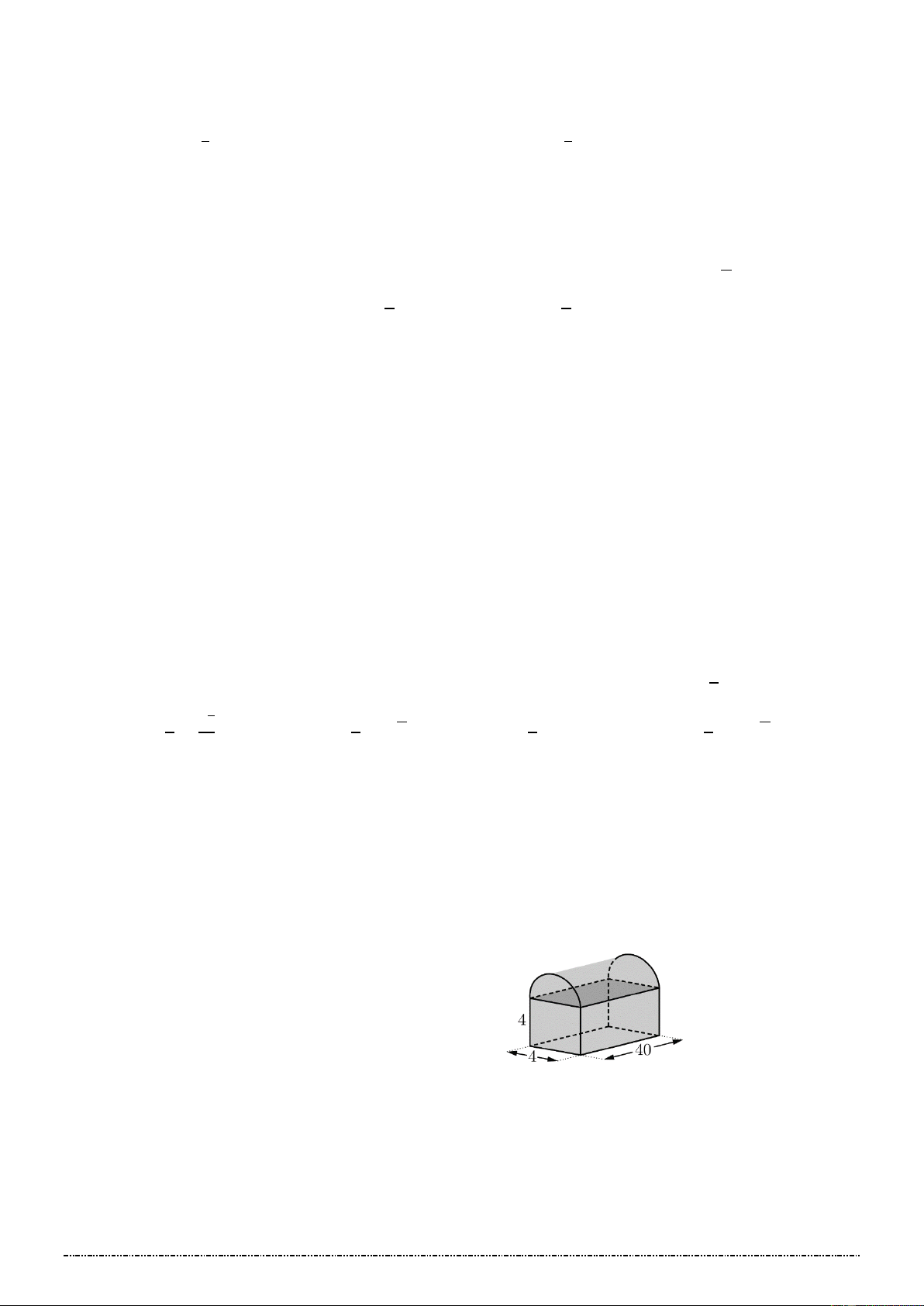
Câu 14: [ Mức độ 3] Một hình lập phương có cạnh 4 cm . Người ta sơn đỏ mặt ngoài của hình lập phương
rồi cắt hình lập phương bằng các mặt phẳng song song với các mặt của hình lập phương thành
64 hình lập phương nhỏ có cạnh 1cm . Có bao nhiêu hình lập phương có đúng một mặt được sơn đỏ? Trang 8
Trên con đường thành công không có dấu chân của kẻ lười biếng A. 8 . B. 16 . C. 24 . D. 48 .
Câu 15: [ Mức độ 3] Cho tứ diện ABC .
D Lấy một điểm M giữa A và B , 1 điểm N giữa C và D
bằng 2 mặt phẳng: (MCD) và ( NAB) , ta chia khối đa diện thành 4 khối tứ diện
A. AMCN, AMND, AMCD, BMCN .
B. AMCN, AMN ,
D BMCN, BMND . C. AMC , D AMN ,
D BMCN, BMND .
D. BMCD, BMND, AMCN, AMDN .
Câu 16: [Mức độ 1] Hình nào trong các hình sau không phải là hình đa diện? A. Hình chóp. B. Hình vuông.
C. Hình lập phương. D. Hình lăng trụ.
Câu 17: [Mức độ 1] Cho khối chóp có là n – giác (n  3; n  N ) . Mệnh đề nào sau đây đúng?
A. Số cạnh của khối chóp bằng n +1. .
B. Số mặt của khối chóp bằng 2 . n .
C. Số đỉnh của khối chóp bằng n +1. .
D. Số mặt của khối chóp bằng số đỉnh của nó.
Câu 18: [Mức độ 1] Hình nào dưới đây không phải là một khối đa diện? A. . B. . C. D.
Câu 19: [Mức độ 2] Cho đa diện ( H ) có tất cả các mặt đều là tam giác. Khẳng định nào sau đây đúng?
A Tổng các mặt của ( H ) luôn là một số chẵn.
B. Tổng các mặt của ( H ) luôn gấp đôi tổng số đỉnh của ( H ) .
C. Tổng số các cạnh của ( H ) là một số không chia hết cho 3.
D. Tổng số các cạnh của ( H ) luôn gấp đôi tổng số các mặt của ( H ).
Câu 20: [Mức độ 1] Cho khối lăng trụ tam giác đều ABC.A' B 'C ' . Về phía ngoài khối lăng trụ này ta
ghép thêm một khối lăng trụ tam giác đều bằng với khối lăng trụ đã cho, sao cho hai khối lăng
trụ có chung một mặt bên. Hỏi khối đa diện mới lập thành có mấy cạnh? A. 9. B. 12. C. 15. D. 18
Câu 21: [Mức độ 1] Phân chia khối lăng trụ ABC.A B  C
  bởi hai mặt phẳng ( AB D  ) và ( AB D  ) ta
được các khối nào sau đây?
A. Khối chóp tứ giác . A BDD B
  và khối tứ diện ABDB.
B. Khối chóp tứ giác . A BDD B
  và khối tứ diện ADD B  .
C. Khối chóp tứ giác . A BDD B
  và khối tứ diện AA B  D  .
D. Ba khối tứ diện ABDB , ADD B  và AA B  D  .
Câu 22: [Mức độ 1] Một hình hộp đứng có đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt phẳng đối xứng? A. 4 mặt phẳng. B. 1 mặt phẳng. C. 2 mặt phẳng. D. 3 mặt phẳng. Trang 9
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 23: [Mức độ 1] Hình đa diện nào dưới đây không có tâm đối xứng? A. Tứ diện đều.
B. Bát diện đều. C. Hình lập phương. D. Lăng trụ lục giác đều.
Câu 24: [Mức độ 1] Một hình chóp có 46 cạnh có bao nhiêu mặt? A. 24 . B. 46 . C. 69 . D. 25 .
Câu 25: [Mức độ 2] Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng? A. 3 mặt phẳng. B. 4 mặt phẳng. C. 6 mặt phẳng. D. 9 mặt phẳng.
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
………………………………………………………………………………………………… Trang 10
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HỌC 12 – CHƯƠNG 1
§2. KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA DIỆN ĐỀU
A. PHẦN KIẾN THỨC CHÍNH
I. ĐỊNH NGHĨA CỔ ĐIỂN
1. Định nghĩa
* VD MỞ ĐẦU:
Câu hỏi:
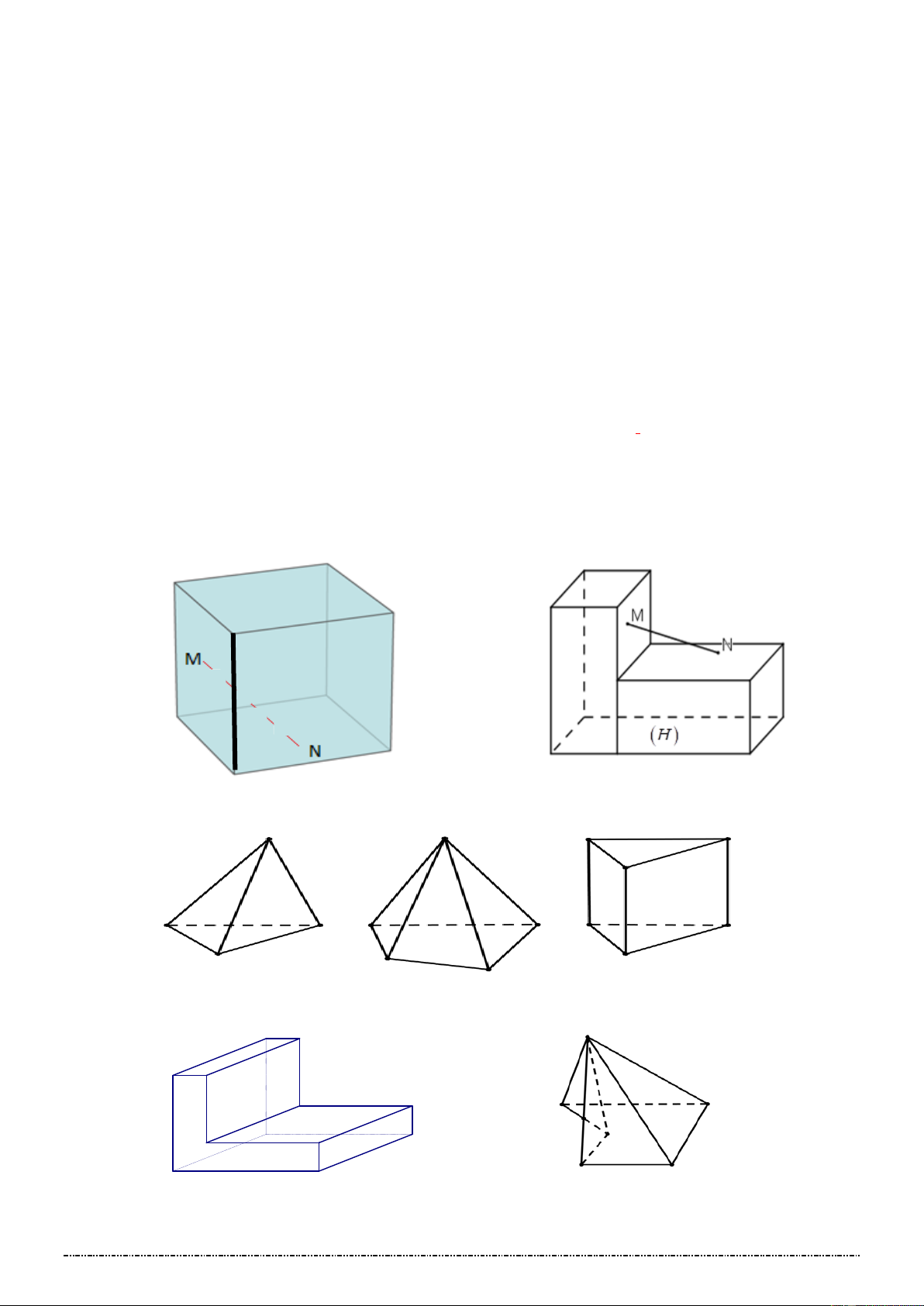
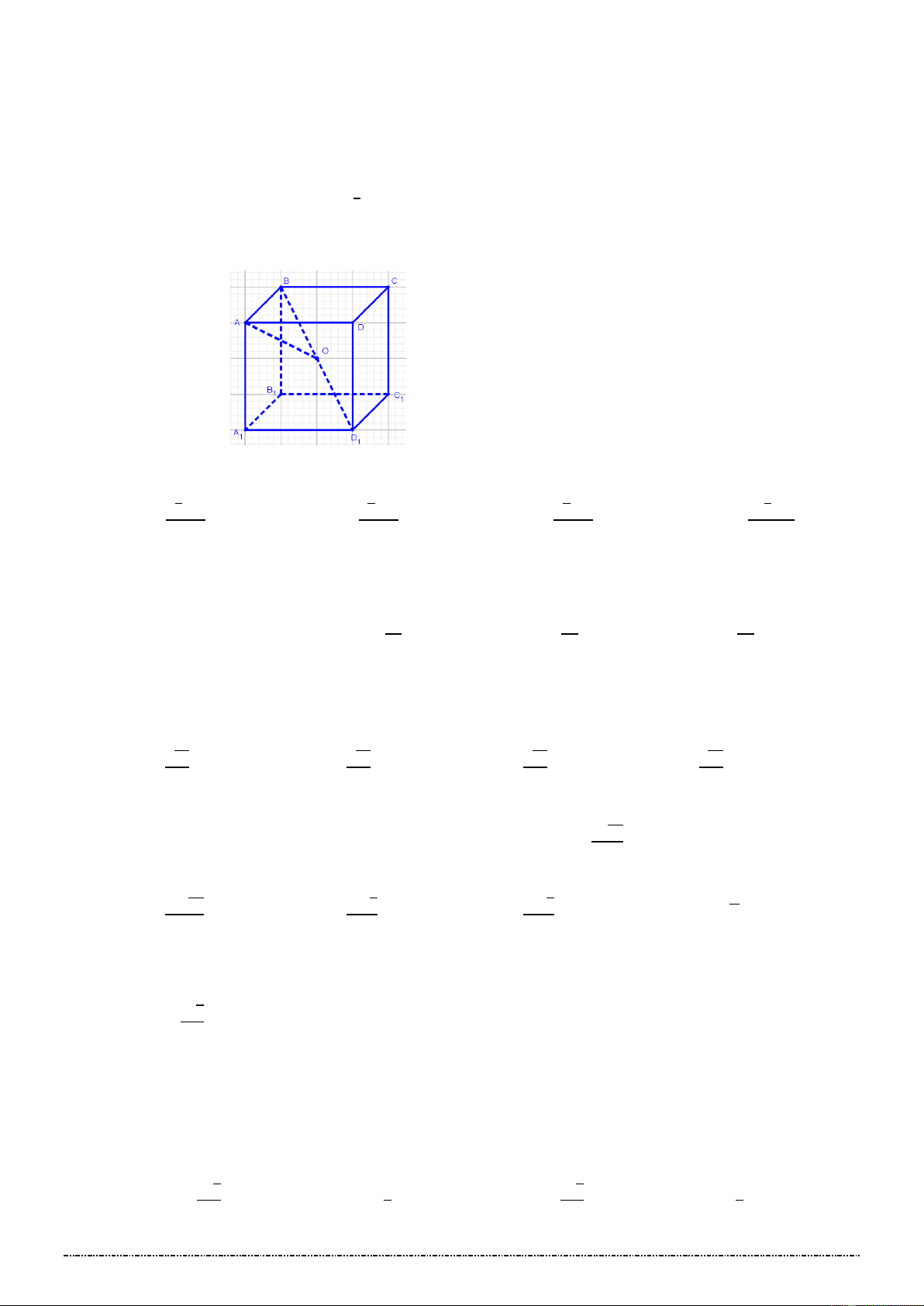
1. Lấy hai điểm M , N thuộc khối lập phương. Có nhận xét gì về vị trí của đoạn thẳng MN và khối lập phương?
……………………………………………………………………………………………………
……………………………………………………………………………………………………
2. Xét hình vẽ dưới đây. Có nhận xét gì về vị trí của đoạn thẳng MN và khối đa diện (H ) ?
……………………………………………………………………………………………………
……………………………………………………………………………………………………
- VD về khối đa diện lồi:
- VD về khối đa diện không phải là đa diện lồi: Trang 11
Trên con đường thành công không có dấu chân của kẻ lười biếng
- VD về khối đa diện đều: * ĐN:
- Khối đa diện ( H ) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của ( H ) luôn
thuộc ( H ) . Khi đó đa diện xác định ( H ) được gọi là đa diện lồi.
- Khối Đa diện đều là khối đa diện lồi có tính chất sau đây:
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại  ; p  q .
* Chú ý:
- Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối
với mỗi mặt phẳng chứa một mặt của nó. -
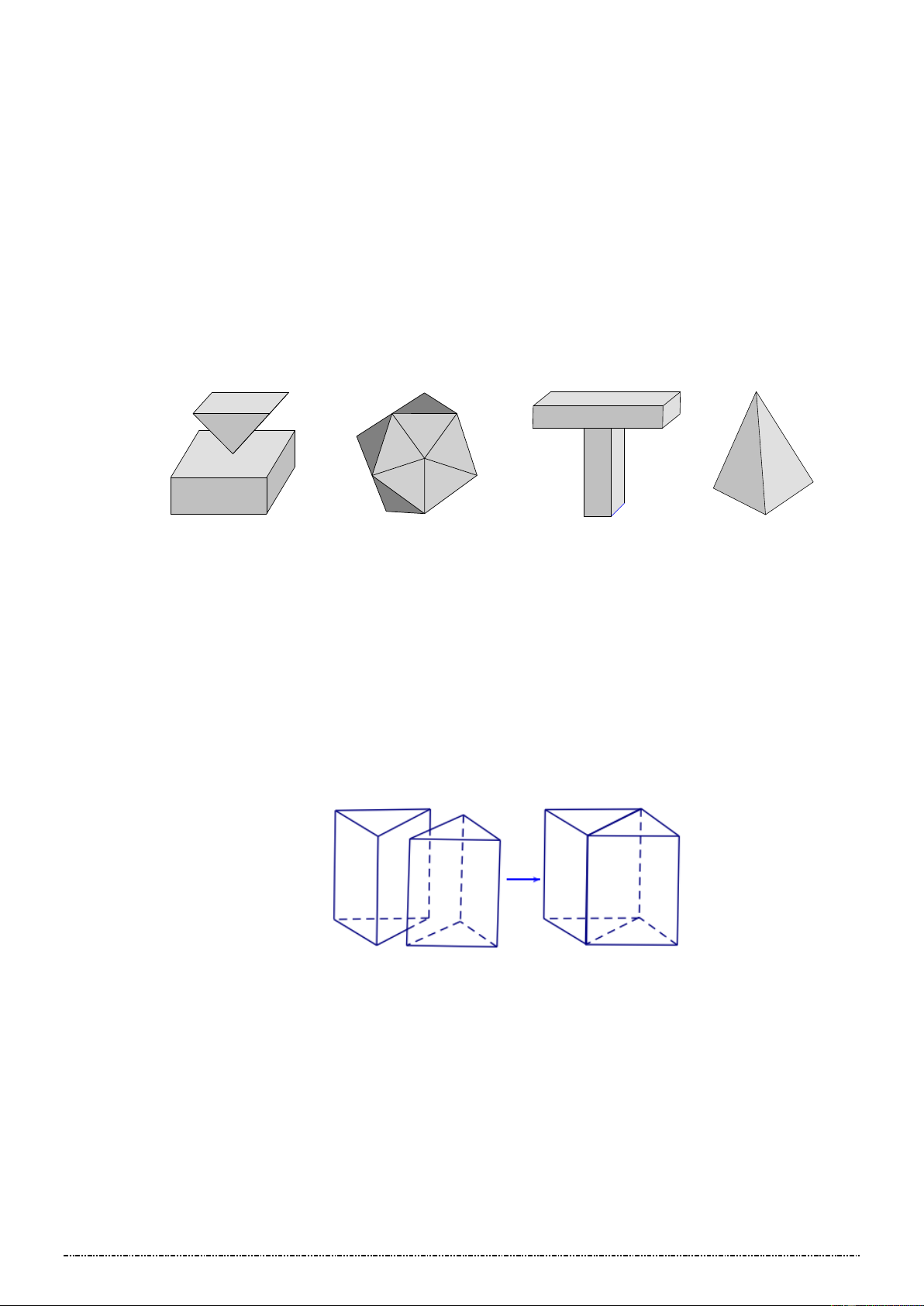
2. Ví dụ *VD1: Hình 1 Hình 2 Hình 3 Hình 4 -
Trong các hình trên, các hình biểu diễn của khối đa diện lồi là hình: …………………………. -
Trong các hình trên, các hình biểu diễn của khối đa diện không phải đa diện lồi là hình: …… *VD2:
Gọi tên các khối đa diện đều sau: Trang 12
Trên con đường thành công không có dấu chân của kẻ lười biếng …………… …………….. …………… …………….. ……………. *VD3:
Trong các khối đa diện đều sau hãy xác định số cạnh ở mỗi mặt và mỗi đỉnh của nó là đỉnh chung
của bao nhiêu mặt ? …………… …………….. …………… …………….. …………….
II. TÍNH CHẤT
1. Định lý
* ĐL: chỉ có năm loại khối đa diện đều. Đó là loại 3;  3 , loại 4;  3 , loại 3;  4 , loại 5;  3 , loại 3;  5 . Loại 3; 
3 : khối tứ diện đều; 4; 
3 : khối lập phương; 3; 
4 : khối bát diện đều; 5;  3 : khối mười hai mặt đều; 3; 
5 : khối hai mươi mặt đều.
2. Ví dụ *VD1:
Cho các đa diện sau: tứ diện đều, hình chóp tứ giác đều, lăng trụ tam giác đều, lập phương, bát diện đều.
- Trong các đa diện trên, đa diện đều gồm:………………………………………………………
- Trong các đa diện trên, đa diện không phải đa diện đều gồm:………………………………… *VD2:
Hoàn thành bảng sau: Trang 13
Trên con đường thành công không có dấu chân của kẻ lười biếng
Tên đa diện Loại
Số mặt
Số đỉnh
Số cạnh Tứ diện đều ………… ………….. …………. ……………
……………………… 4;  3 ………….. …………. ……………
……………………… ………….. 8 6 ……………
……………………… …………..
…………… 20 30
……………………… ………….. 20 …………… 30 *VD3:
Tính diện tích toàn phần của đa diện đều trên (hình vẽ) biết cạnh của đa diện đó là 10 . cm
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
B. LUYỆN TẬP
I. Chữa bài tập SGK
Bài 1 trang 18 -SGK:
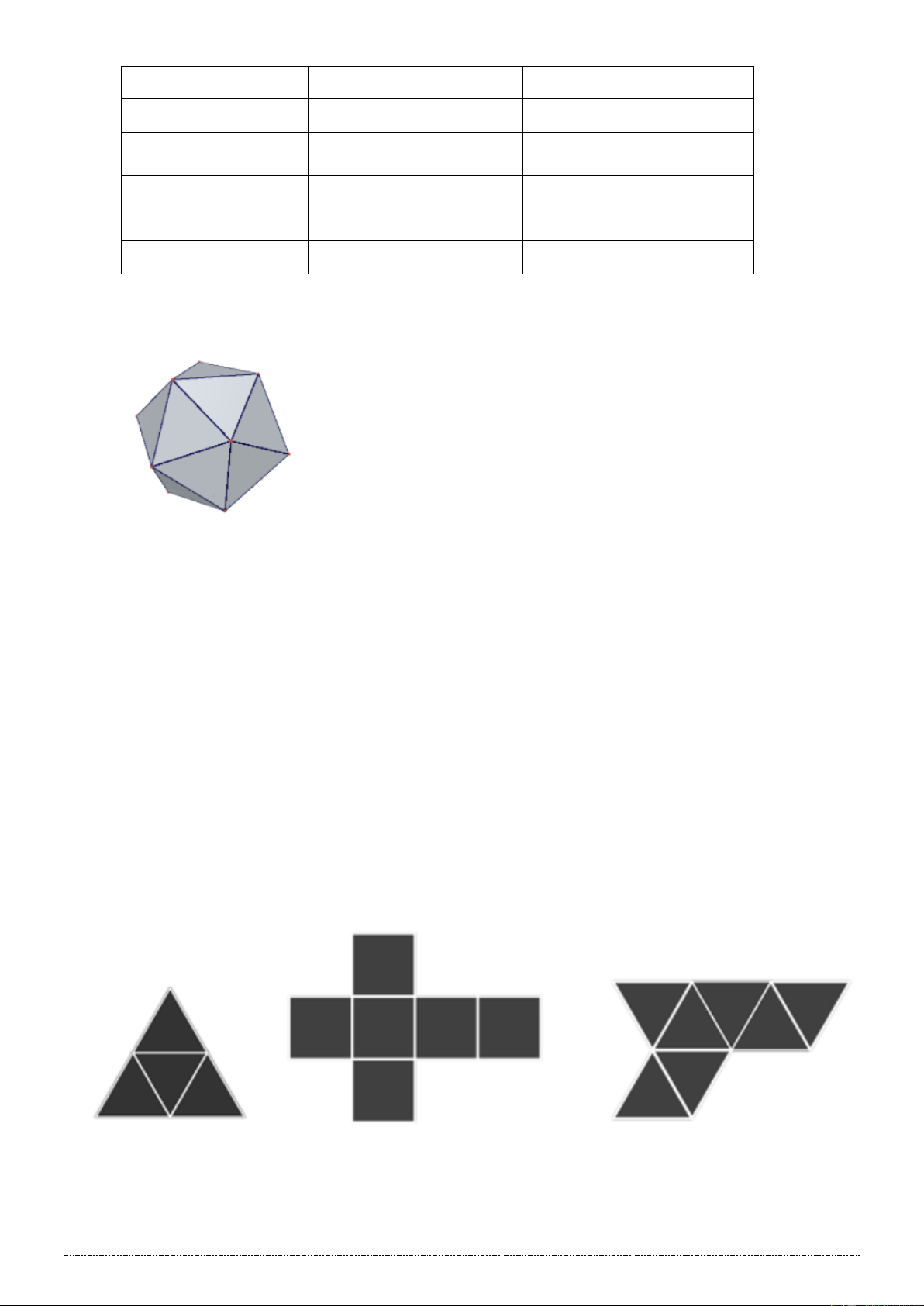
Cắt bìa theo mẫu dưới đây (h.123), gấp theo đường kẻ, rồi dán các mép lại để được các hình tứ diện đều,
hình lập phương và hình bát diện đều.
II. Bài tập trắc nghiệm Trang 14
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 1. [Mức độ 1] Khẳng định nào sau đây là đúng?
A. Tâm các mặt của một hình lập phương là các đỉnh của một hình lập phương.
B. Tâm các mặt của một hình tứ diện đều là các đỉnh của một hình tứ diện đều.
C. Tâm các mặt của một hình tứ diện đều là các đỉnh của một hình lập phương.
D. Tâm các mặt của một hình lập phương là các đỉnh của một hình tứ diện đều.
Câu 2. [Mức độ 1] Khối bát diện đều là khối đa diện đều loại nào ? A. 3;  4 . B. 3;  3 . D. 4;  3 . C.5;  3 .
Câu 3. [Mức độ 2] Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ Khối tứ diện Khối lập Hình 20 đề Bát diện đều Hình 12 mặt đều u phương mặt đều
Mệnh đề nào sau đây đúng?
A. Mọi khối đa diện đều có số mặt là những số chia hết cho 4.
B. Khối lập phương và khối bát diện đều có cùng số cạnh.
C. Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.
D. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh.
Câu 4. [Mức độ 2] Số mặt phẳng đối xứng của khối đa diện đều 4;  3 là A. 3. B. 6. C. 8. D. 9.
Câu 5. [Mức độ 2] Cho hình đa diện đều loại 4; 
3 cạnh a . Gọi S là tổng diện tích tất cả các mặt của
hình đa diện đó. Mệnh đề nào dưới đây đúng? A. 2
S = 4a . B. 2 S = 6a . C. 2
S = 8a . D. 2
S = 10a .
BÀI TẬP VẬN DỤNG Câu 1.
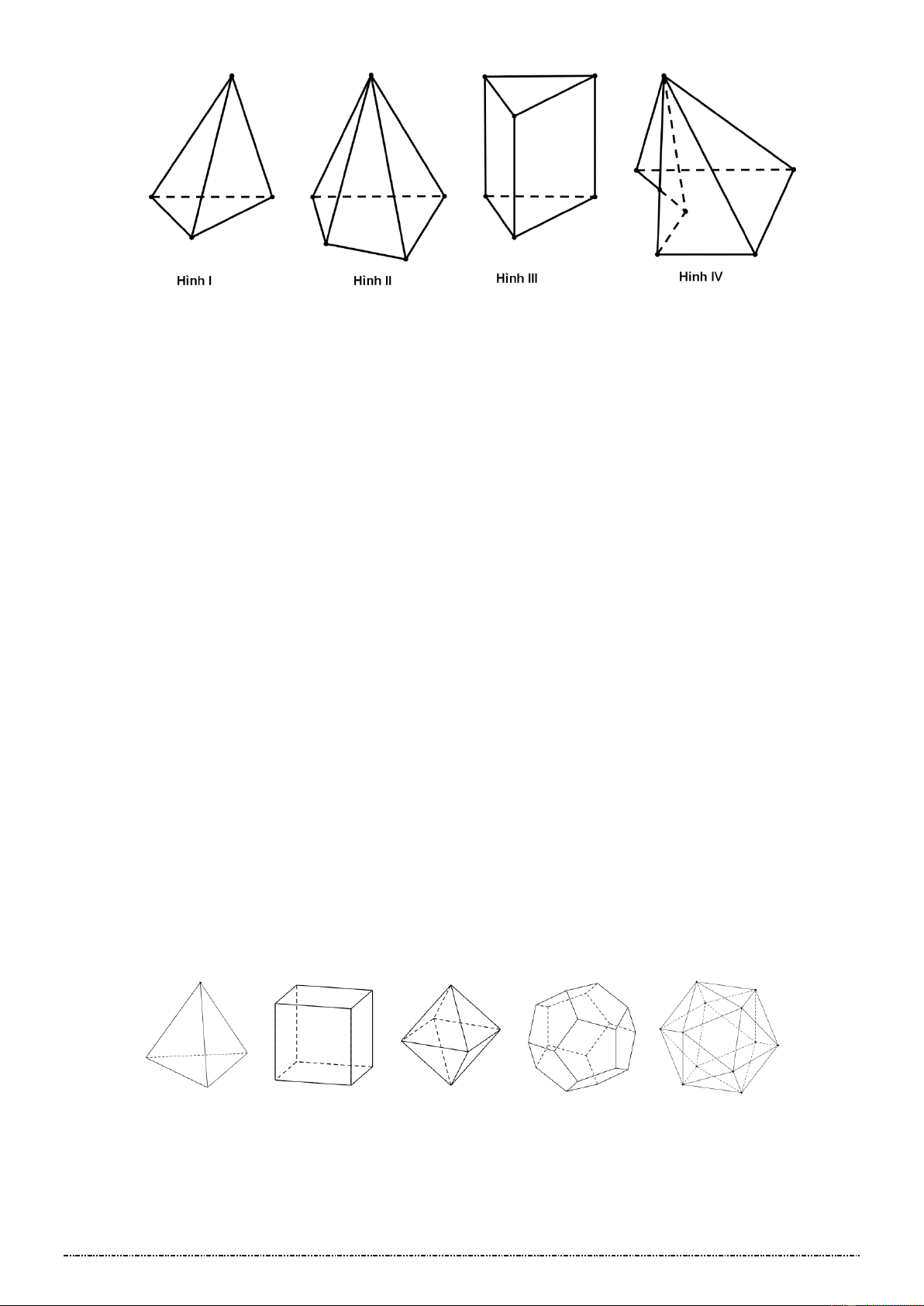
[Mức độ 1] Trong các hình sau, hình nào không phải là đa diện lồi A.Hình 1 B.Hình 2 C.Hình 3 D.Hình 4 Câu 2.
[Mức độ 1] Trong các hình dưới đây, hình nào không phải là đa diện lồi? Trang 15
Trên con đường thành công không có dấu chân của kẻ lười biếng A. Hình (I) . B. Hình (II) .
C. Hình (III) . D. Hình (IV) . Câu 3.
[Mức độ 2] Tâm tất cả các mặt của một hình lập phương là các đỉnh của hình nào trong các hình sau đây?
A. Bát diện đều.
B. Tứ diện đều.
C. Lục giác đều. D. Ngũ giác đều. Câu 4.
[Mức độ 2] Chọn khẳng định đúng
A. Tâm tất cả các mặt của một hình lập phương là các đỉnh của một hình lập phương.
B. Tâm tất cả các mặt của một hình tứ diện đều là các đỉnh của một hình tứ diện đều.
C. Tâm tất cả các mặt của một hình tứ diện đều là các đỉnh của một hình lập phương.
D. Tâm tất cả các mặt của một hình lập phương là các đỉnh của một hình tứ diện đều. Câu 5.
[Mức độ 3] Trung điểm các cạnh của một tứ diện đều tạo thành
A. Các đỉnh của một hình tứ diện đều.
B. Các đỉnh của một hình bát diện đều.
C. Các đỉnh của một hình mười hai mặt đều.
D. Các đỉnh của một hình hai mươi mặt đều. Câu 6.
[Mức độ 2] Trong các mệnh đề sau, mệnh đề nào sai?
A. Tồn tại khối tứ diện là khối đa diện đều.
B. Tồn tại khối lăng trụ đều là khối đa diện đều.
C. Tồn tại khối hộp là khối đa diện đều.
D. Tồn tại khối chóp tứ giác đều là khối đa diện đều. Câu 7.
[Mức độ 2] Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ Khối tứ diện Khối lập Bát diện đều
Hình 12 mặt Hình 20 mặt đều đều phương đều
Mệnh đề nào sau đây đúng? Trang 16
Trên con đường thành công không có dấu chân của kẻ lười biếng
A. Mọi khối đa diện đều có số mặt là những số chia hết cho 4.
B. Khối lập phương và khối bát diện đều có cùng số cạnh.
C. Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.
D. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh. Câu 8.
[Mức độ 2] Khối đa diện đều loại 5; 
3 , diện tích một mặt của khối đa diện đó là 2 3m . Tổng
diện tích các mặt của khối đa diện đó bằng: A. 2 36m . B. 2 24m . C. 2 18m . D. 2 60m . Câu 9.
[Mức độ 2] Cho hình bát diện đều cạnh a . Gọi S là tổng diện tích tất cả các mặt của hình bát
diện đó. Tính S . A. 2
S = 2 3a . B. 2
S = 4 3a . C. 2 S = 8a . D. 2 S = 3a .
Câu 10. [Mức độ 1] Trong các khối đa diện sau: Khối tứ diện, khối lập phương, khối chóp tứ giác, khối
hộp, có mấy khối đa diện lồi? A. 2 . B. 3 . C. 4 . D. 1.
Câu 11. [Mức độ 1] Khối đa diện ( H ) được gọi là khối đa diện lồi nếu
A. Đoạn thẳng nối hai điểm bất kỳ của ( H ) nằm về hai phía đối với ( H ) .
B. Đoạn thẳng nối hai điểm bất kỳ của ( H ) không thuộc ( H ) .
C. Miền trong của nó luôn nằm về 2 phía đối với mỗi mặt phẳng chứa 1 mặt của nó.
D. Đoạn thẳng nối hai điểm bất kỳ của ( H ) luôn thuộc ( H ) .
Câu 12. [Mức độ 1] Chọn khẳng định nào đúng?
A. Khối đa diện đều loại  ; p 
q là khối đa diện đều có p mặt, q đỉnh.
B. Khối đa diện đều loại  ; p 
q là khối đa diện lồi thỏa mãn mỗi mặt của nó là đa giác đều p
cạnh và mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
C. Khối đa diện đều loại  ; p 
q là khối đa diện đều có p cạnh, q mặt.
D. Khối đa diện đều loại  ; p 
q là khối đa diện lồi thỏa mãn mỗi đỉnh của nó là đỉnh chung của
đúng p mặt và mỗi mặt của nó là một đa giác đều q cạnh.
Câu 13. [Mức độ 1] Một hình lăng trụ có 12 cạnh thì có tất cả bao nhiêu đỉnh? A. 8 . B. 12 . C. 4 . D. 6 .
Câu 14. [Mức độ 2] Trong các mệnh đề sau, mệnh đề nào đúng?
A. Khối chóp tứ giác đều là khối đa diện đều loại3;  3 .
B. Khối bát diện đều không phải là khối đa diện lồi.
C. Lắp ghép hai khối hộp luôn được một khối đa diện lồi.
D. Tồn tại hình đa diện có số đỉnh bằng số mặt. Trang 17
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 15. [Mức độ 2] Một người thợ thủ công làm mô hình lồng đèn bát diện đều, mỗi cạnh của bát diện
đó được làm từ các que tre độ dài 8cm . Hỏi người đó cần ít nhất bao nhiêu mét que tre để làm
100 cái đèn (giả sử mối nối giữa các que tre có độ dài không đáng kể)? A. 9600 . B. 96 . C. 6400 . D. 64 .
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 18
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HỌC 12 – CHƯƠNG 1
§3. KHÁI NIỆM VỀ THỂ TÍCH KHỐI ĐA DIỆN
A. PHẦN KIẾN THỨC CHÍNH
I. ĐỊNH NGHĨA CỔ ĐIỂN
1. Định nghĩa
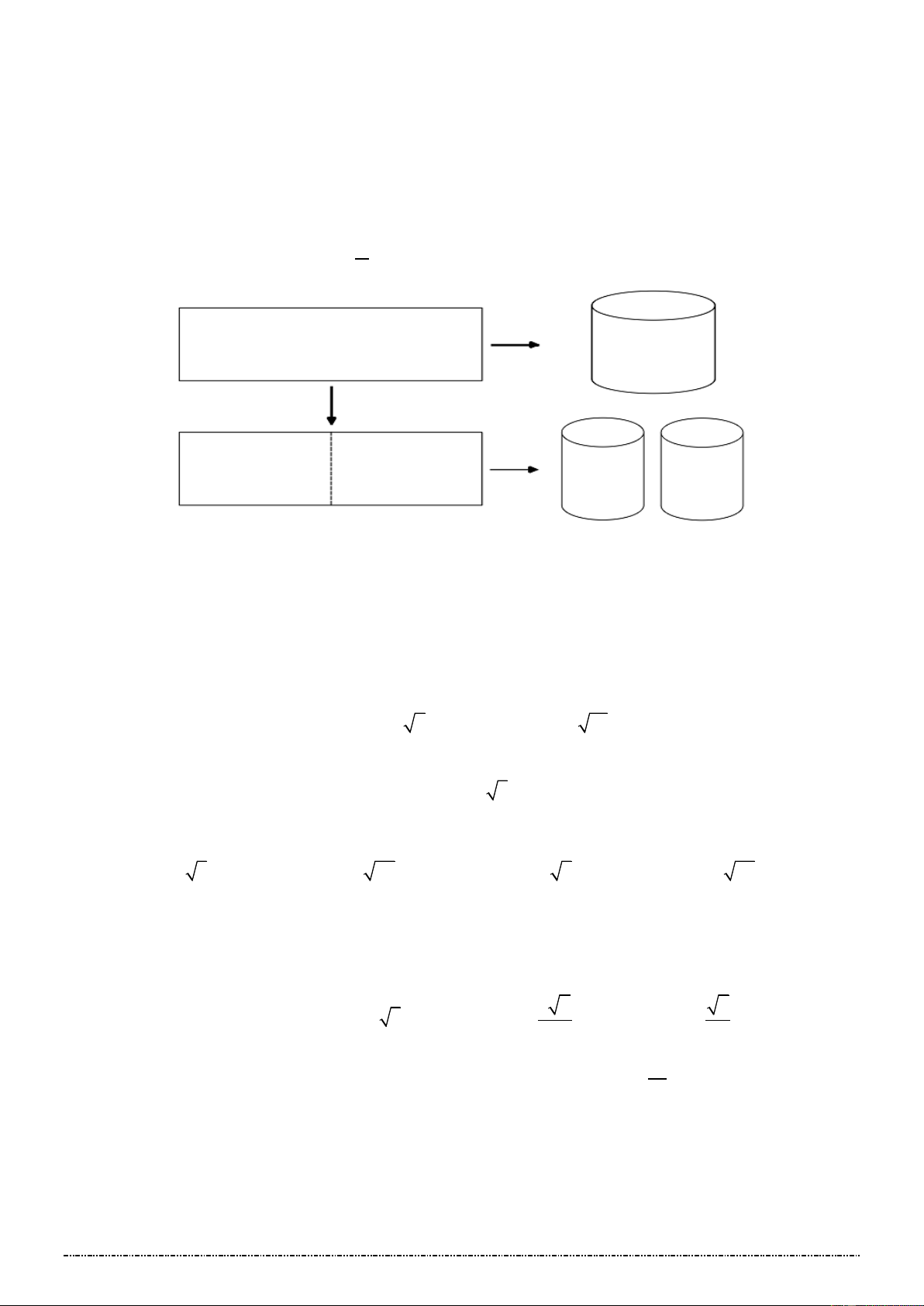
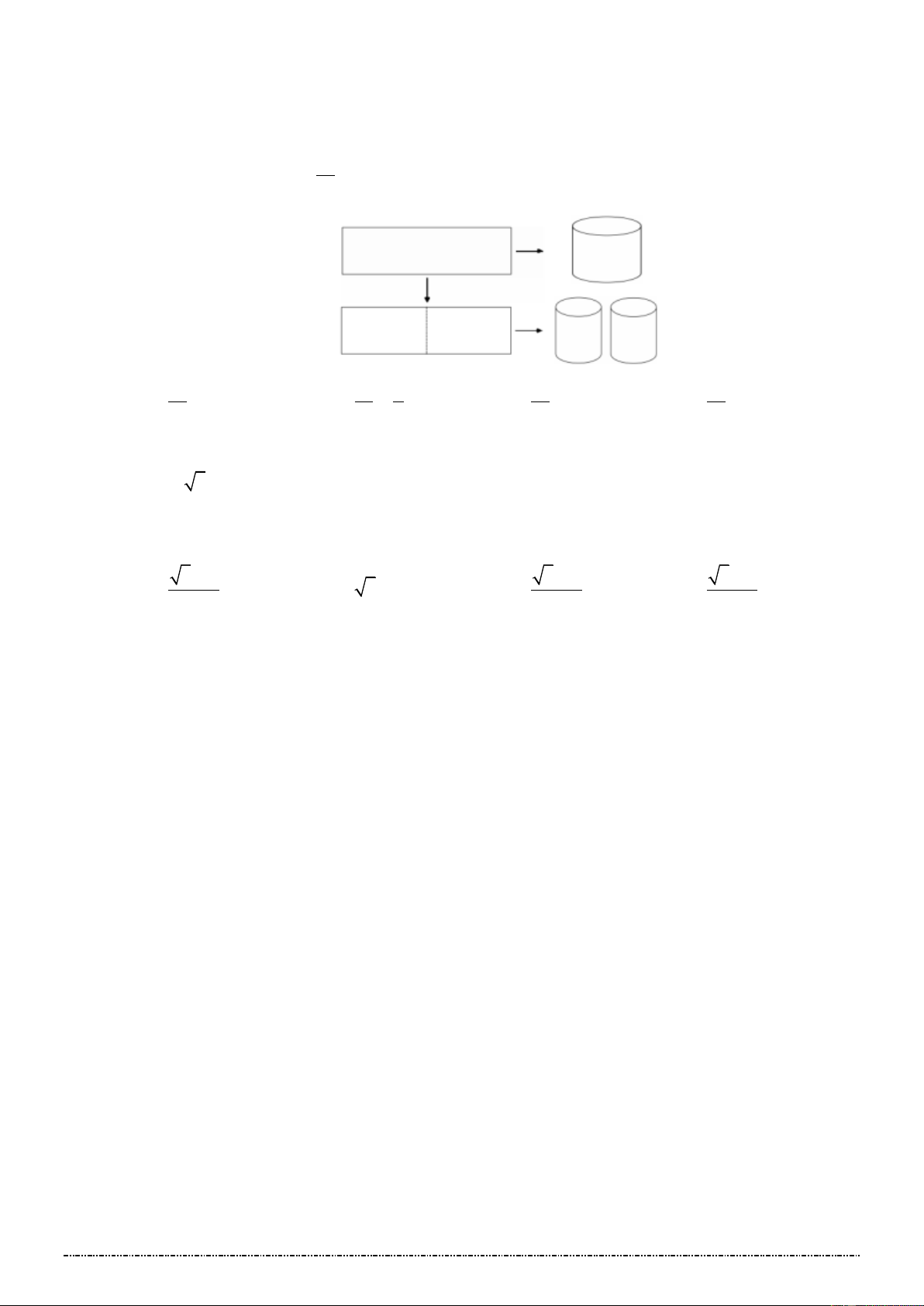
* VD MỞ ĐẦU: Cho khối lập phương có cạnh bằng 1cm (có thể tích 3
1cm ). Các khối đa diện được ghép
từ các khối lập phương có cạnh bằng 1cm (hình vẽ).
a) So sánh thể tích hai khối lập phương (hình vẽ).
b) Tính thể tích V của khối đa diện (hình vẽ).
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
* Định nghĩa: Thể tích của khối đa diện (H) là một số dương duy nhất V(H) thoả mãn các tính chất sau:
a) Nếu (H) là khối lập phương có cạnh bằng 1 thì V(H) = 1.
b) Nếu hai khối đa diện (H1), (H2) bằng nhau thì V(H1)=V(H2).
c) Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H1), (H2) thì V(H) = V(H1) + V(H2).
* Chú ý:
• V(H) cũng được gọi là thể tích của hình đa diện giới hạn khối đa diện (H). Trang 19
Trên con đường thành công không có dấu chân của kẻ lười biếng
• Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị.
2. Ví dụ
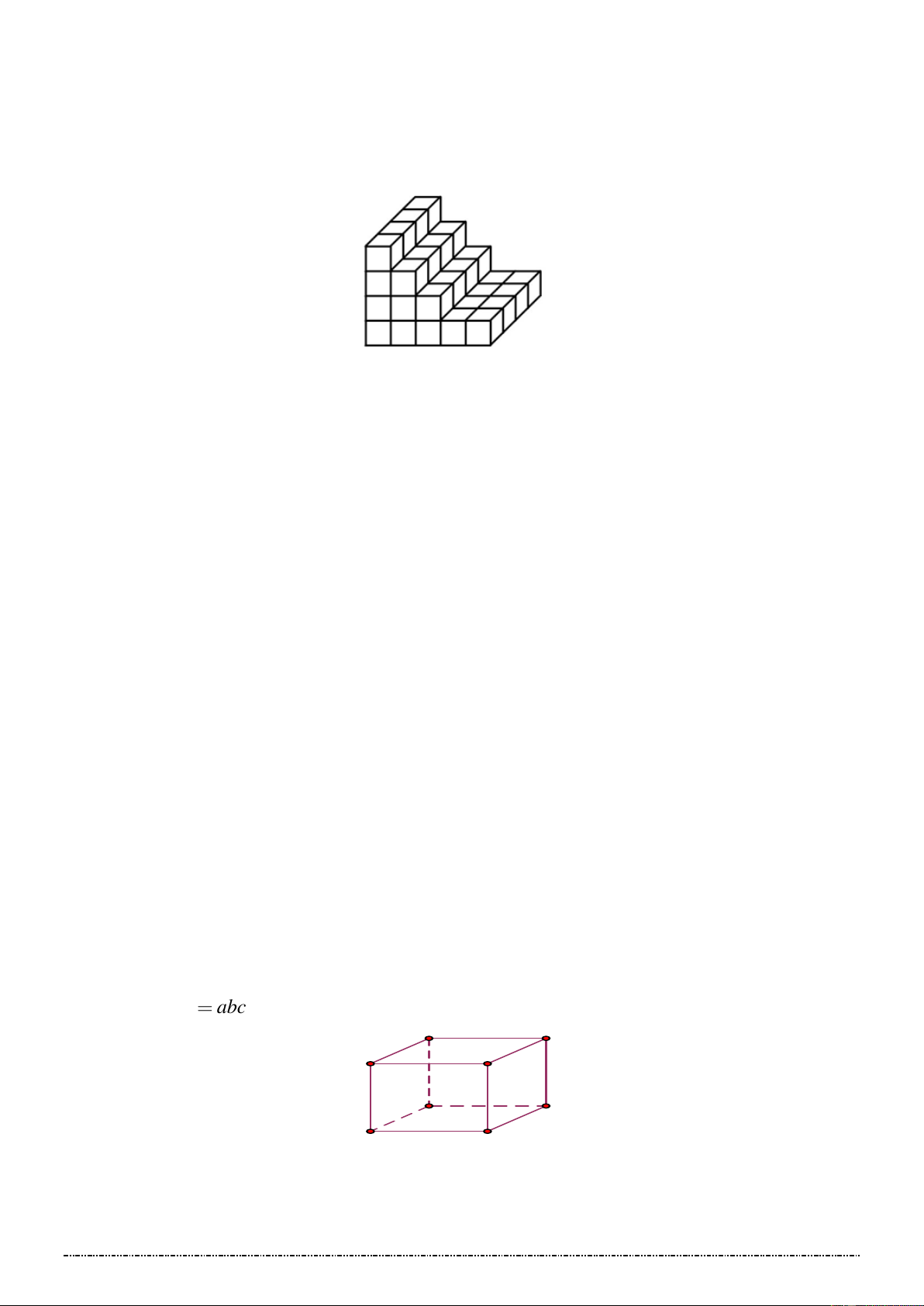
*VD1: Một bậc tam cấp được xếp từ các khối đá hình lập phương có cạnh bằng bằng 1cm như hình vẽ.
Hãy tính thể tích của khối tam cấp?
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
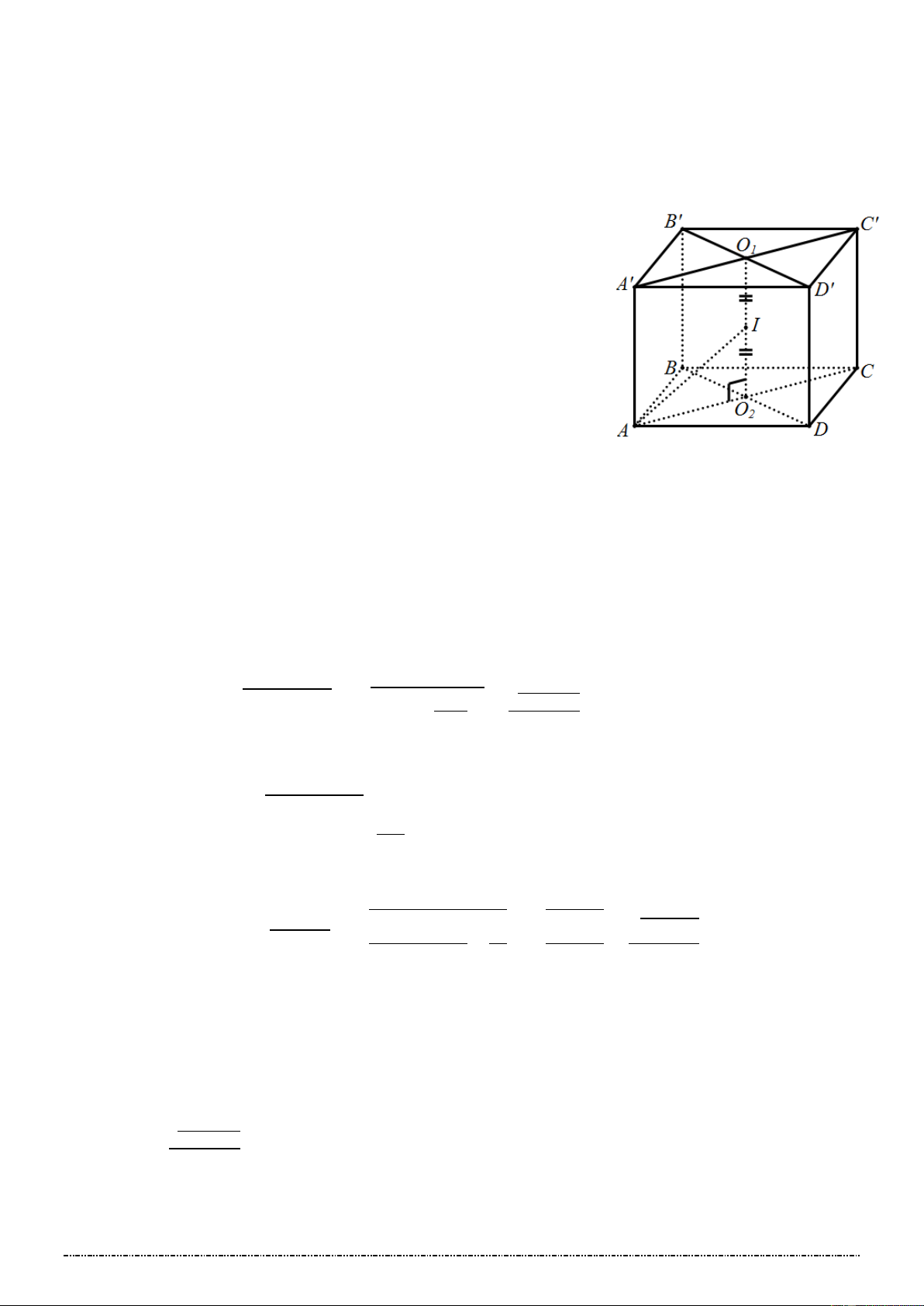
*VD2: Cho khối lập phương ABC . D A B  C  D
  có cạnh bằng 1(m) .Tính thể tích khối lăng trụ ABC.A B  C  .
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
II. TÍNH CHẤT 1. Định lý
* Định lý: Thể tích của một khối hộp chữ nhật bằng tích ba kích thước của nó. V abc . A D B C A D B C
* Định lý: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là V = Bh . Trang 20
Trên con đường thành công không có dấu chân của kẻ lười biếng
* Định lý: Thể tích khối chópcó diện tích đáy B và chiều cao h là 1 V = Bh . 3 3
* Hệ quả: Thể tích của một khối lập phương cạnh a là V a .
2. Ví dụ
*VD1: Cho hình hộp chữ nhật ABC . D A B  C  D
 có đáy là hình vuông, cạnh bên bằng 4a và đường chéo
5a .Tínhthểtích hình hộp chữ nhật này.
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… *VD2:
Cho lăng trụ tam giác ABC.A' B 'C ' có đáy là tam giác đều cạnh a , góc giữa cạnh bên và mặt đáy bằng 0
30 . Hình chiếu của A ' lên ( ABC ) là trung điểm I của BC . Tính thể tích khối lăng trụ.
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 21
Trên con đường thành công không có dấu chân của kẻ lười biếng
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
*VD3: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại B , AB = a , ACB = 60 , cạnh
bên SA vuông góc với mặt đáy và SB hợp với mặt đáy một góc 45 . Tính thể tích V của khối chóp S.ABC .
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
*VD4: Cho hình chóp S.ABCD có đáy là hình vuông ABCD. Mặt bên SAB là tam giác đều có đường cao
SH = 2a 3 và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD.
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
*VD4: Cho hình lăng trụ tam giác ABC.A' B 'C ' .Gọi E và F lần lượt lừ trung điểm của các cạnh AA' và
BB ' .Đường thẳng CE cắt đường thẳng C ' A' tại E . Đường thẳng CF cắt đường thẳng C ' B ' tại
F ' .Gọi V là thể tích khối lăng trụ ABC.A' B 'C ' .
a) Tính thể tích khối chóp C.ABFE theo V . Trang 22
Trên con đường thành công không có dấu chân của kẻ lười biếng
b) Gọi khối đa diện ( H ) là phần còn lại của khối lăng trụ ABC.A' B'C ' sau khi cắt bỏ đi khối
chóp C.ABFE .Tính tỉ số thể tích của ( H ) và của khối chóp C.C ' E ' F '.
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
B. LUYỆN TẬP
I. Chữa bài tập SGK
Bài 1 trang 25 – SGK: Tính thể tích khối tứ diện đều cạnh a.
Bài 2 trang 25 – SGK: Tính thể tích khối bát điện đều cạnh a. Trang 23
Trên con đường thành công không có dấu chân của kẻ lười biếng
Bài 4 trang 25- SGK: Cho hình chóp S.ABC . Trên các tia S ,
A SB, SC lần lượt lấy 3 điểm A', B ', C ' khác V
SA' SB' SC ' S
S.A'B'C ' . Chứng minh: = . . . S V .ABC SA SB SC
Chú ý: Công thức (1) chỉ vận dụng với chóp tam giác.
Hai trong 3 điểm A', B ',C ' có thể trùng với ,
A B,C . Khi đó ta có : S
V .A'B'C SB' SC ' '
Nếu A'  A ta có = . . S V .ABC SB SC S
V .A'B'C SC ' '
Nếu A'  A và B '  B ta có = . S V .ABC SC
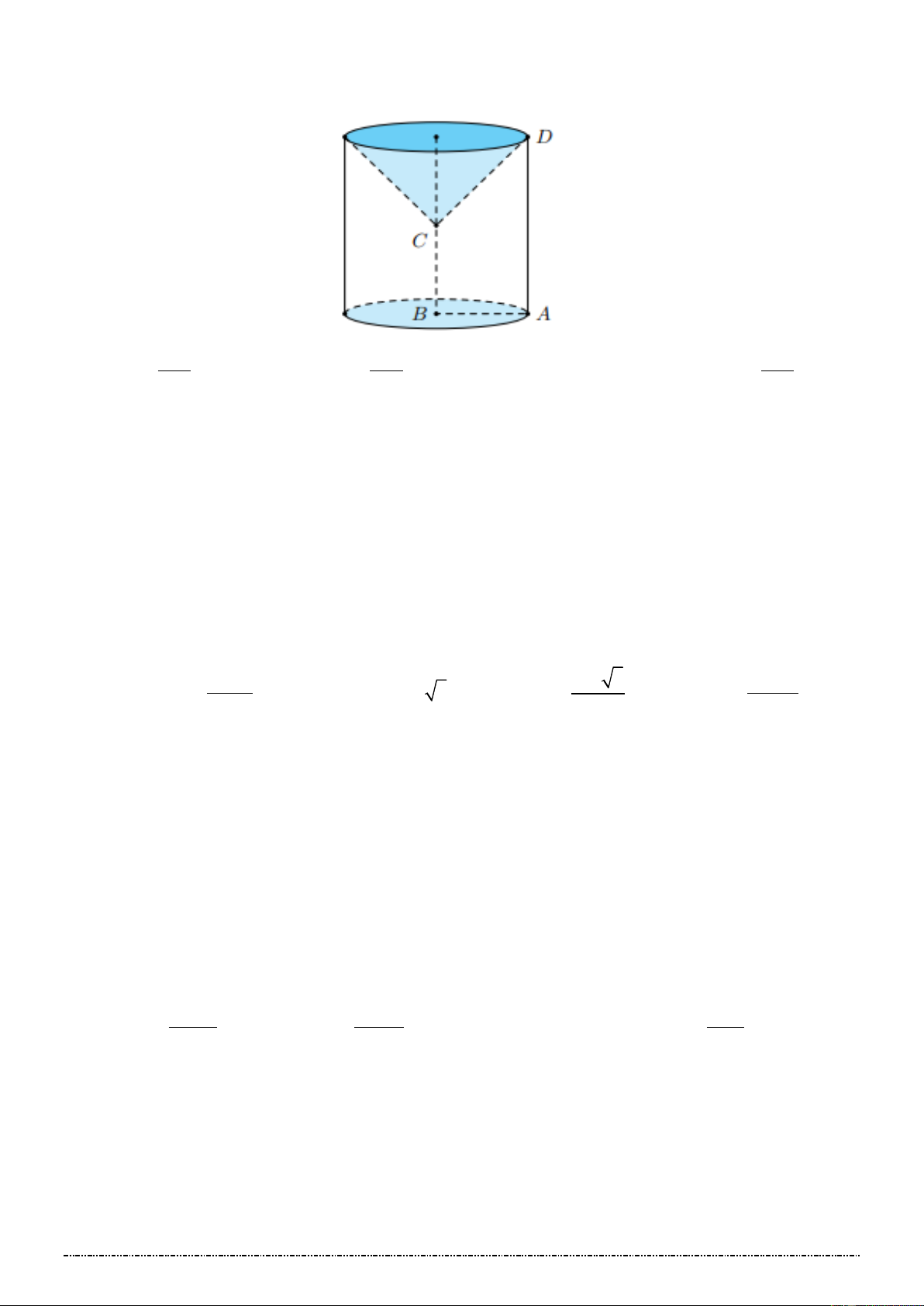
Bài 5 trang 26- SGK: Cho
ABC vuông cân ở A và AB
a . Trên đường thẳng qua C và vuông góc với
mp ABC lấy điểm D sao cho CD a . Mặt phẳng
qua C vuông góc với BD cắt BD tại F
và cắt AD tại E . Tính thể tích khối tứ diện CDFE theo a .
II. Bài tập trắc nghiệm
Câu 1. [Mức độ 1] Thể tích hình lập phương cạnh 3 là A. 6 3 . B. 3 3 . C. 3 . D. 3 .
Câu 2. [Mức độ 1]
Cho khối chóp có đáy là hình vuông cạnh a và chiều cao bằng 2a . Thể tích của
khối chóp đã cho bằng 2 4 A. 3 4a . B. 3 a . C. 3 2a . D. 3 a . 3 3
Câu 3. [Mức độ 1]
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , cạnh bên SA vuông góc với 3 đáy và thể a
tích của khối chóp đó bằng
. Tính cạnh bên SA . 4 a 3 a 3 A. . B. . C. a 3. D. 2a 3. 2 3
Câu 4. [Mức độ 2] Cho khối lăng trụ đứng ABC.A B  C
  có đáy là tam giác đều cạnh a và AA' = 2a
.Thể tích của khối lăng trụ đã cho bằng 3 6a 3 6a 3 6a 3 6a A. . B. . C. . D. . 2 4 6 12
Câu 5. [Mức độ 2] Hình chóp S.ABCD đáy hình thoi, AB = 2a , góc BAD bằng 0 120 . Hình chiếu vuông a
góc của S lên ( ABCD) là I giao điểm của 2 đường chéo, biết SI =
. Khi đó thể tích khối chóp S.ABCD 2 là 3 a 2 3 a 3 3 a 2 3 a 3 A.  B.  C.  D.  9 3 3 9
Câu 6. [Mức độ 2]
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , mặt bên SAB là tam
giác cân tại S và nằm trong mặt phẳng vuông góc với đáy; góc giữa SC và mặt phẳng đáy bằng
45o . Tính thể tích khối chóp S.ABCD bằng: Trang 24
Trên con đường thành công không có dấu chân của kẻ lười biếng 3 a 3 3 a 3 3 a 5 3 a 5 A. . B. . C. . D. . 12 9 24 6
Câu 7. [Mức độ 3]
Cho hình chóp đều S.ABC , góc giữa mặt bên và mặt phẳng đáy ( ABC) bằng 0 60 , 3a
khoảng cách giữa hai đường thẳng SA và BC bằng
. Thể tích của khối chóp S.ABC theo 2 7 a bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 12 18 16 24
Câu 8. [Mức độ 3] Cho hình lăng trụ ABC . D A B  C  D
  có đáy ABCD là hình thoi cạnh a , ABC = 60 .
Chân đường cao hạ từ B trùng với tâm O của đáy ABCD ; góc giữa mặt phẳng (BB C  C  ) với
đáy bằng 60 . Thể tích lăng trụ bằng: 3 3a 3 3 2a 3 3 3a 2 3 3a A. . B. . C. . D. . 8 9 8 4
Câu 9. [Mức độ 3] Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D , AB = AD = a ,
CD = 2a . Hình chiếu của đỉnh S lên mặt ( ABCD) trùng với trung điểm của BD . Biết thể tích 3 a
tứ diện SBCD bằng
. Khoảng cách từ đỉnh A đến mặt phẳng (SBC ) là? 6 a 3 a 2 a 3 a 6 A. . B. . C. . D. . 2 6 6 4
Câu 10. [Mức độ 4] Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc nhau; AB = 6a ,
AC = 7a và AD = 4a . Gọi M , N, P tương ứng là trung điểm các cạnh BC,CD, DB . Tính thể
tích V của khối tứ diện AMNP . 3 28a 3 7a A. 3 V = 7a . B. V = . C. V = . D. 3 V = 14a . 3 2
C. BÀI TẬP TỰ LUYỆN (phần này không làm PPT)
Câu 1.[Mức độ 1] Cho hình lăng trụ đứng có diện tích đáy là 2
3a , độ dài cạnh bên bằng 2a . Thể tích
khối lăng trụ này bằng A. 3 6a . B. 3 3a . C. 3 a . D. 3 2a . Câu 2.
[Mức độ 1] Cho khối chóp .
S ABC có SA vuông góc với đáy, SA = 4 , AB = 6 , BC = 10 và
CA = 8 . Tính thể tích V của khối chóp . S ABC .
A. V = 32 .
B. V = 192 .
C. V = 40 . D. V = 24 . Câu 3.
[Mức độ 2] Cho một hình chóp tam giác đều có cạnh đáy bằng a , góc giữa cạnh bên và mặt phẳng đáy bằng 0
45 . Thể tích khối chóp đó là 3 a 3 3 a 3 a 3 a 3 A. . B. . C. . D. . 12 12 36 36
Câu 4. [Mức độ 2] Cho hình chóp S.ABCD đáy hình chữ nhật, SA vuông góc đáy, AB = a, AD = 2a .
Góc giữa SB và đáy bằng 0
45 . Thể tích khối chóp là 3 a 2 3 2a 3 a 3 a 2 A.  B.  C.  D.  3 3 3 6 Trang 25
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 5.[Mức độ 2] Cho hình chóp S.ABC có AC = a , BC = 2a , 0
ACB = 120 , cạnh bên SA vuông
góc với đáy. Đường thẳng SC tạo với mặt phẳng (SAB) góc 0
30 . Tính thể tích của khối chóp S.ABC . 3 a 105 3 a 105 3 a 105 3 a 105 A. . B. . C. . D. . 28 21 42 7
Câu 6. [Mức độ 2] Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B . Biết S  AB là tam giác
đều và nằm trong mặt phẳng vuông góc với mặt phẳng ( ABC) . Tính thể tích khối chóp S.ABC
biết AB = a , AC = a 3 . 3 a 6 3 a 6 3 a 2 3 a A.  B.  C.  D.  12 4 6 4
Câu 7. [Mức độ2] Lăng trụ đứng ABC. ’ A ’ B ’
C có đáy ABC là tam giác vuông tại ,
A BC = 2a, AB = a . Mặt bên ( B ’
B C’C ) là hình vuông. Khi đó thể tích lăng trụ là 3 a 3 A. . B. 3 3 a 2 . C. 2a 3 . D. 3 a 3 . 3
Câu 8.[Mức độ 3] Cho hình lăng trụ ABC.A' B 'C ' có đáy ABC là tam giác đều cạnh bằng a . Hình chiếu
vuông góc của A' trên ( ABC ) là trung điểm của AB . Mặt phẳng ( AA'C 'C ) tạo với đáy một góc
bằng 45 . Tính thể tích V của khối lăng trụ ABC.A' B 'C ' . 3 3a 3 3a 3 3a 3 3a A. V = . B. V = . C. V = . D. V = . 8 4 2 16
Câu 9. [Mức độ 3] Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a . Tam
giác SAD cân tại S và mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích khối chóp 4 S.ABCD bằng 3
a . Tính khoảng cách h từ B đến mặt phẳng (SCD) . 3 4 3 2 5 6 A. h = a . B. h = a . C. h = a . D. h = a . 3 2 5 3
Câu 10. [Mức độ 4] Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi V là thể tích của khối chóp
S.ABCD và M , N , P lần lượt là trung điểm của các đoạn thẳng SC , SD , AD . Thể tích của
khối tứ diện AMNP bằng 1 1 1 1 A. V . B. V . C. V . D. V . 8 4 16 32
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 26
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HỌC 12– CHƯƠNG 2
§1. KHÁI NIỆM VỀ MẶT TRÒN XOAY
I. SỰ TẠO THÀNH MẶT TRÒN XOAY
Quan sát các hình ảnh sau
Nếu dùng một mặt phẳng song song với đáy cắt những đồ vật này thì thiết diện tạo được là hình
gì?...........................................................................................................................................
I. SỰ TẠO THÀNH MẶT TRÒN XOAY
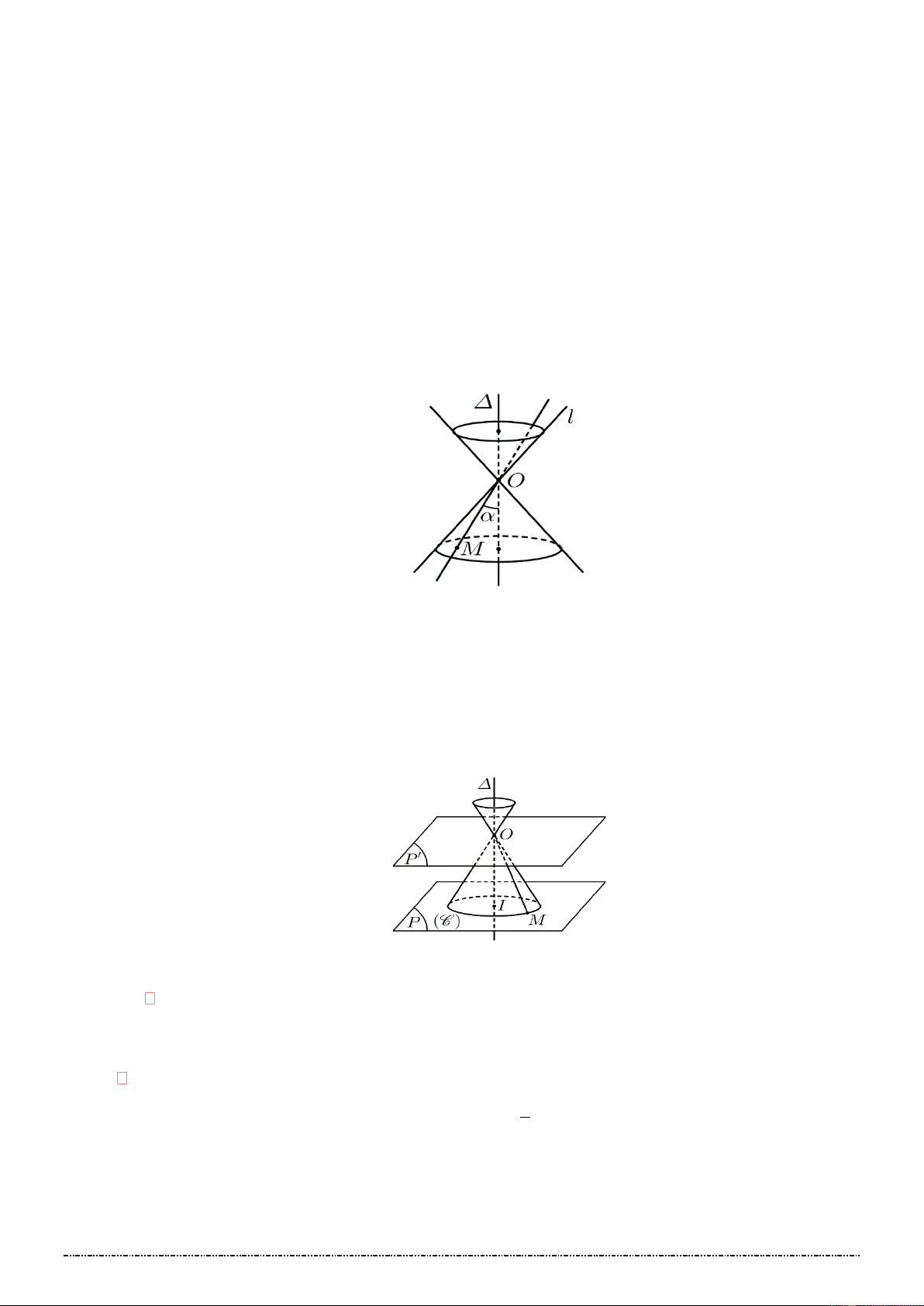
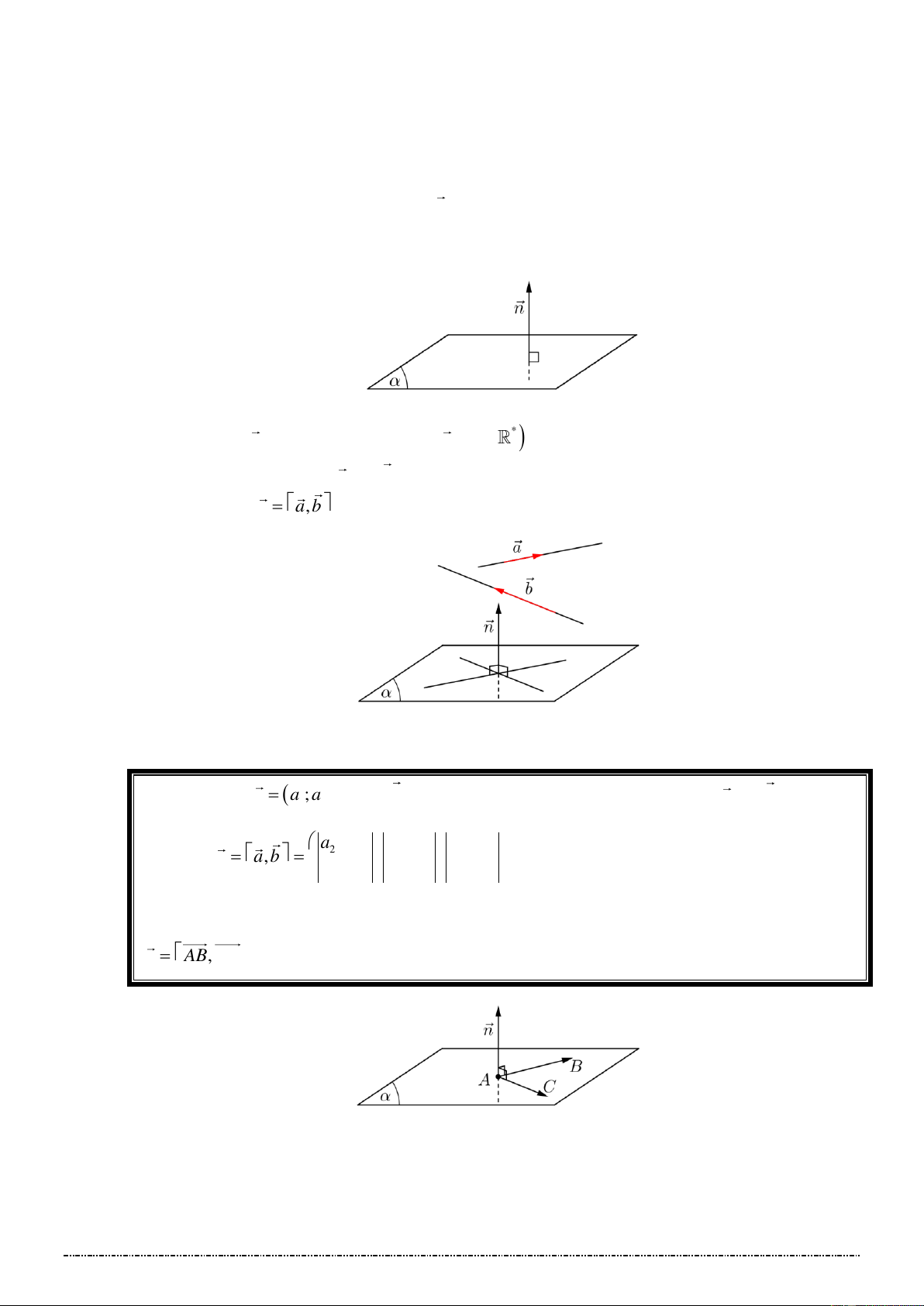
Trong không gian, cho mặt phẳng (P) chứa đường thẳng  và đường (C). Khi quay (P) quay
quanh  một góc 3600 thì:
 Mỗi điểm M (C) vạch ra một đường tròn tâm O   và nằm trên mặt phẳng vuông góc với . 
 Đường (C) sẽ tạo nên một hình được gọi là mặt tròn xoay.
+ Đường (C): Đường sinh của mặt tròn xoay.
+ Đường thẳng  : Trục của mặt tròn xoay.
ĐỒ VẬT NÀO SAU ĐÂY CÓ BỀ MẶT NGOÀI LÀ MẶT TRÒN XOAY? Trang 27
Trên con đường thành công không có dấu chân của kẻ lười biếng II. MẶT NÓN TRÒN XOAY 1. ĐỊNH NGHĨA
Trong mp (P) , cho hai đường thẳng (C) và  cắt nhau tại điểm O và tạo thành góc nhọn  ( 0 0 0    90 ) .
Quay (P) xung quanh  một góc 0 360 .
Đường thẳng (C)sinh ra một hình gọi là mặt nón tròn xoay. + Đỉnh O .
+ Đường thẳng  : Trục
+ Đường thẳng (C) : Đường sinh
+ Góc ở đỉnh O : 2
2.HÌNH NÓN TRÒN XOAY VÀ KHỐI NÓN TRÒN XOAY
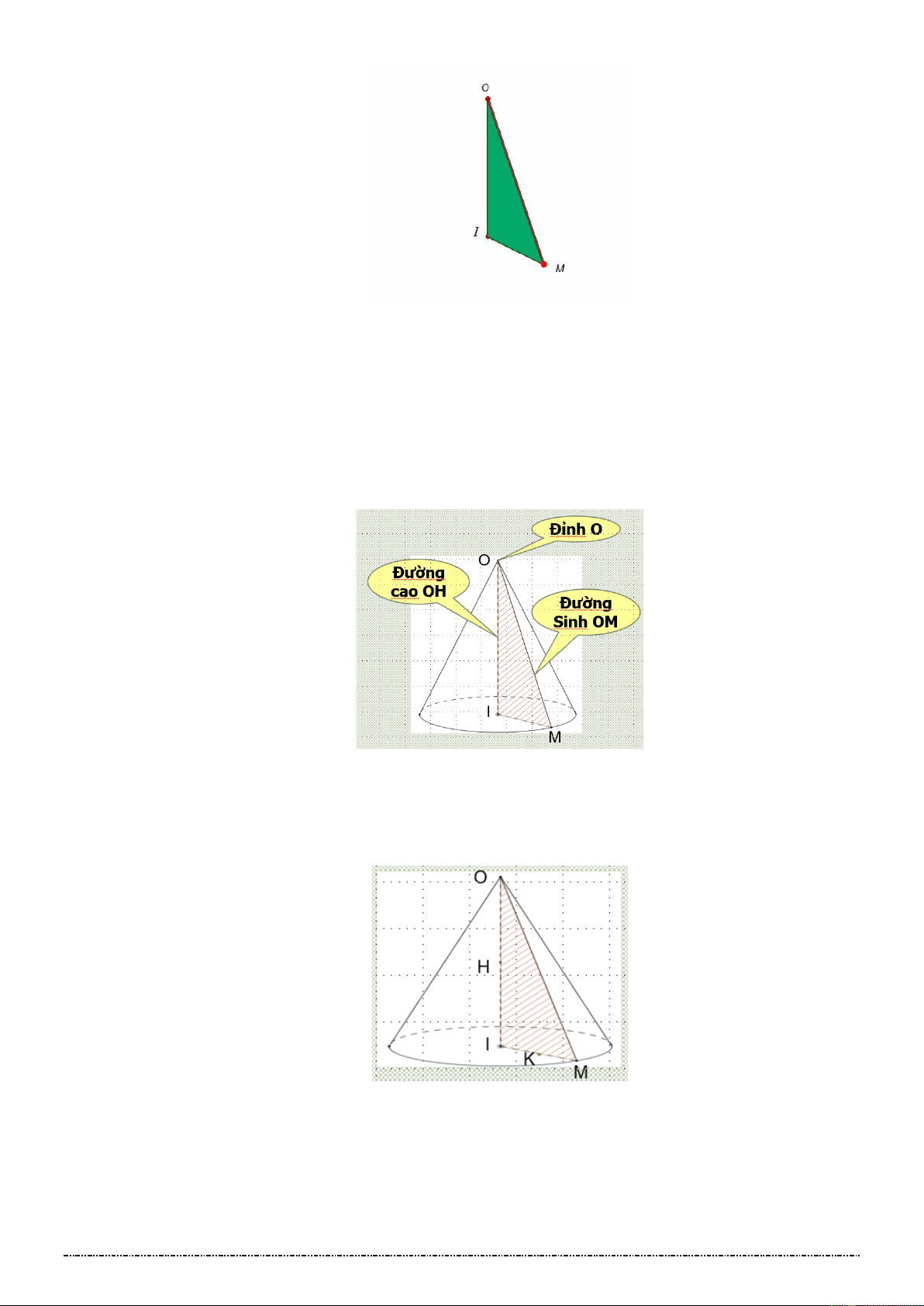
a) Hình nón tròn xoay: Hỏi: Khi quay O
 IM quanh OI , cạnh IM và OM tạo thành hình gì?
 IM tạo thành hình tròn tâm I , bán kính IM – gọi là mặt đáy.
OM tạo thành một phần nón tròn xoay – gọi là mặt xung quanh.
Vậy hình nón hợp của hai phần: Mặt đáy và mặt xung quanh Trang 28
Trên con đường thành công không có dấu chân của kẻ lười biếng Cho O
 IM vuông tại I. Khi quay OMI xung quanh cạnh góc vuông OI thì đường gấp khúc
OMI tạo thành một hình gọi là hình nón tròn xoay. * Gồm hai phần:
– Mặt đáy: Là hình tròn (I, IM)
– Phần mặt xung quanh: Là phần mặt tròn xoay sinh bởi OM quay xung quanh OI .
* Đặc điểm: – Đỉnh: O – Đường cao: OI
– Đường sinh: OM
b) Khối nón tròn xoay:
Phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình nón đó được gọi là khối nón tròn xoay.
– Điểm ngoài: điểm không thuộc khối nón.
– Điểm trong: điểm thuộc khối nón nhưng không thuộc hình nón.
3. DIỆN TÍCH XUNG QUANH CỦA HÌNH NÓN TRÒN XOAY
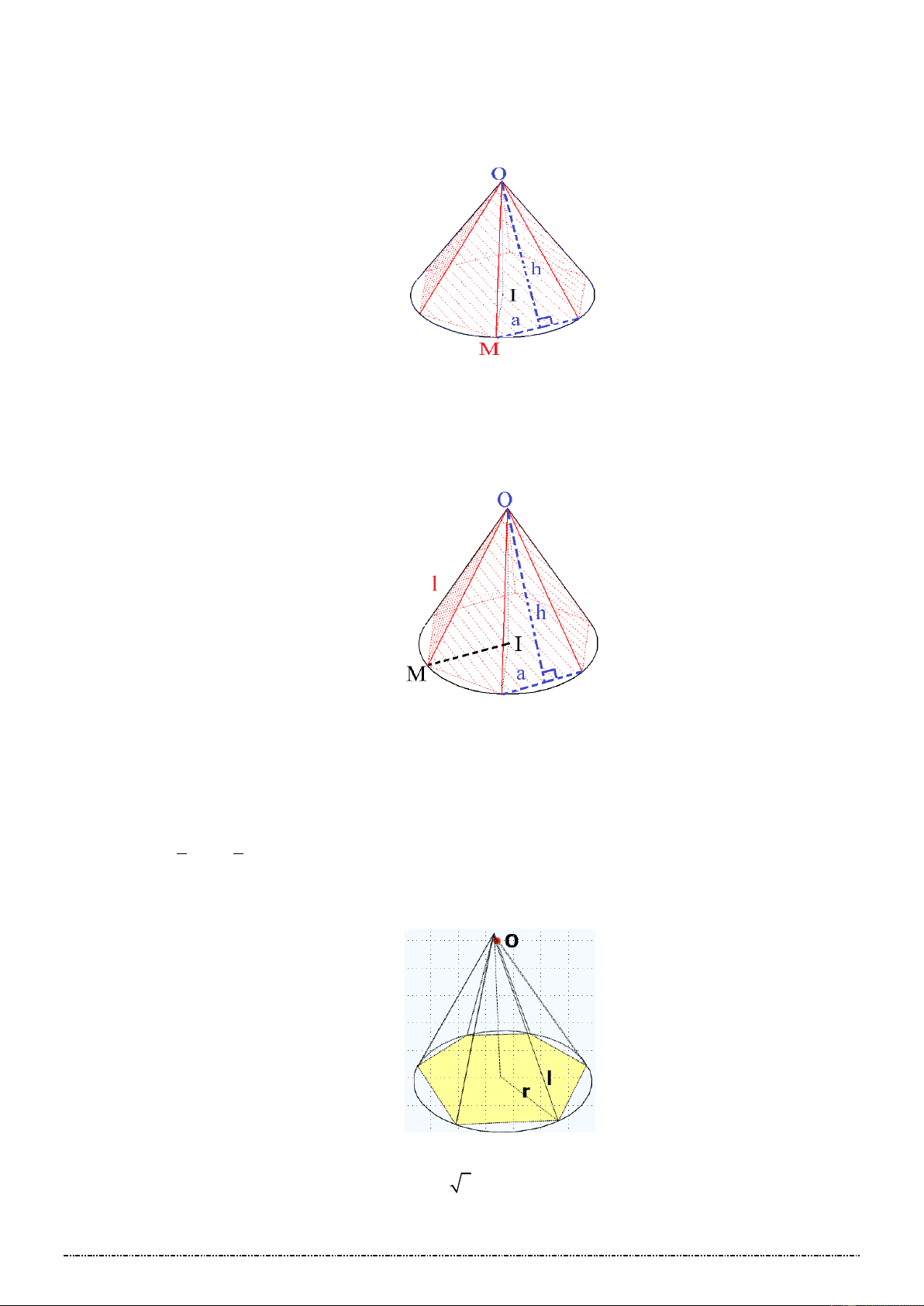
a) Hình chóp nội tiếp hình nón tròn xoay
Một hình chóp được gọi là nội tiếp một hình nón nếu
 đáy của hình chóp là đa giác nội tiếp đường tròn đáy của hình nón Trang 29
Trên con đường thành công không có dấu chân của kẻ lười biếng
 và đỉnh của hình chóp là đỉnh của hình nón
Khi đó ta nói hình nón ngoại tiếp hình chóp
* Định nghĩa: Diện tích xung quanh của hình nón tròn xoay là giới hạn của diện tích xung quanh
của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.
b) Công thức tính diện tích xung quanh của hình nón tròn xoay: S =  rl xq
trong đó: r : bán kính đáy l : độ dài đường sinh
Ghi nhớ: Tổng của diện tích xung quanh và diện tích đáy gọi là diện tích toàn phần 2 S = S + S
=  rl + r tp xq đáy
4. THỂ TÍCH KHỐI NÓN TRÒN XOAY a) Định nghĩa:
Thể tích khối nón tròn xoay là giới hạn của thể tích khối chóp đều nội tiếp khối nón đó khi số
cạnh đáy tăng lên vô hạn
b) Công thức tính thể tích khối nón tròn xoay: 1 1 2 V = .
B h =  r .h 3 3
Trong đó: r: bán kính h: chiều cao
Ví dụ 1: Cho tam giác ABC vuông tại ,
A AB = a 3 và BC = 2 .
a Khi quay tam giác ABC quanh trục
AB ta được một hình nón tròn xoay. Trang 30
Trên con đường thành công không có dấu chân của kẻ lười biếng
a) Tính thể tích khối nón.
b) Tính diện tích xung quanh của hình nón.
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
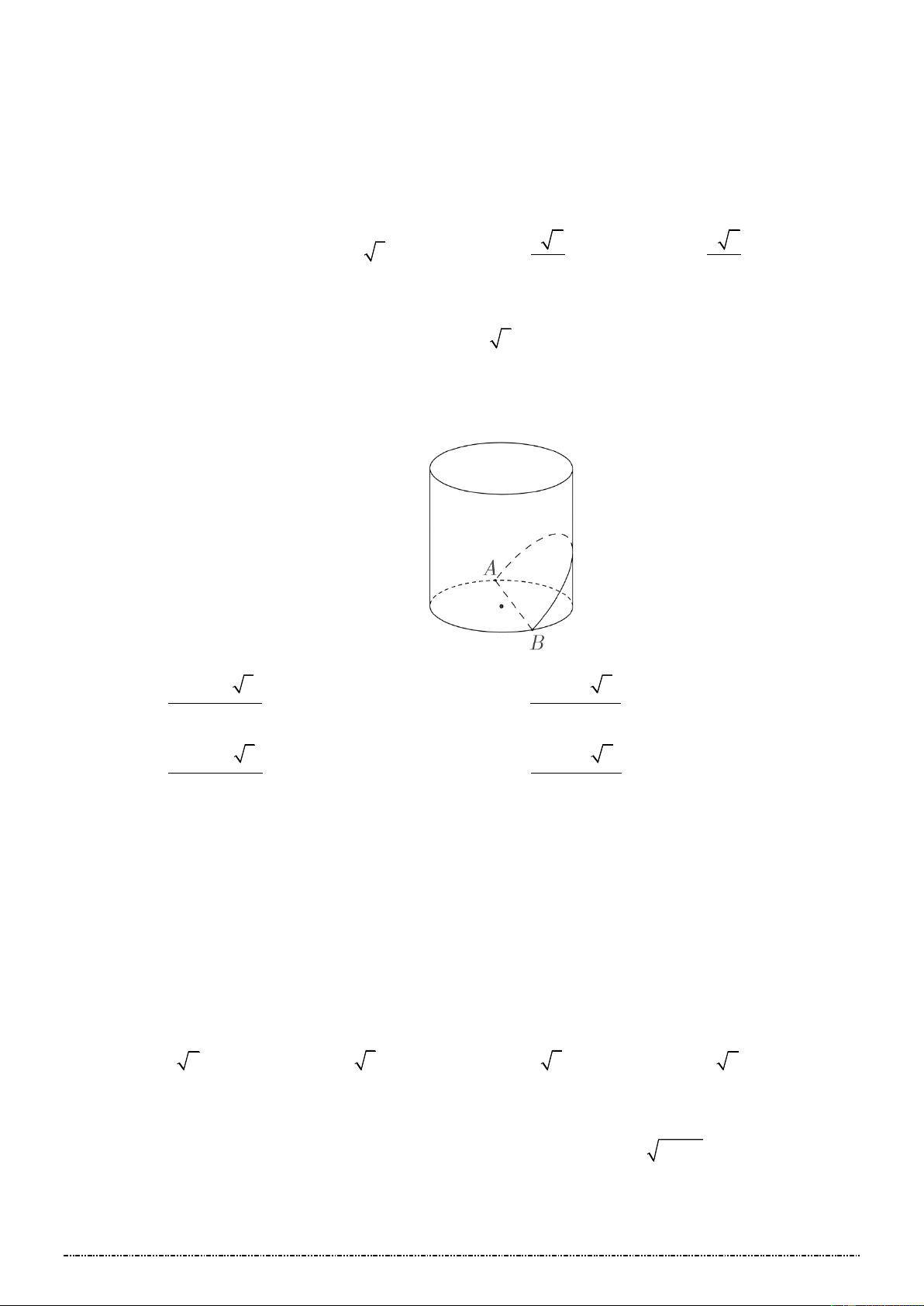
Ví dụ 2: Cắt hình nón đỉnh I bới một mặt phẳng đi qua trục của hình nón ta được một tam giác vuông cân
có cạnh huyền bằng a 2 , BC là dây cung của đường tròn đáy hình nón sao cho mặt phẳng
(IBC) tạo với mặt phẳng chứa đáy hình nón một góc 60. Tính theo a diện tích S của tam giác IBC .
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho đường thẳng l cắt và không vuông góc với  quay quanh  thì ta được
A. Hình nón tròn xoay. B. Mặt nón tròn xoay. C. Khối nón tròn xoay. D. Mặt trụ tròn xoay. Câu 2:
Cho tam giác ABC vuông tại A . Khi quay tam giác ABC (kể cả các điểm trong) quanh cạnh AC ta được A. Khối nón. B. Mặt nón. C. Khối trụ. D. Khối cầu
Câu 3: Mặt phẳng chứa trục của một hình nón cắt hình nón theo thiết diện là:
A. Một hình chữ nhật. B. Một tam giác cân. C. Một đường elip.
D. Một đường tròn.
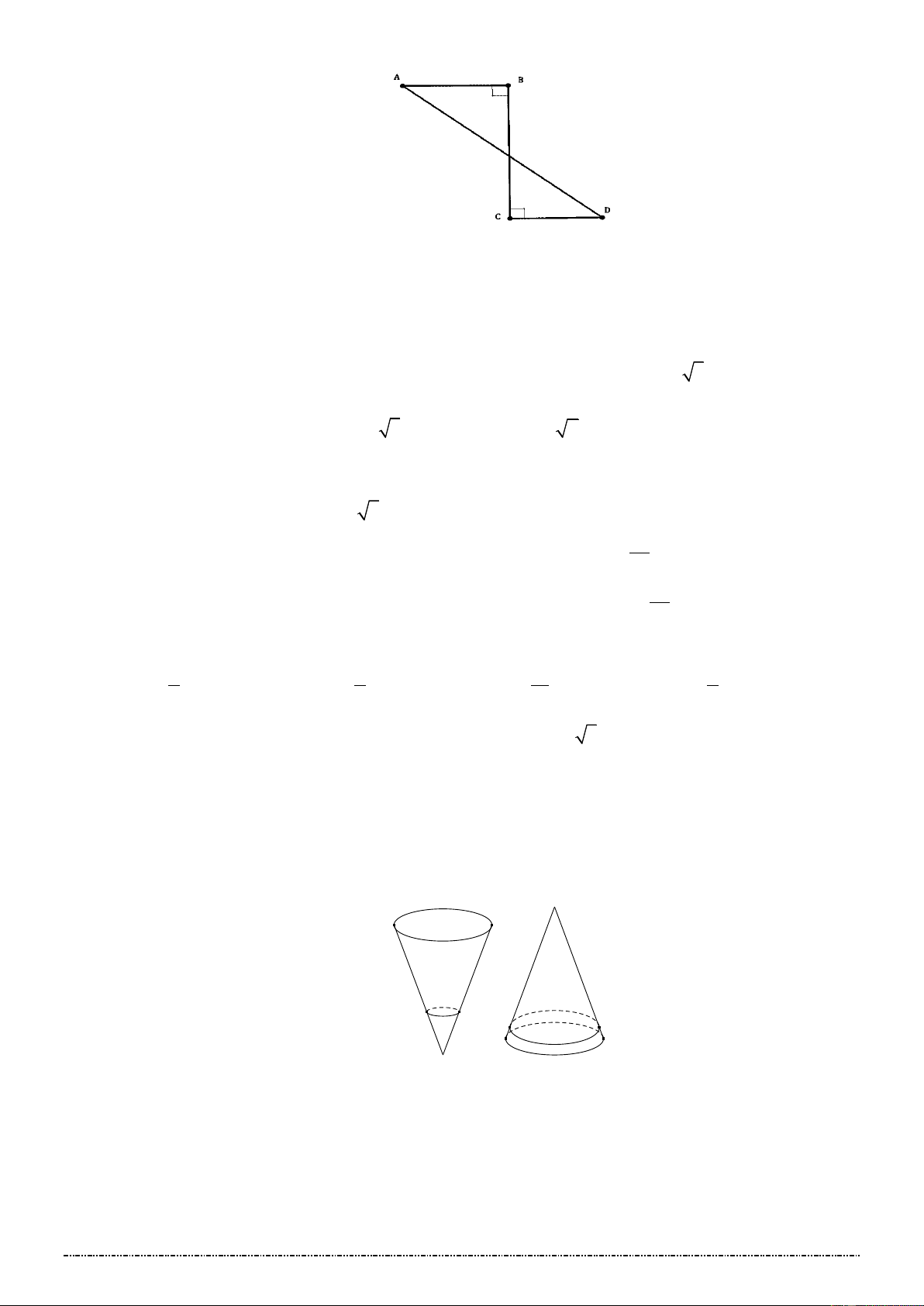
Câu 4: Hình ABCD (như hình bên) khi quay quanh BC thì tạo ra: Trang 31
Trên con đường thành công không có dấu chân của kẻ lười biếng A. Một hình trụ. B. Một hình nón.
C. Một hình nón cụt. D. Hai hình nón. Câu 5:
Gọi l , h , R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Đẳng thức luôn đúng là
A. l = h .
B. R = h . C. 2 2 2
l = h + R . D. 2 2 2
R = h + l .
Câu 6: Trong không gian cho tam giác ABC vuông tại A , AB = a và AC = a 3 . Tính độ dài đường
sinh l của hình nón có được khi quay tam giác ABC xung quanh trục AB .
A. l = a .
B. l = 3a .
C. l = 2a .
D. l = 2a . Câu 7:
Cho hình nón có thiết diện qua đỉnh S tạo với đáy góc 0
60 là tam giác đều cạnh bằng 4cm . Thể
tích của khối nón đó là: A. 3 9 cm . B. 3 4 3 cm . C. 3 3 cm D. 3 7 cm 3 C. 3 πcm . 3 D. 7 πcm . Câu 8 a
: Cho khối nón tròn xoay có đường cao h = a và bán kính đáy 5 r =
. Một mặt phẳng (P) đi 4
qua đỉnh của khối nón và có khoảng cách đến tâm a
O của đáy bằng 3 . Diện tích thiết diện tạo 5
bởi (P) và hình nón là: 5 5 15 7 A. 2 a . B. 2 a . C. 2 a . D. 2 a . 2 4 4 2
Câu 9: Một khối nón có bán kính đáy bằng 2 cm , chiều cao bằng 3 cm . Một mặt phẳng đi qua đỉnh và tạo với đáy một góc 0
60 chia khối nón làm 2 phần. Tính thể tích V phần nhỏ hơn (Tính gần
đúng đến hàng phần trăm). A. 3 V 1, 42 cm . B. 3
V  2, 36 cm . C. 3 V 1,53cm . D. 3 V  2, 47 cm .
Câu 10: Một cái phễu có dạng hình nón. Người ta đổ một lượng nước vào phễu sao cho chiều cao của
lượng nước trong phễu bằng một phần ba chiều cao của phễu. Hỏi nếu bịt miệng phễu rồi lật
ngược phễu lên thì chiều cao của nước bằng bao nhiêu? Biết chiều cao của phễu là 15 cm. A. 0, 5 cm. B. 0, 216 cm. C. 0, 3 cm. D. 0,188 cm. Trang 32
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HỌC 12– CHƯƠNG 2
§1. KHÁI NIỆM VỀ MẶT TRÒN XOAY
A. NHẮC LẠI LÝ THUYẾT
1. Định nghĩa mặt nón
• Trong mặt phẳng (P) cho hai đường thẳng 𝑙 và 𝛥 cắt nhau tại điểm 𝑂 và tạo thành góc  với 0 0
0    90 . Khi quay mặt phẳng (P) quanh 𝛥 thì đường thẳng 𝑙 sinh ra một sinh ra một mặt
tròn xoay được gọi là mặt nón tròn xoay đỉnh 𝑂. Người ta gọi tắt mặt nón tròn xoay là mặt nón.
•  gọi là trục của mặt nón.
• l gọi là đường sinh của mặt nón.
• O gọi là đỉnh của mặt nón.
Góc 2 gọi là góc ở đỉnh của mặt nón
2. Hình nón và khối nón
Cho mặt nón N với trục , đỉnh O và góc ở đỉnh 2. Gọi (P) là mặt phẳng vuông góc với 
tại điểm I khác O (như hình bên). Mặt phẳng (P) cắt mặt nón theo đường tròn (C) có tâm I.
Lại gọi (P ') là mặt phẳng vuông góc với  tại . O Khi đó
Phần mặt nón N giới hạn bởi hai mặt phẳng (P) và (P ') cùng với hình tròn xác định bởi (C)
được gọi là hình nón.
Hình nón cùng với phần bên trong của nó gọi là khối nón
3. Diện tích hình nón và thể tích khối nón
Diện tích xung quanh của hình nón bằng một nửa tích số của độ dài đường tròn đáy và độ dài đường sinh: S =  rl xq
Thể tích khối nón bằng một phần ba tích số diện tích hình tròn đáy và chiều cao: 1 2 V =  r h 3 Trang 33
Trên con đường thành công không có dấu chân của kẻ lười biếng
Ví dụ 1: Một khối nón có thiết diện qua trục là tam giác vuông cân cạnh có cạnh huyền bằng 2a . Tính
diện tích xung quanh, diện tích toàn phần, diện tích thiết diện và thể tích của khối nón đó
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
Bài 3 ( SGK/39). Cho hình nón tròn xoay có đường cao h = 20(cm) , bán kính đáy r = 25(cm) .
a. Tính diện tích xung quanh của hình nón đã cho .
b. Tính thể tích của khối nón được tạo thành bởi hình nón đó.
c. Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa
thiết diện là 12 (cm) . Tính diện tích thiết
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 34
Trên con đường thành công không có dấu chân của kẻ lười biếng
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
Bài 6 ( SGK/ 39). Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam
giác đều cạnh 2a . Tính diện tích xung quanh và thể tích của hình nón đó.
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
Ví dụ 2: Cho hình nón đỉnh I , đường cao SO và có độ dài đường sinh bằng 3cm , góc ở đỉnh bằng 0 60 . 3
Gọi K là điểm thuộc đoạn SO thỏa mãn IO =
IK , cắt hình nón bằng mặt phẳng (P) qua K 2
và vuông góc với IO , khi đó thiết diện tạo thành có diện tích là S . Tính S .
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 35
Trên con đường thành công không có dấu chân của kẻ lười biếng
BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho khối nón có chiều cao h = 5 và bán kính đáy r = 3. Thể tích của khối nón đã cho bằng A. V = 45. B. V = 5 . C. V = 15 . D. V = 20 .
Câu 2: Cho khối nón có thể tích V = 6 và chiều cao h = 4 . Tìm bán kính 𝑟 của khối nón đã cho bằng 2 6 6 3 2 A. r = . B. r = . C. r = . D. r = . 3 2 3 2 Câu 3:
Cho khối nón có thể tích V = 6 và bán kính đáy r = 4 . Tìm chiều cao h của khối nón đã cho bằng A. 9 h = . B. 8 h = . C. 1 h = . D. 8. 8 9 8 Câu 4:
Một hình nón có chiều cao bằng a 3 và bán kính đáy bằng a . Diện tích xung quanh của hình nón bằng A. 2 2 a . B. 2 3 a . C. 2  a . D. 2 3 a . Câu 5:
Cạnh bên của một hình nón bằng 2 .
a Thiết diện qua trục của nó là một tam giác cân có góc ở đỉnh bằng 0
120 . Diện tích toàn phần của hình nón bằng A. 2 6 a . B. 2  (3+ 3). C. 2 2 a (3+ 3) . D. 2  a (3+ 2 3) . Câu 6:
Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác vuông
cân có cạnh góc vuông bằng a . Tính thể tích V của khối nón được tạo nên bởi hình nón đã cho. 3 2 a 3 2 a 3 2 a 3 2 a A. V = . B. V = . C. V = . D. V = . 10 12 4 6
Câu 7. Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác vuông
cân có cạnh góc vuông bằng a . Tính thể tích V của khối nón được tạo nên bởi hình nón đã cho. 3 2 a 3 2 a 3 2 a 3 2 a A. V = . B. V = . C. V = . D. V = . 10 12 4 6
Câu 8. Cho hình nón có thiết diện qua đỉnh S tạo với đáy góc 0
60 là tam giác đều cạnh bằng 4cm . Thể
tích của khối nón đó là: A. 3 9 cm . B. 3 4 3 cm . C. 3 3 cm . D. 3 7 cm .
Câu 9: Một hình nón có chiều cao 2a , bán kính đáy a 2 . Một phẳng phẳng đi qua đỉnh và tạo với mặt
đáy góc 60 . Tính diện tích thiết diện. 2 5 2a 2 4 3a 2 5 3a 2 4 2a A. 3 . B. 3 . C. 3 . D. 3 .
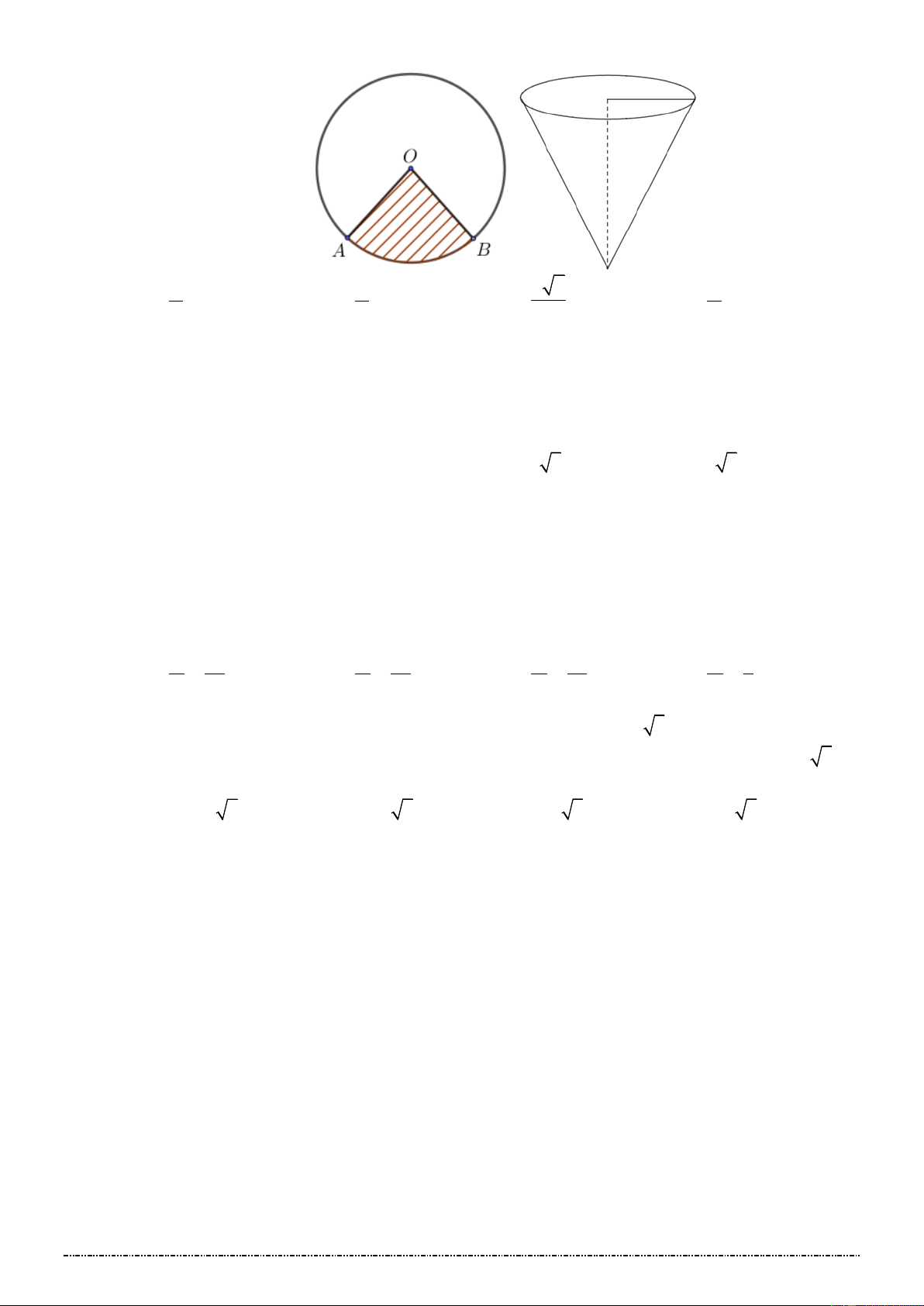
Câu 10: Bạn Hoàn có một tấm bìa hình tròn như hình vẽ, Hoàn muốn biến hình tròn đó thành một hình
cái phễu hình nón. Khi đó Hoàn phải cắt bỏ hình quạt tròn AOB rồi dán hai bán kính OA và OB
lại với nhau (diện tích chỗ dán nhỏ không đáng kể). Gọi x là góc ở tâm hình quạt tròn dùng làm
phễu. Tìm x để thể tích phễu lớn nhất? Trang 36
Trên con đường thành công không có dấu chân của kẻ lười biếng   2 6  A. . B. . C.  . D. . 4 3 3 2
Câu 11: Tại trung tâm một thành phố người ta tạo điểm nhấn bằng cột trang trí hình nón có kích thước
như sau: chiều dài đường sinh l = 10 m , bán kính đáy R = 5m . Biết rằng tam giác SAB là thiết
diện qua trục của hình nón và C là trung điểm SB . Trang trí một hệ thống đèn điện tử chạy từ
A đến C trên mặt nón. Xác định giá trị ngắn nhất của chiều dài dây đèn điện tử. A. 10 m . B. 15m . C. 5 5 m . D. 5 3 m .
Câu 12: Cho hình nón tròn xoay có đỉnh S và đáy là đường tròn C( ;
O R) có thể tích V, với
R = a (a  0) , SO = 3a,O ' SO thỏa mãn OO = x (0  x  3a) . Mặt phẳng ( ) vuông góc
với SO tại O ' cắt hình nón tròn xoay theo giao tuyến là đường tròn (C ') . Khi khối nón đỉnh
O , đáy là đường tròn (C ') đạt giá trị lớn nhất là V , tính tỉ số giữa thể tích khối nón đỉnh O và 1
khối nón đỉnh S . V 23 V 4 V 4 V 1 A. 1 = . B. 1 = . C. 1 = . D. 1 = V 27 V 27 V 23 V 3
Câu 13: Cho hình nón có đỉnh S , đáy là đường tròn tâm O sao cho SO = a 5 , một mặt phẳng ( ) cắt
mặt nón theo hai đường sinh S ,
A SB . Biết khoảng cách từ O đến mặt phẳng ( ) bằng 2 5 và
diện tích tam giác SAB bằng 360 . Thể tích khối nón bằng: A. 1325 5 . B. 265 5 . C.1325 5 . D. 265 5 .
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 37
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HOC 12 – CHƯƠNG 2 §1. MẶT TRÒN XOAY
III. MẶT TRỤ TRÒN XOAY.
1. Định nghĩa
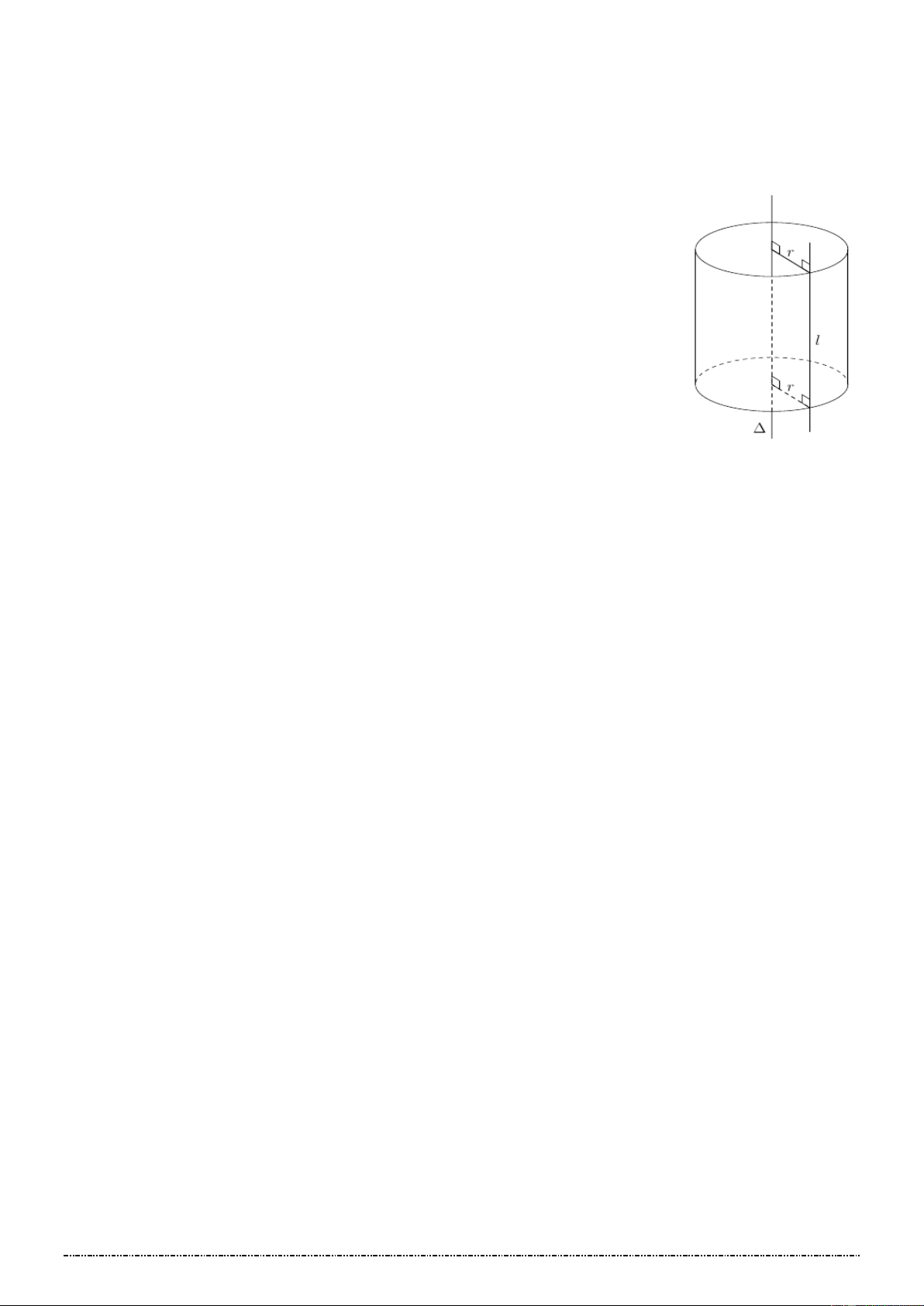
Trong mặt phẳng (𝑃) cho hai đường thẳng ∆ và 𝑙 song song với nhau,
cách nhau một khoảng bằng 𝑟. Khi quay mặt phẳng (𝑃) xung quanh
∆ thì đường thẳng 𝑙 sinh ra một mặt tròn xoay được gọi là mặt trụ
tròn xoay (gọi tắt là mặt trụ)
 ∆ gọi là trục của mặt trụ.
 𝑙 là đường sinh của mặt trụ.
 𝑟 là bán kính của mặt trụ.
2. Hình trụ tròn xoay, khối trụ tròn xoay.
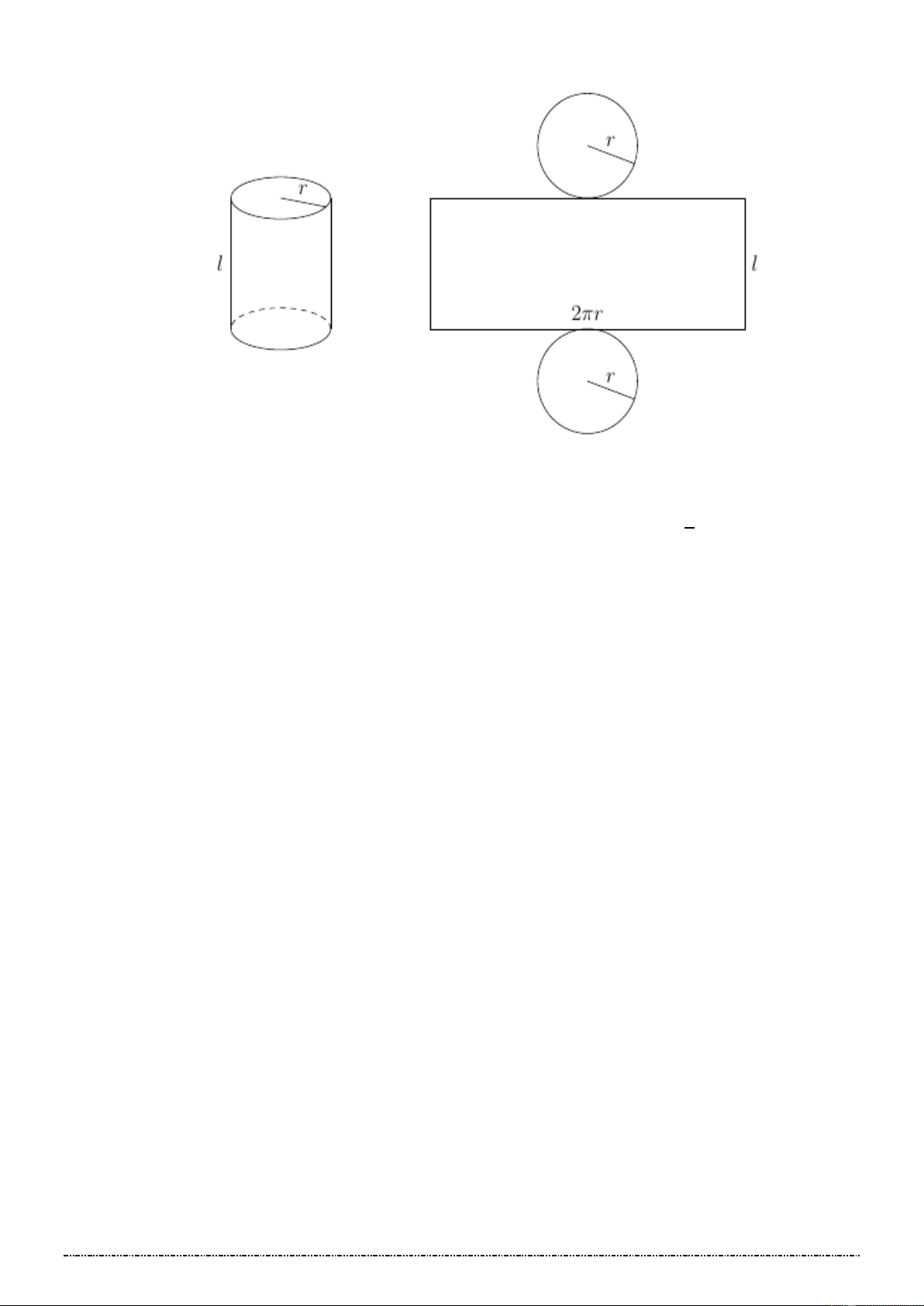
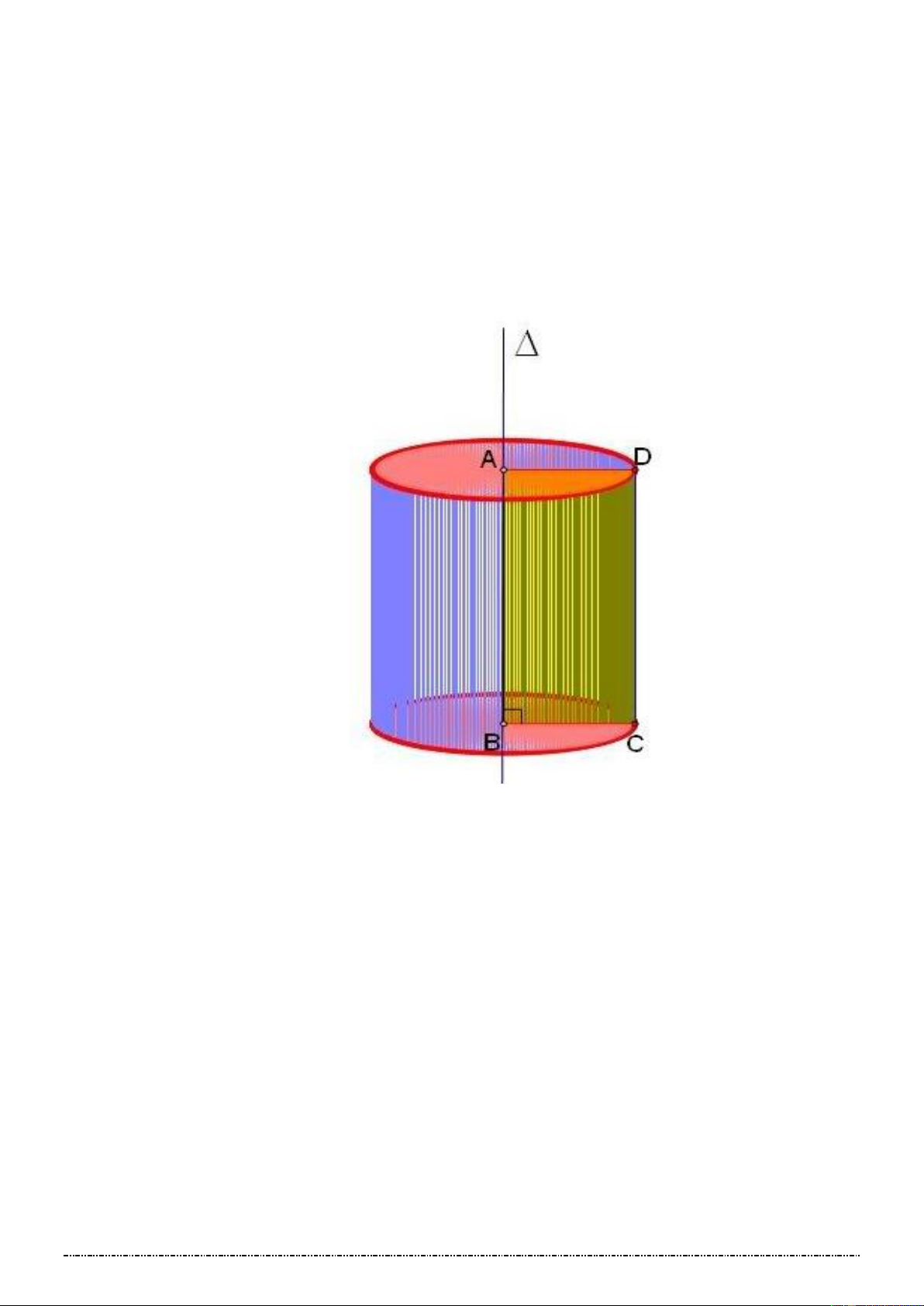
a) Xét hình chữ nhật 𝐴𝐵𝐶𝐷. Khi quay hình đó xung quanh đường thẳng chứa một cạnh (chẳng
hạn cạnh 𝐴𝐵) thì đường gấp khúc 𝐴𝐷𝐶𝐵 tạo thành một hình được gọi là hình trụ tròn xoay
(gọi tắt là hình trụ).
 Hai đáy là hai đường tròn (𝐴; 𝐴𝐷) và (𝐵; 𝐵𝐶).
 Đường sinh là đoạn 𝐶𝐷.
 Mặt xung quanh là mặt do đoạn 𝐶𝐷 tạo thành khi quay.
 Chiều cao ℎ = 𝐴𝐵.
b) Khối trụ tròn xoay là phần không gian được giới hạn bởi một hình trụ và kể cả hình trụ đó.
3. Công thức tính diện tích hình trụ, thể tích khối trụ.
a) Diện tích xung quanh của hình trụ 𝑆𝑥𝑞 = 2𝜋𝑟𝑙
b) Diện tích toàn phần của hình trụ
𝑆𝑡𝑝 = 𝑆𝑥𝑞 + 2. 𝑆đá𝑦 = 2𝜋𝑟𝑙 + 2𝜋𝑟2.
c) Thể tích của khối trụ : 𝑉 = 𝑆đá𝑦. 𝑐ℎ𝑖ề𝑢 𝑐𝑎𝑜 = 𝜋𝑟2ℎ. Trang 38
Trên con đường thành công không có dấu chân của kẻ lười biếng
4. Các ví dụ: *VD1:
Cho hình trụ có hình tròn đáy có bán kính 𝑟 = 𝑎, có chiều cao ℎ = 𝑎√3. Tính diện tích xung
quanh, diện tích toàn phần của hình trụ và thể tích của khối trụ theo 𝑎.
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… *VD2:
Cho hình trụ có hình tròn đáy có bán kính 𝑟 = 𝑎, có thiết diện qua trục là một hình vuông. Tính diện
tích xung quanh, diện tích toàn phần của hình trụ và thể tích của khối trụ theo 𝑎.
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… *VD3:
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh 𝑎 có hai đỉnh liên tiếp 𝐴, 𝐵 nằm trên đường
tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt
phẳng (𝐴𝐵𝐶𝐷) tạo với đáy hình trụ một góc 45°. Tính diện tích xung quanh của hình trụ theo 𝑎.
…………………………………………………………………………………………………… Trang 39
Trên con đường thành công không có dấu chân của kẻ lười biếng
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… *VD4:
Cho một bể bơi mini có dạng hình trụ như hình bên. Giả sử bán kính của bể bơi là 1m, chiều cao
của bể bơi là 0,5m. Hỏi muốn bơm nước đầy bể bơi thì cần bao nhiêu 𝑚3nước?
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………
B. LUYỆN TẬP
Bài tập trắc nghiệm
Câu 1. [Mức độ 1] Cho hình trụ (𝑇) có chiều cao ℎ, độ dài đường sinh 𝑙, bán kính đáy 𝑟. Kí hiệu 𝑆𝑥𝑞 là
diện tích xung quanh của (𝑇). Khẳng định nào sau đây là đúng? A. S =  rh . B. S = 2 rl . C. 2 S = 2 r h . D. S =  rl . xq xq xq xq
Câu 2. [Mức độ 1] Cho hình trụ (T) có chiều cao h, độ dài đường sinh l, bán kính đáy r. Kí hiệu Stp là
diện tích toàn phần của (T). Khẳng định nào sau đây là đúng?
A. S =  rh .
B. S = 2 rl + 2 r . C. 2
S =  rl +  r . D. 2
S = 2 rl + 2 r tp tp tp tp
Câu 3.[Mức độ 1] Cho hình trụ (𝑇) có chiều cao ℎ, độ dài đường sinh 𝑙, bán kính đáy 𝑟. Kí hiệu 𝑉 là thể
tích của khối trụ (𝑇). Khẳng định nào sau đây là đúng? 1
A. V =  rh . B. 2 V =  r h . C. 2
V =  rl . D. 2 V = 2 r h . 3 Trang 40
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 4.[Mức độ 2] Một hình trụ bán kính đáy 𝑟 = 5 cm, chiều cao ℎ = 7 cm. Diện tích xung quanh của hình trụ này là A.  ( 2 35 cm ) . B.  ( 2 70 cm ) . 70 35 C. ( 2 cm ) . D. ( 2 cm ) . 3 3
Câu 5.[Mức độ 2] Một hình trụ bán kính đáy 𝑟 = 𝑎 , độ dài đường sinh 𝑙 = 2𝑎. Diện tích toàn phần của hình trụ này là A. 2 6 a . B. 2 2 a . C. 2 4 a . D. 2 5 a .
Câu 6.[Mức độ 2] Quay hình vuông 𝐴𝐵𝐶𝐷 cạnh 𝑎 xung quanh một cạnh. Thể tích của khối trụ được tạo thành là 1 A. 3  a . B. 3 2 a . C. 3  a . D. 3 3 a . 3
Câu 7.[Mức độ 2] Khối trụ có chiều cao ℎ = 3 cm và bán kính đáy 𝑟 = 2 cm thì có thể tích bằng A.  ( 3 12 cm ) . B.  ( 3 4 cm ) . C.  ( 3 6 cm ) . D.  ( 3 18 cm ) .
Câu 8.[Mức độ 2] Một lon sữa hình trụ có đường kính đáy bằng chiều cao và bằng 1 𝑑𝑚. Thể tích thực của lon sữa đó bằng   A.  ( 3 2 dm ) . B. ( 3 dm ) . C. ( 3 dm ) . D.  ( 3 dm ) . 2 4
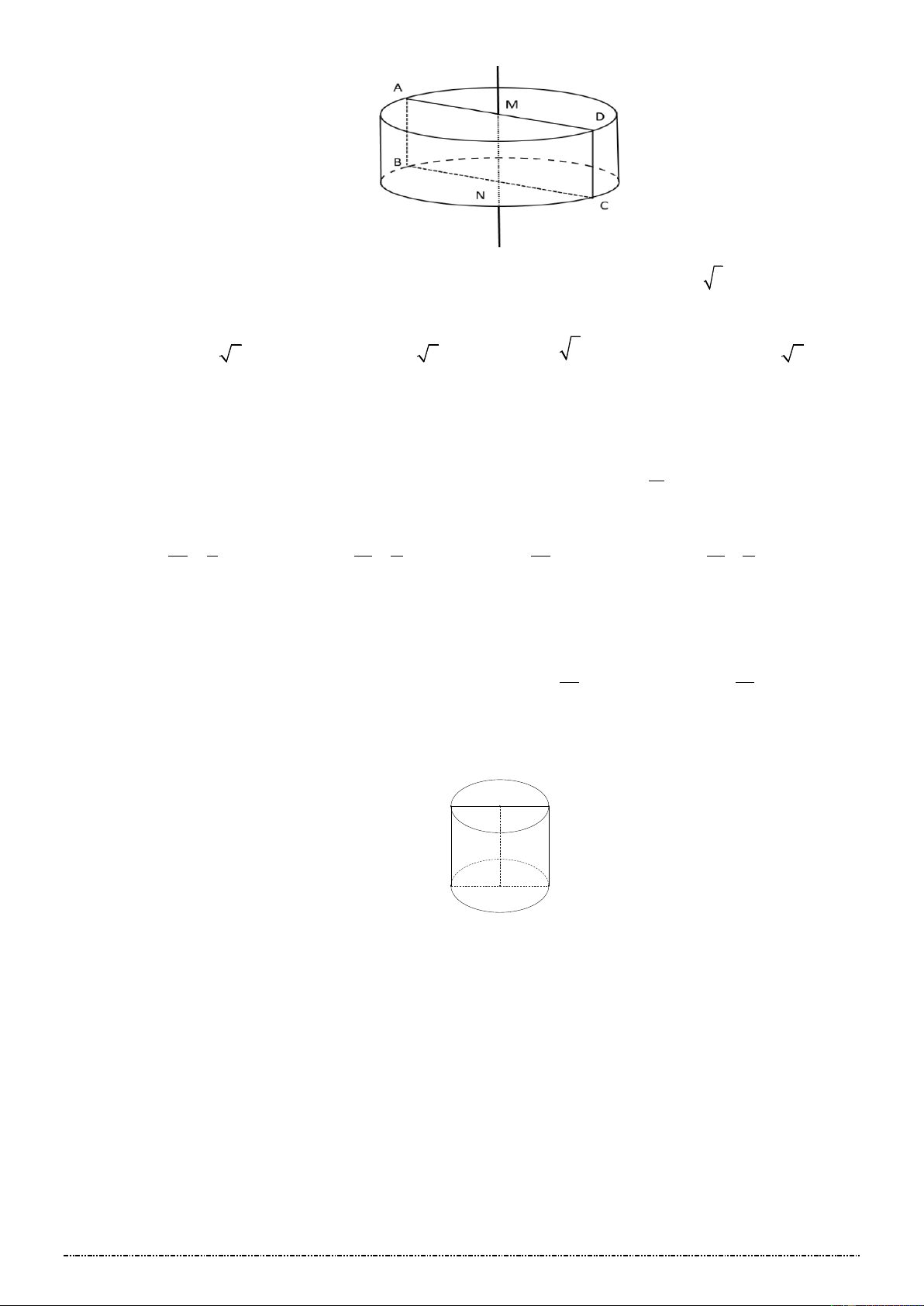
Câu 9.[Mức độ 2] Cho hình vuông 𝐴𝐵𝐶𝐷 cạnh 8 𝑐𝑚. Gọi 𝑀, 𝑁 lần lượt là trung điểm của 𝐴𝐵 và 𝐶𝐷.
Quay hình vuông 𝐴𝐵𝐶𝐷 xung quanh 𝑀𝑁. Diện tích xung quanh của hình trụ tạo thành là A.  ( 2 64 cm ) . B.  ( 2 32 cm ) . C.  ( 2 96 cm ) . D.  ( 2 126 cm ) .
Câu 10.[Mức độ 2] Cho hình chữ nhật 𝐴𝐵𝐶𝐷 có 𝐴𝐵 = 𝑎 và góc 𝐵𝐷𝐶
̂ = 30°. Quay hình chữ nhật này
xung quanh cạnh 𝐴𝐷. Diện tích xung quanh của hình trụ được tạo thành là 2 A. 2 3 a . B. 2 2 3 a . C. 2  a . D. 2 3 a 3 C.
BÀI TẬP TỰ LUYỆN
MỨC NHẬN BIẾT – THÔNG HIỂU
A. A. DẠNG 1. DIỆN TÍCH XUNG QUANH, DIỆN TÍCH TOÀN PHẦN, CHIỀU CAO, BÁN KÍNH ĐÁY, THIẾT DIỆN
Câu 1. (Đề Tham Khảo 2020 Lần 2) Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán
kính đáy r bằng 1
A. 4 rl .
B.  rl .
C.  rl .
D. 2 rl . 3
Câu 2. (Mã 101 - 2020 Lần 1) Cho hình trụ có bán kính đáy R = 8 và độ dài đường sinh l = 3 . Diện tích
xung quanh của hình trụ đã cho bằng: A. 24 . B. 192 . C. 48 . D. 64 . Trang 41
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 3. (Mã 102 - 2020 Lần 1) Cho hình trụ có bán kính đáy r = 4 và độ dài đường sinh l = 3 . Diện tích
xung quanh của hình trụ đã cho bằng A. 48 . B. 12 . C. 16 . D. 24 .
Câu 4. (Mã 103 - 2020 Lần 1) Cho hình trụ có bán kính đáy r = 5 và độ dài đường sinh l = 3 . Diện tích
xung quanh của hình trụ đã cho bằng A. 15 B. 25 .
Câu 5. (Mã 104 - 2020 Lần 1) Cho hình trụ có bán 4 và độ dài đường sinh l = 3 . Diện tích xung quanh
của hình trụ đã cho bằng A. 42 . B. 147 . C. 49 . D. 21 .
Câu 6. (Đề Minh Họa 2020 Lần 1) Cho hình trụ có bán kính đáy bằng 3 . Biết rằng khi cắt hình trụ đã
cho bởi một mặt phẳng qua trục, thiết diện thu được là một hình vuông. Diện tích xung quanh của hình trụ đã cho bằng A. 18 . B. 36 . C. 54 . D. 27 .
Câu 7. (Đề Minh Họa 2017) Trong không gian, cho hình chữ nhật ABCD có AB =1 và AD = 2 . Gọi
M , N lần lượt là trung điểm của AD và BC . Quay hình chữ nhật ABCD xung quanh trục MN , ta được
một hình trụ. Tính diện tích toàn phần S của hình trụ đó. tp
A. S = 10 .
B. S = 2 .
C. S = 6 . D. S = 4 . tp tp tp tp
Câu 8. (Mã 105 2017) Cho hình trụ có diện tích xung quanh bằng 50 và độ dài đường sinh bằng
đường kính của đường tròn đáy. Tính bán kính r của đường tròn đáy. 5 2 5 2
A. r = 5  .
B. r = 5 . C. r = . D. r = . 2 2
Câu 9. (Chuyên Lam Sơn Thanh Hóa 2019) Cho khối trụ (T ) có bán kính đáy R = 1 , thể tích V = 5 .
Tính diện tích toàn phần của hình trụ tương ứng
A. S = 12 .
B. S = 11 .
C. S = 10 . D. S = 7 .
Câu 10. (THPT Lê Quy Đôn Điện Biên 2019) Tính diện tích xung quanh của hình trụ biết hình trụ có
bán kính đáy là a và đường cao là a 3 . A. 2 2 a . B. 2  a . C. 2  a 3 . D. 2 2 a 3 .
B. DẠNG 2. THỂ TÍCH
Câu 11. (Mã 102 - 2020 Lần 2) Cho khối trụ có bán kính đáy bằng r = 5 và chiều cao h = 3 . Thể tích
của khối trụ đã cho bằng A. 5 . B. 30 . C. 25 . D. 75 .
Câu 12. (Mã 103 - 2020 Lần 2) Cho khối trụ có bán kính r = 3và chiều cao h = 4 . Thể tích khối trụ đã cho bằng A. 4 . B. 12 . C. 36 . D. 24 . Trang 42
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 13. (Mã 101 - 2020 Lần 2) Cho khối trụ có bán kính đáy r = 4 và chiều cao h = 3 . Thể tích của
khối trụ đã cho bằng A. 48 . B. 4 . C. 16 . D. 24 .
Câu 14. (Mã 104 - 2020 Lần 2) Cho khối trụ có bán kính đáy r = 3 và chiều cao h = 5 . Thể tích của
khối trụ đã cho bằng A. 45 . B. 5 . C. 15 . D. 30 .
Câu 15. (Mã 103 2018) Thể tích của khối trụ tròn xoay có bán kính đáy r và chiều cao h bằng 4 1 A. 2  r h . B. 2  r h . C. 2  r h . D. 2 rh . 3 3
Câu 16. (Mã 123 2017) Tính thể tích V của khối trụ có bán kính r = 4 và chiều cao h = 4 2 .
A. V = 32 .
B. V = 64 2 .
C. V = 128 .
D. V = 32 2 .
Câu 17. (Chuyên Lê Hồng Phong Nam Định 2019) Thể tích khối trụ có bán kính đáy r = a và chiều
cao h = a 2 bằng 3  a 2 A. 3 4 a 2 . B. 3  a 2 . C. 3 2 a . D. . 3
Câu 18. (Chuyên Lê Quý Đôn Điện Biên 2019) Thiết diện qua trục của một hình trụ là một hình vuông
có cạnh bằng 2a . Tính theo a thể tích khối trụ đó. 2 A. 3  a . B. 3 2 a . C. 3 4 a . D. 3  a . 3
Câu 19. (THPT Lê Quý Đôn Đà Nẵng 2019) Cho hình chữ nhật ABCD có AB = 2BC = 2 . a Tính thể
tích khối tròn xoay khi quay hình phẳng ABCD quanh trục . AD A. 3 4 a . B. 3 2 a . C. 3 8 a . D. 3  a .
Câu 20. (Chuyên Bắc Giang 2019) Cho hình trụ có diện tích toàn phần là 4 và có thiết diện cắt bởi
mặt phẳng qua trục là hình vuông. Tính thể tích khối trụ?  6  6 4 4 6 A. . B. . C. . D. . 12 9 9 9
MỨC VẬN DỤNG 1. Diện tích xung quanh, diện tích toàn phần, chiều cao, bán kính đáy, thiết diện
Câu 21. (Mã 103 - 2019) khoảng bằng 1, thiết diện thu được có diện tích bằng 12 2 . Diện tích xung
quanh của hình trụ đã cho bằng A. 6 10 . B. 6 34 . C. 3 10 . D. 3 34 .
Câu 22. (Mã 101 - 2019) Cho hình trụ có chiều cao bằng 5 3 . Cắt hình trụ đã cho bởi mặt phẳng song
song với trục và cách trục một khoảng bằng 1, thiết diện thu được có diện tích bằng 30 . Diện tích xung
quanh của hình trụ đã cho bằng A. 10 3 . B. 5 39 . C. 20 3 . D. 10 39 . Trang 43
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 23. (Mã 102 - 2019) Cho hình trụ có chiều cao bằng 4 2 . Cắt hình trụ đã cho bởi một mặt phẳng
song song với trục và cách trục một khoảng bằng 2 , thiết diện thu được có diện tích bằng 16 . Diện tích
xung quanh của hình trụ đã cho bằng A. 16 2 . B. 8 2 . C. 12 2 . D. 24 2 .
Câu 24. Cắt hình trụ (T ) bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện tích bằng 2
30cm và chu vi bằng 26 cm . Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy
của hình trụ (T ) . Diện tích toàn phần của (T ) là: 23 69 A.  ( 2 23 cm ) . B. ( 2 cm ) . C. ( 2 cm ) . D.  ( 2 69 cm ) . 2 2
Câu 25. Một hình trụ có bán kính đáy bằng 50 cm và có chiều cao là 50 cm. Một đoạn thẳng AB có
chiều dài là 100 cm và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách d từ đoạn thẳng
đó đến trục hình trụ.
A. d = 50 cm.
B. d = 50 3 cm.
C. d = 25 cm.
D. d = 25 3 cm.
C. D. DẠNG 2. THỂ TÍCH
Câu 26. (Đề Tham Khảo 2020 Lần 2) Cho hình trụ có chiều cao bằng 6a. Biết rằng khi cắt hình trụ đã
cho bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 3a, thiết diện thu được là một
hình vuông. Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng A. 3 216 a . B. 3 150 a . C. 3 54 a . D. 3 108 a .
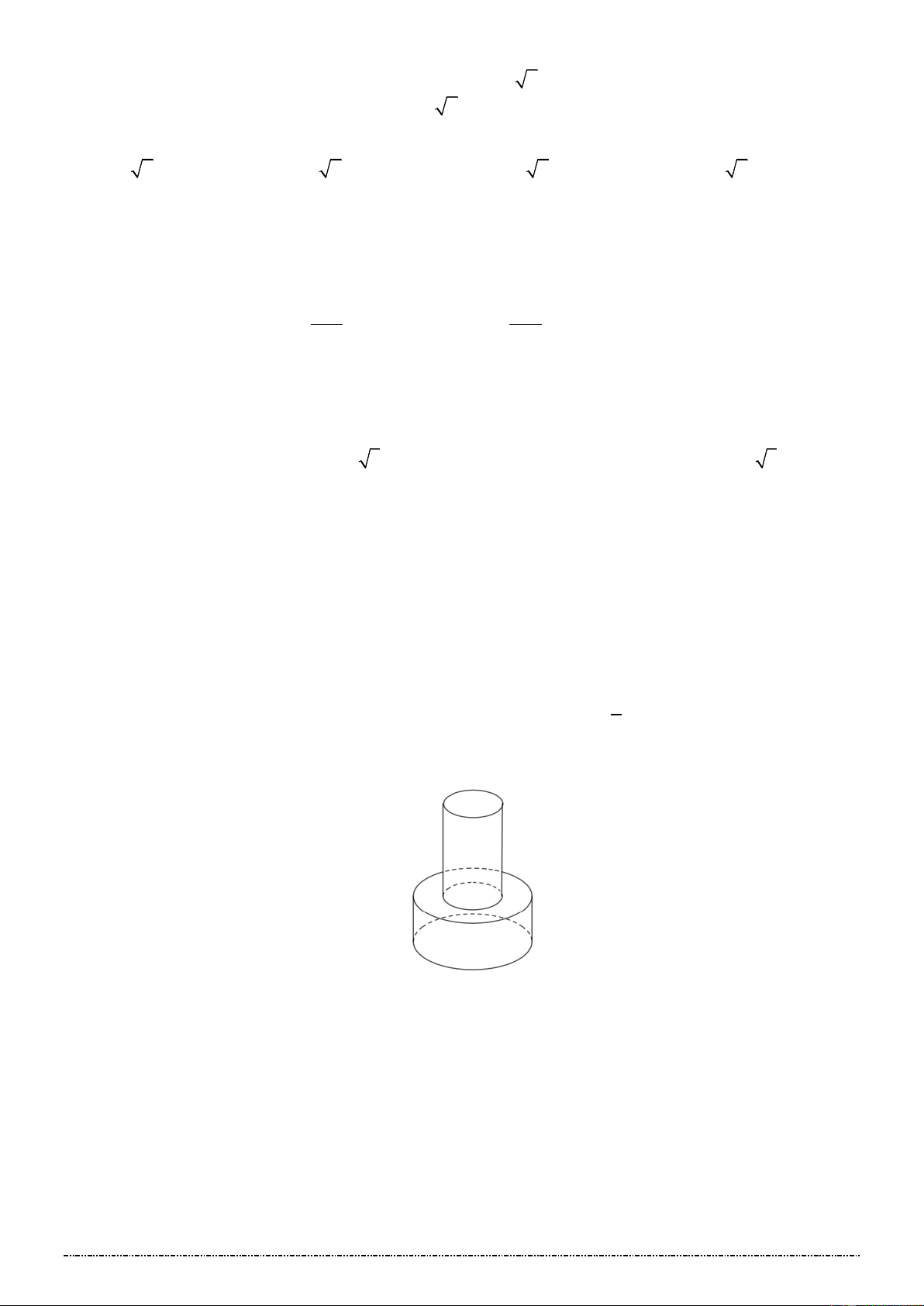
Câu 27. (Đề Tham Khảo 2019) Một khối đồ chơi gồm hai khối trụ ( H , H xếp chồng lên nhau, lần 1 ) ( 2 )
lượt có bán kính đáy và chiều cao tương ứ 1
ng là r , h , r , h thỏa mãn r =
r , h = 2h (tham khảo hình 1 1 2 2 2 1 2 1 2
vẽ). Biết rằng thể tích của toàn bộ khối đồ chơi bằng 3
30cm , thể tích khối trụ ( H bằng 1 ) A. 3 24cm . B. 3 15cm . C. 3 20cm . D. 3 10cm .
Câu 28. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hình trụ có chiều cao bằng 8a . Biết hai điểm ,
A C lần lượt nằm trên hai đáy thỏa AC = 10a , khoảng cách giữa AC và trục của hình trụ bằng 4a .
Thể tích của khối trụ đã cho là A. 3 128 a . B. 3 320 a . C. 3 80 a . D. 3 200 a .
Câu 29. (Sở Hà Nội 2019) Hỏi nếu tăng chiều cao của khối trụ lên 2 lần, bán kính của nó lên 3 lần thì
thể tích của khối trụ mới sẽ tăng bao nhiêu lần so với khối trụ ban đầu? Trang 44
Trên con đường thành công không có dấu chân của kẻ lười biếng A. 36 . B. 6 . C. 18 . D. 12 .
Câu 30. (Chuyên ĐHSPHN - 2018) Cần đẽo thanh gỗ hình hộp có đáy là hình vuông thành hình trụ có
cùng chiều cao. Tỉ lệ thể tích gỗ cần phải đẽo đi ít nhất (tính gần đúng) là A. 30% . B. 50% . C. 21% . D. 11% .
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 45
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HOC 12 – CHƯƠNG 2 §1. MẶT TRÒN XOAY
I. TÓM TẮT KIẾN THỨC VỀ HÌNH NÓN, KHỐI NÓN.
1. Hình nón tròn xoay
Hình thành: Cho 𝛥𝑆𝑂𝑀 vuông tại 𝑂 quay quanh trục 𝑆𝑂, ta được mặt nón như hình trên ℎ = 𝑆𝑂 với:{𝑟 = 𝑂𝑀. 𝑙 = 𝑆𝑀 S l h l l A B r O M
2. Khối nón tròn xoay
- Khối nón tròn xoay là phần không gian được giới hạn bởi hình nón tròn xoay kể cả hình nón đó.
- Các yếu tố của hình nón cũng là của khối nón tương ứng.
3. Các yếu tố của hình nón
Trục của hình nón: 𝑆𝑂
Đường cao: ℎ = 𝑆𝑂 .
Bán kính đáy: 𝑟 = 𝑂𝐴 = 𝑂𝐵 = 𝑂𝑀 .
Đường sinh: 𝑙 = 𝑆𝐴 = 𝑆𝐵 = 𝑆𝑀 . Góc ở đỉnh: 𝐴𝑆𝐵 ̂ = 2𝛼 .
Thiết diện qua trục là 𝛥𝑆𝐴𝐵 cân tại 𝑆.
Góc giữa đường sinh và mặt đáy: 𝑆𝐴𝑂 ̂ = 𝑆𝐵𝑂 ̂ = 𝑆𝑀𝑂 ̂
4. Một số công thức.
Chu vi đáy: 𝑝 = 2𝜋𝑟 .
Diện tích đáy: 𝑆đ = 𝜋𝑟2 . 1 1 Thể tích: 𝑉 = ℎ. 𝑆 ℎ. 𝜋𝑟2 . 3 đ = 3
(liên tưởng đến thể tích khối chóp).
Diện tích xung quanh: 𝑆𝑥𝑞 = 𝜋𝑟𝑙 .
Diện tích toàn phần: 𝑆𝑡𝑝 = 𝑆𝑥𝑞 + 𝑆đ = 𝜋𝑟𝑙 + 𝜋𝑟2 Trang 46
Trên con đường thành công không có dấu chân của kẻ lười biếng
5. Bài tập trắc nghiệm
Dạng 1: Xác định các yếu tố cơ bản của khối nón. Tính diện tích, thể tích.
Câu 1.[Mức độ 1] Cho khối nón có chiều cao ℎ = 3𝑎 và bán kính đáy 𝑟 = 𝑎. Thể tích của khối nón đã cho là 1 A. 3 3 a . B. 3  a . C. 3  a . D. 3 3 a 3
Câu 2.[Mức độ 1] Cho hình nón có đường sinh 𝑙 = 4𝑎 𝑣à 𝑏á𝑛 𝑘í𝑛ℎ đá𝑦 𝑟 = 3𝑎.
Diện tích xung quanh của hình nón đã cho là A. 2 24 a . B. 2 12 a . C. 2 4 a . D. 3𝜋𝑎2.
Câu 3.[Mức độ 1] Cho hình nón có đường sinh 𝑙 = 5 𝑣à 𝑏á𝑛 𝑘í𝑛ℎ đá𝑦 𝑟 = 4.
Diện tích toàn phần của hình nón đã cho bằng A. 16 . B. 44 . C. 24 . D. 72 .
Câu 4.[Mức độ 1] Cho hình nón có đường sinh bằng 10a và đường kính bằng 6a.
Chiều cao của hình nón đã cho bằng A. 8a . B. 2 34a .
C. 109a . D. 91a
Câu 5.[Mức độ 2] Trong không gian, cho tam giác 𝐴𝐵𝐶 vuông tại 𝐴 có 𝐴𝐵 = 𝑎, 𝐴𝐶 = 2𝑎. Khi quay tam
giác 𝐴𝐵𝐶 quanh cạnh góc vuông 𝐴𝐵 thì đường gấp khúc 𝐴𝐶𝐵 tạo thành một hình nón. Diện tích
xung quanh của hình nón đó bằng A. 2 10 a . B. 2 5 a . C. 2 5 a . D. 2 2 5 a
Câu 6.[Mức độ 2] Cắt một hình nón bởi một mặt phẳng qua trục của nó ta được thiết diện là một tam giác
đều có cạnh bằng 2𝑎. Thể tích của khối nón được tạo nên bởi hình nón đã cho bằng 3 2 A. 3 2 a . B. 3 3 a . C. 3  a . D. 3  a 3 3
Câu 7.[Mức độ 2] Cho hình chóp tứ giác đều có cạnh đáy bằng 𝑎 và cạnh bên bằng 4𝑎. Tính diện tích
xung quanh của hình nón có đỉnh trùng với đỉnh hình chóp và đường tròn đáy ngoại tiếp đáy hình chóp đã cho. A. 2 2 a . B. 2 2 2 a . C. 2 3 a . D. 2 4 a
Dạng 2: Thiết diện của khối chóp.
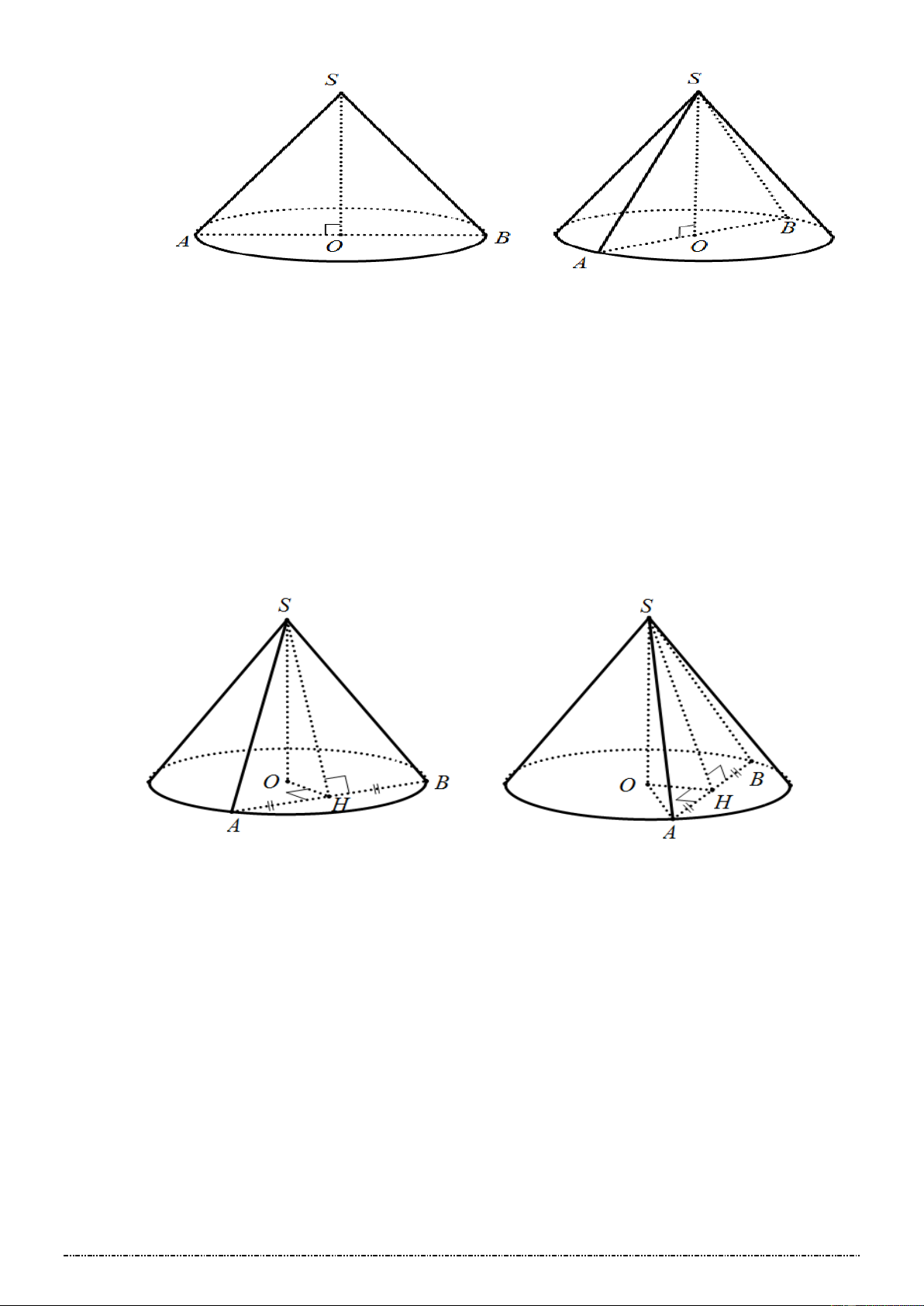
1TRƯỜNG HỢP 1: Thiết diện qua trục của hình nón: 𝑚𝑝(𝑃) đi qua trục của hình nón và cắt mặt nón
theo 2 đường sinh ⇒ Thiết diện là tam giác cân.
. Cách vẽ hình: trên hình vẽ thiết diện là tam giác 𝑆𝐴𝐵. Trang 47
Trên con đường thành công không có dấu chân của kẻ lười biếng
Thiết diện qua trục của hình nón thông thường hay gặp ở một số dạng như:
• Thiết diện qua trục là một tam giác vuông.
• Thiết diện qua trục là một tam giác vuông cân.
• Thiết diện qua trục là một tam giác đều.
• Thiết diện qua trục có góc ở đỉnh bằng số độ cho trước (60° hay 120°). • …..
2TRƯỜNG HỢP 2: Thiết diện qua đỉnh của hình nón: 𝑚𝑝(𝑃) đi qua đỉnh của hình nón và cắt mặt nón
theo 2 đường sinh ⇒ Thiết diện cũng là tam giác cân.
. Cách vẽ hình: trên hình vẽ thiết diện là tam giác 𝑆𝐴𝐵.
 Lưu ý: Khi vẽ thiết diện qua đỉnh, nếu kẻ 𝑂𝐻 ⊥ 𝐴𝐵 thì theo tính chất đường kính và dây cung
của đường tròn (đường kính vuông góc với dây cung thì đi qua trung điểm của dây cung và
ngược lại), thì 𝐻 chính là trung điểm của 𝐴𝐵. Khi đó góc giữa mặt phẳng (𝑆𝐴𝐵) với đường tròn đáy chính là 𝑆𝐻𝑂 ̂.
Thiết diện qua đỉnh của hình nón thông thường hay gặp ở một số dạng như:
• Thiết diện qua đỉnh là một tam giác vuông.
• Thiết diện qua đỉnh là một tam giác vuông cân.
• Thiết diện qua đỉnh là một tam giác đều.
• Thiết diện qua đỉnh có góc tạo bởi thiết diện và trục là số cho trước (60° hay 120°).
• Thiết diện qua đỉnh của hình nón có khoảng cách từ tâm đáy tới mặt phẳng chứa thiết diện là 𝑎(cm). Trang 48
Trên con đường thành công không có dấu chân của kẻ lười biếng
• Thiết diện là một tam giác cân đồng thời tạo với mặt phẳng đường tròn đáy góc cho trước. • …
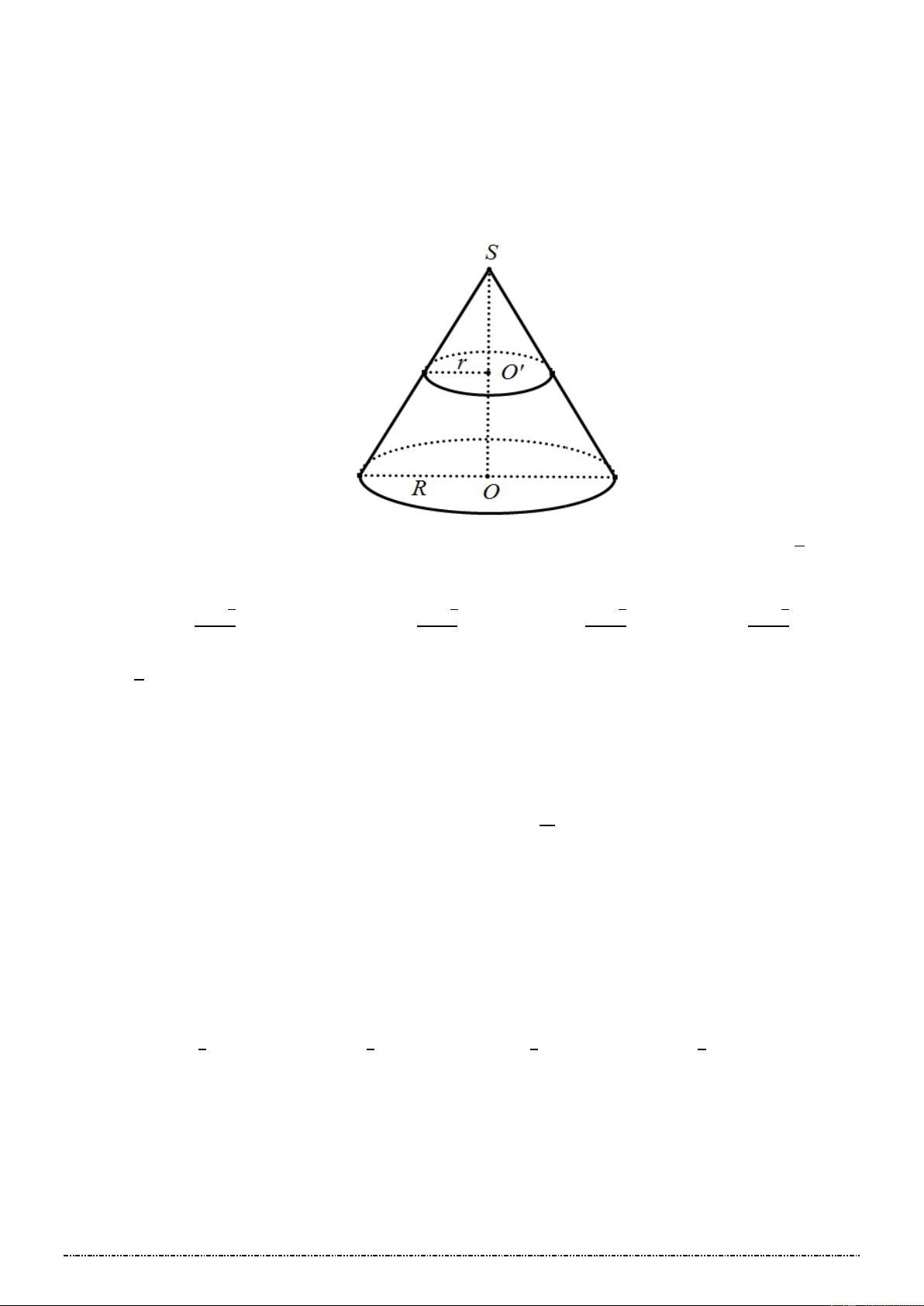
3TRƯỜNG HỢP 3: Thiết diện vuông góc với trục của hình nón và song song với đường tròn đáy hình
nón: 𝑚𝑝(𝑃) vuông góc với trục hình nón ⇒ giao tuyến là một đường tròn.
. Cách vẽ hình: trên hình vẽ, thiết diện là đường tròn tâm 𝑂′.
Câu 1.[Mức độ 2] Cho hình nón có thiết diện qua trục là tam giác vuông có cạnh huyền bằng 𝑎√2. Diện
tích xung quanh 𝑆𝑥𝑞 của hình nón đó bằng 𝜋𝑎2√3 𝜋𝑎2√2 𝜋𝑎2√2 𝜋𝑎2√2 A. 𝑆𝑥𝑞 = . B. 𝑆 . C. 𝑆 . D.𝑆 . 3 𝑥𝑞 = 2 𝑥𝑞 = 6 𝑥𝑞 = 2
Câu 2.[Mức độ 2] Diện tích toàn phần của hình nón có khoảng cách từ tâm của đáy đến đường sinh bằng
√3 và thiết diện qua trục là tam giác đều bằng A. 16𝜋. B. 8𝜋.
C. 20𝜋. D.12𝜋.
Câu 3.[Mức độ 2] Cho một khối nón có bán kính đáy là 9cm, góc giữa đường sinh và mặt đáy là 30°. Tính
diện tích thiết diện của khối nón cắt bởi mặt phẳng đi qua hai đường sinh vuông góc với nhau. 27 A. 27(cm2).
B. 162(cm2). C. . (cm2).
D.54(cm2). 2
Câu 4.[Mức độ 2] Cho hình nón tròn xoay có chiều cao ℎ = 20 và bán kính đáy 𝑟 = 25. Một thiết diện
đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là 12. Tính diện
tích của thiết diện đó. A. 500 . B. 300 . C. 406 . D. 400
Câu 5.[Mức độ 3] Mặt phẳng trung trực của đường cao của một khối nón chia nó ra thành hai khối. Tỉ số
thể tích của khối bé chia khối lớn bằng 𝟏 𝟏 𝟏 𝟏 A. . B. . C. . D. . 𝟓 𝟕 𝟒 𝟖
5. Bài tập trắc nghiệm.
MỨC VẬN DỤNG: NHẬN BIẾT – THÔNG HIỂU tích xung quanh, diện tích toàn phần,
chiều cao, bán kính đáy, thiết diện Trang 49
Trên con đường thành công không có dấu chân của kẻ lười biếng Câu 1.
(Đề Minh Họa 2020 Lần 1) Diện tích xung quanh của hình nón có độ dài đường sinh l và bán kính đáy r bằng 1
A. 4 rl . B. 2 rl .
C.  rl . D.  rl . 3 Câu 2.
(Mã 102 - 2020 Lần 2) Cho hình nón có bán kính đáy r = 2 và độ dài đường sinh l = 7 . Diện
tích xung quanh của hình nón đã cho bằng 14 98 A. 28 . B. 14 . C. . D. . 3 3 Câu 3.
(Mã 101 - 2020 Lần 2) Cho hình nón có bán kính đáy r = 2 và độ dài đường sinh l = 5 . Diện
tích xung quanh của hình nón đã cho bằng 20 10 A. 20 . B. C. 10 . D. . 3 3 Câu 4.
(Mã 104 - 2020 Lần 2) Cho hình nón có bán kính đáy r = 2 và độ dài đường sinh l = 7 . Diện
tích xung quanh của hình nón đã cho bằng 28 14 A. . B. 14 . C. 28 . D. . 3 3 Câu 5.
(KTNL GV Thuận Thành 2 Bắc Ninh 2019) Gọi l, ,
h r lần lượt là độ dài đường sinh, chiều
cao và bán kính mặt đáy của hình nón. Diện tích xung quanh S của hình nón là: xq 1 A. 2 S =  r h . B. S =  rl . C. S =  rh . D. S = 2 rl . xq 3 xq xq xq Câu 6.
(THPT Lê Quy Đôn Điện Biên 2019) Một hình nón có thiết diện qua trục là một tam giác
vuông cân có cạnh góc vuông bằng .
a Tính diện tích xung quanh của hình nón. 2 2 a 2 2  a 2 2  a 2 A. . B. . C. 2  a 2 . D. . 3 4 2 Câu 7.
(THPT Lương Thế Vinh Hà Nội 2019) Cho hình nón có bán kính đáy bằng a và độ dài
đường sinh bằng 2a . Diện tích xung quanh của hình nón đó bằng A. 2 4 a . B. 2 3 a . C. 2 2 a . D. 2 2a . Câu 8.
(Sở Vĩnh Phúc 2019) Cho hình nón có diện tích xung quanh bằng 2
3 a , bán kính đáy bằng a
. Tính độ dài đường sinh của hình nón đó 3a A. 2a 2 . B. . C. 2a . D. 3a . 2 Câu 9.
(THPT - Yên Định Thanh Hóa 2019) Cho khối nón ( N) có thể tích bằng 4 và chiều cao là
3 .Tính bán kính đường tròn đáy của khối nón ( N) . 2 3 4 A. 2 . B. . C. 1. D. . 3 3 Trang 50
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 10. (THPT Trần Nhân Tông - QN -2018) Trong không gian, cho tam giác ABC vuông tại cân
A , gọi I là trung điểm của BC , BC = 2 .Tính diện tích xung quanh của hình nón, nhận được
khi quay tam giác ABC xung quanh trục AI . A. S = 2 . B. S = 2 . C. S = 2 2 . D. S = 4 . xq xq xq xq
BÀI TẬP VẬN DỤNGDạng 2. BThể tích Câu 1.
(Mã 103 - 2019) Thể tích của khối nón có chiều cao h và có bán kính đáy r là 1 4 A. 2 2 r h . B. 2  r h . C. 2  r h . D. 2  r h . 3 3 Câu 2.
(Đề Tham Khảo 2020 Lần 2) Cho khối nón có chiều cao h = 3 và bán kính đáy r = 4 . Thể
tích của khối nón đã cho bằng A. 16 . B. 48 . C. 36 . D. 4 . Câu 3.
(Mã 101 - 2020 Lần 1) Cho khối nón có bán kính đáy r = 5 và chiều cao h = 2 . Thể tích khối nón đã cho bằng: 10 50 A. . B. 10 . C. . D. 50 . 3 3 Câu 4.
(Mã 102 - 2020 Lần 1) Cho khối nón có bán kính đáy r = 4 và chiều cao h = 2 . Thể tích của khối nón đã cho bằng 8  A. . B. 8 32 . C. . D. 32 . 3 3 Câu 5.
(Mã 103 - 2020 Lần 1) Cho khối nón có bán kính r = 2 chiều cao h = 5 . Thể tích của khối nón đã cho bằng 20 10 A. . B. 20 . C. . D. 10 . 3 3 Câu 6.
(Mã 104 - 2020 Lần 1) Cho khối nón có bán kính đáy r = 2 và chiều cao h = 4 . Thể tích của
khối nón đã cho bằng 8 16 A. 8 . B. . C. . D. 16 . 3 3 Câu 7.
(Mã 110 2017) Cho khối nón có bán kính đáy r = 3 và chiều cao h = 4 . Tính thể tích V của khối nón đã cho. 16 3
A. V = 12
B. V = 4
C. V = 16 3 D. V = 3 Câu 8.
(Mã 101 - 2019) Thể tích của khối nón có chiều cao h và bán kính đáy r là 4 1 A. 2  r h . B. 2 2 r h . C. 2  r h . D. 2  r h . 3 3 Câu 9.
(Mã 104 2019) Thể tích khối nón có chiều cao h và bán kính đáy r là Trang 51
Trên con đường thành công không có dấu chân của kẻ lười biếng 1 4 A. 2  r h . B. 2  r h . C. 2 2 r h . D. 2  r h . 3 3
Câu 10. (Mã 102 - 2019) Thể tích của khối nón có chiều cao h và bán kính đáy r là 4 1 A. 2  r h . B. 2  r h . C. 2 2 r h . D. 2  r h . 3 3 MỨC VẬN DỤNG Dạng 2. DẠNG 2.
DIỆN TÍCH XUNG QUANH, DIỆN TÍCH TOÀN PHẦN, CHIỀU CAO, BÁN KÍNH ĐÁY, THIẾT DIỆN
Câu 1. (Đề Tham Khảo 2020 Lần 2) Trong không gian, cho tam giác ABC vuông tại A , AB = a và
AC = 2a . Khi quay tam giác ABC quanh cạnh góc vuông AB thì đường gấp khúc ACB tạo
thành một hình nón. Diện tích xung quanh hình nón đó bằng A. 2 5 a . B. 2 5 a . C. 2 2 5 a . D. 2 10 a .
Câu 2. (Mã 101 - 2020 Lần 1) Cho hình nón có bán kính đáy bằng 2 và góc ở đỉnh bằng 60 . Diện tích
xung quanh của hình nón đã cho bằng 16 3 8 3 A. 8 . B. . C. . D. 16 . 3 3
Câu 3. (Mã 102 - 2020 Lần 1) Cho hình nón có bán kính bằng 5 và góc ở đỉnh bằng 60 . Diện tích
xung quanh của hình nón đã cho bằng  50 3 A. 50 100 3 . B. . C. . D. 100 . 3 3
Câu 4. (Mã 103 - 2020 Lần 1) Cho hình nón có bán kính bằng 3 và góc ở đỉnh bằng 0 60 . Diện tích xung
quanh của hình nón đã cho bằng A. 18 . B. 36 . C. 6 3 . D. 12 3 .
Câu 5. (Mã 104 - 2020 Lần 1) Cho hình nón có bán kính đáy bằng 4 và góc ở đỉnh bằng 0 60 . Diện tích
xung quanh của hình nón đã cho bằng 64 3 32 3 A. . B. 32 . C. 64 . D. . 3 3
Câu 6. (Mã 123 2017) Cho một hình nón có chiều cao h = a và bán kính đáy r = 2a . Mặt phẳng (P) đi
qua S cắt đường tròn đáy tại A và B sao cho AB = 2 3a . Tính khoảng cách d từ tâm của
đường tròn đáy đến (P) . 3a 5a 2a A. d = B. d = C. d =
D. d = a 2 5 2 Trang 52
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 7. (KSCL THPT Nguyễn Khuyến 2019) Cho hình nón đỉnh S , đường cao SO, A và B là hai điể a 3
m thuộc đường tròn đáy sao cho khoảng cách từ O đến (SAB) bằng và 3 0 0
SAO = 30 , SAB = 60 . Độ dài đường sinh của hình nón theo a bằng A. a 2 B. a 3 C. 2a 3 D. a 5
Câu 8. (THPT Cẩm Giàng 2 2019) Cho một hình nón có bán kính đáy bằng a và góc ở đỉnh bằng 60 .
Tính diện tích xung quanh của hình nón đó. 2 2 3 a 2 4 3 a A. 2 S = 4 a . B. S = . C. S = . D. 2 S = 2 a . xq xq 3 xq 3 xq
Câu 9. (THPT Cẩm Giàng 2 2019) Cho đoạn thẳng AB có độ dài bằng 2a , vẽ tia Ax về phía điểm B
sao cho điểm B luôn cách tia Ax một đoạn bằng a . Gọi H là hình chiếu của B lên tia Ax ,
khi tam giác AHB quay quanh trục AB thì đường gấp khúc AHB vẽ thành mặt tròn xoay có
diện tích xung quanh bằng: 2 (3+ 3) 2  (1+ 3) 2  (2+ 2) 2  3 2 a a a a A. . B. . C. . D. . 2 2 2 2
Câu 10. (HSG Bắc Ninh 2019) Cho hình nón có chiều cao h = 20 , bán kính đáy r = 25 . Một thiết diện
đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12 .
Tính diện tích S của thiết diện đó. A. S = 500 . B. S = 400 . C. S = 300 . D. S = 406 .
BÀI TẬP VẬN DỤNG Dạng 3. DẠNG 2. THỂ TÍCH Câu 1.
(Đề Minh Họa 2020 Lần 1) Cho hình nón có chiều cao bằng 2 5 . Một mặt phẳng đi qua
đỉnh hình nón và cắt hình nón theo một thiết diện là tam giác đều có diện tích bằng 9 3 . Thể
tích của khối nón được giới hạn bởi hình nón đã cho bằng 32 5 A. . B. 32 . C. 32 5 . D. 96 . 3 Câu 2.
(KSCL THPT Nguyễn Khuyến 2019) Tính thể tích của hình nón có góc ở đỉnh bằng 60o và
diện tích xung quanh bằng 2 6 a . 3 3 a 2 3 3 a 2 A. V = . B. 3 V = 3 a . C. V = . D. 3 V =  a . 4 4 Câu 3.
(Chuyên Thái Nguyên 2019) Cho tam giác ABC vuông tại A , cạnh AB = 6 , AC = 8 và M là
trung điểm của cạnh AC . Khi đó thể tích của khối tròn xoay do tam giác BMC quanh quanh AB là A. 86 . B. 106 . C. 96 . D. 98 . Câu 4.
(Chuyên Lê Quý Đôn Điện Biên 2019) Cho hình nón có bán kính đáy bằng 2 cm, góc ở đỉnh
bằng 60 . Tính thể tích của khối nón đó. Trang 53
Trên con đường thành công không có dấu chân của kẻ lười biếng 8 3 8 3 8 A. 3 cm . B. 3 8 3 cm . C. 3 cm . D. 3 cm . 9 3 3 Câu 5.
(Việt Đức Hà Nội 2019) Cho tam giác ABC vuông tại A , AB = 6c ,
m AC = 8cm . Gọi V là 1
thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AB và V là thể tích khối nón 2 V
tạo thành khi quay tam giác ABC quanh cạnh AC . Khi đó, tỷ số 1 bằng: V2 3 4 16 9 A. . B. . C. . D. . 4 3 9 16
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 54
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HOC 12 – CHƯƠNG 2 §1. MẶT TRÒN XOAY
I. TÓM TẮT KIẾN THỨC VỀ HÌNH TRỤ, KHỐI TRỤ.
1. Hình trụ tròn xoay.
Xét hình chữ nhật 𝐴𝐵𝐶𝐷. Khi quay hình đó xung quanh đường thẳng chứa một cạnh, chẳng hạn
𝐴𝐵, thì đường gấp khúc 𝐴𝐷𝐶𝐵 tạo thành một hình được gọi là hình trụ tròn xoay.
– Hai đáy (𝐴; 𝑟), (𝐵; 𝑟)
– Đường sinh: 𝑙 = 𝐶𝐷.
– Chiều cao: ℎ = 𝐴𝐵 = 𝐶𝐷.
2. Khối trụ tròn xoay.
Khối trụ tròn xoay là phần không gian được giới hạn bởi một hình trụ tròn xoay kể cả hình trụ đó.
Khối trụ tròn xoay được gọi tắt là khối trụ.
3. Một số công thức về hình nón, khối nón.
- Diện tích đáy của hình trụ : 𝑆đá𝑦 = 𝜋𝑟2.
- Diện tích xung quanh của hình trụ :𝑆𝑥𝑞 = 2𝜋𝑟ℎ.
- Diện tích toàn phần của hình trụ: 𝑆𝑡𝑝 = 𝑆𝑥𝑞 + 2. 𝑆đá𝑦 = 2𝜋𝑟ℎ + 2𝜋𝑟2.
- Chu vi một đáy của hình trụ: 𝐶 = 2𝜋𝑟.
- Thể tích khối trụ : 𝑉 = 𝜋𝑟2ℎ.
II. BÀI TẬP TỰ LUẬN.
Dạng 1: Xác định các yếu tố cơ bản của khối trụ. Tính diện tích, thể tích.
III. BÀI TẬP TRẮC NGHIỆM. Trang 55
Trên con đường thành công không có dấu chân của kẻ lười biếng Câu 1:
[Mức độ 1] Cho hình trụ có bán kính đáy 𝑟 và độ dài đường sinh là ℓ. Thể tích khối trụ được tính theo công thức 1 1
A. 𝑉 = 𝜋𝑟ℓ2.
B. 𝑉 = 𝜋𝑟2ℓ.
C. 𝑉 = 𝜋𝑟2ℓ.
D. 𝑉 = 𝜋𝑟ℓ2. 3 3 Câu 2:
[Mức độ 1] Cho hình trụ có bán kính đáy 𝑟 = 4 và độ dài đường sinh ℓ = 3. Diện tích xung
quanh của hình trụ đã cho bằng A. 48𝜋. B. 12𝜋. C. 16𝜋. D. 24𝜋. Câu 3:
[Mức độ 1] Thể tích của khối trụ có bán kính đáy 𝑟 = 4 và chiều cao ℎ = 4√2 bằng A. 32𝜋. B. 32√2𝜋. C. 64√2𝜋. D. 128𝜋. Câu 4:
[Mức độ 1] Diện tích toàn phần của hình trụ có chiều cao ℎ = 5 và bán kính 𝑟 = 3 bằng A. 48𝜋. B. 48. C. 39. D. 39𝜋. Câu 5:
[Mức độ 2] Khối trụ (𝑇) có bán kính đáy bằng 2 và thể tích bằng 8𝜋. Tính diện tích xung quanh
𝑆𝑥𝑞 của hình trụ (𝑇).
A. 𝑆𝑥𝑞 = 32𝜋.
B. 𝑆𝑥𝑞 = 8𝜋.
C. 𝑆𝑥𝑞 = 16𝜋.
D. 𝑆𝑥𝑞 = 4𝜋. Câu 6:
[Mức độ 2] Cho khối trụ (𝑇) có bán kính đáy bằng 𝑅 và diện tích toàn phần bằng 8𝜋𝑅2. Tính
thể tích 𝑉 của khối trụ (𝑇).
A. 𝑉 = 6𝜋𝑅3.
B. 𝑉 = 3𝜋𝑅3.
C. 𝑉 = 4𝜋𝑅3.
D. 𝑉 = 8𝜋𝑅3. Câu 7:
[Mức độ 2] Cho hình trụ có hai đường tròn đáy là (𝑂; 𝑅) và (𝑂′; 𝑅), 𝑂𝑂′ = ℎ. Gọi 𝐴𝐵 là một đườ ℎ
ng kính của đường tròn (𝑂; 𝑅). Biết rằng tam giác 𝑂′𝐴𝐵 đều. Tính tỉ số ⋅ 𝑅 ℎ ℎ ℎ ℎ A. = √3. B. = √3. C. = 1. D. = 4√3. 𝑅 3 𝑅 𝑅 𝑅
Câu 8: Một hình trụ có bán kính đáy bằng 2cm và có thiết diện qua trục là một hình vuông. Diện tích
xung quanh của hình trụ là A. 3 8 cm . B. 3 4 cm . C. 3 32 cm . D. 3 16 cm . 3
Vì thiết diện qua trục là hình vuông nên ta có h = l = 2r = 4cm . S
= 2rl = 2.2.4 =16cm xq Câu 9:
[Mức độ 2] Một thùng đựng thư được thiết kế như hình vẽ bên, phần phía trên là nửa hình trụ.
Thể tích của thùng đựng thư bằng
A. 320 + 80𝜋.
B. 640 + 40𝜋.
C. 640 + 80𝜋.
D. 640 + 160𝜋.
Câu 10: [Mức độ 2] Trong không gian, cho hình thang 𝐴𝐵𝐶𝐷 vuông tại 𝐴 và 𝐷, có độ dài các cạnh là
𝐴𝐷 = 𝑎, 𝐴𝐵 = 5𝑎, 𝐶𝐷 = 2𝑎. Tính thể tích 𝑉 của vật thể tròn xoay khi quay hình thang trên quanh trục 𝐴𝐵. Trang 56
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 11: [Mức độ 3] Từ một tấm tôn hình chữ nhật kích thước 80cm x 360cm, người ta làm các thùng
đựng nước hình trụ có chiều cao bằng 80cm, theo hai cách sau (xem hình minh họa dưới đây):
C1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
C2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu 𝑉1 là thể tích của thùng gò được theo cách 1 và 𝑉2 là tổng thể tích của hai thùng gò đượ 𝑉
c theo cách 2. Tính tỉ số 2. 𝑉1
Dạng 2: Thiết diện. Câu 1:
[Mức độ 2] Một hình trụ có bán kính đáy bằng a , mặt phẳng qua trục cắt hình trụ theo một
thiết diện có diện tích bằng 2
8a . Tính diện tích xung quanh của hình trụ? A. 2 4 a . B. 2 8 a . C. 2 16 a . D. 2 2 a .
Câu 2: Một khối trụ có bán kính đáy r = 7cm . Khoảng cách hai đáy bằng 10cm . Khi cắt khối trụ bởi một
mặt phẳng song song với trục cách trục 5cm thì diện tích của thiết diện là: A. 2 S = 34cm . B. 2 S = 40 6cm . C. 2 S = 21 31cm . D. 2 S = 38cm . Câu 3:
[Mức độ 2] Cho hình trụ có chiều cao bằng 5 3 . Cắt hình trụ đã cho bởi mặt phẳng song song
với trục và cách trục một khoảng bằng 1, thiết diện thu được có diện tích bằng 30 . Diện tích
xung quanh của hình trụ đã cho bằng A. 10 3 . B. 5 39 . C. 20 3 . D. 10 39 . Câu 4:
[Mức độ 2] Một hình trụ tròn xoay có hai đáy là hai đường tròn (𝑂, 𝑅) và (𝑂′, 𝑅). Biết rằng tồn
tại dây cung 𝐴𝐵 của đường tròn (𝑂, 𝑅)sao cho tam giác 𝑂′𝐴𝐵 đều và góc giữa hai mặt
phẳng (𝑂′𝐴𝐵) và mặt phẳng chứa đường tròn (𝑂, 𝑅) bằng 60°. Tính diện tích xung quanh của hình trụ đã cho. 3 7 6 A. 2 4 R . B. 2 2 3 R . C. 2  R . D. 2  R . 7 7 𝐴𝐷
Câu 5: [Mức độ 3] Cho hình thang 𝐴𝐵𝐶𝐷 vuông tại 𝐴 và 𝐵 với 𝐴𝐵 = 𝐵𝐶 = = 𝑎. Quay hình thang và 2
miền trong của nó quanh đường thẳng chứa cạnh 𝐵𝐶. Tính thể tích 𝑉 của khối tròn xoay được tạo thành. Trang 57
Trên con đường thành công không có dấu chân của kẻ lười biếng 3 5 a 3 4 a 3 5 a A. . B. . C. 3  a . D. . 3 3 3
Câu 6:[Mức độ 3] Cho hình lăng trụ tứ giác đều ABC . D A B  C  D
  có cạnh đáy bằng a
và cạnh bên bằng 4a. Thể tích của khối trụ nội tiếp trong hình lăng trụ là: A. 3 4 a . B. 3 8 a . C. 3 2 a . D. 3  a . III.
BÀI TẬP TỰ LUYỆN ( phần này không làm PPT )
MỨC NHẬN BIẾT – THÔNG HIỂU
A. A. DẠNG 1. DIỆN TÍCH XUNG QUANH, DIỆN TÍCH TOÀN PHẦN, CHIỀU CAO, BÁN KÍNH ĐÁY, THIẾT DIỆN Câu 1.
(THPT - YÊN Định Thanh Hóa 2019) Cắt một khối trụ bởi một mặt phẳng qua trục của nó ta
được thiết diện là một hình vuông có cạnh bằng 3a . Tính diện tích toàn phần của khối trụ. 2 13a  2 a  3 2 27a  A. S = S = a  S = S = tp . B. 2 3 . C. . D. . 6 tp tp 2 tp 2 Câu 2.
(Chuyên Lê Hồng Phong Nam Định 2019) Một hình trụ có diện tích xung quanh bằng 2 4 a
và bán kính đáy là a . Tính độ dài đường cao của hình trụ đó. A. a . B. 2a . C. 3a . D. 4a . Câu 3.
(Chuyên Thái Nguyên 2019) Một hình trụ có bán kính đáy bằng 2cm và có thiết diện qua trục
là một hình vuông. Diện tích xung quanh của hình trụ là A. 3 8p cm . B. 3 4p cm . C. 3 32p cm . D. 3 16p cm . Câu 4.
(THPT Gia Lộc Hải Dương Năm 2019) Cắt một hình trụ bởi một mặt phẳng qua trục của nó,
ta được thiết diện là một hình vuông có cạnh bằng 3a . Tính diện tích toàn phần của hình trụ đã cho. 2 13 a 2 27 a 2 9 a A. . B. . C. 2 9 a . D. . 6 2 2 Câu 5.
(THPT Yên Phong 1 Bắc Ninh 2019) Trong không gian cho hình chữ nhật ABCD có
AB = 1, AD = 2 . Gọi M , N lần lượt là trung điểm của AD và BC . Quay hình chữ nhật đó xung
quanh trục MN ta được một hình trụ. Tính diện tích toàn phần Stp của hình trụ đó. A. S = 4 . S =  S =  S =  tp B. 6 . tp C. 2 . tp D. 10 . tp Trang 58
Trên con đường thành công không có dấu chân của kẻ lười biếng Câu 6.
(Đồng Tháp - 2018) Hình trụ có bán kính đáy bằng a và chiều cao bằng a 3 . Khi đó diện tích
toàn phần của hình trụ bằng 2 A. 2  2 a ( 3 − ) 1 . B. 2  a (1+ 3) . C. a 3 . D. 2 2 a (1+ 3) . Câu 7.
(THPT Kinh Môn - HD - 2018) Cho lập phương có cạnh bằng a và một hình trụ có hai đáy là
hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S1 là diện tích 6 mặt của hình S
lập phương, S2 là diện tích xung quanh của hình trụ. Hãy tính tỉ số 2 . S1 S 1 S  S S  A. 2 = . B. 2 = . C. 2 =  . D. 2 = . S 2 S 2 S S 6 1 1 1 1 Câu 8.
(Chuyên Hùng Vương - Gia Lai - 2018) Một hình trụ có bán kính đáy r = 5cm , chiều cao
h = 7cm . Tính diện tích xung quanh của hình trụ. 70 35 A. S = ( 2 35π cm ) . B. S = ( 2 70π cm ) . C. S = π ( 2 cm ) . D. S = π ( 2 cm ) . 3 3 Câu 9.
(Chuyên ĐH Vinh - 2018) Cắt một hình trụ bằng một mặt phẳng qua trục của nó, ta được thiết
diện là một hình vuông cạnh 2a . Diện tích xung quanh của hình trụ bằng A. 2 2 a . B. 2 8 a . C. 2 4 a . D. 2 16 a .
Câu 10. (THPT Kiến An - Hải Phòng - 2018) Tính diện tích xung quanh của một hình trụ có chiều
cao 20 m , chu vi đáy bằng 5 m . A. 2 50 m . B. 2 50 m . C. 2 100 m . D. 2 100 m .
Câu 11. (Hồng Lĩnh - Hà Tĩnh - 2018)Cho hình chữ nhật ABCD có AB = a , AD = 2a . Thể tích của
khối trụ tạo thành khi quay hình chữ nhật ABCD quanh cạnh AB bằng A. 3 4 a . B. 3  a . C. 3 2a . D. 3 a . Trang 59
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 12. (Chuyên Bắc Ninh - 2018) Trong không gian, cho hình chữ nhật ABCD có AB = 1 và
AD = 2 . Gọi M , N lần lượt là trung điểm của AB và CD . Quay hình chữ nhật đó xung
quanh trục MN , ta được một hình trụ. Tính thể tích V của khối trụ tạo bởi hình trụ đó  A. . B.  . C. 2 . D. 4 . 2
Câu 13. (THPT Trần Phú - Đà Nẵng - 2018) Cho khối trụ có chu vi đáy bằng 4 a và độ dài đường
cao bằng a . Thể tích của khối trụ đã cho bằng 4 A. 2  a . B. 3  a . C. 3 4 a . D. 3 16 a . 3
Câu 14. (THPT Hà Huy Tập - 2018) Cho một khối trụ có diện tích xung quanh của khối trụ bằng 80
. Tính thể tích của khối trụ biết khoảng cách giữa hai đáy bằng 10 . A. 160 . B. 400 . C. 40 . D. 64 .
Câu 15. (Hà Nội - 2018) Cho khối trụ có bán kính hình tròn đáy bằng r và chiều cao bằng h . Hỏi nếu
tăng chiều cao lên 2 lần và tăng bán kính đáy lên 3 lần thì thể tích của khối trụ mới sẽ tăng lên bao nhiêu lần? A. 18 lần. B. 6 lần. C. 36 lần. D. 12 lần.
Câu 16. (THPT Lương Thế Vinh 2018). Cho hình trụ có diện tích toàn phần là 4 và có thiết diện cắt
bởi mặt phẳng qua trục là hình vuông. Tính thể tích khối trụ?  6 4 6  6 4 A. . B. . C. . D. . 9 9 12 9
Câu 17. (Chuyên Phan Bội Châu - Nghệ An - 2018) Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo
thiết diện là hình vuông cạnh a . Thể tích khối trụ đó bằng 3  a 3 a 3  a A. 3  a . B. . C. . D. . 2 3 4
Câu 18. (SGD&ĐT BRVT - 2018) Thiết diện qua trục của một hình trụ là hình vuông có cạnh là 2a
.Thể tích khối trụ được tạo nên bởi hình trụ này là: 3 2 a 3 8 a A. 3 2 a . B. . C. 3 8 a . D. . 3 3
Câu 19. (THPT Kinh Môn - Hải Dương - 2018) Cho một khối trụ (S ) có bán kính đáy bằng a . Biết
thiết diện của hình trụ qua trục là hình vuông có chu vi bằng 8 . Thể tích của khối trụ sẽ bằng A. 8 . B. 4 . C. 2 . D. 16 .
Câu 20. (THPT Gang Thép - 2018)Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là
hình chữ nhật ABCD có AB và CD thuộc hai đáy của khối trụ. Biết AB = 4a , AC = 5a .
Tính thể tích của khối trụ: A. 3 V = 12 a . B. 3 V = 16 a . C. 3 V = 4 a . D. 3 V = 8 a .
MỨC VẬN DỤNG1. Diện tích xung quanh, diện tích toàn phần, chiều cao, bán kính đáy, thiết diện Trang 60
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 21. (THPT Lê Quy Đôn Điện Biên 2019) Một hình trụ tròn xoay có hai đáy là hai đường tròn
(O,R) và (O ,R) . Biết rằng tồn tại dây cung AB của đường tròn (O,R) sao cho tam giác O A
 B đều và góc giữa hai mặt phẳng (O A
 B) và mặt phẳng chứa đường tròn (O, R) bằng 60
. Tính diện tích xung quanh của hình trụ đã cho. 3 7 6 7 A. 2 4 R . B. 2 2 3 R . C. 2  R . D. 2  R . 7 7
Câu 22. (Chuyên Sơn La 2019) Cho khối trụ có bán kính đáy bằng 4 (cm) và chiều cao 5(cm) . Gọi
AB là một dây cung đáy dưới sao cho AB = 4 3(cm) . Người ta dựng mặt phẳng ( P) đi qua
hai điểm A , B và tạo với mặt phẳng đáy hình trụ một góc 60 như hình vẽ. Tính diện tích
thiết diện của hình trụ cắt bởi mặt phẳng ( P) . 8(4 − 3 3) 4 (4 − 3) A. ( 2 cm ) . B. ( 2 cm ) . 3 3 4 (4 − 3 3) 8(4 − 3) C. ( 2 cm ) . D. ( 2 cm ) . 3 3
phương. Gọi S , S lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình 1 2
trụ. Tính S = S + S ( 2 cm ) . 1 2
A. S = 4(2400 +  ) .
B. S = 2400 (4 +  ) . C. S = 2400(4 + 3 ) . D. S = 4(2400 + 3 ) .
Câu 24. (Chuyên Quốc Học Huế 2018) Một hình trụ có diện tích xung quanh bằng 4 , thiết diện qua
trục là hình vuông. Một mặt phẳng ( ) song song với trục, cắt hình trụ theo thiết diện là tứ giác ABB A
  , biết một cạnh của thiết diện là một dây cung của đường tròn đáy của hình trụ và
căng một cung 120 . Tính diện tích thiết diện ABB A   . A. 3 2 . B. 3 . C. 2 3 . D. 2 2 .
Câu 25. (Chuyên Lương Thế Vinh - Đồng Nai - 2018) Ba chiếc bình hình trụ cùng chứa 1 lượng
nước như nhau, độ cao mực nước trong bình II gấp đôi bình I và trong bình III gấp đôi bình
II . Chọn nhận xét đúng về bán kính đáy r , r , r của ba bình 2
y = 6 − x , Ox , III . 1 2 3
A. r , r , r theo thứ tự lập thành cấp số nhân công bội 2 . 1 2 3 Trang 61
Trên con đường thành công không có dấu chân của kẻ lười biếng 1
B. r , r , r theo thứ tự lập thành cấp số nhân công bội . 1 2 3 2
C. r , r , r theo thứ tự lập thành cấp số nhân công bội 2 . 1 2 3 1
D. r , r , r theo thứ tự lập thành cấp số nhân công bội . 1 2 3 2
B. D. DẠNG 2. THỂ TÍCH
Câu 26. (Chuyên ĐHSPHN - 2018) Cần đẽo thanh gỗ hình hộp có đáy là hình vuông thành hình trụ có
cùng chiều cao. Tỉ lệ thể tích gỗ cần phải đẽo đi ít nhất (tính gần đúng) là A. 30% . B. 50% . C. 21% . D. 11% .
Câu 27. Một khối gỗ hình trụ có đường kính 0, 5 m và chiều cao 1 (m) . Người ta đã cắt khối gỗ, phần
còn lại như hình vẽ bên có thể tích là V . Tính V . 3 5 3  A. ( 3 m ) . B. ( 3 m ) . C. ( 3 m ) . D. ( 3 m ) . 16 64 64 16
Câu 28. (Sở Hưng Yên - 2020) Cho hình trụ có O, O là tâm hai đáy. Xét hình chữ nhật ABCD có ,
A B cùng thuộc (O) và C, D cùng thuộc (O) sao cho AB = a 3 , BC = 2a đồng thời
( ABCD) tạo với mặt phẳng đáy hình trụ góc 60. Thể tích khối trụ bằng 3  a 3 3  a 3 A. 3  a 3 . B. . C. . D. 3 2 a 3 . 9 3
Câu 29. (Sở Hà Tĩnh - 2020) Cho khối trụ có hai đáy là (O) và (O) . AB,CD lần lượt là hai đường
kính của (O) và (O) , góc giữa AB và CD bằng 30 , AB = 6 . Thể tích khối tứ diện ABCD
bằng 30 . Thể tích khối trụ đã cho bằng A. 180 . B. 90 . C. 30 . D. 45 .
Câu 30. (Lý Nhân Tông - Bắc Ninh - 2020) Từ một tấm tôn hình chữ nhật kích thước 50 cm x 240 cm ,
người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm , theo hai cách sau (xem
hình minh họa dưới đây):
• Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng. Trang 62
Trên con đường thành công không có dấu chân của kẻ lười biếng
• Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu V là thể tích của thùng gò được theo cách 1 và V là tổng thể tích của hai thùng gò được 1 2 V
theo cách 2. Tính tỉ số 1 . V2 V V 1 V V A. 1 = 1. B. 1 = . C. 1 = 2 . D. 1 = 4 . V V 2 V V 2 2 2 2
Câu 31. (Tiên Du - Bắc Ninh - 2020) Cho hình trụ có hai đáy là hình tròn tâm O và O , chiều cao
h = a 3 . Mặt phẳng đi qua tâm O và tạo với OO một góc 30 , cắt hai đường tròn tâm O và
O tại bốn điểm là bốn đỉnh của một hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng 2
3a . Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng 3 3 a 3 3 a 3 3 a A. . B. 3 3 a . C. . D. . 3 12 4
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 63
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HỌC 12 – CHƯƠNG 2 §2. MẶT CẦU
A. PHẦN KIẾN THỨC CHÍNH
I. Mặt cầu và các khái niệm liên quan đến mặt cầu
I.1. Mặt cầu
Quan sát một số hình ảnh:
Định nghĩa mặt cầu: Tập hợp các điểm M trong không gian cách điểm O cố định một khoảng R gọi là mặt
cầu tâm O, bán kính R, kí hiệu là: S(O; R). Khi đó S(O; R) = {M|OM = R} Chú ý:
* Nếu 2 điểm C, Dnằm trên mặt cầu S(O, R)thì đoạn thẳng CD được gọi là dây cung của mặt cầu (S). Dây
cung AB đi qua tâm O được gọi là một đường kính của mặt cầu (S)
* Một mặt cầu hoàn toàn được xác định nếu biết tâm và bán kính của nó hoặc
biết một đường kính của mặt cầu đó.
Ví dụ (Bài 1/ 49). Tìm tập hợp các điểm M trong không gian luôn nhìn đoạn
thẳng AB cố định dưới một góc vuông.
Giải: Tập hợp các điểm M trong không gian luôn nhìn đoạn thẳng AB cố định
dưới một góc vuông là mặt cầu đường kính AB.
I.2. Vị trí tương đối của một điểm đối với mặt cầu
Câu hỏi: Cho mặt cầuS(O; R)và một điểmAbất kì. Quan sát hình vẽ hãy cho biết B
trong không gian, có bao nhiêu vị trí tương đối giữa điểm A và mặt cầu S(O; R)?
Trả lời: Có 3 vị trí tương đối O
Kết luận: Cho mặt cầuS(O; R)và một điểm A bất kì. Khi đó: A A
Nếu OA = R ⇔ A ∈ S(O; R). Khi đó OA gọi là bán kính mặt cầu. Nếu OA
và OB là hai bán kính sao cho OA ⃗⃗⃗ = −OB
⃗⃗⃗ thì đoạn thẳngAB gọi là một A
đường kính của mặt cầu. Trang 64
Trên con đường thành công không có dấu chân của kẻ lười biếng
Nếu OA < R ⇔ Anằm trong mặt cầu.
Nếu OA > R ⇔ A nằm ngoài mặt cầu.
⇒ Khối cầu S(O; R) là tập hợp tất cả các điểm M sao cho OM ≤ R.
Định nghãi khối cầu: Tập hợp các điểm thuộc mặt cầu S(O; R) cùng với các
điểm nằm trong mặt cầu đó được gọi là khối cầu tâm O bán kính R.
I.3. Biểu diễn mặt cầu:
Hình biểu diễn của mặt cầu là một hình tròn.
Để trực quan người ta vẽ thêm hình biểu diễn của một số đường tròn nằm trên mặt cầu đó.
II. Vị trí tương đối của mặt phẳng và mặt cầu (Hướng dẫn tự học)
Cho mặt cầuS(O; R)và một mp(P). Gọi d là khoảng cách từ tâm O của mặt cầu đến mp(P) và H là
hình chiếu của O trên mp(P) ⇒ d = OH.
Nếu d < R ⇔ mp(P) cắt mặt cầu S(O; R) theo giao tuyến là đường tròn nằm trên mp(P) có tâm
là H và bán kính r = HM = √R2 − d2 = √R2 − OH2 (hình a).
Đặc biệt khi h = 0 mặt phẳng (P) cắt mặt cầu theo một đường tròn lớn có bán kính r = R và (P)
được gọi là mặt phẳng kính
Nếu d > R ⇔ mp(P) không cắt mặt cầu S(O; R) (hình b).
Nếu d = R ⇔ mp(P) có một điểm chung duy nhất. Ta nói mặt cầu S(O; R) tiếp xúc mp(P).
Điểm H: Tiếp điểm của mặt cầu S(O; R) và mặt phẳng (P).
(P) : Mặt phẳng tiếp xúc hay tiếp diện của mặt cầu.
Vậy: +(P) tiếp xúc với mặt cầu S(O; R) tại điểm H ⇔ (P)vuông góc OH tại điểm H.
+ (P) tiếp xúc với mặt cầu S(O; R) ⇔ d(O; (P)) = R. (hình c) d d = Hình a Hình b Hình c
III. Vị trí tương đối của đường thẳng và mặt cầu (Hướng dẫn tự học)
Cho mặt cầuS(O; R)và một đường thẳng Δ. Gọi H là hình chiếu của O trên đường thẳng Δvàd = OHlà
khoảng cách từ tâmOcủa mặt cầu đến đường thẳng Δ. Khi đó:
Nếu d > R ⇔ Δkhông cắt mặt cầuS(O; R).
Nếu d < R ⇔ Δcắt mặt cầuS(O; R)tại hai điểm phân biệt.
Nếu d = R ⇔ Δvà mặt cầu tiếp xúc nhau (tại một điểm duy nhất). Do đó: điều kiện cần và đủ để
đường thẳngΔtiếp xúc với mặt cầu làd = d(O, Δ) = R. Khi đó H được gọi là tiếp điểm và Δ được
gọi là tiếp tuyến của mặt cầu S. Trang 65
Trên con đường thành công không có dấu chân của kẻ lười biếng
Đặc biệt, khi d = 0 thì đường thẳng Δ đi qua tâm O và cắt mặt cầu tại hai điểm A, B. Khi đó AB là đường kính của mặt cầu. d > R d = R d < R
Δ và (S) không có điểm chung Δ tiếp xúc (S) tại H
Δ cắt (S) tại 2 điểm PB Nhận xét:
a) Qua một điểm A nằm trên mặt cầu S(O; R) có vô số tiếp tuyến của mặt cầu đó. Tất cả các tiếp
tuyến này đều vuông góc với bán kính OA của mặt cầu tại A và đều nằm trên mặt phẳng tiếp xúc với mặt cầu tại điểm A đó.
b) Qua một điểm A nằm ngoài mặt cầu S(O; R) có vô số tiếp tuyến với mặt cầu đã cho. Các tiếp
tuyến này tạo thành một mặt nón đỉnh A. Khi đó độ dài các đoạn thẳng kẻ từ A đến các tiếp điểm đều bằng nhau. Chú ý.
+ Mặt cầu nội tiếp hình đa diện nếu mặt cầu đó tiếp xúc với tất cả các mặt của hình đa diện.
+ Mặt cầu ngoại tiếp hình đa diện nếu tất cả các đỉnh của hình đa diện đều nằm trên mặt cầu. Khi
mặt cầu nội tiếp (ngoại tiếp) hình đa diện, người ta cũng nói hình đa diện ngoại tiếp (nội tiếp) mặt cầu.
IV. Công thức tính diện tích và thể tích mặt cầu
• Diện tích mặt cầu: SC = 4πR2 . 4
• Thể tích mặt cầu: VC = πR3 . 3 Ví dụ:
Ví dụ 1: Một mặt cầu (S) có bán kính bằng 2a. Tính diện tích Sc, thể tích Vc của mặt cầu (S).
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 66
Trên con đường thành công không có dấu chân của kẻ lười biếng
……………………………………………………………………………………………………
……………………………………………………………………………………………………
Ví dụ 2: Cho khối cầu (S) có thể tích bằng 36π (cm3). Diện tích mặt cầu bằng bao nhiêu?
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
Ví dụ 3: Thể tích của khối cầu có diện tích mặt cầu bằng 36π.
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
B. LUYỆN TẬP
I. Chữa bài tập SGK
Bài 2 /49. Cho hình chop đều 𝐒. 𝐀𝐁𝐂𝐃có tất cả các cạnh đều bằng 𝐚. Hãy xác định tâm và bán kính
mặt cầu ngoại tiếp hình chop đó.
Gọi O là tâm của đáy⇒ SOlà trục của đường tròn ngoại tiếp đa giác đáy.
Trong mặt phẳng xác định bởiSOvà một cạnh bên mp(SAO), ta vẽ đường
trung trực của cạnhSA và cắt SO tại I ⇒ I là tâm của mặt cầu. SN SI SN.SA SA2 Ta có: ΔSNIΔSOA ⇒ = ⇒Bán kính là R = IS = = = SO SA SO 2SO a2 a = √2 2.√2a/2 2
Bài 3 /49. Tìm tập hợp tâm mặt cầu luôn chứa một đường tròn cố định cho trước Trang 67
Trên con đường thành công không có dấu chân của kẻ lười biếng
Gọi Olà tâm của mặt cầu chứa đường tròn (C)cố định cho trước, như vậy O phải cách đều tất cả các điểm
Mthuộc đường tròn (C), suy ra O nằm trên đường thẳng đi qua tâm H của đường tròn (C) và vuông góc với
mặt phẳng (P) chứa đường tròn (C).
Bài 4 /49. Tìm tập hợp tâm những mặt cầu luôn cùng tiếp xúc với ba cạnh của một tam giác cho trước.
Cho ΔABC, gọi (C) là đường tròn nội tiếp ΔABC, O là tâm đường tròn nội tiếp của (C) ⇒ (C) tiếp xúc ba cạnh của ΔABC.
Gọi I là tâm mặt cẩu (S) chứa đường tròn (C). Suy ra (S)tiếp xúc ba
cạnh của ΔABC, I cách đều tất cả các điểm M nằm trên (C)
Vậy tâm I nằm trên trục đường tròn nội tiếp (C) (là đường thẳng đi qua
O và vuông góc với mặt phẳng chứa (C)).
Bài 7 /49. Cho hình hộp chữ nhật ABCD. A′B′C′D′ có AA′ = a, AB = b, AD = c
a. Hãy xác định tâm và bán kính mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật.
b. Tính bán kính của đường tròn là giao tuyến của mặt phẳng (ABCD) với mặt cầu trên. Giải:
a. Gọi O1O2 lần lượt là tâm đường tròn ngoại tiếp hai đáy hình hộp chữ nhậy. Suy ra O1O2 là trục
đường tròn ngoại tiếp hai đa giác đáy.
Gọi I là trung điểm của O1O2 ⇒ IA = IB = IC = IA′ = IB′ = IC′. Suy ra:
-Trung điểm I của O1O2 là tâm mặt cầu ngoại tiếp lăng trụ. O 2 √a2+b2+c2 -Bán kính: R = IA = √AO2 2 2 1O2 2 + IO2 = √AO2 + ( ) =
.(bằng một nửa đường chéo của hình 2 2 hộp chữ nhật)
Ghi nhớ: Gọi d là đường chéo hình hộp chữ nhật, a, b lần lượt là chiều dài, chiều rộng của đáy, c là chiều
cao của hình hộp ⇒ d = √a2 + b2 + c2.
Đối với hình lập phương cạnh a ⇒ d = √3a2.
b. Bán kính đường tròn giao tuyến của mặt phẳng (ABCD) với mặt cầu trên là a2 + b2 + c2 a2 b2 + c2 √b2 + c2 r = √R2 − d2 = √ − = √ = 4 4 4 2
Bài 10 /49. Cho hình chóp S. ABC có 4 đỉnh đều nằm trên một mặt cầu, SA = a, SB = b, SC = c và 3 cạnh
SA, SB, SCđôi môt vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó. Giải:
Hình chóp S. ABCcó 3 cạnh SA, SB, SCđôi môt vuông góc, lần lượt có độ dài là a, b, c sẽ nội tiếp cùng một
mặt cầu với hình hộp chữ nhật có 3 kích thước là a, b, c. Suy ra bán kính mặt cầu ngoại tiếp khối chóp √a2+b2+c2 S. ABClà R = . 2
Diện tích mặt cầu Sc = 4πR2 = π(a2 + b2 + c2) Trang 68
Trên con đường thành công không có dấu chân của kẻ lười biếng 4 1
Thể tích khối cầu Vc = πR3 = π(a2 + b2 + c2)√a2 + b2 + c2. 3 6
II. Bài tập trắc nghiệm Câu 1.
[Mức độ 1]Cho mặt cầu S(O; r). Chọn khẳng định đúng. A. S(O; r) = {M|OM = r}. B. S(O; r) = {M|OM > r}. C. S(O; r) = {M|OM < r}. D. S(O; r) = {M|OM ≥ r}. Câu 2.
[Mức độ 1]Chọn phát biểu sai.
A. Một mặt cầu được xác định nếu biết đường kính của nó.
B. Một mặt cầu được xác định nếu biết dây cung của nó.
C. Một mặt cầu được xác định nếu tâm và một điểm thuộc mặt cầu đó.
D. Một mặt cầu được xác định nếu biết tâm và bán kính của nó. Câu 3.
[Mức độ 1]Gọi (S) là mặt cầu tâm O, bán kính R; d là khoảng cách từ O đến mặt phẳng (P) với
d < R. Khi đó, số điểm chung giữa (S) và (P) là: A. 2. B. vô số. C. 1. D. 0. Câu 4.
[Mức độ 1]] Khối cầu có bán kính R = 6 có thể tích bằng bao nhiêu? A. 72π. B. 48π. C. 288π. D. 144π. Câu 5.
[Mức độ 1]Thể tích của khối cầu có diện tích mặt cầu bằng 36π. π π A. 9π B. 36π C. D. 9 3 4π Câu 6.
[Mức độ 1] Một hình cầu có thể tích bằng
ngoại tiếp một hình lập phương. 3
Thể tích của khối lập phương đó là 8√3 8 a√3 A. . B. 1. C. . D. . 9 3 2 Câu 7.
[Mức độ 1]Cho mặt cầu S(O; r)và mặt phẳng (P). Gọi d là khoảng cách từ O đến mặt phẳng (P).
Chọn phát biểu đúng.
A. Nếu d = 3 và r = 5 thì mặt phẳng (P) cắt mặt cầu S(O; r).
B. Nếu d = 6và r = 5 thì mặt phẳng (P) tiếp xúc mặt cầu S(O; r).
C. Nếu d = 5và r = 5 thì mặt phẳng (P) và mặt cầu S(O; r) không có điểm chung.
D. Nếu d = 4 và r = 6 thì mặt phẳng (P) cắt mặt cầu S(O; r) theo đường tròn giao tuyến có bán kính là 5.
Câu 9. [Mức độ 1]Trong các mệnh đề sau mệnh đề nào đúng?
A. Mọi hình hộp đều có mặt cầu ngoại tiếp.
B. Mọi hình hộp đứng đều có mặt cầu ngoại tiếp.
C. Mọi hình hộp có một mặt bên vuông góc với đáy đều có mặt cầu ngoại tiếp.
D. Mọi hình hộp chữ nhật đều có mặt cầu ngoại tiếp.
Câu 10. [Mức độ 2]Tính bán kính Rcủa mặt cầu ngoại tiếp một hình lập phương có cạnh bằng 2a. A. R = √3a. B. R = a. C. R = 2√3a. D. R = √3a. 3 Trang 69
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 11. [Mức độ 2]ba điểm phân biệt A, B, C không thẳng hàng. Tập hợp tâm O của các mặt cầu thỏa
mãn điều kiện đi qua hai điểmA, B là:
A. Đường thẳng trung trực của AB.
B. Đường tròn đường kính AB.
C. Đường tròn ngoại tiếp ΔABC.
D. Mặt phẳng trung trực của AB.
Câu 12. [Mức độ 2]Cho hình lập phương ABCD. A1B1C1D1 cạnh a. O là tâm của hình lập phương. Xét a
mặt cầu (S) tâm A bán kính . Khẳng định nào sau đây đúng? 2
A. Điểm B nằm trên (S).
B. Điểm O nằm ngoài(S).
C. Điểm O nằm trong (S).
D. Điểm B nằm trong(S).
Câu 13. [Mức độ 2]
Thể tích của khối cầu ngoại tiếp bát diện đều có cạnh bằng a là: √3πa3 √2πa3 √2πa3 8√2πa3 A. B. . C. . D. . 3 6 3 3
Câu 14. [Mức độ 2]Cho hình lăng trụ tam giác đềuABC. A′B′C′có tất cả các cạnh đều bằng 1.
Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ. 7π 7π 7π A. S = 7π. B. S = . C. S = . D. S = 2 3 6
Câu 15. [Mức độ 3] Cho hình chóp S. ABCD có đáy ABCDlà hình thoi cạnh a, ABC ̂ = 120°, tam giác SAB
đều và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S. ABC. √41 √37 √39 √35 A. a B. a C. a D. a 6 6 6 6
Câu 16. [Mức độ 3]Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a, BAD ̂ = 60° và SA = SB = a SD √15
. Mặt cầu ngoại tiếp hình chóp S. ABD có bán kính bằng
và SA > a. Thể tích khối chóp 5 S. ABCDlà a3√15 a3√5 a3√5 A. . B. . C. . D.a3√5. 3 6 2
Câu 17. [Mức độ 3]Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại B. Biết SA ⊥ (ABC), AB = a, ACB
̂ = 30𝐨, góc giữa (SBC) và (ABC) bằng 60o. Vị trí tương đối giữa mặt cầu tâm A, bán a√3 kính
với mặt phẳng (SBC) là: 2 A. Tiếp xúc.
B. Không có điểm chung.
C. Cắt nhau theo giao tuyến là một đường tròn. D. Cắt nhau theo giao tuyến là đường tròn lớn.
Câu 18. [Mức độ 3] Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại B. Biết SA ⊥ (ABC), AB =
a, góc giữa (SBC) và (ABC) bằng 60o. Mặt cầu S(A; a) cắt mặt phẳng (SBC) theo giao tuyến là
một đường tròn (C). Tính bán kính của(C). a√3 a a√3 a A. r = . B. r = . C. r = . D. r = . 2 2 4 4 Trang 70
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 19. [Mức độ 4] Cho hình chóp S. ABCD có đáy là hình chữ nhật AB = 2a, AD = a√3,
cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SD và mặt phẳng đáy
bằng 300. Diện tích mặt cầu ngoại tiếp hình chóp là. 8πa2 4πa2 A. . B. . C. 4πa2. D. 8πa2.a 3 3
BÀI TẬP TỰ LUYỆN Câu 1.
[Mức độ 1]Tính diện tích mặt cầu biết bán kính mặt cầu đó là R = √2. 2 A. S = 2π. B. S = 4π. C. S = √2π. D. S = π. 32π Câu 2.
[Mức độ 1]Diện tích của mặt cầu có thể tích là R3 bằng 3 A. 2πR2. B. πR2. C. 16πR2. D. 2πR. Câu 3.
[Mức độ 1]Cho mặt cầu S(O; r) và đường thẳng . Gọi H là hình chiếu vuông góc của O lên
đường thẳng Δ. Chọn khẳng định sai.
A. Nếu OH ≤ rthì đường thẳng  cắt mặt cầu S(O; r) tại hai điểm phân biệt.
B. Nếu OH > r thì đường thẳng  và mặt cầu S(O; r) không có điểm chung.
C. Nếu OH = r thì đường thẳng  tiếp xúc với mặt cầu S(O; r) tại H.
D. Nếu OH < r thì đường thẳng  cắt mặt cầu S(O; r) tại hai điểm phân biệt.
Câu 4. [Mức độ 1] Một khối cầu có bán kính 2R thì có thể tích V bằng bao nhiêu? 4πR3 32πR3 24πR3 A. V = 4πR2. B. V = . C. V = . D. V = . 3 3 3
Câu 5. [Mức độ 1] Diện tích của mặt cầu có bán kính 2R bằng 4π(2R)2 = 16πR2. Một hình hộp chữ
nhật có ba kích thước là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó.
Tâm của mặt cầu (S) là:
A. Một đỉnh bất kì của hình hộp chữ nhật.
B. Tâm của một mặt bên của hình hộp chữ nhật.
C. Trung điểm của một cạnh của hình hộp chữ nhật.
D. Tâm của hình hộp chữ nhật. Câu 6.
[Mức độ 1]Cho mặt cầu (S) có tâm I bán kính R = 5 và mặt phẳng (P) cắt (S) theo một đường
tròn (C) có bán kính r = 3. Kết luận nào sau đây là sai?
A. Tâm của (C) là hình chiếu vuông góc của I trên (P).
B.(C) là giao tuyến của (S)và (P).
C. Khoảng cách từ I đến (P)bằng 4.
D.(C)là đường tròn lớn của mặt cầu (S).
Câu 7. [Mức độ 2] Cho hình lăng trụ đứng ABC. A′B′C′ có đáy ABC là tam giác vuông tại B, AA′ = AB = a√2, góc BAC
̂ = 300. Thể tích khối cầu ngoại tiếp hình lăng trụ bằng: √12a3 7√42a3 √42a3 A. . B. . C. . D. 7πa3. 27 27 7 Câu 8.
[Mức độ 2] Cho hình chóp S. ABC, SA ⊥ (ABC). Tam giác ABC vuông tại A, Trang 71
Trên con đường thành công không có dấu chân của kẻ lười biếng
SA = BC = 2a. Bán kính mặt cầu ngoại tiếp khối chóp. a√2 A. a√2. B. . C. a. D. 2a. 2 Câu 9.
[Mức độ 2]Tính bán kính mặt cầu tiếp xúc với tất cả các cạnh của một hình lập phương cạnh a. √2a √3a a a A. . B. . C. . D. . 2 2 2 √2
Câu 10. [Mức độ 2] Cho hình chóp tứ giác đều có tất cả các cạnh bằng 5√2 cm. Tính thể tích V của
khối cầu ngoại tiếp khối chóp trên. 125√2 π A. V = cm3.
B. V = 100π cm3. 3 500π 250 C. V = cm3. D. V = cm3. 3 3
Câu 11. [Mức độ 2] Cho hình hộp chữ nhật có kích thức 2 × 3 × 1.
Tính diện tích mặt cầu ngoại tiếp hình hộp. A. 7π. B. 9π. C. 14π. D. 11π.
Câu 12. [Mức độ 2]Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật với độ dài đường chéo bằng
√2a, cạnh SA có độ dài bằng 2a và vuông góc với mặt phẳng đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S. ABCD ? a√6 2a√6 a√6 a√6 A. . B. . C. . D. . 2 3 12 4
Câu 13. [Mức độ 3] Cho hình chóp tam giác đều S. ABC có đáy ABC là tam giác đều cạnh a, cạnh 2a√3 SA =
. Gọi D là điểm đối xứng của B qua C. Tính bán kính R của mặt cầu ngoại tiếp 3 hình chóp S. ABD.. a√37 a√35 a√39 a√39 A. R = . B. R = . C. R = . D. R = . 6 7 7 7
Câu 14. [Mức độ 3]Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a. SA ⊥ (ABC)và SA = a√3. a√5
Vị trí tương đối giữa mặt cầu tâm A, bán kính
với mặt phẳng (SBC) là: 3 A. Tiếp xúc.
B. Không có điểm chung.
C. Cắt nhau theo giao tuyến là một đường tròn. D. Cắt nhau theo giao tuyến là đường tròn lớn.
Câu 15. [Mức độ 3] Cho hình lăng trụ đứng ABC. A′B′C′ có đáy ABC là tam giác vuông cân tại
A, BC = 3a. Góc giữa đường chéo AB′ của mặt bên B′A′AB với mặt đáy bằng 600. Tính bán
kính mặt cầu ngoại tiếp hình lăng trụ. √10a 3√10a √10a 5√10a A. . B. . C. . D. . 4 4 5 4
Câu 16. [Mức độ 4] Một quả bóng nổi trên mặt hồ khi đóng băng. Khi lấy bóng lên (không làm vỡ bóng)
bóng để lại một lỗ trũng bề ngang 2b đo ở bề mặt trên cùng và sâu a. Bán kính r(a < r < 2b) của quả bóng là: Trang 72
Trên con đường thành công không có dấu chân của kẻ lười biếng a2 + b2 𝐚𝟐 + 𝐛𝟐 a2 + b2 a2 + b2 A. r = . B. 𝐫 = . C. r = . D. r = . 2a 𝐚 b 2b
Câu 17. [Mức độ 4] Cho hình chópS. ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều
và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp khối S. ABCD. 7√21 7√21 7√21 49√21 A. πa3. B. πa3. C. πa3. D. πa3. 54 162 216 36
Câu 19. [Mức độ 4] Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, tam
giác SABđều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N lần lượt là trung điểm các
cạnh AD, DC. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S. DMN. a√102 a√31 a√39 a√39 A. R = . B. R = . C. R = . D. R = . 6 4 6 13
Câu 20. [Mức độ 4] Cho hình nón (N) có góc ở đỉnh bằng 60o, độ dài đường sinh bằng a. Dãy hình
cầu (S1), (S2), (S3), . . ., (Sn), . ..thỏa mãn: (S1) tiếp xúc với mặt đáy và các đường sinh của
hình nón (N); (S2) tiếp xúc ngoài với (S1) và tiếp xúc với các đường sinh của hình nón (N);
(S3) tiếp xúc ngoài với (S2) và tiếp xúc với các đường sinh của hình nón (N). Tính tổng thể
tích các khối cầu (S1), (S2), (S3), . . ., (Sn), . .. theo a. πa3√3 27πa3√3 πa3√3 9πa3√3 A. . B. . C. . D. . 52 52 48 16
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 73
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HỌC 12- CHƯƠNG 3
§1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN
A. PHẦN KIẾN THỨC CHÍNH
I. TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ 1. Hệ tọa độ
Trong không gian, cho ba trục ' ' '
x Ox, y Oy, z Oz vuông góc với nhau từng đôi một, với các vectơ
đơn vị i , j , k và 2 2 2
i = j = k = 1, i . j = j .k = k .i = 0 Trong đó: '
x Ox là trục hoành ' y Oy là trục tung ' z Oz là trục cao
O là gốc tọa độ
Không gian với hệ trục tọa độ Oxyz còn
được gọi là không gian Oxyz .
2. Tọa độ của điểm
Trong không gian Oxyz , điểm M có tọa độ là bộ ba số (x;y;z) khi và chỉ khi OM = xi + y j + zk
Ta viết: M = ( x; y; z) hoặc M ( x; y; z)
*Ví dụ: Cho vectơ OM = i
− + 4 j − 5k. Hãy tìm tọa độ điểm M .
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
3. Tọa độ của vectơ
Trong không gian Oxyz , vectơ a có tọa độ là bộ ba số (a ;a ;a ) khi và chỉ khi 1 2 3
a = a i + a j + a k. 1 2 3
Ta viết: a = (a ;a ;a )hoặc a(a ;a ;a ) . 1 2 3 1 2 3 Trang 74
Trên con đường thành công không có dấu chân của kẻ lười biếng
Chú ý: Trong không gian Oxyz , ta có: M = ( x; y; z)  OM = ( x; y; z ) .
*Ví dụ: Cho vectơ a = 3
− i + 4 j − 5k. Hãy tìm tọa độ điểm a .
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
II. Biểu thức tọa dộ của các phép toán vectơ a. Định lý
Trong không gian Oxyz cho a = ( a ;a ;a ),b = ( b ;b ;b ) . Ta có: 1 2 3 1 2 3
a ) a + b = ( a + b ,a + b ,a + b ) 1 1 2 2 3 3
b ) a − b = ( a − b ,a − b ,a − b ) 1 1 2 2 3 3
c ) k a = k( a ;a ;a ) = ( ka ;ka ;ka ) ( k  ) 1 2 3 1 2 3 b. Hệ quả
Trong không gian Oxyz cho a = ( a ;a ;a ),b = ( b ;b ;b ) . Ta có: 1 2 3 1 2 3 a = b 1 1 
* a = b  a = b 2 2 a = b  3 3
* Xét vectơ 0 có tọa độ là (0;0;0) →
* b  0, a cùng phương b  k   R
a = kb , a = kb , a = kb 1 1 2 2 3 3
* Trong không gian Oxyz cho hai điểm A( x ; y ; z ); B( x ; y ; z ) thì: A A A B B B
AB = ( x − x , y − y ,z − z ) B A B A B A
 x + x y + y z + z 
Nếu M là trung điểm của đoạn AB thì A B A B A B M , ,    2 2 2  c. Ví dụ. Cho a = ( 1
− ;2;3); b = ( 3;0; 5 − ) .
a. Tìm tọa độ của x biết x = 2a − 3b .
b. Tìm tọa độ của x biết 3a − b + 2x = 0 .
......................................................................................................................................................... Trang 75
Trên con đường thành công không có dấu chân của kẻ lười biếng
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
B. Bài tập trắc nghiệm (Chiếu PPT). Câu 1:
[Mức độ 1] Trong không gian Oxyz với hệ tọa độ (O;i; j;k ) cho OA = i
− + 3k . Tọa độ điểm A là A. ( 1 − ;0;3) . B. (0; 1 − ;3) . C. ( 1 − ;3;0) . D. ( 1 − ;3) . Câu 2:
[Mức độ 1] Trong không gian Oxyz, cho điểm M ( 1
− ;2;3) . Tọa độ hình chiếu của M trên trục Ox là A. ( 1 − ;2;0). B. ( 1 − ;0;0).
C. (0;0;3) .
D. (0;2;0) . Câu 3:
[Mức độ 2] Trong không gian Oxyz, cho vectơ OM = i − 3 j + 4k . Gọi M’ là hình chiếu vuông
góc của M trên mp(Oxy). Khi đó tọa độ của điểm M’ là
A. (1;− 3;4) .
B. (1;4;− 3) .
C. (0;0;4) .
D. (1;− 3;0) . Câu 4:
[Mức độ 2] Trong không gian Oxyz, cho hình bình hành ABCD, biết
A(1,0,0); B (0,0, ) 1 ; C (2 1 , , )
1 . Tọa độ điểm D là A. (3 1 , ,0) . B. (3; 1 − ;0) . C. ( 3 − 1 ; ;0) .
D. (1;3;0) . Câu 5:
[Mức độ 2] Cho ba điểm A(2, 1 − , ) 1 ; B (3, 2 − ,− )
1 . Tìm điểm N trên trục x’Ox cách đều A và B.
A. (4;0;0) . B. ( 4 − ;0;0).
C. (1;4;0) .
D. (2;0;4) . Câu 6:
[Mức độ 3] Trong không gian với hệ tọa độ Oxyz, cho A(2; 0; 0), B(0; 3; 1), C(-3; 6; 4). Gọi M
là điểm nằm trên đoạn BC sao cho MC = 2MB . Độ dài đoạn AM là --A. 2 7 . B. 30 . C. 3 3 . D. 29 .
C. BÀI TẬP TỰ LUYỆN Câu 7:
[Mức độ 2] Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a = (1 1 ; ; 2 − ), b = ( 3 − ;0;− ) 1
và điểm A(0;2; )
1 . Tọa độ điểm M thỏa mãn AM = 2a − b là A. M ( 5 − 1 ; ;2) .
B. M (3; 2 − ; ) 1 .
C. M (1;4; 2 − ) .
D. M (5;4; 2 − ) . Câu 8:
[Mức độ 2] Trong không gian với hệ tọa độ Oxyz , cho ba điểm A( 3
− ;4;2) , B( 5
− ;6;2) , C ( 4 − ;7;− ) 1
. Tọa độ điểm D thỏa mãn AD = 2AB + 3AC là Trang 76
Trên con đường thành công không có dấu chân của kẻ lười biếng A. D ( 1 − 0 1 ; 7; 7 − ) . B. D (10 1 ; 7; 7 − ).
C. D (10; 1 − 7;7). D. D ( 1 − 0; 1 − 7;7) . Câu 9:
[Mức độ 2] Trong không gian Oxyz, cho tam giác ABC có tọa độ các đỉnh A( 4;2;3 ) , B(1; 2 − ; 9 − ) và C( 1
− ;2; z ) . Xác định giá trị z để tam giác ABC cân tại A. z = 15 − z =15 z =15 z = 15 − A.  . B.  . C.  . D.  . z = 9 z = 9 − z = 9 z = 9 −
Câu 10: -[Mức độ 3] Trong không gian Oxyz, điểm M nằm trên mặt phẳng (Oxy ) , cách đều ba điểm A(2, 3 − , )
1 ,B (0;4;3) ,C ( 3
− ;2;2) có tọa độ là  17 49   4 13  A. ; ;0   . B. ( 3 − ; 6 − ;7) . C. ( 1 − ; 1 − 3 1 ; 4) . D. ; ;0    25 50   7 14 
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 77
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HỌC 12- CHƯƠNG 3
§1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN
III. TÍCH VÔ HƯỚNG
1. Biểu thức tọa độ của tích vô hướng
* VD MỞ ĐẦU: Cho các vectơ a = (a ;a ;a và b = (b ;b ;b . 1 2 3 ) 1 2 3 )
a) Hãy biểu diễn hai vectơ a,b theo ba vectơ đơn vị i , j ,k .
b) Tính tích vô hướng của hai vectơ a,b theo a ,a ,a ,b ,b ,b . 1 2 3 1 2 3
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
* Định lí: Trong không gian Oxyz, tích vô hướng của hai vectơ a = (a ; a ; a và 1 2 3 )
b = (b ; b ; b được xác định bởi công thức a.b = a b + a b + a b . 1 2 3 ) 1 1 2 2 3 3
Ví dụ 1: Trong không gian Oxyz , cho a = (1; 2; − ) 1 và b = 2
− i + 3 j − 5k . Tính tích vô hướng của hai vectơ a,b .
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
2. Ứng dụng
a) Độ dài của một vectơ
Cho vectơ a = (a ; a ; a , ta có 2 2 2 a =
a + a + a . 1 2 3 ) 1 2 3
b) Khoảng cách giữa hai điểm Trang 78
Trên con đường thành công không có dấu chân của kẻ lười biếng
Cho hai điểm A( x ; y ; z và B( x ; y ; z . Ta có B B B ) A A A )
AB = ( x − x )2 + ( y − y )2 + ( z − z )2 . B A B A B A c) Góc giữa hai vectơ
Gọi  là góc giữa hai vectơ a = (a ; a ; a và b = (b ; b ; b với a và b khác vectơ 0 thì 1 2 3 ) 1 2 3 ) + +
cos  = cos (a,b) a b a b a b 1 1 2 2 3 3 = . 2 2 2 2 2 2
a + a + a . b + b + b 1 2 3 1 2 3
* Chú ý: a ⊥ b  a b + a b + a b = 0. 1 1 2 2 3 3
Ví dụ 2: Trong không gian Oxyz cho hai điểm a = (3; 0; )
1 ,b = (1; −1; − 2) . Hãy tính a + b .
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
Ví dụ 3: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(1; 2
− ;3) , B(0; 1 − ; ) 1 và
C (4;2;− )
1 . Tính độ dài các đoạn thẳng AB, AC và côsin của góc BAC .
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
Ví dụ 4: Trong không gian Oxyz cho hai điểm A(3; 1; − 2) , B ( 1 − ; 2; )
1 . Tìm tọa độ điểm C
trên trục Oz sao cho tam giác ABC vuông tại A.
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
3. Bài tập trắc nghiệm. Câu 1:
Trong không gian với hệ trục tọa độ Oxyz cho hai vectơ a = ( 1 − 1
; ;m) , b = (1;0; ) 1 . Vectơ a vuông góc với b khi A. m = 2 − . B. m = 0 . C. m = 1. D. m = 1 − . Trang 79
Trên con đường thành công không có dấu chân của kẻ lười biếng Câu 2:
Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(3 2 ; ; ) 1 , B ( 1 − 3 ; 2 ; ) ; C (2 4 ; ;− 3) . Tích vô
hướng AB.AC là A. AD . B. 6 − . C. 2 . D. 2 − . Câu 3:
Trong không gian Oxyz, cho vectơ a = (2; 2 − ; 4 − ), b = (1; 1 − ; )
1 . Mệnh đề nào dưới đây sai?
A. a + b = (3; 3 − ; 3
− ) . B. a và b cùng phương.
C. b = 3 . D. a ⊥ b . Câu 4:
Trong không gian Oxyz, cho a, b có độ dài lần lượt là 1 và 2. Biết a + b = 3 khi đó góc giữa 2 vectơ a,b là 4   A. . B. . C. 0 . D. − 3 3 3 Câu 5:
Trong không gian Oxyz cho các điểm A(5 1
; ;5); B (4;3;2); C ( 3 − ; 2 − ; )
1 . Điểm I (a;b;c) là
tâm đường tròn ngoại tiếp tam giác ABC . Tính a + 2b + c . A. 1. B. 3 . C. 6 . D. 9 − . Câu 6:
Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A(1;0;0) , B (0;0; ) 1 , C (2 1 ; ; ) 1 .
Diện tích của tam giác ABC bằng 11 7 6 5 A. . B. . C. . D. , 2 2 2 2
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 80
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HỌC 12- CHƯƠNG 3
§1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN
IV. Phương trình mặt cầu
1. Bài toán mở đầu
Trong không gian với hệ tọa độ Oxyz , cho điểm I (a;b;c) và số dương r . Tìm điều kiện để
điểm M ( x; y; z) nằm trên mặt cầu (S ) tâm I có bán kính r .
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
Nhận xét: Mọi điểm M nằm trên mặt cầu ( S ) đều có tọa độ thỏa mãn phương trình (*).
Phương trình (*) như trên được gọi là phương trình của mặt cầu (S ) .
2. Định lí: Trong không gian Oxyz , mặt cầu ( S ) có tâm I = (a; b; c) bán kính r có phương trình là: ( − )2 +( − )+( − )2 2 2 x a y b z c = r
* Ví dụ 1: Viết phương trình mặt cầu tâm I = (1; − 2; 3) bán kính r = 5.
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
* Ví du 2: Tìm tọa độ tâm I và bán kính r của mặt cầu ( S ) , biết: 2 2 2
a) ( x − 3) + ( y + 4) + ( z − 2) = 16 . 2 2 2 b) ( x + )
1 + ( y − 5) + ( z + 3) = 25 .
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
……………………………………………………………………………………………………. Trang 81
Trên con đường thành công không có dấu chân của kẻ lười biếng
3. Nhận xét Phương trình mặ 2 2 t cầu ( − ) + ( 2 − )+( − ) 2 x a y b z c
= r có thể viết dưới dạng 2 2 2
x + y + z − 2ax − 2by − 2cz + d = 0 với 2 2 2 2
d = a + b + c − r .
Ngược lại những phương trình có dạng 2 2 2
x + y + z − 2ax − 2by − 2cz + d = 0 là phương trình
mặt cầu khi và chỉ khi 2 2 2
a + b + c − d  0 .
Khi đó mặt cầu có tâm I (a;b;c) và bán kính 2 2 2
r = a + b + c − d .
* Ví dụ 3: Trong không gian Oxyz , phương trình nào sau là phương trình mặt cầu? Nếu là
phương trình của một mặt cầu, xác định tọa độ tâm và tính bán kính của nó. a. 2 2 2
x + y + z − 4x + 6 y + 2z +14 = 0 . b. 2 2 2
x + y + z − 8xy + 2 y + 2z + 62 = 0 . c. 2 2 2
3x + y + 2z − 4x + 6 y + 2z − 6 = 0 . d. 2 2 2
x + y + z − 4x + 8y + 2z − 6 = 0 .
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
4. Bài tập trắc nghiệm. Câu 1:
Trong không gian Oxyz , mặt cầu ( S ) : 2 2 2
x + y + z + 2x − 2 y + 6z + 2 = 0 đi qua điểm nào sau đây?
A. Điểm Q (1 1 ; ; 2
− ). B. Điểm M ( 2
− ;3;7) . C. Điểm N (1;3; 2
− ) . D. Điểm P(1;3;0). Câu 2:
Trong không gian Oxyz , mặt cầu tâm I (1; 2
− ;3) bán kính r = 2 có phương trình là 2 2 2 2 2 2 A. ( x − )
1 + ( y + 2) + ( z − 3) = 4 . B. ( x + )
1 + ( y − 2) + ( z + 3) = 4 . 2 2 2 2 2 2 C. ( x − )
1 + ( y + 2) + ( z − 3) = 2 . D. ( x + )
1 + ( y − 2) + ( z + 3) = 2 . Câu 3:
Trong không gian Oxyz cho hai điểm I (1; 2
− ;3) và A(1;0;3). Mặt cầu ( S ) tâm I và đi qua điểm
A có phương trình là 2 2 2 2 2 2 A. ( x − )
1 + ( y + 2) + ( z − 3) = 2 . B. ( x + )
1 + ( y − 2) + ( z + 3) = 4 . Trang 82
Trên con đường thành công không có dấu chân của kẻ lười biếng 2 2 2 2 2 2 C. ( x − )
1 + ( y + 2) + ( z − 3) = 4 . D. ( x + )
1 + ( y − 2) + ( z + 3) = 2 . Câu 4:
Trong không gian Oxyz cho hai điểm A(2; 1
− ;0) và B(0;3; 4
− ). Mặt cầu đường kính AB có phương trình là 2 2 2 2 2 2 A. ( x − ) 1 + ( y − )
1 + ( z − 2) = 3 . B. ( x − ) 1 + ( y − )
1 + ( z + 2) = 3. 2 2 2 2 2 2 C. ( x − ) 1 + ( y − )
1 + ( z − 2) = 9 . D. ( x − ) 1 + ( y − ) 1 + ( z + 2) = 9 . Câu 5:
Trong không gian Oxyz , phương trình nào sau đây là phương trình mặt cầu? A. 2 2 2
2x + 2 y + 2z + 4x + 8y = 0 . B. 2 2 2
x + 2 y + z − 2x + 4 y − 2z −1 = 0 . C. 2 2 2
x + y + z − 2x + 2 y + 2 = 0 . D. 2 2 2
x + y − z − x + y − 5 = 0 . Câu 6:
Trong không gian Oxyz cho mặt cầu ( S ) có phương trình 2 2 2
x + y + z − 2x − 4 y − 6z + 5 = 0
Diện tích của mặt cầu ( S ) là A. 12 . B. 9 . C. 36 . D. 24 . Câu 7:
Trong không gian Oxyz cho ba điểm A(1;3;− ) 1 ,B ( 2 − 1 ; ; ) 1 ;C (4 1
; ;7) . Bán kính r của mặt cầu
đi qua bốn điểm O, A,B,C là 83 77 115 9 A. r = . B. r = . C. r = . D. r = . 2 2 2 2 Câu 8:
Tìm tất cả các giá trị thực của tham số m để phương trình 2 2 2
x + y + z − 2(m − )
1 x + 2(2m − 3) y + 2(2m + )
1 z +11− m = 0
là phương trình của một mặt cầu.
A. m  0 hoặc m  1.
B. 0  m  1 . C. m  1 − hoặc m  2 . D. 1 −  m  2 . Câu 9:
Trong không gian Oxyz cho mặt cầu ( S ) có phương trình 2 2 2
x + y + z − (2m − 2) x + 3my + (6m − 2) z − 7 = 0
Gọi r là bán kính của mặt cầu ( S ) thì giá trị nhỏ nhất của r bằng 377 377 A. 7 . B. . C. 377 . D. . 7 4
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 83
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HỌC 12 – CHƯƠNG 3: PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
§1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN
A. PHẦN KIẾN THỨC CHÍNH
1. Biểu thức tọa độ của các phép toán vectơ
Cho a = (a ;a ;a ,b = b ;b ;b k  1 2 3 ) ( 1 2 3)( )
• a  b = (a  b ;a  b ;a  b 1 1 2 2 3 3 )
• ka = (ka ;ka ;ka 1 2 3 )  a = b 1 1 • 
a = b  a = b 2 2 a = b  3 3
• a cùng phương b (b  0)  a = kb  a = kb 1 1  a a a 1 2 3
 a = kb  = = , b ,b ,b  0 2 2 ( 1 2 3 ) b b b  1 2 3 a = kb  3 3  + + + • x x y y z z 
Toạ độ trung điểm M của đoạn thẳng AB : A B A B A B M ; ;    2 2 2 
• Toạ độ trọng tâm G của tam giác ABC :
 x + x + x y + y + y
z + z + z  A B C A B C A B C G ; ;    3 3 3 
2. Tích vô hướng của 2 vectơ và ứng dụng
Cho a = (a ;a ;a ,b = b ;b ;b 1 2 3 ) ( 1 2 3)
• a.b = a .b + a .b + a .b 1 1 2 2 3 3 • 2 2 2
a = a + a + a 1 2 3 • 2 2 2
AB = AB = ( x − x ) + ( y − y ) + ( z − z ) B A B A B A + + • a.b a b a b a b 1 1 2 2 3 3 cos( a,b ) = = 2 2 2 2 2 2 a . b
a + a + a . b + b + b 1 2 3 1 2 3 B. LUYỆN TẬP
I. Bài tập tự luận sách giáo khoa Trang 84
Trên con đường thành công không có dấu chân của kẻ lười biếng Câu 1:
(Bài 1b/68) Trong không gian Oxyz , cho hai vectơ a = (2; 5
− ;3); b = (0;2;− )
1 ; c = (1;7;2) .
Tính tọa độ vectơ e = a − 4b − 2c . Câu 2:
(Bài 3/68) Trong không gian Oxyz , cho hình hộp ABCD.A' B' C' D' có A(1;0; ) 1 , B (2 1 ; ;2) , D (1; 1 − ; )
1 , C' (4;5; 5
− ) . Tìm tọa độ các đỉnh còn lại của hình hộp. A( 1
− ;2;4) B( 1 − 1
; ;4) C (0;0;4) Câu 3:
Trong không gian Oxyz , cho 3 điểm: , , . Tính
a) Độ dài các đoạn thẳng BA; BC . b) BA.BC .
c) Số đo của góc ABC .
II. Bài tập trắc nghiệm Câu 4:
[Mức độ 2] Trong không gian Oxyz , cho u = ( 1 − ;3; 2
− ) và v = (2;5;− )
1 . Tìm tọa độ của véc
tơ a = 2u − 3v . A. a = ( 8 − ;9;− ) 1 . B. a = ( 8 − ; 9 − ; ) 1 .
C. a = (8; 9 − ;− ) 1 . D. a = ( 8 − ; 9 − ;− ) 1 . Câu 5:
[Mức độ 1] Trong không gian Oxyz , cho a = (1;2; 3 − ) , b = ( 2 − ; 4
− ;6) . Khẳng định nào sau đây là đúng?
A. a = 2b . B. b = 2 − a . C. a = 2 − b .
D. b = 2a . Câu 6:
[Mức độ 2] Trong không gian Oxyz , cho tam giác ABC có A(1;2;− )
1 ; B (2;3; 2
− ); C (1;0; ) 1 .
Tìm tọa độ đỉnh D sao cho ABCD là hình bình hành? A. D (0 1 ; ;2) . B. D (0 1 ; ; 2 − ) . C. D (0; 1 − ;2).
D. D (0; 1 − ; 2 − ) . Câu 7:
[Mức độ 2] Trong không gian Oxyz , cho hình hộp ABCD.A B  C  D
  . Biết tọa độ các đỉnh A( 3 − ;2; )
1 , C (4;2;0) , B( 2 − 1 ; ; )
1 , D(3;5;4) . Tìm tọa độ đỉnh A của hình hộp. A. A' ( 3 − ;3; ) 1 . B. A' ( 3 − ;3;3) . C. A' ( 3 − ; 3 − ; 3 − ) . D. A' ( 3 − ;3; 3 − ) . Câu 8:
[Mức độ 1] Trong không gian Oxyz , cho u = ( 1
− ;3;2) , v = ( 3 − ; 1
− ;2) . Khi đó u.v bằng A. 4 . B. 2 . C. 3 . D. 2 − .
[Mức độ 2] Trong không gian Oxyz , cho a = ( 2 − ; 1
− ;2) , b = (0 1 ; ;− )
1 . Góc giữa hai vectơ a; b Câu 9: bằng A. 0 60 . B. 0 120 . C. 0 45 . D. 0 135 .
Câu 10: [Mức độ 3] Trong không gian Oxyz , cho ba điểm M (2;3;− ) 1 , N ( 1 − 1 ; ; )
1 , P (1;m −1;2) . Tìm
m để tam giác MNP vuông tại N ?
A. m = 2 . B. m = 4 − . C. m = 6 − .
D. m = 0 .
C. BÀI TẬP TỰ LUYỆN
Câu 11: [Mức độ 2] Trong không gian Oxyz , cho ba vectơ a = (1;2;3) , b = (2;2;− )
1 , c = (4;0; 4 − ) .
Tọa độ vectơ d = a − b + 2c là Trang 85
Trên con đường thành công không có dấu chân của kẻ lười biếng A. d = ( 7 − ;0; 4 − ) . B. d = ( 7 − ;0;4) .
C. d = (7;0; 4 − ) .
D. d = (7;0;4) .
Câu 12: [Mức độ 1] Trong không gian Oxyz , cho hai điểm A(2;3;− ) 1 và B ( 4 − 1
; ;9) . Trung điểm I
của đoạn thẳng AB có tọa độ là A. ( 1 − ;2;4) . B. ( 2
− ;4;8) . C. ( 6 − ; 2 − 1 ; 0) . D. (1; 2 − ; 4 − ) .
Câu 13: [Mức độ 2] Trong không gian Oxyz , cho ba điểm A(3;2; ) 1 ,B (1; 1
− ;2),C (1;2;− ) 1 . Tìm tọa độ
điểm M thỏa mãn OM = 2AB − AC . A. M ( 2 − ;6 ; 4 − ).
B. M (2; 6 − ;4 ) . C. M ( 2 − ; 6 − ;4 ). D. M (5;5 ;0 ) .
Câu 14: [Mức độ 2] Trong không gian Oxyz , cho A( 1
− ;2;4), B( 1 − 1
; ;4) , C (0;0;4) . Tính số đo của góc ABC . A. 60O . B. 135 .
C. 120O . D. 45O .
Câu 15: [Mức độ 2] Trong không gian Oxyz , cho ba điểm A( 1
− ;2;0);B( 2 − ; 2
− ;3);C (1;0; 2 − ). Mệnh đề nào sau đây đúng? A. 0 BAC = 30 . B. 0 BAC = 60 . C. 0 BAC = 90 . D. 0 BAC = 120 .
Câu 16: [Mức độ 2] Trong không gian Oxyz , cho bốn điểm A(1;0;0) , B (0 1
; ;0) , C (0;0; ) 1 , D ( 2 − 1 ; ;− )
1 . Tính góc giữa hai đường thẳng AB và CD . A. 0 135 . B. 0 60 . C. 0 90 . D. 0 45 .
Câu 17: [Mức độ 3] Cho ba điểm A(1; 3 − ; ) 1 , B ( 2 − ;6; ) 1 và C (4; 9 − ; 2
− ) . Tìm điểm M trên trục Ox
sao cho vectơ u = MA + MB + MC có độ dài nhỏ nhất.
A. M (1;0;0) .
B. M (4;0;0) .
C. M (3;0;0) .
D. M (2;0;0) .
Câu 18: [Mức độ 3] Trong không gian Oxyz , cho ba điểm A(0;0;− ) 1 , B ( 1 − 1
; ;0) , C (1;0; ) 1 . Tìm tọa
độ điểm M sao cho 2 2 2
3MA + 2MB − MC đạt giá trị nhỏ nhất.  3 1   3 1   3 3   3 1  A. M ; ; 1 −   .
B. M − ; ; 2   .
C. M − ; ; 1 −   .
D. M − ; ; 1 −   .  4 2   4 2   4 2   4 2 
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 86
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HỌC 12- CHƯƠNG 3
§1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN
TIẾT 5. BÀI TẬP PHƯƠNG TRÌNH MẶT CẦU
A. Kiến thức cần nhớ
1) Phương trình mặt cầu (S) dạng 1:
Để viết phương trình mặt cầu ( S ), ta cần tìm tâm I( a;b;c ) và bán kính R. Khi đó:  T âm: I( a;b;c ) 2 2 2 2 ( S ) : 
 ( S ) : ( x − a ) +( y −b ) +( z − c ) = R .  B án kính: R
2) Phương trình mặt cầu (S) dạng 2: Cho 2 2 2
( S ) : x + y + z − 2ax − 2by − 2cz + d = 0 .Với 2 2 2
a + b + c − d  0 là phương trình mặt
cầu dạng 2 tâm I( a;b;c ), bán kính: 2 2 2
R = a + b + c − d  0 . B. Bài tập
Dạng 1. Tìm tâm và bán kính của mặt cầu. Câu 1:
Trong không gian Oxyz , cho mặt cầu có phương trình: 2 2 2
x + y + z + 2x − 6 y − 6 = 0 . Tọa độ tâm I và bán khính của mặt cầu đó.
A. I (1; 3
− ;0);R = 4 . B. I ( 1
− ;3;0);R = 4. C. I ( 1
− ;3;0);R =16 . D. I (1; 3 − ;0);R =16. Câu 2:
Trong không gian Oxyz , cho mặt cầu (S ) 2 2 2
: x + y + z + 2x + 4 y − 2z − m = 0 . Tìm m để bán
kính cầu mặt cầu bằng 4 . A. m = 10 . B. m = 4 . C. m = 2 3 . D. m = 10 . Câu 3:
Trong không gian Oxyz , tìm tất cả các giá trị của m để phương trình 2 2 2
x + y + z + 4x − 2 y + 2z + m = 0 là phương trình của một mặt cầu. A. m  6 . B. m  6 . C. m  6 . D. m  6 .
Dạng 2. Vị trí tương đối của điểm với mặt cầu. Câu 4:
Trong không gian Oxyz , cho mặt cầu 2 2 2
( S ) : ( x −1) + ( y − 2 ) + ( z − 3 ) = 9. Điểm nào sau đây
nằm ngoài mặt cầu (S)? A. M( 1
− ;2;5 ).
B. N( 0;3;2 ) . C. P( 1 − ;6; 1 − ) .
D. Q( 2;4;5 ). Câu 5:
Trong không gian Oxyz , cho mặt cầu 2 2 2
( S ) : x + y + z − 6x − 4 y − 2z = 0 . Điểm nào sau đây
thuộc mặt cầu (S)? A. M (0 1 ; ;− ) 1 .
B. N (0;3;2) . C. P ( 1 − ;6;− ) 1 .
D. Q (1;2;0) . Câu 6:
Trong không gian với hệ tọa độ Oxyz , mặt cầu có phương trình nào sau đây đi qua gốc tọa độ? A. 2 2 2
x + y + z + 2x − 4 y − 2 = 0 . B. 2 2 2
x + y + z − 4 y + 6z − 2 = 0 . Trang 87
Trên con đường thành công không có dấu chân của kẻ lười biếng C. 2 2 2
x + y + z + 2x + 6z = 0 . D. 2 2 2
x + y + z + 2x − 4 y + 6z − 2 = 0 .
Dạng 3. Viết phương trình mặt cầu. Câu 7:
Trong không gian Oxyz , mặt cầu tâm I ( 2 − 1 ; ; )
1 qua điểm A(0;−1; 0) là 2 2 2
A. x + ( y + )2 2 2
1 + z = 9 . B. ( x − 2) + ( y + ) 1 + ( z + ) 1 = 9 . 2 2 2
C. ( x + 2) + ( y − ) 1 + ( z − ) 1 = 9 .
D. x + ( y − )2 2 2 1 + z = 9 . Câu 8:
Trong không gian Oxyz , cho hai điểm M (6;2;− 5) ,N ( 4
− ;0;7) . Viết phương trình mặt cầu
đường kính MN. 2 2 2 2 2 2 A. ( x − ) 1 + ( y − ) 1 + ( z − ) 1 = 62.
B. ( x − 5) + ( y − ) 1 + ( z + 6) = 62 . 2 2 2 2 2 2 C. ( x + ) 1 + ( y + ) 1 + ( z + ) 1 = 62 .
D. ( x + 5) + ( y + ) 1 + ( z − 6) = 62 . Câu 9:
Trong không gian Oxyz, mặt cầu (S ) có tâm I (2 1 ; ;− )
1 , tiếp xúc với mặt phẳng tọa độ (Oyz) .
Phương trình của mặt cầu (S ) là A. ( 2 2 2
x + )2 + ( y + )2 + ( z − )2 2 1 1 = 4 .
B. ( x − 2) + ( y − ) 1 + ( z + ) 1 =1. C. ( 2 2 2
x − )2 + ( y − )2 + ( z + )2 2 1 1 = 4 .
D. ( x + 2) + ( y − ) 1 + ( z + ) 1 = 2 .
Câu 10: Trong không gian Oxyz , cho A( 1
− ;0;0),B(0;0;2),C (0; 3
− ;0) . Tính bán kính mặt cầu ngoại
tiếp tứ diện OABC là 14 14 14 A. . B. . C. . D. 14 3 4 2
Câu 11: Trong không gian Oxyz , cho điểm A(1 1
; ;2) ,B (3;2; 3
− ) . Mặt cầu (S ) có tâm I thuộc Ox và
đi qua hai điểm A,B có phương trình. A. 2 2 2
x + y + z − 8x + 2 = 0 . B. 2 2 2
x + y + z + 8x + 2 = 0 . 2 2 2 2 2 2
C. x + y + z − 4x + 2 = 0 .
D. x + y + z − 8x − 2 = 0 .
Dạng 4. Các bài toán cực trị liên quan đến điểm và mặt cầu. 2 2 2
Câu 12: Trong không gian Oxyz, cho mặt cầu (S ) :( x − )
1 + ( y − 2) + ( z + ) 1 = 9 và hai điểm A(4;3; ) 1 ,B (3 1
; ;3);M là điểm thay đổi trên (S ) . Gọi m,n là giá trị lớn nhất, nhỏ nhất của biểu thức 2 2
P = 2MA − MB . Xác định m − n . A. 64. B. 48. C. 68. D. 60. Trang 88
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HỌC 11 – CHƯƠNG 3
§2. PHƯƠNG TRÌNH MẶT PHẲNG
A. PHẦN KIẾN THỨC CHÍNH
I. Vectơ pháp tuyến của mặt phẳng
➢ Định nghĩa. Cho mặt phẳng ( ) . Nếu vectơ n có giá vuông góc với ( ) thì được gọi là vectơ pháp tuyến (VTPT) của ( ) .
➢ Nhận xét. Nếu vectơ n là VTPT của ( ) thì kn ( * k  ) cũng là VTPT của ().
➢ Chú ý. Nếu hai vectơ a và b không cùng phương và có giá song song hoặc nằm trên mặt
phẳng ( ) thì n = a,b  
 là VTPT của mặt phẳng ( ) .
Tích có hướng của hai vectơ
Cho hai vectơ a = (a ;a ;a và b = (b ;b ;b . Tích có hướng của hai vectơ a và b là 1 2 3 ) 1 2 3 )  a a a a a a  2 3 3 1 1 2
n = a, b  =  ; ;
 = (a b − a b ;a b − b a ;a b − b a . 2 3 3 2 3 1 3 1 1 2 1 2 )   b b b b b b  2 3 3 1 1 2 
Nhận xét. Cho mặt phẳng ( ) đi qua ba điểm A , B , C . Khi đó mp ( ) có một VTPT là
n =  AB, AC    .
➢ Ví dụ 1. Trong không gian Oxyz cho ba điểm không thẳng hàng A(0;1;2) , B(1;−1 ) ;1 và C ( 4 − ;3;2).
a) Tìm tọa độ một VTPT của mặt phẳng đi qua ba điểm A , B , C . Trang 89
Trên con đường thành công không có dấu chân của kẻ lười biếng
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
II. Phương trình tổng quát của mặt phẳng
Trong không gian Oxyz cho mặt phẳng ( ) qua điểm M x ; y ; z và có VTPT n = ( ; A ; B C ) 0 ( 0 0 0 ) . Với M ( ;
x y; z ) bất kì, ta có
M  ( )  n.MM = 0 0
 A(x − x + B y − y + C z − z = 0 1 0 ) ( 0 ) ( 0 ) ( )
 Ax + By + Cz − Ax − By − Cz = 0 0 0 0
 Ax + By + Cz + D = 0 (2)
trong đó, D = −( Ax + By + Cz và 2 2 2
A + B + C  0 . 0 0 0 )
➢ Định nghĩa. Phương trình (2) được gọi là phương trình tổng quát của mặt phẳng ( ) nhận n = ( ; A ; B C ) làm vectơ pháp tuyến.
➢ Ví dụ 1. Trong không gian Oxyz cho ba điểm không thẳng hàng A(0;1;2) , B(1;−1 ) ;1 và C ( 4 − ;3;2) .
a) Tìm tọa độ một VTPT của mặt phẳng đi qua ba điểm A , B , C .
b) Viết phương trình tổng quát của mặt phẳng ( ) . Lời giải.
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 90
Trên con đường thành công không có dấu chân của kẻ lười biếng
……………………………………………………………………………………………………
➢ Ví dụ 2. Trong không gian Oxyz cho (Q) : x − 3y +1 = 0 . Tọa độ một VTPT của mặt phẳng (Q) là A. (1; − 3 ) ;1 . B. ( 3 − ;1;0). C. (1; − 3;0) . D. ( 2 − ;6;− 2) .
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
➢ Ví dụ 3. Trong không gian Oxyz , phương trình nào sau đây không phải là phương trình tổng
quát của mặt phẳng?
A. 2x − y = 0 . B. z +1 = 0 .
C. mx + (2m − )
1 y − z − 2 = 0 .
D. Ax + 2Ay + 3Az − 4 = 0 .
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
2. Các trường hợp riêng
Trong không gian Oxyz cho mặt phẳng ( ) : Ax + By + Cz + D = 0 ( ) 1 .
+ Nếu D = 0 thì mặt phẳng ( ) đi qua gốc tọa độ.
+ Nếu A = 0 thì mặt phẳng ( ) song song hoặc chứa trục Ox .
+ Nếu B = 0 thì mặt phẳng ( ) song song hoặc chứa trục Oy . Trang 91
Trên con đường thành công không có dấu chân của kẻ lười biếng
+ Nếu C = 0 thì mặt phẳng ( ) song song hoặc chứa trục Oz .
II. PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG
2. Các trường hợp riêng
Trong không gian Oxyz cho mặt phẳng ( ) : Ax + By + z C + D = 0 (1)
c)Nếu hai trong ba hệ số , A B, C bằng 0
+ Nếu A = B = 0 và C  0 thì ( ) song song hoặc trùng với mặt phẳng (Oxy) .
+ Nếu A = C = 0 và B  0 thì ( ) song song hoặc trùng với mặt phẳng (Oxz) .
+ Nếu B = C = 0 và A  0 thì ( ) song song hoặc trùng với mặt phẳng (Oyz) . ➢ Nhận xét: Nếu cả bốn hệ số ,
A B, C, D đều khác 0 thì phương trình x y z
Ax + By + Cz + D = 0  + + =1(2). a b c D D Với a = − , b = − D , c = − . A B C
Ta gọi phương trình (2) là phương trình mặt phẳng theo đoạn chắn. Trang 92
Trên con đường thành công không có dấu chân của kẻ lười biếng .
C. LUYỆN TẬP VÀ VẬN DỤNG
BÀI TẬP TRẮC NGHIỆM
Dạng 1. Tìm véc tơ pháp tuyến của mặt phẳng
Bài 1. Trong không gian Oxyz , cho mặt phẳng (Q) : 3y +1 = 0 . Tọa độ một VTPT của mặt phẳng (Q) là: A. (3;1;0) . B. (0;0;3) . C. (3;0;0) . D. (0;3;0)
Bài 2. Trong không gian Oxyz , cho mặt phẳng −x + 3y + 2z +1 = 0 . Tọa độ một VTPT của mặt phẳng là: A. (3; 2 ) ;1 . B. (1;3; 2) . C. (2; − 6; − 4) . D. ( 1 − ;3 ) ;1 .
Bài 3. Trong không gian Oxyz , mặt phẳng ( P) chứa b = (0; 2 )
;1 và song song a = ( 1 − ;2;3) . Mặt phẳng
(P) có VTPT là:
A. n = (2;1; − 4) . B. n = ( 4 − ;1;− 2) .
C. n = (1; − 4; 2) .
D. n = (1; 2; − 4) .
Dạng 2. Viết phương trình mặt phẳng khi biết một điểm và VTPT
Bài 4. Viết phương tình tổng quát của mặt phẳng đi qua điểm N ( 1
− ;2;0) và có VTPT a = (2;2;− 4)
A. 2x + 2 y − 4z + 4 = 0 .
B. −x − 2 y + z − 2 = 0 .
C. x + y − 2z + 2 = 0 .
D. 2x + 2 y − 4z − 2 = 0 .
Bài 5. Viết phương tình tổng quát của mặt phẳng đi qua điểm N ( 1
− ;0;2) và vuông góc với vec tơ
a = (2; 4; − 6)
A. 2x + 4 y − 6z + 5 = 0 .
B. −x − 2 y − 3z + 5 = 0 .
C. x + 2 y − 3z + 7 = 0 .
D. x + 2 y − 3z +10 = 0 .
Dạng 3. Viết phương trình mặt phẳng theo đoạn chắn
Bài 6. Trong không gian Oxyz , cho ba điểm A(1;0;0); B (0; 2
− ;0);C (0;0;5) . Mặt phẳng đi qua 3 điểm ,
A B,C có phương trình là:
A. x − 2 y + 5z = 0 .
B. x − 2 y + 5z −1 = 0 . x y z x y z C. + + = 0 . D. + + = 1. 1 2 − 5 1 2 − 5
Bài 7. Trong không gian Oxyz , mặt phẳng đi qua G (1; 2;3) và cắt các trục ;
Ox Oy; Oz tại điểm , A B, C
với G là trọng tâm ABC 
có phương trình là: x y z x y z x y z
A. x + 2 y + 3z = 0 . B. + + = 1. C. + + = 0. D. + + = 1. 1 2 3 1 2 3 3 6 9 Trang 93
Trên con đường thành công không có dấu chân của kẻ lười biếng
III. ĐIỀU KIỆN ĐỂ HAI MẶT PHẲNG SONG SONG, VUÔNG GÓC
1. Lý thuyết
Cho hai mặt phẳng ( ) : A x + B y + C z + D = 0 và ( ) : A x + B y + C z + 2 = 0 1 1 1 1 1 2 2 2 2 𝑛 ⃗ 1 ⃗ 𝑛 ⃗ 2 ⃗ 𝛼1,2 (   1 ) ( 2 ) ( cắt ( ( vuông góc ( 2 ) 1 ) 2 ) 1 ) = n k n 1 2 ( / /  D  kD n  k n n .n = 0 1 2 1 ) ( 2 ) 1 2 1 2 n = k n 1 2 D  kD 1 2
2. Các ví dụ minh họa
➢ Ví dụ 1. Cho hai mặt phẳng ( ) và ( ) có phương trình ( ) : x − 2y + 3z +1 = 0
( ):2x −4y +6z +1= 0
Có nhận xét gì về vectơ pháp tuyến của chúng?
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
➢ Ví dụ 2. Viết phương trình mặt phẳng ( ) đi qua điểm M (1;− 2;3) và song song với mặt
phẳng ( ) : 2x − 3y + z + 5 = 0 .
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
➢ Ví dụ 3. Viết phương trình mặt phẳng ( ) đi qua hai điểm A(3;1;− )
1 , B (2; −1; 4) và vuông
góc với mặt phẳng (  ) có phương trình: 2x − y + 3z −1 = 0 .
…………………………………………………………………………………………………… Trang 94
Trên con đường thành công không có dấu chân của kẻ lười biếng
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
3. Các bài tập trắc nghiệm
Bài 1. Trong không gian Oxyz cho mặt phẳng ( P) phương trình: 2x − 3y + 4z + 20 = 0 và
(Q):4x −13y −6z + 40 = 0 . Vị trí tương đối của (P) và (Q) là: A. Song song. B. Trùng nhau.
C. Cắt nhưng không vuông góc. D. Vuông góc.
Bài 2. Chọn ngẫu nhiên một số có 4 chữ số. Gọi P là xác suất để tổng các chữ số của số đó là một số lẻ.
Khi đó P bằng:
A. ( P) : 2x − y + z − 5 = 0 và (Q) : 4
− x + 2y − 2z +10 = 0 .
B. ( R) : x − y + z − 3 = 0 và (S ) : 2x − 2 y + 2z + 6 = 0 . x y z
C. (T ) : x − y + z = 0 và ( K ) : − + = 0 . 2 2 2
D. ( X ) : 3x − y + 2z − 3 = 0 và (Z ) : 6x − 2 y − 6 = 0 . Bài 3. Trong không gian Oxyz cho hai mặt phẳng
(P) : x −3y + 2z +1= 0 và
(Q):(2m− )1x + m(1−2m) y +(2m−4)z +14 = 0 . Mặt phẳng (P) ⊥ (Q) khi m bằng bao nhiêu? 3 3 3 A. m = 1; − . B. m = 1 − ;− . C. m = 2 . D. m = . 2 2 2
Bài 4. Trong không gian Oxyz cho hai mặt phẳng ( P) : 2x − y − z − 3 = 0 và (Q) : x − z − 2 = 0 . Tính góc
giữa hai mặt phẳng (P) và (Q) . A. 30 . B. 45 . C. 60 . D. 90 .
Bài 5. Trong không gian Oxyz , cho tứ diện ABCD có A(0; 2;0); B (2;0;0); C (0;0; 2 ); D(0;− 2;0) . Số
đo góc của hai mặt phẳng ( ABC) và ( ACD) là? Trang 95
Trên con đường thành công không có dấu chân của kẻ lười biếng A. 30 . B. 45 . C. 60 . D. 90 .
Bài 6. Trong không gian Oxyz , mặt phẳng ( ) đi qua điểm A(2; −1 )
;1 và vuông góc hai mặt phẳng
(P):2x − z +1= 0 và (Q): y = 0. Phương trình của mặt phẳng ( ) là:
A. 2x + y − 4 = 0 .
B. x + 2z − 4 = 0 .
C. x + 2 y + z = 0 .
D. 2x − y + z = 0 .
Bài 7. Trong không gian với hệ tọa độ Oxyz , cho hai điểm P (2;0; − )
1 ; Q (1; −1;3) và mặt phẳng
(P):3x + 2y − z +5 = 0 . Gọi ( ) là mặt phẳng đi qua P, Q và vuông góc với (P). Phương
trình của ( ) là A. 7
− x +11y + z − 3 = 0.
B. 7x −11y + z −1 = 0 . C. 7
− x +11y + z +15 = 0 .
D. 7x −11y − z +1 = 0 .
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
………………………………………………………………………………………………… Trang 96
Trên con đường thành công không có dấu chân của kẻ lười biếng HH12 – CHƯƠNG 3
§2. PHƯƠNG TRÌNH MẶT PHẲNG
A. PHẦN KIẾN THỨC CHÍNH
I. ĐỊNH NGHĨA CỔ ĐIỂN
1.Khoảng cách từ một điểm đên mặt phẳng.
Trong không gian Oxyz cho điểm M (x ; y ; z và mặt phẳng 0 0 0 )
(): Ax + By +Cz + D = 0. Khi đó khoảng cách từ điểm M đến mặt phẳng ( ) là: (
Ax + By + Cz + D d M , ( )) 0 0 0 = 2 2 2 A + B + C
B. LUYỆN TẬP
I. Các ví dụ
➢ VD1: Tính khoảng cách từ điểm M (1;3;− 2) đến ( ) : 2x − y + 2z +1 = 0 .
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
➢ VD2: Tính khoảng cách giữa hai mặt phẳng song song (P) và(Q) biết: (P) : x + 3y + z −1 = 0
; (Q) : x + 3y + z + 3 = 0 . Lời giải
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
II. Bài tập trắc nghiệm Trang 97
Trên con đường thành công không có dấu chân của kẻ lười biếng Câu 1:
[Mức độ 1] Tính khoảng cách từ điểm M (1; 2 )
;1 đến ( P) : x − 3y + z +15 = 0 . 10 11 A. . B. 11 . C. . D. 11. 11 5 Câu 2:
[Mức độ 1] Trong không gian Oxyz , khoảng cách giữa hai mặt phẳng song song:
(P): x + 2y + 2z −10 = 0 và (Q): x + 2y + 2z −3 = 0 . 8 7 4 A. . B. . C. 3 . D. . 3 3 3 Câu 3:
[Mức độ 2] Trong không gian Oxyz , Mặt cầu ( S ) có tâm I (2;1;3) và tiếp xúc với mặt phẳng
(P): x + 2y + 2z + 2 = 0, phương trình mặt cầu là: 2 2 2 2 2 2 A. ( x − )
1 + ( y − 2) + ( z − 3) = 16 . B. ( x − )
1 + ( y − 2) + ( z − 3) = 4 . 2 2 2 2 2 2 C. ( x + )
1 + ( y + 2) + ( z + 3) = 16 . D. ( x + )
1 + ( y + 2) + ( z + 3) = 4 . Câu 4:
[Mức độ 2] Trong không gian Oxyz ,cho điểm I (2;3;5) phương trình mặt cầu tâm I và tiếp xúc
với mặt phẳng (Oxy) là: 2 2 2 2 2 2
A. ( x − 2) + ( y − 3) + ( z − 5) = 5 .
B. ( x − 2) + ( y − 3) + ( z − 5) = 10 . 2 2 2 2 2 2
C. ( x + 2) + ( y + 3) + ( z + 5) = 25 .
D. ( x − 2) + ( y − 3) + ( z − 5) = 25 . Câu 5:
[Mức độ 2] Trong không gian Oxyz , điểm M thuộc trục Oy và cách đều hai mặt phẳng
(P): x + y − z +1= 0 và (Q): x − y + z −5 = 0có toạ độ là:
A. M (0; − 3;0) .
B. M (0;3;0) .
C. M (0; − 2;0) .
D. M (0;1;0) . Câu 6:
[Mức độ 2] Trong không gian Oxyz , mặt phẳng ( P) : 2x + 2 y − z + 6 = 0 cắt mặt cầu
(S) (x − )2 +( y − )2 +(z − )2 : 1 2 3
= 25 theo một giao tuyến là đường tròn (C). Diện tích của hình tròn (C) là: A. 16 . B. 4 . C. 8 . D. 20 . Câu 7:
[Mức độ 3] Trong không gian Oxyz , cho hai điểm A(2; − 2; 4) , B ( 3 − ;3;− ) 1 và mặt phẳng
(P):2x − y + 2z −8 = 0. Xét M thay đổi và M (P) , giá trị nhỏ nhất của 2 2
2AM + 3BM bằng: A. 145 . B. 135 . C. 105 . D. 108 . Câu 8:
[Mức độ 3] Trong không gian Oxyz , mặt phẳng ( P) đi qua A(1;7; 2) và cách M ( 2 − ;4;− ) 1 một
khoảng cách lớn nhất có phương trình là:
A. ( P) : 3x + 3y + 3z −10 = 0 .
B. ( P) : x + y + z +1 = 0 .
C. ( P) : x + y + z −10 = 0 .
D. ( P) : x + y + z +10 = 0 .
C. BÀI TẬP TỰ LUYỆN Câu 9:
[2H3-2.6-1] (SGD Vĩnh Phúc-2019-2020) Trong không gian Oxyz , khoảng cách từ điểm
M (1; − 4;5) đến mặt phẳng (Oxz) bằng A. 5 . B. 1. C. 42 . D. 4 . Trang 98
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 10: [2H3-2.6-1] (Chuyên Hà Giang - Năm 2019 - 2020) Cho mặt phẳng ( ) : 2x − y + 2z − 6 = 0
và điểm M (2;− 3;5) . Khoảng cách từ M đến mặt phẳng ( ) là 11 5 17 A. 5 . B. . C. . D. . 3 3 3
Câu 11: [2H3-2.6-2] (THPT Lê Văn Thịnh - Bắc Ninh - Năm 2019 - 2020) Trong không gian với hệ
trục toạ độ Oxyz , cho hai mặt phẳng ( ) : x − 2y − 2z + 4 = 0 và ( ) : x − 2y − 2z + 7 = 0 . Tính
khoảng cách giữa hai mặt phẳng ( ) và ( ) . 2 A. 1. B. . C. 6 . D. 3 . 3
Câu 12: [2H3-2.6-2] (SGD Sơn La - Năm 2019-2020) Cho mặt phẳng ( P) : x − 2y + z − 3 = 0 và điểm M ( ;1
m ; 2) với m  . Tìm tất cả cá giá trị của m sao cho khoảng cách từ điểm M đến mặt
phẳng (P) bằng 2 6 . A. m = 9; − m = 15 − .
B. m = 9; m = 15 . C. m = 9; − m =15 .
D. m = 9; m = 15 − .
Câu 13: [2H3-2.6-2] (Chuyên Quang Trung - Lần 01 - Năm 2019 - 2020) Trong không gian với hệ trục
tọa độ Oxyz , khoảng cách từ tâm mặt cầu 2 2 2
x + y + z − 4x − 4y − 4z −1 = 0 đến mặt phẳng
(P): x + 2y + 2z −10 = 0 bằng 7 4 8 A. . B. 0 . C. . D. . 3 3 3
Câu 14: [2H3-2.6-3] (Chuyên Nguyễn Trãi - Hải Dương - Năm 2019-2020) Cho hai điểm A(2;1;− ) 1 , B (0;3; )
1 . Biết tập hợp các điểm M ( ) : x + y + z + 3 = 0 thỏa mãn 2 2
2MA − MB = 4 là đường
tròn có bán kính r . Tính r .
A. r = 2 7 .
B. r = 6 .
C. r = 2 6 .
D. r = 5 .
Câu 15: [2H3-2.6-3] (Chuyên Nguyễn Trãi - Hải Dương - Năm 2019-2020) Cho mặt phẳng ( ) đi
qua hai điểm M (4;0;0) và N (0;0;3) sao cho mặt phẳng ( ) tạo với mặt phẳng (Oyz) một góc bằng 0
60 . Tính khoảng cách từ điểm gốc tọa độ đến mặt phẳng ( ) 3 2 A. 1 . B. . C. . D. 2 . 2 3
Câu 16: [2H3-2.7-2] (Chuyên Phan Bội Châu - Nghệ An - Lần 2 - Năm 2019-2020) Trong không gian
Oxyz , cho mặt cầu (S ) 2 2 2
: x + y + z = 25 và mặt phẳng ( P) : x + 2y + 2z −12 = 0 . Tính bán kính
đường tròn giao tuyến của (S ) và ( P) . A. 4. B. 16. C. 9. D. 3.
Câu 17: [2H3-2.7-2] (Vted - Đề 05 - Năm 2019-2020) Trong không gian Oxyz , mặt cầu
(S) x + y +(z − )2 2 2 : 2
= 9 cắt mặt phẳng (Oxy) theo giao tuyến là một đường tròn có bán kính bằng A. 1. B. 2 . C. 5 . D. 7 . Trang 99
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 18: [2H3-2.7-2] (THPT Đào Duy Từ - Năm 2019 - 2020) Đường tròn giao tuyến của mặt cầu
(S) (x − )2 +( y − )2 +(z − )2 : 3 2 3
= 25 khi cắt bởi mặt phẳng (Oxy) có chu vi bằng A. 8 . B. 4 . C. 2 . D. 10 .
Câu 19: [2H3-2.7-2] (THPT Hoàng Văn Thụ - Nam Định - Lần 2 - Năm 2019 - 2020) Trong không
gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : x + y + z +1 = 0 . Viết phương trình mặt cầu có tâm
I (1;1; 0) và tiếp xúc với mp(P) . A. 2 2 2
(x −1) + ( y −1) + z = 3. B. 2 2 2
(x −1) + ( y −1) + z = 3. C. 2 2 2
(x +1) + ( y +1) + z = 3. D. 2 2 2
(x +1) + ( y +1) + z = 3.
Câu 20: [2H3-2.9-2] (THPT Lương Thế Vinh – Hà Nội – Lần 01 – Năm 2019 - 2020) Trong không
gian Oxyz , cho A(1; 2;5), B (3; 4 )
;1 , C (2;3; − 3), G là trọng tâm tam giác ABC và M là điểm
trên mặt phẳng (Oxz) . Độ dài GM ngắn nhất bằng: A. 3 . B. 4 . C. 1. D. 2 .
Câu 21: [2H3-2.9-3] (THPT Cam Lộ-Quảng Trị-2019-2020) Cho mặt phẳng ( P) : 2x + 2 y − 2z +15 = 0 và mặt cầu (S ) 2 2 2
: x + y + z − 2 y − 2z −1 = 0 . Khoảng cách nhỏ nhất từ một điểm thuộc mặt
phẳng (P) đến một điểm thuộc mặt cầu (S ) là: 3 3 3 3 A. . B. . C. 3 . D. . 2 3 2
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 100
Trên con đường thành công không có dấu chân của kẻ lười biếng HH12 – CHƯƠNG 3
§2. PHƯƠNG TRÌNH MẶT PHẲNG
A. PHẦN KIẾN THỨC CHÍNH
I. ĐỊNH NGHĨA CỔ ĐIỂN
1.Tích có hướng của hai vectơ
Trong không gian Oxyz cho hai vectơ a = (a ; a ; a và b = (b ;b ;b . Khi đó 1 2 3 ) 1 2 3 )
a,b = (a b − a b ;a b − a b ;a b − a b 2 3 3 2 3 1 1 3 1 2 2 1 )   .
2. Phương trình mặt phẳng.
Trong không gian Oxyz mặt phẳng ( P) đi qua điểm M ( x ; y ; z và có một vec tơ pháp tuyến 0 0 0 ) n ( ,
A B, C ) có phương trình dạng: ( P) : A( x − x + B y − y + C z − z = 0 0 ) ( 0 ) ( 0 )
3. Vị trí tương đối của hai mặt phẳng.
Trong không gian Oxyz , cho hai mặt phẳng ( , ( lần lượt có phương trình 2 ) 1 )
( : A x + B y +C z + D = 0, ( : A x + B y +C z + D = 0 , với 2 ) 1 ) 1 1 1 1 2 2 2 2 Gọi  + + + = 1
n ( A ; B ;C là VTPT ( : A x By C z D 0 ; 1 ) 1 1 1 ) 1 1 1 n  + + + = 2 2 2 + +  =
2 ( A ; B ; C là VTPT ( : A x B y C z D 0 , A B C 0 (k 1; 2) . 2 ) 2 2 2 ) 2 2 2 2 k k k Khi đó: (   )  ( )  = 1 n k n2 A B C D 1 1 1 1    = = =
A .B .C .D  0 . 1 2 ( 2 2 2 2 ) D = kD A B C D  1 2 2 2 2 2 (   ) n = kn A B C D || ( ) 1 2 1 1 1 1    = = 
A .B .C  0 1 2 ( 2 2 2 ) D  D A B C D  1 2 2 2 2 2 ( )  ( ) A B C D 1 1 1 1  = = = . 1 2 A B C D 2 2 2 2
( cắt (  A : B :C  A : B :C 2 ) 1 ) 1 1 1 2 2 2 THđặc biệt:
( ⊥   A A + B B +C C = 0. 1 ) ( 2) 1 2 1 2 1 2
4. Góc giữa hai mặt phẳng.
Trong không gian Oxyz , cho hai mặt phẳng ( , ( lần lượt có phương trình 2 ) 1 )
( : A x + B y +C z + D = 0, ( : A x + B y +C z + D = 0 , với 2 ) 1 ) 1 1 1 1 2 2 2 2 Gọi  + + + = 1
n ( A ; B ;C là VTPT ( : A x By C z D 0 ; 1 ) 1 1 1 ) 1 1 1 n  + + + = 2 2 2 + +  =
2 ( A ; B ; C là VTPT ( : A x B y C z D 0 , A B C 0 (k 1; 2) . 2 ) 2 2 2 ) 2 2 2 2 k k k
Góc giữa hai mặt phằng ( , ( và, kí hiệu (( ,  là góc. 1 ) ( 2 )) 2 ) 1 ) 
Từ đó suy ra 0  (( ,   . 1 ) ( 2 )) 2 Trang 101
Trên con đường thành công không có dấu chân của kẻ lười biếng
và có công thức tính như sau: (( + +  ) ( )) = ( n  .n  A A B B C C cos , cos n( 1 2 1 2 1 2  ; n  = = 1 2 1 ) ( 2) ) ( 1) ( 2 ) n( 2 2 2 2 2 2  n 
A + B + C . A + B + C 1 ) ( 2 ) 1 1 1 2 2 2
B. LUYỆN TẬP
I. Các ví dụ
➢ VD1: Cho ba điểm A(5;1;3) , B(1;6;2) , C (5;0;4) . Tìm vectơ pháp tuyến của mặt phẳng (P)
song song với ( ABC) .
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
➢ VD2: Cho ba điểm A(2;−1 )
;1 , B (1;0;3) , P (0; − 2 )
;1 . Viết phương trình mặt phẳng ( P) đi
qua trọng tâm G của ABC 
và vuông góc với BC .
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
➢ VD3: Tìm m + n để (P) : 2x + my + 3z − 5 = 0 song song với (Q) : nx −8y + 6z + 2 = 0 .
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
➢ VD4: Tính góc giữa hai mặt phẳng: (P) : x − 2y − z + 2 = 0 và (Q) : 2x − y + z +1 = 0 .
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
➢ VD5: Tìm m để điểm A( ;
m m −1;1+ 2m) thuộc mặt phẳng ( P) : 2x − y − z +1 = 0 .
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
……………………………………………………………………………………………………. Trang 102
Trên con đường thành công không có dấu chân của kẻ lười biếng
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
II. Bài tập trắc nghiệm Câu 1:
[Mức độ 1] Toạ độ vecto pháp tuyến của mặt phẳng có cặp vecto chỉ phương a = (2;1; 2) , b = (3; 2 ) ;1 là: A. (5;8; − ) 1 . B. (5; − 8 ) ;1 . C. (5; − 8; − ) 1 . D. (5;8 ) ;1 . Câu 2:
[Mức độ 1] Toạ độ vectơ pháp tuyến của mặt phẳng đi qua ba điểm A(1;0; 2) , B (1;1 ) ;1 , C (2;3;0) là? A. (1;1; )1 − . B. (1; 1 − ;− ) 1 . C. (1;1 ) ;1 . D. (1;1; 2 − ) . Câu 3:
[Mức độ 2] Phương trình mặt phẳng trung trực của đoạn thẳng AB với A(1; − 2;3); B ( 3 − ;2 ) ;1 là?
A. 2x − 2 y + z = 0 .
B. 2x − 2 y + z +1 = 0 . C. 2x + 2 y + 2z +1 = 0 . D. 2x + y − z −1 = 0 . Câu 4:
[Mức độ 2] Viết phương trình mặt phẳng ( P) biết ( P) đi qua A(1; − 3; 4) và ( P) song song với
(Q):6x −5y + z +7 = 0
A. 6x − 5y + z + 25 = 0 . B. 6x − 5y + z − 7 = 0 .
C. 6x − 5y + z − 25 = 0 . D. 6x − 5y + z +17 = 0 . Câu 5:
[Mức độ 2] Mặt phẳng ( P) qua G (1; 2;3) cắt các trục toạ độ tại ;
A B; C sao cho G là trọng
tâm của tam giác ABC có phương trình là ax + by + cz −18 = 0 . Gía trị của a + b + c bằng A. 9 . B. 12 . C. 10 . D. 11. Câu 6:
[Mức độ 2] Cho hai mặt phẳng ( P) : 2x + y + mz − 2 = 0 và và (Q) : x + ny + 2z + 8 = 0 song song
với nhau.Tính tổng m + n bằng A. 4, 25 . B. 4, 5 . C. 2, 5 . D. 2, 25 . Câu 7:
[Mức độ 2] Trong không gian Oxyz cho mặt phẳng ( ) 2 m x − y + ( 2 :
m − 2) z + 2 = 0 và ( ) 2
: x + m y − 2z +1 = 0 (m  ) . Tìm m để ( ) ⊥ ( )
A. m = 1.
B. m = 2 .
C. m = 3 .
D. m = 2 . Câu 8:
[Mức độ 2] Tính góc giữa hai mặt phẳng: ( P) : x + z − 4 = 0 và (Oxy) . A. 60o . B. 30o . C. 45o . D. 90o . Câu 9:
[Mức độ 2] Điểm M ( ,
m 1; 6) thuộc mặt phẳng ( P) : x − 2y + z − 5 = 0 khi đó m thuộc khoảng
nào trong các khoảng sau đây? A. (0; 2) . B. ( 2 − ;0) . C. (2; 4) . D. (2;3) .
C. BÀI TẬP TỰ LUYỆN
Câu 10: [2H3-2.1-1] (THPT Ngô Quyền - Hà Nội - Lần 01 - Năm 2018 - 2019) Toạ độ một vectơ pháp
tuyến của mặt phẳng ( ) đi qua ba điểm M (2;0;0) , N (0;− 3;0), P(0;0;4) là Trang 103
Trên con đường thành công không có dấu chân của kẻ lười biếng A. (2; 3 − ;4) . B. ( 6 − ;4; 3 − ). C. ( 6 − ; 4 − ;3) . D. ( 6 − ;4;3).
Câu 11: [2H3-2.1-2] (THPT Cụm Trần Kim Hưng - Hưng Yên - Năm 2018 - 2019) Trong không gian
với hệ tọa độ Oxyz , cho điểm A( 3 − ;−1;3), B( 1 − ;3; )
1 và ( P) là mặt phẳng trung trực của đoạn
thẳng AB . Một vectơ pháp tuyến của (P) có tọa độ là: A. ( 1 − ;3; ) 1 . B. ( 1 − 1 ; ;2). C. ( 3 − ;−1;3) . D. (1;2;− ) 1 .
Câu 12: [2H3-2.4-1] Trong không gian Oxyz , mặt phẳng ( P) : x + y + z − 3 = 0 đi qua điểm nào dưới đây? A. M ( 1 − ;−1;− ) 1 B. N (1;1 ) ;1 C. P ( 3 − ;0;0)
D. Q (0;0; − 3)
Câu 13: [2H3-2.5-1] (Chuyên Phan Bội Châu - Nghệ An - Lần 4 - 2018 - 2019) Trong không gian
Oxyz , cho hai mặt phẳng ( P) : x − 2 y − z +1 = 0 , (Q) : x + y + 2z + 7 = 0 . Tính góc giữa hai mặt phẳng đó. A. o 60 . B. o 45 . C. o 120 . D. o 30 .
Câu 14: [2H3-2.3-1] (THPT Trần Phú - Hải Phòng - Lần 03 - Năm - 2018 -2019) Trong không gian
Oxyz, cho hai mặt phẳng ( P) : x – 2y + 2z – 3 = 0 và (Q) : mx + y – 2z +1 = 0 . Với giá trị nào của
m thì hai mặt phẳng đó vuông góc với nhau?
A. m = 1. B. m = 1 − . C. m = 6 − . D. m = 6 .
Câu 15: n .n = 0  m − 2 − 4 = 0  m = 6 . [2H3-2.11-2] (THPT Trần Phú - Hà Tĩnh - Năm 2019 - 1 2
2020) Trong không gian Oxyz . Cho hai điểm A(2; −1;5) và B (0;1;3 ). Mặt phẳng trung trực
của đoạn thẳng AB có phương trình là
A. x + 3y − z + 3 = 0 .
B. x − y + z − 5 = 0 .
C. x − y + z + 6 = 0 .
D. x + 3y − 5z −1 = 0 .
Câu 16: [2H3-2.11-2] (Love book - Đề số 15 - Năm 2018 - 2019) Cho ba điểm M (0; 2; 0); N (0; 0;1); (
A 3; 2;1) . Lập phương trình mặt phẳng (MNP) . biết điểm P là hình chiếu vuông góc của điểm
A lên trục Ox . x y z x y z x y z x y z A. + + = 1 B. + + = 1 C. + + = 1 D. + + = 1 2 1 3 3 2 1 2 1 1 3 2 1
Câu 17: [2H3-2.5-2] (THPT Nguyễn Khuyến-Lần 5-2018-2019) Trong không gian với hệ trục tọa độ
Oxyz , cho điểm H (2;1; 2) , H là hình chiếu vuông góc của gốc tọa độ O xuống mặt phẳng ( P)
, số đo góc giữa mặt (P) và mặt phẳng (Q) : x + y −11 = 0 0 0 0 0 A. 60 B. 30 C. 45 D. 90
Câu 18: [2H3-2.3-2] (Chuyên Quang Trung - Bình Phước - Lần 05 - Năm 2018 - 2019) Trong không
gian Oxyz , cho A(0;1 )
;1 , B (1;0;0) và mặt phẳng ( P) : x + y + z − 3 = 0 . (Q) là mặt phẳng song
song với (P) đồng thời đường thẳng AB cắt (Q) tại C sao cho CA = 2CB . Mặt phẳng (Q) có phương trình là: 4
A. x + y + z −
= 0 hoặc x + y + z = 0 .
B. x + y + z = 0 . 3 Trang 104
Trên con đường thành công không có dấu chân của kẻ lười biếng 4
C. x + y + z − = 0 .
D. x + y + z − 2 = 0 hoặc x + y + z = 0 . 3
Câu 19: [2H3-2.4-2] (THPT Sơn Tây- Hà Nội- Lần 02- Năm 2018- 2019) Trong không gian với hệ tọa
độ Oxyz , cho mặt phẳng (P) : 2x − 2y + z + 3 = 0 và điểm A(1;− 2;3) . Gọi M ( ; a ;
b c) ( P) sao
cho AM = 4 . Tính a + b + c . 2 8 A. . B. 2 . C. . D. 12 . 3 3
Câu 20: [2H3-2.4-3] (Chuyên Lê Hồng Phong - Nam Định - Lần 01 - Năm 2018 - 2019) Trong không
gian với hệ tọa độ Oxyz , cho mặt phẳng (P) :x + y − z + 2 = 0 và hai điểm A(3;4 ) ;1 ;
B (7; − 4; − 3) . Điểm M ( ; a ;
b c)(a  2) thuộc ( P) sao cho tam giác ABM vuông tại M và có
diện tích nhỏ nhất. Khi đó giá trị biểu thức T = a + b + c bằng: A. T = 6 . B. T = 8 . C. T = 4 . D. T = 0 .
Câu 21: [2H3-2.3-3] (ĐTD - ĐỀ 01 - NĂM 2018-2019) Trong không gian với hệ tọa độ Oxyz , cho điểm
M ( –3; 2; 4) , gọi A , B , C lần lượt là hình chiếu của M trên Ox , Oy , Oz . Mặt phẳng nào sau
đây song song với mp( ABC) ?
A. 4x − 6 y − 3z +12 = 0 .
B. 3x − 6 y − 4z +12 = 0 .
C. 4x − 6 y − 3z −12 = 0 .
D. 6x − 4 y − 3z −12 = 0 .
Câu 22: [2H3-2.5-3] (SGD Đà Nẵng - Năm 2018 - 2019) Trong không gian Oxyz , cho hai điểm
A(1;0;0) , B (0;0 )
;1 và mặt phẳng ( P) : 2x − 2y − z + 5 = 0 . Tọa độ điểm C trên trục Oy sao
cho mặt phẳng ( ABC) hợp với mặt (P) một góc 45 là  2 + 2   1   2 + 2   1  A. C  0; − ; 0    . B. C 0; ;0   . C. C  0; ; 0  
 . D. C 0;− ;0   . 2    4  2    4 
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 105
Trên con đường thành công không có dấu chân của kẻ lười biếng
Chương 3: PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Bài 2: PHƯƠNG TRÌNH MẶT PHẲNG (tiết 5)
A. PHẦN KIẾN THỨC CHÍNH
1. Trong không gian Oxyz cho điểm M ( x ; y ; z và mặt phẳng 0 0 0 )
(P): Ax + By +Cz + D = 0. Khi đó khoảng cách từ điểm M đến mặt phẳng (P) là: (
Ax + By + Cz + D d M , ( P)) 0 0 0 = 2 2 2 A + B + C
2. Cho mặt phẳng (P) : Ax + By + Cz + D = 0 và mặt cầu
(C) (x −a)2 +( y −b)2 +(z −c)2 2 :
= R . Khi đó mặt cầu (C) có tâm I ( ; a ;
b c) và bán kính R
+) Nếu d (M ,(P))  R suy ra (P) và (C) không có điểm chung.
+) Nếu d (M ,(P)) = R suy ra (P) và (C) tiếp xúc nhau.
+) Nếu d (M ,(P))  R suy ra (P) và (C) cắt nhau.
3.Mặt phẳng (P) (Hình 7.5) đi qua ba điểm M ( ; a 0; 0), N (0; ;
b 0), P (0;0;c) trong đó a, b, c đều khác x y z
0 có phương trình ( P) : +
+ = 1. được gọi phương trình mặt phẳng theo đoạn a b c chắn. B. LUYỆN TẬP
I. Các ví dụ minh hoạ Câu 1:
Trong không gian Oxyz cho mặt phẳng (P) : x − 2y + 2z −1 = 0 . Viết phương trình mặt phẳng
(Q) song song và cách mặt phẳng (P) một khoảng bằng 5. Lời giải Trang 106
Trên con đường thành công không có dấu chân của kẻ lười biếng 𝑃 . 𝐴 𝑄
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
……………………………………………………………………………………………………………….. Câu 2:
Trong không gian Oxyz cho hai mặt phẳng (P) :3x − y + 4z + 2 = 0 và (Q) :3x − y + 4z + 8 = 0 .
Viết phương trình mặt phẳng (R) song song và cách đều hai mặt phẳng (P) và (Q) .
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
……………………………………………………………………………………………………………….. Câu 3:
. Trong không gian Oxyz cho mặt phẳng (P) : 2x − y + 2z +1 = 0 và mặt cầu
(C) (x − )2 +( y − )2 +(z − )2 : 1 2 3
= 4. Hãy xét vị trí tương đối giữa (P) và (C)
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
……………………………………………………………………………………………………………….. Câu 4:
Trong không gian Oxyz cho mặt phẳng (P) : 2x − y + 2z + 6 = 0 và mặt cầu
(C) (x − )2 +( y − )2 +(z − )2 : 1 2 3
= 25. Biết (P) và (C) cắt nhau theo giao tuyến là một đường
tròn. Tính bán kính đường tròn đó.
……………………………………………………………………………………………………………….. Trang 107
Trên con đường thành công không có dấu chân của kẻ lười biếng
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
……………………………………………………………………………………………………………….. Câu 5:
Trong không gian Oxyz cho mặt phẳng (P) : x + 2y − 2z −1 = 0. Viết phương trình mặt cầu (C)
tâm I (1;−1;2) và tiếp xúc với (P) .
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
……………………………………………………………………………………………………………….. Câu 6:
Cho hai điểm A(3;5;− )
1 , B(1;1;3) . Tìm tọa độ điểm M thuộc (Oxy) sao cho MA + MB nhỏ nhất?
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..  −  Câu 7:
Trong không gian Oxyz , cho hai điểm M (2; 2; ) 1 , 8 4 8 N ; ; 
 . Viết phương trình mặt cầu có  3 3 3 
tâm là tâm của đường tròn nội tiếp tam giác OMN và tiếp xúc với mặt phẳng (Oxz) .
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
……………………………………………………………………………………………………………….. Trang 108
Trên con đường thành công không có dấu chân của kẻ lười biếng
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
……………………………………………………………………………………………………………….. Câu 8:
Trong không gian với hệ tọa độ Oxyz , cho điểm M ( 2
− ;4;2) . Viết phương trình mặt phẳng (P)
đi qua 3 điểm M , M , M lần lượt là hình chiếu của M trên các trục tọa độ Ox , Oy , Oz . 1 2 3
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………..
II. Bài tập trắc nghiệm Câu 9:
Trong không gian Oxyz , phương trình mặt phẳng ( P) đi qua điểm M (1;3; − 2) , cắt các tia Ox OA OB OC
, Oy , Oz lần lượt tại A , B , C sao cho = = là: 1 2 4
A. 2x − y − z −1 = 0 B + + + = + + + = + + − = . x 2 y 4z 1 0 C. 4x 2 y z 1 0. D. 4x 2 y z 8 0.
Câu 10: Viết phương trình mặt phẳng ( P) qua M (1; 2 )
;1 lần lượt cắt các tia Ox, Oy, Oz tại các điểm ,
A B, C sao cho hình chop . O ABC đều.
A. x − y + z = 0.
B. x + y + z − 4 = 0 . C. x − y + z − 4 = 0 . D x + y + z −1 = 0.
Câu 11: Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A( 2
− ;3;4) , B(8;−5;6) . Hình chiếu
vuông góc của trung điểm I của đoạn AB trên mặt phẳng (Oyz) là điểm nào dưới đây.
A. M (0; −1;5) . B. Q (0;0;5) . C. P (3;0;0) .
D. N (3; −1;5) .
Câu 12: Trong không gian tọa độ Oxyz , cho mặt cầu (S ) có đường kính AB , với A(6; 2; − 5) , B ( 4
− ;0;7). Viết phương trình mặt phẳng (P) tiếp xúc với mặt cầu (S ) tại A .
A. (P) :5x + y – 6z + 62 = 0 .
B. (P) :5x + y – 6z − 62 = 0 .
C. (P) :5x − y – 6z − 62 = 0 .
D. (P) :5x + y + 6z + 62 = 0 . Trang 109
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 13: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng
(P): x −2y + 2z −2 = 0 và điểm I ( 1 − ; 2; − )
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt
mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 5 . A. ( 2 2 2
S ) ( x + )2 + ( y − )2 + ( z + )2 : 1 2 1 = 25.
B. (S ) :(x + )
1 + ( y − 2) + ( z + ) 1 =16. C. ( 2 2 2
S ) ( x − )2 + ( y + )2 + ( z − )2 : 1 2 1 = 34.
D. (S ) :(x + )
1 + ( y − 2) + ( z + ) 1 = 34.
Câu 14: . Trong không gian Oxyz , cho điểm H (2; 1; )
1 . Gọi ( P) là mặt phẳng đi qua H và cắt các trục
tọa độ tại A , B , C sao cho H là trực tâm tam giác ABC . Phương trình mặt phẳng (P) là
A. 2x + y + z − 6 = 0 .
B. x + 2y + z − 6 = 0 . C. x + 2y + 2z − 6 = 0 . D. 2x + y + z + 6 = 0 .
C. BÀI TẬP TỰ LUYỆN
Câu 15: [2H3-2.6-1] (THPT Thạch Thành I-Thanh Hóa-Năm 2018-2019) Trong không gian Oxyz ,
khoảng cách từ điểm A(0;0;5) đến mặt phẳng (P) : x + 2y + 2z − 3 = 0 bằng: 8 7 4 A. . B. . C. 3 . D. . 3 3 3
Câu 16: [2H3-2.6-2] (Vted - Đề số 09 - Năm 2018 - 2019) Trong không gian Oxyz , phương trình mặt
phẳng P song song và cách mặt phẳng Q : x 2y 2z 3 0 một khoảng bằng 1; đồng thời
P không qua O là
A. x + 2 y + 2z +1 = 0 B. x + 2 y + 2z = 0
C. x + 2 y + 2z − 6 = 0 D. x + 2 y + 2z + 3 = 0
Câu 17: [2H3-2.12-1] (Chuyên Quang Trung - Bình Phước - Lần 05 - Năm 2018 - 2019) Trong không
gian Oxyz , mặt phẳng đi qua 3 điểm A(1;0;0) , B (0; 2;0) , C (0;0;3) có phương trình là x y z x y z x y z x y z A. + + = 1. B. + + = 0. C. + + = 1 − . D. + + = 1. 1 2 3 1 2 3 1 2 3 1 1 3
Câu 18: [2H3-2.12-2] (THPT Trần Phú - Hải Phòng - Lần 03 - Năm - 2018 -2019) Trong không gian
Oxyz, cho điểm M (8; − 2; 4) . Gọi ,
A B, C lần lượt là hình chiếu của M trên các trục Ox, Oy,
Oz . Phương trình mặt phẳng đi qua ba điểm ,
A B và C là
A. x + 4 y − 2z − 8 = 0. B. x − 4 y + 2z −18 = 0. C. x + 4 y + 2z − 8 = 0. D. x − 4 y + 2z − 8 = 0.
Câu 19: [2H3-2.12-2] (Vted - Đề số 12 - Năm 2018 - 2019) Trong không gian Oxyz , cho điểm G (1; 4;3)
. Viết phương trình mặt phẳng cắt các trục tọa độ Ox, Oy, Oz lần lượt tại ,
A B, C sao cho
G là trọng tâm của tứ diện OABC . x y z x y z A. + + = 1. B. + + = 1. 3 12 9 4 16 12
C. 3x +12 y + 9z − 78 = 0 .
D. 4x +16 y +12z −104 = 0 .
Câu 20: [2H3-2.6-2] (Vted - Đề số 20 - Năm 2018-2019) Trong không gian Oxyz , cho ba điểm A( ; a 0; 0), B (0; ;
b 0), C (0;0;c) với a, ,
b c là các số thực dương thay đổi thỏa mãn
a + b + c = 3 . Khoảng cách từ gốc tọa độ O đến mặt phẳng ( ABC ) có giá trị lớn nhất bằng 1 3 A. 3 . B. . C. . D. 3 3 . 3 3 Trang 110
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 21: [2H3-2.6-3] (Vted - Đề số 13 - Năm 2018 - 2019) Trong không gian Oxyz, cho ba điểm (
A 1;0;0), B(0;1;0), C(0; 0;1) . Số mặt phẳng đi qua gốc tọa độ O và cách đều ba điểm , A B, C là A. 8 . B. 6 . C. 4 . D. 2 .
Câu 22: [2H3-2.12-3] (ĐTD - Đề 18 - Năm 2018-2019) Trong không gian với hệ trục tọa độ Oxyz , cho
điểm M (3;4;5) . Gọi (P) là mặt phẳng qua M sao cho (P) cắt các trục tọa độ tại các điểm , A
B, C sao cho khoảng cách từ gốc tọa độ tới ( P) là lớn nhất. Thể tích khối tứ diện OABC là? 6250 3125 24 144 A. B. C. D. 3 9 5 5
Câu 23: [2H3-2.8-1] (Chuyên Vinh - Lần 3 - Năm 2018 - 2019) Trong không gian Oxyz , cho điểm
I (1; 2;5) và mặt phẳng ( ) : x − 2y + 2z + 2 = 0 . Phương trình mặt cầu tâm I và tiếp xúc với ( ) là 2 2 2 2 2 2 A. ( x − ) 1
+ ( y − 2) + (z − 5) = 3. B. ( x + ) 1
+ ( y + 2) + (z + 5) = 3. 2 2 2 2 2 2 C. ( x − ) 1
+ ( y − 2) + (z − 5) = 9 . D. ( x + ) 1
+ ( y + 2) + (z + 5) = 9.
Câu 24: [2H3-2.8-2] (THPT Yên Dũng 2 - Bắc Giang - Lần 04 - Năm 2018 - 2019) Trong không gian
với hệ tọa độ Oxyz , cho mặt cầu (S ) có tâm I ( 1
− ;2;0). Biết mặt phẳng (P):3x + y − z −10 = 0
cắt (S ) theo giao tuyến là đường tròn bán kính bằng 2, tính bán kính R của mặt cầu (S ) . 15 13 A. 15 . B. . C. 3 . D. . 2 2
Câu 25: [2H3-2.8-4] (ĐTD - Đề tuần 16 - Năm 2018-2019) Trong không gian với hệ tọa độ Oxyz , cho
mặt phẳng ( P) : x + 2y + z − 4 = 0 . Có tất cả bao nhiêu mặt cầu có tâm nằm trên mặt phẳng ( P)
và tiếp xúc với ba trục tọa độ x 'Ox, y 'Oy, z 'Oz ?
A. 8 mặt cầu
B. 4 mặt cầu
C. 3 mặt cầu D. 1 mặt cầu
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………… Trang 111
Trên con đường thành công không có dấu chân của kẻ lười biếng
HÌNH HỌC 12 – CHƯƠNG 3
§2. PHƯƠNG TRÌNH ĐƯỜNG THẲNG .
Câu hỏi: Nhắc lại phương trình tham số của đường thẳng trong mặt phẳng Oxy?
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
I. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG
1. Vectơ chỉ phương của đường thẳng
Cho đường thẳng . Vectơ u  0 gọi là vectơ chỉ phương của đường thẳng  nếu giá của nó
song song hoặc trùng với . Trang 112
Trên con đường thành công không có dấu chân của kẻ lười biếng Chú ý:
+ Nếu u là vectơ chỉ phương của  thì k.u (k  0) cũng là vectơ chỉ phương của .
+ Nếu đường thẳng  đi qua hai điểm A, B thì AB là một vectơ chỉ phương.
2. Phương trình tham số của đường thẳng Định lí:
Cho đường thẳng  đi qua M (x ; y ; z và có vectơ chỉ phương là u = ( ; a ;
b c) . Điều kiện cần 0 0 0 )
x = x + at 0 và đủ  để điểm M ( ;
x y; z ) nằm trên  là có một số thực t sao cho  y = y + bt . 0
 z = z + ct  0 Định nghĩa:
Phương trình tham số của đường thẳng  đi qua M (x ; y ; z và có vectơ chỉ phương là 0 0 0 ) u = ( ; a ;
b c) là phương trình có dạng
 x = x + at 0 
 y = y + bt , t  1 0 ( )
 z = z + ct  0 Trong đó t là tham số. Chú ý: Nếu a, ,
b c đều khác 0 thì người ta còn có thể viết phương trình của đường thẳng  dưới dạng x − x y − y z − z chính tắc như sau: 0 0 0 = = a b c Nhận xét:
Để viết được phương trình đường thẳng cần biết một điểm thuộc đường thẳng và một véc tơ chỉ
phương của đường thẳng đó.
Ví dụ 1. Trong không gian Oxyz, phương trình tham số của đường thẳng đi qua điểm M (2; 1 − ;3) và có
vectơ chỉ phương u (1;2; 4 − ) là Trang 113
Trên con đường thành công không có dấu chân của kẻ lười biếng x = −1+ 2t  x = 1+ 2t  x = −2 + t  x = 2 + t    
A.  y = −2 − t .
B.  y = 2 − t . C.  y = 1+ 2t . D.  y = 1 − + 2t .     z = 4 + 3t  z = −4 + 3t  z = −3 − 4t  z = 3 − 4t 
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
Ví dụ 2. Trong không gian Oxyz, phương trình chính tắc của đường thẳng đi qua điểm M (2; 1 − ;3) và có
vectơ chỉ phương u (1;2; 4 − ) là x +1 y + 2 z − 4 x −1 y − 2 z + 4 A. = = . B. = = . 2 1 − 3 2 1 − 3 x + 2 y −1 z + 3 x − 2 y +1 z − 3 C. = = . D. = = . 1 2 4 − 1 2 4 −
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
Ví dụ 3. Trong không gian Oxyz, cho điểm A(1; 2;3) và mặt phẳng ( P) có phương trình
3x − 4y + 7z + 2 = 0 . Đường thẳng đi qua A và vuông góc với mặt phẳng ( P) có phương trình là  x = 3 + t  x = 1+ 3t   A.  y = 4
− + 2t ( t  ) .
B.  y = 2 − 4t ( t  ) .   z = 7 + 3t  z = 3 + 7t   x = 1− 3t  x = 1− 4t  
C.  y = 2 − 4t ( t  ) .
D.  y = 2 + 3t ( t  ) .   z = 3 + 7t  z = 3 + 7t 
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
…………………………………………………………………………………………………….. Trang 114
Trên con đường thành công không có dấu chân của kẻ lười biếng
 x = x + at 0 
Chú ý: Cho đường thẳng d :  y = y + bt , t  0
 z = z + ct  0
M  d khi và chỉ khi tồn tại một số t sao cho M ( x + at; y + bt; z + ct 0 0 0 )  x = 2 + t 
Ví dụ 4. Trong không gian Oxyz, cho điểm A(4;3;6) và d :  y = 1− t ( t  ) z = 1 − + 2t 
Tìm tọa độ của điểm M  d sao cho AM = 5 biết hoành độ điểm M là số nguyên. A. M (4; 1 − ;3) . B. M (0;3; 5 − ) . C. M (2;1; − ) 1 .
D. không có M .
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
II. ĐIỀU KIỆN ĐỂ HAI ĐƯỜNG THẲNG SONG SONG, CẮT NHAU, CHÉO NHAU:
x = x + a t 1 1 Cho đườ 
ng thẳng d :  y = y + b t đi qua điểm M ( x ; y ; z , có véc tơ chỉ phương là 1 1 1 ) 1 1
 z = z + c t  1 1
u = a ;b ;c
u = a ;b ;c 1
( 1 1 1) và đường thẳng . có véc tơ chỉ phương là 2 ( 2 2 2)
1. Điều kiện để hai đường thẳng song song: u  = k.u 1 2 d / /d '    M d ' u  = k.u Đặc biệt: 1 2
d  d '    M d
Ví dụ 1. Chứng minh hai đường thẳng sau đây song song: x = 1+ t x = 2 + 2t '  
d :  y = 2t và d ' :  y = 3 + 4t '   z = 3 − t  z = 5 − 2t ' 
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
…………………………………………………………………………………………………….. Trang 115
Trên con đường thành công không có dấu chân của kẻ lười biếng
……………………………………………………………………………………………………..
Ví dụ 2. Chứng minh hai đường thẳng sau đây trùng nhau:  x = 3 − t
x = 2 − 3t '  
d :  y = 4 + t và d ' :  y = 5 + 3t '   z = 5 − 2t  z = 3 − 6t ' 
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
2. Điều kiện để hai đường thẳng cắt nhau:
Hai đường thẳng d và d ' cắt nhau khi và chỉ khi hệ phương trình ẩn t và t ' sau có đúng một nghiệm
x + a t = x + a t ' 1 1 2 2 
 y + b t = y + b t ' I 1 1 2 2 ( )
 z + c t = z + c t '  1 1 2 2 /
Chú ý: Giả sử hệ (I) có nghiệm (t ;t . Để tìm giao điểm M của ta có thể thay t 0 0 ) d và d ' 0 0
vào phương trình tham số của d hoặc /
t vào phương trình tham số của d ' . 0
Ví dụ 3. Tìm giao điểm của hai đường thẳng sau:  x = 1+ t
 x = 2 − 2t '  
d :  y = 2 + 3t và d ' :  y = 2 − + t '   z = 3 − t  z = 1+ 3t ' 
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
…………………………………………………………………………………………………….. Trang 116
Trên con đường thành công không có dấu chân của kẻ lười biếng
3. Điều kiện để hai đường thẳng chéo nhau:
x = x + a t 1 1 
Cho đường thẳng d :  y = y + b t đi qua điểm M ( x ; y ; z , có véc tơ chỉ phương là 1 1 1 ) 1 1
 z = z + c t  1 1
x = x + a t ' 2 2 
u = a ;b ;c  = +
u = a ;b ;c 1
( 1 1 1) và đường thẳng d ': y y b t' có véc tơ chỉ phương là 2 ( 2 2 2) 2 2
 z = z + c t '  2 2
Chú ý: Hai đường thẳng d và d ' chéo nhau khi và chỉ khi u và u không cùng phương và hệ 1 2
x + a t = x + a t ' 1 1 2 2
phương trình  y + b t = y + b t ' vô nghiệm 1 1 2 2
 z + c t = z + c t '  1 1 2 2
Ví dụ 4. Xét vị trí tương đối của hai đường thẳng sau:  x = 1+ 2t  x = 1+ 3t '   d :  y = 1
− + 3t và d ': y = 2 − + 2t '   z = 5 + t  z = 1 − + 2t ' 
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
Củng cố bài học:
Bài học hôm nay các em cần nhớ các nội dung sau
1. Phương trình tham số, phương trình chính tắc của đường thẳng.
2. Các vị trí tương đối của hai đường thẳng. Sơ đồ tư duy:
d đi qua điểm M , có véc tơ chỉ phương là u , d’ có véc tơ chỉ phương là u 1 1 Trang 117
Trên con đường thành công không có dấu chân của kẻ lười biếng
M  d '  d  d ' Xét M và d '
M  d '  d / /d ' Xét u và u 1 2
1 nghiệm  d cắt d '
x + a t = x + a t ' 1 1 2 2 
Xét hệ  y + b t = y + b t ' 1 1 2 2
 z + c t = z + c t '  1 1 2 2
vô nghiệm  d , d ' chéo nhau .
B. LUYỆN TẬP I. BÀI TẬP SGK.
Bài 1 trang 89 – SGK: Viết phương trình tham số của đường thẳng (d) trong mỗi trường hợp sau:
a) (d) đi qua điểm M(5, 4;1) và có vectơ chỉ phương a = (2; 3 − ;1) b) (d) đi qua điểm A(2; 1
− ;3) và vuông góc với mặt phẳng () : x + y − z + 5 = 0 x = 1+ 2t c) (d) đi qua điể  m B(2; 0; 3
− ) và song song với đường thẳng  : y = −3+3t z = 4t 
d) (d) đi qua hai điểm P(1; 2;3) và Q(5;4;4)
Bài 3 trang 90 – SGK: Xét vị trí tương đối của các cặp đường thẳng d và d' cho bởi các phương trình sau: x = 3 − + 2t x = 5 + t   a) d : y = 2 − + 3t và d : y = 1 − − 4t   z = 6 + 4t  z = 20 + t     x = 1+ t x = 1+ 2t     b) d : y = 2 + t và d : y = 1 − + 2t    z = 3 − t  z = 2 − 2t 
Bài 5 trang 90 – SGK: Tìm số giao điểm của đường thẳng d với mặt phẳng ( ) trong các trường hợp sau: x = 12 + 4t 
a) d : y = 9 + 3t và () : 3x + 5y − z − 2 = 0 z =1+ t  Trang 118
Trên con đường thành công không có dấu chân của kẻ lười biếng x = 1+ t 
b) d : y = 2 − t và () : x + 3y + z +1 = 0 z =1+ 2t  x = 1+ t 
c) d :  y = 1+ 2t và
( ) : x + y + z − 4 = 0 z = 2 −3t  x = 3 − + 2t 
Bài 6 trang 90 – SGK: Tính khoảng cách giữa đường thẳng  :  y = −1+ 3t và mặt phẳng z = 1 − + 2t 
( ) : 2x − 2 y + z + 3 = 0 . x = 2 + t 
Bài 7 trang 91- SGK: Cho điểm A(1; 0; 0) và đường thẳng d : y = 1+ 2t z = t 
a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm A trên đường thẳng d .
b) Tìm tọa độ điểm A' đối xứng với A qua đường thẳng d .
Bài 8 trang 91- SGK: Cho điểm M(1; 4; 2) và mặt phẳng  : x + y + z −1 = 0
a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng  .
b) Tìm tọa độ điểm M' đối xứng với M qua mặt phẳng  .
c) Tính khoảng cách từ điểm M đến mặt phẳng  .
Bài 10 trang 91- SGK: Giải bài toán sau đây bằng phương pháp tọa độ:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Tính khoảng cách từ đỉnh A đến các
mặt phẳng (A'BD) và (B'D'C).
II. BÀI TẬP TRẮC NGHIỆM x −1 y − 5 z + 2 Câu 1:
Trong không gian Oxyz, đường thẳng d : = =
có một véc tơ chỉ phương là 3 2 5 −
A. u (1; 5 ; − 2) .
B. u (3 ; 2 ; − 5) . C. u ( 3 − ; 2 ; − 5) .
D. u (2 ; 3 ; − 5) . x − 4 y − 2 z +1 Câu 2:
Trong không gian Oxyz , cho đường thẳng d : = = . Điểm nào dưới 2 5 − 1
đây thuộc d ? A. M (4; 2 ) ;1 . B. Q (2;5 ) ;1 .
C. N (4; 2; − ) 1 . D. P (2; 5 − ) ;1 . Câu 3:
Phương trình tham số của đường thẳng −
d đi qua điểm A(1; 1; 2) và có vectơ chỉ phương
u = (1;2;− 3) là Trang 119
Trên con đường thành công không có dấu chân của kẻ lười biếng x =1+ t x =1+ t x =1 x =1+ t    
A. d :  y = 2 − t .
B. d :  y = 1 − − t .
C. d :  y = 1 − + 3t .
D. d :  y = 1 − + 2t .     z = 3 − + 2t  z = 2 + 2t  z = 2 − 5t  z = 2 − 3t  Câu 4:
Trong không gian, cho điểm A(1; 2; 3) và mặt phẳng (P) : x − z + 2 = 0 . Đường thẳng đi qua A
và vuông góc với mặt phẳng (P) có phương trình là. x = 1− t x = 1− t x = 1+ t x = 1+ t     A.  y = 2 .
B.  y = 2 + t . C.  y = 2 .
D  y = 2 − t .     z = 3 − t  z = 3  z = 3 − t  z = 3  Câu 5:
Trong không gian Oxyz , cho ba điểm A(1; 2;0) , B (1;1; 2) và C (2;3 )
;1 . Đường thẳng đi qua
A và song song với BC có phương trình là x −1 y − 2 z x −1 y − 2 z x +1 y + 2 z x +1 y + 2 z A. = = . B. = = . C. = = . D. = = . 1 2 1 − 3 4 3 3 4 3 1 2 1 − x −1 y z +1 Câu 6:
Trong không gian Oxyz , cho điểm (
A 1; 0; 2) và đường thẳng d : = = . Viết phương 1 1 2
trình đường thẳng  đi qua A , vuông góc và cắt d x −1 y z − 2 x −1 y z − 2 A.  : = = . B.  : = = . 1 3 − 1 1 1 1 x −1 y z − 2 x −1 y z − 2 C.  : = = . D.  : = = . 2 2 1 1 1 1 − x = 2 − 2t  Câu 7:
Trong không gian với hệ trục tọa độ
d :  y = 4t
Oxyz , cho hai đường thẳng 1 và z = 3 − + 6t  x =1− t 
d :  y = 2 + 2t 2
. Khẳng định nào sau đây đúng ? z = 3t   ⊥ A. d d d d d d d d và 2 chéo nhau. B. 1 2 . C. 1 2 . D. 1 2 . 1 x =1+ 2t x = 2 − t   Câu 8:
Trong không gian Oxyz , cho hai đường thẳng d  y = 2 − 2t và d   y = 5
− + 3t . Mệnh đề nào   z = t  z = 4 + t  sau đây đúng?
A. d ⊥ d  .
B. d / /d .
C. d và d chéo nhau.
D. d  d . x = 1+ 3t  Câu 9:
Trong không gian Oxyz , cho điểm M (8;− 4;3) và đường thẳng d : y = 2
− − 2t . Gọi H  là hình z = t 
chiếu vuông góc của M lên d . Khi đó tọa độ của điểm H là
A. H (7;− 6;2) .
B. H (9;− 2;4) . C. H ( 2 − ;0;− ) 1 . D. H (1; − 2 ) ;1 .
C. BÀI TẬP TỰ LUYỆN (phần này không làm PPT) Trang 120
Trên con đường thành công không có dấu chân của kẻ lười biếng
Dạng 1: Véc tơ chỉ phương. x = 1+ t 
Câu 10: [Mức độ 1] Cho d :  y = 2 − 2t (t  ) . Điểm nào sau đây không thuộc đường thẳng d ? z = 3 + t  A. M (0;4;2) . B. N (1;2;3) .
C. P (1; –2;3) . D. Q(2;0;4) . x − 2 y + 2 z
Câu 11: [Mức độ 2] Trong không gian với hệ tọa độ Oxyz , đường thẳng d : = = đi qua 1 2 3
những điểm nào sau đây? A. A( 2 − ;2;0). B. B (2; 2;0) . C. C ( 3 − ;0;3) . D. D (3;0;3) .
Câu 12: [Mức độ 3] Trong hệ trục vuông góc Oxyz, cho hai đường thẳng cắt nhau có phương trình lần − + + − lượ x 2 y 2 z x y 3 z 2 t là d : = = , d : = =
. Một trong hai đường phân giác của các góc 1 1 2 − 2 2 2 1 2 −
tạo bởi d , d có phương trình là 1 2 x = t x = 2 + t x y + 3 z − 2  x − 2 y + 2 z  A. = = . B.  y = 3 − + 3t . C. = = . D. y = 2 − + 3t . 1 3 4 −  1 3 2  z = 2 − 4t.  z = 4 − t. 
Câu 13: [Mức độ 4] Trong không gian (Oxy) cho tam giác ABC có A(2;3;3) , phương trình đường x − 3 y − 3 z − 2
trung tuyến kẻ từ B là = =
, phương trình đường phân giác trong góc C là 1 − 2 1 − x − 2 y − 4 z − 2 = = . Biết rằng u = ( ; m ; n − )
1 là một véc tơ chỉ phương của đường thẳng AB . 2 1 − 1 − 2 2
Tính giá trị biểu thức T = m + n . A. T = 1. B. T = 5 . C. T = 2 . D. T = 10
Dạng 2: Phương trình đường thẳng đi qua 1 điểm, tìm véc tơ chỉ phương.
Câu 14: [Mức độ 1] Phương trình tham số của đường thẳng (d ) đi qua hai điểm A(1;2; 3 − ) và B (3; 1 − ; ) 1 là x = 1+ t x = 1+ 3t x = 1 − + 2t x = 1 − + 2t     A.  y = 2 − + 2t .
B.  y = −2 − t . C.  y = 2 − − 3t .
D.  y = 5 − 3t .     z = 1 − − 3t  z = 3 − + t  z = 3 + 4t  z = 7 − + 4t 
Câu 15: [Mức độ 2] Trong không gian Oxyz , cho mặt phẳng ( P) : 2x + 3y + 2z + 2 = 0 và
(Q): x −3y + 2z +1= 0. Phương trình đường thẳng đi qua gốc tọa độ O và song song với hai
mặt phẳng (P) , (Q) là x y z x y z x y z x y z A. = = . B. = = . C. = = . D. = = . 12 2 9 − 9 12 − 2 − 12 2 − 9 − 9 12 2 − Lời giải
Chọn C [Mức độ 3] Trong không gian với hệ toạ độ Oxyz , cho đường thẳng  là giao tuyến
của hai mặt phẳng ( P) : z −1 = 0 và (Q) : x + y + z − 3 = 0 . Gọi d là đường thẳng nằm trong mặt Trang 121
Trên con đường thành công không có dấu chân của kẻ lười biếng x −1 y − 2 z − 3
phẳng (P) , cắt đường thẳng = =
và vuông góc với đường thẳng  . Phương 1 1 − 1 −
trình của đường thẳng d là x = 3 + t x = 3 − t x = 3 + t x = 3 + t    
A.  y = t .
B.  y = t .
C.  y = t .
D.  y = t − .     z = 1+ t  z = 1  z = 1  z = 1+ t 
Câu 16: [Mức độ 3] Trong không gian với hệ tọa độ Oxyz , cho các điểm A(2;0;0) ; B (0;3;0) ;
C (0;0; 4) . Gọi H là trực tâm tam giác ABC . Tìm phương trình tham số của đường thẳng OH .  x = 4t  x = 3t  x = 6t x = 4t    
A.  y = 3t .
B.  y = 4t .
C.  y = 4t .
D.  y = 3t .     z = −2t  z = 2t  z = 3t  z = 2t 
Dạng 3: Phương trình đường thẳng đi qua 1 điểm, và thỏa mãn điều kiện cho trước.
Câu 17: [Mức độ 1] Phương trình tham số của đường thẳng (d ) đi qua hai điểm A(1;2; 3 − ) và B (3; 1 − ; ) 1 là x = 1+ t x = 1+ 3t x = 1 − + 2t x = 1 − + 2t     A.  y = 2 − + 2t .
B.  y = −2 − t . C.  y = 2 − − 3t .
D.  y = 5 − 3t .     z = 1 − − 3t  z = 3 − + t  z = 3 + 4t  z = 7 − + 4t  x − 2 y + 2 z − 3
Câu 18: [Mức độ 2] Trong không gian Oxyz , cho hai đường thẳng d : = = và 1 2 1 − 1 x = 1− t 
d :  y = 1 + 2t . Đường thẳng  đi qua điểm A( 1; 2; 3) , vuông góc với d và cắt d có phương 2 1 2 z = 1 − + t  trình là x − 1 y − 2 z − 3 x − 1 y − 2 z − 3 A. = = . B. = = . 1 − 3 − 5 − 1 3 5 x − 1 y − 2 z − 3 x − 1 y − 2 z − 3 C. = = . D. = = . 1 3 5 − 1 3 − 5 −
Câu 19: [Mức độ 3] Trong không gian Oxyz , cho tam giác ABC có A(2;3;3) , phương trình đường x − 3 y − 3 z − 2
trung tuyến kẻ từ B là = =
, phương trình đường phân giác trong của góc C là 1 − 2 1 − x − 2 y − 4 z − 2 = =
. Đường thẳng AB có một véc-tơ chỉ phương là 2 1 − 1 − A. u = − . B. u = − . C. u = − . D. u = . 1 (1;2 ) 4 (0;1; ) 2 (1; 1;0) 3 (2;1; ) 1 1 ;1
Câu 20: [Mức độ 3] Trong không gian với hệ tọa độ Oxyz , cho điểm M (2;1;0) và đường thẳng x −1 y +1 z  : = =
. Viết phương trình của đường thẳng d đi qua điểm M , cắt và vuông góc 2 1 1 − với  . x − 2 y −1 z x − 2 y −1 z A. d : = = . B. d : = = . 1 4 1 2 4 − 1 Trang 122
Trên con đường thành công không có dấu chân của kẻ lười biếng x − 2 y −1 z x − 2 y −1 z C. d : = = . D. d : = = . 1 4 − 2 − 1 4 − 1
Dạng 4: Phương trình đường thẳng đi qua 1 điểm, và thỏa mãn điều kiện cắt, vuông góc với đường thẳng cho trước.
Câu 21: [Mức độ 2] Trong không gian với hệ tọa độ Descartes Oxyz , cho điểm M (0; −1; 2) và hai x − y + z − x + y − z − đườ 1 2 3 1 4 2 ng thẳng d : = = , d : = =
. Phương trình đường thẳng đi 1 1 1 − 2 2 2 1 − 4
qua M , cắt cả d và d là 1 2 x y +1 z + 3 x y +1 z − 2 x y +1 z − 2 x y +1 z − 2 A. = = . B. = = . C. = = . D. = = . 9 9 8 − 3 3 − 4 9 9 − 16 9 − 9 16 2 2 x y −1 z + 2
Câu 22: [Mức độ 3] Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d : = = và 1 2 1 − 1 x = 1 − + 2t 
d :  y = 1+ t
. Phương trình đường thẳng vuông góc với (P) : 7x + y − 4z = 0 và cắt hai đường 2 z = 3 
thẳng d , d là 1 2 x − 7 y z + 4 x − 2 y z +1 x + 2 y z −1 x − 2 y z +1 A. = = . B. = = . C. = = . D. = = 2 1 1 7 1 4 − 7 − 1 − 4 7 1 4
Câu 23: [Mức độ 3] Trong không gian với hệ tọa độ Oxyz , cho điểm A(1;0; 2) và đường thẳng x = 1+ t 
d :  y = t
. Phương trình đường thẳng  đi qua A , vuông góc và cắt đường thẳng d là z = 1 − + 2t  x −1 y z − 2 x −1 y z − 2 A.  : = = . B.  : = = . 1 3 2 − 1 1 1 − x −1 y z − 2 x −1 y z − 2 C.  : = = . D.  : = = . 2 4 3 − 1 3 − 1 x − y z +
Câu 24: và đường thẳng d có phương trình: 1 1 = =
. Viết phương trình đường thẳng  đi qua 1 1 2
A , vuông góc và cắt d . x −1 y z − 2 x −1 y z − 2 A.  : = = . B.  : = = . 1 1 1 1 1 1 − x −1 y z − 2 x −1 y z − 2 C.  : = = . D.  : = = . 2 1 1 1 3 − 1
Dạng 5: Phương trình đường thẳng cắt 2 đường thẳng và thỏa mãn 2 điều kiện cho trước. x y z
Câu 25: [Mức độ 2] Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng a : = = ; 1 1 2 − x +1 y z +1 b : = =
và mặt phẳng ( P) : x − y − z = 0. Viết phương trình của đường thẳng d song 2 − 1 1 −
song với (P) , cắt a và b lần lượt tại M và N mà MN = 2. Trang 123
Trên con đường thành công không có dấu chân của kẻ lười biếng 7x + 4 7 y − 4 7z + 8 7x − 4 7 y − 4 7z + 8 A. d : = = . B. d : = = . 3 8 5 − 3 8 5 − 7x −1 7 y + 4 7z + 8 7x − 4 7 y + 4 7z + 8 C. d : = = . D. d : = = . 3 8 5 − 3 8 5 −
Câu 26: [Mức độ 2] Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng phẳng ( P) : 2x − 5y − z = 0 và − + − − hai đườ x 1 y 1 z 3 x y 1 z ng thẳng d : = = ; d : = =
. Viết phương trình đường thẳng  1 1 1 1 − 2 2 1 − 1 −
nằm trên mặt phẳng (P) sao cho  cắt hai đường thẳng d , d . . 1 2 x − 3 y z −1 x y −1 z −1 A.  : = = . B.  : = = 4 1 3 4 1 3 . x − 3 y −1 z −1 x − 3 y −1 z −1 C.  : = = D.  : = = 4 − 1 3 . 4 1 3 . x + 3 y − 2 z −1
Câu 27: [Mức độ 3] Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d : = = 1 1 1 − 2 x − 2 y −1 z +1 , d : = =
và mặt phẳng ( P) : x + 3y + 2z − 5 = 0 . Đường thẳng vuông góc với ( P) 2 2 1 1
, cắt cả d và d có phương trình là: 1 2 x + 3 y + 2 z −1 x y z + 2 A. = = . B. = = . 1 3 2 1 3 2 x + 4 y − 3 z +1 x + 7 y − 6 z + 7 C. = = . D. = = . 1 3 2 1 3 2
Câu 28: [Mức độ 3] Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) : 2x − y + z −10 = 0 và + − − đườ x 2 y 1 z 1 ng thẳng d : = =
. Đường thẳng Δ cắt (P) và d lần lượt tại M và N sao 2 1 1 −
cho A(1;3; 2) là trung điểm MN . Tính độ dài đoạn MN . A. MN = 4 33 .
B. MN = 2 26,5 .
C. MN = 4 16, 5 . D. MN = 2 33 .
Câu 29: [Mức độ 4] Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng ( P) : x + y − z + 2 = 0 và x = 1+ t
x = 3 − t hai đườ  
ng thẳng d : y = t
; d ' : y = 1+ t . Biết rằng có 2 đường thẳng có các đặc điểm: song   z = 2 + 2t  z = 1− 2t  O
song với (P) ; cắt d, d và tạo với d góc 30 . Tính cosin góc tạo bởi hai đường thẳng đó. 1 1 2 1 A. . B. . C. . D. . 5 2 3 2 Khi đó ( 1 cos  ,  = . 1 2 ) 2
Dạng 6: Phương trình đường thẳng giao tuyến của 2 mặt phẳng. Trang 124
Trên con đường thành công không có dấu chân của kẻ lười biếng
Câu 30: [Mức độ 2] Trong không gian với hệ trục tọa độ Oxyz , gọi ( ) là mặt phẳng chứa đường thẳng x − 2 y −1 z  : = =
và vuông góc với mặt phẳng ( ) : x + y + 2z +1 = 0 . Khi đó giao tuyến của 1 1 2 −
hai mặt phẳng ( ) , ( ) có phương trình x − 2 y +1 z x + 2 y −1 z A. = = . B. = = . 1 5 − 2 1 5 − 2 x y +1 z x y +1 z −1 C. = = . D. = = . 1 1 1 − 1 1 1
Câu 31: [Mức độ 3] Cho hai điểm A(3; 3; ) 1 , B (0; 2; )
1 , mặt phẳng ( P) : x + y + z − 7 = 0 . Đường thẳng
d nằm trên ( P) sao cho mọi điểm của d cách đều hai điểm A , B có phương trình là x = t x = t x = t − x = 2t    
A.  y = 7 − 3t .
B.  y = 7 + 3t .
C.  y = 7 − 3t .
D.  y = 7 − 3t .     z = 2t  z = 2t  z = 2t  z = 2t 
Câu 32: [Mức độ 3] Trong không gian với hệ tọa độ Oxyz , gọi ( ) là mặt phẳng chứa đường thẳng  − − có phương trình x 2 y 1 z =
= và vuông góc với mặt phẳng ( ) : x + y − 2z −1 = 0 . Giao 1 1 2
tuyến của ( ) và ( ) đi qua điểm nào trong các điểm sau. A. C (1; 2 ) ;1 . B. D (2;1;0) . C. B (0;1;0) . D. A(2;1 ) ;1 .
Dạng 7: Phương trình đường thẳng vuông góc chung của 2 đường thẳng chéo nhau.
Câu 33: [Mức độ 2] Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng x − 4 y −1 z + 5 − +  x 2 y 3 z : = = và  : =
= . Giả sử M  , N   sao cho MN là đoạn 1 1 2 3 1 − 2 − 2 1 3 1
vuông góc chung của hai đường thẳng  và  . Tính MN . 1 2 A. MN = (5; 5 − ;10) . B. MN = (2; 2 − ; 4) . C. MN = (3; 3 − ;6) . D. MN = (1; 1 − ; 2) x −1 y z + 2
Câu 34: [Mức độ 3] Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d : = = 1 2 1 − 1 x +1 y −1 z − 3 và d : = =
. Đường vuông góc chung của d và d lần lượt cắt d , d tại A và B . 2 1 2 1 2 1 7 1 −
Tính diện tích S của tam giác OAB . 3 6 6 A. S = . B. S = 6 . C. S = . D. S = . 2 2 4
Dạng 8: Phương trình đường thẳng hình chiếu vuông góc lên mặt phẳng. x + 3 y −1 z −1
Câu 35: [Mức độ 2] Trong không gian với hệ tọa độ Oxyz cho đường thẳng d : = = . 2 1 3 −
Hình chiếu vuông góc của d trên mặt phẳng (Oyz) là một đường thẳng có vectơ chỉ phương là
A. u = (0;1;3) . B. u = (0;1; 3 − ). C. u = (2;1; 3 − ) .
D. u = (2;0;0) . Trang 125
Trên con đường thành công không có dấu chân của kẻ lười biếng x −12 y − 9 z −1
Câu 36: [Mức độ 3] Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : = = , và 4 3 1
mặt thẳng ( P): 3x + 5y − z − 2 = 0 . Gọi d 'là hình chiếu của d lên ( P).Phương trình tham số của d ' là x = 62 − t x = 62t x = 62t x = 62t    
A.  y = 25t . B.  y = 25 − t . C.  y = 25 − t . D.  y = 25 − t .     z = 2 − 61t  z = 2 + 61t  z = 2 − + 61t  z = 2 + 61t 
Dạng 9: Phương trình đường thẳng liên quan đến Min - Max.
Câu 37: [Mức độ 2] Trong không gian với hệ tọa độ Oxyz , cho ( P) : x − 2y + 2z − 5 = 0 , A( 3 − ;0 ) ;1 , B (1; 1
− ;3) . Viết phương trình đường thẳng d đi qua A , song song với (P) sao cho khoảng
cách từ B đến d là lớn nhất. x + 3 y z −1 x + 3 y z −1 x −1 y z −1 x + 3 y z −1 A. = = . B. = = . C. = = . D. = = 1 1 − 2 3 2 − 2 1 2 − 2 2 6 − 7 −
Câu 38: [Mức độ 3] Trong không gian Oxyz , cho ba điểm A(0;0; − ) 1 , B ( 1 − ;1;0) , C (1;0 ) ;1 . Tìm điểm 2 2 2
M sao cho 3MA + 2MB − MC đạt giá trị nhỏ nhất.  3 1   3 1   3 3   3 1  A. M ; ; 1 −   . B. M − ; ; 2  . C. M − ; ; 1 −   . D. M − ; ; 1 −   .  4 2   4 2   4 2   4 2 
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
……………………………………………………………………………………………………..
…………………………………………………………………………………………………….. Trang 126

Vở bài học môn Toán 12 phần Hình học

Thông tin :

Tài liệu liên quan:

Hình nón là gì? Công thức tính diện tích xung quanh hình nón | Toán 12

Đề tham khảo kỳ thi tốt nghiệp THPT từ năm 2025 môn Toán

Đề thi thử TN THPT 2025 lần 1 môn Toán trường THPT Lương Tài 2 – Bắc Ninh

Lời giải chi tiết đề tham khảo kỳ thi tốt nghiệp THPT môn Toán từ năm 2025

Đề chọn đội tuyển thi HSG QG môn Toán THPT năm 2024 – 2025 sở GD&ĐT Bắc Giang