
Preview text:
ĐỀ CƯƠNG TOÁN 12 GIỮA KÌ 1 NĂM HỌC 2024-2025
PHẦN I (3 điểm). Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phuơng án.
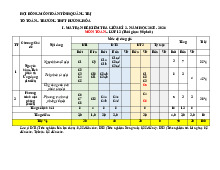
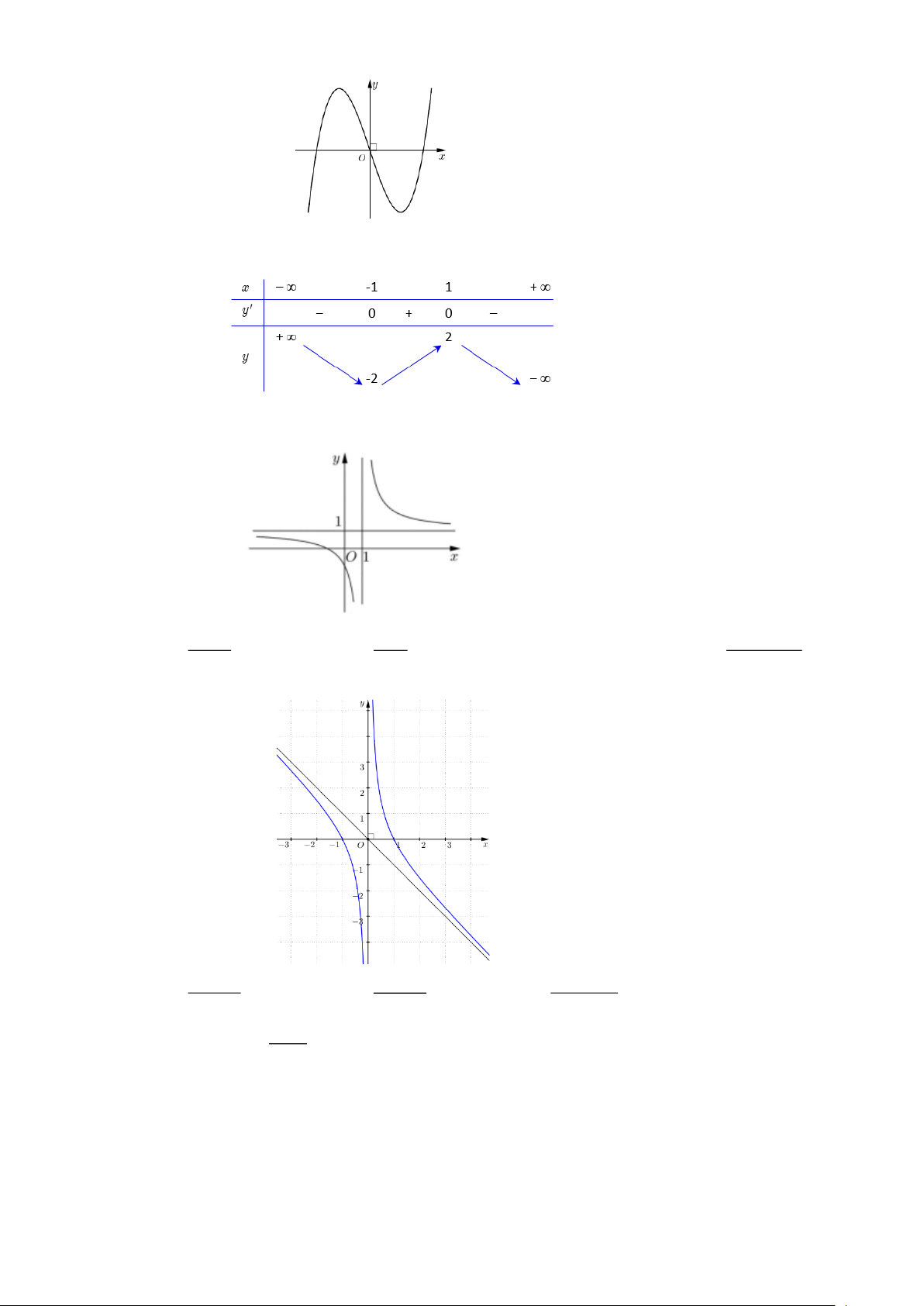
Câu 1.1: Cho hàm số y = f (x) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 2 . B. 3 . C. 0 . D. 4 − .
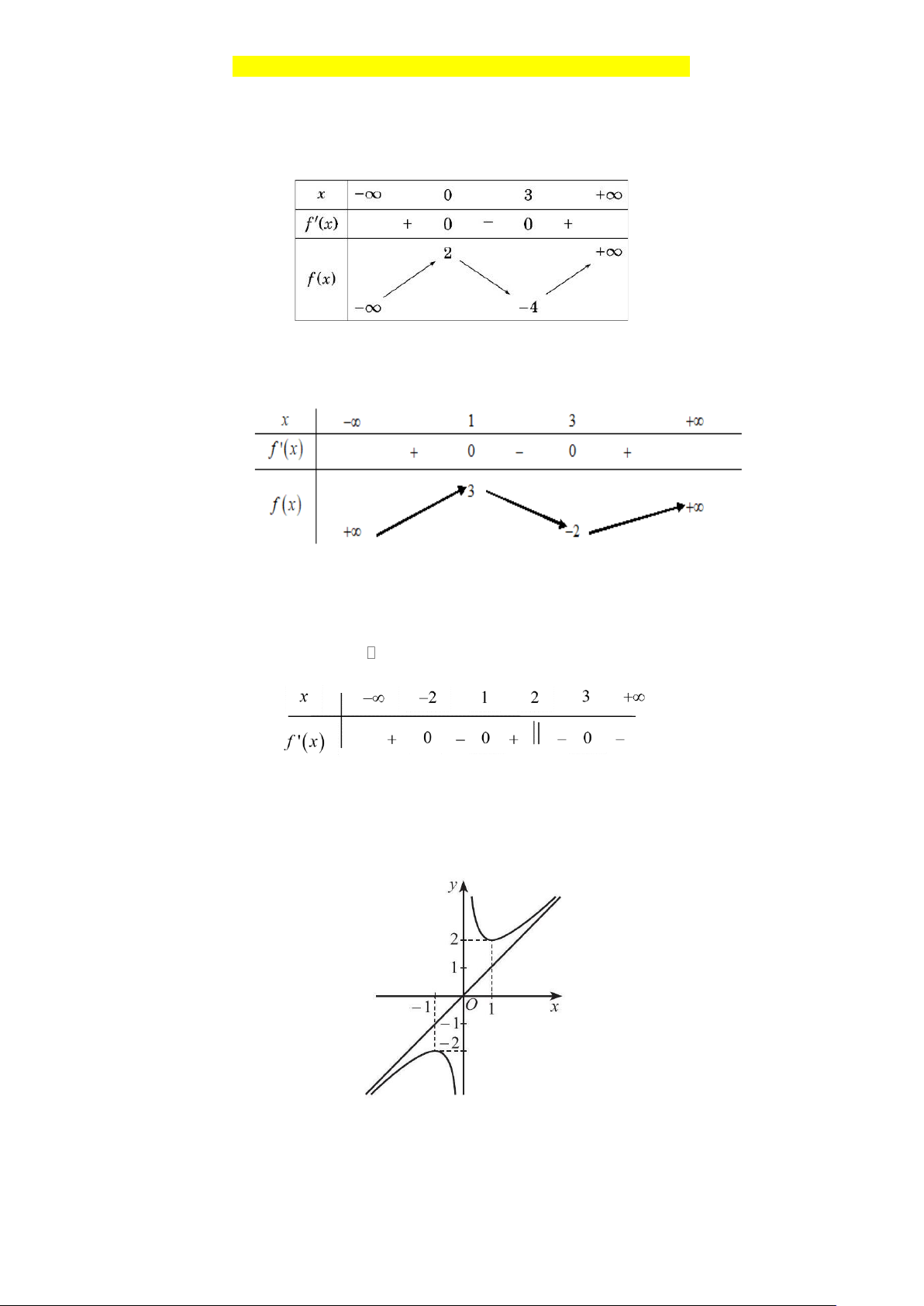
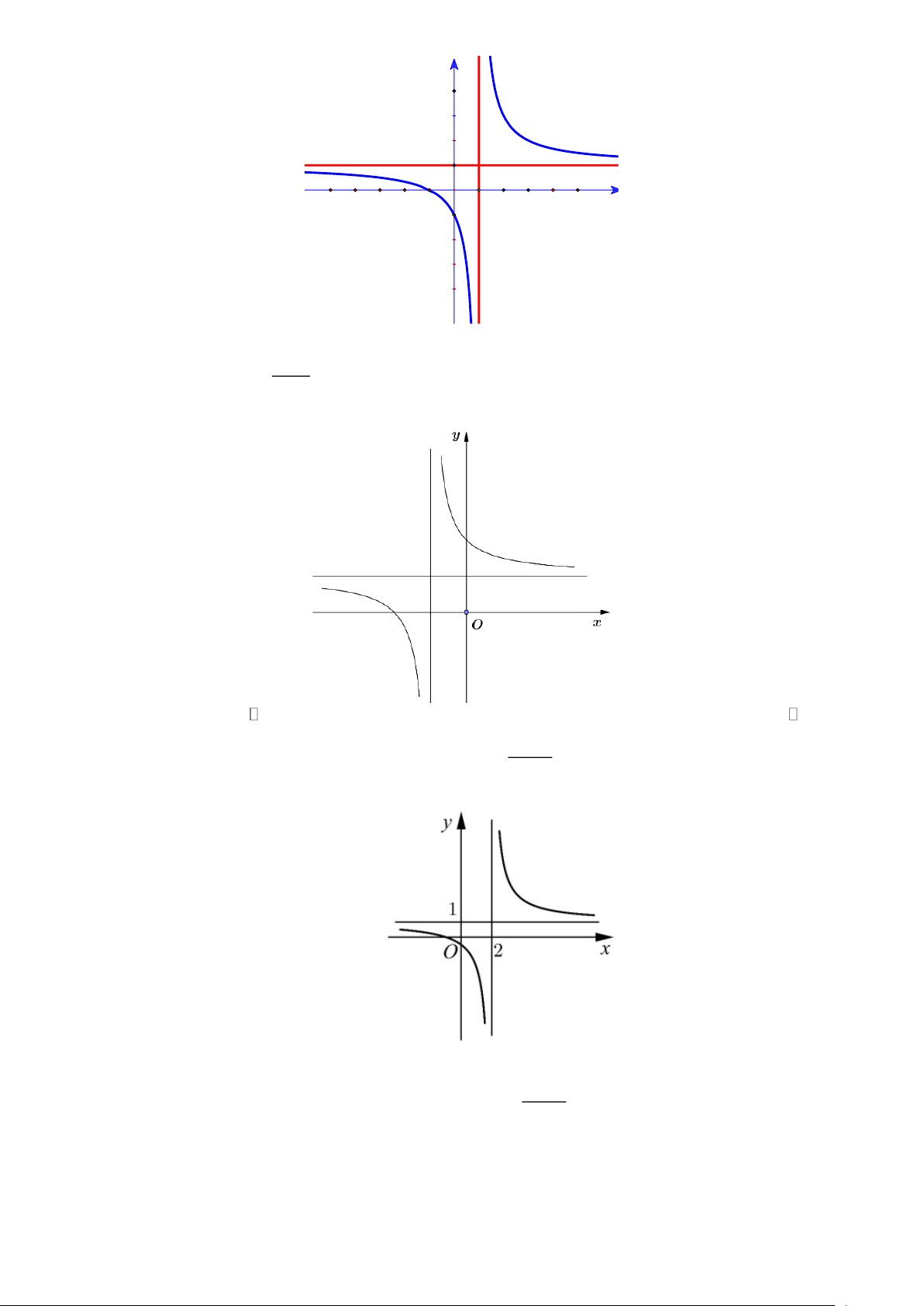
Câu 1.2: Cho hàm số f (x) có bảng biến thiên như sau:
Hàm số f (x) đạt cực đại tại A. x = 2 − . B. x = 3 . C. x = 1 . D. x = 2 .
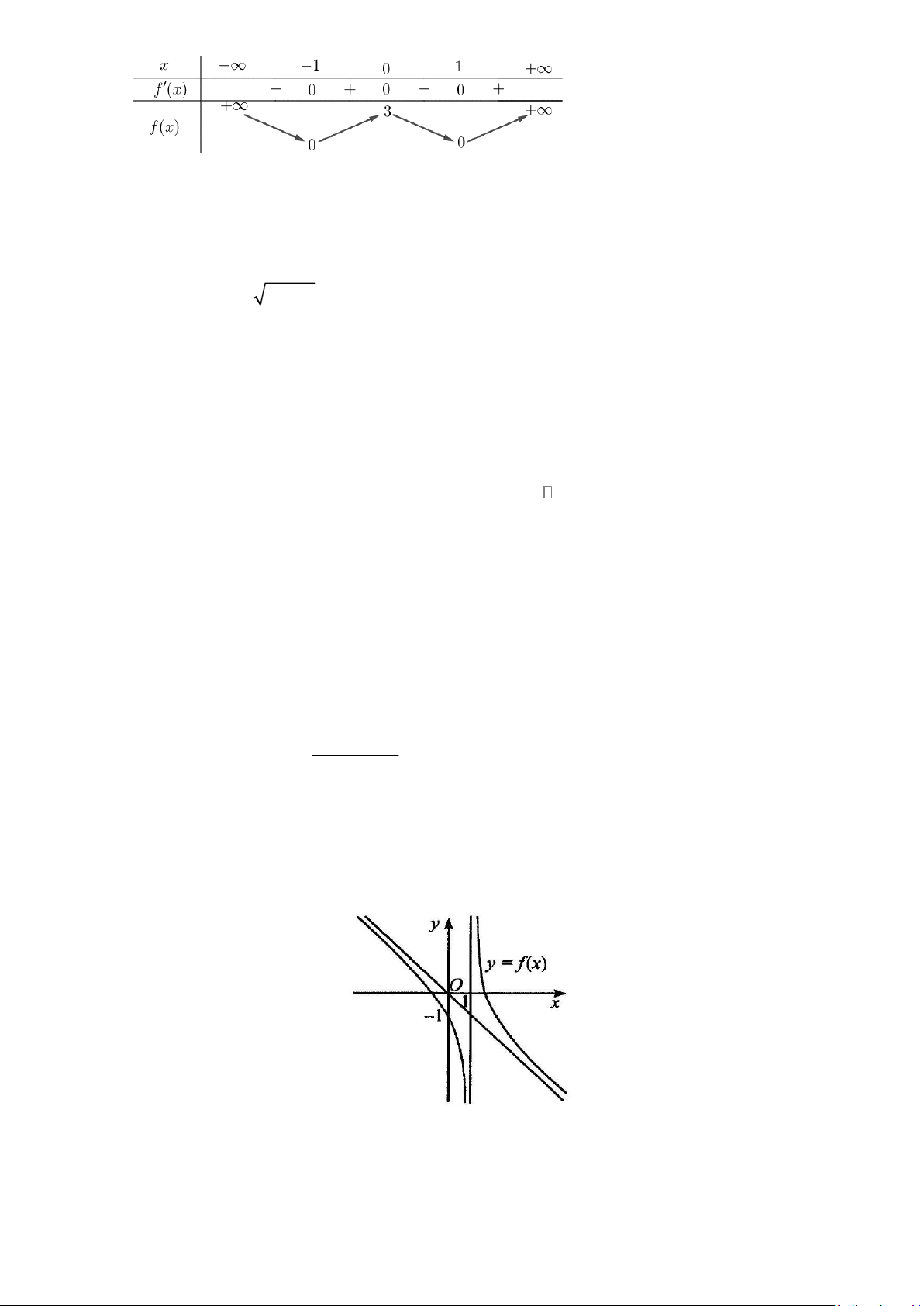
Câu 1.3: Cho hàm số f ( x) liên tục trên và có bảng xét dấu f '( x) như sau:
Số điểm cực đại của hàm số đã cho là: A. 3. B. 1. C. 2. D. 4.
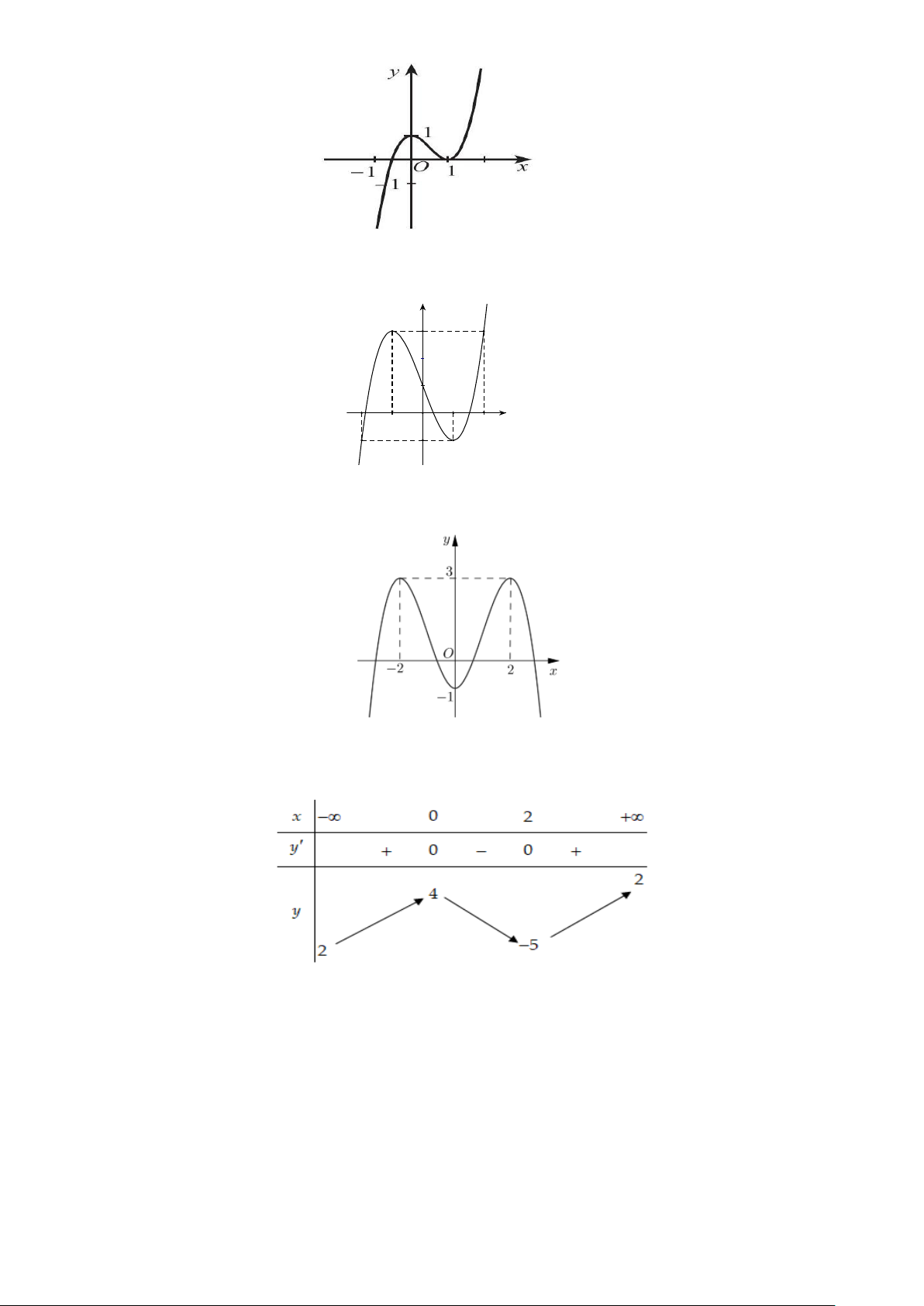
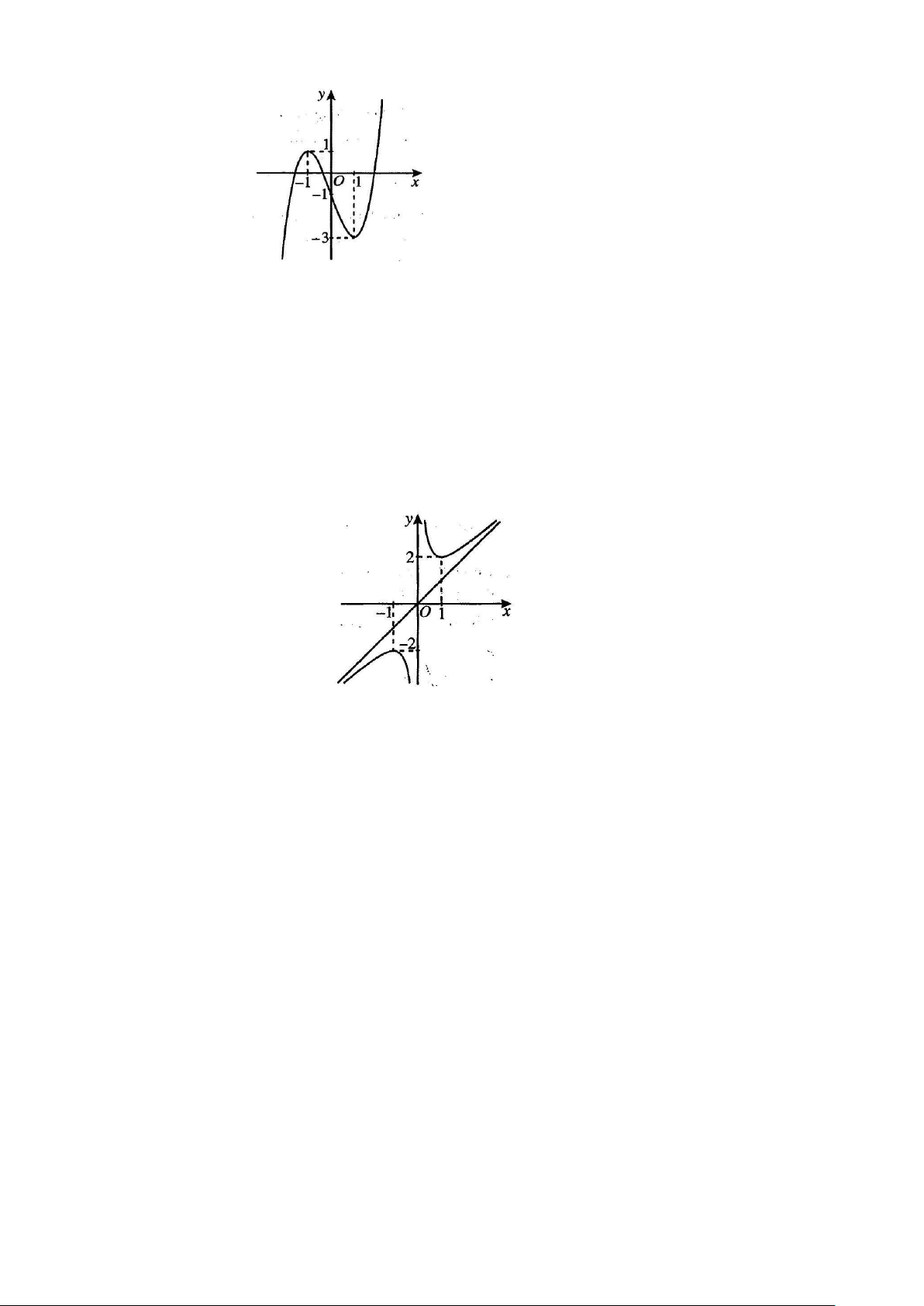
Câu 1.4: Cho hàm số y = f (x) có đồ thị như hình. Hàm số đã cho có điểm cực đại là: A. 1 . B. -1 . C. 2 . D. -2 .
Câu 2.1: Cho hàm số f ( x) có bảng biến thiên như sau: Trang 1
Hàm số đã cho nghịch biến trên khoảng nào sau đây? A. ( ;
− 0). B. n( A) 2 2
= C +C =100 C. ( 1 − ;0). 10 11 D. ( 1 − ;+).
Câu 2.2: Cho hàm số 2
y = 2x +1 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng (0;+ ) .
B. Hàm số đồng biến trên khoảng (−;0) .
C. Hàm số nghịch biến trên khoảng (0;+ ) . D. Hàm số nghịch biến trên khoảng (−1; ) 1 .
Câu 2.3: Cho hàm số y = f (x) liên tục trên R và có đạo hàm f ( x) = ( − x)2 ( x + )3 1 1 (3− x) . Hàm số
y = f (x) đồng biến trên khoảng nào dưới đây? A. ( ) ;1 − . B. (− ; − ) 1 . C. (1;3). D. (3;+ ) .
Câu 2.4: Cho hàm số y = f (x) có đạo hàm trên thỏa mãn f (x) 0, x (1;2) và
f (x) 0, x (2; )
3 . Phát biểu nào sau đây là đúng?
A. Hàm số y = f (x) đồng biến trên cả hai khoảng (1;2) và (2; ) 3 .
B. Hàm số y = f (x) nghịch biến trên cả hai khoảng (1;2) và (2; ) 3 .
C. Hàm số y = f (x) đồng biến trên khoảng (1;2) và nghịch biến trên khoảng (2; ) 3 .
D. Hàm số y = f (x) nghịch biến trên khoảng (1;2) và đồng biến trên khoảng (2; ) 3 . 2
ax + bx + c
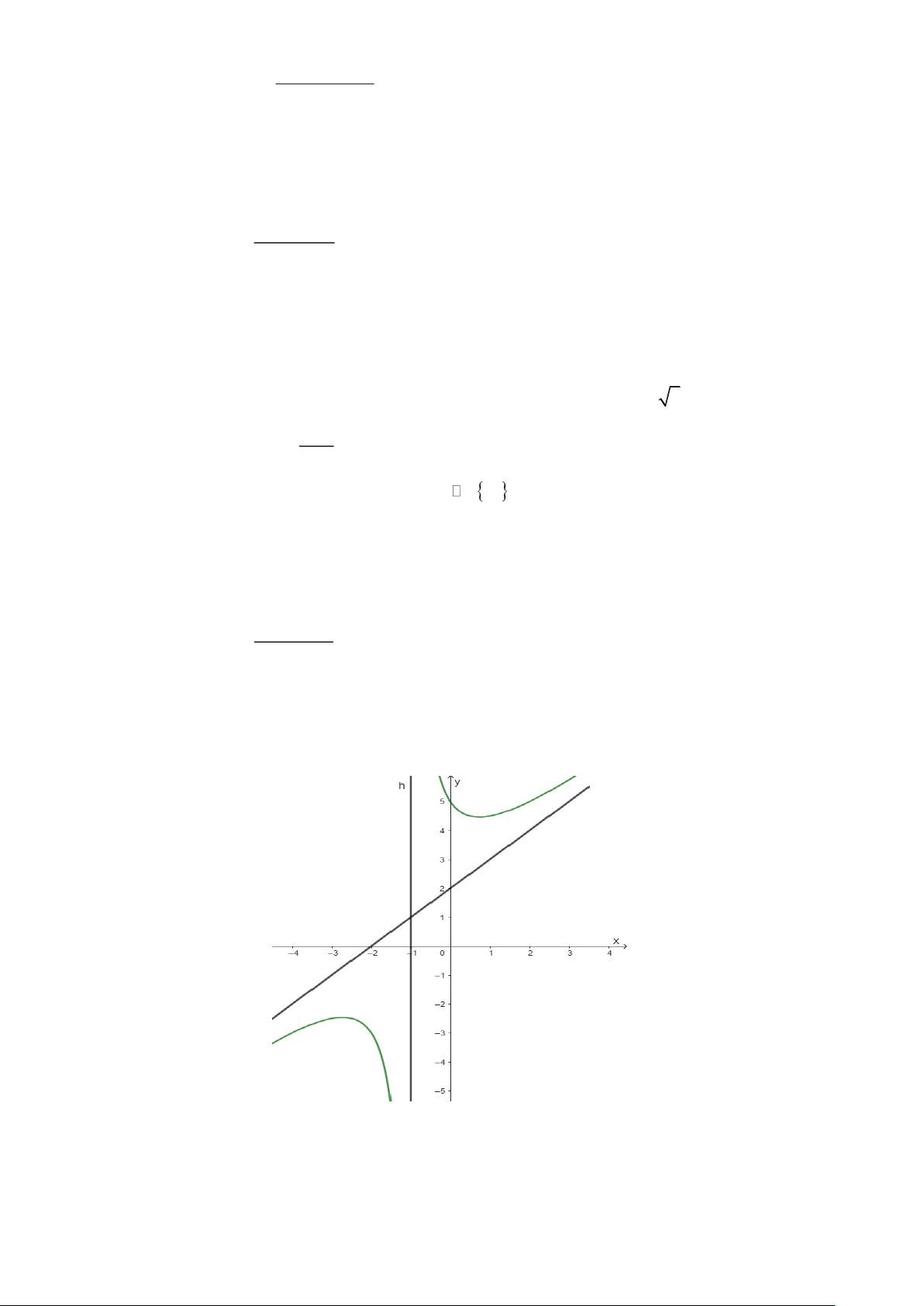
Câu 3.1: Cho hàm số y = f (x) =
có đồ thị như Hình 1. Phát biểu nào sau đây là đúng? mx + n
A. Hàm số y = f (x) nghịch biến trên các khoảng ( − ) ;1 và (1; + ) .
B. Hàm số y = f (x) đồng biến trên các khoảng ( − ) ;1 và (1; + ) .
C. Hàm số y = f (x) đồng biến trên khoảng ( − )
;1 và nghịch biến trên khoảng (1; + ) .
D. Hàm số y = f (x) nghịch biến trên khoảng ( − )
;1 và đồng biến trên khoảng (1; + ) . Hình 1
Câu 3.2: Cho hàm số y = f (x) có đồ thị như hình dưới. Hàm số đã cho đồng biến trên khoảng nào trong các khoảng sau đây? Trang 2 A. (0; ) 1 . B. (0;2) . C. ( 1 − ;0) . D. ( 1 − ; ) 1 .
Câu 3.3: Cho hàm số y = f (x) có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào? y 3 1 2 − 1 1 − O x 2 1 − A. ( 1 − ; ) 1 . B. ( 2 − ;− ) 1 . C. ( 1 − ;2). D. (1;+ ) .
Câu 3.4: Cho hàm số y = f (x) có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào? A. ( 2 − ;0) . B. (−;0) . C. ( 2 − ;2) . D. (0;2).
Câu 4.1: Cho hàm số y = f (x) có bảng biến thiên như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại x = −5 .
B. Hàm số có bốn điểm cực trị.
C. Hàm số đạt cực tiểu tại x = 2 .
D. Hàm số không có cực đại. Trang 3
Câu 4.2: Cho hàm số y = f (x) liên tục trên R và có đồ thị như Hình 4. Hình 4.
Phát biểu nào sau đây là đúng? A. x = 1 − , x =1. B. x = 3 − , x =1. CT CĐ CT CĐ
C. x =1, x = 3 − .
D. x = 1, x = 1 − . CT CĐ CT CĐ
Câu 4.3: Cho hàm số y = f (x) liên tục trên R thoả mãn f (x) f (0), x ( 1 − ; ) 1 ‚ 0 và
f (x) f (2), x (1; ) 3 ‚
2 . Phát biểu nào sau đây là đúng? .
A x = 0, x = 2 .
B. x = 2, x = 0 . CT CĐ CT CĐ C. x = 1 − , x = 3 .
D. x = 3, x = 1 − . CT CĐ CT CĐ
Câu 4.4: Cho hàm số y = f (x) có đồ thị như Hình 5. Hình 5.
Phát biểu nào sau đây là đúng?
A. y =1, y = 2 .
B. y = 2, y = 1 − . CT CĐ CT CĐ C. y = 2 − , y = 2 .
D. y = 2, y = 2 − . CT CĐ CT CĐ
Câu 5.1: Nếu hàm số y = f (x) liên tục trên R thoả mãn f (x) , m x
R và tồn tại aR sao cho
f (a) = m thì:
A. Hàm số y = f (x) đạt giá trị lớn nhất bằng m .
B. Hàm số y = f (x) đạt giá trị cực tiểu bằng m .
C. Hàm số y = f (x) đạt giá trị nhỏ nhất bằng m .
D. Hàm số y = f (x) đạt giá trị cực đại bằng m .
Câu 5.2: Nếu hàm số y = f (x) liên tục trên R thoả mãn f (x) M, x
R và tồn tại aR sao cho
f (a) = M thì:
A. Hàm số đạt giá trị lớn nhất bằng M .
B. Hàm số đạt giá trị cực tiểu bằng M .
C. Hàm số đạt giá trị nhỏ nhất bằng M .
D. Hàm số đạt giá trị cực đại bằng M .
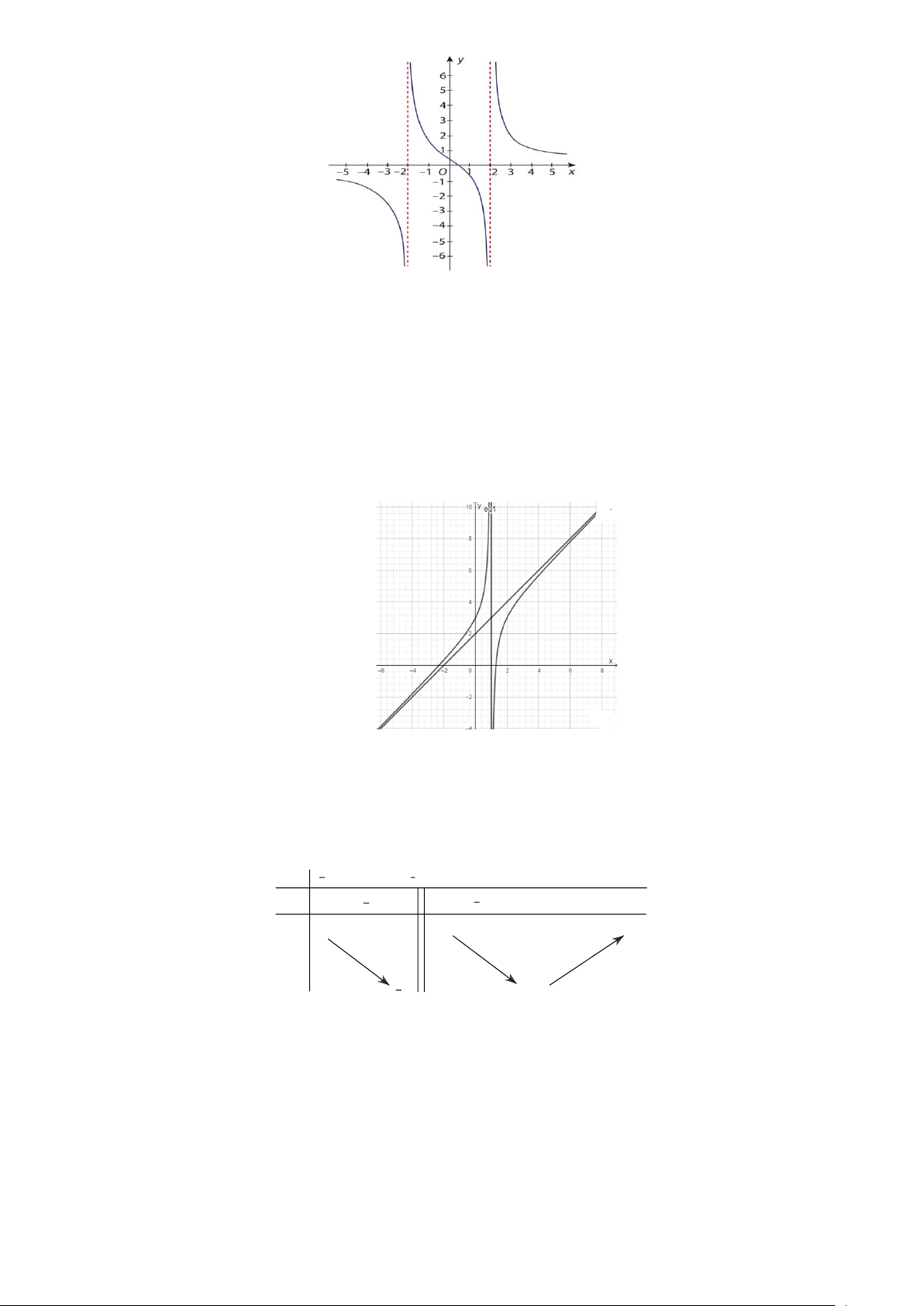
Câu 5.3: Cho hàm số f ( x) có đồ thị trên 3 − ; 3 như hình vẽ. Trang 4
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f ( x) trên 3 − ; 3 lần lượt là
A. M = 3;m = 1 − .
B. M = 4; m = 2 − .
C. M = 3;m = 3 − .
D. M = −1; m = 1.
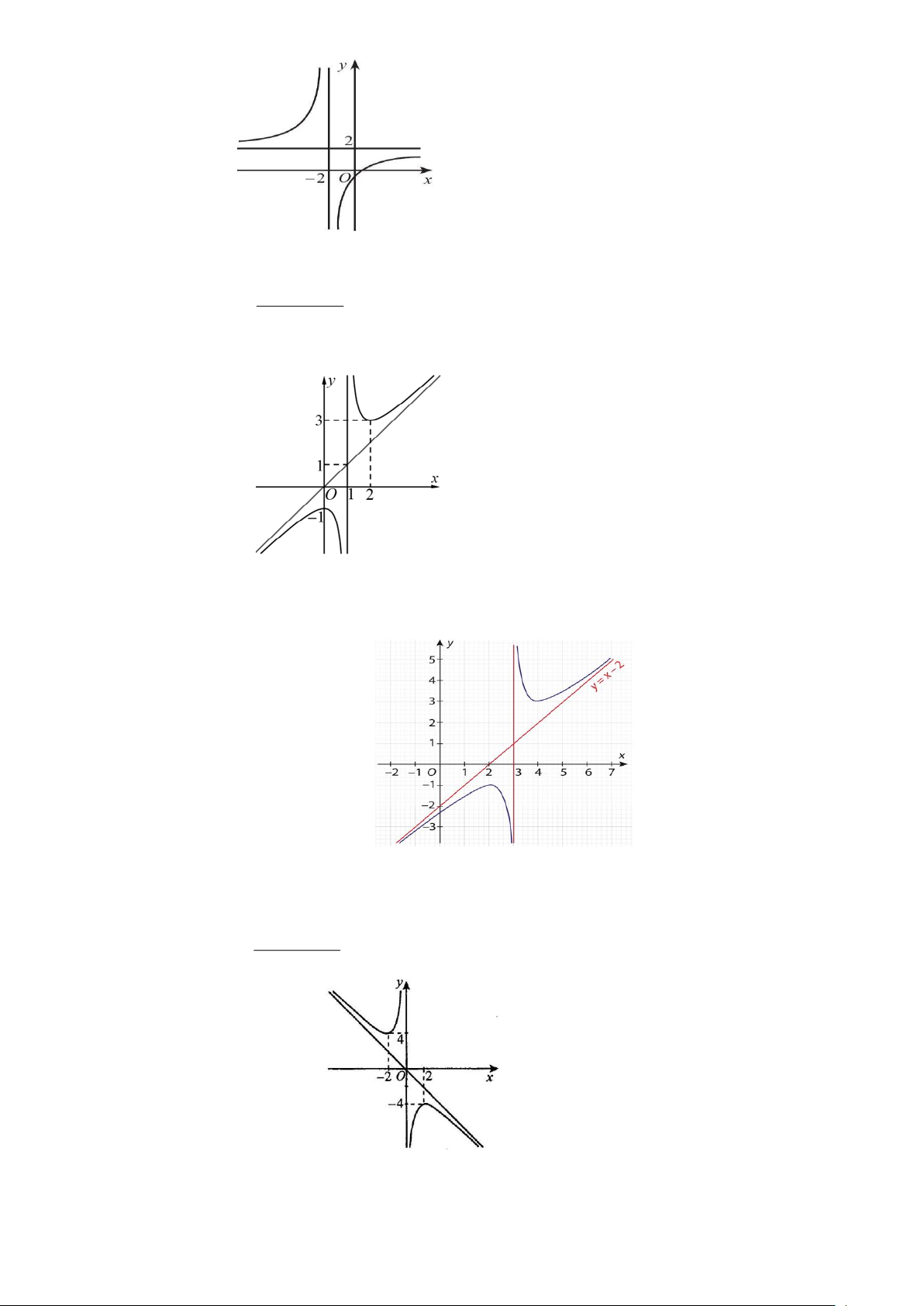
Câu 5.4: Cho hàm số y = f (x) liên tục trên đoạn 1 − ;
3 và có đồ thị như hình vẽ bên. Gọi M và m lần
lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 1 − ;
3 . Giá trị của M − m bằng A. 1. B. 4 . C. 5 . D. 0 .
Câu 6.1: Giá trị nhỏ nhất của hàm số f (x) 3
= x −33x trên đoạn 2;19 bằng A. 72 − . B. 2 − 2 11. C. 58 − . D. 22 11 . 4
Câu 6.2: Tính giá trị nhỏ nhất của hàm số y = 3x +
trên khoảng (0;+). 2 x 33 A. min y = B. 3 min y = 2 9 C. 3 min y = 3 9
D. min y = 7 (0;+) 5 (0;+) (0;+) (0;+)
Câu 6.3: Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số f ( x) 1
= x − x +1 trên 2 đoạn 0;
3 . Tính tổng S = 2m+3M . 7 3
A. S = − .
B. S = − . C. 3 − . D. S = 4 . 2 2 3sin x + 2
Câu 6.4: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = trên đoạn sin x +1 0; . Khi đó giá trị của 2 2
M + m là 2 31 11 41 61 A. . B. . C. . D. . 2 2 4 4 2 − 4x
Câu 7.1: Cho hàm số y = f (x) =
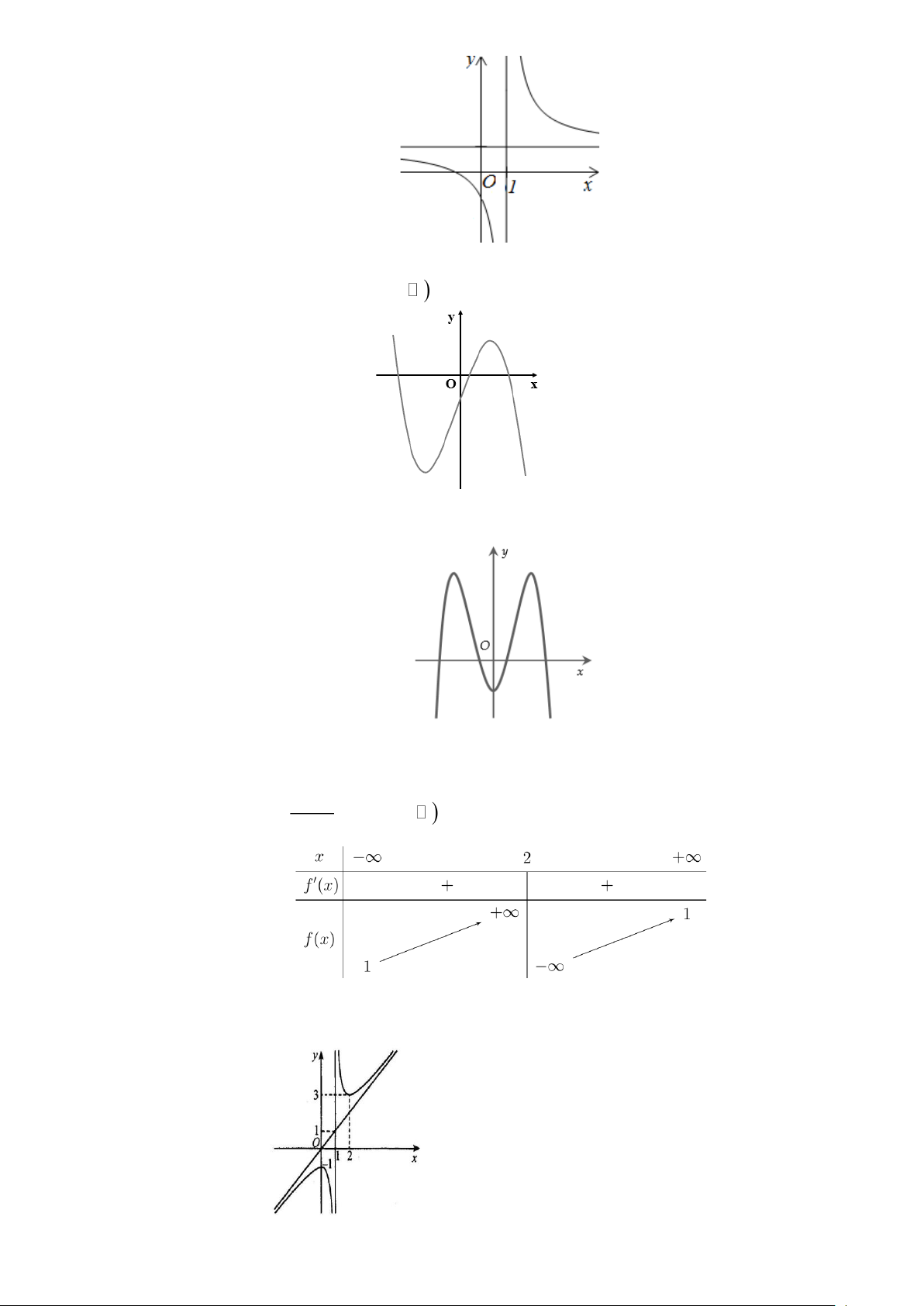
có đồ thị là đường cong như Hình 1. 2 4 − x Trang 5 Hình 1
Đồ thị hàm số trên có bao nhiêu đường tiệm cận đứng? A. 1. B. 2. C. 3. D. 0.
Câu 7.2: Cho hàm số y = f (x) có lim f (x) = và lim f (x) = . Chọn mệnh đề đúng? x 2 →− x→2
A. Đồ thị hàm số đã cho có đúng một tiệm cận đứng.
B. Đồ thị hàm số đã cho không có tiệm cận đứng.
C. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng y = 2 và y = −2 .
D. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x = 2 và x = 2 − .
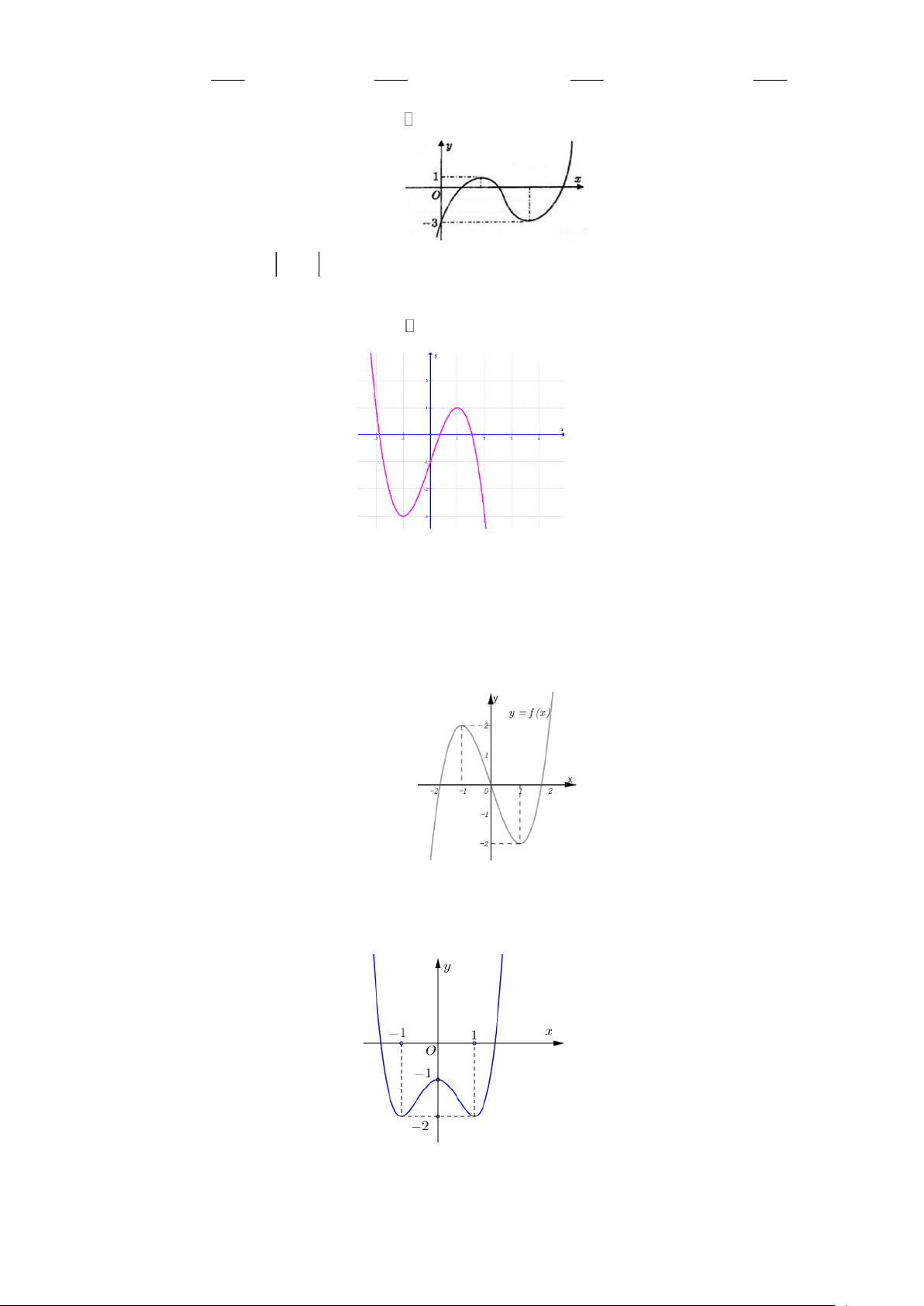
Câu 7.3: Cho đồ thị hàm số y = f (x) như hình bên. Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số đã cho có một tiệm cận đứng và một tiệm cận ngang.
B. Đồ thị hàm số đã cho không có tiệm cận đứng.
C. Đồ thị hàm số đã cho có một tiệm cận ngang và một tiệm cận xiên.
D. Đồ thị hàm số đã cho có một tiệm cận đứng và một tiệm cận xiên.
Câu 7.4: Cho hàm số y = f (x) có bảng biến thiên như hình dưới. x 1 0 + y' || + -1 + 1 y 0
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = f (x) là A.4. B. 3 . C. 2. D. 1.
Câu 8.1: Cho hàm số y = f (x) có đồ thị như hình. Đồ thị hàm số đã cho có đường tiệm cận ngang là Trang 6 A. x = 1 − . B. y = 1 − .
C. x = 2 . D. y = 2 . 2
ax + bx + c
Câu 8.2: Cho hàm số y =
, (am 0) có đồ thị như hình vẽ. Đường thẳng nào sau đây là đường mx + n
tiệm cận xiên của đồ thị hàm số đã cho? A. y = 2 . x B. y = − . x C. y = . x D. y = 2 − . x
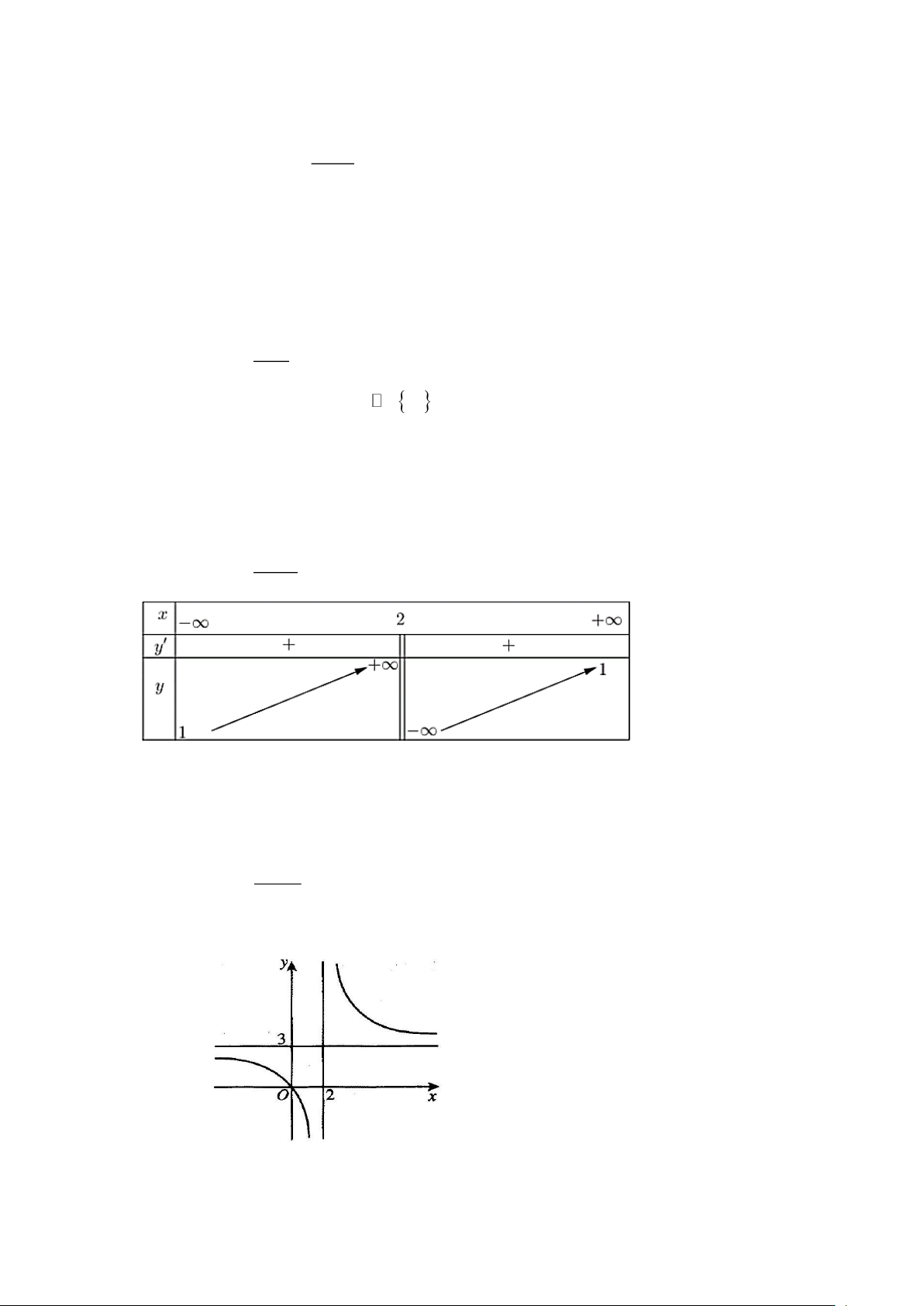
Câu 8.3: Cho hàm số y = f (x) có đồ thị như sau:
Tiệm cận đứng của đồ thị hàm số trên là
A. x = 3.
B. x = 0 .
C. x = 2 . D. y = 3 . 2
ax + bx + c
Câu 8.4: Cho hàm số y =
,(ac 0) có đồ thị như Hình 7. x Hình 7
Đường tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng:
A. Đường thẳng y = x .
B. Đường thẳng y = −x .
C. Đường thẳng x = 0 .
D. Đường thẳng y = 2x . Trang 7
Câu 9.1: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y = x − 3x . B. 3
y = −x + 3x . C. 3 2
y = x − 3x +1. D. 3 2
y = −x + 3x .
Câu 9.2: Hàm số nào dưới đây có bảng biến thiên như sau A 3
y = x − 3x . B. 3
y = −x + 3x . C. 2
y = x − 2x . D. 2
y = −x + 2x .
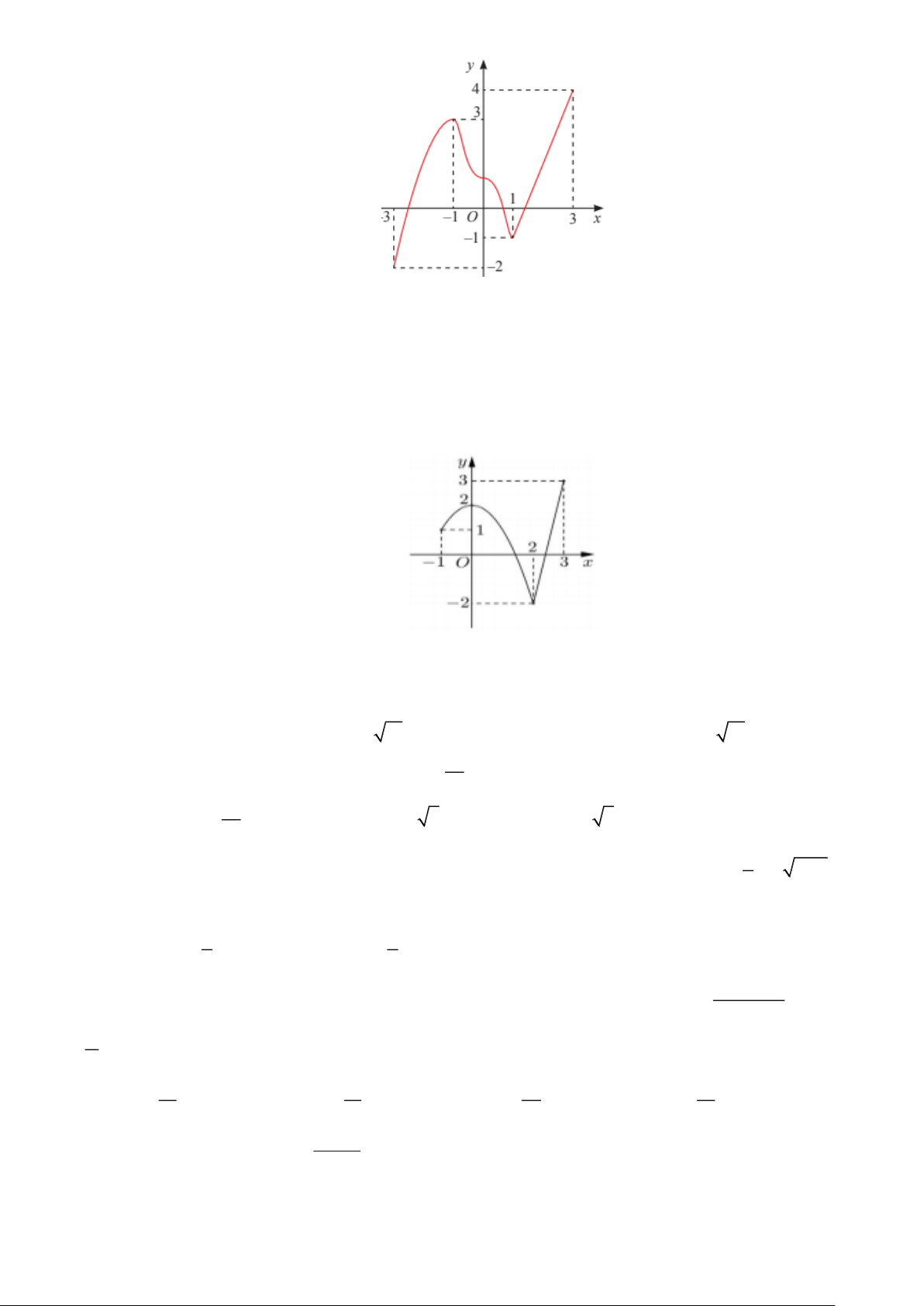
Câu 9.3: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? 2x −1 x +1 2 x − 3x −1 A. y = . B. y = . C. 3 2
y = 2x + x +1. D. y = . x −1 x −1 x − 2
Câu 9.4: Đường cong trong hình là đồ thị của hàm số nào dưới đây? 2 −x +1 2 − x +1 2 x − x +1 A. y = . B. y = . C. y = . D. 3 2
y = x − 3x . x 2x + 2 x −1 x + a
Câu 10.1: Biết hàm số y =
( a là số thực cho trước, a 1
− ) có đồ thị như trong hình bên. Mệnh đề x −1 nào dưới đây đúng? Trang 8 y O x
A. y ' 0, x R .
B. y ' 0, x 1.
C. y ' 0, x R .
D. y ' 0, x 1 . x + a
Câu 10.2: Biết hàm số y =
( a là số thực cho trước, a 1
− ) có đồ thị như hình bên. Mệnh đề nào x +1 dưới đây là đúng? A. y , 0 x .
B. y 0, x 1 − .
C. y 0, x 1 − .
D. y 0, x . ax + b
Câu 10.3: Đường cong ở hình bên là đồ thị của hàm số y =
với a,b,c,d là các số thực. Mệnh đề nào cx + d dưới đây đúng? A.
y 0,x 1. B. y 0,x 1. C. y 0,x 2 . D. y 0,x 2 . ax + b
Câu 10.4: Đường cong ở hình bên là đồ thị của hàm số y =
với a, b, c, d là các số thực. Mệnh đề cx + d nào dưới đây đúng? Trang 9 A.
y 0,x¡ . B.
y 0,x 1. C.
y 0,x 1. D.
y 0,x¡ .
Câu 11.1: Cho hàm số 3
y = ax + 3x + d ( ;
a d ) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?
A. a 0, d 0 .
B. a 0, d 0.
C. a 0, d 0.
D. a 0, d 0 .
Câu 11.2: Cho hàm số 4 2
y = ax + bx + c ( a 0 ) có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A. a 0 , b 0, c 0 .
B. a 0 , b 0 , c 0 .
C. a 0 , b 0, c 0 .
D. a 0 , b 0 , c 0 . ax +
Câu 11.3: Cho hàm số f ( x) 1 = ( , a ,
b c ) có bảng biến thiên như sau: bx + c
Trong các số a, b và c có bao nhiêu số dương? A. 2. B. 3. C. 1. D. 0.
Câu 11.4: Hàm số nào sau đây có đồ thị là đường cong như Hình 1 ? Hình 1 Trang 10 1 1 1 1
A. y = x − .
B. y = −x +
. C. y = −x − . D. y = x + . x −1 x −1 x −1 x −1
Câu 12.1: Cho hàm số y = f (x) liên tục trên và có đồ thị như hình vẽ.
Số nghiệm của phương trình f ( x) = 2 là A. 3 . B. 2 . C. 4 . D. 6 .
Câu 12.2: Cho hàm số y = f (x) liên tục trên có đồ thị như hình vẽ.
Phương trình f (x) = m có ba nghiệm thực phân biệt khi và chỉ khi A. m( 3 − ; ) 1 . B. m 3 − ; 1 . C. m( 1 − ;3) . D. m 1 − ; 3 .
Câu 12.3: Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình bên. Số nghiệm thực của
phương trình f (x) = 1 − là: A. 3 . B. 1. C. 0 . D. 2 .
Câu 12.4: Cho hàm số 4 2
f (x) = ax + bx + c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn 2 − ;
5 của tham số m để phương trình f (x) = m có đúng 2 nghiệm thực phân biệt? A. 1. B. 6. C. 7. D. 5.
PHẦN II (4 điểm). Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1.1 đến câu 4.8. Trong mỗi ý a), b),
c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Trang 11
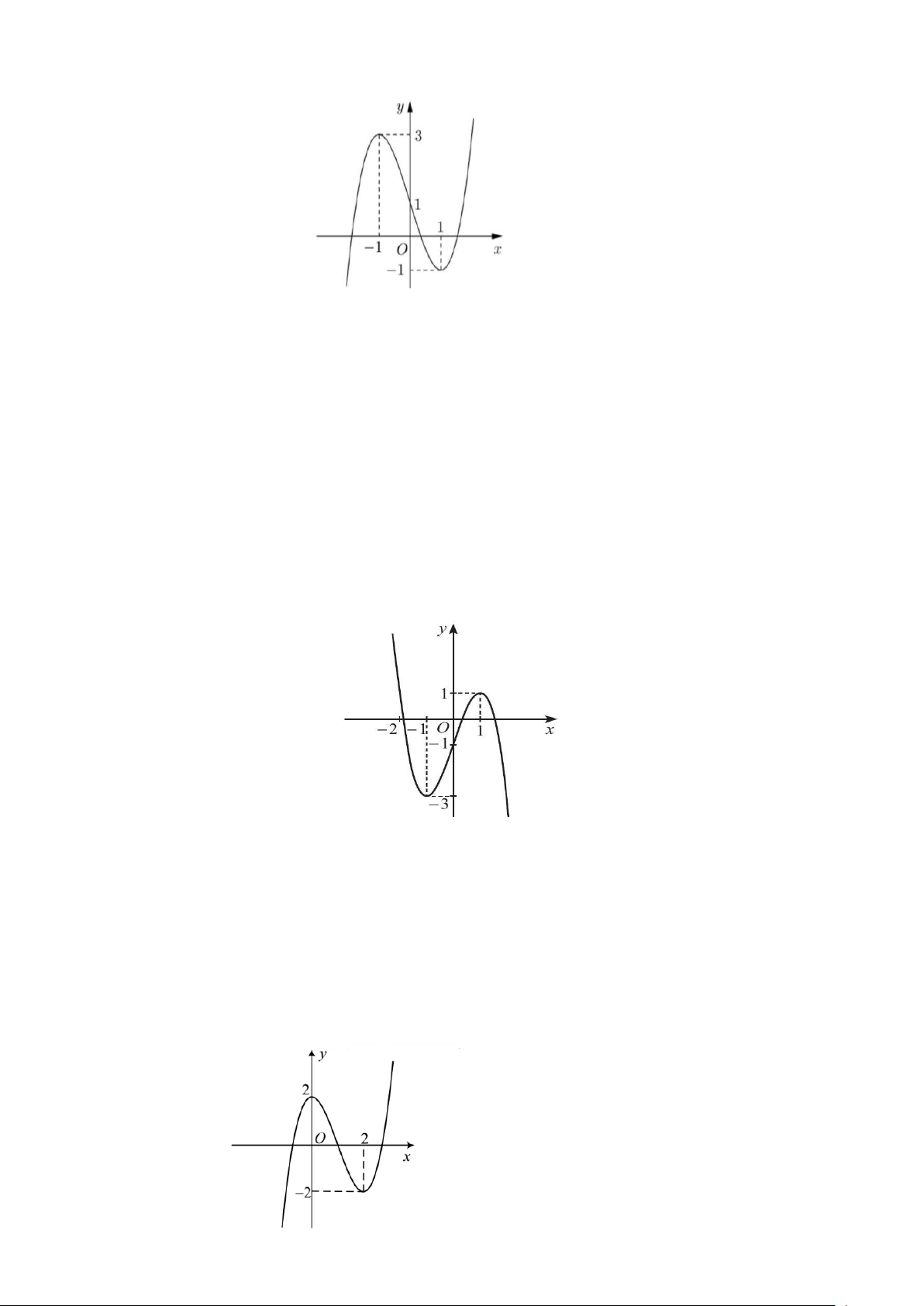
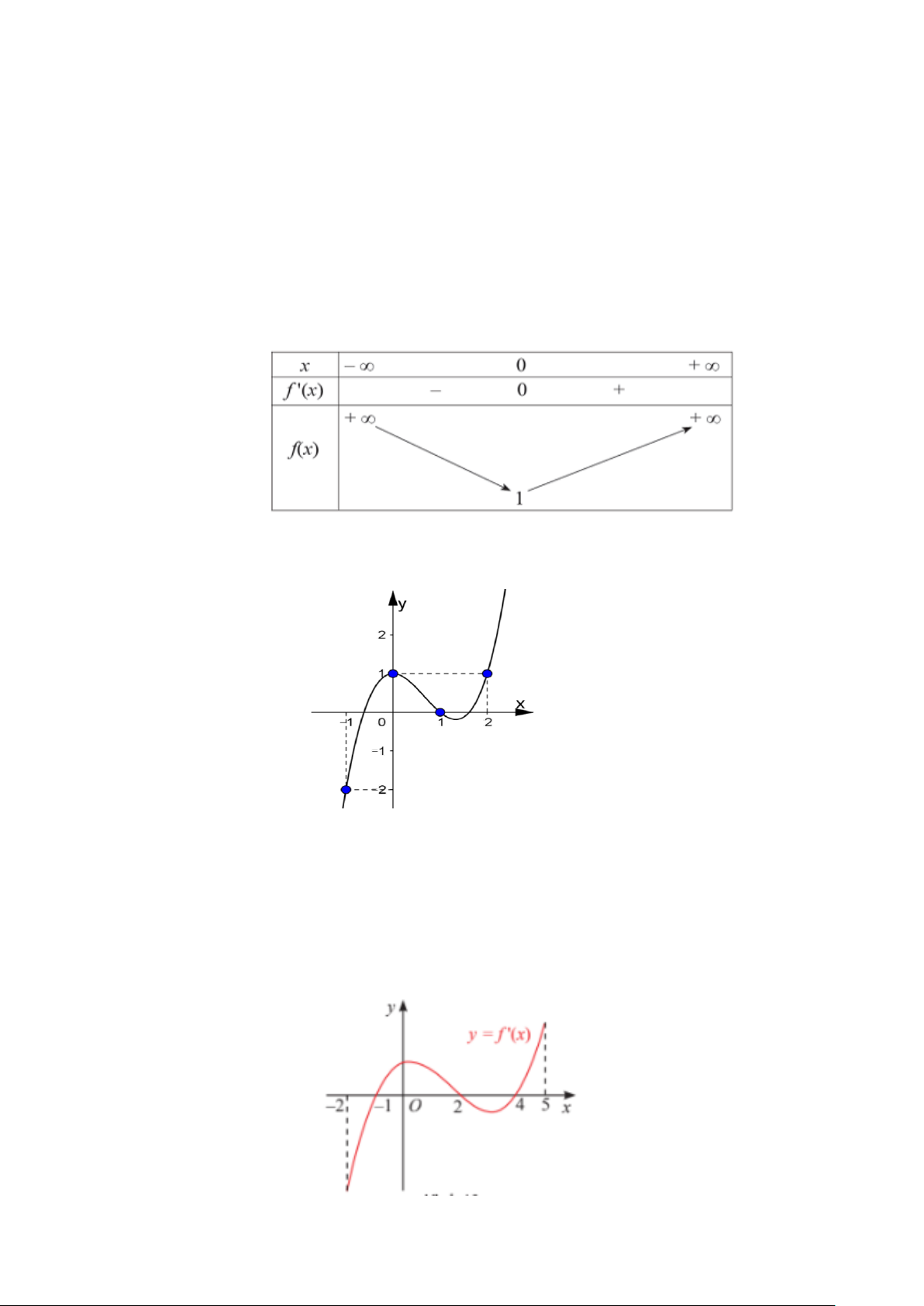
Câu 1.1: Cho hàm số = ( ) 3 2 y
f x = ax + bx + cx + d có đồ thị như hình vẽ dưới đây:
a) Hàm số đạt cực đại tại x = 3.
b) Đồ thị hàm số cắt trục Ox tại điểm có tọa độ (0;1) .
c) Hàm số đồng biến trên khoảng (-1;1).
d) Giá trị lớn nhất của hàm số trên khoảng ( ; − 0) là 3.
Câu 1.2: Cho hàm số f (x) 3 = −x + 3x .
a) f (x) 2 = 3 − x + 3.
b) Hàm số đồng biến trên các khoảng ( − ;− ) 1 và (1;
+ ) ; nghịch biến trên khoảng ( 1 − ; ) 1 .
c) Hàm số đạt cực tiểu tại x = 1
− và đạt cực đại tại x =1.
d) Hàm số có đồ thị như Hình 1 . Hình 1
Câu 1.3: Cho hàm số y = f (x) 3 2
= x −3x −9x + 5.
a) Hàm số đã cho đồng biến trên mỗi khoảng (− ; − ) 1 và (3;+) .
b) Giá trị cực đại của hàm số đã cho là −1.
c) Đồ thị hàm số đã cho đi qua các điểm (0;5), (1; 6 − ),( 1 − ;−10).
d) Đường thẳng y = −22 cắt đồ thị hàm số đã cho tại 3 điểm phân biệt.
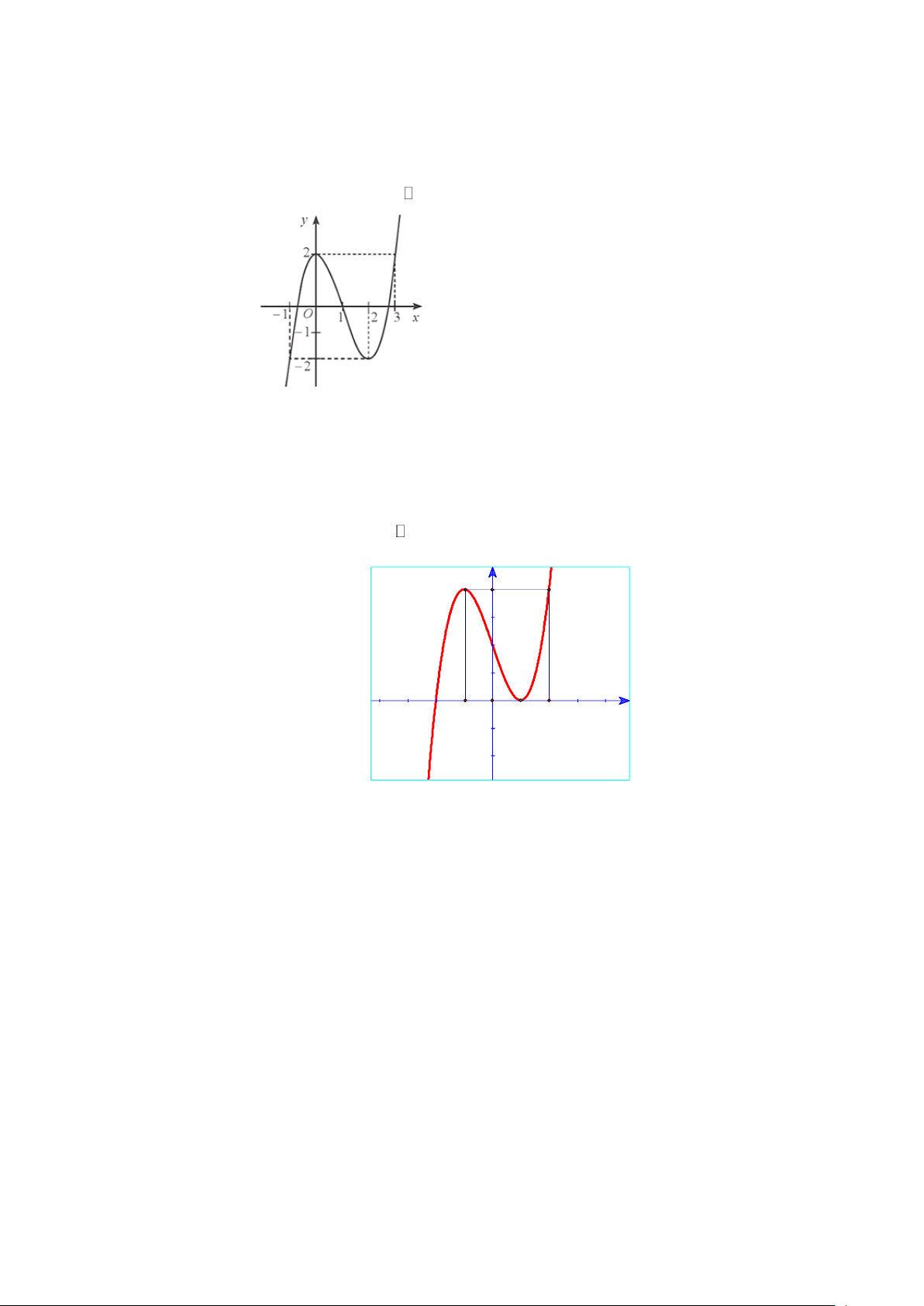
Câu 1.4: Cho hàm số y = f (x) có đồ thị như hình dưới đây. Trang 12
a) Hàm số đã cho đồng biến trên khoảng (2;+ ) .
b) Hàm số đã cho đạt cực đại tại x = 0 ; đạt cực tiểu tại x = 2 .
c) Trên đoạn 0;
2 , giá trị lớn nhất của hàm số đã cho bằng 0 .
d) Phương trình 3 f (x) + 4 = 0 có 3 nghiệm.
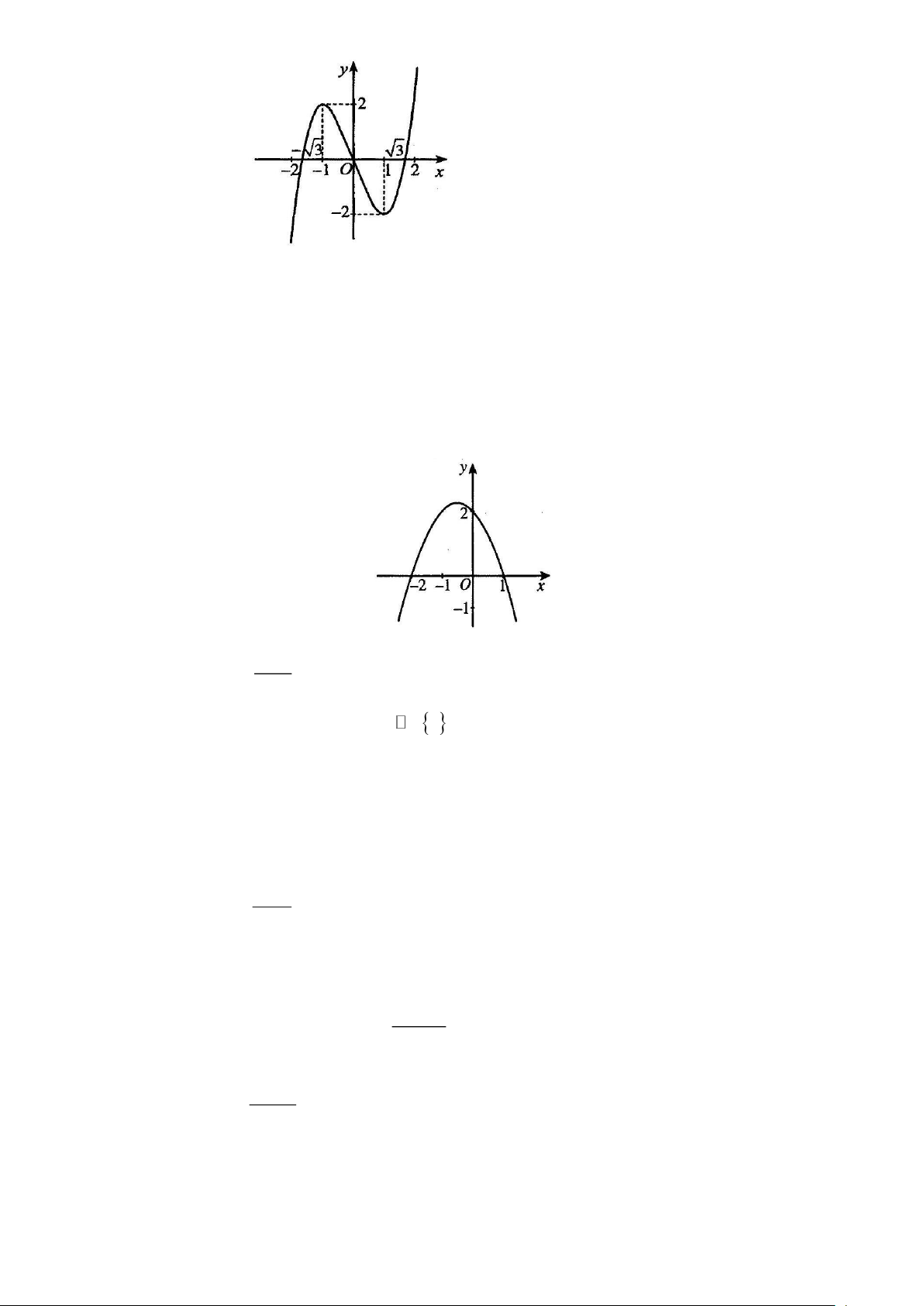
Câu 1.5: Cho hàm số y = f (x) xác định trên và có đồ thị như hình dưới đây.
a) Hàm số đã cho nghịch biến trên các khoảng (− ; − ) 1 và (1;2) .
b) Hàm số đã cho có 2 điểm cực trị. c) Trên đoạn 1 − ;
1 , giá trị lớn nhất của hàm số đã cho bằng 2 .
d) Phương trình 3 f (x) −6 = 0 có duy nhất 1 nghiệm.
Câu 1.6: Cho hàm số y = f (x) liên tục trên và có đồ thị f ( x) như hình bên dưới. y 4 2 -2 O x -1 1 2
a) Hàm số đã cho đồng biến trên các khoảng (− ; 1 − ) và (1;+).
b) Hàm số đã cho có 1 điểm cực trị.
c) Giá trị nhỏ nhất trên đoạn 3 − ; 1 bằng f (−2) .
d) Giá trị f '( ) 3 = 20 .
Câu 1.7: Cho hàm số y = f (x) 3 = x −3x .
a) Tập xác định của hàm số là R .
b) f (x) 2 = 3x +3.
c) f (x) 0 khi x( − ;− ) 1 (1;
+ ); f (x) 0 khi x( 1 − ; ) 1 .
d) Hàm số đã cho có đồ thị như ở Hình 1. Trang 13 Hình 1
Câu 1.8: Cho hàm số y = f (x) 3 2
= ax +bx + cx + d ( , a , b ,
c d là các số thực và a 0) có đồ thị hàm số
f (x) như Hình 13.
a) Điểm cực tiểu của hàm số y = f (x) là x =1. CT
b) Điểm cực đại của hàm số y = f (x) là x = 2 − . CĐ
c) Hàm số y = f (x) đồng biến trên khoảng (0; ) 1 .
d) Hàm số y = f (x) nghịch biến trên khoảng (2025;2026) . Hình 13 x − 2
Câu 2.1: Cho hàm số y = . x +1
a) Tập xác định của hàm số là D = \ 2
b) Đồ thị hàm số có đường tiệm cận đứng là đường thẳng x = 1 − .
c) Đồ thị hàm số có tất cả hai đường tiệm cận.
d) Đồ thị hàm số có tâm đối xứng nằm trên đường thẳng nằm trên đường thẳng
(): x+2y −3= 0.
Câu 2.2: Cho hàm số 2x + 1 y = x - 1
a) Giá trị của hàm số tại điểm x = 2 là f (2) = 5.
b) Giá trị của hàm số tại điểm x = 5là f (5) =11. 3 −
c) Đạo hàm của hàm số là ' f (x) = , x 1. 2 (x −1)
d) Giá trị lớn nhất của hàm số trên đoạn [2; ] 5 bằng 5. 2x + 4
Câu 2.3: Cho hàm số y = . x −1
a) Tập xác định D = R \ 1 .
b) Hàm số đồng biến trên từng khoảng xác định. Trang 14
c) Giao điểm với trục tung là (0; 4 − ) .
d) Toạ độ tâm đối xứng của đồ thị là (1; 4 − ) . x −
Câu 2.4: Cho hàm số y = f ( x) 2 1 =
có đồ thị là (C). x +1
a) Hàm số đã cho nghịch biến trên từng khoảng (− ; − ) 1 và ( 1 − ;+).
b) Hàm số đã cho không có cực trị.
c) (C) có tiệm cận đứng là đường thẳng x = 1
− , tiệm cận ngang là đường thẳng y = 2 .
d) Biết rằng trên (C) có 2 điểm phân biệt mà các tiếp tuyến của (C) tại các điểm đó song song với
đường thẳng y = x . Gọi k là tổng hoành độ của hai điểm đó, khi đó k là một số chính phương. x − 3
Câu 2.5: Cho hàm số y = . x +1
a) Hàm số đã cho đồng biến trên \ 1 − .
b) Hàm số đã cho đạt cực đại tại x = 4 .
c) Đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng x = 1
− , tiệm cận ngang là đường thẳng y = 1.
d) Có 2 023 giá trị nguyên của tham số m thuộc đoạn 2 − 024;202
4 để đường thẳng y = x + 2m
cắt đồ thị hàm số đã cho tại hai điểm nằm về hai phía của trục tung. ax +1
Câu 2.6: Cho hàm số y = ( a, ,
b c là các tham số) có bảng biến thiên như sau: bx + c
a) Hàm số đã cho đồng biến trên các khoảng ( ;2 − ) và (2;+) .
b) Hàm số đã cho có 2 điểm cực trị.
c) Trên khoảng (2;+) , giá trị lớn nhất của hàm số đã cho bằng 1.
d) Giá trị của biểu thức a +b + c bằng 0 . 3x + a
Câu 2.7: Cho hàm số y =
( a, b là các tham số) có đồ thị như Hình 12. x + b
a) Đồ thị hàm số có đường tiệm cận đứng x = 2 . b) b = 2 .
c) Đồ thị hàm số không đi qua gốc tọa độ. d) a = 0 . Hình 12
Câu 2.8: Trong 200 gam dung dịch muối nồng độ 15% , giả sử thêm vào dung dịch x (gam) muối tinh khiết
và được dung dịch có nồng độ f (x)%. Trang 15 100 x + 200
a) Hàm số f (x) ( ) = . x + 30
b) Đạo hàm của hàm số luôn nhận giá trị âm trên khoảng (0; + ).
c) Thêm càng nhiều gam muối tinh khiết thì nồng độ phần trăm càng tăng và không vượt quá 100% .
d) Giới hạn của f (x) khi x dần đến dương vô cực bằng 100 . 2 x − 2x + 2
Câu 3.1: Cho hàm số y = . x −1
a) Tập xác định của hàm số là D = R \ 1
b) Hàm số đạt cực đại tại x = 0
c) Hàm số đạt giá trị nhỏ nhất tại x = 2
d) Khoảng cách giữa hai điểm cực trị của đồ thị hàm số đã cho bằng 2 5 . 1
Câu 3.2: Cho hàm số y = x − 2 − . x + 3
a) Tập xác định của hàm số đã cho là: D = \ − 3 .
b) Tiệm cận đứng của đồ thị hàm số là x = 3.
c) Tiệm cận xiên của đồ thị hàm số là y = x − 2 .
d) Tọa độ tâm đối xứng của đồ thị là I ( 3;1). 2 x + 3x + 3
Câu 3.3: Cho hàm số y =
. Các mệnh đề sau đây đúng hay sai? x +1
a) Tiệm cận đứng của hàm số là x = 1 − .
b) Tiệm cận xiên của đồ thị là y = x − 2 .
c) Hàm số không có cực trị.
d) Hàm số đã cho có đồ thị như vẽ sau: Trang 16
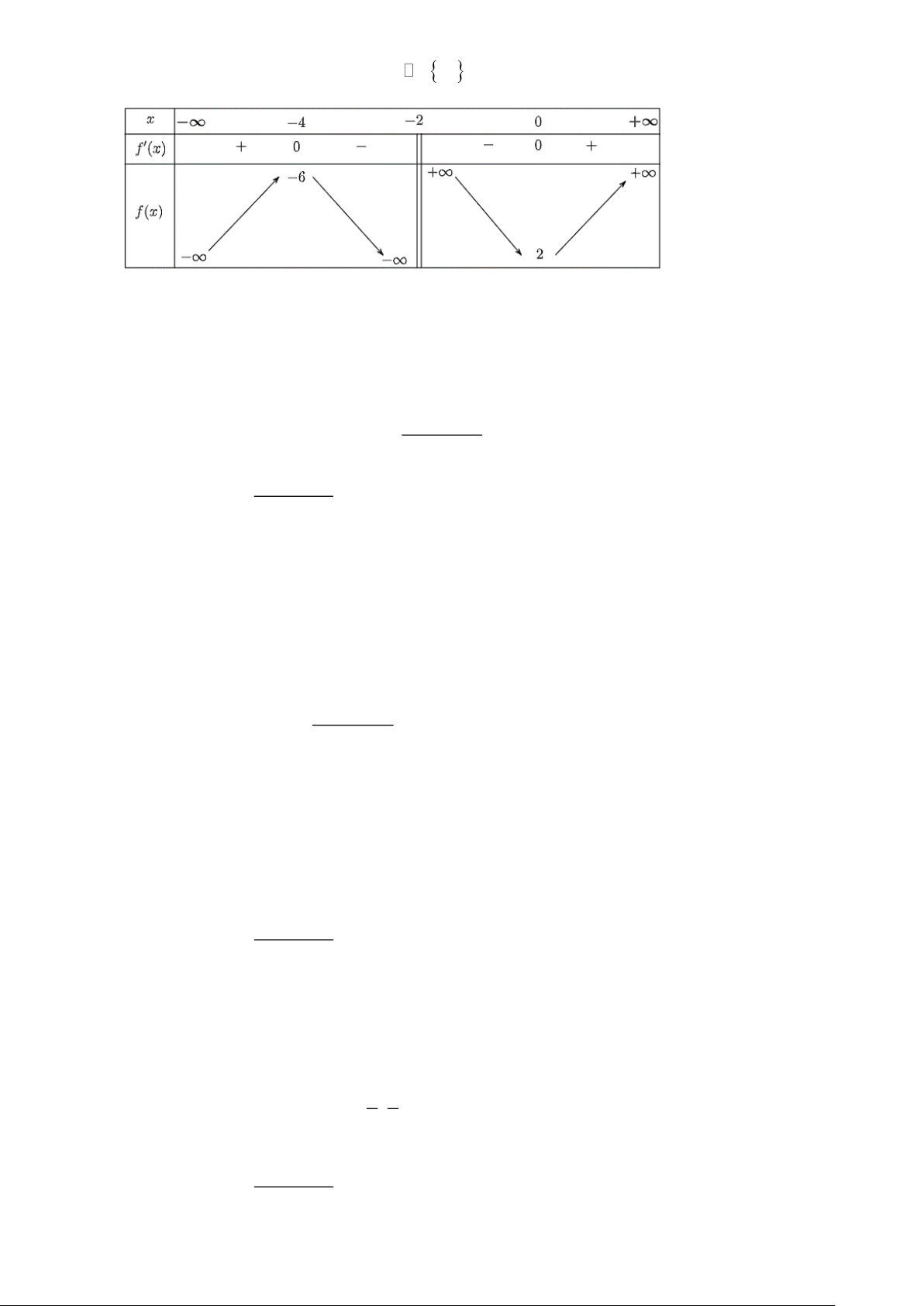
Câu 3.4: Cho hàm số y = f (x) xác định trên \ 2
− và có bảng biến thiên như sau:
a) Hàm số y = f (x) đồng biến trên mỗi khoảng (− ; 4 − ) và (0;+).
b) Giá trị cực tiểu của hàm số đã cho là y = 6 − . CT
c) Hàm số y = f (x) có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 6 − . 2 x + 2x + 4
d) Công thức xác định hàm số là y = . x + 2 2 x − 2x − 3
Câu 3.5: Cho hàm số y = . x − 2
a) Hàm số đã cho đồng biến trên mỗi khoảng ( ;2 − ) và (2;+) .
b) Hàm số đã cho có 2 cực trị.
c) Đồ thị hàm số nhận điểm I (2;2) làm tâm đối xứng.
d) Có 5 điểm thuộc đồ thị hàm số có tọa độ nguyên. 2 x + 4x + 7
Câu 3.6: Cho hàm số y = f ( x) = . x +1
a) Hàm số đã cho nghịch biến trên từng khoảng ( 3 − ;− ) 1 và ( 1 − ; ) 1 .
b) Giá trị cực tiểu của hàm số đã cho là 2 − .
c) Đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng x = 1
− , tiệm cận xiên là đường thẳng y = x + 3 .
d) Đồ thị hàm số y = f (x) đi qua 6 điểm có tọa độ nguyên. 2 x + 3x + 3
Câu 3.7: Cho hàm số y = . x + 2
a) Hàm số đã cho đồng biến trên (− ; − ) 1 và (3;+) .
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng 4 − .
c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm A(0; ) 1 .
d) Phương trình tiếp tuyến của đồ thị hàm số đã cho vuông góc với đường thẳng 3 3
x − 3y − 6 = 0 đi qua điểm B − ; . 2 2 2 −x + x +1
Câu 3.8: Cho hàm số y = có đồ thị (C). x +1
a) Hàm số đã cho nghịch biến trên các khoảng (− ; 2 − ) và (0;+). Trang 17
b) Đồ thị (C) có hai điểm cực trị nằm ở hai phía đối với trục tung.
c) Đồ thị (C) có đường tiệm cận đứng là x = 1
− ; đường tiệm cận xiên là y = −x + 2 .
d) Đồ thị (C) nhận điểm I ( 1
− ;3) làm tâm đối xứng.
Câu 4.1: Cho hàm số ( ) x
f x = e − x . a) ( ) x f x = e +1.
b) f (x) = 0 x = 0 .
c) Bảng biến thiên của hàm số f (x) là
d) Giá trị nhỏ nhất của hàm số đã cho trên R là 1 .
Câu 4.2: Cho hàm số f ( x) có đạo hàm f ( x) liên tục trên R . Hàm f ( x) có đồ thị như hình vẽ.
Các mệnh đề sau đúng hay sai?
a) Giá trị lớn nhất của hàm số trên đoạn 1 − ;2 bằng 1.
b) Hàm số f ( x) đồng biến trên khoảng (−;− ) 1 .
c) Hàm số f ( x) đạt cực đại tại x = 0 .
d) f (0) f ( ) 1 .
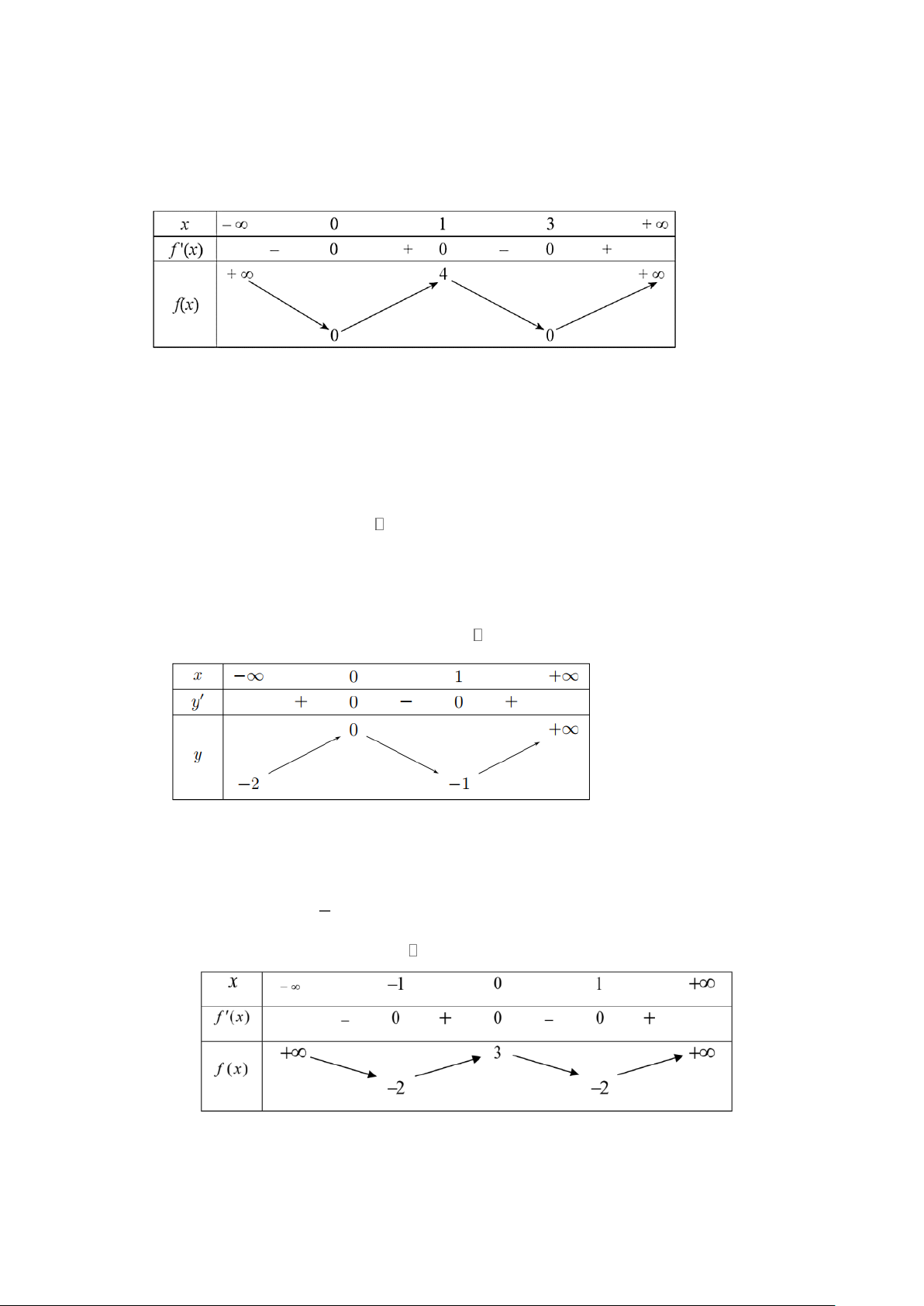
Câu 4.3: Cho hàm số đa thức bậc bốn có đồ thị hàm số y = f '(x) như hình bên dưới.
a) Hàm số y = f (x) đồng biến trên (2;4). Trang 18
b) Hàm số y = f (x) có 2 cực tiểu.
c) Hàm số y = f (x) có giá trị cực đại là f (−1) .
d) f (2) f (4) .
Câu 4.4: Cho hàm số đa thức bậc bốn y = f (x) có bảng biến thiên như sau:
a) Hàm số y = f (x) đồng biến trên mỗi khoảng ( ) ;1 − và (3;+) .
b) Số điểm cực trị của hàm số đã cho là 3 .
c) Hàm số y = f (x) có giá trị nhỏ nhất bằng 0 .
d) Đồ thị của hàm số y = f (x) không có đường tiệm cận.
Câu 4.5: Cho hàm số x
y = e − x + 3 .
a) Hàm số đã cho nghịch biến trên .
b) Hàm số đã cho đạt cực đại tại x = 0 .
c) Đồ thị hàm số cắt trục tung tại điểm có tọa độ là (0;4) .
d) Đồ thị hàm số đã cho không đi qua gốc tọa độ.
Câu 4.6: Cho hàm số y = f (x) xác định, liên tục trên và có bảng biến thiên sau:
a) Hàm số đã cho đồng biến trên ( 1 − ;+ ).
b) Hàm số đã cho đạt cực đại tại x = 0 ; đạt cực tiểu tại x =1.
c) Giá trị nhỏ nhất của hàm số đã cho bằng 2 − .
d) Phương trình f ( x) 3 = − có 1 nghiệm. 2
Câu 4.7: Cho hàm số y = f (x) xác định trên và có bảng biến thiên như sau:
a) Hàm số đã cho nghịch biến trên các khoảng (− ; − ) 1 và (0; ) 1 .
b) Hàm số đã cho có 3 điểm cực trị. c) Trên đoạn 1 − ;
1 , giá trị lớn nhất của hàm số đã cho bằng 3 .
d) Phương trình f (x) + 3 = 0 có 4 nghiệm. Trang 19
Câu 4.8: Trong 9 giây đầu tiên, một chất điểm chuyển động theo phương trình: s(t) 3 2 = t
− + 9t + 21t +1,
trong đó t tính bằng giây và s tính bằng mét.
a) s(t) 2 = 3
− t +18t + 21.
b) s '(t) = 6 − t +18.
c) Phương trình s(t) = 0 có đúng một nghiệm dương là t = 7.
d) Gia tốc của chất điểm tại thời điểm vật dừng lại là 2 36 m / s .
PHẦN III. TỰ LUẬN (3 điểm)
Câu 1 (1 điểm): Khảo sát sự biến thiên và vẽ đồ thị của một hàm số trong ba hàm số sau:
- Hàm số đa thức bậc ba; ax + b
- Hàm số phân thức y =
(c 0, ad −cb 0) ; cx + d 2
ax + bx + c
- Hàm số phân thức y =
(a 0, p 0 , đa thức tử không chia hết cho đa thức mẫu). px + q
Câu 2 (1 điểm): Bài toán liên quan đến các điểm cực trị của đồ thị một trong hai hàm số sau:
- Hàm số đa thức bậc ba; 2
ax + bx + c
- Hàm số phân thức y =
(a 0, p 0 , đa thức tử không chia hết cho đa thức mẫu). px + q
Câu 3 (1 điểm): Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn.
--------------------------HẾT-------------------------- Trang 20