Xử Lý Ảnh Số - Lý Thuyết Và Thực Hành Với Matlab
Trong những năm gần đây, xử lý tín hiệu nói chung và xử lý ảnh nói riêng, đặc biệt là ảnh số phát triển hết sức mạnh mẽ. Các kỹ thuật xử lý ảnh được áp dụng và cập nhật không những trong các công trình cơ bản như thị giác máy tính, mắt nhìn nhân tạo mà cả trong những công nghệ mới nhất như truyền hình sô' IPTV, trong y sinh học và ghi ảnh cộng hưởng từ 3D hay trong robots và người máy. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem!
Môn: Tài liệu Tổng hợp 2.3 K tài liệu
Trường: Tài liệu khác 2.5 K tài liệu
Tác giả:
Preview text:
T S H O V A N S U N G TS. HO VAN SUNG XLT LY ANH SO
I V T H U V e i V f t T H t f C H A N H V 6 l M R T I R B TRUCJNG DAI HRC BUY NH*N _______THU VI$N _______ v /V P . |
NHA XU AT BAN KHOA HOC VA KY THUAT HA NOI LỜI NÓI ĐẦU
Trong những năm gần đây, xử lý tín hiệu nói chung và xử lý ảnh nói riêng,
đặc biệt là ảnh số phát triển hết sức mạnh mẽ. Các kỹ thuật xử lý ảnh được áp dụng
và cập nhật không những trong các công trình cơ bản như thị giác máy tính, mắt
nhìn nhân tạo mà cả trong những công nghệ mới nhất như truyền hình sô' IPTV,
trong y sinh học và ghi ảnh cộng hưởng từ 3D hay trong robots và người máy.
X ử lý ảnh số được phát triển nhằm mục đích số hóa và m ã hóa các bức ảnh
để đơn giản hóa các quá trình truyền thông, in ấn và lưu giữ. Một mục tiêu quan
trọng khác của xử lý ảnh là cải thiện chất lượng và khôi phục ảnh nhằm hiểu biết
nhiều hơn nội dung thông tin chứa trong mỗi bức ảnh; chẳng hạn như cúc bức anh
chụp bề mặt các hành tinh xa xôi do vệ tinh gửi về hoặc các ảnh ỉìội soi, anh cộng
hưởng từ trong khảo sát y học. Một bài toán quan trọng nữa trong xử lý ảnh số là
phân đoạn và mỏ tả ảnh, nhằm tạo nên các ảnh như một tín hiệu lối vào cho một
hệ thống nhìn nhân tạo hay thị giác máy tính nhằm tách các thông tin và đo lường
các đối tượng chứa trong mối bức ảnh thu được. Tất cả các nhiệm vụ trên đều có
chung một mục đích là đáp ứng nhu cầu thông tin và hiểu biết ngàv một lớn của con người.
Đ ể đạt được các mục tiêu nói trên, xử lý ảnh sô' sử dụng các máy tính số làm
công cụ tính toán duy nhất. Hay nói khác di, thành tiãỉ của xử lý ảnh sô' gắn chặt
với các công cụ tính toán số, qua việc lựa chọn và cip dụng các gói phần mềm.
Gói phần mém hiệu quả nhất vẫn là phần mềm MATLAB. Cũng giống như các
môn học khác, hầu hết các khái niệm lý thuyết của xử lý ảnh số dã được cập
nhật trong gói phần mềm này. MATLAB cung cấp một lượng lớn các hàm, các
M-files, giúp ta vận dụng d ể xử lý các hình ảnh trong th ế giới thực. Trong cuốn
sách này, chúng tôi cũng dã tạo được nhiều M-files trong môi trường làm việc
MATLAB, từ những hình ảnh thu được bằng máy ảnh số. Những ảnh này lủ
những ảnh mầu sử dụng trong các chương trình mô phỏng cho các khái niệm lý
thuyết. Ngocù ra, một số ánh mẩu rất điển hình, được mặc định trong hộp câng
cụ của MATLAB (IPT) cũng dược sử dụng, góp phần lỏm phong phú và điển
hình hoá cho các phương pháp phân tích lý thuyết; chẳng hạn như các phép
chiếu xạ Rcuỉon trong khi thu ảnh cộng hưởng từ(MRI).
Các tín hiệu hình ảnh được mô tả bởi mảng dữ liệu nhiều chiều; chúng vừa
có tính chất xác định lẫn thống kê. Biểu diễn ảnh theo quan diêm tín hiệu xác định
dược thể hiện trong chương ỉ. Chương 2 dành cho việc biểu diễn tín hiệu hình ảnh
theo quan điểm thống kê. Chúng tôi dành trọn chương 3 để mô tả những phép biến
dối hai chiều quan trọng nhất. Đó là những phép biến đổi 2D như: DFT-2D, biến
dổi DCT-2D, các phép biến đổi không gian như biến đổi Radon, các phép chiếu 3
'7 -. '»!•:: 77° 7" V ::7 7 7 w
«>« (Weto /wcitaj; tnôt và hai
chiêu. Bởi vì những phép biến đôi này đang đươc s ử d u n o , , ! , - , ", 7 z
„ẬĂ Chương 5 C e d e k ý . L é r ^
aim,¡7 ntu các kỹ ,huJ, Znva ,J h7á z ctjm?x ív "ì í " Í T
v i chrnng 9. chưrrng c u ii cùng cia "ách Z , d c T ì , ỷ , ? hi 7 ,hái
phân đoạn và tách các đường viển, phan lớr iioi rtin p ",!fílíf p l °p p i á n nch, z
7 b S n Z - r Z c Z Z b% T n ó
C tn v ù lọ c ic đ Ịc trưng căng „hư nhện dâng c í c M , 7 2 t i a j h l tranh, bức ánh.
. ng cac đổi tượng cồ trong một bưc
sự thực thi thực tể thế hiện trong các chươnQtr'
r “ c quan ơlem ly tíìllyêt và
Chúng tôi c ố gắng nêu bật các quan điểm lý thúvêt I n r i i i'nêy haậc cèc M ~flles-
trình thực hiện và các ví dụ minh hoạ; giúp „gưài 7 , . . ra nhữn8 chương
quan trọng và ý nghĩa thực tiễn cũng nhưnhưnọ n h ? 7 ?7??'! thức sềl1 sấc hơ" tâm
được trình bầy trong sách .
ns phap thực hiện mồi vấn đề
Xỉí lý ánh là một lĩnh vực rộng lớư, năng đ óm và
soạn cuốn sách này, chúng tôi muốn cung cấp cho b 1
dán' Vì thê khi biên
viên hay các học viên cao học của các trường Đai h o cC -
nhát íà các bạn sinh
thông lẩn Công nghệ Thông tin hay các trường Đai h o i ỉ a ? ngh^’ cả Đi^n tửViễn
kiến thức cơ bản nhất cả V é cơ sở lý thuyết lần những côn 0
h,ọc Tư nhién' "h‘~f»g
có thê tiếp thu và tự mình mô phỏng va piiát triển co
8 ‘‘ 'hực hành đ ể bạn đọc
chúng tôi đã cố gắng chọn lọc và trình bay nhưng nô' ' ì ’ Với m° ng muôn ây’
thực, đồng thời cập nhật được những thông tin va nhan' ung quan trọng vẩ thiết
ảnh hiện đang tồn tạ, hoặc đang được quan tám nghỉén 7,11??!.!™ ! " M t về xừ lý
trình soạn thảo cỏ thê còn có những khiếm khuyéi. Chun !'-; !?! "í"*” tro"8 quá
ơn và mong quí độc giả góp ý đ ể làn tái bản sau cuốn !drì 1
xtn chủ" thằnh cảm
aư<?c hoàn thiện hơn. Tác giả 4 CHƯƠNG 1
BIỂU DIỄN ẢNH THEO QUAN ĐlỂM t í n h i ệ u
1.1. XỬ LÝ ẢNH SỐ LÀ Gì ?
Một bức ảnh một màu được định nghĩa như một hàm của độ sáng 2 chiều (2-
D) f(x,y); ưong đó X và y là hai biến số không gian. Giá trị của hàm f tại điểm (x,y)
tỉ lệ với độ sáng của ảnh tại điểm đó nên được gọi là cường độ của ảnh; nó chính là
mức xám của ảnh tại điểm (x,y) đó. Nếu ta có một bức ảnh nhiều mầu, thì hàm f là
một véctơ, mỗi thành phần của véctơ biểu thị độ sáng của ảnh tại điểm (x,y) tương
ứng với một dải mẩu xác định.
Ảnh số là ảnh f(x,y) được số hóa cả về tọa độ không gian lẳn vế độ sáng. Nó
được biểu thị bằng một mảng số nguyên 2 chiều. Giá trị của độ sáng đã được số hóa
thì gọi là giá trị của mức xám. Như vậy, một ảnh sô' được biểu thị bans một mảng
dữ liệu với một số lượng hữu hạn các phần tử, mỗi phần tử có một vị trí và giá trị
riêng biệt. Mỗi phần từ của mảng này dược gọi là một pixel, hay pel cho một phần tử của một bức tranh.
Xử lý ảnh số sử dụng các máy tính số; chúng được phát triển để đáp ứng ba
vấn đề chính yếu liên quan đến các bức tranh và ảnh là:
• Sô' hóa và mã hóa các bức ảnh để đơn giản hóa các quá trình truyền
thông, in ấn và lưu giữ ảnh.
• Cái thiện chất lượng và khôi phục ảnh để hiểu biết nhiều hơn nội dung
thỏng tin chứa trong mỗi bức ảnh, chẳng hạn như các bức ảnh chụp bề
mặt các hành tinh xa xôi khác do vệ tinh gửi về hoặc các ảnh nội soi,
cộng hưởng từ trong khảo sát y học.
• Phân đoạn và mô tả ảnh, nhằm tạo nên các ảnh như một tín hiệu lối
vào cho một hệ thống nhìn nhân tạo hoặc để tách các thông tin chứa trong một ảnh thu dược.
1.2. BIỂU DIỄN MỘT ẢNH s ố 1.2.1. Ảnh sô là gì?
Như đã nói, một ảnh có thể được biểu diễn như một hàm hai chiều f(x,y);
trong dó X và y là hai biến sô' không gian. Giá trị của hàm f ứng với giá trị của cặp
tọa độ (x,y) được gọi là cường độ của ảnh tại điểm đó. Nó chính là độ sáng của ảnh
tại điểm dó. Thuật ngữ mức xám dùng để chỉ cường độ của các ảnh đơn mầu. Các
ảnh mầu là tổ hợp của các ảnh 2-D thành phần. Chẳng hạn, trong hệ thống mầu
RGB, một ảnh mầu chứa ba ảnh thành phần là đỏ (R), xanh lá cây (G) và xanh nước
biển (B). Vì thế, nhiều kỹ thuật xử lý ảnh đơn mầu có thể mở rộng cho các ảnh da
mầu bằng cách xử lý ba ảnh thành phần này một cách riêng biệt.
Một ảnh có thể là liên tục cả về các biến sô' không gian X và y cũng như vể
biên dộ f. Việc chuyển đổi một ảnh liên tục thành một ảnh sò cẩn phải thực hiện
quá trình sô' hóa cả biến số không gian lân biên độ. Sô' hóa các giá trị tọa độ được
gọi là sự lấy mẫic, còn sô' hóa các giá trị biên độ được gọi là lượng tử hóa. Khi đó,
X, y và các giá trị biên độ của f là những đại lượng rời rạc và hữu hạn. Những ảnh
như vậy được gọi là ảnh số. 5
1.2.2. Biểu diễn ảnh dưới dạng ma trận
Trong một ảnh, mỗi pixel tương úng với một phẩn của một vật thể vật lý
trong thế giới thực 3D. Vật thể vật lý này được minh họa bởi các ánh sang phan xa
và hấp thụ trên vật thể đó. Ánh sáng phản xạ đi đến biến tử (camera chẳng han) và
tạo ra ảnh f(x,y). Cường độ ánh sáng phản xạ thu được tại môi vị trí của vât thể đac
trưng cho giá trị của mỗi phần tử ảnh tại vị trí đó. Mồi phần tử ảnh gọi la môt pixel
ảnh. Giá trị của môi pixel đặc trưng cho cường độ sáng tại vị trí đo, nen no cũng
được gọi là mức xám. ' 5
Nhờ sự lây mâu và lượng tử hóa ảnh f(x,y) ta sẽ thu được môt ma trân tao
thành từ những số thực Ma trận với các phần tử số thực đó còn được gọi là in d Z
dữ liệu ảnh. Môi phân tư của ma trận đó được gọi là một pixel. Giả sir ma trận CO M
hàng và N cột, ta nói rằng ảnh có kích thước MxN. Các giá trị của các tọa đô (X V)
là những đại lượng rời rạc. Đối với một ảnh số, các tọa độ X va y la nhtog gia tri
nguyên; X chạy từ 0 dên M -l ; còn y chạy từ 0 đến N -l. Với nhũng qui đinh này thì
một ảnh sô được biếu thị dưới dạng ma trận sau* f ^ f( 0 ,0) f ( 0 ,l ) f(0 , N - ỉ ) f ( ỉ ,0 ) f ( U ) f ị l , N -1 ) m , 2 ) m - i . N - 1 )
, .,Tr0n! T ột SÔ tài liệu’ chẳng hạn như trong MATI AR - , , biểu thị dưới dạng '
g MAfLAB, một ảnh số còn được f(l,2 ) f ( l,N ) f(2 ,l) f(2,2) f(2,N ) f(M ,l) f(M ,2) f(M ,N )
Rõ ràng, cả hai cách biểu diễn là nh.v
(1.1) dịch gốc tọa độ sang phả 1 đớn vị; CO nghîaTa f n T ) h?,ng ỉ.hAức
ta sẽ sử dụng biểu diễn (1.2) để mô ta anh số VrV ' h Ù. I Đê thuf n hện,
< , I N và 1 < j < M ký hiéu ;Ị T p t i l ì m à đ í t t . ‘ĩ 1 « « ? 1
trong vùng 0 < f(i,j) S G . Chẳng han phẩn (ơ r i1 f i'| Va C'ỏl 1 ^ Ẻ tr' củu năm
thứ 5 và cột thứ 3 của ma trân f. TTiong fhirrVn ’
' -g á [r-’C“a p xel nam ở hàng
ma trận vuông NxN. Ma trận lxN thì đươc goi fà’ ng|r á \ ta , ểu diễn ảnh dưới dạng - 1' * I /
1X11 auvc gọi là môt véctơ hàng trone khi ma tríìn
Mv I thí tiược gọ là mộ,
cộ,. Ma trận 2x2 là mộ, lô !n,Z g. ■
Đối với môt ảnh số thì eiá tri I*n ’ _ s- . , _
thi đướidáng G = 2" Vơ calhbiều diễn „ ít' í? * í
P “ ầ p lhườnê dược biểu
mọt anh °o cd kích thutSc MxN là: y b" b c í " *i mỄ h° a hay 6 b = MxNxm (1.3)
Chẳrig hạn, một ảnh 512x512 với 256 mức xám (m=8) cần 2.097.+S2 bít hoặc
262.144 bytes 8 bít. Vì vậy để giảm bớt lượng bít cần lưu giữ trong bộ nhớ, cần phải
giảm m và N mà không làm giảm chất lượng của ảnh. Việc giảm m và N liên quan đến
một đại lượng rất quan trọng trong xử lý ảnh, đó là độ phân giải của ảnh.
Độ phân giải của một ảnh biểu thị có bao nhiêu chi tiết chứa trong ảnh mà ta
còn có thể phân biệt được. Rõ ràng là, độ phân giải của một ảnh phụ thuộc cả kích
thước N của ảnh lẫn độ lớn m cùa các pixel. Nếu giữ m không đổi và tăng N thì trên
ảnh sẽ xuất hiện hiệu ícng bàn cờ, còn nếu giữ N không đổi và tăng m thì các đường
viền của ảnh sẽ bị sai lệch nhiều. Thực tế cho thấy một bức tranh càng nhiều chi tiết
thì nó được cải thiện càng ít khi giữ N không đổi và tăng m. Do đó đối với những
bức họa có nhiều chi tiết, chẳng hạn như bức họa các đám mây, thì sô' lượng các
mức xám không đóng vai trò quan trọng.
Trong MATLAB, các ma trận được lưu giữ dưới dạng các biến với các tên như A, a, RGB, real_aray,....
1.2.3. Các qui định về tọa độ
Các vị trí trong một ảnh có thể biểu thị trong nhiều hệ tọa độ khác nhau tuỳ
thuộc vào ngữ cảnh. Ớ dây, ta chi xét hai hệ tọa dộ chính. Đó là hệ tọa độ pixel va
hệ tọa độ không gian. Tọa độ pixel
Phương pháp thuận tiện nhất để biểu thị các vị trí của một ảnh là sử dụng các
tọa độ pixel. Tror.g hệ tọa độ này, ảnh dược xử lý như một lưới các phẩn từ rời rạc
sắp xếp từ trên xuống dưới và từ trái sang phải như trên hình 1.1 sau đây.
Đối với các tọa độ pixel thì thành phần r (hàng) tăng từ trên xuống dưới,
trong khi thành phần c (cột) thì tăng từ trái sang phải. Các tọa độ pixel là những giá
trị nguyên bắt đầu từ 1 đến hết chiều dài của hàng và cột. 7
Giữa toa độ pixel yà tọa độ đùng để mô tả một ma trận là hoàn toàn tương
đương. Sự tương đương này^giúp ta hiểu rõ hơn quan hệ giữa ma trận dữ lieu ảnh va
cách để hiển thị ảnh đó. Chang hạn, dữ liệu đối với pixel ờ hàng thứ 5 và côt 3 đứơc
lưu giữ trong phần tử ma trận (5,3).
Các tọa độ không gian
Như đã nói, trong hệ tọa độ pixel, một pixel được xử lý như môt đơn vi rời
rạc được xác định ^ một cách duy nhất nhờ một cặp tọa độ riêng rẽ chẩng han như
(5,3). Với each biểu diễn này thì một vị trí như (5.5,3.2) ìà không CO y nghia nữa
Tuy nhiên, trong hệ tọa độ không gian, các vị trí trong một ảnh là những vi trí trông
một mặt phẳng, được mô tả bằng một cặp tọa độ(x,y), không phải là (r, c) nhir trong
hệ tọa độ pixel. Với hệ tọa độ không gian này, thì VỊ trí (5.5, 3.2) lại có ý nghía
Hình 1.2 minh họa một hệ tọa độ không gian được sử dụng để mô tả các ảnh
Lưu ý rằng y tăng từ trên xuống dưới như trên hĩnh 1.2. O S 1 2 3 4 4.i 0.5- 1 2 . 3 4 " 4.5 ' y Ỷ
Hình 1.2. Hệ tọa độ không gian.
Từ hai hình vẽ trên ta thấy, trong hệ tọa độ không gian, tâm điểm của pixel
nào đó đổng nhất với các tọa độ pixel của pixel đó. Tuy nhiên, hai hệ tọa độ con có
sự khác nhau là vị trí của ảnh ở góc trái trên cùng là (1,1) trong khi ơ tọa đọ không
gian, nó lại là (0.1), 0.5). Sự khác nhau này là do hệ tọa độ pixel là rời rạc, trong khi
hệ tọa độ không gian là liên tục. Sự khác nhau nữa là thứ tự của các thanh phần nam
ngang và thăng đứng trong các hệ tọa độ này: trong hệ toa đô pixel là (r,c), trong
khi hệ tọa độ không gian là (x,y).
Như vậỵ, nệu tọa độ không gian (x,y) chỉ nhận những giá trị nguyên, bắt đầu
từ lđến hết chiểu dài của ảnh; nghĩa là X kéo dài từ 1,2, ..., N và y kéo dài từ 1 2 •••*
đông thơi chọn X =c; y = r, thì tọa độ không gian sẽ đồng nhất với hệ tọa đô
pixel. VỚI cách lam này thì các tọa độ không gian của một ảnh tương úmg vơi các
tọa độ pixel cua anh đó. Chăng hạn tâm điểm của pixel ở hàng 5 và côt 3 có toa đô không gian là x=3; y=5.
1.2. 4. Bỉểu diễn ảnh dưới dạng véctơ
Trong xử lý ảnh, đê thuận tiện cho việc tính toán, các mảng dữ liệu ảnh NxN
thường được viết dưới dạng véctơ. Với cách biểu diễn này thì mảng dữ liệu ảnh f(nj
,n2), với 1 < n, < N và 1 < n2 < N được chuyển thành véctơ N2X1 f có dạng như sau: 8 N f = S N „ f V „ (1.4) n = l
trong dó Vn là véctơ cột có dạng như sau: r 0 hàng 0 hàng n - 1 1 hàng n vn = 0 hàng n + 1 (1.5) _ 0 J hàng N
còn véctơ Nn cũng là véctơ cột có dạng: o
ma trận N X N các phần tử 0 1 0 0 0 0 1 0 0 N.. -
ma trận đơn vi N X N ( 1.6) ‘1 0 . 0 1 o
ma trận N X N các phần tử 0
Rõ ràng, nếu f là một véctơ N2x 1, như biểu thị trong (1.4), thì chúng ta có
thể tìm được ma trận f, NxN có cột đầu tiên của nó là N phần tử đầu tiên của véctơ
f, cột thứ hai là N phần tử tiếp theo của véctơ f , . .. như biểu thức (1.7) sau đây f = Z N T fVnT (1.7) n n = l
Ví dụ 1.1. Hãy biểu diễn ma trận ảnh 3x3 sau đây dưới dạng véctơ f 12 f 13 f = f 21 f 22 f 23 f 31 f 32 f 33 9
Để giải quyết bài toán này, trước tiên ta phải xác định các ma trận v„. Với T '0' '0' v,= 0 ,v2 = 1 .v,= 0 0 0 1
theo (1.6) ta thu dược 3 ma trận Nn là " l 0 0 ' ' o 0 0 ' ' o 0 0 “ 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 N , = 0 0 0 , n 2 = 0 1 0 , n 3 = 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 fll f 21 «31 f 12
f = N,fV, + N2fV2 + N,fVj = f22 ( 1.8) f32 «13 «23 f33
côt thii^ƠI f32 ïà^thanh1 nhắ ưft! d| ng véctơ này thl Phần tử của ma trận ở hàng thứ 3
cọt tmr 2, 132 là thành phần thứ 6 của véctơ f, được ký hiệu la f(6).
1.3. CÁC TOÁN TỬ TUYÊN TÍNH TÁC ĐỘNG LÊN ẢNH
1.3.1. Các toán tỉr tuyến tính đươc mot fnrono ¿a
cac phép toán lên trường ảnh lối vào để thu inven tính r» ' 01 ra'
sô cac toan rá trong xử lý ảnh là những toán tử
pixel cua môt°trưrm a^ i ° ' ánJ ử
trường ảnh 1Ố1 ra thu được là một tổ hợp các
nhX. nhân nh-tr U g ánh lối vào. Các phép toán này bao gổm các phép chồng chất,
phep nhan chập, phép biên đổi unitary và phép lọc tuyến tính. 10
Giả sử ta cỏ mảng ảnh lối vào f(n,,n2) có kích thước là N ixN2. Nếu tác động
toán tử tuyến tính lên trường ảnh lối vào này, ta sẽ thu được một ảnh mới g(m bm2)
có kích thước mới M|XM2, được xác định từ biểu thức (1.9) sau: N| N 2
g(m„m2) = 2 ] ^ f ( n 1,n 2)h(n1,n 2 ;m1,m2) (1.9) nl=l n2=l
Trong đó h ( n j , n 2 ;m i,m 2 )được gọi là hàm mở rộng điểm hay còn được
gọi là đáp ứng xung của hệ thống xử lý ảnh 2D. Hàm mở rộng điểm
h (n Ị,ri2 ;m i,m 2 ) cho biết giá trị của pixel lối vào tại vị trí (n,,n2) ảnh hưởng như
thế nào đến giá trị của pixel lối ra tại vị trí (m, ,m2). Nếu phép toán chỉ phụ thuộc
vào khoảng cách tương đối giữa pixel lối vào và lối ra mà không ảnh hưởng đến vi
trí của mỗi pixel, thì toán tử đó được biểu thị bằng hàm mở rộng điểm bất biến dịch
(shift invariant). Hàm này sẽ có dạng:
h (n 1, n 2 ;m 1,m 2 ) = h(m Ị - n l t m 2 - n 2 ) (1.10)
Khi dó, ảnh lối ra g(m,,m2) được xác định bằng công thức: Ni N 2
g(m„m2)= ^ ^ f ( n 1, n2)h(m1- n ! , m 2 - n 2) (1.11) nl=l n2=l
Biểu thức (1.11) mô tả phép nhân chập hai dãy thời gian rời rạc trong không
gian 2 chiều. Vậy, nếu toán tử tác động lên ảnh là một toán tử bất biến dịch thì ảnh
lối ra thu được sẽ bằng nhân chập giữa ảnh lối vào với đáp ứng xung của hệ thống
xử lý tín hiệu 2D h ( n i,r i2 ;m i,m 2 ) .
Trong MATLAB, phép nhân chập (1.11) được thực hiện để lọc ảnh hoặc thực
hiện các phép bien đổi tuyến tính lên ảnh. Để thực hiện phép nhân chập giữa cẩc
ảnh, ta dùng hàm con\'2 có cú pháp như sau c = conv2(A,B) c = conv2(hcol,hrow,A) c = conv2(...,’shape')
Hàm c = conv2(A,B) tính nhân chập giữa hai ảnh A và B. Nếu một trong hai
ma trận là mạch lọc FIR hai chiéu, thì ma trận kia tương đương với một ảnh đà
được lọc. Phương pháp lọc đó được gọi là lọc tuyến tính hai chiều. Kích thước của
ma trận ảnh c thu được bằng tổng số chiều tương ứng của hai ma trận A và B trừ đi 1 đơn vị. Cómghĩa là
size(C) = [mA+mn- l , nA+nB- l ]
Hàm c = conv2(hcol,hrow,A) trước tiên nhân chập A với véctơ hcol dọc
theo các hàng, sau đó với hrow dọc theo các cột. Nếu hcol một véctơ cột và hrow
là véctơ hàng, thì trường hợp này được tính như c = conv2(hcol*hrow,A).
Hàm c = conv2(...,'shape') cho ra một phần con được qui định trong tham số 'shape'.
Ví dụ 1.2. Giả sử ta có ma trận ảnh
sl= [-i -1 -1; -1 8 -l; -1 -1 -1]';
Ma trận của hàm lọc là A=zeros(10); 11 A(3:7,3:7) = ones(5);
Nhân chập 2 chiéu giữa hai ma trận này dùng lệnh HI = cõnv2(A,sl)
kết quả thu được ảnh mới có ma trận ảnh HI = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 -2 -3 -3 -3 -2 -1 0 0 0 0 0 -2 5 3 3 3 5 -2 0 0 0 0 0 -3 3 0 0 0 3 -3 0 0 0 0 0 -3 3 0 0 0 3 -3 0 0 0 0 0 -3 3 0 0 0 3 -3 0 0 0 0 0 -2 5 3 3 3 5 -2 0 0 0 0 0 -1 -2 -3 -3 -3 -2 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Bây giờ vẽ đồ thị ma ưận ảnh này với lệnh mesh(Hl), sẽ thu được ảnh trên hình 1.3. 0 0
Hình 1.3. Ảnh đã được lọc của ví dụ 1.2.
Quan hệ giữa ảnh lối vào và ảnh lối ra được mô tả một cách thuận lợi hơn,
nếu ta sử dụng cách biểu diễn véctơ. Thật vậy, nếu ma trận ảnh lối vào và ra là
những ma trận vuông: ma trận lối vào có kích thước NxN và lối ra có kích thước
MxM; ở đây, ta chọn N| = N2 =N và M| = M2 =M. Khi dó, dưới dạng véctơ, thì ảnh
lối vào sẽ được mố tả bằng véctơ tơ ảnh f N2X1; còn ảnh lối ra sẽ là véctơ ảnh lối ra
g M2x 1 . Nếu^toán tử tác động là tuyến tính, thì nó có thể được biểu thị bàng ma
trận vuông H N2xN2 . Khi đó, hệ thức (1.9) mô tả quan hệ giữa ảnh lối vào và ảnh
lối ra sau khi tác động được biểu thị dưới dạng đơn giản hơn là: g = Hf ( 1.12) 12
Phương trình này chính là phương ưình cơ bản của xử lý ảnh tuyến tính.
Ma trận H N2xN2 có thể được phân thành MxN các ma trận con H mn và được viết dưới dạng: ' H n H 12 H 1n h 2i h 22 h 2N H = (1.13) H Ml H M2 H MN
Thay (1.7) vào (1.12) , ta sẽ thu được quan hệ giữa véctơ ảnh lối ra g với ma trận ảnh lối vào f: g = £ ; H N nfVn (1.14) n = l
Từ (1.14) ta cũng tìm được ma trận ảnh lối ra theo công thức: M g = £ M m gU m (1.15) m = l
Thay (1.14) vào (1.15), ta tìm được quan hệ giữa ma trận ảnh lối ra g và ma trận ảnh lối vào f: M N / \
ê - £ 2 > J , H N „ ) f ( V n U n l) (1.16) m = 1 n = 1 hay M M N IN / \
= £ £ ( « „ , „ ) f ( v „ u m ) (1.17) m = l n=l
ở đây ta đã sử dụng ma trận H mn= M ^ H N n (1.18)
Bây giờ, chúng ta xét một sô' trường hợp riêng:
1. Nếu toán tử tuyến tính H có thể phán tách được, có nghĩa là hàm mở rộng
điểm ảnh hưởng đến các hàng và cột của ma trận ảnh lối vào là dộc lập với nhau.
Khi đó nó có thể được viết dưới dạng
h (n 1, n 2;m 1,m 2 ) = h c (n 1, m 1)h r (n 2 , m 2 ) (1.19)
Khi đó ma trận ảnh lối ra g(m,,m2) liên hệ với ma trận ảnh lối vào f(n,,n2) dưới dạng N N g(m „m ,)=
h c tn ^ iT i!) ^ f ( n 1, n 2 )h r ( n 1, m 2 ) ( 1.20) nl=l n2=l Hay dưới dạng ma trân 13 g = H / H j (1.21)
Trong (ló, Hc và Hr là những ma trận hàng và cột liên hệ với ma trận H như sau H = HcHr (1.22)
Ví dụl.3. Toán tử tuyến tính là một ma trận H 9x9. Hãy tìm các ma
trận con Hmn. Vì ma trận H có 9 hàng và 9 cột, nên ta phân ra được
3 ma trận con Hmn; các ma trận con cũng là các ma trận vuồng có
3 hàng và 3 cột, được phân chia như sau: h u h)2 h 13 h 14 hl5 h 16 h ị7 h 18 h |9 h 21 h 2-> h 23 h 24 h95 h 26 h 27 h 28 h 29 h 3l h 32 h 33 h 34 h 35 h36 h 37 00 h 39 h 4 i h 42 h 43 h 44 h 45 h 46 h 47 h 48 h49 h 5l h 52 h 53 h 54 h55 h 56 h 57 h 58 h 59 h 61 h 62 h 63 h 64 h 65. h 66 h 67 h 68 h 69 h 7Ị h 72 h 73 h 74 h 75 h 76 h 77 h 78 h 79 h 81 h 82 h 83 h 84 h 85 h 86 h 87 h 88 h 89 h 9I h 92 h 93 h 94 h95 h 96 h 97 họ8 h 99 i
So sánh với ma trận (1.13) ta thấy ma trận con H23 trong trường hợp này sẽ có dạng hA1 0 K 0 I r h59 s K 0 0 K i ^68
ứng với m = 2 (hàng thứ 2 và n =3 (cột thứ 3) trong ma trận phân khối (1.13).
Ma trận này cũng hoàn toàn được xác định nếu dùng hệ thức (1.18) với M = N. Có nghĩa là 14 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0
1.3.2. Mục đích của xử lý ảnh suy từ các phép biến đổi
Từ phương trình cơ bản (1.12) và những hệ quả rút ra từ phương trình đó, ta
thấy mục tiêu của xử lý ảnh giải quyết bốn vần đề chính yếu sau:
• Cho ảnh lối vào f, ta phải chọn ma trận biến đổi H, hay Hc và H r dể sao cho
ảnh thu được g có chất lượng tốt hơn f, theo một sô' tiêu chuẩn nào dấy. Đấy
chính là vấn để cải thiện chất lượng ảnh.
• Cho ảnh f, phải chọn ma trận biến đổi H, hay Hc và H r để sao cho ảnh thu
được g được biểu thị ít bít hơn f mà không làm mất nhiều chi tiết. Đó chính
là vấn đẻ nén ánh.
• Cho ảnh f, phải chọn ma trận biến đổi H hay Hc và Hr để sao cho ảnh thu
được g làm nổi bật một số nét điển hình của f. Đó chính là bài toán tạo ảnh
trong mắt nhìn tự dộng.
• Cuối cùng là bài toán khôi phnc ánh. Đó là bài toán biết các mẫu ảnh lối ra g
và các dữ liệu của hàm mở rộng phô h(n|,n2,m|,m2), khôi phục lại ảnh f. 1.4. ĐỌC ẢNH
Để đọc ảnh f trong môi trường MATLAB, người ta dùng hàm itnread với cú pháp sau
/ = imread('tẻn file') chẳng hạn / = imread('rice.png')
đọc ảnh JFEG rice dưới dạng ma trận f. Trong ví dụ này, hàm imread đọc file từ
một thư mục hiện hành. Cách đơn giản nhất để đọc một ảnh từ một thư mục riêng là
bao gồm cầ đường dẫn đến thư mục đó. Ví dụ
/ = imreadị 'D :\myìmage\rice .pn q ') ;
đọc ảnh từ danh mục gọi myimage trong ổ D; trong khi
/ = imreadự\myimage\rice .png' );
dọc ảnh từ thư mục con myimage của thư mục hiện hành. Bảng B l.l sau đây liệt kê
một số định dạng được trợ giúp bởi hai hàm imread và imnrite. 15
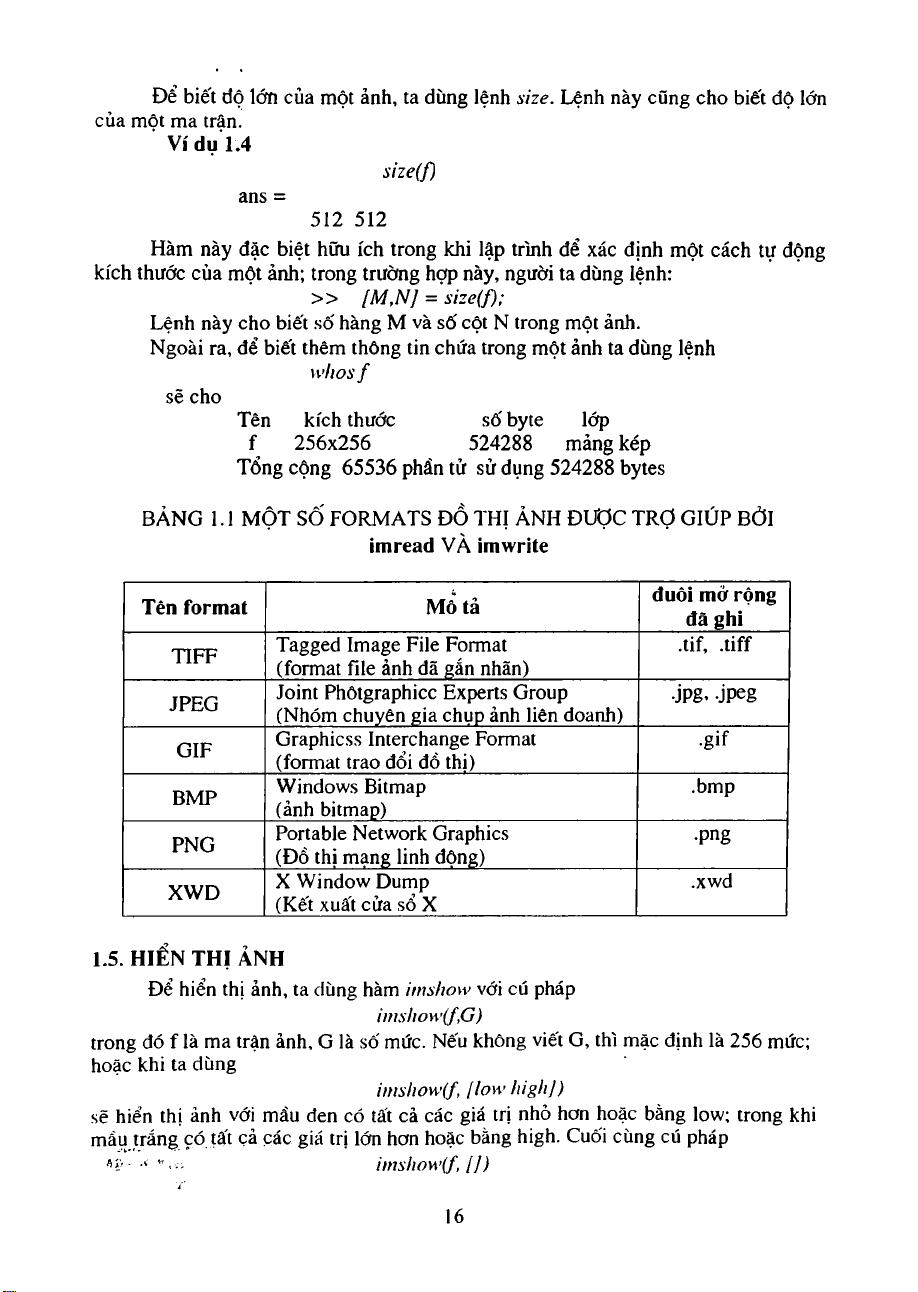
Để biết đô lớn của một ảnh, ta dùng lệnh size. Lệnh này cũng cho biết độ lớn của một ma trận. Ví dụ 1.4 size(f) ans = 512 512
Hàm này đặc biệt hữu ích trong khi lập trình để xác định một cách tự động
kích thước của một ảnh; trong trường hợp này, người ta dùng lệnh:
>> [M,N] = size(f);
Lệnh này cho biết số hàng M và sô' cột N trong một ảnh.
Ngoài ra, để biết thêm thông tin chứa trong một ảnh ta dùng lệnh wltos / sẽ cho Tên kích thước số byte lớp f 256x256 524288 mảng kép
Tổng cộng 65536 phần tử sử dụng 524288 bytes
BẢNG 1.1 MỘT SỐ FORMATS Đ ồ THỊ ẢNH ĐƯỢC TRỢ GIÚP BỞI imread VÀ imwrite đuôi mở rộng Tên format Mô tả đã ghi Tagged Image File Format .tif, .tiff TIFF
(format file ảnh đã gắn nhãn)
Joint Phôtgraphicc Experts Group .jpg, .jpeg JPEG
(Nhóm chuyên gia chụp ảnh liên doanh) Graphicss Interchange Format GIF •gif
(format trao đổi đồ thị) Windows Bitmap .bmp BMP (ảnh bitmap) Portable Network Graphics PNG •png
(Đồ thị mạng linh động) X Window Dump .xwd XWD (Kết xuất cửa sổ X 1.5. HIỂN THỊ ẢNH
Để hiển thị ảnh, ta dùng hàm imshow với cú pháp ỉmshowịf,G)
trong đó f là ma trận ảnh, G là số mức. Nếu không viết G, thì mặc định là 256 mức; hoặc khi ta dùng imshow(f, [low high])
sẽ hiển thị ảnh với mầu đen có tất cả các giá trị nhỏ hơn hoặc bằng low; trong khi
mầu trắng có tất ọả các giấ trị lớn hơn hoặc bằng high. Cuối cùng cú pháp •e'ư ■ A imshow(f, [Ị) 16
có low là giá trị cực tiểu của ảnh còn high là giá trị cực đại của f. Dạng hiển thị sau
cùng này rất thích hợp để hiển thị các ảnh có vùng động lực thấp hoặc các ảnh có giá trị âm và dương.
Người ta cũng thường dùng hàm p ixvađ
ể hiển thị các thông tin về các pixel
ảnh. Hàm này hiển thị một con trỏ nằm ngay trên ảnh. Khi dịch con trỏ này thì giá
trị của các pixel tương ứng sẽ được hiển thị và xuất hiện ở dưới cửa sổ hình. Nếu là
ảnh mầu, thì tọa độ và các thành phần đỏ (R), xanh lá cây (G) và xanh nước biển
cũng sẽ hiện ra. Nếu kích phím trái chuột và ấn giữ thì hiển thị cả khoảng
cách Euler giữa vị trí dầu và vị trí hiện thòi của con trỏ. Ví dụ 1.5.
f = imread('D:\Documenls and SettingsYlTsMy DocumentsXAnh Gia dinli\hoahong.bmp'); whos f imshow(f), figure, imshow(f,[]) kết quả là Tốn Kích thước số bytes loại f 0x3 159390 Hints array
Độ lớn tổng cộng là 159390 phần từ sử dụng 159390 bytes.
Nếu ảnh f vừa mới hiển thị khi dùng lfinh imshow(f) tạo ra ánh I(1.4a) có độ
nét kém, thì ta có thể dùng lệnh ¡m slio w (f,I)sẽ cho ành tốt hơ c n ó cha như t lượng trên hình 1.4(b).
Nếu muốn hiển thị mọt anh khác, g, trẽn cùng một man hình vội f thỉ dùng lệnh ¡inahowtf), figure, Hình 1 .4 a) Ảnh thu được trong b) dùng lệnh imshow(f,
Ví dụ 1.6. Chảng hạn ta dùng lệnh
>> / = im readị 'stafDSP.jpg'); » g=imread('D:\Documents a n d Settings\TT\My t Y W
‘ê í ỉ ‘A‘ọ c tu v NH0N dinh\hoadao.bmp’); THƯ VIỆN W D • 4 4 ^ 4 17
>> imshow(f), figure, imshow(g)
sẽ thu được hai ảnh trong hình 1.5 a và b, cùng hiển thị trên màn hình . a ) b )
Hình 1.5. Hai ảnh thu được trong ví dụ 1.6 dùng lệnh imslunvự), figure, imshow(g). 1.6. VIẾT ẢNH
Để viết ảnh vào trong đĩa, ta dùng hàm imwrite có cú pháp
iimvriteự, 'tên file )
Với cú pháp này, thì chuỗi ký tự chứa trong tên file phải chứa các định dạng
nh.r froné bảné 11 Ngoài ra, môt dinh dạng mong muốn cũng có thể dược xác
định với biến số loi vào thứ 3 Chăng hạn lệnh sau dây viết ảnh f vào một file đã lấy tên là patient 1 l_runl
imwrite(f, 'patientl ì J n u l MJ )
Nếu tên file không chứa các .hOng .in v í dưỉmg dẫn UûimwrtK sẽ lưu me
vào ,hu mực hiên hành' Hàm imwri.e c« .hí c d ĩ !
d ín h d ạ n g c ù a m è « lự a chçn. chẳng hạn, dõi V « các ảnh J P E G , ngư« Ta Ihưỉmg dỉịng cú pháp: , imri„ ơ; 18
trong đó q là một số nguyên nằm giữa 0 và 100 (số càng nhỏ thì độ hư hại do nén JPEG càng cao).
Để nén ảnh và thu được các thong tin chi tiết hơn , ta dùng lệnh imfinfo tên file
Ở đây tên file là tên file hoàn chỉnh của ảnh lưu trong đĩa. Chẳng hạn gõ imfinfo pout.tif ans =
Filename: ’C:\MATLAB7\toolbox\images\imdemos\pout.tif
FileModDate: '04-Dec-2000 13:57:50' FileSize: 69004 Format: 'tif FormatVersion: [] Width: 240 Height: 291 Bit Depth: 8 ColorType: 'grayscale' FormatSignature: [73 73 42 0] ByteOrder: 'little-endian' NewSubfileType: 0 BitsPerSample: 8 Compression: 'PackBits'
Photometriclnterpretation: 'BlacklsZero' StripOffsets: [9x1 double] SamplesPerPixel: 1 RowsPerStrip: 34 StripByteCounts: [9x1 double] XResolution: 72 YResolution: 72 ResolutionUnit: 'Inch' Colormap: [] GrayResponseUnit: 0.0100 MaxSampleValue: 255 MinSampleValue: 0 Thresholding: 1.
Các thông tin hiển thị bởi imfinfo có thể được thu vào trong cấu trúc biến.
Chẳng hạn, gọi cấu trúc biến của ảnh trên là K, ta có:
K = imfinfoCpout.tif)
Với lệnh này, ta đã lưu tất cả các thông tin được phát ra trong khi dùng lệnh
imfinfo vào trong biến K. Chẳng hạn, dộ rộng và độ cao của ảnh được lưu trong cấu
trúc K.Height và K.Width. Và để tính tỉ số nén cho ảnh "pout.tif’, ta dùng lệnh
>> K=imfinfo('poiit.tif);
>> image_bvtes=K.Width* K.Heiglỉt*K.BitDepth/8;
> > compressed_bytes=K.F ileSize;
>> compression ratio-image Jyytes!compressed bytes compressionjatio = 1.0121 19
Đối với các ảnh có định dạng tif hàm imwriîe có cú pháp tổng quát hơn dạng:
imwrỉie(f, 'filename.tì', compression, 'parameter', 'resolution', ịcolres rowresj)
Trong đó 1parameter' có thể có một trong các giá trị sau: none' là không nén;
' pac kbits' chỉ sự nén pac kbit (mặc định cho các ảnh không phải nhị phân) và 'ccitt'
chỉ sự nén ccitt (mặc định cho các ảnh nhị phân). Mảng 1x2 [colres rowres] chứa
hai số nguyên đặc trưng cho độ phân giải cột và hàng đo bằng số điểm trên một đơn
vị, mặc định là [72 72]. Nếu kích thước của ảnh đo bằng inch, thì colres là số điểm
(pixel) trong 1 inch (dpi) theo hướng thẳng dứng và tương tự đối với roxvres theo
hướng ngang. I beo qui dịnh, độ phùn giải là đại lượng vô hướng, res, tương ứng với
cách viết [resSị resị. Ví dụ một ảnh 8 bít, có định dạng jpg, tại 200 dpi, kích thước 450x450 pixe s ls tương tương ứn ứ g n vớ v i ớ i 2,25x2,25 inh in s. hs . Nếu Nế muốn lư l u ư u g eiữ iữ ảnh ản nà n y à ^ tr r on o n g e
định dạng tif ,5x1,5 inh trong khi vẫn giữ nguyên lượng pixel là 450x450, thì dùng lệnh: im im\\r w i n te te (fJ, 's \ u t. itf i , f 'compresion', compresión, 'n ’non o e n ', e . 'ré ré oỉution', olution\ res)
Trong d i véctơ [colres rowres] dược xác dịnh bằng cách nhủn 200 dpi với tỉ|
số 2,25/1,5 đươc 300 dpi; hoặc dơn giản hơn ta dùng lệnh
res = routidị200*2.25/1.5);
im\vrite(f, 'st.tV, compression, 'none', resolution', res)
Trong đo lẹnh round làm tròn dến giá trị nguyỏn gần nhất. Cần lưu ý rằng số
lượng pixel không thay doi do lệnh này chỉ làm cho thang chia của ảnh à thay dổi.
Ảnh gốc 450x ISO với 200 dpi có kích thước 2,25x2,25 inh; còn ảnh mới 300 dpi
dồng nhất với Anh gốc, chỉ khác là 450x450 pixel dược phán bố (leu trên diện tích
1,5x1,5 inh. Cách lam này thường xuyên dược sử dụng đổ điều chinh kích thước
của ảnh mà khỏng hy sinh dợ plum giải.
Để chuyên tải nội tiling của cửa sd hình vào trong đĩa, ta sử dụng hai cách:
thứ nhất sử dụng menu flic pull-down trong cửa sổ hình, sau dỏ chọn Export. Với
dộng thái này, người ta ( o the chọn vị trí, tén file và (lịnh dạng. Đổ dưa dược nhiều
tham số hơn nữa, ta dùng lẹnli
print /no ((/déformât - t resno - filename
y d:.'_7 ;Ọ‘ là HÔ hỉnh trong cưa sổ hình mong muốn; fîlcfprmat là một trong
những dịnh dạng I lia hang 1.1; fresno la dọ phán giãi tínlì bang dpi. Çhang han de
chuyển tải nội lung cùa círa sổ binh 1.2a như một file, til với dộ phân g ai 300 dpi,
dưới tên file là hi IVS bin. ta dùng lộnh
print I duff ’ rĩOOhì res - hull ;
Lệnh này sõ gửi lile hi tv's hin 1 .tir vào thư mục hiện hành. Neu ta chỉ gõ
print thì MATLAIi se in noi clung cua cửa sỏ hình sau cùng.
1.7. CÁC LỚP D ữ LIỆU: CÁC PHƯƠNG PHÁP MÃ HÓA CƯỜNG ĐỘ
Trong MATLAB, để biểu diễn ảnh, người ta dùng 4 loại dữ liệu khác nhau;
mỗi loại dữ liệu có thể được lưu giữ dưới nhiều định dạng khác nhau. Điểu đó phản
ánh tính phong phú và đa dạng của một bứcJiiih (mầu sắc, mức xám, độ đen trắng,
độ tương phản,...). Vấn đề phải làm sao lột tả được hết các chi tiết của ảnh và lưu
giữ có hiệu quả trong các bộ nhớ. Đây là một việc làm khó khăn, bởi vì để mồ tả
hết các chi tiết phải cần một mảng dữ liệu có kích thước rất lớn. Ví dụ một ảnh 400 20