Câu hỏi:
26/04/2025 145Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x - 1)² + (y - 2)² + (z - 3)² = 9, điểm A(0; 0; 2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là đường tròn (C) có diện tích nhỏ nhất?
A
(P): x - 2y + 3z - 6 = 0
B
(P): x + 2y + 3z - 6 = 0
C
(P): 3x + 2y + 2z - 4 = 0
D
(P): x + 2y + z - 2 = 0
Đáp án chính xác
Trả lời:
 Trả lời bởi Docx
Trả lời bởi Docx
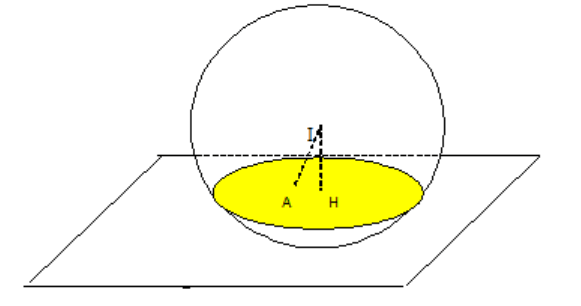
Mặt cầu có tâm I(1; 2; 3), R = 3. Ta có IA(-1; -2; -1) ⇒ = √6 < R. Mặt khác IH ≤ IA nên bán kính của đường tròn giao tuyến min khi H ≡ A. Do đó mp cần tìm nhận làm VTPT và qua A(0; 0; 2) có dạng: x + 2y + z - 2 = 0.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu hỏi 2 / 15
Xem đáp án »
04/04/2025
244
Câu hỏi 6 / 15
Xem đáp án »
04/04/2025
207
Câu hỏi 7 / 15
Xem đáp án »
26/04/2025
193
Câu hỏi 8 / 15
Xem đáp án »
04/04/2025
190
Câu hỏi 10 / 15
Xem đáp án »
05/04/2025
179
Câu hỏi 12 / 15
Xem đáp án »
04/04/2025
175
Câu hỏi 14 / 15
Xem đáp án »
04/04/2025
172
Câu hỏi 15 / 15
Xem đáp án »
04/04/2025
171