Câu hỏi:
04/04/2025 187Trong không gian với hệ trục Oxyz, cho hai điểm A(0; 2; -4), B(-3; 5; 2). Tìm tọa độ điểm M sao cho MA² + 2MB² đạt giá trị nhỏ nhất.
A
M(-1; 3; 2)
B
M(-2; 4; 0)
Đáp án chính xác
C
M(-3; 7; -2)
D
M(-3; 8; -2)
Trả lời:
 Trả lời bởi Docx
Trả lời bởi Docx
Gọi M(x; y; z)
Khi đó: AM² = x² + (y - 2)² + (z + 4)²
BM² = (x + 3)² + (y - 5)² + (z - 2)²
Theo bài ra:
MA² + 2MB² = x² + (y - 2)² + (z + 4)² + 2(x + 3)² + 2(y - 5)² + 2(z - 2)²
= 3(x² + y² + z² + 4x - 8y + 32)
= 3(x + 2)² + (y - 4)² + z² + 12) 3.12
= 36
Vậy (MA² + 2MB²)min = 36
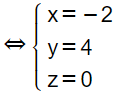
Vậy M(-2; 4; 0) thỏa ycbt.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu hỏi 2 / 15
Xem đáp án »
04/04/2025
244
Câu hỏi 6 / 15
Xem đáp án »
04/04/2025
207
Câu hỏi 7 / 15
Xem đáp án »
26/04/2025
193
Câu hỏi 8 / 15
Xem đáp án »
04/04/2025
190
Câu hỏi 9 / 15
Xem đáp án »
05/04/2025
179
Câu hỏi 11 / 15
Xem đáp án »
04/04/2025
175
Câu hỏi 13 / 15
Xem đáp án »
04/04/2025
172
Câu hỏi 14 / 15
Xem đáp án »
04/04/2025
170