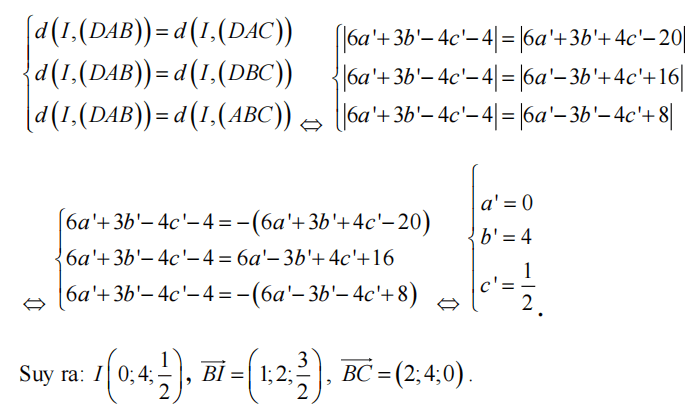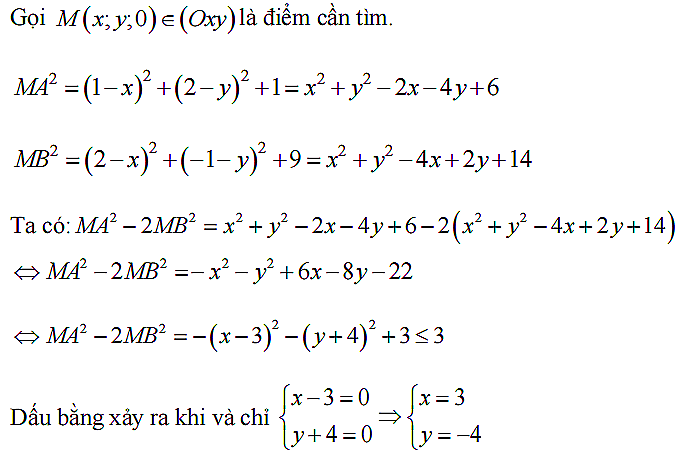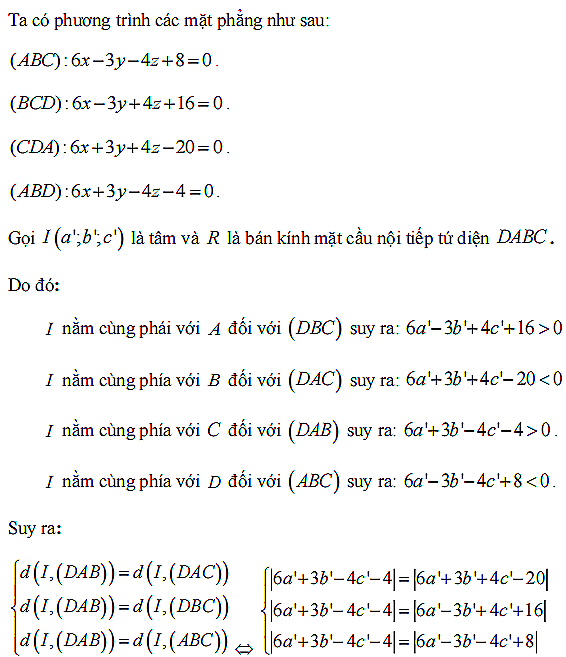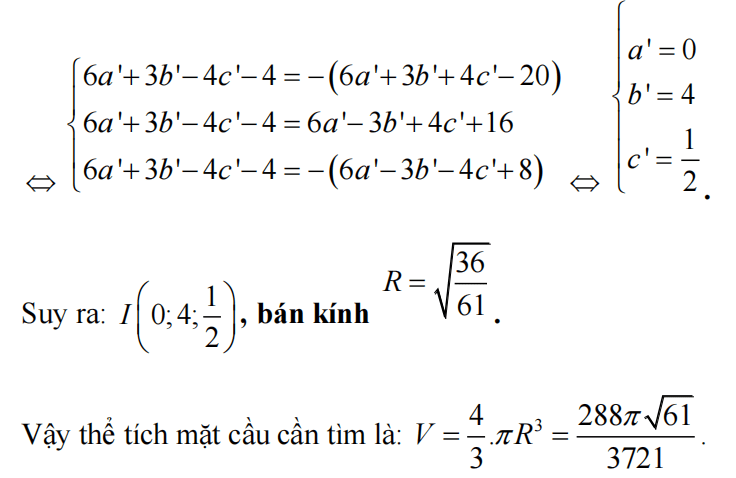Quiz: TOP 205 câu hỏi trắc nghiệm môn Toán vận dụng cao phương pháp tọa độ trong không gian Oxyz (có đáp án và lời giải) | Đề thi THPTQG môn Toán năm 2023
Câu hỏi trắc nghiệm

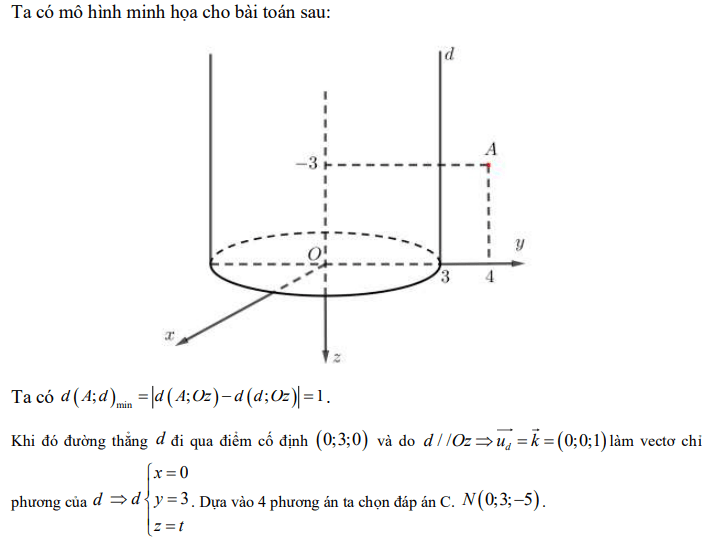


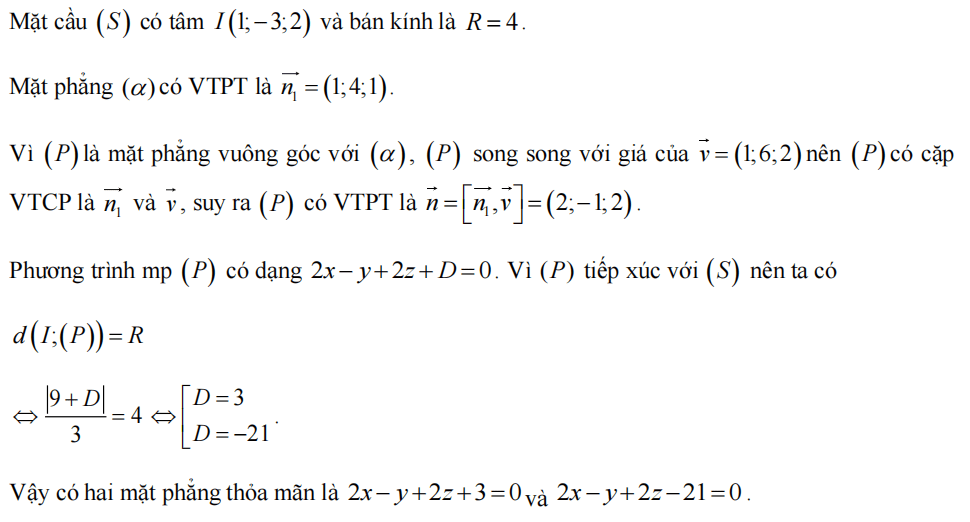
Trong không gian với hệ tọa độ Oxyz, phương trình tổng quát của mp(α) qua hai điểm A(2; -1; 4) B(3; 2; -1) và vuông góc với mp(β): x + y + 2z - 3 = 0 là: ![]()



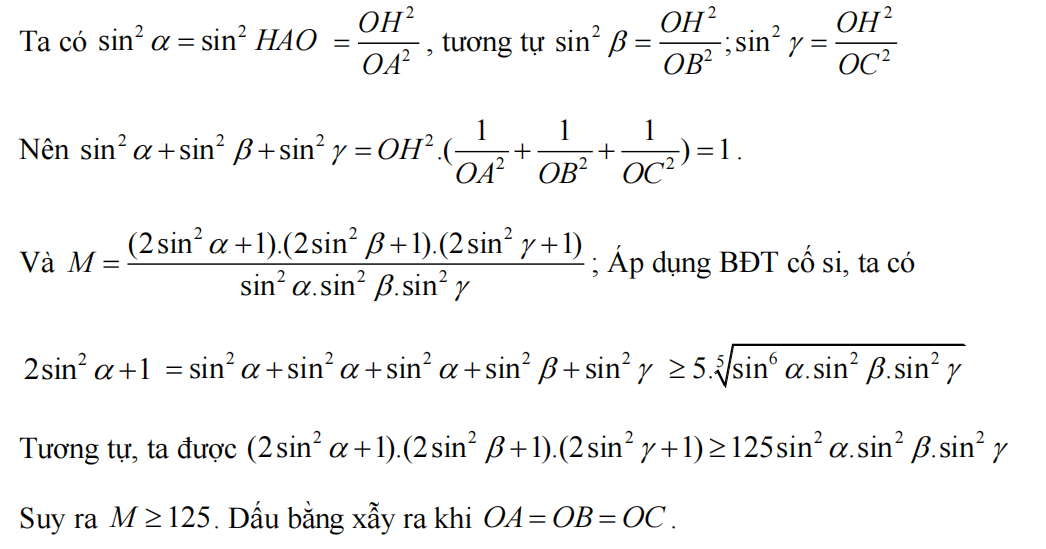
Thoả mãn yêu cầu:
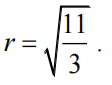
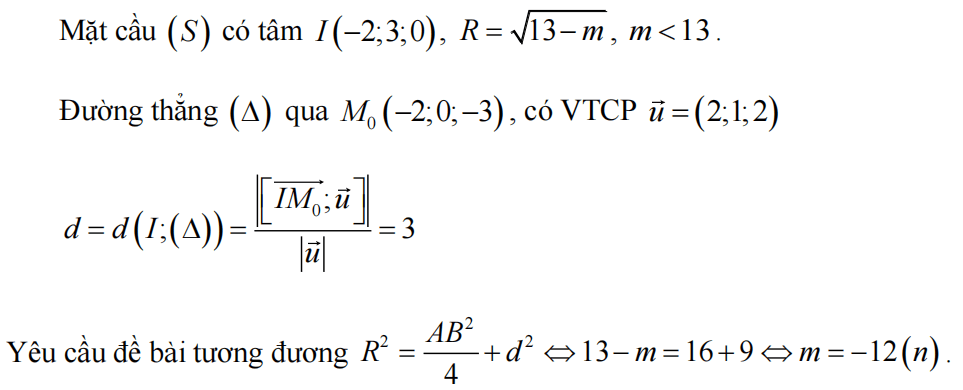
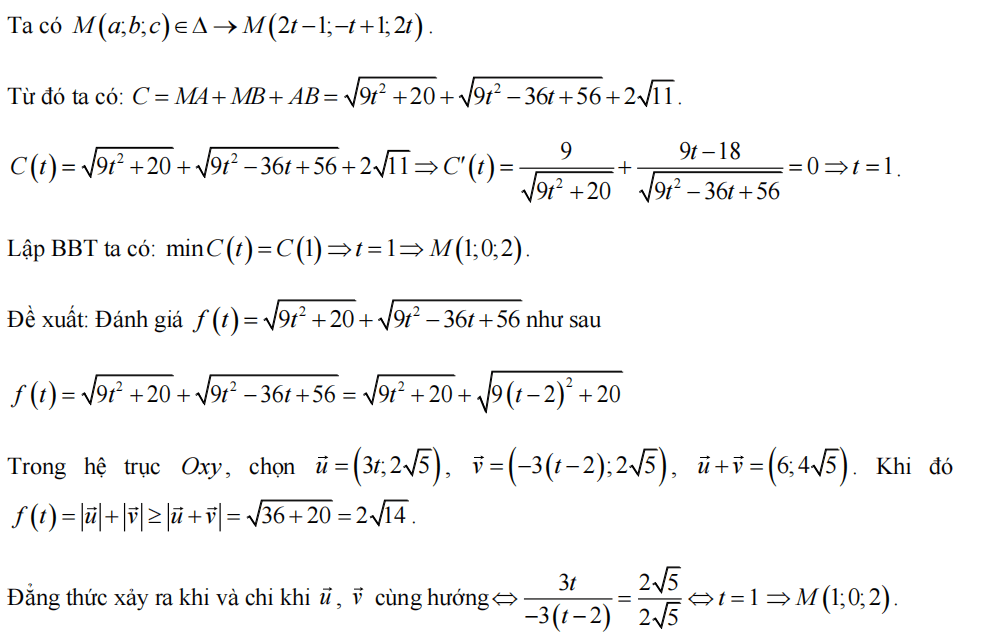

Gọi M(x; y; z)
Khi đó: AM² = x² + (y - 2)² + (z + 4)²
BM² = (x + 3)² + (y - 5)² + (z - 2)²
Theo bài ra:
MA² + 2MB² = x² + (y - 2)² + (z + 4)² + 2(x + 3)² + 2(y - 5)² + 2(z - 2)²
= 3(x² + y² + z² + 4x - 8y + 32)
= 3(x + 2)² + (y - 4)² + z² + 12) 3.12
= 36
Vậy (MA² + 2MB²)min = 36
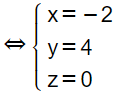
Vậy M(-2; 4; 0) thỏa ycbt.
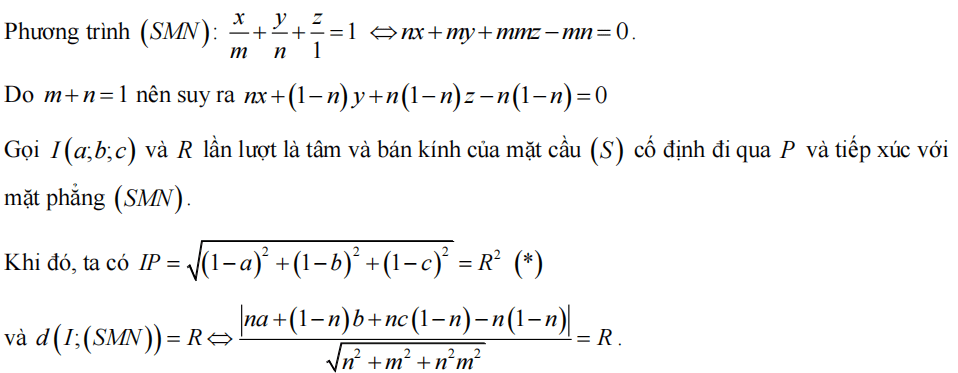
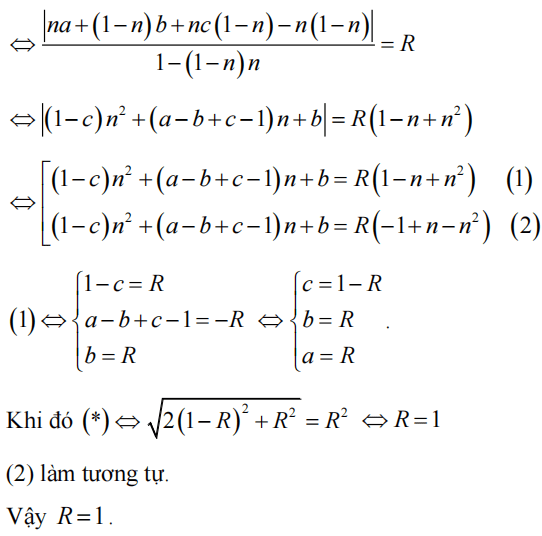

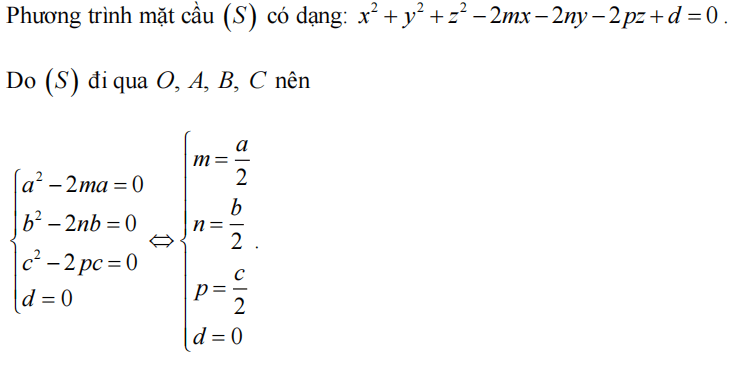
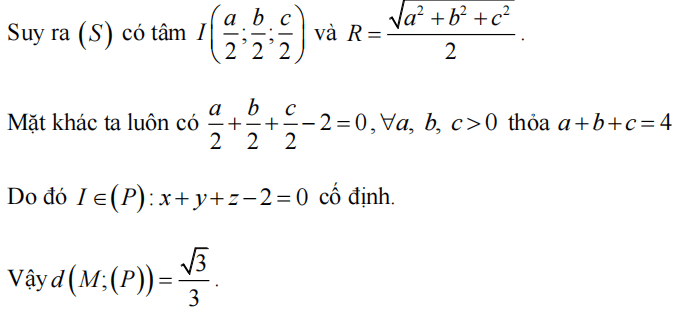
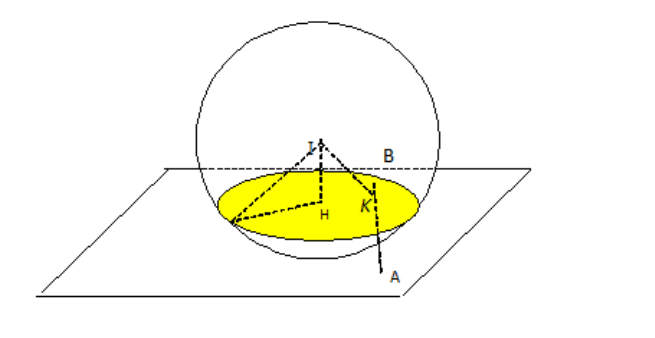

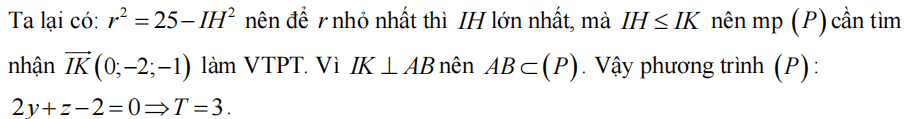
Mặt cầu có tâm I(1; 2; 3), R = 4. Ta có IA = IB = √5 < R. Tương tự bài trên ta có K(0; 1; 2) là trung điểm AB nên mp (P): -x - y + z + 3 = 0.
=> Chọn B
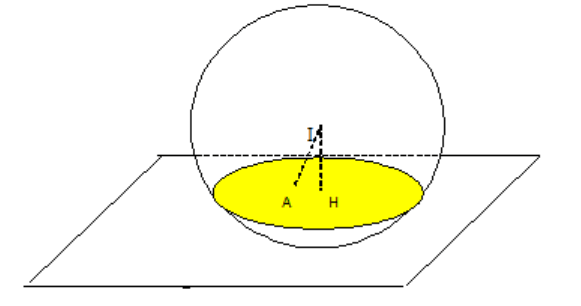
Mặt cầu có tâm I(1; 2; 3), R = 3. Ta có IA(-1; -2; -1) ⇒
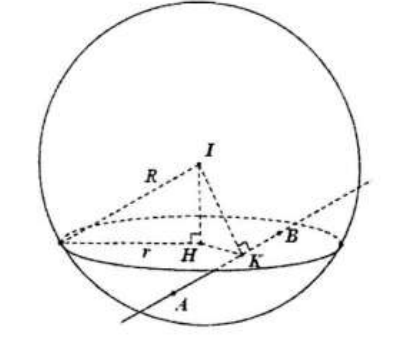

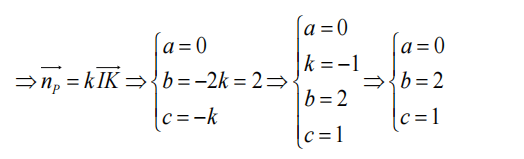
Δ cắt d tại N(-2 + 2t, 1 + t, 1 - t). Ta có A là trung điểm của cạnh MN nên M(4 - 2t, 5 - t, 3 + t).
Vì M ∈ (P) nên ta có: 2(4 - 2t) - (5 - t) + (3 + t) - 10 = 0 ⇔ t = -2
Suy ra: M(8; 7; 1) và N(-6; -1; 3) ⇒ đường thẳng Δ là đường thẳng đi qua M và N
⇒ Phương trình Δ là: ![]()
Phương trình chính tắc của đường thẳng Δ đi qua A, vuông góc và cắt đường thẳng d là: ![]()
Phương trình của đường thẳng Δ đi qua điểm M cắt và vuông góc với đường thẳng d là:
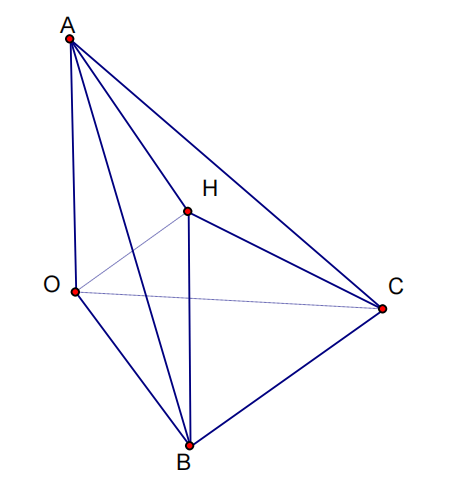
Phương trình (OAB) là: -y + 2z = 0.
Phương trình (OAC) là: 2y + z = 0.
Phương trình (OBC) là: x - z = 0.
Phương trình (ABC) là: 5x + 3y + 4z - 15 = 0.
Gọi I(a'; b'; c') là tâm mặt cầu nội tiếp tứ diện OABC.
Do đó:
- I nằm cùng phía với A đối với (OBC) suy ra: (a' - c') > 0.
- I nằm cùng phía với B đối với (OAC) suy ra: (2b' + c') > 0.
- I nằm cùng phía với C đối với (OAB) suy ra: (-b' + 2c') > 0.
- I nằm cùng phía với O đối với (ABC) suy ra: (5a' + 3b' + 4c' - 15) < 0.
Suy ra:
Suy ra: Đường thẳng d có vecto chỉ phương là Vậy điểm là điểm cần tìm. Vì