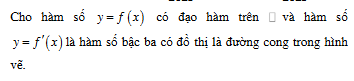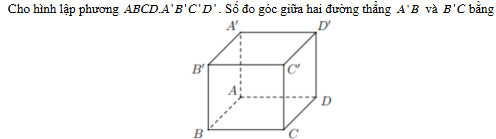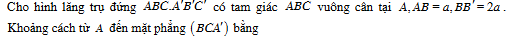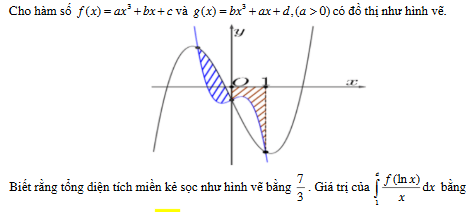Quiz: TOP 43 câu hỏi trắc nghiệm Đề ôn thi tốt nghiệp THPT 2025 toán phát triển minh họa có đáp án - Đề 12 (có đáp án) | Đề Thi THPT Quốc Gia
Câu hỏi trắc nghiệm
Điều kiện . Phương trình đã cho trở thành
Đối chiếu điều kiện, ta được nghiệm duy nhất của phương trình là
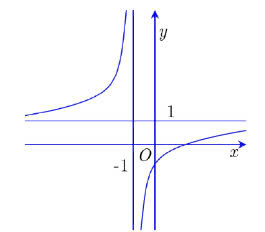
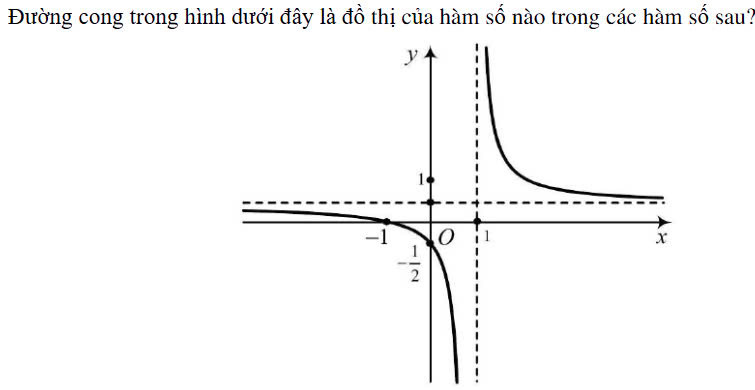
Đồ thị hàm số có TCN là: Loại A,B,C
Do nên ta có điều kiện:
Vậy tập xác định của hàm số là
Trong không gian , cho đường thẳng d. Vector là một vector chỉ phương của d
Điểm là điểm biểu diễn số phức , suy ra .
Vậy phần ảo của bằng 1
Hàm số y = f(x) nghịch biến trên
Một khối lập phương có thể tích bằng 64 cm3. Độ dài mỗi cạnh của khối lập phương đó bằng 4cm
Tập nghiệm của bất phương trình là
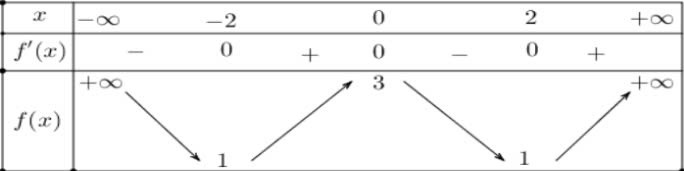
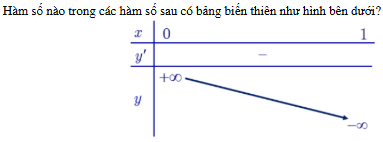
Hàm số có bảng biến thiên như hình dưới là y =
 x - y + 2z - 12 = 0
x - y + 2z - 12 = 0
cho hàm số f(x) có đạo hàm f'(x)= x(x+2)2; Số điểm cực trị của hàm số đã cho là 1
Cho hàm số f(x) liên tục trên R và có . Khi đó bằng 13
Biết bằng -2
Thể tích V của khối chóp bằng 4a3
Cho hai số phức z1 = 2+3i, z2 = -1-4i. Phần thực của số phức 2z1 + z2 là 3
Cho hình trụ có diện tích xung quanh bằng và độ dài đường cao bằng . bán kính đáy của đường tròn đáy của hình trụ đã cho là R = 9a
Một lớp có 35 học sinh. Có cách chọn 1 học sinh làm lớp trưởng và 1 học sinh làm lớp phó học tập
Cho . Khẳng định đúng là F(x) =
Số giao điểm của đồ thị và trục hoành. là 1
Cắt hình trụ bởi một mặt phẳng qua trục, ta được thiết diện là một hình vuông có chu vi là 8. Diện tích xung quanh của hình trụ đã cho bằng 4
Cho cấp số cộng với u1. Khi đó số 2023 là số hạng thứ 226
Cho hai số phức z1 và z2. Phần thực của số phức z1.z2 bằng -8
Cho số phức thỏa mãn . Môđun của số phức bằng
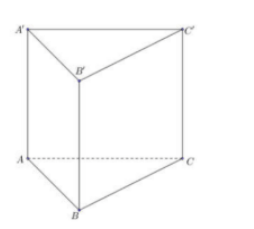
Số đo góc giữa hai đường thẳng A'B và B'C bằng 60
Khoảng cách từ A đến mặt phẳng (BCA') bằng
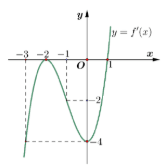
Cho hàm số xác định trên , có đạo hàm . Hàm số đồng biến trên khoảng
Một hộp có 6 viên bi xanh, 4 viên bi đỏ và 5 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, xác suất để 5 viên bi được chọn có đủ ba màu và số viên bi đỏ lớn hơn số viên bi vàng là
Nếu bằng 10
Giá trị lớn nhất của hàm số y = là
Giả sử a,b là các số thực dương tùy ý thỏa mãn a2b3 = 44. Mệnh đề đúng là 2log2a + 3log2b = 8
Phương trình mặt cầu đi qua và có tâm thuộc mặt phẳng là: x2 + y2 + z2 - 14y - 6z + 9 = 0
Trong không gian với hệ tọa độ , cho điểm và hai đường thẳng , phương trình đường thẳng đi qua điểm , vuông góc với đường thẳng và cắt đường thẳng
Cho các số thực a,b,c thuộc khoảng và . Giá trị của biểu thức logab + logbc2 bằng 1
tập hợp tất cả các giá trị của tham số m sao cho hàm số y = nghịch biến trên khoảng (-1;1) là
Giá trị của bằng
Giá trị của | 2z1 -z2| bằng 2
Thể tích của khối lăng trụ ABC.A'B'C' là 12a3