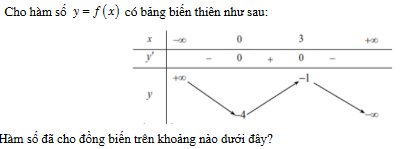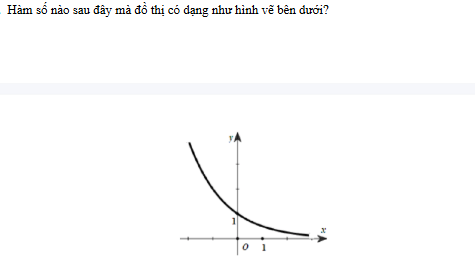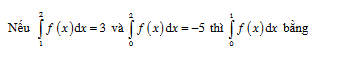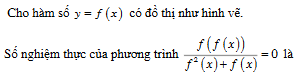Quiz: TOP 50 câu hỏi trắc nghiệm đề thi thử TN môn Toán 2025 THPT Chuyên Thái Bình giải chi tiết ( có đáp án ) | Đề thi THPT Quốc Gia
Câu hỏi trắc nghiệm
![]()
Tập xác định của hàm số là ![]()
Hàm số đã cho đồng biến trên khoảng (0;3)
bằng
Thể tích của khối chóp có diện tích đáy bằng và chiều cao bằng là
Hàm số nghịch biến trên R là
Đạo hàm của hàm số y = là y' =
![]()
![]()
Khai triển có 200 số hạng
Cho cấp số cộng () với = 3 và = 9. Công sai của cấp số cộng đã cho bằng 6
![]() là
là ![]()
Giá trị nhỏ nhất của hàm số y = trên đoạn [2;3] bằng 5
Trong không gian Oxyz, hình chiếu vuông góc của điểm M(3;1;-1) trên trục Oy có tọa độ là (0;1;0)
Hàm số nào sau đây có đúng một điểm cực trị là
Cho khối nón có bán kính đáy r = và chiều cao h =4. Tính thể tích của khối nón đã cho là 4
Khẳng định đúng là a > 0, b < 0, c < 0
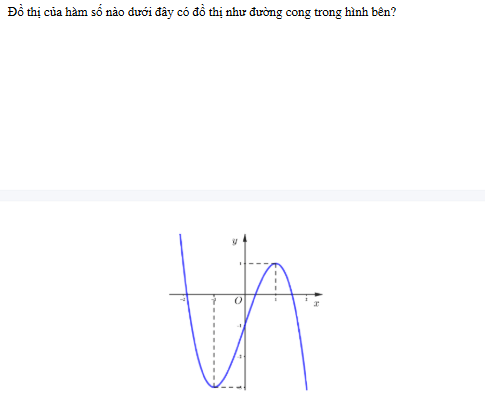
Đồ thị của hàm số có đường cong trong hình bên là
Tiệm cận ngang của đồ thị hàm số y = là đường thẳng y = 0
 là
là ![]()
Cho và . Mệnh đề đúng là m + n = mn
Cho khối hộp chữ nhật ABCD.A'B'C'D' , biết AB = a; BC =2a; AC' = . Thể tích của khối hộp đó là 8
Phương trình có nghiệm là x =3
Biết F (x) = là một nguyên hàm của hàm số f(x) trên i. Khi đó bằng
Tập nghiệm của bất phương trình là
Hàm số mà đồ thị có dạng như hình vẽ là y = (
![]() -8
-8
Cho hàm số F(x) thỏa mãn F'(x) = 3-5cos x và F (0) = 5. Mệnh đề đúng là
F(x)= 3x - 5sin x +5
Trong không gian Oxyz, biết mặt phẳng ax + by + cz + 5 = 0 qua hai điểm A(3;1;-1), B(2;-1;4) và vuông góc với (P): 2x - y + 3z + 4=0. Giá trị của a - b + c bằng 9
![]() 6
6
![]() 10
10
bằng
Cho hình trụ có bán kính đáy bằng R và chiều cao bằng . Mặt phẳng () song song với trục của hình trụ và cách trục một khoảng bằng . Diện tích thiết diện của hình trụ cắt bởi mặt phẳng () là
Trong không gian với hệ tọa độ , cho hai điểm , . Phương trình mặt phẳng trung trực của đoạn thẳng có dạng . Khi đó bằng -4
Gọi là hai nghiệm của phương trình .
Cho tập . Từ tập lập được 72 số tự nhiên gồm 3 chữ số và chia hết cho 3
Biết () là hai nghiệm của phương trình và , với là hai số nguyên dương. . = 14
Số giá trị nguyên của tham số để bất phương trình nghiệm đúng với mọi là 1
Cho hình lập phương cạnh , là trung điểm . Khoảng cách từ đến mặt phẳng bằng
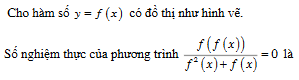 3
3
Giả sử ; a,b R. ab = -6
T = f(a-b+c-d -3) = -1
Có giá trị nguyên của tham số để đồ thị hàm số có đúng ba điểm cực trị và ba điểm cực trị đó tạo thành tam giác có diện tích lớn hơn 4. là 2
Cho hình chóp có đáy là tam giác đều cạnh , cạnh vuông góc với mặt phẳng . Gọi là trọng tâm tam giác ; lần lượt là trung điểm của và . Thể tích của khối tứ diện bằng
Một người bán gạo muốn đóng một thùng tôn đựng gạo thể tích không đổi bằng V = 5, thùng tôn hình hộp chữ nhật có đáy là hình vuông, không nắp. Trên thị trường, giá tôn làm đáy thùng là , giá tôn làm mặt xung quanh thùng là . người bán gạo đó đóng thùng đựng gạo với cạnh đáy bằng 2m
Số giá trị nguyên của tham số để hàm số đồng biến trên khoảng là 2
Có 15 số nguyên để với mỗi có đúng 2 số thực thỏa mãn bất phương trình
Cho hình chóp có đáy là tam giác đều cạnh , cạnh vuông góc với mặt phẳng đáy và . Gọi là trung điểm của . cosin của góc là
cos
Cho hàm số có đạo hàm liên tục, nhận giá trị dương trên , và thỏa mãn , . = 2
Trong không gian với hệ tọa độ , cho mặt phẳng và mặt cầu . Giả sử và sao cho cùng phương với vectơ và khoảng cách giữa và lớn nhất. 3
Cho hàm số Biết rằng (với ) là số thực sao cho phương trình có 6 nghiệm thực phân biệt thỏa mãn tổng các nghiệm âm bằng